Η εξίσωση του Fermat για τον εκθέτη n=3. Μία στοιχειώδης προσέγγιση
|
|
|
- Δευκαλίων Παπανδρέου
- 9 χρόνια πριν
- Προβολές:
Transcript
1 Η εξίσωση του Fermat για τον εκθέτη n=3. Μία στοιχειώδης προσέγγιση Αλέξανδρος Γ. Συγκελάκης 6 Απριλίου 2006 Περίληψη Θέµα της εργασίας αυτής, είναι η απόδειξη οτι η εξίσωση x 3 + y 3 = z 3 όπου xyz 0, δεν έχει ακέραιες λύσεις. Είναι η µερική περίπτωση του Τελευταίου Θεωρήµατος του Fermat για n = 3. Ο Euler, έδωσε δύο αποδείξεις για το ϑέµα αυτό. Η µία, ήταν πολύ καινοτόµος χρησιµοποιώντας άρρητους αριθµούς. υστυχώς ο Euler, έκανε ένα λάθος στους ισχυρισ- µούς του στην απόδειξη αυτή. Παρα ταύτα η µέθοδος αυτή, αποκάλυψε µία πολλά υποσχόµενη προσεγγιση για το τελευταίο Θεώρηµα του Fermat µε το οποίο ασχολήθηκαν αργότερα οι Gauss, Dirichlet και Kummer αλλά και πολλοί άλλοι σύγχρονοι µαθηµατικοί µέχρι και τον A. Wiles, ο οποίος και έδωσε την ολοκληρωµένη απόδειξη του Θεωρήµατος (199). Η δεύτερη απόδειξη (αυτή που παρουσιάζεται και στην εργασία αυτή), είναι πολυ ευρηµατική, χρησιµοποιώντας όµως µεθόδους, µόνο στοιχειώδους Θεωρίας Αριθµών. 1 Γενικές Προτάσεις και Λήµµατα Λήµµα 1.1 Μπορούµε να ϕέρουµε την εξίσωση x n +y n = z n σε µία µορφή, τέτοια ώστε τα x, y, z, να είναι πρώτοι µεταξύ τους ανα δύο. Απόδειξη Εστω (x, y) = d. Τότε x = dx, y = dy, µε (x, y ) = 1, και x n + y n = ( z ) n. ( d z ) n z Άρα Z, οπότε από γνωστή άσκηση, d d Z. Θέτουµε τότε z d = z, οπότε καταλήγουµε στην x n + y n = z n. Είναι εύκολο τώρα να δούµε οτι (x, z ) = 1 και (y, z ) = 1, διότι εαν π.χ. ο πρώτος p διαιρεί τους x, z, τότε p/y n δηλαδή p/y που αντιβαίνει στην (x, y ) = 1. Παρατήρηση : Βάσει του Λήµµατος (1.1) µπορούµε στο εξής να υποθέτουµε οτι στην εξίσωση x 3 + y 3 = z 3, που µελετούµε, οι x, y, z είναι ανα δύο πρώτοι µεταξύ τους. Επίσης x y z x. Τµήµα Μαθηµατικών, Πανεπιστήµιο Κρήτης 1
2 Επεται οτι ένας ακριβώς είναι άρτιος. Μπορούµε χωρίς ϐλάβη της γενικότητος, να υποθέσουµε τον z άρτιο και τους x, y περιττούς. (Εαν π.χ. ο x είναι άρτιος, τότε ( z) 3 + y 3 = ( x) 3 και ϑέτουµε όπου z το x και όπου x το z). Μπορούµε να υποθέσουµε τον z ϑετικό (διαφορετικά ϑα γράφαµε ( x) 3 + ( y) 3 = ( z) 3 και ϑα αντικαθιστούσαµε τους x, y, z από τους x, y, z αντιστοίχως). Αλλά τότε λόγω της z 3 = (x + y)(x 2 xy +y 2 ) = (x+y) [ (x y 2 )2 + 3y2 ], ο x+y είναι ϑετικός. Λόγω συµ- µετρίας του ϱόλου των x, y και της x y µπορούµε να υποθέσουµε x > y. Συνοψίζοντας : Από εδώ και στο εξής, εξίσωση του Fermat, εννοούµε την x 3 +y 3 = z 3 όπου x y z 0,οι x, y, z είναι ανα δύο πρώτοι µεταξύ τους,z άρτιος, x > y και x + y > 0, άρα z > 0. Θεώρηµα 1.1 Εαν η εξίσωση του Fermat x 3 + y 3 = z 3 έχει λύση, υπάρχουν ακέραιοι p, q ϑετικοί πρώτοι µεταξύ τους και διαφορετικής αρτιότητος 1, τέτοιοι ώστε x = p + q, y = p q και z 3 = 2p(p 2 + 3q 2 ). Αφού ο z είναι άρτιος, οι x, y είναι περιττοί άρα µπορούµε να ϑέσουµε x + y = 2p, x y = 2q όπου οι ακέραιοι p, q είναι > 0 (ϐλέπε παρατήρηση πιο πάνω). Από την άσκηση 1 του Β Φυλλαδίου έχουµε ότι (p, q) = (x + y, x y ) = 1 και ένας ακριβώς από τους q, p είναι άρτιος. Τέλος x = p+q, 2 2 y = p q οπότε η εξίσωσή µας γράφεται : (p + q) 3 + (p q) 3 = z 3 δηλαδή 2p(p 2 + 3q 2 ) = z 3. Λήµµα 1.2 Εαν οι πρώτοι µεταξύ τους ακέραιοι p, q, έχουν διαφορετική αρτιότητα τότε (2p, p 2 + 3q 2 ) = 1 ή 3 ανάλογα µε το αν 3 p ή 3 p αντίστοιχα. Εστω (2p, p 2 + 3q 2 ) = t. Ο p 2 + 3q 2 είναι περιττός, άρα ο t είναι περιττός. Συνεπώς p 0 (mod t) και p 2 + 3q 2 0 (mod t). Ο συνδιασµός των δύο σχέσεων δίνει 3q 2 0 (mod t). Αν είναι t > 1, τότε (q, t) = 1 (διότι t p), άρα και (q 2, t) = 1. Επεται οτι 3 0 (mod t), δηλαδή t 3. Άρα t = 1 ή t = 3. Λήµµα 1.3 Ισχύει η ταυτότητα (a 2 +kb 2 )(c 2 +kd 2 ) = (ac kbd) 2 +k(ad+bc) 2 της οποίας εµείς ϑα κάνουµε χρήση για k = 3. 1 Λέγοντας οτι δύο αριθµοί έχουν ίδια αρτιότητα, εννοούµε οτι και οι δύο είναι άρτιοι ή και οι δύο περιττοί και κατ επέκτασιν, δύο αριθµοί έχουν διαφορετική αρτιότητα όταν ένας εκ των δύο είναι άρτιος και ο άλλος περιττός (Πρόκειται για µετάφραση της αγγλικής λέξεως parity). 2
3 Λήµµα 1. Εαν το 2 διαιρεί ένα ακέραιο της µορφής +3, τότε και το διαιρεί τον αριθµό αυτό και το πηλίκο της διαίρεσης αυτής δια, είναι ένας ακέραιος της ίδιας µορφής. Εστω 2 a 2 = 3b 2. Τότε παρατηρούµε ότι τα a, b έχουν την ίδια αρτιότητα. Εαν και οι δύο είναι άρτιοι, τότε a = 2c, b = 2d και a 2 +3b 2 = (2c) 2 +3(2d) 2 = (c 2 + 3d 2 ). Εαν είναι και οι δύο είναι περιττοί, τότε το διαιρεί έναν ακριβώς εκ των a + b, a b (Άσκηση 1, Φυλλάδιο Β ). Θα δείξουµε οτι εαν (a + b) το Λήµµα ισχύει (η περίπτωση (a b) είναι εντελώς ανάλογη). Καταρχήν, (a 2 + 3b 2 ) = ( )(a 2 + 3b 2 ) = (a 3b) 2 + 3(a + b) 2 (πρβλ. Λήµµα 1.3) και αφού a 3b = (a + b) b, άρα a 3b. Συνεπώς a 2 + 3b 2. Αφού όµως a 3b και a + b, γνωρίζουµε οτι υπάρχουν ακέραιοι u, v τέτοιοι ώστε a 3b = u και a + b = v. Λυνοντας ως προς a, b, έχουµε a = u + 3v, b = v u και µε απλές πράξεις διαπιστώνουµε οτι a2 + 3b 2 = u 2 + 3v 2. Λήµµα 1.5 Εαν ένας πρώτος της µορφής + 3 διαιρεί το a 2 + 3b 2, τότε υπάρχουν ακέραιοι c, d τέτοιοι ώστε : a 2 + 3b 2 = (p 2 + 3q 2 )(c 2 + 3d 2 ). Εστω p 2 + 3q 2 πρώτος και ας υποθέσουµε ότι (p 2 + 3q 2 ) (a 2 + 3b 2 ). Τότε υπάρχει ακέραιος k, τέτοιος ώστε a 2 + 3b 2 = k(p 2 + 3q 2 ) και τότε, µε απλές πράξεις, έχουµε (pb aq)(pb + aq) = (p 2 + 3q 2 )(b 2 q 2 k) Άρα ο πρώτος p 2 + 3q 2 διαιρεί ένα τουλάχιστον από τους παράγοντες του αριστερού µέλους. Άρα για ε = 1 ή 1, (pb + εaq) = (p 2 + 3q 2 )d, όπου ο d είναι κάποιος ακέραιος. Οµως, (p 2 +3q 2 )(a 2 +3b 2 ) = (pa ε3qb) 2 +3(pb+εaq) 2 (Λήµµα 1.3), άρα p 2 +3q 2 pa ε3qb (1.1) και ϑέτουµε pa 3εqb = c(p 2 + 3q 2 ) για κάποιο c Z. Άρα λόγω και της (1.1), (p 2 + 3q 2 )(a 2 + 3b 2 ) = (pa 3εqb) 2 + 3(pb + εaq) 2 = [c(p 2 + 3q 2 )] 2 + 3[d(p 2 + 3q 2 )] 2 Άρα τελικά, (a 2 + 3b 2 ) = (p 2 + 3q 2 )(c 2 + 3d 2 ). = (p 2 + 3q 2 ) 2 (c 2 + 3d 2 ) Λήµµα 1.6 Εαν ο ακέραιος a 2 + 3b 2 έχει ένα περιττό παράγοντα > 1, που δεν είναι της ίδιας µορφής, τότε και το πηλίκο έχει ενα παράγοντα, που δεν είναι της ίδιας µορφής. 3
4 Εστω a 2 + 3b 2 ο ελάχιστος ακέραιος µε την ιδιότητα της εκφώνησης. a 2 + 3b 2 = kg και ο k > 1 είναι περιττός + 3. Άρα g > 1. Τότε Εαν ο g έχει περιττό διαιρέτη > 1, τότε ισχυριζόµαστε ότι κάθε περιττός πρώτος διαιρέτης του g δεν είναι της µορφής + 3. Πράγµατι, εαν ο p 2 + 3q 2 είναι περιττός πρώτος διαιρέτης του g, τότε g = (p 2 + 3q 2 )g 1 και από το Λήµµα (1.5), a2 + 3b 2 p 2 + 3q 2 = c2 + 3d 2, άρα c 2 + 3d 2 = kg 1 και αυτό αντιβαίνει στον τρόπο που επιλέξαµε τον a 2 + 3b 2. Εαν ο g δεν έχει περιττό διαιρέτη > 1, τότε g = 2 n, n 1. Επειδή 2 a 2 + 3b 2, το Λήµµα (1.) µας λέει οτι a 2 + 3b 2 (άρα n 2) και ακόµη, a 2 +3b 2 = c 2 + 3d 2. Άρα c 2 + 3d 2 = k2 n 2 και ερχόµαστε ξανά σε αντίφαση µε την επιλογή του a 2 + 3b 2. Θεώρηµα 1.2 Εαν p, q ϑετικοί αριθµοί, πρώτοι µεταξύ τους, διαφορετικής αρτιότητας και έτσι ώστε ο ακέραιος p 2 + 3q 2 να είναι τέλειος κύβος, τότε, υπάρχουν αριθµοί A, B, τέτοιοι ώστε : p = A 3 9AB 2 q = 3A 2 B 3B 3 (A, B) = 1 Θα δουλέψουµε στο σώµα Q(ω) µε ω 2 +ω+1 = 0. Είναι γνωστό οτι οι µονάδες του δακτυλίου Z(ω) είναι οι {1, ω, ω 2 }. Αφού ο p 2 + 3q 2 είναι τέλειος κύβος, άρα υπάρχει περιττός ακέραιος u (οι p, q έχουν διαφορετική αρτιότητα) τέτοιος ώστε p 2 + 3q 2 = u 3 δηλαδή (p + i 3q)(p i 3q) = u 3. Οµως i 3 = 2ω + 1 και η παραπάνω σχέση γράφεται [(p+q)+2qω] [(p q) 2qω] = u 3. Οµως εαν Μ.Κ. ((p+q)+2qω, (p q) 2qω) µονάδα, τότε πρέπει να υπάρχει πρώτος αριθµός π Q(ω), µε π (p + q) + 2qω και π (p q) 2qω, απ οπου π 2p και π 2q(2ω + 1). Εστω π 2p. Τότε π 2 ή π p (i) Εστω π 2. Τότε αφού N(π) και N(π) 1 (π πρώτος άρα όχι µονάδα) ο N(π) είναι άρτιος. Από την άλλη αφού π 2 και π (p + q) + 2qω, έχουµε π p + q δηλαδή N(π) (p + q) 2 και επειδή N(π) άρτιος καταλήγουµε σε άτοπο αφού (p + q) 2 =περιττός λόγω του οτι τα p, q έχουν διαφορετική αρτιότητα. (ii) Εστω π p. Τότε καθώς π 2q(2ω + 1) έχουµε π q ή π (2ω + 1) και εαν π q καταλήγουµε σε άτοπο λόγω της (p, q) = 1. Απ την άλλη, εαν π (2ω + 1)
5 τότε καθώς ο 2ω + 1 είναι πρώτος, έχουµε π = ε(2ω + 1), µε ε=µονάδα. Άρα N(π) = N(2ω + 1) = 3 και καθώς π p έχω 3 N(p) δηλαδή 3 p. Άρα p = 3p 1 για κάποιο ακέραιο p 1. Τότε 9p q2 = u 3 απ όπου 3 u δηλαδή u = 3u 1 για κάποιο ακέραιο u 1. Αντικαθιστώντας παίρνουµε 3p q2 = 9u 3 1, απ όπου 3 q, άτοπο καθώς (p, q) = 1. Συνεπώς ((p + q) + 2qω, (p q) 2qω) = µονάδα. Άρα κάθε ένας από αυτούς τους παράγοντες είναι της µορφής «(τέλειος κύβος) (µονάδα)». Άρα (p + q) + 2qω = (a + bω) 3 ή ω(a + bω) 3 ή ω 2 (a + bω) 3. Εαν ήταν (p + q) + 2qω = ω(a + bω) 3, τότε αναπτύσοντας την ταυτότητα ϑα έπαιρνα 2q = a 3 3a 2 b + b 3 και p + q = 3a 2 b + 3ab 2. Συνδιάζοντας οτι p, q διαφορετικής αρτιότητας, και παίρνοντας περιπτώσεις για τα a, b καταλήγουµε πολύ εύκολα σε άτοπο. Με όµοιο σκεπτικό απορρίπτεται και η περίπτωση να έχουµε (p + q) + 2qω = ω 2 (a + bω) 3. Τέλος εαν (p + q) + 2qω = (a + bω) 3 τότε παίρνω p + q = a 3 3ab 2 + b 3, 2q = 3a 2 b 3ab 2. Με απλές δοκιµές ϐρίσκω οτι a, b είναι περιττοί. Υπάρχουν λοιπόν ακέραιοι A, B τέτοιοι ώστε a = A + B, b = A B µε (A, B) = 1, και αντικαθιστώντας παραπάνω τις τιµές των a, b, παίρνουµε q = 3A 2 B 3B 3, p = A 3 9AB 2, όπως ακριβώς χρειαζόµασταν. Θεώρηµα 1.3 εν υπάρχει λύση (x, y, z) της εξίσωσης του Fermat, τέτοια ώστε να ικανοποιεί τις συνθήκες του Θεωρήµατος 1.1 και να ισχύει (2p, p 2 + 3q 2 ) = 1. Εστω οτι υπάρχει ελάχιστη λύση (x, y, z) υπό την έννοια οτι το γινόµενο xyz είναι ελάχιστο και ϑα ϐρω µία λύση της οποίας η απόλυτη τιµή του γινοµένου ϑα είναι µικρότερη, συνεπώς µε την µέθοδο της άπειρης καθόδου καταλήγουµε σε άτοπο : Σύµφωνα µε την Άσκηση 3 του Φυλλαδίου Β, οι 2p και p 2 + 3q 2 είναι τέλειοι κύβοι. Οµως σύµφωνα µε το Θεώρηµα 1.2, υπάρχουν ακέραιοι a, b τέτοιοι ώστε p = a 3 9ab 2, q = 3a 2 b 3b 3, (a, b) = 1 και οι a, b έχουν διαφορετική αρτιότητα. Επίσης 3 a διότι διαφορετικά οι p, q ϑα ήταν συγχρόνως διαιρετοί δια 3. Οµως 2p = 2a 3 18ab 2 = (2a)(a 3b)(a+3b), και είναι απλή άσκηση να δείξει κανείς ότι οι 2a, a 3b, a + 3b είναι ανα δύο πρώτοι µεταξύ τους, ϐασισµένοι στο ότι οι a ± 3b είναι περιττοί, οι a, b πρώτοι µεταξύ τους και 3 a. Συνεπώς καθένας απ τους 2a, a 3b, a+3b είναι τέλειος κύβος, άρα υπάρχουν ακέραιοι A, B, C τέτοιοι ώστε : 2a = A 3, a 3b = B 3, a + 3b = C 3. Αυτό όµως δίνει µια καινούρια λύση στην εξίσωση του Fermat καθώς A 3 = 2a = (a 3b) + (a + 3b) = B 3 + C 3, και είναι αναγκαστικά µικρότερη απ την x, y, z, αφού A 3 B 3 C 3 = 2a(a 3b)(a + 3b) = 2 p ενώ z 3 = 2p(p 2 + 3q 2 ) (πρβλ. Θεώρηµα 1.1). Συνεπώς A 3 B 3 C 3 < x 3 y 3 z 3 άρα ABC < xyz, άτοπο διότι είχαµε επιλέξει τη λύση (x, y, z) της εξίσωσης του Fermat έτσι ώστε ο xyz να είναι ελάχιστος. 5
6 Θεώρηµα 1. εν υπάρχει λύση (x, y, z) της εξίσωσης του Fermat, τέτοια ώστε να ικανοποιεί τις συνθήκες του Θεωρήµατος 1.1 και να ισχύει (2p, p 2 + 3q 2 ) = 3. Εστω οτι υπάρχει ελάχιστη λύση (x, y, z) υπό την έννοια οτι το z είναι ελάχιστο και ϑα καταλήξω σε µία άλλη µικρότερη λύση, συνεπώς µε την µέθοδο της άπειρης καθόδου καταλήγουµε σε άτοπο : Καταρχήν το 3 διαιρεί τον p, αλλά δεν διαιρεί τον q καθώς 3 2p και (p, q) = 1. Άρα υπάρχει s τέτοιο ώστε : p = 3s και 2p(p 2 + 3q 2 ) = 2 3s(3 3s 2 + 3q 2 ) = 18s(q 2 + 3s 2 ). Αφήνεται στον αναγνώστη ν αποδείξει οτι (18s, q 2 + 3s 2 ) = 1 καθώς πρόκειται για άσκηση ϱουτίνας. Από το Θεώρηµα 1.1 έχουµε ότι ο 2p(p 2 + 3q 2 ) είναι τέλειος κύβος, δηλαδή ο 18s(q 2 + 3s 2 ) είναι τέλειος κύβος. Από την Άσκηση 3 του Φυλλαδίου Β και το γεγονός οτι (18s, q 2 +3s 2 ) = 1, συµπεραίνουµε οτι καθένας απ τους q 2 +3s 2 και 18s, είναι τέλειος κύβος. Άρα, σύµφωνα µε το Θεώρηµα 1.2, αφού ο q 2 + 3s 2 είναι τέλειος κύβος, υπάρχουν a, b τέτοιοι ώστε : q = a 3 9ab 2, s = 3a 2 b 3b 3, (a, b) = 1. Οµως τέλειος κύβος είναι και ο 18s = 3 3 2b(a + b)(a b), άρα ο 2b(a b)(a + b) είναι τέλειος κύβος. Είναι και πάλι άσκηση ϱουτίνας ν αποδείξει κανείς οτι οι 2b, a b, a + b είναι ανα δύο πρώτοι µεταξύ τους. Άρα κάθε ένας από αυτούς είναι κύβος, οπότε υπάρχουν ακέραιοι A, B, C τέτοιοι ώστε : 2b = A 3, a b = B 3, a+b = C 3. Αυτό όµως δίνει µια καινούρια λύση στην εξίσωση του Fermat, καθώς A 3 = 2b = (a + b) (a b) = C 3 B 3 δηλαδή A 3 + B 3 = C 3. Οµως C 3 = a + b < s = 3b(a b)(a + b) < p. Οµως z 3 = 2p(p 2 + 3q 2 ) (πρβλ. Θεώρηµα 1.1 και αρχική παρατήρηση). Ετσι οδηγούµαστε σε µία άλλη λύση της εξισώσεως του Fermat, µικρότερη της προηγούµενης, αφού εαν z 3 = 2p(p 2 + 3q 2 ), τότε καθώς C 3 < p < 2p(p 2 + 3q 2 ) = z 3, έχουµε C 3 < z 3 απ οπου C < z και έχουµε τελειώσει. Άρα λοιπόν δεν υπάρχει λύση της εξίσωσης του Fermat ούτε όταν (2p, p 2 + 3q 2 ) = 3. 2 Η εξίσωση του Fermat για τον εκθέτη n=3 είναι αδύνατη Ας υποθέσουµε οτι έχουµε λύσεις της εξίσωσης του Fermat Τότε από το Θεώρηµα 1.1, ϑα υπάρχουν p, q τέτοιοι ώστε : (p, q) = 1 Οι p, q είναι ϑετικοί Εχουν διαφορετική αρτιότητα Ο ακέραιος 2p(p 2 + 3q 2 ) είναι τέλειος κύβος Επίσης ξέρουµε οτι (2p, p 2 + 3q 2 ) = 1 ή 3 (Λήµµα 1.2) Εαν (2p, p 2 + 3q 2 ) = 1 τότε δεν υπάρχει λύση της εξίσωσης του Fermat (Θεώρηµα 1.3). 6
7 Εαν (2p, p 2 + 3q 2 ) = 3 τότε τότε δεν υπάρχει και πάλι λύση της εξίσωσης του Fermat (Θεώρηµα 1.). Και στις δύο περιπτώσεις λοιπόν, καταλήγουµε σε άτοπο, πράγµα που δηλώνει οτι η εξίσωση του Fermat δεν έχει ακέραιες λύσεις για τον εκθέτη n = 3. Αναφορές [1] H. M. Edwards, Fermat s Last Theorem: A Genetic Introduction to Algebraic Number Theory p [2] P. Ribenboim, Fermat s Last Theorem for Amateurs p [3] Larry Freeman, 7
2 o Καλοκαιρινό σχολείο Μαθηµατικών Νάουσα 2008
 2 o Καλοκαιρινό σχολείο Μαθηµατικών Νάουσα 2008 Μικρό Θεώρηµα του Fermat, η συνάρτηση του Euler και Μαθηµατικοί ιαγωνισµοί Αλέξανδρος Γ. Συγκελάκης ags@math.uoc.gr Αύγουστος 2008 Αλεξανδρος Γ. Συγκελακης
2 o Καλοκαιρινό σχολείο Μαθηµατικών Νάουσα 2008 Μικρό Θεώρηµα του Fermat, η συνάρτηση του Euler και Μαθηµατικοί ιαγωνισµοί Αλέξανδρος Γ. Συγκελάκης ags@math.uoc.gr Αύγουστος 2008 Αλεξανδρος Γ. Συγκελακης
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 3
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 3 ιδασκοντες: Α. Μπεληγιάννης - Σ. Παπαδάκης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt.html Τετάρτη 13 Μαρτίου 2013 Ασκηση 1. Αφού ϐρείτε την
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 3 ιδασκοντες: Α. Μπεληγιάννης - Σ. Παπαδάκης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt.html Τετάρτη 13 Μαρτίου 2013 Ασκηση 1. Αφού ϐρείτε την
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ. Λυσεις Ασκησεων - Φυλλαδιο 2
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt016/nt016.html Πέµπτη 7 Οκτωβρίου 016 Ασκηση 1. Βρείτε όλους
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt016/nt016.html Πέµπτη 7 Οκτωβρίου 016 Ασκηση 1. Βρείτε όλους
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 2
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt014/nt014.html https://sites.google.com/site/maths4edu/home/14
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt014/nt014.html https://sites.google.com/site/maths4edu/home/14
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 3
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 3 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt2014/nt2014.html https://sites.google.com/site/maths4edu/home/14
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 3 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt2014/nt2014.html https://sites.google.com/site/maths4edu/home/14
Μάθηµα Θεωρίας Αριθµών Ε.Μ.Ε
 Μάθηµα Θεωρίας Αριθµών Ε.Μ.Ε 1. Να αποδειχθεί ότι κάθε ϑετικός ακέραιος αριθµός n 6, µπορεί να γραφεί στη µορφή όπου οι a, b, c είναι ϑετικοί ακέραιοι. n = a + b c,. Να αποδειχθεί ότι για κάθε ακέραιο
Μάθηµα Θεωρίας Αριθµών Ε.Μ.Ε 1. Να αποδειχθεί ότι κάθε ϑετικός ακέραιος αριθµός n 6, µπορεί να γραφεί στη µορφή όπου οι a, b, c είναι ϑετικοί ακέραιοι. n = a + b c,. Να αποδειχθεί ότι για κάθε ακέραιο
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 9
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 9 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt2014/nt2014.html https://sites.google.com/site/maths4edu/home/14
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 9 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt2014/nt2014.html https://sites.google.com/site/maths4edu/home/14
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ. Λυσεις Ασκησεων - Φυλλαδιο 3
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο 3 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt2016/nt2016.html Πέµπτη 3 Νοεµβρίου 2016 Ασκηση 1. Αφού ϐρείτε
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο 3 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt2016/nt2016.html Πέµπτη 3 Νοεµβρίου 2016 Ασκηση 1. Αφού ϐρείτε
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 8
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 8 ιδασκοντες: Α. Μπεληγιάννης - Σ. Παπαδάκης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt.html Τετάρτη Μαΐου 013 Ασκηση 1. Βρείτε τις τάξεις των
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 8 ιδασκοντες: Α. Μπεληγιάννης - Σ. Παπαδάκης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt.html Τετάρτη Μαΐου 013 Ασκηση 1. Βρείτε τις τάξεις των
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ. Λυσεις Ασκησεων - Φυλλαδιο 9
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο 9 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt2016/nt2016.html Πέµπτη 12 Ιανουαρίου 2017 Ασκηση 1. Εστω
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο 9 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt2016/nt2016.html Πέµπτη 12 Ιανουαρίου 2017 Ασκηση 1. Εστω
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Λυσεις Ασκησεων - Φυλλαδιο 1
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Λυσεις Ασκησεων - Φυλλαδιο ιδασκοντες: Α. Μπεληγιάννης - Σ. Παπαδάκης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt.html Τετάρτη 7 Φεβρουαρίου 03 Ασκηση. είξτε ότι
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Λυσεις Ασκησεων - Φυλλαδιο ιδασκοντες: Α. Μπεληγιάννης - Σ. Παπαδάκης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt.html Τετάρτη 7 Φεβρουαρίου 03 Ασκηση. είξτε ότι
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ. Λυσεις Ασκησεων - Φυλλαδιο 7
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο 7 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uo.gr/abelga/numbertheory/nt2016/nt2016.html Πέµπτη 7 εκεµβρίου 2016 Ασκηση 1. Για κάθε
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο 7 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uo.gr/abelga/numbertheory/nt2016/nt2016.html Πέµπτη 7 εκεµβρίου 2016 Ασκηση 1. Για κάθε
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 7
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 7 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uo.gr/abelga/numbertheory/nt2014/nt2014.html https://stes.google.com/ste/maths4edu/home/14
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 7 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uo.gr/abelga/numbertheory/nt2014/nt2014.html https://stes.google.com/ste/maths4edu/home/14
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ. Προτεινοµενες Ασκησεις - Φυλλαδιο 9
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Προτεινοµενες Ασκησεις - Φυλλαδιο 9 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt2015/nt2015.html Παρασκευή 29 Μαίου 2015 Ασκηση 1.
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Προτεινοµενες Ασκησεις - Φυλλαδιο 9 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt2015/nt2015.html Παρασκευή 29 Μαίου 2015 Ασκηση 1.
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 6
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 6 ιδασκοντες: Α. Μπεληγιάννης - Σ. Παπαδάκης Ιστοσελιδα Μαθηµατος : htt://users.uoi.gr/abeligia/numbertheory/nt.html Σάββατο 20 Απριλίου 2013 Ασκηση 1. 1) είξτε ότι η
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 6 ιδασκοντες: Α. Μπεληγιάννης - Σ. Παπαδάκης Ιστοσελιδα Μαθηµατος : htt://users.uoi.gr/abeligia/numbertheory/nt.html Σάββατο 20 Απριλίου 2013 Ασκηση 1. 1) είξτε ότι η
ΑΛΓΕΒΡΙΚΕΣ ΟΜΕΣ Ι. Ασκησεις - Φυλλαδιο 2
 ΑΛΓΕΒΡΙΚΕΣ ΟΜΕΣ Ι Τµηµα Β Ασκησεις - Φυλλαδιο 2 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2016/asi2016.html Πέµπτη 3 Μαρτίου 2016 Αν (G, ) είναι
ΑΛΓΕΒΡΙΚΕΣ ΟΜΕΣ Ι Τµηµα Β Ασκησεις - Φυλλαδιο 2 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2016/asi2016.html Πέµπτη 3 Μαρτίου 2016 Αν (G, ) είναι
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ. Λυσεις Ασκησεων - Φυλλαδιο 6
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο 6 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : htt://users.uoi.gr/abeligia/numbertheory/nt2016/nt2016.html Πέµπτη 23 Νεµβρίου 2016 Ασκηση 1. Αν N, να
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο 6 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : htt://users.uoi.gr/abeligia/numbertheory/nt2016/nt2016.html Πέµπτη 23 Νεµβρίου 2016 Ασκηση 1. Αν N, να
Κεφάλαιο 2. Παραγοντοποίηση σε Ακέραιες Περιοχές
 Κεφάλαιο Παραγοντοποίηση σε Ακέραιες Περιοχές Γνωρίζουµε ότι στο Ÿ κάθε στοιχείο εκτός από το 0 και τα ± γράφεται ως γινόµενο πρώτων αριθµών κατά τρόπο ουσιαστικά µοναδικό Από τη Βασική Άλγεβρα ξέρουµε
Κεφάλαιο Παραγοντοποίηση σε Ακέραιες Περιοχές Γνωρίζουµε ότι στο Ÿ κάθε στοιχείο εκτός από το 0 και τα ± γράφεται ως γινόµενο πρώτων αριθµών κατά τρόπο ουσιαστικά µοναδικό Από τη Βασική Άλγεβρα ξέρουµε
HY118- ιακριτά Μαθηµατικά. Παράδειγµα άµεσης απόδειξης. Μέθοδοι αποδείξεως για προτάσεις της µορφής εάν-τότε. 08 - Αποδείξεις
 HY118- ιακριτά Μαθηµατικά Παρασκευή, 06/03/2015 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Το υλικό των διαφανειών έχει βασιστεί σε διαφάνειες του Kees van Deemter, από το University of Aberdeen 3/8/2015
HY118- ιακριτά Μαθηµατικά Παρασκευή, 06/03/2015 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Το υλικό των διαφανειών έχει βασιστεί σε διαφάνειες του Kees van Deemter, από το University of Aberdeen 3/8/2015
3 o Καλοκαιρινό Μαθηµατικό σχολείο Ε.Μ.Ε. Λεπτοκαρυά Πιερίας 2009
 3 o Καλοκαιρινό Μαθηµατικό σχολείο Ε.Μ.Ε. Λεπτοκαρυά Πιερίας 2009 ιαιρετότητα και Ισοτιµίες Β και Γ Λυκείου Αλέξανδρος Γ. Συγκελάκης ags@math.uoc.gr Ιούλιος 2009 1 ιαιρετοτητα και Ισοτιµιες ΠΡΟΛΟΓΟΣ Το
3 o Καλοκαιρινό Μαθηµατικό σχολείο Ε.Μ.Ε. Λεπτοκαρυά Πιερίας 2009 ιαιρετότητα και Ισοτιµίες Β και Γ Λυκείου Αλέξανδρος Γ. Συγκελάκης ags@math.uoc.gr Ιούλιος 2009 1 ιαιρετοτητα και Ισοτιµιες ΠΡΟΛΟΓΟΣ Το
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 6
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 6 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : htt://users.uoi.gr/abeligia/numbertheory/nt204/nt204.html htts://sites.google.com/site/maths4eu/home/4
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 6 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : htt://users.uoi.gr/abeligia/numbertheory/nt204/nt204.html htts://sites.google.com/site/maths4eu/home/4
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις Επαναληψης
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις Επαναληψης ιδασκοντες: Α. Μπεληγιάννης - Σ. Παπαδάκης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt.html Τετάρτη 22 Μαΐου 2013 Ασκηση 1. (1) Να λυθεί η γραµµική
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις Επαναληψης ιδασκοντες: Α. Μπεληγιάννης - Σ. Παπαδάκης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt.html Τετάρτη 22 Μαΐου 2013 Ασκηση 1. (1) Να λυθεί η γραµµική
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ. Ασκησεις - Επανάληψης. ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος :
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Ασκησεις - Επανάληψης ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt015b/nt015b.html Πέµπτη 1 Ιανουαρίου 016 Ασκηση 1. (1) Να λυθεί
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Ασκησεις - Επανάληψης ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt015b/nt015b.html Πέµπτη 1 Ιανουαρίου 016 Ασκηση 1. (1) Να λυθεί
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ. Ασκησεις - Φυλλαδιο 5
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 5 ιδασκοντες: Α Μπεληγιάννης - Σ Παπαδάκης Ιστοσελιδα Μαθηµατος : http://usersuogr/abelga/numbertheory/nthtml Τετάρτη 10 Απριλίου 2013 Ασκηση 1 Θεωρούµε τις αριθµητικές
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 5 ιδασκοντες: Α Μπεληγιάννης - Σ Παπαδάκης Ιστοσελιδα Μαθηµατος : http://usersuogr/abelga/numbertheory/nthtml Τετάρτη 10 Απριλίου 2013 Ασκηση 1 Θεωρούµε τις αριθµητικές
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ. Ασκησεις Επαναληψης. ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος :
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Ασκησεις Επαναληψης ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt015/nt015.html Τρίτη Ιουνίου 015 Ασκηση 1. (1) Να λυθεί η γραµµική
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Ασκησεις Επαναληψης ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt015/nt015.html Τρίτη Ιουνίου 015 Ασκηση 1. (1) Να λυθεί η γραµµική
Αλγεβρικες οµες Ι Ασκησεις - Φυλλαδιο 2
 Αλγεβρικες οµες Ι Ασκησεις - Φυλλαδιο 2 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδες Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2014/asi2014.html, https://sites.google.com/site/maths4edu/home/algdom114
Αλγεβρικες οµες Ι Ασκησεις - Φυλλαδιο 2 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδες Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2014/asi2014.html, https://sites.google.com/site/maths4edu/home/algdom114
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» (ε) Κάθε συγκλίνουσα ακολουθία άρρητων αριθµών συγκλίνει σε άρρητο αριθµό.
 Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο : Ακολουθίες πραγµατικών αριθµών Α Οµάδα Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς αιτιολογήστε πλήρως την απάντησή σας α Κάθε
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο : Ακολουθίες πραγµατικών αριθµών Α Οµάδα Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς αιτιολογήστε πλήρως την απάντησή σας α Κάθε
Αλγεβρικες οµες Ι Ασκησεις - Φυλλαδιο 5
 Αλγεβρικες οµες Ι Ασκησεις - Φυλλαδιο 5 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi.html Παρασκευή 16 & Τετάρτη 21 Νοεµβρίου
Αλγεβρικες οµες Ι Ασκησεις - Φυλλαδιο 5 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi.html Παρασκευή 16 & Τετάρτη 21 Νοεµβρίου
2 o Καλοκαιρινό σχολείο Μαθηµατικών Νάουσα 2008
 2 o Καλοκαιρινό σχολείο Μαθηµατικών Νάουσα 2008 ιαιρετότητα και Ισοτιµίες Αλέξανδρος Γ. Συγκελάκης ags@math.uoc.gr Αύγουστος 2008 Αλεξανδρος Γ. Συγκελακης Στη µνήµη του δασκάλου µου, Χάρη Βαφειάδη... www.math.uoc.gr/
2 o Καλοκαιρινό σχολείο Μαθηµατικών Νάουσα 2008 ιαιρετότητα και Ισοτιµίες Αλέξανδρος Γ. Συγκελάκης ags@math.uoc.gr Αύγουστος 2008 Αλεξανδρος Γ. Συγκελακης Στη µνήµη του δασκάλου µου, Χάρη Βαφειάδη... www.math.uoc.gr/
Αλγεβρικες οµες Ι Ασκησεις - Φυλλαδιο 2
 Αλγεβρικες οµες Ι Ασκησεις - Φυλλαδιο 2 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi.html Τετάρτη 17 Οκτωβρίου 2012 Ασκηση 1.
Αλγεβρικες οµες Ι Ασκησεις - Φυλλαδιο 2 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi.html Τετάρτη 17 Οκτωβρίου 2012 Ασκηση 1.
ΚΕΦΑΛΑΙΟ 2: Ηµιαπλοί ακτύλιοι
 ΚΕΦΑΛΑΙΟ 2: Ηµιαπλοί ακτύλιοι Είδαµε στο κύριο θεώρηµα του προηγούµενου κεφαλαίου ότι κάθε δακτύλιος διαίρεσης έχει την ιδιότητα κάθε πρότυπο είναι ευθύ άθροισµα απλών προτύπων. Εδώ θα χαρακτηρίσουµε όλους
ΚΕΦΑΛΑΙΟ 2: Ηµιαπλοί ακτύλιοι Είδαµε στο κύριο θεώρηµα του προηγούµενου κεφαλαίου ότι κάθε δακτύλιος διαίρεσης έχει την ιδιότητα κάθε πρότυπο είναι ευθύ άθροισµα απλών προτύπων. Εδώ θα χαρακτηρίσουµε όλους
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ. Λυσεις Ασκησεων - Φυλλαδιο 1
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο 1 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt01b/nt01b.html Πέµπτη 1 Οκτωβρίου 01 Ασκηση 1. είξτε ότι
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο 1 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt01b/nt01b.html Πέµπτη 1 Οκτωβρίου 01 Ασκηση 1. είξτε ότι
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές»
 Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο : Το σύνολο των πραγµατικών αριθµών Α Οµάδα Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς αιτιολογήστε πλήρως την απάντησή σας) α)
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο : Το σύνολο των πραγµατικών αριθµών Α Οµάδα Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς αιτιολογήστε πλήρως την απάντησή σας) α)
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 7
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 7 ιδασκοντες: Α. Μπεληγιάννης - Σ. Παπαδάκης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt.html Τετάρτη 15 Μαΐου 2013 Ασκηση 1. Εστω n 3 ακέραιος.
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 7 ιδασκοντες: Α. Μπεληγιάννης - Σ. Παπαδάκης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt.html Τετάρτη 15 Μαΐου 2013 Ασκηση 1. Εστω n 3 ακέραιος.
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 2
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 2 ιδασκοντες: Α. Μπεληγιάννης - Σ. Παπαδάκης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt.html Τετάρτη 6 Μαρτίου 2013 Ασκηση 1. Βρείτε όλους τους
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 2 ιδασκοντες: Α. Μπεληγιάννης - Σ. Παπαδάκης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt.html Τετάρτη 6 Μαρτίου 2013 Ασκηση 1. Βρείτε όλους τους
Το θεώρημα της Sophie Germain και η εξίσωση του Fermat για τον εκθέτη n=4 Στοιχειώδεις προσεγγίσεις
 Το θεώρημα της Sophie Germain και η εξίσωση του Fermat για τον εκθέτη n=4 Στοιχειώδεις προσεγγίσεις Μαρία Παρασύρη 1 και Δέσποινα Χριστοφόρου 1 10 Απριλίου 006 Περίληψη Σκοπός της παρούσης εργασίας είναι
Το θεώρημα της Sophie Germain και η εξίσωση του Fermat για τον εκθέτη n=4 Στοιχειώδεις προσεγγίσεις Μαρία Παρασύρη 1 και Δέσποινα Χριστοφόρου 1 10 Απριλίου 006 Περίληψη Σκοπός της παρούσης εργασίας είναι
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ. Λυσεις Ασκησεων - Φυλλαδιο 1
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο 1 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt016/nt016.html Πέµπτη 13 Οκτωβρίου 016 Ασκηση 1. είξτε ότι
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο 1 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt016/nt016.html Πέµπτη 13 Οκτωβρίου 016 Ασκηση 1. είξτε ότι
τη µέθοδο της µαθηµατικής επαγωγής για να αποδείξουµε τη Ϲητούµενη ισότητα.
 Αριστοτελειο Πανεπιστηµιο Θεσσαλονικης Τµηµα Μαθηµατικων Εισαγωγή στην Αλγεβρα Τελική Εξέταση 15 Φεβρουαρίου 2017 1. (Οµάδα Α) Εστω η ακολουθία Fibonacci F 1 = 1, F 2 = 1 και F n = F n 1 + F n 2, για n
Αριστοτελειο Πανεπιστηµιο Θεσσαλονικης Τµηµα Μαθηµατικων Εισαγωγή στην Αλγεβρα Τελική Εξέταση 15 Φεβρουαρίου 2017 1. (Οµάδα Α) Εστω η ακολουθία Fibonacci F 1 = 1, F 2 = 1 και F n = F n 1 + F n 2, για n
Εισαγωγή στη Θεωρία Αριθµών για το Λύκειο. Ασκήσεις
 Εισαγωγή στη Θεωρία Αριθµών για το Λύκειο Σηµειώσεις Προετοιµασίας για Μαθηµατικούς ιαγωνισµούς Ασκήσεις Αλέξανδρος Γ. Συγκελάκης ags@math.uoc.gr Νοέµβριος 2012 1 Ασκησεις στη Θεωρια Αριθµων 1 Μαθηµατική
Εισαγωγή στη Θεωρία Αριθµών για το Λύκειο Σηµειώσεις Προετοιµασίας για Μαθηµατικούς ιαγωνισµούς Ασκήσεις Αλέξανδρος Γ. Συγκελάκης ags@math.uoc.gr Νοέµβριος 2012 1 Ασκησεις στη Θεωρια Αριθµων 1 Μαθηµατική
ΑΛΓΕΒΡΙΚΕΣ ΟΜΕΣ Ι. Ασκησεις - Φυλλαδιο 4
 ΑΛΓΕΒΡΙΚΕΣ ΟΜΕΣ Ι Τµηµα Β Ασκησεις - Φυλλαδιο 4 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2017/asi2017.html Παρασκευή 7 Απριλίου 2017 Ασκηση 1.
ΑΛΓΕΒΡΙΚΕΣ ΟΜΕΣ Ι Τµηµα Β Ασκησεις - Φυλλαδιο 4 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2017/asi2017.html Παρασκευή 7 Απριλίου 2017 Ασκηση 1.
ΑΛΓΕΒΡΙΚΕΣ ΟΜΕΣ Ι. Επιλυση Ασκησεων - Φυλλαδιο 2
 ΑΛΓΕΒΡΙΚΕΣ ΟΜΕΣ Ι Τµηµα Β Επιλυση Ασκησεων - Φυλλαδιο 2 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2017/asi2017.html Παρασκευή 24 Μαρτίου 2017
ΑΛΓΕΒΡΙΚΕΣ ΟΜΕΣ Ι Τµηµα Β Επιλυση Ασκησεων - Φυλλαδιο 2 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2017/asi2017.html Παρασκευή 24 Μαρτίου 2017
ΚΕΦΑΛΑΙΟ 4: Ριζικό του Jacobson
 ΚΕΦΑΛΑΙΟ 4: Ριζικό του Jacobso Είδαµε στο προηγούµενο κεφάλαιο ότι κάθε ηµιαπλός δακτύλιος είναι δακτύλιος του Art. Επειδή υπάρχουν παραδείγµατα δακτυλίων του Art που δεν είναι ηµιαπλοί, πχ Z 2, > 1, τίθεται
ΚΕΦΑΛΑΙΟ 4: Ριζικό του Jacobso Είδαµε στο προηγούµενο κεφάλαιο ότι κάθε ηµιαπλός δακτύλιος είναι δακτύλιος του Art. Επειδή υπάρχουν παραδείγµατα δακτυλίων του Art που δεν είναι ηµιαπλοί, πχ Z 2, > 1, τίθεται
ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ ΚΕΦΑΛΑΙΟ 1 ο. 2= p=q 2 p =2q
 ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ ΚΕΦΑΛΑΙΟ ο. Υποθέτουµε ότι ο είναι ρητός. ηλαδή, υποθέτουµε p ότι υπάρχουν φυσικοί αριθµοί p και q τέτoιοι ώστε : =, p και q δεν έχουν q κοινούς διαιρέτες. Παρατηρούµε ότι ο άρτιος αριθµός.
ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ ΚΕΦΑΛΑΙΟ ο. Υποθέτουµε ότι ο είναι ρητός. ηλαδή, υποθέτουµε p ότι υπάρχουν φυσικοί αριθµοί p και q τέτoιοι ώστε : =, p και q δεν έχουν q κοινούς διαιρέτες. Παρατηρούµε ότι ο άρτιος αριθµός.
Συνεχή Κλάσματα. Εμμανουήλ Καπνόπουλος Α.Μ 282
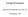 Συνεχή Κλάσματα Εμμανουήλ Καπνόπουλος Α.Μ 282 5 Νοεμβρίου 204 Ορισμός και ιδιότητες: Ορισμός: Έστω a 0, a, a 2,...a n ανεξάρτητες μεταβλητές, n N σχηματίζουν την ακολουθία {[a 0, a,..., a n ] : n N} όπου
Συνεχή Κλάσματα Εμμανουήλ Καπνόπουλος Α.Μ 282 5 Νοεμβρίου 204 Ορισμός και ιδιότητες: Ορισμός: Έστω a 0, a, a 2,...a n ανεξάρτητες μεταβλητές, n N σχηματίζουν την ακολουθία {[a 0, a,..., a n ] : n N} όπου
f (x) = l R, τότε f (x 0 ) = l. = lim (0) = lim f(x) = f(x) f(0) = xf (ξ x ). = l. Εστω ε > 0. Αφού lim f (x) = l R, υπάρχει δ > 0
 Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο 5: Παράγωγος Α Οµάδα. Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς (αιτιολογήστε πλήρως την απάντησή σας). (α) Αν η f είναι παραγωγίσιµη
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο 5: Παράγωγος Α Οµάδα. Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς (αιτιολογήστε πλήρως την απάντησή σας). (α) Αν η f είναι παραγωγίσιµη
Το θεώρημα του Fermat για Ν=3
 Είναι αδύνατον μια κυβική δύναμη να γραφεί ως άθροισμα δυο κυβικών δυνάμεων ή μια τέταρτη δύναμη να γραφεί ως άθροισμα δύο τέταρτων δυνάμεων και γενικά οποιαδήποτε δύναμη μεγαλύτερη του τετραγώνου είναι
Είναι αδύνατον μια κυβική δύναμη να γραφεί ως άθροισμα δυο κυβικών δυνάμεων ή μια τέταρτη δύναμη να γραφεί ως άθροισμα δύο τέταρτων δυνάμεων και γενικά οποιαδήποτε δύναμη μεγαλύτερη του τετραγώνου είναι
Αλγεβρικες οµες Ι Ασκησεις - Φυλλαδιο 5
 Αλγεβρικες οµες Ι Ασκησεις - Φυλλαδιο 5 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδες Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2014/asi2014.html, https://sites.google.com/site/maths4edu/home/algdom114
Αλγεβρικες οµες Ι Ασκησεις - Φυλλαδιο 5 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδες Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2014/asi2014.html, https://sites.google.com/site/maths4edu/home/algdom114
ΜΕΘΟ ΟΛΟΓΙΑ ΚΑΙ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΩΝ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Β ΤΑΞΗΣ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ
 ΜΕΘΟ ΟΛΟΓΙΑ ΚΑΙ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΩΝ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Β ΤΑΞΗΣ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ 4. ΜΕΘΟ ΟΛΟΓΙΑ ΚΑΙ ΑΣΚΗΣΕΙΣ ΣΤH Α. ΘΕΩΡΙΑ ΜΕΘΟ ΟΛΟΓΙΑ ΜΑΘΗΜΑΤΙΚΗ ΕΠΑΓΩΓΗ Εάν ζητείται να δειχθεί ισότητα ή ανίσωση
ΜΕΘΟ ΟΛΟΓΙΑ ΚΑΙ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΩΝ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Β ΤΑΞΗΣ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ 4. ΜΕΘΟ ΟΛΟΓΙΑ ΚΑΙ ΑΣΚΗΣΕΙΣ ΣΤH Α. ΘΕΩΡΙΑ ΜΕΘΟ ΟΛΟΓΙΑ ΜΑΘΗΜΑΤΙΚΗ ΕΠΑΓΩΓΗ Εάν ζητείται να δειχθεί ισότητα ή ανίσωση
< 1 για κάθε k N, τότε η σειρά a k συγκλίνει. +, τότε η η σειρά a k αποκλίνει.
 Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο 3: Σειρές πραγµατικών αριθµών Α Οµάδα. Εστω ( ) µια ακολουθία πραγµατικών αριθµών. Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς (αιτιολογήστε
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο 3: Σειρές πραγµατικών αριθµών Α Οµάδα. Εστω ( ) µια ακολουθία πραγµατικών αριθµών. Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς (αιτιολογήστε
Πολυώνυµα - Πολυωνυµικές εξισώσεις
 4 ΚΕΦΑΛΑΙΟ Πολυώνυµα - Πολυωνυµικές εξισώσεις Ορισµός πολυωνύµου Ονοµάζoυµε ΠΟΛΥΩΝΥΜΟ του κάθε παράσταση της µορφής α ν ν +α ν- ν- + +α +α 0, ν ΙΝ και α 0, α,, α ν-, α ν ΙR. Παρατηρήσεις α. Τα α ν ν, α
4 ΚΕΦΑΛΑΙΟ Πολυώνυµα - Πολυωνυµικές εξισώσεις Ορισµός πολυωνύµου Ονοµάζoυµε ΠΟΛΥΩΝΥΜΟ του κάθε παράσταση της µορφής α ν ν +α ν- ν- + +α +α 0, ν ΙΝ και α 0, α,, α ν-, α ν ΙR. Παρατηρήσεις α. Τα α ν ν, α
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ. Λυσεις Ασκησεων - Φυλλαδιο 4
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο 4 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt2016/nt2016.html Πέµπτη 10 Νοεµβρίου 2016 Ασκηση 1. Να ϐρεθούν
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο 4 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt2016/nt2016.html Πέµπτη 10 Νοεµβρίου 2016 Ασκηση 1. Να ϐρεθούν
ΚΕΦΑΛΑΙΟ 4ο: ΠΟΛΥΩΝΥΜΑ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ
 ΚΕΦΑΛΑΙΟ 4ο: ΠΟΛΥΩΝΥΜΑ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ ) Copyright 2015 Αποστόλου Γιώργος Αποστόλου Γεώργιος apgeorge2004@yahoocom Αδεια χρήσης 3η Εκδοση, Ιωάννινα, Σεπτέµβριος 2015 Περιεχόµενα 1 ΠΟΛΥΩΝΥΜΑ-ΠΟΛΥΩΝΥΜΙΚΕΣ
ΚΕΦΑΛΑΙΟ 4ο: ΠΟΛΥΩΝΥΜΑ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ ) Copyright 2015 Αποστόλου Γιώργος Αποστόλου Γεώργιος apgeorge2004@yahoocom Αδεια χρήσης 3η Εκδοση, Ιωάννινα, Σεπτέµβριος 2015 Περιεχόµενα 1 ΠΟΛΥΩΝΥΜΑ-ΠΟΛΥΩΝΥΜΙΚΕΣ
Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου 4
 Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου 4 ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθος Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://wwwmathuoigr/ abeligia/linearalgebrai/laihtml
Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου 4 ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθος Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://wwwmathuoigr/ abeligia/linearalgebrai/laihtml
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ. Ασκησεις - Φυλλαδιο 5. ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος :
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Ασκησεις - Φυλλαδιο 5 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt205/nt205.html ευτέρα 27 Απριλίου 205 Ασκηση. είξτε ότι για κάθε
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Ασκησεις - Φυλλαδιο 5 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt205/nt205.html ευτέρα 27 Απριλίου 205 Ασκηση. είξτε ότι για κάθε
HY118- ιακριτά Μαθηµατικά
 HY118- ιακριτά Μαθηµατικά Παρασκευή, 04/03/2016 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Το υλικό των διαφανειών έχει βασιστεί σε διαφάνειες του Kees van Deemter, από το University of Aberdeen 3/4/2016
HY118- ιακριτά Μαθηµατικά Παρασκευή, 04/03/2016 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Το υλικό των διαφανειών έχει βασιστεί σε διαφάνειες του Kees van Deemter, από το University of Aberdeen 3/4/2016
Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης
 Τίτλος Μαθήματος: Αλγεβρικές Δομές Ι Ενότητα: Οι Οµάδες τάξης pq, p, q: πρώτοι αριθµοί Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης Τμήμα: Μαθηματικών 246 6. Οι Οµάδες τάξης
Τίτλος Μαθήματος: Αλγεβρικές Δομές Ι Ενότητα: Οι Οµάδες τάξης pq, p, q: πρώτοι αριθµοί Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης Τμήμα: Μαθηματικών 246 6. Οι Οµάδες τάξης
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ. Λυσεις Ασκησεων - Φυλλαδιο 5
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο 5 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt206/nt206.html Πέµπτη 6 Νεµβρίου 206 Ασκηση. Να δειχθεί ότι
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο 5 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt206/nt206.html Πέµπτη 6 Νεµβρίου 206 Ασκηση. Να δειχθεί ότι
Αλγεβρικες οµες Ι Ασκησεις - Φυλλαδιο 4 1 2
 Αλγεβρικες οµες Ι Ασκησεις - Φυλλαδιο 4 1 2 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi.html Πέµπτη 27 εκεµβρίου 2012 Ασκηση
Αλγεβρικες οµες Ι Ασκησεις - Φυλλαδιο 4 1 2 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi.html Πέµπτη 27 εκεµβρίου 2012 Ασκηση
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 4
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 4 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt2014/nt2014.html https://sites.google.com/site/maths4edu/home/14
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 4 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt2014/nt2014.html https://sites.google.com/site/maths4edu/home/14
ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων
 ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων Μελετάµε εδώ τη συνθήκη της αύξουσας αλυσίδας υποπροτύπων και τη συνθήκη της φθίνουσας αλυσίδας υποπροτύπων. Αυτές συνδέονται µεταξύ τους µε την έννοια της συνθετικής σειράς
ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων Μελετάµε εδώ τη συνθήκη της αύξουσας αλυσίδας υποπροτύπων και τη συνθήκη της φθίνουσας αλυσίδας υποπροτύπων. Αυτές συνδέονται µεταξύ τους µε την έννοια της συνθετικής σειράς
Αλγεβρικες οµες Ι Ασκησεις - Φυλλαδιο 3
 Αλγεβρικες οµες Ι Ασκησεις - Φυλλαδιο 3 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi.html Παρασκευή 2 Οκτωβρίου 2012 Ασκηση 1.
Αλγεβρικες οµες Ι Ασκησεις - Φυλλαδιο 3 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi.html Παρασκευή 2 Οκτωβρίου 2012 Ασκηση 1.
Υπερβατικοί Αριθµοί και Θεώρηµα του Liouville
 Υπερβατικοί Αριθµοί και Θεώρηµα του Liouville Χρήστος Κονταράτος 14 Νοεµβρίου 2014 1 Περιεχόµενα 1 Εισαγωγή 3 2 Το Θεώρηµα του Liouville 4 3 Η Υπερβατικότητα του ξ 6 4 Αριθµοί του Liouville 8 2 1 Εισαγωγή
Υπερβατικοί Αριθµοί και Θεώρηµα του Liouville Χρήστος Κονταράτος 14 Νοεµβρίου 2014 1 Περιεχόµενα 1 Εισαγωγή 3 2 Το Θεώρηµα του Liouville 4 3 Η Υπερβατικότητα του ξ 6 4 Αριθµοί του Liouville 8 2 1 Εισαγωγή
ΑΛΓΕΒΡΙΚΕΣ ΟΜΕΣ Ι. Ασκησεις - Φυλλαδιο 9
 ΑΛΓΕΒΡΙΚΕΣ ΟΜΕΣ Ι Τµηµα Β Ασκησεις - Φυλλαδιο 9 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2016/asi2016.html Πέµπτη 12 Μαίου 2016 Ασκηση 1. Εστω
ΑΛΓΕΒΡΙΚΕΣ ΟΜΕΣ Ι Τµηµα Β Ασκησεις - Φυλλαδιο 9 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2016/asi2016.html Πέµπτη 12 Μαίου 2016 Ασκηση 1. Εστω
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 4
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 4 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt2014/nt2014.html https://sites.google.com/site/maths4edu/home/14
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 4 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt2014/nt2014.html https://sites.google.com/site/maths4edu/home/14
1.7 ΙΑΙΡΕΣΗ ΠΟΛΥΩΝΥΜΩΝ
 1 1.7 ΙΑΙΡΕΣΗ ΠΟΛΥΩΝΥΜΩΝ ΘΕΩΡΙΑ 1. Ταυτότητα Ευκλείδειας διαίρεσης : Για δύο οποιαδήποτε πολυώνυµα (x) και δ(x) µε δ(x) µπορούµε να βρούµε δύο άλλα πολυώνυµα π(x) και υ(x) τέτοια ώστε να ισχύει (x) = δ(x)π(x)
1 1.7 ΙΑΙΡΕΣΗ ΠΟΛΥΩΝΥΜΩΝ ΘΕΩΡΙΑ 1. Ταυτότητα Ευκλείδειας διαίρεσης : Για δύο οποιαδήποτε πολυώνυµα (x) και δ(x) µε δ(x) µπορούµε να βρούµε δύο άλλα πολυώνυµα π(x) και υ(x) τέτοια ώστε να ισχύει (x) = δ(x)π(x)
ΑΛΓΕΒΡΙΚΕΣ ΟΜΕΣ Ι. Ασκησεις - Φυλλαδιο 4
 ΑΛΓΕΒΡΙΚΕΣ ΟΜΕΣ Ι Τµηµα Β Ασκησεις - Φυλλαδιο 4 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2016/asi2016.html Πέµπτη 31 Μαρτίου 2016 Υπενθυµίζουµε
ΑΛΓΕΒΡΙΚΕΣ ΟΜΕΣ Ι Τµηµα Β Ασκησεις - Φυλλαδιο 4 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2016/asi2016.html Πέµπτη 31 Μαρτίου 2016 Υπενθυµίζουµε
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ. Ασκησεις - Φυλλαδιο 4. ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος :
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Ασκησεις - Φυλλαδιο 4 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt2015/nt2015.html ευτέρα 30 Μαρτίου 2015 Ασκηση 1. Να ϐρεθούν όλοι
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Ασκησεις - Φυλλαδιο 4 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt2015/nt2015.html ευτέρα 30 Μαρτίου 2015 Ασκηση 1. Να ϐρεθούν όλοι
4.2 4.3 ΕΥΚΛΕΙ ΕΙΑ ΙΑΙΡΕΣΗ ΙΑΙΡΕΤΟΤΗΤΑ
 1 4.2 4.3 ΕΥΚΛΕΙ ΕΙΑ ΙΑΙΡΕΣΗ ΙΑΙΡΕΤΟΤΗΤΑ ΘΕΩΡΙΑ 1. Θεώρηµα Αν α, β ακέραιοι µε β 0, τότε υπάρχουν µοναδικοί ακέραιοι κ και υ, έτσι ώστε α = κβ + υ µε 0 υ < β. 2. Τέλεια διαίρεση Αν το υπόλοιπο υ της Ευκλείδειας
1 4.2 4.3 ΕΥΚΛΕΙ ΕΙΑ ΙΑΙΡΕΣΗ ΙΑΙΡΕΤΟΤΗΤΑ ΘΕΩΡΙΑ 1. Θεώρηµα Αν α, β ακέραιοι µε β 0, τότε υπάρχουν µοναδικοί ακέραιοι κ και υ, έτσι ώστε α = κβ + υ µε 0 υ < β. 2. Τέλεια διαίρεση Αν το υπόλοιπο υ της Ευκλείδειας
Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης
 Τίτλος Μαθήματος: Αλγεβρικές Δομές Ι Ενότητα: Τάξη στοιχείων και Οµάδων - Κυκλικές (Υπο-)Οµάδες Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης Τμήμα: Μαθηματικών 222 3.1. ύναµη
Τίτλος Μαθήματος: Αλγεβρικές Δομές Ι Ενότητα: Τάξη στοιχείων και Οµάδων - Κυκλικές (Υπο-)Οµάδες Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης Τμήμα: Μαθηματικών 222 3.1. ύναµη
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΑΡΤΙΟΙ) Λυσεις Ασκησεων - Φυλλαδιο 4
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ Λυσεις Ασκησεων - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai018/lai018html Παρασκευή 3 Νοεµβρίου 018 Ασκηση
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ Λυσεις Ασκησεων - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai018/lai018html Παρασκευή 3 Νοεµβρίου 018 Ασκηση
Πρώτα και Μεγιστοτικά Ιδεώδη
 Κεφάλαιο 10 Πρώτα και Μεγιστοτικά Ιδεώδη Στο παρόν Κεφάλαιο ϑα µελετήσουµε ειδικούς τύπους ιδεωδών σε έναν δακτύλιο και την επίδραση που έχουν οι επιπλέον ιδιότητες τις οποίες ικανοποιούν τα ιδεώδη αυτά
Κεφάλαιο 10 Πρώτα και Μεγιστοτικά Ιδεώδη Στο παρόν Κεφάλαιο ϑα µελετήσουµε ειδικούς τύπους ιδεωδών σε έναν δακτύλιο και την επίδραση που έχουν οι επιπλέον ιδιότητες τις οποίες ικανοποιούν τα ιδεώδη αυτά
Όνοµα: Λιβαθινός Νικόλαος 2291
 ΠΡΩΤΗ ΆΣΚΗΣΗ ΣΤΗΝ ΚΡΥΠΤΟΓΡΑΦΙΑ Όνοµα: Λιβαθινός Νικόλαος 9 Ηµεροµηνία: 3/5/003 Άσκηση ώστε όλες τις υποοµάδες των Z και Ζ 5 * Προκειµένου να δώσουµε τις υποοµάδες θα πρέπει αρχικά να ορίσουµε τα σύνολα
ΠΡΩΤΗ ΆΣΚΗΣΗ ΣΤΗΝ ΚΡΥΠΤΟΓΡΑΦΙΑ Όνοµα: Λιβαθινός Νικόλαος 9 Ηµεροµηνία: 3/5/003 Άσκηση ώστε όλες τις υποοµάδες των Z και Ζ 5 * Προκειµένου να δώσουµε τις υποοµάδες θα πρέπει αρχικά να ορίσουµε τα σύνολα
ιδασκοντες: x R y x y Q x y Q = x z Q = x z y z Q := x + Q Τετάρτη 10 Οκτωβρίου 2012
 ιδασκοντες: Αλγεβρικες οµες Ι Ασκησεις - Φυλλαδιο 1 Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi.html Τετάρτη 10 Οκτωβρίου 2012 Ασκηση 1.
ιδασκοντες: Αλγεβρικες οµες Ι Ασκησεις - Φυλλαδιο 1 Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi.html Τετάρτη 10 Οκτωβρίου 2012 Ασκηση 1.
Εισαγωγή στην Τοπολογία
 Ενότητα: Συνεκτικότητα Γεώργιος Κουµουλλής Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε
Ενότητα: Συνεκτικότητα Γεώργιος Κουµουλλής Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε
Αρµονική Ανάλυση. Ενότητα: Το ϑεώρηµα παρεµβολής του Riesz και η ανισότητα Hausdorff-Young. Απόστολος Γιαννόπουλος.
 Ενότητα: Το ϑεώρηµα παρεµβολής του Riesz και η ανισότητα Hausdorff-Young Απόστολος Γιαννόπουλος Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Ενότητα: Το ϑεώρηµα παρεµβολής του Riesz και η ανισότητα Hausdorff-Young Απόστολος Γιαννόπουλος Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
1 Οι πραγµατικοί αριθµοί
 1 Οι πραγµατικοί αριθµοί 1.1 Σύνολα αριθµών Το σύνολο των ϕυσικών αριθµών N = {1, 2, 3,...} Το σύνολο των ακεραίων Z = {... 3, 2, 1, 0, 1, 2, 3,...}. Οι ακέραιοι διαµερίζονται σε άρτιους και περιττούς
1 Οι πραγµατικοί αριθµοί 1.1 Σύνολα αριθµών Το σύνολο των ϕυσικών αριθµών N = {1, 2, 3,...} Το σύνολο των ακεραίων Z = {... 3, 2, 1, 0, 1, 2, 3,...}. Οι ακέραιοι διαµερίζονται σε άρτιους και περιττούς
Γραµµική Αλγεβρα Ι. Ενότητα: ιανυσµατικοί χώροι. Ευάγγελος Ράπτης. Τµήµα Μαθηµατικών
 Ενότητα: ιανυσµατικοί χώροι Ευάγγελος Ράπτης Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
Ενότητα: ιανυσµατικοί χώροι Ευάγγελος Ράπτης Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
(x) = δ(x) π(x) + υ(x)
 Μάθηµα 12 Κεφάλαιο 4ο: Πολυώνυµα Πολυωνυµικές Εξισώσεις Θεµατικές Ενότητες: Α. ιαίρεση Πολυωνύµων Β. Σχήµα Horner Η ταυτότητα της Ευκλείδειας διαίρεσης Αν ( χ), δ ( χ) δύο πολυώνυµα µε δ ( χ) 0 και βαθµούς
Μάθηµα 12 Κεφάλαιο 4ο: Πολυώνυµα Πολυωνυµικές Εξισώσεις Θεµατικές Ενότητες: Α. ιαίρεση Πολυωνύµων Β. Σχήµα Horner Η ταυτότητα της Ευκλείδειας διαίρεσης Αν ( χ), δ ( χ) δύο πολυώνυµα µε δ ( χ) 0 και βαθµούς
Ακρότατα υπό συνθήκη και οι πολλαπλασιαστές του Lagrange
 64 Ακρότατα υπό συνθήκη και οι πολλαπλασιαστές του Lagrage Ας υποθέσουµε ότι ένας δεδοµένος χώρος θερµαίνεται και η θερµοκρασία στο σηµείο,, Τ, y, z Ας υποθέσουµε ότι ( y z ) αυτού του χώρου δίδεται από
64 Ακρότατα υπό συνθήκη και οι πολλαπλασιαστές του Lagrage Ας υποθέσουµε ότι ένας δεδοµένος χώρος θερµαίνεται και η θερµοκρασία στο σηµείο,, Τ, y, z Ας υποθέσουµε ότι ( y z ) αυτού του χώρου δίδεται από
2
 ήµητρα Χαµηλάκη ΕΦΑΡΜΟΓΕΣ ΤΗΣ ΑΛΓΕΒΡΙΚΗΣ ΘΕΩΡΙΑΣ ΑΡΙΘΜΩΝ ΣΤΗΝ ΕΠΙΛΥΣΗ ΙΟΦΑΝΤΙΚΩΝ ΕΞΙΣΩΣΕΩΝ Πτυχιακή Εργασία Παρουσιάσθηκε στις 22-6-2000 Επιβλέπων Καθηγητής ΝΓ Τζανάκης Τµήµα Μαθηµατικών Πανεπιστήµιο Κρήτης
ήµητρα Χαµηλάκη ΕΦΑΡΜΟΓΕΣ ΤΗΣ ΑΛΓΕΒΡΙΚΗΣ ΘΕΩΡΙΑΣ ΑΡΙΘΜΩΝ ΣΤΗΝ ΕΠΙΛΥΣΗ ΙΟΦΑΝΤΙΚΩΝ ΕΞΙΣΩΣΕΩΝ Πτυχιακή Εργασία Παρουσιάσθηκε στις 22-6-2000 Επιβλέπων Καθηγητής ΝΓ Τζανάκης Τµήµα Μαθηµατικών Πανεπιστήµιο Κρήτης
Τελική Εξέταση 10 Φεβρουαρίου 2017 ιάρκεια εξέτασης 2 ώρες και 30 λεπτά
 Αριστοτελειο Πανεπιστηµιο Θεσσαλονικης Τµηµα Μαθηµατικων Αλγεβρικές οµές ΙΙ 1. Εστω ότι R Z 3 [x]. Τελική Εξέταση 10 Φεβρουαρίου 2017 ιάρκεια εξέτασης 2 ώρες 30 λεπτά (αʹ) Να αποδείξετε ότι ο R είναι περιοχή
Αριστοτελειο Πανεπιστηµιο Θεσσαλονικης Τµηµα Μαθηµατικων Αλγεβρικές οµές ΙΙ 1. Εστω ότι R Z 3 [x]. Τελική Εξέταση 10 Φεβρουαρίου 2017 ιάρκεια εξέτασης 2 ώρες 30 λεπτά (αʹ) Να αποδείξετε ότι ο R είναι περιοχή
Αριθµοί Liouville. Ιωάννης Μπαρµπαγιάννης
 Αριθµοί Liouville Ιωάννης Μπαρµπαγιάννης Εισαγωγή Η ϑεωρία των υπερβατικών αριθµών έχει ως αφετηρία µια ϕηµισµένη εργασία του Liouville, το 844, ο οποίος περιέγραψε µια κλάση πραγµατικών αριθµών οι οποίοι
Αριθµοί Liouville Ιωάννης Μπαρµπαγιάννης Εισαγωγή Η ϑεωρία των υπερβατικών αριθµών έχει ως αφετηρία µια ϕηµισµένη εργασία του Liouville, το 844, ο οποίος περιέγραψε µια κλάση πραγµατικών αριθµών οι οποίοι
Θεωρια Αριθµων Προβληµατα
 Θεωρια Αριθµων Προβληµατα Μιχάλης Κολουντζάκης Τµήµα Μαθηµατικών και Εφαρµοσµένων Μαθηµατικών Πανεπιστήµιο Κρήτης Βούτες 700 3 Ηράκλειο 6 Απριλίου 205 Πολλές από τις παρακάτω ασκήσεις είναι από το ϐιβλίο
Θεωρια Αριθµων Προβληµατα Μιχάλης Κολουντζάκης Τµήµα Μαθηµατικών και Εφαρµοσµένων Μαθηµατικών Πανεπιστήµιο Κρήτης Βούτες 700 3 Ηράκλειο 6 Απριλίου 205 Πολλές από τις παρακάτω ασκήσεις είναι από το ϐιβλίο
1 Ορισµός ακολουθίας πραγµατικών αριθµών
 ΜΑΣ 02. Απειροστικός Λογισµός Ι Ορισµός ακολουθίας πραγµατικών αριθµών Ορισµός.. Ονοµάζουµε ακολουθία πραγµατικών αριθµών κάθε απεικόνιση του συνόλου N των ϕυσικών αριθµών, στο σύνολο R των πραγµατικών
ΜΑΣ 02. Απειροστικός Λογισµός Ι Ορισµός ακολουθίας πραγµατικών αριθµών Ορισµός.. Ονοµάζουµε ακολουθία πραγµατικών αριθµών κάθε απεικόνιση του συνόλου N των ϕυσικών αριθµών, στο σύνολο R των πραγµατικών
µηδενικό πολυώνυµο; Τι ονοµάζουµε βαθµό του πολυωνύµου; Πότε δύο πολυώνυµα είναι ίσα;
 ΘΕΩΡΙΑ ΠΟΛΥΩΝΥΜΩΝ 1. Τι ονοµάζουµε µονώνυµο Μονώνυµο ονοµάζεται κάθε γινόµενο το οποίο αποτελείται από γνωστούς και αγνώστους (µεταβλητές ) πραγµατικούς αριθµούς. Ο γνωστός πραγµατικός αριθµός ονοµάζεται
ΘΕΩΡΙΑ ΠΟΛΥΩΝΥΜΩΝ 1. Τι ονοµάζουµε µονώνυµο Μονώνυµο ονοµάζεται κάθε γινόµενο το οποίο αποτελείται από γνωστούς και αγνώστους (µεταβλητές ) πραγµατικούς αριθµούς. Ο γνωστός πραγµατικός αριθµός ονοµάζεται
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΑΡΤΙΟΙ) Λυσεις Ασκησεων - Φυλλαδιο 2
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Λυσεις Ασκησεων - Φυλλαδιο ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai8/lai8html Παρασκευή 6 Οκτωβρίου 8 Υπενθυµίζουµε
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Λυσεις Ασκησεων - Φυλλαδιο ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai8/lai8html Παρασκευή 6 Οκτωβρίου 8 Υπενθυµίζουµε
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 1
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β ΑΡΤΙΟΙ Ασκησεις - Φυλλαδιο 1 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/liearalgebrai/lai2018/lai2018html Παρασκευή 12 Οκτωβρίου 2018 Ασκηση 1
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β ΑΡΤΙΟΙ Ασκησεις - Φυλλαδιο 1 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/liearalgebrai/lai2018/lai2018html Παρασκευή 12 Οκτωβρίου 2018 Ασκηση 1
ιαιρετότητα Στοιχεία Θεωρίας Αριθµών «Ο Αλγόριθµος της ιαίρεσης» Αριθµητική Υπολοίπων 0 r < d και a = d q +r
 ιαιρετότητα Στοιχεία Θεωρίας Αριθµών ο a διαιρεί τον b: συµβολισµός: a b Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς a b και a c a (b + c) a b a bc, για κάθε c Z +
ιαιρετότητα Στοιχεία Θεωρίας Αριθµών ο a διαιρεί τον b: συµβολισµός: a b Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς a b και a c a (b + c) a b a bc, για κάθε c Z +
G = a. H = g n. a m = a nq+r = a nq a r = (a n ) q a r = a r = (a n ) q a m. h = a m = a nq = (a n ) q a n
 236 5. Ταξινόµηση Κυκλικών Οµάδων και των Υποοµάδων τους Στην παρούσα ενότητα ϑα ταξινοµήσουµε τις κυκλικές οµάδες, τις υποοµάδες τους, και τους γεννήτο- ϱές τους. Οι ταξινοµήσεις αυτές ϑα ϐασιστούν στην
236 5. Ταξινόµηση Κυκλικών Οµάδων και των Υποοµάδων τους Στην παρούσα ενότητα ϑα ταξινοµήσουµε τις κυκλικές οµάδες, τις υποοµάδες τους, και τους γεννήτο- ϱές τους. Οι ταξινοµήσεις αυτές ϑα ϐασιστούν στην
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ ΑΡΧΗ ΤΗΣ ΜΑΘΗΜΑΤΙΚΗΣ ΕΠΑΓΩΓΗΣ
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ - 11 - ΚΕΦΑΛΑΙΟ 4 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ ΑΡΧΗ ΤΗΣ ΜΑΘΗΜΑΤΙΚΗΣ ΕΠΑΓΩΓΗΣ Έστω Ρ(ν) ένας ισχυρισµός, ο οποίος αναφέρεται στους θετικούς ακέραιους Αν: i) o ισχυρισµός είναι αληθής για τον ακέραιο 1,
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ - 11 - ΚΕΦΑΛΑΙΟ 4 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ ΑΡΧΗ ΤΗΣ ΜΑΘΗΜΑΤΙΚΗΣ ΕΠΑΓΩΓΗΣ Έστω Ρ(ν) ένας ισχυρισµός, ο οποίος αναφέρεται στους θετικούς ακέραιους Αν: i) o ισχυρισµός είναι αληθής για τον ακέραιο 1,
Οι Φυσικοί Αριθμοί. Παρατήρηση: Δεν στρογγυλοποιούνται αριθμοί τηλεφώνων, Α.Φ.Μ., κωδικοί αριθμοί κλπ. Πρόσθεση Φυσικών αριθμών
 Οι Φυσικοί Αριθμοί Γνωρίζουμε ότι οι αριθμοί είναι ποσοτικές έννοιες και για να τους γράψουμε χρησιμοποιούμε τα αριθμητικά σύμβολα. Οι αριθμοί μετρούν συγκεκριμένα πράγματα και φανερώνουν το πλήθος της
Οι Φυσικοί Αριθμοί Γνωρίζουμε ότι οι αριθμοί είναι ποσοτικές έννοιες και για να τους γράψουμε χρησιμοποιούμε τα αριθμητικά σύμβολα. Οι αριθμοί μετρούν συγκεκριμένα πράγματα και φανερώνουν το πλήθος της
α) f(x(t), y(t)) = 0,
 Ρητές καμπύλες Μια επίπεδη αλγεβρική καμπύλη V (f) είναι το σύνολο όλων των σημείων του επιπέδου K 2 που μηδενίζουν κάποιο συγκεκριμένο ανάγωγο πολυώνυμο f K[x, y], δηλαδή V (f) = {(x 0, y 0 ) K 2 f(x
Ρητές καμπύλες Μια επίπεδη αλγεβρική καμπύλη V (f) είναι το σύνολο όλων των σημείων του επιπέδου K 2 που μηδενίζουν κάποιο συγκεκριμένο ανάγωγο πολυώνυμο f K[x, y], δηλαδή V (f) = {(x 0, y 0 ) K 2 f(x
Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου 8
 Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου 8 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Βοηθος Ασκησεων: Χ. Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://www.math.uoi.gr/ abeligia/linearalgebrai/lai.html
Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου 8 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Βοηθος Ασκησεων: Χ. Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://www.math.uoi.gr/ abeligia/linearalgebrai/lai.html
Κεφάλαιο 9. Οµάδες συγκεκριµένης τάξης. 9.1 Οµάδες τάξης pq. Z p 2 και Z p Z p.
 Κεφάλαιο 9 Οµάδες συγκεκριµένης τάξης Στο κεφάλαιο αυτό ϑα εφαρµόσουµε τη ϑεωρία που αναπτύχθηκε στα προηγούµενα κεφάλαια για να περιγράψουµε οµάδες τάξης pq, όπου p, q είναι διακεκριµένοι πρώτοι αριθµοί,
Κεφάλαιο 9 Οµάδες συγκεκριµένης τάξης Στο κεφάλαιο αυτό ϑα εφαρµόσουµε τη ϑεωρία που αναπτύχθηκε στα προηγούµενα κεφάλαια για να περιγράψουµε οµάδες τάξης pq, όπου p, q είναι διακεκριµένοι πρώτοι αριθµοί,
2.1 Διαιρετότητα, ισοϋπόλοιποι αριθμοί. q Z, a = b q + r.
 Κεφάλαιο 2 Θεωρία Αριθμών Κύριες βιβλιογραφικές αναφορές για αυτό το Κεφάλαιο είναι οι Hardy and Wright 1979 και Graham, Knuth, and Patashnik 1994. 2.1 Διαιρετότητα, ισοϋπόλοιποι αριθμοί Θεώρημα 2.1 Αν
Κεφάλαιο 2 Θεωρία Αριθμών Κύριες βιβλιογραφικές αναφορές για αυτό το Κεφάλαιο είναι οι Hardy and Wright 1979 και Graham, Knuth, and Patashnik 1994. 2.1 Διαιρετότητα, ισοϋπόλοιποι αριθμοί Θεώρημα 2.1 Αν
Κεφάλαιο 6. Πεπερασµένα παραγόµενες αβελιανές οµάδες. Z 4 = 1 και Z 2 Z 2.
 Κεφάλαιο 6 Πεπερασµένα παραγόµενες αβελιανές οµάδες Στο κεφάλαιο αυτό ϑα ταξινοµήσουµε τις πεπερασµένα παραγόµενες αβελιανές οµάδες. Αυτές οι οµάδες είναι από τις λίγες περιπτώσεις οµάδων µε µία συγκεκριµένη
Κεφάλαιο 6 Πεπερασµένα παραγόµενες αβελιανές οµάδες Στο κεφάλαιο αυτό ϑα ταξινοµήσουµε τις πεπερασµένα παραγόµενες αβελιανές οµάδες. Αυτές οι οµάδες είναι από τις λίγες περιπτώσεις οµάδων µε µία συγκεκριµένη
Γενικές Παρατηρήσεις. Μη Κανονικές Γλώσσες - Χωρίς Συµφραζόµενα (1) Το Λήµµα της Αντλησης. Χρήση του Λήµµατος Αντλησης.
 Γενικές Παρατηρήσεις Μη Κανονικές Γλώσσες - Χωρίς Συµφραζόµενα () Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Υπάρχουν µη κανονικές γλώσσες, π.χ., B = { n n n }. Αυτό
Γενικές Παρατηρήσεις Μη Κανονικές Γλώσσες - Χωρίς Συµφραζόµενα () Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Υπάρχουν µη κανονικές γλώσσες, π.χ., B = { n n n }. Αυτό
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΠΕΡΙΤΤΟΙ) Λυσεις Ασκησεων - Φυλλαδιο 3
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΠΕΡΙΤΤΟΙ) Λυσεις Ασκησεων - Φυλλαδιο ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/aeligia/linearalgerai/lai07/lai07html Παρασκευή Νοεµβρίου 07 Ασκηση Αν
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΠΕΡΙΤΤΟΙ) Λυσεις Ασκησεων - Φυλλαδιο ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/aeligia/linearalgerai/lai07/lai07html Παρασκευή Νοεµβρίου 07 Ασκηση Αν
4.2 ΕΥΚΛΕΙΔΕΙΑ ΔΙΑΙΡΕΣΗ
 14 4 ΕΥΚΛΕΙΔΕΙΑ ΔΙΑΙΡΕΣΗ Ας υποθέσουμε ότι θέλουμε να βρούμε το πηλίκο και το υπόλοιπο της διαίρεσης του με τον Σύμφωνα με το γνωστό αλγόριθμο της διαίρεσης, το πηλίκο θα είναι ένας ακέραιος κ, τέτοιος,
14 4 ΕΥΚΛΕΙΔΕΙΑ ΔΙΑΙΡΕΣΗ Ας υποθέσουμε ότι θέλουμε να βρούμε το πηλίκο και το υπόλοιπο της διαίρεσης του με τον Σύμφωνα με το γνωστό αλγόριθμο της διαίρεσης, το πηλίκο θα είναι ένας ακέραιος κ, τέτοιος,
Κεφάλαιο 8. Η οµάδα S n. 8.1 Βασικές ιδιότητες της S n
 Κεφάλαιο 8 Η οµάδα S n Στο κεφάλαιο αυτό ϑα µελετήσουµε την οµάδα µεταθέσεων ή συµµετρική οµάδα S n εφαρµόζοντας τη ϑεωρία που αναπτύχθηκε στα προηγούµενα κε- ϕάλαια. Η σηµαντικότητα της S n εµφανίστηκε
Κεφάλαιο 8 Η οµάδα S n Στο κεφάλαιο αυτό ϑα µελετήσουµε την οµάδα µεταθέσεων ή συµµετρική οµάδα S n εφαρµόζοντας τη ϑεωρία που αναπτύχθηκε στα προηγούµενα κε- ϕάλαια. Η σηµαντικότητα της S n εµφανίστηκε
