PRORAČUN VJETRENIH MREŽA
|
|
|
- Δαίδαλος Κοσμόπουλος
- 6 χρόνια πριν
- Προβολές:
Transcript
1 Vjetreje rudka PRORAČUN VJETRENIH MREŽA Povjes razvoj Strujaje zraka kroz jaske provodke spada u područje ehake fluda. Jedu od prvh teorjskh studja vezao uz vjetreje rudčkh prostorja apsao je Atkso 854. gode pod aslovo «Teorja vjetreja rudka». Početko 0. stoljeća pojavo se z radova koj razatraju uvjete strujaja u jedo vjetreo provodku. Važ radov za razvoj ove dscple su «Tehka obračua vodovodh reža» (Adrjašev 93.) «Aalza strujaja u vodovod toplovod režaa» (Hardy Cross 936.), gdje su prkazae osove teorjske postavke za proraču vjetreh reža. Zako strujaja fluda cjeva je eleara pa se u proračua javlja z elearh jedadžb za čje rješavaje ctra autor predlažu tegrale postupke. Iteratv postupak H. Crosas, D.R. Scott F.B. Hsley prjel su a rješavaje vjetreh reža rudka «Vetlato Network Theory»). Izuzev ctrah radova, postoje radov koj se bave etodaa proračua jedostavh vjetreh sustava l se predlažu razlčt teratv postupc. U jedostave vjetree reže ubrajao vjetree reže sa sključvo paralel vjetre graaa l sa al broje djagoalh graa. Iteratv postupc oogućuju, teorjsk, rješeje svake vjetree reže. U praks, vjetree reže za čje je rješavaje potrebo postavt vše od deset jedadžb, zbog dugotrajost postupka rješavaju se prjeo račuala. Ogračeost aaltčkog rješavaja problea strujaja u slože vjetre režaa, te velk začaj rješavaja ovog problea za rudarsku zaost praksu, uvjetoval su razvoj odelske tehke. Modelraja vjetree reže Postoje razlčt fzkal prstup odelraju vjetreh reža. Model koj korste koprra zrak eposredo sulraju vjetreu režu, pa se teelje geoetrjske slčost strujaja određuju velče strujaja u stvaroj vjetreoj rež. Aalog elektrč odel teelje se a slčost osovh zakoa strujaja vjetreh elektrčh reža. Od aalogh elektrčh odela razvla su se aaloga račuala koja su ogla rješt ajsložeje vjetree reže. Aalogo račualo FLUAC (Electroc Flud Aalyser) razvje je u Japau 959. gode (Resources Research Isttut of Japa Methods of Solvg Me Vetlato Network Proble) ogao je rješavat reže sa preko 0 graa. Nešto kasje tvrtka Motaforschug GbH z Düsseldorfa razvja stroj u koje se kvadrat zako sulra elektroehačk. Ovaj stroj ubrzo je zajeje ov, gdje se u eleetu, slčo kao kod Fluaca, parabole sulrae sa 3 do 5 pravaca (Verfahre der Wetteretzberechug). Rješavaje vjetreh reža prjeo aalogh strojeva ogračee je točost, a obzro da se zrađuju sključvo sao za sulraje vjetreh reža, relatvo su skup. Razvoj prjea dgtalh račuala alaz velko opravdaje u ovo području gdje je za dobvaje rezultata potrebo dugo vrjee obzro a velk broj ateatčkh operacja. Prjeo dgtalh račuala teratvh etoda proračua zadatak odeđvaja vjetreh velča u vjetre režaa ože se satrat rješe. D. Vrklja Proraču vjetree reže
2 Vjetreje rudka Defraje zadaća Svaka graa vjetree reže kao čtava vjetrea reža opsa je sa tr osove velče: otporo R, kg/ 7 protoko Q, 3 /s depresjo (pad tlaka) h, Pa U praks se javljaju zadac razh tpova glede određvaja osovh velča vjetree reže: Sloboda raspodjela zraka u vjetreoj rež uz pozate otpore vjetreh provodka R pozate zvore depresja h (prrode ujete) potrebo je utvrdt glavu ulazu (zlazu) protoče kolče zraka po pojed graaa vjetree reže, Regulacja vjetree reže za pozate otpore graa vjetree reže R pozate (tražee) kolče zraka u pojed graaa vjetree reže Q potrebo je utvrdt velče dodath otpora, Stablost vjetreh reža zrada plaova obrae spašavaja z rudka SLOBODNA RASPODJELA ZRAKA U VJETRENOJ MREŽI Postavljaje jedadžb Proraču vjetreh reža teelj se a ekolko osov zakoa ehake fluda. a. za -tu grau (docu) vjetree reže vrjed relacja zeđu depresje (pada tlaka), otpora grae protoče kolče Q: h =R Q, opčeto = što prozlaz z Darcy-Wesebachove relacje za depresju λ ρ L O Q h = 8F 3, Pa gdje je λ - koefcjet treja vjetreog provodka (bezdezoal broj) ρ - gustoća zraka, kg/ 3 F površa poprečog presjeka vjetreog provodka, Q kolča zraka koja struj vjetre provodko, 3 /s O opseg vjetreog provodka, D. Vrklja Proraču vjetree reže
3 Vjetreje rudka U svakoj vjetreoj rež ože se postavt g jedadžb oblka h=r Q, gdje g ozačava broj graa u vjetreoj rež. Otpor R u jedadžb je kostata velča već je u ovsost o hrapavost K Reyoldsovo broju Re: R = f (Re, K ) b. za estšljv flud vrjed zako čvora: sua kolča zraka koje ulaze u čvor jedaka je su kolča zraka koj zlaze z čvora. Mateatčk je ovaj zako zraže zrazo: Q = = 0 gdje je broj graa koje ulaze u čvor Q ulaze, odoso zlaze kolče zraka u čvoru, 3 /s Kolče zraka koje ulaze u čvor suprotog su predzaka od kolča zraka koje zlaze z čvora. Može se uočt da se kod svakog ovog čvora javlja ova graa, odoso ova kolča zraka, os kod posljedjeg čvora u vjetreoj rež koj je kopora sključvo od pozath kolča zraka. To zač da se u vjetreoj rež ože postavt č- ezavsh jedadžb oblka Q = 0. c. zako zatvoreh vjetreh puteva (krugova) zražava se relacjo: = D k = h ± ± hp hv = = j= j = 0 Uvrštavaje zraza za h =R Q dobjeo D k = ± ± R Q hp = = j= hv j = 0 broj graa a zatvoreo vjetreo putu k ozaka zatvoreog vjetreog puta broj vetlatora uutar zatvoreog vjetreog puta h depresja (pad tlaka) u -toj gra zatvoreog vjetreog puta hp - zos prrode depresje u -toj gra zatvoreog vjetreog puta hv j - zos depresje j-tog vetlatora a zatvoreo vjetreo putu Zako zatvoreog vjetreog puta glas da je sua svh depresja, utrošeh prozvedeh, a zatvoreo vjetreo putu jedaka ul. Drug rječa, ože se reć, da su utrošee prozvedee depresje oraju bt u ravotež (jedake), uutar zatvoreog vjetreog puta. Jedadžba se dade postavt za svak zatvore vjetre put u vjetreoj rež. Pr obračuu ovh depresja, sjer kretaja, odoso suraja zosa depresja a zatvoreo vjetreo putu je prozvolja. Pr obračuu je važo da se orao vratt u točku (zatvort krug) z koje D. Vrklja Proraču vjetree reže 3
4 Vjetreje rudka so kreul u oblazak vjetreog puta. Poztva sjer kretaja (strujaja) odgovara kretaju kazaljk a satu. Sve grae a zatvoreo vjetreo putu koje aju sjer strujaja stovjeta sjeru kretaja kazaljke a satu aju poztva zos utrošee depresje. Sve grae a zatvoreo vjetreo putu koje aju sjer strujaja suprota sjeru kretaja kazaljke a satu aju egatva zos utrošee depresje.vjetre putev (krugov) sa graaa koje koucraju sa površo (prostorje otvaraja jae, trasporte l vjetree podzee prostorje) zatvaraju se preko atosfere. U ovaj obraču uključee su prozvedee depresje, prroda ujeta. Izos sjer djelovaja prrode depresje ora se posebo obračuat. Izos prrode depresje ovsa je o kotaa pojedh čvorova a zatvoreo vjetreo putu, odoso o vssk razlkaa zeđu čvorova zatvoreog vjetreog puta te o gustoćaa zraka u graaa zatvoreog vjetreog puta. Sjer djelovaja prrode depresje, općeto je + l -, odoso u sjeru kretaja kazaljke a satu l suproto kretaju kazaljke a satu. Ujete depresje su vetlator, blo glav (u ulazo l zlazo djelu jae) l pooć (uutar pojedh graa u rež). Sjer djelovaja depresje vetlatora, općeto je + l -, odoso u sjeru kretaja kazaljke a satu l suproto kretaju kazaljke a satu. Buduć utrošea depresja a predzak + (odgovara sjeru strujaja zrače struje u gra) ajčešće sjer djelovaja depresje vetlatora je (prozvedee depresja koja ora adokadt utrošeu depresju). Međut, ako se a zatvoreo vjetreo putu alaz dva l vše vetlatora, koj ogu bt u razlčt eđusob pozcjaa te radt u razlčt reža, kopresjsko l ssajuće, ože doć do stuacja u koja djelovaje depresje jedog vetlatora je suproto djelovaju depresje drugoga vetlatora. Poseba slučaj jest ako ao pooće vetlatore uutar graa vjetree reže, gdje pooć vetlator ože at fukcju regulacje vjetree reže, odoso regulacju kolča zraka u pojed graaa reže. Stoga, predzake vetlatora treba blježt općeto ±. Jedadžbe zatvoreh vjetreh puteva su kvadrate za koje e postoj aaltčko rješeje u opće oblku. U praks se javljaju raz slučajev velča stotjak vše putova, tj. sustav sa stotu vše elearh jedadžb. Potreba broj jedadžb za rješavaje slobode raspodjele zraka u rež Broj epozath protoka u vjetreoj rež jedak je broju graa g. Ukupa broj velča Q, R h u vjetreoj rež je 3g. Otpor za svake grae je zada pa je potrebo utvrdt g epozaca. Ukupa broj raspoložvh jedadžb: č- broj raspoložvh jedadžb oblka Q = = 0 (č-broj čvorova u vjetreoj rež) g broj raspoložvh jedadžb oblka h =R Q (g broj graa u vjetreoj rež) D. Vrklja Proraču vjetree reže 4
5 Vjetreje rudka p broj raspoložvh jedadžb oblka R Q ± hp ± hv = 0 = = p broj zatvoreh vjetreh puteva u vjetreoj rež j= j Potreba broj jedadžb x: g=č-+g+x x=g-č+ Gorja relacja predstavlja zraz za odeđvaje potrebog broja jedadžb x, oblka h = 0 kolko je za rješeje vjetree reže potrebo postavt. Taj broj ujedo predstavlja broj osovh zatvoreh vjetreh puteva u vjetreoj rež. Razvdo je da se u vjetreoj rež dade forrat već broj jedadžb a zatvoreo vjetreo putu oblka h = 0, eđut jedadžbe svh zatvoreh vjetreh puteva su ezavse. Razatraje potrebog broja jedadžb razvdo je da se u eodvs jedadžbaa ora pojavt svaka graa vjetree reže bare jedo. Relacjo h =R Q defraa je depresja _ te grae vjetree reže. Prroda depresja uos se redovto u proraču kao kostata velča. Međut, prroda depresja ovsa je o kolčaa zrače struje, proje teperature odoso gustoć zraka. Vetlator kao ujet (točkast) zvor depresje također oraju bt uključe u jedadžbu. Buduć se depresja vetlatora jeja projeo kolče zrače struje to se kod proračua ora uvažt karakterstka vetlatora. Karakterstka vetlatora redovto je krvulja všeg reda. U rado djelu ova krvulja se dade zrazt jedadžbo pravca, jedadžbo parabole l evetualo jedadžbo všeg reda: Jedadžba pravca Jedadžba parabole Jedadžba všeg reda h vj =a j Q +b j h vj =a j Q + b j Q +c j h vj =a j Q 3 + b j Q +c j Q +d j gdje je h vj depresja vetlatora, Pa a j, b j, c j, d j koefcjet jedadžbe vetlatora Q kolča zraka koju daje vetlator, 3 /s j ozaka vetlatora u rež ozaka grae Najčešće se prjejuje jedadžba parabole. Krvulja vetlatora ože bt eka druga vrsta jedadžbe, o oa ora bt jedozača. Svako otporu jae, odoso krvulj otpora jae, ora odgovarat sao jeda rada točka vetlatora sještea a krvulj vetlatora.. D. Vrklja Proraču vjetree reže 5
6 Vjetreje rudka Rješavaje sustava jedadžb teratv postupko Jedadžbe zatvoreh vjetreh puteva predstavlju sste elearh jedadžb sa epozaca. Kod rješeja sstea su a potreb sv korje jedadžb. Za rješavaje ovakvog sustava jedadžb ajprjerej je teratv postupak. U obzr dolaze teratv postupc koj se teelje a Newtoovoj l Lagrageovoj etod. Metoda Hardy Crossa razvjea je kao specfča za rješavaje raspodjele protočh kolča u vodovod režaa. Ova etoda joj slče pozate etode praktčk su ble eprjejve u praks, kod rješavaja sstea sa vše desetaka jedadžb, do razvoja dgtalh račuala koj u kratko vreeu ogu zvest potreb velk broj račuskh operacja. Iteratva etoda Hardy Crossa Metoda polaz od relacje opće jedažbe depresje u -toj vjetreoj gra h =R Q, Pa prošreje u oblk h = R( Q p + ΔQ), Pa gdje je h depresja u -toj vjetreoj gra, Pa R otpor -te grae vjetree reže, kg/ 7 Q p pretpostavljea početa kolča zraka u -toj gra, 3 /s ΔQ poprava kolča zraka u -toj gra, 3 /s Razvoje zraza u Taylorov red h = R ( Q + ΔQ ) = R ( Q + Q ΔQ + ΔQ Q o +...) Uz pretpostavku alog popravka ožeo zaeart sve člaove Taylorovog reda s ekspoeto popravka već od pa a ostaje zraz h = R Q + R Q ΔQ Ukolko se ovaj zraz prje a cjel zatvore k-t vjetre put, odoso sve grae uutar zatvoreog vjetreog puta h k = = R Q A + = R ΔQQ = 0 D. Vrklja Proraču vjetree reže 6
7 Vjetreje rudka odakle sljed zraz za popravak za k-t zatvore vjetre put gdje je Δ Q RQ A = 3 k =, / = R Q A predzak (sgu) ovsa o podudaraju sjera oblaska a zatvoreo vjetreo putu (sjer kretaja kazaljke a satu bljež se sa plus) sjera strujaja (pretpostavljeog) u toj vjetreoj gra zatvoreog vjetreog puta A = + - sjer strujaja u -toj vjetreoj gra k-tog zatvoreog vjetreog puta poklapa se sa poztv sjero oblaska u k-to zatvoreo vjetreo putu A = - - sjer strujaja u -toj vjetreoj gra k-tog zatvoreog vjetreog puta suprota je sa poztv sjero oblaska u k-to zatvoreo vjetreo putu s Gorj zraz predstavlja popravak kolča u pojed graaa uutar zatvoreog vjetreog puta bez da su uključe zvor depresje, prrod ujet. Uključvaje zvora depresje, prrode depresje depresje vetlatora, zraz za popravak kolča u pojed graaa zatvoreog vjetreog puta glas gdje je ΔQ RQ A ± hv j ± hpk = j= 3 k =, / ' ' RQ ± hv j ± h pk = j= hv j depresja j-tog vetlatora a k-to zatvoreo vjetreo putu, hv ' j dervacja depresje j-tog vetlatora a k-to zatvoreo vjetreo putu, - broj vetlatora a k-to zatvoreo vjetreo putu ( je blo koj prrod broj) R otpor -te grae vjetree reže, kg/ 7 Q pretpostavljea početa kolča zraka u -toj gra, 3 /s ΔQ k poprava kolča zraka za k-t zatvore vjetre put, 3 /s broj graa a zatvoreo vjetreo putu ( je blo koj prrod broj) h pk prroda depresja a k-to zatvoreo vjetreo putu, Pa h ' pk dervacja prrode depresje a k-to zatvoreo vjetreo putu, Pa s D. Vrklja Proraču vjetree reže 7
8 Vjetreje rudka Dobve zoso popravka ΔQ k za k-t zatvore vjetre krug popravljaju se kolče zraka u -t graaa k-tog zatvoreog kruga Q ' =Q +Δ Q, 3 /s gdje je Q ' popravljea kolča zraka u -toj gra k-tog zatvoreog vjetreog kruga, 3 /s Q početa (pretpostavljea) kolča zraka u -toj gra k-tog zatvoreog vjetreog kruga, 3 /s ΔQ popravak kolča zraka za -te grae k-tog zatvoreog vjetreog kruga, 3 /s Iteratv postupak se zvod sve dok popravak kolča zraka ΔQ k za zatvoree vjetree krugove e zadovolj postavlje krterj, koj se postavlja ovso o aje za koj se zvod proraču, prjerce ΔQ k <0, 3 /s. Izos popravka kolča zraka ΔQ k ora se tjeko teratvog postupka u odgovarajuć vjetre krugova sajvat što zač da cjel postupak kovergra prblžava se eko rješeju. Ukolko dođe do dvergecje popravh kolča to upućuje a pogrešo postavljee ulaze podatke l a pogrešku tjeko saog postupka. Iteratv postupak započje pretpostavko raspodjele kolče zraka po pojed graaa vjetree reže, suklado zakou čvora da je sua kolča u čvoru jedaka 0, što podrazujeva pretpostavku ukuph ulazh/zlazh kolča z vjetree reže. O toe kolko je pretpostavljea kolča daleko odoso blzu stvaroj kolč koja će se dobt rješeje teratvog postupka ovs trajaje saog teratvog postupka. Os kolča zraka za pojede grae vjetree reže pretpostavlja se sjer strujaja zraka u pojed graaa. Ukolko se pretpostav pogreša sjer strujaja zraka u ekoj gra, tjeko teratvog postupka kolče zraka u toj gra popraju egatve vrjedost. U to slučaju postupak se e prekda, ego se astavlja dok se e spu postavlje krterj spra vrjedost popravka. U rezultata teratvog postupka kostatra se kolča zraka u gra gdje je projeje sjer strujaja sprav sjer strujaja u toj gra. Prroda depresja u k-to zatvoreo vjetreo krugu hp k uza se da je kostata velča, akar u stvarost oa to je ego ovs o protoč kolčaa zraka kroz vjetreu režu, kao što to ovs depresja vetlatora. Stoga se u azvku zraza za popravak kolča dervacja prrode depresje jedaka 0. Za obraču prrode depresje u zatvore vjetre krugova potrebo je pozavat kote pojedh čvorh točaka, kote ulaza zlaza z jae, te gustoće jaskog zaraka u pojed graaa vjetree reže, odoso u čvorova vjetree reže. D. Vrklja Proraču vjetree reže 8
9 Vjetreje rudka REGULACIJA VJETRENE MREŽE Zadaća regulacje je doprea određeh potrebh kolča zaraka u određee grae vjetree reže. Za razlku od slobode raspodjele zraka gdje se zrak slobodo raspodjeljuje po graaaa (docaa) vjetree reže ovso o uvjeta koj vladaju u rež, kod regulacje se zahtjevaju u jedoj l vše graa vjetree reže, određee potrebe protoče kolče zraka. Potrebe kolče zraka u pojed graaa vjetree reže dktrae su rudarsk propsa teelje kojh se proračuavaju. Potrebe kolče zraka proračuavaju se poajčešće teelje broja zaposleka u ja (radlštu), agažrae rudarske ehazacje (jhove sage), kolče plova z stjeskog asva koj prtču u jasku atosferu, razblažvaja plskh produkata raja drugo. Najveć potrošać zraka u ja su otkopa radlšta gdje se zvod eksploatacja (dobvaje) erale srove. Otkopa radlšta su jesta u ja sa ajvećo kocetracjo djelatka rudarske (otkope) ehazacje gdje se zvod koturaa rada aktvost, poekad kroz sve tr sjee. Shodo toe otkopa radlšta zahtjevaju ajveće kolče zraka. Pojedostavljeo, ostale vjetree provodke, ožeo satrat sao trasport puteva za dopreu zraka do otkoph radlšta. Na taj ač, zadaća regulacje se doekle pojedostavljuje, reducraje regulacjskh zahvata a određe aj broj graa vjetree reže u koja se alaze otkopa radlšta. Sekudaro, potrebo je zvest regulacjske zahvate za osguraje kolča zraka u pooć, servs sadržaja poput skladšta eksplozva, radoca, puph postrojeja toe slčo. Ove prostorje uobčajeo se sještaju u kratk spojeva zeđu ulazog (svježe zrače struje) zlazog (strošee zrače struje) djela vjetree reže. Za dopreu potrebe kolče zraka u određee grae vjetree reže zvode se regulacjsk zahvat. Regulacjsk zahvato jeja se, sajuje l povećava, otpor grae kroz koj se žel arut određea protoča kolča zraka (veća l aja). Regulacjsk zahvata postže se željea preraspodjela kolča zraka uutar graa vjetree reže. Regulacja vjetree reže zvod se postavljaje jedadžb oblka Σh=0 (sua depresja a zatvoreo vjetreo putu jedaka je ul). = R Q ± ΔR r Q r + = hp ± j= hv j = 0 - ozaka grae a zatvoreo vjetreo putu R otpor -te grae a zatvoreo vjetreo putu, kg -7 Q kolča zraka u -toj gra zatvoreog vjetreog puta broj graa a zatvoreo vjetreo putu ΔR r popravak otpora u r- toj gra zatvoreog vjetreog puta Q r zahtjevaa kolča zraka u r-toj gra zatvoreog vjetreog puta broj vetlatora uutar zatvoreog vjetreog puta h depresja (pad tlaka) u -toj gra zatvoreog vjetreog puta hp - zos prrode depresje u -toj gra zatvoreog vjetreog puta hv j - zos depresje j-tog vetlatora a zatvoreo vjetreo putu D. Vrklja Proraču vjetree reže 9
10 Vjetreje rudka Broj potrebh jedadžb Σh=0 za regulacju odgovora broju graa koje je potrebo regulrat. Rješeja se za grae u koja se žele projet protoče kolče zraka, dobjaju popravc otpora ±ΔR r. Nov otpor R ' r regulrae vjetree graa pr toe je jedak: R' r = R r ±ΔR r Projee otpora u pojed graaa vjetree reže utječu a projeu ukupog otpora vjetree reže. Ovso o toe u ko sslu se jeja otpor regulrae grae razlkujeo: poztvu regulacju egatvu regulacju Poztva regulacja podrazujeva povečaje otpora regulrae grae, odoso sajeje protoče kolče zraka u toj gra. Negatva regulacja podrazujeva sajeje otpora regulrae grae, odoso povečaje protoče kolče zraka u toj gra. U stručoj lteratur pojed autor drugačje (verzo, suproto) defraju začeje (poja) poztve egatve regulacje. To je stoga jer se u defcj referra a kolče zraka u gra a e a otpore graa (poztva regulacja zač povečaje kolča zraka, odoso sajeje otpora grae a egatva regulacja zač sajeje kolča zraka, odoso povečaje otpora grae). Regulacja se ačelo provod: u ajveće presjeku vjetree reže u određe graaa vjetree reže Regulacja u ajveće presjeku vjetree reže Najveć presjek vjetree reže, satra se presjek u koje je zbroj protočh kolča zraka jedak ulazoj (zlazoj) kolč zraka u vjetreu režu. Prethodo se za vjetreu sheu, proračua sloboda raspodjela zraka u pojed graaa vjetree reže. Kod ovog tpa regulacje regulraju se sve grae u ajveće presjeku os jede. Kroz svaku grau koja se žel regulrat polaže se jeda regulacjska jedadža oblka Σh=0. Regulacjske jedadžbe obavezo obuhvaćaju grau u kojoj se alaz glav vetlator. U grae koje se žele regulrat uvrštavaju se tražee (zahtjevae) protoče kolče zraka. Kolče zraka u ostal graaa vjetree reže predodređee su zahtjeva kolčaa zraka u ajveće (regulrao) presjeku jae. Raspodjela se određuje suklado zakou ΣQ č =0 (sua kolča u čvoru je jedaka ul, odoso koje kolče zraka ulaze u čvor tolke kolče oraju zać z čvora). Ako kolče zraka u ostal graaa je oguće odredt a taj ač, kolče se određuju provođeje teratvog postupka u podrež (aa). U pojed regulacjsk D. Vrklja Proraču vjetree reže 0
11 Vjetreje rudka jedadžbaa oblka Σh=0 a zatvore vjetre puteva, proračuavaju se zos popravaka otpora ΔR. Prethodo se, za postavljee regulacjske jedadžbe, sptuje a koje je zatvoreo vjetreo putu zos utrošee depresje ajveć. U toj gra regulacja se e zvod (ΔR=0), dok se popravc otpora u ostal graaa proračuavaju. Popravc otpora pojedh graa su poztv (+ΔR), otpor pojedh graa se povećavaju, pa se rad sključvo o poztvoj regulacj vjetree reže. Posljedca sključvo poztvh regulacjskh zahvata je povečaje ukupog otpora vjetree reže. Regulacja u određe graaa vjetree reže Regulacja u određe graaa vjetree reže ože bt sključvo poztva, sključvo egatva l ješovta. Mješovta regulacja podrazujeva da se jeda l vše graa regulraju poztvo te jeda l vše graa egatvo. Isključvo egatva l poztva regulacja podrazujeva projeu ukupog otpora reže. Mješovtu regulacju oguće je zvest a ač da se ukup otpor jae kao posljedca regulacjskh zahvata e jeja, drug rječa da vetlator ostaje radt u stoj radoj točk, odoso a sto eergetsko vou. Kroz svaku grau koja se žel regulrat polaže se jeda regulacjska jedadža oblka Σh=0. Regulacjske jedadžbe obavezo obuhvaćaju grau u kojoj se alaz glav vetlator. U grae koje se žele regulrat uvrštavaju se tražee (zahtjevae) protoče kolče zraka. Podreža Podreža je sječe, zdvoje, do vjetree reže. Za podrežu vrjede ste zakotost kao za vjetreu režu. Kolče zraka Q u koje ulaze u podrežu oraju bt jedake kolčaa zraka koje zlaze z podreže Q : ΣQ u = ΣQ Podreža se zolra u slučajeva rješavaja regulacjskh zadaća. Izlazo-ulaze grae u podrežu predstavljaju grae u koja je potrebo zvest regulacju. Da b ogl rješt regulacjske jedadžbe, odoso popravke otpora ΔR u graaa koje se regulraju, orao zat protoče kolče, odoso slobodu raspodjelu zraka u ostal graaa reže. Ova sloboda raspodjela zraka e odgovara početoj, stvaroj, slobodoj raspodjel. Možeo govort o uvjetovaoj slobodoj raspodjel, uvjetovaoj zahtjeva kolčaa zraka u pojed graaa vjetree reže. Pod t zada uvjeta uutar podreže se teratv postupko određuju protoče kolče zraka po pojed graaa potrebe za rješavaje regulacjskh jedadžb. Negatva regulacja vjetree grae zvod se a ač da se saj jez otpor. Na sajvaje otpora grae ože se djelovat: prošreje poprečog presjeka vjetree prostorje sajeje koefcjeta otpora vjetreog provodka Oba avedea postupka za sajeje otpora vjetree grae provođeje egatve regulacje su skup tehološko zahtjev. Stoga je u stvar rudčk uvjeta, poekad, ukolko je D. Vrklja Proraču vjetree reže
12 Vjetreje rudka užo sajt otpore grae u clju povećaja dobavh kolča zraka, praktčje zradt potpuo ovu prostorju tražeh karakterstka (većeg poprečog presjeka ajeg koefcjeta otpora) koja će supstturat u vjetreoj she star vjetre provodk. Novozgrađea graa ože os toga bt kraće dulje će se dobje aj otpor. Troškovo tehčk prhvatljvo rješeje je ugradja pooćog vetlatora u grau kroz koju se žel povećat protok zraka. Izos depresje pooćog vetlatora h pv proporcoala je proračuatoj proje otpora vjetreog provodka -ΔR zahtjevaoj protočoj kolč zraka Q: h pv =-ΔR Q, Pa Ugradjo pooćog vetlatora odgovarajuće depresje stvaro se e sajuje otpor grae koja se regulra al se postže traže efekt: povećaje protoče kolče zraka dovođeje dodatog zvora depresje u regulrau grau. Poztvu regulacju, povećaje otpora vjetree grae, zato je laše zvest, u tehčko troškovo sslu od egatve regulacje. Poztva regulacja zvod se ugradjo regulacjske pregrade u regulrau grau, če se sajuje površa poprečog svjetlog presjeka vjetree prostorje a taj ač povećava je otpor. D. Vrklja Proraču vjetree reže
13 Vjetreje rudka STABILNOST VJETRENE MREŽE Nastupaje razlčth esreća-akcdeata u pojed djelova vjetree reže jejaju se uvjet uutar vjetree reže koj ogu utjecat a paraetre zrače struje: - oečšćeja jaskog zraka, - projeu otpora pojedh graa ukupog otpora vjetree reže, - kolče zraka - sheu vjetree reže. Sve to ože utjecat a sgurost zvođeja rudarskh radova te ugrozt zdravlje žvote zaposleka u ja. U clju studraja uvjeta koj astaju astupaje razlčth vrsta akcdeata u razlčt djelova jae sulraju se razlčte stuacje posljedce a paraetre zrače struje. Iz ovakovh studja zaključuje se a plaove spašavaja u određe kokret akcdet stuacjaa. jae: Najčešća vrsta akcdeata koja utječe a stablost vjetree reže sheu vjetreja požar eksplozje zarušavaje vjetreh provodka provale plova Požar eksplozje u rudca sa podzeo eksploatacjo, uatoč jeraa zaštte, još uvjek su jeda od ajčešćh uzroka esreća čje su posljedce velk broj ljudskh žrtava velka aterjala šteta. Posljedce požara ovse o teztetu pozcj požara uutar vjetree reže. U požara razvjaju se vrlo otrov plov, u prvo redu ugljč ooksd. Kako se otrov plov d šre jask prostorjaa štete posljedce šre se a ogo već prostor od sae lokacje požara. Sulraje jesta požara u vjetreoj rež te raspodjela kolča zraka sjerova strujaja zraka kao posljedca požara začajo je u clju zalažeja prevetvh jera zrad plaova obrae rudka. Prblž zos depresje h p uzrokovae požaro: h p Δz Δt = ρ g, Pa T Δz vsska razlka vjetreog puta sa požaro, Δt porast teperature uzrokova požaro, o C T teperatura zraka prje astupaja požara, o C ρ - sredja gustoća jaskog zraka, kg/ 3 Požar eksplozje prvestveo utječu a projeu prrode depresje jae, projeo teperature jaskog zraka u određe djelova jae. Projea zosa, pa D. Vrklja Proraču vjetree reže 3
14 Vjetreje rudka oguće sjera prrode depresje, ože utjecat a kolče zraka kako ulazh kolča tako raspodjele po pojed djelova jae. Za sulraje pojave požara u pojed točkaa vjetree reže, potrebo je zračuat prrode (toplske) depresje koje prozvod požar u pojed zatvore vjetre krugova vjetree reže. Ov podac uzaju se zat kao ulaz podac za proraču reže. Potpuo l djeločo zatvaraje jaskog vjetreog provodka kao posljedca prodora vode, zarušavaja stjee l slčo uos se u proraču kao povečaje otpora dotčog vjetreog provodka.. Zarušavaje jaskh vjetreh provodka ože bt razlčtog tezteta, od djeločog do potpuog zatvaraja svjetlog, protočog profla, pojedh vjetreh provodka. Zarušavaje vjetreh provodka ogu uzrokovat rudarske aktvost l prrode pojave (potres, gorsk udar). Ovso o teztetu zarušavaja jeju se odgovarajuće otpor pojedh graa (doca) vjetree reže l dolaz do projee shee vjetree reže (u slučaju potpuog zatvaraja vjetreog provodka). Projea otpora pojedh doca vjetree reže, l potpuo prekdaje pojedh doca, utče a ukup otpor vjetree reže (općeto povećaje otpora), te projeu ulazh (zlazh) kolča te raspodjelu kolča zraka po pojed graaa vjetree reže. Ovso o položaju vjetree grae uutar vjetree reže te o velč projee otpora to ože at začaje posljedce glede kolča protoka sjera strujaja. Potpuo zatvaraje vjetree grae ožeo sulrat a dva ača: -zbacvaje dotče grae z vjetree shee jae l -uvrštavaje velkog otpora Drug ač povećava broj teratvh koraka za postzaje rješeja al je jedostavj u prpre. D. Vrklja Proraču vjetree reže 4
Metoda najmanjih kvadrata
 Metoda ajmajh kvadrata Moday, May 30, 011 Metoda ajmajh kvadrata (MNK) MNK smo već uvel u proučavaju leare korelacje; gdje smo tražl da suma kvadrata odstupaja ekspermetalh točaka od pravca koj h a ajbolj
Metoda ajmajh kvadrata Moday, May 30, 011 Metoda ajmajh kvadrata (MNK) MNK smo već uvel u proučavaju leare korelacje; gdje smo tražl da suma kvadrata odstupaja ekspermetalh točaka od pravca koj h a ajbolj
odvodi u okoliš? Rješenje 1. zadatka Zadano: q m =0,5 kg/s p 1 =1 bar =10 5 Pa zrak w 1 = 15 m/s z = z 2 -z 1 =100 m p 2 =7 bar = Pa
 .vježba iz Terodiaike rješeja zadataka 1. Zadatak Kopresor usisava 0,5 kg/s zraka tlaka 1 bar i 0 o C, tlači ga i istiskuje u eizolirai tlači cjevovod. Na ulazo presjeku usise cijevi brzia je 15 /s. Izlazi
.vježba iz Terodiaike rješeja zadataka 1. Zadatak Kopresor usisava 0,5 kg/s zraka tlaka 1 bar i 0 o C, tlači ga i istiskuje u eizolirai tlači cjevovod. Na ulazo presjeku usise cijevi brzia je 15 /s. Izlazi
Polarizacija. Procesi nastajanja polarizirane svjetlosti: a) refleksija b) raspršenje c) dvolom d) dikroizam
 Polarzacja Proces asajaja polarzrae svjelos: a refleksja b raspršeje c dvolom d dkrozam Freselove jedadžbe Svjelos prelaz z opčkog sredsva deksa loma 1 u sredsvo deksa loma, dolaz do: refleksje (prema
Polarzacja Proces asajaja polarzrae svjelos: a refleksja b raspršeje c dvolom d dkrozam Freselove jedadžbe Svjelos prelaz z opčkog sredsva deksa loma 1 u sredsvo deksa loma, dolaz do: refleksje (prema
Reverzibilni procesi
 Reverzbln proces Reverzbln proces: proces pr koja sste nkada nje vše od beskonačno ale vrednost udaljen od ravnoteže, beskonačno ala proena spoljašnjh uslova ože vratt sste u blo koju tačku, proena ože
Reverzbln proces Reverzbln proces: proces pr koja sste nkada nje vše od beskonačno ale vrednost udaljen od ravnoteže, beskonačno ala proena spoljašnjh uslova ože vratt sste u blo koju tačku, proena ože
Vježba 1. Analiza i sinteza sistema regulacije brzine vrtnje istosmjernog motora
 ortorjske vježe z predet ootk uprvljje prozvod sste Vjež Vjež Alz stez sste regulcje rze vrtje stosjerog otor Clj vježe: Stez regultor rze vrtje stosjerog otor pooću etod tehčkog setrčog optu Alzrt dčko
ortorjske vježe z predet ootk uprvljje prozvod sste Vjež Vjež Alz stez sste regulcje rze vrtje stosjerog otor Clj vježe: Stez regultor rze vrtje stosjerog otor pooću etod tehčkog setrčog optu Alzrt dčko
Riješeni zadaci: Nizovi realnih brojeva
 Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Linearna korelacija. Vrijedi: (1) 1 r 1
 Leara korelacja Korelacja je mjera leare zavsost dvju serja podataka 1,,..., 1,,...,. Drugm rječma, ako su točke 1, 1,,,..., gruprae oko regresjskog pravca, oda govormo da su podatc korelra learo korelra.
Leara korelacja Korelacja je mjera leare zavsost dvju serja podataka 1,,..., 1,,...,. Drugm rječma, ako su točke 1, 1,,,..., gruprae oko regresjskog pravca, oda govormo da su podatc korelra learo korelra.
Moguća i virtuelna pomjeranja
 Dnamka sstema sa vezama Moguća vrtuelna pomjeranja f k ( r 1,..., r N, t) = 0 (k = 1, 2,..., K ) df k dt = r + t = 0 d r = r dt moguća pomjeranja zadovoljavaju uvjet: df k = d r + dt = 0. t δ r = δx +
Dnamka sstema sa vezama Moguća vrtuelna pomjeranja f k ( r 1,..., r N, t) = 0 (k = 1, 2,..., K ) df k dt = r + t = 0 d r = r dt moguća pomjeranja zadovoljavaju uvjet: df k = d r + dt = 0. t δ r = δx +
Aritmetički i geometrijski niz
 Zadac sa prethodh prjemh spta z matematke a Beogradskom uverztetu Artmetčk geometrjsk z. Artmetčk z. 00. FF Zbr prvh dvadeset člaova artmetčkog za čj je prv čla, a razlka A) 0 B) C) D) 880 E) 878. 000.
Zadac sa prethodh prjemh spta z matematke a Beogradskom uverztetu Artmetčk geometrjsk z. Artmetčk z. 00. FF Zbr prvh dvadeset člaova artmetčkog za čj je prv čla, a razlka A) 0 B) C) D) 880 E) 878. 000.
Dimenzioniranje SN/NN kabela i transformatora
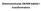 Dmezoraje SN/NN kabela trasformatora Za NN mrežu prkazau slkom potrebo je odredt presjek glavh adzemh trofazh zvoda te moofazh podzvoda obzrom a dozvolje pad apoa kod krajjeg potrošača od 6% dozvoljeu
Dmezoraje SN/NN kabela trasformatora Za NN mrežu prkazau slkom potrebo je odredt presjek glavh adzemh trofazh zvoda te moofazh podzvoda obzrom a dozvolje pad apoa kod krajjeg potrošača od 6% dozvoljeu
REGRESIJSKA ANALIZA. U razvoju regresijske analize najznačajniju ulogu su imali: Carl Friedrich Gauss ( ) Francis Galton (
 SEMINAR U razvoju regresjske aalze ajzačajju ulogu su mal: Carl Fredrch Gauss (822 9) Fracs Galto (822 9) Karl Pearso (857 936) George Udy Yule (87 95) SEMINAR Regresjska aalza je matematčko-statstčk postupak
SEMINAR U razvoju regresjske aalze ajzačajju ulogu su mal: Carl Fredrch Gauss (822 9) Fracs Galto (822 9) Karl Pearso (857 936) George Udy Yule (87 95) SEMINAR Regresjska aalza je matematčko-statstčk postupak
1. ODREĐIVANJE NETOČNOSTI MJERENJA
 . ODREĐIVANJE NETOČNOSTI MJERENJA. Opće Mjereja razh fzkalh ostalh velča rezultat se e ogu provest apsoluto točo. Usljed tehčkh ekooskh razloga potrebo je etočost jereja svest a ajaju oguću jeru, sa što
. ODREĐIVANJE NETOČNOSTI MJERENJA. Opće Mjereja razh fzkalh ostalh velča rezultat se e ogu provest apsoluto točo. Usljed tehčkh ekooskh razloga potrebo je etočost jereja svest a ajaju oguću jeru, sa što
1.4 Tangenta i normala
 28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
RAČUNANJE SA PRIBLIŽNIM VREDNOSTIMA BROJEVA
 RAČUNANJE SA PRIBLIŽNIM VREDNOSTIMA BROJEVA PRIBLIŽNI BROJ I GREŠKA tača vredost ekog broja X prblža vredost ekog broja X apsoluta greška Δ = X X graca apsolute greške (gorja graca) relatva greška X X
RAČUNANJE SA PRIBLIŽNIM VREDNOSTIMA BROJEVA PRIBLIŽNI BROJ I GREŠKA tača vredost ekog broja X prblža vredost ekog broja X apsoluta greška Δ = X X graca apsolute greške (gorja graca) relatva greška X X
TEHNIČKI FAKULTET SVEUČILIŠTA U RIJECI Zavod za elektroenergetiku. Prijelazne pojave. Osnove elektrotehnike II: Prijelazne pojave
 THNIČKI FAKUTT SVUČIIŠTA U IJI Zavod za elekroenergek Sdj: Preddplomsk srčn sdj elekroehnke Kolegj: Osnove elekroehnke II Noselj kolegja: v. pred. mr.sc. Branka Dobraš, dpl. ng. el. Prjelazne pojave Osnove
THNIČKI FAKUTT SVUČIIŠTA U IJI Zavod za elekroenergek Sdj: Preddplomsk srčn sdj elekroehnke Kolegj: Osnove elekroehnke II Noselj kolegja: v. pred. mr.sc. Branka Dobraš, dpl. ng. el. Prjelazne pojave Osnove
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
Ekonometrija 5. Ekonometrija, Osnovne studije. Predavač: Aleksandra Nojković
 Ekoometja 5 Ekoometja, Osove studje Pedavač: Aleksada Nojkovć Stuktua pedavaja Klasč dvostuk (všestuk) lea egeso model - metod ONK. Petpostavke všestukog KLM. Koelacja u všestukom KLM. Oča kogova. Dvostuk
Ekoometja 5 Ekoometja, Osove studje Pedavač: Aleksada Nojkovć Stuktua pedavaja Klasč dvostuk (všestuk) lea egeso model - metod ONK. Petpostavke všestukog KLM. Koelacja u všestukom KLM. Oča kogova. Dvostuk
UNIVERZITET U NIŠU FAKULTET ZAŠTITE NA RADU U NIŠU TEHNIČKA MEHANIKA - PREZENTACIJA PREDAVANJA PREDAVANJE
 UNIVERZITET U NIŠU FAKULTET ZAŠTITE NA RADU U NIŠU TEHNIČKA MEHANIKA - PREZENTACIJA PREDAVANJA - - 4. PREDAVANJE - Dr Darko Mhajlov, doc. 1. ČAS Sredšte (cetar) sstema paralelh sla; Težšte krutog tela;
UNIVERZITET U NIŠU FAKULTET ZAŠTITE NA RADU U NIŠU TEHNIČKA MEHANIKA - PREZENTACIJA PREDAVANJA - - 4. PREDAVANJE - Dr Darko Mhajlov, doc. 1. ČAS Sredšte (cetar) sstema paralelh sla; Težšte krutog tela;
Z A L I H E ... PREMA KARAKTERISTICI POPUNJAVANJA ZALIHA PODELA MODELA JE NA:
 Školska / Vežbe zalhe I deo Z A L I H E o DEFINISANJE POJMA o BINA PIANJA o MODELI-PODELA o SAIČKI MODELI-MODEL NOVOGODIŠNJE JELKE o DIMAMIČKI MODELI-HARISOV MODEL o NADOGRADNJA HARISOVOG MODELA: POPUSI,
Školska / Vežbe zalhe I deo Z A L I H E o DEFINISANJE POJMA o BINA PIANJA o MODELI-PODELA o SAIČKI MODELI-MODEL NOVOGODIŠNJE JELKE o DIMAMIČKI MODELI-HARISOV MODEL o NADOGRADNJA HARISOVOG MODELA: POPUSI,
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
3. OSNOVNI POKAZATELJI TLA
 MEHANIKA TLA: Onovni paraetri tla 4. OSNONI POKAZATELJI TLA Tlo e atoji od tri faze: od čvrtih zrna, vode i vazduha i njihovo relativno učešće e opiuje odgovarajući pokazateljia.. Specifična težina (G)
MEHANIKA TLA: Onovni paraetri tla 4. OSNONI POKAZATELJI TLA Tlo e atoji od tri faze: od čvrtih zrna, vode i vazduha i njihovo relativno učešće e opiuje odgovarajući pokazateljia.. Specifična težina (G)
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
4.1 Zakon inercije prvi Newtonov zakon
 FIZIK podloge za studj strojarsta 4. Daka 1 4.1 Zako ercje pr Newtoo zako Daka šr keatčke aalze uzajuć u obzr ase tjela (aterjale točke). Prje sega zučaa osost gbaja o slaa koje ga zazaju (pokreut auto
FIZIK podloge za studj strojarsta 4. Daka 1 4.1 Zako ercje pr Newtoo zako Daka šr keatčke aalze uzajuć u obzr ase tjela (aterjale točke). Prje sega zučaa osost gbaja o slaa koje ga zazaju (pokreut auto
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
1.1. Pregled najvažnijih izraza i pojmova
 Teorja formacje, kapactet dskretog komukacjskog kaala, Markovljev lac Pregled ajvažjh zraza pojmova Dskreto bezmemorjsko zvoršte Izvoršte X X = {x,,x,,x } [p(x ) = [p(x) = [p(x ) p(x ) p(x ) X dskreta
Teorja formacje, kapactet dskretog komukacjskog kaala, Markovljev lac Pregled ajvažjh zraza pojmova Dskreto bezmemorjsko zvoršte Izvoršte X X = {x,,x,,x } [p(x ) = [p(x) = [p(x ) p(x ) p(x ) X dskreta
II. ANALITIČKA GEOMETRIJA PROSTORA
 II. NLITIČK GEMETRIJ RSTR I. I (Točka. Ravia.) d. sc. Mia Rodić Lipaović 9./. Točka u postou ( ; i, j, k ) Kateijev pavokuti koodiati sustav k i j T T (,, ) oložaj točke u postou je jedoačo odeñe jeim
II. NLITIČK GEMETRIJ RSTR I. I (Točka. Ravia.) d. sc. Mia Rodić Lipaović 9./. Točka u postou ( ; i, j, k ) Kateijev pavokuti koodiati sustav k i j T T (,, ) oložaj točke u postou je jedoačo odeñe jeim
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
MODELI TEMELJENI NA DIFERENCIJALNIM JEDNADŽBAMA VIŠEG REDA I NA SUSTAVIMA DIFERENCIJALNIH JEDNADŽBI
 MODELI TEMELJENI NA DIFERENCIJALNIM JEDNADŽBAMA VIŠEG REDA I NA SUSTAVIMA DIFERENCIJALNIH JEDNADŽBI MATEMATIČKO NJIHALO Jedadžba koja osuje gbaje matematčkog jala rozlaz z drugog Newtoovog zakoa r ma F
MODELI TEMELJENI NA DIFERENCIJALNIM JEDNADŽBAMA VIŠEG REDA I NA SUSTAVIMA DIFERENCIJALNIH JEDNADŽBI MATEMATIČKO NJIHALO Jedadžba koja osuje gbaje matematčkog jala rozlaz z drugog Newtoovog zakoa r ma F
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
Parcijalne molarne veličine
 arcale molare velče 2.5.5. Hemsk potecal 2.5.6. 2.5.6.2. arcale molare velče. Ukolko e kolča supstace u sstemu promelva zbog razmee matere zmeđu sstema okole zbog reverzble hemske reakce l reverzble razmee
arcale molare velče 2.5.5. Hemsk potecal 2.5.6. 2.5.6.2. arcale molare velče. Ukolko e kolča supstace u sstemu promelva zbog razmee matere zmeđu sstema okole zbog reverzble hemske reakce l reverzble razmee
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
PRESECI SA PRSLINOM - VELIKI EKSCENTRICITET
 TEORJA ETONSKH KONSTRUKCJA 1 PRESEC SA PRSLNO - VELK EKSCENTRCTET ČSTO SAVJANJE - SLOODNO DENZONSANJE Poznato: Nepoznato: - statčk tcaj za pojedna opterećenja ( ) - sračnato - kvaltet materjala (, σ v
TEORJA ETONSKH KONSTRUKCJA 1 PRESEC SA PRSLNO - VELK EKSCENTRCTET ČSTO SAVJANJE - SLOODNO DENZONSANJE Poznato: Nepoznato: - statčk tcaj za pojedna opterećenja ( ) - sračnato - kvaltet materjala (, σ v
Cauchyjev teorem. Postoji više dokaza ovog teorema, a najjednostvniji je uz pomoć Greenove formule: dxdy. int C i Cauchy Riemannovih uvjeta.
 auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI. NEUTRALNI ELEMENT GRUPOIDA.
 KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI NEUTRALNI ELEMENT GRUPOIDA 1 Grupoid (G, ) je asocijativa akko važi ( x, y, z G) x (y z) = (x y) z Grupoid (G, ) je komutativa akko važi ( x, y G) x y = y x Asocijativa
KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI NEUTRALNI ELEMENT GRUPOIDA 1 Grupoid (G, ) je asocijativa akko važi ( x, y, z G) x (y z) = (x y) z Grupoid (G, ) je komutativa akko važi ( x, y G) x y = y x Asocijativa
3n an = 4n3/2 +2n+ n 5n 3/2 +5n+2 n a 2 n = n 2. ( 2) n Dodatak. = 0, lim n! 2n 6n + 1
 Nizovi 5 a = 5 +3+ + 6 a = 3 00 + 00 3 +5 7 a = +)+) ) 3 3 8 a = 3 +3+ + +3 9 a = 3 5 0 a = 43/ ++ 5 3/ +5+ a = + + a = + ) 3 a = + + + 4 a = 3 3 + 3 ) 5 a = +++ 6 a = + ++ 3 a = +)!++)! +3)! a = ) +3
Nizovi 5 a = 5 +3+ + 6 a = 3 00 + 00 3 +5 7 a = +)+) ) 3 3 8 a = 3 +3+ + +3 9 a = 3 5 0 a = 43/ ++ 5 3/ +5+ a = + + a = + ) 3 a = + + + 4 a = 3 3 + 3 ) 5 a = +++ 6 a = + ++ 3 a = +)!++)! +3)! a = ) +3
Dinamika krutog tijela. 14. dio
 Dnaka kutog tjela 14. do 1 Pojov: 1. Vekto sle F (tanslacja). Moent sle (otacja) 3. Moent toost asa 4. Rad kutog tjela A 5. Knetka enegja E k 6. Moent kolna gbanja 7. u oenta kolne gbanja oenta sle M (
Dnaka kutog tjela 14. do 1 Pojov: 1. Vekto sle F (tanslacja). Moent sle (otacja) 3. Moent toost asa 4. Rad kutog tjela A 5. Knetka enegja E k 6. Moent kolna gbanja 7. u oenta kolne gbanja oenta sle M (
Frekvencijska karakteristika Prijenosna funkcija Granična frekvencija Rezonantna frekvencija RLC krugova Električni filtri
 5 MREŽNE KARAKTERISTIKE Frekecjska karakterstka Prjeosa fukcja Grača frekecja Rezoata frekecja RLC krugoa Elektrč fltr Mreže karakterstke 5.. Frekecjske karakterstke AC strujh krugoa Mreže karakterstke
5 MREŽNE KARAKTERISTIKE Frekecjska karakterstka Prjeosa fukcja Grača frekecja Rezoata frekecja RLC krugoa Elektrč fltr Mreže karakterstke 5.. Frekecjske karakterstke AC strujh krugoa Mreže karakterstke
Općenito, iznos normalne deformacije u smjeru normale n dan je izrazom:
 Otporost mterijl. Zdtk ZDTK: U točki čeliče kostrukije postvlje su tri osjetil z mjereje deformij prem slii. ri opterećeju kostrukije izmjeree su reltive ormle (dužiske deformije: b ( - b 3 - -6 - ( b
Otporost mterijl. Zdtk ZDTK: U točki čeliče kostrukije postvlje su tri osjetil z mjereje deformij prem slii. ri opterećeju kostrukije izmjeree su reltive ormle (dužiske deformije: b ( - b 3 - -6 - ( b
AKSIOMATIKA TEORIJE VEROVATNOĆE
 AKSIOMATIKA TEORIJE VEROVATNOĆE E Aksomatka teorje verovatoće Polaz se od osovh stavova, tzv. aksoma, a osovu kojh se sve ostale osobe mogu dokazat. Za posmatra prostor el. shoda aksomatzacja daje odgovore
AKSIOMATIKA TEORIJE VEROVATNOĆE E Aksomatka teorje verovatoće Polaz se od osovh stavova, tzv. aksoma, a osovu kojh se sve ostale osobe mogu dokazat. Za posmatra prostor el. shoda aksomatzacja daje odgovore
I N Ž E N J E R S K A M A T E M A T I K A 1
 I N Ž E N J E R S K A M A T E M A T I K A Oaj koj cje praksu bez teorjskh osova slča je moreplovcu koj ulaz u brod bez krme busole e zajuć kuda se plov. ( LEONARDO DA VINCI ) P r e d a v a j a z a d r
I N Ž E N J E R S K A M A T E M A T I K A Oaj koj cje praksu bez teorjskh osova slča je moreplovcu koj ulaz u brod bez krme busole e zajuć kuda se plov. ( LEONARDO DA VINCI ) P r e d a v a j a z a d r
Pismeni ispit iz matematike GRUPA A 1. Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj, zatim naći 4 z.
 Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
F (t) F (t) F (t) OGLEDNI PRIMJER SVEUČILIŠTE J.J.STROSSMAYERA U OSIJEKU ZADATAK
 OGLEDNI PRIMJER ZADAAK Odredte dnamčke karakterstke odzv armranobetonskog okvra C-C prkazanog na slc s prpadajućom tlorsnom površnom, na zadanu uzbudu tjekom prve tr sekunde, ako je konstrukcja prje djelovanja
OGLEDNI PRIMJER ZADAAK Odredte dnamčke karakterstke odzv armranobetonskog okvra C-C prkazanog na slc s prpadajućom tlorsnom površnom, na zadanu uzbudu tjekom prve tr sekunde, ako je konstrukcja prje djelovanja
Prof. dr. sc. Maja Biljan-August Prof. dr. sc. Snježana Pivac Doc. dr. sc. Ana Štambuk 2. IZDANJE. Poglavlje 2.
 Prof. dr. sc. Maja Blja-August Prof. dr. sc. Sježaa Pvac Doc. dr. sc. Aa Štambuk UPORABA STATISTIKE U EKONOMIJI. IZDANJE Poglavlje. REGRESIJSKA I KORELACIJSKA ANALIZA Ekoomsk fakultet Sveučlšta u Rjec
Prof. dr. sc. Maja Blja-August Prof. dr. sc. Sježaa Pvac Doc. dr. sc. Aa Štambuk UPORABA STATISTIKE U EKONOMIJI. IZDANJE Poglavlje. REGRESIJSKA I KORELACIJSKA ANALIZA Ekoomsk fakultet Sveučlšta u Rjec
Građevinski fakultet, Beograd
 Građesk fakule Beogra Eksploaaa zaša pozeh oa Obašea ežbe VEŽBA Pree ežbe e raspor aere u porozo sre. raspora eača presala zako oržaa ase pree a supsau koa se rasporue. Oržae ase rasporoae supsae ože a
Građesk fakule Beogra Eksploaaa zaša pozeh oa Obašea ežbe VEŽBA Pree ežbe e raspor aere u porozo sre. raspora eača presala zako oržaa ase pree a supsau koa se rasporue. Oržae ase rasporoae supsae ože a
Elektrotehnički fakultet univerziteta u Beogradu 16.maj Odsek za Softversko inžinjerstvo
 Elektrotehnčk fakultet unverzteta u Beogradu 6.maj 8. Odsek za Softversko nžnjerstvo Performanse računarskh sstema Drug kolokvjum Predmetn nastavnk: dr Jelca Protć (35) a) () Posmatra se segment od N uzastonh
Elektrotehnčk fakultet unverzteta u Beogradu 6.maj 8. Odsek za Softversko nžnjerstvo Performanse računarskh sstema Drug kolokvjum Predmetn nastavnk: dr Jelca Protć (35) a) () Posmatra se segment od N uzastonh
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
Mate Vijuga: Rijeseni zadaci iz matematike za srednju skolu
 7. KOMPLEKSNI BROJEVI 7. Opc pojmov Kompleksn brojev su sastavljen dva djela: Realnog djela (Re) magnarnog djela (Im) Promatrajmo broj a+ b = + 3 Realn do jednak je Re : Imagnarna jednca: = - l = (U elektrotehnc
7. KOMPLEKSNI BROJEVI 7. Opc pojmov Kompleksn brojev su sastavljen dva djela: Realnog djela (Re) magnarnog djela (Im) Promatrajmo broj a+ b = + 3 Realn do jednak je Re : Imagnarna jednca: = - l = (U elektrotehnc
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
( x) ( ) dy df dg. =, ( x) e = e, ( ) ' x. Zadatak 001 (Marinela, gimnazija) Nađite derivaciju funkcije f(x) = a + b x. ( ) ( )
 Zadatak (Mariela, gimazija) Nađite derivaciju fukcije f() a + b c + d Rješeje Neka su f(), g(), h() fukcije ezavise varijable, a f (), g (), h () derivacije tih fukcija po Osova pravila deriviraja Derivacija
Zadatak (Mariela, gimazija) Nađite derivaciju fukcije f() a + b c + d Rješeje Neka su f(), g(), h() fukcije ezavise varijable, a f (), g (), h () derivacije tih fukcija po Osova pravila deriviraja Derivacija
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI)
 IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
5. Karakteristične funkcije
 5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
Obrada empirijskih podataka
 Obrada emprjskh podataka deskrptva statstka opsvaje podataka z uzorka l populacje u form osovh parametara osove vrste podataka po astaku varjable (upotreba razlčth mjerh ljestvca) se mogu klasfcrat a:.
Obrada emprjskh podataka deskrptva statstka opsvaje podataka z uzorka l populacje u form osovh parametara osove vrste podataka po astaku varjable (upotreba razlčth mjerh ljestvca) se mogu klasfcrat a:.
4. Trigonometrija pravokutnog trokuta
 4. Trigonometrij prvokutnog trokut po školskoj ziri od Dkić-Elezović 4. Trigonometrij prvokutnog trokut Formule koje koristimo u rješvnju zdtk: sin os tg tg ktet nsuprot kut hipotenuz ktet uz kut hipotenuz
4. Trigonometrij prvokutnog trokut po školskoj ziri od Dkić-Elezović 4. Trigonometrij prvokutnog trokut Formule koje koristimo u rješvnju zdtk: sin os tg tg ktet nsuprot kut hipotenuz ktet uz kut hipotenuz
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
7 Algebarske jednadžbe
 7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
INTEGRALNI RAČUN. Teorije, metodike i povijest infinitezimalnih računa. Lucija Mijić 17. veljače 2011.
 INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
Dvanaesti praktikum iz Analize 1
 Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
ZBIRKA POTPUNO RIJEŠENIH ZADATAKA
 **** IVANA SRAGA **** 1992.-2011. ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE POTPUNO RIJEŠENI ZADACI PO ŽUTOJ ZBIRCI INTERNA SKRIPTA CENTRA ZA PODUKU α M.I.M.-Sraga - 1992.-2011.
**** IVANA SRAGA **** 1992.-2011. ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE POTPUNO RIJEŠENI ZADACI PO ŽUTOJ ZBIRCI INTERNA SKRIPTA CENTRA ZA PODUKU α M.I.M.-Sraga - 1992.-2011.
a M a A. Može se pokazati da je supremum (ako postoji) jedinstven pa uvodimo oznaku sup A.
 3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
Obrada signala
 Obrada signala 1 18.1.17. Greška kvantizacije Pretpostavka je da greška kvantizacije ima uniformnu raspodelu 7 6 5 4 -X m p x 1,, za x druge vrednosti x 3 x X m 1 X m = 3 x Greška kvantizacije x x x p
Obrada signala 1 18.1.17. Greška kvantizacije Pretpostavka je da greška kvantizacije ima uniformnu raspodelu 7 6 5 4 -X m p x 1,, za x druge vrednosti x 3 x X m 1 X m = 3 x Greška kvantizacije x x x p
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
10.1. Bit Error Rate Test
 .. Bt Error Rat Tst.. Bt Error Rat Tst Zadata. Izračuat otrba broj rth formacoh bta u BER tstu za,, ogršo dttovaa bta a rjmu, tao da s u sstmu sa brzoom sgalzacj od Mbs mož tvrdt da j vrovatoća grš rosa
.. Bt Error Rat Tst.. Bt Error Rat Tst Zadata. Izračuat otrba broj rth formacoh bta u BER tstu za,, ogršo dttovaa bta a rjmu, tao da s u sstmu sa brzoom sgalzacj od Mbs mož tvrdt da j vrovatoća grš rosa
10. REGRESIJA I KORELACIJA
 0. REGRESIJA I KORELACIJA Jospa Perkov, prof., pred. Jedodmezoala aalza stražvaje vaje jede pojave predočee ee statstčkm zom ezavso od drugh, statstčkm metodama (grafčko tabelaro prkazvaje za, zračuavaje
0. REGRESIJA I KORELACIJA Jospa Perkov, prof., pred. Jedodmezoala aalza stražvaje vaje jede pojave predočee ee statstčkm zom ezavso od drugh, statstčkm metodama (grafčko tabelaro prkazvaje za, zračuavaje
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
1.1. Napisati relaciju kojom je moguće odrediti ukupan broj elektrona na nekoj orbiti: n
 I ES EES - VAIJANA Zadatak bro... Nasat relacu koom e moguće odredt ukua bro elektroa a eko orbt: l 0 ( Z 0 l + ) [ + 3 + 5 + ( ) ].. Nasat relacu koa ovezue kocetrace elektroa šula kod čstog (trsc) oluvodča:.3.
I ES EES - VAIJANA Zadatak bro... Nasat relacu koom e moguće odredt ukua bro elektroa a eko orbt: l 0 ( Z 0 l + ) [ + 3 + 5 + ( ) ].. Nasat relacu koa ovezue kocetrace elektroa šula kod čstog (trsc) oluvodča:.3.
Dinamika krutog tijela ( ) Gibanje krutog tijela. Gibanje krutog tijela. Pojmovi: C. Složeno gibanje. A. Translacijsko gibanje krutog tijela. 14.
 Pojmo:. Vektor se F (transacja). oment se (rotacja) Dnamka krutog tjea. do. oment tromost masa. Rad krutog tjea A 5. Knetka energja k 6. oment kona gbanja 7. u momenta kone gbanja momenta se f ( ) Gbanje
Pojmo:. Vektor se F (transacja). oment se (rotacja) Dnamka krutog tjea. do. oment tromost masa. Rad krutog tjea A 5. Knetka energja k 6. oment kona gbanja 7. u momenta kone gbanja momenta se f ( ) Gbanje
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
Newtonovi aksiomi: MEHANIKA II. Zadaci dinamike: I. Aksiom: Zakon inercije. II. Aksiom: Osnovni zakon dinamike. III. Aksiom: Zakon akcije i reakcije
 Newoo ao: MHANIKA II. do: D Aebero prcp Zao dae I. ao: Zao ercje II. ao: Zao baja III. ao: Zao acje reacje (poajaje z ae) I. Ao: Zao ercje Maerjao jeo oa bez djeoaja ajh a zadržaa aje roaja jedoo praocro
Newoo ao: MHANIKA II. do: D Aebero prcp Zao dae I. ao: Zao ercje II. ao: Zao baja III. ao: Zao acje reacje (poajaje z ae) I. Ao: Zao ercje Maerjao jeo oa bez djeoaja ajh a zadržaa aje roaja jedoo praocro
Matematička analiza 1 dodatni zadaci
 Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Komutacija paketa. Komutacija paketa
 Komutacja aketa Baferovaje u komutatorma aketa Da b se redukovala degradacja erformas komutacoog uređaja rouzrokovaa term soljašjm blokrajem, mogu se obezbjedt bafer a: ulazm ortovma /ulazo baferovaje/,
Komutacja aketa Baferovaje u komutatorma aketa Da b se redukovala degradacja erformas komutacoog uređaja rouzrokovaa term soljašjm blokrajem, mogu se obezbjedt bafer a: ulazm ortovma /ulazo baferovaje/,
TRIGONOMETRIJSKE FUNKCIJE I I.1.
 TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
Granične vrednosti realnih nizova
 Graiče vredosti realih izova Fukcija f : N R, gde je N skup prirodih brojeva a R skup realih brojeva, zove se iz realih brojeva ili reala iz. Opšti čla iza f je f(), N, i običo se obeležava sa f, dok se
Graiče vredosti realih izova Fukcija f : N R, gde je N skup prirodih brojeva a R skup realih brojeva, zove se iz realih brojeva ili reala iz. Opšti čla iza f je f(), N, i običo se obeležava sa f, dok se
radni nerecenzirani materijal za predavanja
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Kažemo da je funkcija f : a, b R u točki x 0 a, b postiže lokalni minimum ako postoji okolina O(x 0 ) broja x 0 takva da je
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Kažemo da je funkcija f : a, b R u točki x 0 a, b postiže lokalni minimum ako postoji okolina O(x 0 ) broja x 0 takva da je
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
Matematika 1 - vježbe. 11. prosinca 2015.
 Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
DINAMIKA. Dinamički sistem - pogon sa motorom jednosmerne struje: N: u f Ulazi Izlazi (?) U opštem slučaju ovaj DS je NELINEARAN!!!!
 DINAMIKA Dnčk sste - ogon s otoro jednoserne struje: N: { DS } u u Ulz Izlz (?),,, [ ] θ U ošte slučju ovj DS je NELINEAAN!!!! BLOK DIJAGAM MAEMAIČKOG MODELA POGONA Iz jednčne ndukt u e e Iz Njutnove jednčne
DINAMIKA Dnčk sste - ogon s otoro jednoserne struje: N: { DS } u u Ulz Izlz (?),,, [ ] θ U ošte slučju ovj DS je NELINEAAN!!!! BLOK DIJAGAM MAEMAIČKOG MODELA POGONA Iz jednčne ndukt u e e Iz Njutnove jednčne
Zavrxni ispit iz Matematiqke analize 1
 Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Pismeni ispit iz OTPORNOSTI MATERIJALA I - grupa A
 Psmen spt z OTPORNOSTI MATERIJALA I - grupa A 1. Kruta poluga ABC se oslanja pomoću dvje špke BD CE kao na slc desno. Špka BD, dužne 0.5 m, zrađena je od čelka (E AB 10 GPa) ma poprečn presjek od 500 mm.
Psmen spt z OTPORNOSTI MATERIJALA I - grupa A 1. Kruta poluga ABC se oslanja pomoću dvje špke BD CE kao na slc desno. Špka BD, dužne 0.5 m, zrađena je od čelka (E AB 10 GPa) ma poprečn presjek od 500 mm.
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
TRIGONOMETRIJA TROKUTA
 TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
Geodetski fakultet, dr. sc. J. Beban-Brkić Predavanja iz Matematike OSNOVNI TEOREMI DIFERENCIJALNOG RAČUNA
 Geodetski akultet dr s J Beba-Brkić Predavaja iz Matematike OSNOVNI TEOREMI DIFERENCIJALNOG RAČUNA Teoremi koje ćemo avesti u ovom poglavlju su osovi teoremi koji osiguravaju ispravost primjea diereijalog
Geodetski akultet dr s J Beba-Brkić Predavaja iz Matematike OSNOVNI TEOREMI DIFERENCIJALNOG RAČUNA Teoremi koje ćemo avesti u ovom poglavlju su osovi teoremi koji osiguravaju ispravost primjea diereijalog
( , treći kolokvij) 3. Na dite lokalne ekstreme funkcije z = x 4 + y 4 2x 2 + 2y 2 3. (20 bodova)
 A MATEMATIKA (.6.., treći kolokvij. Zadana je funkcija z = e + + sin(. Izračunajte a z (,, b z (,, c z.. Za funkciju z = 3 + na dite a diferencijal dz, b dz u točki T(, za priraste d =. i d =.. c Za koliko
A MATEMATIKA (.6.., treći kolokvij. Zadana je funkcija z = e + + sin(. Izračunajte a z (,, b z (,, c z.. Za funkciju z = 3 + na dite a diferencijal dz, b dz u točki T(, za priraste d =. i d =.. c Za koliko
Ekonometrija 4. Ekonometrija, Osnovne studije. Predavač: Aleksandra Nojković
 Ekonometrja 4 Ekonometrja, Osnovne studje Predavač: Aleksandra Nojkovć Struktura predavanja Nelnearne zavsnost Prmene u ekonomskoj analz Prmer nelnearne zavsnost Isptujemo zavsnost zmeđu potrošnje dohotka.
Ekonometrja 4 Ekonometrja, Osnovne studje Predavač: Aleksandra Nojkovć Struktura predavanja Nelnearne zavsnost Prmene u ekonomskoj analz Prmer nelnearne zavsnost Isptujemo zavsnost zmeđu potrošnje dohotka.
x pojedinačnih rezultata:
 ovarjaca koefcjet korelacje Sredja vrjedost stadardo odstupaje Prlkom poavljaja mjereja, uz ste (kolko je to moguće uvjete (st mjertelj, mjer strumet, mjera metoda okol uvjet, eke stale fzkale velče, dobt
ovarjaca koefcjet korelacje Sredja vrjedost stadardo odstupaje Prlkom poavljaja mjereja, uz ste (kolko je to moguće uvjete (st mjertelj, mjer strumet, mjera metoda okol uvjet, eke stale fzkale velče, dobt
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
( , 2. kolokvij)
 A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
VILJUŠKARI. 1. Viljuškar se koristi za utovar standardnih euro-pool paleta na drumsko vozilo u sistemu prikazanom na slici.
 VILJUŠKARI 1. Viljuškar e korii za uoar andardnih euro-pool palea na druko ozilo u ieu prikazano na lici. PALETOMAT a) Koliko reba iljuškara da bi ree uoara kaiona u koji aje palea bilo anje od 6 in, ako
VILJUŠKARI 1. Viljuškar e korii za uoar andardnih euro-pool palea na druko ozilo u ieu prikazano na lici. PALETOMAT a) Koliko reba iljuškara da bi ree uoara kaiona u koji aje palea bilo anje od 6 in, ako
Funkcije dviju varjabli (zadaci za vježbu)
 Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
Pomorske radio komunikacije
 7.. Poorske rado kokaje MODLACIE Modlaja - rasporaje prebavaje sgala oraje sa osovog rekvejskog podrčja basebad a rekvejsko podrčje koje je pogodo za odašljaje elekroageskh valova passbad. Razloz:.već
7.. Poorske rado kokaje MODLACIE Modlaja - rasporaje prebavaje sgala oraje sa osovog rekvejskog podrčja basebad a rekvejsko podrčje koje je pogodo za odašljaje elekroageskh valova passbad. Razloz:.već
PRIMJER 3. MATLAB filtdemo
 PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
Akvizicija tereta. 5660t. Y= masa drva, X=masa cementa. Na brod će se ukrcati 1733 tona drva i 3927 tona cementa.
 Akvizicija tereta. Korisna nosivost broda je 6 t, a na brodu ia 8 cu. ft. prostora raspoloživog za sještaj tereta pod palubu. Navedeni brod treba krcati drvo i ceent, a na palubu ože aksialno ukrcati 34
Akvizicija tereta. Korisna nosivost broda je 6 t, a na brodu ia 8 cu. ft. prostora raspoloživog za sještaj tereta pod palubu. Navedeni brod treba krcati drvo i ceent, a na palubu ože aksialno ukrcati 34
Numerička matematika 2. kolokvij (1. srpnja 2009.)
 Numerička matematika 2. kolokvij (1. srpnja 29.) Zadatak 1 (1 bodova.) Teorijsko pitanje. (A) Neka je G R m n, uz m n, pravokutna matrica koja ima puni rang po stupcima, tj. rang(g) = n. (a) Napišite puni
Numerička matematika 2. kolokvij (1. srpnja 29.) Zadatak 1 (1 bodova.) Teorijsko pitanje. (A) Neka je G R m n, uz m n, pravokutna matrica koja ima puni rang po stupcima, tj. rang(g) = n. (a) Napišite puni
