Φυσική Ι 1ο εξάμηνο. Γεώργιος Γκαϊντατζής Επίκουρος Καθηγητής. Τμήμα Μηχανικών Παραγωγής & Διοίκησης Δημοκρίτειο Πανεπιστήμιο Θράκης.

Transcript

1 Φυσική Ι 1ο εξάμηνο Γεώργιος Γκαϊντατζής Επίκουρος Καθηγητής Τμήμα Μηχανικών Παραγωγής & Διοίκησης Δημοκρίτειο Πανεπιστήμιο Θράκης 4 ο μάθημα

2 Κεφάλαιο 7 Έργο και Ενέργεια

3 Έργο σε μια διάσταση Νόμοι διατήρησης: ενέργειας ορμής στροφορμής μάζας W = F x Δx 1 Joule = 1 J = 1 N m = 1 kg m 2 /s 2 1 ft lbf = 1ft 1 lbf = 1,356 J

4 Έργο σε μια διάσταση

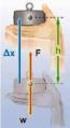
5 Έργο σε μια διάσταση Ο άνθρωπος παράγει έργο (όχι χρήσιμο) στην πραγματικότητα, αλλά επειδή Δx=0 φαίνεται ότι δεν παράγεται έργο (η ανθρώπινη μηχανή θα ήταν πιο αποδοτική αν είχε προβλεφθεί μηχανισμός ακαμψίας) Αν ο άνθρωπος κινείται μέσα σε ανελκυστήρα, τότε Δx>0 και επειδή η μετατόπιση και η δύναμη είναι ομόρροπες έργο θετικό Στο σύστημα αναφοράς του εδάφους, η μπάλλα κινείται προς τα πάνω και παράγεται επάνω της έργο. Στο σύστημα αναφοράς του ανελκυστήρα, η μπάλλα ηρεμεί και δεν παράγεται έργο επάνω της. Αρα, πριν τον υπολογισμό του έργου πρέπει να καθοριστεί σαφώς το σύστημα αναφοράς.

6 Έργο σε μια διάσταση Έστω ότι η δύναμη είναι συνάρτηση της θέσης F x =F x (x). Τότε το ολικό έργο είναι: W i= n 1 = ΔWi = i= 0 i= n 1 i= 0 Fx( xi) Δx b W = x F x) dx a ( = εμβαδό που περιορίζεται από την καμπύλη της συνάρτησης

7 Έργο σε μια διάσταση W b = Fx ( x) dx = ( kx) dx a b a = k [ 1 ] x = k( b a ) 2 b a 2

8 Πολλαπλασιασμός διανυσμάτων Εσωτερικό Γινόμενο (δίνει αριθμό, όχι διάνυσμα) Εξωτερικό Γινόμενο (δίνει διάνυσμα)

9 Έργο σε τρεις διαστάσεις Σχήμα. Σταθερή δύναμη F δρα κατά τη μετατόπιση Δr. Fcosθ είναι η συνιστώσα της F κατά μήκος της Δr. W=FΔr cosθ = F Δr = FxΔx + FyΔy + FzΔz Εργο + ή ανάλογα με τη γωνία θ (F, Δr ομόροπα, αντίροπα) Για δύναμη κάθετη στη φορά της κίνησης W=0 (π.χ. κεντρομόλος, δύναμη Ν κάθετη σε σώμα που ολισθαίνει κτλ. )

10 Έργο σε τρεις διαστάσεις Επειδή W=FΔr cosθ = F Δr = FxΔx + FyΔy + FzΔz και Το έργο που παράγεται από τη βαρύτητα εξαρτάται μόνο από τη μεταβολή του ύψους Δz.

11 Έργο παραγόμενο από μεταβλητή δύναμη σε τρεις διαστάσεις 0 ) ( cos = + + = + + = = = P P z P P y P P x P P z y x P P P P F dz F dy F dx F dz F dy F dx d dr F W r F θ ΔW = F Δr cosθ

12 -T sinφ + S =0 Tcosφ mg = 0 S = mg tanφ W = 5, P P 2 Fxdx = 1 P 2m P mg tanφdx = mgl sinφdφ = mgl[ cosφ] 0 P 5,7 0 2m P mg tanφd ( l sinφ) = 0 5,7 0 0 = mgl(1 cos 0,10) = 600 9,8 20 0,0050 = Το έργο που παράγεται από τη βαρύτητα με z 1 =-l, z 2 =-l(cos5,7 0 ) είναι: W = -mg(-l cos5,7 0 +l) = -mgl(1-cos5,7 0 ) = -590 J 0 mg tanφ( l cosφdφ) = 590J

13 Κινητική ενέργεια Η ποσότητα Κ = ½ mυ 2 ονομάζεται κινητική ενέργεια σωματιδίου. Η μεταβολή της κινητικής ενέργειας ισούται με το έργο που παράγεται πάνω στο σωματίδιο από την ολική δύναμη Κ 2 - Κ 1 = ΔΚ = W (θεώρημα έργου ενέργειας) K = p 2 /2m (ορμή p=mu)

14 Κινητική ενέργεια Πίνακας. Μερικές τιμές κινητικής ενέργειας.

15 Βαρυτική δυναμική ενέργεια Δυναμική ενέργεια η ικανότητα ενός σωματιδίου να παράγει έργο εξαιτίας της θέσης του στο χώρο ησυνάρτηση mgz ονομάζεται βαρυτική δυναμική ενέργεια του σωματιδίου αν η μόνη δύναμη που επιδρά σε σωματίδιο είναι το βάρος του, τότε: W = BΔz = -mg(z 2 -z 1 ) = -mgz 2 +mgz 1 = K 2 -K 1 = ½ mυ 2 2 ½mυ 2 1 K 1 + mgz 1 = K 2 + mgz 2 K + mgz = [σταθ.] = Ε (μηχανική ενέργεια σωματιδίου) (Νόμοςδιατήρησηςμηχανικήςενέργειας)

16 Ε 1 =Ε 2 ½mυ mgz 1 =½mυ 2 2 +mgz 2 mgz 1 = ½ mυ 22 υ 2 = 54 m/s

17

18

19 Σύνοψη

20 Ασκήσεις

21 Ασκήσεις

22 Ασκήσεις

23 Ασκήσεις

24 Ασκήσεις

25 Κεφάλαιο 8 Διατήρηση της ενέργειας

26 Σύνοψη κεφ. 7

27 Σύνοψη κεφ. 7 αν η μόνη δύναμη που επιδρά σε σωματίδιο είναι το βάρος του, τότε: W = BΔz = -mg(z 2 -z 1 ) = -mgz 2 +mgz 1 = K 2 -K 1 = ½ mυ 2 2 ½mυ 2 1 K + mgz = Ε (μηχανική ενέργεια σωματιδίου) = [σταθερά] Νόμοςδιατήρησηςμηχανικήςενέργειας (ενός σωματιδίου που κινείται υπό την επίδραση της βαρύτητας) Εδώ διατύπωση του γενικού νόμου διατήρησης της μηχανικής ενέργειας (όταν (και) άλλες δυνάμεις δρουν πάνω στο σωματίδιο)

28 Διατηρητική δύναμη Μια δύναμη F είναι διατηρητική, όταν το έργο αυτής της δύναμης εξαρτάται από τη θέση των τελικών σημείων P 1 και P 2 και όχι από το σχήμα του δρόμου ανάμεσα στα σημεία (βλ. Σχήμα). το έργο μιας διατηρητικής δύναμης είναι μηδέν για οποιαδήποτε διαδρομή συμπληρώνει ένα κλειστό δρόμο (Σχήμα) ή Παραδείγματα διατηρητικής δύναμης: βαρύτητα? δύναμη ελατηρίου? δύναμη κινητικής τριβής?

29 Δυναμική ενέργεια Διατηρητικής δύναμης

30 Δυναμική ενέργεια Διατηρητικής δύναμης Έστω διατηρητική δύναμη F. Έστω σημείο αναφοράς P 0 με δυναμική ενέργεια U(P 0 ). Σε οποιοδήποτε άλλο σημείο P η τιμή της δυναμικής ενέργειας είναι: Τότε, η μεταβολή της δυναμικής ενέργειας ανάμεσα στα σημεία P 1 και P 2 προσδιορίζεται:

31 Δυναμική ενέργεια Διατηρητικής δύναμης Επειδή η μεταβολή της κινητικής ενέργειας ισούται με το έργο δηλαδή Ε = Κ + U (νόμοςδιατήρησηςτηςμηχανικήςενέργειας)

32 Δυναμική ενέργεια Διατηρητικής δύναμης

33 Δυναμική ενέργεια Διατηρητικής δύναμης

34 Η αρχική ενέργεια στο σημείο x 1 =-6cm είναι: Ε =½mυ 12 +½ kx 12 = 0 + ½ kx 1 2 Ηενέργειαστοx 2 = 0 cm είναι: E = ½ mυ 22 +½ kx 2 2 = ½ mυ Άρα, ½kx 12 = ½ mυ 22 υ 2 = = k / mx1 12m / s

35 Μη διατηρητική δύναμη ΔΚ + ΔU =ΔΕ = W μη διατηρητική Όχι τόσο χρήσιμη, όσο η σχέση που ισχύει όταν δεν υπάρχουν διατηρητικές δυνάμεις (υπολογισμός θέσης-ταχύτητας από τη σχέση ΔΚ+ΔU=0, βλ. παραπάνω παραδείγματα), διότι η τιμή της W μη διατηρητική δεν εξαρτάται μόνο από τη μεταβολή της θέσης αλλά και από τιςλεπτομέρειεςτηςκίνησης, και άρα το W μη διατηρητική δεν μπορεί να υπολογιστεί επακριβώς εκτός και αν γίνουν γνωστές οι λεπτομέρειες της κίνησης

36 Μη διατηρητική δύναμη

37 Υπολογισμός της δύναμης από τη δυναμική ενέργεια Και στην περίπτωση που dy=0 και dz=0, έτσι ώστε du = - F x dx Fy U = y Fz U = z ή Fx = U x Αν για παράδειγμα η δυναμική ενέργεια ελατηρίου είναι: U(x)= ½ kx 2, τότε : F x U = x 1 ( k = 2 x x 2 ) = kx

38 Άλλες μορφές ενέργειας Θερμότητα: Χημική ενέργεια: Πυρηνική ενέργεια: η άτακτη κινητική και δυναμική ενέργεια των ατόμων ενός σώματος, π.χ. εξαιτίας της τριβής. κινητική και δυναμική ενέργεια των ηλεκτρονίων στοεσωτερικότωνατόμων κινητική και δυναμική ενέργεια των πρωτονίων και νετρονίων στο εσωτερικό των πυρήνων των ατόμων Μονάδες: 1 ev = 1, J 1 kw h = J 1 kcal = 4, J 1 Btu = 1, J

39 Πίνακας. Μερικές ενέργειες

40 Μάζα και ενέργεια Η ενέργεια μπορεί να μετατραπεί σε μάζα και αντίστροφα (θεωρία σχετικότητας Einstein): E = mc 2 (c = 3, m/s) ή Δm = ΔΕ/c 2 δηλ. η ενέργεια έχει μάζα, δηλ. κάθε φορά που η ενέργεια ενός σώματος μεταβάλλεται, ημάζατου(και το βάρος του) μεταβάλλονται. Όταν π.χ. αυξάνει η κινητική ενέργεια ενός σώματος, ημάζατου(και το βάρος του) αυξάνει. Σε μικρές ταχύτητες η αύξηση της μάζας είναι ανεπαίσθητη, αλλά όταν π.χ. η ταχύτητα στοιχειωδών σωματιδίων φθάνει στο 0, c η μάζα τους είναι φορές μεγαλύτερη από τη μάζα του ηλεκτρονίου που ηρεμεί.

41 Μάζα και ενέργεια Άρα, οι νόμοι διατήρησης της μάζας και της ενέργειας δεν είναι δύο ανεξάρτητοι νόμοι, αλλά ο ένας εξυπακούει τον άλλο. π.χ. η αντίδραση σχάσης 1 kg U αποδίδει ενέργεια 8, J. Η αντίδραση διατηρεί την ενέργεια, μετασχηματίζοντας την πυρηνική σε θερμότητα, φως και κινητική ενέργεια, αλλά δεν αλλάζει τη συνολική ποσότητα της ενέργειας (θάλαμος αντιδραστήρα ερμητικά κλειστός και θερμικά μονωμένος). Αν ανοιχτεί, θα διαφύγει φως και θερμότητα και θα έχει χαθεί το 0,1% της μάζας του U. Το ίδιο φαινόμενο συμβαίνει και σε μια χημική (εξώθερμη) αντίδραση, όπου η μάζα των καταλοίπων είναι ελαφρώς μικρότερη (μη μετρήσιμη) από την αρχική μάζα.

42 Ισχύς Μέση Ισχύς: Στιγμιαία ισχύς: Μονάδες: P μέση = ΔW/Δt P = dw/dt 1 watt = 1 W = 1 J/s 1 horsepower = 1 hp = 550 ft lbf/s = 745,7 W P = ΔW/Δt = FΔz/Δt = Fυ =mgυ =900 kg 9,8 m/s 2 1,8m/s = 1, W = 4 1hp = 1,6 10 W = 746 W 21hp

43 Αφού η επιτάχυνση κατά μήκος του δρόμου είναι μηδέν,

44

45 Πίνακας. Μερικές τιμές ισχύος

46 Σύνοψη

47 Σύνοψη

48 Ασκήσεις