! = wr = mg(l/2)"µ# (1)
|
|
|
- Πραξιτέλης Φιλιππίδης
- 6 χρόνια πριν
- Προβολές:
Transcript
1 Οµογενής ράβδος µάζας m και µήκους L, µπορεί να στρέφεται χωρίς τριβή περί σταθερό οριζόντιο άξονα που διέρχεται από το ένα άκρο της Ο. Εκτρέπουµε τη ράβδο από τη θέση ευσταθούς ισορ ροπίας της κατα γωνία φ και την αφήνουµε ελεύθερη. Να µελετη θεί η κίνησή της. Δίνεται η επιτάχυνση g της βαρύτητας και η ρο πή αδράνειας Ι=mL /3 της ράβδου περί άξονα που διέρχεται από το άκρο της Ο και είναι κάθετος στη ράβδο. ΛΥΣΗ: Θεωρούµε τη ράβδο σε µια τυχαία θέση (τ), όπου η γωνιακή εκτρο πή της από την κατακόρυφη διεύθυνση Οz (θέση ευσταθούς ισορροπίας) είναι φ. Στη θέση αυτή η ράβδος δέχεται το βάρος της w και τη δύναµη δεσµού από τον άξονα περιστροφής της. Η συνολική ροπή των δύο αυτών δυνάµεων περί τον άξονά της ράβδου αποτελεί ροπή επαναφοράς µε µέτρο: = wr = mg(l/)"µ# (1) Εφαρµόζοντας για τη ράβδο στη θέση αυτή τον θεµελιώδη νόµο της στρο φικής κίνησης, µε θετική φορά περιστροφής την φορά κατά την οποία η γω νιακή εκτροπή φ αυξανεται, παίρνουµε τη σχέση: I d = -" (1) ml 3 d = -mg L "µ d + 3g L "µ = d + k "µ = () µε k =3g/L. H () αποτελεί την διαφορική εξίσωση της στροφικής κίνησης της ράβδου, η λύση της οποίας είναι εξαιρετικά περίπλοκη, λόγω της παρου
2 σίας του όρου ηµφ. Πράγµατι αν αναπτύξουµε το ηµφ σε σειρά Maclau rin η () γράφεται: d + " k $ # % ' = (3) & δηλαδή έχουµε να αντιµετωπίσουµε µια µη γραµµική διαφορική εξίσωση δευτέρας τάξεως, της οποίας η λύση κάτω από δεδοµένες αρχικές συνθήκες δεν επιτυγχάνεται αναλύτικά, αλλά µόνο µε γραφικό τρόπο µέσω κατάλλη λου προγράµµατος ηλεκτρονικού υπολογιστή (λόγου χάρη του προγράµµα τος Mathematika) και µάλιστα η γραφική αυτή λύση προσεγγίζει εξαιρετικά την πραγµατικότητα. Στην ειδική περίπτωση που η γωνιακή εκτροπή φ παίρνει µικρές τιµές που µας επιτρέπουν να γράψουµε την προσεγγιστική σχέση ηµφ φ(rad), τότε η πιο πάνω εξίσωση παίρνει τη µορφή: d + k = (4) η οποία αναφέρεται στον στροφικό αρµονικό ταλαντωτή και δέχεται λύ ση της µορφής: = " #µ (kt + $) (5) όπου οι σταθερές Φ και θ θα προκύψουν από τις αρχικές συνθήκες (φ) t= και (dφ/) t= της ράβδου κατα τρόπο ανάλογο µε εκείνο του µονοδιάστατου αρµονικού ταλαντωτή. Υπολογισµός της περιόδου κίνησης της ράβδου. Εφαρµόζοντας για τη ράβδο την αρχή διατήρησης της µηχανικής ενέργειας κατά την µετάβασή της από την αρχική της θέση (α) όπου αφήνεται ελεύ θερη, µέχρι την τυχαία θέση (τ) παίρνουµε τη σχέση: ( ) + I + = -mg L "#$ - "#$ % d$ ( ' * & ) ml " d % $ ' 3 # & = mgl (()* - ()* ) d = ± 3g ( L "#$ - "#$ ) = ± 3g & L %µ - %µ ) ( ' + * = ± L 3g d "µ ( / ) - "µ ( / ) (6)
3 Ολόκληρώνοντας την (6) µε όρια ολοκλήρωσης για την γωνία φ τα φ και παίρνουµε την ποσότητα Τ/4, όπου Τ η περίοδος της περιοδικής στροφικής ταλάντωσης της ράβδου. Έτσι θα έχουµε τη σχέση: T 4 = L 3g d # (7) "µ ( / ) - "µ ( / ) Θέτοντας ηµ(φ /)=α µε <α<1 και ηµ(φ/)=αz µε <z <1 η (7) γράφεται: T = 4 L 3g d # (8) " 1 - z Όµως ισχύουν και οι σχέσεις: 1 "# % $ ( ' * d$ = +dz 1 & ) 1 - µ " d" = #dz d = "dz 1 - #µ ( / ) = "dz 1 - " z µε αποτέλεσµα η σχέση (8) να γράφεται: T = 8 L 3g 1 dz " (9) (1 - z )(1 - z ) To ολοκλήρωµα που εµφανίζεται στο δέυτερο µέλος της (9) αποτελεί το λεγόµενο ελλειπτικό ολοκλήρωµα πρώτου είδους και δεν υπολογίζε ται συµβατικά, αλλά µόνο αν η ολοκληρωτέα συνάρτηση αναπτυχθεί σε σει ρά Maclaurin. O τελικός υπολογισµός καταλήγει στη σχέση: T = L * 3g 1 + " 1 %, $ ' # & +, ) (µ + " 1.3 % $ ' #.4& ) (µ 4 + " % $ ' #.4.6& ) - (µ /. / Mε το πρόγραµµα Mathematika µπορεί να επαληθευθεί µε µεγάλη προσέγγι ση η τελευταία σχέση. P.M. fysikos Mια λεπτή τροχαλία ακτίνας R έχει στερεωθεί σε οριζόντιο λείο τραπέζι, ώστε να µη µπορεί να περιστρέφεται. Στο αυλάκι της τρο χαλίας έχει στερεωθεί το άκρο αβαρούς και µη εκτατού νήµατος
4 µήκους α στο άλλο άκρο του οποίου έχει δεθεί µικρό σφαιρίδιο µάζας m που ακουµπάει στο τραπέζι. Την χρονική στιγµή t= το σφαιρίδιο ωθείται απότοµα µε αποτέλεσµα να αποκτά ταχύτητα v της οποίας ο φορέας είναι κάθετος προς το τεντωµένο νήµα και τότε αυτό αρχίζει να τυλίγεται στο αυλάκι της τροχαλίας. i) Να εκφράσετε σε συνάρτηση µε το χρόνο τo µήκος του νήµατος. ii) Nα δείξετε ότι τα κέντρα καµπυλότητας της τροχιάς που διαγρά φει το σφαιρίδιο βρίσκονται στο αυλάκι της τροχαλίας. iii) Eάν η αντοχή θραύσεως του νήµατος είναι T =mg, όπου g το µέτρο της επιτάχυνσης της βαρύτητας, να βρεθεί η χρονική στιγµή που σπάει το νήµα. ΛΥΣΗ: i) Kαθώς το νήµα τυλίγεται στο αυλάκι της τροχαλίας δεν συµβαί νει ανταλλαγή ενέργειας µεταξύ του σφαιριδίου και της τροχαλίας που συνε χώς παραµένει ακίνητη. Αυτό σηµαίνει ότι η κινητική ενέργεια του σφαιρι δίου δεν µεταβάλλεται στην διάρκεια της κίνησής του, δηλαδή δεν µεταβάλ λεται το µέτρο της ταχύτητάς του. Άρα η τάση T του νήµατος επί του σφαιριδίου είναι συνεχώς κάθετη στο διάνυσµα της ταχύτητάς του, δηλαδή αποτελεί για το σφαιρίδιο κεντροµόλο δύναµη. Ας εξετάσουµε το σφαιρίδιο σε µια τυχαία θέση της τροχιάς του της οποίας η επιβατική ακτίνα ως προς το Ο είναι r. Aναλύουµε την ταχύτητα v του σφαιριδίου στην ακτινική συνιστώσα v r και στην κάθετη προς την ακτίνα συνιστώσα v K και επειδή η v r είναι αντίρροπη της επιβατικής ακτίνας θα ισχύει η σχέση: dr = -v dr r = -vµ" = -v R r rdr = -v R (1) όπου φ η γωνία του νήµατος µε την επιβατική ακτίνα r στη θέση όπου εξε τάζουµε το σφαιρίδιο. Ολοκληρώνοντας τη σχέση (1) παίρνουµε: r / = - v Rt + όπου σταθερά ολοκλήρωσης που θα βρεθεί από την αρχική συνθήκη ότι για t= είναι r =α +R. Έτσι η προηγούµενη σχέση για t= δίνει = (α +R )/ δηλαδή θα ισχύει:
5 r = -v Rt + + R r = -v Rt + + R r - R = -v Rt + L = -v Rt + () όπου L το µήκος του νήµατος στην θέση που εξετάζουµε το σφαιρίδιο. H () αποτελεί την ζητούµενη σχέση. ii) Εξάλλου εφαρµόζοντας για το σφαιρίδιο το νόµο της στροφορµής περί το σηµείο Ο, µε θετική φορά εκείνη κατά την οποία στρέφεται το σφαιρίδιο, παίρνουµε τη σχέση: dl = -TR d(mrv ) K = -TR d(mrv"#$) = -TR d(mrvl/ r) = -TR d(mv L) = -TR mv dl = -TR (3) όπου Τ το µέτρο της τάσεως του νήµατος. Διαφορίζοντας τη σχέση () παίρ νουµε: LdL = -v R dl = -v R (4) L Συνδυάζοντας τις σχέσεις (3) και (4) παίρνουµε: R$ mv # -v " L% & = -TR T = mv L (5) Επειδή η τάση του νήµατος σε κάθε θέση του σφαιριδίου λειτουργεί ως κεν τροµόλος δύναµη, από την (5) προκύπτει ότι η ακτίνα καµπυλότητας της τροχιάς του σφαιριδίου είναι σε κάθε σηµείο της ίση µε το αντίστοιχο µήκος του νήµατος. Το γεγονός αυτό σηµαίνει ότι τα κέντρα καµυλότητας της τρο χιάς του σφαιριδίου βρίσκονται στο αυλάκι της τροχαλίας. iii) Συνδυάζοντας τις σχέσεις (5) και () παίρνουµε: T = m v 4 L - v Rt H πιο πάνω σχέση εφαρµοζόµενη τη στιγµή t * που επίκειται η θραύση του νήµατος δίνει: m g = m 4 v L L - v Rt * = v 4 - v Rt * g
6 v Rt * = L - v 4 g t * = L g 4 - v v Rg P.M. fysikos Ένας λεπτός κυκλικός δίσκος ακτίνας R, εκτοξεύεται κατά τέτοιο τρόπο, ώστε τη στιγµή που έρχεται σε επαφή µε το οριζόντιο έδα φος να έχει µόνο µεταφορική ταχύτητα v παράλληλη προς αυτό. i) Λαµβάνοντας επί του επιπέδου κίνησης του δίσκου ένα ορθογώ νιο σύστηµα αξόνων Οxy, όπου Ο το σηµείο επαφής του δίσκου µε το οριζόντιο έδαφος τη στιγµή t=, να δείξετε ότι το διάνυσµα θέσε ως r K του στιγµιαίου κέντρου περιστροφής του δίσκου ως προς το Ο, ικανοποιεί τη διανυσµατική σχέση: r K = r + ( " v ) όπου r, v το διάνυσµα θέσεως και η ταχύτητα αντιστοίχως του κέντρου µάζας του δίσκου και η γωνιακή ταχύτητα περιστρο φής του περί το κέντρο µάζας. ii) Χρησιµοποιώντας την παραπάνω σχέση να βρείτε σε συνάρτηση µε τον χρόνο τις συντεταγµένες του στιγµιαίου κέντρου περιστρο φής του δίσκου στο σύστηµα Οxy. Δίνονται ο συντελεστής τριβής ολίσθησης n µεταξύ του δίσκου και του εδάφους, η επιτάχυνση g της βαρύτητας και η ροπή αδράνειας Ι=mR / δίσκου ως προς άξο να που διέρχεται από το κέντρο του και είναι κάθετος στο επίπεδό του. ΛΥΣΗ: i) Από τη στιγµή που ο δίσκος έρχεται σ επαφή µε το οριζόντιο έδαφος δέχεται το βάρος του w και τη δύναµη επαφής από το έδαφος, η οποία αναλύεται στην κάθετη αντίδραση N που είναι κατακόρυφη και την τριβή ολίσθησης T που είναι αντίρροπη της αρχικής ταχύτητας v του κέντρου του δίσκου. Ο δίσκος εκτελεί υπό την επίδραση των δυνάµεων αυτών επίπεδη κίνηση που αποτελείται από µια µεταφορική ολίσθηση που έχει κατεύθυνση ίδια µε την κατεύθυνση της v και µια δεξιόστροφη περισ τροφή περί άξονα που διέρχεται από το κέντρο του και είναι κάθετος στο επί πεδό του. Η επίπεδη αυτή κίνηση µπορεί να θεωρηθεί ως γνήσια περιστρο φή περί άξονα που διέρχεται από το στιγµιαίο κέντρο περιστροφής Κ και είναι κάθετος στο επίπεδο του δίσκου. Aς επιχειρήσουµε να καθορίσουµε κάποια στιγµή την θέση του στιγµιαίου κέντρου περιστροφής Κ του δίσκου ως προς την αρχή Ο του αδρανειακού συστήµατος αναφοράς Οxy. H ταχύ τητα v K του K κατά την θεωρoύµενη χρονική στιγµή είναι µηδενική και θα ισχύει η σχέση:
7 = v + ( " r ) ( " r ) = - v (1) όπου r το διάνυσµα θέσεως του Κ ως προς το κέντρο µάζας του δίσκου. Πολ λαπλασιάζοντας εξωτερικά και τα δύο µέλη της (1) µε το διάνυσµα παίρ νουµε τη σχέση: [ " ( " r )] = -( " v ) Σχήµα α Σχήµα β η οποία µε βάση την διανυσµατική ταυτότητα: γράφεται: [ " (# " $ )] = ( % $ )# - ( %# ) $ ( " r ) - ( " ) r = -( # v ) ( " r ) - r = -( # v ) () Όµως τα διανύσµατα και r είναι µεταξύ τους κάθετα, που σηµαίνει ότι το εσωτερικό τους γινόµενο είναι µηδενικό, οπότε η σχέση () γράφεται: - r = -( " v ) r = ( " v ) (3) Aπό το σχήµα (α) προκύπτει r + r = r K, οπότε η (3) γράφεται: ( r K - r ) = ( " v ) r K = r + ( " v ) (4) ii) Eάν x K, y K είναι οι συντεταγµένες του στιγµιαίου κέντρου περιστρο φής Κ του δίσκου. ύστερα από χρόνο t αφότου ήλθε σε επαφή µε το ορι ζόντιο έδαφος και i, j τα µοναδιαία διανύσµατα των αξόνων Ox, Oy αντι στοίχως, θα έχουµε τις σχέσεις: r K = x K i + y K j και ( " v ) = -v j οπότε η (4) γράφεται: x K i + y K j = x i + R j + -v j
8 " x K i + y K j = x i + R - v $ # % ' & j x K = x " # y K = R - v / $ (5) όπου x η τετµηµένη του κέντρου µάζας του δίσκου την στιγµή που το εξετάζουµε. Εξάλλου εφαρµόζοντας για την µεταφορική κίνηση του δίσ κου τον δεύτερο νόµο του Νεύτωνα παίρνουµε τη σχέση: T = ma nmg = ma a = ng (6) Aπό την (6) παρατηρούµε ότι η το µέτρο της επιβράδυνσης a του κέντρου µάζας είναι σταθερή, οπότε το µέτρο της ταχύτητάς του την χρονική στιγµή t θα είναι: v = v - ngt (7) ενώ την ίδια στιγµή η τετµηµένη του κέντρου µάζας θα είναι: x = v t - ngt / (8) Εφαρµόζοντας για την περιστροφική κίνηση του δίσκου τον θεµελιώδη νόµο της στροφικής κίνησης παίρνουµε: TR = I' nmgr = (mr / )' '= ng / R δηλαδή η γωνιακή επιτάχυνση ' του δίσκου είναι σταθερή, που σηµαί νει ότι το µέτρο της γωνιακής του ταχύτητας την χρονική στιγµή t θα είναι: = 't = ngt / R (9) Όµως το µέτρο της v µειώνεται µε τον χρόνο, ενώ το µέτρο της αυξάνεται και κάποια στιγµή t * θα συµβεί ωr=v. Tη στιγµή αυτή θα µηδενιστεί η ταχύτητα των σηµείων επαφής του δίσκου µε το οριζόντιο έδαφος, δηλαδή δεν θα υπάρχει σχετική κίνηση των σηµείων αυτών µε το έδαφος, µε αποτέλεσµα να µηδενιστεί η στατική τριβή. O χρόνος t * θα προκύψει από τη σχέση: v - ngt * = ngt * t * = v /3ng (1) Έτσι από την στιγµή t * και µετά ο δίσκος θα κυλίεται ισοταχώς πάνω στο οριζόντιο έδαφος και τo µέτρο της ταχύτητας v * του κέντρου µάζας θα δίνεται από τη σχέση: (1) v * = v - ngt * v * = v - ngv /3ng = v /3 (11) Συνδυάζοντας τις σχέσεις (5), (7), (8) και (9) παίρνουµε:
9 x K = v t - ngt / " y K =(3ngRt - v R)/ ngt# µε t v /3ng Τη στιγµή t * που αρχίζει η κύλιση οι σχέσεις (1) δίνουν x =5v /18ng και y K =, ενώ για t * > το σηµείο επαφής του δίσκου µε το οριζόντιο έδαφος θα αποτελει το στιγµιαίο κέντρο περιστροφής του δίσκου. P.M. fysikos Ένα ελαστικό και οµογενές σώµα σχήµατος ορθογωνίου παραλ ληλεπιπέδου ύψους h και µάζας m, προσκρούει σε τραχύ οριζόν τιο έδαφος µε ταχύτητα v και υπό γωνία προσπτώσεως φ. Την στιγµή της κρούσεως η επαφή του σώµατος µε το έδαφος γίνεται µέσω της ευρύτερης έδρας του, που έχει µήκος α. i) Να βρείτε την απαιτούµενη συνθήκη, ώστε τη στιγµή που τό σώµα εγκαταλείπει το έδαφος να κινείται κατακόρυφα; Σε ποιο ύψος θα φθάσει το σώµα στην περίπτωση αυτή; ii) Εάν ο συντελεστής τριβής ολίσθησης του σώµατος είναι ο µισός του µέγιστου επιτρεπόµενου για ασφαλή ολίσθησή του, τότε παρα τηρούµε ότι το σώµα εγκαταλείπει το έδαφος υπό γωνία ανακλά σεως θ<φ. Να βρεθεί στην περίπτωση αυτή σε ποιο ύψος ανέρχεται το σώµα υπεράνω του εδάφους. Δίνεται η επιτάχυνση g της βαρύ τητας. ΛΥΣΗ: i) Yποθέτουµε ότι το σώµα κατά τον χρόνο συµπίεσής του και αποσυµπίεσής του ολισθαίνει πάνω στο οριζόντιο έδαφος χωρίς να ανατρέ πεται. Οι δυνάµεις που δέχεται είναι το βάρος του w και η πλάγια αντίδρα ση του εδάφους, που αναλύεται στην τριβή ολίσθησης T, αντίρροπη της οριζόντιας συνιστώσας v x της ταχύτητας πρόσπτωσης v και την κάθετη Σχήµα α. Σχήµα β. αντίδραση, της οποίας το µέτρο µεταβάλλεται λόγω της ελαστικής παραµόρ φωσης του σώµατος (σχ. β). Εάν N είναι η µέση τιµή της κάθετης αντίδρα
10 σης κατά τον χρόνο Δt της επαφής του σώµατος µε το έδαφος µπορούµε να ισχυριστούµε ότι η N είναι σταθερή και ότι ο φορέας της είναι µετατο πισµένος κατα x σε σχέση µε το κέντρο µάζας του σώµατος (σχήµα β). Εφαρµόζοντας για το κέντρο µάζας και κατά την οριζόντια διευθυνση τον δεύτερο νόµο κίνησης του Νεύτωνα παίρνουµε τη σχέση: T = ma nn = ma a = nn/ m (1) όπου a η επιβράδυνση του σώµατος και n o συντελεστής τριβής ολίσθησης µεταξύ αυτού και του οριζοντίου επιπέδου. Όµως το σώµα δεν έχει περιστρο φή περί το κέντρο µάζας του, οπότε ισχύει η σχέση: Th / - Nx = nnh / = Nx x = nh / () Αλλά η απόσταση x ωφείλει να ικανοποιεί τη σχέση x α/, η οποία µε βάση την () γράφεται: nh / " / n " / h (3) H (3) εκφράζει ότι η µεγαλύτερη τιµή που επιτρέπεται να λάβει ο συντελε στής τριβής, ώστε το σώµα να ολισθαίνει χωρίς να ανατρέπεται είναι α/h. Επειδή θέλουµε το σώµα να εγκαταλείπει το έδαφος µε κατακόρυφη ταχύ τητα, αυτό σηµαίνει ότι κατά τον χρόνο Δt που επιβραδύνεται ολισθαίνον τας η οριζόντια συνιστώσα της ταχύτητάς του µηδενίζεται, οπότε θα ισχύει η σχέση: (1) v µ" - a#t = t = v "µ# /a t = mv "µ# /nn Nt = mv "µ# /n (4) Εξάλλου την στιγµή που το σώµα εγκαταλείπει το έδαφος έχει κατακόρυφή ταχύτητα v ', της οπoίας το µέτρο υπολογίζεται από το γεγονός ότι µέσω του έργου της τριβής T το σώµα απώλεσε κινητική ενεργεια ίση µε mv x /, οπότε θα ισχύει: mv' = mv - mv x v' = v - v "µ # v' = v "#$ % v' = v "#$% (5) Εφαρµόζοντας για το σώµα το θεώρηµα ώθησης ορµής κατά τον κατακόρυφο άξονα και για τον χρόνο Δt παίρνουµε τη σχέση: (5) mv' - (-mv ) = N"t - mg"t mv "#$ = N%t - mg%t (6) Θεωρώντας αµελήτέα την ώθηση του βάρους του σώµατος σε σχέση µε την ώθηση της δύναµης N, η σχέση (5) γράφεται:
11 (4) mv "#$ = N%t mv "#$ = mv %µ$ /n (3) n = "" / "" / # $ /h (7) H (7) αποτελεί την ζητούµενη συνθηκη. Aν Η είναι το ύψος στο οποίο ανέρ χεται το σώµα αφού εγκαταλείψει το έδαφος, θα ισχυει: mv' = mgh H = v' (5) g H = v "# $ g (6) ii) Eάν αλλάξουµε τον συντελεστή τριβής ολίσθησης είναι δυνατόν το σώµα να εγκαταλείψει το έδαφος πριν µηδενιστεί η οριζόντια συνιστώσα της ταχύ τητάς του, που σηµαίνει ότι την στιγµή του αποχωρισµού το σώµα έχει οριζόντια ταχύτητα v ' x της οποίας το µέτρο υπολογίζεται από τη σχέση: v' x = v µ" - a'#t'= v µ" - nn'#t' m v' x = v µ" - #N'$t' hm (7) Σχήµα γ. όπου Δt ο νέος χρόνος επαφής του σώµατος µε το έδαφος, a ' η νέα επιβρά δυνση του σώµατος και N ' η νέα µέση κάθετη αντίδραση του εδάφους. Eξάλλου εάν v ' είναι η κατακόρυφη συνιστώσα της ταχύτητας ανάκλασης του σώµατος θα ισχύει, σύµφωνα µε το θεώρηµα ώθησης-ορµής κατά τον κατακόρυφο άξονα, η σχέση: m(v' +v ) = N'"t' (8) Συνδυάζοντας τις σχέσεις (7) και (8) παίρνουµε: v' x = v µ" - #(v' $ +v $ ) h v' x + v' " h = v #µ$ - v " h v' "#$ + %v' h = v &µ# - % v '()# h
12 & v' "#$ + % ) & ( + = v ' h,µ# - % -./# ) * "µ# - $ %&'# / h- ( + v' * ' h = v, / (9) * + (#) + $ / h. Όµως την στιγµή που το σώµα εγκαταλείπει το έδαφος έχει µεταφορική µό νο κίνηση, διότι η τιµή του συντελεστού τριβής αποκλείει την περιστροφή του περί το κέντρο µάζας του, οπότε όταν το κέντρο µάζας βρεθεί στην ανώ τατη θέση της παραβολικής τροχιάς που διαγράφει θα έχει ταχύτητα v ' x και σύµφωνα µε την αρχή διατήρησης της µηχανικής ενέργειας θα ισχύει η σχέ ση: mv' + mv' x = mgh + mv' x mv' (9) = mgh ) µ" - # $%&" / h, gh = v +. * '"( + # / h - H = v g ) µ" - # $%&" / h, +. * '"( + # / h - P.M. fysikos H τροχιά ενός υλικού σηµείου είναι µια κυκλοειδής καµπύλη (βλέ πε σχήµα), µε παραµετρικές εξισώσεις της µορφής: x = (" - #µ") ' ( y = (1 - $%&") ) µε " # και α θετική σταθερή ποσότητα. Να δείξετε ότι η ακτίνα καµπυλό τητας R της κυκλοειδούς καµπύλης σ ένα σηµείο της δίνεται από τη σχέση: R = 4"µ (# / ) όπου θ η τιµή της παραµέτρου που αντιστοιχεί στο σηµείο αυτό. ΛΥΣΗ: Εξετάζουµε το υλικό σηµείο σε µια τυχαία θέση Μ της κυκλοειδούς τροχιάς του, µε συντεταγµένες x και y ως προς το ορθογώνιο σύστηµα αξόνων Οxy. Εάν v είναι η ταχύτητα του υλικού σηµείου στην θέση αυτή, a η κεντροµόλος επιτάχυνσή του και R η ακτίνα καµπυλότητας της τροχι άς, θα ισχύει η σχέση: a = v /R R = v /a (1)
13 Εξάλλου για τις προβολές v x, v y της ταχύτητας v στους άξονες Οx, Oy αντιστοίχως, έχουµε τις σχέσεις: v x v y = dx = dx d d = " d ( d - #µ ) d = " ( 1 - $%& ) () = dy = dy d d = " d ( d 1 - #$% ) d = "&µ (3) Σχήµα α. όπου ο ρυθµός µεταβολής της παραµέτρου θ. Για το µέτρο της v ισχύει η σχέση: v = v x + v y (),(3) v = ( 1 - "#$%) + "µ v = ( 1 + "#$ % - "#$% + &µ %) v = ( 1 - "#$%) v = 4 "µ (# / ) (4) Εάν a x, a y είναι οι προβολές της επιτάχυνσης a του υλικού σηµείου, θα έχουµε τις σχέσεις: a x = dv x = dv x d d () και a x = d ( "- "#$%" ) = d "- "#$%" - " d(#$%") $ # " & % a x = " (1-"#$)+%µ # $ (5) a y = dv y (3) a y = d ( "µ# # ) = ( $%&# # +"µ# #) (6) Οι προβολές a κx, a κy των a x και a y αντιστοίχως στη διεύθυνση της ακτίνας καµπυλότητας ΜΚ (σχήµα α) δίνουν το µέτρο της κεντροµόλου επιτάχυν σης του υλικού σηµείου, µέσω της σχέσεως:
14 v a = a x - a y = a x "µ# - a y $%&# = a y x v - a v x y v = 1 v a v - a v (7) x y y x Η σχέση (1) µε βάση την (7) παίρνει τη µορφή: R = v 3 (4) a x v y - a y v x R = [4 "µ (# / )] 3 / a x v y - a y v x 3 (8) Εξάλλου µε βάση τις σχέσεις (), (3), (5) και (6) µπορούµε να υπολογίσουµε την ποσότητα a x v y -a y v x, δηλαδή θα έχουµε: a x v y - a y v x = " -#$%" " + &µ"" ( ) &µ"" - - ( "#$% % +&µ% %)( 1-"#$% ) % = (&µ%% %-&µ%"#$% % % + +µ " " 3 - #$%" " 3 - µ" " " +#$%" " 3 µ"#$%" " ") = = ( "µ ## 3 - $%&# # 3 + $%& ## ) 3 = ( 1-$%&# )# 3 (9) Συνδυάζοντας τις σχέσεις (8) και (9) παίρνουµε: R = [4 "µ (# / )] 3 / 1 - $%&# = 8 3 "µ (# / )] 3 / "µ (# / ) = 4"µ (# / ) P.M. fysikos Ένας παρατηρητής ακίνητος επί οριζοντίου εδάφους (αδρανειακός παρατηρητής) καταγράφει την κίνηση ενός σηµείου της περιφέρει ας στεφάνης, η οποία κυλίεται ισοταχώς στο οριζόντιο έδαφος. i) Να βρείτε τις παραµετρικές εξισώσεις της επίπεδης τροχιάς που διαγράφει το σηµείο, αν κατά την αρχή του χρόνου (t=) βρίσκεται στην αρχή του συστήµατος συντεταγµένων. ii) Nα δείξετε ότι κάθε στιγµή η επιτάχυνση του σηµείου κατευθύ νεται προς το κέντρο της στεφάνης, η δε κεντροµόλος επιτάχυν σή του κατευθύνεται προς το σηµείο επαφής Α της στεφάνης µε το οριζόντιο έδαφος και να υπολογίσετε το µέτρο της σε συνάρτηση µε το χρόνο. iii) Nα βρείτε τις παραµετρικές εξισώσεις της γραµµής που διαγρά φει το κέντρο καµπυλότητας της τροχιάς του θεωρούµενου σηµείου της στεφάνης. Δίνεται η ακτίνα r της στεφάνης και η γωνιακή τα χύτητα της περιστροφικής της κίνησης περί το κέντρο της. ΛΥΣΗ: i) Ο αδρανειακός επί του εδάφους παρατηρητής, θεωρώντας την κύλιση της στεφάνης διαπιστώνει ότι ένα οποιοδήποτε σηµείο της M διαγρά
15 φει επίπεδη καµπύλη τροχιά, η δε ταχύτητά του v είναι κάθε στιγµή εφαπτόµενη της τροχιάς αυτής και προκύπτει ως συνισταµένη της οριζόν τιας ταχύτητάς του v που οφείλεται στην µεταφορική κίνηση της στεφάνης Σχήµα b. και της ταχύτητάς του ( " M), που οφείλεται στην περιστροφή της, η οποία είναι εφαπτοµένη της στεφάνης στο θεωρούµενο σηµείο, όπου η σταθερή γωνιακή ταχύτητα περιστροφής της στεφάνης και M το διάνυσµα θέσεως του σηµείου Μ ως προς το κέντρο. Eπειδή τη χρονική στιγµή t= το σηµείο αυτό βρίσκεται στην αρχή Ο του αδρανειακού συστήµατος αναφο ράς Οxψ, η γωνιακή µετατόπιση του διανύσµατος M σε χρόνο t θα είναι ωt, η δε αντίστοιχη x-συντεταγµένη του σηµείου Μ θα είναι: x = OM x = OA - M x A (1) Όµως λόγω της κύλισης της στεφάνης το σηµείο επαφής Α της µε το έδαφος δεν ολισθαίνει πάνω σ αυτό και έτσι το µήκος του τόξου ΜΑ είναι ίσο µε το µήκος OΑ, δηλαδή θα ισχύει ΟΑ=τόξο(ΜΑ)=rωt οπότε η σχέση (1) γράφεται: x = rt - M x A () Eξάλλου από το σχήµα για το µήκος Μ x Α έχουµε: $ M x A = (AM)µ" = rµ #t ' $ & ) µ * % ( - #t ' & ) % ( # M x A = rµ "t & # % ( )*+ "t & % ( = rµ"t (3) $ ' $ ' Συνδυάζοντας τις σχέσεις () και (3) παίρνουµε: x = rt - r"µt = r(t - "µt) (4)
16 H αντίστοιχη ψ-συντεταγµένη του Μ είναι: ( = MM = (AM)"#$% = r&µ 't + ( * - "#$. ), - 't + * - ), $ #t' = r"µ & ) = r(1 - *+,#t) (5) % ( Οι σχέσεις (4) και (5) αποτελούν τις έξισώσεις κίνησης του σηµείου Μ, ή το ίδιο τις παραµετρικές εξισώσεις της τροχιάς του, η οποία ονοµάζεται κυκλο ειδής καµπύλη. ii) Η επιτάχυνση a του Μ ως προς το σύστηµα αναφοράς του εδάφους κάθε στιγµή δίνεται από τη σχέση: # ( ) + % a = a # + d % $ " M & # ( + " d(m) & % ' $ ( = + " M ' " d(m) & $ ( ' # a = " d(m) & % $ ( (6) ' Όµως το δεύτερο µέλος της (6) αποτελεί την κεντροµόλο επιτάχυνση του σηµείου Μ την οφειλόµενη µόνο στην περιστροφική κίνηση της στεφάνης, που σηµαίνει ότι η επιτάχυνση a κατευθύνεται προς το κέντρο της στεφά νης. H κεντροµόλος επιτάχυνση a K της σύνθετης κίνησης του σηµεί ου Μ επί της κυκλοειδούς τροχιάς του είναι η συνιστώσα της a σε διεύθυνση κάθετη προς την ταχύτητα v, που σηµαίνει ότι αυτή κατευθύνεται προς το στιγµιαίο κέντρο περιστροφής της στεφάνης, που δεν είναι άλλο από το σηµείο επαφής Α της στεφάνης µε το οριζόντιο έδαφος. Αυτό προκύπτει από το γεγονός ότι η ΑΜ είναι κάθετη στο διάνυσµα της ταχύτητας v. Εξάλλου το µέτρο της a K θα είναι: & a K = a"# $ - %t ) & ( + = % r,µ %t ) ( + (7) ' * ' * iii) Eάν ρ είναι η ακτίνα της κυκλοειδούς τροχιάς στό σηµείο Μ θα ισχύει: a K = v (7) # r"µ t & % ( = v $ ' ) Για το µέτρο της v ισχύει η σχέση: (8) v = dx $ # & " % + d' $ # & " % (4),(5) v = ( r - r"#$t) + r %µ t v = r + r "#$ t - r "#$t + r %µ t
17 v = r - r "#$t = r (1 - "#$t) = 4r %µ (t / ) (9) Συνδυάζοντας τις σχέσεις (8) και (9) παίρνουµε: ( ) # r"µ t & % $ ' ( = 4r "µ t / ) $ = 4r"µ #t ' & ) (1) % ( Aπό την (1) παρατηρούµε ότι η ακτίνα καµπυλότητας ρ είναι διπλάσια της απόστασης ΑΜ, δηλαδή το κέντρο καµπυλότητας Κ της κυκλοειδούς σε κάθε σηµείο της είναι συµµετρικό του εν λόγω σηµείου, ως προς το σηµείο επαφής Α της στεφάνης µε το έδαφος. Εάν x K, ψ Κ είναι οι συντεταγµένες του Κ, τότε από το σχήµα (β) θα έχουµε: $ x K = OA + AB = rt + AK"µ # - t ' & ) % ( και # x K = rt + r"µ t & # % ( )*+ t & % ( = r(t + "µt) (11) $ ' $ ' ' K = -KB = -(AM)"#$ % - &t * ' &t* ), t = -r-µ ), ( + ( + K = -r(1 - "µ#t) (1) Οι σχέσεις (11) και (1) αποτελούν τις παραµετρικές εξισώσεις της γραµµής K που διαγράφει το κέντρο καµπυλότητας της τροχιάς του σηµείου Μ. P.M. Φυσικός
i) Nα δείξετε ότι, κάθε στιγµή οι ταχύτητες των δύο πιθήκων ως προς το ακίνητο έδαφος είναι ίσες.
 Δύο πιθηκάκια της ίδιας µάζας αναρριχώνται εκ της ηρεµίας κατά µήκος των τµηµάτων του αβαρούς σχοινιού, που διέρχεται από τον λαιµό µιας σταθερής τροχαλίας (σχ. ). H τροχαλία έχει αµελητέα µάζα και µπορεί
Δύο πιθηκάκια της ίδιας µάζας αναρριχώνται εκ της ηρεµίας κατά µήκος των τµηµάτων του αβαρούς σχοινιού, που διέρχεται από τον λαιµό µιας σταθερής τροχαλίας (σχ. ). H τροχαλία έχει αµελητέα µάζα και µπορεί
. Αυτό σηµαίνει ότι το κέντρο µάζας κινείται ευθύγραµµα µε σταθερή επιτάχυνση a! = F!
 Οµογενής κυκλικός δίσκος µάζας m και ακτίνας, βρίσκεται πάνω σε λείο οριζόντιο έδαφος µε τον άξονα συµµετρίας του κατα κόρυφο. Εάν σ ένα σηµείο της περιφέρειας του δίσκου εξασκείται συνεχώς µια σταθερή
Οµογενής κυκλικός δίσκος µάζας m και ακτίνας, βρίσκεται πάνω σε λείο οριζόντιο έδαφος µε τον άξονα συµµετρίας του κατα κόρυφο. Εάν σ ένα σηµείο της περιφέρειας του δίσκου εξασκείται συνεχώς µια σταθερή
µε φορά προς το κυρτό µέρος του σύρµατος (σχήµα α) η οποία µαζί µε την ακτινική συνιστώσα w!
 Το κυκλικό σύρµα του σχήµατος έχει µάζα m/ και είναι κρεµασµένο από κατακόρυφο σπάγκο αµελητέας µάζας αλλά επαρκούς αντοχής. Δύο όµοιες σηµειακές χάντρες, καθε µιά µε µάζα m, αφήνονται ταυτόχρονα από την
Το κυκλικό σύρµα του σχήµατος έχει µάζα m/ και είναι κρεµασµένο από κατακόρυφο σπάγκο αµελητέας µάζας αλλά επαρκούς αντοχής. Δύο όµοιες σηµειακές χάντρες, καθε µιά µε µάζα m, αφήνονται ταυτόχρονα από την
Θεωρούµε στερεό σώµα που εκτελεί ως προς ένα αδρανειακό σύστηµα αναφοράς επίπεδη κίνηση.
 Θεωρούµε στερεό σώµα που εκτελεί ως προς ένα αδρανειακό σύστηµα αναφοράς επίπεδη κίνηση. i) Εάν Κ είναι το στιγµιαίο κέντρο περιστροφής του στερεού κάποια στιγµή και C η αντίστοιχη θέση του κέντρου µάζας
Θεωρούµε στερεό σώµα που εκτελεί ως προς ένα αδρανειακό σύστηµα αναφοράς επίπεδη κίνηση. i) Εάν Κ είναι το στιγµιαίο κέντρο περιστροφής του στερεού κάποια στιγµή και C η αντίστοιχη θέση του κέντρου µάζας
ii) Nα υπολογιστεί η κινητική ενέργεια του συστήµατος σε συνάρτηση µε τον χρόνο. Δίνεται η επιτάχυνση! g της βαρύτητας.
 Στην διάταξη του σχήµατος () η ράβδος ΑΒ είναι οµογενής, έχει µήκος L και µπορεί να στρέφεται περί οριζόντιο άξο να, που διέρχεται από σηµείο Ο ευρισκόµενο σε απόσταση 3L/4 από το άκρο της Α. Η τροχαλία
Στην διάταξη του σχήµατος () η ράβδος ΑΒ είναι οµογενής, έχει µήκος L και µπορεί να στρέφεται περί οριζόντιο άξο να, που διέρχεται από σηµείο Ο ευρισκόµενο σε απόσταση 3L/4 από το άκρο της Α. Η τροχαλία
, της οποίας το µέτρο ικανοποιεί τη σχέση:
 Στην κορυφή της κεκλιµένης έδρας µιας ορθογώνιας σφήνας µάζας M, η οποία ισορροπεί πάνω σε λείο οριζόντιο έδαφος, αφήνεται µικ ρός κύβος µάζας m. Nα δείξετε ότι η σφήνα κινείται στο σύστη µα αναφοράς του
Στην κορυφή της κεκλιµένης έδρας µιας ορθογώνιας σφήνας µάζας M, η οποία ισορροπεί πάνω σε λείο οριζόντιο έδαφος, αφήνεται µικ ρός κύβος µάζας m. Nα δείξετε ότι η σφήνα κινείται στο σύστη µα αναφοράς του
ii) Να δείξετε ότι το σφαιρίδιο εκτελεί µια µη αρµονική περιοδική ταλάντωση, της οποίας να υπολογίσετε την περίοδο.
 Το σύστηµα του σχήµατος αποτελείται από δύο όµοια ελατήρια στα θεράς και φυσικού µήκους α, των οποίων οι άξονες βρίσκονται πάνω στην ευθεία ΑΒ, όπου Α, Β είναι δύο ακλόνητα σηµεία του επιπέδου. Εκτρέπουµε
Το σύστηµα του σχήµατος αποτελείται από δύο όµοια ελατήρια στα θεράς και φυσικού µήκους α, των οποίων οι άξονες βρίσκονται πάνω στην ευθεία ΑΒ, όπου Α, Β είναι δύο ακλόνητα σηµεία του επιπέδου. Εκτρέπουµε
Q του νήµατος που το συγκρατεί, συµφωνα δε µε τον δεύτερο νό µο κίνησης του Νεύτωνα θα ισχύει η σχέση: της τάσεως!
 Αβαρής ράβδος αποτελείται από δύο συνεχόµενα τµήµατα ΟΑ και ΑΒ που είναι ορθογώνια µεταξύ τους. Το άκρο Ο της ράβδου είναι αρθρωµένο σε οριζόντιο έδαφος το δε τµήµα της ΟΑ είναι κατακόρυφο και εφάπτεται
Αβαρής ράβδος αποτελείται από δύο συνεχόµενα τµήµατα ΟΑ και ΑΒ που είναι ορθογώνια µεταξύ τους. Το άκρο Ο της ράβδου είναι αρθρωµένο σε οριζόντιο έδαφος το δε τµήµα της ΟΑ είναι κατακόρυφο και εφάπτεται
i) Nα βρείτε την ταχύτητα του κέντρου της στεφάνης αµέσως µετά την κρού ση, η οποία θεωρείται βραχείας διάρκειας.
 Mια κυκλική στεφάνη ακτίνας R, της οποίας η µάζα θεωρείται συγκεντρωµένη στην περιφέρεια της, κυλίεται ισοταχώς πάνω σε οριζόντιο επίπεδο το δε κέντρο της έχει ταχύτητα v. Kάποια στιγµή η στε φάνη προσκρούει
Mια κυκλική στεφάνη ακτίνας R, της οποίας η µάζα θεωρείται συγκεντρωµένη στην περιφέρεια της, κυλίεται ισοταχώς πάνω σε οριζόντιο επίπεδο το δε κέντρο της έχει ταχύτητα v. Kάποια στιγµή η στε φάνη προσκρούει
ΜΕΡΟΣ Γ! 2η οµάδα λυµένων παραδειγµάτων
 ΜΕΡΟΣ Γ η οµάδα λυµένων παραδειγµάτων Στις άκρες αβαρούς και λεπτής ράβδου µηκούς L, έχουν στερεωθεί δύο όµοιες σφαίρες, µάζας m και ακτίνας R, το δε σύστηµα στρέφεται µε σταθερή γωνιακή ταχύτητα περί
ΜΕΡΟΣ Γ η οµάδα λυµένων παραδειγµάτων Στις άκρες αβαρούς και λεπτής ράβδου µηκούς L, έχουν στερεωθεί δύο όµοιες σφαίρες, µάζας m και ακτίνας R, το δε σύστηµα στρέφεται µε σταθερή γωνιακή ταχύτητα περί
ii) Nα βρείτε την µέγιστη γωνιακή ταχύτητα της ράβδου.
 Oµογενής ράβδος σταθερής διατοµής, µάζας m και µήκους L, µπορεί να στρέφεται περί οριζόντιο άξονα που διέρχεται από το ένα άκρο της. Όταν η ράβδος βρίσκεται στην θέση ευσταθούς ισορροπίας εφαρµόζεται στο
Oµογενής ράβδος σταθερής διατοµής, µάζας m και µήκους L, µπορεί να στρέφεται περί οριζόντιο άξονα που διέρχεται από το ένα άκρο της. Όταν η ράβδος βρίσκεται στην θέση ευσταθούς ισορροπίας εφαρµόζεται στο
από τον κατακόρυφο τοίχο, της οποίας ο φορέας είναι οριζόντιος και την δύναµη επα φής N!
 Οµογενής συµπαγής κύβος ακµής α και µάζας m, ισορροπεί ακουµπώντας µε µια ακµή του σε κατακόρυφο τοίχο και µε µια του έδρα σε κεκλιµένο επίπεδο γωνίας κλίσεως φ ως προς τον ορίζοντα, όπως φαίνεται στο
Οµογενής συµπαγής κύβος ακµής α και µάζας m, ισορροπεί ακουµπώντας µε µια ακµή του σε κατακόρυφο τοίχο και µε µια του έδρα σε κεκλιµένο επίπεδο γωνίας κλίσεως φ ως προς τον ορίζοντα, όπως φαίνεται στο
i) Nα βρεθεί η επιτάχυνση του κέντρου Κ της τροχαλίας την στιγµή t=0 αµέσως µετά την θραύση του νήµατος.
 H τροχαλία του σχήµατος () µάζας m και ακτίνας R, ισορροπεί εξαρτηµένη από τα νήµατα ΑΒ και ΓΔ τα οποία είναι ισο κεκλιµένα ως προς την οριζόντια διεύθυνση κατα γωνία φ. Κάποια στιγµή κόβουµε το νήµα ΑΒ
H τροχαλία του σχήµατος () µάζας m και ακτίνας R, ισορροπεί εξαρτηµένη από τα νήµατα ΑΒ και ΓΔ τα οποία είναι ισο κεκλιµένα ως προς την οριζόντια διεύθυνση κατα γωνία φ. Κάποια στιγµή κόβουµε το νήµα ΑΒ
όπου Μ η µάζα της Γης την οποία θεωρούµε σφαίρα οµογενή, G η παγκόσµια σταθερά της βαρύτητας και L!
 Είναι γνωστό ότι, όταν ένα σώµα κινείται µέσα στο βαρυτικό πεδίο της Γης υπό την επίδραση µόνο της Νευτώνειας έλξεως, η τροχιά που διαγράφει το κέντρο µάζας του είναι επίπεδη και µάλιστα το επίπεδό της
Είναι γνωστό ότι, όταν ένα σώµα κινείται µέσα στο βαρυτικό πεδίο της Γης υπό την επίδραση µόνο της Νευτώνειας έλξεως, η τροχιά που διαγράφει το κέντρο µάζας του είναι επίπεδη και µάλιστα το επίπεδό της
διέρχεται από το σηµείο τοµής Ο των φορέων του βάρους w! της ράβδου και της οριζόντιας αντίδρασης A!
 Η οµογενής ράβδος ΑΒ του σχήµατος έχει βά ρος w και στηρίζεται διά του άκρου της Α σε τραχύ κεκλιµένο επί πεδο γωνίας κλίσεως φ ως προς τον ορίζοντα, ενώ το άλλο της άκρο Β ακουµπάει σε λείο κατακόρυφο
Η οµογενής ράβδος ΑΒ του σχήµατος έχει βά ρος w και στηρίζεται διά του άκρου της Α σε τραχύ κεκλιµένο επί πεδο γωνίας κλίσεως φ ως προς τον ορίζοντα, ενώ το άλλο της άκρο Β ακουµπάει σε λείο κατακόρυφο
i) Nα βρείτε την επιτάχυνση του κέντρου της τροχαλίας τ 1.
 Στην διάταξη του σχήµατος 1) οι τροχαλίες τ 1 και τ έχουν την ίδια µάζα Μ που θεωρείται συγκεντρωµένη στην περι φέρειά τους και την ίδια ακτίνα R. Στο αυλάκι της σταθερής τροχα λίας τ έχει περιτυλιχθεί
Στην διάταξη του σχήµατος 1) οι τροχαλίες τ 1 και τ έχουν την ίδια µάζα Μ που θεωρείται συγκεντρωµένη στην περι φέρειά τους και την ίδια ακτίνα R. Στο αυλάκι της σταθερής τροχα λίας τ έχει περιτυλιχθεί
ΛΥΣΗ: Έστω O η θέση ισορροπίας του σφαιριδίου. Στη θέση αυτή το σφαι ρίδιο δέχεται το βάρος του w!, τη δύναµη F
 Ένα ιδανικό ελατήριο σταθεράς k κόβεται σε δύο τµήµατα µε µήκη L και L. Η µία άκρη κάθε τµήµατος συνδέεται στέρεα µε µικρό σφαιρίδιο µάζας m και οι ελέυθερες άκρες τους στερεώνονται σε ακλόνητα σηµεία
Ένα ιδανικό ελατήριο σταθεράς k κόβεται σε δύο τµήµατα µε µήκη L και L. Η µία άκρη κάθε τµήµατος συνδέεται στέρεα µε µικρό σφαιρίδιο µάζας m και οι ελέυθερες άκρες τους στερεώνονται σε ακλόνητα σηµεία
(τρίτος νόµος του Νεύτωνα) και την πλάγια αντίδραση του οριζόντιου εδάφους, η οποία αναλύεται στην τριβή ολίσθησης T!
 Επί της κεκλιµένης έδρας µιας ορθογώνιας και ισοσκελούς σφήνας µάζας m, η οποία ισορροπεί πάνω σε οριζόντιο έδαφος, αφήνεται µικρός κύβος µάζας m. Μεταξύ του κύβου και της σφήνας δεν υπάρχει τριβή, ενώ
Επί της κεκλιµένης έδρας µιας ορθογώνιας και ισοσκελούς σφήνας µάζας m, η οποία ισορροπεί πάνω σε οριζόντιο έδαφος, αφήνεται µικρός κύβος µάζας m. Μεταξύ του κύβου και της σφήνας δεν υπάρχει τριβή, ενώ
της οποίας ο φορέας σχηµατί ζει γωνία φ=π/6 µε την κατακόρυφη διεύθυνση και ανακλάται µε αντίστοιχη γωνία φ=π/4.
 Οριζόντιος δίσκος µάζας Μ ισορροπεί στηριζόµε νος στο πάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k, του οποίου το άλλο άκρο στηρίζεται στο έδαφος (σχήµα 1). Ένα µικρό σφαιρίδιο µάζας m, προσκρούει
Οριζόντιος δίσκος µάζας Μ ισορροπεί στηριζόµε νος στο πάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k, του οποίου το άλλο άκρο στηρίζεται στο έδαφος (σχήµα 1). Ένα µικρό σφαιρίδιο µάζας m, προσκρούει
i) τον λόγο των µαζών των δύο σφαιριδίων, ώστε αυτά µετά την κρού ση τους να φθάνουν στις αρχικές τους θέσεις και
 Δύο αβαρή και µη εκτατά νήµατα του ίδιου µή κους είναι στερεωµένα στο ίδιο σηµείο Ο, ενώ στις ελεύθερες άκρες των νηµάτων είναι δεµένα δύο σφαιρίδια, µε µάζες 1 και. Eκτρέ πουµε τα σφαιρίδια από την θέση
Δύο αβαρή και µη εκτατά νήµατα του ίδιου µή κους είναι στερεωµένα στο ίδιο σηµείο Ο, ενώ στις ελεύθερες άκρες των νηµάτων είναι δεµένα δύο σφαιρίδια, µε µάζες 1 και. Eκτρέ πουµε τα σφαιρίδια από την θέση
τα µοναδιαία διανύσµατα των αξόνων Οx, Oy, Oz αντιστοί χως. Η αντίστοιχη στροφορµή L!
 Στο ένα άκρο ράβδου µήκους L και αµελητέας µά ζας, έχει στερεωθεί σφαιρίδιο µάζας m. Η ράβδος είναι ακίνητη πάνω σε λείο οριζόντιο επίπεδο Οxy, µε το σφαιρίδιο στο σηµείο, και το άλλο της άκρο στο σηµείο
Στο ένα άκρο ράβδου µήκους L και αµελητέας µά ζας, έχει στερεωθεί σφαιρίδιο µάζας m. Η ράβδος είναι ακίνητη πάνω σε λείο οριζόντιο επίπεδο Οxy, µε το σφαιρίδιο στο σηµείο, και το άλλο της άκρο στο σηµείο
( ) ( ) 2 1 K = K = m 2. ! = v 2 + v 1 R + r (3) H (1) λόγω της (3) γράφεται: R - v 2. + v 1. v 2. r > 0 (4) ! v K. + v 1 )R - v 2. = v 2. - v.
 Το καρούλι του σχήµατος κυλίεται χωρίς ολίσ θηση πάνω σε οριζόντιο δοκάρι, που ολισθαίνει επί οριζοντίου έδα φους µε ταχύτητα v η οποία έχει την κατεύθυνση του δοκαριού. Η κύλιση του καρουλιού επιτυγχάνεται
Το καρούλι του σχήµατος κυλίεται χωρίς ολίσ θηση πάνω σε οριζόντιο δοκάρι, που ολισθαίνει επί οριζοντίου έδα φους µε ταχύτητα v η οποία έχει την κατεύθυνση του δοκαριού. Η κύλιση του καρουλιού επιτυγχάνεται
ακτινικής διεύθυνσης και στην οριακή τριβή T!"
 Λεπτή κυκλική στεφάνη ακτίνας R και µάζας m, ισορρο πεί εφαπτόµενη σε δύο υποστηρίγµατα A και Γ, όπως φαίνεται στο σχήµα (1. Eάν ο συντελεστής οριακής τριβής µεταξύ της στεφάνης και των υποστη ριγµάτων
Λεπτή κυκλική στεφάνη ακτίνας R και µάζας m, ισορρο πεί εφαπτόµενη σε δύο υποστηρίγµατα A και Γ, όπως φαίνεται στο σχήµα (1. Eάν ο συντελεστής οριακής τριβής µεταξύ της στεφάνης και των υποστη ριγµάτων
Ένα διαστηµόπλοιο µάζας M, κινείται στο διά στηµα µε σταθερή ταχύτητα V!
 Ένα διαστηµόπλοιο µάζας M, κινείται στο διά στηµα µε σταθερή ταχύτητα V 0. O πιλότος του θέλει ν αλλάξει τη διεύθυνση κίνησης του διαστηµόπλοιου, ώστε η νέα διεύθυνση να γίνει κάθετη προς την αρχική. Για
Ένα διαστηµόπλοιο µάζας M, κινείται στο διά στηµα µε σταθερή ταχύτητα V 0. O πιλότος του θέλει ν αλλάξει τη διεύθυνση κίνησης του διαστηµόπλοιου, ώστε η νέα διεύθυνση να γίνει κάθετη προς την αρχική. Για
την αρχή Ο του ΟΧY, που είναι ένα αδρανειακό σύστηµα αναφοράς. Εάν
 Ένα στερεό σώµα εκτελεί επίπεδη κίνηση, όταν οι αποστάσεις των υλικών του σηµείων από ένα ορισµένο επίπεδο αναφοράς (ε, παραµένουν αµετάβλητες µε τον χρόνο. Για την µελέτη της επίπεδης κίνησης στερεού
Ένα στερεό σώµα εκτελεί επίπεδη κίνηση, όταν οι αποστάσεις των υλικών του σηµείων από ένα ορισµένο επίπεδο αναφοράς (ε, παραµένουν αµετάβλητες µε τον χρόνο. Για την µελέτη της επίπεδης κίνησης στερεού
Οµογενής σφαίρα µάζας m και ατίνας R, ισορροπεί πάνω σε λείο οριζόντιο επίπεδο. Κάποια στιγµή ενεργεί στην σφαίρα οριζόντια ώθηση!!
 Οµογενής σφαίρα µάζας και ατίνας R, ισορροπεί πάνω σε λείο οριζόντιο επίπεδο. Κάποια στιγµή ενεργεί στην σφαίρα οριζόντια ώθηση βραχείας διάρκειας, της οποίας ο φορέας βρίσκε ται άνωθεν του κέντρου της
Οµογενής σφαίρα µάζας και ατίνας R, ισορροπεί πάνω σε λείο οριζόντιο επίπεδο. Κάποια στιγµή ενεργεί στην σφαίρα οριζόντια ώθηση βραχείας διάρκειας, της οποίας ο φορέας βρίσκε ται άνωθεν του κέντρου της
Δίνεται η ροπή αδράνειας I=mL 2 /3 της ράβδου ως προς τον άξονα περιστροφής της, η επιτάχυνση! g της βαρύτητας και ότι π 2!10.
 Oµογενής ράβδος σταθερής διατοµής, µάζας m και µήκους L, µπορεί να στρέφεται περί οριζόντιο άξονα που διέρχεται από το ένα άκρο της. Όταν η ράβδος βρίσκεται στην θέση ευσταθούς ισορροπίας της εφαρµόζεται
Oµογενής ράβδος σταθερής διατοµής, µάζας m και µήκους L, µπορεί να στρέφεται περί οριζόντιο άξονα που διέρχεται από το ένα άκρο της. Όταν η ράβδος βρίσκεται στην θέση ευσταθούς ισορροπίας της εφαρµόζεται
(σχ. 1). Εφαρ µόζοντας για την µεταφορική συνιστώσα της κύλισης του δίσκου τον
 Oµογενής λεπτός δίσκος ακτίνας R και µάζας m, ακινητεί επί οριζόντιου εδάφους µε το οποίο παρουσιάζει συντελεστή οριακής τριβής µ το δε επιπεδό του είναι κατακόρυφο,. Κάποια στιγµή εφαρµόζεται στο κέντρο
Oµογενής λεπτός δίσκος ακτίνας R και µάζας m, ακινητεί επί οριζόντιου εδάφους µε το οποίο παρουσιάζει συντελεστή οριακής τριβής µ το δε επιπεδό του είναι κατακόρυφο,. Κάποια στιγµή εφαρµόζεται στο κέντρο
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ
 ΠΡΟΒΛΗΜΑ 1 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ Η λεπτή, ομογενής ράβδος ΟΑ του σχήματος έχει μήκος, μάζα και μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο γύρω από οριζόντιο ακλόνητο άξονα (άρθρωση) που διέρχεται
ΠΡΟΒΛΗΜΑ 1 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ Η λεπτή, ομογενής ράβδος ΟΑ του σχήματος έχει μήκος, μάζα και μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο γύρω από οριζόντιο ακλόνητο άξονα (άρθρωση) που διέρχεται
, σταθερής κατεύθυνσης, της οποίας το µέτρο µεταβάλλεται µε τον χρόνο t, σύµφωνα µε την σχέση:
 Σώµα µάζας m σχήµατος ορθογώνιου κιβωτίου, ισορροπεί πάνω σε τραχύ οριζόντιο επίπεδο και στην άνω επιφάνειά του έχει τοποθετηθεί σώµα µάζας m/. Κάποια στιγµή που λαµβάνε ται ως αρχή µέτρησης του χρόνου
Σώµα µάζας m σχήµατος ορθογώνιου κιβωτίου, ισορροπεί πάνω σε τραχύ οριζόντιο επίπεδο και στην άνω επιφάνειά του έχει τοποθετηθεί σώµα µάζας m/. Κάποια στιγµή που λαµβάνε ται ως αρχή µέτρησης του χρόνου
A! Κινηµατική άποψη. Σχήµα 1 Σχήµα 2
 A Κινηµατική άποψη Θεωρούµε στερεό σώµα σε τυχαία κίνηση, η οποία εξέταζεται από ένα αδρα νειακό σύστηµα αναφοράς ΟXYZ. Εφοδιάζουµε το σώµα µε κινητό σύστηµα συντεταγµένων xyz ακλόνητα συνδεδεµένο µε αυτό,
A Κινηµατική άποψη Θεωρούµε στερεό σώµα σε τυχαία κίνηση, η οποία εξέταζεται από ένα αδρα νειακό σύστηµα αναφοράς ΟXYZ. Εφοδιάζουµε το σώµα µε κινητό σύστηµα συντεταγµένων xyz ακλόνητα συνδεδεµένο µε αυτό,
i) Να δείξετε ότι: F max = (m 1 + m 2 όπου! g η επιτάχυνση της βαρύτητας.
 Δύο σώµατα Σ και Σ µε αντίστοιχες µάζες m και m, είναι στερεωµένα στις άκρες ενός κατακόρυφου αβαρούς ελατηρίου, όπως φαίνεται στο σχήµα. Εξασκούµε στο σώµα Σ κατακόρυφη δύναµη µε φορά προς τα κάτω, της
Δύο σώµατα Σ και Σ µε αντίστοιχες µάζες m και m, είναι στερεωµένα στις άκρες ενός κατακόρυφου αβαρούς ελατηρίου, όπως φαίνεται στο σχήµα. Εξασκούµε στο σώµα Σ κατακόρυφη δύναµη µε φορά προς τα κάτω, της
i) Το επίπεδο της τροχαλίας είναι οριζόντιο και το έδαφος λείο.
 Πάνω σε οριζόντιο έδαφος ηρεµεί µια τροχαλία µάζας m και ακτίνας R. Στο αυλάκι της τροχαλίας έχει περιτυλιχ θεί αβαρές νήµα στο ελεύθερο άκρο Α του οποίου εξασκείται σταθε ρή οριζόνια δύναµη F. Eάν µέχρις
Πάνω σε οριζόντιο έδαφος ηρεµεί µια τροχαλία µάζας m και ακτίνας R. Στο αυλάκι της τροχαλίας έχει περιτυλιχ θεί αβαρές νήµα στο ελεύθερο άκρο Α του οποίου εξασκείται σταθε ρή οριζόνια δύναµη F. Eάν µέχρις
Τροχός ακτίνας R κυλίεται χωρίς ολίσθηση κατά µήκος οριζόντιου αυλακιού, το δε κέντρο µάζας του C έχει σταθερή ταχύτητα v!
 Τροχός ακτίνας R κυλίεται χωρίς ολίσθηση κατά µήκος οριζόντιου αυλακιού, το δε κέντρο µάζας του C έχει σταθερή ταχύτητα v C. Σε σηµείο της περιφέρειας του τροχου έχει αρθρωθεί το ένα άκρο Β µιας λεπτής
Τροχός ακτίνας R κυλίεται χωρίς ολίσθηση κατά µήκος οριζόντιου αυλακιού, το δε κέντρο µάζας του C έχει σταθερή ταχύτητα v C. Σε σηµείο της περιφέρειας του τροχου έχει αρθρωθεί το ένα άκρο Β µιας λεπτής
i) το πλάτος ταλάντωσης του καροτσιού µετά την ενσωµάτωση του σφαιριδίου σ' αυτό και
 Ένα καροτσάκι που περιέχει άµµο, συνολικής µάζας M, εκτελεί οριζόντια αρµονική ταλάντωση σε λείο επίπεδο, µε τη βοήθεια ιδανικού οριζόντιου ελατηρίου σταθεράς k. Ένα σφαιρίδιο µάζας m
Ένα καροτσάκι που περιέχει άµµο, συνολικής µάζας M, εκτελεί οριζόντια αρµονική ταλάντωση σε λείο επίπεδο, µε τη βοήθεια ιδανικού οριζόντιου ελατηρίου σταθεράς k. Ένα σφαιρίδιο µάζας m
Eφαρµόζοντας στο τρίγωνο OAΣ το θεώρηµα του συνηµιτόνου παίρνουµε:
 ΘΕΜΑ 6o Η κυκλική τροχαλία του σχήµατος (1) έχει µάζα Μ και ακτίνα R, είναι σε επαφή µε οριζόντιο δάπεδο (ε), ενώ στον άξονά της έχει πακτωθεί αβαρής ράβδος µήκους L, στο ελεύθερο ακρο της οποίας έχει
ΘΕΜΑ 6o Η κυκλική τροχαλία του σχήµατος (1) έχει µάζα Μ και ακτίνα R, είναι σε επαφή µε οριζόντιο δάπεδο (ε), ενώ στον άξονά της έχει πακτωθεί αβαρής ράβδος µήκους L, στο ελεύθερο ακρο της οποίας έχει
διέρχεται από το σηµείο Ο της ράβδου, υπό την επίδραση των βαρών m 1 από τον άξονα περιστροφής, που αναλύεται στην οριζόντια συνιστώσα!
 Θεωρήστε οριζόντια ράβδο αµελητέας µάζας, η οποία µπορεί να περιστρέφεται περί σταθερό οριζόντιο άξονα κάθετο στη ράβδο. Στα άκρα της υπάρχουν δυο διαφορετικές σηµειακές µάζες m, m, που οι αντίστοιχες
Θεωρήστε οριζόντια ράβδο αµελητέας µάζας, η οποία µπορεί να περιστρέφεται περί σταθερό οριζόντιο άξονα κάθετο στη ράβδο. Στα άκρα της υπάρχουν δυο διαφορετικές σηµειακές µάζες m, m, που οι αντίστοιχες
. Εάν η σφαίρα κυλίεται πάνω στο δοκάρι να βρείτε: i) την επιτάχυνση του δοκαριού και του κέντρου της σφαίρας, στο σύστηµα αναφοράς του δαπέδου και
 Οµογενής σφαίρα µάζας m και ακτίνας R είναι ακίνητη πάνω σε οριζόντιο δοκάρι µάζας Μ και µήκους L, που µπορεί να ολισθαίνει χωρίς τριβή επί οριζοντίου δαπέδου. Η σφαίρα εφάπτεται στο δεξιό άκρο Β του δοκαριού
Οµογενής σφαίρα µάζας m και ακτίνας R είναι ακίνητη πάνω σε οριζόντιο δοκάρι µάζας Μ και µήκους L, που µπορεί να ολισθαίνει χωρίς τριβή επί οριζοντίου δαπέδου. Η σφαίρα εφάπτεται στο δεξιό άκρο Β του δοκαριού
i) Nα αποδείξετε ότι το σώµα τελικά θα ηρεµήσει ως προς το δοκάρι και να βρείτε την κοινή τους ταχύτητα στο σύστηµα αναφοράς του εδάφους.
 Ένα δοκάρι µεγάλου µήκους και µάζας M, είναι ακίνητο πάνω σε λείο οριζόντιο έδαφος. Στο ένα άκρο του δοκαριού βρίσκεται ξύλινο σώµα µάζας m, το οποίο παρουσιάζει µε την επιφά νεια του δοκαριού συντελεστή
Ένα δοκάρι µεγάλου µήκους και µάζας M, είναι ακίνητο πάνω σε λείο οριζόντιο έδαφος. Στο ένα άκρο του δοκαριού βρίσκεται ξύλινο σώµα µάζας m, το οποίο παρουσιάζει µε την επιφά νεια του δοκαριού συντελεστή
δεν ολισθαίνει πάνω σ αυτό και έτσι το µήκος του τόξου ΜΑ είναι ίσο µε το µήκος OΑ, δηλαδή θα ισχύει ΟΑ=τόξο(ΜΑ)=Rωt οπότε η σχέση (1) γράφεται:
 Ένας παρατηρητής ακίνητος επί οριζοντίου εδάφους αδρανειακός παρατηρητής) καταγράφει την κίνηση ενός oρισµένου σηµείου της περιφέρειας µιας κυκλικής στεφάνης, η οποία κυλίεται ισοταχώς στο έδαφος. i) Να
Ένας παρατηρητής ακίνητος επί οριζοντίου εδάφους αδρανειακός παρατηρητής) καταγράφει την κίνηση ενός oρισµένου σηµείου της περιφέρειας µιας κυκλικής στεφάνης, η οποία κυλίεται ισοταχώς στο έδαφος. i) Να
Σχήµα 20. οι οριζόντιες συνιστώσες των ταχυτήτων v! προσπτώσεως και ανακλάσεως αντιστοίχως του σφαιριδίου, T!
 Ένα στερεό σώµα εκτελεί επίπεδη κίνηση και δύο σηµεία αυτού βρίσκονται κάποια στιγµή t στις θέσεις Α(,) και Β(,α) του επιπέδου κίνησής του (x,y) Εάν οι ταχύτητες των σηµείων αυτών έχουν το ίδιο µέτρο v
Ένα στερεό σώµα εκτελεί επίπεδη κίνηση και δύο σηµεία αυτού βρίσκονται κάποια στιγµή t στις θέσεις Α(,) και Β(,α) του επιπέδου κίνησής του (x,y) Εάν οι ταχύτητες των σηµείων αυτών έχουν το ίδιο µέτρο v
Yλικό σηµείο κινείται στο επίπεδο Οxy διαγράφον τας καµπύλη τροχιά, η οποία περιγράφεται από την σχέση:
 Yλικό σηµείο κινείται στο επίπεδο Οxy διαγράφον τας καµπύλη τροχιά, η οποία περιγράφεται από την σχέση: y = Αηµωx όπου Α, ω σταθερές και θετικές ποσότητες. Εάν το υλικό σηµείο κατά τον άξονα x κινείται
Yλικό σηµείο κινείται στο επίπεδο Οxy διαγράφον τας καµπύλη τροχιά, η οποία περιγράφεται από την σχέση: y = Αηµωx όπου Α, ω σταθερές και θετικές ποσότητες. Εάν το υλικό σηµείο κατά τον άξονα x κινείται
των Α και Β αντιστοίχως είναι παράλληλες (σχ. 12) που σηµαί Σχήµα 11 Σχήµα 12
 Δύο ακριβώς όµοιες λεπτές ράβδοι OA και AB µήκους L και µάζας m, αρθρώνονται στο σηµείο Α το δε άκρο Ο της ΟΑ αρθρώνεται σε σταθερό υποστήριγµα, ενώ το άκρο Β της ΑΒ µπο ρεί να ολισθαίνει πάνω σε λείο
Δύο ακριβώς όµοιες λεπτές ράβδοι OA και AB µήκους L και µάζας m, αρθρώνονται στο σηµείο Α το δε άκρο Ο της ΟΑ αρθρώνεται σε σταθερό υποστήριγµα, ενώ το άκρο Β της ΑΒ µπο ρεί να ολισθαίνει πάνω σε λείο
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013
 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013 ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1- Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013 ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1- Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ. Α5. α. Λάθος β. Λάθος γ. Σωστό δ. Λάθος ε. Σωστό
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. γ. Α. δ. Α3. γ. Α4. γ. Α5. α. Λάθος β. Λάθος γ. Σωστό δ. Λάθος ε. Σωστό ΘΕΜΑ B B1. Σωστή απάντηση είναι η
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. γ. Α. δ. Α3. γ. Α4. γ. Α5. α. Λάθος β. Λάθος γ. Σωστό δ. Λάθος ε. Σωστό ΘΕΜΑ B B1. Σωστή απάντηση είναι η
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος Ι Ενδεικτικές Λύσεις Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος Ι Ενδεικτικές Λύσεις Θέµα Α Α.1. Η γωνιακή επιτάχυνση ενός οµογενούς δίσκου που στρέφεται γύρω από σταθερό άξονα, που διέρχεται από το κέντρο
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος Ι Ενδεικτικές Λύσεις Θέµα Α Α.1. Η γωνιακή επιτάχυνση ενός οµογενούς δίσκου που στρέφεται γύρω από σταθερό άξονα, που διέρχεται από το κέντρο
. Εάν η κρούση της ράβ δου µε το οριζόντιο έδαφος είναι τελείως ελαστική, να βρείτε:
 Μια λεπτή λαστιχένια ράβδος ΑΒ µήκους L και µάζας m, εκτελεί ελεύθερη πτώση χώρίς να περιστρέφεται και κάποια στιγµή το άκρο της Α συναντά λείο οριζόντιο έδαφος. Την στιγµή αυτή η ράβδος έχει κλίση φ ως
Μια λεπτή λαστιχένια ράβδος ΑΒ µήκους L και µάζας m, εκτελεί ελεύθερη πτώση χώρίς να περιστρέφεται και κάποια στιγµή το άκρο της Α συναντά λείο οριζόντιο έδαφος. Την στιγµή αυτή η ράβδος έχει κλίση φ ως
από την άρθρωση και της δύναµης επαφής από τον τοίχο που αναλύεται στην στατική τριβη T!
 Tο ένα άκρο A οµογενούς ράβδου AB αρθρώνεται σε οριζόντιο επίπεδο, ενώ το άλλο της άκρο Β εφάπτεται κατακόρυ φου τοίχου, µε τον οποίο η ράβδος παρουσιάζει συντελεστή οριακής τριβής µ. H άρθρωση της ράβδου
Tο ένα άκρο A οµογενούς ράβδου AB αρθρώνεται σε οριζόντιο επίπεδο, ενώ το άλλο της άκρο Β εφάπτεται κατακόρυ φου τοίχου, µε τον οποίο η ράβδος παρουσιάζει συντελεστή οριακής τριβής µ. H άρθρωση της ράβδου
i) Να δείξετε ότι αν για µια τιµή της γωνίας θ η ράβδος ισορροπεί, η ισορροπία αυτή είναι αδιάφορη.
 Η ράβδος του σχήµατος έχει µήκος L, βάρος w και στηρίζεται διά του άκρου της Α επί λείου τοίχου, ενώ το άλλο άκρο της Β ακουµπά ει σε λεία κοίλη επιφάνεια. Η τοµή της επιφάνειας µε κατακόρυφο επίπεδο που
Η ράβδος του σχήµατος έχει µήκος L, βάρος w και στηρίζεται διά του άκρου της Α επί λείου τοίχου, ενώ το άλλο άκρο της Β ακουµπά ει σε λεία κοίλη επιφάνεια. Η τοµή της επιφάνειας µε κατακόρυφο επίπεδο που
, που είναι στατική τριβή µε κατεύθυνση αντίθετη της ταχύτητας του κέντρου µάζας C 1 της σφαίρας (σχήµα 1) και η δύναµη επαφής!
 Δύο οµογενείς σφαίρες Α και Β, της ίδιας ακτίνας R µε αντίστοιχες µάζες m και m είναι ακίνητες επί οριζοντίου εδάφους και εφάπ τονται µεταξύ τους. Κάποια στιγµή που λαµβάνεται ως αρχή µέτρη σης του χρόνου
Δύο οµογενείς σφαίρες Α και Β, της ίδιας ακτίνας R µε αντίστοιχες µάζες m και m είναι ακίνητες επί οριζοντίου εδάφους και εφάπ τονται µεταξύ τους. Κάποια στιγµή που λαµβάνεται ως αρχή µέτρη σης του χρόνου
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Σάββατο 24 Φλεβάρη 2018 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Σάββατο 24 Φλεβάρη 2018 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4
ii) ii) Nα καθορίσετε το είδος της ισορροπίας της ράβδου.
 Oµογενής ράβδος Γ, βάρους w και µήκους L, είναι αρθρωµένη στο ένα άκρο της όπως φαίνεται στο σχήµα (), ενώ το άλλο άκρο της είναι δεµένο σε νήµα που διέρχεται από µικρή ακίνητη τροχαλία O, η οποία βρίσκεται
Oµογενής ράβδος Γ, βάρους w και µήκους L, είναι αρθρωµένη στο ένα άκρο της όπως φαίνεται στο σχήµα (), ενώ το άλλο άκρο της είναι δεµένο σε νήµα που διέρχεται από µικρή ακίνητη τροχαλία O, η οποία βρίσκεται
Kινηµατική άποψη της επίπεδης κίνησης
 Kινηµατική άποψη της επίπεδης κίνησης Θα λέµε ότι ένα στερεό σώµα εκτελεί επίπεδη κίνηση, όταν οι αποστάσεις των υλικών του σηµείων από ένα ορισµένο επίπεδο αναφοράς (ε), παραµέ νουν αµετάβλητες µε το
Kινηµατική άποψη της επίπεδης κίνησης Θα λέµε ότι ένα στερεό σώµα εκτελεί επίπεδη κίνηση, όταν οι αποστάσεις των υλικών του σηµείων από ένα ορισµένο επίπεδο αναφοράς (ε), παραµέ νουν αµετάβλητες µε το
ΘΕΩΡΗΜΑ Α! του σώ µατος ισχύει η σχέση: η επιβατική ακτίνα ως προς το σηµείο P του τυχαίου υλικού σηµείου του στερεού µάζας m i και v!
 ΘΕΩΡΗΜΑ Α Ο ρυθµός µεταβολής της στροφορµής στερεού σώµατος, θεωρούµενης περί ένα σηµείο του ή της επεκτάσεώς του και αναφερόµενης σε κάποιο αδρανειακό σύστηµα, είναι κάθε στιγµή ίσος µε την συνολική ροπή
ΘΕΩΡΗΜΑ Α Ο ρυθµός µεταβολής της στροφορµής στερεού σώµατος, θεωρούµενης περί ένα σηµείο του ή της επεκτάσεώς του και αναφερόµενης σε κάποιο αδρανειακό σύστηµα, είναι κάθε στιγµή ίσος µε την συνολική ροπή
και όταν φθάσει στο σηµείο Γ αρχίζει να κινείται στο κυκλικό του τµήµα που έχει την µορφή λείου τεταρτο κυκλίου ακτίνας R.
 Το σώµα Σ του σχήµατος (α) έχει µάζα και µπορεί να ολισθαίνει πάνω σε λείο οριζόντιο έδαφος. Ένα µικρό σφαιρίδιο µάζας m κινείται αρχικά πάνω στο οριζόντιο τµήµα του σώµατος µε ταχύτητα v 0 και όταν φθάσει
Το σώµα Σ του σχήµατος (α) έχει µάζα και µπορεί να ολισθαίνει πάνω σε λείο οριζόντιο έδαφος. Ένα µικρό σφαιρίδιο µάζας m κινείται αρχικά πάνω στο οριζόντιο τµήµα του σώµατος µε ταχύτητα v 0 και όταν φθάσει
( ) ω ( ) = 0. Aπό τις σχέσεις (2) προκύπτει ή ότι το διάνυσµα v K. είναι κάθετο στα διανύσµα τα r A
 Θεωρούµε στερεό σώµα που εκτελεί ως προς ένα αδρανειακό σύστηµα αναφοράς επίπεδη κίνηση και έστω (S) η κύρια* τοµή του στερεού κατά µια τυχαία χρονική στιγµή t. Να δείξετε ότι το αντίστοιχο προς την κύρια
Θεωρούµε στερεό σώµα που εκτελεί ως προς ένα αδρανειακό σύστηµα αναφοράς επίπεδη κίνηση και έστω (S) η κύρια* τοµή του στερεού κατά µια τυχαία χρονική στιγµή t. Να δείξετε ότι το αντίστοιχο προς την κύρια
Οµογενής ράβδος µάζας m και µήκους L, κρατεί ται οριζόντια ακουµπώντας σε σταθερή ακίδα που απέχει απόσταση x από το κέντρο µάζας C της ράβδου.
 Οµογενής ράβδος µάζας m και µήκους L, κρατεί ται οριζόντια ακουµπώντας σε σταθερή ακίδα που απέχει απόσταση x από το κέντρο µάζας C της ράβδου. i) Να βρεθεί η απόσταση x, ώστε την στιγµή που η ράβδος αφήνεται
Οµογενής ράβδος µάζας m και µήκους L, κρατεί ται οριζόντια ακουµπώντας σε σταθερή ακίδα που απέχει απόσταση x από το κέντρο µάζας C της ράβδου. i) Να βρεθεί η απόσταση x, ώστε την στιγµή που η ράβδος αφήνεται
1. Για το σύστηµα που παριστάνεται στο σχήµα θεωρώντας ότι τα νήµατα είναι αβαρή και µη εκτατά, τις τροχαλίες αµελητέας µάζας και. = (x σε μέτρα).
 Θέμα ο. ια το σύστηµα που παριστάνεται στο σχήµα θεωρώντας ότι τα νήµατα είναι αβαρή και µη εκτατά, τις τροχαλίες αµελητέας µάζας και M= M = M, υπολογίστε την επιτάχυνση της µάζας. ίνεται το g. (0) Λύση.
Θέμα ο. ια το σύστηµα που παριστάνεται στο σχήµα θεωρώντας ότι τα νήµατα είναι αβαρή και µη εκτατά, τις τροχαλίες αµελητέας µάζας και M= M = M, υπολογίστε την επιτάχυνση της µάζας. ίνεται το g. (0) Λύση.
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ. Άσκηση 1. (Κινητική ενέργεια λόγω περιστροφής. Έργο και ισχύς σταθερής ροπής)
 ΕΚΦΩΝΗΣΕΣ ΑΣΚΗΣΕΩΝ Άσκηση 1 (Κινητική ενέργεια λόγω περιστροφής Έργο και ισχύς σταθερής ροπής) Ένας κύβος και ένας δίσκος έχουν ίδια μάζα και αφήνονται από το ίδιο ύψος να κινηθούν κατά μήκος δύο κεκλιμένων
ΕΚΦΩΝΗΣΕΣ ΑΣΚΗΣΕΩΝ Άσκηση 1 (Κινητική ενέργεια λόγω περιστροφής Έργο και ισχύς σταθερής ροπής) Ένας κύβος και ένας δίσκος έχουν ίδια μάζα και αφήνονται από το ίδιο ύψος να κινηθούν κατά μήκος δύο κεκλιμένων
[1kgm 2, 5m/s, 3,2cm, 8rad/s][1kgm 2, 5m/s, 3,2cm, 8rad/s]
![[1kgm 2, 5m/s, 3,2cm, 8rad/s][1kgm 2, 5m/s, 3,2cm, 8rad/s] [1kgm 2, 5m/s, 3,2cm, 8rad/s][1kgm 2, 5m/s, 3,2cm, 8rad/s]](/thumbs/61/46095927.jpg) ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 5: ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ ΚΑΙ ΕΡΓΟ ΔΥΝΑΜΗΣ ΣΤΗ ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ 34. Μία κατακόρυφη ράβδος μάζας μήκους, μπορεί να περιστρέφεται στο κατακόρυφο επίπεδο γύρω από
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 5: ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ ΚΑΙ ΕΡΓΟ ΔΥΝΑΜΗΣ ΣΤΗ ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ 34. Μία κατακόρυφη ράβδος μάζας μήκους, μπορεί να περιστρέφεται στο κατακόρυφο επίπεδο γύρω από
Υλικό σηµείο µάζας m, κινείται εντός δυναµικού πεδίου δεχόµενο ελκτική κεντρική δύναµη F!
 Υλικό σηµείο µάζας, κινείται εντός δυναµικού πεδίου δεχόµενο ελκτική κεντρική δύναµη F (), η οποία ακολουθεί τον νόµο του αντιστρόφου τετραγώνου της απόστασης από το ελκτι κό κέντρο Ο, δηλαδή περιγράφεται
Υλικό σηµείο µάζας, κινείται εντός δυναµικού πεδίου δεχόµενο ελκτική κεντρική δύναµη F (), η οποία ακολουθεί τον νόµο του αντιστρόφου τετραγώνου της απόστασης από το ελκτι κό κέντρο Ο, δηλαδή περιγράφεται
! =A'B=C!! C! = R" (1)
 Οµογενής κύβος ακµής α ισορροπεί επί ακλό νητης σφαιρικής επιφάνειας ακτίνας R, µε το κέντρο µάζας του ακριβώς πάνω από την κορυφή Α της επιφάνειας. Εάν µεταξύ του κύβου και της σφαιρικής επιφάνειας υπάρχει
Οµογενής κύβος ακµής α ισορροπεί επί ακλό νητης σφαιρικής επιφάνειας ακτίνας R, µε το κέντρο µάζας του ακριβώς πάνω από την κορυφή Α της επιφάνειας. Εάν µεταξύ του κύβου και της σφαιρικής επιφάνειας υπάρχει
Ένα σώµα µε µεγάλη µάζα Μ, κινείται µε σταθερή
 Ένα σώµα µε µεγάλη µάζα Μ, κινείται µε σταθερή ταχύτητα µέτρου V 0 πάνω σε λείο οριζόντιο έδαφος κατευθυνόµενο προς κατακόρυφο τοίχο. Το σώµα κάποια στιγµή συγκρούεται ελα στικά και µετωπικά µε µια µπάλα
Ένα σώµα µε µεγάλη µάζα Μ, κινείται µε σταθερή ταχύτητα µέτρου V 0 πάνω σε λείο οριζόντιο έδαφος κατευθυνόµενο προς κατακόρυφο τοίχο. Το σώµα κάποια στιγµή συγκρούεται ελα στικά και µετωπικά µε µια µπάλα
Γ ΤΑΞΗ ΤΜΗΜΑ ΟΝΟΜΑ. ΘΕΜΑ 1ο. 7 mr 5. 1 mr. Μονάδες 5. α. 50 W β. 100 W γ. 200 W δ. 400 W
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΟΝΟΜΑ ΤΜΗΜΑ ΕΠΑΝΑΛΗΠΤΙΚΟ ΙΑΓΩΝΙΣΜΑ ΤΕΤΑΡΤΗ 8 ΜΑΡΤΙΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ) ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1ο Στις ερωτήσεις 1-4 να γράψετε
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΟΝΟΜΑ ΤΜΗΜΑ ΕΠΑΝΑΛΗΠΤΙΚΟ ΙΑΓΩΝΙΣΜΑ ΤΕΤΑΡΤΗ 8 ΜΑΡΤΙΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ) ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1ο Στις ερωτήσεις 1-4 να γράψετε
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ. Η ενέργεια ταλάντωσης ενός κυλιόμενου κυλίνδρου
 A A N A B P Y A 9 5 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Η ενέργεια ταλάντωσης ενός κυλιόμενου κυλίνδρου Στερεό σώμα με κυλινδρική συμμετρία (κύλινδρος, σφαίρα, σφαιρικό κέλυφος, κυκλική στεφάνη κλπ) μπορεί να
A A N A B P Y A 9 5 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Η ενέργεια ταλάντωσης ενός κυλιόμενου κυλίνδρου Στερεό σώμα με κυλινδρική συμμετρία (κύλινδρος, σφαίρα, σφαιρικό κέλυφος, κυκλική στεφάνη κλπ) μπορεί να
του σφαιριδίου κατευθύνεται προς τα κάτω και σχηµατίζει µε την κατακόρυφη διεύθυνση γωνία φ.
 Μικρό σφαιρίδιο µάζας m, προσπίπτει σε σηµεί ο Α της περιφέρειας ενός δακτυλιδιού ακτίνας R, το οποίο µπορεί να περιστρέφεται περί οριζόντιο άξονα που διέρχεται από ένα σηµείο του Ο. Η ταχύτητα πρόσπτωσης
Μικρό σφαιρίδιο µάζας m, προσπίπτει σε σηµεί ο Α της περιφέρειας ενός δακτυλιδιού ακτίνας R, το οποίο µπορεί να περιστρέφεται περί οριζόντιο άξονα που διέρχεται από ένα σηµείο του Ο. Η ταχύτητα πρόσπτωσης
ΜΕΡΟΣ Γ! 1η οµάδα λυµένων παραδειγµάτων
 ΜΕΡΟΣ Γ 1η οµάδα λυµένων παραδειγµάτων Ένας τροχός, µάζας m η οποία θεωρείται συγ κεντωµενη στην περιφέρειά του, περιστρέφεται περί οριζόντιο άξονα ασήµαντης µάζας, ο οποίος διέρχεται από το κέντρο του
ΜΕΡΟΣ Γ 1η οµάδα λυµένων παραδειγµάτων Ένας τροχός, µάζας m η οποία θεωρείται συγ κεντωµενη στην περιφέρειά του, περιστρέφεται περί οριζόντιο άξονα ασήµαντης µάζας, ο οποίος διέρχεται από το κέντρο του
i) τον λόγο των µαζών των δύο σφαιριδίων, ώστε αυτά µετά την κρού ση τους να φθάνουν στις αρχικές τους θέσεις και
 Δύο αβαρή και µη εκτατά νήµατα του ίδιου µή κους είναι στερεωµένα στο ίδιο σηµείο Ο, ενώ στις ελεύθερες άκρες των νηµάτων είναι δεµένα δύο σφαιρίδια, µε µάζες 1 και. Eκτρέ πουµε τα σφαιρίδια από την θέση
Δύο αβαρή και µη εκτατά νήµατα του ίδιου µή κους είναι στερεωµένα στο ίδιο σηµείο Ο, ενώ στις ελεύθερες άκρες των νηµάτων είναι δεµένα δύο σφαιρίδια, µε µάζες 1 και. Eκτρέ πουµε τα σφαιρίδια από την θέση
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ» 5 o ΔΙΑΓΩΝΙΣΜΑ ΑΠΡΙΛΙΟΣ 2017: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ
 5 o ΔΙΑΓΩΝΙΣΜΑ ΑΠΡΙΛΙΟΣ 017: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. γ. Α. δ. Α3. γ. Α4. γ. Α5. α. Λάθος β. Λάθος γ. Σωστό
5 o ΔΙΑΓΩΝΙΣΜΑ ΑΠΡΙΛΙΟΣ 017: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. γ. Α. δ. Α3. γ. Α4. γ. Α5. α. Λάθος β. Λάθος γ. Σωστό
(ΘΕΜΑ 17ο)
 Εισαγωγικά: Με το πρόβληµα της αλληλεπίδρασης δύο µαζών, µέσω αβαρούς και µη εκτατού νήµατος παρουσία οµογενούς βαρυτικού πεδίου, είχα ασχοληθεί και στο παρελθόν παρουσιάζοντάς το στην ιστοσελίδα µου µε
Εισαγωγικά: Με το πρόβληµα της αλληλεπίδρασης δύο µαζών, µέσω αβαρούς και µη εκτατού νήµατος παρουσία οµογενούς βαρυτικού πεδίου, είχα ασχοληθεί και στο παρελθόν παρουσιάζοντάς το στην ιστοσελίδα µου µε
θα επιβρα δύνεται. Επειδή η F! /Μ και θα ισχύει η σχέση: /t!
 Ξύλινο κιβώτιο µάζας M κινείται πάνω σε λείο οριζόντιο δάπεδο µε ταχύτητα µέτρου v 0. Ένα βλήµα µάζας m, κινούµενο αντίρροπα προς το κιβώτιο προσπίπτει σ αυτό µε ταχύ τητα µέτρου v 0 και εξέρχεται από
Ξύλινο κιβώτιο µάζας M κινείται πάνω σε λείο οριζόντιο δάπεδο µε ταχύτητα µέτρου v 0. Ένα βλήµα µάζας m, κινούµενο αντίρροπα προς το κιβώτιο προσπίπτει σ αυτό µε ταχύ τητα µέτρου v 0 και εξέρχεται από
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος ΙΙ Ενδεικτικές Λύσεις Κυριακή 28 Φλεβάρη 2016 Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος ΙΙ Ενδεικτικές Λύσεις Κυριακή 28 Φλεβάρη 2016 Θέµα Α Α.1. Ενα στερεό σώµα περιστρέφεται γύρω από ακλόνητο άξονα. Εάν διπλασιαστεί η στροφορµή
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος ΙΙ Ενδεικτικές Λύσεις Κυριακή 28 Φλεβάρη 2016 Θέµα Α Α.1. Ενα στερεό σώµα περιστρέφεται γύρω από ακλόνητο άξονα. Εάν διπλασιαστεί η στροφορµή
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 3 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση,
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 3 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση,
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ» 5 o ΔΙΑΓΩΝΙΣΜΑ ΜΑΡΤΙΟΣ 2017: ΘΕΜΑΤΑ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία
i) Nα δείξετε ότι αν το σύστηµα αφεθεί ελεύθερο η τροχαλία τ 1 δεν µπορεί να κυλίεται, άλλά µόνο να ισσρροπεί ή να ολισθαίνει.
 Στην διάταξη του σχήµατος η τροχαλία τ 1 έχει µάζα m 1 και ακτίνα R και στο αυλάκι της έχει περιτυλιχθεί αβαρές νήµα, το οποίο διέρ χεται από τον λαιµό της µικρής τροχαλίας τ στο δε άκρο του έχει δε θεί
Στην διάταξη του σχήµατος η τροχαλία τ 1 έχει µάζα m 1 και ακτίνα R και στο αυλάκι της έχει περιτυλιχθεί αβαρές νήµα, το οποίο διέρ χεται από τον λαιµό της µικρής τροχαλίας τ στο δε άκρο του έχει δε θεί
όπου y το µήκος του σχοινιού στο κατακόρυφο σκέλος του σωλήνα, v το κοινό µέτρο των ταχυτήτων v!
 Ένας σωλήνας µεγάλου µήκους έχει καµφθεί σε ορθή γωνία και είναι στερεωµένος, ώστε το ένα σκέλος του να είναι οριζόντιο και το άλλό κατακόρυφο, όπως φαίνεται στο σχήµα 1). Ένα σχοινί µήκους L, του οποίου
Ένας σωλήνας µεγάλου µήκους έχει καµφθεί σε ορθή γωνία και είναι στερεωµένος, ώστε το ένα σκέλος του να είναι οριζόντιο και το άλλό κατακόρυφο, όπως φαίνεται στο σχήµα 1). Ένα σχοινί µήκους L, του οποίου
i) Να δείξετε ότι η κίνηση του συστήµατος των δύο σφαιριδίων είναι περιοδική και να υπολογίσετε την περίοδο της.
 Ένα σφαιρίδιο Σ 1 µάζας m, είναι στερεωµένο στο άκρο ιδανικού ελατηρίου σταθεράς k, του οποίου το άλλο άκρο είναι ακλόνητο όπως φαίνεται στο σχήµα (α). Το σφαιρίδιο µπορεί να κινείται χωρίς τριβή πάνω
Ένα σφαιρίδιο Σ 1 µάζας m, είναι στερεωµένο στο άκρο ιδανικού ελατηρίου σταθεράς k, του οποίου το άλλο άκρο είναι ακλόνητο όπως φαίνεται στο σχήµα (α). Το σφαιρίδιο µπορεί να κινείται χωρίς τριβή πάνω
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 1: ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ [Υποκεφάλαιο 4.2 Οι κινήσεις των στερεών σωμάτων του σχολικού βιβλίου]
![ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 1: ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ [Υποκεφάλαιο 4.2 Οι κινήσεις των στερεών σωμάτων του σχολικού βιβλίου] ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 1: ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ [Υποκεφάλαιο 4.2 Οι κινήσεις των στερεών σωμάτων του σχολικού βιβλίου]](/thumbs/52/29790189.jpg) ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
Κεφάλαιο 6β. Περιστροφή στερεού σώματος γύρω από σταθερό άξονα
 Κεφάλαιο 6β Περιστροφή στερεού σώματος γύρω από σταθερό άξονα Ροπή Ροπή ( ) είναι η τάση που έχει μια δύναμη να περιστρέψει ένα σώμα γύρω από κάποιον άξονα. d είναι η κάθετη απόσταση του άξονα περιστροφής
Κεφάλαιο 6β Περιστροφή στερεού σώματος γύρω από σταθερό άξονα Ροπή Ροπή ( ) είναι η τάση που έχει μια δύναμη να περιστρέψει ένα σώμα γύρω από κάποιον άξονα. d είναι η κάθετη απόσταση του άξονα περιστροφής
ii) Nα βρεθεί η κινητική ενέργεια της σφαίρας, όταν το δοκάρι έχει µετατοπιστεί κατά S ως προς το έδαφος.
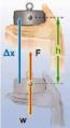 Στην διάταξη του σχήµατος () το δοκάρι Δ έχει µάζα Μ και µπορεί να ολισθαίνει πάνω σε λείο κεκλιµένο επίπεδο γωνίας κλίσεως φ ως προς τον ορίζοντα. Κάποια στιγµή που λαµβά νεται ως αρχή µέτρησης του χρόνου
Στην διάταξη του σχήµατος () το δοκάρι Δ έχει µάζα Μ και µπορεί να ολισθαίνει πάνω σε λείο κεκλιµένο επίπεδο γωνίας κλίσεως φ ως προς τον ορίζοντα. Κάποια στιγµή που λαµβά νεται ως αρχή µέτρησης του χρόνου
) ω ω. L λίγο πριν. . Nα βρεθούν:
 Δύο σφαιρίδια A, B µάζας m το καθένα συνδέονται µεταξύ τους µε αβαρές και µη εκτατό νήµα µήκους L, ηρεµούν δε πάνω σε οριζόντιο τραπέζι ευρισκόµενα σε απόσταση α
Δύο σφαιρίδια A, B µάζας m το καθένα συνδέονται µεταξύ τους µε αβαρές και µη εκτατό νήµα µήκους L, ηρεµούν δε πάνω σε οριζόντιο τραπέζι ευρισκόµενα σε απόσταση α
6ο ιαγώνισµα - Μηχανική Στερεού Σώµατος Ι. Θέµα Α
 6ο ιαγώνισµα - Μηχανική Στερεού Σώµατος Ι Ηµεροµηνία : 10 Μάρτη 2013 ιάρκεια : 3 ώρες Ονοµατεπώνυµο: Βαθµολογία % Θέµα Α Στις ερωτήσεις Α.1 Α.4 επιλέξτε την σωστη απάντηση [4 5 = 20 µονάδες] Α.1. Στερεό
6ο ιαγώνισµα - Μηχανική Στερεού Σώµατος Ι Ηµεροµηνία : 10 Μάρτη 2013 ιάρκεια : 3 ώρες Ονοµατεπώνυµο: Βαθµολογία % Θέµα Α Στις ερωτήσεις Α.1 Α.4 επιλέξτε την σωστη απάντηση [4 5 = 20 µονάδες] Α.1. Στερεό
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β ΛΥΚΕΙΟΥ (ΠΡΟΕΤΟΙΜΑΣΙΑ) ΗΜΕΡΟΜΗΝΙΑ: 19/03/2017 (ΑΠΑΝΤΗΣΕΙΣ) ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 206-207 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β ΛΥΚΕΙΟΥ (ΠΡΟΕΤΟΙΜΑΣΙΑ) ΗΜΕΡΟΜΗΝΙΑ: 9/03/207 (ΑΠΑΝΤΗΣΕΙΣ) ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 206-207 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β ΛΥΚΕΙΟΥ (ΠΡΟΕΤΟΙΜΑΣΙΑ) ΗΜΕΡΟΜΗΝΙΑ: 9/03/207 (ΑΠΑΝΤΗΣΕΙΣ) ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό
Διαγώνισμα Γ Λυκείου Θετικού προσανατολισμού. Διαγώνισμα Μηχανική Στερεού Σώματος. Σάββατο 24 Φεβρουαρίου Θέμα 1ο
 Διαγώνισμα Μηχανική Στερεού Σώματος Σάββατο 24 Φεβρουαρίου 2018 Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να επιλέξτε την σωστή απάντηση (4 5 = 20 μονάδες ) 1.1. Ένας δίσκος στρέφεται γύρω από άξονα που
Διαγώνισμα Μηχανική Στερεού Σώματος Σάββατο 24 Φεβρουαρίου 2018 Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να επιλέξτε την σωστή απάντηση (4 5 = 20 μονάδες ) 1.1. Ένας δίσκος στρέφεται γύρω από άξονα που
περί το κέντρο της σφαίρας, ονοµάζεται δε τριβή κυλίσεως. Tο µέτρο της τρι βής κυλίσεως είναι προφανώς ανάλογο του µέτρου της N,!
 Θεωρούµε µια βαρειά σφαίρα, η οποία ισορροπεί επί σχετικά µαλακού εδάφους, ώστε να προκαλεί σ αυτό µια µικρή παραµόρφωση. Λόγω της συµµετρίας που παρουσιάζει η παραµόρφωση αυτή, ως προς την κατακόρυφη
Θεωρούµε µια βαρειά σφαίρα, η οποία ισορροπεί επί σχετικά µαλακού εδάφους, ώστε να προκαλεί σ αυτό µια µικρή παραµόρφωση. Λόγω της συµµετρίας που παρουσιάζει η παραµόρφωση αυτή, ως προς την κατακόρυφη
γ) το μέτρο της γωνιακής ταχύτητας του δίσκου τη στιγμή κατά την οποία έχει ξετυλιχθεί όλο το σχοινί.
 1. Ο ομογενής και ισοπαχής δίσκος του σχήματος έχει ακτίνα και μάζα, είναι οριζόντιος και μπορεί να περιστρέφεται, χωρίς τριβές, γύρω από κατακόρυφο ακλόνητο άξονα που διέρχεται από το κέντρο του. Ο δίσκος
1. Ο ομογενής και ισοπαχής δίσκος του σχήματος έχει ακτίνα και μάζα, είναι οριζόντιος και μπορεί να περιστρέφεται, χωρίς τριβές, γύρω από κατακόρυφο ακλόνητο άξονα που διέρχεται από το κέντρο του. Ο δίσκος
ΦΥΣΙΚΗ Ο.Π Β Λ-Γ Λ ΧΡΗΣΤΟΣ ΚΑΡΑΒΟΚΥΡΟΣ ΙΩΑΝΝΗΣ ΤΖΑΓΚΑΡΑΚΗΣ
 ΦΥΣΙΚΗ Ο.Π Β Λ-Γ Λ 25/11/2018 ΧΡΗΣΤΟΣ ΚΑΡΑΒΟΚΥΡΟΣ ΙΩΑΝΝΗΣ ΤΖΑΓΚΑΡΑΚΗΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί
ΦΥΣΙΚΗ Ο.Π Β Λ-Γ Λ 25/11/2018 ΧΡΗΣΤΟΣ ΚΑΡΑΒΟΚΥΡΟΣ ΙΩΑΝΝΗΣ ΤΖΑΓΚΑΡΑΚΗΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος Ενδεικτικές Λύσεις Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος Ενδεικτικές Λύσεις Θέµα Α Α.1. Ενας δίσκος στρέφεται γύρω από άξονα που διέρχεται από το κέντρο του και είναι κάθετος στο επίπεδό του. Η τιµή
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος Ενδεικτικές Λύσεις Θέµα Α Α.1. Ενας δίσκος στρέφεται γύρω από άξονα που διέρχεται από το κέντρο του και είναι κάθετος στο επίπεδό του. Η τιµή
ΦΥΕ14-5 η Εργασία Παράδοση
 ΦΥΕ4-5 η Εργασία Παράδοση.5.9 Πρόβληµα. Συµπαγής οµογενής κύλινδρος µάζας τυλιγµένος µε λεπτό νήµα αφήνεται να κυλίσει από την κορυφή κεκλιµένου επιπέδου µήκους l και γωνίας φ (ϐλέπε σχήµα). Το ένα άκρο
ΦΥΕ4-5 η Εργασία Παράδοση.5.9 Πρόβληµα. Συµπαγής οµογενής κύλινδρος µάζας τυλιγµένος µε λεπτό νήµα αφήνεται να κυλίσει από την κορυφή κεκλιµένου επιπέδου µήκους l και γωνίας φ (ϐλέπε σχήµα). Το ένα άκρο
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΑΥΕΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/2014
 ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΑΥΕΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/04 ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΑΥΕΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/04 ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα
Επαναληπτικό διαγώνισµα Ταλαντώσεις Στερεό σώµα
 Επαναληπτικό διαγώνισµα Ταλαντώσεις Στερεό σώµα Θέµα ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις -4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Ένα σηµειακό
Επαναληπτικό διαγώνισµα Ταλαντώσεις Στερεό σώµα Θέµα ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις -4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Ένα σηµειακό
i) την ενέργεια που πρέπει να προσφερθεί στο σφαιρίδιο,
 Tο σφαιρίδιο του σχήµατος ισορροπεί πάνω στο λείο οριζόντιο δαπεδο, ενώ τα οριζόντια ελατήρια είναι τεντωµένα. H απόσταση των σηµείων στήριξης των δύο ελατηρίων είναι 3α, ενώ τα ελατήρια έχουν το ίδιο
Tο σφαιρίδιο του σχήµατος ισορροπεί πάνω στο λείο οριζόντιο δαπεδο, ενώ τα οριζόντια ελατήρια είναι τεντωµένα. H απόσταση των σηµείων στήριξης των δύο ελατηρίων είναι 3α, ενώ τα ελατήρια έχουν το ίδιο
v = r r + r θ θ = ur + ωutθ r = r cos θi + r sin θj v = u 1 + ω 2 t 2
 ΑΠΑΝΤΗΣΕΙΣ ΣΤΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΦΥΣΙΚΉΣ Ι ΤΜΗΜΑ ΧΗΜΕΙΑΣ, 9 ΙΑΝΟΥΑΡΙΟΥ 019 ΚΏΣΤΑΣ ΒΕΛΛΙΔΗΣ, cvellid@phys.uoa.r, 10 77 6895 ΘΕΜΑ 1: Σώµα κινείται µε σταθερή ταχύτητα u κατά µήκος οριζόντιας ράβδου που περιστρέφεται
ΑΠΑΝΤΗΣΕΙΣ ΣΤΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΦΥΣΙΚΉΣ Ι ΤΜΗΜΑ ΧΗΜΕΙΑΣ, 9 ΙΑΝΟΥΑΡΙΟΥ 019 ΚΏΣΤΑΣ ΒΕΛΛΙΔΗΣ, cvellid@phys.uoa.r, 10 77 6895 ΘΕΜΑ 1: Σώµα κινείται µε σταθερή ταχύτητα u κατά µήκος οριζόντιας ράβδου που περιστρέφεται
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος Ι
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος Ι Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Κυριακή 24 Γενάρη 2016 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος Ι Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Κυριακή 24 Γενάρη 2016 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4
i) Nα εκφράσετε σε συνάρτηση µε τον χρόνο την γωνιακή ταχύτητα της τροχαλίας.
 Στην διάταξη του σχήµατος ) οι δύο κυκλικοί δίσκοι Δ, Δ έχουν την ιδια ακτίνα R και αντίστοιχες µάζες m, m µπορούν δε να κυλίωνται χωρίς ολίσθηση κατά µήκος δύο κεκλιµέ νων επιπέδων που είναι µεταξύ τους
Στην διάταξη του σχήµατος ) οι δύο κυκλικοί δίσκοι Δ, Δ έχουν την ιδια ακτίνα R και αντίστοιχες µάζες m, m µπορούν δε να κυλίωνται χωρίς ολίσθηση κατά µήκος δύο κεκλιµέ νων επιπέδων που είναι µεταξύ τους
ΟΡΟΣΗΜΟ. Ισχύει: α. L 1. και Κ 1 β. 2L 1 =2L 2 =L 2. και 2Κ 1 γ. L 1
 61 Η κινητική ενέργεια ενός δίσκου μάζας m και ακτίνας R που εκτελεί στροφική κίνηση, εξαρτάται: α Μόνο από την γωνιακή του ταχύτητα β Μόνο από την μάζα και την ακτίνα του γ Μόνο από την γωνιακή του ταχύτητα,
61 Η κινητική ενέργεια ενός δίσκου μάζας m και ακτίνας R που εκτελεί στροφική κίνηση, εξαρτάται: α Μόνο από την γωνιακή του ταχύτητα β Μόνο από την μάζα και την ακτίνα του γ Μόνο από την γωνιακή του ταχύτητα,
Α. Ροπή δύναµης ως προς άξονα περιστροφής
 Μηχανική στερεού σώµατος, Ροπή ΡΟΠΗ ΔΥΝΑΜΗΣ Α. Ροπή δύναµης ως προς άξονα περιστροφής Έστω ένα στερεό που δέχεται στο άκρο F Α δύναµη F όπως στο σχήµα. Στο Ο διέρχεται άξονας περιστροφής κάθετος στο στερεό
Μηχανική στερεού σώµατος, Ροπή ΡΟΠΗ ΔΥΝΑΜΗΣ Α. Ροπή δύναµης ως προς άξονα περιστροφής Έστω ένα στερεό που δέχεται στο άκρο F Α δύναµη F όπως στο σχήµα. Στο Ο διέρχεται άξονας περιστροφής κάθετος στο στερεό
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 3: ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ - ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ
 ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 3: ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ - ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ 12. Ένας οριζόντιος ομογενής δίσκος ακτίνας μπορεί να περιστρέφεται χωρίς τριβές, γύρω από κατακόρυφο
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 3: ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ - ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ 12. Ένας οριζόντιος ομογενής δίσκος ακτίνας μπορεί να περιστρέφεται χωρίς τριβές, γύρω από κατακόρυφο
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος ΙΙ
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος ΙΙ Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Κυριακή 28 Φλεβάρη 2016 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος ΙΙ Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Κυριακή 28 Φλεβάρη 2016 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΘΕΤ. & ΤΕΧΝ. ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΘΕΤ. & ΤΕΧΝ. ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Α Στις ημιτελείς προτάσεις Α1-Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α1.
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΘΕΤ. & ΤΕΧΝ. ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Α Στις ημιτελείς προτάσεις Α1-Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α1.
