UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA FAKULTETA ZA MATEMATIKO IN FIZIKO Študijski program: Matematika in fizika ZVOK V TROBILIH DIPLOMSKO DELO
|
|
|
- Τῑτάν Αλαφούζος
- 6 χρόνια πριν
- Προβολές:
Transcript
1 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA FAKULTETA ZA MATEMATIKO IN FIZIKO Študijski program: Matematika in fizika ZVOK V TROBILIH DIPLOMSKO DELO Mentor: dr. Bojan Golli, izr. prof. Kandidat: Simon Turk Ljubljana, november 2011
2 Zahvala Zahvaljujem se profesorju Bojanu Golliju za strokovno pomoč in nasvete pri nastajanju diplomskega dela, Gregorju Tarmanu za pomoč pri meritvah in Stanislavu Avscu za material, in nasvete pri izbiri le tega, potreben za izdelavo cevi prisekanega stoˇzca. Zahvaljujem se staršem za podporo pri študiju.
3 Povzetek V diplomskem delu predstavim glavne značilnosti trobil in princip njihovega delovanja. Podrobneje opišem zgradbo trobente. Sledi teoretična obravnava cilindričnih, neprisekanih stožčastih, Salmonovih in Besselovih cevi. V nadaljevanju se osredotočim na opis akustičnih lastnosti cevi v obliki prisekanega stoˇzca, za katero izpeljem analitične izraze za odvisnost akustičnega tlaka in akustičnega prostorninskega toka od razdalje ter za resonančne frekvence cevi. Teoretične ugotovitve z meritvami preverim na modelu cevi v obliki prisekanega stoˇzca. Na koncu preverim, kateri model cevi je ustrezen za opis resonančnih frekvenc trobente. Ugotovim, da je to model prisekanega stožca. Ključne besede: resonančne frekvence cevi, akustična impedanca, valovna enačba, akustični tlak, akustični prostorninski tok I
4 Sound in Brass Instruments -Abstract In the diploma thesis I present the main characteristics of the brass instruments and the principles how they work. I describe in detail the stucture of the trumpet. The theoretical treatment of cylindrical, conical, Salmon s and Bessel s tubes are outlined. In the following I focus on the description of acoustical properties of the truncated conical tube, for which I derive analytical expressions for the dependence of the acoustical pressure and the flow rate on the distance, as well as for resonant frequencies. I check the theoretical predictions on a model of the truncated conical tube. At the end I examine which model of a tube is suitable for the description of resonant frequencies of the trumpet. Key words: resonant frequency in tubes, acoustics impedance, wave equation, acoustics pressure, flow rate II
5 Kazalo 1 Uvod 1 2 Fizikalne osnove nastanka zvoka v trobilih Opis trobil Zvok v cilindričnih ceveh Stoječe valovanje Resonančne frekvence zaprtih in odprtih cevi Hitrost delov zraka pri zvoku v ceveh Akustični prostorninski tok Akustična impedanca Odboj in prepustnost valovanja na izhodu cevi Stožčaste cevi Neprisekane stoˇzčaste cevi Websterjeva enačba Salmonove cevi Besselove cevi Prisekane stoˇzčaste cevi Tlak v cevi prisekanega stoˇzca Resonančne frekvence prisekane stoˇzčaste cevi Meritve tlaka v cevi prisekanega stožca Analiza meritev Resonančne frekvence trobil Model cilindrične cevi Model stožčaste cevi Model Besselove cevi III
6 5 Zaključek 59 Literatura 78 IV
7 1 Uvod Pihala in trobila so sestavljena iz cevi zelo različnih oblik. Razlikujejo pa se ne le po obliki, temveč tudi po zvenu. Ta je posledica oblike cevi. Cev flavte je popolnoma ravna in ima po skoraj vsej svoji dolžini konstanten premer. Cev sopran saksofona ali oboe je v obliki stoˇzca z majhnim hitro razširjajočim se delom na koncu cevi. Brez teˇzav slišimo, da se zven flavte zelo razlikuje od zvena sopran saksofona ali oboe. Prav tako brez težav slišimo, da se zven klarineta zelo razlikuje od zvena sopran saksofona, katerega oblika je na prvi pogled podobna klarinetu. Prava posebnost glede oblike cevi inštrumentov pa so trobila. Cev trobil sestavlja del cevi s konstantnim presekom, temu sledi stožčast del in na koncu odmevnik. Odmevnik je del cevi na izhodu inštrumenta, ki se zelo močno razširi. Princip delovanja trobil in fizikalno ozadje nastanka zvoka v trobilih me zanima tudi zato, ker sam igram trobento. Kot dijaka in študenta me je pri fiziki iz tega razloga posebej pritegnila in zanimala obravnava valovanja in zvoka. To pomeni, da glasbeni inštrumenti lahko sluˇzijo kot motivacija pri obravnavi valovanja in zvoka. Obravnava glasbenih inštrumentov pri poučevanju fizike se mi zdi zelo uporabna, saj lahko nekatere pojme pri fiziki zvoka, kot so vozli in hrbti valovanja, frekvenca, valovna dolžina, razloˇzimo na primerih glasbenih inštrumentov, kot so kitara, flavta in klarinet. V drugem poglavju diplomskega dela so teoretična izhodišča. Ta so podana izključno na podlagi strokovne literature. Opisane so glavne značilnosti trobil in princip njihovega delovanja, podrobneje zgradba trobente. Opisani so nekateri osnovni pojmi, ki jih bomo uporabljali v nadaljevanju diplomske naloge. V tem poglavju je tudi teoretična obravnava cilin- 1
8 dričnih, neprisekanih stoˇzčastih, Salmonovih in Besselovih cevi. Salmonove in Besselove cevi so uporabne pri opisu hitro razširjajočih se delov, ki so zelo značilni prav za trobila. Kot model trobente sem uporabil cev prisekanega stožca, ker je zanjo razmeroma enostavno dobiti analitične izraze za polje akustičnega tlaka in iz tega izpeljati resonančne frekvence, ter ker je enostavno narediti model take cevi in na njem izvesti meritve. V tretjem poglavju sem s pomočjo literature računsko izpeljal enačbe, ki opisujejo potek tlaka in resonančne frekvence v cevi prisekanega stožca. Resonančne frekvence v cevi prisekanega stoˇzca so nekje med resonančnimi frekvencami na eni strani zaprte in na obeh straneh odprte cilindrične cevi ter niso harmonično razporejene. Opisal sem meritve v cevi prisekanega stožca in analiziral podatke, ki sem jih pridobil z meritvami. Primerjal sem rezultate meritev in računskih spoznanj o cevi prisekanega stoˇzca. V četrtem poglavju na podlagi ugotovitev iz drugega in tretjega poglavja analiziram ustreznost modelov cilindrične in stožčaste cevi za trobento. Ugotovim, da je model cevi prisekanega stožca ustrezen za obravnavo resonančnih frekvenc trobente. V zadnjem delu četrtega poglavja je zanimiv primer iz literature, pri katerem uporabimo model Besselovih cevi za razlago spreminjanja resonančnih frekvenc francoskega oziroma lovskega roga. 2
9 2 Fizikalne osnove nastanka zvoka v trobilih 2.1 Opis trobil Trobila uvrščamo med aerofona 1 glasbila [1]. V to skupino spadajo poleg trobil tudi pihala. Glavna značilnost, ki loči trobila od pihal, je način vzbujanja valovanja. Trobilci valovanje v trobilih vzbujajo z nihanjem ustnic. Frekvenco in amplitudo nihanja ustnic lahko s posebnimi tehnikami nadzorujejo. Trobilni inštrumenti za razliko od pihal praviloma nimajo stranskih odprtin v cevi, s pomočjo katerih bi lahko spreminjali višino tona. Izjema so rogovi iz ˇzivalskih rogov s štirimi odprtinami, ki se danes ne uporabljajo več v glasbi, ter cink, serpent in ofikleide (glej sliko 1), ki so bili popularni v začetku 19. stoletja. Z razvojem kakovostnejših trobil z Slika 1: Levo cink, sredina serpent, desno ofikleida [2], [3] in [4]. 1 Za to skupino glasbil je značilno, da so sestavljene iz različnih oblik cevi, ki omejujejo določen zračni stolpec. Pod določenimi pogoji se v tem zračnem stolpcu vzpostavi stoječe valovanje, ki se iz izhoda inštrumenta širi v prostor kot zvok. 3
10 ventili (glej sliko 4 in 2) so trobila s stranskimi odprtinami hitro utonila v pozabo. Trobila, ki se danes uporabljajo za izvajanje glasbe, so sestavljena iz štirih glavnih delov. Ti so ustnik, cev, podaljški in lijak (glej sliko 2) [1]. Ustnik olajša trobilcu vzbujanje valovanja v inštrumentu. Cev in podaljški cevi omejujejo zračni stolpec, v katerem se vzpostavljajo stoječa valovanja. Lijak je potreben za pravo barvo tona in glasnost trobila. Višino tona se pri trobilih spreminja s kombinacijo tehnike vzbujanja višjih resonančnih frekvenc cevi in z dodajanjem podaljškov cevi, oziroma z iztegom cevi pri pozavnah. Trobilec s posebno tehniko niha ustnici z ustrezno resonančno frekvenco trobila in na ta način proizvede ustrezen ton. Pri trobilih se za izvajanje različnih tonov uporablja 10 in več resonančnih frekvenc v posamezni cevi in podaljšku cevi. Vzemimo trobento za predstavnika trobil (glej sliko 2). Posamezne trobente se med sabo malo razlikujejo po obliki, vendar so te razlike za našo obravnavo zanemarljivo majhne. Celotna dolžina cevi trobente z ustnikom je pribliˇzno 137 cm [1]. Cev trobente se začne z ustnikom (glej sliko 3). Kotel ustnika ima premer pribliˇzno 16 mm in globino pribliˇzno 8 mm [5]. Premer grla ustnika je približno 3, 6 mm (glej sliko 3). Grlo ustnika je najožji del cevi trobente. Od grla do izhoda ustnika je cev dolga 6, 5 cm. Ta se stoˇzčasto razširi na pribliˇzno 9 mm. Cev trobente se nato počasi stoˇzčasto razširja v dolˇzini 12 do 24 cm do končnega premera 11 do 12 mm. Cev je nato cilindrična 2 do približno 44 cm pred izhodom cevi. Od tu naprej se močneje razširja vse do izhoda cevi, katerega premer je pribliˇzno 12 cm. V drugi polovici cilindričnega dela cevi se nahajajo ventili (glej sliko 4 in 2). S pritiskom na ventile preusmerimo zrak skozi doda- 2 Cilindrične cevi imajo konstanten premer. 4
11 Slika 2: Trobenta in njeni glavni deli. Slika 3: Ustnik trobente. tno dolˇzino cevi imenovano podaljˇsek. Trobenta ima tri podaljˇske. Prvi je dolg pribliˇzno 9 cm in zniˇza ton trobente za pol tona. Drugi podaljˇsek je dolg pribliˇzno 16, 5 cm in zniˇza ton trobente za cel ton. Tretji podaljˇsek je dolg pribliˇzno 27 cm, ta zniˇza ton trobente za ton in pol. S kombinacijami teh treh podaljˇskov lahko trobilec izvede vse tone med posameznimi resonanˇcnimi frekvencami cevi brez podaljˇskov. 5
12 Slika 4: Périnetov ventil trobente [6]. 2.2 Zvok v cilindričnih ceveh Stoječe valovanje V zraku se valovanje širi longitudinalno. To pomeni, da so odmiki zraka, po katerem se širi valovanje, vzporedni s smerjo širjena valovanja. Odmiki pri zvoku so zelo majhni in jih je praktično nemogoče meriti. Merimo pa lahko akustični tlak 3. Zato se bomo v nadaljevanju bolj kot odmikom in hitrosti delov zraka pri valovanju posvečali akustičnemu tlaku. Pri realnih inštrumentih zavoji cevi nimajo velikega vpliva na zven inštrumenta. Zato lahko cev z zavoji obravnavamo kot ravno. Če zanemarimo interakcije 3 Akustični tlak je razlika med povprečnim in trenutnim zračnim tlakom. 6
13 zraka s stenami cilindrične cevi, se zvok širi le v eni smeri. Označimo jo z x. Pri opisu valovanja v stoˇzčastih ceveh bomo smer širjenja zvoka označevali z r, ker je polje akustičnega tlaka odvisno le od razdalje od temena stožca. Splošna oblika enačbe, ki opisuje spreminjanje akustičnega tlaka pri širjenju valovanja po zraku v smeri osi x je p(x, t) = A sin(kx ± ωt), (1) kjer A predstavlja amplitudo valovanja, k je valovni vektor in ω kotna hitrost širjenja valovanja [1]. Znak minus med členoma kx in ωt v enačbi (1) pomeni, da se valovanje širi v smeri osi x. Znak plus med tema členoma pa pomeni, da se valovanje širi v nasprotni smeri. Pri širjenju valovanja v cevi se od idealno odprtega ali idealno zaprtega konca cevi 4 valovanje odbije. Valovanje se po odboju širi v nasprotno smer. Tako pride v cevi do medsebojnega vpliva dveh valovanj, ki ga imenujemo interferenca. Valovanji, ki potujeta v nasprotnih smereh se seštejeta. To opišemo z enačbo Z adicijskim izrekom p(x, t) = A sin(kx ωt) + A sin(kx + ωt). (2) sin(α β) + sin(α + β) = 2 sin( α + β 2 enačbo (2) prepišemo v obliko, ki opisuje stoječe valovanje ) cos( α β ) (3) 2 p(x, t) = 2A sin(kx) cos(ωt). (4) V enačbi za stoječe valovanje je amplituda valovanja 2A sin(kx) odvisna od lege. Tako je na nekaterih mestih, kjer je sin(kx) = 0, amplituda stoječega valovanja enaka 0. Ta mesta imenujemo vozli valovanja. Na drugih mestih, kjer je sin(kx) = 1, je amplituda stoječega valovanja maksimalna. 4 Idealno odprt je tisti konec cevi, pri katerem je hrbet odmikov in vozel tlaka. Idealno zaprt pa je tisti konec cevi, pri katerem je hrbet tlaka in vozel odmikov. 7
14 Ta mesta imenujemo hrbti valovanja. Frekvence stoječega valovanja imenujemo resonančne frekvence. Valovni vektor in kotno hitrost valovanja določimo z upoštevanjem robnih pogojev Resonančne frekvence zaprtih in odprtih cevi Nekatera pihala in trobila lahko v prvem pribliˇzku obravnavamo kot ravne idealno odprte ali zaprte cilindrične cevi. Flavto lahko v prvem približku obravnavamo kot na obeh koncih idealno odprto cilindrično cev [7]. Inštrumente kot je klarinet, lahko obravnavamo kot na vhodnem koncu idealno zaprto in na izhodnem koncu idealno odprto cilindrično cev. Cev na vhodnem koncu zapira jeziček. Za cevi, odprte na obeh koncih, v najenostavnejšem modelu velja, da je akustični tlak na obeh koncih cevi enak nič [7]. Tako dobimo pogoj k n = nπ/l, kjer je L dolˇzina cevi in n N. Valovni vektor in kotna hitrost valovanja sta povezana z enačbo ω = ck, kjer je c hitrost širjenja valovanja. Resonančne frekvence, ki se lahko pojavijo v taki, na obeh straneh odprti cevi, so enake ν n = nc/2l. Najniˇzjo moˇzno resonančno frekvenco ν 1 v cevi imenujemo osnovna resonančna frekvenca. Ostale resonančne frekvence so večkratniki osnovne resonančne frekvence (ν n = nν 1 ). V cilindričnih ceveh, v katerih vzbujamo stoječe valovanje z jezički oziroma vibrirajočimi ustnicami, je konec cevi, v katerega pihamo, zaprt [7]. Zato je tam vozel odmika in hrbet akustičnega tlaka. Drug konec cevi je odprt, zato je na tem mestu hrbet odmika in vozel akustičnega tlaka. Tako imamo drugačne začetne pogoje kot pri na obeh straneh odprti cevi. Osnovna resonančna frekvenca je v tem primeru enaka ν 1 = c/4l. Višje resonančne frekvence cevi pa so lihi mnogokratniki osnovne resonančne frekvence (ν n = (2n 1)ν 1 ). V tem primeru na enem koncu odprte in na 8
15 drugem koncu zaprte cevi so razmerja frekvenc ν 1 : ν 2 : ν 3... ν n enaka 1 : 3 : 5... (2n 1) Hitrost delov zraka pri zvoku v ceveh Postavimo cev v koordinatni sistem tako, da je začetek cevi na mestu x = 0 in konec cevi na mestu x = L. Amplitudo akustičnega tlaka, ki se širi v smeri osi x, označimo z A. Amplitudo akustičnega tlaka, ki se širi v nasprotni smeri, pa označimo z B. Tlak v cevi s kompleksnim zapisom opišemo s splošno enačbo p(x, t) = (Ae ikx + Be ikx )e iωt e βt, (5) kjer s faktorjem e βt v opis valovanja akustičnega tlaka v cevi vključimo še dušenje. Kompleksni zapis valovanja akustičnega tlaka smo izbrali, ker na ta način v obravnavo lažje vključimo časovne in krajevne fazne premike. Konstanti A in B sta lahko kompleksni. Tako lahko poleg amplitude s konstantama A in B opišemo tudi fazo valovanja. Na primer ie ikx = e i(kx π/2), kar ustreza faznemu premiku π/2. Pri ustrezni izbiri konstant A in B ter predpostavki, da pri valovanju v cevi ni dušenja (β = 0), enačba (5) postane ekvivalentna enačbi (4) v razdelku Povezavo med akustičnim tlakom in hitrostjo delov zraka dobimo z upoštevanjem drugega Newtonovega zakona (F = ma) na majhnem kvadru zraka dv [10]. Vpliv sile teže dela zraka in sile vzgona na del zraka lahko zanemarimo, saj je rezultanta teh dveh sil zanemarljivo majhna v primerjavi z gradientno silo akustičnega tlaka (F gr = dvgradp). Prav tako je pri obravnavi zvoka zaradi majhne amplitude odmikov totalni odvod hitrosti po času približno enak parcialnemu odvodu hitrosti po času a = dv/dt v/ t. Drugi Newtonov zakon za del zraka tako zapišemo 9
16 v obliki ρ 0 v t = gradp, (6) kjer ρ 0 prestavlja povprečno gostoto zraka. Če zanemarimo vpliv sten cilindrične cevi in vzamemo, da je cilindrična cev popolnoma ravna, so odmiki vzporedni z osjo x in so neodvisni od koordinat y in z. Zato lahko v tem primeru namesto gradp v enačbi (6) uporabimo p/ x in nadaljujemo z skalarnim zapisom Akustični prostorninski tok ρ 0 v t = p x. (7) Pri obravnavi širjenja valovanja po različnih ceveh, predvsem tistih, katerih presek se s krajem spreminja, je koristno namesto trenutne hitrosti premikanja delov zraka uporabljati akustični prostorninski tok U(x, t) [7]. Ta je definiran kot skalarni produkt med ploskvijo preseka cevi in trenutno hitrostjo delov zraka na mestu x U(x, t) = S(x) v(x, t). (8) Enačbo (7) lahko dodatno preoblikujemo tako, da na levi strani enačbe števec in imenovalec pomnoˇzimo s presekom cevi na mestu x, S(x). Enačbo (7) tako zapišemo v obliki ρ 0 S U t = p x. (9) Parcialni odvod akustičnega prostorninskega toka po času dobimo tako, da parcialni odvod akustičnega tlaka po legi x p x = ik( Ae ikx + Be ikx )e (iω β)t (10) 10
17 vstavimo v enačbo (9) in dobimo Z integriranjem enačbe (11) dobimo U t = S ρ 0 ik(ae ikx Be ikx )e (iω β)t. (11) U = S ρ Akustična impedanca ik iω β (Ae ikx Be ikx )e (iω β)t. (12) Pri nekaterih izračunih je uporabna akustična impedanca Z. Ta je definirana kot kvocient med akustičnim tlakom in akustičnim prostorninskim tokom Z = p a U. (13) Pri tem je potrebno poudariti, da je v enačbi (13) akustični in ne trenutni tlak. V nadaljevanju bomo večinoma uporabljali akustični tlak, zato bomo indeks a pri simbolu akustičnega tlaka izpuščali. [7] Pomen akustične impedance lahko predstavimo z analogijo na impedanco v električnih vezjih. Akustični tlak p je analogen električni napetosti, akustični prostorninski tok U električnemu toku in akustična impedanca Z impedanci elementov v električnih vezjih. Pri obravnavi električnih nihajnih krogov si večkrat pomagamo s kompleksnim zapisom električne napetosti, električnega toka in impedance elementov električnega nihajnega kroga. S takim zapisom laˇzje v obravnavo vključimo fazo valovanja. Podobno tudi pri obravnavi zvoka včasih uporabimo kompleksni zapis akustičnega tlaka, akustičnega prostorninskega toka in akustične impedance. Na ta način bolj enostavno upoštevamo krajevni in časovni fazni premik med akustičnim tlakom in akustičnim prostorninskim tokom. Z enačbo (5), ki opisuje, kako se spreminja akustični tlak v cevi, in enačbo (12), ki opisuje, kako se spreminja akustični prostorninski tok v 11
18 cevi, zapišemo akustično impedanco z enačbo Ae Z(x) = ikx + Be ikx Z 0 Ae ikx, (14) Beikx kjer je Z 0 = (iω β)ρ 0 /(iks) karakteristična impedanca cevi [8]. Če predpostavimo, da ni dušenja, se izraz karakteristične impedance cevi poenostavi do oblike Z 0 primeru brez dušenja. = cρ/s. Karakteristična impedanca cevi realna v Z akustično impedanco lahko analiziramo resonančne frekvence dveh vrst cilindričnih cevi iz razdelka 2.2.2: 1. Na vhodu in izhodu idealno odprta cev (pribliˇzek flavte). 2. Na vhodu idealno zaprta in na izhodu idealno odprta cev (pribliˇzek klarineta). Na idealno odprtem koncu cevi je akustična impedanca enaka nič, saj je na tistem mestu vozel tlaka in hrbet akustičnega prostorninskega toka. Na idealno zaprtem koncu cevi pa je situacija ravno obratna. Zato je tam akustična impedanca neskončna. Po tem razmisleku dobimo v prvem primeru dva začetna pogoja: Z(x = 0) = 0 in Z(x = L) = 0. Z upoštevanjem prvega začetnega pogoja Z(0) = Z 0 (A + B)/(A B) = 0 dobimo zahtevo A = B. S to zahtevo in drugim začetnim pogojem dobimo naslednjo zahtevo [9] Z(x = L) = Z 0 e ikl e ikl e ikl + e ikl = 0 Z 0 sh(ikl) ch(ikl) = 0 12
19 iz 0 tg(kl) = 0. (15) Iz zahteve (15) dobimo moˇzne rešitve za valovni vektor k = nπ/l, ki se ujemajo z ugotovitvami iz razdelka 2.2.2, ko smo obravnavali na obeh koncih odprto cev brez uporabe akustične impedance. Podobno postopamo v drugem primeru, ki se razlikuje od prvega po tem, da je vhod cevi zaprt. Začetna pogoja sta v tem primeru: Z(x = 0) = in Z(x = L) = 0. Z upoštevanjem prvega začetnega pogoja Z(0) = Z 0 (A + B)/(A B) = dobimo zahtevo A = B. S to zahtevo in drugim začetnim pogojem dobimo naslednjo zahtevo [9] Z(x = L) = Z 0 e ikl + e ikl Ae ikl e ikl = 0 Z 0 = ch(ikl) sh(ikl) = 0 iz 0 ctg(kl) = 0. (16) Iz zahteve (16) dobimo moˇzne rešitve za valovni vektor k = (2n 1)π/2L. Resonančne frekvence se izraˇzajo z enačbo ν n = (2n 1)c/4L, ki se ujema z ugotovitvami iz razdelka [8] Odboj in prepustnost valovanja na izhodu cevi V razdelku smo predpostavili, da se valovanje od idealno odprtega ali idealno zaprtega konca cevi odbije. Z akustično impedanco lahko to pokažemo z računom. Na koncu cevi (x = L) določa razmerje tlaka in prostorninskega pretoka impedanco Z L Z L = Z 0 (Ae ikl + Be ikl ) (Ae ikl Be ikl ) (17) 13
20 B A = e 2ikL Z L Z 0 Z L + Z 0. (18) Odbojni koeficient R je definiran kot razmerje jakosti zvoka vpadnega zvočnega valovanja j v in jakosti zvoka odbitega zvočnega valovanja j o. Ker je jakost zvočnega valovanja sorazmerna s kvadratom efektivnega akustičnega tlaka j p 2 e f, (19) lahko reflekcijski koeficient izrazimo z amplitudo akustičnega tlaka vpadnega valovanja in amplitudo akustičnega tlaka odbitega valovanja. Efektivni akustični tlak vpadnega valovanja je po definiciji enak p 2 e f v = 1 t0 p v 2 dt. (20) t 0 Kvadrat absolutne vrednosti akustičnega tlaka vpadnega valovanja je 0 p v 2 = p p = A Ae ikx e ikx e iωt e iωt = A A = A 2. (21) Tako je p 2 e f v = A 2. Podobno je kvadrat absolutne vrednosti akustičnega tlaka odbitega valovanja p v 2 = p p = B Be ikx e ikx e iωt e iωt = B B = B 2. (22) Kvadrat efektivne vrednosti akustičnega tlaka odbitega valovanja je p 2 e f o = B 2. Reflekcijski koeficient se tako izraˇza z enačbo R = j o j v = p2 e f o p 2 e f v = B 2 A 2 = Z L Z 0 Z L + Z 0 Iz enačbe 23) je očitno, da na izhodu cevi ni odboja, če je Z L 2. (23) = Z 0. To pomeni, da se vse valovanje iz izhoda cevi izseva v prostor. Popoln odboj nastane v primerih, če je Z L = 0 ali če je Z L =. Ker za cevi brez dušenja karakteristična impedanca cevi Z 0 nima imaginarnega dela, pride do popolnega odboja tudi, če ima Z L samo imaginarno komponento. [8] 14
21 Vsa trobila imajo veliko vhodno akustično impedanco. Pri veliki vhodni akustični impedanci valovanje v cevi z ustnicami laˇzje vzbudimo. Če je upor zraka v cevi dovolj velik, nihanje ustnic z odrivanjem zraka ustvari zgoščine in razredčine, ki se širijo po cevi kot valovanje. V nasprotnem primeru, ko je akustična impedanca na vhodu cevi zelo majhna, zrak v cevi ne predstavlja dovolj velikega upora. Ustnice v tem primeru z nihanjem v cevi ne ustvarjajo zgoščin in razredčin zraka, temveč se zrak samo premika, oziroma meša. Za nastanek zvoka v cevi je torej potrebna velika akustična impedanca na vhodu cevi. Ko se cev konča, se akustična impedanca naenkrat močno zmanjša. Iz enačbe (23) lahko sklepamo, da se v tem primeru večino zvoka od izhoda cevi odbije. Tako se zelo malo zvoka izseva v prostor. Da se bo več zvoka iz cevi izsevalo v prostor, moramo zagotoviti nek dober prehod iz velike impedance na vhodu inštrumenta do majhne impedance na izhodu inštrumenta. 2.3 Stoˇzčaste cevi Skupni lastnosti trobil sta njihova glasnost in njihov hitro razširjajoč se lijak. Zato je pri obravnavi trobil dobro raziskati zvok v ceveh, ki se razširjajo. Poleg cilindričnih cevi bomo obravnavali tudi stoˇzčaste cevi. Te se enakomerno razširjajo. Iskanja funkcije, ki podaja spreminjanje akustičnega tlaka v takih ceveh se bomo lotili z valovno enačbo 2 p = 1 c 2 2 p t 2. (24) Če zanemarimo interakcije s stenami cevi, je tlak v stoˇzčasti cevi odvisen le od razdalje do temena stoˇzca [7]. Zato si lahko reševanje valovne enačbe poenostavimo z vpeljavo sferičnih koordinat. Tako bo tlak odvisen 15
22 od ene same spremenljivke. Laplaceov operator ima v sferičnih koordinatah ob predpostavki, da je akustični tlak v cevi odvisen le od razdalje od izhodišča (p = p(r)), obliko 2 = 1/r 2 / r r 2 / r [10]. Valovna enačba ima v sferičnih koordinatah obliko 1 r 2 r r2 r p = 1 c 2 2 p t 2. (25) Enačbo (25) lahko zapišemo v bolj kompaktni obliki z uporabo nastavka p = R/r. 1 r 2 1 r 2 r r2 r ( r r2 R r R r r ( R r + R r + r 2 R r 2 1 r 2 2 R r 2 R r = 1 2 R c 2 t 2 r ) = 1 1 c 2 r ) 2 R t 2 = R c 2 r t 2 = 1 c 2 2 R t 2. (26) Valovna enačba v tej obliki je po obliki zelo podobna valovni enačbi za cilindrične cevi v kartezičnih koordinatah [7]. Če iščemo stacionarne rešitve, ki so oblike p(r, t) = p(r)e iωt, kjer je ω kotna hitrost valovanja, se enačba (26) poenostavi do oblike 2 R r 2 + k2 R = 0, (27) kjer je k valovni vektor in se izraža s kotno hitrostjo kot k = ω/c. Z reševanjem poenostavljene valovne enačbe stoječega valovanja, enačbe (27), dobimo splošno rešitev R = C 1 cos kr + C 2 sin kr. (28) Splošna rešitev, ki opisuje spreminjanje akustičnega tlaka je ( ) cos kr sin kr p(r, t) = C 1 + C 2 e iωt. (29) r r 16
23 2.3.1 Neprisekane stoˇzčaste cevi Nekatere glasbene inštrumente kot sta sopran saksofon in oboa lahko v prvem pribliˇzku obravnavamo kot na izhodu odprte neprisekane stoˇzčaste cevi [7]. Najprej obravnavajmo spreminjanje tlaka znotraj stoˇzčaste cevi. Iz splošne rešitve (enačba (29)), ki opisuje spreminjanje akustičnega tlaka v stožčastih ceveh, lahko z upoštevanjem robnih pogojev pridemo do bolj natančne enačbe. V enačbi (29) člen cos kr/r za neprisekano stoˇzčastno cev ne pride v poštev, saj mora imeti v temenu stoˇzca (pri r = 0) tlak končno vrednost. Temu zadošča člen sin kr/r, saj je sin kr lim r 0 r = k. Enačbo (29) lahko za primer cevi neprisekanega stoˇzca zapišemo krajše kot p = C sin kr e iωt. (30) r Pri valovanjih, ki se širijo v na izhodu odprti stožčasti cevi, dobimo ob upoštevanju robnega pogoja p(l) = 0, kjer je L višina stoˇzčaste cevi, vrednosti, ki jih lahko zavzema valovni vektor k n = nπ/l, kjer je n naravno število. Resonančne frekvence ν n v tem primeru zavzemajo vrednosti nc/2l. Te zavzemajo enake vrednostih kot v primeru enako dolge na obeh koncih odprte cilindrične cevi. Vendar je potrebno poudariti, da poteka akustičnega tlaka v stoˇzčasti cevi in na obeh straneh odprti cilindrični cevi nista enaka kljub temu, da so resonančne frekvence obeh cevi enake. Do največjih razlik v obliki funkcije tlaka pride na začetku cevi v prvi polovici valovne dolˇzine (glej sliko 5). Resonančne frekvence cilindrične cevi ν n, ki je na vhodu zaprta in na izhodu odprta, zavzemajo vrednosti (c/4l)(2n 1), kjer je n naravno število. Najnižja resonančna frekvenca stožčastega inštrumenta z jezičkom na eni strani, kot sta na primer sopran 17
24 Slika 5: Primerjava akustičnega tlaka v stoˇzčasti (modra krivulja) in cilindrični (rdeča krivulja) cevi dolžine 35 cm. Stožčasta cev je neprisekana, cilindrična cev je odprta na obeh straneh. Slika prikazuje 6. resonančno frekvenco (n = 6). saksofon in oboa, je po zgornjih izračunih enaka ν s1 = c/2l. Dvakrat višja (oktavo višja) od najnižje resonančne frekvence stožčastega inštrumenta je resonančna frekvenca cilindričnega inštrumenta iste dolžine, katere vhod je zaprt in izhod odprt. Enaka je ν c1 = c/4l. Primer takega inštrumenta je klarinet. Iz slike 5 oziroma iz enačbe (30) lahko opazimo, da so hrbti tlaka obratno sorazmerni z oddaljenostjo od koordinatnega izhodišča za razliko od primerov v cilindričnih ceveh, kjer so hrbti tlaka vzdolˇz cevi konstantni [7]. Vendar samo s podatki o amplitudi tlaka vzdolˇz cevi ne moremo veliko povedati o tem, kolikšen delež valovanja se od odprtega konca cevi odbije in kolikšen delež valovanja se izseva v prostor. To nam omogoča akustična impedanca cevi. Za izračun te potrebujemo podatek o akustičnem prostorninskem toku. Do njega pridemo preko drugega Newtonovega zakona, ki ga uporabimo na delu zraka v cevi dv (glej sliko 6) [10]. 18
25 Z upoštevanjem predpostavke, da sta totalni in parcialni odvod hitrosti po Slika 6: Osnovne oznake, ki so potrebne za izpeljavo akustičnega prostorninskega toka v stožcu. Oznaka dv predstavlja prostornino zraka med ploskvama S(r) in S(r + dr) ter stenami cevi. Oznaki p(r) in p(r + dr) predstavljata tlak na mestih r in r + dr. času pri obravnavi zvoka pribliˇzno enaka (dv/dt v/ t), lahko drugi Newtonov zakon za del zraka dv zapišemo v obliki m v t = p(r + dr)s(r + dr) + p(r)s(r). (31) Ploskev S je sorazmerna s kvadratom oddaljenosti od koordinatnega izhodišča (S r 2 ). Iz vektorske enačbe (31) lahko preidemo na skalarno, saj so vsi vektorji vzporedni z vektorjem r. Enačbo (31) lahko tako zapišemo v poenostavljeni obliki m v t = K(p(r + dr)(r + dr)2 p(r)s(r)) 19
26 ρkr 2 dr v t = K(p(r + dr)(r + dr)2 p(r)s(r)) ρ U t = K(p(r + dr)(r + dr)2 p(r)s(r)) ρ U t = K (pr2 ), (32) r kjer je ρ gostota zraka in K sorazmernostna konstanta med S in r 2 (S = Kr 2 ). Odvajamo desno stran enačbe (32) in dobimo ρ U t = K (r2 p) r = C(sin kr + kr cos kr)e iωt. (33) Z integriranjem enačbe (33) po času dobimo enačbo, ki opisuje krajevno in časovno spreminjanje akustičnega prostorninskega toka v cevi neprisekanega stožca U = C ρkc [sin(kr) + kr cos(kr)] ( i)eiωt. (34) Faktor i pred eksponentom e iωt pomeni, da je faza valovanja akustičnega prostorninskega toka premaknjeno za π/2 glede na fazo valovanja akustičnega tlaka. Vendar fazni premik ne vpliva na lego vozlov in hrbtov valovanja. Krajevno odvisnost valovanja akustičnega prostorninskega toka opisuje enačba U = C [sin(kr) + kr cos(kr)]. (35) ρkc Slika 7 prikazuje spreminjanje tlaka in prostorninskega pretoka v odvisnosti od lege v stoˇzčasti cevi. Za razliko od cilindrične cevi opazimo, da se vrhovi tlaka ne prekrivajo več z vozli akustičnega prostorninskega toka. To je še posebej očitno na začetku cevi. Hrbti akustičnega prostorninskega toka se povečujejo sorazmerno z razdaljo od temena stoˇzca, hrbti tlaka pa se z razdaljo od temena stoˇzca zmanjšujejo obratno sorazmerno. Stoˇzčasti del cevi tako deluje kot akustični transformator, ki spreminja visoko impedanco na vhodu cevi, v nizko impedanco na odprtem koncu cevi. V tako 20
27 Slika 7: Odvisnost tlaka in akustičnega prostorninskega toka v odvisnosti od lege v stoˇzčasti cevi za četrto resonančno frekvenco (n = 4). Cev je dolga 35 cm. oblikovanih menzurah se veliko večji del valovanja iz izhoda inštrumenta izseva v prostor. [7] 2.4 Websterjeva enačba Čeprav je veliko trobilnih inštrumentov sestavljenih iz večjih delov cilindričnih cevi, imajo vsa trobila na koncu cevi hitro razpirajoč se del, imenovan lijak. Tipična trobilna inštrumenta sta trobenta in pozavna. Njuna cev je približno polovico dolžine približno cilindrična. Ostali del sestavlja rahlo razpirajoča se cev in proti koncu cevi hitro razpirajoč se del cevi (lijak). Ostale vrste trobil imajo na začetku daljši stoˇzčast del. Dober predstavnik takih trobil je rog. Fizikalni vpogled v vpliv oblike menzure na resonančne frekvence tipičnih trobil nam omogoča tako imenovana Websterjeva enačba. Ime se je 21
28 obdrˇzalo, kljub temu da originalno izvira iz časov Bernoullija [8]. Websterjevo enačbo dobimo iz valovne enačbe ob predpostavki ravnih valovnih front. Zapišemo jo kot ( 1 S p ) = 1 2 p S x x c 2 t 2, (36) kjer S predstavlja presek cevi na mestu x. Če predpostavimo, da se cev ne razširja prehitro, se lahko s pribliˇzkom ravne valovne fronte kar dobro pribliˇzamo eksaktnim rezultatom in ohranimo bistveno fiziko. Če naredimo zamenjavo p = ψ S in iščemo rešitve stoječega valovanja (ψ(x)e iωt ), ima enačba (36) obliko 2 ψ x 2 + [ ( ω ) 2 1 c a 2 ] a x 2 ψ = 0, (37) v kateri je radij cevi a funkcija lege x [7]. Če člene zgornje enačbe malo premešamo, dobimo enačbo ( ω c ) 2 2 ψ ψ = x a a x 2 ψ (38) in opazimo, da je enačba (37) analogna stacionarni enodimenzionalni Schrödingerjevi enačbi [11] Eψ = h2 2 ψ + V(x)ψ. (39) 2m x2 E v prvem členu enačbe (39) predstavlja skupno energijo delca. Ta je analogna členu (ω/c) 2 v enačbi (38). Člen 1/a 2 a/ x 2 ψ v enačbi (38) je analogen členu V(x)ψ v Schrödingerjevi enačbi (39), ki predstavlja potencialno energijo. Člen 2 ψ/ x 2 iz enačbe (38) je analogen členu h 2 /2m 2 ψ/ x 2, ki predstavlja kinetično energijo v Schrödingerjevi enačbi (39), kjer je h Planckova konstanta in m masa delca. Zgornja analogija nam pomaga razumeti, kako oblika cevi vpliva na valovanje akustičnega tlaka v cevi. 22
29 Valovanje akustičnega tlaka v cevi obravnavamo analogno, kot obravnavamo delec pri kvantni mehaniki, ki se giblje v potencialu. Oblika te cevi določa neke vrste potencial cevi, ki vpliva na širjenje valovanja akustičnega tlaka v cevi. V členu enačbe (38), ki je analogen potencialu v Schrödingerjevi enačbi, a predstavlja radij cevi. Z uporabo pojma ukrivljenosti cevi κ = 1/R, kjer je R radij ukrivljenosti, lahko potencial cevi zapišemo bolj kompaktno [12]. Fizikalno ukrivljenost interpretiramo kot stopnjo spreminjanja tangentnega vektorja t vzdolˇz krivulje. Naj bo s dolˇzina loka krivulje med izbrano izhodiščno točko in opazovano točko na krivulji. Ukrivljenost cevi zapišemo z enačbo t s = a s x. (40) Pri dovolj majhnih spremembah ukrivljenosti cevi je a/ x a/ s. Radij ukrivljenosti cevi je v tem približku R ( 2 a/ x 2 ) 1. Potencial cevi v enačbi (38) lahko zapišemo kot 1/aR. Valovanje akustičnega tlaka v cevi začne eksponentno pojemati, ko je 1/aR > (ω/c) 2. (41) Podobno pričakujemo tudi pri kvantni mehaniki za delec, ki naleti na potencialno bariero, katere potencial je večji od energije delca. Na ta način lahko določimo kritično frekvenco ω c, nad katero obstajajo rešitve enačbe (37), ki opisujejo stoječe valovanje ω > ω c = c ar. (42) Za frekvence valovanja, ki so manjše od kritične frekvence ω c, rešitve enačbe (37) eksponentno pojemajo, kot e x/δ e iωt, kjer je δ = c/ ω 2 c ω 2. [7] Širjenje zvočnega valovanja v cevi je analogno širjenju valov, s katerimi opišemo delec v krajevno spreminjajočem se potencialu. Če je ukrivljenost cevi dovolj velika, se valovanje odbije preden doseže odprt izhod 23
30 inštrumenta. Vendar tako kot lahko delec v kvantni mehaniki tunelira skozi potencialno bariero, lahko valovanje akustičnega tlaka z manjšo frekvenco od kritične frekvence tunelira skozi hitro razširjajoč se del cevi v prostor [7]. Za take razširjajoče cevi, lahko iz enačbe (42) izrazimo pogoj, pri katerem se valovanje od razširjajočega dela cevi odbije. ω 2 odb. < c2 ar ar < 1 k 2 odb. (2π) 2 ar < λ odb. (43) Ko se cev razširja, se polmer cevi a povečuje. Hkrati se zmanjšuje radij ukrivljenosti R. Pri lijakih trobil se ukrivljenost cevi povečuje hitreje kot polmer cevi. To pomeni, da se radij ukrivljenosti cevi manjša hitreje kot polmer cevi. Iz pogoja (43) lahko sklepamo, da, za valovanja z manjšo valovno dolžino, točka odboja nastopi pozneje kot za valovanja z večjo valovno dolžino. Efektivna dolžina takih cevi, katerih premer se hitro povečuje s krajem, je krajša za nizke resonančne frekvence kot efektivna dolˇzina cevi visokih resonančnih frekvenc. To prikazuje slika Salmonove cevi Za cevi, ki se hitro razširjajo, a/ x ni več približno enak a/ s. Pribli- ˇzek ( 2 a/ x 2 ) 1 = R zato ni več ustrezen. Pri izračunu potenciala cevi pribliˇzka 1/(aR) ne moremo več uporabljati. Uporabiti moramo izraz 1/a 2 a/ x 2. Skupina posebnih oblik cevi, imenovanih Salmonove cevi, je za teoretično obravnavo zelo uporabna. Z njimi lahko pribliˇzno opišemo nekatere oblike delov cevi tipičnih trobil in jih analitično enostavno rešimo [8]. 24
31 Skupna značilnost Salmonovih cevi je v tem, da je potencial cevi in s tem kritična frekvenca ω c konstanten po celotni dolˇzini cevi. To zahtevo po konstantnem potencialu cevi zapišemo z diferencialno enačbo kjer je m 2 konstanta. Rešitve enačbe (44) so 2 a x 2 am2 = 0, (44) a = Ae mx + Be mx. (45) V bolj priročni obliki lahko zgornjo enačbo (45) zapišemo z uporabo hiperboličnih funkcij a = a 0 (cosh mx + T sinh mx), (46) kjer je T parameter, ki določa obliko Salmonove funkcije. Enačbo (37) lahko zapišemo v poenostavljeni obliki kot 2 ψ x 2 + [ ( ω ) 2 m 2] ψ = 0. (47) c Funkcije, ki opisujejo valovanje akustičnega tlaka v takih ceveh, imajo splošno obliko p(x) = p 0 a e i( k 2 m 2x ωt), (48) kjer je k = ω/c. Za cevi, pri katerih je k 2 > m 2, obstajajo rešitve enačbe, ki opisujejo stoječe valovanje. Za cevi, pri katerih to ne velja, je valovanje akustičnega tlaka v cevi eksponentno dušeno. Skupina cevi, ki jih opisuje enačba (46), ima tri degenerirane oblike. Prva je v primeru, ko je parameter T = 1. V tem primeru ima enačba (46) obliko eksponentne funkcije a = a 0 e mx. (49) Radij cevi se z lego eksponentno povečuje. Drugi degeneriran primer enačbe (46) je pri vrednosti parametra T = 0. V tem primeru je funkcija, 25
32 ki opisuje spreminjanje radija cevi z lego enaka a = a 0 cosh mx. (50) Za razliko od eksponentne funkcije radija cevi funkcija hiperboličnega kosinusa omogoča gladko sklopitev s cilindrično cevjo, saj je na mestu x = 0 odvod te funkcije po legi enak 0. Tretja degeneracija enačbe (46) je s parametrom T = x/x 0 m pri pogoju, da gre m proti 0. Tako dobimo degenerirano enačbo a = a 0 (1 + x/x 0 ). (51) Cevi, ki jih opisuje enačba (51), so stožčaste s temenom stožca pri x = x 0. V posebnem primeru, ko je x x 0, enačba (51) opisuje cilindrično cev. Potencial cevi je v teh primerih stoˇzčaste in cilindrične cevi enak 0, kar je v skladu s tem, da cilindrične in stoˇzčaste cevi nimajo kritične frekvence, pod katero bi bilo valovanje akustičnega tlaka eksponentno dušeno. Za Salmonove cevi, ki jih opisuje eksponentna funkcija ali funkcija hiperboličnega kosinusa, velja, da se valovanje s frekvenco, večjo od kritične frekvence ν c = mc/(2π), prosto širi vzdolˇz zračnega stolpca. Za frekvence širjenja valovanja, ki so manjše od kritične frekvence ν c, je valovanje eksponentno dušeno. 2.6 Besselove cevi Naslednja zanimiva skupina oblik cevi so Besselove cevi. Zanimive so, ker z njimi lahko opišemo realne zelo hitro razpirajoče se lijake, ki sestavljajo večino trobilnih inštrumentov [8]. Za te oblike cevi lahko analitično rešimo enačbo (37). Definirane so kot a = Bx m. Za določene vrednosti parametra m dobimo v okviru Besselovih funkcij nekatere degenerirane oblike. Če je parameter m = 0, dobimo funkcije oblike a = B, ki opisujejo cilindrične 26
33 cevi. Pri parametru m = 1 dobimo funkcije oblike a = Bx, ki opisujejo stoˇzčaste cevi. Enačba (37) se za Besselove cevi zapiše kot [ ( ω ) 2 m(m + 1) c 2 ψ x 2 + x 2 ] ψ = 0. (52) Če predpostavimo, da so valovne fronte v cevi ravne, so rešitve zgornje enačbe [9] ψ(x) = x 1 2 Jm+ 1 2 (kx). (53) Akustični tlak se s krajem od odprtega izhoda cevi proti vhodu spreminja po enačbi p(x) = Ax m+ 1 2 Jm+ 1 2 (kx), (54) kjer je J m+ 1 2 (kx) cilindrična oziroma Besselova funkcija reda m + 1/2, po kateri so take cevi dobile ime. Analitična rešitev nam pomaga pri obravnavi inštrumentov z zelo hitro razširjajočim se lijakom [8]. Pri tem se moramo zavedati, da so vsi ti izračuni narejeni na podlagi predpostavke ravne valovne fronte, ki pa za hitro razširjajoče cevi ni več ustrezna, saj je lahko na nekaterih mestih ukrivljenost valovne fronte celo večja od ukrivljenosti cevi. O tem se lahko prepričamo s kratkim razmislekom. V približku ravne valovne fronte je potencial cevi Besselovih cevi oblike m(m + 1)/x 2. Ta narašča v neskončnost, ko gre x proti 0. Potencial cevi narašča v neskončnost, ko se pribliˇzujemo izhodu cevi (glej sliko 8a ). Torej se bi moralo vse valovanje odbiti od odprtega izhoda cevi in se nebi nič valovanja izsevalo iz odprtega izhoda cevi. Boljši približek realni situaciji je približek sferičnih valovnih front (glej sliko 8b). Kljub velikim napakam zaradi pribliˇzka ravne valovne fronte, si lahko s temi izračuni ustvarimo pribliˇzno predstavno o vplivu hitro razširjajočega lijaka na resonančne frekvence [7]. Pomembna stvar pri tej obravnavi 27
34 Slika 8: Grafa prikazujeta potencial cevi v odvisnosti od lege v a) približku ravne valovne fronte in b) pribliˇzku sferične valovne fronte [8]. je način, kako hitro razširjajoč se del menzure potiska vozle akustičnega tlaka proti vhodu cevi. Efektivna dolžina cevi je zato skrajšana in resonančne frekvence se zvišajo. Ta pojav prikazuje slika 9. Efekt teh je najbolj opazen pri niˇzjih resonančnih frekvencah. Hitro razširjajoč se lijak in tudi vse menzure z navzven obrnjeno ukrivljenostjo sten cevi uničujejo harmoničnost resonančnih frekvenc. To je splošen rezultat za vse cevi z hitro razširjajočim lijakom. Zavedati se moramo, da na lego vozlov vpliva tudi ukrivljenost valovne fronte, kar malo spremeni frekvence resonanc. Vendar za kvalitativen opis zadoščajo tudi zgornji izračuni, v katerih smo vzeli približek ravne valovne fronte. 28
35 Slika 9: Osnovni in četrti nihajni način v Besselovi cevi z m = 1/2, dolˇzine 1, 5 m. Rdeča črta predstavlja amplitudo akustičnega tlaka v Besselovi cevi z m = 1/2, zelena črta pa k Besslovi funkciji ekstrapolirano sinusno funkcijo. Na zgornjem grafu je osnovni nihajni način, na spodnjem pa četrti. 29
36 3 Prisekane stoˇzčaste cevi Cev neprisekanega stoˇzca, ki smo jo obravnavali v razdelku 2.3.1, za trobila ni dober približek. Dodajanje ustnika oziroma mikrofona na vhod cevi zahteva, da teme stožca odrežemo in tako uporabljamo cev prisekanega stoˇzca. To lahko spremeni resonančne frekvence v stoˇzčasti cevi. 3.1 Tlak v cevi prisekanega stoˇzca Enačba (29) opisuje spreminjanje akustičnega tlaka znotraj stoˇzčaste cevi. Postavimo cev prisekanega stožca v koordinatni sistem, kot kaže slika 10. Črtkane črte prikazujejo navidezni del stoˇzca in polne črte prisekan stoˇzec. Oznaka d predstavlja razdaljo od koordinatnega izhodišča do vhoda cevi prisekanega stožca. Oznaka L predstavlja dolžino cevi prisekanega stožca. Oznaki r 1 in r 2 predstavljata polmer vhoda cevi in polmer izhoda cevi. Za Slika 10: Postavitev cevi prisekanega stožca v koordinatni sistem. razliko od primera neprisekanega stožca, v tem primeru ne moremo kar predpostaviti, da je člen enačbe (29), A cos(kr)/r, enak nič, saj vrednost tega člen na vhodu cevi ni neskončna. Enačbo (29) za primer prisekane 30
37 stoˇzčaste cevi zapišimo v bolj kompaktni obliki kot p(r) = C sin(kr + δ). (55) r Za opis valovanja v cevi je bolj pregledno, če je vhod cevi postavljen v koordinatno izhodišče. Zato moramo enačbo (55) popraviti. Dobimo enačbo p(r) = C sin(k(r + l)), (56) r + d kjer je l = d + δ/k in d razdalja od navideznega temena stoˇzca do vhoda cevi. Do koeficienta l pridemo s predpostavko, da je na vhodu cevi maksimum akustičnega tlaka. Tako dobimo pogoj p (r + d) = 0 iz katerega izhaja enačba [ C sin(kl) d 2 + k cos(kl) ] = 0 d dk cos(kl) = sin(kl) tg(kl) = dk l = arctg(dk), (57) k ki povezuje koeficient l z razdaljo vhoda cevi prisekanega stoˇzca do navideznega temena stoˇzca d. 3.2 Resonančne frekvence prisekane stoˇzčaste cevi Podobno kot v razdelku bomo tudi v tem razdelku z upoštevanjem robnih pogojev prišli do vrednosti, ki jih lahko zavzema valovni vektor v resonancah. Iz valovnega vektorja bomo nato sklepali na resonančne frekvence. Poleg predpostavke, da je na vhodu cevi maksimum akustičnega tlaka, ki smo jo uporabili v razdelku 3.1, na tem mestu uporabimo še predpostavko, da je na koncu cevi akustični tlak enak 0. Na ta način dobimo dva robna pogoja: 31
38 1. p (d) = 0 in 2. p(d + L) = 0, ki ju uporabimo pri reševanju enačbe (55). 1. Iz enačbe (55) in prvega začetnega pogoja, dobimo enačbo [ ] sin(k(d + δ)) k cos(k(d + δ)) A d 2 + = 0. (58) d Konstanta A v enačbi (58) mora biti različna od 0, saj v nasprotnem primeru dobimo samo trivialno rešitev. Enačbo (58) delimo z A in mnoˇzimo z d 2. Dobimo enačbo kd cos(k(d + δ)) = sin(k(d + δ)). (59) Enačbo (59) delimo s cos(k(d + δ)). Dobimo enačbo tg(k(d + δ)) = kd. (60) 2. Iz enačbe (55) in drugega začetnega pogoja dobimo enačbo sin(k(d + L + δ)) A d + L = 0. (61) Enačbo (61) delimo s konstanto A in mnoˇzimo z d + L. enačbo Dobimo sin(k(d + L + δ)) = 0. (62) Z osnovnimi obrazci trigonometričnih funkcij, sin(α ± β) = sin α cos β ± cos α sin β, zapišimo enačbo (62) v obliki sin(k(d + δ)) cos(kl) + cos(k(d + δ)) sin(kl) = 0. (63) Enačbo (63) delimo s cos(k(d + δ)). Dobimo enačbo tg(k(d + δ)) cos(kl) + sin(kl) = 0. (64) 32
39 Z uporabo enačbe (60) lahko enačbo (64) zapišemo kot kd cos(kl) + sin(kl) = 0. (65) Enačbo (65) delimo s cos(kl). Dobimo enačbo tg(kl) = kd. (66) Dobili smo enačbo, ki povezuje dolˇzino cevi L z razdaljo od koordinatnega izhodišča do vhoda cevi d. S podobnimi trikotniki (glej sliko 10) lahko določimo povezavo med dolžino cevi L in razdaljo med izhodiščem koordinatnega sistema in vhodom cevi d d r 1 = d + L r 2. (67) Zapišemo lahko enačbo, ki opisuje, kako se d spreminja z L v odvisnosti od razmerja polmerov R = r 2 /r 1 d = Z enačbo (68) lahko enačbo (66) prepišemo v obliko L R 1. (68) tg(kl) = kl R 1. (69) Iz enačbe (69) lahko sklepamo na resonančne frekvence v stoˇzčasti cevi, ki je zelo podobna cilindrični cevi. V limiti, ko postaja stoˇzčasta cev cilindrična, gre razmerje polmera izhoda in polmera vhoda cevi proti 1. Enačba (69) ima obliko tg(kl) =. Valovni vektor k lahko v tem primeru zavzema vrednosti (π/(2l))(2n 1). Resonančne frekvence v taki cevi so (c/(4l))(2n 1). Ta rezultat se ujema z izračuni na vhodu zaprte cilindrične cevi iz razdelka Do drugega limitnega primera pridemo, ko postaja premer cevi na vhodu zanemarljivo majhen v primerjavi 33
40 s premerom cevi na izhodu. Taka cev postaja podobna cevi neprisekanega stoˇzca. V limiti, ko gre razmerje R proti neskončno, ima enačba (69) obliko tg(kl) = 0. Valovni vektor k lahko v tem limitnem primeru zavzema vrednosti k = nπ/l. Tudi ta rezultat limitnega primera se ujema z izračunanimi rezultati v razdelku Opazimo lahko, da so resonančne frekvence v teh dveh primerih harmonično razporejene. To pomeni, da so višje resonančne frekvence vsi mnogokratniki osnovne (najnižje) resonančne frekvence. Za cevi med limitnima primeroma resonančne frekvence niso več harmonično razporejene. Odvisnost valovnega vektorja k od dolˇzine cevi lahko razberemo iz grafa na sliki 11. Na njem so narisane tri funkcije. Funkcija tg(kl) (rdeča črta), ki predstavlja levo stran enačbe (69), in funkciji f 1 (zelena črta) in f 2 (modra črta), ki sta oblike f 1,2 = kl R 1,2 1. predstavljata desno stran enačbe (69) za vrednosti razmerja polmerov izhoda in vhoda cevi R 1 = 1, 1 in R 2 = 10. Valovni vektor k je sorazmeren s frekvenco ν. Frekvenca se z valovnim vektorjem izraža z enačbo ν = kc/(2π), kjer je c hitrost širjenja valovanja. Rešitve enačbe (69) so x koordinate presečišča funkcije na levi strani enačbe (tg(kl)) in funkcije na desni strani enačbe ( kl/(r 1)). Na sliki 11 so presečišča označena s točkami od T1 do T6. Resonančne frekvence, ki smo jih s takim postopkom dobili za 35 cm dolgo cev prisekanega stoˇzca z razmerjem polmera izhoda in vhoda cevi R = 10, so v tabeli 1. Za primerjavo so v četrtem in petem stolpca tabele 1 resonančne frekvence na obeh straneh odprte cilindrične cevi enake dolžine in resonančne frekvence na vhodu zaprte in izhodu odprte cilindrične cevi enake dolˇzine. Iz tabele 1 lahko razberemo, da je prva resonančna frekvenca cevi prisekanega stoˇzca bolj podobna resonančni frekvenci na obeh straneh odprte cilindrične cevi kot resonančni Ti 34
41 Slika 11: Graf je namenjen grafičnemu reševanju enačbe (69). n kl ν[hz] ν o [Hz] ν z [Hz] 1 2, , , , , Tabela 1: Prvih pet resonančnih frekvenc 35 cm dolgih cevi. frekvenci na vhodu zaprte cilindrične cevi. Peta resonančna frekvenca cevi prisekanega stoˇzca je nasprotno bolj podobna resonančni frekvenci na vhodu zaprte cilindrične cevi kot resonančni frekvenci na obeh straneh odprte cevi. Do te ugotovitve lahko pridemo tudi direktno iz grafa na sliki 11. Oglejmo si najprej primer majhnih vrednosti valovnega vektorja. Če skle- 35
42 pamo iz enačbe (69), da je k = arctg( kl R 1 ) L 0, (70) ugotovimo, da mora biti kl/(r 1) 0 in posledično kl R 1. Z enačbo (68) lahko pogoj napišemo v bolj kompaktni obliki kd(r 1) (R 1) kd 1 oziroma d 2πλ. (71) V primeru velikih vrednostih valovnega vektorja iz enačbe (69) sklepamo, da je k = arctg( kl R 1 ) L π 2L (72) in ugotovimo, da mora biti kl/(r 1). Posledično velja kl R 1. Z enačbo (68) lahko pogoj napišemo v bolj kompaktni obliki kd(r 1) (R 1) kd 1 oziroma d 2πλ. (73) 36
43 3.3 Meritve tlaka v cevi prisekanega stoˇzca Teoretična ugotovitev, da so resonančne frekvence v cevi lahko neharmonično razporejene, je na prvi pogled malo nenavadna. Z namenom preveriti teoretične rezultate sem izvedel meritve tlaka v cevi prisekanega stožca. Postavitev meritve prikazujeta slika 12 in skica na sliki 13. Slika 12: 1 Stojalo za cev, 2 Mikrofon, 3 Cev prisekanega stoˇzca, 4 Palica za mikrofon, 5 Stojalo za mikrofon, 6 Stojalo za ravnilo, 7 Ravnilo, 8 Ojačevalnik, 9 Napajanje ojačevalnika, 10 Osciloskop, 11 Generator sinusne napetosti, 12 Stojalo za zvočnik, 13 Zvočnik. Iz trdne umetne mase sem izdelal cev prisekanega stoˇzca z višino 35 cm, z vhodom cevi premera 2 cm in izhodom premera 20 cm. Cev prisekanega stožca sem pripel s stojalom za cev tako, da je bila simetrijska os cevi 37
44 Slika 13: 1 Generator sinusne napetosti, 2 Zvočnik, 3 Stoˇzčasta cev, 4 Mikrofon, 5 Ojačevalnik, 6 Osciloskop. prisekanega stoˇzca vodoravna. K vhodu cevi sem s pomočjo stojala postavil zvočnik. Zvočnik sem postavil tako, da je bila membrana zvočnika 5 mm ali manj oddaljena od vhoda cevi. Premer membrane zvočnika je 4 cm. Zvočnik sem priklopil na generator sinusne napetosti. Z generatorjem sinusne napetosti sem lahko reguliral amplitudo napetosti ter frekvenco med 400 Hz in 3000 Hz. Na ta način sem lahko dosegel, da je membrana zvočnika nihala z ustrezno frekvenco in amplitudo. Majhen mikrofon premera 4 mm sem prilepil na dolgo tanko palico. Palico sem postavil na stojalo, ki je palico podpiralo na dveh točkah. Stojalo sem dvignil na tako višino in obrnil v tako smer, da se je palica lahko gibala le v smeri simetrijske osi prisekanega stožca. Nad palico sem s stojalom za ravnilo pripel ravnilo tik nad palico. Na palici sem si izbral referenčno točko in na ta način meril premike palice in mikrofona vzdolˇz simetrijske osi prisekanega stožca. Napetost iz mikrofona sem preko ojačevalnika, katerega sem napajal z napetostjo 8 V in 8 V, peljal na osciloskop. Iz osciloskopa sem lahko odčital frekvenco valovanja in amplitudo napetosti. Amplituda napetosti je sorazmerna z amplitudo akustičnega tlaka. Na ta način sem preko amplitude napetosti, ki sem jo odčital na osciloskopu meril ampli- 38
45 tudo akustičnega tlaka na mestu, kjer je bil postavljen mikrofon. Meritev sem postavil tako, da se je zvok iz cevi lahko prosto širil ven. S tem sem preprečil nastanek stoječega valovanja, ki bi bilo posledica odboja valovanja od kakšne stene. Meritve sem začel tako, da sem mikrofon postavil čim bliˇze vhodu cevi. Tam sem, po izračunih iz razdelka 3.1, pričakoval hrbet akustičnega tlaka pri stoječem valovanju vseh resonančnih frekvenc. Spreminjal sem frekvenco zvočnika ter na osciloskopu opazoval spreminjanje amplitude. Frekvence, pri katerih sem opazil lokalni maksimum amplitude, sem si izpisal ter jih označil kot potencialne resonančne frekvence cevi prisekanega stožca. Nato sem brez premikanja zvočnika odstranil cev prisekanega stožca ter pri frekvenčnem območju okrog posameznih potencialnih resonančnih frekvenc izmeril amplitudo akustičnega tlaka na različnih oddaljenostih od mikrofona. S tem sem pokazal, da maksimumi akustičnega tlaka niso nastali zaradi stoječega valovanja, ki ni povezano s cevjo. Izmerki so zapisani v prilogi 1 in grafično predstavljeni na slikah 14, 15 in 16. Prepričati se je potrebno še, da posamezni maksimumi akustičnega tlaka niso posledica frekvenčne karakteristike zvočnika in mikrofona. Frekvenčno karakteristiko zvočnika in mikrofona sem izmeril tako, da sem blizu zvočnika postavil mikrofon in pri različnih frekvencah odčital amplitudo tlaka. Izmerki so zapisani v prilogi 2 in grafično predstavljeni na sliki 17. Na ta način sem dobil tri frekvence, pri katerih se je pojavil maksimum akustičnega tlaka, ki ni posledica stoječega valovanja, ki bi nastalo zaradi odboja od kakšnih predmetov, ali posebne frekvenčne karakteristike mikrofona in zvočnika. Za te frekvence sem predpostavil, da so resonančne frekvence cevi prisekanega stoˇzca. Brez premikanja mikrofona sem postavil cev prisekanega stožca na prvotno mesto in pričel z merjenji 39
46 amplitude tlaka v odvisnosti od lege mikrofona pri resonančnih frekvencah. Izmerki so zapisani v prilogi 3 in grafično prestavljeni na slikah 18, 19 in Analiza meritev Pri analiziranju izmerjenih podatkov in risanju grafov sem si pomagal z računalniškim programom Gnuplot. Pri določanju funkcije, ki se najbolj prilega izmerkom je program Gnuplot zelo uporaben. Dovolj je, da poznamo obliko funkcije za katero menimo, da se bo najbolj prilegala izmerkom, na primer y(x) = A sin(kx + δ), in približno vrednost nekaterih njenih parametrov, na primer k = 2 in δ = π/2. S programom Gnuplot lahko izračunamo vrednosti parametrov, za katere se dana funkcija najbolj prilega izmerkom. Najprej sem analiziral meritve amplitude akustičnega tlaka v odvisnosti od razdalje od zvočnika brez cilindrične cevi. Iz predpostavke, da v tem primeru ni stoječega valovanja, sledi, da se amplituda akustičnega tlaka spreminja obratno sorazmerno z razdaljo. Na ta način sem določil obliko funkcije, ki se najbolj prilega izmerkom kot p(r) = a r + d. (74) S programom Gnuplot sem določil parametra funkcije a in d, podana z enačbo (74). Parametri in statistična napaka parametrov funkcije, ki jih določi program Gnuplot, so predstavljeni v tabeli 2. Ker nas absolutna amplituda akustičnega tlaka pri obravnavi resonančnih frekvenc ne zanima, bomo v nadaljevanju amplitudo akustičnega tlaka navajali v relativnih (brezdimenzijskih) enotah. Meritve in funkcije, ki se najbolj prilagajo meritvam so predstavljene na slikah 14, 15 in 16. Nato sem grafično predstavil 40
47 Slika 14: Meritve amplitude akustičnega tlaka v odvisnosti od razdalje mikrofona od zvočnika na frekvenčnem območju od 1100 Hz do 1220 Hz. Slika 15: Meritve amplitude akustičnega tlaka v odvisnosti od razdalje mikrofona od zvočnika na frekvenčnem območju od 1500 Hz do 1800 Hz. meritve frekvenčne karakteristike zvočnika in mikrofona (glej sliko 17). Iz grafa na sliki 17 razberemo, da v bližnji okolici resonančnih frekvenc ni 41
48 Slika 16: Meritve amplitude akustičnega tlaka v odvisnosti od razdalje mikrofona od zvočnika na frekvenčnem območju od 1850 Hz do 2250 Hz. Vrednost pri frekvenci Parameter 1176 Hz 1660 Hz 2077 Hz a 0.029(1 ± 0.020) 0.032(1 ± 0.029) 0.038(1 ± 0.025) d 0.014(1 ± 0.028) m 0.015(1 ± 0.041) 0.019(1 ± 0.036) m Tabela 2: Vrednosti parametrov pri prilagajanju funkcije p(r) izmerkom amplitude akustičnega tlaka v odvisnosti od razdalje do zvočnika brez cevi. Meritve so bile izvedene na območju frekvenc resonančnih frekvenc cevi. Poleg vrednosti parametrov so navedene njihove statistične napake, ki jih je določil program Gnuplot. maksimumov frekvenčne karakteristike zvočnika in mikrofona. Na podlagi tega sklepamo, da so izmerjene frekvence 1176 Hz, 1660 Hz in 2077 Hz res resonančne frekvence cevi prisekanega stožca. Za določitev funkcije, ki se najbolj prilega meritvam odvisnosti akustičnega tlaka od lege v cevi prisekanega stoˇzca pri resonančnih frekvencah, moramo najprej ugotoviti obliko funkcije. V razdelku 3.1 smo prišli 42
49 Slika 17: Meritve odvisnosti amplitude akustičnega tlaka od frekvence zvočnika. Mikrofon je bil postavljen na razdalji 3 cm od zvočnika. do ugotovitve, da se tlak v cevi prisekanega stoˇzca spreminja po enačbi (56). Zavedati se moramo, da smo merili le amplitudo, zato moramo pri prilagajanju funkcije meritvam vzeti absolutno vrednost funkcije v enačbi (56). Dobimo funkcijo p(r) = C sin(k(r + l)) r + d. (75) Približno oceno valovnega vektorja k lahko dobimo iz podatka o resonančni frekvenci iz enačbe k = (2π/c)ν. Pribliˇzno oceno konstante C dobimo iz enačbe p(0) C /k, kjer smo s C označili amplitudo pri vhodu cevi. Parameter d je približno razdalja med navideznim temenom prisekanega stožca in vhodom cevi. Izračunamo ga lahko preko enačbe (68). Ta parameter je enak pri vseh treh resonančnih frekvencah. Parameter l lahko izračunamo po enačbi (57). Pri izmerkih je opazno, da moramo pri prilagajanju funkcije izmerkom, poleg oblike enačbe (56) upoštevati tudi neke vrste ozadje. Zato moramo za boljše prilagajanje enačbe izmerkom 43
50 enačbi (75) dodati še člen b/(x + d). Funkcija, ki jo bomo v nadaljevanju prilagajali meritvam ima obliko p(r) = C sin(k(r + l)) r + d + b x + d. (76) Prilagajali bomo parametre k, C, d, l in b. Parametri in njihove napake so predstavljeni v tabeli 3. Vrednost pri frekvenci Parameter 1176 Hz 1660 Hz 2077 Hz k 21.6m 1 ± 0.2m m 1 ± 0.2m m 1 ± 0.3m 1 C ± ± ± d 0.042m ± 0.001m 0.038m ± 0.001m 0.039m ± 0.001m l 0.033m ± 0.002m 0.026m ± 0.001m 0.027m ± 0.001m b ± ± ± Tabela 3: Vrednosti parametrov pri prilagajanju funkcije p(r) izmerkom amplitude akustičnega tlaka v odvisnosti od razdalje do zvočnika. Meritve so bile izvedene pri resonančnih frekvencah cevi. Poleg vrednosti parametrov so navedene njihove statistične napake, ki jih je določil program Gnuplot. Preverimo v kolikšni meri se parametri dobljeni s prilagajanjem izmerkom ujemajo s pričakovanimi vrednostmi. Parameter d predstavlja razdaljo od vhoda cevi do navideznega temena stoˇzca. Ta je za našo cev pri vseh meritvah enaka 0, 35m ± 0, 01m d = = 0, 038m ± 0, 005m. (77) 0,2m±0,01m 0,02m±0,002m 1 Vse dobljene vrednosti parametra d (glej tabelo 3) se v okviru natančnosti ujemajo z vrednostjo v enačbi 77. Pri 10 C in 50 % vlažnosti je hitrost širjenja zvoka v zraku 337 m/s [7]. Napako pri meritvi frekvence je 2 44
51 %. Iz podatkov o frekvenci in hitrosti širjenja zvoka izračunamo vrednosti valovnega vektorja. Te prikazuje tabela 4. Opazimo, da so odstopanja izračunanih vrednosti valovnega vektorja (glej tabelo 4) in vrednosti dobljene s prilagajanjem funkcije meritvam (glej tabelo 3) nekoliko večja, vendar se v okviru natančnosti ujemajo. ν k ν [m 1 ] 1176 Hz 21, 9 ± 0, Hz 31, 0 ± 0, Hz 38, 7 ± 0, 8 Tabela 4: Iz hitrosti širjenja zvoka in resonančnih frekvenc izračunane vrednosti valovnih vektorjev. Prilagajanje funkcij meritvam in meritve same so predstavljene na slikah 18, 19 in 20. Rdeča krivulja predstavlja funkcijo p(r), ki ima obliko enačbe (76). Modra krivulja predstavlja funkcijo p 1 (r), ki ima obliko enačbe (56). Parametri te funkcije a, k, l in d so enaki kot pri funkciji p(r). Funkcija p 1 (r) ponazarja odvisnost akustičnega tlaka v cevi prisekanega stoˇzca, kot smo jo izračunali v razdelku 3.1. Efektivno dolžino cevi lahko določimo iz grafov na slikah 18, 19 in 20. Efektivna dolžina cevi je dolžina, ki bi jo imela idealna cev (brez dušenja in iztočnih popravkov) pri enakih frekvencah. Pri cevi, ki jo obravnavamo, je efektivna dolˇzina cevi kar razdalja od vhodu cevi najbliˇzjega maksimuma do izhodu cevi najbližjega minimuma akustičnega tlaka. Dobljeni rezultati so predstavljeni v tabeli 5. S podatki o efektivni dolžini cevi lahko popravimo vrednosti resonančnih frekvenc v tabeli 1. Nove vrednosti so zapisane v tretjem stolpcu tabele 6. Iz vrednosti valovnih vektorjev, ki smo jih dobili pri prilagajanju funkcije p(r), katero opisuje enačba (76), in 45
52 Slika 18: Izmerjena amplituda akustičnega tlaka v odvisnosti od lege v cevi prisekanega stoˇzca pri resonančni frekvenci 1176 Hz. Slika 19: Izmerjena amplituda akustičnega tlaka v odvisnosti od lege v cevi prisekanega stožca pri resonančni frekvenci 1660 Hz. iz podatka o hitrosti širjenja zvoka, izračunamo valovnim vektorjem pripadajoče resonančne frekvence. Izračunani podatki so zapisani v drugem 46
53 Slika 20: Izmerjena amplituda akustičnega tlaka v odvisnosti od lege v cevi prisekanega stoˇzca pri resonančni frekvenci 2077 Hz. n L e f [m] 3 0, , , 39 Tabela 5: Efektivna dolˇzina cevi prisekanega stoˇzca, na kateri smo izvajali meritve. Dobili smo jo grafično iz grafov na slikah 18, 19 in 20. stolpcu tabele 6. V prvem stolpcu tabele 6 so zapisane direktno izmerjene resonančne frekvence cevi prisekanega stoˇzca. Iz tabele 6 lahko razberemo, da se resonančne frekvence dobljene na vse tri načine v okviru natančnosti ujemajo. Oglejmo si še, kako se v cevi prisekanega stožca spreminja akustična impedanca. Da jo lahko izračunamo, moramo najprej izračunati akustični prostorninski tok U(x). Izračunamo ga z enačbo (34), ki povezuje aku- 47
54 ν mer ν f it ν teo 1176Hz ± 50Hz 1160Hz ± 10Hz 1170Hz 1660Hz ± 50Hz 1650Hz ± 10Hz 1650Hz 2077Hz ± 50Hz 2020Hz ± 20Hz 2020Hz Tabela 6: Primerjava resonančnih frekvenc. stični tlak in akustični prostorninski tok. Z odvajanjem z r 2 pomnoˇzene enačbe p(r, t) = [ sin(k(r + l)) a + b ] e iωt, (78) r + d r + d ki opisuje spreminjanje akustičnega tlaka v cevi prisekanega stožca, dobimo odvod akustičnega prostorninskega toka po času [ C ( (r + 2d) sin(k(r + l))+ U t = K ρ r (r + d) 2 +k(r + d) cos(k(r + l)) ) ] + b(r + 2d) e iωt. (79) Z integriranjem enačbe (79) dobimo odvisnost akustičnega prostorninskega toka od lege v cevi U(r) = K k [ r (r + d) 2 C ( (r + 2d) sin(k(r + l))+ ] +k(r + d) cos(k(r + l)) ) + b(r + 2d) e iωt. (80) Na sliki 21 je prikazan akustični tlak s členom ozadja. Dodali smo ga pri analizi meritev odvisnosti akustičnega tlaka od lege v cevi prisekanega stožca pri resonančnih frekvencah (glej enačbo (76)). Iz enačbe (76), ki opisuje akustični tlak, smo izračunali akustični prostorninski tok. Iz enačbe (56), ki ne vsebuje člena ozadja, dobimo odvisnost akustičnega prostorninskega toka od lege v cevi kot U(r) = K C k r (r + d) 2 [ (r + 2d) sin(k(r + l)) + k(r + d) cos(k(r + l)) 48 ]. (81)
55 Slika 21: Akustični tlak in akustični prostorninski tok v odvisnosti od lege v cevi prisekanega stoˇzca za četrto resonančno frekvenco (n = 4). Cev je dolga 35 cm. Akustični tlak in akustični prostorninski tok brez člena ozadja v odvisnost od lege v cevi sta prikazana na sliki 22. Slika 22: Akustični tlak in akustični prostorninski tok brez člena ozadja v odvisnosti od lege v cevi prisekanega stožca za četrto resonančno frekvenco (n = 4). Cev je dolga 35 cm. 49
56 Iz slik (21) in (22) lahko razberemo, da se proti izhodu stoˇzčaste cevi akustični prostorninski tok povečuje in akustični tlak zmanjšuje. Torej tudi cev prisekanega stožca deluje kot akustični transformator, ki spreminja veliko akustično impedanco na vhodu cevi v majhno akustično impedanco na izhodu cevi. 50
57 4 Resonančne frekvence trobil 4.1 Model cilindrične cevi Preverimo, ali je model cilindrične cevi ustrezen za obravnavo trobente. V cevi trobente lahko brez uporabe ventilov trobilec izvede tone zapisane v tabeli 7. Cev trobente je dolˇzine pribliˇzno 137 cm. Na vhodu je Ton b 1 f 1 b 2 d 2 f 2 ν [Hz] Tabela 7: Toni in pripadajoče frekvence. zaprta s trobilčevimi ustnicami in na izhodu odprta. V takih ceveh so resonančne frekvence ν n = (c/(4l))(2n 1) (glej razdelek 2.2.2), kjer je c hitrost zvoka, ki je pri temperaturi 20 C in normalnem zračnem tlaku 1013 mbar približno 343, 4 m/s. Najnižja frekvenca take cevi je ν 1 63 Hz. Višje resonančne frekvence so lihi mnogokratniki osnovne frekvence. Najniˇzja resonančna frekvenca enako dolge na obeh straneh odprte cevi je dvakrat večja ν Hz. Njene višje resonančne frekvence so vsi mnogokratniki najnižje resonančne frekvence. Natančne dolžine cevi trobente ne poznamo. Prav tako ne poznamo efektivne dolžine cilindrične cevi, s pomočjo katere ˇzelimo opisati trobento. S prilagajanjem efektivne dolˇzine cilindrične cevi, lahko doseˇzemo najboljše moˇzno ujemanje med frekvencami trobente in frekvencami, ki jih napoveduje model cilindričnih cevi. Prva frekvenca trobente je lahko druga ali tretja resonančna frekvenca cilindrične cevi. S programom Gnuplot za obliko funkcije ν z (n) = c 4L e f (2n 1), poiščimo vrednost parametra L e f, pri katerem se funkcija najbolj ujema s frekvencami trobente. Za hitrost širjenja zvoka 51
58 sem vzel 343, 4 m/s. Pri prilagajanju efektivne dolˇzine na vhodu zaprte cilindrične cevi dobimo dva rezultata. a) Prva frekvenca trobente je druga resonančna frekvenca zaprte cilindrične cevi. Parameter efektivne dolˇzine je L e f = 1, 3m ± 0, 03m. b) Prva frekvenca trobente je tretja resonančna frekvenca zaprte cilindrične cevi. Parameter efektivne dolžine je L e f = 1, 63m ± 0, 03m. Oglejmo si še kolikšno ujemanje lahko dobimo z modelom na obeh koncih odprte cilindrične cevi. Oblika funkcije je v tem primeru ν o (n) = c 2L e f n, kjer sem za c vzel vrednost 343, 4 m/s. Pri prilagajanju efektivne dolžine na obeh koncih odprte cilindrične cevi, dobimo dva rezultata: a) Prva frekvenca trobente je druga resonančna frekvenca zaprte cilindrične cevi. Parameter efektivne dolˇzine je L e f = 1, 472m ± 0, 003m. b) Prva frekvenca trobente je tretja resonančna frekvenca zaprte cilindrične cevi. Parameter efektivne dolžine je L e f = 1, 81m ± 0, 06m. Najmanjše odstopanje dobimo z modelom na obeh straneh odprte cilindrične cevi in ne z modelom na vhodu zaprte cilindrične cevi. To se lepo vidi iz grafov na slikah 23 in 24 Za cilindrične cevi velja pribliˇzek [8] L e f = L(1 + 0, 61m 1 a), (82) s katerim lahko izračunamo efektivno dolžino cevi. V enačbi (82) smo z L e f označili efektivno dolžino cevi, z L dejansko dolžino cevi in z a polmer cevi v metrih. Pri igranju trobente, na frekvenco tonov vpliva veliko dejavnikov. Najpomembnejša sta temperatura v prostoru in tehnika igranja posameznega trobilca. Te vplive lahko trobilci kompenzirajo z iztegom 52
59 Slika 23: Model odprte (ν o ) in na vhodu zaprte (ν z ) cilindrične cevi pri predpostavki, da je prva frekvenca trobente druga resonančna frekvenca cilindrične cevi. Slika 24: Model odprte (ν o ) in na vhodu zaprte (ν z ) cilindrične cevi pri predpostavki, da je prva frekvenca trobente tretja resonančna frekvenca cilindrične cevi. (podaljšanjem) cevi. Trobenti se pri kompenzaciji z iztegom, cev lahko podaljša ali skrajša tudi za 2 cm. Izračunajmo efektivno podaljšanje cilin- 53
60 drične cevi, s katero opisujemo trobento. Največjo efektivno dolˇzino bomo dobili, če bomo za polmer cevi, s katero opisujemo trobento, vzeli največji polmer cevi trobente. Ta je 6 cm. Efektivna dolžina take cevi je L e f = (1, 37m ± 0, 02m)(1 + 0, 61m 1 0, 06m) = 1, 42m ± 0, 02m. (83) Ugotovimo, da se v cilindričnih ceveh vrednosti dobljene s prilagajanjem efektivne dolžine cevi v okviru napak ne ujemajo z izračunom v enačbi (83). Vse vrednosti s prilagajanjem dobljene efektivne dolˇzine so večje od izračunane efektivne dolˇzine. Izjema je a) primer pri zaprti cilindrični cevi, katerega efektivna dolžina je opazno krajša od dejanske dolžine. Ta rezultat je napačen, saj po enačbi (82) efektivna dolžina cevi ne more biti krajša od dejanske dolˇzine. To, da so vrednosti s prilagajanjem dobljene efektivne dolˇzine cevi večje od izračunanih, pomeni, da za neujemanje z izračunom efektivne dolžine cevi ni kriva napačna izbira polmera cevi trobente. Izbrali smo namreč največji polmer cevi. To pomeni največje možno efektivno podaljšanje dejanske dolˇzine cevi. Model cilindrične cevi za trobento ni ustrezen. Bolj ustrezen je model stožčaste cevi. 4.2 Model stoˇzčaste cevi V razdelku 4.1 smo ugotovili, da se resonančne frekvence na obeh straneh odprte cilindrične cevi zelo dobro ujemajo s frekvencami trobente. Dobro ujemanje resonančnih frekvenc s frekvencami trobente bomo dosegli z modelom, katerega resonančne frekvence so enake kot frekvence v cilindrični na obeh straneh odprti cevi. Resonančne frekvence v cevi neprisekanega stoˇzca (glej razdelek 2.3.1) so enake kot resonančne frekvence na obeh koncih odprte cilindrične cevi (glej razdelek 2.2.2). Z modelom cevi neprise- 54
61 kanega stoˇzca se lahko dobro pribliˇzamo frekvencam trobente. Kljub ujemanju v frekvencah, model neprisekane stoˇzčaste cevi ni ustrezen za opis trobente, ker moramo pri dodajanju ustnika na cev, teme stožca odstraniti (glej razdelek 3). Iz računskih izpeljav v razdelku 3.2 lahko ugotovimo, da so za prisekane stoˇzčaste cevi, katerih prisekani deli so majhni v primerjavi z valovno dolˇzino valovanja v cevi, resonančne frekvence zelo podobne resonančnim frekvencam neprisekane stožčaste cevi. Pričakujemo lahko, da se bodo nižje resonančne frekvence modela cevi prisekanega stoˇzca bolj ujemale kot višje resonančne frekvence. Vzemimo pribliˇzek, da je cev trobente po celotni dolˇzini popolnoma stožčasta. Razmerje njunih premerov (glej razdelek 2.1) je približno R = d izh. 120mm d vh. 3, 6mm 33. (84) To razmerje je kar veliko. Pribliˇzno trikrat večje je od razmerja pri cevi prisekanega stoˇzca, ki smo jo uporabljali pri meritvah v razdelku 3.3. Na Slika 25: Graf je namenjen grafičnemu reševanju enačbe (69). sliki 25 je graf, s katerim podobno kot v razdelku 3.2 poiščemo vrednosti 55
62 kl pri resonancah v cevi prisekanega stoˇzca. Vrednosti kl, ugotovljene iz grafa na sliki 25, so zapisane v tabeli 8. Ker ne poznamo efektivne dolˇzine n kl 1 0, 97π 2 1, 94π 3 2, 91π 4 3, 89π 5 4, 86π n kl 6 5, 84π 7 6, 81π 8 7, 79π 9 8, 77π 10 9, 76π Tabela 8: Grafično dobljene vrednosti resonančnih frekvenc prisekane stoˇzčaste cevi z razmerjem polmerov R = 33. cevi, s programom Gnuplot poiščimo najbolj ustrezno efektivno dolˇzino. Iščemo ujemanje resonančnih frekvenc prisekanega stožca ν pr.s. in resonančnih frekvenc na obeh straneh odprte cilindrične ν o.cil., ki so zelo podobne frekvencam trobente (glej razdelek 4.1). ν pr.s. = ν o.cil (kl)c 2πL e f.s. = nc 2πL e f.c. (kl) = L e f.s. L e f.c. n (85) V enačbi (85) smo z L e f.s. označili efektivno dolˇzino cevi prisekanega stoˇzca in z L e f.c. efektivno dolžino na obeh straneh odprte cilindrične cevi. Vzemimo obliko funkcije y(x) = L e f.s. L e f.c. x in s prilagajanjem parametra L e f.s. poiščimo funkcijo, ki se najbolj prilagaja vrednostim iz tabele 8. Pri vrednosti parametra L e f.s. = 1, 4337 m se funkcija y(x) najbolj prilagaja pričakovanim vrednostim. Odstopanje je le 0, 06 %. Prilagajanje funkcije y(x) pričakovanim vrednostim je prikazano na grafu slike 26. Z zgornjo 56
63 Slika 26: Prilagajanje funkcije y(x) vrednostim iz tabele 8 obravnavo smo ugotovili, da z modelom cevi prisekanega stoˇzca lahko doseˇzemo dobro ujemanje med resonančnimi frekvencami cevi in frekvencami trobente. Efektivna dolžina take cevi prisekanega stožca je 1, 43 m. Iz grafičnega določanja efektivne dolžine cevi prisekanega stožca (glej tabelo 5) ugotovimo, da s pribliˇzkom v enačbi (82) lahko opišemo efektivno dolˇzino cevi prisekanega stoˇzca, v kateri smo izvajali meritve. Pri tem moramo za polmer cevi vzeti polmer izhoda cevi L e f = 0, 35m(1 + 0, 61m 1 0, 2m) = 0, 39m. Efektivna dolžina cevi prisekanega stožca, s katero opišemo cev trobente, se v okviru napak ujema z izračunom efektivne dolˇzine trobente v enačbi (83). 57
64 4.3 Model Besselove cevi S sliko 9 si lahko predstavljamo, na kakšen način lahko igralec francoskega (glej sliko 27) ali lovskega roga pomembno vpliva na višino tona s premikanjem roke v notranjost lijaka. S potiskom roke v lijak se akustične Slika 27: Francoski rog lastnosti lijaka spremenijo [7]. Postanejo bolj podobne lastnostim počasi razširjajočega lijaka. Na ta način se zmanjša učinek efektivnega skrajšanja cevi zaradi hitro razširjajočega lijaka. Višino tona lahko na ta način zniža tudi za polton. Zniˇzanje tona za polton pomeni, da se frekvenca valovanja zmanjša (1 12 2) krat. Višino tona lahko igralec francoskega roga s premikanjem roke še bolj v notranjost inštrumenta tudi zviša za pribliˇzno pol tona. S tem z roko skoraj popolnoma zapre notranjost menzure. To povzroči velike spremembe robnih pogojev. Efektivna dolˇzina cevi se zmanjša. Zaradi povečanja akustične impedance na izhodu inštrumenta, se večji del valovanja od izhoda inštrumenta odbije. Zvok, ki ga oddaja inštrument, je tišji, v njem pa je prisotnih tudi več višjih harmonskih frekvenc. To zaznamo kot bistveno spremembo barve zvoka inštrumenta. 58
Diferencialna enačba, v kateri nastopata neznana funkcija in njen odvod v prvi potenci
 Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Tretja vaja iz matematike 1
 Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 5. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Funkcijske vrste. Matematika 2. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 2. april Gregor Dolinar Matematika 2
 Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 21. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 14. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 10. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 22. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Matematika 2. Diferencialne enačbe drugega reda
 Matematika 2 Diferencialne enačbe drugega reda (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) y 6y + 8y = 0, (b) y 2y + y = 0, (c) y + y = 0, (d) y + 2y + 2y = 0. Rešitev:
Matematika 2 Diferencialne enačbe drugega reda (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) y 6y + 8y = 0, (b) y 2y + y = 0, (c) y + y = 0, (d) y + 2y + 2y = 0. Rešitev:
Delovna točka in napajalna vezja bipolarnih tranzistorjev
 KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
Kvantni delec na potencialnem skoku
 Kvantni delec na potencialnem skoku Delec, ki se giblje premo enakomerno, pride na mejo, kjer potencial naraste s potenciala 0 na potencial. Takšno potencialno funkcijo zapišemo kot 0, 0 0,0. Slika 1:
Kvantni delec na potencialnem skoku Delec, ki se giblje premo enakomerno, pride na mejo, kjer potencial naraste s potenciala 0 na potencial. Takšno potencialno funkcijo zapišemo kot 0, 0 0,0. Slika 1:
PONOVITEV SNOVI ZA 4. TEST
 PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
diferencialne enačbe - nadaljevanje
 12. vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 diferencialne enačbe - nadaljevanje Ortogonalne trajektorije Dana je 1-parametrična družina krivulj F(x, y, C) = 0. Ortogonalne
12. vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 diferencialne enačbe - nadaljevanje Ortogonalne trajektorije Dana je 1-parametrična družina krivulj F(x, y, C) = 0. Ortogonalne
Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba.
 1. Osnovni pojmi Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba. Primer 1.1: Diferencialne enačbe so izrazi: y
1. Osnovni pojmi Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba. Primer 1.1: Diferencialne enačbe so izrazi: y
*M * Osnovna in višja raven MATEMATIKA NAVODILA ZA OCENJEVANJE. Sobota, 4. junij 2011 SPOMLADANSKI IZPITNI ROK. Državni izpitni center
 Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Funkcije več spremenljivk
 DODATEK C Funkcije več spremenljivk C.1. Osnovni pojmi Funkcija n spremenljivk je predpis: f : D f R, (x 1, x 2,..., x n ) u = f (x 1, x 2,..., x n ) kjer D f R n imenujemo definicijsko območje funkcije
DODATEK C Funkcije več spremenljivk C.1. Osnovni pojmi Funkcija n spremenljivk je predpis: f : D f R, (x 1, x 2,..., x n ) u = f (x 1, x 2,..., x n ) kjer D f R n imenujemo definicijsko območje funkcije
VALOVANJE UVOD POLARIZACIJA STOJEČE VALOVANJE ODBOJ, LOM IN UKLON INTERFERENCA
 VALOVANJE 10.1. UVOD 10.2. POLARIZACIJA 10.3. STOJEČE VALOVANJE 10.4. ODBOJ, LOM IN UKLON 10.5. INTERFERENCA 10.6. MATEMATIČNA OBDELAVA INTERFERENCE IN STOJEČEGA VALOVANJA 10.1. UVOD Valovanje je širjenje
VALOVANJE 10.1. UVOD 10.2. POLARIZACIJA 10.3. STOJEČE VALOVANJE 10.4. ODBOJ, LOM IN UKLON 10.5. INTERFERENCA 10.6. MATEMATIČNA OBDELAVA INTERFERENCE IN STOJEČEGA VALOVANJA 10.1. UVOD Valovanje je širjenje
Kotne in krožne funkcije
 Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
1. Trikotniki hitrosti
 . Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
. Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
Frekvenčna analiza neperiodičnih signalov. Analiza signalov prof. France Mihelič
 Frekvenčna analiza neperiodičnih signalov Analiza signalov prof. France Mihelič Vpliv postopka daljšanja periode na spekter periodičnega signala Opazujmo družino sodih periodičnih pravokotnih impulzov
Frekvenčna analiza neperiodičnih signalov Analiza signalov prof. France Mihelič Vpliv postopka daljšanja periode na spekter periodičnega signala Opazujmo družino sodih periodičnih pravokotnih impulzov
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 15. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
Tema 1 Osnove navadnih diferencialnih enačb (NDE)
 Matematične metode v fiziki II 2013/14 Tema 1 Osnove navadnih diferencialnih enačb (NDE Diferencialne enačbe v fiziki Večina osnovnih enačb v fiziki je zapisana v obliki diferencialne enačbe. Za primer
Matematične metode v fiziki II 2013/14 Tema 1 Osnove navadnih diferencialnih enačb (NDE Diferencialne enačbe v fiziki Večina osnovnih enačb v fiziki je zapisana v obliki diferencialne enačbe. Za primer
vezani ekstremi funkcij
 11. vaja iz Matematike 2 (UNI) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 ekstremi funkcij več spremenljivk nadaljevanje vezani ekstremi funkcij Dana je funkcija f(x, y). Zanimajo nas ekstremi nad
11. vaja iz Matematike 2 (UNI) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 ekstremi funkcij več spremenljivk nadaljevanje vezani ekstremi funkcij Dana je funkcija f(x, y). Zanimajo nas ekstremi nad
IZPIT IZ ANALIZE II Maribor,
 Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
Definicija. definiramo skalarni produkt. x i y i. in razdaljo. d(x, y) = x y = < x y, x y > = n (x i y i ) 2. i=1. i=1
 Funkcije več realnih spremenljivk Osnovne definicije Limita in zveznost funkcije več spremenljivk Parcialni odvodi funkcije več spremenljivk Gradient in odvod funkcije več spremenljivk v dani smeri Parcialni
Funkcije več realnih spremenljivk Osnovne definicije Limita in zveznost funkcije več spremenljivk Parcialni odvodi funkcije več spremenljivk Gradient in odvod funkcije več spremenljivk v dani smeri Parcialni
11. Valovanje Valovanje. = λν λ [m] - Valovna dolžina. hitrost valovanja na napeti vrvi. frekvence lastnega nihanja strune
![11. Valovanje Valovanje. = λν λ [m] - Valovna dolžina. hitrost valovanja na napeti vrvi. frekvence lastnega nihanja strune 11. Valovanje Valovanje. = λν λ [m] - Valovna dolžina. hitrost valovanja na napeti vrvi. frekvence lastnega nihanja strune](/thumbs/79/79968210.jpg) 11. Valovanje Frekvenca ν = 1 t 0 hitrost valovanja c = λ t 0 = λν λ [m] - Valovna dolžina hitrost valovanja na napeti vrvi frekvence lastnega nihanja strune interferenca valovanj iz dveh enako oddaljenih
11. Valovanje Frekvenca ν = 1 t 0 hitrost valovanja c = λ t 0 = λν λ [m] - Valovna dolžina hitrost valovanja na napeti vrvi frekvence lastnega nihanja strune interferenca valovanj iz dveh enako oddaljenih
Osnove elektrotehnike uvod
 Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
VEKTORJI. Operacije z vektorji
 VEKTORJI Vektorji so matematični objekti, s katerimi opisujemo določene fizikalne količine. V tisku jih označujemo s krepko natisnjenimi črkami (npr. a), pri pisanju pa s puščico ( a). Fizikalne količine,
VEKTORJI Vektorji so matematični objekti, s katerimi opisujemo določene fizikalne količine. V tisku jih označujemo s krepko natisnjenimi črkami (npr. a), pri pisanju pa s puščico ( a). Fizikalne količine,
1. Definicijsko območje, zaloga vrednosti. 2. Naraščanje in padanje, ekstremi. 3. Ukrivljenost. 4. Trend na robu definicijskega območja
 ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
NEPARAMETRIČNI TESTI. pregledovanje tabel hi-kvadrat test. as. dr. Nino RODE
 NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 12. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
Analiza 2 Rešitve 14. sklopa nalog
 Analiza Rešitve 1 sklopa nalog Navadne diferencialne enačbe višjih redov in sistemi diferencialnih enačb (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) 6 + 8 0, (b)
Analiza Rešitve 1 sklopa nalog Navadne diferencialne enačbe višjih redov in sistemi diferencialnih enačb (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) 6 + 8 0, (b)
8. Diskretni LTI sistemi
 8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * NAVODILA ZA OCENJEVANJE. Petek, 12. junij 2015 SPLOŠNA MATURA
 Državni izpitni center *M543* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Petek,. junij 05 SPLOŠNA MATURA RIC 05 M543 M543 3 IZPITNA POLA Naloga Odgovor Naloga Odgovor Naloga Odgovor Naloga Odgovor
Državni izpitni center *M543* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Petek,. junij 05 SPLOŠNA MATURA RIC 05 M543 M543 3 IZPITNA POLA Naloga Odgovor Naloga Odgovor Naloga Odgovor Naloga Odgovor
matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):
![matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij): matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):](/thumbs/87/96579490.jpg) 4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
Numerično reševanje. diferencialnih enačb II
 Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
Matematika. Funkcije in enačbe
 Matematika Funkcije in enačbe (1) Nariši grafe naslednjih funkcij: (a) f() = 1, (b) f() = 3, (c) f() = 3. Rešitev: (a) Linearna funkcija f() = 1 ima začetno vrednost f(0) = 1 in ničlo = 1/. Definirana
Matematika Funkcije in enačbe (1) Nariši grafe naslednjih funkcij: (a) f() = 1, (b) f() = 3, (c) f() = 3. Rešitev: (a) Linearna funkcija f() = 1 ima začetno vrednost f(0) = 1 in ničlo = 1/. Definirana
MATEMATIČNI IZRAZI V MAFIRA WIKIJU
 I FAKULTETA ZA MATEMATIKO IN FIZIKO Jadranska cesta 19 1000 Ljubljan Ljubljana, 25. marec 2011 MATEMATIČNI IZRAZI V MAFIRA WIKIJU KOMUNICIRANJE V MATEMATIKI Darja Celcer II KAZALO: 1 VSTAVLJANJE MATEMATIČNIH
I FAKULTETA ZA MATEMATIKO IN FIZIKO Jadranska cesta 19 1000 Ljubljan Ljubljana, 25. marec 2011 MATEMATIČNI IZRAZI V MAFIRA WIKIJU KOMUNICIRANJE V MATEMATIKI Darja Celcer II KAZALO: 1 VSTAVLJANJE MATEMATIČNIH
Na pregledni skici napišite/označite ustrezne točke in paraboli. A) 12 B) 8 C) 4 D) 4 E) 8 F) 12
 Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * FIZIKA NAVODILA ZA OCENJEVANJE. Petek, 10. junij 2016 SPLOŠNA MATURA
 Državni izpitni center *M16141113* SPOMLADANSKI IZPITNI ROK FIZIKA NAVODILA ZA OCENJEVANJE Petek, 1. junij 16 SPLOŠNA MATURA RIC 16 M161-411-3 M161-411-3 3 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor
Državni izpitni center *M16141113* SPOMLADANSKI IZPITNI ROK FIZIKA NAVODILA ZA OCENJEVANJE Petek, 1. junij 16 SPLOŠNA MATURA RIC 16 M161-411-3 M161-411-3 3 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor
Transformator. Delovanje transformatorja I. Delovanje transformatorja II
 Transformator Transformator je naprava, ki v osnovi pretvarja napetost iz enega nivoja v drugega. Poznamo vrsto različnih izvedb transformatorjev, glede na njihovo specifičnost uporabe:. Energetski transformator.
Transformator Transformator je naprava, ki v osnovi pretvarja napetost iz enega nivoja v drugega. Poznamo vrsto različnih izvedb transformatorjev, glede na njihovo specifičnost uporabe:. Energetski transformator.
Vaja: Odbojnostni senzor z optičnimi vlakni. Namen vaje
 Namen vaje Spoznavanje osnovnih fiber-optičnih in optomehanskih komponent Spoznavanje načela delovanja in praktične uporabe odbojnostnega senzorja z optičnimi vlakni, Delo z merilnimi instrumenti (signal-generator,
Namen vaje Spoznavanje osnovnih fiber-optičnih in optomehanskih komponent Spoznavanje načela delovanja in praktične uporabe odbojnostnega senzorja z optičnimi vlakni, Delo z merilnimi instrumenti (signal-generator,
Gimnazija Krˇsko. vektorji - naloge
 Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
Splošno o interpolaciji
 Splošno o interpolaciji J.Kozak Numerične metode II (FM) 2011-2012 1 / 18 O funkciji f poznamo ali hočemo uporabiti le posamezne podatke, na primer vrednosti r i = f (x i ) v danih točkah x i Izberemo
Splošno o interpolaciji J.Kozak Numerične metode II (FM) 2011-2012 1 / 18 O funkciji f poznamo ali hočemo uporabiti le posamezne podatke, na primer vrednosti r i = f (x i ) v danih točkah x i Izberemo
Booleova algebra. Izjave in Booleove spremenljivke
 Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
ZVOK UVOD HITROST ZVOKA V SNOVI JAKOST IN GLASNOST ZVOKA DOPPLERJEV POJAV MACHOV STOŽEC UVOD
 ZVOK 11.1. UVOD 11.2. HITROST ZVOKA V SNOVI 11.3. JAKOST IN GLASNOST ZVOKA 11.4. DOPPLERJEV POJAV 11.5. MACHOV STOŽEC 11.1. UVOD Zvok je longitudinalno valovanje, ki ga človeško uho zaznava. Skozi prazen
ZVOK 11.1. UVOD 11.2. HITROST ZVOKA V SNOVI 11.3. JAKOST IN GLASNOST ZVOKA 11.4. DOPPLERJEV POJAV 11.5. MACHOV STOŽEC 11.1. UVOD Zvok je longitudinalno valovanje, ki ga človeško uho zaznava. Skozi prazen
VAJE IZ NIHANJA. 3. Pospešek nihala na vijačno vzmet je: a. stalen, b. največji v skrajni legi, c. največji v ravnovesni legi, d. nič.
 VAJE IZ NIHANJA Izberi pravilen odgovor in fizikalno smiselno utemelji svojo odločitev. I. OPIS NIHANJA 1. Slika kaže nitno nihalo v ravnovesni legi in skrajnih legah. Amplituda je razdalja: a. Od 1 do
VAJE IZ NIHANJA Izberi pravilen odgovor in fizikalno smiselno utemelji svojo odločitev. I. OPIS NIHANJA 1. Slika kaže nitno nihalo v ravnovesni legi in skrajnih legah. Amplituda je razdalja: a. Od 1 do
Najprej zapišemo 2. Newtonov zakon za cel sistem v vektorski obliki:
 NALOGA: Po cesi vozi ovornjak z hirosjo 8 km/h. Tovornjak je dolg 8 m, širok 2 m in visok 4 m in ima maso 4 on. S srani začne pihai veer z hirosjo 5 km/h. Ob nekem času voznik zaspi in ne upravlja več
NALOGA: Po cesi vozi ovornjak z hirosjo 8 km/h. Tovornjak je dolg 8 m, širok 2 m in visok 4 m in ima maso 4 on. S srani začne pihai veer z hirosjo 5 km/h. Ob nekem času voznik zaspi in ne upravlja več
Reševanje sistema linearnih
 Poglavje III Reševanje sistema linearnih enačb V tem kratkem poglavju bomo obravnavali zelo uporabno in zato pomembno temo linearne algebre eševanje sistemov linearnih enačb. Spoznali bomo Gaussovo (natančneje
Poglavje III Reševanje sistema linearnih enačb V tem kratkem poglavju bomo obravnavali zelo uporabno in zato pomembno temo linearne algebre eševanje sistemov linearnih enačb. Spoznali bomo Gaussovo (natančneje
Kontrolne karte uporabljamo za sprotno spremljanje kakovosti izdelka, ki ga izdelujemo v proizvodnem procesu.
 Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
Kotni funkciji sinus in kosinus
 Kotni funkciji sinus in kosinus Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z oznako cos x, DEFINICIJA V PRAVOKOTNEM TRIKOTNIKU: Kotna funkcija sinus je definirana kot razmerje
Kotni funkciji sinus in kosinus Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z oznako cos x, DEFINICIJA V PRAVOKOTNEM TRIKOTNIKU: Kotna funkcija sinus je definirana kot razmerje
SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK
 SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK
 1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
FAKULTETA ZA STROJNIŠTVO Matematika 4 Pisni izpit 22. junij Navodila
 FAKULTETA ZA STROJNIŠTVO Matematika 4 Pisni izpit 22 junij 212 Ime in priimek: Vpisna št: Navodila Pazljivo preberite besedilo naloge, preden se lotite reševanja Veljale bodo samo rešitve na papirju, kjer
FAKULTETA ZA STROJNIŠTVO Matematika 4 Pisni izpit 22 junij 212 Ime in priimek: Vpisna št: Navodila Pazljivo preberite besedilo naloge, preden se lotite reševanja Veljale bodo samo rešitve na papirju, kjer
Integralni račun. Nedoločeni integral in integracijske metrode. 1. Izračunaj naslednje nedoločene integrale: (a) dx. (b) x 3 +3+x 2 dx, (c) (d)
 Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
UPOR NA PADANJE SONDE V ZRAKU
 UPOR NA PADANJE SONDE V ZRAKU 1. Hitrost in opravljena pot sonde pri padanju v zraku Za padanje v zraku je odgovorna sila teže. Poleg sile teže na padajoče telo deluje tudi sila vzgona, ki je enaka teži
UPOR NA PADANJE SONDE V ZRAKU 1. Hitrost in opravljena pot sonde pri padanju v zraku Za padanje v zraku je odgovorna sila teže. Poleg sile teže na padajoče telo deluje tudi sila vzgona, ki je enaka teži
11. Vaja: BODEJEV DIAGRAM
 . Vaja: BODEJEV DIAGRAM. Bodejev diagram sestavljata dva grafa: a) amplitudno frekvenčni diagram in b) fazno frekvenčni diagram Decibel je enota za razmerje dveh veličin. Definicija: B B 0log0 A A db Bodejeve
. Vaja: BODEJEV DIAGRAM. Bodejev diagram sestavljata dva grafa: a) amplitudno frekvenčni diagram in b) fazno frekvenčni diagram Decibel je enota za razmerje dveh veličin. Definicija: B B 0log0 A A db Bodejeve
13. Jacobijeva metoda za računanje singularnega razcepa
 13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
Navadne diferencialne enačbe
 Navadne diferencialne enačbe Navadne diferencialne enačbe prvega reda V celotnem poglavju bo y = dy dx. Diferencialne enačbe z ločljivima spremeljivkama Diferencialna enačba z ločljivima spremeljivkama
Navadne diferencialne enačbe Navadne diferencialne enačbe prvega reda V celotnem poglavju bo y = dy dx. Diferencialne enačbe z ločljivima spremeljivkama Diferencialna enačba z ločljivima spremeljivkama
Slika 1: Hitrost razširjanja motnje v napeti vrvi
 Študijsko gradivo za študente kemijske tehnologije: FIZIKA Mehanika (valovanje) - B. Borštnik 1 F n F vdt cdt Slika 1: Hitrost razširjanja motnje v napeti vrvi F Valovanje Mehansko valovanje Naštejmo nekaj
Študijsko gradivo za študente kemijske tehnologije: FIZIKA Mehanika (valovanje) - B. Borštnik 1 F n F vdt cdt Slika 1: Hitrost razširjanja motnje v napeti vrvi F Valovanje Mehansko valovanje Naštejmo nekaj
cot x ni def. 3 1 KOTNE FUNKCIJE POLJUBNO VELIKEGA KOTA (A) Merske enote stopinja [ ] radian [rad] 1. Izrazi kot v radianih.
![cot x ni def. 3 1 KOTNE FUNKCIJE POLJUBNO VELIKEGA KOTA (A) Merske enote stopinja [ ] radian [rad] 1. Izrazi kot v radianih. cot x ni def. 3 1 KOTNE FUNKCIJE POLJUBNO VELIKEGA KOTA (A) Merske enote stopinja [ ] radian [rad] 1. Izrazi kot v radianih.](/thumbs/72/66438140.jpg) TRIGONOMETRIJA (A) Merske enote KOTNE FUNKCIJE POLJUBNO VELIKEGA KOTA stopinja [ ] radian [rad] 80 80 0. Izrazi kot v radianih. 0 90 5 0 0 70. Izrazi kot v stopinjah. 5 8 5 (B) Definicija kotnih funkcij
TRIGONOMETRIJA (A) Merske enote KOTNE FUNKCIJE POLJUBNO VELIKEGA KOTA stopinja [ ] radian [rad] 80 80 0. Izrazi kot v radianih. 0 90 5 0 0 70. Izrazi kot v stopinjah. 5 8 5 (B) Definicija kotnih funkcij
Poglavje 7. Poglavje 7. Poglavje 7. Regulacijski sistemi. Regulacijski sistemi. Slika 7. 1: Normirana blokovna shema regulacije EM
 Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
Kvadratne forme. Poglavje XI. 1 Definicija in osnovne lastnosti
 Poglavje XI Kvadratne forme V zadnjem poglavju si bomo ogledali še eno vrsto preslikav, ki jih tudi lahko podamo z matrikami. To so tako imenovane kvadratne forme, ki niso več linearne preslikave. Kvadratne
Poglavje XI Kvadratne forme V zadnjem poglavju si bomo ogledali še eno vrsto preslikav, ki jih tudi lahko podamo z matrikami. To so tako imenovane kvadratne forme, ki niso več linearne preslikave. Kvadratne
Fazni diagram binarne tekočine
 Fazni diagram binarne tekočine Žiga Kos 5. junij 203 Binarno tekočino predstavljajo delci A in B. Ti se med seboj lahko mešajo v različnih razmerjih. V nalogi želimo izračunati fazni diagram take tekočine,
Fazni diagram binarne tekočine Žiga Kos 5. junij 203 Binarno tekočino predstavljajo delci A in B. Ti se med seboj lahko mešajo v različnih razmerjih. V nalogi želimo izračunati fazni diagram take tekočine,
DUŠENO NIHANJE IN RESONANCA
 Politehnika Nova Gorica Šola za znanosti o okolju Univerzitetni študijski program OKOLJE Seminarska naloga DUŠENO NIHANJE IN RESONANCA Mentor: Doc.dr. Iztok Arčon Avtor: Nastja Tomšič Razred: 1.letnik
Politehnika Nova Gorica Šola za znanosti o okolju Univerzitetni študijski program OKOLJE Seminarska naloga DUŠENO NIHANJE IN RESONANCA Mentor: Doc.dr. Iztok Arčon Avtor: Nastja Tomšič Razred: 1.letnik
SEMINARSKA NALOGA Funkciji sin(x) in cos(x)
 FAKULTETA ZA MATEMATIKO IN FIZIKO Praktična Matematika-VSŠ(BO) Komuniciranje v matematiki SEMINARSKA NALOGA Funkciji sin(x) in cos(x) Avtorica: Špela Marinčič Ljubljana, maj 2011 KAZALO: 1.Uvod...1 2.
FAKULTETA ZA MATEMATIKO IN FIZIKO Praktična Matematika-VSŠ(BO) Komuniciranje v matematiki SEMINARSKA NALOGA Funkciji sin(x) in cos(x) Avtorica: Špela Marinčič Ljubljana, maj 2011 KAZALO: 1.Uvod...1 2.
1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου...
 ΑΠΟΖΗΜΙΩΣΗ ΘΥΜΑΤΩΝ ΕΓΚΛΗΜΑΤΙΚΩΝ ΠΡΑΞΕΩΝ ΣΛΟΒΕΝΙΑ 1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου... 3 1 1. Έντυπα αιτήσεων
ΑΠΟΖΗΜΙΩΣΗ ΘΥΜΑΤΩΝ ΕΓΚΛΗΜΑΤΙΚΩΝ ΠΡΑΞΕΩΝ ΣΛΟΒΕΝΙΑ 1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου... 3 1 1. Έντυπα αιτήσεων
Oddelek za fiziko. Seminar 4. Akustika flavte. Mihael Gojkošek Astronomsko-geofizikalna smer. Mentor: dr. Daniel Svenšek
 Oddelek za fiziko Seminar 4 Akustika flavte Mihael Gojkošek Astronomsko-geofizikalna smer Mentor: dr. Daniel Svenšek 22. maj 2009 Kazalo 1 Povzetek 2 2 Kratka zgodovina razvoja flavte 3 3 Kaj se pravzaprav
Oddelek za fiziko Seminar 4 Akustika flavte Mihael Gojkošek Astronomsko-geofizikalna smer Mentor: dr. Daniel Svenšek 22. maj 2009 Kazalo 1 Povzetek 2 2 Kratka zgodovina razvoja flavte 3 3 Kaj se pravzaprav
D f, Z f. Lastnosti. Linearna funkcija. Definicija Linearna funkcija f : je definirana s predpisom f(x) = kx+n; k,
 Linearna funkcija Linearna funkcija f : je definirana s predpisom f(x) = kx+n; k, n ᄀ. k smerni koeficient n začetna vrednost D f, Z f Definicijsko območje linearne funkcije so vsa realna števila. Zaloga
Linearna funkcija Linearna funkcija f : je definirana s predpisom f(x) = kx+n; k, n ᄀ. k smerni koeficient n začetna vrednost D f, Z f Definicijsko območje linearne funkcije so vsa realna števila. Zaloga
Podobnost matrik. Matematika II (FKKT Kemijsko inženirstvo) Diagonalizacija matrik
 Podobnost matrik Matematika II (FKKT Kemijsko inženirstvo) Matjaž Željko FKKT Kemijsko inženirstvo 14 teden (Zadnja sprememba: 23 maj 213) Matrika A R n n je podobna matriki B R n n, če obstaja obrnljiva
Podobnost matrik Matematika II (FKKT Kemijsko inženirstvo) Matjaž Željko FKKT Kemijsko inženirstvo 14 teden (Zadnja sprememba: 23 maj 213) Matrika A R n n je podobna matriki B R n n, če obstaja obrnljiva
Matematika vaja. Matematika FE, Ljubljana, Slovenija Fakulteta za Elektrotehniko 1000 Ljubljana, Tržaška 25, Slovenija
 Matematika 1 3. vaja B. Jurčič Zlobec 1 1 Univerza v Ljubljani, Fakulteta za Elektrotehniko 1000 Ljubljana, Tržaška 25, Slovenija Matematika FE, Ljubljana, Slovenija 2011 Določi stekališča zaporedja a
Matematika 1 3. vaja B. Jurčič Zlobec 1 1 Univerza v Ljubljani, Fakulteta za Elektrotehniko 1000 Ljubljana, Tržaška 25, Slovenija Matematika FE, Ljubljana, Slovenija 2011 Določi stekališča zaporedja a
Tokovi v naravoslovju za 6. razred
 Tokovi v naravoslovju za 6. razred Bojan Golli in Nada Razpet PeF Ljubljana 7. december 2007 Kazalo 1 Fizikalne osnove 2 1.1 Energija in informacija............................... 3 2 Projekti iz fizike
Tokovi v naravoslovju za 6. razred Bojan Golli in Nada Razpet PeF Ljubljana 7. december 2007 Kazalo 1 Fizikalne osnove 2 1.1 Energija in informacija............................... 3 2 Projekti iz fizike
Matematika I (VS) Univerza v Ljubljani, FE. Melita Hajdinjak 2013/14. Pregled elementarnih funkcij. Potenčna funkcija. Korenska funkcija.
 1 / 46 Univerza v Ljubljani, FE Potenčna Korenska Melita Hajdinjak Matematika I (VS) Kotne 013/14 / 46 Potenčna Potenčna Funkcijo oblike f() = n, kjer je n Z, imenujemo potenčna. Število n imenujemo eksponent.
1 / 46 Univerza v Ljubljani, FE Potenčna Korenska Melita Hajdinjak Matematika I (VS) Kotne 013/14 / 46 Potenčna Potenčna Funkcijo oblike f() = n, kjer je n Z, imenujemo potenčna. Število n imenujemo eksponent.
Domače naloge za 2. kolokvij iz ANALIZE 2b VEKTORSKA ANALIZA
 Domače naloge za 2. kolokvij iz ANALIZE 2b VEKTORSKA ANALIZA. Naj bo vektorsko polje R : R 3 R 3 dano s predpisom R(x, y, z) = (2x 2 + z 2, xy + 2yz, z). Izračunaj pretok polja R skozi površino torusa
Domače naloge za 2. kolokvij iz ANALIZE 2b VEKTORSKA ANALIZA. Naj bo vektorsko polje R : R 3 R 3 dano s predpisom R(x, y, z) = (2x 2 + z 2, xy + 2yz, z). Izračunaj pretok polja R skozi površino torusa
Iterativno reševanje sistemov linearnih enačb. Numerične metode, sistemi linearnih enačb. Numerične metode FE, 2. december 2013
 Numerične metode, sistemi linearnih enačb B. Jurčič Zlobec Numerične metode FE, 2. december 2013 1 Vsebina 1 z n neznankami. a i1 x 1 + a i2 x 2 + + a in = b i i = 1,..., n V matrični obliki zapišemo:
Numerične metode, sistemi linearnih enačb B. Jurčič Zlobec Numerične metode FE, 2. december 2013 1 Vsebina 1 z n neznankami. a i1 x 1 + a i2 x 2 + + a in = b i i = 1,..., n V matrični obliki zapišemo:
Univerza v Novi Gorici Fakulteta za znanosti o okolju Okolje (I. stopnja) Meteorologija 2013/2014. Energijska bilanca pregled
 Univerza v Novi Gorici Fakulteta za znanosti o okolu Okole (I. stopna) Meteorologia 013/014 Energiska bilanca pregled 1 Osnovni pomi energiski tok: P [W = J/s] gostota energiskega toka: [W/m ] toplota:q
Univerza v Novi Gorici Fakulteta za znanosti o okolu Okole (I. stopna) Meteorologia 013/014 Energiska bilanca pregled 1 Osnovni pomi energiski tok: P [W = J/s] gostota energiskega toka: [W/m ] toplota:q
Matematične metode v fiziki II. B. Golli, PeF
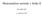 Matematične metode v fiziki II B. Golli, PeF 8. september 2014 2 Kazalo 1 Navadne diferencialne enačbe (NDE) 5 1.1 Uvod.............................................. 5 1.1.1 Diferencialne enačbe v fiziki.............................
Matematične metode v fiziki II B. Golli, PeF 8. september 2014 2 Kazalo 1 Navadne diferencialne enačbe (NDE) 5 1.1 Uvod.............................................. 5 1.1.1 Diferencialne enačbe v fiziki.............................
PROCESIRANJE SIGNALOV
 Rešive pisega izpia PROCESIRANJE SIGNALOV Daum: 7... aloga Kolikša je ampliuda reje harmoske kompoee arisaega periodičega sigala? f() - -3 - - 3 Rešiev: Časova fukcija a iervalu ( /,/) je lieara fukcija:
Rešive pisega izpia PROCESIRANJE SIGNALOV Daum: 7... aloga Kolikša je ampliuda reje harmoske kompoee arisaega periodičega sigala? f() - -3 - - 3 Rešiev: Časova fukcija a iervalu ( /,/) je lieara fukcija:
Vaje iz MATEMATIKE 8. Odvod funkcije., pravimo, da je funkcija f odvedljiva v točki x 0 z odvodom. f (x f(x 0 + h) f(x 0 ) 0 ) := lim
 Študij AHITEKTURE IN URBANIZMA, šol l 06/7 Vaje iz MATEMATIKE 8 Odvod funkcije f( Definicija: Naj bo f definirana na neki okolici točke 0 Če obstaja lim 0 +h f( 0 h 0 h, pravimo, da je funkcija f odvedljiva
Študij AHITEKTURE IN URBANIZMA, šol l 06/7 Vaje iz MATEMATIKE 8 Odvod funkcije f( Definicija: Naj bo f definirana na neki okolici točke 0 Če obstaja lim 0 +h f( 0 h 0 h, pravimo, da je funkcija f odvedljiva
Zaporedna in vzporedna feroresonanca
 Visokonapetostna tehnika Zaporedna in vzporedna feroresonanca delovanje regulacijskega stikala T3 174 kv Vaja 9 1 Osnovni pogoji za nastanek feroresonance L C U U L () U C () U L = U L () U C = ωc V vezju
Visokonapetostna tehnika Zaporedna in vzporedna feroresonanca delovanje regulacijskega stikala T3 174 kv Vaja 9 1 Osnovni pogoji za nastanek feroresonance L C U U L () U C () U L = U L () U C = ωc V vezju
Odvode odvisnih spremenljivk po neodvisni spremenljivki bomo označevali s piko: Sistem navadnih diferencialnih enačb prvega reda ima obliko:
 4 Sisemi diferencialnih enačb V prakičnih primerih večkra naleimo na več diferencialnih enačb, ki opisujejo določen pojav in so medsebojno povezane edaj govorimo o sisemih diferencialnih enačb V eh enačbah
4 Sisemi diferencialnih enačb V prakičnih primerih večkra naleimo na več diferencialnih enačb, ki opisujejo določen pojav in so medsebojno povezane edaj govorimo o sisemih diferencialnih enačb V eh enačbah
1 Fibonaccijeva stevila
 1 Fibonaccijeva stevila Fibonaccijevo število F n, kjer je n N, lahko definiramo kot število načinov zapisa števila n kot vsoto sumandov, enakih 1 ali Na primer, število 4 lahko zapišemo v obliki naslednjih
1 Fibonaccijeva stevila Fibonaccijevo število F n, kjer je n N, lahko definiramo kot število načinov zapisa števila n kot vsoto sumandov, enakih 1 ali Na primer, število 4 lahko zapišemo v obliki naslednjih
7. VAJA IZ MEHANIKE TRDNIH TELES. (tenzor deformacij II) (tenzor majhnih deformacij in rotacij, kompatibilitetni pogoji)
 7. VAJA IZ MEHANIKE TRDNIH TELES (tenzor deformacij II) (tenzor majhnih deformacij in rotacij, kompatibilitetni pogoji) NALOGA 1: Pomik deformabilnega telesa je glede na kartezijski koordinatni sistem
7. VAJA IZ MEHANIKE TRDNIH TELES (tenzor deformacij II) (tenzor majhnih deformacij in rotacij, kompatibilitetni pogoji) NALOGA 1: Pomik deformabilnega telesa je glede na kartezijski koordinatni sistem
MERITVE LABORATORIJSKE VAJE
 UNIVERZA V MARIBORU FAKULTETA ZA ELEKTROTEHNIKO, RAČUNALNIŠTVO IN INFORMATIKO 000 Maribor, Smetanova ul. 17 Študijsko leto: 011/01 Skupina: 9. MERITVE LABORATORIJSKE VAJE Vaja št.: 10.1 Merjenje z digitalnim
UNIVERZA V MARIBORU FAKULTETA ZA ELEKTROTEHNIKO, RAČUNALNIŠTVO IN INFORMATIKO 000 Maribor, Smetanova ul. 17 Študijsko leto: 011/01 Skupina: 9. MERITVE LABORATORIJSKE VAJE Vaja št.: 10.1 Merjenje z digitalnim
POROČILO 3.VAJA DOLOČANJE REZULTANTE SIL
 POROČILO 3.VAJA DOLOČANJE REZULTANTE SIL Izdba aje: Ljubjana, 11. 1. 007, 10.00 Jan OMAHNE, 1.M Namen: 1.Preeri paraeogramsko praio za doočanje rezutante nezporedni si s skupnim prijemaiščem (grafično)..dooči
POROČILO 3.VAJA DOLOČANJE REZULTANTE SIL Izdba aje: Ljubjana, 11. 1. 007, 10.00 Jan OMAHNE, 1.M Namen: 1.Preeri paraeogramsko praio za doočanje rezutante nezporedni si s skupnim prijemaiščem (grafično)..dooči
Električne lastnosti vodov. Ohmske upornosti. Induktivnost vodov. Kapacitivnost vodov. Odvodnost vodov. Vod v svetlobi telegrafske enačbe.
 Električne lastnosti vodov Ohmske upornosti. Induktivnost vodov. Kapacitivnost vodov. Odvodnost vodov. Vod v svetlobi telegrafske enačbe. Primarne konstante vodov Če opazujemo električni vod iz istega
Električne lastnosti vodov Ohmske upornosti. Induktivnost vodov. Kapacitivnost vodov. Odvodnost vodov. Vod v svetlobi telegrafske enačbe. Primarne konstante vodov Če opazujemo električni vod iz istega
V tem poglavju bomo vpeljali pojem determinante matrike, spoznali bomo njene lastnosti in nekaj metod za računanje determinant.
 Poglavje IV Determinanta matrike V tem poglavju bomo vpeljali pojem determinante matrike, spoznali bomo njene lastnosti in nekaj metod za računanje determinant 1 Definicija Preden definiramo determinanto,
Poglavje IV Determinanta matrike V tem poglavju bomo vpeljali pojem determinante matrike, spoznali bomo njene lastnosti in nekaj metod za računanje determinant 1 Definicija Preden definiramo determinanto,
p 1 ENTROPIJSKI ZAKON
 ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
Navadne diferencialne enačbe
 Navadne diferencialne enačbe (študijsko gradivo) Matija Cencelj 1. maja 2003 2 Kazalo 1 Uvod 5 1.1 Preprosti primeri......................... 8 2 Diferencialne enačbe prvega reda 11 2.1 Ločljivi spremenljivki.......................
Navadne diferencialne enačbe (študijsko gradivo) Matija Cencelj 1. maja 2003 2 Kazalo 1 Uvod 5 1.1 Preprosti primeri......................... 8 2 Diferencialne enačbe prvega reda 11 2.1 Ločljivi spremenljivki.......................
Tabele termodinamskih lastnosti vode in vodne pare
 Univerza v Ljubljani Fakulteta za strojništvo Laboratorij za termoenergetiko Tabele termodinamskih lastnosti vode in vodne pare po modelu IAPWS IF-97 izračunano z XSteam Excel v2.6 Magnus Holmgren, xsteam.sourceforge.net
Univerza v Ljubljani Fakulteta za strojništvo Laboratorij za termoenergetiko Tabele termodinamskih lastnosti vode in vodne pare po modelu IAPWS IF-97 izračunano z XSteam Excel v2.6 Magnus Holmgren, xsteam.sourceforge.net
primer reševanja volumskega mehanskega problema z MKE
 Reševanje mehanskih problemov z MKE primer reševanja volumskega mehanskega problema z MKE p p RAK: P-XII//74 Reševanje mehanskih problemov z MKE primer reševanja volumskega mehanskega problema z MKE L
Reševanje mehanskih problemov z MKE primer reševanja volumskega mehanskega problema z MKE p p RAK: P-XII//74 Reševanje mehanskih problemov z MKE primer reševanja volumskega mehanskega problema z MKE L
Osnove matematične analize 2016/17
 Osnove matematične analize 216/17 Neža Mramor Kosta Fakulteta za računalništvo in informatiko Univerza v Ljubljani Kaj je funkcija? Funkcija je predpis, ki vsakemu elementu x iz definicijskega območja
Osnove matematične analize 216/17 Neža Mramor Kosta Fakulteta za računalništvo in informatiko Univerza v Ljubljani Kaj je funkcija? Funkcija je predpis, ki vsakemu elementu x iz definicijskega območja
Če je električni tok konstanten (se ne spreminja s časom), poenostavimo enačbo (1) in dobimo enačbo (2):
 ELEKTRIČNI TOK TEOR IJA 1. Definicija enote električnega toka Električni tok je gibanje električno nabitih delcev v trdnih snoveh (kovine, polprevodniki), tekočinah ali plinih. V kovinah se gibljejo prosti
ELEKTRIČNI TOK TEOR IJA 1. Definicija enote električnega toka Električni tok je gibanje električno nabitih delcev v trdnih snoveh (kovine, polprevodniki), tekočinah ali plinih. V kovinah se gibljejo prosti
Naloge iz vaj: Sistem togih teles C 2 C 1 F A 1 B 1. Slika 1: Sile na levi in desni lok.
 1 Rešene naloge Naloge iz vaj: Sistem togih teles 1. Tročleni lok s polmerom R sestavljen iz lokov in je obremenjen tako kot kaže skica. Določi sile podpor. Rešitev: Lok razdelimo na dva loka, glej skico.
1 Rešene naloge Naloge iz vaj: Sistem togih teles 1. Tročleni lok s polmerom R sestavljen iz lokov in je obremenjen tako kot kaže skica. Določi sile podpor. Rešitev: Lok razdelimo na dva loka, glej skico.
Matematično modeliranje 3. poglavje Dinamično modeliranje: diferencialne enačbe, sistemi diferencialnih enačb
 Matematično modeliranje 3. poglavje Dinamično modeliranje: diferencialne enačbe, sistemi diferencialnih enačb Fakulteta za računalništvo in informatiko Univerza v Ljubljani 2017/2018 Za kaj rabimo diferencialne
Matematično modeliranje 3. poglavje Dinamično modeliranje: diferencialne enačbe, sistemi diferencialnih enačb Fakulteta za računalništvo in informatiko Univerza v Ljubljani 2017/2018 Za kaj rabimo diferencialne
Kotne funkcije poljubnega kota. Osnovne zveze med funkcijamo istega kota. Uporaba kotnih funkcij v poljubnem trikotniku. Kosinusni in sinusni izrek.
 DN#3 (januar 2018) 3A Teme, ki jih preverja domača naloga: Kotne funkcije poljubnega kota. Osnovne zveze med funkcijamo istega kota. Uporaba kotnih funkcij v poljubnem trikotniku. Kosinusni in sinusni
DN#3 (januar 2018) 3A Teme, ki jih preverja domača naloga: Kotne funkcije poljubnega kota. Osnovne zveze med funkcijamo istega kota. Uporaba kotnih funkcij v poljubnem trikotniku. Kosinusni in sinusni
Slika 5: Sile na svetilko, ki je obešena na žici.
 4. poglavje: Sile 5. Cestna svetilka visi na sredi 10 m dolge žice, ki je napeta čez cesto. Zaradi teže svetilke (30 N) se žica za toliko povesi, da pride sredina za 30 cm niže kot oba konca. Kako močno
4. poglavje: Sile 5. Cestna svetilka visi na sredi 10 m dolge žice, ki je napeta čez cesto. Zaradi teže svetilke (30 N) se žica za toliko povesi, da pride sredina za 30 cm niže kot oba konca. Kako močno
Dragi polinom, kje so tvoje ničle?
 1 Dragi polinom, kje so tvoje ničle? Vito Vitrih FAMNIT - Izlet v matematično vesolje 17. december 2010 Polinomi: 2 Polinom stopnje n je funkcija p(x) = a n x n + a n 1 x n 1 +... + a 1 x + a 0, a i R.
1 Dragi polinom, kje so tvoje ničle? Vito Vitrih FAMNIT - Izlet v matematično vesolje 17. december 2010 Polinomi: 2 Polinom stopnje n je funkcija p(x) = a n x n + a n 1 x n 1 +... + a 1 x + a 0, a i R.
Funkcija je predpis, ki vsakemu elementu x iz definicijskega območja D R priredi neko število f (x) R.
 II. FUNKCIJE 1. Osnovni pojmi 2. Sestavljanje funkcij 3. Pregled elementarnih funkcij 4. Zveznost Kaj je funkcija? Definicija Funkcija je predpis, ki vsakemu elementu x iz definicijskega območja D R priredi
II. FUNKCIJE 1. Osnovni pojmi 2. Sestavljanje funkcij 3. Pregled elementarnih funkcij 4. Zveznost Kaj je funkcija? Definicija Funkcija je predpis, ki vsakemu elementu x iz definicijskega območja D R priredi
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
