Matematično modeliranje 3. poglavje Dinamično modeliranje: diferencialne enačbe, sistemi diferencialnih enačb
|
|
|
- ψυχή Θεοδωρίδης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Matematično modeliranje 3. poglavje Dinamično modeliranje: diferencialne enačbe, sistemi diferencialnih enačb Fakulteta za računalništvo in informatiko Univerza v Ljubljani 2017/2018 Za kaj rabimo diferencialne enačbe? Z diferencialnimi enačbami opišemo deterministične procese: nek znan zakon določa zvezo med neko količino, ki je odvisna od ene spremenljivke (na primer od časa), in pa hitrostjo (pospeškom,... ) njenega spreminjanja. Če je odvisnih spremenljvik več, dobimo sistem diferencialnih enačb. Z diferencialno enačbo zapišemo fizikalne, kemijske, informacijske,... zakone, z njimi modeliramo obnašanja kompleksnih sistemov v ekonomiji, ekologiji, medicini,... Obravnavali bomo navadne diferencialne enačbe in sisteme: neodvisna spremenljivka je ena sama, na primer čas (ne pa parcialnih diferencialnih enačb, kjer je neodvisnih spremenljivk več).
2 Diferencialna enačba reda n: F (x, y, y,..., y (n) ) = 0 Rešitev diferencialne enačbe reda n je funkcija y = y(x), ki je vsaj n krat odvedljiva zadošča identiteti F (x, y(x), y (x),..., y (n) (x)) = 0 za vsak x. Primeri Toplotni zakon: T (t) je temperatura homogenega telesa (pločevinke piva) ob času t, T 0 začetna temperatura ob času t 0 = 0, T tmeperatura okolja, k konstanta (toplotna prevodnost) T = k(t T ) Radioaktivni razpad: y(t) količina radioaktivnega izotopa ob času t, t 1/2 razpolovni čas: ẏ(t) = ky(t), k = log 2 t 1/2 Radiometrično datiranje (carbon dating): (Willard Libby, 1949, Nobelova nagrada za kemijo 1960) določanje starosti organskih izkopanin na podlagi razmerja med nestabilnim izotopom C 14 stabilnim C 12.
3 Primer: navpični met Žogico z maso 1kg vržemo v zrak z začetno hitrostjo v 0 = 25 m/s in počakamo, da pade na tla ob predpostavki, da zračnega upora ni, ob predpostavki, da velja linearni zakon upora: F u = kv. Vprašanje: Ali bo dlje letela navzgor ali navzdol? Primerjava Enačba Hitrost in pot žoge Rešitev ma = F g v = 10 v(t) = t + 25 x(t) = t 2 /2 + 25t ma = F u F g v = v 10 v(t) = 10(1 e t ) x(t) =...
4 Diferencialna enačba 1. reda y = f (x, y) Spološna rešitev: enoparametrična družina funkcij y = y(x, C). Začetni problem je diferencialna enačba skupaj z začetnim pogojem: y = f (x, y), y(x 0 ) = y 0 Partikularna rešitev je funkcija iz splošne rešitve, ki reši začetni problem. Singularna rešitev: posebna rešitev, ki ne spada v splošno rešitev. Velika večina diferencialnih enačb analitično ni rešljivih! Linearna DE 1. reda y + f (x)y = g(x) Splošna rešitev je vsota y(x) = y p (x) + Cy h (x), kjer je y p ena partikularna rešitev, Cy h pa splošna rešitve homogene enačbe. Partikularno rešitev dobimo z variacijo konstante, tj. z nastavko, y p = C(x)y h, kjer C ni več konstanta ampak neznana funkcija. Primer: x 2 y + xy = 1, y(1) = 2
5 Grafično reševanje Diferencialna enačba y = f (x, y) v vsaki točki (x, y) iz definicijskega območja funkcije f (x, y) določa smer, v kateri gre rešitev enačbe skozi to točko. Dobimo polje smeri. Splošna rešitev je družina krivulj, ki ustreza temu polju: skozi vsako točko gre natanko ena krivulja y = y(x), ki ima tangento v smeri, predpisani s poljem smeri. Partikularna rešitev je krivulja iz te družine, ki gre skozi eno konkretno točko (x 0, y 0 ), tj. zadošča začetnemu pogoju y(x 0 ) = y 0. Primer: zakoni rasti y(t) je velikost populacije (na primer zajcev ali bakterij) ob času t. Naravna rast: ẏ = ky Rast z omejitvami: ẏ = ky(1 y/y max ) (logistični zakon), y max je kapaciteta okolja, tj. maksimalna populacija, ki se lahko v njem vzdržuje Splošni model ẏ = k(y, t)f (y), ta enačba je analitično rešljiva samo v zelo posebnih primerih
6 y = ky y = ky(1 y) Numerično reševanje Za začetni problem y = f (x, y), y(x 0 ) = y 0 namesto funkcije y(x) iščemo zaporedje približkov y i = y(x i ) za točke na rešitvi, kjer je x i = x 0 + ih in h korak. Obstaja cela vrsta numeričnih metod za reševanje začetnih problemov za diferencialne enačbe 1. reda in sisteme diferencialnih enačb 1. reda.
7 Eulerjeva metoda Najbolj logična in preprosta metoda. Na vsakem koraku naslednjo točko (x i+1, y i+1 ) dobimo tako se za h pomaknemo vzdolž tangente na rešitev skozi (x i, y i ), i = 0,..., i m ax: začetni približek: (x 0, y 0 ) za vsak i > 0 je: x i+1 = x i + h, y i+1 = y i + hf (x i, y i ). Točka (x i+1, y i+1 ) leži na drugi partikularni rešitvi kot (x i, y i ): napaka na vsakem koraku je reda O(h 2 ). Kumulativna napaka z vsakim korakom narašča. Metoda Runge-Kutta Precej bolj natančna, zelo popularna metoda: začetni približek: (x 0, y 0 ) za vsak i > 0 je kjer je x i+1 = x i + h, y i+1 = y i + (k 1 + 2k 2 + 2k 3 + k 4 )/6, k 1 = hf (x i, y i ), k2 = hf (x i + h/2, y i + k 1 /2), k3 = hf (x i + h/2, y i + k 2 /2) in k4 = h f (x i + h, y i + k 3 ) Napaka je precej manjša kot pri Eulerjevi metodi: na vsakem koraku je reda O(h 2 ), kumulativna napaka pa je reda O(h 4 ).
8 Primerjava Rešujemo diferencialno enačbo y = y 1, y(0) = 1, korak je h = 0.3 Rdeča krivulja je prava rešitev y = 2e x 1. Eulerjeva metoda Runge-Kutta Obstoj rešitve Začetni problem y = f (x, y), y(x 0 ) = y 0, kjer je funkcija f (x, y) zvezna in parcialno odvedljiva na y na kvadratu [x 0 a, x 0 + a] [y 0 b, y 0 + b] ima natanko eno rešitev y(x), definirano vsaj za x na intervalu [x 0 α, x 0 + α], kjer je 0 < α a. (Obstajajo boljše ocene... ).
9 Sistemi DE 1. reda Iščemo funkcijo x(t) = (x 1 (t),..., x n (t)), ki zadošča enačbi x = f ( x, t) Izpisano: ẋ 1 = f 1 (x 1,..., x n, t). ẋ n = f n (x 1,..., x n, t) Splošna rešitev je družina parametriziranih krivulj x(t, C 1,..., C n ). Začetni pogoj: x(t 0 ) = x 0 Sistem DE 1. reda za vsak t določa smer tangente x(t) na rešitev skozi točko x(t). Numerične metode za sisteme Rešujemo sistem x = f ( x, t) z začetnim pogojem x(t 0 ) = x 0. Eulerjeva metoda: t i+1 = t i + h, x i+1 = x i + hf ( x i, t i ), i = 1,..., n 1. Runge Kutta: t i+1 = t i + h, x i+1 = x i + ( k k k 3 + k 4 )/6, kjer je k1 = h f ( x i, t i ), k2 = h f ( x i + k 1 /2, t i + h/2), k 3 = h f ( x i + k 2 /2, t i + h/2), k4 = h f ( x i + k 3, t i + h)
10 Sistem je avtonomen, če je funkcija f neodvisna od t: x = f ( x) Za avtonomne sisteme je smer tangente na rešitev odvisna samo od točke x, od časa t pa je neodvisna. Avtonomen sistem dveh DE 1. reda ẋ = f 1 (x, y), ẏ = f 2 (x, y) določa polje smeri v ravnini (x, y). Točke, kjer je x 0 = 0, so stacionarne točke ali ravnovesna stanja sistema. Rešitev sistema x(t) z začetnim pogojem v stacionarni točki x 0 je konstantna funkcija x(t) = x 0. Primer: model plenilec-plen (predator-prey) Dve populaciji, ki živita skupaj, vzajemno vplivata ena na drugo. Zajci Z(t) imajo dovolj hrane in prostora, volkovi V (t) se hranijo z zajci. Če bi živeli vsak zase, bi za zajce veljal zakon naravne rasti, volkovi pa bi hirali: Z = kz, V = rv, k, r > 0. Skupaj pa, (če zanemarimo vse druge vplive) na zajce slabo vpliva število srečanj z volkovi, na volkove pa dobro vpliva število srečanj z zajci: Z = kz azv, V = rv + bvz, a, b > 0.
11 Z = 0.3Z 0.004ZV V = 0.2V ZV Na levi: polje smeri, stacionarne točke so V = 0, Z = 0 in V = k/a, Z = r/b. Na desni: zaporedje približkov za začetni pogoj Z(0) = 500, V (0) = 50 z Eulerjevo metodo, korak h = Linear systems of 1st order DEs A linear system of DEs is of the form ẋ = A(t)x + f (t), where A(t) is an n n matrix with coefficients possibly depending on t (i.e. function of t), and f : R R n is a function. The system is homogeneous is f (t) = 0, has constant coefficients, if the matrix A is constant, i.e. independent of t. A homogeneous system with constatnt coefficients is an autonomous system.
12 An autonomous linear systems of 1st oredr DEs is of the form or in coordinates: ẋ = Ax ẋ 1 = a 11 x 1 + a 12 x a 1n x n ẋ 2 = a 21 x 1 + a 22 x a 2n x n. ẋ n = a n1 x 1 + a n2 x a nn x n : x(t 0 ) = x 0. Poseben primer: A je diagonalna matrika Naj bo A (realna) diagonalna matrika: ẋ 1 λ x 1. =......, ẋ n 0... λ n x n tj. ẋ 1 = λ 1 x 1. ẋ n = λ n x n. Splošna reštev je C 1 e λ 1t C 2 e λ 2t x(t) =. C n e λ nt = C 1e λ 1t C 2e λ 2t C ne λ nt
13 A ima n lastnih vektorjev Če ima A n linearno neodvisnih lastnih vektorjev v 1,... v n, lahko rešitev x(t) zapišemo kot linearno kombinacijo x(t) = ϕ 1 (t) v ϕ n (t) v n. Iz sistema x = A x, dobimo ϕ 1 (t) v ϕ n (t) v n = ϕ 1 (t)λ 1 v ϕ n (t)ϕ n v n, torej za vsak i velja, da je Splošna rešitev sistema je ϕ i (t) = λ i ϕ i (t), torej ϕ i (t) = C i e λ i t. x(t) = C 1 e λ 1t v C n e λ nt v n. Lastne vrednosti λ i so lahko tudi kompleksna števila, v tem primeru je splošna rešitev izražena v kompleksni obliki. Avtonomni sistemi dveh linearnih diferencialnih enačb ẋ 1 = a 11 x 1 + z 12 x 2, ẋ 2 = a 21 x 1 + a 22 x 2. Točka (0, 0) je edina stacionarna točka sistema. Obnašanje rešitev okrog stacionarne točke je odvisno od lastnih vrednosti in lastnih vektorjev matrike A. Če ima matrika dva linearno neodvisna lastna vektorja v 1 in v 2, je splošna rešitev x(t) = C 1 e λ 1t v 1 + C 2 e λ 2t v 2, Konstanti C 1 in C 2 sta določeni z začetnim pogojem: x 0 = C 1 v 1 + C 2 v 2.
14 Primer 1 ẋ 1 = x 1 + x 2, ẋ 2 = 4x 1 2x 2 x 1 (0) = 0, x 2 (0) = 1 Točka (0, 0) je sedlo. Primer 2 ẋ 1 = 2x 1 + 9x 2, ẋ 2 = 2x 1 7x 2 Točka (0, 0) je točkast ponor.
15 A ima kompleksne lastne vrednosti Poglejmo primer matrike 2 2 z lastnima vrednostma in lastnima vektorjema λ 12 = α ± iβ, v 12 = u ± i w. Splošna rešitev je x(t) = C 1 e (α+iβ)t ( u + i w) + C 2 e (α iβ)t ( u i w) = e αt C 1 (cos(βt) u sin(βt) w) + e αt C 2 (sin(βt) u + cos(βt) w) Primer 3 Nihanje: ẋ = v, v = ω 2 x Točka (0, 0) je center.
16 Klasifikacija stacioanrnih točk Realne lastne vrednosti: točkasti izvor: 0 < λ 1 < λ 2 sedlo: λ 1 < 0 < λ 2 točkasti ponor λ 1 < λ 2 < 0 Konjugirano kompleksni lastni vrednosti Vijačni izvor: 0 < Re(λ) Center: Re(λ) = 0) Vijačni ponor Re(λ) < 0, Smer vretnja vijačnice je: pozitivna, če je Im(λ) > 0 in negativna, če je Im(λ) < 0.
17 Nelinearni sistemi ẋ = f 1 (x, y), ẏ = f 2 (x, y) Stacionarne točke: f 1 (x 0, y 0 ) = f 2 (x 0, y 0 ) = 0. Tip stacionarne točke (x 0, y 0 ) določimo tako, da sistem okrog stacionarne točne lineariziramo: [ (f1 ) L f (x, y) = Df (x 0, y 0 )( r r 0 ) = x (x 0, y 0 ) (f 1 ) y (x 0, y 0 ) (f 2 ) x (x 0, y 0 ) (f 2 ) y (x 0, y 0 ) ] in določimo tip stacionarne točke (0, 0) dobljenega linearnega sistema. Primer ẋ = x xy ẏ = xy y Stacionarni točki: (0, 0) in (1, 1) Linearizacija: [ ẋ ẏ ] = V točki (0, 0) dobimo matriko V točki (1, 1) dobimo matriko [ 1 y x y x 1 [ [ ] ], točka je sedlo. ], točka je center.
18 Poleg stacionarnih točk ima lahko nelinearen sistem 2 2 tudi limitne cikle. Limitni cikel je periodična rešitev (x(t), y(t)) za katero velja, da se vse rešitve z začetnim pogojem v neki njegovi okolici tej rešitvi približujejo, ko gre t (ω-limitni cikel) ali ko gre t (α-limitni cikel). Sistemi več diferencialnih enačb 1. reda imajo bistveno bolj zanimivo dinamiko, poleg stacionarnih točk in limitnih ciklov, se lahko pojavijo še kaotični atraktorji. Diferencialne enačbe 2. reda ẍ = f (t, x, ẋ) Splošna rešitev je dvoparametrična družina funkcij x = x(t, C 1, C 2 ). Začetni pogoj: x(t 0 ) = α 0, ẋ(t 0 ) = α 1 Robni pogoj: x(a) = x 0, x(b) = x 1.
19 Diferencialna enačba reda n x (n) = f (t, x, ẋ,..., x (n 1) ) Splošna rešitev je n-parametrična družina fukcij x = x(t, C 1,..., C n ). Partikularna rešitev je določena z začetnim pogojem: x(t 0 ) = α 0,... x (n 1) (t 0 ) = α n 1 ali robnimi pogoji: vrednosti funkcije ali odvodov v različnih točkah. Prevedba na sistem Diferencialni enačbi ẍ = f (t, x, ẋ) lahko priredimo sistem dveh diferencialnih enačb 1. reda: Začetni pogoj [ ẋ v ] [ = v f (x, v, t) ] x(t 0 ) = α 0, ẋ(t 0 ) = α 1 se pri tem prevede na začetni pogoj [ ] x(t0 ) = v(t 0 ) Z robnimi pogoji so težave... [ α0 α 1 ].
20 Podobno lahko vsaki diferencialni enačbi reda n x (n) = f (t, x, ẋ,..., x (n 1) ) priredimo sistem n diferencialnih enačb 1. reda, tako da vpeljemo nove odvisne spremenljivke x 1 = x, x 2 = ẋ,..., x n = x (n 1) in zanje dobimo sistem ẋ 1 ẋ 2. ẋ n = x 2 x 3. f (x, v, t). Linearna DE reda n Homogena: x (n) + a 1 (t)x (n 1) + + a n (t)x = 0 Nehomogena: Začetni pogoj: Robni pogoji: x (n) + a 1 (t)x (n 1) + + a n (t)x = f (t) x(t 0 ) = α 0, ẋ(t 0 ) = α 1,..., x (n 1) (t 0 ) = α n vrednosti funkcije ali odvodov v različnih točkah.
21 Homogena LDE Če sta x 1 in x 2 rešitvi, je tudi poljubna linearna kombinacija C 1 x 1 + C 2 x 2 rešitev. Splošna rešitev je množica vseh linearnih kombinacij y = C 1 x C n x n n različnih linearno neodvisnih rešitev. Če so funkcije a 1 (t),..., a n (t) zvezne, obstaja za poljubne vrednosti α 0,..., α n natanko ena rešitev, ki zadošča začetnemu pogoju x(t 0 ) = α 0, ẋ(t 0 ) = α 1,..., x (n 1) (t 0 ) = α n. Homogena LDE 2. reda s konstantnimi koeficienti aẍ + bẋ + cx = 0 Rešitev je funkcija oblike x = e λt, kjer je λ rešitev kvadratne karakteristične enačbe aλ 2 + bλ + c = 0. Splošna rešitev je linearna kombinacija C 1 x 1 + C 2 x 2, kjer je 1. x 1 = e λ 1t in x 2 = e λ 2t, če ima karakteristična enačba dve realni rešitvi, 2. x 1 = e αt cos βt in x 2 = e αt sin βt, če ima karakteristična enačba kompleksen par rešitev λ 12 = α ± iβ, 3. x 1 = e λt, x 2 = te λt, če ima karakteristična enačba eno dvojno realno rešitev. Homogeni LDE s konstantnimi koeficienti ustreza avtonomen linearen sistem 1. reda.
22 Lastno nihanje Nihanje brez upora: mẍ + kx = 0, m, k > 0, karakterističan enačba mλ 2 + k = 0 ima rešitve λ = ±ωi, ω 2 = k/m, splošna rešitev x(t) = C 1 cos ωt + C 2 sin ωt. Rešitve so periodične s periodo ω. V fazni ravnini (x, v) je stacionarna točka (0, 0) center. Nihanje z uporom: mẍ + βẋ + kx = 0 Ločimo tri primere predušeno nihanje, D = β 2 4km > 0: x(t) = C 1 e λ 1t + C 2 e λ 2t, λ 12 < 0, nihalo drsi proti stabilni legi, kritično dušeno, D = 0: x(t) = C 1 e λt + C 2 te λt, λ < 0, drsalo po enem nihaju drsi proti stabilni legi, dušeno nihanje, D > 0, x(t) = e αt (C 1 cos βt + C 2 sin βt). V fazni ravnini (0, 0) je prvih dveh primerih je točka (0, 0) ponor, v zadnjem pa je vijačni ponor.
23 Nehomogena LDE Če sta x 1 in x 2 rešitvi nehomogene enačbe, je razlika x 1 x 2 rešitev pripadajoče homogene enačbe. Splošna rešitev nehomogene enačbe je vsota x p + x h = x p + C 1 x C n x n, kjer je x p partikularna rešitev nehomogene enačbe, x 1,..., x n pa so linearno neodvisne rešitve homogene enačbe. Partikularno rešitev dobimo s pametnim ugibanjem ali z metodo variacije konstant. Primeri Partikularno rešitev x p lahko pogosto uganemo (ali uganemo vsaj njeno obliko): 1. ẍ + ẋ + x = t 2 2. ẍ 3ẋ + 2x = e 3t, x(0) = 1, ẋ(0) = 0 3. ẍ x = e x
24 Primer: vsiljeno nihanje Nedušeno: mẍ + kx = f (t) Naj bo f (t) = A sin µt: 1. vsiljena frekvenca je drugačna od lastne: µ ω, partikularna rešitev je x p = a sin µt, kjer a določimo tako, da je enačba izpolnjena, splošna rešitev je sestavljeno nihanje x(t) = C 1 sin ωt + C 2 cos ωt + a sin µt. 2. resonanca, vsiljena frekvenca je enaka lastni: µ = ω, x p = at sin ωt, splošna rešitev x(t) = C 1 sin ωt + C 2 cos ωt + at sin µt s časom narašča, ni omejena. Dušeno vsiljeno nihanje: mẍ + βẋ + kx = f (t)...
Diferencialna enačba, v kateri nastopata neznana funkcija in njen odvod v prvi potenci
 Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Funkcije več spremenljivk
 DODATEK C Funkcije več spremenljivk C.1. Osnovni pojmi Funkcija n spremenljivk je predpis: f : D f R, (x 1, x 2,..., x n ) u = f (x 1, x 2,..., x n ) kjer D f R n imenujemo definicijsko območje funkcije
DODATEK C Funkcije več spremenljivk C.1. Osnovni pojmi Funkcija n spremenljivk je predpis: f : D f R, (x 1, x 2,..., x n ) u = f (x 1, x 2,..., x n ) kjer D f R n imenujemo definicijsko območje funkcije
diferencialne enačbe - nadaljevanje
 12. vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 diferencialne enačbe - nadaljevanje Ortogonalne trajektorije Dana je 1-parametrična družina krivulj F(x, y, C) = 0. Ortogonalne
12. vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 diferencialne enačbe - nadaljevanje Ortogonalne trajektorije Dana je 1-parametrična družina krivulj F(x, y, C) = 0. Ortogonalne
Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba.
 1. Osnovni pojmi Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba. Primer 1.1: Diferencialne enačbe so izrazi: y
1. Osnovni pojmi Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba. Primer 1.1: Diferencialne enačbe so izrazi: y
Tretja vaja iz matematike 1
 Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 10. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 5. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Matematika 2. Diferencialne enačbe drugega reda
 Matematika 2 Diferencialne enačbe drugega reda (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) y 6y + 8y = 0, (b) y 2y + y = 0, (c) y + y = 0, (d) y + 2y + 2y = 0. Rešitev:
Matematika 2 Diferencialne enačbe drugega reda (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) y 6y + 8y = 0, (b) y 2y + y = 0, (c) y + y = 0, (d) y + 2y + 2y = 0. Rešitev:
Funkcijske vrste. Matematika 2. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 2. april Gregor Dolinar Matematika 2
 Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 21. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Navadne diferencialne enačbe
 Navadne diferencialne enačbe Navadne diferencialne enačbe prvega reda V celotnem poglavju bo y = dy dx. Diferencialne enačbe z ločljivima spremeljivkama Diferencialna enačba z ločljivima spremeljivkama
Navadne diferencialne enačbe Navadne diferencialne enačbe prvega reda V celotnem poglavju bo y = dy dx. Diferencialne enačbe z ločljivima spremeljivkama Diferencialna enačba z ločljivima spremeljivkama
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 14. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):
![matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij): matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):](/thumbs/87/96579490.jpg) 4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
vezani ekstremi funkcij
 11. vaja iz Matematike 2 (UNI) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 ekstremi funkcij več spremenljivk nadaljevanje vezani ekstremi funkcij Dana je funkcija f(x, y). Zanimajo nas ekstremi nad
11. vaja iz Matematike 2 (UNI) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 ekstremi funkcij več spremenljivk nadaljevanje vezani ekstremi funkcij Dana je funkcija f(x, y). Zanimajo nas ekstremi nad
Tema 1 Osnove navadnih diferencialnih enačb (NDE)
 Matematične metode v fiziki II 2013/14 Tema 1 Osnove navadnih diferencialnih enačb (NDE Diferencialne enačbe v fiziki Večina osnovnih enačb v fiziki je zapisana v obliki diferencialne enačbe. Za primer
Matematične metode v fiziki II 2013/14 Tema 1 Osnove navadnih diferencialnih enačb (NDE Diferencialne enačbe v fiziki Večina osnovnih enačb v fiziki je zapisana v obliki diferencialne enačbe. Za primer
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 22. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Analiza 2 Rešitve 14. sklopa nalog
 Analiza Rešitve 1 sklopa nalog Navadne diferencialne enačbe višjih redov in sistemi diferencialnih enačb (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) 6 + 8 0, (b)
Analiza Rešitve 1 sklopa nalog Navadne diferencialne enačbe višjih redov in sistemi diferencialnih enačb (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) 6 + 8 0, (b)
Definicija. definiramo skalarni produkt. x i y i. in razdaljo. d(x, y) = x y = < x y, x y > = n (x i y i ) 2. i=1. i=1
 Funkcije več realnih spremenljivk Osnovne definicije Limita in zveznost funkcije več spremenljivk Parcialni odvodi funkcije več spremenljivk Gradient in odvod funkcije več spremenljivk v dani smeri Parcialni
Funkcije več realnih spremenljivk Osnovne definicije Limita in zveznost funkcije več spremenljivk Parcialni odvodi funkcije več spremenljivk Gradient in odvod funkcije več spremenljivk v dani smeri Parcialni
*M * Osnovna in višja raven MATEMATIKA NAVODILA ZA OCENJEVANJE. Sobota, 4. junij 2011 SPOMLADANSKI IZPITNI ROK. Državni izpitni center
 Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Na pregledni skici napišite/označite ustrezne točke in paraboli. A) 12 B) 8 C) 4 D) 4 E) 8 F) 12
 Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
IZPIT IZ ANALIZE II Maribor,
 Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 15. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 12. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
Podobnost matrik. Matematika II (FKKT Kemijsko inženirstvo) Diagonalizacija matrik
 Podobnost matrik Matematika II (FKKT Kemijsko inženirstvo) Matjaž Željko FKKT Kemijsko inženirstvo 14 teden (Zadnja sprememba: 23 maj 213) Matrika A R n n je podobna matriki B R n n, če obstaja obrnljiva
Podobnost matrik Matematika II (FKKT Kemijsko inženirstvo) Matjaž Željko FKKT Kemijsko inženirstvo 14 teden (Zadnja sprememba: 23 maj 213) Matrika A R n n je podobna matriki B R n n, če obstaja obrnljiva
Numerično reševanje. diferencialnih enačb II
 Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
1. Definicijsko območje, zaloga vrednosti. 2. Naraščanje in padanje, ekstremi. 3. Ukrivljenost. 4. Trend na robu definicijskega območja
 ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK
 1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
Navadne diferencialne enačbe
 Navadne diferencialne enačbe (študijsko gradivo) Matija Cencelj 1. maja 2003 2 Kazalo 1 Uvod 5 1.1 Preprosti primeri......................... 8 2 Diferencialne enačbe prvega reda 11 2.1 Ločljivi spremenljivki.......................
Navadne diferencialne enačbe (študijsko gradivo) Matija Cencelj 1. maja 2003 2 Kazalo 1 Uvod 5 1.1 Preprosti primeri......................... 8 2 Diferencialne enačbe prvega reda 11 2.1 Ločljivi spremenljivki.......................
Odvode odvisnih spremenljivk po neodvisni spremenljivki bomo označevali s piko: Sistem navadnih diferencialnih enačb prvega reda ima obliko:
 4 Sisemi diferencialnih enačb V prakičnih primerih večkra naleimo na več diferencialnih enačb, ki opisujejo določen pojav in so medsebojno povezane edaj govorimo o sisemih diferencialnih enačb V eh enačbah
4 Sisemi diferencialnih enačb V prakičnih primerih večkra naleimo na več diferencialnih enačb, ki opisujejo določen pojav in so medsebojno povezane edaj govorimo o sisemih diferencialnih enačb V eh enačbah
Osnove matematične analize 2016/17
 Osnove matematične analize 216/17 Neža Mramor Kosta Fakulteta za računalništvo in informatiko Univerza v Ljubljani Kaj je funkcija? Funkcija je predpis, ki vsakemu elementu x iz definicijskega območja
Osnove matematične analize 216/17 Neža Mramor Kosta Fakulteta za računalništvo in informatiko Univerza v Ljubljani Kaj je funkcija? Funkcija je predpis, ki vsakemu elementu x iz definicijskega območja
3.1 Reševanje nelinearnih sistemov
 3.1 Reševanje nelinearnih sistemov Rešujemo sistem nelinearnih enačb f 1 (x 1, x 2,..., x n ) = 0 f 2 (x 1, x 2,..., x n ) = 0. f n (x 1, x 2,..., x n ) = 0. Pišemo F (x) = 0, kjer je x R n in F : R n
3.1 Reševanje nelinearnih sistemov Rešujemo sistem nelinearnih enačb f 1 (x 1, x 2,..., x n ) = 0 f 2 (x 1, x 2,..., x n ) = 0. f n (x 1, x 2,..., x n ) = 0. Pišemo F (x) = 0, kjer je x R n in F : R n
Iterativno reševanje sistemov linearnih enačb. Numerične metode, sistemi linearnih enačb. Numerične metode FE, 2. december 2013
 Numerične metode, sistemi linearnih enačb B. Jurčič Zlobec Numerične metode FE, 2. december 2013 1 Vsebina 1 z n neznankami. a i1 x 1 + a i2 x 2 + + a in = b i i = 1,..., n V matrični obliki zapišemo:
Numerične metode, sistemi linearnih enačb B. Jurčič Zlobec Numerične metode FE, 2. december 2013 1 Vsebina 1 z n neznankami. a i1 x 1 + a i2 x 2 + + a in = b i i = 1,..., n V matrični obliki zapišemo:
Kvadratne forme. Poglavje XI. 1 Definicija in osnovne lastnosti
 Poglavje XI Kvadratne forme V zadnjem poglavju si bomo ogledali še eno vrsto preslikav, ki jih tudi lahko podamo z matrikami. To so tako imenovane kvadratne forme, ki niso več linearne preslikave. Kvadratne
Poglavje XI Kvadratne forme V zadnjem poglavju si bomo ogledali še eno vrsto preslikav, ki jih tudi lahko podamo z matrikami. To so tako imenovane kvadratne forme, ki niso več linearne preslikave. Kvadratne
8. Navadne diferencialne enačbe
 8. Navadne diferencialne enačbe 8.1. Začetni problem prvega reda Iščemo funkcijo y(x), ki zadošča diferencialni enačbi y = f(x, y) in začetnemu pogoju y(x 0 ) = y 0, kjer je f dana dovolj gladka funkcija
8. Navadne diferencialne enačbe 8.1. Začetni problem prvega reda Iščemo funkcijo y(x), ki zadošča diferencialni enačbi y = f(x, y) in začetnemu pogoju y(x 0 ) = y 0, kjer je f dana dovolj gladka funkcija
Kotne in krožne funkcije
 Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK
 SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
INŽENIRSKA MATEMATIKA I
 INŽENIRSKA MATEMATIKA I REŠENE NALOGE za izredne študente VSŠ Tehnično upravljanje nepremičnin Marjeta Škapin Rugelj Fakulteta za gradbeništvo in geodezijo Kazalo Števila in preslikave 5 Vektorji 6 Analitična
INŽENIRSKA MATEMATIKA I REŠENE NALOGE za izredne študente VSŠ Tehnično upravljanje nepremičnin Marjeta Škapin Rugelj Fakulteta za gradbeništvo in geodezijo Kazalo Števila in preslikave 5 Vektorji 6 Analitična
Reševanje sistema linearnih
 Poglavje III Reševanje sistema linearnih enačb V tem kratkem poglavju bomo obravnavali zelo uporabno in zato pomembno temo linearne algebre eševanje sistemov linearnih enačb. Spoznali bomo Gaussovo (natančneje
Poglavje III Reševanje sistema linearnih enačb V tem kratkem poglavju bomo obravnavali zelo uporabno in zato pomembno temo linearne algebre eševanje sistemov linearnih enačb. Spoznali bomo Gaussovo (natančneje
Navadne diferencialne enačbe
 Poglavje 6 Navadne diferencialne enačbe 6.1 Uvod Splošna rešitev navadne diferencialne enačbe n-tega reda F(x, y, y, y,..., y (n) ) = 0 je n-parametrična družina funkcij. Kadar želimo iz splošne rešitve
Poglavje 6 Navadne diferencialne enačbe 6.1 Uvod Splošna rešitev navadne diferencialne enačbe n-tega reda F(x, y, y, y,..., y (n) ) = 0 je n-parametrična družina funkcij. Kadar želimo iz splošne rešitve
UNIVERZA V MARIBORU FAKULTETA ZA KEMIJO IN KEMIJSKO TEHNOLOGIJO MATEMATIKA III
 UNIVERZA V MARIBORU FAKULTETA ZA KEMIJO IN KEMIJSKO TEHNOLOGIJO Petra Žigert Pleteršek MATEMATIKA III Maribor, september 215 ii Kazalo Diferencialni račun vektorskih funkcij 1 1.1 Skalarne funkcije...........................
UNIVERZA V MARIBORU FAKULTETA ZA KEMIJO IN KEMIJSKO TEHNOLOGIJO Petra Žigert Pleteršek MATEMATIKA III Maribor, september 215 ii Kazalo Diferencialni račun vektorskih funkcij 1 1.1 Skalarne funkcije...........................
Nekaj zgledov. J.Kozak Numerične metode II (IŠRM) / 21
 Nekaj zgledov J.Kozak Numerične metode II (IŠRM) 2011-2012 1 / 21 V robnih problemih rešitev diferencialne enačbe zadošča dodatnim pogojem, ki niso vsi predpisani v isti točki. Že osnovna zahteva, kot
Nekaj zgledov J.Kozak Numerične metode II (IŠRM) 2011-2012 1 / 21 V robnih problemih rešitev diferencialne enačbe zadošča dodatnim pogojem, ki niso vsi predpisani v isti točki. Že osnovna zahteva, kot
α i y n i + h β i f n i = 0, Splošni nastavek je k
 10.4 Večkoračne metode Splošni nastavek je k α i y n i + h i=0 k β i f n i = 0, kjer je f i = f(x i, y i ), privzamemo pa še α 0 = 1. Če je β 0 = 0, je metoda eksplicitna, sicer pa implicitna. i=0 Adamsove
10.4 Večkoračne metode Splošni nastavek je k α i y n i + h i=0 k β i f n i = 0, kjer je f i = f(x i, y i ), privzamemo pa še α 0 = 1. Če je β 0 = 0, je metoda eksplicitna, sicer pa implicitna. i=0 Adamsove
13. Jacobijeva metoda za računanje singularnega razcepa
 13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
D f, Z f. Lastnosti. Linearna funkcija. Definicija Linearna funkcija f : je definirana s predpisom f(x) = kx+n; k,
 Linearna funkcija Linearna funkcija f : je definirana s predpisom f(x) = kx+n; k, n ᄀ. k smerni koeficient n začetna vrednost D f, Z f Definicijsko območje linearne funkcije so vsa realna števila. Zaloga
Linearna funkcija Linearna funkcija f : je definirana s predpisom f(x) = kx+n; k, n ᄀ. k smerni koeficient n začetna vrednost D f, Z f Definicijsko območje linearne funkcije so vsa realna števila. Zaloga
Osnove linearne algebre
 Osnove linearne algebre Matrike Matrika razsežnosti n m je A = a 1 1 a 1 2 a 1 m a 2 1 a 2 2 a 2 m a n 1 a n 2 a n m Če je n = m, tedaj matriko imenujemo kvadratna matrika Elementi matrike so lahko realna
Osnove linearne algebre Matrike Matrika razsežnosti n m je A = a 1 1 a 1 2 a 1 m a 2 1 a 2 2 a 2 m a n 1 a n 2 a n m Če je n = m, tedaj matriko imenujemo kvadratna matrika Elementi matrike so lahko realna
Funkcije dveh in več spremenljivk
 Poglavje 3 Funkcije dveh in več spremenljivk 3.1 Osnovni pojmi Definicija 3.1.1. Funkcija dveh spremenljivk je preslikava, ki vsaki točki (x, y) ravninske množice D priredi realno število z = f(x, y),
Poglavje 3 Funkcije dveh in več spremenljivk 3.1 Osnovni pojmi Definicija 3.1.1. Funkcija dveh spremenljivk je preslikava, ki vsaki točki (x, y) ravninske množice D priredi realno število z = f(x, y),
Booleova algebra. Izjave in Booleove spremenljivke
 Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
Afina in projektivna geometrija
 fina in projektivna geometrija tožnice () kiciraj stožnico v evklidski ravnini R, ki je določena z enačbo 6 3 8 + 6 =. Rešitev: tožnica v evklidski ravnini je krivulja, ki jo določa enačba a + b + c +
fina in projektivna geometrija tožnice () kiciraj stožnico v evklidski ravnini R, ki je določena z enačbo 6 3 8 + 6 =. Rešitev: tožnica v evklidski ravnini je krivulja, ki jo določa enačba a + b + c +
Splošno o interpolaciji
 Splošno o interpolaciji J.Kozak Numerične metode II (FM) 2011-2012 1 / 18 O funkciji f poznamo ali hočemo uporabiti le posamezne podatke, na primer vrednosti r i = f (x i ) v danih točkah x i Izberemo
Splošno o interpolaciji J.Kozak Numerične metode II (FM) 2011-2012 1 / 18 O funkciji f poznamo ali hočemo uporabiti le posamezne podatke, na primer vrednosti r i = f (x i ) v danih točkah x i Izberemo
Matematične metode v fiziki II. B. Golli, PeF
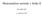 Matematične metode v fiziki II B. Golli, PeF 8. september 2014 2 Kazalo 1 Navadne diferencialne enačbe (NDE) 5 1.1 Uvod.............................................. 5 1.1.1 Diferencialne enačbe v fiziki.............................
Matematične metode v fiziki II B. Golli, PeF 8. september 2014 2 Kazalo 1 Navadne diferencialne enačbe (NDE) 5 1.1 Uvod.............................................. 5 1.1.1 Diferencialne enačbe v fiziki.............................
Dragi polinom, kje so tvoje ničle?
 1 Dragi polinom, kje so tvoje ničle? Vito Vitrih FAMNIT - Izlet v matematično vesolje 17. december 2010 Polinomi: 2 Polinom stopnje n je funkcija p(x) = a n x n + a n 1 x n 1 +... + a 1 x + a 0, a i R.
1 Dragi polinom, kje so tvoje ničle? Vito Vitrih FAMNIT - Izlet v matematično vesolje 17. december 2010 Polinomi: 2 Polinom stopnje n je funkcija p(x) = a n x n + a n 1 x n 1 +... + a 1 x + a 0, a i R.
11.5 Metoda karakteristik za hiperbolične PDE
 11.5 Metoda karakteristik za hiperbolične PDE Hiperbolična kvazi linearna PDE ima obliko au xx + bu xy + cu yy = f, (1) kjer so a, b, c, f funkcije x, y, u, u x in u y, ter velja b 2 4ac > 0. Če predpostavimo,
11.5 Metoda karakteristik za hiperbolične PDE Hiperbolična kvazi linearna PDE ima obliko au xx + bu xy + cu yy = f, (1) kjer so a, b, c, f funkcije x, y, u, u x in u y, ter velja b 2 4ac > 0. Če predpostavimo,
FAKULTETA ZA STROJNIŠTVO Matematika 4 Pisni izpit 22. junij Navodila
 FAKULTETA ZA STROJNIŠTVO Matematika 4 Pisni izpit 22 junij 212 Ime in priimek: Vpisna št: Navodila Pazljivo preberite besedilo naloge, preden se lotite reševanja Veljale bodo samo rešitve na papirju, kjer
FAKULTETA ZA STROJNIŠTVO Matematika 4 Pisni izpit 22 junij 212 Ime in priimek: Vpisna št: Navodila Pazljivo preberite besedilo naloge, preden se lotite reševanja Veljale bodo samo rešitve na papirju, kjer
Domače naloge za 2. kolokvij iz ANALIZE 2b VEKTORSKA ANALIZA
 Domače naloge za 2. kolokvij iz ANALIZE 2b VEKTORSKA ANALIZA. Naj bo vektorsko polje R : R 3 R 3 dano s predpisom R(x, y, z) = (2x 2 + z 2, xy + 2yz, z). Izračunaj pretok polja R skozi površino torusa
Domače naloge za 2. kolokvij iz ANALIZE 2b VEKTORSKA ANALIZA. Naj bo vektorsko polje R : R 3 R 3 dano s predpisom R(x, y, z) = (2x 2 + z 2, xy + 2yz, z). Izračunaj pretok polja R skozi površino torusa
Računski del izpita pri predmetu MATEMATIKA I
 Kemijska tehnologija Visokošolski strokovni program Računski del izpita pri predmetu MATEMATIKA I 29. 8. 2013 Čas reševanja je 75 minut. Navodila: Pripravi osebni dokument. Ugasni in odstrani mobilni telefon.
Kemijska tehnologija Visokošolski strokovni program Računski del izpita pri predmetu MATEMATIKA I 29. 8. 2013 Čas reševanja je 75 minut. Navodila: Pripravi osebni dokument. Ugasni in odstrani mobilni telefon.
Jasna Prezelj DIFERENCIALNE ENAČBE. za finančno matematiko
 Jasna Prezelj DIFERENCIALNE ENAČBE za finančno matematiko Ljubljana 211 naslov: DIFERENCIALNE ENAČBE ZA FINANČNO MATEMATIKO avtorske pravice: Jasna Prezelj izdaja: prva izdaja založnik: samozaložba Jasna
Jasna Prezelj DIFERENCIALNE ENAČBE za finančno matematiko Ljubljana 211 naslov: DIFERENCIALNE ENAČBE ZA FINANČNO MATEMATIKO avtorske pravice: Jasna Prezelj izdaja: prva izdaja založnik: samozaložba Jasna
Matematika. Funkcije in enačbe
 Matematika Funkcije in enačbe (1) Nariši grafe naslednjih funkcij: (a) f() = 1, (b) f() = 3, (c) f() = 3. Rešitev: (a) Linearna funkcija f() = 1 ima začetno vrednost f(0) = 1 in ničlo = 1/. Definirana
Matematika Funkcije in enačbe (1) Nariši grafe naslednjih funkcij: (a) f() = 1, (b) f() = 3, (c) f() = 3. Rešitev: (a) Linearna funkcija f() = 1 ima začetno vrednost f(0) = 1 in ničlo = 1/. Definirana
22. Kdaj sta dva vektorja vzporedna? FGG geodezija UNI Matematika I, 2005/ Kdaj so vektorji a 1, a 2,..., a n linearno neodvisni?
 FGG geodezija UNI Matematika I, 2005/06 1. Definicija enakosti množic (funkcij, kompleksnih števil, urejenih n teric)? 2. Definicija kartezičnega produkta množic A in B. Definicija množice R n. 3. Popolna
FGG geodezija UNI Matematika I, 2005/06 1. Definicija enakosti množic (funkcij, kompleksnih števil, urejenih n teric)? 2. Definicija kartezičnega produkta množic A in B. Definicija množice R n. 3. Popolna
Enočlenske metode veljajo trenutno za najprimernejše metode v numeričnem reševanju začetnih problemov. Skoraj vse sodijo v
 Enočlenske metode J.Kozak Uvod v numerične metode - / 4 Enočlenske metode veljajo trenutno za najprimernejše metode v numeričnem reševanju začetnih problemov. Skoraj vse sodijo v skupino Runge-Kutta metod.
Enočlenske metode J.Kozak Uvod v numerične metode - / 4 Enočlenske metode veljajo trenutno za najprimernejše metode v numeričnem reševanju začetnih problemov. Skoraj vse sodijo v skupino Runge-Kutta metod.
Matematika 1. Gabrijel Tomšič Bojan Orel Neža Mramor Kosta
 Matematika 1 Gabrijel Tomšič Bojan Orel Neža Mramor Kosta 21. april 2008 102 Poglavje 4 Odvod 4.1 Definicija odvoda Naj bo funkcija f definirana na intervalu (a, b) in x 0 točka s tega intervala. Vzemimo
Matematika 1 Gabrijel Tomšič Bojan Orel Neža Mramor Kosta 21. april 2008 102 Poglavje 4 Odvod 4.1 Definicija odvoda Naj bo funkcija f definirana na intervalu (a, b) in x 0 točka s tega intervala. Vzemimo
Vaje iz MATEMATIKE 8. Odvod funkcije., pravimo, da je funkcija f odvedljiva v točki x 0 z odvodom. f (x f(x 0 + h) f(x 0 ) 0 ) := lim
 Študij AHITEKTURE IN URBANIZMA, šol l 06/7 Vaje iz MATEMATIKE 8 Odvod funkcije f( Definicija: Naj bo f definirana na neki okolici točke 0 Če obstaja lim 0 +h f( 0 h 0 h, pravimo, da je funkcija f odvedljiva
Študij AHITEKTURE IN URBANIZMA, šol l 06/7 Vaje iz MATEMATIKE 8 Odvod funkcije f( Definicija: Naj bo f definirana na neki okolici točke 0 Če obstaja lim 0 +h f( 0 h 0 h, pravimo, da je funkcija f odvedljiva
Gimnazija Krˇsko. vektorji - naloge
 Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
Integralni račun. Nedoločeni integral in integracijske metrode. 1. Izračunaj naslednje nedoločene integrale: (a) dx. (b) x 3 +3+x 2 dx, (c) (d)
 Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
MATEMATIKA 1 UNIVERZITETNI ŠTUDIJSKI PROGRAM BIOKEMIJA 1. LETNIK
 abc MATEMATIKA 1 UNIVERZITETNI ŠTUDIJSKI PROGRAM BIOKEMIJA 1. LETNIK ŠTEVILA PRIBLIŽNO RAČUNANJE PRIBLIŽNO RAČUNANJE Ta fosil dinozavra je star 7 milijonov in šest let, pravi paznik v muzeju.??? Ko sem
abc MATEMATIKA 1 UNIVERZITETNI ŠTUDIJSKI PROGRAM BIOKEMIJA 1. LETNIK ŠTEVILA PRIBLIŽNO RAČUNANJE PRIBLIŽNO RAČUNANJE Ta fosil dinozavra je star 7 milijonov in šest let, pravi paznik v muzeju.??? Ko sem
PONOVITEV SNOVI ZA 4. TEST
 PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
8. Posplošeni problem lastnih vrednosti
 8. Posplošeni problem lastnih vrednosti Bor Plestenjak NLA 13. april 2010 Bor Plestenjak (NLA) 8. Posplošeni problem lastnih vrednosti 13. april 2010 1 / 15 Matrični šop Dani sta kvadratni n n matriki
8. Posplošeni problem lastnih vrednosti Bor Plestenjak NLA 13. april 2010 Bor Plestenjak (NLA) 8. Posplošeni problem lastnih vrednosti 13. april 2010 1 / 15 Matrični šop Dani sta kvadratni n n matriki
F (x) = kx. F (x )dx. F = kx. U(x) = U(0) kx2
 F (x) = kx x k F = F (x) U(0) U(x) = x F = kx 0 F (x )dx U(x) = U(0) + 1 2 kx2 x U(0) = 0 U(x) = 1 2 kx2 U(x) x 0 = 0 x 1 U(x) U(0) + U (0) x + 1 2 U (0) x 2 U (0) = 0 U(x) U(0) + 1 2 U (0) x 2 U(0) =
F (x) = kx x k F = F (x) U(0) U(x) = x F = kx 0 F (x )dx U(x) = U(0) + 1 2 kx2 x U(0) = 0 U(x) = 1 2 kx2 U(x) x 0 = 0 x 1 U(x) U(0) + U (0) x + 1 2 U (0) x 2 U (0) = 0 U(x) U(0) + 1 2 U (0) x 2 U(0) =
Uporabna matematika za naravoslovce
 Uporabna matematika za naravoslovce Zapiski predavanj Študijski programi: Aplikativna kineziologija, Biodiverziteta Študijsko leto 203/4 doc.dr. Barbara Boldin Fakulteta za matematiko, naravoslovje in
Uporabna matematika za naravoslovce Zapiski predavanj Študijski programi: Aplikativna kineziologija, Biodiverziteta Študijsko leto 203/4 doc.dr. Barbara Boldin Fakulteta za matematiko, naravoslovje in
Del 5. Vektorske funkcije in funkcije več spremenljivk
 Del 5 Vektorske funkcije in funkcije več spremenljivk POGLAVJE 1 Krivulje v R n 1. Risanje vektorskih funkcij in vektorskih zaporedij Funkcija iz R v R n je podana z dvema podatkoma: z definicijskim območjem,
Del 5 Vektorske funkcije in funkcije več spremenljivk POGLAVJE 1 Krivulje v R n 1. Risanje vektorskih funkcij in vektorskih zaporedij Funkcija iz R v R n je podana z dvema podatkoma: z definicijskim območjem,
Poliedri Ines Pogačar 27. oktober 2009
 Poliedri Ines Pogačar 27. oktober 2009 Pri linearnem programiranju imamo opravka s končnim sistemom neenakosti in končno spremenljivkami, torej je množica dopustnih rešitev presek končno mnogo polprostorov.
Poliedri Ines Pogačar 27. oktober 2009 Pri linearnem programiranju imamo opravka s končnim sistemom neenakosti in končno spremenljivkami, torej je množica dopustnih rešitev presek končno mnogo polprostorov.
Domača naloga 6: dušeno nihanje
 Domača naloga 6: dušeno nihanje Vaje iz predmeta Numerične metode v fiziki Igor Grešovnik Kazalo: 1 Naloga 6a Nihanje... 1.1 Enačbe nihanja... 1. Numerično reševanje problema... 3 1..1 Reševanje sistema
Domača naloga 6: dušeno nihanje Vaje iz predmeta Numerične metode v fiziki Igor Grešovnik Kazalo: 1 Naloga 6a Nihanje... 1.1 Enačbe nihanja... 1. Numerično reševanje problema... 3 1..1 Reševanje sistema
cot x ni def. 3 1 KOTNE FUNKCIJE POLJUBNO VELIKEGA KOTA (A) Merske enote stopinja [ ] radian [rad] 1. Izrazi kot v radianih.
![cot x ni def. 3 1 KOTNE FUNKCIJE POLJUBNO VELIKEGA KOTA (A) Merske enote stopinja [ ] radian [rad] 1. Izrazi kot v radianih. cot x ni def. 3 1 KOTNE FUNKCIJE POLJUBNO VELIKEGA KOTA (A) Merske enote stopinja [ ] radian [rad] 1. Izrazi kot v radianih.](/thumbs/72/66438140.jpg) TRIGONOMETRIJA (A) Merske enote KOTNE FUNKCIJE POLJUBNO VELIKEGA KOTA stopinja [ ] radian [rad] 80 80 0. Izrazi kot v radianih. 0 90 5 0 0 70. Izrazi kot v stopinjah. 5 8 5 (B) Definicija kotnih funkcij
TRIGONOMETRIJA (A) Merske enote KOTNE FUNKCIJE POLJUBNO VELIKEGA KOTA stopinja [ ] radian [rad] 80 80 0. Izrazi kot v radianih. 0 90 5 0 0 70. Izrazi kot v stopinjah. 5 8 5 (B) Definicija kotnih funkcij
Matematično modeliranje. Simpleksna metoda.
 Simpleksna metoda. Drago Bokal, Tanja Gologranc Oddelek za matematiko in računalništvo Fakulteta za naravoslovje in matematiko Univerza v Mariboru Kanonična oblika linearnega programa. min c T x p. p.
Simpleksna metoda. Drago Bokal, Tanja Gologranc Oddelek za matematiko in računalništvo Fakulteta za naravoslovje in matematiko Univerza v Mariboru Kanonična oblika linearnega programa. min c T x p. p.
Matematika I (VS) Univerza v Ljubljani, FE. Melita Hajdinjak 2013/14. Pregled elementarnih funkcij. Potenčna funkcija. Korenska funkcija.
 1 / 46 Univerza v Ljubljani, FE Potenčna Korenska Melita Hajdinjak Matematika I (VS) Kotne 013/14 / 46 Potenčna Potenčna Funkcijo oblike f() = n, kjer je n Z, imenujemo potenčna. Število n imenujemo eksponent.
1 / 46 Univerza v Ljubljani, FE Potenčna Korenska Melita Hajdinjak Matematika I (VS) Kotne 013/14 / 46 Potenčna Potenčna Funkcijo oblike f() = n, kjer je n Z, imenujemo potenčna. Število n imenujemo eksponent.
Funkcija je predpis, ki vsakemu elementu x iz definicijskega območja D R priredi neko število f (x) R.
 II. FUNKCIJE 1. Osnovni pojmi 2. Sestavljanje funkcij 3. Pregled elementarnih funkcij 4. Zveznost Kaj je funkcija? Definicija Funkcija je predpis, ki vsakemu elementu x iz definicijskega območja D R priredi
II. FUNKCIJE 1. Osnovni pojmi 2. Sestavljanje funkcij 3. Pregled elementarnih funkcij 4. Zveznost Kaj je funkcija? Definicija Funkcija je predpis, ki vsakemu elementu x iz definicijskega območja D R priredi
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * FIZIKA NAVODILA ZA OCENJEVANJE. Petek, 10. junij 2016 SPLOŠNA MATURA
 Državni izpitni center *M16141113* SPOMLADANSKI IZPITNI ROK FIZIKA NAVODILA ZA OCENJEVANJE Petek, 1. junij 16 SPLOŠNA MATURA RIC 16 M161-411-3 M161-411-3 3 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor
Državni izpitni center *M16141113* SPOMLADANSKI IZPITNI ROK FIZIKA NAVODILA ZA OCENJEVANJE Petek, 1. junij 16 SPLOŠNA MATURA RIC 16 M161-411-3 M161-411-3 3 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor
DUŠENO NIHANJE IN RESONANCA
 Politehnika Nova Gorica Šola za znanosti o okolju Univerzitetni študijski program OKOLJE Seminarska naloga DUŠENO NIHANJE IN RESONANCA Mentor: Doc.dr. Iztok Arčon Avtor: Nastja Tomšič Razred: 1.letnik
Politehnika Nova Gorica Šola za znanosti o okolju Univerzitetni študijski program OKOLJE Seminarska naloga DUŠENO NIHANJE IN RESONANCA Mentor: Doc.dr. Iztok Arčon Avtor: Nastja Tomšič Razred: 1.letnik
Matematika 1. Gabrijel Tomšič Bojan Orel Neža Mramor Kosta
 Matematika Gabrijel Tomšič Bojan Orel Neža Mramor Kosta 6. november 200 Poglavje 2 Zaporedja in številske vrste 2. Zaporedja 2.. Uvod Definicija 2... Zaporedje (a n ) = a, a 2,..., a n,... je predpis,
Matematika Gabrijel Tomšič Bojan Orel Neža Mramor Kosta 6. november 200 Poglavje 2 Zaporedja in številske vrste 2. Zaporedja 2.. Uvod Definicija 2... Zaporedje (a n ) = a, a 2,..., a n,... je predpis,
DISKRETNA FOURIERJEVA TRANSFORMACIJA
 29.03.2004 Definicija DFT Outline DFT je linearna transformacija nekega vektorskega prostora dimenzije n nad obsegom K, ki ga označujemo z V K, pri čemer ima slednji lastnost, da vsebuje nek poseben element,
29.03.2004 Definicija DFT Outline DFT je linearna transformacija nekega vektorskega prostora dimenzije n nad obsegom K, ki ga označujemo z V K, pri čemer ima slednji lastnost, da vsebuje nek poseben element,
Problem lastnih vrednosti 1 / 20
 Problem lastnih vrednosti 1 / 20 2 / 20 1 Uvod 2 Potenčna metoda 3 Inverzna iteracija 4 QR iteracija 5 Metode za simetrične matrike Sturmovo zaporedje Jacobijeva iteracija 3 / 20 Uvod Naj bo A R n n. Paru
Problem lastnih vrednosti 1 / 20 2 / 20 1 Uvod 2 Potenčna metoda 3 Inverzna iteracija 4 QR iteracija 5 Metode za simetrične matrike Sturmovo zaporedje Jacobijeva iteracija 3 / 20 Uvod Naj bo A R n n. Paru
primer reševanja volumskega mehanskega problema z MKE
 Reševanje mehanskih problemov z MKE primer reševanja volumskega mehanskega problema z MKE p p RAK: P-XII//74 Reševanje mehanskih problemov z MKE primer reševanja volumskega mehanskega problema z MKE L
Reševanje mehanskih problemov z MKE primer reševanja volumskega mehanskega problema z MKE p p RAK: P-XII//74 Reševanje mehanskih problemov z MKE primer reševanja volumskega mehanskega problema z MKE L
Problem lastnih vrednosti
 Problem lastnih vrednosti Naj bo A R n n. Iščemo lastni par, da zanj velja Ax = λx, kjer je x C n, x 0 (desni) lastni vektor, λ C pa lastna vrednost. Vektor y 0, pri katerem je y H A = λy H, je levi lastni
Problem lastnih vrednosti Naj bo A R n n. Iščemo lastni par, da zanj velja Ax = λx, kjer je x C n, x 0 (desni) lastni vektor, λ C pa lastna vrednost. Vektor y 0, pri katerem je y H A = λy H, je levi lastni
Kombinatorika. rekurzivnih enačb in rodovne funkcije. FMF Matematika Finančna matematika. Vladimir Batagelj. Ljubljana, april
 FMF Matematika Finančna matematika Kombinatorika Reševanje rekurzivnih enačb in rodovne funkcije Vladimir Batagelj Math fun: Pascal triangle Ljubljana, april 2008 4. Dec 2012 različica: December 4, 2012
FMF Matematika Finančna matematika Kombinatorika Reševanje rekurzivnih enačb in rodovne funkcije Vladimir Batagelj Math fun: Pascal triangle Ljubljana, april 2008 4. Dec 2012 različica: December 4, 2012
Kontrolne karte uporabljamo za sprotno spremljanje kakovosti izdelka, ki ga izdelujemo v proizvodnem procesu.
 Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
ZBIRKA REŠENIH NALOG IZ MATEMATIKE II
 Univerza v Ljubljani Fakulteta za elektrotehniko Andrej Perne ZBIRKA REŠENIH NALOG IZ MATEMATIKE II Skripta za vaje iz Matematike II (UNI + VSP) Ljubljana, determinante Determinanta det A je število, prirejeno
Univerza v Ljubljani Fakulteta za elektrotehniko Andrej Perne ZBIRKA REŠENIH NALOG IZ MATEMATIKE II Skripta za vaje iz Matematike II (UNI + VSP) Ljubljana, determinante Determinanta det A je število, prirejeno
Osnovne lastnosti odvoda
 Del 2 Odvodi POGLAVJE 4 Osnovne lastnosti odvoda. Definicija odvoda Odvod funkcije f v točki x je definiran z f f(x + ) f(x) (x) =. 0 Ta definicija je smiselna samo v primeru, ko x D(f), ita na desni
Del 2 Odvodi POGLAVJE 4 Osnovne lastnosti odvoda. Definicija odvoda Odvod funkcije f v točki x je definiran z f f(x + ) f(x) (x) =. 0 Ta definicija je smiselna samo v primeru, ko x D(f), ita na desni
Kanonična oblika linearnega programa. Simpleksna metoda. Bazne rešitve kanoničnega linearnega programa.
 Kanonična oblika linearnega programa.. Drago Bokal, Tanja Gologranc Oddelek za matematiko in računalništvo Fakulteta za naravoslovje in matematiko Univerza v Mariboru min c T x p. p. Ax = b x 0 Kako dobimo
Kanonična oblika linearnega programa.. Drago Bokal, Tanja Gologranc Oddelek za matematiko in računalništvo Fakulteta za naravoslovje in matematiko Univerza v Mariboru min c T x p. p. Ax = b x 0 Kako dobimo
ZBIRKA REŠENIH NALOG IZ MATEMATIKE I
 Univerza v Ljubljani Fakulteta za elektrotehniko Andrej Perne ZBIRKA REŠENIH NALOG IZ MATEMATIKE I Skripta za vaje iz Matematike I (UNI + VSP) Ljubljana, množice Osnovne definicije: Množica A je podmnožica
Univerza v Ljubljani Fakulteta za elektrotehniko Andrej Perne ZBIRKA REŠENIH NALOG IZ MATEMATIKE I Skripta za vaje iz Matematike I (UNI + VSP) Ljubljana, množice Osnovne definicije: Množica A je podmnožica
VARIACIJSKE SUBDIVIZIJSKE SHEME
 UNIVERZA V LJUBLJANI FAKULTETA ZA MATEMATIKO IN FIZIKO Seminar za Numerično analizo VARIACIJSKE SUBDIVIZIJSKE SHEME Ljubljana, 004 Marjeta Krajnc . Uvod Subdivizija je postala v zadnjih letih zelo pomembno
UNIVERZA V LJUBLJANI FAKULTETA ZA MATEMATIKO IN FIZIKO Seminar za Numerično analizo VARIACIJSKE SUBDIVIZIJSKE SHEME Ljubljana, 004 Marjeta Krajnc . Uvod Subdivizija je postala v zadnjih letih zelo pomembno
d dx x 2 = 2x d dx x 3 = 3x 2 d dx x n = nx n 1
 d dx x 2 = 2x d dx x 3 = 3x 2 d dx x n = nx n1 x dx = 1 2 b2 1 2 a2 a b b x 2 dx = 1 a 3 b3 1 3 a3 b x n dx = 1 a n +1 bn +1 1 n +1 an +1 d dx d dx f (x) = 0 f (ax) = a f (ax) lim d dx f (ax) = lim 0 =
d dx x 2 = 2x d dx x 3 = 3x 2 d dx x n = nx n1 x dx = 1 2 b2 1 2 a2 a b b x 2 dx = 1 a 3 b3 1 3 a3 b x n dx = 1 a n +1 bn +1 1 n +1 an +1 d dx d dx f (x) = 0 f (ax) = a f (ax) lim d dx f (ax) = lim 0 =
Vaje iz MATEMATIKE 2. Vektorji
 Študij AHITEKTURE IN URBANIZMA, šol. l. 06/7 Vaje iz MATEMATIKE. Vektorji Vektorji: Definicija: Vektor je usmerjena daljica. Oznake: AB, a,... Enakost vektorjev: AB = CD: če lahko vektor AB vzporedno premaknemo
Študij AHITEKTURE IN URBANIZMA, šol. l. 06/7 Vaje iz MATEMATIKE. Vektorji Vektorji: Definicija: Vektor je usmerjena daljica. Oznake: AB, a,... Enakost vektorjev: AB = CD: če lahko vektor AB vzporedno premaknemo
Linearna algebra. Bojan Orel Fakulteta za računalništvo in informatiko
 Linearna algebra Bojan Orel Fakulteta za računalništvo in informatiko 23. februar 205 CIP - Kataložni zapis o publikaciji Narodna in univerzitetna knjižnica, Ljubljana 52.64(075.8)(0.034.2) OREL, Bojan
Linearna algebra Bojan Orel Fakulteta za računalništvo in informatiko 23. februar 205 CIP - Kataložni zapis o publikaciji Narodna in univerzitetna knjižnica, Ljubljana 52.64(075.8)(0.034.2) OREL, Bojan
Poglavje 2. Sistemi linearnih enačb
 Poglavje 2 Sistemi linearnih enačb Najpogostejši problem, na katerega naletimo pri numeričnem računanju, je reševanje sistema linearnih enačb Tak sistem lahko dobimo direktno iz matematične formulacije
Poglavje 2 Sistemi linearnih enačb Najpogostejši problem, na katerega naletimo pri numeričnem računanju, je reševanje sistema linearnih enačb Tak sistem lahko dobimo direktno iz matematične formulacije
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * NAVODILA ZA OCENJEVANJE. Sreda, 3. junij 2015 SPLOŠNA MATURA
 Državni izpitni center *M15143113* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sreda, 3. junij 2015 SPLOŠNA MATURA RIC 2015 M151-431-1-3 2 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor Naloga Odgovor
Državni izpitni center *M15143113* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sreda, 3. junij 2015 SPLOŠNA MATURA RIC 2015 M151-431-1-3 2 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor Naloga Odgovor
Inverzni problem lastnih vrednosti evklidsko razdaljnih matrik
 Univerza v Ljubljani Fakulteta za računalništvo in informatiko Fakulteta za matematiko in fiziko Peter Škvorc Inverzni problem lastnih vrednosti evklidsko razdaljnih matrik DIPLOMSKO DELO UNIVERZITETNI
Univerza v Ljubljani Fakulteta za računalništvo in informatiko Fakulteta za matematiko in fiziko Peter Škvorc Inverzni problem lastnih vrednosti evklidsko razdaljnih matrik DIPLOMSKO DELO UNIVERZITETNI
Matematika. BF Lesarstvo. Zapiski ob predavanjih v šolskem letu 2009/2010
 Matematika BF Lesarstvo Matjaž Željko Zapiski ob predavanjih v šolskem letu 009/00 Izpis: 9 januar 00 KAZALO Kazalo Števila 5 Naravna števila 5 Cela števila 6 3 Racionalna števila 6 4 Realna števila 7
Matematika BF Lesarstvo Matjaž Željko Zapiski ob predavanjih v šolskem letu 009/00 Izpis: 9 januar 00 KAZALO Kazalo Števila 5 Naravna števila 5 Cela števila 6 3 Racionalna števila 6 4 Realna števila 7
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Jaka Cimprič, Jasna Prezelj REŠENE NALOGE IZ ANALIZE 4
 Jaka Cimprič, Jasna Prezelj REŠENE NALOGE IZ ANALIZE 4 Ljubljana naslov: REŠENE NALOGE IZ ANALIZE IV avtorske pravice: Jaka Cimprič, Jasna Prezelj izdaja: prva izdaja založnik: samozaložba Jaka Cimprič
Jaka Cimprič, Jasna Prezelj REŠENE NALOGE IZ ANALIZE 4 Ljubljana naslov: REŠENE NALOGE IZ ANALIZE IV avtorske pravice: Jaka Cimprič, Jasna Prezelj izdaja: prva izdaja založnik: samozaložba Jaka Cimprič
Dodatna poglavja iz linearne algebre za 1. letnik finančne matematike na FMF. Primož Moravec
 Dodatna poglavja iz linearne algebre za 1 letnik finančne matematike na FMF Primož Moravec 13 september 2017 1 CIP - Kataložni zapis o publikaciji Narodna in univerzitetna knjižnica, Ljubljana 51264(0758)
Dodatna poglavja iz linearne algebre za 1 letnik finančne matematike na FMF Primož Moravec 13 september 2017 1 CIP - Kataložni zapis o publikaciji Narodna in univerzitetna knjižnica, Ljubljana 51264(0758)
( , treći kolokvij) 3. Na dite lokalne ekstreme funkcije z = x 4 + y 4 2x 2 + 2y 2 3. (20 bodova)
 A MATEMATIKA (.6.., treći kolokvij. Zadana je funkcija z = e + + sin(. Izračunajte a z (,, b z (,, c z.. Za funkciju z = 3 + na dite a diferencijal dz, b dz u točki T(, za priraste d =. i d =.. c Za koliko
A MATEMATIKA (.6.., treći kolokvij. Zadana je funkcija z = e + + sin(. Izračunajte a z (,, b z (,, c z.. Za funkciju z = 3 + na dite a diferencijal dz, b dz u točki T(, za priraste d =. i d =.. c Za koliko
