ΑΝΩΤΑΤΟ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΑΝΑΤΟΛΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ & ΘΡΑΚΗΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ
|
|
|
- Σαπφώ Πανταζής
- 7 χρόνια πριν
- Προβολές:
Transcript
1 ΑΝΩΤΑΤΟ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΑΝΑΤΟΛΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ & ΘΡΑΚΗΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ «Τμηματοποίηση εικόνων με τη χρήση Ασαφούς Λογικής» Σπουδαστές: Σταύρος Γεωργιάδης ΑΕΜ: 800 Δημήτριος Μαζαράκης ΑΕΜ: 843 Επιβλέπων: Δρ. Γεώργιος Α. Παπακώστας ΚΑΒΑΛΑ 2014
2 Περιεχόμενα Περίληψη...5 Abstract...7 Πρόλογος...9 Κεφάλαιο 1 - Τμηματοποίηση Εικόνων Εισαγωγή Βελτιστοποίηση Ποιότητας Εικόνας Φίλτρο μέσου όρου Median φίλτρο Φίλτρο όξυνσης των ακμών Φίλτρα φωτεινότητας Γραμμικά Φίλτρα Τμηματοποίηση με Κατωφλίωση Τμηματοποίηση βασισμένη σε Αναγνώριση Ακμών Τμηματοποίηση με Ομαδοποίηση(Clustering) Τμηματοποίηση Watershed(Μετασχηματισμός Απορροής) Άλλες Μέθοδοι Εφαρμογή σε διαφόρους κλάδους Προβλήματα...26 Κεφάλαιο2 - Ασαφής Λογική Εισαγωγή Ασαφή Σύνολα...30 [1]
3 2.3 Βασικές Ιδιότητες Ασαφών Συνόλων Πράξεις Ασαφών Συνόλων Συνάρτηση Συμμετοχής Ασαφής Κανόνες Ασαφή Μοντέλα Ασαφές Μοντέλο Mamdani Ασαφές Μοντέλο Takagi-Sugeno-Kang (TSK) Ασαφοποίηση Απo-ασαφοποίηση Εφαρμογές Ασαφούς Λογικής...46 Κεφάλαιο 3- Τμηματοποίηση Εικόνων Ασαφής Λογική Εισαγωγή Ασάφεια και συνάρτηση συμμετοχής Κατανομή γάμα Fuzzy divergence Μεθοδολογία Linear index Quadratic index Fuzzy similarity Fuzzy compactness Μεθοδολογία Intuisionistic Fuzzy divergence Προτεινόμενη συνάρτηση συμμετοχής Συνάρτηση συμμετοχής Διαισθητικά ασαφής δείκτης Μεθοδολογία Intuitionistic Fuzzy C-means...63 [2]
4 3.7.1 Εισαγωγή Παρουσίαση μιας διαισθητικά ασαφής εικόνας Ομαδοποίηση βασισμένη στη διαισθητικά ασαφή διατομή Φάση Αρχικοποίησης Κύριος Βρόγχος Στάδιο Υπολογισμών...66 Κεφάλαιο 4 - Λογισμικό Τμηματοποίησης Εικόνων...69 Κεφάλαιο 5- Πειραματικά Αποτελέσματα Εισαγωγή Ασάφεια και συνάρτηση συμμετοχής Ενότητα Ενότητα Ενότητα Κεφάλαιο 6- Συμπεράσματα Σύνοψη Ασαφείς μέθοδοι Διαισθητικά ασαφείς μέθοδοι(ifs) Ομαδοποίηση(clustering)...92 Βιβλιογραφία...93 [3]
5 [4]
6 Περίληψη Η τμηματοποίηση εικόνας είναι ένα βασικό εργαλείο που λόγο της χρησιμότητάς του έχει εισχωρήσει σε πολλούς κλάδους της επιστήμης της επεξεργασίας εικόνων, με στόχο την εξαγωγή διαφόρων χρήσιμων πληροφοριών. Σκοπός της πτυχιακής εργασίας είναι η μελέτη και ανάπτυξη διαφόρων μεθοδολογιών τμηματοποίησης εικόνων σε αποχρώσεις του γκρι με την χρήση Ασαφούς Λογικής. Στη παρούσα εργασία υλοποιήθηκαν έντεκα αλγόριθμοι τμηματοποίησης με βάση την εύρεση κατωφλίου (κατωφλίωση) από τις οποίες οι έξι γίνονται με μια τιμή κατωφλίου, ενώ οι υπόλοιπες πέντε με δύο τιμές κατωφλίου. Τέλος ο τελευταίος αλγόριθμος υλοποιήθηκε με βάση την μέθοδο της ασαφούς ομαδοποίησης.επίσης, μέσω ενός γραφικού περιβάλλοντος που αναπτύχθηκε παρέχεται η δυνατότητα σύγκρισης της απόδοσης των μεθοδολογιών τμηματοποίησης σε διάφορες πειραματικές εικόνες με την βοήθεια κάποιων δεικτών. [5]
7 [6]
8 Abstract Image segmentation is a basic tool, for that reason its usefulness has run into many areas of science such as image processing to extract various useful information. The purpose of this thesis is to study and develope various methods for the segmentation of gray level images using Fuzzy Logic and clustering. In this paper eleven segmentation algorithms have been implemented based on thresholding. Six of them use one threshold value, while the remaining five are implemented with two threshold values. Finally, the last algorithm was implemented based on the method of the intuitionistic fuzzy c-means. Also, through a developed graphical user interface, we provide the capability to export and compare the performance of the segmentation methods in various experimental images with the help of some performance indices. [7]
9 [8]
10 Πρόλογος Ο άνθρωπος ως ον, βασίζεται στην όραση του για να αναγνωρίσει τον χώρο που τον περιβάλλει. Αυτό γίνεται ανιχνεύοντας τα διάφορα αντικείμενα του χώρου μέσω μιας σειράς εικόνων που λαμβάνει, και αφού τις επεξεργαστεί και ξεχωρίσει τα αντικείμενα από την υπόλοιπη σκηνή, αποκτά μια συνολική αίσθηση του χώρου. Τις τελευταίες δεκαετίες λόγο της ραγδαίας ανάπτυξης της τεχνολογίας και ειδικότερα των υπολογιστών, δημιουργήθηκαν τεχνικές επεξεργασίας εικόνας οι οποίες βελτιώνουν την ποιότητα της εικόνας, ώστε να γίνεται πιο εύκολη η αναγνώριση των αντικειμένων. Γενικότερα από μια σωστά επεξεργασμένη εικόνα μπορούν να ληφθούν χρήσιμες πληροφορίες που δεν μπορούν να ληφθούν από μια μη επεξεργασμένηεικόνα. Στο πρώτο κεφάλαιο της πτυχιακής μελετώνται διάφορες τεχνικές τμηματοποίησης εικόνων. Στο δεύτερο κεφάλαιο μελετάται η έννοια της ασαφούς λογικής, των ασαφών συνόλων και γενικότερα η λειτουργία των ασαφών συστημάτων. Στο τρίτο κεφάλαιο περιγράφονται οι μέθοδοι που έχουν υλοποιηθεί. Στο τέταρτο κεφάλαιο περιγράφετε το λογισμικό που αναπτύχθηκε στα πλαίσια της πτυχιακής καθώς και όλες οι λειτουργιές που παρέχονται στον χρήστη. Στο πέμπτο κεφάλαιο αναλύονται τα πειραματικά αποτελέσματα της κάθε μεθόδου, ενώ με τη χρήση κατάλληλων δείκτών απόδοσης εξάγονται συγκριτικά αποτελέσματα. Στο έκτο κεφάλαιο γίνεται μια σύνοψη της πτυχιακής και καταγράφονται τα συμπεράσματα της κατάτμησης των πειραματικών εικόνων. Τέλος, τέθηκαν οι μελλοντικές χρήσεις της τμηματοποίησης εικόνων με τις διαφορές μεθοδολογίες. [9]
11 Κεφάλαιο 1 - Τμηματοποίηση εικόνας (Image Segmentation) 1.1 Εισαγωγή Η εικόνα σήμερα αποτελεί μία από τις σημαντικότερες πηγές πληροφορίας. Τη συναντούμε είτε ως ακίνητη (φωτογραφία) είτε ως κινούμενη (video). Η ψηφιακή εικόνα αποτελεί ότι πιο σύγχρονο και την συναντούμε, τόσο στο χώρο της ενημέρωσης (Internet), και της εκπαίδευσης όσο και στο χώρο της ψυχαγωγίας αλλά και της υγείας. Μια ψηφιακή εικόνα μπορεί να είναι δυαδική, μονοχρωματική αποχρώσεων του γκρι ή έγχρωμη. H εικόνα μπορεί να οριστεί ως μια δισδιάστατη συνάρτηση f(x,y), όπου τα x,y είναι οι χωρικές συντεταγμένες των εικονοστοιχείων. Σε αυτήν την πτυχιακή θα ασχοληθούμε με την τμηματοποίηση εικόνων που απεικονίζονται με αποχρώσεις του γκρι(grayscale). Στην Εικόνα 1 βλέπουμε μια grayscale εικόνα. Η εύρεση κατωφλίων (thresholds) είναι μια από τις καλύτερες τεχνικές και με βάση αυτή, θα υλοποιήσουμε τις περισσότερες μεθόδους μας. Θα αναλύσουμε ακόμη κάποιες μεθόδους που εφαρμόζονται για τμηματοποίηση σε έγχρωμες εικόνες. Συγκεκριμένα θα αναλύσουμε τις παρακάτω μεθόδους τμηματοποίησης: Τμηματοποίηση με κατωφλίωση Τμηματοποίηση βασισμένη σε αναγνώριση ακμών Τμηματοποίηση με ομαδοποίηση Τμηματοποίηση watershed Άλλες μέθοδοι Όλες οι μεθοδολογίες τμηματοποίησης έχουν ως στόχο την υλοποίηση ενός αλγορίθμου που να μπορεί να λειτουργεί βέλτιστα σε ότι αφορά: Ακρίβεια: Τα αποτελέσματα του αλγορίθμου πρέπει να είναι όσο πιο κοντά γίνεται στο επιθυμητό αποτέλεσμα. [10]
12 Αυτοματοποίηση: Πρέπει να υπάρχει αυτοματοποίηση του αλγορίθμου έτσι ώστε να είναι εύκολη η χρήση του ακόμη και αν ο χρήστης δεν είναι γνώστης του αντικειμένου. Ευστάθεια: Ο αλγόριθμος πρέπει να παράγει τα ίδια αποτελέσματα όσες φορές και αν εκτελείτε στην ίδια εικόνα. Εικόνα 1: Μία grayscale εικόνα. Κατά καιρούς έχουν προταθεί αρκετοί αλγόριθμοι τμηματοποίησης εικόνας οι οποίοι έχουν ως απώτερο σκοπό την πραγματοποίηση μιας καλύτερης τμηματοποίησης. Γενικά όμως οι αλγόριθμοι τμηματοποίησης χωρίζονται κυρίως σε boundary-based (μέθοδοι αναγνώρισης ακμών) και region-based (μέθοδοι ανάπτυξης περιοχών). Και τα δύο είδη χρησιμοποιούν την αντίθεση και το μέγεθος που υπάρχει στην εικόνα ως κριτήρια ομοιογένειας για την υλοποίηση της κατάτμησης. Η ακριβής κατάτμηση πραγματοποιείται με πέντε βασικές προσεγγίσεις. Αυτές είναι: Οι τεχνικές κατωφλιοποίησης, οι οποίες βασίζονται στην λογική ότι τα εικονοστοιχεία με τιμές σε ένα συγκεκριμένο εύρος ανήκουν στο αντικείμενο. [11]
13 Οι boundary-based μέθοδοι, ή τεχνικές αναγνώρισης ακμών οι οποίες βασίζονται στο ότι οι τιμές των εικονοστοιχείων αλλάζουν δραστικά μεταξύ δύο περιοχών. Οι region-based αλγόριθμοι, οι οποίοι ομαδοποιούν pixels σε μεγαλύτερες περιοχές. Επιλέγονται κάποια σημεία της εικόνας και αφού ελεγχθούν εάν τα γειτονικά εικονοστοιχεία τους μέσα στην ίδια περιοχή έχουν παρόμοιες τιμές(διαβάθμιση του γκρι, χρώμα, υφή), χρησιμοποιώντας ένα κριτήριο ομοιογένειας διαχωρίζονται με τα γειτονικά εικονοστοιχεία σε διάφορες περιοχές. Βασική δυσκολία αυτών των αλγορίθμων είναι η επιλογή αυτών των σημείων και των κριτηρίων ομοιογένειας. Οι pixel intensity based μέθοδοι, όπου οι τιμές των εικονοστοιχείων χρησιμοποιούνται για την τμηματοποίηση της εικόνας. Οι topographic region growing (μορφολογικές μέθοδοι), όπως είναι το watershed το οποίο χρησιμοποιεί τις κλίσεις της εικόνας για την τμηματοποίηση της εικόνας. Αυτές οι μέθοδοι ανήκουν στις μη γραμμικές μεθόδους ανάλυσης της εικόνας. Το βασικότερο ερώτημα που γεννιέται είναι ποιός από τους παραπάνω αλγόριθμους τμηματοποίησης είναι ο καταλληλότερος για κάθε εικόνα. Αυτό μπορεί να βρεθεί αν ερωτηθεί κανείς τί θέλουμε να εξάγουμε από την αρχική εικόνα και κατ επέκταση ποιο κριτήριο πρέπει να βελτιστοποιήσει για να αποκτήσουμε το επιθυμητό αποτέλεσμα. Συνδυάζοντας λοιπόν τις ιδιότητες της εικόνας όπως είναι η ένταση της φωτεινότητας, το χρώμα, η υφή, η κίνηση, το βάθος, τον προσανατολισμό, τη συμμετρία, το μέγεθος, καθώς και τα μοντέλα αντικειμένων, μπορούμε να επιλέξουμε την καταλληλότερη μέθοδο τμηματοποίησης [23]. Ένα σημαντικό βήμα πριν την τμηματοποίηση της εικόνας είναι η βελτίωση της ποιότητας της εικόνας ώστε να της δώσει μια καλύτερη μορφή για περαιτέρω επεξεργασία. [12]
14 1.2 Βελτιστοποίηση Ποιότητας Εικόνας Όπως προαναφέρθηκε, για την επιτυχή τμηματοποίηση μιας εικόνας χρειάζονται να εφαρμοστούν διεργασίες πριν την εισαγωγή της σε ένα αλγόριθμο τμηματοποίησης. Οι διεργασίες αυτές αποσκοπούν στην καλύτερη λειτουργία του εκάστοτε αλγορίθμου και στη βελτίωση του αποτελέσματος. Παρακάτω θα δούμε τις πιο σημαντικέςαπό αυτές Φίλτρο μέσου όρου Το φίλτρο μέσου όρου επιδρά σε μια εικόνα f(x,y) και δημιουργεί μια άλλη g(x,y) με βάση τον τύπο: g(x, y) = 1 M f(m, n) m.n S Όπου S είναι η περιοχή γύρω από το κάθε εικονοστοιχείο (x,y), που περιλαμβάνει Μ γειτονικά εικονοστοιχείο. Σε αυτό το φίλτρο η τιμή του κάθε εικονοστοιχείου στην ουσία είναι η μέση τιμή της γειτονίας του εικονοστοιχείου. Το αποτέλεσμα αυτού του φίλτρου είναι η καταστολή του θορύβου μέσω θόλωσης της εικόνας. Στην Εικόνα 2 βλέπουμε την εφαρμογή ενός φίλτρου μέσου όρου [23]. Αρχική Εικόνα Φιλτραρισμένη Εικόνα Εικόνα 2: Εφαρμογή φίλτρου μέσου όρου. [13]
15 1.2.2 Median φίλτρο Το Median φίλτρο είναι παρόμοιο με το φίλτρο μέσου όρου και επίσης χρησιμοποιείται για την καταστολή του θορύβου κατά την προ επεξεργασία της εικόνας. Η διαφορά με το φίλτρο μέσου όρου είναι οτι καταφέρνει και διατηρεί τις ακμές των σχημάτων μετά το φιλτράρισμα της εικόνας, δηλαδή καταστέλλει τον θόρυβο χωρίς να θολώσει την εικόνα. Το Median φίλτρο χρησιμοποιείται κυρίως για να εξαλείψει τον salt and pepper θόρυβο [23] Φίλτρο όξυνσης των ακμών Το φίλτρο όξυνσης των ακμών κάνει την ακριβώς αντίθετη διαδικασία από το φίλτρο μέσου όρου. H άθροιση των τιμών των εικονοστοιχείων επιφέρει θόλωση των λεπτομερειών της εικόνας. Αφού η άθροιση είναι ανάλογη με τη διαδικασία της ολοκλήρωσης, η παραγώγιση θα έχει αντίθετο αποτέλεσμα, ενισχύοντας τις λεπτομέρειες της εικόνας. Τα φίλτρα αυτά χρησιμοποιούνται κυρίως σε θολές εικόνες για την βελτίωση των λεπτομερών [23] Φίλτρα φωτεινότητας Υπάρχουν δύο τεχνικές φίλτρων φωτεινότητας. Αλλαγή της αντίθεσης σε grayscale εικόνες: Η αλλαγή της αντίθεσης σε μια εικόνα επιτυγχάνεται πολλαπλασιάζοντας τις τιμές των εικονοστοιχείων με μια σταθερά. Εξισορρόπηση ιστογράμματος: Το ιστόγραμμα μιας εικόνας είναι η συνάρτηση h(r k ) = n k, όπου n k είναι ο αριθμός των εικονοστοιχείων, και r k η φωτεινότητά τους. Με αυτή την τεχνική κανονικοποιείται το ιστόγραμμα (Εικόνα 3), διαιρώντας κάθε τιμή του με το συνολικό αριθμό των εικονοστοιχείων της εικόνας(n). Επομένως, το κανονικοποιημένο ιστόγραμμα δίνεται από την παρακάτω σχέση: [14]
16 p(r k ) = n k n Η τεχνική εξισορρόπησης ιστογράμματος είναι η βάση για αρκετές μεθόδους επεξεργασίας εικόνας καθώς μπορεί να παρέχει πληροφορίες οι οποίες χρησιμοποιούνται ως συνιστώσες των διαδικασιών συμπίεσης ή κατάτμησης των εικόνων. Αρχική Εικόνα Αρχικό Ιστόγραμμα Τελική Εικόνα Τελικό Ιστόγραμμα Εικόνα 3: Εξισορρόπηση ισογράμματος Γραμμικά Φίλτρα Αυτή η τεχνική χρησιμοποιείται για την εξάλειψη διαφόρων τύπων θορύβου. Το γραμμικό φιλτράρισμα είναι το φιλτράρισμα στο οποίο η τιμή του κάθε εξερχόμενου εικονοστοιχείου είναι ένας γραμμικός συνδυασμός των τιμών των εισερχόμενων γειτονικών εικονοστοιχείων. Ένα γραμμικό φίλτρο είναι το Gaussian. [15]
17 1.3Τμηματοποίηση με Κατωφλίωση Η κατωφλίωση είναι ένα δημοφιλές εργαλείο για την κατάτμηση της εικόνας το οποίο χρησιμοποιείται για την εξαγωγή των αντικειμένων από μια εικόνα. Αν τα αντικείμενα είναι σαφώς διακριτά από το φόντο, η τιμή για την κατάτμηση μπορεί να επιλεγεί εύκολα σύμφωνα με τα σημεία του πολυτροπικού ιστογράμματος. Η ασαφής θεωρία συνόλων εφαρμόζεται στην κατωφλίωση για την διαμέριση της εικόνας σε χρήσιμες περιοχές. Η εφαρμογή των ασαφών εννοιών στην επεξεργασία εικόνας έχει αποκτήσει μεγαλύτερη σημασία λόγω διάφορων λόγων, όπως οι ανακρίβειες των επιπέδων του γκρίζου μιας εικόνας, η ασάφεια σε ορισμένα σημεία, όπως στα όρια μεταξύ των περιοχών της εικόνας κλπ. Οι μετρήσεις, όπως η εντροπία, ο δείκτης της ασάφειας και ο δείκτης της μη ασάφειας μπορούν να χρησιμοποιηθούν ως μια αντικειμενική συνάρτηση η οποία μπορεί να βελτιστοποιηθεί για την τμηματοποίηση των εικόνων. Η τεχνική αυτή λοιπόν έχει βέλτιστη εφαρμογή σε εικόνες στις οποίες τα εικονοστοιχεία του αντικειμένου(object) έχουν διαφορετική απόχρωση από τα εικονοστοιχεία του φόντου(background).η βασική λογική λειτουργίας αυτής της μεθόδου είναι η παρακάτω. Η μετάβαση από τον αναλογικό κόσμο στον ψηφιακό συνεπάγεται τη μετατροπή αναλογικών σημάτων σε ψηφιακά. Έτσι μια πραγματική εικόνα μεταφέρεται στον ψηφιακό κόσμο και απεικονίζεται με μορφή ψηφιακών πινάκων.κατά την κατωφλίωση η εικόνα μετατρέπεται σε δυαδική οπότε κατ επέκταση έχει μόνον δύο στάθμες φωτεινότητας που συνήθως είναι το μαύρο και το άσπρο. Το μαύρο αντιστοιχεί στην τιμή 0 και το άσπρο στην τιμή 1. Επιλέγουμελοιπόν ένα επιθυμητό κατώφλι και ελέγχουμε το επίπεδο γκρι του κάθε εικονοστοιχείου. Η τιμή που μπορεί να έχει το κάθε εικονοστοιχείο είναι από 0 μέχρι 1. Εάν είναι μεγαλύτερη ή ίση της τιμής του κατωφλίου, τότε παίρνει την τιμή 1 ενώ για ένταση μικρότερη από αυτή του κατωφλίου παίρνει την τιμή 0. Έτσι μέσω αυτής της τεχνικής ξεχωρίζουμε κάποια αντικείμενα στην εικόνα τα οποία έχουν ένταση μεγαλύτερη από την τιμή του κατωφλίου. Άρα η τιμή του κατωφλίου πρέπει να επιλέγεται ανάλογα με την φωτεινότητα της εικόνας και των αντικειμένων μέσα σε αυτή. Υπάρχουν λοιπόν κάποια σημαντικά στοιχεία που πρέπει να επισημάνουμε για την μέθοδο αυτή: Η ορθή επιλογή κατωφλίου οδηγεί σε μια επιτυχή τμηματοποίηση. [16]
18 Η επιτυχή τμηματοποίηση μέσω της κατωφλίωσης γίνεται μόνο σε συγκεκριμένες εικόνες στις οποίες δεν υπάρχουν πολλές διακυμάνσεις στη φωτεινότητα τόσο του φόντου όσο και του αντικειμένου. Η επιλογή του κατωφλίου μπορεί να γίνεται χειροκίνητα ή αυτόματα. Για την επίλυση προβλημάτων όπου υπάρχει ανομοιόμορφος φωτισμός και θόρυβος και η μέθοδος αυτή χάνει την αποτελεσματικότητά της, διαχωρίζουμε την εικόνα σε υπόπεριοχές και με την ενίσχυση της αντίθεσης της εικόνας μειώνεται η ανομοιομορφία της φωτεινότητας. Τέτοια προβλήματα συνήθως συναντάμε σε ιατρικές εικόνες όπου υπάρχει ανομοιόμορφος φωτισμός και θόρυβος [17],[20],[11],[23],[19]. Άλλοι μέθοδοι κατωφλίωσης, είναι η probabilistic μέθοδος, η structural μέθοδος όπου αξιολογείται ένα εύρος κατωφλιών σε σχέση με τις δυαδικές εικόνες που προκύπτουν, η τοπική κατωφλίωση όπου η τιμή του κατωφλίου μεταβάλλεται για διάφορες περιοχές της εικόνας και η μέθοδος Otsu (Εικόνα 4). Εικόνα 4: Κατωφλίωση με την μέθοδο Otsu. Μέθοδος Otsu Η βασική ιδέα της μεθόδου Otsu είναι πως οι κατηγορίες οι οποίες διαχωρίστηκαν καλά μπορούν να διακριθούν ως προς τις τιμές έντασης των εικονοστοιχείων τους και αντίστροφα. Με τη μέθοδο Otsu πραγματοποιείται μια κατωφλίωση της εικόνας βασισμένη στο ιστόγραμμα της εικόνας που δημιουργείται αυτόματα στον αλγόριθμο. Ο αλγόριθμος υποθέτει ότι η εικόνα έχει δύο κλάσεις από pixels. [17]
19 Η κατωφλίωση Otsu είναι μια επαναληπτική διαδικασία που για όλες τις πιθανές τιμές κατωφλίου υπολογίζει ένα μέτρο διακύμανσης για τα pixels κάθε πλευράς του κατωφλίου, για παράδειγμα για τα pixels του αντικειμένου και του φόντου. Καθώς προσαρμόζεται το κατώφλι, αυξάνεται η εξάπλωση της μιας συστάδας και μειώνεται η εξάπλωση της άλλης. Ο στόχος είναι η επιλογή του κατωφλίου που ελαχιστοποιεί τη συνδυασμένη εξάπλωση. Το βέλτιστο κατώφλι είναι αυτό που μεγιστοποιεί την μεταξύ τους διακύμανση (ή αντιστρόφως, ελαχιστοποιεί την διακύμανσης εντός της συστάδας) [18]. Διπλή Κατωφλίωση Η διπλή κατωφλίωση είναι μια μέθοδος που εφαρμόζεται συνήθως σε εικόνες στις οποίες το επίπεδο γκρι του φόντου δεν έχει τιμές έντασης μόνο κάτω ή πάνω από τις αντίστοιχες του αντικειμένου. Αυτό σημαίνει ότι έχουμε ένα φόντο που είναι πολύ σκοτεινό σε κάποια σημεία και πολύ φωτεινό σε κάποια άλλα με αποτέλεσμα η απλή κατωφλίωση να μη μπορεί να απομονώσει το αντικείμενο. Παρακάτω στην Εικόνα 5 βλέπουμε ένα απλό παράδειγμα αποτυχίας της απλής κατωφλίωσης. Το συμπέρασμα είναι ότι όποια τιμή κατωφλίωσης και να επιλέξουμε δε θα έχουμε το επιθυμητό αποτέλεσμα καθώς το μόνο που θα καταφέρουμε θα είναι είτε να μαυρίσουμε τα αντικείμενα που βρίσκονται στο αριστερό μέρος της εικόνας, είτε να ασπρίσουμε και άλλα αντικείμενα που βρίσκονται στο κέντρο και αριστερά της εικόνας. Αρχική εικόνα Κατωφλιωμένη εικόνα Εικόνα 5: Αποτυχημένη απλή κατωφλίωση. Για την εύρεση μιας καλύτερης λύσης σε παρόμοιες εικόνες χρησιμοποιούμε την διπλή κατωφλίωση. Στην διπλή κατωφλίωση επιλέγουμε δύο τιμές κατωφλίουτ1 και Τ2. Όταν η τιμή του εικονοστοιχείου βρίσκεται ανάμεσα στις τιμές Τ1 και Τ2 το [18]
20 εικονοστοιχείο γίνεται άσπρο. Σε διαφορετική περίπτωση γίνεται μαύρο. Το μειονέκτημα αυτής της τεχνικής είναι ότι για να είναι αποτελεσματική πρέπει να επιλέξουμε σωστές τιμές κατωφλίου. Στην Εικόνα 6 βλέπουμε ένα παράδειγμα διπλής κατωφλίωσης. Αρχική εικόνα Κατωφλιωμένη εικόνα Εικόνα 6: Διπλή κατωφλίωση. 1.4 Τμηματοποίηση βασισμένη σε Αναγνώριση Ακμών Μια επίσης αποτελεσματική μέθοδος τμηματοποίησης εικόνας είναι η τμηματοποίηση βασισμένη σε αναγνώριση ή αλλιώς ανίχνευση ακμών. Ο στόχος της ανίχνευσης ακμών είναι να μαρκάρει τα σημεία της εικόνας στα οποία το επίπεδο φωτεινότητας αλλάζει απότομα. Ως ακμή ορίζεται η καμπύλη που ακολουθά της διαδρομή της απότομης αλλαγής της φωτεινότητας των εικονοστοιχείων της εικόνας. Στόχος της ανίχνευσης ακμών είναι η κατανόηση των αλλαγών της έντασης της φωτεινότητας μιας εικόνας. Οι απότομες μεταβολές της έντασης της φωτεινότητας της εικόνας συχνά οφείλονται στα χαρακτηριστικά των αντικειμένων όπως το βάθος, η αντανάκλαση κάποιου αντικειμένου ή της επιφάνειας, ο φωτισμός, οι σκιές και άρα ο εντοπισμός των ακμών μας δίνει στοιχεία για τα γεωμετρικά χαρακτηριστικά του αντικειμένου. Οι ακμές είναι συνήθως συνδεδεμένες με τα περιγράμματα των αντικειμένων αφού συνήθως υπάρχει απότομη αλλαγή της φωτεινότητας ανάμεσα στα αντικείμενα και στο φόντο. Για αυτόν τον λόγο η ανίχνευση ακμών χρησιμοποιείται για την τμηματοποίηση της εικόνας. Συνήθως στις εικόνες υπάρχει θόρυβος που επηρεάζει τα αποτελέσματα της ανίχνευσης ακμών, καθώς ο θόρυβος ομαλοποιεί τις απότομες μεταβολές της [19]
21 έντασης της φωτεινότητας, κάτι που κάνει τον εντοπισμό των ακμών δυσκολότερο. Ο θόρυβος μπορεί να αντιμετωπιστεί είτε μέσω της ενίσχυσης της εικόνας (image enhancement), είτε με την ενίσχυση της αντίθεσης της εικόνας, είτε φιλτράροντας τις εικόνες για την εξάλειψη του θορύβου [20],[19]. Η ανίχνευση ακμών γίνεται σε 3 στάδια: Ομαλοποίηση των εντάσεων της εικόνας μέσω φιλτραρίσματος για την καταστολή του θορύβου. Παραγώγιση της ομαλοποιημένης εικόνας μέσω 1ης ή 2ης τάξης παραγώγων, ώστε να ενισχυθούν οι ακμές. Ανίχνευση των ακμών. Μερικοί από τους σημαντικότερους ανιχνευτές ακμών είναι οι παρακάτω: Mέθοδος Sobel: Ο τελεστής Sobel ομαλοποιεί αρκετά την εικόνα καθιστώντας την λιγότερο ευαίσθητη στο θόρυβο. Mέθοδος Prewitt: Τα αποτελέσματα που παράγει είναι παρόμοια με εκείνα του τελεστή Sobel με τη διαφορά ότι δεν είναι τόσο ισοτροπικά. Mέθοδος Canny: Η ανίχνευση ακμών είναι μια μέθοδος ευαίσθητη στο θόρυβο. Ο τελεστής Canny αντιμετωπίζει το πρόβλημα αυτό χρησιμοποιώντας ένα εναλλακτικό τρόπο εύρεσης των ακμών της εικόνας. Mέθοδος LoG (Laplacian of Gaussian) Η μέθοδος LoG είναι παρόμοια με την μέθοδο Canny. Μέσω του λαπλασιανού τελεστή, οι ακμές βρίσκονται στα zero-crossings της LoG. Παρόλα αυτά το βασικό πρόβλημα της LoG είναι ότι για να έχει επιτυχημένα αποτελέσματα πρέπει να τηρούνται κάποια κριτήρια στην εικόνα. Γενικά υπάρχουν πολλές μέθοδοι ανίχνευσης ακμών αλλά μπορούμε να τις εντάξουμε σε δύο κατηγορίες. Στις μεθόδους που μετράνε την ένταση της ακμής, όπως η Sobel και η Prewitt και υπάρχουν οι μέθοδοι που ανιχνεύουν τα zerocrossings όπως οι LoG και η Canny η οποία θεωρείται από τις καλύτερες σε σχέση με τις υπόλοιπες, γιατί επηρεάζεται λιγότερο από την ύπαρξη θορύβου [21],[20]. [20]
22 Στην παρακάτω Εικόνα 7, παρουσιάζονται τα αποτελέσματα εξαγωγής ακμών με την εφαρμογή των προαναφερθέντων μεθόδων. Αρχική Εικόνα Μέθοδος Sobel Μέθοδος Prewitt Μέθοδος LoG Εικόνα 7: Εξαγωγή ακμών με τις μεθόδους που αναφέρθηκαν. 1.5 Τμηματοποίηση με Ομαδοποίηση(Clustering) Οι αλγόριθμοι ομαδοποίησης είναι τεχνικές αναγνώρισης προτύπων που προσπαθούν να διαιρέσουν τον χώρο των χαρακτηριστικών μια εικόνας χρησιμοποιώντας δεδομένα με γνωστές επιγραφές. Ποιο συγκεκριμένα ο αλγόριθμος ξεκινά με μια τυχαία διαμέριση των εικονοστοιχείων σε ομάδες και στη συνέχεια επανατοποθετεί τα εικονοστοιχεία (Εικόνα 8). [21]
23 Οι δημοφιλέστεροι αλγόριθμοι τμηματοποίησης με ομαδοποίηση είναι οι παρακάτω: Ασαφής C-μέσος(fuzzy c-means). Ασαφής Κ-μέσος (fuzzy κ-means)ήisodata αλγόριθμος. Αλγόριθμος μέγιστης προσδοκίας Ο ασαφής C-μέσος πραγματοποιεί τμηματοποίηση βασισμένη στην ασαφή θεωρία συνόλων. Ο Κ-μέσος αλγόριθμος δημιουργεί αρχικά Κ σύνολα. Στη συνέχεια υπολογίζει το μεσαίο του κάθε συνόλου, και υλοποιεί έναν καινούριο διαχωρισμό έτσι ώστε το κάθε σημείο να σχετίζεται με το κοντινότερο μεσαίο. Το μειονέκτημα των c-means και k-means, είναι ότι κάθε φορά ο αριθμός των ομάδων πρέπει να ορίζεται εξαρχής. Τέλος ο αλγόριθμος μέγιστης προσδοκίας είναι μη-παραμετρικός, καθώς τα δεδομένα ακολουθούν ένα γκαουσιανό μοντέλο. Το μοντέλο αυτό οδηγεί σε ομαδοποίηση των δεδομένων γύρω από τα τοπικά μέγιστα [17],[21],[20]. Αρχική εικόνα Ομαδοποιημένη εικόνα Εικόνα 8: Τμηματοποίηση με ομαδοποίηση. [22]
24 1.6 Τμηματοποίηση Watershed(Μετασχηματισμός Απορροής) Η Watershed είναι μια από τις αποτελεσματικότερες τεχνικές τμηματοποίησης. Η λογική αυτής της τεχνικής είναι ότι βλέπει την εικόνα σαν ένα γεωγραφικό τοπίο το οποίο πλημμυρίζεται από νερό και το μόνο που απομένει είναι οι κορυφές των βουνών. Για να εξηγήσουμε πιο σωστά την μέθοδο αυτή, ας φανταστούμε ότι τα τοπικά ελάχιστα της εικόνας είναι πηγές από τις οποίες εισέρχεται το νερό. Καθώς πλημμυρίζεται ο χώρος, σε κάποια σημεία συναντάται το νερό από τις διαφορετικές πηγές. Σε εκείνα τα σημεία ο αλγόριθμος τοποθετεί φράγματα. Η διαδικασία συνεχίζεται μέχρι η στάθμη να καλύψει και την τελευταία κορυφή. Αυτό που απομένει στο τέλος είναι ο διαχωρισμός της εικόνας από τα νοητά αυτά φράγματα που είναι τα watersheds που δημιουργήθηκαν (Εικόνα 9). Εικόνα 9: Watershed μέθοδος. Ο αλγόριθμος αυτός χρησιμοποιείται κυρίως στην τμηματοποίηση ιατρικών εικόνων γιατί είναι απλός για να τον καταλάβει κάποιος.επίσης για τον λόγο του ότι χρησιμοποιεί τα τοπικά ελάχιστα έχει πολύ καλά αποτελέσματα ακόμη και δεν υπάρχουν μεγάλες σε ένταση ακμές. Το μειονέκτημα της μεθόδου είναι η υπέρκατάτμηση η οποία κάνει, η οποία μερικές φορές δεν είναι ουσιαστική. Ειδικά στη περίπτωση όπου η εικόνα επεξεργαστεί πιο πριν, είναι σχεδόν σίγουρο ότι θα υπάρξει υπέρ-κατάτμηση λόγο του μεγάλου πλήθους των catchment basins. Η λύση σε αυτό το πρόβλημα είναι η χρήση markers. Τα markers χρησιμοποιούνται για να μειώσουν τον αριθμό των catchment. Με βάση τους markers που επιλέγουμε έχουμε κάθε φορά διαφορετικό αποτέλεσμα οπότε η επιλογή τους είναι πολύ σημαντική.το επόμενο βήμα είναι να εισαχθούν στην εικόνα καινούργια, από τα οποία θα αρχίζει η διαδικασία του χώρου [11],[19]. Γενικά η τμηματοποίηση watershed εκτελείτε σε τρία στάδια: [23]
25 1. Μη-Γραμμικό Φιλτράρισμα: Σε αυτό το στάδιο γίνεται η απομάκρυνση του θορύβου από την εικόνα έτσι ώστε να έχουμε καλύτερα αποτελέσματα. Επίσης κάποιες φορές γίνεται και ενδυνάμωση των ακμών για την καλύτερη λειτουργία του αλγορίθμου. Στόχος δηλαδή είναι να ετοιμαστεί η εικόνα για την κατάτμηση.για το μη γραμμικό φιλτράρισμα της εικόνας συνήθως χρησιμοποιούνται τα ASF φίλτρα λόγω του ότι καταστέλλουν επιτυχώς τον θόρυβο χωρίς να επηρεάζουν τα περιγράμματα των αντικειμένων της εικόνας. 2. Εξαγωγή Χαρακτηριστών: Στη συνέχεια πραγματοποιείται εξαγωγή και επεξεργασία των χαρακτηριστικών της φιλτραρισμένης εικόνας. Ο στόχος αυτού του σταδίου είναι η εξαγωγή μικρών ομοιογενών περιοχών από την εικόνα οι οποίες θα χρησιμοποιηθούν ως markers. Υπάρχουν δύο είδη markers, οι Inside markers που σχετίζονται με τα αντικείμενα της εικόνας και οι Outside markers που σχετίζονται με το υπόβαθρο της εικόνας. 3. Ανίχνευση Περιγράμματος Περιοχών: Τέλος στο στάδιο αυτό τοποθετούμε τους Inside markers ως τα τοπικά ελάχιστα της εικόνας, και εφαρμόζουμετην watershed για τον εντοπισμό των περιγραμμάτων τα οποία βρίσκονται ανάμεσα στους Inside-Outside markers.[11] 1.7 Άλλες Μέθοδοι Ταξινομητές: Οι Ταξινομητές, ανήκουν στις μεθόδους region-based. Είναι τεχνικές αναγνώρισης προτύπων, που διαχωρίζουν ένα χαρακτηριστικό χώρο, χρησιμοποιώντας σημεία που επιλέγονται μέσα στην εικόνα. Αυτά τα σημεία ονομάζονται labels. Χαρακτηριστικός χώρος θεωρείται οποιαδήποτε συνάρτηση της εικόνας, με πιο γνωστό χαρακτηριστικό χώρο τις εντάσεις της εικόνας. Οι Ταξινομητές, χρειάζονται δεδομένα ομαδοποίησης, τα οποία δίνονται από τον χρήστη και μετά χρησιμοποιούνται ως αναφορές για την δημιουργία νέων δεδομένων, τα οποία κατατέμνονται αυτόματα. [24]
26 Κάποιοι από αυτούς είναι οι εξής : Ταξινομητές του Κοντινότερου Γείτονα : Η βασική ιδέα ανάπτυξης αυτών των κανόνων, είναι ότι τα εικονοστοιχεία που βρίσκονται κοντά στα labels πιθανόν να ανήκουν στην ίδια ομάδα. Χωρισμός των εικονοστοιχείων με ένα άξονα : Εδώ η βασική ιδέα είναι ότι ένας άξονας διαχωρίζει τα εικονοστοιχεία σε ένα διάγραμμα διασποράς με βάσει κάποιακοινά χαρακτηριστικά. Όλα τα εικονοστοιχεία με κοινά χαρακτηριστικά βρίσκονται από την μια πλευρά του άξονα και όλα τα άλλα στην άλλη πλευρά. Σαν αποτέλεσμα έχουμε την δημιουργία δύο κλάσεων Επέκταση περιοχών: Η Επέκταση περιοχών, είναι η τεχνική στην οποία μια συνεχής περιοχή εικόνας, αφαιρείται με βάσει την ένταση ή τις ακμές της εικόνας. Σε αυτή την μέθοδο επιλέγετε ένα αρχικό σημείο και από εκεί και πέρα γίνεται η παραπάνω διαδικασία με βάση κάποια κριτήρια. Τα σημεία επιλογής ονομάζονται seedpoints. Ένα από τα κριτήρια μπορεί να είναι η αύξηση της περιοχής μέχρι να συναντήσει μια ακμή της εικόνας. Το κυριότερο μειονέκτημα της Επέκταση Περιοχών, είναι το γεγονός ότι το αρχικό σημείο (seed point) πρέπει να καθοριστεί με το χέρι. Ακόμη η Επέκταση περιοχών είναι μια μέθοδος που είναι ευαίσθητη στον θόρυβο, ο οποίος όταν είναι έντονος προκαλεί την δημιουργία οπών λόγω της αφαίρεσης περιοχών, ή ακόμη και αποσύνδεση των περιοχών. Τεχνικές δενδροειδούς αναπαράστασης Οι τεχνικές δενδροειδούς αναπαράστασης ανήκουν στην κατηγορία των regionbased αλγορίθμων και είναι τεχνικές βασισμένες σε πυραμιδική αναπαράσταση. Είναι γενικά μια μέθοδος τμηματοποίησης το αποτέλεσμα της οποίας προκύπτει απο τα αποτελέσματα πολλών τμηματοποιήσεων. Από την συλλογή των αρχικών τμηματοποιήσεων για κάθε ζεύγος εικονοστοιχείων εξάγεται μια πιθανότητα, η οποία εμπεριέχει συνολική πληροφορία σε τοπικό επίπεδο. Η τελική τμηματοποίηση προκύπτει από την επεξεργασία αυτού του πεδίου πιθανοτήτων. Πιθανολογικές και Bayesian μέθοδοι Η χρήση αυτής της μεθόδου βασίζεται σε επανεμφανίσεις κάνοντας παράλληλη χρήση πληροφορίας περιοχών και ακμών για τη βελτίωση της απόδοσης, με εφαρμογή σε τμηματοποίηση ακολουθίας εικόνων. Η μέθοδος αυτή έχει [25]
27 ικανοποιητικά αποτελέσματα ακόμη και όταν οι εικόνες έχουν ληφθεί υπό κακές συνθήκες. Τμηματοποίηση με χρήση νευρωνικών δικτύων Είναι μια μέθοδος αυτόματης τμηματοποίησης και ταξινόμησης για φυσικές εικόνες με χρήση νευρωτικών δικτύων [6],[7],[9]. 1.8 Εφαρμογή σε διαφόρους κλάδους Προβλήματα Η ραγδαία εξέλιξη των υπολογιστών, η ψηφιακή επεξεργασία εικόνων, βρήκε εφαρμογή σε πολλούς κλάδους για την επίλυση πολλών προβλημάτων. Οι τεχνικές επεξεργασίας εικόνας έχουν αναπτυχθεί και εφαρμόζονται σε διάφορους τομείς όπως διαστημικά προγράμματα, μελέτη αεροφωτογραφιών και δορυφορικών εικόνων. Σε ότι αφορά τις δορυφορικές εικόνες και τα διαστημικά προγράμματα, πρέπει να προκύψουν όσο το δυνατόν περισσότερα αποτελέσματα από μια κακή εικόνα. Αυτό το φαινόμενο εμφανίζεται συχνά όταν οι εικόνες λαμβάνονται από μη επανδρωμένους δορυφόρους και από διαστημικά οχήματα εξερεύνησης. Η ψηφιακή επεξεργασία εικόνας μπορεί να βελτιώσει την ποιότητα των εικόνων που λαμβάνονται κάτω από εξαιρετικά δυσμενείς συνθήκες. Εικόνες που παρουσιάζουν χωρική διαστρέβλωση, όπως συναντάται σε μια επίπεδη εικόνα που απεικονίζει έναν σφαιρικό πλανήτη, μπορούν επίσης να επεξεργαστούν για ένα καλύτερο αποτέλεσμα. Πολλές μεμονωμένες εικόνες μπορούν επίσης να συνδυαστούν ωστε να ληφθούν σημαντικές πληροφορίες. Για παράδειγμα, μπορεί να εξακριβωθεί μια εναέρια πτήση πάνω από την επιφάνεια ενός απομακρυσμένου πλανήτη. Εφαρμογή βρήκε και στον κλάδο της Ιατρικής, πάνω στις ιατρικές απεικονίσεις, με σκοπό την επισήμανση περιοχών ενδιαφέροντος, καθώς και τον μετασχηματισμό των εικόνων, ώστε να συλλεχθούν οι ζητούμενες πληροφορίες από αυτές.οι ιατρικές απεικονίσεις είναι σύνολο τεχνικών ψηφιακής επεξεργασίας εικόνας, που χρησιμοποιούνται στη δημιουργία και ανάλυση μερών του ανθρώπινου σώματος, με σκοπό την ουσιαστική υποβοήθηση των ιατρών και των επιστημόνων υγείας. [26]
28 Παραδείγματος χάριν, μια ακτινογραφία μπορεί να βοηθήσει έναν ορθοπεδικό χειρουργό να αποφασίσει για το εάν ένα χέρι ή πόδι χρειάζεται να εγχειριστεί μετά από σοβαρό κάταγμα (Εικόνα 10), καθώς και κατά πόσον μια σχετική χειρουργική επέμβαση είχε επιτυχία ή αν το συγκεκριμένο μέλος έχει τελικά ιαθεί. Εικόνα 10: Μία ιατρική εικόνα και η κατωφλιωμένη έκδοση της. Ένα από τα προβλήματα όμως που παρουσιάστηκαν στις ακτινογραφίες, είναι η επικάλυψη που εμφανίζουν μεταξύ τους κάποια μέρη του ανθρωπίνου σώματος. Αυτό έχει αποτέλεσμα να μην μπορούν να γίνουν ορατές οι περιοχές που παρουσιάζουν ενδιαφέρον. Ακόμη ένα παράδειγμα είναι η εξέταση ενός ζωτικού οργάνου, όπως η καρδιά που δεν μπορεί να είναι ορατή λόγο του ότι βρίσκεται πίσω από νεύρα. Η ψηφιακή επεξεργασία εικόνας, μέσω της κατάλληλης επιλογής μεθόδου επεξεργασίας, μπορεί να βοηθήσει σημαντικά τον ιατρό στις σχετικές διαγνώσεις και αποφάσεις του. Παρόλα αυτά δεν είναι πάντα αποτελεσματική η χρήση αυτής της μεθόδου. Παραδείγματος χάριν, μπορεί να είναι εμφανής ο διαχωρισμός του κόκαλου από τον μαλακό ιστό, αλλά δεν διακρίνεται η διαφορά ενός όγκου από ένα ζωτικό όργανο όπως είναι το συκώτι. Ακόμη οι εικόνες ακτινών Χ παρουσιάζουν την ανατομία του ανθρωπίνου σώματος, δηλαδή τη δομή του και όχι τη φυσιολογία, δηλαδή τη λειτουργία του[17],[21],[19]. Γενικά οι ιατρικές εικόνες μπορούν να διακριθούν σε: Δύο διαστάσεων: ακτινογραφίες και οι υπέρηχοι. Τριών διαστάσεων: Υπολογιστική τομογραφία, μαγνητική τομογραφία, τομογραφία εκπομπής ποζιτρονίων και τομογραφία εκπομπής φωτονίου. [27]
29 Τεσσάρων διαστάσεων: Δυναμική αλληλουχία ογκομετρικών δεδομένων από μια δυναμική τομογραφική μελέτη. Πέντε διαστάσεων: Χρονική αλληλουχία ογκομετρικών δεδομένων από μία δυναμική τομογραφική μελέτη, που απεικονίζει επί πλέον την τιμή κάποιας παραμέτρου ενδιαφέροντος (π.χ. μελέτη μαγνητικής φασματοσκοπίας της καρδιάς). [28]
30 Κεφάλαιο 2 - Ασαφής Λογική 2.1 Εισαγωγή Η Κλασική λογική ασχολείται μόνο με προβλήματα όπου τα αποτελέσματα της είναι αληθή ή ψευδή. Για παράδειγμα το ότι 1 +1 = 2 είναι αληθής, απόλυτο, αμετάβλητο, είναι μια μαθηματική αλήθεια. Ωστόσο, υπάρχουν ορισμένα προβλήματα με μεταβλητές απαντήσεις, που δεν βρίσκουν λύση με την κλασική λογική, όπως για παράδειγμα ζητώντας από μια ομάδα ανθρώπων να προσδιορίσουν εάν ο καιρός σήμερα είναι ζεστός, λίγο ζεστός, κρύος κτλ. Η απάντηση στο ερώτημα αυτό εξαρτάται από πολλούς παράγοντες, όπως η ένδυση ή το σωματότυπο ή ακόμη και η διάθεση του κάθε ανθρώπου. Επομένως, η εύρεση λύσης σε ένα τέτοιο πρόβλημα με την κλασική προσέγγιση είναι αδύνατη. Σε αυτά τα προβλήματα λοιπόν εισάγουμε την έννοια της ασαφούς λογικής. Η έννοια της ασαφούς λογικής (Fuzzy Logic) επινοήθηκε από τον Lotfi Zadeh, καθηγητή στο Πανεπιστήμιο της Καλιφόρνιας στο Berkley, και παρουσιάστηκε ως ένας τρόπος για την επεξεργασία των δεδομένων. Αυτή η θεωρία εφαρμόστηκε για τον έλεγχο των συστημάτων μετά το 1970 και αυτό έγινε λόγω της ανεπαρκούς υπολογιστικής ικανότητας που υπήρχε μέχρι εκείνη την εποχή. Ο καθηγητής Zadeh είχε αιτιολογήσει ότι παρόλο που οι άνθρωποι εισάγουν ακριβή, αριθμητικά δεδομένα σε ένα σύστημα, έχουν εξαιρετικό προσαρμοστικό έλεγχο. Εάν οι ελεγκτές ανατροφοδοσίας δεδομένων ενός συστήματος μπορούσαν να προγραμματιστούν ώστε να δέχονται ασαφή δεδομένα, τα συστήματα θα ήταν πολύ πιο αποδοτικά. Για παράδειγμα φανταστείτε ένα αυτοκίνητο με αυτόματο σύστημα φρεναρίσματος, το οποίο ανιχνεύει την απόσταση κάποιου αντικειμένου που υπάρχει μπροστά και ανάλογα με την ταχύτητα του οχήματος πιέζει το πεντάλ του φρένου ώστε να σταματήσει το όχημα πριν από αυτό. Τα ασαφή δεδομένα σε αυτό το παράδειγμα θα μπορούσαν να είναι η θερμοκρασία των ελαστικών, η θερμοκρασία του περιβάλλοντος, ο τύπος των ελαστικών, η κατάσταση των φρένων κτλ. Η ανατροφοδοσία αυτών των δεδομένων θα βοηθούσε στο να έχουμε ένα πολύ καλύτερο αποτέλεσμα. Οι απόψεις του αυτές τον οδήγησαν τελικά στην έκδοση του βιβλίου του με τίτλο «Fuzzy Sets» [14]. [29]
31 Τα ασαφή συστήματα, λόγω της ευκολίας τους να περιγράφουν πολύπλοκα συστήματα βρήκαν μεγάλη αποδοχή από την επιστημονική κοινότητα παρά τις αρχικές αντιδράσεις κυρίως από τον χώρο των μαθηματικών της στατιστικής και των πιθανοτήτων. Από την πρώτη στιγμή πολλά συστήματα δημιουργήθηκαν με σκοπό την επέκταση των ασαφών συστημάτων. Σε αυτήν την πτυχιακή εργασία γίνεται υλοποίηση αυτών των μεθόδων με χρήση του λογισμικού MATLAB και η ενσωμάτωσή τους σε ένα εύχρηστο γραφικό περιβάλλον. Έτσι δίνεται η δυνατότητα στον χρήστη να παρατηρήσει πώς μία εικόνα μετατρέπεται από το πεδίο της φωτεινότητας στο ασαφές πεδίο, στη συνέχεια στο διαισθητικά ασαφές πεδίο και τελικά στο ασαφές πεδίο και στην τελική εικόνα. Η θεωρία των ασαφών συστημάτων επεκτείνει τα κλασικά σύνολα και την κλασική λογική, εισάγοντας τις έννοιες των ασαφών συνόλων και της ασαφούς λογικής αντίστοιχα. Το ασαφές σύνολο είναι ίσως η βασικότερη έννοια του οικοδομήματος της ασαφούς λογικής. 2.2 Ασαφή Σύνολα Η κλασική θεωρία συνόλων εφαρμόζεται σε πολλά επιστημονικά πεδία με μεγάλη επιτυχία, παρόλα αυτά είναι φανερό ότι τα κλασικά σύνολα αδυνατούν να περιγράψουν επαρκώς έννοιες και καταστάσεις οι οποίες χαρακτηρίζονται από μεγάλο βαθμό ασάφειας και απροσδιοριστίας. Αυτό συμβαίνει γιατί στην κλασική θεωρία συνόλων, τα στοιχεία ή ανήκουν ή δεν ανήκουν σε ένα σύνολο. Η έννοια του ασαφούς συνόλου εισήχθη από τον Zadeh το 1965 και δημιούργησε πραγματική επανάσταση στο χώρο των Μαθηματικών. Ο Zadeh παρατήρησε ότι ο παραδοσιακός τρόπος περιγραφής ενός συστήματος που στηρίζεται στην κλασική λογική ότι μια κατάσταση μπορεί να έχει δύο μόνο μορφές ύπαρξης 0 και 1. Στην ουσία εισήγαγε την κλασματοποίηση μεταξύ 1 και 0 της κλασικής λογικής. Δηλαδή δημιούργησε κάποια σύνολα διαβάθμισης μεταξύ των απόλυτων τιμών, τα ασαφή σύνολα. Έτσι, μια τιμή μπορεί να ανήκει σε πολλά υποσύνολα ταυτόχρονα έχοντας για κάθε ένα από αυτά κάποιον βαθμό συμμετοχής. Ο βαθμός συμμετοχής ενός στοιχείου σε ένα σύνολο εξάγεται με τη χρήση της συνάρτησης συμμετοχής. Αν συμβολίσουμε με X ένα από αυτά τα σύνολα και με μ Α (χ) την συνάρτηση συμμετοχής σε αυτό.αν U είναι ο χώρος των στοιχείων χ, τότε ένα ασαφές σύνολο Χ ορίζεται στον U σαν ένα σύνολο διατεταγμένων ζευγών: [30]
32 μ Α (χ): X -> [0,1] με Χ={χ,μ Α (χ) χ U} Η παραπάνω συνάρτηση μας επιστρέφει μια τιμή μεταξύ 0 και 1. Η τιμή αυτή ονομάζεται βαθμός συμμετοχής για κάθε στοιχείο χ, του συνόλου X. Το σύνολο που ορίζεται με τον παραπάνω τρόπο καλείται ασαφές σύνολο. Έτσι όσο πιο κοντά στο 1 είναι η τιμή, τόσο μεγαλύτερο βαθμό συμμετοχής του χ στο σύνολο Χ έχουμε.ανάλογα αν το πεδίο ορισμού U αποτελείται από διακριτά στοιχεία ή είναι ένας συνεχής χώρος, τα ασαφή σύνολα διακρίνονται σε διακριτά και συνεχή αντίστοιχα. Παρακάτω θα δούμε μια απλή εφαρμογή στην οποία εφαρμόζεται η θεωρία ασαφών συνόλων. Για παράδειγμα, σε μία μέτρηση της θερμοκρασίας ενός χώρου για την λειτουργία ενός κλιματιστικού θα μπορούσαμε να ελέγχουμε τη κατάσταση του, χωρίζοντας το φάσμα των θερμοκρασιών σε περιοχές ή σύνολα τιμών. Ανάλογα με την περιοχή στην οποία βρίσκεται η θερμοκρασία, δίνει εντολή για το πώς θα πρέπει να λειτουργήσει το κλιματιστικό. Εικόνα 1: Αναπαράσταση με ασαφή σύνολα. Στην Εικόνα 1, οι έννοιες κρύο, ζεστό, καυτό αντιπροσωπεύουν ένα σύνολο θερμοκρασιών. Η κατακόρυφη γραμμή στην εικόνα αντιπροσωπεύει μια συγκεκριμένη θερμοκρασία που υπάρχει εκείνη τη στιγμή στον χώρο. Το κόκκινο βέλος μπορεί να ερμηνευθεί ως «καυτό». Το πορτοκαλί βέλος (δείχνοντας 0.2) μπορεί να το περιγράψει ως «ελαφρώς ζεστό» και το μπλε βέλος (δείχνοντας 0,8) «αρκετά κρύο». Βλέπουμε δηλαδή ότι το στοιχείο χ ανήκει σε 3 σύνολα, και έχει βαθμό συμμετοχής 0 στο σύνολο καυτό, 0.2 στο σύνολο ελαφρώς ζεστό και 0.8 στο σύνολο κρύο. [31]
33 Αν το πεδίο ορισμού U αποτελείται από διακριτά στοιχεία ή είναι ένας συνεχής χώρος, τα ασαφή σύνολα διακρίνονται σε διακριτά και συνεχή αντίστοιχα. Σε αντίθεση με τα κλασικά σύνολα, ένα ασαφές σύνολο δεν έχει αυστηρά καθορισμένα όρια. Σύμφωνα με τον Zimmermann, το ασαφές σύνολο παρέχει ένα φυσικό τρόπο επεξεργασίας των δεδομένων, σε προβλήματα των οποίων η πηγή ανακρίβειας προέρχεται από την έλλειψη ευκρινώς καθορισμένων κανόνων για τη σχέση των μελών ενός συνόλου, προκειμένου να περιγραφούν οι αντίστοιχες μεταβλητές που χρησιμοποιούνται. Έτσι γίνεται εύκολα αντιληπτό ότι η περιγραφή εννοιών του πραγματικού κόσμου οι οποίες είναι σε μεγάλο βαθμό ασαφείς και ανακριβείς, γίνεται καλύτερα με βάση τομοντέλο του ασαφούς συνόλου. Ένα μειονέκτημα των ασαφών συνόλων είναι η αδυναμία τους να περιγράψουν καταστάσεις αβεβαιότητας της διαθέσιμης πληροφορίας. Η παραπάνω ανάγκη οδήγησε σε μία επέκταση των ασαφών συστημάτων που εισήγαγε ο Atanassov το 1999 με την ονομασία «διαισθητικά ασαφή συστήματα» (Intuitionistic Fuzzy Sets - IFS). Πλέον, όποτε αναφερόμαστε στον όρο «διαισθητικό» θα γίνεται υπό το πρίσμα της θεωρίας των διαισθητικών ασαφών συνόλων που προτάθηκαν από τον Atanassov. Έτσι, τα διαισθητικά ασαφή συστήματα πέρα από τη «θετική πληροφορία» που εκφράζεται με τη συνάρτηση συμμετοχής σε ένα σύνολο, εισάγουν και τη δυνατότητα διατύπωσης «αρνητικής πληροφορίας», μέσω της συνάρτησης μη-συμμετοχής. Επιπλέον, παρέχουν τη δυνατότητα να εκφραστεί μαθηματικά και η έννοια της διστακτικότητας δηλαδή της αβεβαιότητας, γεγονός που οδηγεί στην επαρκέστερη και συνεπώς αντικειμενικότερη αποτύπωση της πραγματικότητας. Οι Vlachos και Sergiadis [15] ερεύνησαν την εφαρμογή των IFS στην περιοχή της ψηφιακής επεξεργασίας εικόνας καθώς και τη θεωρητική προσέγγιση εννοιών που είναι χρήσιμες στις τεχνικές επεξεργασίας. Πιο συγκεκριμένα, διερεύνησαν την εφαρμογή των IFS στην ένταση αντίθεσης, στην ανίχνευση ακμών και στην κατάτμηση ψηφιακών εικόνων. Τέλος, ανέπτυξαν αλγόριθμους για την επεξεργασία ιατρικών εικόνων. 2.3 Βασικές Ιδιότητες Ασαφών Συνόλων Ορισμένες βασικές ιδιότητες των ασαφών συνόλων είναι οι παρακάτω[12],[10]: Σύνολο Υποστήριξης (Support set) Το σύνολο υποστήριξης ενός ασαφούς συνόλου είναι το σύνολο των στοιχείων x στο U για τα οποία έχουμε: [32]
34 supp(a) = {x U\μ Α (x) > 0} Ύψος Ασαφούς Συνόλου (Height) Το ύψος ενός ασαφούς συνόλου Α είναι η μέγιστη τιμή του μ Α (x) στο U και ορίζεται ως εξής: Σύνολο τομής (α-cut set) hgt(a) = max μ Α (x) Το α-cut ενός ασαφούς συνόλου είναι ένα ασαφές σύνολο το οποίο περιέχει όλα τα στοιχεία x Є X που έχουν μεγαλύτερο βαθμό συμμετοχής από μία τιμή α. Πυρήνας(core) Α α = {x X\μ Α (x) a} όπου 0 < α 1 Ο πυρήνας (core) ενός ασαφούς συνόλου είναι το υποσύνολο του πεδίου ορισμού της συνάρτησης συμμετοχής για το οποίο το πεδίο τιμών παίρνει τιμές ίσες με τη μονάδα. Κανονικό ασαφές σύνολο(normalset) core(a) = {x X\μ Α (x) = 1} Είναι το ασαφές σύνολο του οποίου ο πυρήνας δεν είναι κενό σύνολο, δηλαδή υπάρχει τουλάχιστον ένα στοιχείο x τέτοιο ώστε: Κυρτό ασαφές σύνολο (convex fuzzy set) μ Α (x) = 1 Είναι το ασαφές σύνολο το οποίο έχει μονότονα αύξουσα ή μονότονα φθίνουσα συνάρτηση συµµετοχής. 2.4 Πράξεις Ασαφών Συνόλων Ένωση Με την ένωση δύο ασαφών συνόλων Α και Β δημιουργείτε ένα ασαφές σύνολο, το οποίο συμβολίζεται μεa B. Η συνάρτηση συμμετοχής του προκύπτει από τις συναρτήσεις συμμετοχής των Α και Β ως εξής[7],[10]: [33]
35 ( x) ( x) ( x) max[ ( x), ( x)] x X A B A B Τομή Με την ένωση δύο ασαφών συνόλων Α και Β δημιουργείτε ένα ασαφές σύνολο το οποίο συμβολίζεται με A B. Ομοίος η συνάρτηση συμμετοχής του προκύπτει από τις συναρτήσεις συμμετοχής των Α και Β[7]: ( x) ( x) ( x) min[ ( x), ( x)] x X A B A B Συμπλήρωμα Το συμπλήρωμα ενός ασαφούς συνόλου δίνεται από την παρακάτω σχέση[7]: 1 A( x) x X A [34]
36 Γινόμενο Το γινόμενο δύο ασαφών συνόλων Α και Β ορίζεται ως εξής: ( x) ( x) ( x) A B Αλγεβρικό άθροισμα Το αλγεβρικό άθροισμα δύο ασαφών συνόλων Α και Β ορίζεται ως εξής: ( x) ( x) ( x) ( x) ( x) x X A B A B A B 2.5 Συνάρτηση Συμμετοχής Η Συνάρτηση Συμμετοχής είναι μια καμπύλη η οποία μας περιγράφει τον βαθμό στον οποίο κάθε μεταβλητή x διαθέτει μια συγκεκριμένη ιδιότητα στο σύνολο A. Η συνάρτηση μ Α ονομάζεται συνάρτηση συμμετοχής και στην ουσία συμβολίζει το βαθμό συγγένειας του x στο Α. Επειδή στις περισσότερες περιπτώσεις η μεταβλητή x είναι συνεχής χρησιμοποιούμε παραμετροποιημένες συναρτήσεις. Υπάρχουν διάφοροι τύποι συναρτήσεων συμμετοχής. Παρακάτω θα δούμε κάποιες από αυτές [16],[10]. [35]
37 Τριγωνική Συνάρτηση Συμμετοχής (triangle) Η τριγωνική συνάρτηση συμμετοχής ορίζεται πλήρως από τρεις παραμέτρους a,b,c ως εξής: 0 x a x a a x b triangle(x, a, b, c) = b a c x b x c c b { 0 c x Χρησιμοποιώντας τα max και min έχουμε: triangle(x, a, b, c) = max (min ( x a b a, c x c b ), 0) ΤραπεζοειδήςΣυνάρτηση Συμμετοχής trapezoidal Η τραπεζοειδής συνάρτηση συμμετοχής ορίζεται πλήρως από τέσσερις παραμέτρους a,b,c,d ως εξής: x a trapez(x, a, b, c, d) = max (min ( b a, 1, d x d c ), 0) [36]
38 Καμπανοειδής Συνάρτηση Συμμετοχής Η καμπανοειδής συνάρτηση συμμετοχής ορίζεται πλήρως από τρεις παραμέτρους a,b,c ως εξής: bell(x, a, b, c) = x c a 2b Γκαουσιανή Συνάρτηση Συμμετοχής (Gaussian) Η γκαουσιανή συνάρτηση συμμετοχής ορίζεται πλήρως από δύο παραμέτρους σ,c όπου το σ καθορίζει την συνάρτηση συμμετοχής και το c αναπαριστά το κέντρο της συνάρτησης συμμετοχής: gaussian(x, σ, c) = e (x c σ )2 Σιγμοειδής Συνάρτηση Συμμετοχής (sigmoidal) Η σιγμοειδής συνάρτηση συμμετοχής ορίζεται πλήρως από δύο παραμέτρους a,b ως εξής: [37]
39 1 sigm(x, a, b) = 1 + e a(x b) 2.6 Ασαφής Κανόνες Τα ασαφή συστήματα ελέγχου, παίρνουν αποφάσεις με βάση κάποιους ασαφής κανόνες. Οι ασαφείς κανόνες είναι ουσιαστικά υποθετικές προτάσεις και αποτελούν απαραίτητα δομικά στοιχεία συστημάτων εξαγωγής συμπερασμάτων. Ένας ασαφής κανόνας στην πιο απλή μορφή του είναι ο παρακάτω[10]: IF x is A THEN y is B Όπου A και B είναι λεκτικές τιμές των x και y, τα οποία ορίζονται στους χώρους Χ και Y αντίστοιχα. Το αριστερό τμήμα του κανόνα IF x is A, λέγεται τμήμα υπόθεσης και περιγράφει την υπόθεση του κανόνα. Το δεξιό τμήμα, δηλαδή το THEN y is B, είναι το τμήμα συμπεράσματος του κανόνα. Τα ασαφή συστήματα αποτελούνται από μια ασαφή βάση γνώσης (fuzzyknowledgebase) η αποτελείται από μια συλλογή κανόνων IF/THEN της παρακάτω μορφής: IFx 1 isa 1 j and andx n isa n j THEN y is B j όπου τα A 1 j και B j είναι ασαφή σύνολα και τα x n, y είναι γλωσσικές µεταβλητές. [38]
40 2.7 Ασαφή Μοντέλα Γενικά ένας κανόνας από μόνος του δεν μπορεί να σταθεί για την επίλυση των περισσοτέρων πρακτικών προβλημάτων. Από τη δεκαετία του 80 και μέχρι τις αρχές της δεκαετίας του 90 τα περισσότερα από τα ασαφή μοντέλα που υπήρχαν δεν ήταν ικανά να βρουν λύση ακόμη και σε απλά ζητήματα. Γεννήθηκε, λοιπόν, η ανάγκη να δημιουργηθούν μοντέλα τα οποία μέσα από αυτοματοποιημένες διαδικασίες θα μπορούσαν να λύσουν αυτά τα προβλήματα. Αυτό που χρειαζόταν ήταν μια αυτοματοποιημένη διαδικασία που θα συνδύαζε πολλούς κανόνες μεταξύ τους. Η έξοδος του κάθε κανόνα θα ήταν ένα ασαφές σύνολο και τα ασαφή σύνολα που θα προέκυπταν θα συγκεντρώνονταν για να σχηματίσουν ένα ασαφές σύνολο εξόδου από το οποίο μέσω της διαδικασίας της ασαφοποίησης θα μπορούσε να δώσει την τελική τιμή. Πρόσφατα άρχισε να δίνεται μεγάλη προσοχή σε τέτοιες τεχνικές που υποκινούνται από τα δεδομένα που εισάγονται στο σύστημα. Έτσι δημιουργήθηκαν κάποια νέα ασαφή συστήματα τα οποία και ονομάζονται ασαφή μοντέλα. Τα ασαφή συστήµατα είναι κάθε σύστηµα απόφασης και ελέγχου που λειτουργεί σε και μοντελοποιείται µε ασαφείς µμεταβλητές. Τα ασαφή συστήµατα ανήκουν στην κατηγορία των ευφυών συστηµάτων και βρίσκουν εφαρµογή ολοένα και σε περισσότερα πρακτικά προβλήματα. Η γενική δομή των ασαφών συστηµάτων παρουσιάζεται στην παρακάτω Εικόνα 2: Εικόνα 2: Δομή ασαφούς συστήματος. Η πιο γνωστή μεθολογία στα ασαφή συστήματα είναι αναμφισβήτητα η μέθοδος εξαγωγής συμπεράσματος του Mamdani. Μια παρόμοια μέθοδος είναι το μοντέλο Takagi-Sugeno. Οι διαφορές ανάμεσα στα δύο αυτά συστήματα διακρίνονται κυρίως στον τρόπο με τον οποίο σχηματίζεται η έξοδος του συστήματος, καθώς στο μοντέλο του Takagi-Sugeno οι συναρτήσεις συμμετοχής των εξόδων είναι είτε [39]
41 γραμμικές συναρτήσεις είτε σταθερές, πάντα λοιπόν σαφείς, ενώ στα μοντέλα Mamdani είναι ασαφείς ακριβώς όπως και αυτές των εισόδων Ασαφές ΜοντέλοMamdani Η μεθοδολογία αυτή εισήχθηκε το 1975 από τον Ebrahim Mamdani.Το μοντέλο Mamdani λειτουργεί μέσω ενός συστήματος ασαφούς συλλογιστικής ή αλλιώς fuzzy inference system (FIS). Η ασαφής συλλογιστική είναι η διαδικασία κατά την οποία μέσω μιας δεδομένης εισόδου σχηματίζεται η απεικόνιση της εξόδου, χρησιμοποιώντας τις αρχές της ασαφούς λογικής. Η διαδικασία της ασαφούς συλλογιστικής περιλαμβάνει και συνδυάζει όλα όσα αναφέραμε στα προηγούμενα κεφάλαια, δηλαδή τις πράξεις μεταξύ ασαφών συνόλων (ασαφείς τελεστές), τις συναρτήσεις συμμετοχής και τους κανόνες if-then. Η παραπάνω διαδικασία της απεικόνισης των εισόδων στις εξόδους γίνεται μέσα από πέντε βήματα (Εικόνα 3): 1. Ασαφοποίηση: Το πρώτο βήμα έχει να κάνει με την ασαφοποίηση των εισόδων. Δηλαδή, στη διαδικασία της ασαφοποίησης καθορίζεται ο βαθμός κατά τον οποίο οι τιμές των εισόδων ανήκουν στο καθένα από τα ασαφή σύνολα. Αυτό που γίνεται σε αυτό το βήμα είναι μέσα από τις συναρτήσεις συμμετοχής, ο καθορισμός σε ποιο βαθμό κάθε είσοδος ανήκει σε ένα ασαφές σύνολο. Οι είσοδοι είναι αριθμητικές τιμές μέσα στα όρια του χώρου αναφοράς και οι έξοδοι είναι βαθμοί συμμετοχής στο προσδιορισμένο ασαφές σύνολο. Η ασαφοποίηση των εισόδων μπορεί να γίνει είτε με χρήση πίνακα τιμών είτε μέσα από μια συνάρτηση. Παρακάτω θα δούμε κάποιες μεθόδους ασαφοποίησης. 2. Εφαρμογή κανόνων και ασαφών τελεστών: Αφού ασαφοποιηθούν οι είσοδοι εφαρμόζονται οι ασαφείς τελεστές στα υποθετικά μέρη των κανόνων. Αν ένας κανόνας έχει πολλές υποθέσεις, τότε μέσω των τελεστών AND ή OR δίνεται ένα αριθμός που αντιπροσωπεύει το αποτέλεσμα της εκτίμησης του μέρους της υπόθεσης. Δηλαδή, αν ένας κανόνας IF/THEN έχει στο αριστερό τμήμα του if περισσότερα του ενός μέρη, τότε πρέπει να εφαρμοσθούν οι ασαφείς τελεστές ώστε να υπάρχει μόνο ένα νούμερο που αντιπροσωπεύει το αποτέλεσμα της προϋπόθεσης του κανόνα. Οι είσοδοι ενός λογικού τελεστή είναι δύο ή περισσότεροι βαθμοί συμμετοχής που έχουν προκύψει από τις ασαφοποιημένες μεταβλητές εισόδου. Η έξοδος του τελεστή είναι απλά ένας βαθμός αλήθειας. [40]
42 3. Εφαρμογή συνεπαγωγής: Σε αυτό το βήμα εφαρμόζουμε την συνάρτηση συνεπαγωγής. Για να γίνει αυτό όμως, πρέπει να γνωρίζουμε την βαρύτητα του κάθε κανόνα. Ένας κανόνας IF/THEN μπορεί να έχει βαρύτητα από 0 μέχρι 1. Με τον όρο βαρύτητα εννοούμε την έμφαση που δίνει σε σχέση με κάποιον άλλο κανόνα. Συνήθως οι κανόνες έχουν τιμή 1. Έτσι αφού αναθέσουμε την βαρύτητα των κανόνων μπορούμε να εφαρμόσουμε την συνάρτηση συνεπαγωγής. Η έξοδος ενός κανόνα IF/THENείναι ένα ασαφές σύνολο που αντιπροσωπεύεται από μια συνάρτηση. Η έξοδος αυτή αναδιαμορφώνεται με τη χρήση μιας συνάρτησης που που εφαρμόζεταιστο μέρος της υπόθεσης της IF/THEN. Η είσοδος για τη διαδικασία συνεπαγωγής είναι ένας αριθμός που δίνεται από την υπόθεση ενώ η έξοδος είναι ένα νέο ασαφές σύνολο. Αυτή η διαδικασία εφαρμόζεται σε κάθε κανόνα. 4. Συνάθροιση όλων των κανόνων: Στην συνέχεια συγκεντρώνονται οι έξοδοι όλων των κανόνων. Η συνάθροιση είναι μια διαδικασία κατά την οποία όλα τα ασαφή σύνολα που προκύπτουν ως έξοδοι των κανόνων συνδυάζονται ώστε να προκύψει μόνο ένα ασαφές σύνολο. 5. Απο-ασαφοποίηση: Η απο-ασαφοποίηση είναι το τελευταίο βήμα ενός μοντέλου Mamdani. Κατά την απο-ασαφοποίηση μετατρέπεται το ασαφές σύνολο που προκύπτει από το προηγούμενο βήμα, σε έναν αριθμό που θα μας βοηθήσει να πάρουμε κάποιες αποφάσεις. Υπάρχουν πολλοί τρόποι απο-ασαφοποίηση τους οποίους θα δούμε στην επόμενη παράγραφο [16]. [41]
43 Εικόνα 3: Στάδια λειτουργίας ενός ασαφούς συστήματος Ασαφές Μοντέλο Takagi-Sugeno-Kang (TSK) Η μέθοδος Takagi-Sugeno δημιουργήθηκε το 1985, με σκοπό κυρίως την ανάπτυξη μιας μεθόδου παραγωγής ασαφών κανόνων από ένα γνωστό από πριν σύνολο δεδομένων εισόδων-εξόδων, και αναφέρεται απλώς ως μέθοδος Sugeno ενώ τα μοντέλα που παράγονται αναφέρονται ως TSK μοντέλα. Η μέθοδος αυτή, όπως αναφέραμε και στην αρχή του κεφαλαίου είναι εν γένει παρόμοια με τη μέθοδο Mamdani, και περιέχει ακριβώς τα ίδια βήματα που είναι η ασαφοποίηση των εισόδων καθώς και η εφαρμογή των ασαφούς τελεστών. Η βασική διαφορά ανάμεσα στα δύο μοντέλα είναι ότι στο μοντέλο του TSK οι συναρτήσεις συμμετοχής των εξόδων είναι είτε γραμμικές συναρτήσεις είτε σταθερές. [42]
44 Το ασαφές μοντέλο Takagi-Sugeno-Kang αποτελεί ένα από τα κυριότερα μοντέλα τα οποία χρησιμοποιούνται σε πολλές εφαρμογές ανάπτυξης ασαφών συστημάτων. Το μοντέλο TSK υλοποιείται με κανόνες του τύπου: IFx 1 isa 1 j andx 2 isa 2 j and andx n isa n j THEN y j = a 0 j + a 1 j x a n j x n Όπου τα A είναι ασαφή σύνολα, τα a σταθερές και το j παίρνει τιμές 1,2,...,Μ. Συνήθως, το αριστερό κομμάτι του κανόνα είναι ένα πολυώνυμο, αλλά μπορεί να είναι και οποιαδήποτε συνάρτηση που περιγράφει κατάλληλα την έξοδο του μοντέλου. Εάν το πολυώνυμο είναι μηδενικού βαθμού τότε ο κανόνας παίρνει την παρακάτω μορφή: IF x 1 = A and x 2 = B THEN y = a Όπου τα Α και Β είναι ασαφή σύνολα, ενώ το y=a είναι μία σταθερά. Όταν ο κανόνας έχει την παραπάνω μορφή, τότε το μοντέλο έχει έντονη ομοιότητα με αυτό του Mamdani. Εάν το πολυώνυμο είναι πρώτου βαθμού τότε ο κανόνας έχει την μορφή: IFx 1 = A and x 2 = B THEN y = p x 1 + q x 2 + r Όπου τα Α και Β είναι ασαφή σύνολα στο δεξί τμήμα του κανόνα, ενώ τα p,q και r, είναι όλασταθερές. Η έξοδος των συστημάτων TSK προκύπτει με βάση τον σταθμικό μέσο του κάθε επιμέρους κανόνα λαμβάνοντας πάντα υπόψη και την βαρύτητα του κάθε κανόνα όπως και με τη μέθοδο Mamdani. Έχοντας λοιπόν μια είσοδο της μορφής x=[x 1,, x n ] U. Τότε η έξοδος θα είναι ένα f(x) V με την παρακάτω μορφή: y = f(x) = [43] M j=1 yj w j M j=1 w j
45 Όπου τα βάρη w i υπολογίζονται απο τη σχέση: n w j = μ j Αi (x i ) i=1 Τα μοντέλα Takagi-Sugeno, αποτελούν πια ένα ισχυρό εργαλείο της επιστήμης μηχανικών για την μοντελοποίηση σύνθετων συστημάτων. Παρέχουν αποτελεσματικές και υπολογιστικά ελκυστικές λύσεις σε ένα ευρύ φάσμα προβλημάτων, παρουσιάζοντας μια πολλαπλή δομή μοντέλου, ικανή να προσεγγίσει μη γραμμικές δυναμικές, πολλαπλούς τρόπους λειτουργίας καισημαντικές μεταβολές στη δομή και τις παραμέτρους ενός συστήματος [16],[9] Ασαφοποίηση Η εργασία του ασαφοποιητή είναι η απεικόνιση ενός πραγματικού σημείου σε ένα ασαφές σύνολο. Απαραίτητη προϋπόθεση για τη σωστή λειτουργία ενός ασαφοποιητή είναι να περιορίζει την επίδραση του θορύβου στην είσοδο. Τέλος, η μορφή του ασαφοποιητή θα πρέπει να βοηθά ώστε να απλοποιούνται οι διαδικασίες εξαγωγής συμπεράσματος. Οι πιο δημοφιλείς ασαφοποιητές είναι ο ασαφοποιητής Singleton, ο Gaussian και ο τριγωνικός. Ασαφοποιητής Singleton: Ο Singleton απεικονίζει ένα πραγματικό σημείο x U με ένα ασαφές σύνολο A ορισμένο στο U. Η συνάρτηση συμμετοχής έχει τιμή 1 στο y και τιμή 0 σε όλο το υπόλοιπο U. μ Α (x) 1 εαν x = x = { 0 εάν x x Gaussian Ασαφοποιητής: O Gaussian ασαφοποιητής ομοίως απεικονίζει ένα πραγματικό σημείο x U με ένα ασαφές σύνολο A με την παρακάτω συνάρτηση συμμετοχής. 2 μ Α (x) = e (x 1 x 1 a1 ) 2 e (x n x n an ) [44]
46 όπου α i η τυπική απόκλιση της κατανομής Gaussian και το «*» ένας τελεστής t-norm. Τριγωνικός Ασαφοποιητής: Ο τριγωνικός ασαφοποιητής ομοίως απεικονίζει ένα πραγματικό σημείο x U με ένα ασαφές σύνολο A με την παρακάτω συνάρτηση συμμετοχής. μ Α (x) = { (1 x 1 x 1 ) (1 x n x n ) b 1 b n εάν x i x i b i, i = 1,2,, n 0 Διαφορετική περίπτωση Όπου b i είναι η μέγιστη απόκλιση από την κεντρική τιμή x i και το «*» ένας τελεστής t-norm[16] Απo-ασαφοποίηση Μέθοδος απο-ασαφοποίησης Σταθμισμένων Κέντρων (CAD): Κατά την εκτέλεση αυτής της μεθόδου λαμβάνεται ως βάρος w i το μέγιστο της κάθε συνάρτησης συμμετοχής και αντιστοιχίζεται σε κάθε ένα από τα M κέντρα y i. Με αυτό τον τρόπο η μέθοδος ορίζει το y. y = M i=1 M i=1 w i y iw i Μέθοδος απο-ασαφοποίησης MAXIMUM: Σύμφωνα με αυτήν την μέθοδο, η διακριτή τιμή είναι αυτή που αντιστοιχεί στη μέγιστη τιμή συγγένειας του τελικού αποτελέσματος. Αν υπάρχουν περισσότερες από μία τέτοιες τιμές, τότε λαμβάνεται ανάλογα με την περίπτωση είτε ο μέσος όρος τους (μέσος όρος του μεγίστου) ή η μέγιστη τιμή τους (μέγιστη τιμή του μεγίστου) ή η ελάχιστη τιμή τους (ελάχιστη τιμή του μεγίστου). [45]
47 Μέθοδος απο-ασαφοποίησης Cendroid ή κέντρου βάρους(coa): Σύμφωνα με αυτήν την μέθοδο απο-ασαφοποίησης, η διακριτή τιμή είναι αυτή που προκύπτει από το κέντρο βάρους της τελικής συνάρτησης συμμετοχής για την ασαφή παράμετρο εξόδου. Το κέντρο βάρους t κβ, ορίζεται από μια συνάρτηση f(t) και τους καρτεσιανούς άξονεςπου βρίσκονται στη θέση t: t κβ = t f(t)dt f(t)dt Στην περίπτωση που έχουμε ένα διακριτό σύνολο αναφοράς, τα ολοκληρώματα στην παραπάνω σχέση αντικαθίστανται με διακριτό άθροισμα και γίνεται δειγματοληψία Ν σημείων στο σύνολο αναφοράς. Να προσθέσουμε ότι στην περίπτωση που έχει γίνει σύνθεση αποτελεσμάτων από επιμέρους κανόνες και υπάρχουν τυχόν αλληλοεπικαλυπτόμενες περιοχές, αυτές λαμβάνονται υπόψη μία μόνο φορά. Ακόμη, όταν η συνάρτηση συμμετοχής είναι παντού 0, το αποτέλεσμα της απο-ασαφοποίησης ορίζεται κατά σύμβαση[16]. 2.8 Εφαρμογές Ασαφούς Λογικής Η ασαφής λογική είναι σήμερα μια αναγνωρισμένη επιστημονική θεωρία, που βρίσκει εφαρμογή σε πρακτικά κυρίως ζητήματα για την επίλυση ή τουλάχιστον στην επίτευξη καλύτερων λύσεων από αυτές των υπόλοιπων θεωριών, ικανή για την αντιμετώπιση προβλημάτων αβεβαιότητας, καθώς μπορούν να χρησιμοποιηθούν σε εκτιμήσεις στη λήψη αποφάσεων,και σε μηχανικά συστήματα ελέγχου. Η ασαφής λογική έχει σημειώσει τα τελευταία χρόνια μεγάλη ανάπτυξη και έχει καταστεί αξιόπιστο και εύχρηστο εργαλείο σε πολλούς επιστημονικούς κλάδους και όχι μόνο. Για παράδειγμα πολλές οικιακές συσκευές χρησιμοποιούν την ασαφή λογική. Κάποιες απ αυτές είναι τα συστήματα κλιματισμού (τα λεγόμενα inverter) που από μόνα τους έχουν τη δυνατότητα να καθορίζουν πόσο πρέπει να ανεβάσουν τις στροφές της μηχανής, έτσι ώστε ανάλογα με την εσωτερική και εξωτερική θερμοκρασία του χώρο, να έχουν ελάχιστη κατανάλωση ρεύματος, να προσέχουν να μην παγώσει η εξωτερική μονάδα τον χειμώνα άλλα και να κάνουν συντήρηση στον χώρο χωρίς να σταματάνε και να ξεκινάνε συνέχεια καταναλώνοντας μεγάλη ποσότητα ρεύματος. Εκτός από τις οικιακές συσκευές, ασαφή λογική χρησιμοποιούν τα αυτοκίνητα, τα τρένα, τα μετεωρολογικά συστήματα, τα αεροσκάφη κτλ. [46]
48 Ακόμη, η ασαφής λογική χρησιμοποιείται στον κλάδο της ιατρικής για τις διάφορες διαγνώσεις που γίνονται μέσω μηχανημάτων με βάση πιθανοτήτων. Τέλος, παίζει πολύ μεγάλο ρόλο στην επεξεργασία εικόνας αντικείμενο με το οποίο θα ασχοληθούμε στο επόμενο κεφάλαιο. Τα ασαφή συστήματα σημείωσαν επιτυχία εκμεταλλευόμενα σε βάρος των κλασικών συστημάτων, κυρίως λόγω του γεγονότος ότι πολλές διαδικασίες δεν είναι γραμμικές και είναι υπερβολικά περίπλοκες για να μοντελοποιηθούν μαθηματικά. Γενικά η ασαφής λογική βρίσκει λύσεις σε: Πολύπλοκα συστήματα δύσκολα να μοντελοποιηθούν. Συστήματα με συνεχή ροή δεδομένων εισόδου και εξόδου. Συστήματα όπου ο χρήστης του συστήματος εισάγει σε πραγματικό χρόνο τα δεδομένα, ή διατυπώνει τους κανόνες. Συστήματα που είναι από τη φύση τους ασαφή. Σε ότι αφορά τα μειονεκτήματα αυτής της θεωρίας, ένα σημαντικό πρόβλημα είναι ότι τα αποτελέσματά της δεν είναι πάντα σωστά ακριβώς επειδή παρουσιάζονται ως εικασίες. Αντίθετα αυτά της «κλασικής» λογικής είναι πλήρως αξιόπιστα.ένα ακόμη πρόβλημα είναι η ομοιότητα της ασαφούς λογικής με την θεωρία των πιθανοτήτων κάτι που συνήθως μπερδεύει τους χρήστες αυτής της θεωρίας. Πολλοί οπαδοί της μαθηματικής λογικής του 0 και 1 πιστεύουν πως η ασαφής λογική δεν έχει καμία χρησιμότητα, καθώςυποστηρίζουν ότι η περιοχή μεταξύ του 0 και του 1 είναι ανακριβής σε αντίθεση με το πραγματικό 1 ή 0. Αυτό έχει σαν αποτέλεσμα να μην είναι πλήρως αποδεκτή από την επιστημονική κοινότητα μιας και υπάρχει χάσμα μεταξύ των θεωριών. Είναι φανερό ότι η μελλοντική επερχόμενη εξέλιξη της ασαφούς λογικής, θα είναι τεράστια και θα καταλήξει να είναι αναπόσπαστο κομμάτι της επιστήμης και της τεχνολογίας. Ένας πολλά υποσχόμενος τομέας για το μέλλον είναι αυτός που ασχολείται με την τεχνική νοημοσύνη και την δημιουργία ευφυών συστημάτων. Γενικότερα, η ασαφής λογική μπορεί να χρησιμοποιηθεί σε συστήματα υψηλού επιπέδου αυτόματου έλεγχου [13]. [47]
49 Κεφάλαιο 3 - Τμηματοποίηση Εικόνων Ασαφής 3.1 Εισαγωγή Λογική Στο κεφάλαιο αυτό θα αναλυθούν οι μέθοδοι κατωφλίου που τμηματοποιούν μια εικόνα οι οποίες μελετήθηκαν στα πλαίσια της πτυχιακής. Οι μέθοδοι σχετίζονται με την ασαφή λογική όπως έχουμε περιγράψει στα κεφάλαια 1 και 2, εκτός μιας που σχετίζεται με την τεχνική της ομαδοποίησης (clustering). Στην εργασία αυτή, η εικόνα έχει τμηματοποιηθεί χρησιμοποιώντας διάφορες μεθόδους [1],[2] όπως ασαφής απόκλιση(fuzzy divergence) προτεινομένη από τους Chaira και Ray [2], γραμμικούς και τετραγωνικούς δείκτες ασάφειας (linear and quadratic indices of fuzziness), ασαφή πυκνότητα και ασαφή ομοιότητα (fuzzy compactness and fuzzy similarity). Η συνάρτηση συμμετοχής γάμα προτεινομένη από τους Chaira και Ray [2] έχει χρησιμοποιηθεί για την εύρεση των τιμών συμμετοχής των pixel της εικόνας. Η ελαχιστοποίηση των δεικτών ασάφειας αποδίδει την κατάλληλη τιμή κατωφλιού. Παρομοίως, η μεγιστοποίηση των άλλων δυο μέτρων, της ασαφούς πυκνότητας και ομοιότητας σε μια εικόνα, τμηματοποιημένη από μια ιδανική τιμή καωφλίου και η ιδία εικόνα τμηματοποιημένη από μια οποιοιδήποτε αυθαίρετη τιμή αποδίδει το κατάλληλο κατώφλι Ασάφεια και συνάρτηση συμμετοχής Έστω Χ={ f ij, μ(f Ij )}, f ij Χ, είναι μια εικόνα μεγέθους Μ Μ η όποια έχει L επίπεδα και f ij είναι τα γρι επίπεδα των (i,j) pixel της εικόνας Χ. Έστω η μ(f ij ) η τιμή στην συνάρτηση συμμετοχής του (i,j) pixel στην Χ, όπου 0<=μ(f ij )<=1 με μ(f ij )=1 υπάρχει συμμετοχή ενώ με μ(f ij )=0 δεν υπάρχει συμμετοχή. Για μια δεδομένη τιμή κατωφλίου, η συνάρτηση συμμετοχής που προέρχεται από την κατανομή γάμα είναι ανάλογη προς την εκθετική συνάρτηση των αρνητικών της απόλυτης διαφοράς μεταξύ του μέσου όρου της περιοχής στην οποία ανήκει το pixel και το pixel του μέσου γκρι επίπεδου. Είναι επομένως προφανές ότι αυτή είναι αντιστρόφως ανάλογη προς την τιμή συμμετοχής των μελών. Έστω count(f) δηλώνει τον αριθμό των εμφανίσεων του γκρίζου επιπέδου f στην εικόνα. Λαμβάνοντας υπόψη μία ορισμένη οριακή τιμή t, η οποία διαχωρίζει το αντικείμενο και το υπόβαθρο, το μέσο επίπεδο γκρίζου της περιοχής υπόβαθρου δίνεται από τη σχέση: [48]
50 μ 0 = t f=0 f count(f) t f=0 count(f) (1) Και το μέσο γρι επίπεδο του αντικείμενου δίνεται από την σχέση μ1 = L 1 f=t+1 f count(f) L 1 f=t+1 count(f) (2) Η συνάρτηση συμμετοχής του κάθε pixel στην εικόνα εξαρτάται από την συνάφεια της περιοχής στην οποία ανήκει. Οι τιμές συμμετοχής των pixel προσδιορίζονται χρησιμοποιώντας γάμα κατανομή όπως περιγράφετε παρακάτω Κατανομή γάμα Ο γενικός τύπος της συνάρτησης κατανομής γάμα είναι ο f(x) = ((χ v) β )γ 1 exp( (χ v) β ) Γ(χ) x v; γ, β > 0 (3) Όπου γ είναι η παράμετρος σχήματος, και v η παράμετρος θέσης, β παράμετρος κλίμακας και Γ είναι η συνάρτηση γαμα η όποια δίνετε από τον τύπο Γ(γ) = 0 u γ 1 e u du (4) Θα θεωρήσουμε τις παρακάτω περιπτώσεις Περίπτωση 1: Όταν ν=0 και β=1 η συνάρτηση παίρνει την μορφή f(x) = (x)γ 1 exp( x) Γ(χ) χ 0; γ > 0 (5) Η όποια είναι γνωστή ως κανονική γάμα κατανομή Περίπτωση 2: όταν ν 0,β=1και γ=1 η κατανομή γάμα παίρνει την μορφή f(x) = exp( (x ν)) Όπου Γ(1)=1. [49]
51 Αντικαθιστώντας το μ στον τύπο (5) σε μ 0 και μ 1 ξεχωριστά από τους τύπους (1) και (2), η συνάρτηση συμμετοχής για το υπόβαθρο και το αντικείμενο δίνετε ως: μ(f ij ) = exp( c f ij μ 0 )iff ij t, forbackground = exp( c f ij μ 1 )iff ij > t, forobject (6) Όπου t είναι το οποιοδήποτε επιλεγμένο κατώφλι όπως δηλώθηκε πάνω. Στην συνάρτηση συμμετοχής η σταθερά c λαμβάνετε για να εξασφαλίσουμε ότι η τιμή συμμετοχής των μελών του γρι επίπεδου θα είναι μέσα στο διάστημα [0,1].Το c δίνετε από τον τύπο: c = 1 fmax fmin Όπου fmin fmax είναι το ελάχιστο και το μέγιστο γκρι επίπεδο της εικόνας αντίστοιχα. Η απόλυτη τιμή ανάμεσα στην απόσταση της μέσης τιμής της περιοχής στην όποια ένα ανήκει pixel και το γκρι επίπεδο του pixel. Για την κατωφλίωση τριών επίπεδων όπου υπάρχουν τρεις περιοχές στην εικόνα, δυο τιμές κατωφλιού επιλέγονται ώστε 0<=t1<t2<L-1,όπου L είναι η μεγίστη τιμή του γκρι επίπεδου στην εικόνα. Αν επεκτείνουμε την έννοια της πολυκατωφλίωσης η συνάρτηση συμμετοχής στην περίπτωση των τριών επίπεδων παίρνει την μορφή: μ(f ij ) = exp( c f ij μ 0 )iff ij t1 = exp( c f ij μ 1 )ift1 < f ij t2 (7) = exp( c f ij μ 2 )iff ij > t2 Όπου μ 0,μ 1 και μ 2 είναι ο μέσος όρος του γκρι επίπεδου για τις τρεις περιοχές που διαχωρίζονται από τα κατώφλια t1 και t2 και της σταθερά c.η εικόνα χωρίζετε σε τρις περιοχές όπου [0,t1], [t1+1,t2], [t2+1,l-1]. [50]
52 3.2 Fuzzy divergence Εδώ παρουσιάζετε μια νέα μέθοδος με βάση την ελαχιστοποίηση της ασαφούς απόκλισης χρησιμοποιώντας κατανομή γάμα για να προσδιορίσουμε τη συνάρτηση συμμετοχής των pixel της εικόνας. Η μέθοδος ελαχιστοποιεί την απόκλιση μεταξύ των pixels μιας ιδεατής κατωφλιομένης εικόνας και αυτής που θα υποστεί κατωφλιωση. Οι Pal και Pal (1991) χρησιμοποίησαν την κλασική Shannon θεωρία για την τμηματοποίηση μιας εικόνας, χρησιμοποιώντας ασαφή εκθετική εντροπία. Οι Fan και Xie (1999) πρότειναν την ασαφή απόκλιση βασισμένη στην ασαφή εκθετική εντροπία με τη χρήση ενός πινάκα γραμμή. Εδώ η έννοια της απόκλιση των Fan και Xie επεκτείνεται σε μια εικόνα που αντιπροσωπεύετε από ένα πινάκα. Σε μια εικόνα μεγέθους Μ Μ με L διακριτά γκρι επίπεδα έχοντας πιθανότητες L 1 i=0 (p 0,p 1,p 2 p L-1 )η εκθετική εντροπία ορίζετε ως Η = p i e 1 p i Η ασαφής εντροπία μιας εικόνας Α μεγέθους Μ Μ ορίζετε ως: 1 M 1 M 1 i=0 (8) Η(Α) = [(μ n( e 1) Af ij )e 1 μ Af ij + (1 μ A f ij )e μ Af ij j=0 1] Εδώ το n=m 2 και i,j=0,1,2 (M-1). μ A f ij είναι η τιμή συμμετοχής των pixel στην εικόνα και f ij είναι το (i,j)pixel της εικόνας Α. Για δυο εικόνες Α κα Β,στο (i,j)pixel της εικόνας, η διάκριση μεταξύ της μ A f ij και μ B f ij δίνετε από: e μ Af ij / e μ Bf ij = e μ Af ij μb f ij (9) Όπου μ A f ij και μ B f ij είναι οι τιμές συμμετοχής των (i,j)pixel των εικόνων Α και Β. Έτσι η διάκριση μεταξύ των εικόνων δίνετε από: M 1 M 1 D(A, B) = i=0 j=0 (1 (1 μ Α f ij ) e μ Αf ij μ Β f ij μ Α f ij e μ Βf ij μ Α f ij ) (10) [51]
53 Και αντίστοιχα η διάκριση του Β στο Α δίνετε από: M 1 M 1 D(B, Α) = i=0 j=0 (1 (1 μ Β f ij ) e μ Βf ij μ Α f ij μ Α f ij e μ Αf ij μ Β f ij ) (11) Τότε η συνολική ασαφή απόκλιση μεταξύ Α και Β δίνετε απo M 1 i=0 M 1 j=0 D(A, B) = D 1 (A, B) + D 2 (B, A) = (2 (1 μ Α f ij + μ B f ij ) e μ Αf ij μ B f ij (1 μ B f ij + μ Α f ij ) e μ Bf ij μ Α f ij )(12) μεθοδολογία Για δυαδική(bimodal) ή πολυεπίπεδη(multimodal) κατωφλίωση θα ασχοληθούμε με μια μεθοδολογία που βασίζετε στο ιστόγραμμα μιας εικόνας. Η περιοχή μεταξύ δυο διαδοχικών κορυφών είναι η περιοχή για την αναζήτηση. Αν υπάρχουν περισσότερες κοιλάδες (στην περίπτωση του πολυεπίπεδου(multimodal) ιστογράμματος) τότε σημειώνουμε τις κορυφές και οι περιοχές για αναζήτηση είναι οι κοιλάδες ανάμεσα στις κορυφές. Για ιστόγραμμα ενός επίπεδου(unimodal) η γραμμική αναζήτηση χρησιμοποιείτε για την επιλογή του κατωφλίου. Για κάθε κατώφλι,η τιμή συμμετοχής όλων των pixel της εικόνας βρίσκετε με την παρακάτω διαδικασία. Για κάθε τιμή κατωφλιού, η τιμή συμμετοχής της κατωφλιομένης εικόνας συγκρίνετε με μια ιδανικά κατωφλιομένη εικόνα. Οι τιμές συμμετοχής του κάθε pixel σε μια ιδανικά κατωφλιομένη εικόνα λαμβάνονται ως ένα σύνολο. M 1 M 1 D(A, B) = i=0 j=0 (2 (2 μ Α f ij ) e μ Αf ij 1 μ Α f ij e 1 μ Αf ij ) (13) Μια ιδανικά κατωφλιομένη εικόνα είναι αυτή η οποία είναι με ακρίβεια τμηματοποιημένη, ώστε τα pixel της περιοχής αντικείμενου και υπόβαθρου να ανήκουν εντελώς στις περιοχές τους. Από την τιμή απόκλισης του κάθε pixel ανάμεσα στην ιδανικά τμηματοποιμένη εικόνα και την επιλεγμένη εικόνα βρίσκουμε την ασαφή απόκλιση. Αναμένουμε ότι η τιμές συμμετοχής των pixel της τμηματοποιμένης εικόνας και της ιδανικής εικόνας θα είναι κοντά να γίνει καλή κατωφλιωση. Αν ένα pixel βρίσκετε στην περιοχή αντικείμενου η υπόβαθρου θα πρέπει να συμβάλει περισσότερο στην αντίστοιχη περιοχή την όποια ανήκει. Για [52]
54 κάθε κατώφλι η απόκλιση του κάθε pixel ορίζετε από τον τύπο (13) για όλα τα pixel.επιλεγούμε την ελάχιστη απόκλιση με το αντίστοιχο βέλτιστο κατώφλι. Εδώ η ελάχιστη απόκλιση μας δείχνει την συμμετοχή του κάθε pixel αντικείμενου στην περιοχή του αντικείμενου και κάθε pixel του υπόβαθρου στην περιοχή υπόβαθρου. Μετά την κατωφλιώση, η κατωφλιομένη εικόνα μοιάζει με την ιδανικά κατωφλιομένη εικόνα. 3.3Linear index Quadratic index Ο δείκτης ασάφειας ορίζετε ως I(A) = (2 n k )d(a, A ) Όπου d(a, A ), ορίζει την απόσταση ανάμεσα στο A και το κοντινότερο σύνολο του A (αντίστροφος του Α). Το κ ορίζει τον τύπο και τη απόσταση πχ για κ=1 απόσταση Hamming,κ=0.5 ευκλείδεια απόσταση. Ο γραμμικός δείκτης της ασάφειας ορίζετε ως Όπου M 1 M 1 L. I. = ( 2 n ) μ Α (α ij ) μ Α (α ij ) M 1 M 1 i=0 j=0 = ( 2 n ) min (μ Α (α ij ), (1 μ Α (α ij ))) i=0 j=0 μ Α (a ij ) = 0 if μ A (a ij ) 0.5 = 1 if μ A (a ij ) > 0.5 Ο τετραγωνικός δείκτης ασάφειας ορίζετε ως: Μ 1 Μ 1 Q. I. = ( 2 n ) ( ( μ Α (α ij ) μ Α (α ij )) 2 ) i=0 j=0 1 2 [53]
55 1/2 M 1 M 1 = (2/ n ( (min( μ Α (α ij ), (1 μ Α (α ij )))) 2 ) i=0 j=0 Χρησιμοποιώντας τους δείκτες ασάφειας για την τμηματοποίηση από τους τύπους (9),(10), για κάθε κατώφλι, βρίσκουμε την απόσταση μεταξύ της τιμής συμμετοχής των pixel της εικόνας και το κοντινότερου συνόλου του. Το πλησιέστερο σύνολο είναι είτε 0 είτε 1 ανάλογα εάν οι τιμές συμμετοχής είναι μικρότερες η μεγαλύτερες του 0.5. Έδω κατά την χρήση της συνάρτησης γάμα, μια άλλη σταθερά το Ln(0.5)= χρησιμοποιείτε για να ελέγξουμε το εύρος των τιμών συμμετοχής 0.5 μα(i, j) 1 η [0.5,1].Έτσι η συνάρτηση συμμετοχής από τους τύπους (5),(6) τροποποιείτε ως: μα(f ij ) = exp( c f ij μ 0 ) if f ij t, for background = exp( c f ij μ 1 ) if f ij > t, for object Όπου t είναι το οποιοδήποτε επιλεγμένο κατώφλι. Σε αυτή τη γάμα συνάρτηση συμμετοχής όλες οι τιμές συμμετοχής είναι στην περιοχή [0.5,1].Έτσι ενώ υπολογίζουμε τους δείκτες ασάφειας το πλησιέστερο σύνολο είναι 1.Για όλα τα κατώφλια του γκρι επίπεδου στην περιοχή που είναι προς αναζήτηση οι δείκτες ασάφειας υπολογίζονται χρησιμοποιώντας τους τύπους (9),(10). Στη συνέχεια επιλεγούμε την ελάχιστη τιμή ανάμεσα σε όλους τους δείκτες ασάφειας και το αντίστοιχο γκρι επίπεδο επιλέγετε για κατώφλι. Για κάθε κατώφλι, όταν η τιμή συμμετοχής τείνει προς το 1 τότε η απόσταση από το πλησιέστερο σύνολο π.χ 1 είναι μικρότερη, τότε συνεπάγεται ότι ο δείκτης ασάφειας είναι ο ελάχιστος η επιλογή του ελάχιστης τιμής του δείκτη ασάφειας σημαίνει ότι ο διαχωρισμός μεταξύ της υπολογισμένης κατωφλιομένης εικόνας και της ιδανικής εικόνας είναι σωστός Fuzzy similarity Σε αυτή την εργασία ένα νέο είδος μέτρου ομοιότητας για ασαφή σύνολα έχει χρησιμοποιηθεί για τον καθορισμό του κατωφλίου μιας εικόνας όπου οι εικόνες θεωρούνται ως ασαφή εικόνες. Ο Wang (1997) πρότεινε ένα μέτρο ομοιότητας μεταξύ δύο ασαφή συνόλων Α και Β όπου δίνεται από τη σχέση: N 1 S 1 (A, B) = ( 1 n ) min(μ Α(α i ), μ Β (b i )) max (μ Α (α i ), μ B (b i )) i=0 [54]
56 Εδώ η έννοια του Wang έχει επεκταθεί σε εικόνες για καθορισμό κατωφλίου χρησιμοποιώντας γάμα συνάρτηση συμμετοχής. Η ομοιότητα(similarity) μεταξύ δύο εικόνων, Α και Β, μπορεί να δοθεί ως: M 1 M 1 S 1 (A, B) = ( 1 n ) min (μ Α(α ij ), μ Β (b ij )) j=0 i=0 n = M x M max (μ Α (α ij ), μ Β (b ij )) Όπου μ Α (α ij ) και μ Β (b ij ) είναι οι τιμές συμμετοχής των (I,j) pixel, α ij b ij των εικόνων Α και Β αντίστοιχα, η εικόνα Β είναι η ιδανικά τμηματοποιημένη εικόνα η όποια περιγράφετε παρακάτω. Εάν η εικόνα Α είναι σχεδόν προς η ιδανικά τμηματοποιημένη εικόνα, η τιμή ομοιότητας είναι η μέγιστη και η τιμή κατωφλίου που αντιστοιχεί στη μέγιστη τιμή είναι το βέλτιστο κατώφλι. Κατά την χρήση του ασαφούς μέτρου ομοιότητας οι τιμές συμμέτοχης υπολογίζονται χρησιμοποιώντας τις δυο παραπάνω διαδικασίες η ομοιότητα εδώ σημαίνει ότι η κατωφλιομένη εικόνα μοιάζει με την ιδανικά κατωφλιομένη εικόνα. Τώρα αντικαθιστώντας μ Β (b ij ) = 1 στον τύπο(όπως για μια ιδανικά κατωφλιομένη εικόνα, οι τιμές όλων των μελών είναι 1 όπου τα pixel του αντικείμενου κείτονται στην περιοχή του αντικειμένου και τα pixel του υπόβαθρου κείτονται στην περιοχή υπόβαθρου)ο τύπος για την εύρεση του μέτρου έχει τροποποιηθεί ως: M 1 M 1 S 1 (A, B) = ( 1 n ) min(μ Α(α ij ), 1) = ( 1 max (μ Α (α ij ), 1) n ) μ Α(α ij ) j=0 i=0 M 1 M 1 j=0 i=0 Για κάθε κατώφλι οι τιμές ομοιότητας έχουν υπολογιστεί. Όταν η τιμή ομοιότητας σε μια τμηματοποιημένη εικόνα είναι περισσότερο προς την ιδανικά τμηματοποιημένη εικόνα για ένα συγκεκριμένο κατώφλι, η τμηματοποίηση μπορεί να θεωρηθεί ως εξαιρετική. Έτσι, το βέλτιστο κατώφλι είναι η τιμή κατωφλιού στην οποία το ασαφές μέτρο ομοιότητας είναι το μέγιστο. Αυτό συνεπάγεται ότι η κατωφλιομένη εικόνα είναι σχεδόν προς την ιδανικά κατωφλίομένη εικόνα. 3.5 Fuzzy compactness Οι Rosenfeld (1984) και Pal και Rosenfeld (1988) χρησιμοποίησαν τις έννοιες της ψηφιακής γεωμετρίας μιας εικόνας, δηλαδή την ασαφή πυκνότητα για τον καθορισμό κατωφλιού σε μια εικόνα. Ένα ασαφές υποσύνολο μιας εικόνας Α [55]
57 χαρακτηρίζεται από μ Α (Α πινάκας) ή απλά μ (για λόγους απλότητας) του οποίου τα στοιχεία είναι οι τιμές συμμετοχής των Pixel της εικόνας A. Αν μ είναι μια τμηματική σταθερά, σε μια ψηφιακή εικόνα, τότε η περιοχή του μ, δηλαδή α(μ) είναι το σταθμισμένο άθροισμα των περιοχών στις οποίες το μ έχει σαν σταθερά, μη-μηδενικές τιμές. Ως, μ ij είναι το (I,j) στοιχείο του πινάκα συμμετοχής μ διαμορφώνετε από τις τιμές συμμετοχής των pixel α ij δηλ μ Α (α ij ) της εικόνας Α.Εδώ το όνομα της εικόνας Α παραλείπετε για λογούς απλότητας. Μ Μ a(μ) = μ ij (14) i=1 j=1 Για μια τμηματική σταθερά,η περίμετρος του μ έχει οριστεί ως: Μ Μ 1 Μ Μ 1 P(μ) = μ ij μij+1 + μ ij μi+1j (15) i=1 j=1 i=1 j=1 Και η πυκνότητα του μ έχει οριστεί ως: comp(μ) = α(μ)/ρ 2 (μ) (16) Εδώ έχουμε χρησιμοποιήσει τη μεγιστοποίηση της ασαφής πυκνότητας ενός ασαφούς υποσύνολου μιας εικόνας για την επιλογή κατωφλιού χρησιμοποιώντας την συνάρτηση συμμετοχής γάμα που προέρχεται από την συνάρτηση γάμα που περιγράφετε στο Μεθοδολογία Για κάθε κατώφλι οι τιμές συμμετοχής όλων των pixel υπολογίζονται χρησιμοποιώντας τις παραπάνω διαδικασίες. Κατά την χρήση του μέτρου της πυκνότητας από τον τύπο (16) για την ιδανικά κατωφλιομένη εικόνα όπου οι τιμές συμμετοχής όλων των pixel είναι 1(η περιοχή είναι μεγάλη και η περίμετρος πολύ μικρή).ιδανική εικόνα είναι αυτή η οποία είναι ακριβώς κατωφλιομένη έτσι ώστε τα pixel τα οποία είναι στην περιοχή αντικείμενου και υπόβαθρου να ανήκουν εξολοκλήρου στις περιοχές τους. Για την ιδανικά κατωφλιομένη εικόνα, τα pixel του αντικείμενου θα πρέπει να συμβάλουν περισσότερο στις περιοχές του αντικείμενου [56]
58 οι τιμές συμμετοχής όλων των pixel της περιοχής του αντικείμενου μ obj ij πρέπει να είναι 1 ομοίως οι τιμές συμμετοχής των pixel της περιοχής υπόβαθρου μ back ijπρέπει να είναι 1.Ετσι για κάθε κατώφλι όσο περισσότερο οι τιμές συμμέτοχης των pixel είναι προς το 1 τόσο καλύτερη η τμηματοποίηση. Αυτό εξασφαλίζει ότι τα pixel αντικείμενου ανήκουν στην περιοχή αντικειμένου και ομοίως και τα pixel υπόβαθρου στην περιοχή υπόβαθρου, συνεπώς η ασαφή περιοχή γίνετε μεγάλη και η ασαφή περίμετρος μικρότερη για ψηφιακές εικόνες. Αυτό συνεπάγεται ότι η μεγιστοποίηση της πυκνότητας είναι το κριτήριο του κατωφλιού. Το προκύπτον κατώφλι της εικόνα γίνεται ισοδύναμο με την ιδανικά κατωφλιομένη εικόνα. Με αυτόν τον τρόπο, για κάθε κατώφλι, βρίσκουμε την πυκνότητα. Η μεγίστη τιμή πυκνότητας έχει επιλεχτεί και το αντίστοιχο γκρι επίπεδο είναι το βέλτιστο κατώφλι Intuisionistic Fuzzy divergence (Διαισθητικά ασαφές σύνολο) Στην ασαφή θεωρία του Zadeh, ένας βαθμός συμμετοχής αποδίδετε σε κάθε pixel, όπου ο βαθμός της μη συμμετοχής ισούται με το 1 μείον το βαθμό συμμετοχής. Ωστόσο οι άνθρωποι οι οποίοι εκφράζουν τον βαθμό συμμετοχής σε ένα ασαφές σύνολο δεν εκφράζουν τον αντίστοιχο βαθμό μη συμμετοχής στο συμπλήρωμα του 1.Με την προηγούμενη παρατήρηση οι Atanassov και Atanassov και Stoeva εισήγαγαν την έννοια του IFS(διαισθητικά ασαφές σύνολο) [3] που έχει ως στόχο να δείξει ότι η τιμή της συμμετοχής δεν είναι πάντα ίση με 1 μείον το βαθμό μη συμμετοχής, αλλά μπορεί να υπάρχει και κάποιος βαθμός διστακτικότητας. Ένα ασαφές σύνολο Α σε ένα πεπερασμένο σύνολο Χ=[Χ 1,Χ 2 Χ n ] η μαθηματική σχέση ορίζετε ως: Α={(χ,μ Α (χ) χ Χ} Όπου η συνάρτηση μ Α (χ) : --> Χ [0,1] είναι ενα μέτρο συμμετοχής ο βαθμός συμμετοχής ενός στοιχείου χ στο πεπερασμένο σύνολο Χ. Ο Attanassov πρότεινε μια γενίκευση των ασαφών συνόλων που ονομάζετε IFS.Μια IFSΑ σε ένα πεπερασμένο σύνολο Χ ορίζετε μαθηματικά ως: Α={(χ,μ Α (χ),v A (χ)) χ Χ } (17) Όπου οι συναρτήσεις μ Α (χ),v A (χ) : --> Χ [0,1],είναι αντίστοιχα ο βαθμός συμμετοχής και ο βαθμός μη συμμετοχής ενός στοιχείου χ σε ένα πεπερασμένο σύνολο Χ με την απαραίτητη προϋπόθεση. 0 μ Α (χ) +v A (χ) 1 [57]
59 Μπορούμε να παρατηρήσουμε ότι κάθε ασαφές σύνολο είναι μια συγκεκριμένη περίπτωση του IFS. Α={(χ,μ Α (χ),1-μ A (χ)) χ Χ } Πρόσφατα οι Szmidt και Kacpryzk υπογράμμισαν την ανάγκη να λάβουμε υπόψη και μια τρίτη παράμετρο π Α (χ) γνωστή ως διαισθητικά ασαφή δείκτη η βαθμό διστακτικότητας, η όποια προκύπτει λόγο έλλειψης γνώσης η προσωπικού λάθους(personal error) (Attanassov και Stoeva )στον υπολογισμό της απόστασης μεταξύ δυο συνόλων. Έτσι με την εισαγωγή του βαθμού διστακτικότητας η IFS του Α στο Χ ορίζετε ως: Α={(χ,μ Α (χ),v A (χ),π Α (χ)) χ Χ } Με την προϋπόθεση ότι π Α (χ)+μ Α (χ)+v Α (χ)=1 (18) είναι προφανές ότι 0 π Α (χ) 1 για κάθε χ Χ Για την κατασκευή του IFS του Attanassov, χρησιμοποιούμαι διαισθητικά ασαφές γεννήτριες. Από τον ορισμό της ασαφούς διαισθητικά γεννήτριας που δίνετε από τον από Bustince. Μια συνάρτηση φ [0,1] θα ονομάζετε διαισθητικά ασαφή γεννήτρια αν φ(χ) 1-χ χ [0,1] Έτσι σύμφωνα με τον ορισμό φ(0) 1 και φ(1) 0,eδω το συμπλήρωμα της διαισθητικά ασαφής γεννήτριας ασαφές δημιουργείτε από την συνάρτηση της γεννήτριας sugeno.το ασαφές συμπλήρωμα ορίζετε ως: Ν(μ(χ))=g -1 (g(1)-g(μ(χ))) (19) Όπου το g(.)είναι μια αύξουσα συνάρτηση g[0,1] [0,1]. Η κλάση sugeno μπορεί να δημιουργηθεί με την χρήση της ακόλουθης συνάρτησης (20) στο (19). g(μ(χ)) = 1 log (1 + λ. μ(χ)) (20) λ Και ο τύπος της IFS γεννήτριας sugeno γράφετε ως: Ν(μ(χ)) = (1 μ(χ))/ (1 + λ. μ(χ))λ>0 Όπου Ν(1)=0 και Ν(0)=1 [58]
60 Λαμβάνοντας υπόψη τον τύπο IFS γεννήτρια sugeno,το διαισθητικά ασαφές σύνολο γράφετε ως: 1 μ Α (χ) Α IFS = {(x, μ Α (χ), ) χ Χ} 1 + λμ Α (χ) Ο βαθμός διστακτικότητας από τον τύπο (2) π Α (χ) = 1 μ Α (χ) 1 μ Α(χ) 1 + λμ Α (χ) (21) Δεδομένου ότι ο παρονομαστής 1 + λμ Α (χ) είναι μεγαλύτερος του 1,ετσι 1 μ Α (χ) 1+λμ Α (χ) είναι μικρότερο από 1.Η επαλήθευση του IFSμ Α(χ) + vα(χ) έχει ως εξής: μ Α (χ) + 1 μ Α(χ) 1 + λμ Α (χ) μ Α(χ) + 1 μ Α (χ) = 1 Αυτός ο τύπος της IFS γεννήτριας sugeno χρησιμοποιείτε για να δημιουργήσουμε μια διαισθητικά ασαφή εικόνα για την κατωφλίωση μιας εικόνας Προτεινόμενη συνάρτηση συμμετοχής Εδώ η περιορισμένη συνάρτηση λειτουργίας χρησιμοποιείτε για να βρούμε την συνάρτηση συμμετοχής η οποία είναι ένας άλλος τύπος της συνάρτησης συμμετοχής. Αν φ 1 και φ 2 είναι δυο αυτομορφισμοί σε ένα διάστημα μονάδας τότε REF(x, y) = φ 1 1 (1 φ 2 (χ) φ 2 (y) ) Withc(x) = φ 2 1 (1 φ 2 (χ)) Είναι μια περιορισμένη συνάρτηση λειτουργίας. c είναι μια ισχυρή άρνηση όπου c:[0,1] [0,1] είναι μια άρνηση αν πληροί τις ακόλουθες ιδιότητες 1) c(0)=1,c(1)=0; 2) c(χ) c(y), if χ y; Και αυτομορφισμός είναι ένα διάστημα [α,b] είναι μια συνεχή αύξουσα συνάρτηση φ:[α,b] [α,b] έτσι ώστε φ(α)=α και φ(b)=b Ο ορισμός της περιορισμένης συνάρτησης λειτουργίας δίνετε όπως εξακολουθείτε: [59]
61 Μια συνάρτηση REF:[0,1] 2 [0,1] ονομάζετε περιορισμένη συνάρτηση λειτουργίας αν ικανοποιεί τις τους παρακάτω περιορισμούς. 1)REF(x,y)= REF(y,x) για όλαx,y [0,1]; 2)REF(x,y)=1 αν και μόνο ανx=y; 3)REF(x,y)=0 αν και μόνο αν χ=1,y=0 η x=0 y=1; 4)REF(x,y)= )= REF(c(x),c(y)),για όλα τα x,y [0,1],το c είναι μια ισχυρή άρνηση; 5) για όλα τα x,y,z [0,1],εάν x y z, τότε REF(x,y) REF(x,z)και REF(y,z) REF(x,z) Συνάρτηση συμμετοχής Ας θεωρήσουμε φ 2 (χ)=χ. Τότε από τον περιορισμό της συνάρτησης λειτουργίας που αναφέραμε παραπάνω γίνετε. REF(x,y)=φ 1 1 (1 φ 2 (χ) φ 2 (y) ) = φ 1 1 (1 (χ) (y) ). Έτσι,REF(x,y)=φ 1 1 (1 (χ) (y) ) Έστω φ 1 (χ)=ln[x(e-1)+1] όπου e=exp(1) Τότε χρησιμοποιώντας αντίστροφα την συνάρτηση έχουμε Τότε φ 1 1 (χ) = (e x 1)/(e 1) REF(x, y) = (e 1 x y 1)/(e 1) (22) Η εξίσωση (22) ικανοποιεί τις προϋποθέσεις για την περιορισμένη συνάρτηση λειτουργίας οι όποιοι είναι REF(x, y) = REF(y, χ) Όταν χ=y,ref(x, y) = (e 1)/(e 1) = 1 Όταν χ=0,y=1 η χ=1,y=0,ref(x, y) = (e 0 1)/(e 1)= 0 Επίσης για την επιλογή της συνάρτησης αυτομορφισμου φ(χ),η ιδιότητα η όποια είναι μια αύξουσα συνάρτηση πρέπει επίσης να ικανοποιεί την συνθήκη φ(χ)=ln[(e-1)χ+1] όταν χ=0,φ(0)=ln[(e-1)0+1]=ln(1)=0 [60]
62 όταν χ=1,φ(1)=ln[(e-1)1+1]=ln(e)=1 τώρα ο (4) χρησιμοποιείτε για να ορίσει την συνάρτηση συμμετοχής Η συνάρτηση συμμετοχής δηλώνει το να ανήκει ένα pixel σε μια περιοχή. Όσο μικρότερη είναι η διαφορά του γκρι επίπεδου ενός pixel α ij και η μέση τιμή της περιοχής στην οποία ανήκει το pixel,τόσο μεγαλύτερη είναι η τιμή των συμμετοχής και το αντίστροφο. Ας ορίσουμε την συνάρτηση συμμετοχής μ: [0,1] έτσι ώστε: μ(χ)=,ref(x, y) Τότε η συνάρτηση συμμετοχής γίνετε: μ(χ)= = 0.582(e 1 x y 1) (23) Η τιμή την υπολογίζουμε από 1/(exp(1)-1)=0.582.Στον υπολογισμό της συνάρτησης συμμετοχής, χ και y σχετίζονται με το pixel της εικόνας και την μέση τιμή για ένα ορισμένο κατώφλι t αντίστοιχα. Έτσι για ένα ορισμένο κατώφλι t το όποιο διαχωρίζει την περιοχή υποβάθρου και αντικείμενου, η συνάρτηση συμμετοχής από τον τύπο (23) για την περιοχή αντικειμένου γράφετε ως: μ Α (α ij )= = 0.582(e 1 αij m1 1) όταν α ij >t, για το αντικείμενο. Αντίστοιχα η συνάρτηση συμμετοχής μ Α (α ij ) της περιοχής του υποβάθρου είναι μ Α (α ij )= = 0.582(e 1 αij m0 1) αν α ij tυπόβαθρο. (24) Όπου m0,m1 είναι οι μέσοι όροι του γκρι επίπεδου της περιοχής υποβάθρου και αντικειμένου και υπολογίζονται από τον τύπο (1)και (2) στην αρχή του κεφαλαίου στο Όπου count(f) είναι ο αριθμός των εμφανίσεων του γκρι επιπέδου f στην εικόνα. Όταν αij m1 = 0,καμία διάφορα τότε μ Α (α ij )= = 0.582(e 1 1) =1, όταν αij m1 =1,μεγίστη διάφορα τότε μ Α (α ij )= = 0.582(e 0 1)=0. Όσο μικρότερη η διάφορα μεταξύ του γκρι επιπέδου ενός οποιοδήποτε pixel και της μέσης τιμής της περιοχής, τόσο μεγαλύτερη η τιμή συμμετοχής Διαισθητικά ασαφής δείκτης Στην παρούσα μελέτη, χρησιμοποιούμε ένα μέτρο απόστασης που ονομάζεται διαισθητικά ασαφή απόκλιση, όπου υπάρχουν τρεις παράμετροι, ο βαθμός [61]
63 συμμετοχής, ο βαθμός μη συμμετοχής, και ο βαθμός διστακτικότητας (ή διαισθητικά ασαφή δείκτης). Έστω Α={(χ,μ Α (α ij ),v A (α ij )) α ij Χ } και Έστω Β={(χ,μ Β (b ij ),v Β (b ij )) b ij Χ }είναι δυο διαισθητικά ασαφή εικόνες. Εάν μ Α (α ij ) είναι η τιμή συμμετοχής και v A (α ij ) η τιμή μη συμμετοχής των (i,j) της εικόνας Α, τότε ενώ υπολογίζουμε την τιμή συμμετοχής ενός στοιχείου μπορεί να υπάρχει βαθμός διστακτικότητας π Α (α ij ), όπου π Α (α ij )=1- μ Α (α ij )-v A (α ij ).Σε αυτή τη περίπτωση η τιμή συμμετοχής θα είναι σε ένα εύρος το οποίο δίνετε από μ Α (α ij ),{μ Α (α ij )+π Α (α ij )}. Έτσι η απόκλιση των pixel α ij και b ij των εικόνων Α και Β δίνετε από τον τύπο (9) που είναι παρακάτω. Σε αυτή τη μελέτη για κάθε κατώφλι,η κατωφλιομένη εικόνα συγκρίνετε με την ιδανικά κατωφλιομένη εικόνα, όπου οι περιοχές υποβάθρου και του αντικείμενου τμηματοποιούνται με ακρίβεια. Σε μια ιδανικά τμηματοποιημένη εικόνα ο βαθμός συμμετοχής,o βαθμός μη συμμετοχής και ο βαθμός διστακτικότητας όλων των pixel είναι 1,0,0 αντίστοιχα. Έτσι με μ Β (b ij )=1 και π Β (b ij )=0 ο τύπος της διαισθητικά ασαφής απόκλισης απλοποιείτε στον τύπο (10) που φαίνετε παρακάτω.h τιμή του π υπολογίζετε από τον τύπο (5) Μεθοδολογία Η εικόνα πρώτα φιλτράρετε με ένα Gaussian φίλτρο μεγέθους [3,3] με τυπική απόκλιση 0.4. Αυτο το κάνουμε για να εξομαλύνουμε την εικόνα. Γενικά η εικόνα με μεγάλη τυπική απόκλιση γίνετε θολή. Η φιλτραρισμένη εικόνα χωρίζετε σε πολλά παράθυρα, το μέγεθος που επιλέγετε είναι [40,40].Με μικρότερο μέγεθος παράθυρου το κατώφλι επιλεγεί πολλά μικρά σωματίδια και έτσι η απόδοση και ο διαχωρισμός δεν είναι καλός. Με παράθυρα μεγέθους [10,10] και [20,20] βλέπουμε πολύ θόρυβο στην εικόνα. Με μέγεθος [40,40] και [80,80] δεν υπάρχει μεγάλη διάφορα. Για τις πειραματικές εικόνες επιλεγούμε το μέγεθος [40,40].Για εικόνες με ορθογώνιο μέγεθος το μέγεθος παράθυρου επιλέγετε σύμφωνα με το ένα τέταρτο του μεγέθους της εικόνας. Οι τιμές συμμετοχής υπολογίζονται για κάθε παράθυρο χρησιμοποιώντας την συνάρτηση περιορισμένης λειτουργίας. Τότε το διαισθητικά ασαφές σύνολο δημιουργείτε και ο βαθμός διστακτικότητας(hesitation degree) υπολογίζετε. Το λ παίρνει την τιμή 0,8 κατά την δημιουργία του διαισθητικά ασαφές συνόλου. Με αυτή τη τιμή η κατωφλιομένη εικόνα φαίνετε καλύτερη. Αλλάζοντας την τιμή λ η διάφορα είναι πολύ μικρή. Για κάθε κατώφλι, η απόκλιση υπολογίζετε και το γρι επίπεδο που αντιστοιχεί στην ελάχιστη διαισθητικά ασαφή απόκλιση επιλέγετε ως το βέλτιστο κατώφλι του παράθυρου. Αυτό υπολόγιζε για όλα τα παράθυρα της εικόνας. Το τελικό κατώφλι [62]
64 είναι το βέλτιστο κατώφλι μείον το ένα τέταρτο της τυπικής απόκλισης του παράθυρου. opt Final TH = Th window Όπου S.D η τυπική απόκλιση του παράθυρου (1/4)S. D window D IFS (A, B) = [2 (1 μ Α (α ij ) + μ B (b ij )) e μ Α(α ij ) μ B (b ij ) (25) i j (1 μ B (b ij ) + μ Α (α ij )e μ B(b ij ) μ Α (α ij ) ) + 2 (1 μ Α (α ij ) π A (α ij ) + μ B (b ij )) e μ Α(α ij )+π A (α ij ) μ B (b ij ) π B (b ij ) (1 μ B (b ij ) π B (b ij ) + μ Α (α ij ) + π A (α ij ))e μ B(b ij )+(b ij ) μ Α (α ij ) π A (α ij ) ] D IFS (A, B) = [2 (2 μ Α (α ij )) e μ Α(α ij ) 1 μ Α (α ij )e 1 μ Α(α ij i j ) + 2 (26) (2 μ Α (α ij ) π A (α ij )) e μ Α(α ij )+π A (α ij ) 1 (μ Α (α ij ) + π A (α ij ))e 1 μ Α(α ij ) π A (α ij ) ] 3.7 Intuitionistic Fuzzy C-means Εισαγωγή Παρακάτω σχολιάζουμε μια μέθοδο [4] που βασίζετε στην ομαδοποίηση με τη χρήση της διαισθητικά ασαφούς θεωρίας που εξηγούμε στο παραπάνω υποκεφάλαιο Παρουσίαση μιας διαισθητικά ασαφούς εικόνας Μια εικόνα P παρουσιάζετε σαν ένα διαισθητικό ασαφές σύνολο έχοντας q γρι επίπεδα και θ σε εύρος [0,q-1]. Φ = { θ ij, μ Φ (θ ij ), γ Φ (θ ij ) i = 1.. a, j = 1 b} [63]
65 Όπου θ ij είναι η τιμή του P στην θέση (i,j) και μ Φ (θ ij ), γ Φ (θ ij ) είναι οι τιμές συμμετοχής και οι τιμές μη συμμετοχής αντίστοιχα του θ ij στο P. Ως συνάρτηση συμμετοχής και μ Φ (θ) οριζουμε την πιθανοτητα των περιστασεων του γκρι επίπεδου θ [0,q-1]. μ Φ (θ) = h(θ), θ [0,q-1] α β Όπου το h(θ) είναι το τραγανό(crisp) ιστόγραμμα. Ο βαθμός συμμετοχής και μ Φ (θ) ενός γκρι επίπεδου θ σε μια εικόνα υπόκειται σε αβεβαιότητα λόγω του θορύβου. Για να αντιμετωπίσουμε αυτό το πρόβλημα εισάγουμε ένα συντελεστή 1-p(θ) έτσι ώστε το θ να ανήκει λιγότερο σε μια εικόνα, αν το τραγανό ιστόγραμμα h(θ)αποκλίνει περισσότερο από το ασαφές ιστόγραμμαh (θ).το ασαφές ιστόγραμμα ορίζετε ως: Επίσης h (θ) = {(i, j) P μ Θ (θ ij ), i = 1 α, j = 1 b} μ θ (χ) = max (0,1 χ θ ψ ) Όπου ο ψ είναι η παράμετρος που ελέγχει την έκταση του ασαφή αριθμού θ :R [0,1] που αναπαριστά ένα ασαφή γκρι επίπεδο. Όσο το ψ αυξάνετε το ιστόγραμμα φαίνετε πιο λείο και με μεγαλύτερη ανοχή στον θόρυβο από ότι το αντίστοιχο τραγανό ιστόγραμμα. Σύμφωνα με την συνάρτηση συμμετοχής η συνάρτηση μη συμμετοχής του θ ορίζετε ως: γ Φ (θ ij ) = (1 μ(θ)) (1 p(θ)) Ο όρος p(θ) επιλέχτηκε για να είναι ανάλογος της απόσταση μεταξύ του τραγανού και του ασαφούς ιστογράμματος [64]
66 p(θ) = λ max θ h(θ) h (θ) ( h(θ) h (θ) ) Όπου λ [0,1] είναι μια σταθερά και ο παρονομαστής διευκολύνει την κανονικοποιήση. Η έννοια της συνάρτησης της μη συμμετοχής ενός γκρι επιπέδου τιμής θ σε μια εικόνα αυξάνετε κατά ένα συντελεστή που είναι ανάλογη με την ομαλότητα του τραγανού ιστογράμματος. Έτσι καθώς τα επίπεδα θορύβου στην εικόνα αυξάνονται, το τραγανό ιστόγραμμα γίνετε πιο συμπαγές και η διστακτικότητα για τον προσδιορισμό του γκρι επιπέδου της τιμής θ αυξάνετε Ομαδοποίηση βασισμένη στη διαισθητικά ασαφή διατομή Το μέτρο ομοιότητας που έχουμε θέσει από από τη τεχνική της διατομής ιστογράμματος, έχει γενικευτεί για την μέτρηση ομοιότητας των δυο διαισθητικά ασαφή συνόλων. Έστω Α=(Μ Α, Γ Α ) και Β=(Μ Β,Γ Β ) είναι δυο διαισθητικά ασαφή σύνολα όπου Μ Α, Μ Β,Γ Α,,Γ Β F(E) και Ε={χ 1,χ 2 χ n } είναι ένα πεπερασμένο σύνολο, η διαισθητικά ασαφή διατομή ομοιότητας Ζ 1 ανάμεσα σε δυο διαισθητικά ασαφή σύνολα Α και Β υπολογίζετε παρακάτω. Όπου Ζ 1 (Α, Β) = z 1(Μ Α, Μ Β ) + z 1 (Γ Α, Γ Β ) 2 n i=1 min (A (x i ), B (x i )) z 1 (A, B ) = { n max (A (x i ), B (x i )) i=1 Και F(E) είναι το σύνολο όλων των ασαφή υποσυνόλων του Ε, και Μ Α ={μ Α (χ)},γ Α ={γ Α (χ)} χ Ε. Η διαισθητικά ασαφή διατομή είναι ένα μέτρο ομοιότητας Ζ 1 (Α, Β) [0,1]. Ζ 1 (Α, Β) = 1 Α=Β, Ζ 1 (Α, Β) = Ζ 1 (Β, Α), και Ζ 1 (Α, C) Ζ 1 (Α, Β) και Ζ 1 (Α, C) Ζ 1 (Β, C)για A B C F(E) Φάση Αρχικοποίησης Καταρχάς θα πρέπει να επιλέξουμε τον αριθμό των κλάσεων (C) και τους παράγοντες m και ε. Ο m αναπαριστά τον παράγοντα ασάφειας στον αλγόριθμο και βοηθάει στον έλεγχο των μορφών των κλάσεων. Το βασικό χαρακτηριστικό του [65]
67 είναι ότι παράγει μια ισορροπία μεταξύ των τιμών συμμετοχής που είναι κοντά στο 0 ή στο 1 και των ενδιάμεσων τιμών. Το ε είναι το κριτήριο τερματισμού του αλγορίθμου και είναι ένας πολύ μικρός αριθμός. Ουσιαστικά, αν η διαφορά του αποτελέσματος της συνάρτησης λάθους Q (Πίνακας 3.2) σε μια εκτέλεση του αλγορίθμου και του αποτελέσματος στην αμέσως προηγούμενη εκτέλεση, είναι μικρότερη από το ε τότε ο FCM τερματίζει. δηλαδή, Q(t ) Q(t 1) ε, τότε τερμάτισε τον αλγόριθμο (1) Στη συνέχεια, θα πρέπει να αρχικοποιήσουμε και τον πίνακα συμμετοχών με τυχαίες τιμές, αλλά με τον περιορισμό ότι το άθροισμα κάθε στήλης να ισούται με τη μονάδα. Δηλαδή, Αξίζει να αναφέρουμε τη φυσική σημασία του πίνακα συμμετοχών (membership function matrix). Ο πίνακας συμμετοχής περιέχει για κάθε pattern όλες τις τιμές συμμετοχής σε κάθε κλάση. Δηλαδή, το (uij) υποδηλώνει την τιμή συμμετοχής τουpattern (j) στην κλάση(i). Πριν περάσουμε στον κύριο βρόγχο του αλγορίθμου να αναφέρουμε δύο γενικούς περιορισμούς. Πρώτον, ο αλγόριθμος δεν έχει κάποιο νόημα να εκτελεστεί με αριθμό κέντρων ίσο με 1 (C=1), αλλά μόνο με C μεγαλύτερο της μονάδας. Δεύτερον, οι κλάσεις πρέπει να είναι μη-τετριμμένες. Δηλαδή, κάθε κλάση πρέπει να περιλαμβάνει τουλάχιστον ένα pattern, αλλιώς δεν έχει λόγο ύπαρξης Κύριος Βρόγχος Στάδιο Υπολογισμών Το πρώτο βήμα στο κύριο βρόγχο αντιστοιχεί στον υπολογισμό των πρωτοτύπων,δηλαδή των κέντρων των κλάσεων (Vi). Αυτό γίνεται με τη χρήση του πίνακα συμμετοχών και η όλη διαδικασία εξάγει σταθμικούς μέσους όρους (weighted average)που ουσιαστικά είναι τα κέντρα που θέλουμε. Η μαθηματική έκφραση είναι: 1 i c u ik = i k N ( x k v i IFS ) 1 1 m c ( x k v j IFS ) j=1 { u ik = 1, { i I k [66] 1 1 m 0, i I k I k = i I k, I k =
68 Στη συνέχεια θα πρέπει να υπολογίσουμε ξανά τον πίνακα συμμετοχών, αλλά για να το κάνουμε αυτό θα πρέπει πρώτα να βρούμε την απόσταση για κάθε pattern από κάθε κέντρο που υπολογίσαμε στο προηγούμενο βήμα. Πιο αναλυτικά έχουμε τον υπολογισμό του κάθε στοιχείου του πίνακα με τον εξής τύπο 1 i c v i = k=1 (u ik) m x k (u ik ) m N N k=1 Όπως φαίνεται και στο τύπο, ο πίνακας αποστάσεων συμβάλει στο υπολογισμό των τιμών συμμετοχής. Αυτό είναι λογικό γιατί μια τιμή συμμετοχής ενός pattern για μια κλάση πρέπει να εξαρτάται από την απόστασή του από αυτήν. Η σχέση όμως, δεν είναι ανάλογη. Τέλος, θα πρέπει να υπολογίσουμε τη συνάρτηση λάθους και να αποφασίσουμε σύμφωνα με το κριτήριο τερματισμού αν θα ολοκληρωθεί ο FCM. c N J IFS m (U, V) = (u ik ) m x k v i IFS i=1 k=1 Σύμφωνα με τη σχέση 3.5 αποφασίζει ο αλγόριθμος αν θα προχωρήσει σε μία ακόμη επανάληψη του κύριου βρόγχου ή αν θα μας δώσει τα τελικά αποτελέσματα, τα οποία είναι, ο πίνακας συμμετοχών (U), τα κέντρα των κλάσεων (Vi) και τα αποτελέσματα των συναρτήσεων λάθους (Q) σε κάθε επανάληψη. Ένα σημείο που χρίζει ιδιαίτερης προσοχής είναι η δυνατότητα επιλογής της συνάρτησης απόστασης. Μπορούμε να επιλέξουμε, ανάλογα με τη γεωμετρία των δεδομένων μας, την κατάλληλη συνάρτηση απόστασης (Πίνακας 1), ώστε να έχουμε καλύτερα αποτελέσματα. Μπορείτε να συμβουλευτείτε τον παρακάτω Πίνακα για εναλλακτικές συναρτήσεις. Ο κλασσικός FCM έχει ενσωματωμένη την ευκλείδεια απόσταση. [67]
69 Πίνακας 1. Γνωστές συναρτήσεις απόστασης. Συναρτήσεις απόστασης Ευκλείδεια Απόσταση Hamming Απόσταση Tchebyschev Απόσταση Minkowski Απόσταση(γενική περίπτωση) Camberra Απόσταση Εξισώσεις d(x, y) = 2 (x i y i ) 2 n i=1 n d(x, y) = x i y i i=1 d(x, y) = max x i y i, i = 1,2.. n n d(x, y) = p (x i y i ) p. p > 0 n i=1 d(x, y) = x i y i, x x i + y i kai y i > 0 i i=1 [68]
70 Κεφάλαιο 4 - Λογισμικό Τμηματοποίησης Εικόνων Γενικά Γραφικό Περιβάλλον Χρήστη ή Γραφική Διασύνδεση Χρήστη (αγγλικά: Graphical User Interface - GUI) καλείται στην πληροφορική ένα σύνολο γραφικών στοιχείων, τα οποία εμφανίζονται στην οθόνη κάποιας ψηφιακής συσκευής (π.χ. Η/Υ) και χρησιμοποιούνται για την αλληλεπίδραση του χρήστη με τη συσκευή αυτή. Παρέχουν στον τελευταίο, μέσω γραφικών, ενδείξεις και εργαλεία προκειμένου αυτός να φέρει εις πέρας κάποιες επιθυμητές λειτουργίες. Για τον λόγο αυτό δέχονται και είσοδο από τον χρήστη και αντιδρούν ανάλογα στα συμβάντα που αυτός προκαλεί με τη βοήθεια κάποιας συσκευής εισόδου (π.χ. πληκτρολόγιο, ποντίκι). Τα περισσότερα σύγχρονα προγράμματα και λειτουργικά συστήματα υπολογιστών, προσφέρουν στους χρήστες τους κάποιο GUI γιατί αυτός ο τρόπος αλληλεπίδρασης με τον υπολογιστή ταιριάζει αρκετά στην ανθρώπινη εμπειρία και φύση. Σωστά σχεδιασμένα γραφικά προσφέρουν ένα όμορφο, εύχρηστο και λειτουργικό περιβάλλον εργασίας. Πριν από την έλευση και καθιέρωση των GUI ο κανόνας στους μικροϋπολογιστές ήταν η αλληλεπίδραση με τον χρήστη μέσω κάποιου κελύφους γραμμής εντολών. Εισαγωγικά Η δημιουργία του γραφικού περιβάλλοντος (gui) έγινε με το περιβάλλον MATLAB To MATLAB μας προσφέρει μια πληθώρα από λειτουργίες εύχρηστες στον χρήστη που το διαχειρίζεται. [69]
71 Εικόνα 1: Στιγμιότυπο σχεδίασης του GUI. Το περιβάλλον το όποιο διαχειριζόμαστε φαίνεται στην παραπάνω Εικόνα 1, όπου αριστερά βλέπουμε τις λειτουργίες που μας παρέχει, όπως εισαγωγή ετικέτας(statictext) και εικόνας(axes), εισαγωγή button(κουμπί), εισαγωγή πλαισίου(panel) για ομαδοποίηση στοιχείων κτλ. Οι βασικότερες απαιτήσεις του GUI είναι οι εξής: Επιλογή της προς τμηματοποίηση εικόνας. Επιλογή της χρησιμοποιούμενης μεθόδους τμηματοποίησης. Δυνατότητα μέτρησης της ποιότητας τμηματοποίησης με την χρήση κατάλληλων μετρικών. Δυνατότητα πολλαπλής χρήσης των μεθοδολογιών για λόγους σύγκρισης. Στο γραφικό περιβάλλον της παρούσας πτυχιακής υπάρχουν 4 παράθυρα για την εμφάνιση εικόνων, 2 παράθυρα εισόδου και 2 παράθυρα εξόδου αποτελεσμάτων της κατάτμησης-τμηματοποίησης(segmentation) των πειραματικών εικόνων. Για την είσοδο της πειραματικής original εικόνας και της groundtruth εικόνας έχουμε 2 κουμπιά(button) αντίστοιχα για την επιλογή εικόνας ένα αναδυόμενο μενού (popupmenu) όπου έχουμε την δυνατότητα επιλογής της μεθόδου που θέλουμε να επιλέξουμε για την τμηματοποίηση. Για την έξοδο των αποτελεσμάτων υπάρχουν δυο πλαίσια. Ενα πλαίσιο που ονομάζετε results(αποτελέσματα) και ένα ακόμα quality indices (δείκτες ποιότητας). Επίσης υπάρχει ένα πλαίσιο με κάποιες ρυθμίσεις(settings) που αφορούν τις μεθοδολογίες. [70]
72 Δίνετε η δυνατότητα καθαρισμού(clear) όλων των δεδομένων εισόδου και εξόδου με ένα κουμπί push button. Εικόνα 2: Βασικό παράθυρο του GUI. Τέλος όπως μπορούμε να δούμε στην παραπάνω Eικόνα 2 κάτω αριστερά βλέπουμε ένα πλαίσιο με κάποια στοιχεία. Στην μπάρα μενού του γραφικού περιβάλλοντος υπάρχει ένα πράσινο βελάκι, πατώντας το μπορούμε να εκτελέσουμε τις μεθοδολογίες που έχουμε υλοποιήσει και να δούμε αποτελέσματα. Αρχίζοντας, να επισημάνουμε ότι οι πειραματικές εικόνες εκτελούνται διαφορετικά. Πιο συγκεκριμένα υπάρχει η δυνατότητα να φορτώσουμε μια η και δύο εικόνες μαζί, δηλ. αν φορτώσουμε μια εικόνα μόνη(original image) της με την κάθε μεθοδολογία μπορούμε να πάρουμε αποτελέσματα όπως το κατώφλι και μια τιμή της κάθε μεθοδολογίας. Αν φορτώσουμε την original και την ground truth image εκτός από την τιμή κατωφλιού και την τιμή της μεθοδολογίας περνούμε και κάποιους δείκτες ποιότητας για μελλοντική σύγκριση των εικόνων. [71]
73 Εικόνα 3: Παράδειγμα κατωφλιοποίησης εικόνας. Στην εικόνα 3 βλέπουμε την φόρτωση μιας εικόνας, το αποτέλεσμα της τμηματοποίησης και στο πλαίσιο των αποτελεσμάτων μια τιμή κατωφλιού και μια τιμή της μεθοδολογίας. Για κάθε μέθοδο βλέπουμε αποτέλεσμα με το αντίστοιχο αρχικό γράμμα της μεθόδου. Στο παραπάνω παράδειγμα χρησιμοποιήσαμε την μέθοδο Fuzzy_compactness και πήραμε σαν αποτέλεσμα την τιμή C: όπου το C σημαίνει compactness. Αντίστοιχα για κάθε γράμμα των άλλων μεθόδων το S εμφανίζεται για την similarity το Q για την quantratic κτλ. Από κάτω έχουμε επιλέξει μια εικόνα ως original image την εικόνα Rice στο παράδειγμα μας και την αντίστοιχη ground truth image και βλέπουμε ότι στο πλαίσιο των δεικτών ποιότητας μας εμφάνισε αποτελέσματα. [72]
74 Εικόνα 4: Κατωφλιοποίηση με χρηση ground truth image. Βλέπουμε ότι στο πλαίσιο των δεικτών εμφανίστηκαν αποτελέσματα. Ο δείκτης error μας επιστρέφει μια τιμή για την σύγκριση των εικόνων της ground truth και της result1. Οσο μικρότερος ο αριθμός τόσο καλύτερη η τμηματοποίηση. Αυτό φαίνεται αλλώστε και οπτικά. Αν παρατηρήσουμε τις δυο εικόνες υπάρχουν πολλές διαφορές στο κάτω μέρος στο οποίο κάποιοι κόκκοι είναι πιο αχνοί. Ο δείκτης Error είναι μια συνάρτηση που συγκρίνει την ground truth εικόνα με την πειραματική που θα εμφανιστεί μετά την τμηματοποίηση, συγκρίνει τα κοινά pixel(κουκίδες) έχουν οι δυο εικόνες και μας επιστρέφει ένα αποτέλεσμα σφάλματος. Πιο συγκεκριμένα ελέγχει τις εικόνες pixel και με ένα μετρητή βλέπουμε ποσά κοινά έχουμε. Στη συνέχεια αυτός διαιρείται με το μέγεθος της ground truth εικόνας και μας εμφανίζει το σφάλμα. Βασική προϋπόθεση οι εικόνες να είναι ιδίου μεγέθους(size). Ο δείκτης PSNR παίρνει σαν ορίσματα τις δυο εικόνες και μας επιστρέφει και αυτός ένα αριθμό για την μέτρηση της ποιότητας της τμηματοποίησης. Ο δείκτης Q παίρνει σαν ορίσματα τις δυο εικόνες, ένα blocksize που μπορούμε να του αλλάξουμε τιμή από τις ρυθμίσεις και επιστρέφει και αυτός ένα αριθμό για την μέτρηση της ποιότητας. Τέλος ο δείκτης SSIM παίρνει και αυτός σαν ορίσματα 2 εικόνες και ένα L που είναι η μεγίστη τιμή των pixels. [73]
75 Επίσης στις ρυθμίσεις έχουμε και ένα L που είναι μια σταθερά που αν την αλλάξουμε αλλάζει η όψη της πειραματικής εικόνας. Οι τιμές είναι σε ένα εύρος [0,1] με βήμα 0.1. Η σταθερά αυτή χρησιμοποιείτε στην μεθοδολογία Intutionistic fuzzy divergence, που όπως θα δούμε στο κεφάλαιο με τα πειραματικά αποτελέσματα είναι η καλύτερη ποιοτικά για την τμηματοποίηση ιατρικών εικόνων. Οι μέθοδοι τμηματοποίησης δουλεύουν και σε εικόνες που τμηματοποιούνται με 2 τιμές κατωφλιών. Αυτές οι εικόνες έχουν 3 κοιλάδες και ο κώδικας για να τις τμηματοποιήσεις είναι διαφορετικός, για αυτόν τον λόγο έχουμε στο γραφικό περιβάλλον 2 τιμές κατωφλιών T1,T2 και 2 παράθυρα για τα αποτελέσματα. Εικόνα 5: Παράδειγμα χρήσης δύο τιμών κατωφλίων. Βλέπουμε ότι η εικόνα μας είναι ένα δείγμα αίματος μέσα σε ένα δοχείο. Η τμηματοποίηση μας εμφανίζει δυο αποτελέσματα απο τα οποία το ένα αποτέλεσμα είναι σαν αντικείμενο οι κηλίδες αίματος, ενω το δεύτερο αποτέλεσμα παίρνει σαν αντικείμενο όλο το δοχείο. Δηλαδή είναι σαν να έχουμε δυο αντικείμενα και ένα φόντο που τμηματοποιούνται ξεχωριστά. Τέλος μια διαφορετική μέθοδος που υλοποιήθηκε είναι η μέθοδος C-means clustering στην οποία μπορούμε να επιλέξουμε τον αριθμό των clusters(ομάδες) με τα οποία θα γίνει ο διαχωρισμός. Παρακάτω βλέπουμε ένα παράδειγμα εφαρμογής της συγκεκριμένης μεθόδου. [74]
76 Εικόνα 6:Χρηση μεθόδου c-means Η ομαδοποίηση γίνετε με 5 clusters όπως φαίνεται και στην εικόνα. Η επιλογή του αριθμού των clusters γίνεται απο το πεδίο των ρυθμίσεων με εύρος τιμών από [75]
77 Κεφάλαιο 5 - Πειραματικά Αποτελέσματα 5.1 Εισαγωγή Στο κεφάλαιο αυτό θα εξετάσουμε τα αποτελέσματα τμηματοποίησης σε διάφορες πειραματικές εικόνες(original images) με τους αλγόριθμους που έχουμε υλοποιήσει και επίσης θα συγκρίνουμε τα αποτελέσματα των μεθόδων για να δούμε ποια είναι η καλύτερη μέθοδος για την τμηματοποίηση εικόνων και οπτικά και με βάση την ιδανική εικόνα. Θα χωρίσουμε το κεφάλαιο σε τρεις ενότητες. Η πρώτη ενότητα αναφέρεται σε απλές εικόνες(original images) που θα σχολιάσουμε τα αποτελέσματα της τμηματοποίησης και τα αποτελέσματα για την κάθε μέθοδο τιμή κατωφλιού και τιμή αλγόριθμου. Η δεύτερη ενότητα αναφέρεται σε εικόνες για τις οποίες είναι διαθέσιμες οι χειροκίνητα τμηματοποιημένης εικόνες τους(manually segmented image) και μπορούμε να σχολιάσουμε τα αποτελέσματα τμηματοποίησης με βάση κάποιους δείκτες μέτρησης ποιότητας. Τέλος, η τελευταία ενότητα περιγράφει τα αποτελέσματα της ομαδοποίησης(clustering) μέθοδος αξιολόγησης επιδόσεων Για να αξιολογήσουμε την απόδοση των μεθόδων χρησιμοποιούμε την χειροκίνητα τμηματοποιημένη εικόνα(gui). Για όλες τις μεθόδους υπολογίζουμε το σφάλμα ταξινόμησης(error). error = 1 BET BGT + FET FGT BGT + FGT Όπου FGT και BGT είναι οι περιοχές του προσκηνίου και του παρασκηνίου της χειροκίνητα τμηματοποιημένης εικόνας. FET και BET είναι οι περιοχές του προσκηνίου και παρασκηνίου της πειραματικά κατωφλιομένης εικόνας. Αυτό το σφάλμα αντικατοπτρίζει το ποσοστό των pixel που αποδίδονται λάθος σε εύρος από μηδέν η καθόλου σφάλμα, λόγου χάρη όταν η εικόνα είναι επακριβώς τμηματοποιημένη παίρνει την τιμή 1 η όταν είναι λάθος τμηματοποιημένη υπάρχει ποσοστό σφάλματος. Το σφάλμα ταξινόμησης δηλαδή το σφάλμα της πειραματικής τμηματοποιημένης εικόνας σε σχέση με την χειροκίνητα τμηματοποιημένη εικόνα, υπολογίζετε για όλες τις μεθόδους. Παρακάτω θα δούμε και σχετικούς πίνακες. [76]
78 5.2 Ενότητα 1 Οι πειραματικές εικόνες μας είναι 5 στο σύνολο σε μορφή αρχείου jpg,όπως θα δούμε και στις εικόνες παρακάτω με βάση τα ιστογράμματα τους οι εικόνες μπορεί να είναι με μια κορυφή η δυο κορυφές η ακόμα και 3 κορυφές που υπάρχει και για αυτές κατάλληλος κώδικας για να βρει το βέλτιστο κατώφλι για την τμηματοποίηση τον διαχωρισμό του αντικείμενου από το υπόβαθρο. Όπως θα δούμε στην συνέχεια υπάρχουν πίνακες με τα αποτελέσματα τμηματοποίησης για την κάθε μεθοδολογία, τιμή για την εύρεση κατωφλιού ελάχιστη για τις πρώτες(divergence, linear, quantratic) η μέγιστη για τις υπόλοιπες (similarity,compactness). (a) 1 (b) 1 Εικόνα 11 (a) input image,(b) its histogram 1.1 Στην εικόνα 1 έχουμε μια εικόνα cameraman μεγέθους και το ιστόγραμμα που είναι με 2 κορυφές(bimodal).πιο κάτω στον πίνακα 1 μπορούμε να δούμε τις τιμές κατωφλιών(threshold) για την κάθε μέθοδο και την τιμή για το εύρεση του κατωφλίου(tvalue),οι τιμές κατωφλίου είναι όλες πολύ κοντά όπως φαίνετε και οπτικά άλλωστε από τις τμηματοποιημένες εικόνες είναι πανομοιότυπες χωρίς διαφορές. Πίνακας 1 Values Divergence Linear index (c) Quantratic index (d) Fuzzy similarity (e) Fuzzy compactness (f) (b) Threshold Tvalue [77]
79 (l) (m) (n) (o) (p) (q) (a) Εικόνα 2 (a) input image,(b) its histogram (b) 1.2 Στην εικόνα 2 έχουμε μια εικόνα blood1 μεγέθους και το ιστόγραμμα που είναι και αυτό με δυο κορυφές(bimodal).στον πίνακα 2 βλέπουμε τις τιμές κατωφλίου και εδώ οι διαφορές δεν είναι μεγάλες και επίσης οι τμηματοποιημενες εικόνες δεν έχουν μεγάλες διαφορές. [78]
80 Πίνακας 2 Values Divergence Linear index (c) Quantratic index (d) Fuzzy similarity (e) Fuzzy compactness (f) (b) Threshold Tvalue (a) (b) (c) (d) (e) (f) (a) Εικόνα 3 (a) input image,(b) its histogram (b) 1.3 Στην εικόνα 3 έχουμε την εικόνα ic μεγέθους και το ιστόγραμμα της με τις δυο κορυφές πάλι. Οι τιμές κατωφλίου είναι πολύ κοντά σχεδόν [79]
81 πανομοιότυπες τιμές σε όλες τις μεθόδους και οπτικά οι εικόνες δεν έχουν διαφορές. Πίνακας 3 Values Divergence Linear index (c) Quantratic index (d) Fuzzy similarity (e) Fuzzy compactness (f) (b) Threshold Tvalue (a) (b) (c) (d) (e) (f) [80]
82 (a) Εικόνα 4 (a) input image,(b) its histogram (b) 1.4 Στην εικόνα 4 έχουμε μια εικόνα eight μεγέθους και το ιστόγραμμα με τις δυο κορυφές. Οι τιμές κατωφλίου είναι πολύ κοντά και εδώ και τα αποτελέσματα της τμηματοποίησης δεν έχουν διαφορές στις μεθόδους. Πίνακας 4 Values Divergence Linear index (c) Quantratic index (d) Fuzzy similarity (e) Fuzzy compactness (f) (b) Threshold Tvalue [81]
83 (a) (b) (c) (d) (e) (f) (a) Εικόνα 5 (a) input image,(b) its histogram (b) 1.5 Στην εικόνα 5 έχουμε μια εικόνα shot1 μεγέθους και διπλά το ιστόγραμμα με τις τρις κορυφές όπου οι κοιλάδες για την εύρεση κατωφλίου είναι δυο και τα κατώφλια για να τμηματοποιηθεί η εικόνα είναι δυο και όπως έχουμε πει υπάρχει και κατάλληλος κώδικας όπως επίσης τα αποτελέσματα είναι δυο εικόνες. Οι τιμές κατωφλιού είναι παρά πολύ κοντά και οι διαφορές στην κατάτμηση όπως θα δούμε στις εικόνες πιο κάτω είναι μόνο στις σκιές που δημιουργούνται γύρω από το πιατάκι του δείγματος και λίγο μέσα στο δείγμα πολύ καλή κατάτμηση με όλες τις μεθόδους. [82]
84 Πίνακας 5 Values Divergence Linear index (b) Quantratic index (c) Fuzzy similarity (d) Fuzzy compactness (f) (a) Threshold Threshold Tvalue a1 A2 b1 B2 c1 C2 d1 D2 f1 F2 5.3 Ενότητα 2 Οι πειραματικές εικόνες μας που έχουμε τις χειροκίνητα τμηματοποιημένες εκδόσεις τους είναι 5 στο σύνολο. Με την εκχώρηση κάποιων συναρτήσεων με δείκτες που αναφέρονται και στο γραφικό περιβάλλον μπορούμε να δούμε την ποιότητα της τμηματοποίησης και να τις συγκρίνουμε για να δούμε με ποια γίνετε καλύτερη τμηματοποίηση με βάση την χειροκίνητα τμηματοποιημένη εικόνα. Οι μέθοδοι που συγκρίνονται είναι η ασαφή μέθοδος η διαισθητικά ασαφή μέθοδο και η μέθοδος Otsu. Υπάρχει και κατάλληλο πινακάκι για να δούμε το λάθος ταξινόμησης error που έχουμε αναφέρει στην αρχή του κεφαλαίου. Τα αποτελέσματα εμφανίζονται με τιμή λ=0.8 στο Gui υπάρχει δυνατότητα αλλαγής αυτής της τιμής σε εύρος [0,1]. [83]
85 (a) (b) Εικόνα 6 (a) (blood cells) original image, (b) Ground truth image 2.1 Στην εικόνα 6 (a) έχουμε μια εικόνα με κύτταρα αίματος μεγέθους και στην εικόνα (b) έχουμε την ground truth image.τρις οι μέθοδοι που συγκρίνονται με καλύτερη την διαισθητικά ασαφή μέθοδο και τις άλλες δυο στα ιδία επίπεδα οπτικά μιλώντας και στο πίνακα 6 θα δούμε και το λάθος τμηματοποίησης (error). Πίνακας 6 Μέθοδοι τμηματοποίησης Threshold error Fuzzy method (a) Otsu method (b) Intuitionistic method (c) Να συμπληρώσαμε εδώ ότι ότι οι τιμές είναι 2 πρώτες είναι κοντά και οι 3 που έχει τα καλυτέρα αποτελέσματα είναι διαφορετική, επίσης ότι το τελικό κατώφλι βγαίνει με τον περιορισμό του ¼ στην τυπική απόκλιση. (a ) (b) (c) [84]
86 (a) (b) Εικόνα 7 image (blood vessels) (a) original image, (b) Ground truth image 2.1 Στην εικόνα 7 (a) έχουμε μια εικόνα με αιμοφόρα αγγεία μεγέθους και στο (b) την Gti εικόνα. Οπτικά η καλύτερη εικόνα είναι πάλι με την διαισθητικά ασαφή μέθοδο και otsu έχει καλά αποτελέσματα και τελευταία είναι η ασαφή μέθοδος. Στο πίνακα 7 θα δούμε ότι η διαισθητικά έχει μεγάλο λάθος που μάλλον οφείλετε ότι να αγγεία εμφανίζονται κάπου πιο λεπτά και κάπου πιο μεγάλα οπτικά είναι αυτό που μας ενδιαφέρει όμως. (a ) (b) (c) Πίνακας 7 Μέθοδοι τμηματοποίησης Threshold error Fuzzy method (a) Otsu method (b) Intuitionistic method (c) Οι τιμές κατωφλιών έχουν μικρή διάφορα οπτικά η καλύτερη είναι η διαισθητικά ασαφή αν και το λάθος λίγο μεγάλο σε σχέση με τα αλλά και αυτή εμφανίζει καλύτερο αποτέλεσμα χωρίς τον περιορισμό του ¼ στο τελικό κατώφλι και στις άλλες δυο καλή κατάτμηση. [85]
87 (a) Εικόνα 8 (a) original image, (b) Ground truth image (b) 2.3 Στην εικόνα 8 βλέπουμε πάλι μια εικόνα με αιμοφόρα αγγεία λίγο διαφορετική και εδώ η καλύτερη μέθοδος είναι η διαισθητική. (a ) (b) (c) Πίνακας 8 Μέθοδοι τμηματοποίησης Threshold error Fuzzy method (a) Otsu method (b) Intuitionistic method (c) Και εδώ μια διάφορα στις τιμές κατωφλιών να συμπλεύσουμε ότι η εικόνα στην διαισθητικά ασαφή εμφανίζετε καλυτέρα χωρίς τον περιορισμό του ¼ στην τυπική απόκλιση. Αν και καλυτέρα τμηματοποιημένη οπτικά είναι η διαισθητική μέθοδος το λάθος είναι λίγο μεγαλύτερο από τις άλλες μεθόδους. [86]
88 (α) (b) Εικόνα 9 (rice) (a) original image, (b) Ground truth image 2.4 Στην εικόνα 9 riceμεγέθους εδώ τα αποτελέσματα είναι όμοια σχεδόν δεν έχουν τεράστιες διαφορές. (a) (b) (c) Πίνακας 9 Μέθοδοι τμηματοποίησης Threshold error Fuzzy method (a) Otsu method (b) Intuitionistic method (c) Οι διαφορές των κατωφλιών είναι πολύ μικρές με όλες τις μεθόδους έχουμε καλή κατάτμηση στην διαισθητικά ασαφή η κατάτμηση είναι καλύτερη με το βέλτιστο κατώφλι και όχι το τελικό. Οι τιμές errorστα ιδία επίπεδα. Παρακάτω έχουμε τρις πινάκες με τις τιμές των δεικτών απόδοσης της τελικής κατάτμησης για την κάθε εικόνα. [87]
89 Πίνακας 10: blood cells Μεθοδολογίες PSNR Q SSIM Fuzzy method Otsu method Intuitionistic method Πίνακας 11: bood vessels f7 Μεθοδολογίες PSNR Q SSIM Fuzzy method Otsu method Intuitionistic method Πίνακας 12: Blood vessels f8 Μεθοδολογίες PSNR Q SSIM Fuzzy method Otsu method Intuitionistic method Πίνακας 13: rice Μεθοδολογίες PSNR Q SSIM Fuzzy method Otsu method Intuitionistic method [88]
90 5.4 Ενότητα 3 Σε αυτή την ενότητα τα πειράματα πραγματοποιήθηκαν με την μέθοδο της ασαφούς ομαδοποίησης με βάση την διαισθητικά ασαφή θεωρεία. Τρεις οι εικόνες του πειράματος όπως θα δούμε και παρακάτω πιο αναλυτικά naos,naos1,naos2 οι εικόνες. Οι παράμετροι ορίζονται από αρχή ε= και m=0.2 και 4 cluster για να γίνει η τμηματοποίηση. (α) (β) Εικόνα 10 (naos) (a) original image, (b) FCM image (a) (b) Εικόνα 11 (naos2) (a) original image, (b) FCM image [89]
91 (a) (b) Εικόνα 12 image (naos3) (a) original image, (b) FCM image [90]
ΙΑΤΡΙΚΗ ΑΠΕΙΚΟΝΙΣΗ & ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΙΑΤΡΙΚΗΣ ΕΙΚΟΝΑΣ
 ΙΑΤΡΙΚΗ ΑΠΕΙΚΟΝΙΣΗ & ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΙΑΤΡΙΚΗΣ ΕΙΚΟΝΑΣ ΔΡ. Γ. ΜΑΤΣΟΠΟΥΛΟΣ ΕΠ. ΚΑΘΗΓΗΤΗΣ ΣΧΟΛΗ ΗΛΕΚΤΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Επεξεργασία Ιατρικών Εικόνων
ΙΑΤΡΙΚΗ ΑΠΕΙΚΟΝΙΣΗ & ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΙΑΤΡΙΚΗΣ ΕΙΚΟΝΑΣ ΔΡ. Γ. ΜΑΤΣΟΠΟΥΛΟΣ ΕΠ. ΚΑΘΗΓΗΤΗΣ ΣΧΟΛΗ ΗΛΕΚΤΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Επεξεργασία Ιατρικών Εικόνων
Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας. Εισηγητής Αναστάσιος Κεσίδης
 Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας Εισηγητής Αναστάσιος Κεσίδης Τμηματοποίηση εικόνας Τμηματοποίηση εικόνας Γενικά Διαμερισμός μιας εικόνας σε διακριτές περιοχές
Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας Εισηγητής Αναστάσιος Κεσίδης Τμηματοποίηση εικόνας Τμηματοποίηση εικόνας Γενικά Διαμερισμός μιας εικόνας σε διακριτές περιοχές
Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας. Εισηγητής Αναστάσιος Κεσίδης
 Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας Εισηγητής Αναστάσιος Κεσίδης Σημειακή επεξεργασία και μετασχηματισμοί Κατηγορίες μετασχηματισμού εικόνων Σημειακοί μετασχηματισμοί
Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας Εισηγητής Αναστάσιος Κεσίδης Σημειακή επεξεργασία και μετασχηματισμοί Κατηγορίες μετασχηματισμού εικόνων Σημειακοί μετασχηματισμοί
Μάθημα 8 ο. Ανίχνευση Ακμών ΤΜΗΥΠ / ΕΕΣΤ 1
 Μάθημα 8 ο Ανίχνευση Ακμών ΤΜΗΥΠ / ΕΕΣΤ 1 Εισαγωγή (1) Οι ακμές είναι βασικά χαρακτηριστικά της εικόνας. Ένας αποδεκτός ορισμός της ακμής είναι ο ακόλουθος: «Το σύνορο μεταξύ δύο ομοιογενών περιοχών με
Μάθημα 8 ο Ανίχνευση Ακμών ΤΜΗΥΠ / ΕΕΣΤ 1 Εισαγωγή (1) Οι ακμές είναι βασικά χαρακτηριστικά της εικόνας. Ένας αποδεκτός ορισμός της ακμής είναι ο ακόλουθος: «Το σύνορο μεταξύ δύο ομοιογενών περιοχών με
Μάθημα 8 ο. Ανίχνευση Ακμών ΤΜΗΥΠ / ΕΕΣΤ 1
 Μάθημα 8 ο Ανίχνευση Ακμών ΤΜΗΥΠ / ΕΕΣΤ 1 Εισαγωγή (1) Οι ακμές είναι βασικά χαρακτηριστικά της εικόνας Προς το παρόν δεν υπάρχει ακόμα ένας ευρέως αποδεκτός ορισμός της ακμής. Εδώ θα θεωρούμε ως ακμή:
Μάθημα 8 ο Ανίχνευση Ακμών ΤΜΗΥΠ / ΕΕΣΤ 1 Εισαγωγή (1) Οι ακμές είναι βασικά χαρακτηριστικά της εικόνας Προς το παρόν δεν υπάρχει ακόμα ένας ευρέως αποδεκτός ορισμός της ακμής. Εδώ θα θεωρούμε ως ακμή:
Ψηφιακή Επεξεργασία Εικόνας. Σ. Φωτόπουλος ΨΕΕ
 Ψηφιακή Επεξεργασία Εικόνας ΒΕΛΤΙΩΣΗ ΕΙΚΟΝΑΣ ΜΕ ΙΣΤΟΓΡΑΜΜΑ ΔΠΜΣ ΗΕΠ 1/46 Περιλαμβάνει: Βελτίωση (Enhancement) Ανακατασκευή (Restoration) Κωδικοποίηση (Coding) Ανάλυση, Κατανόηση Τμηματοποίηση (Segmentation)
Ψηφιακή Επεξεργασία Εικόνας ΒΕΛΤΙΩΣΗ ΕΙΚΟΝΑΣ ΜΕ ΙΣΤΟΓΡΑΜΜΑ ΔΠΜΣ ΗΕΠ 1/46 Περιλαμβάνει: Βελτίωση (Enhancement) Ανακατασκευή (Restoration) Κωδικοποίηση (Coding) Ανάλυση, Κατανόηση Τμηματοποίηση (Segmentation)
Κατάτµηση Εικόνων: Ανίχνευση Ακµών και Κατάτµηση µε Κατωφλίωση
 ΤΨΣ 50 Ψηφιακή Επεξεργασία Εικόνας Κατάτµηση Εικόνων: Ανίχνευση Ακµών και Κατάτµηση µε Κατωφλίωση Τµήµα ιδακτικής της Τεχνολογίας και Ψηφιακών Συστηµάτων Πανεπιστήµιο Πειραιώς Περιεχόµενα Βιβλιογραφία
ΤΨΣ 50 Ψηφιακή Επεξεργασία Εικόνας Κατάτµηση Εικόνων: Ανίχνευση Ακµών και Κατάτµηση µε Κατωφλίωση Τµήµα ιδακτικής της Τεχνολογίας και Ψηφιακών Συστηµάτων Πανεπιστήµιο Πειραιώς Περιεχόµενα Βιβλιογραφία
ΚΕΦΑΛΑΙΟ 1. Ασαφή Συστήματα. 1.1 Ασαφή Σύνολα. x A. 1, x
 ΚΕΦΑΛΑΙΟ 1 Ασαφή Συστήματα Η τεχνολογική πρόοδος των τελευταίων ετών επέβαλλε τη δημιουργία συστημάτων ικανών να εκτελέσουν προσεγγιστικούς συλλογισμούς, παρόμοιους με αυτούς του ανθρώπινου εγκέφαλου.
ΚΕΦΑΛΑΙΟ 1 Ασαφή Συστήματα Η τεχνολογική πρόοδος των τελευταίων ετών επέβαλλε τη δημιουργία συστημάτων ικανών να εκτελέσουν προσεγγιστικούς συλλογισμούς, παρόμοιους με αυτούς του ανθρώπινου εγκέφαλου.
Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας. Εισηγητής Αναστάσιος Κεσίδης
 Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας Εισηγητής Αναστάσιος Κεσίδης Ακμές και περιγράμματα Ακμές και περιγράμματα Γενικά Μεγάλο τμήμα της πληροφορίας που γίνεται αντιληπτή
Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας Εισηγητής Αναστάσιος Κεσίδης Ακμές και περιγράμματα Ακμές και περιγράμματα Γενικά Μεγάλο τμήμα της πληροφορίας που γίνεται αντιληπτή
ΚΕΦΑΛΑΙΟ 3. Περιγραφή της Μεθόδου ΠΕΡΙΓΡΑΦΗ ΤΗΣ ΜΕΘΟΔΟΥ
 ΚΕΦΑΛΑΙΟ 3 Περιγραφή της Μεθόδου Το αντικείμενο αυτής της εργασίας είναι η χρήση μιας μεθόδου προσέγγισης συναρτήσεων που έχει προταθεί από τον hen-ha huang και ονομάζεται Ασαφώς Σταθμισμένη Παλινδρόμηση
ΚΕΦΑΛΑΙΟ 3 Περιγραφή της Μεθόδου Το αντικείμενο αυτής της εργασίας είναι η χρήση μιας μεθόδου προσέγγισης συναρτήσεων που έχει προταθεί από τον hen-ha huang και ονομάζεται Ασαφώς Σταθμισμένη Παλινδρόμηση
DIP_05 Τμηματοποίηση εικόνας. ΤΕΙ Κρήτης
 DIP_05 Τμηματοποίηση εικόνας ΤΕΙ Κρήτης ΤΜΗΜΑΤΟΠΟΙΗΣΗ ΕΙΚΟΝΑΣ Τμηματοποίηση εικόνας είναι η διαδικασία με την οποία διαχωρίζεται μία εικόνα σε κατάλληλες περιοχές ή αντικείμενα. Για την τμηματοποίηση
DIP_05 Τμηματοποίηση εικόνας ΤΕΙ Κρήτης ΤΜΗΜΑΤΟΠΟΙΗΣΗ ΕΙΚΟΝΑΣ Τμηματοποίηση εικόνας είναι η διαδικασία με την οποία διαχωρίζεται μία εικόνα σε κατάλληλες περιοχές ή αντικείμενα. Για την τμηματοποίηση
Digital Image Processing
 Digital Image Processing Intensity Transformations Πέτρος Καρβέλης pkarvelis@gmail.com Images taken from: R. Gonzalez and R. Woods. Digital Image Processing, Prentice Hall, 2008. Image Enhancement: είναι
Digital Image Processing Intensity Transformations Πέτρος Καρβέλης pkarvelis@gmail.com Images taken from: R. Gonzalez and R. Woods. Digital Image Processing, Prentice Hall, 2008. Image Enhancement: είναι
Κατάτµηση εικόνας σε οµοιόµορφες περιοχές
 KEΣ 03 Αναγνώριση Προτύπων και Ανάλυση Εικόνας Κατάτµηση εικόνας σε οµοιόµορφες περιοχές ΤµήµαΕπιστήµης και Τεχνολογίας Τηλεπικοινωνιών Πανεπιστήµιο Πελοποννήσου Εισαγωγή Κατάτµηση µε πολυκατωφλίωση Ανάπτυξη
KEΣ 03 Αναγνώριση Προτύπων και Ανάλυση Εικόνας Κατάτµηση εικόνας σε οµοιόµορφες περιοχές ΤµήµαΕπιστήµης και Τεχνολογίας Τηλεπικοινωνιών Πανεπιστήµιο Πελοποννήσου Εισαγωγή Κατάτµηση µε πολυκατωφλίωση Ανάπτυξη
Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Ενότητα 8 η : Κατάτμηση Εικόνας
 Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Ενότητα 8 η : Κατάτμηση Εικόνας Καθ. Κωνσταντίνος Μπερμπερίδης Πολυτεχνική Σχολή Μηχανικών Η/Υ & Πληροφορικής Σκοποί ενότητας Εισαγωγή στην κατάτμηση εικόνας Τεχνικές
Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Ενότητα 8 η : Κατάτμηση Εικόνας Καθ. Κωνσταντίνος Μπερμπερίδης Πολυτεχνική Σχολή Μηχανικών Η/Υ & Πληροφορικής Σκοποί ενότητας Εισαγωγή στην κατάτμηση εικόνας Τεχνικές
Τεχνητή Νοημοσύνη (ΥΠ23) 6 ο εξάμηνο Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Ουρανία Χατζή
 Τεχνητή Νοημοσύνη (ΥΠ23) 6 ο εξάμηνο Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Ουρανία Χατζή raniah@hua.gr 1 Ασάφεια (Fuzziness) Ποσοτικοποίηση της ποιοτικής πληροφορίας Οφείλεται κυρίως
Τεχνητή Νοημοσύνη (ΥΠ23) 6 ο εξάμηνο Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Ουρανία Χατζή raniah@hua.gr 1 Ασάφεια (Fuzziness) Ποσοτικοποίηση της ποιοτικής πληροφορίας Οφείλεται κυρίως
DIP_04 Σημειακή επεξεργασία. ΤΕΙ Κρήτης
 DIP_04 Σημειακή επεξεργασία ΤΕΙ Κρήτης ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΕΙΚΟΝΑΣ Σκοπός μιας τέτοιας τεχνικής μπορεί να είναι: η βελτιστοποίηση της οπτικής εμφάνισης μιας εικόνας όπως την αντιλαμβάνεται ο άνθρωπος, η τροποποίηση
DIP_04 Σημειακή επεξεργασία ΤΕΙ Κρήτης ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΕΙΚΟΝΑΣ Σκοπός μιας τέτοιας τεχνικής μπορεί να είναι: η βελτιστοποίηση της οπτικής εμφάνισης μιας εικόνας όπως την αντιλαμβάνεται ο άνθρωπος, η τροποποίηση
Μάθημα 9 ο. Κατάτμηση Εικόνας ΤΜΗΥΠ / ΕΕΣΤ 1
 Μάθημα 9 ο Κατάτμηση Εικόνας ΤΜΗΥΠ / ΕΕΣΤ Εισαγωγή () Η κατάτμηση έχει ως στόχο να υποδιαιρέσει την εικόνα σε συνιστώσες περιοχές και αντικείμενα. Μία περιοχή αναμένεται να έχει ομοιογενή χαρακτηριστικά
Μάθημα 9 ο Κατάτμηση Εικόνας ΤΜΗΥΠ / ΕΕΣΤ Εισαγωγή () Η κατάτμηση έχει ως στόχο να υποδιαιρέσει την εικόνα σε συνιστώσες περιοχές και αντικείμενα. Μία περιοχή αναμένεται να έχει ομοιογενή χαρακτηριστικά
Παρουσίαση Νο. 5 Βελτίωση εικόνας
 Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Παρουσίαση Νο. 5 Βελτίωση εικόνας Εισαγωγή Η βελτίωση γίνεται σε υποκειμενική βάση Η απόδοση εξαρτάται από την εφαρμογή Οι τεχνικές είναι συνήθως ad hoc Τονίζει
Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Παρουσίαση Νο. 5 Βελτίωση εικόνας Εισαγωγή Η βελτίωση γίνεται σε υποκειμενική βάση Η απόδοση εξαρτάται από την εφαρμογή Οι τεχνικές είναι συνήθως ad hoc Τονίζει
Ασαφής Λογική (Fuzzy Logic)
 Ασαφής Λογική (Fuzzy Logic) Ασάφεια: έννοια που σχετίζεται με την ποσοτικοποίηση της πληροφορίας και οφείλεται κυρίως σε μη-ακριβή (imprecise) δεδομένα. Π.χ. "Ο Νίκος είναι ψηλός": δεν προσδιορίζεται με
Ασαφής Λογική (Fuzzy Logic) Ασάφεια: έννοια που σχετίζεται με την ποσοτικοποίηση της πληροφορίας και οφείλεται κυρίως σε μη-ακριβή (imprecise) δεδομένα. Π.χ. "Ο Νίκος είναι ψηλός": δεν προσδιορίζεται με
ΕΠΕΞΕΡΓΑΣΙΑ ΙΑΤΡΙΚΗΣ ΕΙΚΟΝΑΣ
 ΕΠΕΞΕΡΓΑΣΙΑ ΙΑΤΡΙΚΗΣ ΕΙΚΟΝΑΣ Π. ΑΣΒΕΣΤΑΣ Επ. Καθηγητής Τμήμα Μηχανικών Βιοϊατρικής Τεχνολογίας ΤΕΙ Αθήνας Email: pasv@teiath.gr ΠΕΡΙΕΧΟΜΕΝΑ Αναπαράσταση εικόνας Ιστόγραμμα Εξισορρόπηση ιστογράμματος Κατωφλίωση
ΕΠΕΞΕΡΓΑΣΙΑ ΙΑΤΡΙΚΗΣ ΕΙΚΟΝΑΣ Π. ΑΣΒΕΣΤΑΣ Επ. Καθηγητής Τμήμα Μηχανικών Βιοϊατρικής Τεχνολογίας ΤΕΙ Αθήνας Email: pasv@teiath.gr ΠΕΡΙΕΧΟΜΕΝΑ Αναπαράσταση εικόνας Ιστόγραμμα Εξισορρόπηση ιστογράμματος Κατωφλίωση
Μετάδοση Πολυμεσικών Υπηρεσιών Ψηφιακή Τηλεόραση
 Χειμερινό Εξάμηνο 2013-2014 Μετάδοση Πολυμεσικών Υπηρεσιών Ψηφιακή Τηλεόραση 5 η Παρουσίαση : Ψηφιακή Επεξεργασία Εικόνας Διδάσκων: Γιάννης Ντόκας Σύνθεση Χρωμάτων Αφαιρετική Παραγωγή Χρώματος Χρωματικά
Χειμερινό Εξάμηνο 2013-2014 Μετάδοση Πολυμεσικών Υπηρεσιών Ψηφιακή Τηλεόραση 5 η Παρουσίαση : Ψηφιακή Επεξεργασία Εικόνας Διδάσκων: Γιάννης Ντόκας Σύνθεση Χρωμάτων Αφαιρετική Παραγωγή Χρώματος Χρωματικά
K15 Ψηφιακή Λογική Σχεδίαση 7-8: Ανάλυση και σύνθεση συνδυαστικών λογικών κυκλωμάτων
 K15 Ψηφιακή Λογική Σχεδίαση 7-8: Ανάλυση και σύνθεση συνδυαστικών λογικών κυκλωμάτων Γιάννης Λιαπέρδος TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ Η έννοια του συνδυαστικού
K15 Ψηφιακή Λογική Σχεδίαση 7-8: Ανάλυση και σύνθεση συνδυαστικών λογικών κυκλωμάτων Γιάννης Λιαπέρδος TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ Η έννοια του συνδυαστικού
Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Ενότητα 4 η : Βελτίωση Εικόνας. Καθ. Κωνσταντίνος Μπερμπερίδης Πολυτεχνική Σχολή Μηχανικών Η/Υ & Πληροφορικής
 Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Ενότητα 4 η : Βελτίωση Εικόνας Καθ. Κωνσταντίνος Μπερμπερίδης Πολυτεχνική Σχολή Μηχανικών Η/Υ & Πληροφορικής Σκοποί ενότητας Εισαγωγή στις τεχνικές βελτίωσης εικόνας
Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Ενότητα 4 η : Βελτίωση Εικόνας Καθ. Κωνσταντίνος Μπερμπερίδης Πολυτεχνική Σχολή Μηχανικών Η/Υ & Πληροφορικής Σκοποί ενότητας Εισαγωγή στις τεχνικές βελτίωσης εικόνας
ΚΕΣ 03: Αναγνώριση Προτύπων και Ανάλυση Εικόνας. KEΣ 03 Αναγνώριση Προτύπων και Ανάλυση Εικόνας. Κατάτµηση Εικόνων:
 KEΣ 3 Αναγνώριση Προτύπων και Ανάλυση Εικόνας Κατάτµηση Εικόνων: Ανίχνευση Ακµών Τµήµα Επιστήµης και Τεχνολογίας Τηλεπικοινωνιών Πανεπιστήµιο Πελοποννήσου Περιεχόµενα Βιβλιογραφία Περιεχόµενα Ενότητας
KEΣ 3 Αναγνώριση Προτύπων και Ανάλυση Εικόνας Κατάτµηση Εικόνων: Ανίχνευση Ακµών Τµήµα Επιστήµης και Τεχνολογίας Τηλεπικοινωνιών Πανεπιστήµιο Πελοποννήσου Περιεχόµενα Βιβλιογραφία Περιεχόµενα Ενότητας
6-Aνίχνευση. Ακμών - Περιγράμματος
 6-Aνίχνευση Ακμών - Περιγράμματος Ανίχνευση ακμών Μετατροπή 2 εικόνας σε σύνολο ακμών Εξαγωγή βασικών χαρακτηριστικών της εικόνας Πιο «συμπαγής» αναπαράσταση Ανίχνευση ακμών Στόχος: ανίχνευση ασυνεχειών
6-Aνίχνευση Ακμών - Περιγράμματος Ανίχνευση ακμών Μετατροπή 2 εικόνας σε σύνολο ακμών Εξαγωγή βασικών χαρακτηριστικών της εικόνας Πιο «συμπαγής» αναπαράσταση Ανίχνευση ακμών Στόχος: ανίχνευση ασυνεχειών
Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας. Εισηγητής Αναστάσιος Κεσίδης
 Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας Εισηγητής Αναστάσιος Κεσίδης Χωρικά φίλτρα Χωρικά φίλτρα Γενικά Σε αντίθεση με τις σημειακές πράξεις και μετασχηματισμούς, στα
Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας Εισηγητής Αναστάσιος Κεσίδης Χωρικά φίλτρα Χωρικά φίλτρα Γενικά Σε αντίθεση με τις σημειακές πράξεις και μετασχηματισμούς, στα
Μάθημα 9 ο. Κατάτμηση Εικόνας ΤΜΗΥΠ / ΕΕΣΤ 1
 Μάθημα 9 ο Κατάτμηση Εικόνας ΤΜΗΥΠ / ΕΕΣΤ Εισαγωγή () Η κατάτμηση έχει ως στόχο να υποδιαιρέσει την εικόνα σε συνιστώσες περιοχές και αντικείμενα. Μία περιοχή αναμένεται να έχει ομοιογενή χαρακτηριστικά
Μάθημα 9 ο Κατάτμηση Εικόνας ΤΜΗΥΠ / ΕΕΣΤ Εισαγωγή () Η κατάτμηση έχει ως στόχο να υποδιαιρέσει την εικόνα σε συνιστώσες περιοχές και αντικείμενα. Μία περιοχή αναμένεται να έχει ομοιογενή χαρακτηριστικά
Ακαδημαϊκό Έτος , Χειμερινό Εξάμηνο Διδάσκων Καθ.: Νίκος Τσαπατσούλης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ, ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΚΕΣ 3: ΑΝΑΓΝΩΡΙΣΗ ΠΡΟΤΥΠΩΝ ΚΑΙ ΑΝΑΛΥΣΗ ΕΙΚΟΝΑΣ Ακαδημαϊκό Έτος 7 8, Χειμερινό Εξάμηνο Καθ.: Νίκος Τσαπατσούλης ΕΡΩΤΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ Το παρόν
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ, ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΚΕΣ 3: ΑΝΑΓΝΩΡΙΣΗ ΠΡΟΤΥΠΩΝ ΚΑΙ ΑΝΑΛΥΣΗ ΕΙΚΟΝΑΣ Ακαδημαϊκό Έτος 7 8, Χειμερινό Εξάμηνο Καθ.: Νίκος Τσαπατσούλης ΕΡΩΤΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ Το παρόν
Ε.Α.Υ. Υπολογιστική Όραση. Κατάτμηση Εικόνας
 Ε.Α.Υ. Υπολογιστική Όραση Κατάτμηση Εικόνας Γεώργιος Παπαϊωάννου 2015 ΚΑΤΩΦΛΙΩΣΗ Κατωφλίωση - Γενικά Είναι η πιο απλή μέθοδος segmentation εικόνας Χωρίζουμε την εικόνα σε 2 (binary) ή περισσότερες στάθμες
Ε.Α.Υ. Υπολογιστική Όραση Κατάτμηση Εικόνας Γεώργιος Παπαϊωάννου 2015 ΚΑΤΩΦΛΙΩΣΗ Κατωφλίωση - Γενικά Είναι η πιο απλή μέθοδος segmentation εικόνας Χωρίζουμε την εικόνα σε 2 (binary) ή περισσότερες στάθμες
Τεχνικές Μείωσης Διαστάσεων. Ειδικά θέματα ψηφιακής επεξεργασίας σήματος και εικόνας Σ. Φωτόπουλος- Α. Μακεδόνας
 Τεχνικές Μείωσης Διαστάσεων Ειδικά θέματα ψηφιακής επεξεργασίας σήματος και εικόνας Σ. Φωτόπουλος- Α. Μακεδόνας 1 Εισαγωγή Το μεγαλύτερο μέρος των δεδομένων που καλούμαστε να επεξεργαστούμε είναι πολυδιάστατα.
Τεχνικές Μείωσης Διαστάσεων Ειδικά θέματα ψηφιακής επεξεργασίας σήματος και εικόνας Σ. Φωτόπουλος- Α. Μακεδόνας 1 Εισαγωγή Το μεγαλύτερο μέρος των δεδομένων που καλούμαστε να επεξεργαστούμε είναι πολυδιάστατα.
ΔΙΑΡΘΡΩΣΗ ΠΕΡΙΕΧΟΜΕΝΟΥ
 ΑΡΧΙΜΗΔΗΣ ΕΝΙΣΧΥΣΗ ΕΡΕΥΝΗΤΙΚΩΝ ΟΜΑΔΩΝ ΣΤΑ ΤΕΙ 2.2.2.3ζ ΔΙΑΡΘΡΩΣΗ ΠΕΡΙΕΧΟΜΕΝΟΥ ΕΓΧΡΩΜΩΝ ΕΓΓΡΑΦΩΝ Εγχειρίδιο χρήσης λογισμικού ΕΠΙΣΤΗΜΟΝΙΚΟΣ ΥΠΕΥΘΥΝΟΣ: ΣΤΡΟΥΘΟΠΟΥΛΟΣ ΧΑΡΑΛΑΜΠΟΣ ΣΕΡΡΕΣ, ΜΑΙΟΣ 2007 ΠΕΡΙΕΧΟΜΕΝΑ
ΑΡΧΙΜΗΔΗΣ ΕΝΙΣΧΥΣΗ ΕΡΕΥΝΗΤΙΚΩΝ ΟΜΑΔΩΝ ΣΤΑ ΤΕΙ 2.2.2.3ζ ΔΙΑΡΘΡΩΣΗ ΠΕΡΙΕΧΟΜΕΝΟΥ ΕΓΧΡΩΜΩΝ ΕΓΓΡΑΦΩΝ Εγχειρίδιο χρήσης λογισμικού ΕΠΙΣΤΗΜΟΝΙΚΟΣ ΥΠΕΥΘΥΝΟΣ: ΣΤΡΟΥΘΟΠΟΥΛΟΣ ΧΑΡΑΛΑΜΠΟΣ ΣΕΡΡΕΣ, ΜΑΙΟΣ 2007 ΠΕΡΙΕΧΟΜΕΝΑ
Advances in Digital Imaging and Computer Vision
 Advances in Digital Imaging and Computer Vision Lecture and Lab 4 th part 12/3/2018 Κώστας Μαριάς Αναπληρωτής Καθηγητής Επεξεργασίας Εικόνας 21/2/2017 1 Βασικές έννοιες επεξεργασίας Φιλτράρισμα στο χωρικό
Advances in Digital Imaging and Computer Vision Lecture and Lab 4 th part 12/3/2018 Κώστας Μαριάς Αναπληρωτής Καθηγητής Επεξεργασίας Εικόνας 21/2/2017 1 Βασικές έννοιες επεξεργασίας Φιλτράρισμα στο χωρικό
Ψηφιοποίηση και Ψηφιακή Επεξεργασία Εικόνας
 Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων Ψηφιοποίηση και Ψηφιακή Επεξεργασία Εικόνας Ενότητα 11: Επεξεργασία εικόνας Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons εκτός και
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων Ψηφιοποίηση και Ψηφιακή Επεξεργασία Εικόνας Ενότητα 11: Επεξεργασία εικόνας Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons εκτός και
Ενδεικτική πολυ-εργασία 1 - εφαρμογή στην υπολογιστική όραση
 Ενδεικτική πολυ-εργασία 1 - εφαρμογή στην υπολογιστική όραση Εντοπισμός ενός σήματος STOP σε μια εικόνα. Περιγράψτε τη διαδικασία με την οποία μπορώ να εντοπίσω απλά σε μια εικόνα την ύπαρξη του παρακάτω
Ενδεικτική πολυ-εργασία 1 - εφαρμογή στην υπολογιστική όραση Εντοπισμός ενός σήματος STOP σε μια εικόνα. Περιγράψτε τη διαδικασία με την οποία μπορώ να εντοπίσω απλά σε μια εικόνα την ύπαρξη του παρακάτω
DIP_05 Τµηµατοποίηση εικόνας. ΤΕΙ Κρήτης
 DIP_05 Τµηµατοποίηση εικόνας ΤΕΙ Κρήτης ΤΜΗΜΑΤΟΠΟΙΗΣΗ ΕΙΚΟΝΑΣ Τµηµατοποίηση εικόνας είναι η διαδικασία µε την οποία διαχωρίζεται µία εικόνα σε κατάλληλες περιοχές ή αντικείµενα. Για την τµηµατοποίηση εικόνας
DIP_05 Τµηµατοποίηση εικόνας ΤΕΙ Κρήτης ΤΜΗΜΑΤΟΠΟΙΗΣΗ ΕΙΚΟΝΑΣ Τµηµατοποίηση εικόνας είναι η διαδικασία µε την οποία διαχωρίζεται µία εικόνα σε κατάλληλες περιοχές ή αντικείµενα. Για την τµηµατοποίηση εικόνας
ΑΣΚΗΣΗ 3 ΒΕΛΤΙΩΣΗ ΕΙΚΟΝΑΣ ΜΕΛΕΤΗ ΙΣΤΟΓΡΑΜΜΑΤΟΣ. ( ) 1, αν Ι(i,j)=k hk ( ), διαφορετικά
 ΑΣΚΗΣΗ 3 ΒΕΛΤΙΩΣΗ ΕΙΚΟΝΑΣ ΜΕΛΕΤΗ ΙΣΤΟΓΡΑΜΜΑΤΟΣ Αντικείμενο: Εξαγωγή ιστογράμματος εικόνας, απλοί μετασχηματισμοί με αυτό, ισοστάθμιση ιστογράμματος. Εφαρμογή βασικών παραθύρων με την βοήθεια του ΜΑΤLAB
ΑΣΚΗΣΗ 3 ΒΕΛΤΙΩΣΗ ΕΙΚΟΝΑΣ ΜΕΛΕΤΗ ΙΣΤΟΓΡΑΜΜΑΤΟΣ Αντικείμενο: Εξαγωγή ιστογράμματος εικόνας, απλοί μετασχηματισμοί με αυτό, ισοστάθμιση ιστογράμματος. Εφαρμογή βασικών παραθύρων με την βοήθεια του ΜΑΤLAB
Ακαδηµαϊκό Έτος , Χειµερινό Εξάµηνο ιδάσκων Καθ.: Νίκος Τσαπατσούλης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ, ΤΜΗΜΑ Ι ΑΚΤΙΚΗΣ ΤΗΣ ΤΕΧΝΟΛΟΓΙΑΣ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΤΨΣ 50: ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΕΙΚΟΝΑΣ Ακαδηµαϊκό Έτος 005 006, Χειµερινό Εξάµηνο Καθ.: Νίκος Τσαπατσούλης ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ Η εξέταση
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ, ΤΜΗΜΑ Ι ΑΚΤΙΚΗΣ ΤΗΣ ΤΕΧΝΟΛΟΓΙΑΣ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΤΨΣ 50: ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΕΙΚΟΝΑΣ Ακαδηµαϊκό Έτος 005 006, Χειµερινό Εξάµηνο Καθ.: Νίκος Τσαπατσούλης ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ Η εξέταση
Ψηφιακή Επεξεργασία Εικόνας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 2 : Βελτιστοποίηση εικόνας (Image enhancement) Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 2 : Βελτιστοποίηση εικόνας (Image enhancement) Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το
Προβλήματα, αλγόριθμοι, ψευδοκώδικας
 Προβλήματα, αλγόριθμοι, ψευδοκώδικας October 11, 2011 Στο μάθημα Αλγοριθμική και Δομές Δεδομένων θα ασχοληθούμε με ένα μέρος της διαδικασίας επίλυσης υπολογιστικών προβλημάτων. Συγκεκριμένα θα δούμε τι
Προβλήματα, αλγόριθμοι, ψευδοκώδικας October 11, 2011 Στο μάθημα Αλγοριθμική και Δομές Δεδομένων θα ασχοληθούμε με ένα μέρος της διαδικασίας επίλυσης υπολογιστικών προβλημάτων. Συγκεκριμένα θα δούμε τι
ΠΟΛΥΚΡΙΤΗΡΙΑ ΥΠΟΣΤΗΡΙΞΗ ΑΠΟΦΑΣΕΩΝ. Χάρης Δούκας, Πάνος Ξυδώνας, Ιωάννης Ψαρράς
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών Και Μηχανικών Υπολογιστών ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΩΝ ΒΙΟΜΗΧΑΝΙΚΩΝ ΔΙΑΤΑΞΕΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΑΠΟΦΑΣΕΩΝ Εργαστήριο Συστημάτων Αποφάσεων και Διοίκησης ΠΟΛΥΚΡΙΤΗΡΙΑ
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών Και Μηχανικών Υπολογιστών ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΩΝ ΒΙΟΜΗΧΑΝΙΚΩΝ ΔΙΑΤΑΞΕΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΑΠΟΦΑΣΕΩΝ Εργαστήριο Συστημάτων Αποφάσεων και Διοίκησης ΠΟΛΥΚΡΙΤΗΡΙΑ
ΠΟΛΥΚΡΙΤΗΡΙΑ ΥΠΟΣΤΗΡΙΞΗ ΑΠΟΦΑΣΕΩΝ. Χάρης Δούκας, Πάνος Ξυδώνας, Ιωάννης Ψαρράς
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών Και Μηχανικών Υπολογιστών ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΩΝ ΒΙΟΜΗΧΑΝΙΚΩΝ ΔΙΑΤΑΞΕΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΑΠΟΦΑΣΕΩΝ Εργαστήριο Συστημάτων Αποφάσεων και Διοίκησης ΠΟΛΥΚΡΙΤΗΡΙΑ
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών Και Μηχανικών Υπολογιστών ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΩΝ ΒΙΟΜΗΧΑΝΙΚΩΝ ΔΙΑΤΑΞΕΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΑΠΟΦΑΣΕΩΝ Εργαστήριο Συστημάτων Αποφάσεων και Διοίκησης ΠΟΛΥΚΡΙΤΗΡΙΑ
Digital Image Processing
 Digital Image Processing Χωρικό φιλτράρισμα Πέτρος Καρβέλης pkarvelis@gmail.com Images taken from: R. Gonzalez and R. Woods. Digital Image Processing, Prentice Hall, 008. Χωρικού Φιλτράρισμα Η μηχανική
Digital Image Processing Χωρικό φιλτράρισμα Πέτρος Καρβέλης pkarvelis@gmail.com Images taken from: R. Gonzalez and R. Woods. Digital Image Processing, Prentice Hall, 008. Χωρικού Φιλτράρισμα Η μηχανική
Digital Image Processing
 Digital Image Processing Αποκατάσταση εικόνας Αφαίρεση Θορύβου Πέτρος Καρβέλης pkarvelis@gmail.com Images taken from: R. Gonzalez and R. Woods. Digital Image Processing, Prentice Hall, 2008. Αποκατάσταση
Digital Image Processing Αποκατάσταση εικόνας Αφαίρεση Θορύβου Πέτρος Καρβέλης pkarvelis@gmail.com Images taken from: R. Gonzalez and R. Woods. Digital Image Processing, Prentice Hall, 2008. Αποκατάσταση
z = c 1 x 1 + c 2 x c n x n
 Τεχνολογικό Εκπαιδευτικό Ιδρυμα Κεντρικής Μακεδονίας - Σέρρες Τμήμα Μηχανικών Πληροφορικής Γραμμικός Προγραμματισμός & Βελτιστοποίηση Δρ. Δημήτρης Βαρσάμης Καθηγητής Εφαρμογών Δρ. Δημήτρης Βαρσάμης Μάρτιος
Τεχνολογικό Εκπαιδευτικό Ιδρυμα Κεντρικής Μακεδονίας - Σέρρες Τμήμα Μηχανικών Πληροφορικής Γραμμικός Προγραμματισμός & Βελτιστοποίηση Δρ. Δημήτρης Βαρσάμης Καθηγητής Εφαρμογών Δρ. Δημήτρης Βαρσάμης Μάρτιος
Ψηφιακή Επεξεργασία Εικόνας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 3 : Αποκατάσταση εικόνας (Image Restoration) Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το παρόν
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 3 : Αποκατάσταση εικόνας (Image Restoration) Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το παρόν
DIP_01 Εισαγωγή στην ψηφιακή εικόνα. ΤΕΙ Κρήτης
 DIP_01 Εισαγωγή στην ψηφιακή εικόνα ΤΕΙ Κρήτης Πληροφορίες Μαθήματος ιαλέξεις Πέμπτη 12:15 15:00 Αιθουσα Γ7 ιδάσκων:. Κοσμόπουλος Γραφείο: Κ23-0-15 (ισόγειο( κλειστού γυμναστηρίου) Ωρες γραφείου Τε 16:00
DIP_01 Εισαγωγή στην ψηφιακή εικόνα ΤΕΙ Κρήτης Πληροφορίες Μαθήματος ιαλέξεις Πέμπτη 12:15 15:00 Αιθουσα Γ7 ιδάσκων:. Κοσμόπουλος Γραφείο: Κ23-0-15 (ισόγειο( κλειστού γυμναστηρίου) Ωρες γραφείου Τε 16:00
Στο στάδιο ανάλυσης των αποτελεσµάτων: ανάλυση ευαισθησίας της λύσης, προσδιορισµός της σύγκρουσης των κριτηρίων.
 ΠΕΡΙΛΗΨΗ Η τεχνική αυτή έκθεση περιλαµβάνει αναλυτική περιγραφή των εναλλακτικών µεθόδων πολυκριτηριακής ανάλυσης που εξετάσθηκαν µε στόχο να επιλεγεί η µέθοδος εκείνη η οποία είναι η πιο κατάλληλη για
ΠΕΡΙΛΗΨΗ Η τεχνική αυτή έκθεση περιλαµβάνει αναλυτική περιγραφή των εναλλακτικών µεθόδων πολυκριτηριακής ανάλυσης που εξετάσθηκαν µε στόχο να επιλεγεί η µέθοδος εκείνη η οποία είναι η πιο κατάλληλη για
Γενικά Στοιχεία Ηλεκτρονικού Υπολογιστή
 Γενικά Στοιχεία Ηλεκτρονικού Υπολογιστή 1. Ηλεκτρονικός Υπολογιστής Ο Ηλεκτρονικός Υπολογιστής είναι μια συσκευή, μεγάλη ή μικρή, που επεξεργάζεται δεδομένα και εκτελεί την εργασία του σύμφωνα με τα παρακάτω
Γενικά Στοιχεία Ηλεκτρονικού Υπολογιστή 1. Ηλεκτρονικός Υπολογιστής Ο Ηλεκτρονικός Υπολογιστής είναι μια συσκευή, μεγάλη ή μικρή, που επεξεργάζεται δεδομένα και εκτελεί την εργασία του σύμφωνα με τα παρακάτω
Ανάλυση και επεξεργασία εικόνων DICOM με τη χρήση Matlab
 ΑΣΚΗΣΗ 8 Ανάλυση και επεξεργασία εικόνων DICOM με τη χρήση Matlab 1. Περιγραφή του προτύπου DICOM Η ψηφιακή επεξεργασία ιατρικής εικόνας ξεκίνησε παράλληλα με την ανάπτυξη ενός προτύπου για τη μεταφορά
ΑΣΚΗΣΗ 8 Ανάλυση και επεξεργασία εικόνων DICOM με τη χρήση Matlab 1. Περιγραφή του προτύπου DICOM Η ψηφιακή επεξεργασία ιατρικής εικόνας ξεκίνησε παράλληλα με την ανάπτυξη ενός προτύπου για τη μεταφορά
Μέθοδοι Μηχανών Μάθησης για Ευφυή Αναγνώριση και ιάγνωση Ιατρικών εδοµένων
 Μέθοδοι Μηχανών Μάθησης για Ευφυή Αναγνώριση και ιάγνωση Ιατρικών εδοµένων Εισηγητής: ρ Ηλίας Ζαφειρόπουλος Εισαγωγή Ιατρικά δεδοµένα: Συλλογή Οργάνωση Αξιοποίηση Data Mining ιαχείριση εδοµένων Εκπαίδευση
Μέθοδοι Μηχανών Μάθησης για Ευφυή Αναγνώριση και ιάγνωση Ιατρικών εδοµένων Εισηγητής: ρ Ηλίας Ζαφειρόπουλος Εισαγωγή Ιατρικά δεδοµένα: Συλλογή Οργάνωση Αξιοποίηση Data Mining ιαχείριση εδοµένων Εκπαίδευση
(Computed Tomography, CT)
 Υπολογιστική Τοµογραφία (Computed Tomography, CT) Κωσταρίδου Ελένη Αναπληρώτρια Καθηγήτρια Ιατρικής Φυσικής Εργαστήριο Ιατρικής Φυσικής, Τµήµα Ιατρικής, Πανεπιστήµιο Πατρών Περιεχόµενα µαθήµατος Φυσικό
Υπολογιστική Τοµογραφία (Computed Tomography, CT) Κωσταρίδου Ελένη Αναπληρώτρια Καθηγήτρια Ιατρικής Φυσικής Εργαστήριο Ιατρικής Φυσικής, Τµήµα Ιατρικής, Πανεπιστήµιο Πατρών Περιεχόµενα µαθήµατος Φυσικό
Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος
 Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος Χιωτίδης Γεώργιος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος Χιωτίδης Γεώργιος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Ενότητα 2: Οι Θεµελιώδεις Αρχές των Ψηφιακών Εικόνων
 Ενότητα 2: Οι Θεµελιώδεις Αρχές των Ψηφιακών Εικόνων Δειγµατοληψία και Κβαντισµός: Μια εικόνα (µπορεί να) είναι συνεχής τόσο ως προς τις συντεταγµένες x, y όσο και ως προς το πλάτος. Για να τη µετατρέψουµε
Ενότητα 2: Οι Θεµελιώδεις Αρχές των Ψηφιακών Εικόνων Δειγµατοληψία και Κβαντισµός: Μια εικόνα (µπορεί να) είναι συνεχής τόσο ως προς τις συντεταγµένες x, y όσο και ως προς το πλάτος. Για να τη µετατρέψουµε
ΦΙΛΤΡΟ KALMAN ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ
 1 ΦΙΛΤΡΟ KALMAN ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ Σε αυτό το μέρος της πτυχιακής θα ασχοληθούμε λεπτομερώς με το φίλτρο kalman και θα δούμε μια καινούρια έκδοση του φίλτρου πάνω στην εφαρμογή της γραμμικής εκτίμησης διακριτού
1 ΦΙΛΤΡΟ KALMAN ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ Σε αυτό το μέρος της πτυχιακής θα ασχοληθούμε λεπτομερώς με το φίλτρο kalman και θα δούμε μια καινούρια έκδοση του φίλτρου πάνω στην εφαρμογή της γραμμικής εκτίμησης διακριτού
Περί της Ταξινόμησης των Ειδών
 Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Σχολή Θετικών Επιστημών Τμήμα Φυσικής 541 24 Θεσσαλονίκη Καθηγητής Γεώργιος Θεοδώρου Tel.: +30 2310998051, Ιστοσελίδα: http://users.auth.gr/theodoru Περί της Ταξινόμησης
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Σχολή Θετικών Επιστημών Τμήμα Φυσικής 541 24 Θεσσαλονίκη Καθηγητής Γεώργιος Θεοδώρου Tel.: +30 2310998051, Ιστοσελίδα: http://users.auth.gr/theodoru Περί της Ταξινόμησης
ΕΥΦΥΗΣ ΕΛΕΓΧΟΣ. Ενότητα #3: Αρχή της Επέκτασης - Ασαφείς Σχέσεις. Αναστάσιος Ντούνης Τμήμα Μηχανικών Αυτοματισμού Τ.Ε.
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΥΦΥΗΣ ΕΛΕΓΧΟΣ Ενότητα #3: Αρχή της Επέκτασης - Ασαφείς Σχέσεις Αναστάσιος Ντούνης Τμήμα Μηχανικών Αυτοματισμού Τ.Ε. Άδειες Χρήσης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΥΦΥΗΣ ΕΛΕΓΧΟΣ Ενότητα #3: Αρχή της Επέκτασης - Ασαφείς Σχέσεις Αναστάσιος Ντούνης Τμήμα Μηχανικών Αυτοματισμού Τ.Ε. Άδειες Χρήσης
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
ΔΙΑΧΩΡΙΣΤΙΚΗ ΟΜΑΔΟΠΟΙΗΣΗ
 ΔΙΑΧΩΡΙΣΤΙΚΗ ΟΜΑΔΟΠΟΙΗΣΗ Εισαγωγή Τεχνικές διαχωριστικής ομαδοποίησης: Ν πρότυπα k ομάδες Ν>>k Συνήθως k καθορίζεται από χρήστη Διαχωριστικές τεχνικές: επιτρέπουν πρότυπα να μετακινούνται από ομάδα σε
ΔΙΑΧΩΡΙΣΤΙΚΗ ΟΜΑΔΟΠΟΙΗΣΗ Εισαγωγή Τεχνικές διαχωριστικής ομαδοποίησης: Ν πρότυπα k ομάδες Ν>>k Συνήθως k καθορίζεται από χρήστη Διαχωριστικές τεχνικές: επιτρέπουν πρότυπα να μετακινούνται από ομάδα σε
Πρόβλημα 29 / σελίδα 28
 Πρόβλημα 29 / σελίδα 28 Πρόβλημα 30 / σελίδα 28 Αντιμετάθεση / σελίδα 10 Να γράψετε αλγόριθμο, οποίος θα διαβάζει τα περιεχόμενα δύο μεταβλητών Α και Β, στη συνέχεια να αντιμεταθέτει τα περιεχόμενά τους
Πρόβλημα 29 / σελίδα 28 Πρόβλημα 30 / σελίδα 28 Αντιμετάθεση / σελίδα 10 Να γράψετε αλγόριθμο, οποίος θα διαβάζει τα περιεχόμενα δύο μεταβλητών Α και Β, στη συνέχεια να αντιμεταθέτει τα περιεχόμενά τους
ΑΣΑΦΗΣ ΛΟΓΙΚΗ. Οικονόμου Παναγιώτης Δρ. Ε. Παπαγεωργίου 1
 ΑΣΑΦΗΣ ΛΟΓΙΚΗ Ασαφή Σύνολα Συναρτήσεις Συμμετοχής Λεκτικοί Κανόνες Πράξεις Ασαφών Συνόλων Ασαφής Συνεπαγωγές Αποασαφοποίηση Παραδείγματα Ασαφών Συστημάτων Οικονόμου Παναγιώτης 1 Ασάφεια Έννοια που σχετίζεται
ΑΣΑΦΗΣ ΛΟΓΙΚΗ Ασαφή Σύνολα Συναρτήσεις Συμμετοχής Λεκτικοί Κανόνες Πράξεις Ασαφών Συνόλων Ασαφής Συνεπαγωγές Αποασαφοποίηση Παραδείγματα Ασαφών Συστημάτων Οικονόμου Παναγιώτης 1 Ασάφεια Έννοια που σχετίζεται
Μάθημα 10 ο. Περιγραφή Σχήματος ΤΜΗΥΠ / ΕΕΣΤ 1
 Μάθημα 10 ο Περιγραφή Σχήματος ΤΜΗΥΠ / ΕΕΣΤ 1 Εισαγωγή (1) Η περιγραφή μίας περιοχής μπορεί να γίνει: Με βάση τα εξωτερικά χαρακτηριστικά (ακμές, όρια). Αυτή η περιγραφή προτιμάται όταν μας ενδιαφέρουν
Μάθημα 10 ο Περιγραφή Σχήματος ΤΜΗΥΠ / ΕΕΣΤ 1 Εισαγωγή (1) Η περιγραφή μίας περιοχής μπορεί να γίνει: Με βάση τα εξωτερικά χαρακτηριστικά (ακμές, όρια). Αυτή η περιγραφή προτιμάται όταν μας ενδιαφέρουν
Επεξεργασία Χαρτογραφικής Εικόνας
 Επεξεργασία Χαρτογραφικής Εικόνας Διδάσκων: Αναγνωστόπουλος Χρήστος Κώδικες μετρήσεων αντικειμένων σε εικόνα Χρωματικά μοντέλα: Munsell, HSB/HSV, CIE-LAB Κώδικες μετρήσεων αντικειμένων σε εικόνες Η βασική
Επεξεργασία Χαρτογραφικής Εικόνας Διδάσκων: Αναγνωστόπουλος Χρήστος Κώδικες μετρήσεων αντικειμένων σε εικόνα Χρωματικά μοντέλα: Munsell, HSB/HSV, CIE-LAB Κώδικες μετρήσεων αντικειμένων σε εικόνες Η βασική
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ. Μια παράσταση που περιέχει πράξεις με μεταβλητές (γράμματα) και αριθμούς καλείται αλγεβρική, όπως για παράδειγμα η : 2x+3y-8
 ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
Ψηφιακή Επεξεργασία Εικόνων
 Ψηφιακή Επεξεργασία Εικόνων Εικόνα : αναπαράσταση των πραγμάτων Επεξεργασία : βελτίωση, ανάλυση, αντίληψη Βασικές έννοιες και μεθοδολογίες ψηφιακής επεξεργασίας εικόνων Θεμελιώδη θέματα για την περιοχή
Ψηφιακή Επεξεργασία Εικόνων Εικόνα : αναπαράσταση των πραγμάτων Επεξεργασία : βελτίωση, ανάλυση, αντίληψη Βασικές έννοιες και μεθοδολογίες ψηφιακής επεξεργασίας εικόνων Θεμελιώδη θέματα για την περιοχή
Σημαντικές χρονολογίες στην εξέλιξη της Υπολογιστικής Τομογραφίας
 Σημαντικές χρονολογίες στην εξέλιξη της Υπολογιστικής Τομογραφίας 1924 - μαθηματική θεωρία τομογραφικής ανακατασκευής δεδομένων (Johann Radon) 1930 - κλασσική τομογραφία (A. Vallebona) 1963 - θεωρητική
Σημαντικές χρονολογίες στην εξέλιξη της Υπολογιστικής Τομογραφίας 1924 - μαθηματική θεωρία τομογραφικής ανακατασκευής δεδομένων (Johann Radon) 1930 - κλασσική τομογραφία (A. Vallebona) 1963 - θεωρητική
ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΔΙΑΚΡΙΤΩΝ ΕΝΑΛΛΑΚΤΙΚΩΝ ΣΕ ΠΡΟΒΛΗΜΑΤΑ ΣΧΕΔΙΑΣΜΟΥ ΚΑΙ ΣΥΝΘΕΣΗΣ ΔΙΕΡΓΑΣΙΩΝ
 ΜΕΡΟΣ ΙΙ ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΔΙΑΚΡΙΤΩΝ ΕΝΑΛΛΑΚΤΙΚΩΝ ΣΕ ΠΡΟΒΛΗΜΑΤΑ ΣΧΕΔΙΑΣΜΟΥ ΚΑΙ ΣΥΝΘΕΣΗΣ ΔΙΕΡΓΑΣΙΩΝ 36 ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΔΙΑΚΡΙΤΩΝ ΕΝΑΛΛΑΚΤΙΚΩΝ ΣΕ ΠΡΟΒΛΗΜΑΤΑ ΣΧΕΔΙΑΣΜΟΥ ΚΑΙ ΣΥΝΘΕΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Πολλές από τις αποφάσεις
ΜΕΡΟΣ ΙΙ ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΔΙΑΚΡΙΤΩΝ ΕΝΑΛΛΑΚΤΙΚΩΝ ΣΕ ΠΡΟΒΛΗΜΑΤΑ ΣΧΕΔΙΑΣΜΟΥ ΚΑΙ ΣΥΝΘΕΣΗΣ ΔΙΕΡΓΑΣΙΩΝ 36 ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΔΙΑΚΡΙΤΩΝ ΕΝΑΛΛΑΚΤΙΚΩΝ ΣΕ ΠΡΟΒΛΗΜΑΤΑ ΣΧΕΔΙΑΣΜΟΥ ΚΑΙ ΣΥΝΘΕΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Πολλές από τις αποφάσεις
Συστήματα συντεταγμένων
 Κεφάλαιο. Για να δημιουργήσουμε τρισδιάστατα αντικείμενα, που μπορούν να παρασταθούν στην οθόνη του υπολογιστή ως ένα σύνολο από γραμμές, επίπεδες πολυγωνικές επιφάνειες ή ακόμη και από ένα συνδυασμό από
Κεφάλαιο. Για να δημιουργήσουμε τρισδιάστατα αντικείμενα, που μπορούν να παρασταθούν στην οθόνη του υπολογιστή ως ένα σύνολο από γραμμές, επίπεδες πολυγωνικές επιφάνειες ή ακόμη και από ένα συνδυασμό από
E[ (x- ) ]= trace[(x-x)(x- ) ]
![E[ (x- ) ]= trace[(x-x)(x- ) ] E[ (x- ) ]= trace[(x-x)(x- ) ]](/thumbs/55/36021260.jpg) 1 ΦΙΛΤΡΟ KALMAN ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ Σε αυτό το μέρος της πτυχιακής θα ασχοληθούμε λεπτομερώς με το φίλτρο kalman και θα δούμε μια καινούρια έκδοση του φίλτρου πάνω στην εφαρμογή της γραμμικής εκτίμησης διακριτού
1 ΦΙΛΤΡΟ KALMAN ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ Σε αυτό το μέρος της πτυχιακής θα ασχοληθούμε λεπτομερώς με το φίλτρο kalman και θα δούμε μια καινούρια έκδοση του φίλτρου πάνω στην εφαρμογή της γραμμικής εκτίμησης διακριτού
ΠΕΙΡΑΜΑΤΙΚΕΣ ΠΡΟΣΟΜΟΙΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 4. είναι η πραγματική απόκριση του j δεδομένου (εκπαίδευσης ή ελέγχου) και y ˆ j
 Πειραματικές Προσομοιώσεις ΚΕΦΑΛΑΙΟ 4 Όλες οι προσομοιώσεις έγιναν σε περιβάλλον Matlab. Για την υλοποίηση της μεθόδου ε-svm χρησιμοποιήθηκε το λογισμικό SVM-KM που αναπτύχθηκε στο Ecole d Ingenieur(e)s
Πειραματικές Προσομοιώσεις ΚΕΦΑΛΑΙΟ 4 Όλες οι προσομοιώσεις έγιναν σε περιβάλλον Matlab. Για την υλοποίηση της μεθόδου ε-svm χρησιμοποιήθηκε το λογισμικό SVM-KM που αναπτύχθηκε στο Ecole d Ingenieur(e)s
Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας. Παρουσίαση 12 η. Θεωρία Χρώματος και Επεξεργασία Έγχρωμων Εικόνων
 Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Παρουσίαση 12 η Θεωρία Χρώματος και Επεξεργασία Έγχρωμων Εικόνων Εισαγωγή (1) Το χρώμα είναι ένας πολύ σημαντικός παράγοντας περιγραφής, που συχνά απλουστεύει κατά
Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Παρουσίαση 12 η Θεωρία Χρώματος και Επεξεργασία Έγχρωμων Εικόνων Εισαγωγή (1) Το χρώμα είναι ένας πολύ σημαντικός παράγοντας περιγραφής, που συχνά απλουστεύει κατά
ΕΥΦΥΗΣ ΕΛΕΓΧΟΣ. Ενότητα #8: Βελτιστοποίηση Συστημάτων Ασαφούς Λογικής. Αναστάσιος Ντούνης Τμήμα Μηχανικών Αυτοματισμού Τ.Ε.
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΥΦΥΗΣ ΕΛΕΓΧΟΣ Ενότητα #8: Βελτιστοποίηση Συστημάτων Ασαφούς Λογικής Αναστάσιος Ντούνης Τμήμα Μηχανικών Αυτοματισμού Τ.Ε. Άδειες
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΥΦΥΗΣ ΕΛΕΓΧΟΣ Ενότητα #8: Βελτιστοποίηση Συστημάτων Ασαφούς Λογικής Αναστάσιος Ντούνης Τμήμα Μηχανικών Αυτοματισμού Τ.Ε. Άδειες
ΑΝΤΩΝΙΟΣ ΛΥΡΩΝΗΣ ΧΑΝΙΑ 2011. Σκοπός Εργασίας Εντοπισμός πλίνθων σε σειρά ορθοφωτογραφιών και εξαγωγή δισδιάστατης αποτύπωσης των τειχών.
 1 ΑΝΤΩΝΙΟΣ ΛΥΡΩΝΗΣ ΧΑΝΙΑ 2011 2 Σκοπός Εργασίας Εντοπισμός πλίνθων σε σειρά ορθοφωτογραφιών και εξαγωγή δισδιάστατης αποτύπωσης των τειχών. Ενδεδειγμένες και αξιόπιστες μέθοδοι αποτύπωσης Εμπειρικές Τοπογραφικές
1 ΑΝΤΩΝΙΟΣ ΛΥΡΩΝΗΣ ΧΑΝΙΑ 2011 2 Σκοπός Εργασίας Εντοπισμός πλίνθων σε σειρά ορθοφωτογραφιών και εξαγωγή δισδιάστατης αποτύπωσης των τειχών. Ενδεδειγμένες και αξιόπιστες μέθοδοι αποτύπωσης Εμπειρικές Τοπογραφικές
 Β Γραφικές παραστάσεις - Πρώτο γράφημα Σχεδιάζοντας το μήκος της σανίδας συναρτήσει των φάσεων της σελήνης μπορείτε να δείτε αν υπάρχει κάποιος συσχετισμός μεταξύ των μεγεθών. Ο συνήθης τρόπος γραφικής
Β Γραφικές παραστάσεις - Πρώτο γράφημα Σχεδιάζοντας το μήκος της σανίδας συναρτήσει των φάσεων της σελήνης μπορείτε να δείτε αν υπάρχει κάποιος συσχετισμός μεταξύ των μεγεθών. Ο συνήθης τρόπος γραφικής
4.4 Μετατροπή από μία μορφή δομής επανάληψης σε μία άλλη.
 4.4 Μετατροπή από μία μορφή δομής επανάληψης σε μία άλλη. Η μετατροπή μιας εντολής επανάληψης σε μία άλλη ή στις άλλες δύο εντολές επανάληψης, αποτελεί ένα θέμα που αρκετές φορές έχει εξεταστεί σε πανελλαδικό
4.4 Μετατροπή από μία μορφή δομής επανάληψης σε μία άλλη. Η μετατροπή μιας εντολής επανάληψης σε μία άλλη ή στις άλλες δύο εντολές επανάληψης, αποτελεί ένα θέμα που αρκετές φορές έχει εξεταστεί σε πανελλαδικό
ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟ 1: ΕΙΣΑΓΩΓΗ
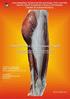 ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟ 1: ΕΙΣΑΓΩΓΗ 1.1 ΕΙΣΑΓΩΓΗ 1.1 1.2 ΤΙ ΕΙΝΑΙ ΜΙΑ ΨΗΦΙΑΚΗ ΕΙΚΟΝΑ 1.2 1.3 ΠΛΗΘΟΣ BITS ΜΙΑΣ ΕΙΚΟΝΑΣ 1.4 1.4 ΕΥΚΡΙΝΕΙΑ ΕΙΚΟΝΑΣ 1.5 1.5 ΕΠΙΠΕ Α BITS ΜΙΑΣ ΕΙΚΟΝΑΣ 1.8 1.6 Η ΦΥΣΗ ΤΟΥ ΧΡΩΜΑΤΟΣ
ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟ 1: ΕΙΣΑΓΩΓΗ 1.1 ΕΙΣΑΓΩΓΗ 1.1 1.2 ΤΙ ΕΙΝΑΙ ΜΙΑ ΨΗΦΙΑΚΗ ΕΙΚΟΝΑ 1.2 1.3 ΠΛΗΘΟΣ BITS ΜΙΑΣ ΕΙΚΟΝΑΣ 1.4 1.4 ΕΥΚΡΙΝΕΙΑ ΕΙΚΟΝΑΣ 1.5 1.5 ΕΠΙΠΕ Α BITS ΜΙΑΣ ΕΙΚΟΝΑΣ 1.8 1.6 Η ΦΥΣΗ ΤΟΥ ΧΡΩΜΑΤΟΣ
Δρ. Βασίλειος Γ. Καμπουρλάζος Δρ. Ανέστης Γ. Χατζημιχαηλίδης
 Μάθημα 2ο Δρ. Ανέστης Γ. Χατζημιχαηλίδης Τμήμα Μηχανικών Πληροφορικής Τ.Ε. ΤΕΙ Ανατολικής Μακεδονίας και Θράκης 2016-2017 Ασαφή Συστήματα 2 Η ασαφής λογική προτάθηκε το 1965 από τον Prof. Lotfi Zadeh
Μάθημα 2ο Δρ. Ανέστης Γ. Χατζημιχαηλίδης Τμήμα Μηχανικών Πληροφορικής Τ.Ε. ΤΕΙ Ανατολικής Μακεδονίας και Θράκης 2016-2017 Ασαφή Συστήματα 2 Η ασαφής λογική προτάθηκε το 1965 από τον Prof. Lotfi Zadeh
ΠΑΡΟΥΣΙΑΣΗ ΣΤΑΤΙΣΤΙΚΩΝ ΔΕΔΟΜΕΝΩΝ
 ο Κεφάλαιο: Στατιστική ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΟΡΙΣΜΟΙ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Πληθυσμός: Λέγεται ένα σύνολο στοιχείων που θέλουμε να εξετάσουμε με ένα ή περισσότερα χαρακτηριστικά. Μεταβλητές X: Ονομάζονται
ο Κεφάλαιο: Στατιστική ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΟΡΙΣΜΟΙ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Πληθυσμός: Λέγεται ένα σύνολο στοιχείων που θέλουμε να εξετάσουμε με ένα ή περισσότερα χαρακτηριστικά. Μεταβλητές X: Ονομάζονται
Τηλεπισκόπηση. Τηλεπισκόπηση. Τηλεπισκόπηση. Τηλεπισκόπηση. Τηλεπισκόπηση. Τηλεπισκόπηση 24/6/2013. Ψηφιακή Ανάλυση Εικόνας. Ψηφιακή Ανάλυση Εικόνας
 Η βελτίωση ασχολείται με την τροποποίηση των εικόνων ώστε να είναι πιο κατάλληλες για την ανθρώπινη όραση. Ανεξάρτητα από το βαθμό της ψηφιακής παρέμβασης, η οπτική ανάλυση παίζει σπουδαίο ρόλο σε όλα
Η βελτίωση ασχολείται με την τροποποίηση των εικόνων ώστε να είναι πιο κατάλληλες για την ανθρώπινη όραση. Ανεξάρτητα από το βαθμό της ψηφιακής παρέμβασης, η οπτική ανάλυση παίζει σπουδαίο ρόλο σε όλα
Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας. Εισηγητής Αναστάσιος Κεσίδης
 Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας Εισηγητής Αναστάσιος Κεσίδης Εισαγωγή Τι είναι η εικόνα; Μια οπτική αναπαράσταση με την μορφή μιας συνάρτησης f(x, y) όπου η
Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας Εισηγητής Αναστάσιος Κεσίδης Εισαγωγή Τι είναι η εικόνα; Μια οπτική αναπαράσταση με την μορφή μιας συνάρτησης f(x, y) όπου η
Ραδιομετρική Ενίσχυση - Χωρική Επεξεργασία Δορυφορικών Εικόνων
 Πανεπιστήμιο Θεσσαλίας Πολυτεχνική Σχολή Τμήμα Μηχανικών Χωροταξίας Πολεοδομίας και Περιφερειακής Ανάπτυξης Ραδιομετρική Ενίσχυση - Χωρική Επεξεργασία Δορυφορικών Εικόνων Ιωάννης Φαρασλής Τηλ : 24210-74466,
Πανεπιστήμιο Θεσσαλίας Πολυτεχνική Σχολή Τμήμα Μηχανικών Χωροταξίας Πολεοδομίας και Περιφερειακής Ανάπτυξης Ραδιομετρική Ενίσχυση - Χωρική Επεξεργασία Δορυφορικών Εικόνων Ιωάννης Φαρασλής Τηλ : 24210-74466,
Τηλεπισκόπηση. Τηλεπισκόπηση. Τηλεπισκόπηση. Τηλεπισκόπηση. Τηλεπισκόπηση 24/6/2013. Τηλεπισκόπηση. Κ. Ποϊραζίδης ΤΑΞΙΝΟΜΗΣΗ ΕΙΚΟΝΑΣ
 ΤΑΞΙΝΟΜΗΣΗ ΕΙΚΟΝΑΣ Κ. Ποϊραζίδης Η ταξινόμηση εικόνας αναφέρεται στην ερμηνεία με χρήση υπολογιστή των τηλεπισκοπικών εικόνων. Παρόλο που ορισμένες διαδικασίες έχουν τη δυνατότητα να συμπεριλάβουν πληροφορίες
ΤΑΞΙΝΟΜΗΣΗ ΕΙΚΟΝΑΣ Κ. Ποϊραζίδης Η ταξινόμηση εικόνας αναφέρεται στην ερμηνεία με χρήση υπολογιστή των τηλεπισκοπικών εικόνων. Παρόλο που ορισμένες διαδικασίες έχουν τη δυνατότητα να συμπεριλάβουν πληροφορίες
I. ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. math-gr
 I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
ΗΥ562 Προχωρημένα Θέματα Βάσεων Δεδομένων Efficient Query Evaluation over Temporally Correlated Probabilistic Streams
 ΗΥ562 Προχωρημένα Θέματα Βάσεων Δεδομένων Efficient Query Evaluation over Temporally Correlated Probabilistic Streams Αλέκα Σεληνιωτάκη Ηράκλειο, 26/06/12 aseliniotaki@csd.uoc.gr ΑΜ: 703 1. Περίληψη Συνεισφοράς
ΗΥ562 Προχωρημένα Θέματα Βάσεων Δεδομένων Efficient Query Evaluation over Temporally Correlated Probabilistic Streams Αλέκα Σεληνιωτάκη Ηράκλειο, 26/06/12 aseliniotaki@csd.uoc.gr ΑΜ: 703 1. Περίληψη Συνεισφοράς
Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας. Παρουσίαση Νο. 1. Εισαγωγή
 Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Ακαδημαϊκό Έτος 2015-16 Παρουσίαση Νο. 1 Εισαγωγή Τι είναι η εικόνα; Οτιδήποτε μπορούμε να δούμε ή να απεικονίσουμε Π.χ. Μια εικόνα τοπίου αλλά και η απεικόνιση
Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Ακαδημαϊκό Έτος 2015-16 Παρουσίαση Νο. 1 Εισαγωγή Τι είναι η εικόνα; Οτιδήποτε μπορούμε να δούμε ή να απεικονίσουμε Π.χ. Μια εικόνα τοπίου αλλά και η απεικόνιση
ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΑΡΧΕΣ ΤΗΣ ΕΠΙΣΤΗΜΗΣ ΤΩΝ Η/Υ
 ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΑΡΧΕΣ ΤΗΣ ΕΠΙΣΤΗΜΗΣ ΤΩΝ Η/Υ ΜΕΡΛΙΑΟΥΝΤΑΣ ΣΤΕΦΑΝΟΣ, ΠΕ19 ΚΕΦΑΛΑΙΟ 3 Αλγόριθμοι 3. Αλγόριθμοι 2 3. Αλγόριθμοι 3.1 Η έννοια του αλγορίθμου 3.2 Χαρακτηριστικά αλγορίθμου 3.3 Ανάλυση αλγορίθμων
ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΑΡΧΕΣ ΤΗΣ ΕΠΙΣΤΗΜΗΣ ΤΩΝ Η/Υ ΜΕΡΛΙΑΟΥΝΤΑΣ ΣΤΕΦΑΝΟΣ, ΠΕ19 ΚΕΦΑΛΑΙΟ 3 Αλγόριθμοι 3. Αλγόριθμοι 2 3. Αλγόριθμοι 3.1 Η έννοια του αλγορίθμου 3.2 Χαρακτηριστικά αλγορίθμου 3.3 Ανάλυση αλγορίθμων
ΙΑ ΟΧΙΚΕΣ ΒΕΛΤΙΩΣΕΙΣ
 Tel.: +30 2310998051, Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Σχολή Θετικών Επιστημών Τμήμα Φυσικής 541 24 Θεσσαλονίκη Καθηγητής Γεώργιος Θεοδώρου Ιστοσελίδα: http://users.auth.gr/theodoru ΙΑ ΟΧΙΚΕΣ ΒΕΛΤΙΩΣΕΙΣ
Tel.: +30 2310998051, Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Σχολή Θετικών Επιστημών Τμήμα Φυσικής 541 24 Θεσσαλονίκη Καθηγητής Γεώργιος Θεοδώρου Ιστοσελίδα: http://users.auth.gr/theodoru ΙΑ ΟΧΙΚΕΣ ΒΕΛΤΙΩΣΕΙΣ
ΔΕΙΓΜΑ ΠΡΙΝ ΤΙΣ ΔΙΟΡΘΩΣΕΙΣ - ΕΚΔΟΣΕΙΣ ΚΡΙΤΙΚΗ
 Συναρτήσεις Προεπισκόπηση Κεφαλαίου Τα μαθηματικά είναι μια γλώσσα με ένα συγκεκριμένο λεξιλόγιο και πολλούς κανόνες. Πριν ξεκινήσετε το ταξίδι σας στον Απειροστικό Λογισμό, θα πρέπει να έχετε εξοικειωθεί
Συναρτήσεις Προεπισκόπηση Κεφαλαίου Τα μαθηματικά είναι μια γλώσσα με ένα συγκεκριμένο λεξιλόγιο και πολλούς κανόνες. Πριν ξεκινήσετε το ταξίδι σας στον Απειροστικό Λογισμό, θα πρέπει να έχετε εξοικειωθεί
Μαθηματικά Μοντέλα Βιολογίας & Φυσιολογίας
 Μαθηματικά Μοντέλα Βιολογίας & Φυσιολογίας ΘΕΩΡΙΑ Γ Εξαμηνο Τμήμα Μηχανικών Βιοϊατρικής / ΠΑΔΑ Υπ. Καθηγ. 1 ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΙΑΤΡΙΚΩΝ ΕΙΚΟΝΩΝ ΑΠΕΙΚΟΝΙΣΗ CT ΤΩΝ ΠΝΕΥΜΟΝΩΝ #10 2 1 Ιατρική Εικόνα Πηγή ανατομικών
Μαθηματικά Μοντέλα Βιολογίας & Φυσιολογίας ΘΕΩΡΙΑ Γ Εξαμηνο Τμήμα Μηχανικών Βιοϊατρικής / ΠΑΔΑ Υπ. Καθηγ. 1 ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΙΑΤΡΙΚΩΝ ΕΙΚΟΝΩΝ ΑΠΕΙΚΟΝΙΣΗ CT ΤΩΝ ΠΝΕΥΜΟΝΩΝ #10 2 1 Ιατρική Εικόνα Πηγή ανατομικών
ΤΜΗΜΑΤΟΠΟΙΗΣΗ ΟΡΘΟΠΕΔΙΚΩΝ ΔΕΔΟΜΕΝΩΝ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΥΣΤΗΜΑΤΩΝ ΜΕΤΑΔΟΣΗΣ ΠΛΗΡΟΦΟΡΙΑΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΤΜΗΜΑΤΟΠΟΙΗΣΗ ΟΡΘΟΠΕΔΙΚΩΝ ΔΕΔΟΜΕΝΩΝ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΥΣΤΗΜΑΤΩΝ ΜΕΤΑΔΟΣΗΣ ΠΛΗΡΟΦΟΡΙΑΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΤΜΗΜΑΤΟΠΟΙΗΣΗ ΟΡΘΟΠΕΔΙΚΩΝ ΔΕΔΟΜΕΝΩΝ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ
Βιομηχανικοί Ελεγκτές
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τ.Τ Βιομηχανικοί Ελεγκτές Ενότητα #7: Ευφυής Ελεγκτής Μέρος Α Κωνσταντίνος Αλαφοδήμος Τμήματος Μηχανικών Αυτοματισμού Τ.Ε. Άδειες Χρήσης Το παρόν
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τ.Τ Βιομηχανικοί Ελεγκτές Ενότητα #7: Ευφυής Ελεγκτής Μέρος Α Κωνσταντίνος Αλαφοδήμος Τμήματος Μηχανικών Αυτοματισμού Τ.Ε. Άδειες Χρήσης Το παρόν
ΠΟΛΥΚΡΙΤΗΡΙΑ ΥΠΟΣΤΗΡΙΞΗ ΑΠΟΦΑΣΕΩΝ
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών Και Μηχανικών Υπολογιστών ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΩΝ ΒΙΟΜΗΧΑΝΙΚΩΝ ΔΙΑΤΑΞΕΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΑΠΟΦΑΣΕΩΝ Εργαστήριο Συστημάτων Αποφάσεων και Διοίκησης ΠΟΛΥΚΡΙΤΗΡΙΑ
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών Και Μηχανικών Υπολογιστών ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΩΝ ΒΙΟΜΗΧΑΝΙΚΩΝ ΔΙΑΤΑΞΕΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΑΠΟΦΑΣΕΩΝ Εργαστήριο Συστημάτων Αποφάσεων και Διοίκησης ΠΟΛΥΚΡΙΤΗΡΙΑ
x 2,, x Ν τον οποίον το αποτέλεσμα επηρεάζεται από
 Στη θεωρία, θεωρία και πείραμα είναι τα ΘΕΩΡΙΑ ΣΦΑΛΜΑΤΩΝ... υπό ισχυρή συμπίεση ίδια αλλά στο πείραμα είναι διαφορετικά, A.Ensten Οι παρακάτω σημειώσεις περιέχουν τα βασικά σημεία που πρέπει να γνωρίζει
Στη θεωρία, θεωρία και πείραμα είναι τα ΘΕΩΡΙΑ ΣΦΑΛΜΑΤΩΝ... υπό ισχυρή συμπίεση ίδια αλλά στο πείραμα είναι διαφορετικά, A.Ensten Οι παρακάτω σημειώσεις περιέχουν τα βασικά σημεία που πρέπει να γνωρίζει
ΚΕΦΑΛΑΙΟ 18. 18 Μηχανική Μάθηση
 ΚΕΦΑΛΑΙΟ 18 18 Μηχανική Μάθηση Ένα φυσικό ή τεχνητό σύστηµα επεξεργασίας πληροφορίας συµπεριλαµβανοµένων εκείνων µε δυνατότητες αντίληψης, µάθησης, συλλογισµού, λήψης απόφασης, επικοινωνίας και δράσης
ΚΕΦΑΛΑΙΟ 18 18 Μηχανική Μάθηση Ένα φυσικό ή τεχνητό σύστηµα επεξεργασίας πληροφορίας συµπεριλαµβανοµένων εκείνων µε δυνατότητες αντίληψης, µάθησης, συλλογισµού, λήψης απόφασης, επικοινωνίας και δράσης
ΔΙΑΧΕΙΡΙΣΗ ΓΛΩΣΣΙΚΩΝ ΜΕΤΑΒΛΗΤΩΝ. Πολυκριτήρια Ανάλυση Αποφάσεων
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών Και Μηχανικών Υπολογιστών ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΩΝ ΒΙΟΜΗΧΑΝΙΚΩΝ ΔΙΑΤΑΞΕΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΑΠΟΦΑΣΕΩΝ Εργαστήριο Συστημάτων Αποφάσεων και Διοίκησης ΔΙΑΧΕΙΡΙΣΗ
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών Και Μηχανικών Υπολογιστών ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΩΝ ΒΙΟΜΗΧΑΝΙΚΩΝ ΔΙΑΤΑΞΕΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΑΠΟΦΑΣΕΩΝ Εργαστήριο Συστημάτων Αποφάσεων και Διοίκησης ΔΙΑΧΕΙΡΙΣΗ
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ Π ΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ Π ΕΡΙΒΑΛΛΟΝ
 ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΠΑΙΔΑΓΩΓΙΚΟ ΙΝΣΤΙΤΟΥΤΟ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ Π ΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ Π ΕΡΙΒΑΛΛΟΝ Κ Υ Κ Λ Ο Υ Π Λ Η Ρ Ο Φ Ο Ρ Ι Κ Η Σ Κ Α Ι Υ Π Η Ρ Ε Σ Ι Ω Ν Τ Ε Χ Ν Ο Λ Ο Γ Ι Κ Η
ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΠΑΙΔΑΓΩΓΙΚΟ ΙΝΣΤΙΤΟΥΤΟ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ Π ΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ Π ΕΡΙΒΑΛΛΟΝ Κ Υ Κ Λ Ο Υ Π Λ Η Ρ Ο Φ Ο Ρ Ι Κ Η Σ Κ Α Ι Υ Π Η Ρ Ε Σ Ι Ω Ν Τ Ε Χ Ν Ο Λ Ο Γ Ι Κ Η
Βασικές Έννοιες Ασαφών Συνόλων
 Ασάφεια (Fuzziness) Έννοια που σχετίζεται με την ποσοτικοποίηση της πληροφορίας και οφείλεται κυρίως σε μη-ακριβή (imprecise) δεδομένα. "Ο Νίκος είναι ψηλός Το πρόβλημα οφείλεται στην αντίληψη που έχει
Ασάφεια (Fuzziness) Έννοια που σχετίζεται με την ποσοτικοποίηση της πληροφορίας και οφείλεται κυρίως σε μη-ακριβή (imprecise) δεδομένα. "Ο Νίκος είναι ψηλός Το πρόβλημα οφείλεται στην αντίληψη που έχει
ΕΝΟΤΗΤΑ III ΒΑΣΙΚΕΣ ΜΕΘΟ ΟΙ ΑΝΑΛΥΣΗΣ
 ΕΝΟΤΗΤΑ III ΒΑΣΙΚΕΣ ΜΕΘΟ ΟΙ ΑΝΑΛΥΣΗΣ Βασικός τελικός στόχος κάθε επιστηµονικής τεχνολογικής εφαρµογής είναι: H γενική βελτίωση της ποιότητας του περιβάλλοντος Η βελτίωση της ποιότητας ζωής Τα µέσα µε τα
ΕΝΟΤΗΤΑ III ΒΑΣΙΚΕΣ ΜΕΘΟ ΟΙ ΑΝΑΛΥΣΗΣ Βασικός τελικός στόχος κάθε επιστηµονικής τεχνολογικής εφαρµογής είναι: H γενική βελτίωση της ποιότητας του περιβάλλοντος Η βελτίωση της ποιότητας ζωής Τα µέσα µε τα
Θέματα Προγραμματισμού Η/Υ
 Πρόγραμμα Μεταπτυχιακών Σπουδών Πληροφορική και Υπολογιστική Βιοϊατρική Θέματα Προγραμματισμού Η/Υ Ενότητα 1: Εισαγωγή Θεματική Ενότητα: Εισαγωγή στον Προγραμματισμό ΘΕΜΑΤΑ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Η/Υ Θεματική
Πρόγραμμα Μεταπτυχιακών Σπουδών Πληροφορική και Υπολογιστική Βιοϊατρική Θέματα Προγραμματισμού Η/Υ Ενότητα 1: Εισαγωγή Θεματική Ενότητα: Εισαγωγή στον Προγραμματισμό ΘΕΜΑΤΑ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Η/Υ Θεματική
Αριθμητική εύρεση ριζών μη γραμμικών εξισώσεων
 Αριθμητική εύρεση ριζών μη γραμμικών εξισώσεων Με τον όρο μη γραμμικές εξισώσεις εννοούμε εξισώσεις της μορφής: f( ) 0 που προέρχονται από συναρτήσεις f () που είναι μη γραμμικές ως προς. Περιέχουν δηλαδή
Αριθμητική εύρεση ριζών μη γραμμικών εξισώσεων Με τον όρο μη γραμμικές εξισώσεις εννοούμε εξισώσεις της μορφής: f( ) 0 που προέρχονται από συναρτήσεις f () που είναι μη γραμμικές ως προς. Περιέχουν δηλαδή
ΠΟΛΥΚΡΙΤΗΡΙΑ ΥΠΟΣΤΗΡΙΞΗ ΑΠΟΦΑΣΕΩΝ. Χάρης ούκας, Πάνος Ξυδώνας, Ιωάννης Ψαρράς
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών Και Μηχανικών Υπολογιστών ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΩΝ ΒΙΟΜΗΧΑΝΙΚΩΝ ΙΑΤΑΞΕΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΑΠΟΦΑΣΕΩΝ Εργαστήριο Συστημάτων Αποφάσεων και ιοίκησης ΠΟΛΥΚΡΙΤΗΡΙΑ
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών Και Μηχανικών Υπολογιστών ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΩΝ ΒΙΟΜΗΧΑΝΙΚΩΝ ΙΑΤΑΞΕΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΑΠΟΦΑΣΕΩΝ Εργαστήριο Συστημάτων Αποφάσεων και ιοίκησης ΠΟΛΥΚΡΙΤΗΡΙΑ
