Some Useful Distributions
|
|
|
- Βασιλική Λούλης
- 6 χρόνια πριν
- Προβολές:
Transcript
1 Chapter 10 Some Useful Distributions Definition 101 The population median is any value MED(Y ) such that P (Y MED(Y )) 05 andp (Y MED(Y )) 05 (101) Definition 10 The population median absolute deviation is MAD(Y )=MED( Y MED(Y ) ) (10) Definition 103 The gamma function Γ(x) = t x 1 e t dt for x>0 0 Some properties of the gamma function follow i) Γ(k) =(k 1)! for integer k 1 ii) Γ(x +1)=x Γ(x) forx>0 iii) Γ(x) =(x 1) Γ(x 1) for x>1 iv) Γ(05) = π 1
2 101 The Beta Distribution If Y has a beta distribution, Y beta(δ, ν), then the probability density function (pdf) of Y is f(y) = where δ>0, ν>0and0 y 1 VAR(Y )= Γ(δ + ν) Γ(δ)Γ(ν) yδ 1 (1 y) ν 1 E(Y )= δ δ + ν δν (δ + ν) (δ + ν +1) Γ(δ + ν) f(y) = Γ(δ)Γ(ν) I [0,1](y)exp[(δ 1) log(y)+(ν 1) log(1 y)] is a P REF Hence Θ = (0, ) (0, ), η 1 = δ 1, η = ν 1and Ω=( 1, ) ( 1, ) If δ =1,thenW = log(1 Y ) EXP(1/ν) Hence T n = log(1 Y i ) G(n, 1/ν) andifr> n then Tn r is the UMVUE of E(Tn)= r 1 Γ(r + n) ν r Γ(n) If ν =1,thenW = log(y ) EXP(1/δ) Hence T n = log(y i ) G(n, 1/δ) andandifr> n then Tn r is the UMVUE of E(Tn)= r 1 Γ(r + n) δ r Γ(n) 10 The Bernoulli and Binomial Distributions If Y has a binomial distribution, Y BIN(k,ρ), then the probability mass function (pmf) of Y is ( ) k f(y) =P (Y = y) = ρ y (1 ρ) k y y 13
3 for y =0, 1,,k where 0 <ρ<1 If ρ =0,P(Y =0)=1=(1 ρ) k while if ρ =1,P(Y = k) =1=ρ k The moment generating function m(t) =[(1 ρ)+ρe t ] k, and the characteristic function c(t) =[(1 ρ)+ρe it ] k E(Y )=kρ VAR(Y )=kρ(1 ρ) The Bernoulli (ρ) distribution is the binomial (k = 1,ρ) distribution The following normal approximation is often used when kρ(1 ρ) > 9 Hence Y N(kρ, kρ(1 ρ)) P (Y y) Φ ( ) y +05 kρ kρ(1 ρ) Also ( 1 1 P (Y = y) exp 1 ) (y kρ) kρ(1 ρ) π kρ(1 ρ) See Johnson, Kotz and Kemp (199, p 115) This approximation suggests that MED(Y ) kρ, andmad(y ) 0674 kρ(1 ρ) Hamza (1995) states that E(Y ) MED(Y ) max(ρ, 1 ρ) and shows that E(Y ) MED(Y ) log() If k is large and kρ small, then Y Poisson(kρ) If Y 1,, Y n are independent BIN(k i,ρ)then Y i BIN( k i,ρ) ( ) [ ] k f(y) = (1 ρ) k ρ exp log( y 1 ρ )y is a 1P REF in ρ if k is known Thus Θ = (0, 1), ( ) ρ η =log 1 ρ 14
4 and Ω = (, ) Assume that Y 1,, Y n are iid BIN(k, ρ), then T n = Y i BIN(nk,ρ) If k is known, then the likelihood L(ρ) =cρ yi (1 ρ) nk y i, and the log likelihood Hence log(l(ρ)) = d +log(ρ) y i +(nk y i )log(1 ρ) d dρ log(l(ρ)) = yi + nk y i ( 1) set =0, 1 ρ ρ or (1 ρ) y i = ρ(nk y i ), or y i = ρnk or ˆρ = Y i /(nk) d dρ log(l(ρ)) = yi ρ nk yi < 0 (1 ρ) if 0 < y i <nkhence kˆρ = Y is the UMVUE, MLE and MME of kρ if k is known 103 The Burr Distribution If Y has a Burr distribution, Y Burr(φ, λ), then the pdf of Y is φy φ 1 f(y) = 1 λ (1 + y φ ) 1 λ +1 where y, φ, and λ are all positive The cdf of Y is [ ] log(1 + y φ ) F (y)=1 exp =1 (1 + y φ ) 1/λ for y > 0 λ MED(Y )=[e λ log() 1] 1/φ See Patel, Kapadia and Owen (1976, p 195) W =log(1+y φ )isexp(λ) 15
5 f(y) = 1 [ 1 λ φyφ 1 1+y exp 1 ] φ λ log(1 + yφ ) I(y >0) is a one parameter exponential family if φ is known If Y 1,, Y n are iid Burr(λ, φ), then T n = log(1 + Y φ i ) G(n, λ) If φ is known, then the likelihood L(λ) =c 1 [ λ exp 1 ] log(1 + y φ n i λ ), log(1 + y φ i ) Hence and the log likelihood log(l(λ)) = d n log(λ) 1 λ d n log(1 + y φ log(l(λ)) = dλ λ + i ) λ or log(1 + y φ i )=nλ or set =0, log(1 + Y φ i ) ˆλ = n d dλ log(l(λ)) = n λ log(1 + y φ λ i ) λ=ˆλ = ṋ λ nˆλ ˆλ 3 = n ˆλ < 0 Thus ˆλ is the UMVUE and MLE of λ if φ is known If φ is known and r> n, thent r n is the UMVUE of E(Tn)=λ r r Γ(r + n) Γ(n) 104 The Cauchy Distribution If Y has a Cauchy distribution, Y C(µ, σ), then the pdf of Y is f(y) = σ π 1 σ +(y µ) = 1 πσ[1 + ( y µ σ ) ] 16
6 where y and µ are real numbers and σ>0 The cumulative distribution function (cdf) of Y is F (y) = 1 π [arctan(y µ σ )+π/] See Ferguson (1967, p 10) This family is a location scale family that is symmetric about µ The moments of Y do not exist, but the chf of Y is c(t) =exp(itµ t σ) MED(Y )=µ, the upper quartile = µ + σ, and the lower quartile = µ σ MAD(Y )=F 1 (3/4) MED(Y )=σ If Y 1,, Y n are independent C(µ i,σ i ), then n n a i Y i C( a i µ i, i=1 i=1 n a i σ i ) In particular, if Y 1,, Y n are iid C(µ, σ), then Y C(µ, σ) 105 The Chi Distribution If Y has a chi distribution (also called a p dimensional Rayleigh distribution), Y chi(p,σ), then the pdf of Y is i=1 f(y) = yp 1 e 1 σ y σ p p 1 Γ(p/) where y 0andσ, p > 0 This is a scale family if p is known E(Y )=σ 1+p Γ( ) Γ(p/) +p VAR(Y )=σ Γ( ) ( Γ( 1+p Γ(p/) ) ), Γ(p/) and r+p E(Y r )= r/ r Γ( σ ) Γ(p/) 17
7 for r> p The mode is at σ p 1forp 1 See Cohen and Whitten (1988, ch 10) Note that W = Y G(p/, σ ) If p =1, then Y has a half normal distribution, Y HN(0,σ ) If p =, then Y has a Rayleigh distribution, Y R(0,σ) If p =3, then Y has a Maxwell Boltzmann distribution (also known as a Boltzmann distribution or a Maxwell distribution), Y MB (0,σ) If p is an integer and Y chi(p, 1), then Y χ p Since f(y) = 1 p 1 Γ(p/)σ p I(y >0) exp[(p 1) log(y) 1 σ y ], this family appears to be a P REF Θ = (0, ) (0, ), η 1 = p 1, η = 1/(σ ), and Ω = ( 1, ) (, 0) If p is known then y p 1 f(y) = p 1 Γ(p/) I(y >0) 1 [ ] 1 σ exp p σ y appears to be a 1P REF If Y 1,, Y n are iid chi(p, σ), then If p is known, then the likelihood and the log likelihood Hence or y i = npσ or T n = Y i G(np/, σ ) L(σ )=c 1 1 exp[ σnp y σ i ], log(l(σ )) = d np log(σ ) 1 σ y i d d(σ ) log(σ )= np σ + 1 (σ ) y i set =0, ˆσ = Y i np 18
8 d d(σ ) log(l(σ )) = np y (σ ) i (σ ) 3 = np σ =ˆσ (ˆσ ) npˆσ (ˆσ ) 3 = np (ˆσ ) < 0 Thus ˆσ is the UMVUE and MLE of σ when p is known If p is known and r> np/, then T r n is the UMVUE of E(Tn)= r r σ r Γ(r + np/) Γ(np/) 106 The Chi square Distribution If Y has a chi square distribution, Y χ p, then the pdf of Y is f(y) = y p 1 e y p Γ( p ) where y 0andp is a positive integer The mgf of Y is ( ) p/ 1 m(t) = =(1 t) p/ 1 t for t<1/ The chf ( ) p/ 1 c(t) = 1 it E(Y )=p VAR(Y )=p Since Y is gamma G(ν = p/,λ=), E(Y r )= r Γ(r + p/),r> p/ Γ(p/) MED(Y ) p /3 See Pratt (1968, p 1470) for more terms in the expansion of MED(Y ) Empirically, p MAD(Y ) 1483 (1 9p ) p 19
9 There are several normal approximations for this distribution The Wilson Hilferty approximation is ( ) 1 Y 3 N(1 p 9p, 9p ) See Bowman and Shenton (199, p 6) This approximation gives and P (Y x) Φ[(( x p )1/3 1+/9p) 9p/], χ p,α p(z α 9p +1 9p )3 where z α is the standard normal percentile, α =Φ(z α ) The last approximation is good if p> 14 log(α) See Kennedy and Gentle (1980, p 118) This family is a one parameter exponential family, but is not a REF since the set of integers does not contain an open interval 107 The Double Exponential Distribution If Y has a double exponential distribution (or Laplace distribution), Y DE(θ, λ), then the pdf of Y is f(y) = 1 ( ) λ exp y θ λ where y is real and λ>0 The cdf of Y is ( ) y θ F (y) =05exp if y θ, λ and ( ) (y θ) F (y) =1 05exp if y θ λ This family is a location scale family which is symmetric about θ The mgf m(t) =exp(θt)/(1 λ t ) for t < 1/λ, and the chf c(t) =exp(θit)/(1 + λ t ) 0
10 E(Y )=θ, and MED(Y )=θ VAR(Y )=λ,and MAD(Y )=log()λ 0693λ Hence λ =MAD(Y )/ log() 1443MAD(Y ) To see that MAD(Y )=λlog(), note that F (θ + λ log()) = 1 05 = 075 The maximum likelihood estimators are ˆθ MLE =MED(n) and ˆλ MLE = 1 n Y i MED(n) n A 100(1 α)% confidence interval (CI) for λ is ( n i=1 Y i MED(n), ) n i=1 Y i MED(n), χ n 1,1 χ α n 1, α and a 100(1 α)% CI for θ is MED(n) ± z n 1 α/ i=1 Y i MED(n) n n z1 α/ i=1 where χ p,α and z α are the α percentiles of the χ p and standard normal distributions, respectively See Patel, Kapadia and Owen (1976, p 194) W = Y θ EXP(λ) f(y) = 1 [ ] 1 λ exp y θ λ is a one parameter exponential family in λ if θ is known If Y 1,, Y n are iid DE(θ, λ) then If θ is known, then the likelihood T n = Y i θ G(n, λ) L(λ) =c 1 [ 1 λ exp n λ and the log likelihood ] yi θ, log(l(λ)) = d n log(λ) 1 λ yi θ 1
11 Hence d n log(l(λ)) = dλ λ + 1 yi θ set =0 λ or y i θ = nλ or Yi θ ˆλ = n d dλ log(l(λ)) = n λ yi θ = ṋ λ 3 λ nˆλ = n ˆλ 3 ˆλ < 0 λ=ˆλ Thus ˆλ is the UMVUE and MLE of λ if θ is known 108 The Exponential Distribution If Y has an exponential distribution, Y EXP(λ), then the pdf of Y is where λ>0 The cdf of Y is f(y) = 1 λ exp ( y ) I(y 0) λ F (y) =1 exp( y/λ), y 0 This distribution is a scale family The mgf m(t) =1/(1 λt) for t<1/λ, and the chf c(t) =1/(1 iλt) E(Y )=λ, and VAR(Y )=λ W =λy χ Since Y is gamma G(ν =1,λ), E(Y r )=λγ(r +1)forr> 1 MED(Y )=log()λ and MAD(Y ) λ/0781 since it can be shown that exp(mad(y )/λ) =1+exp( MAD(Y )/λ)
12 Hence 0781 MAD(Y ) λ The classical estimator is ˆλ = Y n and the 100(1 α)% CI for E(Y )=λ is ( n i=1 Y i, ) n i=1 Y i χ n,1 χ α n, α where P (Y χ n, )=α/ ify is χ n See Patel, Kapadia and Owen (1976, α p 188) f(y) = 1 [ ] 1 λ I(y >0) exp λ y is a 1P REF Hence Θ = (0, ), η = 1/λ and Ω = (, 0) Suppose that Y 1,, Y n are iid EXP(λ), then T n = Y i G(n, λ) The likelihood and the log likelihood L(λ) = 1 λ n exp [ 1 λ yi ], log(l(λ)) = n log(λ) 1 λ yi Hence or y i = nλ or d n log(l(λ)) = dλ λ + 1 set yi =0, λ ˆλ = Y Since d dλ log(l(λ)) = n λ yi λ 3 λ=ˆλ = ṋ λ nˆλ ˆλ 3 = n ˆλ < 0, the ˆλ is the UMVUE, MLE and MME of λ If r> n, thentn r is the UMVUE of E(Tn r Γ(r + n) )=λr Γ(n) 3
13 109 The Two Parameter Exponential Distribution If Y has a parameter exponential distribution, Y EXP(θ, λ) then the pdf of Y is f(y) = 1 ( ) λ exp (y θ) I(y θ) λ where λ>0 The cdf of Y is F (y)=1 exp[ (y θ)/λ)], y θ This family is an asymmetric location-scale family The mgf m(t) =exp(tθ)/(1 λt) for t<1/λ, and the chf c(t) =exp(itθ)/(1 iλt) E(Y )=θ + λ, and VAR(Y )=λ MED(Y )=θ + λ log() and MAD(Y ) λ/0781 Hence θ MED(Y ) 0781 log()mad(y ) See Rousseeuw and Croux (1993) for similar results Note that 0781 log() 144 To see that 0781MAD(Y ) λ, note that 05 = θ+λ log()+mad θ+λ log() MAD 1 exp( (y θ)/λ)dy λ =05[ e MAD/λ + e MAD/λ ] assuming λ log() > MAD Plug in MAD = λ/0781 to get the result If θ is known, then f(y) =I(y θ) 1 [ ] 1 λ exp (y θ) λ 4
14 is a 1P REF in λ Y θ EXP(λ) Let ˆλ = (Yi θ) n Then ˆλ is the UMVUE and MLE of λ if θ is known If Y 1,, Y n are iid EXP(θ, λ), then the likelihood L(θ, λ) = 1 [ 1 λ exp ] (yi θ) I(y n (1) θ), λ and the log likelihood log(l(λ)) = [ n log(λ) 1 λ (yi θ)]i(y (1) θ) For any fixed λ>0, the log likelihood is maximized by maximizing θ Hence ˆθ = Y (1), and the profile log likelihood is log(l(λ y (1) )) = n log(λ) 1 λ (yi y (1) ) is maximized by ˆλ = 1 n n i=1 (y i y (1) ) Hence the MLE ( (ˆθ, ˆλ) = Y (1), 1 n ) n (Y i Y (1) ) =(Y (1), Y Y (1) ) i= The F Distribution If Y has an F distribution, Y F (ν 1,ν ), then the pdf of Y is f(y) = Γ( ν 1+ν ) Γ(ν 1 /)Γ(ν /) ( ) ν1 / ν1 where y>0andν 1 and ν are positive integers ν y (ν 1 )/ ) (ν1 +ν )/ ( 1+( ν 1 ν )y and E(Y )= ν ν, ν > 5
15 ( ) ν (ν 1 + ν ) VAR(Y )= ν ν 1 (ν 4), ν > 4 E(Y r )= Γ( ν 1+r )Γ( ν ( ) r ) r ν, r < ν / Γ(ν 1 /)Γ(ν /) ν 1 Suppose that X 1 and X are independent where X 1 χ ν 1 and X χ ν Then W = (X 1/ν 1 ) (X /ν ) F (ν 1,ν ) If W t ν,theny = W F (1,ν) 1011 The Gamma Distribution If Y has a gamma distribution, Y G(ν, λ), then the pdf of Y is f(y) = yν 1 e y/λ λ ν Γ(ν) where ν, λ, and y are positive The mgf of Y is ( ) ν 1/λ m(t) = 1 t = λ for t<1/λ The chf c(t) = ( ) ν 1 1 iλt ( 1 ) ν 1 λt E(Y )=νλ VAR(Y )=νλ E(Y r )= λr Γ(r + ν) if r> ν (103) Γ(ν) Chen and Rubin (1986) show that λ(ν 1/3) < MED(Y ) <λν= E(Y ) Empirically, for ν>3/, MED(Y ) λ(ν 1/3), and MAD(Y ) λ ν
16 This family is a scale family for fixed ν, soify is G(ν, λ) thency is G(ν, cλ) for c>0 If W is EXP(λ) thenw is G(1,λ) If W is χ p, then W is G(p/, ) Some classical estimates are given next Let [ w =log y n geometric mean(n) where geometric mean(n) =(y 1 y y n ) 1/n Then Thom s estimate (Johnson and Kotz 1970a, p 188) is ˆν 05( w/3 ) w Also w w ˆν MLE w for 0 <w 0577, and ] ˆν MLE w w w( w + w ) for 0577 <w 17 If W>17then estimation is much more difficult, but a rough approximation is ˆν 1/w for w>17 See Bowman and Shenton (1988, p 46) and Greenwood and Durand (1960) Finally, ˆλ = Y n /ˆν Notice that ˆβ may not be very good if ˆν <1/17 Several normal approximations are available The Wilson Hilferty approximation says that for ν>05, Y 1/3 N Hence if Y is G(ν, λ) and ( (νλ) 1/3 (1 1 1 ), (νλ)/3 9ν 9ν α = P [Y G α ], ) then [ 1 G α νλ z α 9ν ν ] 3 where z α is the standard normal percentile, α =Φ(z α ) Bowman and Shenton (1988, p 101) include higher order terms 7
17 f(y) = [ ] 1 1 I(y >0) exp y +(ν 1) log(y) λ ν Γ(ν) λ is a P REF Hence Θ = (0, ) (0, ), η 1 = 1/λ, η = ν 1and Ω=(, 0) ( 1, ) If Y 1,, Y n are independent G(ν i,λ)then Y i G( ν i,λ) If Y 1,, Y n are iid G(ν, λ), then T n = Y i G(nν, λ) Since f(y) = 1 Γ(ν) exp[(ν 1) log(y)]i(y >0) 1 [ ] 1 λ exp ν λ y, Y is a 1P REF when ν is known If ν is known, then the likelihood [ 1 1 L(β) =c exp λnν λ The log likelihood yi ] log(l(λ)) = d nν log(λ) 1 λ yi Hence or y i = nνλ or d nν log(l(λ)) = dλ λ + yi λ ˆλ = Y/ν set =0, d nν log(l(λ)) = dλ λ yi λ 3 λ=ˆλ = nν ˆλ nνˆλ ˆλ 3 Thus Y is the UMVUE, MLE and MME of νλ if ν is known = nν ˆλ < 0 8
18 101 The Generalized Gamma Distribution If Y has a generalized gamma distribution, Y GG(ν, λ, φ), then the pdf of Y is f(y) = φyφν 1 λ φν Γ(ν) exp( yφ /λ φ ) where ν, λ, φ and y are positive This family is a scale family with scale parameter λ if φ and ν are known E(Y r )= λr Γ(ν)+ 1 φ Γ(ν) if r> φν (104) If φ and ν are known, then f(y) = φyφν 1 Γ(ν) [ ] 1 1 I(y >0) exp λφν λ φ yφ, which is a one parameter exponential family W = Y φ G(ν, λ φ ) If Y 1,, Y n are iid GG((ν, λ, φ) where φ and ν are known, then T n = n i=1 Y φ i G(nν, λ φ ), and Tn r is the UMVUE of E(Tn)=λ r φr Γ(r + nν) Γ(nν) for r> nν 1013 The Generalized Negative Binomial Distribution If Y has a generalized negative binomial distribution, Y GNB(µ, κ), then the pmf of Y is ( ) κ ( Γ(y + κ) κ f(y) =P (Y = y) = 1 κ ) y Γ(κ)Γ(y +1) µ + κ µ + κ for y =0, 1,, where µ>0andκ>0 This distribution is a generalization of the negative binomial (κ, ρ) distribution with ρ = κ/(µ + κ) andκ>0is an unknown real parameter rather than a known integer 9
19 The mgf is [ κ m(t) = κ + µ(1 e t ) for t< log(µ/(µ + κ)) E(Y )=µ and VAR(Y )=µ + µ /κ If Y 1,, Y n are iid GNB(µ, κ), then n i=1 Y i GNB(nµ, nκ) When κ is known, this distribution is a 1P REF IfY 1,, Y n are iid GNB(µ, κ) whereκ is known, then ˆµ = Y is the MLE, UMVUE and MME of µ 1014 The Geometric Distribution If Y has a geometric distribution, Y geom(ρ) then the pmf of Y is ] κ f(y) =P (Y = y) =ρ(1 ρ) y for y =0, 1,, and 0 <ρ<1 The cdf for Y is F (y) =1 (1 ρ) y+1 for y 0andF (y)=0fory<0 Here y is the greatest integer function, eg, 77 =7 E(Y )=(1 ρ)/ρ VAR(Y )=(1 ρ)/ρ Y NB(1,ρ) Hence the mgf of Y is for t< log(1 ρ) m(t) = ρ 1 (1 ρ)e t f(y) = ρ exp[log(1 ρ)y] is a 1P REF Hence Θ = (0, 1), η =log(1 ρ) andω=(, 0) If Y 1,, Y n are iid geom(ρ), then T n = Y i NB(n,ρ) The likelihood L(ρ) =ρ n exp[log(1 ρ) y i ], 30
20 and the log likelihood log(l(ρ)) = n log(ρ)+log(1 ρ) y i Hence d dρ log(l(ρ)) = n ρ 1 set yi =0 1 ρ or n(1 ρ)/ρ = y i or n nρ ρ y i =0or ˆρ = n n + Y i d n log(l(ρ)) = dρ ρ yi (1 ρ) < 0 Thus ˆρ is the MLE of ρ The UMVUE, MLE and MME of (1 ρ)/ρ is Y 1015 The Half Cauchy Distribution If Y has a half Cauchy distribution, Y HC(µ, σ), then the pdf of Y is f(y) = πσ[1 + ( y µ σ ) ] where y µ, µ is a real number and σ>0 The cdf of Y is F (y) = π arctan(y µ σ ) for y µ and is 0, otherwise This distribution is a right skewed locationscale family MED(Y )=µ + σ MAD(Y )=07305σ 1016 The Half Logistic Distribution If Y has a half logistic distribution, Y HL(µ, σ), then the pdf of y is f(y) = exp( (y µ)/σ) σ[1 + exp ( (y µ)/σ)] 31
21 where σ>0, y µ and µ are real The cdf of Y is F (y) = exp[(y µ)/σ] 1 1+exp[(y µ)/σ)] for y µ and 0 otherwise This family is a right skewed location scale family MED(Y )=µ +log(3)σ MAD(Y )=067346σ 1017 The Half Normal Distribution If Y has a half normal distribution, Y HN(µ, σ ), then the pdf of Y is f(y) = (y µ) exp ( ) πσ σ where σ>0andy µ and µ is real Let Φ(y) denote the standard normal cdf Then the cdf of Y is F (y) =Φ( y µ σ ) 1 for y > µ and F (y) = 0, otherwise E(Y )=µ + σ /π µ σ VAR(Y )= σ (π ) σ π This is an asymmetric location scale family that has the same distribution as µ + σ Z where Z N(0, 1) Note that Z χ 1 Hence the formula for the rth moment of the χ 1 random variable can be used to find the moments of Y MED(Y )=µ σ MAD(Y )= σ f(y) = [ I(y >µ)exp πσ ( 1 )(y µ) σ is a 1P REF if µ is known Hence Θ = (0, ), η= 1/(σ )andω= (, 0) 3 ]
22 W =(Y µ) G(1/, σ ) If Y 1,, Y n are iid HN(µ, σ ), then T n = (Y i µ) G(n/, σ ) If µ is known, then the likelihood L(σ )=c 1 [ σ exp ( 1 n σ ) ] (y i µ), and the log likelihood Hence log(l(σ )) = d n log(σ ) 1 σ (yi µ) d d(σ ) log(l(σ )) = or (y i µ) = nσ or n (σ ) + 1 (σ ) (yi µ) set =0, ˆσ = 1 n (Yi µ) d d(σ ) log(l(σ )) = n (σ ) (yi µ) ) (σ ) 3 = n σ =ˆσ (ˆσ ) nˆσ ( ˆσ ) 3 = n ˆσ < 0 Thus ˆσ is the UMVUE and MLE of σ if µ is known If r> n/ andifµ is known, then Tn r is the UMVUE of E(T r n)= r σ r Γ(r + n/)/γ(n/) 1018 The Hypergeometric Distribution If Y has a hypergeometric distribution, Y HG(C, N C, n), then the data set contains N objects of two types There are C objects of the first type (that you wish to count) and N C objects of the second type Suppose that n objects are selected at random without replacement from the N objects 33
23 Then Y counts the number of the n selected objects that were of the first type The pmf of Y is ( C N C ) y)( f(y) =P (Y = y) = n y ( N n) where the integer y satisfies max(0,n N + C) y min(n, C) The right inequality is true since if n objects are selected, then the number of objects of the first type must be less than or equal to both n and C The first inequality holds since n Y counts the number of objects of second type Hence n Y N C Let p = C/N Then E(Y )= nc N = np and VAR(Y )= nc(n C) N n N N 1 = np(1 p)n n N 1 If n is small compared to both C and N C then Y BIN(n, p) If n is large but n is small compared to both C and N C then Y N(np, np(1 p)) 1019 The Inverse Gaussian Distribution If Y has an inverse Gaussian distribution, Y IG(θ, λ), then the pdf of Y is [ ] λ λ(y θ) f(y) = πy exp 3 θ y where y, θ, λ > 0 The mgf is m(t) =exp [ ( )] λ 1 1 θ t θ λ for t < λ/(θ ) See Datta (005) and Schwarz and Samanta (1991) for additional properties The chf is [ ( )] λ φ(t) =exp 1 1 θ it θ λ 34
24 E(Y )=θ and f(y) = VAR(Y )= θ3 λ is a two parameter exponential family If Y 1,, Y n are iid IG(θ, λ), then [ λ 1 λ π eλ/θ I(y >0) exp y3 θ y λ ] 1 y n Y i IG(nθ, n λ) and Y IG(θ, nλ) i=1 If λ is known, then the likelihood and the log likelihood L(θ) =ce nλ/θ exp[ λ θ yi ], Hence or y i = nθ or log(l(θ)) = d + nλ θ λ θ yi d nλ log(l(θ)) = + λ set yi =0, dθ θ θ 3 ˆθ = Y d nλ log(l(θ)) = dθ θ 3 3λ yi θ 4 θ=ˆθ = nλ ˆθ 3 3nλˆθ ˆθ 4 = nλ ˆθ 3 < 0 Thus Y is the UMVUE, MLE and MME of θ if λ is known If θ is known, then the likelihood [ λ ] L(λ) =cλ n/ (yi θ) exp, θ y i 35
25 and the log likelihood Hence or log(l(λ)) = d + n log(λ) λ θ (yi θ) y i d dλ log(l(λ)) = n λ 1 θ (yi θ) y i ˆλ = nθ (yi θ) y i d n log(l(λ)) = dλ λ < 0 Thus ˆλ is the MLE of λ if θ is known set =0 Another parameterization of the inverse Gaussian distribution takes θ = λ/ψ so that f(y) = [ λ π e λψ 1 ψ I[y >0] exp y3 y λ ] 1, y where λ>0andψ 0 HereΘ=(0, ) [0, ), η 1 = ψ/, η = λ/ and Ω=(, 0] (, 0) Since Ω is not an open set, this is a parameter full exponential family that is not regular If ψ is known then Y is a 1P REF, but if λ is known the Y is a one parameter full exponential family When ψ = 0,Y has a one sided stable distribution with index 1/ See Barndorff Nielsen (1978, p 117) 100 The Inverted Gamma Distribution If Y has an inverted gamma distribution, Y INVG(ν, λ), then the pdf of Y is 1 f(y) = y ν+1 Γ(ν) I(y >0) 1 ( ) 1 λ exp 1 ν λ y where λ, ν and y are all positive It can be shown that W =1/Y G(ν, λ) This family is a scale family with scale parameter τ =1/λ if ν is known 36
26 If ν is known, this family is a 1 parameter exponential family If Y 1,, Y n are iid INVG(ν, λ) andν is known, then T n = n 1 i=1 Y i G(nν, λ) andtn r is the UMVUE of r Γ(r + nν) λ Γ(nν) for r> nν 101 The Largest Extreme Value Distribution If Y has a largest extreme value distribution (or Gumbel distribution), Y LEV (θ, σ), then the pdf of Y is f(y) = 1 σ exp( (y θ θ )) exp[ exp( (y σ σ ))] where y and θ are real and σ>0 The cdf of Y is F (y)=exp[ exp( ( y θ σ ))] This family is an asymmetric location scale family with a mode at θ The mgf m(t) =exp(tθ)γ(1 σt) for t < 1/σ E(Y ) θ σ, and VAR(Y )=σ π / σ and MED(Y )=θ σ log(log()) θ σ MAD(Y ) σ W =exp( (Y θ)/σ) EXP(1) f(y) = 1 σ eθ/σ e y/σ exp [ e θ/σ e y/σ] is a one parameter exponential family in θ if σ is known 37
27 If Y 1,, Y n are iid LEV(θ, σ)where σ is known, then the likelihood and the log likelihood L(σ) =ce nθ/σ exp[ e θ/σ e y i/σ ], Hence or or or log(l(θ)) = d + nθ σ eθ/σ e y i/σ d dθ log(l(θ)) = n σ 1 eθ/σ e y i /σ set =0, σ e θ/σ e y i/σ = n, e θ/σ = n e y i /σ, ( ) n ˆθ =log e Y i /σ Since d 1 log(l(θ)) = dθ σ eθ/σ e yi/σ < 0, ˆθ is the MLE of θ 10 The Logarithmic Distribution If Y has a logarithmic distribution, then the pmf of Y is f(y) =P (Y = y) = 1 θ y log(1 θ) y for y =1,, and 0 <θ<1 The mgf m(t) = log(1 θet ) log(1 θ) for t< log(θ) E(Y )= 1 θ log(1 θ) 1 θ 38
28 1 1 f(y) = log(1 θ) y exp(log(θ)y) is a 1P REF Hence Θ = (0, 1), η=log(θ) andω=(, 0) If Y 1,, Y n are iid logarithmic (θ), then Y is the UMVUE of E(Y ) 103 The Logistic Distribution If Y has a logistic distribution, Y L(µ, σ), then the pdf of y is f(y) = where σ>0andy and µ are real The cdf of Y is F (y) = exp ( (y µ)/σ) σ[1 + exp ( (y µ)/σ)] 1 1+exp( (y µ)/σ) = exp ((y µ)/σ) 1+exp((y µ)/σ) This family is a symmetric location scale family The mgf of Y is m(t) =πσte µt csc(πσt) for t < 1/σ, and the chf is c(t) =πiσte iµt csc(πiσt) wherecsc(t) is the cosecant of t E(Y )=µ, and MED(Y )=µ VAR(Y )=σ π /3, and MAD(Y )=log(3)σ σ Hence σ =MAD(Y )/ log(3) The estimators ˆµ = Y n and S = 1 n n 1 i=1 (Y i Y n ) are sometimes used Note that if q = F L(0,1) (c) = ec q then c =log( 1+e c 1 q ) Taking q = 9995 gives c = log(1999) 76 To see that MAD(Y )=log(3)σ, notethatf (µ +log(3)σ) =075, F (µ log(3)σ) =05, and 075 = exp (log(3))/(1 + exp(log(3))) 39
29 104 The Log-Cauchy Distribution If Y has a log Cauchy distribution, Y LC(µ, σ), then the pdf of Y is f(y) = 1 πσy[1 + ( log(y) µ σ ) ] where y>0, σ>0andµ is a real number This family is a scale family with scale parameter τ = e µ if σ is known It can be shown that W =log(y ) has a Cauchy(µ, σ) distribution 105 The Log-Logistic Distribution If Y has a log logistic distribution, Y LL(φ, τ), then the pdf of Y is f(y) = φτ(φy)τ 1 [1 + (φy) τ ] where y>0, φ>0andτ>0 The cdf of Y is F (y)=1 1 1+(φy) τ for y>0 This family is a scale family with scale parameter σ = φ 1 if τ is known MED(Y )=1/φ It can be shown that W =log(y ) has a logistic(µ = log(φ),σ =1/τ) distribution Hence φ = e µ and τ =1/σ Kalbfleisch and Prentice (1980, p 7-8) suggest that the log-logistic distribution is a competitor of the lognormal distribution 106 The Lognormal Distribution If Y has a lognormal distribution, Y LN(µ, σ ), then the pdf of Y is ( ) 1 (log(y) µ) f(y) = y πσ exp σ 40
30 where y>0andσ>0andµ is real The cdf of Y is ( ) log(y) µ F (y) =Φ for y>0 σ where Φ(y) is the standard normal N(0,1) cdf This family is a scale family with scale parameter τ = e µ if σ is known and E(Y )=exp(µ + σ /) VAR(Y )=exp(σ )(exp(σ ) 1) exp(µ) For any r, E(Y r )=exp(rµ + r σ /) MED(Y )=exp(µ) and exp(µ)[1 exp( 06744σ)] MAD(Y ) exp(µ)[1 + exp(06744σ)] f(y) = 1 [ 1 1 π σ exp( µ σ )1 I(y 0) exp y σ (log(y)) + µ ] σ log(y) is a P REF Hence Θ = (, ) (0, ), η 1 = 1/(σ ),η = µ/σ and Ω=(, 0) (, ) Note that W =log(y ) N(µ, σ ) f(y) = 1 π 1 σ [ ] 1 1 I(y 0) exp (log(y) µ) y σ is a 1P REF if µ is known, If Y 1,, Y n are iid LN(µ, σ )whereµ is known, then the likelihood L(σ )=c 1 [ 1 σ exp ] (log(yi ) µ), n σ and the log likelihood log(l(σ )) = d n log(σ ) 1 (log(yi ) µ) σ Hence d d(σ ) log(l(σ )) = n σ + 1 (log(yi ) µ) set =0, (σ ) 41
31 or (log(y i ) µ) = nσ or Since ˆσ = d (log(yi ) µ) n d(σ ) log(l(σ )) = n (σ ) (log(yi ) µ) (σ ) 3 = n σ =ˆσ (ˆσ ) nˆσ (ˆσ ) 3 = n (ˆσ ) < 0, ˆσ is the UMVUE and MLE of σ if µ is known Since T n = [log(y i ) µ] G(n/, σ ), if µ is known and r> n/ then Tn r is UMVUE of E(T r n )=r σ r Γ(r + n/) Γ(n/) If σ is known, f(y) = [ I(y 0) exp( π σ y σ (log(y)) )exp( µ µ ] σ )exp σ log(y) is a 1P REF If Y 1,, Y n are iid LN(µ, σ ), where σ is known, then the likelihood [ L(µ) =c exp( nµ µ σ )exp ] log(yi ), σ and the log likelihood log(l(µ)) = d nµ σ + µ σ log(yi ) Hence d nµ log(yi ) set log(l(µ)) = + =0, dµ σ σ or log(y i )=nµ or log(yi ) ˆµ = n Note that d n log(l(µ)) = dµ σ < 0 4
32 Since T n = log(y i ) N(nµ, nσ ), ˆµ is the UMVUE and MLE of µ if σ is known When neither µ nor σ are known, the log likelihood log(l(σ )) = d n log(σ ) 1 (log(yi ) µ) σ Let w i =log(y i ) then the log likelihood is log(l(σ )) = d n log(σ ) 1 (wi µ), σ which is equivalent to the normal N(µ, σ ) log likelihood Hence the MLE (ˆµ, ˆσ) = 1 n W i, 1 n (W i W ) n n i=1 Hence inference for µ and σ is simple Use the fact that W i =log(y i ) N(µ, σ ) and then perform the corresponding normal based inference on the W i For example, a the classical (1 α)100% CI for µ when σ is unknown is S W S W (W n t n 1,1 α, W n + t n 1,1 α ) n n where S W = i=1 n n 1 ˆσ = 1 n 1 n (W i W ), and P (t t n 1,1 α )=1 α/ whent is from a t distribution with n 1 degrees of freedom Compare Meeker and Escobar (1998, p 175) 107 The Maxwell-Boltzmann Distribution If Y has a Maxwell Boltzmann distribution, Y MB(µ, σ), then the pdf of Y is (y µ) e 1 σ f(y) = (y µ) σ 3 π where µ is real, y µ and σ>0 This is a location scale family i=1 E(Y )=µ + σ 1 Γ(3/) 43
33 [ Γ( 5 VAR(Y )=σ ) ( ) ] 1 Γ(3/) Γ(3/) MED(Y )= µ σ and MAD(Y )= σ This distribution a one parameter exponential family when µ is known Note that W =(Y µ) G(3/, σ ) If Z MB(0,σ), then Z chi(p = 3,σ), and for r> 3 The mode of Z is at σ r+3 E(Z r )= r/ r Γ( σ ) Γ(3/) 108 The Negative Binomial Distribution If Y has a negative binomial distribution (also called the Pascal distribution), Y NB(r,ρ), then the pmf of Y is ( ) r + y 1 f(y) =P (Y = y) = ρ r (1 ρ) y y for y =0, 1, where 0 <ρ<1 The moment generating function for t< log(1 ρ) E(Y )=r(1 ρ)/ρ, and [ m(t) = ρ 1 (1 ρ)e t ] r VAR(Y )= r(1 ρ) ρ ( ) r + y 1 f(y) =ρ r exp[log(1 ρ)y] y is a 1P REF in ρ for known r Ω=(, 0) Thus Θ = (0, 1), η= log(1 ρ) and 44
34 If Y 1,, Y n are independent NB(r i,ρ), then Yi NB( r i,ρ) If Y 1,, Y n are iid NB(r, ρ), then If r is known, then the likelihood and the log likelihood Hence or or nr ρnr ρ y i =0or T n = Y i NB(nr, ρ) L(p) =cρ nr exp[log(1 ρ) y i ], log(l(ρ)) = d + nr log(ρ)+log(1 ρ) y i d nr log(l(ρ)) = dρ ρ 1 set yi =0, 1 ρ 1 ρ ρ nr = y i, ˆρ = nr nr + Y i d nr 1 log(l(ρ)) = yi < 0 dρ ρ (1 ρ) Thus ˆρ is the MLE of p if r is known Y is the UMVUE, MLE and MME of r(1 ρ)/ρ if r is known 109 The Normal Distribution If Y has a normal distribution (or Gaussian distribution), Y N(µ, σ ), then the pdf of Y is ( ) 1 (y µ) f(y) = exp πσ σ 45
35 where σ>0andµ and y are real Let Φ(y) denote the standard normal cdf Recall that Φ(y) = 1 Φ( y) The cdf F (y) ofy does not have a closed form, but ( ) y µ F (y) =Φ, σ and Φ(y) 05(1 + 1 exp( y /π) ) for y 0 See Johnson and Kotz (1970a, p 57) The moment generating function is m(t) =exp(tµ + t σ /) The characteristic function is c(t) =exp(itµ t σ /) E(Y )=µ and VAR(Y )=σ E[ Y µ r ]=σ r r/ Γ((r +1)/) π for r> 1 If k is an integer, then E(Y k )=(k 1)σ E(Y k )+µe(y k 1 ) See Stein (1981) and Casella and Berger (1990, p 187) MED(Y )=µ and MAD(Y )=Φ 1 (075)σ 06745σ Hence σ =[Φ 1 (075)] 1 MAD(Y ) 1483MAD(Y ) This family is a location scale family which is symmetric about µ Suggested estimators are Y n =ˆµ = 1 n n i=1 Y i and S = S Y = 1 n 1 n (Y i Y n ) i=1 The classical (1 α)100% CI for µ when σ is unknown is S Y S Y (Y n t n 1,1 α, Y n + t n 1,1 α ) n n 46
36 where P (t t n 1,1 α )=1 α/ whent is from a t distribution with n 1 degrees of freedom If α =Φ(z α ), then z α m c o + c 1 m + c m 1+d 1 m + d m + d 3 m 3 where m =[ log(1 α)] 1/, c 0 =515517, c 1 =080853, c =001038, d 1 =143788, d =018969, d 3 = , and 05 α For 0 <α<05, z α = z 1 α See Kennedy and Gentle (1980, p 95) To see that MAD(Y )=Φ 1 (075)σ, note that 3/4 =F (µ +MAD)sinceY is symmetric about µ However, ( ) y µ F (y) =Φ σ and ( ) 3 µ +Φ 1 4 =Φ (3/4)σ µ σ So µ +MAD=µ +Φ 1 (3/4)σ Cancel µ from both sides to get the result [ 1 1 f(y) = πσ exp( µ σ )exp σ y + µ ] σ y is a P REF Hence Θ = (0, ) (, ), η 1 = 1/(σ ),η = µ/σ and Ω=(, 0) (, ) If σ is known, [ ] 1 1 [ f(y) = exp πσ σ y exp( µ µ ] σ )exp σ y is a 1P REF Also the likelihood L(µ) =c exp( nµ σ )exp [ µ σ yi ] 47
37 and the log likelihood Hence or nµ = y i,or log(l(µ)) = d nµ σ + µ σ yi d nµ yi log(l(µ)) = + dµ σ σ ˆµ = Y set =0, Since d n log(l(µ)) = dµ σ < 0 and since T n = Y i N(nµ, nσ ), Y is the UMVUE, MLE and MME of µ if σ is known If µ is known, [ ] 1 1 f(y) = exp (y µ) πσ σ is a 1P REF Also the likelihood L(σ )=c 1 [ 1 σ exp ] (yi µ) n σ and the log likelihood log(l(σ )) = d n log(σ ) 1 σ (yi µ) Hence d dµ log(l(σ )) = n σ + 1 (yi µ) set =0, (σ ) or nσ = (y i µ),or ˆσ (Yi µ) = n Note that d dµ log(l(σ )) = n (σ ) (yi µ) (σ ) 3 = n σ =ˆσ (ˆσ ) nˆσ (ˆσ ) 3 48
38 = n (ˆσ ) < 0 Since T n = (Y i µ) G(n/, σ ), ˆσ is the UMVUE and MLE of σ if µ is known Note that if µ is known and r> n/, then Tn r is the UMVUE of E(T r n)= r σ r Γ(r + n/) Γ(n/) 1030 The One Sided Stable Distribution If Y has a one sided stable distribution (with index 1/), Y OSS(σ), then the pdf of Y is ( ) 1 σ 1 f(y) = σ exp πy 3 y for y>0andσ>0 This distribution is a scale family with scale parameter σ and a 1P REF Whenσ =1,Y INVG(ν =1/,λ =)where INVG stands for inverted gamma This family is a special case of the inverse Gaussian IG distribution It can be shown that W = 1/Y G(1/, /σ) This distribution is even more outlier prone than the Cauchy distribution See Feller (1971, p 5) and Lehmann (1999, p 76) For applications see Besbeas and Morgan (004) 1 Y i G(n/, /σ) Hence If Y 1,, Y n are iid OSS(σ) thent n = n i=1 T n /n is the UMVUE (and MLE) of 1/σ and Tn r is the UMVUE of for r> n/ 1 r Γ(r + n/) σ r Γ(n/) 1031 The Pareto Distribution If Y has a Pareto distribution, Y PAR(σ, λ), then the pdf of Y is f(y) = 1 λ σ1/λ y 1+1/λ 49
39 where y σ, σ > 0, and λ>0 ThemodeisatY = σ The cdf of Y is F (y) =1 (σ/y) 1/λ for y>µ This family is a scale family when λ is fixed for λ<1 E(Y )= σ 1 λ E(Y r )= σr for r<1/λ 1 rλ MED(Y )=σ λ X =log(y/σ)isexp(λ) andw =log(y )isexp(θ =log(σ),λ) f(y) = 1 λ σ1/λ I[y σ]exp [ (1 + 1λ ] )log(y) = 1 1 I[y σ]exp [ (1 + 1λ ] σ λ )log(y/σ) is a one parameter exponential family if σ is known If Y 1,, Y n are iid PAR(σ, λ) then T n = log(y i /σ) G(n, λ) If σ is known, then the likelihood L(λ) =c 1 [ (1 λ exp + 1 n λ ) ] log(y i /σ), and the log likelihood log(l(λ)) = d n log(λ) (1 + 1 λ ) log(y i /σ) Hence d n log(l(λ)) = dλ λ + 1 log(yi /σ) set =0, λ or log(y i /σ) =nλ or log(yi /σ) ˆλ = n 50
40 d dλ log(l(λ)) = n λ log(yi /σ) λ 3 = λ=ˆλ n ˆλ nˆλ ˆλ 3 = n ˆλ < 0 Hence ˆλ is the UMVUE and MLE of λ if σ is known If σ is known and r> n, thentn r is the UMVUE of E(Tn)=λ r r Γ(r + n) Γ(n) If neither σ nor λ are known, notice that f(y) = 1 [ ( )] 1 log(y) log(σ) y λ exp I(y σ) λ Hence the likelihood L(λ, σ) =c 1 λ n exp [ n ( ) ] log(yi ) log(σ) I(y (1) σ), i=1 λ and the log likelihood is [ log L(λ, σ) = d n log(λ) n ( ) ] log(yi ) log(σ) I(y (1) σ) i=1 λ Let w i =log(y i )andθ =log(σ), so σ = e θ Then the log likelihood is [ n ( ) ] wi θ log L(λ, θ) = d n log(λ) I(w (1) θ), λ which is equivalent to the log likelihood of the EXP(θ, λ) distribution Hence (ˆλ, ˆθ) =(W W (1),W (1) ), and by invariance, the MLE i=1 (ˆλ, ˆσ) =(W W (1),Y (1) ) 51
41 103 The Poisson Distribution If Y has a Poisson distribution, Y POIS(θ), then the pmf of Y is f(y) =P (Y = y) = e θ θ y for y =0, 1,, where θ>0 If θ =0,P(Y =0)=1=e θ The mgf of Y is m(t) =exp(θ(e t 1)), and the chf of Y is c(t) =exp(θ(e it 1)) E(Y )=θ, and Chen and Rubin (1986) and Adell and Jodrá (005) show that 1 < MED(Y ) E(Y ) < 1/3 VAR(Y )=θ The classical estimator of θ is ˆθ = Y n The approximations Y N(θ, θ) and Y N( θ, 1) are sometimes used y! f(y) =e θ 1 y! exp[log(θ)y] is a 1P REF ThusΘ=(0, ), η=log(θ) andω=(, ) If Y 1,, Y n are independent POIS(θ i )then Y i POIS( θ i ) If Y 1,, Y n are iid POIS(θ) then The likelihood and the log likelihood T n = Y i POIS(nθ) L(θ) =ce nθ exp[log(θ) y i ], log(l(θ)) = d nθ +log(θ) y i Hence or y i = nθ, or d dθ log(l(θ)) = n + 1 set yi =0, θ ˆθ = Y 5
42 d dθ log(l(θ)) = yi < 0 θ unless y i =0 Hence Y is the UMVUE and MLE of θ 1033 The Power Distribution If Y has a power distribution, Y POW(λ), then the pdf of Y is f(y) = 1 λ y 1 λ 1, where λ>0and0 y 1 The cdf of Y is F (y) =y 1/λ for 0 y 1 MED(Y )=(1/) λ W = log(y )isexp(λ) Y beta(δ =1/λ, ν =1) f(y) = 1 λ I [0,1](y)exp [( 1λ ] 1) log(y) = 1 λ I [0,1](y)exp [(1 1λ ] )( log(y)) is a 1P REF ThusΘ=(0, ), η=1 1/λ and Ω = (, 1) If Y 1,, Y n are iid POW(λ), then T n = log(y i ) G(n, λ) The likelihood L(λ) = 1 [( λ exp 1 n λ 1) ] log(y i ), and the log likelihood log(l(λ)) = n log(λ)+( 1 λ 1) log(y i ) Hence d n log(l(λ)) = dλ λ log(yi ) λ set =0, 53
43 or log(y i )=nλ, or ˆλ = log(y i ) n d dλ log(l(λ)) = n λ log(yi ) λ 3 = ṋ λ + nˆλ ˆλ 3 Hence ˆλ is the UMVUE and MLE of λ If r> n, thentn r is the UMVUE of = n ˆλ < 0 E(Tn)=λ r r Γ(r + n) Γ(n) λ=ˆλ 1034 The Rayleigh Distribution If Y has a Rayleigh distribution, Y R(µ, σ), then the pdf of Y is [ f(y) = y µ exp 1 ( ) ] y µ σ σ where σ>0, µ is real, and y µ See Cohen and Whitten (1988, Ch 10) This is an asymmetric location scale family The cdf of Y is [ F (y) =1 exp 1 ( ) ] y µ σ for y µ, andf (y) =0, otherwise E(Y )=µ + σ π/ µ σ VAR(Y )=σ (4 π)/ 04904σ MED(Y )=µ + σ log(4) µ σ Hence µ MED(Y ) 655MAD(Y )andσ 30MAD(Y ) Let σd =MAD(Y ) If µ =0, and σ =1, then 05 =exp[ 05( log(4) D) ] exp[ 05( log(4) + D) ] 54
44 Hence D and MAD(Y ) σ It can be shown that W =(Y µ) EXP(σ ) Other parameterizations for the Rayleigh distribution are possible Note that f(y) = 1 [ σ (y µ)i(y µ)exp 1 ] (y µ) σ appears to be a 1P REF if µ is known If Y 1,, Y n are iid R(µ, σ), then T n = (Y i µ) G(n, σ ) If µ is known, then the likelihood [ L(σ 1 )=c exp 1 ] (yi µ), σn σ and the log likelihood log(l(σ )) = d n log(σ ) 1 (yi µ) σ Hence d d(σ ) log(l(σ )) = n σ + 1 (yi µ) set =0, σ or (y i µ) =nσ, or ˆσ (Yi µ) = n d d(σ ) log(l(σ )) = n (σ ) n (ˆσ ) nˆσ (ˆσ ) 3 = (yi µ) (σ ) 3 = σ =ˆσ n (ˆσ ) < 0 Hence ˆσ is the UMVUE and MLE of σ if µ is known If µ is known and r> n, thent r n is the UMVUE of E(T r n )=r σ 55 r Γ(r + n) Γ(n)
45 1035 The Smallest Extreme Value Distribution If Y has a smallest extreme value distribution (or log-weibull distribution), Y SEV (θ, σ), then the pdf of Y is f(y) = 1 σ exp(y θ θ )exp[ exp(y σ σ )] where y and θ are real and σ>0 The cdf of Y is F (y) =1 exp[ exp( y θ σ )] This family is an asymmetric location-scale family with a longer left tail than right E(Y ) θ 05771σ, and VAR(Y )=σ π / σ MED(Y )=θ σlog(log()) MAD(Y ) σ Y is a one parameter exponential family in θ if σ is known If Y has a SEV(θ, σ) distribution, then W = Y has an LEV( θ, σ) distribution 1036 The Student s t Distribution If Y has a Student s t distribution, Y t p, then the pdf of Y is f(y) = Γ( p+1 ) y p+1 (1 + (pπ) 1/ Γ(p/) p ) ( ) where p is a positive integer and y is real This family is symmetric about 0 The t 1 distribution is the Cauchy(0, 1) distribution If Z is N(0, 1) and is independent of W χ p, then Z ( W p )1/ is t p E(Y )=0forp MED(Y )=0 56
46 VAR(Y )=p/(p ) for p 3, and MAD(Y )=t p,075 where P (t p t p,075 )=075 If α = P (t p t p,α ), then Cooke, Craven, and Clarke (198, p 84) suggest the approximation t p,α p[exp( w α p ) 1)] where w α = z α(8p +3) 8p +1, z α is the standard normal cutoff: α =Φ(z α ), and 05 α If 0 <α<05, then t p,α = t p,1 α This approximation seems to get better as the degrees of freedom increase 1037 The Truncated Extreme Value Distribution If Y has a truncated extreme value distribution, Y TEV(λ), then the pdf of Y is f(y) = 1 ( ) λ exp y ey 1 λ where y>0andλ>0 The cdf of Y is [ ] (e y 1) F (y)=1 exp λ for y>0 MED(Y )=log(1+λlog()) W = e Y 1isEXP(λ) f(y) = 1 [ ] 1 λ ey I(y 0) exp λ (ey 1) is a 1P REF Hence Θ = (0, ), η= 1/λ and Ω = (, 0) If Y 1,, Y n are iid TEV(λ), then T n = (e Y i 1) G(n, λ) 57
47 The likelihood L(λ) =c 1 [ 1 λ exp n λ and the log likelihood ] log(e y i 1), log(l(λ)) = d n log(λ) 1 λ log(e y i 1) Hence d n log(e y log(l(λ)) = dλ λ + i 1) λ or log(e y i 1) = nλ, or ˆλ = log(e Y i 1) n d dλ log(l(λ)) = n λ log(e y i 1) λ 3 = ṋ λ nˆλ ˆλ 3 = n ˆλ < 0 Hence ˆλ is the UMVUE and MLE of λ If r> n, thentn r is the UMVUE of E(Tn)=λ r r Γ(r + n) Γ(n) 1038 The Uniform Distribution set =0, λ=ˆλ If Y has a uniform distribution, Y U(θ 1,θ ), then the pdf of Y is 1 f(y) = I(θ 1 y θ ) θ θ 1 The cdf of Y is F (y) =(y θ 1 )/(θ θ 1 )forθ 1 y θ This family is a location-scale family which is symmetric about (θ 1 + θ )/ By definition, m(0) = c(0) = 1 For t 0, the mgf of Y is m(t) = etθ e tθ 1 (θ θ 1 )t, 58
48 and the chf of Y is c(t) = eitθ e itθ 1 (θ θ 1 )it E(Y )=(θ 1 + θ )/, and MED(Y )=(θ 1 + θ )/ VAR(Y )=(θ θ 1 ) /1, and MAD(Y )=(θ θ 1 )/4 Note that θ 1 =MED(Y ) MAD(Y )andθ =MED(Y )+MAD(Y ) Some classical estimates are ˆθ 1 = y (1) and ˆθ = y (n) 1039 The Weibull Distribution If Y has a Weibull distribution, Y W (φ, λ), then the pdf of Y is f(y) = φ λ yφ 1 e yφ λ where λ, y, and φ are all positive For fixed φ, this is a scale family in σ = λ 1/φ The cdf of Y is F (y) =1 exp( y φ /λ) fory>0 E(Y )=λ 1/φ Γ(1 + 1/φ) VAR(Y )=λ /φ Γ(1 + /φ) (E(Y )) E(Y r )=λ r/φ Γ(1 + r φ ) for r> φ MED(Y )=(λ log()) 1/φ Note that λ = (MED(Y ))φ log() W = Y φ is EXP(λ) W =log(y ) has a smallest extreme value SEV(θ =log(λ 1/φ ),σ =1/φ) distribution f(y) = φ [ ] 1 λ yφ 1 I(y 0) exp λ yφ is a one parameter exponential family in λ if φ is known 59
49 If Y 1,, Y n are iid W (φ, λ), then T n = Y φ i If φ is known, then the likelihood and the log likelihood L(λ) =c 1 λ n exp [ 1 λ G(n, λ) log(l(λ)) = d n log(λ) 1 λ ] y φ i, y φ i Hence or y φ i = nλ, or d n log(l(λ)) = dλ λ + y φ i λ Y φ i ˆλ = n d dλ log(l(λ)) = n λ y φ i λ 3 set =0, λ=ˆλ = ṋ λ nˆλ ˆλ 3 Hence ˆλ is the UMVUE and MLE of λ If r> n, thentn r is the UMVUE of = n ˆλ < 0 E(Tn)=λ r r Γ(r + n) Γ(n) 1040 The Zeta Distribution If Y has a Zeta distribution, Y Zeta(ν), then the pmf of Y is f(y) =P (Y = y) = 1 y ν ζ(ν) 60
50 where ν>1andy =1,, 3, Here the zeta function ζ(ν) = y=1 1 y ν for ν>1 This distribution is a one parameter exponential family E(y) = ζ(ν 1) ζ(ν) for ν>, and VAR(Y )= ζ(ν ) ζ(ν) [ ζ(ν 1) ζ(ν) for ν>3 E(Y r ζ(ν r) )= ζ(ν) for ν>r+1 This distribution is sometimes used for count data, especially by linguistics for word frequency See Lindsey (004, p 154) 1041 Complements Many of the distribution results used in this chapter came from Johnson and Kotz (1970a,b) and Patel, Kapadia and Owen (1976) Cohen and Whitten (1988), Ferguson (1967), Castillo (1988), Cramér (1946), Kennedy and Gentle (1980), Lehmann (1983), Meeker and Escobar (1998), Bickel and Doksum (1977), DeGroot and Schervish (001), Hastings and Peacock (1975) and Leemis (1986) also have useful results on distributions Also see articles in Kotz and Johnson (198ab, 1983ab, 1985ab, 1986, 1988ab) Often an entire book is devoted to a single distribution, see for example, Bowman and Shenton (1988) ] 61
Some Useful Distributions
 Chapter 0 Some Useful Distributios Defiitio 0 The populatio media is ay value MED(Y ) such that P(Y MED(Y )) 05 ad P(Y MED(Y )) 05 (0) Defiitio 0 The populatio media absolute deviatio is MAD(Y ) = MED(
Chapter 0 Some Useful Distributios Defiitio 0 The populatio media is ay value MED(Y ) such that P(Y MED(Y )) 05 ad P(Y MED(Y )) 05 (0) Defiitio 0 The populatio media absolute deviatio is MAD(Y ) = MED(
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
An Inventory of Continuous Distributions
 Appendi A An Inventory of Continuous Distributions A.1 Introduction The incomplete gamma function is given by Also, define Γ(α; ) = 1 with = G(α; ) = Z 0 Z 0 Z t α 1 e t dt, α > 0, >0 t α 1 e t dt, α >
Appendi A An Inventory of Continuous Distributions A.1 Introduction The incomplete gamma function is given by Also, define Γ(α; ) = 1 with = G(α; ) = Z 0 Z 0 Z t α 1 e t dt, α > 0, >0 t α 1 e t dt, α >
Lecture 34 Bootstrap confidence intervals
 Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Solution Series 9. i=1 x i and i=1 x i.
 Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Theorem 8 Let φ be the most powerful size α test of H
 Testing composite hypotheses Θ = Θ 0 Θ c 0 H 0 : θ Θ 0 H 1 : θ Θ c 0 Definition 16 A test φ is a uniformly most powerful (UMP) level α test for H 0 vs. H 1 if φ has level α and for any other level α test
Testing composite hypotheses Θ = Θ 0 Θ c 0 H 0 : θ Θ 0 H 1 : θ Θ c 0 Definition 16 A test φ is a uniformly most powerful (UMP) level α test for H 0 vs. H 1 if φ has level α and for any other level α test
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
Bayesian statistics. DS GA 1002 Probability and Statistics for Data Science.
 Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
Homework for 1/27 Due 2/5
 Name: ID: Homework for /7 Due /5. [ 8-3] I Example D of Sectio 8.4, the pdf of the populatio distributio is + αx x f(x α) =, α, otherwise ad the method of momets estimate was foud to be ˆα = 3X (where
Name: ID: Homework for /7 Due /5. [ 8-3] I Example D of Sectio 8.4, the pdf of the populatio distributio is + αx x f(x α) =, α, otherwise ad the method of momets estimate was foud to be ˆα = 3X (where
6. MAXIMUM LIKELIHOOD ESTIMATION
 6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
5.4 The Poisson Distribution.
 The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
Estimation for ARMA Processes with Stable Noise. Matt Calder & Richard A. Davis Colorado State University
 Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
FORMULAS FOR STATISTICS 1
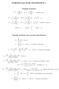 FORMULAS FOR STATISTICS 1 X = 1 n Sample statistics X i or x = 1 n x i (sample mean) S 2 = 1 n 1 s 2 = 1 n 1 (X i X) 2 = 1 n 1 (x i x) 2 = 1 n 1 Xi 2 n n 1 X 2 x 2 i n n 1 x 2 or (sample variance) E(X)
FORMULAS FOR STATISTICS 1 X = 1 n Sample statistics X i or x = 1 n x i (sample mean) S 2 = 1 n 1 s 2 = 1 n 1 (X i X) 2 = 1 n 1 (x i x) 2 = 1 n 1 Xi 2 n n 1 X 2 x 2 i n n 1 x 2 or (sample variance) E(X)
Section 7.6 Double and Half Angle Formulas
 09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
The Simply Typed Lambda Calculus
 Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Solutions to Exercise Sheet 5
 Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
Problem Set 3: Solutions
 CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
Every set of first-order formulas is equivalent to an independent set
 Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
Μηχανική Μάθηση Hypothesis Testing
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
Math 6 SL Probability Distributions Practice Test Mark Scheme
 Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
Introduction to the ML Estimation of ARMA processes
 Introduction to the ML Estimation of ARMA processes Eduardo Rossi University of Pavia October 2013 Rossi ARMA Estimation Financial Econometrics - 2013 1 / 1 We consider the AR(p) model: Y t = c + φ 1 Y
Introduction to the ML Estimation of ARMA processes Eduardo Rossi University of Pavia October 2013 Rossi ARMA Estimation Financial Econometrics - 2013 1 / 1 We consider the AR(p) model: Y t = c + φ 1 Y
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Lecture 7: Overdispersion in Poisson regression
 Lecture 7: Overdispersion in Poisson regression Claudia Czado TU München c (Claudia Czado, TU Munich) ZFS/IMS Göttingen 2004 0 Overview Introduction Modeling overdispersion through mixing Score test for
Lecture 7: Overdispersion in Poisson regression Claudia Czado TU München c (Claudia Czado, TU Munich) ZFS/IMS Göttingen 2004 0 Overview Introduction Modeling overdispersion through mixing Score test for
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
 Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
APPENDICES APPENDIX A. STATISTICAL TABLES AND CHARTS 651 APPENDIX B. BIBLIOGRAPHY 677 APPENDIX C. ANSWERS TO SELECTED EXERCISES 679
 APPENDICES APPENDIX A. STATISTICAL TABLES AND CHARTS 1 Table I Summary of Common Probability Distributions 2 Table II Cumulative Standard Normal Distribution Table III Percentage Points, 2 of the Chi-Squared
APPENDICES APPENDIX A. STATISTICAL TABLES AND CHARTS 1 Table I Summary of Common Probability Distributions 2 Table II Cumulative Standard Normal Distribution Table III Percentage Points, 2 of the Chi-Squared
Second Order RLC Filters
 ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
Probability and Random Processes (Part II)
 Probability and Random Processes (Part II) 1. If the variance σ x of d(n) = x(n) x(n 1) is one-tenth the variance σ x of a stationary zero-mean discrete-time signal x(n), then the normalized autocorrelation
Probability and Random Processes (Part II) 1. If the variance σ x of d(n) = x(n) x(n 1) is one-tenth the variance σ x of a stationary zero-mean discrete-time signal x(n), then the normalized autocorrelation
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
 Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 19/5/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
6.3 Forecasting ARMA processes
 122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
SCITECH Volume 13, Issue 2 RESEARCH ORGANISATION Published online: March 29, 2018
 Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Finite Field Problems: Solutions
 Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +
[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R + k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +](/thumbs/73/69566903.jpg) Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
Uniform Convergence of Fourier Series Michael Taylor
 Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
 Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Lecture 21: Properties and robustness of LSE
 Lecture 21: Properties and robustness of LSE BLUE: Robustness of LSE against normality We now study properties of l τ β and σ 2 under assumption A2, i.e., without the normality assumption on ε. From Theorem
Lecture 21: Properties and robustness of LSE BLUE: Robustness of LSE against normality We now study properties of l τ β and σ 2 under assumption A2, i.e., without the normality assumption on ε. From Theorem
Exercise 2: The form of the generalized likelihood ratio
 Stats 2 Winter 28 Homework 9: Solutions Due Friday, March 6 Exercise 2: The form of the generalized likelihood ratio We want to test H : θ Θ against H : θ Θ, and compare the two following rules of rejection:
Stats 2 Winter 28 Homework 9: Solutions Due Friday, March 6 Exercise 2: The form of the generalized likelihood ratio We want to test H : θ Θ against H : θ Θ, and compare the two following rules of rejection:
SCHOOL OF MATHEMATICAL SCIENCES G11LMA Linear Mathematics Examination Solutions
 SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Lecture 12: Pseudo likelihood approach
 Lecture 12: Pseudo likelihood approach Pseudo MLE Let X 1,...,X n be a random sample from a pdf in a family indexed by two parameters θ and π with likelihood l(θ,π). The method of pseudo MLE may be viewed
Lecture 12: Pseudo likelihood approach Pseudo MLE Let X 1,...,X n be a random sample from a pdf in a family indexed by two parameters θ and π with likelihood l(θ,π). The method of pseudo MLE may be viewed
= λ 1 1 e. = λ 1 =12. has the properties e 1. e 3,V(Y
 Stat 50 Homework Solutions Spring 005. (a λ λ λ 44 (b trace( λ + λ + λ 0 (c V (e x e e λ e e λ e (λ e by definition, the eigenvector e has the properties e λ e and e e. (d λ e e + λ e e + λ e e 8 6 4 4
Stat 50 Homework Solutions Spring 005. (a λ λ λ 44 (b trace( λ + λ + λ 0 (c V (e x e e λ e e λ e (λ e by definition, the eigenvector e has the properties e λ e and e e. (d λ e e + λ e e + λ e e 8 6 4 4
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ
 ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ ΕΛΕΝΑ ΦΛΟΚΑ Επίκουρος Καθηγήτρια Τµήµα Φυσικής, Τοµέας Φυσικής Περιβάλλοντος- Μετεωρολογίας ΓΕΝΙΚΟΙ ΟΡΙΣΜΟΙ Πληθυσµός Σύνολο ατόµων ή αντικειµένων στα οποία αναφέρονται
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ ΕΛΕΝΑ ΦΛΟΚΑ Επίκουρος Καθηγήτρια Τµήµα Φυσικής, Τοµέας Φυσικής Περιβάλλοντος- Μετεωρολογίας ΓΕΝΙΚΟΙ ΟΡΙΣΜΟΙ Πληθυσµός Σύνολο ατόµων ή αντικειµένων στα οποία αναφέρονται
Approximation of distance between locations on earth given by latitude and longitude
 Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Aquinas College. Edexcel Mathematical formulae and statistics tables DO NOT WRITE ON THIS BOOKLET
 Aquinas College Edexcel Mathematical formulae and statistics tables DO NOT WRITE ON THIS BOOKLET Pearson Edexcel Level 3 Advanced Subsidiary and Advanced GCE in Mathematics and Further Mathematics Mathematical
Aquinas College Edexcel Mathematical formulae and statistics tables DO NOT WRITE ON THIS BOOKLET Pearson Edexcel Level 3 Advanced Subsidiary and Advanced GCE in Mathematics and Further Mathematics Mathematical
Statistics 104: Quantitative Methods for Economics Formula and Theorem Review
 Harvard College Statistics 104: Quantitative Methods for Economics Formula and Theorem Review Tommy MacWilliam, 13 tmacwilliam@college.harvard.edu March 10, 2011 Contents 1 Introduction to Data 5 1.1 Sample
Harvard College Statistics 104: Quantitative Methods for Economics Formula and Theorem Review Tommy MacWilliam, 13 tmacwilliam@college.harvard.edu March 10, 2011 Contents 1 Introduction to Data 5 1.1 Sample
Tridiagonal matrices. Gérard MEURANT. October, 2008
 Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Math221: HW# 1 solutions
 Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Congruence Classes of Invertible Matrices of Order 3 over F 2
 International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
HOMEWORK#1. t E(x) = 1 λ = (b) Find the median lifetime of a randomly selected light bulb. Answer:
 HOMEWORK# 52258 李亞晟 Eercise 2. The lifetime of light bulbs follows an eponential distribution with a hazard rate of. failures per hour of use (a) Find the mean lifetime of a randomly selected light bulb.
HOMEWORK# 52258 李亞晟 Eercise 2. The lifetime of light bulbs follows an eponential distribution with a hazard rate of. failures per hour of use (a) Find the mean lifetime of a randomly selected light bulb.
derivation of the Laplacian from rectangular to spherical coordinates
 derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
Second Order Partial Differential Equations
 Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Concrete Mathematics Exercises from 30 September 2016
 Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Section 9.2 Polar Equations and Graphs
 180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
HISTOGRAMS AND PERCENTILES What is the 25 th percentile of a histogram? What is the 50 th percentile for the cigarette histogram?
 HISTOGRAMS AND PERCENTILES What is the 25 th percentile of a histogram? The point on the horizontal axis such that of the area under the histogram lies to the left of that point (and to the right) What
HISTOGRAMS AND PERCENTILES What is the 25 th percentile of a histogram? The point on the horizontal axis such that of the area under the histogram lies to the left of that point (and to the right) What
5. Choice under Uncertainty
 5. Choice under Uncertainty Daisuke Oyama Microeconomics I May 23, 2018 Formulations von Neumann-Morgenstern (1944/1947) X: Set of prizes Π: Set of probability distributions on X : Preference relation
5. Choice under Uncertainty Daisuke Oyama Microeconomics I May 23, 2018 Formulations von Neumann-Morgenstern (1944/1947) X: Set of prizes Π: Set of probability distributions on X : Preference relation
Overview. Transition Semantics. Configurations and the transition relation. Executions and computation
 Overview Transition Semantics Configurations and the transition relation Executions and computation Inference rules for small-step structural operational semantics for the simple imperative language Transition
Overview Transition Semantics Configurations and the transition relation Executions and computation Inference rules for small-step structural operational semantics for the simple imperative language Transition
Exercises to Statistics of Material Fatigue No. 5
 Prof. Dr. Christine Müller Dipl.-Math. Christoph Kustosz Eercises to Statistics of Material Fatigue No. 5 E. 9 (5 a Show, that a Fisher information matri for a two dimensional parameter θ (θ,θ 2 R 2, can
Prof. Dr. Christine Müller Dipl.-Math. Christoph Kustosz Eercises to Statistics of Material Fatigue No. 5 E. 9 (5 a Show, that a Fisher information matri for a two dimensional parameter θ (θ,θ 2 R 2, can
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Instruction Execution Times
 1 C Execution Times InThisAppendix... Introduction DL330 Execution Times DL330P Execution Times DL340 Execution Times C-2 Execution Times Introduction Data Registers This appendix contains several tables
1 C Execution Times InThisAppendix... Introduction DL330 Execution Times DL330P Execution Times DL340 Execution Times C-2 Execution Times Introduction Data Registers This appendix contains several tables
Quadratic Expressions
 Quadratic Expressions. The standard form of a quadratic equation is ax + bx + c = 0 where a, b, c R and a 0. The roots of ax + bx + c = 0 are b ± b a 4ac. 3. For the equation ax +bx+c = 0, sum of the roots
Quadratic Expressions. The standard form of a quadratic equation is ax + bx + c = 0 where a, b, c R and a 0. The roots of ax + bx + c = 0 are b ± b a 4ac. 3. For the equation ax +bx+c = 0, sum of the roots
Appendix to On the stability of a compressible axisymmetric rotating flow in a pipe. By Z. Rusak & J. H. Lee
 Appendi to On the stability of a compressible aisymmetric rotating flow in a pipe By Z. Rusak & J. H. Lee Journal of Fluid Mechanics, vol. 5 4, pp. 5 4 This material has not been copy-edited or typeset
Appendi to On the stability of a compressible aisymmetric rotating flow in a pipe By Z. Rusak & J. H. Lee Journal of Fluid Mechanics, vol. 5 4, pp. 5 4 This material has not been copy-edited or typeset
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
Gaussian related distributions
 Gaussian related distributions Santiago Aja-Fernández June 19, 009 1 Gaussian related distributions 1. Gaussian: ormal PDF: MGF: Main moments:. Rayleigh: PDF: MGF: Raw moments: Main moments: px = 1 σ π
Gaussian related distributions Santiago Aja-Fernández June 19, 009 1 Gaussian related distributions 1. Gaussian: ormal PDF: MGF: Main moments:. Rayleigh: PDF: MGF: Raw moments: Main moments: px = 1 σ π
Fourier Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Fractional Colorings and Zykov Products of graphs
 Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
[1] P Q. Fig. 3.1
![[1] P Q. Fig. 3.1 [1] P Q. Fig. 3.1](/thumbs/79/80362156.jpg) 1 (a) Define resistance....... [1] (b) The smallest conductor within a computer processing chip can be represented as a rectangular block that is one atom high, four atoms wide and twenty atoms long. One
1 (a) Define resistance....... [1] (b) The smallest conductor within a computer processing chip can be represented as a rectangular block that is one atom high, four atoms wide and twenty atoms long. One
A Note on Intuitionistic Fuzzy. Equivalence Relation
 International Mathematical Forum, 5, 2010, no. 67, 3301-3307 A Note on Intuitionistic Fuzzy Equivalence Relation D. K. Basnet Dept. of Mathematics, Assam University Silchar-788011, Assam, India dkbasnet@rediffmail.com
International Mathematical Forum, 5, 2010, no. 67, 3301-3307 A Note on Intuitionistic Fuzzy Equivalence Relation D. K. Basnet Dept. of Mathematics, Assam University Silchar-788011, Assam, India dkbasnet@rediffmail.com
( y) Partial Differential Equations
 Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate
Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate
Asymptotic distribution of MLE
 Asymptotic distribution of MLE Theorem Let {X t } be a causal and invertible ARMA(p,q) process satisfying Φ(B)X = Θ(B)Z, {Z t } IID(0, σ 2 ). Let ( ˆφ, ˆϑ) the values that minimize LL n (φ, ϑ) among those
Asymptotic distribution of MLE Theorem Let {X t } be a causal and invertible ARMA(p,q) process satisfying Φ(B)X = Θ(B)Z, {Z t } IID(0, σ 2 ). Let ( ˆφ, ˆϑ) the values that minimize LL n (φ, ϑ) among those
P AND P. P : actual probability. P : risk neutral probability. Realtionship: mutual absolute continuity P P. For example:
 (B t, S (t) t P AND P,..., S (p) t ): securities P : actual probability P : risk neutral probability Realtionship: mutual absolute continuity P P For example: P : ds t = µ t S t dt + σ t S t dw t P : ds
(B t, S (t) t P AND P,..., S (p) t ): securities P : actual probability P : risk neutral probability Realtionship: mutual absolute continuity P P For example: P : ds t = µ t S t dt + σ t S t dw t P : ds
Arithmetical applications of lagrangian interpolation. Tanguy Rivoal. Institut Fourier CNRS and Université de Grenoble 1
 Arithmetical applications of lagrangian interpolation Tanguy Rivoal Institut Fourier CNRS and Université de Grenoble Conference Diophantine and Analytic Problems in Number Theory, The 00th anniversary
Arithmetical applications of lagrangian interpolation Tanguy Rivoal Institut Fourier CNRS and Université de Grenoble Conference Diophantine and Analytic Problems in Number Theory, The 00th anniversary
CRASH COURSE IN PRECALCULUS
 CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
ORDINAL ARITHMETIC JULIAN J. SCHLÖDER
 ORDINAL ARITHMETIC JULIAN J. SCHLÖDER Abstract. We define ordinal arithmetic and show laws of Left- Monotonicity, Associativity, Distributivity, some minor related properties and the Cantor Normal Form.
ORDINAL ARITHMETIC JULIAN J. SCHLÖDER Abstract. We define ordinal arithmetic and show laws of Left- Monotonicity, Associativity, Distributivity, some minor related properties and the Cantor Normal Form.
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 6/5/2006
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Ολοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα είναι μικρότεροι το 1000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Διάρκεια: 3,5 ώρες Καλή
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Ολοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα είναι μικρότεροι το 1000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Διάρκεια: 3,5 ώρες Καλή
Srednicki Chapter 55
 Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Trigonometric Formula Sheet
 Trigonometric Formula Sheet Definition of the Trig Functions Right Triangle Definition Assume that: 0 < θ < or 0 < θ < 90 Unit Circle Definition Assume θ can be any angle. y x, y hypotenuse opposite θ
Trigonometric Formula Sheet Definition of the Trig Functions Right Triangle Definition Assume that: 0 < θ < or 0 < θ < 90 Unit Circle Definition Assume θ can be any angle. y x, y hypotenuse opposite θ
Additional Results for the Pareto/NBD Model
 Additional Results for the Pareto/NBD Model Peter S. Fader www.petefader.com Bruce G. S. Hardie www.brucehardie.com January 24 Abstract This note derives expressions for i) the raw moments of the posterior
Additional Results for the Pareto/NBD Model Peter S. Fader www.petefader.com Bruce G. S. Hardie www.brucehardie.com January 24 Abstract This note derives expressions for i) the raw moments of the posterior
DERIVATION OF MILES EQUATION FOR AN APPLIED FORCE Revision C
 DERIVATION OF MILES EQUATION FOR AN APPLIED FORCE Revision C By Tom Irvine Email: tomirvine@aol.com August 6, 8 Introduction The obective is to derive a Miles equation which gives the overall response
DERIVATION OF MILES EQUATION FOR AN APPLIED FORCE Revision C By Tom Irvine Email: tomirvine@aol.com August 6, 8 Introduction The obective is to derive a Miles equation which gives the overall response
Practice Exam 2. Conceptual Questions. 1. State a Basic identity and then verify it. (a) Identity: Solution: One identity is csc(θ) = 1
 Conceptual Questions. State a Basic identity and then verify it. a) Identity: Solution: One identity is cscθ) = sinθ) Practice Exam b) Verification: Solution: Given the point of intersection x, y) of the
Conceptual Questions. State a Basic identity and then verify it. a) Identity: Solution: One identity is cscθ) = sinθ) Practice Exam b) Verification: Solution: Given the point of intersection x, y) of the
STAT200C: Hypothesis Testing
 STAT200C: Hypothesis Testing Zhaoxia Yu Spring 2017 Some Definitions A hypothesis is a statement about a population parameter. The two complementary hypotheses in a hypothesis testing are the null hypothesis
STAT200C: Hypothesis Testing Zhaoxia Yu Spring 2017 Some Definitions A hypothesis is a statement about a population parameter. The two complementary hypotheses in a hypothesis testing are the null hypothesis
Jesse Maassen and Mark Lundstrom Purdue University November 25, 2013
 Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
ω ω ω ω ω ω+2 ω ω+2 + ω ω ω ω+2 + ω ω+1 ω ω+2 2 ω ω ω ω ω ω ω ω+1 ω ω2 ω ω2 + ω ω ω2 + ω ω ω ω2 + ω ω+1 ω ω2 + ω ω+1 + ω ω ω ω2 + ω
 0 1 2 3 4 5 6 ω ω + 1 ω + 2 ω + 3 ω + 4 ω2 ω2 + 1 ω2 + 2 ω2 + 3 ω3 ω3 + 1 ω3 + 2 ω4 ω4 + 1 ω5 ω 2 ω 2 + 1 ω 2 + 2 ω 2 + ω ω 2 + ω + 1 ω 2 + ω2 ω 2 2 ω 2 2 + 1 ω 2 2 + ω ω 2 3 ω 3 ω 3 + 1 ω 3 + ω ω 3 +
0 1 2 3 4 5 6 ω ω + 1 ω + 2 ω + 3 ω + 4 ω2 ω2 + 1 ω2 + 2 ω2 + 3 ω3 ω3 + 1 ω3 + 2 ω4 ω4 + 1 ω5 ω 2 ω 2 + 1 ω 2 + 2 ω 2 + ω ω 2 + ω + 1 ω 2 + ω2 ω 2 2 ω 2 2 + 1 ω 2 2 + ω ω 2 3 ω 3 ω 3 + 1 ω 3 + ω ω 3 +
CHAPTER 48 APPLICATIONS OF MATRICES AND DETERMINANTS
 CHAPTER 48 APPLICATIONS OF MATRICES AND DETERMINANTS EXERCISE 01 Page 545 1. Use matrices to solve: 3x + 4y x + 5y + 7 3x + 4y x + 5y 7 Hence, 3 4 x 0 5 y 7 The inverse of 3 4 5 is: 1 5 4 1 5 4 15 8 3
CHAPTER 48 APPLICATIONS OF MATRICES AND DETERMINANTS EXERCISE 01 Page 545 1. Use matrices to solve: 3x + 4y x + 5y + 7 3x + 4y x + 5y 7 Hence, 3 4 x 0 5 y 7 The inverse of 3 4 5 is: 1 5 4 1 5 4 15 8 3
