webpage :

ϕ be a scalar field. The gradient is the vector field defined by

Amn Halloc Math Ecss E-mal : amn@sthths bpa : sthths/amn MATH EXERCISES GRADIENT DIVERGENCE CURL DEL NABLA OERATOR LALACIAN OERATOR CONTINUITY AND NAVIER-STOKES EQUATIONS VECTOR RODUCTS I and thn scala

ϕ be a scalar field. The gradient is the vector field defined by

Amn Halloc Math Ecss E-mal : amn@sthths bpa : sthths/amn MATH EXERCISES GRADIENT DIVERGENCE CURL DEL NABLA OERATOR LALACIAN OERATOR CONTINUITY AND NAVIER-STOKES EQUATIONS VECTOR RODUCTS I an thn scala

webpage :

Amin Haliloic Mah Eciss E-mail : amin@shkhs wbpa : wwwshkhs/amin MATH EXERISES GRADIENT DIVERGENE URL DEL NABLA OERATOR LALAIAN OERATOR ONTINUITY AND NAVIER-STOKES EQUATIONS VETOR RODUTS I and hn scala

ECE 222b Applied Electromagnetics Notes Set 3b

C b Appl lcomancs Nos S 3b Insuco: Pof. Val Loman Dpamn of lccal an Compu nnn Unvs of Calfona San Do Rflcon an Tansmsson. Nomal ncnc T R T R Fs fn h manc fls: 3 Rflcon an Tansmsson T R T R T R T R R T

ELE 3310 Tutorial 11. Reflection of plane waves Wave impedance of the total field

L 0 Tuto Rfcton of pn wvs Wv mpdnc of th tot fd Rfcton of M wvs Rfcton tks pc whn n M wv hts on bound. Pt of th wv gts fctd, nd pt of t gts tnsmttd. Popgton dctons nd mptuds of th fctd nd tnsmttd wvs dpnd

ECE 222b Applied Electromagnetics Notes Set 3a

C b lid lcomagnics Nos S 3a Insuco: Pof. Viali Lomakin Damn of lcical and Comu ngining Univsi of Califonia San Digo Unifom Plan Wavs Consid Mawll s quaions: In a losslss mdium ε and µ a al and σ : Sinc

Matrices and Determinants

Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z

Answers - Worksheet A ALGEBRA PMT. 1 a = 7 b = 11 c = 1 3. e = 0.1 f = 0.3 g = 2 h = 10 i = 3 j = d = k = 3 1. = 1 or 0.5 l =

C ALGEBRA Answers - Worksheet A a 7 b c d e 0. f 0. g h 0 i j k 6 8 or 0. l or 8 a 7 b 0 c 7 d 6 e f g 6 h 8 8 i 6 j k 6 l a 9 b c d 9 7 e 00 0 f 8 9 a b 7 7 c 6 d 9 e 6 6 f 6 8 g 9 h 0 0 i j 6 7 7 k 9

Homework 8 Model Solution Section

MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx

26 28 Find an equation of the tangent line to the curve at the given point Discuss the curve under the guidelines of Section

SECTION 5. THE NATURAL LOGARITHMIC FUNCTION 5. THE NATURAL LOGARITHMIC FUNCTION A Click here for answers. S Click here for solutions. 4 Use the Laws of Logarithms to epand the quantit.. ln ab. ln c. ln

LAPLACE TRANSFORM TABLE

LAPLACE TRANSFORM TABLE Th Laplac afom of am mpl fuco a gv h Tabl. Fuco U mpul U Sp U Ramp Expoal Rpad Roo S Co Polyomal Dampd Dampd co f δ u -a -a co,,... -a -a co F / / /a /a / /!/ /a a/a Thom : Shf

Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------

Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin

Reflection & Transmission

Rflc & Tasmss 4 D. Ray Kw Rflc & Tasmss - D. Ray Kw Gmc Opcs (M wavs flc fac - asmss cdc.. Sll s Law: s s 3. Ccal agl: s c / 4. Tal flc wh > c ly f > Rflc & Tasmss - D. Ray Kw Pla Wav λ wavfs λ λ. < ;

A Predator Prey Model with Discrete Time Delay Considering Different Growth Function of Prey

Avancs n Al Mahmacal Boscncs. ISSN 8-998 Volm, Nmb,. -6 Innaonal Rsach Pblcaon Hos h://www.hos.com A Pao P Mol wh Dsc Tm Dla Consng Dffn Gowh Fncon of P M.A. Ha Damn of Al Mahmacs Unvs of Wsn Onao, Lonon,

Mock Exam 7. 1 Hong Kong Educational Publishing Company. Section A 1. Reference: HKDSE Math M Q2 (a) (1 + kx) n 1M + 1A = (1) =

Mock Eam 7 Mock Eam 7 Section A. Reference: HKDSE Math M 0 Q (a) ( + k) n nn ( )( k) + nk ( ) + + nn ( ) k + nk + + + A nk... () nn ( ) k... () From (), k...() n Substituting () into (), nn ( ) n 76n 76n

Errata Sheet. 2 k. r 2. ts t. t t ... cos n W. cos nx W. W n x. Page Location Error Correction 2 Eq. (1.3) q dt. W/m K. 100 Last but 6 2.

Eaa S Pag can E Ccn Eq. (. q q k W/ K k W/ K A A 6 n as bu 6 s q lns s q T k T k Q.. Wall s aus n gvn Wall s aus a an C. 7 n, lf kc cs ( s sn kc cs ( s sn s f cs k sn cs k sn quan C ( s C ( s an ln 6 sn

General theorems of Optical Imaging systems

Gnral thorms of Optcal Imagng sstms Tratonal Optcal Imagng Topcs Imagng qualt harp: mags a pont sourc to a pont Dstorton fr: mags a shap to a smlar shap tgmatc Imagng Imags a pont sourc to a nfntl sharp

Calculus and Differential Equations page 1 of 17 CALCULUS and DIFFERENTIAL EQUATIONS

alculus and Diffrnial Equaions pag of 7 ALULUS and DIFFERENTIAL EQUATIONS Th following 55 qusions concrn calculus and diffrnial quaions. In his vrsion of h am, h firs choic is always h corrc on. In h acual

( ) ρ ρ + + = + d dt. ME 309 Formula Sheet. dp g dz = ρ. = f +ΣΚ and HS. +α + z = +α + z. δ =δ = δ =θ= τ =ρ =ρ. Page 1 of 7. Basic Equations.

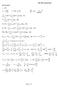Basic Eqaions ME 9 Fomla Shee R µ F F A A ηv V el η η A Vssem ( ) V el A F F V A ( ) S B XYZ XYZ el g F F a V V A S B / XYZ el M M A V ( ) S B el ( ) Q W ev e A hee V e g ino on el V consan (o invisci

! " #! $ %&! '( #)!' * +#, " -! %&! "!! ! " #$ % # " &' &'... ()* ( +, # ' -. + &', - + &' / # ' -. + &' (, % # , 2**.

! " #! $ %&! '( #)!' * +#, " -! %&! "!!! " #$ % # " &' &'... ()* ( +, # ' -. + &', - + &' / 0123 4 # ' -. + &' (, % #. -5 0126, 2**., 2, + &' %., 0, $!, 3,. 7 8 ', $$, 9, # / 3:*,*2;

!!" #7 $39 %" (07) ..,..,.. $ 39. ) :. :, «(», «%», «%», «%» «%». & ,. ). & :..,. '.. ( () #*. );..,..'. + (# ).

1 00 3 !!" 344#7 $39 %" 6181001 63(07) & : ' ( () #* ); ' + (# ) $ 39 ) : : 00 %" 6181001 63(07)!!" 344#7 «(» «%» «%» «%» «%» & ) 4 )&-%/0 +- «)» * «1» «1» «)» ) «(» «%» «%» + ) 30 «%» «%» )1+ / + : +3

Sarò signor io sol. α α. œ œ. œ œ œ œ µ œ œ. > Bass 2. Domenico Micheli. Canzon, ottava stanza. Soprano 1. Soprano 2. Alto 1

Sarò signor io sol Canzon, ottava stanza Domenico Micheli Soprano Soprano 2 Alto Alto 2 Α Α Sa rò si gnor io sol del mio pen sie io sol Sa rò si gnor io sol del mio pen sie io µ Tenor Α Tenor 2 Α Sa rò

Written Examination. Antennas and Propagation (AA ) April 26, 2017.

Written Examination Antennas and Propagation (AA. 6-7) April 6, 7. Problem ( points) Let us consider a wire antenna as in Fig. characterized by a z-oriented linear filamentary current I(z) = I cos(kz)ẑ

4.5 SUMMARY OF CURVE SKETCHING. Click here for answers. Click here for solutions. y cos x sin x. x 2 x 3 4. x 1 x y x 3 x

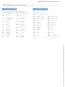SECTION.5 SUMMARY OF CURVE SKETCHING.5 SUMMARY OF CURVE SKETCHING A Click here for answers. S Click here for solutions. 9. 8 Use the guidelines of this section to sketch the curve. cos sin. 5. 6 8 7. cot..

Multi-dimensional Central Limit Theorem

Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t tme

Το άτομο του Υδρογόνου

Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες

Trigonometry 1.TRIGONOMETRIC RATIOS

Trigonometry.TRIGONOMETRIC RATIOS. If a ray OP makes an angle with the positive direction of X-axis then y x i) Sin ii) cos r r iii) tan x y (x 0) iv) cot y x (y 0) y P v) sec x r (x 0) vi) cosec y r (y

2. Chemical Thermodynamics and Energetics - I

. Chemical Thermodynamics and Energetics - I 1. Given : Initial Volume ( = 5L dm 3 Final Volume (V = 10L dm 3 ext = 304 cm of Hg Work done W = ext V ext = 304 cm of Hg = 304 atm [... 76cm of Hg = 1 atm]

MA6451-PROBABILITY & RANDOM PROCESS. UNIT-IV-CORRELATION AND SPECTRAL DENSITIES By K.VIJAYALAKSHMI Dept. of Applied mathematics

M645-POBBILIY & NDOM POCESS UNI-IV-COELION ND SPECL DENSIIES By K.VIJYLKSHMI Dp. of pplid mhmics COELION ND SPECL DENSIIES Dfiniion: uo Corrlion h uo Corrlion of rndom procss {x}is dfind by xx xx im vrg

Κεφάλαιο 2 Διαχείριση Σηµάτων σε Ψηφιακά Συστήµατα Ελέγχου

Κεφάλαιο 2 Διαχείριση Σηµάτων σε Ψηφιακά Συστήµατα Ελέγχου u Μετατροπή Αναλογικού Σήµατος σε Ψηφιακό (A/D Conversion) Ο µετασχηµατισµός Ζ u Μαθηµατική Ανάλυση της Διαδικασίας A/D Μετατροπή Ψηφιακού Σήµατος

[ ] [ ] ( ) 1 1 ( 1. ( x) Q2bi

NSW BOS Mhics Esio Soluios 8 F dowlod d pi fo wwwiuco Do o phoocopy opyigh 8 iuco Q L u 5 d ( ) c u u 5 Q Qc ( ) ( ) d 5 u d c d d l c d [ ] [ ] ( ) d l ( ) l l Qd L u fo > ( ) u d Wh u ; wh u d d ( u

Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού.

Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού. Περιοδικός πίνακας: α. Είναι µια ταξινόµηση των στοιχείων κατά αύξοντα

SUPPLEMENTAL INFORMATION. Fully Automated Total Metals and Chromium Speciation Single Platform Introduction System for ICP-MS

Electronic Supplementary Material (ESI) for Journal of Analytical Atomic Spectrometry. This journal is The Royal Society of Chemistry 2018 SUPPLEMENTAL INFORMATION Fully Automated Total Metals and Chromium

C M. V n: n =, (D): V 0,M : V M P = ρ ρ V V. = ρ

»»...» -300-0 () -300-03 () -3300 3.. 008 4 54. 4. 5 :.. ;.. «....... :. : 008. 37.. :....... 008.. :. :.... 54. 4. 5 5 6 ... : : 3 V mnu V mn AU 3 m () ; N (); N A 6030 3 ; ( ); V 3. : () 0 () 0 3 ()

16. 17. r t te 2t i t 1. 18 19 Find the derivative of the vector function. 19. r t e t cos t i e t sin t j ln t k. 31 33 Evaluate the integral.

SECTION.7 VECTOR FUNCTIONS AND SPACE CURVES.7 VECTOR FUNCTIONS AND SPACE CURVES A Click here for answers. S Click here for soluions. Copyrigh Cengage Learning. All righs reserved.. Find he domain of he

Multi-dimensional Central Limit Theorem

Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t ();

ibemo Kazakhstan Republic of Kazakhstan, West Kazakhstan Oblast, Aksai, Pramzone, BKKS office complex Phone: ; Fax:

C 1 D 1. AB = a, AD = b, AA1 = c. a, b, c : (1) AC 1 ; : (1) AB + BC + CC1, AC 1 = BC = AD, CC1 = AA 1, AC 1 = a + b + c. (2) BD 1 = BD + DD 1,

1 1., BD 1 B 1 1 D 1, E F B 1 D 1. B = a, D = b, 1 = c. a, b, c : (1) 1 ; () BD 1 ; () F; D 1 F 1 (4) EF. : (1) B = D, D c b 1 E a B 1 1 = 1, B1 1 = B + B + 1, 1 = a + b + c. () BD 1 = BD + DD 1, BD =

Average Run Length of Control Chart for ARX(1) Process with Exponential White Noise

Glol Jonl o P nd Appld Mc. ISSN 97-768 Vol, N 6, pp. 4-5 Rc Ind Plcon p://.plcon.co/gp. Avg Rn Lng o Conol C o AR Poc Exponnl W No Pypon Pc Dpn o Sc, Fcly o Scnc, Slpkon Unvy, Sncnd Plc cp, Nkon Po, 7,

1 B0 C00. nly Difo. r II. on III t o. ly II II. Di XR. Di un 5.8. Di Dinly. Di F/ / Dint. mou. on.3 3 D. 3.5 ird Thi. oun F/2. s m F/3 /3.

. F/ /3 3. I F/ 7 7 0 0 Mo ode del 0 00 0 00 A 6 A C00 00 0 S 0 C 0 008 06 007 07 09 A 0 00 0 00 0 009 09 A 7 I 7 7 0 0 F/.. 6 6 8 8 0 00 0 F/3 /3. fo I t o nt un D ou s ds 3. ird F/ /3 Thi ur T ou 0 Fo

ΓΗ ΚΑΙ ΣΥΜΠΑΝ. Εικόνα 1. Φωτογραφία του γαλαξία μας (από αρχείο της NASA)

ΓΗ ΚΑΙ ΣΥΜΠΑΝ Φύση του σύμπαντος Η γη είναι μία μονάδα μέσα στο ηλιακό μας σύστημα, το οποίο αποτελείται από τον ήλιο, τους πλανήτες μαζί με τους δορυφόρους τους, τους κομήτες, τα αστεροειδή και τους μετεωρίτες.

HONDA. Έτος κατασκευής

Accord + Coupe IV 2.0 16V (CB3) F20A2-A3 81 110 01/90-09/93 0800-0175 11,00 2.0 16V (CB3) F20A6 66 90 01/90-09/93 0800-0175 11,00 2.0i 16V (CB3-CC9) F20A8 98 133 01/90-09/93 0802-9205M 237,40 2.0i 16V

Example Sheet 3 Solutions

Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note

b. Use the parametrization from (a) to compute the area of S a as S a ds. Be sure to substitute for ds!

MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.

(... )..!, ".. (! ) # - $ % % $ & % 2007

(! ), "! ( ) # $ % & % $ % 007 500 ' 67905:5394!33 : (! ) $, -, * +,'; ), -, *! ' - " #!, $ & % $ ( % %): /!, " ; - : - +', 007 5 ISBN 978-5-7596-0766-3 % % - $, $ &- % $ % %, * $ % - % % # $ $,, % % #-

,, #,#, %&'(($#(#)&*"& 3,,#!4!4! +&'(#,-$#,./$012 5 # # %, )

!! "#$%&'%( (%)###**#+!"#$ ',##-.#,,, #,#, /01('/01/'#!2#! %&'(($#(#)&*"& 3,,#!4!4! +&'(#,-$#,./$012 5 # # %, ) 6###+! 4! 4! 4,*!47! 4! (! 8!9%,,#!41! 4! (! 4!5),!(8! 4! (! :!;!(7! (! 4! 4!!8! (! 8! 4!!8(!44!

ΦΥΣΙΚΑ ΜΕΓΕΘΗ Αριθμητικά ή Μονόμετρα μεγέθη: Όγκος Μάζα Χρόνος Ενέργεια κ.λ.π. Διανυσματικά μεγέθη: Μετατόπιση Δύναμη Ορμή Διανυσματικοί τελεστές

ΦΥΣΙΚΑ ΜΕΓΕΘΗ Αριθμητικά ή Μονόμετρα μεγέθη: Όγκος Μάζα Χρόνος Ενέργεια κ.λ.π. Διανυσματικά μεγέθη: Μετατόπιση Δύναμη Ορμή Διανυσματικοί τελεστές κ.λ.π. ΔΙΑΝΥΣΜΑΤΑ Παράσταση διανύσματος ΔΙΑΝΥΣΜΑΤΑ ΒΑΣΙΚΕΣ

Appendix A. Curvilinear coordinates. A.1 Lamé coefficients. Consider set of equations. ξ i = ξ i (x 1,x 2,x 3 ), i = 1,2,3

Appendix A Curvilinear coordinates A. Lamé coefficients Consider set of equations ξ i = ξ i x,x 2,x 3, i =,2,3 where ξ,ξ 2,ξ 3 independent, single-valued and continuous x,x 2,x 3 : coordinates of point

StringMassCylinder2. Clear["Global`*"] r = R * {Cos[theta[t]], Sin[theta[t]]} + u * {Sin[theta[t]], -Cos[theta[t]]}

StringMassCylinder2 In[2224]:= In[297]:= Out[297]= Clear["Global`*"] r = R * {Cos[theta[t]], Sin[theta[t]]} + u * {Sin[theta[t]], -Cos[theta[t]]} {R Cos[theta[t]] + u Sin[theta[t]], - u Cos[theta[t]] +

SOLUTIONS & ANSWERS FOR KERALA ENGINEERING ENTRANCE EXAMINATION-2018 PAPER II VERSION B1

SOLUTIONS & ANSWERS FOR KERALA ENGINEERING ENTRANCE EXAMINATION-8 PAPER II VERSION B [MATHEMATICS]. Ans: ( i) It is (cs5 isin5 ) ( i). Ans: i z. Ans: i i i The epressin ( i) ( ). Ans: cs i sin cs i sin

ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?

Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least

Boundary-Layer Flow over a Flat Plate Approximate Method

Bounar-aer lo oer a lat Plate Approimate Metho Transition Turbulent aminar The momentum balance on a control olume o the bounar laer leas to the olloing equation: + () The approimate metho o bounar laer

Exercises 10. Find a fundamental matrix of the given system of equations. Also find the fundamental matrix Φ(t) satisfying Φ(0) = I. 1.

Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given

Αλληλεπίδραση ακτίνων-χ με την ύλη

Άσκηση 8 Αλληλεπίδραση ακτίνων-χ με την ύλη Δ. Φ. Αναγνωστόπουλος Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων Ιωάννινα 2013 Άσκηση 8 ii Αλληλεπίδραση ακτίνων-χ με την ύλη Πίνακας περιεχομένων

( y) Partial Differential Equations

Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate

Reminders: linear functions

Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U

19. ATOMS, MOLECULES AND NUCLEI HOMEWORK SOLUTIONS

. ATOMS, MOLECULES AND NUCLEI HOMEWORK SOLUTIONS. Givn :.53 Å 3?? n n ε πm n n Radius of n t Bo obit, n n ε πm n n 3 n 3 n 3 (3) () (.53).77Å n n ( ) () (.53) 53 Å. Givn : 3 7.7 x m? n n ε πm Radius of

Ι ΙΟΤΗΤΕΣ ΤΩΝ ΑΤΟΜΩΝ. Παππάς Χρήστος Επίκουρος Καθηγητής

ΗΛΕΚΤΡΟΝΙΚΗ ΟΜΗ ΚΑΙ Ι ΙΟΤΗΤΕΣ ΤΩΝ ΑΤΟΜΩΝ Παππάς Χρήστος Επίκουρος Καθηγητής ΤΟ ΜΕΓΕΘΟΣ ΤΩΝ ΑΤΟΜΩΝ Ατομική ακτίνα (r) : ½ της απόστασης μεταξύ δύο ομοιοπυρηνικών ατόμων, ενωμένων με απλό ομοιοπολικό δεσμό.

CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS

CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =

Finite Field Problems: Solutions

Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The

Spherical Coordinates

Spherical Coordinates MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Spherical Coordinates Another means of locating points in three-dimensional space is known as the spherical

SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM

SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max

D Alembert s Solution to the Wave Equation

D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique

ΠΕΡΙΟΔΙΚΟΣ ΠΙΝΑΚΑΣ ΣΤΟΙΧΕΙΩΝ

ΠΕΡΙΟΔΙΚΟΣ ΠΙΝΑΚΑΣ ΣΤΟΙΧΕΙΩΝ Περίοδοι περιοδικού πίνακα Ο περιοδικός πίνακας αποτελείται από 7 περιόδους. Ο αριθμός των στοιχείων που περιλαμβάνει κάθε περίοδος δεν είναι σταθερός, δηλ. η περιοδικότητα

ΝΟΜΟΣ ΤΗΣ ΠΕΡΙΟ ΙΚΟΤΗΤΑΣ : Οι ιδιότητες των χηµικών στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού.

1. Ο ΠΕΡΙΟ ΙΚΟΣ ΠΙΝΑΚΑΣ Οι άνθρωποι από την φύση τους θέλουν να πετυχαίνουν σπουδαία αποτελέσµατα καταναλώνοντας το λιγότερο δυνατό κόπο και χρόνο. Για το σκοπό αυτό προσπαθούν να οµαδοποιούν τα πράγµατα

derivation of the Laplacian from rectangular to spherical coordinates

derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used

MathCity.org Merging man and maths

MathCity.org Merging man and maths Exercise 10. (s) Page Textbook of Algebra and Trigonometry for Class XI Available online @, Version:.0 Question # 1 Find the values of sin, and tan when: 1 π (i) (ii)

Lifting Entry (continued)

ifting Entry (continued) Basic planar dynamics of motion, again Yet another equilibrium glide Hypersonic phugoid motion Planar state equations MARYAN 1 01 avid. Akin - All rights reserved http://spacecraft.ssl.umd.edu

Convection Derivatives February 17, E+01 1.E-01 1.E-02 1.E-03 1.E-04 1.E-05 1.E-06 1.E-07 1.E-08 1.E-09 1.E-10. Error

onvcton rvtvs brry 7, nt Volm Mtho or onvcton rvtvs Lrry rtto Mchncl ngnrng 69 omttonl l ynmcs brry 7, Otln Rv nmrcl nlyss bscs oncl rslts or son th sorc nlyss Introc nt-volm mtho or convcton Not n or

3.4. Click here for solutions. Click here for answers. CURVE SKETCHING. y cos x sin x. x 1 x 2. x 2 x 3 4 y 1 x 2. x 5 2

SECTION. CURVE SKETCHING. CURVE SKETCHING A Click here for answers. S Click here for solutions. 9. Use the guidelines of this section to sketch the curve. cos sin. 5. 6 8 7 0. cot, 0.. 9. cos sin. sin

Commutative Monoids in Intuitionistic Fuzzy Sets

Commutative Monoids in Intuitionistic Fuzzy Sets S K Mala #1, Dr. MM Shanmugapriya *2 1 PhD Scholar in Mathematics, Karpagam University, Coimbatore, Tamilnadu- 641021 Assistant Professor of Mathematics,

Φασματοσκοπία υπεριώδους-ορατού (UV-Vis)

Καλαϊτζίδου Κυριακή Φασματοσκοπία υπεριώδους-ορατού (UV-Vis) Μέθοδος κυανού του μολυβδαινίου Προσθήκη SnCl 2 και (NH 4 ) 6 Mo 7 O 24 4H 2 O στο δείγμα Μέτρηση στα 690nm Μέτρηση 10-12min μετά από την προσθήκη

#%" )*& ##+," $ -,!./" %#/%0! %,!

-!"#$% -&!'"$ & #("$$, #%" )*& ##+," $ -,!./" %#/%0! %,! %!$"#" %!#0&!/" /+#0& 0.00.04. - 3 3,43 5 -, 4 $ $.. 04 ... 3. 6... 6.. #3 7 8... 6.. %9: 3 3 7....3. % 44 8... 6.4. 37; 3,, 443 8... 8.5. $; 3

George S. A. Shaker ECE477 Understanding Reflections in Media. Reflection in Media

Geoge S. A. Shake C477 Udesadg Reflecos Meda Refleco Meda Ths hadou ages a smplfed appoach o udesad eflecos meda. As a sude C477, you ae o equed o kow hese seps by hea. I s jus o make you udesad how some

Fourier Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics

Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)

Vidyamandir Classes. Solutions to Revision Test Series - 2/ ACEG / IITJEE (Mathematics) = 2 centre = r. a

Per -.(D).() Vdymndr lsses Solutons to evson est Seres - / EG / JEE - (Mthemtcs) Let nd re dmetrcl ends of crcle Let nd D re dmetrcl ends of crcle Hence mnmum dstnce s. y + 4 + 4 6 Let verte (h, k) then

EE512: Error Control Coding

EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3

m 1, m 2 F 12, F 21 F12 = F 21

m 1, m 2 F 12, F 21 F12 = F 21 r 1, r 2 r = r 1 r 2 = r 1 r 2 ê r = rê r F 12 = f(r)ê r F 21 = f(r)ê r f(r) f(r) < 0 f(r) > 0 m 1 r1 = f(r)ê r m 2 r2 = f(r)ê r r = r 1 r 2 r 1 = 1 m 1 f(r)ê r r 2 = 1 m

TeSys contactors a.c. coils for 3-pole contactors LC1-D

References a.c. coils for 3-pole contactors LC1-D Control circuit voltage Average resistance Inductance of Reference (1) Weight Uc at 0 C ± 10 % closed circuit For 3-pole " contactors LC1-D09...D38 and

Graded Refractive-Index

Graded Refractive-Index Common Devices Methodologies for Graded Refractive Index Methodologies: Ray Optics WKB Multilayer Modelling Solution requires: some knowledge of index profile n 2 x Ray Optics for

Laplace s Equation in Spherical Polar Coördinates

Laplace s Equation in Spheical Pola Coödinates C. W. David Dated: Januay 3, 001 We stat with the pimitive definitions I. x = sin θ cos φ y = sin θ sin φ z = cos θ thei inveses = x y z θ = cos 1 z = z cos1

Space Physics (I) [AP-3044] Lecture 1 by Ling-Hsiao Lyu Oct Lecture 1. Dipole Magnetic Field and Equations of Magnetic Field Lines

Space Physics (I) [AP-344] Lectue by Ling-Hsiao Lyu Oct. 2 Lectue. Dipole Magnetic Field and Equations of Magnetic Field Lines.. Dipole Magnetic Field Since = we can define = A (.) whee A is called the

Section 8.3 Trigonometric Equations

99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.

ECE Spring Prof. David R. Jackson ECE Dept. Notes 2

ECE 634 Spring 6 Prof. David R. Jackson ECE Dept. Notes Fields in a Source-Free Region Example: Radiation from an aperture y PEC E t x Aperture Assume the following choice of vector potentials: A F = =

Μεταφορά Πρότυπο διασποράς. Ευκίνητη φάση. Περιβάλλον κινητοποίησης στοιχείων. Περιβάλλον απόθεσης στοιχείων

Ευκίνητη φάση Μεταφορά Πρότυπο διασποράς Περιβάλλον κινητοποίησης στοιχείων Περιβάλλον απόθεσης στοιχείων ΣΤΑΔΙΟ ΠΕΡΙΒΑΛΛΟΝ ΒΑΘΟΥΣ ΠΕΡΒΑΛΛΟΝ ΕΠΙΦΑΝΕΙΑΣ ΠΡΩΤΟΓΕΝΕΣ Διάχυση μετάλλων σε περιβάλλοντα πετρώματα

van der Waals Ν Bohr Ν

Ν ( )Ν φ ) ( Ν van der Waals Ν Ν Χ Χ Θ Θ Ν ) ( ( ) ( Ν ( ( Bohr Ν ΝΆ (, )Ν Ν,, ) ) Ν ) Ν 1. Γ /,,,. φ. m, Ό V, P, Θ PV=nRT Van der Waals (P+n2a/V2)(V-nb)=nRT = b= : T Ω Γ φ ( Φ 24/10/2012, ) 11.00-13.00

ΘΕΡΜΟΚΗΠΙΑΚΕΣ ΚΑΛΛΙΕΡΓΕΙΕΣ ΕΚΤΟΣ ΕΔΑΦΟΥΣ ΘΡΕΠΤΙΚΑ ΔΙΑΛΥΜΑΤΑ

ΘΕΡΜΟΚΗΠΙΑΚΕΣ ΚΑΛΛΙΕΡΓΕΙΕΣ ΕΚΤΟΣ ΕΔΑΦΟΥΣ ΘΡΕΠΤΙΚΑ ΔΙΑΛΥΜΑΤΑ Θρεπτικό διάλυμα Είναι ένα αραιό υδατικό διάλυμα όλων των θρεπτικών στοιχείων που είναι απαραίτητα για τα φυτά, τα οποία βρίσκονται διαλυμένα

Numerical Analysis FMN011

Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =

k k ΚΕΦΑΛΑΙΟ 1 G = (V, E) V E V V V G E G e = {v, u} E v u e v u G G V (G) E(G) n(g) = V (G) m(g) = E(G) G S V (G) S G N G (S) = {u V (G)\S v S : {v, u} E(G)} G v S v V (G) N G (v) = N G ({v}) x V (G)

SCHOOL OF MATHEMATICAL SCIENCES G11LMA Linear Mathematics Examination Solutions

SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)

α A G C T 國立交通大學生物資訊及系統生物研究所林勇欣老師

A G C T Juks and Cantor s (969) on-aramtr modl A T C G A G 0 0 0-3 C T A() A( t ) ( 3 ) ( ) A() A() ( 3 ) ( ) A( A( A( A( t ) A( 3 A( t ) ( ) A( A( Juks and Cantor s (969) on-aramtr modl A( A( t ) A( d

Κεφάλαιο 2 Διαχείριση Σηµάτων σε Ψηφιακά Συστήµατα Ελέγχου

Κεφάλαιο 2 Διαχείριση Σηµάτων σε Ψηφιακά Συστήµατα Ελέγχου u Μετατροπή Αναλογικού Σήµατος σε Ψηφιακό (A/D Conversion) Ο µετασχηµατισµός Ζ u Μαθηµατική Ανάλυση της Διαδικασίας A/D Μετατροπή Ψηφιακού Σήµατος

MACCHINE A FLUIDO 2 CORRELAZIONE RENDIMENTO TURBINA A GAS S.F. SMITH

MACCHINE A FLUIDO CORRELAZIONE RENDIMENTO TURBINA A GAS S.F. SMITH MACCHINE A FLUIDO STADIO R.5 * 4 4 fs f 4 ( ) L MACCHINE A FLUIDO STADIO R.5 ϑ S ϑr a tan ( ) ξ.5 ( ϑ / 9) / 4 ( ) 3 MACCHINE A FLUIDO

ITU-R P (2012/02) &' (

ITU-R P.530-4 (0/0) $ % " "#! &' ( P ITU-R P. 530-4 ii.. (IPR) (ITU-T/ITU-R/ISO/IEC).ITU-R http://www.itu.int/itu-r/go/patents/en. ITU-T/ITU-R/ISO/IEC (http://www.itu.int/publ/r-rec/en ) () ( ) BO BR BS

Appendix A. Stability of the logistic semi-discrete model.

Ecological Archiv E89-7-A Elizava Pachpky, Rogr M. Nib, and William W. Murdoch. 8. Bwn dicr and coninuou: conumr-rourc dynamic wih ynchronizd rproducion. Ecology 89:8-88. Appndix A. Sabiliy of h logiic

ME 365: SYSTEMS, MEASUREMENTS, AND CONTROL (SMAC) I

ME 365: SYSTEMS, MEASUREMENTS, AND CONTROL SMAC) I Dynamicresponseof 2 nd ordersystem Prof.SongZhangMEG088) Solutions to ODEs Forann@thorderLTIsystem a n yn) + a n 1 y n 1) ++ a 1 "y + a 0 y = b m u m)

Appendix to On the stability of a compressible axisymmetric rotating flow in a pipe. By Z. Rusak & J. H. Lee

Appendi to On the stability of a compressible aisymmetric rotating flow in a pipe By Z. Rusak & J. H. Lee Journal of Fluid Mechanics, vol. 5 4, pp. 5 4 This material has not been copy-edited or typeset

2. THEORY OF EQUATIONS. PREVIOUS EAMCET Bits.

EAMCET-. THEORY OF EQUATIONS PREVIOUS EAMCET Bits. Each of the roots of the equation x 6x + 6x 5= are increased by k so that the new transformed equation does not contain term. Then k =... - 4. - Sol.

i i (3) Derive the fixed-point iteration algorithm and apply it to the data of Example 1.

Howor#3 urvval Aalyss Na: Huag Xw 黃昕蔚 Quso: uppos ha daa ( follow h odl ( ( > ad <

CNS.1 Compressible Navier-Stokes Time Averaged

CNS.1 Compressble Naver-Sokes Tme Averaged Insananeos flow conservaon prncples, compressble flow D M : L( ρ) = ρ + ( ρ ) = 0 x ρ D P : L( ρ ) = + ρ + pδ = 0 x D E : L( ρe) = ( ρe+ ρ / ) + ( ρh+ ρ / q)