1. Kaj je procesno inženirstvo? Procesno inženirstvo (procesna tehnika) je tehnično področje, ki se ukvarja s pripravljanjem in spreminjanjem snovi.
|
|
|
- Ἰσμήνη Ελευθερόπουλος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 1. Kaj je procesno inženirstvo? Procesno inženirstvo (procesna tehnika) je tehnično področje, ki se ukvarja s pripravljanjem in spreminjanjem snovi. 2. Kaj je glavna značilnost disperznega snovnega sistema? Pojem disperzni sistem tako pomeni drobno porazdelitev delcev ene snovi v drugi snovi. Delci so lahko: o trdne snovi (zrna), o kapljevine (kapljice) ali o plini (mehurčki). Prednost disperznega sistema: o velika površina med razpršeno (disperzno) in zvezno (tekočina) snovjo. 3. Kateri sta dve glavni področji procesnega strojništva? Mehanska procesna tehnika Toplotno-snovna procesna tehnika 4. Kateri so temeljni procesi (postopki), na katerih temelji naša civilizacija? Postopki spremembe energije in spremembe snovi so temeljni procesi, na katerih temelji naša civilizacija. 5. Kaj je glavna naloga okoljskega inženirstva (strojništva)? Zmanjšati neželene učinke človeških aktivnosti (predvsem industrijskih) na okolje. Najpomembnejši načini: o snovanje naprav in strojev z upoštevanjem vidika njihovih emisij (vpliva na okolje). o zmanjševanje vpliva emisij na okolje. o modeliranje razširjanja polutantov v okolju (voda, zemlja, zrak) in tehniško ukrepanje. 6. Kaj so glavni cilji v postopkih spremembe snovi v procesni in okoljski tehniki? Cilj postopkov je pridobitev snovi s točno določenimi lastnostmi. 7. Katera znanja potrebujemo pri določanju količine snovi, ki jo lahko v procesnem postopku spremenimo? Termodinamika. 8. Katera znanja potrebujemo pri določanju časa za potek procesnega postopka? Prenos toplote in snovi v tekočinah. 9. Kaj je značilno za heterogeno zmes? Heterogene zmesi so vse tiste zmesi, za katere ne veljajo pogoji homogenih zmesi. Heterogeno snov lahko na mehanski način ločimo v tiste osnovne dele ali faze, iz katerih je sestavljena. 10. Kaj je faza v procesni tehniki? Je homogen del heterogene snovi. 11. Katero je splošno pravilo za izračun snovnih lastnosti zmesi? Zmesi imajo drugačne lastnosti kot osnovne sestavine. Najboljša možnost: meritev lastnosti. Gostota zmesi je seštevek delnih gostot: o (gostota vode v aeracijskem bazenu?) o Izračun mešalno pravilo za sestavini kjer uporabimo ρ = ρ1 + ρ2 o dve sestavini, prostorninske deleže: o npr. specifična toplotna kapaciteta 12. V kakšnem stanju se začnejo vsi tehniški postopki v procesni in okoljski tehniki? Surovina
2 13. Kaj je suspenzija? Suspénzija je zmes tekočine (običajno kapljevine, redkeje plina) in v njej netopne trdne snovi. Delci trdne snovi so v tekočini dispergirani v obliki majhnih delcev. Fizikalno gledano gre za neobstojen heterogen sistem. Delci trdne snovi po navadi namreč težijo k posedanju (sedimentaciji) zaradi delovanja sile težnosti. 14. Kakšne vrste tekočine je zobna krema? Plastična tekočina 15. Kateri so pogoji ravnotežja v večsestavinskem sistemu? Mehansko, toploto in snovno ravnotežje. 16. Kdaj je doseženo ravnotežje pri prenosu toplote? dt = 0 -> T 1 = T Kateri režim prenosa toplote upoštevamo, če dimenzioniramo toplotno napravo z upoštevanjem izpada pogonskega agregata za vzdrževanje pretoka hladilnega/grelnega medija? Toplotni tok; Q=k x A 18. Kateri procesni parameter je najpomembnejši pri praznjenju silosa? Nasipni kot je pomemben procesni parameter o če želimo, da se bodo v sloju delci začeli premikati, mora biti kot (npr. nagib površine v silosu) večji kot nasipni kot. 19. Kateri način porazdelitve delcev je prikazan na spodnji sliki? Diferencialna ali frakcijska Integralna ali kumulativna 20. Kateri so osnovni mehanizmi mešanja? 21. Kaj je emulgiranje? Z emulgiranjem označujemo porazdelitev kapljic ene kapljevine (disperzna faza) v drugi kapljevini (zvezna faza), s katero se ne mešajo. Uporaba: o pospešitev prenosa snovi (ekstrakcija kapljevito - kapljevito), ali upočasnitev procesa ločevanja obeh kapljevin (emulzijske barve, hladilno-mazalne emulzije). Emulgiranje je izvedljivo predvsem v turbulentnem režimu toka. 22. Kaj je suspendiranje? Suspendiranje ali porazdelitev trdnih delcev v kapljevini z mešanjem zasledimo v številnih osnovnih procesnih postopkih: ekstrakciji trdno - kapljevito, kristalizaciji, homogenizaciji itn Kaj je zaplinjevanje? Je razprševanje plina v kapljevini 24. S kakšnim mešalom lahko mešamo vročo plastično maso? 25. Kaj je pogoj za začetek nekega procesa s prenosom snovi in toplote? Sprememba snovi, ki je posledica prenosa snovi med fazami, je odvisna od neravnotežnih pogojev v nekem delu procesne naprave.
3 26. Ali sta lahko dve fazi v ravnotežju, če obstaja na medfazni meji (vmesni površini) razlika v koncentraciji snovi? NE 27. Katere tri kriterije podobnosti morata izpolnjevati dva sistema, da ju imenujemo podobna? Geometrijska podobnost Kinematična podobnost Dinamična podobnost 28. Katera sta dva načina merilnega prenosa? Podobnostna teorija in računalniška dinamika tekočin. 29. Kateri so glavni vplivi na sušenje vlažne snovi? Na sušenje pomembno vplivajo: o Razmere v vlažni snovi Količina vlage Način vezave vlage Struktura snovi (porozna, polna) o Razmere v sušilnem plinu Temperatura Vlažnost plina 30. Za uparitev katerega dela vlage v vlažni snovi je potreben najdaljši čas sušenja? Če je snov porozna, se največ časa pri sušenju porabi za odstranjevanje (uparjanje) vlage v notranjosti snovi. 31. Kateremu stanju vlažnega zraka (kot sušilnega plina) se moramo pri sušenju nujno izogniti? Nenasičenemu področju. 32. Ali je smiselno sušiti higroskopsko snov do popolne osušitve materiala? Ne ni. 33. Kakšna je definicija vlažnosti snovi, ki jo sušimo (xg)? x G = m w m G,s 34. Čemu je namenjeno segrevanje sušilnega plina? Zagotovimo zadosten toplotni tok, ki se porabi za uparjanje vlage iz vlažne snovi. Povečamo sposobnost plina, da sprejme količine uparjene 35. Kaj je glavni namen postopka uparjanja v procesni tehniki? Namen uparjanja v procesni tehniki je koncentriranje raztopine = povečevanje deleža topljenca v zmesi - raztopini 36. Kateri je najpomembnejši parameter pri toplotnem ovrednotenju uparjalnika? Specifična poraba grelne pare 37. Kaj se najpogosteje uporablja kot grelni medij za uparjalnik? Nasičena para 38. Kaj je vzrok izločanja kristalov pri kristalizaciji iz raztopine? V primeru kristalizacije iz raztopine je stopnja podhladitve le okoli 1-2 K. Odločilni vpliv na rast kristalov ima prenos snovi. 39. Kaj je glavni vzrok za ločevanje sestavin iz kapljevite zmesi pri postopku destilacije? Vzrok ločevanja: različne temperature vrelišč oziroma različna hlapnost posameznih sestavin v kapljeviti zmesi. 40. Katera naprava je najbolj značilna za destilacijo in rektifikacijo? Domač kuhalnik alkohola (šnopsa) 41. Kaj je rektifikacija? Ponovitev destilacije na dobljenem produktu poveča delež alkohola. 42. S katerim postopkom ločujemo surovo nafto v posamezne delne zmesi? Frakcijska destilacija: ločevanje zmesi, v delne zmesi na osnovi območij temperatur vrelišč sestavin (ločevanje surove nafte).
4 43. Kaj je postopek absorpcije? ločitev ene ali več sestavin iz zmesi plinov s pomočjo: o fizikalnega raztapljanja v ustrezni kapljevini topilu, imenovanem absorbens, o kemijske reakcije s topilom. 44. Ali je potrebno absorpcijske stolpe hladiti? zaradi nižje učinkovitosti absorpcije pri povišani temperature je potrebno, absorpcijske stolpe hladiti. 45. Na kaj se pri postopku adsorpcije veže plinska sestavina? Trdno porozno snov 46. Kateri fazi moramo na koncu postopka ekstrakcije ločiti? ločitev faz: o filtriranje, o centrifugiranje 47. Ali je pri ekstrakciji smiselno segrevati topilo? Da 48. Kateri so dejavniki, ki pomembno vplivajo na uspešnost ekstrakcije? Velikost delcev Izbira topila Temperatura v sistemu Mešanje Razlika v koncentraciji 49. Kako povečamo izplen ekstrakcije (zmanjšanje deleža topljenca iz vstopne zmesi)? Z ločevanjem topila in topljenca 50. S katero napravo bi izločili kapljice iz toka plinov? Z vztrajnostim kolektorjem 51. Kaj je cikloniranje? Cikloniranje je izločanje trdnih delcev iz tekoče zmesi (plin, kapljevina) na osnovi delovanja centrifugalne sile. 52. Kateri filter je najpogosteje uporabljen v procesni tehniki? filtriranje skozi filtrno pogačo - najbolj pogosto v procesni tehniki, za koncentrirane suspenzije. 53. S katerimi filtri lahko iz velikih pretokov prašnega zraka odstranimo najmanjše delce? Elektrostatični ter elektro aktivni filtri 54. Katero mešalo je primernejše za suspendiranje? Prednost imajo aksialna mešala s smerjo črpanja proti dnu posode. 55. Katero mešalo je primernejše za razprševanje plina? Tisto z najvišjimi vrtilnimi hitrostmi 56. Kaj je glavna naloga mokrega kalcitnega postopka? Razžvepljevanje 57. Kateri ločevalni proces ni del mokrega kalcitnega postopka? 58. Kaj pomeni kratica BPK v okoljski tehniki? Biološka potreba po kisiku 59. Kaj pomeni kratica KPK v okoljski tehniki? Kemijska potreba po kisiku 60. Katere snovi so v največji meri prisotne v odpadnih vodah? Organske spojine
5 61. Kaj pomeni kratica TOC v okoljski tehniki? Skupni organski ogljik Total organic carbon Količino vseh organskih snovi (biološko razgradljivih in nerazgradljivih) v vodi ocenjujemo na osnovi določanja skupnega organskega ogljika -TOC kajti ogljik nastopa praktično v vseh molekulah organskih spojin 62. V kateri stopnji čiščenja odpadnih vod v biološki čistilni napravi se izvaja biološko čiščenje vode? 2. Stopnji 63. Kateri postopek se danes v večini primerov uporablja za biološko čiščenje odpadnih voda? Postopek s poživljenim blatom. 64. Katere so glavne prednosti sežiga blat iz čistilnih naprav? 65. Kaj sodi med tehnike ponovne uporabe trdnih odpadkov? 66. Kaj sodi med tehnike čiščenja onesnaženega zraka? Absorpcija, adsorpcija, kondenzacija, zgorevanje.
Termodinamika vlažnega zraka. stanja in spremembe
 Termodinamika vlažnega zraka stanja in spremembe Termodinamika vlažnega zraka Najpogostejši medij v sušilnih procesih konvektivnega sušenja je VLAŽEN ZRAK Obravnavamo ga kot dvokomponentno zmes Suhi zrak
Termodinamika vlažnega zraka stanja in spremembe Termodinamika vlažnega zraka Najpogostejši medij v sušilnih procesih konvektivnega sušenja je VLAŽEN ZRAK Obravnavamo ga kot dvokomponentno zmes Suhi zrak
ENERGETSKI STROJI. Energetski stroji. UNIVERZA V LJUBLJANI, FAKULTETA ZA STROJNIŠTVO Katedra za energetsko strojništvo
 ENERGETSKI STROJI Uvod Pregled teoretičnih osnov Hidrostatika Dinamika tekočin Termodinamika Podobnostni zakoni Volumetrični stroji Turbinski stroji Energetske naprave Podobnostni zakoni Kriteriji podobnosti
ENERGETSKI STROJI Uvod Pregled teoretičnih osnov Hidrostatika Dinamika tekočin Termodinamika Podobnostni zakoni Volumetrični stroji Turbinski stroji Energetske naprave Podobnostni zakoni Kriteriji podobnosti
Funkcijske vrste. Matematika 2. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 2. april Gregor Dolinar Matematika 2
 Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 5. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Diferencialna enačba, v kateri nastopata neznana funkcija in njen odvod v prvi potenci
 Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Logatherm WPL 14 AR T A ++ A + A B C D E F G A B C D E F G. kw kw /2013
 WP 14 R T d 9 10 11 53 d 2015 811/2013 WP 14 R T 2015 811/2013 WP 14 R T Naslednji podatki o izdelku izpolnjujejo zahteve uredb U 811/2013, 812/2013, 813/2013 in 814/2013 o dopolnitvi smernice 2010/30/U.
WP 14 R T d 9 10 11 53 d 2015 811/2013 WP 14 R T 2015 811/2013 WP 14 R T Naslednji podatki o izdelku izpolnjujejo zahteve uredb U 811/2013, 812/2013, 813/2013 in 814/2013 o dopolnitvi smernice 2010/30/U.
Osnove elektrotehnike uvod
 Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK
 1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
PONOVITEV SNOVI ZA 4. TEST
 PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
Kotne in krožne funkcije
 Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 21. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Delovna točka in napajalna vezja bipolarnih tranzistorjev
 KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
NEPARAMETRIČNI TESTI. pregledovanje tabel hi-kvadrat test. as. dr. Nino RODE
 NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
Prenos toplote prenos energije katerega pogojuje razlika temperatur temperatura je krajevno od točke do točke različna
 PRENOS OPOE Def. Prenos toplote prenos energije katerega pogojuje razlika temperatur temperatura je krajevno od točke do točke različna Načini prenosa toplote: PREVAJANJE (kondukcija, PRESOP (konvekcija
PRENOS OPOE Def. Prenos toplote prenos energije katerega pogojuje razlika temperatur temperatura je krajevno od točke do točke različna Načini prenosa toplote: PREVAJANJE (kondukcija, PRESOP (konvekcija
UNIVERZA V LJUBLJANI, FAKULTETA ZA STROJNIŠTVO Katedra za energetsko strojništvo VETRNICA. v 2. v 1 A 2 A 1. Energetski stroji
 Katedra za energetsko strojništo VETRNICA A A A Katedra za energetsko strojništo Katedra za energetsko strojništo VETRNICA A A A Δ Δp p p Δ Katedra za energetsko strojništo Teoretična moč etrnice Določite
Katedra za energetsko strojništo VETRNICA A A A Katedra za energetsko strojništo Katedra za energetsko strojništo VETRNICA A A A Δ Δp p p Δ Katedra za energetsko strojništo Teoretična moč etrnice Določite
ZAKLJUČNI PROCESI V BIOTEHNOLOGIJI. Membranski separacijski procesi koncentriranje ali čiščenje
 ZAKLJUČNI PROCESI V BIOTEHNOLOGIJI Membranski separacijski procesi koncentriranje ali čiščenje 5 glavnih stopenj pri izolaciji bioproduktov Predobdelava razbitje celic stabilizacija sterilizacija flokulacija
ZAKLJUČNI PROCESI V BIOTEHNOLOGIJI Membranski separacijski procesi koncentriranje ali čiščenje 5 glavnih stopenj pri izolaciji bioproduktov Predobdelava razbitje celic stabilizacija sterilizacija flokulacija
RANKINOV KROŽNI PROCES Seminar za predmet JTE
 RANKINOV KROŽNI PROCES Seminar za predmet JTE Rok Krpan 16.12.2010 Mentor: izr. prof. Iztok Tiselj Carnotov krožni proces Iz štirih sprememb: dveh izotermnih in dveh izentropnih (reverzibilnih adiabatnih)
RANKINOV KROŽNI PROCES Seminar za predmet JTE Rok Krpan 16.12.2010 Mentor: izr. prof. Iztok Tiselj Carnotov krožni proces Iz štirih sprememb: dveh izotermnih in dveh izentropnih (reverzibilnih adiabatnih)
1. Trikotniki hitrosti
 . Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
. Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 14. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
ZAKLJUČNI PROCESI V BIOTEHNOLOGIJI. Membranski separacijski procesi koncentriranje ali čiščenje
 ZAKLJUČNI PROCESI V BIOTEHNOLOGIJI Membranski separacijski procesi koncentriranje ali čiščenje 5 glavnih stopenj pri izolaciji bioproduktov Predobdelava razbitje celic stabilizacija sterilizacija flokulacija
ZAKLJUČNI PROCESI V BIOTEHNOLOGIJI Membranski separacijski procesi koncentriranje ali čiščenje 5 glavnih stopenj pri izolaciji bioproduktov Predobdelava razbitje celic stabilizacija sterilizacija flokulacija
1. Definicijsko območje, zaloga vrednosti. 2. Naraščanje in padanje, ekstremi. 3. Ukrivljenost. 4. Trend na robu definicijskega območja
 ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
Tabele termodinamskih lastnosti vode in vodne pare
 Univerza v Ljubljani Fakulteta za strojništvo Laboratorij za termoenergetiko Tabele termodinamskih lastnosti vode in vodne pare po modelu IAPWS IF-97 izračunano z XSteam Excel v2.6 Magnus Holmgren, xsteam.sourceforge.net
Univerza v Ljubljani Fakulteta za strojništvo Laboratorij za termoenergetiko Tabele termodinamskih lastnosti vode in vodne pare po modelu IAPWS IF-97 izračunano z XSteam Excel v2.6 Magnus Holmgren, xsteam.sourceforge.net
ZAKLJUČNI PROCESI V BIOTEHNOLOGIJI. Membranski separacijski procesi: diafiltracija, elektrodializa, reverzna osmoza, pervaporacija
 ZAKLJUČNI PROCESI V BIOTEHNOLOGIJI Membranski separacijski procesi: diafiltracija, elektrodializa, reverzna osmoza, pervaporacija Membranski separacijski procesi v biotehnologiji proces mikrofiltracija
ZAKLJUČNI PROCESI V BIOTEHNOLOGIJI Membranski separacijski procesi: diafiltracija, elektrodializa, reverzna osmoza, pervaporacija Membranski separacijski procesi v biotehnologiji proces mikrofiltracija
Tretja vaja iz matematike 1
 Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 22. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Simbolni zapis in množina snovi
 Simbolni zapis in množina snovi RELATIVNA MOLEKULSKA MASA ON MOLSKA MASA Relativna molekulska masa Ker so atomi premajhni, da bi jih merili z običajnimi tehtnicami, so ugotovili, kako jih izračunati. Izražamo
Simbolni zapis in množina snovi RELATIVNA MOLEKULSKA MASA ON MOLSKA MASA Relativna molekulska masa Ker so atomi premajhni, da bi jih merili z običajnimi tehtnicami, so ugotovili, kako jih izračunati. Izražamo
p 1 ENTROPIJSKI ZAKON
 ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
Fazni diagram binarne tekočine
 Fazni diagram binarne tekočine Žiga Kos 5. junij 203 Binarno tekočino predstavljajo delci A in B. Ti se med seboj lahko mešajo v različnih razmerjih. V nalogi želimo izračunati fazni diagram take tekočine,
Fazni diagram binarne tekočine Žiga Kos 5. junij 203 Binarno tekočino predstavljajo delci A in B. Ti se med seboj lahko mešajo v različnih razmerjih. V nalogi želimo izračunati fazni diagram take tekočine,
Aleš Mrhar. kinetični ni vidiki. Izraženo s hitrostjo in maso, dx/dt očistkom
 Izločanje zdravilnih učinkovin u iz telesa: kinetični ni vidiki Biofarmacija s farmakokinetiko Univerzitetni program Farmacija Aleš Mrhar Izločanje učinkovinu Izraženo s hitrostjo in maso, dx/ k e U očistkom
Izločanje zdravilnih učinkovin u iz telesa: kinetični ni vidiki Biofarmacija s farmakokinetiko Univerzitetni program Farmacija Aleš Mrhar Izločanje učinkovinu Izraženo s hitrostjo in maso, dx/ k e U očistkom
SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK
 SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
Laboratorij za termoenergetiko. Vodikove tehnologije in PEM gorivne celice
 Laboratorij za termoenergetiko Vodikove tehnologije in PEM gorivne celice Pokrivanje svetovnih potreb po energiji premog 27% plin 22% biomasa 10% voda 2% sonce 0,4% veter 0,3% nafta 32% jedrska 6% geoterm.
Laboratorij za termoenergetiko Vodikove tehnologije in PEM gorivne celice Pokrivanje svetovnih potreb po energiji premog 27% plin 22% biomasa 10% voda 2% sonce 0,4% veter 0,3% nafta 32% jedrska 6% geoterm.
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * FIZIKA NAVODILA ZA OCENJEVANJE. Petek, 10. junij 2016 SPLOŠNA MATURA
 Državni izpitni center *M16141113* SPOMLADANSKI IZPITNI ROK FIZIKA NAVODILA ZA OCENJEVANJE Petek, 1. junij 16 SPLOŠNA MATURA RIC 16 M161-411-3 M161-411-3 3 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor
Državni izpitni center *M16141113* SPOMLADANSKI IZPITNI ROK FIZIKA NAVODILA ZA OCENJEVANJE Petek, 1. junij 16 SPLOŠNA MATURA RIC 16 M161-411-3 M161-411-3 3 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor
Izločanje zdravilnih učinkovin iz telesa:
 Izločanje zdravilnih učinkovin iz telesa: kinetični vidiki Biofarmacija s farmakokinetiko Aleš Mrhar Izločanje učinkovin Izraženo s hitrostjo in maso, dx/dt = k e U očistkom in volumnom, Cl = k e V Hitrost
Izločanje zdravilnih učinkovin iz telesa: kinetični vidiki Biofarmacija s farmakokinetiko Aleš Mrhar Izločanje učinkovin Izraženo s hitrostjo in maso, dx/dt = k e U očistkom in volumnom, Cl = k e V Hitrost
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 10. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου...
 ΑΠΟΖΗΜΙΩΣΗ ΘΥΜΑΤΩΝ ΕΓΚΛΗΜΑΤΙΚΩΝ ΠΡΑΞΕΩΝ ΣΛΟΒΕΝΙΑ 1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου... 3 1 1. Έντυπα αιτήσεων
ΑΠΟΖΗΜΙΩΣΗ ΘΥΜΑΤΩΝ ΕΓΚΛΗΜΑΤΙΚΩΝ ΠΡΑΞΕΩΝ ΣΛΟΒΕΝΙΑ 1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου... 3 1 1. Έντυπα αιτήσεων
8. Diskretni LTI sistemi
 8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
Zaporedna in vzporedna feroresonanca
 Visokonapetostna tehnika Zaporedna in vzporedna feroresonanca delovanje regulacijskega stikala T3 174 kv Vaja 9 1 Osnovni pogoji za nastanek feroresonance L C U U L () U C () U L = U L () U C = ωc V vezju
Visokonapetostna tehnika Zaporedna in vzporedna feroresonanca delovanje regulacijskega stikala T3 174 kv Vaja 9 1 Osnovni pogoji za nastanek feroresonance L C U U L () U C () U L = U L () U C = ωc V vezju
Booleova algebra. Izjave in Booleove spremenljivke
 Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
Energije in okolje 1. vaja. Entalpija pri kemijskih reakcijah
 Entalpija pri kemijskih reakcijah Pri obravnavi energijskih pretvorb pri kemijskih reakcijah uvedemo pojem entalpije, ki popisuje spreminjanje energije sistema pri konstantnem tlaku. Sistemu lahko povečamo
Entalpija pri kemijskih reakcijah Pri obravnavi energijskih pretvorb pri kemijskih reakcijah uvedemo pojem entalpije, ki popisuje spreminjanje energije sistema pri konstantnem tlaku. Sistemu lahko povečamo
Kontrolne karte uporabljamo za sprotno spremljanje kakovosti izdelka, ki ga izdelujemo v proizvodnem procesu.
 Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
Separacijski procesi zapiski predavanj
 10.Ekstrakcija 10.1Uvod Ekstrakcija je operacija, s katero odstranjujemo iz trdnih ali tekočih zmesi topne komponente s topilom. Ekstrakcija sestoji iz dveh zaporednih postopkov, in sicer v prvem spravimo
10.Ekstrakcija 10.1Uvod Ekstrakcija je operacija, s katero odstranjujemo iz trdnih ali tekočih zmesi topne komponente s topilom. Ekstrakcija sestoji iz dveh zaporednih postopkov, in sicer v prvem spravimo
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * NAVODILA ZA OCENJEVANJE. Sreda, 3. junij 2015 SPLOŠNA MATURA
 Državni izpitni center *M15143113* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sreda, 3. junij 2015 SPLOŠNA MATURA RIC 2015 M151-431-1-3 2 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor Naloga Odgovor
Državni izpitni center *M15143113* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sreda, 3. junij 2015 SPLOŠNA MATURA RIC 2015 M151-431-1-3 2 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor Naloga Odgovor
+105 C (plošče in trakovi +85 C) -50 C ( C)* * Za temperature pod C se posvetujte z našo tehnično službo. ϑ m *20 *40 +70
 KAIFLEX ST Tehnični podatki Material Izjemno fleksibilna zaprtocelična izolacija, fleksibilna elastomerna pena (FEF) Opis Uporaba Temperaturno območje Toplotna prevodnost W/(m K ) pri različnih srednjih
KAIFLEX ST Tehnični podatki Material Izjemno fleksibilna zaprtocelična izolacija, fleksibilna elastomerna pena (FEF) Opis Uporaba Temperaturno območje Toplotna prevodnost W/(m K ) pri različnih srednjih
Gradniki TK sistemov
 Gradniki TK sistemov renos signalov v višji rekvenčni legi Vsebina Modulacija in demodulacija Vrste analognih modulacij AM M FM rimerjava spektrov analognih moduliranih signalov Mešalniki Kdaj uporabimo
Gradniki TK sistemov renos signalov v višji rekvenčni legi Vsebina Modulacija in demodulacija Vrste analognih modulacij AM M FM rimerjava spektrov analognih moduliranih signalov Mešalniki Kdaj uporabimo
IZPIT IZ ANALIZE II Maribor,
 Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
Vaja: Odbojnostni senzor z optičnimi vlakni. Namen vaje
 Namen vaje Spoznavanje osnovnih fiber-optičnih in optomehanskih komponent Spoznavanje načela delovanja in praktične uporabe odbojnostnega senzorja z optičnimi vlakni, Delo z merilnimi instrumenti (signal-generator,
Namen vaje Spoznavanje osnovnih fiber-optičnih in optomehanskih komponent Spoznavanje načela delovanja in praktične uporabe odbojnostnega senzorja z optičnimi vlakni, Delo z merilnimi instrumenti (signal-generator,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):
![matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij): matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):](/thumbs/87/96579490.jpg) 4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
Osnovne stehiometrijske veličine
 Osnovne stehiometrijske veličine Stehiometrija (grško: stoiheion snov, metron merilo) obravnava količinske odnose pri kemijskih reakcijah. Fizikalne veličine, s katerimi kemik najpogosteje izraža količino
Osnovne stehiometrijske veličine Stehiometrija (grško: stoiheion snov, metron merilo) obravnava količinske odnose pri kemijskih reakcijah. Fizikalne veličine, s katerimi kemik najpogosteje izraža količino
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * NAVODILA ZA OCENJEVANJE. Petek, 12. junij 2015 SPLOŠNA MATURA
 Državni izpitni center *M543* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Petek,. junij 05 SPLOŠNA MATURA RIC 05 M543 M543 3 IZPITNA POLA Naloga Odgovor Naloga Odgovor Naloga Odgovor Naloga Odgovor
Državni izpitni center *M543* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Petek,. junij 05 SPLOŠNA MATURA RIC 05 M543 M543 3 IZPITNA POLA Naloga Odgovor Naloga Odgovor Naloga Odgovor Naloga Odgovor
Poglavje 7. Poglavje 7. Poglavje 7. Regulacijski sistemi. Regulacijski sistemi. Slika 7. 1: Normirana blokovna shema regulacije EM
 Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
Integralni račun. Nedoločeni integral in integracijske metrode. 1. Izračunaj naslednje nedoločene integrale: (a) dx. (b) x 3 +3+x 2 dx, (c) (d)
 Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
Tokovi v naravoslovju za 6. razred
 Tokovi v naravoslovju za 6. razred Bojan Golli in Nada Razpet PeF Ljubljana 7. december 2007 Kazalo 1 Fizikalne osnove 2 1.1 Energija in informacija............................... 3 2 Projekti iz fizike
Tokovi v naravoslovju za 6. razred Bojan Golli in Nada Razpet PeF Ljubljana 7. december 2007 Kazalo 1 Fizikalne osnove 2 1.1 Energija in informacija............................... 3 2 Projekti iz fizike
Kvantni delec na potencialnem skoku
 Kvantni delec na potencialnem skoku Delec, ki se giblje premo enakomerno, pride na mejo, kjer potencial naraste s potenciala 0 na potencial. Takšno potencialno funkcijo zapišemo kot 0, 0 0,0. Slika 1:
Kvantni delec na potencialnem skoku Delec, ki se giblje premo enakomerno, pride na mejo, kjer potencial naraste s potenciala 0 na potencial. Takšno potencialno funkcijo zapišemo kot 0, 0 0,0. Slika 1:
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
MOTORJI Z NOTRANJIM ZGOREVANJEM
 MOTORJI Z NOTRANJIM ZGOREVANJEM Dvotaktni Štititaktni Motorji z notranjim zgorevanjem Motorji z zunanjim zgorevanjem izohora: Otto motor izohora in izoterma: Stirling motor izobara: Diesel motor izohora
MOTORJI Z NOTRANJIM ZGOREVANJEM Dvotaktni Štititaktni Motorji z notranjim zgorevanjem Motorji z zunanjim zgorevanjem izohora: Otto motor izohora in izoterma: Stirling motor izobara: Diesel motor izohora
Namen določanja vlažnost lesa
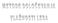 Namen določanja vlažnost lesa V svežem lesu določitev količine vode v lesu Pred izvajanjem sušenja izbira pravilnega programa sušenja Med izvajanjem sušilnega postopka primerjava dejanskega stanja s programiranim
Namen določanja vlažnost lesa V svežem lesu določitev količine vode v lesu Pred izvajanjem sušenja izbira pravilnega programa sušenja Med izvajanjem sušilnega postopka primerjava dejanskega stanja s programiranim
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 12. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
ČHE AVČE. Konzorcij RUDIS MITSUBISHI ELECTRIC SUMITOMO
 ČHE AVČE Konzorcij RUDIS MITSUBISHI ELECTRIC SUMITOMO MONTAŽA IN DOBAVA AGREGATA ČRPALKA / TURBINA MOTOR / GENERATOR S POMOŽNO OPREMO Anton Hribar d.i.s OSNOVNI TEHNIČNI PODATKI ČRPALNE HIDROELEKTRARNE
ČHE AVČE Konzorcij RUDIS MITSUBISHI ELECTRIC SUMITOMO MONTAŽA IN DOBAVA AGREGATA ČRPALKA / TURBINA MOTOR / GENERATOR S POMOŽNO OPREMO Anton Hribar d.i.s OSNOVNI TEHNIČNI PODATKI ČRPALNE HIDROELEKTRARNE
13. Jacobijeva metoda za računanje singularnega razcepa
 13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
Kotni funkciji sinus in kosinus
 Kotni funkciji sinus in kosinus Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z oznako cos x, DEFINICIJA V PRAVOKOTNEM TRIKOTNIKU: Kotna funkcija sinus je definirana kot razmerje
Kotni funkciji sinus in kosinus Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z oznako cos x, DEFINICIJA V PRAVOKOTNEM TRIKOTNIKU: Kotna funkcija sinus je definirana kot razmerje
ZBIRKA REŠENIH PROBLEMOV IN NALOG
 Izr. Prof. dr. Andrej Kitanovski Asist. dr. Urban Tomc Prof. dr. Alojz Poredoš ZBIRKA REŠENIH PROBLEMOV IN NALOG Učni pripomoček pri predmetu Prenos toplote in snovi Ljubljana, 2017 V tem delu so zbrane
Izr. Prof. dr. Andrej Kitanovski Asist. dr. Urban Tomc Prof. dr. Alojz Poredoš ZBIRKA REŠENIH PROBLEMOV IN NALOG Učni pripomoček pri predmetu Prenos toplote in snovi Ljubljana, 2017 V tem delu so zbrane
2.1. MOLEKULARNA ABSORPCIJSKA SPEKTROMETRIJA
 2.1. MOLEKULARNA ABSORPCJSKA SPEKTROMETRJA Molekularna absorpcijska spektrometrija (kolorimetrija, fotometrija, spektrofotometrija) temelji na merjenju absorpcije svetlobe, ki prehaja skozi preiskovano
2.1. MOLEKULARNA ABSORPCJSKA SPEKTROMETRJA Molekularna absorpcijska spektrometrija (kolorimetrija, fotometrija, spektrofotometrija) temelji na merjenju absorpcije svetlobe, ki prehaja skozi preiskovano
II. gimnazija Maribor PROJEKTNA NALOGA. Mentor oblike: Mirko Pešec, prof. Predmet: kemija - informatika
 II. gimnazija Maribor PROJEKTNA NALOGA Mentor vsebine: Irena Ilc, prof. Avtor: Andreja Urlaub Mentor oblike: Mirko Pešec, prof. Predmet: kemija - informatika Selnica ob Dravi, januar 2005 KAZALO VSEBINE
II. gimnazija Maribor PROJEKTNA NALOGA Mentor vsebine: Irena Ilc, prof. Avtor: Andreja Urlaub Mentor oblike: Mirko Pešec, prof. Predmet: kemija - informatika Selnica ob Dravi, januar 2005 KAZALO VSEBINE
OSNOVE HIDROSTATIKE. - vede, ki preučuje mirujoče tekočine
 OSNOVE HIDROSTATIKE - vede, ki preučuje mirujoče tekočine HIDROSTATIKA Značilnost, da je sila na katero koli točko v tekočini enaka iz vseh smeri. Če ta pogoj o ravnovesju sil ne velja, se tekočina premakne
OSNOVE HIDROSTATIKE - vede, ki preučuje mirujoče tekočine HIDROSTATIKA Značilnost, da je sila na katero koli točko v tekočini enaka iz vseh smeri. Če ta pogoj o ravnovesju sil ne velja, se tekočina premakne
ARHITEKTURA DETAJL 1, 1:10
 0.15 0.25 3.56 0.02 0.10 0.12 0.10 SESTV S2 polimer-bitumenska,dvoslojna(po),... 1.0 cm po zahtevah SIST DIN 52133 in nadstandardno, (glej opis v tehn.poročilu), npr.: PHOENIX STR/Super 5 M * GEMINI P
0.15 0.25 3.56 0.02 0.10 0.12 0.10 SESTV S2 polimer-bitumenska,dvoslojna(po),... 1.0 cm po zahtevah SIST DIN 52133 in nadstandardno, (glej opis v tehn.poročilu), npr.: PHOENIX STR/Super 5 M * GEMINI P
Podobnost matrik. Matematika II (FKKT Kemijsko inženirstvo) Diagonalizacija matrik
 Podobnost matrik Matematika II (FKKT Kemijsko inženirstvo) Matjaž Željko FKKT Kemijsko inženirstvo 14 teden (Zadnja sprememba: 23 maj 213) Matrika A R n n je podobna matriki B R n n, če obstaja obrnljiva
Podobnost matrik Matematika II (FKKT Kemijsko inženirstvo) Matjaž Željko FKKT Kemijsko inženirstvo 14 teden (Zadnja sprememba: 23 maj 213) Matrika A R n n je podobna matriki B R n n, če obstaja obrnljiva
Katedra za farmacevtsko kemijo. Sinteza mimetika encima SOD 2. stopnja: Mn 3+ ali Cu 2+ salen kompleks. 25/11/2010 Vaje iz Farmacevtske kemije 3 1
 Katedra za farmacevtsko kemijo Sinteza mimetika encima SOD 2. stopnja: Mn 3+ ali Cu 2+ salen kompleks 25/11/2010 Vaje iz Farmacevtske kemije 3 1 Sinteza kompleksa [Mn 3+ (salen)oac] Zakaj uporabljamo brezvodni
Katedra za farmacevtsko kemijo Sinteza mimetika encima SOD 2. stopnja: Mn 3+ ali Cu 2+ salen kompleks 25/11/2010 Vaje iz Farmacevtske kemije 3 1 Sinteza kompleksa [Mn 3+ (salen)oac] Zakaj uporabljamo brezvodni
Načini vodenja bioprocesov Bioreaktorji Zaključni procesi
 Načini vodenja bioprocesov Bioreaktorji Zaključni procesi Načini obratovanja Šaržni Šaržni z napajanjem substrata ali gojenje z dohranjevanjem.. Kontinuirno gojenje. V Načini vodenja bioprocesov Šaržni
Načini vodenja bioprocesov Bioreaktorji Zaključni procesi Načini obratovanja Šaržni Šaržni z napajanjem substrata ali gojenje z dohranjevanjem.. Kontinuirno gojenje. V Načini vodenja bioprocesov Šaržni
Transformator. Delovanje transformatorja I. Delovanje transformatorja II
 Transformator Transformator je naprava, ki v osnovi pretvarja napetost iz enega nivoja v drugega. Poznamo vrsto različnih izvedb transformatorjev, glede na njihovo specifičnost uporabe:. Energetski transformator.
Transformator Transformator je naprava, ki v osnovi pretvarja napetost iz enega nivoja v drugega. Poznamo vrsto različnih izvedb transformatorjev, glede na njihovo specifičnost uporabe:. Energetski transformator.
Osnove sklepne statistike
 Univerza v Ljubljani Fakulteta za farmacijo Osnove sklepne statistike doc. dr. Mitja Kos, mag. farm. Katedra za socialno farmacijo e-pošta: mitja.kos@ffa.uni-lj.si Intervalna ocena oz. interval zaupanja
Univerza v Ljubljani Fakulteta za farmacijo Osnove sklepne statistike doc. dr. Mitja Kos, mag. farm. Katedra za socialno farmacijo e-pošta: mitja.kos@ffa.uni-lj.si Intervalna ocena oz. interval zaupanja
MODERIRANA RAZLIČICA
 Dr`avni izpitni center *N07143132* REDNI ROK KEMIJA PREIZKUS ZNANJA Maj 2007 NAVODILA ZA VREDNOTENJE NACIONALNO PREVERJANJE ZNANJA b kncu 3. bdbja MODERIRANA RAZLIČICA RIC 2007 2 N071-431-3-2 NAVODILA
Dr`avni izpitni center *N07143132* REDNI ROK KEMIJA PREIZKUS ZNANJA Maj 2007 NAVODILA ZA VREDNOTENJE NACIONALNO PREVERJANJE ZNANJA b kncu 3. bdbja MODERIRANA RAZLIČICA RIC 2007 2 N071-431-3-2 NAVODILA
Difuzijsko in kinetično zgorevanje tekočega naftnega plina
 Univerza v Ljubljani Fakulteta za strojništvo Aškerčeva 6 1 Ljubljana, Slovenija telefon: 1 477 12 faks: 1 251 85 67 www.fs.uni-lj.si e-mail: dekanat@fs.uni-lj.si Katedra za energetsko strojništvo Laboratorij
Univerza v Ljubljani Fakulteta za strojništvo Aškerčeva 6 1 Ljubljana, Slovenija telefon: 1 477 12 faks: 1 251 85 67 www.fs.uni-lj.si e-mail: dekanat@fs.uni-lj.si Katedra za energetsko strojništvo Laboratorij
Laboratorij za termoenergetiko. Vodikove tehnologije
 Laboratorij za termoenergetiko Vodikove tehnologije Pokrivanje svetovnih potreb po energiji premog 27% plin 22% biomasa 10% voda 2% sonce 0,4% veter 0,3% nafta 32% jedrska 6% geoterm. 0,2% biogoriva 0,2%
Laboratorij za termoenergetiko Vodikove tehnologije Pokrivanje svetovnih potreb po energiji premog 27% plin 22% biomasa 10% voda 2% sonce 0,4% veter 0,3% nafta 32% jedrska 6% geoterm. 0,2% biogoriva 0,2%
1. TVORBA ŠIBKEGA (SIGMATNEGA) AORISTA: Največ grških glagolov ima tako imenovani šibki (sigmatni) aorist. Osnova se tvori s. γραψ
 TVORBA AORISTA: Grški aorist (dovršnik) izraža dovršno dejanje; v indikativu izraža poleg dovršnosti tudi preteklost. Za razliko od prezenta ima aorist posebne aktivne, medialne in pasivne oblike. Pri
TVORBA AORISTA: Grški aorist (dovršnik) izraža dovršno dejanje; v indikativu izraža poleg dovršnosti tudi preteklost. Za razliko od prezenta ima aorist posebne aktivne, medialne in pasivne oblike. Pri
NOVE GENERACIJE GORILNIKOV IN ZNIŽEVANJE CO 2
 NOVE GENERACIJE GORILNIKOV IN ZNIŽEVANJE CO 2 Martin Klančišar Weishaupt d.o.o., Celje 1. Gorilniki kot naprave za zgorevanje različnih energentov so v svojem razvoju dosegli zavidljivo raven učinkovitosti
NOVE GENERACIJE GORILNIKOV IN ZNIŽEVANJE CO 2 Martin Klančišar Weishaupt d.o.o., Celje 1. Gorilniki kot naprave za zgorevanje različnih energentov so v svojem razvoju dosegli zavidljivo raven učinkovitosti
Nekateri primeri sklopov izpitnih vprašanj pri predmetu Naključni pojavi
 Nekateri primeri sklopov izpitnih vprašanj pri predmetu Naključni pojavi 1. Izpeljite Binomsko porazdelitev in pokažite kako pridemo iz nje do Poissonove porazdelitve? 2. Kako opišemo naključne lastnosti
Nekateri primeri sklopov izpitnih vprašanj pri predmetu Naključni pojavi 1. Izpeljite Binomsko porazdelitev in pokažite kako pridemo iz nje do Poissonove porazdelitve? 2. Kako opišemo naključne lastnosti
Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba.
 1. Osnovni pojmi Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba. Primer 1.1: Diferencialne enačbe so izrazi: y
1. Osnovni pojmi Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba. Primer 1.1: Diferencialne enačbe so izrazi: y
Gimnazija Krˇsko. vektorji - naloge
 Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
Krogelni ventil MODUL
 Krogelni ventil MODUL Izdaja 0115 KV 2102 (PN) KV 2102 (PN) KV 2122(PN1) KV 2122(PN1) KV 2142RA KV 2142MA (PN) KV 2142TR KV 2142TM (PN) KV 2162 (PN) KV 2162 (PN) Stran 1 Dimenzije DN PN [bar] PN1 [bar]
Krogelni ventil MODUL Izdaja 0115 KV 2102 (PN) KV 2102 (PN) KV 2122(PN1) KV 2122(PN1) KV 2142RA KV 2142MA (PN) KV 2142TR KV 2142TM (PN) KV 2162 (PN) KV 2162 (PN) Stran 1 Dimenzije DN PN [bar] PN1 [bar]
L-400 TEHNIČNI KATALOG. Talni konvektorji
 30 50 30-00 TEHIČI KATAOG 300 Talni konvektorji TAI KOVEKTORJI Talni konvektorji z naravno konvekcijo TK Talni konvektorji s prisilno konvekcijo TKV, H=105 mm, 10 mm Talni konvektorji s prisilno konvekcijo
30 50 30-00 TEHIČI KATAOG 300 Talni konvektorji TAI KOVEKTORJI Talni konvektorji z naravno konvekcijo TK Talni konvektorji s prisilno konvekcijo TKV, H=105 mm, 10 mm Talni konvektorji s prisilno konvekcijo
Numerično reševanje. diferencialnih enačb II
 Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
PROCESIRANJE SIGNALOV
 Rešive pisega izpia PROCESIRANJE SIGNALOV Daum: 7... aloga Kolikša je ampliuda reje harmoske kompoee arisaega periodičega sigala? f() - -3 - - 3 Rešiev: Časova fukcija a iervalu ( /,/) je lieara fukcija:
Rešive pisega izpia PROCESIRANJE SIGNALOV Daum: 7... aloga Kolikša je ampliuda reje harmoske kompoee arisaega periodičega sigala? f() - -3 - - 3 Rešiev: Časova fukcija a iervalu ( /,/) je lieara fukcija:
Uporaba toplotnih izmenjevalcev v postopku pranja
 Leonardo da Vinci Project Trajnostni razvoj v industrijskih procesih pranja 5. Modul Energija v pralnicah Poglavje 4 Uporaba toplotnih izmenjevalcev v postopku pranja 5. Modul Energija v pralnicah Poglavje
Leonardo da Vinci Project Trajnostni razvoj v industrijskih procesih pranja 5. Modul Energija v pralnicah Poglavje 4 Uporaba toplotnih izmenjevalcev v postopku pranja 5. Modul Energija v pralnicah Poglavje
SNOVNE in ENERGIJSKE BILANCE
 SNOVNE in ENERGIJSKE BILANCE MODELIRANJE PROCESOV Matematični modeli nam med drugim omogočajo spoznavanje procesov ter vpliv parametrov modela na potek procesnih spremenljivk. Z modelom poskušamo opisati
SNOVNE in ENERGIJSKE BILANCE MODELIRANJE PROCESOV Matematični modeli nam med drugim omogočajo spoznavanje procesov ter vpliv parametrov modela na potek procesnih spremenljivk. Z modelom poskušamo opisati
Frekvenčna analiza neperiodičnih signalov. Analiza signalov prof. France Mihelič
 Frekvenčna analiza neperiodičnih signalov Analiza signalov prof. France Mihelič Vpliv postopka daljšanja periode na spekter periodičnega signala Opazujmo družino sodih periodičnih pravokotnih impulzov
Frekvenčna analiza neperiodičnih signalov Analiza signalov prof. France Mihelič Vpliv postopka daljšanja periode na spekter periodičnega signala Opazujmo družino sodih periodičnih pravokotnih impulzov
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
*M * Osnovna in višja raven MATEMATIKA NAVODILA ZA OCENJEVANJE. Sobota, 4. junij 2011 SPOMLADANSKI IZPITNI ROK. Državni izpitni center
 Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Gospodarjenje z energijo
 Sočasna proizvodnja toplote in električne energije Značilnosti: zelo dobra pretvorba primarne energije v sekundarno in končno energijo 75 % - 90 % primarne energije se spremeni v želeno obliko uporaba
Sočasna proizvodnja toplote in električne energije Značilnosti: zelo dobra pretvorba primarne energije v sekundarno in končno energijo 75 % - 90 % primarne energije se spremeni v želeno obliko uporaba
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
Stehiometrija za študente veterine
 Univerza v Ljubljani Veterinarska fakulteta Stehiometrija za študente veterine Učbenik s praktičnimi primeri Petra Zrimšek Ljubljana, 01 Petra Zrimšek Stehiometrija za študente veterine Izdajatelj: Univerza
Univerza v Ljubljani Veterinarska fakulteta Stehiometrija za študente veterine Učbenik s praktičnimi primeri Petra Zrimšek Ljubljana, 01 Petra Zrimšek Stehiometrija za študente veterine Izdajatelj: Univerza
The Thermal Comfort Properties of Reusable and Disposable Surgical Gown Fabrics Original Scientific Paper
 24 The Thermal Comfort Properties of Surgical Gown Fabrics 1 1 2 1 2 Termofiziološke lastnosti udobnosti kirurških oblačil za enkratno in večkratno uporabo december 2008 marec 2009 Izvleček Kirurška oblačila
24 The Thermal Comfort Properties of Surgical Gown Fabrics 1 1 2 1 2 Termofiziološke lastnosti udobnosti kirurških oblačil za enkratno in večkratno uporabo december 2008 marec 2009 Izvleček Kirurška oblačila
a) Kateri tip hibridnih orbital na klorovem atomu uporabimo? a) Kateri tip hibridnih orbital na fosforjevem atomu uporabimo?
 76. Narišite strukturo karbonatnega iona. Upoštevajte dejstvo, da so vse vezi enako dolge. Kateri tip hibridizacije na ogljikovem atomu moramo uporabiti? Ogljik je element 4. skupine. a) sp 2 b) sp 3 c)
76. Narišite strukturo karbonatnega iona. Upoštevajte dejstvo, da so vse vezi enako dolge. Kateri tip hibridizacije na ogljikovem atomu moramo uporabiti? Ogljik je element 4. skupine. a) sp 2 b) sp 3 c)
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
SEKUNDARNE VEZE međumolekulske veze
 PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
Univerza v Novi Gorici Fakulteta za znanosti o okolju Okolje (I. stopnja) Meteorologija 2013/2014. Energijska bilanca pregled
 Univerza v Novi Gorici Fakulteta za znanosti o okolu Okole (I. stopna) Meteorologia 013/014 Energiska bilanca pregled 1 Osnovni pomi energiski tok: P [W = J/s] gostota energiskega toka: [W/m ] toplota:q
Univerza v Novi Gorici Fakulteta za znanosti o okolu Okole (I. stopna) Meteorologia 013/014 Energiska bilanca pregled 1 Osnovni pomi energiski tok: P [W = J/s] gostota energiskega toka: [W/m ] toplota:q
Separacijski procesi zapiski predavanj
 8.2 Kolone Kolone so najbolj značilen del destilacijske naprave. Po obliki delimo rektifikacijske kolone v kolone s polnilom in v kolone s prekati. Kolone s polnilom so stoječi ozki in visoki valji, napolnjeni
8.2 Kolone Kolone so najbolj značilen del destilacijske naprave. Po obliki delimo rektifikacijske kolone v kolone s polnilom in v kolone s prekati. Kolone s polnilom so stoječi ozki in visoki valji, napolnjeni
reologija Andreja Zupančič Valant UL FKKT Katedra za kemijsko biokemijsko in ekološko inženirstvo
 reologija Andreja Zupančič Valant UL FKKT Katedra za kemijsko biokemijsko in ekološko inženirstvo 1 Modul 2 Viskoelastično obnašanje strukturiranih tekočin Določanje viskoelastičnih lastnosti tekočin in
reologija Andreja Zupančič Valant UL FKKT Katedra za kemijsko biokemijsko in ekološko inženirstvo 1 Modul 2 Viskoelastično obnašanje strukturiranih tekočin Določanje viskoelastičnih lastnosti tekočin in
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
