Izr. prof. dr. Dominik Vodnik, Katedra za aplikativno botaniko, ekologijo in fiziologijo rastlin govorilne ure: torek od 10 h -12 h
|
|
|
- Παύλος Αγγελοπούλου
- 7 χρόνια πριν
- Προβολές:
Transcript
1 FIZIOLOGIJA RASTLIN Univerza v Ljubljani Biotehniška fakulteta Oddelek za agronomijo predavanja 60 ur vaje 30 ur Izr. prof. dr. Dominik Vodnik, Katedra za aplikativno botaniko, ekologijo in fiziologijo rastlin govorilne ure: torek od 10 h -12 h Obveznosti študenta: prisotnost na vajah + poročanje o rezultatih kolokvij (vaje) pisni izpit (+ ustni, po potrebi) 3 poletni in 3 jesenski izpitni roki + izredni izpitni roki
2 FIZIOLOGIJA RASTLIN - študijska literatura Taiz, L. / Zeiger, E., Plant Physiology. Tretja izdaja. Sinauer Associates, Inc. Publishers, Sunderland, 690 s. Hopkins, W. G Introduction to Plant Physiology. Druga izdaja. John Wiley and Sons, New York 512 s. Salisbury, F. B. / Ross, C. W., Plant Physiology. Ćetrta izdaja. Wadsworth Publishing Company, Belmont, 682 s. Denffer, D. / Ziegler, H., Botanika - Morfologija in fiziologija. Školska knjiga, Zagreb, 586 s. Gogala, N., Slikovno gradivo za študij fiziologije rastlin. Biotehniška fakulteta, Ljubljana. Marschner, H., Mineral nutrition of higher plants. Druga izdaja. Academic Press, London, 889 s. Nilsen, E. T. / Orcutt, D. M., The physiology of plants under stress. John Wiley & Sons, New York, 689 s.
3 ekologija agronomske tehnologije biotehnologija mikrobiologija fitopatologija pedologija fiziologija rastlin kemija, fizika biokemija botanika genetika
4 FIZIOLOGIJA RASTLIN - TEMATSKI SKLOPI PRESKRBA Z VODO IN MINERALNIMI HRANILI FIZIOLOGIJA PRESNOVE (RASTLINSKA BIOKEMIJA) RAST IN RAZVOJ
5 FIZIOLOGIJA RASTLIN - TEMATSKI SKLOPI VODA IN MINERALNA HRANILA - voda in rastlinska celica - vodna bilanca rastline, transport vode - mineralna prehrana - transport in translokacija (razporejanje) BIOKEMIJA IN METABOLIZEM - svetlobne in temotne reakcije fotosinteze - fiziologija in ekofiziologija fotosinteze - transport po floemu - dihanje - asimilacija mineralnih hranil - sekundarni metabolizem RAST IN RAZVOJ - rast, razvoj in diferenciacija - vpliv rdeče in modre svetlobe na rastline - rastlinski rastni hormoni - vpliv okoljskih dejavnikov na rast in razvoj - fiziologija stresa
6 VODA IN RASTLINSKA CELICA Univerza v Ljubljani Biotehniška fakulteta Oddelek za agronomijo
7 Poikilohidre rastline Homojohidre rastline zelo suh zrak kutikula zelo vlažen zrak voda
8 predstavlja 80-95% biomase neolesenelih tkiv, ca. 50% mase olesenelih tkiv za 1g biomase rastlina prečrpa 500g vode H 2 O CO 2
9 Rastlinska celica
10 Lastnosti vode Molekula vode je polarna. Vodikove vezi Fizikalne lastnosti velika specifična toplota (4184 J g -1 K -1 ) velika latentna izparilna toplota ( 44 kj mol -1 ) površinska napetost kohezija vodikove vezi med posameznimi molekulami vode adhezija privlačne sile med molekulami vode in neko površino kapilarnost relativno velika natezna trdnost
11 Pomen vode sodeluje v večini pomembnejših fizioloških procesov je glavni medij za transport metabolitov je dobro topilo za ione in različne polarne organske metabolite (hidratacijski ovoj okoli ionov oz. nabitih molekul) vodne molekule protein
12 Pomen vode sodeluje v večini pomembnejših fizioloških procesov je glavnij medij za transport metabolitov je dobro topilo za ione in različne polarne organske metabolite (hidratacijski ovoj okoli ionov oz. nabitih molekul) znotrajcelični tlak (TURGOR) potreben za normalen potek fizioloških procesov, mehanska stabilnost voda je v rastlinski celici tudi reaktant oz. substrat (fotoliza vode v fotosintezi, hidroliza škroba ipd.)
13 Transport vode difuzija masni tok
14 Difuzija naključno, a progresivno gibanje molekul s področja z veliko prosto energijo na področje z majhno prosto energijo (če ni drugih sil npr. po koncentracijskem gradientu). Difuzijo opisuje Fick-ov zakon J s (gostota toka) = -D s (δc s /δx) [mol m -2 s -1 ] D s = difuzijski koeficient (konstanta, s katero označujemo zmožnost gibanja neke snovi v določenem mediju m -2 s -1 )
15 Začetno stanje Vmesno stanje Ravnotežno stanje Koncentracijski profil Koncentracija Položaj v posodi
16 Difuzija je zelo učinkovit transport, če gre za majhne razdalje, ne pa pri velikih razdaljah. Za celične dimenzije 50 µm = sek, za daljše poti 1m = 30 let! Z difuzijo se voda giblje pri: transportu vode med apoplastom in simplastom transportu vode preko membran transportu vode iz tal v apoplast korenine (delno) pri prehodu vode iz apoplasta v zrak medceličnih prostorov lista pri prehodu iz medceličnih prostorov lista v ozračje
17 Masni (volumski) tok je gibanje molekul po gradientu tlaka odvisno je od polmera vodnika (r), viskoznosti tekočine (η) in gradienta tlaka (δψ/δx). Hitrost volumskega toka opisuje Poiseuille-ov zakon: Jv Π r = 8 η 4 δ Ψp δ x [m 3 s -1 ] Masni tok je neodvisen od koncentracijskih gradientov, če tinevplivajonaviskoznost.
18 Z masnim tokom se voda transportira pri: transportu vode v ksilemu transportu vode v tleh transportu vode v apoplastu transportu vode v floemu Masni tok je glavna oblika transporta vode na daljše razdalje.
19 Rastlinska celica
20 Oliogosaharidne verige glikoproteinov Zunanjost celice Lipidna dvoplast Notranjost celice Periferni membranski protein Integralni membranski protein Periferni membranski protein Z lipidom sidrani membranski protein
21 V rastlinsko celico lahko voda prehaja: skozi membrano - z difuzijo skozi pore, ki jih imenujemo akvaporini - z masnim tokom Akvaporini za vodo specifične pore. Celica lahko kontrolira propustnost membrane za vodo, tako da regulira odprtje/zaprtje akvaporinov (fosforilacija AK v proteinu akvaporina).
22 zunanjost celice vodne molekule akvaporin fosfolipidna dvoplast citoplazma
23 Osmoza Biološke membrane (plazmalema, tonoplast) so selektivno prepustne. Skozi plazmalemo lažje prehajajo voda in druge nenabite manjše molekule, za večje in nabite molekule je prehajanje težje, za to so potrebni posebni prenašalni mehanizmi. Oliogosaharidne verige glikoproteinov Zunanjost celice Lipidna dvoplast Notranjost celice Periferni membranski protein Integralni membranski protein Periferni membranski protein Z lipidom sidrani membranski protein
24 Osmoza Biološke membrane (plazmalema, tonoplast) so selektivno prepustne. Skozi plazmalemo lažje prehajajo voda in druge nenabite manjše molekule, za večje in nabite molekule je prehajanje težje, za to so potrebni posebni prenašalni mehanizmi. Osmoza je neto tok vode skozi selektivno prepustno membrano, ki razmejuje dve raztopini z različnimi koncentracijami topljenca. Gibanje vode koncentracijski gradient + gradient tlaka Smer in hitrost toka sta odvisna od seštevka obeh gradientov, ki ga opisuje gradient vodnega potenciala.
25 osmotski tlak Pfeffer-jeva celica: «polpropustna membrana«glina + CuFe(CN)6 20% vodna raztopina sladkorja 100% voda Rastlinska celica: koncentracija topljencev v notranjosti celice je navadno 0.5 do 1 mol večja kot v zunanjosti celice, med organeli je koncentracija precej izenačena koncentracija v apoplastu molalna
26 Vodni potencial Vodni potencial (Ψ w ) je mera za razpoložljivost vode v nekem sistemu. Enota za vodni potencial je pascal (Pa Nm -2 J m -3 ). Je relativna količina. Navadno ga izražamo kot razliko med potencialom v danih pogojih in potencialom, izmerjenim v standardnih pogojih. Referenčni vodni potencial ima čista voda pri atmosferskem tlaku in okoljski temperaturi (Ψ w ). Ψ w rastlinske celice je negativen. Na vodni potencial vplivajo štirje glavni dejavniki: koncentracija (s) potencial raztopine = osmotski potencial Ψ s tlak (p) potencial tlaka Ψ p gravitacija (g) gravitacijski potencial Ψ g interakcije vodnih molekul s površino (m) matrični potencial Ψ m ψ w = ψ s + ψ p + ψ g + (ψ m )
27 Ψ s... potencial raztopine = osmotski potencial (Π), ( < 0) Ψ s = - RTc s van't Hoff-ova enačba: R = plinska konstanta, 8.31 J mol -1 K -1 m -3 T = absolutna temperatura, K c s = osmolalnost raztopine, mol kg -1 Ψ p... potencial tlaka = hidrostatski tlak raztopine (P), pozitiven tlak veča vodni potencial, negativni ga zmanjšuje Potencial tlaka v celicah = turgorski tlak ali turgor ( > 0). Ψ p je lahko tudi negativen - v ksilemu in celičnih stenah (tenzija).
28 Ψ g... gravitacijski potencial = potencial, ki ga ima voda na večji višini v primerjavi z vodo na referenčni višini ψ g = ρ w gh (10m 0.1 MPa) Ψ m... matrični potencial = potencial matriksa, opisuje zmanjšanje proste energije vode na račun tvorbe tankega sloja vode (1-2 sloja molekul vode) na površini talnih delcev, celične stene in drugega materiala. ψ w = ψ w ψ s = + ψ s ψ p + + ψ p ψ g
29 Sistem z velikim ψ w bo vodo oddajal sistemu z manjšim ψ w. Tudi v celico in iz nje voda prehaja glede na gradient vodnega potenciala. ψ w ψ w
30 Ravnotežje = ni neto toka vode preko membrane ψ w ψ w
31 + čista voda pri atm. tlaku raztopina pri atm. tlaku ψ p raztopina pri različnem tlaku ψ w - ψ s čista voda pri povečanem tlaku + ψ w -
32 Čista voda 0.1 M razt. saharoze Neturgescentna celica Celica po vzpostavitvi ravnotežja
33 Turgescentna celica 0.3 M razt. saharoze Celica po vzpostavitvi ravnotežja
34 ψ w = ψ s + ψ m ψ w = ψ s + ψ p
35 ψ w = ψ s + ψ m ψ s ψ w = 0 ψ m ψ w ψ w = ψ s + ψ p (- 0.9 MPa) + (+ 0.3 MPa) ψ w = 0 = MPa ψ s ψ w ψ p
36 Posamezne komponente vodnega potenciala so spremenljive Ψ S celica -0.5 MPadobro zalivane rastline (solata, kumare fižol) do -1.2 MPa bolj tipično -2.5 MPakorenine sladkorne pese, jagode vinske trte - halofiti apoplast -0.1 do 0 MPa Ψ P celica 0.1 do 1 MPa dobro zalivane rastline apoplast ksilem - 1 MPa ali manjši (spremenljiv, odvisen od transpiracije, lahko tudi pozitiven = koreninski tlak)
37 Ψs = do -7.3(?) MPa
38 pomanjkanje vode osmotska prilagoditev brez osmotske prilagoditve
39 Merjenje vodnega potenciala (glej skripta vaje!) tlačna sonda tlačna (Scholandrova) komora psihrometer krioskopski osmometer
40 Tlačna sonda
41 Tlačna (Scholandrova) komora
42 Kako določiti vsebnost oz. razpoložljivost vode v tkivu? (1) Relativna vsebnost vode - relative water content (RWC) RWC = sveza masa suha masa masa ob saturaciji suha masa 100 (2) Vodni potencial (Ψ)
43 Relativna vsebnost vode - relative water content (RWC) RWC = sveza masa suha masa masa ob saturaciji suha masa 100 -Ψ RWC
44 Kaj se dogaja z vodnim potencialom in njegovimi komponentami, ko celica izgublja vodo? Vodni potencial (MPa) popoln turgor naklon Relativni celični volumen Höflerjev diagram turgor = 0 ΔΨ= ε (ΔV/ V) ε prostorninski razteznostni modul Elastičnost cel. stene ( ε = elastičnost) ε ni konstanten, ampak pada s padcem turgorja celica izgubi relativno malo vode vendar se to zelo pozna na padcu turgorja (Ψp).10% Ψp = 0 kostaε in Ψp majhna, na vodni potencial najbolj vplivajo spremembe Ψs
45 Prostorninski razteznostni moduli se pri različnih rastlinah razlikujejo in odražajo prilagoditev tkiva različnih vrst na zmanjšano razpoložljivost vode
46 Transport vode J v = L p (Δψ w ) [ m 3 m -2 s -1 ] J v hitrost transporta (toka) vode L p hidravlična prevodnost membrane (m 3 m -2 s -1 MPa -1 ) J v = L p (ψ m (a) - ψ p(p) + σ (ψ s (a) - ψ s (p) ) J v hitrost transporta (toka) vode L p hidravlična prevodnost membrane (m 3 m -2 s -1 MPa -1 ) σ reflekcijski koeficient [ 0,1 ]; σ = 1 če membrano prehaja samo voda
47 TLA IN VODA Univerza v Ljubljani Biotehniška fakulteta Oddelek za agronomijo
48 Fizikalno kemične lastnosti tal tekstura struktura delež organske snovi Rast rastline razpoložljivost mineralnih hranil in vode rast korenin (prezračenost, ne prevelika zbitost prodiranje korenin)
49 Gravimetrično določena količinavodev tleh(θ m ): razmerje med maso vode v talnem vzorcu in njegovo suho maso (%) Volumska (prostorninska) vsebnost vode v tleh (θ v ) θ m množena z navidezno gostoto tal (%)
50 Poljska kapaciteta - količina vode, ki ostane v tleh potem, ko iz z vodo nasičenih tal odteče voda zaradi gravitacije Točka venenja - je tisti vodni potencial tal, pri katerem rastlina ne more več vzpostaviti turgorja, četudi popolnoma omeji transpiracijo (npr. preko noči, čeprav je zalita). To pomeni, da je vodni potencial tal mnajši ali enak osmotskemu potencialu (ψ s ) rastline
51 Vodni potencial tal Ψ w = Ψ s + Ψ m Ψ s MPa normalna tla MPa slana tla Ψ m blizu 0 MPa tla nasičena z vodo -1 do -2 MPa izsušena tla fine teksture Ψ m = - 2T / r T površinska napetost 7.28 x 10-8 MPa
52 Ψ m = -2T / r T površinska napetost vode 7.28 x 10-8 MPa m r polmer r = 2.98 µm Ψ m = MPa
53 Ψ m = -2T / r r = µm Ψ m = -1.5 MPa
54 Aparat za merjenje matričnega potenciala tal
55 Vodni potencial tal (-MPa) pesek glina peščena ilovica Vsebnost vode (utežni %)
56 Gibanje vode v tleh Infiltracija (nasičen tok vode navzdol, po dežju ali zalivanju) nenasičen tok vode - horizontalno, h koreninam - navzgor (izparevanje, razlike v T horizontov ) Voda s v tleh giblje z masnim tokom. Rastlina s črpanjem vode v bližini korenin zmanjša vodni potencial tal, nastala tlačna razlika pa je osnova za masni tok. Hitrost toka je odvisna od velikosti tlačne razlike in od hidravlične prevodnosti tal. Ta je odvisna od teksture in od vsebnosti vode v tleh (več vode, boljša prevodnost)
57 Hidravlična prevodnost tal (m h -1 MPa -1 ) poljska kapaciteta točka venenja vodni potencial tal (MPa)
58 korenina koreninski lasek voda peščeni delec glineni delec zrak
59 VODA in RASTLINA (sprejem, transport in oddajanje vode) Univerza v Ljubljani Biotehniška fakulteta Oddelek za agronomijo
60
61 Poikilohidre rastline Homojohidre rastline zelo suh zrak kutikula zelo vlažen zrak voda
62 zračni prostori v listu ksilem prečni prerez korenine tla
63 Prečni prerez stebla epidermis skorja -korteks stržen ksilem floem žilni kambij
64 Prečni prerez korenine epidermis skorja - korteks pericikel endodermis floem žilni kambij ksilem koreninski lasek
65 Lastnosti korenin, pomembne za učinkovito absorpcijo vode velika skupna dolžina in površina veliko razmerje med površino korenin (A R ) in površino listov (A L ) A R : A L =
66
67
68 Vsebnost vode v tleh vpliva na razrast korenin suha tla vlažna tla
69
70 suberinizacija in lignifikacija zmanjšujeta prevodnost Počasno vstopanje vode in soli zaradi zmanjšane prevodnosti izoblikovan (diferenciran) metaksilem začetek suberinizacije in lignifikacije endodermisa Najhitrejše vstopanje vode in soli centralni cilinder - žila primarna skorja (korteks) diferenciacija protoksilema cona podaljševanja diferenciacija primarnega floema meristematska cona Počasno vstopanje vode in soli Relativno nepropustno za vodo koreninska čepica
71 Ex - neizgrajen eksodermis En - endodermis s Casparijevo progo (CB) P - protoksilem (izgrajen) EM - zgodnji metaksilem (izgrajen) LM - neizgrajen pozni metaksilem Ex - izgrajen eksodermis endodermis z asimetrično odebeljenimi celičnimi stenami, izgrajen protoksilem in zgodnji metaksilem, neizgrajen pozni metaksilem Isto, kot pri (B) z izgrajenim poznim metaksilemom Prečni rez primarne korenine koruze (Zea mays) v različnih razvojnih stadijih, UV mikroskopija, berberinm, analinsko modro, tuloidinsko modro.
72 Radialni transport vode endodermis Casparijev trak simplastna pot + transcelična pot pericikel korteks ksilem floem epidermis apoplastna pot
73 Radialni transport vode - shema Protoplast (Σ = SIMPLAST) Celična stena (Σ = APOPLAST) SIMPLASTNA POT vakuola APOPLASTNA POT Casparijeva proga rizodermis korteks (skorja) endodermis parenhim centralnega cilindra ksilem
74 Upornost radialnemu toku vode naj bi bila enakomerno razporejena po radialnem preseku korenine. Endodermis relativno dobro prepušča vodo (upornost toku vode je majhna), hkrati pa predstavlja oviro za vračanje ionov iz centralnega cilindra v korteks. To omogoča učinkovit sprejem vode in učinkovito absorpcijo mineralnih hranil. Rezultat omejevanja ionov v centralnem cilindru je tudi koreninski tlak.
75 Aksialni transport - transport po ksilemu perforirane končne celične stene traheje traheide piknje
76 Aksialni transport vode (transport vode po ksilemu) Hidravlična prevodnost elementov ksilema je dobra (ni membran). Tlak, ki je potreben, da pri znani geometriji ksilemskih elementov (r = 40 µm, µm) dosežemo eksperimentalno izmerjene hitrosti toka (4 mm s -1, ), je ocenjen na 0.02 MPa m -1. za transport vode v 100 m visoko drevo potrebujemo ca. 3 MPa tlačne razlike Od kod ta tlačna razlika? tlak v koreninah ali podtlak v nadzemnem delu
77 Koreninski tlak in gutacija Pozitivni hidrostatski tlak se vzpostavi v ksilemu zaradi akumulacije ionov v ksilemski tekočini (zmanjšanje Ψs privzem vode Ψp). Pojavi se pri dobro zalivanih rastlinah v pogojih velike zračne vlage oz. majhne transpiracije. Znaša lahko od 0.05 do 0.5 MPa. Ksilemski tlak lahko povzroči izhajanje vode iz hidatod na listih, pojav imenujemo gutacija
78 Nastanek koreninskega tlaka Ioni mineralnih hranil se aktivnim transportom sprejmejo v simplast in nakopičijo v centralnem cilindru korenine. Endodermis preprečuje uhajanje ionov iz centralnega cilindra, v katerem zaradi kopičenja ionov pada osmotski potencial. Pride do osmotskega učinka, t.j. vstopa vode v centralni cilinder, to pa poveča hidrostatski tlak nastane koreninski tlak
79 Ali je gonilna sila toka vode po ksilemu podtlak, ki nastaja v nadzemnih delih rastline? evaporacija
80 vakuola celična stena plazmalema vodni film kloroplast citoplazma izhlapevanje
81
82 vakuola celična stena plazmalema vodni film kloroplast izhlapevanje polmer krivine (µm) hidrostatski tlak (MPa) citoplazma plazmalema zrak evaporacija evaporacija evaporacija celulozne mikrofibrile - prečno meja voda/zrak citoplazma celična stena voda v cel. steni
83 Transpiracijski tok razlaga kohezijsko-tenzijska teorija kohezijsko-tenzijska teorija gonilna sila za tok vode po ksilemu je podtlak (tenzija), ki nastaja zaradi izhlapevanja vode iz površine celičnih sten mezofilnih celic. Nastajajo mikroskopsko majhni meniski vode, katerih polmer je z večjim izsuševanjem vedno manjši. Temu ustrezno pa narašča negativni tlak (Ψp = -2T/r). Da je tok pod takšnim podtlakom mogoč, je potrebna posebna anatomska prilagoditev prevajalnih celic. Sekundarne odebelitve celičnihstenomogočajo potrebno mehansko trdnost. Kohezijske sile med molekulami vode omogočajo, da se stolpec vode ne prekine.
84 Sprejem vode v korenino (absorpcija vode) Absorpcija vode v rastlino poteka na osnovi razlike v vodnem potencialu tal in korenine. Ta gradient pa ima pri rastlinah, ki hitro oddajajo vodo in rastlinah, ki jo oddajajo počasi, različni osnovi: majhna transpiracija aktivna ali osmotska absorpcija vode velika transpiracija vlek vode skozi korenine Tok vode iz tal v korenine in navzgor v nadzemni del rastline lahko opišemo kot tok tekočine skuzi niz elementov, ki gradijo rastlino. Ti elementi imajo različno hidravlično prevodnost in se pojavljajo v zaporedju (upornosti se seštevajo) ali vzporedno (prevodnosti se seštevajo).
85 Prečni prerez korenine epidermis skorja - korteks pericikel endodermis floem žilni kambij ksilem koreninski lasek
86 evaporacija vode iz celičnih sten zmanjšanje Ψ v celicah kohezija vodnih molekul v ksilemu, kapilarna geometrija ksilema embolije manjši Ψ v koreninah v primerjavi s tlemi, privzem vode povečana absorpcijska površina
87 Prevelika tenzija (ob slabi razpoložljivosti vode), lahko privede do pretrganja vodnih stolpcev v ksilemu Rastline se razlikujejo po vrednosti vodnega potenciala, pri katerem pride do kavitacije vrsta Ψ cav (MPa) Ilex aquifolium Acer campestre Prunus mahaleb Quercus ilex Laurus nobilis Ceratonia siliqua
88 Vodni potencial atmosfere Razmerja med koncentracijo vodne pare (c wv ), tlakom vodne pare (p wv ), relativno vlago (RH) in vodnim potencialom (Ψ) c wv (mol m-3) p wv (kpa) RH Ψw (MPa) neskončno Podatki so izračunani po enačbi: Ψw = (RT/V w ) ln(rh) za temperaturo 20 C Za transpiracijo je odločilna razlika v c wv, oz. razlika v p wv, ne pa RH. Ta razlika je temperaturno odvisna.
89 vodni potencial in njegove komponente (MPa) Ψw Ψp Ψs Ψg Ψzrak zrak RH% (50%) intercelular lista celična stena mezofila (na vukuola, mezofil (na 10m) ksilem, list (na 10m) ksilem, korenine (ob površini) vakuola, korenine (ob tla ob koreninah tla 10 mm od korenin Opomba: Ψzrak = (RT/Vw) ln(rh)
90 Transpiracija voda prehaja iz lista v atmosfero predvsem skozi listne reže mehanizem tega transporta je difuzija, osnova pa koncentracijski gradient vodne pare, ki ga lahko opišemo tudi z uporabo koncepta vodnega potenciala Ψw = (RT/V w ) ln(rh). deficit tlaka vodne pare razlika razlika v koncentraciji v tlaku vodne vodne pare pare C p wv (list) C wv (zrak) wv (list) - p wv (zrak) transpiracija: E = (mol m -2 s -1 ) r s + r b upornost listnih rež upornost mejne plasti zraka
91 odprtina listne reže c wv (zrak) upornost mejne plasti zraka (r b ) upornost listnih rež (r s ) kutikula c wv (list)
92 Listne reže = stomata anatomska zgradba število razporeditev vgreznjenost
93 epidermalne celice radialno orientirane celulozne mikrofibrile epidermalne celice radialno orientirane celulozne mikrofibrile celici zapiralki pora celici zapiralki pora celici spremljevalki kompleks reže
94 Regulacija transpiracije Mehanizem delovanja listnih rež mehanizem odpiranja/zapiranja je sprememba Ψs (črpanje K + v celico) in posledično sprememba Ψp v celicah zapiralkah) [K + ] v celici Ψ s Ψ P odprtje reže [K + ] v celici Ψ s Ψ P zaprtje reže
95 Regulatorni dejavniki, ki uravnavajo zapiranje/odpiranje rež koncentracija CO 2 v celicah ( CO 2 odprtje rež) svetloba (posredno preko fotosintezne aktivnosti + vpliv modre svetlobe) vodni potencial lista (zapiranje pri vodnem potencialu do -1.5 MPa, tudi podnevi - neposredni učinki, hormonalna kontrola preko abscizinske kisline) temperatura, hlajenje veter
96 relativna povprečna odprtina listne reže tema normalno stanje CO 2, H 2 O malo CO 2 sukulenti močan sušni stres normalno stanje CO 2, H 2 O čas oblačen dan svetloba visoka temperatura močna svetloba šibka svetloba tipičen dan. tipična rastlina zelo suha tla povečan CO 2 nekatere rastline močan veter ali sušni stres polnoč poldne čas dneva polnoč
97 Dnevni hod transpiracije ob različni vsebnosti vode v tleh (krivulje 1-5): reže odprte reže zaprte Evaporacija 1 - neomejena transpiracija 2 - omejevanje transpiracije z opoldanskim zapiranjem rež 3 - popolno zaprtje rež opoldne 4 permanentno zaprtje rež, le kutikularna transpiracija 5 močno zmanjšana transpiracija zaradi poškodb membran Transpiracija kutik. stomat. sončni vzhod poldne sončni zahod siva površina prikazuje območje, v katerem je transpiracija izključno kutikularna
98 Dnevni hod transpiracije pri 2-letnih sadikah bora (Pinus radiata): a dobro zalivane, b 9 dni brez zalivanja, c 12 dni brez zalivanja Transpiracija (mmol H2O m -2 h -1 ) Čas dneva (h)
99 Prevodnost listnih rež uravnava hormon abscizinska kislina
100 sončna svetloba epidermalne celica evaporacija celica zapiralke H 2 O CO 2 reže se zaprejo K + H 2 0 ABA K + H 2 0 Ψ Ψ ABA H 2 O reže se odprejo vstop CO 2 fotosinteza zniža CO 2
101 celice mezofila palisadni parenhim ksilem mejna plast zraka kutikula zgornji epidermis substomatalna votlina velika vsebnost vodne pare malo CO 2 spodnji epidermis kutikula upornost mejne plasti zraka vodna para majhna vsebnost vodne pare stomatalna upornost CO 2 velika koncentracija CO 2 celica zapiralka mejna plast zraka
102 Prevodnost listnih rež ter kompromis fotosinteza/transpiracija H 2 O CO 2
103 učinkovitost izrabe vode: water use efficiency (WUE) molov asimiliranega CO 2 WUE = molov H 2 O, oddane s transpiracijo
104 Spremembe vodnega potenciala tal, korenin in lista, v primeru napredujoče suše tla Vodni potencial (MPa) list korenine Čas (dnevi)
105 Glej tudi poglavje vodni stres!!! Dodatna literatura Kramer, P.J., Boyer, J.S Water relations in plants and soils. Academic Press. 495s. članki v reviji Journal of Experimental Botany. Posebna izdaja: Treatise in Experimental Botany: Water Relations, 1998.
VODA IN RASTLINSKA CELICA
 VODA IN RASTLINSKA CELICA Univerza v Ljubljani Biotehniška fakulteta Oddelek za agronomijo Poikilohidre rastline Homojohidre rastline zelo suh zrak kutikula zelo vlažen zrak voda Rastlinska celica Lastnosti
VODA IN RASTLINSKA CELICA Univerza v Ljubljani Biotehniška fakulteta Oddelek za agronomijo Poikilohidre rastline Homojohidre rastline zelo suh zrak kutikula zelo vlažen zrak voda Rastlinska celica Lastnosti
TRANSPORT RAZTOPIN. Agronomija - UNI
 TRANSPORT RAZTOPIN Agronomija - UNI Transport na celičnem nivoju oz. transport preko membrane je osnova za transport na višjih nivojih (tkiva). Pomen biološki membran (plazmalema, tonoplast,...) homeostaza
TRANSPORT RAZTOPIN Agronomija - UNI Transport na celičnem nivoju oz. transport preko membrane je osnova za transport na višjih nivojih (tkiva). Pomen biološki membran (plazmalema, tonoplast,...) homeostaza
TRANSPORT RAZTOPIN. Agronomija - UNI 2005/06
 TRANSPORT RAZTOPIN Transport na celičnem nivoju oz. transport preko membrane je osnova za transport na višjih nivojih (tkiva). Pomen biološki membran (plazmalema, tonoplast,...) homeostaza rastlinske celice
TRANSPORT RAZTOPIN Transport na celičnem nivoju oz. transport preko membrane je osnova za transport na višjih nivojih (tkiva). Pomen biološki membran (plazmalema, tonoplast,...) homeostaza rastlinske celice
CO2 + H2O sladkor + O2
 VAJA 5 FOTOSINTEZA CO2 + H2O sladkor + O2 Meritve fotosinteze CO 2 + H 2 O sladkor + O 2 Fiziologija rastlin laboratorijske vaje SVETLOBNE REAKCIJE (tilakoidna membrana) TEMOTNE REAKCIJE (stroma kloroplasta)
VAJA 5 FOTOSINTEZA CO2 + H2O sladkor + O2 Meritve fotosinteze CO 2 + H 2 O sladkor + O 2 Fiziologija rastlin laboratorijske vaje SVETLOBNE REAKCIJE (tilakoidna membrana) TEMOTNE REAKCIJE (stroma kloroplasta)
Termodinamika vlažnega zraka. stanja in spremembe
 Termodinamika vlažnega zraka stanja in spremembe Termodinamika vlažnega zraka Najpogostejši medij v sušilnih procesih konvektivnega sušenja je VLAŽEN ZRAK Obravnavamo ga kot dvokomponentno zmes Suhi zrak
Termodinamika vlažnega zraka stanja in spremembe Termodinamika vlažnega zraka Najpogostejši medij v sušilnih procesih konvektivnega sušenja je VLAŽEN ZRAK Obravnavamo ga kot dvokomponentno zmes Suhi zrak
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 5. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Funkcijske vrste. Matematika 2. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 2. april Gregor Dolinar Matematika 2
 Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
FOTOSINTEZA. Univerza v Ljubljani Biotehniška fakulteta Oddelek za agronomijo. Agronomija - VSŠ 2005/06
 FOTOSINTEZA Univerza v Ljubljani Biotehniška fakulteta Oddelek za agronomijo Agronomija - VSŠ 2005/06 svetloba H 2 O CO 2 C 6 H 12 O 6 + O 2 Agronomija - VSŠ 2005/06 fotosinteza = sinteza organskih spojin
FOTOSINTEZA Univerza v Ljubljani Biotehniška fakulteta Oddelek za agronomijo Agronomija - VSŠ 2005/06 svetloba H 2 O CO 2 C 6 H 12 O 6 + O 2 Agronomija - VSŠ 2005/06 fotosinteza = sinteza organskih spojin
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 22. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Tabele termodinamskih lastnosti vode in vodne pare
 Univerza v Ljubljani Fakulteta za strojništvo Laboratorij za termoenergetiko Tabele termodinamskih lastnosti vode in vodne pare po modelu IAPWS IF-97 izračunano z XSteam Excel v2.6 Magnus Holmgren, xsteam.sourceforge.net
Univerza v Ljubljani Fakulteta za strojništvo Laboratorij za termoenergetiko Tabele termodinamskih lastnosti vode in vodne pare po modelu IAPWS IF-97 izračunano z XSteam Excel v2.6 Magnus Holmgren, xsteam.sourceforge.net
1. Trikotniki hitrosti
 . Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
. Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 21. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 14. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Razvoj homojohidrih rastlin iz poikilohidrih pomeni prehod iz vode na kopno in je povezan z razvojem vakuoliziranih celic
 VAKUOLA Nastanek: iz ER, diktiosomov Zgradba: enojna membrana, vsebina: A) vodne vakuole B) Vakuole s hidrofobno vsebino C) Vakuole z emulzijami Različna pojavnost glede na število in zgradbo v odvisnosti
VAKUOLA Nastanek: iz ER, diktiosomov Zgradba: enojna membrana, vsebina: A) vodne vakuole B) Vakuole s hidrofobno vsebino C) Vakuole z emulzijami Različna pojavnost glede na število in zgradbo v odvisnosti
Osnove elektrotehnike uvod
 Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
PONOVITEV SNOVI ZA 4. TEST
 PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
Univerza v Novi Gorici Fakulteta za znanosti o okolju Okolje (I. stopnja) Meteorologija 2013/2014. Energijska bilanca pregled
 Univerza v Novi Gorici Fakulteta za znanosti o okolu Okole (I. stopna) Meteorologia 013/014 Energiska bilanca pregled 1 Osnovni pomi energiski tok: P [W = J/s] gostota energiskega toka: [W/m ] toplota:q
Univerza v Novi Gorici Fakulteta za znanosti o okolu Okole (I. stopna) Meteorologia 013/014 Energiska bilanca pregled 1 Osnovni pomi energiski tok: P [W = J/s] gostota energiskega toka: [W/m ] toplota:q
ΦΥΣΙΟΛΟΓΙΑ ΦΥΤΩΝ ΝΕΡΟ ΚΑΙ ΦΥΤΙΚΟ ΚΥΤΤΑΡΟ ΔΙΑΠΝΟΗ ΚΑΙ ΥΔΑΤΙΚΕΣ ΣΧΕΣΕΙΣ ΦΥΤΟΥ- ΕΔΑΦΟΥΣ-ΑΤΜΟΣΦΑΙΡΑΣ X. K. KITΣAKH
 ΦΥΣΙΟΛΟΓΙΑ ΦΥΤΩΝ ΝΕΡΟ ΚΑΙ ΦΥΤΙΚΟ ΚΥΤΤΑΡΟ ΔΙΑΠΝΟΗ ΚΑΙ ΥΔΑΤΙΚΕΣ ΣΧΕΣΕΙΣ ΦΥΤΟΥ- ΕΔΑΦΟΥΣ-ΑΤΜΟΣΦΑΙΡΑΣ X. K. KITΣAKH Οι ιδιότητες του νερού και συνέπειές τους Δομή μορίου: ηλεκτρικό δίπολο, γέφυρες υδρογόνου-οξυγόνου
ΦΥΣΙΟΛΟΓΙΑ ΦΥΤΩΝ ΝΕΡΟ ΚΑΙ ΦΥΤΙΚΟ ΚΥΤΤΑΡΟ ΔΙΑΠΝΟΗ ΚΑΙ ΥΔΑΤΙΚΕΣ ΣΧΕΣΕΙΣ ΦΥΤΟΥ- ΕΔΑΦΟΥΣ-ΑΤΜΟΣΦΑΙΡΑΣ X. K. KITΣAKH Οι ιδιότητες του νερού και συνέπειές τους Δομή μορίου: ηλεκτρικό δίπολο, γέφυρες υδρογόνου-οξυγόνου
Logatherm WPL 14 AR T A ++ A + A B C D E F G A B C D E F G. kw kw /2013
 WP 14 R T d 9 10 11 53 d 2015 811/2013 WP 14 R T 2015 811/2013 WP 14 R T Naslednji podatki o izdelku izpolnjujejo zahteve uredb U 811/2013, 812/2013, 813/2013 in 814/2013 o dopolnitvi smernice 2010/30/U.
WP 14 R T d 9 10 11 53 d 2015 811/2013 WP 14 R T 2015 811/2013 WP 14 R T Naslednji podatki o izdelku izpolnjujejo zahteve uredb U 811/2013, 812/2013, 813/2013 in 814/2013 o dopolnitvi smernice 2010/30/U.
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * NAVODILA ZA OCENJEVANJE. Petek, 12. junij 2015 SPLOŠNA MATURA
 Državni izpitni center *M543* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Petek,. junij 05 SPLOŠNA MATURA RIC 05 M543 M543 3 IZPITNA POLA Naloga Odgovor Naloga Odgovor Naloga Odgovor Naloga Odgovor
Državni izpitni center *M543* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Petek,. junij 05 SPLOŠNA MATURA RIC 05 M543 M543 3 IZPITNA POLA Naloga Odgovor Naloga Odgovor Naloga Odgovor Naloga Odgovor
Tretja vaja iz matematike 1
 Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Zemlja in njeno ozračje
 Zemlja in njeno ozračje Pojavi v ozračju se dogajajo na zelo različnih časovnih in prostorskih skalah Prostorska skala Pojav 1 cm Turbulenca, sunki vetra 1 m 1 km 10 km 100 km 1000 in več km Tornadi Poplave,
Zemlja in njeno ozračje Pojavi v ozračju se dogajajo na zelo različnih časovnih in prostorskih skalah Prostorska skala Pojav 1 cm Turbulenca, sunki vetra 1 m 1 km 10 km 100 km 1000 in več km Tornadi Poplave,
KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK
 1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
+105 C (plošče in trakovi +85 C) -50 C ( C)* * Za temperature pod C se posvetujte z našo tehnično službo. ϑ m *20 *40 +70
 KAIFLEX ST Tehnični podatki Material Izjemno fleksibilna zaprtocelična izolacija, fleksibilna elastomerna pena (FEF) Opis Uporaba Temperaturno območje Toplotna prevodnost W/(m K ) pri različnih srednjih
KAIFLEX ST Tehnični podatki Material Izjemno fleksibilna zaprtocelična izolacija, fleksibilna elastomerna pena (FEF) Opis Uporaba Temperaturno območje Toplotna prevodnost W/(m K ) pri različnih srednjih
Poglavje 7. Poglavje 7. Poglavje 7. Regulacijski sistemi. Regulacijski sistemi. Slika 7. 1: Normirana blokovna shema regulacije EM
 Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
VODA IN MINERALNA HRANILA
 VODA IN MINERALNA HRANILA - voda in rastlinska celica - vodna bilanca rastline, transport vode - mineralna prehrana - transport in translokacija (razporejanje) BIOKEMIJA IN METABOLIZEM - svetlobne in temotne
VODA IN MINERALNA HRANILA - voda in rastlinska celica - vodna bilanca rastline, transport vode - mineralna prehrana - transport in translokacija (razporejanje) BIOKEMIJA IN METABOLIZEM - svetlobne in temotne
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * FIZIKA NAVODILA ZA OCENJEVANJE. Petek, 10. junij 2016 SPLOŠNA MATURA
 Državni izpitni center *M16141113* SPOMLADANSKI IZPITNI ROK FIZIKA NAVODILA ZA OCENJEVANJE Petek, 1. junij 16 SPLOŠNA MATURA RIC 16 M161-411-3 M161-411-3 3 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor
Državni izpitni center *M16141113* SPOMLADANSKI IZPITNI ROK FIZIKA NAVODILA ZA OCENJEVANJE Petek, 1. junij 16 SPLOŠNA MATURA RIC 16 M161-411-3 M161-411-3 3 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor
Simbolni zapis in množina snovi
 Simbolni zapis in množina snovi RELATIVNA MOLEKULSKA MASA ON MOLSKA MASA Relativna molekulska masa Ker so atomi premajhni, da bi jih merili z običajnimi tehtnicami, so ugotovili, kako jih izračunati. Izražamo
Simbolni zapis in množina snovi RELATIVNA MOLEKULSKA MASA ON MOLSKA MASA Relativna molekulska masa Ker so atomi premajhni, da bi jih merili z običajnimi tehtnicami, so ugotovili, kako jih izračunati. Izražamo
Diferencialna enačba, v kateri nastopata neznana funkcija in njen odvod v prvi potenci
 Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Zemlja in njeno ozračje
 Zemlja in njeno ozračje Pojavi v ozračju se dogajajo na zelo različnih časovnih in prostorskih skalah Prostorska skala Pojav 1 cm Turbulenca, sunki vetra 1 m 1 km 10 km 100 km 1000 in več km Tornadi Poplave,
Zemlja in njeno ozračje Pojavi v ozračju se dogajajo na zelo različnih časovnih in prostorskih skalah Prostorska skala Pojav 1 cm Turbulenca, sunki vetra 1 m 1 km 10 km 100 km 1000 in več km Tornadi Poplave,
Katedra za aplikativno botaniko ekologijo in fiziologijo rastlin Gradiva za študente
 Katedra za aplikativno botaniko ekologijo in fiziologijo rastlin Gradiva za študente Naslov Besedilo, fotografija in obdelava slik: Boris Turk Izdelava preparatov: Gabrijel Leskovec, Boris Turk Boris Turk,
Katedra za aplikativno botaniko ekologijo in fiziologijo rastlin Gradiva za študente Naslov Besedilo, fotografija in obdelava slik: Boris Turk Izdelava preparatov: Gabrijel Leskovec, Boris Turk Boris Turk,
Fotosinteza, meritve fotosinteze. Ekofiziologija in mineralna prehrana rastlin 2005/06
 Fotosinteza, meritve fotosinteze Ekofiziologija in mineralna prehrana rastlin 2005/06 SVETLOBNE REKACIJE (tilakoidna membrana) TEMOTNE REAKCIJE (stroma kloroplasta) Ekofiziologija in mineralna prehrana
Fotosinteza, meritve fotosinteze Ekofiziologija in mineralna prehrana rastlin 2005/06 SVETLOBNE REKACIJE (tilakoidna membrana) TEMOTNE REAKCIJE (stroma kloroplasta) Ekofiziologija in mineralna prehrana
Fazni diagram binarne tekočine
 Fazni diagram binarne tekočine Žiga Kos 5. junij 203 Binarno tekočino predstavljajo delci A in B. Ti se med seboj lahko mešajo v različnih razmerjih. V nalogi želimo izračunati fazni diagram take tekočine,
Fazni diagram binarne tekočine Žiga Kos 5. junij 203 Binarno tekočino predstavljajo delci A in B. Ti se med seboj lahko mešajo v različnih razmerjih. V nalogi želimo izračunati fazni diagram take tekočine,
Razvoj homojohidrih rastlin iz poikilohidrih pomeni prehod iz vode na kopno in je povezan z razvojem vakuoliziranih celic
 VAKUOLA Nastanek: iz ER, diktiosomov Zgradba: enojna membrana, vsebina: A) vodne vakuole B) Vakuole s hidrofobno vsebino C) Vakuole z emulzijami Različna pojavnost glede na število in zgradbo v odvisnosti
VAKUOLA Nastanek: iz ER, diktiosomov Zgradba: enojna membrana, vsebina: A) vodne vakuole B) Vakuole s hidrofobno vsebino C) Vakuole z emulzijami Različna pojavnost glede na število in zgradbo v odvisnosti
Fotosinteza, meritve fotosinteze. Ekofiziologija in mineralna prehrana rastlin
 Fotosinteza, meritve fotosinteze Ekofiziologija in mineralna prehrana rastlin 6CO 2 + 6H 2 O C 6 H 12 O 6 + 6O 2 redukcija oksidacija Ekofiziologija in mineralna prehrana rastlin Ekofiziologija in mineralna
Fotosinteza, meritve fotosinteze Ekofiziologija in mineralna prehrana rastlin 6CO 2 + 6H 2 O C 6 H 12 O 6 + 6O 2 redukcija oksidacija Ekofiziologija in mineralna prehrana rastlin Ekofiziologija in mineralna
UNIVERZITETNI ŠTUDIJ KMETIJSTVO - AGRONOMIJA
 Biotehniška fakulteta Oddelek za agronomijo Dominik VODNIK FIZIOLOGIJA RASTLIN PRAKTIČNE VAJE UNIVERZITETNI ŠTUDIJ KMETIJSTVO - AGRONOMIJA Ljubljana, 2001 1 KAZALO 1. MINERALNA PREHRANA RASTLIN... 4 Vaja
Biotehniška fakulteta Oddelek za agronomijo Dominik VODNIK FIZIOLOGIJA RASTLIN PRAKTIČNE VAJE UNIVERZITETNI ŠTUDIJ KMETIJSTVO - AGRONOMIJA Ljubljana, 2001 1 KAZALO 1. MINERALNA PREHRANA RASTLIN... 4 Vaja
SINTEZA SAHAROZE IN ŠKROBA
 SINTEZA SAHAROZE IN ŠKROBA Univerza v Ljubljani Biotehniška fakulteta Oddelek za agronomijo Stroma kloroplasta Škrob (primarni ali asimilacijski) Calvinov cikel Sladkor (trioza) Sladkor (trioza) Pi Sladkor
SINTEZA SAHAROZE IN ŠKROBA Univerza v Ljubljani Biotehniška fakulteta Oddelek za agronomijo Stroma kloroplasta Škrob (primarni ali asimilacijski) Calvinov cikel Sladkor (trioza) Sladkor (trioza) Pi Sladkor
Delovna točka in napajalna vezja bipolarnih tranzistorjev
 KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
UNIVERZA V LJUBLJANI, FAKULTETA ZA STROJNIŠTVO Katedra za energetsko strojništvo VETRNICA. v 2. v 1 A 2 A 1. Energetski stroji
 Katedra za energetsko strojništo VETRNICA A A A Katedra za energetsko strojništo Katedra za energetsko strojništo VETRNICA A A A Δ Δp p p Δ Katedra za energetsko strojništo Teoretična moč etrnice Določite
Katedra za energetsko strojništo VETRNICA A A A Katedra za energetsko strojništo Katedra za energetsko strojništo VETRNICA A A A Δ Δp p p Δ Katedra za energetsko strojništo Teoretična moč etrnice Določite
Transformator. Delovanje transformatorja I. Delovanje transformatorja II
 Transformator Transformator je naprava, ki v osnovi pretvarja napetost iz enega nivoja v drugega. Poznamo vrsto različnih izvedb transformatorjev, glede na njihovo specifičnost uporabe:. Energetski transformator.
Transformator Transformator je naprava, ki v osnovi pretvarja napetost iz enega nivoja v drugega. Poznamo vrsto različnih izvedb transformatorjev, glede na njihovo specifičnost uporabe:. Energetski transformator.
SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK
 SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
FOTOSINTEZA Wan Hill primerjal rastlinsko fotosintezo s fotosintezo BAKTERIJ
 FOTOSINTEZA FOTOSINTEZA je proces, pri katerem s pomočjo svetlobne energijje nastajajo v živih celicah organske spojine. 1772 Priestley RASTLINA slab zrak dober zrak Rastlina s pomočjo svetlobe spreminja
FOTOSINTEZA FOTOSINTEZA je proces, pri katerem s pomočjo svetlobne energijje nastajajo v živih celicah organske spojine. 1772 Priestley RASTLINA slab zrak dober zrak Rastlina s pomočjo svetlobe spreminja
2.1. MOLEKULARNA ABSORPCIJSKA SPEKTROMETRIJA
 2.1. MOLEKULARNA ABSORPCJSKA SPEKTROMETRJA Molekularna absorpcijska spektrometrija (kolorimetrija, fotometrija, spektrofotometrija) temelji na merjenju absorpcije svetlobe, ki prehaja skozi preiskovano
2.1. MOLEKULARNA ABSORPCJSKA SPEKTROMETRJA Molekularna absorpcijska spektrometrija (kolorimetrija, fotometrija, spektrofotometrija) temelji na merjenju absorpcije svetlobe, ki prehaja skozi preiskovano
ZAKLJUČNI PROCESI V BIOTEHNOLOGIJI. Membranski separacijski procesi: diafiltracija, elektrodializa, reverzna osmoza, pervaporacija
 ZAKLJUČNI PROCESI V BIOTEHNOLOGIJI Membranski separacijski procesi: diafiltracija, elektrodializa, reverzna osmoza, pervaporacija Membranski separacijski procesi v biotehnologiji proces mikrofiltracija
ZAKLJUČNI PROCESI V BIOTEHNOLOGIJI Membranski separacijski procesi: diafiltracija, elektrodializa, reverzna osmoza, pervaporacija Membranski separacijski procesi v biotehnologiji proces mikrofiltracija
IZPIT IZ ANALIZE II Maribor,
 Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
P E D O L O G I J A. Tema: Voda u tlu
 MEĐUSVEUČILIŠNI STUDIJ MEDITERANSKA POLJOPRIVREDA P E D O L O G I J A Tema: Voda u tlu Doc.dr.sc. Aleksandra BENSA i Dr.sc. Boško MILOŠ Autorizirana prezentacija Split, 2011/12. Cilj Objasniti odnose između
MEĐUSVEUČILIŠNI STUDIJ MEDITERANSKA POLJOPRIVREDA P E D O L O G I J A Tema: Voda u tlu Doc.dr.sc. Aleksandra BENSA i Dr.sc. Boško MILOŠ Autorizirana prezentacija Split, 2011/12. Cilj Objasniti odnose između
Zakaj proučevati tla?
 Zakaj proučevati tla? medij za rast rastlin in pridelkov produkcija in absorbcija plinov medij za rast mikroorganizmov habitat za živali veliki integrator vseh delov terestričnega ekosistema vir za proučevanje
Zakaj proučevati tla? medij za rast rastlin in pridelkov produkcija in absorbcija plinov medij za rast mikroorganizmov habitat za živali veliki integrator vseh delov terestričnega ekosistema vir za proučevanje
STRES- VODA : POMANKANJE SUŠA
 STRES- VODA : POMANKANJE SUŠA pomanjkanje vode; veliko izhlapevanje; osmotsko vezana voda; zmrzla tla; plitva tla časovna dimenzija sušnega stresa gradient stanja vode v rastlini; pomen stanja vode v celotnem
STRES- VODA : POMANKANJE SUŠA pomanjkanje vode; veliko izhlapevanje; osmotsko vezana voda; zmrzla tla; plitva tla časovna dimenzija sušnega stresa gradient stanja vode v rastlini; pomen stanja vode v celotnem
Statistična analiza. doc. dr. Mitja Kos, mag. farm. Katedra za socialno farmacijo Univerza v Ljubljani- Fakulteta za farmacijo
 Statistična analiza opisnih spremenljivk doc. dr. Mitja Kos, mag. arm. Katedra za socialno armacijo Univerza v Ljubljani- Fakulteta za armacijo Statistični znaki Proučevane spremenljivke: statistični znaki
Statistična analiza opisnih spremenljivk doc. dr. Mitja Kos, mag. arm. Katedra za socialno armacijo Univerza v Ljubljani- Fakulteta za armacijo Statistični znaki Proučevane spremenljivke: statistični znaki
SEKUNDARNE VEZE međumolekulske veze
 PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
Booleova algebra. Izjave in Booleove spremenljivke
 Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
FIZIOLOGIJA STRESA. Univerza v Ljubljani Biotehniška fakulteta Oddelek za agronomijo. Agronomija - UNI
 FIZIOLOGIJA STRESA Univerza v Ljubljani Biotehniška fakulteta Oddelek za agronomijo Agronomija - UNI Stres vzrok: kakršnakoli sprememba okoljskih dejavnikov, ki ima za posledico zmanjšano rast rastline
FIZIOLOGIJA STRESA Univerza v Ljubljani Biotehniška fakulteta Oddelek za agronomijo Agronomija - UNI Stres vzrok: kakršnakoli sprememba okoljskih dejavnikov, ki ima za posledico zmanjšano rast rastline
Razvoj homojohidrih rastlin iz poikilohidrih pomeni prehod iz vode na kopno in je povezan z razvojem vakuoliziranih celic
 VAKUOLA Nastanek: iz ER, diktiosomov Zgradba: enojna membrana, vsebina: A) vodne vakuole B) Vakuole s hidrofobno vsebino C) Vakuole z emulzijami Različna pojavnost glede na število in zgradbo v odvisnosti
VAKUOLA Nastanek: iz ER, diktiosomov Zgradba: enojna membrana, vsebina: A) vodne vakuole B) Vakuole s hidrofobno vsebino C) Vakuole z emulzijami Različna pojavnost glede na število in zgradbo v odvisnosti
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
TEŽKE KOVINE IN RASTLINE
 TEŽKE KOVINE IN RASTLINE Univerza v Ljubljani Biotehniška fakulteta Oddelek za agronomijo TEŽKE KOVINE (TK) V TLEH PRIVZEM KOVIN V RASTLINE FITOTOKSIČNOST TEŽKIH KOVIN TOLERANCA RASTLIN NA TEŽKE KOVINE
TEŽKE KOVINE IN RASTLINE Univerza v Ljubljani Biotehniška fakulteta Oddelek za agronomijo TEŽKE KOVINE (TK) V TLEH PRIVZEM KOVIN V RASTLINE FITOTOKSIČNOST TEŽKIH KOVIN TOLERANCA RASTLIN NA TEŽKE KOVINE
II. gimnazija Maribor PROJEKTNA NALOGA. Mentor oblike: Mirko Pešec, prof. Predmet: kemija - informatika
 II. gimnazija Maribor PROJEKTNA NALOGA Mentor vsebine: Irena Ilc, prof. Avtor: Andreja Urlaub Mentor oblike: Mirko Pešec, prof. Predmet: kemija - informatika Selnica ob Dravi, januar 2005 KAZALO VSEBINE
II. gimnazija Maribor PROJEKTNA NALOGA Mentor vsebine: Irena Ilc, prof. Avtor: Andreja Urlaub Mentor oblike: Mirko Pešec, prof. Predmet: kemija - informatika Selnica ob Dravi, januar 2005 KAZALO VSEBINE
Kotne in krožne funkcije
 Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
Integralni račun. Nedoločeni integral in integracijske metrode. 1. Izračunaj naslednje nedoločene integrale: (a) dx. (b) x 3 +3+x 2 dx, (c) (d)
 Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
Rizosfera procesi, ki vplivajo na razopložljivost mineralnih hranil. Ekofiziologija in mineralna prehrana rastlin 2005/06
 Rizosfera procesi, ki vplivajo na razopložljivost mineralnih hranil Ekofiziologija in mineralna prehrana rastlin 2005/06 Literatura Marschner H. (1995) Mineral nutrition of higher plants. Poglavje 15:
Rizosfera procesi, ki vplivajo na razopložljivost mineralnih hranil Ekofiziologija in mineralna prehrana rastlin 2005/06 Literatura Marschner H. (1995) Mineral nutrition of higher plants. Poglavje 15:
Prenos toplote prenos energije katerega pogojuje razlika temperatur temperatura je krajevno od točke do točke različna
 PRENOS OPOE Def. Prenos toplote prenos energije katerega pogojuje razlika temperatur temperatura je krajevno od točke do točke različna Načini prenosa toplote: PREVAJANJE (kondukcija, PRESOP (konvekcija
PRENOS OPOE Def. Prenos toplote prenos energije katerega pogojuje razlika temperatur temperatura je krajevno od točke do točke različna Načini prenosa toplote: PREVAJANJE (kondukcija, PRESOP (konvekcija
RANKINOV KROŽNI PROCES Seminar za predmet JTE
 RANKINOV KROŽNI PROCES Seminar za predmet JTE Rok Krpan 16.12.2010 Mentor: izr. prof. Iztok Tiselj Carnotov krožni proces Iz štirih sprememb: dveh izotermnih in dveh izentropnih (reverzibilnih adiabatnih)
RANKINOV KROŽNI PROCES Seminar za predmet JTE Rok Krpan 16.12.2010 Mentor: izr. prof. Iztok Tiselj Carnotov krožni proces Iz štirih sprememb: dveh izotermnih in dveh izentropnih (reverzibilnih adiabatnih)
FARMAKOKINETIKA. Hitrosti procesov Farmakokinetični ni parametri Aplikacija. Tatjana Irman Florjanc
 FARMAKOKINETIKA Hitrosti procesov Farmakokinetični ni parametri Aplikacija Tatjana Irman Florjanc Inštitut za farmakologijo in eksperimentalno toksikologijo, MF, Univerza v Ljubljani V praksi - kontrola
FARMAKOKINETIKA Hitrosti procesov Farmakokinetični ni parametri Aplikacija Tatjana Irman Florjanc Inštitut za farmakologijo in eksperimentalno toksikologijo, MF, Univerza v Ljubljani V praksi - kontrola
KONSTRUKTORSKA GRADBENA FIZIKA. Analiza ios aplikacije Condensation in primerjava z analitično dobljenimi rezultati
 KONSTRUKTORSKA GRADBENA FIZIKA Analiza ios aplikacije Condensation in primerjava z analitično dobljenimi rezultati Timotej Čižek štud. leto 2013/2014 Condensation je preprosta aplikacija, ki deluje na
KONSTRUKTORSKA GRADBENA FIZIKA Analiza ios aplikacije Condensation in primerjava z analitično dobljenimi rezultati Timotej Čižek štud. leto 2013/2014 Condensation je preprosta aplikacija, ki deluje na
Kotni funkciji sinus in kosinus
 Kotni funkciji sinus in kosinus Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z oznako cos x, DEFINICIJA V PRAVOKOTNEM TRIKOTNIKU: Kotna funkcija sinus je definirana kot razmerje
Kotni funkciji sinus in kosinus Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z oznako cos x, DEFINICIJA V PRAVOKOTNEM TRIKOTNIKU: Kotna funkcija sinus je definirana kot razmerje
Tokovi v naravoslovju za 6. razred
 Tokovi v naravoslovju za 6. razred Bojan Golli in Nada Razpet PeF Ljubljana 7. december 2007 Kazalo 1 Fizikalne osnove 2 1.1 Energija in informacija............................... 3 2 Projekti iz fizike
Tokovi v naravoslovju za 6. razred Bojan Golli in Nada Razpet PeF Ljubljana 7. december 2007 Kazalo 1 Fizikalne osnove 2 1.1 Energija in informacija............................... 3 2 Projekti iz fizike
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
*M * Osnovna in višja raven MATEMATIKA NAVODILA ZA OCENJEVANJE. Sobota, 4. junij 2011 SPOMLADANSKI IZPITNI ROK. Državni izpitni center
 Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 12. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
Jure Stojan 2. predavanje termodinamične osnove, encimske katalize encimska kataliza časovni potek encimske reakcije začetna hitrost
 FFA: Laboratorijska medicina, Molekularna encimologija, 2010/2011 3.predavanje Jure Stojan 2. predavanje termodinamične osnove, encimske katalize encimska kataliza časovni potek encimske reakcije začetna
FFA: Laboratorijska medicina, Molekularna encimologija, 2010/2011 3.predavanje Jure Stojan 2. predavanje termodinamične osnove, encimske katalize encimska kataliza časovni potek encimske reakcije začetna
NEPARAMETRIČNI TESTI. pregledovanje tabel hi-kvadrat test. as. dr. Nino RODE
 NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
Laboratorij za termoenergetiko. Vodikove tehnologije in PEM gorivne celice
 Laboratorij za termoenergetiko Vodikove tehnologije in PEM gorivne celice Pokrivanje svetovnih potreb po energiji premog 27% plin 22% biomasa 10% voda 2% sonce 0,4% veter 0,3% nafta 32% jedrska 6% geoterm.
Laboratorij za termoenergetiko Vodikove tehnologije in PEM gorivne celice Pokrivanje svetovnih potreb po energiji premog 27% plin 22% biomasa 10% voda 2% sonce 0,4% veter 0,3% nafta 32% jedrska 6% geoterm.
Aleš Mrhar. kinetični ni vidiki. Izraženo s hitrostjo in maso, dx/dt očistkom
 Izločanje zdravilnih učinkovin u iz telesa: kinetični ni vidiki Biofarmacija s farmakokinetiko Univerzitetni program Farmacija Aleš Mrhar Izločanje učinkovinu Izraženo s hitrostjo in maso, dx/ k e U očistkom
Izločanje zdravilnih učinkovin u iz telesa: kinetični ni vidiki Biofarmacija s farmakokinetiko Univerzitetni program Farmacija Aleš Mrhar Izločanje učinkovinu Izraženo s hitrostjo in maso, dx/ k e U očistkom
PROUČEVANJE OSMOZE PRI DVEH RAZLIČNIH RASTLINSKIH TKIVIH
 II. gimnazija Maribor Trg Miloša Zidanška 1 PROUČEVANJE OSMOZE PRI DVEH RAZLIČNIH RASTLINSKIH TKIVIH SABINA MLAKAR, 4.B BIOLOGIJA MENTORICA: PROF. ALENKA PRAPOTNIK ZALAR 1. Cilji eksperimenta Namen vaje
II. gimnazija Maribor Trg Miloša Zidanška 1 PROUČEVANJE OSMOZE PRI DVEH RAZLIČNIH RASTLINSKIH TKIVIH SABINA MLAKAR, 4.B BIOLOGIJA MENTORICA: PROF. ALENKA PRAPOTNIK ZALAR 1. Cilji eksperimenta Namen vaje
Mehanika fluidov. Statika tekočin. Tekočine v gibanju. Lastnosti tekočin, Viskoznost.
 Mehanika fluidov Statika tekočin. Tekočine v gibanju. Lastnosti tekočin, Viskoznost. 1 Statika tekočin Če tekočina miruje, so vse sile, ki delujejo na tekočino v ravnotežju. Masne volumske sile: masa tekočine
Mehanika fluidov Statika tekočin. Tekočine v gibanju. Lastnosti tekočin, Viskoznost. 1 Statika tekočin Če tekočina miruje, so vse sile, ki delujejo na tekočino v ravnotežju. Masne volumske sile: masa tekočine
vaja Kvan*ta*vno določanje proteinov. 6. vaja Kvan*ta*vno določanje proteinov. 6. vaja Kvan*ta*vno določanje proteinov
 28. 3. 11 UV- spektrofotometrija Biuretska metoda Absorbanca pri λ=28 nm (A28) UV- spektrofotometrija Biuretska metoda vstopni žarek intenziteta I Lowrijeva metoda Bradfordova metoda Bradfordova metoda
28. 3. 11 UV- spektrofotometrija Biuretska metoda Absorbanca pri λ=28 nm (A28) UV- spektrofotometrija Biuretska metoda vstopni žarek intenziteta I Lowrijeva metoda Bradfordova metoda Bradfordova metoda
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * NAVODILA ZA OCENJEVANJE. Sreda, 3. junij 2015 SPLOŠNA MATURA
 Državni izpitni center *M15143113* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sreda, 3. junij 2015 SPLOŠNA MATURA RIC 2015 M151-431-1-3 2 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor Naloga Odgovor
Državni izpitni center *M15143113* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sreda, 3. junij 2015 SPLOŠNA MATURA RIC 2015 M151-431-1-3 2 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor Naloga Odgovor
1. Definicijsko območje, zaloga vrednosti. 2. Naraščanje in padanje, ekstremi. 3. Ukrivljenost. 4. Trend na robu definicijskega območja
 ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
OSNOVE HIDROSTATIKE. - vede, ki preučuje mirujoče tekočine
 OSNOVE HIDROSTATIKE - vede, ki preučuje mirujoče tekočine HIDROSTATIKA Značilnost, da je sila na katero koli točko v tekočini enaka iz vseh smeri. Če ta pogoj o ravnovesju sil ne velja, se tekočina premakne
OSNOVE HIDROSTATIKE - vede, ki preučuje mirujoče tekočine HIDROSTATIKA Značilnost, da je sila na katero koli točko v tekočini enaka iz vseh smeri. Če ta pogoj o ravnovesju sil ne velja, se tekočina premakne
Osnove sklepne statistike
 Univerza v Ljubljani Fakulteta za farmacijo Osnove sklepne statistike doc. dr. Mitja Kos, mag. farm. Katedra za socialno farmacijo e-pošta: mitja.kos@ffa.uni-lj.si Intervalna ocena oz. interval zaupanja
Univerza v Ljubljani Fakulteta za farmacijo Osnove sklepne statistike doc. dr. Mitja Kos, mag. farm. Katedra za socialno farmacijo e-pošta: mitja.kos@ffa.uni-lj.si Intervalna ocena oz. interval zaupanja
13. Jacobijeva metoda za računanje singularnega razcepa
 13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 15. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
TRDNOST (VSŠ) - 1. KOLOKVIJ ( )
 TRDNOST (VSŠ) - 1. KOLOKVIJ (17. 12. 03) Pazljivo preberite besedilo vsake naloge! Naloge so točkovane enakovredno (vsaka 25%)! Pišite čitljivo! Uspešno reševanje! 1. Deformiranje telesa je podano s poljem
TRDNOST (VSŠ) - 1. KOLOKVIJ (17. 12. 03) Pazljivo preberite besedilo vsake naloge! Naloge so točkovane enakovredno (vsaka 25%)! Pišite čitljivo! Uspešno reševanje! 1. Deformiranje telesa je podano s poljem
matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):
![matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij): matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):](/thumbs/87/96579490.jpg) 4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
Zupan, M., Grčman, H., Kočevar, H. Navodila za vaje iz pedologije
 Tekstura tal 5 1. TEKSTURA TAL Tla so sestavljena iz trdne, tekoče in plinaste faze. Trdna faza tal je sestavljena iz mineralnih delcev različnih velikosti (pesek, melj, glina) in organske snovi. Tekstura
Tekstura tal 5 1. TEKSTURA TAL Tla so sestavljena iz trdne, tekoče in plinaste faze. Trdna faza tal je sestavljena iz mineralnih delcev različnih velikosti (pesek, melj, glina) in organske snovi. Tekstura
МЕХАНИКА НА ФЛУИДИ (AFI, TI, EE)
 Zada~i za program 2 po predmetot МЕХАНИКА НА ФЛУИДИ (AFI, TI, EE) Предметен наставник: Проф. д-р Методија Мирчевски Асистент: Виктор Илиев (rok za predavawe na programot - 07. i 08. maj 2010) (во термини
Zada~i za program 2 po predmetot МЕХАНИКА НА ФЛУИДИ (AFI, TI, EE) Предметен наставник: Проф. д-р Методија Мирчевски Асистент: Виктор Илиев (rok za predavawe na programot - 07. i 08. maj 2010) (во термини
Če je električni tok konstanten (se ne spreminja s časom), poenostavimo enačbo (1) in dobimo enačbo (2):
 ELEKTRIČNI TOK TEOR IJA 1. Definicija enote električnega toka Električni tok je gibanje električno nabitih delcev v trdnih snoveh (kovine, polprevodniki), tekočinah ali plinih. V kovinah se gibljejo prosti
ELEKTRIČNI TOK TEOR IJA 1. Definicija enote električnega toka Električni tok je gibanje električno nabitih delcev v trdnih snoveh (kovine, polprevodniki), tekočinah ali plinih. V kovinah se gibljejo prosti
1. Splošna varnostna priporočila za ravnanje z biološkim materialom. 2. Opredelitev nekaterih kemijskih pojmov
 Splošni del 1. Splošna varnostna priporočila za ravnanje z biološkim materialom Pri ravnanju z biološkim materialom veljajo splošna varnostna priporočila: biološki material je potencialno kužen in nevaren;
Splošni del 1. Splošna varnostna priporočila za ravnanje z biološkim materialom Pri ravnanju z biološkim materialom veljajo splošna varnostna priporočila: biološki material je potencialno kužen in nevaren;
Kontrolne karte uporabljamo za sprotno spremljanje kakovosti izdelka, ki ga izdelujemo v proizvodnem procesu.
 Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
p 1 ENTROPIJSKI ZAKON
 ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
Kvantni delec na potencialnem skoku
 Kvantni delec na potencialnem skoku Delec, ki se giblje premo enakomerno, pride na mejo, kjer potencial naraste s potenciala 0 na potencial. Takšno potencialno funkcijo zapišemo kot 0, 0 0,0. Slika 1:
Kvantni delec na potencialnem skoku Delec, ki se giblje premo enakomerno, pride na mejo, kjer potencial naraste s potenciala 0 na potencial. Takšno potencialno funkcijo zapišemo kot 0, 0 0,0. Slika 1:
Razvoj homojohidrih rastlin iz poikilohidrih pomeni prehod iz vode na kopno in je povezan z razvojem vakuoliziranih celic
 VAKUOLA Nastanek: iz ER, diktiosomov Zgradba: enojna membrana, vsebina: A) vodne vakuole B) Vakuole s hidrofobno vsebino C) Vakuole z emulzijami Različna pojavnost glede na število in zgradbo v odvisnosti
VAKUOLA Nastanek: iz ER, diktiosomov Zgradba: enojna membrana, vsebina: A) vodne vakuole B) Vakuole s hidrofobno vsebino C) Vakuole z emulzijami Različna pojavnost glede na število in zgradbo v odvisnosti
Namen določanja vlažnost lesa
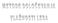 Namen določanja vlažnost lesa V svežem lesu določitev količine vode v lesu Pred izvajanjem sušenja izbira pravilnega programa sušenja Med izvajanjem sušilnega postopka primerjava dejanskega stanja s programiranim
Namen določanja vlažnost lesa V svežem lesu določitev količine vode v lesu Pred izvajanjem sušenja izbira pravilnega programa sušenja Med izvajanjem sušilnega postopka primerjava dejanskega stanja s programiranim
Izločanje zdravilnih učinkovin iz telesa:
 Izločanje zdravilnih učinkovin iz telesa: kinetični vidiki Biofarmacija s farmakokinetiko Aleš Mrhar Izločanje učinkovin Izraženo s hitrostjo in maso, dx/dt = k e U očistkom in volumnom, Cl = k e V Hitrost
Izločanje zdravilnih učinkovin iz telesa: kinetični vidiki Biofarmacija s farmakokinetiko Aleš Mrhar Izločanje učinkovin Izraženo s hitrostjo in maso, dx/dt = k e U očistkom in volumnom, Cl = k e V Hitrost
13. poglavje: Energija
 13. poglavje: Energija 1. (Naloga 3) Koliko kilovatna je peč za hišno centralno kurjavo, ki daje 126 MJ toplote na uro? Podatki: Q = 126 MJ, t = 3600 s; P =? Če peč z močjo P enakomerno oddaja toploto,
13. poglavje: Energija 1. (Naloga 3) Koliko kilovatna je peč za hišno centralno kurjavo, ki daje 126 MJ toplote na uro? Podatki: Q = 126 MJ, t = 3600 s; P =? Če peč z močjo P enakomerno oddaja toploto,
1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου...
 ΑΠΟΖΗΜΙΩΣΗ ΘΥΜΑΤΩΝ ΕΓΚΛΗΜΑΤΙΚΩΝ ΠΡΑΞΕΩΝ ΣΛΟΒΕΝΙΑ 1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου... 3 1 1. Έντυπα αιτήσεων
ΑΠΟΖΗΜΙΩΣΗ ΘΥΜΑΤΩΝ ΕΓΚΛΗΜΑΤΙΚΩΝ ΠΡΑΞΕΩΝ ΣΛΟΒΕΝΙΑ 1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου... 3 1 1. Έντυπα αιτήσεων
ARHITEKTURA DETAJL 1, 1:10
 0.15 0.25 3.56 0.02 0.10 0.12 0.10 SESTV S2 polimer-bitumenska,dvoslojna(po),... 1.0 cm po zahtevah SIST DIN 52133 in nadstandardno, (glej opis v tehn.poročilu), npr.: PHOENIX STR/Super 5 M * GEMINI P
0.15 0.25 3.56 0.02 0.10 0.12 0.10 SESTV S2 polimer-bitumenska,dvoslojna(po),... 1.0 cm po zahtevah SIST DIN 52133 in nadstandardno, (glej opis v tehn.poročilu), npr.: PHOENIX STR/Super 5 M * GEMINI P
Opća bilanca tvari - = akumulacija u dif. vremenu u dif. volumenu promatranog sustava. masa unijeta u dif. vremenu u dif. volumen promatranog sustava
 Opća bilana tvari masa unijeta u dif. vremenu u dif. volumen promatranog sustava masa iznijeta u dif. vremenu iz dif. volumena promatranog sustava - akumulaija u dif. vremenu u dif. volumenu promatranog
Opća bilana tvari masa unijeta u dif. vremenu u dif. volumen promatranog sustava masa iznijeta u dif. vremenu iz dif. volumena promatranog sustava - akumulaija u dif. vremenu u dif. volumenu promatranog
8. Diskretni LTI sistemi
 8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
vaja Izolacija kromosomske DNA iz vranice in hiperkromni efekt. DNA RNA Protein. ime deoksirbonukleinska kislina ribonukleinska kislina
 transkripcija translacija Protein 12. vaja Izolacija kromosomske iz vranice in hiperkromni efekt sladkorji deoksiriboza riboza glavna funkcija dolgoročno shranjevanje genetskih informacij prenos informacij
transkripcija translacija Protein 12. vaja Izolacija kromosomske iz vranice in hiperkromni efekt sladkorji deoksiriboza riboza glavna funkcija dolgoročno shranjevanje genetskih informacij prenos informacij
