VIJČANI SPOJEVI. Pomoćni nastavni materijali uz kolegij "Konstrukcijski elementi I" Ak. godina 2006./07.
|
|
|
- Χθόνια Κουντουριώτης
- 9 χρόνια πριν
- Προβολές:
Transcript
1 VIJČANI SPOJEVI Pomoćni nastavni materijali uz kolegij "Konstrukcijski elementi I" Ak. godina 2006./07. Nositelji kolegija: Prof. dr. sc. Božidar Križan Doc. dr. sc. Saša Zelenika - 1 -
2 VIJČANI SPOJEVI NAVOJ Navojna linija (zavojna linija, zavojnica) nastaje namatanjem hipotenuze pravokutnog trokuta na cilindar. γ γ h 1 - navojna linija, 2 - odmotana navojna linija, tj. hipotenuza pravokutnog trokuta, h - uspon Kut uspona navoja: tan γ = h d π 2 Kad bi po navojnoj liniji oko cilindra namatali žice trokutastog, pravokutnog ili drugih presjeka, dobili bi navoje trokutastog, pravokutnog ili drugih profila zuba: Vijak ima vanjski navoj, izrađen na vanjskoj površini cilindra. Matica ima unutarnji navoj izrađen u cilindričnom provrtu. Unutarnji navoj može biti izrađen i u provrtu u nekom strojnom dijelu. Matica koja se na vijku okrene za 360, napravit će u aksijalnom smjeru put koji je jednak usponu h
3 Najčešće vrste navoja: g) a) Metrički navoj; najčešći standardni navoj b) Fini metrički navoj; ima manju dubinu navoja i korak od normalnog metričkog navoja c) Whitworth-ov cijevni navoj; tradicionalni cijevni navoj porijekolom iz Velike Britanije d) Trapezni navoj; za vretena, ima manje trenje od metričkog navoja e) Pilasti navoj; za vretena, ima manje trenje od trapeznog, ali podnosi opterećenja samo u jednom smjeru f) Obli navoj; za spojnice željezničkih vagona, neosjetljiv na oštećenje i prljavštinu g) Obli elektro-navoj (Edisonov navoj); za grla žarulja i električne osigurače Navoji mogu biti: - desnovojni koji su standardni - lijevovojni za posebne namjene: ventili plinskih boca, natezači čelične užadi Desnovojni navoj Lijevovojni navoj - 3 -
4 Oznake: γ h a) Vijak i matica: - d = vanjski nazivni promjer vijka - d 2 = srednji promjer navoja (bokova) - d 3 = promjer korijena navoja vijka (promjer jezgre); za metričke navoje je d 3 = d 1,22687 P - P = korak navoja (udaljenost između dva susjedna zupca) - β = kut nagiba boka zuba (kut profila) - D 1 = unutarnji promjer navoja matice - m = visina matice - h = uspon navoja - γ = kut uspona b) Profil metričkog ISO navoja: - H 1 = nosiva dubina navoja - h 3 = dubina navoja - R = polumjer zaobljenja u korijenu navoja - 4 -
5 c) Prema kvaliteti izrade, tj. hrapavosti i točnosti izmjera i oblika, vijci i matice se dijele u sljedeće klase (DIN 267): - F - fina - A - srednja - za opću upotrebu - B - srednje gruba - C - gruba Navoj može imati jedan ili više početaka pa se govori o jednovojnom ili viševojnom navoju. Viševojni navoji imaju veći uspon h. h=p h=2p P h=3p P Jednovojni navoj Dvovojni navoj Trovojni navoj Označavanje navoja na crtežima: a) Metrički navoj, npr. M 12; broj označava vanjski promjer d = 12 mm. b) Fini metrički navoj ima manju dubinu navoja i korak od normalnog metričkog navoja, npr. M 3 x 0,35; d = 3 mm, P = 0,35 mm. c) Whitworth-ov cijevni navoj: - vanjski navoj, npr. G 3/4; prema DIN ISO 228; unutarnji promjer cijevi je 3/4 ". - vanjski navoj, npr. R 3/4 za spojeve gdje je unutarnji navoj cilindričan, a vanjski koničan 1:16; prema DIN 2999 i DIN 3858; unutarnji promjer cijevi je 3/4 ". - unutarnji cijevni navoj se označava G p 3/4, odnosno R p 3/4. d) Trapezni navoj: - npr. Tr 36 x 6; d = 36 mm, P = 6 mm. - npr. Tr 52 x 24 P8; d = 52 mm, h = 24 mm, P = 8 mm (trovojni navoj) - 5 -
6 VRSTE VIJČANIH SPOJEVA Vijčani spojevi su najčešće korištena vrsta rastavljivih spojeva. Glavni elementi vijčanog spoja su: 1. Vijak na kojem je izrađen vanjski navoj 2. Matica ili cilindrični provrt u strojnom dijelu u kojima je izrađen unutarnji navoj 3. Podložna pločica ili osigurač - po potrebi. Vijak s maticom (pričvrsni vijak) Vijak u provrtu s unutarnjim navojem (pričvrsni vijak) Postoje vijci koji pomoću svrdla na vrhu sami u metalu buše rupu i urezuju navoj: Neke vrste vijaka za metal, ciglu i beton same u provrtu urezuju unutarnji navoj. Vrste vijčanih spojeva s obzirom na namjenu: 1. Pričvrsni vijčani spojevi: - za međusobno spajanje dijelova (gornja slika) - za napinjanje čelične užadi: okretanjem dvostruke matice se uške međusobno približavaju, odnosno udaljavaju Desni navoj Dvostruka matica Lijevi navoj - 6 -
7 2. Pokretni vijčani spojevi ili "vijčani pogoni": rotacijsko gibanje vijka (vretena) se pretvara u uzdužno pomicanje matice ili vijka (vretena) pri čemu je ponekad bitno proizvesti veliku aksijalnu silu. Primjeri: - vretena na prešama: proizvodi se velika aksijalna sila - vretena na tokarskim i drugim obradnim strojevima - vretena u ventilima - 7 -
8 3. Vijčani spojevi za podešavanje: - za podešavanje ventila motora, sigurnosnih ventila i sl. Vijak za podešavanje - kao noge služe za niveliranje kućanskih aparata (npr. hladnjaka), strojeva, kioska i sl. 4. Brtveni vijci: služe kao čepovi, npr. na karteru automobilskog motora. Čep - 8 -
9 5. Mjerni vijci: kod mjernih uređaja, npr. mikrometarske mjerke, okretanjem vijka u fiksnoj matici pomiče se mjerni tanjurić Mjerni tanjurić na vrhu vijka VIJCI k Najčešće vrste pričvrsnih vijaka: a) Vijak sa šestostranom glavom; b) Vijak za točno nalijeganje (kalibrirani vijak); c) Vijak s cilindričnom glavom; d) Vijak s cilindričnom glavom s unutarnjim šesterokutom (za imbus-ključ); e) Vijak s upuštenom glavom; f) Vijak s upuštenom lećastom glavom; g) Vijak s nareckanom glavom za ručno pritezanje; h) Vijak sa samorežućim navojem; i) Vijak za lim (sličnog koničnog oblika su vijci za drvo); k) Vijak s uškom; l) Vijak s prstenastom glavom; m) Svorni vijak; n) Zatik s navojem; o) Čep s navojem - 9 -
10 - Vijci pod a), b) i o) se pritežu ključevima za šesterokutne glave i matice; - Vijci pod c), e), f), g), h), i) i n) se pritežu izvijačem s plosnatim vrhom; - Vijak pod d) se priteže inbus-ključem; - Vijci pod k) i l) se pritežu podesnim alatom; - Vijak pod g) i svorni vijak pod m) se uvrću ručno. Prostor potreban za pritezanje i otpuštanje vijka ovisi o vrsti vijka, odnosno potrebnoj vrsti ključa. Najmanje je mjesta potrebno za inbus-vijke pa se oni mogu smjestiti neposredno jedan uz drugi. Osim plosnatog izvijača se koriste i drugi oblici. Torx-sistem je dobar jer se sila na maticu ili glavu vijka ne prenosi po nekoliko linija nego po nekoliko površina. Razne vrste izvijača Torx-izvijač - dodir na površini Šesterostrani alat - linijski dodir
11 Najčešći materijal za izradu vijaka je čelik visoke istezljivosti kod kojega nema opasnosti od krhkog loma. U elektrotehnici se zbog dobre vodljivosti koristi mjed. Koriste se i laki metali, a u zadnje vrijeme i polimeri (umjetne plastične mase). Čelični vijci se dijele u razrede čvrstoće: Razred čvrstoće vijka R m (N/mm 2 ) R e (N/mm 2 ) R p0,2 (N/mm 2 ) A 5 (%) Odgovarajući materijal Č0370 Č0370 Č0545 Č1330 Č1430 Č1730 Č4130 Č4732 Č5431 Pripadajući razred čvrstoće matice A 5 = relativno izduženje (dilatacija) ε pri lomu (za probnu epruvetu s l 0 =5 d 0 ). Navedene čvrstoće vrijede za temperature do 350 C. Iznad toga treba koristiti specijalne materijale. Oznaka razreda čvrstoće znači: Npr. 6.8: - prvi broj x 100 = 6 x 100 = 600 N/mm 2 = R m - prvi broj x drugi broj x 10 = 6 x 8 x 10 = 480 N/mm 2 = R e Vijci razreda čvrstoće 6.8 i čvršći moraju oznaku razreda čvrstoće imati vidljivo otisnutu na glavi vijka. Duljina navojnog dijela vijka odabire se po konkretnoj potrebi. Ako se vijak uvrće u podlogu, duljina navojnog dijela vijka mora biti veća od dubine uvrtanja l u, osim kod svornih vijaka gdje je jednaka
12 Najmanja dubina uvrtanja l u (mm) 1) Materijal podloge Razred čvrstoće vijka R m 400 N/mm 2 0,8 d 1,2 d - - Čelik 400 R m 600 N/mm 2 0,8 d 1,2 d 1,2 d R m 800 N/mm 2 0,8 d 1,2 d 1,2 d 1,2 d R m >800 N/mm 2 0,8 d 1,2 d 1,0 d 1,0 d Sivi lijev 1,3 d 1,5 d 1,5 d - Cu-slitine 1,3 d 1,3 d - - Čisti aluminij 1,6 d 2,2 d - - Lake Nekaljene Al-slitine 1,2 d 1,6 d - - kovine 2) Kaljene Al-slitine 0,8 d 1,2 d 1,6 d - Bijela kovina, umjetne plastične mase 2,5 d ) Za fine navoje dubina uvrtanja treba biti za 25 % veća. 2) Za dinamička opterećenja treba dubinu uvrtanja povećati za oko 20 %. Os vijka treba biti na primjerenoj udaljenosti R od ruba: Materijal podloge Čelik Sivi lijev, Cu-slitine Lake kovine Bijela kovina, umjetne plastične mase R min 0,75 d 0,8 d 1,0 d 1,25 d Dubina rupe s navojem treba za oko tri koraka (3 P) biti veća od dubine uvrtanja l u, kako se ne bi dogodilo da vijak dođe do kraja navoja prije nego što su dijelovi koje treba spojiti dobro pritegnuti
13 MATICE Najčešće vrste matica: a) Šesterostrana matica; b) Šesterostrana zatvorena matica; c) Četverostrana matica; d) Matica s čeonim urezom; e) Matica s rupama po obodu; f) Nareckana matica; g) Krilasta matica (za ručno pritezanje); h) Krunasta matica Čelične matice se dijele u razrede čvrstoće: Razred čvrstoće R m (N/mm 2 ) Oznaka razreda čvrstoće znači: Npr. 6: - broj x 100 = 6 x 100 = 600 N/mm 2 = R m Matice većih čvrstoća moraju na sebi imati otisnutu oznaku razreda čvrstoće
14 PODLOŽNE PLOČICE Podložne pločice (podloške) su najčešće okruglog oblika, s rupom kroz koju prolazi vijak. Ne osiguravaju vijak od odvrtanja i koriste se u sljedećim slučajevima: - kad je površina podloge na koju dolaze matica ili glava vijka loše obrađena, tj. kad je neravna, - kad je rupa za vijak u podlozi znatno veća od promjera vijka, - kad se spoj često rastavlja, kako se ne bi oštetila podloga, - kad je podloga mekana, kako bi se povećala površina na koju se ostvaruje pritisak - kad je podloga kosa, što je slučaj kod spajanja U ili I-profila Obična podložna pločica Podložna pločica za profilirane nosače OSIGURANJE VIJČANOG SPOJA OD ODVRTANJA Osiguranje vijčanog spoja od odvrtanja kod statičkih opterećenja nije potrebno, ali se primjenjuje kod dinamičkih opterećenja. Naime, nakon pritezanja vijka dolazi do djelomičnog slijeganja hrapavosti dodirnih površina, može doći do puzanja materijala vijka, a može doći i do lokalnih plastičnih deformacija. Sve to, potpomognuto promjenama opterećenja i eventualnim vibracijama, može rezultirati otpuštanjem vijčanog spoja. U pravilu su dobro proračunati, oblikovani i pritegnuti vijčani spojevi već osigurani protiv neželjenog odvrtanja. To prije svega vrijedi za visokoopterećene spojeve s elastičnim vijcima razreda čvrstoće 8.8 i više, uz male hrapavosti dodirnih površina
15 a) Osiguranje oblikom Osiguranje oblikom se postiže: - rascjepkom s običnom ili krunastom maticom; rascjepka prolazi kroz poprečni provrt u vijku i - sigurnosnim limom s izdancima; jedan izdanak se priljubi uz maticu, a drugi savije oko ruba. a) Osiguranje od odvrtanja pomoću rascjepke; b) Osiguranje od odvrtanja pomoću sigurnosnog lima b) Osiguranje silom Umetanjem posebnih opružnih elemenata se osigurava aksijalna sila prednapona i pri djelovanju najveće radne sile, makar je došlo do slijeganja hrapavosti ili plastičnih deformacija. Ovi elementi su u obliku rasječenih, zakrivljenih ili tanjurastih prstena (pločica), a izrađeni su od opružnog čelika. Nazivaju se i "elastične podloške". Razne zupčaste i lepezaste prstenaste pločice se svojim zupcima utiskuju u podlogu, povećavaju trenje i tako sprečavaju odvrtanje. Ovakvo osiguranje nije primjenjivo na tvrdim kaljenim površinama. Veće trenje i sprečavanje odvrtanja matice se postiže i sigurnosnom limenom maticom od opružnog čelika koja s unutarnje strane ima više jezičaca koji se zabijaju u navoj. Česta je upotreba dvije matice - kontramatice manje visine koja se priteže na podlogu i normalne matice koja se priteže na kontramaticu ( u praksi
16 se često matice montiraju obratno - slika). Matice mogu biti i jednake. Vanjska matica sprečava otpuštanje unutarnje, a na površini njihovog dodira se javlja i dodatno trenje. Za jednokratnu upotrebu se koriste matice s uloškom od umjetne plastične mase u koji vijak urezuje navoj. a) Rasječeni elastični prsteni; b) Zakrivljeni elastični prsteni; c) Tanjurasta elastična pločica; d) i e) Zupčaste pločice; f) i g) Lepezaste pločice; h) Sigurnosna limena matica; i) Sigurnosna matica s poliamidnim uloškom za jednokratnu upotrebu Tanjuraste i zupčaste elastične pločice se mogu integrirati s glavom vijka, odnosno maticom. a) b) Integrirana izvedba osigurača: a) Osiguranje tanjurastom elastičnom pločicom kod vijka; b) Osiguranje ozubljenjem kod vijka i matice Matica s protumaticom c) Osiguranje materijalom Vrši se lijepljenjem navoja umjetnim smolama. Često se koristi ljepilo "Loctite" kojim se mogu postići vodonepropusni spojevi, npr. kod spajanja cijevi. Moguće je i zavarivanje glave vijka ili matice za podlogu za što postoje i posebni vijci i matice
17 Efikasnost osiguranja od ovrtanja je prikazana u dijagramu ovisnosti pada sile prednapona F V o broju promjena opterećenja N. F V Broj promjena opterećenja N A - Loctite, B - tanjurasta elastična pločica integrirana s glavom vijka, C - zupčasta pločica integrirana s glavom vijka, D - matica s poliamidnim uloškom, E - vijak sa zupčastom pločicom, F - vijak s lepezastom pločicom, G - neosigurani vijčani spoj. Linija za rasječene elastične prstene se nalazi između linija F i G. SILE I MOMENTI U VIJČANOM SPOJU Radi pojednostavljenja se razmatra navoj pravokutnog profila, a matica se svodi na jedan element na promjeru d 2. Na element djeluju neke elementarne sile, ali će se radi jednostavnosti odmah računati s ukupnim silama. Prilikom pritezanja matice se taj element uklinjuje između podloge i navoja vijka
18 Promatrani element (odnosno matica) može se dalje okretati samo ako se vijak produlji i podloga sabije (skrati). To će se pri daljnjem pritezanju i dogoditi, što znači da će vijak biti opterećen aksijalnom vlačnom silom F, a podloga istom silom tlačno. Za guranje elementa tj. matice uz kosinu pod kutem uspona γ, potrebna je tangencijalna (obodna) sila F t. Na mjestu dodira elementa matice i navoja vijka djeluju normalna sila F N i sila trenja F tr, a s podloge se još prenosi i sila F. Kad se vijčani spoj priteže, može se zamisliti da se matica "penje" po navoju. Tangencijalna sila F = F tan( γ + ρ' ) t Sila trenja F tr = F N µ ' G = F N tan ρ' µ G ' = korigirani faktor trenja na navoju čija veličina ovisi o materijalu vijka i ' matice, površinskoj obradi i podmazanosti. Okvirno je µ G = 0,09...0,20. Najčešće ' je µ G 0,12. ρ' = kut trenja Da bi se proizvela sila F t, odnosno aksijalna sila u vijku F, treba djelovati momentom pritezanja na navoju d2 d M 2 G = Ft = F tan( γ + ρ' )
19 Kad se vijčani spoj otpušta, matica se "spušta" po navoju i tu se razlikuju dva slučaja: - Ako je kut trenja manji od kuta uspona, tj. ρ' < γ, element matice pri spuštanju treba pridržavati silom F t da bi bio u ravnoteži: F t = F tan( γ ρ' ) Kad sila F t ne bi djelovala, matica bi se sama "spustila" (otpustila) i u tom slučaju vijčani spoj ne bi bio samokočan. Ovakvi vijci moraju imati veliki kut uspona γ, a to se može postići samo viševojnim navojima. - Ako je kut trenja veći od kuta uspona, tj. ρ' > γ, onda (γ ρ') odnosno tan (γ ρ') postaju negativni. Slijedi da je tangencijalna (obodna) sila F t negativna, odnosno ona će imati suprotni smjer djelovanja. Dakle, da bi se matica spuštala, treba ju dodatno gurati silom F t i u tom slučaju je vijčani spoj samokočan. Za metričke navoje s γ 2,5 je samokočnost osigurana ako je µ ' 0,04, a to je praktički uvijek
20 Budući da se bokovi zuba navoja, osim kod pravokutnog profila, nalaze pod određenim kutem β, stvarna normalna sila F N ' bit će nešto veća, a time će veća biti i sila trenja. ' FN F N = β cos 2 U praksi se računa tako da se normalna sila smatra istom, a u istom omjeru se povećava stvarni faktor trenja µ G, čime se množenjem sile i faktora trenja dobiva ista sila trenja. Korigirani računski faktor trenja je jednak ' µ G µ G = β cos 2 ' Za metrički navoj s β = 60 je µ G = 1,155 µ G = tan ρ'. ' Za trapezni navoj s β = 30 je µ G = 1,035 µ G, pa je trenje manje nego na metričkom navoju. Prilikom pritezanja vijčanog spoja, matica treba svladati uspon navoja na vijku za što se troši oko 27 % momenta M G, te trenje na navoju za što se troši oko 73 % momenta M G. Prilikom pritezanja, matica klizi po podlozi gdje se također javlja trenje. Dodir se ostvaruje po prstenastoj površini između promjera rupe za vijak d h i vanjskog promjera oslonca glave vijka ili matice d w. d w 0,9 s za šesterostrane vijke i matice (s = otvor ključa) d w = promjer glave inbus-vijka
21 Srednji polumjer na kojemu se ostvaruje trenje iznosi (d h + d w )/4. Sila trenja na podlozi: F tr K = F µ K µ K = faktor trenja na podlozi. Raspon vrijednosti je sličan kao i na navoju. Moment za svladavanje trenja na podlozi M K = F µ K d h + d 4 w Prilikom pritezanja vijčanog spoja treba svladati moment na navoju i moment na podlozi M A = M G + M K Moment pritezanja vijčanog spoja kod koga će se u vijku javiti sila F je dakle M A d + = 2 dh d F tan( γ + ρ' ) + µ K 2 4 w NAČINI PRITEZANJA VIJČANOG SPOJA Sila u vijku mora prilikom pritezanja biti u dopuštenim granicama da ne bi došlo do plastičnih deformacija ili pucanja vijka. a) Ručno pritezanje ključem Dužina ključa L je prilagođena veličini vijka i prosječnoj ručnoj sili, kako moment pritezanja M A ne bi bio prevelik i doveo do oštećenja vijka. Ova se metoda primjenjuje za vijke korištene za sporedne svrhe
22 Ručna sila N L 21 d b) Pritezanje pneumatskim ili električnim alatom Moment pritezanja se može grubo podesiti. Služi za serijsko pritezanje vijaka. c) Pritezanje momentnim ključem Preciznije od prethodnih načina je pritezanje momentnim ključem. Kod momentog ključa se jedan njegov dio deformira sukladno veličini momenta pritezanja M A, dok na drugi neopterećeni dio moment ne djeluje i on se ne deformira. Kod jedne vrste momentog ključa je deformabilni dio torzijska opruga u obliku šipke na kojoj je i kazaljka. Pri pritezanju se šipka uvija i kazaljka rotira. Kazaljka pokazuje moment pritezanja na skali koja je vezana za drugi neopterećeni dio u obliku cijevi
23 Kod jedne druge vrste momentnog ključa se prethodno na skali postavi željeni moment pritezanja. Kad se taj moment postigne, dolazi do međusobnog pomaka nekih dijelova momentnog ključa i čuje se zvučni signal. d) Hidrauličko pritezanje Kod veoma velikih vijaka je pritezanje ključem neprikladno ili nemoguće jer je moment pritezanja prevelik, a točnost postizanja aksijalne sile F u vijku bi bila mala. Takav je slučaj kod vijaka za pričvršćenje poklopaca cilindra velikih motora ili kod preša. Kako sili F u vijku odgovara određeno izduženje vijka f S, hidrauličkim uređajem se vijak izduži za f S, matica se rukom ili podesnim alatom malo pritegne i hidraulički uređaj ukloni. Vijak ostaje izdužen za iznos f S i opterećen silom F. Za razliku od prethodnih načina pritezanja, vijak nije opterećen torzijski. 1 - dovod ulja pod tlakom, 2 - klip, 3 - tlačni cilindar, 4 - natezna matica spojena s vijkom koju potiskuje klip
24 SLUČAJEVI OPTEREĆENJA VIJČANOG SPOJA Definicije: Sila prednapona F V je statička vlačna sila koja se u vijku javlja nakon pritezanja vijčanog spoja. Nakon pritezanja je i podloga opterećena tlačnom silom iste veličine F V. Radna sila F A je vlačna sila koja djeluje na vijak nakon pritezanja, a može biti statička ili dinamička. 1. Vijčani spoj bez prednapona F V = 0 Vijak, tj navoj na završetku kuke je spojen s maticom. Spoj nije pritegnut, a težina kuke se zanemaruje. 1 - teretna kuka s navojem, 2 - matica, 3 - osigurač protiv odvrtanja matice, 4 - aksijalni kuglični ležaj Teret F A (statička radna sila) izaziva u vijku vlačno naprezanje σ V F = A A S σ dop
25 Površina presjeka preko koje se prenosi sila je A S d2 + d = π 4 = 2 ds π 4 Re σdop = ν odnosno R σdop = ν p0,2 Faktor sigurnosti ν = 1,25...1,5, maksimalno do 6, npr. kod dizala. 2. Vijčani spoj s prednaponom (prednapregnuti vijčani spoj) Prilikom pritezanja vijčanog spoja u vijku se javlja aksijalna sila prednapona F V koja direktno zavisi od momenta pritezanja M A = M G + M K : F V = d 2 2 tan M ( γ + ρ' ) A + µ K d h + d 4 w a) F V > 0; F A = 0 Ako dodatne aksijalne radne sile F A nema ili je zanemariva, vijčani spoj će biti statički opterećen: - vlačno naprezanje F σ v = A V S
26 - torzijsko naprezanje τ t = M W G p = F V d2 tan( γ + ρ' ) 2 3 ds π 16 d S d = 2 + d 2 3 Ekvivalentno naprezanje 2 v 2 t σe = σ + 3 τ σ dop Re σdop = ν odnosno R σdop = ν p0,2 Faktor sigurnosti ν = 1,25...1,5..., ovisno o primjeni, opasnosti i sl. Za ovakve vijke se najčešće koristi ručno pritezanje ključem gdje sama duljina ključa onemogućava prevelika naprezanja. Na ključ se ne smiju stavljati nastavci, npr. cijevi, jer je onda moment pritezanja prevelik. b) F V > 0; F A > 0 FV > 0, FA = 0 Dodatna radna sila F A djeluje na vijak pritegnut silom prednapona F V. Radna sila može biti statička ili dinamička. p a) Vijci poklopca posude pod tlakom; b) Vijci koji nose viseći ležaj
27 Ovako opterećeni vijci imaju statički dio naprezanja usljed sile prednapona te dodatni statički ili dinamički dio naprezanja uslijed radne sile. Radna sila dodatno izdužuje već izduženi vijak i smanjuje silu u podlozi (spojenim dijelovima) pa se i podloga izdužuje. Slučaj opterećenja prednapregnutog vijčanog spoja s dinamičkom radnom silom F A je najznačajniji i najteži i bit će obrađen detaljno. PODATLJIVOST I KRUTOST VIJKA I PODLOGE Gradivo je detaljno izloženo na predavanjima. Slika V1: Elastični vijci Slika V2: Primjer za proračun koeficijenta podatljivosti vijka
28 Slika V3: Primjer za proračun koeficijenta podatljivosti podloge DEFORMACIJSKI DIJAGRAM VIJČANOG SPOJA Gradivo je detaljno izloženo na predavanjima. Slika V4: Deformacije vijka i podloge F A p a) b) c)
29 UTJECAJ HVATIŠTA RADNE SILE Gradivo je detaljno izloženo na predavanjima. Slika V5: Faktor rasterećenja podloge n n 0,25 n 0,5 n 0,
30 DEFORMACIJSKI DIJAGRAM ZA RAZNE SLUČAJEVE OPTEREĆENJA Radi jednostavnosti, bit će prikazan samo donji dio dijagrama. a) Statičko opterećenje silom prednapona F V. Radna sila F A = 0. Sile u vijku i podlozi su jednake. b) Statičko opterećenje silom prednapona F V i statičkom radnom silom F A. Sile u vijku i podlozi su različite i nepromjenljive. Primjer: vijčani spoj na prirubnici posude pod konstantnim tlakom. c) Nakon pritezanja silom F V, vijčani spoj je opterećen dinamički radnom silom koja varira između nule i vrijednosti F A. Sila u vijku će varirati između F V i F S, a u podlozi između F V i F K. Dinamička sila u vijku iznosi ±F SA /2. Primjer: vijčani spoj na poklopcu cilindra klipnog kompresora
31 d) Nakon pritezanja silom F V, vijčani spoj je opterećen dinamički radnom silom koja varira između F A ' i F A ''. Sila u vijku će varirati između F S ' i F S '', a u podlozi između F K ' i F K ''. Dinamička sila u vijku iznosi ±(F S '' F S ')/2. PREDNOST KORIŠTENJA ELASTIČNIH VIJAKA U dinamički opterećenim konstrukcijama bezuvjetno treba težiti što nižoj vrijednosti dinamičke sile ±F SA /2 ili ±(F S '' F S ')/2, kako bi što teže došlo do zamora materijala i zamornog loma. Dinamička će sila biti to manja što je veća podatljivost vijka. Podatljiviji se vijak može dobiti: - stanjenjem struka na promjer d T = ((0,7...)0,85...0,95) d 3 ("elastični vijak"): - bušenjem rupe uzduž vijka: - povećanjem duljine vijka, što znači da se moraju koristiti dodatne čahure:
32 Na gornjim izvedbama je postignut i mali faktor rasterećenja podloge n što također rezultira podatljivijim vijkom. Vijak sa stanjenim strukom može se opteretiti manjom silom prednapona, ali će se još znatnije smanjiti dinamička komponenta pa time i opasnost od zamornog loma. Podatljivi vijak Sila Obični vijak d T = 0,9 d 3 d T = 0,7 d 3 F V 100 % 80 % 50 % F SA 100 % 60 % 38 % Iz usporedbe deformacijskih dijagrama za "kruti" i "elastični" vijak za jednake sile F V i F A može se dobro uočiti smanjenje dinamičke sile F SA. "Kruti" vijak "Elastični" podatljivi vijak
33 NAPREZANJA U VIJKU Gradivo je detaljno izloženo na predavanjima. Slika V6: Smithov dijagram σ R m R e (R p0,2 ) R d0 +R d-1 R a R dg κ =0 R dd κ= 1 R a σ m R d-1 Slika V7: Opterećenje navoja matica Normalna tlačna matica Matica s rasteretnim utorom Vlačna matica
34 POPREČNO OPTEREĆENI VIJČANI SPOJEVI Ako sila djeluje okomito na os vijka, vijčani spoj je poprečno opterećen. Takvi su slučajevi kod sklopova gdje se prenosi okretni moment, npr. kod vijaka kojima se spajaju polovice krutih kolutnih spojki ili kod spojeva glavina s vijencem pužnog kola. Načini prenošenja poprečne sile F Q su sljedeći: a) Izvedba pomoću dosjednog (kalibriranog) vijka je dobra za promjenjive sile. Dosjed je H7/k6, izrada je skupa. Vijak je u poprečnom presjeku opterećen posmično (tangencijalno) i kod preopterećenja je moguća njegova trajna deformacija. b) Običan vijak prolazi kroz uzdužno razrezanu elastičnu čahuru izrađenu od čelika za opruge. Provrt ne zahtijeva toleranciju (obično bušenje). Posmično je opterećena čahura koja zbog svoje elastičnosti može ublažiti udare. c) Poprečnu silu preuzima čahura s dosjedom u provrtu koja je posmično opterećena
35 Posmično naprezanje za navedene slučajeve je τ s = F Q A τ sdop A = površina poprečnog presjeka vijka ili čahure opterećena smicanjem Dopušteno posmično naprezanje: τ s dop 0,6 R e za statičko opterećenje τ s dop 0,5 R e za ishodišno dinamičko opterećenje τ s dop 0,4 R e za izmjenično dinamičko opterećenje Površinski pritisak između vijka ili čahure i površine provrta je p = F Q d s p dop Dopušteni površinski pritisak: p dop 1,2 R e za statičko opterećenje i žilavi materijal p dop 0,9 R e za dinamičko opterećenje i žilavi materijal p dop 0,75 R m za statičko opterećenje i krhki materijal p dop 0,6 R m za dinamičko opterećenje i krhki materijal d) Vijak je pritegnut takvom silom prednapona F V koja na naliježnoj površini proizvodi silu trenja F T = F V µ 0 koja je veća od poprečne sile F Q. Proračun će biti prikazan za slučaj da se sila trenja postiže pomoću dva vijka i da se trenje javlja na dvije površine:
36 Svaki vijčani spoj proizvodi silu na podlozi F K. Ukupna sila trenja mora za faktor sigurnosti ν biti veća od poprečne sile: F K µ 0 i z = ν F Q Materijal Faktor trenja mirovanja µ 0 Glatke neodmašćene površine 0,1...0,15 Čelik/čelik - suho 0,15...0,2 Čelik/sivi lijev, čelik/bronca - suho 0,18...0,25 Sivi lijev/ sivi lijev, sivi lijev/ bronca - suho 0,22...0,26 Konstrukcije od Č Č0561 u visokogradnji i mostogradnji 0,5 i = broj površina na kojima se ostvaruje trenje (na slici i=2) z = broj vijaka ( na slici z=2) ν = 1,2...1,3 za opće strojarstvo i visokogradnju, ν = 1,6 za mostogradnju i dizalice Sila na podlozi F K = ν F µ 0 Q i z Budući da nema radne sile, sila u podlozi je jednaka minimalnoj sili prednapona F V min pa će biti F M min = F K + F Z Naprezanje u vijku treba kontrolirati na najveću montažnu silu prednapona F M max = α A F M min
37 POKRETNI VIJČANI SPOJEVI (VIJČANI POGONI) Služe za pretvorbu rotacijskog gibanja vijka u uzdužno gibanje matice ili vijka pa se nazivaju i vijčanim pogonima. Vijak se naziva vreteno i može biti velike duljine. Pokretni vijčani spojevi, tj. vretena, primjenjuju se kod obradnih strojeva, ventila, zasuna, klavirskih stolica itd. Vretena na tokarskim i drugim obradnim strojevima Vretena u ventilima
38 Kod preša se okretni moment pretvara u veliku aksijalnu silu. Za brzo uzdužno gibanje se koriste višenavojna vretena. Kao navoji se najčešće koriste trapezni jer imaju manje trenje od metričkih. Ako je opterećenje samo u jednom smjeru, mogu se koristiti i pilasti navoji gdje je nagib na opterećenoj strani navoja samo 3 pa je trenje još manje: µ ' G µ G = µ cos3 G Za torzijski moment na vretenu T će aksijalna sila biti F = d 2 T tan( γ + 2 ρ ') Ona će izazvati pritisak na navojima vretena i matice. Zbog stalnog klizanja navoja matice po navoju vretena, dodirni pritisak na navojima ne smije biti velik, kako ne bi došlo do habanja. Srednji dodirni pritisak mora biti manji od dopuštenog: F p = pdop π 2 2 ( d D1 ) z 0,75 4 Samo oko 75% navoja u matici nosi opterećenje Broj navoja u matici Površina jednog navoja (na 360 o ); D 1 = unutarnji promjer matice
39 Materijal vretena/matice Trajni pogon Čelik/čelik 8 Čelik/sivi lijev 5 Čelik/bronca 10 Kaljeni čelik/bronca 15 Čelik/plastika p dop (N/mm 2 ) Povremeni (sprekidani) pogon Rijetki pogon s malim brzinama i dobrim podmazivanjem +50% +100% Visina matice m = z P Usvajanje dimenzija vretena: a) Kod vlačno opterećenih vretena i kratkih tlačno opterećenih vretena kod kojih ne postoji opasnost od izvijanja potrebna se površina presjeka računa prema dopuštenom normalnom naprezanju. A 3 = 2 3 d π F 4 σ dop Za statička opterećenja: σ dop = R e /1,5 Za dinamička opterećenja: σ dop = R d /2 b) Kod tlačno opterećenih dugačkih vretena (kao na primjeru vretena za prešu) postoji opasnost od izvijanja. Promjer vretena se računa po formuli d 3 1, 2 2 k 4 F ν l d 3 (mm), F (N), l k (mm), E (N/mm 2 ) E Faktor sigurnosti ν Računska duljina izvijanja l k 0,7 l l = tlačno opterećena duljina vretena U novije se vrijeme kod alatnih strojeva radi veće točnosti koriste kuglična navojna vretena i matice, gdje je trenje klizanja zamijenjeno manjim trenjem kotrljanja. Kuglice se kotrljaju unutar navoja koji je u obliku polukružnog utora. Kod pomicanja matice uzduž vretena, kuglice recirkuliraju unutar nje
40 - 40 -
41 - 41 -
3525$&8158&1(',=$/,&(6$1$92-1,095(7(120
 Srednja masinska skola OSOVE KOSTRUISAJA List1/8 355$&8158&1(',=$/,&(6$1$9-1,095(7(10 3ROD]QLSRGDFL maksimalno opterecenje Fa := 36000 visina dizanja h := 440 mm Rucna sila Fr := 350 1DYRMQRYUHWHQR optereceno
Srednja masinska skola OSOVE KOSTRUISAJA List1/8 355$&8158&1(',=$/,&(6$1$9-1,095(7(10 3ROD]QLSRGDFL maksimalno opterecenje Fa := 36000 visina dizanja h := 440 mm Rucna sila Fr := 350 1DYRMQRYUHWHQR optereceno
NOSIVI DIJELOVI MEHATRONIČKIH KONSTRUKCIJA
 NOSIVI DIJELOVI MEHATRONIČKIH KONSTRUKCIJA Zavareni spojevi - I. dio 1 ZAVARENI SPOJEVI Nerastavljivi spojevi Upotrebljavaju se prije svega za spajanje nosivih mehatroničkih dijelova i konstrukcija 2 ŠTO
NOSIVI DIJELOVI MEHATRONIČKIH KONSTRUKCIJA Zavareni spojevi - I. dio 1 ZAVARENI SPOJEVI Nerastavljivi spojevi Upotrebljavaju se prije svega za spajanje nosivih mehatroničkih dijelova i konstrukcija 2 ŠTO
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
PRORAČUN GLAVNOG KROVNOG NOSAČA
 PRORAČUN GLAVNOG KROVNOG NOSAČA STATIČKI SUSTAV, GEOMETRIJSKE KARAKTERISTIKE I MATERIJAL Statički sustav glavnog krovnog nosača je slobodno oslonjena greda raspona l11,0 m. 45 0 65 ZAŠTITNI SLOJ BETONA
PRORAČUN GLAVNOG KROVNOG NOSAČA STATIČKI SUSTAV, GEOMETRIJSKE KARAKTERISTIKE I MATERIJAL Statički sustav glavnog krovnog nosača je slobodno oslonjena greda raspona l11,0 m. 45 0 65 ZAŠTITNI SLOJ BETONA
Konstruisanje. Dobro došli na... SREDNJA MAŠINSKA ŠKOLA NOVI SAD DEPARTMAN ZA PROJEKTOVANJE I KONSTRUISANJE
 Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri
 Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
VIJČANI SPOJ VIJCI HRN M.E2.257 PRIRUBNICA HRN M.E2.258 BRTVA
 VIJČANI SPOJ PRIRUBNICA HRN M.E2.258 VIJCI HRN M.E2.257 BRTVA http://de.wikipedia.org http://de.wikipedia.org Prirubnički spoj cjevovoda na parnom stroju Prirubnički spoj cjevovoda http://de.wikipedia.org
VIJČANI SPOJ PRIRUBNICA HRN M.E2.258 VIJCI HRN M.E2.257 BRTVA http://de.wikipedia.org http://de.wikipedia.org Prirubnički spoj cjevovoda na parnom stroju Prirubnički spoj cjevovoda http://de.wikipedia.org
NERASTAVLJIVE VEZE I SPOJEVI. Zakovični spojevi
 NERASTAVLJIVE VEZE I SPOJEVI Zakovični spojevi Zakovice s poluokruglom glavom - za čelične konstrukcije (HRN M.B3.0-984), (lijevi dio slike) - za kotlove pod tlakom (desni dio slike) Nazivni promjer (sirove)
NERASTAVLJIVE VEZE I SPOJEVI Zakovični spojevi Zakovice s poluokruglom glavom - za čelične konstrukcije (HRN M.B3.0-984), (lijevi dio slike) - za kotlove pod tlakom (desni dio slike) Nazivni promjer (sirove)
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
INTEGRALNI RAČUN. Teorije, metodike i povijest infinitezimalnih računa. Lucija Mijić 17. veljače 2011.
 INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
TRIGONOMETRIJA TROKUTA
 TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
Ĉetverokut - DOMAĆA ZADAĆA. Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke.
 Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
RIJEŠENI ZADACI I TEORIJA IZ
 RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
Linearna algebra 2 prvi kolokvij,
 1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
TOLERANCIJE I DOSJEDI
 11.2012. VELEUČILIŠTE U RIJECI Prometni odjel OSNOVE STROJARSTVA TOLERANCIJE I DOSJEDI 1 Tolerancije dimenzija Nijednu dimenziju nije moguće izraditi savršeno točno, bez ikakvih odstupanja. Stoga, kada
11.2012. VELEUČILIŠTE U RIJECI Prometni odjel OSNOVE STROJARSTVA TOLERANCIJE I DOSJEDI 1 Tolerancije dimenzija Nijednu dimenziju nije moguće izraditi savršeno točno, bez ikakvih odstupanja. Stoga, kada
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
BETONSKE KONSTRUKCIJE 2
 BETONSE ONSTRUCIJE 2 vježbe, 31.10.2017. 31.10.2017. DATUM SATI TEMATSA CJELINA 10.- 11.10.2017. 2 17.-18.10.2017. 2 24.-25.10.2017. 2 31.10.- 1.11.2017. uvod ponljanje poznatih postupaka dimenzioniranja
BETONSE ONSTRUCIJE 2 vježbe, 31.10.2017. 31.10.2017. DATUM SATI TEMATSA CJELINA 10.- 11.10.2017. 2 17.-18.10.2017. 2 24.-25.10.2017. 2 31.10.- 1.11.2017. uvod ponljanje poznatih postupaka dimenzioniranja
Akvizicija tereta. 5660t. Y= masa drva, X=masa cementa. Na brod će se ukrcati 1733 tona drva i 3927 tona cementa.
 Akvizicija tereta. Korisna nosivost broda je 6 t, a na brodu ia 8 cu. ft. prostora raspoloživog za sještaj tereta pod palubu. Navedeni brod treba krcati drvo i ceent, a na palubu ože aksialno ukrcati 34
Akvizicija tereta. Korisna nosivost broda je 6 t, a na brodu ia 8 cu. ft. prostora raspoloživog za sještaj tereta pod palubu. Navedeni brod treba krcati drvo i ceent, a na palubu ože aksialno ukrcati 34
BETONSKE KONSTRUKCIJE 3 M 1/r dijagrami
 BETONSKE KONSTRUKCIJE 3 M 1/r dijagrami Izv. prof. dr.. Tomilav Kišiček dipl. ing. građ. 0.10.014. Betonke kontrukije III 1 NBK1.147 Slika 5.4 Proračunki dijagrami betona razreda od C1/15 do C90/105, lijevo:
BETONSKE KONSTRUKCIJE 3 M 1/r dijagrami Izv. prof. dr.. Tomilav Kišiček dipl. ing. građ. 0.10.014. Betonke kontrukije III 1 NBK1.147 Slika 5.4 Proračunki dijagrami betona razreda od C1/15 do C90/105, lijevo:
Grafičko prikazivanje atributivnih i geografskih nizova
 Grafičko prikazivanje atributivnih i geografskih nizova Biserka Draščić Ban Pomorski fakultet u Rijeci 17. veljače 2011. Grafičko prikazivanje atributivnih nizova Atributivni nizovi prikazuju se grafički
Grafičko prikazivanje atributivnih i geografskih nizova Biserka Draščić Ban Pomorski fakultet u Rijeci 17. veljače 2011. Grafičko prikazivanje atributivnih nizova Atributivni nizovi prikazuju se grafički
Dimenzioniranje nosaa. 1. Uvjeti vrstoe
 Dimenzioniranje nosaa 1. Uvjeti vrstoe 1 Otpornost materijala prouava probleme 1. vrstoe,. krutosti i 3. elastine stabilnosti konstrukcija i dijelova konstrukcija od vrstog deformabilnog materijala. Moraju
Dimenzioniranje nosaa 1. Uvjeti vrstoe 1 Otpornost materijala prouava probleme 1. vrstoe,. krutosti i 3. elastine stabilnosti konstrukcija i dijelova konstrukcija od vrstog deformabilnog materijala. Moraju
PREDNAPETI BETON Primjer nadvožnjaka preko autoceste
 PREDNAPETI BETON Primjer nadvožnjaka preko autoceste 7. VJEŽBE PLAN ARMATURE PREDNAPETOG Dominik Skokandić, mag.ing.aedif. PLAN ARMATURE PREDNAPETOG 1. Rekapitulacija odabrane armature 2. Određivanje duljina
PREDNAPETI BETON Primjer nadvožnjaka preko autoceste 7. VJEŽBE PLAN ARMATURE PREDNAPETOG Dominik Skokandić, mag.ing.aedif. PLAN ARMATURE PREDNAPETOG 1. Rekapitulacija odabrane armature 2. Određivanje duljina
SPOJEVI S GLAVINOM. Pomoćni nastavni materijali uz kolegij "Konstrukcijski elementi I" Ak. godina 2006./07.
 SPOJEVI S GLAVINOM Pomoćni nastavni materijali uz kolegij "Konstrukcijski elementi I" Ak. godina 2006./07. Nositelji kolegija: Prof. dr. sc. Božidar Križan Doc. dr. sc. Saša Zelenika - 1 - SPOJEVI S GLAVINOM
SPOJEVI S GLAVINOM Pomoćni nastavni materijali uz kolegij "Konstrukcijski elementi I" Ak. godina 2006./07. Nositelji kolegija: Prof. dr. sc. Božidar Križan Doc. dr. sc. Saša Zelenika - 1 - SPOJEVI S GLAVINOM
2. KARAKTERISTIKE MATERIJALA ZA IZRADU VIJAKA I MATICA
 lementi strojeva RDNRGNUI VIJCNI OJ ist:. UVOD Vijcani soj riaa širokoj grui rastavljivih sojeva i restavlja najcešce korišteni nacin vezivanja va ili više elemenata. oj može biti izveen sa jenim ili više
lementi strojeva RDNRGNUI VIJCNI OJ ist:. UVOD Vijcani soj riaa širokoj grui rastavljivih sojeva i restavlja najcešce korišteni nacin vezivanja va ili više elemenata. oj može biti izveen sa jenim ili više
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
a M a A. Može se pokazati da je supremum (ako postoji) jedinstven pa uvodimo oznaku sup A.
 3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
PROSTA GREDA (PROSTO OSLONJENA GREDA)
 ROS GRED (ROSO OSONJEN GRED) oprečna sila i moment savijanja u gredi y a b c d e a) Zadana greda s opterećenjem l b) Sile opterećenja na gredu c) Određivanje sila presjeka grede u presjeku a) Unutrašnje
ROS GRED (ROSO OSONJEN GRED) oprečna sila i moment savijanja u gredi y a b c d e a) Zadana greda s opterećenjem l b) Sile opterećenja na gredu c) Određivanje sila presjeka grede u presjeku a) Unutrašnje
6 Primjena trigonometrije u planimetriji
 6 Primjena trigonometrije u planimetriji 6.1 Trgonometrijske funkcije Funkcija sinus (f(x) = sin x; f : R [ 1, 1]); sin( x) = sin x; sin x = sin(x + kπ), k Z. 0.5 1-6 -4 - -0.5 4 6-1 Slika 3. Graf funkcije
6 Primjena trigonometrije u planimetriji 6.1 Trgonometrijske funkcije Funkcija sinus (f(x) = sin x; f : R [ 1, 1]); sin( x) = sin x; sin x = sin(x + kπ), k Z. 0.5 1-6 -4 - -0.5 4 6-1 Slika 3. Graf funkcije
radni nerecenzirani materijal za predavanja R(f) = {f(x) x D}
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
ČELIČNA UŽAD 6 X 7 + T.J. = 42 6 X 7 + J.J. = 49. Ø 1,5-20 mm 6 X 19 + T.J. = X 19 + J.J. = 133. Ø 3-30 mm
 ČELIČNA UŽAD STANDARD - OPIS Broj žica dimenzije DIN 3053 19 Ø 1-10 mm DIN 3054 37 Ø 3-10 mm DIN 3055 6 X 7 + T.J. = 42 6 X 7 + J.J. = 49 Ø 1,5-20 mm DIN 3060 6 X 19 + T.J. = 114 6 X 19 + J.J. = 133 Ø
ČELIČNA UŽAD STANDARD - OPIS Broj žica dimenzije DIN 3053 19 Ø 1-10 mm DIN 3054 37 Ø 3-10 mm DIN 3055 6 X 7 + T.J. = 42 6 X 7 + J.J. = 49 Ø 1,5-20 mm DIN 3060 6 X 19 + T.J. = 114 6 X 19 + J.J. = 133 Ø
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
SPOJEVI S GLAVINOM. Pomoćni nastavni materijali uz kolegij "Konstrukcijski elementi I" Ak. godina 2010./11.
 SPOJEVI S GLAVINOM Pomoćni nastavni materijali uz kolegij "Konstrukcijski elementi I" Ak. godina 010./11. Nositelji kolegija: Prof. dr. sc. Božidar Križan Prof. dr. sc. Saša Zelenika - 1 - SPOJEVI S GLAVINOM
SPOJEVI S GLAVINOM Pomoćni nastavni materijali uz kolegij "Konstrukcijski elementi I" Ak. godina 010./11. Nositelji kolegija: Prof. dr. sc. Božidar Križan Prof. dr. sc. Saša Zelenika - 1 - SPOJEVI S GLAVINOM
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
SRĐAN PODRUG ELEMENTI STROJEVA
 S V E U Č I L I Š T E U S P L I T U FAKULTET ELEKTROTEHNIKE, STROJARSTVA I BRODOGRADNJE U SPLITU SRĐAN PODRUG ELEMENTI STROJEVA Predavanja za stručni i preddiplomski studij BRODOGRADNJE za školsku godinu
S V E U Č I L I Š T E U S P L I T U FAKULTET ELEKTROTEHNIKE, STROJARSTVA I BRODOGRADNJE U SPLITU SRĐAN PODRUG ELEMENTI STROJEVA Predavanja za stručni i preddiplomski studij BRODOGRADNJE za školsku godinu
zastori sunset curtain Kućište od željeza zaštićeno epoksidnim prahom, opruge od željeza. Lako i brzo se montiraju.
 zastori zastori sunset curtain Kućište od željeza zaštićeno epoksidnim prahom, opruge od željeza. Lako i brzo se montiraju. (mm) (mm) za PROZOR im (mm) tv25 40360 360 400 330x330 tv25 50450 450 500 410x410
zastori zastori sunset curtain Kućište od željeza zaštićeno epoksidnim prahom, opruge od željeza. Lako i brzo se montiraju. (mm) (mm) za PROZOR im (mm) tv25 40360 360 400 330x330 tv25 50450 450 500 410x410
Repetitorij-Dinamika. F i Zakon očuvanja impulsa (ZOI): i p i = j p j. Zakon očuvanja energije (ZOE):
 Repetitorij-Dinamika Dinamika materijalne točke Sila: F p = m a = lim t 0 t = d p dt m a = i F i Zakon očuvanja impulsa (ZOI): i p i = j p j i p ix = j p jx te i p iy = j p jy u 2D sustavu Zakon očuvanja
Repetitorij-Dinamika Dinamika materijalne točke Sila: F p = m a = lim t 0 t = d p dt m a = i F i Zakon očuvanja impulsa (ZOI): i p i = j p j i p ix = j p jx te i p iy = j p jy u 2D sustavu Zakon očuvanja
Matematička analiza 1 dodatni zadaci
 Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Teorijske osnove informatike 1
 Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Riješeni zadaci: Nizovi realnih brojeva
 Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
Strukture podataka i algoritmi 1. kolokvij 16. studenog Zadatak 1
 Strukture podataka i algoritmi 1. kolokvij Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i službeni šalabahter. Predajete samo papire koje ste dobili. Rezultati i uvid u kolokvije: ponedjeljak,
Strukture podataka i algoritmi 1. kolokvij Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i službeni šalabahter. Predajete samo papire koje ste dobili. Rezultati i uvid u kolokvije: ponedjeljak,
ZASTORI SUNSET CURTAIN Kućište od željeza zaštićeno epoksidnim prahom, opruge od željeza. Lako i brzo se montiraju.
 ZSTORI ZSTORI SUNSET URTIN Kućište od željeza zaštićeno epoksidnim prahom, opruge od željeza. Lako i brzo se montiraju. ŠIRIN (mm) VISIN (mm) Z PROZOR IM. (mm) TV25 40360 360 400 330x330 TV25 50450 450
ZSTORI ZSTORI SUNSET URTIN Kućište od željeza zaštićeno epoksidnim prahom, opruge od željeza. Lako i brzo se montiraju. ŠIRIN (mm) VISIN (mm) Z PROZOR IM. (mm) TV25 40360 360 400 330x330 TV25 50450 450
1 Promjena baze vektora
 Promjena baze vektora Neka su dane dvije različite uredene baze u R n, označimo ih s A = (a, a,, a n i B = (b, b,, b n Svaki vektor v R n ima medusobno različite koordinatne zapise u bazama A i B Zapis
Promjena baze vektora Neka su dane dvije različite uredene baze u R n, označimo ih s A = (a, a,, a n i B = (b, b,, b n Svaki vektor v R n ima medusobno različite koordinatne zapise u bazama A i B Zapis
PRILOG. Tab. 1.a. Dozvoljena trajna opterećenja bakarnih pravougaonih profila u(a) za θ at =35 C i θ=30 C, (θ tdt =65 C)
 PRILOG Tab. 1.a. Dozvoljena trajna opterećenja bakarnih pravougaonih profila u(a) za θ at =35 C i θ=30 C, (θ tdt =65 C) Tab 3. Vrednosti sačinilaca α i β za tipične konstrukcije SN-sabirnica Tab 4. Minimalni
PRILOG Tab. 1.a. Dozvoljena trajna opterećenja bakarnih pravougaonih profila u(a) za θ at =35 C i θ=30 C, (θ tdt =65 C) Tab 3. Vrednosti sačinilaca α i β za tipične konstrukcije SN-sabirnica Tab 4. Minimalni
Izravni posmik. Posmična čvrstoća tla. Laboratorijske metode određivanja kriterija čvratoće ( c i φ )
 Posmična čvrstoća tla Posmična se čvrstoća se često prikazuje Mohr-Coulombovim kriterijem čvrstoće u - σ dijagramu c + σ n tanφ Kriterij čvrstoće C-kohezija φ -kut trenja c + σ n tan φ φ c σ n Posmična
Posmična čvrstoća tla Posmična se čvrstoća se često prikazuje Mohr-Coulombovim kriterijem čvrstoće u - σ dijagramu c + σ n tanφ Kriterij čvrstoće C-kohezija φ -kut trenja c + σ n tan φ φ c σ n Posmična
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
DIMENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE
 TEORIJA ETONSKIH KONSTRUKCIJA T- DIENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE 3.5 f "2" η y 2 D G N z d y A "" 0 Z a a G - tačka presek koja određje položaj sistemne
TEORIJA ETONSKIH KONSTRUKCIJA T- DIENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE 3.5 f "2" η y 2 D G N z d y A "" 0 Z a a G - tačka presek koja određje položaj sistemne
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
ISPIT GRUPA A - RJEŠENJA
 Pismeni ispit iz OTPORNOSTI MATERIJALA I - grupa A 1. Kruta poluga AB oslonjena je na dva čelična štapa u A i B i opterećena trouglastim opterećenjem, kao na slici desno. Ako su oba štapa iste dužine L,
Pismeni ispit iz OTPORNOSTI MATERIJALA I - grupa A 1. Kruta poluga AB oslonjena je na dva čelična štapa u A i B i opterećena trouglastim opterećenjem, kao na slici desno. Ako su oba štapa iste dužine L,
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
 Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
1.4 Tangenta i normala
 28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f
 IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
(P.I.) PRETPOSTAVKA INDUKCIJE - pretpostavimo da tvrdnja vrijedi za n = k.
 1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
SVEUČILIŠTE U MOSTARU GRAĐEVINSKI FAKULTET
 SVEUČILIŠTE U MOSTRU GRĐEVINSKI FKULTET Kolegij: Osnove betonskih konstrukcija k. 013/014 god. 8. pismeni (dodatni) ispit - 10.10.014. god. Zadatak 1 Dimenzionirati i prikazati raspored usvojene armature
SVEUČILIŠTE U MOSTRU GRĐEVINSKI FKULTET Kolegij: Osnove betonskih konstrukcija k. 013/014 god. 8. pismeni (dodatni) ispit - 10.10.014. god. Zadatak 1 Dimenzionirati i prikazati raspored usvojene armature
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
NOMENKLATURA ORGANSKIH SPOJEVA. Imenovanje aromatskih ugljikovodika
 NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
Zavod za tehnologiju, Katedra za alatne strojeve: GLODANJE
 Glodanje je postupak obrade odvajanjem čestica (rezanjem) obradnih površina proizvoljnih oblika. Izvodi se na alatnim strojevima, glodalicama, pri čemu je glavno (rezno) gibanje kružno kontinuirano i pridruženo
Glodanje je postupak obrade odvajanjem čestica (rezanjem) obradnih površina proizvoljnih oblika. Izvodi se na alatnim strojevima, glodalicama, pri čemu je glavno (rezno) gibanje kružno kontinuirano i pridruženo
PROSTORNI STATIČKI ODREĐENI SUSTAVI
 PROSTORNI STATIČKI ODREĐENI SUSTAVI - svi elementi ne leže u istoj ravnini q 1 Z F 1 F Y F q 5 Z 8 5 8 1 7 Y y z x 7 X 1 X - svi elementi su u jednoj ravnini a opterećenje djeluje izvan te ravnine Z Y
PROSTORNI STATIČKI ODREĐENI SUSTAVI - svi elementi ne leže u istoj ravnini q 1 Z F 1 F Y F q 5 Z 8 5 8 1 7 Y y z x 7 X 1 X - svi elementi su u jednoj ravnini a opterećenje djeluje izvan te ravnine Z Y
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
( , 2. kolokvij)
 A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
Riješeni zadaci: Limes funkcije. Neprekidnost
 Riješeni zadaci: Limes funkcije. Neprekidnost Limes funkcije Neka je 0 [a, b] i f : D R, gdje je D = [a, b] ili D = [a, b] \ { 0 }. Kažemo da je es funkcije f u točki 0 jednak L i pišemo f ) = L, ako za
Riješeni zadaci: Limes funkcije. Neprekidnost Limes funkcije Neka je 0 [a, b] i f : D R, gdje je D = [a, b] ili D = [a, b] \ { 0 }. Kažemo da je es funkcije f u točki 0 jednak L i pišemo f ) = L, ako za
ČVRSTOĆA 13. GEOMETRIJSKE KARAKTERISTIKE RAVNIH PRESJEKA ŠTAPA
 ČVRSTOĆA 13. GEOMETRIJSKE KARAKTERISTIKE RAVNIH PRESJEKA ŠTAPA STATIČKI MOMENTI I MOMENTI INERCIJE RAVNIH PLOHA Kao što pri aksijalnom opterećenju štapa apsolutna vrijednost naprezanja zavisi, između ostalog,
ČVRSTOĆA 13. GEOMETRIJSKE KARAKTERISTIKE RAVNIH PRESJEKA ŠTAPA STATIČKI MOMENTI I MOMENTI INERCIJE RAVNIH PLOHA Kao što pri aksijalnom opterećenju štapa apsolutna vrijednost naprezanja zavisi, između ostalog,
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
l r redukovana dužina (zavisno od dužine i načina vezivanja)
 Vežbe 6 IZVIJANJE 1 IZVIJANJE Izvijanje se javlja kod aksijalno napregnutih štapova na pritisak, kada imaju relativno veliku dužinu u odnosu na površinu poprečnog preseka. Zbog postojanja geometrijskih
Vežbe 6 IZVIJANJE 1 IZVIJANJE Izvijanje se javlja kod aksijalno napregnutih štapova na pritisak, kada imaju relativno veliku dužinu u odnosu na površinu poprečnog preseka. Zbog postojanja geometrijskih
Matematika 1 - vježbe. 11. prosinca 2015.
 Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
1.1. Zavojne Ravni torzijski štapovi Zavojna fleksijska opruga: 2.2. Spiralna fleksijska
 Nastavna jedinica: OPUGE (elementi za spajanje rastavljivi spojevi) S. Zelenika KEI 7.ppt Definicija: Opruge: Opruge svrsishodnim oblikovanjem i upotrebom visokoelastičnih materijala mogu mehanički rad
Nastavna jedinica: OPUGE (elementi za spajanje rastavljivi spojevi) S. Zelenika KEI 7.ppt Definicija: Opruge: Opruge svrsishodnim oblikovanjem i upotrebom visokoelastičnih materijala mogu mehanički rad
TEORIJA BETONSKIH KONSTRUKCIJA 79
 TEORIJA BETOSKIH KOSTRUKCIJA 79 Primer 1. Odrediti potrebn površin armatre za stb poznatih dimenzija, pravogaonog poprečnog preseka, opterećen momentima savijanja sled stalnog ( g ) i povremenog ( w )
TEORIJA BETOSKIH KOSTRUKCIJA 79 Primer 1. Odrediti potrebn površin armatre za stb poznatih dimenzija, pravogaonog poprečnog preseka, opterećen momentima savijanja sled stalnog ( g ) i povremenog ( w )
konst. Električni otpor
 Sveučilište J. J. Strossmayera u sijeku Elektrotehnički fakultet sijek Stručni studij Električni otpor hmov zakon Pri protjecanju struje kroz vodič pojavljuje se otpor. Georg Simon hm je ustanovio ovisnost
Sveučilište J. J. Strossmayera u sijeku Elektrotehnički fakultet sijek Stručni studij Električni otpor hmov zakon Pri protjecanju struje kroz vodič pojavljuje se otpor. Georg Simon hm je ustanovio ovisnost
INTELIGENTNO UPRAVLJANJE
 INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
ZAVARENI SPOJEVI (elementi za spajanje nerastavljivi spojevi)
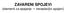 ZAVARENI SPOJEVI (elementi za spajanje nerastavljivi spojevi) Zavarivanje = spajanje dijelova koji su na mjestu spoja dovođenjem topline omekšani ili rastopljeni, uz dodavanje dodatnog materijala ili bez
ZAVARENI SPOJEVI (elementi za spajanje nerastavljivi spojevi) Zavarivanje = spajanje dijelova koji su na mjestu spoja dovođenjem topline omekšani ili rastopljeni, uz dodavanje dodatnog materijala ili bez
Proizvoljno opterećenje tijela može zahtijevati složenu analizu naprezanja i deformacija,
 1. Osnove čvrstoće 1.1. Pojam i vrste opterećenja Nauka o čvrstoći proučava utjecaj vanjskih sila i momenata na ponašanje čvrstih (realnih) tijela. Djelovanje vanjskih sila i momenata na tijelo naziva
1. Osnove čvrstoće 1.1. Pojam i vrste opterećenja Nauka o čvrstoći proučava utjecaj vanjskih sila i momenata na ponašanje čvrstih (realnih) tijela. Djelovanje vanjskih sila i momenata na tijelo naziva
35(7+2'1,3525$&8195$7,/$GLPHQ]LRQLVDQMHYUDWLOD
![35(7+2'1,3525$&8195$7,/$GLPHQ]LRQLVDQMHYUDWLOD 35(7+2'1,3525$&8195$7,/$GLPHQ]LRQLVDQMHYUDWLOD](/thumbs/60/45174330.jpg) Predmet: Mašinski elementi Proraþun vratila strana 1 Dimenzionisati vratilo elektromotora sledecih karakteristika: ominalna snaga P 3kW Broj obrtaja n 14 min 1 Shema opterecenja: Faktor neravnomernosti
Predmet: Mašinski elementi Proraþun vratila strana 1 Dimenzionisati vratilo elektromotora sledecih karakteristika: ominalna snaga P 3kW Broj obrtaja n 14 min 1 Shema opterecenja: Faktor neravnomernosti
4. STATIČKI PRORAČUN STUBIŠTA
 JBAG 4. STATIČKI PRORAČUN STUBIŠTA PROGRA IZ KOLEGIJA BETONSKE I ZIDANE KONSTRUKCIJE 9 5 SVEUČILIŠTE U ZAGREBU JBAG 4. Statiči proračun stubišta 4.. Stubišni ra 4... Analiza opterećenja 5 5 4 6 8 5 6 0
JBAG 4. STATIČKI PRORAČUN STUBIŠTA PROGRA IZ KOLEGIJA BETONSKE I ZIDANE KONSTRUKCIJE 9 5 SVEUČILIŠTE U ZAGREBU JBAG 4. Statiči proračun stubišta 4.. Stubišni ra 4... Analiza opterećenja 5 5 4 6 8 5 6 0
Geometrijske karakteristike poprenih presjeka nosaa. 9. dio
 Geometrijske karakteristike poprenih presjeka nosaa 9. dio 1 Sile presjeka (unutarnje sile): Udužna sila N Poprena sila T Moment uvijanja M t Moment savijanja M Napreanja 1. Normalno napreanje σ. Posmino
Geometrijske karakteristike poprenih presjeka nosaa 9. dio 1 Sile presjeka (unutarnje sile): Udužna sila N Poprena sila T Moment uvijanja M t Moment savijanja M Napreanja 1. Normalno napreanje σ. Posmino
4. STATIČKI PRORAČUN STUBIŠTA
 JBG 4. STTIČKI PRORČUN STUBIŠT PROGR IZ KOLEGIJ BETONSKE I ZIDNE KONSTRUKCIJE 9 6 5 5 SVEUČILIŠTE U ZGREBU JBG 4. Statiči proračun stubišta 4.. Stubišni ra 4... naliza opterećenja 5 5 4 6 8 0 Slia 4..
JBG 4. STTIČKI PRORČUN STUBIŠT PROGR IZ KOLEGIJ BETONSKE I ZIDNE KONSTRUKCIJE 9 6 5 5 SVEUČILIŠTE U ZGREBU JBG 4. Statiči proračun stubišta 4.. Stubišni ra 4... naliza opterećenja 5 5 4 6 8 0 Slia 4..
MATERIJALI I MEHANIČKA SVOJSTVA MATERIJALA. Prof. dr. sc. Ivica Kladarić
 MATERIJALI I MEHANIČKA SVOJSTVA MATERIJALA Statički vlačni pokus Prof. dr. sc. Ivica Kladarić 1 UVOD Metalni materijali najviše se upotrebljavaju u tehničkoj praksi zbog povoljnih mehaničkih, tehnoloških,
MATERIJALI I MEHANIČKA SVOJSTVA MATERIJALA Statički vlačni pokus Prof. dr. sc. Ivica Kladarić 1 UVOD Metalni materijali najviše se upotrebljavaju u tehničkoj praksi zbog povoljnih mehaničkih, tehnoloških,
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
Kolegij: Konstrukcije Rješenje zadatka 2. Okno Građevinski fakultet u Zagrebu. Efektivna. Jedinična težina. 1. Glina 18,5 21,
 Kolegij: Konstrukcije 017. Rješenje zadatka. Okno Građevinski fakultet u Zagrebu 1. ULAZNI PARAETRI. RAČUNSKE VRIJEDNOSTI PARAETARA ATERIJALA.1. Karakteristične vrijednosti parametara tla Efektivna Sloj
Kolegij: Konstrukcije 017. Rješenje zadatka. Okno Građevinski fakultet u Zagrebu 1. ULAZNI PARAETRI. RAČUNSKE VRIJEDNOSTI PARAETARA ATERIJALA.1. Karakteristične vrijednosti parametara tla Efektivna Sloj
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
šupanijsko natjecanje iz zike 2017/2018 Srednje ²kole 1. grupa Rje²enja i smjernice za bodovanje 1. zadatak (11 bodova)
 šupanijsko natjecanje iz zike 017/018 Srednje ²kole 1. grupa Rje²enja i smjernice za bodovanje 1. zadatak (11 bodova) U prvom vremenskom intervalu t 1 = 7 s automobil se giba jednoliko ubrzano ubrzanjem
šupanijsko natjecanje iz zike 017/018 Srednje ²kole 1. grupa Rje²enja i smjernice za bodovanje 1. zadatak (11 bodova) U prvom vremenskom intervalu t 1 = 7 s automobil se giba jednoliko ubrzano ubrzanjem
Funkcije dviju varjabli (zadaci za vježbu)
 Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
Zdaci iz trigonometrije trokuta Izračunaj ostale elemente trokuta pomoću zadanih:
 Zdaci iz trigonometrije trokuta... 1. Izračunaj ostale elemente trokuta pomoću zadanih: a) a = 1 cm, α = 66, β = 5 ; b) a = 7.3 cm, β =86, γ = 51 ; c) b = 13. cm, α =1 48`, β =13 4`; d) b = 44.5 cm, α
Zdaci iz trigonometrije trokuta... 1. Izračunaj ostale elemente trokuta pomoću zadanih: a) a = 1 cm, α = 66, β = 5 ; b) a = 7.3 cm, β =86, γ = 51 ; c) b = 13. cm, α =1 48`, β =13 4`; d) b = 44.5 cm, α
OSOVINE I VRATILA. Pomoćni nastavni materijali uz kolegij "Konstrukcijski elementi I" Ak. godina 2011./12.
 OSOVINE I VRATILA Pomoćni nastavni materijali uz kolegij "Konstrukcijski elementi I" Ak. godina 2011./12. Nositelj kolegija: Prof. dr. sc. Božidar Križan - 1 - OSOVINE I VRATILA Funkcija, opterećenja,
OSOVINE I VRATILA Pomoćni nastavni materijali uz kolegij "Konstrukcijski elementi I" Ak. godina 2011./12. Nositelj kolegija: Prof. dr. sc. Božidar Križan - 1 - OSOVINE I VRATILA Funkcija, opterećenja,
Zadatak 4b- Dimenzionisanje rožnjače
 Zadatak 4b- Dimenzionisanje rožnjače Rožnjača je statičkog sistema kontinualnog nosača raspona L= 5x6,0m. Usvaja se hladnooblikovani šuplji profil pravougaonog poprečnog preseka. Raster rožnjača: λ r 2.5m
Zadatak 4b- Dimenzionisanje rožnjače Rožnjača je statičkog sistema kontinualnog nosača raspona L= 5x6,0m. Usvaja se hladnooblikovani šuplji profil pravougaonog poprečnog preseka. Raster rožnjača: λ r 2.5m
Linearna algebra 2 prvi kolokvij,
 Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
VJEŽBE 3 BIPOLARNI TRANZISTORI. Slika 1. Postoje npn i pnp bipolarni tranziostori i njihovi simboli su dati na slici 2 i to npn lijevo i pnp desno.
 JŽ 3 POLAN TANZSTO ipolarni tranzistor se sastoji od dva pn spoja kod kojih je jedna oblast zajednička za oba i naziva se baza, slika 1 Slika 1 ipolarni tranzistor ima 3 izvoda: emitor (), kolektor (K)
JŽ 3 POLAN TANZSTO ipolarni tranzistor se sastoji od dva pn spoja kod kojih je jedna oblast zajednička za oba i naziva se baza, slika 1 Slika 1 ipolarni tranzistor ima 3 izvoda: emitor (), kolektor (K)
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE GODINE 8. RAZRED TOČNI ODGOVORI
 21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
 TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
