Elektronska struktura atoma
|
|
|
- Πράξις Ρόκας
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Elektronska struktura atoma Raderfordov atomski model jezgro u sredini pozitivno naelektrisano skoro sva masa jezgru veoma malo Elektroni kruže oko jezgra elektrostatičke interakcije ih drže da ne napuste jegro centrifugalna sila ih drži da ne padnu na jezgro mala masa velika zapremina
2 Talasi - elektromagnetno zračenje Elektromagnetno zračenje prenosi energiju kroz prostor Karakteriše ga talasna dužina (λ) i frekvencija (ν) Brzina e-m zračenja (c) u vakuumu je 3,00 x 10 8 m/s Takoñe bitna relacija koja poizilazi iz svega ovoga je: λν=c
3 Talasi - elektromagnetno zračenje Spektar e-m zračenja
4 Kvantna teorija Svetlost se ponaša kao talas interferencija, difrakcija, refleksija... sasvim se lepo uklapa u sve zakone talasne mehanike. Ipak tri stvari kod svetlosti se nikako nisu mogle objasniti talasnom prirodom: 1. Emisija svetlosti sa usijanih objekata (crno telo) 2. Fotoelektrični efekat izbijanje elektrona sa površine metala pomoću svetlosti 3. Emisija svetlosti sa pobuñenih atoma gasa emisioni spektri (neonska lampa)
5 Emisija svetlosti sa usijanih objekata Obična sijalica je usijana volframova žica koja kada se zagreje emituje belu svetlost. Talasna dužina emitovane svetlost zavisi od temperature tela crveno usijana tela su hladnija od usijanih tela koja emituju belu svetlost Ovo je objasnio Max Planck i ustanovio prve principe kvantne teorije On je pretpostavio da atomi mogu da primaju ili otpuštaju energiju samo u malim diskretnim komadima. Najmanja količina energije koja se može emitovati ili apsorbovati elekromagnetnim zračenjem se zove kvant.
6 Emisija svetlosti sa usijanih objekata Energija svakog pojedinačnog kvanta svetlosti je jednaka konstanti puta frekvencija svetlosti E=hν h Plankova konstanta 6,63 x Js Po kvantnoj teoriji energija se uvek emituje ili apsorbuje kao celobrojni umnožak hν. Ako neki atom emituje ukupno energiju od 3hν kažemo da je taj atom emitovao tri kvanta energije. Takoñe kvantna teorija predviña da će energija svakog tela biti kvantirana to znači da može da ima samo odreñene vrednosti.
7 Emisija svetlosti sa usijanih objekata Npr. moja potencijalna energija je kvantirana kada se penjem uz stepenište
8 Fotoelektrični efekat Ajnštajn je pomoću Plankove teorije objasnio fotoelektrični efekat Izbacivanje elektrona sa površine metala pomoću svetlosti
9 Fotoelektrični efekat Potrebna je svetlost odreñene talasne dužine ili kraće. Brzina izbačenih elektrona ne zavisi od intenziteta svetlosti već samo od talasne dužine Broj izbačenih elektrona zavisi od intenziteta svetlosi
10 Fotoelektrični efekat Ajnštajnovo objašnjenje zračenje koje pogaña metal se sastoji od malih paketa energije koje je nazvao foton i koji se ponaša kao čestica Kada foton pogodi metal on nestane i preda svoju energiju elektronu metala Jonizaciona energija energija koja je potrebna da se elektron izbaci iz potencijalne jame jezgra tj. da se odvoji od privlačnog uticaja jezgra Ukoliko je energija fotona mala elektron ne može da napusti jezgro i ništa se ne dešava Ako je energija fotona dovoljno velika elektroni napuštaju jezgra
11 Fotoelektrični efekat Ako je energija fotona znatno veća višak energije fotona se pretvara u kinetičku energiju tih elektrona Dvojna priroda svetlosti i kao talas i kao čestica
12 Emisija svetlosti sa pobuñenih atoma linijski emisioni spektri Laser daje snop svetlosti samo jedne talasne dužine monohromatska svetlost Sijalica daje svetlost različitih talasnih dužina polihromatska svetlost
13 Emisija svetlosti sa pobuñenih atoma linijski emisioni spektri Kada svetlost sunca ili volframove sijalice... propustimo kroz prizmu ona se prelama i razlaže po talasim dužinama (svetlost različitih talasnih dužina se različito prelama) Sve talasne dužine se nalaze u beloj svetlosti, nema praznih mesta takvi spektri se zovu kontinualni spektri
14 Emisija svetlosti sa pobuñenih atoma linijski emisioni spektri Kada se gasovi pod niskim pritiskom stave u zatvorenu staklenu cev i kroz njih propusti struja oni daju nešto drugačiji spektar. Neon svetli crvenkasto narandžasto, narijum žuto... Ovakvi spektri se zovu linijski spektri
15 Emisija svetlosti sa pobuñenih atoma linijski emisioni spektri Linijski spektar vodonika je jako interesantan. Ima 4 linije i prilično su pravilno rasporeñenje. Balmer je otkrio (1885.) (a kasnije Ridberg primenio) da talasne dužine tih traka se mogu izraziti pomoću formule 1 = λ R H R H 1 n n 2 2 = 1, m 1
16 Borov atomski model Na odgovor zašto je ovo tako jednostavno se čekalo 30 godina Pretpostavka: Elektroni se kreću po kružnim putanjama oko jezgra Po klasičnoj fizici ako bi se tako kretali morali bi konstantno da emituju zračenje i gube energiju i veoma brzo bi pali na jezgro Bor je pretpostavio da poznati zakoni fizike ne važe na atomskom nivou
17 Borov atomski model Borov atomski model se zasniva na tri postulata 1. Samo orbite odreñenog radijusa, koje odgovaraju odreñenim energijama elektrona su dozvoljene da ih zauzimaju elektroni u atomu 2. Elektron koji se nalazi u dozvoljenoj orbiti ima odgovarajuću energiju i nalazi se u dozvoljenom energetskom stanju. Elektron koji se nalazi u dozvoljenom energetskom stanju neće otpuštati energiju i neće pasti na jezgro 3. Elektron apsorbuje i emituje energiju samo kada prelazi iz jednog dozvoljenog stanja u drugo. Ova energija se emituje ili apsorbje u vidu elektromagnetnog zračenja tj. fotona energije E=hν
18 Borov atomski model Polazeći od ova tri postulata i koristeći klasične jednačine kretanja i interakcije izmeñu naelektrisanja Bor je izračunao energije koje odgovaraju svakoj orbiti vodonikovog atoma E = 2, J 2 n n kvantni broj, označava broj orbite Enargija orbita je negativna i što je negativnija atom će biti stabilniji ukoliko se elektron nalazi u toj orbiti Stanje najniže energije n=1 se zove osnovno stanje, ako se elektron nalazi u nekoj višoj orbiti n=2,3... atom se nalazi u pobuñenom stanju
19 Borov atomski model
20 Borov atomski model Kada n postane beskonačno energija elektrona je nula. Tada se elektron nalazi izvan uticaja jezgra jonizovan je E = 2, J 2 n Treći postulat apsorpcija i emisija elektromagnetnog zračenja kada elektron prelazi sa jedne na dugu dozvoljenu orbitu. Emisija emitovanog ili apsorbovanog zračenja će biti jednaka razlici u energiji izmeću dve orbite E = E f E i = hν E = hν = hc = 2,18 10 λ J n n f i
21 Borov atomski model Talasni dužina emitovanog ili apsorbovanog fotona će biti: c λ = = ν hc E Ako zamenimo E i izrazimo sve kao 1/λ dobijamo: 1 = λ 2,18 10 hc 18 J n 1 2 f 1 n 2 i Što odgovara Ridbergovoj jednačini za talasne dužine traka u spektru vodonika
22 Limiti Borovog atomskog modela Odlično radi samo prilikom objašnjavanja spektra atomskog vodonika, za sve ostale atome postoje značajne greške Opisuje elektron samo kao česticu ne uzima u obzir njegovu talasnu prirodu Danas značajan samo kao korak u pravom smeru ka otkrivanju prave prirode atoma Jedino što je preživelo od Borovog atomskog modela je: 1. Elektroni postoje samo na odreñenim diskretnim (diskretno - ima jednu vrednost) energetskim nivoima, koji su opisni kvantnim brojevima 2. Pri prelasku elektrona sa jednog nivoa na drugi emituje se ili se apsorbuje energija
23 Talasna priroda materije Zračenje se ponaša i kao čestica i kao talas Luj de Brolji proučavao da li se onda i materija možda u nekim okolnostima ponaša kao talas Da li se elektron koji kruži oko jezgra može posmatrati kao talas? De Brolji predložio da se elektronu (ili svakoj materiji) može pridružiti odgovarajući talas sa talasnom dužinom koja zavisi od mase i brzine te čestice (materije) mv impuls = λ Ovi talasi se zovu talasi materije h mv
24 Talasna priroda materije Za elektrone koji se kreću oko jezgra talasna dužina pridruženih talasa se nalazi negde u oblasti X zraka. Za velike objekte (npr tenisku lopticu) talasna dužina pridruženog talasa je tako mala da je daleko od bilo čega što možemo eksperimentalno opaziti (izračunajte i uverite se) De Broljijeva teorija je i eksperimentalno potvñena elektroni se ponašaju kao talasi difraktuju se, interferiraju... Elektronski mikroskop
25 Hajzenbergov princip neodreñenosti Problem sa talasnom prorodom materije talas se prostire kroz prostor i njegva lokacija nije tačno definisana Ako elektronu pridružimo talas da li onda možemo precizno odrediti njegovu lokaciju? Hajzenberg je zaključio da dvojna priroda materije postavlja fundamentalna ograničenja o tome koliko precizno možemo odrediti lokaciju i impuls nekog objekta Ovo ograničenje postaje bitno jedino kad radimo sa subatomskim česticama (i atomima na temperaturi blizu 0 K) Hajzenbergov princip neodreñenosti primenjen na elektrone u atomu : fundamentalno je nemoguće znati tačan impuls elektrona i njegov polozaj u prostoru
26 Hajzenbergov princip neodreñenosti Hajzenberg je matematički predstavio neodreñenost položaja elektrona x i neodreñenost njegovog impulsa mv kao: x mv Implikacije principa neodreñenosti: Masa elektrona je 9,11x10-31 kg a prosečna brzina u H atomu 5x10 6 m/s. Neka je neodreñenost brzine 1% - v= 5x10 4 m/s i da je to jedina neodreñenost u impulsu tada je neodreñenost položaja elektrona: h 4π x h 4πm v 6, π (9, Js kg)( m ) s = m
27 Hajzenbergov princip neodreñenosti Prečnik vodonikovog atoma je 2x10-10 m to znači da je neodreñenost položaja elektrona pet puta veća od samog atoma. Mi nemamo pojma gde se taj elektron nalazi u atomu.
28 Kvantna mehanika i atomske orbitale godine Šredingerova jednačina HΨ = EΨ Uključena i talasna i čestična priroda elektrona. Ψ je talasna funkcija elektrona i ona potpuno opisuje talas koji je pridružen elektronu i nema fizički smisao Rešenja Šredingerove jednačine za atom vodonika daju iste rezultate kao i Borove jednačine Ipak rešavanjem Šredingerove jednačine ne možemo da doñemo do saznanja o položaju elektrona Jedino do čega možemo da doñemo je verovatnoća da će elektron biti u odreñenom delu prostora tog trenutka
29 Kvantna mehanika i atomske orbitale Ajnštajn predložio da je Ψ 2 mera verovatnoće nalaženja elektrona u odgovarajućem delu prostora. Zato se i Ψ 2 zove gustina verovatnoće Računanjem Ψ 2 za razne delove prostora oko atomskog jezgra dolazi se do mape elektronske gustine oko jezra Mapa elektronske gustine za elektron vodonikovog atoma u svom osnovnom stanju
30 Kvantna mehanika i atomske orbitale Borov atomski model koristi orbite i jedan kvantni broj n koji odreñuje energiju elektrona u tim orbitama Kvantno mehanički pristup se zasniva na talasnoj funkciji Ψ koja samo opisuje talas pridružen elektronu Te talasne funkcije se još zovu i orbitale i one zajedno sa energijom elektrona predstavljaju rešnje Šredingerove jednačine Da bi mogli da napišemo ispravnu talasnu funkciju koja će pravilno reprezentovati talas pridružen elektronu treba nam 3 (4) kvantna broja
31 Kvantna mehanika i atomske orbitale 1. Glavni kvantni broj (n) uvek ima pozitivne vrednosti (1,2,3,4 ). On nam generalno govori o veličini orbitale i energiji elektrona u toj orbitali 2. Azimutalni (sporedni) kvantni broj (l) ima vrednosti od 0 do n-1 (ima tačno n vrednosti). On definiše oblik orbitale. Vrednost l se ne piše prilikom predstavljanja orbitale već se koriste slova s, p, d, f... l vrednost Slovna oznaka s p d f g h 3. Magnetni kantni broj (m l ) definiše orijentaciju orbitale u prostoru. Ima vrednosti od l do +l uključujući nulu Npr za l=2 m l će imati vrednosti -2, -1, 0, 1, 2 m l uvek ima 2l+1 vrednosti
32 Kvantna mehanika i atomske orbitale Sve orbitale sa istom vrednošću n čine jednu elektronsku ljusku ili elektronski nivo Sve orbitale sa istom n i l vrednošću čine jedan elektronski podnivo (npr 2p podnivo, 3d podnivo..)
33 Kvantna mehanika i atomske orbitale Energije orbitala atoma vodonika
34 Izgled orbitala Sve s orbitale su sfernog oblika (jer je l=0 i m l =0) Čvorovi mesta u kojima je verovatnoća nalaženja elektrona jednaka nuli 1s orbitala nema čvorova (osim onog na jezgru) 2s ima jedan sferni čvor 3s ima dva sferna čvora
35 Izgled orbitala Verovatnoća nalaženja elektrona se definiše kao Ψ 2 podeljena sa kvadratom rastojanja od jezgra r 2 p Ψ r 2 2
36 Izgled orbitala Standardan način prikazivanja orbitala je kao granična površina koja obuhata (najčešće) 90% verovatnoće nalaženja elektrona unutar nje
37 Izgled orbitala p orbitale se javljaju tek na nivoima sa n 2 Za sve njih l=1 a m l može imati vrednosti -1, 0, 1 Znači ima ukupno tri p orbitale u podnivou Umesto da se obeležavaju kao 2p -1, 2p 0, 2p 1 usvojene su oznake 2p x, 2p y, 2p z
38 Izgled orbitala d orbitale se javljaju tek na nivoima sa n 3 Za sve njih l=2 a m l može imati vrednosti -2,-1, 0, 1,2 Znači ima ukupno pet d orbitala u podnivou Umesto da se obeležavaju kao 3d -2, 3d -1, 3d 0, 3d 1, 3d 2 usvojene su oznake 3d xz, 3d xz, 3d yz, 3d x2-y2 i 3d z2
39 Izgled orbitala f orbitale se javljaju tek na nivoima sa n 4 Za sve njih l=3 a m l može imati vrednosti -3,-2,-1, 0, 1,2,3 Znači ima ukupno sedam f orbitala u podnivou
40 Višeelektronski atomi Svi ovi rezultati do sada su se odnosili na vodonikov atom Kod vodonika energija elektrona u nekoj orbitali je odreñena samo glavnim kvantnim brojem n Znači elektron u 2s i 2p orbitali ima istu energiju *Ne može se govoriti o energiji orbitale već samo o energiji elektrona kada se nalazi u odgovarajućoj orbitali mada se često koristi izraz energija orbitale ali se uvek misli na energiju elektrona u toj orbitali *Kada se u orbitali ne nalazi elektron ona ne postoji i zove se prazna ili virtuelna orbitala prazne orbitale su veoma zgodne kada se rade izračunavanja i zato ću ih često pominjati tokom predavanja ali u prirodi one ne postoje
41 Višeelektronski atomi Kada u atomu postoji više elektrona situacija se bitno menja jer u razmatranje ulazi još jedan bitan član meñuelektronsko odbijanje Da bi u datom trenutku mogli da izračunamo meñuelektronsko odbijanje dva elektrona moramo znati gde se ti elektroni nalaze, a kvantna mehanika nam ne daje taj podatak 1 4πε e1e r E 2 = Danas postoji veliki broj načina na koji se računa meñuelektronsko odbijanje to je pravac u kome se danas razvija kvantna hemija 0
42 Višeelektronski atomi Meñuelektronsko odbijanje utiče na to da se energije orbitala unutar jednog nivoa razdvoje po podnivoima, sada više 2s i 2p orbitale nemaju istu energiju Na svu sreću meñuelektronsko odbijanje ne utiče na izgled i oblik orbitala (već samo na njihovu energiju) tako da orbitale višeelektronskih atoma imaju isti izgled orbitala kao i atom vodonika
43 Višeelektronski atomi U višeelektronskim atomima energija orbitala sa istim glavnim kvantnim brojem n raste sa porastom azimutalnog kvantnog broja l Tako je raspored orbitala ne četvrtom nivou (n=4): 4s (l=0) < 4p (l=1) < 4d (l=2) < 4f (l=3) Ovde je bitno naglasiti da orbitala koje pripadaju istom podnivou (npr. 3d) ostaju degenerisane tj. iste energije
44 Četvrti kvantni broj - spin Štern Gerlahov ogled (1921. godine) otkriće spina elektrona Zrak atoma srebra ([Kr]4d 10 5s 1 ) propuštan je kroz nehomogeno magnetno polje. Zrak se podelio na dva dela. Znači atomi srebra nisu identični, postoji neka mala razlika izmeñu njih Ta razlika je magnetne prirode
45 Četvrti kvantni broj - spin Objašnjenje Štern-Gerlahovih rezultata dali Ulenbk i Goudsmit uvodeći da elektron ima specijalnu osobinu koja se zove spin. Spin je inherentno svojstvo materije Objašnjenje spina za studente prve godine (klasična fizika): Elektron je naelektrisana čestica sfernog oblika koja se okreće. Kada se u klasičnoj fizici neka naelektrisana sfera okreće oko svoje ose tada ona indukuje magnetno polje. Smer magnetnog polja zavisi od smera okretanja sfere.
46 Četvrti kvantni broj - spin Objašnjenje spina za studente prve godine (klasična fizika): Pošto elektron može da se okreće oko svoje ose na samo dva načina (sa leva na desno i sa desna na levo) onda će imati i samo dve moguće vrednosti spina. Znači spin elekrona je kvantiran. Spin elektrona se predstavlja spinskim kvantnim brojem m s i može imati samo dve vrednosti +½ i -½ Danas se zna da sve elementarne čestice imaju svoj spin ali je danas prihvaćeno objašnjenje spina previše komplikovano za ovaj kurs. Spin je inherentno svojstvo materije
47 Kratko obnavljanje - kvantni brojevi Svaki elektron u atomu (uvek se nalazi u nekoj orbitali tog atoma, jer nema kud drugde) je potpuno opisan sa 4 kvantna broja: 1. Glavni kvantni broj (n) govori o veličini orbitale i energiji elektrona u toj orbitali 2. Azimutalni (sporedni) kvantni broj (l) definiše oblik orbitale i kod višeelektronskih atoma utiče na energiju elektrona (orbitale). Energija elektrona je potpuno odreñena sa n i l 3. Magnetni kantni broj (m l ) definiše orijentaciju orbitale u prostoru. Ne odreñuje energiju elektrona (orbitale) 4. Spinski kvantni broj definiše spin elektrona. Ima samo dve vrednosti
48 Paulijev princip isključivosti Wolfgang Pauli veliki teoretičar Princip opisuje svojstvo prirode, ne može se prekršiti nikada Paulijev princip: dva elektrona u istom atomu ne mogu imati ista sva četiri kvantna broja Sam Paulijev princip je mnogo komplikovaniji i govori o svojstvu antisimetričnosti talasne funkcije prilikom izmene elektrona ali je za sada dovoljno ovoliko. Posledice Paulijevog principa su te da se u jednu orbitalu (definisanu sa prva tri kvantna broja n, l i m l ) mogu smestiti samo dva elektrona različitih spinova
49 Elektronska konfiguracija Da bi mogli da odredimo raspored elektrona u svakom atomu dovoljno je znamo relativne energije orbitala i Paulijev princip Raspored elektrona u atomu nekog elementa se zove još i elektronska konfiguracija tog elementa Osnovno stanje nekog atoma je najstabilnije stanje i karakteriše se time što su svi elektroni u najnižem mogućem energetskom stanju Kada pišemo elektronsku konfiguraciu nekog atoma popunjavamo orbitale po porastu energije sa najviše po dva elektrona u svakoj orbitali Tako će osnovno stanje vodonika biti jedan elektron u 1s orbitali i to se piše kao: H: 1s 1 ili
50 Elektronska konfiguracija Sledeći je helijum. On ima dva elektrona i oba mogu da stanu u isitu orbitalu (ako su im spinovi različiti) tako da će elektronska konfiguracija helijuma biti sa potpuno popunjenom 1s obitalom: He: 1s 2 ili Prvo se piše ime orbitale (1s) pa onda u njenom superskiptu se navodi broj elektrona u toj orbitali Strelica na gore predstavlja elektron sa spinom +½ a na dole sa spinom -½ Kada se u nekoj orbitali nalaze dva elektrona različitih spinova (a samo takvi mogu biti u istoj orbitali) onda se ona zove popunjenja. Orbitala sa jednim elektronom se zove polupopunjena (po konvenciji se uzima da je u njoj elektron sa spinom +½) a bez elektrona - prazna
51 Elektronska konfiguracija Litijum ima tri elektrona. Treći elektron ne može u 1s orbitalu već mora u prvu sledeću po energiji. To je 2s orbitala pa je elektonska konfiguracija litijuma: Li: 1s 2 2s 1 ili
52 Elektronska konfiguracija Berilijum ima četiri elektrona i četvrti elektron popunjava 2s orbitalu: Be: 1s 2 2s 2 Bor ima pet elektrona i pošto su i 1s i 2s pune peti elektron mora da ide u neku (bilo koju od tri postojeće) 2p orbitalu: B: 1s 2 2s 2 2p 1 Ugljenik ima šest elektrona i šesti elektron opet ide u 2p obitalu. Ali pošto ima tri 2p orbitale pitanje je da li će šesti elektron ići u polupopunjenu 2p orbitalu (u kojoj se već nalazi peti elektron) ili u jednu (bilo koju) od dve prazne 2p orbitale. Ovaj problem se rešava primenom Hundovog pravila
53 Elektronska konfiguracija Hundovo pravilo Hundovo pravilo kaže: Za degenerisane obitale najniže energetsko stanje je ono u kome je broj elektrona sa istim spinom maksimalan To znači da će šesti elektron ugljenika ići u jednu od dve prazne 2p orbitale. Hundovo pravilo se zasniva na činjnici da se elektroni meñusobno odbijaju jer su istorodno naelektrisani. Zbog toga teže da budu što je dalje moguće jedan od drugog.
54 Elektronska konfiguracija Hundovo pravilo Poštujući Hundovo pravilo popunjavamo dalje 2p orbitale do neona:
55 Elektronska konfiguracija valentni i unutrašnji elektroni Posle neona (1s 2 2s 2 2p 6 ) ide natrijum sa 11 elektrona. Nema više mesta u prvoj i drugoj ljusci pa moramo otvoriti treću ljusku koja počinje sa 3s orbitalom pa je natrijum: Na: 1s 2 2s 2 2p 6 3s 1 Ovo se može i skraćeno napisati kao Na: [Ne]3s 1 1s 2 2s 2 2p 6 elektroni su zamenjeni sa [Ne] jer predstavljaju elektronsku konfiguraciju neona plemenitog gasa. Ovi elektroni sa hemijske tačke gledišta nisu posebno zanimljivi i ne utiču značajno na hemijske osobine natrijuma. Ovi elektroni se zovu unutrašnji elektroni 3s 1 elektron je mnogo zanimljiviji za hemičare i on se zove valentni elektron.
56 Elektronska konfiguracija prelazni metali Popunjavanje 3s i 3p orbitala elemenata iz treće periode (Na Ar) ide isto kao i popunjavanje druge periode i tako dolazimo do argona sa 1s 2 2s 2 2p 6 3s 2 3p 6. Nakon toga očekivali bi da počnu da se popunjavaju 3d orbitale (treći nivo ima tri podnivoa s, p i d) ali posle argona ide kalijum sa: K: [Ar]4s 1 4s orbitala ide pre 3d obitale jer je njena energija nešto niža
57 Elektronska konfiguracija prelazni metali Nakon kalijuma ide kalcijum sa [Ar]4s 2 pa tek onda počinje popunjavanje 3d orbitala i to poštujući Hundovo pravilo. Ovi elementi kojima su 3d elektroni valentni elektroni se zovu preazni metali. U četvrtoj periodi (kao i u petoj i šestoj) ima ih deset jer ima pet d orbitala. Nakon cinka, počinje popunjavanje 4p orbitala i kod sledećih šest elemenata se ove orbitale popunjavaju
58 Elektronska konfiguracija lantanoidi i aktinoidi Peta perioda je ista kao i četvrta s tim što se popunjavaju 5s, 4d i 5p orbitale. Šesta perioda je nešto komplikovanija. Počinje sa popunjavanjem 6s orbitale (Cs i Ba) i nakon toga počinju da se popunjavaju 4f orbitale. Prvi u ovom redu je element lantan pa se narednih 14 elemenata (zbog sedam 4f orbitala) zovu lantanoidi 4f i 5d orbitale su jako blizu energetski pa često dolazi do toga da se elektroni nalaze i u 4f i u 5d (pogledajte La, Ce, Gd)
59 Elektronska konfiguracija lantanoidi i aktinoidi Takoñe u nekim periodnim sistemima se lantan vodi kao d element (ide ispod itrijuma) a cer je prvi lantanoid a u nekima je lutecijum (broj 71) ispod itrijuma a lantan je prvi lantanoid U IUPAC-ovom peridnom sistemu i La i Lu su lantanoidi (ima ih ukupno 15) a mesto ispod itrijuma je ostavljeno prazno. Isti slučaj je i sa aktinoidima koji su f elementi u sedmoj periodi periodnog sistema.
60 Elektronska konfiguracija lantanoidi i aktinoidi Trenutno važeći IUPAC-ov periodni sistem elemenata
61 Elektronska konfiguracija i periodni sistem Svi pripadnici iste grupe imaju istu elektronsku konfiguraciju velentne ljuske, samo se glavni kvantni broj menja. Zato elementi koji pripadaju istoj grupi imaju veoma slične hemijske osobine 13
62 Elektronska konfiguracija i periodni sistem U periodnom sistemu postoji podela na s, p, d i f elemente u zavisnosti od toga u kojem se podnivou nalaze valentni elektroni
63 Izuzeci u periodnom sistemu Kada su različiti podnivoi blizu tada razlika u energiji potrebnoj za sparivanje spinova dva elektrona u istu orbitalu može biti veća od razlike u energiji dva podnivoa pa dolazi do anomalija u elektronskoj konfiguraciji elemenata. Najbolji primer toga je hrom koji bi trebao da bude: Cr: [Ar]4s 2 3d 4 Ali je (zbog maksimalnog broja nesparenih spinova) Sličan izuzetak je i bakar koji je Cr: [Ar]4s 1 3d 5 Cu: [Ar]4s 1 3d 10 Ovakvi izuzeci se javljaju još kod 5d, 6d, 4f i 5f elemenata ali nisu hemijski značajni.
64 Izuzeci u periodnom sistemu
65 Efektivno naelektrisanje jezgra Koliku privlačnu silu jezgra oseća svaki elektron? Za atom vodonika odgovor je prilično jasan elektron oseća privlačnu sila 1+ jezgra koja zavisi samo od elektron-jezgro rastojanja Ali šta je sa višeelektronskim atomima? Kod njih osim jezgroelektron privlačne sile postoje i elektron-elektron odbojne sile. Da bi odredili koliko je jako svaki elektron vezan za jezgro i ove odbojne sile se moraju uzeti u obzir. Za precizna izračunavanja potrebna su nam elektron-elektron rastojanja!!!!
66 Efektivno naelektrisanje jezgra Naelektrisanje jezgra koje osećaju valentni elektroni efektivno naeletrisanje jezgra - se može proceniti primenom veoma jednostavnih Slaterovih pravila: Prvo se elektroni grupišu i svaka grupa odvoji zagradama (1s)(2s2p)(3s3p)(3d)(4s4p)(4d)(4f)(5s5p) Svi elektroni nadesno od posmatrane grupe ne smanjuju naelektrisanje jezra 2. Elektroni iz iste grupe smanjuju naelektrisanje jezgra za 0,35 3. Svaki elektron iz n-1 nivoa smanjuje naelektrisanje jezgra za s i p elektrone za vrednost 0,85 4. Svaki elektron iz nivoa n-2 smanjuje nelektrisanje jezgra za 1 5. Za f i d elektrone svaki elektron koji je levo od njih smanjuje naelektrisanje jezgra za 1
67 Efektivno naelektrisanje jezgra Primer: koliko je efektivno naelektrisanje jezgra koje osećaju 2p elektroni bora, ugljenika, azota, kiseonika i fluora B: (1s 2 )(2s 2 2p 1 ) S= 2x0,85 + 2x0,35=2,4 Z eff =5-2,4= 2,6 B C: (1s 2 )(2s 2 2p 2 ) S= 2x0,85 + 3x0,35=2,75 Z eff =6-2,75= 3,25 C N: (1s 2 )(2s 2 2p 3 ) S= 2x0,85 + 4x0,35=3,1 Z eff =7-3,1= 3,9 N O: (1s 2 )(2s 2 2p 4 ) S= 2x0,85 + 5x0,35=3,45 Z eff =8-3,45= 4,55 O F: (1s 2 )(2s 2 2p 5 ) S= 2x0,85 + 6x0,35=3,8 Z eff =9-3,8= 5,2 F
68 Veličine atoma Veličine atoma se najlakše izražavaju atomskim poluprečnicima Postoje dve vrste atomskih poluprečnika: Nevezivni (van der Waalsovi) rastojanje do koga atomi mogu da priñu jedan drugome dok elektronski oblaci ne počnu da im se odbijaju Vezivni (kovalentni) polovina rastojanja izmeñu jezgara kada su atomi kovalentno vezani
69 Veličine atoma
70 Veličine atoma
71 Veličine atoma
72 Periodični trendovi atomskih poluprečnika 1. Atomski poluprečnici opadaju sa leva nadesno u istoj periodi. Ovo se najlakše objašnjava preko povećanja efektivnog nelektrisanja jezgra na valentne elektrone (primer pre par slajdova) 2. Atomski poluprečnici rastu odozgo nadole u grupi.ovo se objašava povećanjem glavnog kvantnog broja valentnih elektrona. Što je veći glavni kvantni broj elektron provodi više vremena na većem rastojanju od jezgra a time je i atomski poluprečnik veći.
73 Jonski poluprečnici Svi jonski poluprečnici su eksperimentalno odreñeni na osnovu rastojanja izmeñu jona u kristalnim rešetkama jonskih jedinjenja. Katjoni su uvek manji od atoma od kojih su nastali jer se izbacuje elektron iz najudaljenije orbitale a i smanjuje se elektron-elektron odbijanje tj. povećava se efektivno naelektrisanje jezgra Što je katjon više naelektrisan jonski poluprečnik će biti manji Ajoni su uvek veći od atoma od kojih su nastali jer dodatak elektrona neutralnom atomu povećava elektron-elektron odbijanje i tera elektrone da se rasprostru na veću zapreminu Što je anjon više naelektrisan jonski poluprečnik mu je veći
74 Jonski poluprečnici
75 Jonizaciona energija Jonizaciona energija nekog atoma ili jona je minimalna energija koja je potrebna za uklanjanje elektrona iz osnovnog stanja tog atoma ili jona u gasovitom stanju Dva energetski suprotna procesa: 1. Uklanjanjem elektrona se on odvaja od pozitivnog jezgra i energija sistema raste 2. U nastalom katjonu smanjuju se elektron-elektron odbojne interakcije i energija sistema opada Jonizaciona energija je uvek pozitivna jer se uvek više energije izgubi zbog uklanjanja elektrona iz orbitale nego što se oslobodi zbog smanjenja elektron-elektron odbijanja
76 Jonizaciona energija Prva jonizaciona energija I 1 je energija potrebna za uklanjanje prvog elektrona iz neutralnog atoma: Na(g) Na + (g) + e - Druga jonizaciona energija I 2 je energija potrebna za uklanjanje drugog elektrona iz jedanput naelektisanog katjona Na + (g) Na 2+ (g) + e -
77 Jonizaciona energija Druga jonizaciona energija je uvek veća od prve jer se uklanja elektron iz već pozitivno naelektrisanog jona Veliki skok u vrednosima jonizacione energije nastaje kada počnu da se jonizuju unutrašnji elektroni
78 Jonizaciona energija u periodnom sistemu Prva jonizaciona energija raste po periodi i opada po grupi. To je potpuno u skladu sa podacima o atomskim radijusima što je atom manji elektron je jače vezan i teže se jonizuje
79 Jonizaciona energija u periodnom sistemu
80 Jonizaciona energija u periodnom sistemu Par odstupanja Be ima veću I 1 od B N ima veću I 1 od O OBJASNITE pomoću elektronskih konfiguracija za date atome!!!
81 Afinitet prema elektronu Suprotno od energije jonizacije afinitet prema elektronu je energija koja se oslobodi ili veže kada se jedan elektron doda neutralnom atomu u gasovitom stanju. Ovde opet imamo dva energetski suprotna procesa: 1. Energija sistema se snižava jer se dodati elektron nalazi blizu pozitivnog jezgra atoma 2. Energija sistema raste jer se dodatkom novog elektrona povećava elektron-elektron odbijanje Ukoliko je 1 veće od 2 afinitet prema elektronu će imati negativnu vrednost (češći slučaj) a ukoliko je 2 veće od 1 onda će imati pozitivnu vrednost (reñi slučaj) Cl(g) + e - Cl - (g)
82 Afinitet prema elektronu Afinitet prema elektronu raste (negativniji je) u periodi (sa leva na desno) a opada u grupi (odozgo nadole) Svi plemeniti gasovi imaju afinitet prema elektronu veći od nula. Zašto? Be, Mg imaju isto veći od nula a svi ostali elementi iz druge grupe (Ca i Sr) veoma male negativne vrednosti. Zašto? Azot takoñe ima afinitet prema elektronu veći od nule.
83 Afinitet prema elektronu Uputstva za rešavanje problema sa prethodnog slajda: Dobro razmislite u koju orbitalu se dodaje novi elektron (ako je orbitala prazna lakše ćemo dodati elektron nega oko je polupopunjena zašto). Pokušajte da predvidite (izračunajte) efektivno naelektrisanje jezgra koje će osećati novododati elektron. Da li se razlikuje efektivno naelektrisanje jezgra koje osećaju ostali elektroni u atomu i u anjonu Šta se dešava sa elektron-elektron odbijanjima prilikom dodatka novog elektrona? Po čemu su karakteristični svi elementi kod kojih je afinitet prema elektronu veći od nule? Odgovore obavezno dostaviti na terminu obnavljanja
84 Podela periodnog sistema metali, nemetali i metaloidi Svi elementi periodnog sistema se mogu podeliti u tri grupe metali, nemetali i metaloidi (plemeniti gasovi ne pripadaju nijednoj od ovih grupa) Metali se nalaze levo u periodnom sistemu i oko ¾ elemenata su metali. Nemetali su sa desne strane a metaloidi izmeñu njih
85 Metali Osobine metala: Imaju specifičan metalni sjaj, uglavnom srebrnaste boje Kovnost mogu da se kuju tj. izvlače u listove Elastični su mogu da se izvlače u žice Dobri provodnici toplote i elektriciteta Uglavnom su čvrstog agregatnog stanja na sobnoj temperaturi osim žive koja mrzne na -39 o C Imaju veoma male jonizacione energije i relativno lako grade pozitivne jone U hemijskim reakcijama se oksiduju (gube elektrone)
86 Metali Osobine metala: Metali iz glavnih grupa periodnog sistema otpuštaju elektrone da bi postili stabilnu konfiguraciju plemenitog gasa Prelazni metali često mogu postajati u više jonskih stanja nemaju nikakve veze sa stabilnom konfiguracijom plemenitog gasa
87 Metali Osobine metala: Sa nemetalima uglavnom daju jonska jedinjenja Jedinjenja metala sa metalima se zovu legure Većina oksida metala je bazna, reaguju sa vodom dajući baze, reaguju sa kiselinama dajući soli
88 Nemetali Osobine nemetala: Nemaju neku uniformnu pojavu, sedam njih postoje kao dvoatomni molekuli od čega pet kao gasovi (H 2, N 2, O 2, F 2, Cl 2 ), jedan kao tečnost (Br 2 ) a jedan kao čvrsta supstanca (I 2 ). Svi ostali nemetali postoje kao čvrste supstance koje mogu biti veoma tvrde (dijamant) ili veoma meke (sumpor) Tačke topljenja su im generalno niže nego metalima mada ima izuzetaka (dijamant se topi na 3570 o C) Loše provode toplotu i struju Imaju znatno veću energiju jonizacije od metala i veoma retko grade pozitivne jone Imaju negativne afinitete prema elektronu i lako grade anjone da bi postigli elektronsku konfiguraciju plemenitog gasa
89 Nemetali Osobine nemetala: Sa metalima daju uglavnom jonska jedinjenja Sa drugim nemetalima daju isključivo kovalentna jedinjenja Njihovi oksidi, halidi, hidridi su ili gasovi ili tečnosti ili čvrsta jedinjenja niske tačke topljenaja Oksidi metala su kiseli, sa vodom daju kiseline, sa bazama daju soli
90 Nemetali Razlika u jonizacionim energijama metala i nemetala
91 Metaloidi Metaloidi imaju osobine koje se nalaze izmeñu osobina metala i nemetala. Na primer elementarni silicijum izgleda kao metal ali ne može da se kuje i loše provodi toplotu i elektricitet. Neki nemetali (pogotovo silicijum) su poluprovodnici i koriste se za izradu čipova
Elektronska struktura atoma
 Elektronska struktura atoma Raderfordov atomski model jezgro u sredini pozitivno naelektrisano skoro sva masa u jezgru veoma malo Elektroni kruže oko jezgra elektrostatičke interakcije ih drže da ne napuste
Elektronska struktura atoma Raderfordov atomski model jezgro u sredini pozitivno naelektrisano skoro sva masa u jezgru veoma malo Elektroni kruže oko jezgra elektrostatičke interakcije ih drže da ne napuste
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
STRUKTURA ATOMA. Dalton (1803) Tomson (1904) Raderford (1911) Bor (1913) Šredinger (1926)
 Dalton (1803) Tomson (1904) Raderford (1911) Bor (1913) Šredinger (1926) TALASNO MEHANIČKI MODEL ATOMA Hipoteza de Brolja Elektroni i fotoni imaju dvojnu prirodu: talasnu i korpuskularnu. E = hν E = mc
Dalton (1803) Tomson (1904) Raderford (1911) Bor (1913) Šredinger (1926) TALASNO MEHANIČKI MODEL ATOMA Hipoteza de Brolja Elektroni i fotoni imaju dvojnu prirodu: talasnu i korpuskularnu. E = hν E = mc
PERIODNI SISTEM ELEMENATA
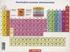 PERIODNI SISTEM ELEMENATA 1/43 PERIODNI SISTEM ELEMENATA - Kratka istorija Otkriće elemenata do danas otktiveno još 11 elemenata 2011. IUPAC potvrdio otkriće 2 nova elementa: Flerovijum (Fl, Z = 114) i
PERIODNI SISTEM ELEMENATA 1/43 PERIODNI SISTEM ELEMENATA - Kratka istorija Otkriće elemenata do danas otktiveno još 11 elemenata 2011. IUPAC potvrdio otkriće 2 nova elementa: Flerovijum (Fl, Z = 114) i
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
HEMIJSKA VEZA TEORIJA VALENTNE VEZE
 TEORIJA VALENTNE VEZE Kovalentna veza nastaje preklapanjem atomskih orbitala valentnih elektrona, pri čemu je region preklapanja između dva jezgra okupiran parom elektrona. - Nastalu kovalentnu vezu opisuje
TEORIJA VALENTNE VEZE Kovalentna veza nastaje preklapanjem atomskih orbitala valentnih elektrona, pri čemu je region preklapanja između dva jezgra okupiran parom elektrona. - Nastalu kovalentnu vezu opisuje
SASTAV MATERIJE STRUKTURA ATOMA I PERODNI SISTEM ELEMENATA
 SASTAV MATERIJE STRUKTURA ATOMA I PERODNI SISTEM ELEMENATA Atomi su veoma sitne čestice Još niko nije uspeo da vidi atom Još nije konstruisan takav mikroskop koji će omogućiti da se vidi atom Najbolji
SASTAV MATERIJE STRUKTURA ATOMA I PERODNI SISTEM ELEMENATA Atomi su veoma sitne čestice Još niko nije uspeo da vidi atom Još nije konstruisan takav mikroskop koji će omogućiti da se vidi atom Najbolji
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
SPEKTROSKOPIJA SPEKTROSKOPIJA
 Spektroskopija je proučavanje interakcija elektromagnetnog zraka (EMZ) sa materijom. Elektromagnetno zračenje Proces koji se odigrava Talasna dužina (m) Energija (J) Frekvencija (Hz) γ-zračenje Nuklearni
Spektroskopija je proučavanje interakcija elektromagnetnog zraka (EMZ) sa materijom. Elektromagnetno zračenje Proces koji se odigrava Talasna dužina (m) Energija (J) Frekvencija (Hz) γ-zračenje Nuklearni
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
TALASNO-MEHANI MEHANIČKI MODEL ATOMA
 TALASNO-MEHANI MEHANIČKI MODEL ATOMA TALASNO-MEHANI MEHANIČKI MODEL ATOMA Kompton (19): svetlost ima i talasnu i korpuskularnu prirodu. Luj De Brolj (193): elektron ima i korpuskularnu i talasnu prirodu.
TALASNO-MEHANI MEHANIČKI MODEL ATOMA TALASNO-MEHANI MEHANIČKI MODEL ATOMA Kompton (19): svetlost ima i talasnu i korpuskularnu prirodu. Luj De Brolj (193): elektron ima i korpuskularnu i talasnu prirodu.
STRUKTURA ATOMA. Dalton (1803) Tomson (1904) Raderford (1911) Bor (1913) Šredinger (1926)
 Dalton (803) Tomson (904) Raderford (9) Bor (93) Šredinger (96) OTKRIĆA OSNOVNIH SASTOJAKA ATOMA Do početka XX veka važila je Daltonova atomska teorija o nedeljivosti atoma. Karjem XIX i početkom XX veka
Dalton (803) Tomson (904) Raderford (9) Bor (93) Šredinger (96) OTKRIĆA OSNOVNIH SASTOJAKA ATOMA Do početka XX veka važila je Daltonova atomska teorija o nedeljivosti atoma. Karjem XIX i početkom XX veka
Osnovne teoreme diferencijalnog računa
 Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
SEKUNDARNE VEZE međumolekulske veze
 PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
KVADRATNA FUNKCIJA. Kvadratna funkcija je oblika: Kriva u ravni koja predstavlja grafik funkcije y = ax + bx + c. je parabola.
 KVADRATNA FUNKCIJA Kvadratna funkcija je oblika: = a + b + c Gde je R, a 0 i a, b i c su realni brojevi. Kriva u ravni koja predstavlja grafik funkcije = a + b + c je parabola. Najpre ćemo naučiti kako
KVADRATNA FUNKCIJA Kvadratna funkcija je oblika: = a + b + c Gde je R, a 0 i a, b i c su realni brojevi. Kriva u ravni koja predstavlja grafik funkcije = a + b + c je parabola. Najpre ćemo naučiti kako
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
Teorijske osnove informatike 1
 Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Verovatnoća i Statistika I deo Teorija verovatnoće (zadaci) Beleške dr Bobana Marinkovića
 Verovatnoća i Statistika I deo Teorija verovatnoće zadaci Beleške dr Bobana Marinkovića Iz skupa, 2,, 00} bira se na slučajan način 5 brojeva Odrediti skup elementarnih dogadjaja ako se brojevi biraju
Verovatnoća i Statistika I deo Teorija verovatnoće zadaci Beleške dr Bobana Marinkovića Iz skupa, 2,, 00} bira se na slučajan način 5 brojeva Odrediti skup elementarnih dogadjaja ako se brojevi biraju
ASIMPTOTE FUNKCIJA. Dakle: Asimptota je prava kojoj se funkcija približava u beskonačno dalekoj tački. Postoje tri vrste asimptota:
 ASIMPTOTE FUNKCIJA Naš savet je da najpre dobro proučite granične vrednosti funkcija Neki profesori vole da asimptote funkcija ispituju kao ponašanje funkcije na krajevima oblasti definisanosti, pa kako
ASIMPTOTE FUNKCIJA Naš savet je da najpre dobro proučite granične vrednosti funkcija Neki profesori vole da asimptote funkcija ispituju kao ponašanje funkcije na krajevima oblasti definisanosti, pa kako
Doc. dr Milena Đukanović
 Doc. dr Milena Đukanović milenadj@ac.me ATOMSKA STRUKTURA MATERIJE: 500 g.p.n.e. Empedokle svijet se sastoji od četiri osnovna elementa: zemlja, vazduh, vatra i voda. 400 g.p.n.e. Demokrit svijet je sagrađen
Doc. dr Milena Đukanović milenadj@ac.me ATOMSKA STRUKTURA MATERIJE: 500 g.p.n.e. Empedokle svijet se sastoji od četiri osnovna elementa: zemlja, vazduh, vatra i voda. 400 g.p.n.e. Demokrit svijet je sagrađen
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
 Kvantna optika Toplotno zračenje Apsorpciona sposobnost tela je sposobnost apsorbovanja energije zračenja iz intervala l, l+ l na površini tela ds za vreme dt. Apsorpciona moć tela je sposobnost apsorbovanja
Kvantna optika Toplotno zračenje Apsorpciona sposobnost tela je sposobnost apsorbovanja energije zračenja iz intervala l, l+ l na površini tela ds za vreme dt. Apsorpciona moć tela je sposobnost apsorbovanja
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
SISTEMI NELINEARNIH JEDNAČINA
 SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
 TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo Najpre da se podsetimo tablice i osnovnih pravila:. C0.. (. ( n n n-. (a a lna 6. (e e 7. (log a 8. (ln ln a (>0 9. ( 0 0. (>0 (ovde je >0 i a >0. (cos. (cos - π. (tg kπ cos. (ctg
IZVODI ZADACI (I deo Najpre da se podsetimo tablice i osnovnih pravila:. C0.. (. ( n n n-. (a a lna 6. (e e 7. (log a 8. (ln ln a (>0 9. ( 0 0. (>0 (ovde je >0 i a >0. (cos. (cos - π. (tg kπ cos. (ctg
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE GODINE 8. RAZRED TOČNI ODGOVORI
 21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
2log. se zove numerus (logaritmand), je osnova (baza) log. log. log =
 ( > 0, 0)!" # > 0 je najčešći uslov koji postavljamo a još je,, > 0 se zove numerus (aritmand), je osnova (baza). 0.. ( ) +... 7.. 8. Za prelazak na neku novu bazu c: 9. Ako je baza (osnova) 0 takvi se
( > 0, 0)!" # > 0 je najčešći uslov koji postavljamo a još je,, > 0 se zove numerus (aritmand), je osnova (baza). 0.. ( ) +... 7.. 8. Za prelazak na neku novu bazu c: 9. Ako je baza (osnova) 0 takvi se
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze:
 Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze: Jonska, Kovalentna i Metalna Luisovi simboli veoma zgodan
Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze: Jonska, Kovalentna i Metalna Luisovi simboli veoma zgodan
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f
 IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Elektrotehnički fakultet univerziteta u Beogradu 17.maj Odsek za Softversko inžinjerstvo
 Elektrotehnički fakultet univerziteta u Beogradu 7.maj 009. Odsek za Softversko inžinjerstvo Performanse računarskih sistema Drugi kolokvijum Predmetni nastavnik: dr Jelica Protić (35) a) (0) Posmatra
Elektrotehnički fakultet univerziteta u Beogradu 7.maj 009. Odsek za Softversko inžinjerstvo Performanse računarskih sistema Drugi kolokvijum Predmetni nastavnik: dr Jelica Protić (35) a) (0) Posmatra
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
3. razred gimnazije- opšti i prirodno-matematički smer ALKENI. Aciklični nezasićeni ugljovodonici koji imaju jednu dvostruku vezu.
 ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
5. Karakteristične funkcije
 5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
INTELIGENTNO UPRAVLJANJE
 INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
( ) ( ) 2 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET. Zadaci za pripremu polaganja kvalifikacionog ispita iz Matematike. 1. Riješiti jednačine: 4
 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
PID: Domen P je glavnoidealski [PID] akko svaki ideal u P je glavni (generisan jednim elementom; oblika ap := {ab b P }, za neko a P ).
![PID: Domen P je glavnoidealski [PID] akko svaki ideal u P je glavni (generisan jednim elementom; oblika ap := {ab b P }, za neko a P ). PID: Domen P je glavnoidealski [PID] akko svaki ideal u P je glavni (generisan jednim elementom; oblika ap := {ab b P }, za neko a P ).](/thumbs/74/70316766.jpg) 0.1 Faktorizacija: ID, ED, PID, ND, FD, UFD Definicija. Najava pojmova: [ID], [ED], [PID], [ND], [FD] i [UFD]. ID: Komutativan prsten P, sa jedinicom 1 0, je integralni domen [ID] oblast celih), ili samo
0.1 Faktorizacija: ID, ED, PID, ND, FD, UFD Definicija. Najava pojmova: [ID], [ED], [PID], [ND], [FD] i [UFD]. ID: Komutativan prsten P, sa jedinicom 1 0, je integralni domen [ID] oblast celih), ili samo
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
I HEMIJSKI ZAKONI I STRUKTURA SUPSTANCI
 dr Ljiljana Vojinović-Ješić I HEMIJSKI ZAKONI I STRUKTURA SUPSTANCI ZAKON STALNIH MASENIH ODNOSA (I stehiometrijski zakon, Prust, 1799) Maseni odnos elemenata u datom jedinjenju je stalan, bez obzira na
dr Ljiljana Vojinović-Ješić I HEMIJSKI ZAKONI I STRUKTURA SUPSTANCI ZAKON STALNIH MASENIH ODNOSA (I stehiometrijski zakon, Prust, 1799) Maseni odnos elemenata u datom jedinjenju je stalan, bez obzira na
Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze:
 Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze: Jonska, Kovalentna i Metalna Luisovi simboli veoma zgodan
Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze: Jonska, Kovalentna i Metalna Luisovi simboli veoma zgodan
KVADRATNA FUNKCIJA. Kvadratna funkcija je oblika: Kriva u ravni koja predstavlja grafik funkcije y = ax + bx + c. je parabola.
 KVADRATNA FUNKCIJA Kvadratna funkcija je oblika: a + b + c Gde je R, a 0 i a, b i c su realni brojevi. Kriva u ravni koja predstavlja grafik funkcije a + b + c je parabola. Najpre ćemo naučiti kako izgleda
KVADRATNA FUNKCIJA Kvadratna funkcija je oblika: a + b + c Gde je R, a 0 i a, b i c su realni brojevi. Kriva u ravni koja predstavlja grafik funkcije a + b + c je parabola. Najpre ćemo naučiti kako izgleda
NOMENKLATURA ORGANSKIH SPOJEVA. Imenovanje aromatskih ugljikovodika
 NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
XI dvoqas veжbi dr Vladimir Balti. 4. Stabla
 XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
Zavrxni ispit iz Matematiqke analize 1
 Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
5 Ispitivanje funkcija
 5 Ispitivanje funkcija 3 5 Ispitivanje funkcija Ispitivanje funkcije pretodi crtanju grafika funkcije. Opšti postupak ispitivanja funkcija koje su definisane eksplicitno y = f() sadrži sledeće elemente:
5 Ispitivanje funkcija 3 5 Ispitivanje funkcija Ispitivanje funkcije pretodi crtanju grafika funkcije. Opšti postupak ispitivanja funkcija koje su definisane eksplicitno y = f() sadrži sledeće elemente:
4.7. Zadaci Formalizam diferenciranja (teorija na stranama ) 343. Znajući izvod funkcije x arctg x, odrediti izvod funkcije x arcctg x.
 4.7. ZADACI 87 4.7. Zadaci 4.7.. Formalizam diferenciranja teorija na stranama 4-46) 340. Znajući izvod funkcije arcsin, odrediti izvod funkcije arccos. Rešenje. Polazeći od jednakosti arcsin + arccos
4.7. ZADACI 87 4.7. Zadaci 4.7.. Formalizam diferenciranja teorija na stranama 4-46) 340. Znajući izvod funkcije arcsin, odrediti izvod funkcije arccos. Rešenje. Polazeći od jednakosti arcsin + arccos
INTEGRALNI RAČUN. Teorije, metodike i povijest infinitezimalnih računa. Lucija Mijić 17. veljače 2011.
 INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
1. razred gimnazije- opšti i prirodno-matematički smer STRUKTURA MOLEKULA HEMIJSKA VEZA
 EMIJSKE VEZE 1 razred gimnazije- opšti i prirodno-matematički smer STRUKTURA MLEKULA Molekul je najsitnija čestica koja se sastoji od dva ili više istih atoma, a to su molekuli elemenata: Cl 2, 2, N 2,
EMIJSKE VEZE 1 razred gimnazije- opšti i prirodno-matematički smer STRUKTURA MLEKULA Molekul je najsitnija čestica koja se sastoji od dva ili više istih atoma, a to su molekuli elemenata: Cl 2, 2, N 2,
MEHANIKA FLUIDA. Isticanje kroz otvore sa promenljivim nivoom tečnosti
 MEHANIKA FLUIDA Isticanje kroz otvore sa promenljivim nivoom tečnosti zadatak Prizmatična sud podeljen je vertikalnom pregradom, u kojoj je otvor prečnika d, na dve komore Leva komora je napunjena vodom
MEHANIKA FLUIDA Isticanje kroz otvore sa promenljivim nivoom tečnosti zadatak Prizmatična sud podeljen je vertikalnom pregradom, u kojoj je otvor prečnika d, na dve komore Leva komora je napunjena vodom
7 Algebarske jednadžbe
 7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
III VEŽBA: FURIJEOVI REDOVI
 III VEŽBA: URIJEOVI REDOVI 3.1. eorijska osnova Posmatrajmo neki vremenski kontinualan signal x(t) na intervalu definisati: t + t t. ada se može X [ k ] = 1 t + t x ( t ) e j 2 π kf t dt, gde je f = 1/.
III VEŽBA: URIJEOVI REDOVI 3.1. eorijska osnova Posmatrajmo neki vremenski kontinualan signal x(t) na intervalu definisati: t + t t. ada se može X [ k ] = 1 t + t x ( t ) e j 2 π kf t dt, gde je f = 1/.
S t r a n a 1. 1.Povezati jonsku jačinu rastvora: a) MgCl 2 b) Al 2 (SO 4 ) 3 sa njihovim molalitetima, m. za so tipa: M p X q. pa je jonska jačina:
 S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
OBRTNA TELA. Vladimir Marinkov OBRTNA TELA VALJAK
 OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
Atomska fizika Sadržaj
 Kvantna svojstva elektromagnetnog zračenja. Ultravioletna katastrofa 363 Plankov zakon zračenja. Bolcmanov i Vinov zakon. 365 Fotoelektrični efekat 367 Komptonovo rasejanje 370 Talasna priroda materije.
Kvantna svojstva elektromagnetnog zračenja. Ultravioletna katastrofa 363 Plankov zakon zračenja. Bolcmanov i Vinov zakon. 365 Fotoelektrični efekat 367 Komptonovo rasejanje 370 Talasna priroda materije.
Inženjerska grafika geometrijskih oblika (5. predavanje, tema1)
 Inženjerska grafika geometrijskih oblika (5. predavanje, tema1) Prva godina studija Mašinskog fakulteta u Nišu Predavač: Dr Predrag Rajković Mart 19, 2013 5. predavanje, tema 1 Simetrija (Symmetry) Simetrija
Inženjerska grafika geometrijskih oblika (5. predavanje, tema1) Prva godina studija Mašinskog fakulteta u Nišu Predavač: Dr Predrag Rajković Mart 19, 2013 5. predavanje, tema 1 Simetrija (Symmetry) Simetrija
Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne
 Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne metode (rentgenska kristalografija, NMR spektroskopija...)
Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne metode (rentgenska kristalografija, NMR spektroskopija...)
VJEŽBE 3 BIPOLARNI TRANZISTORI. Slika 1. Postoje npn i pnp bipolarni tranziostori i njihovi simboli su dati na slici 2 i to npn lijevo i pnp desno.
 JŽ 3 POLAN TANZSTO ipolarni tranzistor se sastoji od dva pn spoja kod kojih je jedna oblast zajednička za oba i naziva se baza, slika 1 Slika 1 ipolarni tranzistor ima 3 izvoda: emitor (), kolektor (K)
JŽ 3 POLAN TANZSTO ipolarni tranzistor se sastoji od dva pn spoja kod kojih je jedna oblast zajednička za oba i naziva se baza, slika 1 Slika 1 ipolarni tranzistor ima 3 izvoda: emitor (), kolektor (K)
Atomska fizika Sadržaj
 Kvantna svojstva elektromagnetnog zračenja. Ultravioletna katastrofa 79 Plankov zakon zračenja. Bolcmanov i Vinov zakon. 81 Fotoelektrični efekat 83 Komptonovo rasejanje 86 Atomska fizika Sadržaj Atomski
Kvantna svojstva elektromagnetnog zračenja. Ultravioletna katastrofa 79 Plankov zakon zračenja. Bolcmanov i Vinov zakon. 81 Fotoelektrični efekat 83 Komptonovo rasejanje 86 Atomska fizika Sadržaj Atomski
MATEMATIKA 2. Grupa 1 Rexea zadataka. Prvi pismeni kolokvijum, Dragan ori
 MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
Strukture podataka i algoritmi 1. kolokvij 16. studenog Zadatak 1
 Strukture podataka i algoritmi 1. kolokvij Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i službeni šalabahter. Predajete samo papire koje ste dobili. Rezultati i uvid u kolokvije: ponedjeljak,
Strukture podataka i algoritmi 1. kolokvij Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i službeni šalabahter. Predajete samo papire koje ste dobili. Rezultati i uvid u kolokvije: ponedjeljak,
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI)
 IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
Osnovne veličine, jedinice i izračunavanja u hemiji
 Osnovne veličine, jedinice i izračunavanja u hemiji Pregled pojmova veličina i njihovih jedinica koje se koriste pri osnovnim izračunavanjima u hemiji dat je u Tabeli 1. Tabela 1. Veličine i njihove jedinice
Osnovne veličine, jedinice i izračunavanja u hemiji Pregled pojmova veličina i njihovih jedinica koje se koriste pri osnovnim izračunavanjima u hemiji dat je u Tabeli 1. Tabela 1. Veličine i njihove jedinice
APROKSIMACIJA FUNKCIJA
 APROKSIMACIJA FUNKCIJA Osnovni koncepti Gradimir V. Milovanović MF, Beograd, 14. mart 2011. APROKSIMACIJA FUNKCIJA p.1/46 Osnovni problem u TA Kako za datu funkciju f iz velikog prostora X naći jednostavnu
APROKSIMACIJA FUNKCIJA Osnovni koncepti Gradimir V. Milovanović MF, Beograd, 14. mart 2011. APROKSIMACIJA FUNKCIJA p.1/46 Osnovni problem u TA Kako za datu funkciju f iz velikog prostora X naći jednostavnu
Skup svih mogućih ishoda datog opita, odnosno skup svih elementarnih događaja se najčešće obeležava sa E. = {,,,... }
 VEROVTNOĆ - ZDI (I DEO) U računu verovatnoće osnovni pojmovi su opit i događaj. Svaki opit se završava nekim ishodom koji se naziva elementarni događaj. Elementarne događaje profesori različito obeležavaju,
VEROVTNOĆ - ZDI (I DEO) U računu verovatnoće osnovni pojmovi su opit i događaj. Svaki opit se završava nekim ishodom koji se naziva elementarni događaj. Elementarne događaje profesori različito obeležavaju,
DALTONOV ATOMSKI MODEL Nastao je čitavih 2300 godina posle DEMOKRITA!
 DALTONOV ATOMSKI MODEL Nastao je čitavih 2300 godina posle DEMOKRITA! Polazna znanja zakoni o: Održanju mase Stalnom (utvrdjenom) sastavu Umnoženim odnosima Zakon o održanju mase masa supstance ne menja
DALTONOV ATOMSKI MODEL Nastao je čitavih 2300 godina posle DEMOKRITA! Polazna znanja zakoni o: Održanju mase Stalnom (utvrdjenom) sastavu Umnoženim odnosima Zakon o održanju mase masa supstance ne menja
kvantovanim elektronskim orbitama. set matematičkih i konceptualnih alata je stvoren do godine
 Dr Dejan Gvozdić Fizika : Elementi atomske i kvantne fizike 04 Dr Dejan Gvozdić.900. godina Rad Ma Planck-a na problemu zračenja crnog tela uvođenje kvanta energije.. 93. godina Niels Bohr predlog modela
Dr Dejan Gvozdić Fizika : Elementi atomske i kvantne fizike 04 Dr Dejan Gvozdić.900. godina Rad Ma Planck-a na problemu zračenja crnog tela uvođenje kvanta energije.. 93. godina Niels Bohr predlog modela
a M a A. Može se pokazati da je supremum (ako postoji) jedinstven pa uvodimo oznaku sup A.
 3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne
 Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne metode (rentgenska kristalografija, NMR spektroskopija...)
Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne metode (rentgenska kristalografija, NMR spektroskopija...)
Linearna algebra 2 prvi kolokvij,
 Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
MEĐUMOLEKULSKE SILE JON-DIPOL DIPOL VODONIČNE NE VEZE DIPOL DIPOL-DIPOL DIPOL-INDUKOVANI INDUKOVANI JON-INDUKOVANI DISPERZNE SILE
 MEĐUMLEKULSKE SILE JN-DIPL VDNIČNE NE VEZE DIPL-DIPL JN-INDUKVANI DIPL DIPL-INDUKVANI INDUKVANI DIPL DISPERZNE SILE MEĐUMLEKULSKE SILE jake JNSKA VEZA (metal-nemetal) KVALENTNA VEZA (nemetal-nemetal) METALNA
MEĐUMLEKULSKE SILE JN-DIPL VDNIČNE NE VEZE DIPL-DIPL JN-INDUKVANI DIPL DIPL-INDUKVANI INDUKVANI DIPL DISPERZNE SILE MEĐUMLEKULSKE SILE jake JNSKA VEZA (metal-nemetal) KVALENTNA VEZA (nemetal-nemetal) METALNA
KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI. NEUTRALNI ELEMENT GRUPOIDA.
 KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI NEUTRALNI ELEMENT GRUPOIDA 1 Grupoid (G, ) je asocijativa akko važi ( x, y, z G) x (y z) = (x y) z Grupoid (G, ) je komutativa akko važi ( x, y G) x y = y x Asocijativa
KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI NEUTRALNI ELEMENT GRUPOIDA 1 Grupoid (G, ) je asocijativa akko važi ( x, y, z G) x (y z) = (x y) z Grupoid (G, ) je komutativa akko važi ( x, y G) x y = y x Asocijativa
1 Promjena baze vektora
 Promjena baze vektora Neka su dane dvije različite uredene baze u R n, označimo ih s A = (a, a,, a n i B = (b, b,, b n Svaki vektor v R n ima medusobno različite koordinatne zapise u bazama A i B Zapis
Promjena baze vektora Neka su dane dvije različite uredene baze u R n, označimo ih s A = (a, a,, a n i B = (b, b,, b n Svaki vektor v R n ima medusobno različite koordinatne zapise u bazama A i B Zapis
Linearna algebra 2 prvi kolokvij,
 1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
Atomska fizika Sadržaj
 Atomska fizika Sadržaj Kvantna svojstva elektromagnetnog zračenja. 86 Ultravioletna katastrofa 87 Plankov zakon zračenja. Bolcmanov i Vinov zakon. 88 Fotoelektrični efekat 90 Komptonovo rasejanje 93 Atomski
Atomska fizika Sadržaj Kvantna svojstva elektromagnetnog zračenja. 86 Ultravioletna katastrofa 87 Plankov zakon zračenja. Bolcmanov i Vinov zakon. 88 Fotoelektrični efekat 90 Komptonovo rasejanje 93 Atomski
Jednodimenzionalne slučajne promenljive
 Jednodimenzionalne slučajne promenljive Definicija slučajne promenljive Neka je X f-ja def. na prostoru verovatnoća (Ω, F, P) koja preslikava prostor el. ishoda Ω u skup R realnih brojeva: (1)Skup {ω/
Jednodimenzionalne slučajne promenljive Definicija slučajne promenljive Neka je X f-ja def. na prostoru verovatnoća (Ω, F, P) koja preslikava prostor el. ishoda Ω u skup R realnih brojeva: (1)Skup {ω/
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
 Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Osnove elektrotehnike I popravni parcijalni ispit VARIJANTA A
 Osnove elektrotehnike I popravni parcijalni ispit 1..014. VARIJANTA A Prezime i ime: Broj indeksa: Profesorov prvi postulat: Što se ne može pročitati, ne može se ni ocijeniti. A C 1.1. Tri naelektrisanja
Osnove elektrotehnike I popravni parcijalni ispit 1..014. VARIJANTA A Prezime i ime: Broj indeksa: Profesorov prvi postulat: Što se ne može pročitati, ne može se ni ocijeniti. A C 1.1. Tri naelektrisanja
( , 2. kolokvij)
 A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
RAČUNSKE VEŽBE IZ PREDMETA POLUPROVODNIČKE KOMPONENTE (IV semestar modul EKM) IV deo. Miloš Marjanović
 Univerzitet u Nišu Elektronski fakultet RAČUNSKE VEŽBE IZ PREDMETA (IV semestar modul EKM) IV deo Miloš Marjanović MOSFET TRANZISTORI ZADATAK 35. NMOS tranzistor ima napon praga V T =2V i kroz njega protiče
Univerzitet u Nišu Elektronski fakultet RAČUNSKE VEŽBE IZ PREDMETA (IV semestar modul EKM) IV deo Miloš Marjanović MOSFET TRANZISTORI ZADATAK 35. NMOS tranzistor ima napon praga V T =2V i kroz njega protiče
Linijski spektri. Užarena čvrsta tijela, tekućine i gasovi pri visokom pritisku i temperaturi emitiraju svjetlost s kontinuiranim valnim duljinama
 Bohrov model atoma Linijski spektri Daćemo malo detaljniji opis linijskih spektara jer ih je Borov model atoma uspio objasniti (za atom hidrogena) Užarena čvrsta tijela, tekućine i gasovi pri visokom pritisku
Bohrov model atoma Linijski spektri Daćemo malo detaljniji opis linijskih spektara jer ih je Borov model atoma uspio objasniti (za atom hidrogena) Užarena čvrsta tijela, tekućine i gasovi pri visokom pritisku
Fizika. Dualna priroda elektromagnetnog zračenja. Princip rada lasera. za studente Geodezije i geomatike. Doc.dr Ivana Stojković
 Fizika za studente Geodezije i geomatike Dualna priroda elektromagnetnog zračenja Princip rada lasera Docdr Ivana Stojković Istorijski razvoj shvatanja prirode svetlosti Korpuskularna teorija svetlosti
Fizika za studente Geodezije i geomatike Dualna priroda elektromagnetnog zračenja Princip rada lasera Docdr Ivana Stojković Istorijski razvoj shvatanja prirode svetlosti Korpuskularna teorija svetlosti
