I HEMIJSKI ZAKONI I STRUKTURA SUPSTANCI
|
|
|
- ÊἙρμῆς Ελευθερίου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 dr Ljiljana Vojinović-Ješić I HEMIJSKI ZAKONI I STRUKTURA SUPSTANCI ZAKON STALNIH MASENIH ODNOSA (I stehiometrijski zakon, Prust, 1799) Maseni odnos elemenata u datom jedinjenju je stalan, bez obzira na način njegovog nastanka. Tako, na primer, u ugljenik(iv)-oksidu, CO 2, maseni odnos ugljenika, C, i kiseonika, O, je uvek 3:8, odnosno ugljenik(iv)-oksid sadrži 27,27 % C i 72,73 % O. Evo nekoliko primera jednačina hemijskih reakcija u kojima nastaje CO 2 : C + O 2 CO 2 CaCO 3 CaO+ CO 2 CaCO HCl CaCl 2 + CO 2 + H 2 O ZAKON UMNOŽENIH (VIŠESTRUKIH) MASENIH ODNOSA (II stehiometrijski zakon, Dalton, 1802) Ako dva elementa grade više jedinjenja, onda različite mase jednog elementa koje jedine se sa istom masom drugog elementa, stoje među sobom u odnosu malih celih brojeva. Tako, prilikom građenja vode, H 2 O, vodonik, H, i kiseonik, O, se jedine u masenom odnosu 1:8, međutim vodonik i kiseonik se
2 Zbirka zadataka za pripremanje prijemnog ispita iz hemije mogu jediniti i u odnosu 1:16 kada nastaje vodonik-peroksid, H 2 O 2, tako da je maseni odnos vodonika i kiseonika u ovim jedinjenjima 1:2. ZAKON STALNIH ZAPREMINSKIH ODNOSA (III stehiometrijski zakon, Gej-Lisak, 1805) Zapremine gasova koji međusobno reaguju, kao i zapremine gasovitih proizvoda reakcije, stoje u odnosu malih celih brojeva pri istim uslovima temperature i pritiska. Primeri: 2H 2(g) +O 2(g) 2H 2 O (g) Dve zapremine vodonika se jedine sa jednom zapreminom kiseonika dajući dve zapremine vodene pare (odnos zapremina je 2:1:2) ili, prilikom građenja amonijaka: N 2(g) +3H 2(g) 2NH 3(g) jedna zapremina azota se jedini sa tri zapremine vodonika dajući dve zapremine amonijaka. U ovom slučaju odnos zapremina je 1:3:2. AVOGADROV ZAKON (Avogadro, 1811) Avogadro je pretpostavio da atomi gasova ne postoje kao izolovane čestice, već da su okupljeni u grupe koje se sastoje od malog broja atoma. Ove grupe Avogadro je nazvao molekulima. Molekuli gasa se u prostoru kreću kao celina i stupaju u hemijske reakcije. Na onovu hipoteze o postojanju molekula gasa Avogadro je postavio zakon stalnih zapreminskih odnosa: jednake zapremine različitih gasova pri istoj temperaturi i pritisku sadrže isti broj molekula. Na primer: 2 3H 2(g) + N 2(g) 2NH 3(g)
3 I Hemijski zakoni i struktura supstanci Tri zapremine vodonika reaguju sa jednom zapreminom azota i daju dve zapremine amonijaka. Pošto iste zapremine sadrže isti broj molekula možemo reći da tri dvoatomna molekula vodonika reaguje sa jednim dvoatomnim molekulom azota dajući dva četiriatomna molekula amonijaka. Kao što se vidi, broj molekula pre i posle reakcije ne mora da bude isti, ali broj atoma ostaje nepromenjen. STVARNE I RELATIVNE ATOMSKE I MOLEKULSKE MASE. MOL I MOLARNA ZAPREMINA Atomi su realne, veoma sitne čestice supstance koji se ne mogu dalje deliti pri hemijskoj reakciji. Stvarne (apsolutne) mase atoma su veoma male vrednosti. Na primer, masa atoma vodonika je m a (H)=1, kg, te se u praksi koriste veličine kao što su relativna atomska masa, Ar, i relativna molekulska masa, Mr. Relativna atomska masa, Ar, je neimenovani broj koji pokazuje koliko puta je prosečna masa atoma nekog elementa, ugljenikovog izotopa 12 C, (u): m a, veća od 1/12 mase atoma Relativna molekulska masa, Mr, jednaka je zbiru relativnih atomskih masa svih atoma koji ulaze u sastav molekula i pokazuje koliko puta je prosečna masa nekog molekula, m m Ar = = m C u a 1/12 12 a ( ) a m m, veća od 1/12 mase atoma ugljenikovog izotopa 12 C: m m Mr = = m C u m 1/12 12 a( ) m 1/12 mase atoma ugljenikovog izotopa 12 C je unificirana jedinica atomske mase, u, i iznosi 1, kg. 3
4 Zbirka zadataka za pripremanje prijemnog ispita iz hemije Osnovna SI jedinica za količinu supstance, n, je mol. Jedan mol je količina supstance definisane hemijske formule, koja sadrži onoliko formulskih jedinica koliko ima atoma u 12 g ugljenikovog izotopa 12 C. Količina supstance je odnos broja jedinki supstance, N, i Avogadrove konstante, N A (N A =6, mol -1 ): n = N N A [ mol] Masa Avogadrovog broja definisanih formulskih jedinica je molarna masa, M. Molarna masa se izračunava množenjem odgovarajuće relativne atomske, odnosno relativne molekulske mase mernom jedinicom g/mol: M = Ar g/mol, kada računamo molsku masu atoma, odnosno M = Mr g/mol kada računamo molsku masu molekula. Masa supstance, m, jednaka je proizvodu molarne mase i količine supstance: m= M n [g] Molarna zapremina gasa, Vm, definiše se kao odnos zapremine gasovite supstance, V, i njene količine: V Vm = dm mol n 3 [ / ] Pri normalnim uslovima (T=273,15 K i p= Pa) molarna zapremina bilo kog gasa iznosi 22,4 dm 3 /mol (Vm=22,4 dm 3 /mol). U 12 g ugljenikovog izotopa 12 C (1 mol) nalazi se 6, atoma, (6, je Avogadrov broj). 4
5 I Hemijski zakoni i struktura supstanci STRUKTURA ATOMA I NJIHOVE ELEKTRONSKE KONFIGURACIJE Svaki atom se sastoji od jezgra (nukleusa) i omotača. U jezgru se nalaze pozitivno naelektrisani protoni, p +, i čestice bez naelektrisanja neutroni, n. Oko jezgra kreću se negativno naelektrisani elektroni, e -. Atom elementa A X definisan Z je atomskim ili rednim brojem, Z, i masenim brojem, A. Atomski broj Z je broj protona u jezgru datog atoma (a on je jednak broju elektrona u datom atomu jer je atom elektroneutralan!). Maseni broj, A, zbir je broja protona i broja neutrona u jezgru datog atoma: Z = N(p + ) = N(e - ), A = N(p + ) + N(n) Atomi istog elementa koji imaju različite masene brojeve nazivaju se izotopi. Na primer, izotopi kiseonika su: O, O, O Stanje svakog elektrona u atomu definisano je kvantnim brojevima. Postoje četiri kvantna broja: Glavni kvantni broj, n, određuje broj energetskih nivoa u atomu. Za normalna (nepobuđena) stanja atoma može imati vrednosti od 1 do 7. Sporedni (azimutski) kvantni broj, l, određuje broj podnivoa, odnosno prostorni oblik orbitala (s, p, d, f), sa vrednostima od 0 do n-1. Magnetni kvantni broj, m l, određuje prostornu orijentaciju i broj orbitala (podpodnivoa) u pojedinim energetskim podnivoima. Može imati vrednosti od l do l, uključujući i nulu. 5
6 Zbirka zadataka za pripremanje prijemnog ispita iz hemije Spinski kvantni broj, m s, odnosi se na tzv. spin elektrona, tj. na njegovu rotaciju oko sopstvene ose u dva suprotna smera: desno ili levo, te može imati samo dve vrednosti: +1/2 i -1/2. Maksimalni broj elektrona u energetskom nivou je 2n 2, a u odgovarajućim podnivoima prikazan je u tabeli: Podnivo s p d f Broj elektrona Redosled popunjavanja orbitala elektronima vrši se postupno dodavanjem elektrona. Pri tome elektron prvo zaposeda stabilniju orbitalu. Ovde je zastupljen princip po kome su najstabilniji sistemi oni sa najmanjom energijom. Prilikom popunjavanja orbitala mora se poštovati Paulijev princip zabrane i Hundovo pravilo. Paulijev princip zabrane: u jednom atomu ne mogu da se nađu dva elektrona koji imaju ista sva četiri kvantna broja, ili jedna orbitala može da sadrži najviše dva elektrona suprotnog spina. Hundovo pravilo: orbitale iste energije popunjavaju se tako da se u svaku od njih smešta po jedan elektron istog spina, nakon čega dolazi do sparivanja po spinu. Redosled popunjavanja orbitala elektronima je: 1s 2s 2p 3s 3p 4s 3d 4p 5s 4d 5p 6s... Elektronske konfiguracije nekih atoma i njihovih jona: 6 atoma natrijuma : 11 Na: 1s 2 2s 2 2p 6 3s 1, natrijumovog jona: 11 Na + : 1s 2 2s 2 2p 6, atoma hlora: 17 Cl: 1s 2 2s 2 2p 6 3s 2 3p 5, hloridnog jona: 17 Cl - : 1s 2 2s 2 2p 6 3s 2 3p 6
7 I Hemijski zakoni i struktura supstanci Prema elektronskoj konfiguraciji elementi u periodnom sistemu elemenata (PSE) su podeljeni na s-, p-, d- i f-elemente. U s-elemente, osim vodonika i helijuma, se ubrajaju elementi prve i druge grupe PSE (alkalni i zemnoalkalni metali). p-elementi počinju popunjavanje p-podnivoa i čine ih elementi od 13. do 18. grupe. Među njima najviše je nemetala, pa potom metala i metaloida. Elementi koji počinju popunjavanje d-podnivoa zovu se i prelazni metali, a čine ih elementi od 3. do 12. grupe PSE. U f-elemente, čiji atomi popunjavaju f-podnivoe, ubrajaju se lantanoidi i aktinoidi. I ovi elementi su metali. HEMIJSKA VEZA Jonska veza nastaje između atoma metala i atoma nemetala i to prelaskom elektrona sa atoma metala na atom nemetala. Atomi metala lako otpuštaju elektrone (imaju malu energiju jonizacije ), a atomi nemetala ih lako primaju (imaju veliki afinitet prema elektronu ). Pri tome nastaju joni sa elektronskom konfiguracijom odgovarajućeg plemenitog gasa koji se privlače elektrostatičkim silama. Jonska jedinjenja su na sobnoj temperaturi čvrste kristalne supstance (NaCl, KF, CaCl 2, Na 2 O, CaO...), sa visokom tačkom topljenja i ključanja, dobro se rastvaraju u vodi, a njihovi vodeni rastvori i njihovi rastopi provode električnu struju. Kovalentna veza se gradi između atoma nemetala stvaranjem zajedničkih elektronskih parova, pri čemu atomi postižu konfiguraciju najbližeg plemenitog gasa. U zavisnosti od broja elektronskih parova kovalentna veza može biti jednostruka, dvostruka ili trostruka (1, 2, ili 3 elektronska para). U molekulu Energija jonizacije je ona količina energije koju je neophodno utrošiti za udaljavanje elektrona od atoma u gasovitom stanju, pri čemu se ove čestice prevode u katjone u gasovitom stanju. Afinitet prema elektronu je sposobnost atoma da primi elektron u valentni nivo, a energija koja se pri tom oslobađa ili utroši naziva se energijom elektronskog afiniteta 7
8 Zbirka zadataka za pripremanje prijemnog ispita iz hemije vodonika, na primer, veza je jednostruka, H-H, u molekulu kiseonika dvostruka, O=O, a u molekulu azota trostruka, N N. Kovalentna veza može biti nepolarna i polarna. Veza između dva ista atoma (H 2, O 2, N 2 ) je nepolarna i u takvoj vezi zajednički elektronski parovi su simetrično raspoređeni u prostoru između atomskih jezgara. Polarna kovalentna veza nastaje između atoma različite elektronegativnosti. Atom elementa veće elektronegativnosti jače privlači vezivne elektrone zbog čega se na tom atomu javlja delimično negativno naelektrisanje (δ - ), a na manje elektronegativnom atomu delimično pozitivno naelektrisanje (δ + ). Tako, na primer, u molekulu fluorovodonika elektronski par je pomeren ka fluoru, pa se na atomu fluora javlja delimično negativno, a na atomu vodonika delimično pozitivno naelektrisanje: δ + δ H F. Jedinjenja sa kovalentnom vezom su na sobnoj temperaturi gasovi ili tečnosti, ređe čvrste supstance, sa niskim tačkama ključanja i topljenja. Nepolarna kovalentna jedinjenja se dobro rastvaraju u nepolarnim rastvaračima, a ne rastvaraju se u vodi i drugim polarnim rastvaračima. Polarna kovalentna jedinjenja se dobro rastvaraju u vodi i polarnim rastvaračima, a nerastvaraju se u nepolarnim. Vodonična veza predstavlja poseban slučaj dipol-dipol interakcija. Naime, ova veza nastaje između molekula u kojima je atom vodonika kovalentno vezan za neki jako elektronegativan atom (F, O, N). Primeri ovakve veze su HF i H 2 O. δ + δ δ + δ Vodonična veza se prikazuje isprekidanom crtom: H F H F 8
9 HEMIJSKE FORMULE I Hemijski zakoni i struktura supstanci Hemijske formule su simbolički prikazi hemijskih struktura (molekuli, joni...). Svaka hemijska formula ima: a) kvalitativno i b) kvantitativno značenje. Tako, na primer, NH 3 znači da je u pitanju amonijak u čiji sastav ulaze azot i vodonik. Ovo je kvalitativno značenje formule NH 3. Iz kvantitativnog značenja 1 molekula NH 3 možemo odrediti: 1. maseni odnos: m(nh 3 ) : m(n) : m(h) = Mr(NH 3 ) : Ar(N) : 3Ar(H) 2. odnos broja čestica: N(NH 3 ) : N(N) : N(H) = 1 : 1 : 3 3. količinski odnos: n(nh 3 ) : n(n) : n(h) = 1 : 1 : 3. Hemijske formule mogu biti: Empirijske - kao najjednostavnije moguće formule, prikazuju najmanji odnos broja atoma u molekulu (empirijska formula vodonik-peroksida je HO), Molekulske - daju stvarni odnos broja atoma u molekulu (molekulska formula vodonik-peroksida je H 2 O 2 ), Strukturne - prikazuju način povezivanja atoma u molekulu: H-O-O-H. 9
10 Zbirka zadataka za pripremanje prijemnog ispita iz hemije ZADACI: 1. Pri nastanku jednog određenog hemijskog jedinjenja elementi se jedine: a) u proizvoljnim masenim odnosima b) u stalnim masenim odnosima c) u zavisnosti od vrste jedinjenja; nekada u stalnim, nekada u proizvoljnim masenim odnosima d) u zavisnosti od načina dobijanja tog jedinjenja 2. Koji se od sledećih parova supstanci može upotrebiti za ilustraciju zakona umnoženih masenih odnosa: a) O 2 i O 3 b) NO 2 i CO 2 c) H 2 O i H 2 O 2 3. Koji od sledećih parova supstanci ilustruje zakon umnoženih masenih odnosa: a) SO 2 i H 2 SO 4 b) CO i CO 2 c) NaCl i KCl 4. U ½ mola mola CaSO 4 ugrađeno je: a) 32 g kiseonika b) 1 mol atoma kalcijuma c) atoma sumpora. (A r (Ca) = 40; A r (S) = 32; A r (O) = 16) 10
11 I Hemijski zakoni i struktura supstanci 5. Koliko ima molekula u jednoj kapi vode mase 90 mg? (N A = ) a) b) c) 1, d) U 0,5 mola molekula kiseonika ima: a) 6, molekula b) 3, molekula c) 3, molekula 7. U količini od 0,5 mola Br 2 broj molekula broma je: a) b) c) 0, Mesto elementa u periodnom sistemu elemenata određeno je: a) relativnom atomskom masom b) relativnom molekulskom masom c) atomskim brojem d) brojem neutrona u jezgru atoma 9. U jednom molu atoma elementa atomskog broja 11 i masenog broja 23 broj protona je: a) 11 b) 23 c) d)
12 Zbirka zadataka za pripremanje prijemnog ispita iz hemije Nuklid elementa 13 X ima: a) isti broj protona i neutrona b) veći broj protona od neutrona c) veći broj neutrona od protona 11. Elektronska konfiguracija atoma nekog elementa je: 1s 2 2s 2 2p 3. a) atom elementa ima 3 nesparena elektrona b) atom elementa ima 3 valentna elektrona c) element pripada trećoj periodi d) element pripada 13. (IIIA) grupi 12. Elektronska konfiguracija atoma nekog elementa je : 1s 2 2s 2 2p 6 3s 2 3p 4 a) atom elementa ima 4 valentna elektrona b) atom elementa ima 2 nesparena elektrona c) element pripada 14. (IVA) grupi PSE d) element pripada 3. periodi PSE Zaokružiti slova ispred tačnih tvrdnji. 13. Elektronska konfiguracija atoma kiseonika je: a) 1s 2 2s 2 2p 3 b) 1s 2 2s 2 2p 5 c) 1s 2 2s 2 2p 4 12
13 I Hemijski zakoni i struktura supstanci 14. Elektronska konfiguracija atoma nekog elementa je: 1s 2 2s 2 2p 6 3s 2 3p 3 a) atom elementa ima 2 nesparena elektrona b) atom elementa ima 3 valentna elektrona c) element pripada 15. (VA) grupi PSE d) element pripada 3. periodi PSE Zaokružiti slova ispred tačnih tvrdnji. 15. Elektronska struktura atoma nekog elementa je: 1s 2 2s 2 2p 6 3s 2 3p 5, a njegovog jona 1s 2 2s 2 2p 6 3s 2 3p 6. To znači da je: a) jon pozitivnog naboja b) jon negativnog naboja c) prečnik jona veći od prečnika atoma d) prečnik jona manji od prečnika atoma e) broj protona u jonu i atomu je isti Zaokružiti slova ispred tačnih tvrdnji. 16. Izotopi su: a) atomi istog elementa različitog masenog broja b) atomi istog elementa koji sadrže jednak broj neutrona c) atomi različitih elemenata koji sadrže jednak broj neutrona 17. Treći energetski nivo sastoji se od: a) dve s-orbitale b) tri p-orbitale c) pet d-orbitala d) jedne s- i tri p-orbitale e) jedne s-, tri p- i pet d-orbitala. 13
14 Zbirka zadataka za pripremanje prijemnog ispita iz hemije 18. Elektronska struktura atoma nekog elementa je: 1s 2 2s 2 2p 6 3s 2 3p 5. Koje od navedenih tvrdnji nisu tačne za dati element: a) ima atomski broj 17 b) ima 7 valentnih elektrona c) ima malu elektronegativnost d) pripada s-elementima e) nalazi se u sedmoj grupi i trećoj periodi 19. 1/ grama je masa: a) jednog mola atoma vodonika b) jednog mola molekula vodonika c) atoma vodonika d) jednog atoma vodonika e) jednog molekula vodonika f) ni jedna tvrdnja nije tačna 20. Peroksidni (O 2 2- ) jon ima: a) 20 elektrona b) 16 elektrona c) 18 elektrona (Z(O)=8) 21. Koliko najviše elektrona može da sadrži : a) drugi energetski nivo b) treći energetski nivo 14
15 22. Hemijski element čiji atomi imaju elektronsku konfiguraciju: 1s 2 2s 2 2p 6 3s 2 3p 6 4s 2 3d 2 nalazi se u: I Hemijski zakoni i struktura supstanci a) 3. periodi i 4. (IVB) grupi Periodnog sistema elemenata b) 4. periodi i 12. (IIB) grupi Periodnog sistema elemenata c) 4. periodi i 4. (IVB) grupi Periodnog sistema elemenata d) 4. periodi i 14. (IVA) grupi Periodnog sistema elemenata e) 3. periodi i 12. (IIB) grupi Periodnog sistema elemenata 23. Atom hemijskog elementa koji se nalazi u trećoj periodi i 14. (IVA) grupi PSE ima elektronsku konfiguraciju: a) 1s 2 2s 2 2p 6 3s 2 b) 1s 2 2s 2 2p 6 3s 2 3p 6 4s 2 c) 1s 2 2s 2 2p 6 3s 2 3p 2 d) 1s 2 2s 2 2p 6 3s 2 3d U atomu hemijskog elementa čiji je atomski broj 20, elektronima su popunjeni: a) 1s, 2s, 3s, 3p i popunjava se 3d podnivo b) 1s, 2s, 2p, 3s, 3p i popunjava se 4p podnivo c) 1s, 2s, 2p, 3s, 3p, 4s podnivoe d) 1s, 2s, 2p, 3s, 3p, 3d, 4s podnivoe e) 1s, 2s, 2p 3s, 3p i popunjava se 3d podnivo 25. Najjače izražene osobine metala ima hemijski element čiji atomi imaju elektronsku konfiguraciju: a) 1s 2 2s 2 b) 1s 2 2s 2 2p 3 c) 1s 1 d) 1s 2 2s 2 2p 4 e) 1s 2 2s 2 2p 5 15
16 Zbirka zadataka za pripremanje prijemnog ispita iz hemije 26. Jonski karakter veze raste u nizu: a) H 2, HCl, KCl, KF b) HCl, KCl, KF, H 2 c) KCl, KF, H 2, HCl d) KF, H 2, HCl, KCl 27. Jonski karakter veze raste u nizu: a) Na 2 O, MgO, Al 2 O 3, P 4 O 10, SO 3 b) MgO, Al 2 O 3, Na 2 O, P 4 O 10, SO 3 c) SO 3, P 4 O 10, Al 2 O 3, MgO, Na 2 O d) SO 3, P 4 O 10, MgO, Al 2 O 3, Na 2 O 28. Niz u kojem se nalaze samo jedinjenja sa kovalentnom vezom je: a) HCl, H 2 O, NaCl, CaO b) CH 4, H 2 O, CO 2, NO c) HCl, H 2 S, CaCl 2, Na 2 O d) KCl, H 2 S, CO, H 2 O Kovalentna veza se stvara ako se elektronegativnost atoma elemenata koji se vezuju: a) u velikoj meri razlikuje b) u maloj meri razlikuje c) ne razlikuje d) elektronegativnost nema uticaja na stvaranje kovalentne veze Zaokružiti slova ispred tačnih tvrdnji. 16
17 I Hemijski zakoni i struktura supstanci 30. σ-veza nastaje: a) preklapanjem odgovarajućih atomskih orbitala duž ose koja spaja jezgra atoma učesnika veze b) potpunim prelaskom elektrona sa jednog na drugi atom c) bočnim preklapanjem p-orbitala 31. π-veza nastaje : a) preklapanjem odgovarajućih atomskih orbitala duž internuklearne ose b) potpunim prelaskom elektrona sa jednog na drugi atom c) bočnim preklapanjem p-orbitala 32. Zaokružiti slovo ispred formule koja sadrži samo kovalentnu vezu: a) Na 3 PO 4 b) NaH 2 PO 4 c) H 3 PO Zaokružiti slovo ispred simbola para hemijskih elemenata koji grade kovalentno jedinjenje: a) Na i Cl b) H i N c) K i F 34. U molekulu N 2 veza je: a) jednostruka b) dvostruka c) trostruka 17
18 Zbirka zadataka za pripremanje prijemnog ispita iz hemije 35. Molekuli vode i amonijaka su: a) planarni b) molekul H 2 O je linearan c) molekul H 2 O nije linearan, a molekul NH 3 je piramidalan d) nepolarni e) polarni 36. Sledeći niz molekula rasporediti prema porastu polarnosti veze H 2 O, CCl 4, CH 4, NH 3, NF 3, ako su poznate elektronegativnosti: H = 2,1; C = 2,5; Cl = 3,0; N = 3,0; O = 3,5; F = 4, Prikazane molekule poređati u niz prema porastu kovalentnog karaktera veze: HF, HCl, KCl, LiCl, Cl 2, ako je elektronegativnost : H= 2,1; F= 4,0; Cl= 3,0; K=: 0,8; Li= 1, Koji je red veze u molekulima: a) azota b) fosfora c) kiseonika d) hlora 39. Niz koji ilustruje povećanje polarnosti veze je : a) H-S, H-O, H-Cl; b) H-Cl, H-O, H-S; c) H-Br, H-Cl, H-F. 18
Osnovne veličine, jedinice i izračunavanja u hemiji
 Osnovne veličine, jedinice i izračunavanja u hemiji Pregled pojmova veličina i njihovih jedinica koje se koriste pri osnovnim izračunavanjima u hemiji dat je u Tabeli 1. Tabela 1. Veličine i njihove jedinice
Osnovne veličine, jedinice i izračunavanja u hemiji Pregled pojmova veličina i njihovih jedinica koje se koriste pri osnovnim izračunavanjima u hemiji dat je u Tabeli 1. Tabela 1. Veličine i njihove jedinice
HEMIJSKA VEZA TEORIJA VALENTNE VEZE
 TEORIJA VALENTNE VEZE Kovalentna veza nastaje preklapanjem atomskih orbitala valentnih elektrona, pri čemu je region preklapanja između dva jezgra okupiran parom elektrona. - Nastalu kovalentnu vezu opisuje
TEORIJA VALENTNE VEZE Kovalentna veza nastaje preklapanjem atomskih orbitala valentnih elektrona, pri čemu je region preklapanja između dva jezgra okupiran parom elektrona. - Nastalu kovalentnu vezu opisuje
SEKUNDARNE VEZE međumolekulske veze
 PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
Pri međusobnom spajanju atoma nastaje energetski stabilniji sistem. To se postiže:
 HEMIJSKE VEZE Pri međusobnom spajanju atoma nastaje energetski stabilniji sistem. To se postiže: - prelaskom atoma u pozitivno i negativno naelektrisane jone koji se međusobno privlače, jonska veza - sparivanjem
HEMIJSKE VEZE Pri međusobnom spajanju atoma nastaje energetski stabilniji sistem. To se postiže: - prelaskom atoma u pozitivno i negativno naelektrisane jone koji se međusobno privlače, jonska veza - sparivanjem
HEMIJSKA VEZA ŠTA DRŽI STVARI (ATOME) ZAJEDNO?
 HEMIJSKA VEZA ŠTA DRŽI STVARI (ATOME) ZAJEDNO? U OKVIRU OVOG POGLAVLJA ĆEMO RADITI Jonska i kovalentna veza. Metalna veza. Elektronska teorija hemijske veze. Struktura molekula. Međumolekulske interakcije.
HEMIJSKA VEZA ŠTA DRŽI STVARI (ATOME) ZAJEDNO? U OKVIRU OVOG POGLAVLJA ĆEMO RADITI Jonska i kovalentna veza. Metalna veza. Elektronska teorija hemijske veze. Struktura molekula. Međumolekulske interakcije.
1. razred gimnazije- opšti i prirodno-matematički smer STRUKTURA MOLEKULA HEMIJSKA VEZA
 EMIJSKE VEZE 1 razred gimnazije- opšti i prirodno-matematički smer STRUKTURA MLEKULA Molekul je najsitnija čestica koja se sastoji od dva ili više istih atoma, a to su molekuli elemenata: Cl 2, 2, N 2,
EMIJSKE VEZE 1 razred gimnazije- opšti i prirodno-matematički smer STRUKTURA MLEKULA Molekul je najsitnija čestica koja se sastoji od dva ili više istih atoma, a to su molekuli elemenata: Cl 2, 2, N 2,
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
U stvaranju hemijske veze među atomima učestvuju samo elektroni u najvišem energetskom nivou valentni elektroni
 HEMIJSKA VEZA ELEKTRONSKA TEORIJA VALENCE U stvaranju hemijske veze među atomima učestvuju samo elektroni u najvišem energetskom nivou valentni elektroni Atomi teže da postignu oktet elektrona na poslednjem
HEMIJSKA VEZA ELEKTRONSKA TEORIJA VALENCE U stvaranju hemijske veze među atomima učestvuju samo elektroni u najvišem energetskom nivou valentni elektroni Atomi teže da postignu oktet elektrona na poslednjem
Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze:
 Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze: Jonska, Kovalentna i Metalna Luisovi simboli veoma zgodan
Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze: Jonska, Kovalentna i Metalna Luisovi simboli veoma zgodan
MEĐUMOLEKULSKE SILE JON-DIPOL DIPOL VODONIČNE NE VEZE DIPOL DIPOL-DIPOL DIPOL-INDUKOVANI INDUKOVANI JON-INDUKOVANI DISPERZNE SILE
 MEĐUMLEKULSKE SILE JN-DIPL VDNIČNE NE VEZE DIPL-DIPL JN-INDUKVANI DIPL DIPL-INDUKVANI INDUKVANI DIPL DISPERZNE SILE MEĐUMLEKULSKE SILE jake JNSKA VEZA (metal-nemetal) KVALENTNA VEZA (nemetal-nemetal) METALNA
MEĐUMLEKULSKE SILE JN-DIPL VDNIČNE NE VEZE DIPL-DIPL JN-INDUKVANI DIPL DIPL-INDUKVANI INDUKVANI DIPL DISPERZNE SILE MEĐUMLEKULSKE SILE jake JNSKA VEZA (metal-nemetal) KVALENTNA VEZA (nemetal-nemetal) METALNA
Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze:
 Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze: Jonska, Kovalentna i Metalna Luisovi simboli veoma zgodan
Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze: Jonska, Kovalentna i Metalna Luisovi simboli veoma zgodan
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
STRUKTURA ATOMA. Dalton (1803) Tomson (1904) Raderford (1911) Bor (1913) Šredinger (1926)
 Dalton (1803) Tomson (1904) Raderford (1911) Bor (1913) Šredinger (1926) TALASNO MEHANIČKI MODEL ATOMA Hipoteza de Brolja Elektroni i fotoni imaju dvojnu prirodu: talasnu i korpuskularnu. E = hν E = mc
Dalton (1803) Tomson (1904) Raderford (1911) Bor (1913) Šredinger (1926) TALASNO MEHANIČKI MODEL ATOMA Hipoteza de Brolja Elektroni i fotoni imaju dvojnu prirodu: talasnu i korpuskularnu. E = hν E = mc
n (glavni ) 1, 2, 3,.. veličina orbitale i njena energija E= -R(1/n 2 )
 Kvantni brojevi Jedna atomska orbitala je definisana sa tri kvantna broja n l m l Elektroni su rasporedjeni u nivoima i podnivoima n l definiše nivo definiše podnivo ukupni broj orbitala u podnivou: 2
Kvantni brojevi Jedna atomska orbitala je definisana sa tri kvantna broja n l m l Elektroni su rasporedjeni u nivoima i podnivoima n l definiše nivo definiše podnivo ukupni broj orbitala u podnivou: 2
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
3. razred gimnazije- opšti i prirodno-matematički smer ALKENI. Aciklični nezasićeni ugljovodonici koji imaju jednu dvostruku vezu.
 ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
S t r a n a 1. 1.Povezati jonsku jačinu rastvora: a) MgCl 2 b) Al 2 (SO 4 ) 3 sa njihovim molalitetima, m. za so tipa: M p X q. pa je jonska jačina:
 S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
HEMIJA. eksterna provjera znanja učenika na kraju iii ciklusa osnovne škole. školska 2012/2013. godina UPUTSTVO
 HEMIJA eksterna provjera znanja učenika na kraju iii ciklusa osnovne škole školska 2012/2013. godina UPUTSTVO Ne otvarajte test dok vam test-administrator ne kaže da možete početi sa radom. Dozvoljen pribor:
HEMIJA eksterna provjera znanja učenika na kraju iii ciklusa osnovne škole školska 2012/2013. godina UPUTSTVO Ne otvarajte test dok vam test-administrator ne kaže da možete početi sa radom. Dozvoljen pribor:
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
Teorijske osnove informatike 1
 Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
Elektronska struktura atoma
 Elektronska struktura atoma Raderfordov atomski model jezgro u sredini pozitivno naelektrisano skoro sva masa jezgru veoma malo Elektroni kruže oko jezgra elektrostatičke interakcije ih drže da ne napuste
Elektronska struktura atoma Raderfordov atomski model jezgro u sredini pozitivno naelektrisano skoro sva masa jezgru veoma malo Elektroni kruže oko jezgra elektrostatičke interakcije ih drže da ne napuste
Elektronska struktura atoma
 Elektronska struktura atoma Raderfordov atomski model jezgro u sredini pozitivno naelektrisano skoro sva masa u jezgru veoma malo Elektroni kruže oko jezgra elektrostatičke interakcije ih drže da ne napuste
Elektronska struktura atoma Raderfordov atomski model jezgro u sredini pozitivno naelektrisano skoro sva masa u jezgru veoma malo Elektroni kruže oko jezgra elektrostatičke interakcije ih drže da ne napuste
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
 TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
1s 2 2s 2 2p 2. C-atom. Hibridne atomske orbitale. sp 3 hibridizacija. sp 3. Elektronska konfiguracija ugljenika: aktivacija. ekscitovano stanje
 PREAVAJE 2. Ugljenik je u organskim jedinjenjima četvorovalentan. Elektronska konfiguracija ugljenika: 1s 2 2 2p 2 dva nesparena elektrona -atom oc.dr Mirjana Abramović 2p osnovno stanje aktivacija 2p
PREAVAJE 2. Ugljenik je u organskim jedinjenjima četvorovalentan. Elektronska konfiguracija ugljenika: 1s 2 2 2p 2 dva nesparena elektrona -atom oc.dr Mirjana Abramović 2p osnovno stanje aktivacija 2p
Idealno gasno stanje-čisti gasovi
 Idealno gasno stanje-čisti gasovi Parametri P, V, T i n nisu nezavisni. Odnos između njih eksperimentalno je utvrđeni izražava se kroz gasne zakone. Gasni zakoni: 1. ojl-maritov: PVconst. pri konstantnim
Idealno gasno stanje-čisti gasovi Parametri P, V, T i n nisu nezavisni. Odnos između njih eksperimentalno je utvrđeni izražava se kroz gasne zakone. Gasni zakoni: 1. ojl-maritov: PVconst. pri konstantnim
SASTAV MATERIJE STRUKTURA ATOMA I PERODNI SISTEM ELEMENATA
 SASTAV MATERIJE STRUKTURA ATOMA I PERODNI SISTEM ELEMENATA Atomi su veoma sitne čestice Još niko nije uspeo da vidi atom Još nije konstruisan takav mikroskop koji će omogućiti da se vidi atom Najbolji
SASTAV MATERIJE STRUKTURA ATOMA I PERODNI SISTEM ELEMENATA Atomi su veoma sitne čestice Još niko nije uspeo da vidi atom Još nije konstruisan takav mikroskop koji će omogućiti da se vidi atom Najbolji
Kovalentna veza , CO 2. U molekulima H 2
 Kovalentna veza U molekulima H 2, N 2, O 2, CO 2, NH 3, H 2 O,... ili molekulima organskih jedinjenja ne postoje joni. To je veza između atoma i ona se bitno razlikuje od jonske veze a naziva se kovalentnom
Kovalentna veza U molekulima H 2, N 2, O 2, CO 2, NH 3, H 2 O,... ili molekulima organskih jedinjenja ne postoje joni. To je veza između atoma i ona se bitno razlikuje od jonske veze a naziva se kovalentnom
Ispitna pitanja iz Osnova hemije
 I grupa pitanja Ispitna pitanja iz Osnova hemije 1. Hijerarhija materijala, smeše, metode razdvajanja smeša Materija: supstance i energija (polje). Supstance se dele na homogene i heterogene supstance.
I grupa pitanja Ispitna pitanja iz Osnova hemije 1. Hijerarhija materijala, smeše, metode razdvajanja smeša Materija: supstance i energija (polje). Supstance se dele na homogene i heterogene supstance.
Verovatnoća i Statistika I deo Teorija verovatnoće (zadaci) Beleške dr Bobana Marinkovića
 Verovatnoća i Statistika I deo Teorija verovatnoće zadaci Beleške dr Bobana Marinkovića Iz skupa, 2,, 00} bira se na slučajan način 5 brojeva Odrediti skup elementarnih dogadjaja ako se brojevi biraju
Verovatnoća i Statistika I deo Teorija verovatnoće zadaci Beleške dr Bobana Marinkovića Iz skupa, 2,, 00} bira se na slučajan način 5 brojeva Odrediti skup elementarnih dogadjaja ako se brojevi biraju
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
NOMENKLATURA ORGANSKIH SPOJEVA. Imenovanje aromatskih ugljikovodika
 NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE GODINE 8. RAZRED TOČNI ODGOVORI
 21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
( ) ( ) 2 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET. Zadaci za pripremu polaganja kvalifikacionog ispita iz Matematike. 1. Riješiti jednačine: 4
 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
XI dvoqas veжbi dr Vladimir Balti. 4. Stabla
 XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
SISTEMI NELINEARNIH JEDNAČINA
 SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne
 Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne metode (rentgenska kristalografija, NMR spektroskopija...)
Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne metode (rentgenska kristalografija, NMR spektroskopija...)
PERIODNI SISTEM ELEMENATA
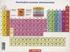 PERIODNI SISTEM ELEMENATA 1/43 PERIODNI SISTEM ELEMENATA - Kratka istorija Otkriće elemenata do danas otktiveno još 11 elemenata 2011. IUPAC potvrdio otkriće 2 nova elementa: Flerovijum (Fl, Z = 114) i
PERIODNI SISTEM ELEMENATA 1/43 PERIODNI SISTEM ELEMENATA - Kratka istorija Otkriće elemenata do danas otktiveno još 11 elemenata 2011. IUPAC potvrdio otkriće 2 nova elementa: Flerovijum (Fl, Z = 114) i
Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne
 Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne metode (rentgenska kristalografija, NMR spektroskopija...)
Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne metode (rentgenska kristalografija, NMR spektroskopija...)
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
OSNOVNA ŠKOLA HEMIJA
 OSNOVNA ŠKOLA HEMIJA Zadatak broj Bodovi 1. 8 2. 8 3. 6 4. 10 5. 10 6. 6 7. 10 8. 8 9. 8 10. 10 11. 8 12. 8 Ukupno 100 Za izradu testa planirano je 120 minuta. U toku izrade testa učenici mogu koristiti
OSNOVNA ŠKOLA HEMIJA Zadatak broj Bodovi 1. 8 2. 8 3. 6 4. 10 5. 10 6. 6 7. 10 8. 8 9. 8 10. 10 11. 8 12. 8 Ukupno 100 Za izradu testa planirano je 120 minuta. U toku izrade testa učenici mogu koristiti
5. Karakteristične funkcije
 5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
JONSKA VEZA (metal-nemetal) KOVALENTNA VEZA (nemetal-nemetal) METALNA VEZA (metal-metal) jake H N. prelazne VODONIČNA VEZA H F
 HEMIJSKE VEZE HEMIJSKE VEZE I GRAĐA JEDINJENJA,, I deo Postoje tri osnovna tipa veza (primarne veze) i one imaju najveći uticaj na svojstva jedinjenja. Pored njih postoje i dopunske (sekundarne) veze između
HEMIJSKE VEZE HEMIJSKE VEZE I GRAĐA JEDINJENJA,, I deo Postoje tri osnovna tipa veza (primarne veze) i one imaju najveći uticaj na svojstva jedinjenja. Pored njih postoje i dopunske (sekundarne) veze između
U unutrašnja energija H entalpija S entropija G 298. G Gibsova energija TERMOHEMIJA I TERMODINAMIKA HEMIJSKA TERMODINAMIKA
 HEMIJSKA TERMODINAMIKA Bavi se energetskim promenama pri odigravanju hemijskih reakcija. TERMODINAMIČKE FUNKCIJE STANJA U unutrašnja energija H entalpija S entropija Ako su određene na standardnom pritisku
HEMIJSKA TERMODINAMIKA Bavi se energetskim promenama pri odigravanju hemijskih reakcija. TERMODINAMIČKE FUNKCIJE STANJA U unutrašnja energija H entalpija S entropija Ako su određene na standardnom pritisku
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
GASNO STANJE.
 GASNO STANJE http://www.ffh.bg.ac.rs/geografi_fh_procesi.html AGREGATNA STANJA MATERIJE Četiri agregatna stanja materije na osnovu stepena uređenosti, tj. odnosa termalne energije čestica i energije međumolekulskih
GASNO STANJE http://www.ffh.bg.ac.rs/geografi_fh_procesi.html AGREGATNA STANJA MATERIJE Četiri agregatna stanja materije na osnovu stepena uređenosti, tj. odnosa termalne energije čestica i energije međumolekulskih
KVADRATNA FUNKCIJA. Kvadratna funkcija je oblika: Kriva u ravni koja predstavlja grafik funkcije y = ax + bx + c. je parabola.
 KVADRATNA FUNKCIJA Kvadratna funkcija je oblika: = a + b + c Gde je R, a 0 i a, b i c su realni brojevi. Kriva u ravni koja predstavlja grafik funkcije = a + b + c je parabola. Najpre ćemo naučiti kako
KVADRATNA FUNKCIJA Kvadratna funkcija je oblika: = a + b + c Gde je R, a 0 i a, b i c su realni brojevi. Kriva u ravni koja predstavlja grafik funkcije = a + b + c je parabola. Najpre ćemo naučiti kako
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Zavrxni ispit iz Matematiqke analize 1
 Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
HEMIJA ELEMENATA VODONIK
 HEMIJA ELEMENATA Najrasprostranjeniji element u Vasioni (88,6 at.%). Na trećem mestu po rasprostranjenosti na Zemlji (15 at.%, iza O i Si). Prvi, najlakši i najjednostavniji element (1 p + i 1 e ). SVOJSTVA
HEMIJA ELEMENATA Najrasprostranjeniji element u Vasioni (88,6 at.%). Na trećem mestu po rasprostranjenosti na Zemlji (15 at.%, iza O i Si). Prvi, najlakši i najjednostavniji element (1 p + i 1 e ). SVOJSTVA
Prirodno-matematički fakultet Društvo matematičara i fizičara Crne Gore
 Prirodno-matematički fakultet Društvo matematičara i fizičara Crne Gore OLIMPIJADA ZNANJA 018. Rješenja zadataka iz HEMIJE za VIII razred osnovne škole 1. Posmatrati sliku i izračunati: a) masu kalijum-permanganata
Prirodno-matematički fakultet Društvo matematičara i fizičara Crne Gore OLIMPIJADA ZNANJA 018. Rješenja zadataka iz HEMIJE za VIII razred osnovne škole 1. Posmatrati sliku i izračunati: a) masu kalijum-permanganata
DALTONOV ATOMSKI MODEL Nastao je čitavih 2300 godina posle DEMOKRITA!
 DALTONOV ATOMSKI MODEL Nastao je čitavih 2300 godina posle DEMOKRITA! Polazna znanja zakoni o: Održanju mase Stalnom (utvrdjenom) sastavu Umnoženim odnosima Zakon o održanju mase masa supstance ne menja
DALTONOV ATOMSKI MODEL Nastao je čitavih 2300 godina posle DEMOKRITA! Polazna znanja zakoni o: Održanju mase Stalnom (utvrdjenom) sastavu Umnoženim odnosima Zakon o održanju mase masa supstance ne menja
Kiselo bazni indikatori
 Kiselo bazni indikatori Slabe kiseline ili baze koje imaju različite boje nejonizovanog i jonizovanog oblika u rastvoru Primer: slaba kiselina HIn(aq) H + (aq) + In (aq) nejonizovani oblik jonizovani oblik
Kiselo bazni indikatori Slabe kiseline ili baze koje imaju različite boje nejonizovanog i jonizovanog oblika u rastvoru Primer: slaba kiselina HIn(aq) H + (aq) + In (aq) nejonizovani oblik jonizovani oblik
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
TALASNO-MEHANI MEHANIČKI MODEL ATOMA
 TALASNO-MEHANI MEHANIČKI MODEL ATOMA TALASNO-MEHANI MEHANIČKI MODEL ATOMA Kompton (19): svetlost ima i talasnu i korpuskularnu prirodu. Luj De Brolj (193): elektron ima i korpuskularnu i talasnu prirodu.
TALASNO-MEHANI MEHANIČKI MODEL ATOMA TALASNO-MEHANI MEHANIČKI MODEL ATOMA Kompton (19): svetlost ima i talasnu i korpuskularnu prirodu. Luj De Brolj (193): elektron ima i korpuskularnu i talasnu prirodu.
Zadaci iz trigonometrije za seminar
 Zadaci iz trigonometrije za seminar FON: 1. Vrednost izraza sin 1 cos 6 jednaka je: ; B) 1 ; V) 1 1 + 1 ; G) ; D). 16. Broj rexea jednaqine sin x cos x + cos x = sin x + sin x na intervalu π ), π je: ;
Zadaci iz trigonometrije za seminar FON: 1. Vrednost izraza sin 1 cos 6 jednaka je: ; B) 1 ; V) 1 1 + 1 ; G) ; D). 16. Broj rexea jednaqine sin x cos x + cos x = sin x + sin x na intervalu π ), π je: ;
OBRTNA TELA. Vladimir Marinkov OBRTNA TELA VALJAK
 OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
INTELIGENTNO UPRAVLJANJE
 INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
RIJEŠENI ZADACI I TEORIJA IZ
 RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
C 273,15, T 273,15, 1 1 C 1 50 C 273,15 K 50K 323,15K 50K 373,15K C 40 C 40 K
 1 Zadatak temperatura K- C Telo A se nalazi na temperaturi 50 C i zagreje se za 50 K. Telo B se nalazi na temperaturi 313 K.i zagreje se za 40 C. Koje je telo toplije posle zagravanja i kolika je razlika
1 Zadatak temperatura K- C Telo A se nalazi na temperaturi 50 C i zagreje se za 50 K. Telo B se nalazi na temperaturi 313 K.i zagreje se za 40 C. Koje je telo toplije posle zagravanja i kolika je razlika
STRUKTURA ATOMA. Dalton (1803) Tomson (1904) Raderford (1911) Bor (1913) Šredinger (1926)
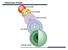 Dalton (803) Tomson (904) Raderford (9) Bor (93) Šredinger (96) OTKRIĆA OSNOVNIH SASTOJAKA ATOMA Do početka XX veka važila je Daltonova atomska teorija o nedeljivosti atoma. Karjem XIX i početkom XX veka
Dalton (803) Tomson (904) Raderford (9) Bor (93) Šredinger (96) OTKRIĆA OSNOVNIH SASTOJAKA ATOMA Do početka XX veka važila je Daltonova atomska teorija o nedeljivosti atoma. Karjem XIX i početkom XX veka
3. Koliko g Fe može da se dobije iz 463,1 g rude gvoždja koja sadrži 50 % minerala magnetita (Fe 3 O 4 ) i 50 % jalovine?
 PRIJEMNI ISPIT IZ HEMIJE NA RUDARSKO-GEOLOŠKOM FAKULTETU UNIVERZITETA U BEOGRADU Katedra za hemiju; Prof. dr Slobodanka Marinković I) Oblasti 1. Jednostavna izračunavanja u hemiji (mol, molska masa, Avogadrov
PRIJEMNI ISPIT IZ HEMIJE NA RUDARSKO-GEOLOŠKOM FAKULTETU UNIVERZITETA U BEOGRADU Katedra za hemiju; Prof. dr Slobodanka Marinković I) Oblasti 1. Jednostavna izračunavanja u hemiji (mol, molska masa, Avogadrov
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
Ĉetverokut - DOMAĆA ZADAĆA. Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke.
 Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri
 Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
radni nerecenzirani materijal za predavanja R(f) = {f(x) x D}
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
MEHANIKA FLUIDA. Isticanje kroz otvore sa promenljivim nivoom tečnosti
 MEHANIKA FLUIDA Isticanje kroz otvore sa promenljivim nivoom tečnosti zadatak Prizmatična sud podeljen je vertikalnom pregradom, u kojoj je otvor prečnika d, na dve komore Leva komora je napunjena vodom
MEHANIKA FLUIDA Isticanje kroz otvore sa promenljivim nivoom tečnosti zadatak Prizmatična sud podeljen je vertikalnom pregradom, u kojoj je otvor prečnika d, na dve komore Leva komora je napunjena vodom
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
Pripremila i uredila: Doc. dr. sc. Blaženka Foretić OSNOVE KEMIJSKOG RAČUNANJA
 Pripremila i uredila: Doc. dr. sc. Blaženka Foretić OSNOVE KEMIJSKOG RAČUNANJA Relativna skala masa elemenata: atomska jedinica mase 1/12 mase atoma ugljika C-12. Unificirana jedinica atomske mase (u)
Pripremila i uredila: Doc. dr. sc. Blaženka Foretić OSNOVE KEMIJSKOG RAČUNANJA Relativna skala masa elemenata: atomska jedinica mase 1/12 mase atoma ugljika C-12. Unificirana jedinica atomske mase (u)
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI)
 IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
Osnovne teoreme diferencijalnog računa
 Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
Riješeni zadaci: Nizovi realnih brojeva
 Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
PRIRUČNIK ZA PRIJEMNI ISPIT
 PRIRUČNIK ZA PRIJEMNI ISPIT 1 OPŠTA I NEORGANSKA HEMIJA Visoka škola strukovnih studija Aranđelovac PRIRUČNIK ZA POLAGANJE PRIJEMNOG ISPITA IZ HEMIJE ARANĐELOVAC, 2017. 2 PRIRUČNIK ZA PRIJEMNI ISPIT PREDGOVOR
PRIRUČNIK ZA PRIJEMNI ISPIT 1 OPŠTA I NEORGANSKA HEMIJA Visoka škola strukovnih studija Aranđelovac PRIRUČNIK ZA POLAGANJE PRIJEMNOG ISPITA IZ HEMIJE ARANĐELOVAC, 2017. 2 PRIRUČNIK ZA PRIJEMNI ISPIT PREDGOVOR
7 Algebarske jednadžbe
 7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
PID: Domen P je glavnoidealski [PID] akko svaki ideal u P je glavni (generisan jednim elementom; oblika ap := {ab b P }, za neko a P ).
![PID: Domen P je glavnoidealski [PID] akko svaki ideal u P je glavni (generisan jednim elementom; oblika ap := {ab b P }, za neko a P ). PID: Domen P je glavnoidealski [PID] akko svaki ideal u P je glavni (generisan jednim elementom; oblika ap := {ab b P }, za neko a P ).](/thumbs/74/70316766.jpg) 0.1 Faktorizacija: ID, ED, PID, ND, FD, UFD Definicija. Najava pojmova: [ID], [ED], [PID], [ND], [FD] i [UFD]. ID: Komutativan prsten P, sa jedinicom 1 0, je integralni domen [ID] oblast celih), ili samo
0.1 Faktorizacija: ID, ED, PID, ND, FD, UFD Definicija. Najava pojmova: [ID], [ED], [PID], [ND], [FD] i [UFD]. ID: Komutativan prsten P, sa jedinicom 1 0, je integralni domen [ID] oblast celih), ili samo
MATEMATIKA 2. Grupa 1 Rexea zadataka. Prvi pismeni kolokvijum, Dragan ori
 MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
TOPLOTA. Primjeri. * TERMODINAMIKA Razmatra prenos energije i efekte tog prenosa na sistem.
 1.OSNOVNI POJMOVI TOPLOTA Primjeri * KALORIKA Nauka o toploti * TERMODINAMIKA Razmatra prenos energije i efekte tog prenosa na sistem. * TD SISTEM To je bilo koje makroskopsko tijelo ili grupa tijela,
1.OSNOVNI POJMOVI TOPLOTA Primjeri * KALORIKA Nauka o toploti * TERMODINAMIKA Razmatra prenos energije i efekte tog prenosa na sistem. * TD SISTEM To je bilo koje makroskopsko tijelo ili grupa tijela,
KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI. NEUTRALNI ELEMENT GRUPOIDA.
 KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI NEUTRALNI ELEMENT GRUPOIDA 1 Grupoid (G, ) je asocijativa akko važi ( x, y, z G) x (y z) = (x y) z Grupoid (G, ) je komutativa akko važi ( x, y G) x y = y x Asocijativa
KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI NEUTRALNI ELEMENT GRUPOIDA 1 Grupoid (G, ) je asocijativa akko važi ( x, y, z G) x (y z) = (x y) z Grupoid (G, ) je komutativa akko važi ( x, y G) x y = y x Asocijativa
Prirodno-matematički fakultet Društvo matematičara I fizičara Crne Gore
 Prirodno-matematički fakultet Društvo matematičara I fizičara Crne Gore OLIMPIJADA ZNANJA 2018. Rješenja zadataka iz HEMIJE za IX razred osnovne škole 1. Koju zapreminu, pri standardnim uslovima, zauzimaju
Prirodno-matematički fakultet Društvo matematičara I fizičara Crne Gore OLIMPIJADA ZNANJA 2018. Rješenja zadataka iz HEMIJE za IX razred osnovne škole 1. Koju zapreminu, pri standardnim uslovima, zauzimaju
a M a A. Može se pokazati da je supremum (ako postoji) jedinstven pa uvodimo oznaku sup A.
 3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
dr.sc. M. Cetina, doc. Tekstilno-tehnološki fakultet, Zavod za primijenjenu kemiju
 Kovalentna veza Za razliku od ionske veze gdje se veza ostvaruje prijenosom elektrona, kod kovalentne veze ona se ostvaruje tako da u toj vezi atomi dijele jedan ili više zajedničkih elektronskih parova.
Kovalentna veza Za razliku od ionske veze gdje se veza ostvaruje prijenosom elektrona, kod kovalentne veze ona se ostvaruje tako da u toj vezi atomi dijele jedan ili više zajedničkih elektronskih parova.
Grafičko prikazivanje atributivnih i geografskih nizova
 Grafičko prikazivanje atributivnih i geografskih nizova Biserka Draščić Ban Pomorski fakultet u Rijeci 17. veljače 2011. Grafičko prikazivanje atributivnih nizova Atributivni nizovi prikazuju se grafički
Grafičko prikazivanje atributivnih i geografskih nizova Biserka Draščić Ban Pomorski fakultet u Rijeci 17. veljače 2011. Grafičko prikazivanje atributivnih nizova Atributivni nizovi prikazuju se grafički
TRIGONOMETRIJSKE FUNKCIJE I I.1.
 TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
