Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze:
|
|
|
- Κλήμης Μοσχοβάκης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze: Jonska, Kovalentna i Metalna Luisovi simboli veoma zgodan način predstavljanja s i p elemenata i veza izmeñu njih. Luisovi simboli nisu praktični za predstavljanje d elemenata. Valentni elektroni se predstavjaju tačkicama na sve 4 strane od simbola elemenata (to je zgodna podudarnost jer s i p elementi imaju 4 orbitale u koje se smeštaju valentni elektroni jednu s i tri p).
2 Hemijska veza Dve tačkice predstavljaju popunjenu orbitalu a jedna polupopunjenu d elektroni se ne predstavljaju Luisovim simbolima
3 Pravilo okteta Elektronska konfiguracija plemenitih gasova je veoma stabilna. Oni imaju veliku jonizacionu energiju, mali afinitet prema elektronu i hemijski su inertni Stoga ostali atomi se jedine u jedinjenja težeći da dobiju elektronsku konfiguraciju najbližeg plemenitog gasa. Iz ovog opažanja je proisteklo pravilo okteta: Atomi će gubiti ili dobijati ili deliti elektrone da bi postigli elektronsku konfiguraciju plemenitog gasa Ovo je pravilo, što znači da ima izuzetaka
4 Jonska veza Jonska veza se tumači kao elektrostatičko privlačenje izmeñu različito naelektrisanih jona Uglavnom nastaje izmeñu katjona metala i anjona nemetala Kada metalni Na reaguje sa gasovitim Cl nastaje jonska veza Na(s) + ½Cl 2 (g) NaCl(s) H o f = -410,9 kj
5 Jonska veza Ova veza se tumači kao da je elektron sa atoma natrijuma prešao potpuno na atom hlora. Nastali katjoni i anjoni su se udružili u trodimenzionalnu kristalnu rešetku i povezani su samo elektrostatičkim silama
6 Jonska veza Standardne entalpije nastajanja svih jonskih jedinjenja su veoma negativne nastajanje jonskih jedinjenja je egzoterman proces Prilikom nastajanja jonkih jedine sa dešavaju tri stvari: 1. Uklanja se elektron sa atoma metala da bi nastao katjon. Za ovo je potrebno utošiti energiju jonizacije to je uvek endotermno 2. Dodaje se elektron atomu nemetala da bi se dobio anjon afinitet prema elektronu - uglavnom egzoterman proces (elementi koji imaju mali ili pozitivan afinitet prema elektronu ne grade anjone) 3. Nastali katjon i anjon se spajaju u čvrsto jonsko jedinjenje
7 Jonska veza Energije sva tri procesa prilikom grañenja NaCl iz natrijuma i hlora su: 1. Na(g) Na + (g) + e - I 1 = +496 kj/mol 2. Cl(g) + e - Cl - (g) Ea= -349 kj/mol 3. Na + (g) + Cl - (g) NaCl(s) H= -788 kj/mol H u trećoj reakciji se naziva energija kristalne rešetke i ona se definiše kao energija koju je potrebno uložiti da bi se potpuno razdvojio jedan mol čvrstog kristalnog jonskog jedinjenja na jone u gasovitom stanju Na(s) + ½Cl 2 (g) NaCl(s) H o f= -410,9 kj
8 Jonska veza Energija kristalne rešetke zavisi isključivo od naelektrisanja, veličine i načina pakovanja jona koji čine jonsko jedinjenje. 1 = 4πε Q1Q d E el 2 Što su joni manji i više naelektrisani i energija kristalne rešetke će rasti. Pakovanje jona u rešetku zavisi od brojnih faktora od kojih je najvažniji odnos izmeñu veličina katjona i anjona. Generalno, ako su katjon i anjoj približo istih veličina pakovanje će biti gušće i energija kristalne rešetke veća. 0
9 Joni prelaznih metala Ne ponašaju se u skladu sa pravilom okteta, jer moraju da otpuste ili prime previše elektrona da bi postigli elektronsku konfiguraciju plemenitog gasa. Npr. gvožñe Fe: [Ar]3d 6 4s 2 bi moralo da otpusti 8 elektrona da bi postiglo elektronsku konfiguraciju argona ili da primi 10 elektrona da bi postiglo elektronsku konfiguraciju kriptona. To je nemoguće jer najčešće srećemo katjone koji su 1+, 2+ i 3+ i anjone koji su 1-, 2- i 3-.
10 Joni prelaznih metala Veoma važno pravilo kod odreñivanja elektronske konfiguracije jona prelaznh metala: kada se stvara katjon uvek se elektron uzima iz onog podnivoa koji ima veći glavni kvantni broj n Tako će kod gvožña prvo se jonizovati 4s elektroni pa tek onda 3d elektroni. Inače gvožñe gradi stabilne 2+ i 3+ katjone Fe: [Ar]3d 6 4s 2 Fe 2+ : [Ar]3d 6 Fe 3+ : [Ar]3d 5
11 Kovalentna veza Mnogo više ima jedinjenja sa kovalentnom nego sa jonskom vezom. Dok su jonska jedinjenja uglavnom čvrste supstance velike tačke topljenja kovalentna jedinjenja su mnogo raznovrsnija Luis je zaključio da atomi ne moraju da otpuštaju ili primaju elektrone da bi postigli elektronsku konfiguraciju plemenitog gasa već da mogu i dele elektrone. Na primer, vodonik ima jedan elektron u 1s orbitali. Najbliži plemeniti gas je helijum sa dva elektrona u 1s orbitali. Znači, dva atoma vodonika mogu da udruže svoje elektrone i postignu elektronsku konfiguraciju helijuma
12 Kovalentna veza Nastajanje kovalentne veze sve sile koje učestvuju: Privlačenje izmeñu jezgra jednog atoma i elektrona drugog atoma Odbijanje izmeñu elektrona dva atoma Odbijanje izmeñu jezgara dva atoma
13 Kovalentna veza Kvantno mehanički proračuni na H 2 molekulu su pokazali da dolazi do nagomilavanja elektronske gustine izmeñu dva jezgra. Znači molekul H 2 postoji zato što su dva jezgra elektrostatički privučena za koncentrovano negativno naelektrisanje (elektrone) izmeñu njih. Zajednički elektronski par ustvari deluje kao lepak koji drži jezgra zajedno
14 Kovalentna veza Prikazivanje kovalentne veze Luisovim simbolima Zajednički elektronski par se u Luisovim strukturama obično predstavlja crticom Kiseoniku trebaju 2 elektrona da bi dobio elektronsku konfiguraciju neona pa će se jedinita sa dva atoma vodonika, azotu trebaju 3 elektrona, ugljeniku 4...
15 Kovalentna veza višestruke veze Kovalentna veza izmeñu dva atoma koji dele jedan zajednički elektronski par se zove prosta kovalentna veza ili samo prosta veza koja se predstavlja jednom crticom Kada dva atoma dele dva elektronska para tada nastaje dvostruka veza koja se predstavlja sa dve crtice Ukoliko atomi dele tri elektronska para tada nastaje trostruka veza
16 Kovalentna veza višestruke veze Pravilo: Dvostruka veza je uvek jača i kraća od proste veze a trostruka je jača i kraća i od dvostruke i od proste!!!
17 Polarnost kovalentne veze Postoje dve vrste kovalentne veze po polarnosti: Polarna kovalentna veza Nepolarna kovalentna veza Nepolarna kovalentna veza nastaje izmeñu atoma istog elementa. U H 2 molekulu oba atoma podjednako dele zajednički elektronski par Polarna kovalentna veza nastaje izmeñu atoma različitih elemenata. Tu jedan atom jače privlači zajednički elektronski par nego drugi atom. Zbog toga su elektroni pomereni ka atomu koji ih jače privlači i on postaje delom negativno naelektrisan dok atom koji slabije privlači elektrone postaje delom pozitivno naelektrisan. Jonska veza se može posmatrati kao drastični primer polarne kovalentne veze gde su oba elektrona iz para kompletno prešla na atom koji ih jače privlači
18 Elektronegativnost - Polarnost kovalentne veze Kako mi da znamo koji atom jače privlači elektrone? Usvojen je pojam elektronegativnosti koji se definiše kao: Elektronegativnost je sposobnost atoma da u molekulu privuče elektronski par Što je veća elektronegativnost atoma to će jače privlačiti zajednički elektronski par. Mulliken je odredio elektronegativnost atoma svakog elementa na osnovu energije jonizacije i afiniteta prema elektronu χ = I 1 + EA 2
19 Elektronegativnost - Polarnost kovalentne veze χ = I 1 + EA 2 Jonizaciona energija nam govori koliko dati atom čvrsto drži svoje elektrone Afinitet prema elektronu nam govori koliko dati atom želi da privuče druge elektrone Danas se koristi Poulingova skala elektronegativnosti koja se zasniva na merenju energije disocijacije veza Uzeto je da je elektronegativnost fluora (najelektronegativnijeg elementa) 4,0 a cezijuma (najmanje elektronegativnog) 0,7
20 Elektronegativnost - Polarnost kovalentne veze Paulingova skala elektronegativnosti
21 Elektronegativnost - Polarnost kovalentne veze Paulingova skala elektronegativnosti Vrednost elektronegativnosti raste po periodi a opada u grupi
22 Elektronegativnost - Polarnost kovalentne veze Sada kada znamo pojam elektronegativnosti možemo na osnovu razlika elektronegativnosti da odredimo koja će veza biti polarna a koja nepolarna Npr. Jedinjenje F 2 HF LiF Razlika 4,0-4,0= 0 4,0 2.1 = 1,9 4,0 1,0 = 3,0 elektroneg. Tip veze nepolarna polarna jonska U jedinjenju HF je polarna veza jer je zajednički elektronski par pomeren ka atomu fluora tj. elektronska gustina oko elektronegativnijeg fluora je veća.
23 Elektronegativnost - Polarnost kovalentne veze Zbog toga će u delu prostora oko fluora biti višak elektrona i to će biti negativno naelektrisani deo molekula HF. U delu oko atoma vodonika će biti manjak elektrona i to će biti pozitivno naelektrisani deo molekula HF Ovakva raspodela naelektrisanja se predstavlja kao: Gde simboli δ+ i δ- predstavljaju parcijalno pozitivna i parcijalno negativna naelektrisanja.
24 Elektronegativnost - Polarnost kovalentne veze Ovo je potvrñeno i kvantno mehaničkim proračunima. Kada se izračuna raspodela elektronske gustine za molekle F 2, HF i HLi dobijaju se sledeće slike: Plavom bojom su obeleženi regioni sa malom elektronskom gustinom a crvenom oni sa velikom elektronskom gustinom
25 Elektronegativnost - Polarnost kovalentne veze Pošto molekul HF ima svoj pozitivan i negativan kraj za njega kažemo da je polaran molekul Polarnost molekula HF se može prikazati na dva načina: Polarnost je veoma važna osobina molekula i mnoge hemijske i fizičke osobine molekula zavise od njihove polarnosti Ali da li postoji skala polarnosti, da li su neki molekuli polarniji od drugih? Kako se može kvantitativno izraziti polarnost?
26 Elektronegativnost - Polarnost kovalentne veze Diplolni momenat je mera za kvantitativno izražavanje polarnosti nekog molekula. Svaki polarni molekul ima i svoj dipolni momenat (µ) Kada se dva jednaka i suprotna naelektrisanja Q nalaze na nekom rastojanju r tada je veličina diplonog momenta takvog sistema data sa: µ= Qr Dipolni momenat je vektorska veličina Jedinica za diploni momenat je kulon-metar (Cm) a češće se izražava u Debajima (D). Jedan Debaj iznosi 3,34 x kulon-metara
27 Elektronegativnost - Polarnost kovalentne veze Dipolni momenat i razlika elektronegativnosti Što je veća razlika elektronegatvnosti izmeñu atoma koji čine dvoatomni molekul to će i dipolni momenat tog molekula biti veći
28 Elektronegativnost - Polarnost kovalentne veze Dipolni momenat kod višeatomskih molekula veoma zavisi od geometrije molekula. CO 2 uprkos velikoj razlici u elektronegativnosti izmeñu C (2,5) i O (3,5) nema dipolni momenat jer je linearan molekul i vektorski zbir dipola C=O veza je nula Voda koja nije linearan molekul ima veoma veliki dipolni momenat
29 Elektronegativnost - Polarnost kovalentne veze Slično je i za metan (CH 4 ). Kada se odreñuje ukupni dipolni momenat celog molekula moraju se vektorski sabrati dipoli svih veza koje čine molekul
30 Formalna naelektrisanja Prilikom pisanja Luisovih formula često možemo napisati više od jedne moguće strukture. Odreñivanje koja je struktura najverovatnija se može uraditi i pomoću formalnih naelektrisanja atoma. Prilikom odreñivanja formalnih naelektrisanja: 1. Prvo se napiše Luisova formula molekula 2. Svi nedeljeni (nevezivni) elektroni se pripišu atomu na kome se nalaze 3. Vezivni elektroni se dodeljuju po jedan svakom atomu u vezi 4. Formalno naelektrisanje je jednako broju valentnih elektrona u izolovanom atomu, minus broj elektrona koji su dodeljeni tom atomu na osnovu Luisove strukture
31 Formalna naelektrisanja Primer: Odrediti formalna naelektrisanja C i N atoma u CN - jonu Na atomu C imamo 2 nevezivna elektrona i na atomu N imamo 2 nevezivna elektrona 3. Imamo 3 vezivna elektronska para izmeñu atoma C i N. Ukupno 6 vezivnih elektrona, od toga 3 dajemo atomu C a 3 atomu N 4. C ima 4 valentna elektona pa mu je formalno naelektrisanje 4 (2+3)= -1. N ima 5 valentnih elektrona pa mu je formalno naelektrisanje 5-(2+3) = 0. Tako da su formalna naelektrisanja u CN - jonu:
32 Formalna naelektrisanja Za molekul CO 2 možemo napisati dve Luisove formule Stabilnija i verovatnija će biti prva struktura jer su u njoj formalna naelektrisanja bliža nuli. Kada imamo dve ili više Luisove strukture za isti molekul verovatnija će biti ona kod koje su: (1)formalna naelektrisanja svih atoma što bliža nuli (2)sva negativna naelektrisanja se nalaze na elektronegatvnim atomima
33 Rezonantne strukture Za molekul ozona O 3 možemo napisati dve Luisove formule koje se u suštini ne razlikuju. Ovakve strukture koje se razlikuju samo po načinju smeštanja elektrona se zovu rezonantne strukture Meñutim precizna merenja su pokazala da u ozonu ne postoji jedna prosta i jedna dvostruka veza već da su obe veze po dužini i energiji negde izmeñu proste i dvostruke. Znači ozon se nalazi negde izmeñu ove dve strukture (ne prelazi iz jedne u drugu već je upravo njihova mešavina kao kad pomešamo plavu i žutu boju pa dobijemo zelenu zelena nije čas plava čas žuta već je zelena). Ipak struktura ozona se pravilno prikazuje:
34 Rezonantne strukture Ovo znači da je prava struktura ozona izmeñu ove dve rezonantne strukture NO 3- anjon ima tri rezonantne strukture
35 Izuzeci od pravila okteta Već smo videli da pravilo okteta ne važi za jone prelaznih metala. Ima još izuzetaka od pravila okteta: 1. Molekuli sa neparnim brojem valentnih elektrona 2. Molekuli u kojima jedan atom ima manje od osam elektrona 3. Molekuli u kojima jedan atom ima više od osam elektrona
36 Izuzeci od pravila okteta 1. Molekuli sa neparnim brojem valentnih elektrona Najpoznatiji primeri molekula sa neparnim brojem elektrona su ClO 2, NO i NO 2 Kod ovih molekula je nemoguće izvršiti sparivanje elektrona i jedan atom uvek ostaje bez okteta. NO ima 11 valentnih elektrona i njegove Luisove formule su: Ovakvi molekuli često podležu dimerizaciji da bi dostigli stabilnu elektronsku konfiguraciju 2NO 2 N 2 O 4
37 Izuzeci od pravila okteta 2. Molekuli u kojima jedan atom ima manje od osam elektrona Ovakav slučaj odstupanja od pravila okteta se najčešće javlja kod jedinjenja bora i berilijuma. BF 3 Meñutim možemo napisati i ovakve Luisove strukture gde je zadovoljeno pravilo okteta za sve atome ali se formalno pozitivno naelektrisanje nalazi na atomu fluora (najelektronegativniji atom) pa su ove strukture malo verovatne
38 Izuzeci od pravila okteta 2. Molekuli u kojima jedan atom ima manje od osam elektrona Ovi molekuli su Luisove kiseline jer na centralnom atomu postoji jedna prazna valentna orbitala. Oni će reagovati sa Luisovim bazama koje imaju na centralnom atomu jedan nevezivni elektronski par dajući soli. U solima svi atomi imaju pun oktet
39 Izuzeci od pravila okteta 3. Molekuli u kojima jedan atom ima više od osam elektrona Najčešći tip odstupanja od pravila okteta. Primer PCl 5 Ovde oko atoma fosfora imamo 10 elektrona. Toliko elektrona ne može da stane u 3s i 3p orbitale fosfora. Moramo proširiti valentnu ljusku fosfora sa (praznim) 3d orbitalama koje su sledeće po energiji. Ostali primer ovog narušavanja pravila okteta su SF 4, AsF 6-, ICl 4 - Naravno odgovarajuća analogna jedinjenja sa centralnim atomom iz druge periode kao što su NF 5 ili OF 4 ne postoje. Zašto?
Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze:
 Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze: Jonska, Kovalentna i Metalna Luisovi simboli veoma zgodan
Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze: Jonska, Kovalentna i Metalna Luisovi simboli veoma zgodan
Pri međusobnom spajanju atoma nastaje energetski stabilniji sistem. To se postiže:
 HEMIJSKE VEZE Pri međusobnom spajanju atoma nastaje energetski stabilniji sistem. To se postiže: - prelaskom atoma u pozitivno i negativno naelektrisane jone koji se međusobno privlače, jonska veza - sparivanjem
HEMIJSKE VEZE Pri međusobnom spajanju atoma nastaje energetski stabilniji sistem. To se postiže: - prelaskom atoma u pozitivno i negativno naelektrisane jone koji se međusobno privlače, jonska veza - sparivanjem
SEKUNDARNE VEZE međumolekulske veze
 PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
HEMIJSKA VEZA ŠTA DRŽI STVARI (ATOME) ZAJEDNO?
 HEMIJSKA VEZA ŠTA DRŽI STVARI (ATOME) ZAJEDNO? U OKVIRU OVOG POGLAVLJA ĆEMO RADITI Jonska i kovalentna veza. Metalna veza. Elektronska teorija hemijske veze. Struktura molekula. Međumolekulske interakcije.
HEMIJSKA VEZA ŠTA DRŽI STVARI (ATOME) ZAJEDNO? U OKVIRU OVOG POGLAVLJA ĆEMO RADITI Jonska i kovalentna veza. Metalna veza. Elektronska teorija hemijske veze. Struktura molekula. Međumolekulske interakcije.
HEMIJSKA VEZA TEORIJA VALENTNE VEZE
 TEORIJA VALENTNE VEZE Kovalentna veza nastaje preklapanjem atomskih orbitala valentnih elektrona, pri čemu je region preklapanja između dva jezgra okupiran parom elektrona. - Nastalu kovalentnu vezu opisuje
TEORIJA VALENTNE VEZE Kovalentna veza nastaje preklapanjem atomskih orbitala valentnih elektrona, pri čemu je region preklapanja između dva jezgra okupiran parom elektrona. - Nastalu kovalentnu vezu opisuje
U stvaranju hemijske veze među atomima učestvuju samo elektroni u najvišem energetskom nivou valentni elektroni
 HEMIJSKA VEZA ELEKTRONSKA TEORIJA VALENCE U stvaranju hemijske veze među atomima učestvuju samo elektroni u najvišem energetskom nivou valentni elektroni Atomi teže da postignu oktet elektrona na poslednjem
HEMIJSKA VEZA ELEKTRONSKA TEORIJA VALENCE U stvaranju hemijske veze među atomima učestvuju samo elektroni u najvišem energetskom nivou valentni elektroni Atomi teže da postignu oktet elektrona na poslednjem
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
1. razred gimnazije- opšti i prirodno-matematički smer STRUKTURA MOLEKULA HEMIJSKA VEZA
 EMIJSKE VEZE 1 razred gimnazije- opšti i prirodno-matematički smer STRUKTURA MLEKULA Molekul je najsitnija čestica koja se sastoji od dva ili više istih atoma, a to su molekuli elemenata: Cl 2, 2, N 2,
EMIJSKE VEZE 1 razred gimnazije- opšti i prirodno-matematički smer STRUKTURA MLEKULA Molekul je najsitnija čestica koja se sastoji od dva ili više istih atoma, a to su molekuli elemenata: Cl 2, 2, N 2,
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
JONSKA VEZA (metal-nemetal) KOVALENTNA VEZA (nemetal-nemetal) METALNA VEZA (metal-metal) jake H N. prelazne VODONIČNA VEZA H F
 HEMIJSKE VEZE HEMIJSKE VEZE I GRAĐA JEDINJENJA,, I deo Postoje tri osnovna tipa veza (primarne veze) i one imaju najveći uticaj na svojstva jedinjenja. Pored njih postoje i dopunske (sekundarne) veze između
HEMIJSKE VEZE HEMIJSKE VEZE I GRAĐA JEDINJENJA,, I deo Postoje tri osnovna tipa veza (primarne veze) i one imaju najveći uticaj na svojstva jedinjenja. Pored njih postoje i dopunske (sekundarne) veze između
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
n (glavni ) 1, 2, 3,.. veličina orbitale i njena energija E= -R(1/n 2 )
 Kvantni brojevi Jedna atomska orbitala je definisana sa tri kvantna broja n l m l Elektroni su rasporedjeni u nivoima i podnivoima n l definiše nivo definiše podnivo ukupni broj orbitala u podnivou: 2
Kvantni brojevi Jedna atomska orbitala je definisana sa tri kvantna broja n l m l Elektroni su rasporedjeni u nivoima i podnivoima n l definiše nivo definiše podnivo ukupni broj orbitala u podnivou: 2
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
I HEMIJSKI ZAKONI I STRUKTURA SUPSTANCI
 dr Ljiljana Vojinović-Ješić I HEMIJSKI ZAKONI I STRUKTURA SUPSTANCI ZAKON STALNIH MASENIH ODNOSA (I stehiometrijski zakon, Prust, 1799) Maseni odnos elemenata u datom jedinjenju je stalan, bez obzira na
dr Ljiljana Vojinović-Ješić I HEMIJSKI ZAKONI I STRUKTURA SUPSTANCI ZAKON STALNIH MASENIH ODNOSA (I stehiometrijski zakon, Prust, 1799) Maseni odnos elemenata u datom jedinjenju je stalan, bez obzira na
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne
 Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne metode (rentgenska kristalografija, NMR spektroskopija...)
Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne metode (rentgenska kristalografija, NMR spektroskopija...)
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
5. Karakteristične funkcije
 5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
3. razred gimnazije- opšti i prirodno-matematički smer ALKENI. Aciklični nezasićeni ugljovodonici koji imaju jednu dvostruku vezu.
 ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne
 Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne metode (rentgenska kristalografija, NMR spektroskopija...)
Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne metode (rentgenska kristalografija, NMR spektroskopija...)
MEĐUMOLEKULSKE SILE JON-DIPOL DIPOL VODONIČNE NE VEZE DIPOL DIPOL-DIPOL DIPOL-INDUKOVANI INDUKOVANI JON-INDUKOVANI DISPERZNE SILE
 MEĐUMLEKULSKE SILE JN-DIPL VDNIČNE NE VEZE DIPL-DIPL JN-INDUKVANI DIPL DIPL-INDUKVANI INDUKVANI DIPL DISPERZNE SILE MEĐUMLEKULSKE SILE jake JNSKA VEZA (metal-nemetal) KVALENTNA VEZA (nemetal-nemetal) METALNA
MEĐUMLEKULSKE SILE JN-DIPL VDNIČNE NE VEZE DIPL-DIPL JN-INDUKVANI DIPL DIPL-INDUKVANI INDUKVANI DIPL DISPERZNE SILE MEĐUMLEKULSKE SILE jake JNSKA VEZA (metal-nemetal) KVALENTNA VEZA (nemetal-nemetal) METALNA
Kovalentna veza , CO 2. U molekulima H 2
 Kovalentna veza U molekulima H 2, N 2, O 2, CO 2, NH 3, H 2 O,... ili molekulima organskih jedinjenja ne postoje joni. To je veza između atoma i ona se bitno razlikuje od jonske veze a naziva se kovalentnom
Kovalentna veza U molekulima H 2, N 2, O 2, CO 2, NH 3, H 2 O,... ili molekulima organskih jedinjenja ne postoje joni. To je veza između atoma i ona se bitno razlikuje od jonske veze a naziva se kovalentnom
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
 TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
Teorijske osnove informatike 1
 Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
SISTEMI NELINEARNIH JEDNAČINA
 SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
ASIMPTOTE FUNKCIJA. Dakle: Asimptota je prava kojoj se funkcija približava u beskonačno dalekoj tački. Postoje tri vrste asimptota:
 ASIMPTOTE FUNKCIJA Naš savet je da najpre dobro proučite granične vrednosti funkcija Neki profesori vole da asimptote funkcija ispituju kao ponašanje funkcije na krajevima oblasti definisanosti, pa kako
ASIMPTOTE FUNKCIJA Naš savet je da najpre dobro proučite granične vrednosti funkcija Neki profesori vole da asimptote funkcija ispituju kao ponašanje funkcije na krajevima oblasti definisanosti, pa kako
S t r a n a 1. 1.Povezati jonsku jačinu rastvora: a) MgCl 2 b) Al 2 (SO 4 ) 3 sa njihovim molalitetima, m. za so tipa: M p X q. pa je jonska jačina:
 S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
NOMENKLATURA ORGANSKIH SPOJEVA. Imenovanje aromatskih ugljikovodika
 NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
2log. se zove numerus (logaritmand), je osnova (baza) log. log. log =
 ( > 0, 0)!" # > 0 je najčešći uslov koji postavljamo a još je,, > 0 se zove numerus (aritmand), je osnova (baza). 0.. ( ) +... 7.. 8. Za prelazak na neku novu bazu c: 9. Ako je baza (osnova) 0 takvi se
( > 0, 0)!" # > 0 je najčešći uslov koji postavljamo a još je,, > 0 se zove numerus (aritmand), je osnova (baza). 0.. ( ) +... 7.. 8. Za prelazak na neku novu bazu c: 9. Ako je baza (osnova) 0 takvi se
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Verovatnoća i Statistika I deo Teorija verovatnoće (zadaci) Beleške dr Bobana Marinkovića
 Verovatnoća i Statistika I deo Teorija verovatnoće zadaci Beleške dr Bobana Marinkovića Iz skupa, 2,, 00} bira se na slučajan način 5 brojeva Odrediti skup elementarnih dogadjaja ako se brojevi biraju
Verovatnoća i Statistika I deo Teorija verovatnoće zadaci Beleške dr Bobana Marinkovića Iz skupa, 2,, 00} bira se na slučajan način 5 brojeva Odrediti skup elementarnih dogadjaja ako se brojevi biraju
Elektronska struktura atoma
 Elektronska struktura atoma Raderfordov atomski model jezgro u sredini pozitivno naelektrisano skoro sva masa u jezgru veoma malo Elektroni kruže oko jezgra elektrostatičke interakcije ih drže da ne napuste
Elektronska struktura atoma Raderfordov atomski model jezgro u sredini pozitivno naelektrisano skoro sva masa u jezgru veoma malo Elektroni kruže oko jezgra elektrostatičke interakcije ih drže da ne napuste
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo Najpre da se podsetimo tablice i osnovnih pravila:. C0.. (. ( n n n-. (a a lna 6. (e e 7. (log a 8. (ln ln a (>0 9. ( 0 0. (>0 (ovde je >0 i a >0. (cos. (cos - π. (tg kπ cos. (ctg
IZVODI ZADACI (I deo Najpre da se podsetimo tablice i osnovnih pravila:. C0.. (. ( n n n-. (a a lna 6. (e e 7. (log a 8. (ln ln a (>0 9. ( 0 0. (>0 (ovde je >0 i a >0. (cos. (cos - π. (tg kπ cos. (ctg
Osnovne veličine, jedinice i izračunavanja u hemiji
 Osnovne veličine, jedinice i izračunavanja u hemiji Pregled pojmova veličina i njihovih jedinica koje se koriste pri osnovnim izračunavanjima u hemiji dat je u Tabeli 1. Tabela 1. Veličine i njihove jedinice
Osnovne veličine, jedinice i izračunavanja u hemiji Pregled pojmova veličina i njihovih jedinica koje se koriste pri osnovnim izračunavanjima u hemiji dat je u Tabeli 1. Tabela 1. Veličine i njihove jedinice
Skup svih mogućih ishoda datog opita, odnosno skup svih elementarnih događaja se najčešće obeležava sa E. = {,,,... }
 VEROVTNOĆ - ZDI (I DEO) U računu verovatnoće osnovni pojmovi su opit i događaj. Svaki opit se završava nekim ishodom koji se naziva elementarni događaj. Elementarne događaje profesori različito obeležavaju,
VEROVTNOĆ - ZDI (I DEO) U računu verovatnoće osnovni pojmovi su opit i događaj. Svaki opit se završava nekim ishodom koji se naziva elementarni događaj. Elementarne događaje profesori različito obeležavaju,
Ispitna pitanja iz Osnova hemije
 I grupa pitanja Ispitna pitanja iz Osnova hemije 1. Hijerarhija materijala, smeše, metode razdvajanja smeša Materija: supstance i energija (polje). Supstance se dele na homogene i heterogene supstance.
I grupa pitanja Ispitna pitanja iz Osnova hemije 1. Hijerarhija materijala, smeše, metode razdvajanja smeša Materija: supstance i energija (polje). Supstance se dele na homogene i heterogene supstance.
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
KVADRATNA FUNKCIJA. Kvadratna funkcija je oblika: Kriva u ravni koja predstavlja grafik funkcije y = ax + bx + c. je parabola.
 KVADRATNA FUNKCIJA Kvadratna funkcija je oblika: = a + b + c Gde je R, a 0 i a, b i c su realni brojevi. Kriva u ravni koja predstavlja grafik funkcije = a + b + c je parabola. Najpre ćemo naučiti kako
KVADRATNA FUNKCIJA Kvadratna funkcija je oblika: = a + b + c Gde je R, a 0 i a, b i c su realni brojevi. Kriva u ravni koja predstavlja grafik funkcije = a + b + c je parabola. Najpre ćemo naučiti kako
Osnovne teoreme diferencijalnog računa
 Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
Zavrxni ispit iz Matematiqke analize 1
 Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
XI dvoqas veжbi dr Vladimir Balti. 4. Stabla
 XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
 Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI)
 IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
1s 2 2s 2 2p 2. C-atom. Hibridne atomske orbitale. sp 3 hibridizacija. sp 3. Elektronska konfiguracija ugljenika: aktivacija. ekscitovano stanje
 PREAVAJE 2. Ugljenik je u organskim jedinjenjima četvorovalentan. Elektronska konfiguracija ugljenika: 1s 2 2 2p 2 dva nesparena elektrona -atom oc.dr Mirjana Abramović 2p osnovno stanje aktivacija 2p
PREAVAJE 2. Ugljenik je u organskim jedinjenjima četvorovalentan. Elektronska konfiguracija ugljenika: 1s 2 2 2p 2 dva nesparena elektrona -atom oc.dr Mirjana Abramović 2p osnovno stanje aktivacija 2p
Elektronska struktura atoma
 Elektronska struktura atoma Raderfordov atomski model jezgro u sredini pozitivno naelektrisano skoro sva masa jezgru veoma malo Elektroni kruže oko jezgra elektrostatičke interakcije ih drže da ne napuste
Elektronska struktura atoma Raderfordov atomski model jezgro u sredini pozitivno naelektrisano skoro sva masa jezgru veoma malo Elektroni kruže oko jezgra elektrostatičke interakcije ih drže da ne napuste
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f
 IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Ovo nam govori da funkcija nije ni parna ni neparna, odnosno da nije simetrična ni u odnosu na y osu ni u odnosu na
 . Ispitati tok i skicirati grafik funkcij = Oblast dfinisanosti (domn) Ova funkcija j svuda dfinisana, jr nma razlomka a funkcija j dfinisana za svako iz skupa R. Dakl (, ). Ovo nam odmah govori da funkcija
. Ispitati tok i skicirati grafik funkcij = Oblast dfinisanosti (domn) Ova funkcija j svuda dfinisana, jr nma razlomka a funkcija j dfinisana za svako iz skupa R. Dakl (, ). Ovo nam odmah govori da funkcija
PID: Domen P je glavnoidealski [PID] akko svaki ideal u P je glavni (generisan jednim elementom; oblika ap := {ab b P }, za neko a P ).
![PID: Domen P je glavnoidealski [PID] akko svaki ideal u P je glavni (generisan jednim elementom; oblika ap := {ab b P }, za neko a P ). PID: Domen P je glavnoidealski [PID] akko svaki ideal u P je glavni (generisan jednim elementom; oblika ap := {ab b P }, za neko a P ).](/thumbs/74/70316766.jpg) 0.1 Faktorizacija: ID, ED, PID, ND, FD, UFD Definicija. Najava pojmova: [ID], [ED], [PID], [ND], [FD] i [UFD]. ID: Komutativan prsten P, sa jedinicom 1 0, je integralni domen [ID] oblast celih), ili samo
0.1 Faktorizacija: ID, ED, PID, ND, FD, UFD Definicija. Najava pojmova: [ID], [ED], [PID], [ND], [FD] i [UFD]. ID: Komutativan prsten P, sa jedinicom 1 0, je integralni domen [ID] oblast celih), ili samo
PERIODNI SISTEM ELEMENATA
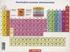 PERIODNI SISTEM ELEMENATA 1/43 PERIODNI SISTEM ELEMENATA - Kratka istorija Otkriće elemenata do danas otktiveno još 11 elemenata 2011. IUPAC potvrdio otkriće 2 nova elementa: Flerovijum (Fl, Z = 114) i
PERIODNI SISTEM ELEMENATA 1/43 PERIODNI SISTEM ELEMENATA - Kratka istorija Otkriće elemenata do danas otktiveno još 11 elemenata 2011. IUPAC potvrdio otkriće 2 nova elementa: Flerovijum (Fl, Z = 114) i
Trigonometrijske nejednačine
 Trignmetrijske nejednačine T su nejednačine kd kjih se nepznata javlja ka argument trignmetrijske funkcije. Rešiti trignmetrijsku nejednačinu znači naći sve uglve kji je zadvljavaju. Prilikm traženja rešenja
Trignmetrijske nejednačine T su nejednačine kd kjih se nepznata javlja ka argument trignmetrijske funkcije. Rešiti trignmetrijsku nejednačinu znači naći sve uglve kji je zadvljavaju. Prilikm traženja rešenja
RAČUNSKE VEŽBE IZ PREDMETA POLUPROVODNIČKE KOMPONENTE (IV semestar modul EKM) IV deo. Miloš Marjanović
 Univerzitet u Nišu Elektronski fakultet RAČUNSKE VEŽBE IZ PREDMETA (IV semestar modul EKM) IV deo Miloš Marjanović MOSFET TRANZISTORI ZADATAK 35. NMOS tranzistor ima napon praga V T =2V i kroz njega protiče
Univerzitet u Nišu Elektronski fakultet RAČUNSKE VEŽBE IZ PREDMETA (IV semestar modul EKM) IV deo Miloš Marjanović MOSFET TRANZISTORI ZADATAK 35. NMOS tranzistor ima napon praga V T =2V i kroz njega protiče
7 Algebarske jednadžbe
 7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
Linearna algebra 2 prvi kolokvij,
 1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
Dvanaesti praktikum iz Analize 1
 Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
1 Promjena baze vektora
 Promjena baze vektora Neka su dane dvije različite uredene baze u R n, označimo ih s A = (a, a,, a n i B = (b, b,, b n Svaki vektor v R n ima medusobno različite koordinatne zapise u bazama A i B Zapis
Promjena baze vektora Neka su dane dvije različite uredene baze u R n, označimo ih s A = (a, a,, a n i B = (b, b,, b n Svaki vektor v R n ima medusobno različite koordinatne zapise u bazama A i B Zapis
SKUPOVI I SKUPOVNE OPERACIJE
 SKUPOVI I SKUPOVNE OPERACIJE Ne postoji precizna definicija skupa (postoji ali nama nije zanimljiva u ovom trenutku), ali mi možemo koristiti jednu definiciju koja će nam donekle dočarati šta su zapravo
SKUPOVI I SKUPOVNE OPERACIJE Ne postoji precizna definicija skupa (postoji ali nama nije zanimljiva u ovom trenutku), ali mi možemo koristiti jednu definiciju koja će nam donekle dočarati šta su zapravo
INTEGRALNI RAČUN. Teorije, metodike i povijest infinitezimalnih računa. Lucija Mijić 17. veljače 2011.
 INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
OBRTNA TELA. Vladimir Marinkov OBRTNA TELA VALJAK
 OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Matematička analiza 1 dodatni zadaci
 Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
4.7. Zadaci Formalizam diferenciranja (teorija na stranama ) 343. Znajući izvod funkcije x arctg x, odrediti izvod funkcije x arcctg x.
 4.7. ZADACI 87 4.7. Zadaci 4.7.. Formalizam diferenciranja teorija na stranama 4-46) 340. Znajući izvod funkcije arcsin, odrediti izvod funkcije arccos. Rešenje. Polazeći od jednakosti arcsin + arccos
4.7. ZADACI 87 4.7. Zadaci 4.7.. Formalizam diferenciranja teorija na stranama 4-46) 340. Znajući izvod funkcije arcsin, odrediti izvod funkcije arccos. Rešenje. Polazeći od jednakosti arcsin + arccos
a M a A. Može se pokazati da je supremum (ako postoji) jedinstven pa uvodimo oznaku sup A.
 3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
radni nerecenzirani materijal za predavanja R(f) = {f(x) x D}
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
VJEŽBE 3 BIPOLARNI TRANZISTORI. Slika 1. Postoje npn i pnp bipolarni tranziostori i njihovi simboli su dati na slici 2 i to npn lijevo i pnp desno.
 JŽ 3 POLAN TANZSTO ipolarni tranzistor se sastoji od dva pn spoja kod kojih je jedna oblast zajednička za oba i naziva se baza, slika 1 Slika 1 ipolarni tranzistor ima 3 izvoda: emitor (), kolektor (K)
JŽ 3 POLAN TANZSTO ipolarni tranzistor se sastoji od dva pn spoja kod kojih je jedna oblast zajednička za oba i naziva se baza, slika 1 Slika 1 ipolarni tranzistor ima 3 izvoda: emitor (), kolektor (K)
RIJEŠENI ZADACI I TEORIJA IZ
 RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
Kiselo bazni indikatori
 Kiselo bazni indikatori Slabe kiseline ili baze koje imaju različite boje nejonizovanog i jonizovanog oblika u rastvoru Primer: slaba kiselina HIn(aq) H + (aq) + In (aq) nejonizovani oblik jonizovani oblik
Kiselo bazni indikatori Slabe kiseline ili baze koje imaju različite boje nejonizovanog i jonizovanog oblika u rastvoru Primer: slaba kiselina HIn(aq) H + (aq) + In (aq) nejonizovani oblik jonizovani oblik
INTELIGENTNO UPRAVLJANJE
 INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
Deljivost. 1. Ispitati kada izraz (n 2) 3 + n 3 + (n + 2) 3,n N nije deljiv sa 18.
 Deljivost 1. Ispitati kada izraz (n 2) 3 + n 3 + (n + 2) 3,n N nije deljiv sa 18. Rešenje: Nazovimo naš izraz sa I.Važi 18 I 2 I 9 I pa možemo da posmatramo deljivost I sa 2 i 9.Iz oblika u kom je dat
Deljivost 1. Ispitati kada izraz (n 2) 3 + n 3 + (n + 2) 3,n N nije deljiv sa 18. Rešenje: Nazovimo naš izraz sa I.Važi 18 I 2 I 9 I pa možemo da posmatramo deljivost I sa 2 i 9.Iz oblika u kom je dat
( ) ( ) 2 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET. Zadaci za pripremu polaganja kvalifikacionog ispita iz Matematike. 1. Riješiti jednačine: 4
 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE GODINE 8. RAZRED TOČNI ODGOVORI
 21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
STRUKTURA ATOMA. Dalton (1803) Tomson (1904) Raderford (1911) Bor (1913) Šredinger (1926)
 Dalton (1803) Tomson (1904) Raderford (1911) Bor (1913) Šredinger (1926) TALASNO MEHANIČKI MODEL ATOMA Hipoteza de Brolja Elektroni i fotoni imaju dvojnu prirodu: talasnu i korpuskularnu. E = hν E = mc
Dalton (1803) Tomson (1904) Raderford (1911) Bor (1913) Šredinger (1926) TALASNO MEHANIČKI MODEL ATOMA Hipoteza de Brolja Elektroni i fotoni imaju dvojnu prirodu: talasnu i korpuskularnu. E = hν E = mc
Riješeni zadaci: Nizovi realnih brojeva
 Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
III VEŽBA: FURIJEOVI REDOVI
 III VEŽBA: URIJEOVI REDOVI 3.1. eorijska osnova Posmatrajmo neki vremenski kontinualan signal x(t) na intervalu definisati: t + t t. ada se može X [ k ] = 1 t + t x ( t ) e j 2 π kf t dt, gde je f = 1/.
III VEŽBA: URIJEOVI REDOVI 3.1. eorijska osnova Posmatrajmo neki vremenski kontinualan signal x(t) na intervalu definisati: t + t t. ada se može X [ k ] = 1 t + t x ( t ) e j 2 π kf t dt, gde je f = 1/.
Strukture podataka i algoritmi 1. kolokvij 16. studenog Zadatak 1
 Strukture podataka i algoritmi 1. kolokvij Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i službeni šalabahter. Predajete samo papire koje ste dobili. Rezultati i uvid u kolokvije: ponedjeljak,
Strukture podataka i algoritmi 1. kolokvij Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i službeni šalabahter. Predajete samo papire koje ste dobili. Rezultati i uvid u kolokvije: ponedjeljak,
APROKSIMACIJA FUNKCIJA
 APROKSIMACIJA FUNKCIJA Osnovni koncepti Gradimir V. Milovanović MF, Beograd, 14. mart 2011. APROKSIMACIJA FUNKCIJA p.1/46 Osnovni problem u TA Kako za datu funkciju f iz velikog prostora X naći jednostavnu
APROKSIMACIJA FUNKCIJA Osnovni koncepti Gradimir V. Milovanović MF, Beograd, 14. mart 2011. APROKSIMACIJA FUNKCIJA p.1/46 Osnovni problem u TA Kako za datu funkciju f iz velikog prostora X naći jednostavnu
Ĉetverokut - DOMAĆA ZADAĆA. Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke.
 Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
radni nerecenzirani materijal za predavanja
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Kažemo da je funkcija f : a, b R u točki x 0 a, b postiže lokalni minimum ako postoji okolina O(x 0 ) broja x 0 takva da je
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Kažemo da je funkcija f : a, b R u točki x 0 a, b postiže lokalni minimum ako postoji okolina O(x 0 ) broja x 0 takva da je
Reverzibilni procesi
 Reverzbln proces Reverzbln proces: proces pr koja sste nkada nje vše od beskonačno ale vrednost udaljen od ravnoteže, beskonačno ala proena spoljašnjh uslova ože vratt sste u blo koju tačku, proena ože
Reverzbln proces Reverzbln proces: proces pr koja sste nkada nje vše od beskonačno ale vrednost udaljen od ravnoteže, beskonačno ala proena spoljašnjh uslova ože vratt sste u blo koju tačku, proena ože
Teorija molekulskoi orbitala linearna kombinacija atomskih orbitala(lcao)
 Teorija molekulskoi orbitala linearna kombinacija atomskih orbitala(lcao) Kada je elektron u blizini jezgre jednog atoma onda njegova valna funkcija sliči atomskoj orbitali tog atoma. Zbrajanjem atomskih
Teorija molekulskoi orbitala linearna kombinacija atomskih orbitala(lcao) Kada je elektron u blizini jezgre jednog atoma onda njegova valna funkcija sliči atomskoj orbitali tog atoma. Zbrajanjem atomskih
Antene. Srednja snaga EM zračenja se dobija na osnovu intenziteta fluksa Pointingovog vektora kroz sferu. Gustina snage EM zračenja:
 Anene Transformacija EM alasa u elekrični signal i obrnuo Osnovne karakerisike anena su: dijagram zračenja, dobiak (Gain), radna učesanos, ulazna impedansa,, polarizacija, efikasnos, masa i veličina, opornos
Anene Transformacija EM alasa u elekrični signal i obrnuo Osnovne karakerisike anena su: dijagram zračenja, dobiak (Gain), radna učesanos, ulazna impedansa,, polarizacija, efikasnos, masa i veličina, opornos
