Übung 7 - Verfahren zur Lösung linearer Systeme, Gittereigenschaften
|
|
|
- Βακχος Ακρίδας
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Übung 7 - Verfahren zur Lösung linearer Systeme, Gittereigenschaften Musterlösung C. Baur, M. Schäfer Fachgebiet für Numerische Berechnungsverfahren im Maschinenbau TU Darmstadt FNB /31
2 Aufg.1 - LU Zerlegung Theorie Gegeben ist das lineares Gleichungssystem A φ = b? A = L U L/U - untere/obere Dreiecksmatrix LU - Zerlegung basiert auf Gauß - Elimination, Direktes Verfahren! Wenn LU - Zerlegung vorliegt, dann mit rekursiven Algorithmen! A φ = LU φ = b L y = b und U φ = y TU Darmstadt FNB /31
3 Aufg. 1 - Algorithmus A = a ij U mit Gauß-Elimination n n L = l ij n 1 Schritte, A 0 = A U = A n 1 a k ij a k ij = a k 1 ij, i k, 1 < j < n = a k 1 ij ak 1 ik a k kk n n U = u ij n n a k kj, i > k, 1 < j < n l ii = 1 l ij = 0, i < j l ij = u ji u ii, i > j 1 < i, j < n TU Darmstadt FNB /31
4 Aufg. 1 - Matrix A = a E a N a W a S a P Matrix A kommt z.b. aus einer FV Diskretisierung des Gebiets. TU Darmstadt FNB /31
5 Aufg. 1 - LU - Zerlegung U L TU Darmstadt FNB / = = 0
6 Aufg. 2 - Matrix 2 1 a S a W 4 3 a P a N φ 1 φ 2 φ 3 φ 4 = Matrix aus einer FV Diskretisierung des Gebiets. a i P φ i + nb a E a i nb φ nb = b i, i = 1,...,4 A φ = b A L + A D + A U φ = b TU Darmstadt FNB /31
7 Aufg. 2 - Iterative Verfahren A φ = b Bφ + A Bφ = b φ = B 1 b A B φ φ k+1 = = B 1 b + B 1 B A φ I B 1 A φ k + B 1 b Die Formel gilt für alle drei Iterationsverfahren! TU Darmstadt FNB /31
8 Aufg. 2 - Jacobi Verfahren, Allgemein φ k+1 i = 1 a i b i P nb = φ k i φ k i + 1 = φ k i + 1 a i P a i P a i nbφ k nb b i nb b i a i Pφ k i nb a i nb φk nb a i nbφ k nb in Matrix-Schreibweise φ k+1 = φ k + A 1 D b Aφ k = I A 1 D A φ k + A 1 D b für Jacobi-Verfahren: B = A D TU Darmstadt FNB /31
9 Aufg. 2 - Jacobi Verfahren k = 0 : φ k = 0 aus Startlösung φ k+1 1 = 1 a 1 b 1 a 1 N φk 2 a1 E φk 3 P φ k+1 2 = 1 a 2 P φ k+1 3 = 1 a 3 P φ k+1 4 = 1 a 4 P b 2 a 2 S φk 1 a2 E φk 4 b 3 a 3 W φk 1 a3 N φk 4 b 4 a 4 W φk 2 a4 S φk 3 TU Darmstadt FNB /31
10 Aufg. 2 - Jacobi Verfahren, Endergebnisse k φ 1 φ 2 φ 3 φ 4 Res ε = ε = TU Darmstadt FNB /31
11 Aufg. 2 - Gauß Seidel Verfahren, Allgemein φ k+1 i = 1 b i a i P in Matrix-Schreibweise nb=w,s a i nb φk+1 nb nb=n,e a i nb φk nb φ k+1 = A 1 D b A L φ k+1 A U φ k A D + A L φ k+1 = b A A D + A L }{{} φ k+1 = für Gauß-Seidel B = A D + A L! A U I A D + A L 1 A + A D + A L 1 b k φ φ k TU Darmstadt FNB /31
12 Aufg. 2 - Gauß Seidel Verfahren k = 0 : φ k = 0 aus Startlösung φ k+1 1 = 1 a 1 b 1 a 1 N φk 2 a1 E φk 3 P φ k+1 2 = 1 a 2 P φ k+1 3 = 1 a 3 P φ k+1 4 = 1 a 4 P b 2 a 2 S φk+1 1 a 2 E φk 4 b 3 a 3 W φk+1 1 a 3 N φk 4 b 4 a 4 W φk+1 2 a 4 S φk+1 3 TU Darmstadt FNB /31
13 Aufg. 2 - Gauß Seidel Verfahren, Endergebnisse k φ 1 φ 2 φ 3 φ 4 Res ε = ε = TU Darmstadt FNB /31
14 Aufg. 2 - SOR Verfahren wie Gauß-Seidel, aber mit Parameter ω φ k+1 i = φ k i + ω b i a i a i Pφ k i P in Matrix-Schreibweise φ k+1 = φ k + ωa 1 D nb=w,s a i nbφ k+1 nb nb=n,e a i nbφ k nb b A D φ k A L φ k+1 A U φ k 1 ω A Dφ k+1 = 1 ω A Dφ k + b A D φ k A L φ k+1 A U φ k 1 ω A D + A L φ k+1 = 1 ω A D A D A }{{ U } φ k + b A L A φ k+1 = I B 1 A φ k + B 1 b, mit B = 1 ω A D + A L TU Darmstadt FNB /31
15 Aufg. 2 - SOR Verfahren k = 0 : φ k = 0 aus Startlösung, wähle ω = 1.1 Φ 1 1 = ω a 1 P Φ 1 2 = ω a 2 P Φ 1 3 = ω a 3 P Φ 1 4 = ω a 4 P b 2 a 2 S Φ1 3 b 3 a 3 W Φ1 1 b 4 a 4 W Φ1 2 a4 S Φ1 3 Φ 1 1 = Φ1 2 = Φ 1 3 = Φ1 4 = TU Darmstadt FNB /31
16 Aufg. 2 - SOR Verfahren, Endergebnisse ω Iter für ε = TU Darmstadt FNB /31
17 Aufg. 3 - Matrix a S a P a W a N a E φ 1 φ 2 φ 3 φ 4 φ 5 φ 6 = Matrix aus einer FV Diskretisierung des Gebiets. TU Darmstadt FNB /31
18 Aufg. 3 - ILU Verfahren Zerlegung in LU mit L und U, dünn besetzt wie A. A LU Iterationsverfahren mit B = LU! LUφ LUφ + Aφ = b LUφ k+1 LUφ k = b Aφ k LU φ k = r k mit φ k = φ k+1 φ k und r k = b Aφ k TU Darmstadt FNB /31
19 Aufg. 3 - LU Approximation l 11 P l 12 S lp 12 ls 13 lp 13 lw 21 lp 21 lw 22 ls 22 lp 22 lw 23 ls 23 lp 23 A L U = 1 u 11 1 u 12 cp 11 cn 11 cse 11 ce 11 cs 12 cp 12 cn 12 cse 12 ce 12 cnw 13 c13 S cp 13 cn 13 cse 13 ce 13 cw 21 c21 NW c21 S cp 21 cn 21 cse 21 cw 22 c22 NW c22 S cp 22 cn 22 cw 23 c23 NW N ue 11 N ue 12 c23 S cp 23 1 ue 13 1 un 21 1 un 22 1 = C A = TU Darmstadt FNB /31
20 Aufg. 3 - LU Approximation Berechnung der Werte in Matrix C aus LU c ij W = lij W c ij NW = lij W ui 1,j N c ij S = l ij S c ij P = l ij P + lij W ui 1,j E + l ij S ui,j 1 N c ij N = u ij N lij P c ij SE = l ij S ui,j 1 E c ij E = u ij E lij P Wir wissen C = A + N, es muß Nφ 0 gelten, damit LUφ Aφ. TU Darmstadt FNB /31
21 Aufg. 3 - Ansatz von Stone Ausdrücken der Nachbarn SE und NW NW N φ SE = αφ E + φ S φ P W P E φ NW = αφ N + φ W φ P Verteilung der Anteile der zusätzlichen S SE Diagonalen auf die anderen! c W φ W + c NW α φ N + φ W φ P + c S φ S + c P φ P + c N φ N + c SE α φ E + φ S φ P + c E φ E = φ W c W + αc NW +φ }{{} S c S + αc SE +φ N c N + αc NW }{{}}{{} =a W =a S =a N + φ E c E + αc SE +φ P c P + α c NW + c SE A }{{}}{{} =a E =a P TU Darmstadt FNB /31
22 Aufg. 3 - ILU Koeffizientenvergleich l ij S = a ij W = cij W + αcij NW = lij W + αlij W ui 1,j N a ij S 1 + αu i,j 1 E l ij P = a ij P + α l ij W = l ij W ui 1,j N u ij N = aij N + αlij S ui,j 1 E l ij P u ij E = aij E + αlij S ui,j 1 E l ij P a ij W 1 + αu i 1,j N +l ij S ui,j 1 E l ij W ui 1,j E l ij S ui,j 1 N TU Darmstadt FNB /31
23 Aufg. 3 - LU Zerlegung mit α = 0.92 L = U = TU Darmstadt FNB /31
24 Aufg. 3 - ILU 1. Iteration k = 0 : φ k = 0 aus Startlösung 2 LU Φ 0 = b AΦ 0 = b = Vorwärts einsetzen: Ly 0 = r 0 Rückwärts einsetzen: U Φ 0 = y 0 2 y 0 = Φ 0 = TU Darmstadt FNB /31
25 Aufg. 3 - Konjugierte Gradienten Problem: Löse A φ = b Alternative Formulierung: Minima des F φ = 1 Aφ,φ b,φ, φ,ψ Skalarprodukt 2 φ,ψ = ψ,φ, φ 1 + φ 2,ψ = φ 1,ψ + φ 2,ψ αφ,ψ = αφ,ψ, φ,φ > 0 φ 0 Bedingung für Extrema: φ F φ A φ b = 0 TU Darmstadt FNB /31
26 Aufg. 3 - Konjugierte Gradienten Für symmetrische Aφ, ψ = φ, Aψ und positiv definite Aφ, φ > 0, φ 0 Matrix, sind beide Formulierungen äquivalent! F φ + φ F φ = b, φ b, φ F φ+ 1 Aφ, φ + Aφ, φ + A φ, φ + A φ, φ = 2 }{{} 2Aφ, φ F φ + Aφ b, φ + 1 A φ, φ F φ }{{} 2 =0 F φ + φ F φ = 1 A φ, φ > 0 2 TU Darmstadt FNB /31
27 Aufg. 3 - CG Iteratives Verfahren φ k+1 = φ k + α φ k φ k - Startlösung ; φ k - Suchrichtung ; α - Schrittlänge Für festes φ k und φ k, wird α berechnet aus α F φ k + α φ k = 0 [ F φ k + Aφ k b, α φ k + 1 Aα φ k, α φ k] = 0 α [ 2 F φ k + α Aφ k b, φ k + 1 α 2 α2 A φ k, φ k] = 0 Aφ k b, φ k + α A φ k, φ k = 0 r k, φ k α = A φ k, φ k mit r k = b Aφ k TU Darmstadt FNB /31
28 Aufg. 3 - CG Iteratives Verfahren Bestimmung von φ k : mit Rekursionsformel! r φ k+1 = r k+1 k+1, r k+1 + r k φk, r k damit ist sicher gestellt, daß A φ k+1, φ i für alle i = 1,...,k Vektoren φ i, i = 1,...,k + 1 sind konjugiert bezüglich A! TU Darmstadt FNB /31
29 Aufg. 3 - CG Algorithmus Initialisierung: r 0 = b Aφ k φ 0 = r 0 β 0 = r 0, r 0 Iteration: α k = β k A φ k, φ k φ k+1 = φ k + α k φ k r k+1 = r k α k A φ k β k+1 = r k+1, r k+1 φ k+1 = r k+1 + βk+1 β k φ k TU Darmstadt FNB /31
30 Aufg. 3 - CG 1. Iteration TU Darmstadt FNB /31 k = 0 : r 0 = b AΦ 0 = b = Φ 0 = r 0 β 0 = r 0 r 0 = 456 α 0 = β0 Φ 0 A Φ0 = = mit Φ 0 A Φ 0 = Φ =
31 Aufg. 3 - CG 1. Iteration Φ 1 = Φ 0 + α 0 Φ 0 = β 1 = r 1 r 1 = Φ 1 = r 1 + β1 β 0 Φ0 = r 1 = r 0 α 0 A Φ 0 = TU Darmstadt FNB /31
3 Lösungen zu Kapitel 3
 3 Lösungen zu Kapitel 3 31 Lösungen der Aufgaben zu Abschnitt 31 311 Lösung Die Abbildung D : { R 4 R 4 R 4 R 4 R, a 1, a 2, a 3, a 4 ) D( a 1, a 2, a 3, a 4 ) definiere eine Determinantenform (auf R 4
3 Lösungen zu Kapitel 3 31 Lösungen der Aufgaben zu Abschnitt 31 311 Lösung Die Abbildung D : { R 4 R 4 R 4 R 4 R, a 1, a 2, a 3, a 4 ) D( a 1, a 2, a 3, a 4 ) definiere eine Determinantenform (auf R 4
18. Normale Endomorphismen
 18. Normale Endomorphismen 18.1. Die adjungierte lineare Abbildung Seien V, W K-Vektorräume mit Skalarprodukt, V,, W Lemma: Sei φ Hom(V, W ). Falls Ψ Hom(W, V ) mit der Eigenschaft so ist Ψ hierdurch eindeutig
18. Normale Endomorphismen 18.1. Die adjungierte lineare Abbildung Seien V, W K-Vektorräume mit Skalarprodukt, V,, W Lemma: Sei φ Hom(V, W ). Falls Ψ Hom(W, V ) mit der Eigenschaft so ist Ψ hierdurch eindeutig
Hauptseminar Mathematische Logik Pcf Theorie (S2A2) Das Galvin-Hajnal Theorem
 Hauptseminar Mathematische Logik Pcf Theorie (S2A2) Das Galvin-Hajnal Theorem Jonas Fiege 21 Juli 2009 1 Theorem 1 (Galvin-Hajnal [1975]) Sei ℵ α eine singuläre, starke Limes-Kardinalzahl mit überabzählbarer
Hauptseminar Mathematische Logik Pcf Theorie (S2A2) Das Galvin-Hajnal Theorem Jonas Fiege 21 Juli 2009 1 Theorem 1 (Galvin-Hajnal [1975]) Sei ℵ α eine singuläre, starke Limes-Kardinalzahl mit überabzählbarer
Geometrische Methoden zur Analyse dynamischer Systeme
 Geometrische Methoden zur Analyse dynamischer Systeme Markus Schöberl markus.schoeberl@jku.at Institut für Regelungstechnik und Prozessautomatisierung Johannes Kepler Universität Linz KV Ausgewählte Kapitel
Geometrische Methoden zur Analyse dynamischer Systeme Markus Schöberl markus.schoeberl@jku.at Institut für Regelungstechnik und Prozessautomatisierung Johannes Kepler Universität Linz KV Ausgewählte Kapitel
Το σύστημα των αξιών της ελληνικής κοινωνίας μέσα στα σχολικά εγχειρίδια της Λογοτεχνίας του Δημοτικού Σχολείου
 ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠ/ΣΗΣ ΔΙΔΑΣΚΑΛΕΙΟ «ΘΕΟΔΩΡΟΣ ΚΑΣΤΑΝΟΣ» Το σύστημα των αξιών της ελληνικής κοινωνίας μέσα στα σχολικά εγχειρίδια της Λογοτεχνίας του Δημοτικού
ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠ/ΣΗΣ ΔΙΔΑΣΚΑΛΕΙΟ «ΘΕΟΔΩΡΟΣ ΚΑΣΤΑΝΟΣ» Το σύστημα των αξιών της ελληνικής κοινωνίας μέσα στα σχολικά εγχειρίδια της Λογοτεχνίας του Δημοτικού
Klausur Strömungsmechanik II Dichte des Fluids ρ F. Viskosität des Fluids η F. Sinkgeschwindigkeit v s. Erdbeschleunigung g
 Name, Matr-Nr, Unterschrift) Klausur Strömungsmechanik II 3 8 Aufgabe a) Einflussgrößen: Partikeldurchmesser d P Partikeldichte ρ P Dichte des Fluids ρ F Viskosität des Fluids η F Sinkgeschwindigkeit v
Name, Matr-Nr, Unterschrift) Klausur Strömungsmechanik II 3 8 Aufgabe a) Einflussgrößen: Partikeldurchmesser d P Partikeldichte ρ P Dichte des Fluids ρ F Viskosität des Fluids η F Sinkgeschwindigkeit v
Formelsammlung zur sphärischen Trigonometrie
 Formelsammlung zur sphärischen Trigonometrie A. Goniometrie A.1. Additionstheoreme für α β für α = β (α ± β) =α cos β ± cos α β ( α) =α cos α cos (α ± β) =cosα cos β β = cos α tan α ± tan β tan (α ± β)
Formelsammlung zur sphärischen Trigonometrie A. Goniometrie A.1. Additionstheoreme für α β für α = β (α ± β) =α cos β ± cos α β ( α) =α cos α cos (α ± β) =cosα cos β β = cos α tan α ± tan β tan (α ± β)
cos(2α) τ xy sin(2α) (7) cos(2(α π/2)) τ xy sin(2(α π/2)) cos(2α) + τ xy sin(2α) (8) (1 + ν) cos(2α) + τ xy (1 + ν) sin(2α) (9)
 Festigkeitslehre Lösung zu Aufgabe 11b Grundsätzliches und Vorüberlegungen: Hookesches Gesetz für den zweidimensionalen Spannungszustand: ε = 1 ( ν (1 ε = 1 ( ν ( Die beiden Messwerte ε = ε 1 und ε = ε
Festigkeitslehre Lösung zu Aufgabe 11b Grundsätzliches und Vorüberlegungen: Hookesches Gesetz für den zweidimensionalen Spannungszustand: ε = 1 ( ν (1 ε = 1 ( ν ( Die beiden Messwerte ε = ε 1 und ε = ε
1 Potentialströmungen
 1 Potentialströmungen Eine Potentialströmung in R D, D = 2, 3, wird durch den (hydrostatischen) Druck p : R, den Fluss q : R D und das Materialgesetz (Darcy) q = κ (p + G) beschrieben. Dabei ist κ der
1 Potentialströmungen Eine Potentialströmung in R D, D = 2, 3, wird durch den (hydrostatischen) Druck p : R, den Fluss q : R D und das Materialgesetz (Darcy) q = κ (p + G) beschrieben. Dabei ist κ der
1. Kapitel I Deskriptive Statistik
 V L ÖSUNGEN 1. Kapitel I Deskriptive Statistik = + + = = = = = + = = = + = = = = = = = = + + + + = = + + + + = = = = = + + + + + + + = B. Auer, H. Rottmann, Statistik und Ökonometrie für Wirtschaftswissenschaftler,
V L ÖSUNGEN 1. Kapitel I Deskriptive Statistik = + + = = = = = + = = = + = = = = = = = = + + + + = = + + + + = = = = = + + + + + + + = B. Auer, H. Rottmann, Statistik und Ökonometrie für Wirtschaftswissenschaftler,
Übungen zu Teilchenphysik 2 SS 2008. Fierz Identität. Handout. Datum: 27. 5. 2008. von Christoph Saulder
 Übungen zu Teilchenphysik 2 SS 2008 Fierz Identität Handout Datum: 27. 5. 2008 von Christoph Saulder 2 Inhaltsverzeichnis Einleitung 5 2 Herleitung der Matrixelemente 7 2. Ansatz...............................
Übungen zu Teilchenphysik 2 SS 2008 Fierz Identität Handout Datum: 27. 5. 2008 von Christoph Saulder 2 Inhaltsverzeichnis Einleitung 5 2 Herleitung der Matrixelemente 7 2. Ansatz...............................
Numerische Methoden für Eigenwertprobleme in der Beschreibung von Drift-Instabilitäten in der Plasma Randzone
 Numerische Methoden für Eigenwertprobleme in der Beschreibung von Drift-Instabilitäten in der Plasma Randzone Dominik Löchel Betreuer: M. Hochbruck und M. Tokar Graduiertenkolleg Dynamik heißer Plasmen
Numerische Methoden für Eigenwertprobleme in der Beschreibung von Drift-Instabilitäten in der Plasma Randzone Dominik Löchel Betreuer: M. Hochbruck und M. Tokar Graduiertenkolleg Dynamik heißer Plasmen
Aufgabe 1 Dreierkette Legt mit den Bild- und Wortkarten eine Dreierkette. Τρεις στη σειρά. Σχηματίστε τριάδες με εικόνες και λέξεις που ταιριάζουν.
 Station Luft Aufgabe 1 Dreierkette Legt mit den Bild- und Wortkarten eine Dreierkette. Τρεις στ σειρά. Σχματίστε τριάδες με εικόνες και λέξεις που ταιριάζουν. der Sturm die Windkraftanlage θύελλα οι ανεμογε
Station Luft Aufgabe 1 Dreierkette Legt mit den Bild- und Wortkarten eine Dreierkette. Τρεις στ σειρά. Σχματίστε τριάδες με εικόνες και λέξεις που ταιριάζουν. der Sturm die Windkraftanlage θύελλα οι ανεμογε
Dozent: Alexander Shnirman Institut für Theorie der Kondensierten Materie
 Sommer-Semester 20 Moderne Theoretische Physik III Statistische Physik Dozent: Alexander Shnirman Institut für Theorie der Kondensierten Materie Di 09:45-:5, Lehmann HS 022, Geb 30.22 Do 09:45-:5, Lehmann
Sommer-Semester 20 Moderne Theoretische Physik III Statistische Physik Dozent: Alexander Shnirman Institut für Theorie der Kondensierten Materie Di 09:45-:5, Lehmann HS 022, Geb 30.22 Do 09:45-:5, Lehmann
Intersection Types. Matthias Putz. Sommersemester 2011
 Intersection TU-München Sommersemester 2011 Themen Zusammenfassung Anwendungsbeispiel 1: chars Programmiersprache C: signed und unsigned chars Wertebereiche: signed char: [ 128, +127] unsigned char: [0,
Intersection TU-München Sommersemester 2011 Themen Zusammenfassung Anwendungsbeispiel 1: chars Programmiersprache C: signed und unsigned chars Wertebereiche: signed char: [ 128, +127] unsigned char: [0,
Jörg Gayler, Lubov Vassilevskaya
 Differentialrechnung: Aufgaben Jörg Gayler, Lubov Vassilevskaya ii Inhaltsverzeichnis. Erste Ableitung der elementaren Funktionen......................... Ableitungsregeln......................................
Differentialrechnung: Aufgaben Jörg Gayler, Lubov Vassilevskaya ii Inhaltsverzeichnis. Erste Ableitung der elementaren Funktionen......................... Ableitungsregeln......................................
B(α, β) B(α + n, β + n x n) α 1 Modus der Be(α, β)-verteilung : α + β 2 α Erwartungswert der Be(α, β)-verteilung : α + β
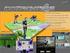 Aufgabe X,..., X n iid G(π) a) Bestimmung der Loglikelihoodfunktion n P L(π) = π( π) xi = π n x ( π) i n = π n ( π) n( x ) Damit folgt: Insgesamt also ˆπ ML = i= l(π) = n log(π) + n( x ) log( π) S(π) =
Aufgabe X,..., X n iid G(π) a) Bestimmung der Loglikelihoodfunktion n P L(π) = π( π) xi = π n x ( π) i n = π n ( π) n( x ) Damit folgt: Insgesamt also ˆπ ML = i= l(π) = n log(π) + n( x ) log( π) S(π) =
DEUTSCHE SCHULE ATHEN ΓΕΡΜΑΝΙΚΗ ΣΧΟΛΗ ΑΘΗΝΩΝ
 Herzlich Willkommen zu unserem Elternabend Übergang aus dem Elternhaus in den Kindergarten Καλωσορίσατε στη συνάντηση γονέων με θέμα τη μετάβαση από το οικογενειακό περιβάλλον στο προνηπιακό τμήμα 1 Überblick
Herzlich Willkommen zu unserem Elternabend Übergang aus dem Elternhaus in den Kindergarten Καλωσορίσατε στη συνάντηση γονέων με θέμα τη μετάβαση από το οικογενειακό περιβάλλον στο προνηπιακό τμήμα 1 Überblick
MATERIALIEN ZUR VORBEREITUNG AUF DIE KLAUSUR INFORMATIK II FÜR VERKEHRSINGENIEURWESEN ANTEIL VON PROF. VOGLER IM WINTERSEMESTER 2011/12
 Fakultät Informatik Institut für Angewandte Informatik, Professur Technische Informationssysteme MATERIALIEN ZUR VORBEREITUNG AUF DIE KLAUSUR INFORMATIK II FÜR VERKEHRSINGENIEURWESEN ANTEIL VON PROF. VOGLER
Fakultät Informatik Institut für Angewandte Informatik, Professur Technische Informationssysteme MATERIALIEN ZUR VORBEREITUNG AUF DIE KLAUSUR INFORMATIK II FÜR VERKEHRSINGENIEURWESEN ANTEIL VON PROF. VOGLER
Optionsbewertung mit FFT
 19.01.2012 Europäische Call Option Wert C T = E[(S(T ) K) + ] Variance Gamma Prozess Dichte γ 2λ x µ λ 1/2 K λ 1/2 (α x µ ) e β(x µ) πγ(λ)(2α) λ 1/2 Charakteristische Funktion (1 izθν + 1 2 σ2 νz 2 ) t
19.01.2012 Europäische Call Option Wert C T = E[(S(T ) K) + ] Variance Gamma Prozess Dichte γ 2λ x µ λ 1/2 K λ 1/2 (α x µ ) e β(x µ) πγ(λ)(2α) λ 1/2 Charakteristische Funktion (1 izθν + 1 2 σ2 νz 2 ) t
Wenn ihr nicht werdet wie die Kinder...
 Wenn ihr nicht werdet wie die Kinder... . Der Memoriam-Garten Schön, dass ich mir keine Sorgen machen muss! Mit dem Memoriam-Garten bieten Ihnen Friedhofsgärtner, Steinmetze
Wenn ihr nicht werdet wie die Kinder... . Der Memoriam-Garten Schön, dass ich mir keine Sorgen machen muss! Mit dem Memoriam-Garten bieten Ihnen Friedhofsgärtner, Steinmetze
Rationales Multilevel Jacobi-Davidson Verfahren für Eigenwertgleichungen in der Plasma Physik
 Rationales Multilevel Jacobi-Davidson Verfahren für Eigenwertgleichungen in der Plasma Physik Dominik Löchel Betreuer: M. Hochbruck und M. Tokar; Kooperation mit D. Reiser Graduiertenkolleg Dynamik heißer
Rationales Multilevel Jacobi-Davidson Verfahren für Eigenwertgleichungen in der Plasma Physik Dominik Löchel Betreuer: M. Hochbruck und M. Tokar; Kooperation mit D. Reiser Graduiertenkolleg Dynamik heißer
α + ω 0 2 = 0, Lösung: α 1,2
 SDOFs Der lineare Einmassenschwinger Bewegungsgleichung m x + c x + k x = f () = p()...krafanregung m x g ()...Weganregung x + ζω x + ω x = f () m, ω = k m, ζ = c mk... Lehr'sches Dämpfungsmaß AB : x(
SDOFs Der lineare Einmassenschwinger Bewegungsgleichung m x + c x + k x = f () = p()...krafanregung m x g ()...Weganregung x + ζω x + ω x = f () m, ω = k m, ζ = c mk... Lehr'sches Dämpfungsmaß AB : x(
α + ω 0 2 = 0, Lösung: α 1,2
 SDOFs Der lineare Einmassenschwinger Bewegungsgleichung m x + c x + k x = f () = p()...krafanregung m x g ()...Weganregung x + 2ζω x + ω 2 x = f () m, ω = k m, ζ = c 2 mk... Lehr'sches Dämpfungsmaß AB
SDOFs Der lineare Einmassenschwinger Bewegungsgleichung m x + c x + k x = f () = p()...krafanregung m x g ()...Weganregung x + 2ζω x + ω 2 x = f () m, ω = k m, ζ = c 2 mk... Lehr'sches Dämpfungsmaß AB
Logik und Beweisbarkeit
 Logik und Beweisbarkeit Kap. I - Aussagenlogik (Sommer 2017) Martin Mundhenk Univ. Jena, Institut für Informatik 19. April 2017 Vorlesung Logik und Beweisbarkeit (Sommer 2017) 1. Aussagenlogik 2. Arithmetik
Logik und Beweisbarkeit Kap. I - Aussagenlogik (Sommer 2017) Martin Mundhenk Univ. Jena, Institut für Informatik 19. April 2017 Vorlesung Logik und Beweisbarkeit (Sommer 2017) 1. Aussagenlogik 2. Arithmetik
Εμπορική αλληλογραφία Ηλεκτρονική Αλληλογραφία
 - Εισαγωγή Sehr geehrter Herr Präsident, Sehr geehrter Herr Präsident, Εξαιρετικά επίσημη επιστολή, ο παραλήπτης έχει ένα ειδικό τίτλο ο οποίος πρέπει να χρησιμοποιηθεί αντί του ονόματος του Sehr geehrter
- Εισαγωγή Sehr geehrter Herr Präsident, Sehr geehrter Herr Präsident, Εξαιρετικά επίσημη επιστολή, ο παραλήπτης έχει ένα ειδικό τίτλο ο οποίος πρέπει να χρησιμοποιηθεί αντί του ονόματος του Sehr geehrter
Ρ Η Μ Α Τ Ι Κ Η Δ Ι Α Κ Ο Ι Ν Ω Σ Η
 Αρ. Φακέλου.: Ku 622.00/3 (Παρακαλούμε να αναφέρεται στην απάντηση) Αριθμός Ρημ. Διακ: 22/14 2 αντίγραφα Συνημμένα: -2- ΑΝΤΙΓΡΑΦΟ Ρ Η Μ Α Τ Ι Κ Η Δ Ι Α Κ Ο Ι Ν Ω Σ Η Η Πρεσβεία της Ομοσπονδιακής Δημοκρατίας
Αρ. Φακέλου.: Ku 622.00/3 (Παρακαλούμε να αναφέρεται στην απάντηση) Αριθμός Ρημ. Διακ: 22/14 2 αντίγραφα Συνημμένα: -2- ΑΝΤΙΓΡΑΦΟ Ρ Η Μ Α Τ Ι Κ Η Δ Ι Α Κ Ο Ι Ν Ω Σ Η Η Πρεσβεία της Ομοσπονδιακής Δημοκρατίας
Weitere Tests bei Normalverteilung
 Tests von Hypothesen über den Erwartungswert Bisher: zweiseitiges Testproblem (Zweiseitiger Einstichproben-t-Test) H : μμ gegen H : μ μ Testentscheidung P- Wert: X μ s(x) : Lehne H ab, wenn T(X) N > t
Tests von Hypothesen über den Erwartungswert Bisher: zweiseitiges Testproblem (Zweiseitiger Einstichproben-t-Test) H : μμ gegen H : μ μ Testentscheidung P- Wert: X μ s(x) : Lehne H ab, wenn T(X) N > t
Hessisches Kultusministerium. Schulbücherkatalog. für den Unterricht in Herkunftssprachen in Verantwortung des Landes Hessen.
 Hessisches Kultusministerium Schulbücherkatalog für den Unterricht in Herkunftssprachen in Verantwortung des Landes Hessen Schuljahr 2013/2014 Unterrichtsmaterialien, die im uftrag des Hessischen Kultusministeriums
Hessisches Kultusministerium Schulbücherkatalog für den Unterricht in Herkunftssprachen in Verantwortung des Landes Hessen Schuljahr 2013/2014 Unterrichtsmaterialien, die im uftrag des Hessischen Kultusministeriums
Mission Berlin. Deutsch lernen und unterrichten Arbeitsmaterialien. Mission Berlin 13 Βοήθεια εκ Θεού
 13 Βοήθεια εκ Θεού Η εκκλησία φαίνεται πως είναι το σωστό µέρος για να πάρει κανείς πληροφορίες. Ο πάστορας εξηγεί στην Άννα τη µελωδία και της λέει ότι είναι το κλειδί για µια µηχανή του χρόνου. Αλλά
13 Βοήθεια εκ Θεού Η εκκλησία φαίνεται πως είναι το σωστό µέρος για να πάρει κανείς πληροφορίες. Ο πάστορας εξηγεί στην Άννα τη µελωδία και της λέει ότι είναι το κλειδί για µια µηχανή του χρόνου. Αλλά
Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α
 Α Ρ Χ Α Ι Α Ι Σ Τ Ο Ρ Ι Α Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α Σ η µ ε ί ω σ η : σ υ ν ά δ ε λ φ ο ι, ν α µ ο υ σ υ γ χ ω ρ ή σ ε τ ε τ ο γ ρ ή γ ο ρ ο κ α ι α τ η µ έ λ η τ ο ύ
Α Ρ Χ Α Ι Α Ι Σ Τ Ο Ρ Ι Α Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α Σ η µ ε ί ω σ η : σ υ ν ά δ ε λ φ ο ι, ν α µ ο υ σ υ γ χ ω ρ ή σ ε τ ε τ ο γ ρ ή γ ο ρ ο κ α ι α τ η µ έ λ η τ ο ύ
ΕΡΓΑΖΟΜΕΝΩΝ Bildung älterer Arbeitnehmer
 ΚΑΤΑΡΤΙΣΗ ΩΡΙΜΩΝ ΕΡΓΑΖΟΜΕΝΩΝ Bildung älterer Arbeitnehmer Kassandra Teliopoulos IEKEP 06/03/06 ΜΕΡΙΚΑ ΣΗΜΕΙΑ ΚΛΕΙΔΙΑ Einige Gedankenansätze!Στις περισσότερες χώρες μέλη της Ε.Ε. μεγάλης ηλικίας εργαζόμενοι
ΚΑΤΑΡΤΙΣΗ ΩΡΙΜΩΝ ΕΡΓΑΖΟΜΕΝΩΝ Bildung älterer Arbeitnehmer Kassandra Teliopoulos IEKEP 06/03/06 ΜΕΡΙΚΑ ΣΗΜΕΙΑ ΚΛΕΙΔΙΑ Einige Gedankenansätze!Στις περισσότερες χώρες μέλη της Ε.Ε. μεγάλης ηλικίας εργαζόμενοι
Strukturgleichungsmodellierung
 Strukturgleichungsmodellierung FoV Methodenlehre FSU-Jena Dipl.-Psych. Norman Rose Strukturgleichungsmodelle mit latenten Variablen Forschungsorientierte Vertiefung - Methodenlehre Dipl.-Psych. Norman
Strukturgleichungsmodellierung FoV Methodenlehre FSU-Jena Dipl.-Psych. Norman Rose Strukturgleichungsmodelle mit latenten Variablen Forschungsorientierte Vertiefung - Methodenlehre Dipl.-Psych. Norman
ΟΔΟΘ ΔΘΖΗΣΘΟΣ Θ,28-32
 ΟΔΟΘ ΔΘΖΗΣΘΟΣ Θ,28-32 Πξώηε Αλάγλωζε Δξκελεία [... ] ρ ξ ε ω 1 δ ε ζ ε π α λ η α π π ζ ε ζ ζ α η 2 1 ΘΔΚΗΠ, ΓΗΘΖ, ΑΛΑΓΘΖ, ΚΝΗΟΑ / ΣΟΖ, ΣΟΔΩΛ: νλνκαηα ηνπ ΡΝ ΑΡΝΛ! Ρν Απξνζσπν Martin Heidegger, Απν Ρν Σι
ΟΔΟΘ ΔΘΖΗΣΘΟΣ Θ,28-32 Πξώηε Αλάγλωζε Δξκελεία [... ] ρ ξ ε ω 1 δ ε ζ ε π α λ η α π π ζ ε ζ ζ α η 2 1 ΘΔΚΗΠ, ΓΗΘΖ, ΑΛΑΓΘΖ, ΚΝΗΟΑ / ΣΟΖ, ΣΟΔΩΛ: νλνκαηα ηνπ ΡΝ ΑΡΝΛ! Ρν Απξνζσπν Martin Heidegger, Απν Ρν Σι
Klausur Strömungslehre
 ...... Name, Matr.-Nr, Unterschrift Klausur Strömungslehre. 3.. Aufgabe a G F A G WV B + V L g G G W + V L g g B V L G g W B L p R T W p a + Wg + h R T W m L L V L m L G pa + Wg + h g W B R T W b G F A
...... Name, Matr.-Nr, Unterschrift Klausur Strömungslehre. 3.. Aufgabe a G F A G WV B + V L g G G W + V L g g B V L G g W B L p R T W p a + Wg + h R T W m L L V L m L G pa + Wg + h g W B R T W b G F A
Mission Berlin. Deutsch lernen und unterrichten Arbeitsmaterialien. Mission Berlin 14 Στο παρελθόν για το µέλλον
 14 Στο παρελθόν για το µέλλον Η Άννα ανακαλύπτει τη µηχανή του χρόνου και µαθαίνει ότι οι τροµοκράτες θέλουν να εξαλείψουν ένα ιστορικό γεγονός. Αλλά ποιο; Ο παίκτης τη στέλνει στη χρονιά 1961. Της µένουν
14 Στο παρελθόν για το µέλλον Η Άννα ανακαλύπτει τη µηχανή του χρόνου και µαθαίνει ότι οι τροµοκράτες θέλουν να εξαλείψουν ένα ιστορικό γεγονός. Αλλά ποιο; Ο παίκτης τη στέλνει στη χρονιά 1961. Της µένουν
Preisliste AB JUNI 2019
 Preisliste AB JUNI 2019 LOVE STORIES Pakete (3H) STATT 690 JETZT 650 - Einmalige Aufnahmepauschale - Brautpaar Shooting inkl. 10 bearbeiteten Bildern digital & mit Abzug bis 15x20cm - Reportage der Trauung
Preisliste AB JUNI 2019 LOVE STORIES Pakete (3H) STATT 690 JETZT 650 - Einmalige Aufnahmepauschale - Brautpaar Shooting inkl. 10 bearbeiteten Bildern digital & mit Abzug bis 15x20cm - Reportage der Trauung
Rotationen und Translationen
 Astrophysikalisches Institut Neunhof Mitteilung sd97211, Januar 2010 1 Rotationen und Translationen Eigentliche Drehungen, Spiegelungen, und Translationen von Kartesischen Koordinaten-Systemen und Kugelkoordinaten-Systemen
Astrophysikalisches Institut Neunhof Mitteilung sd97211, Januar 2010 1 Rotationen und Translationen Eigentliche Drehungen, Spiegelungen, und Translationen von Kartesischen Koordinaten-Systemen und Kugelkoordinaten-Systemen
Kapitel 6 Schweißverbindungen
 Kapitel 6 Schweißverbindungen Alle Angaben beziehen sich auf die 19. Auflage Roloff/Matek Maschinenelemente mit Tabellenbuch und die 15. Auflage Roloff/Matek Aufgabensammlung. Das Aufgabenbuch kann man
Kapitel 6 Schweißverbindungen Alle Angaben beziehen sich auf die 19. Auflage Roloff/Matek Maschinenelemente mit Tabellenbuch und die 15. Auflage Roloff/Matek Aufgabensammlung. Das Aufgabenbuch kann man
Griechisches Staatszertifikat - Deutsch
 ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΡΑΤΙΚΟ ΠΙΣΤΟΠΟΙΗΤΙΚΟ ΓΛΩΣΣΟΜΑΘΕΙΑΣ Griechisches Ministerium für Bildung und Religion Griechisches Staatszertifikat - Deutsch Niveau A1 & A2 Entspricht dem Gemeinsamen
ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΡΑΤΙΚΟ ΠΙΣΤΟΠΟΙΗΤΙΚΟ ΓΛΩΣΣΟΜΑΘΕΙΑΣ Griechisches Ministerium für Bildung und Religion Griechisches Staatszertifikat - Deutsch Niveau A1 & A2 Entspricht dem Gemeinsamen
Auswandern Wohnen. Wohnen - Mieten. Θα ήθελα να ενοικιάσω ένα. Äußern dass man etwas mieten möchte. δωμάτιο Art der Unterbringung
 - Mieten Griechisch Θα ήθελα να ενοικιάσω ένα. Äußern dass man etwas mieten möchte Koreanisch δωμάτιο διαμέρισμα γκαρσονιέρα / στούντιο διαμέρισμα μονοκατοικία ημι-ανεξάρτητο σπίτι σπίτι σε σειρά κατοικιών
- Mieten Griechisch Θα ήθελα να ενοικιάσω ένα. Äußern dass man etwas mieten möchte Koreanisch δωμάτιο διαμέρισμα γκαρσονιέρα / στούντιο διαμέρισμα μονοκατοικία ημι-ανεξάρτητο σπίτι σπίτι σε σειρά κατοικιών
Mission Berlin. Deutsch lernen und unterrichten Arbeitsmaterialien. Mission Berlin 26 Πειράµατα µε τον χρόνο
 26 Πειράµατα µε τον χρόνο Επιστρέφοντας στο παρόν η Άννα προσπαθεί να µπλοκάρει τη µηχανή του χρόνου, αλλά δεν έχει τον κωδικό. Η γυναίκα µε τα κόκκινα εµφανίζεται. Θα χαλάσει η «αρχηγός» τα σχέδια της
26 Πειράµατα µε τον χρόνο Επιστρέφοντας στο παρόν η Άννα προσπαθεί να µπλοκάρει τη µηχανή του χρόνου, αλλά δεν έχει τον κωδικό. Η γυναίκα µε τα κόκκινα εµφανίζεται. Θα χαλάσει η «αρχηγός» τα σχέδια της
Mission Berlin. Deutsch lernen und unterrichten Arbeitsmaterialien. Mission Berlin 25 Απρόοπτες δυσκολίες
 25 Απρόοπτες δυσκολίες Ο χρόνος τελειώνει και η Άννα πρέπει να αποχαιρετήσει τον Paul, για να επιστρέψει στην 9 η Νοεµβρίου 2006. Για την εκπλήρωση της αποστολής της αποµένουν τώρα µόνο 5 λεπτά. Θα φθάσουν;
25 Απρόοπτες δυσκολίες Ο χρόνος τελειώνει και η Άννα πρέπει να αποχαιρετήσει τον Paul, για να επιστρέψει στην 9 η Νοεµβρίου 2006. Για την εκπλήρωση της αποστολής της αποµένουν τώρα µόνο 5 λεπτά. Θα φθάσουν;
 Nr. 544-12/17 Auslosung Klub-Cup 2018 1/8 Final Anlässlich des Freundschaftswettkampfes BL-BS hat unsere Glücksfee Paula Graber folgende Paarungen für den Achtelfinal des Klub-Cup 2018 gezogen
Nr. 544-12/17 Auslosung Klub-Cup 2018 1/8 Final Anlässlich des Freundschaftswettkampfes BL-BS hat unsere Glücksfee Paula Graber folgende Paarungen für den Achtelfinal des Klub-Cup 2018 gezogen
Planheizkörper Carat 5.5. Planheizkörper Typ 11, 20, 21, 22, 33 und Typ 10, 11, 20 und 21 Vertikal /2013
 Planheizkörper Typ 11, 20, 21, 22 und Typ 10, 11, 20 und 21 Vertikal Planheizkörper Typ 11, 20, 21, 22, 33 und Typ 10, 11, 20 und 21 Vertikal Ein- bis dreilagig, Bauhöhen 250, 400, 550 und λ50 mm Anschlussmuffen
Planheizkörper Typ 11, 20, 21, 22 und Typ 10, 11, 20 und 21 Vertikal Planheizkörper Typ 11, 20, 21, 22, 33 und Typ 10, 11, 20 und 21 Vertikal Ein- bis dreilagig, Bauhöhen 250, 400, 550 und λ50 mm Anschlussmuffen
Εμπορική αλληλογραφία Ηλεκτρονική Αλληλογραφία
 - Εισαγωγή ελληνικά Αξιότιμε κύριε Πρόεδρε, γερμανικά Sehr geehrter Herr Präsident, Εξαιρετικά επίσημη επιστολή, ο παραλήπτης έχει ένα ειδικό τίτλο ο οποίος πρέπει να χρησιμοποιηθεί αντί του ονόματος του
- Εισαγωγή ελληνικά Αξιότιμε κύριε Πρόεδρε, γερμανικά Sehr geehrter Herr Präsident, Εξαιρετικά επίσημη επιστολή, ο παραλήπτης έχει ένα ειδικό τίτλο ο οποίος πρέπει να χρησιμοποιηθεί αντί του ονόματος του
Mission Berlin. Deutsch lernen und unterrichten Arbeitsmaterialien. Mission Berlin 04 Σήµατα κινδύνου
 04 Σήµατα κινδύνου Η Άννα βρίσκει στην Kantstraße ένα ρολογάδικο που είναι όµως κλειστό. Μαθαίνει ότι ο ιδιοκτήτης έχει πάει σ ένα καφενείο. Οι δυο τους φαίνεται να γνωρίζονται. Η Άννα έχει ακόµα 100 λεπτά.
04 Σήµατα κινδύνου Η Άννα βρίσκει στην Kantstraße ένα ρολογάδικο που είναι όµως κλειστό. Μαθαίνει ότι ο ιδιοκτήτης έχει πάει σ ένα καφενείο. Οι δυο τους φαίνεται να γνωρίζονται. Η Άννα έχει ακόµα 100 λεπτά.
Harmonischer Oszillator: Bewegungsgleichung. Physik für Mechatroniker WiSe 2008/2009
 Harmonischer Oszillaor: Bewegungsgleichung m F D m& D ω D m && + ω WiSe 8/9 Harmonischer Oszillaor: Energieberachung E ges D + m& D & + m&& & Differenzieren nach cons &( D + m& gil für alle Zeien D + m&
Harmonischer Oszillaor: Bewegungsgleichung m F D m& D ω D m && + ω WiSe 8/9 Harmonischer Oszillaor: Energieberachung E ges D + m& D & + m&& & Differenzieren nach cons &( D + m& gil für alle Zeien D + m&
*1 +3*1 - +3*1. - Ideen zu einer reinen Phänomenologie und Phänomenologischen Philosophie. Zweites Buch., Husserliana
 +3*1 + +3+- + +3*1, +3*+/+3*, +3*1 / 0 +3*1 +3*1 - +3*1 + Ideen zu einer reinen Phänomenologie und Phänomenologischen Philosophie. Erstes Buch., Husserliana Bd III., +3/*, +/* I-II +32. +/*, Ding und Raum
+3*1 + +3+- + +3*1, +3*+/+3*, +3*1 / 0 +3*1 +3*1 - +3*1 + Ideen zu einer reinen Phänomenologie und Phänomenologischen Philosophie. Erstes Buch., Husserliana Bd III., +3/*, +/* I-II +32. +/*, Ding und Raum
u(x, y) =f(x, y) Ω=(0, 1) (0, 1)
 u(x, y) =f(x, y) Ω=(0, 1) (0, 1) u(x, y) =g(x, y) Γ=δΩ ={0, 1} {0, 1} Ω Ω Ω h Ω h h ˆ Ω ˆ u v = fv Ω u = f in Ω v V H 1 (Ω) V V h V h ψ 1,ψ 2,...,ψ N, ˆ ˆ u v = Ω Ω fv v V ˆ ˆ u v = Ω ˆ ˆ u ψ i = Ω Ω Ω
u(x, y) =f(x, y) Ω=(0, 1) (0, 1) u(x, y) =g(x, y) Γ=δΩ ={0, 1} {0, 1} Ω Ω Ω h Ω h h ˆ Ω ˆ u v = fv Ω u = f in Ω v V H 1 (Ω) V V h V h ψ 1,ψ 2,...,ψ N, ˆ ˆ u v = Ω Ω fv v V ˆ ˆ u v = Ω ˆ ˆ u ψ i = Ω Ω Ω
Mission Berlin. Deutsch lernen und unterrichten Arbeitsmaterialien. Mission Berlin 17 Οδοφράγµατα
 17 Οδοφράγµατα 50 λεπτά ακόµα: Ο παίκτης αποφασίζει να τα παίξει όλα για όλα και να εµπιστευθεί την ταµία. Το ράδιο µεταδίδει ότι οι Ανατολικογερµανοί στρατιώτες στήνουν οδοφράγµατα. Αυτό είναι το γεγονός
17 Οδοφράγµατα 50 λεπτά ακόµα: Ο παίκτης αποφασίζει να τα παίξει όλα για όλα και να εµπιστευθεί την ταµία. Το ράδιο µεταδίδει ότι οι Ανατολικογερµανοί στρατιώτες στήνουν οδοφράγµατα. Αυτό είναι το γεγονός
λ + ω 0 2 = 0, Lösung: λ 1,2
 SDOFs Der lineare Einassenschwinger Bewegungsgleichung!!x + c!x + k x = f () = p()...krafanregung!!x g ()...Weganregung!!x + ζω!x + ω x = f (), ω = k, ζ = c k... Lehr'sches Däpfungsaß AB : x( = ) = x,!x(
SDOFs Der lineare Einassenschwinger Bewegungsgleichung!!x + c!x + k x = f () = p()...krafanregung!!x g ()...Weganregung!!x + ζω!x + ω x = f (), ω = k, ζ = c k... Lehr'sches Däpfungsaß AB : x( = ) = x,!x(
PASSANT A: Ja, guten Tag. Ich suche den Alexanderplatz. Können Sie mir helfen?
 03 Για την οδό Kantstraße Η Άννα ξεκινά για την Kantstraße, αλλά καθυστερεί, επειδή πρέπει να ρωτήσει πώς πάνε µέχρι εκεί. Χάνει κι άλλο χρόνο, όταν εµφανίζονται πάλι οι µοτοσικλετιστές µε τα µαύρα κράνη
03 Για την οδό Kantstraße Η Άννα ξεκινά για την Kantstraße, αλλά καθυστερεί, επειδή πρέπει να ρωτήσει πώς πάνε µέχρι εκεί. Χάνει κι άλλο χρόνο, όταν εµφανίζονται πάλι οι µοτοσικλετιστές µε τα µαύρα κράνη
Griechische und römische Rechtsgeschichte
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Griechische und römische Rechtsgeschichte Ενότητα 7: Gortyna Παπακωνσταντίνου Καλλιόπη Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Griechische und römische Rechtsgeschichte Ενότητα 7: Gortyna Παπακωνσταντίνου Καλλιόπη Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Mission Berlin. Deutsch lernen und unterrichten Arbeitsmaterialien. Mission Berlin 05 εν γνωριζόµαστε;
 05 εν γνωριζόµαστε; Η Άννα πηγαίνει το µουσικό κουτί στον ρολογά για να το διορθώσει. Για τον Paul Winkler όµως είναι περισσότερο από µια απλή δουλειά. Νοµίζει ότι ξέρει την Άννα από παλιά. Μα πώς είναι
05 εν γνωριζόµαστε; Η Άννα πηγαίνει το µουσικό κουτί στον ρολογά για να το διορθώσει. Για τον Paul Winkler όµως είναι περισσότερο από µια απλή δουλειά. Νοµίζει ότι ξέρει την Άννα από παλιά. Μα πώς είναι
Griechische und roemische Rechtsgeschichte
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Griechische und roemische Rechtsgeschichte Ενότητα 4: Griechische Rechtsgeschichte Παπακωνσταντίνου Καλλιόπη Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Griechische und roemische Rechtsgeschichte Ενότητα 4: Griechische Rechtsgeschichte Παπακωνσταντίνου Καλλιόπη Άδειες Χρήσης Το παρόν εκπαιδευτικό
Bohrbild im Längsholz. Einstellbereich
 Montageanleitung/Construction Manual GIGANT 120 Fräsbild Art. Nr. K051 a=h x 0,7 im Längsholz Bauzugelassene Holzbauverbindung im Hirnholz 26,5 ±0,25 40 +2-0 h a + 47 Schraubenbild im Längsholz Schraubenbild
Montageanleitung/Construction Manual GIGANT 120 Fräsbild Art. Nr. K051 a=h x 0,7 im Längsholz Bauzugelassene Holzbauverbindung im Hirnholz 26,5 ±0,25 40 +2-0 h a + 47 Schraubenbild im Längsholz Schraubenbild
Eselsbrücken für die Berechnung der Spur von Produkten von Gammamatrizen
 Eselsbrücken für die Berechnung der Spur von Produkten von Gammamatrizen Björn Schemmann Der Autor stellt eine kleine Hilfestellung zur Berechnung von Spuren der Form tr(γ µ 1,..., γ µ 2n ) vor. EINLEITUNG
Eselsbrücken für die Berechnung der Spur von Produkten von Gammamatrizen Björn Schemmann Der Autor stellt eine kleine Hilfestellung zur Berechnung von Spuren der Form tr(γ µ 1,..., γ µ 2n ) vor. EINLEITUNG
Higgs-Mechanismus in der Festkörperphysik
 6.7.2016 Gliederung Einführung 1 Einführung 2 anschaulich in Formeln 3 Superfluides Helium Supraleitung 4 5 in Festkörperphysik meist verbunden mit Supraleitung bekannt: Anregungen durch Symmetriebrechung
6.7.2016 Gliederung Einführung 1 Einführung 2 anschaulich in Formeln 3 Superfluides Helium Supraleitung 4 5 in Festkörperphysik meist verbunden mit Supraleitung bekannt: Anregungen durch Symmetriebrechung
Fragen, ob Gebühren anfallen, wenn man in einem bestimmten Land Geld abhebt
 - Allgemeines Μπορώ να κάνω ανάληψη στην [χώρα] χωρίς να πληρώσω προμήθεια; Kann ich in [Land] gebührenfrei Geld abheben? Fragen, ob Gebühren anfallen, wenn man in einem bestimmten Land Geld abhebt Πόσα
- Allgemeines Μπορώ να κάνω ανάληψη στην [χώρα] χωρίς να πληρώσω προμήθεια; Kann ich in [Land] gebührenfrei Geld abheben? Fragen, ob Gebühren anfallen, wenn man in einem bestimmten Land Geld abhebt Πόσα
Griechisches Staatszertifikat - Deutsch
 ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΡΑΤΙΚΟ ΠΙΣΤΟΠΟΙΗΤΙΚΟ ΓΛΩΣΣΟΜΑΘΕΙΑΣ Griechisches Ministerium für Bildung und Religion Griechisches Staatszertifikat - Deutsch Niveau A1 & A2 Entspricht dem Gemeinsamen
ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΡΑΤΙΚΟ ΠΙΣΤΟΠΟΙΗΤΙΚΟ ΓΛΩΣΣΟΜΑΘΕΙΑΣ Griechisches Ministerium für Bildung und Religion Griechisches Staatszertifikat - Deutsch Niveau A1 & A2 Entspricht dem Gemeinsamen
2015/2016 ΔΙΔΑΚΤΙΚΑ ΒΙΒΛΙΑ
 Klassen 8A/8B/8C Β' Γυμνασίου DEUTSCH/ Verlag Hueber, AusBlick 1 Kursbuch 978-3-19-001860-4 Arbeitsbuch + Audio CD 978-3-19-011860-1 Griechisches Glossar Hueber Hellas 978-960-7396-74-7 Hueber Verlag,
Klassen 8A/8B/8C Β' Γυμνασίου DEUTSCH/ Verlag Hueber, AusBlick 1 Kursbuch 978-3-19-001860-4 Arbeitsbuch + Audio CD 978-3-19-011860-1 Griechisches Glossar Hueber Hellas 978-960-7396-74-7 Hueber Verlag,
Griechische und römische Rechtsgeschichte
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Griechische und römische Rechtsgeschichte Ενότητα 5: die Spartanische Verfassung Παπακωνσταντίνου Καλλιόπη Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Griechische und römische Rechtsgeschichte Ενότητα 5: die Spartanische Verfassung Παπακωνσταντίνου Καλλιόπη Άδειες Χρήσης Το παρόν εκπαιδευτικό
Niveau A1 & A2 PHASE 3 ΚΡΑΤΙΚΟ ΠΙΣΤΟΠΟΙΗΤΙΚΟ ΓΛΩΣΣΟΜΑΘΕΙΑΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙ ΕΙΑΣ, ΙΑ ΒΙΟΥ ΜΑΘΗΣΗΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ
 ΥΠΟΥΡΓΕΙΟ ΠΑΙ ΕΙΑΣ, ΙΑ ΒΙΟΥ ΜΑΘΗΣΗΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΡΑΤΙΚΟ ΠΙΣΤΟΠΟΙΗΤΙΚΟ ΓΛΩΣΣΟΜΑΘΕΙΑΣ Griechisches Ministerium für Bildung, Lebenslanges Lernen und Religionsangelegenheiten Griechisches Staatszertifikat
ΥΠΟΥΡΓΕΙΟ ΠΑΙ ΕΙΑΣ, ΙΑ ΒΙΟΥ ΜΑΘΗΣΗΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΡΑΤΙΚΟ ΠΙΣΤΟΠΟΙΗΤΙΚΟ ΓΛΩΣΣΟΜΑΘΕΙΑΣ Griechisches Ministerium für Bildung, Lebenslanges Lernen und Religionsangelegenheiten Griechisches Staatszertifikat
BIOABFALL. Beantworte folgende Fragen: 1. Welche Farbe hat die Biotonne a) blau b) grün c) gelb d) rot. 2. Was kommt in die Biotonne?
 BIOABFALL Mein Name ist Laura. Zuhause essen wir viel Obst und Gemüse. Die Abfälle, wie zum Beispiel Orangen- oder Kartoffelschalen, aber auch Teeblätter oder Eierschalen, sammeln wir in der Küche in einem
BIOABFALL Mein Name ist Laura. Zuhause essen wir viel Obst und Gemüse. Die Abfälle, wie zum Beispiel Orangen- oder Kartoffelschalen, aber auch Teeblätter oder Eierschalen, sammeln wir in der Küche in einem
Simon Schiffel Implizite Ausfallwahrscheinlichkeiten von Unternehmensanleihen
 Simon Schiffel Implizite Ausfallwahrscheinlichkeiten von Unternehmensanleihen GABLER RESEARCH Simon Schiffel Implizite Ausfallwahrscheinlichkeiten von Unternehmensanleihen Eine empirische Analyse in unterschiedlichen
Simon Schiffel Implizite Ausfallwahrscheinlichkeiten von Unternehmensanleihen GABLER RESEARCH Simon Schiffel Implizite Ausfallwahrscheinlichkeiten von Unternehmensanleihen Eine empirische Analyse in unterschiedlichen
Weihnachtsbrief aus Kindergarten und Vorschule Χριστουγεννιάτικο γράμμα από το προνηπιακό/νηπιακό τμήμα
 Weihnachtsbrief aus Kindergarten und Vorschule Χριστουγεννιάτικο γράμμα από το προνηπιακό/νηπιακό τμήμα 13.12.2016 Liebe Eltern des Kindergartens und der Vorschule, Die Weihnachtszeit ist eingeläutet.
Weihnachtsbrief aus Kindergarten und Vorschule Χριστουγεννιάτικο γράμμα από το προνηπιακό/νηπιακό τμήμα 13.12.2016 Liebe Eltern des Kindergartens und der Vorschule, Die Weihnachtszeit ist eingeläutet.
Hessisches Kultusministerium. Schulbücherkatalog. für den Unterricht in Herkunftssprachen in Verantwortung des Landes Hessen.
 Hessisches Kultusministerium Schulbücherkatalog für den Unterricht in Herkunftssprachen in Verantwortung des Landes Hessen Griechisch Stand: 20.06.2019 Unterrichtsmaterialien, die im Auftrag des Hessischen
Hessisches Kultusministerium Schulbücherkatalog für den Unterricht in Herkunftssprachen in Verantwortung des Landes Hessen Griechisch Stand: 20.06.2019 Unterrichtsmaterialien, die im Auftrag des Hessischen
Mission Berlin. Deutsch lernen und unterrichten Arbeitsmaterialien. Mission Berlin 24 Το ρολόι χτυπάει
 24 Το ρολόι χτυπάει Η Άννα βρίσκει πάλι τη µεταλλική θήκη που είχε κρύψει το 1961, αλλά δεν µπορεί να την ανοίξει, επειδή έχει σκουριάσει. Όταν τελικά τα καταφέρνει, βρίσκει µέσα ένα παλιό κλειδί. Το κλειδί
24 Το ρολόι χτυπάει Η Άννα βρίσκει πάλι τη µεταλλική θήκη που είχε κρύψει το 1961, αλλά δεν µπορεί να την ανοίξει, επειδή έχει σκουριάσει. Όταν τελικά τα καταφέρνει, βρίσκει µέσα ένα παλιό κλειδί. Το κλειδί
4.4 Kreiszylinderschale und Kugelschale
 Flächentrgwerke - WS 05/06 4.4 Kreiszylinderschle und Kugelschle 4.4. Kreiszylinderschle 4.4.. Biegetheorie 4.4.. embrntheorie 4.4..3 Behältertheorie und Rndstörprobleme 4.4. Kugelschle 4.4.. Biegetheorie
Flächentrgwerke - WS 05/06 4.4 Kreiszylinderschle und Kugelschle 4.4. Kreiszylinderschle 4.4.. Biegetheorie 4.4.. embrntheorie 4.4..3 Behältertheorie und Rndstörprobleme 4.4. Kugelschle 4.4.. Biegetheorie
Dr. Christiane Döll Leiterin Luft & Lärm im Umweltamt
 Dr. Christiane Döll Leiterin Luft & Lärm im Umweltamt Dr. Christiane Döll Leiterin Luft & Lärm im Umweltamt Überflug 1.4.2013 05:05 Uhr BR Ost http://casper.umwelthaus.org/dfs/ Dr. Christiane Döll Leiterin
Dr. Christiane Döll Leiterin Luft & Lärm im Umweltamt Dr. Christiane Döll Leiterin Luft & Lärm im Umweltamt Überflug 1.4.2013 05:05 Uhr BR Ost http://casper.umwelthaus.org/dfs/ Dr. Christiane Döll Leiterin
Mission Berlin. Deutsch lernen und unterrichten Arbeitsmaterialien. Mission Berlin 16 Παλιοί γνωστοί
 16 Παλιοί γνωστοί Και το 1961 η Άννα καταδιώκεται από τους ένοπλους µοτοσικλετιστές. Σε αυτή την επικίνδυνη φάση τη βοηθά µια άγνωστη γυναίκα. Αλλά γιατί σπεύδει προς βοήθεια; Μπορεί η Άννα να την εµπιστευθεί;
16 Παλιοί γνωστοί Και το 1961 η Άννα καταδιώκεται από τους ένοπλους µοτοσικλετιστές. Σε αυτή την επικίνδυνη φάση τη βοηθά µια άγνωστη γυναίκα. Αλλά γιατί σπεύδει προς βοήθεια; Μπορεί η Άννα να την εµπιστευθεί;
DEUTSCHE SCHULE ATHEN ΓΕΡΜΑΝΙΚΗ ΣΧΟΛΗ ΑΘΗΝΩΝ
 Herzlich Willkommen zu unserem Elternabend Übergang aus dem Kindergarten in die Vorschule Καλωσορίσατε στη συνάντηση γονέων με θέμα τη μετάβαση από τον παιδικό σταθμό στο νηπιαγωγείο 1 Übergang vom Kindergarten
Herzlich Willkommen zu unserem Elternabend Übergang aus dem Kindergarten in die Vorschule Καλωσορίσατε στη συνάντηση γονέων με θέμα τη μετάβαση από τον παιδικό σταθμό στο νηπιαγωγείο 1 Übergang vom Kindergarten
Εμπορική αλληλογραφία Επιστολή
 - Διεύθυνση Mr. J. Rhodes Rhodes & Rhodes Corp. 212 Silverback Drive California Springs CA 92926 Mr. J. Rhodes Rhodes & Rhodes Corp. 212 Silverback Drive California Springs CA 92926 Αμερικανική γραφή διεύθυνσης:
- Διεύθυνση Mr. J. Rhodes Rhodes & Rhodes Corp. 212 Silverback Drive California Springs CA 92926 Mr. J. Rhodes Rhodes & Rhodes Corp. 212 Silverback Drive California Springs CA 92926 Αμερικανική γραφή διεύθυνσης:
Matrix Algorithms. Παρουσίαση στα πλαίσια του μαθήματος «Παράλληλοι. Αλγόριθμοι» Γ. Καούρη Β. Μήτσου
 Matrix Algorithms Παρουσίαση στα πλαίσια του μαθήματος «Παράλληλοι Αλγόριθμοι» Γ. Καούρη Β. Μήτσου Περιεχόμενα παρουσίασης Πολλαπλασιασμός πίνακα με διάνυσμα Πολλαπλασιασμός πινάκων Επίλυση τριγωνικού
Matrix Algorithms Παρουσίαση στα πλαίσια του μαθήματος «Παράλληλοι Αλγόριθμοι» Γ. Καούρη Β. Μήτσου Περιεχόμενα παρουσίασης Πολλαπλασιασμός πίνακα με διάνυσμα Πολλαπλασιασμός πινάκων Επίλυση τριγωνικού
Auswandern Dokumente Dokumente - Allgemeines Griechisch Koreanisch Dokumente - Persönliche Informationen
 - Allgemeines Πού μπορώ να βρω τη φόρμα για ; Fragen wo man ein Formular findet Πότε εκδόθηκε το [έγγραφο] σας; Fragen wann ein Dokument ausgestellt wurde Πού εκδόθηκε το [έγγραφο] σας; Fragen wo ein Dokument
- Allgemeines Πού μπορώ να βρω τη φόρμα για ; Fragen wo man ein Formular findet Πότε εκδόθηκε το [έγγραφο] σας; Fragen wann ein Dokument ausgestellt wurde Πού εκδόθηκε το [έγγραφο] σας; Fragen wo ein Dokument
22 είκοσι δύο. Κύπρος. Ελλάδα. Ελβετία. Αυστρία. Γερμανία. Από πού είσαι; Είμαι από τη Γερμανία. Εσύ; Από την Κύπρο. Από πού είσαι; Είμαι από
 3 τρί 1. μάθμα Wie heißen die Länder auf Griechisch? Bitte verbinden Sie die Namen mit den richtigen Zeichnungen. Hören Sie dann die Ländernamen und sprechen Sie sie nach. 1.18 Ελλάδα Αυστρία Κύπρος Ελβετία
3 τρί 1. μάθμα Wie heißen die Länder auf Griechisch? Bitte verbinden Sie die Namen mit den richtigen Zeichnungen. Hören Sie dann die Ländernamen und sprechen Sie sie nach. 1.18 Ελλάδα Αυστρία Κύπρος Ελβετία
Aspekte der speziellen Relativitätstheorie
 Aspekte der speziellen Relativitätstheorie Koordinaten x = (x µ ) = x 0 x 1 x 2 x 3 = ( t x ) Aspekte der speziellen Relativitätstheorie Koordinaten x = (x µ ) = x 0 x 1 x 2 x 3 Natürliche Einheiten c
Aspekte der speziellen Relativitätstheorie Koordinaten x = (x µ ) = x 0 x 1 x 2 x 3 = ( t x ) Aspekte der speziellen Relativitätstheorie Koordinaten x = (x µ ) = x 0 x 1 x 2 x 3 Natürliche Einheiten c
Α Ρ Ι Θ Μ Ο Σ : 6.913
 Α Ρ Ι Θ Μ Ο Σ : 6.913 ΠΡΑΞΗ ΚΑΤΑΘΕΣΗΣ ΟΡΩΝ ΔΙΑΓΩΝΙΣΜΟΥ Σ τ η ν Π ά τ ρ α σ ή μ ε ρ α σ τ ι ς δ ε κ α τ έ σ σ ε ρ ι ς ( 1 4 ) τ ο υ μ ή ν α Ο κ τ ω β ρ ί ο υ, η μ έ ρ α Τ ε τ ά ρ τ η, τ ο υ έ τ ο υ ς δ
Α Ρ Ι Θ Μ Ο Σ : 6.913 ΠΡΑΞΗ ΚΑΤΑΘΕΣΗΣ ΟΡΩΝ ΔΙΑΓΩΝΙΣΜΟΥ Σ τ η ν Π ά τ ρ α σ ή μ ε ρ α σ τ ι ς δ ε κ α τ έ σ σ ε ρ ι ς ( 1 4 ) τ ο υ μ ή ν α Ο κ τ ω β ρ ί ο υ, η μ έ ρ α Τ ε τ ά ρ τ η, τ ο υ έ τ ο υ ς δ
 v z cost(z, w) + cost(v, z) < cost(v, w) z v w < > < > v src seq src < src, seq src > w v < src, seq src > v < src, seq src > seq w (src) seq src src seq src > seq w (src) seqw src seq src w src
v z cost(z, w) + cost(v, z) < cost(v, w) z v w < > < > v src seq src < src, seq src > w v < src, seq src > v < src, seq src > seq w (src) seq src src seq src > seq w (src) seqw src seq src w src
English PDFsharp is a.net library for creating and processing PDF documents 'on the fly'. The library is completely written in C# and based
 English PDFsharp is a.net library for creating and processing PDF documents 'on the fly'. The library is completely written in C# and based exclusively on safe, managed code. PDFsharp offers two powerful
English PDFsharp is a.net library for creating and processing PDF documents 'on the fly'. The library is completely written in C# and based exclusively on safe, managed code. PDFsharp offers two powerful
FLASHBACK: Die Spieldose, aha? Sie ist kaputt. Kein Problem Anna, ich repariere sie dir.
 06 Η γυναίκα µε τα κόκκινα Η Άννα συναντά µια γυναίκα που ισχυρίζεται ότι ήταν φίλες το 1961. Κι εκτός αυτού η Άννα τα χάνει µε την πληροφορία ότι την κυνηγά µια γυναίκα ντυµένη στα κόκκινα. Σε κάθε γωνιά
06 Η γυναίκα µε τα κόκκινα Η Άννα συναντά µια γυναίκα που ισχυρίζεται ότι ήταν φίλες το 1961. Κι εκτός αυτού η Άννα τα χάνει µε την πληροφορία ότι την κυνηγά µια γυναίκα ντυµένη στα κόκκινα. Σε κάθε γωνιά
Mathematik. Note. Fußball. Müsli. Stadion
 Seite 5, Übung 1 Fußball Bus Schokolade Auto Stadion Socke Schuh Marmelade Automat Name Adresse Note Mathematik Seite 6, Übung a Auto Name Adresse Schuh Schokolade Mathematik Note Fußball Müsli Stadion
Seite 5, Übung 1 Fußball Bus Schokolade Auto Stadion Socke Schuh Marmelade Automat Name Adresse Note Mathematik Seite 6, Übung a Auto Name Adresse Schuh Schokolade Mathematik Note Fußball Müsli Stadion
English PDFsharp is a.net library for creating and processing PDF documents 'on the fly'. The library is completely written in C# and based
 English PDFsharp is a.net library for creating and processing PDF documents 'on the fly'. The library is completely written in C# and based exclusively on safe, managed code. PDFsharp offers two powerful
English PDFsharp is a.net library for creating and processing PDF documents 'on the fly'. The library is completely written in C# and based exclusively on safe, managed code. PDFsharp offers two powerful
Mission Berlin. Deutsch lernen und unterrichten Arbeitsmaterialien. Mission Berlin 22 Έλα τώρα, κουνήσου
 22 Έλα τώρα, κουνήσου Η Άννα µεταφέρεται στο Βερολίνο του έτους 1989, όπου κυριαρχεί ο ενθουσιασµός για την πτώση του Τείχους. Πρέπει να περάσει µέσα από το πλήθος και να πάρει τη θήκη. Θα τα καταφέρει;
22 Έλα τώρα, κουνήσου Η Άννα µεταφέρεται στο Βερολίνο του έτους 1989, όπου κυριαρχεί ο ενθουσιασµός για την πτώση του Τείχους. Πρέπει να περάσει µέσα από το πλήθος και να πάρει τη θήκη. Θα τα καταφέρει;
K r i t i k i P u b l i s h i n g - d r a f t
 T ij = A Y i Y j /D ij A T ij i j Y i i Y j j D ij T ij = A Y α Y b i j /D c ij b c b c a LW a LC L P F Q W Q C a LW Q W a LC Q C L a LC Q C + a LW Q W L P F L/a LC L/a LW 1.000/2 = 500
T ij = A Y i Y j /D ij A T ij i j Y i i Y j j D ij T ij = A Y α Y b i j /D c ij b c b c a LW a LC L P F Q W Q C a LW Q W a LC Q C L a LC Q C + a LW Q W L P F L/a LC L/a LW 1.000/2 = 500
ἀξιόω! στερέω! ψεύδομαι! συγγιγνώσκω!
 Assimilation νλ λλ νμ μμ νβ/νπ/νφ μβ/μπ/μφ νγ/νκ/νχ γγ/γκ/γχ attisches Futur bei Verben auf -ίζω: -ιῶ, -ιεῖς, -ιεῖ usw. Dehnungsaugment: ὠ- ὀ- ἠ- ἀ-/ἐ- Zur Vorbereitung die Stammveränderungs- und Grundformkarten
Assimilation νλ λλ νμ μμ νβ/νπ/νφ μβ/μπ/μφ νγ/νκ/νχ γγ/γκ/γχ attisches Futur bei Verben auf -ίζω: -ιῶ, -ιεῖς, -ιεῖ usw. Dehnungsaugment: ὠ- ὀ- ἠ- ἀ-/ἐ- Zur Vorbereitung die Stammveränderungs- und Grundformkarten
Griechisches Staatszertifikat - Deutsch
 ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΡΑΤΙΚΟ ΠΙΣΤΟΠΟΙΗΤΙΚΟ ΓΛΩΣΣΟΜΑΘΕΙΑΣ Griechisches Ministerium für Bildung und Religion Griechisches Staatszertifikat - Deutsch Niveau A1 & A2 Entspricht dem Gemeinsamen
ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΡΑΤΙΚΟ ΠΙΣΤΟΠΟΙΗΤΙΚΟ ΓΛΩΣΣΟΜΑΘΕΙΑΣ Griechisches Ministerium für Bildung und Religion Griechisches Staatszertifikat - Deutsch Niveau A1 & A2 Entspricht dem Gemeinsamen
EL Ενωµένη στην πολυµορφία EL A7-0109/298. Τροπολογία. Renate Sommer εξ ονόµατος της Οµάδας PPE
 9.6.2010 A7-0109/298 298 Άρθρο 33 παράγραφος 1 (1) Εκτός από τις µορφές έκφρασης που αναφέρονται στο άρθρο 31 παράγραφοι 2 και 3, η διατροφική δήλωση µπορεί να παρέχεται και µε άλλες µορφές έκφρασης, εφόσον
9.6.2010 A7-0109/298 298 Άρθρο 33 παράγραφος 1 (1) Εκτός από τις µορφές έκφρασης που αναφέρονται στο άρθρο 31 παράγραφοι 2 και 3, η διατροφική δήλωση µπορεί να παρέχεται και µε άλλες µορφές έκφρασης, εφόσον
PUBLIC 5587/18 ADD 1 1 DG G LIMITE EL. Συμβούλιο της Ευρωπαϊκής Ένωσης. Βρυξέλλες, 7 Φεβρουαρίου 2018 (OR. en)
 Conseil UE Συμβούλιο της Ευρωπαϊκής Ένωσης PUBLIC Βρυξέλλες, 7 Φεβρουαρίου 2018 (OR. en) 5587/18 ADD 1 LIMITE PV/CONS 2 ECOFIN 57 ΣΧΕΔΙΟ ΠΡΑΚΤΙΚΩΝ ΣΥΜΒΟΥΛΙΟ ΤΗΣ ΕΥΡΩΠΑΪΚΗΣ ΕΝΩΣΗΣ (Οικονομικά και Δημοσιονομικά
Conseil UE Συμβούλιο της Ευρωπαϊκής Ένωσης PUBLIC Βρυξέλλες, 7 Φεβρουαρίου 2018 (OR. en) 5587/18 ADD 1 LIMITE PV/CONS 2 ECOFIN 57 ΣΧΕΔΙΟ ΠΡΑΚΤΙΚΩΝ ΣΥΜΒΟΥΛΙΟ ΤΗΣ ΕΥΡΩΠΑΪΚΗΣ ΕΝΩΣΗΣ (Οικονομικά και Δημοσιονομικά
ibemo Kazakhstan Republic of Kazakhstan, West Kazakhstan Oblast, Aksai, Pramzone, BKKS office complex Phone: ; Fax:

Preiswerte Energiegewinnung - Polynomiale Eigenwertprobleme
 Preiswerte Energiegewinnung - Polynomiale Eigenwertprobleme Dominik Löchel Betreuer: M. Hochbruck und M. Tokar Graduiertenkolleg Dynamik heißer Plasmen Mathematisches Institut Heinrich-Heine-Universität
Preiswerte Energiegewinnung - Polynomiale Eigenwertprobleme Dominik Löchel Betreuer: M. Hochbruck und M. Tokar Graduiertenkolleg Dynamik heißer Plasmen Mathematisches Institut Heinrich-Heine-Universität
Ηλεκτρισμός 2ο μάθημα
 Μάθημα (τίτλος): Ένα κλειστό κύκλωμα Επίπεδο επάρκειας γλώσσας A1 A2 B1 B2 C1 Τάξη/βαθμίδα: 5η τάξη Αριθμός μαθητών στην τάξη: 11 Αντικείμενο: Φυσική Θέμα: Ηλεκτρισμός Προϋποθέσεις / απαιτήσεις: (π.χ.:
Μάθημα (τίτλος): Ένα κλειστό κύκλωμα Επίπεδο επάρκειας γλώσσας A1 A2 B1 B2 C1 Τάξη/βαθμίδα: 5η τάξη Αριθμός μαθητών στην τάξη: 11 Αντικείμενο: Φυσική Θέμα: Ηλεκτρισμός Προϋποθέσεις / απαιτήσεις: (π.χ.:
 . Zeit: Synoptische Betrachtung # αβ αα a) Allgemeine Abkürzungen Abkürzung Ausführung/Bedeutung AOGCM/GCM (atmosphärisch-ozeanisch gekoppeltes) globales Zirkulations-/Klimamodell (engl.: (atmosphere
. Zeit: Synoptische Betrachtung # αβ αα a) Allgemeine Abkürzungen Abkürzung Ausführung/Bedeutung AOGCM/GCM (atmosphärisch-ozeanisch gekoppeltes) globales Zirkulations-/Klimamodell (engl.: (atmosphere
FLOTT 1 - LEKTION 1. 1 η. S.13, Übungen 1, 2. 2 η ώρα S. 18, Das bin ich! Hausaufgaben: ΑΒ Übungen 3, 4 S. 13 Übungen S S. 19, Ηörverstehen 1
 FLOTT 1 Πλάνο διδασκαλίας* ιδασκαλία σε φροντιστήριο ή ιδιαίτερο µάθηµα : 4 ώρες την εβδοµάδα Σύνολο ωρών ετησίως κατά προσέγγιση: 120-130 (32 εβδοµάδες) Κάθε κεφάλαιο θα πρέπει να διδάσκεται σε συνολικά
FLOTT 1 Πλάνο διδασκαλίας* ιδασκαλία σε φροντιστήριο ή ιδιαίτερο µάθηµα : 4 ώρες την εβδοµάδα Σύνολο ωρών ετησίως κατά προσέγγιση: 120-130 (32 εβδοµάδες) Κάθε κεφάλαιο θα πρέπει να διδάσκεται σε συνολικά
FLASHBACK: Der Mechanismus ist nicht komplett, verstehst du? Es fehlt ein Teil. Seit neunzehnhunderteinundsechzig.
 12 Εκκλησιαστική µουσική Στην Άννα µένουν ακόµα 65 λεπτά. Στην εκκλησία ανακαλύπτει ότι το µουσικό κουτί είναι κοµµάτι που λείπει από το αρµόνιο. Η γυναίκα στα κόκκινα εµφανίζεται και ζητά από την Άννα
12 Εκκλησιαστική µουσική Στην Άννα µένουν ακόµα 65 λεπτά. Στην εκκλησία ανακαλύπτει ότι το µουσικό κουτί είναι κοµµάτι που λείπει από το αρµόνιο. Η γυναίκα στα κόκκινα εµφανίζεται και ζητά από την Άννα
Technisches Handbuch. Pergola Top Star 120X70. metaform Bescha ungssysteme
 02 Technisches Handbuch Pergola Top Star 120X70 Exklusiv von Metaform ΑVΕΕ entworfen, ist es die Innova on bei der professionellen Bescha ung, denn das wegweisende Hebesystem erlaubt es Ihnen, sie an jeder
02 Technisches Handbuch Pergola Top Star 120X70 Exklusiv von Metaform ΑVΕΕ entworfen, ist es die Innova on bei der professionellen Bescha ung, denn das wegweisende Hebesystem erlaubt es Ihnen, sie an jeder
Mission Berlin. Deutsch lernen und unterrichten Arbeitsmaterialien. Mission Berlin 01 Κακά ξυπνητούρια
 01 Κακά ξυπνητούρια Η αποστολή της Άννας είναι να σώσει τη Γερµανία από µια καταστροφή. Πρέπει να λύσει το αίνιγµα και να φυλάγεται από τους άγνωστους µε τα µηχανάκια. Της αποµένουν 130 λεπτά. Αλλά ποιό
01 Κακά ξυπνητούρια Η αποστολή της Άννας είναι να σώσει τη Γερµανία από µια καταστροφή. Πρέπει να λύσει το αίνιγµα και να φυλάγεται από τους άγνωστους µε τα µηχανάκια. Της αποµένουν 130 λεπτά. Αλλά ποιό
Präpositionen ΠΡΟΣ (Ερώτηση με wohin?) nach προς (χώρα χωρίς άρθρο, πόλη, ήπειρο) προς (τοπικό επίρρημα)
 Präpositionen ΠΡΟΣ (Ερώτηση με wohin?) nach προς (χώρα χωρίς άρθρο, πόλη, ήπειρο) Im Sommer fahre ich nach Deutschland, nach Berlin προς (τοπικό επίρρημα) Ich gehe nach oben zu (zum, zur) προς (πρόσωπο,
Präpositionen ΠΡΟΣ (Ερώτηση με wohin?) nach προς (χώρα χωρίς άρθρο, πόλη, ήπειρο) Im Sommer fahre ich nach Deutschland, nach Berlin προς (τοπικό επίρρημα) Ich gehe nach oben zu (zum, zur) προς (πρόσωπο,
ΔΙΔΑΚΤΙΚΑ ΒΙΒΛΙΑ. Klassen 9A/9B/9C Γ' Γυμνασίου Σχολικό έτος 2016/2017
 Klassen 9A/9B/9C Γ' Γυμνασίου DEUTSCH/ Klett Verlag, Mittelpunkt B2 Neu Lehrbuch 978-3-12-676652-4 Arbeitsbuch mit CD 978-3-12-676653-1 Griechisches Glossar 978-960-6891-84-7 Verlag Hueber ENGLISCH / Kurs
Klassen 9A/9B/9C Γ' Γυμνασίου DEUTSCH/ Klett Verlag, Mittelpunkt B2 Neu Lehrbuch 978-3-12-676652-4 Arbeitsbuch mit CD 978-3-12-676653-1 Griechisches Glossar 978-960-6891-84-7 Verlag Hueber ENGLISCH / Kurs
