PFSB* Development and Validation of an MHD Code for Study of Argon plasma Flow Characteristics in the PFSB Thruster

C 1 D 1. AB = a, AD = b, AA1 = c. a, b, c : (1) AC 1 ; : (1) AB + BC + CC1, AC 1 = BC = AD, CC1 = AA 1, AC 1 = a + b + c. (2) BD 1 = BD + DD 1,

1 1., BD 1 B 1 1 D 1, E F B 1 D 1. B = a, D = b, 1 = c. a, b, c : (1) 1 ; () BD 1 ; () F; D 1 F 1 (4) EF. : (1) B = D, D c b 1 E a B 1 1 = 1, B1 1 = B + B + 1, 1 = a + b + c. () BD 1 = BD + DD 1, BD =

19. ATOMS, MOLECULES AND NUCLEI HOMEWORK SOLUTIONS

. ATOMS, MOLECULES AND NUCLEI HOMEWORK SOLUTIONS. Givn :.53 Å 3?? n n ε πm n n Radius of n t Bo obit, n n ε πm n n 3 n 3 n 3 (3) () (.53).77Å n n ( ) () (.53) 53 Å. Givn : 3 7.7 x m? n n ε πm Radius of

Το άτομο του Υδρογόνου

Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες

Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού.

Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού. Περιοδικός πίνακας: α. Είναι µια ταξινόµηση των στοιχείων κατά αύξοντα

Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α

Α Ρ Χ Α Ι Α Ι Σ Τ Ο Ρ Ι Α Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α Σ η µ ε ί ω σ η : σ υ ν ά δ ε λ φ ο ι, ν α µ ο υ σ υ γ χ ω ρ ή σ ε τ ε τ ο γ ρ ή γ ο ρ ο κ α ι α τ η µ έ λ η τ ο ύ

Αλληλεπίδραση ακτίνων-χ με την ύλη

Άσκηση 8 Αλληλεπίδραση ακτίνων-χ με την ύλη Δ. Φ. Αναγνωστόπουλος Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων Ιωάννινα 2013 Άσκηση 8 ii Αλληλεπίδραση ακτίνων-χ με την ύλη Πίνακας περιεχομένων

Accelerator Physics Synchrotron Radiation. A. Bogacz, G. A. Krafft, and T. Zolkin Jefferson Lab Colorado State University Lecture 8

Acclato Physics Synchoton Radiation A. Bogacz, G. A. Kafft, and T. Zolkin Jffson Lab Coloado Stat Univsity Lctu 8 USPAS Acclato Physics Jun 13 Synchoton Radiation Acclatd paticls mit lctomagntic adiation.

Sheet H d-2 3D Pythagoras - Answers

1. 1.4cm 1.6cm 5cm 1cm. 5cm 1cm IGCSE Higher Sheet H7-1 4-08d-1 D Pythagoras - Answers. (i) 10.8cm (ii) 9.85cm 11.5cm 4. 7.81m 19.6m 19.0m 1. 90m 40m. 10cm 11.cm. 70.7m 4. 8.6km 5. 1600m 6. 85m 7. 6cm

DETERMINATION OF DYNAMIC CHARACTERISTICS OF A 2DOF SYSTEM. by Zoran VARGA, Ms.C.E.

DETERMINATION OF DYNAMIC CHARACTERISTICS OF A 2DOF SYSTEM by Zoran VARGA, Ms.C.E. Euro-Apex B.V. 1990-2012 All Rights Reserved. The 2 DOF System Symbols m 1 =3m [kg] m 2 =8m m=10 [kg] l=2 [m] E=210000

Appendix to On the stability of a compressible axisymmetric rotating flow in a pipe. By Z. Rusak & J. H. Lee

Appendi to On the stability of a compressible aisymmetric rotating flow in a pipe By Z. Rusak & J. H. Lee Journal of Fluid Mechanics, vol. 5 4, pp. 5 4 This material has not been copy-edited or typeset

ΓΗ ΚΑΙ ΣΥΜΠΑΝ. Εικόνα 1. Φωτογραφία του γαλαξία μας (από αρχείο της NASA)

ΓΗ ΚΑΙ ΣΥΜΠΑΝ Φύση του σύμπαντος Η γη είναι μία μονάδα μέσα στο ηλιακό μας σύστημα, το οποίο αποτελείται από τον ήλιο, τους πλανήτες μαζί με τους δορυφόρους τους, τους κομήτες, τα αστεροειδή και τους μετεωρίτες.

Estimation of grain boundary segregation enthalpy and its role in stable nanocrystalline alloy design

Supplemental Material for Estimation of grain boundary segregation enthalpy and its role in stable nanocrystalline alloy design By H. A. Murdoch and C.A. Schuh Miedema model RKM model ΔH mix ΔH seg ΔH

SUPPLEMENTAL INFORMATION. Fully Automated Total Metals and Chromium Speciation Single Platform Introduction System for ICP-MS

Electronic Supplementary Material (ESI) for Journal of Analytical Atomic Spectrometry. This journal is The Royal Society of Chemistry 2018 SUPPLEMENTAL INFORMATION Fully Automated Total Metals and Chromium

ΝΟΜΟΣ ΤΗΣ ΠΕΡΙΟ ΙΚΟΤΗΤΑΣ : Οι ιδιότητες των χηµικών στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού.

1. Ο ΠΕΡΙΟ ΙΚΟΣ ΠΙΝΑΚΑΣ Οι άνθρωποι από την φύση τους θέλουν να πετυχαίνουν σπουδαία αποτελέσµατα καταναλώνοντας το λιγότερο δυνατό κόπο και χρόνο. Για το σκοπό αυτό προσπαθούν να οµαδοποιούν τα πράγµατα

!"#!$% &' ( )*+*,% $ &$ -.&01#(2$#3 4-$ #35667

!"#!$% & &' ( )*+*,% $ -*(-$ -.*/% $- &$ -.&01#(2$#3 4-$ #35667 5051 & 00000000000000000000000000000000000000000000000000000000000000000000000000000 9 508&:;&& 0000000000000000000000000000000000000000000000000

Example 1: THE ELECTRIC DIPOLE

Example 1: THE ELECTRIC DIPOLE 1 The Electic Dipole: z + P + θ d _ Φ = Q 4πε + Q = Q 4πε 4πε 1 + 1 2 The Electic Dipole: d + _ z + Law of Cosines: θ A B α C A 2 = B 2 + C 2 2ABcosα P ± = 2 ( + d ) 2 2

Chapter 1 Fundamentals in Elasticity

D. of o. NU Fs s ν ss L. Pof. H L ://s.s.. D. of o. NU. Po Dfo ν Ps s - Do o - M os - o oos : o o w Uows o: - ss - - Ds W ows s o qos o so s os. w ows o fo s o oos s os of o os. W w o s s ss: - ss - -

Chapter 4 : Linear Wire Antenna

Chapt 4 : Lina Wi Antnna nfinitsima Dipo Sma Dipo Finit Lngth Dipo Haf-Wavngth Dipo Lina mnts na o on nfinit Pfct Conductos nfinitsima Dipo Lngth

Ι ΙΟΤΗΤΕΣ ΤΩΝ ΑΤΟΜΩΝ. Παππάς Χρήστος Επίκουρος Καθηγητής

ΗΛΕΚΤΡΟΝΙΚΗ ΟΜΗ ΚΑΙ Ι ΙΟΤΗΤΕΣ ΤΩΝ ΑΤΟΜΩΝ Παππάς Χρήστος Επίκουρος Καθηγητής ΤΟ ΜΕΓΕΘΟΣ ΤΩΝ ΑΤΟΜΩΝ Ατομική ακτίνα (r) : ½ της απόστασης μεταξύ δύο ομοιοπυρηνικών ατόμων, ενωμένων με απλό ομοιοπολικό δεσμό.

Lecture 31. Wire Antennas. Generation of radiation by real wire antennas

Lctu 31 Wi Antnnas n this lctu yu will lan: Gnatin f aiatin by al wi antnnas Sht ipl antnnas Half-wav ipl antnnas Th-half-wav ipl antnnas Small wi lp antnnas magntic ipl antnnas ECE 303 Fall 006 Fahan

ΠΕΡΙΟΔΙΚΟ ΣΥΣΤΗΜΑ ΤΩΝ ΣΤΟΙΧΕΙΩΝ (1) Ηλία Σκαλτσά ΠΕ ο Γυμνάσιο Αγ. Παρασκευής

ΠΕΡΙΟΔΙΚΟ ΣΥΣΤΗΜΑ ΤΩΝ ΣΤΟΙΧΕΙΩΝ (1) Ηλία Σκαλτσά ΠΕ04.01 5 ο Γυμνάσιο Αγ. Παρασκευής Όπως συμβαίνει στη φύση έτσι και ο άνθρωπος θέλει να πετυχαίνει σπουδαία αποτελέσματα καταναλώνοντας το λιγότερο δυνατό

ΠΕΡΙΟΔΙΚΟΣ ΠΙΝΑΚΑΣ ΣΤΟΙΧΕΙΩΝ

ΠΕΡΙΟΔΙΚΟΣ ΠΙΝΑΚΑΣ ΣΤΟΙΧΕΙΩΝ Περίοδοι περιοδικού πίνακα Ο περιοδικός πίνακας αποτελείται από 7 περιόδους. Ο αριθμός των στοιχείων που περιλαμβάνει κάθε περίοδος δεν είναι σταθερός, δηλ. η περιοδικότητα

C M. V n: n =, (D): V 0,M : V M P = ρ ρ V V. = ρ

»»...» -300-0 () -300-03 () -3300 3.. 008 4 54. 4. 5 :.. ;.. «....... :. : 008. 37.. :....... 008.. :. :.... 54. 4. 5 5 6 ... : : 3 V mnu V mn AU 3 m () ; N (); N A 6030 3 ; ( ); V 3. : () 0 () 0 3 ()

W τ R W j N H = 2 F obj b q N F aug F obj b q Ψ F aug Ψ ( ) ϱ t + + p = 0 = 0 Ω f = Γ Γ b ϱ = (, t) = (, t) Ω f Γ b ( ) ϱ t + + p = V max 4 3 2 1 0-1 -2-3 -4-4 -3-2 -1 0 1 2 3 4 x 4 x 1 V mn V max

ECE 222b Applied Electromagnetics Notes Set 3a

C b lid lcomagnics Nos S 3a Insuco: Pof. Viali Lomakin Damn of lcical and Comu ngining Univsi of Califonia San Digo Unifom Plan Wavs Consid Mawll s quaions: In a losslss mdium ε and µ a al and σ : Sinc

!"!# ""$ %%"" %$" &" %" "!'! " #$!

" "" %%"" %" &" %" " " " % ((((( ((( ((((( " %%%% & ) * ((( "* ( + ) (((( (, (() (((((* ( - )((((( )((((((& + )(((((((((( +. ) ) /(((( +( ),(, ((((((( +, 0 )/ (((((+ ++, ((((() & "( %%%%%%%%%%%%%%%%%%%(

Radiation Stress Concerned with the force (or momentum flux) exerted on the right hand side of a plane by water on the left hand side of the plane.

upplement on Radiation tress and Wave etup/et down Radiation tress oncerned wit te force (or momentum flu) eerted on te rit and side of a plane water on te left and side of te plane. plane z "Radiation

, Snowdon. . Frahm.

- :..... ( ). :., Snowdon.. Frohrib Jennige -.[ ]...[ ] Ghannadi-Asl Zahrai..,.[ ]... Frahm Frahm [ ] Den Hartog. mzahrai@ut.ac.ir, hashemif@conwag.com . - Den Hartog g(t)=0 ω f(t)=p 0 sinωt. ω y st =P

Matrices and Determinants

Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z

Parts Manual. Trio Mobile Surgery Platform. Model 1033

Trio Mobile Surgery Platform Model 1033 Parts Manual For parts or technical assistance: Pour pièces de service ou assistance technique : Für Teile oder technische Unterstützung Anruf: Voor delen of technische

Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Σχολή Θετικών Επιστημών Τμήμα Φυσικής Τομέας Θεωρητικής Φυσικής

Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Σχολή Θετικών Επιστημών Τμήμα Φυσικής Τομέας Θεωρητικής Φυσικής Τραϊανού Θάλεια, Χανλαρίδης Σάββας Επιβλέπων καθηγητής: Λαλαζήσης Γεώργιος Πυρηνική Αστροφυσική: Μία

.. ntsets ofa.. d ffeom.. orp ism.. na s.. m ooth.. man iod period I n open square. n t s e t s ofa \quad d ffeom \quad orp ism \quad na s \quad m o

G G - - -- - W - - - R S - q k RS ˆ W q q k M G W R S L [ RS - q k M S 4 R q k S [ RS [ M L ˆ L [M O S 4] L ˆ ˆ L ˆ [ M ˆ S 4 ] ˆ - O - ˆ q k ˆ RS q k q k M - j [ RS ] [ M - j - L ˆ ˆ ˆ O ˆ [ RS ] [ M

Α Ρ Ι Θ Μ Ο Σ : 6.913

Α Ρ Ι Θ Μ Ο Σ : 6.913 ΠΡΑΞΗ ΚΑΤΑΘΕΣΗΣ ΟΡΩΝ ΔΙΑΓΩΝΙΣΜΟΥ Σ τ η ν Π ά τ ρ α σ ή μ ε ρ α σ τ ι ς δ ε κ α τ έ σ σ ε ρ ι ς ( 1 4 ) τ ο υ μ ή ν α Ο κ τ ω β ρ ί ο υ, η μ έ ρ α Τ ε τ ά ρ τ η, τ ο υ έ τ ο υ ς δ

P Œ ²μ, Œ.. ƒê Éμ,. ƒ. ²μ,.. μ. ˆ ˆŸ Œˆ ˆŸ ˆ Š Œ ˆŸ Ÿ - ˆ ˆ ŠˆŒˆ Œ Œˆ ˆ œ ˆ Œ ˆ ŒˆŠ Œ -25

P6-2011-64.. Œ ²μ, Œ.. ƒê Éμ,. ƒ. ²μ,.. μ ˆ ˆŸ Œˆ ˆŸ ˆ Š Œ ˆŸ Ÿ - ˆ ˆ ŠˆŒˆ Œ Œˆ ˆ œ ˆ Œ ˆ ŒˆŠ Œ -25 Œ ²μ... P6-2011-64 ² μ Ö ²Õ³ Ö ± ³ Ö μ Í Ì μ Ò Ö μ-ë Î ± ³ ³ Éμ ³ μ²ó μ ³ ³ ± μé μ Œ -25 μ³μðóõ Ö μ-ë

GEEPLUS VM1614. Force (N) vs Displacement (mm) Peak. Max 'ON' time. Force. Model No. VM

VM1614 2 VM1614 18 VM1614 125 VM1614 1 GEEPLUS VM1614 P 1 is the continuous (1% ED) excitation power at mounted to a massive heatsink at 2 C P 1 5 W Total Mass 15 g T max 13 C Coil Mass 3 g R 2 2.8.2 mh.7

ΠΟΣΟΤΙΚΕΣ ΜΕΘΟΔΟΙ ΔΕΟ 13 ΤΟΜΟΣ Δ ΣΤΑΤΙΣΤΙΚΗ ΓΙΑ ΤΗ ΔΙΟΙΚΗΣΗ ΕΠΙΧΕΙΡΗΣΕΩΝ

ΠΟΣΟΤΙΚΕΣ ΜΕΘΟΔΟΙ ΔΕΟ 13 ΤΟΜΟΣ Δ ΣΤΑΤΙΣΤΙΚΗ ΓΙΑ ΤΗ ΔΙΟΙΚΗΣΗ ΕΠΙΧΕΙΡΗΣΕΩΝ (5) ΑΘΗΝΑ ΜΑΡΤΙΟΣ 2013 1 ΕΠΕΞΗΓΗΣΗ ΤΥΠΩΝ ΚΑΙ ΣΥΜΒΟΛΩΝ ΣΤΑΤΙΣΤΙΚΗΣ ΚΑΤΑΝΟΜΕΣ Τυχαία μεταβλητή είναι μία συνάρτηση η οποία να αντιστοιχεί

Space Physics (I) [AP-3044] Lecture 1 by Ling-Hsiao Lyu Oct Lecture 1. Dipole Magnetic Field and Equations of Magnetic Field Lines

Space Physics (I) [AP-344] Lectue by Ling-Hsiao Lyu Oct. 2 Lectue. Dipole Magnetic Field and Equations of Magnetic Field Lines.. Dipole Magnetic Field Since = we can define = A (.) whee A is called the

!"#$ % &# &%#'()(! $ * +

,!"#$ % &# &%#'()(! $ * + ,!"#$ % &# &%#'()(! $ * + 6 7 57 : - - / :!", # $ % & :'!(), 5 ( -, * + :! ",, # $ %, ) #, '(#,!# $$,',#-, 4 "- /,#-," -$ '# &",,#- "-&)'#45)')6 5! 6 5 4 "- /,#-7 ",',8##! -#9,!"))

Chapter 22 - Heat Engines, Entropy, and the Second Law of Thermodynamics

apter - Heat Engines, Entropy, and te Seond Law o ermodynamis.1 (a).0 J e 0.069 4 or 6.94% 60 J (b) 60 J.0 J J. e eat to melt 1.0 g o Hg is 4 ml 1 10 kg 1.18 10 J kg 177 J e energy absorbed to reeze 1.00

Monolithic Crystal Filters (M.C.F.)

Monolithic Crystal Filters (M.C.F.) MCF (MONOLITHIC CRYSTAL FILTER) features high quality quartz resonators such as sharp cutoff characteristics, low loss, good inter-modulation and high stability over

No No No No No.5. No

0-1 0-2 0-3 0-4 No. 1 1-1 No.2 2-1 No.3 3-1 No.4 4-1 No.5 No.30 30-1 Tokyo) (m) (cm) /ha 1 1062 101 36 58 48 / 139 19 44 1631 3095 375 10.1 ( 1,380 11 N80E dbd 9/17 8/27 2 1062 101 36 58 43 / 139 19 06

Note: Please use the actual date you accessed this material in your citation.

MIT OpeCueWae hp://cw.m.eu 6.13/ESD.13J Elecmagec a pplca, Fall 5 Pleae ue he llwg ca ma: Maku Zah, Ech Ippe, a Dav Sael, 6.13/ESD.13J Elecmagec a pplca, Fall 5. (Maachue Iue Techlgy: MIT OpeCueWae). hp://cw.m.eu

!!" #7 $39 %" (07) ..,..,.. $ 39. ) :. :, «(», «%», «%», «%» «%». & ,. ). & :..,. '.. ( () #*. );..,..'. + (# ).

1 00 3 !!" 344#7 $39 %" 6181001 63(07) & : ' ( () #* ); ' + (# ) $ 39 ) : : 00 %" 6181001 63(07)!!" 344#7 «(» «%» «%» «%» «%» & ) 4 )&-%/0 +- «)» * «1» «1» «)» ) «(» «%» «%» + ) 30 «%» «%» )1+ / + : +3

2. Α ν ά λ υ σ η Π ε ρ ι ο χ ή ς. 3. Α π α ι τ ή σ ε ι ς Ε ρ γ ο δ ό τ η. 4. Τ υ π ο λ ο γ ί α κ τ ι ρ ί ω ν. 5. Π ρ ό τ α σ η. 6.

Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α 1. Ε ι σ α γ ω γ ή 2. Α ν ά λ υ σ η Π ε ρ ι ο χ ή ς 3. Α π α ι τ ή σ ε ι ς Ε ρ γ ο δ ό τ η 4. Τ υ π ο λ ο γ ί α κ τ ι ρ ί ω ν 5. Π ρ ό τ α σ η 6. Τ ο γ ρ α φ ε ί ο 1. Ε ι σ α γ ω

Z L L L N b d g 5 * " # $ % $ ' $ % % % ) * + *, - %. / / + 3 / / / / + * 4 / / 1 " 5 % / 6, 7 # * $ 8 2. / / % 1 9 ; < ; = ; ; >? 8 3 " #

Z L L L N b d g 5 * " # $ % $ ' $ % % % ) * + *, - %. / 0 1 2 / + 3 / / 1 2 3 / / + * 4 / / 1 " 5 % / 6, 7 # * $ 8 2. / / % 1 9 ; < ; = ; ; >? 8 3 " # $ % $ ' $ % ) * % @ + * 1 A B C D E D F 9 O O D H

Lifting Entry (continued)

ifting Entry (continued) Basic planar dynamics of motion, again Yet another equilibrium glide Hypersonic phugoid motion Planar state equations MARYAN 1 01 avid. Akin - All rights reserved http://spacecraft.ssl.umd.edu

P Ò±,. Ï ± ˆ ˆŒˆ Š ƒ ˆŸ. Œ ƒ Œ ˆˆ γ-š Œˆ ƒ ƒˆ 23 ŒÔ. ² μ Ê ². Í μ ²Ó Ò Í É Ö ÒÌ ² μ, É μí±, μ²óï

P15-2012-75.. Ò±,. Ï ± ˆ Œ ˆŸ ˆ, š Œ ˆ ˆŒˆ Š ƒ ˆŸ ˆ ˆ, Œ ƒ Œ ˆˆ γ-š Œˆ ƒ ƒˆ 23 ŒÔ ² μ Ê ² Í μ ²Ó Ò Í É Ö ÒÌ ² μ, É μí±, μ²óï Ò±.., Ï ±. P15-2012-75 ˆ ³ Ö μ Ì μ É, μ Ñ ³ ÒÌ μ É Ì ³ Î ±μ μ μ É μ Íμ Ö ÕÐ

STANDARD LED LAMPS (ROUND TYPES)

Package 3 3 3 1.0 Lead High 3.4 Part No. Chip Material/Emitted Color Wave Length p Lens Appearance Absolute Maximum Ratings Pd (mw) If Electro-optical Data (At ma) Vf (V) Iv (mcd) Typ Max Typ. BL-B4541

a,b a f a = , , r = = r = T

!" #$%" &' &$%( % ) *+, -./01/ 234 5 0462. 4-7 8 74-9:;:; < =>?@ABC>D E E F GF F H I E JKI L H F I F HMN E O HPQH I RE F S TH FH I U Q E VF E WXY=Z M [ PQ \ TE K JMEPQ EEH I VF F E F GF ]EEI FHPQ HI E

Eulerian Simulation of Large Deformations

Eulerian Simulation of Large Deformations Shayan Hoshyari April, 2018 Some Applications 1 Biomechanical Engineering 2 / 11 Some Applications 1 Biomechanical Engineering 2 Muscle Animation 2 / 11 Some Applications

Wb/ Μ. /Α Ua-, / / Βζ * / 3.3. Ηλεκτρομαγνητισμός Ι Μ. 1. Β = k. 3. α) Β = Κ μ Π 2. B-r, 2 10~ ~ 2 α => I = ~ } Α k M I = 20Α

ΛΥΣΗ ΠΡΟΒΛΗΜΑΤΩΝ 3.3 39 3.3. Ηλεκτρομαγνητισμός 1. Β = k 21 9 1Π 2 β = 10 " ίιτκ τ^β = 2 10 " τ 3. α) Β = Κ μ 21 B-r, 2 10~ 5 20 10~ 2 α => I = ~ } Α k M -2 2-10 I = 20Α ϊ)β 2 2Ι = Κ ψ- _ 10' 10^40 7 2

Prey-Taxis Holling-Tanner

Vol. 28 ( 2018 ) No. 1 J. of Math. (PRC) Prey-Taxis Holling-Tanner, (, 730070) : prey-taxis Holling-Tanner.,,.. : Holling-Tanner ; prey-taxis; ; MR(2010) : 35B32; 35B36 : O175.26 : A : 0255-7797(2018)01-0140-07

τροχιακά Η στιβάδα καθορίζεται από τον κύριο κβαντικό αριθµό (n) Η υποστιβάδα καθορίζεται από τους δύο πρώτους κβαντικούς αριθµούς (n, l)

ΑΤΟΜΙΚΑ ΤΡΟΧΙΑΚΑ Σχέση κβαντικών αριθµών µε στιβάδες υποστιβάδες - τροχιακά Η στιβάδα καθορίζεται από τον κύριο κβαντικό αριθµό (n) Η υποστιβάδα καθορίζεται από τους δύο πρώτους κβαντικούς αριθµούς (n,

P ² ± μ. œ Š ƒ Š Ÿƒ ˆŸ Œ œ Œ ƒˆ. μ²μ μ Œ Ê μ μ ±μ Ë Í μ É Í ±μ ³μ²μ (RUSGRAV-13), Œμ ±, Õ Ó 2008.

P3-2009-104.. ² ± μ ˆ ˆ Š Š ˆ œ Š ƒ Š Ÿƒ ˆŸ Œ œ Œ ƒˆ μ²μ μ Œ Ê μ μ ±μ Ë Í μ É Í ±μ ³μ²μ (RUSGRAV-13), Œμ ±, Õ Ó 2008. ² ± μ.. ²μ μ ± μé±²μ μé ÓÕÉμ μ ±μ μ ±μ ÉÖ μé Ö μ³μðóõ É μ μ ³ ²ÒÌ Ô P3-2009-104 ÓÕÉμ

ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΚΡΗΤΗΣ ΤΜΗΜΑ ΦΥΣΙΚΩΝ ΠΟΡΩΝ & ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΤΟΜΕΑΣ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΕΛΕΓΧΟΥ ΠΟΙΟΤΗΤΑΣ Υ ΑΤΙΚΩΝ & Ε ΑΦΙΚΩΝ ΠΟΡΩΝ ΕΠΙΒΑΡΥΝΣΗ ΜΕ ΒΑΡΕΑ ΜΕΤΑΛΛΑ Ε ΑΦΩΝ ΤΗΣ

Lifting Entry 2. Basic planar dynamics of motion, again Yet another equilibrium glide Hypersonic phugoid motion MARYLAND U N I V E R S I T Y O F

ifting Entry Basic planar dynamics of motion, again Yet another equilibrium glide Hypersonic phugoid motion MARYAN 1 010 avid. Akin - All rights reserved http://spacecraft.ssl.umd.edu ifting Atmospheric

APPENDIX I PITTSBURGH NO. 8 WASHABILITY DATA AND RECOVERY- CURVES

APPENDIX I PITTSBURGH NO. 8 WASHABILITY DATA AND RECOVERY- CURVES Seam: Pittsburgh No. 8 Sample: Run-of-Mine Feed Class: 5 x 1 mm Mass (%): 56.26 Individual Sink Float Mass Ash Sulfur Pyritic Heat SG SG

Ó³ Ÿ , º 3(194).. 673Ä677. Š Œ œ ƒˆˆ ˆ ˆŠ. ˆ.. ³ Ì μ, ƒ.. Š ³ÒÏ,ˆ..Š Ö, Ÿ. ʲ ±μ ±

Ó³ Ÿ. 2015.. 12, º 3(194.. 673Ä677 Š Œ œ ƒˆˆ ˆ ˆŠ ˆŸ ˆ Šˆ ˆ ˆ Œ ˆŠ ˆ.. ³ Ì μ, ƒ.. Š ³ÒÏ,ˆ..Š Ö, Ÿ. ʲ ±μ ± Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê ˆ É ÉÊÉ Ö μ Ë ± μ²ó ±μ ± ³ ʱ, Š ±μ, μ²óï μé É ² Ò Ê Ö Ö Î ² Ò Ê²ÓÉ ÉÒ,

Ó³ Ÿ , º 2(131).. 105Ä ƒ. ± Ï,.. ÊÉ ±μ,.. Šμ ² ±μ,.. Œ Ì ²μ. Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê

Ó³ Ÿ. 2006.. 3, º 2(131).. 105Ä110 Š 537.311.5; 538.945 Œ ƒ ˆ ƒ Ÿ ˆŠ ˆ ƒ Ÿ ƒ ˆ œ ƒ Œ ƒ ˆ ˆ Š ˆ 4 ². ƒ. ± Ï,.. ÊÉ ±μ,.. Šμ ² ±μ,.. Œ Ì ²μ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê ³ É É Ö μ ² ³ μ É ³ Í ² Ö Ê³ μ μ ³ É μ μ μ²ö

(... )..!, ".. (! ) # - $ % % $ & % 2007

(! ), "! ( ) # $ % & % $ % 007 500 ' 67905:5394!33 : (! ) $, -, * +,'; ), -, *! ' - " #!, $ & % $ ( % %): /!, " ; - : - +', 007 5 ISBN 978-5-7596-0766-3 % % - $, $ &- % $ % %, * $ % - % % # $ $,, % % #-

16 Electromagnetic induction

Chatr : Elctromagntic Induction Elctromagntic induction Hint to Problm for Practic., 0 d φ or dφ 0 0.0 Wb. A cm cm 7 0 m, A 0 cm 0 cm 00 0 m B 0.8 Wb/m, B. Wb/m,, dφ d BA (B.A) BA 0.8 7 0. 00 0 80 0 8

ITU-R P (2012/02)

ITU-R P.56- (0/0 P ITU-R P.56- ii.. (IPR (ITU-T/ITU-R/ISO/IEC.ITU-R ttp://www.itu.int/itu-r/go/patents/en. (ttp://www.itu.int/publ/r-rec/en ( ( BO BR BS BT F M P RA RS S SA SF SM SNG TF V 0.ITU-R ITU 0..(ITU

Gapso t e q u t e n t a g ebra P open parenthesis N closing parenthesis fin i s a.. pheno mno nd iscovere \ centerline

G q v v G q v H 4 q 4 q v v ˆ ˆ H 4 ] 4 ˆ ] W q K j q G q K v v W v v H 4 z ] q 4 K ˆ 8 q ˆ j ˆ O C W K j ˆ [ K v ˆ [ [; 8 ] q ˆ K O C v ˆ ˆ z q [ R ; ˆ 8 ] R [ q v O C ˆ ˆ v - - ˆ - ˆ - v - q - - v -

Gradient Descent for Optimization Problems With Sparse Solutions

Gradient Descent for Optimization Problems With Sparse Solutions The Harvard community has made this article openly available. Please share how this access benefits you. Your story matters Citation Chen,

Jeux d inondation dans les graphes

Jeux d inondation dans les graphes Aurélie Lagoutte To cite this version: Aurélie Lagoutte. Jeux d inondation dans les graphes. 2010. HAL Id: hal-00509488 https://hal.archives-ouvertes.fr/hal-00509488

Answers to practice exercises

Answers to practice exercises Chapter Exercise (Page 5). 9 kg 2. 479 mm. 66 4. 565 5. 225 6. 26 7. 07,70 8. 4 9. 487 0. 70872. $5, Exercise 2 (Page 6). (a) 468 (b) 868 2. (a) 827 (b) 458. (a) 86 kg (b)

Θερ ικοί Αισθητήρες. Α. Πετρόπουλος - Τεχνολογία των αισθητήρων. 2011. Θερμικοί αισθητήρες. 1. Αισθητήρας Μέτρησης Ροής

Θερ ικοί Αισθητήρες Α. Πετρόπουλος - Τεχνολογία των αισθητήρων. 011 Θερμικοί αισθητήρες 1. Αισθητήρας Μέτρησης Ροής Θερ ικοί Αισθητήρες Α. Πετρόπουλος - Τεχνολογία των αισθητήρων. 011 Συγκεντρωτικά Εφαρμογές

! " #! $ %&! '( #)!' * +#, " -! %&! "!! ! " #$ % # " &' &'... ()* ( +, # ' -. + &', - + &' / # ' -. + &' (, % # , 2**.

! " #! $ %&! '( #)!' * +#, " -! %&! "!!! " #$ % # " &' &'... ()* ( +, # ' -. + &', - + &' / 0123 4 # ' -. + &' (, % #. -5 0126, 2**., 2, + &' %., 0, $!, 3,. 7 8 ', $$, 9, # / 3:*,*2;

means ) ( )- 4 ) ;2 2 , < =- >?6 2 AB )4 AB ) $17,495,00 IJ 0'7 (3- &' ( - KK9 ( ()G ( <). ('2) 100% )7 )!

ارائه شده توسط: سايت ه فا مرجع جديد مقا ت ه شده از ن ت معت K- : means (+ $% &' ( *'.#! ( (.. ( /.0 # 1' 2 1 ('3-2 15 06 7. 8 ( - 4 0 ;2 2 : ('2 9 2.2.# @ < =- >?6 5 ('2 &' / ( 100 m4- xlarge Amazon EC2

Analytical Expression for Hessian

Analytical Expession fo Hessian We deive the expession of Hessian fo a binay potential the coesponding expessions wee deived in [] fo a multibody potential. In what follows, we use the convention that

MAX4147ESD PART 14 SO TOP VIEW. Maxim Integrated Products 1 MAX4147 EVALUATION KIT AVAILABLE ; Rev 1; 11/96 V CC V EE OUT+ IN+ R t SENSE IN-

-; Rev ; / EVALUATION KIT AVAILABLE µ µ PART ESD TEMP. RANGE - C to +5 C PPACKAGE SO TOP VIEW V EE V CC SENSE+ SENSE- R t R t R t R t MAX SENSE OUT SENSE+ SENSE- N.C. SHDN N.C. 3 5 R f R G R f 3 VDSL TRANSFORMER

"BHFC8I7H=CB HC &CH=CB 5B8 &CA9BHIA

ω θ ω = Δθ Δt, θ ω v v = rω ω = v r, r ω α α = Δω Δt, Δω Δt (rad/s)/s rad/s 2 ω α ω α rad/s 2 87.3 rad/s 2 α = Δω Δt Δω Δt α = Δω Δt = 250 rpm 5.00 s. Δω rad/s 2 Δω α Δω = 250 min rev 2π rad rev 60 1 min

http://www.mathematica.gr/forum/viewtopic.php?f=109&t=15584

Επιμέλεια : xr.tsif Σελίδα 1 ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΓΙΑ ΜΑΘΗΤΙΚΟΥΣ ΔΙΑΓΩΝΙΣΜΟΥΣ ΕΚΦΩΝΗΣΕΙΣ ΤΕΥΧΟΣ ΑΣΚΗΣΕΙΣ 101-00 Αφιερωμέν σε κάθε μαθητή πυ ασχλείται ή πρόκειται να ασχληθεί με Μαθηματικύς διαγωνισμύς

MICROMASTER Vector MIDIMASTER Vector

s MICROMASTER Vector MIDIMASTER Vector... 2 1.... 4 2. -MICROMASTER VECTOR... 5 3. -MIDIMASTER VECTOR... 16 4.... 24 5.... 28 6.... 32 7.... 54 8.... 56 9.... 61 Siemens plc 1998 G85139-H1751-U553B 1.

Ó³ Ÿ º 3[120] Particles and Nuclei, Letters No. 3[120]

Ó³ Ÿ. 2004. º 3[120] Particles and Nuclei, Letters. 2004. No. 3[120] Š 621.384.633.5/6 Š ˆ ˆ Šˆ Šˆ Š ˆ Ÿ Ÿ ˆ ˆ.. Œ ϱµ 1,.. µ 1,.. ³ µ 1,. Œ. Ò 1, ƒ.. Ê ±µ 1 Ñ Ò É ÉÊÉ Ö ÒÌ ² µ, Ê Œµ ±µ ± µ Ê É Ò É ÉÊÉ

Study on the Strengthen Method of Masonry Structure by Steel Truss for Collapse Prevention

33 2 2011 4 Vol. 33 No. 2 Apr. 2011 1002-8412 2011 02-0096-08 1 1 1 2 3 1. 361005 3. 361004 361005 2. 30 TU746. 3 A Study on the Strengthen Method of Masonry Structure by Steel Truss for Collapse Prevention

Japanese Fuzzy String Matching in Cooking Recipes

1 Japanese Fuzzy String Matching in Cooking Recipes Michiko Yasukawa 1 In this paper, we propose Japanese fuzzy string matching in cooking recipes. Cooking recipes contain spelling variants for recipe

! " #$% & '()()*+.,/0.

! " #$% & '()()*+,),--+.,/0. 1!!" "!! 21 # " $%!%!! &'($ ) "! % " % *! 3 %,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,0 %%4,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,5

Ηρλνζηνηρεία (Απαξαίηεηα θαη Σνμηθά) ntho@chem.uoa.gr

Ηρλνζηνηρεία (Απαξαίηεηα θαη Σνμηθά) ntho@chem.uoa.gr Οξηζκόο Χο ηρλνζηνηρείν ζεσξείηαη απζαίξεηα θάζε ζηνηρείν πνπ νη απαηηήζεηο ηνπ νξγαληζκνύ καο ζ απηό είλαη κηθξόηεξεο ησλ 25 mg αλά εκέξα Απαξαίηεηα

το περιεχόµενο των οποίων είναι διανεµηµένο µε τον εξής τρόπο: : κάθε πίστα περιέχει

EL Ref. 20620 %$ #"! $,+ *$ ' ' )( '& 4. 3: 046 2 4. 32 1. 0. @ 0.. A A0 ON B D CS SPN R NR KJ A G D R QDC ONR H PC KJ L MN \ [ Z RV RP N S H S A A. 0@ 2 :. ; KJ ^ N \ CV W]P E ] 8 6 2 0 3 6 X _ Z R N

AC 1 = AB + BC + CC 1, DD 1 = AA 1. D 1 C 1 = 1 D 1 F = 1. AF = 1 a + b + ( ( (((

? / / / o/ / / / o/ / / / 1 1 1., D 1 1 1 D 1, E F 1 D 1. = a, D = b, 1 = c. a, b, c : #$ #$ #$ 1) 1 ; : 1)!" ) D 1 ; ) F ; = D, )!" D 1 = D + DD 1, % ) F = D + DD 1 + D 1 F, % 4) EF. 1 = 1, 1 = a + b

m i N 1 F i = j i F ij + F x

N m i i = 1,..., N m i Fi x N 1 F ij, j = 1, 2,... i 1, i + 1,..., N m i F i = j i F ij + F x i mi Fi j Fj i mj O P i = F i = j i F ij + F x i, i = 1,..., N P = i F i = N F ij + i j i N i F x i, i = 1,...,

8η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ1 Ασκήσεις 8 ου Κεφαλαίου

8η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ1 Ασκήσεις 8 ου Κεφαλαίου 1. Ένα σύρμα μεγάλου μήκους φέρει ρεύμα 30 Α, με φορά προς τα αριστερά κατά μήκος του άξονα x. Ένα άλλο σύρμα μεγάλου μήκους φέρει

SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM

SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max

Ax = b. 7x = 21. x = 21 7 = 3.

3 s st 3 r 3 t r 3 3 t s st t 3t s 3 3 r 3 3 st t t r 3 s t t r r r t st t rr 3t r t 3 3 rt3 3 t 3 3 r st 3 t 3 tr 3 r t3 t 3 s st t Ax = b. s t 3 t 3 3 r r t n r A tr 3 rr t 3 t n ts b 3 t t r r t x 3

l 1 p r i = ρ ij α j + w i j=1 ρ ij λ α j j p w i p α j = 1, α j 0, j = 1,..., p j=1 R B B B m j [ρ 1j, ρ 2j,..., ρ Bj ] T = }{{} α + [,,..., ] R B p p α [α 1,..., α p ] [w 1,..., w p ] M m 1 m 2,

Part Numbering. Chip Ferrite Bead for Automotive. D q. (Part Number)

Chip Ferrite Bead for Automotive ing () BL M 18 AG 2 S Z 1 D q w e r t y u i o qproduct ID Product ID BL Chip Ferrite Beads timpedance Expressed by three figures. The unit is in ohm (Ω) at MHz. The first

!! " # $%&'() * & +(&( 2010

!!" #$%&'() *& (&( 00 !! VISNIK OF HE VOLODYMYR DAL EAS UKRAINIAN NAIONAL UNIVERSIY 8 (50) 00 8 (50) 00 HE SCIENIFIC JOURNAL " 996 WAS FOUNDED IN 996 " - - " I IS ISSUED WELVE IMES A YEAR "#$% Founder

ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΙΟΙΚΗΣΗΣ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥ ΩΝ ΜΕΤΑΠΤΥΧΙΑΚΟ ΙΠΛΩΜΑ ΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΜΕ. Ι..Ε.

ΑΣΚΗΣΗ 1 ΟΜΑ Α 2 Στην ακόλουθη άσκηση σας δίνονται τα έξοδα ανά µαθητή και οι ετήσιοι µισθοί (κατά µέσο όρο) των δασκάλων για 51 πολιτείες της Αµερικής. Τα δεδοµένα είναι για τη χρονιά 1985. Οι µεταβλητές

ΘΕΩΡΗΤΙΚΗ ΙΕΡΕΥΝΗΣΗ ΤΟΠΙΚΗΣ ΚΑΤΑΝΟΜΗΣ ΕΝΤΑΣΗΣ ΣΕ ΧΑΛΥΒ ΙΝΑ ΕΛΑΣΜΑΤΑ ΛΟΓΩ ΑΝΗΡΤΗΜΕΝΩΝ ΦΟΡΤΙΩΝ

ΘΕΩΡΗΤΙΚΗ ΙΕΡΕΥΝΗΣΗ ΤΟΠΙΚΗΣ ΚΑΤΑΝΟΜΗΣ ΕΝΤΑΣΗΣ ΣΕ ΧΑΛΥΒ ΙΝΑ ΕΛΑΣΜΑΤΑ ΛΟΓΩ ΑΝΗΡΤΗΜΕΝΩΝ ΦΟΡΤΙΩΝ Ιωάννης Γ. Ραυτογιάννης & Γεώργιος Θ. Μιχάλτσος Εργαστήριο Μεταλλικών Κατασκευών, Σχολή Πολιτικών Μηχανικών

(a b) c = a (b c) e a e = e a = a. a a 1 = a 1 a = e. m+n

Z 6 D 3 G = {a, b, c,... } G a, b G a b = c c (a b) c = a (b c) e a e = e a = a a a 1 = a 1 a = e Q = {0, ±1, ±2,..., ±n,... } m, n m+n m + 0 = m m + ( m) = 0 Z N = {a n }, n = 1, 2... N N Z N = {1, ω,

Αναπληρωτής Καθηγητής Τμήμα Συντήρησης Αρχαιοτήτων και Έργων Τέχνης Πανεπιστήμιο Δυτικής Αττικής - ΣΑΕΤ

Γενική και Ανόργανη Χημεία Περιοδικές ιδιότητες των στοιχείων. Σχηματισμός ιόντων. Στ. Μπογιατζής 1 Αναπληρωτής Καθηγητής Τμήμα Συντήρησης Αρχαιοτήτων και Έργων Τέχνης Π Δ Χειμερινό εξάμηνο 2018-2019 Π

..,..,.. ! " # $ % #! & %

..,..,.. - -, - 2008 378.146(075.8) -481.28 73 69 69.. - : /..,..,... : - -, 2008. 204. ISBN 5-98298-269-5. - -,, -.,,, -., -. - «- -»,. 378.146(075.8) -481.28 73 -,..,.. ISBN 5-98298-269-5..,..,.., 2008,

ELE 3310 Tutorial 11. Reflection of plane waves Wave impedance of the total field

L 0 Tuto Rfcton of pn wvs Wv mpdnc of th tot fd Rfcton of M wvs Rfcton tks pc whn n M wv hts on bound. Pt of th wv gts fctd, nd pt of t gts tnsmttd. Popgton dctons nd mptuds of th fctd nd tnsmttd wvs dpnd

ΗΛΙΑΣΚΟΣ ΦΡΟΝΤΙΣΤΗΡΙΑ. Γενικής Παιδείας Άλγεβρα Β Λυκείου ΥΠΗΡΕΣΙΕΣ ΠΑΙΔΕΙΑΣ ΥΨΗΛΟΥ ΕΠΙΠΕΔΟΥ. Επιμέλεια: Γ. ΦΩΤΟΠΟΥΛΟΣ Σ. ΗΛΙΑΣΚΟΣ

ΗΛΙΑΣΚΟΣ ΦΡΟΝΤΙΣΤΗΡΙΑ ΥΠΗΡΕΣΙΕΣ ΠΑΙΔΕΙΑΣ ΥΨΗΛΟΥ ΕΠΙΠΕΔΟΥ Γενικής Παιδείας Άλγεβρα Β Λυκείου Επιμέλεια: Γ. ΦΩΤΟΠΟΥΛΟΣ Σ. ΗΛΙΑΣΚΟΣ e-mail: info@iliaskos.gr www.iliaskos.gr ΗΛΙΑΣΚΟΣ ΦΡΟΝΤΙΣΤΗΡΙΑ. y y 4 y

( N m 2 /C 2 )( C)( C) J

Electrical Energy and Capacitance Practice 8A, p. 669 Chapter 8. PE electric = 6.3 0 9 J q = q = q p + q n = ().60 0 9 C + ()(0) = 3.0 0 9 C kcqq (8.99 0 9 N /C )(3.0 0 9 C) r = = P Ee lectric 6.3 0 9

) * +, -. + / - 0 1 2 3 4 5 6 7 8 9 6 : ; < 8 = 8 9 >? @ A 4 5 6 7 8 9 6 ; = B? @ : C B B D 9 E : F 9 C 6 < G 8 B A F A > < C 6 < B H 8 9 I 8 9 E ) * +, -. + / J - 0 1 2 3 J K 3 L M N L O / 1 L 3 O 2,

IL - 13 /IL - 18 ELISA PCR RT - PCR. IL - 13 IL - 18 mrna. 13 IL - 18 mrna IL - 13 /IL Th1 /Th2

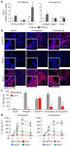344 IL - 13 /IL - 18 1 2 1 2 1 2 1 2 1 2 3 1 2 13 18 IL - 13 /IL - 18 10% / OVA /AL OH 3 5% 16 ~ 43 d 44 d ELISA BALF IL - 13 IL - 18 PCR RT - PCR IL - 13 IL - 18 mrna IL - 13 mrna 0. 01 IL - 18 mrna 0.

The Standard Model. Antonio Pich. IFIC, CSIC Univ. Valencia

http://arxiv.org/pd/0705.464 The Standard Mode Antonio Pich IFIC, CSIC Univ. Vaencia Gauge Invariance: QED, QCD Eectroweak Uniication: SU() Symmetry Breaking: Higgs Mechanism Eectroweak Phenomenoogy Favour

PDF hosted at the Radboud Repository of the Radboud University Nijmegen

PDF hosted at the Radboud Repository of the Radboud University Nijmegen The following full text is a publisher's version. For additional information about this publication click this link. http://hdl.handle.net/2066/52779