INŽENJERSKA GEODEZIJA I
|
|
|
- Αθορ Αλεξόπουλος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 GEODETSKI FAKULTET SVEUČILIŠTE U ZAGREBU KATEDRA ZA INŽENJERSKU GEODEZIJU INŽENJERSKA GEODEZIJA I PREDAVANJA prof. dr. c. Goraa Novakovć goraa. ovakovc@geof.hr INŽENJERSKA GEODEZIJA Ižejerka geodezja je područje geodezje koje e odo a prmjeu geodetkh mjerh utava u projektraju zgradj objekata, te u praćeju jhovh pomaka deformacja tjekom zgradje ekploatacje. Om zgrađeh objekata prate e pomac prrodh objekata - tektok aktva područja. Jeda od oovh zadataka žejerke geodezje je preošeje projekta objekta a plaa a tere. To preošeje azva e ISKOLČENJE. 007./008. Prmjea geodezje u žejerkm radovma IZGRAĐENI OBJEKTI radov veza uz kogradju - željezčke pruge, cete, autocete, motov, tuel, zrače plove luke. radov veza uz vokogradju - velke zgrade, dutrjka potrojeja, tado. radov veza uz eergetku - brae, dalekovod, plovod, aftovod, raferje. zrada projekata regulacje potojećh aelja pr zgradj ovh aelja. 3 PRIRODNI OBLICI ZEMLJINE POVRŠINE Rajed, klzšta, odro, vulka; općeto va tektok aktva područja. Prmjea žejerke geodezje: praćeje gbaja Zemlje kore, klzaja l ljegaja tla l. Potreba praćeja utvrđvaja atalh pomaka l deformacja tla l građeve, eophod u rad poduzmaja mjera gurot l aacje th objekata. 4
2 PROJEKTIRANJE I PROJEKT Idej projekt Ukupa rad oko kompletraja ve potrebe dokumetacje za gradju ekog objekta azva e projektraje, a va potreba dokumetacja č jedu cjelu koja e azva projekt tog objekta. Svak građevk objekt, od zaml do puštaja u ekploatacju, prolaz kroz ekolko faza u kojma u prut odgovarajuć radov. Prema amje raz razrade, projekt e razvrtavaju a (Zako o gradj NN 75/03): dej projekt glav projekt zvedbe projekt. 5 Idej projekt je kup međuobo uklađeh acrta dokumeata kojma e daju oova oblkovo fukcoala tehčka rješeja građeve te prkaz mještaja građeve u protoru. Idej projekt, ovo o ložeot tehčkoj truktur građeve, može adržavat druge acrte dokumete ako u o začaj za zradu glavog projekta (op tehološkog potupka tehološke heme, op prmjea određee tehologje građeja, procjeu troškova rad provedbe potupaka jave abave l.). 6 Glav projekt Izvedbe projekt Glav projekt je kup međuobo uklađeh projekata kojma e daje tehčko rješeje građeve, prkaz mještaja građeve u protoru dokazuje pujavaje bth zahtjeva za građevu, kao drugh zahtjeva tehčkh pecfkacja. Glav projekt adrž građevk projekt geodetk projekt, a ovo o amje tehčkoj truktur građeve adrž arhtektok projekt, elektrotehčk projekt trojark projekt. Projekt moraju uvjek adržavat podatke z elaborata koj u polužl kao podloga za jhovu zradu, te projektra vjek uporabe građeve uvjete za jeo održavaje. Izvedbem projektom razrađuje e tehčko rješeje dao glavm projektom. Izvedbe projekt mora bt zrađe u kladu glavm projektom. Razlkuju e: - građevk projekt, - geodetk projekt (grafčk umerčk do) - realzra građevk projekt. 7 8
3 Geodetk radov pr projektraju, građeju koršteju građevkog objekta GEODETSKE PODLOGE ZA PROJEKTIRANJE prkupljaje potojećh po potreb zrada ovh geodetkh podloga, potavljaje orm za točot građeja prema tome točot kolčeja (horzotalog vertkalog), potavljaje odgovarajuće geodetke oove a koje će e kolčavat a zadaom točošću, zbor metode kolčeja ( obzrom a točot), zbor trumetarja prbora, aalza točot zvršeog kolčeja, zmjera zvedeog taja, opažaje vertkalh horzotalh pomaka - zaključc o tablot gurot objekta. 9 Geodetke podloge za projektraje u plaov karte (aalog dgtal) razlčth mjerla. Mjerlo geodetke podloge ov o karaktertkama objekta za koju fazu projektraja e kort. Geodetk projekt e atoj od:. Predhodh ptvaja elaborat predradj za projektraje.. Idejog projekta 3. Glavog projekta zvedbe l detalj projekt. 0. Elaborat predradj za projektraje. Podloge za dej projekt U ovom djelu elaborata aalzra e ekoomka opravdaot zgradje objekta, razlčte varjate zgradje odabraje ajpovoljjeg rješeja l. Rad počje a geodetkm geološkm kartama, foto mcma ptuju e razlčte lokacje budućeg objekta. Nako oblaka terea odabre e ajpovoljja lokacja. Pretprojekt ucrtava e a kartama opć rapored objekta. To je oova za dej projekt. Karte plaov mjerla: :5000 (:0000), :500, :000, :000 (ov o vrt velč objekta). Sadrž rješeja vh tehčkh elemeata objekta, položaj gradlšta u cjel pojedh djelova, kotrukcje pojedh objekata, obm radova l. Služ kao oova za kolčeje plaraog objekta a tere. Na dejom projektu e projektra geodetka oova za kolčeje objekta.
4 3. Podloge za glav projekt - detalj l zvedbe Plaov mjerla: :000, :500, :00, (:00). Glav projekt predtavlja razradu dejog projekta rad crtež za pojede djelove dejog projekta a detaljm rješejma vh djelova objekta a oovu kojh će e zvodt građeje. Plaov karte Pla je vjera lka majeg djela površe Zemlje; v objekt a plau u zadržal t međuob odo oblk kao što ga maju u prrod amo u majem mjerlu. Mjerlo plaova: :500, :000, :000, :500, :5000. Na kart je predtavlje već do površe pa zakrvljeot Zemlje dolaz do zražaja. Karta je maje, deformra geeralzra prkaz Zemlje površe a rav, defraoj određem matematčkm uvjetma. Mjerlo karata: :5000, :0000, :5000, :50000, :00000 tje. 3 4 Točot geodetkh plaova karata Pored poebh uvjeta koj ove o amje, od plaa l karte e zahtjeva da je: toča, potpua, pregleda jaa. Točot geodetkh podloga (aalogh) ov o:. mjerlu. metod maja kartraja 3. kvaltet materjala. Pr projektraju je važo zat koju točot u horzotalom vkom pogledu mogu dat karte plaov, aročto ako e kort za kolčeje objekta a tere. 5. Točot (grafčka) plaova u horzotalom mlu m k azvk mjerla plaa 0, mm grača grafčka točot (to je velča koja e može protm okom, mjerlom, očtat l ajet a kartu).. Točot plaova u vertkalom mlu Vka predodžba terea e može kazat pomoću: -kota(točke geodetke oove, detalje točke) - zohpa (reljef l kofguracja terea). Točot određvaja kota ov o točot metode zmjere. µ hor 0,mm m k 6
5 Točot vkog prkaza terea pomoću zohpa ov o: točot vke zmjere, gutoće raporedu mljeh točaka, točot kartraja, metode terpolacje, mjerlu plaa ekvdtac zohp. Vka točot plaa: µ K + k tgα ver K -točot cjelokupe vke zmjere k - pogreška horzotalog položaja točke α - kut agba terea. 7 GEODETSKA OSNOVA ZA PROJEKTIRANJE I ISKOLČENJE. Geodetka oova za zmjeru terea - ako za projekt e potoje geodetke podloge l potojeće u kvaltete, potrebo je provet zmjeru terea: potavljaju e polgok l tahmetrjk vlakov (točot zmjere propaa Pravlkom). Kako točot rapored točaka takve oove e zadovoljava točot rapored točaka za kolčeje, projektra e ova:. Geodetka oova za kolčeje amotala oova čja je točot propaa projektom, rapored gutoća točaka ov o oblku velč ovog objekta. Geodetka oova za kolčeje zvod e kao: mreža točaka mreža lja. 8 Opće karaktertke mreža za kolčeje Otale karaktertke mreže Mreža e projektra a dejom projektu objekta gdje u već projektra v pomoć objekt koj će lužt u toku građeja. Projekt mreže treba obuhvatt cjelo gradlšte udovoljt vm jegovm potrebama do kraja građeja. Položaja točot točaka mreže treba bt oko puta veća od položaje točot točaka koje defraju glave o objekta. Rad lakšeg račuaja koordata točaka koje defraju o objekta, treba uklopt pojede o u amu mrežu l trace mreže potavt paralelo budućem objektu. 9 Lokale (amotale) mreže za objekte mještee a majem području l gdje e traž voka točot kolčeja praćeja pomaka (motov, brae, tuel). Prključee a oovu mrežu - za objekte mještee a većem području gdje je potrebo međuobo povezvaje za objekata (hdroeergetk utav, regulacje vodotoka, regulacja gradova, komukacje). Po velč - prlagođee velč objekta. Po oblku - ov o karakteru razvedeot objekta, mogućot tablzacje točaka, vrt predvđeh mjereja tadardma projektraja. Točot - mreža je homogea (ve u točke tog reda). Mreža e zjedačava kao cjela. 0
6 Geometrjka defcja geodetke mreže Algebarka defcja geodetke mreže Geodetko pozcoraje je određvaje položaja, tj. koordata jede, dvje l vše točaka a, zad l pod zemlje površe, u odou a prethodo defra koordat utav. Geodetko pozcoraje e djel a: pozcoraje jede točke, relatvo pozcoraje relatv položaj jede točke u odou a drugu, pozcoraje mreže relatv položaj zmeđu tr l vše točaka. Geodetka mreža e defra kao geometrjka kofguracja tr l vše točaka koje u povezae geodetkm mjerejma. Oov pojmov defcje Potrebo je odredt broje vrjedot ekh velča: X, X,... X u - tražee velče (epozace). Mogu potojat eke raje određee velče - dae l pozate velče. L, L,... L - mjeree velče. (za zjedačeje mora bt > u ; broj ezavo mjereh velča već od broja tražeh velča). Broj mjereh velča u je broj eophodh velča. Otale mjeree velče L u+,... L, jh f - u u prekobroje velče broj tupjeva lobode. Defcja geodetke mreže Vrte metode zmjere geodetkh mreža Skup geodetkh točaka a kupom L, L,... L mjereh velča (koje mogu bt razovre - kutov, dulje) azva e geodetkom mrežom, ako e zmeđu th mjereh velča može ać u (u < ) ezavh velča takvh da e blo koj elemet (čja vrta prpada vrt mjereh velča) može zrazt pomoću th u eophodh velča. Prmjer: Na oovu pozath koord. točaka A B (dae velče) treba odredt koordate točaka C D (tražee velče). Izmjere u horzotal kutov α, α, α 3, α 4, α 5, α 6, α 7, α 8 (mjeree velče). 3 VRSTE GEODETSKIH MREŽA (dmezje) Vke D Horzotale D Protore 3D METODE IZMJERE GEODETSKIH MREŽA TERESTRIČKE Tragulacja Trlateracja Kombacja Polgoometrja Luč prejek Nvelma SATELITSKE GNSS GPS, GPS, GLONASS, Galleo 4
7 USPOSTAVA GEODETSKE MREŽE PROJEKT MREŽE. Projekt mreže određuje e kofguracja mreže (oblk mreže broj točaka u mrež) pla mjereja (koje velče mjert kojom točošću - ocjea točot a pror).. Izvedba mreže realzacja mreže a tereu: rekogocraje, tablzacja, zmjera. 3. Aalza mreže. aalza točot a pror. aalza točot a poteror - ako mjereja ako zjedačeja. Projektraje mreže vezao je uz vrtu oobe objekta. Oblk, dmezje, broj točaka položaj mreže, treba e prlagodt objektu okolom tereu. Ova faza provod e prje zlaka a tere (mjereja). Projekt mreže mreže uključuje: adrž: oblk (kofguracju) mreže pla mjereja, a pror ocjeu točot mjereja, zbor: metode mjereja, trumetarja, broja poavljaja mjereja, metode zjedačeja mreže dr. 5 6 Horzotale mreže Oov oblc horzotalh mreža (D) atavak Cetral utav Kombacja Geodetk četverokut Dvotruk geod. četv. Laac geod. četv. Laac trokuta Mreža trokuta Dvotruk cetral utav Laac cetralh utava 7 8
8 Vrte geodetkh mreža za određvaje pomaka deformacja Apolute mreže atoje e od dvje grupe točaka: - oove točke (refereta mreža) a kojh e opažaju: - kotrole točke mještee a objektu. atavak Relatve mreže ve točke alaze e a objektu (opažaju e relatv pomac zmeđu točaka) oove točke kotrole točke 9 30 Smještaj (lokacja) točaka geodetke mreže Idealo projektraa geodetka mreža za zgradju praćeje pomaka brae C Refereta točka blzu potporog zda Kotrole točke a bra D B A Referete točke zvodo Kofguracja apolute mreže za zgradju praćeje betoke brae (oove kotrole točke) 3 3
9 IZVEDBA MREŽE -rekogocraje, - tablzacja galzacja, -zmjera. Stablzacja Točke e tablzraju okruglm betokm tupovma u čjem e cetru potavlja uređaj za prlo cetrraje. Va tupa oko,5 m. Rekogocraje je odabraje ajpovoljjeg položaja točaka a tereu, a da pr tom budu zadovolje određe uvjet. Treba zbjegavat: klzšta, rede parcela, obale rjeka l potoka, rub puta, blzu predmeta (zgrade, ograde, zdov) l terea (rad refrakcje). Om toga treba zbjegavat blzu željezčkh pruga, elektrčh drugh vodova (koj ometaju elektrooptčke valove daljomjera l GPS gale) Sgalzacja Sgalzacja treba odgovarat prcpu prlog cetrraja. Sgale začke - oova karaktertka da e mogu potavt a tu podložu ploču a koju e potavlja trumet. Metode zmjere horzotalh mreža Tragulacja mjere e pravc, tj. kutov. Trlateracja mjere e dulje. Tragotrlateracja mjere e kutov dulje. Polgoometrja mjere e kutov dulje. Prejek lukova mjere e dulje. Vzure marke prlo cetrraje 35 36
10 ANALIZA KVALITETE GEODETSKIH MJERENJA TOČNOST I PRECIZNOST Oov pojmov defcje Točot predtavlja tupaj podudaraja l blkot pravljeog rezultata mjereja tte, odoo dogovoree tte vrjedot mjeree velče. Točo, al je preczo Preczo, al je točo Točot je kvaltatva mjera e kazuje e brojem. Preczot predtavlja tupaj međuobe blkot poovljeh mjereja te velče u propam uvjetma. Preczot je kvattatva mjera kazuje e brojem. 37 N točo preczo Točo preczo 38 Numerčke metode opa podataka mjereja KRITERIJI KVALITETE GEODETSKE IZMJERE Prava vrjedot pogreška (ε ) Najbolja procjea odtupaje (v ) Stupjev lobode broj prekobrojh mjereja (f ) TOČNOST GEODETSKE IZMJERE Varjaca kupa (ozaka σ ). Stadardo odtupaje kupa (ozaka σ). Varjaca uzorka (ozaka ). Stadardo odtupaje uzorka (ozaka ). Stadardo odtupaje rede uzorka (ozaka x ). Mjera egurot brojča kaz o kvaltet rezultata mjereja uz prmjeu oovog parametra - tadardog odtupaja (). 39 PRECIZNOST Slučaja odtupaja međuoba odtupaja poovljeh mjereja te velče. Reducraju e pažljvm mjerejem, korštejem preczog trumeta, mjerejem pr povoljm uvjetma dr. + POUZDANOST Grube pogreške otkrvaju e kotrolm, prekobrojm mjerejma. Sutava odtupaja reducraju e kalbracjom mjere opreme, razlčtm potupcma pr mjereju (obotrao mjereje, velraje z rede dr.). 40
11 TRIANGULACIJSKE MREŽE Točot tragulacjke mreže Tragulacjka mreža je mreža međuobo povezah trokuta. Mjere e kutov (pravc) u pojedm trokutma. Mkrotragulacjke mreže - dulje traca m. Oova kocepcja određvaja koordata tragulacjkh točaka Za određvaje oblka mjerla tragulacjke mreže potrebo je pozavat ve kutove u mrež dulju jede (blo koje) trae. Na temelju th elemeata račuaju e (po uovom poučku) ve otale trace u mrež. Na temelju zmjereh kutova zračuath dulja račuaju e prblže koordate točaka. Deftve koordate dobju e ako zjedačeja. 4 Položaja točot objekta ov o: točot (metod) kolčeja točot mreže a koje e kolčava. Točot mreže, odoo točot određvaja položaja tragulacjkh točaka ov o:. geometrjkom oblku mreže. točot mjereh velča (horzotal kutov, početa traa) 3. pogreškama dah velča (a to e e može utjecat). 4. Geometrjk oblk mreže U prak, oblk mreže ov o vrt velč objekta kofguracj terea. Treba atojat da u oove fgure (trokut) što pravlj da h je što maje. Optmala oblk trokuta je totrača. Povećaje broja trokuta u mrež veće odtupaje od pravlog oblka trokuta utjecat će a majeje leare preczot u mrež polazeć od mjeree trae. Preczot zračuate trae u trokutu U trokutu je mjereo: a, α, β Traž e: traca b preczot zračuate trae b b γ α a c β β b a α Relatvo tadardo odtupaje zračuate trae b, ako u kutov mjere tom preczošću, tj. α β 0 : b a 0 + ( ctg α ctg b a ρ + β ) 43 44
12 Ocjea preczot blo koje trae u mrež (relatvo): b b a + a 3 0 ρ ( ctg α + ctgα ctgβ + ctg β ) Dakle, leara preczot eke zračuate trae ov o: oblku mreže (velč kutova), broju oovh fgura u mrež (), egurot mjereja kutova ( 0 ), egurot mjereja počete trae u mrež ( a ). Ako je α β γ 60 0 b a 0 + b a 3 ρ 45. Negurot pr mjereju kutova Na egurot mjereog kuta utječu: pogreške trumeta egurot ptvaja (kalbracje) trumeta, egurot pr mjereju (pr. loše cetrraje trumeta gala), egurot mjereja (pr. lučaje utave pogreške vzraja pogreška očtaja), vajk uvjet (refrakcja, ttraje zraka), ooba pogreška opažača (fzološke oobe oka). Na temelju vh pojedh egurot (tadardh odtupaja) može e a pror procjet ukupa egurot zmjereog kuta - račua e po zakou o prratu varjac (zbroj pojedh varjac). 46 Varjaca redje vrjedot horzotalog kuta β, zračuata pomoću horzotalh pravaca zmjereh u poavljaja: Izmjera tragulacjke mreže σ σ + σ v oč c β + σ hor. ctg z + (ρ ). 4σ coβ + σ v egurot vzraja, σ oč. egurot očtaja, σ c egurot cetrraja trumeta vzure marke, σ hor. egurot horzotraja trumeta, σ kh egurot određvaja koefcjeta boče refrakcje, dulja vzure lje, z zeta udaljeot vzure lje, k h koefcjet boče refrakcje, R redj radju Zemlje. R σ kh 47 Grua metoda mjere e pravc. Metoda zatvaraja horzota mjere e kutov. Grua metoda trumet optčkm mkrometrom (0," 0,"), mjere tace. 48
13 Metoda zatvaraja horzota Ocjea točot mjereh kutova (prje zjedačeja mreže) Uvjet: α + β + γ + δ Odtupaje (ezatvaraje horzota): f H (α + β + γ + δ) Iz odtupaja od artmetčke rede 0 Grua metoda: grua, pravaca Stadardo odtupaje jedče teže, tj. pravca mjereog u jedom gruu: [ d ] [ d] ( )( ) d razlka pojedh pravca u gruu od artmetčke rede [d] uma vh razlka d jedog te tog pravca z vh grua [d ] zbroj kvadrata razlka d u pojedm gruma Σ [d ] uma zbroja kvadrata razlka Σ [d] zbroj uma vh kvadrata a kvadrat Stadardo odtupaje pravca kao artmetčke rede z vh grua: S p Iz odtupaja zatvaraja horzota f H broj kutova fh - kut mjere u grua: Sk f H kuta odtupaja Ako ma r taca u mrež: [ Sk ] 3. Iz odtupaja zatvaraja trokuta f S r r a horzotu - kut mjere u gruu: broj grua S k T f f 3N Ferrerova formula k S k r [ ] N broj trokuta f kuta odtupaja u trokutma k r Negurot orjetacje (mjerog kuta) položaja određee točke u mrež U proceu projektraja mreže aalzra e, om egurot mjereh kutova, egurot drugh elemeata u mrež: Negurot (tadardo odtupaje) mjerog kuta veze trae -tog trokuta u tragulacjkom lacu. Uzdužo odtupaje krajje točke u lacu trokuta. Uzdužo odtupaje krajje točke u lacu četverokuta. Poprečo odtupaje krajje točke u lacu trokuta. Poprečo odtupaje krajje točke u lacu četverokuta. 5 5
14 TRILATERACIJSKE MREŽE Trlateracjka mreža e također atoj od za međuobo povezah trokuta, al e u ovom lučaju mjere dulje traca. Predot learh mjereja: jedotava rad elektrokm daljomjerma, lakš zbor povoljh uvjeta za opažaje, lakše otvarvaje (mjereje) dugačkh traa, u trog uvjet u pogledu vdljvot vzure marke, voka preczot mjereja. Nedotatak trlateracje: maja mogućot kotrole mjereja. 53 Na oovu zmjereh traca, račuaju e v kutov u pojedm trokutma. Izmjeree u trace a, b c; potrebo je zračuat kutove α, β, γ. b + c a coα bc α tg ( b) ( c) ( a) a+ b+ c Preczot kutova kao fukcja preczot mjereh dulja: α β α b γ a ρ P b ρ P c ρ P + co γ + co β a a a α a b co γ + co c β b b c + co α c β + co α + c P površa trokuta 54 Pod pretpotavkom da u trae mjeree tom preczošću: a b c, dulje traa jedake: a b c, tada je tadardo odtupaje zračuath kutova kao fukcja mjereh dulja: // // // α β γ // k Ako e žel da zračuat kutov u trlateracjkoj mrež budu te preczot kao mjere kutov u trgoometrjkoj mrež, tada relatvo tadardo odtupaje mjereh traa u trlateracjkoj mrež treba bt,4 puta maje u odou a tadardo odtupaje kuth mjereja u trgoometrjkoj mrež. Prmjer: u trgoometrjkoj mrež kutov u zmjere a tadardm odtupajem 3. Da e dobje ta preczot zračuath kutova u trlateracjkoj mrež, duže u toj mrež treba mjert relatvm tadardm odtupajem: odoo // // ρ k, 4 cm/km 55 Varjaca mjeree dulje: λ σ σ σ Φ + σ z + σ c + π σ Φ - tadardo odtupaje određvaja fazog homogeteta Φ σ z, - tadardo odtupaje određvaja pogreške ule z 0 σ c - tadardo odtupaje perodčke pogreške - tadardo odtupaje određvaja deka refrakcje σ Dulja: Φ λ ( m + ) π λ - vala dulja, Φ -faza razlka, m broj valh dulja Negurot pr elektrooptčkom mjereju dulja 56
15 Preczot mjereja dulja elektrooptčkm daljomjerma zražava e pomoću dva djela: kotatog ovog o dulj. σ a + b U kotatom djelu a prkaza je utjecaj pogreške ule, perodčke faze pogreške, dok parametar b koj ov o dulj (pogreška mjerla) predtavlja pogrešku određvaja deka atmoferke refrakcje kalbracje frekvecje. Ukupo tadardo odtupaje mjeree dulje: σ σ + σ m + a + ( b ppm) KOMBINIRANE MREŽE Tragotrlateracjke mreže U tragotrlateracjkoj mrež mjere e kutov dulje. Idealo kombraa mreža je oa koja ma zmjeree ve kutove duže. Pravlo plaraa zmjerea kombraa mreža je ajbolj moguć tp horzotale mreže al zjedačeje takve mreže mora bt provedeo trogom metodom u kojoj e mora uzet što je vše moguće geometrjkh uvjeta. σ σ m - egurot cetrraja trumeta vzure marke IZJEDNAČENJE GEODETSKE MREŽE Clj zjedačeja je: matematčk defrat mrežu, odredt ajbolje procjee tražeh velča, zvršt ocjeu kvaltete dobveh rezultata. Sva zjedačeja e mogu podjelt a:. Prblže metode zjedačeja potupo prblžavaje rješeju.. Stroge metode zjedačeja kada ve mjeree velče tovremeo udjeluju u zjedačeju ako e zjedačeje provod po metod ajmajh kvadrata. Tada e dobju ajbolje procjee tražeh velča. 59 Prblže metode zjedačeja tragulacjke mreže Kod prblže metode zjedačeja ajprje e zadovolje uvjet uutar elemetarh fgura od kojh e atoj mreža (trokut, četverokut). Daljj e uvjet zadovoljavaju potepem prblžavajem. Uvjete jedadžbe:. Uvjete jedadžbe fgura. Uvjete jedadžbe horzota 3. Sue l uvjete jedadžbe oovce Izjedačeje u dvje grupe:. Izjedačeje kutova za uvjet: fgure (trokuta), uvjet zbroja l razlke, uvjet horzota l uvjet polgoa.. Su uvjet l uvjet fkh traa. 60
16 Stroge metode zjedačeja Oova relacja: l / l + v l /T [L / L/... L/ ] - vektor zjedačeh vrjedot opažaja l T [L L... L ] - vektor mjereh velča v T [v v... v ] - vektor popravaka mjereh velča. Vektor popravaka je epozat treba ga odredt zjedačejem. Prcp ajmajh kvadrata - određvaje zjedačeh vrjedot mjereh velča epozaca zadovoljejem uvjeta: v T Pv m. v - vektor popravaka mjereh velča, P - matrca teža mjereh velča. Stroge metode zjedačeja e mogu podjelt a: uvjeto zjedačeje poredo zjedačeje kombacja. 6 Izjedačeje po uvjetm mjerejma Ovaj potupak zjedačeja prmjejuje e kada u ame tražee velče eporedo mjeree, al jhove ajbolje procjee moraju zadovoljt taovte matematčke uvjete. Izjedačejem po uvjetm mjerejma određuju e amo popravc mjereh velča bez uvođeja epozaca - određuju e ajbolje procjee mjereh velča l / ocjee točot mjereh velča zjedačeh mjereh velča. Izjedačeje je moguće ako potoje prekobroja mjereja broj eovh uvjeta. Formraje uvjeth jedadžb. Izjedačee vrjedot moraju zadovoljt eke matematčke uvjete koj mogu bt lear l elear. Learzacja e provod razvojem u Taylorov red dobvaju e koefcjet uvjeth jedadžb euglace uvjeta ω.. Sutav learh uvjeth jedadžb A T v + ω 0 A - matrca koefcjeata uvjeth jedadžb v - vektor popravaka ω - vektor lobodh člaova (ω mjeree - teorjke vrjedot). 6 Uvjete jedadžbe moraju bt međuobo eove. Broj popravaka v odgovara broju mjereh velča. To u epozace koje treba odredt zjedačejem. Popravc moraju zadovoljt prcp zjedačeja (v T Pv m.) trebaju e uklot ve euglace u mjerejma (ω 0) uvođeje korelata (oe u epozace).. Sutav korelath jedadžb v Q ll A k Q ll P - Q ll k - matrca kofaktora mjereh velča - vektor korelata. Broj korelath jedadžb jedak je broju mjereh velča. Uvrštejem korelath () u uvjete jedadžbe () ljed: 3. Sutav ormalh jedadžb A T Q ll A k + ω 0 A T Q ll A N N k + ω 0 N - matrca koefcjeata ormalh jedadžb. 4. Rješejem ormalh jedadžb dobje e vektor korelata: k - N - ω. Uvrštejem vektora korelata (4) u utav korelath jedadžb () zračuaju e popravke v jhovm umrajem a odgovarajućm mjerem velčama l dobju e zjedačee vrjedot mjereh velča l /
17 Ocjea točot a poteror Izjedačeje po poredm mjerejma. Stadardo odtupaje jedče teže (faktor varjace a poteror):. Stadardo odtupaje mjereh velča (a oov prpade teže p ) 0 v T P v f 3. Stadardo odtupaje zjedačeh mjereh velča: lˆ 0 q Člaov pod korjea u djagoal elemet korelacjke matrce zjedačeh mjereh velča Q ˆ ˆ lˆ lˆ ll 0 p 65 Ovaj potupak zjedačeja prmjejuje e kada e tražee velče (epozace) e mogu eporedo zmjert, ego e određuju pomoću ekh drugh, zmjereh velča, a kojma u fukcjk povezae. Općeto, pr zjedačeju poredh mjereja treba odredt u vrjedot epozaca x j (j,,.., u), pomoću mjereh velča l (,,..., ) a a pror pozatm težama p (,,..., ), dat ocjeu preczot vh mjereh tražeh velča. Izjedačeje je moguće amo kada je > u. 66 Izjedačeje po poredm mjerejma provod e u dva koraka:. Račuaje prblžh vrjedot tražeh parametara (koordata točaka) pomoću eophodog broja (u) mjereh velča.. Račuaje prraštaja (korekcja) prblžh vrjedot. To u epozace koje e dobju kao rezultat zjedačeja. 67 Na oov uvođeja prblžh vrjedot epozaca ako learzacje fukcja, ljede:. Jedadžbe popravaka v A x l Prmjeom metode ajmajh kvadrata v T Pv m, prelaz e a:. Sutav ormalh jedadžb A T P A x - A T P l 0 A T P A N, A T P l N x - 0 Rješejem ormalh jedadžb dobju e ajbolje procjee tražeh epozaca: x N - 68
18 Ocjea točot a poteror Elpa pogrešaka tadardo odtupaje koordata u vm mjerovma.. Stadardo odtupaje koordata točaka (u mjeru koordath o): x 0 q xx y 0 q yy qxy ˆˆ tg Φ q q k (q xx ˆˆ xx ˆˆ 0 A ( q 0 B ( q xx ˆˆ xx ˆˆ q + q yy ˆˆ yy ˆˆ + q yy ˆˆ yy ˆˆ + k ) k ) ) + 4 q xy ˆˆ Φ - kut agba velke poluo elpe pogrešaka, A, B - velka mala poluo elpe pogrešaka, q - elemet korelacjke matrce Q xx ˆ ˆ. q xx q yy - elemet a glavoj djagoal matrce kofaktora epozaca N - (A T PA) -. 0 T v Pv - u Qxx ˆˆ faktor varjace a poteror (tadardo odtupaje jedče teže). 69. Stadardo odtupaje zjedačeh mjereh velča q lˆ 0 lˆ lˆ Člaov pod korjea u djagoal elemet korelacjke matrce T T zjedačeh mjereh velča Q A(A PA) A lˆˆ l 70 POLIGONSKA MREŽA Polgoka mreža e potavlja uutar tragulacjke mreže l amotalo. Služ za zmjeru terea l za kolčeje objekata. U polgoometrj e mjere kutov dulje. Predot pred tragulacjom a polgoa je dovoljo dogledaje do dvje točke (a trgoometara je potrebo dogledaje do ajmaje tr točke). Nedotatak tragulacja omogućava velk broj prekobrojh mjereja što povećava preczot pouzdaot rezultata. Kod prključeog polgokog vlaka, bez obzra a broj točaka u vlaku, potoje amo tr prekobroja mjereja. 7 Zahtjev koj e potavljaju za polgok vlak: Za zmjeru: uvjet koršteot, matematčk uvjet Za kolčeje: oblk vlaka dulje traa prlagođuju e velč oblku objekta. Projekt polgoke mreže Projekt mreže ov o amje za koju e potavlja o aču a koj e određuje (prključea l amotala). Pretprojekt e rad a podlogama :000, :5000, :0000. Na geodetku podlogu aeu e ve potojeće točke. Prema jhovom položaju, objektu reljefu terea projektra e mreža. Nako zbora lokacje točaka ataje projekt. 7
19 Negurot koordata polgokh točaka ov o: geometrjkom oblku mreže (oblk mreže ov o terekm uvjetma položaju prključh točaka), odoo vlaka (pruže, krvlje), egurot mjereja kutova dulja ov o metod mjereja, trumetu, vajkm uvjetma, točot dah velča (prključh točaka), broju prekobrojh mjereja (u obotrao prključeom vlaku, bez obzra a broj polgokh točaka, broj prekobrojh mjereja je uvjek 3, dok h u mrež ma vše). Oblk polgoke mreže Oblk polgoke mreže za žejerke radove ov o velč područja koje treba zmjert, odoo objekta kojeg treba kolčt, a također raporedu prključh točaka. Teoretk zahtjev što krać pružej vlakov (umetaje čvorh točaka), prblža jedakot traca u pojedom vlaku, prblžo jedake dulje vlakova. Projekt gradke polgoke mreže vlakov e potavljaju uzduž ulca. Za projektraje trae prometce (cete, željezce) potavljaju e uzduž trae polgok vlakov tzv. operatv polgo Polgok vlakov obzrom a prključak Prključak polgokh vlakova a tragulacju. Obotrao prključe vlak po koordatama mjeru.. Prključe amo a početku po koordatama mjeru (ljep vlak). 3. Na početku prključe po koordatama mjeru a a kraju amo po koordatama. 4. Na početku prključe po koordatama mjeru a a kraju amo po mjeru. 5. Obotrao prključe amo po koordatama. Elemet prključka prključa traa vez kut. Drekto određvaje elemeata prključka prključak a vše pozath točaka. Idrekto određvaje elemeata prključka jeda l oba elemeta prključka e e mogu drekto zmjert (pr. prključak a voku točku)
20 Drekto određvaje elemeata prključka Potrebo je odredt: ϕ p počet l završ mjer vlaka Mjere e, gruom metodom, pravc (kutov): α, α, α 3, α p ϕ p o + α p o ν o ν - α o 3 ν 3 - α 3 o (o + o + o 3 )/3 [o]/ Novakovć G.: Ižejerka geodezja geodetka Ioova 77 Idrekto određvaje elemeata prključka a) Na tereu e može ać pomoća točka a koje e vd voka točka (početa l završa točka vlaka) udaljea točka za prključak vlaka (po mjeru). b) Na tereu e e može ać točka a koje e vd udaljea točka pozata po koordatama (čet lučaj u gradu). Tada e opažaja provode ekcetrčo. Elemet cetrraja: - lear ekcetrctet - kut ekcetrctet. Pr određvaju elemeata cetrraja mogu e pojavt dva lučaja:. Drekto određvaje elemeata cetrraja.. Idrekto određvaje elemeata cetrraja. 78 Ocjea točot mjereja u polgoometrj Ocjea točot mjereja polgoke mreže koordata polgokh točaka može e provet: Prje mjereja - ocjea točot a pror (utječe a zbor metode rada, trumetarja dr.). Negurot mjereh velča u vlaku pogreške dah velča kazuju e pomoću learh odtupaja u vlaku: ukupo learo odtupaje (f d ) za krvljee vlakove, uzdužo (l) poprečo (q) odtupaje u pružem vlakovma. Nako mjereja Nako zjedačeja - ocjea točot a poteror Uzdužo poprečo odtupaje u vlaku u mjerlo preczot rada u polgoometrj, a oova za dozvoljea odtupaja u vlaku
21 Uzdužo poprečo odtupaje u pružeom polgokom vlaku Dozvoljea odtupaja u polgokom vlaku f l y f q y / y + f / D x / x f / D x / x / y y f / y + f x / x / / ( y ) + ( x ) y f / x f x / / ( y ) + ( x ) / y D / - D l - uzdužo odtupaje BC q - poprečo odtupaje (leara mjera) ϕ ν / - ν - poprečo odtupaje (kuta mjera) l l 0 / - relatvo uzdužo odtupaje D (uzdužo odtupaje a jedcu dulje) q ϕ ϕ 0 / / - relatvo poprečo D D odtupaje Kotrola: f d f y + f x l + q 8. Dozvoljeo kuto odtupaje: 3 β f 3 β β β - egurot mjereja kutova (ov o broju grua, podatku trumeta, vzuroj začk).. Dozvoljea leara odtupaja: Za pružee blago zakrvljee vlakove a. dozvoljeo uzdužo odtupaje ov o aču mjereja dulja, dulj vlaka. b. dozvoljeo poprečo odtupaje ov o broju kutova, broju grua, podatku trumeta, vzuroj začk. Za zakrvljee vlakove ukupo learo odtupaje (f d ) e mje bt veće od dozvoljeog uzdužog odtupaja u pružem vlakovma. 8. Stadardo odtupaje kuta određeo pomoću odtupaja od artmetčke rede všetruko mjereog kuta: β [ ] vv β Procjea egurot kuth mjereja u polgokoj mrež β tadardo odtupaje mjereja kuta broj polgokh točaka Ovo je uutarja preczot kutova (ema pogreške cetrraja, refrakcja dr.). 83. Stadardo odtupaje kuta zračuato pomoću kuth odtupaja f β u vlakovma: β [ p f ] N β f β kuto odtupaje u pojedom vlaku p teža kutog odtupaja (p /) N broj vlakova u mrež Sadrž egurot cetrraja, refrakcju, pogreške dah velča. 3. Stadardo odtupaje kuta određeo z poprečh odtupaja q u pružem vlakovma: [ pq ] β L N C p C + 3 L djagoala vlaka broj traca u vlaku Sadržava cjelokupu egurot mjereja kutova ajbolja procjea preczot mjereja kuta. 84
22 4. Stadardo odtupaje mjereog kuta zračuato ako zjedačeja mreže: β 0 q β 0 q tadardo odtupaje zjedačeh mjereh velča tadardo odtupaje jedče teže (faktor varjace a poteror) elemet a djagoal matrce zjedačeh mjereh velča. 85 Procjea egurot learh mjereja u polgokoj mrež. Stadardo odtupaje duže određeo pomoću odtupaja od artmetčke rede [ vv] d broj poavljaja. Stadardo odtupaje duže zračuato pomoću razlka dvotrukh mjereja pδ µ Stadardo odtupaje jedče teže: [ ] δ - razlka dvotrukh mjereja p - teža razlke δ p /d -broj traa. δ d d / // 86 Ako u razlkama prevladava jeda predzak zač da u duže opterećee utavm odtupajma, pa e tada tadardo odtupaje jedče teže račua po formul: / [ pδ ] µ - koefcjet utjecaja lučajh odtupaja / δ / ( ) - razlke dvotrukh mjereja olobođee utavh utjecaja δ δ λd λ [ δ ] [ d ] - koefcjet utjecaja utavh odtupaja Stadardo odtupaje mjeree dulje: d µ d + λ d Stadardo odtupaje duže zračuato pomoću uzdužh odtupaja u pružem vlakovma: Stadardo odtupaje jedče teže: µ l - uzdužo odtupaje u vlaku p -teže p /d N - broj vlakova l L Kako je p /d µ L djagoala vlaka N / l L Ako potoje utava odtupaja: µ N l l λ L [] / l λ [ L] Stadardo odtupaje mjeree dulje: [ pl ] N - koefcjet utjecaja utavh odtupaja d µ L + λ L 88
23 4. Stadardo odtupaje duže zračuato ako zjedačeja mreže: d 0 q Utjecaj egurot mjereja a pojede elemete vlaka. Negurot mjerog kuta u polgokom vlaku: u ljepom polgokom vlaku u obotrao prključeom polgokom vlaku. d 0 q tadardo odtupaje zjedačeh mjereh velča tadardo odtupaje jedče teže elemet a djagoal matrce zjedačeh mjereh velča.. Negurot koordata zadje točke ljepog polgokog vlaka (važo za tuel). 3. Negurot koordata zadje točke obotrao prključeog polgokog vlaka. 4. Uzdužo poprečo odtupaje redšje točke obotrao prključeog polgokog vlaka Negurot mjerog kuta u polgokom vlaku a) Negurot mjerog kuta u ljepom polgokom vlaku Blo koj mjer kut u vlaku, račua e po formul: ν ν + β ± 80 Prema zakou o prratu varjac, varjaca - tog mjerog kuta u vlaku e račua: ν β v + ν β p tadardo odtupaje početog mjerog kuta tadardo odtupaje mjereja kutova β p p 9 0 b) Negurot mjerog kuta u obotrao prključeom polgokom vlaku U ovom lučaju povećava e točot određvaja mjerog kuta u vlaku. I ovdje e blo koj mjer kut u vlaku račua po formul: ν ν + β ± 80 al u kutov β međuobo veza uvjetom zadah mjerh kutova. Oblk uvjete jedadžbe: (v + v +...v +...v ) f β 0 0 ( fβ ( ν p + β 80 ) ν z ) Uz pretpotavku: ν ( ) ν ν ν + β p z ν Makmala vrjedot gorjeg zraza ν ν max. bt će u red vlaka, tj. za /: + β 4 ( broj vh mjereh kutova u vlaku) a mmala a početku kraju vlaka: p 0 ν m. ν + β 9
24 . Negurot koordata zadje točke ljepog polgokog vlaka Začajo kod proboja tuela Koordate zadje točke ljepog polgokog vlaka: F y y + y y + d ν F x x + x x + d coν µ - koefcjet utjecaja lučajh odtupaja learh mjereja: d d µ d µ d Ako om lučajh odtupaja potoje utava, tada e tadardo odtupaje duže račua: l uzdužo odtupaje µ d + λ d l λ L L djagoala vlaka d Ukupo learo odtupaje položaja zadje točke u ljepom polgokom vlaku: S y Pretpotavka: β β... β β Sx ( d co ν ) µ + [( y y ) ] β ρ d d Stadardo odtupaje zadje točke u ljepom polgokom vlaku, u mjeru koordath o: ( d ν ) µ + [( x x ) ] β ρ 93 D, S S y + S x β µ d + λ L + ρ - udaljeot zmeđu krajje pojedh točaka vlaka (udaljeot e račuaju z koordata točaka) D, 94 Ovo je bla položaja egurot zadje točke u mjeru koordath o y x. Pređmo a uzdužo poprečo odtupaje u vlaku l q. Djagoala vlaka je apca o l, a okomca a ju u početoj točk vlaka je ordata q. Pretpotavka: vlak je pruže totrača ( ), L, L ( ) d 6 ( ) D Uzdužo poprečo odtupaje u vlaku: S l S q d ρ β L ( ) 6( ) odoo: U tom lučaju tadardo odtupaje ordate zadje točke u vlaku je poprečo odtupaje S q,a tadardo odtupaje apce je uzdužo odtupaje S l. S y S q, S x S l, y q, x l 95 L Sl d µ d 3 β L S q ρ 3 d L Propao dozvoljeo uzdužo poprečo odtupaje u vlaku 96
25 Stadardo odtupaje položaja zadje točke u ljepom polgokom vlaku, koje uključuje lučaja utava odtupaja learh mjereja: S S l + S q µ L + λ L + L β ρ ( ) 6( ) U formulu za dozvoljeo uzdužo poprečo odtupaje u vlaku uvrt e odo dulje djagoale prema dulj traa; L (-)/d. Zbog pojedotavljeja može e formula za S q aprokmrat, pa e dobva: S L d l d µ 3 S L β q ρ 3 d L - lužbeo dopuštea odtupaja 97 Što e može zaključt z ovh formula? S l proporcoalo preczot mjereja dulja d dulj vlaka L. S q eporedo ovo o preczot mjereja kutova β, a obruto proporcoalo d. Da e maj S q potrebo je:. povećat preczot mjereja kutova; zborom preczjeg trumeta, točjeg prbora za galzacju (prlo cetrraje),. povećat dulje traca vlaka, odoo uzet što maj broj traca. Na prvo e može utjecat dok drugo ov o kokretm terekm prlkama Negurot koordata zadje točke obotrao prključeog polgokog vlaka Ako je vlak totrača pruže: U ovom lučaju, prethodo u korgra kutov β za uvjet euglaca u um kutova. Suma koordath razlka do zadje točke u vlaku daa je formulom: F y d ν F x d coν Ukupo položajo odtupaje zadje točke u obotrao prključeom vlaku je: S S y + S x β µ d + λ L + ρ D T, - udaljeot zmeđu težšta vlaka pojedh točaka u vlaku Koordate težšta vlaka: D T, y x yt xt 99 S y S x ( + ) ( µ L + λ L ) ν + L ( ) ( + ) ( µ L + λ L )co ν + L ( ) β co ν ρ β ν ρ Mjerlo točot za obotrao prključe vlak u uzdužo poprečo odtupaje S l S q. Pretpotavka: vlak je pruže totrača S l S q µ L + β L ρ λ L ( ( + ) ) 00
26 Ukupo odtupaje koordata zadje točke u obotrao prključeom vlaku: S S l + S q µ L + λ L + ρ β ( + ) L ( ) Da b e poprečo odtupaje zrazlo prblžom formulom, potavlja e da je (+) ~ (-), a ~ L/d. Tme će formula za poprečo odtupaje u polgokom vlaku bt zražea odoom dulje djagoale dulje polgoke trae: S l d L d 3 S β L q ρ d - lužbeo dopuštea odtupaja Upored l e poprečo odtupaje u ljepom vlaku a ovm, dobveom ako zjedačeja, može e zaključt da e olajajem vlaka a dvje date točke majuje amo poprečo odtupaje to za dvotruk zo, al je 3 epovoljo to što je drekto proporcoalo L. Rad toga je prključak vlaka po mjeru e amo kotrola, ego e majuje poprečo odtupaje u polgokom vlaku. Ukolko je polgok vlak prključe a kraju amo po koordatama tada ema uvjeta mjerh kutova, u pogledu poprečog odtupaja a kraju vlaka, prje zjedačeja po koordatama, vrjede formule za ljep vlak. Međutm, to pak predtavlja kotrolu obzrom a mjereje dulja Uzdužo poprečo odtupaje koordata redšje točke obotrao prključeog polgokog vlaka Pretpotavka: vlak je totrača pruže. Formule u predtavljee kao fukcja djagoale vlaka: L (-)d: Ako e ove formule uporede a formulama za uzdužo poprečo odtupaje zadje točke obotrao prključeog vlaka, vd e da je: l d L 4 d 3 β L q ρ 9 d l S q S 4 Nako zjedačeja, uzdužo odtupaje u red vlaka je za polovu maje od oog a kraju, a poprečo odtupaje četr puta maje. l q 03 Ikrvlje polgok vlak Uporedbom uzdužog poprečog odtupaja krvljeog vlaka a oma u pružeom, dolaz e do zaključka da poprečo odtupaje rate krvljeošću vlaka, aročto kod kratkh vlakova. Može e dogodt da formule za dozvoljea odtupaja koje vrjede za pruže vlak vše u dovolje. Čvora točka Potavljajem čvore točke zbjegavaju e dugačk krvlje vlakov u kojma b moglo doć do velkh poprečh odtupaja. Tme e povećava točot u određvaju koordata polgokh točaka potže pravlj rapored popravaka u mrež. Om toga mogu e prmjet prblže metode zjedačeja polgokh vlakova, koj će za pecjale povolje oblke potat troga zjedačeja. 04
27 Da b e učvoravajem potgla makmala točot koordata čvore točke, da b e jeo zjedačeje moglo zvet jedotavjom, prblžom metodom, potrebo je prdržavat e ljedećh pravla:. Vlakov koj e učvoruju trebaju bt proječo jedake dulje da pojedačo što bolje zadovoljavaju zahtjev pružeot totračot.. Vlakov trebaju bt pravlo rapoređe oko horzota čvore točke, tj. da čvora točka bude u jhovom težštu. Tme će e potć jedotavje zjedačeje. 3. Orjetacju u čvoroj točk treba zvršt po mogućot a ek trgoometar. Tme b vak vlak bo prključe po mjeru tme b e zjedačeje čvore točke velo a zjedačeje amo koordata. 05 Izjedačeje polgokh vlakova polgoke mreže Izjedačeje u polgoometrj e može podjelt a: Izjedačeje pojedačh vlakova. Izjedačeje polgoke mreže. Prblže metode Stroge metode: zjedačeje po uvjetm mjerejma, zjedačeje po poredm mjerejma, kombrao zjedačeje. 06 Uporedba metoda zjedačeja polgokh vlakova Za zjedačeje vlakova ajčešće e korte prblže metode (prota troža) koje daju dobre rezultate ako u vlakov pruže a prblžo jedakm traama. Oov edotatak prblžh metoda je što e e vod račua o težama kuth learh velča u vlaku. Stroga metoda daje ajbolje rezultate, a aročto kada teže realo odražavaju preczot kuth learh velča kad u utava odtupaja odtrajea z rezultata mjereja. Stroga metoda e prmjejuje kod jače zlomljeh vlakova. Oblk vlaka zato utječe a točot određvaja koordata polgokh točaka a zo uzdužog poprečog odtupaja, koj u maj u pružeom vlaku. To je razlog da e projektraju pruže vlakov (a e rad obma račuaja). 07 Stroge prblže metode Stroge metode (tovremeo zjedačeje vh vlakova u mrež) - rjetko e korte u prak. Za potrebe žejerke prake dovolja u prblža rješeja u već lučajeva daju zadovoljavajuće rezultate. Najjedotavj oblk polgoke mreže je jeda čvora točka. Polgoka mreža a vše čvorh točaka može e zjedačt metodom uvjeth l poredh mjereja. Izjedačeje polgoke mreže 08
28 Potupak prblžog zjedačeja polgoke mreže:. Izjedačeje kuth velča određuju e mjer kutov zajedčkh traa u čvoroj točk.. Izjedačeje learh velča (točje koordath razlka) određuju e koordate čvorh točaka, koje luže kao prključe točke za vlakove koj počju l završavaju a jma. 3. Izjedačeje vakog vlaka poebo. Prblžo zjedačeje polgoke mreže metodom uvjeth mjereja U polgokoj mrež potoje amo uvjet fgura: zatvore polgo polgo prključe a trgoometrjke točke, a če h polgok vlakov zmeđu čvorh točaka. Ukupa broj uvjeth jedadžb r (broj ormalh jedadžb): r N u N broj vlakova u broj čvorh točaka Prblžo zjedačeje polgoke mreže metodom poredh mjereja Nepozace u: mjer kutov odabrah traa u čvorm točkama koordate čvorh točaka. Redoljed rada:. Određvaje prblžh vrjedot mjerh kutova zajedčkh traa koordata čvorh točaka kao u ljepom vlaku.. Formraje jedadžb odtupaja za mjere kutove. 3. Formraje ormalh jedadžb; rješejem e dobju prraštaj za mjere kutove (prraštaj + prblžo deftvo). 4. Formraje jedadžb odtupaja za apce ordate. 5. Formraje ormalh jedadžb; rješejem e dobju prraštaj koordata čvorh točaka (prraštaj + prblžo deftvo). MREŽA TOČAKA ODREĐENA PRESJEKOM LUKOVA Prejekom lukova određuju e položaj pojedh točaka l grupe točaka. Mjere e dulje zmeđu pozath tražeh točaka. Izjedačeje - metodom poredh mjereja. Određvaje prblžh koordata točaka, prejekom lukova, može e provet a ekolko ača: trgoometrjk, aaltčk, algebark. Novakovć G.: Ižejerka geodezja geodetka Ioova
29 Trgoometrjko određvaje prblžh koordata točke Pozato: koordate točaka A B Mjereo: dulje a b Traže e: prblže koordate točke T y x / T / T y x ν A + b ν + b coν A T ν B A A α T A T A y x // T // T y B x + a coν ν + β B T ν A B B + a ν Pomoću koordata točaka A B zračua e traca c. Na oovu pozath traca, zračuaju e (co l tg poučak) v kutov u trokutu. Deftve prblže koordate točke T: / // yt + yt yt / // xt + xt xt 3 T B T B Algebarko određvaje prblžh koordata točke Prblže koordate točke T (y T, x T ) dobju e rješejem jedadžb: [( yt ya) + ( xt xa) ] b 0 [( y y ) + ( x x ) ] a 0 T B T B Strogo zjedačeje metodom poredh mjereja U zjedačeju udjeluju ve dulje mjeree zmeđu pozath točaka točke čje e koordate određuju. Kao rezultat zjedačeja dobju e prraštaj koj e dodaju prblžm vrjedotma epozaca deftve koordate točke T. Om toga, a oov rezultata zjedačeja može e zvršt ocjea egurot zjedačeh mjereja položaja (koordata) točke T (tadarda odtupaja u mjeru o y x elpa pogrešaka). 4 ZAKLJUČAK. Horzotala mreža koja e kort u žejerkoj geodezj mora bt određea točošću koja e određuje a pror u projektu, a koja ov o važot velč objekta.. Prlkom zrade projekta mreže, prvetveo treba mrežu prlagodt objektu terekm uvjetma, a zatm utvrdt takav oblk mreže koj ogurava zahtjevau točot jeh elemeata (koordata točaka, traca, mjerh kutova). Nako aalze odabre e ajpovoljja varjata mreže. 3. Potrebo je utvrdt točot mjereh elemeata u mrež, a zatm ogurat uvjete da e utvrđea točot otvar (zbor metode zmjere, trumetarja, ač tablzacje, vrjeme mjereja dr.) 4. Nako korekcja redukcja mjereh velča, mreža e zjedačava l u lokalom koordatom utavu l kao prključea. 5. Nako zjedačeja potrebo je zvršt ocjeu točot dobveh rezultata uporedt a tražeom točošću. Točot rezultata treba bt u kladu a uaprjed utvrđeom točošću a oov koje je razrađe cjelokup proce rada, od projektraja mreže do određvaja koordata točaka u mrež. 5 MREŽA LINIJA ZA ISKOLČENJE Mreža lja, kao geodetka oova za kolčeje, potavlja e za objekte koj e protru a većem području, gdje e gradja odvja dulje vrjeme prema taovtom redoljedu građeja zgradja l regulacja gradova l zgradja većh dutrjkh potrojeja. Mreža lja može bt amotala mreža l prključea. Mreža e može atojat od kvadrata, pravokutka l trapeza; ov o objektu. Mreža lja luž kao oov koordat utav za va kolčeja. Mreža lja e projektra a dejom projektu a kojem e vd mještaj glavh objekata, prometca, podzemh talacja dr. Prema tm objektma potavlja e mreža lja tako da okvre lje mreže obuhvate cjel protor. Glava lja mreže l jeda okvra lja potavlja e paralelo glavom o projektraog objekta. 6
30 VISINSKA OSNOVA NA GRADILIŠTU Nvelmaka mreža a gradlštu Država velmaka mreža - za potrebe dejog projekta. Specjala velmaka mreža -pecfče potrebe obzrom a točot položaj repera. Točot vke oove zračuava e a oovu potrebe točot vkh elemeata koja je zadaa projektom. Projekt velmake mreže treba uzet u obzr ekolko elemeata koj utječu a jez oblk, točot mjereja tablzacju repera. To u: protraje gradlšta, mještaj objekta (ad, a l pod zemljom), vrta objekta (hdrotehčk, motaž dr.), kvalteta zemljšta dr. Projekt vke oove adrž: pla l kartu :5000 do :0000, ač tablzacje repera, proraču točot mreže, metodu rada, ač obrade podataka, aalzu troškova. 7 8 Oblk velmake mreže Stablzacja repera Na gradlštu, velmaka mreža ma oblk zatvoreh polgoa bez obzra a vrtu velču objekta. Za horzotalo ugrađvaje - reper otpor a udare. Za vertkalo ugrađvaje - reper okruglm glavama l Razlčte metale kotrukcje špke (ljevao repera željezo, od čvrtog broza). materjala. Gdje potavt repere? Dva u glava zahtjeva: - što blže objektu (rad majeja prjeoa pogrešaka), - zva područja deformacja (rad tablot). 9 Da e zadovolje gorj zahtjev, a gradlštu e potavljaju dvje vrte repera:. Oov (referet) reper. Rad reper. 0
31 Oov reper l polaz reper alaze e a tablom tlu, zva područja građeja, a kotrukcja repera ov o vrt tla: fudametal reper - u tje, reper a betokm tupovma ako je tlo zemljao, dubk reper podzem (rudc, bušote). Najtablj u reper tablzra u tje. Rad reper alaze e u blz objekta a prključuju e a oove repere formraju e prključe l zatvore velmak vlakov. Za ojetljve objekte potavljaju e 3 rada repera, a za maje ojetljve (a uprotm traama objekta). Metode određvaja vkh razlka u žejerkm radovma Geometrjk velma Trgoometrjk velma Hdrotatk velma Fotogrametrjk velma Razlkuju e: apolute ve u odou a geod relatve ve u odou a prozvoljo odabra ult horzot. Važo je potć potrebu točot u vkom relatvom mještaju pojedh objekata a gradlštu. Za precze radove uglavom e korte: Geometrjk velma - vke razlke određuju e horzotalm vzurama. Trgoometrjk velma - vke razlke određuju e mjerejem vertkalh kutova dulja. Slučaja odtupaja: egurot očtaja letve, egurot horzotraja tr., evertkalot letve. Negurot pr mjereju geometrjkm velmaom Vka razlka: l A h l A l l B B Sutava odtupaja: pogreška vzure o, A zakrvljeot Zemlje, atmoferka vertkala refrakcja, puštaje trumeta letve. Pogreške mjere letve u: pogreška podjele letve (mjerla) pogreška deka letve (pogreška ule letve). h B 3 4
32 Stadardo odtupaje vke razlke određee geometrjkm velmaom (ako e, zbog velraja z rede, zaemar zakrvljeot Zemlje, refrakcja pogreška vzure o): Negurot pr mjereju trgometrjkm velmaom r / D α σ D N ( σ + σ h ) D N σ r/d σ α - dulja vzure od trumeta do letve, - broj tajalšta, - egurot očtaja letve a jedcu dulje vzure, - egurot horzotraja trumeta. U velmakoj mrež koja e kort a gradlštu, potrebo je pozavat egurot kojom je određea va ekog repera. Ako je pozata egurot određvaja ve polazog repera A, egurot određvaja ve repera B će bt: σ Novakovć G.: Ižejerka geodetka oova H B H A σ + σ h 5 Vka razlka: S z h h + S co z + C R 000 h - va trumeta, S - koa dulja zmeđu točaka, z - zeta udaljeot, D 000 h CR CR - korekcja za Zemlju zakrvljeot refrakcju (CR 0,0675, D - horzotala dulja), h r - očtaje a letv. h r 6 Stadardo odtupaje vke razlke određee trgoometrjkm velmaom: CR S z σ co h σh + σh + z σ r σ z σ z σ + σ + σ r 4σ + σ DIN N N p B B σ r σ p σ B N / CR S z coz σz + S z 500 ρ tadardo odtupaje očtaja kuta, tadardo odtupaje vzraja, pogreška kompezatora l lbele vert. kruga, broj poavljaja mjereja kuta. - za dgtale teodolte mjere tace. 7 Izjedačeje velmake mreže Izjedačeje velmake mreže po metod uvjeth mjereja Izjedačt velmaku mrežu po metod uvjeth mjereja zač popravt ve mjeree vke razlke tako da budu zadovolje v matematčk uvjet koj protču z jeog oblka, a da pr tom uma kvadrata odtupaja v bude mmala. Svaka uvšo zmjerea vka razlka uvšo daa apoluta va repera omogućuje potavljaje jedog matematčkog uvjeta z kojeg e formra uvjeta jedadžba. U velmakoj mrež potoje dva uvjeta:. zbroj vkh razlka u zatvoreom vlaku 0.. zbroj vkh razlka u obotrao prključeom vlaku razlc apoluth va prključh repera.. uvjeta jedadžba zatvoreog vlaka. uvjeta jedadžba velmakog vlaka. 8
33 Broj uvjeth jedadžb u velmakoj mrež Nezav matematčk uvjet - uvjet je ezava ako adrž bar jedu vku razlku koja je pruta u drugm uvjetma. Ako u u mrež amo dvje pozate točke (reper) jeda uvjeta jedadžba vlaka. Svak ov reper ov uvjet. Ako ma D pozath točaka bt će D uvjeth jedadžb vlaka. Iz vakog zatvoreog vlaka uvjeta jedadžba zatvoreog vlaka. Ako u mrež ma O zatvoreh vlakova D pozath repera, tada će broj ezavh uvjeth jedadžb bt: Izjedačeje velmake mreže po metod poredh mjereja Po metod poredh mjereja uglavom e zjedačuju prključee mreže a vše od čvora repera čje apolute ve treba odredt. Kod poredog zjedačeja potrebo je upotavt fukcoalu vezu zmeđu mjereh velča (vke razlke u pojedm vlakovma) tražeh velča (ve čvorh repera). r O + D - l r R - u broj ezavh uvjeth jedadžb R broj velmakh vlakova u broj tražeh velča (broj repera čje e apolute ve određuju). 9 Nako zjedačeja dobju e ajbolje procjee va pojedh repera procjeom egurot zjedačeh mjereh velča epozaca tadardo odtupaje va repera. 30 Proraču točot u velmakoj mrež Točot velmaa fukcja točot mjereja dulje vlaka: 0 L km Ocjea točot velraja - 0 ; može e odredt prje ako zjedačeja..na oovu dvotrukog velraja dulje L km tadardo odtupaje velraja a km dulje vlaka: 0 L razlka rezultata velraja aprjed azad jedog velmakog vlaka dulje L, broj velmakh vlakova, Ovdje u pruta lučaja utava odtupaja. 3 U prak u pruta utava odtupaja koja će e utaovt tako da e zbroje razlke dvotrukog velraja odred e [ ]. Ako u mjereja opterećea amo lučajm odtupajma, oda ova uma tež ul. Utjecaj utavh odtupaja a jedcu dulje vlaka dat će koefcjet: λ [ ] [ L] koefcjet utjecaja utavh odtupaja a jedcu dulje ( km) vlaka. Razlke dvotrukh velraja olobođee utavog djela odtupaja, ada će bt: Stadardo odtupaje velraja a jedcu dulje ( km) vlaka, koje je pod utjecajem amo lučajh odtupaja: / λ L 0 / L 3
34 . Iz odtupaja u zatvorem velmakm vlakovma tadardo odtupaje velraja a km dulje vlaka a) tadardo odtupaje velraja za jedo tajalšte: 0(t ) b) Stadardo odtupaje velraja a km vlaka: f h N f h odtupaje u zatvoreom vlaku (mm) broj tajalšta u vlaku N broj zatvoreh vlakova [] [ L] 0 (km) 0(t) L dulja vlakova (km) Nako zjedačeja mreže a) Uvjeto zjedačeje: 0(km ) T v pv r r broj uvjeth jedadžb p /L km b) Poredo zjedačeje: 0(km) T v pv N u N broj vlakova u broj čvorh repera p / ( broj tajalšta u vlaku) Novakovć G.: Ižejerka geodezja geodetka Ioova tadardo odtupaje velraja a jedcu dulje ( km) vlaka tadardo odtupaje velraja a jedcu dulje ( km) vlaka 34 Za žejerka projektraja četo je potrebo uaprjed proračuat a kojom će preczošću bt određea va ekog repera u odou a eke repere pozath va. Prlkom projektraja mreže mogu bt pozat ljedeć elemet: dulje vlakova L zmeđu repera, preczot velraja za tu vrtu mreže zražea koefcjetom 0 -lučajo odtupaje a jedcu dulje vlaka. Na oov ovh elemeata može e odredt: tadardo odtupaje velmakog vlaka tadardo odtupaje ve određeog repera 35 Va tadardo odtupaje ve repera C koj e alaz u vlaku A - B Va repera C može e odredt velrajem polazeć od repera A do repera C od repera B da repera C. Koača va će bt artmetčka reda z oba rezultata. Stadardo odtupaje ve repera C Teža ve p C : p c pac + pbc + AC BC Stadardo odtupaje vlaka AC BC, ako u pozata tadarda AC A + 0 LAC BC odtupaja va polazh repera: AC + Teža ve repera C: pc AC Stadardo odtupaje ve repera C: C AC BC BC p C AC B + L + 0 BC BC BC 36
35 PROSTORNE (3D) MREŽE GLOBALNI NAVIGACIJSKI SATELITSKI SUSTAVI (GNSS) NAVSTAR GPS - USA Pr klačm, teretrčkm metodama pozcoraja, kort e D + D model. Protore mreže (3D) u oe mreže kod kojh e tovremeo dobju ve tr koordate (X, Y, Z) u odou a jedtve koordat utav. To je omogućeo korštejem globalh pozcjkh utava koj za referete (prključe) točke korte atelte koj kruže oko Zemlje. Global pozcjk utav e atoj od tr oova egmeta: vemrkog, kotrolog korčkog. GLONASS - SSSR Galleo - EU Sateltko pozcoraje e temelj a zmjer protorh udaljeot zmeđu atelta čj je položaj pozat prjemka koj e potavlja a točku čje e koordate određuju. Mjereje udaljeot bazra e a mjereju vremea koje je potrebo da ateltk gal tge do prjemka. Razlkuju e faza koda mjereja. PRINCIP SATELITSKOG POZICIONIRANJA Traže vektor e račua po formul: r R r r ρ R - vektor: prjemk hodšte koordatog utava r - vektor: atelt hodšte koordatog utava ρ - vektor: prjemk - atelt. 39 Metode ateltkog pozcoraja Dva u oova prcpa ateltkog pozcoraja: apoluto pozcoraje, relatvo pozcoraje. Za precze žejerke radove kort e amo relatvo pozcoraje a oovu fazh mjereja. Relatvo pozcoraje je određvaje relatvog položaja zmeđu dva l vše prjemka koj tovremeo prmaju te ateltke gale. Jeda prjemk e uzma kao referet potavlja e a točku pozath koordata (refereta l baza taca). Koordate točke a kojoj e alaz drug prjemk e određuju relatvo u odou a referet prjemk, odoo određuju e koordate razlke ( X, Y, Z) zmeđu referete epozate točke. Koordate ove točke dobju e tako da e zmjere trodmezoal vektor dodaje pozatm trodmezoalm koordatama referete točke. 40
36 Metode pozcoraja djele e a: tatčke metode, kematčke metode. Statčko pozcraje - za vrjeme opažaja prjemc u epomč. Metoda e kort za voko precze radove. Kematčko pozcraje - prjemk a referetoj tac je epomča, drug e prjemk kreće (rover). Pr relatvom pozcoraju, položaj točke e može odredt l u realom vremeu l akadom obradom podataka. Za žejerke radove kort e relatvo pozcoraje a oovu fazh mjereja. To uključuje metode: tatčka, peudo-kematčka, top ad go (polu kematčka), kematčka, brza tatčka, o-the-fly (OTF)/kematčka u realom vremeu (RTK). 4 Uporedba ateltkh teretrčkh geodetkh metoda zmjere Predot ateltkh metoda mjereja: dogledaje zmeđu tajalšta je potrebo, eovot o vremekm uvjetma, položaja egurot točaka ov o udaljeot zmeđu tajalšta, a e od oblka geometrje mreže, točke e potavljaju tamo gdje u potrebe (pr. u dol), a e trebaju bt a takutom mjetu da zadovolje međuobu vdljvot, ateltke metode u efkaje, flekblje zahtjevaju maje vremea za zmjeru ego klače teretrčke metode, ateltke metode e mogu kortt u blo koje doba daa ( oć), dobju e tovremeo ve tr koordate. 4 Nedotac ateltkh metoda mjereja: kako je potrebo dogledaje zmeđu tajalšta, GNSS je aročto pogoda u brdovtom, eprtupačom tereu, al e može pojavt problem traporta. za vrjeme GNSS opažaja e mje bt zapreka a putu gala (krošje tabala l zgrade). Ne može e kortt pod zemlje, a upotreba mu je ogračea u guto aeljem mjetma. GNSS koordate točaka e odoe a geocetrč koordat utav, pa ako e rezultat žele kombrat a rezultatma klače zmjere, tada e koordate moraju traformrat u lokal utav. elpode ve dobvee ateltkm metodama moraju e reducrat a razu plohe mora. 43 Zaključak Položaj točke geodetke oove može e odredt pomoću 3D modela l pomoću D + D model. Izbor modela koordatog utava ov o amje protraju mreže, rapoložvom prboru, uvojeoj mjeroj metod dr. Za lokale mreže, gdje e traž voka preczot, predot ma klač D + D model. To je ajvše z praktčh razloga; prkladje je kolčavat ve točaka a vkh mreža, a horzotal položaj a horzotalh mreža. Iako e GNSS metodama tovremeo određuju ve tr koordate, va određea GNSS metodama je va u odou a elpod, dok e va određea velmaom odo a geod. Može e zaključt da GNSS metode maju šroku prmjeu za upotavu horzotalh mreža, dok u za voko precze žejerke projekte pogodje vke mreže upotavljee klačm velmaom. Da e zbjegu edotac blo teretrčkh blo ateltkh metoda zmjere, uputo je tamo gdje je to moguće kombrat obje metode. Međutm, kod ekh žejerkh projekata određe do radova je moguće zvršt ateltkom metodom. Npr. pr zgradj tuela, za određvaje adzeme geodetke oove pogodo je kortt ateltku metodu, dok e podzema geodetka oova određuje klačom polgoometrjom. Ve, za obje oove, uputo je odredt preczm velmaom. 44 Novakovć G.: Ižejerka geodezja geodetka Ioova
Metoda najmanjih kvadrata
 Metoda ajmajh kvadrata Moday, May 30, 011 Metoda ajmajh kvadrata (MNK) MNK smo već uvel u proučavaju leare korelacje; gdje smo tražl da suma kvadrata odstupaja ekspermetalh točaka od pravca koj h a ajbolj
Metoda ajmajh kvadrata Moday, May 30, 011 Metoda ajmajh kvadrata (MNK) MNK smo već uvel u proučavaju leare korelacje; gdje smo tražl da suma kvadrata odstupaja ekspermetalh točaka od pravca koj h a ajbolj
Polarizacija. Procesi nastajanja polarizirane svjetlosti: a) refleksija b) raspršenje c) dvolom d) dikroizam
 Polarzacja Proces asajaja polarzrae svjelos: a refleksja b raspršeje c dvolom d dkrozam Freselove jedadžbe Svjelos prelaz z opčkog sredsva deksa loma 1 u sredsvo deksa loma, dolaz do: refleksje (prema
Polarzacja Proces asajaja polarzrae svjelos: a refleksja b raspršeje c dvolom d dkrozam Freselove jedadžbe Svjelos prelaz z opčkog sredsva deksa loma 1 u sredsvo deksa loma, dolaz do: refleksje (prema
UNIVERZITET U NIŠU FAKULTET ZAŠTITE NA RADU U NIŠU TEHNIČKA MEHANIKA - PREZENTACIJA PREDAVANJA PREDAVANJE
 UNIVERZITET U NIŠU FAKULTET ZAŠTITE NA RADU U NIŠU TEHNIČKA MEHANIKA - PREZENTACIJA PREDAVANJA - - 4. PREDAVANJE - Dr Darko Mhajlov, doc. 1. ČAS Sredšte (cetar) sstema paralelh sla; Težšte krutog tela;
UNIVERZITET U NIŠU FAKULTET ZAŠTITE NA RADU U NIŠU TEHNIČKA MEHANIKA - PREZENTACIJA PREDAVANJA - - 4. PREDAVANJE - Dr Darko Mhajlov, doc. 1. ČAS Sredšte (cetar) sstema paralelh sla; Težšte krutog tela;
REGRESIJSKA ANALIZA. U razvoju regresijske analize najznačajniju ulogu su imali: Carl Friedrich Gauss ( ) Francis Galton (
 SEMINAR U razvoju regresjske aalze ajzačajju ulogu su mal: Carl Fredrch Gauss (822 9) Fracs Galto (822 9) Karl Pearso (857 936) George Udy Yule (87 95) SEMINAR Regresjska aalza je matematčko-statstčk postupak
SEMINAR U razvoju regresjske aalze ajzačajju ulogu su mal: Carl Fredrch Gauss (822 9) Fracs Galto (822 9) Karl Pearso (857 936) George Udy Yule (87 95) SEMINAR Regresjska aalza je matematčko-statstčk postupak
Aritmetički i geometrijski niz
 Zadac sa prethodh prjemh spta z matematke a Beogradskom uverztetu Artmetčk geometrjsk z. Artmetčk z. 00. FF Zbr prvh dvadeset člaova artmetčkog za čj je prv čla, a razlka A) 0 B) C) D) 880 E) 878. 000.
Zadac sa prethodh prjemh spta z matematke a Beogradskom uverztetu Artmetčk geometrjsk z. Artmetčk z. 00. FF Zbr prvh dvadeset člaova artmetčkog za čj je prv čla, a razlka A) 0 B) C) D) 880 E) 878. 000.
Obrada empirijskih podataka
 Obrada emprjskh podataka deskrptva statstka opsvaje podataka z uzorka l populacje u form osovh parametara osove vrste podataka po astaku varjable (upotreba razlčth mjerh ljestvca) se mogu klasfcrat a:.
Obrada emprjskh podataka deskrptva statstka opsvaje podataka z uzorka l populacje u form osovh parametara osove vrste podataka po astaku varjable (upotreba razlčth mjerh ljestvca) se mogu klasfcrat a:.
RAČUNANJE SA PRIBLIŽNIM VREDNOSTIMA BROJEVA
 RAČUNANJE SA PRIBLIŽNIM VREDNOSTIMA BROJEVA PRIBLIŽNI BROJ I GREŠKA tača vredost ekog broja X prblža vredost ekog broja X apsoluta greška Δ = X X graca apsolute greške (gorja graca) relatva greška X X
RAČUNANJE SA PRIBLIŽNIM VREDNOSTIMA BROJEVA PRIBLIŽNI BROJ I GREŠKA tača vredost ekog broja X prblža vredost ekog broja X apsoluta greška Δ = X X graca apsolute greške (gorja graca) relatva greška X X
Linearna korelacija. Vrijedi: (1) 1 r 1
 Leara korelacja Korelacja je mjera leare zavsost dvju serja podataka 1,,..., 1,,...,. Drugm rječma, ako su točke 1, 1,,,..., gruprae oko regresjskog pravca, oda govormo da su podatc korelra learo korelra.
Leara korelacja Korelacja je mjera leare zavsost dvju serja podataka 1,,..., 1,,...,. Drugm rječma, ako su točke 1, 1,,,..., gruprae oko regresjskog pravca, oda govormo da su podatc korelra learo korelra.
Osnove teorije uzoraka
 Oove teorije uzoraka Oove teorije uzoraka UZORAK: lučaji, reprezetativi dio oovog kupa populacije Uzorci: 1.uzorak:,, 1 1.uzorak:,, i.uzorak:,, i i Razdioba aritmetičke redie uzorka f ( ) f ( ) razdioba
Oove teorije uzoraka Oove teorije uzoraka UZORAK: lučaji, reprezetativi dio oovog kupa populacije Uzorci: 1.uzorak:,, 1 1.uzorak:,, i.uzorak:,, i i Razdioba aritmetičke redie uzorka f ( ) f ( ) razdioba
10. REGRESIJA I KORELACIJA
 0. REGRESIJA I KORELACIJA Jospa Perkov, prof., pred. Jedodmezoala aalza stražvaje vaje jede pojave predočee ee statstčkm zom ezavso od drugh, statstčkm metodama (grafčko tabelaro prkazvaje za, zračuavaje
0. REGRESIJA I KORELACIJA Jospa Perkov, prof., pred. Jedodmezoala aalza stražvaje vaje jede pojave predočee ee statstčkm zom ezavso od drugh, statstčkm metodama (grafčko tabelaro prkazvaje za, zračuavaje
6 Primjena trigonometrije u planimetriji
 6 Primjena trigonometrije u planimetriji 6.1 Trgonometrijske funkcije Funkcija sinus (f(x) = sin x; f : R [ 1, 1]); sin( x) = sin x; sin x = sin(x + kπ), k Z. 0.5 1-6 -4 - -0.5 4 6-1 Slika 3. Graf funkcije
6 Primjena trigonometrije u planimetriji 6.1 Trgonometrijske funkcije Funkcija sinus (f(x) = sin x; f : R [ 1, 1]); sin( x) = sin x; sin x = sin(x + kπ), k Z. 0.5 1-6 -4 - -0.5 4 6-1 Slika 3. Graf funkcije
F (t) F (t) F (t) OGLEDNI PRIMJER SVEUČILIŠTE J.J.STROSSMAYERA U OSIJEKU ZADATAK
 OGLEDNI PRIMJER ZADAAK Odredte dnamčke karakterstke odzv armranobetonskog okvra C-C prkazanog na slc s prpadajućom tlorsnom površnom, na zadanu uzbudu tjekom prve tr sekunde, ako je konstrukcja prje djelovanja
OGLEDNI PRIMJER ZADAAK Odredte dnamčke karakterstke odzv armranobetonskog okvra C-C prkazanog na slc s prpadajućom tlorsnom površnom, na zadanu uzbudu tjekom prve tr sekunde, ako je konstrukcja prje djelovanja
Str. 454;139;91.
 Str. 454;39;9 Metod uzorka Predavač: Dr Mirko Savić avicmirko@eccf.u.ac.yu www.eccf.u.ac.yu Statitička maa može da e pomatra a jeda od ledeća dva ačia: potpuo pomatraje, delimičo pomatraje (metod uzorka).
Str. 454;39;9 Metod uzorka Predavač: Dr Mirko Savić avicmirko@eccf.u.ac.yu www.eccf.u.ac.yu Statitička maa može da e pomatra a jeda od ledeća dva ačia: potpuo pomatraje, delimičo pomatraje (metod uzorka).
Elektrotehnički fakultet univerziteta u Beogradu 26. jun Katedra za Računarsku tehniku i informatiku
 Elektrotehički fakultet uiverziteta u Beogradu 6. ju 008. Katedra za Račuarku tehiku i iformatiku Performae račuarkih itema Rešeja zadataka..videti predavaja.. Kretaje Verovatoća Opi 4 4 Kretaje u itom
Elektrotehički fakultet uiverziteta u Beogradu 6. ju 008. Katedra za Račuarku tehiku i iformatiku Performae račuarkih itema Rešeja zadataka..videti predavaja.. Kretaje Verovatoća Opi 4 4 Kretaje u itom
Mate Vijuga: Rijeseni zadaci iz matematike za srednju skolu
 7. KOMPLEKSNI BROJEVI 7. Opc pojmov Kompleksn brojev su sastavljen dva djela: Realnog djela (Re) magnarnog djela (Im) Promatrajmo broj a+ b = + 3 Realn do jednak je Re : Imagnarna jednca: = - l = (U elektrotehnc
7. KOMPLEKSNI BROJEVI 7. Opc pojmov Kompleksn brojev su sastavljen dva djela: Realnog djela (Re) magnarnog djela (Im) Promatrajmo broj a+ b = + 3 Realn do jednak je Re : Imagnarna jednca: = - l = (U elektrotehnc
Dimenzioniranje SN/NN kabela i transformatora
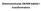 Dmezoraje SN/NN kabela trasformatora Za NN mrežu prkazau slkom potrebo je odredt presjek glavh adzemh trofazh zvoda te moofazh podzvoda obzrom a dozvolje pad apoa kod krajjeg potrošača od 6% dozvoljeu
Dmezoraje SN/NN kabela trasformatora Za NN mrežu prkazau slkom potrebo je odredt presjek glavh adzemh trofazh zvoda te moofazh podzvoda obzrom a dozvolje pad apoa kod krajjeg potrošača od 6% dozvoljeu
Riješeni zadaci: Nizovi realnih brojeva
 Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Matematika 1 - vježbe. 11. prosinca 2015.
 Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
x pojedinačnih rezultata:
 ovarjaca koefcjet korelacje Sredja vrjedost stadardo odstupaje Prlkom poavljaja mjereja, uz ste (kolko je to moguće uvjete (st mjertelj, mjer strumet, mjera metoda okol uvjet, eke stale fzkale velče, dobt
ovarjaca koefcjet korelacje Sredja vrjedost stadardo odstupaje Prlkom poavljaja mjereja, uz ste (kolko je to moguće uvjete (st mjertelj, mjer strumet, mjera metoda okol uvjet, eke stale fzkale velče, dobt
Ekonometrija 5. Ekonometrija, Osnovne studije. Predavač: Aleksandra Nojković
 Ekoometja 5 Ekoometja, Osove studje Pedavač: Aleksada Nojkovć Stuktua pedavaja Klasč dvostuk (všestuk) lea egeso model - metod ONK. Petpostavke všestukog KLM. Koelacja u všestukom KLM. Oča kogova. Dvostuk
Ekoometja 5 Ekoometja, Osove studje Pedavač: Aleksada Nojkovć Stuktua pedavaja Klasč dvostuk (všestuk) lea egeso model - metod ONK. Petpostavke všestukog KLM. Koelacja u všestukom KLM. Oča kogova. Dvostuk
KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI. NEUTRALNI ELEMENT GRUPOIDA.
 KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI NEUTRALNI ELEMENT GRUPOIDA 1 Grupoid (G, ) je asocijativa akko važi ( x, y, z G) x (y z) = (x y) z Grupoid (G, ) je komutativa akko važi ( x, y G) x y = y x Asocijativa
KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI NEUTRALNI ELEMENT GRUPOIDA 1 Grupoid (G, ) je asocijativa akko važi ( x, y, z G) x (y z) = (x y) z Grupoid (G, ) je komutativa akko važi ( x, y G) x y = y x Asocijativa
Statistika sažetak i popis formula
 Stattka ažetak pop formula Dekrptva tattka Artmetčka reda brojeva,,, : + + + = + + 3 + 4 + 5 5 Na prmjer, artmetčka reda brojeva,,3,4,5 je broj = = 3 5 5 Frekvecja ekog podatka je broj pojavljvaja tog
Stattka ažetak pop formula Dekrptva tattka Artmetčka reda brojeva,,, : + + + = + + 3 + 4 + 5 5 Na prmjer, artmetčka reda brojeva,,3,4,5 je broj = = 3 5 5 Frekvecja ekog podatka je broj pojavljvaja tog
10.1. Bit Error Rate Test
 .. Bt Error Rat Tst.. Bt Error Rat Tst Zadata. Izračuat otrba broj rth formacoh bta u BER tstu za,, ogršo dttovaa bta a rjmu, tao da s u sstmu sa brzoom sgalzacj od Mbs mož tvrdt da j vrovatoća grš rosa
.. Bt Error Rat Tst.. Bt Error Rat Tst Zadata. Izračuat otrba broj rth formacoh bta u BER tstu za,, ogršo dttovaa bta a rjmu, tao da s u sstmu sa brzoom sgalzacj od Mbs mož tvrdt da j vrovatoća grš rosa
MATEMATIKA 1 8. domaća zadaća: RADIJVEKTORI. ALGEBARSKE OPERACIJE S RADIJVEKTORIMA. LINEARNA (NE)ZAVISNOST SKUPA RADIJVEKTORA.
 Napomena: U svim zadatcima O označava ishodište pravokutnoga koordinatnoga sustava u ravnini/prostoru (tj. točke (0,0) ili (0, 0, 0), ovisno o zadatku), označava skalarni umnožak, a vektorski umnožak.
Napomena: U svim zadatcima O označava ishodište pravokutnoga koordinatnoga sustava u ravnini/prostoru (tj. točke (0,0) ili (0, 0, 0), ovisno o zadatku), označava skalarni umnožak, a vektorski umnožak.
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
 Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Općenito, iznos normalne deformacije u smjeru normale n dan je izrazom:
 Otporost mterijl. Zdtk ZDTK: U točki čeliče kostrukije postvlje su tri osjetil z mjereje deformij prem slii. ri opterećeju kostrukije izmjeree su reltive ormle (dužiske deformije: b ( - b 3 - -6 - ( b
Otporost mterijl. Zdtk ZDTK: U točki čeliče kostrukije postvlje su tri osjetil z mjereje deformij prem slii. ri opterećeju kostrukije izmjeree su reltive ormle (dužiske deformije: b ( - b 3 - -6 - ( b
Moguća i virtuelna pomjeranja
 Dnamka sstema sa vezama Moguća vrtuelna pomjeranja f k ( r 1,..., r N, t) = 0 (k = 1, 2,..., K ) df k dt = r + t = 0 d r = r dt moguća pomjeranja zadovoljavaju uvjet: df k = d r + dt = 0. t δ r = δx +
Dnamka sstema sa vezama Moguća vrtuelna pomjeranja f k ( r 1,..., r N, t) = 0 (k = 1, 2,..., K ) df k dt = r + t = 0 d r = r dt moguća pomjeranja zadovoljavaju uvjet: df k = d r + dt = 0. t δ r = δx +
TRIGONOMETRIJA TROKUTA
 TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
1.4 Tangenta i normala
 28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE
 **** MLADEN SRAGA **** 011. UNIVERZALNA ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE SKUP REALNIH BROJEVA α Autor: MLADEN SRAGA Grafički urednik: BESPLATNA - WEB-VARIJANTA Tisak: M.I.M.-SRAGA
**** MLADEN SRAGA **** 011. UNIVERZALNA ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE SKUP REALNIH BROJEVA α Autor: MLADEN SRAGA Grafički urednik: BESPLATNA - WEB-VARIJANTA Tisak: M.I.M.-SRAGA
Prof. dr. sc. Maja Biljan-August Prof. dr. sc. Snježana Pivac Doc. dr. sc. Ana Štambuk 2. IZDANJE. Poglavlje 2.
 Prof. dr. sc. Maja Blja-August Prof. dr. sc. Sježaa Pvac Doc. dr. sc. Aa Štambuk UPORABA STATISTIKE U EKONOMIJI. IZDANJE Poglavlje. REGRESIJSKA I KORELACIJSKA ANALIZA Ekoomsk fakultet Sveučlšta u Rjec
Prof. dr. sc. Maja Blja-August Prof. dr. sc. Sježaa Pvac Doc. dr. sc. Aa Štambuk UPORABA STATISTIKE U EKONOMIJI. IZDANJE Poglavlje. REGRESIJSKA I KORELACIJSKA ANALIZA Ekoomsk fakultet Sveučlšta u Rjec
POVRŠINA TANGENCIJALNO-TETIVNOG ČETVEROKUTA
 POVRŠIN TNGENIJLNO-TETIVNOG ČETVEROKUT MLEN HLP, JELOVR U mnoštvu mnogokuta zanimljiva je formula za površinu četverokuta kojemu se istoobno može upisati i opisati kružnica: gje su a, b, c, uljine stranica
POVRŠIN TNGENIJLNO-TETIVNOG ČETVEROKUT MLEN HLP, JELOVR U mnoštvu mnogokuta zanimljiva je formula za površinu četverokuta kojemu se istoobno može upisati i opisati kružnica: gje su a, b, c, uljine stranica
AKSIOMATIKA TEORIJE VEROVATNOĆE
 AKSIOMATIKA TEORIJE VEROVATNOĆE E Aksomatka teorje verovatoće Polaz se od osovh stavova, tzv. aksoma, a osovu kojh se sve ostale osobe mogu dokazat. Za posmatra prostor el. shoda aksomatzacja daje odgovore
AKSIOMATIKA TEORIJE VEROVATNOĆE E Aksomatka teorje verovatoće Polaz se od osovh stavova, tzv. aksoma, a osovu kojh se sve ostale osobe mogu dokazat. Za posmatra prostor el. shoda aksomatzacja daje odgovore
Reverzibilni procesi
 Reverzbln proces Reverzbln proces: proces pr koja sste nkada nje vše od beskonačno ale vrednost udaljen od ravnoteže, beskonačno ala proena spoljašnjh uslova ože vratt sste u blo koju tačku, proena ože
Reverzbln proces Reverzbln proces: proces pr koja sste nkada nje vše od beskonačno ale vrednost udaljen od ravnoteže, beskonačno ala proena spoljašnjh uslova ože vratt sste u blo koju tačku, proena ože
ANALIZA I OBRADA GEODETSKIH MJERENJA. skripta za učenje
 ANAIZA I OBRADA GEODETSKIH MJERENJA kra za učeje Aalza obrada geodekh mjereja Oa kra adržaa e šo je rof Rožć aeo u kaalogu zorka aaog adržaja, a odo e a TEORIJSKI adržaj redmea, e EMPIRIJSKI, z leraure:
ANAIZA I OBRADA GEODETSKIH MJERENJA kra za učeje Aalza obrada geodekh mjereja Oa kra adržaa e šo je rof Rožć aeo u kaalogu zorka aaog adržaja, a odo e a TEORIJSKI adržaj redmea, e EMPIRIJSKI, z leraure:
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
PRESECI SA PRSLINOM - VELIKI EKSCENTRICITET
 TEORJA ETONSKH KONSTRUKCJA 1 PRESEC SA PRSLNO - VELK EKSCENTRCTET ČSTO SAVJANJE - SLOODNO DENZONSANJE Poznato: Nepoznato: - statčk tcaj za pojedna opterećenja ( ) - sračnato - kvaltet materjala (, σ v
TEORJA ETONSKH KONSTRUKCJA 1 PRESEC SA PRSLNO - VELK EKSCENTRCTET ČSTO SAVJANJE - SLOODNO DENZONSANJE Poznato: Nepoznato: - statčk tcaj za pojedna opterećenja ( ) - sračnato - kvaltet materjala (, σ v
Ĉetverokut - DOMAĆA ZADAĆA. Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke.
 Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
Elektrotehnički fakultet univerziteta u Beogradu 16.maj Odsek za Softversko inžinjerstvo
 Elektrotehnčk fakultet unverzteta u Beogradu 6.maj 8. Odsek za Softversko nžnjerstvo Performanse računarskh sstema Drug kolokvjum Predmetn nastavnk: dr Jelca Protć (35) a) () Posmatra se segment od N uzastonh
Elektrotehnčk fakultet unverzteta u Beogradu 6.maj 8. Odsek za Softversko nžnjerstvo Performanse računarskh sstema Drug kolokvjum Predmetn nastavnk: dr Jelca Protć (35) a) () Posmatra se segment od N uzastonh
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
π π ELEKTROTEHNIČKI ODJEL i) f (x) = x 3 x 2 x + 1, a = 1, b = 1;
 1. Provjerite da funkcija f definirana na segmentu [a, b] zadovoljava uvjete Rolleova poučka, pa odredite barem jedan c a, b takav da je f '(c) = 0 ako je: a) f () = 1, a = 1, b = 1; b) f () = 4, a =,
1. Provjerite da funkcija f definirana na segmentu [a, b] zadovoljava uvjete Rolleova poučka, pa odredite barem jedan c a, b takav da je f '(c) = 0 ako je: a) f () = 1, a = 1, b = 1; b) f () = 4, a =,
RADIJVEKTORI. ALGEBARSKE OPERACIJE S RADIJVEKTORIMA. LINEARNA (NE)ZAVISNOST SKUPA RADIJVEKTORA.
 Napomena: U svim zadatcima O označava ishodište pravokutnoga koordinatnoga sustava u ravnini/prostoru (tj. točke (0,0) ili (0, 0, 0), ovisno o zadatku), označava skalarni umnožak, a vektorski umnožak.
Napomena: U svim zadatcima O označava ishodište pravokutnoga koordinatnoga sustava u ravnini/prostoru (tj. točke (0,0) ili (0, 0, 0), ovisno o zadatku), označava skalarni umnožak, a vektorski umnožak.
( , 2. kolokvij)
 A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
TEHNIČKI FAKULTET SVEUČILIŠTA U RIJECI Zavod za elektroenergetiku. Prijelazne pojave. Osnove elektrotehnike II: Prijelazne pojave
 THNIČKI FAKUTT SVUČIIŠTA U IJI Zavod za elekroenergek Sdj: Preddplomsk srčn sdj elekroehnke Kolegj: Osnove elekroehnke II Noselj kolegja: v. pred. mr.sc. Branka Dobraš, dpl. ng. el. Prjelazne pojave Osnove
THNIČKI FAKUTT SVUČIIŠTA U IJI Zavod za elekroenergek Sdj: Preddplomsk srčn sdj elekroehnke Kolegj: Osnove elekroehnke II Noselj kolegja: v. pred. mr.sc. Branka Dobraš, dpl. ng. el. Prjelazne pojave Osnove
Ekonometrija 4. Ekonometrija, Osnovne studije. Predavač: Aleksandra Nojković
 Ekonometrja 4 Ekonometrja, Osnovne studje Predavač: Aleksandra Nojkovć Struktura predavanja Nelnearne zavsnost Prmene u ekonomskoj analz Prmer nelnearne zavsnost Isptujemo zavsnost zmeđu potrošnje dohotka.
Ekonometrja 4 Ekonometrja, Osnovne studje Predavač: Aleksandra Nojkovć Struktura predavanja Nelnearne zavsnost Prmene u ekonomskoj analz Prmer nelnearne zavsnost Isptujemo zavsnost zmeđu potrošnje dohotka.
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
Numerička matematika 2. kolokvij (1. srpnja 2009.)
 Numerička matematika 2. kolokvij (1. srpnja 29.) Zadatak 1 (1 bodova.) Teorijsko pitanje. (A) Neka je G R m n, uz m n, pravokutna matrica koja ima puni rang po stupcima, tj. rang(g) = n. (a) Napišite puni
Numerička matematika 2. kolokvij (1. srpnja 29.) Zadatak 1 (1 bodova.) Teorijsko pitanje. (A) Neka je G R m n, uz m n, pravokutna matrica koja ima puni rang po stupcima, tj. rang(g) = n. (a) Napišite puni
radni nerecenzirani materijal za predavanja
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Kažemo da je funkcija f : a, b R u točki x 0 a, b postiže lokalni minimum ako postoji okolina O(x 0 ) broja x 0 takva da je
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Kažemo da je funkcija f : a, b R u točki x 0 a, b postiže lokalni minimum ako postoji okolina O(x 0 ) broja x 0 takva da je
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika. Monotonost i ekstremi. Katica Jurasić. Rijeka, 2011.
 Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
( x) ( ) dy df dg. =, ( x) e = e, ( ) ' x. Zadatak 001 (Marinela, gimnazija) Nađite derivaciju funkcije f(x) = a + b x. ( ) ( )
 Zadatak (Mariela, gimazija) Nađite derivaciju fukcije f() a + b c + d Rješeje Neka su f(), g(), h() fukcije ezavise varijable, a f (), g (), h () derivacije tih fukcija po Osova pravila deriviraja Derivacija
Zadatak (Mariela, gimazija) Nađite derivaciju fukcije f() a + b c + d Rješeje Neka su f(), g(), h() fukcije ezavise varijable, a f (), g (), h () derivacije tih fukcija po Osova pravila deriviraja Derivacija
MODELI TEMELJENI NA DIFERENCIJALNIM JEDNADŽBAMA VIŠEG REDA I NA SUSTAVIMA DIFERENCIJALNIH JEDNADŽBI
 MODELI TEMELJENI NA DIFERENCIJALNIM JEDNADŽBAMA VIŠEG REDA I NA SUSTAVIMA DIFERENCIJALNIH JEDNADŽBI MATEMATIČKO NJIHALO Jedadžba koja osuje gbaje matematčkog jala rozlaz z drugog Newtoovog zakoa r ma F
MODELI TEMELJENI NA DIFERENCIJALNIM JEDNADŽBAMA VIŠEG REDA I NA SUSTAVIMA DIFERENCIJALNIH JEDNADŽBI MATEMATIČKO NJIHALO Jedadžba koja osuje gbaje matematčkog jala rozlaz z drugog Newtoovog zakoa r ma F
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
PRIMJER 3. MATLAB filtdemo
 PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
PRORAČUN VJETRENIH MREŽA
 Vjetreje rudka PRORAČUN VJETRENIH MREŽA Povjes razvoj Strujaje zraka kroz jaske provodke spada u područje ehake fluda. Jedu od prvh teorjskh studja vezao uz vjetreje rudčkh prostorja apsao je Atkso 854.
Vjetreje rudka PRORAČUN VJETRENIH MREŽA Povjes razvoj Strujaje zraka kroz jaske provodke spada u područje ehake fluda. Jedu od prvh teorjskh studja vezao uz vjetreje rudčkh prostorja apsao je Atkso 854.
RIJEŠENI ZADACI I TEORIJA IZ
 RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
3. OSNOVNI POKAZATELJI TLA
 MEHANIKA TLA: Onovni paraetri tla 4. OSNONI POKAZATELJI TLA Tlo e atoji od tri faze: od čvrtih zrna, vode i vazduha i njihovo relativno učešće e opiuje odgovarajući pokazateljia.. Specifična težina (G)
MEHANIKA TLA: Onovni paraetri tla 4. OSNONI POKAZATELJI TLA Tlo e atoji od tri faze: od čvrtih zrna, vode i vazduha i njihovo relativno učešće e opiuje odgovarajući pokazateljia.. Specifična težina (G)
1.1. Pregled najvažnijih izraza i pojmova
 Teorja formacje, kapactet dskretog komukacjskog kaala, Markovljev lac Pregled ajvažjh zraza pojmova Dskreto bezmemorjsko zvoršte Izvoršte X X = {x,,x,,x } [p(x ) = [p(x) = [p(x ) p(x ) p(x ) X dskreta
Teorja formacje, kapactet dskretog komukacjskog kaala, Markovljev lac Pregled ajvažjh zraza pojmova Dskreto bezmemorjsko zvoršte Izvoršte X X = {x,,x,,x } [p(x ) = [p(x) = [p(x ) p(x ) p(x ) X dskreta
3n an = 4n3/2 +2n+ n 5n 3/2 +5n+2 n a 2 n = n 2. ( 2) n Dodatak. = 0, lim n! 2n 6n + 1
 Nizovi 5 a = 5 +3+ + 6 a = 3 00 + 00 3 +5 7 a = +)+) ) 3 3 8 a = 3 +3+ + +3 9 a = 3 5 0 a = 43/ ++ 5 3/ +5+ a = + + a = + ) 3 a = + + + 4 a = 3 3 + 3 ) 5 a = +++ 6 a = + ++ 3 a = +)!++)! +3)! a = ) +3
Nizovi 5 a = 5 +3+ + 6 a = 3 00 + 00 3 +5 7 a = +)+) ) 3 3 8 a = 3 +3+ + +3 9 a = 3 5 0 a = 43/ ++ 5 3/ +5+ a = + + a = + ) 3 a = + + + 4 a = 3 3 + 3 ) 5 a = +++ 6 a = + ++ 3 a = +)!++)! +3)! a = ) +3
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
Osnove. Uloga algoritama u računarstvu. Algoritmi. Algoritmi kao tehnika
 dr Boba Stojaovć Osove Uloga algortama u račuarstvu Algortm Algortam je strogo defsaa kompjuterska procedura koja uzma vredost l skup vredost, kao ulaz prozvod eku vredost l skup vredost, kao zlaz. Drugm
dr Boba Stojaovć Osove Uloga algortama u račuarstvu Algortm Algortam je strogo defsaa kompjuterska procedura koja uzma vredost l skup vredost, kao ulaz prozvod eku vredost l skup vredost, kao zlaz. Drugm
Matematička analiza 1 dodatni zadaci
 Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Praktikum iz OSNOVA FIZIKE I.
 Praktkum z OSNOVA FIZIKE I. 006./007. Pops vježb:. Pomča mjerka Mkrometarsk vjak Sferometar Vaga. Proučavaje helkodale zavojce Odreñvaje gustoće krutog tjela pomoću damometra 3. Fzkalo jhalo Matematčko
Praktkum z OSNOVA FIZIKE I. 006./007. Pops vježb:. Pomča mjerka Mkrometarsk vjak Sferometar Vaga. Proučavaje helkodale zavojce Odreñvaje gustoće krutog tjela pomoću damometra 3. Fzkalo jhalo Matematčko
II. ANALITIČKA GEOMETRIJA PROSTORA
 II. NLITIČK GEMETRIJ RSTR I. I (Točka. Ravia.) d. sc. Mia Rodić Lipaović 9./. Točka u postou ( ; i, j, k ) Kateijev pavokuti koodiati sustav k i j T T (,, ) oložaj točke u postou je jedoačo odeñe jeim
II. NLITIČK GEMETRIJ RSTR I. I (Točka. Ravia.) d. sc. Mia Rodić Lipaović 9./. Točka u postou ( ; i, j, k ) Kateijev pavokuti koodiati sustav k i j T T (,, ) oložaj točke u postou je jedoačo odeñe jeim
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Dvanaesti praktikum iz Analize 1
 Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
TRIGONOMETRIJSKE FUNKCIJE I I.1.
 TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Primjer - aritmetička sredina = M. x s. Primjer - nastavak. amplituda. vremenski indeks n. orginalni signal šum signal + šum
 Primjer - aritmetička redia Itereata je utav koji luži za glačaje (uredjavaje) lučajih varijacija u igalu. Nerekurzivi digitali filtri x x+ x + + x -poit movig average ytem [ ] + [ ] + [ ] + + [ + ] u
Primjer - aritmetička redia Itereata je utav koji luži za glačaje (uredjavaje) lučajih varijacija u igalu. Nerekurzivi digitali filtri x x+ x + + x -poit movig average ytem [ ] + [ ] + [ ] + + [ + ] u
Osnove kineziometrije i statistike
 Osove kezometrje statstke Prručk za sportske treere 0 P a g e 1 Osov kezometrjsk pojmov Kezometrja je zastvea dscpla koja proučava probleme mjereja u kezologj, odoso probleme kostrukcje, evaluacje prmjee
Osove kezometrje statstke Prručk za sportske treere 0 P a g e 1 Osov kezometrjsk pojmov Kezometrja je zastvea dscpla koja proučava probleme mjereja u kezologj, odoso probleme kostrukcje, evaluacje prmjee
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
4. Trigonometrija pravokutnog trokuta
 4. Trigonometrij prvokutnog trokut po školskoj ziri od Dkić-Elezović 4. Trigonometrij prvokutnog trokut Formule koje koristimo u rješvnju zdtk: sin os tg tg ktet nsuprot kut hipotenuz ktet uz kut hipotenuz
4. Trigonometrij prvokutnog trokut po školskoj ziri od Dkić-Elezović 4. Trigonometrij prvokutnog trokut Formule koje koristimo u rješvnju zdtk: sin os tg tg ktet nsuprot kut hipotenuz ktet uz kut hipotenuz
Iterativne metode - vježbe
 Iterativne metode - vježbe 5. Numeričke metode za ODJ Zvonimir Bujanović Prirodoslovno-matematički fakultet - Matematički odjel 21. studenog 2010. Sadržaj 1 Eulerove metode (forward i backward). Trapezna
Iterativne metode - vježbe 5. Numeričke metode za ODJ Zvonimir Bujanović Prirodoslovno-matematički fakultet - Matematički odjel 21. studenog 2010. Sadržaj 1 Eulerove metode (forward i backward). Trapezna
ZI. NEODREðENI INTEGRALI
 ZI. Nodrđni intgrali 7 ZI. NEODREðENI INTEGRALI. Antidrvacij. Pronañi tri antidrivacij funkcij.. Odrdi sv antidrivacij funkcij.. Pronañi dvij antidrivacij funkcij.. Pronañi antidrivaciju funkcij za koju
ZI. Nodrđni intgrali 7 ZI. NEODREðENI INTEGRALI. Antidrvacij. Pronañi tri antidrivacij funkcij.. Odrdi sv antidrivacij funkcij.. Pronañi dvij antidrivacij funkcij.. Pronañi antidrivaciju funkcij za koju
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Riješeni zadaci: Limes funkcije. Neprekidnost
 Riješeni zadaci: Limes funkcije. Neprekidnost Limes funkcije Neka je 0 [a, b] i f : D R, gdje je D = [a, b] ili D = [a, b] \ { 0 }. Kažemo da je es funkcije f u točki 0 jednak L i pišemo f ) = L, ako za
Riješeni zadaci: Limes funkcije. Neprekidnost Limes funkcije Neka je 0 [a, b] i f : D R, gdje je D = [a, b] ili D = [a, b] \ { 0 }. Kažemo da je es funkcije f u točki 0 jednak L i pišemo f ) = L, ako za
4. Perspektiviteti i perspektivne figure. Desarguesov teorem
 4 Persektvtet ersektvne fgure Desarguesov teorem Promatrajmo rojektvnu ravnnu kao oeratvn rostor u njoj nz točaka ramen ravaca ( ) s vrhom, r čemu točka ne lež na ravcu ( ) na nosocu Jednoznačno obostrano
4 Persektvtet ersektvne fgure Desarguesov teorem Promatrajmo rojektvnu ravnnu kao oeratvn rostor u njoj nz točaka ramen ravaca ( ) s vrhom, r čemu točka ne lež na ravcu ( ) na nosocu Jednoznačno obostrano
Cauchyjev teorem. Postoji više dokaza ovog teorema, a najjednostvniji je uz pomoć Greenove formule: dxdy. int C i Cauchy Riemannovih uvjeta.
 auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
1. Uvod u multivarijatnu statistiku. Prof.dr.sc. N. Bogunović Prof.dr.sc. B. Dalbelo Bašić
 Otkrvaje zaja u skuovma odataka Metoda glavh komoeeta Otkrvaje zaja u skuovma odataka Metoda glavh komoeeta FAKULE ELEKROEHNIKE I RAČUNARSVA Uvod u multvarjatu statstku Profdrs N Boguovć Profdrs B Dalbelo
Otkrvaje zaja u skuovma odataka Metoda glavh komoeeta Otkrvaje zaja u skuovma odataka Metoda glavh komoeeta FAKULE ELEKROEHNIKE I RAČUNARSVA Uvod u multvarjatu statstku Profdrs N Boguovć Profdrs B Dalbelo
Analitička geometrija i linearna algebra. Kartezijev trodimenzionalni pravokutni koordinatni sustav čine 3 međusobno okomite osi: Ox os apscisa,
 Alitičk geoetrij i lier lger Vektori KOORDINATNI SUSTAV Krteijev prvokuti koorditi sustv Krteijev trodieioli prvokuti koorditi sustv čie eđusoo okoite osi: O os pscis O os ordit O os plikt točk O ishodište
Alitičk geoetrij i lier lger Vektori KOORDINATNI SUSTAV Krteijev prvokuti koorditi sustv Krteijev trodieioli prvokuti koorditi sustv čie eđusoo okoite osi: O os pscis O os ordit O os plikt točk O ishodište
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
Više dokaza jedne poznate trigonometrijske nejednakosti u trokutu
 Osječki matematički list 000), 5 9 5 Više dokaza jedne poznate trigonometrijske nejednakosti u trokutu Šefket Arslanagić Alija Muminagić Sažetak. U radu se navodi nekoliko različitih dokaza jedne poznate
Osječki matematički list 000), 5 9 5 Više dokaza jedne poznate trigonometrijske nejednakosti u trokutu Šefket Arslanagić Alija Muminagić Sažetak. U radu se navodi nekoliko različitih dokaza jedne poznate
1. ODREĐIVANJE NETOČNOSTI MJERENJA
 . ODREĐIVANJE NETOČNOSTI MJERENJA. Opće Mjereja razh fzkalh ostalh velča rezultat se e ogu provest apsoluto točo. Usljed tehčkh ekooskh razloga potrebo je etočost jereja svest a ajaju oguću jeru, sa što
. ODREĐIVANJE NETOČNOSTI MJERENJA. Opće Mjereja razh fzkalh ostalh velča rezultat se e ogu provest apsoluto točo. Usljed tehčkh ekooskh razloga potrebo je etočost jereja svest a ajaju oguću jeru, sa što
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI)
 IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
MATEMATIKA Pokažite da za konjugiranje (a + bi = a bi) vrijedi. a) z=z b) z 1 z 2 = z 1 z 2 c) z 1 ± z 2 = z 1 ± z 2 d) z z= z 2
 (kompleksna analiza, vježbe ). Izračunajte a) (+i) ( i)= b) (i+) = c) i + i 4 = d) i+i + i 3 + i 4 = e) (a+bi)(a bi)= f) (+i)(i )= Skicirajte rješenja u kompleksnoj ravnini.. Pokažite da za konjugiranje
(kompleksna analiza, vježbe ). Izračunajte a) (+i) ( i)= b) (i+) = c) i + i 4 = d) i+i + i 3 + i 4 = e) (a+bi)(a bi)= f) (+i)(i )= Skicirajte rješenja u kompleksnoj ravnini.. Pokažite da za konjugiranje
Pismeni ispit iz matematike GRUPA A 1. Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj, zatim naći 4 z.
 Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
VILJUŠKARI. 1. Viljuškar se koristi za utovar standardnih euro-pool paleta na drumsko vozilo u sistemu prikazanom na slici.
 VILJUŠKARI 1. Viljuškar e korii za uoar andardnih euro-pool palea na druko ozilo u ieu prikazano na lici. PALETOMAT a) Koliko reba iljuškara da bi ree uoara kaiona u koji aje palea bilo anje od 6 in, ako
VILJUŠKARI 1. Viljuškar e korii za uoar andardnih euro-pool palea na druko ozilo u ieu prikazano na lici. PALETOMAT a) Koliko reba iljuškara da bi ree uoara kaiona u koji aje palea bilo anje od 6 in, ako
radni nerecenzirani materijal za predavanja R(f) = {f(x) x D}
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Zavrxni ispit iz Matematiqke analize 1
 Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
3. razred gimnazije- opšti i prirodno-matematički smer ALKENI. Aciklični nezasićeni ugljovodonici koji imaju jednu dvostruku vezu.
 ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
