Osnove kineziometrije i statistike
|
|
|
- Ευτέρπη Αναγνωστάκης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Osove kezometrje statstke Prručk za sportske treere 0 P a g e
2 1 Osov kezometrjsk pojmov Kezometrja je zastvea dscpla koja proučava probleme mjereja u kezologj, odoso probleme kostrukcje, evaluacje prmjee mjerh strumeata za procjeu kezološkh feomea. Mjereje je postupak kojm se objektma (ettetma, sptacma) prdružuju brojev l ozake prema određem pravlma u skladu s razvjeost mjereog svojstva (arbuta, karakterstke, oblježja) čme se postže jegova kvatfkacja l klasfkacja. Objekt mjereja l ettet je osoc formacja koje je moguće prkupt ekm postupkom mjereja, a kojma se može opsat staje ekog etteta. Predmet mjereja je određeo svojstvo koje se mjer a objektma mjereja. U ovom prručku predstavlje su mjer strumet (testov) za procjeu motorčko-fukcoalh sposobost morfološkh oblježja. Motorčke sposobost odgovore su za uspješost zvedbe motorčkh aktvost (mafestacja). Fukcoale sposobost odgovore su za trasport stvaraje eergje u ljudskom orgazmu. Uz ovaj term često se korst term zdržljvost (egl. edurace). Slka 1-1. Hpotetsk model strukture motorčko-fukcoalh sposobost. Motorčko-fukcoale sposobost Jakost Brza Izdržljvost Koordacja Aglost Ravoteža Fleksblost Maksmala jakost Brza jedog pokreta Aaeroba zdržljvost Eksplozva jakost Brza frekvecje pokreta Aeroba zdržljvost Repettva jakost Ubrzaje Statčka jakost Maksmala brza trčaja Jakost (egl. stregth) predstavlja sposobost stvaraja sle s cljem savladavaja otpora pomoću volje mšće kotrakcje. Moguće je razlkovat četr osova tpa jakost. To su: 1
3 Maksmala jakost sposobost stvaraja maksmale sle s cljem savladavaja vajskog otopra. Eksplozva jakost sposobost stvaraja maksmale sle u što kraćem vremeu. Repettva jakost sposobost poavljaja određeog pokreta kojm se savladavaju medjala submaksmala optrećeja što duže vrjeme. Repettvu jakost karakterzra zvedba damčkh kretj kod kojh dolaz do azmječh kotrakcja relaksacja agažrah mšća. Statčka jakost sposobost održavaja određeog statčkog položaja što duže vrjeme. Statčku jakost karakterzra zometrčka mšća akcja 1 (statčko aprezaje). Sva četr tpa jakost mogu se dodato dferecrat a: Apsolutu jakost sposobost mfestraja sle za savladavaje opterećeja ekog vajskog objekta (pr. bacaje kugle). Relatva jakost sposobost mafestraja sle za savladavaje opterećeja koje je zravo povezao s vlasttom tjelesom masom (pr. zgbov). Brza pokreta (egl. speed) predstavlja sposobost zvedbe pokreta l kretaja maksmalom brzom bez vajskog otpora. Moguće je razlkovat četr osova tpa brze pokreta. To su: Brza jedostavog pokreta sposobost zvođeja jedostavog pokreta maksmalom brzom. Brza frekvecje pokreta sposobost maksmalo brzog zvođeja poavljajućh pokreta stale ampltude. Ubrzaja sposobost postzaja maksmale brze kretaja u što kraćem vremeu. Maksmala brza kretaja sposobost ajveće moguće brze kretaja. Izdržlvost (egl. edurace) je spostbost orgazma da rad određeog tezteta održava što dulje vrjeme bez smajeja efkasost zvedbe (Maršć, Dzdar Šetja, 2008). Moguće je razlkovat četr osova tpa jakost. To su: Aeroba zdržljovost sposobost odupraja umoru pr damčkom mšćom radu u koj je uključeo vše od 1/6 do 1/7 ukupe skelete muskulature tjekom kojeg teztet rada aktvra vše od 50% maksmale mogućost krvožlog sustava, a uz trajaje 1 Izometrčka mšća akcja predstavlja vrstu mšće akcje kod koje e dolaz do promjee dulje mšća. 2
4 opterećeja od ajmaje 3-5 muta (Joath Kempel, 1987, prema Maršć, Dzdar Šetja, 2008). Aaeroba zdržljvost sposobost odupraja umoru pr damčkm aktvostma submaksmalog l maksmalog tezteta (Maršć, Dzdr Šetja, 2008). Koordacja (egl. coordato) sposobost vremesk prostoro efkasog te eergetsk racoalog zvođeja kompleksh motorčkh zadataka (Sekulć Metkoš, 2007). Aglost (egl. aglty) predstavlja sposobost efkase promjee pravca /l smjera kretaja (Sekulć Metkoš, 2007). Ravoteža (egl. balace) predstavlja sposobost održavaja ravotežog položaja uz aalzu formacja o položaju tjela koje putem kestetčkh vdh podražaja (Sekulć Metkoš, 2007). Fleksblost (egl. flexblty) predstavlja sposobost postzaja maksmale ampltude voljh kretj u jedom l vše zglobova (Sekulć Metkoš, 2007). Morfološka oblježja predstavljaju tjelesu građu ljud. To su: Logtudala dmezoalost skeleta predstavlja morfološko oblježje koje ozačava rast kostju u dulju. Trasverzala dmezoalost skeleta predstavlja morfološko oblježje koje ozačava rast kostju u šru (popreč presjek kost). Volume masa tjela predstavlja morfološko oblježje koje u ajvećoj mjer ozačava kolču mšće mase. Potkožo maso tkvo predstavlja morfološko oblježje koje ozačava kolču potkožog masog tkva. Slka 1-2. Hpotetsk model strukture morfološkh oblježja. Morfološka oblježja Logtudala dmezoalost skeleta Trasverzala dmezoalost skeleta Volume masa tjela Potkožo maso tkvo 3
5 Mjertelj je osoba školovaa za provođeje mjereja. Da b se utjecaj mjertelja a rezultat mjereja sveo a ajmaju moguću mjeru, užo je poštvat stadardzra postupak mjereja. Stadardzra postupak mjereja je precza ops svh postupaka uvjeta u kojma se provod mjereje ekm mjerm strumetom te ača bodovaja vredovaja dobveh rezultata. Mjer strumet l test je operator pomoću kojeg se vrš mjereje, a kojeg če tehčka oprema potreba za mjereje, jeda l vše mjertelja stadardzra postupak mjereja. Mjera skala je skup ozaka l z brojeva kojma je moguće opsat razvjeost mjereog svojstva ekog objekta mjereja. Četr su vrste mjerh skala. To su: Nomala skala je mjera skala bez kvattatvh svojstava kotuteta, a prema kojoj je objekte mjereja moguće klasfcrat u dvje l vše dsjukth kategorja ravopravh po vrjedost (pr. muško žesko, djete adolescet odrasla osoba) Ordala skala je skala ragova, tj. mjera skala prema kojoj je objekte mjereja moguće klasfcrat u dvje l vše dsjukth kategorja ragrah prema vrjedost (pr. skala ragova a prjemom sptu, skala školskh ocjea, skala plasmaa a sveučlšom prvestvu u krosu). Itervala skala je mjera skala koja ma kvattatva svojstva kotutet, vrjedost a skal su ekvdstate, a ulta vrjedost e predstavlja apsoluto odsustvo mjereog svojstva (pr. Celzjeva temperatura ljestvca, skala stadardzrah rezultata, skala T- skorova). Omjera skala je mjera skala koja ma kvattatva svojstva kotutet, vrjedost a skal su ekvdstate, a ulta vrjedost predstavlja apsoluto odsustvo mjereog svojstva (pr. Kelvova temperatura ljestvca, skala jedca apsolutog vremea, metarska skala jedca dulje). 2 Kostrukcja mjerog strumeta Mjer strumet (test) je odgovarajuć operator pomoću kojega se određuje pozcja objekta mjereja a ekoj mjeroj skal kojom se procjejuje predmet mjereja. Koač rezultat mjerog strumeta ukazuje a stupaj razvjeost predmeta mjereja. Kostrukcja mjerog strumeta vrlo je slože proces koj se odvja u pet koraka: defraje predmeta mjereja odabr odgovarajućeg tpa mjerog strumeta zbor podražajh stuacja stadardzacja mjerog postupka utvrđvaje metrjskh karakterstka. 4
6 2.1 Defraje predmeta mjereja Svak mjer strumet korst se za mjereje ekog predmeta mjereja. U kezologj predmet mjereja predstavljaju relevat kezološk feome. Prmjerce, motorčke fukcoale sposobost, morfološka oblježja, stuacjska atjecateljska uspješost u pojedoj kezološkoj aktvost, kvalteta zvedbe ekog tehčkog elemeta td. Zato kostrukcja mjerog strumeta započje preczm defrajem predmeta mjereja. Predmet mjereja ajčešće je ek hpotetsk kostrukt koj je zravo mjerljv. Prmjerce, motorčke sposobost su teorjsk kostrukt koje e možemo zravo mjert, a za koje pretpostavljamo da maju realu egzstecju jer determraju uspješost motorčkog poašaja. Promatrajem motorčkog poašaja ljud, moguće je uočt da ek od jh u većem broju motorčkh aktvost postžu slče rezultate (prmjerce, skokovma, bacajma, sprtovma ), pa je opravdao pretpostavt da postoje ek zajedčk faktor koj determraju uspješost u realzacj th motorčkh aktvost. Zajedčk faktor koj određuju uspješost motorčkog poašaja predstavljaju motorčke sposobost. Dakle, motorčke sposobost su teorjsk kostrukt jer h je emoguće zravo opažat, a tme mjert. Moguće h je samo drekto procjejvat, stoga h zovemo latete dmezje. Slka 2-1. Teorjsk model drektog mjereja (procjee) motorčkh sposobost PREDMET MJERENJA (LATENTNA DIMENZIJA) MOTORIČKE SPOSOBNOSTI MOTORIČKI ZADATAK (maksmalo delako skočt z mjesta suožm odrazom PODRAŽAJNA SITUACIJA (STIMULUS) PROCJENA MOTORIČKA AKTIVNOST (zmjere rezultat skoka u dalj z mjesta suožm dorazom) MANIFESTNA VARIJABLA (REAKCIJA) Općeto se može reć da je svaka motorčka aktvost prozvod motorčkh sposobost podražaje stuacje (slka 2-1). Stoga, mjereć uspješost u određeoj motorčkoj aktvost (mafesta varjabla) koja je zazvaa ekom podražajom stuacjom (motorčk zadatak) možemo zaključvat o stupju razvjeost motorčkh sposobost (lateta dmezja). Ako 5
7 je, prmjerce, predmet mjereja eka motorčka sposobost (pr. eksplozva saga koja se defra kao sposobost geerraja maksmale sle u jedc vremea) koju e možemo drekto mjert, moguće je kostrurat mjer strumet kojm ćemo je drekto procjet pomoću jeh mafestacja (pr. motorčkh aktvost: skokov, bacaja, udarc..). Takav prstup užo ameće problem utvrđvaja pravog predmeta mjereja (valjaost mjerog strumeta). Name, uspješost u ekoj motorčkoj mafestacj koju mjermo kad je pod utjecajem samo jedog faktora, ego većeg broja faktora pa se postavlja ptaje: Što je prav predmet mjereja, tj. koju latetu dmezju procjejujemo ekm motorčkm testom? Problem valjaost mjereja bt će posebo razmatra u poglavlju o metrjskm karakterstkaa. Ovso o predmetu mjereja, valja odabrat prklada tp mjerog strumeta, odoso ač za operacoalzacju odgovarajućeg predmeta mjereja. 2.2 Odabr odgovarajućeg tpa mjerog strumeta Za procjeu relevath kezološkh feomea moguće je korstt ekolko tpova mjerh strumeata: testov tpa papr-olovka ubrajaju se u potpuo objektve mjere strumete jer postgut rezultat e ovse od pogrešc mjeroca (ako je osposoblje za provođeje mjereja), već sključvo o sptaku. Takav tp mjerh strumeata korst se za utvrđvaje kogtvh sposobost, koatvh oblježja, stavova, socjalog statusa, prehrambeh avka td. aparatura za mjereje u ovu skupu mjerh strumeata ubrajaju se raza tehčka pomagala koja u postupku mjereja korst mjerlac. To su, prmjerce, strumet za mjereje morfološkh oblježja (atropometar, kalper td.), fukcoalh sposobost (sprometar, aparatura za mjereje aeroboga aaeroboga kapacteta td.) te motorčkh sposobost (damometar za procjeu mšće sle). Takav tp mjereja je maje objektva od testova tpa papr-olovka jer dobve rezultat u većoj mjer zavse od obučeost mjerlaca. prmjea vježbe (motorčkh zadataka) u ovu skupu mjerh strumeata ubrajaju se razlčt motorčk zadac kojma se u ekoj pozatoj mjer aktvra određea motorčka sposobost. Takav tp mjerh strumeata ajčešće se korst za procjeu motorčkh sposobost (prmjerce, skok udalj s mjesta za procjeu eksplozve sage, okretost a tlu za procjeu koordacje td). Za takav tp mjerh strumeata valja preczo defrat upute za zvođeje zadatka, uvjete u kojma se zadatak zvod, pomagala ač jhova koršteja kako b se mmzrale pogreške mjereja. subjektva procjea mjeroca često se za procjeu ekh složeh sposobost, zaja vješta, odoso kvaltete zvedbe korst subjektva procjea kompeteth mjerlaca (prmjerce, u sportskoj gmastc, klzaju a ledu, skokovma u vodu td.). 6
8 Veća mjereja u atropološkm zaostma obavlja se pomoću kompozth mjerh strumeata. Kompozt mjer strumet se sastoj od većeg čestca (egl. tem), a koje mogu bt: ptaja/zadac (papr-olovka), poavljaa mjereja (aparatura, motorčk zadac) suc (subjektva procjea). Tako dobve rezultat razlčtm se statstčkm postupcma kodezraju, a daljje obrade provode se a kodezram rezultatma. 2.3 Izbor podražajh stuacja Nako preczog defraja predmeta mjereja odabra odgovarajućeg tpa mjerog strumeta valja proučt u kojm stuacjama se mafestra predmet mjereja, odoso koje su to aktvost u kojma se ajbolje očtuje predmet mjereja. Stoga je potrebo zvršt klasfkacju selekcju podražajh stuacja koje su smptomatske za odgovarajuć predmet mjereja. Tako, prmjerce, ako je predmet mjereja eka kogtva sposobost, koatvo oblježje, stavov, raza zaja z ekog područja l sl., moguće je korstt test tpa paprolovka koj će bt sastavlje od većeg broja čestca. Kvalteta mjerog strumeta bt će determraa zborom čestca kojma se aktvra predmet mjereja. Zato pr zboru čestca treba vodt brgu o sljedećem: čestce moraju bt kratko jaso defrae svaka čestca mora bt povezaa s predmetom mjereja čestce moraju bt prlagođee cljaoj populacj sptaka čestce moraju varrat po tež složeost kako b uspješo razlkovale sptake po predmetu mjereja. Za procjeu ekh složeh sposobost, zaja vješta (prmjerce, uspješost u sportskoj gmastc, klzaju a ledu, skokovma u vodu, uspješost košarkaša td.) je uvjek moguće kostrurat objektv mjer strumet, već smo prslje korstt subjektvu procjeu stručjaka (sudaca). Kvalteta ovakvog tpa mjerog strumeta ovst će o jasoć odabru krterja (mjerla), skal procjee te raz sudačke kompetetost skustva. Prmjerce, ako je predmet mjereja kvalteta košarkaša, oda je potrebo preczo defrat krterjsk sustav koj će obuhvatt sve relevate aspekte predmeta mjereja (pr. raza prtska u obra, pomagaje u obra, skakačka uspješost u obra ), defrat mjeru skalu (pr. ocjee od 1 do 5) te krterje koje moraju sput ocjejvač (pr. košarkašk treer 1. lge). Ako je predmet mjereja eka motorčka sposobost (pr. eksplozva saga), potrebo je odabrat oe motorčke zadatke koj će u ajvećoj mjer zazvat aktvacju maksmale sle u što kraćoj jedc vremea (pr. suož skok udalj s mjesta, bacaje medcke s prsa, sprt 20 metara td.). Nako zbora kasfkacje podražajh stuacja, svaku od jh je potrebo preczo opsat, odoso stadardzrat. 7
9 2.4 Stadardzacja postupka mjereja Stadardzacja mjerog postupka podrazumjeva precza ops svh postupaka uvjeta u kojma se provod mjereje ekm mjerm strumetom te ača bodovaja vredovaja dobveh rezultata. Name, svako mjereje astoj sključt mjeročev utjecaj a rezultate mjereja, odoso tež objektvost. Stoga je stadardzacja mjerog postupka bta preduvjet objektvost mjereja. Oa omogućava zjedačavaje svh uvjeta mjereja za sve sptake. Stadardzacja mjerog postupka obuhvaća: azv šfru mjerog strumeta tehčk ops, odoso kostrukcjske karakterstke ops postupka mjereja uputu sptaku ač određvaja rezultata sptaka. Sv važ podac o mjerom postupku moraju bt avede kako b mjer strumet bo upotrebljv u praks. Nazv: Šfra: Tehčk ops: Ops mjerog postupka: Skok udalj s mjesta MFESDM Zatvorea prostorja ajmajh dmezja 6 2 metra. Od zda se postave take strujače tako da ukupa dulja strujača e bude maja od 4,5 m. Strujače su fksrae s jede strae zdom, a s druge strae stopalma dvojce pomagača. Na strujač se ozač početa (odskoča) lja 80 cm od zda. Od počete lje a udaljost od 2 metra pa sve do 3,3 metra ozače se svakh 5 cm paralele lje duge 30 cm. Isptak stae bosm stopalma do samog ruba počete lje ležma prema zdu. Zadatak je sptaka suožm odrazom skočt prema aprjed što je moguće dalje. Zadatak je završe ako što sptak zvede 4 uspješa skoka. Neuspješm skokom smatra se: skok ako dvostrukog odraza (poskoka) u mjestu prje skoka skok ako prestupa počete lje skok koj je zvede suožm odrazom skok kojem prethod dokorak skok ako kojeg sptak dodre strujaču za peta skok ako kojeg sptak pr doskoku sjede Uputa sptaku: Određvaje rezultata: Zadatak se demostrra objašjava: Vaš je zadatak da staete za počete lje suožm odrazom skočte što vše možete prema aprjed. Doskok mora bt a dvje oge. U slučaju espravog skoka, zadatak se poavlja. Ako je zadatak jasa, prpremte se za početak. Rezultat u testu zražava se u cetmetrma, a određuje se kao artmetčka sreda 4 uspješa skoka. 8
10 2.5 Utvrđvaje metrjskh karakterstka Nako kostrukcje prelmare forme mjerog strumeta valja ga emprjsk provjert te tako doć do koače verzje mjerog strumeta sa zadovoljavajućm metrjskm karakterstkama. Prvu formu testa treba provjert a plot-uzorku koj će po karakterstkama bt slča populacj za koju se test kostrura. Tme se dobje emprjska osova za tzv. aalzu čestca (egl. tem aalyss). Pod aalzom čestca podrazumjeva se z postupaka pomoću kojh procjejujemo težu valjaost čestca. Ako se rad o mjerom strumetu tpa papr-olovka, teža čestca se provjerava tzv. deksom lakoće (teže) koj je pokazatelj dskrmatvost svake čestce. Ideks lakoće svake čestce predstavlja proporcju sptaka koj su taj zadatak uspješo rješl (p=u/, gdje je u broj sptaka koj su uspješo rješl zadatak, a ukupa broj sptaka). Odgovarajućm zborom zadataka s obzrom a jhovu težu, moguće je utjecat a osjetljvost mjerog strumeta. Zadac e b smjel bt pretešk prelaga jer b u tm slučajevma slabo razlkoval sptake. Stoga veća čestca treba mat deks lakoće koj se kreće oko p=0,5 te podjedak maj broj čestca čj je deks lakoće maj već od 0,5. Valjaost čestca moguće je procjet kao prosječu korelacju zmeđu čestca. Što se čestce međusobo vše slažu, to m je veća kolča zajedčke varjace, odoso čestce maju vše stog predmeta mjereja. Pomoću aalze teže valjaost čestca braju se čestce za koač oblk testa. Pravlm zborom čestca utječemo a metrjske karakterstke cjelog mjerog strumeta. Prmjerce, odgovarajućm zborom raspodjelom čestca s obzrom a deks lakoće utječemo a osjetljvost, dok korelacjom zmeđu čestca utječemo a pouzdaost djagostčku valjaost. Nako zrade koačog oblka mjerog strumeta a reprezetatvm se uzorcma sptaka utvrđuju metrjske karakterstke. Pr tome valja aglast da se utvrđee metrjske karakterstke uvjek odose a određeu populacju a čjm su reprezetatvm uzorcma utvrđee, a kako e a sve sptake. 3 Metrjske karakterstke Svak mjer strumet užo mora bt dobrh metrjskh karakterstka kako b jme dobve podac bl upotrebljv. To su: pouzdaost objektvost homogeost osjetljvost valjaost. 9
11 3.1 Pouzdaost Pouzdaost je metrjska karakterstka koja se odos a točost mjereja, tj. a ezavsost mjereja od esstematskh pogrešaka. Problem pouzdaost veže se uz problem kozstetost (dosljedost) rezultata u poovljem mjerejma. U svakom mjerom postupku a rezultate djeluju, osm velče predmeta mjereja, ek sstematsk esstematsk faktor. Sstematsk faktor mogu zazvat stal porast l pad rezultata (prmjerce, učeje, umor, razvoj td.) te h je moguće kotrolrat uklot. Njhov se utjecaj može tumačt kao stvara promjea u velč predmeta mjereja te su zamljv teorj pouzdaost. Nesstematsk faktor uzrokuju slučaje varjacje rezultata mjereja te utječu a epouzdaost mjereja jer promjee koje t faktor zazvaju su posljedca promjee predmeta mjereja. Upravo jhovm uzrocma posljedcama bav se teorja pouzdaost. U kezološkm mjerejma pogreške mjereja ajčešće astaju kao rezultat: mjereja razlčth mjerlaca razlčth mjereja stog mjeroca varraja mjeree karakterstke u tjeku daa (prmjerce, tjelesa vsa varra oko 1 cm u tjeku daa) mjereja razlčtom mjerom aparaturom (prmjerce, ejedako baždarea mjera aparatura) slučajh pogrešaka pr prmje blo kojeg mjerog strumeta. Prema tome, a smajeje pogreške mjereja moguće je utjecat dobrom uvježbaošću mjerlaca, prdržavajem stadardzraog postupka mjereja, kvaltetom mjerom opremom koja se redovto baždar te provođejem mjereja u sto vrjeme l u vrlo kratkom vremeskom razmaku. 3.2 Objektvost Objektvost je mjera karakterstka kojom se određuje ezavsost rezultata mjereja od mjeroca. Postupak mjereja smatra se objektvm ako razlčt mjeroc mjereć, ste sptake, dolaze do sth rezultata. Dakle, što je već stupaj slagaja zmeđu rezultata sptaka koje su dobl razlčt mjeroc, to je objektvost mjereja veća. Postupak za utvrđvaje objektvost ekog mjereja u kome sudjeluje već broj mjerlaca detča je metod tere kozstecje za utvrđvaje pouzdaost kompozth mjerh strumeata, s tom razlkom da su pr subjektvoj procje čestce mjereja mjeroc, odoso suc. Stoga se objektvost mjereja može povećat uključvajem većeg broja sudaca čje se ocjee trebaju u što većoj mjer međusobo slagat. To se postže prdržavajem stadardzraog postupka mjereja. Na vsoku razu objektvost ove vrste mjereja utječe kompetetost uvježbaost ocjejvača (zaje skustvo), stablost osoba lčost mjeroca, krterj pravla mjereja, svojstva testa (prmjerce, objektvj su testov koj maju jedozača ključ za ocjejvaje, o koj od sptaka traže jedostavje reakcje, u kojma se korst 10
12 suvremea tehologja sl.), buduć da se tako može zbjeć utjecaj ocjejvača a koaču ocjeu. 3.3 Homogeost Homogeost je svojstvo kompozth testova koje pokazuje kolko rezultat sptaka u svm čestcama zavse od stog predmeta mjereja l detče kombacje razlčth predmeta mjereja. Homogeost, kao metrjska karakterstka, ma važu ulogu pr opsvaju mjerh strumeata jer o joj ovs djagostčka vrjedost testa. Name, ako je ek test homoge to zač da se o predmetu mjereja jedozačo može zaključvat, odoso, ako je test heteroge, usprkos mogućoj pragmatčoj valjaost, je moguće utvrdt u kojem omjeru razlčte sposobost l osobe sptaka utječu a rezultat u testu. Stoga je, usprkos majoj ekoomčost, u praks bolje korstt vše homogeh testova za predkcju eke složee krterjske varjable ego jeda heteroge test. To stoga jer je moguće preczo utvrdt strukturu čmbeka odgovorh za uspješost u krterjskoj varjabl, odoso moguće je dozat zašto etko postže bolje, a etko lošje rezultate u krterjskoj varjabl, što te testove č upotrebljvma u djagostčke svrhe. 3.4 Osjetljvost Osjetljvost predstavlja svojstvo mjerog strumeta da uspješo razlkuje sptake po predmetu mjereja. Ako, prmjerce, ekm mjerm strumetom dobjemo detče rezultate dvaju sptaka, to e mora začt jedak stupaj razvjeost predmeta mjereja, već može bt zak slabje osjetljvost mjerog strumeta. Isto tako, rezultat ula u broju zgbova e mora začt potpuu odsutost predmeta mjereja (repettve sage), već je uzrok tome vjerojato slaba osjetljvost mjerog strumeta, tj. jegova eprmjereost određeoj populacj. To se često događa kada se ek mjer strumet kostrurra za selekcorau populacju (vrhusk sportaš), a prmjejuje se a eselekcoraoj populacj kojoj strumet je težsk prmjere. 3.5 Valjaost S obzrom a to da se mjer strumet kostruraju zato da procjejuju određe predmet mjereja koj može bt relatvo jedostava (pr. eko morfološko oblježje), al vrlo slože (pr. eka motorčka sposobost), postavlja se ptaje što u stvar određe mjer strumet mjer, odoso kakva mu je valjaost. S obzrom a clj mjereja, valjaost mjerh strumeata možemo promatrat sa dva osova stajalšta: Ako je clj mjereja utvrđvaje staja, odoso raze pojedh atropološkh oblježja ekog sptaka, tada se rad o tzv. djagostčkoj valjaost. 11
13 Ako je clj mjereja progozrat uspješost u ekoj aktvost a temelju rezultata prkupljeh ekm mjerm strumetom, tada se rad o tzv. pragmatčoj l progostčkoj valjaost. Djagostčkoj valjaost je osov clj utvrdt što određe test mjer, odoso koj mu je predmet mjereja. Prema aču utvrđvaja, moguće je razlkovat dva osova tpa djagostčke valjaost. To su aprora faktorska valjaost. Kod aprore valjaost zaključvaje o predmetu mjereja temelj se a logčkoj aalz postupka mjereja testovog sadržaja koj dovod do odgovarajuće reakcje sptaka, što može sugerrat aktvraje eke hpotetske latete dmezje (predmeta mjereja). Prema tome, aprora valjaost je prozvod ekspermetale provjere, pa se e zražava kokretm koefcjetom valjaost. Stoga se aprora valjaost občo korst za postavljaje hpoteze o predmetu mjereja koja se potvrđuje l opovrgava ekspermetalom provjerom. Faktorska valjaost astoj utvrdt koj se predmet mjereja sptuje određem mjerm strumetom, odoso u kojoj mjer svak od jegovh faktora uvjetuje varjablost dobveh rezultata. S obzrom a to da se u pravlu jedm mjerm strumetom žel procjet jeda faktor, oda se faktorskom valjaošću utvrđuje kolko ek test dobro mjer oaj faktor za čje je mjereje kostrura. Kod faktorske valjaost zaključvaje o predmetu mjereja temelj se a rezultatma faktorske aalze, odoso ekspermetalo se utvrđuje kolkom proporcjom ek faktor sudjeluje u varjac rezultata testa. Pragmatčka l progostčka valjaost ekog testa pokazuje kolko uspješo, odoso s kolkom sgurošću možemo predvdjet uspjeh u ekoj praktčoj aktvost a temelju rezultata tog testa. Prmjerce, kakva je mogućost progozraja uspjeha u ekoj atletskoj dscpl (pr. trčaju a 100 m) a temelju rezultata dobveh upotrebom ekog testa (pr. skoka udalj s mjesta). Dakle, problem pragmatčke valjaost svod se a utvrđvaje eke mjere povezaost zmeđu varjable dobvee mjerejem određee skupe etteta ekm testom (predktorska l ezavsa varjabla) varjable koja opsuje uspješost th etteta u ekoj aktvost (krterjska l zavsa varjabla). U kezološkm stražvajma, krterjske predktorske varjable mogu bt jedodmezoale všedmezoale. Osm toga mogu bt procjejee ekom kvaltatvom l kvattatvom mjerom skalom. Upravo o avedem karakterstkama varjabl ovs ač utvrđvaja pragmatčke valjaost. 12
14 4. Osov statstčk pojmov 4.1 Podatak Pod pojmom podatak l formacja podrazumjeva se određea kvattatva l kvaltatva vrjedost kojom je opsao određeo oblježje ekog objekta, stvar, osobe, pojave, procesa,odoso, etteta. Prtom je važo aglast da se statstka bav obradom podataka koj međusobo varraju. Name, kada b sv prkuplje podac bl jedak, oda e b bl predmetom statstčke aalze, jer b jeda podatak opsvao sve druge podatke. Osm toga, predmet statstčke aalze su podac koj se zvode po ekoj zadaoj matematčkoj fukcj, prmjerce, logartamsk brojev slčo, već su to podac varjabltet kojh mora bt zraz prrode pojave koja se stražuje. Tako, prmjerce, tjelesa vsa djece stog spola dob je jedaka te se je varjabltet e može točo defrat matematčkom formulom, već se opsuje određem statstčkm pokazateljma. 4.2 Ettet Statstka se bav obradom podataka koj opsuju određea oblježja, svojstva, karakterstke ekog skupa osoba, objekata, stvar, pojava, procesa sl. Svaka jedka toga skupa azva se ettet os formacje koje je moguće prkupt ekm postupkom mjereja. U kezološkm stražvajma ettet su ajčešće ljud, al mogu bt sportske ekpe, tehčk elemet, zadac u gr td. 4.3 Populacja uzorak etteta Skup svh etteta čja su oblježja predmet statstčke aalze ajčešće se azva populacja etteta (statstčk skup, uverzum etteta). Populacja etteta može bt beskoača l koača skup etteta (e). Prema Šošću (2004), beskoača populacja predstavlja hpotetč skup s beskoačo mogo elemeata (etteta) koj su u svez s ekm statstčkm (stohastčkm) procesom. Ako se proces poavlja beskoačo u stm uvjetma, jegov su shod elemet beskoače populacje. Prmjerce, ako a st ač u stm uvjetma beskoačo bacamo pravla ovčć, tada je pozato uaprjed što će bt rezultat bacaja (psmo l glava), a postupak se teoretsk može zvodt beskoačo. Dakle, rad se o statstčkom procesu čj su shod elemet beskoače populacje. Za razlku od beskoače populacje, koja ma beskoača broj etteta, koaču populacju predstavlja pojmovo, prostoro vremesk defra koača skup etteta. Prmjerce, "studet prve gode Kezološkog fakulteta Sveučlšta u Zagrebu školske gode 2002/2003". Ettet koj prpadaju ovako defraoj populacj jedak su po općm oblježjma, a to su: pojmovo - studet prve gode Kezološkog fakulteta, prostoro - Sveučlšta u Zagrebu, vremesk - u školskoj god 2000/
15 Dakle, pojmovo određeje populacje defra što je ettet koja su jegova opća svojstva, prostoro određeje određuje geografsko područje za koje su veza ettet, a vremesko povezuje ettete s određeom vremeskom jedcom l razdobljem. Podskup etteta zabra z populacje u skladu s ekm pravlom, a s cljem da je što bolje reprezetra, azva se uzorak etteta. Ako je uzorak dobar reprezetat, predstavk populacje z koje je zabra, oda rezultat (zaključc) dobve a uzorku, uz određeu pogrešku, vrjede za populacju. Ettet se u uzorak mogu brat a raze ače, što određuje vrste uzoraka. 4.4 Vrste uzoraka etteta Najjedostavja podjela uzoraka je a amjere slučaje uzorke. Pod amjerm uzorcma podrazumjevaju se o uzorc u koje su ettet bra prema ekom subjektvom stavu stražvača o jhovoj reprezetatvost l se uzorak formra odabrom lako l treuto dostuph etteta (prgod uzorak). Uzorak će bt dobar reprezetat populacje ako je za svak ettet jedaka vjerojatost da budu zabra, odoso ako se zadovolj uvjet slučajog odabra etteta. S obzrom a to da se uzorc braju s cljem da što bolje reprezetraju populacju z koje su zabra, lako je uočt da će pogreška procjee statstčkh pokazatelja bt to maja što je efektv uzorka blž broju etteta u populacj. Ovso o aču zbora etteta, odoso uzorkovaju 2 moguće je razlkovat ekolko vrsta slučajh uzoraka. To su: jedostav slučaj uzorak - formra se tako da svakom ettetu eke populacje osguramo jedaku vjerojatost (šasu) zbora (prmjerce, uz pomoć bubja za loto, geeratora slučajh brojeva sl.). terval uzorak - formra se tako da se sv ettet eke populacje poredaju (pr. po abecedom redu) te da se, ako slučajog zbora prvog etteta, bra svak treć, pet, odoso -t ettet. Ovaj ač braja etteta ma karakterstke jedostavog slučajog uzorka ako su ettet esstematsk poreda. stratfcra uzorak - formra se tako da se populacja podjel prema ekm važm oblježjma (pr. spol, dob sl.) u stratume (slojeve, podpopulacje) z kojh se slučajm odabrom braju ettet. Broj etteta brah z svakog stratuma mora bt proporcoala velč pojedog stratuma u populacj. grup uzorak - formra se tako da se z eke populacje slučajm zborom braju cjele grupe (pr. ako se stražuje sredjoškolska populacja u ekoj držav, slučajm zborom bra se uzorak škole, a sv učec škola koje su odabrae če uzorak etteta). 2 uzorkovaje (egl. samplg) predstavlja postupak kojm se z populacje bra uzorak etteta. 14
16 Slka 4-1: Vrste uzoraka amjer prgod slučaj jedostav slučaj zorak terval uzorak stratfcra uzorak grup uzorak 4.5 Varjabla Iako ettet eke populacje maju međusobo jedaka opća oblježja (prmjerce, studet su Kezološkog fakulteta Sveučlšta u Zagrebu u šk. god. 2000/2001.), o se razlkuju po drugm oblježjma (osobama, sposobostma, zajma td.), prmjerce, po morfološkm oblježjma (tjelesa vsa, tjelesa teža, raspo ruku, opseg podlaktce...), motorčkm sposobostma (rezultatma postgutm u razm motorčkm zadacma temeljem kojh se procjejuju pr. eksplozva saga, brza, koordacja...), stuacjskoj uspješost grača l ekpe (broj skokova u obra, broj asstecja...) td. U zastvem stražvajma pod pojmom varjabla podrazumjeva se određeo oblježje (svojstvo) koje oblkom l stupjem varra među ettetma, odoso po kojem ettet mogu bt st l razlčt. To svojstvo mora bt operacoalo defrao, odoso sv postupc za jegovo opažaje l mjereje moraju bt preczo opsa. 4.6 Vrste varjabl Razlčta oblježja, odoso varjable (osobe, sposobost sl.) mogu se pojavljvat u razlčtm oblcma stupjevma. Prmjerce: oblježje spol javlja se u dva oblka: muškarc žee. Takva se oblježja azvaju alteratvma. Školske ocjee se u Hrvatskoj javljaju u 5 razlčth oblka (edovolja, dovolja, dobar, vrlo dobar odlča). Tjelesa vsa vrlo je promjejva može se zrazt razlčtm vrjedostma koje ukazuju a stupaj razvjeost mjereog oblježja td. No usprkos takvoj razolkost, moguće je varjable podjelt a kvaltatve kvattatve. Kvaltatve varjable još se azvaju kategorjalma, a mogu bt omale ordale (redosljeda). Za razlku od kvaltatvh varjabl kojma se zražavaju eumerčka svojstva etteta, kvattatve varjable umerčk zražavaju stupaj razvjeost mjereog svojstva, a dobvee su mjerejem ekog oblježja etteta tervalom omjerom mjerom ljestvcom. Osm toga, kvattatve varjable mogu bt dskrete koturae. Dskrete varjable zražavaju koača broj vrjedost mjereog svojstva uvjek su određee cjelm brojem. Dobvaju se postupkom prebrojavaja (pr. broj sklekova, broj skokova u obra apadu...), dok koturae varjable mogu poprmt blo koju 15
17 umerčku vrjedost, a dobvaju se mjerejem (pr. mjereje vremea, kolče, udaljeost ). Slka 4-2: Vrste varjabl kvaltatve omale ordale kvattatve tervale omjere dskrete koturae 4.7 Populacja uzorak varjabl Populacja l uvezum varjabl W = {wj; j = 1,2, } predstavlja skup svh mogućh varjabl kojma se može opsat staje ekog etteta. Podskup varjabl V = {vj; j = 1,2,,m}, a temelju eke teorje zabra z populacje varjabl, azva se uzorak varjabl. 4.8 Matrca podataka Matrca podataka je skup podataka dobveh opsom skupa etteta E = {e ; = 1,...,} ekm skupom varjabl V = {vj ; j = 1,...,m} smješteh tako da svak redak sadrž podatke kojma je pojed ettet e opsa s m varjabl, dok svak stupac sadrž podatke etteta u pojedoj varjabl vj. Tablca 4-1: Prmjer matrce podataka ENTITETI SPOL TM TVI Šme M Mate M Marko M
18 5. Osov postupc za uređvaje prkazvaje podataka Nako prkupljaja, podatke je potrebo prpremt za odgovarajuću statstčku obradu. S obzrom da se u posljedje vrjeme statstčka obrada obavlja sključvo pomoću specjalzrah račualh programa za statstčko-grafčku obradu podataka (SPSS, STATISTICA td.), prkupljee podatke potrebo je pohrat u datoteke (fleove). Gotovo sv programsk prozvod za statstčko-grafčku obradu podataka zahtjevaju uos podataka u oblku tablce l matrce. U prvom se koraku uz, pomoć odgovarajućh programskh alata, formra tablca čju velču određuje broj etteta (broj etteta određuje broj redaka) broj varjabl (broj varjabl određuje broj stupaca). Zatm se, prema potreb, meuju varjable (stupc) ettet (rec) te se uose prkuplje podac. Prmjer tablce s podacma koja je kreraa u progamskom sustavu STATISTICA prkaza je u tablc 5-1. Tablca 5-1. Tablca podataka 20 etteta opsah 3 varjablama kreraa je u programskom sustavu STATISTICA ENTITETI SPOL POZ OKI AV M B 4 EM M B 3 KV M B 4 MD M B 3 MM M K 3 NM M K 2 NK M K 3 SA M K 3 SS M C 2 VM M C 3 VD M C 3 VI M C 5 BM Z B 3 ML Z B 3 GG Z B 4 KD Z B 3 RM Z K 1 NK Z K 3 MD Z K 5 SJ Z K 3 SS Z C 4 TD Z C 3 VJ Z C 2 VS Z C 2 S obzrom da je uos podataka mukotrpa vrlo važa do svakog stražvaja (jer o točost ueseh podataka ovs koača upotrebljvost rezultata dobveh statstčkom aalzom), 17
19 brza uosa može se povećat prkladm kodrajem podataka. Kodraje se občo korst kod kvaltatvh varjabl, gdje se odgovarajućoj kategorj (oblku kvaltatvog oblježja) prdružuju brojev l ozake. Prmjerce, varjabl spol koja ma dva oblka muškarc žee, mogu se dodjelt ozaka M za muške osobe, a Z za žeske osobe l 1 za muškarce, a 2 za žee. Tablca 5-2 prkazuje kodu lstu koja je korštea za uos podataka z tablce 5-1. Tablca 5-2. Prmjer kode lste Kratko me varjable Dugo me varjable Oblc (vrjedost) varjable SPOL Spol Muškarc M Žee POZ Pozcja u gr Bek B Krlo Cetar OKI Ocjea kvaltete grača Vrlo slaba kvalteta 1 Kod Slaba kvalteta 2 Dobra kvalteta 3 Vrlo dobara kvalteta 4 Izvrsa kvalteta 5 Z K C 5.1 Grupraje podataka Teško je zvest odgovarajuće zaključke o promatram pojavama, samo a temelju prkupljeh podataka, stoga h je potrebo statstčk uredt prklado prkazat. Podac se uređuju gruprajem, odoso razvrstavajem podataka prema oblcma (kategorjama, klasama, razredma) mjereog svojstva. Tako grupra podac se, rad bolje pregledost, prkazuju pomoću tablca grafkoa. Prmjerce, ako je sptu z Kvattatvh metoda prstupo određe broj studeata moguće h je gruprat prema postgutom uspjehu, a to zač ajmaje u dvje kategorje (su položl položl su) l, preczje, u 5 kategorja (edovolja, dovolja, dobar, vrlo dobar odlča). Grupraje predstavlja statstčk postupak razvrstavaja etteta s stm oblkom oblježja u određe broj dsjukth podskupova (podskupov koj emaju zajedčkh člaova). Prtom je važo aglast da se prlkom grupraja sv ettet moraju razvrstat da svak ettet može bt čla samo jedog podskupa (grupe, kategorje, klase, razreda). Dakle, grupraje je postupak sažmaja velkog broja podataka, koj prpadaju osovom skupu, u maj broj podskupova. Broj etteta koj prpadaju stoj kategorj (klas, razredu) azva se frekvecja. Zbroj frekvecja svh grupa jedak je ukupom broju etteta. Ako se ettet grupraju po jedom oblježju (prmjerce, spolu), oda se takvo grupraje azva jedodmezoalo, a ako se grupraju a temelju većeg broja oblježja, oda se azva všedmezoalo grupraje. 18
20 Tablca 5-3 prkazuje jedodmezoalo grupraje etteta. Grupraje se zvod a temelju jede varjable uspjeh a sptu. Od ukupo 40 studeata koj su prstupl psmeom djelu spta, 25 h je položlo spt, a 15 je položlo. Tablca 5-3. Prmjer jedodmezoalog grupraja prema uspjehu a sptu uspjeh a sptu frekvecija su položl 25 položl 15 ukupo 40 Tablca 5-4 prkazuje dvodmezoalo grupraje jer se grupraje zvod po dvje varjable: spol uspjeh a sptu. Isptu je prstuplo 26 studeata 14 studetca. Od 26 studeata, 16 h je položlo spt, a 10 jest, dok od 14 studetca 9 h je položlo, a 5 jest. Tablca 5-4. Prmjer dvodmezoalog grupraja prema spolu uspjehu a sptu spol su položl položl ukupo muškarc žee ukupo Grupraje grafčko prkazvaje kvaltatvh podataka Kvaltatv podac grupraju se tako da se ettet razvrstaju u određe broj kategorja. Prmjerce, oblježje uspjeh a sptu ma dva oblka (omala mjera skala): su položl položl su. Grupraje se zvod razvrstavajem etteta koj su položl spt u kategorju položl, a koj su u kategorju su položl (tablca 5-5). Tablca 5-5. Grupraje etteta prema uspjehu a sptu (dvje kategorje: su položl položl) uspjeh a sptu frekvecija % su položl 25 62,5 položl 15 37,5 ukupo Ettete je moguće gruprat prema ocje dobveoj a sptu (ordala mjera skala). U tom slučaju postoj pet stupjevah kategorja te h je potrebo avest od ajže prema ajvšoj l obruto (tablca 5-6). 19
21 Tablca 5-6. Grupraje etteta prema uspjehu a sptu (pet kategorja: edovolja, dovolja, dobar, vrlo dobar, odlča) uspjeh a sptu frekvecija % edovolja 25 62,5 dovolja 8 20 dobar 3 7,5 vrlo dobar 2 5 odlča 2 5 ukupo Rad lakšeg zaključvaja o prolazost a sptu, moguće je zračuat relatve frekvecje. Relatva frekvecja zračua se kao omjer frekvecje određee kategorje zbroja frekvecja svh kategorja (ukupog broja etteta). pg = fg/; %g = fg/ 100; g = 1,..,k gdje je pg relatva frekvecja zražea u proporcj grupe g (g = 1,..,k) fg frekvecja u grup g %g relatva frekvecja zražea u postotku ukupa broj etteta k broj kategorja (grupa). Prmjerce, relatva frekvecja za kategorju edovolja zos 62,5% (tablca 5-6) jer je %g = fg/ 100 = 25/ = 62,5 % Rad jedostavjeg uočavaja zorjeg prkazvaja dobveh rezultata, često se korste grafčk prkaz. Kvaltatv podac ajčešće se prkazuju pomoću grafkoa stupaca, grafkoa redaka strukturog kruga. Grafko stupaca je površsk grafko koj se crta u pravokutom koordatom sustavu. Na os x alaze se oblc oblježja (kategorje), a a os y alaze se frekvecje. Pravokutc su jedakh osovca (šra), a vsa m je određea frekvecjom prpadajuće kategorje (slka 5-1). 20
22 Slka 5-1. Grafko stupaca edovolja dovolja dobar vrlo dobar odlča f Grafko redaka je površsk grafko koj se također crta u pravokutom koordatom sustavu. Na os y alaze se oblc oblježja (kategorje), a a os x alaze se frekvecje. Pravokutc su jedakh osovca (vsa), a dulja m je određea prpadajućom frekvecjom (slka 5-2). Slka 5-2. Grafko redaka odlča vrlo dobar dobar dovolja edovolja
23 Struktur krug ajčešće se korst za prkaz relatvh frekvecja (slka 5-3). Slka 5-3. Struktur krug 5.2 Grupraje grafčko prkazvaje kvattatvh podataka Vrlo jedostava postupak za sređvaje kvatatvh podataka predstavlja sortraje l ragraje. Ako se podac žu od ajmaje do ajveće vrjedost, oda se takvo sortraje azva uzlazo, a ako se žu od ajveće do ajmaje, oda se azva slazo. Sortraje omogućava uočavaje ajmaje (mmale) vrjedost ajveće (maksmale) vrjedost temeljem kojh je moguće zračuat total raspo rezultata. R = xmax xm gdje je R total raspo rezultata xmax maksmala vrjedost xm mmala vrjedost. Veća kolča kvattatvh dskreth podataka s majm brojem mogućh vrjedost ajčešće se sređuje postupkom grupraja. Postupak grupraja provod se razvrstavajem etteta u podskupove prema vrjedostma kvattatvog oblježja to tako da jeda podskup če ettet s jedom vrjedost kvattatvog oblježja. Broj etteta s jedakom vrjedost kvattatvog oblježja predstavlja frekvecju grupe, a uređe z kvattatvh vrjedost s prpadajućm frekvecjama dstrbucju frekvecja. Prmjerce, tablca 5-7 prkazuje broj osobh pogrešaka 18 košarkaša a jedoj košarkaškoj utakmc. 22
24 Tablca 5-7. Broj osobh pogrešaka (OP) 17 košarkaša a jedoj košarkaškoj utakmc ENTITETI OP ERJA-M 2 KRST-V 1 MILA-D 4 MILL-M 3 NORI-M 1 NOVO-K 4 SAMA-A 2 SUBO-S 3 VANJ-M 5 VOLO-D 3 VUJI-I 2 BAZD-M 3 BLAS-M 3 GIRI-G 4 KRUN-D 3 MALI-M 3 MAMI-M 2 Nako uzlazog sortraja podataka (tablca 5-8), lako se uočava ajmaja (1) ajveća vrjedost (5). Tablca 5-8. Broj osobh pogrešaka (OP) 17 košarkaša a jedoj košarkaškoj utakmc ako uzlazog sortraja ENTITETI OP KRST-V 1 NORI-M 1 MAMI-M 2 ERJA-M 2 SAMA-A 2 VUJI-I 2 MILL-M 3 SUBO-S 3 VOLO-D 3 BAZD-M 3 BLAS-M 3 KRUN-D 3 MALI-M 3 NOVO-K 4 GIRI-G 4 MILA-D 4 VANJ-M 5 23
25 S obzrom da dskreta varjabla osoba pogreška ma mal broj mogućh vrjedost (1, 2, 3, 4 5), dstrbucja frekvecja sastojat će se od 5 grupa s prpadajućm frekvecjama (tablca 5-9). Tablca 5-9. Grupraje etteta prema varjabl broj osobh pogrešaka Broj osobh pogrešaka frekvecja Ukupo 17 Dstrbucju frekvecja, prkazau u tablc 5-9, moguće je grafčk prkazat pomoću hstograma polgoa frekvecja. Slka 5-4. Hstogram frekvecja Hstogram frekvecja je površsk grafčk prkaz dstrbucje frekvecja u kojem se umerčke vrjedost oblježja upsuju a sred pravokutka jedakh osovca čja će vsa ovst o velč frekvecje (slka 5-4). 24
26 Slka 5-5. Polgo frekvecja Polgo frekvecja je ljsk grafčk prkaz dstrbucje frekvecja koj astaje spajajem točaka položaj kojh je u koordatom sustavu određe umerčkom vrjedošću oblježja velčom frekvecje (slka 5-5). Ako dskreta varjabla ma velk broj mogućh vrjedost l ako se rad o koturaoj varjabl, podac se grupraju u maj broj razreda. Za uspješo grupraje potrebo je odredt prklada broj razreda jhovu velču terval razreda. Broj razreda prje svega ovs o broju etteta ajčešće se kreće zmeđu pet petaest. Prmjerce, u tablc 5-10 prkazao je grupraje 60 judaša u 5 razreda u varjabl skok udalj s mjesta. Vdljvo je da je ajveć broj etteta u trećem razredu (26 l %), odoso da ajveć broj judaša u skoku udalj s mjesta postže vrjedost koje se alaze u tervalu zmeđu cm, dok se broj etteta s boljm lošjm rezultatma smajuje. Tablca Apsolute relatve frekvecje Iterval razreda f rf (%) 120<x<= ,67 140<x<= ,00 160<x<= ,33 180<x<= ,67 200<x<= ,33 Dobvee frekvecje (apsolute relatve) moguće je također grafčk prkazat hstogramom (slka 5-6) polgoom frekvecja (slka 5-7). Hstogram frekvecjacrta se tako da osovcu pravokutka određuje terval razreda, a vsu frekvecja pojedog razreda. 25
27 Slka 5-6. Hstogram frekvecja s razredma <x<= <x<= <x<= <x<= <x<=220 Polgo frekvecja astaje spajajem točaka čje su koordate određee sredom pojedog razreda frekvecjom tog razreda. Slka 5-7. Polgo frekvecja s razredma x< <x<= <x<= <x<= <x<= <x<= <x 26
28 Ako se frekvecje (apsolute l relatve) svakog sljedećeg razreda zbrajaju sa sumom frekvecja predhodh razreda, dobju se kumulatve frekvecje (tablca 5-11). Tablca Apsolute relatve kumulatve frekvecje Iterval razreda cf crf (%) 120,000<x<=140, ,67 140,000<x<=160, ,67 160,000<x<=180, ,00 180,000<x<=200, ,67 200,000<x<=220, ,00 Kumulatve frekvecje pokazuju kolko je etteta (apsoluto l relatvo) kojma je vrjedost jedaka l maja od gorje grace razreda čja je frekvecja ušla u kumulatv z. Prmjerce, a temelju tablce vdljvo je da je 39 l 65 % sptaka skočlo u dalj s mjesta do 180 cm, a 21 (60-39=21) l 35 % (100-65=35) vše od 180 cm. Kumulatve frekvecje također se prkazuju hstogramom l polgoom frekvecja (slka 5-8). Slka 5-8. Kumulatv polgo relatvh frekvecja <x<= <x<= <x<= <x<= <x<=220 27
29 6 Deskrptv pokazatelj Deskrptv pokazatelj korste se za ops varjabl, a djele se a mjere cetrale tedecje l sredšje mjere, mjere varjablost l dsperzje te mjere asmetrje zdužeost dstrbucje. 6.1 Mjere cetrale tedecje l sredšje mjere Zajedčko oblježje mjera cetrale tedecje l sredšjh mjera jest da svaka od jh predstavlja jedu vrjedost koja b trebala bt dobra zamjea za skup svh pojedačh vrjedost, odoso jhov ajbolj reprezetat. Dakle, težja je mjera cetrale tedecje da ukažu a vrjedost oko koje postoj tedecja grupraja rezultata, odoso ukazuju a rezultat koj ma ajveću vjerojatost pojavljvaja. Postoj ekolko mjera cetrale tedecje koje se razlkuju prema aču utvrđvaja mogućostma prmjee. Tako se ajčešće razlkuju potpue položaje mjere cetrale tedecje. Potpue mjere cetrale tedecje zračuavaju se a temelju svh podataka. To su: artmetčka sreda, geometrjska sreda harmojska sreda. Nasuprot jma, mod medja su određe položajem u uređeom zu podataka. S obzrom a prrodu varjabl, u kezološkm stražvajma ajčešće se korste artmetčka sreda, mod medja, dok se ostale mjere cetrale tedecje rjetko prmjeuju Artmetčka sreda l prosječa vrjedost Artmetčka sreda svakako je ajčešće korštea mjera cetrale tedecje. Izračuava se kao omjer zbroja svh vrjedost eke varjable ukupog broja etteta gdje je = 1,,, a predstavlja broj etteta. x 1 Prmjer: 10 etteta postglo je sljedeće rezultate u ekom motorčkom testu: 1, 2, 2, 3, 3, 3, 3, 4, 4, 5. Artmetčka sreda je x Artmetčka sreda račua se samo za kvattatve varjable sljedećh je karakterstka: x zbroj odstupaja vrjedost svh pojedačh rezultata od artmetčke srede jedaka je ul, odoso artmetčka sreda predstavlja težšte rezultata. 1 x x 0 28
30 zbroj kvadrrah odstupaja svh pojedačh vrjedost od artmetčke srede je mmala. 1 2 x x m artmetčka sreda uvjek se alaz zmeđu mmale maksmale vrjedost. x x m x max S obzrom a to da je artmetčka sreda potpua mjera cetrale tedecje, odoso da a jeu vrjedost podjedako utječu rezultat svh etteta, podloža je promjeama pod utjecajem zrazto skh l vsokh pojedčh vrjedost, što može zato utjecat a jeu reprezetatvost Mod l domata vrjedost Mod l domata vrjedost je oa vrjedost kvaltatve l kvattatve varjable koja se ajčešće pojavljuje, odoso koja je ajveće frekvecje. Mod djel dstrbucju uređeh podataka a rastuć padajuć do. Određvaje modale vrjedost kod kvaltatvh dskreth kvattatvh varjabl svod se a utvrđvaje vrjedost s ajvećom frekvecjom. Prmjer: 10 etteta je postglo sljedeće rezultate u ekom motorčkom testu: 1, 2, 2, 3, 3, 3, 3, 4, 4, 5. Mod je jedak μo = Medja l cetrala vrjedost Ocjea Medja je vrjedost koja se alaz a sred uređeog za podataka (uzlazo l slazo sortraog), odoso vrjedost koja uređe z podataka djel a dva jedakobroja djela. Medja je moguće odredt za egruprae gruprae ordale te kvattatve dskrete koturae varjable. Medja egruprah podataka moguće je odredt ako uzlazog l slazog uređeja (sortraja) podataka. Ako je broj podataka epara, oda medja predstavlja vrjedost sredšjeg člaa tj. etteta (xr) f 29
31 μe = xr gdje je r = (+1)/2 Ako je broj podataka para, oda je medja jedak artmetčkoj sred vrjedost dvaju sredšjh člaova uređeog za. μe =(xr1+xr2)/2 gdje je r1=/2, a r2 =(/2)+1 Prmjer: Neka je 15 etteta (epara z) zmjereo ekm testom, a rezultat su uređe po velč: x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11 x 12 x 13 x 14 x Medja je 8. podatak po redu μe = x8 = 3 jer je r = (+1)/2 = (15+1)/2 = 8 Ako je 16 etteta (para z) zmjereo ekm testom, a rezultat su uređe po velč x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11 x 12 x 13 x 14 x 15 x oda se medja odred kao artmetčka sreda podatka po redu μe= (x8+x9)/2 = (3+3)/2=3 jer je r1 = /2=16/2=8, a r2 = /2+1=16/2+1=9 Na medja mod e utječu ekstremo vsok l sk rezultat pa bolje reprezetraju poztvo egatvo asmetrčo dstrburae varjable. 6.2 Mjere varjablost l dsperzje Za dobru deskrpcju aalzrae pojave je dostato samo zračuat mjere cetrale tedecje. Ako se rezultat etteta grupraju oko eke sredšje vrjedost, oda odgovarajuća mjera cetrale tedecje može bt dobar reprezetat aalzrah podataka. Ako rezultat malo varraju oko artmetčke srede, oda h oa bolje reprezetra ego kad podac zato varraju. Dvje se varjable, koje se e razlkuju po mjer cetrale tedecje, mogu razlkovat po raspršeost (dsperzj) podataka. Kada b podac bl međusobo jedak, tada e b blo varjablost, a tedecja grupraja rezultata bla b maksmala. Ako b se pr mjereju ekog oblježja a ekoj mjeroj skal uvjek dobvale razlčte vrjedost, tada e b blo kakvog grupraja rezultata, a varjablost b bla maksmala (slka 6-2). 30
32 Slka 6-2. Prkaz dva ekstrema slučaja: 1. ema varjablost (maksmalo grupraje rezultata); 2. maksmala varjablost (ema grupraja rezultata) F REZULTATI REZULTATI U stvarost se, međutm, takv ekstrem slučajev gotovo kad e događaju, već se prkuplje podac uglavom, maje l vše, grupraju oko eke sredšje vrjedost. Grupraje se može procjet mjerama varjablost l dsperzje. Za ops dsperzje varjabl u kezološkm stražvajma ajčešće se korste total raspo, terkvartl, varjaca stadarda devjacja Total raspo Total raspo (Rtot) je ajjedostavja mjera varjablost, a utvrđuje se kao razlka zmeđu maksmale (xmax) mmale (xm) vrjedost. Rtot = xmax - xm Total raspo se skazuje u mjerm jedcama varjable, a s obzrom da zavs samo od dva podatka (maksmalog mmalog), ekstrem rezultat zato utječu a jegovu vrjedost. Osm toga, lako je uočt da se s povećajem broja etteta u uzorku občo povećava total raspo jer se povećava vjerojatost uključvaja etteta s ekstremm (maksmalm mmalm) vrjedostma. Stoga je raspo vrlo esgura mjera varjablost Varjaca stadarda devjacja Stupaj raspršeost moguće je procjet putem odstupaja rezultata etteta od eke sredšje vrjedost, ajčešće artmetčke srede. Dakle, potrebo je zračuat odstupaja vrjedost svakog etteta u određeoj varjabl od artmetčke srede te varjable. d x x Temeljem th odstupaja (d) moguće je zračuat mjeru varjablost jer veća odstupaja ukazuju a veću raspršeost podataka. Iz toga sljed da je stupaj varjablost podataka moguće skazat putem artmetčke srede zračuath odstupaja. Međutm, takva b operacja kao rezultat dala ulu jer je artmetčka sreda težšte rezultata, odoso zbroj odstupaja svh pojedačh rezultata od artmetčke srede jedak je ul. 31
33 1 d 0 Ovaj problem moguće je rješt kvadrrajem. Na taj ač dobveo prosječo kvadrato odstupaje rezultata etteta od artmetčke srede varjable azva se varjaca. 2 2 ( x x) 1 1 d 2 S obzrom a to da je varjaca prosječo kvadrato odstupaje, otežao je jezo terpretraje. Da b se zračuata mjera raspršeost svela a mjeru jedcu varjable, potrebo je z varjace zračuat drug korje. Tako zračuata mjera varjablost azva se stadarda devjacja (σ). 2 ( x x) Žel l se zračuat stadarda devjacja ekog uzorka etteta, temeljem koje se procjejuje stadarda devjacja populacje koje je odabra uzorak reprezetat, oda se stadarda devjacja račua s azvkom -1 umjesto. d 2 s 1 2 ( x x ) 1 Dakle, ako se žel utvrdt stadarda devjacja eke skupe podataka, oda je spravo zračuat stadardu devjacju sa u azvku. Ako se žel zaključvat o populacj z koje su rezultat odabra, oda je spravo račuaje stadarde devjacje sa -1 u azvku. 32
34 Prmjer: 10 etteta je postglo sljedeće rezultate u ekom motorčkom testu. Varjacu stadardu devjacju moguće je zračuat ovm postupkom x x -x (x -x) x (x x ) ,2 1, Koefcjet varjablost Stadarda devjacja se skazuje u mjerm jedcama promatraog oblježja pa jeza vrjedost ovs o stupju varjablost mjerm jedcama. Stoga je moguće zravo uspoređvat stadarde devjacje vše razlčth varjabl. Za usporedbu razlčth varjabl korst se koefcjet varjablost (V) koj pokazuje kolk postotak vrjedost artmetčke srede zos stadarda devjacja, odoso zračuava se kao omjer stadarde devjacje (s) artmetčke srede (x) pomože sa 100. V s 100 x Koefcjet varjablost pokazuje u kojoj varjabl sta grupa etteta maje l vše varra te koja grupa maje l vše varra u stoj varjabl. 33
35 6.3 Mjere asmetrje dstrbucje (egl. skewess) Ako su frekvecje rezultata u ekoj varjabl ravomjero raspodjeljee ljevo deso od prosječe vrjedost, tada se rad o smetrčoj dstrbucj podataka (slka 6-3). Kod umodale (dstrbucja koja ma jedu modalu vrjedost) smetrče dstrbucje artmetčka sreda, mod medja jedake su vrjedost. Ako frekvecje rezultata su ravomjero raspodjeljee ljevo deso od prosječe vrjedost, tada se rad o poztvo l egatvo asmetrčoj dstrbucj podataka. Slka 6-3. Smetrča umodala dstrbucja x o e Ako se veća etteta gruprala u zo žh vrjedost s ekolcom ekstremo vsokh vrjedost, takva se dstrbucja podataka zove poztvo asmetrča (slka 4). Kod poztvo asmetrče dstrbucje artmetčka sreda, mod medja su međusobo jedak. Najveću vrjedost ma artmetčka sreda, zatm medja pa mod. 34
36 Slka 6-4. Poztvo asmetrča dstrbucja rezultata o e x Kod egatvo asmetrče dstrbucje (slka 5) grupraje etteta je u zo všh vrjedost, a majm brojem etteta u zo ekstremo skh vrjedost (obruto od poztvo asmetrče dstrbucje podataka). U egatvo asmetrčm dstrbucjama artmetčka sreda je ajmaja, a zatm po velč sljede medja mod (x < me < mo). Slka 6-5. Negatvo asmetrča dstrbucja rezultata x e o 35
37 Koefcjet asmetrje se zračuava preko trećeg mometa oko srede (m3) stadarde devjacje podgute a treću potecju (σ 3 ) m a3 3 3 gdje je m x x treć momet oko srede. Ako je suma poztvh odstupaja podguth a treću potecju veća od egatve (treća potecja kao epara e mjeja predzak), tada će a3 bt već od ule, što ukazuje a poztvo asmetrču dstrbucju, odoso, ako je a3 maj od ule, oda se rad o egatvoj asmetrj dstrbucje jer je suma egatvh odstupaja podguth a treću potecju veća od sume poztvh. Dakle, o vrjedost trećeg mometa oko srede (m3) ovs da l će a3 bt poztvog l egatvog predzaka buduć da je stadarda devjacja u azvku uvjek poztva. Ako je a3 jedak ul, dstrbucja je smetrča. Stadardom devjacjom poštava se utjecaj mjere jedce varjable, odoso zračuata vrjedost se stadardzra te se tako zračuat koefcjet asmetrje ajčešće kreće u tervalu od -2 do +2, a kod zrazto asmetrčh dstrbucja može bt zva tog tervala. Očto je da kod asmetrčo dstrburah podataka artmetčka sreda eće bt ajpogodja mjera cetrale tedecje jer e predstavlja ajveć broj etteta (ajvjerojatj rezultat) Mjere zdužeost dstrbucje (egl. kurtoss) Dstrbucja podataka može bt maje l vše zdužea, odoso spljoštea, što ukazuje a veću homogeost, odoso heterogeost podataka. Ako je kocetracja frekvecja oko odgovarajuće sredšje vrjedost veća od teoretske ormale dstrbucje, tada je vrh dstrbucje vš od vrha ormale dstrbucje. I obruto, što je kocetracja frekvecja oko sredšje vrjedost maja, to je vrh dstrbucje ž od ormale dstrbucje. Stupaj spljošteost l zdužeost dstrbucje zražava se koefcjetom a4, a zračuava se preko četvrtog mometa oko srede (m4) stadarde devjacje podgute a četvrtu potecju (σ 4 ). m a4 4 4 Četvrt momet oko srede zračua se formulom m 4 1 x x 4 Ako je koefcjet spljošteost: 36
38 a4=3 dstrbucja je mezokurtča ormala a4>3 dstrbucja je leptokurtča zdužea a4<3 dstrbucja je platkurtča spljoštea (slka 6-6). Slka 6-6. Platkurtča, mezokurtča leptokurtča dstrbucja podataka platkurtča mezokurtča leptokurtča 37
39 7. Normala dstrbucja Normala dstrbucja sguro je ajvažja ajčešće korštea koturaa teoretska dstrbucja u statstčkm aalzama (slka 7-1). Nazva se još Gaussovom dstrbucjom jer se smatra da ju je Gauss prv matematčk defrao. Za slučaju koturau varjablu x kaže se da ma ormalu dstrbucju s parametrma μ σ ako je gdje je μ artmetčka sreda σ stadarda devjacja π = 3, e =2, f(x) σ 1 2Π e 2 1 xμ 2 σ Slka 7-1. Normala dstrbucja s parametrma μ σ. x o e Ako su vrjedost zražee u stadardzraom oblku z = (x μ)/σ oda se formula ormale dstrbucje svod a oblk f ( z ) 1 e 2 s parametrma μ = 0 σ=1. U sportskoj praks često je važje utvrdt vjerojatost postzaja boljeg l lošjeg rezultata od eke vrjedost. 2 z 2 38
40 Moguće je uočt da je ormala dstrbucja zvoastog oblka, umodala zrcalo smetrča u odosu a artmetčku sredu. Artmetčka sreda, modus medja su jedak. Normala dstrbucja je defraa artmetčkom sredom stadardom devjacjom. Proteže se u tervalu od - do +, a vjerojatost da se dogod vrjedost u tervalu: od -1 σ do +1 σ je 68,27 % od -2 σ do +2 σ je 95,45 % od -3 σ do +3 σ je 99,73 %, odoso od -1,96 σ do + 1,96 σ je 95 % od -2,58 σ do + 2,58 σ je 99 %. 39
41 8. Stadardzacja podataka (z - vrjedost) Za prkupljaje podataka a ekom uzorku etteta korste se razlčt mjer strumet, pa su rezultat zraže u razlčtm mjerm jedcama. Stoga je usporedba vrjedost etteta u razlčtm varjablama zato otežaa. Ovaj problem se rješava postupkom trasformacje orgalh vrjedost eke varjable u tzv. stadardzrae l z-vrjedost. Postupak stadardzacje provod se pomoću formule gdje je z stadardzra rezultat etteta x orgala vrjedost sptaka x artmetčka sreda s stadarda devjacja. z x x, s Iz avedee formule lako je uočt da se stadardzraa vrjedost zračuava određvajem odstupaja etteta od artmetčke srede (cetrraje rezultata), koje se potom podjel stadardom devjacjom. Dakle, stadardzraa vrjedost je relatva mjera odstupaja svakog etteta od artmetčke srede, zražea u djelovma stadarde devjacje. Praktča prmjea trasformacje orgalh podataka u z-vrjedost razmotrt će se u sljedećm prmjerma. Prmjer: Deset učeka atjecalo se u tr atletske dscple: skok udalj (SD), trčaje a 100 metara (T100m) bacaje kugle (BK) postglo rezultate avedee u tablc 8-1. Tablca 8-1. Rezultat 10 učeka u tr atletske dscple Uček SD T100m BK AB ,6 561 DF ,9 550 JG ,7 538 KL ,0 490 DD ,2 518 ED ,1 551 TB ,5 589 ZN ,3 602 RG ,5 547 EN ,8 510 Potrebo je utvrdt ukupa poredak učeka a ovom atjecaju. Dakle, problem se svod a ragraje većeg broja etteta opsah većm brojem varjabl. S obzrom a to da su 40
42 rezultat učeka u avedem dscplama zraže razlčtm mjerm jedcama, je opravdao kodezrat rezultate jhovm jedostavm zbrajajem, već h je prethodo potrebo trasformrat u z-vrjedost. Cjel postupak moguće je provest u ekolko koraka. Prv korak: Izračuat artmetčku sredu stadardu devjacju za svaku varjablu (tablca 8-2). Tablca 8-2. Artmetčke srede stadarde devjacje SD T100m BK as 370,4 13,36 545,6 sd 45,66 0,73 34,21 Drug korak: Trasformrat orgale podatake u z-vrjedost a temelju zračuath artmetčkh sreda stadardh devjacja. Prmjerce, stadardzra rezultat učeka AB u dscpl skok udalj (SD) zračua se prema formul z AB, SD ,4 11,4 0,25 45,66 45,66 Na st ač trasformraju se rezultat ostalh učeka u sve tr dscple. Rezultat su prkaza u tablc 8-3. Tablca 8-3. Stadardzra rezultat 10 učeka u tr atletske dscple SD T100M BK AB -0,25 0,33 0,45 DF -1,08 0,74 0,13 JG -0,53 0,46-0,22 KL -0,84 0,87-1,63 DD 1,74-1,58-0,81 ED -1,24 1,01 0,16 TB 0,87-1,17 1,27 ZN 1,20-1,44 1,65 RG -0,03 0,19 0,04 EN 0,17 0,60-1,04 Treć korak: Prje kodezacje rezultata (zbrojem l prosječom vrjedošću), potrebo je varjable koje su obruto skalrae pomožt s -1, odoso promjet m predzak. Name, varjabla trčaje a 100 metara (T100m) je obruto skalraa, što zač da veća umerčka vrjedost predstavlja lošj rezultat. Stoga tu varjablu treba pomožt s -1. Nako ovog postupka dobju se rezultat prkaza u tablc
43 Tablca 8-4. Stadardzra rezultat 10 učeka u tr atletske dscple ako što je varjabla T100M pomožea sa -1 SD T100M BK AB -0,25-0,33 0,45 DF -1,08-0,74 0,13 JG -0,53-0,46-0,22 KL -0,84-0,87-1,63 DD 1,74 1,58-0,81 ED -1,24-1,01 0,16 TB 0,87 1,17 1,27 ZN 1,20 1,44 1,65 RG -0,03-0,19 0,04 EN 0,17-0,60-1,04 Četvrt korak: Kodezrat stadardzrae vrjedost artmetčkom sredom, odoso zračuavajem prosječe z-vrjedost za svakog učeka u avedem dscplama. Prmjerce, prosječa z-vrjedost učeka AB zračua se formulom z AB z AB,SD z AB, T100 3 z AB,BK 0,25 ( 0,33) 0,45 0,04 3 Na st ač zračuaju se prosječ rezultat ostalh učeka u sve tr dscple. Rezultat su prkaza u tablc 8-5. Tablca 8-5. Prosječ stadardzra rezultat 10 učeka u tr atletske dscple Z AB -0,04 DF -0,56 JG -0,41 KL -1,11 DD 0,84 ED -0,70 TB 1,10 ZN 1,43 RG -0,06 EN -0,49 Pet korak: Slazo (od većega k majem) poredat učeke po zračuatoj prosječoj z- vrjedost. Koača redosljed učeka prkaza je u tablc
44 Tablca 8-6. Ragra prosječ stadardzra rezultat 10 učeka u tr atletske dscple Uček Rag Z ZN 1 1,43 TB 2 1,10 DD 3 0,84 AB 4-0,04 RG 5-0,06 JG 6-0,41 EN 7-0,49 DF 8-0,56 ED 9-0,70 KL 10-1,11 Dakle, ajbolj je uček ZN, zatm sljed uček TB pa uček DD td. Ovaj postupak u sportu može bt vrlo korsta za provođeje selekcje. Prmjer: Izmjereo je 257 dječaka testom za procjeu eksplozve sage skok udalj s mjesta. Artmetčka sreda zosla je 215 cm, a stadarda devjacja 12 cm. Uček XY postgao je rezultat 230 cm. Potrebo je procjet postotak (%) broj učeka koj su postgl lošj rezultat od učeka XY. Prvo je potrebo zračuat z-vrjedost sptaka XY, a oa zos z XY , Uz pretpostavku da su rezultat ormalo dstrbura, moguće je procjet vjerojatost boljeg rezultata uz pomoć tablce A (str. 59). Name, vjerojatost da se postge bolj rezultat od odgovarajuće z-vrjedost odgovara površ spod ormale dstrbucje od zadae z- vrjedost do desoga kraja krvulje (slka 8-1). 43
45 Slka 8-1. Površa spod ormale dstrbucje odgovara vjerojatost da ek rezultat bude bolj l lošj od zadae z vrjedost p = 0,8943 p = 0,1057 1,25 Dakle, za vrjedost z=1,25 odgovara površa spod ormale dstrbucje od p=0,1057, l zražeo u postotku 10,57%, što zražava vjerojatost da se postge bolj rezultat od sptaka XY. z = 1,25 p = 0, ,57 % Vjerojatost postzaja lošjeg rezultata jedaka je 1-0,1057=0,8943, odoso 89,43 %. Na temelju procjejee vjerojatost može se zračuat broj sptaka s boljm, odoso lošjm rezultatom. S obzrom a to da je d d p, odoso % 100, gdje je p proporcja ( p= 0,1057) d do cjele (broj učeka s boljm rezultatom od z = 1,25) cjela (ukupa broj učeka = 257), oda je d p 0, ,16 27 učeka s boljm, odoso, = 230 učeka s lošjm rezultatom. 44
46 Praktča korst od stadardzacje rezultata ogleda se u mogućost grafčkog prkazvaja rezultata etteta u većem broju varjabl koje opsuju jegov atropološk profl (slka 8-2). Slka 8-2. Grafčk prkaz profla treraost sportaša SDM NEB T20m KUS BP TR IP SKL T12m Legeda: SDM - skok udalj s mjesta, IP - skret palcom, NEB ertmčo bubjaje, SKL sklekov, T12m trčaje 12 muta, T20m - trčaje 20 m, KUS korac u strau, BP brza provlaka, TR tapg rukom. To omogućava, prmjerce, uočavaje staja člaca odgovorh za uspješost u određeoj sportskoj aktvost, odoso određvaje profla staja treraost sportaša (slka 8-2). Na temelju slke 8-2 može se uočt u kojm je testovma sptak postgao dobre, a u kojma loše rezultate, odoso a što b trebalo obratt pozorost pr programraju trega u sljedećem razdoblju. 45
Obrada empirijskih podataka
 Obrada emprjskh podataka deskrptva statstka opsvaje podataka z uzorka l populacje u form osovh parametara osove vrste podataka po astaku varjable (upotreba razlčth mjerh ljestvca) se mogu klasfcrat a:.
Obrada emprjskh podataka deskrptva statstka opsvaje podataka z uzorka l populacje u form osovh parametara osove vrste podataka po astaku varjable (upotreba razlčth mjerh ljestvca) se mogu klasfcrat a:.
REGRESIJSKA ANALIZA. U razvoju regresijske analize najznačajniju ulogu su imali: Carl Friedrich Gauss ( ) Francis Galton (
 SEMINAR U razvoju regresjske aalze ajzačajju ulogu su mal: Carl Fredrch Gauss (822 9) Fracs Galto (822 9) Karl Pearso (857 936) George Udy Yule (87 95) SEMINAR Regresjska aalza je matematčko-statstčk postupak
SEMINAR U razvoju regresjske aalze ajzačajju ulogu su mal: Carl Fredrch Gauss (822 9) Fracs Galto (822 9) Karl Pearso (857 936) George Udy Yule (87 95) SEMINAR Regresjska aalza je matematčko-statstčk postupak
Metoda najmanjih kvadrata
 Metoda ajmajh kvadrata Moday, May 30, 011 Metoda ajmajh kvadrata (MNK) MNK smo već uvel u proučavaju leare korelacje; gdje smo tražl da suma kvadrata odstupaja ekspermetalh točaka od pravca koj h a ajbolj
Metoda ajmajh kvadrata Moday, May 30, 011 Metoda ajmajh kvadrata (MNK) MNK smo već uvel u proučavaju leare korelacje; gdje smo tražl da suma kvadrata odstupaja ekspermetalh točaka od pravca koj h a ajbolj
x pojedinačnih rezultata:
 ovarjaca koefcjet korelacje Sredja vrjedost stadardo odstupaje Prlkom poavljaja mjereja, uz ste (kolko je to moguće uvjete (st mjertelj, mjer strumet, mjera metoda okol uvjet, eke stale fzkale velče, dobt
ovarjaca koefcjet korelacje Sredja vrjedost stadardo odstupaje Prlkom poavljaja mjereja, uz ste (kolko je to moguće uvjete (st mjertelj, mjer strumet, mjera metoda okol uvjet, eke stale fzkale velče, dobt
Aritmetički i geometrijski niz
 Zadac sa prethodh prjemh spta z matematke a Beogradskom uverztetu Artmetčk geometrjsk z. Artmetčk z. 00. FF Zbr prvh dvadeset člaova artmetčkog za čj je prv čla, a razlka A) 0 B) C) D) 880 E) 878. 000.
Zadac sa prethodh prjemh spta z matematke a Beogradskom uverztetu Artmetčk geometrjsk z. Artmetčk z. 00. FF Zbr prvh dvadeset člaova artmetčkog za čj je prv čla, a razlka A) 0 B) C) D) 880 E) 878. 000.
10. REGRESIJA I KORELACIJA
 0. REGRESIJA I KORELACIJA Jospa Perkov, prof., pred. Jedodmezoala aalza stražvaje vaje jede pojave predočee ee statstčkm zom ezavso od drugh, statstčkm metodama (grafčko tabelaro prkazvaje za, zračuavaje
0. REGRESIJA I KORELACIJA Jospa Perkov, prof., pred. Jedodmezoala aalza stražvaje vaje jede pojave predočee ee statstčkm zom ezavso od drugh, statstčkm metodama (grafčko tabelaro prkazvaje za, zračuavaje
1.1. Pregled najvažnijih izraza i pojmova
 Teorja formacje, kapactet dskretog komukacjskog kaala, Markovljev lac Pregled ajvažjh zraza pojmova Dskreto bezmemorjsko zvoršte Izvoršte X X = {x,,x,,x } [p(x ) = [p(x) = [p(x ) p(x ) p(x ) X dskreta
Teorja formacje, kapactet dskretog komukacjskog kaala, Markovljev lac Pregled ajvažjh zraza pojmova Dskreto bezmemorjsko zvoršte Izvoršte X X = {x,,x,,x } [p(x ) = [p(x) = [p(x ) p(x ) p(x ) X dskreta
Polarizacija. Procesi nastajanja polarizirane svjetlosti: a) refleksija b) raspršenje c) dvolom d) dikroizam
 Polarzacja Proces asajaja polarzrae svjelos: a refleksja b raspršeje c dvolom d dkrozam Freselove jedadžbe Svjelos prelaz z opčkog sredsva deksa loma 1 u sredsvo deksa loma, dolaz do: refleksje (prema
Polarzacja Proces asajaja polarzrae svjelos: a refleksja b raspršeje c dvolom d dkrozam Freselove jedadžbe Svjelos prelaz z opčkog sredsva deksa loma 1 u sredsvo deksa loma, dolaz do: refleksje (prema
Linearna korelacija. Vrijedi: (1) 1 r 1
 Leara korelacja Korelacja je mjera leare zavsost dvju serja podataka 1,,..., 1,,...,. Drugm rječma, ako su točke 1, 1,,,..., gruprae oko regresjskog pravca, oda govormo da su podatc korelra learo korelra.
Leara korelacja Korelacja je mjera leare zavsost dvju serja podataka 1,,..., 1,,...,. Drugm rječma, ako su točke 1, 1,,,..., gruprae oko regresjskog pravca, oda govormo da su podatc korelra learo korelra.
RAČUNANJE SA PRIBLIŽNIM VREDNOSTIMA BROJEVA
 RAČUNANJE SA PRIBLIŽNIM VREDNOSTIMA BROJEVA PRIBLIŽNI BROJ I GREŠKA tača vredost ekog broja X prblža vredost ekog broja X apsoluta greška Δ = X X graca apsolute greške (gorja graca) relatva greška X X
RAČUNANJE SA PRIBLIŽNIM VREDNOSTIMA BROJEVA PRIBLIŽNI BROJ I GREŠKA tača vredost ekog broja X prblža vredost ekog broja X apsoluta greška Δ = X X graca apsolute greške (gorja graca) relatva greška X X
AKSIOMATIKA TEORIJE VEROVATNOĆE
 AKSIOMATIKA TEORIJE VEROVATNOĆE E Aksomatka teorje verovatoće Polaz se od osovh stavova, tzv. aksoma, a osovu kojh se sve ostale osobe mogu dokazat. Za posmatra prostor el. shoda aksomatzacja daje odgovore
AKSIOMATIKA TEORIJE VEROVATNOĆE E Aksomatka teorje verovatoće Polaz se od osovh stavova, tzv. aksoma, a osovu kojh se sve ostale osobe mogu dokazat. Za posmatra prostor el. shoda aksomatzacja daje odgovore
Prof. dr. sc. Maja Biljan-August Prof. dr. sc. Snježana Pivac Doc. dr. sc. Ana Štambuk 2. IZDANJE. Poglavlje 2.
 Prof. dr. sc. Maja Blja-August Prof. dr. sc. Sježaa Pvac Doc. dr. sc. Aa Štambuk UPORABA STATISTIKE U EKONOMIJI. IZDANJE Poglavlje. REGRESIJSKA I KORELACIJSKA ANALIZA Ekoomsk fakultet Sveučlšta u Rjec
Prof. dr. sc. Maja Blja-August Prof. dr. sc. Sježaa Pvac Doc. dr. sc. Aa Štambuk UPORABA STATISTIKE U EKONOMIJI. IZDANJE Poglavlje. REGRESIJSKA I KORELACIJSKA ANALIZA Ekoomsk fakultet Sveučlšta u Rjec
Ekonometrija 5. Ekonometrija, Osnovne studije. Predavač: Aleksandra Nojković
 Ekoometja 5 Ekoometja, Osove studje Pedavač: Aleksada Nojkovć Stuktua pedavaja Klasč dvostuk (všestuk) lea egeso model - metod ONK. Petpostavke všestukog KLM. Koelacja u všestukom KLM. Oča kogova. Dvostuk
Ekoometja 5 Ekoometja, Osove studje Pedavač: Aleksada Nojkovć Stuktua pedavaja Klasč dvostuk (všestuk) lea egeso model - metod ONK. Petpostavke všestukog KLM. Koelacja u všestukom KLM. Oča kogova. Dvostuk
LEKCIJE IZ OSNOVA STATISTIKE I TEORIJE VJEROJATNOSTI. Ivica Gusić
 LEKCIJE IZ OSNOVA STATISTIKE I TEORIJE VJEROJATNOSTI Ivca Gusć Uvod u matematčku statstku Pojam matematčke statstke. Pojedostavljeo rečeo, matematčka statstka je zastvea dscpla koja z pozavaja određeh
LEKCIJE IZ OSNOVA STATISTIKE I TEORIJE VJEROJATNOSTI Ivca Gusć Uvod u matematčku statstku Pojam matematčke statstke. Pojedostavljeo rečeo, matematčka statstka je zastvea dscpla koja z pozavaja određeh
Moguća i virtuelna pomjeranja
 Dnamka sstema sa vezama Moguća vrtuelna pomjeranja f k ( r 1,..., r N, t) = 0 (k = 1, 2,..., K ) df k dt = r + t = 0 d r = r dt moguća pomjeranja zadovoljavaju uvjet: df k = d r + dt = 0. t δ r = δx +
Dnamka sstema sa vezama Moguća vrtuelna pomjeranja f k ( r 1,..., r N, t) = 0 (k = 1, 2,..., K ) df k dt = r + t = 0 d r = r dt moguća pomjeranja zadovoljavaju uvjet: df k = d r + dt = 0. t δ r = δx +
Riješeni zadaci: Nizovi realnih brojeva
 Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
1. ODREĐIVANJE NETOČNOSTI MJERENJA
 . ODREĐIVANJE NETOČNOSTI MJERENJA. Opće Mjereja razh fzkalh ostalh velča rezultat se e ogu provest apsoluto točo. Usljed tehčkh ekooskh razloga potrebo je etočost jereja svest a ajaju oguću jeru, sa što
. ODREĐIVANJE NETOČNOSTI MJERENJA. Opće Mjereja razh fzkalh ostalh velča rezultat se e ogu provest apsoluto točo. Usljed tehčkh ekooskh razloga potrebo je etočost jereja svest a ajaju oguću jeru, sa što
F (t) F (t) F (t) OGLEDNI PRIMJER SVEUČILIŠTE J.J.STROSSMAYERA U OSIJEKU ZADATAK
 OGLEDNI PRIMJER ZADAAK Odredte dnamčke karakterstke odzv armranobetonskog okvra C-C prkazanog na slc s prpadajućom tlorsnom površnom, na zadanu uzbudu tjekom prve tr sekunde, ako je konstrukcja prje djelovanja
OGLEDNI PRIMJER ZADAAK Odredte dnamčke karakterstke odzv armranobetonskog okvra C-C prkazanog na slc s prpadajućom tlorsnom površnom, na zadanu uzbudu tjekom prve tr sekunde, ako je konstrukcja prje djelovanja
Dimenzioniranje SN/NN kabela i transformatora
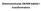 Dmezoraje SN/NN kabela trasformatora Za NN mrežu prkazau slkom potrebo je odredt presjek glavh adzemh trofazh zvoda te moofazh podzvoda obzrom a dozvolje pad apoa kod krajjeg potrošača od 6% dozvoljeu
Dmezoraje SN/NN kabela trasformatora Za NN mrežu prkazau slkom potrebo je odredt presjek glavh adzemh trofazh zvoda te moofazh podzvoda obzrom a dozvolje pad apoa kod krajjeg potrošača od 6% dozvoljeu
OPISNA STATISTIKA GRAFIČKE METODE. Pravila kolokvija PROMJENE RASPOREDA: Dozvoljene formule s weba (M. Grbić) HISTOGRAMI
 PROMJENE RASPOREDA: Kolegij SOM (prvi kolokvij) Opća fizika (predavaje) Numerička matematika Stari termi. ožujka -h. ožujka -h. ožujka -h Novi termi. ožujka -h. ožujka -h. travja - Pravila kolokvija Dozvoljee
PROMJENE RASPOREDA: Kolegij SOM (prvi kolokvij) Opća fizika (predavaje) Numerička matematika Stari termi. ožujka -h. ožujka -h. ožujka -h Novi termi. ožujka -h. ožujka -h. travja - Pravila kolokvija Dozvoljee
KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI. NEUTRALNI ELEMENT GRUPOIDA.
 KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI NEUTRALNI ELEMENT GRUPOIDA 1 Grupoid (G, ) je asocijativa akko važi ( x, y, z G) x (y z) = (x y) z Grupoid (G, ) je komutativa akko važi ( x, y G) x y = y x Asocijativa
KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI NEUTRALNI ELEMENT GRUPOIDA 1 Grupoid (G, ) je asocijativa akko važi ( x, y, z G) x (y z) = (x y) z Grupoid (G, ) je komutativa akko važi ( x, y G) x y = y x Asocijativa
UNIVERZITET U NIŠU FAKULTET ZAŠTITE NA RADU U NIŠU TEHNIČKA MEHANIKA - PREZENTACIJA PREDAVANJA PREDAVANJE
 UNIVERZITET U NIŠU FAKULTET ZAŠTITE NA RADU U NIŠU TEHNIČKA MEHANIKA - PREZENTACIJA PREDAVANJA - - 4. PREDAVANJE - Dr Darko Mhajlov, doc. 1. ČAS Sredšte (cetar) sstema paralelh sla; Težšte krutog tela;
UNIVERZITET U NIŠU FAKULTET ZAŠTITE NA RADU U NIŠU TEHNIČKA MEHANIKA - PREZENTACIJA PREDAVANJA - - 4. PREDAVANJE - Dr Darko Mhajlov, doc. 1. ČAS Sredšte (cetar) sstema paralelh sla; Težšte krutog tela;
Dvanaesti praktikum iz Analize 1
 Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Reverzibilni procesi
 Reverzbln proces Reverzbln proces: proces pr koja sste nkada nje vše od beskonačno ale vrednost udaljen od ravnoteže, beskonačno ala proena spoljašnjh uslova ože vratt sste u blo koju tačku, proena ože
Reverzbln proces Reverzbln proces: proces pr koja sste nkada nje vše od beskonačno ale vrednost udaljen od ravnoteže, beskonačno ala proena spoljašnjh uslova ože vratt sste u blo koju tačku, proena ože
1. Uvod u multivarijatnu statistiku. Prof.dr.sc. N. Bogunović Prof.dr.sc. B. Dalbelo Bašić
 Otkrvaje zaja u skuovma odataka Metoda glavh komoeeta Otkrvaje zaja u skuovma odataka Metoda glavh komoeeta FAKULE ELEKROEHNIKE I RAČUNARSVA Uvod u multvarjatu statstku Profdrs N Boguovć Profdrs B Dalbelo
Otkrvaje zaja u skuovma odataka Metoda glavh komoeeta Otkrvaje zaja u skuovma odataka Metoda glavh komoeeta FAKULE ELEKROEHNIKE I RAČUNARSVA Uvod u multvarjatu statstku Profdrs N Boguovć Profdrs B Dalbelo
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
PRESECI SA PRSLINOM - VELIKI EKSCENTRICITET
 TEORJA ETONSKH KONSTRUKCJA 1 PRESEC SA PRSLNO - VELK EKSCENTRCTET ČSTO SAVJANJE - SLOODNO DENZONSANJE Poznato: Nepoznato: - statčk tcaj za pojedna opterećenja ( ) - sračnato - kvaltet materjala (, σ v
TEORJA ETONSKH KONSTRUKCJA 1 PRESEC SA PRSLNO - VELK EKSCENTRCTET ČSTO SAVJANJE - SLOODNO DENZONSANJE Poznato: Nepoznato: - statčk tcaj za pojedna opterećenja ( ) - sračnato - kvaltet materjala (, σ v
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
 Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
Statistika sažetak i popis formula
 Stattka ažetak pop formula Dekrptva tattka Artmetčka reda brojeva,,, : + + + = + + 3 + 4 + 5 5 Na prmjer, artmetčka reda brojeva,,3,4,5 je broj = = 3 5 5 Frekvecja ekog podatka je broj pojavljvaja tog
Stattka ažetak pop formula Dekrptva tattka Artmetčka reda brojeva,,, : + + + = + + 3 + 4 + 5 5 Na prmjer, artmetčka reda brojeva,,3,4,5 je broj = = 3 5 5 Frekvecja ekog podatka je broj pojavljvaja tog
PROCJENE PARAMETARA POPULACIJE
 PROCJENE PARAMETARA POPULACIJE Iferecijala statistika je skup postupaka kojima se a osovi rezultata iz uzorka doose zaključci o populaciji. INFERENCIJALNA STATISTIKA Procjee parametara Testiraje hipoteza
PROCJENE PARAMETARA POPULACIJE Iferecijala statistika je skup postupaka kojima se a osovi rezultata iz uzorka doose zaključci o populaciji. INFERENCIJALNA STATISTIKA Procjee parametara Testiraje hipoteza
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
Mate Vijuga: Rijeseni zadaci iz matematike za srednju skolu
 7. KOMPLEKSNI BROJEVI 7. Opc pojmov Kompleksn brojev su sastavljen dva djela: Realnog djela (Re) magnarnog djela (Im) Promatrajmo broj a+ b = + 3 Realn do jednak je Re : Imagnarna jednca: = - l = (U elektrotehnc
7. KOMPLEKSNI BROJEVI 7. Opc pojmov Kompleksn brojev su sastavljen dva djela: Realnog djela (Re) magnarnog djela (Im) Promatrajmo broj a+ b = + 3 Realn do jednak je Re : Imagnarna jednca: = - l = (U elektrotehnc
a M a A. Može se pokazati da je supremum (ako postoji) jedinstven pa uvodimo oznaku sup A.
 3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
Ekonometrija 4. Ekonometrija, Osnovne studije. Predavač: Aleksandra Nojković
 Ekonometrja 4 Ekonometrja, Osnovne studje Predavač: Aleksandra Nojkovć Struktura predavanja Nelnearne zavsnost Prmene u ekonomskoj analz Prmer nelnearne zavsnost Isptujemo zavsnost zmeđu potrošnje dohotka.
Ekonometrja 4 Ekonometrja, Osnovne studje Predavač: Aleksandra Nojkovć Struktura predavanja Nelnearne zavsnost Prmene u ekonomskoj analz Prmer nelnearne zavsnost Isptujemo zavsnost zmeđu potrošnje dohotka.
Granične vrednosti realnih nizova
 Graiče vredosti realih izova Fukcija f : N R, gde je N skup prirodih brojeva a R skup realih brojeva, zove se iz realih brojeva ili reala iz. Opšti čla iza f je f(), N, i običo se obeležava sa f, dok se
Graiče vredosti realih izova Fukcija f : N R, gde je N skup prirodih brojeva a R skup realih brojeva, zove se iz realih brojeva ili reala iz. Opšti čla iza f je f(), N, i običo se obeležava sa f, dok se
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
ZBIRKA POTPUNO RIJEŠENIH ZADATAKA
 **** IVANA SRAGA **** 1992.-2011. ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE POTPUNO RIJEŠENI ZADACI PO ŽUTOJ ZBIRCI INTERNA SKRIPTA CENTRA ZA PODUKU α M.I.M.-Sraga - 1992.-2011.
**** IVANA SRAGA **** 1992.-2011. ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE POTPUNO RIJEŠENI ZADACI PO ŽUTOJ ZBIRCI INTERNA SKRIPTA CENTRA ZA PODUKU α M.I.M.-Sraga - 1992.-2011.
Praktikum iz OSNOVA FIZIKE I.
 Praktkum z OSNOVA FIZIKE I. 006./007. Pops vježb:. Pomča mjerka Mkrometarsk vjak Sferometar Vaga. Proučavaje helkodale zavojce Odreñvaje gustoće krutog tjela pomoću damometra 3. Fzkalo jhalo Matematčko
Praktkum z OSNOVA FIZIKE I. 006./007. Pops vježb:. Pomča mjerka Mkrometarsk vjak Sferometar Vaga. Proučavaje helkodale zavojce Odreñvaje gustoće krutog tjela pomoću damometra 3. Fzkalo jhalo Matematčko
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
II. ANALITIČKA GEOMETRIJA PROSTORA
 II. NLITIČK GEMETRIJ RSTR I. I (Točka. Ravia.) d. sc. Mia Rodić Lipaović 9./. Točka u postou ( ; i, j, k ) Kateijev pavokuti koodiati sustav k i j T T (,, ) oložaj točke u postou je jedoačo odeñe jeim
II. NLITIČK GEMETRIJ RSTR I. I (Točka. Ravia.) d. sc. Mia Rodić Lipaović 9./. Točka u postou ( ; i, j, k ) Kateijev pavokuti koodiati sustav k i j T T (,, ) oložaj točke u postou je jedoačo odeñe jeim
4.1. Počeci, razvoj, značaj i definicija statistike
 Glava 4: U V O D U O P Š T U I M A T E M A T I Č K U S T A T I S T I K U 4.. Počec, razvoj, začaj defcja statste Pr zučavaju Teorje vjerovatoće upozal smo se sa em pojmovma oje proučava l a ojma se zasva
Glava 4: U V O D U O P Š T U I M A T E M A T I Č K U S T A T I S T I K U 4.. Počec, razvoj, začaj defcja statste Pr zučavaju Teorje vjerovatoće upozal smo se sa em pojmovma oje proučava l a ojma se zasva
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
Osnove. Uloga algoritama u računarstvu. Algoritmi. Algoritmi kao tehnika
 dr Boba Stojaovć Osove Uloga algortama u račuarstvu Algortm Algortam je strogo defsaa kompjuterska procedura koja uzma vredost l skup vredost, kao ulaz prozvod eku vredost l skup vredost, kao zlaz. Drugm
dr Boba Stojaovć Osove Uloga algortama u račuarstvu Algortm Algortam je strogo defsaa kompjuterska procedura koja uzma vredost l skup vredost, kao ulaz prozvod eku vredost l skup vredost, kao zlaz. Drugm
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Matematička analiza 1 dodatni zadaci
 Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
radni nerecenzirani materijal za predavanja
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Kažemo da je funkcija f : a, b R u točki x 0 a, b postiže lokalni minimum ako postoji okolina O(x 0 ) broja x 0 takva da je
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Kažemo da je funkcija f : a, b R u točki x 0 a, b postiže lokalni minimum ako postoji okolina O(x 0 ) broja x 0 takva da je
Klasični linearni regresioni model (KLRM)
 Profesor Zorca Mladeovć Klasč lear regreso model (KLRM) Zorca Mladeovć Ključe teme Postavka pretpostavke KLRM Svojstva ocea parametara u KLRM Elemet statstčkog zaključvaja u KLRM Predvđaje u KLRM Ekoomsk
Profesor Zorca Mladeovć Klasč lear regreso model (KLRM) Zorca Mladeovć Ključe teme Postavka pretpostavke KLRM Svojstva ocea parametara u KLRM Elemet statstčkog zaključvaja u KLRM Predvđaje u KLRM Ekoomsk
Osnove teorije uzoraka
 Oove teorije uzoraka Oove teorije uzoraka UZORAK: lučaji, reprezetativi dio oovog kupa populacije Uzorci: 1.uzorak:,, 1 1.uzorak:,, i.uzorak:,, i i Razdioba aritmetičke redie uzorka f ( ) f ( ) razdioba
Oove teorije uzoraka Oove teorije uzoraka UZORAK: lučaji, reprezetativi dio oovog kupa populacije Uzorci: 1.uzorak:,, 1 1.uzorak:,, i.uzorak:,, i i Razdioba aritmetičke redie uzorka f ( ) f ( ) razdioba
7 Algebarske jednadžbe
 7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
KRIVULJE RASPODJELE. Doc.dr.sc. Vesna Denić-Jukić
 KRIVULJE RASPODJELE Doc.dr.sc. Vesna Denć-Jukć Krvulje raspodjele predstavljaju zakon vjerojatnost pojave neke hdrološke velčne. Za slučajnu varjablu X kažemo da je poznata ako znamo zakon njene raspodjele.
KRIVULJE RASPODJELE Doc.dr.sc. Vesna Denć-Jukć Krvulje raspodjele predstavljaju zakon vjerojatnost pojave neke hdrološke velčne. Za slučajnu varjablu X kažemo da je poznata ako znamo zakon njene raspodjele.
Procjena parametara. Zadatak 4.1 Neka je X 1, X 2,..., X n slučajni uzorak iz populacije s konačnim očekivanjem µ i varijancom σ 2.
 4 Procjea parametara Neka je X slučaja varijabla čiju distribuciju proučavamo. Defiicija: Slučaji uzorak duljie za X je iz od ezavisih i jedako distribuiraih slučajih varijabli X 1, X,..., X koje imaju
4 Procjea parametara Neka je X slučaja varijabla čiju distribuciju proučavamo. Defiicija: Slučaji uzorak duljie za X je iz od ezavisih i jedako distribuiraih slučajih varijabli X 1, X,..., X koje imaju
TEHNIČKI FAKULTET SVEUČILIŠTA U RIJECI Zavod za elektroenergetiku. Prijelazne pojave. Osnove elektrotehnike II: Prijelazne pojave
 THNIČKI FAKUTT SVUČIIŠTA U IJI Zavod za elekroenergek Sdj: Preddplomsk srčn sdj elekroehnke Kolegj: Osnove elekroehnke II Noselj kolegja: v. pred. mr.sc. Branka Dobraš, dpl. ng. el. Prjelazne pojave Osnove
THNIČKI FAKUTT SVUČIIŠTA U IJI Zavod za elekroenergek Sdj: Preddplomsk srčn sdj elekroehnke Kolegj: Osnove elekroehnke II Noselj kolegja: v. pred. mr.sc. Branka Dobraš, dpl. ng. el. Prjelazne pojave Osnove
Pismeni ispit iz OTPORNOSTI MATERIJALA I - grupa A
 Psmen spt z OTPORNOSTI MATERIJALA I - grupa A 1. Kruta poluga ABC se oslanja pomoću dvje špke BD CE kao na slc desno. Špka BD, dužne 0.5 m, zrađena je od čelka (E AB 10 GPa) ma poprečn presjek od 500 mm.
Psmen spt z OTPORNOSTI MATERIJALA I - grupa A 1. Kruta poluga ABC se oslanja pomoću dvje špke BD CE kao na slc desno. Špka BD, dužne 0.5 m, zrađena je od čelka (E AB 10 GPa) ma poprečn presjek od 500 mm.
radni nerecenzirani materijal za predavanja R(f) = {f(x) x D}
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
nepoznati parametar θ jednak broju θ 0, u oznaci H 0 (θ =θ 0 ), je primer proste hipoteze. Ako hipoteza nije prosta, onda je složena.
 Testiraje parametarskih hipoteza Pretpostavka (hipoteza) o parametru raspodele se zove parametarska hipoteza. Postupak jeog potvrđivaja ili odbacivaja a osovu podataka iz uzorka je parametarski test. t
Testiraje parametarskih hipoteza Pretpostavka (hipoteza) o parametru raspodele se zove parametarska hipoteza. Postupak jeog potvrđivaja ili odbacivaja a osovu podataka iz uzorka je parametarski test. t
ODRŽAVANJE POUZDANOST TEHNIČKIH SUSTAVA
 Ver. 3.0.09. Predmeti astavik: dr. sc. I. Čala, izv. prof. Obrada: dr. sc. /77 S A D R Ž A J. POUZDANOST. ANALIZA POUZDANOSTI ELEMENATA. Začajke pouzdaosti. Fukcije razdioba u teoriji pouzdaosti.3 Simulacija
Ver. 3.0.09. Predmeti astavik: dr. sc. I. Čala, izv. prof. Obrada: dr. sc. /77 S A D R Ž A J. POUZDANOST. ANALIZA POUZDANOSTI ELEMENATA. Začajke pouzdaosti. Fukcije razdioba u teoriji pouzdaosti.3 Simulacija
Korelacijska i regresijska analiza
 Korelacjska regresjska analza Odnos među pojavama Odnos među pojavama može bt: determnstčk l funkconaln stohastčk l statstčk Kod determnstčkoga se odnosa za svaku vrjednost jedne pojave točno zna vrjednost
Korelacjska regresjska analza Odnos među pojavama Odnos među pojavama može bt: determnstčk l funkconaln stohastčk l statstčk Kod determnstčkoga se odnosa za svaku vrjednost jedne pojave točno zna vrjednost
I N Ž E N J E R S K A M A T E M A T I K A 1
 I N Ž E N J E R S K A M A T E M A T I K A Oaj koj cje praksu bez teorjskh osova slča je moreplovcu koj ulaz u brod bez krme busole e zajuć kuda se plov. ( LEONARDO DA VINCI ) P r e d a v a j a z a d r
I N Ž E N J E R S K A M A T E M A T I K A Oaj koj cje praksu bez teorjskh osova slča je moreplovcu koj ulaz u brod bez krme busole e zajuć kuda se plov. ( LEONARDO DA VINCI ) P r e d a v a j a z a d r
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI)
 IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
1.4 Tangenta i normala
 28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Linearna algebra 2 prvi kolokvij,
 Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
VJEROVATNOĆA-POJAM. Definicija vjerovatnoće Σ = f x f. f f. f x f. f f ... = Σ = Σ. i...
 VJEROVATNOĆA-OJAM Defiicija vjerovatoće f f f f f f f m X i i... ) + + + Σ p p p p f f f f f i i i i i i i ) )... ) )... + + + Σ + + Σ + Σ Σ Σ µ µ Aditivo i multiplikativo pravilo. Ako su E i E slučaji
VJEROVATNOĆA-OJAM Defiicija vjerovatoće f f f f f f f m X i i... ) + + + Σ p p p p f f f f f i i i i i i i ) )... ) )... + + + Σ + + Σ + Σ Σ Σ µ µ Aditivo i multiplikativo pravilo. Ako su E i E slučaji
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
10.1. Bit Error Rate Test
 .. Bt Error Rat Tst.. Bt Error Rat Tst Zadata. Izračuat otrba broj rth formacoh bta u BER tstu za,, ogršo dttovaa bta a rjmu, tao da s u sstmu sa brzoom sgalzacj od Mbs mož tvrdt da j vrovatoća grš rosa
.. Bt Error Rat Tst.. Bt Error Rat Tst Zadata. Izračuat otrba broj rth formacoh bta u BER tstu za,, ogršo dttovaa bta a rjmu, tao da s u sstmu sa brzoom sgalzacj od Mbs mož tvrdt da j vrovatoća grš rosa
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Ratomir Paunović i Radovan Omorjan, Tehnološki fakultet u Novom Sadu
 PREDGOVOR Ova kjga predstavlja uvod u statstku amejea je pre svega studetma prmejeh tehčkh auka, kao žejerma. Psal smo je sa cljem da pomogemo zateresovaom čtaocu da razume pravlo korst osove statstčke
PREDGOVOR Ova kjga predstavlja uvod u statstku amejea je pre svega studetma prmejeh tehčkh auka, kao žejerma. Psal smo je sa cljem da pomogemo zateresovaom čtaocu da razume pravlo korst osove statstčke
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE
 **** MLADEN SRAGA **** 011. UNIVERZALNA ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE SKUP REALNIH BROJEVA α Autor: MLADEN SRAGA Grafički urednik: BESPLATNA - WEB-VARIJANTA Tisak: M.I.M.-SRAGA
**** MLADEN SRAGA **** 011. UNIVERZALNA ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE SKUP REALNIH BROJEVA α Autor: MLADEN SRAGA Grafički urednik: BESPLATNA - WEB-VARIJANTA Tisak: M.I.M.-SRAGA
TRIGONOMETRIJSKE FUNKCIJE I I.1.
 TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
Dinamika krutog tijela ( ) Gibanje krutog tijela. Gibanje krutog tijela. Pojmovi: C. Složeno gibanje. A. Translacijsko gibanje krutog tijela. 14.
 Pojmo:. Vektor se F (transacja). oment se (rotacja) Dnamka krutog tjea. do. oment tromost masa. Rad krutog tjea A 5. Knetka energja k 6. oment kona gbanja 7. u momenta kone gbanja momenta se f ( ) Gbanje
Pojmo:. Vektor se F (transacja). oment se (rotacja) Dnamka krutog tjea. do. oment tromost masa. Rad krutog tjea A 5. Knetka energja k 6. oment kona gbanja 7. u momenta kone gbanja momenta se f ( ) Gbanje
Riješeni zadaci: Limes funkcije. Neprekidnost
 Riješeni zadaci: Limes funkcije. Neprekidnost Limes funkcije Neka je 0 [a, b] i f : D R, gdje je D = [a, b] ili D = [a, b] \ { 0 }. Kažemo da je es funkcije f u točki 0 jednak L i pišemo f ) = L, ako za
Riješeni zadaci: Limes funkcije. Neprekidnost Limes funkcije Neka je 0 [a, b] i f : D R, gdje je D = [a, b] ili D = [a, b] \ { 0 }. Kažemo da je es funkcije f u točki 0 jednak L i pišemo f ) = L, ako za
( , 2. kolokvij)
 A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
Jednostavna regresiona analiza
 Profesor Zorca Mladeovć Jedostava regresoa aalza Zorca Mladeovć Struktura predavaja Polaza deja prmer Populacoa uzoračka regresoa prava Metod očh ajmajh kvadrata Korelacja Jedostave eleare zavsost Ekoomsk
Profesor Zorca Mladeovć Jedostava regresoa aalza Zorca Mladeovć Struktura predavaja Polaza deja prmer Populacoa uzoračka regresoa prava Metod očh ajmajh kvadrata Korelacja Jedostave eleare zavsost Ekoomsk
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
METODA SEČICE I REGULA FALSI
 METODA SEČICE I REGULA FALSI Zadatak: Naći ulu fukcije f a itervalu (a,b), odoso aći za koje je f()=0. Rešeje: Prvo, tražimo iterval (a,b) a kome je fukcija eprekida, mootoa i važi: f(a)f(b)
METODA SEČICE I REGULA FALSI Zadatak: Naći ulu fukcije f a itervalu (a,b), odoso aći za koje je f()=0. Rešeje: Prvo, tražimo iterval (a,b) a kome je fukcija eprekida, mootoa i važi: f(a)f(b)
Elektrotehnički fakultet univerziteta u Beogradu 16.maj Odsek za Softversko inžinjerstvo
 Elektrotehnčk fakultet unverzteta u Beogradu 6.maj 8. Odsek za Softversko nžnjerstvo Performanse računarskh sstema Drug kolokvjum Predmetn nastavnk: dr Jelca Protć (35) a) () Posmatra se segment od N uzastonh
Elektrotehnčk fakultet unverzteta u Beogradu 6.maj 8. Odsek za Softversko nžnjerstvo Performanse računarskh sstema Drug kolokvjum Predmetn nastavnk: dr Jelca Protć (35) a) () Posmatra se segment od N uzastonh
Elektrotehnički fakultet univerziteta u Beogradu 26. jun Katedra za Računarsku tehniku i informatiku
 Elektrotehički fakultet uiverziteta u Beogradu 6. ju 008. Katedra za Račuarku tehiku i iformatiku Performae račuarkih itema Rešeja zadataka..videti predavaja.. Kretaje Verovatoća Opi 4 4 Kretaje u itom
Elektrotehički fakultet uiverziteta u Beogradu 6. ju 008. Katedra za Račuarku tehiku i iformatiku Performae račuarkih itema Rešeja zadataka..videti predavaja.. Kretaje Verovatoća Opi 4 4 Kretaje u itom
Linearna algebra 2 prvi kolokvij,
 1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
Parcijalne molarne veličine
 arcale molare velče 2.5.5. Hemsk potecal 2.5.6. 2.5.6.2. arcale molare velče. Ukolko e kolča supstace u sstemu promelva zbog razmee matere zmeđu sstema okole zbog reverzble hemske reakce l reverzble razmee
arcale molare velče 2.5.5. Hemsk potecal 2.5.6. 2.5.6.2. arcale molare velče. Ukolko e kolča supstace u sstemu promelva zbog razmee matere zmeđu sstema okole zbog reverzble hemske reakce l reverzble razmee
Teorijske osnove informatike 1
 Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
transformacija j y i x x promatramo dva koordinatna sustava S i S sa zajedničkim ishodištem z z Homogene funkcije Ortogonalne transformacije
 promatramo dva oordnatna sustava S S sa zaednčm shodštem z z y y x x blo o vetor možemo raspsat u baz, A = A x + Ay + Az = ( A ) + ( A ) + ( A ) (1) sto vred za ednčne vetore sustava S = ( ) + ( ) + (
promatramo dva oordnatna sustava S S sa zaednčm shodštem z z y y x x blo o vetor možemo raspsat u baz, A = A x + Ay + Az = ( A ) + ( A ) + ( A ) (1) sto vred za ednčne vetore sustava S = ( ) + ( ) + (
10 = 1 + = = 1.1. Vježba 001 U banku je danas uloženo kn. Kolika je vrijednost tog uloga na kraju treće godine ako je C C
 Zadatak (Des, ekoomska škola) U baku je daas uložeo k. Kolka je vrjedost tog uloga a kraju ete gode ako je obraču kamata slože, godšj dekurzva? Godšja kamata stoa je. Rješeje Postuak o kojem se kamate
Zadatak (Des, ekoomska škola) U baku je daas uložeo k. Kolka je vrjedost tog uloga a kraju ete gode ako je obraču kamata slože, godšj dekurzva? Godšja kamata stoa je. Rješeje Postuak o kojem se kamate
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Str. 454;139;91.
 Str. 454;39;9 Metod uzorka Predavač: Dr Mirko Savić avicmirko@eccf.u.ac.yu www.eccf.u.ac.yu Statitička maa može da e pomatra a jeda od ledeća dva ačia: potpuo pomatraje, delimičo pomatraje (metod uzorka).
Str. 454;39;9 Metod uzorka Predavač: Dr Mirko Savić avicmirko@eccf.u.ac.yu www.eccf.u.ac.yu Statitička maa može da e pomatra a jeda od ledeća dva ačia: potpuo pomatraje, delimičo pomatraje (metod uzorka).
4. Perspektiviteti i perspektivne figure. Desarguesov teorem
 4 Persektvtet ersektvne fgure Desarguesov teorem Promatrajmo rojektvnu ravnnu kao oeratvn rostor u njoj nz točaka ramen ravaca ( ) s vrhom, r čemu točka ne lež na ravcu ( ) na nosocu Jednoznačno obostrano
4 Persektvtet ersektvne fgure Desarguesov teorem Promatrajmo rojektvnu ravnnu kao oeratvn rostor u njoj nz točaka ramen ravaca ( ) s vrhom, r čemu točka ne lež na ravcu ( ) na nosocu Jednoznačno obostrano
3. razred gimnazije- opšti i prirodno-matematički smer ALKENI. Aciklični nezasićeni ugljovodonici koji imaju jednu dvostruku vezu.
 ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
(P.I.) PRETPOSTAVKA INDUKCIJE - pretpostavimo da tvrdnja vrijedi za n = k.
 1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
Glava 5 Z-TRANSFORMACIJA I NJENE PRIMJENE U ANALIZI DISKRETNIH LTI ISTEMA
 Glava 5 Z-TRANSFORMACIJA I NJENE PRIMJENE U ANALIZI DISKRETNIH LTI ISTEMA Trasformacoe tehke su moća alat a aalu sgala LTI sstema. U ovoj glav ćemo uvest -trasformacju, opsat jee osobe mogućost prmjee
Glava 5 Z-TRANSFORMACIJA I NJENE PRIMJENE U ANALIZI DISKRETNIH LTI ISTEMA Trasformacoe tehke su moća alat a aalu sgala LTI sstema. U ovoj glav ćemo uvest -trasformacju, opsat jee osobe mogućost prmjee
PRIMJERI RJEŠENIH ZADATAKA IZ STATISTIKE
 PRIMJERI RJEŠENIH ZADATAKA IZ STATISTIKE Obuhvaćene cjelne su: Srednje vrjednost (, Me, Mo ) Mjere dsperzje ( δ², δ, Q, Q, Iq, Vq, V ) Standardzrano oblježje ( z ) Mjere asmetrje zaobljenost ( α α 4 )
PRIMJERI RJEŠENIH ZADATAKA IZ STATISTIKE Obuhvaćene cjelne su: Srednje vrjednost (, Me, Mo ) Mjere dsperzje ( δ², δ, Q, Q, Iq, Vq, V ) Standardzrano oblježje ( z ) Mjere asmetrje zaobljenost ( α α 4 )
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
