Univerzita Karlova v Praze
|
|
|
- Φιλομήνα Κλυμένη Αθανασιάδης
- 9 χρόνια πριν
- Προβολές:
Transcript
1 Univerzita Karlova v Praze Přírodovědecká fakulta Katedra fyzikální a makromolekulární chemie Aplikace explicitně korelovaných multireferenčních metod spražených klastrů Aplication of explicitly correlated multi-reference coupled cluster methods Diplomová práca Bc. Jakub Lang Vedoucí práce: Mgr. Jiří Pittner Dr. rer. nat., DSc. Praha 2014
2
3 Prohlášení Prohlašuji, že jsem záverečnou práci zpracoval samostatně a že jsem uvedl všechny použité informační zdroje a literaturu. Tato práce ani její podstatná čast nebyla předložena k získaní jiného nebo stejného akademického titulu. V Praze, Jakub Lang
4
5 Abstrakt Metody Coupled cluster patří v současnosti mezi standardní kvantově-chemické metody. Tyhle metody však nejsou schopny kvalitativně popsat systémy s kvazidegenerovanými orbitaly, kde je jednorefereční přístup klasických coupled cluster metod nedostatečný. Tyhle systémy se vyznačují příspěvky statické korelace, na popis které je potřeba využít multireferenční přístup. Multireferenční coupled cluster metody vyvinuté v naší skupině jsou schopny popsat jak statickou, tak i dynamickou korelaci a dovolují tak počítat dřív problematické systémy. Ve spojení s explicitní korelací, která je schopna zlepšit popis elektronického cuspu, je možné dosáhnout vynikající výsledky zkonvergované do úplné báze a s méně nasycenými bázemi. Takhle urychlená konvergence je následně uplatněna ve výpočtu doposud výpočetně náročných systémů. V téhle práci jsou prezentovány multireferenční coupled cluster výpočty tranzitních stavů izomerizace bicyklobutánu a explicitně korelované výpočty molekuly tetrametylénetánu. 5
6
7 Abstract Nowdays, coupled cluster method belongs to one of the most used quantum chemical methods. However, the single-reference coupled cluster methods are not able to describe systems where the static correlation have an important role. Multireference coupled cluster methods developed in our group can describe both static and dynamic correlation and can be used for problematic systems. Together with explicitly correlated wavefunction, which can properly describe the electronic cusp and speed up the convergence to the complete basis set limit, they are able to calculate computationally demanding diradicals. Multireference CC calculations of tetramethylenethane have been perforemd and the performance of explicitly correlated version is discussed. Calculations of the isomerization of bicyclobutane using the multireference approach are presented as well. 7
8
9 Pod akovanie Týmto by som rád pod akoval svojmu školitel ovi za vedenie pri príprave tohto textu, samotných výpočtov, trpezlivosti s mojou osobou a zároveň možnosti podiel at sa tomto výskume. Kolegom Dr. Liborovi Veisovi, Dr. Jiřími Brabcovi, Dr. Ondřejovi Demelovi a Dr. Michalovi Taranovi z Ústavu Fyzikální chemie J. Heyrovského AV ČR. Taktiež by som chcel pod akovat samotnému vedeniu ústavu, ktoré mi dovolilo využit výpočtových clustrov na jej pôde. Samotný výskum bol podporený grantom z GAČR (č. p. 208/11/2222). 9
10
11 Obsah 1 Úvod 17 2 Elektrónová korelácia Dynamická a statická korelácia R12 metódy História R12 metód Korelačný faktor Projekčný operátor Viacelektrónové integrály Coupled Cluster metódy Úvod do CC metód CCSD(T) metóda Normálne usporiadaný Hamiltonián CCSD energia a amplitúdy T korekcie Multirefenčné Coupled Cluster metódy Klasické multireferenčné metódy MRCC R12 prístup Izomerizácia bicyklo[1.1.0]butánu Bicyklo[1.1.0]bután
12 12 Obsah 5.2 Výpočtové detaily Výsledky a diskusia Zhrnutie Explicitne korelované výpočty Tetrametylénetán Výpočtové detaily Výsledky a diskusia Zhrnutie Záver 72
13 Zoznam obrázkov 1.1 Diagram rozdelenia energie Problematika presného riešenia Schrödingerovej rovnice Vlnová funkcia atómu hélia s jedným fixovaným elektrónom Disociácia molekuly H Porovnanie R12 a F12 kor. faktoru Efekt parametru γ na bázu Diagram integrálu Ψ 0 ˆF N ˆT1 Ψ CCSD apmlitúdové rovnice Obsadené molekulové orbitály Neobsadené molekulové orbitály Optimalizované geometrie reaktantu a produktu Optimalizované geometrie tranzitných stavov PES izomerizácie bicbut tbut MRCC PES izomerizácie bicbut tbut Korelácia energetického rozdielu medzi dists a conts Relatívne energie vôči reaktantu D 2 geometria tetrametylénetánu optimalizovaná na úrovni MP2/6-31G HOMO-LUMO orbitály molekuly TME
14 14 Zoznam obrázkov 6.3 Konvergencia k CBS
15 Zoznam tabuliek 3.1 Závislost parametru γ na náboji jadra Výpočtová náročnost jednotlivých CC aproximácií Najdôležitejšie determinanty pre conts Najdôležitejšie determinanty pre dists Entalpie conts pri 0 K Relatívne energie (kcal/mol) voči bicyklobutánu Absolútne energie TME(E h ) pre MRCC-F Absolútne energie TME(E h ) pre klas. MRCC CBS limita TME(E h ) pre MRCC-F
16
17 Kapitola 1 Úvod L udstvo sa už od nepamäti snaží nájst nástroje, ako vysvetlit experimenty v rôznych vedeckých oboroch a ako tieto zistenia následne využit. Tieto teoretické metódy umožňujú skúmat mechanizmy, ktoré nie sú pozorovatel né experimentálne. V tomto zmysle výpočtová chémia umožňuje vysvetlit alebo predpovedat skutočnosti pozorované v chemických reakciách. Kvantová chémia si kladie za úlohu popísat svet na úrovni elektrónových a molekulárnych štruktúr. Už od jej začiatku sa jej to darilo vel mi dobre. 1 Dokázala spočítat vlastnosti a štruktúru jednoduchých systémov ako atóm vodíka, hélia a d alších jednoduchších molekúl. V súčastnosti je však potrebné popísat ovel a väčšie systémy. Či už sú to lieky, ktoré reagujú v našom tele, vznik molekúl v medzihviezdnych hmlovinách, ktoré by mohli raz viest k vzniku života podobného nášmu alebo aj samotné bielkoviny tvoriace naše telá. Tieto tradičné metódy začínajú zlyhávat s vzrastajúcim počtom valenčných elektrónov, respektíve v systémoch, kde korelačná energia hrá dôležitú úlohu. Nanešt astie metódy s ktorými prišla kvantová chémia na začiatku jej existencie už nie sú dostačujúce a je potreba príst na nové a lepšie. Na rad prichádzajú metódy ako konfiguračná interakcia (CI), Density Functional Theory (DFT), coupled cluster (CC) a iné. Tieto metódy umožňujú úspešne popísat vlastnosti zložitejších molekúl, ako napríklad F 2, CH 4, CO 3 a d alšie. 17
18 18 Kapitola 1. Úvod Jednou z najpoužívanejších metód je metóda CCSD(T) a považovaná za takzvanú gold standard. Avšak aj táto metóda prichádza na pokraj svojej použitel nosti a nie je ju možné použit na výpočet niektorých systémov ako sú napríklad diradikály alebo i zdanlivo triviálny popis disociácie väzieb, v takýchto je tradičný popis systému pomocou jednej referenčnej vlnovej funkcie nedostačujúci. Nie len pre výpočet týchto molekúl boli navrhnuté multireferenčné metódy, ktoré sa dokážu s podobnými t ažkost ami vysporiadat. Tieto metódy sú však už výpočtovo náročnejšie a dostávajú sa do kolízie s Moorovým zákonom, ked sú súčasné počítače už príliš pomalé. Full CI metóda je napríklad schopná získat až 100% korelačnej energie. Toto je však uskutočnitel né len pre malé systémy a to z toho dôvodu, že matice potrebné na výpočet nadobúdajú obrovské rozmery s tým ako vzrastá počet potrebných determinantov popisujúcich daný systém. Z tohto dôvodu vznikajú zlepšenia, ktoré sa snažia zrýchlit tieto výpočty či už na úrovni implementácií (Optimized Virtual Orbital Space b, Frozen Natural Orbitals) alebo nadstavby nad metódami, ktoré nám pomáhajú popísat systém s menšími bázami c ako sú práve explicitne korelované metódy. V rámci tejto diplomovej práce boli získané korelačné energie pre niekol ko systémov. Ako prvé boli spočítané tranzitné stavy vznikajúce pri izomerizácii bicyklobutánu. Výsledným produktom je trans-buta-1,3-dién, ktorý je v súčastnosti využívaný hlavne v gumárenskom priemysle alebo ako kopolymér v rôznych polyméroch. Samotná izomerizácia je zaujímavá tým, že môže prebiehat niekol kými mechanizmami a to konrotačným alebo disrotačným. V prípade konrotačného stavu bolo publikovaných niekol ko štúdií popisujúcich tento stav a jeho aka Coupled Clusters Singles Doubles with T correction b Implementácia tejto metódy v programe ACES II bola predmetom mojej bakalárskej práce c Väčšina kvantovo chemických výpočtov je založená na popise vlnovej funkcie pomocou lineárnej kombinácii iných funkcii vid. d alej.
19 19 tivačnú bariéru vo vynikajúcej zhode s experimentmi. Avšak pre disrotačný stav neboli až do nedávna príliš presné výsledky, kedže tento stav vykazuje silné diradikálne vlastnosti. 2 V práci sú prezentované prvé výsledky získané pomocou Brillouin-Wignerovej 3 6 a Mukherjeeho coupled cluster metódy, 7, 8 ktoré boli vyvinuté práve ako metódy schopné popísat diradikály a systémy s kvázidegenerovanými orbitálmi, kedy je potreba popísat systém pomocou viacerých referenčných vlnových funkcií. Obe metódy patria medzi multireferenčné State-specific coupled cluster metódy, 9 ktoré sa ukazujú ako vhodný nástupcovia klasických coupled cluster. Samotné metódy dokázali popísat konrotačný stav vo vel mi dobrej zhode s experimentom a pre disrotačný stav dosiahli podobne dobré výsledky. Výsledky získané pomocou týchto multireferenčných metód sú prezentované v kapitole 5. Ďalším počítaným systémom je molekula tetrametylénetánu. Tetrametylénetán patrí do skupiny takzvaných disjunktných diradikálov a je zaujímavý tým, že jeho orbitály sú skoro degenerované a donedávna nebolo isté či je základný stav tejto molekuly singlet alebo triplet. Práve preto nebolo do súčastnosti možné teoreticky predpovedat správne molekulárne spektrá, chemickú reaktivitu a iné vlastnosti. Z tohto dôvodu sa javia multireferenčné metódy ako potencionálne vhodný nástroj pre popis elektrónovej štruktúry a energie tetrametylénetánu. Čo dokazujú aj výsledky publikované v nedávnych rokoch, ktoré využili mutltireferečných coupled cluster metód a ukazujú, že multiplicita základného stavu je singlet. Aj vzhl adom k týmto publikáciám boli multireferenčné výpočty na tejto molekule spočítané pre singletový stav 10 s použitím explicitnej korelácie, ktorá je schopná urýchlit konvergenciu k úplnej báze. A tak aj napriek komplexnosti tohto systému, ktorá zabraňuje použitiu dostatočne nasýtených bází, je možné spočítat tento systém vel mi presne. V kapitole 7 sú následne zhrnuté výsledky a diskutované dôsledky týchto výpočtov. V prvých štyroch kapitolách sú priblížené teoretické základy metód, použitých pri získaní potrebných výsledkov. Po-
20 20 Kapitola 1. Úvod sledná kapitola následne pozostáva z dodatku o druhom kvantovaní s jeho detailnejším popisom. Popis pohybu viacerých elektrónov predstavuje jeden z najväčších problémov v oblasti problematiky popisu molekúl v rámci kvantovej chémie a to navzdory tomu, že máme k dispozícii Schrödingerovu rovnicu), ktorá popisuje všetky častice systému a. V súčastnosti sme schopný vyriešit časovo nezávislú Schrödingerovu rovnicu (1.1) pre jeden elektrón v poli nepohybujúcich sa kladne nabitých častíc(jadier). 1 Ĥ ψ = E ψ (1.1) Na výpočet zložitejších a väčších systémov je potreba využit rôznych aproximácii. Jedním zo základných riešení je použitie aproximácie vlnovej funkcie ψ pomocou súčinu vlnových funkcií neinteragujúcich častic, takzvaný Hartreeho produkt. Ψ = φ 1 (1)φ 2 (2)φ 3 (3)... φ n (n), (1.2) kde je funkcia φ i (j) nazývaná spinorbitálom a je konštruovaná ako súčin priestorovej a spinovej vlnovej funkcie ψ i (r j ), χ i (r j ) respektívne. φ i (j) = ψ i (r j )χ i (r j ) (1.3) Spinová funkcia môže v tomto prípade nadobúdat hodnoty α a β v závislosti na z-tovej zložke momentu hybnosti danej častice, v tomto prípade elektrónu. Táto funkcia (1.2) však nie je schopná splnit Fermiho podmienku nerozlíšitel nosti častíc b a Schrödingeorva rovnica nezahrňuje relativistické efekty elektrónov pohybujúcich sa rýchlost ami blízkymi rýchlosti svetla ako sú napríklad elektróny v t ažších prvkoch. Tieto efekty zahrnul až Paul Dirac do rozšírenej rovnice nesúcej jeho meno tzv. Diracovej rovnice b prípad pre dva fermióny
21 21 φ 1 (1)φ 2 (2) = ±φ 1 (2)φ 2 (1), (1.4) čo je vidno na tom ak vo vlnovej funkcii (1.2) permutujeme dve častice medzi sebou. Ako riešenie sa ukazuje vlnová funkcia v tvare tzv. Slaterova determinantu (1.5) 11, 12 φ 1 (rx 1 ) φ 2 (x 1 ) φ N (x 1 ) Ψ = 1 φ 1 (x 2 ) φ 2 (x 2 ) φ N (x 2 ) N! (1.5). φ 1 (x N ) φ 2 (x N ) φ N (x N ) Takto upravená vlnová funkcia už aproximáciou pre skutočnú vlnovú funkciu spĺňa Fermiho podmienku a je dobrou Vd aka takto upravenej vlnovej funkcii a za použitia metódy LCAO(Linear Combination of Atomic Orbitals) sme následne schopní kvalitatívne popísat elektrónovú štruktúru molekúl. Táto metóda dostala meno po svojich objavitel och a nazýva sa Hartree-Fockova metoda (HF). Nanešt astie Hartree Fockova metóda nedokáže správne popísat elektrónovú koreláciu, práve z dôvodu užitia vlnovej funkcie v súčinom tvare a. Energia, ktorá je rovná rozdielu skutočnej energie odpovedajúcej presnému riešeniu Schrödingerovej rovnice a energie získanej z HF metódy sa nazýva energia korelačná a zodpovedá chýbajúcemu popisu chovania elektrónov v systéme. 13 E corr = E 0 E HF (1.6) a Pri použití vlnovej funkcie ako súčinu jednočasticových vlnových funkcií dochádza k strate informácie o vzájomnej korelácii častíc a a tie sa medzi sebou necítia, teda jednotlivé častice sa tak pohybujú v priemernom elektrickom poli ostatných častíc
22 22 Kapitola 1. Úvod Obr. 1.1: Diagram rozdelenia energie Diagram rozdelenia energie na základe jednotlivých výpočtov. Horná čiara predstavuje energetické minimum, ktoré je schopná dosiahnut HF metóda, d alej pokračujú post-hf metódy, full CI a relativistické energie. Nakoniec sa dostávame na presnú energiu systému. Na získanie tejto chybajúcej energie bolo navrhnutých niekol ko teórií a na nich postavených výpočtových metód. Medzi najvýznamnejšie patria metódy ako sú napríklad už spomínaná konfiguračná interakcia, 14, 15 poruchová teória a metóda coupled cluster, 16 ktoré sa v súčastnosti stali štandardnými metódami v kvantovej chémii. Jednou z najpoužívanejších sa stala metóda CC, ktorá má najväčšiu šancu na systematické zlepšovanie presnosti v podobe zväčšovania úrovne exitácií v excitačnom operátore. Toto zodpovedá konvencii v menovaní jednotlivých aproximácii CCD, CCSD, CCSD(T), CCSDT, CCSDTQ 17, 18 až po úplné zahrnutie všetkých možných excitácií, kde je CC metóda ekvivalentná full CI. Ďalší problém sa dotýka všetkých teórií založených na teórii molekulových orbitálov (MO) a to je neúplnost použitej báze, ktorá by v ideálnom prípade mala byt nekonečne vel ká.
23 23 Obr. 1.2: Problematika presného riešenia Schrödingerovej rovnice. So zlepšujúcou sa presnost ou aproximatívneho modelu sa približujeme k presnému riešeniu (osa x) avšak taktiež je potrebné spresňovat popis vlnovej funkcie pomocou bázových funkcii tz. zvýšit počet bázových funkcií. Problém neúplnej báze je v súčastnosti možné riešit niekol kými spôsobmi, medzi ne patrí extrapolácia do úplnej báze (CBS) a alebo zavedenie korelácie závislej na vzdialenosti medzi elektrónmi priamo do rozvoja vlnovej funkcie. Ako výhodnejšie riešenie z vyššie uvedených sa ukazuje explicitná korelácia, ktorá je schopná zlepšit popis molekuly cez vlnovú funkciu na rozdiel od CBS metódy, ktorá získa len energiu systému. Základom CBS metódy je aproximatívne určenie energie s nekonečne vel kou bázou. Táto báza je v princípe schopná získat presnú energiu pre danú výpočtovú metódu. Túto bázu avšak nie je možné z pochopitel ných dôvodov použit a preto boli navrhnuté extrapolačné schémy, ktoré sú schopné získat približnú energiu pre túto nekonečnú bázu. Tieto extrapolácie využívajú báz a Complete Basis Set
24 24 Kapitola 1. Úvod ako sú napríklad Dunningsove korelačne konzistenté báze cc-pvxz, 19 kde X je kardinálne číslo báze, ktoré so zvyšujúcim X zlepšuje schopnost báze získat korelačnú energiu. Extrapolácie do CBS následne extrapolujú energiu pre CBS pomocou energií získaných z cc-pvxz výpočtov a to podl a vzt ahu pre extrapoláciu HF energie a E SCF x = CBS SCF + Ae Bx, (1.7) pre získanie korelačnej energie E corr x = CBS corr + Ax 3, (1.8) Hlavným ciel om tejto práce je ukázat účinnost explicitne korelovaných metód, implementovaných do multireferenčných coupled cluster metód na popis energií systémoch kvázidegenerovaných diradikálov a jej porovnanie s klasickými metódami.
25 Kapitola 2 Elektrónová korelácia 2.1 Dynamická a statická korelácia Základom aplikácií explicitne korelovaných metód je zlepšenie popisu chovania elektrónov vel mi blízko seba, kde dochádza k vzniku takzvanej cusp singularity. Tento cusp vzniká ako dôsledok divergencie Coulombického členu Hamiltionánu 1/r, avšak lokálna energia systému, definovaná ako E lok (r) = Ĥψ(r) ψ(r) (2.1) sa v celom priestore nemení a to v prípade ak ψ zodpovedá presnej vlnovej funkcii. Coulombická interakcia teda musí byt vyrovnaná zvyšným členom Hamiltionánu, teda kinetickým členom ˆT = 2 2m 2. Ako dôsledok musí vlnová funkcia splnit Katovu podmienku (2.2) pre dva elektróny s opačnými spinmi a pre jadro-elektrón. 23 ( ( ) ψ(r ij ) r ij ψ(r ij ) r ij ) r ij 0 r ij 0 = 1 2 ψ(r ij = 0) = Zψ(r ij = 0) (2.2) Aproximatívne funkcie založené na metóde MO LCAO nedokážu túto podmienku splnit, čo spôsobuje divergenciu v okolí potencionálnej kolízie dvoch 25
26 26 Kapitola 2. Elektrónová korelácia elektrónov. Kedže tento región je vel mi malý, celková energia nie je podstatne ovplyvnená touto divergenciou a energiu systému je možne vel mi presne opísat pomocou jedno-elektrónových funkcií. Nanešt astie tento cusp silne ovplyvňuje konvergenciu vlnových funkcií minimalizovaných vo variačných výpočtoch využívajúcich hladkých funkcií (napr. Gaussovské funkcie). Toto ukazuje sa ako vel ký problém pri počítaní náročných výpočtov (väčšie báze). Ako jedno z riešení sa ukazuje zahrnutie lineárneho členu zodpovedajúcemu vzájomnej vzdialenosti elektrónov podl a rovnice. ( ψ(r i, r j ) = ψ(r ij = 0) ) 2 r ij +... (2.3) Tohto využil Hylleraas vo svojej vlnovej funkcii, využívajúc lineárneho člena popisujúceho vzájomnú vzdialenost elektrónov na výpočet atómu hélia (2.4) Ψ Hylleraas = e αs klm c klm s k t 2l u m, (2.4) kde zvolil súradnicový systém definovaný ako s = r 1 + r 2, t = r 1 r 2 a u = r 12. Pomocou tejto funkcie bol Hylleraas schopný popísat energiu atómu hélia s presnost ou na 0.01eV. Na obrázku 2.1 v časti (a) je vykreslený rozdiel medzi Hylleraaasovovou funkciou (2.4) a Hartree-Fockovskou funkciou. V časti (b) je vykreslený rozdiel pre geminálnu funkciu s explicitným riešením pre vzájomnú vzdialenost oboch elektrónov. A ako je možné vidiet na obrázku v časti (c) je rozdiel medzi častami (a) a (b) je minimálny a geminálne funkcie dokážu správne popísat elektronický cusp. Na prácach Hylleraasa pokračovali James a Coolidge, 27 neskôr Kolos s Wolniewiczom, 28, 29 ktorým sa podarilo vel mi presne popísat molekulu vodíku a, ale pri pokusoch o aplikácie na väčšie systémy sa potýkali s problémami príliš zložitých integrálov. a so započítanými relativistickými príspevkami
27 2.1. Dynamická a statická korelácia 27 Obr. 2.1: Vlnová funkcia atómu hélia s jedným fixovaným elektrónom. Čast (a) rozdiel medzi Hylleraasovou a Hartree Fockovskou vlnovou funkciou.v časti (b) graf zodpovedá F12 geminálnej funkcii s faktorom 1 a 0 a (c) zodpovedá ich vzájomnému rozdielu. Zdroj [27] Hylleraasove funkcie a ich rozšírenia od Jamesa, Coolidga a Kolosa, Wolniewicza predstavujú ideálne nástroje pre popis korelačného cuspu a pre jednoduché systémy boli úspešne aplikované (Obr. 2.1). So vzrastajúcou zložitost ou systému dochádza prílišnému skomplikovaniu integrálov, ktoré už nie je možné riešit analyticky. Jedným z riešení sa ukazuje návrat ku tradičným gaussovským funkciám v tvare (2.5), pre ktoré boli už v 60-tych rokoch boli navrhnuté analytické riešenia pre ich súčiny a derivácie30, 31 G α,r ijk (r) = N α ijk (x R x) i (y R y ) j (z R z ) k e α(r R)2. (2.5) Na základe týchto funkcií boli následne navrhnuté takzvané exponencionálne korelované gaussiany (ECG) v tvare G α,r ijk (r) = N α ijk (x R x) i (y R y ) j (z R z ) k e α r R 2 m γ m r r m 2, (2.6) ktoré tvoria výsledné bázové funkcie. Počas minulého storočia sa ukázalo, že teória ECG dokáže zreprodukovat skvelé výsledky pre cusp. Nanešt astie
28 28 Kapitola 2. Elektrónová korelácia je táto metóda príliš časovo náročná a to z toho dôvodu, že je potrebné optimalizovat n bas (3N +N(N + 1)/2) nelineárnych členov, kde n bas je počet bázových funkcií a N je počet elektrónov v systéme. 32, 36, 37 Iným spôsobom ako sa vysporiadat s explicitnou koreláciou sú transkorelované metódy, ktoré využívajú podobne transformovaného Hamiltionánu38, 39 H = e ĈĤeĈ, (2.7) kde Ĉ = ij r 12. (2.8) Takto transformovaný Hamiltionán je nazývaný transkorelovaný ale vd aka tejto transformácii sa stáva nehermitovským, čo značne obmedzuje jeho využitie. Použitie tejto metódy spolu s Hausdorffovým rozvojom a však zaručuje, že vo výsledných rovniciach vystupujú nanajvýš troj-elektrónové integrály. V súčastnosti sa využíva hlavne v kvantových Monte Carlo metódach (QMC) Statická korelácia Ďalším problémom popisu elektrónovej korelácie je takzvaná statická korelácia, ktorá nie je spojená s Coulombickou dierou ale s nedostatočným popisom systému pomocou jednodeterminantnej vlnovej funkcie. Táto korelácia má na rozdiel od dynamickej (Coulombickej) d alekosiahlu povahu a je závislá na miešaní niekol kých vlnových funkcií popisujúcich daný systém. Sú to systémy, kde hrá dominantnú úlohu viac ako jedna jednodeterminantná vlnová funkcia. V rámci Hartree-Fockovskej metódy je možné získat čast statickej korelácie pri použití tzv. Unrestricted Hartree-Fock metódy (UHF) ako je vidiet na obrázku 2.2. Vlnová funkcia v RHF prípade pre molekulu a Campbell-Baker-Hausdorffova formula e ˆB Âe ˆB = Â + [Â, ˆB] + 1 2! [[Â, ˆB], ˆB] + 1 3! [[[Â, ˆB], ˆB], ˆB] +...
29 2.1. Dynamická a statická korelácia 29 Obr. 2.2: Disociácia molekuly H 2. Neprerušovaná čiara zodpovedá energii získanej z Restricted Hartree-Fockovej metódy a pri väčšom oddialení jadier preceňuje väzbovú energiu molekuly z dôvodu prítomnosti iónového príspevku vo vlnovej funkcii. Prerušovaná čiara následne reprezentuje UHF riešenie ktoré popisuje disociáciu vodíka ovel a presnejšie. 43 vodíka je definovaná ako ψ = Âσ(α) (1)σ (β) (2), (2.9) kde σ (α) = 1 2 (1s α A + 1sβ B ) a 1sα A respektíve 1sβ B zodpovedajú orbitálom centrovaným na jednotlivé jadrá. Dosadením σ α a σ β do rovnice 2.7 dostaneme rovnicu 2.8, kde je zrejmé, že RHF vlnová funkcia pozostáva z kovalentnej a iónovej časti, kde oba elektróny populujú jedno z jadier čo zodpovedá ne-fyzikálnej podstate disociácie molekuly vodíku. ( ψ = 1 2Â 1s α A1s β B + 1sα B1s β A + 1s α } {{ } A1s β A + 1sα B1s β B } {{ } kovalentný člen iónový člen ) (2.10) Narozdiel od RHF metódy UHF metóda poskytuje správny popis disociácie a to z toho dôvodu, že jednotlivé spinorbitály majú svoje vlastné priestorové funkcie. UHF metóda nanešt astie trpí takzvanou spinovou kontamináciou, kedy výsledná vlnová funkcia nie je vlastnou funkciou operátoru
30 30 Kapitola 2. Elektrónová korelácia spinu Ŝ2. Toto spôsobuje problém ak chceme využit UHF vlnovú funkciu v pokročilejších metódach (CC, MBPT,...). Ďalším spôsobom ako popísat statickú koreláciu je zahrnút do vlnovej funkcie viaceré referencie tz. viacero Slaterových determinantov a, čo je základom pre multireferenčné metódy ako sú MRCI, MRCC at d. a Napríklad dve referencie popisujúce obsadenie dvoch skoro degenerovaných orbitálov.
31 Kapitola 3 R12 metódy 3.1 História R12 metód Jednými z prvých pionierov explicitne korelovaných výpočtov boli Kuztelnigg a Klopper, 44 ktorí však prišli s odlišným prístupom ako priamym započítaním explicitnej korelácie v rozvoji bázových funkcií a túto metódu nazvali R12 metóda. Ich teória bola založená na konfiguračne interakčnom rozvoji vlnovej funkcie. Tento postup najprv aplikovali na Møller Plessetovu MP2 metódu, kde využili vlnovej funkcie v tvare Ψ = ˆR Φ + Ψ CI, (3.1) kde ˆR je operátor zahrňujúci explicitnú koreláciu častíc. Využili taktiež faktu, že príspevok k druhému rádu energie získaný z MP2 metódy je možné rozložit do súčtu párových príspevkov a. Párova funkcia potom získava tvar45, 46 u ij = v ij + w ij, (3.2) kde v ij = kl c kl ij ˆQ 12 f 12 kl (3.3) a Platí to len v prípade ak sú párové funkcie navzájom ortogonálne k priestoru obsadených orbitálov. 31
32 32 Kapitola 3. R12 metódy a w ij = ab t ab ij ab. (3.4) Operátor ˆQ 12 je projekčný operátor zaručujúci silnú ortogonalitu, f 12 je korelačný faktor. Tento faktor je zväčša rovný r 12 vtedy je metóda nazývaná R12 takto zvolený faktor bol používaný ako jeden z prvých, avšak v súčastnosti sú v užívaní aj iné faktory ako napríklad exponenciála potom sa jedná o novšie metódu ako napríklad F12. Výsledná energia systému môže byt následne získaná minimalizáciou Hylleraasovho funkcionálu H(u ij ). H(u ij ) u ij ˆF 1 + ˆF 2 ɛ i ɛ j u ij + 2 u ij r 1 ij u ij > ɛ 2 ij (3.5) Dosadením explicitne korelovanej funkcie 2.8 do 2.11 dostávame rovnice v ktorých vystupujú 3 až 4 elektrónové integrály ako sú ij r 12 Ô 1 r 1 12 ij = ijk r 12r 1 13 kji ij r 12 Ô 1 ˆK1 r 1 12 ij = ijkl r 12r 1 14 r 34 lkji (3.6) tie sú však výpočtovo príliš nákladné a je potreba d alšej aproximácie navzdory tomu, že takto definovaná MP2 metóda konverguje vel mi rýchlo. MP2 rovnice je možné následne rozdelit na klasickú čast a R12 korekciu, toto umožňuje implementáciu R12 kódov do už momentálne implementovaných podprogramov. Súčasné implementácie MP2-R12/F12 metód využívajú najmä rezolúcie jednotky(ri) ako náhrady viac centrických integrálov pre následné zrýchlenie výpočtov. 47, Korelačný faktor Väčšina povôdných prác na R12 metódach bola založená na korelačnom faktore v lineárnom tvare f(r 12 ) = r 12 (3.7)
33 3.2. Korelačný faktor 33 Takto zvolený faktor popisuje korelačný cusp (2.2) a jeho lineárnu povahu vlnovej funkcie v tomto okolí vel mi dobre. Avšak prináša sebou problém viac centrických integrálov ako sú troj až štvor-elektronové integrály, ktoré nie je možné vyjadrit v analytickom tvare. Taktiež nedokáže adekvátne popísat elektrónovú koreláciu vo väčšej vzdialenosti od cuspu, kde explicitný člen neklesá dostatočne rýchlo (viz. obrázok 3.1). V roku 1996 prišli Persson a Obr. 3.1: Porovnanie R12 a F12 kor. faktoru Porovnanie R12 a F12 korelačných faktorov (c = 0.49,γ = 0.81a 0 1 s optimalizovaným faktorom pre singletový stav hélia 9 Taylor s nápadom aproximovat chovanie lineárneho člena pomocou rozvoja geminálnych gaussiánov. 55, 56 Ψ = e [ α(r 1+r 2 )] ( c 0 + v c v e ( γvr2 12 )) (3.8) Spolu s optimalizáciou všetkých parametrov boli schopní získat 98%-99% korelačnej energie pre atóm neónu a molekuly vodíku. Ďalším logickým kro-
34 34 Kapitola 3. R12 metódy kom je modifikovat lineárny člen pomocou gaussovskej funkcie v tvare 57 f(r 12 ) = r 12 e ( γr2 12 ) r12 + O(r 3 12) (3.9) čo má za následok správne chovanie korelačného faktoru vo vel kých vzdialenostiach od cuspu. Avšak aby bola funkcia schopná popísat samotný cusp, je potrebné aby faktor γ 12 bol vel mi malý čo naopak neutralizuje výhodu gaussiánu. 57, 58 Na túto prácu nadviazal v roku 2004 Ten-no a zamenil Gaussián za Slaterov geminál v tvare f(r 12 ) = 1 e ( γr 12) = γr 12 + O(r 2 12) (3.10) Takto definovaný faktor sa neskôr stal súčast ou najpoužívanejších metód, pre ktoré Ten-no vytvoril jedny z prvých implementácii. 59 Tieto implementácie v tej dobe používaných postupov napomohli k rozšíreniu R12 metód ako jednej zo štandardných kvantovo chemických metód. 60, 61 Slaterove geminály môžu byt následne substituované rozvojom v gaussovských gemináloch za vzniku korelačného faktoru f(r 12 ) = 1 v c v e ( γvr2 12 ) γr γ2 r O(r 3 12). (3.11) Klopper a Tew neskôr študovali korelačný faktor v tvare Slaterovho geminálu vynásobeného lineárnym členom a po porovnaní výsledkov a vzájomných príspevkov explicitných členov došli k záveru, že chýbajúci kvadratický člen v 3.10 prispieva významnou mierou k popisu elektrónovej korelácie. 60 Metódy so Slaterovými geminálmi boli nazvané F12 metódy z dôvodu rozlíšenia od pôvodnej metódy R12, ktorá zahrnuje korelačný faktor ako lineárnu vzdialenost dvoch elektrónov. Výpočty s F12 korelačnými faktormi sú schopné popísat korelačnú energiu na rovnakej úrovni presnosti ako metódy R12 s korelačne konzistentnou bázou väčšou o jedno až dve kardinálne čísla tz. aug-cc-pvnz aug-cc-pv(n-1,2)z. Toto je v prípade vel kých bázi ako sú quadruple a pentuple úspora takmer v stovkách bázových funkcií a redukcia
35 3.2. Korelačný faktor 35 Tabul ka 3.1: Aproximácia korelačného člena (cγ 1 (1 e ( γr12 )) na optimálny popis explicitnej korelácie atómu hélia a jeho izolektrónové katióny a porovnanie s tienením náboja jadra pre konštanty a = , b = a c = Z γ(a 1 0 ) a(z b) v časových úsporách takmer o jeden rád. Pri použití špeciálne zostavovaných a zoptimalizovaných bázových funkcií pre explicitne korelované výpočty môže byt úspora voči štandardným výpočtom bez explicitnej korelácie ešte väčšia a. Čo sa týka samotného faktoru γ ten je závislý hlavne na samotných jadrách ako je vidiet z tabul ky 3.1. S vzrastajúcim nábojom jadra dochádza k zmenšovaniu oblasti cuspu a tým pádom k zväčšovaniu samotného parametru γ. Jedným z riešení, ako obíst túto závislost, je optimalizácia bázových funkcií na určenú hodnotu γ parametru(obr. 3.2). 9 a Tieto báze boli pomenované ako cc-pvxz-f12
36 36 Kapitola 3. R12 metódy Obr. 3.2: Efekt parametru γ na bázu Porovnanie závislosti strednej hodnoty odchýlky korelačnej energie (kj mol 1 získanej z CCSD(F12)/cc-pVnZ-F12 výpočtov na parametre γ pre 58 molekúl, kde n=d(krížik) a T(bodka). Prebraté z Projekčný operátor Ďalším úskalím R12 metód je výber projekčného operátoru ˆQ 12. V súčastnosti najviac používaným je projekčný operátor na podpriestor obsadených Hartree- Fockovských orbitálov v tvare 63 ˆQ 12 = (1 Ô1)(1 Ô2) ˆV 1 ˆV2, (3.12) kde Ô 1 = i ψ i (1) ψ i (1) (3.13) ˆV 1 = a ψ a (1) ψ a (1) (3.14) taktiež nazývaný Ansatz 2. 64, 65 Počas vývoja R12 metód bolo navrhnutých niekol ko d alších projekčných operátorov ako je ortogonalizácia fun-
37 3.3. Projekčný operátor 37 kcií ˆQ 12 f(r 12 ) kl voči všetkým orbitálom dvojicou Klopper a Kutzelnigg(3.8). 63 ˆQ 12 = (1 ˆP 1 ˆP2 )(1 Ô1)(1 Ô2) = 1 Ô1(1 ˆP 2 ) (1 ˆP 1 )Ô2 ˆP 1 ˆP2, (3.15) kde ˆP 1 je definované ako ˆP 1 = p ψ p (1) ψ p (1) (3.16) K rovnakému tvaru projekčného operátoru sa je možné tiež dostat skrz ortogonalizáciou ˆQ 12 f(r 12 ) kl voči virtualným orbitálom. Toho je možné docielit definovaním operátoru ˆV 1 = a ψ a (1) ψ a (1) a redefinovaním operátoru ˆQ 12. ˆQ 12 = (1 ˆV 1 ˆV2 )(1 Ô1)(1 Ô2) = (1 Ô1)(1 Ô2) ˆV 1 ˆV2 (3.17) = 1 Ô1(1 ˆP 2 ) (1 ˆP 1 )Ô2 ˆP 1 ˆP2, V prípade, ak nie sú zavedené žiadne aproximácie či už na model projekčného operátoru alebo samotných výpočtov integrálov sú vyššie uvedené rovnice ekvivalentné a nezáleží na tom či funkcie ˆQ 12 f(r 12 ) kl sú ortogonalizované voči akémukol vek podpriestoru orbitálov. Na druhu zvoleného projekčného operátoru následne závisí zložitost výsledných algebraických rovníc a s tým spojené viac-elektrónové integrály. Jedným z prvých návrhov bolo použitie rezolúcie jednotky ako spôsobu aproximácie projekčných operátorov Ô 1 a Ô2 a to tak, že tieto integrály sú nahradené súčinom Ô1 ˆP 2 a ˆP 1Ô2, kde ˆP 1 je definované ako projekčný operátor na ortonormálnu pomocnú bázu {ψ p }. 63, 66 Táto báza môže byt rovná pôvodnému rozvoju Hartree- Fockovských orbitálov kde operátor ˆQ 12 nadobúda tvaru ˆQ 12 1 ˆP 1 ˆP2 (3.18)
38 38 Kapitola 3. R12 metódy a ˆP 1 je rovné ˆP 1 alebo je táto pomocná báza 66 odlišná od Hartree-Fockovskej a ˆQ 12 je definovaná ako ˆQ 12 = (1 ˆV 1 ˆV2 )(1 Ô1)(1 Ô2) = 1 Ô1(1 ˆP 2 ) (1 ˆP 1 )Ô2 ˆP 1 ˆP2 (3.19) 1 Ô1( ˆP 2 ˆP 2 ) ( ˆP 1 ˆP 1 )Ô2 ˆP 1 ˆP2, Na rozdiel od projekčného operátoru Ansatz 1, Ansatz 2 dokáže zvýšit rýchlost konvergencie post Hartree-Fockovských výpočtov korelačných energií avšak cenou za toto zrýchlenie je coupling medzi klasickou a R12 korekciou. 67 Následkom toho je nemožnost separovat tieto príspevky, čo vedie k zložitejšej implementácií v zdrojovom kóde. 3.4 Viacelektrónové integrály Ako bolo spomenuté vyššie na vyriešenie problému viac-elektrónových integrálov boli navrhnuté viaceré metódy, v súčastnosti je však najpoužívanejšou rezolúcia jednotky (RI), ktorá využíva takzvanej pomocnej báze a dokáže aproximovat troj elektrónové integrály ako súčin dvoj-elektrónových. ij r 12 Ô 1 r 1 12 kl p ij r 12 mp mp r 1 12 kl (3.20) Aby bola zabezpečená správnost RI, je treba aby pomocná báza bola dostatočne vel ká. V 1985 ukázal Kutzelnigg, 68 že nasýtenost pomocnej báze musí byt 3L occ, čo vo vtedajšej dobe predstavovalo problém, kedže ako pomocná báza bola používaná báza molekulových orbitálov. Toto však spôsobovalo, že Hartree-Fockovská báza používaná na výpočty by musela byt vel mi vel ká. Ako riešenie sa ukázalo použitie externej báze slúžiacej len pre správnu aproximáciu RI. 66 Túto bázu nazval Klopper Auxuliary Basis Set (ABS), avšak aj táto báza musí byt dostatočne vel ká aby sa zabránilo chybám vo výpočtoch integrálov. Našt astie však už takáto vel ká báza nezat ažuje hlavný výpočet. Ďalšou alternatívou k ABS je takzvaná ABS+, ktorá v
39 3.4. Viacelektrónové integrály 39 sebe zahrňuje samotnú Hartree-Fockovskú bázu. 65 Ako úspešné riešenie sa tiež ukazuje aproximácia členu (1 ˆP 1 ) priamo ako ˆP 1 = (1 ˆP 1 ) α ψ α (1) ψ α (1), (3.21) kde α je orbitál z takzvaného komplementárneho priestoru ABS (CABS) a. Ak CABS ešte obsahuje Hartree-Fockovskú bázu je tento prístup analogicky nazvaný CABS+. Odlišnými prístupmi k výpočtu viac-elektrónových integrálov je numerická kvadratúra daných integrálov a metóda aproximácie hustoty (density fitting). Obe majú svoje výhody aj nevýhody. V poslednej dobe dochádza k snahám skombinovat uvedené metódy a zjednodušit tak výpočet viac-elektrónových integrálov. a Complementary Auxuliary Basis Set
40 Kapitola 4 Coupled Cluster metódy 4.1 Úvod do CC metód Jednou z najpoužívanejších metód na výpočet korelačnej energie taktiež nazývaných post Hartreee-Fockovské metódy je metóda Coupled Cluster (CC). Jej prvé základy siahajú ku H. Kümmlovi až do konca 50-tych rokov, ked bola výhradne používaná v rámci jadrovej fyziky a chemikmi nedotknutá. 69, 70 To sa zmenilo v roku 1966 ked Jiří Čížek vydal prvý článok na téma coupled cluster metód 16 a následne v roku 1972 spolu s Josefom Paldusom uverejnili ich spoločný článok s aplikáciou CC metódy na cyklické polyény. 71, 72 Základnou premisou CC metód je rozvoj korelovanej vlnovej funkcie v exponenciálnej forme Ψ CC = e ˆT Ψ 0, (4.1) kde ˆT je takzvaný clusterový operátor, ktorý je definovaný ako ˆT = n ˆT n, (4.2) s ˆT n = ( 1 n! )2 ij...,ab... t ab... ij... a aa b... a ja i. (4.3) 40
41 4.1. Úvod do CC metód 41 Tabul ka 4.1: Škálovanie coupled cluster metód s korešpondujúcimi názvami jednotlivých metód ˆT = ˆT 1 + ˆT 2 CCSD O(N 6 ) ˆT = ˆT 1 + ˆT 2 + ˆT 3 CCSDT O(N 8 ) ˆT = ˆT 1 + ˆT 2 + ˆT 3 + ˆT 4 CCSDTQ O(N 10 ) Takto zvolený operátor môže byt následne omedzený na rôzne hodnoty n (n max = N elek ), ktoré určujú stupeň excitácie. Podl a zvoleného stupňa excitácie sa jednotlivé metódy nazývaju CCSD (n = 2),CCSDT (n = 3),CCSDTQ (n = 4) atd (tab. 4.1). Najpoužívanejšou metódou je CCSD, kde clusterové operátory sú definované ako ˆT 1 = i ˆt i = ia t a i a aa i, (4.4) a ˆT 2 = 1 ˆt ij = 1 t ab ij a 2 4 aa b a ja i. (4.5) ij ijab V prípade úplného rozvoja ˆT operátora sú rovnice ekvivalentné rovniciam pre full CI a je možné vyjadrit CI rozvojové konštanty pomocou ˆT n. (1 + Ĉ) Ψ 0 = e ˆT Ψ 0 Ĉ 1 = ˆT 1 Ĉ 2 = ˆT ˆT 2 1 (4.6) Ĉ 3 = ˆT 3 + ˆT 1 ˆT ˆT Dosadením takto vytvorenej funkcie do Schrödingerovej rovnice (1.1) a projektovaním na referenčnú funkcie Ψ 0 zl ava dostávame energiu pre CC metódu. Ĥe ˆT Ψ 0 = Ee ˆT Ψ 0, (4.7)
42 42 Kapitola 4. Coupled Cluster metódy Ψ 0 Ĥe ˆT Ψ 0 = E Ψ 0 e ˆT Ψ 0 = E, (4.8) kde využijeme toho, že výraz Ψ 0 Ψ CC = 1, vd aka ortogonalite báze Slaterových determinantov. Clusterové amplitúdy (t a i, tab ij,atd) je následne možné získat projektovaním zl ava excitovanou vlnovou funkciou na rovnicu 4.7 a. Aby bolo možné vyriešit uvedené rovnice je treba transformovat exponencionálu do mocninovej rady. Vložením tejto rady do rovnice 4.8 dostávame Ψ 0 Ĥ(1 + ˆT + ˆT ˆT ) Ψ 0 = E. (4.9) Táto séria je však konečná a to z dôvodu, že Hamiltonián je dvojelektrónový operátor a ˆT obsahuje len excitačné operátory. Podl a Slaterových pravidiel sú maticové elementy dvojelektrónových operátorov medzi dvomi Slaterovými determinantmi líšiacimi sa o viac ako dva spinorbitály nulové. Výsledná rovnica tak obsahuje len prvé tri členy. Ψ 0 Ĥ Ψ 0 + Ψ 0 Ĥ ˆT Ψ 0 + Ψ 0 Ĥ ˆT 2 2 Ψ 0 = E (4.10) Analogicky amplitúdové rovnice sa dajú odovodit podobne. Vhodnejší postup pre získanie prakticky využitel ných rovníc je vynásobenie 4.7 funkciou Ψ 0 e ˆT zl ava a využitie Campbell-Baker-Hausdorffovo rovnice čo vedie na vnorený rozvoj komutátorov medzi Hamiltoniánon Ĥ a clustrovým operátorom ˆT. Ψ 0 Ĥ + [Ĥ, ˆT ] [[Ĥ, ˆT ], ˆT ] [[[Ĥ, ˆT ], ˆT ], ˆT ] [[[[Ĥ, ˆT ], ˆT ], ˆT ], ˆT ] +... Ψ 0 (4.11) Podobne ako v predchádzajúcom prípade je tento rozvoj konečný, protože Hamiltonián obsahuje v rámci teórie druhého kvantovania najviac štyri kreačné/anihilačné operátory. Každý komutátor s operátorom ˆT eliminuje jeden operátor druhého kvantovania, tak že rozvoj (4.11) končí po piatom členu. a Na riešenie amplitúd t ab ij potrebujeme získat rovnicu Ψ ab ij Ĥe ˆT Ψ 0 = E Ψ ab e ˆT Ψ 0 a podobne pre dal šie amplitúdy. ij
43 4.2. CCSD(T) metóda CCSD(T) metóda Normálne usporiadaný Hamiltonián Základom CCSD(T) metódy je CCSD metóda, 73 ktorej rovnice sú riešené iteratívne a následne je spočítaná neiteratívna korekcia pre triexcitované príspevky. S využitím Wickového teorému 74 a kontrakcií párov kreačných a anihilačných operátorov a je možné transformovat Hamiltonián Ĥ na takzvaný normal product Hamiltonián 1675 Ĥ N ˆF N + ˆV N = ˆF N + ˆV N + Ψ 0 Ĥ Ψ 0 Ψ 0 Ĥ Ψ 0 (4.12) = Ĥ Ψ 0 Ĥ Ψ 0, kde N značí normal product a operátory ˆF N a ˆV N sú jednoelektrónové a dvojelektrónové operátory Hamiltoniánu. Ψ 0 Ĥ Ψ 0 nie je nič iné ako energia referenčnej vlnovej funkcie b a teda ĤN je možné chápat ako operátor korelačnej energie. Dosadením clustrového operátoru vo forme ˆT CCSD = ˆT 1 + ˆT 2 do podobnostne transformovaného Hamiltoniánu H e ˆT Ĥ N e ˆT dostávame H = ĤN + [ĤN, ˆT 1 ] + [ĤN, ˆT 1 ] [[ĤN, ˆT 1 ], ˆT 1 ] +[[ĤN, ˆT 1 ], ˆT 2 ] +... (4.13) CCSD energia a amplitúdy Do výsledného tvar H však prispievajú len connected členy a H nadobúda tvar H = ĤN(1 + ˆT 1 + ˆT ˆT 1 2 ) C (4.14) a Pre prípad jednoelektrónových operátorov je definovaný súčin a pa q = {a pa q} + {a pa q}, viz. Dodatok A b Čo je vo väčšine prípadov Hartreee-Fockovská energia
44 44 Kapitola 4. Coupled Cluster metódy Dosadením za ĤN z rovnice 4.12 dostávame H = ( ˆF N + ˆV N + ˆF N ˆT1 + ˆF N ˆT ˆF N ˆT ˆV N ˆT1 + ˆV N ˆT ˆV N ˆT 2 1 ) C, Následne využitím druhého kvantovania a Wickovho teorému, môžme dospiet ku členom v tvaroch. Ψ 0 ( ˆF N ˆT1 ) C Ψ 0 = 1 f pq t a i Ψ 0 {a 2 pa q }{a aa i } Ψ 0 = f ia t a i pq ai ai Ψ 0 ( ˆF N ˆT2 ) C Ψ 0 = 1 f pq t ab ij Ψ 0 {a 4 pa q }{a aa b a ia j } Ψ 0 = 0 pq aibj Ψ 0 ( ˆF 2 N ˆT 1 ) C Ψ 0 = 1 f pq t a i t b j Ψ 0 {a 2 pa q }{a aa i }{a b a j} Ψ 0 Ψ 0 = 0 pq aibj Ψ 0 ( ˆV N ˆT1 ) C Ψ 0 = 1 pq rs Ψ 0 {a 4 pa q }{a aa b a ia j } 1 t a i {a 2 aa i } Ψ 0 = 0 pqrs ai (4.15) Druhou možnost ou je použitie diagramatického prístupu (Obr. 4.1), ktorý dovol uje ovel a rýchlejšie odvodenie potrebných členov, ktorých je v prípade amplitúdových rovnic pre ˆT 3 je niekol ko stoviek. Aplikovaním H na vlnovú... Obr. 4.1: Diagram integrálu Ψ 0 ˆF N ˆT1 Ψ 0 Príklad diagramatického zobrazenia integrálu Ψ 0 ˆF N ˆT1 Ψ 0 funkciu Ψ 0, vynásobením zl ava a dosadením členov z 4.15 dostávame výraz pre korelačnú energiu v tvare. E corr E CCSD E 0 = Ψ 0 H Ψ 0 (4.16)
45 4.2. CCSD(T) metóda 45 respektíve E corr = ia f ia t a i aibj ij ab t ab ij ij ab t a i t b j. (4.17) aibj Kde sme využili faktu, že Ψ 0 H Ψ 0 = 0. Ďalej je možné využit toho, že ak je Ψ 0 = Ψ HF tak podl a Brillouinového pravidla f ia = 0 a to tak, že Ψ 0 H ˆT 1 Ψ 0 = Ψ 0 ( ˆF N ˆT1 + ˆV N ˆT1 ) Ψ 0 = 0 (4.18) takže v rovnici 4.17 vypadne prvý člen. Ak sa zanedbá druhý člen jedna sa o CCD teóriu, kde ˆT = T 1. Rovnica 4.17 však nie je obmedzená len pre CCSD metódu ale je použitel ná pre všetky ostatné CC metódy (CCSDT, CCSDTQ atd ) 76 a to z toho dôvodu, že kontrahované príspevky medzi clustrovými operátormi pre vyššie excitácie a Hamiltoniánom sú nulové. To však neznamená že energia je pre všetky metódy rovnaká, kedže jednotlivé clustrové operátory prispievajú do rovnice 4.17 cez amplitúdy t ab ij a ta i. Obr. 4.2: CCSD apmlitúdové rovnice Amplitúdové rovnice pre CCSD metódu obsahujúce ˆT 2 príspevky
46 46 Kapitola 4. Coupled Cluster metódy Amplitúdové rovnice je možné získat analogickým prístupom a to projektovaním zl ava na H Ψ 0, v tomto prípade pomocou excitovaných vlnových funkcií Ψ a i Ψ a ab ij Ψ a i H Ψ 0 = 0 Ψ ab H Ψ 0 = 0 ij (4.19) Vyjadrením všetkých príspevkov od členov v connected Hamiltoniánu dostávame takzvané ˆT 1 a ˆT 2 amplitúdové rovnice. Amplitúdové rovnice sú iteratívne riešené kým nedochádza k splneniu daných konvergenčných podmienok T korekcie V minulom desat ročí už bolo preukázané, že triple a vyššie excitácie prispievajú výraznou mierou ku korelačnej energii a teda aj k popisu molekulárnych vlastností. Naneštastie, CCSDT a vyššie aproximácie clustrového operátoru sú príliš výpočtovo náročné a aplikovatel né len na malé systémy. V priebehu vývoja CC metód bolo navrhnutých niekol ko druhov triple korekcií ku CCSD energii. Jednou z prvých bolo využitie triple príspevkov ku štvrtému rádu poruchovej teórie (MBPT(4)).Táto aproximácia bola nazvaná CCSD[T]. 17 Neskôr sa však ukázalo, že je potrebný d alší člen, kedže E [4] DT často preceňuje interakcie a je potrebné toto zníženie kompenzovat práve d alším členom v rozvoji. 18, 77 Týmto členom je príspevok piateho rádu zahrnujúci single excitácie. E CCSD(T ) = E CCSD + E [4] DT + E[5] ST (4.20) Oba príspevky sú následne definované ako E [4] DT = ijkabc E [5] ST = ijkabc t ab ij Ψ ab ij Ĥ ˆT [2] 3 Ψ 0 t abc ijk Ψa [2] i Ĥ ˆT 3 Ψ 0, (4.21) kde ˆT [2] 3 sú aproximované ˆT 3 amplitúdy.
47 4.3. Multirefenčné Coupled Cluster metódy Multirefenčné Coupled Cluster metódy Klasické multireferenčné metódy Ako bolo spomenuté v sekcii 2.1 klasické jednoreferenčné metódy nedokážu popísat statickú koreláciu, ktorej príspevky sú významné u systémov so skoro degenerovanými orbitálmi ako sú napríklad biradikály. V týchto prípadoch je výhodne definovat referenčnú vlnovú funkciu ako lineárnu kombináciu viacerých konfigurácií. Jednou z prvých multireferenčných metód bola metóda MCSCF (Multi-configurational self-consistent field), ktorá je rozšírením Hartreee- Fockovskej metódy pre prípad viacerých konfigurácii. Ψ P M ω = Cµ ω Φ µ (4.22) µ=1 Naneštastie podobne ako klasická HF metóda nedokáže popísat dynamickú koreláciu. Ďalšími pokusmi bolo analogické rozšírenie pre konfiguračnú interakciu, v ktorej prípade je to priamočiare riešenie a následne aj post HF metódy ako sú MBPT, CC a d alšie. V súčastnosti existuje niekol ko spôsobov ako definovat multireferenčnú vlnovú funkciu metódy coupled cluster. Jedným z nich sú prístupy založené na Jeziorski-Monkhorstovom ansatze (4.22) 78 takzvané Hilbert space metódy. ˆΩ ω = M µ=1 e ˆT ( µ) ω Φ µ Φ µ (4.23) Ψ ω = Ω ω Ψ P ω (4.24) Tieto metódy sa d alej delia na State-Universal metódy(succ) a State- Specific(SSCC). SUCC metódy umožňujú získat energie pre viac stavov v rámci jednej iterácie ale trpia konvergenčnými problémami tzv. Intruder stavov a. State-Specific síce dokážu spočítat v rámci jedného výpočtu len jednu a Tieto stavy vznikajú ak sú jednotlivé referenčné determinanty energeticky príliš blízko, čo následne spôsobuje problémy s divergenciou počas samotných výpočtov
48 48 Kapitola 4. Coupled Cluster metódy energiu pre jeden stav, avšak netrpia intruder stavmi. Prvou SSCC metódou bola Brillouin-Wignerova metóda (MR BWCC) navrhnutá Hubáčom. 79, 80 Nanešt astie MR BWCC trpí problémom size-extenzivity spôsobenej unlinked členmi v clustrových rovniciach. Ďalšou state-specific metódou navrhnutou Mukherjeem je Mukherjee Coupled Cluster metóda (MR MkCC). 7 Pomocou Jeziorski-Monkhorstovho (4.22) operátoru je možné definovat presnú vlnovú funkciu a. Na takto definovanú vlnovú funkciu je následne aplikovaný takzvaný efektívny Hamiltoniánon Ĥeff, ktorý je definovaný v tvare Ĥ eff = ˆP ĤΩ ω ˆP, (4.25) kde ˆP je projekčný operátor na priestor konfigurácií. Prepísaním Hamiltoniánu ako Ĥ = Ĥµµ + ĤN(µ) (4.26) a dosadením tohto Hamiltoniánu do 4.25 dostávame rovnicu pre efektívny Hamiltonián Ĥ eff νµ = Ĥµµδ νµ + Φ ν ĤN(µ)e T (µ) Φ µ (4.27) Túto rovnicu je nad alej možné zjednodušit a to tak, že z druhého členu ostanú len connected členy. Amplitúdové rovnice je možné získat dosadením do zovšeobecnenej Blochovej rovnice. [Ĥe ˆT µ Φ µ c ω µ E ω e ˆT µ Φ µ c ω µ] = 0 (4.28) µ Do tohto bodu sú obe teórie MR BWCC a MR MkCC zhodné b. Z tejto rovnice je následne nemožné získat dostatočný počet rovníc pre jej riešenie a je potreba pridat určité rovnice obsahujúce podmienky pre riešenie tohto systému. Avšak výber týchto podmienok nie je unikátny a je možné ich a Predpokladá sa intermediálna normalizácia Ψ ω Ψ P ω, ktorá zaručuje nulové amplitúdy pre vnútorné excitácie v priestore všetkých konfigurácií b Mimo diagonálny člen zodpovedá práve interným excitáciám trasformujúcimi Φ ν na Φ µ
49 4.3. Multirefenčné Coupled Cluster metódy 49 zostrojit niekol ko. Podl a týchto podmienok je možné odvodit MR BWCC a MR MkCC. 3 5, 7, 8, 79, 80 BWCC V prípade BWCC je to podmienka, že jednotlivé členy v sumácii 4.28 sú po vynásobení zl ava vlnovými funkciami Φ θ, ktoré sú súčast ou podpriestoru tvoreného excitáciami z referenčných vlnových funkcií Φ µ a to tak, že počet excitácií nepresahuje počet excitácií v ˆT a Následne je Hamiltonián rozdelený podl a 4.26 a amplitúdové rovnice dostávajú tvar (E ω Ĥµµ) Φ ν e ˆT (µ) Φ µ = Φ ν ĤN(µ)e ˆT (µ) Φ µ C+DC,L + Φ ν e ˆT (µ) Φ µ UL, (4.29) kde UL sú unlinked členy a C+DC,L sú linked členy.ďalšími úpravami sa pravá strana zredukuje len na príspevky od linked členov. MkCC Alternatívnym riešením 4.28 je využitie rezolúcie jednotky 7 v tvare = ν 1 = e ˆT (µ) e ˆT (µ) e ˆT (µ) Φ ν Φ ν e ˆT (µ) + e ˆT (µ) ˆQe ˆT (µ), (4.30) kde ˆQ je opät projekčný operátor. Dosadením tejto rovnice do 4.28 a zámenou indexov ν za µ v člene obsahujúcom Ĥeff νµ dostávame { } e ˆT (ν) Φ µ Ĥeff µν c ω µ+e ˆT (µ) ˆQe ˆT (µ) Ĥe ˆT (µ) Φ µ c ω µ E ω e ˆT (µ) Φ µ c ω µ = 0, µ ν (4.31) Kde jednotlivé sumácie v zložených zátvorkách sú rovné nule, čo je práve nutná podmienka v MkCC metóde. Amplitúdové rovnice potom dostávame vynásobením každého členu v sumácii zl ava členom Φ θ e ˆT (µ) Tieto podmienky môžu následne zabezpečit medzi iným aj size-extenzivitu MR MkCC, ktorá chýba v prípade MR BWCCSD. MR MkCC je však a Pre prípad jednoreferenčnej CCSD metódy by boli tieto funkcie totožné s Ψ a i a Ψ ab ij
50 50 Kapitola 4. Coupled Cluster metódy naopak zat ažená orbitálnou invariancou v prípade rotácie v priestore aktivných orbitálov. Na zabezpečenie size-extenzivity v prípade MR BWCC je treba spočítat externú a posteriori korekciu, nazvanú tiež Hubáčovou korekciou. 81, MRCC R12 prístup Analogicky ku klasickým R12 metódam je do vlnovej funkcie zahrnutá explicitná korelácia v tvare f(r 12 ). V prípade CC R metód je nahradenie clustrového operátora ˆT za takzvaný globálny excitačný operátor, ktorý je definovaný ako Ŝ(µ) = ˆT (µ) + ˆR(µ), (4.32) kde ˆR(µ) je operátor zabezpečujúci explicitnú koreláciu. Tento postup je rovnaký pre jednorefenčné CC (SR CC) a84 a pre MR CC metódy. 86, 87 Operátor ˆR(µ) je definovaný analogicky ku clusterovému operátoru ako súčet jednotlivých korelačných operátorov. Jedno a dvojčasticové korelačné operátory sú definované následovne ˆR 1 = c i k R k i = c i k ˆR 2 = 1 4 cij kl kl R ij = 1 ( cij kl kl F αβãαβ ij + F kj αj ãα i (4.33) ) kl F αbãαb ij, (4.34) kde maticové elementy F zodpovedajú integrálom s operátorom f(r 12 ). Na základe tejto funkcie sú jednotlivé metódy rozdelené na R12 (f 12 = r 12 ) alebo F12 (f 12 = 1 e γr 12 ) , 88 Pri predpoklade všeobecnej Brillouinovej podmienky (GBC) b príspevky ku ˆR 1 vymiznú. V prípade ak je normal a V prípade jednoreferenčnej coupled cluster metódy je µ = 1, čo zodpovedá práve jednej referenčnej vlnovej funkcii. b Generalized Brillouin Condition f α i = 0
51 4.3. Multirefenčné Coupled Cluster metódy 51 product Hamiltonián 89 rozdelený na dve časti s každou zodpovedajúcou klasickej báze a komplementárnej, je možné príspevky v clusterových rovniciach rozdelit na členy zahrnujúce len klasickú bázu a CABS bázu. 65 Ĥ N (µ) = ĤN(µ) AO + ĤN(µ) comp, (4.35) kde ĤN(µ) AO zodpovedá klasickej báze vzniklej lineárnou kombináciou atómových orbitálov a ĤN(µ) comp komplementárnej báze. Ĥ N (µ) AO sa dá d alej definovat ako Ĥ N (µ) AO = fp q (µ)a p q(µ) grs pqa pg rs(µ), (4.36) a a sú normálne usporiadané excitačné operátory. V prípade MR MkCC 87 dostáva efektívny Hamiltonián tvar H eff µµ = Ψ µ Ĥ Ψ µ + Ψ µ e ˆT (µ) Ĥ AO N e ˆT (µ) Ψ µ + Ψ µ e Ŝ(µ) Ĥ comp N eŝ(µ) Ψ µ (4.37) Podobne ako v jednoreferenčných CC metódach je potreba iterovat ˆT amplitúdové rovnice ale zároveň aj ˆR rovnice, obsahujúce explicitnú korekciu. V prípade MR MkCC boli v rámci implementácie explicitnej korelovanej metódy ˆR amplitúdy c ij kl aproximované v rámci SP ansatzu9059 a to vzt ahom c ij kl = 3 8 δ ikδ jl δ ilδ kj. (4.38) A teda nie sú optimalizované v každej iterácii. Z tohto dôvodu sú rovnice pre efektívny Hamiltonián rozšírené o členy µ ˆR(µ) e Ŝ(µ) eŝ(µ) Φ µ (4.39) pre H eff µµ a H eff µν je klasický člen F12 metódy vynásobený ešte členom (1 + µ ˆR(µ) e Ŝ(µ) eŝ(µ) Φ µ ). (4.40) Zároveň boli zanedbané coupling príspevky 91 a rozvoj F12 členov bol aproximovaný podl a [88,89].
52 Kapitola 5 Izomerizácia bicyklo[1.1.0]butánu Popis disrotačného a konrotačného tranzitného stavu Stúdium konrotačného a disrotačného mechanizmu izomerizácie bolo prevedené ako validácia multireferenčných CC metód a to menovite Brilloiun- Wignerovej metódy a Mukherjeeho metódy. Pôvodné výpočty pomocou jednoreferenčných CC metód nedokázali popísat správne konrotačný a disrotačný tranzitný stav. 92 V následujúcej kapitole budú prezentované výsledky pre tieto dva tranzitné stavy. 5.1 Bicyklo[1.1.0]bután Jedny z prvých experimentálnych výsledkov boli prevedené až v 60-tych rokoch 93 a ukázali, že bicyklobután izomerizuje cez konrotačný mechanizmus v súlade s Woodward-Hoffmannovými orbitálnymi pravidlami. Na tieto experimenty onedlho nadviazali viaceré teoretické práce94, 95 využívajúce multireferenčnej konfiguračnej interakcie, 96 poruchovej teórie a CCSD(T). 92 Všetky tieto práce boli schopné popísat konrotačný mechanizmus v dob- 52
53 5.2. Výpočtové detaily 53 rej zhode s experimentom avšak v prípade disrotačného mechanizmu neboli tieto výsledky jednoznačné. Toto je spôsobené tým, že disrotačný tranzitný stav (dists) má silný biradikálový charakter. S popisom disrotačného tranzitného stavu má problém aj jedna z najpoužívanejších metód CCSD(T), ktorá vel mi dobre popisuje bicyklobután (bicbut), konrotačný tranzitný stav (conts) a aj samotný produkt trans butadién (tbut), avšak pre dists predpovedá aktivačnú bariéru nižšiu ako je aktivačná bariéra conts Výpočtové detaily Oba reakčné mechanizmy začínajú u reaktantu bicyklobutánu, po prejdení konrotačným a disrotačným tranzitným stavom konvergujú v lokálnom minime buta-1,3-dién (v gauche forme). Tento systém následne prechádza izomerizáciou cez nízko položenú aktivačnú bariéru na finálny produkt transbuta- 1,3-dién. Predmetom práce bol popis jednotlivých tranzitných stavov tak ako aj reaktantu a produktu pomocou kvantovo chemických výpočtov. Geometrie (Obr Obr. 5.2) všetkých uvedených systémov boli optimalizované na úrovni CASSCF(10,10) s použitými bázami cc-pvdz a cc-pvtz. 19 Na popis všetkých zmien ku ktorým dochádza pri izomerizácii (napríklad rozpad kruhu) bol použitý aktivný priestor obsahujúci 5 okupovaných molekulárnych orbitálov korešpondujúcich s väzbami bicyklobutánového kruhu(c1- C2, C1-C3, C2-C3, C2-C4, C3-C4). 2 Ako zbylých 5 molekúlárnich orbitálov boli vybrané anti-väzbové orbitály ku vyššie uvedeným obsadeným väzbovým molekulovým orbitálom. Multireferenčná SCF dokáže popísat statickú koreláciu avšak trpí podobným nedostatkom ako klasická SCF metóda a to tým, že neobsahuje rigorózne zahrnutie dynamickej korelácie. Z toho dôvodu boli v minulosti na tomto systéme prevedené výpočty na úrovni MCQDPT2, MRCI a CR-CCSD(T). Výpočty na úrovni MR CC sú vôbec jedny z prvých prevedených na tomto systéme.
54 54 Kapitola 5. Izomerizácia bicyklo[1.1.0]butánu (a) MO orbitál č. 11 (b) MO orbitál č. 12 (c) MO orbitál č. 13 (d) MO orbitál č. 14 (e) MO orbitál č. 15 Obr. 5.1: Obsadené molekulové orbitály Elektrónová hustota obsadených molekulových orbitálov použitých ako aktívne mol. orbitály vo výpočtu CASSCF(10,10)
55 5.2. Výpočtové detaily 55 (a) MO orbitál č. 16 (b) MO orbitál č. 17 (c) MO orbitál č. 18 (d) MO orbitál č. 19 (e) MO orbitál č. 20 Obr. 5.2: Neobsadené molekulové orbitály Elektrónová hustota neobsadených molekulových orbitálov použitých ako aktívne mol. orbitály vo výpočtu CASSCF(10,10)
56 56 Kapitola 5. Izomerizácia bicyklo[1.1.0]butánu Z CASSCF výpočtov sa ukázalo, že nakol ko nemá konrotačný TS silný biradikálový charakter, v celkovej vlnovej funkcii sa aktívne podiel a aj biexcitovaný determinant(ψ 1... ψhomo 0 ψ2 LUMO ) (Tab5.1). V prípade, dists je tento príspevok ešte väčší a oba determinanty (Hartree-Fockovský a biexcitovaný (ψ 1... ψhomo 0 ψ2 LUMO )) sú takmer degenerované. (a) bicbut C 2v (b) tbut C 2h Obr. 5.3: Optimalizované geometrie reaktantu a produktu Uvedené geometrie sú v Ångströmoch pre CASSCF(10,10)/cc-pVDZ, kurziva CASSCF(10,10)/cc-pVTZ a tučne experimentálne hodnoty Tabul ka 5.1: Najdôležitejšie determinanty pre conts CASSCF(10,10)/cc-pVDZ CASSCF(10,10)/cc-pVTZ Determinant Koeficienty
57 5.2. Výpočtové detaily 57 (a) dists C 1 (b) conts C 1 Obr. 5.4: Optimalizované geometrie tranzitných stavov Uvedené geometrie sú v Ångströmoch pre CASSCF(10,10)/cc-pVDZ a kurziva CASSCF(10,10)/cc-pVTZ Tabul ka 5.2: Najdôležitejšie determinanty pre dists CASSCF(10,10)/cc-pVDZ CASSCF(10,10)/cc-pVTZ Determinant Koeficienty Na oboch geometriách boli následne prevedené výpočty metódami MRCC (MR BWCCSD(T) 6, 79, 97 a MR MkCCSD(T)) 7, 98, 99 a taktiež aj poruchové korekcie druhého rádu pre samotné CASSCF energie (CASPT2) a. Výpočty na reaktantoch a produktoch boli prevedné klasickou jednoreferenčnou CCSD(T), kedže oba systémy vykazujú jednoreferenčný charakter a rozdiel medzi energiami získanými z jednoreferenčných a multireferenčných metód je takmer nulový. Pre výpočet tranzitných stavov bol použitý modelový priestor tvorený HF determinantom, biexcitovaním HF determinantom a dvomi degea Oprava ku chýbajúcej dynamickej korelácii SCF metód, pomocou poruchovej metódy
58 58 Kapitola 5. Izomerizácia bicyklo[1.1.0]butánu nerovanými monoexcitovanými HF determinantami z HOMO orbitálu do LUMO orbitálu. Ako štartovacie molekulové orbitály boli použíté tak Hartree-Fockovské ako aj orbitály zo samotných CASSCF výpočtov. Všetky multireferenčné coupled cluster výpočty boli prevedené s použitím programového balíka ACES II, optimalizácie geometrií a CASPT2 v programoch MOLPRO 2012, 100 GAUSSIAN a NWCHEM Výsledky a diskusia Geometrie optimalizované na CASSCF(10.10) v cc-pvdz bázi sú vo vel mi dobrej zhode s experimentom. Pre molekulu bicyklobutánu je maximálny rozdiel medzi optimalizovanou geometriou a experimentálnou okolo Å v prípade väžby C2-C3. Pre transbutadiénu je tento rozdiel ešte menší a najväčší rozdiel je taktiež v dlžke väžby C2-C Å. Geometria optimalizovaná na úrovni cc-pvtz je dokonca o 0.01 Å presnejšia a takmer zhodná s experimentálnou hodnotou v rámci experimentálnej chyby. Na získanie správnej geometrie tranzitných stavov boli aplikované výpočty IRC, 103 ktoré úspešne spojili tranzitné stavy s produktami a rekreantami. Počas izomerizácie cez konrotačný mechanizmus dochádza k disociácii väzby C1-C3 a súčasnej rotácii väzieb C1-C2 a C2-C3 a vzniká charakteristický dihedrálny uhol medzi H6, H5, C2 a C Dlžka väzby C2-C3 zostáva takmer rovnaká, ale väzba C1-C2 sa medzitým stáva kratšia o Å v cc-pvdz bázi a 0.07 Å v cc-pvtz respektíve a získava čiastočný π charakter čo zodpovedá 24% biradikálneho charakteru. 2 Pre optimalizáciu dists je dôležité správne popísat miešanie tripletovej a singletovej vlnovej funkcie a využit metódy ktorá dokáže popísat biradikály, tz. aspoň MCSCF. K dôkazu silného miešania dvoch spinových stavov služi aj tripletový stav ležiaci len okolo 3 kcal/mol nižšie ako disrotačný tranzitný stav. 2, 92
59 5.3. Výsledky a diskusia 59 Relatívne energie ku reaktantu popisujúce stacionárne body pozdlž reakčnej koordináty pre konrotačný a disrotačný mechanizmus izomerizácie bicyklobutánu získané z multireferenčných coupled cluster výpočtov sú uvedené v tabul ke 5.3. Experimentálna hodnota pre aktivačnú bariéru je 40.6 ± 2.5 kcal/mol a blízkost výpočtov k tejto hodnote môže slúžit ako porovnanie presnosti výpočtu v prípade disrotačného tranzitného stavu. Túto hodnotu sa podarilo zreprodukovat v rámci chyby meriania, dôležitá je však otázka biradikálu a to disrotačného tranzitného stavu. V zhode s experimentom má disrotačný mechanizmus vyššiu aktivačnú bariéru. Z obrázku 5.3 je vidiet, že CCSD(T) metóda predpovedá konrotačný stav nižšie položený ako disrotačný stav, kedže ako už bolo spomenuté jednoreferenčná CCSD(T) nedokáže popísat statickú koreláciu. Taktiež je vidno, že multikonfiguračné SCF metódy sú schopné popísat statickú koreláciu v prípade disrotačného stav a tento stav sa dostáva energeticky vyššie ako conts. Ich reprodukovaná energia je kcal/mol a kcal/mol pre CASSCF/cc-pvDZ a CASPT2/cc-pvDZ. V prípade cc-pvtz to je kcal/mol a kcal/mol. Nanešt astie nedokážu popísat dynamickú koreláciu a celkovo nadhodnocujú energie pre všetky systémy. Dynamickú koreláciu dokáže čiastočne popísat CASPT2 metóda, avšak jej popis nie je tak dobrý ako u CCSD(T) metódy, ktorá v sebe zahrňuje príspevky vyšších rádov ako druhého, čo sa zobrazuje na nižšie položených energiách v prípade CCSD(T)(Obr. 5.5).
60 60 Kapitola 5. Izomerizácia bicyklo[1.1.0]butánu CCSD(T)/cc-pVTZ CASSCF(10,10)/cc-pVDZ CASSCF(10,10)/cc-pVTZ CASPT2(10,10)/cc-pVDZ CASPT2(10,10)/cc-pVTZ Energia(Hartree) bicbut dists conts tbut Obr. 5.5: PES izomerizácie bicbut tbut Popis PES konrotačného a disrotačného mechanizmu v rámci MCSSCF a porovnanie s CCSD(T) metódou nezahrňujúcou statickú koreláciu V prípade aplikácie multireferenčných coupled cluster metód (tab. 5.3) sa ukazuje, že pre Brilloiun-Wignerovu metódu je báza cc-pvdz príliš malá a ňou vytvorená vlnová funkcia nedokáže popísat konrotačný stav v presnej zhode s experimentom. Metóda je však schopná popísat statickú koreláciu správne a stavia disrotačný tranzitný stav vyššie ako konrotačný (Obr. 5.6). Rozdiel medzi BWCCSD a BWCCSD(T) respektíve je 5.28± 2.5 kcal/mol a 4.03 ± 2.5 kcal/mol. Mukherjeeho CCSD(T) metóda je naopak schopná popísat konrotačný stav aj s cc-pvdz bázou a MkCCSD(T) energia je kcal/mol a kcal/mol (pre HF orbitály a CASSCF orbitály) sú vel mi blízko experimentálnej. Vdaka tomuto je možné usudzovat, že MRCCSD(T) metódy sú schopné správne popísat disrotačný tranzitný stav. CCSD(T) predpovedá takmer dists aktivačnú energiu okolo 25.7 kcal/mol čo je asi o 17.5 kcal/mol nižšie ako conts. Multireferenčné Coupled Cluster metódy predpovedajú energetický rozdiel medzi disrotačným a konrotačným stavom
61 5.3. Výsledky a diskusia 61 až okolo 81 kcal/mol BWCCSD/cc-pVDZ BWCCSD(T)/cc-pVDZ MkCCSD/cc-pVDZ MkCCSD(T)/cc-pVDZ Energia(Hartree) bicbut dists conts tbut Obr. 5.6: MRCC PES izomerizácie bicbut tbut Popis PES konrotačného a disrotačného mechanizmu v rámci MRCC metód, ktoré správne popisujú poradie tranzitných stavov Pri aplikácii väčšej báze už dochádza k vyrovnaniu rozdielov medzi BWCCSD(T) a experimentálnymi hodnotami(tab.5.4). Tam je síce CCSD energia vyššie a konrotačný stav je viac de-stabilizovaný, avšak pri započítaniu triple korekcie dôležitej pre popis tripletovej časti vlnovej funkcie, sa bariéra znížila z kcal/mol na 38.7 kcal/mol čo zodpovedá experimentálnej hodnote (Experimentálna hodnota je 40.6 ± 2.5 kcal/mol). U MkCCSD/MkCCSD(T) je tento rozdiel ešte menší a hodnota MkCCSD(T) bariéry je kcal/mol. S väčšou bázou sa taktiež stabilizoval disrotačný tranzitný stav a to v priemere na hodnotu kcal/mol( MkCCSD(T)). Z obr. 5.6 je vidiet, že rozdiel medzi disrotačným a konrotačným tranzitným stavom je zhruba 20 kcal/mol. Naneštastie z obr. 5.6 je očividné, že neexistuje žiadna korelácia medzi použitou metódou a energetickým rozdielom medzi tranzitnými stavmi.
62 62 Kapitola 5. Izomerizácia bicyklo[1.1.0]butánu Tabul ka 5.3: Aktivačné bariéry opravené o príslušné hodnoty ZPE pre konrotačný tranzitný stav spočítané v bázi cc-pvdz, cc-pvdz a cc-pvqz. cc-pvdz c cc-pvtz d CASSCF CASPT BWCCD a BWCCSD(T) a MkCCSD a MkCCSD(T) a BWCCD b BWCCSD(T) b MkCCSD b MkCCSD(T) b Experiment 40.6 ±2.5 a HF orbitály, b CASSCF orbitály, c geometria optimalizovaná v cc-pvdz bázi, d CASSCF(10,10)/cc-pvTZ geometrie "./gap_pvtz.dat" using 2:xticlabels(1) Rel. energia BWCCSD BWCCSD(T) BWCCSD/cas BWCCSD(T)/cas MKCCSD MKCCSD(T) Metoda Obr. 5.7: Korelácia energetického rozdielu medzi dists a conts Rozdiel medzi energiami(kcal/mol) conts a dists a ich korelácia skrz MRCC metódy
63 5.4. Zhrnutie 63 Tabul ka 5.4: Relatívne energie (kcal/mol) tranzitných stavov(kcal/mol) voči bicyklobutánu získane z MRCC cc-pvdz c cc-pvtz d dis. TS con. TS dis. TS con. TS MR BWCCSD a nekonv MR BWCCSD(T) a nekonv MR MkCCSD a nekonv MR MkCCSD(T) a nekonv MR BWCCSD b MR BWCCSD(T) b MR MkCCSD b nekonv MR MkCCSD(T) b nekonv Experiment 40.6 c 40.6 c a HF orbitály, b Použité orbitály z CASSCF výpočtov, c exp. odchylka ± 2.5 Na obr. 5.8 sú následne zobrazené oba reakčné mechanizmy ako konrotačný tak aj disrotačný a ich relatívne energie voči reaktantu bicyklobutánu. 5.4 Zhrnutie V tejto kapitole boli zhrnuté výsledky pre multireferenčný popis izomerizácie bicyklobutánu ako validácie multireferenčných coupled cluster metód na výpočet biradikálov. Samotná izomerizácia prebieha dvoma mechanizmami a to konrotačným(obr. 5.2a), ktorý mal biradikálny TS (24% ) a disrotačným(obr. 5.2b). Disrotačný stav dists slúžiaci ako model biradikálu je na základe experimentov a základných empirických kvantovo chemických
64 64 Kapitola 5. Izomerizácia bicyklo[1.1.0]butánu pravidiel (Woodward-Hoffmannove pravidlá) považovaný za vyššie ležiaci. Túto skutočnost sa podarilo overit a výsledky všetkých multireferenčných coupled cluster metód súhlasia s danými predpokladmi. Obr. 5.8: Relatívne energie vôči reaktantu Relatívne BWCCSD(T) a MkCCSD(T)[kurzíva] energie pre tranzitné stavy a produkt pozdlž reakčnej koordináty. Všetky uvedené energie sú v kcal/mol. Samotným metódam sa podarilo reprodukovat experimentálne hodnoty. Metódy BWCCSD(T) a MkCCSD(T) poskytli hodnoty kcal/mol, kcal/mol a kcal/mol a kcal/mol v cc-pvdz bazi a cc-pvtz respektíve, čo súhlasí s experimentom v rámci experimentálnej presnosti. Z výsledkov je teda možné usudzovat, že multireferenčné coupled cluster výpočty sa ukazujú ako nástrojom pre výpočet biradikálov a iných podobných systémov zo skoro degenerovanými orbitálmi.
65 Kapitola 6 Explicitne korelované výpočty 6.1 Tetrametylénetán Tetrametylénetán (TME) je jeden z najzaujímavejších disjunktných biradikálov. Už prvé EPR experimenty 104 ukazovali, že singletový a tripletový stav sú skoro degenerované a tripletový stav leží vel mi blízko pod singletom. Jedny z prvých výpočtov ukázali, že triplet leží asi o 1 kcal/mol pod singletovým stavom v prípade D 2 geometrie (obr. 6.1). Ďalšie experimenty ukázali singletový stav 2 kcal/mol pod tripletovým stavom. Tento rozdiel sa pokúsil vysvetlit Clifford 109 a poukázal na to, že tieto experimentálne rozdiely môžu byt vysvetlené práve D 2 geometriou a to tak, že experimenty boli zmerané pre tripletovú geometriu. Ako jedny z prvých pokročilých výpočtov boli výpočty Filatova 110 využívajúce metódy spin-restricted open-shell Kohn Sham DFT a spin-restricted ensemble-reference Kohn-Sham DFT. Tieto výpočty ukázali, že oba stavy v D 2 geometrii sú takmer degenerované. Predmetom tejto štúdie je demonštrácia explicitne korelovaných F12 metód na tomto systéme a porovnanie s klasickými multireferenčnými coupled cluster metódami. 65
66 66 Kapitola 6. Explicitne korelované výpočty (a) TME bočný pohl ad (b) TME frontálny pohl ad Obr. 6.1: D 2 geometria tetrametylénetánu optimalizovaná na úrovni MP2/6-31G 6.2 Výpočtové detaily Geometria pre študovaný singletový stav tetrametylénetánu bola získaná z MP2 výpočtov za použitia báze 6-31G s fixným uhl om 51 10, 104, 110 medzi jednotlivými ramenami. Tieto výpočty boli prevedené v programe MOLPRO Pre následné klasické multireferenčné a F12 multireferenčné výpočty boli ako referenčné funkcie použité funkcie popisujúce základný stav (GS) a vlnové funkcie popisujúce single a double excitácie z HOMO orbitálu do LUMO orbitálu. Ďalej bola využitá symetria študovanej molekuly a mono excitované vlnové funkcie neboli zahrnuté v multireferenčných výpočtoch, nakol ko ich príspevky sú nulové. Na výpočet energií s využitím multireferenčnej coupled cluster teórie boli vybrané BWCCSD, BWCCSD(T) 6, 97 a MkCCSD,MkCCSD(T) 98, 99 a ich rozšírenia pre explicitne korelované výpočty (xxccsd-f12, xxccsd(t)-f12). 86, 87, 111 Rovnako ako v predchádzajúcom prípade boli pre multireferenčné výpočty využité HF orbitály a orbitály z CASSCF(8,8) výpočtov. Klasické multi-
67 6.3. Výsledky a diskusia 67 (a) HOMO orbitál (b) LUMO orbitál Obr. 6.2: HOMO-LUMO orbitály molekuly TME Elektrónová hustota HOMO a LUMO molekulových orbitálov referenčné coupled cluster výpočty boli spočítané pre báze cc-pvdz, ccpvtz 19 a výpočty s použitím explicitnej korelácie s bázami cc-pvdz, ccpvdz-f12 a cc-pvtz. 19, 112 Pre bázu cc-pvqz bola nad alej spočítaná SCF HF energia a to z dôvodu, že daný systém popísaný cc-pvqz bázou sa stal výpočtovo príliš náročný pre post HF metódy ako sú multireferečné coupled cluster metódy. Samotné multireferenčné coupled cluster výpočty boli prevedené v programe ACES II a NWCHEM, výpočty CASSCF(8,8) v programe MOLPRO a explicitne korelované výpočty v program DIRCCR Výsledky a diskusia V tabul ke 6.1 je možné vidiet absolútne energie pre tetrametylénetán. Na porovnanie, výsledky z klasických multireferenčných výpočtov sú taktiež zahrnuté. Na prvý pohl ad je vidiet, že absolútne energie spočítané metódou MR BWCCSD a BWCCSD(T) v bázi cc-pvdz sú ovel a nižšie ako ostatné energie. Po preskúmaní váh jednotlivých referencií vo výpočtoch v bázi cc-pvdz a cc-pvtz, ktoré boli zhodne 0.72 HOMO 2 LUMO 0 a 0.68 HOMO 0 LUMO 2 pre všetky výpočty je možné vyvodit, že chyba nie je súčast ou explicitne korelovaných výpočtov ale skôr problémom cc-pvdz bázi. Tomuto tiež na-
Vzorce pre polovičný argument
 Ma-Go-15-T List 1 Vzorce pre polovičný argument RNDr Marián Macko U: Vedel by si vypočítať hodnotu funkcie sínus pre argument rovný číslu π 8? Ž: Viem, že hodnota funkcie sínus pre číslo π 4 je Hodnota
Ma-Go-15-T List 1 Vzorce pre polovičný argument RNDr Marián Macko U: Vedel by si vypočítať hodnotu funkcie sínus pre argument rovný číslu π 8? Ž: Viem, že hodnota funkcie sínus pre číslo π 4 je Hodnota
AerobTec Altis Micro
 AerobTec Altis Micro Záznamový / súťažný výškomer s telemetriou Výrobca: AerobTec, s.r.o. Pionierska 15 831 02 Bratislava www.aerobtec.com info@aerobtec.com Obsah 1.Vlastnosti... 3 2.Úvod... 3 3.Princíp
AerobTec Altis Micro Záznamový / súťažný výškomer s telemetriou Výrobca: AerobTec, s.r.o. Pionierska 15 831 02 Bratislava www.aerobtec.com info@aerobtec.com Obsah 1.Vlastnosti... 3 2.Úvod... 3 3.Princíp
Matematika prednáška 4 Postupnosti a rady 4.5 Funkcionálne rady - mocninové rady - Taylorov rad, MacLaurinov rad
 Matematika 3-13. prednáška 4 Postupnosti a rady 4.5 Funkcionálne rady - mocninové rady - Taylorov rad, MacLaurinov rad Erika Škrabul áková F BERG, TU Košice 15. 12. 2015 Erika Škrabul áková (TUKE) Taylorov
Matematika 3-13. prednáška 4 Postupnosti a rady 4.5 Funkcionálne rady - mocninové rady - Taylorov rad, MacLaurinov rad Erika Škrabul áková F BERG, TU Košice 15. 12. 2015 Erika Škrabul áková (TUKE) Taylorov
Motivácia Denícia determinantu Výpo et determinantov Determinant sú inu matíc Vyuºitie determinantov. Determinanty. 14. decembra 2010.
 14. decembra 2010 Rie²enie sústav Plocha rovnobeºníka Objem rovnobeºnostena Rie²enie sústav Príklad a 11 x 1 + a 12 x 2 = c 1 a 21 x 1 + a 22 x 2 = c 2 Dostaneme: x 1 = c 1a 22 c 2 a 12 a 11 a 22 a 12
14. decembra 2010 Rie²enie sústav Plocha rovnobeºníka Objem rovnobeºnostena Rie²enie sústav Príklad a 11 x 1 + a 12 x 2 = c 1 a 21 x 1 + a 22 x 2 = c 2 Dostaneme: x 1 = c 1a 22 c 2 a 12 a 11 a 22 a 12
Goniometrické rovnice a nerovnice. Základné goniometrické rovnice
 Goniometrické rovnice a nerovnice Definícia: Rovnice (nerovnice) obsahujúce neznámu x alebo výrazy s neznámou x ako argumenty jednej alebo niekoľkých goniometrických funkcií nazývame goniometrickými rovnicami
Goniometrické rovnice a nerovnice Definícia: Rovnice (nerovnice) obsahujúce neznámu x alebo výrazy s neznámou x ako argumenty jednej alebo niekoľkých goniometrických funkcií nazývame goniometrickými rovnicami
Ekvačná a kvantifikačná logika
 a kvantifikačná 3. prednáška (6. 10. 004) Prehľad 1 1 (dokončenie) ekvačných tabliel Formula A je ekvačne dokázateľná z množiny axióm T (T i A) práve vtedy, keď existuje uzavreté tablo pre cieľ A ekvačných
a kvantifikačná 3. prednáška (6. 10. 004) Prehľad 1 1 (dokončenie) ekvačných tabliel Formula A je ekvačne dokázateľná z množiny axióm T (T i A) práve vtedy, keď existuje uzavreté tablo pre cieľ A ekvačných
Matematika Funkcia viac premenných, Parciálne derivácie
 Matematika 2-01 Funkcia viac premenných, Parciálne derivácie Euklidovská metrika na množine R n všetkých usporiadaných n-íc reálnych čísel je reálna funkcia ρ: R n R n R definovaná nasledovne: Ak X = x
Matematika 2-01 Funkcia viac premenných, Parciálne derivácie Euklidovská metrika na množine R n všetkých usporiadaných n-íc reálnych čísel je reálna funkcia ρ: R n R n R definovaná nasledovne: Ak X = x
Obvod a obsah štvoruholníka
 Obvod a štvoruholníka D. Štyri body roviny z ktorých žiadne tri nie sú kolineárne (neležia na jednej priamke) tvoria jeden štvoruholník. Tie body (A, B, C, D) sú vrcholy štvoruholníka. strany štvoruholníka
Obvod a štvoruholníka D. Štyri body roviny z ktorých žiadne tri nie sú kolineárne (neležia na jednej priamke) tvoria jeden štvoruholník. Tie body (A, B, C, D) sú vrcholy štvoruholníka. strany štvoruholníka
1. Limita, spojitost a diferenciálny počet funkcie jednej premennej
 . Limita, spojitost a diferenciálny počet funkcie jednej premennej Definícia.: Hromadný bod a R množiny A R: v každom jeho okolí leží aspoň jeden bod z množiny A, ktorý je rôzny od bodu a Zadanie množiny
. Limita, spojitost a diferenciálny počet funkcie jednej premennej Definícia.: Hromadný bod a R množiny A R: v každom jeho okolí leží aspoň jeden bod z množiny A, ktorý je rôzny od bodu a Zadanie množiny
SUPPLEMENTARY INFORMATION
 Capture of Elusive Hydroxymethylene and its Fast Disappearance through Tunnelling Peter R. Schreiner a, Hans Peter Reisenauer a, Frank Pickard b, Andrew C. Simmonett b, Wesley D. Allen b, Edit Mátyus c
Capture of Elusive Hydroxymethylene and its Fast Disappearance through Tunnelling Peter R. Schreiner a, Hans Peter Reisenauer a, Frank Pickard b, Andrew C. Simmonett b, Wesley D. Allen b, Edit Mátyus c
Moderné vzdelávanie pre vedomostnú spoločnosť Projekt je spolufinancovaný zo zdrojov EÚ M A T E M A T I K A
 M A T E M A T I K A PRACOVNÝ ZOŠIT II. ROČNÍK Mgr. Agnesa Balážová Obchodná akadémia, Akademika Hronca 8, Rožňava PRACOVNÝ LIST 1 Urč typ kvadratickej rovnice : 1. x 2 3x = 0... 2. 3x 2 = - 2... 3. -4x
M A T E M A T I K A PRACOVNÝ ZOŠIT II. ROČNÍK Mgr. Agnesa Balážová Obchodná akadémia, Akademika Hronca 8, Rožňava PRACOVNÝ LIST 1 Urč typ kvadratickej rovnice : 1. x 2 3x = 0... 2. 3x 2 = - 2... 3. -4x
1. písomná práca z matematiky Skupina A
 1. písomná práca z matematiky Skupina A 1. Vypočítajte : a) 84º 56 + 32º 38 = b) 140º 53º 24 = c) 55º 12 : 2 = 2. Vypočítajte zvyšné uhly na obrázku : β γ α = 35 12 δ a b 3. Znázornite na číselnej osi
1. písomná práca z matematiky Skupina A 1. Vypočítajte : a) 84º 56 + 32º 38 = b) 140º 53º 24 = c) 55º 12 : 2 = 2. Vypočítajte zvyšné uhly na obrázku : β γ α = 35 12 δ a b 3. Znázornite na číselnej osi
Hartree-Fock Theory. Solving electronic structure problem on computers
 Hartree-Foc Theory Solving electronic structure problem on computers Hartree product of non-interacting electrons mean field molecular orbitals expectations values one and two electron operators Pauli
Hartree-Foc Theory Solving electronic structure problem on computers Hartree product of non-interacting electrons mean field molecular orbitals expectations values one and two electron operators Pauli
HASLIM112V, HASLIM123V, HASLIM136V HASLIM112Z, HASLIM123Z, HASLIM136Z HASLIM112S, HASLIM123S, HASLIM136S
 PROUKTOVÝ LIST HKL SLIM č. sklad. karty / obj. číslo: HSLIM112V, HSLIM123V, HSLIM136V HSLIM112Z, HSLIM123Z, HSLIM136Z HSLIM112S, HSLIM123S, HSLIM136S fakturačný názov výrobku: HKL SLIMv 1,2kW HKL SLIMv
PROUKTOVÝ LIST HKL SLIM č. sklad. karty / obj. číslo: HSLIM112V, HSLIM123V, HSLIM136V HSLIM112Z, HSLIM123Z, HSLIM136Z HSLIM112S, HSLIM123S, HSLIM136S fakturačný názov výrobku: HKL SLIMv 1,2kW HKL SLIMv
M6: Model Hydraulický systém dvoch zásobníkov kvapaliny s interakciou
 M6: Model Hydraulický ytém dvoch záobníkov kvapaliny interakciou Úlohy:. Zotavte matematický popi modelu Hydraulický ytém. Vytvorte imulačný model v jazyku: a. Matlab b. imulink 3. Linearizujte nelineárny
M6: Model Hydraulický ytém dvoch záobníkov kvapaliny interakciou Úlohy:. Zotavte matematický popi modelu Hydraulický ytém. Vytvorte imulačný model v jazyku: a. Matlab b. imulink 3. Linearizujte nelineárny
Electronic Supplementary Information DFT Characterization on the Mechanism of Water Splitting Catalyzed by Single-Ru-substituted Polyoxometalates
 Electronic Supplementary Information DFT Characterization on the Mechanism of Water Splitting Catalyzed by Single-Ru-substituted Polyoxometalates Zhong-Ling Lang, Guo-Chun Yang, Na-Na Ma, Shi-Zheng Wen,
Electronic Supplementary Information DFT Characterization on the Mechanism of Water Splitting Catalyzed by Single-Ru-substituted Polyoxometalates Zhong-Ling Lang, Guo-Chun Yang, Na-Na Ma, Shi-Zheng Wen,
ARMA modely čast 2: moving average modely (MA)
 ARMA modely čast 2: moving average modely (MA) Beáta Stehlíková Časové rady, FMFI UK, 2014/2015 ARMA modely časť 2: moving average modely(ma) p.1/24 V. Moving average proces prvého rádu - MA(1) ARMA modely
ARMA modely čast 2: moving average modely (MA) Beáta Stehlíková Časové rady, FMFI UK, 2014/2015 ARMA modely časť 2: moving average modely(ma) p.1/24 V. Moving average proces prvého rádu - MA(1) ARMA modely
7. FUNKCIE POJEM FUNKCIE
 7. FUNKCIE POJEM FUNKCIE Funkcia f reálnej premennej je : - každé zobrazenie f v množine všetkých reálnych čísel; - množina f všetkých usporiadaných dvojíc[,y] R R pre ktorú platí: ku každému R eistuje
7. FUNKCIE POJEM FUNKCIE Funkcia f reálnej premennej je : - každé zobrazenie f v množine všetkých reálnych čísel; - množina f všetkých usporiadaných dvojíc[,y] R R pre ktorú platí: ku každému R eistuje
Start. Vstup r. O = 2*π*r S = π*r*r. Vystup O, S. Stop. Start. Vstup P, C V = P*C*1,19. Vystup V. Stop
 1) Vytvorte algoritmus (vývojový diagram) na výpočet obvodu kruhu. O=2xπxr ; S=πxrxr Vstup r O = 2*π*r S = π*r*r Vystup O, S 2) Vytvorte algoritmus (vývojový diagram) na výpočet celkovej ceny výrobku s
1) Vytvorte algoritmus (vývojový diagram) na výpočet obvodu kruhu. O=2xπxr ; S=πxrxr Vstup r O = 2*π*r S = π*r*r Vystup O, S 2) Vytvorte algoritmus (vývojový diagram) na výpočet celkovej ceny výrobku s
Numerická matematika - výcuc LS 2009/2010, FMFI UK
 Numerická matematika - výcuc LS 2009/2010, FMFI UK Cyby a nepresnosti reportujte na kovac zavináč fotopriestor.sk 16. mája 2010 1 Úvod 1.1 Literatúra Babušíková, Slodička, Weisz - Numerické metódy Mila
Numerická matematika - výcuc LS 2009/2010, FMFI UK Cyby a nepresnosti reportujte na kovac zavináč fotopriestor.sk 16. mája 2010 1 Úvod 1.1 Literatúra Babušíková, Slodička, Weisz - Numerické metódy Mila
Η ΑΝΘΥΦΑΙΡΕΤΙΚΗ ΕΡΜΗΝΕΙΑ ΤΗΣ ΕΞΩΣΗΣ ΤΗΣ ΠΟΙΗΣΗΣ ΣΤΟ ΔΕΚΑΤΟ ΒΙΒΛΙΟ ΤΗΣ ΠΟΛΙΤΕΙΑΣ ΤΟΥ ΠΛΑΤΩΝΟΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ MΑΘΗΜΑΤΙΚΩΝ ΤΜΗΜΑ ΜΕΘΟΔΟΛΟΓΙΑΣ, ΙΣΤΟΡΙΑΣ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΣΤΑΤΙΣΤΙΚΗΣ ΤΜΗΜΑ ΕΠΙΣΤΉΜΩΝ ΑΓΩΓΉΣ & ΘΕΩΡΙΑΣ ΤΗΣ ΕΠΙΣΤΗΜΗΣ ΤΜΗΜΑ ΦΙΛΟΣΟΦΙΑΣ, ΠΑΙΔΑΓΩΓΙΚΗΣ &
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ MΑΘΗΜΑΤΙΚΩΝ ΤΜΗΜΑ ΜΕΘΟΔΟΛΟΓΙΑΣ, ΙΣΤΟΡΙΑΣ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΣΤΑΤΙΣΤΙΚΗΣ ΤΜΗΜΑ ΕΠΙΣΤΉΜΩΝ ΑΓΩΓΉΣ & ΘΕΩΡΙΑΣ ΤΗΣ ΕΠΙΣΤΗΜΗΣ ΤΜΗΜΑ ΦΙΛΟΣΟΦΙΑΣ, ΠΑΙΔΑΓΩΓΙΚΗΣ &
Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy
 Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2012/2013 Jednotkový koreň(unit root),diferencovanie časového radu, unit root testy p.1/18
Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2012/2013 Jednotkový koreň(unit root),diferencovanie časového radu, unit root testy p.1/18
Spojité rozdelenia pravdepodobnosti. Pomôcka k predmetu PaŠ. RNDr. Aleš Kozubík, PhD. 26. marca Domovská stránka. Titulná strana.
 Spojité rozdelenia pravdepodobnosti Pomôcka k predmetu PaŠ Strana z 7 RNDr. Aleš Kozubík, PhD. 6. marca 3 Zoznam obrázkov Rovnomerné rozdelenie Ro (a, b). Definícia.........................................
Spojité rozdelenia pravdepodobnosti Pomôcka k predmetu PaŠ Strana z 7 RNDr. Aleš Kozubík, PhD. 6. marca 3 Zoznam obrázkov Rovnomerné rozdelenie Ro (a, b). Definícia.........................................
Základné poznatky molekulovej fyziky a termodynamiky
 Základné poznatky molekulovej fyziky a termodynamiky Opakovanie učiva II. ročníka, Téma 1. A. Príprava na maturity z fyziky, 2008 Outline Molekulová fyzika 1 Molekulová fyzika Predmet Molekulovej fyziky
Základné poznatky molekulovej fyziky a termodynamiky Opakovanie učiva II. ročníka, Téma 1. A. Príprava na maturity z fyziky, 2008 Outline Molekulová fyzika 1 Molekulová fyzika Predmet Molekulovej fyziky
Ma-Go-20-T List 1. Obsah trojuholníka. RNDr. Marián Macko
 Ma-Go-0-T List 1 Obsah trojuholníka RNDr Marián Macko U: Čo potrebuješ poznať, aby si mohol vypočítať obsah trojuholníka? Ž: Potrebujem poznať jednu stranu a výšku na túto stranu, lebo základný vzorec
Ma-Go-0-T List 1 Obsah trojuholníka RNDr Marián Macko U: Čo potrebuješ poznať, aby si mohol vypočítať obsah trojuholníka? Ž: Potrebujem poznať jednu stranu a výšku na túto stranu, lebo základný vzorec
Cvičenie č. 4,5 Limita funkcie
 Cvičenie č. 4,5 Limita funkcie Definícia ity Limita funkcie (vlastná vo vlastnom bode) Nech funkcia f je definovaná na nejakom okolí U( ) bodu. Hovoríme, že funkcia f má v bode itu rovnú A, ak ( ε > )(
Cvičenie č. 4,5 Limita funkcie Definícia ity Limita funkcie (vlastná vo vlastnom bode) Nech funkcia f je definovaná na nejakom okolí U( ) bodu. Hovoríme, že funkcia f má v bode itu rovnú A, ak ( ε > )(
Το άτομο του Υδρογόνου
 Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες
Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες
Prechod z 2D do 3D. Martin Florek 3. marca 2009
 Počítačová grafika 2 Prechod z 2D do 3D Martin Florek florek@sccg.sk FMFI UK 3. marca 2009 Prechod z 2D do 3D Čo to znamená? Ako zobraziť? Súradnicové systémy Čo to znamená? Ako zobraziť? tretia súradnica
Počítačová grafika 2 Prechod z 2D do 3D Martin Florek florek@sccg.sk FMFI UK 3. marca 2009 Prechod z 2D do 3D Čo to znamená? Ako zobraziť? Súradnicové systémy Čo to znamená? Ako zobraziť? tretia súradnica
ΙΩΑΝΝΗ ΑΘ. ΠΑΠΑΪΩΑΝΝΟΥ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΓΕΩΠΟΝΙΑΣ, ΔΑΣΟΛΟΓΙΑΣ ΚΑΙ ΦΥΣΙΚΟΥ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΤΜΗΜΑ ΓΕΩΠΟΝΙΑΣ ΤΟΜΕΑΣ ΑΓΡΟΤΙΚΗΣ ΟΙΚΟΝΟΜΙΑΣ ΙΩΑΝΝΗ ΑΘ. ΠΑΠΑΪΩΑΝΝΟΥ Πτυχιούχου Γεωπόνου Κατόχου Μεταπτυχιακού
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΓΕΩΠΟΝΙΑΣ, ΔΑΣΟΛΟΓΙΑΣ ΚΑΙ ΦΥΣΙΚΟΥ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΤΜΗΜΑ ΓΕΩΠΟΝΙΑΣ ΤΟΜΕΑΣ ΑΓΡΟΤΙΚΗΣ ΟΙΚΟΝΟΜΙΑΣ ΙΩΑΝΝΗ ΑΘ. ΠΑΠΑΪΩΑΝΝΟΥ Πτυχιούχου Γεωπόνου Κατόχου Μεταπτυχιακού
rs r r â t át r st tíst Ó P ã t r r r â
 rs r r â t át r st tíst P Ó P ã t r r r â ã t r r P Ó P r sã rs r s t à r çã rs r st tíst r q s t r r t çã r r st tíst r t r ú r s r ú r â rs r r â t át r çã rs r st tíst 1 r r 1 ss rt q çã st tr sã
rs r r â t át r st tíst P Ó P ã t r r r â ã t r r P Ó P r sã rs r s t à r çã rs r st tíst r q s t r r t çã r r st tíst r t r ú r s r ú r â rs r r â t át r çã rs r st tíst 1 r r 1 ss rt q çã st tr sã
ARMA modely čast 2: moving average modely (MA)
 ARMA modely čast 2: moving average modely (MA) Beáta Stehlíková Časové rady, FMFI UK, 2011/2012 ARMA modely časť 2: moving average modely(ma) p.1/25 V. Moving average proces prvého rádu - MA(1) ARMA modely
ARMA modely čast 2: moving average modely (MA) Beáta Stehlíková Časové rady, FMFI UK, 2011/2012 ARMA modely časť 2: moving average modely(ma) p.1/25 V. Moving average proces prvého rádu - MA(1) ARMA modely
Laplace Expansion. Peter McCullagh. WHOA-PSI, St Louis August, Department of Statistics University of Chicago
 Laplace Expansion Peter McCullagh Department of Statistics University of Chicago WHOA-PSI, St Louis August, 2017 Outline Laplace approximation in 1D Laplace expansion in 1D Laplace expansion in R p Formal
Laplace Expansion Peter McCullagh Department of Statistics University of Chicago WHOA-PSI, St Louis August, 2017 Outline Laplace approximation in 1D Laplace expansion in 1D Laplace expansion in R p Formal
Matematika 2. časť: Analytická geometria
 Matematika 2 časť: Analytická geometria RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk Súradnicové
Matematika 2 časť: Analytická geometria RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk Súradnicové
Komplexné čísla, Diskrétna Fourierova transformácia 1
 Komplexné čísla, Diskrétna Fourierova transformácia Komplexné čísla C - množina všetkých komplexných čísel komplexné číslo: z = a + bi, kde a, b R, i - imaginárna jednotka i =, t.j. i =. komplexne združené
Komplexné čísla, Diskrétna Fourierova transformácia Komplexné čísla C - množina všetkých komplexných čísel komplexné číslo: z = a + bi, kde a, b R, i - imaginárna jednotka i =, t.j. i =. komplexne združené
Τίτλος: Eνεργά δυναμικά στη θεωρία συναρτησιακών του πρώτου πίνακα πυκνότητας
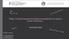 Τίτλος: Eνεργά δυναμικά στη θεωρία συναρτησιακών του πρώτου πίνακα πυκνότητας Μπουσιάδη Σοφία Τριμελής επιτροπή: Ν. Λαθιωτάκης (Ε.Ι.Ε) Ι. Λελίδης (Ε.Κ.Π.Α) Ι. Πετσαλάκης (Ε.Ι.Ε) Περιεχόμενα Εισαγωγή στην
Τίτλος: Eνεργά δυναμικά στη θεωρία συναρτησιακών του πρώτου πίνακα πυκνότητας Μπουσιάδη Σοφία Τριμελής επιτροπή: Ν. Λαθιωτάκης (Ε.Ι.Ε) Ι. Λελίδης (Ε.Κ.Π.Α) Ι. Πετσαλάκης (Ε.Ι.Ε) Περιεχόμενα Εισαγωγή στην
ΚΕΙΜΕΝΟΚΕΝΤΡΙΚΗ ΘΕΩΡΙΑ: ΘΕΩΡΗΤΙΚΟ ΠΛΑΙΣΙΟ ΚΑΙ ΠΕΙΡΑΜΑΤΙΚΗ ΕΦΑΡΜΟΓΗ ΣΕ ΣΠΠΕ ΜΕ ΣΤΟΧΟ ΤΟΝ ΠΕΡΙΒΑΛΛΟΝΤΙΚΟ ΓΡΑΜΜΑΤΙΣΜΟ ΤΩΝ ΜΑΘΗΤΩΝ
 ΚΕΙΜΕΝΟΚΕΝΤΡΙΚΗ ΘΕΩΡΙΑ: ΘΕΩΡΗΤΙΚΟ ΠΛΑΙΣΙΟ ΚΑΙ ΠΕΙΡΑΜΑΤΙΚΗ ΕΦΑΡΜΟΓΗ ΣΕ ΣΠΠΕ ΜΕ ΣΤΟΧΟ ΤΟΝ ΠΕΡΙΒΑΛΛΟΝΤΙΚΟ ΓΡΑΜΜΑΤΙΣΜΟ ΤΩΝ ΜΑΘΗΤΩΝ ΤΣΙΓΚΟΥ Α. 1, και ΝΟΥΤΣΟΥ Α. 1 1 9 ο Δημοτικό Σχολείο Μεγάρων e-mail: atsig@tee.gr,
ΚΕΙΜΕΝΟΚΕΝΤΡΙΚΗ ΘΕΩΡΙΑ: ΘΕΩΡΗΤΙΚΟ ΠΛΑΙΣΙΟ ΚΑΙ ΠΕΙΡΑΜΑΤΙΚΗ ΕΦΑΡΜΟΓΗ ΣΕ ΣΠΠΕ ΜΕ ΣΤΟΧΟ ΤΟΝ ΠΕΡΙΒΑΛΛΟΝΤΙΚΟ ΓΡΑΜΜΑΤΙΣΜΟ ΤΩΝ ΜΑΘΗΤΩΝ ΤΣΙΓΚΟΥ Α. 1, και ΝΟΥΤΣΟΥ Α. 1 1 9 ο Δημοτικό Σχολείο Μεγάρων e-mail: atsig@tee.gr,
Život vedca krajší od vysnívaného... s prírodou na hladine α R-P-R
 Život vedca krajší od vysnívaného... s prírodou na hladine α R-P-R Ako nadprirodzené stretnutie s murárikom červenokrídlym naformátovalo môj profesijný i súkromný život... Osudové stretnutie s murárikom
Život vedca krajší od vysnívaného... s prírodou na hladine α R-P-R Ako nadprirodzené stretnutie s murárikom červenokrídlym naformátovalo môj profesijný i súkromný život... Osudové stretnutie s murárikom
ΚEΦΑΛΑΙΟ 1. Πίνακες. Από τα παραπάνω γίνεται αντιληπτό ότι κάθε γραµµή και στήλη ενός πίνακα A ορίζει µονοσήµαντα τη θέση κάθε στοιχείου A
 ΚEΦΑΛΑΙΟ Πίνακες Εστω και είναι το σώµα των πραγµατικών και των µιγαδικών αριθµών αντιστοίχως Στο εξής όταν γράφουµε F θα εννοούµε είτε το είτε το Ορισµός Eστω F = ή και m, Κάθε ορθογώνια διάταξη m A F
ΚEΦΑΛΑΙΟ Πίνακες Εστω και είναι το σώµα των πραγµατικών και των µιγαδικών αριθµών αντιστοίχως Στο εξής όταν γράφουµε F θα εννοούµε είτε το είτε το Ορισµός Eστω F = ή και m, Κάθε ορθογώνια διάταξη m A F
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
 Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Pevné ložiská. Voľné ložiská
 SUPPORTS D EXTREMITES DE PRECISION - SUPPORT UNIT FOR BALLSCREWS LOŽISKA PRE GULIČKOVÉ SKRUTKY A TRAPÉZOVÉ SKRUTKY Výber správnej podpory konca uličkovej skrutky či trapézovej skrutky je dôležité pre správnu
SUPPORTS D EXTREMITES DE PRECISION - SUPPORT UNIT FOR BALLSCREWS LOŽISKA PRE GULIČKOVÉ SKRUTKY A TRAPÉZOVÉ SKRUTKY Výber správnej podpory konca uličkovej skrutky či trapézovej skrutky je dôležité pre správnu
Řečtina I průvodce prosincem a začátkem ledna prezenční studium
 Řečtina I průvodce prosincem a začátkem ledna prezenční studium Dobson číst si Dobsona 9. až 12. lekci od 13. lekce už nečíst (minulý čas probírán na stažených slovesech velmi matoucí) Bartoň pořídit si
Řečtina I průvodce prosincem a začátkem ledna prezenční studium Dobson číst si Dobsona 9. až 12. lekci od 13. lekce už nečíst (minulý čas probírán na stažených slovesech velmi matoucí) Bartoň pořídit si
DuPont Suva. DuPont. Thermodynamic Properties of. Refrigerant (R-410A) Technical Information. refrigerants T-410A ENG
 Technical Information T-410A ENG DuPont Suva refrigerants Thermodynamic Properties of DuPont Suva 410A Refrigerant (R-410A) The DuPont Oval Logo, The miracles of science, and Suva, are trademarks or registered
Technical Information T-410A ENG DuPont Suva refrigerants Thermodynamic Properties of DuPont Suva 410A Refrigerant (R-410A) The DuPont Oval Logo, The miracles of science, and Suva, are trademarks or registered
An experimental and theoretical study of the gas phase kinetics of atomic chlorine reactions with CH 3 NH 2, (CH 3 ) 2 NH, and (CH 3 ) 3 N
 Electronic Supplementary Material (ESI) for Physical Chemistry Chemical Physics. This journal is the Owner Societies 2015 An experimental and theoretical study of the gas phase kinetics of atomic chlorine
Electronic Supplementary Material (ESI) for Physical Chemistry Chemical Physics. This journal is the Owner Societies 2015 An experimental and theoretical study of the gas phase kinetics of atomic chlorine
Technical Information T-9100 SI. Suva. refrigerants. Thermodynamic Properties of. Suva Refrigerant [R-410A (50/50)]
![Technical Information T-9100 SI. Suva. refrigerants. Thermodynamic Properties of. Suva Refrigerant [R-410A (50/50)] Technical Information T-9100 SI. Suva. refrigerants. Thermodynamic Properties of. Suva Refrigerant [R-410A (50/50)]](/thumbs/89/98928029.jpg) d Suva refrigerants Technical Information T-9100SI Thermodynamic Properties of Suva 9100 Refrigerant [R-410A (50/50)] Thermodynamic Properties of Suva 9100 Refrigerant SI Units New tables of the thermodynamic
d Suva refrigerants Technical Information T-9100SI Thermodynamic Properties of Suva 9100 Refrigerant [R-410A (50/50)] Thermodynamic Properties of Suva 9100 Refrigerant SI Units New tables of the thermodynamic
Electronic Supplementary Information:
 Electronic Supplementary Information: 2 6 5 7 2 N S 3 9 6 7 5 2 S N 3 9 Scheme S. Atom numbering for thione and thiol tautomers of thioacetamide 3 0.6 0. absorbance 0.2 0.0 0.5 0.0 0.05 0.00 N 2 Ar km/mol
Electronic Supplementary Information: 2 6 5 7 2 N S 3 9 6 7 5 2 S N 3 9 Scheme S. Atom numbering for thione and thiol tautomers of thioacetamide 3 0.6 0. absorbance 0.2 0.0 0.5 0.0 0.05 0.00 N 2 Ar km/mol
Approximation of distance between locations on earth given by latitude and longitude
 Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Διευθύνοντα Μέλη του mathematica.gr
 Το «Εικοσιδωδεκάεδρον» παρουσιάζει ϑέματα που έχουν συζητηθεί στον ιστότοπο http://www.mathematica.gr. Η επιλογή και η ϕροντίδα του περιεχομένου γίνεται από τους Επιμελητές του http://www.mathematica.gr.
Το «Εικοσιδωδεκάεδρον» παρουσιάζει ϑέματα που έχουν συζητηθεί στον ιστότοπο http://www.mathematica.gr. Η επιλογή και η ϕροντίδα του περιεχομένου γίνεται από τους Επιμελητές του http://www.mathematica.gr.
Supporting Information
 Supporting Information rigin of the Regio- and Stereoselectivity of Allylic Substitution of rganocopper Reagents Naohiko Yoshikai, Song-Lin Zhang, and Eiichi Nakamura* Department of Chemistry, The University
Supporting Information rigin of the Regio- and Stereoselectivity of Allylic Substitution of rganocopper Reagents Naohiko Yoshikai, Song-Lin Zhang, and Eiichi Nakamura* Department of Chemistry, The University
Úvod do lineárnej algebry. Monika Molnárová Prednášky
 Úvod do lineárnej algebry Monika Molnárová Prednášky 2006 Prednášky: 3 17 marca 2006 4 24 marca 2006 c RNDr Monika Molnárová, PhD Obsah 2 Sústavy lineárnych rovníc 25 21 Riešenie sústavy lineárnych rovníc
Úvod do lineárnej algebry Monika Molnárová Prednášky 2006 Prednášky: 3 17 marca 2006 4 24 marca 2006 c RNDr Monika Molnárová, PhD Obsah 2 Sústavy lineárnych rovníc 25 21 Riešenie sústavy lineárnych rovníc
β) ψ τάξης ως προς Β,
 3.3 Νο μος ταχυ τητας - Μηχανισμο ς αντι δρασης αντιδράσεις ονοµάζονται απλές ή στοιχειώδεις; αντιδράσεις ονοµάζονται πολύπλοκες; Τι ονοµάζεται νόµος ταχύτητας µιας χηµικής Πως προσδιορίζεται ο νόµος της
3.3 Νο μος ταχυ τητας - Μηχανισμο ς αντι δρασης αντιδράσεις ονοµάζονται απλές ή στοιχειώδεις; αντιδράσεις ονοµάζονται πολύπλοκες; Τι ονοµάζεται νόµος ταχύτητας µιας χηµικής Πως προσδιορίζεται ο νόµος της
FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Univerzita Komenského, Bratislava. Aproximácia implicitne definovaných
 FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Univerzita Komenského, Bratislava Katedra algebry, geometrie a didaktiky matematiky Aproximácia implicitne definovaných plôch v E 3 DIPLOMOVÁ PRÁCA Bratislava,
FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Univerzita Komenského, Bratislava Katedra algebry, geometrie a didaktiky matematiky Aproximácia implicitne definovaných plôch v E 3 DIPLOMOVÁ PRÁCA Bratislava,
C. Kontaktný fasádny zatepľovací systém
 C. Kontaktný fasádny zatepľovací systém C.1. Tepelná izolácia penový polystyrén C.2. Tepelná izolácia minerálne dosky alebo lamely C.3. Tepelná izolácia extrudovaný polystyrén C.4. Tepelná izolácia penový
C. Kontaktný fasádny zatepľovací systém C.1. Tepelná izolácia penový polystyrén C.2. Tepelná izolácia minerálne dosky alebo lamely C.3. Tepelná izolácia extrudovaný polystyrén C.4. Tepelná izolácia penový
Príklady na precvičovanie Fourierove rady
 Príklady na precvičovanie Fourierove rady Ďalším významným typom funkcionálnych radov sú trigonometrické rady, pri ktorých sú jednotlivé členy trigonometrickými funkciami. Konkrétne, jedná sa o rady tvaru
Príklady na precvičovanie Fourierove rady Ďalším významným typom funkcionálnych radov sú trigonometrické rady, pri ktorých sú jednotlivé členy trigonometrickými funkciami. Konkrétne, jedná sa o rady tvaru
Electronic Supplementary Information
 Electronic Supplementary Information The preferred all-gauche conformations in 3-fluoro-1,2-propanediol Laize A. F. Andrade, a Josué M. Silla, a Claudimar J. Duarte, b Roberto Rittner, b Matheus P. Freitas*,a
Electronic Supplementary Information The preferred all-gauche conformations in 3-fluoro-1,2-propanediol Laize A. F. Andrade, a Josué M. Silla, a Claudimar J. Duarte, b Roberto Rittner, b Matheus P. Freitas*,a
Math 6 SL Probability Distributions Practice Test Mark Scheme
 Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
EPR spektroskopia. E E(M s
 EPR spektroskopia Elektrónová paramagnetická rezonancia (EPR) patrí do skupiny magnetických rezonančných metód. Najširšie uplatnenie z rezonančných metód zaznamenáva jadrová magnetická rezonancia, ktorá
EPR spektroskopia Elektrónová paramagnetická rezonancia (EPR) patrí do skupiny magnetických rezonančných metód. Najširšie uplatnenie z rezonančných metód zaznamenáva jadrová magnetická rezonancia, ktorá
Photo-Induced Self-Assembly of Pt(II)-Linked Rings and Cages via the Photolabilization of a Pt(II) Pyridine Bond
 Photo-Induced Self-Assembly of Pt(II)-Linked Rings and Cages via the Photolabilization of a Pt(II) Pyridine Bond Ken-ichi Yamashita, Kei-ichi Sato, Masaki Kawano and Makoto Fujita* Contents; Figure S1.
Photo-Induced Self-Assembly of Pt(II)-Linked Rings and Cages via the Photolabilization of a Pt(II) Pyridine Bond Ken-ichi Yamashita, Kei-ichi Sato, Masaki Kawano and Makoto Fujita* Contents; Figure S1.
Einsteinove rovnice. obrázkový úvod do Všeobecnej teórie relativity. Pavol Ševera. Katedra teoretickej fyziky a didaktiky fyziky
 Einsteinove rovnice obrázkový úvod do Všeobecnej teórie relativity Pavol Ševera Katedra teoretickej fyziky a didaktiky fyziky (Pseudo)historický úvod Gravitácia / Elektromagnetizmus (Pseudo)historický
Einsteinove rovnice obrázkový úvod do Všeobecnej teórie relativity Pavol Ševera Katedra teoretickej fyziky a didaktiky fyziky (Pseudo)historický úvod Gravitácia / Elektromagnetizmus (Pseudo)historický
Κεφάλαιο 6 ιανυσµατικοί χώροι...1
 6. ιανυσµατικοί χώροι Σελίδα από 5 Κεφάλαιο 6 ιανυσµατικοί χώροι ιανυσµατικοί χώροι... 6. ιανυσµατικοί χώροι... 6. Υποχώροι...7 6. Γραµµικοί συνδυασµοί... 6. Γραµµική ανεξαρτησία...9 6.5 Άθροισµα και ευθύ
6. ιανυσµατικοί χώροι Σελίδα από 5 Κεφάλαιο 6 ιανυσµατικοί χώροι ιανυσµατικοί χώροι... 6. ιανυσµατικοί χώροι... 6. Υποχώροι...7 6. Γραµµικοί συνδυασµοί... 6. Γραµµική ανεξαρτησία...9 6.5 Άθροισµα και ευθύ
7 Mechanika tuhého telesa
 105 7 Mechanika tuhého telesa V tejto kapitole sú popísané základy dynamiky sústavy hmotných bodov a tuhého telesa. Zovšeobecnia sa vzorce pre pohyb, rýchlosť a zrýchlenie takýchto sústav pomocou ťažiska.
105 7 Mechanika tuhého telesa V tejto kapitole sú popísané základy dynamiky sústavy hmotných bodov a tuhého telesa. Zovšeobecnia sa vzorce pre pohyb, rýchlosť a zrýchlenie takýchto sústav pomocou ťažiska.
KATEDRA DOPRAVNEJ A MANIPULAČNEJ TECHNIKY Strojnícka fakulta, Žilinská Univerzita
 132 1 Absolútna chyba: ) = - skut absolútna ochýlka: ) ' = - spr. relatívna chyba: alebo Chyby (ochýlky): M systematické, M náhoné, M hrubé. Korekcia: k = spr - = - Î' pomerná korekcia: Správna honota:
132 1 Absolútna chyba: ) = - skut absolútna ochýlka: ) ' = - spr. relatívna chyba: alebo Chyby (ochýlky): M systematické, M náhoné, M hrubé. Korekcia: k = spr - = - Î' pomerná korekcia: Správna honota:
ΤΡΙΤΕΚΝΟΣ ΠΙΝΑΚΑΣ ΚΛΑΔΟΥ
 112 134 ΑΒΑΤΑΓΓΕΛΟΥ ΣΟΦΙΑ ΣΠΥΡΙΔΩΝΑΣ ΚΑΣΣΙΑΝΗ ΠΕ70 Δάσκαλοι ΟΧΙ Β 150 19 Κέρκυρα ΔΙΕΥΘΥΝΣΗ Π.Ε. ΚΕΡΚΥΡΑΣ 32 35 ΑΒΡΑΜΙΔΟΥ ΜΑΡΙΚΑ ΔΗΜΗΤΡΙΟΣ ΣΟΦΙΑ ΠΕ70 Δάσκαλοι ΟΧΙ Β 42 28,133 Ζάκυνθος ΔΙΕΥΘΥΝΣΗ Π.Ε. ΖΑΚΥΝΘΟΥ
112 134 ΑΒΑΤΑΓΓΕΛΟΥ ΣΟΦΙΑ ΣΠΥΡΙΔΩΝΑΣ ΚΑΣΣΙΑΝΗ ΠΕ70 Δάσκαλοι ΟΧΙ Β 150 19 Κέρκυρα ΔΙΕΥΘΥΝΣΗ Π.Ε. ΚΕΡΚΥΡΑΣ 32 35 ΑΒΡΑΜΙΔΟΥ ΜΑΡΙΚΑ ΔΗΜΗΤΡΙΟΣ ΣΟΦΙΑ ΠΕ70 Δάσκαλοι ΟΧΙ Β 42 28,133 Ζάκυνθος ΔΙΕΥΘΥΝΣΗ Π.Ε. ΖΑΚΥΝΘΟΥ
DuPont Suva 95 Refrigerant
 Technical Information T-95 SI DuPont Suva refrigerants Thermodynamic Properties of DuPont Suva 95 Refrigerant (R-508B) The DuPont Oval Logo, The miracles of science, and Suva, are trademarks or registered
Technical Information T-95 SI DuPont Suva refrigerants Thermodynamic Properties of DuPont Suva 95 Refrigerant (R-508B) The DuPont Oval Logo, The miracles of science, and Suva, are trademarks or registered
ΟΡΙΣΤΙΚΟΣ ΠΙΝΑΚΑΣ ΩΦΕΛΟΥΜΕΝΩΝ (ΑΛΦΑΒΗΤΙΚΑ) ΑΝΑ ΔΗΜΟ ΔΟΜΗΣ
 ΑΓΓΕΛΟΥ ΑΘΑΝΑΣΙΑ - ΜΑΡΙΑ 22900 74,33 ΑΓΓΕΛΟΥ ΦΙΛΙΠΠΑ - ΑΡΓΥΡΩ 20191 Α1.1 - Βρεφονηπιακός Σταθμός "Η παρεούλα μας" ΑΓΓΕΛΟΥ ΑΝΑΣΤΑΣΙΑ 83231 87,77 ΒΙΡΛΑΣ ΙΩΑΝΝΗΣ 21836 Γ - Κοινωνική Προσπάθεια (ΚΔΑΠ) (Α'
ΑΓΓΕΛΟΥ ΑΘΑΝΑΣΙΑ - ΜΑΡΙΑ 22900 74,33 ΑΓΓΕΛΟΥ ΦΙΛΙΠΠΑ - ΑΡΓΥΡΩ 20191 Α1.1 - Βρεφονηπιακός Σταθμός "Η παρεούλα μας" ΑΓΓΕΛΟΥ ΑΝΑΣΤΑΣΙΑ 83231 87,77 ΒΙΡΛΑΣ ΙΩΑΝΝΗΣ 21836 Γ - Κοινωνική Προσπάθεια (ΚΔΑΠ) (Α'
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
þÿ Ç»¹º ³µÃ ± : Ãż²» Ä Â
 Neapolis University HEPHAESTUS Repository School of Economic Sciences and Business http://hephaestus.nup.ac.cy Master Degree Thesis 2015 þÿ Ç»¹º ³µÃ ± : Ãż²» Ä Â þÿãå½±¹ã ¼±Ä¹º  ½ ¼ Ãͽ  þÿ±à ĵ»µÃ¼±Ä¹º
Neapolis University HEPHAESTUS Repository School of Economic Sciences and Business http://hephaestus.nup.ac.cy Master Degree Thesis 2015 þÿ Ç»¹º ³µÃ ± : Ãż²» Ä Â þÿãå½±¹ã ¼±Ä¹º  ½ ¼ Ãͽ  þÿ±à ĵ»µÃ¼±Ä¹º
Συνεργασία Μουσείου και Σχολείου. Ο ρόλος των Μουσειοπαιδαγωγών ΕΠΙΣΤΗΜΟΝΙΚΗ ΑΝΑΚΟΙΝΩΣΗ 1
 ΕΠΙΣΤΗΜΟΝΙΚΗ ΑΝΑΚΟΙΝΩΣΗ 1 Συνεργασία Μουσείου και Σχολείου Ο ρόλος των Μουσειοπαιδαγωγών Ράπτου Θεοδοσία δασκάλα- μουσειοπαιδαγωγός αποσπασμένη στο Παιδαγωγικό Τμήμα Δημοτικής Εκπαίδευσης Πανεπιστημίου
ΕΠΙΣΤΗΜΟΝΙΚΗ ΑΝΑΚΟΙΝΩΣΗ 1 Συνεργασία Μουσείου και Σχολείου Ο ρόλος των Μουσειοπαιδαγωγών Ράπτου Θεοδοσία δασκάλα- μουσειοπαιδαγωγός αποσπασμένη στο Παιδαγωγικό Τμήμα Δημοτικής Εκπαίδευσης Πανεπιστημίου
Exercises 10. Find a fundamental matrix of the given system of equations. Also find the fundamental matrix Φ(t) satisfying Φ(0) = I. 1.
 Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
Φύλλο1. ΠΕΡΙΟΧΗ ΠΡΟΣΛΗΨΗΣ ΑΒΡΑΜΙΔΟΥ ΜΑΡΙΚΑ ΔΗΜΗΤΡΙΟΣ Γ Αθηνών ΑΒΡΑΜΙΔΟΥ ΣΟΦΙΑ ΔΗΜΗΤΡΙΟΣ Λασίθι ΑΓΓΕΛΗ ΑΝΔΡΟΜΑΧΗ ΒΑΣΙΛΕΙΟΣ
 ΕΠΩΝΥΜΟ ΟΝΟΜΑ ΠΑΤΡΩΝΥΜΟ ΠΕΡΙΟΧΗ ΠΡΟΣΛΗΨΗΣ ΑΒΡΑΜΙΔΟΥ ΜΑΡΙΚΑ ΔΗΜΗΤΡΙΟΣ Γ Αθηνών ΑΒΡΑΜΙΔΟΥ ΣΟΦΙΑ ΔΗΜΗΤΡΙΟΣ Λασίθι ΑΓΓΕΛΗ ΑΝΔΡΟΜΑΧΗ ΒΑΣΙΛΕΙΟΣ Α Ανατ. Αττικής ΑΓΓΕΛΟΠΟΥΛΟΥ ΚΩΝΣΤΑΝΤΙΝΑ ΠΑΝΑΓΙΩΤΗΣ Αχαία ΑΓΓΕΛΟΠΟΥΛΟΥ
ΕΠΩΝΥΜΟ ΟΝΟΜΑ ΠΑΤΡΩΝΥΜΟ ΠΕΡΙΟΧΗ ΠΡΟΣΛΗΨΗΣ ΑΒΡΑΜΙΔΟΥ ΜΑΡΙΚΑ ΔΗΜΗΤΡΙΟΣ Γ Αθηνών ΑΒΡΑΜΙΔΟΥ ΣΟΦΙΑ ΔΗΜΗΤΡΙΟΣ Λασίθι ΑΓΓΕΛΗ ΑΝΔΡΟΜΑΧΗ ΒΑΣΙΛΕΙΟΣ Α Ανατ. Αττικής ΑΓΓΕΛΟΠΟΥΛΟΥ ΚΩΝΣΤΑΝΤΙΝΑ ΠΑΝΑΓΙΩΤΗΣ Αχαία ΑΓΓΕΛΟΠΟΥΛΟΥ
Το αντικείμενο αυτό είναι χειροποίητο από 100% οικολογικό βαμβάκι, με φυτικές βαφές και φυτική κόλλα.
 Cotton leather paper Με υπερηφάνια σας παρουσιάζουμε μια νέα σειρά χειροποίητων προϊόντων το...cotton leather paper. Το αντικείμενο αυτό είναι χειροποίητο από 100% οικολογικό βαμβάκι, με φυτικές βαφές
Cotton leather paper Με υπερηφάνια σας παρουσιάζουμε μια νέα σειρά χειροποίητων προϊόντων το...cotton leather paper. Το αντικείμενο αυτό είναι χειροποίητο από 100% οικολογικό βαμβάκι, με φυτικές βαφές
DuPont Suva 95 Refrigerant
 Technical Information T-95 ENG DuPont Suva refrigerants Thermodynamic Properties of DuPont Suva 95 Refrigerant (R-508B) The DuPont Oval Logo, The miracles of science, and Suva, are trademarks or registered
Technical Information T-95 ENG DuPont Suva refrigerants Thermodynamic Properties of DuPont Suva 95 Refrigerant (R-508B) The DuPont Oval Logo, The miracles of science, and Suva, are trademarks or registered
Affine Weyl Groups. Gabriele Nebe. Summerschool GRK 1632, September Lehrstuhl D für Mathematik
 Affine Weyl Groups Gabriele Nebe Lehrstuhl D für Mathematik Summerschool GRK 1632, September 2015 Crystallographic root systems. Definition A crystallographic root system Φ is a finite set of non zero
Affine Weyl Groups Gabriele Nebe Lehrstuhl D für Mathematik Summerschool GRK 1632, September 2015 Crystallographic root systems. Definition A crystallographic root system Φ is a finite set of non zero
ΠΑΥΛΙΝΑ 609315 ΠΕ11 25,5 ΚΑΒΑΛΑΣ ΑΝΑΤ. ΑΤΤΙΚΗ
 ΕΛΛΕΙΜΑΤΙΚΕΣ - ΠΛΕΟΝΑΣΜΑΤΙΚΕΣ 1 1 ΑΒΑΝΙΔΗ ΑΝΝΑ 593587 ΠΕ70 14 ΚΟΡΙΝΘΙΑ Α ΑΘΗΝΩΝ 2 ΑΒΕΡΚΙΑΔΟΥ ΠΑΤΑΡΙΝΣΚΑ ΠΑΥΛΙΝΑ 609315 ΠΕ11 25,5 ΚΑΒΑΛΑΣ ΑΝΑΤ. ΑΤΤΙΚΗ 3 ΑΒΟΥΡΗ ΑΙΚΑΤΕΡΙΝΗ 590405 ΠΕ16 36,917 ΖΑΚΥΝΘΟΣ ΣΕΡΡΕΣ
ΕΛΛΕΙΜΑΤΙΚΕΣ - ΠΛΕΟΝΑΣΜΑΤΙΚΕΣ 1 1 ΑΒΑΝΙΔΗ ΑΝΝΑ 593587 ΠΕ70 14 ΚΟΡΙΝΘΙΑ Α ΑΘΗΝΩΝ 2 ΑΒΕΡΚΙΑΔΟΥ ΠΑΤΑΡΙΝΣΚΑ ΠΑΥΛΙΝΑ 609315 ΠΕ11 25,5 ΚΑΒΑΛΑΣ ΑΝΑΤ. ΑΤΤΙΚΗ 3 ΑΒΟΥΡΗ ΑΙΚΑΤΕΡΙΝΗ 590405 ΠΕ16 36,917 ΖΑΚΥΝΘΟΣ ΣΕΡΡΕΣ
ΠΕΡΙ ΑΠΕΙΛΟΥΜΕΝΩΝ ΖΩΩΝ...ΑΝΘΡΩΠΩΝ ΕΡΓΑ.
 ΠΕΡΙ ΑΠΕΙΛΟΥΜΕΝΩΝ ΖΩΩΝ...ΑΝΘΡΩΠΩΝ ΕΡΓΑ. ΤΣΟΧΑΝΤΑΡΙΔΟΥ Μ. 2 ο Νηπιαγωγείο Αγ. Ι. Ρέντη και Διεύθυνση Πρωτοβάθμιας Εκπαίδευσης Πειραιά e-mail: martha_tso@hotmail.com ΠΕΡΙΛΗΨΗ Η έννοια του περιβάλλοντος είναι
ΠΕΡΙ ΑΠΕΙΛΟΥΜΕΝΩΝ ΖΩΩΝ...ΑΝΘΡΩΠΩΝ ΕΡΓΑ. ΤΣΟΧΑΝΤΑΡΙΔΟΥ Μ. 2 ο Νηπιαγωγείο Αγ. Ι. Ρέντη και Διεύθυνση Πρωτοβάθμιας Εκπαίδευσης Πειραιά e-mail: martha_tso@hotmail.com ΠΕΡΙΛΗΨΗ Η έννοια του περιβάλλοντος είναι
Zrýchľovanie vesmíru. Zrýchľovanie vesmíru. o výprave na kraj vesmíru a čo tam astronómovia objavili
 Zrýchľovanie vesmíru o výprave na kraj vesmíru a čo tam astronómovia objavili Zrýchľovanie vesmíru o výprave na kraj vesmíru a čo tam astronómovia objavili Zrýchľovanie vesmíru o výprave na kraj vesmíru
Zrýchľovanie vesmíru o výprave na kraj vesmíru a čo tam astronómovia objavili Zrýchľovanie vesmíru o výprave na kraj vesmíru a čo tam astronómovia objavili Zrýchľovanie vesmíru o výprave na kraj vesmíru
Srednicki Chapter 55
 Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Parametre ovplyvňujúce spotrebu paliva automobilu
 1 Portál pre odborné publikovanie ISSN 1338-0087 Parametre ovplyvňujúce spotrebu paliva automobilu Matej Juraj Elektrotechnika, Strojárstvo 20.03.2013 Nasledujúci príspevok pojednáva o fyzikálnych veličinách,
1 Portál pre odborné publikovanie ISSN 1338-0087 Parametre ovplyvňujúce spotrebu paliva automobilu Matej Juraj Elektrotechnika, Strojárstvo 20.03.2013 Nasledujúci príspevok pojednáva o fyzikálnych veličinách,
! "# $ % $&'& () *+ (,-. / 0 1(,21(,*) (3 4 5 "$ 6, ::: ;"<$& = = 7 + > + 5 $?"# 46(A *( / A 6 ( 1,*1 B"',CD77E *+ *),*,*) F? $G'& 0/ (,.
 ! " #$%&'()' *('+$,&'-. /0 1$23(/%/4. 1$)('%%'($( )/,)$5)/6%6 7$85,-9$(- /0 :/986-$, ;2'$(2$ 1'$-/-$)('')5( /&5&-/ 5(< =(4'($$,'(4 1$%$2/996('25-'/(& ;/0->5,$ 1'$-/%'')$(($/3?$%9'&-/?$( 5(< @6%-'9$
! " #$%&'()' *('+$,&'-. /0 1$23(/%/4. 1$)('%%'($( )/,)$5)/6%6 7$85,-9$(- /0 :/986-$, ;2'$(2$ 1'$-/-$)('')5( /&5&-/ 5(< =(4'($$,'(4 1$%$2/996('25-'/(& ;/0->5,$ 1'$-/%'')$(($/3?$%9'&-/?$( 5(< @6%-'9$
AΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ
 AΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΕΙΔΙΚΕΥΣΗΣ ΠΡΟΣΤΑΣΙΑ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΚΑΙ ΒΙΩΣΙΜΗ ΑΝΑΠΤΥΞΗ ΔΙΕΡΕΥΝΗΣΗ ΤΩΝ ΠΙΕΣΕΩΝ ΣΤΟ ΠΕΡΙΒΑΛΛΟΝ
AΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΕΙΔΙΚΕΥΣΗΣ ΠΡΟΣΤΑΣΙΑ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΚΑΙ ΒΙΩΣΙΜΗ ΑΝΑΠΤΥΞΗ ΔΙΕΡΕΥΝΗΣΗ ΤΩΝ ΠΙΕΣΕΩΝ ΣΤΟ ΠΕΡΙΒΑΛΛΟΝ
LP N to BD* C-C = BD C-C to BD* O-H = LP* C to LP* B =5.
 Electronic Supplementary Material (ESI) for Physical Chemistry Chemical Physics. This journal is the Owner Societies 2016 MS No.: CP-ART-03-2016-002134.R1 Optical Response and Gas Sequestration Properties
Electronic Supplementary Material (ESI) for Physical Chemistry Chemical Physics. This journal is the Owner Societies 2016 MS No.: CP-ART-03-2016-002134.R1 Optical Response and Gas Sequestration Properties
PRUŽNOSŤ A PEVNOSŤ PRE ŠPECIÁLNE INŽINIERSTVO
 ŽILINSKÁ UNIVERZITA V ŽILINE Fakulta špeciálneho inžinierstva Doc. Ing. Jozef KOVAČIK, CSc. Ing. Martin BENIAČ, PhD. PRUŽNOSŤ A PEVNOSŤ PRE ŠPECIÁLNE INŽINIERSTVO Druhé doplnené a upravené vydanie Určené
ŽILINSKÁ UNIVERZITA V ŽILINE Fakulta špeciálneho inžinierstva Doc. Ing. Jozef KOVAČIK, CSc. Ing. Martin BENIAČ, PhD. PRUŽNOSŤ A PEVNOSŤ PRE ŠPECIÁLNE INŽINIERSTVO Druhé doplnené a upravené vydanie Určené
Review: Molecules = + + = + + Start with the full Hamiltonian. Use the Born-Oppenheimer approximation
 Review: Molecules Start with the full amiltonian Ze e = + + ZZe A A B i A i me A ma ia, 4πε 0riA i< j4πε 0rij A< B4πε 0rAB Use the Born-Oppenheimer approximation elec Ze e = + + A A B i i me ia, 4πε 0riA
Review: Molecules Start with the full amiltonian Ze e = + + ZZe A A B i A i me A ma ia, 4πε 0riA i< j4πε 0rij A< B4πε 0rAB Use the Born-Oppenheimer approximation elec Ze e = + + A A B i i me ia, 4πε 0riA
Prednáška Fourierove rady. Matematická analýza pre fyzikov IV. Jozef Kise lák
 Prednáška 6 6.1. Fourierove rady Základná myšlienka: Nech x Haφ 1,φ 2,...,φ n,... je ortonormálny systém v H, dá sa tento prvok rozvinút do radu x=c 1 φ 1 + c 2 φ 2 +...,c n φ n +...? Ako nájdeme c i,
Prednáška 6 6.1. Fourierove rady Základná myšlienka: Nech x Haφ 1,φ 2,...,φ n,... je ortonormálny systém v H, dá sa tento prvok rozvinút do radu x=c 1 φ 1 + c 2 φ 2 +...,c n φ n +...? Ako nájdeme c i,
Výpočet. sledu skrátenia koľajníc v zloženom oblúku s krajnými prechodnicami a s medziľahlou prechodnicou a. porovnanie
 Výpočet sledu skrátenia koľajníc v zloženo oblúku s krajnýi prechodnicai a s edziľahlou prechodnicou a porovnanie výsledkov výpočtového riešenia a grafického riešenia Príloha.4 Výpočet sledu skrátenia
Výpočet sledu skrátenia koľajníc v zloženo oblúku s krajnýi prechodnicai a s edziľahlou prechodnicou a porovnanie výsledkov výpočtového riešenia a grafického riešenia Príloha.4 Výpočet sledu skrátenia
Electronic Supplementary Information (ESI)
 Electronic Supplementary Material (ESI) for Dalton Transactions. This journal is The Royal Society of Chemistry 2016 Electronic Supplementary Information (ESI) CPh 3 as a functional group in P-heterocyclic
Electronic Supplementary Material (ESI) for Dalton Transactions. This journal is The Royal Society of Chemistry 2016 Electronic Supplementary Information (ESI) CPh 3 as a functional group in P-heterocyclic
A N A L I S I S K U A L I T A S A I R D I K A L I M A N T A N S E L A T A N S E B A G A I B A H A N C A M P U R A N B E T O N
 I N F O T E K N I K V o l u m e 1 5 N o. 1 J u l i 2 0 1 4 ( 61-70) A N A L I S I S K U A L I T A S A I R D I K A L I M A N T A N S E L A T A N S E B A G A I B A H A N C A M P U R A N B E T O N N o v i
I N F O T E K N I K V o l u m e 1 5 N o. 1 J u l i 2 0 1 4 ( 61-70) A N A L I S I S K U A L I T A S A I R D I K A L I M A N T A N S E L A T A N S E B A G A I B A H A N C A M P U R A N B E T O N N o v i
ΠΕΡΙΦΕΡΕΙΑΚΗ ΕΝΟΤΗΤΑ ΑΤΤΙΚΗΣ ΚΕΝΤΡΙΚΟΥ ΤΟΜΕΑ 17 ΠΕ ΑΤΤΙΚΗΣ ΚΕΝΤΡΙΚΟΥ ΤΟΜΕΑ 33 ΔΕ ΑΤΤΙΚΗΣ ΚΕΝΤΡΙΚΟΥ ΤΟΜΕΑ 41 ΠΕ/ΤΕ ΑΤΤΙΚΗΣ ΚΕΝΤΡΙΚΟΥ ΤΟΜΕΑ 69 ΥΕ
 A/A 1 2 3 4 ΕΠΙΒΛΕΠΩΝ ΦΟΡΕΑΣ ΕΚΠΑΙΔΕΥΣΗΣ Α ΑΘΗΝΑΣ ΕΚΠΑΙΔΕΥΣΗΣ Α ΑΘΗΝΑΣ ΕΚΠΑΙΔΕΥΣΗΣ Α ΑΘΗΝΑΣ ΕΚΠΑΙΔΕΥΣΗΣ Α ΑΘΗΝΑΣ ΥΠΗΡΕΣΙΑ ΤΟΠΟΘΕΤΗΣΗΣ ΔΙΟΙΚΗΤΙΚΗ ΠΕΡΙΦΕΡΕΙΑ ΠΕΡΙΦΕΡΕΙΑΚΗ ΕΝΟΤΗΤΑ ΑΡΙΘΜΟΣ ΘΕΣΕΩΝ ΕΠΙΠΕΔΟ ΕΚΠΑΙΔΕΥΣΗΣ
A/A 1 2 3 4 ΕΠΙΒΛΕΠΩΝ ΦΟΡΕΑΣ ΕΚΠΑΙΔΕΥΣΗΣ Α ΑΘΗΝΑΣ ΕΚΠΑΙΔΕΥΣΗΣ Α ΑΘΗΝΑΣ ΕΚΠΑΙΔΕΥΣΗΣ Α ΑΘΗΝΑΣ ΕΚΠΑΙΔΕΥΣΗΣ Α ΑΘΗΝΑΣ ΥΠΗΡΕΣΙΑ ΤΟΠΟΘΕΤΗΣΗΣ ΔΙΟΙΚΗΤΙΚΗ ΠΕΡΙΦΕΡΕΙΑ ΠΕΡΙΦΕΡΕΙΑΚΗ ΕΝΟΤΗΤΑ ΑΡΙΘΜΟΣ ΘΕΣΕΩΝ ΕΠΙΠΕΔΟ ΕΚΠΑΙΔΕΥΣΗΣ
Διπλωματική εργασία: Τα κίνητρα των παιδιών προσχολικής ηλικίας για μάθηση
 ΤΜΗΜΑ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΚΑΙ ΤΗΣ ΑΓΩΓΗΣ ΣΤΗΝ ΠΡΟΣΧΟΛΙΚΗ ΗΛΙΚΙΑ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΚΑΤΕΥΘΥΝΣΗ: ΚΟΙΝΩΝΙΚΗ ΘΕΩΡΙΑ, ΠΟΛΙΤΙΚΗ ΚΑΙ ΠΡΑΚΤΙΚΕΣ ΣΤΗΝ ΕΚΠΑΙΔΕΥΣΗ Διπλωματική εργασία: Τα κίνητρα
ΤΜΗΜΑ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΚΑΙ ΤΗΣ ΑΓΩΓΗΣ ΣΤΗΝ ΠΡΟΣΧΟΛΙΚΗ ΗΛΙΚΙΑ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΚΑΤΕΥΘΥΝΣΗ: ΚΟΙΝΩΝΙΚΗ ΘΕΩΡΙΑ, ΠΟΛΙΤΙΚΗ ΚΑΙ ΠΡΑΚΤΙΚΕΣ ΣΤΗΝ ΕΚΠΑΙΔΕΥΣΗ Διπλωματική εργασία: Τα κίνητρα
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
ΑΚΑ ΗΜΙΑ ΕΜΠΟΡΙΚΟΥ ΝΑΥΤΙΚΟΥ ΜΑΚΕ ΟΝΙΑΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ
 ΑΚΑ ΗΜΙΑ ΕΜΠΟΡΙΚΟΥ ΝΑΥΤΙΚΟΥ ΜΑΚΕ ΟΝΙΑΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΘΕΜΑ : ΥΠΟΒΡΥΧΙΕΣ ΚΟΠΕΣ ΚΑΙ ΣΥΓΚΟΛΛΗΣΕΙΣ ΑΣΦΑΛΕΙΑ ΥΤΩΝ ΣΠΟΥ ΑΣΤΗΣ : [ΥΦΑΝΤΗΣ ΡΑΦΑΗΛ] ΑΜ : [4187] ΗΜΕΡΟΜΗΝΙΑ ΠΑΡΑ ΟΣΗΣ : 9/1/2013
ΑΚΑ ΗΜΙΑ ΕΜΠΟΡΙΚΟΥ ΝΑΥΤΙΚΟΥ ΜΑΚΕ ΟΝΙΑΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΘΕΜΑ : ΥΠΟΒΡΥΧΙΕΣ ΚΟΠΕΣ ΚΑΙ ΣΥΓΚΟΛΛΗΣΕΙΣ ΑΣΦΑΛΕΙΑ ΥΤΩΝ ΣΠΟΥ ΑΣΤΗΣ : [ΥΦΑΝΤΗΣ ΡΑΦΑΗΛ] ΑΜ : [4187] ΗΜΕΡΟΜΗΝΙΑ ΠΑΡΑ ΟΣΗΣ : 9/1/2013
Aπειλεί τους μισθούς στον ιδιωτικό τομέα
 36Ô Ú. Ê ÏÏÔ 10.597 Àƒø 1,30 TETAPTH 10 NOEMBPIOY 2010 www.enet.gr apple Ú ÂÈ ÓÙÔ ÁÈ appleúfiûıâù Ì ÙÚ È ÌËÓ ÂÈ Î È ÛÙËÓ ÙÚfiÈÎ Ë EıÓÈÎ ÓÔÌÔÛappleÔÓ EÏÏËÓÈÎÔ EÌappleÔÚ Ô, ÓÔÓÙ ÛÙÔÈ Â ÁÈ ÂappleÈ- Î Ó ÓÂ
36Ô Ú. Ê ÏÏÔ 10.597 Àƒø 1,30 TETAPTH 10 NOEMBPIOY 2010 www.enet.gr apple Ú ÂÈ ÓÙÔ ÁÈ appleúfiûıâù Ì ÙÚ È ÌËÓ ÂÈ Î È ÛÙËÓ ÙÚfiÈÎ Ë EıÓÈÎ ÓÔÌÔÛappleÔÓ EÏÏËÓÈÎÔ EÌappleÔÚ Ô, ÓÔÓÙ ÛÙÔÈ Â ÁÈ ÂappleÈ- Î Ó ÓÂ
A Lambda Model Characterizing Computational Behaviours of Terms
 A Lambda Model Characterizing Computational Behaviours of Terms joint paper with Silvia Ghilezan RPC 01, Sendai, October 26, 2001 1 Plan of the talk normalization properties inverse limit model Stone dualities
A Lambda Model Characterizing Computational Behaviours of Terms joint paper with Silvia Ghilezan RPC 01, Sendai, October 26, 2001 1 Plan of the talk normalization properties inverse limit model Stone dualities
March 14, ( ) March 14, / 52
 March 14, 2008 ( ) March 14, 2008 1 / 52 ( ) March 14, 2008 2 / 52 1 2 3 4 5 ( ) March 14, 2008 3 / 52 I 1 m, n, F m n a ij, i = 1,, m; j = 1,, n m n F m n A = a 11 a 12 a 1n a 21 a 22 a 2n a m1 a m2 a
March 14, 2008 ( ) March 14, 2008 1 / 52 ( ) March 14, 2008 2 / 52 1 2 3 4 5 ( ) March 14, 2008 3 / 52 I 1 m, n, F m n a ij, i = 1,, m; j = 1,, n m n F m n A = a 11 a 12 a 1n a 21 a 22 a 2n a m1 a m2 a
k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +
[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R + k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +](/thumbs/73/69566903.jpg) Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Ψηφιακό Μουσείο Ελληνικής Προφορικής Ιστορίας: πώς ένας βιωματικός θησαυρός γίνεται ερευνητικό και εκπαιδευτικό εργαλείο στα χέρια μαθητών
 Μ. Τζακώστα, Α. Σφακιανάκη & Α. Πατσιάς Ψηφιακό Μουσείο Ελληνικής Προφορικής Ιστορίας: πώς ένας βιωματικός θησαυρός γίνεται ερευνητικό και εκπαιδευτικό εργαλείο στα χέρια μαθητών Abstract In this paper
Μ. Τζακώστα, Α. Σφακιανάκη & Α. Πατσιάς Ψηφιακό Μουσείο Ελληνικής Προφορικής Ιστορίας: πώς ένας βιωματικός θησαυρός γίνεται ερευνητικό και εκπαιδευτικό εργαλείο στα χέρια μαθητών Abstract In this paper
PRIEMER DROTU d = 0,4-6,3 mm
 PRUŽINY PRUŽINY SKRUTNÉ PRUŽINY VIAC AKO 200 RUHOV SKRUTNÝCH PRUŽÍN PRIEMER ROTU d = 0,4-6,3 mm èíslo 3.0 22.8.2008 8:28:57 22.8.2008 8:28:58 PRUŽINY SKRUTNÉ PRUŽINY TECHNICKÉ PARAMETRE h d L S Legenda
PRUŽINY PRUŽINY SKRUTNÉ PRUŽINY VIAC AKO 200 RUHOV SKRUTNÝCH PRUŽÍN PRIEMER ROTU d = 0,4-6,3 mm èíslo 3.0 22.8.2008 8:28:57 22.8.2008 8:28:58 PRUŽINY SKRUTNÉ PRUŽINY TECHNICKÉ PARAMETRE h d L S Legenda
PREHĽAD ZÁKLADNÝCH VZORCOV A VZŤAHOV ZO STREDOŠKOLSKEJ MATEMATIKY. Pomôcka pre prípravný kurz
 KATEDRA APLIKOVANEJ MATEMATIKY A INFORMATIKY STROJNÍCKA FAKULTA TU KOŠICE PREHĽAD ZÁKLADNÝCH VZORCOV A VZŤAHOV ZO STREDOŠKOLSKEJ MATEMATIKY Pomôcka pre prípravný kurz 8 ZÁKLADNÉ ALGEBRAICKÉ VZORCE ) (a±b)
KATEDRA APLIKOVANEJ MATEMATIKY A INFORMATIKY STROJNÍCKA FAKULTA TU KOŠICE PREHĽAD ZÁKLADNÝCH VZORCOV A VZŤAHOV ZO STREDOŠKOLSKEJ MATEMATIKY Pomôcka pre prípravný kurz 8 ZÁKLADNÉ ALGEBRAICKÉ VZORCE ) (a±b)
Αλληλεπίδραση ακτίνων-χ με την ύλη
 Άσκηση 8 Αλληλεπίδραση ακτίνων-χ με την ύλη Δ. Φ. Αναγνωστόπουλος Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων Ιωάννινα 2013 Άσκηση 8 ii Αλληλεπίδραση ακτίνων-χ με την ύλη Πίνακας περιεχομένων
Άσκηση 8 Αλληλεπίδραση ακτίνων-χ με την ύλη Δ. Φ. Αναγνωστόπουλος Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων Ιωάννινα 2013 Άσκηση 8 ii Αλληλεπίδραση ακτίνων-χ με την ύλη Πίνακας περιεχομένων
Termodynamika. Doplnkové materiály k prednáškam z Fyziky I pre SjF Dušan PUDIŠ (2008)
 ermodynamika nútorná energia lynov,. veta termodynamická, Izochorický dej, Izotermický dej, Izobarický dej, diabatický dej, Práca lynu ri termodynamických rocesoch, arnotov cyklus, Entroia Dolnkové materiály
ermodynamika nútorná energia lynov,. veta termodynamická, Izochorický dej, Izotermický dej, Izobarický dej, diabatický dej, Práca lynu ri termodynamických rocesoch, arnotov cyklus, Entroia Dolnkové materiály
