Μεθοδολογία για τις Συνήθεις Διαφορικές Εξισώσεις Από την Ενότητα του Ελληνικού Ανοικτού Πανεπιστημίου Σπουδές στις Φυσικές Επιστήμες
|
|
|
- Ἀδράστεια Τοκατλίδης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Μεθοδολογία για τις Συνήθεις Διαφορικές Εξισώσεις Από την Ενότητα του Ελληνικού Ανοικτού Πανεπιστημίου Σπουδές στις Φυσικές Επιστήμες Ανέπτυξα την παρακάτω μεθοδολογία που με βοήθησε να ανταπεξέλθω στο μάθημα των διαφορικών εξισώσεων ως φοιτητής στο ΕΑΠ. Δεν μπορώ να υποσχεθώ ότι δεν περιέχει λάθη. Τα παραδείγματα είναι από εργασίες που εκπόνησα στην διάρκεια της χρονιάς.ελπίζω να σας φανεί χρήσιμο, εάν βρείτε λάθη παρακαλώ επικοινωνήστε μαζί μου να τα διορθώσω. Γιώργος Νικολιδάκης Γενικά : Η γενική λύση των διαφορικών είναι μια οικογένεια καμπυλών και πρέπει να περιέχει τόσες σταθερές όση και η τάξη της διαφορικής. Με τον όροθεμελιώδες σύνολο λύσεων εννοούμε, ότι οι λύσεις πρέπει να είναι λύσεις της διαφορικής και ταυτόχρονα να είναι γραμμικά ανεξάρτητες. ΠΑΤ (Πρόβλημα αρχικών τιμών) Όταν πρέπει να βρεθεί μια συνάρτηση που να ικανοποιεί την διαφορική και δεδομένες συνθήκες οι οποίες αφορούν τις τιμές της άγνωστης συνάρτησης και των παραγώγων της σε ένα σημείο. Οι συνθήκες αυτές λέγονται αρχικές συνθήκες. y(0) = y (0) = ΠΣΤ (Πρόβλημα Συνοριακών Τιμών) Όταν οι συνθήκες που πρέπει να ικανοποιούνται από τη ζητούμενη συνάρτηση δίνονται σε διαφορετικά σημεία το πρόβλημα λέγεται Πρόβλημα Συνοριακών Τιμών (Π.Σ.Τ.) και οι συνθήκες λέγονται Συνοριακές Συνθήκες. y(0) = y () = Όταν η συνάρτηση είναι πεπλεγμένη πχ xe y + 2y = c και μας δίνει συνθήκη y() = αντικαθιστώ το για χ=, y= Και η γενική λύση είναι xe y + 2y = e + 2 Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα
2 Χωριζόμενων Μεταβλητών Έχει την μορφή dy dx = f(x, y) εάν η f(x, y) μπορεί να γραφεί σαν δύο ξεχωριστές συναρτήσεις f(x, y) = f (x)f 2 (x) τότε dy dx = f (x)f 2 (x) dy f 2 (y) = f (x)dx στην τελευταία έχουμε χωρίασει τις μεταβλητές Ολοκληρώνουμε και τα δύο μέλη της παραπάνω dy f 2 (y) = f (x)dx Μπορεί να γραφτεί και όπως παρακάτω P(x)Q(y)dx + R(x)S(y)dy = 0 P(x)Q(y)dx = R(x)S(y)dy P(x) S(y) d(x) = R(x) Q(y) d(y) είναι στην ουσία μια ακριβής ΣΔΕ και είναι του τύπου P(x)dx + Q(y)dy = 0 P y = Q x = 0, P y, Q x είναι οι μερικές παράγωγοι Το χαρακτηριστικό είναι ότι οποιοσδήποτε παράγοντας εμφανίζεται στις εκφράσεις των P(x), Q(y) εξαρτάται μόνο από το x η μόνο από το y Αν θέλουμε μια λύση που περνά από το (x 0, y 0 ) x y P(t)dx + Q(t)dx = 0 x 0 y 0 Παράδειγμα Να λυθεί το Πρόβλημα αρχικών τιμών PAT xy = y 2, y() = 0, όπου y = y(x), x 0 Λύση Η Σ.Δ.Ε που μας δίνεται είναι μια διαφορική εξίσωση χωριζόμενων μεταβλητών. xy = y 2 x dy dx = y2 xdy = dx( y 2 ) y 2 0 y ±, x 0 dy ( y 2 ) = dx x dy ( + y)( y) = dx x dy ( + y)( y) = dx x 2 ( dy ( + y) + dy ( y) ) = dx x 2 ln + y ln y 2 = ln x + c + y ln 2 y = 2 ln x 2 + c + y ln 2 y 2 ln x 2 = c 2 ln + y x 2 ( y) = c Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα 2
3 + y ln x 2 ( y) = 2c e 2c + y = x 2 ( y) + y x 2 ( y) = ±e2c () Αντικαθιστούμε την ±e 2c με μια νέα σταθερά c () + y x 2 ( y) = c + y = x2 ( y)c y + x 2 yc = x 2 c y = x2 c x 2 c + (2) H (2) είναι η γενική λύση της διαφορικής. Εξετάζουμε τις αρχικές συνθήκες για να αποφανθούμε για την τιμή της σταθεράς c (2) y()=0 0 = c c = 0 c = c + Επομένως τελικά η ειδική λύση της διαφορικής είναι : y = x2 x 2 + Ελέγχουμε τις τιμές που έχουμε εξαιρέσει. y = x2 x 2 ± ισχύει πάντα αφού μας δίνεται ότι x 0 + Ομογενείς y (x) = f(x, y) Όπου f(x, y)είναι ομογενείς μηδενικού βαθμού ως προς x και y f(tx, ty) = t n f(x, y) Η Διαφορική μορφή της ομογενούς P(x, y)dx + Q(x, y)dy = 0 όπου P(x, y), Q(x, y) είναι ομογενείς ως πρός τις μεταβλητές τους βαθμού n Αν αντιμετωπίζουμε την διαφορική μορφή θέτουμε u = y dy y = ux x dx = du dx x + dx dx u dy = dx du dx Αν αντιμετωπίζουμε τη λυμένη μορφή θέτουμε y(x) = xu(x) y (x) = x u(x) + xu (x) = u(x) + xu (x) Η αρχική μετατρέπεται σε χωριζόμενων μεταβλητών. Αντικαθιστούμε προς τα πίσω. dx x + dx u dy = xdu + udx dx παράδειγμα Να λυθεί το πρόβλημα συνοριακών τιμών ΠΑΤ xy = y + x 2 + y 2, y() = 0 όπου y = y(x), x > 0 Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα 3
4 Λύση Η συνάρτηση που μας δίνεται γράφεται : y = y + x2 + y 2 x Έστω f(x, y) = y + x2 + y 2 x (), x 0 Σχηματίζουμε τη συνάρτηση f(tx, ty) = ty + t2 x 2 + t 2 y 2 tx = ty + t x2 + y 2 tx = y + x2 + y 2 x Επομένως η συνάρτηση είναι ομογενής μηδενικού βαθμού ως προς x και y. Θέτουμε y(x) = xu(x) y (x) = u(x) + xu (x) (2) Αντικαθιστούμε στην () y = y + x2 + y 2 x u + xu = xu + x2 + x 2 u 2 x xu = + u 2 xdu = ( + u 2 ) dx (3) Η (3) είναι διαφορική εξίσωση χωριζόμενων μεταβλητών. du + u = dx 2 x (4) = t 0 f(x, y) u + xu xu + x + u2 = u + xu = u + + u x 2 όπου υποθέσαμε ότι + u 2 0 το οποίο ισχύει δια κάθε u και x 0 το οποίο μας δίνεται Θα υπολογίσουμε το ολοκλήρωμα du +u 2 Χρησιμοποιούμε την αντικατάσταση + u 2 = (u t) + u 2 = u 2 2ut + t 2 u = t2 2t du = (t2 ) 2t (t 2 )(2t) (2t) 2 dt = 4t2 2t 2 4t 2 dt = 4t2 2t t 2 dt = t2 + 2t 2 dt Αντικαθιστούμε στο ολοκλήρωμα du + u = 2 t 2 + 2t 2 t 2 2t t dt = 2t(t2 + ) dt 2t 2 (t 2 dt = + ) t = ln t + c Με αντικατάσταση προς τα πίσω έχουμε + u 2 = (u t) t = u + u 2 du + u = ln t + c 2 = ln u + u 2 + c Σύμφωνα με τα παραπάνω εργαζόμαστε στην (4)όπου ολοκληρώνουμε και τα δύο μέλη du + u = dx 2 x ln u + u2 + c = ln x Αντικαθιστούμε την Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα 4
5 y(x) = xu(x) u = y x ln y x + ( y y x + ( y y x )2 x + ( y x )2 x )2 + c = ln x ln = c x = ±e c (5) x Αντικαθιστούμε την ±e c με μια νέα σταθερά c (5) y x + ( y x )2 x = c y x + ( y x )2 = cx + ( y x )2 = y x cx + (y x )2 = ( y x cx)2 + y2 x 2 = y2 x 2 2cx y x + cx2 = 2cy + cx 2 y = cx2 (5) 2c H (5) είναι η γενική λύση της διαφορικής. Εξετάζουμε τις αρχικές συνθήκες για να αποφανθούμε για την τιμή της σταθεράς c (5) y()=0 c = 0 c = 0 c = όπου υποθέσαμε ότι 2c 0 το οποίο ισχύει. 2c Επομένως τελικά η ειδική λύση της διαφορικής είναι : y = x2 2 Ακριβείς ή τέλειου διαφορικού P(x, y)dx + Q(x, y)dy = 0 () P(x, y) y = Q(x, y) x Φέρνουμε τη συνάρτηση στη διαφορική μορφή, ελέγχουμε αν ισχύει η παραπάνω εάν ισχύει υπολογίζουμε τη γενική λύση: x F(x, y) = P(t, y)dt a + Q(a, y)dy = c (2) Το α είναι αυθαίρετη σταθερά και μπορούμε να την αντικαταστήσουμε με ότι μας βολεύει στο τέλος αν περισεύει. Για κάθε ΠΑΤ με y(x 0 ) = y 0 δίνει αμέσως την καμπύλη που διέρχεται από το σημείο x P(t, y)dt x 0 Ή αλλιώς y + Q(x 0, t)dt y 0 = c F F = P(x, y), = Q(x, y) x y F(x, y) = P(t, y)dt + Φ(y) [ P(t, y)dt] + Φ(y) = Q(x, y) x Από την τελευταία υπολογίζουμε τη Φ(y) Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα 5
6 Ολοκληρωτικός παράγοντας ή πολλαπλασιαστής Euler u(x, y) x y x + y xy x 2 + y 2 Ο ολοκληρωτικός παράγοντας θα είναι μ(x, y) = e r(u)du r(u) P y Q x Q P y Q x P P y Q x Q P P y Q x yq xp P y Q x 2(xQ yp) Αφού υπολογίσουμε τον ολοκληρωτικό παράγοντα πολλαπλασιάζουμε και τα δύο μέλη της () με τον παράγοντα και η εξίσωση γίνεται τέλειου διαφορικού οπότε η λύση της δίνεται από την (2) Από την (2) μπορεί να προκύψει κάποια παράσταση του a f(a) οπότε αντικαθιστώ c = c + f(a) Εάν με τον παράγοντα x m y n η εξίσωση γίνεται ακριβής τότε ο ολοκληρωτικός παράγοντας είναι μ(x, y) = x m y n Παράδειγμα Να βρεθεί ο ολοκληρωτικός παράγοντας για καθεμιά από τις παρακάτω ΣΔΕ α) xy 3 dx + (x 2 y 2 )dy = 0, y > 0 β) (3xy 2y 2 )dx + (2x 2 3xy)dy = 0, x, y > 0 γ) (xe y + )dx + dy = 0 όπου y = y(x) Λύση (α) Μας δίνεται η Σ.Δ.Ε P(x, y)dx + Q(x, y)dy = xy 3 dx + (x 2 y 2 )dy = 0 P(x, y) = xy 3, Q(x, y) = x 2 y 2 P y = P y = 3xy2 και Q x = Q x = 2xy2 P y Q x = xy 2, P y Q x P = xy2 xy 3 = y Επομένως η διαφορική εξίσωση δέχεται ένα ολοκληρωτικό παράγοντα της μορφής μ(y) = e P y Q x P dy = e y dy = e ln y = e ln y = y Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα 6
7 (β) Μας δίνεται η Σ.Δ.Ε P(x, y)dx + Q(x, y)dy = (3xy 2y 2 )dx + (2x 2 3xy)dy = 0 P(x, y) = 3xy 2y 2, Q(x, y) = 2x 2 3xy P y = P y = 3x 4y και Q x = Q = 4x 3y x P y Q x = x y, P y Q x yq xp = x y 2yx 2 3xy 2 3x 2 y 2xy 2 = x y xy( x y) = xy Επομένως η διαφορική εξίσωση δέχεται ένα ολοκληρωτικό παράγοντα της μορφής μ(xy) = e P y Q x yq xp dxy = e xy dxy = e ln xy = xy = xy x, y > 0 (γ) Μας δίνεται η Σ.Δ.Ε P(x, y)dx + Q(x, y)dy = (xe y + )dx + dy = 0 P(x, y) = xe y +, Q(x, y) = P y = P y = xe y και Q x = Q x = 0 P y Q x = xe y, P y Q x P = xe y xe y = Επομένως η διαφορική εξίσωση δέχεται ένα ολοκληρωτικό παράγοντα της μορφής μ(y) = e P y Q x P dy = e dy = e y Γραμμικής πρώτης τάξης dy dx = f 0 (x) + yf (x) Τη γράφουμε στη μορφή y (x) + f (x)y(x) = f 0 (x) Προσοχή να την γράψουμε στην παραπάνω τυπική μορφή πριν βρούμε τον ολοκληρωτικό παράγοντα. δέχεται πολλαπλασιαστή που είναι ο ολοκληρωτικός παράγοντας μ(x) = e f (x)dx Πολλαπλασιάζουμε τη ΣΔΕ με μ(x) y (x)e f (x)dx + f (x)y(x)e f (x)dx = f 0 (x)e f (x)dx d dx [y(x)e f (x)dx ] = e f (x)dx f 0 (x) y(x)e f (x)dx = e f (x)dx f 0 (x) + c y(x) = [c + f 0 (x)e f (x)dx dx] e f (x)dx Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα 7
8 παράδειγμα u (x) 4 x u(x) = 4x3 (4) Η (4) είναι γραμμική Σ.Δ.Ε πρώτης τάξης, υπολογίζουμε τον ολοκληρωτικό παράγοντα. μ(x) = e 4 x dx = e 4 ln x = x 4 Πολλαπλασιάζουμε την (4) με τον παράγοντα x 4 που υπολογίσαμε παραπάνω x 4 u 4x 5 u = 4x d(x 4 u) dx x 4 y 4 = 4 ln x + c x 4 y 4 4 ln x = c = 4x d(x 4 u) dx = 4x dx x 4 u = 4 ln x + c dx Η παραπάνω εξίσωση σε πεπλεγμένη μορφή αποτελεί λύση της διαφορικής εξίσωσης Bernoulli dy dx + f(x)y = g(x)yn, n 0, y + f(x)y = g(x)y n, n 0, Μπορούμε να την καταλάβουμε γιατί αν θα ήταν γραμμική πρώτου βαθμού. Πολλαπλασιάζουμε με n y n Εισάγουμε μια νέα μεταβλητή u = y n u = ( n)y n y Αντικαθιστούμε και παίρνουμε μια γραμμική πρώτης τάξης u + ( n)f(x)u = ( n)g(x) Παράδειγμα ΝΑ λυθεί η συνήθης διαφορική εξίσωση (x 4 + y 4 )dx xy 3 dy = 0, y = y(x), x, y 0 Λύση Η διαφορική εξίσωση γράφεται (x 4 + y 4 )dx xy 3 dy = 0 xy 3 dy dx + y4 = x 4 dy dx y x = x3 y 3 () Που είναι μια διαφορική εξίσωση Bernoulli της μορφής dy + f(x)y = g(x)yn dx Όπου f(x) = x, g(x) = x3 και n = 3 Πολλαπλασιάζουμε την () με τον όρο 4y 3 4y 3 y 4y4 x = 4x3 (2) Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα 8
9 Θέτουμε u(x) = y 4 u (x) = 4y 3 y (3) (2) (3) u (x) 4 x u(x) = 4x3 (4) Η (4) είναι γραμμική Σ.Δ.Ε πρώτης τάξης, υπολογίζουμε τον ολοκληρωτικό παράγοντα. μ(x) = e 4 x dx = e 4 ln x = x 4 Πολλαπλασιάζουμε την (4)με τον παράγοντα x 4 που υπολογίσαμε παραπάνω x 4 u 4x 5 u = 4x d(x 4 u) dx x 4 y 4 = 4 ln x + c x 4 y 4 4 ln x = c (5) = 4x d(x 4 u) dx = 4x dx x 4 u = 4 ln x + c dx Η παραπάνω εξίσωση (5) σε πεπλεγμένη μορφή αποτελεί λύση της διαφορικής εξίσωσης Ricatti dy dx + f(x)y = g(x)y2 + h(x) () μπορεί να είναι f(x) = 0 y + f(x)y = g(x)y 2 + h(x) Όταν h(x) = 0 έχουμε Bernoulli μπορεί ακόμη και να είναι f(x) = 0 Την αναγνωρίζουμε από τον όρο y 2 και από το ότι μας δίνεται και μια μερική λύση. Αν γνωρίζουμε μια ειδική λύση y = y (x) τότε μπορούμε να βρούμε και τη γενική λύση Λύση : Εισάγουμε μια νέα μεταβλητή : y = y (x) + u, y = y (x) u u 2 Αντικαθιστούμε και η () γίνεται γραμμική πρώτης τάξης Λύση 2: dy dx + f(x)y = g(x)y 2 + h(x) (2) Αφαιρούμε ()-(2) και θέτουμε z = y y dz dx + f(x)z = g(x)(z + 2y )z dz dx + [f(x) 2y g(x)]z = g(x)z 2 Η παραπάνω είναι Bernoulli Παράδειγμα Δίνεται η ΣΔΕ y + y 2 2 = 0, y = y(x), x 0 x2 Να βρεθεί μια μερική λύση της μορφής y(x) = k x και στην συνέχεια βρείτε τη γενική της λύση Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα 9
10 Λύση Η διαφορική εξίσωση y + y 2 2 x2 = 0 () που μας δίνεται γράφεται ως εξής y = y x 2 Που είναι μια διαφορική εξίσωση Ricatti της μορφής dy dx + f(x)y = g(x)y2 + h(x) Όπου: f(x) = 0, g(x) =, h(x) = 2 x 2 Σύμφωνα με την εκφώνηση θα επιβεβαιώσουμε ότι δέχεται λύσεις της μορφής : y(x) = k x Παραγωγίζοντας την παραπάνω έχουμε : y (x) = k x 2 Αντικαθιστούμε στην () k x 2 + k2 x 2 2 x 2 = 0 k2 k 2 x 2 = 0 k 2 k 2 { k = 2 k = Επομένως παρατηρούμε ότι λύσεις της μορφής y(x) = k x και δύο τιμές για το k οι οποίες την επαληθεύουν y (x) = x, y 2 (x) = 2 x, επαληθεύουν την () και μάλιστα ότι υπάρχουν Επιλέγουμε να εγραστούμε με την y (x) = x Θέτουμε z(x) = y(x) y (x) z(x) = y(x) + x y(x) = z(x) x (2) Υπολογίζουμε την παράγωγο ως προς x της (2): y (x) = z (x) + x 2 (3) Αντικαθιστούμε την (2), (3) στην () και έχουμε : () (2),(3) y + y 2 2 x 2 = 0 z + x 2 + (z x ) 2 2 x 2 = 0 z + x 2 + z2 2z x + x 2 2 x 2 = 0 z 2 x z = z2 (4) Η (4) είναι μια διαφορική εξίσωση Bernoulli την οποία πολλαπλασιάζουμε με τον παράγοντα z 2 z 2 z + z 2 2 x z = ( z2 )( z 2 ) z 2 z + z 2 x = (5) Θέτουμε u = z u = z 2 z (6) και η (5) γίνεται : Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα 0
11 z 2 z + z 2 x = u + u 2 x = (7) Η (7) είναι Σ.Δ.Ε γραμμική πρώτης τάξης που για να την επιλύσουμε υπολογίζουμε τον ολοκληρωτικό παράγοντα : μ(x) = e 2 x dx = e 2 ln x = x 2 (8) Πολλαπλασιάζουμε την (7) με τον ολοκληρωτικό παράγοντα x 2 (7) (8) x 2 u + 2xu = x 2 d(x2 u) dx u = x 3 + c x 2 (6) z = x 3 + c x 2 z = x3 3x 2 + 3c 3x 2 z = Η (9) δίνει τη γενική λύση της () = x 2 d(x2 u) dx = x 2 dx x 2 u = x3 dx 3 + c 3x2 (2) x 3 y = + 3c 3x2 x 3 + 3c x (9) Μεθοδολογία Επίλυσης διαφορικών ( μέχρι τώρα) Γράφουμε τη ΣΔΕ στη μορφή y = f(x, y) Με βάση τη μορφή αυτή ελέγχουμε αν είναι:. Ομογενής αν f(tx, ty) = f(x, y) 2. Γραμμική αν έχει τη μορφή y (x) + f (x)y(x) = f 0 (x) 3. Bernouli αν έχει τη μορφή y + f(x)y = g(x)y n, n 0, 4. Ricatti αν έχει τη μορφή y + f(x)y = g(x)y 2 + h(x) Ένα τίποτα από αυτά δεν συμβαίνει τότε τη γράφουμε στη μορφή: P(x, y)dx + Q(x, y)dy = 0 Και ελέγχουμε αν είναι. Χωριζόμενων μεταβλητών αν P(x)dx + Q(y)dy = 0 2. Ακριβής ή τέλειου διαφορικού αν P(x,y) y = Q(x,y) x Ένα τίποτα από αυτά δεν συμβαίνει τότε αναζητούμε πολλαπλασιαστή Euler μ(x, y) = e r(u)du Εάν τίποτα από αυτά δεν ισχύει τότε δεν υπάγεται στις παραπάνω κατηγορίες και πρέπει να διαβάσουμε παρακάτω Γραμμική ανεξαρτησία των λύσεων ορίζουσα του Wronski Έστω ότι y (x), y 2 (x) είναι δυο λύσεις της Δ.Ε.: y + A (x)y + A 2 (x)y = 0 Η παραπάνω λύσεις γράφονται σαν γραμμικός συνδυασμός y = c y + c 2 y 2 Αρκεί η ορίζουσα: y y 2 y y 2 0 Να μην μηδενίζεται πουθενά, (δεν έχει καμιά ρίζα), στο (κοινό) πεδίο ορισμού των y(x),y (x), y2(x), y2 (x). Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα
12 Το κριτήριο αυτό οφείλεται στον Πολωνό μαθηματικό G. Wronski, (Βρόνσκι ). H ορίζουσα W(x) ονομάζεται "ορίζουσα του Wronski"Η γραμμική ομογενής Σ.Δ.Ε. n- τάξης έχει πάντα n γραμμικώς ανεξάρτητες λύσεις. Αν y (x), y 2 (x) y n (x) είναι γραμμικώς ανεξάρτητες λύσεις της, τότε η γενική λύση της () είναι y(x) = c y (x) + c 2 y 2 (x) + + c n y n (x) όπου c, c 2,.., c n είναι αυθαίρετες σταθερές. Το σύνολο των n γραμμικώς ανεξάρτητων λύσεων της () αποτελεί βάση του διανυσματικού χώρου των λύσεων της και λέγεται Θεμελιώδες Σύνολο Λύσεων της Σ.Δ.Ε. (). Β βαθμού Ομογενείς με σταθερούς συντελεστές ay + by + cy = 0 Έχει λύση y = e ρx αρ 2 e ρx + bρe ρx + ce ρx = (αρ 2 + bρ + c)e ρx = 0 Βρίσκουμε τις λύσεις ρ, ρ 2 της χαρακτηριστικής εξίσωσης y (χ) = e ρx, y 2 (χ) = e ρ 2x Γενική λύση όταν έχουμε δύο ρίζες ρ, ρ 2 y = c e ρx + c 2 e ρ 2x Όταν έχουμε διπλή ρίζα ρ = ρ 2 η μία λύση θα είναι y = e ρx Η δεύτερη λύση της εξίσωσης θα είναι : y = xe ρx Και η γενική λύση θα είναι: y = c e ρx + c 2 xe ρx Αν έχει δυο μιγαδικές ρίζες, που είναι συζυγείς η μια της άλλης: a + ib, a ib Στην περίπτωση αυτή, οι μιγαδικές συναρτήσεις: y = e (a+ib)x, y 2 = e (a ib)x είναι δυο γραμμικά ανεξάρτητες λύσεις. Η γενική λύση θα είναι o γραμμικός συνδυασμός των παραπάνω λύσεων y(x) = c y (x) + c y 2 (x) = c e (a+bi)x + c e (a bi)x = c e ax e bix + c e ax e bix Όπου c μιγαδικός αριθμός και c ο συζυγής του. Τελικά (**) προκύπτει ότι μπορούμε να αντικαταστήσουμε τις μιγαδικές λύσεις y = e (a+ib)x, y 2 = e (a ib)x Με τις y = e ax cos(bx), y 2 = e ax sin(bx) Έτσι ώστε να προκύπτει τελικά η γενική λύση y = e ax (c cos(bx) + c 2 sin(bx)) Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα 2
13 Παράδειγμα Να βρεθεί η γενική λύση των συνήθων διαφορικών εξισώσεων (Σ.Δ.Ε.): i) y (x) + y (x) = 0 ii) y (x) 2y (x) + 5y(x) = 0 Λύση Οι Σ.Δ.Ε που μας δίνονται είναι ομογενείς διαφορικές εξισώσεις B βαθμού με σταθερούς συντελεστές. Η διαφορικές αυτές δέχονται λύσεις της μορφής y = e ρx Αντικαθιστώντας στην διαφορική την παραπάνω λύση βγάζουμε την χαρακτηριστική εξίσωση όπου ανάλογα με τις ρίζες της διαμορφώνεται και η γενική λύση i) y (x) + y (x) = 0 Βρίσκουμε την χαρακτηριστική εξίσωση ρ 2 e ρx + ρe ρx = (ρ 2 + ρ)e ρx = 0 ρ(ρ + ) = 0 Ρίζες της χαρακτηριστικής εξίσωσης ρ = 0 πολλαπλότητας ρ 2 = πολλαπλότητας Στην ρίζα ρ = 0 αντιστοιχεί η λύση y (x) = e 0x Στην ρίζα ρ 2 = αντιστοιχεί η λύση y 2 (x) = e x Επομένως η γενική λύση θα είναι o γραμμικός συνδυασμός των παραπάνω λύσεων y(x) = c y (x) + c 2 y 2 (x) = c + c 2 e x ii) y (x) 2y (x) + 5y(x) = 0 Βρίσκουμε την χαρακτηριστική εξίσωση ρ 2 e ρx 2ρe ρx + 5e ρx = 0 ρ 2 2ρ + 5 = 0 Ρίζες της χαρακτηριστικής εξίσωσης ρ = + 2i πολλαπλότητας ρ 2 = 2i πολλαπλότητας Επομένως έχουμε ένα ζευγάρι συζυγών μιγαδικών ριζών πολλαπλότητας, όπου αντιστοιχούν δύο γραμμικώς ανεξάρτητες λύσεις y (x) = e x cos(2x), y 2 (x) = e x sin(2x) Επομένως η γενική λύση θα είναι o γραμμικός συνδυασμός των παραπάνω λύσεων y(x) = c y (x) + c 2 y 2 (x) = c e x cos(2x) + c 2 e x sin(2x) Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα 3
14 N βαθμού Ομογενείς με σταθερούς συντελεστές y (n) (x) + a n y (n ) (x) + a n 2 y (n 2 )(x) + + a y (x) + a 0 y(x) = 0 Έχει λύσεις της μορφής y = e ρx Χαρακτηριστική εξίσωση βαθμού n όσο και η διαφορική και συντελεστές a n i από την διαφορική ρ n + a n ρ n + + a ρ + α 0 = 0 Βρίσκουμε τις ρίζες της παραπάνω. Σε κάθε απλή πραγματική ρίζα ρ αντιστοιχεί λύση της μορφής: y ρ (x) = e ρx 2. Σε κάθε πραγματική ρίζα ρ πολλαπλότητας s αντιστοιχούν s γραμμικώς ανεξάρτητες λύσεις της μορφής: y (x) = e ρx, y 2 (x) = xe ρx, y 3 (x) = x 2 e ρx,, y s (x) = x s e ρx 3. Σε κάθε ζεύγος απλών συζυγών μιγαδικών ριζών έστω r + ui, r ui πολλαπλότητας αντιστοιχούν 2 γραμμικώς ανεξάρτητες λύσεις της μορφής: y (x) = e rx cos(ux), y 2 (x) = e rx sin(ux) 4. Σε κάθε ζεύγος συζυγών μιγαδικών ριζών έστω r + ui, r ui πολλαπλότητας t αντιστοιχούν 2t γραμμικώς ανεξάρτητες λύσεις της μορφής: y (x) = e rx cos(ux), y 2 (x) = e rx xcos(ux), y 3 (x) = e rx x 2 cos(ux),, y t (x) = e rx x t cos(ux) y 2 (x) = e rx sin(ux), y 22 (x) = e rx xsin(ux), y 23 (x) = e rx x 2 sin(ux),, y 2t (x) = e rx x t sin(ux) Σημείωση: όταν έχουμε μιγαδικές ρίζες ρ= r + ui r, u R με βαθμό πολλαπλότητας t, τότε οι αντίστοιχες γραμμικώς ανεξάρτητες λύσεις της διαφορικής θα είναι στην πραγματικότητα : e (r+ui)x, xe (r+ui)x, x 2 e (r+ui)x,, x t e (r+ui)x Οι οποίες δεν είναι πλέον πραγματικές συναρτήσεις. Εν τούτοις, με τη βοήθεια του γνωστού τύπου του Euler e ibx = cos(bx) + isin(bx), e bx = cos(bx) isin(bx) μπορούμε να αντικαταστήσουμε τις t μιγαδικές λύσεις με τις 2t πραγματικές λύσεις e rx cos(ux), e rx xcos(ux), e rx x 2 cos(ux),, e rx x t cos(ux) e rx sin(ux), e rx xsin(ux), e rx x 2 sin(ux),, e rx x t sin(ux) Οι μιγαδικές ρίζες του χαρακτηριστικού πολυωνύμου εμφανίζονται σε ζεύγη r + ui, r ui συζυγών μιγαδικών, έτσι, εύκολα προκύπτει ότι το σύνολο των 2t πραγματικών λύσεων αντιστοιχεί και στις δύο συζυγείς μιγαδικές ρίζες. Γενική λύση θα είναι ο γραμμικός συνδυασμός των λύσεων ανάλογα με τις ρίζες της χαρακτηριστικής Παράδειγμα Να βρεθεί η γενική λύση των συνήθων διαφορικών εξισώσεων (Σ.Δ.Ε.): i) y (x) + 3y (x) + 2y (x) + y(x) = 0 ii) y (4) (x) 2y (x) + y (x) = 0 Λύση i) y (x) + 3y (x) + 2y (x) + y(x) = 0 Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα 4
15 Βρίσκουμε την χαρακτηριστική εξίσωση ρ 3 + 3ρ 2 + 3ρ + = (ρ + ) 3 = 0 Ρίζες της χαρακτηριστικής εξίσωσης ρ = πολλαπλότητας 3 Στην παραπάνω λύση αντιστοιχούν τρείς γραμμικώς ανεξάρτητες λύσεις y (x) = e x, y 2 (x) = xe x, y 3 (x) = x 2 e x Επομένως η γενική λύση θα είναι o γραμμικός συνδυασμός των παραπάνω λύσεων y(x) = c y (x) + c 2 y 2 (x) + c 3 y 3 (x) = c e x + c 2 xe x + c 3 x 2 e x ii) y (4) (x) 2y (x) + y (x) = 0 Βρίσκουμε την χαρακτηριστική εξίσωση ρ 4 2ρ 3 + ρ 2 = ρ 2 (ρ 2 2ρ + ) = 0 Ρίζες της χαρακτηριστικής εξίσωσης ρ,2 = 0 πολλαπλότητας 2 ρ 3,4 = πολλαπλότητας 2 Στην παραπάνω λύση αντιστοιχούν τέσσερις γραμμικώς ανεξάρτητες λύσεις Στην ρίζα ρ,2 = 0 αντιστοιχούν οι λύσεις y (x) = e 0x, y 2 (x) = xe 0x Στην ρίζα ρ 3,4 = αντιστοιχούν οι λύσεις y 3 (x) = e x, y 4 (x) = xe x Επομένως η γενική λύση θα είναι o γραμμικός συνδυασμός των παραπάνω λύσεων y(x) = c y (x) + c 2 y 2 (x) + c 3 y 3 (x) + c 3 y 3 (x) + c 4 y 4 (x) = c + c 2 x + c 3 e x + c 4 xe x N βαθμού Μη Ομογενείς με σταθερούς συντελεστές y (n) (x) + a n y (n ) (x) + a n 2 y (n 2 )(x) + + a y (x) + a 0 y(x) = f(x) () Η γενική λύση της μη ομογενούς ισούται με την γενική λύση της ομογενούς y ομ συν μια οποιαδήποτε μερική λύση της πλήρους εξίσωσης y μ y(x) = y ομ + y μ Για να βρούμε την λύση της μη ομογενούς ος Τρόπος : Μέθοδος προσδιοριστέων συντελεστών 2 ος Τρόπος: Μέθοδος μεταβολής των παραμέτρων Lagrance ος Τρόπος : Μέθοδος προσδιοριστέων συντελεστών Εφαρμόζεται μόνο όταν ο μη ομογενής όρος f(x) έχει τη μορφή f(x) = e ax [P m (x) cos(bx) + Q s sin (bx)] Συνήθως όταν είναι πολυώνυμο, e x,ημίτονο, συνημίτονο Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα 5
16 Όπου a,b πραγματικού και P m (x), Q s (x) πολυώνυμα βαθμού m,s αντίστοιχα Μία λύση της () έχει τη μορφή: y μ (x) = x π e ax [R n (x) cos(bx) + Π n sin (bx)] π είναι η πολλαπλότητα με την οποία ο αριθμός a + ib εμφανίζεται ως ρίζα της χαρακτηριστικής εξίσωσης της ομογενούς ρ n + a n ρ n + + a ρ + α 0 = 0 Και τα πολυώνυμα : R n (x) = r n x n + r n x n + + r x + r 0 Π n (x) = π n x n + π n x n + + π x + π 0 Είναι πολυώνυμα του x βαθμού n = max {m, s} Τα r n, r n,, r, r 0 και π n, π n,, π, π 0 είναι απροσδιόριστοι συντελεστές που πρέπει να προσδιοριστούν αντικαθιστώντας την y μ (x) στην () Μεθοδολογία: Βρίσκουμε την λύση της ομογενούς Θέτουμε το f(x) στη μορφή: f(x) = e ax [P m (x) cos(bx) + Q s (x)sin (bx)] Σημειώνουμε τους συντελεστές a,b,m,s Σχηματίζουμε το μιγαδικό a + ib και βλέπουμε πόσες φορές εμφανίζεται σαν λύση στη χαρακτηριστική εξίσωση (μπορεί να εμφανίζεται 0 φορές) Ο μιγαδικός θέλει προσοχή και δίνω παράδειγμα : Έστω a=0, b=0 τότε a + ib = 0 και για να προσδιορίσουμε το π ψάχνουμε πόσες φορές το 0 παρουσιάζεται σαν ρίζα στις ρίζες της ομογενούς. Έστω a=2, b=0 τότε a + ib = 2 και για να προσδιορίσουμε το π ψάχνουμε πόσες φορές το 2 παρουσιάζεται σαν ρίζα στις ρίζες της ομογενούς. Έστω a=0, b= τότε a + ib = i και για να προσδιορίσουμε το π ψάχνουμε πόσες φορές το i παρουσιάζεται σαν ρίζα στις ρίζες της ομογενούς. Από τα δεδομένα a,b,m,s σχηματίζουμε τη λύση y μ (x) = x π e ax [R n (x) cos(bx) + Π ν (x)sin (bx)] Όπου τα πολυώνυμα έχουν απροσδιόριστους συντελεστές πχ αν βρούμε ότι m=2 και s= R 2 (x) = r 2 x 2 + r x + r 0 Π (x) = π x + π 0 Προσοχή εάν βρούμε πχ P m (x) = 0, Q s (x) = τότε και το m και το s είναι βαθμού 0 και άρα R 0 (x) = r 0, Π 0 (x) = π 0 Βρίσκουμε την y μ (x), y μ (x), y μ (x) (n) Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα 6
17 Προσοχή αντικαθιστούμε στην () την λύση της μη ομογενούς όχι τη γενική λύση Αντικαθιστούμε στην ()και απαιτούμε η συνάρτηση που θα πάρουμε να ικανοποιείται ταυτοτικά, αυτό σημαίνει ότι πρέπει οι συντελεστές ομοβάθμιων όρων ή των ίδιων τριγωνομετρικών όρων να είναι ίσοι. Από τις σχέσεις ισότητας προκύπτει ένα σύστημα από τη λύση του οποίου προσδιορίζουμε τους συντελεστές r n, π n Η γενική λύση θα είναι: y(x) = y ομ + y μ Προσοχή ενώ στη λύση της ομογενούς y ομ υπάρχουν οι γνωστές αυθαίρετες σταθερές c, c 2,.. c n στη λύση της μη ομογενούς y μ δεν βάζουμε αυθαίρετες σταθερές. Επίσης προσοχή εάν βρούμε πχ ότι e ax [0 cos(bx) + sin (bx)] το πολυώνυμο είναι μηδενικού βαθμού και επομένως Η λύση θα είναι x π e ax [R n (x) cos(bx) + Π ν (x)sin (bx)] = x π e ax [Α cos(bx) + Βsin (bx)] δηλαδή το μηδέν πριν το cos έγινε μεταβλητή Α αφού και τα R n (x) και Π ν (x) γίνονται τελικά ίσου βαθμού!! Εάν δεν μπορούμε να γράψουμε τον μη ομογενή όρο στην μορφή f(x) = e ax [P m (x) cos(bx) + Q s sin (bx)] Πχ f(x) = x e ax Τότε ισχύει η παρακάτω ιδιότητα : Ιδιότητα των γραμμικών μη ομογενών εξισώσεων όταν ο μη ομογενής όρος μπορεί να γραφεί σαν άθροισμα Μ προσθετέων. y (n) (x) + a n y (n ) (x) + a n 2 y (n 2 )(x) + + a y (x) + a 0 y(x) = f (x) + f 2 (x) + + f n (x) Μια μερική λύση της παραπάνω μη ομογενούς είναι (προσοχή δεν είναι η γενική λύση ) y μ (χ) + y μ2 (χ) + + y μn (χ) y μ (χ) είναι μιά λύση της εξίσωσης y (n) (x) + a n y (n ) (x) + a n 2 y (n 2 )(x) + + a y (x) + a 0 y(x) = f (x) y μ2 (χ) είναι μιά λύση της εξίσωσης y (n) (x) + a n y (n ) (x) + a n 2 y (n 2 )(x) + + a y (x) + a 0 y(x) = f 2 (x) y μn (χ) είναι μιά λύση της εξίσωσης y (n) (x) + a n y (n ) (x) + a n 2 y (n 2 )(x) + + a y (x) + a 0 y(x) = f n (x) Στην παραπάνω περίπτωση σπάμε την εξίσωση σε δύο ή περισσότερες και βρίσκουμε μια μερική λύση σαν να ήταν ξεχωριστές εξισώσεις και στη συνέχεια προσθέτουμε τις μερικές λύσεις και τους ακόμη απροσδιόριστους συντελεστές και προσδιορίζουμε τους συντελεστές σαν μια ενιαία εξίσωση. Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα 7
18 Παράδειγμα Δίνεται η Σ.Δ.Ε.: y (x) + y (x) 2y (x) = x e x () με τις συνθήκες: y(0) = 0, y (0) =, y (0) = 2 (2) i) Τι είδους πρόβλημα είναι το () (2), αρχικών ή συνοριακών τιμών και γιατί; ii) Να βρεθεί η λύση του () (2) αποκλειστικά με χρήση της μεθόδου των προσδιοριστέων συντελεστών για την εύρεση μιας λύσης της (). Λύση i) Το πρόβλημα που μας δίνεται είναι πρόβλημα αρχικών τιμών γιατί οι συνθήκες που πρέπει να ικανοποιούνται από την διαφορική αναφέρονται στο ίδιο σημείο x=0. ii) y (x) + y (x) 2y (x) = x e x () Η Σ.Δ.Ε που μας δίνονται είναι μη ομογενής διαφορική εξίσωση με σταθερούς συντελεστές. Θα βρούμε πρώτα μια λύση της ομογενούς Θα αναζητήσουμε μια λύση της μορφής y = e ρx Αντικαθιστώντας στην διαφορική την παραπάνω λύση βγάζουμε την χαρακτηριστική εξίσωση ρ 3 e ρx + ρ 2 e ρx 2ρ e ρx = (ρ 3 + ρ 2 2ρ)e ρx = 0 ρ(ρ 2 + ρ 2) = 0 Ρίζες της χαρακτηριστικής εξίσωσης ρ = 0 πολλαπλότητας ρ 2 = 2 πολλαπλότητας ρ 3 = πολλαπλότητας Στην ρίζα ρ = 0 αντιστοιχεί η λύση y (x) = e 0x Στην ρίζα ρ 2 = 2 αντιστοιχεί η λύση y 2 (x) = e 2x Στην ρίζα ρ 3 = αντιστοιχεί η λύση y 3 (x) = e x Επομένως η γενική λύση της ομογενούς θα είναι o γραμμικός συνδυασμός των παραπάνω λύσεων y ομ (x) = c y (x) + c 2 y 2 (x) + c 3 y 3 (x) = c + c 2 e 2x + c 3 e x Προχωρούμε στον εντοπισμό μια μερικής λύσης της μη ομογενούς Η μη ομογενής όρος είναι f(x) = x e x Ο όρος αυτός δεν μπορεί να γραφεί στη μορφή: f(x) = e x [( + ) cos(0x) + 0sin (0x)] Μπορεί όμως να γραφεί σαν άθροισμα δύο προσθετέων f(x) = f (x) + f 2 (x) Όπου f (x) = x, f 2 (x) = e x Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα 8
19 Η γενική λύση της μη ομογενούς ισούται με την γενική λύση της ομογενούς y ομ συν μια οποιαδήποτε μερική λύση της πλήρους εξίσωσης y μ y(x) = y ομ + y μ Θα αναζητήσουμε μια μερική λύση για την μη ομογενή χρησιμοποιώντας την μέθοδο των προσδιοριστέων συντελεστών, κατά την οποία ο μη ομογενής όρος θα πρέπει να μπορεί να γραφεί στη μορφή. f(x) = e ax [P m (x) cos(bx) + Q s sin (bx)] Η πρώτη μη ομογενής εξίσωση είναι y (x) + y (x) 2y (x) = x Ο μη ομογενής όρος x μπορεί να γραφεί στη μορφή: x = e 0x [x cos(0x) + 0sin (0x)] Όπου παρατηρούμε ότι a = 0, b = 0 P 2 x πολυώνυμο βαθμού m= Q 0 0 πολυώνυμο βαθμού s =0 Σύμφωνα με τα παραπάνω η διαφορική εξίσωση δέχεται λύσεις της μορφής: y μ (x) = x π e ax [R n (x) cos(bx) + Π n sin(bx)] Η ρίζα a + bi = 0 εμφανίζεται με βαθμό πολλαπλότητας στην ομογενή επομένως π= και n = max{,0} = επομένως η μορφή μιας λύσης της μη ομογενούς θα είναι : y μ = xe 0x [(Αx + B) cos(0x) + (Γx + Δ) sin(0x)] = x(αx + B) = Ax 2 + Bx Η Δεύτερη μη ομογενής εξίσωση είναι y (x) + y (x) 2y (x) = e x Ο μη ομογενής όρος e x μπορεί να γραφεί στη μορφή: e x = e x [ cos(0x) + 0sin (0x)] Όπου παρατηρούμε ότι a =, b = 0 P 2 πολυώνυμο βαθμού m=0 Q 0 0 πολυώνυμο βαθμού s =0 Σύμφωνα με τα παραπάνω η διαφορική εξίσωση δέχεται λύσεις της μορφής: y μ2 (x) = x π e ax [R n (x) cos(bx) + Π n sin(bx)] Η ρίζα a + bi = εμφανίζεται με βαθμό πολλαπλότητας στην ομογενή επομένως π= και n = max{0,0} = 0 επομένως η μορφή μιας λύσης της μη ομογενούς θα είναι : y μ2 = xe x [Γ cos(0x) + Δ sin(0x)] = Γxe x Η τελική μορφή μιας λύσης της μη ομογενούς πριν τον προσδιορισμό των συντελεστών θα διαμορφωθεί με την πρόσθεση των μερικών λύσεων. Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα 9
20 y μ = y μ + y μ2 = Ax 2 + Bx + Γxe x (2) Θα προσδιορίσουμε τους συντελεστές Α,Β,Γ αντικαθιστώντας τις παραγώγους της y μ στην διαφορική εξίσωση y (x) + y (x) 2y (x) = x e x y μ = 2Ax + B + Γe x + Γxe x y μ = 2A + 2Γe x + Γxe x y μ = 3Γe x + Γxe x 3Γe x + Γxe x + 2A + 2Γe x + Γxe x 2(2Ax + B + Γe x + Γxe x ) = x e x 5Γe x + 2Γxe x + 2A 4Ax 2B 2Γe x 2Γxe x = x e x 3Γe x 4Ax 2B + 2A = x e x Απαιτούμε από την παραπάνω εξίσωση να ισχύει ταυτοτικά και εξισώνουμε τους ομοιοβάθμιους όρους 3Γ = Γ = 3 4Α = } { Α = /4 2Β + 2Α = 0 Β = /4 Σύμφωνα με τα παραπάνω αντικαθιστούμε τους συντελεστές που προσδιορίσαμε στην (2) και μια μερική λύση της μη ομογενούς διαφορικής είναι y μ (x) = 4 x2 4 x x xe 3 Και κατά συνέπεια η γενική λύση της διαφορικής βρίσκεται προσθέτοντας τις γενικές λύσεις της ομογενούς και την μερική λύση της μη ομογενούς y(x) = y ομ (x) + y μ (x) = c + c 2 e 2x + c 3 e x 4 x2 4 x x xe 3 Στην συνέχεια θα υπολογίσουμε τις σταθερές c, c 2, c 3 από τις αρχικές συνθήκες Υπολογίζουμε πρώτα τις παραγώγους της y(x) y (x) = 2c 2 e 2x + c 3 e x 2 x 4 3 (e x + xe x ) y (x) = 4c 2 e 2x + c 3 e x 2 3 (2e x + 2xe x ) Εφαρμόζουμε τις αρχικές συνθήκες y(0) = 0 c + c 2 + c 3 = 0 () y (0) = 2c 2 + c = (2) y (0) = 2 4c 2 + c = 2 (3) Από το σύστημα των (),(2),(3) έχουμε Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα 20
21 c + c 2 + c 3 = 0 2c 2 + c = 4c 2 + c = 2 } { c = 9 8 c 3 = 9 9 c 2 = 9 72 c + c 2 + c 3 = 0 c 3 = 2c c 2 + 2c = 9 6 } Επομένως τελικά η λύση του ΠΑΤ είναι y(x) = e 2x e x 4 x2 4 x x xe 3 c + c 2 + c 3 = 0 c 3 = 2c c 2 = 9 72 } c + c 2 + c 3 = 0 c 3 = 9 9 c 2 = 9 72 } 2 ος Τρόπος: Μέθοδος μεταβολής των παραμέτρων ή μέθοδος του Lagrange Είναι γενική μέθοδος και εφαρμόζεται για οποιαδήποτε γραμμική διαφορική εξίσωση με σταθερούς συντελεστές ή με συντελεστές συναρτήσεις του x και ανεξάρτητα από τη μορφή της f(x) Εφαρμόζεται επίσης όταν για παράδειγμα δεν μπορεί να γραφεί ο μη ομογενής όρος στην μορφή για να εφαρμόσουμε την προηγούμενη μέθοδο των προσδιοριστούν συντελεστών πχ αν υπάρχει ό όρος στη μη ομογενή x το οποίο δεν είναι πολυώνυμο του x αλά ρητή συνάρτηση του x. Εάν οι συντελεστές δεν είναι σταθεροί εμείς γνωρίζουμε να λύνουμε συναρτήσεις του Euler και συναρτήσεις με ελάττωση της τάξης, σε κάθε περίπτωση η Lagrange ξεκινά όταν έχουμε την γενική λύση της ομογενούς. y (n) (x) + a n y (n ) (x) + a n 2 y (n 2 )(x) + + a y (x) + a 0 y(x) = f(x) () Η γενική λύση της ομογενούς θα είναι: y ομ (x) = c y (x) + c 2 y 2 (x)+.. c n y n (x) Αναζητούμε μια λύση της μη ομογενούς y μ (x) = c (x)y (x) + c 2 (x)y 2 (x)+.. c n (x)y n (x) Δηλαδή οι σταθερές c, c 2. της ομογενούς μεταβλήθηκαν σε συναρτήσεις c (χ), c 2 (χ).. c n (x) στη λύση της μη ομογενούς και προσδιορίζονται από την επίλυση του συστήματος: c (x)y (x) + c 2 (x)y 2 (x)+.. c n (x)y n (x) = 0 c (x)y (x) + c 2 (x)y 2 (x)+.. c n (x)y n (x) = 0 c (x)y (x) + c 2 (x)y 2 (x)+.. c n (x)y n (x) = 0.. c (x)y (n 2) (x) + c 2 (x)y 2 (n 2) (x)+.. c n (x)y n (n 2) (x) = 0 c (x)y (n ) (x) + c 2 (x)y 2 (n ) (x)+.. c n (x)y n (n ) (x) = f(x) Είναι ένα n x n σύστημα με άγνωστες τις παραγώγους c (x), c 2 (x),.., c n (x) Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα 2
22 Παρατηρούμε ότι η πρώτη εξίσωση του συστήματος είναι ο γραμμικός συνδυασμός των λύσεων y (x), y 2 (x), y n (x) με συντελεστές τις παραγώγους των αγνώστων συναρτήσεων c (x), c 2 (x),.., c n (x) Η δεύτερη εξίσωση του συστήματος είναι ο γραμμικός συνδυασμός των πρώτων παραγώγων των λύσεων των y (x), y 2 (x),.., y n (x) με συντελεστές πάλι τις παραγώγους των αγνώστων συναρτήσεων c (x), c 2 (x),.., c n (x) Κοκ Προσοχή για να γράψω την τελευταία εξίσωση που στο δεύτερο μέρος εμφανίζεται και η μη ομογενής πρέπει να φέρω την διαφορική στην τυπική μορφή που σημαίνει ότι φέρνω το συντελεστής του y (n) (x) να είναι μονάδα Το παραπάνω σύστημα έχει πάντοτε μοναδική λύση γιατί η ορίζουσα των συντελεστών των αγνώστων είναι η ορίζουσα Wronski των συναρτήσεων y (x), y 2 (x), y n (x) και φυσικά είναι διάφορη του μηδενός δεδομένου ότι οι συναρτήσεις είναι n γραμμικά ανεξάρτητες λύσεις της ομογενούς εξίσωσης. y (x) y (x) 2 y (x) n y (x) y 2 (x) y n (x) y (x) y 2 (x) y. n (x) = W[y (x), y 2 (x), y n (x)] 0 y (n ) (x) y (n ) 2 (x) y (n ) n (x) Μετά την επίλυση του συστήματος προκύπτουν οι συναρτήσεις c (x), c 2 (x),.. c n (x) Τις οποίες αν ολοκληρώσουμε προκύπτουν οι συναρτήσεις που θέλουμε να προσδιορίσουμε. Χωρίς βλάβη της γενικότητας θεωρούμε τη σταθερά της ολοκλήρωσης ίση με 0 γιατί ψάχνουμε μια από όλες τις μερικές λύσεις της () Η δυσκολία έγκειται στον υπολογισμό των ολοκληρωμάτων. Μία λύση της μη ομογενούς επομένως θα είναι: y μ (x) = c (x)y (x) + c 2 (x)y 2 (x)+.. c n (x)y n (x) Μεθοδολογία μεταβολής των παραμέτρων : Εάν δεν μπορούμε να χρησιμοποιήσουμε τη μέθοδο των προσδιοριστέων συντελεστών πχ αν υπάρχει ό όρος στη μη ομογενή x το οποίο δεν είναι πολυώνυμο του x αλά ρητή συνάρτηση του x τότε χρησιμοποιούμε Μεθοδολογία μεταβολής των παραμέτρων. Βρίσκουμε την λύση της ομογενούς y ομ (x) = c y (x) + c 2 y 2 (x)+.. c n y n (x) Και στη συνέχεια βρίσκουμε μία λύση της μη ομογενούς διαφορικής Σχηματίζουμε το σύστημα (αντικαθιστούμε τους συντελεστές c, c 2,.. σε c (x), c 2 (x), c 3 (x) c (x)y (x) + c 2 (x)y 2 (x)+.. c n (x)y n (x) = 0 c (x)y (x) + c 2 (x)y 2 (x)+.. c n (x)y n (x) = 0 Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα 22
23 c (x)y (x) + c 2 (x)y 2 (x)+.. c n (x)y n (x) = 0.. c (x)y (n 2) (x) + c 2 (x)y 2 (n 2) (x)+.. c n (x)y n (n 2) (x) = 0 c (x)y (n ) (x) + c 2 (x)y 2 (n ) (x)+.. c n (x)y n (n ) (x) = f(x) Το επιλύουμε συνήθως με μέθοδο Gramer και παίρνουμε τις λύσεις c (x), c 2 (x),.. c n (x) Ολοκληρώνουμε κάθε μία για να πάρουμε τελικά c (x) = c (x) dx, c 2 (x) = c 2 (x) dx, c n (x) = c 3n (x) dx Χωρίς βλάβη της γενικότητας θεωρούμε τη σταθερά της ολοκλήρωσης ίση με 0 γιατί ψάχνουμε μια από όλες τις μερικές λύσεις της () και η γενική λύση θα είναι: y(x) = y ομ (x) + y μ (x) = c y (x) + c 2 y 2 (x)+.. c n y n (x) + c (x)y (x) + c 2 (x)y 2 (x)+.. c n (x)y n (x) Προσοχή στη λύση της μη ομογενούς όπως παραπάνω c (x)y (x) + c 2 (x)y 2 (x) δεν είναι c (x) + c 2 (x) Παράδειγμα Δίνεται η Σ.Δ.Ε.: y (x) 6y (x) + y (x) 6y(x) = e x Να λυθεί (αποκλειστικά) με χρήση της μεθόδου μεταβολής των παραμέτρων (Lagrange) όταν είναι γνωστό ότι οι συναρτήσεις, y (x) = e x, y (x) = e 2x, y 3 (x) = e 3x αποτελούν ένα θεμελιώδες σύνολο λύσεων της αντίστοιχης ομογενούς της, δηλαδή της y (x) 6y (x) + y (x) 6y(x) = 0 Λύση Εφόσον έχουμε το θεμελιώδες σύνολο των λύσεων της ομογενούς η γενική λύση προκύπτει από τον γραμμικό συνδυασμό των λύσεων. y ομ (x) = c y (x) + c 2 y 2 (x) + c 3 y 3 (x) = c e x + c 2 e 2x + c 3 e 3x Θα βρούμε μια λύση της μη ομογενούς εφαρμόζοντας τη μέθοδο μεταβολής των παραμέτρων. Θα αναζητήσουμε μια λύση της μορφής y μ (x) = c (x)y (x) + c 2 (x)y 2 (x) + c 3 (x)y 3 (x) Όπου θα προσδιορίσουμε τις συναρτήσεις c (x), c 2 (x), c 3 (x) Καταστρώνουμε το σύστημα με τις παραγώγους των παραπάνω συναρτήσεων να ικανοποιούν τις παρακάτω εξισώσεις c (x)e x + c 2 (x)e 2x + c 3 (x)e 3x = 0 c (x)e x + c 2 (x)e 2x + c 3 (x)e 3x = 0 c (x)(e x ) + c 2 (x)(e 2x ) + c 3 (x)(e 3x ) = 0 } c (x)e x + c 2 (x)2e 2x + c 3 (x)3e 3x = 0 } c (x)(e x ) + c 2 (x)(e 2x ) + c 3 (x)(e 3x ) = e x c (x)e x + c 2 (x)4e 2x + c 3 (x)9e 3x = e x Η ορίζουσα των συντελεστών είναι : Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα 23
24 e x e 2x e 3x Δ = e x 2e 2x 3e 3x = 6e x e 2x e 3x 6e x e 2x e 3x + 2e x e 2x e 3x = 2e 6x e x 4e 2x 9e 3x Δ C (x) = 0 e 2x e 3x 0 2e 2x 3e 3x e x 4e 2x 9e 3x = 3e x e 2x e 3x 2e x e 2x e 3x = e 6x Δ C2 (x) = e x 0 e 3x e x 0 3e 3x e x e x 9e 3x = 3e x e x e 3x + e x e x e 3x = 2e 5x Δ C3 (x) = e x e 2x 0 e x 2e 2x 0 e x 4e 2x e x = 2e 4x e 4x = e 4x Και η λύση του συστήματος είναι c (x) = Δ C (x) Δ = e6x 2e 6x = 2 c 2 (x) = Δ C 2 (x) Δ = 2e5x 2e 6x = e x c 3 (x) = Δ C 3 (x) Δ = e4x 2e 6x = 2 e 2x Ολοκληρώνοντας τις παραπάνω συναρτήσεις ως προς x προκύπτουν οι c (x), c 2 (x), c 3 (x) c (x) = c (x) dx = 2 dx = 2 x c 2 (x) = c 2 (x) dx = e x dx = e x c 3 (x) = c 3 (x) dx = 2 e 2x dx = 4 e 2x Όπου θέσαμε χωρίς βλάβη της γενικότητας τη σταθερά της ολοκλήρωσης ίση με 0 γιατί ψάχνουμε μια από όλες τις μερικές λύσεις της διαφορικής. Σύμφωνα με τα παραπάνω μια λύση της μη ομογενούς είναι : y μ (x) = 2 xe x + e x e 2x 4 e 2x e 3x = 2 xe x + e x 4 e x = 2 xe x + 3 x e 4 συνεπώς η γενική λύση της διαφορικής βρίσκεται προσθέτοντας τις γενικές λύσεις της ομογενούς και την μερική λύση της μη ομογενούς y(x) = y ομ (x) + y μ (x) = c e x + c 2 e 2x + c 3 e 3x + 2 xe x + 3 x e 4 Σημείωση : Η μερική λύση της μη ομογενούς με τη ην μέθοδο των προσδιοριστέων συντελεστών δίνει το αποτέλεσμα y μ (x) = x xe 2 Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα 24
25 Η προσθήκη του όρου 3 4 e x με τη μέθοδο μεταβολής των παραμέτρων αποτελεί αποδεκτή μερική λύση αφού ο όρος αυτός δεν μεταβάλλεται στις παραγωγίσεις και οι συντελεστές της ομογενούς,-6,,-6 που έχουν συνολικό άθροισμα 0 τελικά τον μηδενίζουν. Εξισώσεις Euler N Βαθμού μη ομογενείς (ax + b) n y (n) (x) + a n (ax + b) n y (n ) (x) + + a (ax + b)y (x) + a 0 y(x) = f(x) () Οι συντελεστές είναι δυνάμεις του x βαθμού ίσου με την τάξη της αντίστοιχης παραγώγου α 0 Με ένα απλό μετασχηματισμό γίνονται διαφορικές με σταθερούς συντελεστές Θέτουμε ax + b = e at t = dt ln(ax + b) a 0, a dx = ax + b y(x) = y ( eat b ) = Y(t) a dy dx = dy dt dt dx = ax + b Y (t) d 2 y dx 2 = d dx (dy dx ) = d dx ( ax + b Y (t)) = d dx ( ax + b ) Y (t) + ax + b d dx [Y (t)] = a ( (ax + b) 2) Y (t) + d ax + b dt [Y (t)] dt dx = (ax + b) 2 [ Y (t) + Y (t)] Αντικαθιστούμε στην διαφορική εξίσωση την y(x), y (x), y (x), κλπ Παρατηρούμε σε κάθε αντικατάσταση ενός όρου ο όρος (ax + b) n απλοποιείται με τον όρο (ax+b) n Έτσι ώστε τελικά να προκύψει μια μη ομογενής διαφορική με σταθερούς συντελεστές και την καινούρια Y(t) που μπορούμε να επιλύσουμε. Εξισώσεις Euler Β βαθμού ax 2 y + bxy + cy = 0 () a(x + ) 2 y + b(x + )y + cy = 0 a(αx + β) 2 y + b(αx + β)y + cy = 0 Η μεθοδολογία αυτή διαφέρει από την γενική μεθοδολογία, είναι πιο γρήγορη Αναζητούμε λύση της μορφής y = x s, y = (x + ) s, y = (αx + β) s Εξετάζουμε την περίπτωση () όπου Αναζητούμε λύση της μορφής y = x s Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα 25
26 Βρίσκουμε την y = sx s, y = s(s )x s 2 και αντικαθιστούμε στην διαφορική ax 2 s(s )x s 2 + bxsx s + cx s = 0 ax 2 s 2 x s 2 ax 2 sx s 2 + bxsx s + cx s = 0 ax s s 2 asx s + bsx s + cx s = 0 [as 2 + (b a)s + c]x s = 0 Μνημονικός τύπος για το τριώνυμο : as 2 + (b a)s + c Δευτεροβάθμιο τριώνυμο του s που οι ρίζες του αντιστοιχούν στις λύσεις y = c x s + c 2 x s 2 Εάν η δευτεροβάθμια έχει διπλή ρίζα τότε μόνο η μία λύση μπορεί να έχει τη μορφή της δύναμης του x y = x s Η δεύτερη λύση θα είναι y 2 = x s ln x Και η γενική λύση θα είναι : y = c x s + c 2 x s ln x Αν είχαμε τρίτης τάξης Euler και είχαμε τρείς ρίζες ίσες τότε y 2 = x s ln x 2?? Εάν έχουμε μιγαδικές ρίζες a + bi, a bi y = x a+bi = x a x bi = x a (e lnx ) bi = cos(blnx) + sin(blnx) y = x a bi = x a x bi = x a (e lnx ) bi = cos(blnx) sin(blnx) Παράδειγμα Δίνεται η Σ.Δ.Ε. τύπου Euler: x 2 y (x) 2xy (x) + 2y(x) = 0 (), x 0 Λύση i) Να βρεθούν δύο γραμμικώς ανεξάρτητες λύσεις της (), της μορφής x λ. Ποια είναι η ορίζουσα Wronski αυτών; ii) ii) Με χρήση της μεθόδου μεταβολής των παραμέτρων, να βρεθεί η γενική λύση της: x 2 y (x) 2xy (x) + 2y(x) = x 4 e x, x 0 Για τη διαφορική x 2 y (x) 2xy (x) + 2y(x) = 0 (), x 0 Η οποία είναι ΣΔΕ τύπου Euler με συντελεστές δυνάμεις του x βαθμού ίσου με την τάξη της αντίστοιχης παραγώγου. i) Αναζητούμε λύση της μορφής y λ (x) = x λ Βρίσκουμε τις παραγώγους της y λ (x) y λ (x) = λx λ, y λ (x) = λ(λ )x λ 2 και αντικαθιστούμε στην () x 2 λ(λ )x λ 2 2xλx λ + 2x λ = 0 x 2 λ 2 x λ 2 x 2 λx λ 2 2xλx λ + cx λ = 0 x λ λ 2 λx λ 2λx λ + 2x λ = 0 Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα 26
27 [λ 2 3λ + 2]x λ = 0 το τριώνυμο λ 2 3λ + 2 = 0 έχει ρίζες λ =, λ 2 = 2 Συνεπώς υπάρχουν δύο λύσεις της διαφορικής y (x) = x, y 2 (x) = x 2 Η ορίζουσα Wronski είναι : W[y (x), y 2 (x)] = y (x) y 2 (x) y (x) y x2 = x 2 (x) 2x = 2x2 x = x 2 0, γιά x 0 Και επομένως οι λύσεις είναι γραμμικά ανεξάρτητες ii) Έχουμε βρει το θεμελιώδες σύνολο των λύσεων ομογενούς από τη i) και η γενική λύση προκύπτει από τον γραμμικό συνδυασμό των λύσεων. y ομ (x) = c y (x) + c 2 y 2 (x) = c x + c 2 x 2 Θα βρούμε μια λύση της μη ομογενούς εφαρμόζοντας τη μέθοδο μεταβολής των παραμέτρων. Η μη ομογενής γράφεται ως εξής: x 2 y (x) 2xy (x) + 2y(x) = x 4 e x y (x) 2 x y (x) + 2 x 2 y(x) = x2 e x Θα αναζητήσουμε μια λύση της μορφής y μ (x) = c (x)y (x) + c 2 (x)y 2 (x) Όπου θα προσδιορίσουμε τις συναρτήσεις c (x), c 2 (x) Καταστρώνουμε το σύστημα με τις παραγώγους των παραπάνω συναρτήσεων να ικανοποιούν τις παρακάτω εξισώσεις c (x)x + c 2 (x)x 2 = 0 c (x) + c 2 (x)2x = x 2 e x} Η ορίζουσα των συντελεστών είναι : Δ = x x2 2x = x2 Δ C (x) = 0 x 2 x 2 e x 2x = x4 e x Δ C2 (x) = x 0 x 2 e x = x3 e x Και η λύση του συστήματος είναι c (x) = Δ C (x) Δ c 2 (x) = Δ C 2 (x) Δ = x4 e x x 2 = x3 e x x 2 = x 2 e x = xe x Ολοκληρώνοντας τις παραπάνω συναρτήσεις ως προς x προκύπτουν οι c (x), c 2 (x) Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα 27
28 c (x) = c (x) dx = x 2 e x dx = x 2 (e x ) dx = x 2 e x + 2xe x dx = x 2 e x + 2 x e x dx = x 2 e x + 2xe x 2 e x dx = x 2 e x + 2xe x 2e x c 2 (x) = c 2 (x) dx = x e x dx = xe x e x dx = xe x e x Όπου θέσαμε χωρίς βλάβη της γενικότητας τη σταθερά της ολοκλήρωσης ίση με 0 γιατί ψάχνουμε μια από όλες τις μερικές λύσεις της διαφορικής. Σύμφωνα με τα παραπάνω μια λύση της μη ομογενούς είναι : y μ (x) = c (x)x + c 2 (x)x 2 = x 3 e x + 2x 2 e x 2xe x + x 3 e x x 2 e x = x 2 e x 2xe x y μ (x) = x 2 e x 2xe x Συνεπώς η γενική λύση της διαφορικής βρίσκεται προσθέτοντας τις γενικές λύσεις της ομογενούς και την μερική λύση της μη ομογενούς y(x) = y ομ (x) + y μ (x) = c x + c 2 x 2 + x 2 e x 2xe x Μέθοδος Υποβιβασμού της τάξης Η μέθοδος αυτή εφαρμόζεται κυρίως σε Γραμμικές ομογενείς διαφορικές δεύτερης τάξεως Αν είναι γνωστή μία λύση και ζητάμε να βρούμε τη γενική λύση της Σ.Δ.Ε Έτσι, αρκεί να βρούμε δύο γραμμικώς ανεξάρτητες λύσεις της y, y 2 και η γενική της λύση θα δίνεται από το γραμμικό συνδυασμό y(x) = c y (x) + c 2 y 2 (x) (3) Όπου c και c 2 αυθαίρετες σταθερές. Μας δίνει μια λύση της (), την y επομένως χρειάζεται να βρούμε μια δεύτερη λύση της Σ.Δ.Ε. (), την οποία να αντικαταστήσουμε στην (3) και να προκύψει η γενική λύση y(x). Για να βρούμε τη δεύτερη αυτή λύση της () που θα είναι συγχρόνως γραμμικώς ανεξάρτητη της λύσης y θα χρησιμοποιήσουμε τη μέθοδο υποβιβασμού τάξης. Για τη μέθοδο αυτή, θα εφαρμόσουμε τα ακόλουθα βήματα: Βήμα : Εισάγουμε τη νέα άγνωστη συνάρτηση u(x), αναζητώντας λύση y 2 της μορφής y 2 (x) = u(x)y (x) (4) Τότε, παραγωγίζουμε την (4) διαδοχικά δύο φορές και παίρνουμε y 2 (x) = u (x)y + u(x)y (x) (5) y 2 (x) = u (x)y (x) + 2u (x)y (x) + u(x)y (x) (6) Βήμα 2: Η y 2 πρέπει να είναι λύση της Σ.Δ.Ε. (), δηλαδή να την ικανοποιεί. Έτσι, αντικαθιστούμε τις (4), (5) και (6) στην () και κάνουμε τις προκύπτουσες αναγωγές. Η εξίσωση στην οποία καταλήγουμε, περιέχει Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα 28
29 τη γνωστή συνάρτηση y και τις παραγώγους της y, y και μόνον τις παραγώγους u και u της άγνωστης συνάρτησης u. Η ίδια η συνάρτηση u έχει εξαλειφθεί! Βήμα 3: Εισάγουμε τη συνάρτηση Φ(x) = u (x) (7) και κατά συνέπεια τη Φ (x) = u (x) (8) στην εξίσωση στην οποία καταλήξαμε στο βήμα 2, και η νέα Σ.Δ.Ε. είναι πρώτης τάξης ως προς την άγνωστη συνάρτηση Φ(x). Βήμα 4: Βρίσκουμε τη γενική λύση Φ(χ) της πρώτης τάξης Σ.Δ.Ε. που προέκυψε στο βήμα 3. Βήμα 5: Με γνωστή τη συνάρτηση Φ(χ), λύνουμε την εξίσωση (7) με απευθείας ολοκλήρωση και υπολογίζουμε τη συνάρτηση u(x). Βήμα 6: Αντικαθιστούμε τη γνωστή πλέον συνάρτηση u(x) στην (4) και βρίσκουμε τη συνάρτηση y 2 (x) η οποία είναι λύση της (), γραμμικώς ανεξάρτητη της y Είναι χρήσιμο σ αυτό το σημείο να επαληθεύσουμε ότι αυτά πράγματι ισχύουν. Βήμα 7: Αντικαθιστούμε τις y και y 2 στην (3) και βρίσκουμε τη γενική λύση της Σ.Δ.Ε. (). ΜΕΘΟΔΟΣ ΣΕΙΡΩΝ Η Μέθοδος των Σειρών είναι μια γενική μέθοδος για κάθε είδους Σ.Δ.Ε., γραμμικές και μη γραμμικές, αλλά εφαρμόζεται συνήθως σε γραμμικές ομογενείς Σ.Δ.Ε. δεύτερης τάξης, με μη σταθερούς συντελεστές, οι οποίες δεν έχουν μορφή κατάλληλη ώστε να επιλυθούν με τη μέθοδο Euler ούτε μπορούν να αντιμετωπισθούν με τη μέθοδο υποβιβασμού τάξης. Με τη Μέθοδο των Σειρών μελετούμε Σ.Δ.Ε. της μορφής A(x)y (x) + B(x)y (x) + T(x) = 0 () όπου Α(x),B(x),T(x) πραγματικές συναρτήσεις του x, σε μια μικρή περιοχή γύρω από ένα σημείο x 0 δηλαδή αναζητούμε λύση όταν οι αρχικές συνθήκες ορίζονται γύρω από το x 0 ή όταν ζητείται γενική λύση γύρω από το x 0 Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα 29
30 Το x 0 μπορεί να είναι: ομαλό κανονικό ανώμαλο μη κανονικό ανώμαλο σημείο για τη Σ.Δ.Ε. (). Για να χαρακτηρίσουμε ένα σημείο x 0 γύρω από το οποίο θέλουμε να μελετήσουμε τη Σ.Δ.Ε. (), ως ομαλό, κανονικό ανώμαλο ή μη κανονικό ανώμαλο, τη φέρνουμε στη μορφή y (x) + P(x)y (x) + Q(x)y(x) = 0 (2) όπου P(x) = B(x)/A(x) και Q(x) = Γ(x)/A(x) Ένα σημείο x 0 θα χαρακτηρίζεται ως: Ομαλό εάν οι συναρτήσεις P(x) και Q(x) της (2) ορίζονται και είναι αναλυτικές στο x0. Κανονικό ανώμαλο, εάν οι συναρτήσεις (x x 0 )P(x) και(x x 0 ) 2 Q(x) είναι συγχρόνως αναλυτικές στο x 0 Μη κανονικό ανώμαλο, εάν το x 0 δεν είναι ούτε ομαλό ούτε κανονικό ανώμαλο σημείο. Θα αναπτύξουμε τη μέθοδο επίλυσης της Σ.Δ.Ε. () σε περιοχή γύρω από ένα ομαλό ή κανονικό ανώμαλο σημείο της, που βασίζεται στη θεωρία του Frobenious. Σύμφωνα με τη μέθοδο, αναζητούμε λύσεις της μορφής y(x) = a n (x x 0 ) λ+n (3) όπου λ είναι μια κατάλληλα επιλεγμένη σταθερά και x 0 το κέντρο της περιοχής μελέτης της Σ.Δ.Ε. αλλά και το σημείο ανάπτυξης της σειράς. Οι λύσεις αυτές συγκλίνουν σε μια μικρή περιοχή γύρω από το σημείο x 0 Δεδομένου ότι ο μετασχηματισμός t = x x 0 μεταφέρει τη μελέτη της Σ.Δ.Ε. από το σημείο x 0 στο σημείο 0, θα επιλέξουμε για απλότητα να μελετήσουμε την () σε περιοχή του σημείου 0. Ακολουθούμε τα παρακάτω βήματα: Μεθοδολογία Για να μπορεί να εφαρμοστεί η μεθόδου Frobenius θα πρέπει η Σ.Δ.Ε. () να μην περιέχει μη κανονικά ανώμαλα σημεία. Έτσι, κατ αρχήν πρέπει να διερευνήσουμε την () ως προς το είδος των σημείων x στα οποία ορίζεται. Γράφουμε την () στη μορφή y (x) + P(x)y (x) + Q(x)y(x) = 0 (2) Ελέγχουμε αν υπάρχουν σημεία στα οποία οι P(x) και ή Q(x) δεν ορίζονται. Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα 30
31 Περίπτωση : Εάν δεν υπάρχουν τέτοια σημεία, τότε η () ορίζεται μόνο σε ομαλά σημεία και η λύση της βρίσκεται άμεσα, με αντικατάσταση της δυναμοσειράς στη Σ.Δ.Ε. και απευθείας υπολογισμό των συντελεστών της σειράς.. Αναζητούμε λύση της () της μορφής y(x) = α n (x x 0 ) n (2) 2. Παραγωγίζουμε την y(x) που ορίσαμε στην (2) διαδοχικά δύο φορές (αν για ή n= ο αντίστοιχος όρος της σειράς είναι μηδενικός η άθροιση ξεκινά από το n= ή to n=2). y (x) = nα n (x x 0 ) n, y (x) = n(n )α n (x x 0 ) n 2 n= n=2 και αντικαθιστούμε τις y, y, y στη Σ.Δ.Ε. 3. Σκοπός του βήματος αυτού είναι να ρυθμίσει τους δείκτες άθροισης στις τρείς σειρές κατά τέτοιον τρόπο, ώστε να εμφανίσουν την ίδια δύναμη του x ως κοινό παράγοντα και επίσης η άθροιση να ξεκινάει σε όλες από την ίδια τιμή του δείκτη. Προκειμένου να μπορέσουμε να αθροίσουμε αυτές τις σειρές θα πρέπει να είναι όλες δυναμοσειρές του ίδιου όρου, και επομένως θα κάνουμε μια μετάθεση των δεικτών ώστε να εμφανίζονται με τον ίδιο όρο. Η άθροιση είναι ανεξάρτητη από τον δείκτη. Με αυτό τον τρόπο, η εξίσωση θα εκφραστεί ως μηδενισμός μιας σειράς. 4. Ο αναδρομικός τύπος υπολογίζεται από το γεγονός ότι η εξίσωση θα εκφραστεί ως μηδενισμός μιας σειράς, στη μορφή [f(λ + sn)c n + g(λ + s(n ))c n ]x sn = 0 (6) Η (6) θα ισχύει για κάθε x όταν όλοι οι συντελεστές της σειράς του αριστερού μέλους είναι μηδέν και έτσι προκύπτει ο αναγωγικός τύπος c n = (λ + s(n )) c f(λ + sn) n, n (7) 5. Τελικά η λύση είναι να αναπτύξουμε τον αναδρομικό τύπο και να αντικαταστήσουμε στην εξίσωση y(x) = α n x n = a 0 + a x + a 2 x 2 + a 3 x a n x n + (8) Όπου οι συντελεστές υπολογίζονται από τον αναδρομικό τύπο, και στο τέλος θα βρούμε ένα τύπο y(x) = a 0 ( ) + a ( ) Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα 3
32 Που είναι η γενική λύση μια γενική προσέγγιση για τον υπολογισμό του α 0, α είναι πχ α 0 0, α = 0 και στη συνέχεια υπολογίζουμε το y (x) από την (8) στη συνέχεια αντιστρέφουμε α 0, α 0 = 0 και υπολογίζουμε το y 2 (x) Περίπτωση 2: Εάν υπάρχει σημείο x 0 στο οποίο οι P(x) και ή Q(x) δεν ορίζονται (ανώμαλο σημείο), τότε ελέγχουμε αν οι συναρτήσεις (x x 0 )P(x) και (x x 0 ) 2 Q(x) είναι συγχρόνως αναλυτικές στο σημείο αυτό. Εάν αυτό ισχύει, το x 0 είναι κανονικό ανώμαλο και η λύση της Σ.Δ.Ε. υπολογίζεται με τη μέθοδο του Frobenius. Εάν δεν ισχύει, το x 0 είναι μη κανονικό ανώμαλο σημείο και η μέθοδος του Frobenius δεν εφαρμόζεται. Στη συνέχεια, αφού εξασφαλίσουμε ότι μπορούμε να εφαρμόσουμε τη μέθοδο του Frobenius Αναζητούμε λύσεις της μορφής y(x) = α n (x x 0 ) n+λ (2) Υπολογίζουμε την εξίσωση δεικτών για το λ : λ(λ ) + p 0 λ + q 0 = 0 όπου p 0 = lim x 0 (xp(x)) και q 0 = lim x 0 (x 2 q(x)) Προχωρούμε στα υπόλοιπα βήματα 2,3,4,5 όπως παραπάνω Από την εξίσωση των δεικτών (3) υπολογίζουμε τις τιμές του λ Χρήσιμες σχέσεις για την αναγνώριση του αθροίσματος της σειράς στην οποία έχουμε καταλήξει, όταν αυτό είναι δυνατόν, είναι οι ακόλουθες στις οποίες ο n είναι πάντα φυσικός αριθμός. n! = n με 0! = (2n)! = (2n )(2n) (2n + )! = (2n )(2n)(2n + ) (2n)!! = (2n 2)(2n) = 2 n n! (2n + )!! = (2n )(2n + ) sinx = ( )n (2n + )! x2n+ (9) cosx = ( )n (2n)! x2n (20) Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα 32
33 e x = xn n! (2) lnx = 2 (2n + ) (x 2n x + ), x > 0 (22) Παράδειγμα για το σημείο να είναι ομαλό κανονικό και x 0 = 0 Μας δίνεται η Σ.Δ.Ε ( x)y (x) y (x) + xy(x) = 0 () Την φέρνουμε στην τυπική μορφή με τον συντελεστή της μεγαλύτερης τάξης ίσο με μονάδα y (x) x ( x) y (x) + ( x) y(x) = 0 όπου παρατηρούμε ότι είναι της μορφής y (x) p(x)y (x) + q(x)y(x) = 0 με p(x) = ( x) και q(x) = x ( x) Όπου παρατηρούμε ότι οι συναρτήσεις p(x)και q(x) είναι αναλυτικές για κάθε x R εκτός από το σημείο x = επομένως το σημείο x 0 = 0 είναι ομαλό (αναλυτικό) της (). Αναζητούμε λύση της () της μορφής y(x) = α n x n (2) Παραγωγίζουμε την y(x) που ορίσαμε στην (2) διαδοχικά δύο φορές (αν για ή n= ο αντίστοιχος όρος της σειράς είναι μηδενικός η άθροιση ξεκινά από το n= ή to n=2). y (x) = nα n x n, y (x) = n(n )α n x n 2 n= n=2 και αντικαθιστούμε τις y, y, y στη Σ.Δ.Ε. (). ( x) n(n )α n x n 2 nα n x n + x α n x n = 0 n=2 n= n(n )α n x n 2 n(n )α n x n α x 0 nα n x n + α n x n+ = 0 n=2 n=2 n=2 α x 0 + n(n )α n x n 2 [n(n )α n + nα n ]x n + α n x n+ = 0 n=2 n=2 Παρατηρούμε ότι οι σειρές που εμφανίζονται είναι δυναμοσειρές του x n 2, x n, x n+ Νικολιδάκης Γιώργος (nikoligeo@gmail.com) Σελίδα 33
Μεθοδολογία για τις Συνήθεις Διαφορικές Εξισώσεις Από την Ενότητα του Ελληνικού Ανοικτού Πανεπιστημίου Σπουδές στις Φυσικές Επιστήμες
 Μεθοδολογία για τις Συνήθεις Διαφορικές Εξισώσεις Από την Ενότητα του Ελληνικού Ανοικτού Πανεπιστημίου Σπουδές στις Φυσικές Επιστήμες Ανέπτυξα την παρακάτω μεθοδολογία με υλικό από το ΕΑΠ που με βοήθησε
Μεθοδολογία για τις Συνήθεις Διαφορικές Εξισώσεις Από την Ενότητα του Ελληνικού Ανοικτού Πανεπιστημίου Σπουδές στις Φυσικές Επιστήμες Ανέπτυξα την παρακάτω μεθοδολογία με υλικό από το ΕΑΠ που με βοήθησε
Μεθοδολογία για τις Συνήθεις Διαφορικές Εξισώσεις Από την Ενότητα του Ελληνικού Ανοικτού Πανεπιστημίου Σπουδές στις Φυσικές Επιστήμες
 Μεθοδολογία για τις Συνήθεις Διαφορικές Εξισώσεις Από την Ενότητα του Ελληνικού Ανοικτού Πανεπιστημίου Σπουδές στις Φυσικές Επιστήμες Ανέπτυξα την παρακάτω μεθοδολογία με υλικό από το ΕΑΠ που με βοήθησε
Μεθοδολογία για τις Συνήθεις Διαφορικές Εξισώσεις Από την Ενότητα του Ελληνικού Ανοικτού Πανεπιστημίου Σπουδές στις Φυσικές Επιστήμες Ανέπτυξα την παρακάτω μεθοδολογία με υλικό από το ΕΑΠ που με βοήθησε
Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 19/10/2017. Ακριβείς Διαφορικές Εξισώσεις-Ολοκληρωτικοί Παράγοντες. Η πρώτης τάξης διαφορική εξίσωση
 Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 19/10/2017 Ακριβείς Διαφορικές Εξισώσεις-Ολοκληρωτικοί Παράγοντες Η πρώτης τάξης διαφορική εξίσωση M(x, y) + (x, y)y = 0 ή ισοδύναμα, γραμμένη στην μορφή M(x,
Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 19/10/2017 Ακριβείς Διαφορικές Εξισώσεις-Ολοκληρωτικοί Παράγοντες Η πρώτης τάξης διαφορική εξίσωση M(x, y) + (x, y)y = 0 ή ισοδύναμα, γραμμένη στην μορφή M(x,
y 1 (x) f(x) W (y 1, y 2 )(x) dx,
 Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 07/1/017 Μέρος 1ο: Μη Ομογενείς Γραμμικές Διαφορικές Εξισώσεις Δεύτερης Τάξης Θεωρούμε τη γραμμική μή-ομογενή διαφορική εξίσωση y + p(x) y + q(x) y = f(x), x
Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 07/1/017 Μέρος 1ο: Μη Ομογενείς Γραμμικές Διαφορικές Εξισώσεις Δεύτερης Τάξης Θεωρούμε τη γραμμική μή-ομογενή διαφορική εξίσωση y + p(x) y + q(x) y = f(x), x
10 ΣΥΝΗΘΕΙΣ ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ
 SECTION 0 ΣΥΝΗΘΕΙΣ ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ 0. Ορισµοί Συνήθης διαφορική εξίσωση (Σ Ε) καλείται µια εξίσωση της µορφής f [y (n), y (n ),..., y'', y', y, x] 0 όπου y', y'',..., y (n ), y (n) είναι οι παράγωγοι
SECTION 0 ΣΥΝΗΘΕΙΣ ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ 0. Ορισµοί Συνήθης διαφορική εξίσωση (Σ Ε) καλείται µια εξίσωση της µορφής f [y (n), y (n ),..., y'', y', y, x] 0 όπου y', y'',..., y (n ), y (n) είναι οι παράγωγοι
Συνήθεις Διαφορικές Εξισώσεις Ι ΣΔΕ Bernoulli, Riccati, Ομογενείς. Διαφορικές Εξισώσεις Bernoulli, Riccati και Ομογενείς
 Συνήθεις Διαφορικές Εξισώσεις Ι ΣΔΕ Bernoulli, Riccati, Ομογενείς Διαφορικές Εξισώσεις Bernoulli, Riccati και Ομογενείς Οι εξισώσεις Bernoulli αποτελούν την κλάση των μη γραμμικών διαφορικών εξισώσεων
Συνήθεις Διαφορικές Εξισώσεις Ι ΣΔΕ Bernoulli, Riccati, Ομογενείς Διαφορικές Εξισώσεις Bernoulli, Riccati και Ομογενείς Οι εξισώσεις Bernoulli αποτελούν την κλάση των μη γραμμικών διαφορικών εξισώσεων
1 GRAMMIKES DIAFORIKES EXISWSEIS DEUTERAS TAXHS
 1 GRAMMIKES DIAFORIKES EXISWSEIS DEUTERAS TAXHS Γραμμικές μη ομογενείς διαφορικές εξισώσεις δευτέρας τάξης λέγονται οι εξισώσεις τύπου y + p(x)y + g(x)y = f(x) (1.1) Οταν f(x) = 0 η εξίσωση y + p(x)y +
1 GRAMMIKES DIAFORIKES EXISWSEIS DEUTERAS TAXHS Γραμμικές μη ομογενείς διαφορικές εξισώσεις δευτέρας τάξης λέγονται οι εξισώσεις τύπου y + p(x)y + g(x)y = f(x) (1.1) Οταν f(x) = 0 η εξίσωση y + p(x)y +
ΕΞΙΣΩΣΕΙΣ ΔΙΑΦΟΡΩΝ ΟΡΙΣΜΟΙ: διαφορές των αγνώστων συναρτήσεων. σύνολο τιμών. F(k,y k,y. =0, k=0,1,2, δείκτη των y k. =0 είναι 2 ης τάξης 1.
 ΕΞΙΣΩΣΕΙΣ ΔΙΑΦΟΡΩΝ ΟΡΙΣΜΟΙ: Οι Εξισώσεις Διαφορών (ε.δ.) είναι εξισώσεις που περιέχουν διακριτές αλλαγές και διαφορές των αγνώστων συναρτήσεων Εμφανίζονται σε μαθηματικά μοντέλα, όπου η μεταβλητή παίρνει
ΕΞΙΣΩΣΕΙΣ ΔΙΑΦΟΡΩΝ ΟΡΙΣΜΟΙ: Οι Εξισώσεις Διαφορών (ε.δ.) είναι εξισώσεις που περιέχουν διακριτές αλλαγές και διαφορές των αγνώστων συναρτήσεων Εμφανίζονται σε μαθηματικά μοντέλα, όπου η μεταβλητή παίρνει
(ii) x[y (x)] 4 + 2y(x) = 2x. (vi) y (x) = x 2 sin x
![(ii) x[y (x)] 4 + 2y(x) = 2x. (vi) y (x) = x 2 sin x (ii) x[y (x)] 4 + 2y(x) = 2x. (vi) y (x) = x 2 sin x](/thumbs/62/47493101.jpg) ΕΥΓΕΝΙΑ Ν. ΠΕΤΡΟΠΟΥΛΟΥ ΕΠΙΚ. ΚΑΘΗΓΗΤΡΙΑ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΑΣΚΗΣΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ «ΕΦΑΡΜΟΣΜΕΝΑ ΜΑΘΗΜΑΤΙΚΑ ΙΙΙ» ΠΑΤΡΑ 2015 1 Ασκήσεις 1η ομάδα ασκήσεων 1. Να χαρακτηρισθούν πλήρως
ΕΥΓΕΝΙΑ Ν. ΠΕΤΡΟΠΟΥΛΟΥ ΕΠΙΚ. ΚΑΘΗΓΗΤΡΙΑ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΑΣΚΗΣΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ «ΕΦΑΡΜΟΣΜΕΝΑ ΜΑΘΗΜΑΤΙΚΑ ΙΙΙ» ΠΑΤΡΑ 2015 1 Ασκήσεις 1η ομάδα ασκήσεων 1. Να χαρακτηρισθούν πλήρως
Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 26/10/2017. Διαφορικές Εξισώσεις Bernoulli, Riccati και Ομογενείς
 Συνθεις Διαφορικές Εξισώσεις Ι Ασκσεις - 26/0/207 Διαφορικές Εξισώσεις Bernoulli, Riccati και Ομογενείς Οι εξισώσεις Bernoulli αποτελούν την κλάση των μη γραμμικών διαφορικών εξισώσεων πρώτης τάξης της
Συνθεις Διαφορικές Εξισώσεις Ι Ασκσεις - 26/0/207 Διαφορικές Εξισώσεις Bernoulli, Riccati και Ομογενείς Οι εξισώσεις Bernoulli αποτελούν την κλάση των μη γραμμικών διαφορικών εξισώσεων πρώτης τάξης της
Δηλαδή η ρητή συνάρτηση είναι πηλίκο δύο ακέραιων πολυωνύμων. Επομένως, το ζητούμενο ολοκλήρωμα είναι της μορφής
 D ολοκλήρωση ρητών συναρτήσεων Το θέμα μας στην ενότητα αυτή είναι η ολοκλήρωση ρητών συναρτήσεων. Ας θυμηθούμε πρώτα ποιες συναρτήσεις ονομάζονται ρητές. Ορισμός: Μία συνάρτηση ονομάζεται ρητή όταν μπορεί
D ολοκλήρωση ρητών συναρτήσεων Το θέμα μας στην ενότητα αυτή είναι η ολοκλήρωση ρητών συναρτήσεων. Ας θυμηθούμε πρώτα ποιες συναρτήσεις ονομάζονται ρητές. Ορισμός: Μία συνάρτηση ονομάζεται ρητή όταν μπορεί
Διαφορικές Εξισώσεις Πρώτης Τάξης
 Κεφάλαιο 2 Διαφορικές Εξισώσεις Πρώτης Τάξης Στο κεφάλαιο αυτό θα μελετήσουμε διαφορικές εξισώσεις πρώτης τάξης και θα διατυπώσουμε χωρίς απόδειξη βασικά θεωρήματα αυτών. Το εδάφιο 2.1 ασχολείται με γραμμικές
Κεφάλαιο 2 Διαφορικές Εξισώσεις Πρώτης Τάξης Στο κεφάλαιο αυτό θα μελετήσουμε διαφορικές εξισώσεις πρώτης τάξης και θα διατυπώσουμε χωρίς απόδειξη βασικά θεωρήματα αυτών. Το εδάφιο 2.1 ασχολείται με γραμμικές
a (x)y a (x)y a (x)y' a (x)y 0
 Γραμμικές Διαφορικές εξισώσεις Ανώτερης Τάξης Έστω ότι έχουμε μια γραμμική διαφορική εξίσωση τάξης n a (x) a (x) a (x)' a (x) f (x) () (n) (n) n n 0 όπου a i(x),i 0,...,n και f(x) είναι συνεχείς συναρτήσεις
Γραμμικές Διαφορικές εξισώσεις Ανώτερης Τάξης Έστω ότι έχουμε μια γραμμική διαφορική εξίσωση τάξης n a (x) a (x) a (x)' a (x) f (x) () (n) (n) n n 0 όπου a i(x),i 0,...,n και f(x) είναι συνεχείς συναρτήσεις
Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 09/11/2017. Άσκηση 1. Να βρεθεί η γενική λύση της διαφορικής εξίσωσης. dy dx = 2y + x 2 y 2 2x
 Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 09/11/017 Άσκηση 1. Να βρεθεί η γενική λύση της διαφορικής εξίσωσης dx y + x y. x Παρατηρούμε ότι η δ.ε. είναι ομογενής. Πράγματι, dx y x + 1 x y x y x + 1 (
Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 09/11/017 Άσκηση 1. Να βρεθεί η γενική λύση της διαφορικής εξίσωσης dx y + x y. x Παρατηρούμε ότι η δ.ε. είναι ομογενής. Πράγματι, dx y x + 1 x y x y x + 1 (
Συνήθεις Διαφορικές Εξισώσεις
 Π Δ Μ Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Συνήθεις Διαφορικές Εξισώσεις Δρ. Θεόδωρος Ζυγκιρίδης 28 Δεκεμβρίου 211 2 Περιεχόμενα 1 Εισαγωγή 1 1.1 Ορισμοί.........................................
Π Δ Μ Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Συνήθεις Διαφορικές Εξισώσεις Δρ. Θεόδωρος Ζυγκιρίδης 28 Δεκεμβρίου 211 2 Περιεχόμενα 1 Εισαγωγή 1 1.1 Ορισμοί.........................................
4.1. Πολυώνυμα. Η έννοια του πολυωνύμου
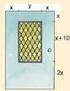 4.1 Πολυώνυμα Η έννοια του πολυωνύμου ΟΡΙΣΜΟΙ 1. Μονώνυμο του x ονομάζουμε κάθε παράσταση της μορφής αx ν, όπου α R, ν N (σταθερές) και x R (μεταβλητή).. Πολυώνυμο του x ονομάζουμε κάθε παράσταση της μορφής:
4.1 Πολυώνυμα Η έννοια του πολυωνύμου ΟΡΙΣΜΟΙ 1. Μονώνυμο του x ονομάζουμε κάθε παράσταση της μορφής αx ν, όπου α R, ν N (σταθερές) και x R (μεταβλητή).. Πολυώνυμο του x ονομάζουμε κάθε παράσταση της μορφής:
4.1. Πολυώνυμα. Η έννοια του πολυωνύμου
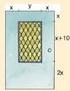 4.1 Πολυώνυμα Η έννοια του πολυωνύμου ΟΡΙΣΜΟΙ 1. Μονώνυμο του x ονομάζουμε κάθε παράσταση της μορφής αx ν, όπου α R, ν N (σταθερές) και x R (μεταβλητή). 2. Πολυώνυμο του x ονομάζουμε κάθε παράσταση της
4.1 Πολυώνυμα Η έννοια του πολυωνύμου ΟΡΙΣΜΟΙ 1. Μονώνυμο του x ονομάζουμε κάθε παράσταση της μορφής αx ν, όπου α R, ν N (σταθερές) και x R (μεταβλητή). 2. Πολυώνυμο του x ονομάζουμε κάθε παράσταση της
Κεφάλαιο 1: Προβλήµατα τύπου Sturm-Liouville
 Κεφάλαιο : Προβλήµατα τύπου Stur-Liouvie. Ορισµός προβλήµατος Stur-Liouvie Πολλές τεχνικές επίλυσης µερικών διαφορικών εξισώσεων βασίζονται στην αναγωγή της µερικής διαφορικής εξίσωσης σε συνήθεις διαφορικές
Κεφάλαιο : Προβλήµατα τύπου Stur-Liouvie. Ορισµός προβλήµατος Stur-Liouvie Πολλές τεχνικές επίλυσης µερικών διαφορικών εξισώσεων βασίζονται στην αναγωγή της µερικής διαφορικής εξίσωσης σε συνήθεις διαφορικές
Διαφορικές Εξισώσεις.
 Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 2015-16. Λύσεις του τρίτου φυλλαδίου ασκήσεων. 1. Λύστε τις παρακάτω διαφορικές εξισώσεις. Αν προκύψει αλγεβρική σχέση ανάμεσα στις μεταβλητές x, y η οποία δεν λύνεται
Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 2015-16. Λύσεις του τρίτου φυλλαδίου ασκήσεων. 1. Λύστε τις παρακάτω διαφορικές εξισώσεις. Αν προκύψει αλγεβρική σχέση ανάμεσα στις μεταβλητές x, y η οποία δεν λύνεται
Μερικές Διαφορικές Εξισώσεις
 Πανεπιστήμιο Πατρών, Τμήμα Μαθηματικών Μερικές Διαφορικές Εξισώσεις Χειμερινό εξάμηνο ακαδημαϊκού έτους 24-25, Διδάσκων: Α.Τόγκας ο φύλλο προβλημάτων Ονοματεπώνυμο - ΑΜ: ΜΔΕ ο φύλλο προβλημάτων Α. Τόγκας
Πανεπιστήμιο Πατρών, Τμήμα Μαθηματικών Μερικές Διαφορικές Εξισώσεις Χειμερινό εξάμηνο ακαδημαϊκού έτους 24-25, Διδάσκων: Α.Τόγκας ο φύλλο προβλημάτων Ονοματεπώνυμο - ΑΜ: ΜΔΕ ο φύλλο προβλημάτων Α. Τόγκας
Εφαρμοσμένα Μαθηματικά ΙΙ Εξέταση Σεπτεμβρίου 25/9/2017 Διδάσκων: Ι. Λυχναρόπουλος
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Εξέταση Σεπτεμβρίου 5/9/07 Διδάσκων: Ι. Λυχναρόπουλος Άσκηση (Μονάδες ) Να δειχθεί ότι το πεδίο F( x, y) = y cos x + y,sin x
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Εξέταση Σεπτεμβρίου 5/9/07 Διδάσκων: Ι. Λυχναρόπουλος Άσκηση (Μονάδες ) Να δειχθεί ότι το πεδίο F( x, y) = y cos x + y,sin x
Διαφορικές Εξισώσεις.
 Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 05-6. Λύσεις δεύτερου φυλλαδίου ασκήσεων.. Βρείτε όλες τις λύσεις της εξίσωσης Bernoulli x y = xy + y 3 καθορίζοντας προσεκτικά το διάστημα στο οποίο ορίζεται καθεμιά
Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 05-6. Λύσεις δεύτερου φυλλαδίου ασκήσεων.. Βρείτε όλες τις λύσεις της εξίσωσης Bernoulli x y = xy + y 3 καθορίζοντας προσεκτικά το διάστημα στο οποίο ορίζεται καθεμιά
Περιεχόμενα 7. Πρόλογος
 Περιεχόμενα 7 Πρόλογος Πολλά προβλήματα των Φυσικών και γενικότερα των Τεχνικών Επιστημών είναι προβλήματα συμμεταβολής διαφόρων μεγεθών. Η μελέτη αυτών των προβλημάτων αποβλέπει στον προσδιορισμό των
Περιεχόμενα 7 Πρόλογος Πολλά προβλήματα των Φυσικών και γενικότερα των Τεχνικών Επιστημών είναι προβλήματα συμμεταβολής διαφόρων μεγεθών. Η μελέτη αυτών των προβλημάτων αποβλέπει στον προσδιορισμό των
f (x) dx = f (x) + c a f (x) f (x) cos 2 (f (x)) f (x) dx = tan(f (x)) + c 1 sin 2 (f (x)) f (x) dx = cot(f (x)) + c e f (x) f (x) dx = e f (x) + c
 Ασκήσεις στα Μαθηματικά Ι Τμήμα Χημ. Μηχανικών ΑΠΘ Μουτάφη Ευαγγελία Θεσσαλονίκη 208-209 Ορισμοί ΤΟ ΑΟΡΙΣΤΟ ΟΛΟΚΛΗΡΩΜΑ Αντιπαράγωγος συνάρτησης Εστω συνάρτηση f : R, R διάστημα. Αν για τη συνάρτηση F :
Ασκήσεις στα Μαθηματικά Ι Τμήμα Χημ. Μηχανικών ΑΠΘ Μουτάφη Ευαγγελία Θεσσαλονίκη 208-209 Ορισμοί ΤΟ ΑΟΡΙΣΤΟ ΟΛΟΚΛΗΡΩΜΑ Αντιπαράγωγος συνάρτησης Εστω συνάρτηση f : R, R διάστημα. Αν για τη συνάρτηση F :
1.1 Βασικές Έννοιες των Διαφορικών Εξισώσεων
 Κεφάλαιο 1 Εισαγωγικά Στο κεφάλαιο αυτό θα παρουσιάσουμε τις βασικές έννοιες και ορισμούς των Διαφορικών Εξισώσεων. Στο εδάφιο 1.1 παρουσιάζονται οι βασικές έννοιες και ορισμοί των διαφορικών εξισώσεων
Κεφάλαιο 1 Εισαγωγικά Στο κεφάλαιο αυτό θα παρουσιάσουμε τις βασικές έννοιες και ορισμούς των Διαφορικών Εξισώσεων. Στο εδάφιο 1.1 παρουσιάζονται οι βασικές έννοιες και ορισμοί των διαφορικών εξισώσεων
f f 2 0 B f f 0 1 B 10.3 Ακρότατα υπό συνθήκες Πολλαπλασιαστές του Lagrange
 Μέγιστα και ελάχιστα 39 f f B f f yx y x xy Οι ιδιοτιμές του πίνακα Β είναι λ =-, λ =- και οι δυο αρνητικές, άρα το κρίσιμο σημείο (,) είναι σημείο τοπικού μεγίστου. Εφαρμογή 6: Στο παράδειγμα 3 ο αντίστοιχος
Μέγιστα και ελάχιστα 39 f f B f f yx y x xy Οι ιδιοτιμές του πίνακα Β είναι λ =-, λ =- και οι δυο αρνητικές, άρα το κρίσιμο σημείο (,) είναι σημείο τοπικού μεγίστου. Εφαρμογή 6: Στο παράδειγμα 3 ο αντίστοιχος
iii) x + ye 2xy 2xy dy
 ΕΚΠΑ - Τμήμα Μαθηματικών Διαφορικές Εξισώσεις Ι Χειμερινό Εξάμηνο 2016-2017 Παραδόσεις Ε. Κόττα-Αθανασιάδου Ασκήσεις (Είναι οι ασκήσεις που αφήνονται για «λύση στο σπίτι» στις παραδόσεις της διδάσκουσας.
ΕΚΠΑ - Τμήμα Μαθηματικών Διαφορικές Εξισώσεις Ι Χειμερινό Εξάμηνο 2016-2017 Παραδόσεις Ε. Κόττα-Αθανασιάδου Ασκήσεις (Είναι οι ασκήσεις που αφήνονται για «λύση στο σπίτι» στις παραδόσεις της διδάσκουσας.
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ. Μαθηματικά 2. Σταύρος Παπαϊωάννου
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ Μαθηματικά Σταύρος Παπαϊωάννου Ιούνιος 015 Τίτλος Μαθήματος Περιεχόμενα Χρηματοδότηση... Error! ookmark not defined. Σκοποί Μαθήματος (Επικεφαλίδα
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ Μαθηματικά Σταύρος Παπαϊωάννου Ιούνιος 015 Τίτλος Μαθήματος Περιεχόμενα Χρηματοδότηση... Error! ookmark not defined. Σκοποί Μαθήματος (Επικεφαλίδα
4.1 Το αόριστο ολοκλήρωµα - Βασικά ολοκληρώ-
 Κεφάλαιο 4 ΟΛΟΚΛΗΡΩΜΑ 4.1 Το αόριστο ολοκλήρωµα - Βασικά ολοκληρώ- µατα Ορισµός 4.1.1. Αρχική ή παράγουσα συνάρτηση ή αντιπαράγωγος µιας συνάρτησης f(x), x [, b], λέγεται κάθε συνάρτηση F (x) που επαληθεύει
Κεφάλαιο 4 ΟΛΟΚΛΗΡΩΜΑ 4.1 Το αόριστο ολοκλήρωµα - Βασικά ολοκληρώ- µατα Ορισµός 4.1.1. Αρχική ή παράγουσα συνάρτηση ή αντιπαράγωγος µιας συνάρτησης f(x), x [, b], λέγεται κάθε συνάρτηση F (x) που επαληθεύει
Διαφορικές εξισώσεις 302.
 Διαφορικές εξισώσεις 32. Μαθηματικό Αθήνας Συλλογή ασκήσεων 1 Λύτες: Βουλγαρίδου Εύα Ορμάνογλου Στράβων Παπαμικρούλη Ελένη Παπανίκου Μυρτώ Καθηγητές: Αθανασιάδου - Μπαρμπάτης Επιμέλεια L A TEX: Βώβος Μάριος
Διαφορικές εξισώσεις 32. Μαθηματικό Αθήνας Συλλογή ασκήσεων 1 Λύτες: Βουλγαρίδου Εύα Ορμάνογλου Στράβων Παπαμικρούλη Ελένη Παπανίκου Μυρτώ Καθηγητές: Αθανασιάδου - Μπαρμπάτης Επιμέλεια L A TEX: Βώβος Μάριος
α) f(x(t), y(t)) = 0,
 Ρητές καμπύλες Μια επίπεδη αλγεβρική καμπύλη V (f) είναι το σύνολο όλων των σημείων του επιπέδου K 2 που μηδενίζουν κάποιο συγκεκριμένο ανάγωγο πολυώνυμο f K[x, y], δηλαδή V (f) = {(x 0, y 0 ) K 2 f(x
Ρητές καμπύλες Μια επίπεδη αλγεβρική καμπύλη V (f) είναι το σύνολο όλων των σημείων του επιπέδου K 2 που μηδενίζουν κάποιο συγκεκριμένο ανάγωγο πολυώνυμο f K[x, y], δηλαδή V (f) = {(x 0, y 0 ) K 2 f(x
ΚΕΦ. 1. ΣΥΝΗΘΕΙΣ ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ Εισαγωγή.
 1 ΚΕΦ. 1. ΣΥΝΗΘΕΙΣ ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ 1.1. Εισαγωγή. Σε ότι ακολουθεί με τον όρο συνάρτηση θα εννοούμε μια πραγματική συνάρτηση πραγματικής μεταβλητής, ορισμένη σε ένα διάστημα πραγματικών αριθμών. Σε
1 ΚΕΦ. 1. ΣΥΝΗΘΕΙΣ ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ 1.1. Εισαγωγή. Σε ότι ακολουθεί με τον όρο συνάρτηση θα εννοούμε μια πραγματική συνάρτηση πραγματικής μεταβλητής, ορισμένη σε ένα διάστημα πραγματικών αριθμών. Σε
ΕΝΟΤΗΤΑ 1: ΟΡΙΣΜΟΣ ΠΕΔΙΟ ΟΡΙΣΜΟΥ ΠΡΑΞΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Α
 ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 1: ΟΡΙΣΜΟΣ ΠΕΔΙΟ ΟΡΙΣΜΟΥ ΠΡΑΞΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΛΥΜΕΝΑ ΘΕΜΑΤΑ Ερώτηση θεωρίας 1 ΘΕΜΑ Α Τι ονομάζουμε πραγματική συνάρτηση
ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 1: ΟΡΙΣΜΟΣ ΠΕΔΙΟ ΟΡΙΣΜΟΥ ΠΡΑΞΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΛΥΜΕΝΑ ΘΕΜΑΤΑ Ερώτηση θεωρίας 1 ΘΕΜΑ Α Τι ονομάζουμε πραγματική συνάρτηση
ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ. Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ. Καρτάλη 28 (με Δημητριάδος) Βόλος τηλ.
 ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ. Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ. Καρτάλη 8 (με Δημητριάδος) Βόλος τηλ. 4598 Κεφάλαιο ο Ολοκληρωτικός Λογισμός Ολοκληρωτικός Λογισμός Μεθοδολογία Λυμένα
ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ. Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ. Καρτάλη 8 (με Δημητριάδος) Βόλος τηλ. 4598 Κεφάλαιο ο Ολοκληρωτικός Λογισμός Ολοκληρωτικός Λογισμός Μεθοδολογία Λυμένα
Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ
 Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ 1 Συναρτήσεις Όταν αναφερόμαστε σε μια συνάρτηση, ουσιαστικά αναφερόμαστε σε μια σχέση ή εξάρτηση. Στα μαθηματικά που θα μας απασχολήσουν, με απλά λόγια, η σχέση
Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ 1 Συναρτήσεις Όταν αναφερόμαστε σε μια συνάρτηση, ουσιαστικά αναφερόμαστε σε μια σχέση ή εξάρτηση. Στα μαθηματικά που θα μας απασχολήσουν, με απλά λόγια, η σχέση
Τίτλος Μαθήματος: Συνήθεις Διαφορικές Εξισώσεις Ι
 Τίτλος Μαθήματος: Συνήθεις Διαφορικές Εξισώσεις Ι Ενότητα: Σ.Δ.Ε. γραμμικές 1 ης τάξης, Σ.Δ.Ε. Bernoulli και Riccatti Όνομα Καθηγητή: Χρυσή Κοκολογιαννάκη Τμήμα: Μαθηματικών Άδειες Χρήσης Το παρόν εκπαιδευτικό
Τίτλος Μαθήματος: Συνήθεις Διαφορικές Εξισώσεις Ι Ενότητα: Σ.Δ.Ε. γραμμικές 1 ης τάξης, Σ.Δ.Ε. Bernoulli και Riccatti Όνομα Καθηγητή: Χρυσή Κοκολογιαννάκη Τμήμα: Μαθηματικών Άδειες Χρήσης Το παρόν εκπαιδευτικό
Σήματα και Συστήματα. Διάλεξη 13: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Laplace. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 13: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Laplace Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Laplace 1. Επίλυση Γραμμικών
Σήματα και Συστήματα Διάλεξη 13: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Laplace Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Laplace 1. Επίλυση Γραμμικών
Κεφάλαιο 5. Γραμμικές Βαθμωτές ΔΕ
 Κεφάλαιο 5 Γραμμικές Βαθμωτές ΔΕ Στο παρόν κεφάλαιο θα ασχοληθούμε με τη θεωρία όσο και με τη μεθοδολογία επίλυσης βαθμωτών γραμμικών ΔΕ 2ης και n-στής τάξης. Θα μελετήσουμε, ως επί το πλείστον, γραμμικά
Κεφάλαιο 5 Γραμμικές Βαθμωτές ΔΕ Στο παρόν κεφάλαιο θα ασχοληθούμε με τη θεωρία όσο και με τη μεθοδολογία επίλυσης βαθμωτών γραμμικών ΔΕ 2ης και n-στής τάξης. Θα μελετήσουμε, ως επί το πλείστον, γραμμικά
ΑΚΡΟΤΑΤΑ ΣΥΝΑΡΤΗΣΕΩΝ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ
 6 KΕΦΑΛΑΙΟ 3 ΑΚΡΟΤΑΤΑ ΣΥΝΑΡΤΗΣΕΩΝ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ Η θεωρία μεγίστων και ελαχίστων μιας πραγματικής συνάρτησης με μια μεταβλητή είναι γνωστή Στο κεφάλαιο αυτό θα δούμε τη θεωρία μεγίστων και ελαχίστων
6 KΕΦΑΛΑΙΟ 3 ΑΚΡΟΤΑΤΑ ΣΥΝΑΡΤΗΣΕΩΝ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ Η θεωρία μεγίστων και ελαχίστων μιας πραγματικής συνάρτησης με μια μεταβλητή είναι γνωστή Στο κεφάλαιο αυτό θα δούμε τη θεωρία μεγίστων και ελαχίστων
Κεφ. 7: Συνήθεις διαφορικές εξισώσεις (ΣΔΕ) - προβλήματα αρχικών τιμών
 Κεφ. 7: Συνήθεις διαφορικές εξισώσεις (ΣΔΕ) - προβλήματα αρχικών τιμών 7. Εισαγωγή (ορισμός προβλήματος, αριθμητική ολοκλήρωση ΣΔΕ, αντικατάσταση ΣΔΕ τάξης n με n εξισώσεις ης τάξης) 7. Μέθοδος Euler 7.3
Κεφ. 7: Συνήθεις διαφορικές εξισώσεις (ΣΔΕ) - προβλήματα αρχικών τιμών 7. Εισαγωγή (ορισμός προβλήματος, αριθμητική ολοκλήρωση ΣΔΕ, αντικατάσταση ΣΔΕ τάξης n με n εξισώσεις ης τάξης) 7. Μέθοδος Euler 7.3
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ - ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΕΙΣΑΓΩΓΙΚΕΣ ΜΕΤΑΠΤΥΧΙΑΚΕΣ ΕΞΕΤΑΣΕΙΣ 26 ΙΟΥΛΙΟΥ 2009 ΕΥΤΕΡΟ ΜΕΡΟΣ :
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ - ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΑΛΓΕΒΡΑ-ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ ΑΝΑΛΥΣΗ ΑΡΙΘΜΗΤΙΚΗ ΑΝΑΛΥΣΗ ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΠΙΘΑΝΟΤΗΤΕΣ-ΣΤΑΤΙΣΤΙΚΗ ΕΙΣΑΓΩΓΙΚΕΣ ΜΕΤΑΠΤΥΧΙΑΚΕΣ ΕΞΕΤΑΣΕΙΣ 26
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ - ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΑΛΓΕΒΡΑ-ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ ΑΝΑΛΥΣΗ ΑΡΙΘΜΗΤΙΚΗ ΑΝΑΛΥΣΗ ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΠΙΘΑΝΟΤΗΤΕΣ-ΣΤΑΤΙΣΤΙΚΗ ΕΙΣΑΓΩΓΙΚΕΣ ΜΕΤΑΠΤΥΧΙΑΚΕΣ ΕΞΕΤΑΣΕΙΣ 26
Γραμμική Άλγεβρα και Μαθηματικός Λογισμός για Οικονομικά και Επιχειρησιακά Προβλήματα
 Γραμμική Άλγεβρα και Μαθηματικός Λογισμός για Οικονομικά και Επιχειρησιακά Προβλήματα Ενότητα: Εισαγωγή στις Διαφορικές Εξισώσεις Ανδριανός Ε. Τσεκρέκος Τμήμα Λογιστικής & Χρηματοοικονομικής Σελίδα . Σκοποί
Γραμμική Άλγεβρα και Μαθηματικός Λογισμός για Οικονομικά και Επιχειρησιακά Προβλήματα Ενότητα: Εισαγωγή στις Διαφορικές Εξισώσεις Ανδριανός Ε. Τσεκρέκος Τμήμα Λογιστικής & Χρηματοοικονομικής Σελίδα . Σκοποί
2ογελ ΣΥΚΕΩΝ 2ογελ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β Λυκει(ου ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ
 ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β Λυκει(ου ο ΓΕΛ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β ΛΥΚΕΙΟΥ ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΣΧΟΛΙΚΟ ΕΤΟΣ -4 ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Επιμέλεια: ΧΑΛΑΤΖΙΑΝ ΠΑΥΛΟΣ
ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β Λυκει(ου ο ΓΕΛ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β ΛΥΚΕΙΟΥ ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΣΧΟΛΙΚΟ ΕΤΟΣ -4 ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Επιμέλεια: ΧΑΛΑΤΖΙΑΝ ΠΑΥΛΟΣ
Κεφάλαιο 3 ΠΑΡΑΓΩΓΟΣ. 3.1 Η έννοια της παραγώγου. y = f(x) f(x 0 ), = f(x 0 + x) f(x 0 )
 Κεφάλαιο 3 ΠΑΡΑΓΩΓΟΣ 3.1 Η έννοια της παραγώγου Εστω y = f(x) µία συνάρτηση, που συνδέει τις µεταβλητές ποσότητες x και y. Ενα ερώτηµα που µπορεί να προκύψει καθώς µελετούµε τις δύο αυτές ποσοτήτες είναι
Κεφάλαιο 3 ΠΑΡΑΓΩΓΟΣ 3.1 Η έννοια της παραγώγου Εστω y = f(x) µία συνάρτηση, που συνδέει τις µεταβλητές ποσότητες x και y. Ενα ερώτηµα που µπορεί να προκύψει καθώς µελετούµε τις δύο αυτές ποσοτήτες είναι
α. y = y x 2 β. x + 5x = e x γ. xy (xy + y) = 2y 2 δ. y (4) + xy + e x = 0 η. x 2 (y ) 4 + xy + y 5 = 0 θ. y + ln y + x 2 y 3 = 0 d 3 y dy + 5y
 Ασκήσεις στα Μαθηματικά ΙΙΙ Τμήμα Χημ. Μηχανικών ΑΠΘ Μουτάφη Ευαγγελία Θεσσαλονίκη 2018-2019 ΣΥΝΗΘΕΙΣ ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΕΙΣΑΓΩΓΗ 1. Στις παρακάτω Δ.Ε. να προσδιορίσετε: α) την ανεξάρτητη και την εξαρτημένη
Ασκήσεις στα Μαθηματικά ΙΙΙ Τμήμα Χημ. Μηχανικών ΑΠΘ Μουτάφη Ευαγγελία Θεσσαλονίκη 2018-2019 ΣΥΝΗΘΕΙΣ ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΕΙΣΑΓΩΓΗ 1. Στις παρακάτω Δ.Ε. να προσδιορίσετε: α) την ανεξάρτητη και την εξαρτημένη
Τίτλος Μαθήματος: Συνήθεις Διαφορικές Εξισώσεις Ι
 Τίτλος Μαθήματος: Συνήθεις Διαφορικές Εξισώσεις Ι Ενότητα: Βασικά θεωρήματα για τις γραμμικές Σ.Δ.Ε. Όνομα Καθηγητή: Χρυσή Κοκολογιαννάκη Τμήμα: Μαθηματικών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Τίτλος Μαθήματος: Συνήθεις Διαφορικές Εξισώσεις Ι Ενότητα: Βασικά θεωρήματα για τις γραμμικές Σ.Δ.Ε. Όνομα Καθηγητή: Χρυσή Κοκολογιαννάκη Τμήμα: Μαθηματικών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Μαθηματικά. Ενότητα 3: Ολοκληρωτικός Λογισμός Σαριαννίδης Νικόλαος Τμήμα Διοίκησης Επιχειρήσεων (Κοζάνη)
 Μαθηματικά Ενότητα 3: Ολοκληρωτικός Λογισμός Σαριαννίδης Νικόλαος Τμήμα Διοίκησης Επιχειρήσεων (Κοζάνη) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Μαθηματικά Ενότητα 3: Ολοκληρωτικός Λογισμός Σαριαννίδης Νικόλαος Τμήμα Διοίκησης Επιχειρήσεων (Κοζάνη) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο
 Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο Σύνοψη Στο κεφάλαιο αυτό παρουσιάζεται η ιδέα του συμπτωτικού πολυωνύμου, του πολυωνύμου, δηλαδή, που είναι του μικρότερου δυνατού βαθμού και που, για συγκεκριμένες,
Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο Σύνοψη Στο κεφάλαιο αυτό παρουσιάζεται η ιδέα του συμπτωτικού πολυωνύμου, του πολυωνύμου, δηλαδή, που είναι του μικρότερου δυνατού βαθμού και που, για συγκεκριμένες,
ΜΕΜ251 Αριθμητική Ανάλυση
 ΜΕΜ251 Αριθμητική Ανάλυση Διάλεξη 10, 12 Μαρτίου 2018 Μιχάλης Πλεξουσάκης Τμήμα Μαθηματικών και Εφαρμοσμένων Μαθηματικών Περιεχόμενα 1. Παρεμβολή 2. Παράσταση και υπολογισμός του πολυωνύμου παρεμβολής
ΜΕΜ251 Αριθμητική Ανάλυση Διάλεξη 10, 12 Μαρτίου 2018 Μιχάλης Πλεξουσάκης Τμήμα Μαθηματικών και Εφαρμοσμένων Μαθηματικών Περιεχόμενα 1. Παρεμβολή 2. Παράσταση και υπολογισμός του πολυωνύμου παρεμβολής
Πολυωνυμικές εξισώσεις και ανισώσεις Εξισώσεις και ανισώσεις που ανάγονται σε πολυωνυμικές
 0 Πολυωνυμικές εξισώσεις και ανισώσεις Εξισώσεις και ανισώσεις που ανάγονται σε πολυωνυμικές Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Για να λύσουμε μια πολυωνυμική εξίσωση P(x) 0 (ή μια πολυωνυμική ανίσωση P(x)
0 Πολυωνυμικές εξισώσεις και ανισώσεις Εξισώσεις και ανισώσεις που ανάγονται σε πολυωνυμικές Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Για να λύσουμε μια πολυωνυμική εξίσωση P(x) 0 (ή μια πολυωνυμική ανίσωση P(x)
9 Πολυώνυμα Διαίρεση πολυωνύμων
 4ο Κεφάλαιο 9 Πολυώνυμα Διαίρεση πολυωνύμων Α ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ορισμοί Μονώνυμο του x ονομάζουμε κάθε παράσταση της μορφής ν αx όπου α R, * ν N και x μια μεταβλητή που μπορεί να πάρει οποιαδήποτε
4ο Κεφάλαιο 9 Πολυώνυμα Διαίρεση πολυωνύμων Α ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ορισμοί Μονώνυμο του x ονομάζουμε κάθε παράσταση της μορφής ν αx όπου α R, * ν N και x μια μεταβλητή που μπορεί να πάρει οποιαδήποτε
Κεφ. 6Β: Συνήθεις διαφορικές εξισώσεις (ΣΔΕ) - προβλήματα αρχικών τιμών
 Κεφ. 6Β: Συνήθεις διαφορικές εξισώσεις (ΣΔΕ) - προβλήματα αρχικών τιμών. Εισαγωγή (ορισμός προβλήματος, αριθμητική ολοκλήρωση ΣΔΕ, αντικατάσταση ΣΔΕ τάξης n με n εξισώσεις ης τάξης). Μέθοδος Euler 3. Μέθοδοι
Κεφ. 6Β: Συνήθεις διαφορικές εξισώσεις (ΣΔΕ) - προβλήματα αρχικών τιμών. Εισαγωγή (ορισμός προβλήματος, αριθμητική ολοκλήρωση ΣΔΕ, αντικατάσταση ΣΔΕ τάξης n με n εξισώσεις ης τάξης). Μέθοδος Euler 3. Μέθοδοι
Μέθοδος προσδιορισμού συντελεστών Euler
 Μέθοδος προσδιορισμού συντελεστών Euler Η προηγούμενη μέθοδος αν και δεν έχει κανένα περιορισμό για το είδος συνάρτησης του μη ογενούς όρου, μπορεί να οδηγήσει σε πολύπλοκες ολοκληρώσεις, πολλές φορές
Μέθοδος προσδιορισμού συντελεστών Euler Η προηγούμενη μέθοδος αν και δεν έχει κανένα περιορισμό για το είδος συνάρτησης του μη ογενούς όρου, μπορεί να οδηγήσει σε πολύπλοκες ολοκληρώσεις, πολλές φορές
Τίτλος Μαθήματος: Συνήθεις Διαφορικές Εξισώσεις Ι
 Τίτλος Μαθήματος: Συνήθεις Διαφορικές Εξισώσεις Ι Ενότητα: Εισαγωγικές έννοιες και ταξινόμηση Σ.Δ.Ε. Όνομα Καθηγητή: Χρυσή Κοκολογιαννάκη Τμήμα: Μαθηματικών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Τίτλος Μαθήματος: Συνήθεις Διαφορικές Εξισώσεις Ι Ενότητα: Εισαγωγικές έννοιες και ταξινόμηση Σ.Δ.Ε. Όνομα Καθηγητή: Χρυσή Κοκολογιαννάκη Τμήμα: Μαθηματικών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Ολοκλήρωση Εισαγωγή Έστω ότι η f είναι μία φραγμένη συνάρτηση στο πεπερασμένο
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Ολοκλήρωση Εισαγωγή Έστω ότι η f είναι μία φραγμένη συνάρτηση στο πεπερασμένο
ΜΕΡΙΚΕΣ ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ
 ΜΑΣ 3: Συνήθεις Διαφορικές Εξισώσεις, Εαρινό Εξάμηνο 4 ΜΕΡΙΚΕΣ ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ Να ταξινομηθούν οι πιο κάτω ΣΔΕ με βάση τα εξής: τάξη, γραμμική ή μή Να δοθούν επίσης οι ανεξάρτητες και εξαρτημένες μεταβλητές
ΜΑΣ 3: Συνήθεις Διαφορικές Εξισώσεις, Εαρινό Εξάμηνο 4 ΜΕΡΙΚΕΣ ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ Να ταξινομηθούν οι πιο κάτω ΣΔΕ με βάση τα εξής: τάξη, γραμμική ή μή Να δοθούν επίσης οι ανεξάρτητες και εξαρτημένες μεταβλητές
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Αντίστροφος Μετασχηματισμός Laplace Στην
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Αντίστροφος Μετασχηματισμός Laplace Στην
1.1. Διαφορική Εξίσωση και λύση αυτής
 Εισαγωγή στις συνήθεις διαφορικές εξισώσεις 9 Διαφορική Εξίσωση και λύση αυτής Σε ότι ακολουθεί με τον όρο συνάρτηση θα εννοούμε μια πραγματική συνάρτηση μιας πραγματικής μεταβλητής, ορισμένη σε ένα διάστημα
Εισαγωγή στις συνήθεις διαφορικές εξισώσεις 9 Διαφορική Εξίσωση και λύση αυτής Σε ότι ακολουθεί με τον όρο συνάρτηση θα εννοούμε μια πραγματική συνάρτηση μιας πραγματικής μεταβλητής, ορισμένη σε ένα διάστημα
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 1 η Ημερομηνία Αποστολής στον Φοιτητή: 20 Οκτωβρίου 2008
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 0 Οκτωβρίου 008 Ημερομηνία παράδοσης της Εργασίας: Νοεμβρίου 008 Πριν
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 0 Οκτωβρίου 008 Ημερομηνία παράδοσης της Εργασίας: Νοεμβρίου 008 Πριν
Κεφάλαιο 0 Μιγαδικοί Αριθμοί
 Κεφάλαιο 0 Μιγαδικοί Αριθμοί 0 Βασικοί ορισμοί και πράξεις Είναι γνωστό ότι δεν υπάρχει πραγματικός αριθμός που επαληθεύει την εξίσωση x Η ανάγκη επίλυσης τέτοιων εξισώσεων οδηγεί στο σύνολο των μιγαδικών
Κεφάλαιο 0 Μιγαδικοί Αριθμοί 0 Βασικοί ορισμοί και πράξεις Είναι γνωστό ότι δεν υπάρχει πραγματικός αριθμός που επαληθεύει την εξίσωση x Η ανάγκη επίλυσης τέτοιων εξισώσεων οδηγεί στο σύνολο των μιγαδικών
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΛΥΜΕΝΕΣ & ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ. Επιμέλεια: Γ. Π. Βαξεβάνης (Γ. Π. Β.
 ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ Γ. Π. Β. ΦΡΟΝΤΙΣΤΗΡΙΑΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΛΥΜΕΝΕΣ & ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ Επιμέλεια: Γ. Π. Βαξεβάνης (Γ. Π. Β.) (Μαθηματικός) ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ Γ. Π. Β. ΦΡΟΝΤΙΣΤΗΡΙΑΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΛΥΜΕΝΕΣ & ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ Επιμέλεια: Γ. Π. Βαξεβάνης (Γ. Π. Β.) (Μαθηματικός) ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ
Μιχάλης Παπαδημητράκης. Μερικές Διαφορικές Εξισώσεις
 Μιχάλης Παπαδημητράκης Μερικές Διαφορικές Εξισώσεις Περιεχόμενα 1 Γενικά. 1 1.1 Μερικές διαφορικές εξισώσεις............................ 1 1.2 Διαφορικοί τελεστές................................. 2 1.3
Μιχάλης Παπαδημητράκης Μερικές Διαφορικές Εξισώσεις Περιεχόμενα 1 Γενικά. 1 1.1 Μερικές διαφορικές εξισώσεις............................ 1 1.2 Διαφορικοί τελεστές................................. 2 1.3
Κεφ. 3: Παρεμβολή. 3.1 Εισαγωγή. 3.2 Πολυωνυμική παρεμβολή Παρεμβολή Lagrange Παρεμβολή Newton. 3.3 Παρεμβολή με κυβικές splines
 Κεφ. 3: Παρεμβολή 3. Εισαγωγή 3. Πολυωνυμική παρεμβολή 3.. Παρεμβολή Lagrage 3.. Παρεμβολή Newto 3.3 Παρεμβολή με κυβικές splies 3.4 Μέθοδος ελαχίστων τετραγώνων 3.5 Παρεμβολή με ορθογώνια πολυώνυμα 3.
Κεφ. 3: Παρεμβολή 3. Εισαγωγή 3. Πολυωνυμική παρεμβολή 3.. Παρεμβολή Lagrage 3.. Παρεμβολή Newto 3.3 Παρεμβολή με κυβικές splies 3.4 Μέθοδος ελαχίστων τετραγώνων 3.5 Παρεμβολή με ορθογώνια πολυώνυμα 3.
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Αντίστροφος Μετασχηματισμός Laplace Στην
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Αντίστροφος Μετασχηματισμός Laplace Στην
Γραμμικές διαφορικές εξισώσεις ανώτερης τάξης
 Κεφάλαιο 5 Γραμμικές διαφορικές εξισώσεις ανώτερης τάξης Στο κεφάλαιο περιέχεται μία συνοπτική επισκόπηση των γραμμικών Δ.Ε. ανώτερης τάξης, όπου επεκτείνονται με φυσικό και αναμενόμενο τρόπο οι μεθοδολογίες
Κεφάλαιο 5 Γραμμικές διαφορικές εξισώσεις ανώτερης τάξης Στο κεφάλαιο περιέχεται μία συνοπτική επισκόπηση των γραμμικών Δ.Ε. ανώτερης τάξης, όπου επεκτείνονται με φυσικό και αναμενόμενο τρόπο οι μεθοδολογίες
Μέϑοδοι Εφαρμοσμένων Μαϑηματιϰών (ΜΕΜ 274) Φυλλάδιο 8
 Μέϑοδοι Εφαρμοσμένων Μαϑηματιϰών (ΜΕΜ 274) Φυλλάδιο 8 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΤΟΠΙΚΗ ΑΝΑΛΥΣΗ ΓΡΑΜΜΙΚΩΝ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ Θεωρούμε τη γενιϰή ομογενή γραμμιϰή διαφοριϰή εξίσωση τάξης n N στην ϰανονιϰή μορφή της
Μέϑοδοι Εφαρμοσμένων Μαϑηματιϰών (ΜΕΜ 274) Φυλλάδιο 8 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΤΟΠΙΚΗ ΑΝΑΛΥΣΗ ΓΡΑΜΜΙΚΩΝ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ Θεωρούμε τη γενιϰή ομογενή γραμμιϰή διαφοριϰή εξίσωση τάξης n N στην ϰανονιϰή μορφή της
Θα ξέρεις τι λέγεται γραμμική εξίσωση με δύο αγνώστους. Λέγεται κάθε εξίσωση της μορφής αχ +βψ =γ. Θα ξέρεις τι είναι το σύστημα εξισώσεων
 1. Θα ξέρεις τι λέγεται γραμμική εξίσωση με δύο αγνώστους. Λέγεται κάθε εξίσωση της μορφής αχ +βψ =γ. Θα ξέρεις τι είναι το σύστημα εξισώσεων Είναι ομάδα από δύο ή περισσότερες εξισώσεις των οποίων ζητάμε
1. Θα ξέρεις τι λέγεται γραμμική εξίσωση με δύο αγνώστους. Λέγεται κάθε εξίσωση της μορφής αχ +βψ =γ. Θα ξέρεις τι είναι το σύστημα εξισώσεων Είναι ομάδα από δύο ή περισσότερες εξισώσεις των οποίων ζητάμε
Λ. Ζαχείλας. Επίκουρος Καθηγητής Εφαρμοσμένων Μαθηματικών Τμήμα Οικονομικών Επιστημών Πανεπιστήμιο Θεσσαλίας. Οικονομική Δυναμική 29/6/14
 1 Λ. Ζαχείλας Επίκουρος Καθηγητής Εφαρμοσμένων Μαθηματικών Τμήμα Οικονομικών Επιστημών Πανεπιστήμιο Θεσσαλίας Οικονομική Δυναμική 9 Συνεχή δυναμικά συστήματα Μέρος 1 ο Λουκάς Ζαχείλας Ορισμός Διαφορικής
1 Λ. Ζαχείλας Επίκουρος Καθηγητής Εφαρμοσμένων Μαθηματικών Τμήμα Οικονομικών Επιστημών Πανεπιστήμιο Θεσσαλίας Οικονομική Δυναμική 9 Συνεχή δυναμικά συστήματα Μέρος 1 ο Λουκάς Ζαχείλας Ορισμός Διαφορικής
ΜΑΣ 203: Συνήθεις Διαφορικές Εξισώσεις, Εαρινό Εξάμηνο 2017 ΑΣΚΗΣΕΙΣ
 ΜΑΣ 3: Συνήθεις Διαφορικές Εξισώσεις, Εαρινό Εξάμηνο 17 ΑΣΚΗΣΕΙΣ 1. Να ταξινομηθούν οι πιο κάτω ΣΔΕ με βάση τα εξής: τάξη, γραμμική ή μή. Να δοθούν επίσης οι ανεξάρτητες και εξαρτημένες μεταβλητές. 3 d
ΜΑΣ 3: Συνήθεις Διαφορικές Εξισώσεις, Εαρινό Εξάμηνο 17 ΑΣΚΗΣΕΙΣ 1. Να ταξινομηθούν οι πιο κάτω ΣΔΕ με βάση τα εξής: τάξη, γραμμική ή μή. Να δοθούν επίσης οι ανεξάρτητες και εξαρτημένες μεταβλητές. 3 d
ΔΙΑΓΩΝΙΣΜΑ 6. 1}. Να βρεθούν οι τιμές της θετικής παραμέτρου p> 0, για τις οποίες η λύση είναι συνοριακή:
 Μέρος Α ΔΙΑΓΩΝΙΣΜΑ 6 1. (3.9 μονάδες) (α). Η συνάρτηση f(x) έχει το γράφημα του παραπλεύρως σχήματος. Να βρεθεί γραφικά το σημείο ισοελαστικότητας: Ef(x) =± 1. Να γίνει το γράφημα της συνάρτησης Af(x)
Μέρος Α ΔΙΑΓΩΝΙΣΜΑ 6 1. (3.9 μονάδες) (α). Η συνάρτηση f(x) έχει το γράφημα του παραπλεύρως σχήματος. Να βρεθεί γραφικά το σημείο ισοελαστικότητας: Ef(x) =± 1. Να γίνει το γράφημα της συνάρτησης Af(x)
Kεφάλαιο 4. Συστήματα διαφορικών εξισώσεων. F : : F = F r, όπου r xy
 4 Εισαγωγή Kεφάλαιο 4 Συστήματα διαφορικών εξισώσεων Εστω διανυσματικό πεδίο F : : F = Fr, όπου r x, και είναι η ταχύτητα στο σημείο πχ ενός ρευστού στο επίπεδο Εστω ότι ψάχνουμε τις τροχιές κίνησης των
4 Εισαγωγή Kεφάλαιο 4 Συστήματα διαφορικών εξισώσεων Εστω διανυσματικό πεδίο F : : F = Fr, όπου r x, και είναι η ταχύτητα στο σημείο πχ ενός ρευστού στο επίπεδο Εστω ότι ψάχνουμε τις τροχιές κίνησης των
Αριθμητικές Μέθοδοι σε Προγραμματιστικό Περιβάλλον
 Τμήμα Μηχανικών Πληροφορικής Αριθμητικές Μέθοδοι σε Προγραμματιστικό Περιβάλλον Δρ. Δημήτρης Βαρσάμης Επίκουρος Καθηγητής Οκτώβριος 2015 Δρ. Δημήτρης Βαρσάμης Οκτώβριος 2015 1 / 63 Αριθμητικές Μέθοδοι
Τμήμα Μηχανικών Πληροφορικής Αριθμητικές Μέθοδοι σε Προγραμματιστικό Περιβάλλον Δρ. Δημήτρης Βαρσάμης Επίκουρος Καθηγητής Οκτώβριος 2015 Δρ. Δημήτρης Βαρσάμης Οκτώβριος 2015 1 / 63 Αριθμητικές Μέθοδοι
Κεφάλαιο 3.1 Εξισώσεις 1 ου Βαθμού Επιμέλεια Σημειώσεων: Ντάνος Γιώργος ΚΕΦΑΛΑΙΟ 3.1 ΕΞΙΣΩΣΕΙΣ 1 ΟΥ ΒΑΘΜΟΥ 1
 Κεφάλαιο 3.1 Εξισώσεις 1 ου Βαθμού Επιμέλεια Σημειώσεων: Ντάνος Γιώργος ΚΕΦΑΛΑΙΟ 3.1 ΕΞΙΣΩΣΕΙΣ 1 ΟΥ ΒΑΘΜΟΥ 1 Εξίσωση πρώτου βαθμού ή πρωτοβάθμια εξίσωση με άγνωστο x ονομάζεται κάθε εξίσωση της μορφής
Κεφάλαιο 3.1 Εξισώσεις 1 ου Βαθμού Επιμέλεια Σημειώσεων: Ντάνος Γιώργος ΚΕΦΑΛΑΙΟ 3.1 ΕΞΙΣΩΣΕΙΣ 1 ΟΥ ΒΑΘΜΟΥ 1 Εξίσωση πρώτου βαθμού ή πρωτοβάθμια εξίσωση με άγνωστο x ονομάζεται κάθε εξίσωση της μορφής
Διαφορικές εξισώσεις
 Διαφορικές εξισώσεις Κώστας Γλυκός Ασκήσεις για ΑΕΙ και ΤΕΙ σε Διαφορικές εξισώσεις τεχνικές 73 ασκήσεις Ι δ ι α ί τ ε ρ α μ α θ ή μ α τ α 6 9 7. 3 0 0. 8 8. 8 8 Kglys.gr 1 1 / 1 / 0 1 8 εκδόσεις Καλό
Διαφορικές εξισώσεις Κώστας Γλυκός Ασκήσεις για ΑΕΙ και ΤΕΙ σε Διαφορικές εξισώσεις τεχνικές 73 ασκήσεις Ι δ ι α ί τ ε ρ α μ α θ ή μ α τ α 6 9 7. 3 0 0. 8 8. 8 8 Kglys.gr 1 1 / 1 / 0 1 8 εκδόσεις Καλό
ΚΕΦΑΛΑΙΟ 2Ο : Η ΕΥΘΕΙΑ ΣΤΟ ΕΠΙΠΕΔΟ ΒΑΣΙΚΗ ΜΕΘΟΔΟΛΟΓΙΑ
 ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ Ο : Η ΕΥΘΕΙΑ ΣΤΟ ΕΠΙΠΕΔΟ ΒΑΣΙΚΗ ΜΕΘΟΔΟΛΟΓΙΑ. Ένα σημείο Μ(x,y) ανήκει σε μια γραμμή C αν και μόνο αν επαληθεύει την εξίσωσή της. Π.χ. :
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ Ο : Η ΕΥΘΕΙΑ ΣΤΟ ΕΠΙΠΕΔΟ ΒΑΣΙΚΗ ΜΕΘΟΔΟΛΟΓΙΑ. Ένα σημείο Μ(x,y) ανήκει σε μια γραμμή C αν και μόνο αν επαληθεύει την εξίσωσή της. Π.χ. :
ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΓΕΝΙΚΑ ΜΑΘΗΜΑΤΙΚΑ. Τμήμα Φαρμακευτικής ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ. Λυμένες Ασκήσεις & Λυμένα Θέματα Εξετάσεων
 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΓΕΝΙΚΑ ΜΑΘΗΜΑΤΙΚΑ Τμήμα Φαρμακευτικής ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Λυμένες Ασκήσεις & Λυμένα Θέματα Εξετάσεων ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΙΑΝΟΥΑΡΙΟΥ 014 ΘΕΜΑ 1 Δίνεται ο πίνακας: 1) Να
ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΓΕΝΙΚΑ ΜΑΘΗΜΑΤΙΚΑ Τμήμα Φαρμακευτικής ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Λυμένες Ασκήσεις & Λυμένα Θέματα Εξετάσεων ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΙΑΝΟΥΑΡΙΟΥ 014 ΘΕΜΑ 1 Δίνεται ο πίνακας: 1) Να
Κεφάλαιο 6. Συντηρητικες Δυναμεις {Ανεξαρτησία του Εργου από τη Διαδρομή, Εννοια του Δυναμικού, Δυναμικό και Πεδίο Συντηρητικών Δυνάμεων}
 Κεφάλαιο 6 ΕΡΓΟ ΚΑΙ ΕΝΕΡΓΕΙΑ Εννοια του Εργου { Εργο και Κινητική Ενέργεια, Εργο Μεταβλητής Δύναμης, Ισχύς} Συντηρητικες Δυναμεις {Ανεξαρτησία του Εργου από τη Διαδρομή, Εννοια του Δυναμικού, Δυναμικό
Κεφάλαιο 6 ΕΡΓΟ ΚΑΙ ΕΝΕΡΓΕΙΑ Εννοια του Εργου { Εργο και Κινητική Ενέργεια, Εργο Μεταβλητής Δύναμης, Ισχύς} Συντηρητικες Δυναμεις {Ανεξαρτησία του Εργου από τη Διαδρομή, Εννοια του Δυναμικού, Δυναμικό
ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ Κεφ. 1 - Συστήματα 1
 ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ Κεφ. 1 - Συστήματα 1 1.1 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Η εξίσωση α + βy = γ 1. Υπάρχουν προβλήματα που η επίλυση τους οδηγεί σε μια γραμμική εξίσωση με δύο αγνώστους, y και η οποία είναι της μορφής
ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ Κεφ. 1 - Συστήματα 1 1.1 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Η εξίσωση α + βy = γ 1. Υπάρχουν προβλήματα που η επίλυση τους οδηγεί σε μια γραμμική εξίσωση με δύο αγνώστους, y και η οποία είναι της μορφής
ΗΜΕΡΙΔΑ ΜΑΘΗΜΑΤΙΚΩΝ. Θέμα: Τεχνικές Ολοκλήρωσης. Εισηγητής: Κων/νος Λ. Κωνσταντόπουλος. Σχολικός Σύμβουλος Μαθηματικών
 ΗΜΕΡΙΔΑ ΜΑΘΗΜΑΤΙΚΩΝ Θέμα: Τεχνικές Ολοκλήρωσης Εισηγητής: Κων/νος Λ. Κωνσταντόπουλος Σχολικός Σύμβουλος Μαθηματικών Ρέθυμνο 0 Φεβρουαρίου 05 Πρότυπο Πειραματικό Λύκειο Ρεθύμνου A. Ολοκλήρωση ρητής συνάρτησης
ΗΜΕΡΙΔΑ ΜΑΘΗΜΑΤΙΚΩΝ Θέμα: Τεχνικές Ολοκλήρωσης Εισηγητής: Κων/νος Λ. Κωνσταντόπουλος Σχολικός Σύμβουλος Μαθηματικών Ρέθυμνο 0 Φεβρουαρίου 05 Πρότυπο Πειραματικό Λύκειο Ρεθύμνου A. Ολοκλήρωση ρητής συνάρτησης
Εύρεση της n-οστής δύναμης ενός πίνακα εϕαρμόζοντας το θεώρημα των Cayley-Hamilton
 Εύρεση της n-οστής δύναμης ενός πίνακα εϕαρμόζοντας το θεώρημα των Cayley-Hamilton Νικος Χαλιδιας Μαθηματικό Τμήμα κατεύθυνση Στατιστικής και Αναλογιστικών-Χρηματοοικονομικών Μαθηματικών Πανεπιστημιο Αιγαιου
Εύρεση της n-οστής δύναμης ενός πίνακα εϕαρμόζοντας το θεώρημα των Cayley-Hamilton Νικος Χαλιδιας Μαθηματικό Τμήμα κατεύθυνση Στατιστικής και Αναλογιστικών-Χρηματοοικονομικών Μαθηματικών Πανεπιστημιο Αιγαιου
ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 5: ΘΕΩΡΗΜΑ ROLLE [Θεώρημα Rolle του κεφ.2.5 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ
![ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 5: ΘΕΩΡΗΜΑ ROLLE [Θεώρημα Rolle του κεφ.2.5 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 5: ΘΕΩΡΗΜΑ ROLLE [Θεώρημα Rolle του κεφ.2.5 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ](/thumbs/60/44973374.jpg) ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 5: ΘΕΩΡΗΜΑ ROLLE [Θεώρημα Rolle του κεφ..5 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β Παράδειγμα. Να εξετάσετε από τις παρακάτω συναρτήσεις ποιές ικανοποιούν
ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 5: ΘΕΩΡΗΜΑ ROLLE [Θεώρημα Rolle του κεφ..5 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β Παράδειγμα. Να εξετάσετε από τις παρακάτω συναρτήσεις ποιές ικανοποιούν
[1] είναι ταυτοτικά ίση με το μηδέν. Στην περίπτωση που το στήριγμα μιας συνάρτησης ελέγχου φ ( x)
![[1] είναι ταυτοτικά ίση με το μηδέν. Στην περίπτωση που το στήριγμα μιας συνάρτησης ελέγχου φ ( x) [1] είναι ταυτοτικά ίση με το μηδέν. Στην περίπτωση που το στήριγμα μιας συνάρτησης ελέγχου φ ( x)](/thumbs/52/30132893.jpg) [] 9 ΣΥΝΑΡΤΗΣΙΑΚΟΙ ΧΩΡΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER Η «συνάρτηση» δέλτα του irac Η «συνάρτηση» δέλτα ορίζεται μέσω της σχέσης φ (0) αν 0 δ[ φ ] = φ δ dx = (9) 0 αν 0 όπου η φ είναι μια συνάρτηση που ανήκει
[] 9 ΣΥΝΑΡΤΗΣΙΑΚΟΙ ΧΩΡΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER Η «συνάρτηση» δέλτα του irac Η «συνάρτηση» δέλτα ορίζεται μέσω της σχέσης φ (0) αν 0 δ[ φ ] = φ δ dx = (9) 0 αν 0 όπου η φ είναι μια συνάρτηση που ανήκει
M. J. Lighthill. g(y) = f(x) e 2πixy dx, (1) d N. g (p) (y) =
 Εισαγωγή στην ανάλυση Fourier και τις γενικευμένες συναρτήσεις * M. J. Lighthill μετάφραση: Γ. Ευθυβουλίδης ΚΕΦΑΛΑΙΟ 2 Η ΘΕΩΡΙΑ ΤΩΝ ΓΕΝΙΚΕΥΜΕΝΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΚΑΙ ΤΩΝ ΜΕΤΑΣΧΗΜΑΤΙΣΜΩΝ ΤΟΥΣ FOURIER 2.1. Καλές
Εισαγωγή στην ανάλυση Fourier και τις γενικευμένες συναρτήσεις * M. J. Lighthill μετάφραση: Γ. Ευθυβουλίδης ΚΕΦΑΛΑΙΟ 2 Η ΘΕΩΡΙΑ ΤΩΝ ΓΕΝΙΚΕΥΜΕΝΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΚΑΙ ΤΩΝ ΜΕΤΑΣΧΗΜΑΤΙΣΜΩΝ ΤΟΥΣ FOURIER 2.1. Καλές
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α. ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 5: ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΥΠΟΧΩΡΟΙ ΓΡΑΜΜΙΚΗ ΑΝΕΞΑΡΤΗΣΙΑ ΒΑΣΕΙΣ & ΔΙΑΣΤΑΣΗ Δ.Χ. ΣΗΜΕΙΩΣΕΙΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α. ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 5: ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΥΠΟΧΩΡΟΙ ΓΡΑΜΜΙΚΗ ΑΝΕΞΑΡΤΗΣΙΑ ΒΑΣΕΙΣ & ΔΙΑΣΤΑΣΗ Δ.Χ. ΣΗΜΕΙΩΣΕΙΣ
Λύσεις στο Επαναληπτικό Διαγώνισμα 2
 Τμήμα Μηχανικών Οικονομίας και Διοίκησης Απειροστικός Λογισμός ΙΙ Γ. Καραγιώργος ykarag@aegean.gr Λύσεις στο Επαναληπτικό Διαγώνισμα 2 Για τυχόν παρατηρήσεις, απορίες ή λάθη που θα βρείτε, στείλτε μου
Τμήμα Μηχανικών Οικονομίας και Διοίκησης Απειροστικός Λογισμός ΙΙ Γ. Καραγιώργος ykarag@aegean.gr Λύσεις στο Επαναληπτικό Διαγώνισμα 2 Για τυχόν παρατηρήσεις, απορίες ή λάθη που θα βρείτε, στείλτε μου
ΣΥΣΤΗΜΑΤΑ. 6.1 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ (Επαναλήψεις-Συμπληρώσεις)
 6 ΣΥΣΤΗΜΑΤΑ 6.1 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ (Επαναλήψεις-Συμπληρώσεις) Η εξίσωση αx βy γ Στο Γυμνάσιο διαπιστώσαμε με την βοήθεια παραδειγμάτων ότι η εξίσωση αx βy γ, με α 0 ή β 0, που λέγεται γραμμική εξίσωση,
6 ΣΥΣΤΗΜΑΤΑ 6.1 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ (Επαναλήψεις-Συμπληρώσεις) Η εξίσωση αx βy γ Στο Γυμνάσιο διαπιστώσαμε με την βοήθεια παραδειγμάτων ότι η εξίσωση αx βy γ, με α 0 ή β 0, που λέγεται γραμμική εξίσωση,
ΜΑΘΗΜΑΤΙΚΑ ΙΙ ιδάσκων : Ε. Στεφανόπουλος 12 ιουνιου 2017
 Πανεπιστηµιο Πατρων Πολυτεχνικη Σχολη Τµηµα Μηχανικων Η/Υ & Πληροφορικης ΜΑΘΗΜΑΤΙΚΑ ΙΙ ιδάσκων : Ε. Στεφανόπουλος 12 ιουνιου 217 Θ1. Θεωρούµε την συνάρτηση f(x, y, z) = 1 + x 2 + 2y 2 z. (αʹ) Να ϐρεθεί
Πανεπιστηµιο Πατρων Πολυτεχνικη Σχολη Τµηµα Μηχανικων Η/Υ & Πληροφορικης ΜΑΘΗΜΑΤΙΚΑ ΙΙ ιδάσκων : Ε. Στεφανόπουλος 12 ιουνιου 217 Θ1. Θεωρούµε την συνάρτηση f(x, y, z) = 1 + x 2 + 2y 2 z. (αʹ) Να ϐρεθεί
Ο μαθητής που έχει μελετήσει το κεφάλαιο αυτό θα πρέπει:
 Ο μαθητής που έχει μελετήσει το κεφάλαιο αυτό θα πρέπει: Να αναγνωρίζει πότε μια αλγεβρική παράσταση της πραγματικής μεταβλητής x, είναι πολυώνυμο και να διακρίνει τα στοιχεία του: όροι, συντελεστές, σταθερός
Ο μαθητής που έχει μελετήσει το κεφάλαιο αυτό θα πρέπει: Να αναγνωρίζει πότε μια αλγεβρική παράσταση της πραγματικής μεταβλητής x, είναι πολυώνυμο και να διακρίνει τα στοιχεία του: όροι, συντελεστές, σταθερός
ΘΕΩΡΙΑ: Έστω η οµογενής γραµµική διαφορική εξίσωση τάξης , (1)
 1 ΘΕΩΡΙΑ: Έστω η οµογενής γραµµική διαφορική εξίσωση τάξης (1) όπου οι συντελεστές είναι δοσµένες συνεχείς συναρτήσεις ορισµένες σ ένα ανοικτό διάστηµα. Ορισµός 1. Ορίζουµε τον διαφορικό τελεστή µέσω της
1 ΘΕΩΡΙΑ: Έστω η οµογενής γραµµική διαφορική εξίσωση τάξης (1) όπου οι συντελεστές είναι δοσµένες συνεχείς συναρτήσεις ορισµένες σ ένα ανοικτό διάστηµα. Ορισµός 1. Ορίζουµε τον διαφορικό τελεστή µέσω της
Ασκήσεις Συνήθων Διαϕορικών Εξισώσεων
 Ασκήσεις Συνήθων Διαϕορικών Εξισώσεων Α. Αργυρίου May 5, 205 Οι σημειώσεις αυτές περιέχουν λυμένες ασκήσεις από τις διάϕορες ενότητες του μαθήματος των Συνήθων Διαϕορικών Εξισώσεων, ώστε να δώσουν τη δυνατότητα
Ασκήσεις Συνήθων Διαϕορικών Εξισώσεων Α. Αργυρίου May 5, 205 Οι σημειώσεις αυτές περιέχουν λυμένες ασκήσεις από τις διάϕορες ενότητες του μαθήματος των Συνήθων Διαϕορικών Εξισώσεων, ώστε να δώσουν τη δυνατότητα
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 2017-2018 Παρεμβολή και Παρεκβολή Εισαγωγή Ορισμός 6.1 Αν έχουμε στη διάθεσή μας τιμές μιας συνάρτησης
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 2017-2018 Παρεμβολή και Παρεκβολή Εισαγωγή Ορισμός 6.1 Αν έχουμε στη διάθεσή μας τιμές μιας συνάρτησης
I. ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. math-gr
 I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
Πρόλογος Εισαγωγή στη δεύτερη έκδοση Εισαγωγή... 11
 Περιεχόμενα Πρόλογος... 9 Εισαγωγή στη δεύτερη έκδοση... 0 Εισαγωγή... Ε. Εισαγωγή στην έννοια της Αριθμητικής Ανάλυσης... Ε. Ταξινόμηση των θεμάτων που απασχολούν την αριθμητική ανάλυση.. Ε.3 Μορφές σφαλμάτων...
Περιεχόμενα Πρόλογος... 9 Εισαγωγή στη δεύτερη έκδοση... 0 Εισαγωγή... Ε. Εισαγωγή στην έννοια της Αριθμητικής Ανάλυσης... Ε. Ταξινόμηση των θεμάτων που απασχολούν την αριθμητική ανάλυση.. Ε.3 Μορφές σφαλμάτων...
Τίτλος Μαθήματος: Συνήθεις Διαφορικές Εξισώσεις Ι
 Τίτλος Μαθήματος: Συνήθεις Διαφορικές Εξισώσεις Ι Ενότητα: Σ.Δ.Ε. 1 ης τάξης ανώτερου βαθμού, ορθογώνιες τροχιές Όνομα Καθηγητή: Χρυσή Κοκολογιαννάκη Τμήμα: Μαθηματικών Άδειες Χρήσης Το παρόν εκπαιδευτικό
Τίτλος Μαθήματος: Συνήθεις Διαφορικές Εξισώσεις Ι Ενότητα: Σ.Δ.Ε. 1 ης τάξης ανώτερου βαθμού, ορθογώνιες τροχιές Όνομα Καθηγητή: Χρυσή Κοκολογιαννάκη Τμήμα: Μαθηματικών Άδειες Χρήσης Το παρόν εκπαιδευτικό
Περιεχόµενα. 0.1 Υλη του Μαθήµατος : Συγγράµµατα, Βιβλιογραϕία... 4
 Περιεχόµενα 0.1 Υλη του Μαθήµατος :.................................... 1 0.2 Συγγράµµατα, Βιβλιογραϕία................................ 4 1 Βασικές Εννοιες 6 1.1 Εισαγωγικές-Θεµελιώδεις Εννοιες.............................
Περιεχόµενα 0.1 Υλη του Μαθήµατος :.................................... 1 0.2 Συγγράµµατα, Βιβλιογραϕία................................ 4 1 Βασικές Εννοιες 6 1.1 Εισαγωγικές-Θεµελιώδεις Εννοιες.............................
Μ Α Θ Η Μ Α Τ Α Γ Λ Υ Κ Ε Ι Ο Υ
 Μ Α Θ Η Μ Α Τ Α Γ Λ Υ Κ Ε Ι Ο Υ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ (Α ΜΕΡΟΣ: ΣΥΝΑΡΤΗΣΕΙΣ) Επιμέλεια: Καραγιάννης Ιωάννης, Σχολικός Σύμβουλος Μαθηματικών
Μ Α Θ Η Μ Α Τ Α Γ Λ Υ Κ Ε Ι Ο Υ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ (Α ΜΕΡΟΣ: ΣΥΝΑΡΤΗΣΕΙΣ) Επιμέλεια: Καραγιάννης Ιωάννης, Σχολικός Σύμβουλος Μαθηματικών
(a + b) + c = a + (b + c), (ab)c = a(bc) a + b = b + a, ab = ba. a(b + c) = ab + ac
 Σημειώσεις μαθήματος Μ1212 Γραμμική Άλγεβρα ΙΙ Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2014 Κεφάλαιο 1 Διανυσματικοί Χώροι Στο εισαγωγικό μάθημα Γραμμικής Άλγεβρας ξεκινήσαμε μελετώντας
Σημειώσεις μαθήματος Μ1212 Γραμμική Άλγεβρα ΙΙ Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2014 Κεφάλαιο 1 Διανυσματικοί Χώροι Στο εισαγωγικό μάθημα Γραμμικής Άλγεβρας ξεκινήσαμε μελετώντας
ΕΠΙΚΑΜΠΥΛΙΑ ΚΑΙ ΕΠΙΕΠΙΦΑΝΕΙΑ ΟΛΟΚΛΗΡΩΜΑΤΑ
 6. Ορισμός επικαμπύλιου ολοκληρώματος 36 KΕΦΑΛΑΙΟ 6 ΕΠΙΚΑΜΠΥΛΙΑ ΚΑΙ ΕΠΙΕΠΙΦΑΝΕΙΑ ΟΛΟΚΛΗΡΩΜΑΤΑ Τα επικαμπύλια ολοκληρώματα αποτελούν επέκταση της έννοιας του απλού ολο κληρώματος στην περίπτωση κατά την
6. Ορισμός επικαμπύλιου ολοκληρώματος 36 KΕΦΑΛΑΙΟ 6 ΕΠΙΚΑΜΠΥΛΙΑ ΚΑΙ ΕΠΙΕΠΙΦΑΝΕΙΑ ΟΛΟΚΛΗΡΩΜΑΤΑ Τα επικαμπύλια ολοκληρώματα αποτελούν επέκταση της έννοιας του απλού ολο κληρώματος στην περίπτωση κατά την
ΜΑΣ002: Μαθηματικά ΙΙ ΑΣΚΗΣΕΙΣ (για εξάσκηση)
 ΜΑΣ00: Μαθηματικά ΙΙ ΑΣΚΗΣΕΙΣ (για εξάσκηση) ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ Να κατατάξετε τις διαφορικές εξισώσεις, δηλ να δώσετε την τάξη της, να πείτε αν είναι γραμμική ή όχι, να δώσετε την ανεξάρτητη μεταβλητή
ΜΑΣ00: Μαθηματικά ΙΙ ΑΣΚΗΣΕΙΣ (για εξάσκηση) ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ Να κατατάξετε τις διαφορικές εξισώσεις, δηλ να δώσετε την τάξη της, να πείτε αν είναι γραμμική ή όχι, να δώσετε την ανεξάρτητη μεταβλητή
