Μέχριτώραηµελέτητωντυχαίωνδιαδικασιώνέγινεστοπεδίοτουχρόνου (µέσητιµή, συναρτήσεις αυτοσυσχέτισης, αµοιβαίου συσχετισµού και συµµεταβολής).
|
|
|
- Νατάσσα Κουβέλης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Μέχριτώραηµελέτητωντυχαίωνδιαδικασιώνέγινεστοπεδίοτουχρόνου (µέσητιµή, συναρτήσεις αυτοσυσχέτισης, αµοιβαίου συσχετισµού και συµµεταβολής. Στη συνέχεια οι τυχαίες διαδικασίες θα µελετηθούν στο πεδίο συχνότητας. Για ένα νοµοτελειακό σήµα x ( οι φασµατικές ιδιότητες περιγράφονται από το µετασχηµατισµό Fourier ( x( j π e d ( είναιηφασµατικήπυκνότητατάσης (volage densiy specrum Το σήµα x( µπορεί να ανακτηθεί µε τον αντίστροφο µετασχηµατισµό Fourier x ( ( e j π d Η περιγραφή τυχαίας διαδικασίας µέσω του φάσµατος πυκνότητας τάσης δεν είναι πάντα εφικτή. Γιατολόγοαυτόχρησιµοποιούµετηφασµατικήπυκνότηταισχύος.
2 Φασµατικά Χαρακτηριστικά Τυχαίας ιαδικασίας Ηµέσηισχύς µιαςτυχαίαςδιαδικασίας (δίνεται + [ ] + [ ( ] E ( d lim lim E d Ορίζουµε τη Φασµατική Πυκνότητας Ισχύος της τυχαίας διαδικασίας ως ( E lim [ ( ] οπότε η µέση ισχύς της διαδικασίας βρίσκεται µε το ολοκλήρωµα + ( d 4-
3 Ιδιότητες της Φασµατικής Πυκνότητας Ισχύος ( ( ( όταν η είναι πραγµατική 3 Η είναι πραγµατική ( [ [ ] 4 ( d A E ( + 5 F A[ R (, +τ ] ( ( Αν η ( είναι τουλάχιστον στατική (µε την ευρεία έννοια τότε R F ( τ ( R ( τ ( e j π τ dτ ( R τ e j π τ ( dτ 4-3
4 Παράδειγµα (συνηµιτονοειδές κύµα µε τυχαία φάση Για τη τυχαία διαδικασία ( A cos ( π + Θ όπου Θ τυχαία µεταβλητή οµοιόµορφα κατανεµηµένη στο διάστηµα [ π να βρεθεί η συνάρτηση αυτοσυσχέτισης και η φασµατική πυκνότητα ισχύος της τυχαίας διαδικασίας. Απάντηση x ( ; ϑ A cos( π + ϑ x ( ; ϑ A cos( π + ϑ x ( ; ϑ 3 Acos( π + ϑ3 x ( ; ϑ 4 A cos( π + ϑ4 Η συνάρτηση αυτοσυσχέτισης της τυχαίας διαδικασίας είναι A R ( τ cos( π τ Η φασµατική πυκνότητα ισχύος της τυχαίας διαδικασίας είναι A 4 δ ( + A ( δ + 4 R (τ A [ δ( + ( ] ( A 4 ( Τυχαίες διαδικασίες στο πεδίο συχνοτήτων δ τ 4-4
5 Παράδειγµα (τυχαίο δυαδικό κύµα ίνεται η τυχαία διαδικασία της οποίας τα δείγµατα συνάρτησης είναι η έξοδος ενός ψηφιακού διαµορφωτή ο οποίος στα δυαδικά ψηφία και αντιστοιχεί ορθογώνιους παλµούς µε πλάτη A και A αντίστοιχα και χρονικής διάρκεια. Ναβρεθείησυνάρτησηαυτοσυσχέτισηςκαιηφασµατικήπυκνότηταισχύοςτηςδιαδικασίας. x k ( A A d είγµα συνάρτησης τυχαίου δυαδικού κύµατος Τοχρονικόδιάστηµα d είναιδείγµατυχαίαςµεταβλητής d οµοιόµορφακατανεµηµένηςστο διάστηµα [, Τ (, d d d, αλλιώς Υποθέτοντας ότι τα δυαδικά ψηφία και είναι ισοπίθανα έχουµε E[(]. 4-5
6 x ( Αν > οιτυχαίεςµεταβλητέςλαµβάνονταισεδιαφορετικάχρονικάδιαστήµαταπαλµών και λόγω της ανεξαρτησίας είναι [ ( ( ] E[ ( ] E[ ( ] R (, E x ( d x 3( d ( ( 4-6
7 Αν < και <, οιτυχαίεςµεταβλητές ( καιχ( λαµβάνονταιστοίδιοχρονικό διάστηµαπαλµούανκαιµόνοαντοχρονικόδιάστηµα d ικανοποιείτην < d d < < τ d x ( x ( d x 3( d ( ( 4-7
8 Η συνάρτηση αυτοσυσχέτισης της τυχαίας διαδικασίας είναι [ ] ( (, ( E R Αν > οιτυχαίεςµεταβλητέςλαµβάνονταισεδιαφορετικάχρονικάδιαστήµαταπαλµών και λόγω της ανεξαρτησίας είναι [ ] [ ] [ ] ( ( ( (, ( E E E R Αν < και <, οιτυχαίεςµεταβλητές ( καιχ( λαµβάνονταιστοίδιοχρονικό διάστηµαπαλµούανκαιµόνοαντοχρονικόδιάστηµα d ικανοποιείτην d <. Η υποσυσθήκηµέσητιµή E[( ( d ] δίνεταιως [ ] < αλλιώς,, ( ( A E d d Ολοκληρώνονταςγιαόλεςτιςτιµέςτηςµεταβλητής d έχουµε [ ] ( d A d d A d d A E d ( ( ( 4-8
9 Η συνάρτηση αυτοσυσχέτισης της τυχαίας διαδικασίας είναι R ( τ A ( τ,, τ < τ R (τ A τ Χρησιµοποιώντας το µετασχηµατισµό Fourier του τριγωνικού παλµού η φασµατική πυκνότητα ισχύος της τυχαίας διαδικασίας είναι ( A sinc ( ( A
10 Η Gaussian τυχαία µεταβλητή Η συνάρτηση πυκνότητας πιθανότητας είναι ( x m ( σ x e πσ όπου mείναιηµέσητιµήκαισ ηδιασπορά ( x πσ,67 πσ,68 m σ m m+ σ Η συνάρτηση πυκνότητας πιθανότητας της Gaussian τυχαίας µεταβλητής x 4-
11 Μέσο Τετραγωνικό Εύρος Ζώνης της Φασµατικής Πυκνότητας Ισχύος Γνωρίζουµε ότι η διασπορά είναι ένα µέτρο του ανοίγµατος της συνάρτησης πυκνότηταςπιθανότητας. Η ανάλογη ποσότητα για την κανονικοποιηµένη φασµατική πυκνότητα ισχύος µίαςτυχαίαςδιαδικασίαςείναιτοµέσοτετραγωνικόεύροςζώνης rms (roo mean squared bandwidh η οποία συµβολίζεται ως W rms ( rad/sec Αν η διαδικασία είναι βασικής ζώνης το µέσο τετραγωνικό εύρος ζώνης δίνεται από W rms ω ( ω ( ω dω dω 4-
12 Παράδειγµα ίνεται η τυχαία διαδικασία που έχει τη φασµατική πυκνότητα ισχύος ( ω [ + ( ω / ] Να προσδιοριστεί το µέσο τετραγωνικό εύρος ζώνης Λύση W rms ω ( ω ( ω dω dω + ω + ( ω ( ω dω dω ω [ ( ω / ] [ ( ω / ] dω dω 5π 5π 5 π W rad rms 5π sec (ω 5 4 W rms ω rad sec 4-
13 Ορίζουµεως διαφασµατική πυκνότητα ισχύοςγια τις τυχαίες διαδικασίες ( και Y( ( F[ ( τ ] Y R Y Επειδή ισχύει R Y ( τ R ( τ h ( έχουµε τ Y ( ( H ( Ενώ επειδή ισχύει Y R Y ( τ R ( έχουµε τ Y ( ( ( H( Y 4-3
14 Τυχαίες ιαδικασίες και Γραµµικά Συστήµατα ( H ( ( Y Γιατηµέσητιµήσυνόλουτηςεξόδουέχουµε m H ( m Y m H ( Για τις συναρτήσεις φασµατικής πυκνότητας ισχύος έχουµε H ( Y ( ( H ( ( H ( ( ( H( Y H ( ( ( H( Y 4-4
15 Φασµατική Πυκνότητα Ισχύος του Αθροίσµατος ιαδικασιών ίνονται οι W τυχαίες διαδικασίες ( και Y( και ορίζεται η τυχαία διαδικασία Z ( ( + Y ( Η συνάρτηση αυτοσυσχέτισης της Z( είναι R ( τ R ( τ + R ( τ + R ( τ + R ( τ ZZ και η φασµατική πυκνότητα ισχύος της Z( είναι Z YY ( ( + ( + Re[ ( ] Y Y Y Y Αν οι δύο διαδικασίες είναι ασυσχέτιστες τότε R Y (τ m m Y τουλάχιστον από τις διαδικασίες έχει µέση τιµή ίση µε το µηδέν τότε και αν µία ( ( ( Z + Y 4-5
16 Μίξη τυχαίας διαδικασίας µε συνηµιτονοειδή τυχαία διαδικασία R YY, Πολλαπλασιατής ( ( ( A cos( ( A cos π Η συνάρτηση αυτoσυσχέτισης της εξόδου είναι Y π ( + τ E[ Y( Y( +τ ] E [ A ( ( + τ cos( π cos( π + τ ] π [ cos( π τ + cos( π + τ ] A R ( τ π παρατηρούµεότιηr (, + τ εξαρτάταιαπότο έτσι A A [ R ( + τ ] lim R (, τ YY, + YY d lim A ( π τ d+ lim R ( τ cos( 4π + τ A R ( τ cos π d A R π ( ( τ cos τ 4-6
17 Γνωρίζουµε για τη φασµατική πυκνότητα ισχύος Εποµένως η φασµατική πυκνότητα ισχύος της εξόδου του πολλαπλασιαστή είναι A F [ R (, +τ ] ( YY YY ( 4 + ( [ ] A A F R ( τ cos( π τ [ + ( ] YY ( ( YY ( A 4 YY (
18 Λευκός Θόρυβος Μία συνάρτηση δείγµατος n( µίας W τυχαίας διαδικασίας N( ονοµάζεται λευκός θόρυβος αν N N ( Η συνάρτηση αυτοσυσχέτισης της διαδικασίας είναι ( N δ ( R ( τ τ NN R NN (τ N ( N δ ( τ N τ 4-8
19 Παρατηρούµε N ( d Ο θερµικός θόρυβος έχει φασµατική πυκνότητα ισχύος N ( ( e h h k h k e h k h N ( h k k Όπου h 6,6 k, joule secείναι η σταθερά του lanck και joule/kelv inη σταθερά του olzmann Ο θερµικός θόρυβος αποτελεί µία καλή προσέγγιση λευκού θορύβου αφού διατηρεί σταθερή τιµή για µία µεγάλη σχετικά περιοχή συχνοτήτων, πράγµατι N N (,9 N (,9 4-9
20 Θερµικός Θόρυβος (Θόρυβος Johnson Αν n( είναι η στιγµιαία τάση στα άκρα µίας αντίστασης R λόγω θερµικής κίνησης των ηλεκτρονίων, η συνάρτηση πυκνότητας πιθανότητας της n( ακολουθεί στατιστική Gausse, µε µέση τιµή ίση µε µηδέν, δηλαδή, ( υ e σ π υ σ Η διακύµανση του θερµικού θορύβου είναι ίσηµε (υ π m σ σ [ ] n ( n ( 4 k R d Vols E υ H n ( ισούται αριθµητικά µε την ισχύ του θορύβου ανά µονάδα αντίστασης Έχουµε τα δύο Ισοδύναµα Θορύβου κυκλώµατα µίας αντίστασης. Ισοδύναµο θορύβου της αντίστασης R κατά hevenin Ισοδύναµο θορύβου της αντίστασης R κατά Noron 4-
21 Πηγές θερµικού θορύβου Κάθε φυσική αντίσταση µπορεί να µοντελοποιηθεί µε µία πηγή θορύβου σε σειρά µε µία αθόρυβη αντίσταση. n( R (ενθόρυβη R L R (αθόρυβη E n ( R L Η έξοδος n( της πηγής θορύβου χαρακτηρίζεται ως δείγµα συνάρτησης της τυχαίας διαδικασίας N(. Η φασµατική πυκνότητα ισχύος του θερµικού θορύβου που εµφανίζεται στα άκρα αντίστασης R είναι R h V R ( h k e Hz Σε θερµοκρασία δωµατίου αποδεικνύεται ότι φασµατική πυκνότητα ισχύος είναι περίπου R ( k R V Hz e h k h k +, εποµένως, η 4-
22 Αν η αντίσταση αυτή συνδεθεί µε αντίσταση φόρτου R L µεταφερόµενη ισχύ (προσαρµογή όταν η µέγιστη µεταφερόµενη ισχύς είναι R E [ N 4 R L R L ( ] τότε έχουµε µέγιστη Εποµένως η φασµατική πυκνότητα ισχύος του θορύβου στην αντίσταση φόρτου είναι k n ( Το kσυµβολίζεταισυνήθωςµεν,εποµένωςηφασµατικήπυκνότηταισχύοςτου θερµικού θορύβου γενικά εκφράζεται ως ( N n W Hz W Hz 4-
23 Ιδανικά φίλτρα H ( Ζώνη αποκοπής c Ζώνη διέλευσης c Ζώνη αποκοπής Ιδανικό βαθυπερατό φίλτρο H ( Ζώνη αποκοπής Ζώνη διέλευσης Ζώνη αποκοπής Ζώνη διέλευσης Ζώνη αποκοπής Ιδανικό ζωνοπερατό φίλτρο 4-3
24 Αν λευκός θόρυβος διέλθει µέσα από ένα ιδανικό φίλτρο βασικής ζώνης (χαµηλοπερατό η έξοδός του θα είναι λευκός θόρυβος περιορισµένου εύρους ζώνης µε φασµατική πυκνότητα ισχύος, < <, αλλιως ɺ N ( και συνάρτηση αυτοσυσχέτισης ή N, < <, αλλιως ɺ ( N R NN ( τ / / N e j π τ d R NN ( τ sin ( π τ π τ R NN (τ N N ( τ 4-4
25 Αν λευκός θόρυβος διέλθει µέσα από ένα ιδανικό φίλτρο διέλευσης ζώνης (ζωνοπερατό συχνοτήτων η έξοδος θα είναι λευκός ζωνοπερατός θόρυβος µε φασµατική πυκνότητα ισχύος και συνάρτηση αυτοσυσχέτισης R, < < +, αλλιως ɺ N ( sin ( π τ ( τ cos (π NN π τ τ R NN (τ N ( τ
26 Παράδειγµα Μία τυχαία διαδικασία θορύβου είναι στατική µε την ευρεία έννοια (W και έχει συνάρτηση αυτοσυσχέτισης R NN ( τ e a τ Να προσδιοριστεί η φασµατική πυκνότητα ισχύος της τυχαίας διαδικασίας θορύβου. Λύση a a + (π Από το γνωστό ζευγάρι µετασχηµατισµού Fourier F NN ( a a + (π e a R (τ a,5 a, 9 ( a a 5 5 τ (sec, 5, 5 ( Hz 4-6
27 Ισοδύναµο Εύρος Ζώνης Θορύβου Ορίζουµεωςισοδύναµοεύροςζώνηςθορύβουτοεύροςζώνης neq ενόςιδανικού φίλτρου που αφήνει να περάσει την ίδια ολική ισχύ θορύβου µε την πραγµατική διάταξη, αν στην είσοδό του δεχόταν τον ίδιο λευκό θόρυβο. Η ισχύς θορύβου στην έξοδο του πραγµατικού φίλτρου πραγ N H ( d N H ( d Η ισχύς θορύβου στην έξοδο του ιδανικού φίλτρου ιδαν neq neq N H ( d N H ( neq Το ισοδύναµο εύρος ζώνης θορύβου H ( d H ( neq 4-7
28 Η συνάρτηση µεταφοράς ισχύος (power ranser uncion πραγµατικού και του ιδανικού του φίλτρου H ( H max neq neq Το τετράγωνο του µέτρου της απόκρισης συχνότητας του πραγµατικού φίλτρου H I ( Ίσα εµβαδά H max neq neq Το τετράγωνο του µέτρου της απόκρισης συχνότητας του ιδανικού φίλτρου 4-8
29 Θερµικός Θόρυβος από κύκλωµα RC R C y ( x ( ( k R R C y ( Y ( Κύκλωµα RC Ισοδύναµο θορύβου Απόκριση συχνότητας του κυκλώµατος RC H ( H ( Z C Z + C Z R + j π RC + j Απόκριση ισχύος του κυκλώµατος RC 4-9
30 Η συνάρτηση φασµατικής πυκνότητας ισχύος της εξόδου του κυκλώµατος Y k ( R Y ( ( H ( Y ( k R + ( Η συνάρτηση αυτοσυσχέτισης εξόδου (τ R YY k C R Y ( τ k C e τ RC k C Ηισχύςτηςέξοδου RC RC τ y RY ( k C 4-3
31 Ενεργός θερµοκρασία θορύβου Στα συστήµατα επικοινωνίας, όταν χρησιµοποιούµε ενισχυτές για να ανυψώσουµε τη στάθµη ενόςσήµατος, ενισχύεταιεπίσηςκαι οθόρυβοςπουδιαβρώνειτοσήµα. Επειδή κάθε ενισχυτής έχει πεπερασµένο εύρος-ζώνης, µπορούµε να αναπαραστήσουµε έναν ενισχυτή ως ένα φίλτρο µε απόκριση συχνότητας H(. Ας υπολογίσουµε την έξοδο ενός ενισχυτήότανστηνείσοδότουσυνδεθείπηγήθερµικούθορύβου. Πηγή θερµικού θορύβου Προσαρµογή Ενισχυτής H( Προσαρµογή Φόρτος Θερµικός θόρυβος που εφαρµόζεται σε φόρτο µέσω ενισχυτή. Η ισχύς του θορύβου στην έξοδο του τετραπόλου (ενισχυτής είναι + N nos N ( H ( + d H ( d neq N H ( max όπου H ( max είναι η µέγιστη διαθέσιµη απολαβή ισχύος του τετραπόλου Ενεργός θερµοκρασία θορύβου Εικόνα θορύβου 4-3
32 Κάθε τετράπολο στην πράξη παρέχει επιπρόσθετο θόρυβο στην έξοδό του εξαιτίας θορύβου που δηµιουργείται εσωτερικά. Εποµένως η ισχύς του θορύβου στην έξοδό του ενισχυτή µπορεί να εκφρασθεί ως + no neq N H ( max + noi neq ks H ( max όπου nοi είναι η ισχύς της εξόδου του ενισχυτή εξαιτίας του θορύβου που παράγεται εσωτερικά. Εποµένως, no Ας ορίσουµε την ποσότητα noi neq k H ( max s + neq k H ( max ενερ neq noi k H ( ως ενεργό θερµοκρασία θορύβου (eecive noise του τετραπόλου (ενισχυτή. Τότε ισχύει max no neq k H ( max s+ ( Έτσι, ερµηνεύουµε το θόρυβο εξόδου ως προερχόµενον από µία πηγή θερµικού θορύβου σε θερµοκρασία s + ενερ στηνείσοδοενόςισοδύναµουιδανικούτετραπόλου. ενερ noi Ενεργός θερµοκρασία θορύβου Εικόνα θορύβου 4-3
33 Θερµοκρασία θορύβου ενός τετραπόλου Πηγή ενεργού θερµοκρασίας Ενθόρυβο Τετράπολο + no nos noi Ωςενεργόθερµοκρασίαενόςτετραπόλου, ορίζουµε την θερµοκρασίατ ενερ µίας θερµικής πηγής θορύβου που θα έπρεπε να βάλουµε στην είσοδο του τετραπόλου αν ήταν αθόρυβο, για ναδώσειστηνέξοδότουισχύ noi ίσηµετηνπρόσθετηισχύτουτετραπόλου. k neq Αθόρυβο Τετράπολο + no nos noi k ενερ neq + ενερ Αθόρυβο Τετράπολο + no nos noi 4-33
34 Μίαπηγήσήµατος µεισχύ si στηνείσοδοενός ενισχυτήδηµιουργεί ισχύεξόδου Πηγή σήµατος si Προσαρµογή Ενισχυτής H( so Προσαρµογή Φόρτος Σήµα που εφαρµόζεται σε φόρτο µέσω ενισχυτή. so H ( max si Έτσι το NR της εξόδου του ενισχυτή είναι N εξοδ so no N H ( H ( max max neq si (+ ενερ / s N neq si (+ ενερ / s (+ ενερ / s N εισοδ Παρατηρείστεότιτο NR εξόδου υποβαθµίζεται κατάτο συντελεστή ( + ενερ / s. Έτσιτο ενερ είναιέναµέτροτουθορύβουπουεισάγειοενισχυτής. Ιδανικόςενισχυτήςείναιεκείνος γιατονοποίοισχύει ενερ. Ενεργός θερµοκρασία θορύβου Εικόνα θορύβου 4-34
35 Λειτουργική Εικόνα Θορύβου Λειτουργική εικόνα θορύβου ενός τετραπόλου ορίζεται ο λόγος της ισχύος του θορύβου στην έξοδο no προςτηνισχύτουθορύβουστηνέξοδοενόςιδανικού (αθόρυβου τετραπόλου. F op F op Εναλλακτικός ορισµός της λειτουργικής εικόνας θορύβου τετραπόλου είναι ( ( N N no nos εισοδ εξοδ Λογαριθµίζοντας και τα δύο µέλη της Εξίσωσης, λαµβάνουµε εξοδ F op log log + log F N N Εποµένως το log F παριστά τις απώλειες στο NR εξαιτίας του επιπρόσθετου θορύβου που εισάγει ο ενισχυτής. Σε πολλούς ενισχυτές χαµηλού θορύβου, όπως οι λυχνίες διαδιδόµενου κύµατος, η εικόνα θορύβου έχει τιµή κάτω από 3d. Οι συµβατικοί ενισχυτές ολοκληρωµένων κυκλωµάτων παρουσιάζουν εικόνα θορύβου µεταξύ 6-7 d. εισοδ 4-35
36 Η λειτουργική εικόνα θορύβου και η ενεργός θερµοκρασία τετραπόλου συνδέονται µε την F op no nos nos + nos noi noi + + nos ενερ s ΑνυποθέσουµεότιτοτετράπολοοδηγείταιαπόπηγήµεενεργόθερµοκρασίαθορύβουΤ ο 9 Κ τότε ορίζεται η εικόνα θορύβου αναφοράς F + ενερ 4-36
37 Θόρυβος από γραµµή µεταφοράς ή υποβιβαστή Ορίζουµε ως απώλεια L το λόγο της ισχύος εξόδου προς την ισχύ εισόδου G L εξοδ εισοδ Αποδεικνύεται ότι η ενεργός θερµοκρασία προσαρµοσµένης γραµµής µεταφοράς που βρίσκεταισεθερµοκρασίατ περ είναι ενερ L ( περ Η εικόνα θορύβου της προσαρµοσµένης γραµµής µεταφοράς που βρίσκεται σε θερµοκρασία Τ περ είναι F L 4-37
38 Θερµοκρασία Θορύβου Συστήµατος Τετραπόλων σε Σειρά k s neq G Τετράπολο G G3 Τετράπολο Τετράπολο 3 nos+ noi k ενερ neq k ενερ neq k ενερ 3 neq k s neq G ολικ Τετράπολο + nos noi k ενερ ολικ neq Η συνολική ενεργός θερµοκρασία θορύβου για συνδεδεµένα σε σειρά τετράπολα είναι ενερ ενερ oλ ενερ + + G G ενερ 3 G 4-38
39 Θερµοκρασία Συστήµατος Ορίζουµε ως θερµοκρασία συστήµατος Τ Συσ το άθροισµα της ολικής θερµοκρασίας θορύβουτ ενερολικ. όλουτουδέκτησυντηνθερµοκρασίαθορύβουτηςκεραίαςτ κερ + Συσ κερ ενερ ολικ κερ Κεραία G κερ in RF Γραµµή µεταφοράς ενερ ολικ έκτης G in G k ( κερ + ενερολικ neq N ολικ G k( G + in κερ ενερ ολικ k in neq Συσ neq 4-39
40 Άσκηση Σ' ένασύστηµαεπικοινωνίαςτοσήµαλήψης r( s( + n( διέρχεταιµέσααπόέναιδανικό LF µε εύρος-ζώνης W και µοναδιαία απολαβή. Η συνιστώσα του σήµατος s( έχει φασµατική πυκνότητα ισχύος s ( + ( όπου είναι το 3-d εύρος-ζώνης. Η συνιστώσα θορύβου n( έχει φασµατική πυκνότητα ισχύος N / γιαόλεςτιςσυχνότητες. α Υπολογίστεκαισχεδιάστετο NR ωςσυνάρτησητουλόγου W/. β Ποιο είναι το εύρος-ζώνης W του φίλτρου το οποίο δίνει µέγιστο NR; 4-4
41 Άσκηση Η είσοδος στο σύστηµα είναι η κυµατοµορφή του αθροίσµατος σήµατος και θορύβου r( A c cos(π c + n( όπου n( είναι συνάρτηση δείγµα µιας διαδικασίας λευκού θορύβου µε φασµατική πυκνότητα ισχύος N /. α Υπολογίστε και σχεδιάστε την απόκριση συχνότητας του φίλτρου RC. β Σχεδιάστε την απόκριση συχνότητας του συνολικού συστήµατος. γ Υπολογίστετο NR στηνέξοδοτουιδανικού LF υποθέτονταςότι W > c. Σχεδιάστε το NR ως συνάρτηση του W για σταθερές τιµές των R και C. r ( C R Ιδανικό LF Έξοδος 4-4
42 4-4
43 Άσκηση Ένα τηλεφωνικό κανάλι συνεστραµµένου ζεύγους µε χαρακτηριστική σύνθετη αντίσταση Z c 3 Ωτερµατίζεταισεφορτίο Z L 3 Ω. Ητηλεφωνικήγραµµήέχειµήκος Kmκαι παρουσιάζει απώλειες d/km. α Ανηµέσηεκπεµπόµενη ισχύς είναι dm, υπολογίστε την ισχύ λήψης R, ανη τηλεφωνική γραµµή δεν περιλαµβάνει επαναλήπτες. β Αν χρησιµοποιηθούν επαναλήπτες µε απολαβή d για την ενίσχυση του σήµατος στο κανάλι και αν κάθε επαναλήπτης απαιτεί στην είσοδο στάθµη ισχύος dm, υπολογίστε τον αριθµότωνεπαναληπτώνκαιτηναπόστασηµεταξύτους. Η εικόνα θορύβου κάθε επαναλήπτη είναι 6d. 4-43
44 Άσκηση Μία κεραία προσανατολισµένη προς µια κατεύθυνση στον ουρανό έχει ενεργό θερµοκρασία θορύβου 5Κ. Η κεραία οδηγεί το λαµβανόµενο σήµα στον προενισχυτή ο οποίος έχει απολαβή 35dσ' έναεύρος-ζώνης MHz, καιεικόναθορύβουαναφοράς d. α Υπολογίστε την ενεργό θερµοκρασία θορύβου στην είσοδο του προενισχυτή. β Βρείτε την ισχύ θορύβου στην έξοδο του προενισχυτή. 4-44
45 Άσκηση Μία κεραία έχει ενεργό θερµοκρασία θορύβου 5 Κ. Η κεραία οδηγεί το λαµβανόµενο σήµα στο δέκτη µέσω γραµµής µεταφοράς η οποία βρίσκεται σε φυσική θερµοκρασία 8Κ και έχει απώλεια ίση µε,76d. Ο δέκτης έχει ισοδύναµο εύρος ζώνης θορύβου ίσο µε 6 Hz και ενεργό θερµοκρασία θορύβου ίση µε 7 Κ. Να υπολογιστούν α ηενεργόθερµοκρασίαθορύβουτουσυστήµατος, β η λειτουργική εικόνα θορύβου του συστήµατος και γ η ισχύ θορύβου στην έξοδο του συστήµατος. 4-45
Στη συνέχεια οι τυχαίες διαδικασίες θα µελετηθούν στο πεδίο συχνότητας. ( t) X( f)
 Μέχρι τώρα η µελέτη των τυχαίων διαδικασιών έγινε στο πεδίο του χρόνου (µέση τιµή, συναρτήσεις αυτοσυσχέτισης, αµοιβαίου συσχετισµού και συµµεταβολής. Στη συνέχεια οι τυχαίες διαδικασίες θα µελετηθούν
Μέχρι τώρα η µελέτη των τυχαίων διαδικασιών έγινε στο πεδίο του χρόνου (µέση τιµή, συναρτήσεις αυτοσυσχέτισης, αµοιβαίου συσχετισµού και συµµεταβολής. Στη συνέχεια οι τυχαίες διαδικασίες θα µελετηθούν
Επεξεργασία Στοχαστικών Σημάτων
 Επεξεργασία Στοχαστικών Σημάτων Σεραφείμ Καραμπογιάς Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Μέχρι τώρα η μελέτη των τυχαίων διαδικασιών έγινε στο πεδίο του χρόνου (μέση τιμή, συναρτήσεις
Επεξεργασία Στοχαστικών Σημάτων Σεραφείμ Καραμπογιάς Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Μέχρι τώρα η μελέτη των τυχαίων διαδικασιών έγινε στο πεδίο του χρόνου (μέση τιμή, συναρτήσεις
Τηλεπικοινωνιακά Συστήματα Ι
 Τηλεπικοινωνιακά Συστήματα Ι Διάλεξη 3: Ο Θόρυβος στα Τηλεπικοινωνιακά Συστήματα Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα Εισαγωγή Τύποι Θορύβου Θερμικός θόρυβος Θόρυβος βολής Θόρυβος περιβάλλοντος
Τηλεπικοινωνιακά Συστήματα Ι Διάλεξη 3: Ο Θόρυβος στα Τηλεπικοινωνιακά Συστήματα Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα Εισαγωγή Τύποι Θορύβου Θερμικός θόρυβος Θόρυβος βολής Θόρυβος περιβάλλοντος
Η Έννοια της τυχαίας ιαδικασίας
 Η Έννοια της τυχαίας ιαδικασίας Η έννοια της τυχαίας διαδικασίας, βασίζεται στην επέκταση της έννοιας της τυχαίας µεταβλητής, ώστε να συµπεριλάβει το χρόνο. Σεκάθεαποτέλεσµα s k ενόςπειράµατοςτύχης αντιστοιχούµε,
Η Έννοια της τυχαίας ιαδικασίας Η έννοια της τυχαίας διαδικασίας, βασίζεται στην επέκταση της έννοιας της τυχαίας µεταβλητής, ώστε να συµπεριλάβει το χρόνο. Σεκάθεαποτέλεσµα s k ενόςπειράµατοςτύχης αντιστοιχούµε,
ΑΝΑΠΤΥΓΜA - ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ. Περιγράψουµε τον τρόπο ανάπτυξης σε σειρά Fourier ενός περιοδικού αναλογικού σήµατος.
 3. ΚΕΦΑΛΑΙΟ ΑΝΑΠΤΥΓΜA - ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ Περιγράψουµε τον τρόπο ανάπτυξης σε σειρά Fourier ενός περιοδικού αναλογικού σήµατος. Ορίσουµε το µετασχηµατισµό Fourier ενός µη περιοδικού
3. ΚΕΦΑΛΑΙΟ ΑΝΑΠΤΥΓΜA - ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ Περιγράψουµε τον τρόπο ανάπτυξης σε σειρά Fourier ενός περιοδικού αναλογικού σήµατος. Ορίσουµε το µετασχηµατισµό Fourier ενός µη περιοδικού
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER
 4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Υπολογίζουµε εύκολα τον αντίστροφο Μετασχηµατισµό Fourier µιας συνάρτησης χωρίς να καταφεύγουµε στην εξίσωση ανάλυσης. Υπολογίζουµε εύκολα την απόκριση
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Υπολογίζουµε εύκολα τον αντίστροφο Μετασχηµατισµό Fourier µιας συνάρτησης χωρίς να καταφεύγουµε στην εξίσωση ανάλυσης. Υπολογίζουµε εύκολα την απόκριση
Επεξεργασία Στοχαστικών Σημάτων
 Επεξεργασία Στοχαστικών Σημάτων Ψηφιακή Μετάδοση Αναλογικών Σημάτων Σεραφείμ Καραμπογιάς Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Ψηφιακή Μετάδοση Αναλογικών Σημάτων Τα σύγχρονα συστήματα
Επεξεργασία Στοχαστικών Σημάτων Ψηφιακή Μετάδοση Αναλογικών Σημάτων Σεραφείμ Καραμπογιάς Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Ψηφιακή Μετάδοση Αναλογικών Σημάτων Τα σύγχρονα συστήματα
Βέλτιστα γραµµικά χρονικά αναλλοίωτα συστήµατα Συστήµατα που ελαχιστοποιούν το µέσο-τετραγωνικό σφάλµα
 Σεραφείµ Καραµπογιάς Βέλτιστα γραµµικά χρονικά αναλλοίωτα συστήµατα Ο Wiener εέτασε το προβληµα της εκτίµησης µίας επιθυµητής κυµατοµορφής σήµατος s παρουσία προσθετικού θορύβου n, βάση του λαµβανόµενου
Σεραφείµ Καραµπογιάς Βέλτιστα γραµµικά χρονικά αναλλοίωτα συστήµατα Ο Wiener εέτασε το προβληµα της εκτίµησης µίας επιθυµητής κυµατοµορφής σήµατος s παρουσία προσθετικού θορύβου n, βάση του λαµβανόµενου
Συναρτήσεις Συσχέτισης
 Συναρτήσεις Συσχέτισης Για ένα σήµα ενέργειας ορίζεται η συνάρτηση αυτοσυσχέτισης R + ( τ = ( τ ( τ = ( ( τ d = ( + τ + ( d Για ένα σήµα ισχύος ορίζεται η µέση χρονική συνάρτηση αυτοσυσχέτισης R ( τ =
Συναρτήσεις Συσχέτισης Για ένα σήµα ενέργειας ορίζεται η συνάρτηση αυτοσυσχέτισης R + ( τ = ( τ ( τ = ( ( τ d = ( + τ + ( d Για ένα σήµα ισχύος ορίζεται η µέση χρονική συνάρτηση αυτοσυσχέτισης R ( τ =
Τι είναι σήµα; Ωςσήµαορίζεταιέναφυσικόµέγεθοςτοοποίοµεταβάλλεταισεσχέσηµετοχρόνοή το χώρο ή µε οποιαδήποτε άλλη ανεξάρτητη µεταβλητή ή µεταβλητές.
 Τι είναι σήµα; Ωςσήµαορίζεταιέναφυσικόµέγεθοςτοοποίοµεταβάλλεταισεσχέσηµετοχρόνοή το χώρο ή µε οποιαδήποτε άλλη ανεξάρτητη µεταβλητή ή µεταβλητές. Παραδείγµατα: Σήµα οµιλίας Πίεση P() Σήµα εικόνας y I
Τι είναι σήµα; Ωςσήµαορίζεταιέναφυσικόµέγεθοςτοοποίοµεταβάλλεταισεσχέσηµετοχρόνοή το χώρο ή µε οποιαδήποτε άλλη ανεξάρτητη µεταβλητή ή µεταβλητές. Παραδείγµατα: Σήµα οµιλίας Πίεση P() Σήµα εικόνας y I
Τι είναι σήµα; Σεραφείµ Καραµπογιάς
 Τι είναι σήµα; Σεραφείµ Καραµπογιάς Ωςσήµαορίζεταιέναφυσικόµέγεθοςτοοποίοµεταβάλλεταισεσχέσηµετοχρόνοή το χώρο ή µε οποιαδήποτε άλλη ανεξάρτητη µεταβλητή ή µεταβλητές Παραδείγµατα: Σήµα οµιλίας Σήµα εικόνας
Τι είναι σήµα; Σεραφείµ Καραµπογιάς Ωςσήµαορίζεταιέναφυσικόµέγεθοςτοοποίοµεταβάλλεταισεσχέσηµετοχρόνοή το χώρο ή µε οποιαδήποτε άλλη ανεξάρτητη µεταβλητή ή µεταβλητές Παραδείγµατα: Σήµα οµιλίας Σήµα εικόνας
Υπολογίζουμε εύκολα τον αντίστροφο Μετασχηματισμό Fourier μιας συνάρτησης χωρίς να καταφεύγουμε στην εξίσωση ανάλυσης.
 4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Υπολογίζουμε εύκολα τον αντίστροφο Μετασχηματισμό Fourir μιας συνάρτησης χωρίς να καταφεύγουμε στην εξίσωση ανάλυσης. Υπολογίζουμε εύκολα την απόκριση
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Υπολογίζουμε εύκολα τον αντίστροφο Μετασχηματισμό Fourir μιας συνάρτησης χωρίς να καταφεύγουμε στην εξίσωση ανάλυσης. Υπολογίζουμε εύκολα την απόκριση
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER
 4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Σκοπός του κεφαλαίου είναι να παρουσιάσει μερικές εφαρμογές του Μετασχηματισμού Fourier (ΜF). Ειδικότερα στο κεφάλαιο αυτό θα περιγραφούν έμμεσοι τρόποι
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Σκοπός του κεφαλαίου είναι να παρουσιάσει μερικές εφαρμογές του Μετασχηματισμού Fourier (ΜF). Ειδικότερα στο κεφάλαιο αυτό θα περιγραφούν έμμεσοι τρόποι
Εισαγωγή στη Σχεδίαση RF Κυκλωμάτων
 Εισαγωγή στη Σχεδίαση F Κυκλωμάτων Κεφάλαιο,.3 Βασικές έννοιες Σχεδίασης F Κυκλωμάτων Σωτήριος Ματακιάς, 0-3, Σχεδίαση Τηλεπικοινωνιακών LI Κυκλωμάτων, Κεφάλαιο /34 Φασματική πυκνότητα ισχύος Power pectral
Εισαγωγή στη Σχεδίαση F Κυκλωμάτων Κεφάλαιο,.3 Βασικές έννοιες Σχεδίασης F Κυκλωμάτων Σωτήριος Ματακιάς, 0-3, Σχεδίαση Τηλεπικοινωνιακών LI Κυκλωμάτων, Κεφάλαιο /34 Φασματική πυκνότητα ισχύος Power pectral
ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER
 4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Υπολογίζουµε εύκολα τον αντίστροφο Μετασχηµατισµό Fourir µιας συνάρτησης χρίς να καταφεύγουµε στην εξίσση ανάλυσης. Υπολογίζουµε εύκολα την απόκριση συχνότητας
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Υπολογίζουµε εύκολα τον αντίστροφο Μετασχηµατισµό Fourir µιας συνάρτησης χρίς να καταφεύγουµε στην εξίσση ανάλυσης. Υπολογίζουµε εύκολα την απόκριση συχνότητας
X(t) = A cos(2πf c t + Θ) (1) 0, αλλού. 2 cos(2πf cτ) (9)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 05-6 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λυµένες Ασκήσεις - Τυχαίες ιαδικασίες Ασκηση. Εστω
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 05-6 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λυµένες Ασκήσεις - Τυχαίες ιαδικασίες Ασκηση. Εστω
2. ΚΕΦΑΛΑΙΟ ΕΙΣΑΓΩΓΗ ΣΤΑ ΣΥΣΤΗΜΑΤΑ. Γενικά τι είναι σύστηµα - Ορισµός. Τρόποι σύνδεσης συστηµάτων.
 2. ΚΕΦΑΛΑΙΟ ΕΙΣΑΓΩΓΗ ΣΤΑ ΣΥΣΤΗΜΑΤΑ Γενικά τι είναι - Ορισµός. Τρόποι σύνδεσης συστηµάτων. Κατηγορίες των συστηµάτων ανάλογα µε τον αριθµό και το είδος των επιτρεποµένων εισόδων και εξόδων. Ιδιότητες των
2. ΚΕΦΑΛΑΙΟ ΕΙΣΑΓΩΓΗ ΣΤΑ ΣΥΣΤΗΜΑΤΑ Γενικά τι είναι - Ορισµός. Τρόποι σύνδεσης συστηµάτων. Κατηγορίες των συστηµάτων ανάλογα µε τον αριθµό και το είδος των επιτρεποµένων εισόδων και εξόδων. Ιδιότητες των
Παράδειγµα ενός ηλεκτρικού συστήµατος
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Εισαγωγή στα Σήµατα Εισαγωγή στα Συστήµατα Ανάπτυγµα - Μετασχηµατισµός Fourier Μετασχηµατισµός aplace Μετασχηµατισµός Z Εφαρµογές Παράδειγµα ενός ηλεκτρικού συστήµατος A R B i( ) i
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Εισαγωγή στα Σήµατα Εισαγωγή στα Συστήµατα Ανάπτυγµα - Μετασχηµατισµός Fourier Μετασχηµατισµός aplace Μετασχηµατισµός Z Εφαρµογές Παράδειγµα ενός ηλεκτρικού συστήµατος A R B i( ) i
Επεξεργασία Στοχαστικών Σημάτων
 Επεξεργασία Στοχαστικών Σημάτων Σεραφείμ Καραμπογιάς Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Η Έννοια της τυχαίας Διαδικασίας Η έννοια της τυχαίας διαδικασίας βασίζεται στην επέκταση
Επεξεργασία Στοχαστικών Σημάτων Σεραφείμ Καραμπογιάς Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Η Έννοια της τυχαίας Διαδικασίας Η έννοια της τυχαίας διαδικασίας βασίζεται στην επέκταση
Σήματα και Συστήματα. Διάλεξη 10: Γραμμικά Φίλτρα. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 10: Γραμμικά Φίλτρα Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Γραμμικά Φίλτρα 1. Ιδανικά Γραμμικά Φίλτρα Ιδανικό Κατωδιαβατό Φίλτρο Ιδανικό Ανωδιαβατό Φίλτρο Ιδανικό Ζωνοδιαβατό
Σήματα και Συστήματα Διάλεξη 10: Γραμμικά Φίλτρα Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Γραμμικά Φίλτρα 1. Ιδανικά Γραμμικά Φίλτρα Ιδανικό Κατωδιαβατό Φίλτρο Ιδανικό Ανωδιαβατό Φίλτρο Ιδανικό Ζωνοδιαβατό
ΑΝΑΠΤΥΓΜA - ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ. Περιγράψουμε τον τρόπο ανάπτυξης σε σειρά Fourier ενός περιοδικού αναλογικού σήματος.
 3. ΚΕΦΑΛΑΙΟ ΑΝΑΠΤΥΓΜA - ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ OURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ Περιγράψουμε τον τρόπο ανάπτυξης σε σειρά ourir ενός περιοδικού αναλογικού σήματος. Ορίσουμε το μετασχηματισμό ourir ενός μη περιοδικού
3. ΚΕΦΑΛΑΙΟ ΑΝΑΠΤΥΓΜA - ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ OURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ Περιγράψουμε τον τρόπο ανάπτυξης σε σειρά ourir ενός περιοδικού αναλογικού σήματος. Ορίσουμε το μετασχηματισμό ourir ενός μη περιοδικού
( x) Η ΕΝΝΟΙΑ ΤΗΣ ΤΥΧΑΙΑΣ ΜΕΤΑΒΛΗΤΗΣ - ΠΙΘΑΝΟΤΗΤΑΣ. Βασικά αξιώµατα και ιδιότητες της πιθανότητας. Σεραφείµ Καραµπογιάς
 Η ΕΝΝΟΙΑ ΤΗΣ ΤΥΧΑΙΑΣ ΜΕΤΑΒΛΗΤΗΣ - ΠΙΘΑΝΟΤΗΤΑΣ Βασικά αξιώµατα και ιδιότητες της πιθανότητας Σεραφείµ Καραµπογιάς Η αθροιστική συνάρτηση κατανοµής cumulaive diribuio ucio CDF µίας τυχαίας µεταβλητής X ορίζεται
Η ΕΝΝΟΙΑ ΤΗΣ ΤΥΧΑΙΑΣ ΜΕΤΑΒΛΗΤΗΣ - ΠΙΘΑΝΟΤΗΤΑΣ Βασικά αξιώµατα και ιδιότητες της πιθανότητας Σεραφείµ Καραµπογιάς Η αθροιστική συνάρτηση κατανοµής cumulaive diribuio ucio CDF µίας τυχαίας µεταβλητής X ορίζεται
Κεφάλαιο 3 ο : ΕΙΣΑΓΩΓΗ στις ΤΗΛΕΠΙΚΟΙΝΩΝΙΕΣ. ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟ ΚΥΜΑ και ΤΕΧΝΙΚΕΣ ΙΑΜΟΡΦΩΣΗΣ
 Μάθηµα 1ο Θέµα Εισαγωγή στις τηλεπικοινωνίες 1. Τι ορίζουµε µε τον όρο τηλεπικοινωνία; 2. Ποιες οι βασικότερες ανταλλασσόµενες πληροφορίες, ανάλογα µε τη φύση και το χαρακτήρα τους; 3. Τι αποκαλούµε ποµπό
Μάθηµα 1ο Θέµα Εισαγωγή στις τηλεπικοινωνίες 1. Τι ορίζουµε µε τον όρο τηλεπικοινωνία; 2. Ποιες οι βασικότερες ανταλλασσόµενες πληροφορίες, ανάλογα µε τη φύση και το χαρακτήρα τους; 3. Τι αποκαλούµε ποµπό
Λύσεις Θεµάτων Εξεταστικής Ιανουαρίου 2009 Mάθηµα: «Ψηφιακές Επικοινωνίες» G F = 0.8 T F = 73 0 K
 Λύσεις Θεµάτων Εξεταστικής Ιανουαρίου 9 Mάθηµα: «Ψηφιακές Επικοινωνίες» Θέµα 1 ο (3%) A =6 o K P R = 1pWatt SNR IN G LNA =13dB LNA =3 K LNA G F =.8 F = 73 K Φίλτρο G = db F = 8 db Ενισχυτής IF SNR OU 1.
Λύσεις Θεµάτων Εξεταστικής Ιανουαρίου 9 Mάθηµα: «Ψηφιακές Επικοινωνίες» Θέµα 1 ο (3%) A =6 o K P R = 1pWatt SNR IN G LNA =13dB LNA =3 K LNA G F =.8 F = 73 K Φίλτρο G = db F = 8 db Ενισχυτής IF SNR OU 1.
Ασκήσεις στα Συστήµατα Ηλεκτρονικών Επικοινωνιών Κεφάλαιο 3 ο : ΕΙΣΑΓΩΓΗ στις ΤΗΛΕΠΙΚΟΙΝΩΝΙΕΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟ ΚΥΜΑ και ΤΕΧΝΙΚΕΣ ΙΑΜΟΡΦΩΣΗΣ
 Κεφάλαιο 3 ο : ΕΙΣΑΓΩΓΗ στις ΤΗΛΕΠΙΚΟΙΝΩΝΙΕΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟ ΚΥΜΑ και ΤΕΧΝΙΚΕΣ ΙΑΜΟΡΦΩΣΗΣ 1. Ποµπός ΑΜ εκπέµπει σε φέρουσα συχνότητα 1152 ΚΗz, µε ισχύ φέροντος 10KW. Η σύνθετη αντίσταση της κεραίας είναι
Κεφάλαιο 3 ο : ΕΙΣΑΓΩΓΗ στις ΤΗΛΕΠΙΚΟΙΝΩΝΙΕΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟ ΚΥΜΑ και ΤΕΧΝΙΚΕΣ ΙΑΜΟΡΦΩΣΗΣ 1. Ποµπός ΑΜ εκπέµπει σε φέρουσα συχνότητα 1152 ΚΗz, µε ισχύ φέροντος 10KW. Η σύνθετη αντίσταση της κεραίας είναι
ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 12η διάλεξη
 ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 12η διάλεξη ηµήτρης-αλέξανδρος Τουµπακάρης Τµήµα ΗΜ&ΤΥ, Πανεπιστήµιο Πατρών 2 Ιουνίου 2015 ηµήτρης-αλέξανδρος Τουµπακάρης Προχ. Θέµατα Θεωρίας Πληροφορίας 12η
ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 12η διάλεξη ηµήτρης-αλέξανδρος Τουµπακάρης Τµήµα ΗΜ&ΤΥ, Πανεπιστήµιο Πατρών 2 Ιουνίου 2015 ηµήτρης-αλέξανδρος Τουµπακάρης Προχ. Θέµατα Θεωρίας Πληροφορίας 12η
Στοχαστικές Ανελίξεις
 Ντετερμινιστικά Σήματα - Τυχαία Σήματα Ταξινόμηση των σημάτων ανάλογα με τη βεβαιότητα όσο αφορά την τιμή τους κάθε χρονική στιγμή. Τα ντετερμινιστικά σήματα μπορούν να αναπαρασταθούν σαν πλήρως καθορισμένες
Ντετερμινιστικά Σήματα - Τυχαία Σήματα Ταξινόμηση των σημάτων ανάλογα με τη βεβαιότητα όσο αφορά την τιμή τους κάθε χρονική στιγμή. Τα ντετερμινιστικά σήματα μπορούν να αναπαρασταθούν σαν πλήρως καθορισμένες
Τι είναι σήμα; Παραδείγματα: Σήμα ομιλίας. Σήμα εικόνας. Σεισμικά σήματα. Ιατρικά σήματα
 Τι είναι σήμα; Σεραφείμ Καραμπογιάς Ως σήμα ορίζεται ένα φυσικό μέγεθος το οποίο μεταβάλλεται σε σχέση με το χρόνο ή το χώρο ή με οποιαδήποτε άλλη ανεξάρτητη μεταβλητή ή μεταβλητές. Παραδείγματα: Σήμα
Τι είναι σήμα; Σεραφείμ Καραμπογιάς Ως σήμα ορίζεται ένα φυσικό μέγεθος το οποίο μεταβάλλεται σε σχέση με το χρόνο ή το χώρο ή με οποιαδήποτε άλλη ανεξάρτητη μεταβλητή ή μεταβλητές. Παραδείγματα: Σήμα
NRZ Non return to zero: Οι άσσοι καταλαµβάνουν ολόκληρη τη διάρκεια bit. (Μικρό Bandwidth)
 ιαµόρφωση Αποδιαµόρφωση ) Μορφές Σηµάτων NRZ No rtur to zro: Οι άσσοι καταλαµβάνουν ολόκληρη τη διάρκεια bit. (Μικρό adwidth) RZ Rtur to zro : Ανάµεσα σε δύο άσσους µεσολαβεί ένα κενό διάστηµα (Μεγαλύτερο
ιαµόρφωση Αποδιαµόρφωση ) Μορφές Σηµάτων NRZ No rtur to zro: Οι άσσοι καταλαµβάνουν ολόκληρη τη διάρκεια bit. (Μικρό adwidth) RZ Rtur to zro : Ανάµεσα σε δύο άσσους µεσολαβεί ένα κενό διάστηµα (Μεγαλύτερο
ΦΙΛΤΡΑ ΜΕ ΠΑΘΗΤΙΚΑ ΣΤΟΙΧΕΙΑ
 ΦΙΛΤΡΑ ΜΕ ΠΑΘΗΤΙΚΑ ΣΤΟΙΧΕΙΑ Τα φίλτρα είναι ηλεκτρικά δικτυώματα που αφήνουν να περνούν απαραμόρφωτα ηλεκτρικά σήματα μέσα σε συγκεκριμένες ζώνες συχνοτήτων και ταυτόχρονα μηδενίζουν κάθε άλλο ηλεκτρικό
ΦΙΛΤΡΑ ΜΕ ΠΑΘΗΤΙΚΑ ΣΤΟΙΧΕΙΑ Τα φίλτρα είναι ηλεκτρικά δικτυώματα που αφήνουν να περνούν απαραμόρφωτα ηλεκτρικά σήματα μέσα σε συγκεκριμένες ζώνες συχνοτήτων και ταυτόχρονα μηδενίζουν κάθε άλλο ηλεκτρικό
Εισαγωγή στις Τηλεπικοινωνίες. Δομή της παρουσίασης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Εφαρμογές της Ανάλυσης Fourier Αθανάσιος
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Εφαρμογές της Ανάλυσης Fourier Αθανάσιος
Συστήματα Επικοινωνιών
 Συστήματα Επικοινωνιών Ενότητα 2: Μαθιόπουλος Παναγιώτης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Περιγραφή ενότητας Τυχαίες Διαδικασίες: Ορισμοί, Μέσες τιμές συνόλου (Ensemble averages),
Συστήματα Επικοινωνιών Ενότητα 2: Μαθιόπουλος Παναγιώτης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Περιγραφή ενότητας Τυχαίες Διαδικασίες: Ορισμοί, Μέσες τιμές συνόλου (Ensemble averages),
Ψηφιακή Επεξεργασία Σηµάτων. ηµήτριος Βαρσάµης Καθηγητής Εφαρµογών
 Ψηφιακή Επεξεργασία Σηµάτων ηµήτριος Βαρσάµης Καθηγητής Εφαρµογών Πεδίο Συχνοτήτων Απόκριση συχνότητας LTI συστήµατος µε συνάρτηση µεταφοράς Hz). Σε ένα LTI σύστηµα µε συνάρτησηµεταφοράς Hz), εφόσον ο
Ψηφιακή Επεξεργασία Σηµάτων ηµήτριος Βαρσάµης Καθηγητής Εφαρµογών Πεδίο Συχνοτήτων Απόκριση συχνότητας LTI συστήµατος µε συνάρτηση µεταφοράς Hz). Σε ένα LTI σύστηµα µε συνάρτησηµεταφοράς Hz), εφόσον ο
Εισαγωγή στη Σχεδίαση RF Κυκλωμάτων
 Εισαγωγή στη Σχεδίαση RF Κυκλωμάτων Κεφάλαιο,.. Βασικές έννοιες Σχεδίασης RF Κυκλωμάτων Σωτήριος Ματακιάς, 0-, Σχεδίαση Τηλεπικοινωνιακών VLSI Κυκλωμάτων, Κεφάλαιο / In=Inerfirer IP Παράδειγμα ω,ω = in,ou
Εισαγωγή στη Σχεδίαση RF Κυκλωμάτων Κεφάλαιο,.. Βασικές έννοιες Σχεδίασης RF Κυκλωμάτων Σωτήριος Ματακιάς, 0-, Σχεδίαση Τηλεπικοινωνιακών VLSI Κυκλωμάτων, Κεφάλαιο / In=Inerfirer IP Παράδειγμα ω,ω = in,ou
Μαθηµατική Παρουσίαση των FM και PM Σηµάτων
 Μαθηµατική Παροσίαση των FM και PM Σηµάτων Ένα γωνιακά διαµορφωµένο σήµα, πο αναφέρεται επίσης και ως εκθετικά διαµορφωµένο σήµα, έχει τη µορφή u os j [ ] { π + jφ π + φ Re e } Σεραφείµ Καραµπογιάς Ορίζοµε
Μαθηµατική Παροσίαση των FM και PM Σηµάτων Ένα γωνιακά διαµορφωµένο σήµα, πο αναφέρεται επίσης και ως εκθετικά διαµορφωµένο σήµα, έχει τη µορφή u os j [ ] { π + jφ π + φ Re e } Σεραφείµ Καραµπογιάς Ορίζοµε
Συστήµατα τα οποία χαρακτηρίζονται από γραµµικές εξισώσεις διαφορών µε σταθερούς συντελεστές
 Συστήµατα τα οποία χαρακτηρίζονται από γραµµικές εξισώσεις διαφορών µε σταθερούς συντελεστές x h γραµµική εξίσωση διαφορών µε σταθερούς συντελεστές της µορφής x µπορεί να θεωρηθεί ως ένας αλγόριθµος υπολογισµού
Συστήµατα τα οποία χαρακτηρίζονται από γραµµικές εξισώσεις διαφορών µε σταθερούς συντελεστές x h γραµµική εξίσωση διαφορών µε σταθερούς συντελεστές της µορφής x µπορεί να θεωρηθεί ως ένας αλγόριθµος υπολογισµού
HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών. στο χώρο της συχνότητας
 HMY 49: Εισαγωγή στην Επεξεργασία Ψηφιακών Σημάτων Διάλεξη 3: Σήματα και Συστήματα διακριτού χρόνου Διάλεξη 3: Σήματα και Συστήματα διακριτού χρόνου στο χώρο της συχνότητας Μιγαδικά εκθετικά σήματα και
HMY 49: Εισαγωγή στην Επεξεργασία Ψηφιακών Σημάτων Διάλεξη 3: Σήματα και Συστήματα διακριτού χρόνου Διάλεξη 3: Σήματα και Συστήματα διακριτού χρόνου στο χώρο της συχνότητας Μιγαδικά εκθετικά σήματα και
0, αλλιώς. Σεραφείµ Καραµπογιάς. Παράδειγµα 1 Η πηγή X(t) είναι στατική Gaussian µε µέση τιµή µηδέν και φασµατική πυκνότητα ισχύος.
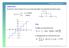 Παράδειγµα Η πηγή X(t) είναι στατική Gussin µε µέση τιµή µηδέν και φασµατική πυκνότητα ισχύος S X ( f ) 70, f < 00Hz 0, αλλιώς S X ( f ) 00 00 f 50 Λύση: 60 40 0 30 0 0 30 0 40 60 Ο ρυθµός που απαιτείται
Παράδειγµα Η πηγή X(t) είναι στατική Gussin µε µέση τιµή µηδέν και φασµατική πυκνότητα ισχύος S X ( f ) 70, f < 00Hz 0, αλλιώς S X ( f ) 00 00 f 50 Λύση: 60 40 0 30 0 0 30 0 40 60 Ο ρυθµός που απαιτείται
Ιατρικά Ηλεκτρονικά. Χρήσιμοι Σύνδεσμοι. ΙΑΤΡΙΚΑ ΗΛΕΚΤΡΟΝΙΚΑ - ΔΙΑΛΕΞΗ 5α. Σημειώσεις μαθήματος: E mail:
 Ιατρικά Ηλεκτρονικά Δρ. Π. Ασβεστάς Τμήμα Μηχανικών Βιοϊατρικής Τεχνολογίας Τ.Ε Χρήσιμοι Σύνδεσμοι Σημειώσεις μαθήματος: http://medisp.bme.teiath.gr/eclass/courses/tio127/ E mail: pasv@teiath.gr 2 1 Περιοδικά
Ιατρικά Ηλεκτρονικά Δρ. Π. Ασβεστάς Τμήμα Μηχανικών Βιοϊατρικής Τεχνολογίας Τ.Ε Χρήσιμοι Σύνδεσμοι Σημειώσεις μαθήματος: http://medisp.bme.teiath.gr/eclass/courses/tio127/ E mail: pasv@teiath.gr 2 1 Περιοδικά
Επομένως το εύρος ζώνης του διαμορφωμένου σήματος είναι 2.
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΠΛΗ ΓΙΑ ΤΙΣ ΕΞΕΤΑΣΕΙΣ ΘΕΜΑ Το φέρον σε ένα σύστημα DSB διαμόρφωσης είναι c t A t μηνύματος είναι το m( t) sin c( t) sin c ( t) ( ) cos 4 c και το σήμα. Το διαμορφωμένο σήμα διέρχεται
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΠΛΗ ΓΙΑ ΤΙΣ ΕΞΕΤΑΣΕΙΣ ΘΕΜΑ Το φέρον σε ένα σύστημα DSB διαμόρφωσης είναι c t A t μηνύματος είναι το m( t) sin c( t) sin c ( t) ( ) cos 4 c και το σήμα. Το διαμορφωμένο σήμα διέρχεται
ΑΝΑΠΤΥΓΜA -ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ
 3. ΚΕΦΑΛΑΙΟ ΑΝΑΠΤΥΓΜA -ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ Περιγράψουµε τον τρόπο ανάπτυξης σε σειρά Fourier ενός περιοδικού αναλογικού σήµατος. Ορίσουµε το µετασχηµατισµό Fourier ενός µη περιοδικού
3. ΚΕΦΑΛΑΙΟ ΑΝΑΠΤΥΓΜA -ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ Περιγράψουµε τον τρόπο ανάπτυξης σε σειρά Fourier ενός περιοδικού αναλογικού σήµατος. Ορίσουµε το µετασχηµατισµό Fourier ενός µη περιοδικού
ΚΕΦΑΛΑΙΟ 2. Ανάλυση Ηλεκτρικού Σήµατος
 ΚΕΦΑΛΑΙΟ Ανάλυση Ηλεκτρικού Σήµατος. Εισαγωγή Τα σήµατα εξόδου από µετρητικές διατάξεις έχουν συνήθως τη µορφή ηλεκτρικών σηµάτων. Πριν από την καταγραφή ή περαιτέρω επεξεργασία, ένα σήµα υφίσταται µια
ΚΕΦΑΛΑΙΟ Ανάλυση Ηλεκτρικού Σήµατος. Εισαγωγή Τα σήµατα εξόδου από µετρητικές διατάξεις έχουν συνήθως τη µορφή ηλεκτρικών σηµάτων. Πριν από την καταγραφή ή περαιτέρω επεξεργασία, ένα σήµα υφίσταται µια
ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ ΕΞΕΤΑΣΤΙΚΗΣ ΠΕΡΙΟ ΟΥ ΙΟΥΝΙΟΥ 2004., η οποία όµως µπορεί να γραφεί µε την παρακάτω µορφή: 1 e
 ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΣΥΣΤΗΜΑΤΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΥΣΗΣ ΗΛΕΚΤΡΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ ΜΑΘΗΜΑ: ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΩΝ ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ ΕΞΕΤΑΣΤΙΚΗΣ ΠΕΡΙΟ ΟΥ ΙΟΥΝΙΟΥ 4 AΣΚΗΣΗ () [ ] (.5)
ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΣΥΣΤΗΜΑΤΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΥΣΗΣ ΗΛΕΚΤΡΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ ΜΑΘΗΜΑ: ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΩΝ ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ ΕΞΕΤΑΣΤΙΚΗΣ ΠΕΡΙΟ ΟΥ ΙΟΥΝΙΟΥ 4 AΣΚΗΣΗ () [ ] (.5)
Όταν θα έχουµε τελειώσει το Κεφάλαιο αυτό θα µπορούµε να:
 6. ΚΕΦΑΛΑΙΟ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Όταν θα έχουµε τελειώσει το Κεφάλαιο αυτό θα µπορούµε να: ορίσουµε το Μετασχηµατισµό Laplace (ML) και το Μονόπλευρο Μετασχηµατισµό Laplace (MML) και να περιγράψουµε
6. ΚΕΦΑΛΑΙΟ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Όταν θα έχουµε τελειώσει το Κεφάλαιο αυτό θα µπορούµε να: ορίσουµε το Μετασχηµατισµό Laplace (ML) και το Μονόπλευρο Μετασχηµατισµό Laplace (MML) και να περιγράψουµε
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2014-2015 Κβάντιση Δρ. Ν. Π. Σγούρος 2 Αναλογικά Ψηφιακά Σήματα Αναλογικό Σήμα x t, t [t min, t max ], x [x min, x max ] Δειγματοληψία t n, x t x n, n = 1,, N Κβάντιση x n x(n) 3 Αλφάβητο
Συμπίεση Δεδομένων 2014-2015 Κβάντιση Δρ. Ν. Π. Σγούρος 2 Αναλογικά Ψηφιακά Σήματα Αναλογικό Σήμα x t, t [t min, t max ], x [x min, x max ] Δειγματοληψία t n, x t x n, n = 1,, N Κβάντιση x n x(n) 3 Αλφάβητο
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ. Εισαγωγή στα Σήµατα Εισαγωγή στα Συστήµατα Ανάπτυγµα - Μετασχηµατισµός Fourier Μετασχηµατισµός Z
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Εισαγωγή στα Σήµατα Εισαγωγή στα Συστήµατα Ανάπτυγµα - Μετασχηµατισµός Fourier Μετασχηµατισµός Laplace Μετασχηµατισµός Z Εφαρµογές Παράδειγµα ενός ηλεκτρικού συστήµατος Σύστηµα Παράδειγµα
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Εισαγωγή στα Σήµατα Εισαγωγή στα Συστήµατα Ανάπτυγµα - Μετασχηµατισµός Fourier Μετασχηµατισµός Laplace Μετασχηµατισµός Z Εφαρµογές Παράδειγµα ενός ηλεκτρικού συστήµατος Σύστηµα Παράδειγµα
ΕΚΠΑΙΔΕΥΤΙΚΟ ΕΠΟΠΤΙΚΟ ΥΛΙΚΟ
 ΤΕΙ ΣΤΕΡΕΑΣ ΕΛΛΑΔΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ ΕΚΠΑΙΔΕΥΤΙΚΟ ΕΠΟΠΤΙΚΟ ΥΛΙΚΟ ΗΛΕΚΤΡΟΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΜΕΤΡΗΣΕΙΣ Χ. ΤΣΩΝΟΣ ΛΑΜΙΑ 2013 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
ΤΕΙ ΣΤΕΡΕΑΣ ΕΛΛΑΔΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ ΕΚΠΑΙΔΕΥΤΙΚΟ ΕΠΟΠΤΙΚΟ ΥΛΙΚΟ ΗΛΕΚΤΡΟΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΜΕΤΡΗΣΕΙΣ Χ. ΤΣΩΝΟΣ ΛΑΜΙΑ 2013 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Τελεστικοί Ενισχυτές. Σπύρος Νικολαΐδης Αναπληρωτής Καθηγητής Τομέας Ηλεκτρονικής & ΗΥ Τμήμα Φυσικής
 Τελεστικοί Ενισχυτές Σπύρος Νικολαΐδης Αναπληρωτής Καθηγητής Τομέας Ηλεκτρονικής & ΗΥ Τμήμα Φυσικής Ο ιδανικός τελεστικός ενισχυτής Είσοδος αντιστροφής Ισοδύναμα Είσοδος μη αντιστροφής A( ) A d 2 1 2 1
Τελεστικοί Ενισχυτές Σπύρος Νικολαΐδης Αναπληρωτής Καθηγητής Τομέας Ηλεκτρονικής & ΗΥ Τμήμα Φυσικής Ο ιδανικός τελεστικός ενισχυτής Είσοδος αντιστροφής Ισοδύναμα Είσοδος μη αντιστροφής A( ) A d 2 1 2 1
Συστήµατα τα οποία χαρακτηρίζονται από γραµµικές εξισώσεις διαφορών µε σταθερούς συντελεστές
 Συστήµατα τα οποία χαρακτηρίζονται από γραµµικές εξισώσεις διαφορών µε σταθερούς συντελεστές x h γραµµική εξίσωση διαφορών µε σταθερούς συντελεστές της µορφής x µπορεί να θεωρηθεί ως ένας αλγόριθµος υπολογισµού
Συστήµατα τα οποία χαρακτηρίζονται από γραµµικές εξισώσεις διαφορών µε σταθερούς συντελεστές x h γραµµική εξίσωση διαφορών µε σταθερούς συντελεστές της µορφής x µπορεί να θεωρηθεί ως ένας αλγόριθµος υπολογισµού
Διάρκεια εξέτασης 2 ώρες
 ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΗΣ ΤΕΙ ΠΕΙΡΑΙΑ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ B ΠΕΡΙΟΔΟΥ ΕΑΡΙΝΟΥ 007-08 Η/Ν ΦΙΛΤΡΑ Εξεταστής: Καθηγητής Ηρ. Γ. Δηµόπουλος Διάρκεια εξέτασης ώρες 0.09.008 ΖΗΤΗΜΑ (5 µονάδες Tο εικονιζόµενο κανονικοποιηµένο
ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΗΣ ΤΕΙ ΠΕΙΡΑΙΑ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ B ΠΕΡΙΟΔΟΥ ΕΑΡΙΝΟΥ 007-08 Η/Ν ΦΙΛΤΡΑ Εξεταστής: Καθηγητής Ηρ. Γ. Δηµόπουλος Διάρκεια εξέτασης ώρες 0.09.008 ΖΗΤΗΜΑ (5 µονάδες Tο εικονιζόµενο κανονικοποιηµένο
Επαναληπτικές Ασκήσεις για το µάθηµα Ψηφιακή Επεξεργασία Σηµάτων
 Άσκηση η α) Πώς θα µετρήσετε πρακτικά πόσο κοντά είναι ένα σήµα σε λευκό θόρυβο; Αναφέρατε 3 διαφορετικές µεθόδους (κριτήρια) για την απόφαση: "Ναι, πρόκειται για σήµα που είναι πολύ κοντά σε λευκό θόρυβο"
Άσκηση η α) Πώς θα µετρήσετε πρακτικά πόσο κοντά είναι ένα σήµα σε λευκό θόρυβο; Αναφέρατε 3 διαφορετικές µεθόδους (κριτήρια) για την απόφαση: "Ναι, πρόκειται για σήµα που είναι πολύ κοντά σε λευκό θόρυβο"
Ψηφιακές Τηλεπικοινωνίες. Βέλτιστος Δέκτης
 Ψηφιακές Τηλεπικοινωνίες Βέλτιστος Δέκτης Σύνδεση με τα Προηγούμενα Επειδή το πραγματικό κανάλι είναι αναλογικό, κατά τη διαβίβαση ψηφιακής πληροφορίας, αντιστοιχίζουμε τα σύμβολα σε αναλογικές κυματομορφές
Ψηφιακές Τηλεπικοινωνίες Βέλτιστος Δέκτης Σύνδεση με τα Προηγούμενα Επειδή το πραγματικό κανάλι είναι αναλογικό, κατά τη διαβίβαση ψηφιακής πληροφορίας, αντιστοιχίζουμε τα σύμβολα σε αναλογικές κυματομορφές
ΑΝΑΛΥΣΗ ΣΗΜΑΤΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΜΕ ΤΟ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟ FOURIER
 ΑΝΑΛΥΣΗ ΣΗΜΑΤΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΜΕ ΤΟ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟ FOURIER Ανάλυση σημάτων και συστημάτων Ο μετασχηματισμός Fourier (DTFT και DFT) είναι σημαντικότατος για την ανάλυση σημάτων και συστημάτων Εντοπίζει
ΑΝΑΛΥΣΗ ΣΗΜΑΤΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΜΕ ΤΟ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟ FOURIER Ανάλυση σημάτων και συστημάτων Ο μετασχηματισμός Fourier (DTFT και DFT) είναι σημαντικότατος για την ανάλυση σημάτων και συστημάτων Εντοπίζει
Συστήµατα τα οποία χαρακτηρίζονται από γραµµικές εξισώσεις διαφορών µε σταθερούς συντελεστές
 Συστήµατα τα οποία χαρακτηρίζονται από γραµµικές εξισώσεις διαφορών µε σταθερούς συντελεστές x h γραµµική εξίσωση διαφορών µε σταθερούς συντελεστές της µορφής x µπορεί να θεωρηθεί ως ένας αλγόριθµος υπολογισµού
Συστήµατα τα οποία χαρακτηρίζονται από γραµµικές εξισώσεις διαφορών µε σταθερούς συντελεστές x h γραµµική εξίσωση διαφορών µε σταθερούς συντελεστές της µορφής x µπορεί να θεωρηθεί ως ένας αλγόριθµος υπολογισµού
Μεταβατική Ανάλυση - Φάσορες. Κατάστρωση διαφορικών εξισώσεων. Μεταβατική απόκριση. Γενικό μοντέλο. ,, ( ) είναι γνωστές ποσότητες (σταθερές)
 Μεταβατική Ανάλυση - Φάσορες Πρόσθετες διαφάνειες διαλέξεων Αλέξανδρος Πίνο Δεκέμβριος 2017 Γενικό μοντέλο Απόκριση κυκλώματος πρώτης τάξης, δηλαδή με ένα μόνο στοιχείο C ή L 3 Μεταβατική απόκριση Ξαφνική
Μεταβατική Ανάλυση - Φάσορες Πρόσθετες διαφάνειες διαλέξεων Αλέξανδρος Πίνο Δεκέμβριος 2017 Γενικό μοντέλο Απόκριση κυκλώματος πρώτης τάξης, δηλαδή με ένα μόνο στοιχείο C ή L 3 Μεταβατική απόκριση Ξαφνική
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ. Εργαστήριο 8 ο. Αποδιαμόρφωση PAM-PPM με προσαρμοσμένα φίλτρα
 Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΨΗΦΙΑΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Εργαστήριο 8 ο Αποδιαμόρφωση PAM-PPM με προσαρμοσμένα φίλτρα Βασική Θεωρία Σε ένα σύστημα μετάδοσης
Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΨΗΦΙΑΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Εργαστήριο 8 ο Αποδιαμόρφωση PAM-PPM με προσαρμοσμένα φίλτρα Βασική Θεωρία Σε ένα σύστημα μετάδοσης
Συστήματα Επικοινωνιών
 Συστήματα Επικοινωνιών Ενότητα 11: Ψηφιακή Διαμόρφωση Μέρος Α Μιχαήλ Λογοθέτης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Περιγραφή διαμόρφωσης παλμών κατά
Συστήματα Επικοινωνιών Ενότητα 11: Ψηφιακή Διαμόρφωση Μέρος Α Μιχαήλ Λογοθέτης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Περιγραφή διαμόρφωσης παλμών κατά
Κεφάλαιο 1 ο. Βασικά στοιχεία των Κυκλωμάτων
 Κεφάλαιο 1 ο Βασικά στοιχεία των Κυκλωμάτων Ένα ηλεκτρικό/ηλεκτρονικό σύστημα μπορεί εν γένει να παρασταθεί από ένα κυκλωματικό διάγραμμα ή δικτύωμα, το οποίο αποτελείται από στοιχεία δύο ακροδεκτών συνδεδεμένα
Κεφάλαιο 1 ο Βασικά στοιχεία των Κυκλωμάτων Ένα ηλεκτρικό/ηλεκτρονικό σύστημα μπορεί εν γένει να παρασταθεί από ένα κυκλωματικό διάγραμμα ή δικτύωμα, το οποίο αποτελείται από στοιχεία δύο ακροδεκτών συνδεδεμένα
MAJ. MONTELOPOIHSH II
 MAJ MONTELOPOIHSH II ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΕΑΡΙΝΟ ΕΞΑΜΗΝΟ 009 ΦΥΛΛΑΔΙΟ ΑΣΚΗΣΕΩΝ ΙV Οι ασκήσεις είναι από το βιβλίο του Simon Haykin Θα ακολουθήσει ακόμη ένα φυλλάδιο τις επόμενες μέρες Άσκηση
MAJ MONTELOPOIHSH II ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΕΑΡΙΝΟ ΕΞΑΜΗΝΟ 009 ΦΥΛΛΑΔΙΟ ΑΣΚΗΣΕΩΝ ΙV Οι ασκήσεις είναι από το βιβλίο του Simon Haykin Θα ακολουθήσει ακόμη ένα φυλλάδιο τις επόμενες μέρες Άσκηση
Εισαγωγή. Προχωρημένα Θέματα Τηλεπικοινωνιών. Ανάκτηση Χρονισμού. Τρόποι Συγχρονισμού Συμβόλων. Συγχρονισμός Συμβόλων. t mt
 Προχωρημένα Θέματα Τηλεπικοινωνιών Συγχρονισμός Συμβόλων Εισαγωγή Σε ένα ψηφιακό τηλεπικοινωνιακό σύστημα, η έξοδος του φίλτρου λήψης είναι μια κυματομορφή συνεχούς χρόνου y( an x( t n ) n( n x( είναι
Προχωρημένα Θέματα Τηλεπικοινωνιών Συγχρονισμός Συμβόλων Εισαγωγή Σε ένα ψηφιακό τηλεπικοινωνιακό σύστημα, η έξοδος του φίλτρου λήψης είναι μια κυματομορφή συνεχούς χρόνου y( an x( t n ) n( n x( είναι
HMY 220: Σήματα και Συστήματα Ι
 HMY 220: Σήματα και Συστήματα Ι Βασικές Έννοιες Σήματα Κατηγορίες Σημάτων Συνεχούς/ Διακριτού Χρόνου, Αναλογικά/ Ψηφιακά Μετασχηματισμοί Σημάτων Χρόνου: Αντιστροφή, Κλιμάκωση, Μετατόπιση Πλάτους Βασικά
HMY 220: Σήματα και Συστήματα Ι Βασικές Έννοιες Σήματα Κατηγορίες Σημάτων Συνεχούς/ Διακριτού Χρόνου, Αναλογικά/ Ψηφιακά Μετασχηματισμοί Σημάτων Χρόνου: Αντιστροφή, Κλιμάκωση, Μετατόπιση Πλάτους Βασικά
Εφαρμογή στις ψηφιακές επικοινωνίες
 Δειγματοληψία Εφαρμογή στις ψηφιακές επικοινωνίες Γεννήτρια σήματος RF, (up converter Ενισχυτής) Προενισχυτής down-converter Ψηφιοποιητής σήματος RF Μονάδα ψηφ. επεξεργασίας Μονάδα ψηφ. επεξεργασίας 100
Δειγματοληψία Εφαρμογή στις ψηφιακές επικοινωνίες Γεννήτρια σήματος RF, (up converter Ενισχυτής) Προενισχυτής down-converter Ψηφιοποιητής σήματος RF Μονάδα ψηφ. επεξεργασίας Μονάδα ψηφ. επεξεργασίας 100
6. Τελεστικοί ενισχυτές
 6. Τελεστικοί ενισχυτές 6. Εισαγωγή Ο τελεστικός ενισχυτής (OP AMP) είναι ένας ενισχυτής με μεγάλη απολαβή στον οποίο προσαρτάται ανάδραση, ώστε να ελέγχεται η λειτουργία του. Χρησιμοποιείται για την πραγματοποίηση
6. Τελεστικοί ενισχυτές 6. Εισαγωγή Ο τελεστικός ενισχυτής (OP AMP) είναι ένας ενισχυτής με μεγάλη απολαβή στον οποίο προσαρτάται ανάδραση, ώστε να ελέγχεται η λειτουργία του. Χρησιμοποιείται για την πραγματοποίηση
Επεξεργασία Στοχαστικών Σημάτων
 Επεξεργασία Στοχαστικών Σημάτων Βέλτιστα γραμμικά χρονικά αναλλοίωτα συστήματα Σεραφείμ Καραμπογιάς Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Βέλτιστα γραμμικά χρονικά αναλλοίωτα συστήματα
Επεξεργασία Στοχαστικών Σημάτων Βέλτιστα γραμμικά χρονικά αναλλοίωτα συστήματα Σεραφείμ Καραμπογιάς Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Βέλτιστα γραμμικά χρονικά αναλλοίωτα συστήματα
Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 5 : Θόρυβος Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Είδη θορύβου Περιγραφή θορύβου Θεώρημα Shannon Hartley Απόδοση ισχύος και εύρους
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 5 : Θόρυβος Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Είδη θορύβου Περιγραφή θορύβου Θεώρημα Shannon Hartley Απόδοση ισχύος και εύρους
h(t τ k ) X (t) = X (t) = (shot noise). 3/28 4/28
 Θόρυβος Στοχαστικά συστήματα & επικοινωνίες 6 Δεκεμβρίου 2012 1/28 2/28 Ο θόρυβος βολής εμφανίζεται στις ηλεκτρονικές συσκευές, όπως οι δίοδοι και τα τρανζίστορ, εξαιτίας της διακριτής φύσης της ροής του
Θόρυβος Στοχαστικά συστήματα & επικοινωνίες 6 Δεκεμβρίου 2012 1/28 2/28 Ο θόρυβος βολής εμφανίζεται στις ηλεκτρονικές συσκευές, όπως οι δίοδοι και τα τρανζίστορ, εξαιτίας της διακριτής φύσης της ροής του
Μοντέλο συστήματος αποδιαμόρφωσης παρουσία θορύβου
 Μοντέλο συστήματος αποδιαμόρφωσης παρουσία θορύβου Επίδοση παρουσία θορύβου Η ανάλυση της επίδοσης των συστημάτων διαμόρφωσης παρουσία θορύβου είναι εξαιρετικά σημαντική για τη σχεδίαση των διαφόρων επικοινωνιακών
Μοντέλο συστήματος αποδιαμόρφωσης παρουσία θορύβου Επίδοση παρουσία θορύβου Η ανάλυση της επίδοσης των συστημάτων διαμόρφωσης παρουσία θορύβου είναι εξαιρετικά σημαντική για τη σχεδίαση των διαφόρων επικοινωνιακών
Στοχαστικές Ανελίξεις
 Ντετερμινιστικά Σήματα - Τυχαία Σήματα Ταξινόμηση των σημάτων ανάλογα με τη βεβαιότητα όσο αφορά την τιμή τους κάθε χρονική στιγμή. Τα ντετερμινιστικά σήματα μπορούν να αναπαρασταθούν σαν πλήρως καθορισμένες
Ντετερμινιστικά Σήματα - Τυχαία Σήματα Ταξινόμηση των σημάτων ανάλογα με τη βεβαιότητα όσο αφορά την τιμή τους κάθε χρονική στιγμή. Τα ντετερμινιστικά σήματα μπορούν να αναπαρασταθούν σαν πλήρως καθορισμένες
Ψηφιακές Τηλεπικοινωνίες. Διαμόρφωση Παλμών κατά Πλάτος
 Ψηφιακές Τηλεπικοινωνίες Διαμόρφωση Παλμών κατά Πλάτος Διαμόρφωση Παλμών κατά Πλάτος Είπαμε ότι κατά την ψηφιακή μετάδοση μέσα από αναλογικό κανάλι κάθε σύμβολο αντιστοιχίζεται σε μια κυματομορφή σήματος
Ψηφιακές Τηλεπικοινωνίες Διαμόρφωση Παλμών κατά Πλάτος Διαμόρφωση Παλμών κατά Πλάτος Είπαμε ότι κατά την ψηφιακή μετάδοση μέσα από αναλογικό κανάλι κάθε σύμβολο αντιστοιχίζεται σε μια κυματομορφή σήματος
Ευαισθησία πειράµατος (Signal to noise ratio = S/N) ιάρκεια πειράµατος (signal averaging)) ιάρκεια 1,38 1,11 0,28 5,55. (h) πειράµατος.
 Γιατί NMR µε παλµούς; Ευαισθησία πειράµατος (Signal to noise ratio = S/N) ιάρκεια πειράµατος (signal averaging)) Πυρήνας Φυσική αφθονία (%) ν (Hz) Ταχύτητα σάρωσης (Hz/s) Αριθµός σαρώσεων 1 Η 99,985 1000
Γιατί NMR µε παλµούς; Ευαισθησία πειράµατος (Signal to noise ratio = S/N) ιάρκεια πειράµατος (signal averaging)) Πυρήνας Φυσική αφθονία (%) ν (Hz) Ταχύτητα σάρωσης (Hz/s) Αριθµός σαρώσεων 1 Η 99,985 1000
ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 2015 ΕΚΦΩΝΗΣΕΙΣ
 ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 05 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α. Αν οι συναρτήσεις f, g είναι παραγωγίσιµες στο R, να αποδείξετε ότι: f + g ' = f ' + g ', R Μονάδες 7 Α. Πότε λέµε ότι µια συνάρτηση
ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 05 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α. Αν οι συναρτήσεις f, g είναι παραγωγίσιµες στο R, να αποδείξετε ότι: f + g ' = f ' + g ', R Μονάδες 7 Α. Πότε λέµε ότι µια συνάρτηση
Επικοινωνίες I FM ΔΙΑΜΟΡΦΩΣΗ. Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Επικοινωνίες I ΔΙΑΜΟΡΦΩΣΗ ΓΩΝΙΑΣ FM ΔΙΑΜΟΡΦΩΣΗ Σήμα FM Η ακόλουθη εξίσωση δίδει την ισοδύναμη για τη διαμόρφωση συχνότητας έκφραση
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Επικοινωνίες I ΔΙΑΜΟΡΦΩΣΗ ΓΩΝΙΑΣ FM ΔΙΑΜΟΡΦΩΣΗ Σήμα FM Η ακόλουθη εξίσωση δίδει την ισοδύναμη για τη διαμόρφωση συχνότητας έκφραση
Το σήμα εξόδου ενός διαμορφωτή συμβατικού ΑΜ είναι:
 Άσκηση 1 Το σήμα εξόδου ενός διαμορφωτή συμβατικού ΑΜ είναι: i. Προσδιορίστε το σήμα πληροφορίας και το φέρον. ii. Βρείτε το δείκτη διαμόρφωσης. iii. Υπολογίστε το λόγο της ισχύος στις πλευρικές ζώνες
Άσκηση 1 Το σήμα εξόδου ενός διαμορφωτή συμβατικού ΑΜ είναι: i. Προσδιορίστε το σήμα πληροφορίας και το φέρον. ii. Βρείτε το δείκτη διαμόρφωσης. iii. Υπολογίστε το λόγο της ισχύος στις πλευρικές ζώνες
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ. Θ.Ε. ΠΛΗ22 ( ) 2η Γραπτή Εργασία
 Θ.Ε. ΠΛΗ 0-3 η Γραπτή Εργασία Στόχος: Η η ΑΠΑΝΤΗΣΕΙΣ εργασία αποσκοπεί στην κατανόηση των συστατικών στοιχείων των αναλογικών διαμορφώσεων, της δειγματοληψίας, και της μετατροπής του αναλογικού σήματος
Θ.Ε. ΠΛΗ 0-3 η Γραπτή Εργασία Στόχος: Η η ΑΠΑΝΤΗΣΕΙΣ εργασία αποσκοπεί στην κατανόηση των συστατικών στοιχείων των αναλογικών διαμορφώσεων, της δειγματοληψίας, και της μετατροπής του αναλογικού σήματος
Σήματα και Συστήματα. Διάλεξη 1: Σήματα Συνεχούς Χρόνου. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 1: Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Εισαγωγή στα Σήματα 1. Σκοποί της Θεωρίας Σημάτων 2. Κατηγορίες Σημάτων 3. Χαρακτηριστικές Παράμετροι
Σήματα και Συστήματα Διάλεξη 1: Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Εισαγωγή στα Σήματα 1. Σκοποί της Θεωρίας Σημάτων 2. Κατηγορίες Σημάτων 3. Χαρακτηριστικές Παράμετροι
Θ.Ε. ΠΛΗ22 ( ) 2η Γραπτή Εργασία
 Θ.Ε. ΠΛΗ22 (2012-13) 2η Γραπτή Εργασία Στόχος: Η 2 η εργασία αποσκοπεί στην κατανόηση των συστατικών στοιχείων των αναλογικών διαμορφώσεων, της δειγματοληψίας, και της μετατροπής του αναλογικού σήματος
Θ.Ε. ΠΛΗ22 (2012-13) 2η Γραπτή Εργασία Στόχος: Η 2 η εργασία αποσκοπεί στην κατανόηση των συστατικών στοιχείων των αναλογικών διαμορφώσεων, της δειγματοληψίας, και της μετατροπής του αναλογικού σήματος
Να σχεδιαστεί ένας ενισχυτής κοινού εκπομπού (σχ.1) με τα εξής χαρακτηριστικά: R 2.3 k,
 Να σχεδιαστεί ένας ενισχυτής κοινού εκπομπού (σχ) με τα εξής χαρακτηριστικά: 3 k, 50, k, S k και V 5 α) Nα υπολογιστούν οι τιμές των αντιστάσεων β) Να επιλεγούν οι χωρητικότητες C, CC έτσι ώστε ο ενισχυτής
Να σχεδιαστεί ένας ενισχυτής κοινού εκπομπού (σχ) με τα εξής χαρακτηριστικά: 3 k, 50, k, S k και V 5 α) Nα υπολογιστούν οι τιμές των αντιστάσεων β) Να επιλεγούν οι χωρητικότητες C, CC έτσι ώστε ο ενισχυτής
Ασκήσεις στο µάθηµα «Επισκόπηση των Τηλεπικοινωνιών»
 Ασκήσεις στο µάθηµα «Επισκόπηση των Τηλεπικοινωνιών» Άσκηση 1 Πρόκειται να µεταδώσουµε δυαδικά δεδοµένα σε RF κανάλι µε. Αν ο θόρυβος του καναλιού είναι Gaussian - λευκός µε φασµατική πυκνότητα W, να βρεθεί
Ασκήσεις στο µάθηµα «Επισκόπηση των Τηλεπικοινωνιών» Άσκηση 1 Πρόκειται να µεταδώσουµε δυαδικά δεδοµένα σε RF κανάλι µε. Αν ο θόρυβος του καναλιού είναι Gaussian - λευκός µε φασµατική πυκνότητα W, να βρεθεί
ΕΠΙΔΡΑΣΗ ΤΟΥ ΘΟΡΥΒΟΥ ΣΤΑ ANΑΛΟΓΙΚΑ ΣΥΣΤΗΜΑΤΑ ΔΙΑΒΙΒΑΣΗΣ ΣΗΜΑΤΟΣ. Προσθετικός Λευκός Gaussian Θόρυβος (Additive White Gaussian Noise-AWGN
 ΡΗ 009-10 16/1/009 3:4 μμ ΕΠΙΔΡΑΣΗ ΤΟΥ ΘΟΡΥΒΟΥ ΣΤΑ ANΑΛΟΓΙΚΑ ΣΥΣΤΗΜΑΤΑ ΔΙΑΒΙΒΑΣΗΣ ΣΗΜΑΤΟΣ Προσθετικός Λευκός Gaussian Θόρυβος (Additive White Gaussian Noise-AWGN AWGN) ΕΠΙΔΡΑΣΗ ΤΟΥ ΘΟΡΥΒΟΥ ΣΕ ΜΕΤΑΔΟΣΗ
ΡΗ 009-10 16/1/009 3:4 μμ ΕΠΙΔΡΑΣΗ ΤΟΥ ΘΟΡΥΒΟΥ ΣΤΑ ANΑΛΟΓΙΚΑ ΣΥΣΤΗΜΑΤΑ ΔΙΑΒΙΒΑΣΗΣ ΣΗΜΑΤΟΣ Προσθετικός Λευκός Gaussian Θόρυβος (Additive White Gaussian Noise-AWGN AWGN) ΕΠΙΔΡΑΣΗ ΤΟΥ ΘΟΡΥΒΟΥ ΣΕ ΜΕΤΑΔΟΣΗ
Τηλεπικοινωνιακά Συστήματα ΙΙ
 Τηλεπικοινωνιακά Συστήματα ΙΙ Διάλεξη 1: Χωρητικότητα Καναλιών Το θεώρημα Shannon - Hartley Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα 1. Δυαδική σηματοδοσία 2. Μορφές δυαδικής σηματοδοσίας 3.
Τηλεπικοινωνιακά Συστήματα ΙΙ Διάλεξη 1: Χωρητικότητα Καναλιών Το θεώρημα Shannon - Hartley Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα 1. Δυαδική σηματοδοσία 2. Μορφές δυαδικής σηματοδοσίας 3.
ΘΕΜΑΤΑ & ΛΥΣΕΙΣ ΕΞΕΤΑΣΕΩΝ
 ΘΕΜΑΤΑ & ΛΥΣΕΙΣ ΕΞΕΤΑΣΕΩΝ Μάθημα: Επικοινωνίες ΙΙ. Εξεταστική Περίοδος: B Θερινή, 14 Σεπτεμβρίου 2009. ΕΙΣΗΓΗΤΗΣ: Αναστάσιος Παπατσώρης Θέμα 1 ο (25 μονάδες) Ένα ADSL modem λειτουργεί με ταχύτητα downloading
ΘΕΜΑΤΑ & ΛΥΣΕΙΣ ΕΞΕΤΑΣΕΩΝ Μάθημα: Επικοινωνίες ΙΙ. Εξεταστική Περίοδος: B Θερινή, 14 Σεπτεμβρίου 2009. ΕΙΣΗΓΗΤΗΣ: Αναστάσιος Παπατσώρης Θέμα 1 ο (25 μονάδες) Ένα ADSL modem λειτουργεί με ταχύτητα downloading
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών. HY-215: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς ιδάσκοντες : Γ. Στυλιανού, Γ.
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-15: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ - Ενδεικτικές Λύσεις ιάρκεια : 3 ώρες Ρήτρα τελικού :
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-15: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ - Ενδεικτικές Λύσεις ιάρκεια : 3 ώρες Ρήτρα τελικού :
ΘΕΜΑ 2 1. Υπολογίστε την σχέση των δύο αντιστάσεων, ώστε η συνάρτηση V
 Θέµατα εξετάσεων Θ. Κυκλωµάτων & Σηµάτων Σας προσφέρω τα περισσότερα θέµατα που έχουν τεθεί στις εξετάσεις τα τελευταία χρόνια ελπίζοντας ότι θα ασχοληθείτε µαζί τους κατά την προετοιµασία σας. Τα θέµατα
Θέµατα εξετάσεων Θ. Κυκλωµάτων & Σηµάτων Σας προσφέρω τα περισσότερα θέµατα που έχουν τεθεί στις εξετάσεις τα τελευταία χρόνια ελπίζοντας ότι θα ασχοληθείτε µαζί τους κατά την προετοιµασία σας. Τα θέµατα
Τηλεπικοινωνιακά Συστήματα Ι
 Τηλεπικοινωνιακά Συστήματα Ι Διάλεξη 12: Βασικές Αρχές και Έννοιες Ψηφιακών Επικοινωνιών Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα 1. Παράγοντες που επηρεάζουν τη σχεδίαση τηλεπικοινωνιακών
Τηλεπικοινωνιακά Συστήματα Ι Διάλεξη 12: Βασικές Αρχές και Έννοιες Ψηφιακών Επικοινωνιών Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα 1. Παράγοντες που επηρεάζουν τη σχεδίαση τηλεπικοινωνιακών
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙςΤΗΜΗς & ΤΕΧΝΟΛΟΓΙΑς ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΜΔΕ Προηγμένα Τηλεπικοινωνιακά Συστήματα και Δίκτυα Διάλεξη 2 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst233
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙςΤΗΜΗς & ΤΕΧΝΟΛΟΓΙΑς ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΜΔΕ Προηγμένα Τηλεπικοινωνιακά Συστήματα και Δίκτυα Διάλεξη 2 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst233
Ψηφιακές Τηλεπικοινωνίες
 Ψηφιακές Τηλεπικοινωνίες Θεωρία Πληροφορίας: Χωρητικότητα Καναλιού Χωρητικότητα Καναλιού Η θεωρία πληροφορίας περιλαμβάνει μεταξύ άλλων: κωδικοποίηση πηγής κωδικοποίηση καναλιού Κωδικοποίηση πηγής: πόση
Ψηφιακές Τηλεπικοινωνίες Θεωρία Πληροφορίας: Χωρητικότητα Καναλιού Χωρητικότητα Καναλιού Η θεωρία πληροφορίας περιλαμβάνει μεταξύ άλλων: κωδικοποίηση πηγής κωδικοποίηση καναλιού Κωδικοποίηση πηγής: πόση
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 17 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη 3 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst15
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 17 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη 3 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst15
Σεραφείµ Καραµπογιάς ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Εισαγωγή στα Σήµατα Εισαγωγή στα Συστήµατα Ανάπτυγµα - Μετασχηµατισµός Fourier Μετασχηµατισµός Laplace Μετασχηµατισµός z Εφαρµογές 1. ΚΕΦΑΛΑΙΟ ΕΙΣΑΓΩΓΗ ΣΤΑ ΣΗΜΑΤΑ Γενική εικόνα τι
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Εισαγωγή στα Σήµατα Εισαγωγή στα Συστήµατα Ανάπτυγµα - Μετασχηµατισµός Fourier Μετασχηµατισµός Laplace Μετασχηµατισµός z Εφαρµογές 1. ΚΕΦΑΛΑΙΟ ΕΙΣΑΓΩΓΗ ΣΤΑ ΣΗΜΑΤΑ Γενική εικόνα τι
ΚΕΦΑΛΑΙΟ 5 Ο : ΣΥΝΤΟΝΙΣΜΟΣ ΑΠΛΩΝ ΗΛΕΚΤΡΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ
 ΚΕΦΑΛΑΙΟ 5 Ο : ΣΥΝΤΟΝΙΣΜΟΣ ΑΠΛΩΝ ΗΛΕΚΤΡΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ 1 Ο συντονισμός είναι μια κατάσταση κατά την οποία το φανταστικό μέρος της σύνθετης αντίστασης ενός κυκλώματος RCL μηδενίζεται. Αυτό συμβαίνει γιατί
ΚΕΦΑΛΑΙΟ 5 Ο : ΣΥΝΤΟΝΙΣΜΟΣ ΑΠΛΩΝ ΗΛΕΚΤΡΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ 1 Ο συντονισμός είναι μια κατάσταση κατά την οποία το φανταστικό μέρος της σύνθετης αντίστασης ενός κυκλώματος RCL μηδενίζεται. Αυτό συμβαίνει γιατί
Τελεστικοί Ενισχυτές
 Τελεστικοί Ενισχυτές Ο Τελεστικός Ενισχυτής (ΤΕ) αποτελεί ένα ιδιαίτερο είδος ενισχυτή, το οποίο έχει ευρύτατη αποδοχή ως δομικό στοιχείο των ηλεκτρονικών κυκλωμάτων. Η μεγάλη του δημοτικότητα οφείλεται
Τελεστικοί Ενισχυτές Ο Τελεστικός Ενισχυτής (ΤΕ) αποτελεί ένα ιδιαίτερο είδος ενισχυτή, το οποίο έχει ευρύτατη αποδοχή ως δομικό στοιχείο των ηλεκτρονικών κυκλωμάτων. Η μεγάλη του δημοτικότητα οφείλεται
10-Μαρτ-2009 ΗΜΥ Παραθύρωση Ψηφιακά φίλτρα
 -Μαρτ-9 ΗΜΥ 49. Παραθύρωση Ψηφιακά φίλτρα . Παραθύρωση / Ψηφιακά Φίλτρα -Μαρτ-9 Είδη παραθύρων Bartlett τριγωνικό: n, n Blacman: πn 4πn.4.5cos +.8cos, n < . Παραθύρωση / Ψηφιακά Φίλτρα -Μαρτ-9 3 Hamming:
-Μαρτ-9 ΗΜΥ 49. Παραθύρωση Ψηφιακά φίλτρα . Παραθύρωση / Ψηφιακά Φίλτρα -Μαρτ-9 Είδη παραθύρων Bartlett τριγωνικό: n, n Blacman: πn 4πn.4.5cos +.8cos, n < . Παραθύρωση / Ψηφιακά Φίλτρα -Μαρτ-9 3 Hamming:
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ
 Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 8 ο : Προσαρμοσμένα Φίλτρα Βασική
Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 8 ο : Προσαρμοσμένα Φίλτρα Βασική
Συστήματα Επικοινωνιών ΙI
 + Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI FSK, MSK Πυκνότητα φάσματος ισχύος βασικής ζώνης + Ιστοσελίδα nιστοσελίδα του μαθήματος: n https://eclass.uowm.gr/courses/icte302/
+ Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI FSK, MSK Πυκνότητα φάσματος ισχύος βασικής ζώνης + Ιστοσελίδα nιστοσελίδα του μαθήματος: n https://eclass.uowm.gr/courses/icte302/
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ Θ.Ε. ΠΛΗ22 ( ) ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ #1 ΑΠΑΝΤΗΣΕΙΣ
 Θ.Ε. ΠΛΗ (0-3) ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ # ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Στόχος της άσκησης είναι η εξοικείωση με γραφικές παραστάσεις βασικών σημάτων και πράξεις, καθώς και τον υπολογισμό ΜΣ Fourier βασικών σημάτων με τη χρήση
Θ.Ε. ΠΛΗ (0-3) ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ # ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Στόχος της άσκησης είναι η εξοικείωση με γραφικές παραστάσεις βασικών σημάτων και πράξεις, καθώς και τον υπολογισμό ΜΣ Fourier βασικών σημάτων με τη χρήση
Εξεταστική Ιανουαρίου 2007 Μάθηµα: «Σήµατα και Συστήµατα»
 Εξεταστική Ιανουαρίου 27 Μάθηµα: «Σήµατα και Συστήµατα» Θέµα 1 ο (3%) Έστω δύο διακριτά σήµατα: x(n) = {1,,, -1} και h(n) = {1,, 1} µε το πρώτο δείγµα να αντιστοιχεί σε n= και για τα δύο. Υπολογίστε τα
Εξεταστική Ιανουαρίου 27 Μάθηµα: «Σήµατα και Συστήµατα» Θέµα 1 ο (3%) Έστω δύο διακριτά σήµατα: x(n) = {1,,, -1} και h(n) = {1,, 1} µε το πρώτο δείγµα να αντιστοιχεί σε n= και για τα δύο. Υπολογίστε τα
Εισαγωγή. Ακουστικό. Μικρόφωνο
 Εισαγωγή Ο σκοπός του συστήµατος επικοινωνίας είναι να µεταδώσει πληροφορία (ransmission of informaion) από ένα σηµείο του χώρου, που λέγεται πηγή, σε ένα άλλο σηµείο, που είναι ο προορισµός χρήσης. Κατά
Εισαγωγή Ο σκοπός του συστήµατος επικοινωνίας είναι να µεταδώσει πληροφορία (ransmission of informaion) από ένα σηµείο του χώρου, που λέγεται πηγή, σε ένα άλλο σηµείο, που είναι ο προορισµός χρήσης. Κατά
ΕΥΑΙΣΘΗΣΙΑ ΗΛΕΚΤΡΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ
 ΤΕΙ ΠΕΙΡΑΙΑ -ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΝΙΚΩΝ ΦΙΛΤΡΩΝ ΧΕΙΜΕΡΙΝΟ 2017-18 ΕΥΑΙΣΘΗΣΙΑ ΗΛΕΚΤΡΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ 1. ΕΥΑΙΣΘΗΣΙΑ Ενα κύκλωµα, το οποίο κάνει µια συγκεκριµένη λειτουργία εκφραζόµενη
ΤΕΙ ΠΕΙΡΑΙΑ -ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΝΙΚΩΝ ΦΙΛΤΡΩΝ ΧΕΙΜΕΡΙΝΟ 2017-18 ΕΥΑΙΣΘΗΣΙΑ ΗΛΕΚΤΡΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ 1. ΕΥΑΙΣΘΗΣΙΑ Ενα κύκλωµα, το οποίο κάνει µια συγκεκριµένη λειτουργία εκφραζόµενη
Να εξετάσετε αν είναι συναρτήσεις πυκνότητας πιθανότητας, κι αν είναι να υπολογίσετε τη συνάρτηση κατανομής πιθανότητας F x (x).
 Κεφάλαιο 2, άσκηση 1: Δίνονται οι συναρτήσεις: α) 2, β), Να εξετάσετε αν είναι συναρτήσεις πυκνότητας πιθανότητας, κι αν είναι να υπολογίσετε τη συνάρτηση κατανομής πιθανότητας F x (x). Λύση : Για να είναι
Κεφάλαιο 2, άσκηση 1: Δίνονται οι συναρτήσεις: α) 2, β), Να εξετάσετε αν είναι συναρτήσεις πυκνότητας πιθανότητας, κι αν είναι να υπολογίσετε τη συνάρτηση κατανομής πιθανότητας F x (x). Λύση : Για να είναι
Παλμοκωδική Διαμόρφωση. Pulse Code Modulation (PCM)
 Παλμοκωδική Διαμόρφωση Pulse Code Modulation (PCM) Pulse-code modulation (PCM) Η PCM είναι ένας στοιχειώδης τρόπος διαμόρφωσης που δεν χρησιμοποιεί φέρον! Το μεταδιδόμενο (διαμορφωμένο) σήμα PCM είναι
Παλμοκωδική Διαμόρφωση Pulse Code Modulation (PCM) Pulse-code modulation (PCM) Η PCM είναι ένας στοιχειώδης τρόπος διαμόρφωσης που δεν χρησιμοποιεί φέρον! Το μεταδιδόμενο (διαμορφωμένο) σήμα PCM είναι
ΘΕΜΑ 1 ο. α. τα μήκη κύματος από 100m έως 50m ονομάζονται κύματα νύχτας και τα μήκη κύματος από 50m έως 10m ονομάζονται κύματα ημέρας.
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΤΑΞΗ ΕΠΑΛ (ΟΜΑΔΑ Α ) & ΜΑΘΗΜΑΤΩΝ ΕΙΔΙΚΟΤΗΤΑΣ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 06/05/016 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΗΛΕΚΤΡΟΝΙΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ 1 ο ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΤΑΞΗ ΕΠΑΛ (ΟΜΑΔΑ Α ) & ΜΑΘΗΜΑΤΩΝ ΕΙΔΙΚΟΤΗΤΑΣ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 06/05/016 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΗΛΕΚΤΡΟΝΙΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ 1 ο ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ
