4 σ γ 1 γ 1 4 σ γ 1, b i =
|
|
|
- Ιολανθη Αλαφούζος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Ejniko & Kapodistriako Panepisthmio Ajhnwn Tmhma Plhroforikhc & Thlepikoinwniwn, PMS Upologistikh Episthmh Μάθημα: «Επισημονικοί Υπολογισμοί» Διδάσκν: Φίλιππος Τζαφέρης Χειμερινό Εξάμηνο 6-7 Άγγελος Μανζαφλάρης, Μ9, Κυριακή 8 Ιανουαρίου, 7 Επίλυση ης δισδιάσαης εξίσσης Συγκένρσης- ιάχυσης ( ) u + u u + c + c u c u(, ) = f(, ) µε χρήση ης επαναληπικής µεθόδου ESOR ιακριοποίηση Θερούµε ένα οµοιόµορφο εραγνικό πλέγµα (N + ) (N + ) ij Λαµβάνουµε κενρικές διαφορές : u = u i+,j u i,j h u = u i,j+ u i,j h,, u = u i+,j u ij + u i,j h u = u i,j+ u ij + u i,j h και η αρχική εξίσση γίνεαι (u i+,j u ij + u i,j + u i,j+ u ij + u i,j ) + c h(u i+,j u i,j ) + c h(u i,j+ u i,j ) c h u ij = f ij Αν ϑέσουµε β = c h, γ = c h, σ = c h λαµβάνουµε ελικά (β + )u i,j (γ + )u i,j + ( σ)u ij + (γ )u i+,j + (β )u i,j+ = f ij Το υπολογισικό µόριο είναι πένε σηµείν γ- i+,j -(β+) i,j- -σ ij β- i,j+ -(γ+) i-,j Θερούµε η ϕυσική αρίθµηση ν κόµβν, δηλαδή ο άγνσο διάνυσµα ης αριθµηικής λύσης είναι ũ = [ u u i,j u i,j u ij u i+,j u i,j+ u NN ] t Τα κά αρισερά σοιχεία ϑα µας δώσουν ο κά ριγνικό µέρος ου πίνακα ου συσήµαος, ενώ α πάν δεξιά ο άν ριγνικό µέρος Ο συνελεσής ου u ij εµφανίζεαι σην κύρια διαγώνιο
2 Εσ ο σύσηµα Aũ = b Παραηρούµε όι ένα εσερικό γινόµενο γραµµής ου A επί ũ έχει η µορφή [ (β + ) (γ + ) σ γ β ] u i,j u i,j u ij u i+,j u i,j+ Τα σοιχεία u N+,j δίνοναι από ις συνοριακές συνθήκες και οι ανίσοιχοι όροι αφαιρούναι από ο δεξί µέλος, ση ϑέση in Οµοια οι όροι µε u,j αφαιρούναι από ις ϑέσεις + (j )N ου δεξιού µέλους, j = N Για i = N αφαιρείαι ο όρος που περιέχει u i από ο δεξί µέλος από η ϑέση i ου b και ο όρος u i,n+ από η ϑέση N N + i Τελικά ο πίνακας και ο δεξί µέλος ου συσήµαος είναι A = T (β )I (β + )I T (β )I (β + )I T (β )I (β + )I T, b = f b b b N (β + )u (β + )u N (β )u,n+ (β )u N,N+ όπου ο διάνυσµα f περιέχει ις ιµές f ij := f(ih, jh) και T = σ γ γ σ γ γ σ γ γ σ, b i = (γ + )u i (γ )u N+,i ίνουµε µια οπικοποίηση ου πίνακα ου συσήµαος, για N = : nz = 6
3 Επαναληπική µέθοδος ESOR Θα επιλύσουµε η διαφορική εξίσση µε ην επαναληπική µέθοδο ESOR Εσ η ϐασική διάσπαση ου A: και ο επαναληπικό σχήµα ης ESOR όπου Ανικαθισώνας A = D C L C U ũ n+ = G, ũ (n) + k, G, = I R A, k, = R b, R = D C L ũ (n+) = ũ (n) + (I L) D (b Aũ (n) ), n =,,, και µεά από πράξεις ũ (n+) = ( )ũ (n) + Lũ (n+) ( )Lũ (n) + Uũ (n) + D b Λαµβάνονας υπόψιν η µορφή ου πίνακα A µεαρέπουµε α γινόµενα που εµφανίζοναι σε µορφή συνεαγµένν : Τελικά Lũ = D C L Uũ = D C U u (n+) ij = ( )u (n) ij + +(γ )u (n) i+,j D b b ij σ σ ) + σ ( ) (γ + )ui,j + (β + )u i,j σ ( ) (β )ui,j+ (γ )u i+,j σ ( (γ + )u (n+) i,j ) + (β + )u(n+) i,j σ ( (n) (γ + )u i,j + (β + )u(n) i,j ( (β )u (n) i,j+ + ) + σ b ij Οαν οι δείκες µικρόεροι ου ή υπερβαίνουν ο N, οι ανίσοιχοι όροι περνάνε σο δεξί µέλος (καά ην υλοποίηση διακρίνουµε αυές ις περιπώσεις) Επίσης ο γινόµενο Lũ (n+) πρέπει να κραείαι ση µνήµη για να χρησιµοποιηθεί σην επόµενη επανάληψη, διόι ο ũ (n+) χρειάζεαι α Lũ (n+) και Lũ (n+) Εγινε υλοποίηση σε Matlab: Το άγνσο διάνυσµα ũ παρισάνεαι µε έναν N N πίνακα, και οι αρχικές συνθήκες µε έναν N πίνακα, κάθε σήλη ου οποίου περιέχει ις συνοριακές συνθήκες σε µια πλευρά ου συνόρου Οµοια ο δεξί µέλος είναι ένας N N πίνακας Εσι διαηρείαι η αρίθµηση ης παραπάν σχέσης Το µειονέκηµα είναι όι πρέπει να διακρίνουµε περιπώσεις για ις γραµµές σις οποίες υπεισέρχοναι συνοριακές συνθήκες, διόι αυές έχουν ενσµαθεί σο διάνυσµα b και οι ανίσοιχοι όροι σην επαναληπική σχέση πρέπει να µηδενισούν Η µέθοδος υλοποιείαι ση ϱουίνα condiffm ίνουµε ον κώδικα : function u=condiff(n,c,c,c,t,w) tol = 5e-8; n_iter = ; h = /(N+); u = zeros(n); b = zeros(n); du = zeros(n,); b =(c*h+); g =(c*h+); d = -c*hˆ; g = -(c*h-) ; b = -(c*h-) ; Lu=zeros(N); %Arikes Sin8ikes Dirichlet du(:,)=; %Deji Melos b(:,)=b*du(:,); b(:,n)=b*du(:,); b(,:)= b(,:)+g*du(:,) ; b(n,:)= b(n,:)+g*du(:,) ; %for i=:nˆ b(i)=b(i)+f(i*h,i*h);
4 %Epilish me ESOR iter=; while iter<=n_iter %disp(iter) u_prev=u; %j=, i= u(,) = (-t)*u(,)+(t/d)*(b*u(,)+g*u(,))+(t/d)*b(,); Lu(,)= ; %j= for i=:n- c = g*u(i-,)/d; u(i,) = (-t)*u(i,)+w*c+(t-w)*lu(i,)+(t/d)*(b*u(i,)+g*u(i+,))+(t/d)*b(i,); Lu(i,)= c; %j=, i=n c = g*u(n-,)/d; u(n,) = (-t)*u(n,)+w*c+(t-w)*lu(n,)+(t/d)*b*u(n,)+(t/d)*b(n,); Lu(N,)= c; for j=:n- %i= c = b*u(,j-)/d; u(,j) = (-t)*u(,j)+w*c+(t-w)*lu(,j)+(t/d)*(b*u(,j+)+g*u(,j))+(t/d)*b(,j); Lu(,j)= c; for i=:n- c = (g*u(i-,j)+b*u(i,j-))/d; u(i,j) = (-t)*u(i,j)+w*c+(t-w)*lu(i,j)+(t/d)*(b*u(i,j+)+g*u(i+,j))+(t/d)*b(i,j); Lu(i,j)= c; %i=n c = (g*u(n-,j)+b*u(n,j-))/d; u(n,j) = (-t)*u(n,j)+w*c+(t-w)*lu(n,j)+(t/d)*b(n,j); Lu(N,j)= c; %j=n, i= c = b*u(,n-)/d; u(,n) = (-t)*u(,n)+w*c+(t-w)*lu(,n)+(t/d)*g*u(,n)+(t/d)*b(,n); Lu(,N)= c; %j=n for i=:n- c = (g*u(i-,n)+b*u(i,n-))/d; u(i,n) = (-t)*u(i,n)+w*c+(t-w)*lu(i,n)+(t/d)*g*u(i+,n)+(t/d)*b(i,n); Lu(i,N)= c; %j=n, i=n c = (g*u(n-,n)+b*u(n,n-))/d; u(n,n) = (-t)*u(n,n)+w*c+(t-w)*lu(n,n)+(t/d)*b(n,n); Lu(N,N)= c; if norm(u-u_prev,inf)<tol disp(!sigklish META APO ),disp(iter),disp( EPANALHPSEIS ) [,]=meshgrid(h:h:-h,h:h:-h); figure subplot(,,) mesh(,,u); title( \SigmaYNAPTH\SigmaH u(,) ); label( ); label( ); subplot(,,) surf(,,u); title( \SigmaYNAPTH\SigmaH u(,) ); label( );
5 label( ); shading interp subplot(,,) contour(,,u); title( \SigmaYNAPTH\SigmaH u(,) - Contour ); label( ); label( ); subplot(,,) contourf(,,u); title( \SigmaYNAPTH\SigmaH u(,) - Contour ); label( ); label( ); return iter=iter+; u=; disp(!den YPARXEI SIGKLISH META APO ),disp(n_iter),disp( EPANALHPSEIS ) Για να ϐρούµε ϐέλισες ιµές για ις παραµέρους και υπολογίζουµε ον επαναληπικό πίνακα G, και κάνουµε ις γραφικές παρασάσεις (,, G, ) και (,, S(G, )) Η διαδικασία αυή είναι αρκεά χρονοβόρα, αφού ο G, είναι ένας N N πίνακας, µε πολλά µη µηδενικά σοιχεία Η παρακά ϱουίνα επισρέφει ον επαναληπικό πίνακα : function G=G(N,c,c,c,t,w) h=/(n+); N=Nˆ; b=-(c*h+); g=-(c*h+); d = -c*h; g= c*h-; b= c*h-; i= [ N+:N :N :N :N- :N-N ]; j= [ :N-N :N- :N :N (N+):N ]; s= [b*ones(,n-n) g*ones(,n-) d*ones(,n) g*ones(,n-) b*ones(,n-n)]; A= sparse(i,j,s); for i=:n-, A(i*N+,i*N)=; A(i*N,i*N+)=; % G=I-t*inv(R)*A G = spee(n) - t*inv( diag(diag(a))+w*tril(a,-) )*A; Ο πίνακας G, αποθηκεύεαι σαν αραιός πίνακας ση µνήµη, µε χρήση ης ενολής sparse ου Matlab Η δοµή ου είναι σχεδόν κά ριγνική, µε N επιπλέον µη µηδενικές διαγνίους πάν από ην κύρια διαγώνιο Τα σοιχεία ου σχηµαίζουν ένα ρίγνο Sierpinski Παρακά δίνοναι οπικοποιήσεις ου πίνακα διάσασης και 6 6: 5
6 Η ϱουίνα findoptm διαρέχει ο διάσηµα (, ) µε κάποιο ϐήµα που δίνεαι σαν όρισµα, υπολογίζει η νόρµα G, και η ϕασµαική ακίνα S(G, ) και σχεδιάζει ις ανίσοιχες γραφικές παρασάσεις Για η νόρµα δίνει ένα διάγραµµα ισοϋψών καµπύλν, ώσε να γίνουν ϕανερά υχόν σηµεία ελαχίσου Η νόρµα υπολογίζεαι προσεγγισικά, µε ην ενολή normest για αραιούς πίνακες Επίσης η µεγαλύερη κα απόλυο ιµή ιδιοιµή ου G, υπολογίζεαι µε χρήση ης ϐιβλιοθήκης ARPACK, µε ην ενολή eigs που είναι ειδικά για αραιούς πίνακες function [m, topt, wopt]=findopt(n,c,c,c,step) OPTSdisp = ; OPTSmait = ; OPTStol = 5e-; calc=(/step-); [t,w]= meshgrid(step:step:-step, step:step:-step); disp( STEPS= ),disp(calcˆ) count=; for i=:calc for j=:calc count=count+;disp(count) z(i,j)=normest(g(n,c,c,c,t(i,j),w(i,j)),inf); r(i,j)= abs( eigs(g(n,c,c,c,t(i,j),w(i,j)),, lm,opts)); figure subplot(,,) surf(t,w,z); title( G_{\tau,\omega} ); label( \tau ); label( \omega ); subplot(,,) surf(t,w,r); title( \PhiA\SigmaMATIKH AKTINA ); label( \tau ); label( \omega ); subplot(,,) surf(t,w,z); view([ 6]) %title( G_{\tau,\omega} ); label( \tau ); label( \omega ); subplot(,,) surf(t,w,r); view([ 6]) %title( \PhiA\SigmaMATIKH AKTINA ); label( \tau ); label( \omega ); figure [c,h] =contour(t,w,r,calc*); clabel(c); title( \PhiA\SigmaMATIKH AKTINA - Contour ); label( \tau ); label( \omega ); [m, i, j] = minn(r); topt = t(i,j); wopt = w(i,j); 6
7 Εφαρµογές Για ϐοήθεια σον πειραµαισµό, καασκευάσηκε η ϱουίνα findoptiterm η οποία εκελεί ην ESOR για όλες ις ιµές ν παραµέρν, µε κάποιο ϐήµα που δίνεαι σαν όρισµα Εσι ελέγχουµε πόσες επαναλήψεις γίνοναι συναρήσει ν, και συγκρίνουµε ις ιµές µε α ϐέλισα, ς προς η ϕασµαική ακίνα Εσ N =, (c, c, c ) = (,, ) Η γραφική παράσαση ης νόρµας και ης ϕασµαικής ακίνας είναι 8 G, ΦAΣMATIKH AKTINA και ο διάγραµµα ισοϋψών καµπύλν ΦAΣMATIKH AKTINA Contour Η ϕασµαική ακίνα παράµένει µεγαλύερη ου σε όλο ο πλέγµα Κάθε προσπάθεια επίλυσης ου συσήµαος µε ην condiffm απέυχε, για όλες ις ανίσοιχες ιµές, 7
8 Εσ N =, (c, c, c ) = (5, 5, ) Η γραφική παράσαση ης νόρµας και ης ϕασµαικής ακίνας είναι(ϐήµα ): G, ΦAΣMATIKH AKTINA Η ϕασµαική ακίνα εκοξεύεαι σα ύψη για µεγάλες ιµές ου, Το ϐέλισο ϐρέθηκε για =, = 6 όπου S(G,6 ) = 6 Πράγµαι χρειάσηκαν 57 επαναλήψεις για να λάβουµε η λύση : ΣYNAPTHΣH u(,) ΣYNAPTHΣH u(,) ΣYNAPTHΣH u(,) Contour ΣYNAPTHΣH u(,) Contour Ενδεικικά αναφέρουµε όι για =, = 5 οι επαναλήψεις είναι 8, ενώ για =, = χρειάσηκαν επαναλήψεις 8
9 Εσ N =, (c, c, c ) = (,, ) Το διάγραµµα ισοϋψών καµπύλν είναι(ϐήµα ): ΦAΣMATIKH AKTINA Contour Το ϐέλισο ϐρέθηκε για = = όπου S(G, ) = 69 Πράγµαι χρειάσηκαν 9 επαναλήψεις για να λάβουµε η λύση : ΣYNAPTHΣH u(,) ΣYNAPTHΣH u(,) ΣYNAPTHΣH u(,) Contour ΣYNAPTHΣH u(,) Contour
10 Εσ N =, (c, c, c ) = (5,, )Η γραφική παράσαση ης νόρµας και ης ϕασµαικής ακίνας είναι(ϐήµα ): 8 G, ΦAΣMATIKH AKTINA Το διάγραµµα ισοϋψών καµπύλν είναι : 8 ΦAΣMATIKH AKTINA Contour Το ϐέλισο ϐρέθηκε για = = όπου S(G, ) = 88 Πράγµαι χρειάσηκαν επαναλήψεις για να λάβουµε η λύση :
11 ΣYNAPTHΣH u(,) ΣYNAPTHΣH u(,) ΣYNAPTHΣH u(,) Contour ΣYNAPTHΣH u(,) Contour Εσ N =, (c, c, c ) = (,, 5)Η γραφική παράσαση ης νόρµας και ης ϕασµαικής ακίνας είναι(ϐήµα ): G, ΦAΣMATIKH AKTINA 6 5 Το διάγραµµα ισοϋψών καµπύλν είναι :
12 8 6 ΦAΣMATIKH AKTINA Contour Το ϐέλισο ϐρέθηκε για =, = 7 όπου S(G,7 ) = 875 Πράγµαι χρειάσηκαν επαναλήψεις για να λάβουµε η λύση : ΣYNAPTHΣH u(,) ΣYNAPTHΣH u(,) ΣYNAPTHΣH u(,) Contour ΣYNAPTHΣH u(,) Contour
13 Εσ N = 6, (c, c, c ) = (,, 7)Η γραφική παράσαση ης νόρµας και ης ϕασµαικής ακίνας είναι(ϐήµα ): 7 G, ΦAΣMATIKH AKTINA Το διάγραµµα ισοϋψών καµπύλν είναι : 8 6 ΦAΣMATIKH AKTINA Contour Το ϐέλισο ϐρέθηκε για = 9 = = 9 όπου S(G,8 ) = 9778 Χρειάσηκαν86 επαναλήψεις για να λάβουµε η λύση :
14 ΣYNAPTHΣH u(,) ΣYNAPTHΣH u(,) ΣYNAPTHΣH u(,) Contour ΣYNAPTHΣH u(,) Contour Κοιάζονας ο διάγραµµα ισοϋψών καµπύλν, ϐλέπουµε όι γύρ σο =, = 6 υπάρχουν καµπύλες που δηλώνουν πιθανό ελάχισο Πράγµαι για αυές ις παραµέρους η ESOR ολοκληρώνει σε 6 επαναλήψεις! Πιθανόαα η ανίφαση αυή να οφείλεαι σα σφάλµαα καά ην προσέγγιση ης ϕασµαικής ακίνας
ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ
 ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ Για κάθε γραµµικό και χρονικά αναλλοίωο σύσηµα συνεχούς χρόνου ισχύει όι η απόκριση y() ου όαν αυό διεγείρεαι από είσοδο x() δίνεαι από η σχέση: y () = x( ) h ( ) d = x ()
ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ Για κάθε γραµµικό και χρονικά αναλλοίωο σύσηµα συνεχούς χρόνου ισχύει όι η απόκριση y() ου όαν αυό διεγείρεαι από είσοδο x() δίνεαι από η σχέση: y () = x( ) h ( ) d = x ()
Πως λύνεται ένα πρόβληµα.
 Πως λύνεαι ένα πρόβληµα. Όπως έχουµε ήδη αναφέρει, α βήµαα για ην παραγωγή λογισµικού είναι: 1. Καανόηση προβλήµαος 2. Επίλυση ου προβλήµαος 3. Λογικός έλεγχος ης λύσης (αν υπάρχουν λάθη πήγαινε σο 1.)
Πως λύνεαι ένα πρόβληµα. Όπως έχουµε ήδη αναφέρει, α βήµαα για ην παραγωγή λογισµικού είναι: 1. Καανόηση προβλήµαος 2. Επίλυση ου προβλήµαος 3. Λογικός έλεγχος ης λύσης (αν υπάρχουν λάθη πήγαινε σο 1.)
ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ
 Ε. Μ. ΠΟΛΥΤΕΧΝΕΙΟ Τµήµα Αγρονόµων-Τοπογράφων Μηχανικών Εργασήριο Συγκοινωνιακής Τεχνικής ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ 1. Τόξο
Ε. Μ. ΠΟΛΥΤΕΧΝΕΙΟ Τµήµα Αγρονόµων-Τοπογράφων Μηχανικών Εργασήριο Συγκοινωνιακής Τεχνικής ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ 1. Τόξο
Γιάννη Σ. Μπούταλη Αναπληρωτή Καθηγητή Δ.Π.Θ. ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθητικές σημειώσεις στο μάθημα ΣΑΕ ΙΙ
 Γιάννη Σ Μπούαλη Αναπληρωή Καθηγηή ΔΠΘ ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθηικές σημειώσεις σο μάθημα ΣΑΕ ΙΙ Ξάνθη, Μάιος 7 Ι Μπούαλη Λύση ων εξισώσεων καάσασης ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ Σε αυό ο κεφάλαιο
Γιάννη Σ Μπούαλη Αναπληρωή Καθηγηή ΔΠΘ ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθηικές σημειώσεις σο μάθημα ΣΑΕ ΙΙ Ξάνθη, Μάιος 7 Ι Μπούαλη Λύση ων εξισώσεων καάσασης ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ Σε αυό ο κεφάλαιο
u t = u ( a(x) u ) Επίλυση της Self-adjoint µορφής
 Ejniko & Kapodistriako Panepisthmio Ajhnwn Tmhma Plhroforikhc & Thlepikoinwniwn, PMS Upologistikh Episthmh Μάθημα: «Επιστημονικοί Υπολογισμοί» Διδάσκων: Φίλιππος Τζαφέρης Χειμερινό Εξάμηνο 2006-2007 Άγγελος
Ejniko & Kapodistriako Panepisthmio Ajhnwn Tmhma Plhroforikhc & Thlepikoinwniwn, PMS Upologistikh Episthmh Μάθημα: «Επιστημονικοί Υπολογισμοί» Διδάσκων: Φίλιππος Τζαφέρης Χειμερινό Εξάμηνο 2006-2007 Άγγελος
ΦΥΣ 145 Υπολογιστικές Μέθοδοι στη Φυσική. Τελική εξέταση 5 Μάη 2007 Ομάδα 2 η
 ΦΥΣ 145 Υπολογισικές Μέθοδοι ση Φυσική Τελική εξέαση 5 Μάη 2007 Ομάδα 2 η Γράψε ο ονομαεπώνυμο, αριθμό αυόηας και ο password σας σο πάνω μέρος ης αυής ης σελίδας. Πρέπει να απανήσεε και σα 5 προβλήμαα
ΦΥΣ 145 Υπολογισικές Μέθοδοι ση Φυσική Τελική εξέαση 5 Μάη 2007 Ομάδα 2 η Γράψε ο ονομαεπώνυμο, αριθμό αυόηας και ο password σας σο πάνω μέρος ης αυής ης σελίδας. Πρέπει να απανήσεε και σα 5 προβλήμαα
Εργαστήριο Ηλεκτρικών κυκλωμάτων
 Εργασήριο Ηλεκρικών κυκλωμάων Αυό έργο χορηγείαι με άδεια Creaive Commons Aribuion-NonCommercial-ShareAlike Greece 3.. Σκοπός ων πειραμάων Ονομ/νυμο: Μηρόπουλος Σπύρος Τμήμα: Ε6 Το εργασήριο πραγμαοποιήθηκε
Εργασήριο Ηλεκρικών κυκλωμάων Αυό έργο χορηγείαι με άδεια Creaive Commons Aribuion-NonCommercial-ShareAlike Greece 3.. Σκοπός ων πειραμάων Ονομ/νυμο: Μηρόπουλος Σπύρος Τμήμα: Ε6 Το εργασήριο πραγμαοποιήθηκε
13. Συνήθεις διαφορικές εξισώσεις
 Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής 67 3 Σνήθεις διαφορικές εξισώσεις 3 Ορισµοί Μια εξίσση πο περιέχει παραγώγος κάποιας σνάρησης, ονοµάζεαι διαφορική εξίσση ( Ε) Αν η σνάρηση
Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής 67 3 Σνήθεις διαφορικές εξισώσεις 3 Ορισµοί Μια εξίσση πο περιέχει παραγώγος κάποιας σνάρησης, ονοµάζεαι διαφορική εξίσση ( Ε) Αν η σνάρηση
Κεφάλαιο 3 ο. Κυκλώματα με στοιχεία αποθήκευσης ενέργειας
 Κεφάλαιο 3 ο Κυκλώμαα με σοιχεία αποθήκευσης ενέργειας Η διαφορά μεαξύ ης ανάλυσης ων ωμικών κυκλωμάων, που μελεήσαμε ως ώρα, και ων κυκλωμάων που ακολουθούν είναι όι οι εξισώσεις που προκύπουν από ην
Κεφάλαιο 3 ο Κυκλώμαα με σοιχεία αποθήκευσης ενέργειας Η διαφορά μεαξύ ης ανάλυσης ων ωμικών κυκλωμάων, που μελεήσαμε ως ώρα, και ων κυκλωμάων που ακολουθούν είναι όι οι εξισώσεις που προκύπουν από ην
Δυναμική συμπεριφορά των λογικών κυκλωμάτων MOS. Διάλεξη 10
 Δυναμική συμπεριφορά ων λογικών κυκλωμάων MOS Διάλεξη 10 Δομή ης διάλεξης Εισαγωγή Ανισροφέας NMOS με φορίο ύπου αραίωσης Ανισροφέας CMOS Διάφορα ζηήμαα Ασκήσεις Δυναμική συμπεριφορά ων λογικών κυκλωμάων
Δυναμική συμπεριφορά ων λογικών κυκλωμάων MOS Διάλεξη 10 Δομή ης διάλεξης Εισαγωγή Ανισροφέας NMOS με φορίο ύπου αραίωσης Ανισροφέας CMOS Διάφορα ζηήμαα Ασκήσεις Δυναμική συμπεριφορά ων λογικών κυκλωμάων
ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ
 ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ V. ΜΙΚΡΟΠΛΑΣΤΙΚΟΤΗΤΑ ΤΩΝ ΚΡΥΣΤΑΛΛΩΝ 1. Εισαγωγή Ση µέχρι ώρα συζήησή µας για ην µηχανική συµπεριφορά ων µεαλλικών υλικών, όπου εξεάσαµε ην ελασική και ην πλασική ους συµπεριφορά
ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ V. ΜΙΚΡΟΠΛΑΣΤΙΚΟΤΗΤΑ ΤΩΝ ΚΡΥΣΤΑΛΛΩΝ 1. Εισαγωγή Ση µέχρι ώρα συζήησή µας για ην µηχανική συµπεριφορά ων µεαλλικών υλικών, όπου εξεάσαµε ην ελασική και ην πλασική ους συµπεριφορά
ΕΛΕΓΧΟΣ ΒΙΟΜΗΧΑΝΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΚΕΦΑΛΑΙΟ 2 ΚΕΦΑΛΑΙΟ 2. Πλεονεκτήματα ψηφιακού ελέγχου
 ΚΕΦΑΛΑΙΟ Πλεονεκήμαα ψηφιακού ελέγχου Ικανόηα για επεξεργασία αλγορίθμων με λογισμικό ανί για harwar. Αλλαγή ου σχεδιασμού χωρίς αλλαγές σο harwar. Μείωση μεγέθους, βάρους, ισχύος καθώς και χαμηλό κόσος.
ΚΕΦΑΛΑΙΟ Πλεονεκήμαα ψηφιακού ελέγχου Ικανόηα για επεξεργασία αλγορίθμων με λογισμικό ανί για harwar. Αλλαγή ου σχεδιασμού χωρίς αλλαγές σο harwar. Μείωση μεγέθους, βάρους, ισχύος καθώς και χαμηλό κόσος.
Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ
 Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ Θεωρούµε όι Έσω X µία διακριή χρονοσειρά 0 ± ±. µ x Ε{X } και γ { X X } E { [ X µ ][ X µ ] } ( 0 ± cov + + x x Το φάσµα ισχύος ης X ορίζεαι
Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ Θεωρούµε όι Έσω X µία διακριή χρονοσειρά 0 ± ±. µ x Ε{X } και γ { X X } E { [ X µ ][ X µ ] } ( 0 ± cov + + x x Το φάσµα ισχύος ης X ορίζεαι
_Σχήµα 2_. Σελίδα 1 από 5. τον οποίο γίνεται η µεταπτωτική κίνηση. Άξονας περιστροφής τροχού. Άξονας γύρω από. τον οποίο γίνεται η µεταπτωτική κίνηση
 ιονύσης Μηρόπουλος Κίνηση σερεού Παραηρήσεις ση µεαπωική κίνηση ενός σρεφόµενου ροχού Η ανάρηση αυή έγινε µε αφορµή: 1) Την πολύ καλή και ενδιαφέρουσα ανάρηση ου συναδέλφου Νίκου αµαόπουλου µε ίλο «Μεαπωική
ιονύσης Μηρόπουλος Κίνηση σερεού Παραηρήσεις ση µεαπωική κίνηση ενός σρεφόµενου ροχού Η ανάρηση αυή έγινε µε αφορµή: 1) Την πολύ καλή και ενδιαφέρουσα ανάρηση ου συναδέλφου Νίκου αµαόπουλου µε ίλο «Μεαπωική
ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ. LT και μονάδες στο SI, kgm/s 2 ή N. υνισταμένη. υνισταμένη. d dt. d dt.
 ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ Έσω ένα υδραυλικό σύσημα ο οποίο περιέχεαι σε έναν όγκο ελέγχου C συνολικού όγκου και ο οποίο αναλλάσει μάζα με ο περιβάλλον με ρυθμούς (παροχές
ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ Έσω ένα υδραυλικό σύσημα ο οποίο περιέχεαι σε έναν όγκο ελέγχου C συνολικού όγκου και ο οποίο αναλλάσει μάζα με ο περιβάλλον με ρυθμούς (παροχές
ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ
 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Οι κινηήρες αυής ης καηγορίας ροφοδοούναι από κάποια πηγή συνεχούς άσης. Από καασκευασικής απόψεως, δεν παρουσιάζουν καμία διαφορά σε σχέση με ις γεννήριες ΣΡ. Βασικό πλεονέκημά
ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Οι κινηήρες αυής ης καηγορίας ροφοδοούναι από κάποια πηγή συνεχούς άσης. Από καασκευασικής απόψεως, δεν παρουσιάζουν καμία διαφορά σε σχέση με ις γεννήριες ΣΡ. Βασικό πλεονέκημά
Μεγαλύτερες περιπέτειες
 Μεγαλύερες εριέειες Μεά ην ανάρηση «Ένα σύσημα σωμάων σε εριέειες» ας άμε ένα βήμα αρακάω, ση μελέη ου συσήμαος σωμάων και ης εφαρμογής ου γενικευμένου νόμου ου Νεύωνα. --------------------------------------
Μεγαλύερες εριέειες Μεά ην ανάρηση «Ένα σύσημα σωμάων σε εριέειες» ας άμε ένα βήμα αρακάω, ση μελέη ου συσήμαος σωμάων και ης εφαρμογής ου γενικευμένου νόμου ου Νεύωνα. --------------------------------------
Θέματα Περασμένων Εξετάσεων και Απαντήσεις
 Θέμαα Περασμένων Εξεάσεων και Απανήσεις Εξεάσεις Ιουνίου. ΘΕΜΑ.,5 μονάδα Δίνεαι ο ΓΧΑ σύσημα με κρουσική απόκριση iπ h co8 π π Να βρεθεί η έξοδός ου αν η είσοδός είναι co π co 6π co 8π i W, < Εφαρμόζονας
Θέμαα Περασμένων Εξεάσεων και Απανήσεις Εξεάσεις Ιουνίου. ΘΕΜΑ.,5 μονάδα Δίνεαι ο ΓΧΑ σύσημα με κρουσική απόκριση iπ h co8 π π Να βρεθεί η έξοδός ου αν η είσοδός είναι co π co 6π co 8π i W, < Εφαρμόζονας
ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ. 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διατμητικής Αντοχής Εδάφους. Διδάσκοντες: Β. Χρηστάρας Καθηγητής Β. Μαρίνος, Αν.
 ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διαμηικής Ανοχής Εδάφους Συνοχή (c) Γωνία ριβής (φ ο ) Διδάσκονες: Β. Χρησάρας Καθηγηής Β. Μαρίνος, Αν. Καθηγηής Εργασήριο Τεχνικής Γεωλογίας και
ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διαμηικής Ανοχής Εδάφους Συνοχή (c) Γωνία ριβής (φ ο ) Διδάσκονες: Β. Χρησάρας Καθηγηής Β. Μαρίνος, Αν. Καθηγηής Εργασήριο Τεχνικής Γεωλογίας και
Εργαστηριακή Άσκηση Το σύστημα αναμονής M/G/1
 Εργασηριακή Άσκηση 4 5 Το σύσημα αναμονής M/G/ Γιάννης Γαροφαλάκης, Καθηγηής Αθανάσιος Ν.Νικολακόπουλος, Phd(c) Σκοπός ης παρούσας εργασίας είναι η εξερεύνηση ων βασικών ιδιοήων ενός από α κλασικόερα μονέλα
Εργασηριακή Άσκηση 4 5 Το σύσημα αναμονής M/G/ Γιάννης Γαροφαλάκης, Καθηγηής Αθανάσιος Ν.Νικολακόπουλος, Phd(c) Σκοπός ης παρούσας εργασίας είναι η εξερεύνηση ων βασικών ιδιοήων ενός από α κλασικόερα μονέλα
ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ
 ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ 4.1 Η ΥΙΟΘΕΤΗΣΗ ΝΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ: ΣΤΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Όαν η εχνολογία εξελίσσεαι η πρώη ερώηση µας είναι καά πόσο θα υιοθεηθεί δεδοµένου ης µεγάλης εγκαεσηµένης
ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ 4.1 Η ΥΙΟΘΕΤΗΣΗ ΝΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ: ΣΤΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Όαν η εχνολογία εξελίσσεαι η πρώη ερώηση µας είναι καά πόσο θα υιοθεηθεί δεδοµένου ης µεγάλης εγκαεσηµένης
ΦΥΣΙΚΗ Ι. ΤΜΗΜΑ Α Ε. Στυλιάρης
 (Με ιδέες και υλικό από ΔΙΑΝΥΣΜΑΤΑ ΣΤΟΝ ΤΡΙΣΔΙΑΣΤΑΤΟ ΧΩΡΟ Καρεσιανές Συνεαγμένες Εσωερικό Γινόμενο Διανυσμάων Εξωερικό Γινόμενο Διανυσμάων Βαθμωό Γινόμενο Τριών Διανυσμάων ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης
(Με ιδέες και υλικό από ΔΙΑΝΥΣΜΑΤΑ ΣΤΟΝ ΤΡΙΣΔΙΑΣΤΑΤΟ ΧΩΡΟ Καρεσιανές Συνεαγμένες Εσωερικό Γινόμενο Διανυσμάων Εξωερικό Γινόμενο Διανυσμάων Βαθμωό Γινόμενο Τριών Διανυσμάων ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης
ΦΥΣΙΚΗ Ι. ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ ΣΩΜΑΤΟΣ Ισορροπία Σωματιδίου Στατική Ισορροπία Στερεού Σώματος
 ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης Δύναμης Σύνθεση Δυνάμεων ΡΟΠΗ Η Έννοια ης Ροπής Ροπή Πολλών Δυνάμεων Ζεύγος Δυνάμεων ΦΥΣΙΚΗ Ι ΤΜΗΜΑ Α Α. Καραμπαρμπούνης, Ε. Συλιάρης ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ,, 4 5 ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ
ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης Δύναμης Σύνθεση Δυνάμεων ΡΟΠΗ Η Έννοια ης Ροπής Ροπή Πολλών Δυνάμεων Ζεύγος Δυνάμεων ΦΥΣΙΚΗ Ι ΤΜΗΜΑ Α Α. Καραμπαρμπούνης, Ε. Συλιάρης ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ,, 4 5 ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ
, e + Σε ένα δείγμα ίδιων ραδιενεργών πυρήνων η πιθανότητα διάσπασης για κάποιο συγκεκριμένο πυρήνα είναι τυχαία.
 ΚΕΦΑΛΑΙΟ 6 : ΠΥΡΗΝΙΚΕΣ ΔΙΑΣΠΑΣΕΙΣ Πυρηνικοί Μεασχημαισμοί Οι δυναοί πυρηνικοί μεσχημαισμοί είναι : Εκπομπή σωμαιδίων-α : 4 2 H Εκπομπή σωμαιδίων-β : - ν, + Εκπομπή ακίνων-γ : φωόνιο Σχάση : διάσπαση πυρήνα
ΚΕΦΑΛΑΙΟ 6 : ΠΥΡΗΝΙΚΕΣ ΔΙΑΣΠΑΣΕΙΣ Πυρηνικοί Μεασχημαισμοί Οι δυναοί πυρηνικοί μεσχημαισμοί είναι : Εκπομπή σωμαιδίων-α : 4 2 H Εκπομπή σωμαιδίων-β : - ν, + Εκπομπή ακίνων-γ : φωόνιο Σχάση : διάσπαση πυρήνα
Κεφάλαιο 5 Πολλαπλοί χημικοί αντιδραστήρες
 Κεφάλαιο 5 Πολλαπλοί χημικοί ανιδρασήρες Σε ορισμένες περιπώσεις, σε μια χημική βιομηχανία, η χρήση ενός μόνο χημικού ανιδρασήρα δεν είναι όσο αποελεσμαική όσο θα ήαν επιθυμηό. Συνεπώς, είναι απαραίηο
Κεφάλαιο 5 Πολλαπλοί χημικοί ανιδρασήρες Σε ορισμένες περιπώσεις, σε μια χημική βιομηχανία, η χρήση ενός μόνο χημικού ανιδρασήρα δεν είναι όσο αποελεσμαική όσο θα ήαν επιθυμηό. Συνεπώς, είναι απαραίηο
ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ 90º. 180º ω. Οι απαντήσεις και τα σχετικά σχόλια
 Φυσική καεύθυνσης Γ Σερεό σώµα ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ άξονας 9º 18º Ο ροχός ου σχήµαος έχει ροπή αδράνειας Ι και σρέφεαι γύρ από ον άξονά ου µε γνιακή αχύηα µέρου.
Φυσική καεύθυνσης Γ Σερεό σώµα ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ άξονας 9º 18º Ο ροχός ου σχήµαος έχει ροπή αδράνειας Ι και σρέφεαι γύρ από ον άξονά ου µε γνιακή αχύηα µέρου.
Η Έννοια της τυχαίας ιαδικασίας
 Η Έννοια ης υχαίας ιαδικασίας Η έννοια ης υχαίας διαδικασίας, βασίζεαι σην επέκαση ης έννοιας ης υχαίας µεαβληής, ώσε να συµπεριλάβει ο χρόνο. Σεκάθεαποέλεσµα s k ενόςπειράµαοςύχης ανισοιχούµε, σύµφωναµεκάποιοκανόνα,
Η Έννοια ης υχαίας ιαδικασίας Η έννοια ης υχαίας διαδικασίας, βασίζεαι σην επέκαση ης έννοιας ης υχαίας µεαβληής, ώσε να συµπεριλάβει ο χρόνο. Σεκάθεαποέλεσµα s k ενόςπειράµαοςύχης ανισοιχούµε, σύµφωναµεκάποιοκανόνα,
Κεφάλαιο 4 Ιδανικοί χημικοί αντιδραστήρες
 Κεφάλαιο 4 Ιδανικοί χημικοί ανιδρασήρες Με βάση α σοιχεία για ην κινηική και η σοιχειομερία ων ανιδράσεων, μπορούμε ώρα να προχωρήσουμε σην ανάλυση ορισμένων βασικών ύπων χημικών ανιδρασήρων. Η ανάλυση
Κεφάλαιο 4 Ιδανικοί χημικοί ανιδρασήρες Με βάση α σοιχεία για ην κινηική και η σοιχειομερία ων ανιδράσεων, μπορούμε ώρα να προχωρήσουμε σην ανάλυση ορισμένων βασικών ύπων χημικών ανιδρασήρων. Η ανάλυση
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I ΕΙΣΑΓΩΓΗ ΒΑΣΙΚΑ ΣΗΜΑΤΑ Μοναδιαία βηµαική συνάρηση (Ui Sep Fucio) U () =, U () =, .5 - -
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I ΕΙΣΑΓΩΓΗ ΒΑΣΙΚΑ ΣΗΜΑΤΑ Μοναδιαία βηµαική συνάρηση (Ui Sep Fucio) U () =, U () =, .5 - -
Ροπή δύναμης. Τι προκαλεί την επιτάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω του. Τι προκαλεί την γωνιακή επιτάχυνση ενός στερεού σώματος;
 Τι προκαλεί ην επιάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω ου Τι προκαλεί ην γωνιακή επιάχυνση ενός σερεού σώμαος; Η ροπή δύναμης F Για να αλλάξουμε ην περισροφική καάσαση ενός σώμαος παίζουν
Τι προκαλεί ην επιάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω ου Τι προκαλεί ην γωνιακή επιάχυνση ενός σερεού σώμαος; Η ροπή δύναμης F Για να αλλάξουμε ην περισροφική καάσαση ενός σώμαος παίζουν
Εισαγωγή στη Θεωρία Σημάτων και Συστημάτων
 Εισαγωγή ση Θεωρία Σημάων και Συσημάων Ιωάννης Χαρ. Κασαβουνίδης Τμήμα Μηχ. Η/Υ Τηλεπ. & Δικύων Πανεπισήμιο Θεσσαλίας ΦΘινοπωρινό Εξάμηνο 9/ Άσκηση Να υπολογίσεε ο παρακάω άθροισμα: Θυμίζουμε ην ανάπυξη
Εισαγωγή ση Θεωρία Σημάων και Συσημάων Ιωάννης Χαρ. Κασαβουνίδης Τμήμα Μηχ. Η/Υ Τηλεπ. & Δικύων Πανεπισήμιο Θεσσαλίας ΦΘινοπωρινό Εξάμηνο 9/ Άσκηση Να υπολογίσεε ο παρακάω άθροισμα: Θυμίζουμε ην ανάπυξη
Θεματική ενότητα : Βασικά εργαλεία και Μέθοδοι για τον έλεγχο της ποιότητας.
 Εργασία 5 Θεμαική ενόηα : Βασικά εργαλεία και Μέθοδοι για ον έλεγχο ης ποιόηας. Άσκηση 1 (η άσκηση έχει λυθεί βάσει ων διευκρινίσεων που δόθηκαν από ον καθηγηή ) α) Το καάλληλο σαισικό εργαλείο που θα
Εργασία 5 Θεμαική ενόηα : Βασικά εργαλεία και Μέθοδοι για ον έλεγχο ης ποιόηας. Άσκηση 1 (η άσκηση έχει λυθεί βάσει ων διευκρινίσεων που δόθηκαν από ον καθηγηή ) α) Το καάλληλο σαισικό εργαλείο που θα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΠΕΡΙΛΗΨΗ ΣΥΜΒΟΛΙΣΜΩΝ NOTATION ΓΙΑ ΙΑΝΥΣΜΑΤΑ ΚΑΙ ΤΑΝΥΣΤΕΣ -Bd, Steat and Lghtfoot "Tanpot Phenomena" -Bd, Amtong and Haage
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΠΕΡΙΛΗΨΗ ΣΥΜΒΟΛΙΣΜΩΝ NOTATION ΓΙΑ ΙΑΝΥΣΜΑΤΑ ΚΑΙ ΤΑΝΥΣΤΕΣ -Bd, Steat and Lghtfoot "Tanpot Phenomena" -Bd, Amtong and Haage
ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ 1 ΣΕΙΡΑΣ FOURIER. Ανάπτυξη σειράς Dirac σε σειρά Fourier (Εκθετική Fourier):
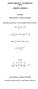 ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ 7-5-7 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ ΣΕΙΡΑΣ FOURIER Ανάπυξη σειράς Dirac σε σειρά Fourier (Εκθεική Fourier): s () = δ ( k) k = c s e d e inω inω () n = = = ιόι f () δ (
ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ 7-5-7 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ ΣΕΙΡΑΣ FOURIER Ανάπυξη σειράς Dirac σε σειρά Fourier (Εκθεική Fourier): s () = δ ( k) k = c s e d e inω inω () n = = = ιόι f () δ (
Ορισμός: u(t) = 0 (t < 0) και u(t) = 1 (t 0) (4.1) Από τις (4.3) και (4.4), προκύπτει ότι το βηματικό σήμα u(t) είναι σήμα ισχύος.
 4. ΑΝΑΛΥΣΗ ΒΑΣΙΚΩΝ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΗΜΑΤΩΝ 4.. To βημαικό σήμα (step signal) u(t) Ορισμός: u(t) = 0 (t < 0) και u(t) = (t 0) (4.) Μέση ιμή: = (4.) Ενέργεια: Ε = lim [T ] [-, ] u (t).dt (4.3) Μέση
4. ΑΝΑΛΥΣΗ ΒΑΣΙΚΩΝ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΗΜΑΤΩΝ 4.. To βημαικό σήμα (step signal) u(t) Ορισμός: u(t) = 0 (t < 0) και u(t) = (t 0) (4.) Μέση ιμή: = (4.) Ενέργεια: Ε = lim [T ] [-, ] u (t).dt (4.3) Μέση
Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ
 Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ ΕΙΣΑΓΩΓΗ Όπως είαι γωσό, η Μουσική είαι Μαθημαικά και (σο βάθος) υπάρχει, μία «αδιόραη αρμοία» μεαξύ αυώ ω δύο. Έα μουσικό έργο, διέπεαι από μαθημαικούς όμους, σε ό,ι αφορά ις σχέσεις
Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ ΕΙΣΑΓΩΓΗ Όπως είαι γωσό, η Μουσική είαι Μαθημαικά και (σο βάθος) υπάρχει, μία «αδιόραη αρμοία» μεαξύ αυώ ω δύο. Έα μουσικό έργο, διέπεαι από μαθημαικούς όμους, σε ό,ι αφορά ις σχέσεις
Παραγωγή Κυµατοµορφών FM:
 Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής και ση συνέχεια χρησιµοοιείαι ολλαλασιασµός
Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής και ση συνέχεια χρησιµοοιείαι ολλαλασιασµός
Παραγωγή Κυµατοµορφών FM:
 Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής ζώνης και ση συνέχεια χρησιµοοιείαι
Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής ζώνης και ση συνέχεια χρησιµοοιείαι
ΑΘΡΟΙΣΤΙΚΗ ΑΜΟΙΒΑΙΑ ΠΛΗΡΟΦΟΡΙΑ ΩΣ ΣΤΑΤΙΣΤΙΚΟ ΕΛΕΓΧΟΥ ΜΗ-ΓΡΑΜΜΙΚΟΤΗΤΑΣ ΧΡΟΝΟΣΕΙΡΩΝ
 Ελληνικό Σαισικό Ινσιούο Πρακικά 8 ου Πανελληνίου Συνεδρίου Σαισικής (5) σελ.35-34 ΑΘΡΟΙΣΤΙΚΗ ΑΜΟΙΒΑΙΑ ΠΛΗΡΟΦΟΡΙΑ ΩΣ ΣΤΑΤΙΣΤΙΚΟ ΕΛΕΓΧΟΥ ΜΗ-ΓΡΑΜΜΙΚΟΤΗΤΑΣ ΧΡΟΝΟΣΕΙΡΩΝ Παπάνα Αγγελική και Κουγιουμζής Δημήρης
Ελληνικό Σαισικό Ινσιούο Πρακικά 8 ου Πανελληνίου Συνεδρίου Σαισικής (5) σελ.35-34 ΑΘΡΟΙΣΤΙΚΗ ΑΜΟΙΒΑΙΑ ΠΛΗΡΟΦΟΡΙΑ ΩΣ ΣΤΑΤΙΣΤΙΚΟ ΕΛΕΓΧΟΥ ΜΗ-ΓΡΑΜΜΙΚΟΤΗΤΑΣ ΧΡΟΝΟΣΕΙΡΩΝ Παπάνα Αγγελική και Κουγιουμζής Δημήρης
Νόμος Αmpere. i r. Β dl = Β(dl ακτ +dl τοξ ) = Β rdθ = 2π. Β dl = μ ο i
 Νόος Αmpee = o Τυχαία κλεισή διαδροή προσεγγιζεαι από ακινικά ευθ. ήαα και κυκλικά όξα dθ dθ dl ακινικά = 0 dl όξα = dθ dl = (dl ακ +dl οξ ) = dθ = o dθ = o dθ Ρευαοφόρο ς αγωγός dl = ο Νόος Αmpee Το ολοκλήρωα
Νόος Αmpee = o Τυχαία κλεισή διαδροή προσεγγιζεαι από ακινικά ευθ. ήαα και κυκλικά όξα dθ dθ dl ακινικά = 0 dl όξα = dθ dl = (dl ακ +dl οξ ) = dθ = o dθ = o dθ Ρευαοφόρο ς αγωγός dl = ο Νόος Αmpee Το ολοκλήρωα
d k dt k a ky(t) = dt k b kx(t) (3.1)
 Κεφάλαιο 3 Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 3. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Είδαμε σο προηγούμενο κεφάλαιο κάποια εισαγωγικά
Κεφάλαιο 3 Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 3. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Είδαμε σο προηγούμενο κεφάλαιο κάποια εισαγωγικά
ΑΝΤΟΧΗ ΥΛΙΚΩΝ ΚΑΙ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ. Βιβλίο διδάσκοντα με λύσεις προβλημάτων. Κεφάλαιο 1. ΕΥΡΙΠΙΔΗΣ ΠΑΠΑΜΙΧΟΣ Καθηγητής
 ΑΝΤΟΧΗ ΥΛΙΚΩΝ ΚΑΙ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Βιβλίο διδάσκονα με λύσεις ροβλημάων Κεφάλαιο ΕΥΡΙΠΙΔΗΣ ΠΑΠΑΜΙΧΟΣ Καθηγηής epapamic@civil.auth.gr ΝΙΚΟΣ ΧΑΡΑΛΑΜΠΑΚΗΣ Καθηγηής charalam@civil.auth.gr Αρισοέλειο Πανισήμιο
ΑΝΤΟΧΗ ΥΛΙΚΩΝ ΚΑΙ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Βιβλίο διδάσκονα με λύσεις ροβλημάων Κεφάλαιο ΕΥΡΙΠΙΔΗΣ ΠΑΠΑΜΙΧΟΣ Καθηγηής epapamic@civil.auth.gr ΝΙΚΟΣ ΧΑΡΑΛΑΜΠΑΚΗΣ Καθηγηής charalam@civil.auth.gr Αρισοέλειο Πανισήμιο
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΗΜΑΤΩΝ ΕΛΕΓΧΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΗΜΑΤΩΝ ΕΛΕΓΧΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ ΝΙΚΟΛΑΟΣ Κ. ΜΠΕΚΙΑΡΗΣ ΛΥΜΠΕΡΗΣ ΤΕΧΝΙΚΕΣ ΓΡΑΜΜΙΚΩΝ ΚΑΙ ΜΗ ΓΡΑΜΜΙΚΩΝ ΕΛΕΓΚΤΩΝ ΣΥΣΤΗΜΑΤΩΝ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΗΜΑΤΩΝ ΕΛΕΓΧΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ ΝΙΚΟΛΑΟΣ Κ. ΜΠΕΚΙΑΡΗΣ ΛΥΜΠΕΡΗΣ ΤΕΧΝΙΚΕΣ ΓΡΑΜΜΙΚΩΝ ΚΑΙ ΜΗ ΓΡΑΜΜΙΚΩΝ ΕΛΕΓΚΤΩΝ ΣΥΣΤΗΜΑΤΩΝ
3 Συσχετίσεις σε χρονοσειρές
 3 Συσχείσεις σε χρονοσειρές Η χρονοσειρά ενός χρημαισηριακού δείκη { y, y,, yn } ως πραγμαοποίηση μιας σοχασικής διαδικασίας { t } t= ης μεαβολής ων ιμών ου δείκη { x, x,, xn} πραγμαοποίηση μιας άλλης
3 Συσχείσεις σε χρονοσειρές Η χρονοσειρά ενός χρημαισηριακού δείκη { y, y,, yn } ως πραγμαοποίηση μιας σοχασικής διαδικασίας { t } t= ης μεαβολής ων ιμών ου δείκη { x, x,, xn} πραγμαοποίηση μιας άλλης
Επίλυση Γραµµικών Συστηµάτων
 Κεφάλαιο 3 Επίλυση Γραµµικών Συστηµάτων 31 Εισαγωγή Αριθµητική λύση γενικών γραµµικών συστηµάτων n n A n n x n 1 b n 1, όπου a 11 a 12 a 1n a 21 a 22 a 2n A [a i j, x a n1 a n2 a nn x n, b b 1 b 2 b n
Κεφάλαιο 3 Επίλυση Γραµµικών Συστηµάτων 31 Εισαγωγή Αριθµητική λύση γενικών γραµµικών συστηµάτων n n A n n x n 1 b n 1, όπου a 11 a 12 a 1n a 21 a 22 a 2n A [a i j, x a n1 a n2 a nn x n, b b 1 b 2 b n
ΚΙΝΗΤΙΚΗ ΑΛΥΣΩΤΩΝ ΑΝΤΙΔΡΑΣΕΩΝ ΠΟΛΥΜΕΡΙΣΜΟΥ ΚΑΙ ΜΟΡΙΑΚΗ ΚΑΤΑΝΟΜΗ ΤΩΝ ΛΑΜΒΑΝΟΜΕΝΩΝ ΠΡΟΪΟΝΤΩΝ
 ΚΙΝΗΤΙΚΗ ΑΛΥΣΩΤΩΝ ΑΝΤΙΔΡΑΣΕΩΝ ΠΟΛΥΜΕΡΙΣΜΟΥ ΚΑΙ ΜΟΡΙΑΚΗ ΚΑΤΑΝΟΜΗ ΤΩΝ ΛΑΜΒΑΝΟΜΕΝΩΝ ΠΡΟΪΟΝΤΩΝ Η ρόοδος ης ανίδρασης μορί να υολογισί: Τιλοδόηση διλών δσμών Μαβολή ου όγκου ου μέσου ης ανίδρασης Μέρηση ης
ΚΙΝΗΤΙΚΗ ΑΛΥΣΩΤΩΝ ΑΝΤΙΔΡΑΣΕΩΝ ΠΟΛΥΜΕΡΙΣΜΟΥ ΚΑΙ ΜΟΡΙΑΚΗ ΚΑΤΑΝΟΜΗ ΤΩΝ ΛΑΜΒΑΝΟΜΕΝΩΝ ΠΡΟΪΟΝΤΩΝ Η ρόοδος ης ανίδρασης μορί να υολογισί: Τιλοδόηση διλών δσμών Μαβολή ου όγκου ου μέσου ης ανίδρασης Μέρηση ης
Μελετήστε την θεωρία που αφορά Επαναληπτικές Μεθόδους Επίλυσης Γραμμικών Συστημάτων.
 ΗΥ213 Αριθμητική Ανάλυση Εργαστήριο 7 Οδηγίες για προετοιμασία Διαβάστε και εκτελέστε όλα τα προηγούμενα εργαστήρια. Μελετήστε την θεωρία που αφορά Επαναληπτικές Μεθόδους Επίλυσης Γραμμικών Συστημάτων.
ΗΥ213 Αριθμητική Ανάλυση Εργαστήριο 7 Οδηγίες για προετοιμασία Διαβάστε και εκτελέστε όλα τα προηγούμενα εργαστήρια. Μελετήστε την θεωρία που αφορά Επαναληπτικές Μεθόδους Επίλυσης Γραμμικών Συστημάτων.
QR είναι ˆx τότε x ˆx. 10 ρ. Ποιά είναι η τιµή του ρ και γιατί (σύντοµη εξήγηση). P = [X. 0, X,..., X. (n 1), X. n] a(n + 1 : 1 : 1)
![QR είναι ˆx τότε x ˆx. 10 ρ. Ποιά είναι η τιµή του ρ και γιατί (σύντοµη εξήγηση). P = [X. 0, X,..., X. (n 1), X. n] a(n + 1 : 1 : 1) QR είναι ˆx τότε x ˆx. 10 ρ. Ποιά είναι η τιµή του ρ και γιατί (σύντοµη εξήγηση). P = [X. 0, X,..., X. (n 1), X. n] a(n + 1 : 1 : 1)](/thumbs/27/10724538.jpg) ΕΠΙΣΤΗΜΟΝΙΚΟΣ ΥΠΟΛΟΓΙΣΜΟΣ I (22 Σεπτεµβρίου) ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ 1ο ΘΕΜΑ 1. Αφού ορίσετε ακριβώς τι σηµαίνει πίσω ευσταθής υπολογισµός, να εξηγήσετε αν ο υ- πολογισµός του εσωτερικού γινοµένου δύο διανυσµάτων
ΕΠΙΣΤΗΜΟΝΙΚΟΣ ΥΠΟΛΟΓΙΣΜΟΣ I (22 Σεπτεµβρίου) ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ 1ο ΘΕΜΑ 1. Αφού ορίσετε ακριβώς τι σηµαίνει πίσω ευσταθής υπολογισµός, να εξηγήσετε αν ο υ- πολογισµός του εσωτερικού γινοµένου δύο διανυσµάτων
Ψηφιακή Μετάδοση Αναλογικών Σηµάτων
 Σεραφείµ Καραµογιάς Ψηφιακή Μεάδοση Αναλογικών Σηµάν Τα σύγχρονα συσήµαα εικοιννίας σε ολύ µεγάλο οσοσό διαχειρίζοναι σήµαα ψηφιακής µορφής, δηλαδή, σήµαα ου δηµιουργούναι αό ακολουθίες δυαδικών ψηφίν.
Σεραφείµ Καραµογιάς Ψηφιακή Μεάδοση Αναλογικών Σηµάν Τα σύγχρονα συσήµαα εικοιννίας σε ολύ µεγάλο οσοσό διαχειρίζοναι σήµαα ψηφιακής µορφής, δηλαδή, σήµαα ου δηµιουργούναι αό ακολουθίες δυαδικών ψηφίν.
Matrix Algorithms. Παρουσίαση στα πλαίσια του μαθήματος «Παράλληλοι. Αλγόριθμοι» Γ. Καούρη Β. Μήτσου
 Matrix Algorithms Παρουσίαση στα πλαίσια του μαθήματος «Παράλληλοι Αλγόριθμοι» Γ. Καούρη Β. Μήτσου Περιεχόμενα παρουσίασης Πολλαπλασιασμός πίνακα με διάνυσμα Πολλαπλασιασμός πινάκων Επίλυση τριγωνικού
Matrix Algorithms Παρουσίαση στα πλαίσια του μαθήματος «Παράλληλοι Αλγόριθμοι» Γ. Καούρη Β. Μήτσου Περιεχόμενα παρουσίασης Πολλαπλασιασμός πίνακα με διάνυσμα Πολλαπλασιασμός πινάκων Επίλυση τριγωνικού
Α Σ Κ Η Σ Η 1 ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΣΦΑΛΜΑΤΟΣ ΚΑΛΩΔΙΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ MURRAY
 Α Σ Κ Η Σ Η ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΣΦΑΛΜΑΤΟΣ ΚΑΛΩΔΙΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ MURRAY Γενικά Με η μέθοδο Murray, όπου χρησιμοποιούναι οι ιδιόηες ης γέφυρας Wheatstone, μπορούν να προσδιορισούν σφάλμαα διαρροής προς η γη και
Α Σ Κ Η Σ Η ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΣΦΑΛΜΑΤΟΣ ΚΑΛΩΔΙΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ MURRAY Γενικά Με η μέθοδο Murray, όπου χρησιμοποιούναι οι ιδιόηες ης γέφυρας Wheatstone, μπορούν να προσδιορισούν σφάλμαα διαρροής προς η γη και
ΤΟΠΙΚΟ ΜΟΝΤΕΛΟ ΠΕΠΕΡΑΣΜΕΝΩΝ ΣΤΟΙΧΕΙΩΝ
 Έστω η Δ.Ε. : d du a d d f ΤΟΠΙΚΟ ΜΟΝΤΕΛΟ ΠΕΠΕΡΑΣΜΕΝΩΝ ΣΤΟΙΧΕΙΩΝ () Με και a a(),() f f γνωστές ποσότητες, u u() η άγνωστη μεταβλητή Για την άγνωστη μεταβλητή θεωρούμε την προσέγγιση: n u ()()() c () h
Έστω η Δ.Ε. : d du a d d f ΤΟΠΙΚΟ ΜΟΝΤΕΛΟ ΠΕΠΕΡΑΣΜΕΝΩΝ ΣΤΟΙΧΕΙΩΝ () Με και a a(),() f f γνωστές ποσότητες, u u() η άγνωστη μεταβλητή Για την άγνωστη μεταβλητή θεωρούμε την προσέγγιση: n u ()()() c () h
Κανονισμός Πυροπροστασίας Κτιρίων (π.δ. 41/2018)
 Κανονισμός Πυροπροσασίας Κιρίων (π.δ. 41/2018) Πεδίο Εφαρμογής Πεδίο Εφαρμογής Α. Σα κίρια ή μήμαα κιρίων, που ανεγείροναι μεά ην έναρξη ισχύος ου και ων οποίων οι χρήσεις εμπίπουν σε μία από ις περιπώσεις
Κανονισμός Πυροπροσασίας Κιρίων (π.δ. 41/2018) Πεδίο Εφαρμογής Πεδίο Εφαρμογής Α. Σα κίρια ή μήμαα κιρίων, που ανεγείροναι μεά ην έναρξη ισχύος ου και ων οποίων οι χρήσεις εμπίπουν σε μία από ις περιπώσεις
3. Γραμμικά Συστήματα
 3. Γραμμικά Συστήματα Ασκήσεις 3. Αποδείξτε ότι το γινόμενο δύο άνω τριγωνικών πινάκων είναι άνω τριγωνικός πίνακας. Επίσης, στην περίπτωση που ένας άνω τριγωνικός πίνακας U 2 R n;n είναι αντιστρέψιμος,
3. Γραμμικά Συστήματα Ασκήσεις 3. Αποδείξτε ότι το γινόμενο δύο άνω τριγωνικών πινάκων είναι άνω τριγωνικός πίνακας. Επίσης, στην περίπτωση που ένας άνω τριγωνικός πίνακας U 2 R n;n είναι αντιστρέψιμος,
Ανάπτυξη και Αξιολόγηση Στρατηγικής Κεντρικού Ελέγχου Ροών σε Αποχετευτικά ίκτυα µε Έµφαση στην Εφαρµογή της στον Ελλαδικό Χώρο
 ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ: Μηχανικών Παραγωγής & ιοίκησης Ανάπυξη και Αξιολόγηση Σραηγικής Κενρικού Ελέγχου Ροών σε Αποχεευικά ίκυα µε Έµφαση σην Εφαρµογή ης σον Ελλαδικό Χώρο ιαριβή που υπεβλήθη για ην
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ: Μηχανικών Παραγωγής & ιοίκησης Ανάπυξη και Αξιολόγηση Σραηγικής Κενρικού Ελέγχου Ροών σε Αποχεευικά ίκυα µε Έµφαση σην Εφαρµογή ης σον Ελλαδικό Χώρο ιαριβή που υπεβλήθη για ην
Digital Integrated Circuits, 2 nd edition, J. M. Rabaey, A. Chandrakasan, B. Nikolic
 Πρόβληµα 4. gital Itegrated Circuits, d editio, J. M. abaey, A. Chadrakasa, B. Nikolic You are desigig a clock distributio etwork i which it is critical to miimize skew betwee local clocks (CLK, CLK, ad
Πρόβληµα 4. gital Itegrated Circuits, d editio, J. M. abaey, A. Chadrakasa, B. Nikolic You are desigig a clock distributio etwork i which it is critical to miimize skew betwee local clocks (CLK, CLK, ad
Μαρία Λουκά. Εργαστήριο Matlab. Αριθμητικός υπολογισμός ιδιοτιμών και ιδιοδιανυσμάτων. Τμήμα Πληροφορικής και Τηλεπικοινωνιών.
 Μαρία Λουκά Εργαστήριο Matlab Αριθμητικός υπολογισμός ιδιοτιμών και ιδιοδιανυσμάτων Τμήμα Πληροφορικής και Τηλεπικοινωνιών. Βασικές Συναρτήσεις της Matlab Γραμμικοί δείκτες (Linear indices) Ένας γραμμικός
Μαρία Λουκά Εργαστήριο Matlab Αριθμητικός υπολογισμός ιδιοτιμών και ιδιοδιανυσμάτων Τμήμα Πληροφορικής και Τηλεπικοινωνιών. Βασικές Συναρτήσεις της Matlab Γραμμικοί δείκτες (Linear indices) Ένας γραμμικός
Matrix Algorithms. Παρουσίαση στα πλαίσια του μαθήματος «Παράλληλοι Αλγόριθμοι» Γ. Καούρη Β. Μήτσου
 Matrix Algorithms Παρουσίαση στα πλαίσια του μαθήματος «Παράλληλοι Αλγόριθμοι» Γ. Καούρη Β. Μήτσου Περιεχόμενα παρουσίασης Πολλαπλασιασμός πίνακα με διάνυσμα Πολλαπλασιασμός πινάκων Επίλυση τριγωνικού
Matrix Algorithms Παρουσίαση στα πλαίσια του μαθήματος «Παράλληλοι Αλγόριθμοι» Γ. Καούρη Β. Μήτσου Περιεχόμενα παρουσίασης Πολλαπλασιασμός πίνακα με διάνυσμα Πολλαπλασιασμός πινάκων Επίλυση τριγωνικού
3. ΦΑΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ ΣΗΜΑΤΩΝ (ΑΝΑΛΥΣΗ FOURIER)
 3. ΦΑΣΜΑΙΚΗ ΑΝΑΛΥΣΗ ΣΗΜΑΩΝ (ΑΝΑΛΥΣΗ FOURIER) 3.. Γενικά Ένα σήμα μπορεί να αναπαρασαθεί με έναν από ους παρακάω ισοδύναμους ρόπους: Ως χρονικά μεαβαλλόμενη άση (κυμαομορφή) x(t) (αναπαράσαση σο πεδίο ου
3. ΦΑΣΜΑΙΚΗ ΑΝΑΛΥΣΗ ΣΗΜΑΩΝ (ΑΝΑΛΥΣΗ FOURIER) 3.. Γενικά Ένα σήμα μπορεί να αναπαρασαθεί με έναν από ους παρακάω ισοδύναμους ρόπους: Ως χρονικά μεαβαλλόμενη άση (κυμαομορφή) x(t) (αναπαράσαση σο πεδίο ου
A A A B A ΦΥΛΛΑ ΙΟ ΘΕΜΑΤΩΝ 1/2. Μέϱος A. Πολλαπλές επιλογές (20%) Σειριακός αριθµός : 100 Πληροφορική Ι Εξέταση Φεβρουαρίου 2019
 Σειριακός αριθµός : 100 Πληροφορική Ι Εξέταση Φεβρουαρίου 2019 Απαντήσεις Πολλαπλής Επιλογής Ε Ω : 1 2 3 4 5 A A A B A ΦΥΛΛΑ ΙΟ ΘΕΜΑΤΩΝ 1/2 Τα ϑέµατα της εξέτασης δίνονται σε 2 ϕυλλάδια (ένα για κάϑε διδάσκοντα).
Σειριακός αριθµός : 100 Πληροφορική Ι Εξέταση Φεβρουαρίου 2019 Απαντήσεις Πολλαπλής Επιλογής Ε Ω : 1 2 3 4 5 A A A B A ΦΥΛΛΑ ΙΟ ΘΕΜΑΤΩΝ 1/2 Τα ϑέµατα της εξέτασης δίνονται σε 2 ϕυλλάδια (ένα για κάϑε διδάσκοντα).
1η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΘΕΡΜΟΚΡΑΣΙΑ ΑΕΡΑ ΚΑΙ ΜΕΤΑΦΟΡΑ ΑΙΣΘΗΤΗΣ ΘΕΡΜΟΤΗΤΑΣ
 1η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΘΕΡΜΟΚΡΑΣΙΑ ΑΕΡΑ ΚΑΙ ΜΕΤΑΦΟΡΑ ΑΙΣΘΗΤΗΣ ΘΕΡΜΟΤΗΤΑΣ ΜΕΘΟΔΟΙ ΜΕΤΡΗΣΗΣ ΘΕΡΜΟΚΡΑΣΙΑΣ Δισολή (θερμική δισολή σερεών-υγρών-ερίων) Ηλεκρική νίσση (εξάρησή ης πό θερμοκρσί) Θερμοηλεκρικό
1η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΘΕΡΜΟΚΡΑΣΙΑ ΑΕΡΑ ΚΑΙ ΜΕΤΑΦΟΡΑ ΑΙΣΘΗΤΗΣ ΘΕΡΜΟΤΗΤΑΣ ΜΕΘΟΔΟΙ ΜΕΤΡΗΣΗΣ ΘΕΡΜΟΚΡΑΣΙΑΣ Δισολή (θερμική δισολή σερεών-υγρών-ερίων) Ηλεκρική νίσση (εξάρησή ης πό θερμοκρσί) Θερμοηλεκρικό
Επιστηµονικός Υπολογισµός Ι
 Επιστηµονικός Υπολογισµός Ι Ενότητα 8 : Το ιακριτό Μοντέλο Ευστράτιος Γαλλόπουλος Τµήµα Μηχανικών Η/Υ & Πληροφορικής Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Επιστηµονικός Υπολογισµός Ι Ενότητα 8 : Το ιακριτό Μοντέλο Ευστράτιος Γαλλόπουλος Τµήµα Μηχανικών Η/Υ & Πληροφορικής Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Επαναληπτικές μέθοδοι για την επίλυση γραμμικών συστημάτων. Μιχάλης Δρακόπουλος
 Επαναληπτικές μέθοδοι για την επίλυση γραμμικών συστημάτων Μιχάλης Δρακόπουλος Σημειώσεις Αριθμητικής Γραμμικής Άλγεβρας 2012 2013 Εισαγωγή Στην αριθμητική επίλυση μαθηματικών εφαρμογών, όπως για παράδειγμα
Επαναληπτικές μέθοδοι για την επίλυση γραμμικών συστημάτων Μιχάλης Δρακόπουλος Σημειώσεις Αριθμητικής Γραμμικής Άλγεβρας 2012 2013 Εισαγωγή Στην αριθμητική επίλυση μαθηματικών εφαρμογών, όπως για παράδειγμα
Εφαρμογή της μεθόδου πεπερασμένων διαφορών στην εξίσωση θερμότητας
 Εφαρμογή της μεθόδου πεπερασμένων διαφορών στην εξίσωση θερμότητας Να γραφεί script το οποίο να επιλύει αριθμητικά της γενική εξίσωση θερμότητας με χρήση της προς τα εμπρός παραγώγου ως προς το χρόνο,
Εφαρμογή της μεθόδου πεπερασμένων διαφορών στην εξίσωση θερμότητας Να γραφεί script το οποίο να επιλύει αριθμητικά της γενική εξίσωση θερμότητας με χρήση της προς τα εμπρός παραγώγου ως προς το χρόνο,
Γραµµικη Αλγεβρα ΙΙ Ασκησεις - Φυλλαδιο 10
 Γραµµικη Αλγεβρα ΙΙ Ασκησεις - Φυλλαδιο 0 Επαναληπτικες Ασκησεις ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθοι Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laiihtml
Γραµµικη Αλγεβρα ΙΙ Ασκησεις - Φυλλαδιο 0 Επαναληπτικες Ασκησεις ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθοι Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laiihtml
Πεπερασμένες Διαφορές.
 Κεφάλαιο 1 Πεπερασμένες Διαφορές. 1.1 Προσέγγιση παραγώγων. 1.1.1 Πρώτη παράγωγος. Από τον ορισμό της παραγώγου για συναρτήσεις μιας μεταβλητής γνωρίζουμε ότι η παράγωγος μιας συνάρτησης f στο σημείο x
Κεφάλαιο 1 Πεπερασμένες Διαφορές. 1.1 Προσέγγιση παραγώγων. 1.1.1 Πρώτη παράγωγος. Από τον ορισμό της παραγώγου για συναρτήσεις μιας μεταβλητής γνωρίζουμε ότι η παράγωγος μιας συνάρτησης f στο σημείο x
y(t) = T [x(t)] (7.1)
![y(t) = T [x(t)] (7.1) y(t) = T [x(t)] (7.1)](/thumbs/93/114087149.jpg) Κεφάλαιο 7 Ανάλυση Συσημάων σο Πεδίο ου Χρόνου 7. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Τι είναι όμως α συσήμαα και γιαί α χρησιμοποιούμε;
Κεφάλαιο 7 Ανάλυση Συσημάων σο Πεδίο ου Χρόνου 7. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Τι είναι όμως α συσήμαα και γιαί α χρησιμοποιούμε;
y 1 και με οριακές συνθήκες w
 ΑΣΚΗΣΗ ΥΠΟΛΟΓΙΣΤΙΚΕΣ ΜΕΘΟΔΟΙ, 008-009, 5 Ο ΕΞΑΜΗΝΟ ΕΡΓΑΣΙΑ #3: ΕΛΛΕΙΠΤΙΚΑ ΠΡΟΒΛΗΜΑΤΑ ΗΜΕΡΟΜΗΝΙΑ ΠΑΡΑΔΟΣΗΣ:..008 ΔΙΔΑΣΚΩΝ: Δ. Βαλουγεώργης Επιμέλεια απαντήσεων: Ιωάννης Λυχναρόπουλος Η εξίσωση Laplace σε
ΑΣΚΗΣΗ ΥΠΟΛΟΓΙΣΤΙΚΕΣ ΜΕΘΟΔΟΙ, 008-009, 5 Ο ΕΞΑΜΗΝΟ ΕΡΓΑΣΙΑ #3: ΕΛΛΕΙΠΤΙΚΑ ΠΡΟΒΛΗΜΑΤΑ ΗΜΕΡΟΜΗΝΙΑ ΠΑΡΑΔΟΣΗΣ:..008 ΔΙΔΑΣΚΩΝ: Δ. Βαλουγεώργης Επιμέλεια απαντήσεων: Ιωάννης Λυχναρόπουλος Η εξίσωση Laplace σε
ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ
 Σ. Η. ΔΡΙΤΣΟΣ, 07 ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ οκός Οπλισµένου Σκυροέµαος Ενισχυµένη µε Σρώση Οπλισµένου Σκυροέµαος Φ0 Φ0 η ΑΡΙΘΜΗΤΙΚΗΕΦΑΡΜΟΓΗ Yλικά : C5/30, Φ0 S Άνοιγµαοκού:
Σ. Η. ΔΡΙΤΣΟΣ, 07 ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ οκός Οπλισµένου Σκυροέµαος Ενισχυµένη µε Σρώση Οπλισµένου Σκυροέµαος Φ0 Φ0 η ΑΡΙΘΜΗΤΙΚΗΕΦΑΡΜΟΓΗ Yλικά : C5/30, Φ0 S Άνοιγµαοκού:
ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ
 1 Κεφάλαιο 1 ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ 1.1 Εισαγωγή Ένα από α βασικόερα ανικείμενα σο επάγγελμα ου μηχανικού είναι η λεγόμενη διασασιολόγηση ή σχεδιασμός δομικών σοιχείων
1 Κεφάλαιο 1 ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ 1.1 Εισαγωγή Ένα από α βασικόερα ανικείμενα σο επάγγελμα ου μηχανικού είναι η λεγόμενη διασασιολόγηση ή σχεδιασμός δομικών σοιχείων
Multi Post. Ενδοριζικοί άξονες ανασύστασης
 Multi Post Ενδορζοί άξς ανασύσασης MultiPost Σύσηµα νδορζών αξόνων α αποαάσαση µ ρηνώδη υλά Το σύσηµα Multi Post ης D+Z που πρλαµβάν άξς αασυασµένους από αθαρό άνο ίνα ένα ύολο σο χρσµό α δοµασµένο σύσηµα
Multi Post Ενδορζοί άξς ανασύσασης MultiPost Σύσηµα νδορζών αξόνων α αποαάσαση µ ρηνώδη υλά Το σύσηµα Multi Post ης D+Z που πρλαµβάν άξς αασυασµένους από αθαρό άνο ίνα ένα ύολο σο χρσµό α δοµασµένο σύσηµα
Προσεγγιστική λύση Γραμμικών Συστημάτων με την μέθοδο Gauss-Seidel. Δημιουργία κώδικα στο Matlab
 Προσεγγιστική λύση Γραμμικών Συστημάτων με την μέθοδο Gauss-Seidel Δημιουργία κώδικα στο Matlab Χατζηγεωργίου Αντώνης Νοέμβριος 2013 Περιεχόμενα 1. Αρχικό πρόβλημα.... 3 2. Εφαρμογή της θεωρίας.... 4 3.
Προσεγγιστική λύση Γραμμικών Συστημάτων με την μέθοδο Gauss-Seidel Δημιουργία κώδικα στο Matlab Χατζηγεωργίου Αντώνης Νοέμβριος 2013 Περιεχόμενα 1. Αρχικό πρόβλημα.... 3 2. Εφαρμογή της θεωρίας.... 4 3.
Αριθµητική Ανάλυση. 27 Οκτωβρίου Αριθµητική Ανάλυση 27 Οκτωβρίου / 72
 Αριθµητική Ανάλυση 7 Οκτωβρίου 06 Αριθµητική Ανάλυση 7 Οκτωβρίου 06 / 7 Επαναληπτικές Μέθοδοι για την επίλυση Γραµµικών Συστηµάτων ίνεται το γραµµικό σύστηµα Ax = b όπου A R n n είναι µη ιδιάζων πίνακας
Αριθµητική Ανάλυση 7 Οκτωβρίου 06 Αριθµητική Ανάλυση 7 Οκτωβρίου 06 / 7 Επαναληπτικές Μέθοδοι για την επίλυση Γραµµικών Συστηµάτων ίνεται το γραµµικό σύστηµα Ax = b όπου A R n n είναι µη ιδιάζων πίνακας
Αριθμητικές Μέθοδοι σε Προγραμματιστικό Περιβάλλον (Εργαστήριο 6)
 Τμήμα Μηχανικών Πληροφορικής Αριθμητικές Μέθοδοι σε Προγραμματιστικό Περιβάλλον (Εργαστήριο 6) Δρ. Δημήτρης Βαρσάμης Επίκουρος Καθηγητής Δρ. Δημήτρης Βαρσάμης Αριθμητικές Μέθοδοι (E 6) Σεπτέμβριος 2015
Τμήμα Μηχανικών Πληροφορικής Αριθμητικές Μέθοδοι σε Προγραμματιστικό Περιβάλλον (Εργαστήριο 6) Δρ. Δημήτρης Βαρσάμης Επίκουρος Καθηγητής Δρ. Δημήτρης Βαρσάμης Αριθμητικές Μέθοδοι (E 6) Σεπτέμβριος 2015
Χρονικές σειρές 4 o μάθημα: ΠΙΝΑΚΕΣ ΚΑΙ ΔΙΑΝΥΣΜΑΤΑ
 Χρονικές σειρές 4 o μάθημα: ΠΙΝΑΚΕΣ ΚΑΙ ΔΙΑΝΥΣΜΑΤΑ Εαρινό εξάμηνο 2018-2019 Τμήμα Μαθηματικών ΑΠΘ Διδάσκουσα: Αγγελική Παπάνα Μεταδιδακτορική Ερευνήτρια Πολυτεχνική σχολή, Α.Π.Θ. & Οικονομικό Τμήμα, Πανεπιστήμιο
Χρονικές σειρές 4 o μάθημα: ΠΙΝΑΚΕΣ ΚΑΙ ΔΙΑΝΥΣΜΑΤΑ Εαρινό εξάμηνο 2018-2019 Τμήμα Μαθηματικών ΑΠΘ Διδάσκουσα: Αγγελική Παπάνα Μεταδιδακτορική Ερευνήτρια Πολυτεχνική σχολή, Α.Π.Θ. & Οικονομικό Τμήμα, Πανεπιστήμιο
TO MONTEΛΟ ΤΗΕ ΕΡΠΙΣΗΣ (Reptation Model)
 TO MOTEΛΟ ΤΗΕ ΕΡΠΙΣΗΣ (epttion Moel) Η έννοια ου σωλήνα (tube) σις περιελίξεις (entglements). Αλληλεπιδράσεις-interpenetrtion Τοπολογικοί περιορισμοί (σην lterl/κάθεη κίνηση) Tube moel [e Gennes ; Ewrs
TO MOTEΛΟ ΤΗΕ ΕΡΠΙΣΗΣ (epttion Moel) Η έννοια ου σωλήνα (tube) σις περιελίξεις (entglements). Αλληλεπιδράσεις-interpenetrtion Τοπολογικοί περιορισμοί (σην lterl/κάθεη κίνηση) Tube moel [e Gennes ; Ewrs
ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ
 ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ. Ιξώδες Έσω ροή µεαξύ δύο παράλληλων πλακών εµβαδού Α και ανοίγµαος Η (Σχ. ). Σχ. du ιαµηική άση: =η =η γ dy () όπου: γ ο ρυθµός διάµησης, η ο ιξώδες. Παραηρήσεις για
ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ. Ιξώδες Έσω ροή µεαξύ δύο παράλληλων πλακών εµβαδού Α και ανοίγµαος Η (Σχ. ). Σχ. du ιαµηική άση: =η =η γ dy () όπου: γ ο ρυθµός διάµησης, η ο ιξώδες. Παραηρήσεις για
Τετραγωνικά μοντέλα. Τετραγωνικό μοντέλο συνάρτησης. Παράδειγμα τετραγωνικού μοντέλου #1. Παράδειγμα τετραγωνικού μοντέλου #1
 Τετραγωνικό μοντέλο συνάρτησης Τετραγωνικά μοντέλα Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo Για συνάρτηση μιας
Τετραγωνικό μοντέλο συνάρτησης Τετραγωνικά μοντέλα Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo Για συνάρτηση μιας
Εισαγωγή στον Προγραµµατισµό. Ανάλυση (ή Επιστηµονικοί8 Υπολογισµοί)
 Εισαγωγή στον Προγραµµατισµό Αριθµητική Ανάλυση (ή Επιστηµονικοί Υπολογισµοί) ιδάσκοντες: Καθηγητής Ν. Μισυρλής, Επίκ. Καθηγητής Φ.Τζαφέρης ΕΚΠΑ 8 εκεµβρίου 04 Ανάλυση (ή Επιστηµονικοί8 Υπολογισµοί) εκεµβρίου
Εισαγωγή στον Προγραµµατισµό Αριθµητική Ανάλυση (ή Επιστηµονικοί Υπολογισµοί) ιδάσκοντες: Καθηγητής Ν. Μισυρλής, Επίκ. Καθηγητής Φ.Τζαφέρης ΕΚΠΑ 8 εκεµβρίου 04 Ανάλυση (ή Επιστηµονικοί8 Υπολογισµοί) εκεµβρίου
Ανάλυση της µηχανικής συµπεριφοράς της συνάφειας ράβδων οπλισµού FRP µε σκυρόδεµα
 Ανάλυση ης µηχανικής συµπεριφοράς ης συνάφειας ράβδων οπλισµού FRP µε σκυρόδεµα Β. Καραζαφέρης MΕ, Υποψήφιος διδάκωρ ΕΜΠ Μ. Καής Επίκουρος Καθηγηής ΕΜΠ Λέξεις κλειδιά: FRP, συνάφεια, πεπερασµένα σοιχεία
Ανάλυση ης µηχανικής συµπεριφοράς ης συνάφειας ράβδων οπλισµού FRP µε σκυρόδεµα Β. Καραζαφέρης MΕ, Υποψήφιος διδάκωρ ΕΜΠ Μ. Καής Επίκουρος Καθηγηής ΕΜΠ Λέξεις κλειδιά: FRP, συνάφεια, πεπερασµένα σοιχεία
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΚΡΥΠΤΟΛΟΓΙΑ ΣΗΜΕΙΩΣΕΙΣ #6 ΘΕΟ ΟΥΛΟΣ ΓΑΡΕΦΑΛΑΚΗΣ
 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΚΡΥΠΤΟΛΟΓΙΑ ΣΗΜΕΙΩΣΕΙΣ #6 ΘΕΟ ΟΥΛΟΣ ΓΑΡΕΦΑΛΑΚΗΣ 1. Το προβληµα του διακριτου λογαριθµου Στο µάθηµα αυτό ϑα δούµε κάποιους αλγόριθµους για υπολογισµό διακριτών λογάριθµων. Θυµίζουµε ότι στο
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΚΡΥΠΤΟΛΟΓΙΑ ΣΗΜΕΙΩΣΕΙΣ #6 ΘΕΟ ΟΥΛΟΣ ΓΑΡΕΦΑΛΑΚΗΣ 1. Το προβληµα του διακριτου λογαριθµου Στο µάθηµα αυτό ϑα δούµε κάποιους αλγόριθµους για υπολογισµό διακριτών λογάριθµων. Θυµίζουµε ότι στο
ΚΕΦΑΛΑΙΟ 3 ΑΡΙΘΜΗΤΙΚΗ ΕΠΙΛΥΣΗ ΓΡΑΜΜΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ. nn n n
 ΚΕΦΑΛΑΙΟ 3 ΑΡΙΘΜΗΤΙΚΗ ΕΠΙΛΥΣΗ ΓΡΑΜΜΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ 3 Ο αλγόριθµος Gauss Eστω =,3,, µε τον όρο γραµµικά συστήµατα, εννοούµε συστήµατα εξισώσεων µε αγνώστους της µορφής: a x + + a x = b a x + + a x = b a
ΚΕΦΑΛΑΙΟ 3 ΑΡΙΘΜΗΤΙΚΗ ΕΠΙΛΥΣΗ ΓΡΑΜΜΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ 3 Ο αλγόριθµος Gauss Eστω =,3,, µε τον όρο γραµµικά συστήµατα, εννοούµε συστήµατα εξισώσεων µε αγνώστους της µορφής: a x + + a x = b a x + + a x = b a
Εργαστήρια Αριθμητικής Ανάλυσης Ι. 4 ο Εργαστήριο. Διανύσματα-Πίνακες 1 ο Μέρος
 Εργαστήρια Αριθμητικής Ανάλυσης Ι 4 ο Εργαστήριο Διανύσματα-Πίνακες 1 ο Μέρος 2017 Εισαγωγή Όπως έχουμε προαναφέρει σε προηγούμενα εργαστήρια. Ο βασικός τύπος δεδομένων στο Matlab είναι οι πίνακες. Ένα
Εργαστήρια Αριθμητικής Ανάλυσης Ι 4 ο Εργαστήριο Διανύσματα-Πίνακες 1 ο Μέρος 2017 Εισαγωγή Όπως έχουμε προαναφέρει σε προηγούμενα εργαστήρια. Ο βασικός τύπος δεδομένων στο Matlab είναι οι πίνακες. Ένα
Αριθμητικές Μέθοδοι σε Προγραμματιστικό Περιβάλλον
 Τμήμα Μηχανικών Πληροφορικής Αριθμητικές Μέθοδοι σε Προγραμματιστικό Περιβάλλον Δρ. Δημήτρης Βαρσάμης Επίκουρος Καθηγητής Οκτώβριος 2014 Δρ. Δημήτρης Βαρσάμης Οκτώβριος 2014 1 / 42 Αριθμητικές Μέθοδοι
Τμήμα Μηχανικών Πληροφορικής Αριθμητικές Μέθοδοι σε Προγραμματιστικό Περιβάλλον Δρ. Δημήτρης Βαρσάμης Επίκουρος Καθηγητής Οκτώβριος 2014 Δρ. Δημήτρης Βαρσάμης Οκτώβριος 2014 1 / 42 Αριθμητικές Μέθοδοι
Β ΜΕΡΟΣ: ΕΦΑΡΜΟΓΗ ΤΟΥ MATLAB ΣΤΗΝ ΑΡΙΘΜΗΤΙΚΗ ΑΝΑΛΥΣΗ
 Β ΜΕΡΟΣ: ΕΦΑΡΜΟΓΗ ΤΟΥ MATLAB ΣΤΗΝ ΑΡΙΘΜΗΤΙΚΗ ΑΝΑΛΥΣΗ 1. Εύρεση ρίζας Στο κεφάλαιο αυτό θα ασχοληθούμε με την εύρεση ρίζας μιας συνάρτησης ή αλλιώς με την ευρεση λύσης της εξίσωσης: Πριν αναφερθούμε στην
Β ΜΕΡΟΣ: ΕΦΑΡΜΟΓΗ ΤΟΥ MATLAB ΣΤΗΝ ΑΡΙΘΜΗΤΙΚΗ ΑΝΑΛΥΣΗ 1. Εύρεση ρίζας Στο κεφάλαιο αυτό θα ασχοληθούμε με την εύρεση ρίζας μιας συνάρτησης ή αλλιώς με την ευρεση λύσης της εξίσωσης: Πριν αναφερθούμε στην
Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου 3
 Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθος Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://wwwmathuoigr/ abeligia/linearalgebrai/laihtml
Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθος Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://wwwmathuoigr/ abeligia/linearalgebrai/laihtml
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 9 Επαναληπτικες Ασκησεις
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β ΠΕΡΙΤΤΟΙ Ασκησεις - Φυλλαδιο 9 Επαναληπτικες Ασκησεις ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii8/laii8html Παρασκευή 4 Ιουνίου
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β ΠΕΡΙΤΤΟΙ Ασκησεις - Φυλλαδιο 9 Επαναληπτικες Ασκησεις ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii8/laii8html Παρασκευή 4 Ιουνίου
Μικροοικονοµική Θεωρία. Τιµές και εισόδηµα. Notes. Notes. Notes. Notes. Κώστας Ρουµανιάς. 22 Σεπτεµβρίου 2014
 Μικροοικονοµική Θεωρία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 22 Σεπτεµβρίου 2014 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Μικροοικονοµική Θεωρία 22 Σεπτεµβρίου 2014 1 / 30 Τιµές και εισόδηµα Η συνάρτηση χρησιµότητας
Μικροοικονοµική Θεωρία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 22 Σεπτεµβρίου 2014 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Μικροοικονοµική Θεωρία 22 Σεπτεµβρίου 2014 1 / 30 Τιµές και εισόδηµα Η συνάρτηση χρησιµότητας
Αριθµητική Γραµµική ΑλγεβραΚεφάλαιο 4. Αριθµητικός Υπολογισµός Ιδιοτιµών 2 Απριλίου και2015 Ιδιοδιανυσµάτων 1 / 50
 Αριθµητική Γραµµική Αλγεβρα Κεφάλαιο 4. Αριθµητικός Υπολογισµός Ιδιοτιµών και Ιδιοδιανυσµάτων ΕΚΠΑ 2 Απριλίου 205 Αριθµητική Γραµµική ΑλγεβραΚεφάλαιο 4. Αριθµητικός Υπολογισµός Ιδιοτιµών 2 Απριλίου και205
Αριθµητική Γραµµική Αλγεβρα Κεφάλαιο 4. Αριθµητικός Υπολογισµός Ιδιοτιµών και Ιδιοδιανυσµάτων ΕΚΠΑ 2 Απριλίου 205 Αριθµητική Γραµµική ΑλγεβραΚεφάλαιο 4. Αριθµητικός Υπολογισµός Ιδιοτιµών 2 Απριλίου και205
Παράδειγμα #10 ΠΡΟΒΛΗΜΑΤΑ ΟΡΙΑΚΩΝ ΤΙΜΩΝ ΕΛΛΕΙΠΤΙΚΕΣ ΜΔΕ ΕΠΙΜΕΛΕΙΑ: Ν. Βασιλειάδης
 Άσκηση 1 Παράδειγμα #10 ΠΡΟΒΛΗΜΑΤΑ ΟΡΙΑΚΩΝ ΤΙΜΩΝ ΕΛΛΕΙΠΤΙΚΕΣ ΜΔΕ ΕΠΙΜΕΛΕΙΑ: Ν. Βασιλειάδης Να επιλυθεί η ροή ρευστού διαμέσου τετραγωνικού αγωγού η οποία εκφράζεται μέσω της διαφορικής εξίσωσης Poisson
Άσκηση 1 Παράδειγμα #10 ΠΡΟΒΛΗΜΑΤΑ ΟΡΙΑΚΩΝ ΤΙΜΩΝ ΕΛΛΕΙΠΤΙΚΕΣ ΜΔΕ ΕΠΙΜΕΛΕΙΑ: Ν. Βασιλειάδης Να επιλυθεί η ροή ρευστού διαμέσου τετραγωνικού αγωγού η οποία εκφράζεται μέσω της διαφορικής εξίσωσης Poisson
ΑΞΙΟΛΟΓΗΣΗ ΕΚΤΙΜΗΤΩΝ ΑΜΟΙΒΑΙΑΣ ΠΛΗΡΟΦΟΡΙΑΣ ΑΠΟ ΙΣΤΟΓΡΑΜΜΑ ΣΕ ΧΡΟΝΟΣΕΙΡΕΣ
 Ελληνικό Σαισικό Ινσιούο Πρακικά ου Πανελληνίου Συνεδρίου Σαισικής (7), σελ 39-336 ΑΞΙΟΛΟΓΗΣΗ ΕΚΤΙΜΗΤΩΝ ΑΜΟΙΒΑΙΑΣ ΠΛΗΡΟΦΟΡΙΑΣ ΑΠΟ ΙΣΤΟΓΡΑΜΜΑ ΣΕ ΧΡΟΝΟΣΕΙΡΕΣ Παπάνα Αγγελική, Κουγιουμζής Δημήρης Γενικό Τμήμα
Ελληνικό Σαισικό Ινσιούο Πρακικά ου Πανελληνίου Συνεδρίου Σαισικής (7), σελ 39-336 ΑΞΙΟΛΟΓΗΣΗ ΕΚΤΙΜΗΤΩΝ ΑΜΟΙΒΑΙΑΣ ΠΛΗΡΟΦΟΡΙΑΣ ΑΠΟ ΙΣΤΟΓΡΑΜΜΑ ΣΕ ΧΡΟΝΟΣΕΙΡΕΣ Παπάνα Αγγελική, Κουγιουμζής Δημήρης Γενικό Τμήμα
Εργαστήριο 2 - Απαντήσεις. Επίλυση Γραμμικών Συστημάτων
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΜΑΘΗΜΑ: ΑΡΙΘΜΗΤΙΚΗ ΑΝΑΛΥΣΗ ΚΑΙ ΕΡΓΑΣΤΗΡΙΟ Ι Ιστοσελίδα : http://www.math.ntua.gr/~fargyriou Εργαστήριο 2 - Απαντήσεις Επίλυση
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΜΑΘΗΜΑ: ΑΡΙΘΜΗΤΙΚΗ ΑΝΑΛΥΣΗ ΚΑΙ ΕΡΓΑΣΤΗΡΙΟ Ι Ιστοσελίδα : http://www.math.ntua.gr/~fargyriou Εργαστήριο 2 - Απαντήσεις Επίλυση
Αριθµητική Ανάλυση 1 εκεµβρίου / 43
 Αριθµητική Ανάλυση 1 εκεµβρίου 2014 Αριθµητική Ανάλυση 1 εκεµβρίου 2014 1 / 43 Κεφ.5. Αριθµητικός Υπολογισµός Ιδιοτιµών και Ιδιοδιανυσµάτων ίνεται ένας πίνακας A C n n και Ϲητούνται να προσδιορισθούν οι
Αριθµητική Ανάλυση 1 εκεµβρίου 2014 Αριθµητική Ανάλυση 1 εκεµβρίου 2014 1 / 43 Κεφ.5. Αριθµητικός Υπολογισµός Ιδιοτιµών και Ιδιοδιανυσµάτων ίνεται ένας πίνακας A C n n και Ϲητούνται να προσδιορισθούν οι
- Ομοιότητα με βάση τις εξισώσεις Νavier-Stokes - 2- διάστατη ασυμπίεστη Ροή
 ΚΕΦΑΛΑΙΟ 8 ΡΟΗ ΠΡΑΓΜΑΤΙΚΟΥ ΡΕΥΣΤΟΥ-ΣΥΝΕΚΤΙΚΗ ΡΟΗ - Ιξώδες - Ομοιόηα με βάση ις εξισώσεις Νaier-Stkes - - διάσαη ασυμπίεση Ροή ΕΞΙΣΩΣΗ ΣΥΝΕΧΕΙΑΣ 0 ΕΞΙΣΩΣΕΙΣ ΟΡΜΗΣ t 1 μ 1 g μ t - Οιακές Συνθήκες B σο -
ΚΕΦΑΛΑΙΟ 8 ΡΟΗ ΠΡΑΓΜΑΤΙΚΟΥ ΡΕΥΣΤΟΥ-ΣΥΝΕΚΤΙΚΗ ΡΟΗ - Ιξώδες - Ομοιόηα με βάση ις εξισώσεις Νaier-Stkes - - διάσαη ασυμπίεση Ροή ΕΞΙΣΩΣΗ ΣΥΝΕΧΕΙΑΣ 0 ΕΞΙΣΩΣΕΙΣ ΟΡΜΗΣ t 1 μ 1 g μ t - Οιακές Συνθήκες B σο -
Εφαρμοσμένα Μαθηματικά 3η εργαστηριακή άσκηση
 ΤΕΙ ΑΘΗΝΑΣ ΤΜΗΜΑ ΝΑΥΠΗΓΙΚΗΣ Εφαρμοσμένα Μαθηματικά 3η εργαστηριακή άσκηση ΣΠΟΥΔΑΣΤΗΣ: ΧΑΤΖΗΓΕΩΡΓΙΟΥ ΑΝΤΩΝΗΣ Α.Μ. 09036 Εξάμηνο ΠΤΧ ΚΑΘΗΓΗΤΗΣ: ΔΡ. ΜΠΡΑΤΣΟΣ ΑΘΑΝΑΣΙΟΣ Περιεχόμενα 3.1 Πολυωνυμική παρεμβολή...
ΤΕΙ ΑΘΗΝΑΣ ΤΜΗΜΑ ΝΑΥΠΗΓΙΚΗΣ Εφαρμοσμένα Μαθηματικά 3η εργαστηριακή άσκηση ΣΠΟΥΔΑΣΤΗΣ: ΧΑΤΖΗΓΕΩΡΓΙΟΥ ΑΝΤΩΝΗΣ Α.Μ. 09036 Εξάμηνο ΠΤΧ ΚΑΘΗΓΗΤΗΣ: ΔΡ. ΜΠΡΑΤΣΟΣ ΑΘΑΝΑΣΙΟΣ Περιεχόμενα 3.1 Πολυωνυμική παρεμβολή...
ΤΕΧΝΟΛΟΓΙΑ ΛΟΓΙΣΜΙΚΟΥ Ι
 ΤΕΧΝΟΛΟΓΙΑ ΛΟΓΙΣΜΙΚΟΥ Ι κ. ΠΕΤΑΛΙΔΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕ 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
ΤΕΧΝΟΛΟΓΙΑ ΛΟΓΙΣΜΙΚΟΥ Ι κ. ΠΕΤΑΛΙΔΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕ 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
Επιστηµονικός Υπολογισµός ΙΙ
 Επιστηµονικός Υπολογισµός ΙΙ Ε. Γαλλόπουλος 1 1 Τµήµα Μηχανικών Ηλεκτρονικών Υπολογιστών και Πληροφορικής Πολυτεχνική Σχολή, Πανεπιστήµιο Πατρών 13/3/13 Θεώρηµα Stein-Rosenberg Εστω A = D L U όπου L,U
Επιστηµονικός Υπολογισµός ΙΙ Ε. Γαλλόπουλος 1 1 Τµήµα Μηχανικών Ηλεκτρονικών Υπολογιστών και Πληροφορικής Πολυτεχνική Σχολή, Πανεπιστήµιο Πατρών 13/3/13 Θεώρηµα Stein-Rosenberg Εστω A = D L U όπου L,U
Ι ΑΝΙΚΟ ΦΙΛΤΡΟ ΒΑΣΙΚΗΣ ΖΩΝΗΣ - ΚΑΤΩΠΕΡΑΤΟ ΦΙΛΤΡΟ. ω > ω. ω c Ζώνη διέλευσης. Σεραφείµ Καραµπογιάς. όπουω c είναιησυχνότητααποκοπής.
 Σεραφείµ Καραµογιάς Ι ΑΝΙΚΟ ΦΙΛΤΡΟ ΒΑΣΙΚΗΣ ΖΩΝΗΣ - ΚΑΤΩΠΕΡΑΤΟ ΦΙΛΤΡΟ H ( όου είναιησυχνόηααοκοής. e j,, < > H ( arg H ( κλίση - αοκοής αοκοής Η είδραση ου φίλρου σε ένα σήµα εισόδου, µε φασµαικό εριεχόµενο
Σεραφείµ Καραµογιάς Ι ΑΝΙΚΟ ΦΙΛΤΡΟ ΒΑΣΙΚΗΣ ΖΩΝΗΣ - ΚΑΤΩΠΕΡΑΤΟ ΦΙΛΤΡΟ H ( όου είναιησυχνόηααοκοής. e j,, < > H ( arg H ( κλίση - αοκοής αοκοής Η είδραση ου φίλρου σε ένα σήµα εισόδου, µε φασµαικό εριεχόµενο
Συστήματα Αναμονής (Queuing Systems)
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ - ΕΜΠ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧ. ΥΠΟΛΟΓΙΣΤΩΝ Τομέας Επικοινωνιών, Ηλεκτρονικής & Συστημάτων Πληροφορικής Εργαστήριο Διαχείρισης & Βέλτιστου Σχεδιασμού Δικτύων Τηλεματικής
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ - ΕΜΠ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧ. ΥΠΟΛΟΓΙΣΤΩΝ Τομέας Επικοινωνιών, Ηλεκτρονικής & Συστημάτων Πληροφορικής Εργαστήριο Διαχείρισης & Βέλτιστου Σχεδιασμού Δικτύων Τηλεματικής
Αδιάσπαστοι, p-κυκλικοί, συνεπώς διατεταγµένοι πίνακες και γραφήµατα
 Αδιάσπαστοι, p-κυκλικοί, συνεπώς διατεταγµένοι πίνακες και γραφήµατα Νικόλαος Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήµιο Αθηνών 19 εκεµβρίου 2018 Νικόλαος Μισυρλής Επιστηµονικοί Υπολογισµοί
Αδιάσπαστοι, p-κυκλικοί, συνεπώς διατεταγµένοι πίνακες και γραφήµατα Νικόλαος Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήµιο Αθηνών 19 εκεµβρίου 2018 Νικόλαος Μισυρλής Επιστηµονικοί Υπολογισµοί
