ΚΙΝΗΣΙΚΗ ΘΕΩΡΙΑ ΣΩΝ ΑΕΡΙΩΝ. Χάρθσ Βάρβογλθσ Σμιμα Φυςικισ Πανεπιςτιμιο Θεςςαλονίκθσ
|
|
|
- Ζήνων Κορνάρος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΚΙΝΗΣΙΚΗ ΘΕΩΡΙΑ ΣΩΝ ΑΕΡΙΩΝ Χάρθσ Βάρβογλθσ Σμιμα Φυςικισ Πανεπιςτιμιο Θεςςαλονίκθσ
2 Ατομικι κεωρία Αρχαίοι Ζλλθνεσ: Λεφκιπποσ και Δθμόκριτοσ Πειραματικά δεδομζνα: Νόμοι των αερίων: Boyle ( ) & Mariotte ( ) Βάροσ αντιδρϊντων-προϊόντων ςε χθμικζσ αντιδράςεισ: Lavoisier ( ) Αναβίωςθ τθσ ατομικισ κεωρίασ: John Dalton ( ) Ενδιαφζρον ςθμείο: οι νόμοι των αερίων υποδθλϊνουν τθν φπαρξθ μορίων οι νόμοι τθσ Χθμείασ υποδθλϊνουν τθν φπαρξθ ατόμων Αλλά τα άτομα αποτελοφνται από πρωτόνια, νετρόνια και θλεκτρόνια! Σα πρωτόνια και τα νετρόνια αποτελοφνται από quarks! Αντίκετα με τθν κακθμερινι αντίλθψθ, τα πειράματα δείχνουν ότι κάκε φορά που είχαμε τθ δυνατότθτα να «χτυπιςουμε δυνατά» ζνα ςωματίδιο, βρικαμε ότι δεν ιταν ςτοιχειϊδεσ! τθ ςφγχρονθ String Theory τα «ςτοιχειϊδθ ςωμάτια» είναι χορδζσ, δθλ. μονοδιάςτατα (1-D) αντικείμενα, με μικοσ ~10-35 m, δθλαδι μικρότερο από τθν «κλαςικι» διάμετρο ενόσ πρωτονίου!
3 Κινθτικι κεωρία των αερίων Ιδανικό (τζλειο) αζριο: το «ιδανικό» μοντζλο για τθν περιγραφι τθσ Θερμοδυναμικισ. Daniel Bernoulli (ζνασ από τα εννζα διάςθμα μζλθ τθσ οικογζνειασ): pv = ⅓Nm<v 2 >. Maxwell: ςυνάρτθςθ «κατανομισ» (ορκότερα ςυνάρτθςθ πυκνότθτασ πικανότθτασ), dn = f(v)dv. Με τθν μορφι f(v) = (2π) -3/2 exp(-mv 2 /2kT), που πρότεινε ο Maxwell, βρίςκουμε τθ ςχζςθ pv = NkT (νόμοσ του Clapeyron). Ο Clausius πίςτευε ότι όλα τα μόρια κινοφνται με τθν ίδια «μζςθ ταχφτθτα», αλλά με τυχαίεσ διευκφνςεισ. Ερϊτθςθ: είναι θ f(v) μοναδικι; Ο Boltzmann πίςτευε ότι το απζδειξε (H- Theorem), ςιμερα υπάρχει και άλλθ άποψθ (Tsallis non-extensive entropy). Από τισ δφο παραπάνω ςχζςεισ βρίςκουμε ότι: Τ = ⅓(m/k)<v 2 >. Η κερμοκραςία είναι ζνα μζτρο τθσ άτακτθσ («χαοτικισ») κινθτικισ ενζργειασ των μορίων!
4 υνάρτθςθ κατανομισ Maxwell-Bolztmann f(v)
5 φγχρονθ κινθτικι κεωρία τθν κλαςική κινθτικι κεωρία, θ ελεφκερθ διαδρομι ακολουκεί κατανομι Gauss, οπότε είναι γνωςτό ότι μετά από N «βιματα» θ κατανομι του τελικοφ ςθμείου είναι επίςθσ Gaussian (Κεντρικό Οριακό Θεϊρθμα, ΚΟΘ). Τπάρχουν και άλλεσ κατανομζσ (πζρα από τθν Gaussian) με τθν ίδια (αυτο-όμοια) ιδιότθτα; Γενίκευςθ τθσ κατανομισ Gauss (Lévy-Montroll). Οι κατανομζσ Lévy τθσ ελεφκερθσ διαδρομισ οδθγοφν ςε μια αυτόόμοια κίνθςθ των μορίων των αερίων που δεν ικανοποιεί το ΚΟΘ. Φρακταλικι διάςταςθ τθσ τροχιάσ ενόσ μορίου ςε μια κατανομι Lévy (ζναντι ακζραιασ ςτθν περίπτωςθ τθσ Gaussian). Θερμοδυναμικι non-equilibrium (Ilya Prigogine). Non-extensive Θερμοδυναμικι και γενικευμζνη εντροπία (Tsallis).
6 Συχαίοι βθματιςμοί Gaussian - Lévy φγκριςθ των τροχιϊν μιασ διαδικαςίασ Gauss (αριςτερά) και Lévy (δεξιά). Και οι δφο τροχιζσ είναι ςτατιςτικά αυτό-όμοιεσ. Η τροχιά τθσ διαδικαςίασ Lévy χαρακτθρίηεται από δομι νθςίδων ςμθνϊν από μικρότερα βιματα, τα οποία ςυνδζονται με ζνα μεγαλφτερα βιματα. Και οι δφο βθματιςμοί ζχουν ςχεδιαςκεί για τον ίδιο αρικμό βθμάτων ( 7000).
7 Ο Maxwell και το Εργαςτιριο Cavendish Ο ανεψιόσ του Cavendish,Chancellor του Πανεπιςτθμίου του Cambridge, ςυνειςζφερε 6,300 ζναντι του κόςτουσ ανζγερςθσ ενόσ εργαςτθρίου Φυςικισ (του πρϊτου ςτον κόςμο!), με τον όρο ότι τα Κολλζγια κα πλιρωναν τον μιςκό ενόσ κακθγθτι Πειραματικισ Φυςικισ. Η κζςθ προςφζρκθκε αρχικά ςτον Kelvin. Όταν αρνικθκε, προςφζρκθκε ςτον Helmholtz, που αρνικθκε επίςθσ. Σότε ο Kelvin πρότεινε τον «προςτατευόμενό του» (ςτο Cambridge), Maxwell. Τπιρχε ζνασ όροσ: ο νζοσ κακθγθτισ κα ζπρεπε να διαβάςει και να δθμοςιεφςει τα χειρόγραφα του Henry Cavendish. Ο Maxwell πιρε τθ κζςθ και μετακόμιςε ςτο Cambridge πριν από τθν ολοκλιρωςθ του κτθρίου. Εκτζλεςε πολλά από τα αρχικά πειράματά του με τθ βοικεια τθσ γυναίκασ του, ςτθν κουηίνα του ςπιτιοφ του. Διάδοχοι: Lord Rayleigh, JJ Thomson, Rutherford, Lawrence Bragg. The Seventh Duke of Devonshire, William Cavendish
8 Σα πειράματα του Maxwell Ο Clausius είχε ειςαγάγει τθν ζννοια τθσ μζςησ ελεφθερησ διαδρομήσ, l. Μποροφμε να βροφμε, κεωρθτικά, ότι το ιξϊδεσ ενόσ αερίου δίνεται από τθ ςχζςθ 1 3 v, όπου v vf () v dv. Εξάλλου, μπορεί να αποδειχκεί ότι, όπου κ είναι θ διατομι των μορίων και ρ θ πυκνότθτά του. m 2 Από τα παραπάνω βλζπουμε ότι το ιξϊδεσ, μ, είναι ανεξάρτθτο του ρ, m v Η φυςικι ερμθνεία αυτοφ του «παράδοξου» αποτελζςματοσ δόκθκε (ορκά) από τον Maxwell, και ςχετίηεται με τθ μεταφορά ορμισ. Επιπλζον, επειδι T = ⅓(m/k)<v 2 > μ ~ T 1/2, αλλά ο Maxwell βρικε πειραματικά (ςτθν κουηίνα του!) ότι μ ~ T! Ερμθνεία: Σα μόρια δεν είναι «ςκλθρζσ» ςφαίρεσ, αλλά (αρνθτικά, ςτθν επιφάνεια!) φορτιςμζνα ςωματίδια. Σο μοντζλο του ιδανικοφ αερίου ζχει τα όριά του! (κα επανζλκουμε ςε αυτό ςτθ Θεωρία του Χάουσ).
9 Σο βζλοσ του χρόνου: Ludwig Boltzmann ( ) Γνωςτόσ από τον νόμο (με τον κακθγθτι του) των Stefan- Boltzmann, Ε = ςt 4. χζςθ εντροπίασ- πικανότθτασ: S = k logw Αντιςτρεπτότθτα των εξιςϊςεων τθσ Φυςικισ και το βζλοσ του χρόνου. Παράδειγμα: θ εξίςωςθ Λφςθ: x = v t + x 0 dx dt v Για τισ αρχικζσ ςυνκικεσ x 0 = 0 και (dx/dt) 0 = 5 θ λφςθ είναι x = 5t. Για ζνα άλλο ηεφγοσ αρχικϊν ςυνκθκϊν, x 0 = 0 και (dx/dt) 0 = 5, θ αντίςτοιχθ λφςθ είναι x = 5t. Η δεφτερθ λφςθ είναι θ πρϊτθ, αν αντικαταςτιςουμε t όπου t!
10 Βζλοσ του χρόνου και εντροπία Όλεσ οι εξιςϊςεισ των άλλων κεφαλαίων τθσ Φυςικισ (όχι μόνο τθσ κλαςικισ!) είναι ςυμμετρικζσ ωσ προσ τον χρόνο. Πϊσ λοιπόν ςυμβαίνει ότι ςτον «πραγματικό» κόςμο ζχουμε μια κακαρι εικόνα του χρόνου που «περνά» (παρελκόν -> μζλλον); Παραδείγματα: θ κραφςθ ενόσ ποτθριοφ θ διάχυςθ ενόσ αρϊματοσ. Προςπάκειεσ του Boltzmann να λφςει το πρόβλθμα διαμάχεσ με πολλοφσ επιςτιμονεσ (επόμενθ διαφάνεια), κεϊρθμα-h (1872) => S = -NkH. Σο κεϊρθμα τθσ επανάλθψθσ του Poincaré και θ εκτίμθςθ του Boltzmann για τον αναγκαίο χρόνο (ςτα Μακθματικά μόνο δφο αρικμοί είναι απόλυτοι: το 0 και το ). Άραγε ο χρόνοσ ςχετίηεται με κάποια αφξουςα ςυνάρτθςθ; Hawking (αρχικά): διαςτολι του φμπαντοσ (τελικά): αφξθςθ τθσ εντροπίασ (γενικευμζνθ με τθν επιφάνεια των μελανϊν οπϊν) χζςθ με τθ Θεωρία του Χάουσ;
11 Διαμάχεσ του Boltzmann Πρϊτθ: Loschmidt vs. Boltzmann Loschmidt: Σα μθχανικά ςυςτιματα είναι αντιςτρεπτά, θ Θερμοδυναμικι όχι. Ο Boltzmann απάντθςε: Εμπρόσ λοιπόν, αντιςτρζψτε τεσ (τισ ταχφτθτεσ των μορίων) Δεφτερθ: Zermelo vs. Boltzmann Zermelo: Δεδομζνων πολφ γενικϊν ςυνκθκϊν, κάκε ςφςτθμα κα επιςτρζψει αυκαίρετα κοντά ςτθν αρχικι κατάςταςι του (κεϊρθμα επανόδου -recurrence theoremτου Poincaré). Άρα θ μθ αντιςτρεπτι προςζγγιςθ ςε μια τελικι κατάςταςθ είναι αδφνατθ. Η «ςιβυλλικι» απάντθςθ του Boltzmann: Θζλετε να περιμζνετε τόςο πολφ;
12 Σο τραγικό τζλοσ των Maxwell & Boltzmann Ο Maxwell πζκανε ςε θλικία 48 ετϊν, από καρκίνο του ςτομάχου. Η μθτζρα του είχε πεκάνει από τθν ίδια αιτία ςτθν ίδια θλικία! Ο Boltzmann αυτοκτόνθςε ςε θλικία 62 ετϊν. Τπζφερε από διπολικι διαταραχι.
ςυςτιματα γραμμικϊν εξιςϊςεων
 κεφάλαιο 7 Α ςυςτιματα γραμμικϊν εξιςϊςεων αςικζσ ζννοιεσ Γραμμικά, λζγονται τα ςυςτιματα εξιςϊςεων ςτα οποία οι άγνωςτοι εμφανίηονται ςτθν πρϊτθ δφναμθ. Σα γραμμικά ςυςτιματα με δφο εξιςϊςεισ και δφο
κεφάλαιο 7 Α ςυςτιματα γραμμικϊν εξιςϊςεων αςικζσ ζννοιεσ Γραμμικά, λζγονται τα ςυςτιματα εξιςϊςεων ςτα οποία οι άγνωςτοι εμφανίηονται ςτθν πρϊτθ δφναμθ. Σα γραμμικά ςυςτιματα με δφο εξιςϊςεισ και δφο
Διάδοση θερμότητας σε μία διάσταση
 Διάδοση θερμότητας σε μία διάσταση Η θεωρητική μελζτη που ακολουθεί πραγματοποιήθηκε με αφορμή την εργαςτηριακή άςκηςη μζτρηςησ του ςυντελεςτή θερμικήσ αγωγιμότητασ του αλουμινίου, ςτην οποία διαγωνίςτηκαν
Διάδοση θερμότητας σε μία διάσταση Η θεωρητική μελζτη που ακολουθεί πραγματοποιήθηκε με αφορμή την εργαςτηριακή άςκηςη μζτρηςησ του ςυντελεςτή θερμικήσ αγωγιμότητασ του αλουμινίου, ςτην οποία διαγωνίςτηκαν
ΑΝΣΙΣΡΟΦΗ ΤΝΑΡΣΗΗ. f y x y f A αντιςτοιχίηεται ςτο μοναδικό x A για το οποίο. Παρατθριςεισ Ιδιότθτεσ τθσ αντίςτροφθσ ςυνάρτθςθσ 1. Η. f A τθσ f.
 .. Αντίςτροφθ ςυνάρτθςθ Ζςτω θ ςυνάρτθςθ : A θ οποία είναι " ". Τότε ορίηεται μια νζα ςυνάρτθςθ, θ μζςω τθσ οποίασ το κάκε ιςχφει y. : A με Η νζα αυτι ςυνάρτθςθ λζγεται αντίςτροφθ τθσ. y y A αντιςτοιχίηεται
.. Αντίςτροφθ ςυνάρτθςθ Ζςτω θ ςυνάρτθςθ : A θ οποία είναι " ". Τότε ορίηεται μια νζα ςυνάρτθςθ, θ μζςω τθσ οποίασ το κάκε ιςχφει y. : A με Η νζα αυτι ςυνάρτθςθ λζγεται αντίςτροφθ τθσ. y y A αντιςτοιχίηεται
ΑΞΙΟΛΟΓΗΣΗ ΕΚΠΑΙΔΕΥΤΙΚΟΥ
 ΑΞΙΟΛΟΓΗΣΗ ΕΚΠΑΙΔΕΥΤΙΚΟΥ Ειςαγωγή Τπάρχουν τρία επίπεδα ςτα οποία καλείςτε να αξιολογιςετε το εργαςτιριο D-ID: Νζα κζματα Σεχνολογία Διδακτικι Νέα θέματα Σο εργαςτιριο κα ειςαγάγουν τουσ ςυμμετζχοντεσ
ΑΞΙΟΛΟΓΗΣΗ ΕΚΠΑΙΔΕΥΤΙΚΟΥ Ειςαγωγή Τπάρχουν τρία επίπεδα ςτα οποία καλείςτε να αξιολογιςετε το εργαςτιριο D-ID: Νζα κζματα Σεχνολογία Διδακτικι Νέα θέματα Σο εργαςτιριο κα ειςαγάγουν τουσ ςυμμετζχοντεσ
ΧΗΥΙΑΚΟ ΔΚΠΑΙΔΔΤΣΙΚΟ ΒΟΗΘΗΜΑ «ΥΤΙΚΗ ΘΔΣΙΚΗ ΚΑΙ ΣΔΦΝΟΛΟΓΙΚΗ ΚΑΣΔΤΘΤΝΗ» ΦΥΣΙΚΗ ΘΔΤΙΚΗΣ ΚΑΙ ΤΔΧΝΟΛΟΓΙΚΗΣ ΚΑΤΔΥΘΥΝΣΗΣ ΘΔΜΑ Α ΘΔΜΑ Β
 4 o ΔΙΓΩΝΙΜ ΠΡΙΛΙΟ 04: ΔΝΔΔΙΚΣΙΚΔ ΠΝΣΗΔΙ ΦΥΣΙΚΗ ΘΔΤΙΚΗΣ ΚΙ ΤΔΧΝΟΛΟΓΙΚΗΣ ΚΤΔΥΘΥΝΣΗΣ 4 ο ΔΙΓΩΝΙΣΜ ΔΝΔΔΙΚΤΙΚΔΣ ΠΝΤΗΣΔΙΣ ΘΔΜ. β. β 3. α 4. γ 5. α.σ β.σ γ.λ δ.σ ε.λ. ΘΔΜ Β Σωςτι είναι θ απάντθςθ γ. Έχουμε ελαςτικι
4 o ΔΙΓΩΝΙΜ ΠΡΙΛΙΟ 04: ΔΝΔΔΙΚΣΙΚΔ ΠΝΣΗΔΙ ΦΥΣΙΚΗ ΘΔΤΙΚΗΣ ΚΙ ΤΔΧΝΟΛΟΓΙΚΗΣ ΚΤΔΥΘΥΝΣΗΣ 4 ο ΔΙΓΩΝΙΣΜ ΔΝΔΔΙΚΤΙΚΔΣ ΠΝΤΗΣΔΙΣ ΘΔΜ. β. β 3. α 4. γ 5. α.σ β.σ γ.λ δ.σ ε.λ. ΘΔΜ Β Σωςτι είναι θ απάντθςθ γ. Έχουμε ελαςτικι
Διαγώνισμα Χημείας Γ Λυκείου στα Κεφάλαια 1-4
 Διαγώνισμα Χημείας Γ Λυκείου στα Κεφάλαια 1-4 Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-5 και δίπλα το γράμμα που αντιςτοιχεί ςτθ
Διαγώνισμα Χημείας Γ Λυκείου στα Κεφάλαια 1-4 Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-5 και δίπλα το γράμμα που αντιςτοιχεί ςτθ
ΜΑΘΗΜΑΤΙΚΑ Α Γυμνασίου
 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΜΑΘΗΜΑΤΙΚΑ Α Γυμνασίου Ενότητα 1β: Ισότητα - Εξίσωση ΠΑΙΔΑΓΩΓΙΚΟ ΙΝΣΤΙΤΟΥΤΟ ΥΠΗΡΕΣΙΑ ΑΝΑΠΤΥΞΗΣ ΠΡΟΓΡΑΜΜΑΤΩΝ ΜΑΘΗΜΑΤΙΚΑ Α Γυμνασίου Ενότητα 1β: Ισότητα - Εξίσωση Συγγραφή:
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΜΑΘΗΜΑΤΙΚΑ Α Γυμνασίου Ενότητα 1β: Ισότητα - Εξίσωση ΠΑΙΔΑΓΩΓΙΚΟ ΙΝΣΤΙΤΟΥΤΟ ΥΠΗΡΕΣΙΑ ΑΝΑΠΤΥΞΗΣ ΠΡΟΓΡΑΜΜΑΤΩΝ ΜΑΘΗΜΑΤΙΚΑ Α Γυμνασίου Ενότητα 1β: Ισότητα - Εξίσωση Συγγραφή:
Ανταλλαγι δυο ταυτόςθμων κβαντικών ςωματιδίων. r 2. r 2 r 1. ,r 1. r 1. r, r r. , r
 Ανταλλαγι δυο ταυτόςθμων κβαντικών ςωματιδίων Μποηόνια - Φερμιόνια ςπιν ακζραιο ςπιν θμι-ακζραιο 5 ςυμμετρικι Ψ αντι-ςυμμετρικι Ψ φωτόνια μεςόνια Γκλουόνια κλπ θλεκτρόνια πρωτόνια νετρόνια Μιόνια κλπ β
Ανταλλαγι δυο ταυτόςθμων κβαντικών ςωματιδίων Μποηόνια - Φερμιόνια ςπιν ακζραιο ςπιν θμι-ακζραιο 5 ςυμμετρικι Ψ αντι-ςυμμετρικι Ψ φωτόνια μεςόνια Γκλουόνια κλπ θλεκτρόνια πρωτόνια νετρόνια Μιόνια κλπ β
Ποσοτικές Μέθοδοι Δρ. Χάϊδω Δριτσάκη
 Ποσοτικές Μέθοδοι Δρ. Χάϊδω Δριτσάκη MSc Τραπεζική & Χρηματοοικονομική Τεχνολογικό Εκπαιδευτικό Ίδρυμα Δυτικής Μακεδονίας Western Macedonia University of Applied Sciences Κοίλα Κοζάνης 50100 Kozani GR
Ποσοτικές Μέθοδοι Δρ. Χάϊδω Δριτσάκη MSc Τραπεζική & Χρηματοοικονομική Τεχνολογικό Εκπαιδευτικό Ίδρυμα Δυτικής Μακεδονίας Western Macedonia University of Applied Sciences Κοίλα Κοζάνης 50100 Kozani GR
ΘΕΡΜΟΔΤΝΑΜΙΚΗ Ι. Ενότθτα 4: Πρϊτοσ Θερμοδυναμικόσ Νόμοσ. ογομϊν Μπογοςιάν Πολυτεχνικι χολι Σμιμα Χθμικϊν Μθχανικϊν
 ΘΕΡΜΟΔΤΝΑΜΙΚΗ Ι Ενότθτα 4: Πρϊτοσ Θερμοδυναμικόσ Νόμοσ ογομϊν Μπογοςιάν Πολυτεχνικι χολι Σμιμα Χθμικϊν Μθχανικϊν κοποί ενότθτασ κοπόσ τθσ ενότθτασ αυτισ είναι θ περιγραφι των οριςμϊν και των κεμελιωδϊν
ΘΕΡΜΟΔΤΝΑΜΙΚΗ Ι Ενότθτα 4: Πρϊτοσ Θερμοδυναμικόσ Νόμοσ ογομϊν Μπογοςιάν Πολυτεχνικι χολι Σμιμα Χθμικϊν Μθχανικϊν κοποί ενότθτασ κοπόσ τθσ ενότθτασ αυτισ είναι θ περιγραφι των οριςμϊν και των κεμελιωδϊν
8 τριγωνομετρία. βαςικζσ ζννοιεσ. γ ςφω. εφω και γ. κεφάλαιο
 κεφάλαιο 8 τριγωνομετρία Α βαςικζσ ζννοιεσ τθν τριγωνομετρία χρθςιμοποιοφμε τουσ τριγωνομετρικοφσ αρικμοφσ, οι οποίοι ορίηονται ωσ εξισ: θμω = απζναντι κάκετθ πλευρά υποτείνουςα Γ ςυνω = εφω = προςκείμενθ
κεφάλαιο 8 τριγωνομετρία Α βαςικζσ ζννοιεσ τθν τριγωνομετρία χρθςιμοποιοφμε τουσ τριγωνομετρικοφσ αρικμοφσ, οι οποίοι ορίηονται ωσ εξισ: θμω = απζναντι κάκετθ πλευρά υποτείνουςα Γ ςυνω = εφω = προςκείμενθ
Επαναληπτικό Διαγώνισμα Φυσικη ς Α Λυκει όυ
 Επαναληπτικό Διαγώνισμα Φυσικη ς Α Λυκει όυ Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα που αντιςτοιχεί ςτθ
Επαναληπτικό Διαγώνισμα Φυσικη ς Α Λυκει όυ Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα που αντιςτοιχεί ςτθ
Θεωρία του Χάουσ. Χάρθσ Βάρβογλθσ Τμιμα Φυςικισ Πανεπιςτιμιο Θεςςαλονίκθσ
 Θεωρία του Χάουσ Χάρθσ Βάρβογλθσ Τμιμα Φυςικισ Πανεπιςτιμιο Θεςςαλονίκθσ Laplace και Αιτιοκρατία - I O Laplace ςτο βιβλίο του πάνω ςτισ Πικανότθτεσ: Μποροφμε να κεωροφμε τθν παροφςα κατάςταςθ του Σφμπαντοσ
Θεωρία του Χάουσ Χάρθσ Βάρβογλθσ Τμιμα Φυςικισ Πανεπιςτιμιο Θεςςαλονίκθσ Laplace και Αιτιοκρατία - I O Laplace ςτο βιβλίο του πάνω ςτισ Πικανότθτεσ: Μποροφμε να κεωροφμε τθν παροφςα κατάςταςθ του Σφμπαντοσ
Πόςο εκτατό μπορεί να είναι ζνα μη εκτατό νήμα και πόςο φυςικό. μπορεί να είναι ζνα μηχανικό ςτερεό. Συνιςταμζνη δφναμη versus «κατανεμημζνησ» δφναμησ
 Πόςο εκτατό μπορεί να είναι ζνα μη εκτατό νήμα και πόςο φυςικό μπορεί να είναι ζνα μηχανικό ςτερεό. Συνιςταμζνη δφναμη versus «κατανεμημζνησ» δφναμησ Για τθν ανάδειξθ του κζματοσ κα λφνουμε κάποια προβλιματα
Πόςο εκτατό μπορεί να είναι ζνα μη εκτατό νήμα και πόςο φυςικό μπορεί να είναι ζνα μηχανικό ςτερεό. Συνιςταμζνη δφναμη versus «κατανεμημζνησ» δφναμησ Για τθν ανάδειξθ του κζματοσ κα λφνουμε κάποια προβλιματα
Διαγώνισμα Φυσική ς Κατευ θυνσής Γ Λυκει ου - Ταλαντώσεις
 Διαγώνισμα Φυσική ς Κατευ θυνσής Γ Λυκει ου - Ταλαντώσεις Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα που αντιςτοιχεί
Διαγώνισμα Φυσική ς Κατευ θυνσής Γ Λυκει ου - Ταλαντώσεις Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα που αντιςτοιχεί
Πλαγιογώνια Συςτήματα Συντεταγμζνων Γιϊργοσ Καςαπίδθσ
 Πρόλογοσ το άρκρο αυτό κα δοφμε πωσ διαμορφϊνονται κάποιεσ ζννοιεσ όπωσ το εςωτερικό γινόμενο διανυςμάτων, οι ςυνκικεσ κακετότθτασ και παραλλθλίασ διανυςμάτων και ευκειϊν, ο ςυντελεςτισ διευκφνςεωσ διανφςματοσ
Πρόλογοσ το άρκρο αυτό κα δοφμε πωσ διαμορφϊνονται κάποιεσ ζννοιεσ όπωσ το εςωτερικό γινόμενο διανυςμάτων, οι ςυνκικεσ κακετότθτασ και παραλλθλίασ διανυςμάτων και ευκειϊν, ο ςυντελεςτισ διευκφνςεωσ διανφςματοσ
Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο του Άβακα
 Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο του Άβακα Αυτζσ οι οδθγίεσ ζχουν ςτόχο λοιπόν να βοθκιςουν τουσ εκπαιδευτικοφσ να καταςκευάςουν τισ δικζσ τουσ δραςτθριότθτεσ με το μοντζλο του Άβακα. Παρουςίαςη
Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο του Άβακα Αυτζσ οι οδθγίεσ ζχουν ςτόχο λοιπόν να βοθκιςουν τουσ εκπαιδευτικοφσ να καταςκευάςουν τισ δικζσ τουσ δραςτθριότθτεσ με το μοντζλο του Άβακα. Παρουςίαςη
Παράςταςη ςυμπλήρωμα ωσ προσ 1
 Δρ. Χρήστος Ηλιούδης Θζματα διάλεξησ ΣΤ1 Προςθεςη αφαίρεςη ςτο ΣΤ1 2 ή ΣΤ1 Ονομάηουμε ςυμπλιρωμα ωσ προσ μειωμζνθ βάςθ R ενόσ μθ προςθμαςμζνου αρικμοφ Χ = ( Χ θ-1 Χ θ-2... Χ 0 ) R ζναν άλλον αρικμό Χ'
Δρ. Χρήστος Ηλιούδης Θζματα διάλεξησ ΣΤ1 Προςθεςη αφαίρεςη ςτο ΣΤ1 2 ή ΣΤ1 Ονομάηουμε ςυμπλιρωμα ωσ προσ μειωμζνθ βάςθ R ενόσ μθ προςθμαςμζνου αρικμοφ Χ = ( Χ θ-1 Χ θ-2... Χ 0 ) R ζναν άλλον αρικμό Χ'
Μάκθςθ Κατανομϊν Πικανότθτασ και Ομαδοποίθςθ
 Μάκθςθ Κατανομϊν Πικανότθτασ και Ομαδοποίθςθ Κϊςτασ Διαμαντάρασ Τμιμα Πλθροφορικισ ΤΕΙ Θεςςαλονίκθσ 1 Μάκθςθ κατανομισ πικανότθτασ Σε όλθ τθν ανάλυςθ μζχρι τϊρα ζγινε ςιωπθρά θ παραδοχι ότι γνωρίηουμε
Μάκθςθ Κατανομϊν Πικανότθτασ και Ομαδοποίθςθ Κϊςτασ Διαμαντάρασ Τμιμα Πλθροφορικισ ΤΕΙ Θεςςαλονίκθσ 1 Μάκθςθ κατανομισ πικανότθτασ Σε όλθ τθν ανάλυςθ μζχρι τϊρα ζγινε ςιωπθρά θ παραδοχι ότι γνωρίηουμε
ΘΕΡΜΟΔΤΝΑΜΙΚΗ Ι. Ενότθτα 1: Βαςικά χαρακτθριςτικά τθσ Θερμοδυναμικισ. ογομϊν Μπογοςιάν Πολυτεχνικι χολι Σμιμα Χθμικϊν Μθχανικϊν
 ΘΕΡΜΟΔΤΝΑΜΙΚΗ Ι Ενότθτα 1: Βαςικά χαρακτθριςτικά τθσ Θερμοδυναμικισ ογομϊν Μπογοςιάν Πολυτεχνικι χολι Σμιμα Χθμικϊν Μθχανικϊν κοποί ενότθτασ κοπόσ τθσ ενότθτασ αυτισ είναι θ περιγραφι των οριςμϊν και και
ΘΕΡΜΟΔΤΝΑΜΙΚΗ Ι Ενότθτα 1: Βαςικά χαρακτθριςτικά τθσ Θερμοδυναμικισ ογομϊν Μπογοςιάν Πολυτεχνικι χολι Σμιμα Χθμικϊν Μθχανικϊν κοποί ενότθτασ κοπόσ τθσ ενότθτασ αυτισ είναι θ περιγραφι των οριςμϊν και και
Ένα πρόβλθμα γραμμικοφ προγραμματιςμοφ βρίςκεται ςτθν κανονικι μορφι όταν:
 Μζθοδος Simplex Η πλζον γνωςτι και περιςςότερο χρθςιμοποιουμζνθ μζκοδοσ για τθν επίλυςθ ενόσ γενικοφ προβλιματοσ γραμμικοφ προγραμματιςμοφ, είναι θ μζκοδοσ Simplex θ οποία αναπτφχκθκε από τον George Dantzig.
Μζθοδος Simplex Η πλζον γνωςτι και περιςςότερο χρθςιμοποιουμζνθ μζκοδοσ για τθν επίλυςθ ενόσ γενικοφ προβλιματοσ γραμμικοφ προγραμματιςμοφ, είναι θ μζκοδοσ Simplex θ οποία αναπτφχκθκε από τον George Dantzig.
ΛΕΙΣΟΤΡΓΙΚΆ ΤΣΉΜΑΣΑ. 2 ο Εργαςτιριο Διαχείριςθ Διεργαςιϊν
 ΛΕΙΣΟΤΡΓΙΚΆ ΤΣΉΜΑΣΑ 2 ο Εργαςτιριο Διαχείριςθ Διεργαςιϊν Τπόβακρο (1/3) τουσ παλαιότερουσ υπολογιςτζσ θ Κεντρικι Μονάδα Επεξεργαςίασ (Κ.Μ.Ε.) μποροφςε κάκε ςτιγμι να εκτελεί μόνο ζνα πρόγραμμα τουσ ςφγχρονουσ
ΛΕΙΣΟΤΡΓΙΚΆ ΤΣΉΜΑΣΑ 2 ο Εργαςτιριο Διαχείριςθ Διεργαςιϊν Τπόβακρο (1/3) τουσ παλαιότερουσ υπολογιςτζσ θ Κεντρικι Μονάδα Επεξεργαςίασ (Κ.Μ.Ε.) μποροφςε κάκε ςτιγμι να εκτελεί μόνο ζνα πρόγραμμα τουσ ςφγχρονουσ
ΒΙΟΛΟΓΟΙ ΓΙΑ ΦΥΣΙΚΟΥΣ
 ΦΥΣΙΚΗ vs ΒΙΟΛΟΓΙΑ ΒΙΟΛΟΓΟΙ ΓΙΑ ΦΥΣΙΚΟΥΣ «Προτείνω να αναπτφξουμε πρώτα αυτό που κα μποροφςε να ζχει τον τίτλο: «ιδζεσ ενόσ απλοϊκοφ φυςικοφ για τουσ οργανιςμοφσ». Κοντολογίσ, τισ ιδζεσ που κα μποροφςαν
ΦΥΣΙΚΗ vs ΒΙΟΛΟΓΙΑ ΒΙΟΛΟΓΟΙ ΓΙΑ ΦΥΣΙΚΟΥΣ «Προτείνω να αναπτφξουμε πρώτα αυτό που κα μποροφςε να ζχει τον τίτλο: «ιδζεσ ενόσ απλοϊκοφ φυςικοφ για τουσ οργανιςμοφσ». Κοντολογίσ, τισ ιδζεσ που κα μποροφςαν
ΟΙΚΙΑΚΗ ΟΙΚΟΝΟΜΙΑ ΑΡΙΘΜΟ ΑΝΑΠΛΗΡΩΣΩΝ
 ΟΙΚΙΑΚΗ ΟΙΚΟΝΟΜΙΑ ΔΙΟΡΙΜΟΙ ΜΟΝΙΜΩΝ ΚΑΘΗΓΗΣΩΝ ΟΙΚΙΑΚΗ ΟΙΚΟΝΟΜΙΑ ΑΡΙΘΜΟ ΔΙΟΡΙΘΕΝΣΩΝ 2006-2007 34 2007-2008 40 2008-2009 38 2009-2010 25 2010-2011 13 ΤΝΟΛΟ: 150 ΔΙΟΡΙΜΟΙ ( ΜΕΟ ΟΡΟ 30 ΔΙΟΡΙΜΟΙ ΑΝΑ ΕΣΟ) Με
ΟΙΚΙΑΚΗ ΟΙΚΟΝΟΜΙΑ ΔΙΟΡΙΜΟΙ ΜΟΝΙΜΩΝ ΚΑΘΗΓΗΣΩΝ ΟΙΚΙΑΚΗ ΟΙΚΟΝΟΜΙΑ ΑΡΙΘΜΟ ΔΙΟΡΙΘΕΝΣΩΝ 2006-2007 34 2007-2008 40 2008-2009 38 2009-2010 25 2010-2011 13 ΤΝΟΛΟ: 150 ΔΙΟΡΙΜΟΙ ( ΜΕΟ ΟΡΟ 30 ΔΙΟΡΙΜΟΙ ΑΝΑ ΕΣΟ) Με
Επαναληπτικό Διαγώνισμα Φυσικη ς Α Λυκει όυ Ε.Ο.Κ. και Ε.Ο.Μ.Κ.
 Επαναληπτικό Διαγώνισμα Φυσικη ς Α Λυκει όυ Ε.Ο.Κ. και Ε.Ο.Μ.Κ. Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα
Επαναληπτικό Διαγώνισμα Φυσικη ς Α Λυκει όυ Ε.Ο.Κ. και Ε.Ο.Μ.Κ. Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα
Πανελλαδικε σ Εξετα ςεισ Γ Τα ξησ Ημερη ςιου και Δ Τα ξησ Εςπερινου Γενικου Λυκει ου
 Ζνωςθ Ελλινων Χθμικϊν Πανελλαδικε σ Εξετα ςεισ Γ Τα ξησ Ημερη ςιου και Δ Τα ξησ Εςπερινου Γενικου Λυκει ου Χημεία 03/07/2017 Τμιμα Παιδείασ και Χθμικισ Εκπαίδευςθσ 0 Πανελλαδικε σ Εξετα ςεισ Γ Τα ξησ Ημερη
Ζνωςθ Ελλινων Χθμικϊν Πανελλαδικε σ Εξετα ςεισ Γ Τα ξησ Ημερη ςιου και Δ Τα ξησ Εςπερινου Γενικου Λυκει ου Χημεία 03/07/2017 Τμιμα Παιδείασ και Χθμικισ Εκπαίδευςθσ 0 Πανελλαδικε σ Εξετα ςεισ Γ Τα ξησ Ημερη
Διαγώνισμα Φυσική ς Α Λυκει ου Δυναμική σε μι α δια στασή και στο επι πεδο
 Διαγώνισμα Φυσική ς Α Λυκει ου Δυναμική σε μι α δια στασή και στο επι πεδο Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα
Διαγώνισμα Φυσική ς Α Λυκει ου Δυναμική σε μι α δια στασή και στο επι πεδο Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα
ΚΩΝΣΑΝΣΙΝΟ ΑΛ. ΝΑΚΟ ΜΑΘΗΜΑΣΙΚΟ M.Sc ΧΟΛΙΚΟ ΤΜΒΟΤΛΟ Πτυχ. ΚΟΙΝΩΝΙΚΗ ΟΙΚΟΝΟΜΙΑ
 1 ΚΩΝΣΑΝΣΙΝΟ ΑΛ. ΝΑΚΟ ΜΑΘΗΜΑΣΙΚΟ M.Sc ΧΟΛΙΚΟ ΤΜΒΟΤΛΟ Πτυχ. ΚΟΙΝΩΝΙΚΗ ΟΙΚΟΝΟΜΙΑ.ΣΙΡΚΑ 8 και ΑΝΣΤΠΑ 30100 ΑΓΡΙΝΙΟ Email: nakosk@sch.gr Σηλ 64105400 κι.69749695 ΜΕΓΙΣΑ-ΕΛΑΧΙΣΑ ΧΩΡΙ ΠΑΡΑΓΩΓΟΤ 3 ΕΙΣΑΓΩΓΗ Σα
1 ΚΩΝΣΑΝΣΙΝΟ ΑΛ. ΝΑΚΟ ΜΑΘΗΜΑΣΙΚΟ M.Sc ΧΟΛΙΚΟ ΤΜΒΟΤΛΟ Πτυχ. ΚΟΙΝΩΝΙΚΗ ΟΙΚΟΝΟΜΙΑ.ΣΙΡΚΑ 8 και ΑΝΣΤΠΑ 30100 ΑΓΡΙΝΙΟ Email: nakosk@sch.gr Σηλ 64105400 κι.69749695 ΜΕΓΙΣΑ-ΕΛΑΧΙΣΑ ΧΩΡΙ ΠΑΡΑΓΩΓΟΤ 3 ΕΙΣΑΓΩΓΗ Σα
Κριτθριο αξιολόγηςησ χημείασ προςανατολιςμοφ Γ Λυκείου
 ΘΕΜΑ Α. Στισ παρακάτω ερωτήςεισ πολλαπλήσ επιλογήσ Α1 έωσ και Α4 να επιλέξετε το γράμμα που αντιςτοιχεί ςτη ςωςτή απάντηςη. Α1. Ο αρικμόσ οξείδωςθσ του C ςτθν φορμαλδεΰδθ είναι : α. 0 β. -1 γ. +1 δ. +2
ΘΕΜΑ Α. Στισ παρακάτω ερωτήςεισ πολλαπλήσ επιλογήσ Α1 έωσ και Α4 να επιλέξετε το γράμμα που αντιςτοιχεί ςτη ςωςτή απάντηςη. Α1. Ο αρικμόσ οξείδωςθσ του C ςτθν φορμαλδεΰδθ είναι : α. 0 β. -1 γ. +1 δ. +2
Σ ΤΑΤ Ι Σ Τ Ι Κ Η. Statisticum collegium V
 Σ ΤΑΤ Ι Σ Τ Ι Κ Η i Statisticum collegium V Στατιςτική Συμπεραςματολογία Ι Σημειακζσ Εκτιμήςεισ Διαςτήματα Εμπιςτοςφνησ Στατιςτική Συμπεραςματολογία (Statistical Inference) Το πεδίο τθσ Στατιςτικισ Συμπεραςματολογία,
Σ ΤΑΤ Ι Σ Τ Ι Κ Η i Statisticum collegium V Στατιςτική Συμπεραςματολογία Ι Σημειακζσ Εκτιμήςεισ Διαςτήματα Εμπιςτοςφνησ Στατιςτική Συμπεραςματολογία (Statistical Inference) Το πεδίο τθσ Στατιςτικισ Συμπεραςματολογία,
Γενικά Μαθηματικά ΙΙ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Γενικά Μαθηματικά ΙΙ Ενότητα 10 η : Εφαρμογζσ Διανυςματικών Συναρτιςεων Λουκάσ Βλάχοσ Κακθγθτισ Αςτροφυςικισ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Γενικά Μαθηματικά ΙΙ Ενότητα 10 η : Εφαρμογζσ Διανυςματικών Συναρτιςεων Λουκάσ Βλάχοσ Κακθγθτισ Αςτροφυςικισ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό
Διαγώνισμα Φυσική ς Α Λυκει ου Έργο και Ενε ργεια
 Διαγώνισμα Φυσική ς Α Λυκει ου Έργο και Ενε ργεια Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα που αντιςτοιχεί
Διαγώνισμα Φυσική ς Α Λυκει ου Έργο και Ενε ργεια Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα που αντιςτοιχεί
Γράφοι. Δομζσ Δεδομζνων Διάλεξθ 9
 Γράφοι Δομζσ Δεδομζνων Διάλεξθ 9 Περιεχόμενα Γράφοι Γενικζσ ζννοιεσ, οριςμόσ, κτλ Παραδείγματα Γράφων Αποκικευςθ Γράφων Βαςικοί Οριςμοί Γράφοι και Δζντρα Διάςχιςθ Γράφων Περιοδεφων Πωλθτισ Γράφοι Οριςμόσ:
Γράφοι Δομζσ Δεδομζνων Διάλεξθ 9 Περιεχόμενα Γράφοι Γενικζσ ζννοιεσ, οριςμόσ, κτλ Παραδείγματα Γράφων Αποκικευςθ Γράφων Βαςικοί Οριςμοί Γράφοι και Δζντρα Διάςχιςθ Γράφων Περιοδεφων Πωλθτισ Γράφοι Οριςμόσ:
ΘΕΡΜΟΔΤΝΑΜΙΚΗ Ι. Ενότθτα 3: Μθδενικόσ Νόμοσ - Ζργο. ογομϊν Μπογοςιάν Πολυτεχνικι χολι Σμιμα Χθμικϊν Μθχανικϊν
 ΘΕΡΜΟΔΤΝΑΜΙΚΗ Ι Ενότθτα 3: Μθδενικόσ Νόμοσ - Ζργο ογομϊν Μπογοςιάν Πολυτεχνικι χολι Σμιμα Χθμικϊν Μθχανικϊν κοποί ενότθτασ κοπόσ τθσ ενότθτασ αυτισ είναι θ περιγραφι των οριςμϊν και των κεμελιωδϊν εννοιϊν
ΘΕΡΜΟΔΤΝΑΜΙΚΗ Ι Ενότθτα 3: Μθδενικόσ Νόμοσ - Ζργο ογομϊν Μπογοςιάν Πολυτεχνικι χολι Σμιμα Χθμικϊν Μθχανικϊν κοποί ενότθτασ κοπόσ τθσ ενότθτασ αυτισ είναι θ περιγραφι των οριςμϊν και των κεμελιωδϊν εννοιϊν
Προχωρθμζνα Θζματα Συςτθμάτων Ελζγχου
 ΠΑΝΕΠΙΣΗΜΙΟ ΑΙΓΑIΟΤ & ΑΕΙ ΠΕΙΡΑΙΑ Σ.Σ. Σμήματα Ναυτιλίας και Επιχειρηματικών Τπηρεσιών & Μηχ. Αυτοματισμού ΣΕ Π.Μ.. «Νέες Σεχνολογίες στη Ναυτιλία και τις Μεταφορές» Προχωρθμζνα Θζματα Συςτθμάτων Ελζγχου
ΠΑΝΕΠΙΣΗΜΙΟ ΑΙΓΑIΟΤ & ΑΕΙ ΠΕΙΡΑΙΑ Σ.Σ. Σμήματα Ναυτιλίας και Επιχειρηματικών Τπηρεσιών & Μηχ. Αυτοματισμού ΣΕ Π.Μ.. «Νέες Σεχνολογίες στη Ναυτιλία και τις Μεταφορές» Προχωρθμζνα Θζματα Συςτθμάτων Ελζγχου
ΑΔΡΑΝΕΙΑ ΜΑΘΗΣΕ: ΜΑΡΙΑΝΝΑ ΠΑΡΑΘΤΡΑ ΑΝΑΣΑΗ ΠΟΤΛΙΟ ΠΑΝΑΓΙΩΣΗ ΠΡΟΔΡΟΜΟΤ ΑΝΑΣΑΙΑ ΠΟΛΤΧΡΟΝΙΑΔΟΤ ΙΩΑΝΝΑ ΠΕΝΓΚΟΤ
 ΑΔΡΑΝΕΙΑ ΜΑΘΗΣΕ: ΜΑΡΙΑΝΝΑ ΠΑΡΑΘΤΡΑ ΑΝΑΣΑΗ ΠΟΤΛΙΟ ΠΑΝΑΓΙΩΣΗ ΠΡΟΔΡΟΜΟΤ ΑΝΑΣΑΙΑ ΠΟΛΤΧΡΟΝΙΑΔΟΤ ΙΩΑΝΝΑ ΠΕΝΓΚΟΤ Οριςμόσ: Με τον όρο αδράνεια ςτθ Φυςικι ονομάηεται θ χαρακτθριςτικι ιδιότθτα των ςωμάτων να αντιςτζκονται
ΑΔΡΑΝΕΙΑ ΜΑΘΗΣΕ: ΜΑΡΙΑΝΝΑ ΠΑΡΑΘΤΡΑ ΑΝΑΣΑΗ ΠΟΤΛΙΟ ΠΑΝΑΓΙΩΣΗ ΠΡΟΔΡΟΜΟΤ ΑΝΑΣΑΙΑ ΠΟΛΤΧΡΟΝΙΑΔΟΤ ΙΩΑΝΝΑ ΠΕΝΓΚΟΤ Οριςμόσ: Με τον όρο αδράνεια ςτθ Φυςικι ονομάηεται θ χαρακτθριςτικι ιδιότθτα των ςωμάτων να αντιςτζκονται
Η αυτεπαγωγή ενός δακτυλίου
 Η αυτεπαγωγή ενός δακτυλίου Υποκζςτε ότι κρατάτε ςτο χζρι ςασ ζναν μεταλλικό δακτφλιο διαμζτρου πχ 5 cm. Ζνασ φυςικόσ πικανότθτα κα προβλθματιςτεί: τι αυτεπαγωγι ζχει άραγε; Νομίηω κα ιταν μια καλι ιδζα
Η αυτεπαγωγή ενός δακτυλίου Υποκζςτε ότι κρατάτε ςτο χζρι ςασ ζναν μεταλλικό δακτφλιο διαμζτρου πχ 5 cm. Ζνασ φυςικόσ πικανότθτα κα προβλθματιςτεί: τι αυτεπαγωγι ζχει άραγε; Νομίηω κα ιταν μια καλι ιδζα
Διδάςκων: Κακθγθτισ Αλζξανδροσ Ριγασ υνεπικουρία: πφρογλου Ιωάννθσ
 ΔΗΜΟΚΡΙΣΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΡΑΚΗ ΣΜΗΜΑ ΗΛΕΚΣΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΤΠΟΛΟΓΙΣΩΝ ΣΟΜΕΑ ΣΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΚΑΙ ΔΙΑΣΗΜΙΚΗ Βιοϊατρική Σεχνολογία 9 ο Εξάμηνο Διδάςκων: Κακθγθτισ Αλζξανδροσ Ριγασ υνεπικουρία:
ΔΗΜΟΚΡΙΣΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΡΑΚΗ ΣΜΗΜΑ ΗΛΕΚΣΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΤΠΟΛΟΓΙΣΩΝ ΣΟΜΕΑ ΣΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΚΑΙ ΔΙΑΣΗΜΙΚΗ Βιοϊατρική Σεχνολογία 9 ο Εξάμηνο Διδάςκων: Κακθγθτισ Αλζξανδροσ Ριγασ υνεπικουρία:
ΝΟΜΟΙ ΚΙΝΗΗ ΠΛΑΝΗΣΩΝ ΣΟΤ ΚΕΠΛΕΡ
 ΝΟΜΟΙ ΚΙΝΗΗ ΠΛΑΝΗΣΩΝ ΣΟΤ ΚΕΠΛΕΡ 1. Νόμοσ των ελλειπτικών τροχιών Η τροχιζσ των πλανθτϊν είναι ελλείψεισ, των οποίων τθ μία εςτία κατζχει ο Ήλιοσ. Προφανϊσ όλοι οι πλανιτεσ του ίδιου πλανθτικοφ ςυςτιματοσ
ΝΟΜΟΙ ΚΙΝΗΗ ΠΛΑΝΗΣΩΝ ΣΟΤ ΚΕΠΛΕΡ 1. Νόμοσ των ελλειπτικών τροχιών Η τροχιζσ των πλανθτϊν είναι ελλείψεισ, των οποίων τθ μία εςτία κατζχει ο Ήλιοσ. Προφανϊσ όλοι οι πλανιτεσ του ίδιου πλανθτικοφ ςυςτιματοσ
Δυναμικι Μθχανϊν I. Διάλεξθ 16. Χειμερινό Εξάμθνο 2013 Τμιμα Μθχανολόγων Μθχ., ΕΜΠ
 Δυναμικι Μθχανϊν I Διάλεξθ 16 Χειμερινό Εξάμθνο 2013 Τμιμα Μθχανολόγων Μθχ., ΕΜΠ 1 Ανακοινϊςεισ Office Hours: Δευτζρα 1-3 μμ, Εργαςτιριο Εμβιομθχανικισ, Ιςόγειο Κτθρίου Μ (210 772-1516) DMmeche2013@gmail.com
Δυναμικι Μθχανϊν I Διάλεξθ 16 Χειμερινό Εξάμθνο 2013 Τμιμα Μθχανολόγων Μθχ., ΕΜΠ 1 Ανακοινϊςεισ Office Hours: Δευτζρα 1-3 μμ, Εργαςτιριο Εμβιομθχανικισ, Ιςόγειο Κτθρίου Μ (210 772-1516) DMmeche2013@gmail.com
Απάντηση ΘΕΜΑ1 ΘΕΜΑ2. t=t 1 +T/2. t=t 1 +3T/4. t=t 1 +T ΔΙΑΓΩΝΙΣΜΑ ΣΕ ΤΑΛΑΝΤΩΣΕΙΣ-ΚΥΜΑΤΑ 1) (Β), 2. (Γ), 3. (Γ), 4. (Γ), 5. (Δ).
 Απάντηση ΘΕΜΑ1 1) (Β), 2. (Γ), 3. (Γ), 4. (Γ), 5. (Δ). ΘΕΜΑ2 Α)Ανάκλαςθ ςε ακίνθτο άκρο. Το προςπίπτον κφμα ςε χρόνο Τ/2 κα ζχει μετακινθκεί προσ τα δεξιά κατά 2 τετράγωνα όπωσ φαίνεται ςτο ςχιμα. Για
Απάντηση ΘΕΜΑ1 1) (Β), 2. (Γ), 3. (Γ), 4. (Γ), 5. (Δ). ΘΕΜΑ2 Α)Ανάκλαςθ ςε ακίνθτο άκρο. Το προςπίπτον κφμα ςε χρόνο Τ/2 κα ζχει μετακινθκεί προσ τα δεξιά κατά 2 τετράγωνα όπωσ φαίνεται ςτο ςχιμα. Για
ΦΥΕ 14 ΑΚΑΔ. ΕΤΟΣ Η ΕΡΓΑΣΙΑ. Ημερομηνία παράδοςησ: 12 Νοεμβρίου (Όλεσ οι αςκιςεισ βακμολογοφνται ιςοτίμωσ με 10 μονάδεσ θ κάκε μία)
 ΦΥΕ ΑΚΑΔ. ΕΤΟΣ 007-008 Η ΕΡΓΑΣΙΑ Ημερομηνία παράδοςησ: Νοεμβρίου 007 (Όλεσ οι αςκιςεισ βακμολογοφνται ιςοτίμωσ με 0 μονάδεσ θ κάκε μία) Άςκηςη α) Να υπολογιςκεί θ προβολι του πάνω ςτο διάνυςμα όταν: (.
ΦΥΕ ΑΚΑΔ. ΕΤΟΣ 007-008 Η ΕΡΓΑΣΙΑ Ημερομηνία παράδοςησ: Νοεμβρίου 007 (Όλεσ οι αςκιςεισ βακμολογοφνται ιςοτίμωσ με 0 μονάδεσ θ κάκε μία) Άςκηςη α) Να υπολογιςκεί θ προβολι του πάνω ςτο διάνυςμα όταν: (.
ΝΟΜΟ ΣΟΤ BOYLE(βαςιςμζνο ςε πείραμα)
 2ο ΠΕΙΡΑΜΑΣΙΚΟ ΛΤΚΕΙΟ ΑΘΗΝΩΝ τθσ Κυπραίου Φωτεινισ 'Eτοσ:2012-2013 ΝΟΜΟ ΣΟΤ BOYLE(βαςιςμζνο ςε πείραμα) O Νόμος του Boyle τθ κερμοδυναμικι ο Νόμοσ του Boyle είναι ζνασ από τουσ τρεισ νόμουσ των αερίων.ωσ
2ο ΠΕΙΡΑΜΑΣΙΚΟ ΛΤΚΕΙΟ ΑΘΗΝΩΝ τθσ Κυπραίου Φωτεινισ 'Eτοσ:2012-2013 ΝΟΜΟ ΣΟΤ BOYLE(βαςιςμζνο ςε πείραμα) O Νόμος του Boyle τθ κερμοδυναμικι ο Νόμοσ του Boyle είναι ζνασ από τουσ τρεισ νόμουσ των αερίων.ωσ
Ζρευνα ικανοποίθςθσ τουριςτϊν
 Ζρευνα ικανοποίθςθσ τουριςτϊν Ammon Ovis_Ζρευνα ικανοποίθςθσ τουριςτϊν_ Ραδιοςτακμόσ Flash 96 1 ΣΤΟΙΧΕΙΑ ΔΕΙΓΜΑΤΟΣ Σο δείγμα περιλαμβάνει 332 τουρίςτεσ από 5 διαφορετικζσ θπείρουσ. Οι περιςςότεροι εξ αυτϊν
Ζρευνα ικανοποίθςθσ τουριςτϊν Ammon Ovis_Ζρευνα ικανοποίθςθσ τουριςτϊν_ Ραδιοςτακμόσ Flash 96 1 ΣΤΟΙΧΕΙΑ ΔΕΙΓΜΑΤΟΣ Σο δείγμα περιλαμβάνει 332 τουρίςτεσ από 5 διαφορετικζσ θπείρουσ. Οι περιςςότεροι εξ αυτϊν
ΑΝΑΚΟΙΝΩΗ ΜΕΣΑΒΑΣΙΚΩΝ ΡΤΘΜΙΕΩΝ ΓΙΑ ΣΙ ΑΛΛΑΓΕ ΣΟ ΠΡΟΓΡΑΜΜΑ ΠΟΤΔΩΝ ΣΟΤ ΣΜΗΜΑΣΟ ΜΗΧ. ΣΕΧΝΟΛΟΓΙΑ ΑΕΡΟΚΑΦΩΝ
 ΑΝΑΚΟΙΝΩΗ ΜΕΣΑΒΑΣΙΚΩΝ ΡΤΘΜΙΕΩΝ ΓΙΑ ΣΙ ΑΛΛΑΓΕ ΣΟ ΠΡΟΓΡΑΜΜΑ ΠΟΤΔΩΝ ΣΟΤ ΣΜΗΜΑΣΟ ΜΗΧ. ΣΕΧΝΟΛΟΓΙΑ ΑΕΡΟΚΑΦΩΝ Πλοι οι ςπουδαςτζσ ακολουκοφν το νζο πρόγραμμα ςπουδών από το παρόν εξάμθνο που βρίςκονται. Για τα
ΑΝΑΚΟΙΝΩΗ ΜΕΣΑΒΑΣΙΚΩΝ ΡΤΘΜΙΕΩΝ ΓΙΑ ΣΙ ΑΛΛΑΓΕ ΣΟ ΠΡΟΓΡΑΜΜΑ ΠΟΤΔΩΝ ΣΟΤ ΣΜΗΜΑΣΟ ΜΗΧ. ΣΕΧΝΟΛΟΓΙΑ ΑΕΡΟΚΑΦΩΝ Πλοι οι ςπουδαςτζσ ακολουκοφν το νζο πρόγραμμα ςπουδών από το παρόν εξάμθνο που βρίςκονται. Για τα
ΘΥ101: Ειςαγωγι ςτθν Πλθροφορικι
 Παράςταςη κινητήσ υποδιαςτολήσ ςφμφωνα με το πρότυπο ΙΕΕΕ Δρ. Χρήστος Ηλιούδης το πρότυπο ΙΕΕΕ 754 ζχει χρθςιμοποιθκεί ευρζωσ ςε πραγματικοφσ υπολογιςτζσ. Το πρότυπο αυτό κακορίηει δφο βαςικζσ μορφζσ κινθτισ
Παράςταςη κινητήσ υποδιαςτολήσ ςφμφωνα με το πρότυπο ΙΕΕΕ Δρ. Χρήστος Ηλιούδης το πρότυπο ΙΕΕΕ 754 ζχει χρθςιμοποιθκεί ευρζωσ ςε πραγματικοφσ υπολογιςτζσ. Το πρότυπο αυτό κακορίηει δφο βαςικζσ μορφζσ κινθτισ
Slide 1. Εισαγωγή στη ψυχρομετρία
 Slide 1 Εισαγωγή στη ψυχρομετρία 1 Slide 2 Σφντομη ειςαγωγή ςτη ψυχρομετρία. Διάγραμμα Mollier (πίεςησ-ενθαλπίασ P-H) Σο διάγραμμα Mollier είναι μία γραφικι παράςταςθ ςε ζναν άξονα ςυντεταγμζνων γραμμϊν
Slide 1 Εισαγωγή στη ψυχρομετρία 1 Slide 2 Σφντομη ειςαγωγή ςτη ψυχρομετρία. Διάγραμμα Mollier (πίεςησ-ενθαλπίασ P-H) Σο διάγραμμα Mollier είναι μία γραφικι παράςταςθ ςε ζναν άξονα ςυντεταγμζνων γραμμϊν
ΛΕΙΣΟΤΡΓΙΚΆ ΤΣΉΜΑΣΑ. 7 θ Διάλεξθ Διαχείριςθ Μνιμθσ Μζροσ Γ
 ΛΕΙΣΟΤΡΓΙΚΆ ΤΣΉΜΑΣΑ 7 θ Διάλεξθ Διαχείριςθ Μνιμθσ Μζροσ Γ ελιδοποίθςθ (1/10) Σόςο θ κατάτμθςθ διαμεριςμάτων ςτακεροφ μεγζκουσ όςο και θ κατάτμθςθ διαμεριςμάτων μεταβλθτοφ και άνιςου μεγζκουσ δεν κάνουν
ΛΕΙΣΟΤΡΓΙΚΆ ΤΣΉΜΑΣΑ 7 θ Διάλεξθ Διαχείριςθ Μνιμθσ Μζροσ Γ ελιδοποίθςθ (1/10) Σόςο θ κατάτμθςθ διαμεριςμάτων ςτακεροφ μεγζκουσ όςο και θ κατάτμθςθ διαμεριςμάτων μεταβλθτοφ και άνιςου μεγζκουσ δεν κάνουν
Άπειρεσ κροφςεισ. Τθ χρονικι ςτιγμι. t, ο δακτφλιοσ ςυγκροφεται με τον τοίχο με ταχφτθτα (κζντρου μάηασ) μζτρου
 Άπειρεσ κροφςεισ Δακτφλιοσ ακτίνασ κυλάει ςε οριηόντιο δάπεδο προσ ζνα κατακόρυφο τοίχο όπωσ φαίνεται ςτο ςχιμα. Ο ςυντελεςτισ τριβισ ίςκθςθσ του δακτυλίου με το δάπεδο είναι, ενϊ ο τοίχοσ είναι λείοσ.
Άπειρεσ κροφςεισ Δακτφλιοσ ακτίνασ κυλάει ςε οριηόντιο δάπεδο προσ ζνα κατακόρυφο τοίχο όπωσ φαίνεται ςτο ςχιμα. Ο ςυντελεςτισ τριβισ ίςκθςθσ του δακτυλίου με το δάπεδο είναι, ενϊ ο τοίχοσ είναι λείοσ.
Επαναληπτικές Ασκήσεις στα κευ 1 και 2
 Επαναληπτικές Ασκήσεις στα κευ 1 και 2 1. Αζριο με όγκο 0,004 m 3 κερμαίνεται με ςτακερι πίεςθ p =1,2 atm μζχρι ο όγκοσ του να γίνει 0,006 m 3. Τπολογίςτε το ζργο που παράγει το αζριο. Δίνεται 1 atm =
Επαναληπτικές Ασκήσεις στα κευ 1 και 2 1. Αζριο με όγκο 0,004 m 3 κερμαίνεται με ςτακερι πίεςθ p =1,2 atm μζχρι ο όγκοσ του να γίνει 0,006 m 3. Τπολογίςτε το ζργο που παράγει το αζριο. Δίνεται 1 atm =
Η άςκθςθ αποτελεί τροποποιθμζνθ εκδοχι του κζματοσ φυςικισ, τθσ Ευρωπαϊκισ Ολυμπιάδασ Φυςικών Επιςτθμών 2009_επιμζλεια κζματοσ: Κώςτασ Παπαμιχάλθσ
 ΕΚΦΕ Αχαρνών Η άςκθςθ αποτελεί τροποποιθμζνθ εκδοχι του κζματοσ φυςικισ, τθσ Ευρωπαϊκισ Ολυμπιάδασ Φυςικών Επιςτθμών 9_επιμζλεια κζματοσ: Κώςτασ Παπαμιχάλθσ Εφαρμογζσ τθσ Αρχισ του Αρχιμιδθ & τθσ ςυνκικθσ
ΕΚΦΕ Αχαρνών Η άςκθςθ αποτελεί τροποποιθμζνθ εκδοχι του κζματοσ φυςικισ, τθσ Ευρωπαϊκισ Ολυμπιάδασ Φυςικών Επιςτθμών 9_επιμζλεια κζματοσ: Κώςτασ Παπαμιχάλθσ Εφαρμογζσ τθσ Αρχισ του Αρχιμιδθ & τθσ ςυνκικθσ
Πειραματικι Ψυχολογία (ΨΧ66)
 Πειραματικι Ψυχολογία (ΨΧ66) Διάλεξη 7 Σεχνικζσ για τθν επίτευξθ ςτακερότθτασ Πζτροσ Ροφςςοσ Μζθοδοι για την επίτευξη του ελζγχου Μζςω του κατάλλθλου ςχεδιαςμοφ του πειράματοσ (ςτόχοσ είναι θ εξάλειψθ
Πειραματικι Ψυχολογία (ΨΧ66) Διάλεξη 7 Σεχνικζσ για τθν επίτευξθ ςτακερότθτασ Πζτροσ Ροφςςοσ Μζθοδοι για την επίτευξη του ελζγχου Μζςω του κατάλλθλου ςχεδιαςμοφ του πειράματοσ (ςτόχοσ είναι θ εξάλειψθ
ΡΑΝΕΛΛΘΝΙΕΣ ΕΞΕΤΑΣΕΙΣ 2014 ΧΗΜΕΙΑ ΘΕΤΙΚΘΣ ΚΑΤΕΥΘΥΝΣΘΣ
 ΡΑΝΕΛΛΘΝΙΕΣ ΕΞΕΤΑΣΕΙΣ 2014 ΧΗΜΕΙΑ ΘΕΤΙΚΘΣ ΚΑΤΕΥΘΥΝΣΘΣ Θζμα Α Α1: γ, Α2: β, Α3: α, Α4: β, A5: β Θζμα Β Β1: Σ ι Λ (ελλιπισ διατφπωςθ), Λ, Σ, Σ, Σ Β2: α) Οι διαφορζσ μεταξφ ς και π δεςμοφ είναι: α. Στον ς
ΡΑΝΕΛΛΘΝΙΕΣ ΕΞΕΤΑΣΕΙΣ 2014 ΧΗΜΕΙΑ ΘΕΤΙΚΘΣ ΚΑΤΕΥΘΥΝΣΘΣ Θζμα Α Α1: γ, Α2: β, Α3: α, Α4: β, A5: β Θζμα Β Β1: Σ ι Λ (ελλιπισ διατφπωςθ), Λ, Σ, Σ, Σ Β2: α) Οι διαφορζσ μεταξφ ς και π δεςμοφ είναι: α. Στον ς
ΧΕΔΙΑΜΟ ΠΡΟΪΟΝΣΩΝ ΜΕ Η/Τ
 ΧΕΔΙΑΜΟ ΠΡΟΪΟΝΣΩΝ ΜΕ Η/Τ ΚΑΜΠΤΛΕ ΕΛΕΤΘΕΡΗ ΜΟΡΦΗ Χριςιμεσ για τθν περιγραφι ομαλών και ελεφκερων ςχθμάτων Αμάξωμα αυτοκινιτου, πτερφγια αεροςκαφών, ςκελετόσ πλοίου χιματα χαρακτιρων κινουμζνων ςχεδίων Περιγραφι
ΧΕΔΙΑΜΟ ΠΡΟΪΟΝΣΩΝ ΜΕ Η/Τ ΚΑΜΠΤΛΕ ΕΛΕΤΘΕΡΗ ΜΟΡΦΗ Χριςιμεσ για τθν περιγραφι ομαλών και ελεφκερων ςχθμάτων Αμάξωμα αυτοκινιτου, πτερφγια αεροςκαφών, ςκελετόσ πλοίου χιματα χαρακτιρων κινουμζνων ςχεδίων Περιγραφι
ΘΕΡΜΟΔΤΝΑΜΙΚΗ IΙ. Ενότθτα 4: Χθμικζσ αντιδράςεισ αερίων τακερά Χθμικισ Ιςορροπίασ Πρότυπθ Ελεφκερθ Ενζργεια
 ΘΕΡΜΟΔΤΝΑΜΙΚΗ IΙ Ενότθτα 4: Χθμικζσ αντιδράςεισ αερίων τακερά Χθμικισ Ιςορροπίασ Πρότυπθ Ελεφκερθ Ενζργεια ογομών Μπογοςιάν Πολυτεχνικι χολι Σμιμα Χθμικών Μθχανικών κοποί ενότθτασ κοπόσ τθσ ενότθτασ αυτισ
ΘΕΡΜΟΔΤΝΑΜΙΚΗ IΙ Ενότθτα 4: Χθμικζσ αντιδράςεισ αερίων τακερά Χθμικισ Ιςορροπίασ Πρότυπθ Ελεφκερθ Ενζργεια ογομών Μπογοςιάν Πολυτεχνικι χολι Σμιμα Χθμικών Μθχανικών κοποί ενότθτασ κοπόσ τθσ ενότθτασ αυτισ
ΟΝΟΜΑΣΕΠΩΝΤMΟ: ΗΜΕΡΟΜΗΝΙΑ: ΕΙΡΑ: 3 ΕΞΕΣΑΣΕΑ ΤΛΗ: ΗΛΕΚΣΡΙΚΟ ΠΕΔΙΟ- ΜΑΓΝΗΣΙΚΟ ΠΕΔΙΟ- ΕΠΑΓΩΓΗ
 ΜΑΘΗΜΑ /ΣΑΞΗ: ΦΤΙΚΗ ΚΑΣΕΤΘΤΝΗ / Β ΛΤΚΕΙΟΤ ΟΝΟΜΑΣΕΠΩΝΤMΟ: ΗΜΕΡΟΜΗΝΙΑ: ΕΙΡΑ: 3 ΕΞΕΣΑΣΕΑ ΤΛΗ: ΗΛΕΚΣΡΙΚΟ ΠΕΔΙΟ- ΜΑΓΝΗΣΙΚΟ ΠΕΔΙΟ- ΕΠΑΓΩΓΗ ΘΕΜΑ Α 1. Δφο ςθμειακά φορτία απζχον μεταξφ τοσ απόςταςθ r και θ δναμικι
ΜΑΘΗΜΑ /ΣΑΞΗ: ΦΤΙΚΗ ΚΑΣΕΤΘΤΝΗ / Β ΛΤΚΕΙΟΤ ΟΝΟΜΑΣΕΠΩΝΤMΟ: ΗΜΕΡΟΜΗΝΙΑ: ΕΙΡΑ: 3 ΕΞΕΣΑΣΕΑ ΤΛΗ: ΗΛΕΚΣΡΙΚΟ ΠΕΔΙΟ- ΜΑΓΝΗΣΙΚΟ ΠΕΔΙΟ- ΕΠΑΓΩΓΗ ΘΕΜΑ Α 1. Δφο ςθμειακά φορτία απζχον μεταξφ τοσ απόςταςθ r και θ δναμικι
Αυτόνομοι Πράκτορες. Αναφορά Εργασίας Εξαμήνου. Το αστέρι του Aibo και τα κόκαλα του
 Αυτόνομοι Πράκτορες Αναφορά Εργασίας Εξαμήνου Το αστέρι του Aibo και τα κόκαλα του Jaohar Osman Η πρόταςθ εργαςίασ που ζκανα είναι το παρακάτω κείμενο : - ξ Aibo αγαπάει πάρα πξλύ ρα κόκαλα και πάμρα ρα
Αυτόνομοι Πράκτορες Αναφορά Εργασίας Εξαμήνου Το αστέρι του Aibo και τα κόκαλα του Jaohar Osman Η πρόταςθ εργαςίασ που ζκανα είναι το παρακάτω κείμενο : - ξ Aibo αγαπάει πάρα πξλύ ρα κόκαλα και πάμρα ρα
lim x και lim f(β) f(β). (β > 0)
 . Δίνεται θ παραγωγίςιμθ ςτο * α, β + ( 0 < α < β ) ςυνάρτθςθ f για τθν οποία ιςχφουν: f(α) lim (-) a και lim ( f(β)) = Να δείξετε ότι: α. f(α) < α και f(β) > β β. Αν g() = τότε θ C f και C g ζχουν ζνα
. Δίνεται θ παραγωγίςιμθ ςτο * α, β + ( 0 < α < β ) ςυνάρτθςθ f για τθν οποία ιςχφουν: f(α) lim (-) a και lim ( f(β)) = Να δείξετε ότι: α. f(α) < α και f(β) > β β. Αν g() = τότε θ C f και C g ζχουν ζνα
Δείκτεσ απόδοςθσ υλικών
 Δείκτεσ απόδοςθσ υλικών Κάκε ςυνδυαςμόσ λειτουργίασ, περιοριςμϊν και ςτόχων, οδθγεί ςε ζνα μζτρο τθσ απόδοςθσ τθσ λειτουργίασ του εξαρτιματοσ και περιζχει μια ομάδα ιδιοτιτων των υλικϊν. Αυτι θ ομάδα των
Δείκτεσ απόδοςθσ υλικών Κάκε ςυνδυαςμόσ λειτουργίασ, περιοριςμϊν και ςτόχων, οδθγεί ςε ζνα μζτρο τθσ απόδοςθσ τθσ λειτουργίασ του εξαρτιματοσ και περιζχει μια ομάδα ιδιοτιτων των υλικϊν. Αυτι θ ομάδα των
Τεχνικζσ Ανάλυςησ Διοικητικών Αποφάςεων
 Τεχνικζσ Ανάλυςησ Διοικητικών Αποφάςεων Ενότητα 3: υςτιματα ουρϊν αναμονισ Κακθγθτισ Γιάννθσ Γιαννίκοσ χολι Οργάνωςθσ και Διοίκθςθσ Επιχειριςεων Σμιμα Διοίκθςθσ Επιχειριςεων Σκοποί ενότητασ Μελζτθ ςυςτθμάτων
Τεχνικζσ Ανάλυςησ Διοικητικών Αποφάςεων Ενότητα 3: υςτιματα ουρϊν αναμονισ Κακθγθτισ Γιάννθσ Γιαννίκοσ χολι Οργάνωςθσ και Διοίκθςθσ Επιχειριςεων Σμιμα Διοίκθςθσ Επιχειριςεων Σκοποί ενότητασ Μελζτθ ςυςτθμάτων
ΑΠΟΣΕΛΕΜΑΣΑ ΑΞΙΟΛΟΓΗΗ ΣΟΤ ΔΙΔΑΚΣΙΚΟΤ ΕΡΓΟΤ ΣΩΝ ΤΠΟΧΡΕΩΣΙΚΩΝ ΜΑΘΗΜΑΣΩΝ ΕΑΡΙΝΟΤ ΕΞΑΜΗΝΟΤ ΑΚΑΔΗΜΑΪΚΟΤ ΕΣΟΤ
 ΑΠΟΣΕΛΕΜΑΣΑ ΑΞΙΟΛΟΓΗΗ ΣΟΤ ΔΙΔΑΚΣΙΚΟΤ ΕΡΓΟΤ ΣΩΝ ΤΠΟΧΡΕΩΣΙΚΩΝ ΜΑΘΗΜΑΣΩΝ ΕΑΡΙΝΟΤ ΕΞΑΜΗΝΟΤ ΑΚΑΔΗΜΑΪΚΟΤ ΕΣΟΤ 2010-2011 Κατά τθ διάρκεια παρακολοφκθςθσ των μακθμάτων του εαρινοφ εξαμινου του ακαδθμαϊκοφ ζτουσ
ΑΠΟΣΕΛΕΜΑΣΑ ΑΞΙΟΛΟΓΗΗ ΣΟΤ ΔΙΔΑΚΣΙΚΟΤ ΕΡΓΟΤ ΣΩΝ ΤΠΟΧΡΕΩΣΙΚΩΝ ΜΑΘΗΜΑΣΩΝ ΕΑΡΙΝΟΤ ΕΞΑΜΗΝΟΤ ΑΚΑΔΗΜΑΪΚΟΤ ΕΣΟΤ 2010-2011 Κατά τθ διάρκεια παρακολοφκθςθσ των μακθμάτων του εαρινοφ εξαμινου του ακαδθμαϊκοφ ζτουσ
Modellus 4.01 Συ ντομοσ Οδηγο σ
 Νίκοσ Αναςταςάκθσ 4.01 Συ ντομοσ Οδηγο σ Περιγραφή Σο είναι λογιςμικό προςομοιϊςεων που ςτθρίηει τθν λειτουργία του ςε μακθματικά μοντζλα. ε αντίκεςθ με άλλα λογιςμικά (π.χ. Interactive Physics, Crocodile
Νίκοσ Αναςταςάκθσ 4.01 Συ ντομοσ Οδηγο σ Περιγραφή Σο είναι λογιςμικό προςομοιϊςεων που ςτθρίηει τθν λειτουργία του ςε μακθματικά μοντζλα. ε αντίκεςθ με άλλα λογιςμικά (π.χ. Interactive Physics, Crocodile
Διαγώνιςμα Γ Λυκείου Ιανουάριοσ2018
 Διαγώνιςμα Γ Λυκείου Ιανουάριοσ08 Διάρκεια Εξζταςησ 3ώρεσ Ονοματεπώνυμο. ΘΕΜΑ Α: Στισ ερωτήςεισ Α ωσ και Α4 επιλζξτε την ςωςτή απάντηςη: Α.Αν το πλάτοσ Α μιασ φκίνουςασ ταλάντωςθσ μεταβάλλεται με το χρόνο
Διαγώνιςμα Γ Λυκείου Ιανουάριοσ08 Διάρκεια Εξζταςησ 3ώρεσ Ονοματεπώνυμο. ΘΕΜΑ Α: Στισ ερωτήςεισ Α ωσ και Α4 επιλζξτε την ςωςτή απάντηςη: Α.Αν το πλάτοσ Α μιασ φκίνουςασ ταλάντωςθσ μεταβάλλεται με το χρόνο
ΕΡΓΑΣΗΡΙΑΚΗ ΑΚΗΗ ΜΕΛΕΣΗ ΣΗ ΚΙΝΗΗ ΩΜΑΣΟ Ε ΠΛΑΓΙΟ ΕΠΙΠΕΔΟ - ΜΕΣΡΗΗ ΣΟΤ ΤΝΣΕΛΕΣΗ ΣΡΙΒΗ ΟΛΙΘΗΗ
 ΕΡΓΑΣΗΡΙΑΚΗ ΑΚΗΗ ΜΕΛΕΣΗ ΣΗ ΚΙΝΗΗ ΩΜΑΣΟ Ε ΠΛΑΓΙΟ ΕΠΙΠΕΔΟ - ΜΕΣΡΗΗ ΣΟΤ ΤΝΣΕΛΕΣΗ ΣΡΙΒΗ ΟΛΙΘΗΗ ΕΚΦΕ Α & Β ΑΝΑΣΟΛΙΚΗ ΑΣΣΙΚΗ τόχοι Μετά το πζρασ τθσ εργαςτθριακισ άςκθςθσ, οι μακθτζσ κα πρζπει να είναι ςε κζςθ:
ΕΡΓΑΣΗΡΙΑΚΗ ΑΚΗΗ ΜΕΛΕΣΗ ΣΗ ΚΙΝΗΗ ΩΜΑΣΟ Ε ΠΛΑΓΙΟ ΕΠΙΠΕΔΟ - ΜΕΣΡΗΗ ΣΟΤ ΤΝΣΕΛΕΣΗ ΣΡΙΒΗ ΟΛΙΘΗΗ ΕΚΦΕ Α & Β ΑΝΑΣΟΛΙΚΗ ΑΣΣΙΚΗ τόχοι Μετά το πζρασ τθσ εργαςτθριακισ άςκθςθσ, οι μακθτζσ κα πρζπει να είναι ςε κζςθ:
Γενικά Μαθηματικά ΙΙ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Γενικά Μαθηματικά ΙΙ Ενότητα 7 η : Σφνκετεσ Συναρτιςεισ Λουκάσ Βλάχοσ Κακθγθτισ Αςτροφυςικισ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Γενικά Μαθηματικά ΙΙ Ενότητα 7 η : Σφνκετεσ Συναρτιςεισ Λουκάσ Βλάχοσ Κακθγθτισ Αςτροφυςικισ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται
ΘΕΜΟΔΥΝΑΜΙΚΘ Ι. Ενότθτα 7: Θεωριματα και ςχζςεισ μερικϊν παραγϊγων Σχζςεισ Maxwell Θερμοδυναμικζσ Καταςτατικζσ Εξιςϊςεισ
 ΘΕΜΟΔΥΝΑΜΙΚΘ Ι Ενότθτα 7: Θεωριματα και ςχζςεισ μερικϊν παραγϊγων Σχζςεισ Maxwell Θερμοδυναμικζσ Καταςτατικζσ Εξιςϊςεισ Σογομϊν Μπογοςιάν Ρολυτεχνικι Σχολι Τμιμα Χθμικϊν Μθχανικϊν Σκοποί ενότθτασ Σκοπόσ
ΘΕΜΟΔΥΝΑΜΙΚΘ Ι Ενότθτα 7: Θεωριματα και ςχζςεισ μερικϊν παραγϊγων Σχζςεισ Maxwell Θερμοδυναμικζσ Καταςτατικζσ Εξιςϊςεισ Σογομϊν Μπογοςιάν Ρολυτεχνικι Σχολι Τμιμα Χθμικϊν Μθχανικϊν Σκοποί ενότθτασ Σκοπόσ
Θεςιακά ςυςτιματα αρίκμθςθσ
 Θεςιακά ςυςτιματα αρίκμθςθσ Δρ. Χρήστος Ηλιούδης αρικμθτικό ςφςτθμα αρίκμθςθσ (Number System) Αξία (value) παράςταςθ Οι αξίεσ (π.χ. το βάροσ μιασ ποςότθτασ μιλων) μποροφν να παραςτακοφν με πολλοφσ τρόπουσ
Θεςιακά ςυςτιματα αρίκμθςθσ Δρ. Χρήστος Ηλιούδης αρικμθτικό ςφςτθμα αρίκμθςθσ (Number System) Αξία (value) παράςταςθ Οι αξίεσ (π.χ. το βάροσ μιασ ποςότθτασ μιλων) μποροφν να παραςτακοφν με πολλοφσ τρόπουσ
Ανάλυςη κλειςτϊν δικτφων
 Ανάλυςη κλειςτϊν δικτφων Θ ανάλυςθ κλειςτϊν δικτφων ςτθρίηεται ςτθ διατιρθςθ τθσ μάηασ και τθσ ενζργειασ. Σε ζνα τυπικό βρόχο ABCDA υπάρχει ζνασ αρικμόσ από κόμβουσ, εδϊ A,B,C,D, ςτουσ οποίουσ ιςχφει θ
Ανάλυςη κλειςτϊν δικτφων Θ ανάλυςθ κλειςτϊν δικτφων ςτθρίηεται ςτθ διατιρθςθ τθσ μάηασ και τθσ ενζργειασ. Σε ζνα τυπικό βρόχο ABCDA υπάρχει ζνασ αρικμόσ από κόμβουσ, εδϊ A,B,C,D, ςτουσ οποίουσ ιςχφει θ
-Έλεγχοσ μπαταρίασ (χωρίσ φορτίο) Ο ζλεγχοσ αυτόσ μετράει τθν κατάςταςθ φόρτιςθ τθσ μπαταρίασ.
 1 -Έλεγχοσ μπαταρίασ (έλεγχοσ επιφανείασ) Ο ζλεγχοσ αυτόσ γίνεται για τθν περίπτωςθ που υπάρχει χαμθλό ρεφμα εκφόρτιςθσ κατά μικοσ τθσ μπαταρίασ -Έλεγχοσ μπαταρίασ (χωρίσ φορτίο) Ο ζλεγχοσ αυτόσ μετράει
1 -Έλεγχοσ μπαταρίασ (έλεγχοσ επιφανείασ) Ο ζλεγχοσ αυτόσ γίνεται για τθν περίπτωςθ που υπάρχει χαμθλό ρεφμα εκφόρτιςθσ κατά μικοσ τθσ μπαταρίασ -Έλεγχοσ μπαταρίασ (χωρίσ φορτίο) Ο ζλεγχοσ αυτόσ μετράει
ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΑΠΟ ΘΕΜΑΤΑ ΤΕΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ
 Λφκειο Ακρόπολθσ 2015 Επιμζλεια Μάριοσ Πουργουρίδθσ ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΑΠΟ ΘΕΜΑΤΑ ΤΕΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 1. Η πιο κάτω μπάλα αφινεται να πζςει από το ςθμείο Α,κτυπά ςτο ζδαφοσ ςτο ςθμείο Ε και αναπθδά ςε μικρότερο
Λφκειο Ακρόπολθσ 2015 Επιμζλεια Μάριοσ Πουργουρίδθσ ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΑΠΟ ΘΕΜΑΤΑ ΤΕΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 1. Η πιο κάτω μπάλα αφινεται να πζςει από το ςθμείο Α,κτυπά ςτο ζδαφοσ ςτο ςθμείο Ε και αναπθδά ςε μικρότερο
Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο τησ Αριθμογραμμήσ
 Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο τησ Αριθμογραμμήσ Αυτζσ οι οδθγίεσ ζχουν ςτόχο να βοθκιςουν τουσ εκπαιδευτικοφσ να καταςκευάςουν τισ δικζσ τουσ δραςτθριότθτεσ με το μοντζλο τθσ Αρικμογραμμισ.
Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο τησ Αριθμογραμμήσ Αυτζσ οι οδθγίεσ ζχουν ςτόχο να βοθκιςουν τουσ εκπαιδευτικοφσ να καταςκευάςουν τισ δικζσ τουσ δραςτθριότθτεσ με το μοντζλο τθσ Αρικμογραμμισ.
Γενικά Μαθηματικά ΙΙ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Γενικά Μαθηματικά ΙΙ Ενότητα 13 η : Επαναλθπτικι Ενότθτα Λουκάσ Βλάχοσ Κακθγθτισ Αςτροφυςικισ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Γενικά Μαθηματικά ΙΙ Ενότητα 13 η : Επαναλθπτικι Ενότθτα Λουκάσ Βλάχοσ Κακθγθτισ Αςτροφυςικισ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται
ΜΑ032: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Εαρινό εξάμηνο , Διδάςκων: Γιώργοσ Γεωργίου ΕΝΔΙΑΜΕΗ ΕΞΕΣΑΗ, 21 Μαρτίου, 2012 Διάρκεια: 2 ώρεσ
 ΜΑ: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Εαρινό εξάμηνο -, Διδάςκων: Γιώργοσ Γεωργίου ΕΝΔΙΑΜΕΗ ΕΞΕΣΑΗ, Μαρτίου, Διάρκεια: ώρεσ ΟΝΟΜΑ: Αρ. Πολ. Σαυτ. Πρόβλημα. Θεωροφμε τα διανφςματα u =,,,, v =,,,4, w =,,,, (α) Υπολογίςτε
ΜΑ: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Εαρινό εξάμηνο -, Διδάςκων: Γιώργοσ Γεωργίου ΕΝΔΙΑΜΕΗ ΕΞΕΣΑΗ, Μαρτίου, Διάρκεια: ώρεσ ΟΝΟΜΑ: Αρ. Πολ. Σαυτ. Πρόβλημα. Θεωροφμε τα διανφςματα u =,,,, v =,,,4, w =,,,, (α) Υπολογίςτε
Πανεπιςτιμιο Κφπρου ΟΙΚ 223: Μακθματικά για οικονομολόγουσ ΙΙ Διδάςκων:
 Πανεπιςτιμιο Κφπρου ΟΙΚ 3: Μακθματικά για οικονομολόγουσ ΙΙ Διδάςκων: Φάμπιο Αντωνίου τοιχεία Επικοινωνίασ: email: fantoniou@aueb.gr ; fabio@ucy.ac.cy Σθλ:893683 Προςωπικι Ιςτοςελίδα: fantoniou.wordpress.com
Πανεπιςτιμιο Κφπρου ΟΙΚ 3: Μακθματικά για οικονομολόγουσ ΙΙ Διδάςκων: Φάμπιο Αντωνίου τοιχεία Επικοινωνίασ: email: fantoniou@aueb.gr ; fabio@ucy.ac.cy Σθλ:893683 Προςωπικι Ιςτοςελίδα: fantoniou.wordpress.com
Δείκτεσ Διαχείριςθ Μνιμθσ. Βαγγζλθσ Οικονόμου Διάλεξθ 8
 Δείκτεσ Διαχείριςθ Μνιμθσ Βαγγζλθσ Οικονόμου Διάλεξθ 8 Δείκτεσ Κάκε μεταβλθτι ςχετίηεται με μία κζςθ ςτθν κφρια μνιμθ του υπολογιςτι. Κάκε κζςθ ςτθ μνιμθ ζχει τθ δικι τθσ ξεχωριςτι διεφκυνςθ. Με άμεςθ
Δείκτεσ Διαχείριςθ Μνιμθσ Βαγγζλθσ Οικονόμου Διάλεξθ 8 Δείκτεσ Κάκε μεταβλθτι ςχετίηεται με μία κζςθ ςτθν κφρια μνιμθ του υπολογιςτι. Κάκε κζςθ ςτθ μνιμθ ζχει τθ δικι τθσ ξεχωριςτι διεφκυνςθ. Με άμεςθ
ΕΦΑΡΜΟΓΕ ΒΑΕΩΝ ΔΕΔΟΜΕΝΩΝ ΣΗ ΝΟΗΛΕΤΣΙΚΗ. Φιλιοποφλου Ειρινθ
 ΕΦΑΡΜΟΓΕ ΒΑΕΩΝ ΔΕΔΟΜΕΝΩΝ ΣΗ ΝΟΗΛΕΤΣΙΚΗ Φιλιοποφλου Ειρινθ Προςθήκη νζων πεδίων Ασ υποκζςουμε ότι μετά τθ δθμιουργία του πίνακα αντιλαμβανόμαςτε ότι ζχουμε ξεχάςει κάποια πεδία. Είναι ζνα πρόβλθμα το οποίο
ΕΦΑΡΜΟΓΕ ΒΑΕΩΝ ΔΕΔΟΜΕΝΩΝ ΣΗ ΝΟΗΛΕΤΣΙΚΗ Φιλιοποφλου Ειρινθ Προςθήκη νζων πεδίων Ασ υποκζςουμε ότι μετά τθ δθμιουργία του πίνακα αντιλαμβανόμαςτε ότι ζχουμε ξεχάςει κάποια πεδία. Είναι ζνα πρόβλθμα το οποίο
Παράςταςη ακεραίων ςτο ςυςτημα ςυμπλήρωμα ωσ προσ 2
 Παράςταςη ακεραίων ςτο ςυςτημα ςυμπλήρωμα ωσ προσ 2 Δρ. Χρήζηος Ηλιούδης Μθ Προςθμαςμζνοι Ακζραιοι Εφαρμογζσ (ςε οποιαδιποτε περίπτωςθ δεν χρειάηονται αρνθτικοί αρικμοί) Καταμζτρθςθ. Διευκυνςιοδότθςθ.
Παράςταςη ακεραίων ςτο ςυςτημα ςυμπλήρωμα ωσ προσ 2 Δρ. Χρήζηος Ηλιούδης Μθ Προςθμαςμζνοι Ακζραιοι Εφαρμογζσ (ςε οποιαδιποτε περίπτωςθ δεν χρειάηονται αρνθτικοί αρικμοί) Καταμζτρθςθ. Διευκυνςιοδότθςθ.
Βαςικι Θεωρία Ημιαγωγών. Κεφάλαιο 1 πφροσ Βλάςςθσ Αναπλθρωτισ Κακθγθτισ
 Βαςικι Θεωρία Ημιαγωγών Κεφάλαιο 1 πφροσ Βλάςςθσ Αναπλθρωτισ Κακθγθτισ Περιεχόμενα Ημιαγωγοί τφπου p Αγωγιμότθτα θμιαγωγoφ τφπoυ p Αντίςταςθ θμιαγωγοφ τφπου p Ρεφματα διάχυςθσ ςε θμιαγωγό χζςθ Einstein
Βαςικι Θεωρία Ημιαγωγών Κεφάλαιο 1 πφροσ Βλάςςθσ Αναπλθρωτισ Κακθγθτισ Περιεχόμενα Ημιαγωγοί τφπου p Αγωγιμότθτα θμιαγωγoφ τφπoυ p Αντίςταςθ θμιαγωγοφ τφπου p Ρεφματα διάχυςθσ ςε θμιαγωγό χζςθ Einstein
Μάρκετινγκ V Κοινωνικό Μάρκετινγκ. Πόπη Σουρμαΐδου. Σεμινάριο: Αναπτφςςοντασ μια κοινωνική επιχείρηςη
 Μάρκετινγκ V Κοινωνικό Μάρκετινγκ Πόπη Σουρμαΐδου Σεμινάριο: Αναπτφςςοντασ μια κοινωνική επιχείρηςη Σφνοψη Τι είναι το Marketing (βαςικι ειςαγωγι, swot ανάλυςθ, τα παλιά 4P) Τι είναι το Marketing Plan
Μάρκετινγκ V Κοινωνικό Μάρκετινγκ Πόπη Σουρμαΐδου Σεμινάριο: Αναπτφςςοντασ μια κοινωνική επιχείρηςη Σφνοψη Τι είναι το Marketing (βαςικι ειςαγωγι, swot ανάλυςθ, τα παλιά 4P) Τι είναι το Marketing Plan
Ιδιότθτεσ πεδίων Γενικζσ.
 Οι ιδιότθτεσ των πεδίων διαφζρουν ανάλογα με τον τφπο δεδομζνων που επιλζγουμε. Ορίηονται ςτο κάτω μζροσ του παρακφρου ςχεδίαςθσ του πίνακα, ςτθν καρτζλα Γενικζσ. Ιδιότθτα: Μζγεκοσ πεδίου (Field size)
Οι ιδιότθτεσ των πεδίων διαφζρουν ανάλογα με τον τφπο δεδομζνων που επιλζγουμε. Ορίηονται ςτο κάτω μζροσ του παρακφρου ςχεδίαςθσ του πίνακα, ςτθν καρτζλα Γενικζσ. Ιδιότθτα: Μζγεκοσ πεδίου (Field size)
Ενθμζρωςθ και προςταςία των καταναλωτών από τουσ κινδφνουσ που απορρζουν από τα χθμικά προϊόντα
 Ενθμζρωςθ και προςταςία των καταναλωτών από τουσ κινδφνουσ που απορρζουν από τα χθμικά προϊόντα Γενικό Χθμείο του Κράτουσ Διεφκυνςθ Περιβάλλοντοσ Δρ. Διμθτρα Δανιιλ Χθμικά προϊόντα Οι χθμικζσ ουςίεσ υπάρχουν
Ενθμζρωςθ και προςταςία των καταναλωτών από τουσ κινδφνουσ που απορρζουν από τα χθμικά προϊόντα Γενικό Χθμείο του Κράτουσ Διεφκυνςθ Περιβάλλοντοσ Δρ. Διμθτρα Δανιιλ Χθμικά προϊόντα Οι χθμικζσ ουςίεσ υπάρχουν
ΚΤΚΛΩΜΑ RLC Ε ΕΙΡΑ (Απόκριςη ςε ημιτονοειδή είςοδο)
 ΚΤΚΛΩΜΑ RLC Ε ΕΙΡΑ (Απόκριςη ςε ημιτονοειδή είςοδο) χήμα Κφκλωμα RLC ςε ςειρά χήμα 2 Διανυςματικι παράςταςθ τάςεων και ρεφματοσ Ζςτω ότι ςτο κφκλωμα του ςχιματοσ που περιλαμβάνει ωμικι, επαγωγικι και χωρθτικι
ΚΤΚΛΩΜΑ RLC Ε ΕΙΡΑ (Απόκριςη ςε ημιτονοειδή είςοδο) χήμα Κφκλωμα RLC ςε ςειρά χήμα 2 Διανυςματικι παράςταςθ τάςεων και ρεφματοσ Ζςτω ότι ςτο κφκλωμα του ςχιματοσ που περιλαμβάνει ωμικι, επαγωγικι και χωρθτικι
ΔΙΑΓΩΝΙΣΜΑ XHMEIAΣ Γ ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΑ:
 ΔΙΑΓΩΝΙΣΜΑ XHMEIAΣ Γ ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΑ: 1-2-3-4-5 Ονοματεπϊνυμο:..... Ημ/νία:.. Σάξθ: Χρονικι Διάρκεια:... Βακμόσ: ΘΕΜΑ Α Για τισ προτάςεισ Α1 ζωσ Α5 να γράψετε ςτο τετράδιό ςασ τον αρικμό τθσ πρόταςθσ
ΔΙΑΓΩΝΙΣΜΑ XHMEIAΣ Γ ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΑ: 1-2-3-4-5 Ονοματεπϊνυμο:..... Ημ/νία:.. Σάξθ: Χρονικι Διάρκεια:... Βακμόσ: ΘΕΜΑ Α Για τισ προτάςεισ Α1 ζωσ Α5 να γράψετε ςτο τετράδιό ςασ τον αρικμό τθσ πρόταςθσ
ΕΡΓΑΣΗΡΙΟ ΕΦΑΡΜΟΜΕΝΗ ΠΛΗΡΟΦΟΡΙΚΗ
 Στο εργαςτιριο αυτό κα δοφμε πωσ μποροφμε να προςομοιϊςουμε μια κίνθςθ χωρίσ τθ χριςθ εξειδικευμζνων εργαλείων, παρά μόνο μζςω ενόσ προγράμματοσ λογιςτικϊν φφλλων, όπωσ είναι το Calc και το Excel. Τα δφο
Στο εργαςτιριο αυτό κα δοφμε πωσ μποροφμε να προςομοιϊςουμε μια κίνθςθ χωρίσ τθ χριςθ εξειδικευμζνων εργαλείων, παρά μόνο μζςω ενόσ προγράμματοσ λογιςτικϊν φφλλων, όπωσ είναι το Calc και το Excel. Τα δφο
α) Στο μιγαδικό επίπεδο οι εικόνεσ δφο ςυηυγϊν μιγαδικϊν είναι ςθμεία ςυμμετρικά ωσ προσ τον πραγματικό άξονα
 ΘΕΜΑ Α ΠΑΝΕΛΛΗΝΙΕ ΕΞΕΣΑΕΙ Γ ΣΑΞΗ ΗΜΕΡΗΙΟΤ ΓΕΝΙΚΟΤ ΛΤΚΕΙΟΤ ΚΑΙ ΕΠΑΛ ΟΜΑΔΑ Β ΔΕΤΣΕΡΑ 8 ΜΑΪΟΤ ΕΞΕΣΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΣΙΚΑ ΘΕΣΙΚΗ ΚΑΙ ΣΕΧΝΟΛΟΓΙΚΗ ΚΑΣΕΤΘΤΝΗ ΤΝΟΛΟ ΕΛΙΔΩΝ: ΣΕΕΡΙ A. Ζςτω μια ςυνάρτθςθ f θ
ΘΕΜΑ Α ΠΑΝΕΛΛΗΝΙΕ ΕΞΕΣΑΕΙ Γ ΣΑΞΗ ΗΜΕΡΗΙΟΤ ΓΕΝΙΚΟΤ ΛΤΚΕΙΟΤ ΚΑΙ ΕΠΑΛ ΟΜΑΔΑ Β ΔΕΤΣΕΡΑ 8 ΜΑΪΟΤ ΕΞΕΣΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΣΙΚΑ ΘΕΣΙΚΗ ΚΑΙ ΣΕΧΝΟΛΟΓΙΚΗ ΚΑΣΕΤΘΤΝΗ ΤΝΟΛΟ ΕΛΙΔΩΝ: ΣΕΕΡΙ A. Ζςτω μια ςυνάρτθςθ f θ
ΔΙΑΓΩΝΙΜΑ ΧΗΜΕΙΑ Γ ΛΤΚΕΙΟΤ. Ημ/νία: Τάξθ: Χρονικι Διάρκεια:.
 ΔΙΑΓΩΝΙΜΑ ΧΗΜΕΙΑ Γ ΛΤΚΕΙΟΤ ΟΞΕΙΔΟΑΝΑΓΩΓΗ ΘΕΡΜΟΧΗΜΕΙΑ ΧΗΜΙΚΗ ΚΙΝΗΣΙΚΗ ΧΗΜΙΚΗ ΙΟΡΡΟΠΙΑ - ΟΡΓΑΝΙΚΗ Ονοματεπϊνυμο:. Ημ/νία: Τάξθ: Χρονικι Διάρκεια:. Βακμόσ: ΘΕΜΑ Α Να επιλζξετε τθ ςωςτι απάντθςθ ςε κακεμιά
ΔΙΑΓΩΝΙΜΑ ΧΗΜΕΙΑ Γ ΛΤΚΕΙΟΤ ΟΞΕΙΔΟΑΝΑΓΩΓΗ ΘΕΡΜΟΧΗΜΕΙΑ ΧΗΜΙΚΗ ΚΙΝΗΣΙΚΗ ΧΗΜΙΚΗ ΙΟΡΡΟΠΙΑ - ΟΡΓΑΝΙΚΗ Ονοματεπϊνυμο:. Ημ/νία: Τάξθ: Χρονικι Διάρκεια:. Βακμόσ: ΘΕΜΑ Α Να επιλζξετε τθ ςωςτι απάντθςθ ςε κακεμιά
Αρχή διατήρηςησ τησ μηχανικήσ ενζργειασ
 Αρχή διατήρηςησ τησ μηχανικήσ ενζργειασ Φφλλο εργαςίασ Α. Όργανα και υλικά που απαιτοφνται Βάςθ παραλλθλόγραμμθ φιγκτιρασ τφπου G Μία (1) ράβδοσ μεταλλικι 80 cm Δφο () ράβδοι μεταλλικζσ 30 cm Δφο () απλοί
Αρχή διατήρηςησ τησ μηχανικήσ ενζργειασ Φφλλο εργαςίασ Α. Όργανα και υλικά που απαιτοφνται Βάςθ παραλλθλόγραμμθ φιγκτιρασ τφπου G Μία (1) ράβδοσ μεταλλικι 80 cm Δφο () ράβδοι μεταλλικζσ 30 cm Δφο () απλοί
Σο θλεκτρικό κφκλωμα
 Σο θλεκτρικό κφκλωμα Για να είναι δυνατι θ ροι των ελεφκερων θλεκτρονίων, για να ζχουμε θλεκτρικό ρεφμα, απαραίτθτθ προχπόκεςθ είναι θ φπαρξθ ενόσ κλειςτοφ θλεκτρικοφ κυκλϊματοσ. Είδθ κυκλωμάτων Σα κυκλϊματα
Σο θλεκτρικό κφκλωμα Για να είναι δυνατι θ ροι των ελεφκερων θλεκτρονίων, για να ζχουμε θλεκτρικό ρεφμα, απαραίτθτθ προχπόκεςθ είναι θ φπαρξθ ενόσ κλειςτοφ θλεκτρικοφ κυκλϊματοσ. Είδθ κυκλωμάτων Σα κυκλϊματα
Γ' ΛΥΚΕΙΟΥ Η ΤΑΞΗ ΤΗΣ ΤΕΛΙΚΗΣ ΕΠΙΛΟΓΗΣ. Στθ ΓϋΛυκείου οι Ομάδεσ Προςανατολιςμοφ είναι τρεισ:
 Γ' ΛΥΚΕΙΟΥ Η ΤΑΞΗ ΤΗΣ ΤΕΛΙΚΗΣ ΕΠΙΛΟΓΗΣ Στθ ΓϋΛυκείου οι Ομάδεσ Προςανατολιςμοφ είναι τρεισ: 1. Ομάδα Ανκρωπιςτικών Σπουδών 2. Ομάδα Οικονομικών, Πολιτικών, Κοινωνικών & Παιδαγωγικών Σπουδών 3. Ομάδα Θετικών
Γ' ΛΥΚΕΙΟΥ Η ΤΑΞΗ ΤΗΣ ΤΕΛΙΚΗΣ ΕΠΙΛΟΓΗΣ Στθ ΓϋΛυκείου οι Ομάδεσ Προςανατολιςμοφ είναι τρεισ: 1. Ομάδα Ανκρωπιςτικών Σπουδών 2. Ομάδα Οικονομικών, Πολιτικών, Κοινωνικών & Παιδαγωγικών Σπουδών 3. Ομάδα Θετικών
Το καλωςόριςμα των μαθητών ςτο Εργαςτήριο Φυςικών Επιςτημών
 Το καλωςόριςμα των μαθητών ςτο Εργαςτήριο Φυςικών Επιςτημών Η ΟΡΙΖΟΝΣΙΑ ΒΟΛΗ ΜΕΑ ΑΠΟ ΣΙ ΝΕΕ ΣΕΧΝΟΛΟΓΙΕ Εισαγωγή Ο καταλλθλότεροσ χϊροσ για ζνα επιτυχθμζνο μάκθμα φυςικισ είναι το εργαςτιριο φυςικϊν επιςτθμϊν.
Το καλωςόριςμα των μαθητών ςτο Εργαςτήριο Φυςικών Επιςτημών Η ΟΡΙΖΟΝΣΙΑ ΒΟΛΗ ΜΕΑ ΑΠΟ ΣΙ ΝΕΕ ΣΕΧΝΟΛΟΓΙΕ Εισαγωγή Ο καταλλθλότεροσ χϊροσ για ζνα επιτυχθμζνο μάκθμα φυςικισ είναι το εργαςτιριο φυςικϊν επιςτθμϊν.
Πωσ δθμιουργώ φακζλουσ;
 Πωσ δθμιουργώ φακζλουσ; Για να μπορζςετε να δθμιουργιςετε φακζλουσ ςτο χαρτοφυλάκιό ςασ ςτο Mahara κα πρζπει να μπείτε ςτο ςφςτθμα αφοφ πατιςετε πάνω ςτο ςφνδεςμο Mahara profiles από οποιοδιποτε ςελίδα
Πωσ δθμιουργώ φακζλουσ; Για να μπορζςετε να δθμιουργιςετε φακζλουσ ςτο χαρτοφυλάκιό ςασ ςτο Mahara κα πρζπει να μπείτε ςτο ςφςτθμα αφοφ πατιςετε πάνω ςτο ςφνδεςμο Mahara profiles από οποιοδιποτε ςελίδα
Workshop Ιστορίας της Τέχνης
 Το Workshop Ιςτορίασ τθσ Τζχνθσ διεξιχκθ τον Οκτϊβριο από το Τμιμα Καλλιτεχνικισ Παιδείασ & Επιμόρφωςθσ του Διμου Πειραιά. Σκοπόσ του εργαςτθρίου ιταν να εμβακφνει ςτθ μελζτθ τριϊν περιόδων τθσ τζχνθσ
Το Workshop Ιςτορίασ τθσ Τζχνθσ διεξιχκθ τον Οκτϊβριο από το Τμιμα Καλλιτεχνικισ Παιδείασ & Επιμόρφωςθσ του Διμου Πειραιά. Σκοπόσ του εργαςτθρίου ιταν να εμβακφνει ςτθ μελζτθ τριϊν περιόδων τθσ τζχνθσ
ΑΓΟΡΕ ΚΑΙ ΑΠΟΣΕΛΕΜΑΣΙΚΟΣΗΣΑ
 ΑΓΟΡΕ ΚΑΙ ΑΠΟΣΕΛΕΜΑΣΙΚΟΣΗΣΑ Ειςαγωγικά το κεφάλαιο αυτό κα εξετάςουμε τα βαςικά ςτοιχεία ςφνδεςθσ του οικονομικοφ και του περιβαλλοντικοφ ςυςτιματοσ τθν βαςικό πλαίςιο μζςα ςτο οποίο κα εξετάςουμε τθ ςχζςθ
ΑΓΟΡΕ ΚΑΙ ΑΠΟΣΕΛΕΜΑΣΙΚΟΣΗΣΑ Ειςαγωγικά το κεφάλαιο αυτό κα εξετάςουμε τα βαςικά ςτοιχεία ςφνδεςθσ του οικονομικοφ και του περιβαλλοντικοφ ςυςτιματοσ τθν βαςικό πλαίςιο μζςα ςτο οποίο κα εξετάςουμε τθ ςχζςθ
Ηλεκτρονικι Επιχειρθςιακι Δράςθ Εργαςτιριο 1
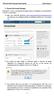 1. Εγκατάςταςη Xampp Προκειμζνου να γίνει θ εγκατάςταςθ κα πρζπει πρϊτα να κατεβάςετε και εγκαταςτιςετε το XAMPP ωσ ακολοφκωσ. 1.1. Πάμε ςτθν ακόλουκθ διεφκυνςθ https://www.apachefriends.org/download.html
1. Εγκατάςταςη Xampp Προκειμζνου να γίνει θ εγκατάςταςθ κα πρζπει πρϊτα να κατεβάςετε και εγκαταςτιςετε το XAMPP ωσ ακολοφκωσ. 1.1. Πάμε ςτθν ακόλουκθ διεφκυνςθ https://www.apachefriends.org/download.html
Ερωτιςεισ & απαντιςεισ για τα ξφλινα πνευςτά
 Τα νύλιμα! ΧΟΡΗΓΟΣ Ερωτιςεισ & απαντιςεισ για τα ξφλινα πνευςτά τα ξφλινα! 1. Γιατί τα λζμε ξφλινα πνευςτά; Πνευςτά ονομάηονται τα όργανα ςτα οποία ο ιχοσ παράγεται μζςα ςε ζνα ςωλινα απ όπου περνάει ο
Τα νύλιμα! ΧΟΡΗΓΟΣ Ερωτιςεισ & απαντιςεισ για τα ξφλινα πνευςτά τα ξφλινα! 1. Γιατί τα λζμε ξφλινα πνευςτά; Πνευςτά ονομάηονται τα όργανα ςτα οποία ο ιχοσ παράγεται μζςα ςε ζνα ςωλινα απ όπου περνάει ο
Τάξη Β. Φυςικθ Γενικθσ Παιδείασ. Τράπεζα ιεμάτων Κεφ.1 ο ΘΕΜΑ Δ. Για όλεσ τισ αςκθςεισ δίνεται η ηλεκτρικθ ςταιερά
 Τάξη Β Φυςικθ Γενικθσ Παιδείασ Τράπεζα ιεμάτων Κεφ.1 ο ΘΕΜΑ Δ Για όλεσ τισ αςκθςεισ δίνεται η ηλεκτρικθ ςταιερά k 2 9 9 10 Nm 2 1. Δφο ακίνθτα ςθμειακά θλεκτρικά φορτία q 1 = - 2 μq και q 2 = + 3 μq, βρίςκονται
Τάξη Β Φυςικθ Γενικθσ Παιδείασ Τράπεζα ιεμάτων Κεφ.1 ο ΘΕΜΑ Δ Για όλεσ τισ αςκθςεισ δίνεται η ηλεκτρικθ ςταιερά k 2 9 9 10 Nm 2 1. Δφο ακίνθτα ςθμειακά θλεκτρικά φορτία q 1 = - 2 μq και q 2 = + 3 μq, βρίςκονται
Διαδικασία με βήματα. 1. Αλλάηω το χρϊμα ςκθνικοφ ςε γκρι(#3333).
 Διαδικασία με βήματα 1. Αλλάηω το χρϊμα ςκθνικοφ ςε γκρι(#3333). 2. Διαλζγω το Polystar Tool. Από τα Options κάνω το Polygon ςε Star και τα υπόλοιπα όπωσ είναι. Ζωγραφίηω ζνα αςτζρι πάνω αριςτερά. Fill
Διαδικασία με βήματα 1. Αλλάηω το χρϊμα ςκθνικοφ ςε γκρι(#3333). 2. Διαλζγω το Polystar Tool. Από τα Options κάνω το Polygon ςε Star και τα υπόλοιπα όπωσ είναι. Ζωγραφίηω ζνα αςτζρι πάνω αριςτερά. Fill
Διορκώνω τισ εργαςίεσ των ςυμφοιτθτών μου
 Διορκώνω τισ εργαςίεσ των ςυμφοιτθτών μου Ένασ φοιτητήσ έγραψε ςτην αναφορά του το παρακάτω: Κατά τθ γνώμθ μου θ πλθροφορία για τισ επιχειριςεισ λαμβάνει πολφ ςθμαντικό ρόλο. Κατά τθ γνώμθ μου, ο ρόλοσ
Διορκώνω τισ εργαςίεσ των ςυμφοιτθτών μου Ένασ φοιτητήσ έγραψε ςτην αναφορά του το παρακάτω: Κατά τθ γνώμθ μου θ πλθροφορία για τισ επιχειριςεισ λαμβάνει πολφ ςθμαντικό ρόλο. Κατά τθ γνώμθ μου, ο ρόλοσ
Ακράτεια οφρων είναι οποιαςδιποτε μορφισ ακοφςια απώλεια οφρων.
 Σί είναι η ακράτεια οφρων; Ακράτεια οφρων είναι οποιαςδιποτε μορφισ ακοφςια απώλεια οφρων. Ποιά είναι η επίπτωςή τησ ςτο γυναικείο πληθυςμό; Γενικά 27% των γυναικών κα παρουςιάςουν κάποιο τφπο ακράτειασ
Σί είναι η ακράτεια οφρων; Ακράτεια οφρων είναι οποιαςδιποτε μορφισ ακοφςια απώλεια οφρων. Ποιά είναι η επίπτωςή τησ ςτο γυναικείο πληθυςμό; Γενικά 27% των γυναικών κα παρουςιάςουν κάποιο τφπο ακράτειασ
assessment.gr USER S MANUAL (users)
 assessment.gr USER S MANUAL (users) Human Factor January 2010 Περιεχόμενα 1. Γενικζσ οδθγίεσ ςυςτιματοσ... 3 1.1 Αρχικι ςελίδα... 3 1.2 Ερωτθματολόγια... 6 1.2.1 Τεςτ Γνϊςεων Γενικοφ Ρεριεχομζνου... 6
assessment.gr USER S MANUAL (users) Human Factor January 2010 Περιεχόμενα 1. Γενικζσ οδθγίεσ ςυςτιματοσ... 3 1.1 Αρχικι ςελίδα... 3 1.2 Ερωτθματολόγια... 6 1.2.1 Τεςτ Γνϊςεων Γενικοφ Ρεριεχομζνου... 6
