Mərkəzi sahə yaxınlaşmasına əsasən atomda elektronun halı nlmlm s

Mühazirə 4. HİDROGENƏBƏNZƏR ATOMLAR ÜÇÜN ŞREDİNGER TƏNLİYİNİN HƏLLİ. Nüvədən və bir elektrondan ibarət sistemlərə hidrogenəbənzər sistemlər deyilir.

Mühazirə. HİDROGENƏBƏNZƏR ATOMLAR ÜÇÜN ŞREDİNGER TƏNLİYİNİN HƏLLİ H He Nüvədə və bir eektroda ibarət sistemərə hidrogeəbəzər sistemər deyiir. + Li + Be + və s. Burada z - üvəi sıra ömrəsi r - üvədə eektroa

x = l divarları ilə hüdudlanmış oblastda baş verir:

Müazirə 3. BİRÖLÇÜLÜ POTNSİAL ÇUXURDA HİSSƏCİYİN HƏRƏKƏTİNİN ŞRDİNGR TƏNLİYİ Tutaq ki, zərrəcik sosuz üür və keçiəz ivarara üuaış fəza obastıa ərəkət eir. Beə obasta potesia çuur eyiir. Divarar keçiəz

TƏQRIBI HESABLAMA ÜSULLARI

YƏƏDOV Də əı ə SS E-ı e və İ əəşı: - eə əə Vəəəov və ƏŞəev ə veşə E eo: İıov - eə ə oe TƏQIBI HESB ÜSUI 5 əəov Y Tə e üı əəə üçü ə Bı: «Bı Uvee» əşı 8 88 ə şə əəə üçü ə Tə o ə üç əə ə B əə ə üı əə ə ə

Azərbaycan Dövlət Aqrar Universiteti. mühəndislik ixtisasları. Aqrar fizika və riyaziyyat. f.-r.e.n., dosent Ağayev Q.Ü.

Azərbayca Dövlət Aqrar Uivrsitti. Fakültə: müədislik ixtisasları Kafdra: Aqrar fizika və riyaziyyat Fə: Fizika Müazirəçi: f.-r..., dost Ağayv Q.Ü. Ədəbiyyat:. Савельев И.В. Общий курс физики. I, II, III

C.S. ƏSGƏROV. ELEKTROMAQNIT SAHƏ NƏZƏRİYYƏSİNİN XÜSUSİ MƏSƏLƏLƏRİ monoqrafiya

CS ƏSGƏROV ELEKTROMQNIT SHƏ NƏZƏRİYYƏSİNİN XÜSUSİ MƏSƏLƏLƏRİ monoqafia ZƏRNƏŞR BKI-07 CS ƏSGƏROV ELEKTROMQNIT SHƏ NƏZƏRİYYƏSİNİN XÜSUSİ MƏSƏLƏLƏRİ monoqafia ZƏRNƏŞR BKI-07 BBK 45 C-4 Rəçilə: əbacan Elmi-Tədqiqat

ibemo Kazakhstan Republic of Kazakhstan, West Kazakhstan Oblast, Aksai, Pramzone, BKKS office complex Phone: ; Fax:

MÜNDƏ R İ CAT. 4.Xarici Dirixle məsələsinin həlli ƏDƏBİYYAT...164

3 MÜNDƏ İ CAT GİİŞ...5 I FƏİL. XÜUİ TÖƏMƏLİ TƏNLİKLƏ. ƏHƏD MƏƏLƏİ...7. fı bə əə çııışı...7.iəb əşə əə əsfı ə o şəə gəəs... 3.Çoəşə əə əsfı...7 4.Xüss öəə əə üçü səhə əsəəə qoş... 5.Xs səh. Koş əsəəs qoş...3

Elektrik dövrələri nəzəriyyəsi fənnindən kollokvium suallarının cavabları

lektk dövələ əzəyyəs fədə kollokv sallaıı cavablaı. KTRİK DÖVRƏSİ ƏRƏYAN VƏ GƏRGİNİYİN MÜSBƏT İSTİQAMƏTƏRİ lektk dövəs dedkdə cəəyaı keçəs tə edə lektk dövəs üç hssədə baətd.. ej əbəy (gəglk və cəəya əbələ)..

Azərbaycan Respublikası Təhsil Nazirliyi Azərbaycan Dövlət Neft Akademiyası. АDNА-nın 90 illik yubilеyinə həsr еdilir

M Ktabaa Aərbaca espubası Təhs Nar Aərbaca Dövət Neft Aadeası АDNА-ı 9 ubеə həsr еdr NЕFTQАZ MƏDƏN MАŞIN VƏ АVАDАNLIQLАININ АVTОMАTLАŞDIILMIŞ LАYIHƏLƏNDIMƏ SISTЕMI VƏ MÜHƏNDIS HЕSАBLАMА MЕTОDLАI (А tех

Fizikadan imtahan suallarının cavabları. (AZ)

Fzkada mtaha suallaıı cavablaı. (AZ). Механики щярякят. Мадди нюгтя. Йол. Йердяйишмя. Madd csmlədə baş veə hə cü dəyşklk hadsə adlaı. Buzu əməs, ldıım çaxması, aqldə cəəya keçəkə stlk ayılması və s. hadsələ

E.Q. Orucov TƏTBİQİ FUNKSİONAL ANALİZİN ELEMENTLƏRİ

E.Q. Orucov TƏTBİQİ FUNKSİONL NLİZİN ELEMENTLƏRİ Baı 8 3 Elmi redator: BDU-u Tətbiqi riyaziyyat afedrasıı müdiri, ME-ı aademii Qasımov M.G. Rəyçilər: fizia-riyaziyyat elmləri dotoru, rofessor İsgədərov

ΛΥΣΕΙΣ ΦΥΛΛΑΔΙΟΥ 6 / ΠΟΛΙΤΙΚΟΙ ΜΗΧΑΝΙΚΟΙ Γραμμικές απεικονίσεις, Αλλαγή βάσης, Ιδιοτιμές, Ιδιοδιανύσματα

ΛΥΣΕΙΣ ΦΥΛΛΑΔΙΟΥ 6 / 009-0 ΠΟΛΙΤΙΚΟΙ ΜΗΧΑΝΙΚΟΙ Γραμμικές απεικονίσεις, Αλλαγή βάσης, Ιδιοτιμές, Ιδιοδιανύσματα Έστω η γραμμική απεικόνιση T : με (α) Βρείτε τον πίνακα της T, I Ως προς την κανονική βάση

RG Tutorial xlc3.doc 1/10. To apply the R-G method, the differential equation must be represented in the form:

G Tuorial xlc3.oc / iear roblem i e C i e C ( ie ( Differeial equaio for C (3 Thi fir orer iffereial equaio ca eaily be ole bu he uroe of hi uorial i o how how o ue he iz-galerki meho o fi ou he oluio.

tel , version 1-7 Feb 2013

!"## $ %&' (") *+ '#),! )%)%' *, -#)&,-'" &. % /%%"&.0. )%# "#",1 2" "'' % /%%"&30 "'' "#", /%%%" 4"," % /%%5" 4"," "#",%" 67 &#89% !"!"# $ %& & # &$ ' '#( ''# ))'%&##& *'#$ ##''' "#$ %% +, %'# %+)% $

AI, A2, A3, A4, A5, A6, A7 AIAI, AIA2, AIA3, AIA4, AIA5, AIA6, AIA7 BI, B2, B3, B4, B5, B6, B7 BIBI, BIB2, BIB3, BIB4, BIB5, BIB6, BIB7

Δίφυλλη θύρα τηλεσκοπικού ανοίγματος Two panel telescopic door AI, A2, A3, A4, A5, A6, A7 Δίφυλλη θύρα τηλεσκοπικού ανοίγματος - A2 Two panel telescopic door - A2 AAI, AA2, AA3, AA4, AA5, AA6, AA7 Δίφυλλη

M.H.Yaqubov, M.A.Nəcəfov Ekstremum məsələləri. Bakı:

Eli redtoru:professor K.Q.Həsəov Rəçilər:fii-riit elləri dotoru,professor H.F.Quliev ı Dövlət Uiversiteti Fii-riit elləri iədi,doset Ş.Ş.Yusubov ı Dövlət Uiversiteti M.H.Yqubov, M.A.Nəcəfov Estreu əsələləri.

Δεν θα γίνονται δεκτές εκπρόθεσμες αιτήσεις ή/και αιτήσεις που δεν είναι πλήρως συμπληρωμένες, με όλα τα απαιτούμενα πιστοποιητικά.

Για Επίσημη Χρήση ΤΟΜΕΑΣ ΦΟΙΤΗΤΙΚΗΣ ΜΕΡΙΜΝΑΣ ΓΡΑΦΕΙΟ ΚΟΙΝΩΝΙΚΗΣ ΣΤΗΡΙΞΗΣ (ΤΗΛ. 22 89 4051, 4021- ΦΑΞ. 22 89 5379) Αρ. Αίτησης:. Όν. Παρ.:. Ημερ. Παραλαβής: Κατηγορία:. ΑΙΤΗΣΗ ΥΠΟΨΗΦΙΩΝ ΓΙΑ ΕΙΣΑΓΩΓΗ ΣΤΟ

ÁÈ Ù apple È È appleô ı apple ÓÂ ÛÙË μã Ù ÍË

ÁÈ Ù apple È È appleô ı apple Ó ÛÙË μã Ù ÍË Δ Àƒ π ø ø º π π π ª Δ ƒàªª π μàƒπ π ø π π π ª Δ Δƒ À π ƒ Àà ƒ ªÀ π π ª ª Δπ ø, π Δ Ã π, ø ƒ ºπ, ƒ Δ ƒ Δπ Δ Δ, ƒπ π ª ª ΚΑΛΟ ΚΑΛΟΚΑΙΡΙ Με το πέρασμα του χρόνου

f(z) 1 + z a lim f (n) (0) n! = 1

ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ & ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΟΜΕΑΣ ΜΑΘΗΜΑΤΙΚΩΝ 3η Σειρά Ασκήσεων στη Μιγαδική Ανάλυση. Υποθέτουμε ότι η f : C C είναι ακέραια συνάρτηση και ότι το όριο Αποδείξτε ότι η f είναι σταθερή.

INFCIRC/540 (Corrected)

INFCIRC/540 (Corrected) ( ) ( ) 2 9.18 17 INFCIRC/540 1998 / 1998 / ...... - - 1 3-2 10-4 11 12 13 14 15 16 17 18 AI/1-3 AII/1-40 2 4 2 9 ( )... ) ("..." )... ) (" " (" " :... :... 1 1.. 2 :... (1)....

Ηλεκτρονική φασματοσκοπία ατόμων

Ηλεκτρονική φασματοσκοπία ατόμων Εξίσωση του chrodger H H H µ µ m e e 4πε r Ζe 4πε r για το άτοµο του υδρογόνου για τα υδρογονοειδή άτοµα He Ζe 4πε r < j Ζe 4πε r j για πολυηλεκτρονικά άτοµα µ m m m e

Batigoal_mathscope.org ñược tính theo công thức

SỐ PHỨC TRONG CHỨNG MINH HÌNH HỌC PHẲNG Batigoal_mathscope.org Hoangquan9@gmail.com I.MỘT SỐ KHÁI NIỆM CƠ BẢN. Khoảng cách giữa hai ñiểm Giả sử có số phức và biểu diễn hai ñiểm M và M trên mặt phẳng tọa

ΥΠΗΡΕΣΙΕΣ ΠΡΟΣΩΠΙΚΟΥ ΔΙΑΧΕΙΡΙΣΗ ΑΠΟΔΟΣΗΣ ΚΑΙ ΣΤΕΛΕΧΩΣΗ

ΥΠΗΡΕΣΙΕΣ ΠΡΟΣΩΠΙΚΟΥ ΔΙΑΧΕΙΡΙΣΗ ΑΠΟΔΟΣΗΣ ΚΑΙ ΣΤΕΛΕΧΩΣΗ ΚΑΤΑΛΟΓΟΣ ΑΠΟΤΕΛΕΣΜΑΤΩΝ ΗΛΕΚΤΡΟΝΙΚΟΥ ΤΕΣΤ ΙΚΑΝΟΤΗΤΩΝ ΓΙΑ ΤΙΣ ΘΕΣΕΙΣ ΩΡΟΜΙΣΘΙΟΥ ΠΡΟΣΩΠΙΚΟΥ ΒΟΗΘΟΙ ΤΗΛΕΞΥΠΗΡΕΤΗΣΗΣ (ΑΡ. ΠΡΟΚΗΡΥΞΗΣ: 2/2017) (ΛΕΥΚΩΣΙΑ

cz+d d (ac + cd )z + bc + dd c z + d

T (z) = az + b cz + d ; a, b, c, d C, ad bc 0 ( ) a b M T (z) = (z) az + b c d cz + d (T T )(z) = T (T (z) (T T )(z) = az+b a + cz+d b c az+b + = (aa + cb )z + a b + b d a z + b cz+d d (ac + cd )z + bc

Πίνακες και ερµάρια. διανοµής. ƒ 2010. Plexo 3 στεγανοί πίνακες από 2 έως 72 στοιχεία (σ. 59) Practibox χωνευτοί πίνακες από 6 έως 36 τοιχεία (σ.

χωνευτοί σ. 56 Nedbox χωνευτοί από 12 έως 56 στοιχεία σ. 58 από 1 έως 6 στοιχεία σ. 62 XL 3 160 από 48 έως 144 στοιχεία και ερµάρια διανοµής ισχύος XL 3 σ. 68 Ράγες, πλάτες στήριξης και µετώπες σ. 77 0

(a b) c = a (b c) e a e = e a = a. a a 1 = a 1 a = e. m+n

Z 6 D 3 G = {a, b, c,... } G a, b G a b = c c (a b) c = a (b c) e a e = e a = a a a 1 = a 1 a = e Q = {0, ±1, ±2,..., ±n,... } m, n m+n m + 0 = m m + ( m) = 0 Z N = {a n }, n = 1, 2... N N Z N = {1, ω,

KURS LAYİHƏSİ AZƏRBAYCAN RESPUBLİKASI TƏHSİL NAZİRLİYİ AZƏRBAYCAN DÖVLƏT NEFT AKADEMİYASI. Fakültə: QNM

AZƏRBAYCAN RESPUBLİKASI TƏHSİL NAZİRLİYİ AZƏRBAYCAN DÖVLƏT NEFT AKADEMİYASI Fakültə QNM Kafedra Qaz və q/k yataqlarının işlənməsi və istismarı Qrup 2378 İxtisas T020500 KURS LAYİHƏSİ Fənn Neft və qaz yataqlarının

MATSEC Intermediate Past Papers Index L. Bonello, A. Vella

2009 MATSEC Intermediate Past Papers Index Louisella Bonello Antonia Vella The Junior College Physics Department 2009 MATSEC INTERMEDIATE PAST PAPERS INDEX WITH ANSWERS TO NUMERICAL PROBLEMS by Louisella

VILJUŠKARI. 1. Viljuškar se koristi za utovar standardnih euro-pool paleta na drumsko vozilo u sistemu prikazanom na slici.

VILJUŠKARI 1. Viljuškar e korii za uoar andardnih euro-pool palea na druko ozilo u ieu prikazano na lici. PALETOMAT a) Koliko reba iljuškara da bi ree uoara kaiona u koji aje palea bilo anje od 6 in, ako

Azərbaycan Dövlət Aqrar Universiteti. mühəndislik ixtisasları. Aqrar fizika və riyaziyyat. f.-r.e.n., dosent Ağayev Q.Ü.

Azərbyc Dövlət Aqrr ivrsitti. Fkültə: mühədislik ixtisslrı Kfdr: Aqrr fizik və riyziyyt Fə: Fizik Mühzirəçi: f.-r..., dost Ağyv Q.Ü. Ədəbiyyt:. Савельев И.В. Общий курс физики. I, II, III т.т. М. 989..

υ η µ η. υ η µ υµ η υ υ υ µ υ η µ η υ. µ υ υ υ η ω µ ω µ υ η ω υ µ υ ω ω ω η ω ω., ω ω,, % #" ".µ, & ". 0, # #'

- 1 - µ µ 1 µ µ" # 2 µ %& µ "' (µ 2 µ %& µ "' ( &% ) 3 µ %µ,, υ η µ η. υµ υ υµ ηµ υµ υ υ η µ υµ η υ υ υ µ υ η µ η υ. µ υ υ υ η ω µ ω µ υ η ω υ ω η υµ ω η υ., µ υµ µ υ ω ω ω η ω ω., ω ω ω, µω µ η µ η η

3. Sərbəst işlərin mövzuları və hazırlanma qaydaları

3. Sərbəst işlərin mövzuları və hazırlanma qaydaları Təhvil verilmə tarixi (həftə) Mövzunun adı və ədəbiyyatın şifri 1. 3 Koordinatları ilə verilmiş nöqtələrin hər üç proyeksiyasını və əyani təsvirini

PHƯƠNG TRÌNH MẶT PHẲNG

CHƯƠNG 2 PHƯƠNG TRÌNH MẶT PHẲNG TÓM TẮT LÝ THUYẾT I. VECTƠ PHÁP TUYẾN (HAY PHÁP VECTƠ) CỦA MẶT PHẲNG Vectơ 0 gọi là vtpt của mặt phẳng a nếu giá của vuông góc mặt phẳng a. Vtpt của mp a thường ký hiệu

Meren virsi Eino Leino

œ_ œ _ q = 72 Meren virsi Eino Leino Toivo Kuua o. 11/2 (1909) c c F c Kun ne F iu L? c œ J J J J œ_ œ_ nœ_ Min ne rien nät, vie ri vä vir ta? Kun ne c c F c Kun ne F iu L? c œ J J J J œ_ œ_ nœ_ Min ne

ΣΤΗΝ ΒΑΣΙΚΗ ΤΟΥΣ ΕΚΔΟΣΗ

4 ΣΤΗΝ ΒΑΣΙΚΗ ΤΟΥΣ ΕΚΔΟΣΗ ΜΟΤΕΡ 800m 3 ΔΥΟ ΕΙΣΟΔΩΝ ΤΡΕΙΣ ΠΕΡΣΙΔΕΣ ΑΛΟΥΜΙΝΙΟΥ ΕΣΩΤΕΡΙΚΕΣ ΗΛΕΚΤΡΟΝΙΚΟΣ ΘΕΡΜΟΣΤΑΤΗΣ ΜΙΑ ΠΕΡΣΙΔΑ ΕΚΤΟΝΩΣΗΣ ΠΕΡΣΙΔΑ ΑΛΟΥΜΙΝΙΟΥ ΕΞΩΤΕΡΙΚΗ ΣΩΛΗΝΕΣ ΑΛΟΥΜΙΝΙΟΥ Φ120 ΚΕΡΑΜΙΚΑ ΚΡΥΣΤΑΛΛΑ

AZƏRBAYCAN RESPUBLİKASI KƏND TƏSƏRRÜFATI NAZİRLİYİ AZƏRBAYCAN RESPUBLİKASI TƏHSİL NAZİRLİYİ AZƏRBAYCAN RESPUBLİKASI TƏHSİL PROBLEMLƏRİ İNSTİTUTU

. Uverstet dı: zərbc Dövlət qrr Uverstet. Fkültə: qrr qtsdt. Kfedr: İforms teologlrı və sstemlər. Fə: Ekoometrk 5. Mühzrəç: dos. S..Məmmədov ZƏRYN RESPULİKSI KƏND TƏSƏRRÜFTI NZİRLİYİ ZƏRYN RESPULİKSI TƏHSİL

A/A Επώνυμο Όνομα 1 ΑΒΑΓΙΑΝΝΗΣ ΙΩΑΝΝΗΣ 2 ΑΓΓΕΛΕΡΟΥ ΑΙΚΑΤΕΡΙΝΗ 3 ΑΓΡΙΤΕΛΛΗΣ ΕΜΜΑΝΟΥΗΛ 4 ΑΘΑΝΑΣΙΑΔΟΥ ΕΥΤΕΡΠΗ - ΑΙΚΑΤΕΡΙΝΗ 5 ΑΘΑΝΑΣΙΑΔΟΥ ΜΑΡΙΑ 6 ΑΘΑΝΑΣΙΟΥ ΙΩΑΝΝΗΣ 7 ΑΘΑΝΑΣΙΟΥ ΜΙΧΑΗΛ 8 ΑΘΑΝΑΣΙΟΥ ΧΡΗΣΤΟΣ 9

Ψηφιακός Έλεγχος. 7 η διάλεξη Υλοποίηση Ψηφιακών Φίλτρων. Ψηφιακός Έλεγχος 1

Ψηφιακός Έλεγχος 7 η διάλεξη Υλοποίηση Ψηφιακών Φίλτρων Ψηφιακός Έλεγχος Υλοποίηση Ψηφιακών φίλτρων Το πρακτικό ενδιαφέρον της υλοποίησης ψηφιακών ρυθμιστών είναι μεγάλο καθώς λαμβάνονται υπόψιν θέματα

!"!# ""$ %%"" %$" &" %" "!'! " #$!

" "" %%"" %" &" %" " " " % ((((( ((( ((((( " %%%% & ) * ((( "* ( + ) (((( (, (() (((((* ( - )((((( )((((((& + )(((((((((( +. ) ) /(((( +( ),(, ((((((( +, 0 )/ (((((+ ++, ((((() & "( %%%%%%%%%%%%%%%%%%%(

OIKONOMIKO ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ

ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΜΗΤΡΩΟ ΕΣΩΤΕΡΙΚΩΝ ΜΕΛΩΝ ΕΠΙΤΡΟΠΩΝ ΓΙΑ ΚΡΙΣΕΙΣ ΕΚΛΟΓΗΣ Η ΕΞΕΛΙΞΗΣ ΣΕ ΘΕΣΕΙΣ ΚΑΘΗΓΗΤΩΝ ΟΠΟΙΑΣΔΗΠΟΤΕ ΒΑΘΜΙΔΑΣ ΜΕ ΓΝΩΣΤΙΚΟ ΠΟΥ ΑΝΗΚΕΙ ΣΤΗΝ ΕΥΡΥΤΕΡΗ ΓΝΩΣΤΙΚΗ ΠΕΡΙΟΧΗ ΤΗΣ ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗΣ A/A

d 2 y dt 2 xdy dt + d2 x

y t t ysin y d y + d y y t z + y ty yz yz t z y + t + y + y + t y + t + y + + 4 y 4 + t t + 5 t Ae cos + Be sin 5t + 7 5 y + t / m_nadjafikhah@iustacir http://webpagesiustacir/m_nadjafikhah/courses/ode/fa5pdf

HEYDƏR ƏLİYEV AZƏRBAYCAN XALQININ ÜMUMMİLLİ LİDERİ

l i n ü ç ü HEYDƏR ƏLİYEV p a e d AZƏRBAYCAN XALQININ ÜMUMMİLLİ LİDERİ Ç ali Çap üçün deil. Nama Qəhrəmanova Məhəmməd Kərimov İlham Hüsenov RİYAZİYYAT0 Öìóìòÿùñèë ìÿêòÿáëÿðèíèí 0-úó ñèíôè ö öí Ðèéàçèééàò

! " #$ (!$ )* ' & )* # & # & ' +, #

! " #$ %%%$&$' %$($% (!$ )* ' & )* # & # & ' +, # $ $!,$$ ' " (!!-!.$-/001 # #2 )!$!$34!$ )$5%$)3' ) 3/001 6$ 3&$ '(5.07808.98: 23*+$3;'$3;',;.8/ *' * $

Đường tròn : cung dây tiếp tuyến (V1) Đường tròn cung dây tiếp tuyến. Giải.

Đường tròn cung dây tiếp tuyến BÀI 1 : Cho tam giác ABC. Đường tròn có đường kính BC cắt cạnh AB, AC lần lượt tại E, D. BD và CE cắt nhau tại H. chứng minh : 1. AH vuông góc BC (tại F thuộc BC). 2. FA.FH

!#$%!& '($) *#+,),# - '($) # -.!, '$%!%#$($) # - '& %#$/0#!#%! % '$%!%#$/0#!#%! % '#%3$-0 4 '$%3#-!#, '5&)!,#$-, '65!.#%

" #$%& '($) *#+,),# - '($) # -, '$% %#$($) # - '& %#$0##% % '$% %#$0##% % '1*2)$ '#%3$-0 4 '$%3#-#, '1*2)$ '#%3$-0 4 @ @ @

A Ï apple ÁÈ ÛÙÔÈ Â ÔÈapple Ï 0,14 0,14 ÓÔÏÔ 0,14 0,14. ÚÔÎ Ù ÔÏ Î È ÌË Î ÎÏÔÊÔÚÔ ÓÙ ÛÙÔÈ Â applefi Î Ù ÛÎÂ 0, ,65 ÓÔÏÔ 0,00 29.

NYMºH E IXEIPH EI E..T.. & EMºIA ø H A.E. AP. MAE 26878/80/B/92/23 - AP..E.MH 71708520000 I O O I MO 31Ë EKEMBPIOY 2015 - ETAIPIKH XPH H (1 IANOYAPIOY - 31 EKEMBPIOY 2015) (XÚËÌ ÙÔÔÈÎÔÓÔÌÈÎ ÛÙÔÈ Â ÛÂ ÎfiÛÙÔ

ΚEΦΑΛΑΙΟ 1. Πίνακες. Από τα παραπάνω γίνεται αντιληπτό ότι κάθε γραµµή και στήλη ενός πίνακα A ορίζει µονοσήµαντα τη θέση κάθε στοιχείου A

ΚEΦΑΛΑΙΟ Πίνακες Εστω και είναι το σώµα των πραγµατικών και των µιγαδικών αριθµών αντιστοίχως Στο εξής όταν γράφουµε F θα εννοούµε είτε το είτε το Ορισµός Eστω F = ή και m, Κάθε ορθογώνια διάταξη m A F

Παναγιώτης Ψαρράκος Αν. Καθηγητής

Ανάλυση Πινάκων Κεφάλαιο 5: Κανονικοί Πίνακες Παναγιώτης Ψαρράκος Αν. Καθηγητής Δ.Π.Μ.Σ. Εφαρμοσμένες Μαθηματικές Επιστήμες Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Τομέας Μαθηματικών Εθνικό

ΑΡΧΕΙΑ ΚΑΙ ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ

ÔØ Ö ΑΡΧΕΙΑ ΚΑΙ ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ Στοκεφάλαιοαυτόθαπαρουσ ιασ τούνμερικέςαπότιςδυνατότητεςπουπαρέχειη βιβλιοθήκη ÉÌσ εαρχείακαθώςκαιτρόποισ ύνδεσ ηςκαιεκτέλεσ ηςερωτημάτων σ εβάσ ειςδεδομένωνº º½ Ηκατηγορία

6. Aπόκριες 7. Πάσχα

TÈ Ù ÍË Â Ó È ÌÔ Ô appleôïèùèûìfi ; 1. O πολιτισµός του τόπου µας 2. Mια επίσκεψη στο µουσείο 3. Tι συµβαίνει στην περιοχή µας; 4. Kάθε τόπος τα έθιµά του και ο χρόνος τα δικά του... 5. Tο βιβλίο των παροιµιών

Η αυτοχειρία στην αρχαία Ελλάδα: Γνώμες των φιλοσόφων

Σύλλογος Αρχαίας Ελληνικής Φιλοσοφίας σὺν Ἀθηνᾷ Η αυτοχειρία στην αρχαία Ελλάδα: Γνώμες των φιλοσόφων Κυριακή, 16 Δεκεμβρίου 2012 ΣΩΚΡΑΤΗΣ aãpeimi de/, w j eãoike, th/meron: keleu/ousi ga\r ¹AqhnaiÍoi.

Answers to practice exercises

Answers to practice exercises Chapter Exercise (Page 5). 9 kg 2. 479 mm. 66 4. 565 5. 225 6. 26 7. 07,70 8. 4 9. 487 0. 70872. $5, Exercise 2 (Page 6). (a) 468 (b) 868 2. (a) 827 (b) 458. (a) 86 kg (b)

MÉTHODES ET EXERCICES

J.-M. MONIER I G. HABERER I C. LARDON MATHS PCSI PTSI MÉTHODES ET EXERCICES 4 e édition Création graphique de la couverture : Hokus Pokus Créations Dunod, 2018 11 rue Paul Bert, 92240 Malakoff www.dunod.com

Suy ra EA. EN = ED hay EI EJ = EN ED. Mặt khác, EID = BCD = ENM = ENJ. Suy ra EID ENJ. Ta thu được EI. EJ Suy ra EA EB = EN ED hay EA

ài tập ôn đội tuyển năm 015 guyễn Văn inh Số 6 ài 1. ho tứ giác ngoại tiếp. hứng minh rằng trung trực của các cạnh,,, cắt nhau tạo thành một tứ giác ngoại tiếp. J 1 1 1 1 hứng minh. Gọi 1 1 1 1 là tứ giác

18x 3x. x + 4 = 1 tənliyinin kökləri hasilini

1. Mərəzləri düzucqlı üçucğın iti ucq təpələrində oln ii çevrənin əsişmə nöqtələrindən iri düzucq təpəsindədir. Üçucğın tetləri sm və sm olrs, çevrələrin əsişmə nöqtələri rsındı məsfəni ) 5, sm ) 8 sm

HÀM NHIỀU BIẾN Lân cận tại một điểm. 1. Định nghĩa Hàm 2 biến. Miền xác định của hàm f(x,y) là miền VD:

. Định nghĩa Hàm biến. f : D M (, ) z= f( M) = f(, ) Miền ác định của hàm f(,) là miền VD: f : D HÀM NHIỀU BIẾN M (, ) z= f(, ) = D sao cho f(,) có nghĩa. Miền ác định của hàm f(,) là tập hợp những điểm

!"#$ %"&'$!&!"(!)%*+, -$!!.!$"("-#$&"%-

!"#$ %"&$!&!"(!)%*+, -$!!.!$"("-#$&"%-.#/."0, .1%"("/+.!2$"/ 3333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333 4.)!$"!$-(#&!- 33333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333

'A Ï apple ÁÈ ÛÙÔÈ Â ÔÈapple Ï 0,01 0,01 ÓÔÏÔ 0,01 0,01 ÓÔÏÔ ÌË Î ÎÏÔÊÔÚÔ ÓÙˆÓ , ,72

TÔ ÚÈÛÙÈÎ EappleÈ ÂÈÚ ÛÂÈ EappleÈappleÏˆÌ ÓˆÓ È ÌÂÚÈÛÌ ÙˆÓ TAM. TZøPTZH E..E. AP..E.MH 71601820000 I O O I MO 31Ë EKEMBPIOY 2016 ETAIPIKH XPH H (1 IANOYAPIOY - 31 EKEMBPIOY 2016) (XÚËÌ ÙÔÔÈÎÔÓÔÌÈÎ ÛÙÔÈ

ΚΕΦΑΛΑΙΟ 9 «Ταλαντώσεις»

ΚΕΦΑΛΑΙΟ 9 «Ταλαντώσεις» Μαρία Κατσικίνη aii@auh.gr uer.auh.gr/~aii Οι έντε αισθήσεις Αντίληψη του εριβάλλοντος Όραση Ακοή Γεύση Αφή Όσφρηση φς ήχος κύματα ηλεκτρομαγνητικά μηχανικά Ταλαντώσεις - κυμάνσεις

]Zp _[ I 8G4G /<4 6EE =A>/8E>4 06? E6/<; 6008:6> /8= 4; /823 ;1A :40 >176/812; 98/< ;76//40823 E182/;G g= = 4/<1

! " #$ # %$ & ' ( ) *+, ( -+./0123 045067/812 15 96:4; 82 /178/? = 1@4> 82/01@A74; B824= 6/87 60/8567/; C 71 04D47/10; C 82/1 /

Προγραμματισμός I (Θ)

Τεχνολογικό Εκπαιδευτικό Ίδρυμα Κεντρικής Μακεδονίας - Σέρρες Τμήμα Μηχανικών Πληροφορικής Προγραμματισμός I (Θ) Δρ. Δημήτρης Βαρσάμης Επίκουρος Καθηγητής Οκτώβριος 2017 Δρ. Δημήτρης Βαρσάμης Οκτώβριος

ΚΩΣΤΑΣ ΜΗΛΙΩΤΗΣ ksperaor@cytanet.com.cy Φαξ: +357 22623924

1/ 5 ΠΡΟΚΗΡΥΞΗ ΔΙΑΓΩΝΙΣΜΟΥ - ΚΑΤΩ ΑΠΟ ΤΑ ΟΡΙΑ ΔΗΜΟΣΙΕΥΣΗΣ - EL ΠΡΟΚΗΡΥΞΗ ΔΙΑΓΩΝΙΣΜΟΥ - ΚΑΤΩ ΑΠΟ ΤΑ ΟΡΙΑ ΔΗΜΟΣΙΕΥΣΗΣ ΤΜΗΜΑ I: ΑΝΑΘΕΤΟΥΣΑ ΑΡΧΗ I.1) ΕΠΩΝΥΜΙΑ, ΔΙΕΥΘΥΝΣΕΙΣ ΚΑΙ ΣΗΜΕΙΟ(Α) ΕΠΑΦΗΣ Επίσημη επωνυμία:

º πo 2: À ª π Ã πƒπ OπO π π ª ƒπø

º πo 2: À ª π Ã πƒπ OπO π π ª ƒπø Η βασική απαίτηση για ένα σύστηµα διαχείρισης ποιότητας είναι ότι ο οργανισµός θα πρέπει να προσδιορίσει και να διαχειριστεί την οικογένεια των απαραίτητων διεργασιών

General 2 2 PT -Symmetric Matrices and Jordan Blocks 1

General 2 2 PT -Symmetric Matrices and Jordan Blocks 1 Qing-hai Wang National University of Singapore Quantum Physics with Non-Hermitian Operators Max-Planck-Institut für Physik komplexer Systeme Dresden,

Τυπολόγιο Υπολογισµού Προσπιπτώµενης Ηλιακής Ακτινοβολίας σε Οριζόντια και Κεκλιµένη Επιφάνεια

Πανεπιστήµι υτικής Μακεδνίας Τµήµα Μηχανικών ιαχείρισης Ενεργειακών Πόρων, Κζάνης λιακή Τεχνική/Φωτβλταϊκά Συστήµατα Επ. Καθ.. Μπύρης Τυπλόγι Υπλγισµύ Πρσπιπτώµενης λιακής Ακτινβλίας σε Οριζόντια και Κεκλιµένη

Μετασχηµατισµοί 2 &3

Μετασχηµατισµοί &3 Περιγράφονται σαν σύνθεση βασικών: µετατόπιση, αλλαγή κλίµακας,περιστροφή, στρέβλωση Χωρίζονται σε γεωµετρικούς (εδώ) και αξόνων (αντίστροφοι) Θέσεις αντικειµένων και φωτεινών πηγών

'A Ï apple ÁÈ ÛÙÔÈ Â ÔÈapple Ï , ,96 ÓÔÏÔ , ,96 ÓÔÏÔ ÌË Î ÎÏÔÊÔÚÔ ÓÙˆÓ , ,99

TOYPI TIKAI E IXEIPH EI «PO.KA.Kø A.E.» AP.M.A.E. 12152/80/B/86/115 - AP..E.MH 123448420000 I O O I MO 31Ë EKEMBPIOY 2017 ETAIPIKH XPH H (1 IANOYAPIOY - 31 EKEMBPIOY 2017) (XÚËÌ ÙÔÔÈÎÔÓÔÌÈÎ ÛÙÔÈ Â ÛÂ ÎfiÛÙÔ

ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Γ ΤΑΞΗΣ ΕΠΑΛ (ΟΜΑ Α Β ) 2010

ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Γ ΤΑΞΗΣ ΕΠΑΛ (ΟΜΑ Α Β ) 00 ΘΕΜΑ Α Στις ερωτήσεις Α-Α3 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία

The effect of curcumin on the stability of Aβ. dimers

The effect of curcumin on the stability of Aβ dimers Li Na Zhao, See-Wing Chiu, Jérôme Benoit, Lock Yue Chew,, and Yuguang Mu, School of Physical and Mathematical Sciences, Nanyang Technological University,

Respublikanın ümumtəhsil məktəblərinin 9-cu sinifləri üçün Cəbr 9 dərsliyi

Respublikanın ümumtəhsil məktəblərinin 9-cu sinifləri üçün Cəbr 9 dərsliyi Müəlliflər: Misir Mərdanov Məmməd Yaqubov Sabir Mirzəyev Ağababa İbrahimov İlham Hüseynov Məhəmməd Kərimov Bakı: Çaşıoğlu, 0.

ĐỀ SỐ 1. ĐỀ SỐ 2 Bài 1 : (3 điểm) Thu gọn các biểu thức sau : Trần Thanh Phong ĐỀ THI HỌC KÌ 1 MÔN TOÁN LỚP O a a 2a

Trần Thanh Phong 0908 456 ĐỀ THI HỌC KÌ MÔN TOÁN LỚP 9 ----0O0----- Bài :Thưc hiên phép tính (,5 đ) a) 75 08 b) 8 4 5 6 ĐỀ SỐ 5 c) 5 Bài : (,5 đ) a a a A = a a a : (a > 0 và a ) a a a a a) Rút gọn A b)

L P I J C B D. Do GI 2 = GJ.GH nên GIH = IJG = IKJ = 90 GJB = 90 GLH. Mà GIH + GIQ = 90 nên QIG = ILG = IQG, suy ra GI = GQ hay Q (BIC).

ài tập ôn đội tuyển I năm 015 Nguyễn Văn inh Số 7 ài 1. (ym). ho tam giác nội tiếp đường tròn (), ngoại tiếp đường tròn (I). G là điểm chính giữa cung không chứa. là tiếp điểm của (I) với. J là điểm nằm

ΚΑΙ ΓΡΑΦΙΚΩΝ. Μοντέλα και Αλγόριθμοι Φωτισμού

ΕΡΓΑΣΤΗΡΙΟ ΠΟΛΥΜΕΣΩΝ ΚΑΙ ΓΡΑΦΙΚΩΝ Γ Ρ Α Φ Ι Κ Α Μοντέλα και Αλγόριθμοι Φωτισμού Φωτισμός Για την ρεαλιστική παράσταση γραφικών χρειάζονται τα εξής: Ένα μοντέλο φωτισμού απλοποιημένη αναπαράσταση των φυσικών

ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ C ΣΕΙΡΑ 6 η

Δημοκρίτειο Πανεπιστήμιο Θράκης Πολυτεχνική Σχολή Τμήμα Μηχανικών Παραγωγής & Διοίκησης Ακαδ. έτος 2016-2017 Τομέας Συστημάτων Παραγωγής Εξάμηνο Β Αναπληρωτής Καθηγητής Στέφανος Δ. Κατσαβούνης ΜΑΘΗΜΑ :

Bakı Dövlət Universiteti. Mühazirəçi: dosent Lalə İslam qızı Vəliyeva

Bakı Dövlət Universiteti Nanomaterialların n kimyəvi ə ifizikası ikas kafedrası Mühazirəçi: dosent Lalə İslam qızı Vəliyeva MÜHAZİRƏ-4 NANOMATERİALLARIN TƏDQİQİNDƏ İSTİFADƏ OLUNAN ÜSULLAR İnsan gözünün

ÕÄÑÏËÇØÉÅÓ ÔÕÐÏÕ Á2 - Á4 ÌÅ ÁÍÔÉÐÁÃÅÔÉÊÇ ÐÑÏÓÔÁÓÉÁ

ÕÄÑÏËÇØÉÅÓ ÔÕÐÏÕ Á - Á ÌÅ ÁÍÔÉÐÁÃÅÔÉÊÇ ÐÑÏÓÔÁÓÉÁ Ç ÅÕÄÏÓ ÁÂÅÅ êáôáóêåõüæåé õäñïëçøßåò Üñäåõóçò ôýðïõ SCHLUMBERGER ïé ïðïßåò áíôáðïêñßíïíôáé ðëþñùò ðñïò ôéò äéåèíåßò ðñïäéáãñáöýò, êáôáóêåõüæïíôáé ìå Þ ùñßò

Müəlliflər (əlifba sırası ilə)

1 Müəlliflər (əlifba sırası ilə) A B C Ç D E Ə Əzimə Nəsibova F G H X Xanım İsmayılova İ J K Könül İsmayılzadə Q L M Magistr OL N O Ö P R Reşad Əbilzadə S Ş Şəbnəm Nuruyeva T Təhmasib Quluzadə Turqut İsmayılov

Déformation et quantification par groupoïde des variétés toriques

Défomation et uantification pa goupoïde de vaiété toiue Fédéic Cadet To cite thi veion: Fédéic Cadet. Défomation et uantification pa goupoïde de vaiété toiue. Mathématiue [math]. Univeité d Oléan, 200.

M c. E M b F I. M a. Chứng minh. M b M c. trong thứ hai của (O 1 ) và (O 2 ).

ài tập ôn đội tuyển năm 015 Nguyễn Văn inh Số 5 ài 1. ho tam giác nội tiếp () có + =. Đường tròn () nội tiếp tam giác tiếp xúc với,, lần lượt tại,,. Gọi b, c lần lượt là trung điểm,. b c cắt tại. hứng

MÜHAZİRƏ - 3. Karbon klasterləri: füllerenlər, nanoborular, nanoalmazlar və qrafen

21 MÜHAZİRƏ - 3 Karbon klasterləri: füllerenlər, nanoborular, nanoalmazlar və qrafen Nano aləmdə hal-hazırda mövcud olan klasterlər içərisində karbon atomundan yarananları həm sadəliyi, həm dayanıqlılığı

Е. S. C Ə F Ə R O V F İ Z İ K A

Е. S. C Ə F Ə R O V F İ Z İ K A Abituriyentlər, orta məktəbin yuxarı sinif şagirdləri, orta məktəb müəllimləri, fizikanı sərbəst öyrənənlər üçün vəsait B A K I - 2013 Elmi redaktor: AMEA-nın Radiasiya

ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΥΦΥΗΣ ΕΛΕΓΧΟΣ. Ενότητα #7: Σύστημα Ασαφούς Λογικής Μαθηματικές Εκφράσεις

ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΥΦΥΗΣ ΕΛΕΓΧΟΣ Ενότητα #7: Σύστημα Ασαφούς Λογικής Μαθηματικές Εκφράσεις Αναστάσιος Ντούνης Τμήμα Μηχανικών Αυτοματισμού Τ.Ε.

ΑΝΑΡΤΗΣΗ ΣΤΟ ΔΙΑΔΥΚΤΙΟ

1 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΥΓΕΙΑΣ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΑΣΦΑΛΙΣΕΩΝ ΠΑΝΕΠΙΣΤΗΜΙΑΚΟ ΓΕΝΙΚΟ ΝΟΣΟΚΟΜΕΙΟ ΙΩΑΝΝΙΝΩΝ Γραφείο : Προμηθειών Ταχ. Δ/νση : Λ. Στ. Νιάρχου : 45500 ΙΩΑΝΝΙΝΑ ΠΡΟΣ: ΑΝΑΡΤΗΣΗ ΣΤΟ ΔΙΑΔΥΚΤΙΟ

Chapter 1 Complex numbers

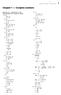Complex numbers MC Qld- Chapter Complex numbers Exercise A Operations on and representations of complex numbers a u ( i) 8i b u + v ( i) + ( + i) + i c u + v ( i) + ( + i) i + + i + 8i d u v ( i) ( + i)

Πανεπιστήμιο Ιωαννίνων Τμήμα Πληροφορικής Δομές Δεδομένων [ΠΛΥ302] Χειμερινό Εξάμηνο 2012

Πανεπιστήμιο Ιωαννίνων Τμήμα Πληροφορικής Δομές Δεδομένων [ΠΛΥ302] Χειμερινό Εξάμηνο 2012 Ενδεικτικές απαντήσεις 1 ου σετ ασκήσεων. Άσκηση 1 Πραγματοποιήσαμε μια σειρά μετρήσεων του χρόνου εκτέλεσης τριών

934 Ν. 9<Π)/94. Ε.Ε. Παρ. 1(H) Αρ. 2863,43.94

Ε.Ε. Παρ. 1(H) Αρ. 286,4.94 94 Ν. 9

UDC. An Integral Equation Problem With Shift of Several Complex Variables 厦门大学博硕士论文摘要库

ß¼ 0384 9200852727 UDC Î ± À» An Integral Equation Problem With Shift of Several Complex Variables Û Ò ÖÞ Ô ²» Ý Õ Ø ³ÇÀ ¼ 2 0 º 4 Ñ ³ÇÙÐ 2 0 º Ñ Ä ¼ 2 0 º Ñ ÄÞ Ê Ã Ö 20 5  Š¾ º ½ É É Ç ¹ ¹Ý É ½ ÚÓÉ

14.5mm 14.5mm

This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication. Citation information: DOI 1.119/JETCAS.218.289582,

ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ C ΣΕΙΡΑ 6 η

Δημοκρίτειο Πανεπιστήμιο Θράκης Πολυτεχνική Σχολή Τμήμα Μηχανικών Παραγωγής & Διοίκησης Ακαδ. έτος 2017-2018 Τομέας Συστημάτων Παραγωγής Εξάμηνο Β Αναπληρωτής Καθηγητής Στέφανος Δ. Κατσαβούνης ΜΑΘΗΜΑ :

ΑΣΣΟΣ - ΚΟΡΙΝΘΙΑΣ. α/α: KOΡ 04

ΑΣΣΟΣ - ΚΟΡΙΝΘΙΑΣ α/α: KOΡ 04 Τοποθεσία Ακινήτου Το ακίνητο με εμβαδόν 4985 μ. βρίσκεται επί της Π.Ε.Ο Κορίνθου - Πατρών 6 χιλ. μετά την Κόρινθο, δεξιά, και 9 χιλ. πριν το Κιάτο. ΕΥΡΥΤΕΡΗ ΠΕΡΙΟΧΗ ΠΙΝΑΚΑΣ

Nayma Qəhrəmanova Məhəmməd Kərimov İlham Hüseynov RİYAZİYYAT 10

Nama Qəhrəmanova Məhəmməd Kərimov İlham Hüsenov RİYAZİYYAT 0 Ümumtəhsil məktəblərinin 0-cu sinfi üçün Riaziat fənni üzrə dərsliin METODİK VƏSAİTİ Bu nəşrlə bağlı irad və təkliflərinizi radius_n@hotmail.com

Distributed by: www.jameco.com -800-83-4242 The content and copyrights of the attached material are the property of its owner. φ δ δ φ φφ φ 86 δ φ δ An explanation of the taping dimensions can be found

d 4 1 q M 2 q 2 M 2 q 2 M 2 226/389

Μη αβελιανές θεωρίες - Yang-Mills θεωρίες Η μικρή ακτίνα δράσης των ασθενών αλληλεπιδράσεων μας οδηγεί στο συμπέρασμα ότι τα σωματίδια υπεύθυνα για αυτήν την αλληλεπίδραση (τα αντίστοιχα σωματίδια βαθμίδας)

!"#$%& '!(#)& a<.21c67.<9 /06 :6>/ 54.6: 1. ]1;A76 _F -. /06 4D26.36 <> A.:4D6:6C C4/4 /06 D:43? C</ O=47?6C b*dp 12 :1?6:E /< D6 3:4221N6C 42 D:A6 O=

! " #$% & '( )*+, -. /012 3045/67 8 96 57626./ 4. 4:;74= 69676.36 D426C

Πανεπιστήμιο Ιωαννίνων Τμήμα Μηχανικών Η/Υ και Πληροφορικής Δομές Δεδομένων [ΠΛΥ302] Χειμερινό Εξάμηνο 2013

Πανεπιστήμιο Ιωαννίνων Τμήμα Μηχανικών Η/Υ και Πληροφορικής Δομές Δεδομένων [ΠΛΥ302] Χειμερινό Εξάμηνο 2013 Λυμένες Ασκήσεις Σετ Α: Ανάλυση Αλγορίθμων Άσκηση 1 Πραγματοποιήσαμε μια σειρά μετρήσεων του

Q B Y A P O 4 O 6 Z O 5 O 1 O 2 O 3

ài tập ôn đội tuyển năm 2015 guyễn Văn Linh Số 8 ài 1. ho tam giác nội tiếp đường tròn () có là tâm nội tiếp. cắt () lần thứ hai tại J. Gọi ω là đường tròn tâm J và tiếp xúc với,. Hai tiếp tuyến chung

linear motions: surge, sway, and heave rotations: roll, pitch, and yaw

heave yaw when the ship is treated as a rigid body, it has six degrees of freedom: three linear motions and three rotations as indicated in the figure at the left: body-fixed axes pitch, v roll, u sway

ΠΑΡΑΡΤΗΜΑ ΙΙ ΔΗΜΟΣ ΑΛΕΞΑΝΔΡΟΥΠΟΛΗΣ. Πόλη: ΑΛΕΞΑΝΔΡΟΥΠΟΛΗ Ταχ. κώδικας: Χώρα: Ελλάδα 681 00 ΕΛΛΑΔΑ-GR Σημείο(-α) επαφής: Τεχνική Υπηρεσία

ΠΑΡΑΡΤΗΜΑ ΙΙ ΕΥΡΩΠΑΪΚΗ ΕΝΩΣΗ Δημοσίευση στο συμπλήρωμα της Επίσημης Εφημερίδας της Ευρωπαϊκής Ένωσης 2, rue Mercier, L-2985 Luxembourg Φαξ: (352) 29 29 42 670 Ηλεκτρονικό ταχυδρομείο: mp-ojs@opoce.cec.eu.int

PHÉP TÍNH VI PHÂN HÀM MỘT BIẾN

9//6 CHƯƠNG Đạo hàm ại mộ điểm PHÉP TÍNH VI PHÂN HÀM MỘT BIẾN Địh ghĩa: Đạo hàm của hàm f ại điểm a, ký hiệ f (a) là: f ' a lim a f f a (ế giới hạ à ồ ại hữ hạ). Chú ý: đặ h=-a, a có: f ' a a f a h f a

HOC360.NET - TÀI LIỆU HỌC TẬP MIỄN PHÍ. đến va chạm với vật M. Gọi vv, là vận tốc của m và M ngay. đến va chạm vào nó.

HOC36.NET - TÀI LIỆU HỌC TẬP IỄN PHÍ CHỦ ĐỀ 3. CON LẮC ĐƠN BÀI TOÁN LIÊN QUAN ĐẾN VA CHẠ CON LẮC ĐƠN Phương pháp giải Vật m chuyển động vận tốc v đến va chạm với vật. Gọi vv, là vận tốc của m và ngay sau