POGOJI ZA UPORABO SISTEMA PRISTOJBIN NA ZRAČNIH POTEH IN PLAČILNI POGOJI
|
|
|
- Τελεσφόρος Κοτζιάς
- 6 χρόνια πριν
- Προβολές:
Transcript
1 Priloga 2 POGOJI ZA UPORABO SISTEMA PRISTOJBIN NA ZRAČNIH POTEH IN PLAČILNI POGOJI [Besedilo je potrdila Razširjena komisija. Veljati je začelo 1. oktobra 2007.] Izdano v letu 2007 (Ta različica nadomesti izdajo št /2.)
2 POGOJI ZA UPORABO SISTEMA PRISTOJBIN NA ZRAČNIH POTEH 1. ČLEN 1. Pristojbina se zaračuna za vsak let, izveden v skladu s postopki, določenimi za izvajanje standardov in priporočene prakse Mednarodne organizacije za civilno letalstvo, opravljen v zračnem prostoru v pristojnosti držav pogodbenic. Za namen pristojbin na zračnih poteh se zračni prostor razdeli na območja zaračunavanja pristojbin na zračnih poteh, ki jih določijo države pogodbenice in so navedena v seznamu v Dodatku 1 teh pogojev. 2. Pristojbina pomeni plačilo stroškov, ki jih imajo države pogodbenice v zvezi z navigacijskimi napravami in storitvami na zračnih poteh ter v zvezi z izvajanjem sistema pristojbin na zračnih poteh, pa tudi stroškov, ki jih ima EUROCONTROL z izvajanjem tega sistema. 3. Za pristojbine, ki nastanejo v določenem območju zaračunavanja, ki je v pristojnosti ene izmed držav pogodbenic, se lahko predpiše plačilo davka na dodano vrednost (Value Added Tax; v nadaljnjem besedilu: VAT). V tem primeru lahko EUROCONTROL ta davek zaračunava pod pogoji in v skladu s pravili, o katerih se je dogovoril z zadevno državo. 4. Pristojbine, ki nastanejo v določenem območju zaračunavanja, so lahko predmet ene ali več spodbujevalnih shem. EUROCONTROL lahko uvede spodbujevalno shemo pod pogoji in v skladu s pravili, o katerih se je dogovoril z zadevno državo. 5. Oseba, ki mora plačati pristojbino, je oseba, ki je upravljala zrakoplov v času izvedbe leta. Če identiteta operatorja ni znana, se šteje, da je operator zrakoplova njegov lastnik, razen če dokaže, katera druga oseba ga je upravljala v omenjenem času. 2. ČLEN Za vsak let, ki vstopi v zračni prostor z območji zaračunavanja, ki so navedena v seznamu v Dodatku 1 teh pogojev, se zaračuna enotna pristojbina (R), ki je enaka vsoti pristojbin za letenje v zadevnem zračnem prostoru z območji zaračunavanja, in sicer: R = Σ r i. n Posamezna pristojbina (r i ) za lete v območju zaračunavanja (i) se izračuna v skladu z določbami v 3. členu. 3. ČLEN Pristojbina za let v danem območju zaračunavanja (i) se izračuna po naslednji formuli: ri = ti x Ni, pri čemer (ri) pomeni pristojbino, (ti) ceno za enoto storitve in (Ni) število enot storitve v zvezi s takim letom. 4. ČLEN Število enot storitve iz prejšnjega člena, označeno z (N i ), se za določen let izračuna s formulo: Ni = di x p, kjer je (d i ) količnik razdalje v zvezi z območjem zaračunavanja (i), (p) pa je količnik teže (mase) zadevnega zrakoplova.
3 5. ČLEN 1. Količnik razdalje (d i ) se izračuna tako, da se število kilometrov razdalje velikega kroga deli s sto (100), in sicer med: letališčem odhoda v območju zaračunavanja oziroma točko vstopa v to območje (i) in prvim namembnim letališčem v območju zaračunavanja oziroma točko izhoda iz tega območja (i). Omenjeni vstopna in izstopna točka sta tisti točki, kjer zračna pot, opisana v načrtu leta, prečka lateralne meje omenjenega območja zaračunavanja. Ta načrt leta vključuje vse spremembe, ki jih operator izvede v prvotno prijavljenem načrtu leta, in vse spremembe, potrjene s strani operatorja, ki so posledica ukrepov upravljanja pretoka zračnega prometa. 2. Vendar pa za tiste lete, ki se končajo na letališču, s katerega je zrakoplov vzletel, in med katerimi ni bilo nobenega vmesnega pristanka (krožni leti), velja člen 5.1, razen v naslednjih dveh primerih: a) za krožne lete, ki potekajo izključno v enem območju zaračunavanja, se količnik razdalje izračuna tako, da se število kilometrov razdalje po velikem krogu med letališčem in točko, ki je od njega najbolj oddaljena, deli s sto (100) in pomnoži z dve (2); b) za krožne lete, ki potekajo v več kot enem območju zaračunavanja, velja člen 5.1, razen za tisto območje zaračunavanja, ki zajema točko, ki je od letališča najbolj oddaljena. V tem primeru se količnik razdalje izračuna tako, da skupno število kilometrov razdalje po velikem krogu med točko vstopa v območje zaračunavanja in najbolj oddaljeno točko in od te najbolj oddaljene točke do točke izhoda iz območja zaračunavanja deli s sto (100). 3. Za vsak vzlet z ozemlja države pogodbenice in za vsak pristanek na ozemlju države pogodbenice se razdalja, ki se upoševa, zmanjša za dvajset (20) kilometrov. 6. ČLEN 1. Količnik teže (mase) (p) izražen kot številka z dvema decimalnima mestoma je kvadratni koren iz količnika števila največje dovoljene vzletne mase zrakoplova izražene v metričnih tonah z enomestnim decimalnim številom, ki je navedena v spričevalu o plovnosti, letalskem priročniku ali drugem ustreznem uradnem dokumentu, in števila petdeset (50), in sicer: p = najv. dov. vzlet. teža (masa) zrakoplova 50. Kadar organom, ki so odgovorni za izterjavo pristojbin, največja dovoljena vzletna masa zrakoplova ni znana, se za izračun količnika teže (mase) upošteva znana teža (masa) najtežjega zrakoplova istega tipa. 2. Za zrakoplov, ki ima več različnih dovoljenih največjih vzletnih tež (mas), se količnik teže (mase) izračuna na osnovi najvišje dovoljene vzletne teže (mase), ki jo za takšen zrakoplov predpiše država, v kateri je zrakoplov registriran.
4 3. Kadar operator zadnji delovni dan koledarskega meseca, v katerem je prišlo do sprememb v njegovi floti, in najmanj enkrat letno obvesti EUROCONTROL, da upravlja z dvema ali več zrakoplovi, ki so različice istega tipa, se za izračun količnika teže (mase) za vsak zrakoplov tega tipa uporabi povprečje največjih dovoljenih vzletnih tež (mas) vseh njegovih zrakoplovov istega tipa. Količnik teže (mase) se izračunava za vsak tip zrakoplova in za vsakega operatorja vsaj enkrat letno. 7. ČLEN 1. Cena za enoto storitve (t i ) se določi v evrih. 2. Razen v primerih, ko prizadeta država določi drugače, se cena za enoto storitve za območje zaračunavanja, v katerem evro ni nacionalna valuta, preračunava mesečno na podlagi povprečnih mesečnih menjalnih tečajev med evrom in nacionalno valuto, ki so veljali v mesecu pred mesecem, ko je bil let izveden. Uporabljal se bo menjalni tečaj po Reutersovem izračunu mesečnega povprečja zaključnih dnevnih tečajev na podlagi dnevnih borznih cen ponudbe. 8. ČLEN 1. Oproščeni plačila pristojbine so naslednji leti: a. leti zrakoplovov, katerih največja dovoljena vzletna teža (masa) znaša manj kot dve (2) metrični toni; b. leti, namenjeni izključno prevozom, na službeni poti, vladajočega monarha in njegove/njene ožje družine, voditeljev držav, voditeljev vlad in vladnih ministrov. V teh primerih mora biti to utemeljeno z ustrezno oznako statusa ali opombo v načrtu leta; c. leti, namenjeni iskanju in reševanju (SAR), če jih odobri ustrezen pristojni organ. 2. Poleg tega države članice v zvezi z določenim območjem zaračunavanja v njihovi pristojnosti oprostijo plačila pristojbin: a. vojaške lete, ki jih izvede zrakoplov katere koli države; b. trenažne lete, izvedene izključno zaradi pridobitve licence ali v primeru pilotskega dela posadke razreda (rating), če to utemeljuje označba v načrtu leta. Leti morajo biti izvedeni izključno znotraj območja zaračunavanja. Leti ne smejo služiti prevozu potnikov in/ali tovora niti preletu zrakoplova na določen kraj ali preletu iz tehničnih razlogov; c. lete, izvedene izključno z namenom preverjanja ali testiranja opreme na zemlji, uporabljene ali namenjene za pomoč zračnemu prometu, razen preletov zadevnih zrakoplovov na določen kraj; d. lete, ki se končajo na letališču, s katerega je zrakoplov vzletel, in med katerimi ni prišlo do nobenega vmesnega pristanka (krožni leti); e. lete, ki se izvajajo izključno v pogojih VHR znotraj območja zaračunavanja; f. humanitarne lete, ki jih odobri ustrezen pristojni organ; g. carinske in policijske lete.
5 9. ČLEN Pristojbina se plačuje na poslovnem sedežu EUROCONTROLA v skladu s plačilnimi pogoji, določenimi v Dodatku 2 teh pogojev. Obračunska enota je evro. 10. ČLEN Države pogodbenice objavijo Pogoje uporabe sistema pristojbin na zračnih poteh in cene za enoto storitve.
6 Dodatek 1 OBMOČJA ZARAČUNAVANJA PRISTOJBIN NA ZRAČNIH POTEH Ime območja Opis zračnega prostora Država(-e) zaračunavanja pogodbenica(-e) Albanija Tirana Letalsko informativno območje Republika Albanija Tirana Zgornje letalsko informativno območje Nemčija Hannover Zgornje letalsko informativno območje Zvezna republika Nemčija Rhein Zgornje letalsko informativno območje Bremen Letalsko informativno območje Langen Letalsko informativno območje München Letalsko informativno območje Armenija Yerevan Letalsko informativno območje Republika Armenija 1 Avstrija Dunaj Letalsko informativno območje Republika Avstrija Belgija Luksemburg Bruselj Zgornje letalsko informativno območje Kraljevina Belgija Bruselj Letalsko informativno območje Vojvodina Luksemburg Bosna in Hercegovina Sarajevo Zgornje letalsko informativno območje Bosna in Hercegovina Sarajevo Letalsko informativno območje Bolgarija Sofija Letalsko informativno območje Republika Bolgarija Varna Letalsko informativno območje Ciper Nikozija Letalsko informativno območje Republika Ciper Hrvaška Zagreb Letalsko informativno območje Hrvaška republika Zagreb Zgornje letalsko informativno območje Danska Kopenhagen Letalsko informativno območje Kraljevina Danska Kontinentalna Španija Madrid Zgornje letalsko informativno območje Kraljevina Španija Madrid Letalsko informativno območje Barcelona Zgornje letalsko informativno območje Barcelona Letalsko informativno območje 1 Še ni tehnično vključena.
7 Ime območja Opis zračnega prostora Država(-e) zaračunavanja pogodbenica(-e) Kanarski otoki Kanarski otoki Zgornje letalsko informativno območje Kraljevina Španija Kanarski otoki Letalsko informativno območje Finska Finska Zgornje letalsko informativno območje Republika Finska Finska Letalsko informativno območje Francija Francija Zgornje letalsko informativno območje Francoska republika Pariz Letalsko informativno območje Brest Letalsko informativno območje Bordeaux Letalsko informativno območje Marseille Letalsko informativno območje Reims Letalsko informativno območje Združeno kraljestvo Škotska Zgornje letalsko informativno območje Združeno kraljestvo Velike Škotska Letalsko informativno območje Britanije in Severne Irske London Zgornje letalsko informativno območje London Letalsko informativno območje Grčija Atene Zgornje letalsko informativno območje Helenska republika Atene Letalsko informativno območje Madžarska Budimpešta Letalsko informativno območje Republika Madžarska Irska Shannon Zgornje letalsko informativno območje Irska Shannon Letalsko informativno območje Shannon Oceansko tranzitno območje, katerega meje so določene z naslednjimi koordinatami: 51 sever 15 zahod, 51 sever 8 zahod, 48 30' sever 8 zahod, 49 sever 15 zahod, 51 sever 15 zahod na in nad FL55 Severno oceansko tranzitno območje, katerega meje so določene z naslednjimi koordinatami: 57 sever 15 zahod, 54 sever 15 zahod, 57 sever 10 zahod, sever 10 zahod na in nad FL55 Italija Milano Zgornje letalsko informativno območje Italijanska republika Milano Letalsko informativno območje Rim Zgornje letalsko informativno območje Rim Letalsko informativno območje Brindisi Zgornje letalsko informativno območje Brindisi Letalsko informativno območje
8 Ime območja Opis zračnega prostora Država(-e) zaračunavanja pogodbenica(-e) Litva Vilnius Letalsko informativno območje Republika Litva 1 Nekdanja jugoslovanska Skopje Letalsko informativno območje Nekdanja jugoslovanska republika Makedonija republika Makedonija Malta Malta Zgornje letalsko informativno območje Republika Malta Malta Letalsko informativno območje Moldavija Chisinau Letalsko informativno območje Republika Moldavija Norveška Norveška Zgornje letalsko informativno območje Kraljevina Norveška Norveška Zgornje letalsko informativno območje Bodø Oceansko letalsko informativno območje Nizozemska Amsterdam Letalsko informativno območje Kraljevina Nizozemska Poljska Varšava Letalsko informativno območje Republika Poljska 1 Lizbona Lizbona Zgornje letalsko informativno območje Portugalska republika Lizbona Letalsko informativno območje Santa Maria Santa Maria Letalsko informativno območje Portugalska republika Romunija Bukarešta Letalsko informativno območje Romunija Beograd Beograd Zgornje letalsko informativno območje Republika Srbija Beograd Letalsko informativno območje Republika Črna gora Slovaška Bratislava Letalsko informativno območje Slovaška republika Slovenija Ljubljana Letalsko informativno območje Republika Slovenija Švedska Švedska Zgornje letalsko informativno območje Kraljevina Švedska Švedska Letalsko informativno območje 1 Še ni tehnično vključena.
9 Ime območja Opis zračnega prostora Država(-e) zaračunavanja pogodbenica(-e) Švica Švica Zgornje letalsko informativno območje Švicarska konfederacija Švica Letalsko informativno območje Češka republika Praga Letalsko informativno območje Češka republika Turčija Ankara Letalsko informativno območje Republika Turčija Istanbul Letalsko informativno območje Ukrajina Kijev Letalsko informativno območje Ukrajina 1 Simferopol' Letalsko informativno območje Odesa Letalsko informativno območje Kharkiv Letalsko informativno območje Lvov Letalsko informativno območje
10 PLAČILNI POGOJI Dodatek 2 1. KLAVZULA 1. Zaračunani zneski se plačajo na poslovnem sedežu EUROCONTROLA v Bruslju. 2. Ne glede na to, bo EUROCONTROL vplačila na račune, ki so v državah pogodbenicah ali v drugih državah v njegovem imenu odprti v bančnih ustanovah, ki so jih določili organi, pooblaščeni za izvajanje sistema pristojbin na zračnih poteh, sprejel kot izpolnitev dolžnikove plačilne obveznosti. 3. Znesek pristojbine zapade v plačilo z dnem, ko je let izveden. Datum valutacije, do katerega mora EUROCONTROL prejeti plačilo, mora biti označen na računu in znaša 30 dni od datuma računa. 2. KLAVZULA 1. Znesek pristojbine se plača v evrih, razen v primerih, določenih v drugem odstavku te klavzule. 2. Vsak uporabnik, ki ima domicil v eni izmed držav pogodbenic, lahko vsakič, ko pristojbino plačuje v določeni bančni ustanovi, ki je v državi njegovega domicila, to pristojbino poravna v konvertibilni valuti te države. 3. Vsakič, ko uporabnik uporabi storitev v skladu s prejšnjim odstavkom, se zneski, izraženi v evrih, preračunajo v državno valuto na podlagi dnevnih menjalnih tečajev, kot veljajo za komercialne transakcije glede na datum valutacije in kraj plačila. 3. KLAVZULA Šteje se, da je EUROCONTROL prejel plačilo na dan valutacije, ko je dolžni znesek nakazan v dobro dogovorjenega bančnega računa EUROCONTROLA. Datum valutacije je datum, ko EUROCONTROL lahko dvigne nakazilo. 4. KLAVZULA 1. Plačilo mora spremljati poročilo, v katerem so navedeni podatki, na katere lete se plačilo nanaša, datumi in zneski v evrih v zvezi s plačanimi računi in z morebitnimi odštetimi zneski dobropisov. Zahteva glede prikazovanja zneskov na računih v evrih velja tudi za tiste uporabnike, ki bodo uporabljali možnost, da omenjene zneske poravnajo v svoji valuti. 2. Kadar plačila ne spremlja poročilo, opisano v prejšnjem odstavku, iz katerega je razvidno, za plačilo katerega računa ali računov je neki znesek namenjen, bo EUROCONTROL z zneskom najprej poravnal: obresti, nato pa račune z najstarejšim datumom zapadlosti. 5. KLAVZULA 1. Pritožbe na račune se predložijo EUROCONTROLU v pisni ali elektronski obliki, ki jo EUROCONTROL pred tem odobri. Zadnji rok, do katerega mora EUROCONTROL sprejeti pritožbe, je označen na računu in znaša 60 dni od datuma računa. 2. Šteje se, da je pritožba vložena z dnem, ko jo je EUROCONTROL prejel.
11 3. Pritožbe morajo biti natančno opisane, priložena pa morajo biti tudi ustrezna dokazila. 4. Vložitev pritožbe še ni zadosten razlog, da bi plačnik od zaračunanega zneska kar koli odštel, razen če to dovoli EUROCONTROL. 5. Kadar se EUROCONTROL in uporabnik pojavljata hkrati kot dolžnik in upnik, ni mogoče pobotati terjatev brez predhodnega pristanka EUROCONTROLA. 6. KLAVZULA 1. Vsaka pristojbina, ki ni poravnana v roku zapadlosti v plačilo, se lahko poveča za znesek obresti, izračunane po tisti obrestni meri, ki jo pristojni organi določijo in države pogodbenice objavijo v skladu z 10. členom glede pogojev uporabe sistema. Obresti, ki se imenujejo obresti za zapadla plačila, so navadne obresti, ki se izračunavajo za vsak dan posebej na neplačano zapadlo vsoto. 2. Obresti se obračunajo in zaračunajo v evrih. 7. KLAVZULA Če dolžnik ne plača dolžnega zneska, se lahko sprejmejo ukrepi za njegovo prisilno izterjavo. Ti ukrepi lahko vključujejo odpoved storitev, zadržanje zrakoplova ali druge izvršilne ukrepe v skladu z veljavno zakonodajo.
1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου...
 ΑΠΟΖΗΜΙΩΣΗ ΘΥΜΑΤΩΝ ΕΓΚΛΗΜΑΤΙΚΩΝ ΠΡΑΞΕΩΝ ΣΛΟΒΕΝΙΑ 1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου... 3 1 1. Έντυπα αιτήσεων
ΑΠΟΖΗΜΙΩΣΗ ΘΥΜΑΤΩΝ ΕΓΚΛΗΜΑΤΙΚΩΝ ΠΡΑΞΕΩΝ ΣΛΟΒΕΝΙΑ 1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου... 3 1 1. Έντυπα αιτήσεων
Funkcijske vrste. Matematika 2. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 2. april Gregor Dolinar Matematika 2
 Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 5. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 14. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Diferencialna enačba, v kateri nastopata neznana funkcija in njen odvod v prvi potenci
 Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK
 1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 22. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 21. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Tretja vaja iz matematike 1
 Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
IZPIT IZ ANALIZE II Maribor,
 Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 10. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Integralni račun. Nedoločeni integral in integracijske metrode. 1. Izračunaj naslednje nedoločene integrale: (a) dx. (b) x 3 +3+x 2 dx, (c) (d)
 Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
PONOVITEV SNOVI ZA 4. TEST
 PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
Kotne in krožne funkcije
 Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
Kontrolne karte uporabljamo za sprotno spremljanje kakovosti izdelka, ki ga izdelujemo v proizvodnem procesu.
 Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK
 SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 15. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * NAVODILA ZA OCENJEVANJE. Sreda, 3. junij 2015 SPLOŠNA MATURA
 Državni izpitni center *M15143113* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sreda, 3. junij 2015 SPLOŠNA MATURA RIC 2015 M151-431-1-3 2 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor Naloga Odgovor
Državni izpitni center *M15143113* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sreda, 3. junij 2015 SPLOŠNA MATURA RIC 2015 M151-431-1-3 2 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor Naloga Odgovor
Gimnazija Krˇsko. vektorji - naloge
 Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
Osnove elektrotehnike uvod
 Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
Booleova algebra. Izjave in Booleove spremenljivke
 Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
Na pregledni skici napišite/označite ustrezne točke in paraboli. A) 12 B) 8 C) 4 D) 4 E) 8 F) 12
 Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
8. Diskretni LTI sistemi
 8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
Splošno o interpolaciji
 Splošno o interpolaciji J.Kozak Numerične metode II (FM) 2011-2012 1 / 18 O funkciji f poznamo ali hočemo uporabiti le posamezne podatke, na primer vrednosti r i = f (x i ) v danih točkah x i Izberemo
Splošno o interpolaciji J.Kozak Numerične metode II (FM) 2011-2012 1 / 18 O funkciji f poznamo ali hočemo uporabiti le posamezne podatke, na primer vrednosti r i = f (x i ) v danih točkah x i Izberemo
1. Definicijsko območje, zaloga vrednosti. 2. Naraščanje in padanje, ekstremi. 3. Ukrivljenost. 4. Trend na robu definicijskega območja
 ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 12. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
POROČILO 3.VAJA DOLOČANJE REZULTANTE SIL
 POROČILO 3.VAJA DOLOČANJE REZULTANTE SIL Izdba aje: Ljubjana, 11. 1. 007, 10.00 Jan OMAHNE, 1.M Namen: 1.Preeri paraeogramsko praio za doočanje rezutante nezporedni si s skupnim prijemaiščem (grafično)..dooči
POROČILO 3.VAJA DOLOČANJE REZULTANTE SIL Izdba aje: Ljubjana, 11. 1. 007, 10.00 Jan OMAHNE, 1.M Namen: 1.Preeri paraeogramsko praio za doočanje rezutante nezporedni si s skupnim prijemaiščem (grafično)..dooči
NEPARAMETRIČNI TESTI. pregledovanje tabel hi-kvadrat test. as. dr. Nino RODE
 NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
*M * Osnovna in višja raven MATEMATIKA NAVODILA ZA OCENJEVANJE. Sobota, 4. junij 2011 SPOMLADANSKI IZPITNI ROK. Državni izpitni center
 Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Numerično reševanje. diferencialnih enačb II
 Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):
![matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij): matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):](/thumbs/87/96579490.jpg) 4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
7 Značilnosti poučevanja v razredu
 7 Značilnosti poučevanja v razredu Na začetku tega poglavja so predstavljeni podatki o velikosti in sestavi matematičnih razredov, ki bodo pomagali razumeti matematične dosežke učenca ter jih uvrstiti
7 Značilnosti poučevanja v razredu Na začetku tega poglavja so predstavljeni podatki o velikosti in sestavi matematičnih razredov, ki bodo pomagali razumeti matematične dosežke učenca ter jih uvrstiti
PRILOGA VI POTRDILO O SKLADNOSTI. (Vzorci vsebine) POTRDILO O SKLADNOSTI ZA VOZILO HOMOLOGIRANEGA TIPA
 PRILOGA VI POTRDILA O SKLADNOSTI (Vzorci vsebine) A POTRDILO O SKLADNOSTI ZA VOZILO HOMOLOGIRANEGA TIPA Stran 1 POTRDILO O SKLADNOSTI ZA VOZILO HOMOLOGIRANEGA TIPA (1) (številka potrdila o skladnosti:)
PRILOGA VI POTRDILA O SKLADNOSTI (Vzorci vsebine) A POTRDILO O SKLADNOSTI ZA VOZILO HOMOLOGIRANEGA TIPA Stran 1 POTRDILO O SKLADNOSTI ZA VOZILO HOMOLOGIRANEGA TIPA (1) (številka potrdila o skladnosti:)
1. Trikotniki hitrosti
 . Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
. Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
CM707. GR Οδηγός χρήσης... 2-7. SLO Uporabniški priročnik... 8-13. CR Korisnički priručnik... 14-19. TR Kullanım Kılavuzu... 20-25
 1 2 3 4 5 6 7 OFFMANAUTO CM707 GR Οδηγός χρήσης... 2-7 SLO Uporabniški priročnik... 8-13 CR Korisnički priručnik... 14-19 TR Kullanım Kılavuzu... 20-25 ENG User Guide... 26-31 GR CM707 ΟΔΗΓΟΣ ΧΡΗΣΗΣ Περιγραφή
1 2 3 4 5 6 7 OFFMANAUTO CM707 GR Οδηγός χρήσης... 2-7 SLO Uporabniški priročnik... 8-13 CR Korisnički priručnik... 14-19 TR Kullanım Kılavuzu... 20-25 ENG User Guide... 26-31 GR CM707 ΟΔΗΓΟΣ ΧΡΗΣΗΣ Περιγραφή
Delovna točka in napajalna vezja bipolarnih tranzistorjev
 KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
ΠΡΙΤΣΙΝΑΔΟΡΟΣ ΛΑΔΙΟΥ ΑΕΡΟΣ ΓΙΑ ΠΡΙΤΣΙΝΙΑ M4/M12 ΟΔΗΓΙΕΣ ΧΡΗΣΗΣ - ΑΝΤΑΛΛΑΚΤΙΚΑ
 GR ΠΡΙΤΣΙΝΑΔΟΡΟΣ ΛΑΔΙΟΥ ΑΕΡΟΣ ΓΙΑ ΠΡΙΤΣΙΝΙΑ M4/M12 ΟΔΗΓΙΕΣ ΧΡΗΣΗΣ - ΑΝΤΑΛΛΑΚΤΙΚΑ H OLJLAJNYOMÁSÚ SZEGECSELŐ M4/M12 SZEGECSEKHEZ HASZNÁLATI UTASÍTÁS - ALKATRÉSZEK SLO OLJNO-PNEVMATSKI KOVIČAR ZA ZAKOVICE
GR ΠΡΙΤΣΙΝΑΔΟΡΟΣ ΛΑΔΙΟΥ ΑΕΡΟΣ ΓΙΑ ΠΡΙΤΣΙΝΙΑ M4/M12 ΟΔΗΓΙΕΣ ΧΡΗΣΗΣ - ΑΝΤΑΛΛΑΚΤΙΚΑ H OLJLAJNYOMÁSÚ SZEGECSELŐ M4/M12 SZEGECSEKHEZ HASZNÁLATI UTASÍTÁS - ALKATRÉSZEK SLO OLJNO-PNEVMATSKI KOVIČAR ZA ZAKOVICE
+105 C (plošče in trakovi +85 C) -50 C ( C)* * Za temperature pod C se posvetujte z našo tehnično službo. ϑ m *20 *40 +70
 KAIFLEX ST Tehnični podatki Material Izjemno fleksibilna zaprtocelična izolacija, fleksibilna elastomerna pena (FEF) Opis Uporaba Temperaturno območje Toplotna prevodnost W/(m K ) pri različnih srednjih
KAIFLEX ST Tehnični podatki Material Izjemno fleksibilna zaprtocelična izolacija, fleksibilna elastomerna pena (FEF) Opis Uporaba Temperaturno območje Toplotna prevodnost W/(m K ) pri različnih srednjih
MATEMATIČNI IZRAZI V MAFIRA WIKIJU
 I FAKULTETA ZA MATEMATIKO IN FIZIKO Jadranska cesta 19 1000 Ljubljan Ljubljana, 25. marec 2011 MATEMATIČNI IZRAZI V MAFIRA WIKIJU KOMUNICIRANJE V MATEMATIKI Darja Celcer II KAZALO: 1 VSTAVLJANJE MATEMATIČNIH
I FAKULTETA ZA MATEMATIKO IN FIZIKO Jadranska cesta 19 1000 Ljubljan Ljubljana, 25. marec 2011 MATEMATIČNI IZRAZI V MAFIRA WIKIJU KOMUNICIRANJE V MATEMATIKI Darja Celcer II KAZALO: 1 VSTAVLJANJE MATEMATIČNIH
p 1 ENTROPIJSKI ZAKON
 ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
13. Jacobijeva metoda za računanje singularnega razcepa
 13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
Bočna zvrnitev upogibno obremenjenih elementov s konstantnim prečnim prerezom
 D. Beg, študijsko gradivo za JK, april 006 KK FGG UL Bočna zvrnitev upogibno obremenjenih elementov s konstantnim prečnim prerezom Nosilnost na bočno zvrnitev () Elemente, ki niso bočno podprti in so upogibno
D. Beg, študijsko gradivo za JK, april 006 KK FGG UL Bočna zvrnitev upogibno obremenjenih elementov s konstantnim prečnim prerezom Nosilnost na bočno zvrnitev () Elemente, ki niso bočno podprti in so upogibno
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
1 Mednarodna primerjava matematičnih dosežkov
 1 Mednarodna primerjava matematičnih dosežkov Prvo poglavje vsebuje rezultate preverjanja znanja matematike med osnovnošolci v četrtem in osmem razredu za vsako sodelujočo državo ali šolski sistem. Dodani
1 Mednarodna primerjava matematičnih dosežkov Prvo poglavje vsebuje rezultate preverjanja znanja matematike med osnovnošolci v četrtem in osmem razredu za vsako sodelujočo državo ali šolski sistem. Dodani
ARHITEKTURA DETAJL 1, 1:10
 0.15 0.25 3.56 0.02 0.10 0.12 0.10 SESTV S2 polimer-bitumenska,dvoslojna(po),... 1.0 cm po zahtevah SIST DIN 52133 in nadstandardno, (glej opis v tehn.poročilu), npr.: PHOENIX STR/Super 5 M * GEMINI P
0.15 0.25 3.56 0.02 0.10 0.12 0.10 SESTV S2 polimer-bitumenska,dvoslojna(po),... 1.0 cm po zahtevah SIST DIN 52133 in nadstandardno, (glej opis v tehn.poročilu), npr.: PHOENIX STR/Super 5 M * GEMINI P
- Geodetske točke in geodetske mreže
 - Geodetske točke in geodetske mreže 15 Geodetske točke in geodetske mreže Materializacija koordinatnih sistemov 2 Geodetske točke Geodetska točka je točka, označena na fizični površini Zemlje z izbrano
- Geodetske točke in geodetske mreže 15 Geodetske točke in geodetske mreže Materializacija koordinatnih sistemov 2 Geodetske točke Geodetska točka je točka, označena na fizični površini Zemlje z izbrano
Kotni funkciji sinus in kosinus
 Kotni funkciji sinus in kosinus Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z oznako cos x, DEFINICIJA V PRAVOKOTNEM TRIKOTNIKU: Kotna funkcija sinus je definirana kot razmerje
Kotni funkciji sinus in kosinus Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z oznako cos x, DEFINICIJA V PRAVOKOTNEM TRIKOTNIKU: Kotna funkcija sinus je definirana kot razmerje
Vaje iz MATEMATIKE 8. Odvod funkcije., pravimo, da je funkcija f odvedljiva v točki x 0 z odvodom. f (x f(x 0 + h) f(x 0 ) 0 ) := lim
 Študij AHITEKTURE IN URBANIZMA, šol l 06/7 Vaje iz MATEMATIKE 8 Odvod funkcije f( Definicija: Naj bo f definirana na neki okolici točke 0 Če obstaja lim 0 +h f( 0 h 0 h, pravimo, da je funkcija f odvedljiva
Študij AHITEKTURE IN URBANIZMA, šol l 06/7 Vaje iz MATEMATIKE 8 Odvod funkcije f( Definicija: Naj bo f definirana na neki okolici točke 0 Če obstaja lim 0 +h f( 0 h 0 h, pravimo, da je funkcija f odvedljiva
ODLOK O KOMUNALNEM PRISPEVKU V OBČINI VRHNIKA neuradno prečiščeno besedilo. 1. člen
 - Odlok o komunalnem prispevku v Občini Vrhnika (Naš časopis, št. 427/2015) - Odlok o spremembah in dopolnitvah Odloka o komunalnem prispevku v Občini Vrhnika (Naš časopis, št. 440/16) ODLOK O KOMUNALNEM
- Odlok o komunalnem prispevku v Občini Vrhnika (Naš časopis, št. 427/2015) - Odlok o spremembah in dopolnitvah Odloka o komunalnem prispevku v Občini Vrhnika (Naš časopis, št. 440/16) ODLOK O KOMUNALNEM
Iterativno reševanje sistemov linearnih enačb. Numerične metode, sistemi linearnih enačb. Numerične metode FE, 2. december 2013
 Numerične metode, sistemi linearnih enačb B. Jurčič Zlobec Numerične metode FE, 2. december 2013 1 Vsebina 1 z n neznankami. a i1 x 1 + a i2 x 2 + + a in = b i i = 1,..., n V matrični obliki zapišemo:
Numerične metode, sistemi linearnih enačb B. Jurčič Zlobec Numerične metode FE, 2. december 2013 1 Vsebina 1 z n neznankami. a i1 x 1 + a i2 x 2 + + a in = b i i = 1,..., n V matrični obliki zapišemo:
PROCESIRANJE SIGNALOV
 Rešive pisega izpia PROCESIRANJE SIGNALOV Daum: 7... aloga Kolikša je ampliuda reje harmoske kompoee arisaega periodičega sigala? f() - -3 - - 3 Rešiev: Časova fukcija a iervalu ( /,/) je lieara fukcija:
Rešive pisega izpia PROCESIRANJE SIGNALOV Daum: 7... aloga Kolikša je ampliuda reje harmoske kompoee arisaega periodičega sigala? f() - -3 - - 3 Rešiev: Časova fukcija a iervalu ( /,/) je lieara fukcija:
Definicija. definiramo skalarni produkt. x i y i. in razdaljo. d(x, y) = x y = < x y, x y > = n (x i y i ) 2. i=1. i=1
 Funkcije več realnih spremenljivk Osnovne definicije Limita in zveznost funkcije več spremenljivk Parcialni odvodi funkcije več spremenljivk Gradient in odvod funkcije več spremenljivk v dani smeri Parcialni
Funkcije več realnih spremenljivk Osnovne definicije Limita in zveznost funkcije več spremenljivk Parcialni odvodi funkcije več spremenljivk Gradient in odvod funkcije več spremenljivk v dani smeri Parcialni
1. TVORBA ŠIBKEGA (SIGMATNEGA) AORISTA: Največ grških glagolov ima tako imenovani šibki (sigmatni) aorist. Osnova se tvori s. γραψ
 TVORBA AORISTA: Grški aorist (dovršnik) izraža dovršno dejanje; v indikativu izraža poleg dovršnosti tudi preteklost. Za razliko od prezenta ima aorist posebne aktivne, medialne in pasivne oblike. Pri
TVORBA AORISTA: Grški aorist (dovršnik) izraža dovršno dejanje; v indikativu izraža poleg dovršnosti tudi preteklost. Za razliko od prezenta ima aorist posebne aktivne, medialne in pasivne oblike. Pri
I. SPLOŠNE DOLOČBE. 1. člen (namen)
 Na podlagi drugega odstavka 19. člena Zakona o varstvu okolja (Uradni list RS, št. 39/06 uradno prečiščeno besedilo in 49/06 ZMetD) izdaja Vlada Republike Slovenije U R E D B O o pogojih, pod katerimi
Na podlagi drugega odstavka 19. člena Zakona o varstvu okolja (Uradni list RS, št. 39/06 uradno prečiščeno besedilo in 49/06 ZMetD) izdaja Vlada Republike Slovenije U R E D B O o pogojih, pod katerimi
DISKRETNA FOURIERJEVA TRANSFORMACIJA
 29.03.2004 Definicija DFT Outline DFT je linearna transformacija nekega vektorskega prostora dimenzije n nad obsegom K, ki ga označujemo z V K, pri čemer ima slednji lastnost, da vsebuje nek poseben element,
29.03.2004 Definicija DFT Outline DFT je linearna transformacija nekega vektorskega prostora dimenzije n nad obsegom K, ki ga označujemo z V K, pri čemer ima slednji lastnost, da vsebuje nek poseben element,
Osnove matematične analize 2016/17
 Osnove matematične analize 216/17 Neža Mramor Kosta Fakulteta za računalništvo in informatiko Univerza v Ljubljani Kaj je funkcija? Funkcija je predpis, ki vsakemu elementu x iz definicijskega območja
Osnove matematične analize 216/17 Neža Mramor Kosta Fakulteta za računalništvo in informatiko Univerza v Ljubljani Kaj je funkcija? Funkcija je predpis, ki vsakemu elementu x iz definicijskega območja
P R A V I L N I K o spremembah in dopolnitvah Pravilnika prometni signalizaciji in prometni opremi na cestah
 OSNUTEK Na podlagi osmega odstavka 9. člena Zakona o cestah (Uradni list RS, št. 109/10, 48/12, 36/14 odl. US in 46/15) minister za infrastrukturo izdaja P R V I L N I K o spremembah in dopolnitvah Pravilnika
OSNUTEK Na podlagi osmega odstavka 9. člena Zakona o cestah (Uradni list RS, št. 109/10, 48/12, 36/14 odl. US in 46/15) minister za infrastrukturo izdaja P R V I L N I K o spremembah in dopolnitvah Pravilnika
Tabele termodinamskih lastnosti vode in vodne pare
 Univerza v Ljubljani Fakulteta za strojništvo Laboratorij za termoenergetiko Tabele termodinamskih lastnosti vode in vodne pare po modelu IAPWS IF-97 izračunano z XSteam Excel v2.6 Magnus Holmgren, xsteam.sourceforge.net
Univerza v Ljubljani Fakulteta za strojništvo Laboratorij za termoenergetiko Tabele termodinamskih lastnosti vode in vodne pare po modelu IAPWS IF-97 izračunano z XSteam Excel v2.6 Magnus Holmgren, xsteam.sourceforge.net
Primeri: naftalen kinolin spojeni kinolin
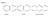 Primeri: naftalen kinolin spojeni kinolin 3 skupne strani 7 skupnih strani 5 skupnih strani 6 skupnih atomov 8 skupnih atomov 6 skupnih atomov orto spojen sistem orto in peri spojena sistema mostni kinolin
Primeri: naftalen kinolin spojeni kinolin 3 skupne strani 7 skupnih strani 5 skupnih strani 6 skupnih atomov 8 skupnih atomov 6 skupnih atomov orto spojen sistem orto in peri spojena sistema mostni kinolin
DOKUMENTI 1. o pristopu Helenske republike k Evropskim skupnostim. Uradni list Republike Slovenije Mednarodne pogodbe Št. 7 /
 Uradni list Republike Slovenije Mednarodne pogodbe Št. 7 / 23. 3. 2004 / Stran 3247 DOKUMENTI 1 o pristopu Helenske republike k Evropskim skupnostim 1 Uradni list Evropskih skupnosti, št. L 291, 19. november
Uradni list Republike Slovenije Mednarodne pogodbe Št. 7 / 23. 3. 2004 / Stran 3247 DOKUMENTI 1 o pristopu Helenske republike k Evropskim skupnostim 1 Uradni list Evropskih skupnosti, št. L 291, 19. november
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
STANDARD1 EN EN EN
 PRILOGA RADIJSKE 9,000-20,05 khz naprave kratkega dosega: induktivne aplikacije 315 600 khz naprave kratkega dosega: aktivni medicinski vsadki ultra nizkih moči 4516 khz naprave kratkega dosega: železniške
PRILOGA RADIJSKE 9,000-20,05 khz naprave kratkega dosega: induktivne aplikacije 315 600 khz naprave kratkega dosega: aktivni medicinski vsadki ultra nizkih moči 4516 khz naprave kratkega dosega: železniške
Matematika 1. Gregor Dolinar. 2. januar Fakulteta za elektrotehniko Univerza v Ljubljani. Gregor Dolinar Matematika 1
 Mtemtik 1 Gregor Dolinr Fkultet z elektrotehniko Univerz v Ljubljni 2. jnur 2014 Gregor Dolinr Mtemtik 1 Izrek (Izrek o povprečni vrednosti) Nj bo m ntnčn spodnj mej in M ntnčn zgornj mej integrbilne funkcije
Mtemtik 1 Gregor Dolinr Fkultet z elektrotehniko Univerz v Ljubljni 2. jnur 2014 Gregor Dolinr Mtemtik 1 Izrek (Izrek o povprečni vrednosti) Nj bo m ntnčn spodnj mej in M ntnčn zgornj mej integrbilne funkcije
15106/15 ADD 1 /mr HR
 Vijeće Europske unije Bruxelles, 14. prosinca 2015. (OR. en) Međuinstitucijski predmet: 2015/0283 (COD) 15106/15 ADD 1 PRIJEDLOG Od: Datum primitka: 3. prosinca 2015. Za: CODIF 112 CODEC 1683 DRS 75 ETS
Vijeće Europske unije Bruxelles, 14. prosinca 2015. (OR. en) Međuinstitucijski predmet: 2015/0283 (COD) 15106/15 ADD 1 PRIJEDLOG Od: Datum primitka: 3. prosinca 2015. Za: CODIF 112 CODEC 1683 DRS 75 ETS
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
Matematika vaja. Matematika FE, Ljubljana, Slovenija Fakulteta za Elektrotehniko 1000 Ljubljana, Tržaška 25, Slovenija
 Matematika 1 3. vaja B. Jurčič Zlobec 1 1 Univerza v Ljubljani, Fakulteta za Elektrotehniko 1000 Ljubljana, Tržaška 25, Slovenija Matematika FE, Ljubljana, Slovenija 2011 Določi stekališča zaporedja a
Matematika 1 3. vaja B. Jurčič Zlobec 1 1 Univerza v Ljubljani, Fakulteta za Elektrotehniko 1000 Ljubljana, Tržaška 25, Slovenija Matematika FE, Ljubljana, Slovenija 2011 Določi stekališča zaporedja a
1. izpit iz Diskretnih struktur UNI Ljubljana, 17. januar 2006
 1. izpit iz Diskretnih struktur UNI Ljubljana, 17. januar 2006 1. Dana je množica predpostavk p q r s, r t, s q, s p r, s t in zaključek t r. Odloči, ali je sklep pravilen ali napačen. pravilen, zapiši
1. izpit iz Diskretnih struktur UNI Ljubljana, 17. januar 2006 1. Dana je množica predpostavk p q r s, r t, s q, s p r, s t in zaključek t r. Odloči, ali je sklep pravilen ali napačen. pravilen, zapiši
POROČILO. št.: P 1100/ Preskus jeklenih profilov za spuščen strop po točki 5.2 standarda SIST EN 13964:2004
 Oddelek za konstrkcije Laboratorij za konstrkcije Ljbljana, 12.11.2012 POROČILO št.: P 1100/12 680 01 Presks jeklenih profilov za spščen strop po točki 5.2 standarda SIST EN 13964:2004 Naročnik: STEEL
Oddelek za konstrkcije Laboratorij za konstrkcije Ljbljana, 12.11.2012 POROČILO št.: P 1100/12 680 01 Presks jeklenih profilov za spščen strop po točki 5.2 standarda SIST EN 13964:2004 Naročnik: STEEL
Fazni diagram binarne tekočine
 Fazni diagram binarne tekočine Žiga Kos 5. junij 203 Binarno tekočino predstavljajo delci A in B. Ti se med seboj lahko mešajo v različnih razmerjih. V nalogi želimo izračunati fazni diagram take tekočine,
Fazni diagram binarne tekočine Žiga Kos 5. junij 203 Binarno tekočino predstavljajo delci A in B. Ti se med seboj lahko mešajo v različnih razmerjih. V nalogi želimo izračunati fazni diagram take tekočine,
PRILOGE. k predlogu. direkitve Evropskega parlamenta in Sveta. o kakovosti vode, namenjene za prehrano ljudi (prenovitev)
 EVROPSKA KOMISIJA Bruselj, 1.2.2018 COM(2017) 753 final ANNEXES 1 to 6 PRILOGE k predlogu direkitve Evropskega parlamenta in Sveta o kakovosti vode, namenjene za prehrano ljudi (prenovitev) {SWD(2017)
EVROPSKA KOMISIJA Bruselj, 1.2.2018 COM(2017) 753 final ANNEXES 1 to 6 PRILOGE k predlogu direkitve Evropskega parlamenta in Sveta o kakovosti vode, namenjene za prehrano ljudi (prenovitev) {SWD(2017)
1. VAJA IZ TRDNOSTI. (linearna algebra - ponovitev, Kroneckerjev δ i j, permutacijski simbol e i jk )
 VAJA IZ TRDNOSTI (lnearna algebra - ponovtev, Kroneckerev δ, permutacsk smbol e k ) NALOGA : Zapš vektor a = [, 2,5,] kot lnearno kombnaco vektorev e = [,,,], e 2 = [,2,3,], e 3 = [2,,, ] n e 4 = [,,,]
VAJA IZ TRDNOSTI (lnearna algebra - ponovtev, Kroneckerev δ, permutacsk smbol e k ) NALOGA : Zapš vektor a = [, 2,5,] kot lnearno kombnaco vektorev e = [,,,], e 2 = [,2,3,], e 3 = [2,,, ] n e 4 = [,,,]
Spoznajmo sedaj definicijo in nekaj osnovnih primerov zaporedij števil.
 Zaporedja števil V matematiki in fiziki pogosto operiramo s približnimi vrednostmi neke količine. Pri numeričnemu računanju lahko npr. število π aproksimiramo s števili, ki imajo samo končno mnogo neničelnih
Zaporedja števil V matematiki in fiziki pogosto operiramo s približnimi vrednostmi neke količine. Pri numeričnemu računanju lahko npr. število π aproksimiramo s števili, ki imajo samo končno mnogo neničelnih
1 Fibonaccijeva stevila
 1 Fibonaccijeva stevila Fibonaccijevo število F n, kjer je n N, lahko definiramo kot število načinov zapisa števila n kot vsoto sumandov, enakih 1 ali Na primer, število 4 lahko zapišemo v obliki naslednjih
1 Fibonaccijeva stevila Fibonaccijevo število F n, kjer je n N, lahko definiramo kot število načinov zapisa števila n kot vsoto sumandov, enakih 1 ali Na primer, število 4 lahko zapišemo v obliki naslednjih
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Zakon o spremembah zakona o financiranju občin zfo-1
 Gregorčičeva 20 25, Sl-1001 Ljubljana T: +386 1 478 1000 F: +386 1 478 1607 E: gp.gs@gov.si http://www.vlada.si/ I. UVOD Zakon o spremembah zakona o financiranju občin zfo-1 1. OCENA STANJA IN RAZLOGI
Gregorčičeva 20 25, Sl-1001 Ljubljana T: +386 1 478 1000 F: +386 1 478 1607 E: gp.gs@gov.si http://www.vlada.si/ I. UVOD Zakon o spremembah zakona o financiranju občin zfo-1 1. OCENA STANJA IN RAZLOGI
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
Kotne funkcije poljubnega kota. Osnovne zveze med funkcijamo istega kota. Uporaba kotnih funkcij v poljubnem trikotniku. Kosinusni in sinusni izrek.
 DN#3 (januar 2018) 3A Teme, ki jih preverja domača naloga: Kotne funkcije poljubnega kota. Osnovne zveze med funkcijamo istega kota. Uporaba kotnih funkcij v poljubnem trikotniku. Kosinusni in sinusni
DN#3 (januar 2018) 3A Teme, ki jih preverja domača naloga: Kotne funkcije poljubnega kota. Osnovne zveze med funkcijamo istega kota. Uporaba kotnih funkcij v poljubnem trikotniku. Kosinusni in sinusni
D f, Z f. Lastnosti. Linearna funkcija. Definicija Linearna funkcija f : je definirana s predpisom f(x) = kx+n; k,
 Linearna funkcija Linearna funkcija f : je definirana s predpisom f(x) = kx+n; k, n ᄀ. k smerni koeficient n začetna vrednost D f, Z f Definicijsko območje linearne funkcije so vsa realna števila. Zaloga
Linearna funkcija Linearna funkcija f : je definirana s predpisom f(x) = kx+n; k, n ᄀ. k smerni koeficient n začetna vrednost D f, Z f Definicijsko območje linearne funkcije so vsa realna števila. Zaloga
17261/13 lst 1 DG B 4B
 SVET EVROPSKE UNIJE Bruselj, 3. december 2013 (05.12) (OR. en) 17261/13 DENLEG 146 SAN 502 AGRI 812 SPREMNI DOPIS Pošiljatelj: Evropska komisija Datum prejema: 2. december 2013 Prejemnik: generalni sekretariat
SVET EVROPSKE UNIJE Bruselj, 3. december 2013 (05.12) (OR. en) 17261/13 DENLEG 146 SAN 502 AGRI 812 SPREMNI DOPIS Pošiljatelj: Evropska komisija Datum prejema: 2. december 2013 Prejemnik: generalni sekretariat
Univerza v Ljubljani Fakulteta za računalništvo in informatiko MATEMATIKA. Polona Oblak
 Univerza v Ljubljani Fakulteta za računalništvo in informatiko MATEMATIKA Polona Oblak Ljubljana, 04 CIP - Kataložni zapis o publikaciji Narodna in univerzitetna knjižnica, Ljubljana 5(075.8)(0.034.) OBLAK,
Univerza v Ljubljani Fakulteta za računalništvo in informatiko MATEMATIKA Polona Oblak Ljubljana, 04 CIP - Kataložni zapis o publikaciji Narodna in univerzitetna knjižnica, Ljubljana 5(075.8)(0.034.) OBLAK,
Shefferjeva polinomska zaporedja
 Shefferjeva polinomska zaporedja Marko Razpet Matematični kolokviji Ljubljana, 23. marca 2006 Page 1 of 63 Predstavljen bo osnovni koncept umbralnega računa, kakršnega sta razvila Gian-Carlo Rota in Steven
Shefferjeva polinomska zaporedja Marko Razpet Matematični kolokviji Ljubljana, 23. marca 2006 Page 1 of 63 Predstavljen bo osnovni koncept umbralnega računa, kakršnega sta razvila Gian-Carlo Rota in Steven
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * FIZIKA NAVODILA ZA OCENJEVANJE. Petek, 10. junij 2016 SPLOŠNA MATURA
 Državni izpitni center *M16141113* SPOMLADANSKI IZPITNI ROK FIZIKA NAVODILA ZA OCENJEVANJE Petek, 1. junij 16 SPLOŠNA MATURA RIC 16 M161-411-3 M161-411-3 3 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor
Državni izpitni center *M16141113* SPOMLADANSKI IZPITNI ROK FIZIKA NAVODILA ZA OCENJEVANJE Petek, 1. junij 16 SPLOŠNA MATURA RIC 16 M161-411-3 M161-411-3 3 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor
SATCITANANDA. F = e E sila na naboj. = ΔW e. Rudolf Kladnik: Fizika za srednješolce 3. Svet elektronov in atomov
 Ruolf Klnik: Fizik z srenješolce Set elektrono in too Električno olje (11), gibnje elce električne olju Strn 55, nlog 1 Kolikšno netost or releteti elektron, se njego kinetičn energij oeč z 1 kev? Δ W
Ruolf Klnik: Fizik z srenješolce Set elektrono in too Električno olje (11), gibnje elce električne olju Strn 55, nlog 1 Kolikšno netost or releteti elektron, se njego kinetičn energij oeč z 1 kev? Δ W
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
Matematika. Funkcije in enačbe
 Matematika Funkcije in enačbe (1) Nariši grafe naslednjih funkcij: (a) f() = 1, (b) f() = 3, (c) f() = 3. Rešitev: (a) Linearna funkcija f() = 1 ima začetno vrednost f(0) = 1 in ničlo = 1/. Definirana
Matematika Funkcije in enačbe (1) Nariši grafe naslednjih funkcij: (a) f() = 1, (b) f() = 3, (c) f() = 3. Rešitev: (a) Linearna funkcija f() = 1 ima začetno vrednost f(0) = 1 in ničlo = 1/. Definirana
Svet Evropske unije Bruselj, 19. junij 2015 (OR. en)
 Svet Evropske unije Bruselj, 19. junij 2015 (OR. en) Medinstitucionalna zadeva: 2015/0105 (NLE) 9356/15 UD 125 ZAKONODAJNI AKTI IN DRUGI INSTRUMENTI Zadeva: UREDBA SVETA o spremembi Uredbe (EU) št. 1388/2013
Svet Evropske unije Bruselj, 19. junij 2015 (OR. en) Medinstitucionalna zadeva: 2015/0105 (NLE) 9356/15 UD 125 ZAKONODAJNI AKTI IN DRUGI INSTRUMENTI Zadeva: UREDBA SVETA o spremembi Uredbe (EU) št. 1388/2013
( , 2. kolokvij)
 A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
3. VAJA IZ TRDNOSTI. Rešitev: Pomik v referenčnem opisu: u = e y 2 e Pomik v prostorskem opisu: u = ey e. e y,e z = e z.
 3. VAJA IZ TRDNOSTI (tenzor deformacij) (pomiki togega telesa, Lagrangev in Eulerjev opis, tenzor velikih deformacij, tenzor majhnih deformacij in rotacij, kompatibilitetni pogoji) NALOGA 1: Gumijasti
3. VAJA IZ TRDNOSTI (tenzor deformacij) (pomiki togega telesa, Lagrangev in Eulerjev opis, tenzor velikih deformacij, tenzor majhnih deformacij in rotacij, kompatibilitetni pogoji) NALOGA 1: Gumijasti
Podobnost matrik. Matematika II (FKKT Kemijsko inženirstvo) Diagonalizacija matrik
 Podobnost matrik Matematika II (FKKT Kemijsko inženirstvo) Matjaž Željko FKKT Kemijsko inženirstvo 14 teden (Zadnja sprememba: 23 maj 213) Matrika A R n n je podobna matriki B R n n, če obstaja obrnljiva
Podobnost matrik Matematika II (FKKT Kemijsko inženirstvo) Matjaž Željko FKKT Kemijsko inženirstvo 14 teden (Zadnja sprememba: 23 maj 213) Matrika A R n n je podobna matriki B R n n, če obstaja obrnljiva
1. člen (vsebina) 2. člen (pomen izrazov)
 Na podlagi 64.e člena Energetskega zakona (Uradni list RS, št. 27/07 uradno prečiščeno besedilo in 70/08) in za izvrševanje četrte alinee tretjega odstavka 42. člena Zakona o spremembah in dopolnitvah
Na podlagi 64.e člena Energetskega zakona (Uradni list RS, št. 27/07 uradno prečiščeno besedilo in 70/08) in za izvrševanje četrte alinee tretjega odstavka 42. člena Zakona o spremembah in dopolnitvah
Funkcije več spremenljivk
 DODATEK C Funkcije več spremenljivk C.1. Osnovni pojmi Funkcija n spremenljivk je predpis: f : D f R, (x 1, x 2,..., x n ) u = f (x 1, x 2,..., x n ) kjer D f R n imenujemo definicijsko območje funkcije
DODATEK C Funkcije več spremenljivk C.1. Osnovni pojmi Funkcija n spremenljivk je predpis: f : D f R, (x 1, x 2,..., x n ) u = f (x 1, x 2,..., x n ) kjer D f R n imenujemo definicijsko območje funkcije
vezani ekstremi funkcij
 11. vaja iz Matematike 2 (UNI) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 ekstremi funkcij več spremenljivk nadaljevanje vezani ekstremi funkcij Dana je funkcija f(x, y). Zanimajo nas ekstremi nad
11. vaja iz Matematike 2 (UNI) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 ekstremi funkcij več spremenljivk nadaljevanje vezani ekstremi funkcij Dana je funkcija f(x, y). Zanimajo nas ekstremi nad
Klasifikacija blizu Kelerovih mnogostrukosti. konstantne holomorfne sekcione krivine. Kelerove. mnogostrukosti. blizu Kelerove.
 Klasifikacija blizu Teorema Neka je M Kelerova mnogostrukost. Operator krivine R ima sledeća svojstva: R(X, Y, Z, W ) = R(Y, X, Z, W ) = R(X, Y, W, Z) R(X, Y, Z, W ) + R(Y, Z, X, W ) + R(Z, X, Y, W ) =
Klasifikacija blizu Teorema Neka je M Kelerova mnogostrukost. Operator krivine R ima sledeća svojstva: R(X, Y, Z, W ) = R(Y, X, Z, W ) = R(X, Y, W, Z) R(X, Y, Z, W ) + R(Y, Z, X, W ) + R(Z, X, Y, W ) =
Matematika 2. Diferencialne enačbe drugega reda
 Matematika 2 Diferencialne enačbe drugega reda (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) y 6y + 8y = 0, (b) y 2y + y = 0, (c) y + y = 0, (d) y + 2y + 2y = 0. Rešitev:
Matematika 2 Diferencialne enačbe drugega reda (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) y 6y + 8y = 0, (b) y 2y + y = 0, (c) y + y = 0, (d) y + 2y + 2y = 0. Rešitev:
Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba.
 1. Osnovni pojmi Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba. Primer 1.1: Diferencialne enačbe so izrazi: y
1. Osnovni pojmi Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba. Primer 1.1: Diferencialne enačbe so izrazi: y
nipulating Crane (dvigalo za manipulacijo z gorivom v bazenu za izrabljeno gorivo).
 Uradni list Republike Slovenije Internet: http:www.uradni-list.si Št. 11 Ljubljana, ponedeljek 11. 2. 2002 Uradne objave e-pošta: objave@uradni-list.si ISSN 1318-9182 Leto XII Javna naročila po Zakonu
Uradni list Republike Slovenije Internet: http:www.uradni-list.si Št. 11 Ljubljana, ponedeljek 11. 2. 2002 Uradne objave e-pošta: objave@uradni-list.si ISSN 1318-9182 Leto XII Javna naročila po Zakonu
Poglavje 7. Poglavje 7. Poglavje 7. Regulacijski sistemi. Regulacijski sistemi. Slika 7. 1: Normirana blokovna shema regulacije EM
 Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
10973/16 ADD 5 MKW/kok DGC 1A
 Svet Evropske unije Bruselj, 14. september 2016 Medinstitucionalna zadeva: 2016/0206 (NLE) 10973/16 ADD 5 WTO 195 SERVICES 20 FDI 16 CDN 12 ZAKONODAJNI AKTI IN DRUGI INSTRUMENTI Zadeva: Celoviti gospodarski
Svet Evropske unije Bruselj, 14. september 2016 Medinstitucionalna zadeva: 2016/0206 (NLE) 10973/16 ADD 5 WTO 195 SERVICES 20 FDI 16 CDN 12 ZAKONODAJNI AKTI IN DRUGI INSTRUMENTI Zadeva: Celoviti gospodarski
Univerza v Ljubljani FS & FKKT. Varnost v strojništvu
 Univerza v Ljubljani FS & FKKT Varnost v strojništvu doc.dr. Boris Jerman, univ.dipl.inž.str. Govorilne ure: med šolskim letom: srede med 9:00 in 11:30 pisarna: FS - 414 telefon: 01/4771-414 boris.jerman@fs.uni-lj.si,
Univerza v Ljubljani FS & FKKT Varnost v strojništvu doc.dr. Boris Jerman, univ.dipl.inž.str. Govorilne ure: med šolskim letom: srede med 9:00 in 11:30 pisarna: FS - 414 telefon: 01/4771-414 boris.jerman@fs.uni-lj.si,
V tem poglavju bomo vpeljali pojem determinante matrike, spoznali bomo njene lastnosti in nekaj metod za računanje determinant.
 Poglavje IV Determinanta matrike V tem poglavju bomo vpeljali pojem determinante matrike, spoznali bomo njene lastnosti in nekaj metod za računanje determinant 1 Definicija Preden definiramo determinanto,
Poglavje IV Determinanta matrike V tem poglavju bomo vpeljali pojem determinante matrike, spoznali bomo njene lastnosti in nekaj metod za računanje determinant 1 Definicija Preden definiramo determinanto,
