Capitolul 3 EŞANTIONAREA ŞI CUANTIZAREA IMAGINILOR
|
|
|
- Κύρα Μπλέτσας
- 6 χρόνια πριν
- Προβολές:
Transcript
1 Capioll 3 EŞANTIONAREA ŞI CUANTIZAREA IMAGINILOR 3. INTRODUCERE Penr prelcrarea digială a imaginilor c ajorl ni calclaor avem nevoie de forma digială a acesora, respeciv de o marice compsă din "cvine" binare de dimensini finie. Penr digiizare, imaginea se eşanionează c ajorl nei reţele discree, iar fiecare eşanion (sa piel), ese caniza folosind n nmăr fini de biţi. Penr afişare, imaginea digială se convereşe din no în formă analogică. O meodă simplă de eşanionare ese eplorarea (scanarea) imaginii, linie dpă linie, şi eşanionarea fiecărei linii. De eempl, camera video c b vidicon sa având n dispoziiv videocapor de ip CCD, face o asemenea scanare a imaginii chiar în procesl de capare. Ale ipri de imagini, cm ar fi filmele sa paginile ipărie, se scanează în mod analog, c ajorl nor echipamene nmie scanere. În figra 3. ese prezena principil de obţinere a imaginilor digiale, precm şi ransformarea inversă în formă analogică. f(,y) f s (,y) (m,n) Eşanionare Canizare Calclaor Calclaor (m,n) Digiizare Conversie D/A Monior Redare Fig 3. Eşanionarea, canizarea şi afişarea imaginilor 45
2 Cap.3 Eşanionarea şi canizarea imaginilor Sandarde de elevizine Da fiind fapl că marea majoriae a imaginilor folosie în aplicaţiile zale sn obţine pornind de la imagini de elevizine, considerăm ilă prezenarea sccină a sandardelor de elevizine în clori folosie în momenl de faţă. Ese vorba de sandardl nord-american - NTSC ("Naional Television Sysem Commiee"), cel german - PAL ("Phase Alernaion Line") şi de cel francez - SECAM ("Seqeniel a Memoire"), c arii diferie de răspândire în diferie ţări şi coninene. Siseml NTSC foloseşe 55 linii de baleiaj şi o frecvenţă de eplorare pe vericală de 6 Hz. Semnall videocomple color se poae scrie ca : () = Y() + I() cos(πf sc + ϕ) + Q () sin (πf sc + ϕ) (3.) nde ϕ = 33, iar f sc ese frecvenţa sbprăoarei de crominanţă. Termenii Y() şi (I, Q) reprezină componenele de lminanţă, respeciv de crominanţă, care se obţin prin ransformări liniare ale semnalelor primare de cloare E R, E B, E G. Lărgimea de bandă a semnalli Y() ese de 4, MHz, iar a semnalelor I() şi Q() ese de,3 şi respeciv,5 MHz. Frecvenţa sbprăoarei de crominanţă ese de 3,58 MHz, ceea ce reprezină a 455-a armonică a f h / (f h - frecvenţa liniilor în NTSC Hz.). Siseml SECAM foloseşe o eplorare înreţesă c 65 de linii, c 5 de cadre/secndă. Pe fiecare linie se ransmie semnall de lminanţă Y() şi câe nl dinre semnalele de crominanţă D R () sa D B () modlae în frecvenţă. Folosirea acesi ip de modlaţie ese posibilă ocmai daoriă ransmisiei secvenţiale a semnalelor de crominanţă. Sbprăoarele celor doă semnale de cloare a frecvenţele respeciv de 4,5 şi 4,4 MHz. Siseml PAL ese n sisem simlan, la fel ca şi siseml NTSC (cele doă informaţii de crominanţă se ransmi simlan, pe fiecare linie) dar se deosebeşe esenţial de acesa prin modaliaea de ransmisie aleasă. Penr diminarea erorilor de fază, nl dinre semnalele de crominanţă se ransmie c o fază ce alernanează c 8 dpă fiecare linie. Semnall videocomple color PAL reprezină sma dinre semnall de lminanţă, semnalele de crominanţă, la care se adagă, eviden, celelale componene ale semnalli TV color: salvele de sincronizare a clorii şi semnalele de singere şi sincronizare. Semnall videocomple color PAL are rmăoarea formă maemaică: () = Y() + U() cos πf sc + (-) m V() sin πf sc (3.) nde m ese indicele liniei. Semnalele de crominanţă a aceeaşi bandă de frecvenţă, de,3 MHz, iar sbprăoarea ese la 4,43 MHz. Având în vedere schimbarea fazei li V() dpă fiecare linie, precm şi dependenţa semnalelor n nmai de imp ci şi de coordonaele spaţiale ale fiecări pnc din imagine, semnall videocomple color PAL se mai poae scrie: (,y,) = Y(,y,) + U(,y,) cos [πf sc + (πf h /4)y - (6πf v /8)] + + V(,y,) sin [πf sc - (πf h /4)y -(6πf v /8)] (3.3) Aceasă relaţie se ilizează penr implemenarea algorimilor de eşanionare a semnalli de elevizine color PAL. Se po dedce din relaţia (3.3) paramerii 46
3 PRELUCRAREA DIGITALĂ A IMAGINILOR semnalli TV care a imporanţă din pncl de vedere al eoriei eşanionării şi se po face evenale prelcrări ale acesia, dpă cm se va vedea în paragrafele rmăoare. Relaţii similare se po scrie şi penr celelale semnale de elevizine în clori. 3. TEORIA EŞANTIONĂRII ÎN SPAŢIUL BIDIMENSIONAL Imagini c specr limia Procesl de digiizare aplica imaginilor poae fi înţeles prin modelarea c ajorl semnalelor c specr limia. Deşi în realiae imaginile c specr limia sn rare, oşi ele po fi aproimae în genere ca fncţii c specr limia. F(ξ, ξ ) ξ ξ y ξ ξ -ξ ξ ξ -ξ y -ξ y ξ Transformaa Forier a fncţiei c specr limia Reginea de definiţie Fig. 3. Transformarea Forier a fncţiilor c specr limia Fncţia f(,y) se nmeşe fncţie c specr limia dacă ransformaa sa Forier F(ξ,,ξ ) ese zero în afara nei regini delimiae din planl frecvenţei (fig.3.): F( ξ, ξ), ξ ξ, ξ ξy = > > (3.4) nde ξ şi ξ y se nmesc lărgimile de bandă, respeciv y. Dacă specrl are o simerie circlară, anci lărgimea de bandă va fi ξ =ξ =ξ y. Eşanionarea Eşanionarea poae fi şor înţeleasă dacă ne adcem amine că ransformaa Forier a nei fncţii eşanionae ese dplical scala respeciv periodic al ransformaei Forier a fncţiei originale. Penr a demonsra aceasa, vom considera o y y Fig. 3.3 Reţea de eşanionare imagine eşanionaă ideal, care se reprezină ca n ablo bidimensional de fncţii Dirac dela, siae pe o reţea drepnghilară c pasl, y (fig. 3.3), definiă de: 47
4 Cap.3 Eşanionarea şi canizarea imaginilor gp(, y;, y) = δ (, y y) (3.5) m= n= Imaginea eşanionaă ese definiă prin rmăoarea ecaţie: f( y, ) = f( yg, ) ( y, ;, y) = f( m n, y) δ ( m y, n y) (3.6) s p mn, = Transformaa Forier a fncţiei g p c pasl, y ese o fncţie c pasl (/, / y) noaă c G p şi ese definiă de: G ( ξ, ξ ) = Forier{ g (, y;, y)} = ξ, ξ δ( ξ ξ, ξ lξ ) p p s ys s ys l, = = ξs, ξysgp( ξ, ξ ; /, / y) (3.7) nde ξ s =/, ξ ys =/ y. Prin aplicarea proprieăţii de mliplicare din domenil imp, ransformaa Forier a imaginii eşanionae f s (,y) va fi: F ( ξ, ξ ) = F( ξ, ξ ) G ( ξ, ξ ) = ξ ξ F( ξ, ξ ) δ( ξ ξ, ξ lξ ) s p s ys s ys l, = = ξξ F( ξ ξ, ξ lξ ) s ys s ys l, = (3.8) Din ecaţia (3.8), ransformaa Forier a imaginii eşanionae ese replica periodică şi, respeciv, scalaă a ransformaei Forier a imaginii de inrare, pe o reţea al cărei pas ese (ξ,ξ ) (fig.3.4). ξ / ξ ys ξ ys -ξ y ξ y ξ y R R / y R 3 R ξ ξ s -ξ ξ ξ s ξ s ξ Fig.3.4 Specrl imaginii eşanionae Refacerea imaginii ilizând eşanioanele sale Din proprieaea de niciae a ransformaei Forier se şie că, dacă specrl imaginii originale se poae reface folosind specrl imaginii eşanionae, anci vom pea obţine şi imaginea inerpolaă pe baza imaginii eşanionae. Dacă frecvenţele de eşanionare pe cele doă ae, şi y, sn de doă ori mai mari decâ lărgimea de bandă, respeciv dacă: ξ > ξ, ξ > ξ (3.9) s ys y 48
5 PRELUCRAREA DIGITALĂ A IMAGINILOR sa dacă inervalele de eşanionare sn mai mici decâ jmăae din (/lărgimea de bandă) corespnzăoare, <, y < (3.) ξ ξ y anci F(ξ,ξ ) poae fi refăcă prinr-o filrare rece jos c caracerisica de frecvenţă: (, ) ( ξξ ), ( ξ, ξ ) R, ]n res H ξ ξ = s ys (3.) nde R ese orice regine ale cărei margini R se află Ţn sprafaţa cprinsă Ţnre drepnghirile R şi R, aşa cm se poae observa şi din fig.3.4. Vom pea deci scrie: ~ F( ξ, ξ ) = H( ξ, ξ ) F ( ξ, ξ ) = F( ξ, ξ ) (3.) s rezlând ocmai imaginea refăcă prin filrarea imaginii eşanionae. Raa Nyqis, efecl "alias" şi frecvenţele de sprapnere Valorile minime ale raei de eşanionare, ξ, ξ y, se nmesc raele Nyqis sa frecvenţele Nyqis. Complemenarele din domenil imp se nmesc inervale Nyqis. Teoria eşanionării precizează că o imagine c specr limia, eşanionaă c frecvenţele Nyqis, poae fi refăcă fără nici o eroare prin filrarea imaginii eşanionae. Uneori, dacă frecvenţele de eşanionare sn mai mici decâ frecvenţele Nyqis, respeciv: ξ < ξ, ξ < ξ s ys y anci replicile periodice ale li F(ξ,ξ ) se vor sprapne, rezlând n specr disorsiona F s (ξ,ξ ) (fig. 3.5), de nde rezlă că F(ξ,ξ ) n va mai pea fi refăc c eaciae. ξ ξ y ξ y ξ Fig. 3.5 Efecl "alias" - frecvenţele de sprapnere Frecvenţele mai mari decâ jmăae din frecvenţele de eşanionare (mai mari decâ ξ s, respeciv ξ ys din figra 3.4) se nmesc frecvenţe de sprapnere. Aceasă sprapnere parţială de perioade sccesive din specr cazează apariţia frecvenţelor de sprapnere în imaginea originală. Fenomenl se nmeşe efec "alias". Erorile de "alias" n po fi eliminae prin filrarea ce rmează ransformării. El poae fi înlăra ξ ξ 49
6 Cap.3 Eşanionarea şi canizarea imaginilor nmai prinr-o filrare rece jos a imaginii iniţiale asfel încâ lărgimea de bandă să fie mai mică decâ jmăae din frecvenţa de eşanionare, saisfăcând-se în fell acesa condiţia (3.9). Teorema eşanionării O imagine c specr limia f(,y) care saisface condiţia (3.4) şi care ese eşanionaă niform pe o reţea drepnghilară c pasl (, y), poae fi refăcă fără erori din valorile eşanioanelor f(m, n y), dacă şi nmai dacă raa de eşanionare ese mai mare decâ raa Nyqis : = ξs > ξ = ξys > ξ y y Imaginea reconsiiă ese obţină ilizând rmăoarea formlă de inerpolare: m y m s ys f (, y) f ( m, n y) sin( ξ ) π sin( ξ ) π = mn, ( s m) ( y ys m) = ξ π ξ π (3.3) Ecaţia (3.3) relevă fapl că fncţia f(,y) se obţine prin inerpolarea infiniă a eşanionelor f(m,n y). În pracică însă ese posibilă doar o inerpolare finiă. C oae acesea, se poae spne că eoria eşanionării redce nmărl infini de eşanioane ale fncţiei f(,y), corespnzăoare ariei y, la n singr eşanion. Energia efecli alias reprezină energia acmlaă în domeniile de frecvenţă nde apar sprapneri ale specrelor şi ese egală c energia imaginii în zonele în care specrl aceseia depăşeşe drepnghil R. Spre eempl, o imagine descrisă de fncţia: fy (,) = cos π ( 3+ 4y) ese eşanionaă c = y=,. Fncţia f(,y) ese c specr limia, deoarece: F( ξ, ξ ) = δ( ξ 3, ξ 4 ) + δ( ξ + 3, ξ + 4 ) ese zero penr ξ >3, ξ >4. De aici rezlă că ξ =3, ξ y =4 şi ξ s =ξ ys =/,=5, valori mai mici decâ frecvenţele Nyqis ξ şi ξ y. Specrl imaginii eşanionae ese: F s (, ) 5 ξ ξ = [ δ ( ξ 3,l 5, ξ 4 5l) + δ ( ξ + 3 5, ξ + 4 = 5l)] Penr filrare vom considera n filr care aie frecvenţele mai mari decâ / din frecvenţele de eşanionare:,,5,5,,5,5 H(, ) = 5, înres Aplicând ecaţia (3.), se obţine: ~ F( ξ, ξ ) = δ( ξ, ξ ) + δ( ξ +, ξ + ) care prin ransformare inversă dce la obţinerea imaginii reconsiie: f Ă (,y)=cosπ(+y). Aces rezla ne araă că orice componenă de frecvenţă din imaginea de inrare, care iese din domenil (ξ s /, ξ s /) c ( ξ, ξ y ), ese reprodsă ca o frecvenţă de valoare (ξ s /- ξ, ξ ys /- ξ y ). 5
7 Reţele de eşanionare nerecanglare şi înreţese PRELUCRAREA DIGITALĂ A IMAGINILOR În general ese avanajoasă folosirea reţelelor de eşanionare drepnghilare dacă specrl F(ξ,ξ ) ese limia de drepnghil R. Eisă însă şi reţele de eşanionare nerecanglare care sn ml mai eficiene din pnc de vedere al densiăţii de eşanionare (nmăr de eşanioane/sprafaţă), dacă domenil de definiţie penr F(ξ,ξ ) n ese drepnghilar. Vom la în considerare specrl din figra 3.6.a, care poae fi asemi c forma ni diaman. Penr o reţea recanglară G, inervalele de eşanionare Nyqis vor fi = y= =. Dacă se foloseşe reţeaa de eşanionare G ( ) (fig.3.6.c), obţină prin roirea reţelei G c 45, dar având disanţa înre eşanioane, specrl imaginii eşanionae va fi repea (replica) pe o reţea asemănăoare c G. Din cază că =, efecl "alias" n va apărea, dar densiaea de eşanionare se redce la jmăae. Deci, dacă o imagine n conţine frecvenţe înale simlan în ambele direcţii, anci raa de eşanionare poae fi redsă la jmăae. Aceasă eorie se foloseşe penr înreţeserea liniilor din semnall de elevizine, da fiind fapl că observaorl man ese insensibil la frecvenţele spaţiale înale. Semnall analogic de elevizine poae fi considera ca n semnal ridimensional f(,y,), eşaniona pe (y) respeciv pe (). Dacă ξ şi ξ reprezină frecvenţele, emporală respeciv vericală, anci fig. 3.6.e reprezină proiecţia în planl (ξ,ξ ) a specrli ridimensional al semnalli de elevizine. -/ / ξ / F(ξ, ξ )= / ξ n n -/ - 3 m - - m a) Specrl b) reţea drepnghilară G c) reţea c înreţesere G ξ ξ - ξ ξ d) specrl penr G e) Specrl penr G Fig.3.6 Eşanionarea înreţesă Eşanionarea opimală 5
8 Cap.3 Eşanionarea şi canizarea imaginilor Din cele discae anerior s-a deds fapl că procesl de eşanionare ransformă o fncţie conină f(,y) înr-o secvenţă f (m,n y), din care se poae apoi reface fncţia conină. Prin rmare, coeficienţii oricărei dezvolări în serie convergenă a fncţiei f(,y) po fi consideraţi ca fiind o formă generalizaă de eşanionare. De aici rezlă fapl că eşanionarea n ese resricţionaă la fncţii c specr limia. În cazl fncţiilor c specr limia, fncţiile sinc sn opimale penr refacerea fncţiei originale f(,y) din eşanioanele sale. Penr câmpri aleaoare c specr limia, câmpl aleaor refăc converge spre câmpl original în sensl erorii păraice medii minime. Tabell 3. Fncţii de inerpolare a imaginilor Fncţia de inerpolare nidimensională Reprezenare grafică Definiţia p() Fncţia de inerpolare bidimensională p a (,y)=p()p(y) Răspnsl Ţn frecvenţă p a (ξ,ξ ) p a (ξ,) / Drepnghilar (filr ordinzero) p () - / / rec p( ) p( y) ξ ξ sinc sinc ξ ξ y 4ξ Tringhilar (filr ordinn) p () - / ri p ( ) p ( ) p ( ) p ( y) ξ ξ sinc sinc ξ ξ y 4ξ filr ordin-n n=, păraic n=3, spline cbic p n () p ( ) p ( ) n convol@ii p ( ) p ( y) n n ξ ξ sinc sinc ξ ξ y n+ 4ξ Gassian p g () σ ep πσ σ ( + y ) ep πσ σ [ πσ ξ + ξ ] ep ( ) Sinc sinc y ξ ξ sinc sinc y rec rec y ξ ξ y ξ În general se poae spne că eisă fncţii care sn opimale, în sensl că ele eşanionează o imagine aleaoare, obţinând-se o secvenţă finiă, asfel încâ eroarea medie păraică dinre original şi imaginea refăcă să fie minimă. O asfel de dezvolare ese dezvolarea în serie Karhnen-Loeve a ni câmp aleaor: 5
9 PRELUCRAREA DIGITALĂ A IMAGINILOR f (, y) = a mn, Φ mn, mn, = (3.4) nde {Φ m,n (,y)} sn valorile proprii ale fncţiei de aocorelaţie corespnzăoare câmpli aleaor f(,y), iar a m,n sn variabile aleaoare orogonale. Penr n nmăr da de ermeni, eroarea medie păraică în imaginea refăcă ese minimă în comparaţie c oricare ală fncţie de eşanionare. Aceasă proprieae se foloseşe în domenil ehnicilor de compresie a imaginilor. Penr a face o eşanionare opimală în cazl imaginilor reale, principala dificlae în ilizarea rezlaelor precedene consă în calcll coeficienţilor a m,n, pe când în cazl nei eşanionări convenţionale, folosind fncţia sinc, coeficienţii sn valori simple, şor de obţin. C oae acesea, eoria dezvolării K-L poae fi folosiă ca modaliae de comparaţie penr diferiţi algorimi de procesare a imaginilor. Limiări în procesl de eşanionare şi reconsrcţie Procesele de eşanionare prezenae anerior sn bazae pe concepe idealizane. Imaginile reale n a specr limia, ceea ce dce la apariţia erorilor de ip "alias", care po fi redse prinr-o filrare iniţială a imaginii (înainea eşanionării), dar c dezavanajl aenării frecvenţelor înale. În consecinţă, imaginea va fi înceţoşaă ("blrred"), lcr care se perece şi în procesl de achiziţie, deoarece sisemele de descompnere a imaginii a, în pracică, o aperră finiă. Fncţia de ransfer a filrli rece-jos de reconsrcţie n va fi ideală, aceasa depinzând de aperra sisemli de afişare. Imagine inrare Aperra sisemli de scanare p s (-,-y) g(,y) Sisem de eşanionare ideal, y g s (,y) Sisem de afişare p a (-,-y) g ~ (,y) Model de scaner real Fig. 3.7 Schema-bloc a ni sisem de eşanionare real În figra 3.7 ese prezena n sisem real de eşanionare, respeciv de reconsrcţie a imaginilor. Un sisem perfec de refacere a imaginii necesiă n proces de inerpolare infiniă înre eşanionele f(m,n y). Penr siseml de afişare, asa înseamnă că "spol" acesia rebie să aibă o disribţie a inensiăţii lminoase daă de fncţia sinc, care are o draă infiniă şi prezină lobi negaivi. În abell 3. sn prezenae câeva fncţii folosie penr inerpolare. Inerpolarea bidimensională poae fi realizaă prinr-o sccesine de inerpolări pe rândri, respeciv pe coloane. Filrele de ordin zero respeciv de ordin n, da inerpolări în repe, respeciv liniare înre eşanioane. Filrele de ordin sperior po dce la inerpolări păraice (n=) respeciv spline cbice (n=3). Penr n, filrele de ordinl n po să conveargă spre o fncţie gassiană. 53
10 Cap.3 Eşanionarea şi canizarea imaginilor P a (ξ,) Filr de refacere sa specrl sisemli de afişare -ξ s / ξ s / ξ Specrl imaginii eşanionae Specrl imaginii refăce Specrl imaginii de inrare Pierderile de specr - ξ -ξ s / ξ s / Eroarea de inerpolare Fig. 3.8 Efecl real al inerpolării În figra 3.8 ese prezena efecl real al implemenării inerpolării în refacerea imaginii conine. Rezolţia în frecvenţă, pierdă daoriă filrli de reconsrcţie, depinde de dimensinea lobli principal. Deoarece sinc() n < penr orice, lobl principal al filrli de ordinl n va deveni o mai îngs, pe măsră ce n creşe. Prin rmare, dinre oae fncţiile prezenae în abell 3., filrl de ordin zero ese singrl care prezină pierderi minime de specr (rezolţie), dar va avea eroare maimă de inerpolare. În pracică, inerpolarea c fncţii de ordinl înâi (liniară) oferă n compromis saisfăcăor înre pierderea de rezolţie şi acraeţea imaginii reconsrie. 3.3 CUANTIZAREA IMAGINILOR Pasl lerior eşanionării în digiizarea imaginilor ese canizarea. Un canizor face corespondenţa dinre o variabilă conină şi o variabilă discreă care ia valori dinr-n se fini de nmere {r,, r L }. Aceasă alocare se face în general c o fncţie scară (fig.3.9) şi regla ese rmăoarea: se defineşe { ; =,,L+} n se de ranziţii crescăoare sa nivele de decizie, nde şi L+ sn valoarea Canizor r L I e[ irea canizorl r L r r Eroarea de canizare r Fig. 3.9 Canizor şi fncţia de canizare 54
11 PRELUCRAREA DIGITALĂ A IMAGINILOR minimă şi, respeciv, maimă a li. Dacă ese în inervall (, + ), anci i se alocă nivell r, al -lea nivel de reconsrcţie.cel mai simpl şi mai zal canizor ese cel niform. Considerăm ieşirea ni senzor de imagine c valori înre, şi,. Dacă eşanioanele sn canizae niform c 56 de nivele, anci nivelele de ranziţie şi de reconsrcţie sn: ( ) =, =,..., r = +, =,..., Inervall q= - - =r -r - ese consan penr diferie valori ale li şi ese nmi inerval de canizare. În aces capiol vom la în considerare doar canizarea c memorie zero, care operează la n momen da nmai aspra ni eşanion de inrare, iar valoarea de ieşire depinde nmai de acel eşanion. Asemenea canizori sn ili în ehnicile de codare de imagine ca, de eempl, modlaţia implsrilor în cod (PCM), modlaţia diferenţială PCM, codarea prin ransformări şi alele. Ese de noa că operaţia de canizare ese ireversibilă deoarece, penr o valoare daă de ieşire, n se poae deermina în mod nic valoarea de la inrare. Din aces moiv, n canizor inrodce disorsini, pe care orice meodă de proiecare rebie să încerce să le minimizeze. 3.4 CUANTIZORUL OPTIMAL (LLOYD - MAX) Canizorl opimal în sensl erorii păraice medii, sa, cm se mai nmeşe, canizorl Lloyd-Ma, minimizeză eroarea păraică medie penr n nmăr da de nivele de canizare. Fie o variabilă aleaoare reală scalară, care are o fncţie de probabiliae conină p (). Problema consă în găsirea nivelelor de decizie şi a nivelelor de reconsrcţie r, penr n canizor c L nivele, asfel încâ eroarea păraică medie: să fie minimă. Rescriind aceasa ca: L+ (3.5) e= E[( ' ) ] = ( ' ) p ()d ε = L i+ i= i ( r) p ( ) d i (3.6) condiţiile necesare penr minimizarea li ε se obţin prin diferenţierea ecaţiei în rapor c şi r şi egalând rezlaele c zero: ε = ( r ) ( r) p( ) = L i+ ε = ri p d= L r ( ) ( ) Uilizând fapl că -, simplificarea ecaţiilor anerioare dă: i= i r = + r (3.7) 55
12 Cap.3 Eşanionarea şi canizarea imaginilor r + p ()d p ()d [ ] = = E ϑ (3.8) + nde ϑ ese inervall de ordinl, (, + ). Acese rezlae araă că nivelele opime de ranziţie se găsesc la jmăaea disanţei dinre nivelele de reconsrcţie opimă, care, la rândl lor, se găsesc în cenrl de masă al densiăţii de probabiliae, înre nivelele de ranziţie. Împrenă, ecaţiile (3.7) şi (3.8) sn ecaţii neliniare care rebiesc rezolvae simlan, având dae condiţiile de graniţă şi L+. În pracică, acese ecaţii po fi rezolvae prin meode nmerice ieraive ca, spre eempl, meoda Newon. Anci când nmărl nivelelor de canizare ese mare, o solţie aproimaivă se poae obţine prin modelarea fncţiei densiae de probabiliae p () ca fncţie consană pe inervale (ca în fig. 3.): p( ) p( j), j = ( j + j+ ), j < j+ (3.9) Uilizând aceasă aproimare în ecaţia (3.6) şi făcând minimizările cere, se poae obţine o solţie aproimaivă penr nivelele de decizie: + z + 3 / A [ p ( )] d + L + 3 / [ p ( )] d (3.) nde A= L+ - şi z =(/L)A, =,,L. Aceasă meodă cere ca valorile şi L+, nmie şi pnce de graniţă, să fie finie. Valorile pncelor de graniţă, ce deermină gama dinamică A a canizorli, rebie să fie cnosce înaine de plasarea nivelelor de decizie şi reconsrcţie. O daă ce nivelele { Î a fos deerminae, nivelele de reconsrcţie { Î se po deermina şor ca media li şi +. Disorsinea medie păraică a canizorli se obţine prin: ε = L L + [ p ( )] / d (3.) 3 3 p ( ) j j+ L+ Fig. 3. Aproimarea în repe a fncţiei p() 56
Demodularea (Detectia) semnalelor MA, Detectia de anvelopa
 Deodularea (Deecia) senalelor MA, Deecia de anveloa Deodularea ese recuerarea senalului odulaor din senalul MA. Aceasa se oae face erfec nuai daca s( ) ese de banda liiaa iar Deodularea senalelor MA se
Deodularea (Deecia) senalelor MA, Deecia de anveloa Deodularea ese recuerarea senalului odulaor din senalul MA. Aceasa se oae face erfec nuai daca s( ) ese de banda liiaa iar Deodularea senalelor MA se
CAPITOLUL 4 FUNCŢIONALE LINIARE, BILINIARE ŞI PĂTRATICE
 CAPITOLUL FUNCŢIONALE LINIAE BILINIAE ŞI PĂTATICE FUNCŢIONALE LINIAE BEIA TEOETIC Deiniţia Fie K X un spaţiu vecorial de dimensiune iniă O aplicaţie : X K se numeşe uncţională liniară dacă: ese adiivă
CAPITOLUL FUNCŢIONALE LINIAE BILINIAE ŞI PĂTATICE FUNCŢIONALE LINIAE BEIA TEOETIC Deiniţia Fie K X un spaţiu vecorial de dimensiune iniă O aplicaţie : X K se numeşe uncţională liniară dacă: ese adiivă
ANALIZA SPECTRALĂ A SEMNALELOR ALEATOARE
 ANALIZA SPECRALĂ A SEMNALELOR ALEAOARE. Scopul lucrării Se sudiază caracerizarea în domeniul frecvenţă a semnalelor aleaoare de ip zgomo alb şi zgomo roz şi aplicaţiile aceseia la deerminarea modulelor
ANALIZA SPECRALĂ A SEMNALELOR ALEAOARE. Scopul lucrării Se sudiază caracerizarea în domeniul frecvenţă a semnalelor aleaoare de ip zgomo alb şi zgomo roz şi aplicaţiile aceseia la deerminarea modulelor
(a) se numeşte derivata parţială a funcţiei f în raport cu variabila x i în punctul a.
 Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate.
 Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
SEMINAR TRANSFORMAREA LAPLACE. 1. Probleme. ω2 s s 2, Re s > 0; (4) sin ωt σ(t) ω. (s λ) 2, Re s > Re λ. (6)
 SEMINAR TRANSFORMAREA LAPLACE. Probleme. Foloind proprieaea de liniariae, ă e demonreze urmăoarele: in σ(, Re > ; ( + penru orice C. co σ( h σ( ch σ(, Re > ; ( +, Re > ; (3, Re > ; (4. Să e arae că penru
SEMINAR TRANSFORMAREA LAPLACE. Probleme. Foloind proprieaea de liniariae, ă e demonreze urmăoarele: in σ(, Re > ; ( + penru orice C. co σ( h σ( ch σ(, Re > ; ( +, Re > ; (3, Re > ; (4. Să e arae că penru
Sisteme diferenţiale liniare de ordinul 1
 1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
Metode iterative pentru probleme neliniare - contractii
 Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
CURS METODA OPERAŢIONALĂ DE INTEGRARE A ECUAŢIILOR CU DERIVATE PARŢIALE DE ORDIN II
 CURS METODA OPERAŢIONALĂ DE INTEGRARE A ECUAŢIILOR CU DERIVATE PARŢIALE DE ORDIN II. Utiizarea transformării Lapace Să considerăm probema hiperboică de forma a x + b x + c + d = f(t, x), (t, x) [, + )
CURS METODA OPERAŢIONALĂ DE INTEGRARE A ECUAŢIILOR CU DERIVATE PARŢIALE DE ORDIN II. Utiizarea transformării Lapace Să considerăm probema hiperboică de forma a x + b x + c + d = f(t, x), (t, x) [, + )
Măsurări în Electronică şi Telecomunicaţii 2. Osciloscopul
 2. Osciloscopl 2.5 anall X al osciloscopli Schema bloc a canalli X onţine doă blocri fncţionale nl care asigră sincronizarea, al doilea, care asigră referinţa de imp, făcând posibilă afişarea pe o scară
2. Osciloscopl 2.5 anall X al osciloscopli Schema bloc a canalli X onţine doă blocri fncţionale nl care asigră sincronizarea, al doilea, care asigră referinţa de imp, făcând posibilă afişarea pe o scară
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM 1 electronica.geniu.ro
 Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Curs 4 Serii de numere reale
 Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Dinamica fluidelor. p z. u w y. X x. p z. v w y. Y y. p z. w w y. Z z. w t. v t. = t. dy u. dz v
 Dinamica flielor Relaţia li Bernolli Aceasă relaţie se obţine efecân inegrarea ecaţiilor e mişcare a flielor ieale e o linie e cren. Se orneşe e la siseml e ecaţii e mişcare ala flielor ieale: X Y Z Se
Dinamica flielor Relaţia li Bernolli Aceasă relaţie se obţine efecân inegrarea ecaţiilor e mişcare a flielor ieale e o linie e cren. Se orneşe e la siseml e ecaţii e mişcare ala flielor ieale: X Y Z Se
Transformata Radon. Reconstructia unei imagini bidimensionale cu ajutorul proiectiilor rezultate de-a lungul unor drepte.
 Problema Tranformaa Radon Reconrucia unei imaini bidimenionale cu auorul roieciilor rezulae de-a lunul unor dree. Domeniul de uilizare: Prelucrarea imainilor din domeniul medical Prelucrarea imainilor
Problema Tranformaa Radon Reconrucia unei imaini bidimenionale cu auorul roieciilor rezulae de-a lunul unor dree. Domeniul de uilizare: Prelucrarea imainilor din domeniul medical Prelucrarea imainilor
( ) () t = intrarea, uout. Seminar 5: Sisteme Analogice Liniare şi Invariante (SALI)
 Seminar 5: Sieme Analogice iniare şi Invariane (SAI) SAI po fi caracerizae prin: - ecuaţia diferenţială - funcţia de iem (fd) H() - funcţia pondere h - răpunul indicial a - răpunul la frecvenţă H(j) ăpunul
Seminar 5: Sieme Analogice iniare şi Invariane (SAI) SAI po fi caracerizae prin: - ecuaţia diferenţială - funcţia de iem (fd) H() - funcţia pondere h - răpunul indicial a - răpunul la frecvenţă H(j) ăpunul
Studiul chopperelor de putere individuale
 aboraor: Eleroniă Indsrială Eleronia de Pere Sdil hopperelor de pere individale hopperele de pere a roll de a modifia valoarea medie a ensinii apliae nei sarini, alimenarea irili fiind onsiia de o srsa
aboraor: Eleroniă Indsrială Eleronia de Pere Sdil hopperelor de pere individale hopperele de pere a roll de a modifia valoarea medie a ensinii apliae nei sarini, alimenarea irili fiind onsiia de o srsa
5.5. REZOLVAREA CIRCUITELOR CU TRANZISTOARE BIPOLARE
 5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
Cursul 14 ) 1 2 ( fg dµ <. Deci fg L 2 ([ π, π]). Prin urmare,
![Cursul 14 ) 1 2 ( fg dµ <. Deci fg L 2 ([ π, π]). Prin urmare, Cursul 14 ) 1 2 ( fg dµ <. Deci fg L 2 ([ π, π]). Prin urmare,](/thumbs/85/91744612.jpg) D.Rs, Teoia măsii şi integala Lebesge 6 SERII FOURIER ÎN L ([, ]) Csl 4 6 Seii Foie în L ([, ]) Consideăm spaţil c măsă ([, ], M [,], µ), nde M este σ-algeba mlţimilo măsabile Lebesge, ia µ este măsa Lebesge.
D.Rs, Teoia măsii şi integala Lebesge 6 SERII FOURIER ÎN L ([, ]) Csl 4 6 Seii Foie în L ([, ]) Consideăm spaţil c măsă ([, ], M [,], µ), nde M este σ-algeba mlţimilo măsabile Lebesge, ia µ este măsa Lebesge.
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor X) functia f 1
 Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Planul determinat de normală şi un punct Ecuaţia generală Plane paralele Unghi diedru Planul determinat de 3 puncte necoliniare
 1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor
 Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
3 Minimizarea cu diagramelor KV
 3 Minimizarea c diagramelor KV 3. Prezentare generală Metoda de minimizare c ajtorl diagramelor KarnaghVeitch (diagrame KV) este o metodă grafică de minimizare bazată pe o reprezentare specială a tabelli
3 Minimizarea c diagramelor KV 3. Prezentare generală Metoda de minimizare c ajtorl diagramelor KarnaghVeitch (diagrame KV) este o metodă grafică de minimizare bazată pe o reprezentare specială a tabelli
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE
 DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
ANEXA I. 1. Managementul Ştiinţific (Frederic Winslow Taylor)
 ANEXE 364 Gesinea inegraă a firmei 365 ANEXA I 1. Managemenl Şiinţific Frederic Winslow aylor Frederic Winslow aylor 1856-1915 a fos nl dinre primii care a încerca să creeze o şiinţă a managemenli necesară
ANEXE 364 Gesinea inegraă a firmei 365 ANEXA I 1. Managemenl Şiinţific Frederic Winslow aylor Frederic Winslow aylor 1856-1915 a fos nl dinre primii care a încerca să creeze o şiinţă a managemenli necesară
ELEMENTE DE STABILITATE A SISTEMELOR LINIARE
 6 ELEMENTE DE STABILITATE A SISTEMELOR LINIARE In sudiul sabiliăţii sisemelor se uilizează două concepe: concepul de sabiliae inernă (a sării) şi concepul de sabiliae exernă (a ieşirii) 6 STABILITATEA
6 ELEMENTE DE STABILITATE A SISTEMELOR LINIARE In sudiul sabiliăţii sisemelor se uilizează două concepe: concepul de sabiliae inernă (a sării) şi concepul de sabiliae exernă (a ieşirii) 6 STABILITATEA
III. Serii absolut convergente. Serii semiconvergente. ii) semiconvergentă dacă este convergentă iar seria modulelor divergentă.
 III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
Definiţia generală Cazul 1. Elipsa şi hiperbola Cercul Cazul 2. Parabola Reprezentari parametrice ale conicelor Tangente la conice
 1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
Capitolul I ECUAŢII DIFERENŢIALE. 1 Matematici speciale. Probleme. 1. Să de integreze ecuaţia diferenţială de ordinul întâi liniară
 Mamaici spcial Problm c solţia apioll I EUAŢII DIFERENŢIALE Să d ingrz caţia difrnţială d ordinl înâi liniară g cos d Solţi: Ecaţia omognă aaşaă s: - g sa g d ln - ln cos ln sa Pnr rzolvara caţii cos nomogn
Mamaici spcial Problm c solţia apioll I EUAŢII DIFERENŢIALE Să d ingrz caţia difrnţială d ordinl înâi liniară g cos d Solţi: Ecaţia omognă aaşaă s: - g sa g d ln - ln cos ln sa Pnr rzolvara caţii cos nomogn
V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile
 Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
prin egalizarea histogramei
 Lucrarea 4 Îmbunătăţirea imaginilor prin egalizarea histogramei BREVIAR TEORETIC Tehnicile de îmbunătăţire a imaginilor bazate pe calculul histogramei modifică histograma astfel încât aceasta să aibă o
Lucrarea 4 Îmbunătăţirea imaginilor prin egalizarea histogramei BREVIAR TEORETIC Tehnicile de îmbunătăţire a imaginilor bazate pe calculul histogramei modifică histograma astfel încât aceasta să aibă o
5. FUNCŢII IMPLICITE. EXTREME CONDIŢIONATE.
 5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
a n (ζ z 0 ) n. n=1 se numeste partea principala iar seria a n (z z 0 ) n se numeste partea
 Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
CIRCUITE ELEMENTARE CU AMPLIFICATOARE OPERAȚIONALE
 LUCAEA nr. CICUITE ELEMENTAE CU AMPLIFICATOAE OPEAȚIONALE Scopul lucrării: Se sudiază câeva dinre circuiele elemenare ce se po realiza cu amplificaoare operaţionale (), în care acesea sun considerae ca
LUCAEA nr. CICUITE ELEMENTAE CU AMPLIFICATOAE OPEAȚIONALE Scopul lucrării: Se sudiază câeva dinre circuiele elemenare ce se po realiza cu amplificaoare operaţionale (), în care acesea sun considerae ca
Curs 14 Funcţii implicite. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi"
 Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Proiectarea filtrelor prin metoda pierderilor de inserţie
 FITRE DE MIROUNDE Proiectarea filtrelor prin metoda pierderilor de inserţie P R Puterea disponibila de la sursa Puterea livrata sarcinii P inc P Γ ( ) Γ I lo P R ( ) ( ) M ( ) ( ) M N P R M N ( ) ( ) Tipuri
FITRE DE MIROUNDE Proiectarea filtrelor prin metoda pierderilor de inserţie P R Puterea disponibila de la sursa Puterea livrata sarcinii P inc P Γ ( ) Γ I lo P R ( ) ( ) M ( ) ( ) M N P R M N ( ) ( ) Tipuri
SERII NUMERICE. Definiţia 3.1. Fie (a n ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0
 SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
3. CONVOLUŢIA. Sinteza semnalului de intrare Produsul intre un impuls Dirac intarziat cu k si semnalul x[n] extrage valoarea esantionului x[k]:
![3. CONVOLUŢIA. Sinteza semnalului de intrare Produsul intre un impuls Dirac intarziat cu k si semnalul x[n] extrage valoarea esantionului x[k]: 3. CONVOLUŢIA. Sinteza semnalului de intrare Produsul intre un impuls Dirac intarziat cu k si semnalul x[n] extrage valoarea esantionului x[k]:](/thumbs/82/86941072.jpg) 3. COVOLUŢIA Inroducem operaia de convoluţie in imp discre (suma de convoluie) si in imp coninuu (produsul de convoluie). Calculul răspunsului sisemelor liniare şi invariane in imp, la un semnal de inrare
3. COVOLUŢIA Inroducem operaia de convoluţie in imp discre (suma de convoluie) si in imp coninuu (produsul de convoluie). Calculul răspunsului sisemelor liniare şi invariane in imp, la un semnal de inrare
Componente şi Circuite Electronice Pasive. Laborator 4. Măsurarea parametrilor mărimilor electrice
 Laborator 4 Măsurarea parametrilor mărimilor electrice Obiective: o Semnalul sinusoidal, o Semnalul dreptunghiular, o Semnalul triunghiular, o Generarea diferitelor semnale folosind placa multifuncţională
Laborator 4 Măsurarea parametrilor mărimilor electrice Obiective: o Semnalul sinusoidal, o Semnalul dreptunghiular, o Semnalul triunghiular, o Generarea diferitelor semnale folosind placa multifuncţională
R R, f ( x) = x 7x+ 6. Determinați distanța dintre punctele de. B=, unde x și y sunt numere reale.
 5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
Erori si incertitudini de măsurare. Modele matematice Instrument: proiectare, fabricaţie, Interacţiune măsurand instrument:
 Erori i incertitudini de măurare Sure: Modele matematice Intrument: proiectare, fabricaţie, Interacţiune măurandintrument: (tranfer informaţie tranfer energie) Influente externe: temperatura, preiune,
Erori i incertitudini de măurare Sure: Modele matematice Intrument: proiectare, fabricaţie, Interacţiune măurandintrument: (tranfer informaţie tranfer energie) Influente externe: temperatura, preiune,
a. Caracteristicile mecanice a motorului de c.c. cu excitaţie independentă (sau derivaţie)
 Caracteristica mecanică defineşte dependenţa n=f(m) în condiţiile I e =ct., U=ct. Pentru determinarea ei vom defini, mai întâi caracteristicile: 1. de sarcină, numită şi caracteristica externă a motorului
Caracteristica mecanică defineşte dependenţa n=f(m) în condiţiile I e =ct., U=ct. Pentru determinarea ei vom defini, mai întâi caracteristicile: 1. de sarcină, numită şi caracteristica externă a motorului
5.4. MULTIPLEXOARE A 0 A 1 A 2
 5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
7. Rezolvarea numerică a problemelor la limită pentru ecuaţii cu derivate parţiale de tip eliptic
 Rezolvarea nmerică a problemelor la limită pentr edp de tip eliptic 7 Rezolvarea nmerică a problemelor la limită pentr ecaţii c derivate parţiale de tip eliptic Fie R o mlţime descisă coneă şi mărginită
Rezolvarea nmerică a problemelor la limită pentr edp de tip eliptic 7 Rezolvarea nmerică a problemelor la limită pentr ecaţii c derivate parţiale de tip eliptic Fie R o mlţime descisă coneă şi mărginită
FIZICĂ. Unde elastice. ş.l. dr. Marius COSTACHE
 FZCĂ Unde elasice ş.l. d. Mais COSTCHE Noţini geneale UNDE ELSTCE Unda fenomenl de popagae din apoape în apoape a nei pebaţii peiodice podsa în-n anmi pnc din medil de popagae. Fncţia de ndă descie maemaic
FZCĂ Unde elasice ş.l. d. Mais COSTCHE Noţini geneale UNDE ELSTCE Unda fenomenl de popagae din apoape în apoape a nei pebaţii peiodice podsa în-n anmi pnc din medil de popagae. Fncţia de ndă descie maemaic
Curs 1 Şiruri de numere reale
 Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].
![Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].](/thumbs/72/67648751.jpg) Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
Metode de interpolare bazate pe diferenţe divizate
 Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
Seminar 5 Analiza stabilității sistemelor liniare
 Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
TEMA 9: FUNCȚII DE MAI MULTE VARIABILE. Obiective:
 TEMA 9: FUNCȚII DE MAI MULTE VARIABILE 77 TEMA 9: FUNCȚII DE MAI MULTE VARIABILE Obiective: Deiirea pricipalelor proprietăţi matematice ale ucţiilor de mai multe variabile Aalia ucţiilor de utilitate şi
TEMA 9: FUNCȚII DE MAI MULTE VARIABILE 77 TEMA 9: FUNCȚII DE MAI MULTE VARIABILE Obiective: Deiirea pricipalelor proprietăţi matematice ale ucţiilor de mai multe variabile Aalia ucţiilor de utilitate şi
6 n=1. cos 2n. 6 n=1. n=1. este CONV (fiind seria armonică pentru α = 6 > 1), rezultă
 Semiar 5 Serii cu termei oarecare Probleme rezolvate Problema 5 Să se determie atura seriei cos 5 cos Soluţie 5 Şirul a 5 este cu termei oarecare Studiem absolut covergeţa seriei Petru că cos a 5 5 5 şi
Semiar 5 Serii cu termei oarecare Probleme rezolvate Problema 5 Să se determie atura seriei cos 5 cos Soluţie 5 Şirul a 5 este cu termei oarecare Studiem absolut covergeţa seriei Petru că cos a 5 5 5 şi
SEMINARUL 3. Cap. II Serii de numere reale. asociat seriei. (3n 5)(3n 2) + 1. (3n 2)(3n+1) (3n 2) (3n + 1) = a
 Capitolul II: Serii de umere reale. Lect. dr. Lucia Maticiuc Facultatea de Hidrotehică, Geodezie şi Igieria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucia MATICIUC SEMINARUL 3. Cap. II Serii
Capitolul II: Serii de umere reale. Lect. dr. Lucia Maticiuc Facultatea de Hidrotehică, Geodezie şi Igieria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucia MATICIUC SEMINARUL 3. Cap. II Serii
Seminariile Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reziduurilor
 Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Probleme. c) valoarea curentului de sarcină prin R L şi a celui de la ieşirea AO dacă U I. Rezolvare:
 Pobleme P Pentu cicuitul din fig P, ealizat cu amplificatoae opeaţionale ideale, alimentate cu ±5V, să se detemine: a) elaţia analitică a tensiunii de ieşie valoile tensiunii de ieşie dacă -V 0V +,8V -V
Pobleme P Pentu cicuitul din fig P, ealizat cu amplificatoae opeaţionale ideale, alimentate cu ±5V, să se detemine: a) elaţia analitică a tensiunii de ieşie valoile tensiunii de ieşie dacă -V 0V +,8V -V
Integrala nedefinită (primitive)
 nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
STUDIUL REGIMULUITRANZITORIU AL CIRCUITELOR ELECTRICE
 UNIVERSITATEA "POLITEHNICA" DIN BUCURESTI CATEDRA DE FIZICĂ LABORATORUL ELECTRICITATE SI MAGNETISM BN 119 STUDIUL REGIMULUITRANZITORIU AL CIRCUITELOR ELECTRICE 7 STUDIUL REGIMULUITRANZITORIU AL CIRCUITELOR
UNIVERSITATEA "POLITEHNICA" DIN BUCURESTI CATEDRA DE FIZICĂ LABORATORUL ELECTRICITATE SI MAGNETISM BN 119 STUDIUL REGIMULUITRANZITORIU AL CIRCUITELOR ELECTRICE 7 STUDIUL REGIMULUITRANZITORIU AL CIRCUITELOR
Transformarea Fourier a semnalelor analogice
 ransformarea Fourier a semnalelor analogice O reprezenare specrala aplicabila semnalelor neperiodice hp://shannon.ec.up.ro/eaching/ssis/cap5.pdf ransformarea Fourier penru semnale aperiodice Semnalul ()
ransformarea Fourier a semnalelor analogice O reprezenare specrala aplicabila semnalelor neperiodice hp://shannon.ec.up.ro/eaching/ssis/cap5.pdf ransformarea Fourier penru semnale aperiodice Semnalul ()
3.3. Ecuaţia propagării căldurii
 3 ECUAŢII γ k + k iar din (34 rezuă că a 4Aω δ k (k + + a + (k+ (k+ ω deci 4Aω δ k + a a (k + (k+ ω Conform (9 souţia probemei considerae va fi 4Aω a w ( sin( sin( k+ k+ + a k a (k+ (k+ ω 4Asinω + sin(k+
3 ECUAŢII γ k + k iar din (34 rezuă că a 4Aω δ k (k + + a + (k+ (k+ ω deci 4Aω δ k + a a (k + (k+ ω Conform (9 souţia probemei considerae va fi 4Aω a w ( sin( sin( k+ k+ + a k a (k+ (k+ ω 4Asinω + sin(k+
TEMA 12 SERII DE TIMP
 TEMA SERII DE TIMP Obiecive Cunoaşerea concepelor referioare la seriile de imp Analiza principalelor meode de analiză şi prognoză cu serii de imp Aplicaţii rezolvae Aplicaţii propuse Cuprins Concepe referioare
TEMA SERII DE TIMP Obiecive Cunoaşerea concepelor referioare la seriile de imp Analiza principalelor meode de analiză şi prognoză cu serii de imp Aplicaţii rezolvae Aplicaţii propuse Cuprins Concepe referioare
SEMINAR 14. Funcţii de mai multe variabile (continuare) ( = 1 z(x,y) x = 0. x = f. x + f. y = f. = x. = 1 y. y = x ( y = = 0
 Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
riptografie şi Securitate
 riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
 4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
 10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
Ovidiu Gabriel Avădănei, Florin Mihai Tufescu,
 vidiu Gabriel Avădănei, Florin Mihai Tufescu, Capitolul 6 Amplificatoare operaţionale 58. Să se calculeze coeficientul de amplificare în tensiune pentru amplficatorul inversor din fig.58, pentru care se
vidiu Gabriel Avădănei, Florin Mihai Tufescu, Capitolul 6 Amplificatoare operaţionale 58. Să se calculeze coeficientul de amplificare în tensiune pentru amplficatorul inversor din fig.58, pentru care se
CAPITOLUL 3. FILTRE CU RĂSPUNS INFINIT LA IMPULS
 Capiolul 3 Filre cu răspuns fini la impuls 69 CAPITOLUL 3. FILTRE CU RĂSPUNS INFINIT LA IMPULS 3.. Să se proieceze un FTJ numeric, care lucrează la frecvenţa de eşanionare FS khz, pornind de la filrul
Capiolul 3 Filre cu răspuns fini la impuls 69 CAPITOLUL 3. FILTRE CU RĂSPUNS INFINIT LA IMPULS 3.. Să se proieceze un FTJ numeric, care lucrează la frecvenţa de eşanionare FS khz, pornind de la filrul
Asupra unei inegalităţi date la barajul OBMJ 2006
 Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
Măsurări în Electronică şi Telecomunicaţii 4. Măsurarea impedanţelor
 4. Măsurarea impedanţelor 4.2. Măsurarea rezistenţelor în curent continuu Metoda comparaţiei ceastă metodă: se utilizează pentru măsurarea rezistenţelor ~ 0 montaj serie sau paralel. Montajul serie (metoda
4. Măsurarea impedanţelor 4.2. Măsurarea rezistenţelor în curent continuu Metoda comparaţiei ceastă metodă: se utilizează pentru măsurarea rezistenţelor ~ 0 montaj serie sau paralel. Montajul serie (metoda
Lucrarea Nr. 5 Comportarea cascodei EC-BC în domeniul frecvenţelor înalte
 Lucaea N. 5 opoaea cascode E-B în doenul fecenţelo înale Scopul lucă - edenţeea cauzelo ce deenă copoaea la HF a cascode E-B; - efcaea coespondenţe dne ezulaele obţnue expeenal penu la supeoaă a benz acesu
Lucaea N. 5 opoaea cascode E-B în doenul fecenţelo înale Scopul lucă - edenţeea cauzelo ce deenă copoaea la HF a cascode E-B; - efcaea coespondenţe dne ezulaele obţnue expeenal penu la supeoaă a benz acesu
a. 11 % b. 12 % c. 13 % d. 14 %
 1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
Criptosisteme cu cheie publică III
 Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
11 PORŢI LOGICE Operaţii şi porţi logice. S.D.Anghel - Bazele electronicii analogice şi digitale
 S.D.nghel - azele elecronicii analogice şi digiale PORŢI LOGICE. Operaţii şi porţi logice lgebra care operează numai cu două simboluri, şi, ese mul mai simplă decâ algebra clasică, exisând doar rei operaţii
S.D.nghel - azele elecronicii analogice şi digiale PORŢI LOGICE. Operaţii şi porţi logice lgebra care operează numai cu două simboluri, şi, ese mul mai simplă decâ algebra clasică, exisând doar rei operaţii
CURS 1 completare Automatizare proceselor termoenergetice
 Capitoll 2: Configratii de sistem de reglare atomata 2.1. Tipri de SRA SRA se pot clasifica in: - sisteme de rejectie a pertrbatiilor (c referinta fixa); SRA asigra fnctionarea procesli intr-n regim stationar
Capitoll 2: Configratii de sistem de reglare atomata 2.1. Tipri de SRA SRA se pot clasifica in: - sisteme de rejectie a pertrbatiilor (c referinta fixa); SRA asigra fnctionarea procesli intr-n regim stationar
Aplicaţii ale principiului I al termodinamicii la gazul ideal
 Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Prelucrarea semnalelor
 Prelcrarea emnalelor Facltatea de Electronica i Telecomnicatii, UPT http://hannon.etc.pt.ro/teaching/p/ Tranformarea aplace http://hannon.etc.pt.ro/teaching/p/cap7.pdf Pierre Simon aplace Regim permanent
Prelcrarea emnalelor Facltatea de Electronica i Telecomnicatii, UPT http://hannon.etc.pt.ro/teaching/p/ Tranformarea aplace http://hannon.etc.pt.ro/teaching/p/cap7.pdf Pierre Simon aplace Regim permanent
Componente şi Circuite Electronice Pasive. Laborator 3. Divizorul de tensiune. Divizorul de curent
 Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
REPREZENTAREA MATEMATICA A SISTEMELOR
 EPEZENAEA MAEMAICA A SISEMELO Comporamel i sisem î regim iamic care icle regiml saţioar şi regiml raziori poae fi escris pe baza i moel maemaic, forma i ecaţii algebrice şi i ecaţii ifereţiale oriare sa
EPEZENAEA MAEMAICA A SISEMELO Comporamel i sisem î regim iamic care icle regiml saţioar şi regiml raziori poae fi escris pe baza i moel maemaic, forma i ecaţii algebrice şi i ecaţii ifereţiale oriare sa
Profesor Blaga Mirela-Gabriela DREAPTA
 DREAPTA Fie punctele A ( xa, ya ), B ( xb, yb ), C ( xc, yc ) şi D ( xd, yd ) în planul xoy. 1)Distanţa AB = (x x ) + (y y ) Ex. Fie punctele A( 1, -3) şi B( -2, 5). Calculaţi distanţa AB. AB = ( 2 1)
DREAPTA Fie punctele A ( xa, ya ), B ( xb, yb ), C ( xc, yc ) şi D ( xd, yd ) în planul xoy. 1)Distanţa AB = (x x ) + (y y ) Ex. Fie punctele A( 1, -3) şi B( -2, 5). Calculaţi distanţa AB. AB = ( 2 1)
Seminar 3. Problema 1. a) Reprezentaţi spectrul de amplitudini şi faze pentru semnalul din figură.
 Seminar 3 Problema 1. a) Reprezentaţi spectrul de amplitudini şi faze pentru semnalul din figură. b) Folosind X ( ω ), determinaţi coeficienţii dezvoltării SFE pentru semnalul () = ( ) xt t x t kt şi reprezentaţi
Seminar 3 Problema 1. a) Reprezentaţi spectrul de amplitudini şi faze pentru semnalul din figură. b) Folosind X ( ω ), determinaţi coeficienţii dezvoltării SFE pentru semnalul () = ( ) xt t x t kt şi reprezentaţi
Subiecte Clasa a VIII-a
 Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
4. Măsurarea tensiunilor şi a curenţilor electrici. Voltmetre electronice analogice
 4. Măsurarea tensiunilor şi a curenţilor electrici oltmetre electronice analogice oltmetre de curent continuu Ampl.c.c. x FTJ Protectie Atenuator calibrat Atenuatorul calibrat divizor rezistiv R in const.
4. Măsurarea tensiunilor şi a curenţilor electrici oltmetre electronice analogice oltmetre de curent continuu Ampl.c.c. x FTJ Protectie Atenuator calibrat Atenuatorul calibrat divizor rezistiv R in const.
MARCAREA REZISTOARELOR
 1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
Curs 2 DIODE. CIRCUITE DR
 Curs 2 OE. CRCUTE R E CUPRN tructură. imbol Relația curent-tensiune Regimuri de funcționare Punct static de funcționare Parametrii diodei Modelul cu cădere de tensiune constantă Analiza circuitelor cu
Curs 2 OE. CRCUTE R E CUPRN tructură. imbol Relația curent-tensiune Regimuri de funcționare Punct static de funcționare Parametrii diodei Modelul cu cădere de tensiune constantă Analiza circuitelor cu
INTRODUCERE IN TEORIA SISTEMELOR AUTOMATE
 1 INTRODUCERE IN TEORIA SISTEMELOR AUTOMATE Disciplina Teoria sisemelor auomae consiuie o pune de legăura înre eapa pregăirii ehnice fundamenale şi eapa pregăirii de specialiae, inroducănd o serie de cunoşine,
1 INTRODUCERE IN TEORIA SISTEMELOR AUTOMATE Disciplina Teoria sisemelor auomae consiuie o pune de legăura înre eapa pregăirii ehnice fundamenale şi eapa pregăirii de specialiae, inroducănd o serie de cunoşine,
RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii transversale, scrisă faţă de una dintre axele de inerţie principale:,
 REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
Lucrarea nr.1b - TSA SISTEM. MODEL. CONSTRUCTIA MODELULUI MATEMATIC
 1 SISTEM. MODEL. CONSTRUCTIA MODELULUI MATEMATIC 1. Scopul lucrǎrii Lucrarea are drep scop însuşirea noţiunilor de sysem, model şi analiza posibiliăţilor de consruire a modelului mahemaic penru un sysem
1 SISTEM. MODEL. CONSTRUCTIA MODELULUI MATEMATIC 1. Scopul lucrǎrii Lucrarea are drep scop însuşirea noţiunilor de sysem, model şi analiza posibiliăţilor de consruire a modelului mahemaic penru un sysem
Tratarea numerică a semnalelor
 LUCRAREA 5 Tratarea numerică a semnalelor Filtre numerice cu răspuns finit la impuls (filtre RFI) Filtrele numerice sunt sisteme discrete liniare invariante în timp care au rolul de a modifica spectrul
LUCRAREA 5 Tratarea numerică a semnalelor Filtre numerice cu răspuns finit la impuls (filtre RFI) Filtrele numerice sunt sisteme discrete liniare invariante în timp care au rolul de a modifica spectrul
IV. CUADRIPOLI SI FILTRE ELECTRICE CAP. 13. CUADRIPOLI ELECTRICI
 V. POL S FLTE ELETE P. 3. POL ELET reviar a) Forma fundamentala a ecuatiilor cuadripolilor si parametrii fundamentali: Prima forma fundamentala: doua forma fundamentala: b) Parametrii fundamentali au urmatoarele
V. POL S FLTE ELETE P. 3. POL ELET reviar a) Forma fundamentala a ecuatiilor cuadripolilor si parametrii fundamentali: Prima forma fundamentala: doua forma fundamentala: b) Parametrii fundamentali au urmatoarele
Capitolul 4. Integrale improprii Integrale cu limite de integrare infinite
 Capitolul 4 Integrale improprii 7-8 În cadrul studiului integrabilităţii iemann a unei funcţii s-au evidenţiat douăcondiţii esenţiale:. funcţia :[ ] este definită peintervalînchis şi mărginit (interval
Capitolul 4 Integrale improprii 7-8 În cadrul studiului integrabilităţii iemann a unei funcţii s-au evidenţiat douăcondiţii esenţiale:. funcţia :[ ] este definită peintervalînchis şi mărginit (interval
Esalonul Redus pe Linii (ERL). Subspatii.
 Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
V O. = v I v stabilizator
 Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
2.1 Sfera. (EGS) ecuaţie care poartă denumirea de ecuaţia generală asferei. (EGS) reprezintă osferă cu centrul în punctul. 2 + p 2
 .1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
.1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
* K. toate K. circuitului. portile. Considerând această sumă pentru toate rezistoarele 2. = sl I K I K. toate rez. Pentru o bobină: U * toate I K K 1
 FNCȚ DE ENERGE Fie un n-port care conține numai elemente paive de circuit: rezitoare dipolare, condenatoare dipolare și bobine cuplate. Conform teoremei lui Tellegen n * = * toate toate laturile portile
FNCȚ DE ENERGE Fie un n-port care conține numai elemente paive de circuit: rezitoare dipolare, condenatoare dipolare și bobine cuplate. Conform teoremei lui Tellegen n * = * toate toate laturile portile
Curs 2 Şiruri de numere reale
 Curs 2 Şiruri de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Convergenţă şi mărginire Teoremă Orice şir convergent este mărginit. Demonstraţie Fie (x n ) n 0 un
Curs 2 Şiruri de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Convergenţă şi mărginire Teoremă Orice şir convergent este mărginit. Demonstraţie Fie (x n ) n 0 un
STUDIUL POLARIZĂRII LUMINII
 STUDIUL POLARIZĂRII LUMINII 1. Scopul lucrării Măsurarea inensiăţii luminii care rece prinr-un sisem forma dinr-un polarizor şi un analizor în funcţie de unghiul ϕ dinre planele de polarizare ale polarizorului
STUDIUL POLARIZĂRII LUMINII 1. Scopul lucrării Măsurarea inensiăţii luminii care rece prinr-un sisem forma dinr-un polarizor şi un analizor în funcţie de unghiul ϕ dinre planele de polarizare ale polarizorului
SISTEME DE COMUNICAŢII
 Cap. Siseme de comunicaţii SISTEME DE COMUNICŢII.1 Inroducere Dezvolarea ehnologicǎ în domeniul elecronicii digiale a dus, prinre alele, la dezvolarea unor ehnici avansae de comunicaţii, bazae pe semnale
Cap. Siseme de comunicaţii SISTEME DE COMUNICŢII.1 Inroducere Dezvolarea ehnologicǎ în domeniul elecronicii digiale a dus, prinre alele, la dezvolarea unor ehnici avansae de comunicaţii, bazae pe semnale
Analiza și Prelucrarea Digitală a Semnalelor Video
 Analiza și Prelucrarea Digitală a Semnalelor Video Conf. dr. ing. Radu Ovidiu Preda radu@comm.pub.ro Ș.l. dr. ing. Ionuţ Pirnog ionut@comm.pub.ro Site disciplină: www.comm.pub.ro/preda/apdsv Analiza și
Analiza și Prelucrarea Digitală a Semnalelor Video Conf. dr. ing. Radu Ovidiu Preda radu@comm.pub.ro Ș.l. dr. ing. Ionuţ Pirnog ionut@comm.pub.ro Site disciplină: www.comm.pub.ro/preda/apdsv Analiza și
Cursul Măsuri reale. D.Rusu, Teoria măsurii şi integrala Lebesgue 15
 MĂSURI RELE Cursul 13 15 Măsuri reale Fie (,, µ) un spaţiu cu măsură completă şi f : R o funcţie -măsurabilă. Cum am văzut în Teorema 11.29, dacă f are integrală pe, atunci funcţia de mulţime ν : R, ν()
MĂSURI RELE Cursul 13 15 Măsuri reale Fie (,, µ) un spaţiu cu măsură completă şi f : R o funcţie -măsurabilă. Cum am văzut în Teorema 11.29, dacă f are integrală pe, atunci funcţia de mulţime ν : R, ν()
Subiecte Clasa a VII-a
 lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
7. RETELE ELECTRICE TRIFAZATE 7.1. RETELE ELECTRICE TRIFAZATE IN REGIM PERMANENT SINUSOIDAL
 7. RETEE EECTRICE TRIFAZATE 7.. RETEE EECTRICE TRIFAZATE IN REGIM PERMANENT SINSOIDA 7... Retea trifazata. Sistem trifazat de tensiuni si curenti Ansamblul format din m circuite electrice monofazate in
7. RETEE EECTRICE TRIFAZATE 7.. RETEE EECTRICE TRIFAZATE IN REGIM PERMANENT SINSOIDA 7... Retea trifazata. Sistem trifazat de tensiuni si curenti Ansamblul format din m circuite electrice monofazate in
Captura imaginilor. este necesară o sursă de lumină (λ: lungimea de undă a sursei)
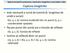 Captura imaginilor este necesară o sursă de lumină (λ: lungimea de undă a sursei) E(x, y, z, λ): lumina incidentă într-un punct (x, y, z coordonatele spațiale) fiecare punct din scenă are o funcție de
Captura imaginilor este necesară o sursă de lumină (λ: lungimea de undă a sursei) E(x, y, z, λ): lumina incidentă într-un punct (x, y, z coordonatele spațiale) fiecare punct din scenă are o funcție de
CIRCUITE INTEGRATE MONOLITICE DE MICROUNDE. MMIC Monolithic Microwave Integrated Circuit
 CIRCUITE INTEGRATE MONOLITICE DE MICROUNDE MMIC Monolithic Microwave Integrated Circuit CUPRINS 1. Avantajele si limitarile MMIC 2. Modelarea dispozitivelor active 3. Calculul timpului de viata al MMIC
CIRCUITE INTEGRATE MONOLITICE DE MICROUNDE MMIC Monolithic Microwave Integrated Circuit CUPRINS 1. Avantajele si limitarile MMIC 2. Modelarea dispozitivelor active 3. Calculul timpului de viata al MMIC
