4η Διάλεξη Οπτικές ίνες
|
|
|
- Ζέφυρος Αθανασίου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 4η Διάλεξη Οπτικές ίνες Γ. Έλληνας, Διάλεξη 4, σελ. 1 Η διάλεξη αυτή αναφέρεται στο κεφ. 3 του βιβλίου του Green και πιο συγκεκριμένα στις ενότητες και 3.8, 3.9. Page 1
2 Περιεχόμενα διάλεξης Ηλεκτρομαγνητικά κύματα Κυματική Εξίσωση Ακριβής Λύση Οπτικών Ινών Ταξινόμηση Τρόπων Αριθμός Τρόπων Γ. Έλληνας, Διάλεξη 4, σελ. 2 Στη διάλεξη θα αναφερθώ γενικά στις οπτικές ίνες, στην ανάκλαση και διάθλαση των φωτεινών ακτίνων με βάση τη γεωμετρική οπτική και τη διάδοση των φωτεινών κυμάτων με βάση τις εξισώσεις Maxwell. Θα παρουσιάσω εμβόλιμα κάποιες βασικές έννοιες κυματικής. Page 2
3 Παράρτημα Κυματική εξίσωση Γ. Έλληνας, Διάλεξη 4, σελ. 3 Η ακριβής μελέτη των οπτικών ινών απαιτεί χρήση των εξισώσεων Maxwell. Υπενθυμίζουμε εδώ κάποιες βασικές γνώσεις ηλεκτρομαγνητικών κυμάτων. Για περισσότερες λεπτομέρειες, ο αναγνώστης θα πρέπει να αναφερθεί στο κεφ. 10 του βιβλίου του Β. Μακιού, Εισαγωγή στον Ηλεκτρομαγνητισμό. Page 3
4 Κυματική εξίσωση ΗΠ Για ομογενές, ισότροπο, γραμμικό διηλεκτρικό μέσο χωρίς απώλειες: όπου 2 2 E E με = 0 2 t = E ε= μ= Ηλεκτρικό πεδίο Διηλεκτρική σταθερά Μαγνητική διαπερατότητα Γ. Έλληνας, Διάλεξη 4, σελ. 4 Ο συνδυασμός των εξισώσεων Maxwell οδηγεί στην κυματική εξίσωση για το ηλεκτρικό πεδίο που φαίνεται στο άνω μέρος της διαφάνειας. Μια ανάλογη εξίσωση ισχύει για το μαγνητικό πεδίο. Ορολογία: Ομογενές: ε = σταθερό Ισότροπο: ε = βαθμωτό μέγεθος Γραμμικό: ε ε(ε) Τέλειο διηλεκτρικό χωρίς απώλειες: σ=0 Page 4
5 Οδεύον κύμα E z = E0 g( t± ) υ όπου όρισα την ταχύτητα διάδοσης (φάσης) του κύματος υ 1 υ = με Γ. Έλληνας, Διάλεξη 4, σελ. 5 Η προηγούμενη εξίσωση έχει λύσεις της μορφής που φαίνεται στο άνω μέρος της διαφάνειας. Οι λύσεις αναπαριστούν οδεύοντα κύματα που κινούνται κατά μήκος του άξονα z με ταχύτητα υ. Το αρνητικό πρόσημο αντιστοιχεί σε κύματα που κινούνται προς τη θετική κατεύθυνση z ενώ το θετικό πρόσημο αντιστοιχεί σε κύματα που κινούνται προς την αρνητική κατεύθυνση z. Page 5
6 Αρμονικό κύμα E = E0 exp( iωt± iβ z) Αναλυτικό σήμα όπου όρισα τη σταθερά διάδοσης β = ω υ E = E0 exp( ± iβ z) Μιγαδική περιβάλλουσα (φάσορας) Γ. Έλληνας, Διάλεξη 4, σελ. 6 Ιδιαίτερο ενδιαφέρον παρουσιάζει η περίπτωση όπου η διαταραχή στο σημείο z=0 είναι περιοδική αρμονική συνάρτηση g(t)=exp(iωt). Αυτή η διαταραχή δημιουργεί οδεύον κύμα της μορφής exp(iωt-iβz), όπου η σταθερά β ονομάζεται σταθερά διάδοσης. Στη συνέχεια θα χρησιμοποιήσουμε μιγαδικές περιβάλλουσες (φάσορες) για να απλοποιήσουμε το μαθηματικό φορμαλισμό. Page 6
7 Άλλοι ορισμοί Μήκος κύματος (χωρική περίοδος κύματος κατά τον άξονα ζ) βλ 2π = 2π β = λ Δείκτης διάθλασης εr μr c n = = υ μ ε Σχετική διηλεκτρική σταθερά r Σχετική μαγνητική διαπερατότητα r Γ. Έλληνας, Διάλεξη 4, σελ. 7 Η χωρική περίοδος του κύματος κατά τον άξονα z λέγεται μήκος κύματος. Εδώ δείχνουμε τους ορισμούς του μήκους κύματος και του δείκτη διάθλασης. Page 7
8 Διανυσματική εξίσωση Helmholtz Ι Η κυματική εξίσωση για το ηλεκτρικό πεδίο για τη μιγαδική περιβάλλουσα είναι 2 2 E+ k E = 0 όπου όρισα τον κυματάριθμο k = ω με Ομοίως για τη μιγαδική περιβάλλουσα του μαγνητικού πεδίου 2 2 H+ k H = 0 Γ. Έλληνας, Διάλεξη 4, σελ. 8 Η κυματική εξίσωση για το ηλεκτρικό πεδίο για τη μιγαδική περιβάλλουσα γράφεται όπως ανωτέρω. Η εξίσωση αυτή ονομάζεται διανυσματική εξίσωση Helmholtz. Μια παρόμοια εξίσωση ισχύει για το διάνυσμα του μαγνητικού πεδίου. Page 8
9 Διανυσματική εξίσωση Helmholtz ΙΙ E n k0 E 0 + = H n k0 H 0 + = όπου όρισα τον κυματάριθμο στο κενό k = ω με Γ. Έλληνας, Διάλεξη 4, σελ. 9 Page 9
10 Ακριβής ανάλυση οπτικής ίνας Γ. Έλληνας, Διάλεξη 4, σελ. 10 Η λύση ακολουθεί την παρουσίαση των κεφ. 1-3 του βιβλίου του Buck. Page 10
11 Υποθέσεις Ιδανικήοπτικήίνα Ομογενής Ισότροπη Γραμμική Χωρίς απώλειες Με ντύμα απείρων διαστάσεων Γ. Έλληνας, Διάλεξη 4, σελ. 11 Page 11
12 Ακριβής ορισμός τρόπου Τρόπος = Λύση της κυματικής εξίσωσης η οποία είναι αρμονική συνάρτηση ως προς το χρόνο (η χωρική του κατανομή δεν μεταβάλλεται κατά την μετάδοση) και ικανοποιεί τις οριακές συνθήκες στη διαχωριστική επιφάνεια μεταξύ πυρήνα και ντύματος Γ. Έλληνας, Διάλεξη 4, σελ. 12 Page 12
13 Λύση εξίσωσης Helmholtz Ι Υποθέτουμε λύση της μορφής Σε κυλινδρικές συντεταγμένες Γ. Έλληνας, Διάλεξη 4, σελ. 13 Υποθέτουμε λύσεις της εξίσωσης Helmholtz ως ανωτέρω. Με αντικατάσταση στη εξίσωση Helmholtz και ανάπτυξη της Λαπλασιανής σε εγκάρσιους και διαμήκεις τελεστές, παίρνουμε τις δύο κάτω εξισώσεις που ισχύουν για τα πεδία στον πυρήνα και το ντύμα. Οι εξισώσεις αυτές ισχύουν και για τις τρεις συνιστώσες των δύο πεδίων. Θα τις λύσουμε για τις διαμήκεις συνιστώσες Εz, Ηz. Page 13
14 Λύση εξίσωσης Helmholtz ΙΙ Θέτω Εκφράζω την εγκάρσια Λαπλασιανή σε κυλινδρικές συντεταγμένες Γενική λύση (υπέρθεση τρόπων & χωρισμός μεταβλητών) Γ. Έλληνας, Διάλεξη 4, σελ. 14 Για συντομία ορίζω δύο καινούριες σταθερές και ξαναγράφω τις εξισώσεις στο κάτωμέροςτης προηγούμενης διαφάνειας υπό γενικευμένη μορφή. Επίσης εκφράζω την εγκάρσια Λαπλασιανή σε κυλινδρικές συντεταγμένες. Η γενική λύση της τελευταίας εξίσωσης αποτελείται από το άθροισμα των μερικών λύσεων (τρόπων). Κάθε τρόπος εκφράζεται ως γινόμενο τριών παραγόντων, κάθε ένας εκ των οποίων εξαρτάται από μία εκ των ανεξάρτητων μεταβλητών. Page 14
15 Λύση εξίσωσης Helmholtz ΙΙΙ Για ένα στοιχειώδη τρόπο Επιμέρους διαφορικές εξισώσεις (Γωνιακή) (Ακτινική) Γ. Έλληνας, Διάλεξη 4, σελ. 15 Κάθε τρόπος πρέπει να ικανοποιεί ανεξάρτητα, κάθε ένας εκ των οποίων εξαρτάται από μία εκ των ανεξάρτητων μεταβλητών. Για ένα τρόπο, η διαφορική εξίσωση της προηγούμενης σελίδας γράφεται ως ανωτέρω. Το αριστερό μέλος της εξίσωσης εξαρτάται μόνο από την ακτίνα r ενώ το δεξί μέλος μόνο από το αζιμούθιο φ. Δεδομένου ότι τα r,φ είναι ανεξάρτητες μεταβλητές, τα δύο μέλη πρέπει να είναι ίσα με μια σταθερά q 2. Αντικαθιστώντας, χωρίζουμε την αρχική εξίσωση σε δυο δευτεροβάθμιες γραμμικές διαφορικές εξισώσεις οι οποίες περιγράφουν τη γωνιακή και την ακτινική εξάρτηση αντίστοιχα. Page 15
16 Λύση γωνιακής ΔΕ Λύση όπου q α Ακέραιος (γωνιακός αριθμός) Αυθαίρετη σταθερά φάσης Γ. Έλληνας, Διάλεξη 4, σελ. 16 Η γωνιακή διαφορική εξίσωση είναι η εξίσωση του αρμονικού ταλαντωτή κι έχει λύσεις αρμονικές συναρτήσεις. Παρατηρούμε ότι οι λύσεις περιέχουν στο όρισμά τους τη σταθερά q και μια σταθερή αυθαίρετη γωνία α. Λόγω περιοδικότητας θα πρέπει το q να είναι ακέραιος αριθμός. Page 16
17 Λύση ακτινικής ΔΕ Εξίσωση Bessel Γενική λύση όπου J q N I q K q q Κανονική συνάρτηση Bessel πρώτου είδους βαθμού q Κανονική συνάρτηση Bessel δεύτερου είδους βαθμού q Τροποποιημένη συνάρτηση Bessel πρώτου είδους βαθμού q Τροποποιημένη συνάρτηση Bessel δεύτερου είδους βαθμού q Γ. Έλληνας, Διάλεξη 4, σελ. 17 Η ακτινική διαφορική εξίσωση είναι η εξίσωση Bessel κι έχει λύσεις κανονικές και τροποποιημένες συναρτήσεις Βessel πρώτου και δεύτερου είδους βαθμού q. Παρατηρούμε ότι οι λύσεις περιέχουν στο όρισμά τους τη σταθερά βt. Οι αυθαίρετες σταθερές Α, Α, Β, Β έχουν σχέσημετοπλάτοςτηςδιαταραχήςπουδιαδίδεται. Απαιτούμε η λύση μέσα στον πυρήνα να παρουσιάζει διακυμάνσεις αλλά όχι ανώμαλα σημεία κι η λύση στο ντύμα να φθίνει με την ακτινική απόσταση από τον άξονα συμμετρίας. Page 17
18 Εξισώσεις Bessel Ι Κανονικές συναρτήσεις Bessel πρώτου είδους Κανονικές συναρτήσεις Bessel δεύτερου είδους Γ. Έλληνας, Διάλεξη 4, σελ. 18 Εδώ βλέπουμε τη γραφική παράσταση των κανονικών συναρτήσεων Βessel πρώτου και δεύτερου είδους βαθμού q. Παρατηρούμε ότι οι πρώτες περιγράφουν ικανοποιητικά διακυμάνσεις στον πυρήνα. Παρατηρούμε ότι οι δεύτερες αντιβαίνουν στην απαίτηση στον πυρήνα να μην παρουσιάζεται απειρισμός. Επομένως διαλέγουμε βt πραγματικό για την περιοχή του πυρήνα και θέτουμε Α =0. Page 18
19 Εξισώσεις Bessel ΙΙ Τροποποιημένες συναρτήσεις Bessel πρώτου είδους Τροποποιημένες συναρτήσεις Bessel δεύτερου είδους Γ. Έλληνας, Διάλεξη 4, σελ. 19 Εδώ βλέπουμε τη γραφική παράσταση των τροποποιημένων συναρτήσεων Βessel πρώτου και δεύτερου είδους βαθμού q. Παρατηρούμε ότι οι πρώτες αντιβαίνουν στη απαίτηση η λύση στο ντύμα να φθίνει με την ακτινική απόσταση από τον άξονα συμμετρίας ενώ οι δεύτερες την ικανοποιούν. Επομένως διαλέγουμε βt φανταστικό για την περιοχή του ντύματος και θέτουμε C =0. Page 19
20 Τελική λύση Ε z, H z Όπου όρισα τις κανονικοποιημένες παραμέτρους Εγκάρσια σταθερά διάδοσης Εγκάρσιος συντελεστής εξασθένησης Γ. Έλληνας, Διάλεξη 4, σελ. 20 ΕδώβλέπουμετιςτελικέςλύσειςγιαταEz, Hz. Page 20
21 Υπολογισμός λοιπών συνιστωσών Από τις εξισώσεις Maxwell Γ. Έλληνας, Διάλεξη 4, σελ. 21 Οι υπόλοιπες συνιστώσες του ηλεκτρικού και μαγνητικού πεδίου σχετίζονται μεταez, Hz μέσω των εξισώσεων Maxwell. Οι τύποι που περιγράφουν την εξάρτηση φαίνονται σε αυτήν τη διαφάνεια. Με απλές παραγωγίσεις υπολογίζω τα Er, Eφ, Hr, Hφ. Page 21
22 Γενική λύση (πυρήνας) Γ. Έλληνας, Διάλεξη 4, σελ. 22 Εδώ φαίνονται οι τελικές λύσεις για όλες τις συνιστώσες του ηλεκτρικού και μαγνητικού πεδίου μέσα στον πυρήνα. Οι τόνοι εκφράζουν παραγώγιση ως προς την ακτινική συνιστώσα. Page 22
23 Γενική λύση (ντύμα) Γ. Έλληνας, Διάλεξη 4, σελ. 23 Εδώ φαίνονται οι τελικές λύσεις για όλες τις συνιστώσες του ηλεκτρικού και μαγνητικού πεδίου μέσα στο ντύμα. Page 23
24 Οριακές συνθήκες Ι Συνέχεια εφαπτομενικών συνιστωσών ΗΠ, ΜΠ: E ( a) = E ( a) z H ( a) = H ( a) z z 1 2 z 1 2 E ( a) = E ( a) φ φ 1 2 H ( a) = H ( a) φ φ 1 2 Γ. Έλληνας, Διάλεξη 4, σελ. 24 Ο υπολογισμός των u, v, β γίνεται από την ικανοποίηση των οριακών συνθηκών στη διαχωριστική επιφάνεια πυρήνα, ντύματος. Πιο συγκεκριμένα, εξισώνουμε τις εφαπτομενικές συνιστώσεςτουηλεκτρικούκαιτουμαγνητικούπεδίουστοr=α. Page 24
25 Οριακές συνθήκες ΙΙ Σύστημα τεσσάρων εξισώσεων με τέσσερις αγνώστους: Μη μηδενική λύση για det[m]=0: Χαρακτηριστική εξίσωση Γ. Έλληνας, Διάλεξη 4, σελ. 25 Προκύπτει έτσι ένα γραμμικό σύστημα τεσσάρων εξισώσεων με τέσσερις αγνώστους. Γιαναέχει μη τετριμμένη (μη μηδενική) λύση θα πρέπει η ορίζουσα των συντελεστών να μηδενίζεται. Αυτό οδηγεί στη χαρακτηριστική εξίσωση (εξίσωση ιδιοτιμών) που αναγράφεται στο κάτω μέρος της διαφάνειας. Page 25
26 Παράμετρος V Ορίζω την αδιάστατη παράμετρο: V = u + w Από τον ορισμό των u,w: 2 2 V = ( n n ) k a = NAk a Εξαρτάται από τις γεωμετρικές παραμέτρους και τη συχνότητα Γ. Έλληνας, Διάλεξη 4, σελ. 26 Ορίζω μια καινούρια παράμετρο V η οποία εξαρτάται από τα γεωμετρικά χαρακτηριστικά της ίνας και τη μήκος κύματος (που κρύβεται μέσα στον κυματάριθμο) του κύματος που πρόκειται να διαδοθεί. Page 26
27 Λύση χαρακτηριστικής εξίσωσης Υπερβατική εξίσωση οπότε αριθμητική λύση Για δεδομένα V, q υπάρχουν m ρίζες Από κάθε ρίζα υπολογίζω β,w,u Γ. Έλληνας, Διάλεξη 4, σελ. 27 Η χαρακτηριστική εξίσωση λύνεται αριθμητικά δεδομένων των V, q έχει δε m ρίζες. Page 27
28 Ταξινόμηση τρόπων Ονομασία Υβριδικοί τρόποι (q>0) TE (q=0, Ε z =0) TM (q=0, Η z =0) Συμβολισμός HEqm, EHqm TE 0 m TM 0 m Γ. Έλληνας, Διάλεξη 4, σελ. 28 Οι διαφορετικές ρίζες της χαρακτηριστικής εξίσωσης αντιστοιχούν σε διαφορετικούς τρόπους με διαφορετικές ταχύτητες διάδοσης. Οι τρόποι ταξινομούνται με βάση τις τιμές των q και m. Page 28
29 Σταθερά διάδοσης β/k 0 Για V<2.405 η ίνα γίνεται μονότροπη! Γ. Έλληνας, Διάλεξη 4, σελ. 29 Εδώ βλέπουμε τη μεταβολή της κανονικοποιημένης σταθεράς διάδοσης β/k0 ως συνάρτηση της παραμέτρου V. Παρατηρούμε ότι για επαρκώς μικρές διαστάσεις του πυρήνα σε σχέση με το μήκος κύματος (V<2.405) μόνο ένας τρόπος μπορεί να διαδοθεί. Αυτός είναι ο τρόπος ΗΕ11, ο οποίος λέγεται και θεμελιώδης τρόπος. Πρέπει να τονιστεί ότι μια ίνα που είναι μονότροπη για ένα συγκεκριμένο μήκος κύματος μπορεί να είναι πολύτροπη για ένα μικρότερο μήκος κύματος. Page 29
30 Προσεγγιστικός υπολογισμός ιδιοτιμών Γ. Έλληνας, Διάλεξη 4, σελ. 30 Η χαρακτηριστική εξίσωση απλοποιείται σημαντικά για μικρά Δ, όπου το n1 είναι περίπου ίσο με το n2. Page 30
31 Απλοποιημένη χαρακτηριστική εξίσωση Μικρά Δ [4, pp ] u Jl 1( u) Kl 1( w) = w J ( u) K ( w) l l όπου 1 l = q+ 1 q 1 TE, TM 0m 0m EH HE qm qm Γ. Έλληνας, Διάλεξη 4, σελ. 31 Θέτοντας n1= n2 στη χαρακτηριστική εξίσωση της διαφάνειας σελ. 41, η χαρακτηριστική εξίσωση γράφεται ως ανωτέρω. Page 31
32 Γραφική λύση (V=2) Γ. Έλληνας, Διάλεξη 4, σελ. 32 Γραφική λύση της χαρακτηριστικής εξίσωσης της προηγούμενης διαφάνειας για V=2 για τους τρόπους ΤE0m, TM0m, HE1m. Το αριστερό μέλος των χαρακτηριστικών εξισώσεων για αυτές τις περιπτώσεις είναι το ίδιο. To δεξί μέρος διαφέρει. Το αντίστροφο του αριστερού μέλους των χαρακτηριστικών εξισώσεων J1(u)/J0(u) μοιάζει με τη συνάρτηση tan(u). Το αντίστροφο του δεξιού μέλους των χαρακτηριστικών εξισώσεων Κ1(w)/K0(w) είναι μια φθίνουσα συνάρτηση στο κάτω ημιεπίπεδο για την περίπτωση ΤEom, TM0m και στο πάνω ημιεπίπεδο για την περίπτωση HE1m. Οι τομές των καμπυλών του αριστερού και του του δεξιού μέλους δίνουν τους διαδοχικούς τρόπους. Στη συγκεκριμένη περίπτωση υπάρχει μόνο μια λύση που αντιστοιχεί στον τρόπο HE11. Page 32
33 Γραφική λύση (V=8) Γ. Έλληνας, Διάλεξη 4, σελ. 33 Γραφική λύση της χαρακτηριστικής εξίσωσης της προηγούμενης διαφάνειας για V=8 για τους τρόπους ΤE0m, TM0m. HE1m. Στη συγκεκριμένη περίπτωση υπάρχουν πέντε λύσεις που αντιστοιχούν σε πέντε διαφορετικούς τρόπους. Page 33
34 Ταξινόμηση τρόπων Γ. Έλληνας, Διάλεξη 4, σελ. 34 Υπάρχει ένα εναλλακτικό σύστημα ταξινόμησης των τρόπων δια την περίπτωση τωνμικρώνδ. Οι τρόποι τώρα συμβολίζονται με LPlm, όπου τα αρχικά LP σημαίνουν γραμμικώς πολωμένοι τρόποι (linearly polarized) καιοιδείκτεςlm αντιστοιχούν στην παράμετρο l της απλοποιημένης χαρακτηριστικής εξίσωσης της σελ. 47 και στο m των τρόπων ΤΕ, ΤΜ και ΕΗ αντίστοιχα. Ο πίνακας αυτός δείχνει τους πρώτους τρόπους LP και την τιμή της παραμέτρου V για την αποκοπή. Τρόποι ΤΕ, ΤΜ και ΕΗ που αντιστοιχούν στα ίδια lm έχουν την ίδια σταθερά διάδοσης (όχι όμως και ταυτόσημα ηλεκτρικά και μαγνητικά πεδία). Μπορούν δε να συνδυαστούν γραμμικά και να δώσουν τρόπους γραμμικά πολωμένους τρόπους σε μια εγκάρσια καρτεσιανή συντεταγμένη χ,ψ. Εξ ου δε κι η ονομασία LP. Page 34
35 Σταθερές διάδοσης Κανονικοποιημένη σταθερά μετάδοσης 2 b = 1 u 2 V D. Gloge, App. Opt. 10, 2252,1971. [2, p.42] Γ. Έλληνας, Διάλεξη 4, σελ. 35 Εδώ βλέπουμε τη μεταβολή της κανονικοποιημένης σταθεράς διάδοσης b ως συνάρτηση της παραμέτρου V για τους τρόπους LP. Παρατηρούμε ότι η καμπύλη 01 αντιστοιχεί στην καμπύλη ΗΕ11 της διαφάνειας της σελ. 45, η καμπύλη11 αντιστοιχεί στις τρεις καμπύλες ΗΕ21, ΤΕ01, ΤΜ01 της διαφάνειας της σελ. 45, οι οποίες για μικρά Δ ταυτίζονται, κοκ. Υπό αυτήν την έννοια, μπορούμε να κατανοήσουμε και την αντιστοιχία μεταξύ των τρόπων, όπως αυτή αναγράφεται στον πίνακα της προηγούμενης διαφάνειας. Page 35
36 Ισοδυναμικές γραμμές I LP 11 LP 12 Γ. Έλληνας, Διάλεξη 4, σελ. 36 Οι τρόποι ΗΕ21, ΤΕ01, ΤΜ01 μπορούν να συνδυαστούν γραμμικά και να δώσουν τέσσερις γραμμικά πολωμένους τρόπους προσανατολισμένους παράλληλα με τις καρτεσιανές συντεταγμένες χ,ψ. Όλοι οι ανωτέρω τρόποι είναι ισοδύναμοι κι αντιστοιχούν σε διαφορετικές μορφές του τρόπου LP11. Στο αριστερό σχήμα φαίνονται οι ισοδυναμικές γραμμές σε μια εγκάρσια τομή της οπτικής ίνας. Ομοίως, οι τρόποι ΗΕ21, ΤΕ02, ΤΜ02 μπορούν να συνδυαστούν γραμμικά και να δώσουν τέσσερις γραμμικά πολωμένους τρόπους που όλοι είναι ισοδύναμοι κι αντιστοιχούν στον τρόπο LP12. Page 36
37 Ισοδυναμικές γραμμές II LP 21 LP 22 Γ. Έλληνας, Διάλεξη 4, σελ. 37 Όπως προηγουμένως για τους τρόπους LP21, LP22. Page 37
38 Δυναμικές γραμμές LP 01 TE 02 Γ. Έλληνας, Διάλεξη 4, σελ. 38 Δυναμικές γραμμές του ηλεκτρικού πεδίου (συνεχείς καμπύλες) και του μαγνητικού πεδίου (διακεκομμένες καμπύλες) στον πυρήνα ίνας βηματικού δείκτη διάθλασης, για δυο διαφορετικούς τρόπους. Page 38
39 Ένταση LP 01 Γ. Έλληνας, Διάλεξη 4, σελ. 39 Κατανομή της έντασης του ηλεκτρομαγνητικού κύματος (ανάλογη του Ε ^2) σε μια εγκάρσια διατομή της οπτικής ίνας για τον θεμελιώδη τρόπο LP01. Η ένταση έχει μέγιστο στο κέντρο του πυρήνα και φθίνει ακτινικά ως συνάρτηση του J0^2, και δεν παρουσιάζει διακυμάνσεις στη γωνιακή κατεύθυνση. Page 39
40 Ένταση LP 11 Γ. Έλληνας, Διάλεξη 4, σελ. 40 Στη γενική περίπτωση ενός τρόπου LPlm υπάρχουν 2l μέγιστα έντασης κατά τη γωνιακή διεύθυνση και m μέγιστα έντασης κατά την ακτινική διεύθυνση. Page 40
41 Ένταση LP 21 Γ. Έλληνας, Διάλεξη 4, σελ. 41 Page 41
42 Ένταση LP 02 Γ. Έλληνας, Διάλεξη 4, σελ. 42 Page 42
43 Ένταση LP 31 Γ. Έλληνας, Διάλεξη 4, σελ. 43 Page 43
44 Ένταση LP 12 Γ. Έλληνας, Διάλεξη 4, σελ. 44 Page 44
45 Ένταση LP 11 Γ. Έλληνας, Διάλεξη 4, σελ. 45 Page 45
46 Φωτογραφίες έντασης τρόπων LP 21 LP 31 LP 12 Γ. Έλληνας, Διάλεξη 4, σελ. 46 Φωτογραφίες της φωτεινής έντασης στην εγκάρσια τομή μιας ίνας για την περίπτωση διαφόρων τρόπων. Αναγνωρίζουμε τους LP12, LP21, LP31 που φαίνονται στις προηγούμενες διαφάνειες. Page 46
47 Αριθμός τρόπων Εξαρτάται από το V N mod es V 2 2 D. Gloge, App. Opt. 10, 2252,1971. [4, p.283] Γ. Έλληνας, Διάλεξη 4, σελ. 47 Ο αριθμός τρόπων εξαρτάται προσεγγιστικά από το τετράγωνο του V. Page 47
48 Αριθμητικό παράδειγμα Ι Δεδομένα Λύση (ίνα με ντύμα) n 1 = 1.46 Δ = 1% λ 0 = 0.85 μm NA = n 1 2Δ = V = 37.9 N mod es V modes Γ. Έλληνας, Διάλεξη 4, σελ. 48 Page 48
49 Αριθμητικό παράδειγμα ΙΙ Λύση (ίνα χωρίς ντύμα) n 2 =1 NA = 1 V = N mod es V2 2 13,800 modes Συμπέρασμα: Υπάρχουν πολύ περισσότεροι τρόποι σε ίνα χωρίς ντύμα Γ. Έλληνας, Διάλεξη 4, σελ. 49 Page 49
50 Θεμελιώδης τρόπος LP 01 iβ z E 0 ( / ) for a ( r, z ) A J ur a e r x = J i z 0( u )/ K 0( w ) K 0( wr / a ) e β for r a Γ. Έλληνας, Διάλεξη 4, σελ. 50 Συνοψίζοντας, η έκφραση του ηλεκτρικού πεδίου για το θεμελιώδη τρόπο δίνεται παραπάνω. Page 50
51 Προσέγγιση LP 01 όπου w το εύρος της δέσμης. Γ. Έλληνας, Διάλεξη 4, σελ. 51 Για απλότητα η συνάρτηση Bessel στην προηγούμενη έκφραση του ηλεκτρικού πεδίου μπορεί να αντικατασταθεί με μια Gaussian. Με κατάλληλη προσαρμογή της παραμέτρου w μπορούμε να έχουμε πολύ καλή προσέγγιση. Page 51
52 Κλάσμα ισχύος στον πυρήνα Βάσει της προσέγγισης Gauss: Για V=2, Pcore/Ptotal=75% V=1, Pcore/Ptotal=20% Συμπέρασμα : Βέλτιστη τιμή 2<V<2.4 Γ. Έλληνας, Διάλεξη 4, σελ. 52 Μόνο ένα μικρό μέρος της φωτεινής ισχύος των κυματοδηγούμενων τρόπων βρίσκεται στον πυρήνα! Χρησιμοποιώντας την προηγούμενη έκφραση του ηλεκτρικού πεδίου μπορεί να δει κανείς ότι για V=1, μόνο 25% της του θεμελιώδους τρόπου βρίσκεται στον πυρήνα. Αν κι αυτό δεν εμποδίζει τη διάδοση, οι παραμικρές ατέλειες (π.χ. μικροκάμψεις της ίνας) κάνουν το φως να διαφεύγει με αποτέλεσμα αυξημένες απώλειες. Ταυτόχρονα, ίνες με λεπτό πυρήνα έχουν μεγαλύτερο πρόβλημα κι απώλειες στις συγκολήσεις και συνδέσεις. Για αυτό το λόγο χρησιμοποιούμε μεγάλα V, μικρότερα όμως από τη συχνότητα αποκοπής, έτσι ώστε η ίνα να παραμένει μονότροπη. Page 52
53 Βιβλιογραφία Ι Άλλα βοηθήματα [1] John M. Senior, "Optical Fiber Communications : Principles and Practice," Prentice Hall, 2nd edition, 1993, ISBN: [2] Paul Diament, Wave Transmission and Fiber Optics, Macmillan, [3] Bahaa E.A. Saleh, M. C. Teich, "Fundamentals of Photonics," Wiley, [4] Dietrich Marcuse, "Theory of dielectric optical waveguides," Academic Press, [5] Simon Ramo, John R. Whinnery, Theodore Van Duzer, "Fields and Waves in Communication Electronics," Wiley, 1993, ISBN: Γ. Έλληνας, Διάλεξη 4, σελ. 53 Page 53
54 Βιβλιογραφία ΙΙ Wim Van Etten and Jan Van Der Plaats, Fundamentals of optical fiber communications, Prentice Hall, 2nd edition, 1991, ISBN: J. Buck, Fundamental of optical fibers, Wiley, 1995, ISBN: Ν. Ουζούνογλου, Τηλεπικοινωνίες Οπτικών Ινών, Εκδόσεις Συμεών, Αθήνα Γ. Έλληνας, Διάλεξη 4, σελ. 54 Page 54
Περιεχόμενα διάλεξης
 4η Διάλεξη Οπτικές ίνες Γ. Έλληνας, Διάλεξη 4, σελ. 1 Περιεχόμενα διάλεξης Ηλεκτρομαγνητικά κύματα Κυματική Εξίσωση Ακριβής Λύση Οπτικών Ινών Ταξινόμηση Τρόπων Αριθμός Τρόπων Γ. Έλληνας, Διάλεξη 4, σελ.
4η Διάλεξη Οπτικές ίνες Γ. Έλληνας, Διάλεξη 4, σελ. 1 Περιεχόμενα διάλεξης Ηλεκτρομαγνητικά κύματα Κυματική Εξίσωση Ακριβής Λύση Οπτικών Ινών Ταξινόμηση Τρόπων Αριθμός Τρόπων Γ. Έλληνας, Διάλεξη 4, σελ.
11 ΧΡΟΝΙΚΑ ΜΕΤΑΒΑΛΛΟΜΕΝΑ ΠΕΔΙΑ
 xx ΤΟΜΟΣ ΙI 11 ΧΡΟΝΙΚΑ ΜΕΤΑΒΑΛΛΟΜΕΝΑ ΠΕΔΙΑ 741 11.1 Διαφορική και ολοκληρωτική μορφή των εξισώσεων Maxwell Ρεύμα μετατόπισης...................................... 741 11.2 Οι εξισώσεις Maxwell σε μιγαδική
xx ΤΟΜΟΣ ΙI 11 ΧΡΟΝΙΚΑ ΜΕΤΑΒΑΛΛΟΜΕΝΑ ΠΕΔΙΑ 741 11.1 Διαφορική και ολοκληρωτική μορφή των εξισώσεων Maxwell Ρεύμα μετατόπισης...................................... 741 11.2 Οι εξισώσεις Maxwell σε μιγαδική
ΛΥΣΕΙΣ ΕΞΙΣΩΣΗΣ ΚΥΜΑΤΟΣ ΣΤΟΥΣ ΚΥΜΑΤΟΔΗΓΟΥΣ ΔΙΑΦΟΡΩΝ ΔΙΑΤΟΜΩΝ
 ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ : Φυσικής και Εφαρμοσμένων Μαθηματικών Μάθημα : Εφαρμοσμένα Μαθηματικά Διδάσκων: Αν. καθηγητής Χρ. Σχοινάς Προαιρετική
ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ : Φυσικής και Εφαρμοσμένων Μαθηματικών Μάθημα : Εφαρμοσμένα Μαθηματικά Διδάσκων: Αν. καθηγητής Χρ. Σχοινάς Προαιρετική
Ανάλυση της κυματοδήγησης στις οπτικές ίνες με την ηλεκτρομαγνητική θεωρία
 Ανάλυση της κυματοδήγησης στις οπτικές ίνες με την ηλεκτρομαγνητική θεωρία Τρόποι διάδοσης ηλεκτρομαγνητικών κυμάτων Στο κενό, τα ηλεκτρομαγνητικά κύματα διαδίδονται έχοντας το ηλεκτρικό πεδίο Ε και το
Ανάλυση της κυματοδήγησης στις οπτικές ίνες με την ηλεκτρομαγνητική θεωρία Τρόποι διάδοσης ηλεκτρομαγνητικών κυμάτων Στο κενό, τα ηλεκτρομαγνητικά κύματα διαδίδονται έχοντας το ηλεκτρικό πεδίο Ε και το
Κεφάλαιο 2 ο Ενότητα 1 η : Μηχανικά Κύματα Θεωρία Γ Λυκείου
 Κεφάλαιο 2 ο Ενότητα 1 η : Μηχανικά Κύματα Θεωρία Γ Λυκείου Τρέχοντα Κύματα Κύμα ονομάζεται η διάδοση μιας διαταραχής σε όλα τα σημεία του ελαστικού μέσου με ορισμένη ταχύτητα. Κατά τη διάδοση ενός κύματος
Κεφάλαιο 2 ο Ενότητα 1 η : Μηχανικά Κύματα Θεωρία Γ Λυκείου Τρέχοντα Κύματα Κύμα ονομάζεται η διάδοση μιας διαταραχής σε όλα τα σημεία του ελαστικού μέσου με ορισμένη ταχύτητα. Κατά τη διάδοση ενός κύματος
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ & ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Η. Ν. Γλύτσης, Tηλ.: 21-7722479 - e-mail:
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ & ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Η. Ν. Γλύτσης, Tηλ.: 21-7722479 - e-mail:
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Ηλίας Γλύτσης, Τηλ. 21-7722479, e-mail:
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Ηλίας Γλύτσης, Τηλ. 21-7722479, e-mail:
Περιεχόμενα διάλεξης
 7η Διάλεξη Οπτικές ίνες Γ. Έλληνας, Διάλεξη 7, σελ. 1 Περιεχόμενα διάλεξης Διασπορά Πόλωσης Γ. Έλληνας, Διάλεξη 7, σελ. Page 1 Πόλωση Γενική θεωρία Γ. Έλληνας, Διάλεξη 7, σελ. 3 Μηχανικό ανάλογο Εγκάρσια
7η Διάλεξη Οπτικές ίνες Γ. Έλληνας, Διάλεξη 7, σελ. 1 Περιεχόμενα διάλεξης Διασπορά Πόλωσης Γ. Έλληνας, Διάλεξη 7, σελ. Page 1 Πόλωση Γενική θεωρία Γ. Έλληνας, Διάλεξη 7, σελ. 3 Μηχανικό ανάλογο Εγκάρσια
Κλασική Ηλεκτροδυναμική Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΤΕΧΝΙΚΕΣ ΥΠΟΛΟΓΙΣΜΟΥ ΗΛΕΚΤΡΙΚΟΥ ΔΥΝΑΜΙΚΟΥ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΤΕΧΝΙΚΕΣ ΥΠΟΛΟΓΙΣΜΟΥ ΗΛΕΚΤΡΙΚΟΥ ΔΥΝΑΜΙΚΟΥ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
Κεφάλαιο 1. Κβαντική Μηχανική ΙΙ - Περιλήψεις, Α. Λαχανάς
 Κεφάλαιο 1 Κβαντική Μηχανική ΙΙ - Περιλήψεις, Α. Λαχανάς 2 Κβαντική Μηχανική ΙΙ - Περιλήψεις, Α. Λαχανάς 1.1 Ατοµο του Υδρογόνου 1.1.1 Κατάστρωση του προβλήµατος Ας ϑεωρήσουµε πυρήνα ατοµικού αριθµού Z
Κεφάλαιο 1 Κβαντική Μηχανική ΙΙ - Περιλήψεις, Α. Λαχανάς 2 Κβαντική Μηχανική ΙΙ - Περιλήψεις, Α. Λαχανάς 1.1 Ατοµο του Υδρογόνου 1.1.1 Κατάστρωση του προβλήµατος Ας ϑεωρήσουµε πυρήνα ατοµικού αριθµού Z
AΠΟΦΑΣΗ της από 3/4/2012 Συνεδρίασης του Δ.Σ. του Τμήματος Φυσικής. ΕΞΕΤΑΣΤΕΑ ΥΛΗ ΦΥΣΙΚΗΣ ΙΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ) Για το 5ο εξάμηνο
 ΕΞΕΤΑΣΤΕΑ ΥΛΗ ΦΥΣΙΚΗΣ ΙΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ) Ι. Ηλεκτρικό φορτίο-διατήρηση φορτίου-κβάντωση φορτίου-νόμος Coulomb-Ενέργεια συστήματος φορτίων-ηλεκτρικό πεδίο-κατανομές φορτίου-ροή, Νόμος Gauss. ΙΙ. Ηλεκτρικό
ΕΞΕΤΑΣΤΕΑ ΥΛΗ ΦΥΣΙΚΗΣ ΙΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ) Ι. Ηλεκτρικό φορτίο-διατήρηση φορτίου-κβάντωση φορτίου-νόμος Coulomb-Ενέργεια συστήματος φορτίων-ηλεκτρικό πεδίο-κατανομές φορτίου-ροή, Νόμος Gauss. ΙΙ. Ηλεκτρικό
Μικροκυματικές Επικοινωνίες & Τεχνολογίες Χιλιοστομετρικών Κυμάτων
 Μικροκυματικές Επικοινωνίες & Τεχνολογίες Χιλιοστομετρικών Κυμάτων ΕΙΣΑΓΩΓΗ - Το μάθημα αυτό πραγματεύεται θεμελιώδεις έννοιες των γραμμών μεταφοράς στην επιστημονική περιοχή των ηλεκτρονικών συστημάτων
Μικροκυματικές Επικοινωνίες & Τεχνολογίες Χιλιοστομετρικών Κυμάτων ΕΙΣΑΓΩΓΗ - Το μάθημα αυτό πραγματεύεται θεμελιώδεις έννοιες των γραμμών μεταφοράς στην επιστημονική περιοχή των ηλεκτρονικών συστημάτων
I. ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. math-gr
 I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
HMY 333 Φωτονική Διάλεξη 07. Ταχύτητα φάσης, ταχύτητα ομάδας και διασπορά. n 2 n O
 Uiersiy of Cyrus Πανεπιστήμιο Κύπρου Uiersiy of Cyrus Πανεπιστήμιο Κύπρου HMY 333 Φωτονική Διάλεξη 7 Ταχύτητα φάσης, ταχύτητα ομάδας και διασπορά Σε ένα μέσο διασποράς, όπως οι οπτικές ίνες, η μορφή του
Uiersiy of Cyrus Πανεπιστήμιο Κύπρου Uiersiy of Cyrus Πανεπιστήμιο Κύπρου HMY 333 Φωτονική Διάλεξη 7 Ταχύτητα φάσης, ταχύτητα ομάδας και διασπορά Σε ένα μέσο διασποράς, όπως οι οπτικές ίνες, η μορφή του
papost/
 Δρ. Παντελής Σ. Αποστολόπουλος Επίκουρος Καθηγητής http://users.uoa.gr/ papost/ papost@phys.uoa.gr ΤΕΙ Ιονίων Νήσων, Τμήμα Τεχνολόγων Περιβάλλοντος ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-2017 Οπως είδαμε
Δρ. Παντελής Σ. Αποστολόπουλος Επίκουρος Καθηγητής http://users.uoa.gr/ papost/ papost@phys.uoa.gr ΤΕΙ Ιονίων Νήσων, Τμήμα Τεχνολόγων Περιβάλλοντος ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-2017 Οπως είδαμε
Περιεχόμενα διάλεξης
 7η Διάλεξη Οπτικές ίνες Γ. Έλληνας, Διάλεξη 7, σελ. 1 Περιεχόμενα διάλεξης Διασπορά Πόλωσης Γ. Έλληνας, Διάλεξη 7, σελ. Page 1 Πόλωση Γενική θεωρία Γ. Έλληνας, Διάλεξη 7, σελ. 3 Μηχανικό ανάλογο Εγκάρσια
7η Διάλεξη Οπτικές ίνες Γ. Έλληνας, Διάλεξη 7, σελ. 1 Περιεχόμενα διάλεξης Διασπορά Πόλωσης Γ. Έλληνας, Διάλεξη 7, σελ. Page 1 Πόλωση Γενική θεωρία Γ. Έλληνας, Διάλεξη 7, σελ. 3 Μηχανικό ανάλογο Εγκάρσια
ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΚΥΜΑΤΑ
 ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΚΥΜΑΤΑ Θέμα1: Α. Η ταχύτητα διάδοσης ενός ηλεκτρομαγνητικού κύματος: α. εξαρτάται από τη συχνότητα ταλάντωσης της πηγής β. εξαρτάται
ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΚΥΜΑΤΑ Θέμα1: Α. Η ταχύτητα διάδοσης ενός ηλεκτρομαγνητικού κύματος: α. εξαρτάται από τη συχνότητα ταλάντωσης της πηγής β. εξαρτάται
2 ο ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΣΤΗ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 δυαδικό ΦΡΟΝΤΙΣΤΗΡΙΑ ο ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΣΤΗ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΔΙΑΡΚΕΙΑ: 3 ώρες ΒΑΘΜΟΣ:.. ΗΜΕΡΟΜΗΝΙΑ: 3// ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΥΠΕΥΘΥΝΟΣ ΚΑΘΗΓΗΤΗΣ: Ατρείδης Γιώργος Θ Ε Μ Α
δυαδικό ΦΡΟΝΤΙΣΤΗΡΙΑ ο ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΣΤΗ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΔΙΑΡΚΕΙΑ: 3 ώρες ΒΑΘΜΟΣ:.. ΗΜΕΡΟΜΗΝΙΑ: 3// ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΥΠΕΥΘΥΝΟΣ ΚΑΘΗΓΗΤΗΣ: Ατρείδης Γιώργος Θ Ε Μ Α
ΚΥΜΑΤΟ ΗΓΗΣΗ. «Μικροοπτικές διατάξεις-ολοκληρωµένα οπτικά»
 ΚΥΜΑΤΟ ΗΓΗΣΗ Επίπεδοι κυµατοδηγοί Προσέγγιση γεωµετρικής οπτικής Προσέγγιση κυµατικής οπτικής και συνοριακών συνθηκών Οπτικές ίνες ιασπορά Μέθοδοι ανάπτυξης κυµατοδηγών Ηχρήση των κυµάτων στις επικοινωνίες
ΚΥΜΑΤΟ ΗΓΗΣΗ Επίπεδοι κυµατοδηγοί Προσέγγιση γεωµετρικής οπτικής Προσέγγιση κυµατικής οπτικής και συνοριακών συνθηκών Οπτικές ίνες ιασπορά Μέθοδοι ανάπτυξης κυµατοδηγών Ηχρήση των κυµάτων στις επικοινωνίες
Περιοχές Ακτινοβολίας Κεραιών
 Κεραίες ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ Δημοσθένης Βουγιούκας Αναπληρωτής Καθηγητής Τμήμα Μηχανικών Πληροφοριακών & Επικοινωνιακών Συστημάτων Περιοχές Ακτινοβολίας Κεραιών 2 1 Σημειακή Πηγή 3 Κατακόρυφα Πολωμένο
Κεραίες ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ Δημοσθένης Βουγιούκας Αναπληρωτής Καθηγητής Τμήμα Μηχανικών Πληροφοριακών & Επικοινωνιακών Συστημάτων Περιοχές Ακτινοβολίας Κεραιών 2 1 Σημειακή Πηγή 3 Κατακόρυφα Πολωμένο
ΠΕΡΙΕΧΟΜΕΝΑ ΤΟΜΟΣ Ι ΕΙΣΑΓΩΓΗ 1
 ΤΟΜΟΣ Ι ΕΙΣΑΓΩΓΗ 1 1 ΟΙ ΒΑΣΙΚΟΙ ΝΟΜΟΙ ΤΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟΥ ΠΕΔΙΟΥ 7 1.1 Μονάδες και σύμβολα φυσικών μεγεθών..................... 7 1.2 Προθέματα φυσικών μεγεθών.............................. 13 1.3 Αγωγοί,
ΤΟΜΟΣ Ι ΕΙΣΑΓΩΓΗ 1 1 ΟΙ ΒΑΣΙΚΟΙ ΝΟΜΟΙ ΤΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟΥ ΠΕΔΙΟΥ 7 1.1 Μονάδες και σύμβολα φυσικών μεγεθών..................... 7 1.2 Προθέματα φυσικών μεγεθών.............................. 13 1.3 Αγωγοί,
ΣΕΜΦΕ ΕΜΠ Φυσική ΙΙΙ (Κυματική) Διαγώνισμα επί πτυχίω εξέτασης 02/06/2017 1
 ΣΕΜΦΕ ΕΜΠ Φυσική ΙΙΙ (Κυματική) Διαγώνισμα επί πτυχίω εξέτασης /6/7 Διάρκεια ώρες. Θέμα. Θεωρηστε ενα συστημα δυο σωματων ισων μαζων (μαζας Μ το καθενα) και δυο ελατηριων (χωρις μαζα) με σταθερες ελατηριων
ΣΕΜΦΕ ΕΜΠ Φυσική ΙΙΙ (Κυματική) Διαγώνισμα επί πτυχίω εξέτασης /6/7 Διάρκεια ώρες. Θέμα. Θεωρηστε ενα συστημα δυο σωματων ισων μαζων (μαζας Μ το καθενα) και δυο ελατηριων (χωρις μαζα) με σταθερες ελατηριων
2-1 ΕΙΣΑΓΩΓΗ 2-2 ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ
 ΕΞΩΦΥΛΛΟ 43 Εικ. 2.1 Κύμα στην επιφάνεια της θάλασσας. 2-1 ΕΙΣΑΓΩΓΗ Η έννοια «κύμα», από τις πιο βασικές έννοιες της φυσικής, χρησιμοποιήθηκε για την περιγραφή φαινομένων που καλύπτουν ένα ευρύ φάσμα.
ΕΞΩΦΥΛΛΟ 43 Εικ. 2.1 Κύμα στην επιφάνεια της θάλασσας. 2-1 ΕΙΣΑΓΩΓΗ Η έννοια «κύμα», από τις πιο βασικές έννοιες της φυσικής, χρησιμοποιήθηκε για την περιγραφή φαινομένων που καλύπτουν ένα ευρύ φάσμα.
Κλασική Ηλεκτροδυναμική
 Κλασική Ηλεκτροδυναμική Ενότητα 22: Κυματοπακέτα-Κυματοδηγοί Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι να παρουσιάσει την έννοια του κυματοπακέτου,
Κλασική Ηλεκτροδυναμική Ενότητα 22: Κυματοπακέτα-Κυματοδηγοί Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι να παρουσιάσει την έννοια του κυματοπακέτου,
HMY 333 Φωτονική Διάλεξη 12 Οπτικοί κυματοδηγοί
 4 Hsiu. Ha Ανάκλαση και μετάδοση του φωτός σε μια διηλεκτρική επαφή HMY 333 Φωτονική Διάλεξη Οπτικοί κυματοδηγοί i i i r i si c si v c hp://www.e.readig.ac.u/clouds/awell/ c 3 Γωνία πρόσπτωσης < κρίσιμη
4 Hsiu. Ha Ανάκλαση και μετάδοση του φωτός σε μια διηλεκτρική επαφή HMY 333 Φωτονική Διάλεξη Οπτικοί κυματοδηγοί i i i r i si c si v c hp://www.e.readig.ac.u/clouds/awell/ c 3 Γωνία πρόσπτωσης < κρίσιμη
ΕΡΓΑΣΙΑ ΣΤΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ
 ΕΡΓΑΣΙΑ ΣΤΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Τι ονομάζεται μηχανικό κύμα; Να περιγράψετε το μηχανισμό διάδοσής του. 2. Τι χρειάζεται για να δημιουργηθεί και να διαδοθεί ένα μηχανικό κύμα; Διαδίδονται
ΕΡΓΑΣΙΑ ΣΤΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Τι ονομάζεται μηχανικό κύμα; Να περιγράψετε το μηχανισμό διάδοσής του. 2. Τι χρειάζεται για να δημιουργηθεί και να διαδοθεί ένα μηχανικό κύμα; Διαδίδονται
ΚΥΜΑΤΙΚΗ-ΟΠΤΙΚΗ 1. Σχήµα 1 Σχήµα 2
 ΚΥΜΑΤΙΚΗ-ΟΠΤΙΚΗ The law of natue ae witten in the language of mathematic G.Galileo God ued beautiful mathematic in ceating the wold P.Diac ΣΥΝΤΟΜΗ ΜΑΘΗΜΑΤΙΚΗ ΕΙΣΑΓΩΓΗ Α. ΣΤΟΙΧΕΙΑ ΙΑΝΥΣΜΑΤΙΚΗΣ ΑΝΑΛΥΣΗΣ.Ροή
ΚΥΜΑΤΙΚΗ-ΟΠΤΙΚΗ The law of natue ae witten in the language of mathematic G.Galileo God ued beautiful mathematic in ceating the wold P.Diac ΣΥΝΤΟΜΗ ΜΑΘΗΜΑΤΙΚΗ ΕΙΣΑΓΩΓΗ Α. ΣΤΟΙΧΕΙΑ ΙΑΝΥΣΜΑΤΙΚΗΣ ΑΝΑΛΥΣΗΣ.Ροή
Γ ΛΥΚΕΙΟΥ ΚΥΜΑΤΑ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ. Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός.
 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΚΥΜΑΤΑ Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός / Βασικές Έννοιες Η επιστήμη της Φυσικής συχνά μελετάει διάφορες διαταραχές που προκαλούνται και διαδίδονται στο χώρο.
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΚΥΜΑΤΑ Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός / Βασικές Έννοιες Η επιστήμη της Φυσικής συχνά μελετάει διάφορες διαταραχές που προκαλούνται και διαδίδονται στο χώρο.
, όπου οι σταθερές προσδιορίζονται από τις αρχικές συνθήκες.
 Στην περίπτωση της ταλάντωσης µε κρίσιµη απόσβεση οι δύο γραµµικώς ανεξάρτητες λύσεις εκφυλίζονται (καταλήγουν να ταυτίζονται) Στην περιοχή ασθενούς απόσβεσης ( ) δύο γραµµικώς ανεξάρτητες λύσεις είναι
Στην περίπτωση της ταλάντωσης µε κρίσιµη απόσβεση οι δύο γραµµικώς ανεξάρτητες λύσεις εκφυλίζονται (καταλήγουν να ταυτίζονται) Στην περιοχή ασθενούς απόσβεσης ( ) δύο γραµµικώς ανεξάρτητες λύσεις είναι
ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΣΥΜΠΛΗΡΩΜΑ ΘΕΩΡΙΑΣ
 ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΣΥΜΠΛΗΡΩΜΑ ΘΕΩΡΙΑΣ 1. ΕΓΚΑΡΣΙΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ Κύματα κατά μήκος τεντωμένου νήματος Στο τεντωμένο με δύναμη νήμα του Σχήματος 1.1α δημιουργούμε μια εγκάρσια διαταραχή (παράλληλη με τη διεύθυνση
ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΣΥΜΠΛΗΡΩΜΑ ΘΕΩΡΙΑΣ 1. ΕΓΚΑΡΣΙΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ Κύματα κατά μήκος τεντωμένου νήματος Στο τεντωμένο με δύναμη νήμα του Σχήματος 1.1α δημιουργούμε μια εγκάρσια διαταραχή (παράλληλη με τη διεύθυνση
7. Ταλαντώσεις σε συστήµατα µε πολλούς βαθµούς ελευθερίας
 7 Ταλαντώσεις σε συστήµατα µε πολλούς βαθµούς ελευθερίας Συζευγµένες ταλαντώσεις Βιβλιογραφία F S Crawford Jr Κυµατική (Σειρά Μαθηµάτων Φυσικής Berkeley, Τόµος 3 Αθήνα 979) Κεφ H J Pai Φυσική των ταλαντώσεων
7 Ταλαντώσεις σε συστήµατα µε πολλούς βαθµούς ελευθερίας Συζευγµένες ταλαντώσεις Βιβλιογραφία F S Crawford Jr Κυµατική (Σειρά Μαθηµάτων Φυσικής Berkeley, Τόµος 3 Αθήνα 979) Κεφ H J Pai Φυσική των ταλαντώσεων
ΚΕΦΑΛΑΙΟ 2ο: ΜΗΧΑΝΙΚΑ- ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ.
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
max 0 Eκφράστε την διαφορά των δύο θετικών λύσεων ώς πολλαπλάσιο του ω 0, B . Αναλύοντας το Β σε σειρά άπειρων όρων ώς προς γ/ω 0 ( σειρά
 . Να αποδείξετε ότι σε ένα ταλαντούμενο σύστημα ενός βαθμού ελευθερίας, μάζας και σταθεράς ελατηρίου s με πολύ ασθενή απόσβεση (γω, όπου γ r/, r η σταθερά αντίστασης και s/ ) το πλήρες εύρος στο μισό του
. Να αποδείξετε ότι σε ένα ταλαντούμενο σύστημα ενός βαθμού ελευθερίας, μάζας και σταθεράς ελατηρίου s με πολύ ασθενή απόσβεση (γω, όπου γ r/, r η σταθερά αντίστασης και s/ ) το πλήρες εύρος στο μισό του
r r r r r r r r r r r
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 0 ΜΑÏΟΥ 011 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ) ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ:
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 0 ΜΑÏΟΥ 011 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ) ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ:
Ηλεκτρομαγνητισμός. Μαγνητικό πεδίο. Νίκος Ν. Αρπατζάνης
 Ηλεκτρομαγνητισμός Μαγνητικό πεδίο Νίκος Ν. Αρπατζάνης Μαγνητικοί πόλοι Κάθε μαγνήτης, ανεξάρτητα από το σχήμα του, έχει δύο πόλους. Τον βόρειο πόλο (Β) και τον νότιο πόλο (Ν). Μεταξύ των πόλων αναπτύσσονται
Ηλεκτρομαγνητισμός Μαγνητικό πεδίο Νίκος Ν. Αρπατζάνης Μαγνητικοί πόλοι Κάθε μαγνήτης, ανεξάρτητα από το σχήμα του, έχει δύο πόλους. Τον βόρειο πόλο (Β) και τον νότιο πόλο (Ν). Μεταξύ των πόλων αναπτύσσονται
Διαγώνισμα Φυσικής Κατεύθυνσης Γ Λυκείου
 Διαγώνισμα Φυσικής Κατεύθυνσης Γ Λυκείου Ζήτημα 1 ον 1.. Ένα σημειακό αντικείμενο εκτελεί απλή αρμονική ταλάντωση. Τις χρονικές στιγμές που το μέτρο της ταχύτητας του αντικειμένου είναι μέγιστο, το μέτρο
Διαγώνισμα Φυσικής Κατεύθυνσης Γ Λυκείου Ζήτημα 1 ον 1.. Ένα σημειακό αντικείμενο εκτελεί απλή αρμονική ταλάντωση. Τις χρονικές στιγμές που το μέτρο της ταχύτητας του αντικειμένου είναι μέγιστο, το μέτρο
Experiments are the only means of knowledge. Anyother is poetry and imagination. M.Plank 2 ΟΙ ΕΞΙΣΩΣΕΙΣ ΤΟΥ MAXWELL
 ΚΥΜΑΤΙΚΗ-ΟΠΤΙΚΗ 7 xpeiments ae the only means o knowledge. Anyothe is poety and imagination. M.Plank 2 ΟΙ ΕΞΙΣΩΣΕΙΣ ΤΟΥ MAXWLL Σε µια πρώτη παρουσίαση του θέµατος δίνονται οι εξισώσεις του Maxwell στο
ΚΥΜΑΤΙΚΗ-ΟΠΤΙΚΗ 7 xpeiments ae the only means o knowledge. Anyothe is poety and imagination. M.Plank 2 ΟΙ ΕΞΙΣΩΣΕΙΣ ΤΟΥ MAXWLL Σε µια πρώτη παρουσίαση του θέµατος δίνονται οι εξισώσεις του Maxwell στο
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα. ΔΙΑΛΕΞΗ 21 Κυματική ΦΥΣ102 1
 Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 21 Κυματική ΦΥΣ102 1 Χαρακτηριστικά Διάδοσης Κύματος Όλα τα κύματα μεταφέρουν ενέργεια.
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 21 Κυματική ΦΥΣ102 1 Χαρακτηριστικά Διάδοσης Κύματος Όλα τα κύματα μεταφέρουν ενέργεια.
website:
 Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 31 Μαρτίου 2019 1 Δυνάμεις μάζας και επαφής Δυνάμεις μάζας ή δυνάμεις όγκου ονομάζονται οι δυνάμεις που είναι
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 31 Μαρτίου 2019 1 Δυνάμεις μάζας και επαφής Δυνάμεις μάζας ή δυνάμεις όγκου ονομάζονται οι δυνάμεις που είναι
Δίκτυα Τηλεπικοινωνιών. και Μετάδοσης
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Δίκτυα Τηλεπικοινωνιών και Μετάδοσης Σύστημα μετάδοσης με οπτικές ίνες Tο οπτικό φέρον κύμα μπορεί να διαμορφωθεί είτε από αναλογικό
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Δίκτυα Τηλεπικοινωνιών και Μετάδοσης Σύστημα μετάδοσης με οπτικές ίνες Tο οπτικό φέρον κύμα μπορεί να διαμορφωθεί είτε από αναλογικό
(ΚΕΦ 32) f( x x f( x) x z y
 (ΚΕΦ 3) f( x x f( x) x z y ΣΥΝΟΨΗ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΥ J. C. Maxwell (~1860) συνόψισε τη δουλειά ως τότε για το ηλεκτρικό και μαγνητικό πεδίο σε 4 εξισώσεις. Όμως, κατανόησε ότι οι εξισώσεις αυτές (όπως
(ΚΕΦ 3) f( x x f( x) x z y ΣΥΝΟΨΗ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΥ J. C. Maxwell (~1860) συνόψισε τη δουλειά ως τότε για το ηλεκτρικό και μαγνητικό πεδίο σε 4 εξισώσεις. Όμως, κατανόησε ότι οι εξισώσεις αυτές (όπως
Βασικές διαδικασίες παραγωγής πολωμένου φωτός
 Πόλωση του φωτός Βασικές διαδικασίες παραγωγής πολωμένου φωτός πόλωση λόγω επιλεκτικής απορρόφησης - διχρωισμός πόλωση λόγω ανάκλασης από μια διηλεκτρική επιφάνεια πόλωση λόγω ύπαρξης δύο δεικτών διάθλασης
Πόλωση του φωτός Βασικές διαδικασίες παραγωγής πολωμένου φωτός πόλωση λόγω επιλεκτικής απορρόφησης - διχρωισμός πόλωση λόγω ανάκλασης από μια διηλεκτρική επιφάνεια πόλωση λόγω ύπαρξης δύο δεικτών διάθλασης
( ) ( ) ( )z. HMY Φωτονική. Διάλεξη 08 Οι εξισώσεις του Maxwell. r = A r. B r. ˆ det = Βαθμωτά και διανυσματικά μεγέθη
 HMY - Φωτονική Διάλεξη 8 Οι εξισώσεις του Mawell Βαθμωτά και διανυσματικά μεγέθη Πολλαπλασιασμός Πρόσθεση διανυσμάτων Βαθμωτό: το μέγεθος που για τον προσδιορισμό του χρειάζεται μόνο το μέτρο του και η
HMY - Φωτονική Διάλεξη 8 Οι εξισώσεις του Mawell Βαθμωτά και διανυσματικά μεγέθη Πολλαπλασιασμός Πρόσθεση διανυσμάτων Βαθμωτό: το μέγεθος που για τον προσδιορισμό του χρειάζεται μόνο το μέτρο του και η
ΓΡΑΜΜΕΣ ΜΕΤΑΦΟΡΑΣ. a) Ομοαξονική γραμμή b) Γραμμή εδάφους c) Τρίκλωνη γραμμή d) Δισύρματη γραμμή (συνεστραμμένο καλώδιο)
 ΓΡΑΜΜΕΣ ΜΕΤΑΦΟΡΑΣ a) Ομοαξονική γραμμή b) Γραμμή εδάφους c) Τρίκλωνη γραμμή d) Δισύρματη γραμμή (συνεστραμμένο καλώδιο) 1 ΜΕΤΑΔΟΣΗ ΠΛΗΡΟΦΟΡΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΗ ΖΕΥΞΗ ΠΡΟΒΛΗΜΑΤΑ ΜΕΤΑΔΟΣΗΣ ΕΞΑΣΘΕΝΙΣΗ ΓΡΑΜΜΙΚΕΣ
ΓΡΑΜΜΕΣ ΜΕΤΑΦΟΡΑΣ a) Ομοαξονική γραμμή b) Γραμμή εδάφους c) Τρίκλωνη γραμμή d) Δισύρματη γραμμή (συνεστραμμένο καλώδιο) 1 ΜΕΤΑΔΟΣΗ ΠΛΗΡΟΦΟΡΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΗ ΖΕΥΞΗ ΠΡΟΒΛΗΜΑΤΑ ΜΕΤΑΔΟΣΗΣ ΕΞΑΣΘΕΝΙΣΗ ΓΡΑΜΜΙΚΕΣ
ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑΤΙΚΑ Β ΓΥΜΝΑΣΙΟΥ. ΜΕΡΟΣ 1ο ΑΛΓΕΒΡΑ
 1. Τι καλείται μεταβλητή; ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑΤΙΑ Β ΓΥΜΝΑΣΙΟΥ ΜΕΡΟΣ 1ο ΑΛΓΕΒΡΑ Μεταβλητή είναι ένα γράμμα (π.χ., y, t, ) που το χρησιμοποιούμε για να παραστήσουμε ένα οποιοδήποτε στοιχείο ενός συνόλου..
1. Τι καλείται μεταβλητή; ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑΤΙΑ Β ΓΥΜΝΑΣΙΟΥ ΜΕΡΟΣ 1ο ΑΛΓΕΒΡΑ Μεταβλητή είναι ένα γράμμα (π.χ., y, t, ) που το χρησιμοποιούμε για να παραστήσουμε ένα οποιοδήποτε στοιχείο ενός συνόλου..
Η αριστερή μεριά εξαρτάται μόνο από το z και η δεξιά μόνο από το t, έτσι και οι δυο πρέπει να είναι σταθερές. Καλούμε την σταθερά
 Πρόβλημα 8.3 Πρόβλημα 8.4 Η κυματικ εξίσωση δίνει Ψάχνουμε για λύσεις του τύπου Το τοποθετούμε αυτό και: Διαιρούμε με ZT: Η αριστερ μεριά εξαρτάται μόνο από το z και η δεξιά μόνο από το t, έτσι και οι
Πρόβλημα 8.3 Πρόβλημα 8.4 Η κυματικ εξίσωση δίνει Ψάχνουμε για λύσεις του τύπου Το τοποθετούμε αυτό και: Διαιρούμε με ZT: Η αριστερ μεριά εξαρτάται μόνο από το z και η δεξιά μόνο από το t, έτσι και οι
8 η Διάλεξη Ηλεκτρομαγνητική ακτινοβολία, φαινόμενα συμβολής, περίθλαση
 11//17 8 η Διάλεξη Ηλεκτρομαγνητική ακτινοβολία, φαινόμενα συμβολής, περίθλαση Φίλιππος Φαρμάκης Επ. Καθηγητής 1 Ηλεκτρομαγνητισμός Πως συνδέονται ο ηλεκτρισμός με τον μαγνητισμό; Πως παράγονται τα κύματα;
11//17 8 η Διάλεξη Ηλεκτρομαγνητική ακτινοβολία, φαινόμενα συμβολής, περίθλαση Φίλιππος Φαρμάκης Επ. Καθηγητής 1 Ηλεκτρομαγνητισμός Πως συνδέονται ο ηλεκτρισμός με τον μαγνητισμό; Πως παράγονται τα κύματα;
Σήματα και Συστήματα. Διάλεξη 1: Σήματα Συνεχούς Χρόνου. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 1: Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Εισαγωγή στα Σήματα 1. Σκοποί της Θεωρίας Σημάτων 2. Κατηγορίες Σημάτων 3. Χαρακτηριστικές Παράμετροι
Σήματα και Συστήματα Διάλεξη 1: Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Εισαγωγή στα Σήματα 1. Σκοποί της Θεωρίας Σημάτων 2. Κατηγορίες Σημάτων 3. Χαρακτηριστικές Παράμετροι
ΘΕΩΡΗΤΙΚΗ ΜΗΧΑΝΙΚΗ ΙΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΝΟΜΙΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΣΠΟΥΔ ΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΑΣΚΗΣΕΙΣ ΑΝΑΛΥΤΙΚΗΣ ΔΥΝΑΜΙΚΗΣ Μεθοδολογία Κλεομένης Γ. Τσιγάνης Λέκτορας ΑΠΘ Πρόχειρες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΝΟΜΙΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΣΠΟΥΔ ΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΑΣΚΗΣΕΙΣ ΑΝΑΛΥΤΙΚΗΣ ΔΥΝΑΜΙΚΗΣ Μεθοδολογία Κλεομένης Γ. Τσιγάνης Λέκτορας ΑΠΘ Πρόχειρες
Σφαίρα σε ράγες: Η συνάρτηση Lagrange. Ν. Παναγιωτίδης
 Η Εξίσωση Euler-Lagrange Σφαίρα σε ράγες: Η συνάρτηση Lagrange Ν. Παναγιωτίδης Έστω σύστημα δυο συγκλινόντων ραγών σε σχήμα Χ που πάνω τους κυλίεται σφαίρα ακτίνας. Θεωρούμε σύστημα συντεταγμένων με οριζόντιους
Η Εξίσωση Euler-Lagrange Σφαίρα σε ράγες: Η συνάρτηση Lagrange Ν. Παναγιωτίδης Έστω σύστημα δυο συγκλινόντων ραγών σε σχήμα Χ που πάνω τους κυλίεται σφαίρα ακτίνας. Θεωρούμε σύστημα συντεταγμένων με οριζόντιους
Επαναληπτικό διαγώνισµα στα Κύµατα
 ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΤΑΙΧΜΙΟ 1 Επαναληπτικό διαγώνισµα στα Κύµατα Θέµα 1 0 Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΤΑΙΧΜΙΟ 1 Επαναληπτικό διαγώνισµα στα Κύµατα Θέµα 1 0 Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
Η Ψ = Ε Ψ. Ψ = f(x, y, z, t, λ)
 Κυματική εξίσωση του Schrödinger (196) Η Ψ = Ε Ψ Η: τελεστής Hamilton (Hamiltonian operator) εκτέλεση μαθηματικών πράξεων επί της κυματοσυνάρτησης Ψ. Ε: ολική ενέργεια των ηλεκτρονίων δυναμική ενέργεια
Κυματική εξίσωση του Schrödinger (196) Η Ψ = Ε Ψ Η: τελεστής Hamilton (Hamiltonian operator) εκτέλεση μαθηματικών πράξεων επί της κυματοσυνάρτησης Ψ. Ε: ολική ενέργεια των ηλεκτρονίων δυναμική ενέργεια
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ. Μαθηματικά 2. Σταύρος Παπαϊωάννου
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ Μαθηματικά Σταύρος Παπαϊωάννου Ιούνιος Τίτλος Μαθήματος Περιεχόμενα Χρηματοδότηση. Σφάλμα! Δεν έχει οριστεί σελιδοδείκτης. Σκοποί Μαθήματος
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ Μαθηματικά Σταύρος Παπαϊωάννου Ιούνιος Τίτλος Μαθήματος Περιεχόμενα Χρηματοδότηση. Σφάλμα! Δεν έχει οριστεί σελιδοδείκτης. Σκοποί Μαθήματος
r r r r r r r r r r r
 http://edu.kliaka.g ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 0 ΜΑÏΟΥ 011 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ)
http://edu.kliaka.g ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 0 ΜΑÏΟΥ 011 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ)
ΦΟΡΤΙΣΜΕΝΟΣ ΑΡΜΟΝΙΚΟΣ ΤΑΛΑΝΤΩΤΗΣ ΜΕΣΑ ΣΕ ΟΜΟΓΕΝΕΣ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ: ΤΕΛΕΣΤΕΣ ΔΗΜΙΟΥΡΓΙΑΣ ΚΑΙ ΚΑΤΑΣΤΡΟΦΗΣ, ΒΑΣΙΚΗ ΚΑΤΑΣΤΑΣΗ, ΕΛΑΧΙΣΤΗ ΕΝΕΡΓΕΙΑ ΣΥΖΗΤΗΣΗ
 ΦΟΡΤΙΣΜΕΝΟΣ ΑΡΜΟΝΙΚΟΣ ΤΑΛΑΝΤΩΤΗΣ ΜΕΣΑ ΣΕ ΟΜΟΓΕΝΕΣ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ: ΤΕΛΕΣΤΕΣ ΔΗΜΙΟΥΡΓΙΑΣ ΚΑΙ ΚΑΤΑΣΤΡΟΦΗΣ, ΒΑΣΙΚΗ ΚΑΤΑΣΤΑΣΗ, ΕΛΑΧΙΣΤΗ ΕΝΕΡΓΕΙΑ ΣΥΖΗΤΗΣΗ Ξεκινώντας από τους τελεστές δημιουργίας και καταστροφής
ΦΟΡΤΙΣΜΕΝΟΣ ΑΡΜΟΝΙΚΟΣ ΤΑΛΑΝΤΩΤΗΣ ΜΕΣΑ ΣΕ ΟΜΟΓΕΝΕΣ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ: ΤΕΛΕΣΤΕΣ ΔΗΜΙΟΥΡΓΙΑΣ ΚΑΙ ΚΑΤΑΣΤΡΟΦΗΣ, ΒΑΣΙΚΗ ΚΑΤΑΣΤΑΣΗ, ΕΛΑΧΙΣΤΗ ΕΝΕΡΓΕΙΑ ΣΥΖΗΤΗΣΗ Ξεκινώντας από τους τελεστές δημιουργίας και καταστροφής
Σύνθεση ή σύζευξη ταλαντώσεων;
 Σύνθεση ή σύζευξη ταλαντώσεων; Σώμα Σ μάζας προσδένεται στο ένα άκρο οριζόντιου ελατηρίου σταθεράς το άλλο άκρο του οποίου είναι ακλόνητα στερεωμένο. Πάνω στο πρώτο σώμα στερεώνεται δεύτερο ελατήριο σταθεράς,
Σύνθεση ή σύζευξη ταλαντώσεων; Σώμα Σ μάζας προσδένεται στο ένα άκρο οριζόντιου ελατηρίου σταθεράς το άλλο άκρο του οποίου είναι ακλόνητα στερεωμένο. Πάνω στο πρώτο σώμα στερεώνεται δεύτερο ελατήριο σταθεράς,
21/11/2013 ETY-202 ETY-202 ΎΛΗ & ΦΩΣ 06. Ο ΑΡΜΟΝΙΚΟΣ ΤΑΛΑΝΤΩΤΗΣ. 1396; office Δ013 ΙΤΕ. Στέλιος Τζωρτζάκης
 stzortz@iesl.forth.gr 1396; office Δ013 ΙΤΕ 2 ΎΛΗ & ΦΩΣ 06. Ο ΑΡΜΟΝΙΚΟΣ ΤΑΛΑΝΤΩΤΗΣ Στέλιος Τζωρτζάκης Ο ΑΡΜΟΝΙΚΟΣ ΤΑΛΑΝΤΩΤΗΣ 1 3 4 Το δυναμικό του αρμονικού ταλαντωτή Η παραβολική προσέγγιση βρίσκει άμεση
stzortz@iesl.forth.gr 1396; office Δ013 ΙΤΕ 2 ΎΛΗ & ΦΩΣ 06. Ο ΑΡΜΟΝΙΚΟΣ ΤΑΛΑΝΤΩΤΗΣ Στέλιος Τζωρτζάκης Ο ΑΡΜΟΝΙΚΟΣ ΤΑΛΑΝΤΩΤΗΣ 1 3 4 Το δυναμικό του αρμονικού ταλαντωτή Η παραβολική προσέγγιση βρίσκει άμεση
Να αιτιολογήσετε την απάντησή σας. Μονάδες 5
 2002 5. Να γράψετε στο τετράδιό σας τη λέξη που συµπληρώνει σωστά καθεµία από τις παρακάτω προτάσεις. γ. Η αιτία δηµιουργίας του ηλεκτροµαγνητικού κύµατος είναι η... κίνηση ηλεκτρικών φορτίων. 1. Ακτίνα
2002 5. Να γράψετε στο τετράδιό σας τη λέξη που συµπληρώνει σωστά καθεµία από τις παρακάτω προτάσεις. γ. Η αιτία δηµιουργίας του ηλεκτροµαγνητικού κύµατος είναι η... κίνηση ηλεκτρικών φορτίων. 1. Ακτίνα
ΤΕΛΟΣ 2ΗΣ ΑΠΟ 4 ΣΕΛΙΔΕΣ
 ΑΡΧΗ 2ΗΣ ΣΕΛΙΔΑΣ ΘΕΜΑ 1 ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 20 ΔΕΚΕΜΒΡΙΟΥ 2014 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΤΕΣΣΕΡΙΣ (4) Α) Για κάθε μία
ΑΡΧΗ 2ΗΣ ΣΕΛΙΔΑΣ ΘΕΜΑ 1 ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 20 ΔΕΚΕΜΒΡΙΟΥ 2014 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΤΕΣΣΕΡΙΣ (4) Α) Για κάθε μία
Από τι αποτελείται το Φως (1873)
 Από τι αποτελείται το Φως (1873) Ο James Maxwell έδειξε θεωρητικά ότι το ορατό φως αποτελείται από ηλεκτρομαγνητικά κύματα. Ηλεκτρομαγνητικό κύμα είναι η ταυτόχρονη διάδοση, μέσω της ταχύτητας του φωτός
Από τι αποτελείται το Φως (1873) Ο James Maxwell έδειξε θεωρητικά ότι το ορατό φως αποτελείται από ηλεκτρομαγνητικά κύματα. Ηλεκτρομαγνητικό κύμα είναι η ταυτόχρονη διάδοση, μέσω της ταχύτητας του φωτός
Δίκτυα Τηλεπικοινωνιών. και Μετάδοσης
 Τεχνοογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πηροφορικής & Επικοινωνιών Δίκτυα Τηεπικοινωνιών και Μετάδοσης Ίνες βηματικού δείκτη (step index fibres) Ίνα βηματικού δείκτη: απότομη (βηματική) μεταβοή του
Τεχνοογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πηροφορικής & Επικοινωνιών Δίκτυα Τηεπικοινωνιών και Μετάδοσης Ίνες βηματικού δείκτη (step index fibres) Ίνα βηματικού δείκτη: απότομη (βηματική) μεταβοή του
website:
 Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ιδρυμα Θεσσαλονίκης Τμήμα Μηχανικών Αυτοματισμού Μαθηματική Μοντελοποίηση Αναγνώριση Συστημάτων Μαάιτα Τζαμάλ-Οδυσσέας 6 Μαρτίου 2017 1 Εισαγωγή Κάθε φυσικό σύστημα
Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ιδρυμα Θεσσαλονίκης Τμήμα Μηχανικών Αυτοματισμού Μαθηματική Μοντελοποίηση Αναγνώριση Συστημάτων Μαάιτα Τζαμάλ-Οδυσσέας 6 Μαρτίου 2017 1 Εισαγωγή Κάθε φυσικό σύστημα
Μάθημα Ακουστικής. Νικόλαος Παλληκαράκης Καθ. Ιατρικής Φυσικής ΠΠ
 Μάθημα Ακουστικής Νικόλαος Παλληκαράκης Καθ. Ιατρικής Φυσικής ΠΠ Περιοδική Κίνηση Μία κίνηση χαρακτηρίζεται σαν περιοδική αν αναπαράγεται απαράλλακτα σε ίσα διαδοχικά χρονικά διαστήματα. Στο χρονικό αυτό
Μάθημα Ακουστικής Νικόλαος Παλληκαράκης Καθ. Ιατρικής Φυσικής ΠΠ Περιοδική Κίνηση Μία κίνηση χαρακτηρίζεται σαν περιοδική αν αναπαράγεται απαράλλακτα σε ίσα διαδοχικά χρονικά διαστήματα. Στο χρονικό αυτό
Σφαίρα σε ράγες: Η συνάρτηση Lagrange. Ν. Παναγιωτίδης
 Σφαίρα σε ράγες: Η συνάρτηση Lagrange Ν. Παναγιωτίδης Έστω σύστημα δυο συγκλινόντων ραγών σε σχήμα Χ που πάνω τους κυλίεται σφαίρα ακτίνας. Θεωρούμε σύστημα συντεταγμένων με οριζόντιους τους άξονες και.
Σφαίρα σε ράγες: Η συνάρτηση Lagrange Ν. Παναγιωτίδης Έστω σύστημα δυο συγκλινόντων ραγών σε σχήμα Χ που πάνω τους κυλίεται σφαίρα ακτίνας. Θεωρούμε σύστημα συντεταγμένων με οριζόντιους τους άξονες και.
ΔΙΑΓΩΝΙΣΜΑ ΘΕΩΡΙΑΣ ΣΤΑ ΚΥΜΑΤΑ(μέχρι ΗΜ) Διάρκεια 90 min
 ΔΙΑΓΩΝΙΣΜΑ ΘΕΩΡΙΑΣ ΣΤΑ ΚΥΜΑΤΑ(μέχρι ΗΜ) Διάρκεια 90 min Θέμα 1 Ερωτήσεις πολαλπλής επιλογής Σε κάθε ερώτηση υπάρχει μόνο μια σωστή απάντηση 1. Η περίοδος (Τ) του κύµατος είναι ίση µε (ποια πρόταση είναι
ΔΙΑΓΩΝΙΣΜΑ ΘΕΩΡΙΑΣ ΣΤΑ ΚΥΜΑΤΑ(μέχρι ΗΜ) Διάρκεια 90 min Θέμα 1 Ερωτήσεις πολαλπλής επιλογής Σε κάθε ερώτηση υπάρχει μόνο μια σωστή απάντηση 1. Η περίοδος (Τ) του κύµατος είναι ίση µε (ποια πρόταση είναι
γ) Να σχεδιάσετε τις γραφικές παραστάσεις απομάκρυνσης - χρόνου, για τα σημεία Α, Β και Γ, τα οποία απέχουν από το ελεύθερο άκρο αντίστοιχα,,
 1. Κατά μήκος μιας ελαστικής χορδής μεγάλου μήκους που το ένα άκρο της είναι ακλόνητα στερεωμένο, διαδίδονται δύο κύματα, των οποίων οι εξισώσεις είναι αντίστοιχα: και, όπου και είναι μετρημένα σε και
1. Κατά μήκος μιας ελαστικής χορδής μεγάλου μήκους που το ένα άκρο της είναι ακλόνητα στερεωμένο, διαδίδονται δύο κύματα, των οποίων οι εξισώσεις είναι αντίστοιχα: και, όπου και είναι μετρημένα σε και
Κεφάλαιο 15 Κίνηση Κυµάτων. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 15 Κίνηση Κυµάτων Περιεχόµενα Κεφαλαίου 15 Χαρακτηριστικά των Κυµάτων Είδη κυµάτων: Διαµήκη και Εγκάρσια Μεταφορά ενέργειας µε κύµατα Μαθηµατική Περιγραφή της Διάδοσης κυµάτων Η Εξίσωση του Κύµατος
Κεφάλαιο 15 Κίνηση Κυµάτων Περιεχόµενα Κεφαλαίου 15 Χαρακτηριστικά των Κυµάτων Είδη κυµάτων: Διαµήκη και Εγκάρσια Μεταφορά ενέργειας µε κύµατα Μαθηµατική Περιγραφή της Διάδοσης κυµάτων Η Εξίσωση του Κύµατος
Πρόλογος. Κατάλογος Σχημάτων
 Περιεχόμενα Πρόλογος Κατάλογος Σχημάτων v xv 1 ΜΔΕ πρώτης τάξης 21 1.1 Γενικότητες........................... 21 1.2 Εισαγωγή............................ 24 1.2.1 Γεωμετρικές θεωρήσεις στο πρόβλημα της
Περιεχόμενα Πρόλογος Κατάλογος Σχημάτων v xv 1 ΜΔΕ πρώτης τάξης 21 1.1 Γενικότητες........................... 21 1.2 Εισαγωγή............................ 24 1.2.1 Γεωμετρικές θεωρήσεις στο πρόβλημα της
1 p p a y. , όπου H 1,2. u l, όπου l r p και u τυχαίο μοναδιαίο διάνυσμα. Δείξτε ότι μπορούν να γραφούν σε διανυσματική μορφή ως εξής.
 ΚΒΑΝΤΟΜΗΧΑΝΙΚΗ Ασκήσεις Κεφαλαίου V Άσκηση : Οι θεμελιώδεις σχέσεις μετάθεσης της στροφορμής επιτρέπουν την ύπαρξη ακέραιων και ημιπεριττών ιδιοτιμών Αλλά για την τροχιακή στροφορμή L r p γνωρίζουμε ότι
ΚΒΑΝΤΟΜΗΧΑΝΙΚΗ Ασκήσεις Κεφαλαίου V Άσκηση : Οι θεμελιώδεις σχέσεις μετάθεσης της στροφορμής επιτρέπουν την ύπαρξη ακέραιων και ημιπεριττών ιδιοτιμών Αλλά για την τροχιακή στροφορμή L r p γνωρίζουμε ότι
Φυσική Γ Θετ. και Τεχν/κης Κατ/σης ΚΥΜΑΤΑ ( )
 ΚΥΜΑΤΑ ( 2.1-2.2) Για τη δημιουργία ενός κύματος χρειάζονται η πηγή της διαταραχής ή πηγή του κύματος, δηλαδή η αιτία που θα προκαλέσει τη διαταραχή και ένα υλικό (μέσο) στο οποίο κάθε μόριο αλληλεπιδρά
ΚΥΜΑΤΑ ( 2.1-2.2) Για τη δημιουργία ενός κύματος χρειάζονται η πηγή της διαταραχής ή πηγή του κύματος, δηλαδή η αιτία που θα προκαλέσει τη διαταραχή και ένα υλικό (μέσο) στο οποίο κάθε μόριο αλληλεπιδρά
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ. Μια παράσταση που περιέχει πράξεις με μεταβλητές (γράμματα) και αριθμούς καλείται αλγεβρική, όπως για παράδειγμα η : 2x+3y-8
 ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
Μάθηµα Γραµµές Μεταφοράς Κυµατοδηγοί & Οπτικές Ίνες Καθ. Θωµάς Σφηκόπουλος
 Μάθηµα Γραµµές Μεταφοράς Κυµατοδηοί & Οπτικές Ίνες Καθ. Θωµάς Σφηκόπουλος Κυµατοδηοί - Μάθηµα 3ο -4ο ΘΝΙΚΟ & ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΠΙΣΤΜΙΟ ΑΘΝΩΝ Τοµέας πικοινωνιών και πεξερασίας Σήµατος Τµήµα Πληροφορικής
Μάθηµα Γραµµές Μεταφοράς Κυµατοδηοί & Οπτικές Ίνες Καθ. Θωµάς Σφηκόπουλος Κυµατοδηοί - Μάθηµα 3ο -4ο ΘΝΙΚΟ & ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΠΙΣΤΜΙΟ ΑΘΝΩΝ Τοµέας πικοινωνιών και πεξερασίας Σήµατος Τµήµα Πληροφορικής
ˆ ˆ. (τελεστής καταστροφής) (τελεστής δημιουργίας) Το δυναμικό του συστήματός μας (αρμονικός ταλαντωτής μέσα σε ομογενές ηλεκτρικό πεδίο) είναι
 ΜΟΝΟΔΙΑΣΤΑΤΟΣ ΑΡΜΟΝΙΚΟΣ ΤΑΛΑΝΤΩΤΗΣ ΜΕΣΕ ΣΕ ΟΜΟΓΕΝΕΣ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ: ΤΕΛΕΣΤΕΣ ΔΗΜΙΟΥΡΓΙΑΣ ΚΑΙ ΚΑΤΑΣΤΡΟΦΗΣ, ΒΑΣΙΚΗ ΚΑΤΑΣΤΑΣΗ, ΕΛΑΧΙΣΤΗ ΕΝΕΡΓΕΙΑ ΣΥΖΗΤΗΣΗ Ξεκινώντας από τους τελεστές δημιουργίας και καταστροφής
ΜΟΝΟΔΙΑΣΤΑΤΟΣ ΑΡΜΟΝΙΚΟΣ ΤΑΛΑΝΤΩΤΗΣ ΜΕΣΕ ΣΕ ΟΜΟΓΕΝΕΣ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ: ΤΕΛΕΣΤΕΣ ΔΗΜΙΟΥΡΓΙΑΣ ΚΑΙ ΚΑΤΑΣΤΡΟΦΗΣ, ΒΑΣΙΚΗ ΚΑΤΑΣΤΑΣΗ, ΕΛΑΧΙΣΤΗ ΕΝΕΡΓΕΙΑ ΣΥΖΗΤΗΣΗ Ξεκινώντας από τους τελεστές δημιουργίας και καταστροφής
Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο
 Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο Σύνοψη Στο κεφάλαιο αυτό παρουσιάζεται η ιδέα του συμπτωτικού πολυωνύμου, του πολυωνύμου, δηλαδή, που είναι του μικρότερου δυνατού βαθμού και που, για συγκεκριμένες,
Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο Σύνοψη Στο κεφάλαιο αυτό παρουσιάζεται η ιδέα του συμπτωτικού πολυωνύμου, του πολυωνύμου, δηλαδή, που είναι του μικρότερου δυνατού βαθμού και που, για συγκεκριμένες,
NTÙÍÉÏÓ ÃÊÏÕÔÓÉÁÓ - ÖÕÓÉÊÏÓ www.geocities.com/gutsi1 -- www.gutsias.gr
 Έστω µάζα m. Στη µάζα κάποια στιγµή ασκούνται δυο δυνάµεις. ( Βλ. σχήµα:) Ποιά η διεύθυνση και ποιά η φορά κίνησης της µάζας; F 1 F γ m F 2 ιατυπώστε αρχή επαλληλίας. M την της Ποιό φαινόµενο ονοµάζουµε
Έστω µάζα m. Στη µάζα κάποια στιγµή ασκούνται δυο δυνάµεις. ( Βλ. σχήµα:) Ποιά η διεύθυνση και ποιά η φορά κίνησης της µάζας; F 1 F γ m F 2 ιατυπώστε αρχή επαλληλίας. M την της Ποιό φαινόµενο ονοµάζουµε
Δίκτυα Τηλεπικοινωνιών. και Μετάδοσης
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Δίκτυα Τηλεπικοινωνιών και Μετάδοσης Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής & Δρ. Στυλιανός Π. Τσίτσος Επίκουρος Καθηγητής
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Δίκτυα Τηλεπικοινωνιών και Μετάδοσης Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής & Δρ. Στυλιανός Π. Τσίτσος Επίκουρος Καθηγητής
α. φ Α < φ Β, u A < 0 και u Β < 0. β. φ Α > φ Β, u A > 0 και u Β > 0. γ. φ Α < φ Β, u A > 0 και u Β < 0. δ. φ Α > φ Β, u A < 0 και u Β > 0.
 ΙΙΑΓΓΩΝΙΙΣΜΑ ΦΦΥΥΣΙΙΚΚΗΣ ΚΚΑΤΤΕΕΥΥΘΥΥΝΣΗΣ ΓΓ ΛΛΥΥΚΚΕΕΙΙΟΥΥ ΚΚυυρρι ιιαακκήή 1133 ΙΙααννοουυααρρί ίίοουυ 001133 Θέμα 1 ο (Μονάδες 5) 1. Στο σχήμα φαίνεται το στιγμιότυπο ενός εγκάρσιου αρμονικού κύματος
ΙΙΑΓΓΩΝΙΙΣΜΑ ΦΦΥΥΣΙΙΚΚΗΣ ΚΚΑΤΤΕΕΥΥΘΥΥΝΣΗΣ ΓΓ ΛΛΥΥΚΚΕΕΙΙΟΥΥ ΚΚυυρρι ιιαακκήή 1133 ΙΙααννοουυααρρί ίίοουυ 001133 Θέμα 1 ο (Μονάδες 5) 1. Στο σχήμα φαίνεται το στιγμιότυπο ενός εγκάρσιου αρμονικού κύματος
1ο Κεφάλαιο: Συστήματα
 ο Κεφάλαιο: Συστήματα Γραμμικά συστήματα i. Ποια εξίσωση λέγεται γραμμική; ii. Πως μεταβάλλεται η ευθεία y, 0 ή 0 για τις διάφορες τιμές των α,β,γ; iii. Τι ονομάζεται λύση μιας γραμμικής εξίσωσης; iv.
ο Κεφάλαιο: Συστήματα Γραμμικά συστήματα i. Ποια εξίσωση λέγεται γραμμική; ii. Πως μεταβάλλεται η ευθεία y, 0 ή 0 για τις διάφορες τιμές των α,β,γ; iii. Τι ονομάζεται λύση μιας γραμμικής εξίσωσης; iv.
ΠΡΑΓΜΑΤΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ
 1 ΚΕΦΑΛΑΙΟ 1 : ΠΡΑΓΜΑΤΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ 11 ΕΙΣΑΓΩΓΗ Σε ότι ακολουθεί συμβολίζουμε με το σύνολο των φυσικών αριθμών και με και R τα σύνολα των ακεραίων των ρητών και των πραγματικών αριθμών
1 ΚΕΦΑΛΑΙΟ 1 : ΠΡΑΓΜΑΤΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ 11 ΕΙΣΑΓΩΓΗ Σε ότι ακολουθεί συμβολίζουμε με το σύνολο των φυσικών αριθμών και με και R τα σύνολα των ακεραίων των ρητών και των πραγματικών αριθμών
Κλασική Ηλεκτροδυναμική Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΗΛΕΚΤΡΟΣΤΑΤΙΚΑ ΠΕΔΙΑ ΣΤΗΝ ΥΛΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΗΛΕΚΤΡΟΣΤΑΤΙΚΑ ΠΕΔΙΑ ΣΤΗΝ ΥΛΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΕΛΕΥΘΕΡΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 73
 ΕΛΕΥΘΕΡΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 73 ΚΕΦΑΛΑΙΟ 4 ΕΛΕΥΘΕΡΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 4.. Εισαγωγή Στο παρόν κεφάλαιο θα μελετηθούν οι ελεύθερες ταλαντώσεις συστημάτων που περιγράφονται
ΕΛΕΥΘΕΡΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 73 ΚΕΦΑΛΑΙΟ 4 ΕΛΕΥΘΕΡΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 4.. Εισαγωγή Στο παρόν κεφάλαιο θα μελετηθούν οι ελεύθερες ταλαντώσεις συστημάτων που περιγράφονται
V. Διαφορικός Λογισμός. math-gr
 V Διαφορικός Λογισμός Παντελής Μπουμπούλης, MSc, PhD σελ blospotcom, bouboulismyschr ΜΕΡΟΣ Η έννοια της Παραγώγου Α Ορισμός Εφαπτομένη καμπύλης συνάρτησης: Έστω μια συνάρτηση και A, ένα σημείο της C Αν
V Διαφορικός Λογισμός Παντελής Μπουμπούλης, MSc, PhD σελ blospotcom, bouboulismyschr ΜΕΡΟΣ Η έννοια της Παραγώγου Α Ορισμός Εφαπτομένη καμπύλης συνάρτησης: Έστω μια συνάρτηση και A, ένα σημείο της C Αν
Κεφάλαιο 0 Μιγαδικοί Αριθμοί
 Κεφάλαιο 0 Μιγαδικοί Αριθμοί 0 Βασικοί ορισμοί και πράξεις Είναι γνωστό ότι δεν υπάρχει πραγματικός αριθμός που επαληθεύει την εξίσωση x Η ανάγκη επίλυσης τέτοιων εξισώσεων οδηγεί στο σύνολο των μιγαδικών
Κεφάλαιο 0 Μιγαδικοί Αριθμοί 0 Βασικοί ορισμοί και πράξεις Είναι γνωστό ότι δεν υπάρχει πραγματικός αριθμός που επαληθεύει την εξίσωση x Η ανάγκη επίλυσης τέτοιων εξισώσεων οδηγεί στο σύνολο των μιγαδικών
ΠΡΟΣΟΧΗ : Nέα Ύλη για τις Κατατακτήριες από 2012 και μετά στην Φυσική Ι. Για το 3ο εξάμηνο. ΕΞΕΤΑΣΤΕΑ ΥΛΗ στο μάθημα ΦΥΣΙΚΗ Ι - ΜΗΧΑΝΙΚΗ
 ΠΡΟΣΟΧΗ : Nέα Ύλη για τις Κατατακτήριες από 2012 και μετά στην Φυσική Ι ΕΞΕΤΑΣΤΕΑ ΥΛΗ στο μάθημα ΦΥΣΙΚΗ Ι - ΜΗΧΑΝΙΚΗ 1. Κινηματική (ευθύγραμμη και καμπυλόγραμμη κίνηση) 2. Σχετική κίνηση-μετασχηματισμοί
ΠΡΟΣΟΧΗ : Nέα Ύλη για τις Κατατακτήριες από 2012 και μετά στην Φυσική Ι ΕΞΕΤΑΣΤΕΑ ΥΛΗ στο μάθημα ΦΥΣΙΚΗ Ι - ΜΗΧΑΝΙΚΗ 1. Κινηματική (ευθύγραμμη και καμπυλόγραμμη κίνηση) 2. Σχετική κίνηση-μετασχηματισμοί
Εφαρμοσμένη Οπτική. Γεωμετρική Οπτική
 Εφαρμοσμένη Οπτική Γεωμετρική Οπτική Κύρια σημεία του μαθήματος Η προσέγγιση της γεωμετρικής οπτικής Νόμοι της ανάκλασης και της διάθλασης Αρχή του Huygens Αρχή του Fermat Αρχή της αντιστρεψιμότητας (principle
Εφαρμοσμένη Οπτική Γεωμετρική Οπτική Κύρια σημεία του μαθήματος Η προσέγγιση της γεωμετρικής οπτικής Νόμοι της ανάκλασης και της διάθλασης Αρχή του Huygens Αρχή του Fermat Αρχή της αντιστρεψιμότητας (principle
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ. Φυσική των Laser ΔΙΑΔΟΣΗ ΗΜ ΚΥΜΑΤΩΝ ΣΕ ΟΠΤΙΚΑ ΜΕΣΑ. Διδάσκων : Επίκ. Καθ. Μ.
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Φυσική των Laser ΔΙΑΔΟΣΗ ΗΜ ΚΥΜΑΤΩΝ ΣΕ ΟΠΤΙΚΑ ΜΕΣΑ Διδάσκων : Επίκ. Καθ. Μ. Μπενής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Φυσική των Laser ΔΙΑΔΟΣΗ ΗΜ ΚΥΜΑΤΩΝ ΣΕ ΟΠΤΙΚΑ ΜΕΣΑ Διδάσκων : Επίκ. Καθ. Μ. Μπενής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΕΞΟΜΟΙΩΣΗ ΠΑΝΕΛΛΗΝΙΩΝ
 e- laboratory ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ http://users.dra.sch.gr/filplatakis ΟΝΟΜΑ ΕΞΟΜΟΙΩΣΗ ΠΑΝΕΛΛΗΝΙΩΝ ΚΥΡΙΑΚΗ 20 ΙΑΝΟΥΑΡΙΟΥ 2008 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΤΕΣΣΕΡΙΣ (4) ΘΕΜΑ
e- laboratory ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ http://users.dra.sch.gr/filplatakis ΟΝΟΜΑ ΕΞΟΜΟΙΩΣΗ ΠΑΝΕΛΛΗΝΙΩΝ ΚΥΡΙΑΚΗ 20 ΙΑΝΟΥΑΡΙΟΥ 2008 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΤΕΣΣΕΡΙΣ (4) ΘΕΜΑ
δ. έχουν πάντα την ίδια διεύθυνση.
 Διαγώνισμα ΦΥΣΙΚΗ Κ.Τ Γ ΛΥΚΕΙΟΥ ΖΗΤΗΜΑ 1 ον 1.. Σφαίρα, μάζας m 1, κινούμενη με ταχύτητα υ1, συγκρούεται μετωπικά και ελαστικά με ακίνητη σφαίρα μάζας m. Οι ταχύτητες των σφαιρών μετά την κρούση α. έχουν
Διαγώνισμα ΦΥΣΙΚΗ Κ.Τ Γ ΛΥΚΕΙΟΥ ΖΗΤΗΜΑ 1 ον 1.. Σφαίρα, μάζας m 1, κινούμενη με ταχύτητα υ1, συγκρούεται μετωπικά και ελαστικά με ακίνητη σφαίρα μάζας m. Οι ταχύτητες των σφαιρών μετά την κρούση α. έχουν
Όταν το ελατήριο έχει μάζα
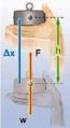 Όταν το ελατήριο έχει μάζα Εισαγωγή Αφορμή για την παρούσα ανάρτηση ήταν η θέση που διατύπωσε ο Γιάννης ο Κυριακόπουλος όσον αφορά στην συχνότητα ταλάντωσης ενός σώματος, το οποίο είναι δεμένο σε ελατήριο
Όταν το ελατήριο έχει μάζα Εισαγωγή Αφορμή για την παρούσα ανάρτηση ήταν η θέση που διατύπωσε ο Γιάννης ο Κυριακόπουλος όσον αφορά στην συχνότητα ταλάντωσης ενός σώματος, το οποίο είναι δεμένο σε ελατήριο
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΦΥΣΙΚΗ, Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΝΟΤΗΤΑ 1: ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ*
 ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΦΥΣΙΚΗ, Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΝΟΤΗΤΑ 1: ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ* διατυπώνουν τον ορισμό του μαγνητικού πεδίου διατυπώνουν και να εφαρμόζουν τον ορισμό της έντασης του μαγνητικού πεδίου διατυπώνουν
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΦΥΣΙΚΗ, Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΝΟΤΗΤΑ 1: ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ* διατυπώνουν τον ορισμό του μαγνητικού πεδίου διατυπώνουν και να εφαρμόζουν τον ορισμό της έντασης του μαγνητικού πεδίου διατυπώνουν
Βασικές Γνώσεις Μαθηματικών Α - Β Λυκείου
 Βασικές Γνώσεις Μαθηματικών Α - Β Λυκείου Αριθμοί 1. ΑΡΙΘΜΟΙ Σύνολο Φυσικών αριθμών: Σύνολο Ακέραιων αριθμών: Σύνολο Ρητών αριθμών: ακέραιοι με Άρρητοι αριθμοί: είναι οι μη ρητοί π.χ. Το σύνολο Πραγματικών
Βασικές Γνώσεις Μαθηματικών Α - Β Λυκείου Αριθμοί 1. ΑΡΙΘΜΟΙ Σύνολο Φυσικών αριθμών: Σύνολο Ακέραιων αριθμών: Σύνολο Ρητών αριθμών: ακέραιοι με Άρρητοι αριθμοί: είναι οι μη ρητοί π.χ. Το σύνολο Πραγματικών
Kεφάλαιο 4. Συστήματα διαφορικών εξισώσεων. F : : F = F r, όπου r xy
 4 Εισαγωγή Kεφάλαιο 4 Συστήματα διαφορικών εξισώσεων Εστω διανυσματικό πεδίο F : : F = Fr, όπου r x, και είναι η ταχύτητα στο σημείο πχ ενός ρευστού στο επίπεδο Εστω ότι ψάχνουμε τις τροχιές κίνησης των
4 Εισαγωγή Kεφάλαιο 4 Συστήματα διαφορικών εξισώσεων Εστω διανυσματικό πεδίο F : : F = Fr, όπου r x, και είναι η ταχύτητα στο σημείο πχ ενός ρευστού στο επίπεδο Εστω ότι ψάχνουμε τις τροχιές κίνησης των
ΗΜ & Διάδοση ΗΜ Κυμάτων
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΗΜ & Διάδοση ΗΜ Κυμάτων Ενότητα : Κυματική Εξίσωση & Επίπεδο ΗΜ Κύμα Σαββαΐδης Στυλιανός Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε. Άδειες
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΗΜ & Διάδοση ΗΜ Κυμάτων Ενότητα : Κυματική Εξίσωση & Επίπεδο ΗΜ Κύμα Σαββαΐδης Στυλιανός Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε. Άδειες
ΟΕΦΕ 2009 Γ' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΦΥΣΙΚΗ
 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 1 ΟΕΦΕ 2009 Γ' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΦΥΣΙΚΗ ΘΕΜΑ 1 Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράμμα που
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 1 ΟΕΦΕ 2009 Γ' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΦΥΣΙΚΗ ΘΕΜΑ 1 Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράμμα που
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Παραγώγιση Εισαγωγή Ορισμός 7. Αν y f x είναι μια συνάρτηση ορισμένη σε ένα διάστημα
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Παραγώγιση Εισαγωγή Ορισμός 7. Αν y f x είναι μια συνάρτηση ορισμένη σε ένα διάστημα
ΘΕΩΡΗΤΙΚΗ ΜΗΧΑΝΙΚΗ ΙΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΝΟΜΙΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΣΠΟΥΔΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΑΣΚΗΣΕΙΣ ΑΝΑΛΥΤΙΚΗΣ ΔΥΝΑΜΙΚΗΣ ( Μεθοδολογία- Παραδείγματα ) Κλεομένης Γ. Τσιγάνης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΝΟΜΙΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΣΠΟΥΔΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΑΣΚΗΣΕΙΣ ΑΝΑΛΥΤΙΚΗΣ ΔΥΝΑΜΙΚΗΣ ( Μεθοδολογία- Παραδείγματα ) Κλεομένης Γ. Τσιγάνης
ΚΕΦΑΛΑΙΟ 9 «Κυμάνσεις» Μαρία Κατσικίνη users.auth.gr/~katsiki
 ΚΕΦΑΛΑΙΟ 9 «Κυμάνσεις» Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Σχέση δύναμης - κίνησης Δύναμη σταθερή εφαρμόζεται σε σώμα Δύναμη ανάλογη της απομάκρυνσης (F-kx) εφαρμόζεται σε σώμα Το σώμα
ΚΕΦΑΛΑΙΟ 9 «Κυμάνσεις» Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Σχέση δύναμης - κίνησης Δύναμη σταθερή εφαρμόζεται σε σώμα Δύναμη ανάλογη της απομάκρυνσης (F-kx) εφαρμόζεται σε σώμα Το σώμα
ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης Γ Λυκείου ΓΡΑΠΤΕΣ ΔΟΚΙΜΑΣΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ 2009
 ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης Γ Λυκείου ΓΡΑΠΤΕΣ ΔΟΚΙΜΑΣΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ 009 Θέμα 1ο Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από
ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης Γ Λυκείου ΓΡΑΠΤΕΣ ΔΟΚΙΜΑΣΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ 009 Θέμα 1ο Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από
ΜΔΕ: Αναλυτικό πρόγραμμα - Ύλη Μαθήματος 2018
 1 ΚΕΦΑΛΑΙΟ 1 ΜΔΕ: Αναλυτικό πρόγραμμα - Ύλη Μαθήματος 2018 Αντικείμενο του μαθήματος είναι η μελέτη Μερικών Διαφορικών Εξισώσεων. Τον όρο Μερική Διαφορική Εξίσωση θα συμβολίζουμε με (ΜΔΕ). Η ιστοσελίδα
1 ΚΕΦΑΛΑΙΟ 1 ΜΔΕ: Αναλυτικό πρόγραμμα - Ύλη Μαθήματος 2018 Αντικείμενο του μαθήματος είναι η μελέτη Μερικών Διαφορικών Εξισώσεων. Τον όρο Μερική Διαφορική Εξίσωση θα συμβολίζουμε με (ΜΔΕ). Η ιστοσελίδα
