ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΤΟΥ ΦΟΙΤΗΤΗ ΤΟΥ ΤΜΗΜΑΤΟΣ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΗΣ ΠΟΛΥΤΕΧΝΙΚΗΣ ΣΧΟΛΗΣ ΤΟΥ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ
|
|
|
- Ἡρακλείδης Διδασκάλου
- 7 χρόνια πριν
- Προβολές:
Transcript
1 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ: ΣΥΣΤΗΜΑΤΩΝ ΚΑΙ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΕΡΓΑΣΤΗΡΙΟ: ΓΕΝΙΚΗΣ ΗΛΕΚΤΡΟΤΕΧΝΙΑΣ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΤΟΥ ΦΟΙΤΗΤΗ ΤΟΥ ΤΜΗΜΑΤΟΣ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΗΣ ΠΟΛΥΤΕΧΝΙΚΗΣ ΣΧΟΛΗΣ ΤΟΥ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΣΕΛΙΜΗ ΙΩΑΝΝΗ του ΚΩΝ/ΝΟΥ ΑΡΙΘΜΟΣ ΜΗΤΡΩΟΥ: 6083 ΘΕΜΑ «Η ΑΠΟΔΟΣΗ ΤΟΥ ΓΡΑΜΜΙΚΟΥ ΤΕΤΡΑΓΩΝΙΚΟΥ ΡΥΘΜΙΣΤΗ ΓΙΑ ΜΗ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ» ΕΠΙΒΛΕΠΩΝ ΚΟΥΣΟΥΛΑΣ ΝΙΚΟΛΑΟΣ - ΚΑΘΗΓΗΤΗΣ ΑΡΙΘΜΟΣ ΔΙΠΛΩΜΑΤΙΚΗΣ ΕΡΓΑΣΙΑΣ: ΠΑΤΡΑ, ΟΚΤΩΒΡΙΟΣ
2 2
3 ΠΙΣΤΟΠΟΙΗΣΗ Πιστοποιείται ότι η Διπλωματική Εργασία με θέμα: «Η ΑΠΟΔΟΣΗ ΤΟΥ ΓΡΑΜΜΙΚΟΥ ΤΕΤΡΑΓΩΝΙΚΟΥ ΡΥΘΜΙΣΤΗ ΓΙΑ ΜΗ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ» Του φοιτητή του Τμήματος Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών ΣΕΛΙΜΗ ΙΩΑΝΝΗ ΤΟΥ ΚΩΝ/ΝΟΥ ΑΡΙΘΜΟΣ ΜΗΤΡΩΟΥ: 6083 Παρουσιάστηκε δημόσια και εξετάστηκε στο Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών στις.../../ Ο Διευθυντής του Τομέα Κούσουλας Νικόλαος Καθηγητής Ο Επιβλέπων Κούσουλας Νικόλαος Καθηγητής 3
4 4
5 Αριθμός Διπλωματικής Εργασίας: Θέμα: «Η ΑΠΟΔΟΣΗ ΤΟΥ ΓΡΑΜΜΙΚΟΥ ΤΕΤΡΑΓΩΝΙΚΟΥ ΡΥΘΜΙΣΤΗ ΓΙΑ ΜΗ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ» Φοιτητής: Σελίμης Ιωάννης Επιβλέπων: Κούσουλας Νικόλαος Περίληψη Τα βασικά ερωτήματα που καλύπτονται στη διπλωματική αυτή είναι κατά πόσο ένα δυναμικό σύστημα είναι γραμμικό ή μη γραμμικό, και για την περίπτωση της μη γραμμικότητας, να κατανοηθεί τι σημαίνει να απέχει πολύ ή λίγο από τη γραμμικότητα. Επιπλέον, στην περίπτωση που μπορούμε να γραμμικοποιήσουμε ένα μοντέλο, κατά πόσο αυτό είναι καλό ή κακό, προκειμένου να προχωρήσουμε στο σχεδιασμό ενός ελεγκτή για να πετύχουμε την επιθυμητή συμπεριφορά. Σχετικά με το σχεδιασμό του ελεγκτή, εξετάζονται διάφορα παραδείγματα μη γραμμικών συστημάτων με την LQR και LQG και γίνονται συγκρίσεις όσον αφορά το αποτέλεσμα ελέγχου σε αυτές. 5
6 6
7 Περίληψη Τα βασικά ερωτήματα που καλύπτονται στη διπλωματική αυτή είναι κατά πόσο ένα δυναμικό σύστημα είναι γραμμικό ή μη γραμμικό, και για την περίπτωση της μη γραμμικότητας, να κατανοηθεί τι σημαίνει να απέχει πολύ ή λίγο από τη γραμμικότητα. Επιπλέον, στην περίπτωση που μπορούμε να γραμμικοποιήσουμε ένα μοντέλο, κατά πόσο αυτό είναι καλό ή κακό, προκειμένου να προχωρήσουμε στο σχεδιασμό ενός ελεγκτή για να πετύχουμε την επιθυμητή συμπεριφορά. Σχετικά με το σχεδιασμό του ελεγκτή, εξετάζονται διάφορα παραδείγματα μη γραμμικών συστημάτων με την LQR και LQG και γίνονται συγκρίσεις όσον αφορά το αποτέλεσμα ελέγχου σε αυτές. Πιο συγκεκριμένα, στο κεφάλαιο 1 γίνεται μια εισαγωγή στα μαθηματικά μοντέλα και τη διαδικασία σχεδιασμού ελέγχου, καθώς και την αξιολόγηση της μη γραμμικότητας και την εφαρμογή γραμμικού ελέγχου σε μη γραμμικά συστήματα. Στη συνέχεια, στο κεφάλαιο 2, γίνεται μια αναφορά σχετικά με τη συμπεριφορά των δυναμικών συστημάτων στο χώρο κατάστασης και στη συνέχεια μια εισαγωγή στα είδη συνδέσεων των σύνθετων συστημάτων (σειριακές, παράλληλες συνδέσεις κλπ). Επιπρόσθετα, προσεγγίσεις μικρού γραμμικού κέρδους για έλεγχο μη γραμμικών συστημάτων με ανάπτυξη συγκεκριμένων θεωρημάτων, όπως αυτά προκύπτουν από τη θεωρία και παρουσιάζονται στο κεφάλαιο 3. Το πρακτικό μέρος με ανάπτυξη κώδικα με λογισμικό MATLAB παρουσιάζεται στο κεφάλαιο 4, όπου αναπτύσσονται LQR και LQG σε μη γραμμικά συστήματα, βασισμένα στις τεχνικές βέλτιστου ελέγχου. Στα παραδείγματα που αναπτύσσονται, γίνονται συγκρίσεις μεταξύ των αποτελεσμάτων που δίνει ο σχεδιασμός αυτών των ελεγκτών και γίνεται μια προσπάθεια να συσχετιστούν οι ελεγκτές αυτοί με ένα πραγματικό σύστημα και να καταγραφούν τα αποτελέσματα. Τα αποτελέσματα του σχεδιασμού των ελεγκτών σε μη γραμμικά συστήματα, επιβεβαίωσαν τα θεωρητικά αναμενόμενα αποτελέσματα. Επιπρόσθετα, παραδείγματα εφαρμογής των παραπάνω ελεγκτών παρουσιάζονται στο τέλος του κεφαλαίου σε διάφορες βιομηχανικές εφαρμογές, τονίζοντας τη σημαντικότητα και τη συνεισφορά των συγκεκριμένων τεχνικών ελέγχου. 7
8 Abstract The subject of this thesis is nonlinear systems; Given a dynamic system we examine whether it is nonlinear or not, and in the case of non-linearity, how highly nonlinear the system is. It also checks the linearization of nonlinear systems and how close the linearized model is to the original, in order to proceed to the design of a control scheme based on the linear model. LQR and LQG control schemes were implemented and compared on the initial nonlinear model. 8
9 ΠΕΡΙΕΧΟΜΕΝΑ 1 Εισαγωγή Εισαγωγικές έννοιες Μαθηματικά μοντέλα και σχεδιασμός ελέγχου Βασικά ερωτήματα Αξιολόγηση μη γραμμικότητας Γραμμικά Μοντέλα για μη γραμμικά συστήματα Αξιολόγηση τεχνικής ελέγχου σχετικά με τη μη γραμμικότητα Γραμμικός Έλεγχος Μη Γραμμικών Συστημάτων Κεφάλαιο Μέτρα μη γραμμικοτήτων και Γραμμικά Μοντέλα για Μη Γραμμικά Συστήματα Συστήματα χωρίς μνήμη και συμπεριφορά δυναμικών συστημάτων στο χώρο κατάστασης Συμπεριφορά των Δυναμικών Συστημάτων Σύνθετα Συστήματα Παράλληλες συνδέσεις Σειριακές συνδέσεις, Hammerstein και Wiener συστήματα Διασύνδεση Feedback Κεφάλαιο Μια προσέγγιση μικρού κέρδους για γραμμικό έλεγχο μη γραμμικών συστημάτων Αρχές σθεναρού ελέγχου Σταθερότητα Μη Γραμμικών Συστημάτων με Γραμμικούς Ελεγκτές Θεώρημα Θεώρημα Θεώρημα Θεώρημα Θεώρημα Θεώρημα Θεώρημα Θεώρημα Θεώρημα
10 Θεώρημα Σχεδιασμός σθεναρού ελεγκτή με εγγυημένη Lp-απόδοση Σχέσεις με Γραμμική Σταθεροποίηση Μη Γραμμικών Συστημάτων με χρήση του Μετρικού Χάσματος Συμπεράσματα Kεφάλαιο Έλεγχος με Πλήρη Ανατροφοδότηση Καταστάσεων Γραμμικοποίηση συστήματος ο Θεώρημα Lyapunov Τοποθέτηση Πόλων Βέλτιστος Έλεγχος Linear Quadratic Regulator-LQR Γραμμικός τετραγωνικός Γκαουσιανός έλεγχος (LQG) Παρατηρητές πλήρους κατάστασης Αρχή της διαχωρισιμότητας LQG estimation Βέλτιστος Κέρδος LQ η ΕΦΑΡΜΟΓΗ η ΕΦΑΡΜΟΓΗ η ΕΦΑΡΜΟΓΗ η ΕΦΑΡΜΟΓΗ: LQG & LQR ΣΥΓΚΡΙΣΗ Παρατηρήσεις Εφαρμογές-παραδείγματα LQR-LQG ελεγκτών στη βιομηχανία Κεφάλαιο Συμπεράσματα Μελλοντική έρευνα Παράρτημα Βιβλιογραφία
11 1 Εισαγωγή Ο γραμμικός έλεγχος μπορεί να είναι πιο αποτελεσματικός για τον έλεγχο μιας μη γραμμικής διαδικασίας, επειδή οι γραμμικές τεχνικές σχεδιασμού διευκολύνουν σε μεγάλο βαθμό τη διαδικασία σχεδιασμού και ελέγχου, διότι οι γραμμικοί ελεγκτές επιβάλουν λιγότερες απαιτήσεις σχετικά με την υλοποίηση και λειτουργία, σε σύγκριση με μη γραμμικούς ελεγκτές. Συνεπώς, είναι μια δελεαστική ιδέα να χρησιμοποιήσουμε γραμμικά μοντέλα και γραμμικές μεθόδους σχεδιασμού ελεγκτών, ακόμα και για τα μη γραμμικά συστήματα. Είναι, για παράδειγμα, κοινή πρακτική στη μηχανική ελέγχου να χρησιμοποιούμε μοντέλα που προέρχονται από Jacobiγραμμικοποίηση ( δηλαδή Taylor σειρά πρώτης τάξης που προσεγγίζεται από τις εξισώσεις στο χώρο κατάστασης), αντί πλήρους τάξης μη γραμμικά μοντέλα. Ωστόσο, προκειμένου να εγγυηθούμε την καταλληλότητα ενός γραμμικού μοντέλου ή την εύρυθμη λειτουργία ενός γραμμικού ελεγκτή στην παρουσία της αναντιστοιχίας ενός μοντέλου που προέκυψε από γραμμικοποίηση, απαιτείται μια αυστηρή αιτιολόγηση. Στην προκειμένη διπλωματική εργασία, θα μας απασχολήσει ένα γενικό πλαίσιο για το σχεδιασμό γραμμικών ελεγκτών για μη γραμμικά συστήματα που βασίζονται σε γραμμικά μοντέλα (έπειτα από τη διαδικασία της γραμμικοποίησης), που θα εγγυάται τη σταθερότητα και για το κλειστό μη γραμμικό σύστημα. Ο τρόπος για να ασχοληθεί κανείς με ένα μοντέλο σε μια καθαρά γραμμική ρύθμιση είναι πολύ καλά γνωστή από την θεωρία του σθεναρού ελέγχου. Η σθεναρή σταθερότητα μπορεί να εξασφαλιστεί εάν το κέρδος του σφάλματος της μοντελοποίησης ικανοποιεί ένα ορισμένο εύρος. Αυτό το μικρό κέρδος εξακολουθεί να ισχύει στην περίπτωση ενός μη γραμμικού μοντέλου που διαμορφώνεται από ένα γραμμικό 11
12 μοντέλο. Ωστόσο, το μικρό αυτό κέρδος απαιτεί ένα ευρύ φάσμα των κερδών του σφάλματος μοντελοποίησης. Επιπλέον, αυτό το εύρος πρέπει να είναι αρκετά μικρό, ώστε να αποδειχθεί η σταθερότητα. Οι απαιτήσεις αυτές είναι συχνά υπερβολικές για να ικανοποιηθούν στη γενική περίπτωση μη γραμμικών συστημάτων. Για να αποφευχθεί ο συντηρητισμός που συνδέεται με την ευρεία ανάλυση, η προσέγγιση αυτή παρουσιάζει ως εκ τούτου τη χρήση των κερδών πάνω από σύνολα, ώστε να είναι σε θέση να προβεί σε ανάλυση και σύνθεση σε μια καθορισμένη περιοχή λειτουργίας. Όσον αφορά στην εισαγωγή των κερδών πάνω στη θεωρία συνόλων, ένα φίλτρο εισάγεται στο μοντέλο ή στον ελεγκτή ανάλογα με την εφαρμογή. Ο σχεδιασμός ελεγκτή για μη γραμμικά συστήματα συνεπώς μειώνεται στο σχεδιασμό των ελεγκτών για γραμμικά συστήματα με φίλτρα. Πριν από το σχεδιασμό του ελεγκτή, ένα γραμμικό μοντέλο και το το σφάλμα πρέπει να προσδιορίζονται. Ενώ η γραμμικοποίηση είναι μια κοινή επιλογή για να φτιάξουμε ένα γραμμικό μοντέλο από ένα μη γραμμικό σύστημα, δε χρειάζεται να είναι η καλύτερη επιλογή για συγκεκριμένη περιοχή λειτουργίας. Στην πραγματικότητα, υπάρχουν καταστάσεις στις οποίες άλλα γραμμικά μοντέλα έχουν αποδειχθεί ότι είναι καλύτερα για το σχεδιασμό ελεγκτή από ό, τι το μοντέλο που μας δίνει η γραμμικοποίηση. Αυτό συμβαίνει, γιατί για να κάνουμε γραμμικοποίηση θέτουμε κάποιες προϋποθέσεις που πρέπει να ισχύουν γύρω από μια περιοχή (πχ γύρω από το σημείο ισορροπίας). Συνεπώς, είναι ενδιαφέρον να ψάξει κανείς για το καλύτερο γραμμικό μοντέλο ενός μη γραμμικού συστήματος, που χαρακτηρίζεται από ένα ελάχιστο σφάλμα μοντελοποίησης. Το ελάχιστο αυτό σφάλμα μοντελοποίησης μετρά την ίδια στιγμή τη διαφορά μεταξύ των μη γραμμικών συστημάτων και το σύνολο των γραμμικών συστημάτων, και έτσι παρέχεται ένας τρόπος για να εκτιμηθεί η έκταση της γραμμικότητας του μοντέλου. 12
13 Το σφάλμα μοντελοποίησης επιτρέπει: (i) την αξιολόγηση της ποιότητας ενός συγκεκριμένου γραμμικού μοντέλου, (ii) την άντληση ενός καλύτερου γραμμικού μοντέλου που ελαχιστοποιεί το σφάλμα μοντελοποίησης, και (iii) τη χρήση του σφάλματος μοντελοποίησης του καλύτερου συστήματος ως μέτρο της γραμμικότητας του συστήματος, δεδομένου ότι υπάρχουν διαφορετικοί τρόποι για να καθορίσουν ένα σφάλμα μοντελοποίησης, όπως ένα πρόσθετο σφάλμα, ή πολλαπλά λάθη κατά την είσοδο ή έξοδο, κλπ. 1.1 Εισαγωγικές έννοιες Σε πολλές πρακτικές εφαρμογές, τα μη γραμμικά συστήματα περιγράφονται με εξισώσεις στο χώρο κατάστασης, και θα εστιάσουμε στις ιδιότητες των συστημάτων εισόδου-εξόδου όπου είναι κατάλληλο. Τις περισσότερες φορές, θα θεωρούμε τα γενικά συστήματα P:U Y από ένα σήμα του χώρου U σε ένα άλλο σήμα χώρου Y. Επίσης, θα θεωρήσουμε ότι P0 = 0. Συμβολίζουμε με m τον αριθμό εισόδων, με n τον αριθμό εξόδων και με z τον αριθμό των διανυσμάτων κατάστασης. Η θεωρία της απαγωγής παρέχει έναν τύπο προκειμένου να συσχετίσουμε τις ιδιότητες εισόδου-εξόδου των μη γραμμικών συστημάτων κατά την αναπαράστασή τους στο χώρο κατάστασης (εάν αυτό υπάρχει): x( t) f ( x( t), u( t)) y( t) h( x( t), u( t)) θεωρώντας μηδενικές αρχικές καταστάσεις χωρίς βλάβη της γενικότητας. Για ένα σύστημα που δίνεται σε μορφή εξισώσεων του χώρου κατάστασης,το πεπερασμένο κέρδος μπορεί να χαρακτηριστεί μέσω ανισοτήτων της απαγωγής για t <. 13
14 Ως βασικό εργαλείο, χρησιμοποιούμε τη θεωρία της σκέδασης (dissipativity theory) η οποία παρέχει το πλαίσιο για την ανάλυση και το σχεδιασμό συστημάτων ελέγχου χρησιμοποιώντας μια περιγραφή εισόδων-εξόδων. Πιο συγκεκριμένα, η περιγραφή εισόδων εξόδων επιτρέπει μια προσέγγιση με βάση ξεχωριστές μονάδες στην ανάλυση και τον σχεδιασμό συστημάτων ελέγχου. 1.2 Μαθηματικά μοντέλα και σχεδιασμός ελέγχου Τα μαθηματικά μοντέλα των συστημάτων μπορούν να περιγράψουν και να εξηγήσουν φαινομενολογικές παρατηρήσεις με ένα δομημένο και γενικό τρόπο. Τα μοντέλα διαδραματίζουν θεμελιώδη ρόλο στον τομέα της επιστήμης, επειδή επιτρέπουν να προβλέψουμε φυσικά φαινόμενα και να σχεδιάσουμε τεχνητούς μηχανισμούς. Ένα μοντέλο θεωρείται ότι είναι ένα καλό μοντέλο, εάν επιτρέπει να περιγράψει πειράματα και φαινομενολογικά δεδομένα επαρκώς. Στον έλεγχο, ο σχεδιασμός και η λειτουργία των τεχνικών συστημάτων διευκολύνεται σε μεγάλο βαθμό από τη χρήση μοντέλων. Ειδικά η τήρηση των κανόνων ασφαλείας και οι προδιαγραφές της απόδοσης μπορεί να είναι εγγυημένες με βάση το μοντέλο που ακολουθούμε στην ανάλυση και τις τεχνικές σχεδιασμού. Έτσι, τα μαθηματικά μοντέλα παίζουν σημαντικό ρόλο στη μηχανική συστημάτων, και καταβάλλεται πολύ προσπάθεια για την ανάλυση των μοντέλων των τεχνικών συστημάτων, καθώς επίσης και στον σχεδιασμό τεχνικών που δημιουργούμε τα μοντέλα αυτά. Μια σημαντική ιδιότητα των μαθηματικών μοντέλων των δυναμικών συστημάτων είναι η γραμμικότητα. Εξαιτίας της σχετικά απλής δομής των γραμμικών συστημάτων, για πολλά προβλήματα ελέγχου υπάρχουν διαθέσιμες μέθοδοι που θεωρητικά ακούγονται καλές, καθώς και στην πράξη εφαρμόζονται. Λόγω της ποικιλίας και της σύνθετης συμπεριφοράς μη γραμμικών συστημάτων, εργαλεία για τη μη γραμμική ανάλυση συστημάτων και το σχεδιασμό αντίστοιχων ελεγκτών εμφανίζουν πολύ χαμηλότερο 14
15 επίπεδο αποδοτικότητας. Για να αντιμετωπιστεί η μη γραμμική ανάλυση στα προβλήματα ελέγχου, υπάρχουν δύο εναλλακτικές προσεγγίσεις. Για τα εξαιρετικά μη γραμμικά συστήματα, κάποιες ειδικές μέθοδοι πρέπει να αναπτυχθούν που ενδεχομένως βασίζονται σε ορισμένες φυσικές ιδιότητες της εφαρμογής ή ενδεχομένως σε μαθηματικές ιδιότητες μιας συγκεκριμένης κατηγορίας συστημάτων, όπως μέθοδοι που βασίζονται στην μεταβολή ενέργειας για συστήματα μηχανικού ελέγχου και στη γραμμικοποίηση με χρήση ανάδρασης. Για ελαφρώς μη γραμμικά προβλήματα, μπορεί κανείς να επιχειρήσει να χρησιμοποιήσει τα αντίστοιχα γραμμικά μοντέλα και γραμμικές μεθόδους σχεδιασμού ελεγκτή. Ωστόσο, αυτή η τελευταία προσέγγιση απαιτεί μια αυστηρή αιτιολόγηση, ώστε να εγγυάται την ακρίβεια ενός γραμμικού μοντέλου ή την ορθή λειτουργία ενός γραμμικού ελεγκτή στην παρουσία της μη γραμμικής συμπεριφοράς του συστήματος για το οποίο σχεδιάστηκε. 1.3 Βασικά ερωτήματα Τα βασικά ερωτήματα που πρέπει να καλύψουμε στη διπλωματική αυτή είναι κατά πόσο ένα δεδομένο δυναμικό σύστημα είναι γραμμικό ή μη γραμμικό, και για την περίπτωση της μη γραμμικότητας, να κατανοήσουμε τι σημαίνει να απέχει πολύ ή λίγο από τη γραμμικότητα. Επιπλέον, στην περίπτωση που μπορούμε να γραμμικοποιήσουμε ένα μοντέλο, κατά πόσο αυτό είναι καλό ή κακό, προκειμένου να προχωρήσουμε στο σχεδιασμό ενός ελεγκτή για να πετύχουμε την επιθυμητή συμπεριφορά. Τέλος, όσον αφορά το σχεδιασμό του ελεγκτή, να μπορούμε να εξετάσουμε αν επαρκεί ο σχεδιασμός ενός γραμμικού ελεγκτή για ένα μη γραμμικό σύστημα ή αν πρέπει να καταφύγουμε σε μη γραμμικές τεχνικές σχεδιασμού ενός ελεγκτή. Παρακάτω αναλύουμε τα ερωτήματα αυτά ανά τομέα έτσι ώστε να κατανοήσουμε αρχικά τη φύση τους. 1.4 Αξιολόγηση μη γραμμικότητας Η γραμμικότητα είναι μια καθορισμένη ιδιότητα που χαρακτηρίζεται από τις αρχές της υπέρθεσης και της ομοιογένειας. Εάν αυτές οι αρχές ικανοποιούνται από την συμπεριφορά της εισόδου-εξόδου του δυναμικού συστήματος, ή, 15
16 ακριβέστερα, του μοντέλου του δυναμικού συστήματος, τότε το σύστημα (μοντέλο) θεωρείται γραμμικό. Διαφορετικά λέγεται μη γραμμικό. Εάν ένα μαθηματικό μοντέλο ενός δυναμικού συστήματος δίνεται, η γραμμικότητα μπορεί να ελεγχθεί με τις εξισώσεις του μοντέλου. Για τα συστήματα στο χώρο κατάστασης, η γραμμικότητα μπορεί να είναι ένα θέμα παρουσίασης, και φαινομενικά μη γραμμικά συστήματα μπορούν υπό ορισμένες προϋποθέσεις, να έρθουν σε μια γραμμική μορφή με χρήση κατάλληλων μετασχηματισμών. Εάν δεν υπάρχει λεπτομερές μαθηματικό μοντέλο, τα δεδομένα των μετρήσεων μπορούν να χρησιμοποιηθούν για να αξιολογηθεί κατά πόσον η συμπεριφορά εισόδου-εξόδου μιας διεργασίας είναι γραμμική ή μη γραμμική, δηλαδή αν ένα γραμμικό μοντέλο της διαδικασίας μπορεί να χρησιμοποιηθεί ή όχι. Αν και ο αυστηρός μαθηματικός ορισμός της γραμμικότητας είναι μια καθορισμένη ιδιότητα σωστό- λάθος, μερικές φορές είναι ενδιαφέρον να αναρωτηθούμε αν ένα σύστημα είναι "κοντά στο γραμμικό" ή "μακριά από το γραμμικό". Στη θεωρία του ελέγχου, είναι γνωστό ότι η ανάδραση συμβάλει επίδραση της γραμμικότητας της ελεγχόμενης διαδικασίας.για να είναι σε θέση να αποδειχθεί το γεγονός αυτό σε ένα θεωρητικό πλαίσιο, οι Desoer και Wang εισήγαγαν την ποσότητα: U N inf sup Nu Gu Gg u U σαν μέτρο της μη γραμμικότητας. Ο αριθμός αυτός ποσοτικοποιεί την απόκλιση της συμπεριφοράς ενός συστήματος από τη γραμμικότητα. Στον ορισμό αυτό, το Ν είναι το μη γραμμικό σύστημα υπό εξέταση, το U συμβολίζει το σύνολο των εξεταζόμενων σημάτων εισόδου, και G είναι το σύνολο της σταθερότητας των γραμμικών συστημάτων. Επίσης, ένα δεύτερο μέτρο μπορεί να υπολογιστεί, όπου η παραπάνω ποσότητα κανονικοποιείται από τη νόρμα της εισόδου, U N Nu Gu inf sup Gg u U u 16
17 Το δεύτερο αυτό μέτρο αντιπροσωπεύει το κέρδος του συστήματος που έχει ως αποτέλεσμα τη διαφορά σφάλματος μεταξύ της εξόδου του μη γραμμικού Β συστήματος και ενός γραμμικού μοντέλου G, όπου το G θα επιλεγεί έτσι ώστε να ελαχιστοποιηθεί αυτό το κέρδος. Είναι σημαντικό να σημειωθεί ότι όλα τα μέτρα για τη μη γραμμικότητα που έχουν εξετασθεί είναι μόνο για σταθερά χρονικά συστήματα. Στη μελέτη της μη γραμμικότητας δύο χαρακτηριστικά είναι υψηλής σημασίας: 1. Η προσέγγιση εισόδων-εξόδων παρέχει μια πολύ γενική ρύθμιση για δυναμική μοντελοποίηση των συστημάτων και τον έλεγχο. 2. Η ανάλυση και σύνθεση των μη γραμμικών συστημάτων γίνεται με ένα μη-καθολικό τρόπο. 1.5 Γραμμικά Μοντέλα για μη γραμμικά συστήματα Στο σημείο αυτό δεν ζητάμε απλώς να αξιολογηθεί ο βαθμός της γραμμικότητας, αλλά ζητάμε ένα καλό (ή το καλύτερο δυνατό) γραμμικό μοντέλο για ένα μη γραμμικό σύστημα. Φυσικά υπάρχει ισχυρός δεσμός μεταξύ της αξιολόγησης της γραμμικότητας και της γραμμικής μοντελοποίησης για τα μη γραμμικά συστήματα. Στην πραγματικότητα, το κέρδος με βάση τα μέτρα γραμμικότητας που συζητήθηκαν παραπάνω έχουν ποσοτικοποιηθεί ακριβώς με τη διαφορά μεταξύ των μη γραμμικών συστημάτων και ενός καλύτερου γραμμικού μοντέλου. Αλλά πριν αναλύσουμε αυτή τη σχέση με λεπτομέρεια, είναι σημαντικό να καταστεί το πεδίο του ενδιαφέροντος μας να είναι πιο ακριβές. Σχεδόν όλα τα μέτρα που συζητήθηκαν για τη γραμμικότητα απαιτούν λεπτομερές μη γραμμικό μοντέλο αναφοράς. Παρά το γεγονός ότι μερικά από αυτά μπορεί κατ 'αρχήν, να χρησιμοποιηθούν αποκλειστικά και μόνο με βάση σε στοιχεία της διαδικασίας, δεν είναι ειδικά προσαρμοσμένα σε προβλήματα που εμφανίζονται συνήθως στην αναγνώριση και στην πράξη, όπως ο θόρυβος μέτρησης, ο περιορισμένος αριθμός των πειραμάτων, για παράδειγμα λόγω των μεγάλων χρονικών περιορισμών, ή την ανάγκη για διαδικασία φιλική προς τις εισόδους προσομοίωσης. 17
18 Ως εκ τούτου, το ζήτημα της γραμμικής τεχνικής μοντελοποίησης για μη γραμμικά συστήματα μπορεί να χωριστεί σε δύο κατηγορίες. Η πρώτη τάξη των τεχνικών λύνει το πρόβλημα της αναγνώρισης των γραμμικών μοντέλων, δηλαδή το πρόβλημα του απευθείας καθορισμού ενός γραμμικού μοντέλου από την επεξεργασία δεδομένων και την ίδια στιγμή προκύπτει ένα μέτρο της ποιότητας ή ένα όριο εμπιστοσύνης για το μοντέλο. Το δεύτερο είδος των τεχνικών βοηθά στο να αποκομίσουμε ένα απλουστευμένο γραμμικό μοντέλο από ένα λεπτομερές γραμμικό μοντέλο αναφοράς, και μπορεί να περιγραφεί με τον όρο μείωσης της πολυπλοκότητας του μοντέλου. Και τα δύο θέματα έχουν προκαλέσει μεγάλο ενδιαφέρον κατά την τελευταία εικοσαετία. Τα μέτρα για τη μη γραμμικότητα που βασίζονται επί των κερδών του συστήματος είναι πολύ λεπτά. Πράγματι, το δεύτερο μέτρο γραμμικότητας από Desoer και Wang αντιστοιχεί στην απόσταση μεταξύ των μη γραμμικών Ν συστημάτων υπό εξέταση και μια καλύτερη γραμμική προσέγγιση G * ορίζεται από: U Nu G * u Nu Gu sup N inf sup uu u Gg uu u Αντί να εξετάζει το καλύτερο γραμμικό μοντέλο G *, η έκφραση Nu Gu NG sup uu u μπορεί να χρησιμοποιηθεί για την αξιολόγηση της ποιότητας, για κάθε μοντέλο G. Η έκφραση της νόρμας N G αντιστοιχεί στο κέρδος (άμεσα ή έμμεσα κανόνας) του συστήματος με σφάλμα: E N G. Όλες οι μέθοδοι για την εξαγωγή γραμμικών μοντέλων από τα μη γραμμικά συστήματα βασίζονται σε πρότυπα του σήματος. Το σφάλμα εξόδου e = Nu Gu μεταξύ του μη γραμμικού συστήματος και του γραμμικού μοντέλου του είναι, είτε ένα μέτρο της ποιότητας μοντέλου, ή χρησιμοποιείται για να ορίσει ένα εσωτερικό στοιχείο, ή μια νόρμα για τους τελεστές. Μέχρι στιγμής, η γραμμικότητα θεωρήθηκε σαν μια ιδιότητα του συστήματος, και τα 18
19 αποτελέσματα σε καλά μοντέλα για τα μη γραμμικά συστήματα από φέρουν ένα μικρό σφάλμα πρόβλεψης που αξιολογείται. Στη συνέχεια θέλουμε να αντιμετωπιστεί το ζήτημα αν η εκτίμηση της μη γραμμικότητας ενός συστήματος μπορεί να δώσει μια ιδέα για την εφαρμογή και την καταλληλότητα των γραμμικών τεχνικών ελέγχου. 1.6 Αξιολόγηση τεχνικής ελέγχου σχετικά με τη μη γραμμικότητα Έχει αναγνωριστεί στη βιβλιογραφία ότι, εκτός από παράγοντες όπως η δυναμική της τάξης και αλληλεπίδρασης, η διαδικασία της μη γραμμικότητας είναι ένας από τους κυριότερους παράγοντες που καθορίζουν τη δυσκολία σε ένα πρόβλημα ελέγχου. Σε ένα βιομηχανικό πλαίσιο, κάποιος προσπαθεί να αποφύγει τη μη γραμμική σχεδίαση ελεγκτή γιατί απαιτεί περισσότερο ανθρώπινο δυναμικό και γνώσεις της αναπτυξιακής διαδικασίας και μπορεί να χρειάζεται πιο περίπλοκη διαδικασία (και ως εκ τούτου πιο ακριβό υλικό) και μπορεί να συνεπάγεται υψηλές απαιτήσεις από τους φορείς κατά το στάδιο της υλοποίησης αλλά και της λειτουργίας. Πιο συγκεκριμένα, κάποιος θέλει να μάθει εάν ο γραμμικός σχεδιασμός των ελεγκτών είναι κατάλληλος παρά τη μη γραμμική συμπεριφορά της διαδικασίας. Ο σκοπός του ελέγχου που ενδιαφέρει την εκτίμηση γραμμικότητας είναι να εκτιμήσει κατά πόσο ο γραμμικός έλεγχος είναι επαρκής σε σχέση με την σταθερότητα και την συμπεριφορά του κλειστού βρόχου. Επειδή η συμπεριφορά κλειστού βρόχου είναι πολύ δύσκολο να εκτιμηθεί, πολλοί συγγραφείς αντιμετωπίζουν το πρόβλημα έμμεσα από την εκτίμηση της γραμμικότητας του κατάλληλου ελεγκτή. Η αξιολόγηση σχετικά με τον έλεγχο για μη γραμμικότητα γίνεται για να αποφευχθεί ο άσκοπος σχεδιασμός μη γραμμικών ελεγκτών και έτσι ένας πρωταρχικός στόχος έρχεται στο συμπεράσματα χωρίς να χρειάζεται να σχεδιάσουμε ένα μη γραμμικό ελεγκτή. Στην εργασία αυτή, μας ενδιαφέρει περισσότερο ο τρόπος με τον οποίο ένας γραμμικός ελεγκτής μπορεί πραγματικά να χρησιμοποιηθεί για ένα μη γραμμικό σύστημα σε σχέση με το θεωρητικό κέρδος απόδοσης με τη χρήση 19
20 μη γραμμικών ελεγκτών. Το θέμα της αξιολόγησης του ελέγχου σχετικά με τη γραμμικότητα ως τέτοια εκ τούτου, θα εμφανίζονται από πλευρά σε πλευρά. 1.7 Γραμμικός Έλεγχος Μη Γραμμικών Συστημάτων Αν η αξιολόγηση του έλεγχου σχετικά με τη μη γραμμικότητα δείχνει ότι ο γραμμικός έλεγχος είναι επαρκής, το επόμενο βήμα είναι να σχεδιάσουμε ένα γραμμικό ελεγκτή για το μη γραμμικό σύστημα. Για να επωφεληθούμε από την προηγούμενη ανάλυση για τη μη γραμμικότητα, η διαδικασία σχεδιασμού του ελεγκτή θα πρέπει να πληρεί δύο κριτήρια: Πρώτον, ο σχεδιασμός του ελεγκτή μη γραμμικού συστήματος δεν θα πρέπει να εμπλακεί περισσότερο από ό, τι ο σχεδιασμός του ελεγκτή για ένα γραμμικό σύστημα. Θα πρέπει τουλάχιστον να είναι πολύ πιο εύκολο από ό, τι ένας πλήρης σχεδιασμός μη γραμμικού ελεγκτή, επειδή μια μη γραμμική σχεδίαση ελεγκτή είναι αυτό που θέλουμε να αποφύγουμε. Δεύτερον, η διαδικασία του σχεδιασμού θα πρέπει να εγγυάται τη σταθεροποιησιμότητα, και ιδανική απόδοση του κλειστού βρόχου. Προκειμένου να διασφαλιστεί η σταθερότητα του κλειστού βρόχου, είναι κυρίως τρία είδη των τεχνικών που χρησιμοποιούνται : τεχνικές που βασίζονται σε μικρό κέρδος, τεχνικές που στηρίζονται στην παθητικότητα, καθώς και τεχνικές που περιλαμβάνουν Lyapunov συναρτήσεις. Το μικρό κέρδος και οι passivity-based τεχνικές που επιτρέπουν την εξασφάλιση της σταθερότητας ήδη από την εξέταση του συστήματος και του ελεγκτή χωριστά. Προκειμένου να εξακριβωθεί (ασυμπτωτική) σταθερότητα του κλειστού βρόχου σε μορφή χώρου κατάστασης, η θεωρία Lyapunov χρησιμοποιείται συχνά. Τα αποτελέσματα σταθερότητας που προκύπτουν χρησιμοποιώντας αυτές τις τεχνικές συνήθως είναι εγγύηση της σταθερότητας, όχι μόνο για ένα δεδομένο μη γραμμικό σύστημα, αλλά για μια οικογένεια μη Γραμμικών Συστημάτων, που χαρακτηρίζεται από κέρδος, ή Lipschitz κατάσταση. Έτσι, οι μέθοδοι σχεδιασμού του ελεγκτή που χρησιμοποιούν αυτές τις τεχνικές είναι στην 20
21 πραγματικότητα ισχυρές μέθοδοι ελέγχου που επιτυγχάνουν ισχυρή σταθερότητα για μια ολόκληρη τάξη μη γραμμικών αβεβαιοτήτων. Ένας κλασικός τρόπος περιγραφής για γραμμικό έλεγχο μη γραμμικών συστημάτων είναι η περίπτωση ενός γραμμικού δυναμικού συστήματος με χρήση ανάδρασης με μη γραμμικό στοιχείο χωρίς μνήμη, που συχνά αναφέρεται ως το πρόβλημα της απόλυτης σταθερότητας. Βασιζόμενοι στα αποτελέσματα της σταθερότητας, μπορούν επίσης να βρεθούν τεχνικές σύνθεσης στη βιβλιογραφία. Ένα ιδιαίτερα σημαντικό είδος των στατικών μη γραμμικοτήτων είναι ο κορεσμός των εισόδων, και πολλοί μέθοδοι σχεδιασμού ελεγκτή σε αυτόν τον τομέα που σχετίζονται με τις τεχνικές της απόλυτης σταθερότητας. Με σκοπό να αναλυθεί η σθεναρή σταθερότητα στην παρουσία μη γραμμικών αβεβαιοτήτων σε μια γενικότερη ρύθμιση από ό, τι για γραμμικά δυναμικά συστήματα διασυνδεδεμένα με μη γραμμικότητα χωρίς μνήμη, μπορούμε να θεωρήσουμε ένα μη γραμμικό σύστημα με περιγραφή στο χώρο κατάστασης: x Ax Bu ( x, u) y Cx ( x, u) Ευκολότερες συνθήκες μπορούν να βασιστούν στις διαφορετικές μεταβλητές του μικρού κέρδους και τη συστολή αρχών απεικόνισης (στοιχειώδες- μικρό κέρδος). Για παράδειγμα, χρησιμοποιώντας ένα μη γραμμικό εσωτερικό μοντέλο ελέγχου, με πεπερασμένο κέρδος του κλειστού βρόχου μπορεί να είναι εγγυημένη η σταθερότητα αν ( N L) Q 1, με Ν παριστάνεται η μη γραμμική διαδικασία, με L ένα γραμμικό μοντέλο, και με Q η παράμετρος ελεγκτή IMC που έχει επιλεγεί με βάση το γραμμικό μοντέλο. Το αποτέλεσμα αυτό ισχύει επίσης για έναν τοπικό σχεδιασμό ελεγκτή, το μόνο μειονέκτημα είναι ότι το σύνολο των σημάτων αναφοράς που μπορεί να καθορίζεται έμμεσα. 21
22 Όσον αφορά την αξιολόγηση του έλεγχου σχετικά με γραμμικότητα, η θεωρία του βέλτιστου ελέγχου παρέχει επίσης μια πιθανή προσέγγιση στο σχεδιασμό των γραμμικών ελεγκτών για μη γραμμικά συστήματα. Οι βέλτιστες τροχιές για πολλαπλές αρχικές συνθήκες μπορούν να χρησιμοποιηθούν για το σχεδιασμό της ανεπαρκούς γραμμικής κατάστασης με νόμους ανάδρασης. Αν και έχει αποδειχθεί ότι οι προκύπτοντες γραμμικοί ελεγκτές μπορεί να συμπεριφέρονται εξίσου καλά με έναν βέλτιστο μη γραμμικό ελεγκτή, αλλά δεν εγγυάται ότι θα επιτευχθεί σταθερότητα ή την απόδοση. Όπως και στην περίπτωση της αξιολόγησης της μη γραμμικότητας, βασικό μέλημα για την ανάπτυξη τεχνικών γραμμικής σχεδίασης ελεγκτών για μη γραμμικά συστήματα θα είναι να χρησιμοποιήσουμε μια ρύθμιση που επιτρέπει την αντιμετώπιση της γενικής δυναμικής εισόδου / εξόδου, και που επιτρέπει να εκτελέσουμε μια σύνθεση για καθορισμένη περιοχή λειτουργίας. Αυτά τα δύο σημεία θα είναι τα διακριτικά χαρακτηριστικά της προσέγγισης μας, σε σύγκριση με τις μεθόδους που υπάρχουν στη βιβλιογραφία. 22
23 2 Κεφάλαιο 2.1 Μέτρα μη γραμμικοτήτων και Γραμμικά Μοντέλα για Μη Γραμμικά Συστήματα Τα μέτρα μη γραμμικοτήτων έχουν εισαχθεί στη βιβλιογραφία, προκειμένου να ποσοτικοποιηθεί η ακρίβεια των γραμμικών μοντέλων για μη γραμμικά συστήματα. Στις περισσότερες προσεγγίσεις εισόδου-εξόδου για την αξιολόγηση της μη γραμμικότητας, το σφάλμα εξόδου e = Nu - Gu, δηλαδή η διαφορά μεταξύ της μη γραμμικής διαδικασίας εξόδου y = Nu και της έξοδος ~ y = Gu ενός γραμμικού μοντέλου διαδραματίζει σημαντικό ρόλο. Όπου στο σχήμα αυτό παριστάνεται η γενική μορφή του μέτρου μη γραμμικότητας: U AE, N ( Nu Gu) T inf sup inf N G m, n uu, T 0 u Ggm, n G g T u Όπου g mn, συμβολίζει ένα σύνολο γραμμικών συντελεστών μεταφοράς. Η ερμηνεία της απόστασης του μέτρου γραμμικότητας είναι πολύ ενδιαφέρουσα και σημαντική για να δούμε τη μαθηματική δομή του ορισμού αυτού. Ωστόσο, θέλουμε να επισημαίνουμε ένα διαφορετικό σύστημα ερμηνείας της θεωρίας, δηλαδή η ομοιότητα του ορισμού αυτού με τις τυπικές ρυθμίσεις στον γραμμικό σθεναρό έλεγχο. Ονομάζουμε τη γνωστή μη 23
24 γραμμικότητα στον παραπάνω τύπο προσθετικό σφάλμα μέτρου μη γραμμικότητας του Ν στο U. Στο εξής παρουσιάζουμε τα είδη των σφαλμάτων που προκύπτουν ανάλογα με το σχήμα που έχει ο βρόχος, όπως φαίνεται στον παρακάτω πίνακα: Προσθετικό σφάλμα Πολλαπλασιαστικό σφάλμα εξόδου Αντίστροφο πολλαπλασιαστικό σφάλμα εξόδου Πολλαπλασιαστικό σφάλμα εισόδου Αντίστροφο πολλαπλασιαστικό σφάλμα εισόδου 24
25 Σφάλμα ανάδρασης 2.2 Συστήματα χωρίς μνήμη και συμπεριφορά δυναμικών συστημάτων στο χώρο κατάστασης Στη συνέχεια, έχουμε εξάγει αποτελέσματα σχετικά με τα μέτρα μη γραμμικότητας και στα καλύτερα γραμμικά μοντέλα που βασίζονται σε ειδικές δομικές ιδιότητες των συστημάτων. Θεωρούμε πρώτα συστήματα με μια δεδομένη απόκριση στο χώρο κατάστασης, πριν μπορέσουμε να στρέψουμε την προσοχή μας σε φορείς χωρίς μνήμη. 2.3 Συμπεριφορά των Δυναμικών Συστημάτων Το πρώτο αποτέλεσμα αφορά την αύξηση των σταθερών μη γραμμικών συστημάτων που διαθέτουν μια σταθερή απόκριση του συστήματος σε μια σταθερή εισόδο του συστήματος. Η έξυπνη ιδέα είναι ότι το κέρδος του συστήματος είναι αυτό που οριοθετείται από τα κάτω όρια του κέρδος του όταν η λειτουργία που περιγράφει την σταθερή κατάσταση του γεωμετρικού τόπου. Στην ενότητα αυτή, φάνηκε για το κέρδος και την μέτρηση του προσθετικού λάθους της μη-γραμμικότητας πόσο χαμηλότερα όρια μπορούν να προκύψουν από τη σταθερή συμπεριφορά της κατάστασης ενός συστήματος. Επιπλέον, το κέρδος και το μέτρο γραμμικότητας ενός συστήματος χωρίς μνήμη μπορεί να χαρακτηριστεί από ένα «στατικό» πρόβλημα βελτιστοποίησης που έχει μια ιδιαίτερα απλή λύση στην περίπτωση του βαθμωτού συστήματος. Το αποτέλεσμα για το κάτω όριο είναι οτι επιτρέπει πολύ εύκολα να αποκομίσουμε μια πρώτη εκτίμηση του βαθμού της γραμμικότητας ενός 25
26 γενικού συστήματος. Τα αποτελέσματα για τα συστήματα χωρίς μνήμη δείχνουν ότι σε ένα πρακτικό πλαίσιο, τα δυναμικά γραμμικά μοντέλα δεν μπορούν να προσεγγίσουν ένα μη γραμμικό σύστημα χωρίς μνήμη καλύτερα από ένα γραμμικό μοντέλο χωρίς μνήμη. Επιπλέον, τα αποτελέσματα αυτά θα είναι χρήσιμα για το χαρακτηρισμό των συστημάτων που αποτελούνται από δυναμικά γραμμικά υποσυστήματα και χωρίς μνήμη μη γραμμικά υποσυστήματα. Τα αποτελέσματα σχετικά με τα συστήματα χωρίς μνήμη για το σφάλμα ανάδρασης επιτρέπει μια ενδιαφέρουσα ερμηνεία. Ο τύπος που δίνεται είναι ένας πλήρης αναλογικός στην περίπτωση του προσθετικού λάθους, αν η αντίστροφη μη γραμμική λειτουργία και το αντίστροφο του γραμμικού μοντέλου θεωρείται με καθορισμένο φάσμα εξόδου. Κατά συνέπεια, το βαθμωτό μέτρο του σφάλματος της στατικής ανάδρασης μη γραμμικότητας είναι το μόνο συγκεκριμένο μέτρο μη γραμμικότητας που μπορεί να γενικευτεί σε ασταθή συστήματα (π.χ. λειτουργίες που δεν είναι γραμμικά οριοθετημένες), ενώ εξακολουθούν να παρέχουν μη τετριμμένες τιμές. Εικόνα 2.1 Σχέση εισόδου-εξόδου για την βηματική συνάρτηση και το καλύτερο γραμμικό μοντέλο (αριστερά) και σφάλμα συστήματος Δ (δεξιά) για το σφάλμα ανάδρασης. Σχολιασμός εικόνας Η βηματική συνάρτηση : 26
27 ολοφάνερα δεν έχει πεπερασμένο κέρδος, Κ + =. Το μέτρο του σφάλματος ανατροφοδότησης μη γραμμικότητας, ωστόσο, μπορεί να οριστεί και να αποκτά τιμές Κ + =1, Κ - =0 και Κ * =0.5(Κ + + Κ - )=0.5, για ένα εύρος λειτουργίας u 1, στο οποίο ανήκει το καλύτερο γραμμικό κέρδος Κ=1/ Κ * = Σύνθετα Συστήματα Στην ενότητα αυτή, θα δούμε κάποια αποτελέσματα σχετικά με τα μέτρα μη γραμμικότητας των διασυνδέσεων από δύο υποσυστήματα. Ο στόχος είναι να ορισθούν άνω όρια σε τέτοιες διασυνδέσεις που βασίζονται στα μέτρα των υποσυστημάτων και μόνο. Επιπλέον, αν τα γραμμικά μοντέλα είναι γνωστά για τα υποσυστήματα, όπως συμβαίνει για τις διασυνδέσεις των δυναμικών συστημάτων γραμμικών και χωρίς μνήμη μη γραμμικών συστημάτων, τα αποτελέσματα αυτά προσφέρουν αμέσως γραμμικό μοντέλο που επιτυγχάνουν το σφάλμα μοντελοποίησης που δίνεται από αυτά τα ανώτερα όρια Παράλληλες συνδέσεις Θα εξετάσουμε πρώτα την περίπτωση της παράλληλης σύνδεσης N1 + N2 των δύο συστημάτων Ν1 και Ν2. Η πρόταση που ακολουθεί δείχνει ότι η AE- NLM της την παράλληλη σύνδεση που οριοθετείται από το άθροισμα των επιμέρους μέτρων μη γραμμικότητα. Για αυτή τη σχέση, δεν υπάρχει αντίστοιχη σχέση που να μπορεί να αποδειχθεί για τα άλλα μέτρα μη γραμμικότητας Σειριακές συνδέσεις, Hammerstein και Wiener συστήματα Στη συνέχεια, θεωρούμε συνδέσεις σειράς των συστημάτων. Ειδικότερα, μας ενδιαφέρουν συνδέσεις σειράς ενός γραμμικού και μη γραμμικού συστήματος. 27
28 Η πρώτη περίπτωση είναι μια σύνδεση σε σειρά L Χ Ν ενός μη γραμμικού σύστηματος (N) που ακολουθείται από ένα γραμμικό σύστημα (L). Εάν το μη γραμμικό υποσύστημα είναι χωρίς μνήμη, αυτή είναι η κλασική δομή του συστήματος Hammerstein Διασύνδεση Feedback Δεδομένης της τρίτης κοινής διασύνδεσης, μελετάμε την διασύνδεση ανατροφοδότησης ενός γραμμικού συστήματος L σε ένα εμπροσθόδρομο μονοπάτι και ενός μη γραμμικού συστήματος N στο μονοπάτι ανάδρασης. Ο τελεστής μεταφοράς αυτής της διασύνδεσης μπορεί να γραφτεί ως L (I - NL) - 1. Αν αυτό το μη γραμμικό σύστημα δεν έχει μνήμη, αυτή είναι η κλασική δομή του συστήματος Lurie. Αναμένεται ότι μπορούμε να αντλήσουμε ένα άνω όριο για το μέτρο του σφάλματος μη γραμμικότητας ανατροφοδότησης για αυτού του είδους το σύστημα. 28
29 3 Κεφάλαιο 3.1 Μια προσέγγιση μικρού κέρδους για γραμμικό έλεγχο μη γραμμικών συστημάτων Το πρόβλημα που εξετάζεται στο παρόν κεφάλαιο είναι ο σχεδιασμός ενός γραμμικού C ελεγκτή για το μη γραμμικό σύστημα Ν. Το σύστημα προς έλεγχο δίνεται στο σχήμα 3.1. Δύο εξωγενή σήματα εισέρχονται στο βρόχο ελέγχου που αντιστοιχούν σε αυτό που είναι συνήθως το σήμα διαταραχής στην είσοδο του συστήματος (U1) και το σήμα αναφοράς (U2). Οι ρυθμιζόμενες μεταβλητές είναι οι έξοδοι του ελεγκτή y2 και του συστήματος y1 από τις αντίστοιχες εισόδους τους e2 και e1. Σχήμα 3.1 Η συνηθισμένη προσέγγιση στο σχεδιασμό των γραμμικών ελεγκτών για μη γραμμικά συστήματα είναι η χρήση της γραμμικοποίησης στο σημείο λειτουργίας ως ένα γραμμικό μοντέλο, ο σχεδιασμός ενός γραμμικού C ελεγκτή και να αναλύσει τη σταθερότητα και την απόδοση του κλειστού βρόχου με το μη γραμμικό μοντέλο. Χρησιμοποιώντας αυτή τη μέθοδο, δεν είναι εγγυημένη η σταθερότητα και η απόδοση που μπορεί να γίνει και ο βαθμός της μη γραμμικότητας του συστήματος δεν έχει ληφθεί υπόψη στο στάδιο του σχεδιασμού ελεγκτή. Στην ενότητα αυτή, παρουσιάζεται μια νέα προσέγγιση για το γραμμικό σχεδιασμό των ελεγκτών για τα μη γραμμικά συστήματα που εγγυάται σταθερότητα του κλειστού βρόχου που περιέχει τη μη γραμμική διαδικασία. Η κεντρική ιδέα της μεθόδου είναι να χρησιμοποιηθούν τα αποτελέσματα από την ανάλυση της μη γραμμικότητας στο κεφάλαιο 2. Στην πραγματικότητα, 29
30 όλα τα μέτρα μη γραμμικότητας δίνουν το κέρδος του σφάλματος του συστήματος όταν μια δεδομένη μη γραμμική διαδικασία παρουσιάζεται ως η διασύνδεση ενός (καλύτερου) γραμμικού μοντέλου και του συστήματος με το σφάλμα. Αυτές οι πληροφορίες μπορούν να χρησιμοποιηθούν για έλεγχοαξιολόγηση σχετική με μη γραμμικότητα και γραμμικό σχεδιασμό των ελεγκτών για τα μη γραμμικά συστήματα. Είναι απαραίτητο να σημειωθεί ότι, όπως η μέθοδος που αναπτύχθηκε σε αυτό το κεφάλαιο κάνει χρήση του μέτρου μη γραμμικότητας, αυτό περιορίζεται σε πεπερασμένο κέρδος σταθεροποιήσιμων μη γραμμικών συστημάτων. Έτσι, με σκοπό να μην αφήνουν περιθώρια για αμφιβολία, ο στόχος της προτεινόμενης μεθόδου σχεδιασμού ελεγκτών δεν είναι η σταθεροποίηση ασταθών συστημάτων με γραμμική ανάδραση. Αντ 'αυτού, ο σκοπός αυτών των προσπαθειών είναι να μπορεί να σχεδιαστεί ένας γραμμικός ελεγκτής χρησιμοποιώντας ένα γραμμικό μοντέλο, προκειμένου να ενισχυθεί η ονομαστική απόδοση του συστήματος ελέγχου. Αν και μόνο η σταθερότητα του βρόχου ελέγχου με το μη γραμμικό σύστημα μπορεί να είναι εγγυημένη, ωστόσο, η απόδοση αναμένεται να αυξηθεί. Σχήμα
31 3.2 Αρχές σθεναρού ελέγχου Αρχικά θα αναφερθούμε σε κάποιες αρχές του σθεναρού ελέγχου, προκειμένου να προχωρήσουμε με το σχεδιασμό γραμμικού ελεγκτή για ένα μη γραμμικό σύστημα. Ο στόχος του γραμμικού σθεναρού έλεγχου είναι η σταθεροποίηση ενός δεδομένου γραμμικού G συστήματος, παρά την παρουσία ενός γραμμικού σφάλματος μοντελοποίησης Δ (ή αβεβαιότητας). Η συνήθης αρχικοποίηση σε γραμμικό σθεναρό έλεγχο είναι αυτή που απεικονίζεται στο σχήμα Εδώ, Δ είναι η αβεβαιότητα, το C είναι ο ελεγκτής και P είναι το λεγόμενο γενικευμένο μοντέλο, το οποίο περιέχει ένα μοντέλο της διαδικασίας G και οι πληροφορίες σχετικά με το πώς G, και C είναι αλληλένδετα. Η θεμελιώδης αρχή του γραμμικού σθεναρού έλεγχου μπορεί στη συνέχεια να σκιαγραφηθεί ως εξής: Το σύστημα ελέγχου είναι δυναμικά σταθερό, εάν (α) το σύστημα ελέγχου είναι ονομαστικά σταθερό, δηλαδή σταθερό για Δ= 0, και αν (β) ένα μικρό κέρδος κατάστασης που ικανοποιείται εγγυάται την σταθερότητα της διασύνδεσης των P, C και Δ. Συμβολίζουμε με M το ονομαστικό βρόχο ανάδρασης, δηλαδή τη διασύνδεση των P και C. Έτσι, το ένα αποκτά τη συνήθη M Δ-δομή που απεικονίζεται στο σχήμα Όπως το ονομαστικό σύστημα κλειστού βρόχου M είναι γραμμικό, μπορεί να χωριστεί σε τέσσερα μέρη, di M11 M12 do y M M u (3.1) Σχήμα
32 Το σύστημα κλειστού βρόχου Μ χαρακτηρίζεται σαν σταθερό, αν όλα τα υποσυστήματά του έχουν πεπερασμένο κέρδος. Έχουμε την παρακάτω ανισότητα: m με d m d m u (3.2) i 11 o 12 M και m12 M12, και do di οδηγεί στη δέσμευση Αυτό δίνει: d (1 m ) m u (3.3) o y m d m u (3.4) m με o 22 M και m22 M22, ή y ( m (1 m ) m m ) u (3.5) και το σύστημα κλειστού βρόχου είναι σταθερό και στην παρουσία του όρου του σφάλματος Δ. Για τα γραμμικά συστήματα, μπορεί να αποδειχθεί ότι, αν ο όρος για το μικρό κέρδος δεν πληρούται, τότε υπάρχει ένα γραμμικό δυναμικό σύστημα Δ με κέρδος που αποσταθεροποιεί το κλειστό βρόχο. Με αυτή M 1 την έννοια, ο όρος 11 σθεναρή σταθερότητα στην γραμμική περίπτωση. είναι αναγκαία και ικανή συνθήκη για Ο στόχος αυτού του κεφαλαίου είναι ο παραλληλισμός αυτής της διαδικασίας με σκοπό το σχεδιασμό γραμμικών ελεγκτών για μη γραμμικά συστήματα. Για το σκοπό αυτό, η μη γραμμική διαδικασία είναι χωρισμένη σε ένα γραμμικό μοντέλο G και μια μη γραμμικό όρο σφάλματος. Ας σημειώσουμε ότι υπάρχουν δύο διαφορές στην περίπτωση του γραμμικού σθεναρού έλεγχου. Πρώτον, ο όρος Δ δεν είναι κάτι αβέβαιο, αλλά είναι γνωστός. Ωστόσο, το Δ θα είναι μη γραμμικό (και αυτή είναι η δεύτερη διαφορά). Ας σημειώσουμε ότι, επίσης στη γραμμική περίπτωση, χρησιμοποιώντας τον όρο του μικρού κέρδους εισάγεται συντηρητισμός αν η αβεβαιότητα Δ είναι γνωστή, ενώ στην γραμμική περίπτωση δε χρειάζεται να εισαγάγει το Δ, καθώς τα δεδομένα θα μπορούσαν να χρησιμοποιηθούν απευθείας για το σχεδιασμό των ελεγκτών. 32
33 Στη μη γραμμική περίπτωση, όμως, αυτός ο συντηρητισμός είναι το τίμημα για τη μείωση της πολυπλοκότητας στο στάδιο του σχεδιασμού ελεγκτή (δηλαδή το σχεδιασμό ενός γραμμικού ελεγκτή αντί για έναν σε μια μη γραμμική διαδικασία). Όταν εφαρμόζονται μέθοδοι σθεναρού ελέγχου για το σχεδιασμό των ελεγκτών, αναφέρεται μερικές φορές ότι αυτή η στρατηγική λαμβάνει επίσης υπόψη πιθανά σφάλματα μοντελοποίησης λόγω της μη γραμμικής συμπεριφοράς. Ωστόσο, όπως έχει αναφερθεί σε διάφορα σημεία και παρουσιάζεται με διαφορετικά παραδείγματα, η σφαιρική ανάλυση και σύνθεση για μη γραμμικά συστήματα δεν είναι κατάλληλη σε πολλές περιπτώσεις, επειδή η διαφορά στη συμπεριφορά μεταξύ οποιουδήποτε γραμμικού μοντέλου και μη γραμμικού συστήματος γίνεται αυθαίρετα μεγάλη για μεγάλες περιοχές λειτουργίας. Για παράδειγμα, τα μέτρα της μη γραμμικότητας που εισήχθησαν στο Κεφάλαιο 2 συνήθως λαμβάνουν τη μέγιστη τιμή τους, αν μια μη περιορισμένη περιοχή ληφθεί υπόψη. Αλλά εάν μια περιορισμένη περιοχή ληφθεί υπόψη, η παραπάνω αιτιολογία για ισχυρή σταθερότητα δεν κρατά περισσότερο. Κατά συνέπεια, η κύρια συμβολή αυτού του κεφαλαίου είναι να αλλάξει την υπόθεση ότι το κέρδος του Δ θεωρείται σταθερό σε μια κατάσταση όπου αυτό είναι μόνο η περίπτωση για μια συγκεκριμένη υποομάδα σημάτων. Σε σχεδόν όλες τις εφαρμογές, οι μηχανικοί ελέγχου πρέπει να ασχοληθούν με διαδικασίες των οποίων οι μεταβλητές μπορούν να πάρουν τιμές σε μια συγκεκριμένη περιοχή τιμών μόνο. Κατά συνέπεια, μόνο μη γραμμική συμπεριφορά που παρουσιάζεται για αυτές τις εισόδους παίζει ρόλο στο σχεδιασμό των ελεγκτών. Στη συνέχεια, θα θεωρήσουμε ως εκ τούτου εισόδους που προορίζονται να πάρουν τιμές στο σύνολο: m v R : v v, i 1.. m i imax 3.3 Σταθερότητα Μη Γραμμικών Συστημάτων με Γραμμικούς Ελεγκτές 33
34 Πριν στρέψουμε την προσοχή μας στα κύρια αποτελέσματα, έχουμε αποσαφηνίσει το είδος της σταθερότητας που θέλουμε να επιτευχθεί και παρουσιάζονται κάποια συγκεκριμένα λήμματα για το λόγο αυτό, τα οποία απλά θα αναφέρουμε χωρίς να επεκταθούμε σε βάθος. Σχήμα 3.4 Θεωρούμε το σύστημα που παρουσιάζεται στο σχήμα 3.1. Θεωρούμε ότι το σύστημά μας είναι καλώς ορισμένο και ονομάζουμε τον κλειστό βρόχο σταθερό αν το σύστημα: H :( u u ) ( y, y, e, e ) NC 1, έχει πεπερασμένο κέρδος. Για να ελέγξουμε την σταθερότητα, χρησιμοποιούμε τα παρακάτω προτάσεις: 34
35 3.3.1 Θεώρημα 1 Οι ακόλουθες τρεις εντολές είναι ισοδύναμες: (i) (u1, u2) (y1, y2, Ε1, Ε2) έχει πεπερασμένο κέρδος, (ii) (u1, u2) (y1, y2) έχει πεπερασμένο κέρδος, (iii) (u1, u2) (Ε1, Ε2) έχει πεπερασμένο κέρδος Θεώρημα 2 Σκεφτείτε ένα σύστημα ελέγχου, όχι απαραίτητα γραμμικό, όπως φαίνεται στο σχήμα. 3.3, που ικανοποιεί την αρχή της επαλληλίας. Αν i D m 1 Όπου το Di δηλώνει το σύνολο των σημάτων di που μπορεί να προκύψουν ως εισροές κατά τη διάρκεια λειτουργίας σε κλειστό βρόχο, τότε το κλειστό κύκλωμα είναι σταθερό, δηλαδή το σύστημα u y έχει πεπερασμένο κέρδος Θεώρημα 3 Ο τελεστής κορεσμού Σν που έδωσε (3.6) έχει πεπερασμένο (στοιχειώδες) κέρδος που είναι σταθερό και ισχύει v Θεώρημα 4 Έστω ότι η M είναι το σύστημα ελέγχου στο σχήμα. 3.5 (με το Δ = 0) είναι σταθερό και G είναι ένα πεπερασμένο σταδιακά αυξανόμενο κέρδος σταθερού συστήματος. Υπό αυτές τις συνθήκες, (3.2) και (3.4) ισχύουν και ειδικότερα, το m 11 μπορεί να ληφθεί ως εξής: m I CG C C I G C ( ) ( ) 35
36 3.3.5 Θεώρημα 5 Για την διαδικασία(ν) πεπερασμένου κέρδους, έστω ένα σταθερό μοντέλο G πεπερασμένου αυξητικού κέρδους και ένας πεπερασμένος σταθερός όρος αναντιστοιχίας N G που δίνεται. Επιπλέον, ας υποθέσουμε ότι ένας ελεγκτής C παρέχεται ώστε η απεικόνιση m 11 = C (I + G VC) -1 πεπερασμένο κέρδος. Αν τα κέρδη ικανοποιούν τη σχέση ( ) uv M11 1 τότε το σύστημα ελέγχου στο σχήμα. 3.5 είναι σταθερό, δηλαδή το ( N ) έχει πεπερασμένο κέρδος. H έχει C Η κατάσταση της σταθερότητας παραπάνω μπορεί να χρησιμοποιηθεί για να καθιερωθεί μια διαδικασία σχεδιασμού των ελεγκτών που αποτελείται από τα βήματα: (1) καθορισμός της περιοχής λειτουργίας του U (V) με την επιλογή V i, max, (2) τον υπολογισμό του μέτρου μη γραμμικότητας μέτρο και το U( V), καλύτερο γραμμικό μοντέλο G*,ή να υπολογισθεί ο δείκτης ποιότητας ( ) U V για ένα συγκεκριμένο γραμμικό μοντέλο G, και (3) το σχεδιασμό ενός γραμμικού ελεγκτή C για το κορεσμένο γραμμικό σύστημα G V τέτοιον ώστε: M C( I G C) 1/ uv 1 ( ). 36
37 Σχήμα 3.5 Θα μπορούσε κανείς να υποστηρίξει ότι μετά από όλα αυτά, καταλήγουμε με ένα δύσκολο πρόβλημα σχεδιασμού, καθώς έχουμε να σχεδιάσουμε έναν ελεγκτή που επιτυγχάνει ένα συγκεκριμένο Lp-κέρδος, παρά τον κορεσμό των συστημάτων. Από την άλλη, κατά τη διάρκεια οποιασδήποτε πρακτικού σχεδιασμού ελεγκτή,οι περιορισμοί εισόδου πρέπει να είναι σεβαστοί. Πράγματι, δεν εισάγουμε μια πρόσθετη δυσκολία εδώ, αλλά μάλλον να επωφεληθούν από το γεγονός ότι ο κορεσμός θα πρέπει να ληφθεί υπόψη ούτως ή άλλως, έτσι ώστε η μη γραμμική συμπεριφορά της διαδικασίας αυτής να ληφθεί υπόψη μόνο στην αντίστοιχη περιοχή. Αυτή η διαδικασία έχει αποδειχθεί χρήσιμη και παρουσιάσει ικανοποιητικά αποτελέσματα. Η συνεχιζόμενη έρευνα στον έλεγχο των κορεσμένων συστημάτων υπόσχεται να παραδώσει στο μέλλον πιο αποτελεσματικές μεθόδους που είναι πιο εύκολες στη χρήση τους. Γραμμική σταθεροποίηση των μη γραμμικών συστημάτων στο πολλαπλασιαστικό σφάλμα εξόδου 37
38 Στην περίπτωση του πολλαπλασιαστικού σφάλματος εξόδου, δεν προκύπτουν πρόσθετες δυσκολίες. Η όλη διαδικασία προκύπτει από ένα απότομο όριο για την αρχή της επαλληλίας. Η διασύνδεση και ο κλειστός βρόχος M φαίνεται στο σχήμα Θεώρημα 6 Για την διαδικασία (Ν) πεπερασμένου κέρδους, έστω ένα πεπερασμένο οριακό κέρδος του σταθερού μοντέλου G και ένα κέρδος πεπερασμένο του πολλαπλασιαστικού σφάλματος εξόδου να δίνεται. Εάν ένας ελεγκτής C σταθεροποιεί το γραμμικό κορεσμένο σύστημα G, δηλαδή το κλειστό H κύκλωμα ( G ) C είναι σταθερό, και Όπου ( ) Gu v m11 1 m G C I G C,τότε ο ελεγκτής σταθεροποιεί επίσης 1 11 v ( ) το μη γραμμικό σύστημα κλειστού βρόχου, δηλαδή ( G ) C είναι σταθερό. H Σχήμα
39 Γραμμική σταθεροποίηση των μη γραμμικών συστημάτων στο αντίστροφο πολλαπλασιαστικό σφάλμα εξόδου Το αντίστοιχο αποτέλεσμα μπορεί να επιτευχθεί για το αντίστροφο πολλαπλασιαστικό σφάλμα εξόδου χωρίς δυσκολία. Το σύστημα κλειστού βρόχου με το αντίστροφο πολλαπλασιαστικό σφάλμα εξόδου του μη γραμμικού μοντέλου που συμβάλει για την ανάλυση του συστήματος M φαίνεται στο σχήμα 3.7. Σχήμα Θεώρημα 7 Για την διαδικασία Ν πεπερασμένου σταθερού κέρδους, έστω ένα πεπερασμένο οριακό κέρδος του σταθερού γραμμικού μοντέλου G και ένα πεπερασμένο πολλαπλασιαστικό σφάλμα με σταθερό κέρδος εξόδου Δ να δίνεται. Εάν ένας ελεγκτής C σταθεροποιεί το γραμμικό κορεσμένο G σύστημα, δηλαδή το σύστημα κλειστού βρόχου ( G ) C είναι σταθερό, και H ( ) Nu v m
40 Όπου m 1 11 ( I G C ), τότε ο ελεγκτής σταθεροποιεί επίσης το μη γραμμικό σύστημα κλειστού βρόχου, δηλαδή ( N ) C είναι σταθερό. H Γραμμική σταθεροποίηση των μη γραμμικών συστημάτων στο πολλαπλασιαστικό σφάλμα εισόδου Προκειμένου να διατηρηθεί η επιρροή του u, πρέπει να υποθέσουμε τους αυστηρότερους όρους για τα παραπάνω αποτελέσματα. Το σύστημα απεικονίζεται στο σχήμα. 3.8 για την εξέταση της λειτουργίας κλειστού βρόχου Μ. Σχήμα Θεώρημα 8 Για την διαδικασία Ν πεπερασμένου σταθερού κέρδους, έστω ένα πεπερασμένο οριακό κέρδος του σταθερού γραμμικού μοντέλου G και ένα πεπερασμένο πολλαπλασιαστικό σφάλμα με σταθερό κέρδος εξόδου Δ να δίνεται. Εάν ένας ελεγκτής C δίνεται έτσι ώστε το σύστημα κλειστού βρόχου H ( G ) C να είναι σταθερό και μια από τις προϋποθέσεις (i) ο C είναι γραμμικός και να έχει πεπερασμένο σταθερό κέρδος, 40
41 (ii) το G έχει ένα σταθερό αντίστροφο, (iii)η ( ) είναι το σταδιακό αυξητικό κέρδος που ισχύει, και το 1 I CG C μικρό κέρδος κατάστασης, του οποίου η συνθήκη ( ) uv m11 1 ικανοποιείται, με m CG I CG τότε ο ελεγκτής σταθεροποιεί 1 11 ( ) επίσης το μη γραμμικό κλειστό βρόχο, δηλαδή ( N ) C είναι σταθερό. Το συμπέρασμα αυτό ισχύει επίσης εάν C σταθεροποιεί το σύστημα κλειστού βρόχου και το μικρό κέρδος κατάστασης ικανοποιείται με m C I G C G 1 11 ( ) H Γραμμική σταθεροποίηση των μη γραμμικών συστημάτων με το αντίστροφο πολλαπλασιαστικό σφάλμα εισόδου Με σκοπό να δείξουμε τη σταθερότητα και για τα μη γραμμικά συστήματα κλειστού βρόχου σε αντίστροφο πολλαπλασιαστικό σφάλμα εισόδου (βλ. σχήμα. 3.9), έχουμε και πάλι αναλάβει τις κάπως αυστηρότερους όρους ως προς την πολλαπλασιαστική εγκατάσταση λάθους εισόδου. Σχήμα
42 3.3.9 Θεώρημα 9 Για την διαδικασία Ν πεπερασμένου σταθερού κέρδους, έστω ένα πεπερασμένο οριακό κέρδος του σταθερού γραμμικού μοντέλου G και ένα πεπερασμένο πολλαπλασιαστικό σφάλμα με σταθερό κέρδος εξόδου Δ να δίνεται. Εάν ένας ελεγκτής C δίνεται έτσι ώστε το σύστημα κλειστού βρόχου H ( G ) C να είναι σταθερό και ισχύει μια από τις προϋποθέσεις: (i)ο C είναι γραμμικός και να έχει πεπερασμένο σταθερό κέρδος, (ii) το G έχει ένα σταθερό αντίστροφο, (iii)η ( ) είναι το σταδιακό αυξητικό κέρδος και η συνθήκη 1 I CG C μικρού κέρδους ικανοποιείται με NG 1 u( v) m ( ) 11 m CG I CG τότε ο ελεγκτής σταθεροποιεί επίσης το μη γραμμικό κλειστό βρόχο, δηλαδή ( N ) C είναι σταθερό. Το συμπέρασμα αυτό ισχύει επίσης εάν C σταθεροποιεί το σύστημα κλειστού βρόχου και το μικρό κέρδος κατάσταση ικανοποιείται με m C I G C ( ) G. H Γραμμική σταθεροποίηση των μη γραμμικών συστημάτων στο σφάλμα ανάδρασης Έχουμε και πάλι να υποθέσουμε την πεπερασμένη σταδιακή σταθερότητα για το (γραμμικό κορεσμένο) σύστημα κλειστού βρόχου (σχήμα 3.10), προκειμένου να είμαστε σε θέση να δείξουμε τη σταθερότητα και για το μη γραμμικό σύστημα κλειστού βρόχου. 42
43 Σχήμα Θεώρημα 10 Για την διαδικασία Ν πεπερασμένου σταθερού κέρδους, έστω ένα πεπερασμένο οριακό κέρδος του σταθερού γραμμικού μοντέλου G και ένα πεπερασμένο πολλαπλασιαστικό σφάλμα με σταθερό κέρδος εξόδου Δ να δίνεται. Εάν ένας ελεγκτής C δίνεται έτσι ώστε το σύστημα κλειστού βρόχου H ( G ) C να είναι σταθερό και ισχύει μια από τις προϋποθέσεις: (i)ο C είναι γραμμικός και να έχει πεπερασμένο σταθερό κέρδος, (ii) το G έχει ένα σταθερό αντίστροφο, (iii)η ( I CG ) 1 είναι το σταδιακό αυξητικό κέρδος, και η συνθήκη μικρού κέρδους ικανοποιείται, όπου NG 1 u( v) m 1 11 m G I CG τότε ο ελεγκτής 1 11 ( ) σταθεροποιεί επίσης τη μη γραμμικό κλειστό βρόχο, δηλαδή ( N ) C είναι H 43
44 σταθερό. Το συμπέρασμα αυτό ισχύει επίσης εάν C σταθεροποιεί το σύστημα κλειστού βρόχου και το μικρό κέρδος κατάστασης ικανοποιείται με m I G C 1 11 ( ) G. 3.4 Σχεδιασμός σθεναρού ελεγκτή με εγγυημένη Lp-απόδοση Στόχος μας είναι να προτείνουμε μια διαδικασία σχεδίασης ελεγκτή που μπορεί να τροποποιηθεί ώστε να βελτιωθεί η απόδοση των μη γραμμικών συστημάτων κλειστού βρόχου. Παρά το γεγονός ότι η προσέγγιση που περιγράφεται μπορεί να είναι χρήσιμη, δε δίνεται καμία εγγύηση για την πραγματική απόδοση. Σε ένα γραμμικό σύστημα, η δομημένη μοναδική αξία είναι το κατάλληλο εργαλείο ανάλυσης για την σθεναρή απόδοση. Θα εξετάσουμε μια παρόμοια διαδικασία, προκειμένου να αναλυθεί η απόδοση ενός μη γραμμικού συστήματος. Έστω για μια άλλη μια φορά μια δομή M-Δ που δίνεται στο σχήμα 3.3 (αριστερό μέρος). Ας υποθέσουμε ότι η M έχει ήδη ενσωματωθεί με κατάλληλα βάρη για την απόδοση και έναν ελεγκτή. Αν M 1 και 1, τότε d y d u i o 2 2 d d o i 2 y u 2 2 Επομένως, αποδεικνύουμε ότι το κέρδος L2 οριοθετείται από το ένα. Η διαδικασία μπορεί επίσης να γίνει για άλλα Lp κέρδη, εάν ο κανόνας διάνυσμα επιλέγεται έτσι ώστε να ισχύει: 44
45 x y p p p x y p p p Για να πάρουμε μια γενικότερη εικόνα, θεωρούμε το Σχήμα Προκειμένου να ασχοληθούμε με μια γενική αβεβαιότητα, όχι κατ 'ανάγκην που οριοθετείται από το ένα, εισαγάγαμε το συντελεστή προσαύξησης. Επιπλέον, έχουμε εισαγάγει επιπλέον βαθμούς ελευθερίας εισάγοντας τις πραγματικές παραμέτρους (βαθμωτά) α και β. Με την εφαρμογή της παραπάνω διαδικασίας, αν 1 I 0 I 0 I 0 M M 1 0 ai 0 I 1 0 I a η σθεναρή απόδοση είναι εγγυημένη με y u y u,ή ισοδύναμα. Καθώς οι παράμετροι α και β είναι αυθαίρετοι, μπορούν να επιλέγονται έτσι ώστε να ελαχιστοποιούν την ποσότητα M το συντηρητισμό της προσέγγισης., μειώνοντας Σχήμα 3.11 Ένα κρίσιμο σημείο για την παραπάνω προσέγγιση είναι να τηρεί μια συγκεκριμένη περιοχή της λειτουργίας του για το σύστημα. 45
46 3.5 Σχέσεις με Γραμμική Σταθεροποίηση Μη Γραμμικών Συστημάτων με χρήση του Μετρικού Χάσματος Η μικρή προσέγγιση κέρδους για γραμμικό έλεγχο των μη γραμμικών συστημάτων είναι πολύ ελκυστική λόγω της απλότητας και της διαισθητικής φύσης της. Παρ 'όλα αυτά έχει κάποια μειονεκτήματα. Πρώτα απ ' όλα, μπορεί να εφαρμοστεί μόνο σε σταθερές εγκαταστάσεις. Επιπλέον, το μικρό κέρδος κατάστασης είναι γνωστό ότι είναι συντηρητικό. Ακόμη και στο γραμμικό πλαίσιο, το μικρό κέρδος κατάστασης είναι αρκετό, αλλά δεν είναι απαραίτητο για τη σταθερότητα του κλειστού βρόχου. Το πρόβλημα είναι στην πραγματικότητα ο σχεδιασμός ενός ελεγκτή για το μοντέλο Α, και να εξακριβωθεί ότι ο ανεπτυγμένος ελεγκτής σταθεροποιεί επίσης ο σύστημα Β. Στο γραμμικό πλαίσιο, μια αναγκαία και ικανή συνθήκη μπορεί να προκύψει χρησιμοποιώντας το μετρικό χάσμα (Gap Metric). Το μετρικό χάσμα ως έννοια μπορεί να επεκταθεί και σε μη γραμμικά συστήματα, αλλά η αναγκαιότητα του κριτηρίου έχει χαθεί. Παρ 'όλα αυτά, η προσέγγιση του μετρικού χάσματος συμβάλει στη μείωση της μικρής προσέγγισης σημαντικά. Επιπλέον, το μετρικό χάσμα επιτρέπει, επίσης, την αντιμετώπιση της αστάθειας των συστημάτων και την ανάλυση της σταθερότητας και της απόδοσης για οριοθετημένα σήματα. 3.6 Συμπεράσματα Είναι σημαντικό να γνωρίζουμε σε ποιες περιπτώσεις η απλούστευση που συνάδει με την χρήση γραμμικών μοντέλων για μη γραμμικά συστήματα είναι ανεκτή στη μηχανική ελέγχου. Ο στόχος εδώ είναι η δημιουργία μεθόδων: (1) για την αξιολόγηση της ακρίβειας ενός συγκεκριμένου γραμμικού μοντέλου για ένα δεδομένο μη γραμμικό σύστημα και (2) να αποκομίσουμε βέλτιστα γραμμικά μοντέλα για αυτό το σύστημα, καθώς και (3) για το σχεδιασμό των ελεγκτών για ένα δεδομένο μη γραμμικό σύστημα που βασίζεται σε ένα συγκεκριμένο γραμμικό μοντέλο. 46
47 Προκειμένου να ποσοτικοποιηθεί η ποιότητα ενός συγκεκριμένου γραμμικού μοντέλου και να δημιουργήσουμε ένα βέλτιστο γραμμικό μοντέλο, εισαγάγουμε ένα νέο ενοποιητικό πλαίσιο. Σε αυτό το πλαίσιο, το μη γραμμικό σύστημα παρουσιάζεται ως η διασύνδεση του γραμμικού μοντέλου και ενός μη γραμμικού σφάλματος. Η ποιότητα του μοντέλου μπορεί να μετρηθεί με το κέρδος του σφάλματος του συστήματος και ένα καλύτερο γραμμικό μοντέλο ορίζεται για να επιτευχθεί το μικρότερο δυνατό κέρδος. Πιθανή διασύνδεση δομών περιλαμβάνουν εκείνα που είναι γνωστά από τη θεωρία του σθεναρού ελέγχου. Ο δείκτης ποιότητας μοντέλου από το καλύτερο γραμμικό μοντέλο είναι ένα μέτρο της μη γραμμικότητας στη συμπεριφορά εισόδου-εξόδου της μη γραμμικής διαδικασίας, και δύο μέτρα μη γραμμικότητας γνωστά από τη βιβλιογραφία είναι ειδικές περιπτώσεις του προτεινόμενου πλαισίου. Οι πληροφορίες σχετικά με το γραμμικό μοντέλο και το κέρδος σφάλματος μπορεί στη συνέχεια να χρησιμοποιηθούν για το σχεδιασμό ενός γραμμικού ελεγκτή για το μη γραμμικό σύστημα. Η κύρια συμβολή αυτής της μελέτης για τη γραμμική μοντελοποίηση των μη γραμμικών συστημάτων είναι η παροχή μιας αυστηρής μαθηματικής θεμελίωσης για την παροχή χαρακτηρισμών των μέτρων μη γραμμικότητας και των βέλτιστων γραμμικών μοντέλων για ειδικές τάξεις συστημάτων. Οι δεδομένες συνθήκες υπό τις οποίες το σφάλμα ενός μοντέλου μπορεί να οριστεί με σαφήνεια, παρουσιάζοντας επίσης ότι οι δεδομένοι ορισμοί των μέτρων μη γραμμικότητας και τα βέλτιστα γραμμικά μοντέλα είναι πράγματι σημαντικά. Επίσης, παρατηρήσαμε για το μέτρο του προσθετικού σφάλματος μη γραμμικότητας που η γραμμικοποίηση στο χώρο κατάστασης δίνει ένα μοναδικό τέλειο τοπικό γραμμικό μοντέλο, δηλαδή το μοναδικό γραμμικό μοντέλο που επιτυγχάνει μηδενικό σφάλμα μοντελοποίησης. Αποδείχθηκε ότι η σταθερή συμπεριφορά της κατάστασης καθιερώνει ένα κατώτερο όριο για τα τρία μέτρα μη γραμμικότητας, και ότι σε αυτές τις περιπτώσεις, δυναμικά γραμμικά μοντέλα δεν έχουν κανένα πλεονέκτημα σε σχέση με στατικά γραμμικά μοντέλα για μη γραμμικούς χωρίς μνήμη φορείς. Οι τύποι για τα μέτρα μη γραμμικότητας χωρίς μνήμη ήταν δεδομένοι, και ιδιαίτερα απλές εκφράσεις που λαμβάνονταν για συστήματα χωρίς μνήμη 47
48 βασιζόταν στην έννοια ενός τομέα. Αποδείχθηκε ότι, αν η προσέγγιση είναι γραμμικός συνδυασμός των γραμμικών μοντέλων από μια συγκεκριμένη βάση, το καλύτερο γραμμικό μοντέλο είναι εγγυημένο για να υπάρχει για δύο από τα μέτρα. Εάν ένα αυστηρώς ορισμένο καλύτερο γραμμικό μοντέλο δεν υπάρχει, τότε μια αυθαίρετη προσέγγιση γραμμικού μοντέλου μπορεί να επιτευχθεί. Επίσης κύρια συμβολή αυτής της μελέτης για γραμμικό έλεγχο των μη γραμμικών συστημάτων είναι η σταθερότητα των καταστάσεων και οι διαδικασίες σχεδιασμού ελεγκτή για γραμμικό έλεγχο των μη γραμμικών συστημάτων. Η γενική διαδικασία στηρίζεται στο γεγονός ότι η μη γραμμική μονάδα αναπαρίσταται ως η διασύνδεση ενός γραμμικού μοντέλου και ενός μη γραμμικού όρου σφάλματος. Η ιδέα είναι, στη συνέχεια, να χρησιμοποιηθεί σχεδιασμός ελεγκτή για τη σθεναρή σταθεροποίηση του γραμμικού συστήματος με την παρουσία όρου μη γραμμικής διαταραχής. Κυρίως οποιοδήποτε γραμμικό μοντέλο μπορεί να χρησιμοποιηθεί, αλλά το καλύτερο μοντέλο, με ένα κέρδος σφάλματος που δίνεται από το αντίστοιχο μέτρο μη γραμμικότητας, φάνηκε να είναι μερικές φορές σημαντικά ανώτερο από άλλα μοντέλα. Αυτό εξηγείται από το γεγονός ότι το μικρότερο σφάλμα μοντέλου συνεπάγεται το λιγότερο συντηρητισμό στον σχεδιασμό των ελεγκτών. Το παράδειγμα ενός τοπικά σταθερού συστήματος έδειξε ότι είναι όντως απαραίτητο να γίνει ένα περιφερειακός σχεδιασμός των ελεγκτών. Στην προσέγγισή μας, η περιοχή λειτουργίας περιγράφεται με τον περιορισμό του σύνολο των επιτρεπόμενων σημάτων εισόδου σε ένα συγκεκριμένο σύνολο. Προκειμένου να ενσωματωθούν αυτοί οι περιορισμοί στο σύστημα κλειστού βρόχου, ένα φίλτρο πρέπει να εισαχθεί, στο σύστημα. Η σταθερότητα του κλειστού βρόχου μπορεί στη συνέχεια να είναι εγγυημένη ικανοποιώντας ένα μικρό κέρδος από την κατάσταση του συστήματος από το κέρδος του σφάλματος και το κέρδος του συστήματος κλειστού βρόχου. Η ακριβής μορφή του συστήματος κλειστού βρόχου εξαρτάται από τον τύπο διασύνδεσης που έχουμε επιλέξει και παρουσιάσαμε τα αποτελέσματα για όλες τις δομές διασύνδεσης που ορίζονται προηγουμένως. 48
49 Παρά το γεγονός ότι η προτεινόμενη μέθοδος είναι περιορισμένη σε πεπερασμένο κέρδος σταθερών διαδικασιών, το βασικό πλεονέκτημα είναι ότι ένας γραμμικός ελεγκτής μπορεί να σχεδιαστεί για να επιτευχθεί η επιθυμητή απόδοσης για το γραμμικό μοντέλο, ενώ ακόμα εγγυάται τη σταθερότητα κλειστού βρόχου για τις μη γραμμικές διαδικασίες. Έχει αποδειχθεί ότι η προσέγγιση αυτή μπορεί να οδηγήσει σε καλές επιδόσεις, και ότι είναι, επίσης, εφαρμόσιμη για σχετικές διαδικασίες. Όσον αφορά τους τομείς της αξιολόγησης της μη γραμμικότητας και της γραμμικής μοντελοποίησης για μη γραμμικά συστήματα, τα αποτελέσματα έχουν δείξει ότι δύο γνωστά μέτρα μη γραμμικότητας είναι πιο κοντά από ό, τι ήταν γνωστά πριν. Πολλά θεωρητικά αποτελέσματα έχουν δείξει ότι οι ορισμοί των μέτρων μη γραμμικότητας είναι σύμφωνα με τη διαίσθηση της μηχανικής, π.χ. στην περίπτωση των τοπικών γραμμικών προσεγγίσεων, ενισχύοντας έτσι την εμπιστοσύνη στην χρησιμότητα του πλαισίου. Άλλα αποτελέσματα επιτρέπουν στον χρήστη να αξιολογήσει πιο εύκολα το μέτρο μη γραμμικότητας και την άντληση γραμμικών μοντέλων για ένα σύστημα με γνωστή δομή, όπως Hammerstein και Wiener συστήματα. Επίσης να αποφασίσει εκ των προτέρων αν ένα συγκεκριμένο μέτρο μη γραμμικότητας (ή το δείκτη ποιότητας μοντέλου) είναι κατάλληλο για ένα συγκεκριμένο σύστημα ή όχι. Τα δύο αυτά γεγονότα συμβάλουν στην εφαρμογή του προτεινόμενου πλαισίου. Αντί να αξιολογηθεί το κέρδος του σφάλματος για μια σταθερή ρύθμιση, μπορεί κανείς επίσης, να σκεφτεί την αναζήτηση για ένα βέλτιστο γενικευμένο μοντέλο. Για να είναι σε θέση κανείς να εφαρμόζει τις μεθόδους ανάλυσης και σύνθεσης της μελέτης, η πρόοδος στον υπολογισμό των κερδών μη γραμμικών συστημάτων είναι επιθυμητή. Παρόλο που τα επιμέρους μέτρα μη γραμμικότητας υπολογίζονται με βάση το μοντέλο μόνο, το πλαίσιο επιτρέπει, επίσης, να αξιολογήσει τον έλεγχο που ενδιαφέρει τη μη γραμμικότητα. Η εκτίμηση αυτή μπορεί αφενός να λαμβάνει υπόψη το κατά πόσον οι απαραίτητες προϋποθέσεις σταθερότητας μπορεί να ικανοποιηθούν για το καλύτερο γραμμικό μοντέλο. Από την άλλη πλευρά, τα διάφορα μέτρα μη γραμμικότητας μπορούν να συγκριθούν, και σταθμισμένα 49
50 μέτρα μη γραμμικότητας μπορούν να χρησιμοποιηθούν για την αξιολόγηση της καταλληλότητας των γραμμικών μοντέλων σε σχέση με ένα συγκεκριμένο στόχο. Επιπλέον, η ανάλυση του σχετικού ελέγχου που γίνεται με αυτόν τον τρόπο δεν αναφέρεται μόνο σε ένα φανταστικό καλύτερο γραμμικό ελεγκτή για μια μη γραμμική μονάδα, αλλά από μια συγκεκριμένη διαδικασία σχεδιασμού είναι γνωστό πώς να σχεδιαστεί ένας πραγματικός γραμμικός ελεγκτής. 50
51 4 Kεφάλαιο 4.1 Έλεγχος με Πλήρη Ανατροφοδότηση Καταστάσεων Θεωρούμε σύστημα μονής εισόδου Η βασική ιδέα είναι να χρησιμοποιήσουμε ελεγκτή K ώστε να αλλάξουμε τις ιδιοτιμές του συστήματος, αλλάζοντας τελικά την δυναμική συμπεριφορά του συστήματος. Οι πόλοι του συστήματος κλειστού βρόχου είναι οι ιδιοτιμές του πίνακα Acl = A BK. Θεωρούμε πλήρη ανατροφοδότηση των καταστάσεων (full-state feedback) της μορφής u = r Kx, με u την είσοδο ελέγχου, r την είσοδο αναφοράς, Κ τα κέρδη του ελεγκτή, x τις μεταβλητές κατάστασης. Με βάση το σύστημα και την είσοδο ελέγχου, θα ισχύει Στόχος είναι να βρούμε τις τιμές K, ώστε ο πίνακας Acl να έχει επιθυμητές ιδιότητες, δηλαδή να είναι ευσταθής, με πόλους σε επιθυμητές θέσεις, κλπ. Με τη μέθοδο τοποθέτησης πόλων (pole placement), τοποθετούνται οι πόλοι κλειστού βρόχου σε επιθυμητές θέσεις. Στην περίπτωση ρυθμιστή (regulator), r = 0, όπου δεν υπάρχει εντολή εισόδου, τότε ο νόμος ελέγχου είναι ο γραμμικός συνδιασμός των μεταβλητών κατάστασης 51
52 Για σύστημα n τάξης, θα υπάρχουν n κέρδη (συντελεστές) ανάδρασης K1...Kn, για n ρίζες του συστήματος, υπάρχουν αρκετοί βαθμοί ελευθερίας για τοποθέτηση πόλων με κατάλληλη επιλογή των Κ. 4.2 Γραμμικοποίηση συστήματος Υποθέτουμε ότι η συνάρτηση f(x) μπορεί να αναπτυχθεί στην μορφή : f ( x) Ax g( x) όπου η συνάρτηση g(x) ικανοποιεί την σχέση gx ( ) lim 0 x x 0 Αυτό είναι πάντοτε δυνατό στην περίπτωση που η συνάρτηση f(x) αναπτύσσεται σε σειρά Taylor. Τότε f ( x) f (0) Ax g( x) και η g(x) ικανοποιεί την σχέση γιατί περιέχει όρους τάξεως μεγαλύτερης του 1. Η μήτρα A είναι η Ιακωβιανή της f(x) στο σημείο x=0. Δηλαδή Από αυτό προκύπτει ότι 52
53 f ( x) Ax g( x) γιατί, δεδομένου ότι η x=0 είναι κατάσταση ισορροπίας του συστήματος Σ, ισχύει f(0)=0. Το σύστημα x( t) Ax( t) λέγεται γραμμική προσέγγιση του συστήματος Σ. Με τις προαναφερθείσες υποθέσεις το πρώτο θεώρημα του Lyapunov διατυπώνεται ως εξής: ο Θεώρημα Lyapunov Αν f ( x) Ax g( x) και η συνάρτηση g(x) ικανοποιεί την σχέση : gx ( ) lim 0 x x 0 τότε η ασυμπτωτική ευστάθεια της ισορροπίας x=0 του γραμμικού συστήματος x( t) Ax( t) συνεπάγεται την ασυμπτωτική ευστάθεια της ισορρoπίας x=0 του συστήματος Σ. 4.3 Τοποθέτηση Πόλων Με τη μέθοδο τοποθέτησης πόλων τοποθετούνται όλοι οι πόλοι του συστήματος κλειστού βρόχου σε επιθυμητές θέσεις. Πλεονεκτήματα της μεθόδου είναι η δυνατότητα καθορισμού της επιθυμητής μεταβατικής απόκρισης. Μειονέκτημα θεωρείται η δυσκολία εφαρμογής σε συστήματα με περισσότερες από μία εισόδους/εξόδους και για αυτό εφαρμόζεται συνήθως σε συστήματα SISO. Επίσης παρότι οι πόλοι τοποθετούνται σε επιθυμητές θέσεις, δεν μπορούμε να γνωρίζουμε πόσο απέχουμε από τον βέλτιστο σχεδιασμό, κάτι που είναι εφικτό με τη μέθοδο βέλτιστου ελέγχου. 53
54 Απαραίτητη προυπόθεση ύπαρξης κέρδους Κ κατά την εφαρμογή της μεθόδου τοποθέτησης πόλων είναι οι πίνακες Α, Β του συστήματος να είναι ελέγξιμοι. Δύο είναι τα βασικά ερωτήματα που μας απασχολούν κατά την τοποθέτηση πόλων: Πως θα τοποθετηθούν οι πόλοι στις επιθυμητές θέσεις (υπολογισμός κερδών του ελεγκτή)? Που πρέπει να τοποθετηθούν οι πόλοι κλειστού βρόχου (υπολογισμός πόλων)? Για συστήματα 2ης τάξης, ο υπολογισμός κερδών γίνεται με απλές πράξεις. Για συστήματα μεγαλύτερης τάξης, εφαρμόζεται η μέθοδος Ackermann. Υπάρχουν 3 τεχνικές που βοηθούν στην επιλογή και υπολογισμό των επιθυμητών θέσεων πόλων προκειμένου για pole placement: Κυριαρχούντες πόλοι συστήματος 2ης τάξης Πρωτότυπος σχεδιασμός (Bessel/ITAE) Συμμετρική τοποθέτηση πόλων (LQR-Linear Quadratic Regulator). Στην εργασία αυτή, στόχος είναι η εφαρμογή δυο διαφορετικών τεχνικών βέλτιστου ελέγχου σε 2 μη γραμμικά προβλήματα, καθένα από τα οποία θα αντιστοιχεί σε 1 ου και 2 ου βαθμού γραμμικοποιημένα συστήματα. 4.4 Βέλτιστος Έλεγχος Ο βέλτιστος έλεγχος (optimal control) εισήχθη το 1960, ταυτόχρονα σε ΗΠΑ και πρώην Σοβιετική Ένωση, την εποχή που παρουσίαζε ενδιαφέρον η έρευνα για καθοδήγηση (guidance) και ελιγμούς (maneuvering), κυρίως για στρατιωτικές και διαστημικές εφαρμογές. Ο βέλτιστος έλεγχος επιδιώκει η απόδοση να είναι εκτός από αποδεκτή και βέλτιστη. Στον κλασσικό έλεγχο προσπαθούμε να ελαχιστοποιήσουμε το σφάλμα σε καθορισμένα χρονικά σημεία, π.χ. σφάλμα μόνιμης κατάστασης. Στο βέλτιστο έλεγχο ελαχιστοποιούμε το σφάλμα παντού. Συνάρτηση κόστους ή δείκτης λειτουργικής απόδοσης (ΔΛΑ-performance index) μπορεί να είναι το ολοκλήρωμα σφάλματος J1 ή το ολοκλήρωμα απόλυτης τιμής σφάλματος J2 54
55 Σημαντικό πλεονέκτημα της μεθόδου θεωρείται η δυνατότητα εφαρμογής σε σύστηματα με πολλές εισόδους/πολλές εξόδους (ΜΙΜΟ). Για γραμμικό μοντέλο και τετραγωνική συνάρτηση σφάλματος, το πρόβλημα είναι γνωστό ως Γραμμικό Τετραγωνικό (Linear Quadratic-LQ). Η συνάρτηση κόστους ορίζεται ως όπου Q 0;R > 0 είναι συμμετρικοί, θετικά ορισμένοι πίνακες καταλλήλων διαστάσεων. Αυτή η συνάρτηση κόστους αποτελεί συμβιβασμό (tradeoff) ανάμεσα στην απόσταση της κατάστασης (state) από την αρχή (origin) και το κόστος της εισόδου ελέγχου. 4.5 Linear Quadratic Regulator-LQR Ο βέλτιστος νόμος ελέγχου (Linear Quadratic Regulator-LQR) προκύπτει με ανατροφοδότηση κατάστασης Το κέρδος του ελεγκτή δίνεται από όπου P είναι συμμετρική θετικά ημιορισμένη λύση της αλγεβρικής εξίσωσης Riccati Η τελευταία μπορεί πολύ εύκολα να λυθεί με χρήση της εντολής CARE ή DARE στο Matlab.Έχοντας τον πίνακα P το LQR πρόβλημα μπορεί να λυθεί με γραμμική ανατροφοδότηση κατάστασης με σταθερό κέρδος : 55
56 Το κλειστό σύστημα τώρα διαμορφώνεται ως εξής: Προυποθέσεις για την επίλυση του συστήματος θα πρέπει το σύστημα κλειστού βρόχου να είναι ασυμπτωτικά ευσταθές, δηλαδή ελέγξιμο και παρατηρήσιμο. Οι πίνακες βάρους Q, R αποτελούν επιλογή του μηχανικού και επιδρούν στις μεταβλητές x,u. Συνήθως έχουν διαγώνια μορφή ( = 0), και τα στοιχεία τους καθορίζουν τη συμμετοχή των μεταβλητών κατάστασης και εισόδων ελέγχου στη συνολική συνάρτηση κόστους. Κf είναι ο χρόνος στον οποίο σταματάει η δράση ελέγχου που σημαίνει ότι η δράση ελέγχου είναι μέσα σε ένα συγκεκριμένο χρονικό διάστημα.s είναι ο πίνακας βάρους για την τελική κατάσταση.το βέλτιστο πρόβλημα ελέγχου ονομάζεται γραμμικό τετραγωνικό πρόβλημα (Linear Quadratic). Για την επίλυση αυτού του προβλήματος σχηματίζουμε τον πίνακα Hamilton : Η ενέργεια του συστήματος σχετίζεται με τον παράγοντα xtqx. Κατά τη μεταβατική κατάσταση, πρέπει η ενέργεια να πέφτει γρήγορα στο μηδέν. Η μέγιστη τιμή της σχετίζεται με την υπερακόντιση, ενώ ο χρόνος μείωσης της ενέργειας στο μηδέν σχετίζεται με τον χρόνο αποκατάστασης (settling time). Η ενέργεια ελέγχου σχετίζεται με τον παράγοντα utru. 4.6 Γραμμικός τετραγωνικός Γκαουσιανός έλεγχος (LQG) O σχηματισμός ενός lqr ελεγκτή πάσχει από το πολύ σημαντικό πρόβλημα ότι ο βέλτιστος νόμος ελέγχου : u(k ) = Kx(k ) απαιτεί όλη την κατάσταση να είναι διαθέσιμη για μέτρηση.μια πιθανή λύση για να ξεπεραστεί αυτό το πρόβλημα είναι ο βέλτιστος νόμος ελέγχου που περιγράψαμε παραπάνω να αντικατασταθεί με τον ακόλουθο : u(k ) = Kxˆ(k ) όπου xˆ(k ) δηλώνει μια εκτίμηση της κατάστασης. 56
57 4.7 Παρατηρητές πλήρους κατάστασης Ας θεωρήσουμε μια διεργασία η οποία περιγράφεται από τις ακόλουθες καταστατικές εξισώσεις : Υποθέτουμε τώρα ότι οι καταστάσεις x δεν μπορούν να μετρηθούν και στόχος μας είναι να τις εκτιμήσουμε με βάση την y. Eστω ότι κατασκευάζαμε μια εκτίμηση xˆ(k ) το σύστημα θα γινόταν : xˆ(k + 1) = Axˆ(k ) + Bu(k ) Ορίζουμε το σφάλμα εκτίμησης (estimation error) e = x(k ) xˆ(k ) Αυτό δείχνει ότι όταν το σύστημα είναι ασυμπτωτικά ευσταθές το σφάλμα e συγκλίνει στο μηδέν για κάθε είσοδο u. Στην περίπτωση όμως που o A δεν είναι ευσταθής η εκτίμηση θα μεγαλώνει συνεχώς.για να το αποφύγουμε αυτό εισάγουμε άλλον έναν όρο και παίρνουμε τις εξισώσεις : Ετσι όταν το xˆ(k ) είναι πολύ κοντά στο x(k ) το yˆ (k ) θα είναι πολύ κοντά στο y(k ) και άρα ο όρος L( y(k ) yˆ (k )) δεν θα παίζει κανένα ρόλο.αν όμως το xˆ(k ) φεύγει μακριά από το x(k ) τότε αυτός ο όρος, ευτυχώς, θα διορθώσει το σφάλμα.για να δούμε πως μπορεί να γίνει αυτό ξαναγράφουμε την εξίσωση κατάστασης ως προς το σφάλμα εκτίμησης : Τώρα το e συγκλίνει στο μηδέν αν o πίνακας (A LC) είναι ασυμπτωτικά ευσταθής. Έτσι ακόμα και αν ο A είναι ασταθής μπορούμε να επιλέξουμε έναν πίνακα L τέτοιο ώστε ο πίνακας (A LC) να είναι ασυμπτωτικά ευσταθής.τώρα το αρχικό σύστημα μπορεί να γραφτεί στην μορφή : 57
58 4.8 Αρχή της διαχωρισιμότητας Το πρόβλημα του βέλτιστου τετραγωνικού ελέγχου LQG μπορεί να χωριστεί σε 2 προβλήματα : 1) Την εκτίμηση των καταστάσεων με διαταραχές. 2) Το LQ βέλτιστο έλεγχο με ανατροφοδότηση κατάστασης 4.9 LQG estimation Κάθε επιλογή του πίνακα L που κάνει το A-LC να είναι ασυμπτωτικά ευσταθές θα κάνει την τιμή του xˆ(k ) να συγκλίνει στο x(k ) όσο η εξισώσεις κατάστασης περιγράφονται από την σχέση : Ωστόσο στις πιο πολλές περιπτώσεις οι μετρήσεις επηρεάζονται από θόρυβο το ίδιο και οι καταστάσεις. Έχοντας αυτό υπόψη θα πρέπει να αντικαταστήσουμε το παραπάνω σύστημα καταστατικών εξισώσεων με ένα πιο κατάλληλο που θα έχει την ακόλουθη μορφή : Όπου d είναι διαταραχές και n ο θόρυβος μετρήσεων με χαρακτηριστικά (τα ίδια ισχύουν και για τον n) : 58
59 Με Q να εκφράζει το πλάτος των διαταραχών του συστήματος και R να εκφράζει το πλάτος του θορύβου των μετρήσεων. Η εξίσωση για το λάθος εκτίμησης παίρνει την παρακάτω μορφή : (Υποθέτουμε επίσης ότι τα δυο σήματα n και d είναι μεταξύ τους ανεξάρτητα δηλαδή : T E d( k) n ( k) 0 Εξαιτίας του n και του d γενικά το σφάλμα εκτίμησης δεν θα συγκλίνει στο 0 αλλα θέλουμε ακόμα να το κρατήσουμε σε μια αρκετά χαμηλή τιμή. Στην περίπτωση αυτή θα πρέπει να χρησιμοποιήσουμε φίλτρο Kalman. Με αυτό τον τρόπο μπορεί κάποιος να βρει την βέλτιστη εκτίμηση του xˆ(k ) που ελαχιστοποιεί την συνδιασπορά E (x xˆ)(x xˆ)t και να χρησιμοποιήσει αυτή την εκτίμηση για να αντικαταστήσει την x(k ) στο σχεδιασμό ενός LQ ελεγκτή. Το block διάγραμμα του kalman φίλτρου φαίνεται παρακάτω : Το φίλτρο Kalman έχει περιγραφεί και παραπάνω εδώ ακολουθεί μια πολύ σύντομη περιγραφή : 1) Κατά την μέτρηση 2) Ανάμεσα στις μετρήσεις : 59
60 Διαφορετικές επιλογές των τιμών Q και R οδηγούν σε διαφορετικό πίνακα L. 1) Όταν ο πίνακας R είναι πολύ μικρός (συγκρινόμενος με τον Q) ο θόρυβος μετρήσεων είναι μικρός και το σύστημα ερμηνεύει μια μεγάλη απόκλιση του yˆ (k ) από το y(k ) σαν ένδειξη ότι η εκτίμηση xˆ(k ) για το x(k ) είναι κακή και χρειάζεται διόρθωση.αυτό οδηγεί σε μεγάλους πίνακες L. 2) Όταν ο πίνακας R είναι πολύ μεγάλος ο θόρυβος μετρήσεων είναι πολύ μεγάλος και έτσι ο βέλτιστος παρατηρητής είναι πιο συντηρητικός στην αντίδρασή του σε απότομες μεταβολές του yˆ (k ) από το y(k ). Αυτό οδηγεί σε μικρούς πίνακες L Βέλτιστος Κέρδος LQ Η εύρεση ενός κατάλληλου πίνακα L (ή Κf) τέτοιο ώστε να ελαχιστοποιείται το κριτήριο εκτίμησης : Η λύση του βέλτιστου προβλήματος του LQG είναι ένας πίνακας L διαστάσεων nxk ο οποίος θα δίνεται από την σχέση : Και ο P θα είναι η θετικά ορισμένη λύση της αλγεβρικής εξίσωση Riccati : Όταν κάποιος χρησιμοποιήσει αυτό το βέλτιστο κέρδος στην σχέση : xˆ(k + 1) = (A LC)xˆ(k ) + Bu(k ) + Ly το σύστημα ονομάζεται Kalman-Busy filter. Πολύ σημαντική ιδιότητα ενός τέτοιου συστήματος είναι ο πίνακας A LC να είναι ασυμτωτικά ευσταθής γεγονός που συμβαίνει όταν το σύστημα : 60
61 είναι παρατηρήσιμο και ελέγξιμο (αν θεωρήσουμε σαν μοναδική είσοδο στο σύστημα την d). Όταν η βέλτιστη εκτίμηση γίνει διαθέσιμη μπορεί να χρησιμοποιηθεί για να βρεθεί ο βέλτιστος νόμος ελέγχου Αυτό οδηγεί στον ακόλουθο ελεγκτή μα ανατροφοδότηση εξόδου : Για την διάταξη που θα φανεί παρακάτω το κλειστό σύστημα θα περιγράφεται από τις εξισώσεις : Οι πόλοι του κλειστού συστήματος είναι απλώς οι πόλοι του ντετερμινιστικού LQR συστήματος (ιδιοτιμές του c A Bk ) μαζί με τους πόλους του φίλτρου (ιδιοτιμές του f A k C ) κάτι που ήταν αναμενόμενο άλλωστε από την αρχή της διαχωρισιμότητας κατά τον σχεδιασμό του LQG. 61
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER
 4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Σκοπός του κεφαλαίου είναι να παρουσιάσει μερικές εφαρμογές του Μετασχηματισμού Fourier (ΜF). Ειδικότερα στο κεφάλαιο αυτό θα περιγραφούν έμμεσοι τρόποι
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Σκοπός του κεφαλαίου είναι να παρουσιάσει μερικές εφαρμογές του Μετασχηματισμού Fourier (ΜF). Ειδικότερα στο κεφάλαιο αυτό θα περιγραφούν έμμεσοι τρόποι
Συστήματα Αυτομάτου Ελέγχου ΙΙ. Άσκηση. γραμμάτων του επιθέτου σας (π.χ. για το επίθετο Κοσματόπουλος, οι αριθμοί α ι θα είναι a
 Συστήματα Αυτομάτου Ελέγχου ΙΙ Άσκηση Θεωρείστε το σύστημα με συνάρτηση μεταφοράς: Y ( s) a s 4 3 a3s a U ( s) s a όπου οι αριθμοί α ι αντιστοιχούν στους αντίστοιχους αριθμούς των 4 πρώτων γραμμάτων του
Συστήματα Αυτομάτου Ελέγχου ΙΙ Άσκηση Θεωρείστε το σύστημα με συνάρτηση μεταφοράς: Y ( s) a s 4 3 a3s a U ( s) s a όπου οι αριθμοί α ι αντιστοιχούν στους αντίστοιχους αριθμούς των 4 πρώτων γραμμάτων του
ΜΕΓΙΣΤΙΚΟΣ ΤΕΛΕΣΤΗΣ 18 Σεπτεμβρίου 2014
 ΜΕΓΙΣΤΙΚΟΣ ΤΕΛΕΣΤΗΣ 18 Σεπτεμβρίου 2014 Περιεχόμενα 1 Εισαγωγή 2 2 Μεγιστικός τελέστης στην μπάλα 2 2.1 Βασικό θεώρημα........................ 2 2.2 Γενική περίπτωση μπάλας.................. 6 2.2.1 Στο
ΜΕΓΙΣΤΙΚΟΣ ΤΕΛΕΣΤΗΣ 18 Σεπτεμβρίου 2014 Περιεχόμενα 1 Εισαγωγή 2 2 Μεγιστικός τελέστης στην μπάλα 2 2.1 Βασικό θεώρημα........................ 2 2.2 Γενική περίπτωση μπάλας.................. 6 2.2.1 Στο
Πανεπιστήμιο Πατρών Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών. Διάλεξη 13
 Πανεπιστήμιο Πατρών Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Τομέας Συστημάτων και Αυτομάτου Ελέγχου ΠΡΟΣΑΡΜΟΣΤΙΚΟΣ ΕΛΕΓΧΟΣ Διάλεξη 13 Πάτρα 28 Προσαρμοστικός έλεγχος με μοντέλο αναφοράς
Πανεπιστήμιο Πατρών Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Τομέας Συστημάτων και Αυτομάτου Ελέγχου ΠΡΟΣΑΡΜΟΣΤΙΚΟΣ ΕΛΕΓΧΟΣ Διάλεξη 13 Πάτρα 28 Προσαρμοστικός έλεγχος με μοντέλο αναφοράς
ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΔΙΑΚΡΙΤΩΝ ΕΝΑΛΛΑΚΤΙΚΩΝ ΣΕ ΠΡΟΒΛΗΜΑΤΑ ΣΧΕΔΙΑΣΜΟΥ ΚΑΙ ΣΥΝΘΕΣΗΣ ΔΙΕΡΓΑΣΙΩΝ
 ΜΕΡΟΣ ΙΙ ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΔΙΑΚΡΙΤΩΝ ΕΝΑΛΛΑΚΤΙΚΩΝ ΣΕ ΠΡΟΒΛΗΜΑΤΑ ΣΧΕΔΙΑΣΜΟΥ ΚΑΙ ΣΥΝΘΕΣΗΣ ΔΙΕΡΓΑΣΙΩΝ 36 ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΔΙΑΚΡΙΤΩΝ ΕΝΑΛΛΑΚΤΙΚΩΝ ΣΕ ΠΡΟΒΛΗΜΑΤΑ ΣΧΕΔΙΑΣΜΟΥ ΚΑΙ ΣΥΝΘΕΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Πολλές από τις αποφάσεις
ΜΕΡΟΣ ΙΙ ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΔΙΑΚΡΙΤΩΝ ΕΝΑΛΛΑΚΤΙΚΩΝ ΣΕ ΠΡΟΒΛΗΜΑΤΑ ΣΧΕΔΙΑΣΜΟΥ ΚΑΙ ΣΥΝΘΕΣΗΣ ΔΙΕΡΓΑΣΙΩΝ 36 ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΔΙΑΚΡΙΤΩΝ ΕΝΑΛΛΑΚΤΙΚΩΝ ΣΕ ΠΡΟΒΛΗΜΑΤΑ ΣΧΕΔΙΑΣΜΟΥ ΚΑΙ ΣΥΝΘΕΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Πολλές από τις αποφάσεις
Ψηφιακός Έλεγχος. 6 η διάλεξη Σχεδίαση στο χώρο κατάστασης. Ψηφιακός Έλεγχος 1
 Ψηφιακός Έλεγχος 6 η διάλεξη Σχεδίαση στο χώρο κατάστασης Ψηφιακός Έλεγχος Μέθοδος μετατόπισης ιδιοτιμών Έστω γραμμικό χρονικά αμετάβλητο σύστημα διακριτού χρόνου: ( + ) = + x k Ax k Bu k Εφαρμόζουμε γραμμικό
Ψηφιακός Έλεγχος 6 η διάλεξη Σχεδίαση στο χώρο κατάστασης Ψηφιακός Έλεγχος Μέθοδος μετατόπισης ιδιοτιμών Έστω γραμμικό χρονικά αμετάβλητο σύστημα διακριτού χρόνου: ( + ) = + x k Ax k Bu k Εφαρμόζουμε γραμμικό
1. ΣΤΑΤΙΚΗ ΑΡΙΣΤΟΠΟΙΗΣΗ
 . ΣΤΑΤΙΚΗ ΑΡΙΣΤΟΠΟΙΗΣΗ. Μέγιστα και Ελάχιστα Συναρτήσεων Χωρίς Περιορισμούς Συναρτήσεις μιας Μεταβλητής Εστω f ( x) είναι συνάρτηση μιας μόνο μεταβλητής. Εστω επίσης ότι x είναι ένα σημείο στο πεδίο ορισμού
. ΣΤΑΤΙΚΗ ΑΡΙΣΤΟΠΟΙΗΣΗ. Μέγιστα και Ελάχιστα Συναρτήσεων Χωρίς Περιορισμούς Συναρτήσεις μιας Μεταβλητής Εστω f ( x) είναι συνάρτηση μιας μόνο μεταβλητής. Εστω επίσης ότι x είναι ένα σημείο στο πεδίο ορισμού
Βέλτιστος Έλεγχος Συστημάτων
 Βέλτιστος Έλεγχος Συστημάτων Ενότητα 6: Το γραμμικό τετραγωνικό πρόβλημα βέλτιστης Καθηγητής Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα Αδειοδότησης
Βέλτιστος Έλεγχος Συστημάτων Ενότητα 6: Το γραμμικό τετραγωνικό πρόβλημα βέλτιστης Καθηγητής Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα Αδειοδότησης
Πανεπιστήμιο Πατρών Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών. Διάλεξη 9
 Πανεπιστήμιο Πατρών Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Τομέας Συστημάτων και Αυτομάτου Ελέγχου ΠΡΟΣΑΡΜΟΣΤΙΚΟΣ ΕΛΕΓΧΟΣ Διάλεξη 9 Πάτρα 2008 Ρύθμιση ελαχίστης διασποράς Η στρατηγική
Πανεπιστήμιο Πατρών Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Τομέας Συστημάτων και Αυτομάτου Ελέγχου ΠΡΟΣΑΡΜΟΣΤΙΚΟΣ ΕΛΕΓΧΟΣ Διάλεξη 9 Πάτρα 2008 Ρύθμιση ελαχίστης διασποράς Η στρατηγική
Παράδειγμα 1. Δίνεται ο κάτωθι κλειστός βρόχος αρνητικής ανάδρασης με. Σχήμα 1. στο οποίο εφαρμόζουμε αρνητική ανάδραση κέρδους
 Παράδειγμα 1 Δίνεται ο κάτωθι κλειστός βρόχος αρνητικής ανάδρασης με _ + Σχήμα 1 στο οποίο εφαρμόζουμε αρνητική ανάδραση κέρδους Α) Γράψτε το σύστημα ευθέως κλάδου σε κανονική παρατηρήσιμη μορφή στο χώρο
Παράδειγμα 1 Δίνεται ο κάτωθι κλειστός βρόχος αρνητικής ανάδρασης με _ + Σχήμα 1 στο οποίο εφαρμόζουμε αρνητική ανάδραση κέρδους Α) Γράψτε το σύστημα ευθέως κλάδου σε κανονική παρατηρήσιμη μορφή στο χώρο
ΑΝΑΛΥΣΗ 1 ΠΕΜΠΤΟ ΜΑΘΗΜΑ, Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ 1 ΠΕΜΠΤΟ ΜΑΘΗΜΑ, 17-10-13 Μ. Παπαδημητράκης. 1 Την προηγούμενη φορά αναφέραμε (και αποδείξαμε στην περίπτωση n = 2) το θεώρημα που λέει ότι, αν n N, n 2, τότε για κάθε y 0 υπάρχει μοναδική μηαρνητική
ΑΝΑΛΥΣΗ 1 ΠΕΜΠΤΟ ΜΑΘΗΜΑ, 17-10-13 Μ. Παπαδημητράκης. 1 Την προηγούμενη φορά αναφέραμε (και αποδείξαμε στην περίπτωση n = 2) το θεώρημα που λέει ότι, αν n N, n 2, τότε για κάθε y 0 υπάρχει μοναδική μηαρνητική
Γραφική Λύση & Πρότυπη Μορφή Μαθηματικού Μοντέλου
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Επιχειρησιακή Έρευνα Γραφική Λύση & Πρότυπη Μορφή Μαθηματικού Μοντέλου Η παρουσίαση προετοιμάστηκε από τον Ν.Α. Παναγιώτου Περιεχόμενα Παρουσίασης 1. Προϋποθέσεις Εφαρμογής
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Επιχειρησιακή Έρευνα Γραφική Λύση & Πρότυπη Μορφή Μαθηματικού Μοντέλου Η παρουσίαση προετοιμάστηκε από τον Ν.Α. Παναγιώτου Περιεχόμενα Παρουσίασης 1. Προϋποθέσεις Εφαρμογής
Εφαρμοσμένη Βελτιστοποίηση
 Εφαρμοσμένη Βελτιστοποίηση Ενότητα 1: Το πρόβλημα της βελτιστοποίησης Καθηγητής Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα Αδειοδότησης Το
Εφαρμοσμένη Βελτιστοποίηση Ενότητα 1: Το πρόβλημα της βελτιστοποίησης Καθηγητής Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα Αδειοδότησης Το
Φίλτρα Kalman. Αναλυτικές μέθοδοι στη Γεωπληροφορική. ιατύπωση του βασικού προβλήματος. προβλήματος. μοντέλο. Πρωτεύων μοντέλο
 Φίλτρα Kalman Εξαγωγή των εξισώσεων τους με βάση το κριτήριο ελαχιστοποίησης της Μεθόδου των Ελαχίστων Τετραγώνων. Αναλυτικές Μέθοδοι στη Γεωπληροφορική Μεταπτυχιακό Πρόγραμμα ΓΕΩΠΛΗΡΟΦΟΡΙΚΗ ιατύπωση του
Φίλτρα Kalman Εξαγωγή των εξισώσεων τους με βάση το κριτήριο ελαχιστοποίησης της Μεθόδου των Ελαχίστων Τετραγώνων. Αναλυτικές Μέθοδοι στη Γεωπληροφορική Μεταπτυχιακό Πρόγραμμα ΓΕΩΠΛΗΡΟΦΟΡΙΚΗ ιατύπωση του
Βέλτιστος Έλεγχος Συστημάτων
 Βέλτιστος Έλεγχος Συστημάτων Ενότητα 1: Εισαγωγή Καθηγητής Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα Αδειοδότησης Το παρόν υλικό διατίθεται
Βέλτιστος Έλεγχος Συστημάτων Ενότητα 1: Εισαγωγή Καθηγητής Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα Αδειοδότησης Το παρόν υλικό διατίθεται
Διερευνητική μάθηση We are researchers, let us do research! (Elbers and Streefland, 2000)
 Διερευνητική μάθηση We are researchers, let us do research! (Elbers and Streefland, 2000) Πρόκειται για την έρευνα που διεξάγουν οι επιστήμονες. Είναι μια πολύπλοκη δραστηριότητα που απαιτεί ειδικό ακριβό
Διερευνητική μάθηση We are researchers, let us do research! (Elbers and Streefland, 2000) Πρόκειται για την έρευνα που διεξάγουν οι επιστήμονες. Είναι μια πολύπλοκη δραστηριότητα που απαιτεί ειδικό ακριβό
Η Βασική Δομή Συστημάτων Ελέγχου Κίνησης
 Η Βασική Δομή Συστημάτων Ελέγχου Κίνησης Σύστημα ονομάζουμε ένα σύνολο στοιχείων κατάλληλα συνδεδεμένων μεταξύ τους για να επιτελέσουν κάποιο έργο Είσοδο ονομάζουμε τη διέγερση, εντολή ή αιτία η οποία
Η Βασική Δομή Συστημάτων Ελέγχου Κίνησης Σύστημα ονομάζουμε ένα σύνολο στοιχείων κατάλληλα συνδεδεμένων μεταξύ τους για να επιτελέσουν κάποιο έργο Είσοδο ονομάζουμε τη διέγερση, εντολή ή αιτία η οποία
(είσοδος) (έξοδος) καθώς το τείνει στο.
 Υπενθυμίζουμε ότι αν ένα σύστημα είναι ευσταθές, τότε η απόκριση είναι άθροισμα μίας μεταβατικής και μίας μόνιμης. Δηλαδή, αν το σύστημα είναι ευσταθές όπου και Είθισται, σε ένα σύστημα αυτομάτου ελέγχου
Υπενθυμίζουμε ότι αν ένα σύστημα είναι ευσταθές, τότε η απόκριση είναι άθροισμα μίας μεταβατικής και μίας μόνιμης. Δηλαδή, αν το σύστημα είναι ευσταθές όπου και Είθισται, σε ένα σύστημα αυτομάτου ελέγχου
ΕΛΕΓΧΟΣ ΠΑΡΑΓΩΓΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΛΕΓΧΟΣ ΠΑΡΑΓΩΓΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ Ενότητα: Αναγνώριση Διεργασίας - Προσαρμοστικός Έλεγχος (Process Identification) Αλαφοδήμος Κωνσταντίνος
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΛΕΓΧΟΣ ΠΑΡΑΓΩΓΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ Ενότητα: Αναγνώριση Διεργασίας - Προσαρμοστικός Έλεγχος (Process Identification) Αλαφοδήμος Κωνσταντίνος
Αναγνώριση Προτύπων Ι
 Αναγνώριση Προτύπων Ι Ενότητα 1: Μέθοδοι Αναγνώρισης Προτύπων Αν. Καθηγητής Δερματάς Ευάγγελος Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Αναγνώριση Προτύπων Ι Ενότητα 1: Μέθοδοι Αναγνώρισης Προτύπων Αν. Καθηγητής Δερματάς Ευάγγελος Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Εισαγωγή στην Επιστήμη του Ηλεκτρολόγου Μηχανικού (και στην Τεχνολογία Υπολογιστών;)
 Εισαγωγή στην Επιστήμη του Ηλεκτρολόγου Μηχανικού (και στην Τεχνολογία Υπολογιστών;) Τι είναι αυτό; 1. Διαλέξεις; 2. Σεμινάριο; 3. Μάθημα; 4. Αλλο; Θεωρία Συστημάτων, Θεωρία Αποφάσεων και (αυτόματος) Έλεγχος
Εισαγωγή στην Επιστήμη του Ηλεκτρολόγου Μηχανικού (και στην Τεχνολογία Υπολογιστών;) Τι είναι αυτό; 1. Διαλέξεις; 2. Σεμινάριο; 3. Μάθημα; 4. Αλλο; Θεωρία Συστημάτων, Θεωρία Αποφάσεων και (αυτόματος) Έλεγχος
E [ -x ^2 z] = E[x z]
![E [ -x ^2 z] = E[x z] E [ -x ^2 z] = E[x z]](/thumbs/69/60621176.jpg) 1 1.ΦΙΛΤΡΟ KALMAN ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ Σε αυτήν την διάλεξη θα πάμε στο φίλτρο με περισσότερες λεπτομέρειες, και θα παράσχουμε μια νέα παραγωγή για το φίλτρο Kalman, αυτή τη φορά βασισμένο στην ιδέα της γραμμικής
1 1.ΦΙΛΤΡΟ KALMAN ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ Σε αυτήν την διάλεξη θα πάμε στο φίλτρο με περισσότερες λεπτομέρειες, και θα παράσχουμε μια νέα παραγωγή για το φίλτρο Kalman, αυτή τη φορά βασισμένο στην ιδέα της γραμμικής
Μέρος Β /Στατιστική. Μέρος Β. Στατιστική. Γεωπονικό Πανεπιστήμιο Αθηνών Εργαστήριο Μαθηματικών&Στατιστικής/Γ. Παπαδόπουλος (www.aua.
 Μέρος Β /Στατιστική Μέρος Β Στατιστική Γεωπονικό Πανεπιστήμιο Αθηνών Εργαστήριο Μαθηματικών&Στατιστικής/Γ. Παπαδόπουλος (www.aua.gr/gpapadopoulos) Από τις Πιθανότητες στη Στατιστική Στα προηγούμενα, στο
Μέρος Β /Στατιστική Μέρος Β Στατιστική Γεωπονικό Πανεπιστήμιο Αθηνών Εργαστήριο Μαθηματικών&Στατιστικής/Γ. Παπαδόπουλος (www.aua.gr/gpapadopoulos) Από τις Πιθανότητες στη Στατιστική Στα προηγούμενα, στο
Εφαρμοσμένη Βελτιστοποίηση
 Εφαρμοσμένη Βελτιστοποίηση Ενότητα 3: Αναλυτικές μέθοδοι βελτιστοποίησης για συναρτήσεις μιας μεταβλητής Καθηγητής Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών
Εφαρμοσμένη Βελτιστοποίηση Ενότητα 3: Αναλυτικές μέθοδοι βελτιστοποίησης για συναρτήσεις μιας μεταβλητής Καθηγητής Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών
3.1 Η Αρχή της υπέρθεσης (ή της επαλληλίας)
 ΚΕΦ. 3 Γενικές αρχές της κυματικής 3.1-1 3.1 Η Αρχή της υπέρθεσης (ή της επαλληλίας) 3.1.1 Γενική διατύπωση 3.1. Εύρος ισχύος της αρχής της υπέρθεσης 3.1.3 Μαθηματικές συνέπειες της αρχής της υπέρθεσης
ΚΕΦ. 3 Γενικές αρχές της κυματικής 3.1-1 3.1 Η Αρχή της υπέρθεσης (ή της επαλληλίας) 3.1.1 Γενική διατύπωση 3.1. Εύρος ισχύος της αρχής της υπέρθεσης 3.1.3 Μαθηματικές συνέπειες της αρχής της υπέρθεσης
Ψηφιακός Έλεγχος. 10 η διάλεξη Ασκήσεις. Ψηφιακός Έλεγχος 1
 Ψηφιακός Έλεγχος 10 η διάλεξη Ασκήσεις Ψηφιακός Έλεγχος 1 Άσκηση1 Ασκήσεις Επιθυμούμε να ελέγξουμε την γωνία ανύψωσης μιας κεραίας για να παρακολουθείται η θέση ενός δορυφόρου. Το σύστημα της κεραίας και
Ψηφιακός Έλεγχος 10 η διάλεξη Ασκήσεις Ψηφιακός Έλεγχος 1 Άσκηση1 Ασκήσεις Επιθυμούμε να ελέγξουμε την γωνία ανύψωσης μιας κεραίας για να παρακολουθείται η θέση ενός δορυφόρου. Το σύστημα της κεραίας και
Κύρια σημεία. Η έννοια του μοντέλου. Έρευνα στην εφαρμοσμένη Στατιστική. ΈρευναστηΜαθηματικήΣτατιστική. Αντικείμενο της Μαθηματικής Στατιστικής
 Κύρια σημεία Ερευνητική Μεθοδολογία και Μαθηματική Στατιστική Απόστολος Μπουρνέτας Τμήμα Μαθηματικών ΕΚΠΑ Αναζήτηση ερευνητικού θέματος Εισαγωγή στην έρευνα Ολοκλήρωση ερευνητικής εργασίας Ο ρόλος των
Κύρια σημεία Ερευνητική Μεθοδολογία και Μαθηματική Στατιστική Απόστολος Μπουρνέτας Τμήμα Μαθηματικών ΕΚΠΑ Αναζήτηση ερευνητικού θέματος Εισαγωγή στην έρευνα Ολοκλήρωση ερευνητικής εργασίας Ο ρόλος των
ΔΙΑΧΕΙΡΙΣΗ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΔΙΑΧΕΙΡΙΣΗ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ Συνδυασμένη χρήση μοντέλων προσομοίωσης βελτιστοποίησης. Η μέθοδος του μητρώου μοναδιαίας απόκρισης Νικόλαος
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΔΙΑΧΕΙΡΙΣΗ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ Συνδυασμένη χρήση μοντέλων προσομοίωσης βελτιστοποίησης. Η μέθοδος του μητρώου μοναδιαίας απόκρισης Νικόλαος
ΕΝΑΣ ΔΙΚΡΙΤΗΡΙΟΣ ΑΛΓΟΡΙΘΜΟΣ SIMPLEX
 ΚΕΦΑΛΑΙΟ 3 ΕΝΑΣ ΔΙΚΡΙΤΗΡΙΟΣ ΑΛΓΟΡΙΘΜΟΣ SIMPLEX 3.1 Εισαγωγή Ο αλγόριθμος Simplex θεωρείται πλέον ως ένας κλασικός αλγόριθμος για την επίλυση γραμμικών προβλημάτων. Η πρακτική αποτελεσματικότητά του έχει
ΚΕΦΑΛΑΙΟ 3 ΕΝΑΣ ΔΙΚΡΙΤΗΡΙΟΣ ΑΛΓΟΡΙΘΜΟΣ SIMPLEX 3.1 Εισαγωγή Ο αλγόριθμος Simplex θεωρείται πλέον ως ένας κλασικός αλγόριθμος για την επίλυση γραμμικών προβλημάτων. Η πρακτική αποτελεσματικότητά του έχει
Παρουσίαση 2 η : Αρχές εκτίμησης παραμέτρων Μέρος 1 ο
 Εφαρμογές Ανάλυσης Σήματος στη Γεωδαισία Παρουσίαση η : Αρχές εκτίμησης παραμέτρων Μέρος ο Βασίλειος Δ. Ανδριτσάνος Αναπληρωτής Καθηγητής Γεώργιος Χλούπης Επίκουρος Καθηγητής Τμήμα Μηχανικών Τοπογραφίας
Εφαρμογές Ανάλυσης Σήματος στη Γεωδαισία Παρουσίαση η : Αρχές εκτίμησης παραμέτρων Μέρος ο Βασίλειος Δ. Ανδριτσάνος Αναπληρωτής Καθηγητής Γεώργιος Χλούπης Επίκουρος Καθηγητής Τμήμα Μηχανικών Τοπογραφίας
Μηχανική ΙI. Μετασχηματισμοί Legendre. διπλανό σχήμα ότι η αντίστροφη συνάρτηση dg. λέγεται μετασχηματισμός Legendre της f (x)
 Τμήμα Π Ιωάννου & Θ Αποστολάτου 7/5/000 Μηχανική ΙI Μετασχηματισμοί Legendre Έστω μια πραγματική συνάρτηση f (x) Ορίζουμε την παράγωγο συνάρτηση df (x) της f (x) : ( x) (η γραφική της παράσταση δίνεται
Τμήμα Π Ιωάννου & Θ Αποστολάτου 7/5/000 Μηχανική ΙI Μετασχηματισμοί Legendre Έστω μια πραγματική συνάρτηση f (x) Ορίζουμε την παράγωγο συνάρτηση df (x) της f (x) : ( x) (η γραφική της παράσταση δίνεται
ΦΙΛΤΡΟ KALMAN ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ
 1 ΦΙΛΤΡΟ KALMAN ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ Σε αυτό το μέρος της πτυχιακής θα ασχοληθούμε λεπτομερώς με το φίλτρο kalman και θα δούμε μια καινούρια έκδοση του φίλτρου πάνω στην εφαρμογή της γραμμικής εκτίμησης διακριτού
1 ΦΙΛΤΡΟ KALMAN ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ Σε αυτό το μέρος της πτυχιακής θα ασχοληθούμε λεπτομερώς με το φίλτρο kalman και θα δούμε μια καινούρια έκδοση του φίλτρου πάνω στην εφαρμογή της γραμμικής εκτίμησης διακριτού
Βέλτιστος Έλεγχος Συστημάτων
 Βέλτιστος Έλεγχος Συστημάτων Ενότητα 11: Στοχαστικός βέλτιστος έλεγχος γραμμικών συστημάτων με χρήση τετραγωνικών κριτηρίων (LQG Problem) Καθηγητής Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων
Βέλτιστος Έλεγχος Συστημάτων Ενότητα 11: Στοχαστικός βέλτιστος έλεγχος γραμμικών συστημάτων με χρήση τετραγωνικών κριτηρίων (LQG Problem) Καθηγητής Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων
Έλεγχος Κίνησης
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα 1501 - Έλεγχος Κίνησης Ενότητα: Συστήματα Ελέγχου Κίνησης Μιχαήλ Παπουτσιδάκης Τμήμα Αυτοματισμού Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα 1501 - Έλεγχος Κίνησης Ενότητα: Συστήματα Ελέγχου Κίνησης Μιχαήλ Παπουτσιδάκης Τμήμα Αυτοματισμού Άδειες Χρήσης Το παρόν εκπαιδευτικό
5. (Λειτουργικά) Δομικά Διαγράμματα
 5. (Λειτουργικά) Δομικά Διαγράμματα Γενικά, ένα λειτουργικό δομικό διάγραμμα έχει συγκεκριμένη δομή που περιλαμβάνει: Τις δομικές μονάδες (λειτουργικά τμήματα ή βαθμίδες) που συμβολίζουν συγκεκριμένες
5. (Λειτουργικά) Δομικά Διαγράμματα Γενικά, ένα λειτουργικό δομικό διάγραμμα έχει συγκεκριμένη δομή που περιλαμβάνει: Τις δομικές μονάδες (λειτουργικά τμήματα ή βαθμίδες) που συμβολίζουν συγκεκριμένες
ΠΡΟΣΑΡΜΟΣΤΙΚΟΣ ΕΛΕΓΧΟΣ ΡΟΜΠΟΤΙΚΟΥ ΒΡΑΧΙΟΝΑ ΜΕ ΕΞΑΣΦΑΛΙΣΗ ΠΡΟΚΑΘΟΡΙΣΜΕΝΗΣ ΕΠΙΔΟΣΗΣ ΣΤΟ ΣΦΑΛΜΑ ΠΑΡΑΚΟΛΟΥΘΗΣΗΣ ΤΡΟΧΙΑΣ ΣΤΙΣ ΑΡΘΡΩΣΕΙΣ.
 ΠΡΟΣΑΡΜΟΣΤΙΚΟΣ ΕΛΕΓΧΟΣ ΡΟΜΠΟΤΙΚΟΥ ΒΡΑΧΙΟΝΑ ΜΕ ΕΞΑΣΦΑΛΙΣΗ ΠΡΟΚΑΘΟΡΙΣΜΕΝΗΣ ΕΠΙΔΟΣΗΣ ΣΤΟ ΣΦΑΛΜΑ ΠΑΡΑΚΟΛΟΥΘΗΣΗΣ ΤΡΟΧΙΑΣ ΣΤΙΣ ΑΡΘΡΩΣΕΙΣ. Όλγα Ζωίδη, Ζωή Δουλγέρη Εργαστήριο Αυτοματοποίησης και Ρομποτικής Τμήμα
ΠΡΟΣΑΡΜΟΣΤΙΚΟΣ ΕΛΕΓΧΟΣ ΡΟΜΠΟΤΙΚΟΥ ΒΡΑΧΙΟΝΑ ΜΕ ΕΞΑΣΦΑΛΙΣΗ ΠΡΟΚΑΘΟΡΙΣΜΕΝΗΣ ΕΠΙΔΟΣΗΣ ΣΤΟ ΣΦΑΛΜΑ ΠΑΡΑΚΟΛΟΥΘΗΣΗΣ ΤΡΟΧΙΑΣ ΣΤΙΣ ΑΡΘΡΩΣΕΙΣ. Όλγα Ζωίδη, Ζωή Δουλγέρη Εργαστήριο Αυτοματοποίησης και Ρομποτικής Τμήμα
J-GANNO. Σύντοµη αναφορά στους κύριους στόχους σχεδίασης και τα βασικά χαρακτηριστικά του πακέτου (προέκδοση 0.9Β, Φεβ.1998) Χάρης Γεωργίου
 J-GANNO ΓΕΝΙΚΕΥΜΕΝΟ ΠΑΚΕΤΟ ΥΛΟΠΟΙΗΣΗΣ ΤΕΧΝΗΤΩΝ ΝΕΥΡΩΝΙΚΩΝ ΙΚΤΥΩΝ ΣΤΗ ΓΛΩΣΣΑ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ JAVA Σύντοµη αναφορά στους κύριους στόχους σχεδίασης και τα βασικά χαρακτηριστικά του πακέτου (προέκδοση 0.9Β,
J-GANNO ΓΕΝΙΚΕΥΜΕΝΟ ΠΑΚΕΤΟ ΥΛΟΠΟΙΗΣΗΣ ΤΕΧΝΗΤΩΝ ΝΕΥΡΩΝΙΚΩΝ ΙΚΤΥΩΝ ΣΤΗ ΓΛΩΣΣΑ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ JAVA Σύντοµη αναφορά στους κύριους στόχους σχεδίασης και τα βασικά χαρακτηριστικά του πακέτου (προέκδοση 0.9Β,
ΕΡΓΑΣΤΗΡΙΟ ΣΥΣΤΗΜΑΤΩΝ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΔΙΕΥΘΥΝΤΗΣ ΚΑΘΗΓΗΤΗΣ Γ.Π. ΠΑΠΑΒΑΣΙΛΟΠΟΥΛΟΣ ΣΧΕΔΙΑΣΗ ΣΥΣΤΗΜΑΤΩΝ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΑΣΚΗΣΗ 2
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΗΜΑΤΩΝ ΕΛΕΓΧΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΣΥΣΤΗΜΑΤΩΝ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΔΙΕΥΘΥΝΤΗΣ ΚΑΘΗΓΗΤΗΣ Γ.Π. ΠΑΠΑΒΑΣΙΛΟΠΟΥΛΟΣ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΗΜΑΤΩΝ ΕΛΕΓΧΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΣΥΣΤΗΜΑΤΩΝ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΔΙΕΥΘΥΝΤΗΣ ΚΑΘΗΓΗΤΗΣ Γ.Π. ΠΑΠΑΒΑΣΙΛΟΠΟΥΛΟΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 07-08 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Επικ. Καθηγητής v.koutras@fme.aegea.gr Τηλ: 7035468 Θα μελετήσουμε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 07-08 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Επικ. Καθηγητής v.koutras@fme.aegea.gr Τηλ: 7035468 Θα μελετήσουμε
(1) L{a 1 x 1 + a 2 x 2 } = a 1 L{x 1 } + a 2 L{x 2 } (2) x(t) = δ(t t ) x(t ) dt x[i] = δ[i i ] x[i ] (3) h[i, i ] x[i ] (4)
![(1) L{a 1 x 1 + a 2 x 2 } = a 1 L{x 1 } + a 2 L{x 2 } (2) x(t) = δ(t t ) x(t ) dt x[i] = δ[i i ] x[i ] (3) h[i, i ] x[i ] (4) (1) L{a 1 x 1 + a 2 x 2 } = a 1 L{x 1 } + a 2 L{x 2 } (2) x(t) = δ(t t ) x(t ) dt x[i] = δ[i i ] x[i ] (3) h[i, i ] x[i ] (4)](/thumbs/58/41629922.jpg) Πανεπιστήμιο Θεσσαλίας ΗΥ240: Θεωρία Σημάτων και Συστημάτων Γραμμικά χρονικά μεταβαλλόμενα συστήματα Συνάρτηση συστήματος Ένα σύστημα L απεικονίζει κάθε σήμα εισόδου x σε ένα σήμα εξόδου y, δηλ., συνεχής
Πανεπιστήμιο Θεσσαλίας ΗΥ240: Θεωρία Σημάτων και Συστημάτων Γραμμικά χρονικά μεταβαλλόμενα συστήματα Συνάρτηση συστήματος Ένα σύστημα L απεικονίζει κάθε σήμα εισόδου x σε ένα σήμα εξόδου y, δηλ., συνεχής
Συστήματα Αυτομάτου Ελέγχου ΙΙ Γιώργος Σούλτης 167
 Προσομοίωση πραγματικών συστημάτων στο MATLAB Είδαμε μέχρι τώρα πως μπορούμε να υπολογίσουμε την συνάρτηση μεταφοράς σε πραγματικά συστήματα. Ο υπολογισμός της συνάρτησης μεταφοράς στη ουσία είναι η «γραμμικοποίηση»
Προσομοίωση πραγματικών συστημάτων στο MATLAB Είδαμε μέχρι τώρα πως μπορούμε να υπολογίσουμε την συνάρτηση μεταφοράς σε πραγματικά συστήματα. Ο υπολογισμός της συνάρτησης μεταφοράς στη ουσία είναι η «γραμμικοποίηση»
5. ΤΟ ΓΕΝΙΚΟ ΓΡΑΜΜΙΚΟ ΜΟΝΤΕΛΟ (GENERAL LINEAR MODEL) 5.1 Εναλλακτικά μοντέλα του απλού γραμμικού μοντέλου: Το εκθετικό μοντέλο
 5. ΤΟ ΓΕΝΙΚΟ ΓΡΑΜΜΙΚΟ ΜΟΝΤΕΛΟ (GENERAL LINEAR MODEL) 5.1 Εναλλακτικά μοντέλα του απλού γραμμικού μοντέλου: Το εκθετικό μοντέλο Ένα εναλλακτικό μοντέλο της απλής γραμμικής παλινδρόμησης (που χρησιμοποιήθηκε
5. ΤΟ ΓΕΝΙΚΟ ΓΡΑΜΜΙΚΟ ΜΟΝΤΕΛΟ (GENERAL LINEAR MODEL) 5.1 Εναλλακτικά μοντέλα του απλού γραμμικού μοντέλου: Το εκθετικό μοντέλο Ένα εναλλακτικό μοντέλο της απλής γραμμικής παλινδρόμησης (που χρησιμοποιήθηκε
website:
 Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ιδρυμα Θεσσαλονίκης Τμήμα Μηχανικών Αυτοματισμού Μαθηματική Μοντελοποίηση Αναγνώριση Συστημάτων Μαάιτα Τζαμάλ-Οδυσσέας 6 Μαρτίου 2017 1 Εισαγωγή Κάθε φυσικό σύστημα
Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ιδρυμα Θεσσαλονίκης Τμήμα Μηχανικών Αυτοματισμού Μαθηματική Μοντελοποίηση Αναγνώριση Συστημάτων Μαάιτα Τζαμάλ-Οδυσσέας 6 Μαρτίου 2017 1 Εισαγωγή Κάθε φυσικό σύστημα
Προηγμένος έλεγχος ηλεκτρικών μηχανών
 Προηγμένος έλεγχος ηλεκτρικών μηχανών Ενότητα 3: Βαθμωτός Έλεγχος Ασύχρονων Μηχανών Επαμεινώνδας Μητρονίκας - Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών & Τεχνολογίας Υπολογιστών
Προηγμένος έλεγχος ηλεκτρικών μηχανών Ενότητα 3: Βαθμωτός Έλεγχος Ασύχρονων Μηχανών Επαμεινώνδας Μητρονίκας - Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών & Τεχνολογίας Υπολογιστών
Γραμμικός Προγραμματισμός Μέθοδος Simplex
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Επιχειρησιακή Έρευνα Γραμμικός Προγραμματισμός Μέθοδος Simplex Η παρουσίαση προετοιμάστηκε από τον Ν.Α. Παναγιώτου Περιεχόμενα Παρουσίασης 1. Πρότυπη Μορφή ΓΠ 2. Πινακοποίηση
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Επιχειρησιακή Έρευνα Γραμμικός Προγραμματισμός Μέθοδος Simplex Η παρουσίαση προετοιμάστηκε από τον Ν.Α. Παναγιώτου Περιεχόμενα Παρουσίασης 1. Πρότυπη Μορφή ΓΠ 2. Πινακοποίηση
Βιομηχανικοί Ελεγκτές
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τ.Τ Βιομηχανικοί Ελεγκτές Ενότητα #10: Μοντέρνες Μέθοδοι Αναλογικού Ελέγχου Κωνσταντίνος Αλαφοδήμος Τμήματος Μηχανικών Αυτοματισμού Τ.Ε. Άδειες Χρήσης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τ.Τ Βιομηχανικοί Ελεγκτές Ενότητα #10: Μοντέρνες Μέθοδοι Αναλογικού Ελέγχου Κωνσταντίνος Αλαφοδήμος Τμήματος Μηχανικών Αυτοματισμού Τ.Ε. Άδειες Χρήσης
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Ι
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Ι Προσέγγιση και Ομοιότητα Σημάτων Επιμέλεια: Πέτρος Π. Γρουμπός Καθηγητής Γεώργιος Α. Βασκαντήρας Υπ. Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών & Τεχνολογίας Υπολογιστών Άδειες Χρήσης
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Ι Προσέγγιση και Ομοιότητα Σημάτων Επιμέλεια: Πέτρος Π. Γρουμπός Καθηγητής Γεώργιος Α. Βασκαντήρας Υπ. Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών & Τεχνολογίας Υπολογιστών Άδειες Χρήσης
ΠΡΟΗΓΜΕΝΑ ΣΥΣΤΗΜΑΤΑ ΜΕΤΑΦΟΡΩΝ
 ΠΡΟΗΓΜΕΝΑ ΣΥΣΤΗΜΑΤΑ ΜΕΤΑΦΟΡΩΝ Ενότητα 3: Συστήματα Αυτόματου Ελέγχου Διδάσκων: Γεώργιος Στεφανίδης Πολυτεχνική Σχολή Τμήμα Πολιτικών Μηχανικών Σκοποί ενότητας Στην ενότητα αυτή θα ασχοληθούμε με τα Συστήματα
ΠΡΟΗΓΜΕΝΑ ΣΥΣΤΗΜΑΤΑ ΜΕΤΑΦΟΡΩΝ Ενότητα 3: Συστήματα Αυτόματου Ελέγχου Διδάσκων: Γεώργιος Στεφανίδης Πολυτεχνική Σχολή Τμήμα Πολιτικών Μηχανικών Σκοποί ενότητας Στην ενότητα αυτή θα ασχοληθούμε με τα Συστήματα
ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΜΑΘΗΜΑΤΙΚΗ ΔΙΑΤΥΠΩΣΗ, Διαλ. 2. Ανωτάτη Σχολή Παιδαγωγικής και Τεχνολογικής Εκπαίδευσης 8/4/2017
 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΜΑΘΗΜΑΤΙΚΗ ΔΙΑΤΥΠΩΣΗ, Διαλ. 2 Ανωτάτη Σχολή Παιδαγωγικής και Τεχνολογικής Εκπαίδευσης 8/4/2017 Αντικειμενικοί στόχοι Η μελέτη των βασικών στοιχείων που συνθέτουν ένα πρόβλημα βελτιστοποίησης
ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΜΑΘΗΜΑΤΙΚΗ ΔΙΑΤΥΠΩΣΗ, Διαλ. 2 Ανωτάτη Σχολή Παιδαγωγικής και Τεχνολογικής Εκπαίδευσης 8/4/2017 Αντικειμενικοί στόχοι Η μελέτη των βασικών στοιχείων που συνθέτουν ένα πρόβλημα βελτιστοποίησης
ΑΝΑΛΥΣΗ ΕΥΑΙΣΘΗΣΙΑΣ Εισαγωγή
 1 ΑΝΑΛΥΣΗ ΕΥΑΙΣΘΗΣΙΑΣ Εισαγωγή Η ανάλυση ευαισθησίας μιάς οικονομικής πρότασης είναι η μελέτη της επιρροής των μεταβολών των τιμών των παραμέτρων της πρότασης στη διαμόρφωση της τελικής απόφασης. Η ανάλυση
1 ΑΝΑΛΥΣΗ ΕΥΑΙΣΘΗΣΙΑΣ Εισαγωγή Η ανάλυση ευαισθησίας μιάς οικονομικής πρότασης είναι η μελέτη της επιρροής των μεταβολών των τιμών των παραμέτρων της πρότασης στη διαμόρφωση της τελικής απόφασης. Η ανάλυση
Εξαρτημένες Πηγές και Τελεστικός Ενισχυτής
 Ανάλυση Κυκλωμάτων Εξαρτημένες Πηγές και Τελεστικός Ενισχυτής Φώτης Πλέσσας fplessas@inf.uth.gr Εισαγωγή Οι εξαρτημένες πηγές είναι πολύ ενδιαφέροντα ηλεκτρικά στοιχεία, αφού αποτελούν αναπόσπαστα στοιχεία
Ανάλυση Κυκλωμάτων Εξαρτημένες Πηγές και Τελεστικός Ενισχυτής Φώτης Πλέσσας fplessas@inf.uth.gr Εισαγωγή Οι εξαρτημένες πηγές είναι πολύ ενδιαφέροντα ηλεκτρικά στοιχεία, αφού αποτελούν αναπόσπαστα στοιχεία
E[ (x- ) ]= trace[(x-x)(x- ) ]
![E[ (x- ) ]= trace[(x-x)(x- ) ] E[ (x- ) ]= trace[(x-x)(x- ) ]](/thumbs/55/36021260.jpg) 1 ΦΙΛΤΡΟ KALMAN ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ Σε αυτό το μέρος της πτυχιακής θα ασχοληθούμε λεπτομερώς με το φίλτρο kalman και θα δούμε μια καινούρια έκδοση του φίλτρου πάνω στην εφαρμογή της γραμμικής εκτίμησης διακριτού
1 ΦΙΛΤΡΟ KALMAN ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ Σε αυτό το μέρος της πτυχιακής θα ασχοληθούμε λεπτομερώς με το φίλτρο kalman και θα δούμε μια καινούρια έκδοση του φίλτρου πάνω στην εφαρμογή της γραμμικής εκτίμησης διακριτού
Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος
 Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος Χιωτίδης Γεώργιος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος Χιωτίδης Γεώργιος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Σ ΤΑΤ Ι Σ Τ Ι Κ Η. Statisticum collegium iv
 Σ ΤΑΤ Ι Σ Τ Ι Κ Η i Statisticum collegium iv Στατιστική Συμπερασματολογία Ι Σημειακές Εκτιμήσεις Διαστήματα Εμπιστοσύνης Στατιστική Συμπερασματολογία (Statistical Inference) Το πεδίο της Στατιστικής Συμπερασματολογία,
Σ ΤΑΤ Ι Σ Τ Ι Κ Η i Statisticum collegium iv Στατιστική Συμπερασματολογία Ι Σημειακές Εκτιμήσεις Διαστήματα Εμπιστοσύνης Στατιστική Συμπερασματολογία (Statistical Inference) Το πεδίο της Στατιστικής Συμπερασματολογία,
Βιομηχανικοί Ελεγκτές
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τ.Τ Βιομηχανικοί Ελεγκτές Ενότητα #9: Αναλογικά Συστήματα Ελέγχου Κωνσταντίνος Αλαφοδήμος Τμήματος Μηχανικών Αυτοματισμού Τ.Ε. Άδειες Χρήσης Το παρόν
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τ.Τ Βιομηχανικοί Ελεγκτές Ενότητα #9: Αναλογικά Συστήματα Ελέγχου Κωνσταντίνος Αλαφοδήμος Τμήματος Μηχανικών Αυτοματισμού Τ.Ε. Άδειες Χρήσης Το παρόν
HY213. ΑΡΙΘΜΗΤΙΚΗ ΑΝΑΛΥΣΗ ΕΛΑΧΙΣΤΑ ΤΕΤΡΑΓΩΝΑ AΝΑΛΥΣΗ ΙΔΙΑΖΟΥΣΩΝ ΤΙΜΩΝ
 HY3. ΑΡΙΘΜΗΤΙΚΗ ΑΝΑΛΥΣΗ ΕΛΑΧΙΣΤΑ ΤΕΤΡΑΓΩΝΑ AΝΑΛΥΣΗ ΙΔΙΑΖΟΥΣΩΝ ΤΙΜΩΝ Π. ΤΣΟΜΠΑΝΟΠΟΥΛΟΥ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ Μέθοδος ελαχίστων τετραγώνων Τα σφάλματα
HY3. ΑΡΙΘΜΗΤΙΚΗ ΑΝΑΛΥΣΗ ΕΛΑΧΙΣΤΑ ΤΕΤΡΑΓΩΝΑ AΝΑΛΥΣΗ ΙΔΙΑΖΟΥΣΩΝ ΤΙΜΩΝ Π. ΤΣΟΜΠΑΝΟΠΟΥΛΟΥ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ Μέθοδος ελαχίστων τετραγώνων Τα σφάλματα
Πανεπιστήμιο Πατρών Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών. Διάλεξη 11
 Πανεπιστήμιο Πατρών Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Τομέας Συστημάτων και Αυτομάτου Ελέγχου ΠΡΟΣΑΡΜΟΣΤΙΚΟΣ ΕΛΕΓΧΟΣ Διάλεξη 11 Πάτρα 2008 Προσαρμοστικός LQ έλεγχος για μη ελαχίστης
Πανεπιστήμιο Πατρών Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Τομέας Συστημάτων και Αυτομάτου Ελέγχου ΠΡΟΣΑΡΜΟΣΤΙΚΟΣ ΕΛΕΓΧΟΣ Διάλεξη 11 Πάτρα 2008 Προσαρμοστικός LQ έλεγχος για μη ελαχίστης
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Παραγώγιση Εισαγωγή Ορισμός 7. Αν y f x είναι μια συνάρτηση ορισμένη σε ένα διάστημα
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Παραγώγιση Εισαγωγή Ορισμός 7. Αν y f x είναι μια συνάρτηση ορισμένη σε ένα διάστημα
ΔΙΔΑΣΚΑΛΙΑ ΤΗΣ ΕΝΝΟΙΑΣ ΤΟΥ ΟΡΙΟΥ ΣΥΝΑΡΤΗΣΗΣ
 ΕΠΙΜΟΡΦΩΣΗ ΤΩΝ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΓΙΑ ΤΗΝ ΑΞΙΟΠΟΙΗΣΗ ΚΑΙ ΕΦΑΡΜΟΓΗ ΤΩΝ ΤΠΕ ΣΤΗ ΔΙΔΑΚΤΙΚΗ ΠΡΑΞΗ ΔΙΔΑΣΚΑΛΙΑ ΤΗΣ ΕΝΝΟΙΑΣ ΤΟΥ ΟΡΙΟΥ ΣΥΝΑΡΤΗΣΗΣ ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΕΞ ΑΡΙΣΤΕΡΩΝ ΚΑΙ ΕΚ ΔΕΞΙΩΝ ΣΥΓΓΡΑΦΕΑΣ: ΚΟΥΤΙΔΗΣ ΙΩΑΝΝΗΣ
ΕΠΙΜΟΡΦΩΣΗ ΤΩΝ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΓΙΑ ΤΗΝ ΑΞΙΟΠΟΙΗΣΗ ΚΑΙ ΕΦΑΡΜΟΓΗ ΤΩΝ ΤΠΕ ΣΤΗ ΔΙΔΑΚΤΙΚΗ ΠΡΑΞΗ ΔΙΔΑΣΚΑΛΙΑ ΤΗΣ ΕΝΝΟΙΑΣ ΤΟΥ ΟΡΙΟΥ ΣΥΝΑΡΤΗΣΗΣ ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΕΞ ΑΡΙΣΤΕΡΩΝ ΚΑΙ ΕΚ ΔΕΞΙΩΝ ΣΥΓΓΡΑΦΕΑΣ: ΚΟΥΤΙΔΗΣ ΙΩΑΝΝΗΣ
ΕΛΕΓΚΤΕΣ PID. Ελεγκτής τριών όρων Η συνάρτηση μεταφοράς του PID ελεγκτή είναι η ακόλουθη:
 ΕΛΕΓΚΤΕΣ PID Εισαγωγή Αυτό το βοήθημα θα σας δείξει τα χαρακτηριστικά καθενός από τους τρεις ελέγχους ενός PID ελεγκτή, του αναλογικού (P), του ολοκληρωτικού (I) και του διαφορικού (D) ελέγχου, καθώς και
ΕΛΕΓΚΤΕΣ PID Εισαγωγή Αυτό το βοήθημα θα σας δείξει τα χαρακτηριστικά καθενός από τους τρεις ελέγχους ενός PID ελεγκτή, του αναλογικού (P), του ολοκληρωτικού (I) και του διαφορικού (D) ελέγχου, καθώς και
Ψηφιακή Επεξεργασία Σημάτων
 Ψηφιακή Επεξεργασία Σημάτων Ενότητα 3: Συστήματα Διακριτού Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Συστήματα Διακριτού Χρόνου Εισαγωγή στα Συστήματα Διακριτού Χρόνου Ταξινόμηση Συστημάτων ΔΧ
Ψηφιακή Επεξεργασία Σημάτων Ενότητα 3: Συστήματα Διακριτού Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Συστήματα Διακριτού Χρόνου Εισαγωγή στα Συστήματα Διακριτού Χρόνου Ταξινόμηση Συστημάτων ΔΧ
ΒΑΣΙΚΑ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ ΤΗΣ ΜΕΘΟΔΟΥ SIMPLEX
 ΒΑΣΙΚΑ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ ΤΗΣ ΜΕΘΟΔΟΥ SIMPLEX Θεμελιώδης αλγόριθμος επίλυσης προβλημάτων Γραμμικού Προγραμματισμού που κάνει χρήση της θεωρίας της Γραμμικής Άλγεβρας Προτάθηκε από το Dantzig (1947) και πλέον
ΒΑΣΙΚΑ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ ΤΗΣ ΜΕΘΟΔΟΥ SIMPLEX Θεμελιώδης αλγόριθμος επίλυσης προβλημάτων Γραμμικού Προγραμματισμού που κάνει χρήση της θεωρίας της Γραμμικής Άλγεβρας Προτάθηκε από το Dantzig (1947) και πλέον
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ. Εργαστήριο 8 ο. Αποδιαμόρφωση PAM-PPM με προσαρμοσμένα φίλτρα
 Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΨΗΦΙΑΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Εργαστήριο 8 ο Αποδιαμόρφωση PAM-PPM με προσαρμοσμένα φίλτρα Βασική Θεωρία Σε ένα σύστημα μετάδοσης
Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΨΗΦΙΑΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Εργαστήριο 8 ο Αποδιαμόρφωση PAM-PPM με προσαρμοσμένα φίλτρα Βασική Θεωρία Σε ένα σύστημα μετάδοσης
[1] είναι ταυτοτικά ίση με το μηδέν. Στην περίπτωση που το στήριγμα μιας συνάρτησης ελέγχου φ ( x)
![[1] είναι ταυτοτικά ίση με το μηδέν. Στην περίπτωση που το στήριγμα μιας συνάρτησης ελέγχου φ ( x) [1] είναι ταυτοτικά ίση με το μηδέν. Στην περίπτωση που το στήριγμα μιας συνάρτησης ελέγχου φ ( x)](/thumbs/52/30132893.jpg) [] 9 ΣΥΝΑΡΤΗΣΙΑΚΟΙ ΧΩΡΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER Η «συνάρτηση» δέλτα του irac Η «συνάρτηση» δέλτα ορίζεται μέσω της σχέσης φ (0) αν 0 δ[ φ ] = φ δ dx = (9) 0 αν 0 όπου η φ είναι μια συνάρτηση που ανήκει
[] 9 ΣΥΝΑΡΤΗΣΙΑΚΟΙ ΧΩΡΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER Η «συνάρτηση» δέλτα του irac Η «συνάρτηση» δέλτα ορίζεται μέσω της σχέσης φ (0) αν 0 δ[ φ ] = φ δ dx = (9) 0 αν 0 όπου η φ είναι μια συνάρτηση που ανήκει
Έλεγχος Υποθέσεων. Δρ. Αθανάσιος Δαγούμας, Επ. Καθηγητής Οικονομικής της Ενέργειας & των Φυσικών Πόρων, Πανεπιστήμιο Πειραιώς
 Δρ. Αθανάσιος Δαγούμας, Επ. Καθηγητής Οικονομικής της Ενέργειας & των Φυσικών Πόρων, Πανεπιστήμιο Πειραιώς Η μηδενική υπόθεση είναι ένας ισχυρισμός σχετικά με την τιμή μιας πληθυσμιακής παραμέτρου. Είναι
Δρ. Αθανάσιος Δαγούμας, Επ. Καθηγητής Οικονομικής της Ενέργειας & των Φυσικών Πόρων, Πανεπιστήμιο Πειραιώς Η μηδενική υπόθεση είναι ένας ισχυρισμός σχετικά με την τιμή μιας πληθυσμιακής παραμέτρου. Είναι
iii ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος
 iii ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος xi 1 Αντικείμενα των Πιθανοτήτων και της Στατιστικής 1 1.1 Πιθανοτικά Πρότυπα και Αντικείμενο των Πιθανοτήτων, 1 1.2 Αντικείμενο της Στατιστικής, 3 1.3 Ο Ρόλος των Πιθανοτήτων
iii ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος xi 1 Αντικείμενα των Πιθανοτήτων και της Στατιστικής 1 1.1 Πιθανοτικά Πρότυπα και Αντικείμενο των Πιθανοτήτων, 1 1.2 Αντικείμενο της Στατιστικής, 3 1.3 Ο Ρόλος των Πιθανοτήτων
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ-ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ. ΜΕΡΟΣ Α : Άλγεβρα. Κεφάλαιο 2 ο (Προτείνεται να διατεθούν 12 διδακτικές ώρες) Ειδικότερα:
 ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ-ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΜΕΡΟΣ Α : Άλγεβρα Κεφάλαιο ο (Προτείνεται να διατεθούν διδακτικές ώρες) Ειδικότερα:. -. (Προτείνεται να διατεθούν 5 διδακτικές ώρες).3 (Προτείνεται να διατεθούν
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ-ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΜΕΡΟΣ Α : Άλγεβρα Κεφάλαιο ο (Προτείνεται να διατεθούν διδακτικές ώρες) Ειδικότερα:. -. (Προτείνεται να διατεθούν 5 διδακτικές ώρες).3 (Προτείνεται να διατεθούν
Σημειώσεις διαλέξεων: Βελτιστοποίηση πολυδιάστατων συνεχών συναρτήσεων 1 / 20
 Σημειώσεις διαλέξεων: Βελτιστοποίηση πολυδιάστατων συνεχών συναρτήσεων Ισαάκ Η Λαγαρής 1 Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιον Ιωαννίνων 1 Με υλικό από το υπό προετοιμασία βιβλίο των: Βόγκλη,
Σημειώσεις διαλέξεων: Βελτιστοποίηση πολυδιάστατων συνεχών συναρτήσεων Ισαάκ Η Λαγαρής 1 Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιον Ιωαννίνων 1 Με υλικό από το υπό προετοιμασία βιβλίο των: Βόγκλη,
Περί της Ταξινόμησης των Ειδών
 Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Σχολή Θετικών Επιστημών Τμήμα Φυσικής 541 24 Θεσσαλονίκη Καθηγητής Γεώργιος Θεοδώρου Tel.: +30 2310998051, Ιστοσελίδα: http://users.auth.gr/theodoru Περί της Ταξινόμησης
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Σχολή Θετικών Επιστημών Τμήμα Φυσικής 541 24 Θεσσαλονίκη Καθηγητής Γεώργιος Θεοδώρου Tel.: +30 2310998051, Ιστοσελίδα: http://users.auth.gr/theodoru Περί της Ταξινόμησης
ΚΥΡΙΑ ΣΤΟΙΧΕΙΑ ΜΑΘΗΜΑΤΟΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΠΕΙΡΑΙΑ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΑΥΤΟΜΑΤΙΣΜΟΥ ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ Ι Καθηγητής: Δ. ΔΗΜΟΓΙΑΝΝΟΠΟΥΛΟΣ Εργαστηριακοί Συνεργάτες: Σ. ΒΑΣΙΛΕΙΑΔΟΥ, Α. ΟΙΚΟΝΟΜΙΔΗΣ,
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΠΕΙΡΑΙΑ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΑΥΤΟΜΑΤΙΣΜΟΥ ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ Ι Καθηγητής: Δ. ΔΗΜΟΓΙΑΝΝΟΠΟΥΛΟΣ Εργαστηριακοί Συνεργάτες: Σ. ΒΑΣΙΛΕΙΑΔΟΥ, Α. ΟΙΚΟΝΟΜΙΔΗΣ,
7 ο ΚΕΦΑΛΑΙΟ ΕΡΩΤΗΣΕΙΣ ΑΥΤΟΕΞΕΤΑΣΗΣ. 1) Ποιος είναι ο ρόλος του δέκτη στις επικοινωνίες.
 7 ο ΚΕΦΑΛΑΙΟ ΕΡΩΤΗΣΕΙΣ ΑΥΤΟΕΞΕΤΑΣΗΣ 1) Ποιος είναι ο ρόλος του δέκτη στις επικοινωνίες. Ρόλος του δέκτη είναι να ενισχύει επιλεκτικά και να επεξεργάζεται το ωφέλιμο φέρον σήμα που λαμβάνει και να αποδίδει
7 ο ΚΕΦΑΛΑΙΟ ΕΡΩΤΗΣΕΙΣ ΑΥΤΟΕΞΕΤΑΣΗΣ 1) Ποιος είναι ο ρόλος του δέκτη στις επικοινωνίες. Ρόλος του δέκτη είναι να ενισχύει επιλεκτικά και να επεξεργάζεται το ωφέλιμο φέρον σήμα που λαμβάνει και να αποδίδει
Έλεγχος Κίνησης
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα 1501 - Έλεγχος Κίνησης Ενότητα: Αυτόματος Έλεγχος Συστημάτων Κίνησης Μιχαήλ Παπουτσιδάκης Τμήμα Αυτοματισμού Άδειες Χρήσης Το
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα 1501 - Έλεγχος Κίνησης Ενότητα: Αυτόματος Έλεγχος Συστημάτων Κίνησης Μιχαήλ Παπουτσιδάκης Τμήμα Αυτοματισμού Άδειες Χρήσης Το
Μία μέθοδος προσομοίωσης ψηφιακών κυκλωμάτων Εξελικτικής Υπολογιστικής
 Μία μέθοδος προσομοίωσης ψηφιακών κυκλωμάτων Εξελικτικής Υπολογιστικής Βασισμένο σε μια εργασία των Καζαρλή, Καλόμοιρου, Μαστοροκώστα, Μπαλουκτσή, Καλαϊτζή, Βαλαή, Πετρίδη Εισαγωγή Η Εξελικτική Υπολογιστική
Μία μέθοδος προσομοίωσης ψηφιακών κυκλωμάτων Εξελικτικής Υπολογιστικής Βασισμένο σε μια εργασία των Καζαρλή, Καλόμοιρου, Μαστοροκώστα, Μπαλουκτσή, Καλαϊτζή, Βαλαή, Πετρίδη Εισαγωγή Η Εξελικτική Υπολογιστική
Άσκηση 3. Έλεγχος ανατροφοδότησης κατάστασης dc κινητήρα. Έλεγχος ανατροφοδότησης κατάστασης
 Άσκηση 3 Έλεγχος ανατροφοδότησης κατάστασης dc κινητήρα Έλεγχος ανατροφοδότησης κατάστασης Ένα γραμμικό χρονικά αμετάβλητο (LTI) σύστημα όπως γνωρίζουμε, μπορεί να περιγραφεί στο πεδίο του χρόνου μέσω
Άσκηση 3 Έλεγχος ανατροφοδότησης κατάστασης dc κινητήρα Έλεγχος ανατροφοδότησης κατάστασης Ένα γραμμικό χρονικά αμετάβλητο (LTI) σύστημα όπως γνωρίζουμε, μπορεί να περιγραφεί στο πεδίο του χρόνου μέσω
Βασίλειος Μαχαιράς Πολιτικός Μηχανικός Ph.D.
 Βασίλειος Μαχαιράς Πολιτικός Μηχανικός Ph.D. Μη γραμμικός προγραμματισμός: μέθοδοι μονοδιάστατης ελαχιστοποίησης Πανεπιστήμιο Θεσσαλίας Σχολή Θετικών Επιστημών ΤμήμαΠληροφορικής Διάλεξη 6 η /2017 Τι παρουσιάστηκε
Βασίλειος Μαχαιράς Πολιτικός Μηχανικός Ph.D. Μη γραμμικός προγραμματισμός: μέθοδοι μονοδιάστατης ελαχιστοποίησης Πανεπιστήμιο Θεσσαλίας Σχολή Θετικών Επιστημών ΤμήμαΠληροφορικής Διάλεξη 6 η /2017 Τι παρουσιάστηκε
Βιομηχανικοί Ελεγκτές
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τ.Τ Βιομηχανικοί Ελεγκτές Ενότητα #12: Παραδείγματα Αναλογικών Συστημάτων Ελέγχου Κωνσταντίνος Αλαφοδήμος Τμήματος Μηχανικών Αυτοματισμού Τ.Ε. Άδειες
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τ.Τ Βιομηχανικοί Ελεγκτές Ενότητα #12: Παραδείγματα Αναλογικών Συστημάτων Ελέγχου Κωνσταντίνος Αλαφοδήμος Τμήματος Μηχανικών Αυτοματισμού Τ.Ε. Άδειες
Πίνακας 4.4 Διαστήματα Εμπιστοσύνης. Τιμές που Επίπεδο εμπιστοσύνης. Διάστημα εμπιστοσύνης
 Σφάλματα Μετρήσεων 4.45 Πίνακας 4.4 Διαστήματα Εμπιστοσύνης. Τιμές που Επίπεδο εμπιστοσύνης Διάστημα εμπιστοσύνης βρίσκονται εκτός του Διαστήματος Εμπιστοσύνης 0.500 X 0.674σ 1 στις 0.800 X 1.8σ 1 στις
Σφάλματα Μετρήσεων 4.45 Πίνακας 4.4 Διαστήματα Εμπιστοσύνης. Τιμές που Επίπεδο εμπιστοσύνης Διάστημα εμπιστοσύνης βρίσκονται εκτός του Διαστήματος Εμπιστοσύνης 0.500 X 0.674σ 1 στις 0.800 X 1.8σ 1 στις
Εισόδημα Κατανάλωση 1500 500 1600 600 1300 450 1100 400 600 250 700 275 900 300 800 352 850 400 1100 500
 Εισόδημα Κατανάλωση 1500 500 1600 600 1300 450 1100 400 600 250 700 275 900 300 800 352 850 400 1100 500 Πληθυσμός Δείγμα Δείγμα Δείγμα Ο ρόλος της Οικονομετρίας Οικονομική Θεωρία Διατύπωση της
Εισόδημα Κατανάλωση 1500 500 1600 600 1300 450 1100 400 600 250 700 275 900 300 800 352 850 400 1100 500 Πληθυσμός Δείγμα Δείγμα Δείγμα Ο ρόλος της Οικονομετρίας Οικονομική Θεωρία Διατύπωση της
Κεφάλαιο 5 Κριτήρια απόρριψης απόμακρων τιμών
 Κεφάλαιο 5 Κριτήρια απόρριψης απόμακρων τιμών Σύνοψη Στο κεφάλαιο αυτό παρουσιάζονται δύο κριτήρια απόρριψης απομακρυσμένων από τη μέση τιμή πειραματικών μετρήσεων ενός φυσικού μεγέθους και συγκεκριμένα
Κεφάλαιο 5 Κριτήρια απόρριψης απόμακρων τιμών Σύνοψη Στο κεφάλαιο αυτό παρουσιάζονται δύο κριτήρια απόρριψης απομακρυσμένων από τη μέση τιμή πειραματικών μετρήσεων ενός φυσικού μεγέθους και συγκεκριμένα
Ανασκόπηση θεωρίας ελαχίστων τετραγώνων και βέλτιστης εκτίμησης παραμέτρων
 Τοπογραφικά Δίκτυα και Υπολογισμοί 5 ο εξάμηνο, Ακαδημαϊκό Έτος 2017-2018 Ανασκόπηση θεωρίας ελαχίστων τετραγώνων και βέλτιστης εκτίμησης παραμέτρων Χριστόφορος Κωτσάκης Τμήμα Αγρονόμων και Τοπογράφων
Τοπογραφικά Δίκτυα και Υπολογισμοί 5 ο εξάμηνο, Ακαδημαϊκό Έτος 2017-2018 Ανασκόπηση θεωρίας ελαχίστων τετραγώνων και βέλτιστης εκτίμησης παραμέτρων Χριστόφορος Κωτσάκης Τμήμα Αγρονόμων και Τοπογράφων
Συστήματα Αυτομάτου Ελέγχου
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Συστήματα Αυτομάτου Ελέγχου Ενότητα Α: Γραμμικά Συστήματα Όνομα Καθηγητή: Ραγκούση Μαρία Τμήμα: Ηλεκτρονικών Μηχανικών Τ.Ε. Άδειες
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Συστήματα Αυτομάτου Ελέγχου Ενότητα Α: Γραμμικά Συστήματα Όνομα Καθηγητή: Ραγκούση Μαρία Τμήμα: Ηλεκτρονικών Μηχανικών Τ.Ε. Άδειες
Σύστημα και Μαθηματικά μοντέλα συστημάτων
 Σύστημα και Μαθηματικά μοντέλα συστημάτων Όταν μελετούμε έναν συγκεκριμένο μηχανισμό η μια φυσική διεργασία επικεντρώνουμε το ενδιαφέρον μας στα φυσικά μεγέθη του μηχανισμού τα οποία μας ενδιαφέρει να
Σύστημα και Μαθηματικά μοντέλα συστημάτων Όταν μελετούμε έναν συγκεκριμένο μηχανισμό η μια φυσική διεργασία επικεντρώνουμε το ενδιαφέρον μας στα φυσικά μεγέθη του μηχανισμού τα οποία μας ενδιαφέρει να
ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ ΠΡΩΤΟ ΣΤΟΙΧΕΙΑ ΔΙΑΦΟΡΙΚΟΥ ΛΟΓΙΣΜΟΥ ΣΥΝΑΡΤΗΣΕΩΝ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ 15
 ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ 13 ΜΕΡΟΣ ΠΡΩΤΟ ΣΤΟΙΧΕΙΑ ΔΙΑΦΟΡΙΚΟΥ ΛΟΓΙΣΜΟΥ ΣΥΝΑΡΤΗΣΕΩΝ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ 15 ΚΕΦΑΛΑΙΟ 1: ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ 17 1. Εισαγωγή 17 2. Πραγματικές συναρτήσεις διανυσματικής μεταβλητής
ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ 13 ΜΕΡΟΣ ΠΡΩΤΟ ΣΤΟΙΧΕΙΑ ΔΙΑΦΟΡΙΚΟΥ ΛΟΓΙΣΜΟΥ ΣΥΝΑΡΤΗΣΕΩΝ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ 15 ΚΕΦΑΛΑΙΟ 1: ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ 17 1. Εισαγωγή 17 2. Πραγματικές συναρτήσεις διανυσματικής μεταβλητής
ΣΥΝΟΠΤΙΚΗ ΠΑΡΟΥΣΙΑΣΗ
 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΣΥΝΟΠΤΙΚΗ ΠΑΡΟΥΣΙΑΣΗ ΕΙΣΑΓΩΓΙΚΑ Ι Από το πραγματικό κύκλωμα στο μοντέλο Μαθηματική μοντελοποίηση Η θεωρία κυκλωμάτων είναι
ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΣΥΝΟΠΤΙΚΗ ΠΑΡΟΥΣΙΑΣΗ ΕΙΣΑΓΩΓΙΚΑ Ι Από το πραγματικό κύκλωμα στο μοντέλο Μαθηματική μοντελοποίηση Η θεωρία κυκλωμάτων είναι
ΔΕΙΓΜΑ ΠΡΙΝ ΤΙΣ ΔΙΟΡΘΩΣΕΙΣ - ΕΚΔΟΣΕΙΣ ΚΡΙΤΙΚΗ
 Συναρτήσεις Προεπισκόπηση Κεφαλαίου Τα μαθηματικά είναι μια γλώσσα με ένα συγκεκριμένο λεξιλόγιο και πολλούς κανόνες. Πριν ξεκινήσετε το ταξίδι σας στον Απειροστικό Λογισμό, θα πρέπει να έχετε εξοικειωθεί
Συναρτήσεις Προεπισκόπηση Κεφαλαίου Τα μαθηματικά είναι μια γλώσσα με ένα συγκεκριμένο λεξιλόγιο και πολλούς κανόνες. Πριν ξεκινήσετε το ταξίδι σας στον Απειροστικό Λογισμό, θα πρέπει να έχετε εξοικειωθεί
Άσκηση: Ένα σύστηµα µε είσοδο u(t), έξοδο y(t) και διάνυσµα κατάστασης x(t) = (x 1 (t) x 2 (t)) T περιγράφεται από το ακόλουθο διάγραµµα:
 1 Άσκηση: Ένα σύστηµα µε είσοδο u(t), έξοδο y(t) και διάνυσµα κατάστασης x(t) = (x 1 (t) x 2 (t)) T περιγράφεται από το ακόλουθο διάγραµµα: Όπου Κ R α) Να βρεθεί η περιγραφή στο χώρο κατάστασης και η συνάρτηση
1 Άσκηση: Ένα σύστηµα µε είσοδο u(t), έξοδο y(t) και διάνυσµα κατάστασης x(t) = (x 1 (t) x 2 (t)) T περιγράφεται από το ακόλουθο διάγραµµα: Όπου Κ R α) Να βρεθεί η περιγραφή στο χώρο κατάστασης και η συνάρτηση
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΔΙΟΙΚΗΣΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΔΙΟΙΚΗΣΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 06-07 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Επικ. Καθηγητής v.koutra@fme.aegea.gr Τηλ: 7035468 Θα μελετήσουμε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΔΙΟΙΚΗΣΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 06-07 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Επικ. Καθηγητής v.koutra@fme.aegea.gr Τηλ: 7035468 Θα μελετήσουμε
Η αβεβαιότητα στη μέτρηση.
 Η αβεβαιότητα στη μέτρηση. 1. Εισαγωγή. Κάθε μέτρηση, όσο προσεκτικά και αν έχει γίνει, περικλείει κάποια αβεβαιότητα. Η ανάλυση των σφαλμάτων είναι η μελέτη και ο υπολογισμός αυτής της αβεβαιότητας στη
Η αβεβαιότητα στη μέτρηση. 1. Εισαγωγή. Κάθε μέτρηση, όσο προσεκτικά και αν έχει γίνει, περικλείει κάποια αβεβαιότητα. Η ανάλυση των σφαλμάτων είναι η μελέτη και ο υπολογισμός αυτής της αβεβαιότητας στη
ΣΥΣΤΗΜΑΤΩΝ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΔΙΟΙΚΗΣΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΕΝΟΤΗΤΑ 0: ΒΑΣΙΚΑ ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΚΑΙ ΤΥΠΟΙ ΣΥΣΤΗΜΑΤΩΝ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ Δρ Γιώργος
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΔΙΟΙΚΗΣΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΕΝΟΤΗΤΑ 0: ΒΑΣΙΚΑ ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΚΑΙ ΤΥΠΟΙ ΣΥΣΤΗΜΑΤΩΝ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ Δρ Γιώργος
Κεφάλαιο 12: Υδραυλική ανάλυση δικτύων διανομής
 Κεφάλαιο 12: Υδραυλική ανάλυση δικτύων διανομής Εννοιολογική αναπαράσταση δίκτυων διανομής Σχηματοποίηση: δικτυακή απεικόνιση των συνιστωσών του φυσικού συστήματος ως συνιστώσες ενός εννοιολογικού μοντέλου
Κεφάλαιο 12: Υδραυλική ανάλυση δικτύων διανομής Εννοιολογική αναπαράσταση δίκτυων διανομής Σχηματοποίηση: δικτυακή απεικόνιση των συνιστωσών του φυσικού συστήματος ως συνιστώσες ενός εννοιολογικού μοντέλου
ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΑΥΤΟΜΑΤΙΣΜΟ ΔΙΔΑΣΚΑΛΙΑ ΤΟΥ ΜΑΘΗΜΑΤΟΣ ΑΥΤΟΜΑΤΙΣΜΟΥ ΣΤΑ ΤΕΧΝΟΛΟΓΙΚΑ ΕΠΑΓΓΕΛΜΑΤΙΚΑ ΕΚΠΑΙΔΕΥΤΗΡΙΑ-ΤΕΕ
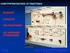 Αφιέρωμα στο Γ Συνέδριο «Τεχνολογία & Αυτοματισμός» ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΑΥΤΟΜΑΤΙΣΜΟ ΔΙΔΑΣΚΑΛΙΑ ΤΟΥ ΜΑΘΗΜΑΤΟΣ ΑΥΤΟΜΑΤΙΣΜΟΥ ΣΤΑ ΤΕΧΝΟΛΟΓΙΚΑ ΕΠΑΓΓΕΛΜΑΤΙΚΑ ΕΚΠΑΙΔΕΥΤΗΡΙΑ-ΤΕΕ Νίκος Γλώσσας Καθηγητής Δευτεροβάθμιας
Αφιέρωμα στο Γ Συνέδριο «Τεχνολογία & Αυτοματισμός» ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΑΥΤΟΜΑΤΙΣΜΟ ΔΙΔΑΣΚΑΛΙΑ ΤΟΥ ΜΑΘΗΜΑΤΟΣ ΑΥΤΟΜΑΤΙΣΜΟΥ ΣΤΑ ΤΕΧΝΟΛΟΓΙΚΑ ΕΠΑΓΓΕΛΜΑΤΙΚΑ ΕΚΠΑΙΔΕΥΤΗΡΙΑ-ΤΕΕ Νίκος Γλώσσας Καθηγητής Δευτεροβάθμιας
Πανεπιστήμιο Πατρών Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών. Διδάσκων: Αντώνιος Τζές
 Πανεπιστήμιο Πατρών Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Τομέας Συστημάτων και Αυτομάτου Ελέγχου ΠΡΟΣΑΡΜΟΣΤΙΚΟΣ ΕΛΕΓΧΟΣ Διδάσκων: Αντώνιος Τζές Πάτρα 2008 Πανεπιστήμιο Πατρών Τμήμα
Πανεπιστήμιο Πατρών Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Τομέας Συστημάτων και Αυτομάτου Ελέγχου ΠΡΟΣΑΡΜΟΣΤΙΚΟΣ ΕΛΕΓΧΟΣ Διδάσκων: Αντώνιος Τζές Πάτρα 2008 Πανεπιστήμιο Πατρών Τμήμα
Στοχαστικές Μέθοδοι στους Υδατικούς Πόρους Φασματική ανάλυση χρονοσειρών
 Στοχαστικές Μέθοδοι στους Υδατικούς Πόρους Φασματική ανάλυση χρονοσειρών Δημήτρης Κουτσογιάννης Τομέας Υδατικών Πόρων και Περιβάλλοντος, Σχολή Πολιτικών Μηχανικών, Εθνικό Μετσόβιο Πολυτεχνείο Αθήνα Επανέκδοση
Στοχαστικές Μέθοδοι στους Υδατικούς Πόρους Φασματική ανάλυση χρονοσειρών Δημήτρης Κουτσογιάννης Τομέας Υδατικών Πόρων και Περιβάλλοντος, Σχολή Πολιτικών Μηχανικών, Εθνικό Μετσόβιο Πολυτεχνείο Αθήνα Επανέκδοση
Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών
 Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών Οι παρούσες σημειώσεις αποτελούν βοήθημα στο μάθημα Αριθμητικές Μέθοδοι του 5 ου εξαμήνου του ΤΜΜ ημήτρης Βαλουγεώργης Καθηγητής Εργαστήριο Φυσικών
Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών Οι παρούσες σημειώσεις αποτελούν βοήθημα στο μάθημα Αριθμητικές Μέθοδοι του 5 ου εξαμήνου του ΤΜΜ ημήτρης Βαλουγεώργης Καθηγητής Εργαστήριο Φυσικών
ΚΕΦΑΛΑΙΟ ΕΚΤΟ: Ανάλυση ευαισθησίας των παραμέτρων του μαθηματικού υποδείγματος. Εφαρμογές χρησιμοποιώντας το R
 ΚΕΦΑΛΑΙΟ ΕΚΤΟ: Ανάλυση ευαισθησίας των παραμέτρων του μαθηματικού υποδείγματος. Εφαρμογές χρησιμοποιώντας το R Σύνοψη Το κεφάλαιο αυτό έχει σκοπό να παρουσιάσει και να υπογραμμίσει τη σημασία της ανάλυσης
ΚΕΦΑΛΑΙΟ ΕΚΤΟ: Ανάλυση ευαισθησίας των παραμέτρων του μαθηματικού υποδείγματος. Εφαρμογές χρησιμοποιώντας το R Σύνοψη Το κεφάλαιο αυτό έχει σκοπό να παρουσιάσει και να υπογραμμίσει τη σημασία της ανάλυσης
Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εργαστήριο Κυκλωμάτων και Μετρήσεων
 Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εργαστήριο Κυκλωμάτων και Μετρήσεων Εργαστήριο 5 Γραμμικότητα (Linearity), Αναλογικότητα (Proportionality), και Επαλληλία (Superposition)
Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εργαστήριο Κυκλωμάτων και Μετρήσεων Εργαστήριο 5 Γραμμικότητα (Linearity), Αναλογικότητα (Proportionality), και Επαλληλία (Superposition)
 Β Γραφικές παραστάσεις - Πρώτο γράφημα Σχεδιάζοντας το μήκος της σανίδας συναρτήσει των φάσεων της σελήνης μπορείτε να δείτε αν υπάρχει κάποιος συσχετισμός μεταξύ των μεγεθών. Ο συνήθης τρόπος γραφικής
Β Γραφικές παραστάσεις - Πρώτο γράφημα Σχεδιάζοντας το μήκος της σανίδας συναρτήσει των φάσεων της σελήνης μπορείτε να δείτε αν υπάρχει κάποιος συσχετισμός μεταξύ των μεγεθών. Ο συνήθης τρόπος γραφικής
Κεφάλαιο 8. Οπτικοποίηση Απαλοιφή
 Κεφάλαιο 8. Οπτικοποίηση Απαλοιφή Oι οπτικές επιδράσεις, που μπορεί να προκαλέσει μια εικόνα στους χρήστες, αποτελούν ένα από τα σπουδαιότερα αποτελέσματα των λειτουργιών γραφικών με Η/Υ. Τον όρο της οπτικοποίησης
Κεφάλαιο 8. Οπτικοποίηση Απαλοιφή Oι οπτικές επιδράσεις, που μπορεί να προκαλέσει μια εικόνα στους χρήστες, αποτελούν ένα από τα σπουδαιότερα αποτελέσματα των λειτουργιών γραφικών με Η/Υ. Τον όρο της οπτικοποίησης
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ
 Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 8 ο : Προσαρμοσμένα Φίλτρα Βασική
Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 8 ο : Προσαρμοσμένα Φίλτρα Βασική
ΚΕΦΑΛΑΙΟ 6 ΠΡΟΒΛΕΨΕΙΣ ΜΕ ΥΠΟΔΕΙΓΜΑΤΑ ΧΡΟΝΟΣΕΙΡΩΝ
 ΚΕΦΑΛΑΙΟ 6 ΠΡΟΒΛΕΨΕΙΣ ΜΕ ΥΠΟΔΕΙΓΜΑΤΑ ΧΡΟΝΟΣΕΙΡΩΝ 6. Εισαγωγή 6. Μονομεταβλητές προβλέψεις Βέλτιστη πρόβλεψη και Θεώρημα βέλτιστης πρόβλεψης Διαστήματα εμπιστοσύνης 6.3 Εφαρμογές A. MILIONIS KEF. 6 08 BEA
ΚΕΦΑΛΑΙΟ 6 ΠΡΟΒΛΕΨΕΙΣ ΜΕ ΥΠΟΔΕΙΓΜΑΤΑ ΧΡΟΝΟΣΕΙΡΩΝ 6. Εισαγωγή 6. Μονομεταβλητές προβλέψεις Βέλτιστη πρόβλεψη και Θεώρημα βέλτιστης πρόβλεψης Διαστήματα εμπιστοσύνης 6.3 Εφαρμογές A. MILIONIS KEF. 6 08 BEA
