REFLEKSNA AKTIVNOST KIČMENE MOŽDINE
|
|
|
- Θεράπων Μαλαξός
- 8 χρόνια πριν
- Προβολές:
Transcript
1 REFLEKSNA AKTIVNOST KIČMENE MOŽDINE
2 Grčki filozofi Hipokrat ( B.C.) Ars longa, vita brevis Aristotel ( B.C.) Mozak centralni organ intelektualne aktivnosti i glavni sezorni organ Povrede glave senzorni i motorni poremecaji Srce je glavni organ ogovoran za pokrete, cula; nervi polaze iz srca i ono ih kontrolise Mozak se sastoji iz cerebeluma i cerebruma
3 R. Dekart ( ) Cogito ergo sum Mozak je glavni organ koji utiče na ponašanje. MEHANISTIČKA TEORIJA PONAŠANJA Zacetnik teorije o refleksnom luku: stimulus izaziva odgovor - promene u spoljašnjoj sredini utiču na periferne krajeve ( nervna vlakna ) što dovodi do centralnih promena (u pinealnoj žlezdi). Nervi su šuplje cevi kroz koje protiču fluidi koji dovode do stimulacije mišića.
4 Sir C. Sherrington ( ) Karakteristike spinalnih refleksa i uticaj viših moždanih struktura (cerebelum i moždano stablo) na refl odgovor. Integrativna uloga nervnog sistema (1906) Ekscitatorne i ihibitorne sinapse u CNS neophodne za integraciju refleksa
5 DESCENDENTI SISTEM Gornji motoneuron Motorni korteks Planiranje, započinjanje i usmeravanje voljnih pokreta Moždano stablo Kontrola položaja, spontana lokomocija BAZALNE GANGLIJE Inicijacija pokreta CEREBELUM Kooridinacija pokreta Interneuroni Koordinacija reflekne aktivnosti Mononeuroni KM Dornji motoneuron KIČMENA MOŽDINA SKELETNI MIŠIĆI
6 Uloge KM 1. SPROVODNA 2. REFLEKSNA 3. AUTONOMNA ULOGA
7 Kičmena moždina dorzalni funikulus dorzalni rogovi Lateralni funikulus Lateralni funikulus lateralni rogovi ventralni rogovi Ventralni funikulus Propriocepcija Propriocepcija, duboki dodir, vibracije Voljni pokreti Propriocepcij, bol, temperatura, laki dodir, pritisak Voljni pokreti
8 Kičmena moždina siva masa ZADNJI ROGOVI SENZORNI, ćelijska tela interneurona - završavaju aferentna vlakna LATERALNI ROGOVI- ćelijska tela autonomnih aferentnih vlakana PREDNJI ROGOVI- MOTORNI, ćelijska tela somatskih eferentnih vlakana Bell Megendijev zakon: ZADNJI ROGOVI SU SENZORNI A PREDNJI SU MOTORNI
9 Kičmena moždina siva masa C6 Th6 L3
10 Intermedio Lateralni rogovi (S2-S4) (Th1-L2) Parasimpatički NS Simpatički NS
11 Motorni neuroni Prednji motorni neuroni Alfa (α) debela mijelinska vlakna, brze,, fine, vešte pokrete, fiziološki fleksori Gama (γ) tanja vlakna, do intrafuzalnih mišićnih vlakana koja čine krajeve mišićnog vretena, niži prag okidanja, tonički aktivni
12 Motorni neuroni dorzolateralni ventromedijalni trakt trakt Motoneuroni ekstremitetnih mišića Motoneuroni aksijalnih mišića fleksor distalni proksimalni ekstenzor
13 Senzorni neuroni Telo neurona RECEPTOR CNS Senzitivno vl akson Po ulasku u k.m., grane senzornog nerva o Završavaju se u sivoj masi- lokalni segmentni refleksi o Prenose signal do viših centara- viši nivoi k.m., moždanog stabla i cerebralnog korteksa
14 Interneuroni-mali inhibitorni neuroni Renšo ćelija z senzornih neurona Ka drugim neuronima Telo neurona α motoneuron Rekurentna grana Inhibiraju motoneurone antagonista Rekurentna inhibicija- Renshaw ćelija - izoštrava signal Glicin
15 Propriospinalna vlakna Multisegmentne veze Integracija polisinaptičkih refleksa koordinacija trupa, gornjih i donjih ekstremiteta Aferentno nervno vlakno Propriospinalni interneuroni
16 Kičmena moždina bela masa Zadnje kolumne Lateralne columne Fissura ventralis Prednje kolumne
17 Kičmena moždina bela masa
18 Kičmena moždina bela masa
19 Refleks AUTOMATSKI ODGOVOR EFEKTORA NA DRAŽENJE RECEPTORA Adekvatna draž
20 Refleksni luk 1. RECEPTOR 2. SENZORNI NEURON AP 3. CENTRALNA SINAPSA Receptorski potencijal 4. EFERNTNI NEURON 5. EFEKTOR Potencijal motorne ploce
21 Refleksi - podela 1. Prema broju sinapsi Monosinaptički Polisinaptički 2. Prema lokalizaciji receptora Eksteroreceptivne Proprioceptivne Autonomne 3. Prema mestu integracije Spinalni Bulbarni Mezencefalički Kortikalni 4. Prema vremenu nastanka Bezuslovni ( urodjeni) Uslovni (stečeni)
22 Refleksi Monosinaptički refleks Skeletni mišić Senzitivni neuron Centralna sinapsa KM Somatski motoneuron Odgovor Efektor Eferentni neuron Jedna sinapsa Polisinaptički refleks Senzitivni neuron Sinapsa 1 Centralna sinapsa KM Interneuron Odgovor Efektor Eferentni neuron Sinapsa 2
23 SPINALNI REFLEKSI o o o o MIOTATSKI REFLEKS (refleks na istezanje) GOLDŽIJEV TETIVNI REFLEKS (obrnuti refleks na istezanje) REFLEKS FLEKSORA UNAKRSNI REFLEKS EKSTENZORA
24 Monosinaptički refleksi Refleks na istezanje (miotatski)
25 Refleks na istezanje (miotatički) 1. RECEPTOR (mišićno vreteno) 2. Aferentno vl 3. Eferentno vl Relaksacija antagnonista 3. Aktivacija motoneurona Inhibitorni interneuron 5. Efektor (kontrakcija mišića)
26 RECIPROČNA INERVACIJA : KADA SE DESI REFLEKS ISTEZANJA, ANTAGONISTIČKI MIŠIĆ SE OPUŠTA 1b aferent vl tetiva Mišićno vreteno Estrafuzalna vl. Isti mišić antagonist
27 Receptor Mišićno vreteno γ eferent Aferent vl Adekvatna draž: Istezanje mišićnog vretena ( dužine) γ dinamička γ statička Primarni završ Sekund. završ Jedra u vrećici Jedra u nizu Visok prag DINAMIČKI ODGOVOR brzo adaptirajuci Nizak prag STATIČKI ODGOVOR Receptor je paralelno vezan sa ekstrafuzal. vl.
28 Mišićno vreteno 1. Dinamički odgovor Primarni završetci - intrafuzalna vlakna sa jedrima u vreći broj impulsa zavisi od brzine istezanja (suprotstavlja se promeni dužine), visok stepen adaptacije Mišićno vreteno detektor dužine Istezanje mišića Mišićno vreteno Intrafuzalna vl Kontrakcija mišića 2. Statički odgovor Primarni i sekundarni završetci - intrafuzalna vlakna sa jedrima u lancu Sporo istežanje, br. impulsa zavisi od dužine mišića održavanje položaja, manji stepen adaptacije Ia ekstrafuzalna vl Frekvenca Ap se tokom istezanja Frekvenca Ap se tokom kontrakcije
29 Mišićno vreteno Istezanje Prestanak istezanja Stimulus Stimulus Primarni Primarni Sekundarni Sekundarni
30 Aferentna vl mišićnog vretena Mišićno vreteno - γ motoneuroni γ statički mn. vlakna sa jedrima u lancu- statičku aktivnost ekstrafuzalna vl γ motoneuroni Statički Dinamički Primarna aff Ia γ dinamički mn. vlakna sa jedrima u vrećici- fazičku aktivnost γ eferentna vlakna sekundarna aff II Intrafuzalna vl Jedra u vrećici Jedra u nizu
31 Uloga γ motoneurona α-γ koaktivacija 1. održava osetljivost mišićnog vretena za vreme kontrakcije Ekstrafuzalna mišićna vl. 2. podešava osetljivost mišićnog vretena Kičmena moždina intrafuzalna mišićna vl. Afernentna vl iz mišićnog vretena Inervacija iz α motoneurona Reflekni luk refleksa na istezanje γ inervacija mišinog vretena Descendentni putevi koaktivacije α i γ motoneurona
32 ALFA GAMA koaktivacija Voljni pokreti Descendentni putevi KONSTANTNO ISTEZANJE α motoneuron γ motoneuron Stimulacija α motoneurona skraćenje mišića Aα vlakno Ia vlakno Aγ vlakno Stimulacija α i γ motoneurona mišić Mišićno vreteno Dužina mišića
33 ALFA MOTO NEURONIMOGU BITI AKTIVIRANI POMOĆU GAMA KRUGA: GAMA MOTO NEURONI DOBIJAJU IMPULSE IZ VIŠIH DELOVA DELUJU NA SKRAĆENJE VRETENA ŠTO UTIČE NA POJAČANO OKIDANJE Ia ŠTO POVEĆAVA AKTIVNOST ALFA MOTO NEURONA DELUJE NA EKSTRA-FUZALNE MIŠIĆE DA SE SKRATE ZBOG KOAKTIVACIJE- GAMA KRUG JE AKTIVIRAN TOKOM SVIH POKRETA I DOPRINOSI EKSCITABILNOSTI I FREKVENCI OKIDANJA U α Mn. γ motoneuroni α motoneuroni
34 Uloga refleksa na istezanje kontrola dužin ine mišića održavanje uspravnog položaja voljne kontrakcije intrafuzalna vlakna - Povratna sprega kapsula mišićnog vretena Ekstrafuzalna vlakna gama motoneuroni Ia gama motoneuroni intrafuzalna vlakna Završetci gama motoneuronac 4. Uporedjuje željenu i aktuelnu dužinu prenosi je do MN i ispravlja grešku izračunava grešku ku,
35 Spinalni i supraspinalni uticaji Modulacija refleksnog odgovora α motoneuron Presinaptička inhibicija mišić Afferent. Iz mišićnog vretena Promena dužine Mišićno vreteno γ motoneuroni
36 UTICAJ VIŠIH CENTARA NA REFLEKS NA ISTEZANJE + STIMULACIJA - INHIBICIJA
37 Polisinaptički refleksi Goldžijev tetivni refleks (obrnuti refleks na istezanje) Refleks fleksora Unakrsni refleks ekstenzora
38 Receptor - Goldžijev tetivni organ Adekvatna draž: snage mišićna vl Receptor je serijski vezan sa ekstrafuzal. vl. Goldžijev tetivni org. detektor napetosti Ib kapsula Kolagena vl tetiva Aktivira se pasivnim istezanjem i Aktivnom mišićnom kontrakcijom - Nizak je prag-
39 EFEKTOR MOTONEURON inhibiran α RECEPTOR Tenzija u tetivi inhibitorni interneuron SENZITIVNI NEURON Ib CNS Interneuroni Kontrakcija antagonističkih mišića α MOTONEURON antagoniste stimulisan ekscitacijsk REFLEKSNI CENTAR interneuron (kičmena moždina) aktivacija inh. interneurona Goldžijev tetivni refleksobrnuti refleks na istezanje
40 1b aferent vl tetiva Mišićno vreteno Estrafuzalna vl. Isti mišić antagonist Aferentna vlakna iz Goldži tetivnog organa (Ib) aktiviraju intern. koji inhibiraju motoneurone sinergista ali ekscitiraju antagoniste.
41 Recipročna inhibicija i recipročna inervacija Fenomen recipročne inhibicije: inhibicija antagonističkih mišića posle, recimo aktivacije refleksa na istezanje Recipročna inervacija neuronski krug koji uzrokuje ovaj recipročni odnos
42 Ib ratna sprega stitna uloga: ečava razvoj rekomerne osti u mišićima Goldžijev tetivni organ Isti mišić sinergist antagonist
43 Refleks na istezanje i Goldžijev tetivni refleks Informacije o sili Goldži tetivni organ interneuroni Centralna kontrola signala α motoneuron Mišić Opterećenje Precizna regulacija AKTIVNOSTI α MOTO- NEURONA ZA OBAVLJANJE SVIH VOLJNIH POKRETA γ motoneuron Informacije o dužini Mišićno vreteno
44 Refleks fleksora DRAŽ nociceptivni stimulus Periferni nervni sistem Centralni nervni sistem 1. Receptor u koži Interneuron Mozak 2. Aferentni put Stimulus Kontrakcija fleksora Relaksacija ekstenzora 4. Eferentni put 3. Centralna sinapsa Odgovor efektora 5. Efektor KARAKTERISTIKE: Dug latentni period (aff. vl., sinapse) Odgovor traje duže od stimulusa naknadno pražnjenje Stereotipni odgovor Povećanje intenziteta draži kraće refleksno vreme prostorna i vremenska sumacija veći br. aktiviranih receptora
45 Naknadno praznjenje reverberantni krugovi Naknadno pražnjenje Trajanje stimulusa REFLEKS EKSTENZORA ( 2OO-500 msec )
46 Aferentna vl iz kože i proprioceptora ipsilateralni fleksori ipsilateralni ekstenzori Kontralateralni fleksori Konralateralni ekstenzori PROCES ŠIRENJA IMPULSA U KM I UKLJUČIVANJE NOVIH MOTO NEURONA - REGRUTACIJA-
47 Unakrsni refleks 4. Unakrsni ekstenzora refleks ekstenzora CNS Održavanje uspravnog položaja Inhib. neuron - Inhib. neuron + Iz CNS Inhibitorni interneuron + - Eksicitatorni interneuron
48 1. DIVERGENTNI KRUGOVI 2. KRUGOVI RECIPROČNE INHIBICIJE IBICIJE 3. PROLONGIRANO PONOVLJENO OKIDANJE
49 REKURENTNA INHIBICIJA OGRANIČAVA AVA TRAJANJE I INTENZITET REFLEKSNOG ODGOVORA isti mišić Renšo ćelija Ia inhibitorni interneuron antagonist
50 RENŠO INHIBICIJA Interneuroni, Inhibitorni REKURENTNA Aksoni motoneurona IPSP
51 REFLEKSI POLOŽAJA I LOKOMOCIJE Pozitivna reakcija podupiranja magnetna Refleksi uspravljanja, pokušaj stajanja Ritmički pokreti jednog ekstremiteta Recipročno koračanje suprotnih ekstremiteta Dijagonalno koračanje sva 4 ekstremiteta Refleks galopiranja
52 Fiziološki Plantarni refleks Patološki (znak Babinski)
53 SPINALNI šok akutno i tranzitorno odsustvo svih funkcija KM PERIFERNA MUSKULATURA JE: MLITAVA (FLAKCIDNA) ili PREDOMINIRA TONUS FLEKSORA Prvo se oporavljaju refleksi fleksora (patelarni)
54 Ni paraplegičan Čovek ni spinalna Životinja NE MOGU DA STOJE kvadriplegija kvadriplegija cervikalni torakalni Prag za reflekse posle oporavka Pada (Refleks fleksora) Minimalna draž dovodi do masovnih refleksa, Svih ekstremiteta paraplegija paraplegija lumbalni sakralni kokcigealni Autonomni refleksi: (pražnjenje bešike i rektuma, seksualni) Vazomocija, termoregulacija
55 SPINALNI ŠOK 1. NEPOSREDNO POSLE TRANSEKCIJE AREFLEKSIJA - Odsustvo motornih, senzitivnih i visceralnih refleksa OPORAVAK (zavisi od ENCEFALIZACIJE) žaba i pacov do nekoliko minuta Pas i mačka- 1-2 h Majmun dani Čovek najmanje 2 nedelje 2. HIPERREFLEKSIJA I MASOVNI REFLEKSI: Reakcije hroničnih spinalnih ljudi niži prag okidanja. Refleksi na istezanje (patelarni refleks) Ili refleks fleksora na bolnu draž
56 Viši delovi NS tonički bombarduju KM (odvajanje SA) prestanak svih funkcija KM Hiperaktivnost- masovni refleksi -Denervaciona hipersenzibilnost na preostale NT iz spinalnih terminala -Kolaterale iz ekscitatornih n
57 Brown-Sequardov sindrom Hemisekcija kičmene moždine Dorzalna kolumna Lateralni kortikospinalni trakt Spinotalamički trakt 1. Na strani lezije: Oduzetost piramidnog tipa ispod lezije Oštećenje taktilne diskriminacije i sezibiliteta za dodir Ostecenje dubokog senzibilteta (dorzalne kolumne) 2. Na suptrotnoj strani: Gubitak senzibilteta za bol i temperaturu (tr. spinothalamicus)
58
59 Teze Funkcionalna organizacija kičmene moždine Uloge kičmene moždine Organizacija refleksnog luka Podela spinalnih somatskih refleksa: monosinaptički (npr. refleksi na istezanje - značaj) polisinaptički (npr. refleks fleksora, Goldžijev tetivni refleks - značaj) Recipročna inervacija i recipročna inhibicija značaj Spinalni šok i hemisekcija kičmene moždine (Brown- Sequard sindrom)
Motorni nervni sistem (1)
FAKULTET ZA SPECIJALNU EDUKACIJU I REHABILITACIJU Medicinska fiziologija - predavanja Motorni nervni sistem (1) Doc. dr Maja Milovanović Sadržaj prezentacije Kičmena moždina, refleksi Motorna kora velikog
Senzorni nervni sistem
FAKULTET ZA SPECIJALNU EDUKACIJU I REHABILITACIJU Medicinska fiziologija - predavanja Senzorni nervni sistem Doc. dr Maja Milovanović Sadržaj prezentacije Senzorni receptori Somatski osećaji Somatosenzorni
Anatomija nervnog sistema
FAKULTET ZA SPECIJALNU EDUKACIJU I REHABILITACIJU Medicinska fiziologija - predavanja Anatomija nervnog sistema Doc. dr Maja Milovanović MOZAK KIČMENA MOŽDINA PETODELNI - SREDNJI MOZAK - MEĐUMOZAK - VELIKI
FIZIOLOŠKE OSNOVE SILE I SNAGE. Prof. dr Dušan Perić
FIZIOLOŠKE OSNOVE ISPOLJAVANJA SILE I SNAGE Prof. dr Dušan Perić Mehanizam mišićne kontrakcije Struktura mišića i mišićnih ovojnica MOTORNA JEDINICA } TELO (SOMA) NERVNE ĆELIJE AKSON TELODENDRON MIŠIĆNA
Nervni sistem (1) Opšta neurofiziologija
FAKULTET ZA SPECIJALNU EDUKACIJU I REHABILITACIJU Medicinska fiziologija - predavanja Nervni sistem (1) Opšta neurofiziologija Doc. dr Maja Milovanović Sadržaj Nervno tkivo Nervna ćelija Potporne ćelije
Novi Sad god Broj 1 / 06 Veljko Milković Bulevar cara Lazara 56 Novi Sad. Izveštaj o merenju
Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
Mozak kao organ. Elementi. Terminologija UVOD U FARMAKOLOGIJU CENTRALNOG NERVNOG SISTEMA ORGANIZACIJA NERVNOG SISTEMA
UVOD U FARMAKOLOGIJU CETRALOG ERVOG SISTEMA Doc. dr Miroslav Savić Institut za farmakologiju Farmaceutski fakultet Univerziteta u Beogradu Mozak kao organ Masa 2-3% ukupne Potrošnja O 2 20% ukupne Potrošnja
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
( ) ( ) 2 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET. Zadaci za pripremu polaganja kvalifikacionog ispita iz Matematike. 1. Riješiti jednačine: 4
UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
INTELIGENTNO UPRAVLJANJE
INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
FARMAKOLOGIJA PERIFERNOG ŽIVČANOG SUSTAVA
FARMAKOLOGIJA PERIFERNOG ŽIVČANOG SUSTAVA Prof. dr. sc. Frane Božić Zavod za farmakologiju i toksikologiju Veterinarski fakultet Sveučilišta u Zagrebu USTROJ ŽIVČANOG SUSTAVA MOZAK KRALJEŽNIČNA MOŽDINA
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE GODINE 8. RAZRED TOČNI ODGOVORI
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
3.1 Granična vrednost funkcije u tački
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
ELEKTROTEHNIČKI ODJEL
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
II. ODREĐIVANJE POLOŽAJA TEŽIŠTA
II. ODREĐIVANJE POLOŽAJA TEŽIŠTA Poožaj težišta vozia predstavja jednu od bitnih konstruktivnih karakteristika vozia s obzirom da ova konstruktivna karakteristika ima veiki uticaj na vučne karakteristike
S t r a n a 1. 1.Povezati jonsku jačinu rastvora: a) MgCl 2 b) Al 2 (SO 4 ) 3 sa njihovim molalitetima, m. za so tipa: M p X q. pa je jonska jačina:
S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
numeričkih deskriptivnih mera.
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
Zavrxni ispit iz Matematiqke analize 1
Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
REGULACIJA ARTERIJSKOG KRVNOG PRITISKA
REGULACIJA ARTERIJSKOG KRVNOG PRITISKA Krvni sudovi - uloge elastične arterije Aortna valvula Levo srce Levi ventrikul mitralna valvula Levi atrijum plućne vene Arteriole kontrola protoka i pritiska Pluća
Autonomni živčani sustav i srž nadbubrežnih žlijezda. Katedra za fiziologiju Medicinski fakultet u Splitu
Autonomni živčani sustav i srž nadbubrežnih žlijezda Prof. dr.. Zoran Valić Katedra za fiziologiju Medicinski fakultet u Splitu dio živčanog sustava koji nadzire većinu visceralnih funkcija tijela arterijski
DIMENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE
TEORIJA ETONSKIH KONSTRUKCIJA T- DIENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE 3.5 f "2" η y 2 D G N z d y A "" 0 Z a a G - tačka presek koja određje položaj sistemne
RIJEŠENI ZADACI I TEORIJA IZ
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
3525$&8158&1(',=$/,&(6$1$92-1,095(7(120
Srednja masinska skola OSOVE KOSTRUISAJA List1/8 355$&8158&1(',=$/,&(6$1$9-1,095(7(10 3ROD]QLSRGDFL maksimalno opterecenje Fa := 36000 visina dizanja h := 440 mm Rucna sila Fr := 350 1DYRMQRYUHWHQR optereceno
Eliminacijski zadatak iz Matematike 1 za kemičare
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
II. ODREĐIVANJE POLOŽAJA TEŽIŠTA
II. ODREĐIVANJE POLOŽAJA TEŽIŠTA Poožaj težišta vozia predstavja jednu od bitnih konstruktivnih karakteristika vozia s obzirom da ova konstruktivna karakteristika ima veiki uticaj na vučne karakteristike
XI dvoqas veжbi dr Vladimir Balti. 4. Stabla
XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
FAKULTET PROMETNIH ZNANOSTI
SVUČILIŠT U ZAGU FAKULTT POMTNIH ZNANOSTI predmet: Nastavnik: Prof. dr. sc. Zvonko Kavran zvonko.kavran@fpz.hr * Autorizirana predavanja 2016. 1 Pojačala - Pojačavaju ulazni signal - Zahtjev linearnost
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Obrada signala
Obrada signala 1 18.1.17. Greška kvantizacije Pretpostavka je da greška kvantizacije ima uniformnu raspodelu 7 6 5 4 -X m p x 1,, za x druge vrednosti x 3 x X m 1 X m = 3 x Greška kvantizacije x x x p
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
POPREČNO-PRUGASTA SKELETNA MUSKULATURA
POPREČNO-PRUGASTA SKELETNA MUSKULATURA Opšta fiziologija sa biofizikom 2014/2015 MUSKULATURA 1.SKELETNA 2.SRČANA 3.GLATKA SKELETNI MIŠIĆ Kost Tetiva Epimisium Epimisium Perimisium Endomisium Mišićno vlakno
PRIMJER 3. MATLAB filtdemo
PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
1 - KROVNA KONSTRUKCIJA : * krovni pokrivač, daska, letva: = 0,60 kn/m 2 * sneg, vetar : = 1,00 kn/m 2
OPTEREĆENJE KROVNE KONSTRUKCIJE : * krovni pokrivač, daska, letva: = 0,60 kn/m 2 * sneg, vetar : = 1,00 kn/m 2 1.1. ROGOVI : * nagib krovne ravni : α = 35 º * razmak rogova : λ = 80 cm 1.1.1. STATIČKI
Funkcija prenosa. Funkcija prenosa se definiše kao količnik z transformacija odziva i pobude. Za LTI sistem: y n h k x n k.
OT3OS1 7.11.217. Definicije Funkcija prenosa Funkcija prenosa se definiše kao količnik z transformacija odziva i pobude. Za LTI sistem: y n h k x n k Y z X z k Z y n Z h n Z x n Y z H z X z H z H z n h
Evolucija kontaktnih tesnih dvojnih sistema W UMa tipa
Evolucija kontaktnih tesnih dvojnih sistema W UMa tipa B.Arbutina 1,2 1 Astronomska opservatorija, Volgina 7, 11160 Beograd, Srbija 2 Katedra za astronomiju, Univerzitet u Beogradu, Studentski trg 16,
SISTEMI NELINEARNIH JEDNAČINA
SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
OSNOVI ELEKTRONIKE VEŽBA BROJ 1 OSNOVNA KOLA SA DIODAMA
ELEKTROTEHNIČKI FAKULTET U BEOGRADU KATEDRA ZA ELEKTRONIKU OSNOVI ELEKTRONIKE SVI ODSECI OSIM ODSEKA ZA ELEKTRONIKU LABORATORIJSKE VEŽBE VEŽBA BROJ 1 OSNOVNA KOLA SA DIODAMA Autori: Goran Savić i Milan
10. STABILNOST KOSINA
MEHANIKA TLA: Stabilnot koina 101 10. STABILNOST KOSINA 10.1 Metode proračuna koina Problem analize tabilnoti zemljanih maa vodi e na određivanje odnoa između rapoložive mičuće čvrtoće i proečnog mičućeg
( , 2. kolokvij)
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
Računarska grafika. Rasterizacija linije
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
Hormoni štitaste žlezde T 4
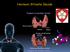Hormoni štitaste žlezde T 4 Morfološke odlike štitaste žlezde TSH Rast žlezde camp - preuzimanje jodida, transkripcija Tg, TPO i aktivnost Na + /I - kotransportera PLC efluks i oksidacija jodida, produkcija
Kaskadna kompenzacija SAU
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Delotvornost aktivnih biljnih principa trenutna dostignuća
Kontinuirana edukacija farmaceuta 6. novembar 2010. Hotel Continental, Beograd odobrenje ZSS B-297 (juli 2010.) Delotvornost aktivnih biljnih principa trenutna dostignuća Prof. dr Nenad Ugrešić, Farmaceutski
LANCI & ELEMENTI ZA KAČENJE
LANCI & ELEMENTI ZA KAČENJE 0 4 0 1 Lanci za vešanje tereta prema standardu MSZ EN 818-2 Lanci su izuzetno pogodni za obavljanje zahtevnih operacija prenošenja tereta. Opseg radne temperature se kreće
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Konstruisanje. Dobro došli na... SREDNJA MAŠINSKA ŠKOLA NOVI SAD DEPARTMAN ZA PROJEKTOVANJE I KONSTRUISANJE
Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
SEKUNDARNE VEZE međumolekulske veze
PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
Srednjenaponski izolatori
Srednjenaponski izolatori Linijski potporni izolatori tip R-ET Komercijalni naziv LPI 24 N ET 1) LPI 24 L ET/5 1)2) LPI 24 L ET/6 1)2) LPI 38 L ET 1) Oznaka prema IEC 720 R 12,5 ET 125 N R 12,5 ET 125
POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE
**** MLADEN SRAGA **** 011. UNIVERZALNA ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE SKUP REALNIH BROJEVA α Autor: MLADEN SRAGA Grafički urednik: BESPLATNA - WEB-VARIJANTA Tisak: M.I.M.-SRAGA
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Ispitivanje toka i skiciranje grafika funkcija
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Pismeni ispit iz matematike GRUPA A 1. Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj, zatim naći 4 z.
Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Matematika 1 - vježbe. 11. prosinca 2015.
Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Elementi spektralne teorije matrica
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Cauchyjev teorem. Postoji više dokaza ovog teorema, a najjednostvniji je uz pomoć Greenove formule: dxdy. int C i Cauchy Riemannovih uvjeta.
auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
Polarizacija. Procesi nastajanja polarizirane svjetlosti: a) refleksija b) raspršenje c) dvolom d) dikroizam
Polarzacja Proces asajaja polarzrae svjelos: a refleksja b raspršeje c dvolom d dkrozam Freselove jedadžbe Svjelos prelaz z opčkog sredsva deksa loma 1 u sredsvo deksa loma, dolaz do: refleksje (prema
Dvanaesti praktikum iz Analize 1
Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
5. PARCIJALNE DERIVACIJE
5. PARCIJALNE DERIVACIJE 5.1. Izračunajte parcijalne derivacije sljedećih funkcija: (a) f (x y) = x 2 + y (b) f (x y) = xy + xy 2 (c) f (x y) = x 2 y + y 3 x x + y 2 (d) f (x y) = x cos x cos y (e) f (x
Grafičko prikazivanje atributivnih i geografskih nizova
Grafičko prikazivanje atributivnih i geografskih nizova Biserka Draščić Ban Pomorski fakultet u Rijeci 17. veljače 2011. Grafičko prikazivanje atributivnih nizova Atributivni nizovi prikazuju se grafički
III VEŽBA: FURIJEOVI REDOVI
III VEŽBA: URIJEOVI REDOVI 3.1. eorijska osnova Posmatrajmo neki vremenski kontinualan signal x(t) na intervalu definisati: t + t t. ada se može X [ k ] = 1 t + t x ( t ) e j 2 π kf t dt, gde je f = 1/.
INŽENJERSTVO NAFTE I GASA. 2. vežbe. 2. vežbe Tehnologija bušenja II Slide 1 of 50
INŽENJERSTVO NAFTE I GASA Tehnologija bušenja II 2. vežbe 2. vežbe Tehnologija bušenja II Slide 1 of 50 Proračuni trajektorija koso-usmerenih bušotina 2. vežbe Tehnologija bušenja II Slide 2 of 50 Proračun
Elektrotehnički fakultet univerziteta u Beogradu 16.maj Odsek za Softversko inžinjerstvo
Elektrotehnčk fakultet unverzteta u Beogradu 6.maj 8. Odsek za Softversko nžnjerstvo Performanse računarskh sstema Drug kolokvjum Predmetn nastavnk: dr Jelca Protć (35) a) () Posmatra se segment od N uzastonh
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
ТЕМПЕРАТУРА СВЕЖЕГ БЕТОНА
ТЕМПЕРАТУРА СВЕЖЕГ БЕТОНА empertur sežeg beton menj se tokom remen i zisi od ećeg broj utijnih prmetr: Početne temperture mešine (n izsku iz mešie), emperture sredine, opote hidrtije ement, Rzmene topote
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
Elektrotehnički fakultet univerziteta u Beogradu 17.maj Odsek za Softversko inžinjerstvo
Elektrotehnički fakultet univerziteta u Beogradu 7.maj 009. Odsek za Softversko inžinjerstvo Performanse računarskih sistema Drugi kolokvijum Predmetni nastavnik: dr Jelica Protić (35) a) (0) Posmatra
Opšte KROVNI POKRIVAČI I
1 KROVNI POKRIVAČI I FASADNE OBLOGE 2 Opšte Podela prema zaštitnim svojstvima: Hladne obloge - zaštita hale od atmosferskih padavina, Tople obloge - zaštita hale od atmosferskih padavina i prodora hladnoće
VISKOZNOST TEČNOSTI Viskoznost
VISKOZNOST VISKOZNOST TEČNOSTI Viskoznost predstavlja otpor kojim se pojedini slojevi tečnosti suprostavljaju kretanju jednog u odnosu na drugi, odnosno to je vrsta unutrašnjeg trenja koja dovodi do protoka
Prvi kolokvijum. y 4 dy = 0. Drugi kolokvijum. Treći kolokvijum
27. septembar 205.. Izračunati neodredjeni integral cos 3 x (sin 2 x 4)(sin 2 x + 3). 2. Izračunati zapreminu tela koje nastaje rotacijom dela površi ograničene krivama y = 3 x 2, y = x + oko x ose. 3.
OBRTNA TELA. Vladimir Marinkov OBRTNA TELA VALJAK
OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
100g maslaca: 751kcal = 20g : E maslac E maslac = (751 x 20)/100 E maslac = 150,2kcal 100g med: 320kcal = 30g : E med E med = (320 x 30)/100 E med =
100g maslaca: 751kcal = 20g : E maslac E maslac = (751 x 20)/100 E maslac = 150,2kcal 100g med: 320kcal = 30g : E med E med = (320 x 30)/100 E med = 96kcal 100g mleko: 49kcal = 250g : E mleko E mleko =
a M a A. Može se pokazati da je supremum (ako postoji) jedinstven pa uvodimo oznaku sup A.
3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
Moguća i virtuelna pomjeranja
Dnamka sstema sa vezama Moguća vrtuelna pomjeranja f k ( r 1,..., r N, t) = 0 (k = 1, 2,..., K ) df k dt = r + t = 0 d r = r dt moguća pomjeranja zadovoljavaju uvjet: df k = d r + dt = 0. t δ r = δx +
TRIGONOMETRIJA TROKUTA
TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
Operacije s matricama
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
TRIGONOMETRIJSKE FUNKCIJE I I.1.
TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
MATEMATIKA 2. Grupa 1 Rexea zadataka. Prvi pismeni kolokvijum, Dragan ori
MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika. Monotonost i ekstremi. Katica Jurasić. Rijeka, 2011.
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
18. listopada listopada / 13
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
Cenovnik spiro kanala i opreme - FON Inžinjering D.O.O.
Cenovnik spiro kanala i opreme - *Cenovnik ažuriran 09.02.2018. Spiro kolena: Prečnik - Φ (mm) Spiro kanal ( /m) 90 45 30 Muf/nipli: Cevna obujmica: Brza diht spojnica: Elastična konekcija: /kom: Ø100
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
Mašinsko učenje. Regresija.
Mašinsko učenje. Regresija. Danijela Petrović May 17, 2016 Uvod Problem predviđanja vrednosti neprekidnog atributa neke instance na osnovu vrednosti njenih drugih atributa. Uvod Problem predviđanja vrednosti
Strukture podataka i algoritmi 1. kolokvij 16. studenog Zadatak 1
Strukture podataka i algoritmi 1. kolokvij Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i službeni šalabahter. Predajete samo papire koje ste dobili. Rezultati i uvid u kolokvije: ponedjeljak,
Računarska grafika. Rasterizacija linije
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Viskoznost predstavlja otpor tečnosti pri proticanju. Viskoznost predstavlja unutrašnje trenje između molekula u fluidu.
VISKOZNOST VISKOZNOST Viskoznost predstavlja otpor tečnosti pri proticanju. Viskoznost predstavlja unutrašnje trenje između molekula u fluidu. VISKOZNOST Da li očekujete da će glicerol imati veću ili manju
Pozicija elektrod: ena elektroda zunaj celice in druga elektroda znotraj celice.
Strnad Petra 1 ŽIVEC IN MIŠICA MEMBRANSKI POTENCIAL 1. Kaj je membranski potencial? Napetostna razlika med notranjostjo in zunanjostjo membrane, ki jo omogočata različna razporeditev ionov med celično
OSNOVE TEHNOLOGIJE PROMETA
OSNOVE TEHNOLOGIJE PROMETA MODUL: Tehnologija teleomuniacijsog rometa FAKULTET PROMETNIH ZNANOSTI Predavači: Doc.dr.sc. Štefica Mrvelj Maro Matulin, dil.ing. Zagreb, ožuja 2009. Oće informacije Konzultacije:
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije