|
|
|
- Νέφθυς Βούλγαρης
- 9 χρόνια πριν
- Προβολές:
Transcript
1
2
3
4
5
6
7
8
9 K.Z. K.Z.
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
cz+d d (ac + cd )z + bc + dd c z + d
T (z) = az + b cz + d ; a, b, c, d C, ad bc 0 ( ) a b M T (z) = (z) az + b c d cz + d (T T )(z) = T (T (z) (T T )(z) = az+b a + cz+d b c az+b + = (aa + cb )z + a b + b d a z + b cz+d d (ac + cd )z + bc
Παραδείγματα Διανυσματικοί Χώροι
Παραδείγματα Διανυσματικοί Χώροι Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με y, V και του πολλαπλασιασμού: με V και
qwφιertyuiopasdfghjklzxερυυξnmηq σwωψerβνtyuςiopasdρfghjklzxcvbn mqwertyuiopasdfghjklzxcvbnφγιmλι qπςπζαwωeτrtνyuτioρνμpκaλsdfghςj
qwφιrtyuiopasdfghjklzερυυξnmηq σwωψrβνtyuςiopasdρfghjklzcvbn mqwrtyuiopasdfghjklzcvbnφγιmλι ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ qπςπζαwωτrtνyuτioρνμpκaλsdfghςj ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ klzcvλοπbnαmqwrtyuiopasdfghjklz
7 Οπτική ενεργότητα. (Σχ.7.1)
- 15-7 Οπτική ενεργότητα Το φαινόµενο της οπτικής ενεργότητας (optical activity) για πρώτη φορά παρατηρήθηκε από τον F. J. Arago το 1811 σε κρύσταλλο Χαλαζία (Σχ.7.1). (Σχ.7.1) Ένα επίπεδο µέτωπο κύµατος
2(z 2) οι εικόνες των z 1
ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ 3: ΓΕΩΜΕΤΡΙΚΗ ΕΡΜΗΝΕΙΑ ΤΟΥ ΜΕΤΡΟΥ - ΤΡΙΓΩΝΙΚΗ ΑΝΙΣΟΤΗΤΑ [Κεφ 3: Μέτρο Μιγαδικού Αριθμού του σχολικού βιβλίου] ΣΗΜΕΙΩΣΕΙΣ Γεωμετρική ερμηνεία του μέτρου Θεωρούμε το
Απόδειξη. Η ιδιότητα(vi) του ορισμού δεν ισχύει στην πράξη αυτή. Πράγματι, έχουμε. 1 (x, y, z) =(1 x, 1 y, 2 1 z) =(x, y, 2z)
1 ιανυσματικοί χώροι Άσκηση 1.1 Στο σύνολο R 3 όλων των διατεταγμένων τριάδων διατηρούμε την πρόσθεση, που ορίσαμε στο αντίστοιχο παράδειγμα, και ορίζουμε εξωτερικό πολλαπλασιασμό με τη σχέση λ(a 1,a 2,a
Κεφάλαιο 4 Σχεδίαση Συστηµάτων Ελέγχου µε Μικροϋπολογιστές - Συνεχής Σχεδίαση
Κεφάλαιο 4 Σχεδίαση Συστηµάτων Ελέγχου µε Μικροϋπολογιστές - Συνεχής Σχεδίαση Επανάληψη στα Συστήµατα από Δειγµατοληπτικά Δεδοµένα στα Πεδία Συχνότητας και Χρόνου Ψηφιακός Έλεγχος µε Συνεχή Σχεδιασµό Χαρακτηριστικά
ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ 2013 ΕΚΦΩΝΗΣΕΙΣ
ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ 3 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α A Έστω f µια συνεχής συνάρτηση σε ένα διάστηµα [α, β] Αν G είναι µια παράγουσα της f στο [α, β], τότε να αποδείξετε ότι: β f () t dt = G ( β) G ( α) a Μονάδες
Εφαρμοσμένα Μαθηματικά ΙΙ 7ο Σετ Ασκήσεων (Λύσεις) Γραμμικά Συστήματα- Απαλοιφή Gauss Επιμέλεια: I. Λυχναρόπουλος
Εφαρμοσμένα Μαθηματικά ΙΙ 7ο Σετ Ασκήσεων (Λύσεις) Γραμμικά Συστήματα- Απαλοιφή Gauss Επιμέλεια: I. Λυχναρόπουλος. Χρησιμοποιείστε απαλοιφή Gauss για να επιλύσετε τα ακόλουθα συστήματα: 5x 8y = 5x= + y
AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ. ( t) f dt = G(β) G(α) A2. Πότε η γραφική παράσταση μιας συνάρτησης f λέμε ότι έχει:
AΡΧΗ ΗΣ ΣΕΛΙΔΑΣ 9 ο ΔΙΑΓΩΝΙΣΜΑ ΕΠΑΝΑΛΗΨΗΣ ΠΡΟΣΟΜΟΙΩΣΗΣ 5o ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΠΕΤΡΟΥΠΟΛΗΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ : ΜΑΘΗΜΑΤΙΚΑ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : Tέσσερις (4) ΘΕΜΑ A Α. Έστω f μια
ΠΑΡΑΡΤΗΜΑ. της. Έκθεσης της Επιτροπής προς το Ευρωπαϊκό Κοινοβούλιο και το Συμβούλιο
ΕΥΡΩΠΑΪΚΗ ΕΠΙΤΡΟΠΗ Βρυξέλλες, 2.6.2014 COM(2014) 312 final ANNEX 1 ΠΑΡΑΡΤΗΜΑ της Έκθεσης της Επιτροπής προς το Ευρωπαϊκό Κοινοβούλιο και το Συμβούλιο για την εφαρμογή της απόφασης-πλαισίου 2008/675/ΔΕΥ
Διαμόρφωση απλής πλευρικής ζώνης (single-sideband SSB)
Διαμόρφωση απλής πλευρικής ζώνης single-sidebnd SSB Διαμόρφωση κατά πλάτος Ι s osπ s [ x os km km ]os x [ km ] km 0 km m: σήμα βασικής ζώνης σήμα διαμόρφωσης : φέρον σήμα s: διαμορφωμένο σήμα k: ευαισθησία
Τα η/µ κύµατα πρέπει να ικανοποιούν όλες τις σχέσεις Maxwell. Στον ελεύθερο χώρο, έχουµε τα παρακάτω ηλεκτρικά πεδία
1 Τα η/µ κύµατα πρέπει να ικανοποιούν όλες τις σχέσεις Mawell. Στον ελεύθερο χώρο, έχουµε τα παρακάτω ηλεκτρικά πεδία e1 = zˆ cos( ωt kz) e = ( ˆ + zˆ) cos( ωt k z ) e 3 = ( ˆ + zˆ) cos( ω t + k) (α) Ικανοποιούν
Σεµινάριο Αυτοµάτου Ελέγχου
Σεµινάριο Αυτοµάτου Ελέγχου Μάθηµα 4 Αναλυτική σύνθεση συστηµάτων αυτοµάτου ελέγχου Με συνθήκη µόνιµου σφάλµατος Με συνθήκη επιθυµητών πόλων Με επιθυµητό πρότυπο Καλλιγερόπουλος 4 1 Αναλυτική Σύνθεση συστηµάτων
Εφαρμοσμένα Μαθηματικά ΙΙ Εξέταση Σεπτεμβρίου 25/9/2017 Διδάσκων: Ι. Λυχναρόπουλος
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Εξέταση Σεπτεμβρίου 5/9/07 Διδάσκων: Ι. Λυχναρόπουλος Άσκηση (Μονάδες ) Να δειχθεί ότι το πεδίο F( x, y) = y cos x + y,sin x
Εφαρμοσμένα Μαθηματικά ΙΙ 7ο Σετ Ασκήσεων (Λύσεις) Ορίζουσες Επιμέλεια: Ι. Λυχναρόπουλος
Εφαρμοσμένα Μαθηματικά ΙΙ 7ο Σετ Ασκήσεων (Λύσεις) Ορίζουσες Επιμέλεια: Ι. Λυχναρόπουλος. Υπολογίστε τις ακόλουθες ορίζουσες a) 4 b) c) a b + a) 4 4 Παρατήρηση: Προσέξτε ότι ο συμβολισμός της ορίζουσας
Παραδείγματα (1 ο σετ) Διανυσματικοί Χώροι
Παραδείγματα ( ο σετ) Διανυσματικοί Χώροι Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με y, V και του πολλαπλασιασμού:
P l+1 (cosa) P l 1 (cosa) 2δ l,0 1
Λεοντσ ίνης Στέφανος Ηλεκτομαγνητισ μός η Σειά Ασ κήσ εων 3 Το ηλεκτικό πεδίο έχει τη μοφή φ σ ε ˆr άα φ σ ε rr Tο δυναμικό σ ε σ φαιικές σ υντεταγμένες φ r, θ Al + B l r l+] l cosθ Για να είναι πεπεασ
ΠΠΜ 220: Στατική Ανάλυση των Κατασκευών Ι
ΠΠΜ 220: Στατική Ανάλυση των Κατασκευών Ι, 2004-4 η Πρόοδος Πανεπιστήµιο Κύπρου Πολυτεχνική Σχολή Τµήµα Πολιτικών Μηχανικών και Μηχανικών Περιβάλλοντος ΠΠΜ 220: Στατική Ανάλυση των Κατασκευών Ι Ακαδηµαϊκό
Προσεγγιστική κατασκευή κανονικού 9-γώνου με κανόνα και διαβήτη
Προσεγγιστική κατασκευή κανονικού 9-γώνου με κανόνα και διαβήτη Η επίκεντρη γωνία ενός κανονικού 9-γώνου είναι: 0 9 0 Η γωνία αυτή δεν κατασκευάζεται με κανόνα και διαβήτη και επομένως ένα κανονικό 9-γωνο
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ «ΠΛΗΡΟΦΟΡΙΚΗ» ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ 4 Ιουνίου 009 Θέμα (0 μονάδες) α) (7 μον) Για τις διάφορες τιμές του k R, να λυθεί το σύστημα y+ kz =
Λυγισμός Ευστάθεια (Euler και Johnson)
Λυγισμός Ευστάθεια (Euler και Johnson) M z P z EI z P z P z z 0 και αν EI k EI P 0 z k z Η λύση της διαφορικής εξίσωσης έχει την μορφή: 1 sin z C kz C cos kz Αν οι οριακές συνθήκες είναι άρθρωση άρθρωση
Κ Α Τ Α Λ Ο Γ Ο Σ 2 0 1 5
Κ Α Τ Α Λ Ο Γ Ο Σ 2 0 5 Η Δομική Εξοπλιστική δραστηριοποιείται στην εισαγωγή και διάθεση ειδών ύδρευσης, αποχέτευσης, θέρμανσης και άρδευσης εδώ και 8 χρόνια. Εκπροσωπεί μεγάλους εμπορικούς οίκους παραγωγής
Ερωτήσεις ανάπτυξης 1. ** 2. ** 3. ** 4. ** 5. ** 6. **
Ερωτήσεις ανάπτυξης 1. ** ίνονται επίπεδο p και τρία µη συνευθειακά σηµεία του Α, Β και Γ καθώς και ένα σηµείο Μ, που δεν συµπίπτει µε το Α. Αν η ευθεία ΑΜ τέµνει την ευθεία ΒΓ, να δείξετε ότι το Μ είναι
1 ΣΤΑΘ.ΜΕ ΦΕΓΓΙΤΗΣ ΚΑΙ ΝΤΙΖΑ 1 ΣΤΑΘ.ΜΕ ΦΕΓΓΙΤΗΣ ΚΑΙ ΝΤΙΖΑ ΣΥΡΟΜΕΝΟ ΜΟΝΟΦΥΛΛΟ
AA ΦΩΤΟΓΡΑΦΙΑ ΠΛΑΤΟΣ ΥΨΟΣ ΣΕΙΡΑ ΧΡΩΜΑ ΓΕΝΙΚΗ ΠΕΡΙΓΡΑΦΗ ΡΟΛΟ ΦΟΡΑ ΤΙΜΗ STOCK ΜΕ ΦΠΑ 23 % ΣΚ0001 1150 2950 ELITE NUSSBAUM 1 ΣΤΑΘ.ΜΕ ΦΕΓΓΙΤΗΣ ΚΑΙ ΝΤΙΖΑ ΑΝΟΙΓΟΜΕΝΗ ΑΡΙΣΤΕΡΑ ΣΚ0002 1055 2965 ELITE NUSSBAUM
Πράξεις διανυσμάτων. Πρόσθεση. Αφαίρεση. Συντεταγμένες στο επίπεδο. Συντεταγμένες διανύσματος και. Συντεταγμένες μέσου ευθυγράμμου τμηματος
ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΚΑΙ ΜΙΓΑΔΙΚΟΙ Πράξεις διανυσμάτων Πρόσθεση Αφαίρεση Συντεταγμένες στο επίπεδο Συντεταγμένες διανύσματος με (x 1, y1) (x, y ) (x x, y y ) 1 Συντεταγμένες μέσου ευθυγράμμου τμηματος
,..., v n. W πεπερασμένα παραγόμενοι και dimv. Τα ακόλουθα είναι ισοδύναμα f είναι ισομορφιμός. f είναι 1-1. f είναι επί.
Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις7: Γραμμικές Απεικονίσεις Βασικά σημεία Ορισμός και παραδείγματα γραμμικών απεικονίσεων Σύνθεση γραμμικών απεικονίσεων, ισομορφισμοί Κάθε γραμμική απεικόνιση f : V W, όπου
u = 0 u = ϕ t + Π) = 0 t + Π = C(t) C(t) C(t) = K K C(t) ϕ = ϕ 1 + C(t) dt Kt 2 ϕ = 0
u = (u, v, w) ω ω = u = 0 ϕ u u = ϕ u = 0 ϕ 2 ϕ = 0 u t = u ω 1 ρ Π + ν 2 u Π = p + (1/2)ρ u 2 + ρgz ω = 0 ( ϕ t + Π) = 0 ϕ t + Π = C(t) C(t) C(t) = K K C(t) ϕ = ϕ 1 + C(t) dt Kt C(t) ϕ ϕ 1 ϕ = ϕ 1 p ρ
1 ΣΤΑΘ.ΜΕ ΦΕΓΓΙΤΗΣ ΚΑΙ ΝΤΙΖΑ 1 ΣΤΑΘ.ΜΕ ΦΕΓΓΙΤΗΣ ΚΑΙ ΝΤΙΖΑ ΣΥΡΟΜΕΝΟ ΜΟΝΟΦΥΛΛΟ
AA ΦΩΤΟΓΡΑΦΙΑ ΠΛΑΤΟΣ ΥΨΟΣ ΣΕΙΡΑ ΧΡΩΜΑ ΓΕΝΙΚΗ ΠΕΡΙΓΡΑΦΗ ΡΟΛΟ ΦΟΡΑ Α ΤΙΜΗ Ρ ΣΤΟΚ Χ ΣΚ0001 1150 2950 ELITE NUSSBAUM 1 ΣΤΑΘ.ΜΕ ΦΕΓΓΙΤΗΣ ΚΑΙ ΝΤΙΖΑ ΑΝΟΙΓΟΜΕΝΗ ΑΡΙΣΤΕΡΑ 305 ΣΚ0002 1055 2965 ELITE NUSSBAUM 1 ΣΤΑΘ.ΜΕ
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 2
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 2 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/linearalgebraii/laii2018/laii2018.html Παρασκευή 16 Μαρτίου 2018
ΣΚΙΑΘΟΣ. Ξενοδοτείο Καη. Διαηροθή Δίκλινο Μονόκλινο. Παιδί. Παιδί. Ενήλικας. 1 ο Παιδί. 3 ος Ενήλικας. 2 ο Παιδί. Καη. Διαηροθή Δίκλινο Μονόκλινο
ΣΚΙΑΘΟΣ Ξενοδοτείο KASSANDRA BAY RESORT & SPA GARDEN VIEW Καη. Διαηροθή Δίκλινο Μονόκλινο 7/7, 11/7, 14/7 1,019 Κ/Ζ 465 465 Γ/Π 18/7, 21/7, 22/8 1,099 Κ/Ζ 465 465 Γ/Π 25/7,28/7 1,159 Κ/Ζ 465 465 Γ/Π 11/8,15/8,18/8
T p =. (1) p = m q. (2)
Υπενύμιση: Συχνά δεν εμφανίζονται όλες οι μεταβλητές μιάς συνάρτησης, πχ. F(,t) = F() = F(t) = F. Έντονη γραφή υποδεικνύει άνυσμα, π.χ. F αντιστοιχεί σε τρείς συνιστώσες, {F x, F y, F z }, στον τρισδιάστατο
Σειρά Προβλημάτων 2 Λύσεις
Σειρά Προβλημάτων 2 Λύσεις Άσκηση 1 Χρησιμοποιώντας τα πιο κάτω κατηγορήματα και σταθερές και υποθέτωντας ως σύμπαν το σύνολο όλων των ανθρώπων, να διατυπώσετε τις προτάσεις που ακολουθούν στον Κατηγορηματικό
t : (x, y) x 2 +y 2 y x
Σύνοψη Κεφαλαίου 5: Αντιστροφική Γεωμετρία Αντιστροφή 1. Η ανάκλαση σε μία ευθεία l στο επίπεδο απεικονίζει ένα σημείο A σε ένα σημείο A που απέχει ίση απόσταση από την l αλλά βρίσκεται στην άλλη πλευρά
Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 19/6/2018 Διδάσκων: Ι. Λυχναρόπουλος
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Άσκηση (Μονάδες.) Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 9/6/08 Διδάσκων: Ι. Λυχναρόπουλος Έστω A= k και w = 3 0. Να βρεθεί η τιμή του k για την οποία
ΘΕΜΑ ΕΚΠΟΝΗΣΗΣ Παράδοση Παραδοτέα (α) (β) (γ) (δ) Βαθμός Φορτία
Πάτρα 5-12-2016 ΘΕΜΑ ΕΚΠΟΝΗΣΗΣ Παράδοση: Ημέρα διεξαγωγής της εξέτασης περίοδος Ιανουαρίου 2017. Παραδοτέα: (α) Τεχνική έκθεση η οποία θα ξεκινά με συμπληρωμένο των πίνακα αριθμητικών δεδομένων (βλ. παρακάτω),
Κεραίες & Ασύρματες Ζεύξεις
Κεραίες & Ασύρματες Ζεύξεις Εισαγωγή στις ΣΤΟΙΧΕΙΟΚΕΡΑΙΕΣ Το μάθημα αυτό πραγματεύεται το αντικείμενο των κεραιών και των Ασύρματων Ζεύξεων. Περιέχει τη θεμελίωση και τις βασικές έννοιες /αρχές που διέπουν
2 η έκδοση Συλλογικού Καταλόγου Ελληνικών Ακαδημαϊκών Βιβλιοθηκών
2 η έκδοση Συλλογικού Καταλόγου Ελληνικών Ακαδημαϊκών Βιβλιοθηκών Η 2 η έκδοση του Συλλογικού Καταλόγου κυκλοφόρησε στις αρχές του 2008, ενώ η εξαγωγή των, από τα τοπικά συστήματα, πραγματοποιήθηκε μεταξύ
ΠPOKHPYΞH ΠΑΝΕΛΛΗΝΙΟΥ ΠPΩTAΘΛHMATΟΣ KARTING 2016
ΟΜΟΣΠΟΝΔΙΑ ΜΗΧΑΝΟΚΙΝΗΤΟΥ ΑΘΛΗΤΙΣΜΟΥ ΕΛΛΑΔΟΣ (O.M.A.E) ΠPOKHPYΞH ΠΑΝΕΛΛΗΝΙΟΥ ΠPΩTAΘΛHMATΟΣ KARTING 2016 ΕΠΙΤΡΟΠΗ ΑΓΩΝΩΝ (ΕΠ.Α.) 1η έκδοση: 11/02/2016 2 η έκδοση: 28/06/2016 H ΕΠΑ/ΟΜΑΕ σύμφωνα με τον ΔΑΚ,
Μπλοκ quickconnect (ταχείας σύνδεσης) 7.05. Μπάρες συνδέσεων πολλαπλών διατομών 7.07. Μπάρες σύνδεσης περονωτές 7.11. Μπάρες σύνδεσης διχαλωτές 7.
Σύνδεση Μπλοκ quickconnect (ταχείας σύνδεσης) 7.05 Κλέμες ράγας 7.06 Μπάρες συνδέσεων πολλαπλών διατομών 7.07 Μπαρέτες 7.08 Ακροδέκτες 7.09 Μπλοκ διανομής 7.10 Μπάρες σύνδεσης περονωτές 7.11 Μπάρες σύνδεσης
Πρόταση ΚΑΝΟΝΙΣΜΟΣ ΤΟΥ ΣΥΜΒΟΥΛΙΟΥ
ΕΥΡΩΠΑΪΚΗ ΕΠΙΤΡΟΠΗ Βρυξέλλες, 7.7.2014 COM(2014) 448 final 2014/0207 (NLE) Πρόταση ΚΑΝΟΝΙΣΜΟΣ ΤΟΥ ΣΥΜΒΟΥΛΙΟΥ για την τροποποίηση του κανονισμού (ΕΚ) αριθ. 1340/2008 του Συμβουλίου, της 8ης Δεκεμβρίου 2008,
3 η έκδοση Συλλογικού Καταλόγου Ελληνικών Ακαδημαϊκών Βιβλιοθηκών
3 η έκδοση Συλλογικού Καταλόγου Ελληνικών Ακαδημαϊκών Βιβλιοθηκών Η 3 η έκδοση του Συλλογικού Καταλόγου κυκλοφόρησε το καλοκαίρι του 2008, ενώ η εξαγωγή των εγγραφών, από τα τοπικά συστήματα, πραγματοποιήθηκε
Βελτίωσητηςεκπαίδευσηςσε ΠανεπιστήμιατηςκεντρικήςΑσίας. καθ. Π. Αξαόπουλος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕΙ Αθηνών
Βελτίωσητηςεκπαίδευσηςσε ΠανεπιστήμιατηςκεντρικήςΑσίας καθ. Π. Αξαόπουλος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕΙ Αθηνών Ενιαίος ΕυρωπαϊκόςΧώρος Ανώτατης Εκπαίδευσης Aναγνωρισιμότητα πτυχίων και ακαδημαϊκών
MOTROL. COMMISSION OF MOTORIZATION AND ENERGETICS IN AGRICULTURE 2014, Vol. 16, No. 5,
MOTROL. COMMISSION OF MOTORIZATION AND ENERGETICS IN AGRICULTURE 2014, Vol. 16, No. 5, 3 14 -, :., 83, 66404 e-mail: chupinvr@istu.irk.ru...,,., -,.,. :,,,,,, -, - [1].,.., [2, 3].,.,,,.,,, [4, 5].,..1.
ΜΕΛΕΤΗ ΣΥΣΤΗΜΑΤΟΣ ΜΑΖΑΣ-ΕΛΑΤΗΡΙΟΥ-ΑΠΟΣΒΕΣΤΗΡΑ
ΤΕΙ ΚΡΗΤΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΙΙ ΜΕΛΕΤΗ ΣΥΣΤΗΜΑΤΟΣ ΜΑΖΑΣ-ΕΛΑΤΗΡΙΟΥ-ΑΠΟΣΒΕΣΤΗΡΑ Μ. Σφακιωτάκης mfak@taff.teicrete.gr Χειµερινό Οκτώβριος εξάµηνο 2010-11 2017 Σύστηµα Μάζας-Ελατηρίου-Αποσβεστήρα
4 η έκδοση Συλλογικού Καταλόγου Ελληνικών Ακαδημαϊκών Βιβλιοθηκών
4 η έκδοση Συλλογικού Καταλόγου Ελληνικών Ακαδημαϊκών Βιβλιοθηκών Η 4 η έκδοση του Συλλογικού Καταλόγου κυκλοφόρησε στις αρχές του 2009, ενώ η εξαγωγή των εγγραφών, από τα τοπικά συστήματα, πραγματοποιήθηκε
dx A β δ: παράμετρος πυκνότητας, πόλωση του μέσου, ενέργεια πλάσματος τι περιμένουμε 1/ 2 πτώση Ένα ελάχιστο: minimum ionizing particle: MIP
de/ Bethe Bloch de πzn rmc e e γ β mc e δ z ln β A β I δ: παράμετρος πυκνότητας, πόλωση του μέσου, ενέργεια πλάσματος 1/ πτώση τι περιμένουμε Ένα ελάχιστο: minimum ionizing particle: MIP 0.1 1 10 100 p/m
Εισαγωγή στην Οικονομική Επιστήμη Ι. Μονοπωλιακός Ανταγωνισμός. Αρ. Διάλεξης: 12
Εισαγωγή στην Οικονομική Επιστήμη Ι Μονοπωλιακός Ανταγωνισμός Αρ. Διάλεξης: 12 Μονοπωλιακός Ανταγωνισμός Ο Μονοπωλιακός Ανταγωνισμός αναφέρεται στην διάρθρωση της αγοράς εκείνης η οποία βρίσκεται μεταξύ
Αναλογικά φίλτρα. Για να επιτύχουµε µια επιθυµητή απόκριση χρειαζόµαστε σηµαντικά λιγότερους συντελεστές γιαένα IIR φίλτροσεσχέσηµετοαντίστοιχο FIR.
Τα IIR φίλτρα είναι επαναληπτικά ή αναδροµικά, µε την έννοια ότι δείγµατα της εξόδου χρησιµοποιούνται από το σύστηµα για τον υπολογισµό τν νέν τιµών της εξόδου σε επόµενες χρονικές στιγµές. Για να επιτύχουµε
Κεφάλαιο 2 ο ανάλυσης ερωτήσεις στις παραγώγους. τότε η f(x) είναι παραγωγίσιμη
Κεφάλαιο 2 ο ανάλυσης ερωτήσεις στις παραγώγους. 1. Αν υπάρχει το lim x x0 f(x) f(x 0 ) x x 0 τότε η f(x) είναι παραγωγίσιμη στο x 0 του Π.Ο της; : όχι. Πρέπει επιπλέον το όριο να είναι πραγματικός αριθμός.
DGC 2A ΣΥΝΕΡΓΑΣΙΑ ΜΕΤΑΞΥ ΤΗΣ ΕΥΡΩΠΑΪΚΗΣ ΕΝΩΣΗΣ ΚΑΙ ΤΟΥ ΚΑΖΑΚΣΤΑΝ. Βρυξέλλες, 7 Μαρτίου 2017 (OR. en) UE-KZ 2301/17
ΣΥΝΕΡΓΑΣΙΑ ΜΕΤΑΞΥ ΤΗΣ ΕΥΡΩΠΑΪΚΗΣ ΕΝΩΣΗΣ ΚΑΙ ΤΟΥ ΚΑΖΑΚΣΤΑΝ Συμβούλιο Συνεργασίας Βρυξέλλες, 7 Μαρτίου 2017 (OR. en) UE-KZ 2301/17 Διοργανικός φάκελος: 2017/0019 (NLE) ΝΟΜΟΘΕΤΙΚΕΣ ΚΑΙ ΑΛΛΕΣ ΠΡΑΞΕΙΣ Θέμα:
ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 69 946778 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 69 946778 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ
Ελληνικό Ανοικτό Πανεπιστήµιο Ενδεικτικές Λύσεις Θεµάτων Τελικών εξετάσεων στη Θεµατική Ενότητα ΦΥΕ34. Ιούλιος 2008 KYMATIKH. ιάρκεια: 210 λεπτά
Κυµατική ΦΥΕ4 5/7/8 Ελληνικό Ανοικτό Πανεπιστήµιο Ενδεικτικές Λύσεις Θεµάτων Τελικών εξετάσεων στη Θεµατική Ενότητα ΦΥΕ4 Ιούλιος 8 KYMATIKH ιάρκεια: λεπτά Θέµα ο (Μονάδες:.5) A) Θεωρούµε τις αποστάσεις
ΜΕΛΕΤΗ ΣΥΣΤΗΜΑΤΟΣ ΜΑΖΑΣ-ΕΛΑΤΗΡΙΟΥ-ΑΠΟΣΒΕΣΤΗΡΑ
ΤΕΙ ΚΡΗΤΗΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΠΡΟΗΓΜΕΝΑ ΣΥΣΤΗΜΑΤΑ ΠΑΡΑΓΩΓΗΣ, ΑΥΤΟΜΑΤΙΣΜΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ ΔΥΝΑΜΙΚΗ & ΕΛΕΓΧΟΣ ΜΕΛΕΤΗ ΣΥΣΤΗΜΑΤΟΣ ΜΑΖΑΣ-ΕΛΑΤΗΡΙΟΥ-ΑΠΟΣΒΕΣΤΗΡΑ Μ. Σφακιωτάκης fak@taff.teirete.gr Χειµερινό
ΠPOKHPYΞH 2018 ΠΑΝΕΛΛΗΝΙΟΥ ΠPΩTAΘΛHMATΟΣ KARTING ΚΥΠΕΛΛΟΥ ΕΛΛΑΔΑΣ KARTING
ΠPOKHPYΞH 2018 ΠΑΝΕΛΛΗΝΙΟΥ ΠPΩTAΘΛHMATΟΣ KARTING ΚΥΠΕΛΛΟΥ ΕΛΛΑΔΑΣ KARTING ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΚΗΡΥΞΗ ΤΙΤΛΩΝ ΠΡΩΤΑΘΛΗΜΑΤΩΝ / ΚΥΠΕΛΛΩΝ / ΕΠΑΘΛΩΝ... 3 1. ΠΑΝΕΛΛΗΝΙΟ ΠΡΩΤΑΘΛΗΜΑ KARTING 2018... 3 2. ΚΥΠΕΛΛΟ ΕΛΛΑΔΑΣ
5 η έκδοση Συλλογικού Καταλόγου Ελληνικών Ακαδημαϊκών Βιβλιοθηκών
5 η έκδοση Συλλογικού Καταλόγου Ελληνικών Ακαδημαϊκών Βιβλιοθηκών Η 5η έκδοση του Συλλογικού Καταλόγου κυκλοφόρησε στις αρχές του 2010, ενώ η εξαγωγή των εγγραφών, από τα τοπικά συστήματα, πραγματοποιήθηκε
ΣΑΕ 1. Σημειώσεις από τις παραδόσεις. Για τον κώδικα σε L A TEX, ενημερώσεις και προτάσεις: https://github.com/kongr45gpen/ece-notes
ΣΑΕ Σημειώσεις από τις παραδόσεις Για τον κώδικα σε L A TEX, ενημερώσεις και προτάσεις: https://github.com/kongr45gpen/ece-notes Οκτώβριος-Ιανουάριος 207 Τελευταία ενημέρωση: 3 Οκτωβρίου 207 Συστήματα
Φυσική Στοιχειωδών Σωματιδίων ΙΙ (8ου εξαμήνου) Μάθημα 4: Οπτικό θεώρημα και συντονισμοί
Φυσική Στοιχειωδών Σωματιδίων ΙΙ (8ου εξαμήνου) Μάθημα 4: Οπτικό θεώρημα και συντονισμοί Λέκτορας Κώστας Κορδάς Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Στοιχειώδη ΙΙ, Αριστοτέλειο Παν. Θ/νίκης, 21 Μαρτίου
Ερωτήσεις για το μάθημα Μη Γραμμικά ΣΑΕ και Εφαρμογές: 10, 11, 15, 16, 17,18
ΕΡΓΑΣΤΗΡΙΟ ΣΥΣΤΗΜΑΤΩΝ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ Διευθυντής Γ.Π. Παπαβασιλόπουλος Τίτλος Άσκησης: Sampling, Quantization, Jitter noise, Chaos Επιμέλεια: Ι. Κορδώνης Υ.Δ., Dr Ε. Σαρρή Ερωτήσεις για το μάθημα Προχωρημένες
ΚΥΠΕΛΛΟΥ ΕΛΛΑΔΑΣ KARTING 2017
ΟΜΟΣΠΟΝΔΙΑ ΜΗΧΑΝΟΚΙΝΗΤΟΥ ΑΘΛΗΤΙΣΜΟΥ ΕΛΛΑΔΟΣ (O.M.A.E) ΠPOKHPYΞH ΠΑΝΕΛΛΗΝΙΟΥ ΠPΩTAΘΛHMATΟΣ KARTING 2017 ΚΥΠΕΛΛΟΥ ΕΛΛΑΔΑΣ KARTING 2017 ΕΠΙΤΡΟΠΗ ΑΓΩΝΩΝ (ΕΠ.Α.) ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΚΗΡΥΞΗ ΤΙΤΛΩΝ ΠΡΩΤΑΘΛΗΜΑΤΩΝ /
Κεθάιαην Επηθακπύιηα θαη Επηθαλεηαθά Οινθιεξώκαηα
Δπηθακπύιηα Οινθιεξώκαηα Κεθάιαην Επηθακπύιηα θαη Επηθαλεηαθά Οινθιεξώκαηα Επηθακπύιηα Οινθιεξώκαηα θαη εθαξκνγέο. Επηθακπύιην Οινθιήξωκα. Έζηω όηη ε βαζκωηή ζπλάξηεζε f(x,y,z) είλαη νξηζκέλε πάλω ζε κία
Radiation Stress Concerned with the force (or momentum flux) exerted on the right hand side of a plane by water on the left hand side of the plane.
upplement on Radiation tress and Wave etup/et down Radiation tress oncerned wit te force (or momentum flu) eerted on te rit and side of a plane water on te left and side of te plane. plane z "Radiation
SCHOOL OF MATHEMATICAL SCIENCES G11LMA Linear Mathematics Examination Solutions
SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
1 ος ΑΓΩΝΑΣ ΠΑΝΕΛΛΗΝΙΟ ΠΡΩΤΑΘΛΗΜΑ ΚΑΡΤ 1 os ΑΓΩΝΑΣ ΚΥΠΕΛΛΟ KARTODROMO 2015 ΣΥΜΠΛΗΡΩΜΑΤΙΚΟΣ ΚΑΝΟΝΙΣΜΟΣ
1 ος ΑΓΩΝΑΣ ΠΑΝΕΛΛΗΝΙΟ ΠΡΩΤΑΘΛΗΜΑ ΚΑΡΤ 1 os ΑΓΩΝΑΣ ΚΥΠΕΛΛΟ KARTODROMO 2015 ΣΥΜΠΛΗΡΩΜΑΤΙΚΟΣ ΚΑΝΟΝΙΣΜΟΣ KARTODROMO Κυριακή 6 Σεπτεμβρίου 2015 Οργάνωση: ΑΓΩΝΙΣΤΙΚΗ ΛΕΣΧΗ ΑΥΤΟΚΙΝΗΤΟΥ ΠΡΟΓΡΑΜΜΑ Έναρξη εγγραφών
ΠΛΗ ΛΥΣΕΙΣ ΕΡΓ_2 ΣΕΛ. 1/11
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: Νοεμβρίου 007 Ημερομηνία παράδοσης της Εργασίας: 4 Δεκεμβρίου 007 Πριν από την λύση κάθε άσκησης καλό
(Equipped with magnetic Shieid)
Power Trnsformer PT-0 PT-310 PT-0 PT-270 PT-260 PT-250 PT-2 PT-2 PT-180 PT-165 PT-160 PT-150 PT-100 PT-95 PT-60 Primry Specifictions Secondry V-0-280V-3V-360V-7m (450m ;ridge rectifier) 75V-0-75V-0.15
Κατερίνα Ζωντανού. Γράμματα. Στη Νεφέλη και στον Αναστάση. K.Z. Εικονογράφηση: Γεωργία Στύλου. από τον
Κατερίνα Ζωντανού Γράμματα από τον Στη Νεφέλη και στον Αναστάση. K.Z. Εικονογράφηση: Γεωργία Στύλου Τ ελευταίες μέρες του χρόνου και ο Αϊ-Βασίλης ετοιμάζεται πυρετωδώς για τη μεγάλη του αποστολή. Έχει
Έντυπο Yποβολής Αξιολόγησης ΓΕ
Έντυπο Yποβολής Αξιολόγησης ΓΕ O φοιτητής συμπληρώνει την ενότητα «Υποβολή Εργασίας» και αποστέλλει το έντυπο σε δύο μη συρραμμένα αντίγραφα (ή ηλεκτρονικά) στον Καθηγητή-Σύμβουλο Ο Καθηγητής-Σύμβουλος
3ος ΑΓΩΝΑΣ ΠΑΝΕΛΛΗΝΙΟY ΠΡΩΤΑΘΛΗΜΑΤΟΣ KARTING 2017 ΣΥΜΠΛΗΡΩΜΑΤΙΚΟΣ ΚΑΝΟΝΙΣΜΟΣ
3ος ΑΓΩΝΑΣ ΠΑΝΕΛΛΗΝΙΟY ΠΡΩΤΑΘΛΗΜΑΤΟΣ KARTING 2017 ΣΥΜΠΛΗΡΩΜΑΤΙΚΟΣ ΚΑΝΟΝΙΣΜΟΣ ΠΙΣΤΑ ΚΑΡΤ SPARTA RACING CIRCUIT ΣΠΑΡΤΗ Κυριακή 7 Μαΐου 2017 Αριθμός Μητρώου 047-4/4/2017 Οργάνωση: ΕΛΛΗΝΙΚΗ ΛΕΣΧΗ ΑΥΤΟΚΙΝΗΤΟΥ
(Equipped with magnetic Shieid)
Power Trnsformer PT-0 PT-310 PT-0 PT-270 PT-260 PT-250 PT-2 PT-2 PT-180 PT-165 PT-160 PT-150 PT-100 PT-95 PT-60 V-0-280V-3V-360V-7m (450m ;ridge rectifier) 75V-0-75V-0.15 6.3V-4( 2) 6.3V-2( 2) 0-10V-160V-180V-800m
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΑΠΑΝΤΗΣΕΙΣ Α ΕΡΓΑΣΙΑΣ. ( 8 µον.) Η άσκηση αυτή αναφέρεται σε διαιρετότητα και ρίζες πολυωνύµων. a. Να λυθεί η εξίσωση
Σηµειώσεις Μιγαδικής Ανάλυσης Θέµης Μήτσης
Σηµειώσεις Μιαδικής Ανάλυσης Θέµης Μήτσης Τµηµα Μαθηµατικων Πανεπιστηµιο Κρητης Ηρακλειο Περιεχόµενα Κεφάλαιο 1. Εισαωικά 5 Η αλεβρική δοµή 5 Η τοπολοική δοµή τού 6 Το εκτεταµένο µιαδικό επίπεδο 7 Συνεκτικότητα
Kεφ. 1 TAΛANTΩΣEIΣ (part 1, pages 1-9)
Mάθημα: Φυσική, Ακαδ. Ετος: 000-00 Tμήμα: Πολιτικών Mηχανικών, Πανεπιστήμιο Πάτρας Eγχειρίδιο: Mαθήματα Φυσικής Παν. Berkeley, τόμος 3: Kυματική Διδάσκων: Αναπληρωτής Καθηγητής Μ. Βελγάκης Kεφ. TAΛANTΩΣEIΣ
ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2014 ΜΑΘΗΜΑΤΙΚΑ κ.κ.
ΜΕΡΟΣ A ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ Στασίνου 36, Γραφ. 102, Στρόβολος 2003, Λευκωσία Τηλ. 357-22378101 Φαξ: 357-22379122 cms@cms.org.cy, www.cms.org.cy ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2014 ΜΑΘΗΜΑΤΙΚΑ κ.κ. Ημερομηνία:
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor X) functia f 1
Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Java 4205 Graphite 10
Java 5 ite 10 i Διατίθενται σε πολλά σχέδια και χρωματικές επιλογές με εναλλακτικές δυνατότητες εγκατάστασης, ένθετοι, υποκαθήμενοι. Ταιριαστές μπαταρίες κουζίνας και αξεσουάρ. Είτε προτιμάτε τη μεγαλύτερη
B Παγκύπριο Μαθητικό Συνέδριο Δημοτικής Εκπαίδευσης «Μικροί Ερευνητές Για Το Περιβάλλον»
00 1 2 Οργανωτική Επιτροπή Γιώργος Γεωργίου, Πρόεδρος Οργανωτικής Επιτροπής Ηλίας Ηλία, Συντονιστής Συνεδρίου Δρ Ανδρέας Χατζηχαμπής, Επιστημονικός Διευθυντής ΚΥΚΠΕΕ Δρ Δήμητρα Χατζηχαμπή, Υπεύθυνη Προγραμμάτων
Ε ΡΓΑ ΛΕΙΑ ΑΕ ΡΟΣ ΠΙΣΤΕΥΕΤΕ ΣΤΗΝ ΕΥΚΟΛΗ ΛΕΙΤΟΥΡΓΙΑ; Βεβαίως! Ειδικά, εάν πρόκειται για δύσκολες εργασίες.
245 Ε ΡΓΑ ΛΕΙΑ ΑΕ ΡΟΣ Μ ε ρ ι κ έ ς φ ο ρ έ ς τ ο μ έ λ λ ο ν β ρ ί σ κ ε τ α ι σ τ o ν α έ ρ α ΠΙΣΤΕΥΕΤΕ ΣΤΗΝ ΕΥΚΟΛΗ ΛΕΙΤΟΥΡΓΙΑ; Βεβαίως! Ειδικά, εάν πρόκειται για δύσκολες εργασίες. Τα εργαλεία πεπιεσμένου
P l+1 (cosa) P l 1 (cosa) 2δ l,0 1
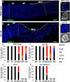Λεοντσ ίνης Στέφανος Ηλεκτομαγνητισ μός 3 η Σειά Ασ κήσ εων 3 Tο δυναμικό λόγω αζιμουθιακής σ υμμετίας θα έχει τη μοφή φ r, θ [ Al + B l r l+] l cosθ Λόγω l Φ οιακών σ υνθηκών έχω: Φ in r R Φ out r R και
1ος ΑΓΩΝΑΣ ΠΑΝΕΛΛΗΝΙΟY ΠΡΩΤΑΘΛΗΜΑΤΟΣ KARTING 2019 ΣΥΜΠΛΗΡΩΜΑΤΙΚΟΣ ΚΑΝΟΝΙΣΜΟΣ ΠΙΣΤΑ KARTODROMO. Οργάνωση: ΑΛΑ - ΑΡΤΕΜΙΣ Αθλητική Ένωση
1ος ΑΓΩΝΑΣ ΠΑΝΕΛΛΗΝΙΟY ΠΡΩΤΑΘΛΗΜΑΤΟΣ KARTING 2019 ΣΥΜΠΛΗΡΩΜΑΤΙΚΟΣ ΚΑΝΟΝΙΣΜΟΣ ΠΙΣΤΑ KARTODROMO Κυριακή 24 Φεβρουαρίου 2019 Αριθμός Μητρώου ΕΠΑ: 003/28.2.2019 Οργάνωση: ΑΛΑ - ΑΡΤΕΜΙΣ Αθλητική Ένωση ΓΡΑΜΜΑΤΕΙΑ
1ος ΑΓΩΝΑΣ ΠΑΝΕΛΛΗΝΙΟ ΠΡΩΤΑΘΛΗΜΑ ΚΑΡΤ ΣΥΜΠΛΗΡΩΜΑΤΙΚΟΣ ΚΑΝΟΝΙΣΜΟΣ
1ος ΑΓΩΝΑΣ ΠΑΝΕΛΛΗΝΙΟ ΠΡΩΤΑΘΛΗΜΑ ΚΑΡΤ ΣΥΜΠΛΗΡΩΜΑΤΙΚΟΣ ΚΑΝΟΝΙΣΜΟΣ KARTODROMO Κυριακή 20 Μαρτίου 2016 Οργάνωση: ΕΛΛΗΝΙΚΗ ΛΕΣΧΗ ΑΥΤΟΚΙΝΗΤΟΥ ΔΥΤΙΚΗΣ ΑΤΤΙΚΗΣ ΠΡΟΓΡΑΜΜΑ Έναρξη εγγραφών Δευτέρα 07 Μαρτίου 2016
5ος ΑΓΩΝΑΣ ΠΑΝΕΛΛΗΝΙΟY ΠΡΩΤΑΘΛΗΜΑΤΟΣ KARTING 2017 ΣΥΜΠΛΗΡΩΜΑΤΙΚΟΣ ΚΑΝΟΝΙΣΜΟΣ
5ος ΑΓΩΝΑΣ ΠΑΝΕΛΛΗΝΙΟY ΠΡΩΤΑΘΛΗΜΑΤΟΣ KARTING 2017 ΣΥΜΠΛΗΡΩΜΑΤΙΚΟΣ ΚΑΝΟΝΙΣΜΟΣ ΠΙΣΤΑ ΚΑΡΤ KARTODROMO ΑΦΙΔΝΕΣ Κυριακή 3 Σεπτεμβρίου 2017 Οργάνωση: ΕΛΛΗΝΙΚΗ ΛΕΣΧΗ ΑΥΤΟΚΙΝΗΤΟΥ ΔΥΤΙΚΗΣ ΑΤΤΙΚΗΣ ΓΡΑΜΜΑΤΕΙΑ ΤΟΥ
Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος
Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με, y V και του πολλαπλασιασμού
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ «ΠΛΗΡΟΦΟΡΙΚΗ» ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) TEΛΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 4 Ιουνίου 7 Από τα κάτωθι Θέµατα καλείστε να λύσετε το ο που περιλαµβάνει ερωτήµατα από όλη την ύλη
4ος ΑΓΩΝΑΣ ΠΑΝΕΛΛΗΝΙΟY ΠΡΩΤΑΘΛΗΜΑΤΟΣ KARTING 2016 ΣΥΜΠΛΗΡΩΜΑΤΙΚΟΣ ΚΑΝΟΝΙΣΜΟΣ
4ος ΑΓΩΝΑΣ ΠΑΝΕΛΛΗΝΙΟY ΠΡΩΤΑΘΛΗΜΑΤΟΣ KARTING 2016 ΣΥΜΠΛΗΡΩΜΑΤΙΚΟΣ ΚΑΝΟΝΙΣΜΟΣ ΠΙΣΤΑ ΚΑΡΤ KARTODROMO ΑΦΙΔΝΕΣ Κυριακή 9 Οκτωβρίου 2016 Αριθμός Μητρώου ΕΠΑ: 124/27.09.2016 Οργάνωση: ΕΛΛΗΝΙΚΗ ΛΕΣΧΗ ΑΥΤΟΚΙΝΗΤΟΥ
9 o PICK - ΛΟΥΞ COLA plus n light
Πάτρα, - Σεπτεμβρίου 60 MINI 1 ΚΑΦΑΝΤΑΡΗΣ ΑΝΑΣΤΑΣΙΟΣ ΚΑΦΑΝΤΑΡΗΣ ΓΙΩΡΓΟΣ GRE FORMULA K IAME MINI 60 VEGA SL 10 2 11 ZORRI MOTORSPORT ΖΗΣΙΜΟΠΟΥΛΟΣ ΓΙΑΝΝΗΣ GRE BIRELARTC28-C8 B LKE R14 VO VEGA SL 10 3 ATHENS
KARTING SUPER CUP 2016 ΣΥΜΠΛΗΡΩΜΑΤΙΚΟΣ ΚΑΝΟΝΙΣΜΟΣ
KARTING SUPER CUP 2016 ΣΥΜΠΛΗΡΩΜΑΤΙΚΟΣ ΚΑΝΟΝΙΣΜΟΣ ΠΙΣΤΑ ΚΑΡΤ KARTODROMO ΑΦΙΔΝΕΣ Κυριακή 4 Δεκεμβρίου 2016 Αριθμός Μητρώου ΕΠΑ: 144-10/11/2016 Οργάνωση: ΕΛΛΗΝΙΚΗ ΛΕΣΧΗ ΑΥΤΟΚΙΝΗΤΟΥ ΔΥΤΙΚΗΣ ΑΤΤΙΚΗΣ ΓΡΑΜΜΑΤΕΙΑ
Ποσοτική Μικροανάλυση Μέθοδος ZAF
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Ποσοτική Μικροανάλυση Μέθοδος ZAF Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Crete Center for Quantum Complexity and Nanotechnology Department
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Ακτομηχανική και λιμενικά έργα
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Διάλεξη 2 η. Επιφανειακοί κυματισμοί- κύματα Γιάννης Ν. Κρεστενίτης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
2 c. cos H 8. u = 50 n
Τεχνολογικό Πανεπιστήµιο Κύπρου Σχολή Μηχανικής και Τεχνολογίας Τµήµα Πολιτικών Μηχανικών και Μηχανικών Γεωπληροφορικής (Κατεύθυνση Πολιτικών Μηχανικών / Τοπογράφων Μηχανικών και Μηχανικών Γεωπληροφορικής)
(Equipped with static shield, magnetic shieid) (Equipped with magnetic Shieid)
New Power Trnsformer PT-0 PT-310 PT-0 PT-270 PT-260 PT-250 PT-2 PT-2 PT-180 PT-160 PT-150 PT-100 PT-95 PT-60 Specifictions (Equipped wit sttic sield, mgnetic sieid) V-0-280V-3V-360V-7m (450m ;ridge rectifier)
3 η ενότητα ΑΠΟΚΡΙΣΗ ΣΥΧΝΟΤΗΤΑΣ ΕΝΙΣΧΥΤΩΝ
ρ. Λάμπρος Μπισδούνης Καθηγητής 3 η ενότητα ΑΠΟΚΡΙΣΗ ΣΥΧΝΟΤΗΤΑΣ ΕΝΙΣΧΥΤΩΝ T.E.I. ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Περιεχόμενα 3 ης ενότητας Στην τρίτη ενότητα θα μελετήσουμε την απόκριση
Εφαρμοσμένα Μαθηματικά ΙΙ 1ο Σετ Ασκήσεων (Λύσεις) Διανύσματα, Ευθείες Επίπεδα, Επιφάνειες 2ου βαθμού Επιμέλεια: Ι. Λυχναρόπουλος
Εφαρμοσμένα Μαθηματικά ΙΙ ο Σετ Ασκήσεων (Λύσεις) Διανύσματα, Ευθείες Επίπεδα, Επιφάνειες ου βαθμού Επιμέλεια: Ι. Λυχναρόπουλος. Βρείτε το διάνυσμα με άκρα το Α(3,-,5) και Β(5,,-) ΑΒ=< 5 3, ( ), 5 >=
(Equipped with static shield, magnetic shieid) (Equipped with magnetic Shieid)
Power Trnsformer PT-0 PT-0 PT-270 PT-260 PT-250 PT-2 PT-2 PT-180 PT-160 PT-0 PT-100 PT-95 PT-60 Specifictions (Equipped wit sttic sield, mgnetic sieid) V-0-280V-3V-360V-7m (450m ;ridge rectifier) 75V-0-75V-0.
Το Φως Είναι Εγκάρσιο Κύμα!
ΓΙΩΡΓΟΣ ΑΣΗΜΕΛΛΗΣ Μαθήματα Οπτικής 3. Πόλωση Το Φως Είναι Εγκάρσιο Κύμα! Αυτό που βλέπουμε με τα μάτια μας ή ανιχνεύουμε με αισθητήρες είναι το αποτέλεσμα που προκύπτει όταν φως με συγκεκριμένο χρώμα -είδος,
EΞΑΝΑΓΚΑΣΜΕΝΕΣ TAΛANTΩΣEIΣ
Kεφ. 3 EΞΑΝΑΓΚΑΣΕΝΕΣ TAΛANTΩΣEIΣ Θα εξετάσυμε τη περίπτση εφαρμγής σ ένα σύστημα μιάς δεδμένης εξτερικής δύναμης η πία να εξαρτάται από τ χρόν (δηλ. τ σύστημα υπβάλλεται σε εξτερική διέγερση. η περίπτση:
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 2 η Ημερομηνία Αποστολής στον Φοιτητή: 28 Νοεμβρίου 2011
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 8 Νοεμβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 6 Ιανουαρίου 0 Οι ασκήσεις
HONDA. Έτος κατασκευής
Accord + Coupe IV 2.0 16V (CB3) F20A2-A3 81 110 01/90-09/93 0800-0175 11,00 2.0 16V (CB3) F20A6 66 90 01/90-09/93 0800-0175 11,00 2.0i 16V (CB3-CC9) F20A8 98 133 01/90-09/93 0802-9205M 237,40 2.0i 16V
TALAR ROSA -. / ',)45$%"67789
TALAR ROSA!"#"$"%$&'$%(" )*"+%(""%$," *$ -. / 0"$%%"$&'1)2$3!"$ ',)45$%"67789 ," %"(%:,;,"%,$"$)$*2