( ) ( ) ( ) ( ) Παράγωγος-Κλίση-Μονοτονία ( ) ( ) β = Άσκηση 1 η : Να βρεθούν οι παράγωγοι των συναρτήσεων: log x. 2 x. ln(x, ( ) 2 x x. Έχουμε.
|
|
|
- Βασιλεύς Ρόκας
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Παράγωγος-Κλίση-Μονοτονία Άσκηση η : Να βρεθούν οι παράγωγοι των συναρτήσεων:, log, ) ln(, e, Λύση: Έχουμε ln ln ( ), f = = e = e R ln ln f ( ) = ( e ) = e ( ln ) = ln = ln, R Γενικά ισχύει: ( a ) = ln a a, με < a ln Έχουμε f ( ) = log =, > ln ln f ( ) = = (ln )' =, > ln ln ln Γενικά ισχύει : ( ) log a =, >, < ln a a Έχουμε f ( ) = ln ( ), (, ] [, + ) τύπος αλλαγής βάσης: log a lnβ β = ln a ( ) ( ) ( ) f ( ) ln( = ) = ln( ) ln( ) = ln( ) = ln( ) =, (, ) (, + ) ln( ) Έχουμε f ( ) e, Έχουμε f ( ) = e = e = e, > = με ( ) ( ) ln ln ( ) = = =, > f e e ( ) f ( ) = ( e ) = e ( ln ) = ( ) ln + ( ln ) = ln + ln ln ( ) ( ) = ln + = ln +, >
2 Άσκηση η :Θεωρούμε την εξίσωση y= +.Να βρεθεί η εξίσωση μεταβολών και να υπολογιστεί πόσο πρέπει να μεταβληθεί το από την τιμή = 4 ώστε η τιμή της συνάρτησης να ελαττωθεί κατά.να επαναληφθεί για την εξίσωση y= ln. Λύση: y f ( ), = = + R Αρχικά, βρίσκουμε την εξίσωση μεταβολών, οπότε έχουμε: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) y= f + f = = = + () Για αρχική τιμή = 4, ζητάμε πόσο θα είναι η μεταβολή του (δηλαδή ) ώστε η συνάρτηση να ελαττωθεί κατά,δηλαδή y=.οπότε από την () έχουμε: ( ) ( ) ( ) ( ) ( ) ( ) y= + = = με διακρίνουσα 8± 5 = 8 4 ( ) = 6> και με ρίζες τις ( ), = = 4± 5 Για = 4,έχουμε f (4) = 7,άρα το y από 7 γίνεται 6,οπότε έχουμε: + = 4 4 5= 5,απορρίπτεται + = = 5,δεκτή Έχουμε y= f ( ) = ln, > Αρχικά, βρίσκουμε την εξίσωση μεταβολών, οπότε έχουμε: 4+ y= f ( + ) f ( ) = ln( + ) ln = ln 4 y= = = e + = e e = 4 ln 4 4
3 Άρα = 4+ 4= e e Άσκηση 3 η : Να επαληθευτεί ο κανόνας αλυσωτής παραγώγισης για τις παρακάτω συνθέσεις: Λύση: { f ( ) = ln, g( ) = e } ( ) Βρίσκουμε την f ( g( )) και στη συνέχεια την παράγωγό της, οπότε έχουμε: f ( g( )) = f ( e ) = ln e = ln e= Άρα ( f ( g( ))) = ( ) = ( ) Εφαρμόζουμε τον κανόνα αλυσωτής παραγώγισης,οπότε έχουμε: ( f ( g( ))) = f ( g( )) g ( ) = f ( e ) ( e ) = e = e αφού f ( ) = (ln ) = { z= ln y, y= + } z= z( y) = z( y( )) = z( ) ( ) Βρίσκουμε την z( y( )) και στην συνέχεια υπολογίζουμε την παράγωγό της, οπότε Έχουμε z z y z ( ) = ( ( )) = ( + ) = ln( + ) Άρα dz = (ln( + )) = ( + ) = d + + ( ) Εφαρμόζουμε τον κανόνα αλυσωτής παραγώγισης, οπότε έχουμε: dz = dz dy = = d dy d y + { z= ln y, y=, = t+ } Έχουμε z= z( y) = z( y( )) = z( y( ( t))) = z( t) ( ) Βρίσκουμε την z( y( ( t))) = z( t) και στη συνέχεια υπολογίζουμε την παράγωγό της, οπότε, έχουμε: z( t) = z( y( ( t))) = z( y(t+ )) = z((t+ ) ) = ln(t+ ) 3
4 Άρα dz 4(t+ ) 4 = (ln(t+ ) ) = ((t+ ) ) = (t+ ) (t+ ) = = dt (t+ ) (t+ ) (t+ ) t+ Εφαρμόζουμε τον κανόνα αλυσωτής παραγώγισης, οπότε έχουμε: dz dz dy d = = = = = = dt dy d dt y y t+ αφού dz = dy, = d, = dy y d dt Άσκηση 4 η : Να υπολογιστεί το βήμα ασυνέχειας της παραγώγου για τις συναρτήσεις: Λύση: Έχουμε f ( ) = min {, }, [, + ) min {, },ma{, } ( ) ή οπότε ο τύπος της συνάρτησης f είναι:, < f ( ) =, Η παράγωγος της f είναι: 4
5 Η βηματική ασυνέχεια της παραγώγου είναι:, < f ( ) =, ) f ( ) = f ( ) f ( ) = lim f ( ) lim f ( ) = = + + f ( + οπότε η f εμφανίζει στο = βηματική ασυνέχεια. Έχουμε f ( ) = ma {, }, [, + ) Σύμφωνα με τα παραπάνω, ο τύπος της f είναι:, < f ( ) =, με, < f ( ) =, Τα γραφήματα των C, C είναι τα ακόλουθα: f ' f Η βηματική ασυνέχεια της παραγώγου είναι: 5
6 + + f ( ) f ( ) = f ( ) f ( ) = lim f ( ) lim f ( ) = = + οπότε η f εμφανίζει στο = βηματική ασυνέχεια. Άσκηση 5 η : Να γίνουν τα γραφήματα των παρακάτω συναρτήσεων στο θετικό διάστημα: Λύση: f ( ) = e, [, + ) e, e, ln, ln, ln + lim f ( ) = f () =,αφού η f είναι συνεχής στο = + ( + ) + lim f ( ) = lim ( e ) = lim = e ( ) lim = lim = lim e = + + e + ( e ) Η f είναι παραγωγίσιμη στο [,+ ) με f ( ) = ( e ) = e + ( ) e = e ( ), f () = (δηλαδή η κλίση της εφαπτομένης της Cf στο = είναι ή σχηματίζει με τον άξονα γωνία 45 ) ( ) + lim f ( ) = lim (( ) e ) = lim = e ( ) lim = lim + + e = lim ( e ) = + ( e ) Στάσιμο σημείο: e > f ( ) = ( ) e = = = R e > f ( ) > ( ) e > > < R e > f ( ) < ( ) e < < > R 6
7 Έχουμε f ( ) = e, [, + ) f () = lim f ( ) lim ( e ) + + ( + )( + ) = = + Η f είναι παραγωγίσιμη στο [,+ ) με f e e e e ( ) = ( ) = + = ( + ), f () = lim f ( ) lim (( ) e + + ( + )( + ) = + = + Στάσιμο σημείο: e > ( ) ( ) ( ) R f = + e = + = = (δεκτή) ή = (απορ.) ( ) ( ) e > ( ) R f > + e = + > < ή > > ( ) ( ) e > ( ) (, ) R f < + e < + < αδύνατη, αφού οπότε η f είναι γνησίως αύξουσα στο [,+ ), άρα η f παρουσιάζει στη θέση = ολικό ελάχιστο το f () =. 7
8 Έχουμε f ( ) = ln, (, + ) ( ) ln + lim f ( ) lim ( ln ) lim lim = = lim ( ) = = = ( + )( + ) lim f ( ) = lim ( ln ) = Η f είναι παραγωγίσιμη στο (,+ ) με f ( ) = ( ln ) = ln + = ln +, > lim f ( ) = lim (ln + ) = + + lim f ( ) = lim (ln + ) =+ + + Στάσιμο σημείο: f ( ) = ln + = ln = = e = e f ( ) > ln + > ln > > e f ( ) < ln + < ln < < < e 8
9 Έχουμε f ( ) = ln, (, + ) ( ) ( ) ( ) 3 ln + lim f ( ) = lim ( ln ) = lim = lim = lim ( ) = ( ) ( + )( + ) lim f ( ) = lim ln = Η f είναι παραγωγίσιμη στο (,+ ) με ln + ln f ( ) = ( ln ) = ln + = + =, > lim f ( ) lim lim ( ln ) ( )( + ) ln + = = + = ( + ) ( + ) ln + lim f ( ) = lim lim lim + + = = = + + Στάσιμο σημείο: ln + > f ( ) = = ln + = ln = = e ln + > f ( ) > > ln + > ln > > e f ( ) < < < e 9
10 Έχουμε f ( ) = ln + = ln +, (, + ) ( ) + ( + ) lim f ( ) = lim (ln + ) = lim (( ln + ) ) = ( + ) = (*) αφού ( ) ln + lim( ln ) = lim lim lim ( ) = = = Άρα lim ( ln + ) = + = (*) + ( + ) + lim f ( ) = lim (ln + ) = Η f είναι παραγωγίσιμη στο ( ) ( )( + ) lim f ( ) = lim + + = lim f ( ) = lim + + = Στάσιμο σημείο:,+ με ( ) ln f = + = =, >
11 f ( ) = = = f ( ) > > > f ( ) < < < < Άσκηση 6 η : Να βρεθούν οι γραμμικές προσεγγίσεις των παρακάτω συναρτήσεων στο =. Λύση: Έχουμε f () = ( ) =, Η f είναι παραγωγίσιμη στο R-{} με f ( ) = = ( ) Είναι f ()= και f () = ( ) = ( ), Άρα η γραμμική προσέγγιση της f στο =, είναι: f () f ()+ f () ( )=+ Η γραμμική προσέγγιση της f στο D f, είναι: o f () f ( )+ f ( ) ( ) Σημείωση: Γραμμική προσέγγιση καλείται η γραμμική συνάρτηση της εφαπτόμενης ευθείας.
12 Έχουμε f () = (+ ) 3, [, + ) Η f είναι παραγωγίσιμη στο (,+ ) με f ( )= (+ ) 3 = 3 (+ ) ( + ) = 3 3 Είναι f ()= ( ) 3 + = και f ()= 3 ( ) 3 +, > ( ) 3 + = 3 Άρα η γραμμική προσέγγιση της f στο =, είναι: f ( ) f ()+ f ()( )=+ 3 Έχουμε f ( )=ln(+ ), R Η f είναι παραγωγίσιμη στο R με f ( )=( ln(+ )) = + Είναι f ()=ln( + ) = και f ()= + = Άρα η γραμμική προσέγγιση της f στο =, είναι: f () f ()+ f () ( )=, δηλαδή ο άξονας. ( + ) = +, R Έχουμε f () = 3 + +, R 3 Η f είναι παραγωγίσιμη στο R με f ( )=( + + ) =3 +, R Είναι f ()= 3 ++= και f ()=3 += Άρα η γραμμική προσέγγιση της f στο =, είναι: f () f ()+ f () ( )=+
13 Άσκηση 7 η : Να γίνουν στο θετικό διάστημα τα γραφήματα των συνεχών συναρτήσεων f (), με f ()=, των οποίων οι παράγωγοι f ( ) έχουν τα παρακάτω γραφήματα. Λύση: Παρατηρούμε ότι f ( ) >, [, + ) (αφού η C f βρίσκεται πάνω από τον άξονα ) τότε η f είναι γνησίως αύξουσα στο [, + ). Επειδή η f είναι γνησίως αύξουσα στο [, + ) τότε ισχύει f ( ) >, [, + ), δηλαδή η f είναι γνήσια κυρτή στο [, + ). Αφού το γράφημα της f είναι ευθεία, τότε το γράφημα της f θα είναι παραβολή με τις παραπάνω ιδιότητες. Επειδή f ()= τότε η C f αρχίζει από το σημείο Ο(,), έχοντας κάποια κλίση, ώστε η εφαπτομένη της στο σημείο Ο(,) να σχηματίζει με τον άξονα γωνία ω, με εφω=α. Επομένως, έχουμε: 3
14 4
15 Παρατηρούμε ότι f ( )>, [, + ), τότε η f είναι γνησίως αύξουσα στο [, + ). : η f είναι γνησίως, τότε ισχύει f ( ) <, [, ) κοίλη. (η f αυξάνεται με φθίνοντα ρυθμό) f = : η f παρουσιάζει στη θέση =, ελάχιστο οπότε πρέπει ( ) =, δηλαδή η f < <+ : η γνήσια κυρτή στο ( ) C παρουσιάζει στο σημείο (, ( )) f, σημείο καμπής. f είναι γνησίως αύξουσα, τότε ισχύει f ( ) >, (, ), δηλαδή η f είναι γνήσια +, οπότε η f είναι +, δηλαδή η f αυξάνεται με αύξοντα ρυθμό. Επομένως, έχουμε :, 5
16 Παρατηρούμε ότι: : η f είναι σταθερή, αφού f ( )=, [, ] Τότε ισχύει f ( )= c, [, ], c R. Όμως, f ()= οπότε πρέπει c =, άρα f ( )=, [, ] = : η f δεν είναι συνεχής στο =, αφού f ( ) = και f ( + ) =+. (έχουμε άπειρη ασυνέχεια της f στο σημείο =. < <+ : Είναι f ( )<, (, + ) άρα η f είναι γνησίως αύξουσα στο (, + ). Επίσης η f είναι γνησίως φθίνουσα στο (, + ), τότε ισχύει f ( )<, (, + ) δηλαδή η f είναι γνήσια κοίλη. 6
17 Άσκηση 8 η : Να βρεθεί με αντίστροφη και με πλεγμένη παραγώγιση η παράγωγος της συνάρτησης y= y( ) που ορίζεται πλεγμένα από την εξίσωση 3 y y = + +. Λύση: d Έχουμε ( y ) = y 3 + y+ τότε '( y) = = 3y + dy οπότε από τον τύπο της αντίστροφης παραγώγισης, έχουμε : dy d = = d 3y + dy Παραγωγίζουμε πλεγμένα ως προς, θεωρώντας το y ως την αντίστοιχη πλεγμένη συνάρτηση του, οπότε έχουμε: =y 3 ()+y()+ = 3 y y + y y (3y + ) = y = 3y + Άσκηση 9 η : Για κάθε μία από τις παρακάτω εξισώσεις, να βρεθούν πλεγμένα οι παράγωγοι του y ως προς και του ως προς, και να γίνει επαλήθευση. Να βρεθούν και τα γραφήματα Λύση: + 3y= 8 (γραμμική εξίσωση) Παραγωγίζουμε πλεγμένα ως προς, θεωρώντας το y ως την αντίστοιχη πλεγμένη συνάρτηση του : 7
18 + 3 y( ) = 8 τότε + 3 y '( ) = y ' = 3 Επαλήθευση: Λύνουμε ως προς y και στη συνέχεια την παραγωγίζουμε ως προς, οπότε έχουμε: + 3y= 8 3y= y= Άρα y = dy d = 3 Παραγωγίζουμε πλεγμένα ως προς y, θεωρώντας το ως την αντίστοιχη πλεγμένη συνάρτηση του y : ( y) + 3y= 8τότε + ' 3= 3 ' = Επαλήθευση: Λύνουμε την εξίσωση ως προς και στην συνέχεια την παραγωγίζουμε ως προς y, οπότε έχουμε: + 3y= 8 = 3y+ 8 3 d 3 ( y) = y+ 4άρα ' = = dy Γράφημα: 4 y 8 3 8
19 Έχουμε : y= y = Παραγωγίζουμε πλεγμένα ως προς, θεωρώντας το y ως την αντίστοιχη πλεγμένη συνάρτηση του : y ( ) = τότε yy ' = y ' = y dy = y ' = d Επαλήθευση: Λύνουμε την εξίσωση ως προς y και στη συνέχεια την παραγωγίζουμε ως προς, οπότε έχουμε: y= τότε y = ( ) = ( ) = Παραγωγίζουμε πλεγμένα ως προς y, θεωρώντας το ως την αντίστοιχη πλεγμένη συνάρτηση του y : y ( y) = τότε y ' = ' = d = y dy Επαλήθευση: Λύνουμε την εξίσωση ως προς και στη συνέχεια την παραγωγίζουμε ως προς y, οπότε έχουμε: y = ( y) = y + τότε '( y) = d = y dy Γράφημα: Έχουμε y 3 + = ( ) Παραγωγίζουμε πλεγμένα ως προς, θεωρώντας το y ως την αντίστοιχη πλεγμένη συνάρτηση του : 9
20 + y( ) = 3τότε () dy y 3 + y ' = y ' = = = y d Επαλήθευση: Λύνουμε την εξίσωση ως προς y και στην συνέχεια την παραγωγίζουμε ως προς,οπότε έχουμε : 9 + y = 3 y = 3 y= ( 3 ) 3 = = = d = Παραγωγίζουμε πλεγμένα ως προς y, θεωρώντας το ως την αντίστοιχη πλεγμένη συνάρτηση dy άρα y ' ( 3 )( 3 ) ( 3 ) του y : ( y) + y = 3 τότε d 3 y ' + = ' = = = y dy y y Επαλήθευση: Λύνουμε την εξίσωση ως προς και στη συνέχεια την παραγωγίζουμε ως προς y, οπότε έχουμε: ( ) y 9 + y = 3 = 3 y ( y) = 3 y τότε d ' = = ( 3 y)( 3 y) = ( 3 y) = 3 y dy y y Γράφημα: ( ) 9 y 9
21 Έχουμε ( ) y = 3 + y = 9 () Παραγωγίζουμε πλεγμένα ως προς, θεωρώντας το y ως την αντίστοιχη πλεγμένη συνάρτηση του : 3 + y 3 ( ) = 9 τότε + = = = y 3 3 y y ' 3 y y ' 3 y ' Επαλήθευση: Λύνουμε την εξίσωση ως προς y και στην συνέχεια την παραγωγίζουμε ως προς,οπότε έχουμε : ( ) y = 9 y = 9 y( ) = 9 3 άρα dy ' ( 9 ) ( ) ( ) ( ) 3 y = = 9 = = = = d 3 3 y () 3 3 ( 9 ) ( y ) 3 3 Παραγωγίζουμε πλεγμένα ως προς y, θεωρώντας το ως την αντίστοιχη πλεγμένη συνάρτηση του y : 3 3 d y ( y ) + y = 9 τότε 3 ' + 3y = 3 ' = 3 y ' = = dy Επαλήθευση: Λύνουμε την εξίσωση ως προς και στη συνέχεια την παραγωγίζουμε ως προς y, οπότε έχουμε: ( ) y = 9 = 9 y ( y) = 9 y 3, άρα d ' ( 9 ) ( ) ( ) ( ) 3 y y y = = y 9 y = 9 y 3 3y = = = dy 3 3 () 3 3 ( 9 y ) ( ) 3 3 Γράφημα: 3 9 y 3 9
22 Άσκηση η : Να επαληθευτεί ο κανόνας σχετιζόμενων ρυθμών για τις παρακάτω παραμετρικές εξισώσεις: t { = t, y= 4 t}, = t, y=, { = 3 t, y= t t+ } 4 Λύση: = t, y= 4t { } Κανόνας Σχετιζόμενων Ρυθμών: dy dy dt y 4 dy d = = = =, αφού = 4, = d d dt dt dt Επαλήθευση: Έχουμε = t t = t= y= 4 = y= 4t y= 4t y= 4t dy οπότε d = t = t, y= 4 Κανόνας Σχετιζόμενων Ρυθμών: dy dy dt y 4 t = = = = =, αφού d d dt t Επαλήθευση: dy d =, = dt 4 dt t Έχουμε ( ) ( ) ( ) = t t = t= t t t y= =, y= y= y= Άρα { = } 3 t, y= t t+ dy ( ) = = ( )( ) = d 4 4 Κανόνας Σχετιζόμενων Ρυθμών: dy dy dt y t 3 = = = = t= = d d dt
23 Επαλήθευση: Έχουμε 3 t = 3 t= ( ) ( ) = 3 t 3 y= = y= y= t t+ y= t 4 y= ( t ) Άρα dy ( ) = = ( )( ) = d 4 4 3
dy df(x) y= f(x) y = f (x), = dx dx θ x m= 1
 I. ΠΑΡΑΓΩΓΟΣ-ΚΛΙΣΗ d df() = f() = f (), = d d.κλίση ευθείας.μεταολές 3.(Οριακός) ρυθμός μεταολής ή παράγωγος 4.Παράγωγοι ασικών συναρτήσεων 5. Κανόνες παραγώγισης 6.Αλυσωτή παράγωγος 7.Μονοτονία 8.Στάσιμα
I. ΠΑΡΑΓΩΓΟΣ-ΚΛΙΣΗ d df() = f() = f (), = d d.κλίση ευθείας.μεταολές 3.(Οριακός) ρυθμός μεταολής ή παράγωγος 4.Παράγωγοι ασικών συναρτήσεων 5. Κανόνες παραγώγισης 6.Αλυσωτή παράγωγος 7.Μονοτονία 8.Στάσιμα
A2. ΠΑΡΑΓΩΓΟΣ-ΚΛΙΣΗ-ΜΟΝΟΤΟΝΙΑ
 A. ΠΑΡΑΓΩΓΟΣ-ΚΛΙΣΗ-ΜΟΝΟΤΟΝΙΑ d df() = f() = f (), = d d.κλίση ευθείας.μεταβολές 3.(Οριακός) ρυθµός µεταβολής ή παράγωγος 4.Παράγωγοι βασικών συναρτήσεων 5. Κανόνες παραγώγισης 6.Αλυσωτή παράγωγος 7.Μονοτονία
A. ΠΑΡΑΓΩΓΟΣ-ΚΛΙΣΗ-ΜΟΝΟΤΟΝΙΑ d df() = f() = f (), = d d.κλίση ευθείας.μεταβολές 3.(Οριακός) ρυθµός µεταβολής ή παράγωγος 4.Παράγωγοι βασικών συναρτήσεων 5. Κανόνες παραγώγισης 6.Αλυσωτή παράγωγος 7.Μονοτονία
ΤΕΣΤ Α2 ΟΜΑΔΑ Ι. παράγωγος είναι αρνητική: f (x) = 1 2x, f
 ΤΕΣΤ Α ΟΜΑΔΑ Ι Θεωρούμε την συνάρτηση: f() = pln(+ ) για, με p>. Να διερευνηθεί αν είναι κυρτή η κοίλη. Να βρεθούν οι τιμές της παραμέτρου p για τις οποίες η μέγιστη τιμή της βρίσκεται στο =.. Η συνάρτηση
ΤΕΣΤ Α ΟΜΑΔΑ Ι Θεωρούμε την συνάρτηση: f() = pln(+ ) για, με p>. Να διερευνηθεί αν είναι κυρτή η κοίλη. Να βρεθούν οι τιμές της παραμέτρου p για τις οποίες η μέγιστη τιμή της βρίσκεται στο =.. Η συνάρτηση
(f,g) f(x,y,v, w) = xy v= 0 x (v,y) = = = = = 3. g(x,y,v,w) = x+ 2y w= 0. (x,y) g g 1 2. Λύση 2. Με πλεγμένη παραγώγιση ως προς v, με σταθερό w :
 ΤΕΣΤ Β.λύσεις ΟΜΑΔΑ Ι Οι εξισώσεις: {=, + = w} ορίζουν πλεγμένα τα {,} ως συναρτήσεις των {,w}. Να βρεθεί η μερική παράγωγος του ως προς. Λύση. Με τους τύπους πλεγμένης παραγώγισης: (,g) (,,, w) = = (,)
ΤΕΣΤ Β.λύσεις ΟΜΑΔΑ Ι Οι εξισώσεις: {=, + = w} ορίζουν πλεγμένα τα {,} ως συναρτήσεις των {,w}. Να βρεθεί η μερική παράγωγος του ως προς. Λύση. Με τους τύπους πλεγμένης παραγώγισης: (,g) (,,, w) = = (,)
I.3 ΔΕΥΤΕΡΗ ΠΑΡΑΓΩΓΟΣ-ΚΥΡΤΟΤΗΤΑ
 I.3 ΔΕΥΤΕΡΗ ΠΑΡΑΓΩΓΟΣ-ΚΥΡΤΟΤΗΤΑ.Δεύτερη παράγωγος.παραβολική προσέγγιση ή επέκταση 3.Κυρτή 4.Κοίλη 5.Ιδιότητες κυρτών/κοίλων συναρτήσεων 6.Σημεία καμπής ΠΑΡΑΡΤΗΜΑ 7.Δεύτερη πλεγμένη παραγώγιση 8.Χαρακτηρισμός
I.3 ΔΕΥΤΕΡΗ ΠΑΡΑΓΩΓΟΣ-ΚΥΡΤΟΤΗΤΑ.Δεύτερη παράγωγος.παραβολική προσέγγιση ή επέκταση 3.Κυρτή 4.Κοίλη 5.Ιδιότητες κυρτών/κοίλων συναρτήσεων 6.Σημεία καμπής ΠΑΡΑΡΤΗΜΑ 7.Δεύτερη πλεγμένη παραγώγιση 8.Χαρακτηρισμός
(iii) Να βρεθεί το δεσμευμένο στάσιμο της συνάρτησης f(x, y) = x + y με τον περιορισμό:
 ΔΙΑΓΩΝΙΣΜΑ 1 (3 μονάδες) (i) Δίνονται οι παραμετρικές εξισώσεις: = ln(t+ 1), y= t + t. Να υπολογιστεί η παράγωγος του ως προς y, όταν t= 0. (ii) Δίνεται η συνάρτηση: f() = p+. Να διερευνηθεί αν είναι κυρτή
ΔΙΑΓΩΝΙΣΜΑ 1 (3 μονάδες) (i) Δίνονται οι παραμετρικές εξισώσεις: = ln(t+ 1), y= t + t. Να υπολογιστεί η παράγωγος του ως προς y, όταν t= 0. (ii) Δίνεται η συνάρτηση: f() = p+. Να διερευνηθεί αν είναι κυρτή
I.3 ΔΕΥΤΕΡΗ ΠΑΡΑΓΩΓΟΣ-ΚΥΡΤΟΤΗΤΑ
 I.3 ΔΕΥΤΕΡΗ ΠΑΡΑΓΩΓΟΣ-ΚΥΡΤΟΤΗΤΑ.Δεύτερη παράγωγος.κυρτή 3.Κοίλη 4.Ιδιότητες κυρτών/κοίλων συναρτήσεων 5.Σημεία καμπής 6.Παραβολική προσέγγιση(επέκταση) ΠΑΡΑΡΤΗΜΑ 7.Δεύτερη πλεγμένη παραγώγιση 8.Χαρακτηρισμός
I.3 ΔΕΥΤΕΡΗ ΠΑΡΑΓΩΓΟΣ-ΚΥΡΤΟΤΗΤΑ.Δεύτερη παράγωγος.κυρτή 3.Κοίλη 4.Ιδιότητες κυρτών/κοίλων συναρτήσεων 5.Σημεία καμπής 6.Παραβολική προσέγγιση(επέκταση) ΠΑΡΑΡΤΗΜΑ 7.Δεύτερη πλεγμένη παραγώγιση 8.Χαρακτηρισμός
ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ 4. [ ] z, w. 3 f x, x 1,3 όπου 3 μιγαδικοί των οποίων οι εικόνες
![ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ 4. [ ] z, w. 3 f x, x 1,3 όπου 3 μιγαδικοί των οποίων οι εικόνες ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ 4. [ ] z, w. 3 f x, x 1,3 όπου 3 μιγαδικοί των οποίων οι εικόνες](/thumbs/55/37062184.jpg) ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ 4 1. i) Να δείξετε ότι υπάρχει μοναδικό 3 3 0 1, ώστε: 3 e, 1 ln 0 + 0 = 0 ii) Δίνεται ο μιγαδικός 3 z = ln + i, > 0 a) Να βρείτε την ελάχιστη απόσταση k της εικόνας του z από την αρχή
ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ 4 1. i) Να δείξετε ότι υπάρχει μοναδικό 3 3 0 1, ώστε: 3 e, 1 ln 0 + 0 = 0 ii) Δίνεται ο μιγαδικός 3 z = ln + i, > 0 a) Να βρείτε την ελάχιστη απόσταση k της εικόνας του z από την αρχή
Λύσεις του διαγωνίσματος στις παραγώγους
 Λύσεις του διαγωνίσματος στις παραγώγους Θέμα ο Α Έστω ότι f ), για κάθε α, ), β) Επειδή η f είναι συνεχής στο θα είναι γνησίως αύξουσα σε κάθε ένα από τα διαστήματα α, ] και [, β) Επομένως, για ισχύει
Λύσεις του διαγωνίσματος στις παραγώγους Θέμα ο Α Έστω ότι f ), για κάθε α, ), β) Επειδή η f είναι συνεχής στο θα είναι γνησίως αύξουσα σε κάθε ένα από τα διαστήματα α, ] και [, β) Επομένως, για ισχύει
και δεν είναι παραγωγίσιμη σε αυτό, σχολικό βιβλίο σελ. 99 Α3. Ορισμός σελ. 73 Α4. α) Λ β) Σ γ) Λ δ) Σ ε) Σ , δηλαδή αρκεί x 1 x
 ΘΕΜΑ Α Α1. Απόδειξη σχολικού βιβλίου σελ. 15 Α. α) Ψ β) Σχήμα 1 και μελέτη της f, όπου η f είναι συνεχής στο και δεν είναι παραγωγίσιμη σε αυτό, σχολικό βιβλίο σελ. 99 Α. Ορισμός σελ. 7 Α. α) Λ β) Σ γ)
ΘΕΜΑ Α Α1. Απόδειξη σχολικού βιβλίου σελ. 15 Α. α) Ψ β) Σχήμα 1 και μελέτη της f, όπου η f είναι συνεχής στο και δεν είναι παραγωγίσιμη σε αυτό, σχολικό βιβλίο σελ. 99 Α. Ορισμός σελ. 7 Α. α) Λ β) Σ γ)
ΟΙΚΟΝΟΜΙΚΑ ΜΑΘΗΜΑΤΙΚΑ
 ΟΙΚΟΝΟΜΙΚΑ ΜΑΘΗΜΑΤΙΚΑ Ι. Δημόπουλος Τμήμα Διοίκησης Μονάδων Υγείας και Πρόνοιας -ΤΕΙ Καλαμάτας ΠΑΡΑΓΩΓΟΣ ΚΑΙ ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ Τοπική μονοτονία Αν μια συνεχής συνάρτηση έχει γνήσια θετική αρνητική παράγωγο
ΟΙΚΟΝΟΜΙΚΑ ΜΑΘΗΜΑΤΙΚΑ Ι. Δημόπουλος Τμήμα Διοίκησης Μονάδων Υγείας και Πρόνοιας -ΤΕΙ Καλαμάτας ΠΑΡΑΓΩΓΟΣ ΚΑΙ ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ Τοπική μονοτονία Αν μια συνεχής συνάρτηση έχει γνήσια θετική αρνητική παράγωγο
αx αx αx αx 2 αx = α e } 2 x x x dx καλείται η παραβολική συνάρτηση η οποία στο x
 A3. ΕΥΤΕΡΗ ΠΑΡΑΓΩΓΟΣ-ΚΥΡΤΟΤΗΤΑ. εύτερη παράγωγος.παραβολική προσέγγιση ή επέκταση 3.Κυρτή 4.Κοίλη 5.Ιδιότητες κυρτών/κοίλων συναρτήσεων 6.Σηµεία καµπής ΠΑΡΑΡΤΗΜΑ 7. εύτερη πλεγµένη παραγώγιση 8.Χαρακτηρισµός
A3. ΕΥΤΕΡΗ ΠΑΡΑΓΩΓΟΣ-ΚΥΡΤΟΤΗΤΑ. εύτερη παράγωγος.παραβολική προσέγγιση ή επέκταση 3.Κυρτή 4.Κοίλη 5.Ιδιότητες κυρτών/κοίλων συναρτήσεων 6.Σηµεία καµπής ΠΑΡΑΡΤΗΜΑ 7. εύτερη πλεγµένη παραγώγιση 8.Χαρακτηρισµός
ΑΠΑΝΤΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ 2012
 ΑΠΑΝΤΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ Θέμα A Α, A, A3 : Θεωρία A4. : α Σ, β Σ, γ Λ, δ Σ, ε Λ Θέμα B Β : Έχουμε z z wi w w zz zz z z zz z z Β : Είναι z z zz z. z 4 4 4 4 4 Αν ω z, τότε ω z z
ΑΠΑΝΤΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ Θέμα A Α, A, A3 : Θεωρία A4. : α Σ, β Σ, γ Λ, δ Σ, ε Λ Θέμα B Β : Έχουμε z z wi w w zz zz z z zz z z Β : Είναι z z zz z. z 4 4 4 4 4 Αν ω z, τότε ω z z
Α1. Θεωρία Σελίδες Σχολικού Βιβλίου ΜΑΘΗΜΑΤΙΚΑ Θετικής& Τεχνολογικής κατεύθυνσης Γ ΛΥΚΕΙΟΥ, ΕΚΔΟΣΗ 2014
 ΑΠΑΝΤΗΣΕΙΣ ΣΤΟ ΠΡΟΣΟΜΟΙΩΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ Γ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ ΤΗΣ ΜΑΡΤΗ ΘΕΜΑ Α Α Θεωρία Σελίδες 33-33 Σχολικού Βιβλίου ΜΑΘΗΜΑΤΙΚΑ Θετικής& Τεχνολογικής κατεύθυνσης Γ ΛΥΚΕΙΟΥ, ΕΚΔΟΣΗ ΑΘεωρία
ΑΠΑΝΤΗΣΕΙΣ ΣΤΟ ΠΡΟΣΟΜΟΙΩΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ Γ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ ΤΗΣ ΜΑΡΤΗ ΘΕΜΑ Α Α Θεωρία Σελίδες 33-33 Σχολικού Βιβλίου ΜΑΘΗΜΑΤΙΚΑ Θετικής& Τεχνολογικής κατεύθυνσης Γ ΛΥΚΕΙΟΥ, ΕΚΔΟΣΗ ΑΘεωρία
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 9 ΙΟΥΝΙΟΥ 2017 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ:
 ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 9 ΙΟΥΝΙΟΥ 7 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΠΛΗΡΕΙΣ ΛΥΣΕΙΣ ΘΕΜΑ Α Α. Σχολικό βιβλίο σελίδα
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 9 ΙΟΥΝΙΟΥ 7 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΠΛΗΡΕΙΣ ΛΥΣΕΙΣ ΘΕΜΑ Α Α. Σχολικό βιβλίο σελίδα
x R, να δείξετε ότι: i)
 ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΨΗΣ Γ ΛΥΚΕΙΟΥ Έστω μια συνάρτηση f παραγωγίσιμη στο R για την οποία ισχύουν: f ( ), f ( ) για κάθε R και f ( ) f ( ) α) Να βρείτε τον τύπο της f για κάθε R g( ) β) Αν g είναι
ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΨΗΣ Γ ΛΥΚΕΙΟΥ Έστω μια συνάρτηση f παραγωγίσιμη στο R για την οποία ισχύουν: f ( ), f ( ) για κάθε R και f ( ) f ( ) α) Να βρείτε τον τύπο της f για κάθε R g( ) β) Αν g είναι
ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΓΕΝΙΚΩΝ ΛΥΚΕΙΩΝ. f ( x) 0 0 2x 0 x 0
 ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΓΕΝΙΚΩΝ ΛΥΚΕΙΩΝ ΑΠΑΝΤΗΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΚΑΙ ΟΙΚΟΝΟΜΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) 8 ΜΑΪΟΥ 6 ΘΕΜΑ Α Α. Θεωρία, βλ. σχολικό βιβλίο
ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΓΕΝΙΚΩΝ ΛΥΚΕΙΩΝ ΑΠΑΝΤΗΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΚΑΙ ΟΙΚΟΝΟΜΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) 8 ΜΑΪΟΥ 6 ΘΕΜΑ Α Α. Θεωρία, βλ. σχολικό βιβλίο
g= x + y 1}. Να βρεθεί γραφικά και αναλυτικά η MR Π(Q) = R(Q) C(Q). Στο παραπλεύρως σχήμα
 ΔΙΑΓΩΝΙΣΜΑ 0 Μέρος Α. (.6 μονάδες) α). Οι μεταβλητές {,,} συνδέονται με τις εξισώσεις κανόνας αλυσωτής παραγώγισης. { = e +, = ln}. Να επαληθευτεί ο β). Οι μεταβλητές {, y} συνδέονται με μια εξίσωση. Για
ΔΙΑΓΩΝΙΣΜΑ 0 Μέρος Α. (.6 μονάδες) α). Οι μεταβλητές {,,} συνδέονται με τις εξισώσεις κανόνας αλυσωτής παραγώγισης. { = e +, = ln}. Να επαληθευτεί ο β). Οι μεταβλητές {, y} συνδέονται με μια εξίσωση. Για
Η f(x) y είναι συνεχής στο [0, 2α], σαν διαφορά των συνεχών f(x) και y = 8αx 8α 2
![Η f(x) y είναι συνεχής στο [0, 2α], σαν διαφορά των συνεχών f(x) και y = 8αx 8α 2 Η f(x) y είναι συνεχής στο [0, 2α], σαν διαφορά των συνεχών f(x) και y = 8αx 8α 2](/thumbs/92/107960223.jpg) 1994 ΘΕΜΑΤΑ 1. ίνεται η συνάρτηση f()=,. Α) Αν ε είναι η εφαπτοµένη της γραφικής παράστασης C της συνάρτησης f στο σηµείο Μ(α, α ), α >, να βρείτε το εµβαδόν του χωρίου που περικλείεται από τη C, την ευθεία
1994 ΘΕΜΑΤΑ 1. ίνεται η συνάρτηση f()=,. Α) Αν ε είναι η εφαπτοµένη της γραφικής παράστασης C της συνάρτησης f στο σηµείο Μ(α, α ), α >, να βρείτε το εµβαδόν του χωρίου που περικλείεται από τη C, την ευθεία
- + Απαντήσεις. Θέμα Β Β1. Από την Cf παρατηρούμε ότι 0. f x για κάθε (0,4) συνεπώς η f είναι γνήσια αύξουσα στο [4, 5] και γνήσια φθίνουσα στο [0,4].
![- + Απαντήσεις. Θέμα Β Β1. Από την Cf παρατηρούμε ότι 0. f x για κάθε (0,4) συνεπώς η f είναι γνήσια αύξουσα στο [4, 5] και γνήσια φθίνουσα στο [0,4]. - + Απαντήσεις. Θέμα Β Β1. Από την Cf παρατηρούμε ότι 0. f x για κάθε (0,4) συνεπώς η f είναι γνήσια αύξουσα στο [4, 5] και γνήσια φθίνουσα στο [0,4].](/thumbs/88/117335912.jpg) ΑΡΧΗ ΗΣ ΣΕΛΙΔΑΣ Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΥΡΙΑΚΗ 3//7 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ Ο.Π ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΠΤΑ (7) Απαντήσεις Θέμα Α Α. Θεωρία σχολικού βιβλίου σελ. 99 Α. Θεωρία σχολικού βιβλίου σελ. 6
ΑΡΧΗ ΗΣ ΣΕΛΙΔΑΣ Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΥΡΙΑΚΗ 3//7 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ Ο.Π ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΠΤΑ (7) Απαντήσεις Θέμα Α Α. Θεωρία σχολικού βιβλίου σελ. 99 Α. Θεωρία σχολικού βιβλίου σελ. 6
Κεφάλαιο 4: Διαφορικός Λογισμός
 ΣΥΓΧΡΟΝΗ ΠΑΙΔΕΙΑ ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Κεφάλαιο 4: Διαφορικός Λογισμός Μονοτονία Συνάρτησης Tζουβάλης Αθανάσιος Κεφάλαιο 4: Διαφορικός Λογισμός Περιεχόμενα Μονοτονία συνάρτησης... Λυμένα παραδείγματα...
ΣΥΓΧΡΟΝΗ ΠΑΙΔΕΙΑ ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Κεφάλαιο 4: Διαφορικός Λογισμός Μονοτονία Συνάρτησης Tζουβάλης Αθανάσιος Κεφάλαιο 4: Διαφορικός Λογισμός Περιεχόμενα Μονοτονία συνάρτησης... Λυμένα παραδείγματα...
2. Έστω η συνάρτηση f :[0, 6] με την παρακάτω γραφική παράσταση.
![2. Έστω η συνάρτηση f :[0, 6] με την παρακάτω γραφική παράσταση. 2. Έστω η συνάρτηση f :[0, 6] με την παρακάτω γραφική παράσταση.](/thumbs/62/47302337.jpg) . Έστω η συνάρτηση f : με την παρακάτω γραφική παράσταση. Α. Να προσδιορίσετε τα διαστήματα στα οποία η f είναι γνησίως αύξουσα, γνησίως φθίνουσα, κυρτή, κοίλη, καθώς και τα τοπικά ακρότατα και τα σημεία
. Έστω η συνάρτηση f : με την παρακάτω γραφική παράσταση. Α. Να προσδιορίσετε τα διαστήματα στα οποία η f είναι γνησίως αύξουσα, γνησίως φθίνουσα, κυρτή, κοίλη, καθώς και τα τοπικά ακρότατα και τα σημεία
και γνησίως αύξουσα στο 0,
 ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ Α Α1. Σχολικό βιβλίο σελ 6 (i) A. Σχολικό βιβλίο σελ 141 Α. Σχολικό βιβλίο σελ 46-47 Α4. α. Λ β. Σ γ. Λ δ. Σ ε. Σ ΘΕΜΑ Β Β1. Ισχύει D f επειδή 1 1 1 Για κάθε η f είναι παραγωγίσιμη
ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ Α Α1. Σχολικό βιβλίο σελ 6 (i) A. Σχολικό βιβλίο σελ 141 Α. Σχολικό βιβλίο σελ 46-47 Α4. α. Λ β. Σ γ. Λ δ. Σ ε. Σ ΘΕΜΑ Β Β1. Ισχύει D f επειδή 1 1 1 Για κάθε η f είναι παραγωγίσιμη
f '(x 0) lim lim x x x x
 Α Θ Ε Μ Α A Θ Ε Ω Ρ Η Μ Α ( F e r m a t ) Έστω μια συνάρτηση ορισμένη σ ένα διάστημα Δ και ένα εσωτερικό σημείο του Δ Αν η παρουσιάζει τοπικό ακρότατο στο και είναι παραγωγίσιμη στο σημείο αυτό, τότε:
Α Θ Ε Μ Α A Θ Ε Ω Ρ Η Μ Α ( F e r m a t ) Έστω μια συνάρτηση ορισμένη σ ένα διάστημα Δ και ένα εσωτερικό σημείο του Δ Αν η παρουσιάζει τοπικό ακρότατο στο και είναι παραγωγίσιμη στο σημείο αυτό, τότε:
ΚΕΦΑΛΑΙΟ 4ο: ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 4: ΕΜΒΑΔΟΝ ΕΠΙΠΕΔΟΥ ΧΩΡΙΟΥ [Κεφ.3.7 Μέρος Β του σχολικού βιβλίου]. ΑΣΚΗΣΕΙΣ
![ΚΕΦΑΛΑΙΟ 4ο: ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 4: ΕΜΒΑΔΟΝ ΕΠΙΠΕΔΟΥ ΧΩΡΙΟΥ [Κεφ.3.7 Μέρος Β του σχολικού βιβλίου]. ΑΣΚΗΣΕΙΣ ΚΕΦΑΛΑΙΟ 4ο: ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 4: ΕΜΒΑΔΟΝ ΕΠΙΠΕΔΟΥ ΧΩΡΙΟΥ [Κεφ.3.7 Μέρος Β του σχολικού βιβλίου]. ΑΣΚΗΣΕΙΣ](/thumbs/54/33927053.jpg) ΚΕΦΑΛΑΙΟ ο: ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ : ΕΜΒΑΔΟΝ ΕΠΙΠΕΔΟΥ ΧΩΡΙΟΥ [Κεφ..7 Μέρος Β του σχολικού βιβλίου]. ΑΣΚΗΣΕΙΣ ΘΕΜΑ Β Άσκηση. Να υπολογίσετε το εμβαδόν του χωρίου που περικλείεται από τη γραφική
ΚΕΦΑΛΑΙΟ ο: ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ : ΕΜΒΑΔΟΝ ΕΠΙΠΕΔΟΥ ΧΩΡΙΟΥ [Κεφ..7 Μέρος Β του σχολικού βιβλίου]. ΑΣΚΗΣΕΙΣ ΘΕΜΑ Β Άσκηση. Να υπολογίσετε το εμβαδόν του χωρίου που περικλείεται από τη γραφική
ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ
 Ιουνίου 4 ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Απαντήσεις Επαναληπτικών Θεμάτων Πανελληνίων Εξετάσεων Ημερησίων Γενικών Λυκείων ΘΕΜΑ Α Α. Σχολικό βιβλίο σελίδα 63. Α. Σχολικό βιβλίο σελίδα 9. Α3. Σχολικό βιβλίο σελίδα
Ιουνίου 4 ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Απαντήσεις Επαναληπτικών Θεμάτων Πανελληνίων Εξετάσεων Ημερησίων Γενικών Λυκείων ΘΕΜΑ Α Α. Σχολικό βιβλίο σελίδα 63. Α. Σχολικό βιβλίο σελίδα 9. Α3. Σχολικό βιβλίο σελίδα
Μαθηματικά Θετικής και Τεχνολογικής Κατεύθυνσης Γ Λυκείου ΚΥΡΤΟΤΗΤΑ - ΣΗΜΕΙΑ ΚΑΜΠΗΣ ΣΥΝΑΡΤΗΣΗΣ
 ΚΥΡΤΟΤΗΤΑ - ΣΗΜΕΙΑ ΚΑΜΠΗΣ ΣΥΝΑΡΤΗΣΗΣ Ορισμός Θεωρούμε μια συνάρτηση f συνεχή σ' ένα διάστημα Δ και παραγωγίσιμη στο εσωτερικό του Δ. α) Θα λέμε ότι η f είναι κυρτή ή στρέφει τα κοίλα άνω στο Δ, αν η f
ΚΥΡΤΟΤΗΤΑ - ΣΗΜΕΙΑ ΚΑΜΠΗΣ ΣΥΝΑΡΤΗΣΗΣ Ορισμός Θεωρούμε μια συνάρτηση f συνεχή σ' ένα διάστημα Δ και παραγωγίσιμη στο εσωτερικό του Δ. α) Θα λέμε ότι η f είναι κυρτή ή στρέφει τα κοίλα άνω στο Δ, αν η f
f(x 2) 5 x 1 α) Να αποδείξετε ότι: i) f (3) = 5 και ii) f (3) = 6 x 2 f(x)
 . Έστω η συνάρτηση = + e. Να μελετήσετε την f ως προς τη μονοτονία.. Να λύσετε την εξίσωση e = 3. Θεωρούμε τη γνησίως μονότονη συνάρτηση g : R R η οποία για κάθε R ικανοποιεί τη σχέση g() + e g() = +.
. Έστω η συνάρτηση = + e. Να μελετήσετε την f ως προς τη μονοτονία.. Να λύσετε την εξίσωση e = 3. Θεωρούμε τη γνησίως μονότονη συνάρτηση g : R R η οποία για κάθε R ικανοποιεί τη σχέση g() + e g() = +.
Κεφάλαιο 2ο: ΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ 2ο ΜΕΡΟΣ
 Κεφάλαιο ο: ΙΑΦΟΡΙΚΟ ΟΓΙΜΟ ο ΜΕΡΟ Ερωτήσεις του τύπου «ωστό - άθος» 1. * Αν η συνάρτηση f είναι παραγωγίσιµη στο R και f (α) f (β), α, β R, α < β, τότε ισχύει f () για κάθε (α, β).. * Αν η συνάρτηση f
Κεφάλαιο ο: ΙΑΦΟΡΙΚΟ ΟΓΙΜΟ ο ΜΕΡΟ Ερωτήσεις του τύπου «ωστό - άθος» 1. * Αν η συνάρτηση f είναι παραγωγίσιµη στο R και f (α) f (β), α, β R, α < β, τότε ισχύει f () για κάθε (α, β).. * Αν η συνάρτηση f
3o Επαναληπτικό Διαγώνισμα 2016
 3o Επαναληπτικό Διαγώνισμα 6 Διάρκεια: 3 ώρες ΘΕΜΑ A A Έστω μια συνάρτηση παραγωγίσιμη σ ένα διάστημα (α,β), με εξαίρεση ίσως ένα σημείο του,στο οποίο όμως η είναι συνεχής Να αποδείξετε ότι Αν () στο (α,
3o Επαναληπτικό Διαγώνισμα 6 Διάρκεια: 3 ώρες ΘΕΜΑ A A Έστω μια συνάρτηση παραγωγίσιμη σ ένα διάστημα (α,β), με εξαίρεση ίσως ένα σημείο του,στο οποίο όμως η είναι συνεχής Να αποδείξετε ότι Αν () στο (α,
********* Β ομάδα Κυρτότητα Σημεία καμπής*********
 ********* Β ομάδα Κυρτότητα Σημεία καμπής********* 5 Για την δύο φορές παραγωγίσιμη στο R συνάρτηση ισχύει: e για κάθε R. Να αποδείξετε ότι η γραφική παράσταση της δεν παρουσιάζει σημείο καμπής. Υποθέτουμε
********* Β ομάδα Κυρτότητα Σημεία καμπής********* 5 Για την δύο φορές παραγωγίσιμη στο R συνάρτηση ισχύει: e για κάθε R. Να αποδείξετε ότι η γραφική παράσταση της δεν παρουσιάζει σημείο καμπής. Υποθέτουμε
Πανελλαδικές εξετάσεις 2015
 Πανελλαδικές εξετάσεις 5 Ενδεικτικές απαντήσεις στο μάθημα «MΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ» Θέμα Α Α Απόδειξη βιβλίο σχολείου σελ(94) Α Ορισμός βιβλίο σχολείου σελ(88) Α Ορισμός βιβλίο
Πανελλαδικές εξετάσεις 5 Ενδεικτικές απαντήσεις στο μάθημα «MΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ» Θέμα Α Α Απόδειξη βιβλίο σχολείου σελ(94) Α Ορισμός βιβλίο σχολείου σελ(88) Α Ορισμός βιβλίο
ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΥΛΗ ΔΙΑΓΩΝΙΣΜΑΤΟΣ:ΠΑΡΑΓΩΓΟΙ
 ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΥΛΗ ΔΙΑΓΩΝΙΣΜΑΤΟΣ:ΠΑΡΑΓΩΓΟΙ ΘΕΜΑ Α Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στο τετράδιό σας τη λέξη Σωστό ή Λάθος δίπλα στο γράμμα που αντιστοιχεί σε κάθε
ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΥΛΗ ΔΙΑΓΩΝΙΣΜΑΤΟΣ:ΠΑΡΑΓΩΓΟΙ ΘΕΜΑ Α Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στο τετράδιό σας τη λέξη Σωστό ή Λάθος δίπλα στο γράμμα που αντιστοιχεί σε κάθε
ΜΑΘΗΜΑΤΙΚΑ ΟΠ- Γ ΓΕΛ 12:50
 ΜΑΘΗΜΑΤΙΚΑ ΟΠ- Γ ΓΕΛ 1:5 Σελίδα από 11 ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ ΕΞΕΤΑΣΗΣ: 11 / 6 / 18 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: Μαθηματικά ΟΠ Γ ΓΕΛ ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ
ΜΑΘΗΜΑΤΙΚΑ ΟΠ- Γ ΓΕΛ 1:5 Σελίδα από 11 ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ ΕΞΕΤΑΣΗΣ: 11 / 6 / 18 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: Μαθηματικά ΟΠ Γ ΓΕΛ ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ
Ασκήσεις Επανάληψης Γ Λυκείου
 Ασκήσεις Επανάληψης Γ Λυκείου Ασκήσεις Επανάληψης σε όλο το εύρος της διδακτέας ύλης Κων/νος Παπασταματίου Κ. Καρτάλη 8 (με Δημητριάδος) Τηλ. 4 598 Θε ματα Δεσμω ν 98- Επιμέλεια Κων/νος Παπασταματίου Σελίδα
Ασκήσεις Επανάληψης Γ Λυκείου Ασκήσεις Επανάληψης σε όλο το εύρος της διδακτέας ύλης Κων/νος Παπασταματίου Κ. Καρτάλη 8 (με Δημητριάδος) Τηλ. 4 598 Θε ματα Δεσμω ν 98- Επιμέλεια Κων/νος Παπασταματίου Σελίδα
ΜΑΘΗΜΑΤΙΚΑ ΟΠ- Γ ΓΕΛ 12:50
 ΜΑΘΗΜΑΤΙΚΑ ΟΠ- Γ ΓΕΛ 1:5 Σελίδα από 11 ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΠΑΓΓΕΛΜΑΤΙΚΟΥ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ ΕΞΕΤΑΣΗΣ: 11 / 6 / 18 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: Μαθηματικά ΟΠ Γ ΓΕΛ ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ
ΜΑΘΗΜΑΤΙΚΑ ΟΠ- Γ ΓΕΛ 1:5 Σελίδα από 11 ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΠΑΓΓΕΛΜΑΤΙΚΟΥ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ ΕΞΕΤΑΣΗΣ: 11 / 6 / 18 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: Μαθηματικά ΟΠ Γ ΓΕΛ ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΚΕΦΑΛΑΙΟ 4ο: ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΘΕΜΑ Α
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΚΕΦΑΛΑΙΟ 4ο: ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΘΕΜΑ Α Άσκηση i. Έστω μια συνάρτηση ορισμένη σε ένα διάστημα Δ. Αν F είναι μια παράγουσα της στο Δ, τότε να αποδείξετε ότι: όλες οι συναρτήσεις της
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΚΕΦΑΛΑΙΟ 4ο: ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΘΕΜΑ Α Άσκηση i. Έστω μια συνάρτηση ορισμένη σε ένα διάστημα Δ. Αν F είναι μια παράγουσα της στο Δ, τότε να αποδείξετε ότι: όλες οι συναρτήσεις της
ln 1. ( ) vii. Να βρείτε το εμβαδόν του χωρίου που περικλείεται από τη C f, τον άξονα η οποία είναι συνεχής στο και για την οποία ισχύει
 Μαθηματικά Γ Λυκείου Θέμα 4o Α Δίνεται η συνάρτηση h ( ), η οποία είναι συνεχής και γνησίως αύξουσα στο διάστημα [, ] β αβ Να δείξετε ότι h d hαβα Β Δίνεται η συνάρτηση f α ( ) ln i Να βρείτε το πεδίο
Μαθηματικά Γ Λυκείου Θέμα 4o Α Δίνεται η συνάρτηση h ( ), η οποία είναι συνεχής και γνησίως αύξουσα στο διάστημα [, ] β αβ Να δείξετε ότι h d hαβα Β Δίνεται η συνάρτηση f α ( ) ln i Να βρείτε το πεδίο
Ερωτήσεις πολλαπλής επιλογής
 Ερωτήσεις πολλαπλής επιλογής. * Έστω µια συνάρτηση f για την οποία ισχύουν οι υποθέσεις του θεωρήµατος του Rolle στο διάστηµα [α, β]. Τότε θα υπάρχει ξ (α, β), ώστε η εφαπτοµένη της C f στο (ξ, f (ξ))
Ερωτήσεις πολλαπλής επιλογής. * Έστω µια συνάρτηση f για την οποία ισχύουν οι υποθέσεις του θεωρήµατος του Rolle στο διάστηµα [α, β]. Τότε θα υπάρχει ξ (α, β), ώστε η εφαπτοµένη της C f στο (ξ, f (ξ))
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΠΑΡΑΣΚΕΥΗ 9 ΙΟΥΝΙΟΥ 2017 Ενδεικτικές απαντήσεις
 ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΠΑΡΑΣΚΕΥΗ 9 ΙΟΥΝΙΟΥ 7 Ενδεικτικές απαντήσεις Θέμα Α Α. Σχολικό βιβλίο σελίδα 35 Α. α. Ψ β. Παράδειγμα η συνάρτηση f ( ) είναι συνεχής στο αλλά όχι παραγωγίσιμη σε αυτό. Α3. Σχολικό
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΠΑΡΑΣΚΕΥΗ 9 ΙΟΥΝΙΟΥ 7 Ενδεικτικές απαντήσεις Θέμα Α Α. Σχολικό βιβλίο σελίδα 35 Α. α. Ψ β. Παράδειγμα η συνάρτηση f ( ) είναι συνεχής στο αλλά όχι παραγωγίσιμη σε αυτό. Α3. Σχολικό
g x είναι συνάρτηση 1 1 στο Ag = R αλλά δεν είναι γνησίως
 ΘΕΜΑ Α Α. Απόδειξη θεωρήματος σελ. 99 σχολικού βιβλίου. Α. α. Ψευδής β. Θεωρούμε τη συνάρτηση, 0 g, 0 η οποία έχει γραφική παράσταση (σχήμα σχολικού βιβλίου σελ.5): y O y=g() Η g είναι συνάρτηση στο Ag
ΘΕΜΑ Α Α. Απόδειξη θεωρήματος σελ. 99 σχολικού βιβλίου. Α. α. Ψευδής β. Θεωρούμε τη συνάρτηση, 0 g, 0 η οποία έχει γραφική παράσταση (σχήμα σχολικού βιβλίου σελ.5): y O y=g() Η g είναι συνάρτηση στο Ag
ΤΕΣΤ Β2.λύσεις ΟΜΑΔΑ Ι
 Η εξίσωση ΤΕΣΤ Β.λύσεις ΟΜΑΔΑ Ι αβ+ α = ορίζει πλεγμένα το ως συνάρτηση των {α,β}. Να βρεθούν η παράγωγος και η ελαστικότητα του ως προς β, στις τιμές: {α=,β =, = }. Λύση. Ο τύπος πλεγμένης παραγώγισης
Η εξίσωση ΤΕΣΤ Β.λύσεις ΟΜΑΔΑ Ι αβ+ α = ορίζει πλεγμένα το ως συνάρτηση των {α,β}. Να βρεθούν η παράγωγος και η ελαστικότητα του ως προς β, στις τιμές: {α=,β =, = }. Λύση. Ο τύπος πλεγμένης παραγώγισης
ΜΑΘΗΜΑΤΙΚΑ - ΠΛΗΡΟΦΟΡΙΚΗ
 ΘΕΜΑ Α ΜΑΘΗΜΑΤΙΚΑ - ΠΛΗΡΟΦΟΡΙΚΗ ΑΠΑΝΤΗΣΕΙΣ ΣΤΑ ΘΕΜΑΤΑ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ Α. Θεωρία (Θεώρημα σελίδα 5 σχολικού βιβλίου) Α. Α) ΨΕΥΔΗΣ Β) Θα δώσουμε ένα αντιπαράδειγμα Έστω η συνάρτηση
ΘΕΜΑ Α ΜΑΘΗΜΑΤΙΚΑ - ΠΛΗΡΟΦΟΡΙΚΗ ΑΠΑΝΤΗΣΕΙΣ ΣΤΑ ΘΕΜΑΤΑ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ Α. Θεωρία (Θεώρημα σελίδα 5 σχολικού βιβλίου) Α. Α) ΨΕΥΔΗΣ Β) Θα δώσουμε ένα αντιπαράδειγμα Έστω η συνάρτηση
x, x (, x ], επειδή η f είναι γνησίως αύξουσα στο (, x0]
![x, x (, x ], επειδή η f είναι γνησίως αύξουσα στο (, x0] x, x (, x ], επειδή η f είναι γνησίως αύξουσα στο (, x0]](/thumbs/102/155315355.jpg) Απαντήσεις στο ο Διαγώνισμα Μαθηματικών Κατεύθυνσης Γ Λυκείου Θέμα ο Α Έστω ότι f( ), για κάθε (, ) (, ) Επειδή η f είναι συνεχής στο θα είναι γνησίως αύξουσα σε κάθε ένα από τα διαστήματα (, ] και [,
Απαντήσεις στο ο Διαγώνισμα Μαθηματικών Κατεύθυνσης Γ Λυκείου Θέμα ο Α Έστω ότι f( ), για κάθε (, ) (, ) Επειδή η f είναι συνεχής στο θα είναι γνησίως αύξουσα σε κάθε ένα από τα διαστήματα (, ] και [,
Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ. Ημερομηνία: Τρίτη 10 Απριλίου 2018 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ
 ΑΠΟ /4/8 ΕΩΣ 4/4/8 ΤΑΞΗ: ΜΑΘΗΜΑ Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Τρίτη Απριλίου 8 Διάρκεια Εξέτασης: ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α Έστω μία συνάρτηση ορισμένη σε ένα διάστημα Δ Αν o
ΑΠΟ /4/8 ΕΩΣ 4/4/8 ΤΑΞΗ: ΜΑΘΗΜΑ Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Τρίτη Απριλίου 8 Διάρκεια Εξέτασης: ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α Έστω μία συνάρτηση ορισμένη σε ένα διάστημα Δ Αν o
ΔΙΑΓΩΝΙΣΜΑ 14. Μέρος Α
 Μέρος Α ΔΙΑΓΩΝΙΣΜΑ 14 1. (4 μονάδες) (α). Να δοθεί το γράφημα μιας συνάρτησης f() της οποίας η παράγωγος έχει το γράφημα του παραπλεύρως σχήματος, και αρχική τιμή f() =. (β). Να βρεθεί συνάρτηση f() σταθερής
Μέρος Α ΔΙΑΓΩΝΙΣΜΑ 14 1. (4 μονάδες) (α). Να δοθεί το γράφημα μιας συνάρτησης f() της οποίας η παράγωγος έχει το γράφημα του παραπλεύρως σχήματος, και αρχική τιμή f() =. (β). Να βρεθεί συνάρτηση f() σταθερής
Τελευταία Επανάληψη. την ευθεία x=1 και τoν x x. 2 1 x. Λύση. x 2 1 x 0, άρα. x 1 x. x x 1. γ) x 1 e x x 1 x e ln x 1 x f x.
 Δίνεται η συνάρτηση ln Τελευταία Επανάληψη α) Να βρείτε το πεδίο ορισμού της β) Να μελετήσετε την ως προς την μονοτονία της γ) Να βρείτε το πλήθος των ριζών της εξίσωσης e, δ) Να υπολογίσετε το εμβαδόν
Δίνεται η συνάρτηση ln Τελευταία Επανάληψη α) Να βρείτε το πεδίο ορισμού της β) Να μελετήσετε την ως προς την μονοτονία της γ) Να βρείτε το πλήθος των ριζών της εξίσωσης e, δ) Να υπολογίσετε το εμβαδόν
( ) ( ) ( 3 ) ( ) = ( ) ( ) ( ) ( ) ( ) ( 1) ( ) (( ) ( )) ( ) + = = και και και και. ζ να ταυτισθούν, δηλαδή θα πρέπει: f x ημ x. 6 x x x.
 Ενδεικτικές Λύσεις Διαγωνίσματος (9--9) ΘΕΜΑ Α A. Απόδειξη σχολικού βιβλίου σελ. 5 Α. α. ψ β. Αντιπαράδειγμα σχολικού βιβλίου σελ. 99 Α. Ορισμός σχολικού βιβλίου σελ. 6 Α4. α) Σ β) Λ γ) Λ δ) Σ ε) Λ ΛΥΣΗ
Ενδεικτικές Λύσεις Διαγωνίσματος (9--9) ΘΕΜΑ Α A. Απόδειξη σχολικού βιβλίου σελ. 5 Α. α. ψ β. Αντιπαράδειγμα σχολικού βιβλίου σελ. 99 Α. Ορισμός σχολικού βιβλίου σελ. 6 Α4. α) Σ β) Λ γ) Λ δ) Σ ε) Λ ΛΥΣΗ
ΕΝΔΕΙΚΤΙΚΕΣ ΛΥΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 2017
 ΕΝΔΕΙΚΤΙΚΕΣ ΛΥΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 7 ΘΕΜΑ Α A Έστω συνάρτηση f, η οποία είναι συνεχής σε ένα διάστημα Δ Αν f σε κάθε εσωτερικό σημείο του Δ, τότε να αποδείξετε ότι η f είναι γνησίως αύξουσα
ΕΝΔΕΙΚΤΙΚΕΣ ΛΥΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 7 ΘΕΜΑ Α A Έστω συνάρτηση f, η οποία είναι συνεχής σε ένα διάστημα Δ Αν f σε κάθε εσωτερικό σημείο του Δ, τότε να αποδείξετε ότι η f είναι γνησίως αύξουσα
Α1. Να διατυπωθεί και να δοθεί η γεωµετρική ερµηνεία του θεωρήµατος Μέσης Τιµής του ιαφορικού Λογισµού. (3 µονάδες)
 Α Να διατυπωθεί και να δοθεί η γεωµετρική ερµηνεία του θεωρήµατος Μέσης Τιµής του ιαφορικού Λογισµού Α Έστω µια συνάρτηση ορισµένη σε ένα διάστηµα Αν η είναι συνεχής στο και ( ) = για κάθε εσωτερικό σηµείο
Α Να διατυπωθεί και να δοθεί η γεωµετρική ερµηνεία του θεωρήµατος Μέσης Τιµής του ιαφορικού Λογισµού Α Έστω µια συνάρτηση ορισµένη σε ένα διάστηµα Αν η είναι συνεχής στο και ( ) = για κάθε εσωτερικό σηµείο
Για να προσδιορίσουμε τη μονοτονία της συνάρτησης η πρέπει να βρούμε το πρόσημο της h, το οποίο εξαρτάται από τη συνάρτηση φ(x) = e x 1
 ΘΕΜΑ Έστω οι συναρτήσεις, g με () και g() ln( + ) +. Να αποδείξετε ότι οι C, C g έχουν ακριβώς ένα κοινό σημείο. Στη συνέχεια να δείξετε ότι στο σημείο αυτό έχουν κοινή εφαπτόμενη, την οποία και να βρείτε.
ΘΕΜΑ Έστω οι συναρτήσεις, g με () και g() ln( + ) +. Να αποδείξετε ότι οι C, C g έχουν ακριβώς ένα κοινό σημείο. Στη συνέχεια να δείξετε ότι στο σημείο αυτό έχουν κοινή εφαπτόμενη, την οποία και να βρείτε.
Μαθηματικά Ο.Π. Γ ΓΕΛ 29/ 04 / 2018 ΘΕΜΑ Α. Α1. Σελίδα 216. Α2.i) Λ ii) Σελίδα 134. Α3. Σελίδα 128
 Γ ΓΕΛ 9/ 4 / 8 Μαθηματικά Ο.Π. ΘΕΜΑ Α Α. Σελίδα 6 Α.i) Λ ii) Σελίδα 34 Α3. Σελίδα 8 Α4. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν γράφοντας στο γράμμα που αντιστοιχεί σε κάθε πρόταση τη λέξη Σωστό
Γ ΓΕΛ 9/ 4 / 8 Μαθηματικά Ο.Π. ΘΕΜΑ Α Α. Σελίδα 6 Α.i) Λ ii) Σελίδα 34 Α3. Σελίδα 8 Α4. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν γράφοντας στο γράμμα που αντιστοιχεί σε κάθε πρόταση τη λέξη Σωστό
ΑΠΑΝΤΗΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 28 ΜΑΪΟΥ 2012
 ΑΠΑΝΤΗΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 8 ΜΑΪΟΥ ΘΕΜΑ Α Α. Ο.Ε.Δ.Β. σελ. 53 Α. Ο.Ε.Δ.Β. σελ. 9 Α3. Ο.Ε.Δ.Β. σελ. 58 Α4. α) Σ β) Σ γ) Λ δ) Λ ε) Λ ΘΕΜΑ Β Β. Ισχύει z z = 4 () Έχουμε από
ΑΠΑΝΤΗΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 8 ΜΑΪΟΥ ΘΕΜΑ Α Α. Ο.Ε.Δ.Β. σελ. 53 Α. Ο.Ε.Δ.Β. σελ. 9 Α3. Ο.Ε.Δ.Β. σελ. 58 Α4. α) Σ β) Σ γ) Λ δ) Λ ε) Λ ΘΕΜΑ Β Β. Ισχύει z z = 4 () Έχουμε από
x, οπότε για x 0 η g παρουσιάζει
 ΜΑΘΗΜΑΤΙΚΑ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ 9 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ (Σε όλη την ύλη) ΘΕΜΑ Α A Βλέπε Σχολικό βιβλίο σελίδα 33 A
ΜΑΘΗΜΑΤΙΚΑ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ 9 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ (Σε όλη την ύλη) ΘΕΜΑ Α A Βλέπε Σχολικό βιβλίο σελίδα 33 A
ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΩΝ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΩΝ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Ο Να εξετάσετε ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λανθασµένες.. Αν η συνάρτηση είναι συνεχής στο
ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΩΝ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Ο Να εξετάσετε ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λανθασµένες.. Αν η συνάρτηση είναι συνεχής στο
ΜΑΘΗΜΑΤΙΚΑ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ. f (f )(x) x f (f )(x) x f (f )(x) (f ) (x)
 ΜΑΘΗΜΑΤΙΚΑ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ 4 Ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α A Βλέπε Σχολικό βιβλίο σελίδα 4 A α) Βλέπε Σχολικό βιβλίο
ΜΑΘΗΜΑΤΙΚΑ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ 4 Ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α A Βλέπε Σχολικό βιβλίο σελίδα 4 A α) Βλέπε Σχολικό βιβλίο
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 11 ΙΟΥΝΙΟΥ 2018 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ
 ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ ΙΟΥΝΙΟΥ 8 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α Θεωρία σχολ βιβλίου σελ 99 Α α ψευδής β g Α Θεωρία
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ ΙΟΥΝΙΟΥ 8 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α Θεωρία σχολ βιβλίου σελ 99 Α α ψευδής β g Α Θεωρία
2.8 ΚΥΡΤΟΤΗΤΑ ΣΗΜΕΙΑ ΚΑΜΠΗΣ ΣΥΝΑΡΤΗΣΗΣ
 8 ΚΥΡΤΟΤΗΤΑ ΣΗΜΕΙΑ ΚΑΜΠΗΣ ΣΥΝΑΡΤΗΣΗΣ 49 ΟΡΙΣΜΟΣ 6 4 Πότε μια συνάρτηση λέγεται κυρτή και πότε κοίλη σε ένα διάστημα Δ ; Απάντηση : Έστω μία συνάρτηση σ υ ν ε χ ή ς σ ένα διάστημα Δ και π α ρ α γ ω γ ί
8 ΚΥΡΤΟΤΗΤΑ ΣΗΜΕΙΑ ΚΑΜΠΗΣ ΣΥΝΑΡΤΗΣΗΣ 49 ΟΡΙΣΜΟΣ 6 4 Πότε μια συνάρτηση λέγεται κυρτή και πότε κοίλη σε ένα διάστημα Δ ; Απάντηση : Έστω μία συνάρτηση σ υ ν ε χ ή ς σ ένα διάστημα Δ και π α ρ α γ ω γ ί
ΜΑΘΗΜΑΤΙΚΑ ΟΙΚΟΝΟΜΙΚΗΣ ΕΠΙΣΤΗΜΗΣ I 22 Διάρκεια εξέτασης: 2 ώρες και 15' 1 (4 μονάδες)
 ΜΑΘΗΜΑΤΙΚΑ ΟΙΚΟΝΟΜΙΚΗΣ ΕΠΙΣΤΗΜΗΣ I Διάρκεια εξέτασης: ώρες και 15' 1 (4 μονάδες) f() α) Να βρεθούν γραφικά τα σημεία ισοελαστικότητας, αν υπάρχουν, της συνάρτησης f() που έχει το γράφημα του παραπλεύρως
ΜΑΘΗΜΑΤΙΚΑ ΟΙΚΟΝΟΜΙΚΗΣ ΕΠΙΣΤΗΜΗΣ I Διάρκεια εξέτασης: ώρες και 15' 1 (4 μονάδες) f() α) Να βρεθούν γραφικά τα σημεία ισοελαστικότητας, αν υπάρχουν, της συνάρτησης f() που έχει το γράφημα του παραπλεύρως
Επιμέλεια: Παναγιώτης Γιαννές
 Λ Υ Σ Ε Ι Σ Θ Ε Μ Α Τ Ω Ν Π Α Ν Ε Λ Λ Η Ν Ι Ω Ν Ε Ξ Ε Τ Α Σ Ε Ω Ν 08 Μ Α Θ Η Μ Α Τ Ι Κ Ω Ν Π Ρ Ο Σ Α Ν Α Τ Ο Λ Ι Σ Μ ΟΥ Επιμέλεια: Παναγιώτης Γιαννές ΘΕΜΑ Α Α Θεωρία σχολικού βιβλίου σελίδα 99 Α α Ο ισχυρισμός
Λ Υ Σ Ε Ι Σ Θ Ε Μ Α Τ Ω Ν Π Α Ν Ε Λ Λ Η Ν Ι Ω Ν Ε Ξ Ε Τ Α Σ Ε Ω Ν 08 Μ Α Θ Η Μ Α Τ Ι Κ Ω Ν Π Ρ Ο Σ Α Ν Α Τ Ο Λ Ι Σ Μ ΟΥ Επιμέλεια: Παναγιώτης Γιαννές ΘΕΜΑ Α Α Θεωρία σχολικού βιβλίου σελίδα 99 Α α Ο ισχυρισμός
ΔΙΑΓΩΝΙΣΜΑ 12., στο ίδιο σύστημα
 Μέρος Α ΔΙΑΓΩΝΙΣΜΑ 1 1. (4 μονάδες) α). Η συνάρτηση () έχει το παραπλεύρως γράφημα. () Να βρεθούν τα γραφήματα της μέσης τιμής: A() = () / και του οριακού ρυθμού: M() = (), στο ίδιο σύστημα συντεταγμένων.
Μέρος Α ΔΙΑΓΩΝΙΣΜΑ 1 1. (4 μονάδες) α). Η συνάρτηση () έχει το παραπλεύρως γράφημα. () Να βρεθούν τα γραφήματα της μέσης τιμής: A() = () / και του οριακού ρυθμού: M() = (), στο ίδιο σύστημα συντεταγμένων.
Γ Ε Ν Ι Κ Ο Δ Ι Α Γ Ω Ν Ι Σ Μ Α Ο Ι Κ Ο Ν Ο Μ Ι Α Σ - Θ Ε Τ Ι Κ Η Σ Γ Τ Α Ξ Η Β. Ρ.
 Γ Ε Ν Ι Κ Ο Δ Ι Α Γ Ω Ν Ι Σ Μ Α Ο Ι Κ Ο Ν Ο Μ Ι Α Σ - Θ Ε Τ Ι Κ Η Σ 6 Γ Τ Α Ξ Η Β. Ρ. Θ Ε Μ Α ο Α. Έστω μια συνάρτηση f ορισμένη στο Δ. Αν η f είναι συνεχής στο Δ και f (χ)= για κάθε εσωτερικό σημείο του
Γ Ε Ν Ι Κ Ο Δ Ι Α Γ Ω Ν Ι Σ Μ Α Ο Ι Κ Ο Ν Ο Μ Ι Α Σ - Θ Ε Τ Ι Κ Η Σ 6 Γ Τ Α Ξ Η Β. Ρ. Θ Ε Μ Α ο Α. Έστω μια συνάρτηση f ορισμένη στο Δ. Αν η f είναι συνεχής στο Δ και f (χ)= για κάθε εσωτερικό σημείο του
ΘΕΜΑΤΑΚΙΑ ΓΕΝΙΚΑ. x 0. 2 x
 ΘΕΜΑ A ΘΕΜΑΤΑΚΙΑ ΓΕΝΙΚΑ. Δίνεται η συνάρτηση f με τύπο: f ( ) ln,,. Να δείξετε ότι η f είναι αντιστρέψιμη και να βρείτε το πεδίο ορισμού της αντίστροφής της.. Να δικαιολογήσετε ότι η εξίσωση f ( ) a, a,
ΘΕΜΑ A ΘΕΜΑΤΑΚΙΑ ΓΕΝΙΚΑ. Δίνεται η συνάρτηση f με τύπο: f ( ) ln,,. Να δείξετε ότι η f είναι αντιστρέψιμη και να βρείτε το πεδίο ορισμού της αντίστροφής της.. Να δικαιολογήσετε ότι η εξίσωση f ( ) a, a,
ΔΙΑΓΩΝΙΣΜΑ 1. Α Μέρος
 Α Μέρος ΔΙΑΓΩΝΙΣΜΑ 1 1. (3.6 μονάδες) (α). Δίνεται η εξίσωση: = 8. Αν το ελαττωθεί από την τιμή = κατά 1%, να εκτιμηθεί η αντίστοιχη ποσοστιαία μεταβολή στην τιμή του. (β). Να διαπιστωθεί ότι η συνάρτηση
Α Μέρος ΔΙΑΓΩΝΙΣΜΑ 1 1. (3.6 μονάδες) (α). Δίνεται η εξίσωση: = 8. Αν το ελαττωθεί από την τιμή = κατά 1%, να εκτιμηθεί η αντίστοιχη ποσοστιαία μεταβολή στην τιμή του. (β). Να διαπιστωθεί ότι η συνάρτηση
ΘΕΜΑ Α. Α1. Θεωρία -απόδειξη θεωρήματος στη σελίδα 262 (μόνο το iii) στο σχολικό βιβλίο.
 ΙΟΥΝΙΟΥ 0 ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΛΥΚΕΙΩΝ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α. Θεωρία -απόδειξη θεωρήματος στη σελίδα 6 (μόνο το iii) στο σχολικό βιβλίο.
ΙΟΥΝΙΟΥ 0 ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΛΥΚΕΙΩΝ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α. Θεωρία -απόδειξη θεωρήματος στη σελίδα 6 (μόνο το iii) στο σχολικό βιβλίο.
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΜΑΘΗΜΑΤΙΚΑ ΤΑΞΗ / ΤΜΗΜΑ : ΘΕΤΙΚΩΝ & ΟΙΚΟΝΟΜΙΚΩΝ ΣΠΟΥΔΩΝ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΤΕΛΙΚΟ ΕΠΑΝΑΛΗΠΤΙΚΟ 2018
 ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΜΑΘΗΜΑΤΙΚΑ ΤΑΞΗ / ΤΜΗΜΑ : ΘΕΤΙΚΩΝ & ΟΙΚΟΝΟΜΙΚΩΝ ΣΠΟΥΔΩΝ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΤΕΛΙΚΟ ΕΠΑΝΑΛΗΠΤΙΚΟ 18 ΑΡΙΘΜΟΣ ΣΕΛΙΔΩΝ : 7 ΘΕΜΑ Α Α1. Πότε η ευθεία : λέγεται κατακόρυφη
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΜΑΘΗΜΑΤΙΚΑ ΤΑΞΗ / ΤΜΗΜΑ : ΘΕΤΙΚΩΝ & ΟΙΚΟΝΟΜΙΚΩΝ ΣΠΟΥΔΩΝ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΤΕΛΙΚΟ ΕΠΑΝΑΛΗΠΤΙΚΟ 18 ΑΡΙΘΜΟΣ ΣΕΛΙΔΩΝ : 7 ΘΕΜΑ Α Α1. Πότε η ευθεία : λέγεται κατακόρυφη
II.6 ΙΣΟΣΤΑΘΜΙΚΕΣ. 1. Γραφήματα-Επιφάνειες: z= 2. Γραμμική προσέγγιση-εφαπτόμενο επίπεδο. 3. Ισοσταθμικές: f(x, y) = c
 II.6 ΙΣΟΣΤΑΘΜΙΚΕΣ.Γραφήματα-Επιφάνειες.Γραμμική προσέγγιση-εφαπτόμενο επίπεδο 3.Ισοσταθμικές 4.Κλίση ισοσταθμικών 5.Διανυσματική ή Ιακωβιανή παράγωγος 6.Ιδιότητες των ισοσταθμικών 7.κυρτότητα των ισοσταθμικών
II.6 ΙΣΟΣΤΑΘΜΙΚΕΣ.Γραφήματα-Επιφάνειες.Γραμμική προσέγγιση-εφαπτόμενο επίπεδο 3.Ισοσταθμικές 4.Κλίση ισοσταθμικών 5.Διανυσματική ή Ιακωβιανή παράγωγος 6.Ιδιότητες των ισοσταθμικών 7.κυρτότητα των ισοσταθμικών
ΛΥΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗ ΘΕΜΑΤΩΝ 5 05/05/2016 ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΛΥΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗ ΘΕΜΑΤΩΝ 5 5/5/6 ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΜΑ ο Α. Τι ορίζουμε ως εφαπτομένη (όχι κατακόρυφη) της γραφικής παράστασης C
ΛΥΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗ ΘΕΜΑΤΩΝ 5 5/5/6 ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΜΑ ο Α. Τι ορίζουμε ως εφαπτομένη (όχι κατακόρυφη) της γραφικής παράστασης C
Υψώνουμε την δοσμένη σχέση στο τετράγωνο οπότε
 ΑΠΑNTHΣΕΙΣ ΣΤA ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ ΠΑΝΕΛΛΑΔΙΚΕΣ ΘΕΜΑ A A Απόδειξη Σελ 53 Α Ορισμός Σελ 9 Α3 Ορισμός Σελ 58 Α4 α) Σ β) Σ γ) Λ δ) Λ ε) Λ ΘΕΜΑ Β Β 4 4 4 Άρα ο γεωμετρικός τόπος των εικόνων των μιγαδικών
ΑΠΑNTHΣΕΙΣ ΣΤA ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ ΠΑΝΕΛΛΑΔΙΚΕΣ ΘΕΜΑ A A Απόδειξη Σελ 53 Α Ορισμός Σελ 9 Α3 Ορισμός Σελ 58 Α4 α) Σ β) Σ γ) Λ δ) Λ ε) Λ ΘΕΜΑ Β Β 4 4 4 Άρα ο γεωμετρικός τόπος των εικόνων των μιγαδικών
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 00 ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Α A. Έστω μια συνάρτηση ορισμένη σε ένα διάστημα. Αν F είναι μια παράγουσα της στο, τότε να αποδείξετε ότι:
ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 00 ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Α A. Έστω μια συνάρτηση ορισμένη σε ένα διάστημα. Αν F είναι μια παράγουσα της στο, τότε να αποδείξετε ότι:
2.8 ΚΥΡΤΟΤΗΤΑ ΣΗΜΕΙΑ ΚΑΜΠΗΣ ΣΥΝΑΡΤΗΣΗΣ
 Ο ΚΕΦΑΛΑΙΟ : ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ 8 ΚΥΡΤΟΤΗΤΑ ΣΗΜΕΙΑ ΚΑΜΠΗΣ ΣΥΝΑΡΤΗΣΗΣ 49 ΟΡΙΣΜΟΣ 6 4 Πότε μια συνάρτηση λέγεται κυρτή και πότε κοίλη σε ένα διάστημα Δ ; Απάντηση : Έστω μία συνάρτηση σ υ ν ε χ ή ς σ ένα
Ο ΚΕΦΑΛΑΙΟ : ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ 8 ΚΥΡΤΟΤΗΤΑ ΣΗΜΕΙΑ ΚΑΜΠΗΣ ΣΥΝΑΡΤΗΣΗΣ 49 ΟΡΙΣΜΟΣ 6 4 Πότε μια συνάρτηση λέγεται κυρτή και πότε κοίλη σε ένα διάστημα Δ ; Απάντηση : Έστω μία συνάρτηση σ υ ν ε χ ή ς σ ένα
Πανελλαδικές εξετάσεις 2017
 Πανελλαδικές εξετάσεις 7 Ενδεικτικές απαντήσεις στο μάθημα «Μαθηματικά ΟΠ» Θέμα Α Α Θεωρία σχολικού βιβλίου σελ 36 Α α) Λ β) H συνάρτηση ( ) είναι παραγωγίσιμη σε αυτό αφού: ( ) () lim lim είναι συνεχής
Πανελλαδικές εξετάσεις 7 Ενδεικτικές απαντήσεις στο μάθημα «Μαθηματικά ΟΠ» Θέμα Α Α Θεωρία σχολικού βιβλίου σελ 36 Α α) Λ β) H συνάρτηση ( ) είναι παραγωγίσιμη σε αυτό αφού: ( ) () lim lim είναι συνεχής
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Δευτέρα 11 Ιουνίου 2018 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ
 ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Δευτέρα Ιουνίου 08 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (Ενδεικτικές Απαντήσεις) ΘΕΜΑ Α Α Απόδειξη θεωρήματος σελ 99 σχολικού βιβλίου
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Δευτέρα Ιουνίου 08 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (Ενδεικτικές Απαντήσεις) ΘΕΜΑ Α Α Απόδειξη θεωρήματος σελ 99 σχολικού βιβλίου
, να αποδείξετε ότι και η συνάρτηση f+g είναι παραγωγίσιμη στο x. και ισχύει. Μονάδες 9 Α2. Έστω μια συνάρτηση f με πεδίο ορισμού το Α και [, ]
![, να αποδείξετε ότι και η συνάρτηση f+g είναι παραγωγίσιμη στο x. και ισχύει. Μονάδες 9 Α2. Έστω μια συνάρτηση f με πεδίο ορισμού το Α και [, ] , να αποδείξετε ότι και η συνάρτηση f+g είναι παραγωγίσιμη στο x. και ισχύει. Μονάδες 9 Α2. Έστω μια συνάρτηση f με πεδίο ορισμού το Α και [, ]](/thumbs/65/52608485.jpg) ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 6-7 ΜΑΘΗΜΑ / ΤΑΞΗ : ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: Μαθηματικά Προσανατολισμού Γ' Λυκείου Θέμα Α Α. Αν οι συναρτήσεις, g είναι παραγωγίσιμες στο, να αποδείξετε ότι και
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 6-7 ΜΑΘΗΜΑ / ΤΑΞΗ : ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: Μαθηματικά Προσανατολισμού Γ' Λυκείου Θέμα Α Α. Αν οι συναρτήσεις, g είναι παραγωγίσιμες στο, να αποδείξετε ότι και
ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ-ΛΑΘΟΥΣ
 ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ-ΛΑΘΟΥΣ 1. Αν f συνεχής στο [α, β] είναι f ( ) d 0 f ( ) 0 2. Αν f συνεχής και γν. αύξουσα στο [α, β] ισχύει ότι: f ( ) d 0. 3. Αν f ( ) d g( ) d, ό f ( ) g( ) ά [, ]. 4. Το σύνολο τιμών
ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ-ΛΑΘΟΥΣ 1. Αν f συνεχής στο [α, β] είναι f ( ) d 0 f ( ) 0 2. Αν f συνεχής και γν. αύξουσα στο [α, β] ισχύει ότι: f ( ) d 0. 3. Αν f ( ) d g( ) d, ό f ( ) g( ) ά [, ]. 4. Το σύνολο τιμών
ΜΑΘΗΜΑΤΙΚΑ ΟΙΚΟΝΟΜΙΚΗΣ ΕΠΙΣΤΗΜΗΣ Ι 15 Διάρκεια εξέτασης: 2 ώρες
 ΜΑΘΗΜΑΤΙΚΑ ΟΙΚΟΝΟΜΙΚΗΣ ΕΠΙΣΤΗΜΗΣ Ι 15 Διάρκεια εξέτασης: ώρες Μέρος Α 1. (4 μονάδες) (α). Να γίνει το γράφημα μιας συνεχούς συνάρτησης f() της οποίας η παράγωγος έχει το γράφημα του παραπλεύρως σχήματος.
ΜΑΘΗΜΑΤΙΚΑ ΟΙΚΟΝΟΜΙΚΗΣ ΕΠΙΣΤΗΜΗΣ Ι 15 Διάρκεια εξέτασης: ώρες Μέρος Α 1. (4 μονάδες) (α). Να γίνει το γράφημα μιας συνεχούς συνάρτησης f() της οποίας η παράγωγος έχει το γράφημα του παραπλεύρως σχήματος.
AΠΑΝΤΗΣΕΙΣ. z z 0 που είναι τριώνυμο με διακρίνουσα. 2 Re z 4Im z R. x 2 y x y 2
 AΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α Βλ σχολ βιβλίο σελ 5 Α Βλ σχολ βιβλίο σελ Α Σ Σ Σ 4 Σ 5 - Λ ΘΕΜΑ Β Β Η εξίσωση () z ισοδυναμεί με την z z που είναι τριώνυμο με διακρίνουσα 4 διότι 4 Άρα οι ρίζες είναι συζυγείς μιγαδικές
AΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α Βλ σχολ βιβλίο σελ 5 Α Βλ σχολ βιβλίο σελ Α Σ Σ Σ 4 Σ 5 - Λ ΘΕΜΑ Β Β Η εξίσωση () z ισοδυναμεί με την z z που είναι τριώνυμο με διακρίνουσα 4 διότι 4 Άρα οι ρίζες είναι συζυγείς μιγαδικές
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Β ΜΕΡΟΣ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 7-8 Β ΜΕΡΟΣ. Δίνεται η τέσσερις φορές παραγωγίσιμη στο συνάρτηση f τέτοια ώστε : f (4) () + f () () = ημ + συν, για κάθε και f() =, f () =, f () = - και f () () =. α) Να βρείτε τον
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 7-8 Β ΜΕΡΟΣ. Δίνεται η τέσσερις φορές παραγωγίσιμη στο συνάρτηση f τέτοια ώστε : f (4) () + f () () = ημ + συν, για κάθε και f() =, f () =, f () = - και f () () =. α) Να βρείτε τον
Οι ασκήσεις βασίζονται στο αξιόλογο φυλλάδιο του Μαθηματικού Μιλτ. Παπαγρηγοράκη, από τις σημειώσεις του για το 4ο Γενικό Λύκειο Χανίων [ <
 Οι ασκήσεις βασίζονται στο αξιόλογο φυλλάδιο του Μαθηματικού Μιλτ. Παπαγρηγοράκη, από τις σημειώσεις του για το 4ο Γενικό Λύκειο Χανίων [008-009 < Mathematica.gr], τον οποίο κι ευχαριστώ ιδιαίτερα για
Οι ασκήσεις βασίζονται στο αξιόλογο φυλλάδιο του Μαθηματικού Μιλτ. Παπαγρηγοράκη, από τις σημειώσεις του για το 4ο Γενικό Λύκειο Χανίων [008-009 < Mathematica.gr], τον οποίο κι ευχαριστώ ιδιαίτερα για
f(x) Af(x) = και Mf(x) = f (x) x
 ΜΑΘΗΜΑΤΙΚΑ ΟΙΚΟΝΟΜΙΚΗΣ ΕΠΙΣΤΗΜΗΣ I Διάρκεια εξέτασης: ώρες και 5' (4 μονάδες) (α). Η συνάρτηση f() έχει το παραπλεύρως γράφημα με πλάγια ασύμπτωτο. Να δοθούν, στο ίδιο σύστημα συντεταγμένων, τα γραφήματα
ΜΑΘΗΜΑΤΙΚΑ ΟΙΚΟΝΟΜΙΚΗΣ ΕΠΙΣΤΗΜΗΣ I Διάρκεια εξέτασης: ώρες και 5' (4 μονάδες) (α). Η συνάρτηση f() έχει το παραπλεύρως γράφημα με πλάγια ασύμπτωτο. Να δοθούν, στο ίδιο σύστημα συντεταγμένων, τα γραφήματα
ΚΕΦΑΛΑΙΟ 3 ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΕΩΝ
 ΚΕΦΑΛΑΙΟ 3 ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΕΩΝ 31 Ορισµοί Ορισµός 311 Εστω f : A f( A), A, f( A) και έστω 0 Α είναι σηµείο συσσώρευσης του συνόλου Α Θα λέµε ότι η f είναι παραγωγίσιµη στο σηµείο 0 εάν υπάρχει λ : Ισοδύναµα:
ΚΕΦΑΛΑΙΟ 3 ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΕΩΝ 31 Ορισµοί Ορισµός 311 Εστω f : A f( A), A, f( A) και έστω 0 Α είναι σηµείο συσσώρευσης του συνόλου Α Θα λέµε ότι η f είναι παραγωγίσιµη στο σηµείο 0 εάν υπάρχει λ : Ισοδύναµα:
( ) f( x ) ΔΙΑΓΩΝΙΣΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ. Επώνυμο: Όνομα: Τμήμα: Ημερομηνία: Α Βαθ. Β Βαθ. Μ.Ο. (ενδεικτικές λύσεις)
 Επώνυμο: Όνομα: Τμήμα: ΤΣΙΜΙΣΚΗ & ΚΑΡΟΛΟΥ ΝΤΗΛ ΓΩΝΙΑ ΤΗΛ : 777 594 ΑΡΤΑΚΗΣ Κ. ΤΟΥΜΠΑ ΤΗΛ : 99 9494 www.sygrono.gr Ημερομηνία: Α Βαθ. Β Βαθ. Μ.Ο. ΔΙΑΓΩΝΙΣΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ (ενδεικτικές
Επώνυμο: Όνομα: Τμήμα: ΤΣΙΜΙΣΚΗ & ΚΑΡΟΛΟΥ ΝΤΗΛ ΓΩΝΙΑ ΤΗΛ : 777 594 ΑΡΤΑΚΗΣ Κ. ΤΟΥΜΠΑ ΤΗΛ : 99 9494 www.sygrono.gr Ημερομηνία: Α Βαθ. Β Βαθ. Μ.Ο. ΔΙΑΓΩΝΙΣΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ (ενδεικτικές
Af(x) = και Mf(x) = f (x) x
 ΜΑΘΗΜΑΤΙΚΑ ΟΙΚΟΝΟΜΙΚΗΣ ΕΠΙΣΤΗΜΗΣ Ι. Λύσεις 9 Διάρκεια εξέτασης: ώρες και 5' (4 μονάδες) (α). Η συνάρτηση f() έχει το παραπλεύρως γράφημα με πλάγια ασύμπτωτο. Να δοθούν, στο ίδιο σύστημα συντεταγμένων,
ΜΑΘΗΜΑΤΙΚΑ ΟΙΚΟΝΟΜΙΚΗΣ ΕΠΙΣΤΗΜΗΣ Ι. Λύσεις 9 Διάρκεια εξέτασης: ώρες και 5' (4 μονάδες) (α). Η συνάρτηση f() έχει το παραπλεύρως γράφημα με πλάγια ασύμπτωτο. Να δοθούν, στο ίδιο σύστημα συντεταγμένων,
ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Γ ΛΥΚΕΙΟΥ 2008
 ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Γ ΛΥΚΕΙΟΥ 8 ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Γ ΛΥΚΕΙΟΥ 8 ΕΠΙΚΑΙΡΟΠΟΙΗΜΕΝΗ ΣΤΟ ΠΛΑΙΣΙΟ ΤΗΣ ΝΕΑΣ ΥΛΗΣ ΜΑΘΗΜΑΤΙΚΑ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ
ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Γ ΛΥΚΕΙΟΥ 8 ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Γ ΛΥΚΕΙΟΥ 8 ΕΠΙΚΑΙΡΟΠΟΙΗΜΕΝΗ ΣΤΟ ΠΛΑΙΣΙΟ ΤΗΣ ΝΕΑΣ ΥΛΗΣ ΜΑΘΗΜΑΤΙΚΑ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ
Μαθηματικά Ο.Π. Γ ΓΕΛ 05/ 05 / 2019 ΘΕΜΑ Α. Α1. Σελίδες Σχολικού Βιβλίου. Α2. Σελίδα 161 Σχολικού Βιβλίου
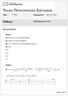 Γ ΓΕΛ 5/ 5 / 9 Μαθηματικά Ο.Π. ΘΕΜΑ Α Α. Σελίδες 4-43 Σχολικού Βιβλίου Α. Σελίδα 6 Σχολικού Βιβλίου Α3. i) Ψ ii) Σελίδα 56 Σχολικού Βιβλίου (Σχόλιο) Α4. α) Λ β) Λ γ) Σ δ) Σ ε) Σ ΘΕΜΑ Β ' ' ' ( ) ( )( )
Γ ΓΕΛ 5/ 5 / 9 Μαθηματικά Ο.Π. ΘΕΜΑ Α Α. Σελίδες 4-43 Σχολικού Βιβλίου Α. Σελίδα 6 Σχολικού Βιβλίου Α3. i) Ψ ii) Σελίδα 56 Σχολικού Βιβλίου (Σχόλιο) Α4. α) Λ β) Λ γ) Σ δ) Σ ε) Σ ΘΕΜΑ Β ' ' ' ( ) ( )( )
ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Γ ΛΥΚΕΙΟΥ 2010 ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 2010
 ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Γ ΛΥΚΕΙΟΥ ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ 3ο : Δίνεται η συνάρτηση f :(,) R με f() η οποία για κάθε (,
ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Γ ΛΥΚΕΙΟΥ ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ 3ο : Δίνεται η συνάρτηση f :(,) R με f() η οποία για κάθε (,
Εξετάσεις 11 Ιουνίου Μαθηματικά Προσανατολισμού Γ Λυκείου ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ
 Εξετάσεις Ιουνίου 8 Μαθηματικά Προσανατολισμού Γ Λυκείου (Θετικών Σπουδών και Σπουδών Οικονομίας-Πληροφορικής) ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΤΣΙΜΙΣΚΗ & ΚΑΡΟΛΟΥ ΝΤΗΛ ΓΩΝΙΑ THΛ: 777 59 ΑΡΤΑΚΗΣ - Κ ΤΟΥΜΠΑ THΛ: 99
Εξετάσεις Ιουνίου 8 Μαθηματικά Προσανατολισμού Γ Λυκείου (Θετικών Σπουδών και Σπουδών Οικονομίας-Πληροφορικής) ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΤΣΙΜΙΣΚΗ & ΚΑΡΟΛΟΥ ΝΤΗΛ ΓΩΝΙΑ THΛ: 777 59 ΑΡΤΑΚΗΣ - Κ ΤΟΥΜΠΑ THΛ: 99
2015zi 2015zi 2015zi 2015zi 4030zi 4030zi z z
 Λύσεις των θεμάτων προσομοίωσης στα Μαθηματικά Θετικής και Τεχνολογικής Κατευθυνσης 15 ΛΥΣΕΙΣ ΘΕΜΑΤΩΝ ΠΡΟΣΟΜΟΙΩΣΗΣ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 15 ΘΕΜΑ Α Α1.
Λύσεις των θεμάτων προσομοίωσης στα Μαθηματικά Θετικής και Τεχνολογικής Κατευθυνσης 15 ΛΥΣΕΙΣ ΘΕΜΑΤΩΝ ΠΡΟΣΟΜΟΙΩΣΗΣ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 15 ΘΕΜΑ Α Α1.
20 επαναληπτικά θέματα
 0 επαναληπτικά θέματα για τα μαθηματικά κατεύθυνσης Γ λυκείου (τεύχος σχολικό έτος 03-04) Γράφουν οι μαθηματικοί: Βέρρας Οδυσσέας Καρύμπαλης Νώντας Κοτσώνης Γιώργος Κώνστας Χάρης Μπούζας Δημήτρης Πετρόπουλος
0 επαναληπτικά θέματα για τα μαθηματικά κατεύθυνσης Γ λυκείου (τεύχος σχολικό έτος 03-04) Γράφουν οι μαθηματικοί: Βέρρας Οδυσσέας Καρύμπαλης Νώντας Κοτσώνης Γιώργος Κώνστας Χάρης Μπούζας Δημήτρης Πετρόπουλος
Απαντήσεις στα Μαθηματικά Κατεύθυνσης 2016
 ΘΕΜΑ Α Απαντήσεις στα Μαθηματικά Κατεύθυνσης 6 Α.. Σχολ. Βιβλίο, Θεωρία, σελ.6-(i) Α.. Σχολ. Βιβλίο, Θεωρία, σελ. 4 Α. Σχολ. Βιβλίο, Θεωρία, σελ. 46,47 Α.4. α. Λ β. Σ γ. Λ δ. Σ ε. Σ ΘΕΜΑ Β B. Η συνάρτηση
ΘΕΜΑ Α Απαντήσεις στα Μαθηματικά Κατεύθυνσης 6 Α.. Σχολ. Βιβλίο, Θεωρία, σελ.6-(i) Α.. Σχολ. Βιβλίο, Θεωρία, σελ. 4 Α. Σχολ. Βιβλίο, Θεωρία, σελ. 46,47 Α.4. α. Λ β. Σ γ. Λ δ. Σ ε. Σ ΘΕΜΑ Β B. Η συνάρτηση
Επαναληπτικά Θέματα Μαθηματικών Γ Λυκείου Κατεύθυνσης
 6 Επαναληπτικά Θέματα Μαθηματικών Γ Λυκείου Κατεύθυνσης ΘΕΜΑ Έστω η συνεχής συνάρτηση f : (, ) R τέτοια ώστε για κάθε να ισχύει: t f ( ) dt. f () t te ( ) α) Να αποδείξετε ότι για κάθε ισχύει: β) Να αποδείξετε
6 Επαναληπτικά Θέματα Μαθηματικών Γ Λυκείου Κατεύθυνσης ΘΕΜΑ Έστω η συνεχής συνάρτηση f : (, ) R τέτοια ώστε για κάθε να ισχύει: t f ( ) dt. f () t te ( ) α) Να αποδείξετε ότι για κάθε ισχύει: β) Να αποδείξετε
ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟ ΛΑΘΟΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ., τότε η f είναι πάντοτε συνεχής στο x., τότε η f είναι συνεχής στο x.
 ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟ ΛΑΘΟΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στο τετράδιό σας την ένδειξη σωστό ή λάθος δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση
ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟ ΛΑΘΟΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στο τετράδιό σας την ένδειξη σωστό ή λάθος δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση
ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Γ ΛΥΚΕΙΟΥ 2016 ΜΑΘΗΜΑΤΙΚΑ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Γ ΛΥΚΕΙΟΥ 6 ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Γ ΛΥΚΕΙΟΥ 6 ΜΑΘΗΜΑΤΙΚΑ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΜΑ ο
ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Γ ΛΥΚΕΙΟΥ 6 ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Γ ΛΥΚΕΙΟΥ 6 ΜΑΘΗΜΑΤΙΚΑ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΜΑ ο
ΘΕΜΑ Α : Α1. Σχολικό βιβλίο σελίδα 253. Α2. Σχολικό βιβλίο σελίδα 191. Α3. Σχολικό βιβλίο σελίδα 150. Α4. Α)Σ β)σ γ)λ δ)λ ε)λ ΘΕΜΑ Β : Β1.
 ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ : ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΙΓΙΚΗΣ Γ ΛΥΚΕΙΟΥ 8 / 05/ 0 ΘΕΜΑ Α : Α Σχολικό βιβλίο σελίδα 53 Α Σχολικό βιβλίο σελίδα 9 Α3 Σχολικό βιβλίο σελίδα 50 Α4 Α)Σ β)σ γ)λ δ)λ ε)λ ΘΕΜΑ Β
ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ : ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΙΓΙΚΗΣ Γ ΛΥΚΕΙΟΥ 8 / 05/ 0 ΘΕΜΑ Α : Α Σχολικό βιβλίο σελίδα 53 Α Σχολικό βιβλίο σελίδα 9 Α3 Σχολικό βιβλίο σελίδα 50 Α4 Α)Σ β)σ γ)λ δ)λ ε)λ ΘΕΜΑ Β
Λύσεις θεμάτων προσομοίωσης 1-Πανελλαδικές Εξετάσεις 2016
 Λύσεις θεμάτων προσομοίωσης -Πανελλαδικές Εξετάσεις 06 Λύσεις θεμάτων ΠΡΟΣΟΜΟΙΩΣΗΣ -- Πανελλαδικών Εξετάσεων 06 Στο μάθημα: «Μαθηματικά Προσανατολισμού Θετικών Σπουδών και Σπουδών Οικονομίας και Πληροφορικής»
Λύσεις θεμάτων προσομοίωσης -Πανελλαδικές Εξετάσεις 06 Λύσεις θεμάτων ΠΡΟΣΟΜΟΙΩΣΗΣ -- Πανελλαδικών Εξετάσεων 06 Στο μάθημα: «Μαθηματικά Προσανατολισμού Θετικών Σπουδών και Σπουδών Οικονομίας και Πληροφορικής»
2. Αν έχουμε μια συνάρτηση f η οποία είναι συνεχής σε ένα διάστημα Δ.
 Κατηγορία η Εύρεση μονοτονίας Τρόπος αντιμετώπισης:. Αν έχουμε μια συνάρτηση f η οποία είναι συνεχής σε ένα διάστημα Δ. Αν f( ) σε κάθε εσωτερικό σημείο του Δ, τότε η f είναι γνησίως αύξουσα σε όλο το
Κατηγορία η Εύρεση μονοτονίας Τρόπος αντιμετώπισης:. Αν έχουμε μια συνάρτηση f η οποία είναι συνεχής σε ένα διάστημα Δ. Αν f( ) σε κάθε εσωτερικό σημείο του Δ, τότε η f είναι γνησίως αύξουσα σε όλο το
Ασκήσεις Επανάληψης Γ Λυκείου
 Ασκήσεις Επανάληψης Γ Λυκείου Ασκήσεις Επανάληψης σε όλο το εύρος της διδακτέας ύλης Κων/νος Παπασταματίου Κ. Καρτάλη 8 (με Δημητριάδος) Τηλ. 4 3 598 Θε ματα ΟΕΦΕ - 5 Επιμέλεια Κων/νος Παπασταματίου Σελίδα
Ασκήσεις Επανάληψης Γ Λυκείου Ασκήσεις Επανάληψης σε όλο το εύρος της διδακτέας ύλης Κων/νος Παπασταματίου Κ. Καρτάλη 8 (με Δημητριάδος) Τηλ. 4 3 598 Θε ματα ΟΕΦΕ - 5 Επιμέλεια Κων/νος Παπασταματίου Σελίδα
h ln 1 γ) Αν η συνάρτηση f είναι συνεχής στο Δ, τότε είναι και παραγωγίσιμη στο Δ.
 ΘΕΜΑ A Α1. α) Να δώσετε τον ορισμό πότε μια συνάρτηση f είναι συνεχής στο (α, β) και πότε στο [α, β]. Σχεδιάστε μια συνάρτηση που είναι συνεχής στο =1 αλλά όχι παραγωγίσιμη β) Να διατυπώσετε τον ορισμό
ΘΕΜΑ A Α1. α) Να δώσετε τον ορισμό πότε μια συνάρτηση f είναι συνεχής στο (α, β) και πότε στο [α, β]. Σχεδιάστε μια συνάρτηση που είναι συνεχής στο =1 αλλά όχι παραγωγίσιμη β) Να διατυπώσετε τον ορισμό
Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ. Ημερομηνία: Πέμπτη 20 Απριλίου 2017 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ
 ΑΠΟ /4/7 έως τις /4/7 ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Πέμπτη Απριλίου 7 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Α Έστω μία συνάρτηση f ορισμένη σε ένα διάστημα
ΑΠΟ /4/7 έως τις /4/7 ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Πέμπτη Απριλίου 7 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Α Έστω μία συνάρτηση f ορισμένη σε ένα διάστημα
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ. Δευτέρα 25-5-2015 ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΛΥΣΕΙΣ. Α4.) α) Λάθος, β) Σωστό, γ) Λάθος, δ) Σωστό, ε) Σωστό
 ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Δευτέρα 5-5-5 ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΛΥΣΕΙΣ ΘΕΜΑ Α Α.) Θεωρία σελ. 94 Α.) Θεωρία σελ.88 Α3.) Θεωρία σελ. 59 Α4.) α) Λάθος, β) Σωστό, γ) Λάθος, δ) Σωστό, ε) Σωστό
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Δευτέρα 5-5-5 ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΛΥΣΕΙΣ ΘΕΜΑ Α Α.) Θεωρία σελ. 94 Α.) Θεωρία σελ.88 Α3.) Θεωρία σελ. 59 Α4.) α) Λάθος, β) Σωστό, γ) Λάθος, δ) Σωστό, ε) Σωστό
