ΣΚΟΡ 6 στατιστική έρευνα του cosmicway.net
|
|
|
- Αδώνια Ζαφειρόπουλος
- 9 χρόνια πριν
- Προβολές:
Transcript
1 ΣΚΟΡ 6 στατιστική έρευνα του cosmicway.net Το σκορ-6 τείνει να γίνει το πιό δηµοφιλές ιπποδροµιακό στοίχηµα. εν είναι υπερβολή ότι το σκορ-6 είναι το µόνο παιχνίδι που µπορεί να σας επιτρέψει να «νικήσετε τον ιππόδροµο», αν πετύχετε µία µεγάλη νίκη. Με το τετραπλό και µε το σύνθετο φορκάστ µπορεί επίσης να γίνει αυτό, αλλά πιστεύουµε ότι µόνο από µεγάλη τύχη µπορεί κανείς να κερδίσει ένα ποσό της τάξεως των 20,000-30,000 ευρώ, όταν προκύψουν τέτοιες αποδόσεις. Φυσικά και έχουµε δει πολλούς που έχουν κερδίσει και µετά έχασαν πολλαπλάσια. Αυτό συνέβη επειδή µεταβλήθηκαν σε «µηχάνηµα παραγωγής χαρτοπόλεµου» αµέσως µετά τη νίκη, κάτι που θα σας προτείναµε να το αποφύγετε! Πως αντιµετωπίζεται το σκορ-6 από τους παίκτες του ιπποδρόµου, από την εποχή που ξεκίνησε, γύρω στο 1998 ; Το 99.9% το αντιµετωπίζει παίζοντας πλήρες σύστηµα, στο ποσό βέβαια που έχει να διαθέσει ο καθένας, π.χ. τέσσερεις τριπλές και δύο διπλές = 324 στήλες = 486 ευρώ. Στην αρχή πιστεύαµε ότι όσοι έπαιζαν έτσι θα το εγκατέλειπαν αµέσως, όπως είχε συµβεί και στο ΠΡΟΠΟ, στο οποίο όσοι έπαιζαν συστηµατικά έβαζαν όρους computer. Στο ΠΡΟΠΟ η «επιβίωση» παίζοντας πλήρες είναι πρακτικά αδύνατη ενώ µε τη χρήση του computer συµµαζεύεται η κατάσταση. Η αλήθεια είναι όµως ότι το πλήρες στο σκορ-6 δεν είναι τόσο απόλυτα καταδικαστικό και γι αυτό όλοι σχεδόν έµειναν σ αυτό, τη στιγµή βέβαια που δεν ξέρουν περισσότερα και πιθανώς να µην έχουν ασχοληθεί ποτέ µε το ΠΡΟΠΟ, όπως συνήθως συνέβαινε µε τους φίλους του ιπποδρόµου ακόµα και την εποχή που το ΠΡΟΠΟ ήταν το «νάµπερ ουάν» δηµοφιλές παιχνίδι. Το ΠΡΟΠΟ είχε 13 αγώνες και 3 πιθανά σηµεία στον καθένα (σ.σ. 14 τώρα). Το σκορ-6 έχειι 6 αγώνες και µέχρι 20 πιθανές εκβάσεις στον καθένα, εκείνο που µετράει όµως είναι το µέγεθος του παρολί, οι αγώνες. Το 6 είναι το µισό του 13 και λιγώτερο και γι αυτό το λόγο παίζοντας πλήρες υπάρχει περίπτωση να πιάσεις αν έχεις καλά προγνωστικά βέβαια. Αλλά και πάλι υπάρχει µειονέκτηµα του πλήρες έναντι του computer, αρκετά αισθητό. Στην πραγµατικότητα τόσο το ΠΡΟΠΟ όσο και το σκορ-6 είναι, κατά µία βασική έννοια, «λυµένα προβλήµατα» από µαθηµατικής άποψης. Ξεκινάµε από µία βασική έννοια, την πιθανότητα, για να το κατανοήσουµε αυτό: Για να απλουστεύσουµε τα πράγµατα θα εξετάσουµε, από δω και µπρός, την περίπτωση δύο ιπποδροµιών µε τέσσερα άλογα στην κάθε µία. Το σκορ-6 το κάνουµε «σκορ-2» αλλά ότι λέµε επεκτείνεται αµέσως και στο σκορ-6 µε τα έξη σκέλη και στα πεδία µε άνω των έξη ίππων. Η πρώτη ιπποδροµία: Ίππος Πιθανότητα νίκης % ΒΙΣΜΑΡΚ 45% ΤΙΡΠΙΤΣ 30% ΣΑΡΝΧΟΡΣΤ 20% ΓΚΑΪΖΕΝΑΟΥ 5% Η δεύτερη ιπποδροµία: Ίππος Πιθανότητα νίκης % ΓΙΑΜ ΓΙΑΜ 35% ΠΙΠ ΜΠΟ 30% ΠΙΤΙ ΣΙΝΓΚ 25% ΚΟ ΚΟ 10%
2 -2- Πως θα πιάσετε αυτό το σκορ-2 ; Μία µέθοδος είναι να παιξουµε τη δυάδα 1-1, τα δύο φαβορί και αν µας γίνει, µας έγινε. Άλλη µέθοδος είναι να παίξουµε 2 διπλές µε τα δύο φαβορί τις κάθε κούρσας, ήτοι το σύστηµα 1-2 / 1-2 που είναι 4 στήλες συνολικά. Στην παραγµατικότητα οι περιπτπώσεις είναι 16 και η κάθε µία έχει τη δικιά της πιθανότητα, που προκύπτει από τον πολλαπλασιασµό. Έχουµε λοιπόν: 1/1 = 0.45 x 0.35 = = 15.75% 1/2 = 0.45 x 0.30 = = 13.50% 1/3 = 0.45 x 0.25 = = 11.25% 1/4 = 0.45 x 0.10 = = 4.50% 2/1 = 0.30 x 0.35 = = 10.50% 2/2 = 0.30 x 0.30 = = 9.00% 2/3 = 0.30 x 0.25 = = 7.50% 2/4 = 0.30 x 0.10 = = 3.00% 3/1 = 0.20 x 0.35 = = 7.00% 3/2 = 0.20 x 0.30 = = 6.00% 3/3 = 0.20 x 0.25 = = 5.00% 3/4 = 0.20 x 0.10 = = 2.00% 4/1 = 0.05 x 0.35 = = 1.75% 4/2 = 0.05 x 0.30 = = 1.50% 4/3 = 0.05 x 0.25 = = 1.25% 4/4 = 0.05 x 0.10 = = 0.50% Οι παραπάνω δυάδες είναι αταξινόµητες. Οι ταξινοµηµένες δυάδες είναι: 1/1 = 15.75% 1/2 = 13.50% 1/3 = 11.25% 2/1 = 10.50% 2/2 = 9.00% 2/3 = 7.50% 3/1 = 7.00% 3/2 = 6.00% 3/3 = 5.00% 1/4 = 4.50% 2/4 = 3.00% 3/4 = 2.00% 4/1 = 1.75% 4/2 = 1.50% 4/3 = 1.25% 4/4 = 0.50% Από τις παραπάνω πράξεις βλέπετε -ήδη- ένα παικτικό λάθος ; Αν παίξουµε τις δύο διπλές 1-2 / 1-2, δεν παίρνουµε τις 4 µεγαλύτερες τύχες, γιατί δεν παίξαµε το 1/3. Παίζοντας το πληράκι 1-2 / 1-2, παίξαµε την 1 η, -2 η -4 η και 5 η τύχη αλλά την πραγµατική τρίτη τύχη δεν την παίξαµε ήτοι το 1/3! Παρατηρούµε επίσης ότι µε τις 4 πρώτες τύχες η πιθανότητα µας να είµαστε µέσα είναι το 51% (γιατί = 51.00). ηλαδή το 1/4 του συνόλου των τυχών περικλείει το 51%.
3 -3- Τώρα καταλάβατε πως αναλύεται το παιχνίδι στις συνιστώσες του. Επίσης πως επεκτείνεται στα 6 σκέλη του σκορ-6 ή στα 4 σκέλη του σκορ-4, θα πρέπει να είναι αυτή τη στιγµή φανερό. εν έχουµε καµία ελπίδα να κάνουµε τις πράξεις µε το χέρι, χωρίς computer, αλλά οι πράξεις που χρειάζονται είναι οι ίδιες, όπως και στο απλουστευµένο παράδειγ- µα µας. Τρία σχόλια που κάνουν όλοι σ αυτό το στάδιο, είναι τα εξής: α) Στο παράδειγµα σας πως, υποτίθεται, προέκυψαν οι ποσοστιαίες πιθανότητες ; β) Εγώ δεν χρησιµοποιώ ποσοστιαίες πιθανότητες. γ) Οι δικές µου ποσοστιαίες πιθανότητες είναι -εν δυνάµει- διαφορετικές από τις δικές σας α) Μπορεί να προέκυψαν από άλλο πρόγραµµα computer που αναλύει χρόνους, επίδραση της σύνθεσης διαδροµής, αναβάτες κλπ (όπως το CosmiC Racing). Μπορεί να προέκυψαν από στατιστικό πρόγραµµα που κάνει «γκάλοπ των experts» του ιπποδρόµου (επίσης εγκεκριµένη µέθοδος) ή µπορεί να προέκυψαν από τα «χιλιάρικα γκανιάν» που ανακοινώνει ο ιππόδροµος. β) Σ αυτή την περίπτωση πάλι το «πλήρες» δεν σας συµφέρει απόλυτα. Ένα είδος συστήµατος «µαύρα-κόκκινα» θα σας εξυπηρετούσε κάπως καλύτερα, αν µάθετε να το χειρίζεστε. Αλλά το σοβαρό πρόβληµα µε τον παίκτη που δεν κάνει χρήση ποσοστών είναι το εξής: Χωρίς ποσοστιαία νούµερα για το κάθε άλογο, πως θα κάνουµε µετρήσεις ; Πως θα ξέρουµε, µε κάποια σχετική ακρίβεια, προς τα που βαδίζουµε ; γ) Όπως ήδη εξηγήσαµε στο (α) υπάρχουν τρεις εγκεκριµένοι τρόποι που ξέρουµε εµείς. Γενικά πιστεύουµε ότι ένας έµπειρος φίλιππος θα έπεφτε κάπου στα σωστά, κάνοντας τη δική του ανάλυση αλλά θα επιµείνουµε στη συνέχεια στα ποσοστά του CosmiC Racing τα οποία είναι καλά και επίσης τα έχουµε φυλαγµένα, για όλες τις παλιές ιπποδροµιακές. Η µεγιστοπιθανη ανάπτυξη των στηλών Στο παράδειγµα µε το σκορ-2 που αναλύσαµε πιό πάνω, κάναµε ήδη µία µεγιστοπίθανη ανάπτυξη, ταξινοµώντας τις 16 στήλες-δυάδες. Στο σκορ-6 οι στήλες είναι αφ ενός εξάδες και αφ ετέρου είναι πολλές, π.χ. µε 7 ίππους στο κάθε σκέλος είναι στήλες. Όµως τα σηµερινά computer είναι γρήγορα και η ταξινόµηση γίνεται εύκολα µε το πάτηµα ενός κουµπιου, µε την προϋπόθεση οι πίνακες µε τα ποσοστά των 6 ιπποδροµιών να είναι συµπληρωµένοι. Η µεγιστοπίθανη ανάπτυξη είναι το πιό σύντοµο µονοπάτι για να φτάσουµε στη νικήτρια στήλη. Με βάση το παράδειγµα µας µε τις δύο κούρσες των τεσσάρων αλόγων, κάντε το εξής πείραµα, το οποίο απαιτεί τη συµµετοχή δύο παικτών: Ο ένας βγάζει τη νικήτρια δυάδα κληρώνοντας µπαλάκια µε βάση τα νούµερα που δίνουµε. Θα κρατάει το νούµερο κρυφό και ο άλλος παίκτης θα προσπαθεί να το µαντέψει προτείνοντας δυάδες. Αν ο παίκτης που µαντεύει ακολουθήσει τη σειρά των ταξινοµηµένων δυάδων θα το βρίσκει µε τον µίνιµουµ αριθµό προσπαθειών. Αν ακολουθήσει οποιαδήποτε άλλη σειρά, θα χρειάζεται παραπάνω προσπάθειες.
4 -4- Μεγιστοπίθανη στατιστική ανάλυση για το σκορ-6: α) Το όριο του «50%» Το όριο του 50% είναι οι 1500 στήλες (2250 ευρώ). β) Οι αποδόσεις µε 1500 στήλες Οι αποδόσεις κυµαίνονται στα 2000 ευρώ, αλλά µε όχι σπάνιες περιπτώσεις για µεγαλύτερες. Το παιχνίδι αποφέρει κέρδος και το αρχικό κεφάλαιο αυξάνεται κατά 150% περίπου. γ) Τζάκποτ Περιορίζοντας τη συµµετοχή σας στις περιπτώσεις που έχει προηγηθεί τζάκποτ µόνο, πρακτικά πετυχαίνετε µεγαλύτερη αύξηση κεφαλαίου, αφού θα πάρετε µερίδιο και από το τζάκποτ και από το ταµείο της ηµέρας. Τα αποτελέσµατα αυτά που βγάλαµε είναι γενικώς ενθαρρυντικά, σε ένα αρκετά µεγάλο κόστος βέβαια (2250 ευρώ ανά συµµετοχή). Πως γίνεται να παίξω ; Για να παίξει κανείς µε αυτή τη µέθοδο, υπάρχουν τα προγράµµατα CosmiC Racing και CosmiC Score Ippo, τα οποία κάνουν την ποσοστιαία ανάπτυξη. Ίσως να υπάρχουν και άλλα προγράµµατα. Το πρόγραµµα computer αφού τροφοδοτηθεί µε τα κατάλληλα δεδοµένα, παράγει δελτία και προσπαθεί πάντα να µειώσει τον αριθµό των δελτίων, να κάνει σύµπτυξη δηλαδή. Αν ζητήσουµε 1500 στήλες π.χ., τότε θα τις βγάλει πρώτα και στη συνέχεια θα προσπαθήσει να τις «δέσει» µεταξύ τους, για να βγουν πληράκια. Στις 1500 στήλες βγαίνουν περίπου πληράκια. Παρά τη µείωση που επιτυγχάνουµε αυτό είναι ένα µεγάλο πρακτικό πρόβληµα. Πως θα παιχτούν αυτά τα πληράκια, χωρίς µάλιστα να γίνει λάθος στη µεταφορά ; Θα πρέπει να ξέρετε ότι µε την παρούσα υποστήριξη που παρέχει ο Ο..Ι.Ε. είναι αρκετά δύσκολο. Αν υπήρχε η διευκόλυνση να τα παίζουµε κατ ευθείαν µε αρχείο computer τύπου zip θα ήταν το άριστο (σ.σ. όπως έχει κάνει πρόσφατα ο Ο.Π.Α.Π. για τα δικά του παιχνίδια). Πως γίνεται να εχει κανείς πιθανότητες κέρδους σε ένα µέρος σαν το Μαρκόπουλο ; Το Μαρκόπουλο είναι επικίνδυνη περιοχή. Πράγµατι! Αυτό που πρέπει να συµβαίνει είναι ότι λόγω του κόστους (1.50 ευρώ η στήλη) δεν έχουν καταφέρει ακόµα να το ξετινάξουν το παιχνίδι. Επίσης λόγω της άγνοιας που επικρατεί σχετικά µε τα συστήµατα. Αυτά, συν το µπόνους των τζάκποτ δηµιουργούν µιά καλή ευκαιρία αυτή τη στιγµή, σε όσους έχουν βέβαια το κεφάλαιο. Γίνεται το computer να µου προτείνει πλήρες σύστηµα ; Το computer µπορεί να βγάλει και πλήρες. Σε σχέση µε το νούµερο των 1500 στηλών που αναφέραµε προηγουµένως, ζητάµε π.χ. να µας βγάλει το πλήρες µε τη µεγαλύτερη πιθανότητα που δεν ξεπερνάει το Τα συστήµατα αυτά είναι όµως υποδεέστερα από αυτά που περιγράψαµε προηγουµένως, για τον ίδιο λόγο που στο απλό παράδειγµα µας µε τις δυάδες οι δύο διπλές ήταν λάθος. εν είναι άχρηστα, είναι όµως υποδεέστερα και έχουµε δει στήλη που κανονικά βγαίνει στο νού- µερο 150 (150 η τύχη) να µην την πετυχαίνει το πλήρες αν δεν ζητήσουµε 1000 στήλες (έχουµε δει και το αντίθετο να γίνεται αλλά σπάνια).
5 -5- Μπορώ να κάνω µικρότερο παιχνίδι µε στήλες ; Το στατιστικά δεδοµένα, µε βάση τις ιπποδροµίες του Μαρκόπουλου πάντα, δείχνουν ότι µε ένα παιχνίδι 200 στηλών οι πιθανότητες είναι 13%. Μπορεί αυτό το παιχνίδι, µε κάπως πιό µειωµένες βέβαια απαιτήσεις, να σας οδηγήσει κάπου. Θα παραχθούν γύρω στα 50 πληράκια που και πάλι αποτελεί «στρες» για τον πράκτορα, εκτός αν κάποια στιγµή ο Ο..Ι.Ε. αποφασίσει να διευκολύνει. copyright cosmicway.net, Φεβρουάριος 2010
ΕΓΧΕΙΡΙΔΙΟ ΛΕΙΤΟΥΡΓΙΑΣ WORLD TILL ΓΙΑ ΤΟ ΙΠΠΟΔΡΟΜΙΑΚΟ ΣΤΟΙΧΗΜΑ. Βασικές οδηγίες - 1:
 ΕΓΧΕΙΡΙΔΙΟ ΛΕΙΤΟΥΡΓΙΑΣ WORLD TILL ΓΙΑ ΤΟ ΙΠΠΟΔΡΟΜΙΑΚΟ ΣΤΟΙΧΗΜΑ Βασικές οδηγίες - 1: 1. Για κάθε επιλογή μπορούμε να χρησιμοποιήσουμε είτε ποντίκι είτε πληκτρολόγιο 2. Η περιοχή Πεδίο θα είναι το πλήκτρο
ΕΓΧΕΙΡΙΔΙΟ ΛΕΙΤΟΥΡΓΙΑΣ WORLD TILL ΓΙΑ ΤΟ ΙΠΠΟΔΡΟΜΙΑΚΟ ΣΤΟΙΧΗΜΑ Βασικές οδηγίες - 1: 1. Για κάθε επιλογή μπορούμε να χρησιμοποιήσουμε είτε ποντίκι είτε πληκτρολόγιο 2. Η περιοχή Πεδίο θα είναι το πλήκτρο
Το 1ο βήμα ανανέωσης. Νέα οθόνη ΚΙΝΟ. Επίσημη οθόνη στατιστικών ΚΙΝΟ από τον ΟΠΑΠ
 ΚΙΝΟ BONUS Το 1ο βήμα ανανέωσης Νέα οθόνη ΚΙΝΟ Επίσημη οθόνη στατιστικών ΚΙΝΟ από τον ΟΠΑΠ Το 2 ο βήμα ανανέωσης Δελτίο με 4 Βήματα για τον «Άπειρο Παίκτη» που παίζει πρώτη φορά Δελτίο με περισσότερες
ΚΙΝΟ BONUS Το 1ο βήμα ανανέωσης Νέα οθόνη ΚΙΝΟ Επίσημη οθόνη στατιστικών ΚΙΝΟ από τον ΟΠΑΠ Το 2 ο βήμα ανανέωσης Δελτίο με 4 Βήματα για τον «Άπειρο Παίκτη» που παίζει πρώτη φορά Δελτίο με περισσότερες
Kεφάλαιο 10. Πόσα υποπαίγνια υπάρχουν εδώ πέρα; 2 υποπαίγνια.
 Kεφάλαιο 10 Θα δούµε ένα δύο παραδείγµατα να ορίσουµε/ µετρήσουµε τα υποπαίγνια και µετά θα λύσουµε και να βρούµε αυτό που λέγεται τέλεια κατά Nash ισορροπία. Εδώ θα δούµε ένα παίγνιο όπου έχουµε µια επιχείρηση
Kεφάλαιο 10 Θα δούµε ένα δύο παραδείγµατα να ορίσουµε/ µετρήσουµε τα υποπαίγνια και µετά θα λύσουµε και να βρούµε αυτό που λέγεται τέλεια κατά Nash ισορροπία. Εδώ θα δούµε ένα παίγνιο όπου έχουµε µια επιχείρηση
ΠΡΟΣΟΜΟΙΩΤΙΚΗ ΜΕΛΕΤΗ ΓΚΑΝΙΟΤΑΣ ΓΙΑ ΤΙΣ ΕΛΛΗΝΙΚΕΣ ΙΠΠΟ ΡΟΜΙΕΣ
 ΠΡΟΣΟΜΟΙΩΤΙΚΗ ΜΕΛΕΤΗ ΓΚΑΝΙΟΤΑΣ ΓΙΑ ΤΙΣ ΕΛΛΗΝΙΚΕΣ ΙΠΠΟ ΡΟΜΙΕΣ Ν.Α. Παπαδάκης (cosmicway.net, ΠΑΝ.Ε.ΦΙΛ.) Αύγουστος 2011 1. Περίληψη Οι πρόσφατες κινήσεις του Υπουργείου των Οικονοµικών και του Ο ΙΕ να επιφέρουν
ΠΡΟΣΟΜΟΙΩΤΙΚΗ ΜΕΛΕΤΗ ΓΚΑΝΙΟΤΑΣ ΓΙΑ ΤΙΣ ΕΛΛΗΝΙΚΕΣ ΙΠΠΟ ΡΟΜΙΕΣ Ν.Α. Παπαδάκης (cosmicway.net, ΠΑΝ.Ε.ΦΙΛ.) Αύγουστος 2011 1. Περίληψη Οι πρόσφατες κινήσεις του Υπουργείου των Οικονοµικών και του Ο ΙΕ να επιφέρουν
Monitor Games BOWLING
 ΠΕΡΙΓΡΑΦΗ ΠΑΙΧΝΙΔΙΟΥ: BOWLING Αναπαράσταση παιχνιδιού Bowling με δύο εικονικούς παίκτες. Κάθε εικονικός παίκτης έχει δύο ευκαιρίες να ρίξει και τις 10 κορύνες ώστε να πετύχει τη μέγιστη βαθμολογία. Το
ΠΕΡΙΓΡΑΦΗ ΠΑΙΧΝΙΔΙΟΥ: BOWLING Αναπαράσταση παιχνιδιού Bowling με δύο εικονικούς παίκτες. Κάθε εικονικός παίκτης έχει δύο ευκαιρίες να ρίξει και τις 10 κορύνες ώστε να πετύχει τη μέγιστη βαθμολογία. Το
Αφού έχετε μπει στη σελίδα pamestoixima.gr, πατάτε πάνω αριστερά, την επιλογή
 1. ΠΩΣ ΠΑΙΖΕΤΑΙ Διαδικασία Αφού έχετε μπει στη σελίδα pamestoixima.gr, πατάτε πάνω αριστερά, την επιλογή "ΣΤΟΙΧΗΜΑ" και μπορείτε να δείτε τις ενότητες που περιγράφονται παρακάτω. Στην αριστερή μπάρα επιλογών
1. ΠΩΣ ΠΑΙΖΕΤΑΙ Διαδικασία Αφού έχετε μπει στη σελίδα pamestoixima.gr, πατάτε πάνω αριστερά, την επιλογή "ΣΤΟΙΧΗΜΑ" και μπορείτε να δείτε τις ενότητες που περιγράφονται παρακάτω. Στην αριστερή μπάρα επιλογών
Οδηγός των νέων δελτίων
 Οδηγός των νέων δελτίων 4-7 Νέα εποχή Η ΟΠΑΠ Α.Ε. στο πλαίσιο της δυναμικής της ανάπτυξης, προχωρά στην αναμόρφωση και ανανέωση των παιχνιδιών της. Με ακόμη πιο λειτουργικό σχεδιασμό, μοντέρνα εμφάνιση
Οδηγός των νέων δελτίων 4-7 Νέα εποχή Η ΟΠΑΠ Α.Ε. στο πλαίσιο της δυναμικής της ανάπτυξης, προχωρά στην αναμόρφωση και ανανέωση των παιχνιδιών της. Με ακόμη πιο λειτουργικό σχεδιασμό, μοντέρνα εμφάνιση
* τη µήτρα. Κεφάλαιο 1o
 Κεφάλαιο 1o Θεωρία Παιγνίων Η θεωρία παιγνίων εξετάζει καταστάσεις στις οποίες υπάρχει αλληλεπίδραση µεταξύ ενός µικρού αριθµού ατόµων. Άρα σε οποιαδήποτε περίπτωση, αν ο αριθµός των ατόµων που συµµετέχουν
Κεφάλαιο 1o Θεωρία Παιγνίων Η θεωρία παιγνίων εξετάζει καταστάσεις στις οποίες υπάρχει αλληλεπίδραση µεταξύ ενός µικρού αριθµού ατόµων. Άρα σε οποιαδήποτε περίπτωση, αν ο αριθµός των ατόµων που συµµετέχουν
Έκδοση 5.8 ΟΡΟΙ ΠΡΟΠΟ ΚΑΙ ΣΤΟΙΧΗΜΑ
 ΣΥΣΤΗΜΑΤΑ ΜΕ COMPUTER Λ ί σ τ α ό ρ ω ν τ ο υ Έκδοση 5.8 ΤΟ ΚΟΡΥΦΑΙΟ ΠΡΟΓΡΑΜΜΑ ΚΑΤΑΣΚΕΥΗΣ ΣΥΣΤΗΜΑΤΩΝ ΜΕ ΥΠΟΛΟΓΙΣΤΗ (PC) ΓΙΑ ΤΑ ΠΑΙΧΝΙ ΙΑ: ΣΤΟΙΧΗΜΑ ΠΡΟΠΟ 14 και 7 ΤΖΟΚΕΡ ΚΙΝΟ ΛΟΤΤΟ ΠΡΟΠΟΓΚΟΛ ΕΞΤΡΑ-5 ΚΑΤΑΣΚΕΥΑΣΤΗΣ:
ΣΥΣΤΗΜΑΤΑ ΜΕ COMPUTER Λ ί σ τ α ό ρ ω ν τ ο υ Έκδοση 5.8 ΤΟ ΚΟΡΥΦΑΙΟ ΠΡΟΓΡΑΜΜΑ ΚΑΤΑΣΚΕΥΗΣ ΣΥΣΤΗΜΑΤΩΝ ΜΕ ΥΠΟΛΟΓΙΣΤΗ (PC) ΓΙΑ ΤΑ ΠΑΙΧΝΙ ΙΑ: ΣΤΟΙΧΗΜΑ ΠΡΟΠΟ 14 και 7 ΤΖΟΚΕΡ ΚΙΝΟ ΛΟΤΤΟ ΠΡΟΠΟΓΚΟΛ ΕΞΤΡΑ-5 ΚΑΤΑΣΚΕΥΑΣΤΗΣ:
Πριν απο λιγα χρονια ημουνα ακριβως σαν εσενα.
 Πριν απο λιγα χρονια ημουνα ακριβως σαν εσενα. Ηξερα οτι υπαρχουν επαγγελματιες παιχτες που κερδιζουν πολλα χρηματα απο το στοιχημα και εψαχνα να βρω τη "μυστικη formula" 'Ετσι κ εσυ. Πηρες μια απο τις
Πριν απο λιγα χρονια ημουνα ακριβως σαν εσενα. Ηξερα οτι υπαρχουν επαγγελματιες παιχτες που κερδιζουν πολλα χρηματα απο το στοιχημα και εψαχνα να βρω τη "μυστικη formula" 'Ετσι κ εσυ. Πηρες μια απο τις
Κεφάλαιο 4. Στο προηγούµενο κεφάλαιο ορίσαµε την ισορροπία κατά Nash και είδαµε ότι µια ισορροπία
 Κεφάλαιο 4 Στο προηγούµενο κεφάλαιο ορίσαµε την ισορροπία κατά Nash και είδαµε ότι µια ισορροπία κατά Nash είναι: (α) ένα διάνυσµα από στρατηγικές, έτσι ώστε δεδοµένων των υπολοίπων στρατηγικών, ο παίκτης
Κεφάλαιο 4 Στο προηγούµενο κεφάλαιο ορίσαµε την ισορροπία κατά Nash και είδαµε ότι µια ισορροπία κατά Nash είναι: (α) ένα διάνυσµα από στρατηγικές, έτσι ώστε δεδοµένων των υπολοίπων στρατηγικών, ο παίκτης
Τα φαβορί ορίζουν το παιχνίδι στα προγνωστικά στοιχήματος
 Τα φαβορί ορίζουν το παιχνίδι στα προγνωστικά στοιχήματος Καλημέρα σε όλους σας, συμπληρώνονται σήμερα οι αγωνιστικές, με τα τελευταία παιχνίδια των πρωταθλημάτων και παρόλα τα λίγα ματς, αυτά έχουν σχετική
Τα φαβορί ορίζουν το παιχνίδι στα προγνωστικά στοιχήματος Καλημέρα σε όλους σας, συμπληρώνονται σήμερα οι αγωνιστικές, με τα τελευταία παιχνίδια των πρωταθλημάτων και παρόλα τα λίγα ματς, αυτά έχουν σχετική
Κεφάλαιο 9 ο Κ 5, 4 4, 5 0, 0 0,0 5, 4 4, 5. Όπως βλέπουµε το παίγνιο δεν έχει καµιά ισορροπία κατά Nash σε αµιγείς στρατηγικές διότι: (ΙΙ) Α Κ
 Κεφάλαιο ο Μεικτές Στρατηγικές Τώρα θα δούµε ένα παράδειγµα στο οποίο κάθε παίχτης έχει τρεις στρατηγικές. Αυτό θα µπορούσε να είναι η µορφή που παίρνει κάποιος µετά που έχει απαλείψει όλες τις αυστηρά
Κεφάλαιο ο Μεικτές Στρατηγικές Τώρα θα δούµε ένα παράδειγµα στο οποίο κάθε παίχτης έχει τρεις στρατηγικές. Αυτό θα µπορούσε να είναι η µορφή που παίρνει κάποιος µετά που έχει απαλείψει όλες τις αυστηρά
Πιθανότητες. Κεφάλαιο Δειγματικός χώρος - Ενδεχόμενα Κατανόηση εννοιών - Θεωρία
 Κεφάλαιο 1 Πιθανότητες 1.1 Δειγματικός χώρος - Ενδεχόμενα 1.1.1 Κατανόηση εννοιών - Θεωρία 1. Ποιό πείραμα λέγεται αιτιοκρατικό και ποιό πείραμα τύχης; 2. Τι ονομάζουμε δειγματικό χώρο ενός πειράματος
Κεφάλαιο 1 Πιθανότητες 1.1 Δειγματικός χώρος - Ενδεχόμενα 1.1.1 Κατανόηση εννοιών - Θεωρία 1. Ποιό πείραμα λέγεται αιτιοκρατικό και ποιό πείραμα τύχης; 2. Τι ονομάζουμε δειγματικό χώρο ενός πειράματος
Οδηγίε παιχνιδιού 3210
 Οδηγίε παιχνιδιού 3210 Copyright - Spiele Bad Rodach 2004 Επιτραπέζιο HABA: 3210 Γενναίοι Ιππότε Ένα συναρπαστικό παιχνίδι δράση με ιππότε, για 2 έω 4 παίκτε ηλικία άνω των 4 ετών. Δημιουργία παιχνιδιού:
Οδηγίε παιχνιδιού 3210 Copyright - Spiele Bad Rodach 2004 Επιτραπέζιο HABA: 3210 Γενναίοι Ιππότε Ένα συναρπαστικό παιχνίδι δράση με ιππότε, για 2 έω 4 παίκτε ηλικία άνω των 4 ετών. Δημιουργία παιχνιδιού:
Κατανόηση προφορικού λόγου
 Κατανόηση προφορικού λόγου Επίπεδο Γ Πρώτη διδακτική πρόταση ΠΡΟΠΟ Ενδεικτική διάρκεια: Ομάδα-στόχος: Διδακτικός στόχος: 1 διδακτική ώρα ενήλικοι μαθητές Γ επιπέδου κατανόηση αθλητικής εκπομπής (τυχερά
Κατανόηση προφορικού λόγου Επίπεδο Γ Πρώτη διδακτική πρόταση ΠΡΟΠΟ Ενδεικτική διάρκεια: Ομάδα-στόχος: Διδακτικός στόχος: 1 διδακτική ώρα ενήλικοι μαθητές Γ επιπέδου κατανόηση αθλητικής εκπομπής (τυχερά
 Πάνω στον πίνακα έχουµε γραµµένο το γινόµενο 1 2 3 4 595. ύο παίκτες Α και Β παίζουν το εξής παιχνίδι. Ο ένας µετά τον άλλο, διαγράφουν από έναν παράγοντα του γινοµένου αρχίζοντας από τον παίκτη Α. Νικητής
Πάνω στον πίνακα έχουµε γραµµένο το γινόµενο 1 2 3 4 595. ύο παίκτες Α και Β παίζουν το εξής παιχνίδι. Ο ένας µετά τον άλλο, διαγράφουν από έναν παράγοντα του γινοµένου αρχίζοντας από τον παίκτη Α. Νικητής
Κρίνονται η πρωτιά και η τρίτη θέση στον 3ο όμιλο
 Κρίνονται η πρωτιά και η τρίτη θέση στον 3ο όμιλο Ολοκληρώθηκαν χτες οι δύο πρώτοι όμιλοι του Copa America και έχουν προκύψει οι ομάδες που θα συνεχίσουν στον θεσμό. Σήμερα, τελειώνει ο τρίτος και τελευταίος
Κρίνονται η πρωτιά και η τρίτη θέση στον 3ο όμιλο Ολοκληρώθηκαν χτες οι δύο πρώτοι όμιλοι του Copa America και έχουν προκύψει οι ομάδες που θα συνεχίσουν στον θεσμό. Σήμερα, τελειώνει ο τρίτος και τελευταίος
ΕΙΣΑΓΩΓΗ. Η Ο.Π.Α.Π. Α.Ε. εισήγαγε στην Ελλάδα τα παιχνίδια στοιχημάτων προκαθορισμένης απόδοσης το έτος 2000, με μεγάλη επιτυχία.
 ΕΙΣΑΓΩΓΗ Η Ο.Π.Α.Π. Α.Ε. εισήγαγε στην Ελλάδα τα παιχνίδια στοιχημάτων προκαθορισμένης απόδοσης το έτος 2000, με μεγάλη επιτυχία. ΤΙ ΕΙΝΑΙ ΤΑ ΠΑΙΧΝΙΔΙΑ ΣΤΟΙΧΗΜΑΤΩΝ Τα στοιχήματα ήταν γνωστά ήδη από την
ΕΙΣΑΓΩΓΗ Η Ο.Π.Α.Π. Α.Ε. εισήγαγε στην Ελλάδα τα παιχνίδια στοιχημάτων προκαθορισμένης απόδοσης το έτος 2000, με μεγάλη επιτυχία. ΤΙ ΕΙΝΑΙ ΤΑ ΠΑΙΧΝΙΔΙΑ ΣΤΟΙΧΗΜΑΤΩΝ Τα στοιχήματα ήταν γνωστά ήδη από την
Βγαίνουν τα ζευγάρια των ημιτελικών του Copa America
 Βγαίνουν τα ζευγάρια των ημιτελικών του Copa America Ολοκληρώνεται σήμερα η προημιτελική φάση του Copa America με το τελευταίο παιχνίδι για αυτή την φάση. Ήδη το πρώτο ζευγάρι των ημιτελικών θα είναι Βραζιλία
Βγαίνουν τα ζευγάρια των ημιτελικών του Copa America Ολοκληρώνεται σήμερα η προημιτελική φάση του Copa America με το τελευταίο παιχνίδι για αυτή την φάση. Ήδη το πρώτο ζευγάρι των ημιτελικών θα είναι Βραζιλία
Φύλλο Εργασίας 3. Μια γρήγορη επανάληψη από τα προηγούμενα
 3 Φύλλο Εργασίας 3 Στο φύλλο εργασιών 3 θα ασχοληθούμε με τις λίστες μια δομή της γλώσσας python που έχει την δομή ενός πίνακα. Θα χρησιμοποιήσουμε τις βασικές εντολές από τις λίστες και θα κατασκευάσουμε
3 Φύλλο Εργασίας 3 Στο φύλλο εργασιών 3 θα ασχοληθούμε με τις λίστες μια δομή της γλώσσας python που έχει την δομή ενός πίνακα. Θα χρησιμοποιήσουμε τις βασικές εντολές από τις λίστες και θα κατασκευάσουμε
Σας καλωσορίζω σήµερα στην Περιφέρεια Αττικής.
 Αξιότιµε κύριε Υπουργέ, Αγαπητοί ήµαρχοι, Σας καλωσορίζω σήµερα στην Περιφέρεια Αττικής. Γνωρίζετε όλοι πως κάθε έργο για να υλοποιηθεί περνά από πολλές φάσεις: µελέτες, εγκρίσεις περιβαλλοντικών όρων,
Αξιότιµε κύριε Υπουργέ, Αγαπητοί ήµαρχοι, Σας καλωσορίζω σήµερα στην Περιφέρεια Αττικής. Γνωρίζετε όλοι πως κάθε έργο για να υλοποιηθεί περνά από πολλές φάσεις: µελέτες, εγκρίσεις περιβαλλοντικών όρων,
Εγκατάσταση της Unity
 Εγκατάσταση της Unity Όπως έχουμε πει, θα χρησιμοποιήσουμε την Unity για να φτιάξουμε τα παιχνίδια μας. Η Unity είναι μια μηχανή παιχνιδιών (game engine). Τι σημαίνει όμως αυτό; Σημαίνει απλά ότι είναι
Εγκατάσταση της Unity Όπως έχουμε πει, θα χρησιμοποιήσουμε την Unity για να φτιάξουμε τα παιχνίδια μας. Η Unity είναι μια μηχανή παιχνιδιών (game engine). Τι σημαίνει όμως αυτό; Σημαίνει απλά ότι είναι
Προωθητικό Υλικό και Οδηγίες Τοποθέτησης
 Προωθητικό Υλικό και Οδηγίες Τοποθέτησης Ιούνιος 205 Επικοινωνία στα σημεία πώλησης Επικοινωνία Λανσαρίσματος 2 Νέα δελτία ΚΙΝΟ για πιο διασκεδαστικό παιχνίδι! Στοχευμένη Επικοινωνία Για άπειρους παίκτες
Προωθητικό Υλικό και Οδηγίες Τοποθέτησης Ιούνιος 205 Επικοινωνία στα σημεία πώλησης Επικοινωνία Λανσαρίσματος 2 Νέα δελτία ΚΙΝΟ για πιο διασκεδαστικό παιχνίδι! Στοχευμένη Επικοινωνία Για άπειρους παίκτες
Διπλά και γκολ μας πληρώνουν την Τετάρτη
 Διπλά και γκολ μας πληρώνουν την Τετάρτη Καλημέρα, πλήρες αγωνιστική ημέρα υπάρχει σήμερα Τετάρτης, διότι υπάρχουν παιχνίδια τόσο από τα κύπελλα, όσο και εμβόλιμες αγωνιστικές στα μεγαλύτερα πρωταθλήματα.
Διπλά και γκολ μας πληρώνουν την Τετάρτη Καλημέρα, πλήρες αγωνιστική ημέρα υπάρχει σήμερα Τετάρτης, διότι υπάρχουν παιχνίδια τόσο από τα κύπελλα, όσο και εμβόλιμες αγωνιστικές στα μεγαλύτερα πρωταθλήματα.
Blackjack: Στρατηγική, συμβουλές και τρόπος παιχνιδιού - ΚΑΛΑΜΠΑΚΑ CITY KALAMPAKA METEOR
 Blackjack: Στρατηγική, συμβουλές και τρόπος παιχνιδιού - ΚΑΛΑΜΠΑΚΑ CITY KALAMPAKA METEOR Τελευταία μέρα του έτους σήμερα, το κουπόνι του πάμε στοίχημα είναι ιδιαιτέρως φτωχό, έτσι δεν θα ασχοληθούμε με
Blackjack: Στρατηγική, συμβουλές και τρόπος παιχνιδιού - ΚΑΛΑΜΠΑΚΑ CITY KALAMPAKA METEOR Τελευταία μέρα του έτους σήμερα, το κουπόνι του πάμε στοίχημα είναι ιδιαιτέρως φτωχό, έτσι δεν θα ασχοληθούμε με
3 ΙΣΟΡΡΟΠΙΕΣ 3 ΙΣΟΡΡΟΠΙΕΣ
 Kεφάλαιο 11 Θα επαναλάβουµε αυτά που είχαµε πει την προηγούµενη φορά. Παραστατικά αν έχουµε το εξής παίγνιο όπου οι δύο παίχτες παίρνουν ταυτόχρονα τις αποφάσεις τους αφού αποφασίσει ο Ι, θα δούµε πόσα
Kεφάλαιο 11 Θα επαναλάβουµε αυτά που είχαµε πει την προηγούµενη φορά. Παραστατικά αν έχουµε το εξής παίγνιο όπου οι δύο παίχτες παίρνουν ταυτόχρονα τις αποφάσεις τους αφού αποφασίσει ο Ι, θα δούµε πόσα
Με το μυαλό στο πρωτάθλημα πολλές ομάδες
 Με το μυαλό στο πρωτάθλημα πολλές ομάδες Καλημέρα σε όλους σας, ιδιαίτερα φτωχό το αγωνιστικό πρόγραμμα, με ελάχιστες επιλογές για το στοίχημα, οι αναμετρήσεις του κυπέλλου, τις κάνουν ακόμα πιο δύσκολες.
Με το μυαλό στο πρωτάθλημα πολλές ομάδες Καλημέρα σε όλους σας, ιδιαίτερα φτωχό το αγωνιστικό πρόγραμμα, με ελάχιστες επιλογές για το στοίχημα, οι αναμετρήσεις του κυπέλλου, τις κάνουν ακόμα πιο δύσκολες.
Κεφάλαιο 8 ο Τ 3, 1-1, -1 Χ -1, -1 1, 3
 Κεφάλαιο 8 ο Συνεχίζουµε µε τις µεικτές στρατηγικές. Θα δούµε τώρα ένα παράδειγµα στο οποίο υπάρχουνε ισορροπίες κατά Nash σε αµιγείς στρατηγικές αλλά πέρα από αυτό υπάρχει και µια ισορροπία κατά Nash
Κεφάλαιο 8 ο Συνεχίζουµε µε τις µεικτές στρατηγικές. Θα δούµε τώρα ένα παράδειγµα στο οποίο υπάρχουνε ισορροπίες κατά Nash σε αµιγείς στρατηγικές αλλά πέρα από αυτό υπάρχει και µια ισορροπία κατά Nash
Επίλυση προβληµάτων. Περιγραφή προβληµάτων Αλγόριθµοι αναζήτησης Αλγόριθµοι τυφλής αναζήτησης Αλγόριθµοι ευρετικής αναζήτησης
 Επίλυση προβληµάτων Περιγραφή προβληµάτων Αλγόριθµοι αναζήτησης Αλγόριθµοι τυφλής αναζήτησης Αλγόριθµοι ευρετικής αναζήτησης! Παιχνίδια δύο αντιπάλων Προβλήµατα ικανοποίησης περιορισµών Γενικά " Ντετερµινιστικά
Επίλυση προβληµάτων Περιγραφή προβληµάτων Αλγόριθµοι αναζήτησης Αλγόριθµοι τυφλής αναζήτησης Αλγόριθµοι ευρετικής αναζήτησης! Παιχνίδια δύο αντιπάλων Προβλήµατα ικανοποίησης περιορισµών Γενικά " Ντετερµινιστικά
Ασκήσεις μελέτης της 6 ης διάλεξης
 Οικονομικό Πανεπιστήμιο Αθηνών, Τμήμα Πληροφορικής Μάθημα: Τεχνητή Νοημοσύνη, 2016 17 Διδάσκων: Ι. Ανδρουτσόπουλος Ασκήσεις μελέτης της 6 ης διάλεξης 6.1. (α) Το mini-score-3 παίζεται όπως το score-4,
Οικονομικό Πανεπιστήμιο Αθηνών, Τμήμα Πληροφορικής Μάθημα: Τεχνητή Νοημοσύνη, 2016 17 Διδάσκων: Ι. Ανδρουτσόπουλος Ασκήσεις μελέτης της 6 ης διάλεξης 6.1. (α) Το mini-score-3 παίζεται όπως το score-4,
ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΠΑΙΧΝΙΔΙΩΝ ΤΗΣ ΟΠΑΠ Α.Ε.
 ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΠΑΙΧΝΙΔΙΩΝ ΤΗΣ ΟΠΑΠ Α.Ε. ΓΝΩΣΗ ΑΜΟΙΒΑΙΑ ΚΕΡΔΗ ΠΡΟΚΑΘΟΡΙΣΜΕΝΑ ΚΕΡΔΗ ΤΥΧΗ Ημερομηνία Έναρξης: 3 Μαρτίου 1996 Αντικείμενο Παιχνιδιού Το παιχνίδι ΠΡΟΠΟΓΚΟΛ αφορά στην πρόβλεψη οκτώ (8) ποδοσφαιρικών
ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΠΑΙΧΝΙΔΙΩΝ ΤΗΣ ΟΠΑΠ Α.Ε. ΓΝΩΣΗ ΑΜΟΙΒΑΙΑ ΚΕΡΔΗ ΠΡΟΚΑΘΟΡΙΣΜΕΝΑ ΚΕΡΔΗ ΤΥΧΗ Ημερομηνία Έναρξης: 3 Μαρτίου 1996 Αντικείμενο Παιχνιδιού Το παιχνίδι ΠΡΟΠΟΓΚΟΛ αφορά στην πρόβλεψη οκτώ (8) ποδοσφαιρικών
Εισπράττουµε περί τα 40 δις ευρώ το χρόνο και ξοδεύουµε περί τα 60. Κατ' αναλογία είναι σαν να βγάζω 1.000 ευρώ το µήνα και να χαλάω 1.500.
 Αφού κανείς από τους επίσηµους φορείς δεν βγαίνει επιτέλους να πει την πολυπόθητη αλήθεια στον ελληνικό λαό αποφάσισα να το κάνω εγώ. Ξέρετε η αλήθεια στα οικονοµικά δεν είναι ούτε θέσφατο, ούτε κρυφή
Αφού κανείς από τους επίσηµους φορείς δεν βγαίνει επιτέλους να πει την πολυπόθητη αλήθεια στον ελληνικό λαό αποφάσισα να το κάνω εγώ. Ξέρετε η αλήθεια στα οικονοµικά δεν είναι ούτε θέσφατο, ούτε κρυφή
ΕΠΙΣΗΜΟΙ ΚΑΝΟΝΕΣ ΤΟΥ ΟΙ ΚΑΡΤΕΣ
 ΕΠΙΣΗΜΟΙ ΚΑΝΟΝΕΣ ΤΟΥ Το SLEUTH είναι ένα φανταστικό παιχνίδι έρευνας για 3 έως 7 παίκτες. Μέσα από έξυπνες ερωτήσεις προς τους αντιπάλους του, κάθε παίκτης συλλέγει στοιχεία και έπειτα, χρησιμοποιώντας
ΕΠΙΣΗΜΟΙ ΚΑΝΟΝΕΣ ΤΟΥ Το SLEUTH είναι ένα φανταστικό παιχνίδι έρευνας για 3 έως 7 παίκτες. Μέσα από έξυπνες ερωτήσεις προς τους αντιπάλους του, κάθε παίκτης συλλέγει στοιχεία και έπειτα, χρησιμοποιώντας
Πλειστηριασμός Για να πλειοδοτήσει κάποιος άξονας θα πρέπει να αναλάβει την υποχρέωση
 Πλειστηριασμός Προκειμένου να περιγράψουμε το χέρι μας στο συμπαίκτη, χρησιμοποιούμε μια ειδική διεθνή γλώσσα τα Μπριτζικά ή Μπριτζιακά. Τα καλά νέα είναι ότι αυτή η γλώσσα έχει μόνο λίγες λεξούλες. Πλειστηριασμός
Πλειστηριασμός Προκειμένου να περιγράψουμε το χέρι μας στο συμπαίκτη, χρησιμοποιούμε μια ειδική διεθνή γλώσσα τα Μπριτζικά ή Μπριτζιακά. Τα καλά νέα είναι ότι αυτή η γλώσσα έχει μόνο λίγες λεξούλες. Πλειστηριασμός
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ Τελικές Εξετάσεις Παρασκευή 16 Οκτωβρίου 2007 ιάρκεια εξέτασης: 3 ώρες (15:00-18:00) ΘΕΜΑ 1
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ Τελικές Εξετάσεις Παρασκευή 16 Οκτωβρίου 2007 ιάρκεια εξέτασης: 3 ώρες (15:00-18:00) ΘΕΜΑ 1
Δύσκολο έξοδο στην Βοσνία για την Εθνική μας
 Δύσκολο έξοδο στην Βοσνία για την Εθνική μας Σήμερα, Τρίτη, διεξάγεται η δεύτερη αγωνιστική των ομίλων των προκριματικών του Euro 2020, με πολλές σημαντικές αναμετρήσεις. Η Εθνική Ελλάδος πηγαίνει στην
Δύσκολο έξοδο στην Βοσνία για την Εθνική μας Σήμερα, Τρίτη, διεξάγεται η δεύτερη αγωνιστική των ομίλων των προκριματικών του Euro 2020, με πολλές σημαντικές αναμετρήσεις. Η Εθνική Ελλάδος πηγαίνει στην
Κανονισµοί Στοιχηµάτων Ιρλανδικών Ιπποδροµιών ΓΚΑΝΙΑΝ ΠΛΑΣΕ
 1 Κανονισµοί Στοιχηµάτων Ιρλανδικών Ιπποδροµιών ΓΚΑΝΙΑΝ Κερδίζει όποιος προβλέψει το άλογο που τερµατίζει πρώτο. ιενεργείται σε όλες τις ιπποδροµίες στις οποίες συµµετέχουν δύο ή περισσότερα άλογα Σε περίπτωση
1 Κανονισµοί Στοιχηµάτων Ιρλανδικών Ιπποδροµιών ΓΚΑΝΙΑΝ Κερδίζει όποιος προβλέψει το άλογο που τερµατίζει πρώτο. ιενεργείται σε όλες τις ιπποδροµίες στις οποίες συµµετέχουν δύο ή περισσότερα άλογα Σε περίπτωση
Ξεκινούν οι αγωνιστικές την Παρασκευή
 Ξεκινούν οι αγωνιστικές την Παρασκευή Λόγω του Πάσχα των Καθολικών έχουμε έντονη δραστηριότητα σήμερα Παρασκευή από αγώνες και ειδικά από τους Άγγλους, που παίζουν μπάλα με την Τσάμπιονσιπ και παρακάτω.
Ξεκινούν οι αγωνιστικές την Παρασκευή Λόγω του Πάσχα των Καθολικών έχουμε έντονη δραστηριότητα σήμερα Παρασκευή από αγώνες και ειδικά από τους Άγγλους, που παίζουν μπάλα με την Τσάμπιονσιπ και παρακάτω.
ΗΜΙΟΥΡΓΙΑ ΠΑΙΧΝΙ ΙΟΥ ΣΤΟ SCRATCH ΒΗΜΑ ΠΡΟΣ ΒΗΜΑ
 ΗΜΙΟΥΡΓΙΑ ΠΑΙΧΝΙ ΙΟΥ ΣΤΟ SCRATCH ΒΗΜΑ ΠΡΟΣ ΒΗΜΑ ΣΕΝΑΡΙΟ ΠΑΙΧΝΙ ΙΟΥ Το παιχνίδι θα αποτελείται από δυο παίκτες, οι οποίοι θα βρίσκονται αντικριστά στις άκρες ενός γηπέδου δεξιά και αριστερά, και µια µπάλα.
ΗΜΙΟΥΡΓΙΑ ΠΑΙΧΝΙ ΙΟΥ ΣΤΟ SCRATCH ΒΗΜΑ ΠΡΟΣ ΒΗΜΑ ΣΕΝΑΡΙΟ ΠΑΙΧΝΙ ΙΟΥ Το παιχνίδι θα αποτελείται από δυο παίκτες, οι οποίοι θα βρίσκονται αντικριστά στις άκρες ενός γηπέδου δεξιά και αριστερά, και µια µπάλα.
Προβλέψεις στο στοίχημα την Παρασκευή
 Προβλέψεις στο στοίχημα την Παρασκευή Ξεκινούν σήμερα οι αγωνιστικές των πρωταθλημάτων, όπως κάθε Παρασκευή. Στην Γαλλική Ligue 1 αρχίζει η 12 η αγωνιστική με μία αναμέτρηση. Συγκεκριμένα, η ουραγός Ντιζόν
Προβλέψεις στο στοίχημα την Παρασκευή Ξεκινούν σήμερα οι αγωνιστικές των πρωταθλημάτων, όπως κάθε Παρασκευή. Στην Γαλλική Ligue 1 αρχίζει η 12 η αγωνιστική με μία αναμέτρηση. Συγκεκριμένα, η ουραγός Ντιζόν
Κεφάλαιο 2ο (α) Αµιγείς Στρατηγικές (β) Μεικτές Στρατηγικές (α) Αµιγείς Στρατηγικές. Επαναλαµβάνουµε:
 Κεφάλαιο 2 ο Μέχρι τώρα δώσαµε τα στοιχεία ενός παιγνίου σε µορφή δέντρου και σε µορφή µήτρας. Τώρα θα ορίσουµε τη στρατηγική στην αναλυτική µορφή του παιγνίου (η στρατηγική ορίζεται από κάθε στήλη ή γραµµή
Κεφάλαιο 2 ο Μέχρι τώρα δώσαµε τα στοιχεία ενός παιγνίου σε µορφή δέντρου και σε µορφή µήτρας. Τώρα θα ορίσουµε τη στρατηγική στην αναλυτική µορφή του παιγνίου (η στρατηγική ορίζεται από κάθε στήλη ή γραµµή
159141,9 64 x n 1 n
 Πιθανότητες Στατιστική: Λύσεις θεμάτων. Φεβρουάριος 9. Σειρά Α Ζήτημα ο : Μία ομάδα φοιτητών μετρά 64 φορές μία απόσταση s που δεν γνωρίζουν. Τα αποτελέσματα των μετρήσεων εμφανίζονται στον διπλανό πίνακα
Πιθανότητες Στατιστική: Λύσεις θεμάτων. Φεβρουάριος 9. Σειρά Α Ζήτημα ο : Μία ομάδα φοιτητών μετρά 64 φορές μία απόσταση s που δεν γνωρίζουν. Τα αποτελέσματα των μετρήσεων εμφανίζονται στον διπλανό πίνακα
BRIDGE ÑÉÓÔÉÍÁ ÓÕÑÁÊÏÐÏÕËÏÕ
 BRIDGE ÃÍÙÑÉÌÉÁ ÌÅ ÔÏ ÁÈËÇÌÁ ÑÉÓÔÉÍÁ ÓÕÑÁÊÏÐÏÕËÏÕ Ξεκινώντας να παίζουμε μπριτζ Γνωριμία με το παιχνίδι Το μπριτζ παίζεται με 4 παίκτες: Τον Βορά, την Ανατολή, το Νότο και τη Δύση! Ο Βοράς είναι συμπαίκτης
BRIDGE ÃÍÙÑÉÌÉÁ ÌÅ ÔÏ ÁÈËÇÌÁ ÑÉÓÔÉÍÁ ÓÕÑÁÊÏÐÏÕËÏÕ Ξεκινώντας να παίζουμε μπριτζ Γνωριμία με το παιχνίδι Το μπριτζ παίζεται με 4 παίκτες: Τον Βορά, την Ανατολή, το Νότο και τη Δύση! Ο Βοράς είναι συμπαίκτης
Η διακριτή συνάρτηση μάζας πιθανότητας δίνεται από την
 Η ΔΙΩΝΥΜΙΚΗ ΚΑΤΑΝΟΜΗ Ενδιαφερόμαστε για την απλούστερη μορφή πειραματικής διαδικασίας, όπου η έκβαση των αποτελεσμάτων χαρακτηρίζεται μόνο ως "επιτυχής" ή "ανεπιτυχής" (δοκιμές Beroulli). Ορίζουμε λοιπόν
Η ΔΙΩΝΥΜΙΚΗ ΚΑΤΑΝΟΜΗ Ενδιαφερόμαστε για την απλούστερη μορφή πειραματικής διαδικασίας, όπου η έκβαση των αποτελεσμάτων χαρακτηρίζεται μόνο ως "επιτυχής" ή "ανεπιτυχής" (δοκιμές Beroulli). Ορίζουμε λοιπόν
ΔΙΕΥΚΡΙΝΙΣΕΙΣ MEGA BOOSTER-ΠΟΔΟΣΦΑΙΡΟ
 ΔΙΕΥΚΡΙΝΙΣΕΙΣ MEGA BOOSTER-ΠΟΔΟΣΦΑΙΡΟ H επιβράβευση αυτή αφορά μόνο pregame στοιχήματα σε 3άδες και πάνω, σε αγορές των πρωταθλημάτων ΕΛΛΑΔΑ ΣΟΥΠΕΡ ΛΙΓΚ, ΑΓΓΛΙΑ ΠΡΕΜΙΕΡ ΛΙΓΚ, ΙΣΠΑΝΙΑ 1Η, ΙΤΑΛΙΑ 1Η, ΓΕΡΜΑΝΙΑ
ΔΙΕΥΚΡΙΝΙΣΕΙΣ MEGA BOOSTER-ΠΟΔΟΣΦΑΙΡΟ H επιβράβευση αυτή αφορά μόνο pregame στοιχήματα σε 3άδες και πάνω, σε αγορές των πρωταθλημάτων ΕΛΛΑΔΑ ΣΟΥΠΕΡ ΛΙΓΚ, ΑΓΓΛΙΑ ΠΡΕΜΙΕΡ ΛΙΓΚ, ΙΣΠΑΝΙΑ 1Η, ΙΤΑΛΙΑ 1Η, ΓΕΡΜΑΝΙΑ
Πατώντας την επιλογή αυτή, ανοίγει ένα παράθυρο που έχει την ίδια μορφή με αυτό που εμφανίζεται όταν δημιουργούμε μία μεταβλητή.
 Λίστες Τι είναι οι λίστες; Πολλές φορές στην καθημερινή μας ζωή, χωρίς να το συνειδητοποιούμε, χρησιμοποιούμε λίστες. Τέτοια παραδείγματα είναι η λίστα του super market η οποία είναι ένας κατάλογος αντικειμένων
Λίστες Τι είναι οι λίστες; Πολλές φορές στην καθημερινή μας ζωή, χωρίς να το συνειδητοποιούμε, χρησιμοποιούμε λίστες. Τέτοια παραδείγματα είναι η λίστα του super market η οποία είναι ένας κατάλογος αντικειμένων
Ημέρα φαβορί στην Serie A
 Ημέρα φαβορί στην Serie A Καλημέρα σας, άλλη ημέρα σήμερα, όπου το αγωνιστικό πρόγραμμα, είναι γεμάτο με σημαντικές αναμετρήσεις, όλων των μεγάλων ομάδων, στα περισσότερα πρωταθλήματα. Σήμερα, θα ασχοληθώ
Ημέρα φαβορί στην Serie A Καλημέρα σας, άλλη ημέρα σήμερα, όπου το αγωνιστικό πρόγραμμα, είναι γεμάτο με σημαντικές αναμετρήσεις, όλων των μεγάλων ομάδων, στα περισσότερα πρωταθλήματα. Σήμερα, θα ασχοληθώ
Ανάλυση Δεδοµένων µε χρήση του Στατιστικού Πακέτου R
 Ανάλυση Δεδοµένων µε χρήση του Στατιστικού Πακέτου R, Επίκουρος Καθηγητής, Τοµέας Μαθηµατικών, Σχολή Εφαρµοσµένων Μαθηµατικών και Φυσικών Επιστηµών, Εθνικό Μετσόβιο Πολυτεχνείο. Περιεχόµενα Εισαγωγή στη
Ανάλυση Δεδοµένων µε χρήση του Στατιστικού Πακέτου R, Επίκουρος Καθηγητής, Τοµέας Μαθηµατικών, Σχολή Εφαρµοσµένων Μαθηµατικών και Φυσικών Επιστηµών, Εθνικό Μετσόβιο Πολυτεχνείο. Περιεχόµενα Εισαγωγή στη
ΔΙΕΥΚΡΙΝΙΣΕΙΣ MEGA BOOSTER-ΠΟΔΟΣΦΑΙΡΟ
 ΔΙΕΥΚΡΙΝΙΣΕΙΣ MEGA BOOSTER-ΠΟΔΟΣΦΑΙΡΟ H επιβράβευση αυτή αφορά μόνο pregame στοιχήματα σε 3άδες και πάνω, σε αγορές των διοργανώσεων ΤΣΑΜΠΙΟΝΣ ΛΙΓΚ και ΓΙΟΥΡΟΠΑ ΛΙΓΚ. εφόσον έχουν απόδοση μεγαλύτερη ή
ΔΙΕΥΚΡΙΝΙΣΕΙΣ MEGA BOOSTER-ΠΟΔΟΣΦΑΙΡΟ H επιβράβευση αυτή αφορά μόνο pregame στοιχήματα σε 3άδες και πάνω, σε αγορές των διοργανώσεων ΤΣΑΜΠΙΟΝΣ ΛΙΓΚ και ΓΙΟΥΡΟΠΑ ΛΙΓΚ. εφόσον έχουν απόδοση μεγαλύτερη ή
ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ
 ΘΕΜΑ 1 ο (2.5 µονάδες) ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ Τελικές εξετάσεις Παρασκευή 28 Σεπτεµβρίου 2007 ιάρκεια: 13:00-16:00
ΘΕΜΑ 1 ο (2.5 µονάδες) ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ Τελικές εξετάσεις Παρασκευή 28 Σεπτεµβρίου 2007 ιάρκεια: 13:00-16:00
Κεφάλαιο 13ο Eπαναλαµβανόµενα παίγνια (Repeated Games)
 Κεφάλαιο 13ο Eπαναλαµβανόµενα παίγνια (Repeated Gaes) Το δίληµµα των φυλακισµένων, όπως ξέρουµε έχει µια και µοναδική ισορροπία η οποία είναι σε αυστηρά κυρίαρχες στρατηγικές. C N C -8, -8 0, -10 N -10,
Κεφάλαιο 13ο Eπαναλαµβανόµενα παίγνια (Repeated Gaes) Το δίληµµα των φυλακισµένων, όπως ξέρουµε έχει µια και µοναδική ισορροπία η οποία είναι σε αυστηρά κυρίαρχες στρατηγικές. C N C -8, -8 0, -10 N -10,
ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΠΑΙΧΝΙΔΙΩΝ ΤΗΣ ΟΠΑΠ Α.Ε.
 ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΠΑΙΧΝΙΔΙΩΝ ΤΗΣ ΟΠΑΠ Α.Ε. ΓΝΩΣΗ ΑΜΟΙΒΑΙΑ ΚΕΡΔΗ ΠΡΟΚΑΘΟΡΙΣΜΕΝΑ ΚΕΡΔΗ ΤΥΧΗ Ημερομηνία Έναρξης Η διεξαγωγή του αριθμολαχείου ξεκίνησε στις 16/11/1997 Αντικείμενο Παιχνιδιού Το ΤΖΟΚΕΡ είναι παιχνίδι
ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΠΑΙΧΝΙΔΙΩΝ ΤΗΣ ΟΠΑΠ Α.Ε. ΓΝΩΣΗ ΑΜΟΙΒΑΙΑ ΚΕΡΔΗ ΠΡΟΚΑΘΟΡΙΣΜΕΝΑ ΚΕΡΔΗ ΤΥΧΗ Ημερομηνία Έναρξης Η διεξαγωγή του αριθμολαχείου ξεκίνησε στις 16/11/1997 Αντικείμενο Παιχνιδιού Το ΤΖΟΚΕΡ είναι παιχνίδι
 ΤΙ ΕΙΝΑΙ ΤΖΟΓΟΣ Με την λέξη τζόγος εννοούμε το ποντάρισμα ή το στοίχημα πάνω σε κάτι που πιστεύουμε ότι θα κερδίσει και εμείς φυσικά θα έχουμε ένα κέρδος.ο τζόγος είναι στο αίμα του κάθε ανθρώπου και η
ΤΙ ΕΙΝΑΙ ΤΖΟΓΟΣ Με την λέξη τζόγος εννοούμε το ποντάρισμα ή το στοίχημα πάνω σε κάτι που πιστεύουμε ότι θα κερδίσει και εμείς φυσικά θα έχουμε ένα κέρδος.ο τζόγος είναι στο αίμα του κάθε ανθρώπου και η
Δύο μονομαχίες στα προημιτελικά του Copa America
 Δύο μονομαχίες στα προημιτελικά του Copa America Συνεχίζονται οι προημιτελικοί του Copa America, όπου με την ολοκλήρωση τους θα προκύψει η τελική τετράδα του θεσμού, διεκδικώντας το μεγάλο τρόπαιο. Σήμερα,
Δύο μονομαχίες στα προημιτελικά του Copa America Συνεχίζονται οι προημιτελικοί του Copa America, όπου με την ολοκλήρωση τους θα προκύψει η τελική τετράδα του θεσμού, διεκδικώντας το μεγάλο τρόπαιο. Σήμερα,
Α. ΑΝΙΣΟΤΗΤΕΣ - ΚΑΝΟΝΕΣ ΑΝΙΣΟΤΗΤΩΝ
 Κεφάλαιο o : Εξισώσεις - Ανισώσεις ΜΑΘΗΜΑ Υποενότητα.: Ανισώσεις ου Βαθµού Θεµατικές Ενότητες:. Ανισότητες - Κανόνες Ανισοτήτων.. Η έννοια της ανίσωσης.. Τρόπος επίλυσης ανισώσεων ου βαθµού. Α. ΑΝΙΣΟΤΗΤΕΣ
Κεφάλαιο o : Εξισώσεις - Ανισώσεις ΜΑΘΗΜΑ Υποενότητα.: Ανισώσεις ου Βαθµού Θεµατικές Ενότητες:. Ανισότητες - Κανόνες Ανισοτήτων.. Η έννοια της ανίσωσης.. Τρόπος επίλυσης ανισώσεων ου βαθµού. Α. ΑΝΙΣΟΤΗΤΕΣ
Κεφάλαιο 9. Έλεγχοι υποθέσεων
 Κεφάλαιο 9 Έλεγχοι υποθέσεων 9.1 Εισαγωγή Όταν παίρνουμε ένα ή περισσότερα τυχαία δείγμα από κανονικούς πληθυσμούς έχουμε τη δυνατότητα να υπολογίζουμε στατιστικά, όπως μέσους όρους, δειγματικές διασπορές
Κεφάλαιο 9 Έλεγχοι υποθέσεων 9.1 Εισαγωγή Όταν παίρνουμε ένα ή περισσότερα τυχαία δείγμα από κανονικούς πληθυσμούς έχουμε τη δυνατότητα να υπολογίζουμε στατιστικά, όπως μέσους όρους, δειγματικές διασπορές
ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΠΑΙΧΝΙΔΙΩΝ ΤΗΣ ΟΠΑΠ Α.Ε.
 ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΠΑΙΧΝΙΔΙΩΝ ΤΗΣ ΟΠΑΠ Α.Ε. ΓΝΩΣΗ ΑΜΟΙΒΑΙΑ ΚΕΡΔΗ ΠΡΟΚΑΘΟΡΙΣΜΕΝΑ ΚΕΡΔΗ ΤΥΧΗ Ημερομηνία Έναρξης Η διεξαγωγή του αριθμολαχείου ξεκίνησε στις 5/12/1990 Αντικείμενο Παιχνιδιού Το ΛΟΤΤΟ είναι ένα
ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΠΑΙΧΝΙΔΙΩΝ ΤΗΣ ΟΠΑΠ Α.Ε. ΓΝΩΣΗ ΑΜΟΙΒΑΙΑ ΚΕΡΔΗ ΠΡΟΚΑΘΟΡΙΣΜΕΝΑ ΚΕΡΔΗ ΤΥΧΗ Ημερομηνία Έναρξης Η διεξαγωγή του αριθμολαχείου ξεκίνησε στις 5/12/1990 Αντικείμενο Παιχνιδιού Το ΛΟΤΤΟ είναι ένα
Το Μπαούλο του κυρ Γιάννη
 Εισαγωγή Το Μπαούλο του κυρ Γιάννη Ο κυρ Γιάννης έχει κληρονομιά ένα παλιό μπαούλο με ό,τι αντικείμενα μπορείς να φανταστείς! Τα ανίψια του, ο Λευτεράκης και η Βασούλα, θέλουν να τα δουν, αλλά για να τα
Εισαγωγή Το Μπαούλο του κυρ Γιάννη Ο κυρ Γιάννης έχει κληρονομιά ένα παλιό μπαούλο με ό,τι αντικείμενα μπορείς να φανταστείς! Τα ανίψια του, ο Λευτεράκης και η Βασούλα, θέλουν να τα δουν, αλλά για να τα
ΔΗΜΙΟΎΡΓΗΣΕ ΤΗ ΔΙΚΉ ΣΟΥ ΜΠΑΝΆΝΑ ΤΖΌΚΕΡ!
 01 ΔΗΜΙΟΎΡΓΗΣΕ ΤΗ ΔΙΚΉ ΣΟΥ ΜΠΑΝΆΝΑ ΤΖΌΚΕΡ! A N A N BA R E K JO Μια μπανάνα μπορεί να κάνει πολλά πράγματα. Είναι νόστιμη, σε γεμίζει ενέργεια για κάθε σωματική ή πνευματική άσκηση και ακόμη και η φλούδα
01 ΔΗΜΙΟΎΡΓΗΣΕ ΤΗ ΔΙΚΉ ΣΟΥ ΜΠΑΝΆΝΑ ΤΖΌΚΕΡ! A N A N BA R E K JO Μια μπανάνα μπορεί να κάνει πολλά πράγματα. Είναι νόστιμη, σε γεμίζει ενέργεια για κάθε σωματική ή πνευματική άσκηση και ακόμη και η φλούδα
ΠΑΝΕΛΛΗΝΙΑ ΟΜΟΣΠΟΝΔΙΑ ΕΠΑΓΓΕΛΜΑΤΙΩΝ ΠΡΑΚΤΟΡΩΝ ΠΑΙΧΝΙΔΙΩΝ ΠΡΟΓΝΩΣΗΣ ΟΠΑΠ
 πάμε στοίχημα Π.Ο.Ε.Π.Π.Π. ΠΑΝΕΛΛΗΝΙΑ ΟΜΟΣΠΟΝΔΙΑ ΕΠΑΓΓΕΛΜΑΤΙΩΝ ΠΡΑΚΤΟΡΩΝ ΠΑΙΧΝΙΔΙΩΝ ΠΡΟΓΝΩΣΗΣ ΟΠΑΠ ΜΑΡΝΗ 56, 104 37 ΑΘΗΝΑ, ΤΗΛ. 210 5223580 FAX: 210 5229289 Αθήνα 19/9/09 Πρόταση αναμόρφωσης Πάμε Στοίχημα
πάμε στοίχημα Π.Ο.Ε.Π.Π.Π. ΠΑΝΕΛΛΗΝΙΑ ΟΜΟΣΠΟΝΔΙΑ ΕΠΑΓΓΕΛΜΑΤΙΩΝ ΠΡΑΚΤΟΡΩΝ ΠΑΙΧΝΙΔΙΩΝ ΠΡΟΓΝΩΣΗΣ ΟΠΑΠ ΜΑΡΝΗ 56, 104 37 ΑΘΗΝΑ, ΤΗΛ. 210 5223580 FAX: 210 5229289 Αθήνα 19/9/09 Πρόταση αναμόρφωσης Πάμε Στοίχημα
Χρήσεις του Η/Υ και Βάσεις Βιολογικών Δεδομένων
 Χρήσεις του Η/Υ και Βάσεις Βιολογικών Δεδομένων 3. Δεδομένα και Στατιστική Επεξεργασία Χριστόφορος Νικολάου Τμήμα Βιολογίας, Πανεπιστήμιο Κρήτης computational-genomics-uoc.weebly.com Χριστόφορος Νικολαου,
Χρήσεις του Η/Υ και Βάσεις Βιολογικών Δεδομένων 3. Δεδομένα και Στατιστική Επεξεργασία Χριστόφορος Νικολάου Τμήμα Βιολογίας, Πανεπιστήμιο Κρήτης computational-genomics-uoc.weebly.com Χριστόφορος Νικολαου,
Από την Α Λυκείου µέχρι το Πανεπιστήµιο
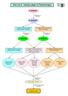 Από την Α Λυκείου µέχρι το Πανεπιστήµιο Α ΛΥΚΕΙΟΥ Β ΛΥΚΕΙΟΥ 1 η οµάδα προσανατολισµού ανθρωπιστικών σπουδών η οµάδα προσανατολισµού θετικών σπουδών 1 η οµάδα προσανατολισµού ανθρωπιστικών σπουδών 3 η οµάδα
Από την Α Λυκείου µέχρι το Πανεπιστήµιο Α ΛΥΚΕΙΟΥ Β ΛΥΚΕΙΟΥ 1 η οµάδα προσανατολισµού ανθρωπιστικών σπουδών η οµάδα προσανατολισµού θετικών σπουδών 1 η οµάδα προσανατολισµού ανθρωπιστικών σπουδών 3 η οµάδα
Από τα Δεδομένα στις Πληροφορίες - Μέρος Ι (Ταξινόμηση, Επιλογή, Μερικά Αθροίσματα)
 Άσκηση 4 Από τα Δεδομένα στις Πληροφορίες - Μέρος Ι (Ταξινόμηση, Επιλογή, Μερικά Αθροίσματα) Σκοπός Η ανάλυση μη αριθμητικών μεθόδων επεξεργασίας δεδομένων. Η συστηματική οργάνωση και ανάλυση δεδομένων
Άσκηση 4 Από τα Δεδομένα στις Πληροφορίες - Μέρος Ι (Ταξινόμηση, Επιλογή, Μερικά Αθροίσματα) Σκοπός Η ανάλυση μη αριθμητικών μεθόδων επεξεργασίας δεδομένων. Η συστηματική οργάνωση και ανάλυση δεδομένων
Ισορροπία (balance) Οι ιδιότητες που δημιουργεί η μέθοδος του ακεραίου τοπ.
 Ισορροπία (balance) Ένας όρος που χρησιμοποιείται συχνά σε θέματα κινήσεων είναι η ισορροπία (balance). Για να προχωρήσουμε παρακάτω πρέπει να ξέρουμε πως να βγάζουμε αποτελέσματα σε ένα τουρνουά ζευγών
Ισορροπία (balance) Ένας όρος που χρησιμοποιείται συχνά σε θέματα κινήσεων είναι η ισορροπία (balance). Για να προχωρήσουμε παρακάτω πρέπει να ξέρουμε πως να βγάζουμε αποτελέσματα σε ένα τουρνουά ζευγών
Τον πρώτο λόγο η Αγγλία με την Σουηδία
 Τον πρώτο λόγο η Αγγλία με την Σουηδία Καλημέρα σας, ολοκληρώνονται σήμερα οι προημιτελικοί του παγκοσμίου κυπέλλου και θα προκύψει το δεύτερο ζευγάρι των ημιτελικών του Μουντιάλ 2018. Η έκπληξη της διοργάνωσης
Τον πρώτο λόγο η Αγγλία με την Σουηδία Καλημέρα σας, ολοκληρώνονται σήμερα οι προημιτελικοί του παγκοσμίου κυπέλλου και θα προκύψει το δεύτερο ζευγάρι των ημιτελικών του Μουντιάλ 2018. Η έκπληξη της διοργάνωσης
Α. ΜΕΣΗ ΤΙΜΗ - ΙΑΜΕΣΟΣ
 ΜΑΘΗΜΑ 17 Κεφάλαιο 4o : Περιγραφική Στατιστική Υποενότητα 4.5: Μέση Τιµή - ιάµεσος Θεµατικές Ενότητες: 1. Μέση Τιµή - ιάµεσος. Α. ΜΕΣΗ ΤΙΜΗ - ΙΑΜΕΣΟΣ ΟΡΙΣΜΟΙ Για πιο σύντοµη, αποδοτική και συγκρίσιµη θεώρηση
ΜΑΘΗΜΑ 17 Κεφάλαιο 4o : Περιγραφική Στατιστική Υποενότητα 4.5: Μέση Τιµή - ιάµεσος Θεµατικές Ενότητες: 1. Μέση Τιµή - ιάµεσος. Α. ΜΕΣΗ ΤΙΜΗ - ΙΑΜΕΣΟΣ ΟΡΙΣΜΟΙ Για πιο σύντοµη, αποδοτική και συγκρίσιµη θεώρηση
Κεφάλαιο 5 R (2, 3) R (3, 0)
 Κεφάλαιο 5 Θα ξεκινήσουµε το κεφάλαιο αυτό βλέποντας ένα ακόµη παράδειγµα αναφορικά µε την ισορροπία που προκύπτει από την οπισθογενή επαγωγή (backwards induction) και την ισορροπία κατά Nash στην στρατηγική
Κεφάλαιο 5 Θα ξεκινήσουµε το κεφάλαιο αυτό βλέποντας ένα ακόµη παράδειγµα αναφορικά µε την ισορροπία που προκύπτει από την οπισθογενή επαγωγή (backwards induction) και την ισορροπία κατά Nash στην στρατηγική
Προγνωστικα από όλη την Ευρώπη
 Προγνωστικα από όλη την Ευρώπη Καλημέρα σας, ενώ το αγωνιστικό πρόγραμμα είναι γεμάτο, αυτό, δεν έχει καθόλου ποιότητα, χωρίς μεγάλες αναμετρήσεις, με ματς από μικρομεσαίες ομάδες. Στην Ελλάδα, δεν γίνονται
Προγνωστικα από όλη την Ευρώπη Καλημέρα σας, ενώ το αγωνιστικό πρόγραμμα είναι γεμάτο, αυτό, δεν έχει καθόλου ποιότητα, χωρίς μεγάλες αναμετρήσεις, με ματς από μικρομεσαίες ομάδες. Στην Ελλάδα, δεν γίνονται
Η παρούσα αξία της επένδυσης αν αυτή υλοποιηθεί άµεσα είναι 0 K 0 1 K
 6. Αβεβαιότητα και µη Αναστρέψιµες Επενδύσεις Στην περίπτωση που µία επένδυση δεν µπορεί να αντιστραφεί χωρίς κόστος, δηλαδή αφού έχει πραγµατοποιηθεί η αγορά κεφαλαιακού εξοπλισµού, κατασκευή κτηρίων
6. Αβεβαιότητα και µη Αναστρέψιµες Επενδύσεις Στην περίπτωση που µία επένδυση δεν µπορεί να αντιστραφεί χωρίς κόστος, δηλαδή αφού έχει πραγµατοποιηθεί η αγορά κεφαλαιακού εξοπλισµού, κατασκευή κτηρίων
ΚΕΦΑΛΑΙΟ 13 ο. Μάντεψε το µυστικό κανόνα µου. Στο κεφάλαιο αυτό, θα προσπαθήσουµε να επιτύχουµε τους εξής στόχους:
 ΚΕΦΑΛΑΙΟ 13 ο Κριτήρια διαιρετότητας Μάντεψε το µυστικό κανόνα µου Στο κεφάλαιο αυτό, θα προσπαθήσουµε να επιτύχουµε τους εξής στόχους: 1. Να µάθεις να ξεχωρίζεις ποιοι αριθµοί διαιρούνται µε το 2, το
ΚΕΦΑΛΑΙΟ 13 ο Κριτήρια διαιρετότητας Μάντεψε το µυστικό κανόνα µου Στο κεφάλαιο αυτό, θα προσπαθήσουµε να επιτύχουµε τους εξής στόχους: 1. Να µάθεις να ξεχωρίζεις ποιοι αριθµοί διαιρούνται µε το 2, το
Πιλόττα. Θεωρείται κάπως περίπλοκο παιχνίδι λόγω μερικών σημαντικών εξαιρέσεων στους κανόνες βασικής ροής, αλλά αυτό το κάνει και ενδιαφέρον.
 Πιλόττα Εισαγωγή Η Πιλόττα είναι ένα πολύ δημοφιλές επιτραπέζιο παιγνίδι με τράπουλα που παίζεται με ιδιαίτερο τρόπο στην Κύπρο, αλλά παραδόξως, όχι ευρέως στην Ελλάδα. Η Πιλόττα μοιάζει αρκετά με το πολύ
Πιλόττα Εισαγωγή Η Πιλόττα είναι ένα πολύ δημοφιλές επιτραπέζιο παιγνίδι με τράπουλα που παίζεται με ιδιαίτερο τρόπο στην Κύπρο, αλλά παραδόξως, όχι ευρέως στην Ελλάδα. Η Πιλόττα μοιάζει αρκετά με το πολύ
Ε Ν Ι Α Ι Ο ΑΝτιµνηµονιακό ΑΓωνιστικό ΚΙνηµα «ΑΝ.ΑΓ.ΚΙ.»- «Αγωνιστική Ενιαία Κινητοποίηση»-Συνεργαζόµενοι ικαστικοί Υπάλληλοι
 Ε Ν Ι Α Ι Ο ΑΝτιµνηµονιακό ΑΓωνιστικό ΚΙνηµα «ΑΝ.ΑΓ.ΚΙ.»- «Αγωνιστική Ενιαία Κινητοποίηση»-Συνεργαζόµενοι ικαστικοί Υπάλληλοι ΛΙΓΑ ΛΟΓΙΑ ΓΙΑ ΝΑ ΓΙΝΕΙ ΜΙΑ ΓΙΟΡΤΗ ΟΠΩΣ ΤΗΣ ΠΡΕΠΕΙ Πολλά και από πολλούς, κατά
Ε Ν Ι Α Ι Ο ΑΝτιµνηµονιακό ΑΓωνιστικό ΚΙνηµα «ΑΝ.ΑΓ.ΚΙ.»- «Αγωνιστική Ενιαία Κινητοποίηση»-Συνεργαζόµενοι ικαστικοί Υπάλληλοι ΛΙΓΑ ΛΟΓΙΑ ΓΙΑ ΝΑ ΓΙΝΕΙ ΜΙΑ ΓΙΟΡΤΗ ΟΠΩΣ ΤΗΣ ΠΡΕΠΕΙ Πολλά και από πολλούς, κατά
www.onlineclassroom.gr
 ΑΣΚΗΣΗ 3 (ΜΟΝΑΔΕΣ 25) Σε ένα αγώνα ποδοσφαίρου οι προπονητές των δύο αντίπαλων ομάδων αποφάσισαν ότι έχουν 4 και 3 επιλογές συστήματος, αντίστοιχα. Η αναμενόμενη διαφορά τερμάτων δίνεται από τον παρακάτω
ΑΣΚΗΣΗ 3 (ΜΟΝΑΔΕΣ 25) Σε ένα αγώνα ποδοσφαίρου οι προπονητές των δύο αντίπαλων ομάδων αποφάσισαν ότι έχουν 4 και 3 επιλογές συστήματος, αντίστοιχα. Η αναμενόμενη διαφορά τερμάτων δίνεται από τον παρακάτω
Ζακόκ. Πεπέκης Κωνσταντίνος
 Ζακόκ Ένα παιχνίδι που έπαιζε η γιαγιά µου όταν ήταν µικρή είναι το ζακόκ. Το ζακόκ είναι παρόµοιο µε το κυνηγητό που παίζουµε τώρα. Για να ξεκινήσει το παιχνίδι τα παιδιά πρέπει να χωριστούν σε 2 οµάδες.
Ζακόκ Ένα παιχνίδι που έπαιζε η γιαγιά µου όταν ήταν µικρή είναι το ζακόκ. Το ζακόκ είναι παρόµοιο µε το κυνηγητό που παίζουµε τώρα. Για να ξεκινήσει το παιχνίδι τα παιδιά πρέπει να χωριστούν σε 2 οµάδες.
ΟΔΗΓΟΣ ΤΥΠΩΝ ΑΜΟΙΒΑΙΟΥ ΙΠΠΟΔΡΟΜΙΑΚΟΥ ΣΤΟΙΧΗΜΑΤΟΣ
 ΟΔΗΓΟΣ ΤΥΠΩΝ ΑΜΟΙΒΑΙΟΥ ΙΠΠΟΔΡΟΜΙΑΚΟΥ ΣΤΟΙΧΗΜΑΤΟΣ Α. ΓΕΝΙΚΕΣ ΠΛΗΡΟΦΟΡΙΕΣ 1. Φορέας Εκμετάλλευσης: Ιπποδρομίες ΑΝΩΝΥΜΗ ΕΤΑΙΡΙΑ (διακριτικός τίτλος «Ιπποδρομίες Α.Ε.») Έδρα: Λ. ΑΘΗΝΩΝ 112 Τ.Κ. 10442 ΑΘΗΝΑ
ΟΔΗΓΟΣ ΤΥΠΩΝ ΑΜΟΙΒΑΙΟΥ ΙΠΠΟΔΡΟΜΙΑΚΟΥ ΣΤΟΙΧΗΜΑΤΟΣ Α. ΓΕΝΙΚΕΣ ΠΛΗΡΟΦΟΡΙΕΣ 1. Φορέας Εκμετάλλευσης: Ιπποδρομίες ΑΝΩΝΥΜΗ ΕΤΑΙΡΙΑ (διακριτικός τίτλος «Ιπποδρομίες Α.Ε.») Έδρα: Λ. ΑΘΗΝΩΝ 112 Τ.Κ. 10442 ΑΘΗΝΑ
ΕΛΛΗΝΙΚΟ ΑΝΟΙΧΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ιακριτά Μαθηµατικά και Μαθηµατική Λογική ΠΛΗ20 Ε ρ γ α σ ί α 1η Συνδυαστική-Σχέσεις-Συναρτήσεις Σκοπός της παρούσας εργασίας είναι η περαιτέρω εξοικείωση µε τις σηµαντικότερες µεθόδους και ιδέες της Συνδυαστικής
ιακριτά Μαθηµατικά και Μαθηµατική Λογική ΠΛΗ20 Ε ρ γ α σ ί α 1η Συνδυαστική-Σχέσεις-Συναρτήσεις Σκοπός της παρούσας εργασίας είναι η περαιτέρω εξοικείωση µε τις σηµαντικότερες µεθόδους και ιδέες της Συνδυαστικής
Γυµνάσιο Σιταγρών Θεατρικοί διάλογοι από τους µαθητές της Α Γυµνασίου. 1 η µέρα. Χιουµορίστας: Καληµέρα παιδιά, πρώτη µέρα στο Γυµνάσιο.
 Ντέµι Ραµά 1 η µέρα Χιουµορίστας: Καληµέρα παιδιά, πρώτη µέρα στο Γυµνάσιο. Κακός µ.: Άντε να δούµε τι θα γίνει αυτή τη χρονιά. ύσκολα θα είναι στο Γυµνάσιο? Καλός µ.: Σιγά να µην είναι δύσκολα, άµα διαβάζεις
Ντέµι Ραµά 1 η µέρα Χιουµορίστας: Καληµέρα παιδιά, πρώτη µέρα στο Γυµνάσιο. Κακός µ.: Άντε να δούµε τι θα γίνει αυτή τη χρονιά. ύσκολα θα είναι στο Γυµνάσιο? Καλός µ.: Σιγά να µην είναι δύσκολα, άµα διαβάζεις
ΜΙΛΩΝΤΑΣ ΣΤΑ ΠΑΙΔΙΑ ΓΙΑ ΤΗΝ ΟΙΚΟΝΟΜΙΚΗ ΚΡΙΣΗ. ΕΛΕΥΘΕΡΙΑ ΚΑΒΒΑΔΙΑ Σύμβουλος Ψυχικής Υγείας
 ΜΙΛΩΝΤΑΣ ΣΤΑ ΠΑΙΔΙΑ ΓΙΑ ΤΗΝ ΟΙΚΟΝΟΜΙΚΗ ΚΡΙΣΗ ΕΛΕΥΘΕΡΙΑ ΚΑΒΒΑΔΙΑ Σύμβουλος Ψυχικής Υγείας 29.05.2015 Ερωτήματα που μας απασχολούν Τι κάνουμε όταν αμφιβάλλουμε για το αν θα τα καταφέρουμε να κρατήσουμε
ΜΙΛΩΝΤΑΣ ΣΤΑ ΠΑΙΔΙΑ ΓΙΑ ΤΗΝ ΟΙΚΟΝΟΜΙΚΗ ΚΡΙΣΗ ΕΛΕΥΘΕΡΙΑ ΚΑΒΒΑΔΙΑ Σύμβουλος Ψυχικής Υγείας 29.05.2015 Ερωτήματα που μας απασχολούν Τι κάνουμε όταν αμφιβάλλουμε για το αν θα τα καταφέρουμε να κρατήσουμε
40 πιόνια 10 x κόκκινο, πορτοκαλί, μαύρο, μπλε. 7 ελέφαντες 3 λιοντάρια 6 κανονικοί 1 σούπερ κροκόδειλοι κροκόδειλος
 Λιοντάρι, Ζέβρα, Ελέφαντας Άγρια, πλατειά, όμορφη χώρα! Παίκτες: 2-4 Ηλικία: από 8 ετών Διάρκεια: περ. 20 λεπτά Andreas Spies Οι κάρτες Υπάρχουν συνολικά 42 οπληφόρα ζώα (γκνου, ζέβρα, αντιλόπη), τα οποία
Λιοντάρι, Ζέβρα, Ελέφαντας Άγρια, πλατειά, όμορφη χώρα! Παίκτες: 2-4 Ηλικία: από 8 ετών Διάρκεια: περ. 20 λεπτά Andreas Spies Οι κάρτες Υπάρχουν συνολικά 42 οπληφόρα ζώα (γκνου, ζέβρα, αντιλόπη), τα οποία
Επαναληπτικέ ς Ασκη σέις ΑΕΠΠ
 Επαναληπτικέ ς Ασκη σέις ΑΕΠΠ Επιμέλεια: Σ. Ασημέλλης 1. Σε ένα ποδοσφαιρικό πρωτάθλημα μετέχουν 16 ομάδες. Κάθε ομάδα παίζει με όλες τις υπόλοιπες ως γηπεδούχος και ως φιλοξενούμενη. Νίκη μιας ομάδας
Επαναληπτικέ ς Ασκη σέις ΑΕΠΠ Επιμέλεια: Σ. Ασημέλλης 1. Σε ένα ποδοσφαιρικό πρωτάθλημα μετέχουν 16 ομάδες. Κάθε ομάδα παίζει με όλες τις υπόλοιπες ως γηπεδούχος και ως φιλοξενούμενη. Νίκη μιας ομάδας
Λίγες επιλογές την Δευτέρα
 Λίγες επιλογές την Δευτέρα Η αγωνιστική στην Σούπερ Λιγκ, ρίχνει την αυλαία της, στην Τρίπολη, όπου το ο τοπικός Αστέρας υποδέχεται την Λαμία. Οι δύο σύλλογοι, είναι χαμηλά στην βαθμολογία, λίγο πάνω από
Λίγες επιλογές την Δευτέρα Η αγωνιστική στην Σούπερ Λιγκ, ρίχνει την αυλαία της, στην Τρίπολη, όπου το ο τοπικός Αστέρας υποδέχεται την Λαμία. Οι δύο σύλλογοι, είναι χαμηλά στην βαθμολογία, λίγο πάνω από
Δυνατές μάχες στον 2ο όμιλο για τη πρόκριση
 Δυνατές μάχες στον 2ο όμιλο για τη πρόκριση Συνεχίζονται οι μάχες στο Copa America, χτες ολοκληρώθηκε ο πρώτος όμιλος και σήμερα τελειώνει ο δεύτερος όμιλος, με πολλές σημαντικές μάχες. Σήμερα, η Αργεντινή
Δυνατές μάχες στον 2ο όμιλο για τη πρόκριση Συνεχίζονται οι μάχες στο Copa America, χτες ολοκληρώθηκε ο πρώτος όμιλος και σήμερα τελειώνει ο δεύτερος όμιλος, με πολλές σημαντικές μάχες. Σήμερα, η Αργεντινή
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΟΛΟΓΙΣΤΩΝ ΖΩΓΡΑΦΟΥ 157 73, ΑΘΗΝΑ ΕΒΓ - ΙΠΛ-2003-1 20 Ιανουαρίου 2003 Σύγκριση Αλγορίθµων
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΟΛΟΓΙΣΤΩΝ ΖΩΓΡΑΦΟΥ 157 73, ΑΘΗΝΑ ΕΒΓ - ΙΠΛ-2003-1 20 Ιανουαρίου 2003 Σύγκριση Αλγορίθµων
οποία ερχόµενη πίσω από τη γραµµή εκκίνησης κτυπήσει την αριθµηµένη µπίλια.
 ΠΑΓΚΟΣΜΙΟΙ ΚΑΝΟΝΙΣΜΟΙ ΟΚΤΑΜΠΑΛΟ 1. Σκοπός του παιχνιδιού. Το παιγνίδι παίζεται µε δηλωµένα χτυπήµατα και παίζεται µε µια άσπρη µπίλια και δεκαπέντε αριθµηµένες µπίλιες από το 1 ως το 15. Ο ένας παίκτης
ΠΑΓΚΟΣΜΙΟΙ ΚΑΝΟΝΙΣΜΟΙ ΟΚΤΑΜΠΑΛΟ 1. Σκοπός του παιχνιδιού. Το παιγνίδι παίζεται µε δηλωµένα χτυπήµατα και παίζεται µε µια άσπρη µπίλια και δεκαπέντε αριθµηµένες µπίλιες από το 1 ως το 15. Ο ένας παίκτης
Κεφάλαιο 9. Έλεγχοι υποθέσεων
 Κεφάλαιο 9 Έλεγχοι υποθέσεων 9.1 Εισαγωγή Όταν παίρνουμε ένα ή περισσότερα τυχαία δείγμα από κανονικούς πληθυσμούς έχουμε τη δυνατότητα να υπολογίζουμε στατιστικά, όπως μέσους όρους, δειγματικές διασπορές
Κεφάλαιο 9 Έλεγχοι υποθέσεων 9.1 Εισαγωγή Όταν παίρνουμε ένα ή περισσότερα τυχαία δείγμα από κανονικούς πληθυσμούς έχουμε τη δυνατότητα να υπολογίζουμε στατιστικά, όπως μέσους όρους, δειγματικές διασπορές
5.1 Συναρτήσεις δύο ή περισσοτέρων µεταβλητών
 Κεφάλαιο 5 ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ 5.1 Συναρτήσεις δύο ή περισσοτέρων µεταβλητών Οταν ένα µεταβλητό µέγεθος εξαρτάται αποκλειστικά από τις µεταβολές ενός άλλου µεγέθους, τότε η σχέση που συνδέει
Κεφάλαιο 5 ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ 5.1 Συναρτήσεις δύο ή περισσοτέρων µεταβλητών Οταν ένα µεταβλητό µέγεθος εξαρτάται αποκλειστικά από τις µεταβολές ενός άλλου µεγέθους, τότε η σχέση που συνδέει
Σχολικός Σύµβουλος ΠΕ03
 Α Σ Κ Η Σ Ε Ι Σ Π Ι Θ Α Ν Ο Τ Η Τ Ω Ν ρ. Παναγιώτης Λ. Θεοδωρόπουλος Σχολικός Σύµβουλος ΠΕ0 e-mail@p-theodoropoulos.gr Πρόλογος Η Θεωρία Πιθανοτήτων είναι ένας σχετικά νέος κλάδος των Μαθηµατικών µε πολλά
Α Σ Κ Η Σ Ε Ι Σ Π Ι Θ Α Ν Ο Τ Η Τ Ω Ν ρ. Παναγιώτης Λ. Θεοδωρόπουλος Σχολικός Σύµβουλος ΠΕ0 e-mail@p-theodoropoulos.gr Πρόλογος Η Θεωρία Πιθανοτήτων είναι ένας σχετικά νέος κλάδος των Μαθηµατικών µε πολλά
Οι παίκτες παίρνουν το ρόλο των χειρότερων πειρατών στο πλήρωμα ενός πλοίου. Ο καπετάνιος σας έχει στη μπούκα, επειδή είστε πολύ τεμπέληδες και
 Οι παίκτες παίρνουν το ρόλο των χειρότερων πειρατών στο πλήρωμα ενός πλοίου. Ο καπετάνιος σας έχει στη μπούκα, επειδή είστε πολύ τεμπέληδες και βλάκες για να αξίζετε μερίδιο στο ρούμι και τα λάφυρα. Επειδή
Οι παίκτες παίρνουν το ρόλο των χειρότερων πειρατών στο πλήρωμα ενός πλοίου. Ο καπετάνιος σας έχει στη μπούκα, επειδή είστε πολύ τεμπέληδες και βλάκες για να αξίζετε μερίδιο στο ρούμι και τα λάφυρα. Επειδή
ροµολόγηση πακέτων σε δίκτυα υπολογιστών
 ροµολόγηση πακέτων σε δίκτυα υπολογιστών Συµπληρωµατικές σηµειώσεις για το µάθηµα Αλγόριθµοι Επικοινωνιών Ακαδηµαϊκό έτος 2011-2012 1 Εισαγωγή Οι παρακάτω σηµειώσεις παρουσιάζουν την ανάλυση του άπληστου
ροµολόγηση πακέτων σε δίκτυα υπολογιστών Συµπληρωµατικές σηµειώσεις για το µάθηµα Αλγόριθµοι Επικοινωνιών Ακαδηµαϊκό έτος 2011-2012 1 Εισαγωγή Οι παρακάτω σηµειώσεις παρουσιάζουν την ανάλυση του άπληστου
Του Βασίλη Παπαδάκη* Οι "μεταγραφές" στο παιδικό ποδόσφαιρο: Ένα παιχνίδι στην πλάτη των Παιδιών από Προπονητές
 Του Βασίλη Παπαδάκη* Τα παιδιά συμμετέχουν σε ένα άθλημα για να διασκεδάσουν, να βελτιώσουν τις δεξιότητές τους, να αποτελέσουν μέλη μιας ομάδας, να κερδίσουν αναγνώριση, καλή φυσική κατάσταση και να ζήσουν
Του Βασίλη Παπαδάκη* Τα παιδιά συμμετέχουν σε ένα άθλημα για να διασκεδάσουν, να βελτιώσουν τις δεξιότητές τους, να αποτελέσουν μέλη μιας ομάδας, να κερδίσουν αναγνώριση, καλή φυσική κατάσταση και να ζήσουν
Διαπιστευτήρια για τον τίτλο Σεβίλλη και Ατλέτικο
 Διαπιστευτήρια για τον τίτλο Σεβίλλη και Ατλέτικο Ένα μεγάλο ντέρμπι περιλαμβάνει σήμερα Κυριακή το πρόγραμμα στο ποδόσφαιρο και δεν είναι άλλο από το Σεβίλλη Ατλέτικο Μαδρίτης, που θα κρίνει πολλά όσον
Διαπιστευτήρια για τον τίτλο Σεβίλλη και Ατλέτικο Ένα μεγάλο ντέρμπι περιλαμβάνει σήμερα Κυριακή το πρόγραμμα στο ποδόσφαιρο και δεν είναι άλλο από το Σεβίλλη Ατλέτικο Μαδρίτης, που θα κρίνει πολλά όσον
Σχολείο εύτερης Ευκαιρίας Αλεξανδρούπολης. Σχολικό Έτος 2006 2007. Σενάριο : Αγιοργιωτάκης Ιωάννης Μαθηµατικός
 Σχολείο εύτερης Ευκαιρίας Αλεξανδρούπολης Σχολικό Έτος 2006 2007 Σενάριο : Αγιοργιωτάκης Ιωάννης Μαθηµατικός Τρίτη 10 Οκτωβρίου στο Σ Ε Αλεξανδρούπολης. 2 η Ώρα : Μαθηµατικά στο Β2. ΙΣΜΑΗΛ : Λεµονιά, θέλω
Σχολείο εύτερης Ευκαιρίας Αλεξανδρούπολης Σχολικό Έτος 2006 2007 Σενάριο : Αγιοργιωτάκης Ιωάννης Μαθηµατικός Τρίτη 10 Οκτωβρίου στο Σ Ε Αλεξανδρούπολης. 2 η Ώρα : Μαθηµατικά στο Β2. ΙΣΜΑΗΛ : Λεµονιά, θέλω
Μια φορά κι ένα γαϊδούρι
 Μια φορά κι ένα γαϊδούρι Ερευνητική Εργασία Α Λυκείου Υπεύθυνοι Καθηγητές Κοκκίνου Ελένη Παπαζέτης Κωνσταντίνος Καϊµακάµης Αθανάσιος Συγγραφική Οµάδα Τσιρίδης Νίκος Ραχωβίτσας Δηµήτρης Σιέλης Χρίστος Σχολικό
Μια φορά κι ένα γαϊδούρι Ερευνητική Εργασία Α Λυκείου Υπεύθυνοι Καθηγητές Κοκκίνου Ελένη Παπαζέτης Κωνσταντίνος Καϊµακάµης Αθανάσιος Συγγραφική Οµάδα Τσιρίδης Νίκος Ραχωβίτσας Δηµήτρης Σιέλης Χρίστος Σχολικό
Παραδοσιακά παιχνίδια
 Ενότητα 11 Περιγράφουμε πώς παίζονται διάφορα παιχνίδια Κατανοούμε και δίνουμε οδηγίες για να παίξουμε παιχνίδια Ξεχωρίζουμε τις εγκλίσεις των ρημάτων Χρησιμοποιούμε απρόσωπα ρήματα Κλίνουμε επίθετα σε
Ενότητα 11 Περιγράφουμε πώς παίζονται διάφορα παιχνίδια Κατανοούμε και δίνουμε οδηγίες για να παίξουμε παιχνίδια Ξεχωρίζουμε τις εγκλίσεις των ρημάτων Χρησιμοποιούμε απρόσωπα ρήματα Κλίνουμε επίθετα σε
11, 12, 13, 14, 21, 22, 23, 24, 31, 32, 33, 34, 41, 42, 43, 44.
 ΤΕΧΝΙΚΕΣ ΚΑΤΑΜΕΤΡΗΣΗΣ Η καταµετρηση ενος συνολου µε πεπερασµενα στοιχεια ειναι ισως η πιο παλια µαθηµατικη ασχολια του ανθρωπου. Θα µαθουµε πως, δεδοµενης της περιγραφης ενος συνολου, να µπορουµε να ϐρουµε
ΤΕΧΝΙΚΕΣ ΚΑΤΑΜΕΤΡΗΣΗΣ Η καταµετρηση ενος συνολου µε πεπερασµενα στοιχεια ειναι ισως η πιο παλια µαθηµατικη ασχολια του ανθρωπου. Θα µαθουµε πως, δεδοµενης της περιγραφης ενος συνολου, να µπορουµε να ϐρουµε
Τίτλος προγράμματος: «Παιχνίδια στο χθες, παιχνίδια στο σήμερα, παιχνίδια δίχως σύνορα» Υπεύθυνη προγράμματος: Μπότη Ευαγγελή Εκπαιδευτικός που
 Τίτλος προγράμματος: «Παιχνίδια στο χθες, παιχνίδια στο σήμερα, παιχνίδια δίχως σύνορα» Υπεύθυνη προγράμματος: Μπότη Ευαγγελή Εκπαιδευτικός που συμμετέχει: Κακάρη Κωνσταντίνα Παρακολουθώντας τα παιδιά
Τίτλος προγράμματος: «Παιχνίδια στο χθες, παιχνίδια στο σήμερα, παιχνίδια δίχως σύνορα» Υπεύθυνη προγράμματος: Μπότη Ευαγγελή Εκπαιδευτικός που συμμετέχει: Κακάρη Κωνσταντίνα Παρακολουθώντας τα παιδιά
Μάθηµα 14. Κεφάλαιο: Στατιστική
 Μάθηµα 4 Κεφάλαιο: Στατιστική Θεµατικές Ενότητες:. Μέτρα θέσης. Εισαγωγή. Για πιο σύντοµη, αποδοτική και συγκρίσιµη θεώρηση της κατανοµής συχνοτήτων µιας µεταβλητής, έχουµε ορίσει και χρησιµοποιούµε κάποια
Μάθηµα 4 Κεφάλαιο: Στατιστική Θεµατικές Ενότητες:. Μέτρα θέσης. Εισαγωγή. Για πιο σύντοµη, αποδοτική και συγκρίσιµη θεώρηση της κατανοµής συχνοτήτων µιας µεταβλητής, έχουµε ορίσει και χρησιµοποιούµε κάποια
2.3. Ασκήσεις σχ. βιβλίου σελίδας 100 104 Α ΟΜΑ ΑΣ
 .3 Ασκήσεις σχ. βιβλίου σελίδας 00 04 Α ΟΜΑ ΑΣ. Έξι διαδοχικοί άρτιοι αριθµοί έχουν µέση τιµή. Να βρείτε τους αριθµούς και τη διάµεσό τους. Αν είναι ο ποιο µικρός άρτιος τότε οι ζητούµενοι αριθµοί θα είναι
.3 Ασκήσεις σχ. βιβλίου σελίδας 00 04 Α ΟΜΑ ΑΣ. Έξι διαδοχικοί άρτιοι αριθµοί έχουν µέση τιµή. Να βρείτε τους αριθµούς και τη διάµεσό τους. Αν είναι ο ποιο µικρός άρτιος τότε οι ζητούµενοι αριθµοί θα είναι
 Τρία συνηθισµένα λάθη που κάνουν µαθητές της Γ Λυκείου σε ασκήσεις του ιαφορικού Λογισµού ρ. Παναγιώτης Λ. Θεοδωρόπουλος πρώην Σχολικός Σύµβουλος ΠΕ3 e-mail@p-thedrpuls.gr Πρόλογος Στην εργασία αυτή επισηµαίνονται
Τρία συνηθισµένα λάθη που κάνουν µαθητές της Γ Λυκείου σε ασκήσεις του ιαφορικού Λογισµού ρ. Παναγιώτης Λ. Θεοδωρόπουλος πρώην Σχολικός Σύµβουλος ΠΕ3 e-mail@p-thedrpuls.gr Πρόλογος Στην εργασία αυτή επισηµαίνονται
