Μικροοικονοµική Θεωρία
|
|
|
- Ιώ Διδασκάλου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Μικροοικονοµική Θεωρία Θεωρία Χρησιµότητας και Προτιµήσεων. Καταναλωτικές Προτιµήσεις: Βασικά Αξιώµατα. Συνολική και οριακή χρησιµότητα Καµπύλη αδιαφορίας ή ισοϋψής καµπύλη χρησιµότητας. Ιστορική Αναδροµή Χαρακτηριστικά Καµπυλών Αδιαφορίας Οριακός λόγος υποκατάστασης Φθίνον Οριακός Λόγος Υποκατάστασης (αφορά κυρτές καµπύλες αδιαφορίας) Είδη Καµπυλών Αδιαφορίας 1
2 Θεωρία Χρησιµότητας και Προτιµήσεων. έσµη ή δεσµίδα ή συνδυασµός κατανάλωσης είναι ένα διάνυσµα Χ= (χ 1, χ 2, χ 3..χ ν ) n που περιέχει αγαθά. Ανήκει σε ένα σύνολο κατανάλωσης Χ ( x X ) όπου X R1 (το Χ υποσύνολο του θετικού τεταρτηµορίου) > : τουλάχιστον τόσο προτιµητέο όσο > : αυστηρά προτιµητέο ~ : αδιάφορο Κάθε συνδυασµός καταναλωτικών αγαθών δίδεται από ένα διατεταγµένο σύνολο µη αρνητικών πραγµατικών αριθµών και απεικονίζεται γεωµετρικά ως ένα σηµείο στο µη αρνητικό τµήµα του σχετικού χώρου. Καταναλωτικές Προτιµήσεις: Βασικά Αξιώµατα. 1. Συγκρισιµότητα Πληρότητα Για οποιουσδήποτε συνδυασµούς αγαθών Α και Β, ο καταναλωτής µπορεί να προσδιορίσει ποιος συνδυασµός του αποφέρει µεγαλύτερη ικανοποίηση. Αν ο Α παρέχει µεγαλύτερη ικανοποίηση από τον Β, τότε λέµε ότι ο Α είναι προτιµητέος έναντι του Β και το αντίστροφο. Αν και οι δυο συνδυασµοί παρέχουν την ίδια ικανοποίηση, τότε λέµε ότι ο καταναλωτής είναι αδιάφορος µεταξύ των Α και Β. 2. Μεταβατικότητα Συνέπεια Αν ο συνδυασµός Α προτιµάται έναντι του συνδυασµού Β και ο Β προτιµάται έναντι του συνδυασµού Γ, τότε ο Α προτιµάται έναντι του. Παρόµοια αν ο καταναλωτής είναι αδιάφορος µεταξύ των συνδυασµών Α και Β και µεταξύ Β και Γ, τότε είναι αδιάφορος και µεταξύ Α και Γ. Το αξίωµα αυτό εξασφαλίζει την εσωτερική συνέπεια των επιλογών του καταναλωτή. Τα σύνολα αδιαφορίας δεν έχουν κοινά σηµεία, δηλαδή οι καµπύλες αδιαφορίας δεν τέµνονται. Ορθολογικός Καταναλωτής: ο καταναλωτής του οποίου οι επιλογές εκπληρούν τις δυο παραπάνω ιδιότητες. 3. Συνεχεία εδοµένου ενός συνδυασµού αγαθών Α, υπάρχουν συνδυασµοί αγαθών, τους οποίους ο καταναλωτής προτιµά έναντι του Α, άλλοι συνδυασµοί έναντι των οποίων ο Α είναι προτιµότερος και τέλος, υπάρχουν οπωσδήποτε συνδυασµοί αγαθών, διάφοροι ποσοτικά του Α, οι οποίοι του παρέχουν την ίδια ικανοποίηση. Άρα οι καµπύλες δεν µπορούν να είναι διακεκοµµένες, αλλά είναι συνεχείς, δεν υπάρχουν δηλαδή ασυνέχειες. 4. Ανακλαστικότητα Το Αξίωµα της Ανακλαστικότητας, σύµφωνα µε το οποίο ένας συνδυασµός είναι εξίσου καλός µε τον εαυτό του. Κάθε δεσµίδα ανήκει σε κάποιο σύνολο αδιαφορίας, έστω και στον εαυτό της. 2
3 Τα παραπάνω 4 αξιώµατα θεωρούνται τα βασικά υπάρχουν όµως και δυο επικουρικά αξιώµατα. 5. Μονοτονικότητα? Ασθενής Μονοτονικότητα: ο καταναλωτής προτιµά µια δεσµίδα που έχει περισσότερες ποσότητες από µια άλλη που έχει λιγότερες. Άρα θέλει και τα δυο αγαθά να έχουν περισσότερη ποσότητα από την άλλη δεσµίδα για να την προτιµήσει. Ισχυρή Μονοτονικότητα: ο καταναλωτής προτιµά µια δεσµίδα αρκεί το ένα αγαθό να είναι σε µεγαλύτερη ποσότητα από το άλλο για να την προτιµήσει. Αντιπροσώπευση Εκπροσώπηση Μια συνάρτηση Μ(χ) που αντίστοιχη έναν αριθµό σε κάθε δεσµίδα κατανάλωσης, αντιπροσωπεύει τις προτιµήσεις του καταναλωτή, δηλαδή αποτελεί συνάρτηση χρησιµότητας. Το µόνο που απαιτείται από την συνάρτηση χρησιµότητας είναι να εκφράζει απλά, την κατάταξη των συνδυασµών των αγαθών κατά τις προτιµήσεις του καταναλωτή, δίδοντας µεγαλύτερη τιµή σε ορισµένους συνδυασµούς έναντι άλλων χωρίς, όµως να έχουν σηµασία οι αριθµοί αυτοί καθαυτοί και, εποµένως και οι µεταξύ τους διαφορές. (µιλάµε για την χρησιµότητα ως τακτικό µέγεθος και όχι ως απόλυτο) Πολλές συναρτήσεις χρησιµότητας µπορούν να περιγράψουν εξίσου καλά τις προτιµήσεις του καταναλωτή: Π.χ. u 1 = u(x,y) = xy & u 2 = u(u) 2 =(xy) 2 x y u 1 u Άρα ο συγκεκριµένος καταναλωτής είναι αδιάφορος µεταξύ των τριών αυτών συνδυασµών παρόλο που η απόλυτη τιµή (αριθµός) της χρησιµότητας διαφέρει. Η απόλυτη τιµή της χρησιµότητας εξαρτάται από τη συγκεκριµένη συνάρτηση χρησιµότητας που θα πάρουµε. Έχοντας µια συνάρτηση, που αντανακλά τις τακτικές προτιµήσεις του καταναλωτή, µπορούµε να κατασκευάσουµε έναν οποιοδήποτε αριθµό εναλλακτικών συναρτήσεων χρησιµότητας που να αντανακλούν τις ίδιες τακτικές προτιµήσεις. Συνολική και οριακή χρησιµότητα Η γενικευµένη µορφή της συνάρτησης χρησιµότητας είναι: u(x 1, x 2,x 3 x v ) όπου: u= συνολική χρησιµότητα και x 1, x 2,x 3 x v = ποσότητες των αγαθών 1,.., ν 3
4 Η οριακή χρησιµότητα είναι: η χρησιµότητα που επιτυγχάνεται από την κατανάλωση u µιας επιπλέον µονάδας του αγαθού X, ux Καµπύλη αδιαφορίας ή ισοϋψής καµπύλη χρησιµότητας. Είναι ο γεωµετρικός τόπος των σηµείων (ή των συνδυασµών αγαθών) µεταξύ των οποίων ο καταναλωτής είναι αδιάφορος. Κάθε σηµείο µιας καµπύλης αδιαφορίας αποφέρει την ίδια συνολική χρησιµότητα µε οποιαδήποτε άλλο σηµείο της ίδιας καµπύλης αδιαφορίας. Αν η συνάρτηση χρησιµότητας δίνεται από τον τύπο u(x 1, x 2,x 3 x v ) όπου χ 1 είναι η καταναλισκόµενη ποσότητα του αγαθού 1, χ 2 είναι η καταναλισκόµενη ποσότητα του αγαθού 2 κ.τ.λ., τότε η καµπύλη αδιαφορίας ορίζεται ως το σύνολο όλων των συνδυασµών των αγαθών (χ 1, χ 2, χ 3, χ v ) που ικανοποιούν την εξίσωση u(x 1, x 2,x 3 x v ) = c όπου c είναι το σταθερό επίπεδο χρησιµότητας για αυτή τη καµπύλη αδιαφορίας. Ένας Χάρτης καµπυλών αδιαφορίας δηµιουργείται αν δοθούν διάφορες τιµές στη σταθερά c της εξίσωσης u(x 1, x 2,x 3 x v ) = c Π.χ. Όταν u(x,y) = xy οι καµπύλες αδιαφορίας δίνονται από την εξίσωση xy=c όπου c είναι η σταθερή τιµή της χρησιµότητας κατά µήκος µιας καµπύλης αδιαφορίας. Τα σηµεία (x,y) : (1,5) και (2,5, 2) βρίσκονται πάνω στην ίδια καµπύλη αδιαφορίας µιας και αποδίδουν την ίδια χρησιµότητα c=5. Έστω ότι αλλάζουµε τις απόλυτες τιµές χρησιµότητας µε την ύψωση τους στο τετράγωνο έτσι ώστε u (x,y) = [u(x,y)] 2 = x 2 y 2. ιαπιστώνουµε ότι βρισκόµαστε πάνω στην ίδια καµπύλη αδιαφορίας αλλά τώρα c=25. Εποµένως οι καµπύλες αδιαφορίας παραµένουν αµετάβλητες (εκτός από τις αριθµητικές ταµπέλες τους) µετά από µονοτονικούς µετασχηµατισµούς της συνάρτησης χρησιµότητας. Ιστορική Αναδροµή Jeremy Bentham 1789 = απόλυτη χρησιµότητα 1. Stanley Jevons 1871, Carl Menger 1871, Leon Warlas 1874 = Απόλυτη, Αθροιστική Χρησιµότητα u= u(x 1 ) + u(x 2 ) + u(x 3 ) +.. u(x n ) 2. Francis Edgeworth 1881, G.B. Antonelli 1886, Irving Fisher 1892 = Μετρήσιµο µέγεθος (απόλυτη χρησιµότητα) αλλά όχι αθροιστική. u(x 1, x 2,x 3 x v ) 3. Vilfredo Pareto 1906 = Τακτική χρησιµότητα Χαρακτηριστικά Καµπυλών Αδιαφορίας 1. Το πεδίο των καµπυλών αδιαφορίας είναι πυκνό. Υπάρχει µια καµπύλη αδιαφορίας που περνά από κάθε σηµείο του χώρου των αγαθών. 4
5 2. Ο χάρτης αδιαφορίας είναι µοναδικός για κάθε καταναλωτή. 3. Οι συνδυασµοί πάνω στην ίδια καµπύλη αδιαφορίας δίνουν την ίδια ικανοποίηση στον καταναλωτή. 4. Κάθε συνδυασµός δεξιά της καµπύλη αδιαφορίας προτιµάται και αριστερά της καµπύλη αδιαφορίας δίνει λιγότερη ικανοποίηση. 5. Καµπύλες αδιαφορίας που παριστούν διαφορετικά επίπεδα προτίµησης δεν µπορούν να τέµνονται. Σηµεία πάνω σε δυο καµπύλες αδιαφορίας: Α, Β, Γ. Τα σηµεία Α,Β ανήκουν στην καµπύλη αδιαφορίας Ι, και τα σηµεία Α, Γ ανήκουν στην καµπύλη αδιαφορίας ΙΙ. Ο καταναλωτής είναι αδιάφορος µεταξύ των συνδυασµών Α και Β αφού ανήκουν στην ίδια καµπύλη αδιαφορίας. Αντίστοιχα ο καταναλωτής είναι αδιάφορος µεταξύ των συνδυασµών Α και Γ αφού ανήκουν στην ίδια καµπύλη αδιαφορίας. Σύµφωνα µε την ιδιότητα της Μεταβατικότητας: οι συνδυασµοί Β, Γ θα πρέπει να µας είναι αδιάφοροι (ταυτίζονται). Εδώ εµφανίζεται µια αντίφαση µιας και οι συνδυασµοί Β, Γ ανήκουν σε ξεχωριστή καµπύλη αδιαφορίας. 6. Μονοτονικές προτιµήσεις η οποία και συνεπάγεται αρνητική κλίση στις καµπύλες αδιαφορίας Αυστηρή Μονοτονικότητα: ο συνδυασµός Α είναι αυστηρά µεγαλύτερος από τον Β διότι έστω ο πρώτος περιέχει περισσότερες µονάδες για κάθε αγαθό σε σχέση µε τον συνδυασµό Β. Στον χώρο των αγαθών αυτό φαίνεται επειδή ο Α βρίσκεται βορειοανατολικά του Β. Αν ο καταναλωτής δεν έχει φτάσει σε σηµείο κορεσµού και για τα δυο αγαθά, τότε προτιµά τον Α από τον Β: κατά συνέπεια οι καµπύλες αδιαφορίας έχουν αρνητική κλίση. Γιατί έστω ότι ο καταναλωτής είναι αδιάφορος µεταξύ των συνδυασµών Γ,, ο Γ δεν µπορεί να περιέχει µεγαλύτερες ποσότητες και των δυο αγαθών από ότι ο και το αντίστροφο (θα είχαµε θετική κλίση). Αντίθετα κάθε συνδυασµός πρέπει να περιέχει µεγαλύτερη ποσότητα του ενός αγαθού και µικρότερη ποσότητα του αλλού. 5
6 Η κλίση τους (δηλ. ο MRS) µειώνεται όσο προχωρούµε από πάνω προς τα κάτω. Αυτό σχετίζεται µε το νόµο της φθίνουσας οριακής χρησιµότητας. Όσο αυξάνεται η ποσότητα του Χ και µειώνεται η ποσότητα του Υ η οριακή χρησιµότητα του Χ µειώνεται ενώ η οριακή χρησιµότητα του Υ αυξάνεται. 7. Κυρτότητα (ή φθίνων οριακός λόγος Υποκατάστασης) ένας καταναλωτής που είναι αδιάφορος ανάµεσα στο Α και το Β θα προτιµούσε αυστηρά έναν γραµµικό συνδυασµό Γ = αα + (1-α)Β από είτε απλά Α είτε απλά Β. Άρα προτιµά µίγµατα. Σε περίπτωση κοίλης καµπύλης αδιαφορίας ο καταναλωτής απεχθάνεται τα µίγµατα. Κυρτές προτιµήσεις -ο σταθµισµένος µέσος όρος δύο αδιάφορων συνδυασµών είναι αυστηρά προτιµότερος από τους δύο ακραίους συνδυασµούς- συνεπάγεται καµπύλες αδιαφορίας κυρτές ως προς την αρχή των αξόνων. Η διαπίστωση της κυρτότητας (ή κοιλότητας) γίνεται πιο εύκολα εάν η καµπύλη βρίσκεται πάνω (κάτω) από την εφαπτόµενη της σε κάθε σηµείο. Οριακός λόγος υποκατάστασης Ο λόγος υποκατάστασης του Υ σε όρους του Χ µετράει τον αριθµό των µονάδων του Υ οι οποίες πρέπει να θυσιαστούν για την απόκτηση µιας επί πλέον µονάδας του Χ, έτσι ώστε ο καταναλωτής να απολαµβάνει το ίδιο επίπεδο ικανοποίησης (να διατηρήσει το επίπεδο χρησιµότητας στην ίδια καµπύλη αδιαφορίας) Η κλίση των καµπυλών αδιαφορίας ονοµάζεται οριακός λόγος υποκατάστασης (marginal rate of substitution, MRS) Ορίζεται µόνο για µετακινήσεις κατά µήκος µιας καµπύλης αδιαφορίας και ποτέ για µετακινήσεις µεταξύ καµπυλών. Y ΟΛΥ= MRS = Χ Έστω ότι η συνάρτηση χρησιµότητας είναι u(x,y). Η µεταβολή της χρησιµότητας που προέρχεται από µια µικρή µεταβολή του χ (ή του y) είναι η οριακή χρησιµότητα του χ u (ή του y). Άρα η οριακή χρησιµότητα του χ είναι ux και η οριακή χρησιµότητα 6
7 u του y είναι uy. Μια καµπύλη αδιαφορίας δίνεται από τον τύπο u(x,y = c µια y σταθερά. Παίρνοντας την ολική παράγωγο βρίσκουµε u ( x, y) dx+ u ( x, y) dy= 0 και λύνοντας ως προς την κλίση της καµπύλης x αδιαφορίας βρίσκουµε ότι: dy ux( x, y) =ΟΛΥ y/ x = dx u ( x, y) y y Άρα ο λόγος υποκαταστάσεως του y µε χ (κλίση) είναι ο λόγος των οριακών χρησιµοτήτων του Χ και του Υ. Φθίνον Οριακός Λόγος Υποκατάστασης (αφορά κυρτές καµπύλες αδιαφορίας) Ο ΟΛΥ του Υ µε Χ µειώνεται σε απόλυτους όρους καθώς το Υ υποκαθίσταται µε το Χ κατά µήκος µιας κυρτής καµπύλης αδιαφορίας. Η κυρτότητα των καµπυλών αδιαφορίας δικαιολογείται συνήθως µε το επιχείρηµα ότι καθώς ο καταναλωτής αποκτά ολοένα και µεγαλύτερες ποσότητες του Χ, η οριακή χρησιµότητα µιας επιπλέον αυξήσεως του Χ µειώνεται. Ενώ αντίθετα η οριακή χρησιµότητα του Υ διαρκώς αυξάνει, µε αποτέλεσµα η µείωση της καταναλώσεως του Υ κατά µια επιπλέον µονάδα να απαιτεί όλο και µεγαλύτερη ποσότητα του Χ για να αντισταθµίσει ο καταναλωτής την απώλεια χρησιµότητας του. ΟΛΥ Υµε Χ =7 αυξάνεται το Χ µια µονάδα, µειώνεται το Υ κατά 7 ΟΛΥ Υµε Χ =5 αυξάνεται το Χ µια µονάδα, µειώνεται το Υ κατά 5 ΟΛΥ Υµε Χ =3 αυξάνεται το Χ µια µονάδα, µειώνεται το Υ κατά 3 Όσο αυξάνεται το Χ τόσο µειώνεται ο ΟΛΥ Υµε Χ εξαιτίας του βαθµιαίου κορεσµού που επέρχεται στον καταναλωτή όταν αυξάνεται η κατανάλωση του Χ. Συνεπώς καθώς αυξάνεται η κατανάλωση του Χ ο καταναλωτής είναι διατεθειµένος να θυσιάσει ολοένα και µικρότερες ποσότητες του Υ για την απόκτηση µιας προσθετής µονάδας του Χ. dy ux( x, y) u =ΟΛΥ y/ x = µειώνεται ux( x. y) dx u ( x, y) y u αυξάνεται uy ( x, y) y Π.χ. ένας καταναλωτής που έχει 1000 λίτρα νερού εβδοµαδιαίως µπορεί να είναι απόλυτα ευχαριστηµένος από την ανταλλαγή ενός λίτρου νερού µε µια φέτα ψωµί. Αν όµως µόνο ένα λίτρο νερού την εβδοµάδα µπορεί να δίσταζε, ίσως να ανταλλάξει ακόµα και ένα ποτήρι νερού έστω και µε ένα ολόκληρο φούρνο ψωµιά. Θεώρηµα: Εάν υποθέσουµε ότι οι προτιµήσεις του καταναλωτή είναι πλήρεις, ανακλαστικές, µεταβατικές και συνεχείς, τότε υπάρχει µια συνεχής συνάρτηση χρησιµότητας, η οποία αντιπροσωπεύει αυτές τις προτιµήσεις. 7
8 Αυστηρά κοίλη συνάρτηση χρησιµότητας + αυστηρά κυρτή καµπύλη αδιαφορίας + φθίνοντας οριακός λόγος υποκαταστάσεως. Τα παραπάνω ισχύουν όταν 2 y y ΟΛΥ Υµε X = < 0και > 0 2 Η συνάρτηση χρησιµότητας τύπου Cobb Douglas προϋπόθεσης. u a b = x y πλήρη τις πιο πάνω Είδη Καµπυλών Αδιαφορίας 1. Οι καµπύλες αδιαφορίας είναι ευθείες γραµµές (U(x,y) = ax + by) για αγαθά τέλεια υποκατάστατα µε MRS = - a / b 2. Οι καµπύλες αδιαφορίας έχουν σχήµα L για αγαθά τέλεια συµπληρωµατικά µε U(x,y) = min(ax, by) µε MRS είτε 0 είτε άπειρος. 3. Στα ουδέτερα αγαθά οι καµπύλες αδιαφορίας είναι κάθετες γραµµές µε MRS παντού άπειρος. 4. Στα ανεπιθύµητα αγαθά η κατεύθυνση αύξουσας προτίµησης των καµπυλών αδιαφορίας είναι προς τα κάτω και δεξιά προς το «αγαθό». 5. Οι καµπύλες αδιαφορίας που παριστάνουν κορεσµένες προτιµήσεις είναι κυκλικές 6. Οι (κυρτές) Καµπύλες Αδιαφορίας εµφανίζουν έναν µειούµενο οριακό λόγο υποκατάστασης Οµοθετικές και Μη Οµοθετικές προτιµήσεις Οµοθετικές συναρτήσεις: ο οριακός λόγος υποκατάστασης στις συναρτήσεις χρησιµότητας εξαρτάται µόνο από το λόγο των ποσοτήτων των δύο αγαθών και όχι από τις συνολικές ποσότητες των δύο αγαθών. Οι οριακές χρησιµότητες και των δύο αγαθών εξαρτώνται από τα Χ και Υ. οι κλίσεις των καµπυλών αδιαφορίας εξαρτώνται µόνο από τον λόγο Υ / Χ και όχι από το πόσο µακριά είναι η καµπύλη από την αρχή των αξόνων. Μη Οµοθετικές συναρτήσεις: ο οριακός λόγος υποκατάστασης στις συναρτήσεις χρησιµότητας εξαρτάται µόνο από την µια ποσότητα του Υ ή Χ. 8
Συνάρτηση χρησιμότητας (utility function): u(x)
 Συνάρτηση χρησιμότητας (utility function): u(x) είναι ένας τρόπος να δώσουμε έναν αριθμό σε κάθε δυνατό συνδυασμό κατανάλωσης, τέτοιο ώστε να δίνονται μεγαλύτεροι αριθμοί στους πλέον προτιμώμενους συνδυασμούς
Συνάρτηση χρησιμότητας (utility function): u(x) είναι ένας τρόπος να δώσουμε έναν αριθμό σε κάθε δυνατό συνδυασμό κατανάλωσης, τέτοιο ώστε να δίνονται μεγαλύτεροι αριθμοί στους πλέον προτιμώμενους συνδυασμούς
Ατομικές Προτιμήσεις και Συνάρτηση Χρησιμότητας - Έστω x=(x 1,,x n ) ένας καταναλωτικός συνδυασμός, όπου x i η ποσότητα του αγαθού i που καταναλώνει
 Ατομικές Προτιμήσεις και Συνάρτηση Χρησιμότητας - Έστω x=(x,,x n ) ένας καταναλωτικός συνδυασμός, όπου x i η ποσότητα του αγαθού i που καταναλώνει το άτομο (i =,,n). - Πρόβλημα καταναλωτή: Κάθε άτομο (καταναλωτής)
Ατομικές Προτιμήσεις και Συνάρτηση Χρησιμότητας - Έστω x=(x,,x n ) ένας καταναλωτικός συνδυασμός, όπου x i η ποσότητα του αγαθού i που καταναλώνει το άτομο (i =,,n). - Πρόβλημα καταναλωτή: Κάθε άτομο (καταναλωτής)
Προτιµήσεις-Υπενθύµιση
 Προτιµήσεις-Υπενθύµιση Διάλεξη 4 x y: To x προτιµάται σαφώς από το y.! x ~ y: Το x και το y προτιµούνται εξίσου. Χρησιµότητα! x y: Το x προτιµάται τουλάχιστο όσο και το y.!1! 1 Προτιµήσεις-Υπενθύµιση Προτιµήσεις-Υπενθύµιση
Προτιµήσεις-Υπενθύµιση Διάλεξη 4 x y: To x προτιµάται σαφώς από το y.! x ~ y: Το x και το y προτιµούνται εξίσου. Χρησιµότητα! x y: Το x προτιµάται τουλάχιστο όσο και το y.!1! 1 Προτιµήσεις-Υπενθύµιση Προτιµήσεις-Υπενθύµιση
Θεωρία Καταναλωτή. Υποδειγματοποίηση της συμπεριφοράς του καταναλωτή. Βασική έννοια: Βελτιστοποίηση υπό περιορισμό.
 Θεωρία Καταναλωτή Υποδειγματοποίηση της συμπεριφοράς του καταναλωτή. Βασική έννοια: Βελτιστοποίηση υπό περιορισμό. Προτιμήσεις (preferences) Εισοδηματικός περιορισμός (budget constraint) Άριστη επιλογή
Θεωρία Καταναλωτή Υποδειγματοποίηση της συμπεριφοράς του καταναλωτή. Βασική έννοια: Βελτιστοποίηση υπό περιορισμό. Προτιμήσεις (preferences) Εισοδηματικός περιορισμός (budget constraint) Άριστη επιλογή
Προτιµήσεις-Υπενθύµιση
 Προτιµήσεις-Υπενθύµιση ιάλεξη 4 Χρησιµότητα x y: To x προτιµάται σαφώς από το y. x y: Το x και το y προτιµούνται εξίσου. y: Το x προτιµάται τουλάχιστο όσο και το y. x f Προτιµήσεις-Υπενθύµιση Προτιµήσεις-Υπενθύµιση
Προτιµήσεις-Υπενθύµιση ιάλεξη 4 Χρησιµότητα x y: To x προτιµάται σαφώς από το y. x y: Το x και το y προτιµούνται εξίσου. y: Το x προτιµάται τουλάχιστο όσο και το y. x f Προτιµήσεις-Υπενθύµιση Προτιµήσεις-Υπενθύµιση
Μικροοικονομική. Θεωρία Συμπεριφοράς Καταναλωτή
 Μικροοικονομική Θεωρία Συμπεριφοράς Καταναλωτή Συνολική και οριακή ρησιμότητα Η κατανάλωση αγαθών συνεπάγεται κάποια ικανοποίηση ή ρησιμότητα για τον καταναλωτή. Συνολική ρησιμότητα (U) είναι η συνολική
Μικροοικονομική Θεωρία Συμπεριφοράς Καταναλωτή Συνολική και οριακή ρησιμότητα Η κατανάλωση αγαθών συνεπάγεται κάποια ικανοποίηση ή ρησιμότητα για τον καταναλωτή. Συνολική ρησιμότητα (U) είναι η συνολική
Διάλεξη 3. Προτιµήσεις. Ορθολογισµός στην οικονοµική. Σχέσεις προτιµήσεων
 Ορθολογισµός στην οικονοµική Διάλεξη 3 Προτιµήσεις!1 Υπόθεση συµπεριφοράς: Ένας λήπτης αποφάσεων επιλέγει πάντοτε τον πλέον προτιµώµενο συνδυασµό από το σύνολο των εναλλακτικών συνδυασµών που έχει στη
Ορθολογισµός στην οικονοµική Διάλεξη 3 Προτιµήσεις!1 Υπόθεση συµπεριφοράς: Ένας λήπτης αποφάσεων επιλέγει πάντοτε τον πλέον προτιµώµενο συνδυασµό από το σύνολο των εναλλακτικών συνδυασµών που έχει στη
ΘΕΩΡΙΑ ΧΡΗΣΙΜΟΤΗΤΑΣ ΚΑΤΑΝΑΛΩΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ
 Ένθετο Κεφάλαιο ΘΕΩΡΙΑ ΧΡΗΣΙΜΟΤΗΤΑΣ ΚΑΤΑΝΑΛΩΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ Μικροοικονομική Ε. Σαρτζετάκης 1 Καταναλωτική συμπεριφορά Σκοπός αυτής της διάλεξης είναι να εξετάσουμε τον τρόπο με τον οποίο οι καταναλωτές
Ένθετο Κεφάλαιο ΘΕΩΡΙΑ ΧΡΗΣΙΜΟΤΗΤΑΣ ΚΑΤΑΝΑΛΩΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ Μικροοικονομική Ε. Σαρτζετάκης 1 Καταναλωτική συμπεριφορά Σκοπός αυτής της διάλεξης είναι να εξετάσουμε τον τρόπο με τον οποίο οι καταναλωτές
Προσφορά Εργασίας Προτιμήσεις και Συνάρτηση Χρησιμότητας ( Χ,Α συνάρτηση χρησιμότητας U(X,A)
 Προσφορά Εργασίας - Έστω ότι υπάρχουν δύο αγαθά Α και Χ στην οικονομία. Το αγαθό Α παριστάνει τα διάφορα καταναλωτικά αγαθά. Το αγαθό Χ παριστάνει τον ελεύθερο χρόνο. Προτιμήσεις και Συνάρτηση Χρησιμότητας
Προσφορά Εργασίας - Έστω ότι υπάρχουν δύο αγαθά Α και Χ στην οικονομία. Το αγαθό Α παριστάνει τα διάφορα καταναλωτικά αγαθά. Το αγαθό Χ παριστάνει τον ελεύθερο χρόνο. Προτιμήσεις και Συνάρτηση Χρησιμότητας
ΘΕΩΡΙΑ ΧΡΗΣΙΜΟΤΗΤΑΣ ΚΑΤΑΝΑΛΩΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ
 ΘΕΩΡΙΑ ΧΡΗΣΙΜΟΤΗΤΑΣ ΚΑΤΑΝΑΛΩΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ Κεφάλαιο 3 Οικονοµικά των Επιχειρήσεων Ε. Σαρτζετάκης 1 Καταναλωτική συµπεριφορά! Σκοπός αυτής της διάλεξης είναι να εξετάσουµε τον τρόπο µε τον οποίο οι καταναλωτές
ΘΕΩΡΙΑ ΧΡΗΣΙΜΟΤΗΤΑΣ ΚΑΤΑΝΑΛΩΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ Κεφάλαιο 3 Οικονοµικά των Επιχειρήσεων Ε. Σαρτζετάκης 1 Καταναλωτική συµπεριφορά! Σκοπός αυτής της διάλεξης είναι να εξετάσουµε τον τρόπο µε τον οποίο οι καταναλωτές
ιάλεξη 3 Προτιµήσεις ~ σηµαίνει ότι το x προτιµάται τουλάχιστο όσο και ~ f Ορθολογισµός στην οικονοµική Σχέσεις προτιµήσεων
 Ορθολογισµός στην οικονοµική ιάλεξη 3 Προτιµήσεις Υπόθεση συµπεριφοράς: Ένας λήπτης αποφάσεων επιλέγει πάντοτε τον πλέον προτιµώµενο συνδυασµό από το σύνολο των εναλλακτικών συνδυασµών που έχει στη διάθεση
Ορθολογισµός στην οικονοµική ιάλεξη 3 Προτιµήσεις Υπόθεση συµπεριφοράς: Ένας λήπτης αποφάσεων επιλέγει πάντοτε τον πλέον προτιµώµενο συνδυασµό από το σύνολο των εναλλακτικών συνδυασµών που έχει στη διάθεση
ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ. Θεωρία Χρησιµότητας και Συµπεριφοράς του Καταναλωτή
 ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ Θεωρία Χρησιµότητας και Συµπεριφοράς του Καταναλωτή Εισαγωγή: Όπως γνωρίζουµε, το οικονοµικό πρόβληµα εστιάζεται στην αποτελεσµατική κατανοµή των ανεπαρκών οικονοµικών πόρων στις εναλλακτικές
ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ Θεωρία Χρησιµότητας και Συµπεριφοράς του Καταναλωτή Εισαγωγή: Όπως γνωρίζουµε, το οικονοµικό πρόβληµα εστιάζεται στην αποτελεσµατική κατανοµή των ανεπαρκών οικονοµικών πόρων στις εναλλακτικές
 ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΘΕΩΡΙΑ-ΜΑΘΗΜΑ ΠΕΜΠΤΟ-ΕΚΤΟ ΕΚΤΟ ΘΕΩΡΙΑ ΧΡΗΣΙΜΟΤΗΤΑΣ-ΙΣΟΡΡΟΠΙΑ ΙΣΟΡΡΟΠΙΑ ΤΟΥ ΚΑΤΑΝΑΛΩΤΗ ΤΜΗΜΑ ΕΠΙΧΕΙΡΗΜΑΤΙΚΟΥ ΣΧΕ ΙΑΣΜΟΥ & ΠΛΗΡΟΦΟΡΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Ακαδηµαϊκό Έτος 2011-2012 ΕΠΙΧ Μικροοικονοµική
ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΘΕΩΡΙΑ-ΜΑΘΗΜΑ ΠΕΜΠΤΟ-ΕΚΤΟ ΕΚΤΟ ΘΕΩΡΙΑ ΧΡΗΣΙΜΟΤΗΤΑΣ-ΙΣΟΡΡΟΠΙΑ ΙΣΟΡΡΟΠΙΑ ΤΟΥ ΚΑΤΑΝΑΛΩΤΗ ΤΜΗΜΑ ΕΠΙΧΕΙΡΗΜΑΤΙΚΟΥ ΣΧΕ ΙΑΣΜΟΥ & ΠΛΗΡΟΦΟΡΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Ακαδηµαϊκό Έτος 2011-2012 ΕΠΙΧ Μικροοικονοµική
ΤΟΥΡΙΣΤΙΚΗ ΟΙΚΟΝΟΜΙΚΗ ΚΕΦΑΛΑΙΟ 6 ΘΕΩΡΙΑ ΠΡΟΤΙΜΗΣΕΩΝ ΚΑΙ ΕΠΙΛΟΓΩΝ ΤΟΥ ΤΟΥΡΙΣΤΑ-ΚΑΤΑΝΑΛΩΤΗ
 ΤΟΥΡΙΣΤΙΚΗ ΟΙΚΟΝΟΜΙΚΗ ΚΕΦΑΛΑΙΟ 6 ΘΕΩΡΙΑ ΠΡΟΤΙΜΗΣΕΩΝ ΚΑΙ ΕΠΙΛΟΓΩΝ ΤΟΥ ΤΟΥΡΙΣΤΑ-ΚΑΤΑΝΑΛΩΤΗ ΘΕΩΡΙΑ ΠΡΟΤΙΜΗΣΕΩΝ ΚΑΙ ΕΠΙΛΟΓΩΝ ΤΟΥ ΤΟΥΡΙΣΤΑ- ΚΑΤΑΝΑΛΩΤΗ ΔΙΑΡΘΡΩΣΗ ΘΕΜΑΤΙΚΩΝ ΕΝΟΤΗΤΩΝ ΚΕΦΑΛΑΙΟΥ Η θεωρία της οριακής
ΤΟΥΡΙΣΤΙΚΗ ΟΙΚΟΝΟΜΙΚΗ ΚΕΦΑΛΑΙΟ 6 ΘΕΩΡΙΑ ΠΡΟΤΙΜΗΣΕΩΝ ΚΑΙ ΕΠΙΛΟΓΩΝ ΤΟΥ ΤΟΥΡΙΣΤΑ-ΚΑΤΑΝΑΛΩΤΗ ΘΕΩΡΙΑ ΠΡΟΤΙΜΗΣΕΩΝ ΚΑΙ ΕΠΙΛΟΓΩΝ ΤΟΥ ΤΟΥΡΙΣΤΑ- ΚΑΤΑΝΑΛΩΤΗ ΔΙΑΡΘΡΩΣΗ ΘΕΜΑΤΙΚΩΝ ΕΝΟΤΗΤΩΝ ΚΕΦΑΛΑΙΟΥ Η θεωρία της οριακής
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος Τμήμα Οικονομικών Επιστημών Μάθημα: Μικροοικονομική Ανάλυση της Κατανάλωσης και της Παραγωγής
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος 2013-2014 Τμήμα Οικονομικών Επιστημών Μάθημα: Μικροοικονομική Ανάλυση της Κατανάλωσης και της Παραγωγής Πρώτο πακέτο ασκήσεων Προθεσμία παράδοσης Παρασκευή 28 Φεβρουαρίου
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος 2013-2014 Τμήμα Οικονομικών Επιστημών Μάθημα: Μικροοικονομική Ανάλυση της Κατανάλωσης και της Παραγωγής Πρώτο πακέτο ασκήσεων Προθεσμία παράδοσης Παρασκευή 28 Φεβρουαρίου
Μικροοικονομική Ι. Ενότητα # 3: Θεωρία επιλογών καταναλωτή Διδάσκων: Πάνος Τσακλόγλου Τμήμα: Διεθνών και Ευρωπαϊκών Οικονομικών Σπουδών
 Μικροοικονομική Ι Ενότητα # 3: Θεωρία επιλογών καταναλωτή Διδάσκων: Πάνος Τσακλόγλου Τμήμα: Διεθνών και Ευρωπαϊκών Οικονομικών Σπουδών Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια
Μικροοικονομική Ι Ενότητα # 3: Θεωρία επιλογών καταναλωτή Διδάσκων: Πάνος Τσακλόγλου Τμήμα: Διεθνών και Ευρωπαϊκών Οικονομικών Σπουδών Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια
Θεωρία Καταναλωτή. Υποδειγματοποίηση της συμπεριφοράς του καταναλωτή. Βασική έννοια: Βελτιστοποίηση υπό περιορισμό.
 Θεωρία Καταναλωτή Υποδειγματοποίηση της συμπεριφοράς του καταναλωτή. Βασική έννοια: Βελτιστοποίηση υπό περιορισμό. Προτιμήσεις (preferences) Εισοδηματικός περιορισμός (budget constraint) Άριστη επιλογή
Θεωρία Καταναλωτή Υποδειγματοποίηση της συμπεριφοράς του καταναλωτή. Βασική έννοια: Βελτιστοποίηση υπό περιορισμό. Προτιμήσεις (preferences) Εισοδηματικός περιορισμός (budget constraint) Άριστη επιλογή
E5 ΣΥΝΑΡΤΗΣΕΙΣ ΣΤΑ ΟΙΚΟΝΟΜΙΚΑ II
 E5 ΣΥΝΑΡΤΗΣΕΙΣ ΣΤΑ ΟΙΚΟΝΟΜΙΚΑ II 1.Εισροές-Συντελεστές παραγωγής.εκροές-παραγόμενα προιόντα 3.Εξωτερικότητες 4.Εισροές-Καταναλωτικά αγαθά 5.Καμπύλες αδιαφορίας 6.Βελτιστοποίηση Σε μια παραγωγική διαδικασία
E5 ΣΥΝΑΡΤΗΣΕΙΣ ΣΤΑ ΟΙΚΟΝΟΜΙΚΑ II 1.Εισροές-Συντελεστές παραγωγής.εκροές-παραγόμενα προιόντα 3.Εξωτερικότητες 4.Εισροές-Καταναλωτικά αγαθά 5.Καμπύλες αδιαφορίας 6.Βελτιστοποίηση Σε μια παραγωγική διαδικασία
Θεωρία παραγωγού. Μικροοικονομική Θεωρία Ι / Διάλεξη 10 / Φ. Κουραντή
 Θεωρία παραγωγού Σκοπεύουμε να εξάγουμε από το πρόβλημα του παραγωγού τις συναρτήσεις ζήτησης παραγωγικών συντελεστών, την συνάρτηση προσφοράς της επιχείρησης και τις συναρτήσεις κόστους και κερδών. 1
Θεωρία παραγωγού Σκοπεύουμε να εξάγουμε από το πρόβλημα του παραγωγού τις συναρτήσεις ζήτησης παραγωγικών συντελεστών, την συνάρτηση προσφοράς της επιχείρησης και τις συναρτήσεις κόστους και κερδών. 1
ΥΠΟΒΑΘΡΟ ΤΗΣ ΖΗΤΗΣΗΣ: Η ΘΕΩΡΙΑ ΕΠΙΛΟΓΗΣ ΤΟΥ ΚΑΤΑΝΑΛΩΤΗ
 ΥΠΟΒΑΘΡΟ ΤΗΣ ΖΗΤΗΣΗΣ: Η ΘΕΩΡΙΑ ΕΠΙΛΟΓΗΣ ΤΟΥ ΚΑΤΑΝΑΛΩΤΗ ΕΙΣΑΓΩΓΗ Ο νόμος της ζήτησης λέει ότι η ποσότητα, που επιθυμούν να αγοράσουν οι καταναλωτές, σχετίζεται αρνητικά με την τιμή. Πίσω από το νόμο αυτό,
ΥΠΟΒΑΘΡΟ ΤΗΣ ΖΗΤΗΣΗΣ: Η ΘΕΩΡΙΑ ΕΠΙΛΟΓΗΣ ΤΟΥ ΚΑΤΑΝΑΛΩΤΗ ΕΙΣΑΓΩΓΗ Ο νόμος της ζήτησης λέει ότι η ποσότητα, που επιθυμούν να αγοράσουν οι καταναλωτές, σχετίζεται αρνητικά με την τιμή. Πίσω από το νόμο αυτό,
Πρώτο πακέτο ασκήσεων
 ΕΚΠΑ Ακαδημαϊκό έτος 208-209 Τμήμα Οικονομικών Επιστημών Μάθημα: Μικροοικονομική Θεωρία Ι Πρώτο πακέτο ασκήσεων Προθεσμία παράδοσης Παρασκευή 6 Νοεμβρίου (στο μάθημα της κ. Κουραντή, του κ. Παπανδρέου
ΕΚΠΑ Ακαδημαϊκό έτος 208-209 Τμήμα Οικονομικών Επιστημών Μάθημα: Μικροοικονομική Θεωρία Ι Πρώτο πακέτο ασκήσεων Προθεσμία παράδοσης Παρασκευή 6 Νοεμβρίου (στο μάθημα της κ. Κουραντή, του κ. Παπανδρέου
Ιδιότητες καµπυλών ζήτησης
 Ιδιότητες καµπυλών ζήτησης Διάλεξη 6 ΖΗΤΗΣΗ Συγκριτική στατική ανάλυση των συναρτήσεων της κανονικής ζήτησης είναι η µελέτη του πώς οι συναρτήσεις κανονικής ζήτησης (, 2,) και (, 2,) αλλάζουν όταν οι τιµές,
Ιδιότητες καµπυλών ζήτησης Διάλεξη 6 ΖΗΤΗΣΗ Συγκριτική στατική ανάλυση των συναρτήσεων της κανονικής ζήτησης είναι η µελέτη του πώς οι συναρτήσεις κανονικής ζήτησης (, 2,) και (, 2,) αλλάζουν όταν οι τιµές,
1. Η ερώτηση ίσως δέχεται διαφορετικές ερμηνείες για το τί ακριβώς εννοούμε
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Οικονομικών Επιστημών Μάθημα: Μικροοικονομική Θεωρία Ι 2015-16 Λύσεις Πρώτου Πακέτου Ασκήσεων 1. Η ερώτηση ίσως δέχεται διαφορετικές ερμηνείες για το τί ακριβώς εννοούμε με το
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Οικονομικών Επιστημών Μάθημα: Μικροοικονομική Θεωρία Ι 2015-16 Λύσεις Πρώτου Πακέτου Ασκήσεων 1. Η ερώτηση ίσως δέχεται διαφορετικές ερμηνείες για το τί ακριβώς εννοούμε με το
Άσκηση 3: Έστω η συνάρτηση χρησιμότητας για δύο αγαθά Χ και Υ έχει τη μορφή Cobb- Douglas U (X,Y) = X o,5 Y 0,5
 ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗΣ Σημείωση: Κάποιες από τις παρακάτω ασκήσεις θα λυθούν στην 3 η και 4 η διάλεξη του μαθήματος (στις ημερομηνίες που αναγράφονται στο πρόγραμμα) και οι υπόλοιπες θα αποτελέσουν προσωπική
ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗΣ Σημείωση: Κάποιες από τις παρακάτω ασκήσεις θα λυθούν στην 3 η και 4 η διάλεξη του μαθήματος (στις ημερομηνίες που αναγράφονται στο πρόγραμμα) και οι υπόλοιπες θα αποτελέσουν προσωπική
Μικροοικονομική Ανάλυση της Κατανάλωσης και της Παραγωγής
 Μικροοικονομική Ανάλυση της Κατανάλωσης και της Παραγωγής Διάλεξη 5: Επιλογή Ανδρέας Παπανδρέου Σχολή Οικονομικών και Πολιτικών Επιστημών Τμήμα Οικονομικών Επιστημών Οικονομικός ορθολογισμός Η βασική παραδοχή
Μικροοικονομική Ανάλυση της Κατανάλωσης και της Παραγωγής Διάλεξη 5: Επιλογή Ανδρέας Παπανδρέου Σχολή Οικονομικών και Πολιτικών Επιστημών Τμήμα Οικονομικών Επιστημών Οικονομικός ορθολογισμός Η βασική παραδοχή
Μικροοικονομία. Ενότητα 4: Θεωρία Χρησιμότητας και Καταναλωτική Συμπεριφορά. Δριτσάκη Χάιδω Τμήμα Λογιστικής και Χρηματοοικονομικής
 Μικροοικονομία Ενότητα 4: Θεωρία Χρησιμότητας και Καταναλωτική Συμπεριφορά Δριτσάκη Χάιδω Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Μικροοικονομία Ενότητα 4: Θεωρία Χρησιμότητας και Καταναλωτική Συμπεριφορά Δριτσάκη Χάιδω Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Μεγιστοποίηση της Χρησιμότητας
 Μεγιστοποίηση της Χρησιμότητας - Πρόβλημα Καταναλωτή: Επιλογή καταναλωτικού συνδυασμού x=(x, x ) υπό ένα σύνολο φυσικών, θεσμικών και οικονομικών περιορισμών κατά τρόπο ώστε να μεγιστοποιεί τη χρησιμότητά
Μεγιστοποίηση της Χρησιμότητας - Πρόβλημα Καταναλωτή: Επιλογή καταναλωτικού συνδυασμού x=(x, x ) υπό ένα σύνολο φυσικών, θεσμικών και οικονομικών περιορισμών κατά τρόπο ώστε να μεγιστοποιεί τη χρησιμότητά
4. Σωστό ή Λάθος (εξηγείστε): Κάποια καταναλωτικά προϊόντα είναι αγαθά επιθυμητά για κάποιες ποσότητες και κακά ανεπιθύμητα για άλλες.
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος 2014-2015 Τμήμα Οικονομικών Επιστημών Μάθημα: Μικροοικονομική Ανάλυση της Κατανάλωσης και της Παραγωγής Πρώτο πακέτο ασκήσεων και λύσεων 1. Σωστό ή Λάθος (εξηγείστε):
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος 2014-2015 Τμήμα Οικονομικών Επιστημών Μάθημα: Μικροοικονομική Ανάλυση της Κατανάλωσης και της Παραγωγής Πρώτο πακέτο ασκήσεων και λύσεων 1. Σωστό ή Λάθος (εξηγείστε):
ΜΕΡΟΣ ΙΙΙ: ΘΕΩΡΙΑ ΠΑΡΑΓΩΓΟΥ ΚΑΙ ΠΡΟΣΦΟΡΑΣ
 ΜΕΡΟΣ ΙΙΙ: ΘΕΩΡΙΑ ΠΑΡΑΓΩΓΟΥ ΚΑΙ ΠΡΟΣΦΟΡΑΣ Τεχνολογία και Συναρτήσεις Παραγωγής -H πλευρά της προσφοράς στην οικονομία μελετάει τη διαδικασία παραγωγής των αγαθών και υπηρεσιών που καταναλώνονται από τα
ΜΕΡΟΣ ΙΙΙ: ΘΕΩΡΙΑ ΠΑΡΑΓΩΓΟΥ ΚΑΙ ΠΡΟΣΦΟΡΑΣ Τεχνολογία και Συναρτήσεις Παραγωγής -H πλευρά της προσφοράς στην οικονομία μελετάει τη διαδικασία παραγωγής των αγαθών και υπηρεσιών που καταναλώνονται από τα
II.6 ΙΣΟΣΤΑΘΜΙΚΕΣ. 1. Γραφήματα-Επιφάνειες: z= 2. Γραμμική προσέγγιση-εφαπτόμενο επίπεδο. 3. Ισοσταθμικές: f(x, y) = c
 II.6 ΙΣΟΣΤΑΘΜΙΚΕΣ.Γραφήματα-Επιφάνειες.Γραμμική προσέγγιση-εφαπτόμενο επίπεδο 3.Ισοσταθμικές 4.Κλίση ισοσταθμικών 5.Διανυσματική ή Ιακωβιανή παράγωγος 6.Ιδιότητες των ισοσταθμικών 7.κυρτότητα των ισοσταθμικών
II.6 ΙΣΟΣΤΑΘΜΙΚΕΣ.Γραφήματα-Επιφάνειες.Γραμμική προσέγγιση-εφαπτόμενο επίπεδο 3.Ισοσταθμικές 4.Κλίση ισοσταθμικών 5.Διανυσματική ή Ιακωβιανή παράγωγος 6.Ιδιότητες των ισοσταθμικών 7.κυρτότητα των ισοσταθμικών
Επιλογές του Καταναλωτή και Αποφάσεις Ζήτησης Εκδόσεις Κριτική
 5 Επιλογές του Καταναλωτή και Αποφάσεις Ζήτησης Τέσσερα βασικά στοιχεία του υποδείγματος επιλογής του καταναλωτή Το εισόδημα του καταναλωτή. Οι τιμές των αγαθών. Οι προτιμήσεις του καταναλωτή. Η υπόθεση
5 Επιλογές του Καταναλωτή και Αποφάσεις Ζήτησης Τέσσερα βασικά στοιχεία του υποδείγματος επιλογής του καταναλωτή Το εισόδημα του καταναλωτή. Οι τιμές των αγαθών. Οι προτιμήσεις του καταναλωτή. Η υπόθεση
Μικροοικονομική Ανάλυση Ι
 Μικροοικονομική Ανάλυση Ι Θεωρία συμπεριφοράς καταναλωτή Ιδιότητες Καμπυλών Αδιαφορίας Συνάρτηση Ωφέλειας και Οριακός Λόγος υποκατάστασης Τμήμα: Αγροτικής Οικονομίας & Ανάπτυξης Διδάσκων: Λαζαρίδης Παναγιώτης
Μικροοικονομική Ανάλυση Ι Θεωρία συμπεριφοράς καταναλωτή Ιδιότητες Καμπυλών Αδιαφορίας Συνάρτηση Ωφέλειας και Οριακός Λόγος υποκατάστασης Τμήμα: Αγροτικής Οικονομίας & Ανάπτυξης Διδάσκων: Λαζαρίδης Παναγιώτης
Άριστες κατά Pareto Κατανομές
 Άριστες κατά Pareto Κατανομές - Ορισμός. Μια κατανομή x = (x, x ) = (( 1, )( 1, )) ονομάζεται άριστη κατά Pareto αν δεν υπάρχει άλλη κατανομή x = ( x, x ) τέτοια ώστε: U j( x j) U j( xj) για κάθε καταναλωτή
Άριστες κατά Pareto Κατανομές - Ορισμός. Μια κατανομή x = (x, x ) = (( 1, )( 1, )) ονομάζεται άριστη κατά Pareto αν δεν υπάρχει άλλη κατανομή x = ( x, x ) τέτοια ώστε: U j( x j) U j( xj) για κάθε καταναλωτή
Οι τιμές των αγαθών προσδιορίζονται στην αγορά από την αλληλεπίδραση των δυνάμεων της ζήτησης και της προσφοράς.
 ΤΙΜΗ ΚΕΦΑΛΑΙΟ ΔΕΥΤΕΡΟ: Η ΖΗΤΗΣΗ Οι τιμές των αγαθών προσδιορίζονται στην αγορά από την αλληλεπίδραση των δυνάμεων της ζήτησης και της προσφοράς. Χρησιμότητα ενός αγαθού, για τον καταναλωτή, είναι η ικανοποίηση
ΤΙΜΗ ΚΕΦΑΛΑΙΟ ΔΕΥΤΕΡΟ: Η ΖΗΤΗΣΗ Οι τιμές των αγαθών προσδιορίζονται στην αγορά από την αλληλεπίδραση των δυνάμεων της ζήτησης και της προσφοράς. Χρησιμότητα ενός αγαθού, για τον καταναλωτή, είναι η ικανοποίηση
Λύσεις Πρώτου Πακέτου Ασκήσεων
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Οικονομικών Επιστημών Μάθημα: Μικροοικονομική Θεωρία Ι 2016-17 Λύσεις Πρώτου Πακέτου Ασκήσεων Άσκηση 1 1. α) Αν βάλουµε την ποσότητα του αγαθού X στον οριζόντιο και την ποσότητα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Οικονομικών Επιστημών Μάθημα: Μικροοικονομική Θεωρία Ι 2016-17 Λύσεις Πρώτου Πακέτου Ασκήσεων Άσκηση 1 1. α) Αν βάλουµε την ποσότητα του αγαθού X στον οριζόντιο και την ποσότητα
Κοινωνικοοικονομική Αξιολόγηση Επενδύσεων Διάλεξη 3 η. Αποτελεσματικότητα και Ευημερία
 Κοινωνικοοικονομική Αξιολόγηση Επενδύσεων Διάλεξη 3 η Αποτελεσματικότητα και Ευημερία Ζητήματα που θα εξεταστούν: Πότε και πως επιτυγχάνεται η οικονομική αποτελεσματικότητα Θεωρήματα των οικονομικών της
Κοινωνικοοικονομική Αξιολόγηση Επενδύσεων Διάλεξη 3 η Αποτελεσματικότητα και Ευημερία Ζητήματα που θα εξεταστούν: Πότε και πως επιτυγχάνεται η οικονομική αποτελεσματικότητα Θεωρήματα των οικονομικών της
Σύνολο ασκήσεων 5. Άσκηση 1. Υπολογίστε τις μερικές παραγώγους ως προς 1 ή κτλ (συμβολισμός ή κτλ) για τις παρακάτω συναρτήσεις
 Σύνολο ασκήσεων 5. Άσκηση 1 Υπολογίστε τις μερικές παραγώγους ως προς 1 ή κτλ (συμβολισμός ή κτλ) για τις παρακάτω συναρτήσεις = 1 3 Για τη συνάρτηση CES (σταθερής ελαστικότητας υποκατάστασης) = ( ) =
Σύνολο ασκήσεων 5. Άσκηση 1 Υπολογίστε τις μερικές παραγώγους ως προς 1 ή κτλ (συμβολισμός ή κτλ) για τις παρακάτω συναρτήσεις = 1 3 Για τη συνάρτηση CES (σταθερής ελαστικότητας υποκατάστασης) = ( ) =
) = 2lnx lnx 2
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Σεπτέµβριος 8 Τµήµα Οικονοµικών Επιστηµών Μάθηµα: Μικροοικονοµική Ι ιδάσκοντες: Β. Ράπανος-Ι Χειάς Εξέταση στη Μικροοικονοµική Ι Στην εξέταση αυτή δίνονται δύο σύνοα το Α και το Β.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Σεπτέµβριος 8 Τµήµα Οικονοµικών Επιστηµών Μάθηµα: Μικροοικονοµική Ι ιδάσκοντες: Β. Ράπανος-Ι Χειάς Εξέταση στη Μικροοικονοµική Ι Στην εξέταση αυτή δίνονται δύο σύνοα το Α και το Β.
Οικονοµικός ορθολογισµός
 Οικονοµικός ορθολογισµός Διάλεξη 5 Επιλογή!1 Η βασική παραδοχή για τη συµπεριφορά του λήπτη αποφάσεων είναι ότι αυτός/αυτή επιλέγει την πλέον προτιµώµενη εναλλακτική επιλογή που του/της είναι διαθέσιµη.
Οικονοµικός ορθολογισµός Διάλεξη 5 Επιλογή!1 Η βασική παραδοχή για τη συµπεριφορά του λήπτη αποφάσεων είναι ότι αυτός/αυτή επιλέγει την πλέον προτιµώµενη εναλλακτική επιλογή που του/της είναι διαθέσιµη.
Κεφάλαιο 1. Θεωρία Ζήτησης
 Κεφάλαιο 1 Θεωρία Ζήτησης Στο κεφάλαιο αυτό υποθέτουµε ότι καταναλωτής εισέρχεται στην αγορά µε πλούτο w > 0 και επιθυµεί να τον ανταλλάξει µε διάνυσµα αγαθών x που να µεγιστοποιεί τις προτιµήσεις του.
Κεφάλαιο 1 Θεωρία Ζήτησης Στο κεφάλαιο αυτό υποθέτουµε ότι καταναλωτής εισέρχεται στην αγορά µε πλούτο w > 0 και επιθυµεί να τον ανταλλάξει µε διάνυσµα αγαθών x που να µεγιστοποιεί τις προτιµήσεις του.
Ανάλυση συγκριτικής στατικής
 Ανάλυση συγκριτικής στατικής Μεταβολή παραμέτρων και σύγκριση δυο στατικών σημείων. Εδώ θα μελετήσουμε τη μεταβολή των συναρτήσεων ζήτησης όταν παρατηρείται: x i p,i 1. μεταβολή όλων των τιμών και του
Ανάλυση συγκριτικής στατικής Μεταβολή παραμέτρων και σύγκριση δυο στατικών σημείων. Εδώ θα μελετήσουμε τη μεταβολή των συναρτήσεων ζήτησης όταν παρατηρείται: x i p,i 1. μεταβολή όλων των τιμών και του
1 Μερική παραγώγιση και μερική παράγωγος
 Περίγραμμα διάλεξης 5 Βιβλίο Chiang και Wainwright (κεφ 74,75,76) 1 Μερική παραγώγιση και μερική παράγωγος Έστω η συνάρτηση (x) όπου x R ή εναλλακτικά γράφουμε ( 1 2 ) Το διάνυσμα x περιέχει τις ανεξάρτητες
Περίγραμμα διάλεξης 5 Βιβλίο Chiang και Wainwright (κεφ 74,75,76) 1 Μερική παραγώγιση και μερική παράγωγος Έστω η συνάρτηση (x) όπου x R ή εναλλακτικά γράφουμε ( 1 2 ) Το διάνυσμα x περιέχει τις ανεξάρτητες
Μικροοικονομική Ανάλυση Ι: Θεωρία Συμπεριφοράς Καταναλωτή
 Μικροοικονομική Ανάλυση Ι: Θεωρία Συμπεριφοράς Καταναλωτή Ανδρέας Δριχούτης, hd Επίκουρος Καθηγητής Τμ. Αγροτικής Οικονομίας & Ανάπτυξης Γεωπονικό Πανεπιστήμιο Αθηνών Ποιες οικονομικές αρχές βρίσκονται
Μικροοικονομική Ανάλυση Ι: Θεωρία Συμπεριφοράς Καταναλωτή Ανδρέας Δριχούτης, hd Επίκουρος Καθηγητής Τμ. Αγροτικής Οικονομίας & Ανάπτυξης Γεωπονικό Πανεπιστήμιο Αθηνών Ποιες οικονομικές αρχές βρίσκονται
Οικονομικά για Μη Οικονομολόγους Ενότητα 2: Θεωρία Καταναλωτή
 Οικονομικά για Μη Οικονομολόγους Ενότητα 2: Θεωρία Καταναλωτή Καθηγητής: Κώστας Τσεκούρας Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Οικονομικών Επιστημών Σκοποί ενότητας Στην ενότητα αυτή παρουσιάζονται
Οικονομικά για Μη Οικονομολόγους Ενότητα 2: Θεωρία Καταναλωτή Καθηγητής: Κώστας Τσεκούρας Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Οικονομικών Επιστημών Σκοποί ενότητας Στην ενότητα αυτή παρουσιάζονται
ΑΝΑ ΚΕΦΑΛΑΙΟ. geeconomy@yahoo.com. Γ Ι Ω Ρ Γ Ο Σ Κ Α Μ Α Ρ Ι Ν Ο Σ Ο Ι Κ Ο Ν Ο Μ Ο Λ Ο Γ Ο Σ ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 2000 2012
 ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 2000 2012 1 ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 2000 2012 ΑΝΑ ΚΕΦΑΛΑΙΟ Στο παρόν είναι συγκεντρωµένες όλες σχεδόν οι ερωτήσεις κλειστού τύπου που
ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 2000 2012 1 ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 2000 2012 ΑΝΑ ΚΕΦΑΛΑΙΟ Στο παρόν είναι συγκεντρωµένες όλες σχεδόν οι ερωτήσεις κλειστού τύπου που
Ποιες οικονομικές αρχές βρίσκονται πίσω από την ζήτηση Θεωρία Συμπεριφοράς του. Καταναλωτή. Θεωρία της Απόλυτης. Θεωρία της Τακτικής Ωφέλειας
 Ποιες οικονομικές αρχές βρίσκονται ; πίσω από την ζήτηση Θεωρία Συμπεριφοράς του Καταναλωτή Θεωρία της Τακτικής Ωφέλειας Θεωρία της Απόλυτης Ωφέλειας Θεωρία των Επιλογών Θεωρία των επιλογών Οικουμενικό
Ποιες οικονομικές αρχές βρίσκονται ; πίσω από την ζήτηση Θεωρία Συμπεριφοράς του Καταναλωτή Θεωρία της Τακτικής Ωφέλειας Θεωρία της Απόλυτης Ωφέλειας Θεωρία των Επιλογών Θεωρία των επιλογών Οικουμενικό
Notes. Notes. Notes. Notes
 Θεωρία Καταναλωτή-Προτιμήσεις Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 3 Οκτωβρίου 2012 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) Θεωρία Καταναλωτή-Προτιμήσεις 3 Οκτωβρίου 2012 1 / 19 Προτιμήσεις καταναλωτών Θέλουμε
Θεωρία Καταναλωτή-Προτιμήσεις Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 3 Οκτωβρίου 2012 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) Θεωρία Καταναλωτή-Προτιμήσεις 3 Οκτωβρίου 2012 1 / 19 Προτιμήσεις καταναλωτών Θέλουμε
Η θεωρία των επιλογών του καταναλωτή
 Η θεωρία των επιλογών του καταναλωτή Ο εισοδηµατικός περιορισµός του καταναλωτή Λίτρα Αριθµός από πίτσες απάνες για (σε ευρώ) απάνες για πίτσα (σε ευρώ) Συνολικές δαπάνες (σε ευρώ) 1 1. 1. 5 9 1 9 1. 1
Η θεωρία των επιλογών του καταναλωτή Ο εισοδηµατικός περιορισµός του καταναλωτή Λίτρα Αριθµός από πίτσες απάνες για (σε ευρώ) απάνες για πίτσα (σε ευρώ) Συνολικές δαπάνες (σε ευρώ) 1 1. 1. 5 9 1 9 1. 1
Τεχνολογίες. Διάλεξη 10. Τεχνολογίες. Συνδυασµοί εισροών. Τεχνολογία
 Τεχνολογίες Διάλεξη 0 Τεχνολογία Τεχνολογία είναι µια διαδικασία µε την οποία εισροές µετατρέπονται σε εκροές. π.χ. εργασία, ένας υπολογιστής, ένας προβολέας, ηλεκτρισµός, κ.α. Συνδυάζονται για την παραγωγή
Τεχνολογίες Διάλεξη 0 Τεχνολογία Τεχνολογία είναι µια διαδικασία µε την οποία εισροές µετατρέπονται σε εκροές. π.χ. εργασία, ένας υπολογιστής, ένας προβολέας, ηλεκτρισµός, κ.α. Συνδυάζονται για την παραγωγή
E1. ΣΥΝΑΡΤΗΣΕΙΣ ΣΤΑ ΟΙΚΟΝΟΜΙΚΑ Ι
 E. ΣΥΝΑΡΤΗΣΕΙΣ ΣΤΑ ΟΙΚΟΝΟΜΙΚΑ Ι.Κόστος.Παραγωγή 3.Χρησιµότητα 4.Ζήτηση-Προσφορά 5.Φόρος. Κόστος Θεωρούµε ότι το κόστος παραγωγής (cost) ενός προιόντος είναι συνάρτηση της ποσότητας παραγωγής (production)
E. ΣΥΝΑΡΤΗΣΕΙΣ ΣΤΑ ΟΙΚΟΝΟΜΙΚΑ Ι.Κόστος.Παραγωγή 3.Χρησιµότητα 4.Ζήτηση-Προσφορά 5.Φόρος. Κόστος Θεωρούµε ότι το κόστος παραγωγής (cost) ενός προιόντος είναι συνάρτηση της ποσότητας παραγωγής (production)
ΣΗΜΕΙΩΣΕΙΣ ΣΤΗ ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΤΜΗΜΑ ΝΑΥΤΙΛΙΑΚΩΝ ΣΠΟΥΔΩΝ ΔΑΠ-ΝΔΦΚ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΕΙΡΑΙΑ
 ΤΜΗΜΑ ΣΗΜΕΙΩΣΕΙΣ ΣΤΗ ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΕΙΡΑΙΑ ΘΕΩΡΙΑ ΣΥΜΠΕΡΙΦΟΡΑΣ ΚΑΤΑΝΑΛΩΤΗ Η οικονομική δραστηριότητα τείνει στην ικανοποίηση των αναγκών του καταναλωτή, ο οποίος με δεδομένο το εισόδημα
ΤΜΗΜΑ ΣΗΜΕΙΩΣΕΙΣ ΣΤΗ ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΕΙΡΑΙΑ ΘΕΩΡΙΑ ΣΥΜΠΕΡΙΦΟΡΑΣ ΚΑΤΑΝΑΛΩΤΗ Η οικονομική δραστηριότητα τείνει στην ικανοποίηση των αναγκών του καταναλωτή, ο οποίος με δεδομένο το εισόδημα
ΚΕΦΑΛΑΙΟ 2 ΘΕΩΡΙΑ ΖΗΤΗΣΗΣ
 ΚΕΦΑΛΑΙΟ 2 ΘΕΩΡΙΑ ΖΗΤΗΣΗΣ Οι τιµές Στην οικονοµία οι τιµές παίζουν βασικό ρόλο. Κατανέµουν τους παραγωγικούς πόρους στις τοµείς όπου υπάρχει µεγαλύτερη ζήτηση µε το πιο αποτελεσµατικό τρόπο. Αυτό το οποίο
ΚΕΦΑΛΑΙΟ 2 ΘΕΩΡΙΑ ΖΗΤΗΣΗΣ Οι τιµές Στην οικονοµία οι τιµές παίζουν βασικό ρόλο. Κατανέµουν τους παραγωγικούς πόρους στις τοµείς όπου υπάρχει µεγαλύτερη ζήτηση µε το πιο αποτελεσµατικό τρόπο. Αυτό το οποίο
3.1 Ανεξάρτητες αποφάσεις - Κατανομή χρόνου μεταξύ εργασίας και σχόλης
 3. ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΑΝΑΛΥΣΗ ΤΗΣ ΑΓΟΡΑΣ ΕΡΓΑΣΙΑΣ (ΝΕΟΚΛΑΣΙΚΟ ΥΠΟΔΕΙΓΜΑ). ΠΡΟΣΦΟΡΑ ΕΡΓΑΣΙΑΣ Ως προσφορά εργασίας ορίζεται το σύνολο των ωρών εργασίας που προσφέρονται προς εκμίσθωση μία δεδομένη χρονική στιγμή.
3. ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΑΝΑΛΥΣΗ ΤΗΣ ΑΓΟΡΑΣ ΕΡΓΑΣΙΑΣ (ΝΕΟΚΛΑΣΙΚΟ ΥΠΟΔΕΙΓΜΑ). ΠΡΟΣΦΟΡΑ ΕΡΓΑΣΙΑΣ Ως προσφορά εργασίας ορίζεται το σύνολο των ωρών εργασίας που προσφέρονται προς εκμίσθωση μία δεδομένη χρονική στιγμή.
(i) Νόμος Ζήτησης. Μικροοικονομία Εξετάζει τη συμπεριφορά του οικονομούντος ατόμου (καταναλωτή, παραγωγού επιχείρησης)
 ΕΙΣΑΩΗ Μικροοικονομία Εξετάζει τη συμπεριφορά του οικονομούντος ατόμου (καταναλωτή, παραγωγού επιχείρησης) Μικροοικονομία ή Θεωρία Τιμών Σημείο αναφοράς είναι ο προσδιορισμός της τιμής ενός αγαθού. Ν Ο
ΕΙΣΑΩΗ Μικροοικονομία Εξετάζει τη συμπεριφορά του οικονομούντος ατόμου (καταναλωτή, παραγωγού επιχείρησης) Μικροοικονομία ή Θεωρία Τιμών Σημείο αναφοράς είναι ο προσδιορισμός της τιμής ενός αγαθού. Ν Ο
Σύνολο ασκήσεων 5. = = ( ) = = ( ) = p ln ( ) Για τη συνάρτηση CES (σταθερής ελαστικότητας υποκατάστασης)
 Σύνολο ασκήσεων 5. Άσκηση 1 Υπολογίστε τις μερικές παραγώγους ως προς 1 ή,, (συμβολισμός ή,, ) για τις παρακάτω συναρτήσεις = 1 3 = ( 1 3 4 )= 1 1 3+5 3 +8ln( 1 )+ 4 = ( ) = +3 + +3 = ( ) = p ln ()+ +
Σύνολο ασκήσεων 5. Άσκηση 1 Υπολογίστε τις μερικές παραγώγους ως προς 1 ή,, (συμβολισμός ή,, ) για τις παρακάτω συναρτήσεις = 1 3 = ( 1 3 4 )= 1 1 3+5 3 +8ln( 1 )+ 4 = ( ) = +3 + +3 = ( ) = p ln ()+ +
αx αx αx αx 2 αx = α e } 2 x x x dx καλείται η παραβολική συνάρτηση η οποία στο x
 A3. ΕΥΤΕΡΗ ΠΑΡΑΓΩΓΟΣ-ΚΥΡΤΟΤΗΤΑ. εύτερη παράγωγος.παραβολική προσέγγιση ή επέκταση 3.Κυρτή 4.Κοίλη 5.Ιδιότητες κυρτών/κοίλων συναρτήσεων 6.Σηµεία καµπής ΠΑΡΑΡΤΗΜΑ 7. εύτερη πλεγµένη παραγώγιση 8.Χαρακτηρισµός
A3. ΕΥΤΕΡΗ ΠΑΡΑΓΩΓΟΣ-ΚΥΡΤΟΤΗΤΑ. εύτερη παράγωγος.παραβολική προσέγγιση ή επέκταση 3.Κυρτή 4.Κοίλη 5.Ιδιότητες κυρτών/κοίλων συναρτήσεων 6.Σηµεία καµπής ΠΑΡΑΡΤΗΜΑ 7. εύτερη πλεγµένη παραγώγιση 8.Χαρακτηρισµός
( ) Κλίση και επιφάνειες στάθµης µιας συνάρτησης. x + y + z = κ ορίζει την επιφάνεια µιας σφαίρας κέντρου ( ) κ > τότε η
 Έστω Κλίση και επιφάνειες στάθµης µιας συνάρτησης ανοικτό και σταθερά ( µε κ f ( ) ορίζει µια επιφάνεια S στον f : ) τότε η εξίσωση, ονοµάζεται συνήθως επιφάνεια στάθµης της f. εξίσωση, C συνάρτηση. Αν
Έστω Κλίση και επιφάνειες στάθµης µιας συνάρτησης ανοικτό και σταθερά ( µε κ f ( ) ορίζει µια επιφάνεια S στον f : ) τότε η εξίσωση, ονοµάζεται συνήθως επιφάνεια στάθµης της f. εξίσωση, C συνάρτηση. Αν
Οµάδες ψηφοφόρων Αρ. Μελών Οµάδων Προτιµήσεις Α 1 x > y > z Β 1 y > z >x Γ 1 z > x > y
 0. Mη Μεταβατικές Συλλογικές Προτιµήσεις Το αξίωµα της µεταβατικότητας στην περίπτωση των προτιµήσεων ενός µεµονωµένου φορέα αποφάσεων, επιτρέπει την επέκταση της ικανότητας σύγκρισης ζευγών επιλογών στο
0. Mη Μεταβατικές Συλλογικές Προτιµήσεις Το αξίωµα της µεταβατικότητας στην περίπτωση των προτιµήσεων ενός µεµονωµένου φορέα αποφάσεων, επιτρέπει την επέκταση της ικανότητας σύγκρισης ζευγών επιλογών στο
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τµήµα Οικονοµικών Επιστηµών Ακαδηµαϊκό έτος (διαβάζουμε κεφ. 4 από Μ. Χλέτσο και σημειώσεις στο eclass)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τµήµα Οικονοµικών Επιστηµών Ακαδηµαϊκό έτος 2016-17 ΠΟΛΙΤΙΚΗ ΟΙΚΟΝΟΜΙΑ ΤΗΣ ΚΟΙΝΩΝΙΚΗΣ ΠΟΛΙΤΙΚΗΣ (διαβάζουμε κεφ. 4 από Μ. Χλέτσο και σημειώσεις στο eclass) 1 ιάλεξη2 Ανταγωνισμός, οικονομική
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τµήµα Οικονοµικών Επιστηµών Ακαδηµαϊκό έτος 2016-17 ΠΟΛΙΤΙΚΗ ΟΙΚΟΝΟΜΙΑ ΤΗΣ ΚΟΙΝΩΝΙΚΗΣ ΠΟΛΙΤΙΚΗΣ (διαβάζουμε κεφ. 4 από Μ. Χλέτσο και σημειώσεις στο eclass) 1 ιάλεξη2 Ανταγωνισμός, οικονομική
9 εύτερη παράγωγος κι εφαρµογές
 9 εύτερη παράγωγος κι εφαρµογές Εστω ότι η y = f x είναι παραγωγίσιµη σε κάποιο διάστηµα το οποίο περιέχει τον x 0 και ότι η f x η οποία ορίζεται στο διάστηµα αυτό έχει µε την σειρά της παράγωγο στο x
9 εύτερη παράγωγος κι εφαρµογές Εστω ότι η y = f x είναι παραγωγίσιµη σε κάποιο διάστηµα το οποίο περιέχει τον x 0 και ότι η f x η οποία ορίζεται στο διάστηµα αυτό έχει µε την σειρά της παράγωγο στο x
Κεφάλαιο 33 Παραγωγή
 HAL R. VARIAN Μικροοικονομική Μια σύγχρονη προσέγγιση 3 η έκδοση Εκδόσεις Κριτική Κεφάλαιο 33 Παραγωγή Ύλη για τη Μίκρο ΙΙ: όλο το κεφάλαιο Οικονομίες ανταλλαγής (αναθεώρηση) Καμία παραγωγή, μόνο αποθέματα,
HAL R. VARIAN Μικροοικονομική Μια σύγχρονη προσέγγιση 3 η έκδοση Εκδόσεις Κριτική Κεφάλαιο 33 Παραγωγή Ύλη για τη Μίκρο ΙΙ: όλο το κεφάλαιο Οικονομίες ανταλλαγής (αναθεώρηση) Καμία παραγωγή, μόνο αποθέματα,
Στον πίνακα που ακολουθεί δίνονται πέντε δέσμες (Α, Β, Γ, Δ και Ε) των αγαθών Χ
 Άσκηση 1 Στον πίνακα που ακολουθεί δίνονται πέντε δέσμες (Α, Β, Γ, Δ και Ε) των αγαθών Χ και Υ. Α Β Γ Δ Ε Χ 90 30 5 55 50 Υ 10 80 40 0 55 Ποιες από τις παρακάτω προτάσεις θεωρείτε ότι αντιστοιχούν σε ορθολογική
Άσκηση 1 Στον πίνακα που ακολουθεί δίνονται πέντε δέσμες (Α, Β, Γ, Δ και Ε) των αγαθών Χ και Υ. Α Β Γ Δ Ε Χ 90 30 5 55 50 Υ 10 80 40 0 55 Ποιες από τις παρακάτω προτάσεις θεωρείτε ότι αντιστοιχούν σε ορθολογική
Α.Ο.Θ ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΑΝΑ ΚΕΦΑΛΑΙΟ
 Α.Ο.Θ ΕΡΩΣΗΕΙ ΚΛΕΙΣΟΤ ΣΤΠΟΤ ΑΝΑ ΚΕΥΑΛΑΙΟ Γ τάξης Γενικοφ Λυκείου ΝΙΚΟ ΠΕΡΟΤΛΑΚΗ Οικονομολόγος, ΙΕΡΑΠΕΣΡΑ Σηλ. 6977246129 ΑΟΘ ΝΙΚΟ ΠΕΡΟΥΛΑΚΗ Οικονομολόγος ελίδα 1 Γ τάξης Γενικοφ Λυκείου ΕΡΩΣΗΕΙ ΚΛΕΙΣΟΤ
Α.Ο.Θ ΕΡΩΣΗΕΙ ΚΛΕΙΣΟΤ ΣΤΠΟΤ ΑΝΑ ΚΕΥΑΛΑΙΟ Γ τάξης Γενικοφ Λυκείου ΝΙΚΟ ΠΕΡΟΤΛΑΚΗ Οικονομολόγος, ΙΕΡΑΠΕΣΡΑ Σηλ. 6977246129 ΑΟΘ ΝΙΚΟ ΠΕΡΟΥΛΑΚΗ Οικονομολόγος ελίδα 1 Γ τάξης Γενικοφ Λυκείου ΕΡΩΣΗΕΙ ΚΛΕΙΣΟΤ
ΕΦΑΡΜΟΣΜΕΝΗ ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΑΣΚΗΣΕΙΣ ΕΙΣΑΓΩΓΗ Ο ΜΗΧΑΝΙΣΜΟΣ ΤΗΣ ΑΓΟΡΑΣ
 ΕΦΑΡΜΟΣΜΕΝΗ ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΑΣΚΗΣΕΙΣ ΕΙΣΑΓΩΓΗ Ο ΜΗΧΑΝΙΣΜΟΣ ΤΗΣ ΑΓΟΡΑΣ Άσκηση 1 Αν το επιτόκιο είναι 10%, ποια είναι η παρούσα αξία των κερδών της Monroe orporation στα επόμενα 5 χρόνια; Χρόνια στο μέλλον
ΕΦΑΡΜΟΣΜΕΝΗ ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΑΣΚΗΣΕΙΣ ΕΙΣΑΓΩΓΗ Ο ΜΗΧΑΝΙΣΜΟΣ ΤΗΣ ΑΓΟΡΑΣ Άσκηση 1 Αν το επιτόκιο είναι 10%, ποια είναι η παρούσα αξία των κερδών της Monroe orporation στα επόμενα 5 χρόνια; Χρόνια στο μέλλον
Μικροοικονοµική Θεωρία
 Μικροοικονοµική Θεωρία Ειδικά Θέµατα της Θεωρίας της Συµπεριφοράς του Καταναλωτή Το Συνολικό Αποτέλεσµα. Το Αποτέλεσµα Υποκατάστασης. Το Εισοδηµατικό Αποτέλεσµα. Κανονικά Αγαθά. Κατώτερα Αγαθά. Παράδοξο
Μικροοικονοµική Θεωρία Ειδικά Θέµατα της Θεωρίας της Συµπεριφοράς του Καταναλωτή Το Συνολικό Αποτέλεσµα. Το Αποτέλεσµα Υποκατάστασης. Το Εισοδηµατικό Αποτέλεσµα. Κανονικά Αγαθά. Κατώτερα Αγαθά. Παράδοξο
ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΘΕΩΡΙΑ
 ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΘΕΩΡΙΑ Τσελεκούνης Μάρκος Επίκουρος Καθηγητής Τμήμα Οικονομικής Επιστήμης mtselek@unipi.gr http://www.unipi.gr/unipi/en/mtselek.html Γραφείο 516 Ώρες Γραφείου: Τετάρτη 12:00-14:00 ΚΕΦΑΛΑΙΟ
ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΘΕΩΡΙΑ Τσελεκούνης Μάρκος Επίκουρος Καθηγητής Τμήμα Οικονομικής Επιστήμης mtselek@unipi.gr http://www.unipi.gr/unipi/en/mtselek.html Γραφείο 516 Ώρες Γραφείου: Τετάρτη 12:00-14:00 ΚΕΦΑΛΑΙΟ
ΑΠΑΝΤΗΤΙΚΟ ΔΕΛΤΙΟ ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΑΕΜ ΕΞΑΜΗΝΟ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΝΟΜΙΚΩΝ, ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΠΟΛΙΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΟΜΕΑΣ: ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΚΑΙ ΠΟΛΙΤΙΚΗΣ ΜΑΘΗΜΑ: Μικροοικονομική Ι ΔΙΔΑΣΚΩΝ: Νίκος
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΝΟΜΙΚΩΝ, ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΠΟΛΙΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΟΜΕΑΣ: ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΚΑΙ ΠΟΛΙΤΙΚΗΣ ΜΑΘΗΜΑ: Μικροοικονομική Ι ΔΙΔΑΣΚΩΝ: Νίκος
Κεφάλαιο 2. Ζήτηση των Αγαθών
 Κεφάλαιο 2 Ζήτηση των Αγαθών Οι τιμές των αγαθών προσδιορίζονται στην αγορά από την αλληλεπίδραση των δυνάμεων της ζήτησης και της προσφοράς (demand & supply). Χρησιμότητα ενός αγαθού είναι η ικανοποίηση
Κεφάλαιο 2 Ζήτηση των Αγαθών Οι τιμές των αγαθών προσδιορίζονται στην αγορά από την αλληλεπίδραση των δυνάμεων της ζήτησης και της προσφοράς (demand & supply). Χρησιμότητα ενός αγαθού είναι η ικανοποίηση
Μικροοικονομική Ανάλυση της Κατανάλωσης και της Παραγωγής
 Μικροοικονομική Ανάλυση της Κατανάλωσης και της Παραγωγής Διάλεξη 10: Τεχνολογία Ανδρέας Παπανδρέου Σχολή Οικονομικών και Πολιτικών Επιστημών Τμήμα Οικονομικών Επιστημών Τεχνολογίες Τεχνολογία είναι μια
Μικροοικονομική Ανάλυση της Κατανάλωσης και της Παραγωγής Διάλεξη 10: Τεχνολογία Ανδρέας Παπανδρέου Σχολή Οικονομικών και Πολιτικών Επιστημών Τμήμα Οικονομικών Επιστημών Τεχνολογίες Τεχνολογία είναι μια
( ) Κλίση και επιφάνειες στάθµης µιας συνάρτησης. x + y + z = κ ορίζει την επιφάνεια µιας σφαίρας κέντρου ( ) κ > τότε η
 Έστω Κλίση και επιφάνειες στάθµης µιας συνάρτησης ανοικτό και σταθερά ( µε κ f ( ) ορίζει µια επιφάνεια S στον f : ) τότε η εξίσωση, ονοµάζεται συνήθως επιφάνεια στάθµης της f. εξίσωση, C συνάρτηση. Αν
Έστω Κλίση και επιφάνειες στάθµης µιας συνάρτησης ανοικτό και σταθερά ( µε κ f ( ) ορίζει µια επιφάνεια S στον f : ) τότε η εξίσωση, ονοµάζεται συνήθως επιφάνεια στάθµης της f. εξίσωση, C συνάρτηση. Αν
Αποτέλεσμα Υποκατάστασης και Αποτέλεσμα Εισοδήματος
 Αποτέλεσμα Υποκατάστασης και Αποτέλεσμα Εισοδήματος (Επιπτώσεις Μεταβολής της Τιμής στη Ζητούμενη Ποσότητα) () Διαγραμματική Παρουσίαση Α. Επιπτώσεις Μεταβολής της Τιμής στα Κανονικά Αγαθά M x / p (Π)
Αποτέλεσμα Υποκατάστασης και Αποτέλεσμα Εισοδήματος (Επιπτώσεις Μεταβολής της Τιμής στη Ζητούμενη Ποσότητα) () Διαγραμματική Παρουσίαση Α. Επιπτώσεις Μεταβολής της Τιμής στα Κανονικά Αγαθά M x / p (Π)
Ελαστικότητες Ζήτησης
 Ελαστικότητες Ζήτησης - Η ευαισθησία της ζητούμενης ποσότητας x σε μεταβολές της τιμής μπορεί να μετρηθεί άμεσα από το λόγο Δx / Δ (ήαπότην παράγωγο x / ). - Αυτό το μέτρο ευαισθησίας έχει το μειονέκτημα
Ελαστικότητες Ζήτησης - Η ευαισθησία της ζητούμενης ποσότητας x σε μεταβολές της τιμής μπορεί να μετρηθεί άμεσα από το λόγο Δx / Δ (ήαπότην παράγωγο x / ). - Αυτό το μέτρο ευαισθησίας έχει το μειονέκτημα
Παραγωγική διαδικασία. Τεχνολογία
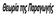 Σκοπός: Η μελέτη της σχέσης εισροών και εκροών Συντελεστές παραγωγής (Εισροές) Παραγωγική διαδικασία Παραγόμενο Προϊόν (Εκροές) Κεφαλαιουχικά αγαθά Εργασία Γή Επιχειρηματικές ή διοικητικές ικανότητες κλπ
Σκοπός: Η μελέτη της σχέσης εισροών και εκροών Συντελεστές παραγωγής (Εισροές) Παραγωγική διαδικασία Παραγόμενο Προϊόν (Εκροές) Κεφαλαιουχικά αγαθά Εργασία Γή Επιχειρηματικές ή διοικητικές ικανότητες κλπ
Διάλεξη 5- Σημειώσεις
 Διάλεξη 5- Σημειώσεις 1 Κοίλες (concave) και κυρτές (convex) συναρτήσεις Σημείωση: Μόνο για συναρτήσεις που είναι συνεχείς σε ένα (κυρτό) διάστημα R και παραγωγίσιμες τουλάχιστον δύο φορές στο εσωτερικό
Διάλεξη 5- Σημειώσεις 1 Κοίλες (concave) και κυρτές (convex) συναρτήσεις Σημείωση: Μόνο για συναρτήσεις που είναι συνεχείς σε ένα (κυρτό) διάστημα R και παραγωγίσιμες τουλάχιστον δύο φορές στο εσωτερικό
Δεύτερο πακέτο ασκήσεων
 ΕΚΠΑ Ακαδημαϊκό έτος 018-019 Τμήμα Οικονομικών Επιστημών Μάθημα: Μικροοικονομική Θεωρία Ι Δεύτερο πακέτο ασκήσεων Προθεσμία παράδοσης Παρασκευή 7 Δεκεμβρίου (στο μάθημα της κ. Κουραντή, του κ. Παπανδρέου
ΕΚΠΑ Ακαδημαϊκό έτος 018-019 Τμήμα Οικονομικών Επιστημών Μάθημα: Μικροοικονομική Θεωρία Ι Δεύτερο πακέτο ασκήσεων Προθεσμία παράδοσης Παρασκευή 7 Δεκεμβρίου (στο μάθημα της κ. Κουραντή, του κ. Παπανδρέου
ΑΠΑΝΤΗΤΙΚΟ ΔΕΛΤΙΟ ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΑΕΜ ΕΞΑΜΗΝΟ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΝΟΜΙΚΩΝ, ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΠΟΛΙΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΟΜΕΑΣ: ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΚΑΙ ΠΟΛΙΤΙΚΗΣ ΜΑΘΗΜΑ: Μικροοικονομική Ι ΔΙΔΑΣΚΩΝ: Νίκος
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΝΟΜΙΚΩΝ, ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΠΟΛΙΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΟΜΕΑΣ: ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΚΑΙ ΠΟΛΙΤΙΚΗΣ ΜΑΘΗΜΑ: Μικροοικονομική Ι ΔΙΔΑΣΚΩΝ: Νίκος
Μικροοικονομική. Ενότητα 3: Ο καταναλωτής επιλέγει να μεγιστοποιήσει τη χρησιμότητά του. Σόρμας Αστέριος Τμήμα Διοίκησης Επιχειρήσεων (Κοζάνη)
 Μικροοικονομική Ενότητα 3: Ο καταναλωτής επιλέγει να μεγιστοποιήσει τη χρησιμότητά του Σόρμας Αστέριος Τμήμα Διοίκησης Επιχειρήσεων (Κοζάνη) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Μικροοικονομική Ενότητα 3: Ο καταναλωτής επιλέγει να μεγιστοποιήσει τη χρησιμότητά του Σόρμας Αστέριος Τμήμα Διοίκησης Επιχειρήσεων (Κοζάνη) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
α β. M x f x. f x x x = = =.
 Κυρτές συναρτήσεις σηµεία καµπής, Έστω συνάρτηση f συνεχής στο [ α β ] και παραγωγίσιµη στο ( α, β ) (α) Αν η f είναι γνησίως αύξουσα στο ( α, β ), τότε η fείναι κυρτή ή στρέφει τα κοίλα πάνω στο [ α,
Κυρτές συναρτήσεις σηµεία καµπής, Έστω συνάρτηση f συνεχής στο [ α β ] και παραγωγίσιµη στο ( α, β ) (α) Αν η f είναι γνησίως αύξουσα στο ( α, β ), τότε η fείναι κυρτή ή στρέφει τα κοίλα πάνω στο [ α,
Πολιτική Οικονομία Ενότητα
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 03: Ζήτηση και προσφορά αγαθών Πολυξένη Ράγκου Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 03: Ζήτηση και προσφορά αγαθών Πολυξένη Ράγκου Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Μικροοικονομική Ανάλυση Ι
 Μικροοικονομική Ανάλυση Ι Θεωρία συμπεριφοράς καταναλωτή Ιδιότητες Συνάρτησης ωφέλειας Εισοδηματικός περιορισμός Τμήμα: Αγροτικής Οικονομίας & Ανάπτυξης Διδάσκων: Λαζαρίδης Παναγιώτης Μαθησιακοί Στόχοι
Μικροοικονομική Ανάλυση Ι Θεωρία συμπεριφοράς καταναλωτή Ιδιότητες Συνάρτησης ωφέλειας Εισοδηματικός περιορισμός Τμήμα: Αγροτικής Οικονομίας & Ανάπτυξης Διδάσκων: Λαζαρίδης Παναγιώτης Μαθησιακοί Στόχοι
Διάλεξη 7. Εξίσωση Slutsky. Οι επιδράσεις µιας µεταβολής της
 Οι επιδράσεις µιας µεταβολής της τιµής Διάλεξη 7 Εξίσωση Slutsk Τι θα συµβεί όταν µειωθεί η τιµή ενός αγαθού; Αποτέλεσµα υποκατάστασης : το αγαθό γίνεται σχετικά πιο φτηνό και γι αυτό ο καταναλωτής υποκαθιστά
Οι επιδράσεις µιας µεταβολής της τιµής Διάλεξη 7 Εξίσωση Slutsk Τι θα συµβεί όταν µειωθεί η τιµή ενός αγαθού; Αποτέλεσµα υποκατάστασης : το αγαθό γίνεται σχετικά πιο φτηνό και γι αυτό ο καταναλωτής υποκαθιστά
I.3 ΔΕΥΤΕΡΗ ΠΑΡΑΓΩΓΟΣ-ΚΥΡΤΟΤΗΤΑ
 I.3 ΔΕΥΤΕΡΗ ΠΑΡΑΓΩΓΟΣ-ΚΥΡΤΟΤΗΤΑ.Δεύτερη παράγωγος.παραβολική προσέγγιση ή επέκταση 3.Κυρτή 4.Κοίλη 5.Ιδιότητες κυρτών/κοίλων συναρτήσεων 6.Σημεία καμπής ΠΑΡΑΡΤΗΜΑ 7.Δεύτερη πλεγμένη παραγώγιση 8.Χαρακτηρισμός
I.3 ΔΕΥΤΕΡΗ ΠΑΡΑΓΩΓΟΣ-ΚΥΡΤΟΤΗΤΑ.Δεύτερη παράγωγος.παραβολική προσέγγιση ή επέκταση 3.Κυρτή 4.Κοίλη 5.Ιδιότητες κυρτών/κοίλων συναρτήσεων 6.Σημεία καμπής ΠΑΡΑΡΤΗΜΑ 7.Δεύτερη πλεγμένη παραγώγιση 8.Χαρακτηρισμός
ΔΗΜΟΣΙΑ ΟΙΚΟΝΟΜΙΚΗ Ι
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΔΗΜΟΣΙΑ ΟΙΚΟΝΟΜΙΚΗ Ι Ενότητα 3: Εργαλεία Κανονιστικής Ανάλυσης Κουτεντάκης Φραγκίσκος Γαληνού Αργυρώ Τμήμα Οικονομικών Επιστημών Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΔΗΜΟΣΙΑ ΟΙΚΟΝΟΜΙΚΗ Ι Ενότητα 3: Εργαλεία Κανονιστικής Ανάλυσης Κουτεντάκης Φραγκίσκος Γαληνού Αργυρώ Τμήμα Οικονομικών Επιστημών Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΑΘΟΥΣ 1. Σε ένα κανονικό αγαθό, όταν αυξάνεται το εισόδηµα των καταναλωτών, τότε αυξάνεται και η συνολική δαπάνη των καταναλωτών 2.
 ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΑΘΟΥΣ 1. Σε ένα κανονικό αγαθό, όταν αυξάνεται το εισόδηµα των καταναλωτών, τότε αυξάνεται και η συνολική δαπάνη των καταναλωτών 2. Το µαγνητόφωνο ενός παιδιού είναι καταναλωτό αγαθό
ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΑΘΟΥΣ 1. Σε ένα κανονικό αγαθό, όταν αυξάνεται το εισόδηµα των καταναλωτών, τότε αυξάνεται και η συνολική δαπάνη των καταναλωτών 2. Το µαγνητόφωνο ενός παιδιού είναι καταναλωτό αγαθό
Κεφάλαιο 1. Ατοµική Θεωρία Λήψης Αποφάσεων. 1.1 Χώρος αγαθών. a = (3, 4, 2), a = (0, 2, 0).
 Κεφάλαιο 1 Ατοµική Θεωρία Λήψης Αποφάσεων 1.1 Χώρος αγαθών Αρχίζουµε τη µελέτη πρώτα µε πεπερασµένες οικονοµίες. Υποθέτουµε ότι στην οικονοµία έχουµε πεπερασµένο πλήθος αγαθών (m αγαθά) που αριθµούνται
Κεφάλαιο 1 Ατοµική Θεωρία Λήψης Αποφάσεων 1.1 Χώρος αγαθών Αρχίζουµε τη µελέτη πρώτα µε πεπερασµένες οικονοµίες. Υποθέτουµε ότι στην οικονοµία έχουµε πεπερασµένο πλήθος αγαθών (m αγαθά) που αριθµούνται
ΑΝΤΑΛΛΑΓΗ. Οι συναρτήσεις χρησιμότητας των ατόμων Α και Β είναι αντίστοιχα. και. και το αρχικό απόθεμα και.
 ΑΝΤΑΛΛΑΓΗ Άσκηση 5 Οι συναρτήσεις χρησιμότητας των ατόμων Α και Β είναι αντίστοιχα u ( x, x ) = x + x 1 2 1 2 και u ( x, x ) = x + x 1 2 1 2 Ω = (2,0) Ω = (0,1) και το αρχικό απόθεμα και. Να προσδιοριστεί
ΑΝΤΑΛΛΑΓΗ Άσκηση 5 Οι συναρτήσεις χρησιμότητας των ατόμων Α και Β είναι αντίστοιχα u ( x, x ) = x + x 1 2 1 2 και u ( x, x ) = x + x 1 2 1 2 Ω = (2,0) Ω = (0,1) και το αρχικό απόθεμα και. Να προσδιοριστεί
Ευχαριστίες... 16 Δύο λόγια από την συγγραφέα... 17
 Περιεχόμενα Ευχαριστίες... 16 Δύο λόγια από την συγγραφέα... 17 ΚΕΦΑΛΑΙΟ 1. Το σύνολο των πραγματικών αριθμών... 19 1.1 Σύνολα αριθμών... 19 1.2 Αλγεβρική δομή του R... 20 1.2.1 Ιδιότητες πρόσθεσης...
Περιεχόμενα Ευχαριστίες... 16 Δύο λόγια από την συγγραφέα... 17 ΚΕΦΑΛΑΙΟ 1. Το σύνολο των πραγματικών αριθμών... 19 1.1 Σύνολα αριθμών... 19 1.2 Αλγεβρική δομή του R... 20 1.2.1 Ιδιότητες πρόσθεσης...
Πρόγραμμα Σπουδών: Διοίκηση Επιχειρήσεων & Οργανισμών Θεματική Ενότητα: ΔΕΟ 34 Οικονομική Ανάλυση & Πολιτική
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ Πρόγραμμα Σπουδών: Διοίκηση Επιχειρήσεων & Οργανισμών Θεματική Ενότητα: ΔΕΟ 34 Οικονομική Ανάλυση & Πολιτική Γραπτή Εργασία # 4 (Δημόσια Οικονομική) Ακαδ. Έτος: 2006-7 Οδηγίες
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ Πρόγραμμα Σπουδών: Διοίκηση Επιχειρήσεων & Οργανισμών Θεματική Ενότητα: ΔΕΟ 34 Οικονομική Ανάλυση & Πολιτική Γραπτή Εργασία # 4 (Δημόσια Οικονομική) Ακαδ. Έτος: 2006-7 Οδηγίες
Notes. Notes. Notes. Notes. A B C x y z y z x z x y
 Κοινωνική επιλογή και Ευημερία Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 3 Δεκεμβρίου 01 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) Κοινωνική επιλογή και Ευημερία 3 Δεκεμβρίου 01 1 / 50 Κοινωνική επιλογή. Κοινωνική επιλογή.
Κοινωνική επιλογή και Ευημερία Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 3 Δεκεμβρίου 01 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) Κοινωνική επιλογή και Ευημερία 3 Δεκεμβρίου 01 1 / 50 Κοινωνική επιλογή. Κοινωνική επιλογή.
4.1 Ζήτηση για Ασφάλιση. Πλήρη κάλυψη.
 4. Ζήτηση για Ασφάλιση. Πλήρη κάλυψη. Η αγορά ασφαλιστικών συµφωνιών είναι µία ιδιαίτερη περίπτωση αγοράς δικαιωµάτων. Αντικείµενο της αγοράς αυτής είναι να δώσει την ευκαιρία µεταβίβασης εισοδήµατος από
4. Ζήτηση για Ασφάλιση. Πλήρη κάλυψη. Η αγορά ασφαλιστικών συµφωνιών είναι µία ιδιαίτερη περίπτωση αγοράς δικαιωµάτων. Αντικείµενο της αγοράς αυτής είναι να δώσει την ευκαιρία µεταβίβασης εισοδήµατος από
ΑΝΑ ΚΕΦΑΛΑΙΟ. geeconomy@yahoo.com. Γ Ι Ω Ρ Γ Ο Σ Κ Α Μ Α Ρ Ι Ν Ο Σ Ο Ι Κ Ο Ν Ο Μ Ο Λ Ο Γ Ο Σ ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 2000 2015
 ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 2000 2015 1 ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 2000 2015 ΑΝΑ ΚΕΦΑΛΑΙΟ Στο παρόν είναι συγκεντρωµένες όλες σχεδόν οι ερωτήσεις κλειστού τύπου που
ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 2000 2015 1 ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 2000 2015 ΑΝΑ ΚΕΦΑΛΑΙΟ Στο παρόν είναι συγκεντρωµένες όλες σχεδόν οι ερωτήσεις κλειστού τύπου που
από την ποσοστιαία μεταβολή της ζητούμενης ποσότητας προς την ποσοστιαία Σχέση ελαστικότητας ζήτησης και κλίση της καμπύλης ζήτησης.
 ΕΛΑΣΤΙΚΟΤΗΤΑ ΖΗΤΗΣΗΣ Ορισμός: Η ελαστικότητα ζήτησης, ενός αγαθού ως προς την τιμή του δίνεται από την ποσοστιαία μεταβολή της ζητούμενης ποσότητας προς την ποσοστιαία μεταβολή της τιμής του. Δηλαδή %
ΕΛΑΣΤΙΚΟΤΗΤΑ ΖΗΤΗΣΗΣ Ορισμός: Η ελαστικότητα ζήτησης, ενός αγαθού ως προς την τιμή του δίνεται από την ποσοστιαία μεταβολή της ζητούμενης ποσότητας προς την ποσοστιαία μεταβολή της τιμής του. Δηλαδή %
0 χ1 χ2 Ι2 χ3 Ι5 Ι3 χ
 ΠΝΕΠΙΣΤΗΜΙΟ ΜΚΕ ΟΝΙΣ - ΤΜΗΜ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΘΗΓΗΤΗΣ ΚΩΣΤΣ ΕΛΕΝΤΖΣ ΠΟΤΕΛΕΣΜΤ ΥΠΟΚΤΣΤΣΗΣ ΚΙ ΕΙΣΟ ΗΜΤΟΣ Ι1 χ/ Ρ=0 χ/ Ρ>0 χ/ Ρ
ΠΝΕΠΙΣΤΗΜΙΟ ΜΚΕ ΟΝΙΣ - ΤΜΗΜ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΘΗΓΗΤΗΣ ΚΩΣΤΣ ΕΛΕΝΤΖΣ ΠΟΤΕΛΕΣΜΤ ΥΠΟΚΤΣΤΣΗΣ ΚΙ ΕΙΣΟ ΗΜΤΟΣ Ι1 χ/ Ρ=0 χ/ Ρ>0 χ/ Ρ
Διεθνές εµπόριο-1 P 1 P 2
 Διεθνές εµπόριο-1 Το διεθνές εµπόριο συµβάλλει στην καλύτερη αξιοποίηση των παραγωγικών πόρων της ανθρωπότητας γιατί ελαχιστοποιεί το κόστος παραγωγής της συνολικής προσφοράς αγαθών και υπηρεσιών που διακινείται
Διεθνές εµπόριο-1 Το διεθνές εµπόριο συµβάλλει στην καλύτερη αξιοποίηση των παραγωγικών πόρων της ανθρωπότητας γιατί ελαχιστοποιεί το κόστος παραγωγής της συνολικής προσφοράς αγαθών και υπηρεσιών που διακινείται
Μαθηματικά. Ενότητα 13: Κυρτότητα Συνάρτησης Σαριαννίδης Νικόλαος Τμήμα Λογιστικής και Χρηματοοικονομικής
 Μαθηματικά Ενότητα 13: Κυρτότητα Συνάρτησης Σαριαννίδης Νικόλαος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Μαθηματικά Ενότητα 13: Κυρτότητα Συνάρτησης Σαριαννίδης Νικόλαος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
I.3 ΔΕΥΤΕΡΗ ΠΑΡΑΓΩΓΟΣ-ΚΥΡΤΟΤΗΤΑ
 I.3 ΔΕΥΤΕΡΗ ΠΑΡΑΓΩΓΟΣ-ΚΥΡΤΟΤΗΤΑ.Δεύτερη παράγωγος.κυρτή 3.Κοίλη 4.Ιδιότητες κυρτών/κοίλων συναρτήσεων 5.Σημεία καμπής 6.Παραβολική προσέγγιση(επέκταση) ΠΑΡΑΡΤΗΜΑ 7.Δεύτερη πλεγμένη παραγώγιση 8.Χαρακτηρισμός
I.3 ΔΕΥΤΕΡΗ ΠΑΡΑΓΩΓΟΣ-ΚΥΡΤΟΤΗΤΑ.Δεύτερη παράγωγος.κυρτή 3.Κοίλη 4.Ιδιότητες κυρτών/κοίλων συναρτήσεων 5.Σημεία καμπής 6.Παραβολική προσέγγιση(επέκταση) ΠΑΡΑΡΤΗΜΑ 7.Δεύτερη πλεγμένη παραγώγιση 8.Χαρακτηρισμός
ΘΕΩΡΙΑ ΤΩΝ ΕΠΙΛΟΓΩΝ ΤΟΥ ΚΑΤΑΝΑΛΩΤΗ I
 ΘΕΩΡΙΑ ΤΩΝ ΕΠΙΛΟΓΩΝ ΤΟΥ ΚΑΤΑΝΑΛΩΤΗ I Τέσσερα σηµαντικά στοιχεία: Το εισόδηµα του καταναλωτή Οι τιµές των αγαθών Οι ροτιµήσεις των καταναλωτών Η υ όθεση ότι ο καταναλωτής λαµβάνει α οφάσεις ου µεγιστο οιούν
ΘΕΩΡΙΑ ΤΩΝ ΕΠΙΛΟΓΩΝ ΤΟΥ ΚΑΤΑΝΑΛΩΤΗ I Τέσσερα σηµαντικά στοιχεία: Το εισόδηµα του καταναλωτή Οι τιµές των αγαθών Οι ροτιµήσεις των καταναλωτών Η υ όθεση ότι ο καταναλωτής λαµβάνει α οφάσεις ου µεγιστο οιούν
Η ΘΕΩΡΙΑ ΤΗΣ ΕΠΙΧΕΙΡΗΣΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΘΗΓΗΤΗΣ ΚΩΣΤΑΣ ΒΕΛΕΝΤΖΑΣ Η ΘΕΩΡΙΑ ΤΗΣ ΕΠΙΧΕΙΡΗΣΗΣ. Μερικές έννοιες Η συνάρτηση παραγωγής (, ), όπου είναι το συνολικό προϊόν και και οι συντελεστές
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΘΗΓΗΤΗΣ ΚΩΣΤΑΣ ΒΕΛΕΝΤΖΑΣ Η ΘΕΩΡΙΑ ΤΗΣ ΕΠΙΧΕΙΡΗΣΗΣ. Μερικές έννοιες Η συνάρτηση παραγωγής (, ), όπου είναι το συνολικό προϊόν και και οι συντελεστές
Διάλεξη 11. Μεγιστοποίηση κέρδους. Οικονοµικό κέρδος. Η ανταγωνιστική επιχείρηση
 Οικονοµικό κέρδος Διάλεξη Μεγιστοποίηση Μια επιχείρηση χρησιµοποιεί εισροές j,m για να παραγάγει n προϊόντα i, n. Τα επίπεδα του προϊόντος είναι,, n. Τα επίπεδα των εισροών είναι,, m. Οι τιµές των προϊόντων
Οικονοµικό κέρδος Διάλεξη Μεγιστοποίηση Μια επιχείρηση χρησιµοποιεί εισροές j,m για να παραγάγει n προϊόντα i, n. Τα επίπεδα του προϊόντος είναι,, n. Τα επίπεδα των εισροών είναι,, m. Οι τιµές των προϊόντων
x r i s t o s t s a g a l i d i s
 ΕΑ-2009 1. Εισαγωγή 1. Πώς προσδιορίζονται οι τιμές των αγαθών στην αγορά; Οι τιμές των αγαθών προσδιορίζονται στην αγορά από την αλληλεπίδραση των δυνάμεων της ζήτησης και της προσφοράς. 2. Η συµπεριφορά
ΕΑ-2009 1. Εισαγωγή 1. Πώς προσδιορίζονται οι τιμές των αγαθών στην αγορά; Οι τιμές των αγαθών προσδιορίζονται στην αγορά από την αλληλεπίδραση των δυνάμεων της ζήτησης και της προσφοράς. 2. Η συµπεριφορά
