Capitolul Elemente de optică fizică Interferenţa undelor de lumină
|
|
|
- Έλλη Βουγιουκλάκης
- 6 χρόνια πριν
- Προβολές:
Transcript
1 Capitolul 9 9. Elemente de optică fizică 9.1. Interferenţa undelor de lumină Aparatele optice interferenţiale funcţionează, în general, pe principiul divizării frontului de undă al radiaţiei electromagnetice coerente. Compunerea constructivă a fronturilor undelor monocromatice coerente determină formarea unei imagini optice, numită tablou de interferenţă. Tabloul de interferenţă al undelor electromagnetice reprezintă locul geometric al tuturor punctelor care aparţin diferenţelor de faze constante şi are aspectul unor maxime, respectiv minime de intensitate ale radiaţiei rezultante Dispozitivul interferenţial al lui Young O experienţă originală a fost propusă de către Thomas Young (1801) pentru demonstrarea caracterului de undă al radiaţiei optice (figura 9.1). Un ecran prevăzut cu o deschidere S sub formă de fantă îngustă dreptunghiulară a fost iluminat prin intermediul unei lentile condensor cu o radiaţie monocromatică de lungime de undă. În spatele primului ecran a fost dispus paralel un al doilea ecran prevăzut cu două fante parelele S 1 şi S foarte înguste, distanţate între ele cu d, dispuse simetric faţă de poziţia fantei centrale. Frontul semicilindric al undei de lumină, originar din sursa liniară S iluminează fantele S 1 şi S şi se propagă în direcţia ecranului de observaţie sub forma undelor semicilindrice. Pătrunderea fluxului de lumină în zona de penumbră este explicată prin teoria ondulatorie a lui Huygens, conform căreia fiecare punct al frontului de undă devine o nouă sursă de oscilaţie pentru undele secundare şi prin suprapunerea undelor secundare se formează frontul undei difractate. Principiul Huygens dă o explicaţie bună în cazul difracţiei pe obstacole cu dimensiuni comparabile cu lungimea de undă a radiaţiei. Fig Schema dispozitivului lui Young pentru demonstrarea interferenţei (a), şi tabloul de interferenţă al luminii în cazul fantelor dreptunghiulare (b) 107
2 În general oscilaţiile surselor luminoase punctiforme S 1 şi S sunt descrise prin variaţiile vectorilor de câmp electric conform ecuaţiei: E s ( t) = E max cos ( ω t + ϕ 0 ) unde E max este amplitudinea vectorului câmp electric. Fiecare sursă emite oscilaţie armonică simplă de aceeaşi pulsaţie, având direcţii paralele de oscilaţie. Aceste oscilaţii în planul ecranului de observaţie vor avea faze diferite în funcţie de distanţele parcurse r 1, respectiv r : E 1( t) = E1max cos( ω t k r1 + ϕ0 ) E ( t) = Emax cos( ω t k r + ϕ0 ), π unde k = este vectorul de undă al oscilaţiei. Oscilaţia undei rezultante în punctul de interferenţă P(r,θ ) va fi suma oscilaţiilor componente descrisă de o ecuaţie de formă: E( r, θ, t) = E1 ( t) + E ( t) = E( r, θ ) cos( ωt k r + ϕ ) 1 În expresie r = ( r1 + r ) reprezintă distanţa medie dintre surse şi punctual de observaţie de pe ecran, respectiv Δ r = r r1 diferenţa de drum optic. Unghiul de fază şi amplitudinea oscilaţiei rezultante sunt exprimate prin relaţiile următoare: E 1max sinϕ1 + E max sinϕ ϕ = arctg E1max cosϕ1 + E max cosϕ ( E ) + ( E ) + ( E ) ( ) Δϕ E( 1max max 1max E max r, θ ) = cos Întrucât intensitatea este proporţională cu pătratul amplitudinii I E( r, θ ), intensitatea luminoasă I( r,θ ) într-un punct P al ecranului se poate exprima prin diferenţa de fază Δ ϕ a undelor coerente: ( E ) + ( E ) + ( E )( E ) cos Δϕ I( θ ) E( r, θ ) = 1max max 1max max În cazul general intensitatea rezultantă prezintă variaţii rapide în timp datorită modificărilor dezordonate ale fazelor de oscilaţie. Ochiul înregistrează în timp pe durata de observaţie doar o valoare mediată a intensităţii radiaţiei. Valoarea medie a intensităţii oscilaţiei rezultante evaluată pe o perioadă de timp T este dată de integrala: T [( E1max ) + ( E max ) + ( E1max )( E max ) cos Δ ] dt 1 I E( r, θ ) = ϕ T 0 Dacă diferenţa de fază Δ ϕ rămâne constantă pe durata de observaţie, atunci integrala termenului care conţine diferenţa de fază de asemenea este o constantă: T 1 T 0 [ ( E )( E ) cos Δϕ] dt = ( E ) ( ) cos Δϕ. 1max max 1max Emax Prin urmare, avem pentru intensitatea rezultantă relaţia:. 108
3 ( E ) + ( E ) + ( E ) ( E ) cos Δϕ, I E( r, θ ) = 1max max 1max max π E( r, θ ) I = I1 + I + I1 I cos Δr adică, în cazul surselor coerente intensitatea oscilaţiei rezultante nu este egală cu suma intensităţilor componente I I 1 + I. E =, respectiv În situaţia când sursele au aceeaşi amplitudine ( 1max ) ( E max ) ( E ) = ( ), avem: intensităţile sunt identice 1max E max Δr I E( r, θ ) = 4 ( Emax ) cos π. Punctele pentru care Δ r = const. vom avea intensitate de aceeaşi valoare, aceste puncte sunt situate pe suprafeţele unor hiperboloizi de revoluţie cu două pânze având focare în punctele S 1 şi S, iar axa lor comună coincide cu direcţia dreptei care uneşte sursele S 1 şi S. Prin urmare, compunerea undelor coerente determină formarea tabloului de maxime şi minime de intensităţi rezultante în funcţie de diferenţa de fază a undelor componente. În cazul recepţionării imaginilor pe un ecran de observaţie plan, intersecţia suprafeţelor de revoluţie ale hiperboloizilor reprezintă franje de interferenţă cu maxime şi minime de intensitate distribuite după o familie de hiperbole. În cazul dispozitivului Young dacă sursele coerente sunt fante liniare paralele, diferenţa de fază este determinată de diferenţa drumurilor optice ale celor două raze: π π Δϕ = ( S P S1P ) Δr. Intensitatea radiaţiei pe ecranul de observaţie se poate evalua din considerentul că, undele provenite de la cele două surse coerente S 1 şi S parcurg distanţele inegale S 1 P, respectiv S P (figura 9..). Fig. 9.. Exprimarea diferenţei de drum în experienţa lui Young cu două fascicule: S- sursă monocromatică, L- lentilă convergentă de focalizare, S 1, S - fante paralele, având rol de surse coerente secundare, E ecran de observaţie a figurii de interferenţă 109
4 Prin aplicarea aproximaţiilor valabile în cazul unghiurilor mici de observaţie, x x avem: sin θ, Δr = d sin θ d. În expresia precedentă x semnifică distanţa D D liniară în planul ecranului de observaţie a punctului P faţă de punctul central O. Prin înlocuirea diferenţei de drum în expresia intensităţii constatăm că valoarea acesteia este maximă de 4E. Dacă undele întâlnite în timp şi în spaţiu sunt în concordanţă de fază sau prezintă un multiplu întreg de π pentru diferenţa de fază a oscilaţiilor componente, obţinem maxime de intensitate (franjă luminoasă). Această condiţie se x obţine dacă diferenţa de drum este Δ r d = k. Astfel, pentru k=0, 1,,... număr D întreg, pe ecranul de observaţie avem locurile punctelor de intensitate maximă corespunzătoare distanţelor: D xmax = k. d Valoarea minimului de intensitate (franjă întunecoasă) se obţine dacă diferenţa de fază este un număr impar de π, adică în acele puncte pentru care diferenţa de drum este x Δr d = (k + 1). D Coordonata punctelor de minim faţă de centrul figurii de interferenţă este dată de relaţia: D xmin = (k + 1). d În expresiile precedente constanta k=0,1,,3, semnifică ordinul maximelor sau minimelor de interferenţă. Valoarea interfranjei reprezintă distanţa dintre franje vecine de acelaşi tip: i = x k +1 x k. D D D Rezultă că valoarea interfranjei i = ( k + 1 ) k este direct d d d proporţională cu lungimea de undă a radiaţiei şi cu distanţa D dintre planul surselor coerente şi planul ecranului de observaţie, respectiv invers proporţională cu distanţa liniară d dintre fante. Adesea în calea razelor de lumină nu avem un mediu optic omogen identic, exemplu în calea radiaţiei provenite de la una din surse se introduce o lamă plan-paralelă transparentă de grosime e. Din această cauză dacă indicele de refracţie a lamei este n>1, franja centrală de ordinul zero şi tot tabloul de interferenţă al sistemului de franje se deplasează către partea în care s-a introdus lama transparentă. În această situaţie diferenţa de drum optic va fi: Δ r = r [ r1 + ( n 1) e] În asemenea situaţii drumul optic suplimentar determinat de lamă face ca poziţia franjei centrale să fie deplasată faţă de poziţia iniţială cu valoarea: e D Δx = ( n 1 ). d În situaţia când radiaţia nu este monocromatică ci este o radiaţie compusă, fiecare lungime de undă va produce în mod independent un tablou propriu de franje de 110
5 interferenţă. În punctul de simetrie al figurii de interferenţă se situează franja centrală de ordinul zero, unde diferenţa de drum este zero pentru toate radiaţiile monocromatice şi apare maximul central în lumina tuturor radiaţiilor monocromatice, adică apare franja albă. În cele două părţi ale maximului central se formează succesiuni de maxime şi minime de diferite ordine, maxime care sunt colorate începând cu violet şi conţin toate nuanţele până la nuanţa roşie. Intensitatea franjelor de interferenţă scade pentru ordine superioare ale franjelor, iar culorile devin mai puţin perceptibile ale căror distribuţie depinde de lăţimea d dintre fantele paralele, respectiv de grosimea deschiderii a fantelor duble. De la o anumită distanţă faţă de franja centrală are loc o suprapunere a poziţiilor diferitelor maxime corespunzătoare diferitelor lungimi de unde, de exemplu franja de ordinul k a radiaţiei roşie coincide cu franja de ordinul k+1 a radiaţiei violete. Această suprapunere determină apariţia culorii albe de ordin superior. În general în cazul iluminării cu lumina albă a fantelor se pot identifica cca. 5 6 maxime de interferenţă colorate de fiecare parte a franjei centrale albe. Dacă oscilaţiile componente nu sunt coerente, ele prezintă faze necorelate în timp, integrala termenului care conţine diferenţa de fază a oscilaţiilor T 1 T 0 [ ( E ) ( E ) cos Δ dt 0 1 max max = ϕ] tinde către zero şi constatăm că: ( E1max ) + ( E max ) I1 I E( r, θ ) = + I. Concluzionăm că, dacă oscilaţiile componente au aceeaşi pulsaţie şi direcţie se disting două situaţii în funcţie de natura diferenţelor de faze: a). Dacă diferenţele de fază ale oscilaţiilor componenete rămân constante în timp, intensitatea rezultantă este staţionară şi prezintă variaţii locale în funcţie de diferenţa fazelor oscilaţiilor coerente. Compunerea unor asemenea oscilaţii coerente dă naştere la formarea interferenţei staţionare. b). În situaţia când diferenţele fazelor oscilaţiilor componente prezintă variaţii rapide în mod aleatoric, intensitatea oscilaţiei rezultante este egală cu suma intensităţilor oscilaţiilor componente. Prin urmare compunerea intensităţilor oscilaţiilor necoerente în timp nu produce fenomenul de interferenţă staţionară şi se observă o însumare a intensităţilor. În practica experimentală a interferenţei adesea sunt folosite interferometre bazate pe divizarea frontului de undă obţinute prin dedublarea fasciculelor sursei de lumină. Un astfel de dispozitiv constituie biprisma-, respectiv oglinzile lui Fresnel Biprisma-Fresnel Augustin Fresnel a descoperit în 1815 un dispozitiv interferenţial nou format din 0 două prisme optice având unghiuri mici de refracţie cca. α 1, unite la bazele lor (figura 9.3.). Unghiul refringent al prismelor fiind mic, distanţa dintre imaginile virtuale S 1 şi S este aproximat prin relaţia d = n 1 α, unde B este distanţa dintre planul ( ) B 111
6 sursei S (care este o fantă liniară cu deschidere paralelă centrată pe muchia biprismei) şi biprisma P). Lumina monocromatică a sursei S este deviată către bazele celor două prisme, care reproduc imaginile virtuale S 1 respectiv S distanţate între ele la d în planul sursei S. Astfel, radiaţiile coerente originale din sursele virtuale S 1 şi S determină prin suprapunerea fluxurilor de lumină un tablou de interferenţă sub forma sistemului de franje paralele cu muchia prismelor. Prin dispunerea ecranului MN, astfel încât să obtureze parţial fasciculul de lumină doar pentru regiunea centrală bc, imaginea de interferenţă formată din franje echidistante se poate identifica doar în regiunea centrală bc a ecranului de observaţie, restul franjelor difuze pe ecran se datorează difracţiei. Fig Biprisma-Fresnel şi imaginile de interferenţă, respectiv franje de difracţie obţinute în experienţa cu biprisma Fresnel Dacă ecranul MN este îndepărtat din calea fasciculului de lumină, fasciculul acoperă regiunea ad al ecranului, iar imaginea de interferenţă a franjelor egal distanţate se poate identifica în poziţii simetrice faţă de centrul ecranului. Această imagine de interferenţă este suprapusă peste imaginea de difracţie situată în partea centrală a ecranului. Sistemul franjelor de interferenţă obţinut în lumina monocromatică a sursei luminoase S se poate utiliza pentru determinarea lungimii de undă a radiaţiei. Acea stă lungime de undă se poate evalua în funcţie de distanţa L=B+C dintre planul surselor şi poziţia ecranului de observaţie, distanţa d dintre sursele coerente, respectiv valoare i= Δ x a interfranjei: d Δx = L 11
7 Oglinzile-Fresnel În cazul oglinzilor Fresnel lumina incidentă de la o fantă S iluminată este reflectată pe două oglinzi plane aşazate sub un unghi reglabil al planelor, pentru o valoare 0 0 foarte mică, apropiată de θ 1... (figura 9.4.). Oglinzile-Fresnel determină câte o imagine virtu ală S 1, respectiv S a sursei S, care este o fantă liniară cu orientare paralelă la muchia M de intersecţie ale oglinzilor. Imaginile S 1 şi S sunt distanţate unghiular la valoarea θ, respectiv la o distanţă liniară d θ r, unde r = SM. Acestea se comportă ca două surse coerente, care determină tabloul de interferenţă a luminii pe un ecran de observaţie dispus paralel cu muchia oglinzilor. Franjele de interferenţă obţinute sunt paralele cu muchia de întâlnire a celor două oglinzi. Fig Geometria dispunerii oglinzilor-fresnel pentru obţinerea interferenţei luminii monocromatice Prin măsurarea mărimilor caracteristice, în mod analog cu metoda biprismei- se poate determina valoarea lungimii de undă a radiaţiei monocromatice utilizate Fresnel, pentru realizarea figurii de interferenţă Oglinda-Lloyd Oglinda-Lloyd reprezintă o suprafaţă plană reflectătoare pentru fasciculul de lumină, prin care fluxul radiaţiei incidente este trimis simultan cu fluxul direct al sursei pe ecranul de observaţie. Sursa de lumină S 1 ce iluminează o fantă liniară, respectiv imaginea acesteia S constituie cele două surse coerente de la care ajung fluxurile de lumină pe ecranul de observaţie şi se formează imaginea de interferenţă a sistemului franjelor paralele (figura 9.5.). 113
8 Fig Oglinda-Lloyd şi sistemul de franje obţinut cu radiaţia optică de lungime = 435,8 nm (a), respectiv cu radiaţia Röntgen cu lungimea de undă = 0,83 nm În cazul oglinzii Lloyd fanta iluminată S 1 şi imaginea acesteia S fiind paralele cu suprafaţa oglinzii, franjele de interferenţă vor fi paralele cu deschiderea fantei de lumină Bilentile-Billet Sistemul de lentile duble Billet (figura 9.6.) este format din două jumătăţi ale unei lentile convergente, care divizează frontul fasciculului incident, respectiv prin unirea fronturilor de undă determină condiţiile formării interferenţei în lumina coerentă a surselor reale I 1 şi I. Aceste surse sunt imaginile reale ale fantei iluminate I reproduse în cele două jumătăţi ale lentilei convergente. Fig Bilentile-Billet pentru formarea interferenţei luminii În dispozitivele prezentate anterior interferenţa luminii se datorează compunerii radiaţiilor coerente obţinute prin divizarea frontului de undă. În cele ce urmează vom prezenta o metodă de interferenţă obţinută prin divizarea amplitudinii undei. Metoda 114
9 aceasta a fost propusă de A.A. Michelson (premiu Nobel în 1907 acordat pentru cercetarea proprietăţii luminii). 9.. Interferenţa fasciculelor multiple Interferenţa pe lame subţiri plane-paralele Apare adesea o imagine fascinant colorată, vizibilă în cazul unei pelicule subţire de ulei întinse pe suprafaţa apei sau în cazul a unei băşici de săpun, etc. Acestea se datoresc reflexiei şi compunerii constructive a undelor luminoase pe suprafeţele plane ale unui mediu optic transparent, fenomen numit interferenţă formată în cazul reflexiilor multiple. Un asemenea fenomen poate fi identificat în urma reflexiilor multiple a unei raze incidente SA pe suprafaţa plană a plăcii de sticlă plan-paralelă. Dacă razele reflectate sunt paralele interferenţa lor are loc la infinit şi observarea razelor se realizează cu ajutorul unei lentile L convergente (figura 9.7.), care adună razele în focarul ei P. Formarea maximelor de interferenţă presupune compunerea razelor reflectate care sosesc cu o diferenţă de drum optic Δr = k, adică pentru un multiplu întreg de lungimi de unde. Minime de interferenţă se for forma în acele poziţii pentru care diferenţa de drum optic Δr = k + 1, adică pentru un multiplu impar de semilungimi de unde. Dacă este ( ) observarea se face cu ochiul liber, rolul lentilei L îndeplineşte cristalinul ochiului şi imaginea P se formează pe retină. Fig Reflexia multiplă a luminiii pe suprafaţa unei lame plan-paralele Să analizăm reflexia în cazul unei raze de lumină incidentă pe suprafaţa lamei de sticlă plan-paralelă şi să determinăm valoarea diferenţei de drum optic între raza incidentă şi reflectată în punctul de pe faţa superioară a lamei, respectiv raza de lumină care suferă reflexie în punctul de pe faţa inferioară a lamei (figura 9.8.). Fie d grosimea lamei L şi indicele de refracţie n pentru radiaţia monocromatică incidentă cu lungimea de undă, unghiul de incidenţă i şi unghiul de refracţie r pe faţa superioară a lamei. După reflexie pe lamă razele (1) şi () din frontul undei 115
10 electromagnetice CD, perpendicular pe direcţia de propagare a razelor (1) şi (), se propagă fără diferenţă de drum până la punctul de focusare M al lentilei convergente L. Diferenţa de drum optic între razele menţionate este cauzată de procesul reflexiei razei () pe suprafaţa inferioară, respectiv diferenţei de drum optic acumulat de raza () în interiorul lamei comparativ cu raza (1). Diferenţa drumurilor optice între cele două raze (1) şi () se poate evalua conform ecuaţiei: Δr ( r ) ( r1 ) = n ( AB + BC) AD În această expresie am luat în considerare faptul că la reflexia razei (1) pe faţa superioară a lamei are loc un salt de fază π în avans (corespunzătoare unei pierderi de drum, care trebuie scăzut din drumul AD). În evaluarea mărimilor avem în vedere ca drumurile parcurse în lamă d AB = BC, AD = AC sin i d tgr sin i. cos r Conform legii refracţiei sin i = n sin r, obţinem pentru segmentul sin r AD = nd, iar pentru diferenţa de drum vom obţine următoarea expresie: cos r Δr = n d cos r + Dacă diferenţa de drum optic al razelor componente este egală cu lungimea de undă a radiaţiei atunci are loc formarea unui maxim în focarul lentilei. şi prin urmare ecuaţia Δr = n d cos r + = k corespunde condiţiei de formare a maximului de interferenţă. În ecuaţie constanta k are semnificaţia ordinului de interferenţă şi are valori k=0, 1,, 3, Pentru formarea minimelor de interferenţă condiţia este: Δr = n d cos r + = ( k + 1) Fig Diferenţa de drum optic între două raze de lumină vecine în urma reflexiei pe suprafeţele superioare respectiv inferioare ale lamei plan-paralele 116
11 În formulele precedente se poate substitui valoarea unghiului de refracţie r cu sin i valoarea unghiului de incidenţă i, astfel cos r = 1 sin r 1, astfel relaţia n diferenţei de drum optic va avea forma Δr = d n sin i +. Lentila convergentă are rolul de a aduna razele paralele în planul ei focal pentru a pune în evidenţă rezultatul compunerii razelor în urma reflexiei multiple Franje de interferenţă de egală incidenţă Dacă placa plan-paralelă este iluminată cu o sursă monocromatică întinsă, razele incidente paralele de radiaţie optică provenite de la diferite puncte ale sursei, se reflectă pe faţa superioară şi inferioară ale lamei tot ca raze paralele. Razelor care au avut unghiuri de incidenţă identice vor prezenta defazaje identice şi vor contribui la formarea franjelor de interferenţă corespunzătoare unei diferenţe de drum definit prin valoarea lui k. Figura de interferenţă obţinută pe un ecran dispus perpendicular pe axa lentilei L în punctul ei focar F va fi format din inele circulare cu maxime, respectiv minime de interferenţă în funcţie de diferenţa lor de fază. Pentru o franjă dată valoarea unghiului r este constantă, prin urmare forma franjei este un inel circular al cărui centru coincide cu punctul de intersecţie al dreptei coborâte perpendicular din poziţia ochiului pe planul de observaţie. Aceste franje corespund unei incidenţe a razelor identic înclinate, de aceea aceste franje le numim franje de egală înclinare sau se mai numesc franje Haidinger. Observaţie: Franjele sunt vizibile în cazul unei surse monocromatice întinse cu condiţia ca lama să fie riguros plan-paralelă. În cazul iluminării lamei cu o sursă de lumină albă are loc suprapunerea sistemelor de franje monocromatice, care determină apariţia luminii albe de ordin superior. În lumină albă lamele subţiri cu grosimi de cca. câţiva microni determină prin reflexie formarea franjelor de interferenţă colorate, irizate. O asemenea situaţie întâlnim şi la observarea franjelor de interferenţă circulare în interferometrul Michelson. Analizând relaţia interferenţei pentru cazul limită, când r = 0 ceea ce înseamnă Δr = n d = k, pentru ordinul franjelor întunecoase obţinute în lumină incidentă n d putem scrie că k =. Întrucât franjele de interferenţă de ordine superioare vor fi observate la unghiuri i şi r din ce în ce mai mare, înseamnă că diferenţele de drum Δ r = n d cos r consecutive vor fi din ce în ce mai mici. Aceste franje vor fi observate cu ochiul liber doar dacă lama este foarte subţire sau dacă observarea se realizează la incidenţă aproape perpendiculară. În alte condiţii de observare, exemplu pentru un unghi mare de observaţie şi/sau lamă groasă, ochiul uman datorită ariei reduse a pupilei ochiului nu poate recepţiona razele reflectate care se distribuie pe o arie mare şi prin urmare ochiul va fi atins de către o singură rază şi nu se pot identifica franjele de intereferenţă. Dacă însă utilizăm o lunetă 117
12 cu deschidere mare vom putea observa sistemul de franje în lumina reflectată de pe o lamă nu neapărat subţire. Intensitatea maximelor de interferenţă prezintă o descreştere, iar minimele încep să prezinte o creştere de intensitate din cauza compunerii unor raze cu amplitudini diferite în urma reflexiilor cu pierderi Interferenţa în lumina transmisă Razele de lumină care suferă refracţie la faţa inferioară a lamei (figura 9.9.) şi părăsesc aceasta sub forma unui flux paralel emergent vor fi adunate cu ajutorul unei lentile convergente dând naştere la fenomenul de intereferenţă în lumina transmisă. Lipsa reflexiei pentru acest fascicul înseamnă că nu apare saltul de fază π şi prin urmare pentru lumina transmisă condiţia maximelor de interferenţă se va obţine conform relaţiei: Δ = n d cos r = k iar pentru minime: Δ = n d cos r = k + 1 ( ) cu k = 0, 1,, 3, valori de numere naturale. Aşadar franjelor luminoase obţinute în lumină reflectată vor corespunde franje întunecoase în lumină transmisă. În situaţia când coeficientul de reflectivitate la suprafeţe are o valoare redusă, interferenţa are loc între două raze care au intensităţi mult diferite: raza transmisă cu intensitate mare, respectiv raza care a suferit două reflexii în lamă, motiv pentru care are un contrast foarte redus. De aceea intensitatea minimelor nu este nulă şi diferă foarte puţin de intensitatea maximelor, astfel figura de interferenţă în lumina transmisă este mai puţin clară. Distribuţia intensităţilor maximelor şi minimelor este prezentată pe figura 9.9. pentru lumina transmisă I T şi pentru lumina reflectată I R în cazul lamei plan-paralele al cărui coeficient de reflexie este r = 0,. Fig Distribuţia intensităţii I franjelor obţinute în lumina reflectată respectiv în lumina transmisă reprezentate în funcţie de unghiul de fază δ dintre razele vecine π δ = nd cos r Franjele de egală înclinare observate în cazul studiului suprafeţelor plan-paralele serveşte pentru evaluarea plan-paralelismului dintre feţele lamei. 118
13 9..4. Franje de interferenţă de egală grosime. Interferenţa pe lame sub formă de pană În situaţia când lama nu este plan-paralelă, adică suprafeţele plane de reflexie formează un unghi mic, razele reflectate către ochiul observatorului formează un flux divergent. Observatorul are impresia că razele reflectate sosesc dintr-un punct din apropierea lamei, şi dacă suprafeţele penei sunt plane, franjele de intereferenţă vor fi nişte dungi drepte localizate la grosimi de aceeaşi valoare a penei. Din aceste considerente ele sunt numite franje de egală grosime (figura 9.10.). Fig Interferenţa în lumină reflectată obţinută în cazul penei subţiri Dacă sursa punctiformă de lumină din punctul P se află la distanţă mare faţă de lamă şi incidenţa razelor 1, respectiv este apropiată de normala suprafeţei (cos r = 1), condiţia pentru formarea în punctul A a unei franje luminoase de interferenţă între fasciculele incidente vecine, pentru care variaţia de grosime a lamei se poate neglija, avem: nd (k + 1) Franjele de interferenţă formate în lumină monocromatică reflectate corespund locurilor de aceeaşi grosime, de aceea franjele se numesc franje de egală grosime. Ele sunt localizate pe suprafaţa lamei reflectante şi se pot observa direct cu ochiul liber acomodat pentru vedere la distanţa suprafeţei. În lumină transmisă intensitatea contrastului franjelor este redusă, ceea ce reduce observabilitatea sistemului de franje. Franjele care se formează în cazul unei pene au orientare paralelă cu muchia penei şi sunt echidistante. Dacă o astfel de pană foarte subţire este iluminată cu lumină albă, franjele de interferenţă vor fi colorate, aşa cum se poate observa în cazul peliculelor subţiri de ulei întinse pe apă sau a unor pene subţiri de aer formate între două plăci de sticlă. O creştere a numărului de ordine a franjelor luminoase cu unitate Δk = 1 pentru o deplasare în lungul lamei cauzează o variaţie de grosimea optică a lamei nd egală cu. Asemenea concluzii au importanţă în evaluarea planeităţii suprafeţelor, orice abatere de la planeitate poate fi sesizată prin modificarea tabloului imaginii de interferenţă. De exemplu, dacă pentru muchia penei imaginea de interferenţă observată în lumina reflectată prezintă o franjă întunecoasă (din cauza lui d=0, Δr = ) a doua franjă 119
14 întunecată apare pentru diferenţa de drum optic egal cu pentru o grosime d= a penei (figura 9.11.). Δr = nd + = 3, adică Fig Formarea figurilor de interferenţă în lumina reflectată pe suprafaţa plăcilor subţiri de sticlă, care delimitează între ele o pană de aer Celelalte franje întunecoase corespund poziţiilor la care grosimea penei de aer 3 corespunde la d = sau d =, etc. Valoarea interfranjei în această dispunere se poate exprima prin tangenta unghiului penei, respectiv diferenţa grosimilor corespunzătoare la dk +1 dk două franje vecine de aceeaşi natură tgα =, aşadar interfranja se exprimă prin i dk +1 dk relaţia: i =. tgα De asemenea putem exprima condiţia de formare a minimelor consecutive prin relaţiile: nd k + = ( k + 1) nd k = ( k + 3) a căror diferenţă ne dă n ( d k + 1 dk ) =, respectiv ( dk + 1 dk ) =. n Prin combinarea expresiilor de mai sus putem exprima valoarea interfranjei în funcţie de lungimea de undă a radiaţiei monocromatice, unghiul penei, respectiv indicele de refracţie al materialului penei: i =. n tgα n α Metoda interferometrică este extrem utilă în caracterizarea suprafeţelor pieselor optice în privinţa planeităţii sau abaterii de formă a suprafeţelor. În cazul când suprafaţa este perfect plană vom observa franje de interferenţă liniare, echidistante, iar în cazul suprafeţelor curbate putem determina abaterea de la planeitate. Acest lucru valorifică faptul că tranziţia de la o franjă la alta este cauzată de o variaţie în grosimea penei egală cu. În general se pot evalua variaţiuni de ordinul 10 i, ceea ce înseamnă denivelări de ordinul. Spre exemplificare, dacă folosim lumina galbenă a sodiului cu 0 10
15 = 589,3 nm se pot determina abateri de la planeitate de valoare 0,589 μm = 0,08 μm Inele de interferenţă a lui Newton În practica de verificare a sfericităţii suprafeţelor convexe se utilizează metoda de evaluare a inelelor Newton (figura 9.1.). Aşa-numitele inele Newton sunt formate pe pana de aer care separă suprafaţa unei lame plane etalon şi suprafaţa sferică convexă investigată a unei lentile. Pana de aer care se formează între suprafeţele cu unghi variabil având simetrie circulară pe punctul de contact între placa P şi suprafaţa lentilei L, în urma iluminării normale cu lumină monocromatică a penei se formează franje de interferenţă de egală grosime dispuse concentric în jurul punctului de contact O. Observarea franjelor în lumina reflectată prezintă aceste franje cu o pată centrală neagră, din cauza faptului că pentru diferenţa de drum optic avem îndeplinită relaţia: Δr = n d cos r + = ( k + 1) ceea ce corespunde pentru k=0, d=0, n=1, i=r=0 la condiţia de minim a intensităţii. Fig Prezentarea schematică a principalilor parametri în studierea inelelor Newton Într-un punct arbitrar M situat pe suprafaţa sferei corespunzător inelului de rază MN=r k cu centrul pe axa verticală OC, grosimea penei fiind d, avem pentru diferenţa de drum optic condiţia: Δr = d +. Putem stabili relaţia de legătură între raza R a sferei, raza inelului de interferenţă r k şi grosimea penei corespunzătoare acestui inel: r k = ON ND = d (R d) dr unde am considerat ca d<<r. 11
16 Astfel grosimea penei pentru inelul luminos de ordinul k este diferenţa de drum optic corespunzător: rk d =, iar R rk rk Δr = + = +. R R În situaţia în care punctul considerat M este situat pe un inel de franjă cu intensitate minimă, impunem condiţia: Δr = + ( k + 1) R k r, din care rezultă pentru raza inelului întunecos de ordinul k valoarea: r k = k R. Conform acestei relaţii razele inelelor întunecoase se succed ca şi rădăcinile pătrate ale numerelor întregi consecutive. În cazul iluminării sistemului cu lumină albă, inelele devin colorate, care începând cu ordinul al 5-lea încep să se suprapună, astfel contribuie la apariţia albului de ordin superior (figura 9.13.). În cazul studierii inelelor în lumină transmisă, vom vedea în punctul de contact o pată luminoasă iar inelele consecutive vor fi mai puţin nete datorită contrastului mai slab. Fig Schema dispozitivului experimental pentru observarea franjelor de interferenţă de egală grosime şi fotografia inelelor Newton 9.3. Aparate interferenţiale. Interferometre Interferometrele permit efectuarea unor determinări cantitative pentru indici de refracţie, distanţe, densităţi, etc. pe baza intrepretării tabloului de interferenţă. Vom face referiri la tipurile mai uzuale de interferometre Interferometrul-Michelson Schema constructivă a interferometrului Michelson este indicată pe figura
17 Fig Schema interferometrului Michelson şi imaginile de interferenţă obţinute în lumină monocromatică pentru diferenţe de drum de valoare mai mare, respectiv mai mică. La trecerea de la o franjă la alta ordinul franjei se modifică cu unitate, aceasta corespunde unei variaţii egală cu în valoarea diferenţei de drum Condiţia obţinerii figurii de interferenţă este utilizarea unei surse întinse de lumină. În calitate de sursă întinsă de lumină monocromatică poate fi utilizată o lampă de sodiu sau cu vapori de mercur. Iluminarea uniformă a câmpului vizual poate fi extinsă la nevoie prin utilizarea unei lame difuze L şi a unei lentile convergente. Faţa posterioară a lamei G 1 este semiargintată în vederea egalizării intensităţilor de lumină divizate în direcţia de propagare (1) şi (). Lamele plan-paralele G 1 şi G au rolul elementelor de compensare pentru egalizarea drumurilor optice ale razelor de lumină. Oglinzile plane metalice M 1 şi M sunt bine şlefuite pentru reflectivitate mărită şi sunt reglate precis cu ajutorul şurubului micrometric V de deplasare, respectiv cu cele de reglaj pentru ortogonalitatea razelor de lumină ca şi pentru modificarea distanţelor străbătute de razele de lumină (1) şi (). Prin reglarea egalităţii distanţelor parcurse de cele două fascicule, în urma reflexiilor pe oglinzile plane M 1 şi M, observatorul E identifică formarea unui sistem de franje circulare de interferenţă. Interferenţa obţinută este cauzată de suprapunerea undelor paralele reflectate de pe cele două oglinzi. În situaţia când diferenţa de drum dintre undele componente satisface condiţia d cosθ = k, vom obţine maxime de interferenţă distribuite pe zone inelare în jurul axei de simetrie. Aceste franje de interferenţă sunt numite franje de egală înclinaţie, dat fiind că aceste franje corespund unei direcţii de observare θ faţă de axa centrală de simetrie a sistemului. Factorul d în expresia precedentă se datorează faptului că, diferenţa de drum între fascicule se acumulează pe o distanţă dublă prin care se deosebesc lungimile braţelor interferometrului. Tehnica interferometrică este utilizabilă pentru controlul uniformităţii suprafeţelor şlefuite la plan-paralelism, pentru măsurarea unor etaloane de lungimi şi măsurea indicilor de refracţie ale mediilor străbătute de către radiaţia studiată. 13
18 Măsurarea indicelui de refracţie al unui mediu optic se bazează pe faptul că, introducerea mediului în calea fasciculului modifică lungimea t a drumului geometric străbătut pentru o valoare a drumului optic egală cu nt. Prin urmare modificarea drumului optic cauzată de introducerea mediului optic investigat este (n-1) t. Deplasarea sistemului de franje exprimată prin numărul franjelor defilate este legată prin relaţia ( n 1) t = ( Δm), după care se poate evalua valoarea n a indicelui de refracţie. Pentru determinarea indicelui de refracţie a gazelor au fost dezvoltate diferite interferometre, cum ar fi cazul interferometrului Jamin, interferometrul Mach-Zehnder şi interferometrul Rayleigh, numite unoeri şi refractometre interferenţiale Interferometrul Mach-Zehnder Acest tip de aparat se mai numeşte şi refractometru-interferenţial, care foloseşte o sursă de lumină monocromatică întinsă şi prin divizarea fasciculului de lumină pe placa semitransparentă P 1 o parte a luminii este trecută prin rezervorul care conţine gazul pentru care dorim să evaluăm valoarea indicelui de refracţie (figura 9.15.), restul fasciculului este condus direct către sistemul de observaţie. Fig Refractometrul interferenţial Mach-Zehnder destinat pentru măsurarea indicelui de refracţie al mediilor omogene Interferometrul Fabry-Perot (figura 9.16) 14
19 Fig Imagini de interferenţă realizate cu interferometrul: a). Michelson, b). Fabry-Perot 9.3. Difracţia undelor luminoase Fenomenul de difracţie a luminii a pus în evidenţă faptul că undele de lumină pot ocoli obstacolele aşezate în calea lor de propagare şi pătrund în zona umbrei geometrice. Acest comportament de abatere de la direcţia de propagare rectilinie, se observă în cazul obstacolelor cu dimensiuni comparabile cu lungimea de undă a radiaţiei studiate. Pentru explicaţia acestui fenomen apelăm la principiul Huygens-Fresnel, care consideră că fiecare punct al frontului de undă se comportă ca o nouă sursă de oscilaţie. Un asemenea punct al frontului de undă emite radiaţii în toate direcţii, care se propagă într-un mediu optic omogen în linie dreaptă. Astfel are loc pătrunderea radiaţiei inclusiv în regiunea umbrei geometrice. În situaţia surselor punctiforme de radiaţie frontul de undă se poate asimila cu o sferă centrată pe sursa de radiaţie, iar în cazul surselor întinse sau a radiaţiei cu fascicule de raze paralele, frontul de undă este aproximat cu planul orientat perpendicular pe direcţia de propagare. În aparatele optice avem de a face cu 15
20 amândouă situaţii, datorită acţiunii elementelor optice asupra radiaţiilor emise de sursele luminoase. În situaţia surselor punctiforme aşezate în punctul focar al lentilei convergente frontul undei sferice se transformă în frontul undei plane, care de regulă este limitat printr-o diafragmă liniară sau circulară în vederea aproximării condiţiilor de paraxialitate a radiaţiei. Acesta se manifestă în faptul că punctele imaginii sunt asociate prin figuri de difracţie, ceea ce reduce puterea de rezoluţie a aparatelor optice. Să trecem în revistă cazurile limită în care sistemele optice sunt afectate de fenomenul de difracţie a luminii Difracţia undelor plane în cazul unei fante dreptunghiulare (difracţia Fraunhofer) Fanta dreptunghiulară este o deschidere îngustă F cu o lăţime neglijabilă în comparaţie cu înălţimea acesteia (figura 9.17.). Fig Prezentarea schematică a fantei dreptunghiulare iluminate şi aproximarea frontului de undă semicilindric printr-o suprafaţă plană Putem considera lungimea fantei ca fiind infinită comparativ cu lărgimea acesteia. Fanta iluminată cu o sursă de radiaţie transmite în domeniul opus sursei un front de undă semicilindric, care pentru distanţe mari se poate aproxima cu un plan. Fie o fantă îngustă F aşezată paralel cu frontul undei plane incidente, situaţie care se poate obţine prin aşezarea perpendiculară a fantei F în calea fasciculului de lumină provenită de la o sursă punctiformă S dispusă în focarul unei lentile C convergente (figura 9.18.). Fig Schema optică a secţiunii sistemului de investigare a fenomenului de difracţie produsă pe o fantă dreptunghiulară în lumină incidentă paralelă (difracţia Fraunhofer) 16
21 Prin divizarea virtuală a deschiderii AB de lăţime a a fantei F în zone elementare paralele cu marginile fantei obţinem în planul frontului de undă fâşii înguste având lăţimi identice dx, care se pot asimila cu sursele elementare de radiaţie a lui Huygens-Fresnel. Sursele elementare au aceeaşi fază de oscilaţie, fiind din acelaşi front al undei incidente, ele trimit radiaţii ce se propagă în toate direcţiile posibile. Intensitatea de radiaţie într-o direcţie arbitrară poate fi evaluată prin însumarea efectelor tuturor radiaţiilor provenite de la sursele elementare. Fie α unghiul în care evaluăm intensitatea radiaţiei difractate faţă de direcţia radiaţiei incidente. Toate radiaţiile paralele care sunt deviate după aceeaşi direcţie α vor fi adunate într-un punct al planului focal al unei lentile convergente L, care are rolul de a focaliza radiaţiile paralele. Pentru simplificarea calculelor admitem că pentru unghiuri mici de difracţie radiaţiile provenite de la diferitele zone elementare au aceeaşi amplitudine în punctul de suprapunere a oscilaţiilor componente. În evaluarea amplitudinii rezultante însumăm amplitudinile oscilaţiilor componente provenite de la toate zonele elementare de lărgime dx. Aceste amplitudini de oscilaţie ale undelor elementare sunt proporţionale cu lărgimea zonelor, adică de i dx = k dx. Pentru amplitudinea undelor emise de întreaga fantă cu lăţime a în direcţia de propagare a radiaţiei incidente, adică pentru α =0 avem: E0 = k a. Expresia oscilaţiei vectorului luminos determinată de zona elementară de lărgime dx din planul fantei se poate descrie prin ecuaţia: E de = 0 dx sinωt a Într-o direcţie arbitrară de propagare a undelor difractate în punctul F α al ecranului de observaţie E oscilaţiile com ponente vor sosi cu faze diferite în funcţie de valoarea drumului optic străbătut de la diferitele poziţii ale surselor elementare. Fazele de oscilaţie vor putea fi evaluate prin considerarea planului frontului de undă difractat faţă de direcţia de propagare a undei incidente. Acest plan este planul undei difractate în direcţia α considerată, corespunzătoare momentului în care frontul undei incidente depăşeşte planul fantei prin ultima undă elementară difractată. Astfel, în planul frontului undei cu direcţia de propagare considerată oscilaţia emisă de o zonă elementară dx situată la distanţa x de marginea de referinţă a fantei va prezenta o diferenţă de drum optic faţă de drumul oscilaţiilor emise de sursa elementară corespunzătoare marginii fantei situată în vecinătatea punctului A, δ = BD = x sinα, respectiv o diferenţă de fază π Δϕ = x sinα. Prin urmare, oscilaţia vectorului câmp electric în planul de propagare AD se poate exprima prin ecua ţia: E π de = 0 dx sin ωt x sinα. a Oscilaţia rezultantă în planul focal F al lentilei convergente va fi determinată prin integrala valorilor extinse pentru coordonatele x ale surselor elementare cuprinse între limitele x=0 şi x=a: 17
22 πasinα a a sin E = = 0 π πa E de sin ωt x sinα dx = E0 sin ωt sinα πasinα 0 0 a Vedem că amplitudinea oscilaţiei rezultante în punctual F α al ecranului prezintă variaţii periodice conform relaţiei: πasinα sin Eα = E 0. πasinα Prin urmare, intensitatea luminoasă, care este proporţională cu pătratul amplitudinii, se poate exprima prin relaţia: πasinα sin I α = I0. πasinα πasinα Folosind substituţia u =, obţinem relaţia care descrie distribuţia intensităţii luminoase în fenomenul de difracţie produsă în lumină monocromatică cu frontul de undă plan incident pe o fantă liniară: sin u Iα = I0. u Analizând relaţia de mai sus, observăm că maximul de intensitate I = I 0 se formează în direcţia undei incidente pentru α = 0, unde u = 0, respectiv avem îndeplinită sin u relaţia lim = 1. u 0 u Minime de intensitate I α = 0 se vor obţine pentru direcţiile unghiulare când sin u = 0, adică pentru condiţia u = kπ, unde k este un număr natural întreg (k =1,, 3, ). πa sinα Prin urmare, pentru condiţia u = = kπ defineşte valorile direcţiilor unghiulare corespunzătoare minimelor de intensitate prin relaţia: sin α = k. a Între minimele de intensitate vor apărea maxime secundare cu intensitate descrescătoare. Poziţia unghiulară a maximelor se poate determina din condiţia de extremum a relaţiei de dependenţă a intensităţii: di α sinu u cosu sinu = I0 = 0 du u u. 18
23 Maximele secundare sunt date de acele valori ale lui u pentru care derivata se anulează. Rezolvarea ecuaţiei conduce la aflarea rădăcinilor acesteia corespunzătoare la ecuaţia u = tgu. Această rezolvare se poate efectua pe cale grafică prin determinarea intersecţiilor curbelor reprezentative y = tgu cu dreptele y = u. Reprezentând gra fic ecuaţia y = tgu pe ntru intervalele caracteristice definite prin π 3π abscisele cu valorile lui u = 0,, π,,..., punctele de intersecţie ale dreptei y = u corespunzătoare bisectoarei cadranului întâi care trece prin origine şi curbele y = tgu, observăm că punctele de intersecţie s unt apropiate setului de valori ale lui 3 π 5π ( k + 1) u =,,... π (figura 9.19.). Fig Metodă grafică de determinare a punctelor de intersecţie a curbelor reprezentative y = tgu, respectiv y = u şi distribuţia intensităţii a franjelor de difracţie observate în lumina radiaţiei monocromatice a razelor paralele Cu cât sunt mai mari valorile lui u cu atât punctele de intersecţie vor fi mai apropiate de valorile π ( k + 1). Prin urmare, maximele secundare se vor forma pentru π sinα u = ( k + 1) = πa, adică pentru acele direcţii unghiulare care satisfac relaţiile: sinα = ( k + 1). a Distribuţia intensităţii maximelor secundare va fi descrisă de ecuaţia: 1 I α = I0, π ( k + 1) 4 19
24 adică, intensitatea maximelor secundare variază cu inversul pătratelor numerelor impare consecutive. Prin urmare, intensitatea maximelor secundare scade repede cu creşterea numărului de ordine k al difracţiei. Maximul secundar de ordinul 1 are o intensitate relativă exprimată în funcţie de intensitatea maximului central I 0 : 1 I I 0 1 = I0 =, π, 9 4 respectiv al doilea maxim secundar va avea intensitatea 1 I = I0 = 0, 0165 I 0. π 5 4 Reprezentarea grafică a distribuţiei intensităţilor luminoase indică o scădere rapidă (figura 9.19b) comparativ cu intensitatea maximului central corespunzătoare 3π valorii lui u=0, respectiv primul maxim secundar corespunzător valorii lui u =. Comportament similar se poate identifica şi în cazul dechiderii circulare (orificiu iris) cu deosebirea că imaginea figurii de difracţie va prezenta zone inelare concentrice alternativ luminoase şi întunecoase. Distribuţia intensităţii relative de asemenea va prezenta o scădere rapidă, cu formarea unei pete luminoase în centrul figurii de difracţie, urmată de inelele concentrice dispuse pe pata centrală Difracţia luminii pe reţeaua optică Reţeaua optică de difracţie este o suprafaţă plană sau curbă prevăzută cu trăsături, (canaluri) liniare, paralele şi echidistante gravate foarte riguros pe suportul reţelei. Zonele paralele echidistante dintre trăsături constituie un sistem de fante fine, separate prin intervale opace. Sunt uzuale reţele optice plane şi reţele optice concave în funcţie de forma suprafeţei optice pe care se realizează trăsăturile (figura 9.0.). Reţelele de difracţie sunt caracterizate prin distanţa d=a+b între două trăsături consecutive numită şi constanta reţelei de difracţie, respectiv prin numărul de trăsături pe unitatea de lungime N, între care se poate scrie relaţia N d = 1 mm. Să considerăm o porţiune de secţiune normală pe planul reţelei optice pe care să trimitem un fascicul paralel de lumină monocromatică. În urma interacţiunii cu reţeaua optică lumina difractată este proiectată pe un ecran cu ajutorul unei lentile convergente L în planul ei focal, astfel obţinem figura de difracţie a luminii monocromatice cu frontul de undă plan. De fapt imaginea observată este rezultatul suprapunerii efectelor de difracţie şi de interferenţă a undelor provenite de la toate fantele reţelei. Toate radiaţiile paralele care sunt difractate într-o direcţie unghiulară α vor fi adunate în F α de lentila convergentă într-o zonă liniară a planului focal. Să evaluăm diferenţa de drum optic dintre două unde elementare ale frontului de undă, care sunt emise din punctele B şi D corespunzătoare ale fantelor vecine. Diferenţa de drum ale radiaţiilor respective se poate exprima prin relaţia: δ = a + b sinα d sin, ( ) α 130
25 în care a este lăţimea zonei opace ale trăsăturii, iar b este lăţimea fantei transparente. Fig.9.0. Schema optică a reţelei de difracţie R cu indicarea unei direcţii α de difracţie a razelor de lumină paralele şi focalizarea razelor pe un ecran de observaţie E cu ajutorul lentilei convergente L În vederea evaluării intensităţii luminoase a benzii de difracţie F α din planul focal al lentilei vom aplica o metodă grafică de compunere a amplitudinilor oscilaţiilor. Prin însumarea amplitudinilor şi fazelor de oscilaţie a undelor luminoase difractate de fantele individuale în direcţia unghiulară α, vom stabili valoarea sumei vectoriale a celor N vectori E i cu defazare relativă între ele la unghiul de fază (figura 9.1.): π π ϕ = δ = d sinα Fig Reprezentarea vectorială prin însumareaa amplitudinilor oscilaţiilor componente (metoda de construcţie a spiralei Cornu) Vectorii oscilaţiilor componente prin însumarea lor determină o linie poligonală care se dispune pe perimetrul unui cerc de rază R. Vectorul rezultant prezentat de vectorul OM are un unghi de fază determinat de suma unghiurilor de fază ale vectorilor 131
26 componenţi. Prin urmare poligonul înscris în cercul de rază R cu valoare a OM razei R = OC =, se închide prin vectorul rezultant de modul E: ϕ sin Nϕ sin Nϕ E = OM = R sin E 1. ϕ sin Având în vedere că valoarea modulului vectorului de oscilaţie electrică E 1 este determinată de difracţia pe o fantă unică, pentru amplitudinea undei rezultante difractate în direcţia unghiulară α avem relaţia: πa sinα Nπd sinα sin sin E = E 0, πa sinα πd sinα sin unde E 0 reprezintă valoarea amplitudinii undei difractate în direcţia fasciculului incident, adică în direcţia pentru care α = 0. Din analiza acestei relaţii putem deduce condiţia formării maximalor şi minimelor de intensitate. Intensitate minimă se obţine pentru condiţia anulării fracţiei, adică pentru πasinα anularea factorului de difracţie sin = 0 sau anulării factorului de interferenţă Nπd sinα sin = 0. Aşadar, condiţia de minim se obţine pentru valorile argumenetelor Nπd sinα πasinα = kπ sau = kπ. Prin urmare unghiurile pentru care sunt îndeplinite k k condiţiile sin α = cu k=1,, 3,, respectiv sin α = cu k=1,, 3 obţinem a Nd minime de intensitate. Maximele de intensitate cu amplitudine E vor fi obţinute în acele direcţii unghiulare pentru care factorul de difracţie şi factorul de intereferenţă au valori maxime. De regulă aceşti factori nu au valori maxime şi minime simultane. Problema în primă aproximaţie se poate discuta în cazul când lăţimea a a fantei este neglijabilă comparativ cu distanţa dintre două fante succesive. Într-o asemenea situaţie maximul central al unei fante individuale este larg şi în interiorul acestui maxim amplitudinea prezintă o variaţie relativ mică, astfel condiţia formării maximului se poate exprima prin relaţia: Nϕ sin E = E d, ϕ sin unde E d este factorul constant care înlocuieşte valoarea factorului de difracţie. Aşadar, maximele de difracţie vor fi localizate pentru direcţiile unghiulare care satisfac condiţia ϕ = kπ, respectiv pentru diferenţele de drum avem îndeplinită condiţia δ = d sin α = k cu valorile k= 0, 1,,. 13
27 Nϕ sin Deşi pentru aceste valori ale lui ϕ raportul 0 = este nedeterminat, limita ϕ 0 sin Nϕ sin raportului are valoarea finită lim = N, prin care amplitudinea maximelor de ϕ kπ ϕ sin intensitate este dată de valoarea E = N Ed. O evaluare mai detaliată pune în evidenţă faptul că între maximele principale se află N-1 minime nule, iar între duoă minime nule se află un maxim secundar, respectiv între două maxime principale se află N- maxime secundare. În planul focal al lentilei convergente constatăm apariţia maximelor principale, care corespund imaginii fantelor, dar apare şi o structură de difracţie asemănătoare cu cea produsă de o fantă singulară. În situaţia când numărul fantelor este foarte mare între maximele principale intensitatea este redusă, astfel dacă observaţia se face cu reţele de difracţie cu constante de reţea foarte mici, maximele apar nete pe un fond aproape lipsit de luminozitate (figura 9..). Fig. 9.. Distribuţia intensităţii radiaţiei difractate în cazul unei reţele optice realizată cu un număr de N=6 trăsături Dacă observaţia este efectuată în lumină albă reţeaua de difracţie dă o distribuţie de imagini colorate ale diferitelor maxime. În direcţia pentru care α = 0 se obţin maxime pentru toate radiaţiile monocromatice din spectrul luminii albe şi suprapunerea radiaţiilor monocromatice reproduce radiaţia albă. În planul imaginii pe o parte şi alta a maximului central apar spectre cu maximele având distribuite culorile radiaţiilor de la violet spre roşu, culoarea violetă fiind situată în partea mai apropiată către maximul central iar culoarea roşie fiind aşezată în exterior. 133
28 Conform relaţiei care defineşte poziţia maximelor de difracţie d sin α = k observăm că maximele vor prezenta distribuţii unghiulare pentru radiaţiile monocromatice, pentru o ordine k a difracţiei radiaţiile cu lungimi de unde mai mari vor fi difractate mai mult. Astfel, spectrul radiaţiei obţinute este un spectru direct contrar spectrului optic descompus de prisma optică. Prin urmare, reţeaua optică îndeplineşte rolul elementului dispersiv în aparate spectrale numite spectrografe cu reţea şi în monocromatoare Carcateristici optice principale şi limitări de performanţă în utilizarea reţelei 9.3.3a. Dispersia unghiulară a reţelei optice O caracteristică de bază al oricărui aparat optic spectral este dispersia unghiulară dα D a elementului dispersiv definit prin raportul D =. d Diferenţiind ecuaţia reţelei optice d sin α = k, pentru variaţia unghiului de difracţie α funcţie de lungimea de undă a radiaţiei incidente, corespunzător unui dα k anumit ordin de interferenţă obţinem: =. d d cosα Prin urmare dispersia unghiulară a reţelei optice este cu atât mai mare cu cât constanta reţelei d este mai mică (densitatea liniilor gravate pe unitatea de lungime este mai mare), respectiv cu cât ordinul k al spectrului de difracţie este mai mare b. Puterea de rozolvare spectrală a reţelei optice. Criteriul de rezoluţie în definirea lui Rayleigh Este cunoscut faptul că imaginile aparatelor optice suferă de anumite aberaţii. Dacă punctele de imagini ale punctelor obiect redate în aparatele optice prezintă figură de difracţie, pentru punctele obiect apropiate figurile de difracţie se vor suprapune (figura 9.3.). Criteriul Rayleigh consideră separarea imaginilor a două puncte obiect îndeplinită, dacă maximul de difracţie al unui punct obiect cade în poziţia minimului de difracţie al punctului obiect vecin. Puterea de rezolvare (sau puterea de separare în diferite radiaţii monocromatice) a fost definită de Rayleigh drept criteriu minim în capacitatea reţelei de difracţie de a separa două puncte obiect adiacente. 134
29 Fig Criteriul de separare în definirea lui Rayleigh pentru definirea puterii de rezoluţie În cazul aparatelor spectrale o cerinţă fundamentală este capacitatea de a distinge diferitele imagini spectrale, exemplu franje de interferenţă redate în lungimi de unde apropiate. Prin urmare puterea de rezoluţie este exprimarea raportului maxim dintre Δ lungimea de undă a radiaţiei utilizate în măsurătoarea, respectiv a intervalului elementar de lungime de undă Δ din vecinătatea lui pentru care aparatul încă mai poate asigura separarea imaginilor afectate de figurile de difracţie. Să evaluăm puterea de rezoluţie a unei reţele optice pe baza criteriului formulat de către Rayleigh. Condiţia Rayleigh impune suprapunerea poziţiei unghiulare pentru maximul central al unei imagini de difracţie obţinută în lumina monocromatică cu lungime de undă, cu primul minim al radiaţiei de lungime de undă + Δ. Pentru maximul principal condiţia unghiulară este exprimată prin relaţia reţelei de difracţie d sin α = k, unde d - este constanta reţelei, lungimea de undă a radiaţiei monocromatice incidente, α unghiul de difracţie. Pentru puterea de rezoluţie a unei reţele de difracţie rezultă expresia = kn, catre arată că puterea de rezoluţie este cu Δ atât mai mare cu cât numărul de trăsături N este mai mare, respectiv cu cât ordinul k al spectrului este mai mare. Acest raport însă nu depined de valaorea constantei de reţea d. Distribuţia luminii în maxime de diferite ordine ale reţelei de difracţie depinde de profilul microscopic al trăsăturilor, fiin caracterizat prin unghiul θ de profil. Remarcăm că unghiul de difracţie este definit faţă de normala planului reţelei, în timp ce unghiul de reflexie γ este măsurat faţă de normala suprafeţei trăsăturii. Pentru creşterea puterii de rezolvare, se lucrează cu spectre de ordine superioare, sub unghiuri mai mici de observare. În utilizarea reţelei de difracţie apare o limitare teoretică pentru unghiul de difracţie α 90, respectiv faptul că distanţa dintre două trăsături consecutive să nu fie mult prea mică decât lungimea de undă a luminii (în situaţia când d << reţeaua optică se comportă ca o oglindă, mai mult reflectând lumina decât să o disperseze). 135
30 Dacă frontul de undă al radiaţiei incidente nu este paralel cu planul reţelei de difracţie, astfel direcţia razelor incidente formează un unghi de incidenţă β cu normala planului reţelei, difernţa de drum optic δ corespunzătoare la două raze de lumină consecutive este dată de relaţia: δ = d (sinα ± sin β ). În această situaţie interferenţa constructivă a undelor elementare va determina maxime de intensitate pentru acele direcţii unghiulare pentru care diferenţa de drum optic este δ = k = k, respectiv minime de difracţie apar pentru diferenţele de drum δ = (k + 1) cu k = 0, ± 1, ±,... În cazul reţelelor de difracţie transparente, numărul maxim de trăsături este limitat prin faptul că, pe măsură ce α se apropie de unghiul maxim al reflexiei interne, tot mai multă lumină se pierde prin reflexie internă. Reţeaua optică poate funcţiona şi în lumină reflectată. Figura 9.4. prezintă schematic funcţionarea reţelei optice prin reflexie. Fig Schema reţelei de difracţie bazată pe reflexia şi difracţia luminii Observaţie importantă: Nu se admite atingerea directă cu degete a ariei trasate pe suprafaţa reţelei optice, întrucât amprentele degetelor înrăutăţesc calităţile reţelei de difracţie! 9.4. Polarizarea luminii Lumina în interacţiunea sa cu substanţa îşi exercită efectul în primul rând prin componenta electrică a câmpului electromagnetic, numită componentă luminoasă. Unda de lumină naturală se caracterizează prin simetrie de rotaţie a vectorului câmp electric cu oscilaţie în plan perpendicular pe direcţia de propagare. Polarizarea luminii naturale înseamnă limitarea direcţiei de oscilaţie a vectorului de câmp electric, fără să existe o simetrie de rotaţie în oscilaţia vectorului luminos. Direcţia de propagare a radiaţiei şi direcţia de oscilaţie a vectorului de câmp electric definesc planul de polarizare sau planul de vibraţie al vectorului luminos E. Polarizarea poate fi realizată 136
31 în procesul de reflexie a luminii sau în cazul refracţiei luminii la traversarea suprafeţei de separaţie a două medii dielectrice. În cazul luminii reflectate oscilaţia câmpului electric are loc după o direcţie perpendiculară pe planul de incidenţă, iar pentru lumina refractată oscilaţia Fig Prezentarea schematică a direcţiilor de oscilaţie a vectorului de câmp electric pentru lumina total polarizată prin reflexie sau prin refracţie pe suprafaţa unui dielectric Lumina fiind o undă transversală, vectorul câmp electric E poate fi asimilat cu suma a două componente ortogonale, care oscilează într-un plan perpendicular pe direcţia de propagare. În cazul luminii plan polarizate, vectorul câmpului electric are o direcţie definită de oscilaţie în planul perpendicular pe direcţia de propagare (figura 9.6.). Fig.9.6. Descompunerea luminii polarizate după două direcţii perpendiculare Intensitatea câmpului electric poate fi scrisă în forma analitică: E = E e 0 i( kz ωt) = E e 0 i( ωt kz) Planul de polarizare poate avea direcţie arbitrară, în particular pentru E x = E y direcţia de vibraţie poate fi orientată la θ = 45 faţă de axele Ox sau Oy. Dacă vectorul E se roteşte în jurul direcţiei de propagare, astfel încât între componentele E şi E există π o diferenţă de fază avem lumină circular polarizată, unde: E = E x e i( ωt kz) + E y e π i( ωt kz + ) x y 137
32 Dacă rotaţia vectorului E coincide cu sensul de rotaţie acelor ceasornicului se spune că avem polarizarea circulară către dreapta, în caz contrar polarizarea circulară către stânga. Lumina polarizată eliptic poate fi considerată ca rezultatul compunerii a două unde coerente polarizate plan (sau liniar) perpendiculare între ele, având o diferenţă de fază între ele ceea ce face ca în timpul propagării vectorul luminos rezultat să descrie (în proiecţie!) o elipsă în planul normal direcţiei de propagare a razei. În experienţa de reflexie consecutivă a luminii incidente naturale pe o suprafaţă dielectrică, reflexia luminii determină modificări în azimutul planelor de oscilaţie, obţinem aşa numita lumină parţial polarizată. La incidenţa pentru care se obţine lumina total polarizată, unghiul de incidenţă i satisface legea lui Brewster: n tgi b = n =, n1 unde n este indicele de refracţie (relativ) al substanţei din care este confecţionată oglinda. În această situaţie unghiul de refracţie satisface condiţia r = π i1, adică raza reflectată şi cea refractată sunt perpendiculare Birefrigenţa cristalelor Un mediu optic se comportă izotrop în raport cu propagarea luminii dacă toate direcţiile de propagare sunt echivalente. Acest lucru întâlnim în cazul mediilor gazoase şi lichide, respectiv la solide aflate în stare amorfă. Însă în cazul solidelor cristaline avem de a face cu o dispunere ordonată a atomilor în reţele cristaline, ceea ce conferă acestora proprietăţi anizotrope faţă de propagarea luminii. Fenomenul de birefrigenţă a fost descoperit în 1669 de Bartholinus, observând imagini duble pentru obiecte privite prin cristalul spat de Islanda (calcită, CaCO 3 ). Cristalelor optic transparente care prezintă anizotropie în propagarea luminii este caracteristică dedublarea razei incidente. Materialele cristalizate în sistemul cubic nu prezintă birefrigenţă datorită simetriei ridicate, însă calcita (carbonatul de calciu) cristalizat în sistemul romboedric prezintă două valori pentru indicele de refracţie. Fig Aspectul cristalografic al calcitei (carbonat de calciu), respectiv în cazul cuarţului cristalin 138
33 Cristalul are o axă cristalografică de simetrie de ordinul 3, fapt ce indică existenţa a trei poziţii echivalente pentru care la o rotire completă în jurul unei axe de simetrie cristalul ajunge în poziţii identice de 3 ori. Această axă constituie şi axă optică pentru cristalul respectiv. Axa optică este singura direcţie în cristal, după care cristalul nu prezintă fenomenul de birefrigenţă. Cristalele optice uniaxe (cum este şi cuarţul) se deosebesc de cristalele optice biaxe, care prezintă două astfel de direcţii (ex. mică, gipsul, etc.). Fig Fenomenul de birefrigenţă observat în cazul cristalului de calcită CaCO3 Fasciculul de lumină naturală incident perpendicular pe faţa cristalului de CaCO 3 se desparte în raze, şi la ieşirea razelor din cristal acestea sunt paralele şi deplasate una faţă de alta, dacă faţa de ieşire a cristalului este paralelă cu cea de intrare. Direcţia razei incidente împreună cu direcţia axului optic determină planul secţiunii principale pentru cristalul respectiv. Fig Descompunerea luminii în componenta ordinară şi cea extraordinară a luminii polarizate în două plane reciproc perpendiculare: direcţia AA reprezintă axa optică a cristalului Raza OO se comportă ca o rază ordinară, cu respectarea legilor opticii geometrice, iar raza IE refractată se numeşte rază extraordinară. Amândouă raze sunt linear polarizate, având însă plane de polarizare ortogonale. Indicele de refracţie a cristalului diferă pentru cele două raze, ba mai mult acestea sunt dependente şi de valoarea unghiului de incidenţă. În interiorul cristalului uniax undele luminoase provenite de la un izvor punctiform S se vor propaga pe distanţe diferite faţă de centrul emisiv: unda ordinară va prezenta un front de undă sferic după toate direcţiile de propagare, iar undele extraordinare vor avea viteze diferite în funcţie de direcţia de propagare. Viteza de propagare a undei extraordinare poate avea valoarea mai mică sau mai mare faţă de viteza undei ordinare, astfel pentru cristalul uniax pozitiv, respectiv pentru cristalul uniax negativ unda extraordinară formează un front de undă elipsoidal. Doar după direcţia axului optic cele două viteze de propagare vor coincide, suprafeţele fronturilor de undă fiind tangente după direcţia axului optic AA'. 139
Planul determinat de normală şi un punct Ecuaţia generală Plane paralele Unghi diedru Planul determinat de 3 puncte necoliniare
 1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
Reflexia şi refracţia luminii.
 Reflexia şi refracţia luminii. 1. Cu cat se deplaseaza o raza care cade sub unghiul i =30 pe o placa plan-paralela de grosime e = 8,0 mm si indicele de refractie n = 1,50, pe care o traverseaza? Caz particular
Reflexia şi refracţia luminii. 1. Cu cat se deplaseaza o raza care cade sub unghiul i =30 pe o placa plan-paralela de grosime e = 8,0 mm si indicele de refractie n = 1,50, pe care o traverseaza? Caz particular
5. FUNCŢII IMPLICITE. EXTREME CONDIŢIONATE.
 5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate.
 Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
(a) se numeşte derivata parţială a funcţiei f în raport cu variabila x i în punctul a.
 Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
- Optica Ondulatorie
 - Optica Ondulatorie *Proiect coordonat de Dna. Prof. Domisoru Daniela *Elevii participanti: Simion Vlad, Codreanu Alexandru, Domnisoru Albert-Leonard *Colegiul National Vasile Alecsandri GALATI *Concursul
- Optica Ondulatorie *Proiect coordonat de Dna. Prof. Domisoru Daniela *Elevii participanti: Simion Vlad, Codreanu Alexandru, Domnisoru Albert-Leonard *Colegiul National Vasile Alecsandri GALATI *Concursul
Metode iterative pentru probleme neliniare - contractii
 Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
STUDIUL DIFRACŢIEI LUMINII
 LUCRAREA NR. 10 STUDIUL DIFRACŢIEI LUMINII Tema lucrării: 1) Etalonarea tamburului unei fante reglabile. Difracţia Fraunhofer 2) Studiul difracţiei Fraunhofer prin mai multe fante paralele. 3) Studiul
LUCRAREA NR. 10 STUDIUL DIFRACŢIEI LUMINII Tema lucrării: 1) Etalonarea tamburului unei fante reglabile. Difracţia Fraunhofer 2) Studiul difracţiei Fraunhofer prin mai multe fante paralele. 3) Studiul
MARCAREA REZISTOARELOR
 1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE
 DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
Ecuaţia generală Probleme de tangenţă Sfera prin 4 puncte necoplanare. Elipsoidul Hiperboloizi Paraboloizi Conul Cilindrul. 1 Sfera.
 pe ecuaţii generale 1 Sfera Ecuaţia generală Probleme de tangenţă 2 pe ecuaţii generale Sfera pe ecuaţii generale Ecuaţia generală Probleme de tangenţă Numim sferă locul geometric al punctelor din spaţiu
pe ecuaţii generale 1 Sfera Ecuaţia generală Probleme de tangenţă 2 pe ecuaţii generale Sfera pe ecuaţii generale Ecuaţia generală Probleme de tangenţă Numim sferă locul geometric al punctelor din spaţiu
Curs 14 Funcţii implicite. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi"
 Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Laborator 5 INTERFEROMETRE
 Laborator 5 INTERFEROMETRE Scopul lucrarii În lucrarea de fańă sunt prezentate unele aspecte legate de interferometrie. Se prezinta functionarea unui modulator optic ce lucreaza pe baza interferentei dintre
Laborator 5 INTERFEROMETRE Scopul lucrarii În lucrarea de fańă sunt prezentate unele aspecte legate de interferometrie. Se prezinta functionarea unui modulator optic ce lucreaza pe baza interferentei dintre
Definiţia generală Cazul 1. Elipsa şi hiperbola Cercul Cazul 2. Parabola Reprezentari parametrice ale conicelor Tangente la conice
 1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
Subiecte Clasa a VIII-a
 Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Curs 4 Serii de numere reale
 Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
2.1 Sfera. (EGS) ecuaţie care poartă denumirea de ecuaţia generală asferei. (EGS) reprezintă osferă cu centrul în punctul. 2 + p 2
 .1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
.1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
R R, f ( x) = x 7x+ 6. Determinați distanța dintre punctele de. B=, unde x și y sunt numere reale.
 5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
STUDIUL INTERFERENŢEI LUMINII CU DISPOZITIVUL LUI YOUNG
 UNIVESITATEA "POLITEHNICA" DIN BUCUEŞTI DEPATAMENTUL DE FIZICĂ LABOATOUL DE OPTICĂ BN - 10 B STUDIUL INTEFEENŢEI LUMINII CU DISPOZITIVUL LUI YOUNG 004-005 STUDIUL INTEFEENŢEI LUMINII CU DISPOZITIVUL LUI
UNIVESITATEA "POLITEHNICA" DIN BUCUEŞTI DEPATAMENTUL DE FIZICĂ LABOATOUL DE OPTICĂ BN - 10 B STUDIUL INTEFEENŢEI LUMINII CU DISPOZITIVUL LUI YOUNG 004-005 STUDIUL INTEFEENŢEI LUMINII CU DISPOZITIVUL LUI
Profesor Blaga Mirela-Gabriela DREAPTA
 DREAPTA Fie punctele A ( xa, ya ), B ( xb, yb ), C ( xc, yc ) şi D ( xd, yd ) în planul xoy. 1)Distanţa AB = (x x ) + (y y ) Ex. Fie punctele A( 1, -3) şi B( -2, 5). Calculaţi distanţa AB. AB = ( 2 1)
DREAPTA Fie punctele A ( xa, ya ), B ( xb, yb ), C ( xc, yc ) şi D ( xd, yd ) în planul xoy. 1)Distanţa AB = (x x ) + (y y ) Ex. Fie punctele A( 1, -3) şi B( -2, 5). Calculaţi distanţa AB. AB = ( 2 1)
5.5. REZOLVAREA CIRCUITELOR CU TRANZISTOARE BIPOLARE
 5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM 1 electronica.geniu.ro
 Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Problema a II - a (10 puncte) Diferite circuite electrice
 Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
III. Serii absolut convergente. Serii semiconvergente. ii) semiconvergentă dacă este convergentă iar seria modulelor divergentă.
 III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
Conice. Lect. dr. Constantin-Cosmin Todea. U.T. Cluj-Napoca
 Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
Sisteme diferenţiale liniare de ordinul 1
 1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
Curs 1 Şiruri de numere reale
 Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Cum folosim cazuri particulare în rezolvarea unor probleme
 Cum folosim cazuri particulare în rezolvarea unor probleme GHEORGHE ECKSTEIN 1 Atunci când întâlnim o problemă pe care nu ştim s-o abordăm, adesea este bine să considerăm cazuri particulare ale acesteia.
Cum folosim cazuri particulare în rezolvarea unor probleme GHEORGHE ECKSTEIN 1 Atunci când întâlnim o problemă pe care nu ştim s-o abordăm, adesea este bine să considerăm cazuri particulare ale acesteia.
Interferenţa şi difracţia undelor electromagnetice
 1 CAPITOLUL 3 Interferenţa şi difracţia undelor electromagnetice 3.1 Fenomenul de interferenţă. Surse coerente şi necoerente În descrierea proprietăţilor undelor am întâlnit diverse situaţii în care două
1 CAPITOLUL 3 Interferenţa şi difracţia undelor electromagnetice 3.1 Fenomenul de interferenţă. Surse coerente şi necoerente În descrierea proprietăţilor undelor am întâlnit diverse situaţii în care două
Metode de interpolare bazate pe diferenţe divizate
 Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile
 Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Algebra si Geometrie Seminar 9
 Algebra si Geometrie Seminar 9 Decembrie 017 ii Equations are just the boring part of mathematics. I attempt to see things in terms of geometry. Stephen Hawking 9 Dreapta si planul in spatiu 1 Notiuni
Algebra si Geometrie Seminar 9 Decembrie 017 ii Equations are just the boring part of mathematics. I attempt to see things in terms of geometry. Stephen Hawking 9 Dreapta si planul in spatiu 1 Notiuni
a n (ζ z 0 ) n. n=1 se numeste partea principala iar seria a n (z z 0 ) n se numeste partea
 Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Seminariile Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reziduurilor
 Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Integrala nedefinită (primitive)
 nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii transversale, scrisă faţă de una dintre axele de inerţie principale:,
 REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
SEMINAR 14. Funcţii de mai multe variabile (continuare) ( = 1 z(x,y) x = 0. x = f. x + f. y = f. = x. = 1 y. y = x ( y = = 0
 Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
Difractia de electroni
 Difractia de electroni 1 Principiul lucrari Verificarea experimentala a difractiei electronilor rapizi pe straturi de grafit policristalin: observarea inelelor de interferenta ce apar pe ecranul fluorescent.
Difractia de electroni 1 Principiul lucrari Verificarea experimentala a difractiei electronilor rapizi pe straturi de grafit policristalin: observarea inelelor de interferenta ce apar pe ecranul fluorescent.
2. Sisteme de forţe concurente...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...3
 SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
Activitatea A5. Introducerea unor module specifice de pregătire a studenţilor în vederea asigurării de şanse egale
 Investeşte în oameni! FONDUL SOCIAL EUROPEAN Programul Operaţional Sectorial pentru Dezvoltarea Resurselor Umane 2007 2013 Axa prioritară nr. 1 Educaţiaşiformareaprofesionalăînsprijinulcreşteriieconomiceşidezvoltăriisocietăţiibazatepecunoaştere
Investeşte în oameni! FONDUL SOCIAL EUROPEAN Programul Operaţional Sectorial pentru Dezvoltarea Resurselor Umane 2007 2013 Axa prioritară nr. 1 Educaţiaşiformareaprofesionalăînsprijinulcreşteriieconomiceşidezvoltăriisocietăţiibazatepecunoaştere
Concurs MATE-INFO UBB, 1 aprilie 2017 Proba scrisă la MATEMATICĂ
 UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ Concurs MATE-INFO UBB, aprilie 7 Proba scrisă la MATEMATICĂ SUBIECTUL I (3 puncte) ) (5 puncte) Fie matricele A = 3 4 9 8
UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ Concurs MATE-INFO UBB, aprilie 7 Proba scrisă la MATEMATICĂ SUBIECTUL I (3 puncte) ) (5 puncte) Fie matricele A = 3 4 9 8
Aplicaţii ale principiului I al termodinamicii la gazul ideal
 Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
SEXTANTUL CUM FUNCŢIONEAZĂ UN SEXTANT?
 SEXTANTUL CUM FUNCŢIONEAZĂ UN SEXTANT? Să considerăm mai întâi (pentru a asigura o descriere fizică riguroasă) două oglinzi plane paralele M 1, M 2 (orientate după direcţia MN PQ), aparţinând spre exemplu
SEXTANTUL CUM FUNCŢIONEAZĂ UN SEXTANT? Să considerăm mai întâi (pentru a asigura o descriere fizică riguroasă) două oglinzi plane paralele M 1, M 2 (orientate după direcţia MN PQ), aparţinând spre exemplu
Olimpiada de Fizică Etapa pe judeţ 4 februarie 2012 Barem
 4 februarie Pagina din 5. subiect (Masa furnicilor) p A.... 5p În cazurile a) şi b) lungimile catetelor sunt L 38cm şi 4R L, 49cm....,75p a) Când partea coborâtoare a punţii este mai lungă timpul total
4 februarie Pagina din 5. subiect (Masa furnicilor) p A.... 5p În cazurile a) şi b) lungimile catetelor sunt L 38cm şi 4R L, 49cm....,75p a) Când partea coborâtoare a punţii este mai lungă timpul total
LUCRAREA NR. 4 DETERMINAREA INDICELUI DE REFRACŢIE AL UNUI SOLID CU AJUTORUL PRISMEI
 LUCRAREA NR. 4 DETERMINAREA INDICELUI DE REFRACŢIE AL UNUI SOLID CU AJUTORUL PRISMEI Tema lucrării: 1) Determinarea unghiului refringent al prismei. ) Determinarea indicelui de refracţie al prismei pentru
LUCRAREA NR. 4 DETERMINAREA INDICELUI DE REFRACŢIE AL UNUI SOLID CU AJUTORUL PRISMEI Tema lucrării: 1) Determinarea unghiului refringent al prismei. ) Determinarea indicelui de refracţie al prismei pentru
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor X) functia f 1
 Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Esalonul Redus pe Linii (ERL). Subspatii.
 Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
Functii Breviar teoretic 8 ianuarie ianuarie 2011
 Functii Breviar teoretic 8 ianuarie 011 15 ianuarie 011 I Fie I, interval si f : I 1) a) functia f este (strict) crescatoare pe I daca x, y I, x< y ( f( x) < f( y)), f( x) f( y) b) functia f este (strict)
Functii Breviar teoretic 8 ianuarie 011 15 ianuarie 011 I Fie I, interval si f : I 1) a) functia f este (strict) crescatoare pe I daca x, y I, x< y ( f( x) < f( y)), f( x) f( y) b) functia f este (strict)
Lectia VII Dreapta si planul
 Planul. Ecuatii, pozitii relative Dreapta. Ecuatii, pozitii relative Aplicatii Lectia VII Dreapta si planul Oana Constantinescu Oana Constantinescu Lectia VII Planul. Ecuatii, pozitii relative Dreapta.
Planul. Ecuatii, pozitii relative Dreapta. Ecuatii, pozitii relative Aplicatii Lectia VII Dreapta si planul Oana Constantinescu Oana Constantinescu Lectia VII Planul. Ecuatii, pozitii relative Dreapta.
LUCRAREA NR. 3 DETERMINAREA DISTANŢEI FOCALE A OGLINZILOR SFERICE
 LUCRAREA NR. 3 DETERMINAREA DISTANŢEI FOCALE A OGLINZILOR SFERICE Tema lucrării: 1) Determinarea distanţei focale a unei oglinzi concave ) Determinarea distanţei focale a unei oglinzi convexe 3) Studiul
LUCRAREA NR. 3 DETERMINAREA DISTANŢEI FOCALE A OGLINZILOR SFERICE Tema lucrării: 1) Determinarea distanţei focale a unei oglinzi concave ) Determinarea distanţei focale a unei oglinzi convexe 3) Studiul
INTENSITATEA ŞI DIFRACŢIA RADIAŢIEI LASER
 UNIVERSITATEA "POLITEHNICA" DIN BUCUREŞTI DEPARTAMENTUL DE FIZICĂ LABORATORUL DE OPTICĂ BN - 1 A INTENSITATEA ŞI DIFRACŢIA RADIAŢIEI LASER INTENSITATEA ŞI DIFRACŢIA RADIAŢIEI LASER 1. Scopul lucrării Lucrarea
UNIVERSITATEA "POLITEHNICA" DIN BUCUREŞTI DEPARTAMENTUL DE FIZICĂ LABORATORUL DE OPTICĂ BN - 1 A INTENSITATEA ŞI DIFRACŢIA RADIAŢIEI LASER INTENSITATEA ŞI DIFRACŢIA RADIAŢIEI LASER 1. Scopul lucrării Lucrarea
Conice - Câteva proprietǎţi elementare
 Conice - Câteva proprietǎţi elementare lect.dr. Mihai Chiş Facultatea de Matematicǎ şi Informaticǎ Universitatea de Vest din Timişoara Viitori Olimpici ediţia a 5-a, etapa I, clasa a XII-a 1 Definiţii
Conice - Câteva proprietǎţi elementare lect.dr. Mihai Chiş Facultatea de Matematicǎ şi Informaticǎ Universitatea de Vest din Timişoara Viitori Olimpici ediţia a 5-a, etapa I, clasa a XII-a 1 Definiţii
 10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
INTERFEROMETRUL MICHELSON
 INTERFEROMETRUL MICHELSON 1. Scopul lucrării - Reglarea montajului optic corespunzător interferometrului Michelson; - Observarea figurii de interferență pe un ecran, constituită din franje luminoase și
INTERFEROMETRUL MICHELSON 1. Scopul lucrării - Reglarea montajului optic corespunzător interferometrului Michelson; - Observarea figurii de interferență pe un ecran, constituită din franje luminoase și
Curs 2 Şiruri de numere reale
 Curs 2 Şiruri de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Convergenţă şi mărginire Teoremă Orice şir convergent este mărginit. Demonstraţie Fie (x n ) n 0 un
Curs 2 Şiruri de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Convergenţă şi mărginire Teoremă Orice şir convergent este mărginit. Demonstraţie Fie (x n ) n 0 un
SERII NUMERICE. Definiţia 3.1. Fie (a n ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0
 SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
1.7. AMPLIFICATOARE DE PUTERE ÎN CLASA A ŞI AB
 1.7. AMLFCATOARE DE UTERE ÎN CLASA A Ş AB 1.7.1 Amplificatoare în clasa A La amplificatoarele din clasa A, forma de undă a tensiunii de ieşire este aceeaşi ca a tensiunii de intrare, deci întreg semnalul
1.7. AMLFCATOARE DE UTERE ÎN CLASA A Ş AB 1.7.1 Amplificatoare în clasa A La amplificatoarele din clasa A, forma de undă a tensiunii de ieşire este aceeaşi ca a tensiunii de intrare, deci întreg semnalul
Optica este o ramură a fizicii care studiază proprietăţile şi natura luminii, modul de producere a acesteia, şi legile propagării şi interacţiunii
 Optica este o ramură a fizicii care studiază proprietăţile şi natura luminii, modul de producere a acesteia, şi legile propagării şi interacţiunii luminii cu substanţa. Optica geometrica este acea parte
Optica este o ramură a fizicii care studiază proprietăţile şi natura luminii, modul de producere a acesteia, şi legile propagării şi interacţiunii luminii cu substanţa. Optica geometrica este acea parte
a. Caracteristicile mecanice a motorului de c.c. cu excitaţie independentă (sau derivaţie)
 Caracteristica mecanică defineşte dependenţa n=f(m) în condiţiile I e =ct., U=ct. Pentru determinarea ei vom defini, mai întâi caracteristicile: 1. de sarcină, numită şi caracteristica externă a motorului
Caracteristica mecanică defineşte dependenţa n=f(m) în condiţiile I e =ct., U=ct. Pentru determinarea ei vom defini, mai întâi caracteristicile: 1. de sarcină, numită şi caracteristica externă a motorului
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor
 Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Toate subiectele sunt obligatorii. Timpul de lucru efectiv este de 3 ore. Se acordă din oficiu 10 puncte. SUBIECTUL I.
 Modelul 4 Se acordă din oficiu puncte.. Fie numărul complex z = i. Calculaţi (z ) 25. 2. Dacă x şi x 2 sunt rădăcinile ecuaţiei x 2 9x+8 =, atunci să se calculeze x2 +x2 2 x x 2. 3. Rezolvaţi în mulţimea
Modelul 4 Se acordă din oficiu puncte.. Fie numărul complex z = i. Calculaţi (z ) 25. 2. Dacă x şi x 2 sunt rădăcinile ecuaţiei x 2 9x+8 =, atunci să se calculeze x2 +x2 2 x x 2. 3. Rezolvaţi în mulţimea
DETERMINAREA LUNGIMII DE UNDA A LUMINII MONOCROMATICE CU AJUTORUL DISPOZITIVULUI YOUNG
 UNIVERSITATEA "POLITEHNICA" DIN BUCURESTI CATEDRA DE FIZICA LABORATORUL DE OPTICÅ BN 121 DETERMINAREA LUNGIMII DE UNDA A LUMINII MONOCROMATICE CU AJUTORUL DISPOZITIVULUI YOUNG 1996 DETERMINAREA LUNGIMII
UNIVERSITATEA "POLITEHNICA" DIN BUCURESTI CATEDRA DE FIZICA LABORATORUL DE OPTICÅ BN 121 DETERMINAREA LUNGIMII DE UNDA A LUMINII MONOCROMATICE CU AJUTORUL DISPOZITIVULUI YOUNG 1996 DETERMINAREA LUNGIMII
Să se arate că n este număr par. Dan Nedeianu
 Primul test de selecție pentru juniori I. Să se determine numerele prime p, q, r cu proprietatea că 1 p + 1 q + 1 r 1. Fie ABCD un patrulater convex cu m( BCD) = 10, m( CBA) = 45, m( CBD) = 15 și m( CAB)
Primul test de selecție pentru juniori I. Să se determine numerele prime p, q, r cu proprietatea că 1 p + 1 q + 1 r 1. Fie ABCD un patrulater convex cu m( BCD) = 10, m( CBA) = 45, m( CBD) = 15 și m( CAB)
 4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
GEOMETRIE PLANĂ TEOREME IMPORTANTE ARII. bh lh 2. abc. abc. formula înălţimii
 GEOMETRIE PLNĂ TEOREME IMPORTNTE suma unghiurilor unui triunghi este 8º suma unghiurilor unui patrulater este 6º unghiurile de la baza unui triunghi isoscel sunt congruente într-un triunghi isoscel liniile
GEOMETRIE PLNĂ TEOREME IMPORTNTE suma unghiurilor unui triunghi este 8º suma unghiurilor unui patrulater este 6º unghiurile de la baza unui triunghi isoscel sunt congruente într-un triunghi isoscel liniile
7. RETELE ELECTRICE TRIFAZATE 7.1. RETELE ELECTRICE TRIFAZATE IN REGIM PERMANENT SINUSOIDAL
 7. RETEE EECTRICE TRIFAZATE 7.. RETEE EECTRICE TRIFAZATE IN REGIM PERMANENT SINSOIDA 7... Retea trifazata. Sistem trifazat de tensiuni si curenti Ansamblul format din m circuite electrice monofazate in
7. RETEE EECTRICE TRIFAZATE 7.. RETEE EECTRICE TRIFAZATE IN REGIM PERMANENT SINSOIDA 7... Retea trifazata. Sistem trifazat de tensiuni si curenti Ansamblul format din m circuite electrice monofazate in
5.4. MULTIPLEXOARE A 0 A 1 A 2
 5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
Asupra unei inegalităţi date la barajul OBMJ 2006
 Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
Capitolul 4. Integrale improprii Integrale cu limite de integrare infinite
 Capitolul 4 Integrale improprii 7-8 În cadrul studiului integrabilităţii iemann a unei funcţii s-au evidenţiat douăcondiţii esenţiale:. funcţia :[ ] este definită peintervalînchis şi mărginit (interval
Capitolul 4 Integrale improprii 7-8 În cadrul studiului integrabilităţii iemann a unei funcţii s-au evidenţiat douăcondiţii esenţiale:. funcţia :[ ] este definită peintervalînchis şi mărginit (interval
DETERMINAREA LUNGIMII DE UNDĂ A RADIAŢIEI LASER CU INTERFEROMETRUL MICHELSON
 UNIVERSITATEA "POLITEHNICA" DIN BUCUREŞTI DEPARTAMENTUL DE FIZICĂ LABORATORUL DE OPTICĂ BN - 122 A DETERMINAREA LUNGIMII DE UNDĂ A RADIAŢIEI LASER CU INTERFEROMETRUL MICHELSON DETERMINAREA LUNGIMII DE
UNIVERSITATEA "POLITEHNICA" DIN BUCUREŞTI DEPARTAMENTUL DE FIZICĂ LABORATORUL DE OPTICĂ BN - 122 A DETERMINAREA LUNGIMII DE UNDĂ A RADIAŢIEI LASER CU INTERFEROMETRUL MICHELSON DETERMINAREA LUNGIMII DE
Seminar 5 Analiza stabilității sistemelor liniare
 Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Capitolul FF.03 Interferenţa luminii
 Capitolul FF.3 Interferenţa luminii Cuvinte-cheie principiul superpoziţiei, fazor, undă staţionară, experienţa lui Wiener, bătăi luminoase, frecvenţă purtătoare, frecvenţă de modulaţie, tren de unde, viteză
Capitolul FF.3 Interferenţa luminii Cuvinte-cheie principiul superpoziţiei, fazor, undă staţionară, experienţa lui Wiener, bătăi luminoase, frecvenţă purtătoare, frecvenţă de modulaţie, tren de unde, viteză
8 Intervale de încredere
 8 Intervale de încredere În cursul anterior am determinat diverse estimări ˆ ale parametrului necunoscut al densităţii unei populaţii, folosind o selecţie 1 a acestei populaţii. În practică, valoarea calculată
8 Intervale de încredere În cursul anterior am determinat diverse estimări ˆ ale parametrului necunoscut al densităţii unei populaţii, folosind o selecţie 1 a acestei populaţii. În practică, valoarea calculată
Modulul 5 OPTICĂ ONDULATORIE
 57 Modulul 5 OPTICĂ ONDULATORIE Conţinutul modulului: 5.1 Generalităţi 5. Reflexia şi refracţia luminii 5.3 Interferenţa luminii 5.4 Difracţia luminii 5.5 Difuzia luminii 5.6 Dispersia luminii 5.7 Polarizarea
57 Modulul 5 OPTICĂ ONDULATORIE Conţinutul modulului: 5.1 Generalităţi 5. Reflexia şi refracţia luminii 5.3 Interferenţa luminii 5.4 Difracţia luminii 5.5 Difuzia luminii 5.6 Dispersia luminii 5.7 Polarizarea
3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...4
 SEMINAR 3 MMENTUL FRŢEI ÎN RAPRT CU UN PUNCT CUPRINS 3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere...1 3.1. Aspecte teoretice...2 3.2. Aplicaţii rezolvate...4 3. Momentul forţei
SEMINAR 3 MMENTUL FRŢEI ÎN RAPRT CU UN PUNCT CUPRINS 3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere...1 3.1. Aspecte teoretice...2 3.2. Aplicaţii rezolvate...4 3. Momentul forţei
Curs 2 DIODE. CIRCUITE DR
 Curs 2 OE. CRCUTE R E CUPRN tructură. imbol Relația curent-tensiune Regimuri de funcționare Punct static de funcționare Parametrii diodei Modelul cu cădere de tensiune constantă Analiza circuitelor cu
Curs 2 OE. CRCUTE R E CUPRN tructură. imbol Relația curent-tensiune Regimuri de funcționare Punct static de funcționare Parametrii diodei Modelul cu cădere de tensiune constantă Analiza circuitelor cu
INTERFEROMETRUL MICHELSON
 UNIVERSITATEA "POLITEHNICA" DIN BUCUREŞTI DEPARTAMENTUL DE FIZICĂ LABORATORUL DE TERMODINAMICA SI FIZICA STATISTICA BN 121 INTERFEROMETRUL MICHELSON INTERFEROMETRUL MICHELSON 1. Scopul lucrării Asamblarea
UNIVERSITATEA "POLITEHNICA" DIN BUCUREŞTI DEPARTAMENTUL DE FIZICĂ LABORATORUL DE TERMODINAMICA SI FIZICA STATISTICA BN 121 INTERFEROMETRUL MICHELSON INTERFEROMETRUL MICHELSON 1. Scopul lucrării Asamblarea
CURS MECANICA CONSTRUCŢIILOR
 CURS 10+11 MECANICA CONSTRUCŢIILOR Conf. Dr. Ing. Viorel Ungureanu CINEMATICA SOLIDULUI RIGID In cadrul cinematicii punctului material s-a arătat ca a studia mişcarea unui punct înseamnă a determina la
CURS 10+11 MECANICA CONSTRUCŢIILOR Conf. Dr. Ing. Viorel Ungureanu CINEMATICA SOLIDULUI RIGID In cadrul cinematicii punctului material s-a arătat ca a studia mişcarea unui punct înseamnă a determina la
Subiecte Clasa a VIII-a
 (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul numarului intrebarii
(40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul numarului intrebarii
COLEGIUL NATIONAL CONSTANTIN CARABELLA TARGOVISTE. CONCURSUL JUDETEAN DE MATEMATICA CEZAR IVANESCU Editia a VI-a 26 februarie 2005.
 SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
a. 11 % b. 12 % c. 13 % d. 14 %
 1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
Subiecte Clasa a VII-a
 lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
Interferenta undelor sau Despre cuplarea a doua antene.
 Interferenta undelor sau Despre cuplarea a doua antene. 1 Bazele teoriei cuplarii antenelor sint similare interferentei undelor invatata in liceu in clasa a 11-a, in capitolul de compunere a oscilatiilor.
Interferenta undelor sau Despre cuplarea a doua antene. 1 Bazele teoriei cuplarii antenelor sint similare interferentei undelor invatata in liceu in clasa a 11-a, in capitolul de compunere a oscilatiilor.
Lectia VI Structura de spatiu an E 3. Dreapta si planul ca subspatii ane
 Subspatii ane Lectia VI Structura de spatiu an E 3. Dreapta si planul ca subspatii ane Oana Constantinescu Oana Constantinescu Lectia VI Subspatii ane Table of Contents 1 Structura de spatiu an E 3 2 Subspatii
Subspatii ane Lectia VI Structura de spatiu an E 3. Dreapta si planul ca subspatii ane Oana Constantinescu Oana Constantinescu Lectia VI Subspatii ane Table of Contents 1 Structura de spatiu an E 3 2 Subspatii
Componente şi Circuite Electronice Pasive. Laborator 3. Divizorul de tensiune. Divizorul de curent
 Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
V O. = v I v stabilizator
 Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Laborator 11. Mulţimi Julia. Temă
 Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
TEST DE EVALUARE SUMATIVA
 TEST DE EVALUARE SUMATIVA Profesor: Merfea Romeo Institutia: COLEGIUL NATIONAL ROMAN-VODA Clasa a IX-a Disciplina: Fizica Continuturi vizate: Reflexia si refractia luminii Obiective: sa defineasca fenomenele
TEST DE EVALUARE SUMATIVA Profesor: Merfea Romeo Institutia: COLEGIUL NATIONAL ROMAN-VODA Clasa a IX-a Disciplina: Fizica Continuturi vizate: Reflexia si refractia luminii Obiective: sa defineasca fenomenele
Captura imaginilor. este necesară o sursă de lumină (λ: lungimea de undă a sursei)
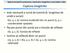 Captura imaginilor este necesară o sursă de lumină (λ: lungimea de undă a sursei) E(x, y, z, λ): lumina incidentă într-un punct (x, y, z coordonatele spațiale) fiecare punct din scenă are o funcție de
Captura imaginilor este necesară o sursă de lumină (λ: lungimea de undă a sursei) E(x, y, z, λ): lumina incidentă într-un punct (x, y, z coordonatele spațiale) fiecare punct din scenă are o funcție de
3. REPREZENTAREA PLANULUI
 3.1. GENERALITĂŢI 3. REPREZENTAREA PLANULUI Un plan este definit, în general, prin trei puncte necoliniare sau prin o dreaptă şi un punct exterior, două drepte concurente sau două drepte paralele (fig.3.1).
3.1. GENERALITĂŢI 3. REPREZENTAREA PLANULUI Un plan este definit, în general, prin trei puncte necoliniare sau prin o dreaptă şi un punct exterior, două drepte concurente sau două drepte paralele (fig.3.1).
prin egalizarea histogramei
 Lucrarea 4 Îmbunătăţirea imaginilor prin egalizarea histogramei BREVIAR TEORETIC Tehnicile de îmbunătăţire a imaginilor bazate pe calculul histogramei modifică histograma astfel încât aceasta să aibă o
Lucrarea 4 Îmbunătăţirea imaginilor prin egalizarea histogramei BREVIAR TEORETIC Tehnicile de îmbunătăţire a imaginilor bazate pe calculul histogramei modifică histograma astfel încât aceasta să aibă o
re se reconstituie imaginea obiectului.
 HOLOGRAFIA Metoda holografiei a fost elaborata în 1948 de catre Denis Gabor, care a descris o metoda prin care se poate obtine imaginea unui obiect din figura generala de difractie produsa de acel obiect.
HOLOGRAFIA Metoda holografiei a fost elaborata în 1948 de catre Denis Gabor, care a descris o metoda prin care se poate obtine imaginea unui obiect din figura generala de difractie produsa de acel obiect.
DIFRACŢIA LUMINII PE FANTE MULTIPLE ŞI REŢELE
 UNIVERSITATEA "POLITEHNICA" DIN BUCUREŞTI DEPARTAMENTUL DE FIZICĂ LABORATORUL DE OPTICĂ BN 1 A DIFRACŢIA LUMINII PE FANTE MULTIPLE ŞI REŢELE DIFRACŢIA LUMINII PE FANTE MULTIPLE ŞI REŢELE 1. Scopul lucrarii
UNIVERSITATEA "POLITEHNICA" DIN BUCUREŞTI DEPARTAMENTUL DE FIZICĂ LABORATORUL DE OPTICĂ BN 1 A DIFRACŢIA LUMINII PE FANTE MULTIPLE ŞI REŢELE DIFRACŢIA LUMINII PE FANTE MULTIPLE ŞI REŢELE 1. Scopul lucrarii
Dreapta in plan. = y y 0
 Dreapta in plan 1 Dreapta in plan i) Presupunem ca planul este inzestrat cu un reper ortonormat de dreapta (O, i, j). Fiecarui punct M al planului ii corespunde vectorul OM numit vector de pozitie al punctului
Dreapta in plan 1 Dreapta in plan i) Presupunem ca planul este inzestrat cu un reper ortonormat de dreapta (O, i, j). Fiecarui punct M al planului ii corespunde vectorul OM numit vector de pozitie al punctului
CUPRINS 5. Reducerea sistemelor de forţe (continuare)... 1 Cuprins..1
 CURS 5 REDUCEREA SISTEMELOR DE FORŢE (CONTINUARE) CUPRINS 5. Reducerea sistemelor de forţe (continuare)...... 1 Cuprins..1 Introducere modul.1 Obiective modul....2 5.1. Teorema lui Varignon pentru sisteme
CURS 5 REDUCEREA SISTEMELOR DE FORŢE (CONTINUARE) CUPRINS 5. Reducerea sistemelor de forţe (continuare)...... 1 Cuprins..1 Introducere modul.1 Obiective modul....2 5.1. Teorema lui Varignon pentru sisteme
Vectori liberi Produs scalar Produs vectorial Produsul mixt. 1 Vectori liberi. 2 Produs scalar. 3 Produs vectorial. 4 Produsul mixt.
 liberi 1 liberi 2 3 4 Segment orientat liberi Fie S spaţiul geometric tridimensional cu axiomele lui Euclid. Orice pereche de puncte din S, notată (A, B) se numeşte segment orientat. Dacă A B, atunci direcţia
liberi 1 liberi 2 3 4 Segment orientat liberi Fie S spaţiul geometric tridimensional cu axiomele lui Euclid. Orice pereche de puncte din S, notată (A, B) se numeşte segment orientat. Dacă A B, atunci direcţia
VII.2. PROBLEME REZOLVATE
 Teoria Circuitelor Electrice Aplicaţii V PROBEME REOVATE R7 În circuitul din fiura 7R se cunosc: R e t 0 sint [V] C C t 0 sint [A] Se cer: a rezolvarea circuitului cu metoda teoremelor Kirchhoff; rezolvarea
Teoria Circuitelor Electrice Aplicaţii V PROBEME REOVATE R7 În circuitul din fiura 7R se cunosc: R e t 0 sint [V] C C t 0 sint [A] Se cer: a rezolvarea circuitului cu metoda teoremelor Kirchhoff; rezolvarea
 11.2 CIRCUITE PENTRU FORMAREA IMPULSURILOR Metoda formării impulsurilor se bazează pe obţinerea unei succesiuni periodice de impulsuri, plecând de la semnale periodice de altă formă, de obicei sinusoidale.
11.2 CIRCUITE PENTRU FORMAREA IMPULSURILOR Metoda formării impulsurilor se bazează pe obţinerea unei succesiuni periodice de impulsuri, plecând de la semnale periodice de altă formă, de obicei sinusoidale.
Optica. Noţiuni generale Reflexia, refracţia şi dispersia luminii Sisteme optice. Elemente de optică ondulatorie
 Optica Noţiuni generale Releia, reracţia şi dispersia luminii Sisteme optice sisteme optice, punct obiect, punct imagine construcţia imaginilor dioptrul seric, sisteme de dioptri oglinzi serice (elemente
Optica Noţiuni generale Releia, reracţia şi dispersia luminii Sisteme optice sisteme optice, punct obiect, punct imagine construcţia imaginilor dioptrul seric, sisteme de dioptri oglinzi serice (elemente
FIZICĂ. Oscilatii mecanice. ş.l. dr. Marius COSTACHE
 FIZICĂ Oscilatii mecanice ş.l. dr. Marius COSTACHE 3.1. OSCILAŢII. Noţiuni generale Oscilaţii mecanice Oscilaţia fenomenul fizic în decursul căruia o anumită mărime fizică prezintă o variaţie periodică
FIZICĂ Oscilatii mecanice ş.l. dr. Marius COSTACHE 3.1. OSCILAŢII. Noţiuni generale Oscilaţii mecanice Oscilaţia fenomenul fizic în decursul căruia o anumită mărime fizică prezintă o variaţie periodică
