Γραφικά Υπολογιστών. Τμήμα Μηχανικών Πληροφορικής ΤΕΙ Ανατολικής Μακεδονίας και Θράκης. Γραφικά Υπολογιστών ΣΤ Εξάμηνο. Δρ Κωνσταντίνος Δεμερτζής
|
|
|
- Ἀλκμήνη Γούναρης
- 6 χρόνια πριν
- Προβολές:
Transcript
1 Τμήμα Μηχανικών Πληροφορικής ΤΕΙ Ανατολικής Μακεδονίας και Θράκης ΣΤ Εξάμηνο Δρ Κωνσταντίνος Δεμερτζής
2 η Σχεδίαση Πολυγώνων και Καμπυλών
3
4 Σχεδίαση Πολυγώνων Τα ευθύγραμμα τμήματα δεν αποτελούν τα μόνα σχήματα που καλούνται να αποτυπωθούν πάνω σε πλεγματικές οθόνες. Τα περισσότερα από τα τελικά σχήματα που σχεδιάζονται, είναι σύνθετα και αποτελούνται μεταξύ άλλων και από πολύγωνα. Παρακάτω εξετάζονται τα πιο συνήθη πολύγωνα και κάποιοι ενδεικτικοί αλγόριθμοι σχεδίασης.
5 Αλγόριθμοι Σχεδίασης Τριγώνου Πολύγραμμα είναι τα σχήματα που ορίζονται από μια σειρά διαδοχικών ευθύγραμμων τμημάτων. Tα πολύγραμμα σχεδιάζονται καλώντας επαναληπτικά τον αλγόριθμο σχεδίασης ευθύγραμμου τμήματος. Το κλειστό πολύγραμμο αποτελεί πολύγωνο. Το πιο απλό πολύγωνο είναι το τρίγωνο και αποτελείται από τρία ευθύγραμμα τμήματα που τέμνονται στις άκρες τους σχηματίζοντας ένα κλειστό σχήμα. Το τρίγωνο είναι πολύ σημαντικό σχήμα για το χώρο των γραφικών καθώς πολλές διαδικασίες εξετάζουν τις επιφάνειες ως τριγωνικά πλέγματα (τριγωνοποίηση). Ως επίπεδα σχήματα, τα πολύγωνα ορίζονται με βάση τις κορυφές τους οι οποίες όταν ενώνονται μεταξύ τους με ακμές ορίζουν: α) ένα τριγωνικό πλέγμα (τα σημεία του σχήματος ανήκουν στις ακμές), β) μια τριγωνική επιφάνεια (χρειάζεται ένας έλεγχος εσωτερικότητας των σημείων για να διαπιστωθεί αν αυτά ανήκουν ή όχι στην επιφάνεια που ορίζεται από τις ακμές).
6 Αλγόριθμοι Σχεδίασης Τριγώνου Ο αλγόριθμος του Bresenham, ως ένας αποδοτικός αλγόριθμος σχεδίασης ευθύγραμμου τμήματος χρησιμοποιείται τρεις φορές, για να σχεδιαστούν οι ακμές του τριγώνου. Ο συγχρονισμός των τριών εκτελέσεων του αλγορίθμου επιτρέπει τη σχεδίαση ανά γραμμή σάρωσης. Για κάθε θέση της γραμμής σάρωσης υπολογίζεται εκ νέου το ευθύγραμμο τμήμα που περιέχει τα εσωτερικά σημεία του τριγώνου και στη συνέχεια χρωματίζονται αυτά τα σημεία αποκαλύπτοντας σταδιακά το επιθυμητό σχήμα.
7 Αλγόριθμοι Σχεδίασης Τριγώνου Στην αρχή τοποθετούνται οι δύο κορυφές πάνω στον οριζόντιο άξονα και υπολογίζονται οι κλίσεις των ευθύγραμμων τμημάτων από την άνω κορυφή προς τη βάση του τριγώνου. Σε κάθε νέα θέση η γραμμή σάρωσης υπολογίζει με βάση τις κλίσεις slope1 και slope2, τις νέες θέσεις των σημείων που ορίζουν την εσωτερική γραμμή. Η drawline (π.χ. Bresenham) είναι η συνάρτηση που καλείται, για να χρωματίσει τα σημεία της γραμμής σάρωσης από το x1 έως το x2. Ο αλγόριθμος που υλοποιεί αυτήν την προσέγγιση παρατίθεται παρακάτω: 1. vertex v1, v2, v3; 2. float slope1 = (v2.x - v1.x) / (v2.y - v1.y); 3. float slope2 = (v3.x - v1.x) / (v3.y - v1.y); 4. float x1 = v1.x; 5. float x2 = v1.x; 6. for (int sliney = v1.y; sline <= v2.y; sline++){ 7. drawline((int)x1, sline, (int)x2, sline); 8. x1+ = slope1; 9. x2+ = slope2; 10. } 11.}
8 Αλγόριθμοι Σχεδίασης Τριγώνου Το παραπάνω παράδειγμα παρουσίαζε τη βολική περίπτωση οι δύο κορυφές του τριγώνου να είναι παράλληλα τοποθετημένες πάνω σε μια οριζόντια ευθεία. Στη γενική περίπτωση, ένα τρίγωνο είναι τοποθετημένο στο 2D επίπεδο, όπως φαίνεται στην Εικόνα παρακάτω:
9 Αλγόριθμοι Σχεδίασης Τριγώνου Η λύση είναι να χωριστεί το τρίγωνο σε δύο μικρότερα τρίγωνα με βάση την οριζόντια γραμμή που διέρχεται από την ενδιάμεση ως προς το ύψος (άξονας y) κορυφή. Το πάνω τρίγωνο σχεδιάζεται με τη βοήθεια του αλγορίθμου που παρουσιάστηκε προηγουμένως, ενώ το κάτω τρίγωνο σχεδιάζεται με μια παραλλαγή του αλγορίθμου που θεωρεί ότι οι πάνω ακμές βρίσκονται στο ίδιο ύψος. Το ποιος αλγόριθμος θα εκτελεστεί κάθε φορά καθορίζεται από τον έλεγχο του τεμαχισμού όπως φαίνεται παρακάτω: 1. sortverticesbyy();// Ταξινόμηση των κορυφών ως προς y 2. if (v2.y == v3.y){ 3. filluprighttriangle(v1, v2, v3); } 4. else if (vt1.y == vt2.y){ 5. fillreversetriangle(v1, v2, v3); 6. } else { 7. Vertice v4 = new Vertice((int)(vt1.x + 8. ((float)(vt2.y - vt1.y) / (float)(vt3.y - vt1.y)) 9.* (vt3.x - vt1.x)), vt2.y); 10.fillUpRightTriangle(g, vt1, vt2, v4); 11.fillReverseTriangle(g, vt2, v4, vt3); 12. } }
10 Αλγόριθμοι Σχεδίασης Τριγώνου Στην αρχή θεωρείται μια λίστα με τις κορυφές του τριγώνου ταξινομημένες ως προς τον άξονα Y. Στη συνέχεια γίνονται μια σειρά έλεγχοι για να διαπιστωθεί αν το τρίγωνο ανήκει ή όχι σε μια από τις βολικές περιπτώσεις (όρθιο ή ανάστροφο τρίγωνο). Αν όχι, τότε τεμαχίζει το τρίγωνο και καλεί τους δύο κατάλληλους αλγορίθμους. Σύμφωνα με μια άλλη προσέγγιση, κάθε τρίγωνο περικλείεται από ένα ορθογώνιο παραλληλόγραμμο του οποίου τα εικονοστοιχεία ελέγχονται αν ανήκουν ή όχι στο τρίγωνο. Με αυτήν την απλή σχετικά τεχνική σχεδιάζεται ένα τρίγωνο χωρίς ταξινόμηση των κορφών του και χωρίς κατάτμηση. Ο έλεγχος εσωτερικότητας των εικονοστοιχείων που περικλείονται από το ορθογώνιο παραλληλόγραμμο καθορίζει ποια εικονοστοιχεία θα χρωματιστούν και ποια όχι.
11 Αλγόριθμοι Σχεδίασης Τριγώνου Ανάκτηση πλαισίου οριοθέτησης του τριγώνου και έλεγχος εσωτερικότητας των εικονοστοιχείων
12 Αλγόριθμοι Σχεδίασης Τριγώνου 1. int maxx = max(v1.x, v2.x, v3.x); 2. int minx = min(v1.x, v2.x, v3.x); 3. int maxy = max(v1.y, v2.y, v3.y); 4. int miny = min(v1.y, v2.y, v3.y); 5. for (int x = minx; x <= maxx; x++){ 6. for (int y = miny; y <= maxy; y++){ 7. if (checkinternal(x,y)){ 8. drawpixel(x, y); 9. } 10.} 11.} Ο κώδικας σχεδίασης τριγώνου με έλεγχο εσωτερικότητας των εικονοστοιχείων
13 Αλγόριθμοι Σάρωσης Πολυγώνου Ο Αλγόριθμος Σάρωσης Πολυγώνου (Scanline polygon fill algorithm) χρησιμοποιείται για να γεμίσει το εσωτερικό ενός πολυγώνου. Η προβληματική αναφέρεται στο ποια εικονοστοιχεία (με βάση τις συντεταγμένες του κέντρου τους) πρέπει να χρωματιστούν για να προκύψει η επιφάνεια που ορίζεται από το πολύγωνο, ή η γραμμή της περιμέτρου στην περίπτωση που δε μας ενδιαφέρουν τα εσωτερικά σημεία. Η σάρωση πολυγώνου βασίζεται στον έλεγχο των σημείων τομής μεταξύ των ακμών του πολυγώνου και της γραμμής σάρωσης. Θεωρούμε γραμμή σάρωσης εκείνη που σαρώνει το πολύγωνο από τη χαμηλότερη θέση (κατά y) έως την υψηλότερη.
14 Αλγόριθμοι Σάρωσης Πολυγώνου Ο αλγόριθμος σάρωσης πολυγώνου ακολουθεί τα παρακάτω βήματα: Βήμα 1: Για κάθε θέση της γραμμής σάρωσης βρες τα σημεία τομής της γραμμής σάρωσης με τις ακμές του πολυγώνου. Βήμα 2: Ταξινόμησε τα σημεία τομής ως προς x. Βήμα 3: Χρωμάτισε τα εικονοστοιχεία που βρίσκονται ανάμεσα σε ζεύγη σημείων τομής [(x1,y1), (x2,y2)] δηλαδή για όσα ισχύει y = y1 = ysl και x1 <= x<= x2, όπου ysl είναι η τρέχουσα θέση της γραμμής σάρωσης. Τα ζεύγη σημείων τομής που προκύπτουν από το δεύτερο βήμα είναι ταξινομημένα ως προς χ, προκειμένου να εφαρμοστεί ο κανόνας των μονών-ζυγών σημείων (έλεγχος ισοτιμίας Parity check). Σύμφωνα με αυτόν τον κανόνα, ξεκινώντας από το αριστερότερο άκρο έχουμε αρχικά μηδέν σημεία τομής.
15 Αλγόριθμοι Σάρωσης Πολυγώνου Ο αλγόριθμος χρωματίζει τα σημεία που βρίσκονται στις περιοχές μονού αριθμού σημείων τομής και δεξιότερα. Αποτέλεσμα της σάρωσης πολυγώνου για τη γραμμή σάρωσης y=3
16 Αλγόριθμοι Σάρωσης Πολυγώνου Υπάρχουν περιπτώσεις που ο παραπάνω αλγόριθμος αποτυγχάνει να αποδώσει με επιτυχία. Τέτοιες περιπτώσεις συμβαίνουν, όταν έχουμε π.χ. μια κορυφή πολυγώνου που βρίσκεται πάνω στη γραμμή σάρωσης. Για το πόσες τομές πρέπει να θεωρήσει ο αλγόριθμος για να λειτουργήσει σωστά, δεν υπάρχει κάποια προφανής λύση που να ισχύει σε όλες τις περιπτώσεις, καθώς άλλοτε μια κορυφή πρέπει να μετρήσει για ένα, δύο ή κανένα σημείο τομής. Στο προηγούμενο παράδειγμα, η κορυφή Ε πρέπει να μετρήσει ως καμία ή δύο, αλλιώς αν μετρήσει ως μία, τότε το τμήμα από το σημείο Ε έως το δεξί άκρο δε θα χρωματιστεί.
17 Αλγόριθμοι Σάρωσης Πολυγώνου Για να αντιμετωπιστούν αυτές οι ιδιάζουσες καταστάσεις, γίνεται μια σειρά από παραδοχές. Δεδομένου ότι κάθε ακμή έχει δύο κορυφές, μόνο η χαμηλότερη κορυφή (κορυφή με το μικρότερο y) θεωρείται έγκυρη. Με αυτόν τον τρόπο θεωρείται ότι υπάρχει μια μικρή μετατόπιση της κορυφής ως προς τον άξονα y, τόσο αμελητέα, ώστε να μην αλλοιώνει την ποιότητα του τελικού αποτελέσματος. Μια δεύτερη παραδοχή θέλει τις οριζόντιες γραμμές να μη μετράνε. Έτσι τα σημεία Α και Γ μετράνε για ένα σημείο τομής το καθένα, τα σημεία Β και Ε μετράνε για μηδέν σημεία τομής και τέλος, τα σημεία Ζ και Δ μετράνε για δύο σημεία. Το μειονέκτημα που εισάγει το παραπάνω σύνολο παραδοχών είναι ότι τα εικονοστοιχεία που βρίσκονται πάνω πάνω σε ένα πολύγωνο δε χρωματίζονται. Το λάθος αυτό θεωρείται ανεκτό, ενώ στην περίπτωση δύο πολυγώνων που μοιράζονται την ίδια ακμή, η αποφυγή χρωματισμού της κοινής ακμής για το κάτω πολύγωνο δεν αποτελεί ουσιαστικό πρόβλημα. Στην περίπτωση που δύο πολύγωνα μοιράζονται την ίδια κάθετη ακμή, τότε η ακμή χρωματίζεται δύο φορές με υπερισχύον το χρώμα του δεύτερου πολυγώνου.
18 Αλγόριθμοι Σάρωσης Πολυγώνου Παρατηρούμε ότι στον αλγόριθμο σάρωσης πολυγώνου τα σημεία τομής των ακμών με τη γραμμή σάρωσης i δε διαφέρουν πολύ από την αμέσως υψηλότερη γραμμή i+1. Αυτό μπορούμε να το εκμεταλλευτούμε για να κάνουμε τον αλγόριθμο πιο γρήγορο και αποδοτικό. Ως παράδειγμα δίνεται το πολύγωνο που φαίνεται στην Εικόνα. Ο πίνακας ακμών του πολυγώνου και οι γραμμές σάρωσης
19 Αλγόριθμοι Σάρωσης Πολυγώνου Δύο διαδοχικά στιγμιότυπα της γραμμής σάρωσης, τα yn και yn+1 διαφέρουν κατά ένα εικονοστοιχείο ως προς τον κάθετο άξονα. Ζητούμενο είναι το πόσο διαφέρουν κατά τον οριζόντιο άξονα. Με βάση την κλίση της ευθείας που δίνεται από τον τύπο: m=(yn+1-yn)/(xn+1-xn) μπορούμε να υπολογίσουμε την οριζόντια μετατόπιση κατά xn+1=χn+1/m. Η παραπάνω συλλογιστική στην πλεγματική οθόνη μπορεί να γραφτεί ως: xn+1=round(xn+1/m), όπου m=δυ/δχ Έτσι, λοιπόν, μπορούμε να διατηρούμε τις τιμές της κάθε γραμμής σάρωσης με τις ακμές του πολυγώνου στη Λίστα Ενεργών Ακμών (ΛΕΑ) και να ελέγχουμε κατά τη μετάβαση από τη μία γραμμή σάρωσης στην επόμενη για το ποιες αλλαγές έχουν επέλθει λόγω της κλίσης της ακμής. Όλες οι ακμές του πολυγώνου διατηρούνται στον Πίνακα Ακμών (ΠΑ).
20 Αλγόριθμοι Σάρωσης Πολυγώνου Μετά τη δημιουργία του Πίνακα Ακμών, ο αλγόριθμος ακολουθεί τα παρακάτω βήματα: 1) Θέσε το Y στο χαμηλότερο Y των εγγραφών του πίνακα ΠΑ 2) Αρχικοποίησε την ΛΕΑ (κενή) 3) Επανάλαβε μέχρι η ΛΕΑ και ο ΠΑ να είναι κενοί (από το Ymin έως το Ymax): 3.1) Μετακίνησε από τον ΠΑ προς την ΛΕΑ τις εγγραφές που έχουν Ymin=Y 3.2) Ταξινόμησε την ΛΕΑ κατά Χ 3.3) Χρωμάτισε τα εικονοστοιχεία της γραμμής σάρωσης χρησιμοποιώντας ζεύγη από συντεταγμένες Χ από την ΛΕΑ. 3.4) Αύξησε την τιμή της γραμμής σάρωσης κατά ) Αφαίρεσε από την ΛΕΑ τις εγγραφές που έχουν Y=Ymax 3.6) Για κάθε μη-κάθετη ακμή στη ΛΕΑ ανανέωσε τα Χ για τη νέα τιμή του Y). Ο αλγόριθμος σάρωσης πολυγώνου (Scan-fill Polygon) μπορεί να γενικευτεί για να χειρίζεται σύνολα πολυγώνων, όταν αυτά είναι ταξινομημένα κατά προτεραιότητα (κατά βάθος zindex).
21 Αλγόριθμοι Σάρωσης Πολυγώνου Μια ιδέα για υλοποίηση του συγκεκριμένου αλγορίθμου παρουσιάζεται παρακάτω: 1. Array ET = readdata(edges[]); 2. Ymin=min(ET[]); 3. AET=null; 4. for (y=ymin; y<=ymax; y++){ 5. MergeSortbyX(ET[y], AET); 6. FillPairsofX(AET); 7. for (int j=0; j=aet.length; j++){ 8. if (edge[j].ymax=y){ 9. remove(edge[j], AET); 10. } 11. Else{ 12.Edge[j].X=edge[j].X+dx/dy; 13. } 14. sortbyx(aet); 15.}
22 Έλεγχος Εσωτερικότητας Σημείων Οι αλγόριθμοι σχεδίασης βασίζονται στον έλεγχο του αν ένα σημείο (εικονοστοιχείο) είναι εσωτερικό ή όχι ενός πολυγώνου. Μια μέθοδος για τον έλεγχο αν το σημείο P ανήκει ή όχι στην επιφάνεια του πολυγώνου Π, το οποίο ορίζεται από την ακολουθία n κορυφών (n1, n2, n-1 με n ακμές), πραγματοποιείται με την αρίθμηση των τομών της ημιευθείας από το P προς το άπειρο. Σύμφωνα με αυτήν την τεχνική ελέγχου ισοτιμίας (parity test), με αφετηρία το σημείο P, θεωρείται μια ημιευθεία προς οποιαδήποτε κατεύθυνση και μετράται ο αριθμός των τομών με τις ακμές του πολυγώνου: Έλεγχος εσωτερικότητας σημείου με έλεγχο ισοτιμίας (parity test)
23 Έλεγχος Εσωτερικότητας Σημείων Αν αυτός ο αριθμός είναι περιττός, τότε το σημείο P βρίσκεται εντός του πολυγώνου Π. Σε αντίθετη περίπτωση, ένας ζυγός αριθμός τομών σημαίνει ότι το σημείο P ανήκει στην εξωτερική περιοχή του Π. Η δεύτερη μέθοδος βασίζεται στην καταμέτρηση του αριθμού των περιελίξεων μιας ακτίνας που ενώνει το σημείο Ρ με την περίμετρο μιας κλειστής καμπύλης Κ για μια πλήρη περιδιάβαση: Έλεγχος εσωτερικότητας σημείου με καταμέτρηση του αριθμού των περιελίξεων
24 Έλεγχος Εσωτερικότητας Σημείων Οι περιελίξεις ορίζονται ως: Για κάθε περιστροφή προς τη θετική φορά (δηλαδή αντίθετα με τους δείκτες του ρολογιού) το Ω(Κ,Ρ) αυξάνεται κατά μία μονάδα. Αντίθετα, η περιστροφή προς την αρνητική φορά (σύμφωνα με τους δείκτες του ρολογιού) αφαιρεί από το Ω (Κ,Ρ) μία μονάδα. Αν στο τέλος ο αριθμός των περιελίξεων είναι περιττός αριθμός, τότε το σημείο Ρ βρίσκεται εντός της κλειστής καμπύλης Κ, διαφορετικά είναι εκτός.
25 Χρωματισμός Εσωτερικού Πολυγώνων Το πρόβλημα του χρωματισμού του εσωτερικού ενός πολυγώνου, δηλαδή σχεδιασμού της επιφάνειας που προσδιορίζεται με βάση μια κλειστή πολυγραμμή μπορεί να διατυπωθεί ως το πρόβλημα επιλογής των εικονοστοιχείων της περιμέτρου και του συνόλου των εσωτερικών εικονοστοιχείων. Για να γεμίσουμε το εσωτερικό ενός πολυγώνου μπορούμε να χρησιμοποιήσουμε τον αλγόριθμο σάρωσης πολυγώνου για να προσδιορίσουμε τα σημεία τομής με τη γραμμή σάρωσης και σε κάθε βήμα σχεδιάζουμε το ευθύγραμμο τμήμα που ενώνει δύο σημεία τομής (PolygonScan-Conversion). Εναλλακτικά μπορούμε να ξεκινήσουμε με ένα εικονοστοιχείο που γνωρίζουμε ότι είναι εσωτερικό του πολυγώνου κα γεμίζουμε τη γειτονική περιοχή μέχρι να συναντήσουμε τα όρια του πολυγώνου. Ο αλγόριθμος εσωτερικού γεμίσματος θεωρεί ότι έχει σχεδιαστεί πρώτα η περίμετρος του πολυγώνου και έχει βρεθεί ένα εσωτερικό σημείο που θα θεωρηθεί ως το σημείο εκκίνησης.
26 Χρωματισμός Εσωτερικού Πολυγώνων Ο ψευδοκώδικας του αλγορίθμου φαίνεται παρακάτω: 1. fillpolygon(x,y){ 2. Color c; 3. C=getColor(x,y); 4. if (c<>fill_color){ 5. setpixel(x,y,color); 6. fillpolygon(x-1,y-1); 7. fillpolygon(x,y+1); 8. fillpolygon(x+1,y+1); 9. fillpolygon(x+1,y); 10.fillPolygon(x+1,y+1); 11.fillPolygon(x,y+1); 12.fillPolygon(x-1,y+1); 13.fillPolygon(x-1,y); 14. } 15.}
27 Χρωματισμός Εσωτερικού Πολυγώνων Η επαναληπτική κλήση της συνάρτησης fillpolygon γίνεται για τα γειτονικά σημεία. Εδώ μπορεί να οριστεί μια γειτονιά είτε πέντε (5) είτε εννέα (9) σημείων όπως φαίνεται στην Εικόνα: Περιοχές εικονοστοιχείων: α) 4 σημείων (αριστερά) και β) 8 σημείων (δεξιά) Για περιοχές με τετραπλή σύνδεση, οι τέσσερις αναδρομικές κλήσεις της fill- Polygon κρίνονται επαρκείς. Σε διαφορετική περίπτωση οι περιοχές με οκταπλή σύνδεση χρειάζονται και τις οκτώ αναδρομικές κλήσεις για να καλύψουν τη γειτονιά των 9 σημείων.
28 Χρωματισμός Εσωτερικού Πολυγώνων Υπάρχουν, όμως, και μειονεκτήματα των δύο προσεγγίσεων. Η τετραπλή σύνδεση ενδέχεται σε ορισμένες περιπτώσεις να σταματά πρόωρα, όπως η περίπτωση στην Εικόνα (πάνω) όπου το πολύγωνο συνεχίζεται προς την πάνω δεξιά κατεύθυνση, αλλά το στένωμα στη μέση κάνει τον αλγόριθμο που βασίζεται στην τετραπλή σύνδεση να σταματήσει, ενώ η οκταπλή σύνδεση του εικονοστοιχείου θα μπορούσε να ολοκληρώσει το γέμισμα. Αντίστοιχα, ούτε η οκταπλή σύνδεση δεν είναι απαλλαγμένη από προβλήματα καθώς όπως φαίνεται στην περίπτωση της Εικόνας (κάτω) υπάρχει διαρροή προς ένα γειτονικό σχήμα:
29 Σχεδίαση Καμπυλών Οι καμπύλες μπορεί να υλοποιηθούν από εξίσωση έλλειψης (κύκλου), υπερβολής, παραβολής ή ακόµη και ζεύγους τεµνόµενων ή παράλληλων ευθειών.
30 Αλγόριθμοι Σχεδίασης Κύκλου Μια άλλη μεγάλη κατηγορία βασικών σχημάτων είναι οι κωνικές τομές. Ξεκινώντας με τον κύκλο που είναι το πιο απλό παράδειγμα κωνικής τομής, τότε από τη γνωστή εξίσωση του κύκλου αν λύσουμε ως προς y: Με αυτόν τον τρόπο υπολογίζονται ζεύγη σημείων (x, y) που χρωματίζονται για να σχεδιαστεί η περίμετρος του κύκλου. Εξετάζοντας τώρα το πρόβλημα της σχεδίασης π.χ. στο δεύτερο οκταμόριο, ο άξονας που μεταβάλλεται γρηγορότερα είναι ο χ. Δηλαδή, αν ένα σημείο διατρέχει τον κύκλο σύμφωνα με τους δείκτες του ρολογιού, τότε η κάθε επόμενη θέση του θα διαφέρει κατά ένα εικονοστοιχείο ως προς τον οριζόντιο άξονα, ενώ ο κάθετος άξονας θα μειώνεται κατά ένα σε κάποιες περιπτώσεις. Η εφαρμογή μιας λύσης που βασίζεται στην εξίσωση του κύκλου αφήνει κενά στη σχεδίαση, πράγμα μη επιτρεπτό. Μάλιστα, όσο αυξάνεται η κλίση, τόσο αυξάνονται και τα κενά που προκύπτουν ενδιάμεσα.
31 Αλγόριθμοι Σχεδίασης Κύκλου O παρακάτω Πίνακας, παρουσιάζει έναν κύκλο ακτίνας r=10 στον οποίο προκύπτουν μη συνεχόμενες για το y τιμές. Βήματα εκτέλεσης του αλγορίθμου σχεδίασης με βάση την εξίσωση του κύκλου από όπου φαίνεται ότι η σχεδίαση δε δίνει ικανοποιητικό αποτέλεσμα διότι δημιουργούνται κενά.
32 Αλγόριθμοι Σχεδίασης Κύκλου Στη συνέχεια θα παρουσιαστούν τρόποι σχεδίασης της περιμέτρου με βάση την οκταπλή συμμετρία που παρουσιάζει το σχήμα του κύκλου. Αυτό σημαίνει ότι αν σχεδιαστεί ένα από τα οκταμόριά του, τα υπόλοιπα τμήματα του κύκλου μπορούν να προκύψουν με εναλλαγή προσήμων στις τιμές των x και y. Αν έχουμε έναν κύκλο ακτίνας r=1 και κέντρο την αρχή των αξόνων, τότε με δεδομένο ένα σημείο (x,y) που ανήκει στον κύκλο μπορούμε να θεωρήσουμε με βεβαιότητα ότι και τα σημεία: [(y, x), (y, -x), (x, -y), (-x, -y), (-y, -x), (-y, x), (-x, y)] ανήκουν επίσης στον ίδιο κύκλο. Αυτό είναι απόρροια της οκταπλής συμμετρίας του κύκλου.
33 Αλγόριθμοι Σχεδίασης Κύκλου Παρατηρούμε ότι σε κάθε μετατόπιση προς τα δεξιά, κατεύθυνση αύξησης του Χ κατά μία μονάδα σε κάθε βήμα, το επόμενο σημείο προς επιλογή είναι είτε το διπλανό του (Xn+1,Yn), είτε το διαγωνίως πιο κάτω (Xn+1,Yn+1), ανάλογα με το πιο από τα δύο βρίσκεται κοντύτερα στον κύκλο, όπως φαίνεται στην Εικόνα: Σχεδίαση με βάση την εξίσωση του κύκλου
34 Αλγόριθμοι Σχεδίασης Κύκλου Αν τώρα θέσουμε έναν παράγοντα μετατόπισης κατά μισό εικονοστοιχείο προς τα πάνω, η συνάρτηση κύκλου γράφεται: Αυτή είναι η μεταβλητή σφάλματος που δίνει την απόφαση για την επιλογή του καταλληλότερου εικονοστοιχείου. Αν η παραπάνω ποσότητα προκύψει μικρότερη του μηδενός, τότε το σημείο ανήκει στο εσωτερικό του κύκλου. Αν είναι μεγαλύτερη του μηδενός, τότε δεν ανήκει στον κύκλο και είναι εξωτερικό σημείο. Τέλος, αν ισούται με μηδέν, τότε είναι σημείο της περιφέρειας του κύκλου. Αν και η μεταβλητή σφάλματος υπολογίζεται ότι πρέπει να αρχικοποιηθεί στην τιμή:
35 Αλγόριθμοι Σχεδίασης Κύκλου Συνολικά η λύση αυτή εκφρασμένη σε ψευδοκώδικα φαίνεται παρακάτω: 1. int x=0; 2. int y=r; 3. int e=-r; 4. while (x <= y) { 5. setpixel(y, x); 6. setpixel (y, -x); 7. setpixel (x, -y); 8. setpixel (-x, -y); 9. setpixel (-y, -x); 10.setPixel (-y, x); 11.setPixel (-x, y); 12. e=e+2*x+1; 13.x=x+1; 14.if (e >= 0) { 15. e=e-2y+2; 16. y=y-1; 17. } }
36 Σχεδίαση Καμπυλών Bezier Οι καμπύλες ελεύθερης μορφής χρησιμοποιούνται κατά κόρον στα γραφικά για να αποδώσουν ποικίλα σχήματα και αντικείμενα σε περιβάλλοντα διανυσματικής σχεδίασης, αλλά και για περιγραφή της κίνησης σε περιβάλλοντα animation. Το πρόβλημα της σχεδίασης καμπυλών μπορεί να λυθεί εφόσον μιλάμε για μοντέλα ομαλών καμπυλών που ορίζονται με μαθηματικό τρόπο. Οι εύκαμπτες καμπύλες (splines) ορίζονται με βάση ένα σύνολο από σημεία ελέγχου όπως είναι οι παραμετρικές καμπύλες Bezier. Ένας αλγόριθμος σχεδίασης, προκειμένου να σχεδιάσει μια καμπύλη Bezier, χρειάζεται να δέχεται ως είσοδό του τη λίστα των σημείων ελέγχου τα οποία θα ορίζουν μοναδικά το σχήμα της καμπύλης (ή της επιφάνειας όταν πρόκειται για γενίκευση σε περισσότερες της μίας διάστασης). Στις καμπύλες Bezier, η μορφή της καμπύλης εξαρτάται μόνο από τα σημεία ελέγχου που ορίζουν την καμπύλη και άρα υπάρχει η επιθυμητή σταθερότητα. Συνήθως χρειάζεται να λυθεί το πρόβλημα της σχεδίασης κυβικής καμπύλης (4 σημεία ελέγχου) καθώς μεγαλύτερης πολυπλοκότητας καμπύλες προκύπτουν από συνδυασμούς διασυνδεμένων καμπυλών (συνέχεια θέσης, κλίσης, καμπυλότητας).
37 Σχεδίαση Καμπυλών Bezier Η καμπύλη Bezier βρίσκεται εντός του κυρτού κελύφους ή περιβλήματος (convex hull) που ορίζεται από τα σημεία ελέγχου της, ενώ παρεμβάλλεται στο πρώτο και στο τελευταίο σημείο διότι P(0)=p0 και P(n)=pn. Αυτό για το πρόβλημα της σχεδίασης σημαίνει ότι το πρώτο και το τελευταίο σημείο της καμπύλης είναι γνωστά, ενώ αναζητούνται τα ενδιάμεσα. Σε περίπτωση συγγραμμικών σημείων ελέγχου προκύπτει ευθύγραμμο τμήμα. Η πολυπλοκότητα της καμπύλης και επομένως και της σχεδίασης είναι ανάλογες με τον αριθμό των σημείων ελέγχου. Έτσι, με n σημεία ελέγχου προκύπτουν n-1 διαδοχικά επίπεδα γραμμικής παρεμβολής για να σχεδιαστεί μια καμπύλη Bezier βαθμού n. Αν B(t) είναι μια καμπύλη Bezier που ορίζεται με βάση τα P0, P1, P2, P3 σημεία ελέγχου και το t παίρνει τιμές στο διάστημα [a, b], τότε για 0 t 1 τα διαστήματα t-a ισούνται με t (το πρώτο τμήμα κάθε ευθύγραμμου τμήματος που ενώνει δύο διαδοχικά σημεία ελέγχου) και το b-t γίνεται 1-t που αντιστοιχεί στο δεύτερο τμήμα.
38 Σχεδίαση Καμπυλών Bezier
39 Σχεδίαση Καμπυλών Bezier Ο ψευδοκώδικας του αλγορίθμου decasteljau ο οποίος παρατίθεται παρακάτω, προϋποθέτει ότι για να σχεδιάσουμε ολόκληρη την καμπύλη, υπολογίζουμε έναένα τα σημεία και τα συνδέουμε με ευθύγραμμα τμήματα, όπως φαίνεται και στις 2 προηγούμενες εικόνες. 1. point tmppoint; 2. double step=0.001; 3. array Points[]=getControlPoints; 4. for (double t=0; t<=1; t+=step){ 5. tmppoint=getcasteljaupoint(length(points)-1, 0, t); 6. setpixel(tmppoint.x, tmppoint.y); } 8. point getcasteljaupoint (int r, int I, double t){ 9. if (r==0) return Points[i]; 10.point p1 = getcasteljaupoint(r-1, i, t); 11.point p2 = getcasteljaupoint(r-1, i+1, t); 12.point respoint; 13.resPoint.X = int((1-t)*p1.x+t*p2.x); 14.resPoint.Y = int((1-t)*p1.y+t*p2.y)); 15.return respoint; }
40 Βιβλιογραφία Σ. Καλαφατούδη, Γραφικά με Υπολογιστή, Εκδόσεις Νέων Τεχνολογιών, Α. Στυλιάδη, Γραφικά με Η/Υ, Εκδόσεις Ζήτη, Θ. Θεοχάρης, Α. Μπέμ, "Γραφικά: Αρχές και Αλγόριθμοι, Εκδόσεις Συμμετρία, Γ. Παρασχάκη, Μ. Παπαδοπούλου, Π. Πατιάς, Σχεδίαση με Η/Υ, Εκδόσεις Ζήτη, J. D. Foley, A. van Dam, S. K. Feiner, J. F. Hughes, R. L. Phillips, Introduction to Computer Graphics, Addison Wesley, Κ. Μουστάκας Ι. Παλιόκας Α. Τσακίρης Δ. Τζοβάρας, (2015), Γραφικά και Εικονική Πραγματικότητα, ISBN: , Λαζαρίνης, Φ, (2015), Πολυμέσα, ISBN: , Γεώργιος Λέπουρας, Αγγελική Αντωνίου, Νίκος Πλαιής, Δημήτρης Χαρίχος, (2015), Ανάπτυξη συστημάτων εικονικής πραγματικότητας, ISBN: ,
Κεφάλαιο 2 - Σχεδίαση
 Κεφάλαιο 2 - Σχεδίαση Σύνοψη Στον τομέα των γραφικών, υπάρχει από τη μια μεριά η μαθηματική περιγραφή των σχημάτων που χαρακτηρίζεται από την ανάλογη αυστηρότητα και από την άλλη οι περιορισμοί της πλεγματικής
Κεφάλαιο 2 - Σχεδίαση Σύνοψη Στον τομέα των γραφικών, υπάρχει από τη μια μεριά η μαθηματική περιγραφή των σχημάτων που χαρακτηρίζεται από την ανάλογη αυστηρότητα και από την άλλη οι περιορισμοί της πλεγματικής
Γραφικά Υπολογιστών. Τμήμα Μηχανικών Πληροφορικής ΤΕΙ Ανατολικής Μακεδονίας και Θράκης. Γραφικά Υπολογιστών ΣΤ Εξάμηνο. Δρ Κωνσταντίνος Δεμερτζής
 Τμήμα Μηχανικών Πληροφορικής ΤΕΙ Ανατολικής Μακεδονίας και Θράκης ΣΤ Εξάμηνο Δρ Κωνσταντίνος Δεμερτζής η Παραμετρική Αναπαράσταση Γεωμετρικών Σχημάτων και Σχεδίαση ευθείας kdemertz@fmenr.duth.gr Αξιολόγηση
Τμήμα Μηχανικών Πληροφορικής ΤΕΙ Ανατολικής Μακεδονίας και Θράκης ΣΤ Εξάμηνο Δρ Κωνσταντίνος Δεμερτζής η Παραμετρική Αναπαράσταση Γεωμετρικών Σχημάτων και Σχεδίαση ευθείας kdemertz@fmenr.duth.gr Αξιολόγηση
5ο Μάθημα Αλγόριθμοι Σχεδίασης Βασικών Σχημάτων
 5ο Μάθημα Αλγόριθμοι Σχεδίασης Βασικών Σχημάτων Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Εισαγωγή Ευθεία Κύκλος Έλλειψη Σύνοψη του σημερινού μαθήματος 1 Εισαγωγή 2 Ευθεία 3 Κύκλος
5ο Μάθημα Αλγόριθμοι Σχεδίασης Βασικών Σχημάτων Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Εισαγωγή Ευθεία Κύκλος Έλλειψη Σύνοψη του σημερινού μαθήματος 1 Εισαγωγή 2 Ευθεία 3 Κύκλος
Γραφικά με υπολογιστές. Διδάσκων: Φοίβος Μυλωνάς. Διάλεξη #07
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Χειμερινό εξάμηνο Γραφικά με υπολογιστές Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διάλεξη #07 Γραμμές και Πολύγωνα: Εισαγωγή Αναπαράσταση 2D και 3D Χρωματισμός πολυγώνων
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Χειμερινό εξάμηνο Γραφικά με υπολογιστές Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διάλεξη #07 Γραμμές και Πολύγωνα: Εισαγωγή Αναπαράσταση 2D και 3D Χρωματισμός πολυγώνων
Εργαστήριο Τεχνολογίας Πολυμέσων & Γραφικών, Τ.Ε.Π Π.Μ, Μάθημα: Γραφικά με Η/Υ
 ΓΡΑΦΙΚΑ Γέμισμα ΑΛΓΟΡΙΘΜΟΙ ΓΕΜΙΣΜΑΤΟΣ Για τις πλεγματικές οθόνες υπάρχουν: Αλγόριθμοι γεμίσματος:, που στηρίζονται στη συνάφεια των pixels του εσωτερικού ενός πολυγώνου Αλγόριθμοι σάρωσης: που στηρίζονται
ΓΡΑΦΙΚΑ Γέμισμα ΑΛΓΟΡΙΘΜΟΙ ΓΕΜΙΣΜΑΤΟΣ Για τις πλεγματικές οθόνες υπάρχουν: Αλγόριθμοι γεμίσματος:, που στηρίζονται στη συνάφεια των pixels του εσωτερικού ενός πολυγώνου Αλγόριθμοι σάρωσης: που στηρίζονται
Γραφικά Υπολογιστών: Σχεδίαση γραμμών (Bresenham), Σχεδίασης Κύκλων, Γέμισμα Πολυγώνων
 1 ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Σχεδίαση γραμμών (Bresenham), Σχεδίασης Κύκλων, Γέμισμα Πολυγώνων Πασχάλης Ράπτης http://aetos.it.teithe.gr/~praptis praptis@it.teithe.gr 2 Περιγραφή
1 ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Σχεδίαση γραμμών (Bresenham), Σχεδίασης Κύκλων, Γέμισμα Πολυγώνων Πασχάλης Ράπτης http://aetos.it.teithe.gr/~praptis praptis@it.teithe.gr 2 Περιγραφή
Γραφικά με Η/Υ Αλγόριθμοι σχεδίασης βασικών 22D D σχημάτων (ευθεία
 Γραφικά με Η/Υ Αλγόριθμοι σχεδίασης βασικών 2D σχημάτων (ευθεία) Σχεδίαση ευθείας θί με σάρωση (παρουσίαση προβλήματος) σχεδίαση ευθείας AB, με σάρωση, όπου A=(0,1) και B=(5,4) ποιο είναι το επόμενο pixel
Γραφικά με Η/Υ Αλγόριθμοι σχεδίασης βασικών 2D σχημάτων (ευθεία) Σχεδίαση ευθείας θί με σάρωση (παρουσίαση προβλήματος) σχεδίαση ευθείας AB, με σάρωση, όπου A=(0,1) και B=(5,4) ποιο είναι το επόμενο pixel
Γραφικά Υπολογιστών. Τμήμα Μηχανικών Πληροφορικής ΤΕΙ Ανατολικής Μακεδονίας και Θράκης. Γραφικά Υπολογιστών ΣΤ Εξάμηνο. Δρ Κωνσταντίνος Δεμερτζής
 Τμήμα Μηχανικών Πληροφορικής ΤΕΙ Ανατολικής Μακεδονίας και Θράκης ΣΤ Εξάμηνο Δρ Κωνσταντίνος Δεμερτζής η Μετασχηματισμοί kdemertz@fmenr.duth.gr Μετασχηματισμοί Κατά τον σχηματισμό του εικονικού κόσμου
Τμήμα Μηχανικών Πληροφορικής ΤΕΙ Ανατολικής Μακεδονίας και Θράκης ΣΤ Εξάμηνο Δρ Κωνσταντίνος Δεμερτζής η Μετασχηματισμοί kdemertz@fmenr.duth.gr Μετασχηματισμοί Κατά τον σχηματισμό του εικονικού κόσμου
Εισαγωγή Αποκοπή ευθείας σε 2Δ Αποκοπή πολυγώνου σε 2Δ Αποκοπή σε 3Δ. 3ο Μάθημα Αποκοπή. Γραφικα. Ευάγγελος Σπύρου
 Εισαγωγή Αποκοπή ευθείας σε 2Δ Αποκοπή πολυγώνου σε 2Δ Αποκοπή σε 3Δ Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Εισαγωγή Αποκοπή ευθείας σε 2Δ Αποκοπή πολυγώνου σε 2Δ Αποκοπή σε
Εισαγωγή Αποκοπή ευθείας σε 2Δ Αποκοπή πολυγώνου σε 2Δ Αποκοπή σε 3Δ Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Εισαγωγή Αποκοπή ευθείας σε 2Δ Αποκοπή πολυγώνου σε 2Δ Αποκοπή σε
ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ
 ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Ξεφυλλίζοντας τα σχολικά βιβλία της Α και Β Λυκείου θα συναντήσουμε τις παρακάτω 10 "βασικές" συναρτήσεις των οποίων τη γραφική παράσταση πρέπει να γνωρίζουμε:
ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Ξεφυλλίζοντας τα σχολικά βιβλία της Α και Β Λυκείου θα συναντήσουμε τις παρακάτω 10 "βασικές" συναρτήσεις των οποίων τη γραφική παράσταση πρέπει να γνωρίζουμε:
Γραφικά με υπολογιστές
 Γραφικά με Υπολογιστές Ενότητα # 3: Εισαγωγή Φοίβος Μυλωνάς Τμήμα Πληροφορικής Φοίβος Μυλωνάς Γραφικά με υπολογιστές 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Γραφικά με Υπολογιστές Ενότητα # 3: Εισαγωγή Φοίβος Μυλωνάς Τμήμα Πληροφορικής Φοίβος Μυλωνάς Γραφικά με υπολογιστές 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Καρτεσιανές συντεταγμένες Γραφική παράσταση συνάρτησης
 Καρτεσιανές συντεταγμένες Γραφική παράσταση συνάρτησης Ορθοκανονικό σύστημα αξόνων ονομάζεται ένα σύστημα από δύο κάθετους άξονες με κοινή αρχή στους οποίους οι μονάδες έχουν το ίδιο μήκος. Υπάρχουν περιπτώσεις
Καρτεσιανές συντεταγμένες Γραφική παράσταση συνάρτησης Ορθοκανονικό σύστημα αξόνων ονομάζεται ένα σύστημα από δύο κάθετους άξονες με κοινή αρχή στους οποίους οι μονάδες έχουν το ίδιο μήκος. Υπάρχουν περιπτώσεις
Η συνάρτηση y = αχ 2. Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd
 Η συνάρτηση y = αχ Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd 1 Η συνάρτηση y = αχ με α 0 Μια συνάρτηση της μορφής y = α + β + γ με α 0 ονομάζεται τετραγωνική συνάρτηση.
Η συνάρτηση y = αχ Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd 1 Η συνάρτηση y = αχ με α 0 Μια συνάρτηση της μορφής y = α + β + γ με α 0 ονομάζεται τετραγωνική συνάρτηση.
Κεφάλαιο 4 ΜΕΤΑΒΟΛΗ ΚΕΝΤΡΟΥ ΑΝΤΩΣΗΣ ΚΑΙ ΜΕΤΑΚΕΝΤΡΟΥ ΛΟΓΩ ΕΓΚΑΡΣΙΑΣ ΚΛΙΣΗΣ
 Κεφάλαιο 4 ΜΕΤΑΒΟΛΗ ΚΕΝΤΡΟΥ ΑΝΤΩΣΗΣ ΚΑΙ ΜΕΤΑΚΕΝΤΡΟΥ ΛΟΓΩ ΕΓΚΑΡΣΙΑΣ ΚΛΙΣΗΣ Σύνοψη Αυτό το κεφάλαιο έχει επίσης επαναληπτικό χαρακτήρα. Σε πρώτο στάδιο διερευνάται η μορφή της καμπύλης την οποία γράφει το
Κεφάλαιο 4 ΜΕΤΑΒΟΛΗ ΚΕΝΤΡΟΥ ΑΝΤΩΣΗΣ ΚΑΙ ΜΕΤΑΚΕΝΤΡΟΥ ΛΟΓΩ ΕΓΚΑΡΣΙΑΣ ΚΛΙΣΗΣ Σύνοψη Αυτό το κεφάλαιο έχει επίσης επαναληπτικό χαρακτήρα. Σε πρώτο στάδιο διερευνάται η μορφή της καμπύλης την οποία γράφει το
ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ
 ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΣΑΝΑΤΛΙΣΜΥ Β ΛΥΚΕΙΥ ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΥ Να δώσετε τους ορισμούς: διάνυσμα, μηδενικό διάνυσμα, μέτρο διανύσματος, μοναδιαίο διάνυσμα Διάνυσμα AB ονομάζεται ένα ευθύγραμμο
ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΣΑΝΑΤΛΙΣΜΥ Β ΛΥΚΕΙΥ ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΥ Να δώσετε τους ορισμούς: διάνυσμα, μηδενικό διάνυσμα, μέτρο διανύσματος, μοναδιαίο διάνυσμα Διάνυσμα AB ονομάζεται ένα ευθύγραμμο
δίου ορισμού, μέσου του τύπου εξαρτημένης μεταβλητής του πεδίου τιμών που λέγεται εικόνα της f για x α f α.
 3.1 Η έννοια της συνάρτησης Ορισμοί Συνάρτηση f από ένα συνόλου Α σε ένα σύνολο Β είναι μια αντιστοιχία των στοιχείων του Α στα στοιχεία του Β, κατά την οποία κάθε στοιχείο του Α αντιστοιχεί σε ένα μόνο
3.1 Η έννοια της συνάρτησης Ορισμοί Συνάρτηση f από ένα συνόλου Α σε ένα σύνολο Β είναι μια αντιστοιχία των στοιχείων του Α στα στοιχεία του Β, κατά την οποία κάθε στοιχείο του Α αντιστοιχεί σε ένα μόνο
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ. Μια παράσταση που περιέχει πράξεις με μεταβλητές (γράμματα) και αριθμούς καλείται αλγεβρική, όπως για παράδειγμα η : 2x+3y-8
 ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
ΣΥΝΑΡΤΗΣΕΩΝ. f3 x = και
 7 ΜΕΛΕΤΗ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Στο κεφάλαιο αυτό θα δούμε πώς, με τη βοήθεια των πληροφοριών που α- ποκτήσαμε μέχρι τώρα, μπορούμε να χαράξουμε με όσο το δυνατόν μεγαλύτερη ακρίβεια τη γραφική παράσταση
7 ΜΕΛΕΤΗ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Στο κεφάλαιο αυτό θα δούμε πώς, με τη βοήθεια των πληροφοριών που α- ποκτήσαμε μέχρι τώρα, μπορούμε να χαράξουμε με όσο το δυνατόν μεγαλύτερη ακρίβεια τη γραφική παράσταση
Οδηγίες για το Geogebra Μωυσιάδης Πολυχρόνης Δόρτσιος Κώστας
 Οδηγίες για το Geogebra Μωυσιάδης Πολυχρόνης Δόρτσιος Κώστας Η πρώτη οθόνη μετά την εκτέλεση του προγράμματος διαφέρει κάπως από τα προηγούμενα λογισμικά, αν και έχει αρκετά κοινά στοιχεία. Αποτελείται
Οδηγίες για το Geogebra Μωυσιάδης Πολυχρόνης Δόρτσιος Κώστας Η πρώτη οθόνη μετά την εκτέλεση του προγράμματος διαφέρει κάπως από τα προηγούμενα λογισμικά, αν και έχει αρκετά κοινά στοιχεία. Αποτελείται
Γραφικά Ι. Ενότητα 2: Αλγόριθμοι Σχεδίασης. Θεοχάρης Θεοχάρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών
 Γραφικά Ι Ενότητα 2: Αλγόριθμοι Σχεδίασης Θεοχάρης Θεοχάρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Ενότητα 2 Αλγόριθμοι Σχεδίασης Σχεδίαση 2Δ οθόνες αποτελούνται από διακριτά πλέγματα
Γραφικά Ι Ενότητα 2: Αλγόριθμοι Σχεδίασης Θεοχάρης Θεοχάρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Ενότητα 2 Αλγόριθμοι Σχεδίασης Σχεδίαση 2Δ οθόνες αποτελούνται από διακριτά πλέγματα
Ορισμός Τετραγωνική ονομάζεται κάθε συνάρτηση της μορφής y = αx 2 + βx + γ με α 0.
 ΜΕΡΟΣ Α. Η ΣΥΝΑΡΤΗΣΗ =α +β+γ,α 0 337. Η ΣΥΝΑΡΤΗΣΗ =α +β+γ ME α 0 Ορισμός Τετραγωνική ονομάζεται κάθε συνάρτηση της μορφής = α + β + γ με α 0. Η συνάρτηση = α +β+γ με α > 0 Η γραφική παράσταση της συνάρτησης
ΜΕΡΟΣ Α. Η ΣΥΝΑΡΤΗΣΗ =α +β+γ,α 0 337. Η ΣΥΝΑΡΤΗΣΗ =α +β+γ ME α 0 Ορισμός Τετραγωνική ονομάζεται κάθε συνάρτηση της μορφής = α + β + γ με α 0. Η συνάρτηση = α +β+γ με α > 0 Η γραφική παράσταση της συνάρτησης
Τι είναι Αποκοπή (clip)?
 Αποκοπή Τι είναι Αποκοπή (clip)? Η διαδικασία απεικόνισης μόνο των τμημάτων των αντικειμένων που βρίσκονται μέσα σε μια περιοχή Από μεγαλύτερη 2Δ σκηνή στην οποία έχουμε ήδη τιμές για τα piels Κατά την
Αποκοπή Τι είναι Αποκοπή (clip)? Η διαδικασία απεικόνισης μόνο των τμημάτων των αντικειμένων που βρίσκονται μέσα σε μια περιοχή Από μεγαλύτερη 2Δ σκηνή στην οποία έχουμε ήδη τιμές για τα piels Κατά την
ΜΕΛΕΤΗ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ
 5 ΜΕΛΕΤΗ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Εισαγωγή Στο κεφάλαιο αυτό θα δούμε πώς, με τη βοήθεια των πληροφοριών που α- ποκτήσαμε μέχρι τώρα, μπορούμε να χαράξουμε με όσο το δυνατόν μεγαλύτερη ακρίβεια τη γραφική παράσταση
5 ΜΕΛΕΤΗ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Εισαγωγή Στο κεφάλαιο αυτό θα δούμε πώς, με τη βοήθεια των πληροφοριών που α- ποκτήσαμε μέχρι τώρα, μπορούμε να χαράξουμε με όσο το δυνατόν μεγαλύτερη ακρίβεια τη γραφική παράσταση
Αλγόριθμοι παράστασης βασικών σχημάτων σε πλεγματικές οθόνες
 Αλγόριθμοι παράστασης βασικών σχημάτων σε πλεγματικές οθόνες Αλγόριθμοι Παράστασης Βασικών Σχημάτων Προσέγγιση μαθηματικών σχημάτων από διακριτά pxels: Ευθύγραμμο τμήμα, κύκλος, κωνικές τομές, πολύγωνο.
Αλγόριθμοι παράστασης βασικών σχημάτων σε πλεγματικές οθόνες Αλγόριθμοι Παράστασης Βασικών Σχημάτων Προσέγγιση μαθηματικών σχημάτων από διακριτά pxels: Ευθύγραμμο τμήμα, κύκλος, κωνικές τομές, πολύγωνο.
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ. Ημερομηνία: Πέμπτη 12 Απριλίου 2018 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ
 ΑΠΟ 0/04/018 ΕΩΣ 14/04/018 ΤΑΞΗ: ΜΑΘΗΜΑ: Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Πέμπτη 1 Απριλίου 018 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α1. Να αποδείξετε ότι η εφαπτομένη ε του κύκλου
ΑΠΟ 0/04/018 ΕΩΣ 14/04/018 ΤΑΞΗ: ΜΑΘΗΜΑ: Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Πέμπτη 1 Απριλίου 018 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α1. Να αποδείξετε ότι η εφαπτομένη ε του κύκλου
ΑΣΚΗΣΕΙΣ ΚΑΤΑ Ι ΑΚΤΙΚΗ ΕΝΟΤΗΤΑ
 Ο ΚΕΦΑΛΑΙΟ ΑΣΚΗΣΕΙΣ ΚΑΤΑ Ι ΑΚΤΙΚΗ ΕΝΟΤΗΤΑ ΣΥΝΟΛΑ ΕΡΩΤΗΣΕΙΣ ΤΥΠΟΥ «ΣΩΣΤΟ ΛΑΘΟΣ». {,3,5,7,... } { / = ν +, ν Ν} =. = {} 0 3. Αν Α Β τότε Α Β = Α 4. 5 {,3,5,7 } 5. Αν Α= {, 3,7} και Β= {,3} 7, τότε Α=Β 6.
Ο ΚΕΦΑΛΑΙΟ ΑΣΚΗΣΕΙΣ ΚΑΤΑ Ι ΑΚΤΙΚΗ ΕΝΟΤΗΤΑ ΣΥΝΟΛΑ ΕΡΩΤΗΣΕΙΣ ΤΥΠΟΥ «ΣΩΣΤΟ ΛΑΘΟΣ». {,3,5,7,... } { / = ν +, ν Ν} =. = {} 0 3. Αν Α Β τότε Α Β = Α 4. 5 {,3,5,7 } 5. Αν Α= {, 3,7} και Β= {,3} 7, τότε Α=Β 6.
Γραμμή. Σημείο. κεφαλαίο γράμμα. Κάθε γραμμή. αποτελείται. Ευθεία κι αν αρχή και χωρίς. τέλος! x x
 1. Οι Πρωταρχικές Γεωμετρικές Έννοιες Σημείο Γραμμή Δεν έχει διαστάσεις!! Υπάρχει μόνο στο μυαλό μας. Συμβολίζεται με κεφαλαίο γράμμα. Κάθε γραμμή αποτελείται από άπειρα σημεία. Ευθεία Δεν είναι εύκολο
1. Οι Πρωταρχικές Γεωμετρικές Έννοιες Σημείο Γραμμή Δεν έχει διαστάσεις!! Υπάρχει μόνο στο μυαλό μας. Συμβολίζεται με κεφαλαίο γράμμα. Κάθε γραμμή αποτελείται από άπειρα σημεία. Ευθεία Δεν είναι εύκολο
Αλγόριθµοι Παράστασης Βασικών Σχηµάτων
 Αλγόριθµοι Παράστασης Βασικών Σχηµάτων Προσέγγιση µαθηµατικών σχηµάτων από διακριτά pixels: Ευθύγραµµο τµήµα, κύκλος, κωνικές τοµές, πολύγωνο. S/W ή H/W. Θέσεις αντικειµένων και φωτεινών πηγών Θέση παρατηρητή
Αλγόριθµοι Παράστασης Βασικών Σχηµάτων Προσέγγιση µαθηµατικών σχηµάτων από διακριτά pixels: Ευθύγραµµο τµήµα, κύκλος, κωνικές τοµές, πολύγωνο. S/W ή H/W. Θέσεις αντικειµένων και φωτεινών πηγών Θέση παρατηρητή
Μεθοδολογία Έλλειψης
 Μεθοδολογία Έλλειψης Έλλειψη ονομάζεται ο γεωμετρικός τόπος των σημείων, των οποίων το άθροισμα των αποστάσεων από δύο σταθερά σημεία Ε και Ε είναι σταθερό και μεγαλύτερο από την απόσταση (ΕΕ ). Στη Φύση
Μεθοδολογία Έλλειψης Έλλειψη ονομάζεται ο γεωμετρικός τόπος των σημείων, των οποίων το άθροισμα των αποστάσεων από δύο σταθερά σημεία Ε και Ε είναι σταθερό και μεγαλύτερο από την απόσταση (ΕΕ ). Στη Φύση
II.6 ΙΣΟΣΤΑΘΜΙΚΕΣ. 1. Γραφήματα-Επιφάνειες: z= 2. Γραμμική προσέγγιση-εφαπτόμενο επίπεδο. 3. Ισοσταθμικές: f(x, y) = c
 II.6 ΙΣΟΣΤΑΘΜΙΚΕΣ.Γραφήματα-Επιφάνειες.Γραμμική προσέγγιση-εφαπτόμενο επίπεδο 3.Ισοσταθμικές 4.Κλίση ισοσταθμικών 5.Διανυσματική ή Ιακωβιανή παράγωγος 6.Ιδιότητες των ισοσταθμικών 7.κυρτότητα των ισοσταθμικών
II.6 ΙΣΟΣΤΑΘΜΙΚΕΣ.Γραφήματα-Επιφάνειες.Γραμμική προσέγγιση-εφαπτόμενο επίπεδο 3.Ισοσταθμικές 4.Κλίση ισοσταθμικών 5.Διανυσματική ή Ιακωβιανή παράγωγος 6.Ιδιότητες των ισοσταθμικών 7.κυρτότητα των ισοσταθμικών
ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ
 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ Άσκηση 1. Έστω ότι η συνάρτηση f: R R είναι γνησίως αύξουσα στο R και η γραφική της παράσταση τέµνει τον άξονα y y στο. Να λύσετε την ανίσωση: f(x 9)
ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ Άσκηση 1. Έστω ότι η συνάρτηση f: R R είναι γνησίως αύξουσα στο R και η γραφική της παράσταση τέµνει τον άξονα y y στο. Να λύσετε την ανίσωση: f(x 9)
Στοιχεία Συναρτήσεων. 1. Να βρεθεί το πεδίο ορισμού των παρακάτω συναρτήσεων: στ. x 1
 Στοιχεία Συναρτήσεων 1. Να βρεθεί το πεδίο ορισμού των παρακάτω συναρτήσεων: 1 α. f() β. f() 3 6 8 3 1 γ. g() δ. g() ( 6)( 5) 4 ε. h() 4 στ. h() 4 ζ. ε. στ. 1 φ() η. 1 1 1 r() 5 6 1 r() 1 5 6 φ() 5. Στις
Στοιχεία Συναρτήσεων 1. Να βρεθεί το πεδίο ορισμού των παρακάτω συναρτήσεων: 1 α. f() β. f() 3 6 8 3 1 γ. g() δ. g() ( 6)( 5) 4 ε. h() 4 στ. h() 4 ζ. ε. στ. 1 φ() η. 1 1 1 r() 5 6 1 r() 1 5 6 φ() 5. Στις
Γραφικά με Η/Υ Αλγ λ ό γ ρ ό ιθ ρ μοι κύκλου & έλλειψης
 Γραφικά με Η/Υ Αλγόριθμοι κύκλου & έλλειψης Τεχνική μέσου σημείου (μέσο έ σημείο Q) NE pixel Q Μέσο σημείο M E pixel P = ( x p, y p ) x x + 1 = p Προηγούμενο pixel Επιλογές για το Επιλογές για το τρέχων
Γραφικά με Η/Υ Αλγόριθμοι κύκλου & έλλειψης Τεχνική μέσου σημείου (μέσο έ σημείο Q) NE pixel Q Μέσο σημείο M E pixel P = ( x p, y p ) x x + 1 = p Προηγούμενο pixel Επιλογές για το Επιλογές για το τρέχων
Διαλέξεις #05 & #06. Διδάσκων: Φοίβος Μυλωνάς. Γραφικά με υπολογιστές. Αλγόριθμος Σχεδίασης Κύκλου Αλγόριθμος Σχεδίασης Έλλειψης
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Χειμερινό εξάμηνο Γραφικά με υπολογιστές Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διαλέξεις #05 & #06 Αλγόριθμος Σχεδίασης Κύκλου Αλγόριθμος Σχεδίασης Έλλειψης Φοίβος
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Χειμερινό εξάμηνο Γραφικά με υπολογιστές Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διαλέξεις #05 & #06 Αλγόριθμος Σχεδίασης Κύκλου Αλγόριθμος Σχεδίασης Έλλειψης Φοίβος
Φύλλο Εργασίας για την y=αx 2
 Πρόβλημα Σε ένα τετραγωνικό περιβόλι πλευράς 10m πρόκειται να χτιστεί μια αποθήκη σχήματος ορθογωνίου, όπως φαίνεται στο διπλανό σχήμα. Α) Να βρεθούν οι διαστάσεις της αποθήκης συναρτήσει του x, αν γνωρίζετε
Πρόβλημα Σε ένα τετραγωνικό περιβόλι πλευράς 10m πρόκειται να χτιστεί μια αποθήκη σχήματος ορθογωνίου, όπως φαίνεται στο διπλανό σχήμα. Α) Να βρεθούν οι διαστάσεις της αποθήκης συναρτήσει του x, αν γνωρίζετε
Γραφικά Υπολογιστών. Τμήμα Μηχανικών Πληροφορικής ΤΕΙ Ανατολικής Μακεδονίας και Θράκης. Γραφικά Υπολογιστών ΣΤ Εξάμηνο. Δρ Κωνσταντίνος Δεμερτζής
 Τμήμα Μηχανικών Πληροφορικής ΤΕΙ Ανατολικής Μακεδονίας και Θράκης ΣΤ Εξάμηνο Δρ Κωνσταντίνος Δεμερτζής η Προαπαιτούμενα για kdemertz@fmenr.duth.gr Αξιολόγηση Μαθήματος Τρόποι αξιολόγησης Γραπτή Εξέταση
Τμήμα Μηχανικών Πληροφορικής ΤΕΙ Ανατολικής Μακεδονίας και Θράκης ΣΤ Εξάμηνο Δρ Κωνσταντίνος Δεμερτζής η Προαπαιτούμενα για kdemertz@fmenr.duth.gr Αξιολόγηση Μαθήματος Τρόποι αξιολόγησης Γραπτή Εξέταση
ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ
 ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ ΚΑΤΑΚΟΡΥΦΗ-ΟΡΙΖΟΝΤΙΑ ΜΕΤΑΤΟΠΙΣΗ ΚΑΜΠΥΛΗΣ Να σχεδιάσετε στο ίδιο σύστημα αξόνων τις γραφικές παραστάσεις των συναρτήσεων: f ()=, g()= +3,h()= -3 Να σχεδιάσετε στο ίδιο σύστημα
ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ ΚΑΤΑΚΟΡΥΦΗ-ΟΡΙΖΟΝΤΙΑ ΜΕΤΑΤΟΠΙΣΗ ΚΑΜΠΥΛΗΣ Να σχεδιάσετε στο ίδιο σύστημα αξόνων τις γραφικές παραστάσεις των συναρτήσεων: f ()=, g()= +3,h()= -3 Να σχεδιάσετε στο ίδιο σύστημα
Συμπεριφορά συναρτήσεως σε κλειστές φραγμένες περιοχές. (x 0, y 0, f(x 0, y 0 ) z = L(x, y)
 11.7. Aκρότατα και σαγματικά σημεία 903 39. Εκτίμηση μέγιστου σφάλματος Έστω ότι u e sin και ότι τα,, και μπορούν να μετρηθούν με μέγιστα δυνατά σφάλματα 0,, 0,6, και / 180, αντίστοιχα. Εκτιμήστε το μέγιστο
11.7. Aκρότατα και σαγματικά σημεία 903 39. Εκτίμηση μέγιστου σφάλματος Έστω ότι u e sin και ότι τα,, και μπορούν να μετρηθούν με μέγιστα δυνατά σφάλματα 0,, 0,6, και / 180, αντίστοιχα. Εκτιμήστε το μέγιστο
Μελέτη της συνάρτησης ψ = α χ 2
 Μελέτη της συνάρτησης ψ = α χ Η γραφική της παράσταση είναι μια καμπύλη που λέγεται παραβολή. Ανάλογα με το πρόσημο του α έχω και τα αντίστοιχα συμπεράσματα. αν α > 0 1) Η γραφική της παράσταση είναι πάνω
Μελέτη της συνάρτησης ψ = α χ Η γραφική της παράσταση είναι μια καμπύλη που λέγεται παραβολή. Ανάλογα με το πρόσημο του α έχω και τα αντίστοιχα συμπεράσματα. αν α > 0 1) Η γραφική της παράσταση είναι πάνω
ΑΛΓΕΒΡΑ B ΛΥΚΕΙΟΥ. Γενικής Παιδείας ΑΠΑΝΤΗΣΕΙΣ ΛΥΣΕΙΣ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ
 ΑΛΓΕΒΡΑ B ΛΥΚΕΙΥ Γενικής Παιδείας ΑΠΑΝΤΗΣΕΙΣ ΛΥΣΕΙΣ ΣΧΛΙΚΥ ΒΙΒΛΙΥ Σχολικό βιβλίο: Απαντήσεις Λύσεις Κεφάλαιο ο: Συστήματα Γραμμικά συστήματα Α ΜΑΔΑΣ Έχουμε: = 4 i = 6 = + = + = = Άρα, η λύση του συστήματος
ΑΛΓΕΒΡΑ B ΛΥΚΕΙΥ Γενικής Παιδείας ΑΠΑΝΤΗΣΕΙΣ ΛΥΣΕΙΣ ΣΧΛΙΚΥ ΒΙΒΛΙΥ Σχολικό βιβλίο: Απαντήσεις Λύσεις Κεφάλαιο ο: Συστήματα Γραμμικά συστήματα Α ΜΑΔΑΣ Έχουμε: = 4 i = 6 = + = + = = Άρα, η λύση του συστήματος
1 ο ΦΥΛΛΑΔΙΟ ΑΣΚΗΣΕΩΝ - ΑΛΓΟΡΙΘΜΟΙ
 Δ.Π.Θ. - Πολυτεχνική Σχολή Τμήμα Μηχανικών Παραγωγής & Διοίκησης Ακαδ. έτος 2017-2018 Τομέας Συστημάτων Παραγωγής Εξάμηνο A Αναπληρωτής Καθηγητής Στέφανος Δ. Κατσαβούνης 03 ΟΚΤ 2017 ΜΑΘΗΜΑ : ΕΙΣΑΓΩΓΗ ΣΤΗΝ
Δ.Π.Θ. - Πολυτεχνική Σχολή Τμήμα Μηχανικών Παραγωγής & Διοίκησης Ακαδ. έτος 2017-2018 Τομέας Συστημάτων Παραγωγής Εξάμηνο A Αναπληρωτής Καθηγητής Στέφανος Δ. Κατσαβούνης 03 ΟΚΤ 2017 ΜΑΘΗΜΑ : ΕΙΣΑΓΩΓΗ ΣΤΗΝ
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ Β ΓΥΜΝΑΣΙΟΥ ΜΕΡΟΣ 1ο «ΑΛΓΕΒΡΑ»
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ Β ΓΥΜΝΑΣΙΥ ΜΕΡΣ ο «ΑΛΓΕΒΡΑ». Να υπολογίσετε την τιμή της παράστασης: Α = ( + ) 4( ) 8, όταν = 0,45. Απλοποιούμε πρώτα την παράσταση : Α = ( + ) 4( ) 8 = = + 6 4 + 4 8
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ Β ΓΥΜΝΑΣΙΥ ΜΕΡΣ ο «ΑΛΓΕΒΡΑ». Να υπολογίσετε την τιμή της παράστασης: Α = ( + ) 4( ) 8, όταν = 0,45. Απλοποιούμε πρώτα την παράσταση : Α = ( + ) 4( ) 8 = = + 6 4 + 4 8
Μεθοδολογία Παραβολής
 Μεθοδολογία Παραβολής Παραβολή είναι ο γεωμετρικός τόπος των σημείων που ισαπέχουν από μια σταθερή ευθεία, την επονομαζόμενη διευθετούσα (δ), και από ένα σταθερό σημείο Ε που λέγεται εστία της παραβολής.
Μεθοδολογία Παραβολής Παραβολή είναι ο γεωμετρικός τόπος των σημείων που ισαπέχουν από μια σταθερή ευθεία, την επονομαζόμενη διευθετούσα (δ), και από ένα σταθερό σημείο Ε που λέγεται εστία της παραβολής.
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΓΕΝΙΚΑ ΘΕΜΑ Α. , έχει κατακόρυφη ασύμπτωτη την x 0.
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΓΕΝΙΚΑ ΘΕΜΑ Α Άσκηση Θεωρούμε τον παρακάτω ισχυρισμό: «Αν η συνάρτηση την» ορίζεται στο τότε δεν μπορεί να έχει κατακόρυφη ασύμπτωτη ) Να χαρακτηρίσετε τον παραπάνω ισχυρισμό γράφοντας
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΓΕΝΙΚΑ ΘΕΜΑ Α Άσκηση Θεωρούμε τον παρακάτω ισχυρισμό: «Αν η συνάρτηση την» ορίζεται στο τότε δεν μπορεί να έχει κατακόρυφη ασύμπτωτη ) Να χαρακτηρίσετε τον παραπάνω ισχυρισμό γράφοντας
Διδάσκων: Φοίβος Μυλωνάς
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Χειμερινό εξάμηνο Γραφικά με υπολογιστές Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διάλεξη #08 Αποκοπή (εισαγωγή) Σημειακή Αποκοπή Αποκοπή Ευθύγραμμων Τμημάτων (line
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Χειμερινό εξάμηνο Γραφικά με υπολογιστές Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διάλεξη #08 Αποκοπή (εισαγωγή) Σημειακή Αποκοπή Αποκοπή Ευθύγραμμων Τμημάτων (line
Κεφ 3 ο. - Συναρτήσεις.
 Μαθηματικά B Γυμνασίου Κεφ 3 ο. - Συναρτήσεις. Μέρος Α. Θεωρία. 1. Τι λέμε συνάρτηση; 2. Με τι αντιστοιχούμε κάθε σημείο Μ στο επίπεδο; 3. Πως λέγεται ο άξονας χ χ και πως ο άξονας ψ ψ; 4. Τι είναι το
Μαθηματικά B Γυμνασίου Κεφ 3 ο. - Συναρτήσεις. Μέρος Α. Θεωρία. 1. Τι λέμε συνάρτηση; 2. Με τι αντιστοιχούμε κάθε σημείο Μ στο επίπεδο; 3. Πως λέγεται ο άξονας χ χ και πως ο άξονας ψ ψ; 4. Τι είναι το
Αλγόριθμοι Ταξινόμησης Μέρος 2
 Αλγόριθμοι Ταξινόμησης Μέρος 2 Μανόλης Κουμπαράκης 1 Προχωρημένοι Αλγόριθμοι Ταξινόμησης Στη συνέχεια θα παρουσιάσουμε τρείς προχωρημένους αλγόριθμους ταξινόμησης: treesort, quicksort και mergesort. 2
Αλγόριθμοι Ταξινόμησης Μέρος 2 Μανόλης Κουμπαράκης 1 Προχωρημένοι Αλγόριθμοι Ταξινόμησης Στη συνέχεια θα παρουσιάσουμε τρείς προχωρημένους αλγόριθμους ταξινόμησης: treesort, quicksort και mergesort. 2
7.1 ΜΕΛΕΤΗ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ
 7.1 ΜΕΛΕΤΗ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ f ( ) 1. Μορφή της συνάρτησης f ( ) Ιδιότητες Έχει πεδίο ορισµού ολο το R Είναι άρτια, άρα συµµετρική ως προς τον άξονα y y Είναι γνησίως φθίνουσα στο διάστηµα (,0] Είναι γνησίως
7.1 ΜΕΛΕΤΗ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ f ( ) 1. Μορφή της συνάρτησης f ( ) Ιδιότητες Έχει πεδίο ορισµού ολο το R Είναι άρτια, άρα συµµετρική ως προς τον άξονα y y Είναι γνησίως φθίνουσα στο διάστηµα (,0] Είναι γνησίως
Η συνάρτηση y = αχ 2 + βχ + γ
 Η συνάρτηση y αχ + βχ + γ Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd 1 Η συνάρτηση y αx + βx + γ με α 0 Μια συνάρτηση της μορφής y αx + βx + γ με α 0 ονομάζεται τετραγωνική
Η συνάρτηση y αχ + βχ + γ Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd 1 Η συνάρτηση y αx + βx + γ με α 0 Μια συνάρτηση της μορφής y αx + βx + γ με α 0 ονομάζεται τετραγωνική
6.1 Η ΕΝΝΟΙΑ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ
 ΟΡΙΣΜΟΣ 6. ΣΥΝΑΡΤΗΣΕΙΣ 6.1 Η ΕΝΝΟΙΑ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ Ονομάζουμε συνάρτηση από ένα σύνολο Α σε ένα σύνολο Β μια διαδικασία (κανόνα) f, με την οποία κάθε στοιχείο του συνόλου Α αντιστοιχίζεται σε ένα ακριβώς
ΟΡΙΣΜΟΣ 6. ΣΥΝΑΡΤΗΣΕΙΣ 6.1 Η ΕΝΝΟΙΑ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ Ονομάζουμε συνάρτηση από ένα σύνολο Α σε ένα σύνολο Β μια διαδικασία (κανόνα) f, με την οποία κάθε στοιχείο του συνόλου Α αντιστοιχίζεται σε ένα ακριβώς
Αλγόριθμοι Σχεδίασης
 Γραφικά & Οπτικοποίηση Κεφάλαιο 2 Αλγόριθμοι Σχεδίασης Σχεδίαση 2Δοθόνες αποτελούνται από διακριτά πλέγματα εικονοστοιχείων (pixels) Σχεδίαση: μετατροπή 2Δ στοιχειωδών σχημάτων σε διακριτή παράσταση εικονοστοιχείων
Γραφικά & Οπτικοποίηση Κεφάλαιο 2 Αλγόριθμοι Σχεδίασης Σχεδίαση 2Δοθόνες αποτελούνται από διακριτά πλέγματα εικονοστοιχείων (pixels) Σχεδίαση: μετατροπή 2Δ στοιχειωδών σχημάτων σε διακριτή παράσταση εικονοστοιχείων
ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1 ΜΑΘΗΜΑ 1 ο +2 ο ΕΝΝΟΙΑ ΔΙΑΝΥΣΜΑΤΟΣ Διάνυσμα ορίζεται ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ένα ευθύγραμμο τμήμα
ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1 ΜΑΘΗΜΑ 1 ο +2 ο ΕΝΝΟΙΑ ΔΙΑΝΥΣΜΑΤΟΣ Διάνυσμα ορίζεται ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ένα ευθύγραμμο τμήμα
ΚΕΦΑΛΑΙΟ 2: ΑΛΓΟΡΙΘΜΟΙ ΕΥΘΕΙΑΣ ΚΥΚΛΟΥ -ΈΛΛΕΙΨΗΣ
 ΚΕΦΑΛΑΙΟ : ΑΛΓΟΡΙΘΜΟΙ ΕΥΘΕΙΑΣ ΚΥΚΛΟΥ -ΈΛΛΕΙΨΗΣ Μια εικόνα μπορεί να περιγραφεί με πολλούς τρόπους. Αν υποθέσουμε ότι έχουμε μια προβολή ψηφιδοπλέγματος, μια εικόνα καθορίζεται πλήρως από το σύνολο των
ΚΕΦΑΛΑΙΟ : ΑΛΓΟΡΙΘΜΟΙ ΕΥΘΕΙΑΣ ΚΥΚΛΟΥ -ΈΛΛΕΙΨΗΣ Μια εικόνα μπορεί να περιγραφεί με πολλούς τρόπους. Αν υποθέσουμε ότι έχουμε μια προβολή ψηφιδοπλέγματος, μια εικόνα καθορίζεται πλήρως από το σύνολο των
4. 1 Η ΣΥΝΑΡΤΗΣΗ Y=AX 2 ME A 0
 ΜΕΡΟΣ Α. Η ΣΥΝΑΡΤΗΣΗ Y=AX ME A 0 5. Η ΣΥΝΑΡΤΗΣΗ Y=AX ME A 0 Ορισμοί Ονομάζουμε συνάρτηση την διαδικασία με την οποία σε κάθε τιμή της μεταβλητής αντιστοιχίζουμε μια μόνο τιμή της μεταβλητής. Ονομάζουμε
ΜΕΡΟΣ Α. Η ΣΥΝΑΡΤΗΣΗ Y=AX ME A 0 5. Η ΣΥΝΑΡΤΗΣΗ Y=AX ME A 0 Ορισμοί Ονομάζουμε συνάρτηση την διαδικασία με την οποία σε κάθε τιμή της μεταβλητής αντιστοιχίζουμε μια μόνο τιμή της μεταβλητής. Ονομάζουμε
Μεθοδολογία Υπερβολής
 Μεθοδολογία Υπερβολής Υπερβολή ονομάζεται ο γεωμετρικός τόπος των σημείων, των οποίων η απόλυτη τιμή της διαφοράς των αποστάσεων από δύο σταθερά σημεία Ε και Ε είναι σταθερή και μικρότερη από την απόσταση
Μεθοδολογία Υπερβολής Υπερβολή ονομάζεται ο γεωμετρικός τόπος των σημείων, των οποίων η απόλυτη τιμή της διαφοράς των αποστάσεων από δύο σταθερά σημεία Ε και Ε είναι σταθερή και μικρότερη από την απόσταση
Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο
 Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο Σύνοψη Στο κεφάλαιο αυτό παρουσιάζεται η ιδέα του συμπτωτικού πολυωνύμου, του πολυωνύμου, δηλαδή, που είναι του μικρότερου δυνατού βαθμού και που, για συγκεκριμένες,
Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο Σύνοψη Στο κεφάλαιο αυτό παρουσιάζεται η ιδέα του συμπτωτικού πολυωνύμου, του πολυωνύμου, δηλαδή, που είναι του μικρότερου δυνατού βαθμού και που, για συγκεκριμένες,
1 ΘΕΩΡΙΑΣ...με απάντηση
 1 ΘΕΩΡΙΑΣ.....με απάντηση ΑΛΓΕΒΡΑ Κεφάλαιο 1 0 Εξισώσεις Ανισώσεις 1. Τι ονομάζεται Αριθμητική και τι Αλγεβρική παράσταση; Ονομάζεται Αριθμητική παράσταση μια παράσταση που περιέχει πράξεις μεταξύ αριθμών.
1 ΘΕΩΡΙΑΣ.....με απάντηση ΑΛΓΕΒΡΑ Κεφάλαιο 1 0 Εξισώσεις Ανισώσεις 1. Τι ονομάζεται Αριθμητική και τι Αλγεβρική παράσταση; Ονομάζεται Αριθμητική παράσταση μια παράσταση που περιέχει πράξεις μεταξύ αριθμών.
ΟΜΑΔΟΠΟΙΗΣΗ ΤΩΝ ΠΑΡΑΤΗΡΗΣΕΩΝ
 9 ο ΜΑΘΗΜΑ ΟΜΑΔΟΠΟΙΗΣΗ ΤΩΝ ΠΑΡΑΤΗΡΗΣΕΩΝ Πότε κάνουμε ομαδοποίηση των παρατηρήσεων; Όταν το πλήθος των τιμών μιας μεταβλητής είναι αρκετά μεγάλο κάνουμε ομαδοποίηση των παρατηρήσεων. Αυτό συμβαίνει είτε
9 ο ΜΑΘΗΜΑ ΟΜΑΔΟΠΟΙΗΣΗ ΤΩΝ ΠΑΡΑΤΗΡΗΣΕΩΝ Πότε κάνουμε ομαδοποίηση των παρατηρήσεων; Όταν το πλήθος των τιμών μιας μεταβλητής είναι αρκετά μεγάλο κάνουμε ομαδοποίηση των παρατηρήσεων. Αυτό συμβαίνει είτε
Εφαρμοσμένα Μαθηματικά ΙΙ 1ο Σετ Ασκήσεων (Λύσεις) Διανύσματα, Ευθείες Επίπεδα, Επιφάνειες 2ου βαθμού Επιμέλεια: Ι. Λυχναρόπουλος
 Εφαρμοσμένα Μαθηματικά ΙΙ ο Σετ Ασκήσεων (Λύσεις) Διανύσματα, Ευθείες Επίπεδα, Επιφάνειες ου βαθμού Επιμέλεια: Ι. Λυχναρόπουλος. Βρείτε το διάνυσμα με άκρα το Α(3,-,5) και Β(5,,-) ΑΒ=< 5 3, ( ), 5 >=
Εφαρμοσμένα Μαθηματικά ΙΙ ο Σετ Ασκήσεων (Λύσεις) Διανύσματα, Ευθείες Επίπεδα, Επιφάνειες ου βαθμού Επιμέλεια: Ι. Λυχναρόπουλος. Βρείτε το διάνυσμα με άκρα το Α(3,-,5) και Β(5,,-) ΑΒ=< 5 3, ( ), 5 >=
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΑΝΑΠΤΥΞΗ ΚΑΙ ΣΧΕΔΙΑΣΗ ΛΟΓΙΣΜΙΚΟΥ Η γλώσσα προγραμματισμού C ΕΡΓΑΣΤΗΡΙΟ 3: Πίνακες, βρόχοι, συναρτήσεις 1 Ιουνίου 2017 Το σημερινό εργαστήριο
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΑΝΑΠΤΥΞΗ ΚΑΙ ΣΧΕΔΙΑΣΗ ΛΟΓΙΣΜΙΚΟΥ Η γλώσσα προγραμματισμού C ΕΡΓΑΣΤΗΡΙΟ 3: Πίνακες, βρόχοι, συναρτήσεις 1 Ιουνίου 2017 Το σημερινό εργαστήριο
ΑΛΓΟΡΙΘΜΟΙ ΕΥΘΕΙΑΣ ΚΥΚΛΟΥ - ΕΛΛΕΙΨΗΣ
 ΚΕΦΑΛΑΙΟ : ΑΛΓΟΡΙΘΜΟΙ ΕΥΘΕΙΑΣ ΚΥΚΛΟΥ - ΕΛΛΕΙΨΗΣ Μια εικόνα μπορεί να περιγραφεί με πολλούς τρόπους. Αν υποθέσουμε ότι έχουμε μια προβολή ψηφιδοπλέγματος, μια εικόνα καθορίζεται πλήρως από το σύνολο των
ΚΕΦΑΛΑΙΟ : ΑΛΓΟΡΙΘΜΟΙ ΕΥΘΕΙΑΣ ΚΥΚΛΟΥ - ΕΛΛΕΙΨΗΣ Μια εικόνα μπορεί να περιγραφεί με πολλούς τρόπους. Αν υποθέσουμε ότι έχουμε μια προβολή ψηφιδοπλέγματος, μια εικόνα καθορίζεται πλήρως από το σύνολο των
ΕΝΟΤΗΤΑ 4 ΕΙΔΗ ΓΡΑΜΜΩΝ, ΕΙΔΗ ΤΡΙΓΩΝΩΝ, ΠΑΡΑΛΛΗΛΟΓΡΑΜΜΑ, ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ
 ΕΝΟΤΗΤΑ 4 ΕΙΔΗ ΓΡΑΜΜΩΝ, ΕΙΔΗ ΤΡΙΓΩΝΩΝ, ΠΑΡΑΛΛΗΛΟΓΡΑΜΜΑ, ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ ΑΡΙΘΜΟΙ Εκτίμηση και μέτρηση Μ3.6 Εκτιμούν, μετρούν, ταξινομούν και κατασκευάζουν γωνίες (με ή χωρίς τη χρήση της
ΕΝΟΤΗΤΑ 4 ΕΙΔΗ ΓΡΑΜΜΩΝ, ΕΙΔΗ ΤΡΙΓΩΝΩΝ, ΠΑΡΑΛΛΗΛΟΓΡΑΜΜΑ, ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ ΑΡΙΘΜΟΙ Εκτίμηση και μέτρηση Μ3.6 Εκτιμούν, μετρούν, ταξινομούν και κατασκευάζουν γωνίες (με ή χωρίς τη χρήση της
Μαθηματική Εισαγωγή Συναρτήσεις
 Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας Διανύσματα Καστοριά,
Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας Διανύσματα Καστοριά,
ΕΝΔΕΙΚΤΙΚΕΣ ΛΥΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 2017
 ΕΝΔΕΙΚΤΙΚΕΣ ΛΥΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 7 ΘΕΜΑ Α A Έστω συνάρτηση f, η οποία είναι συνεχής σε ένα διάστημα Δ Αν f σε κάθε εσωτερικό σημείο του Δ, τότε να αποδείξετε ότι η f είναι γνησίως αύξουσα
ΕΝΔΕΙΚΤΙΚΕΣ ΛΥΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 7 ΘΕΜΑ Α A Έστω συνάρτηση f, η οποία είναι συνεχής σε ένα διάστημα Δ Αν f σε κάθε εσωτερικό σημείο του Δ, τότε να αποδείξετε ότι η f είναι γνησίως αύξουσα
Τάξη B. Μάθημα: Η Θεωρία σε Ερωτήσεις. Επαναληπτικά Θέματα. Επαναληπτικά Διαγωνίσματα. Επιμέλεια: Κώστας Κουτσοβασίλης. α Ε
 Ν β K C Ε -α Ο α Ε Τάξη B Μ -β Λ Μάθημα: Η Θεωρία σε Ερωτήσεις Επαναληπτικά Θέματα Επαναληπτικά Διαγωνίσματα Επιμέλεια: Διανύσματα Ερωτήσεις θεωρίας 1. Πως ορίζεται το διάνυσμα;. Τι λέγεται μηδενικό διάνυσμα;
Ν β K C Ε -α Ο α Ε Τάξη B Μ -β Λ Μάθημα: Η Θεωρία σε Ερωτήσεις Επαναληπτικά Θέματα Επαναληπτικά Διαγωνίσματα Επιμέλεια: Διανύσματα Ερωτήσεις θεωρίας 1. Πως ορίζεται το διάνυσμα;. Τι λέγεται μηδενικό διάνυσμα;
ΤΟΠΙΚΑ ΑΚΡΟΤΑΤΑ ΠΡΟΒΛΗΜΑΤΑ ΑΚΡΟΤΑΤΩΝ
 Ενότητα 1 ΤΟΠΙΚΑ ΑΚΡΟΤΑΤΑ ΠΡΟΒΛΗΜΑΤΑ ΑΚΡΟΤΑΤΩΝ Ασκήσεις για λύση 3 3, < 1). Δίνεται η συνάρτηση f ( ). 6, Να βρείτε : i ) την παράγωγο της f, ii) τα κρίσιμα σημεία της f. ). Να μελετήσετε ως προς τη μονοτονία
Ενότητα 1 ΤΟΠΙΚΑ ΑΚΡΟΤΑΤΑ ΠΡΟΒΛΗΜΑΤΑ ΑΚΡΟΤΑΤΩΝ Ασκήσεις για λύση 3 3, < 1). Δίνεται η συνάρτηση f ( ). 6, Να βρείτε : i ) την παράγωγο της f, ii) τα κρίσιμα σημεία της f. ). Να μελετήσετε ως προς τη μονοτονία
Κεφάλαιο 1: Κίνηση και γεωμετρικά σχήματα
 Ασκήσεις της Ενότητας 2 : Ζωγραφίζοντας με το ΒΥΟΒ -1- α. Η χρήση της πένας Κεφάλαιο 1: Κίνηση και γεωμετρικά σχήματα Υπάρχουν εντολές που μας επιτρέπουν να επιλέξουμε το χρώμα της πένας, καθώς και το
Ασκήσεις της Ενότητας 2 : Ζωγραφίζοντας με το ΒΥΟΒ -1- α. Η χρήση της πένας Κεφάλαιο 1: Κίνηση και γεωμετρικά σχήματα Υπάρχουν εντολές που μας επιτρέπουν να επιλέξουμε το χρώμα της πένας, καθώς και το
Εργασία 2. Παράδοση 20/1/08 Οι ασκήσεις είναι βαθμολογικά ισοδύναμες
 Εργασία Παράδοση 0/1/08 Οι ασκήσεις είναι βαθμολογικά ισοδύναμες 1. Υπολογίστε τα παρακάτω όρια: Α. Β. Γ. όπου x> 0, y > 0 Δ. όπου Κάνετε απευθείας τις πράξεις χωρίς να χρησιμοποιήσετε παραγώγους. Επιβεβαιώστε
Εργασία Παράδοση 0/1/08 Οι ασκήσεις είναι βαθμολογικά ισοδύναμες 1. Υπολογίστε τα παρακάτω όρια: Α. Β. Γ. όπου x> 0, y > 0 Δ. όπου Κάνετε απευθείας τις πράξεις χωρίς να χρησιμοποιήσετε παραγώγους. Επιβεβαιώστε
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ
 ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΒΑΣΙΚΟΙ ΤΥΠΟΙ ΑΠΟ ΤΗΝ ΘΕΩΡΙΑ ΔΙΑΝΥΣΜΑΤΑ ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΔΙΑΝΥΣΜΑΤΟΣ Αρχή και Πέρας Φορέας Διεύθυνση (Συγγραμμικά διανύσματα) Μέτρο Κατεύθυνση (Ομόρροπα Αντίρροπα διανύσματα)
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΒΑΣΙΚΟΙ ΤΥΠΟΙ ΑΠΟ ΤΗΝ ΘΕΩΡΙΑ ΔΙΑΝΥΣΜΑΤΑ ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΔΙΑΝΥΣΜΑΤΟΣ Αρχή και Πέρας Φορέας Διεύθυνση (Συγγραμμικά διανύσματα) Μέτρο Κατεύθυνση (Ομόρροπα Αντίρροπα διανύσματα)
21. ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 4 - ΔΗΜΙΟΥΡΓΩΝΤΑΣ ΜΕ ΤΟ BYOB BYOB. Αλγόριθμος Διαδικασία Παράμετροι
 21. ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 4 - ΔΗΜΙΟΥΡΓΩΝΤΑΣ ΜΕ ΤΟ BYOB BYOB Αλγόριθμος Διαδικασία Παράμετροι Τι είναι Αλγόριθμος; Οι οδηγίες που δίνουμε με λογική σειρά, ώστε να εκτελέσουμε μια διαδικασία ή να επιλύσουμε ένα
21. ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 4 - ΔΗΜΙΟΥΡΓΩΝΤΑΣ ΜΕ ΤΟ BYOB BYOB Αλγόριθμος Διαδικασία Παράμετροι Τι είναι Αλγόριθμος; Οι οδηγίες που δίνουμε με λογική σειρά, ώστε να εκτελέσουμε μια διαδικασία ή να επιλύσουμε ένα
Προτεινόμενο διαγώνισμα Φυσικής Α Λυκείου
 Προτεινόμενο διαγώνισμα Φυσικής Α Λυκείου Θέμα 1 ο Σε κάθε μια από τις παρακάτω προτάσεις 1-5 να επιλέξετε τη μια σωστή απάντηση: 1. Όταν ένα σώμα ισορροπεί τότε: i. Ο ρυθμός μεταβολής της ταχύτητάς του
Προτεινόμενο διαγώνισμα Φυσικής Α Λυκείου Θέμα 1 ο Σε κάθε μια από τις παρακάτω προτάσεις 1-5 να επιλέξετε τη μια σωστή απάντηση: 1. Όταν ένα σώμα ισορροπεί τότε: i. Ο ρυθμός μεταβολής της ταχύτητάς του
) = Απόσταση σημείου από ευθεία. Υπολογισμός Εμβαδού Τριγώνου. και A
 [Επιλογή Ιαν.. Εμβαδόν Τριγώνου ΣΤΟΧΟΙ: Ο µαθητής ϖρέϖει: να είναι ικανός να υϖολογίζει την αϖόσταση σηµείου αϖό ευθεία να είναι ικανός να υϖολογίζει το εµβαδό ενός τριγώνου αϖό τις συντεταγµένες των κορυφών
[Επιλογή Ιαν.. Εμβαδόν Τριγώνου ΣΤΟΧΟΙ: Ο µαθητής ϖρέϖει: να είναι ικανός να υϖολογίζει την αϖόσταση σηµείου αϖό ευθεία να είναι ικανός να υϖολογίζει το εµβαδό ενός τριγώνου αϖό τις συντεταγµένες των κορυφών
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ. Μαθηματικά 2. Σταύρος Παπαϊωάννου
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ Μαθηματικά Σταύρος Παπαϊωάννου Ιούνιος 5 Τίτλος Μαθήματος Περιεχόμενα Χρηματοδότηση... Error! Bookmark not defned. Σκοποί Μαθήματος (Επικεφαλίδα
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ Μαθηματικά Σταύρος Παπαϊωάννου Ιούνιος 5 Τίτλος Μαθήματος Περιεχόμενα Χρηματοδότηση... Error! Bookmark not defned. Σκοποί Μαθήματος (Επικεφαλίδα
Μελέτη της ευθύγραμμης ομαλά μεταβαλλόμενης κίνησης σώματος με χρήση συστήματος φωτοπύλης-χρονομέτρου. Περιγραφή - Θεωρητικές προβλέψεις - Σχεδιασμός
 Εργαστήριο Φυσικής Λυκείου Επιμέλεια: Κ. Παπαμιχάλης Μελέτη της ευθύγραμμης ομαλά μεταβαλλόμενης κίνησης σώματος με χρήση συστήματος φωτοπύλης-χρονομέτρου Περιγραφή - Θεωρητικές προβλέψεις - Σχεδιασμός
Εργαστήριο Φυσικής Λυκείου Επιμέλεια: Κ. Παπαμιχάλης Μελέτη της ευθύγραμμης ομαλά μεταβαλλόμενης κίνησης σώματος με χρήση συστήματος φωτοπύλης-χρονομέτρου Περιγραφή - Θεωρητικές προβλέψεις - Σχεδιασμός
ENOTHTA 1.1 ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ
 ENOTHTA. ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ ΜΕΡΟΣ ο. Πώς προσδιορίζουμε τη θέση των αντικειμένων; A O M B ' y P Ì(,y) Ð Για τον προσδιορισμό της θέσης πάνω σε μία ευθεία πρέπει να έχουμε ένα σημείο της
ENOTHTA. ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ ΜΕΡΟΣ ο. Πώς προσδιορίζουμε τη θέση των αντικειμένων; A O M B ' y P Ì(,y) Ð Για τον προσδιορισμό της θέσης πάνω σε μία ευθεία πρέπει να έχουμε ένα σημείο της
ΑΛΓΕΒΡΑ - ΚΕΦΑΛΑΙΟ 4ο Εξισώσεις - Ανισώσεις Δευτέρου Βαθμού
 ΑΛΓΕΒΡΑ - ΚΕΦΑΛΑΙΟ 4ο Εξισώσεις - Ανισώσεις Δευτέρου Βαθμού 97 98 ΕΡΩΤΗΣΕΙΣ ΑΝΑΠΤΥΞΗΣ 1. Να λυθεί η εξίσωση: 1 1 1 ( x+ )(x ) = x 3 3 9. Αν η εξίσωση (x - 3) λ + 3 = λ x έχει ρίζα τον αριθμό, να υπολογιστεί
ΑΛΓΕΒΡΑ - ΚΕΦΑΛΑΙΟ 4ο Εξισώσεις - Ανισώσεις Δευτέρου Βαθμού 97 98 ΕΡΩΤΗΣΕΙΣ ΑΝΑΠΤΥΞΗΣ 1. Να λυθεί η εξίσωση: 1 1 1 ( x+ )(x ) = x 3 3 9. Αν η εξίσωση (x - 3) λ + 3 = λ x έχει ρίζα τον αριθμό, να υπολογιστεί
Κεφάλαιο 3 Βασική Σχεδίαση και Επεξεργασία
 Περιεχόμενα Πρόλογος... 7 Εισαγωγή... 9 Κεφάλαιο 1: Στοιχεία Λειτουργίας του Υπολογιστή και του προγράμματος AutoCAD... 11 Κεφάλαιο 2: Στοιχεία Λειτουργικού Συστήματος... 15 Κεφάλαιο 3: Βασική Σχεδίαση
Περιεχόμενα Πρόλογος... 7 Εισαγωγή... 9 Κεφάλαιο 1: Στοιχεία Λειτουργίας του Υπολογιστή και του προγράμματος AutoCAD... 11 Κεφάλαιο 2: Στοιχεία Λειτουργικού Συστήματος... 15 Κεφάλαιο 3: Βασική Σχεδίαση
ΑΣΚΗΣΕΙΣ ΘΕΜΑ Β. 0και 4 x 3 0.
 ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 1: ΕΝΝΟΙΑ ΠΡΑΓΜΑΤΙΚΗΣ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ ΣΥΝΑΡΤΗΣΗΣ. IΣΟΤΗΤΑ ΣΥΝΑΡΤΗΣΕΩΝ - ΠΡΑΞΕΙΣ ΜΕ ΣΥΝΑΡΤΗΣΕΙΣ - ΣΥΝΘΕΣΗ ΣΥΝΑΡΤΗΣΕΩΝ [Ενότητα
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 1: ΕΝΝΟΙΑ ΠΡΑΓΜΑΤΙΚΗΣ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ ΣΥΝΑΡΤΗΣΗΣ. IΣΟΤΗΤΑ ΣΥΝΑΡΤΗΣΕΩΝ - ΠΡΑΞΕΙΣ ΜΕ ΣΥΝΑΡΤΗΣΕΙΣ - ΣΥΝΘΕΣΗ ΣΥΝΑΡΤΗΣΕΩΝ [Ενότητα
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΤΗΣ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΤΗΣ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΘΕΜΑ ο _6950 α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του μηδενός, το οποίο να
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΤΗΣ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΘΕΜΑ ο _6950 α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του μηδενός, το οποίο να
α) f(x(t), y(t)) = 0,
 Ρητές καμπύλες Μια επίπεδη αλγεβρική καμπύλη V (f) είναι το σύνολο όλων των σημείων του επιπέδου K 2 που μηδενίζουν κάποιο συγκεκριμένο ανάγωγο πολυώνυμο f K[x, y], δηλαδή V (f) = {(x 0, y 0 ) K 2 f(x
Ρητές καμπύλες Μια επίπεδη αλγεβρική καμπύλη V (f) είναι το σύνολο όλων των σημείων του επιπέδου K 2 που μηδενίζουν κάποιο συγκεκριμένο ανάγωγο πολυώνυμο f K[x, y], δηλαδή V (f) = {(x 0, y 0 ) K 2 f(x
Άσκηση 1 η ( x 2) 2. i) Να βρείτε την τιμή της παράστασης Α, αν χ = 0. ii) Να βρείτε την τιμή της παράστασης Β, αν χ = 2 2 [ 3 8 ( 3) ]
![Άσκηση 1 η ( x 2) 2. i) Να βρείτε την τιμή της παράστασης Α, αν χ = 0. ii) Να βρείτε την τιμή της παράστασης Β, αν χ = 2 2 [ 3 8 ( 3) ] Άσκηση 1 η ( x 2) 2. i) Να βρείτε την τιμή της παράστασης Α, αν χ = 0. ii) Να βρείτε την τιμή της παράστασης Β, αν χ = 2 2 [ 3 8 ( 3) ]](/thumbs/64/51524102.jpg) ά ς w w w.e - m at hs.g r ά έ ί ς ά ά έ ά ς ί ά Άσκηση 1 η i) Να βρείτε την τιμή της παράστασης Α, αν χ = 0 4 2 3 3 6 3 ( x 2) 2 x 1 x x 1 x 2 ii) Να βρείτε την τιμή της παράστασης Β, αν χ = 2 3 27 3 2
ά ς w w w.e - m at hs.g r ά έ ί ς ά ά έ ά ς ί ά Άσκηση 1 η i) Να βρείτε την τιμή της παράστασης Α, αν χ = 0 4 2 3 3 6 3 ( x 2) 2 x 1 x x 1 x 2 ii) Να βρείτε την τιμή της παράστασης Β, αν χ = 2 3 27 3 2
Αριθμητική εύρεση ριζών μη γραμμικών εξισώσεων
 Αριθμητική εύρεση ριζών μη γραμμικών εξισώσεων Με τον όρο μη γραμμικές εξισώσεις εννοούμε εξισώσεις της μορφής: f( ) 0 που προέρχονται από συναρτήσεις f () που είναι μη γραμμικές ως προς. Περιέχουν δηλαδή
Αριθμητική εύρεση ριζών μη γραμμικών εξισώσεων Με τον όρο μη γραμμικές εξισώσεις εννοούμε εξισώσεις της μορφής: f( ) 0 που προέρχονται από συναρτήσεις f () που είναι μη γραμμικές ως προς. Περιέχουν δηλαδή
Ένας απλός και γρήγορος αλγόριθμος για την αποκοπή γραμμών στο Scratch
 Ένας απλός και γρήγορος αλγόριθμος για την αποκοπή γραμμών στο Scratch Ματθές Δημήτριος 1, Μαγουλάς Αντώνιος 2 1 Εκπαιδευτικός Πληροφορικής ΠΕ86, dimmat@gmail.com 2 Εκπαιδευτικός Πληροφορικής ΠΕ03, amagul@yahoo.com
Ένας απλός και γρήγορος αλγόριθμος για την αποκοπή γραμμών στο Scratch Ματθές Δημήτριος 1, Μαγουλάς Αντώνιος 2 1 Εκπαιδευτικός Πληροφορικής ΠΕ86, dimmat@gmail.com 2 Εκπαιδευτικός Πληροφορικής ΠΕ03, amagul@yahoo.com
ΠΕΡΙΓΡΑΦΗ ΤΗΣ ΚΙΝΗΣΗΣ ΤΩΝ ΣΩΜΑΤΩΝ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ ΕΥΘΥΓΡΑΜΜΗ ΟΜΑΛΑ ΜΕΤΑΒΑΛΛΟΜΕΝΗ ΚΙΝΗΣΗ (Ε.Ο.Μ.Κ.) Με διάγραμμα :
 Νόμος Νόμοι Πρότυπο ΠΕΡΙΓΡΑΦΗ ΤΗΣ ΚΙΝΗΣΗΣ ΤΩΝ ΣΩΜΑΤΩΝ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ ΕΥΘΥΓΡΑΜΜΗ ΟΜΑΛΑ ΜΕΤΑΒΑΛΛΟΜΕΝΗ ΚΙΝΗΣΗ (Ε.Ο.Μ.Κ.) Πρότυπο ευθύγραμμης ομαλά μεταβαλλόμενης κίνησης (Ε.Ο.Μ.Κ) Όταν η επιτάχυνση ενός
Νόμος Νόμοι Πρότυπο ΠΕΡΙΓΡΑΦΗ ΤΗΣ ΚΙΝΗΣΗΣ ΤΩΝ ΣΩΜΑΤΩΝ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ ΕΥΘΥΓΡΑΜΜΗ ΟΜΑΛΑ ΜΕΤΑΒΑΛΛΟΜΕΝΗ ΚΙΝΗΣΗ (Ε.Ο.Μ.Κ.) Πρότυπο ευθύγραμμης ομαλά μεταβαλλόμενης κίνησης (Ε.Ο.Μ.Κ) Όταν η επιτάχυνση ενός
Αποκοπή 4.1. Εργα: : & ΣΚΕΠΣΙΣ (ΕΠΕΑΚ - ΥΠΕΠΘ) Τµήµα Πληροφορικής 1 2 (SCS) Θέση παρατηρητή. Θέσεις αντικειµένων και φωτεινών πηγών
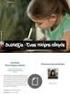 Αποκοπή Αποκοπή αντικειµένου (π.χ. πολυγώνου) ως προς αντικείµενο αποκοπής (π.χ. πολύγωνο, πυραµίδα, κύβος). Για αποφυγή αντεστραµµένης εµφάνισης αντικειµένων όπισθεν παρατηρητή. Για σηµαντική µείωση όγκου
Αποκοπή Αποκοπή αντικειµένου (π.χ. πολυγώνου) ως προς αντικείµενο αποκοπής (π.χ. πολύγωνο, πυραµίδα, κύβος). Για αποφυγή αντεστραµµένης εµφάνισης αντικειµένων όπισθεν παρατηρητή. Για σηµαντική µείωση όγκου
Μαθηματική Εισαγωγή Συναρτήσεις
 Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς Καστοριά, Ιούλιος 14 A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας
Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς Καστοριά, Ιούλιος 14 A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας
Απαλλακτική Εργασία Γραφικά & Εικονική Πραγματικότητα. Παπαπαύλου Χρήστος ΑΜ: 6609
 Απαλλακτική Εργασία Γραφικά & Εικονική Πραγματικότητα Παπαπαύλου Χρήστος ΑΜ: 6609 Αναπαράσταση μοντέλου Το 3D μοντέλο το αποθηκεύουμε στην μνήμη με τις εξής δομές δεδομένων: Λίστα κορυφών Λίστα τριγώνων
Απαλλακτική Εργασία Γραφικά & Εικονική Πραγματικότητα Παπαπαύλου Χρήστος ΑΜ: 6609 Αναπαράσταση μοντέλου Το 3D μοντέλο το αποθηκεύουμε στην μνήμη με τις εξής δομές δεδομένων: Λίστα κορυφών Λίστα τριγώνων
lim είναι πραγµατικοί αριθµοί, τότε η f είναι συνεχής στο x 0. β) Να εξετάσετε τη συνέχεια της συνάρτησης f (x) =
 Ερωτήσεις ανάπτυξης. ** α) Να αποδείξετε ότι αν τα όρια lim - f () - f - είναι πραγµατικοί αριθµοί, τότε η f είναι συνεχής στο. ( ) και β) Να εξετάσετε τη συνέχεια της συνάρτησης f () = lim + στο σηµείο
Ερωτήσεις ανάπτυξης. ** α) Να αποδείξετε ότι αν τα όρια lim - f () - f - είναι πραγµατικοί αριθµοί, τότε η f είναι συνεχής στο. ( ) και β) Να εξετάσετε τη συνέχεια της συνάρτησης f () = lim + στο σηµείο
ΣΧΕΔΙΑΣΗ ΜΗΧΑΝΟΛΟΓΙΚΩΝ ΚΑΤΑΣΚΕΥΩΝ ΜΕ Η/Υ (Computer Aided Design)
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΧΕΔΙΑΣΗ ΜΗΧΑΝΟΛΟΓΙΚΩΝ ΚΑΤΑΣΚΕΥΩΝ ΜΕ Η/Υ (Computer Aided Design) Ενότητα # 2: Στερεοί Μοντελοποιητές (Solid Modelers) Δρ Κ. Στεργίου
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΧΕΔΙΑΣΗ ΜΗΧΑΝΟΛΟΓΙΚΩΝ ΚΑΤΑΣΚΕΥΩΝ ΜΕ Η/Υ (Computer Aided Design) Ενότητα # 2: Στερεοί Μοντελοποιητές (Solid Modelers) Δρ Κ. Στεργίου
ΘΕΩΡΙΑ Α ΓΥΜΝΑΣΙΟΥ. Η διαίρεση καλείται Ευκλείδεια και είναι τέλεια όταν το υπόλοιπο είναι μηδέν.
 ΑΛΓΕΒΡΑ 1 ο ΚΕΦΑΛΑΙΟ ΘΕΩΡΙΑ Α ΓΥΜΝΑΣΙΟΥ 1. Τι είναι αριθμητική παράσταση; Με ποια σειρά εκτελούμε τις πράξεις σε μια αριθμητική παράσταση ώστε να βρούμε την τιμή της; Αριθμητική παράσταση λέγεται κάθε
ΑΛΓΕΒΡΑ 1 ο ΚΕΦΑΛΑΙΟ ΘΕΩΡΙΑ Α ΓΥΜΝΑΣΙΟΥ 1. Τι είναι αριθμητική παράσταση; Με ποια σειρά εκτελούμε τις πράξεις σε μια αριθμητική παράσταση ώστε να βρούμε την τιμή της; Αριθμητική παράσταση λέγεται κάθε
2. Πόσοι ακέραιοι αριθμοί μεταξύ του 10 και του 100 αυξάνονται κατά 9 μονάδες, όταν αντιστραφούν τα ψηφία τους; Γ. Αν, Δ. Αν, τότε. τότε.
 11η Κυπριακή Μαθηματική Ολυμπιάδα πρίλιος 010 Χρόνος: 60 λεπτά ΛΥΚΕΙΟΥ 1. Το τελευταίο ψηφίο του αριθμού 1 3 5 Ε 9 7. Πόσοι ακέραιοι αριθμοί μεταξύ του 10 του 100 αυξάνονται κατά 9 μονάδες όταν αντιστραφούν
11η Κυπριακή Μαθηματική Ολυμπιάδα πρίλιος 010 Χρόνος: 60 λεπτά ΛΥΚΕΙΟΥ 1. Το τελευταίο ψηφίο του αριθμού 1 3 5 Ε 9 7. Πόσοι ακέραιοι αριθμοί μεταξύ του 10 του 100 αυξάνονται κατά 9 μονάδες όταν αντιστραφούν
1 x και y = - λx είναι κάθετες
 Κεφάλαιο ο: ΕΥΘΕΙΑ Ερωτήσεις του τύπου «Σωστό-Λάθος» 1. * Συντελεστής διεύθυνσης μιας ευθείας (ε) είναι η εφαπτομένη της γωνίας που σχηματίζει η ευθεία (ε) με τον άξονα. Σ Λ. * Ο συντελεστής διεύθυνσης
Κεφάλαιο ο: ΕΥΘΕΙΑ Ερωτήσεις του τύπου «Σωστό-Λάθος» 1. * Συντελεστής διεύθυνσης μιας ευθείας (ε) είναι η εφαπτομένη της γωνίας που σχηματίζει η ευθεία (ε) με τον άξονα. Σ Λ. * Ο συντελεστής διεύθυνσης
ΕΠΙΦΑΝΕΙΕΣ ΔΕΥΤΕΡΟΥ ΒΑΘΜΟΥ
 ΚΕΦΑΛΑΙΟ 1 ΕΠΙΦΑΝΕΙΕΣ ΔΕΥΤΕΡΟΥ ΒΑΘΜΟΥ 1 Γενικά Επειδή οι επιφάνειε δευτέρου βαθμού συναντώνται συχνά στη μελέτη των συναρτήσεων πολλών μεταβλητών θεωρούμε σκόπιμο να τι περιγράψουμε στην αρχή του βιβλίου
ΚΕΦΑΛΑΙΟ 1 ΕΠΙΦΑΝΕΙΕΣ ΔΕΥΤΕΡΟΥ ΒΑΘΜΟΥ 1 Γενικά Επειδή οι επιφάνειε δευτέρου βαθμού συναντώνται συχνά στη μελέτη των συναρτήσεων πολλών μεταβλητών θεωρούμε σκόπιμο να τι περιγράψουμε στην αρχή του βιβλίου
 Β Γραφικές παραστάσεις - Πρώτο γράφημα Σχεδιάζοντας το μήκος της σανίδας συναρτήσει των φάσεων της σελήνης μπορείτε να δείτε αν υπάρχει κάποιος συσχετισμός μεταξύ των μεγεθών. Ο συνήθης τρόπος γραφικής
Β Γραφικές παραστάσεις - Πρώτο γράφημα Σχεδιάζοντας το μήκος της σανίδας συναρτήσει των φάσεων της σελήνης μπορείτε να δείτε αν υπάρχει κάποιος συσχετισμός μεταξύ των μεγεθών. Ο συνήθης τρόπος γραφικής
Οδηγίες για το SKETCHPAD Μωυσιάδης Πολυχρόνης - Δόρτσιος Κώστας. Με την εκτέλεση του Sketchpad παίρνουμε το παρακάτω παράθυρο σχεδίασης:
 Οδηγίες για το SKETCHPAD Μωυσιάδης Πολυχρόνης - Δόρτσιος Κώστας Με την εκτέλεση του Sketchpad παίρνουμε το παρακάτω παράθυρο σχεδίασης: παρόμοιο με του Cabri με αρκετές όμως διαφορές στην αρχιτεκτονική
Οδηγίες για το SKETCHPAD Μωυσιάδης Πολυχρόνης - Δόρτσιος Κώστας Με την εκτέλεση του Sketchpad παίρνουμε το παρακάτω παράθυρο σχεδίασης: παρόμοιο με του Cabri με αρκετές όμως διαφορές στην αρχιτεκτονική
Χωρικές σχέσεις και Γεωμετρικές Έννοιες στην Προσχολική Εκπαίδευση
 Χωρικές σχέσεις και Γεωμετρικές Έννοιες στην Προσχολική Εκπαίδευση Ενότητα 6: Γεωμετρικά σχήματα και μεγέθη δύο και τριών διαστάσεων Δημήτρης Χασάπης Τμήμα Εκπαίδευσης και Αγωγής στην Προσχολική Ηλικία
Χωρικές σχέσεις και Γεωμετρικές Έννοιες στην Προσχολική Εκπαίδευση Ενότητα 6: Γεωμετρικά σχήματα και μεγέθη δύο και τριών διαστάσεων Δημήτρης Χασάπης Τμήμα Εκπαίδευσης και Αγωγής στην Προσχολική Ηλικία
ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΠΕΡΙΟΔΟΥ ΜΑΪΟΥ - ΙΟΥΝΙΟΥ ΜΑΘΗΜΑΤΙΚΑ
 ΡΠΤΕΣ ΠΡΟΩΙΚΕΣ ΕΞΕΤΣΕΙΣ ΠΕΡΙΟΔΟΥ ΜΪΟΥ - ΙΟΥΝΙΟΥ ΜΘΗΜΤΙΚ ΣΤ () ΘΕΩΡΙ ΘΕΜ 1: (α) Να χαρακτηρίσετε καθεμία από τις παρακάτω προτάσεις ως «Σωστή» ή «Λάθος» : 1. Η ευθεία με εξίσωση y = 3x περνάει από την αρχή
ΡΠΤΕΣ ΠΡΟΩΙΚΕΣ ΕΞΕΤΣΕΙΣ ΠΕΡΙΟΔΟΥ ΜΪΟΥ - ΙΟΥΝΙΟΥ ΜΘΗΜΤΙΚ ΣΤ () ΘΕΩΡΙ ΘΕΜ 1: (α) Να χαρακτηρίσετε καθεμία από τις παρακάτω προτάσεις ως «Σωστή» ή «Λάθος» : 1. Η ευθεία με εξίσωση y = 3x περνάει από την αρχή
α) γνησίως αύξουσα σε ένα διάστημα Δ του πεδίου ορισμού της (Σχ.α), όταν β) γνησίως φθίνουσα σε ένα διάστημα Δ του πεδίου ορισμού της (Σχ.
 ΜΟΝΟΤΟΝΙΑ. ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ. ΜΟΝΟΤΟΝΙΑ - ΑΚΡΟΤΑΤΑ - ΣΥΜΜΕΤΡΙΕΣ Μια συνάρτηση f λέγεται: α) γνησίως αύξουσα σε ένα διάστημα Δ του πεδίου ορισμού της (Σχ.α), όταν για οποιαδήποτε χ,χ Δ με χ
ΜΟΝΟΤΟΝΙΑ. ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ. ΜΟΝΟΤΟΝΙΑ - ΑΚΡΟΤΑΤΑ - ΣΥΜΜΕΤΡΙΕΣ Μια συνάρτηση f λέγεται: α) γνησίως αύξουσα σε ένα διάστημα Δ του πεδίου ορισμού της (Σχ.α), όταν για οποιαδήποτε χ,χ Δ με χ
