Εισαγωγή Αποκοπή ευθείας σε 2Δ Αποκοπή πολυγώνου σε 2Δ Αποκοπή σε 3Δ. 3ο Μάθημα Αποκοπή. Γραφικα. Ευάγγελος Σπύρου
|
|
|
- Κόριννα Παπακωνσταντίνου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Εισαγωγή Αποκοπή ευθείας σε 2Δ Αποκοπή πολυγώνου σε 2Δ Αποκοπή σε 3Δ Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος
2 Εισαγωγή Αποκοπή ευθείας σε 2Δ Αποκοπή πολυγώνου σε 2Δ Αποκοπή σε 3Δ Σύνοψη του σημερινού μαθήματος 1 Εισαγωγή 2 Αποκοπή ευθείας σε 2Δ 3 Αποκοπή πολυγώνου σε 2Δ 4 Αποκοπή σε 3Δ
3 Εισαγωγή Εισαγωγή Μια βασική πράξη στα γραφικά είναι η αποκοπή (clipping) Η αποκοπή ενός αντικειμένου (πχ ευθύγραμμου τμήματος, πολυγώνου) γίνεται ως προς συγκεκριμένο αντικείμενο αποκοπής (πχ ορθογώνιο παραλληλόγραμμο, πυραμίδα, κύβος) Το αντικείμενο αποκοπής ορίζει το τμήμα του χώρου που ενδιαφέρει τον παρατηρητή σχετικά με το ποιες επιφάνειες μιας σκηνής μπορεί αυτός να δει
4 Εισαγωγή Χρησιμότητα Αποκοπής Η αποκοπή είναι πολύ χρήσιμη για τους εξής λόγους Αποφυγή της λανθασμένης (αντεστραμμένης) εμφάνισης αντικειμένων που βρίσκονται πίσω από τον παρατηρητή Μείωση του όγκου των δεδομένων που προωθούνται προς την αναπαράσταση στην οθόνη Το ενδιαφέρον της αποκοπής εστιάζεται στα αντικείμενα της σκηνής που τέμνουν το αντικείμενο αποκοπής και όχι σε αυτά που βρίσκονται πλήρως εντός ή εκτός της σκηνής
5 Αποκοπή ευθείας σε 2Δ Αποκοπή στις 2 διαστάσεις Για απλούστερη διατύπωση των αλγορίθμων, αλλά και επειδή το τελικό μέσο παράστασης (οθόνη) είναι ορθογώνιο παραλληλόγραμμο, χρησιμοποιείται εδώ ως αντικείμενο αποκοπής ένα ορθογώνιο παραλληλόγραμμο το οποίο και θα αποκαλείται παράθυρο αποκοπής (window)
6 Αποκοπή ευθείας σε 2Δ Σημειακή Αποκοπή Στην περίπτωση αυτή εξετάζεται αν το σημείο P(x, y) βρίσκεται εντός ή εκτός του Ā B C D παραθύρου που ορίζεται από τα σημεία Ā(x min, y min ) και C(x max, y max ) Εάν x min x x max και y min y y max, τότε το P(x, y) βρίσκεται εντός του παραθύρου, διαφορετικά αποκόπτεται
7 Αποκοπή ευθείας σε 2Δ Αλγόριθμος Μέσου Ο απλούστερος αλγόριθμος αποκοπής ευθύγραμμου τμήματος είναι ο αλγόριθμος μέσου Έστω P 1 (x 1, y 1 ) και P 2 (x 2, y 2 ) τα δύο άκρα ενός ευθύγραμμου τμήματος Σε κάθε σημείο P(x, y) του επιπέδου αντιστοιχούν δύο παράμετροι IX, IY με βάση το παράθυρο Οι πιθανές τιμές για τα IX, IY είναι 1, 0, +1 Το επίπεδο χωρίζεται σε 9 περιοχές
8 Εισαγωγή Αποκοπή ευθείας σε 2Δ Αποκοπή πολυγώνου σε 2Δ Αποκοπή σε 3Δ Αποκοπή ευθείας σε 2Δ Αλγόριθμος Μέσου Στο σημείο P 1 (x 1, y 1 ) αντιστοιχούνται οι παράμετροι IX 1, IY 1 και στο P 2 (x 2, y 2 ) οι παράμετροι IX 2, IY 2
9 Αποκοπή ευθείας σε 2Δ Αλγόριθμος Μέσου typedef struct {float x,y} point; midpoint (P1,P2,xmin,xmax,ymin,ymax) point P1,P2; float xmin,xmax,ymin,ymax; point M // calculate IX1,IY1,IX2,IY2 if ((IX1==0)&&(IY1==0)&&(IX2==0)&&(IY2==0)) // P1P2 is inside the window else if ((IX1==IX2)&&(IX1!=0)) ((IY1==IY2)&&(IY1!=0)) //P1P2 is outside the window else Mx=(P1x+P2x)/2; My=(P1y+P2y)/2; midpoint (P1,M,xmin,xmax,ymin,ymax); midpoint (M,P2,xmin,xmax,ymin,ymax);
10 Αποκοπή ευθείας σε 2Δ Αλγόριθμος Cohen-Sutherland Ο αλγόριθμος αρχικά σαν 1ο βήμα εκτελεί έναν υπολογιστικά φθηνό έλεγχο για να αποφανθεί κατά πόσον το ευθύγραμμο τμήμα είναι εξ ολοκλήρου εντός ή εκτός του παραθύρου Εάν μπορεί να ληφθεί μια απόφαση, αποφεύγεται ο δαπανηρός υπολογισμός της τομής
11 Αποκοπή ευθείας σε 2Δ Αλγόριθμος Cohen-Sutherland Εύκολα φαίνεται ότι το Ā B είναι εκτός, αφού οι x συντεταγμένες των άκρων του είναι μικρότερες από x m in Εύκολα φαίνεται ότι το C D είναι εντός, αφού όλες οι συντεταγμένες των άκρων του είναι μεταξύ από x min, x max και y min, y max
12 Αποκοπή ευθείας σε 2Δ Αλγόριθμος Cohen-Sutherland Δεν μπορεί να εξαχθεί συμπέρασμα για τα Ḡ H και Ē F Αναζητείται κάποια πλευρά του παραθύρου που τέμνει είτε η ίδια είτε προέκτασή της το ευθύγραμμο τμήμα Υπολογίζεται το σημείο τομής Εφαρμόζεται αναδρομικά ο αλγόριθμος στα ευθύγραμμα τμήματα που προκύπτουν (πχ για το Ē F τα ĒĪ, Ī F)
13 Αποκοπή ευθείας σε 2Δ Αλγόριθμος Cohen-Sutherland Για να γίνουν αποδοτικά οι έλεγχοι, το επίπεδο του παραθύρου χωρίζεται σε 9 περιοχές Σε κάθε περιοχή αντιστοιχεί ένας κώδικας Ο κώδικας καθορίζεται απο τη θέση της περιοχής σχετικά με τα ημιεπίπεδα των ακμών του παραθύρου
14 Αποκοπή ευθείας σε 2Δ Αλγόριθμος Cohen-Sutherland Κάθε ένα από τα 4 bits του κώδικα έχει τιμή 1 αν η περιοχή βρίσκεται στο ημιεπίπεδο της ακμής που ΔΕΝ περιέχει το παράθυρο, αλλιώς έχει την τιμή 0 1ο bit = 1: περιοχή πάνω από την ευθεία y = y max 2ο bit = 1: περιοχή κάτω από την ευθεία y = y min 3ο bit = 1: περιοχή δεξιά από την ευθεία x = x max 4ο bit = 1: περιοχή αριστερά από την ευθεία x = x max
15 Αποκοπή ευθείας σε 2Δ Αλγόριθμος Cohen-Sutherland Για κάθε άκρο (x, y) ενός ευθυγράμμου τμήματος υπολογίζεται ο κώδικας της περιοχής στην οποία βρίσκεται Αυτό γίνεται αποδοτικά ως εξής: το 1ο bit αντιστοιχεί στο πρόσημο της παράστασης y max y το 2ο bit αντιστοιχεί στο πρόσημο της παράστασης y y min το 3ο bit αντιστοιχεί στο πρόσημο της παράστασης x max x το 4ο bit αντιστοιχεί στο πρόσημο της παράστασης x x min Έχοντας υπολογίσει τους κώδικες c 1, c 2 των άκρων κάποιου ευθύγραμμου τμήματος, το 1ο βήμα της αποκοπής είναι Αν C 1 C 2 = 0000, τότε το ευθύγραμμο τμήμα είναι εντός του παραθύρου Αν C 1 C , τότε το ευθύγραμμο τμήμα είναι εκτός του παραθύρου
16 Αποκοπή ευθείας σε 2Δ Αλγόριθμος Cohen-Sutherland Στην περίπτωση που δεν ισχύει κάτι από τα παραπάνω, προσδιορίζεται ένα σημείο τομής ως εξής Συγκρίνοντας τους κώδικες των άκρων του ευθύγραμμου τμήματος, επιλέγεται η ευθεία μιας ακμής του παραθύρου που αντιστοιχεί σε ένα bit για το οποίο οι κώδικες έχουν διαφορετικές τιμές Υπολογίζεται το σημείο τομής του ευθύγραμμου τμήματος με την ευθεία αυτή Ο αλγόριθμος καλείται αναδρομικά για το ευθύγραμμο τμήμα του οποίου το ένα άκρο είναι το σημείο τομής και το άλλο είναι εκείνο το άκρο του ευθύγραμμου τμήματος του οποίου ο κώδικας έχει τιμή 0 στο bit που αντιστοιχεί στην ευθεία αποκοπής
17 Αποκοπή ευθείας σε 2Δ Αλγόριθμος Cohen-Sutherland CS (P1,P2,xmin,xmax,ymin,ymax) point P1,P2; float xmin,xmax,ymin,ymax; int c1,c2; point I; c1=code(p1); //find P1 code c2=code(p2); //find P2 code if ((c1 c2)==0) // P1P2 is inside the window else if ((c1&&c2)!=0) // P1P2 is outside the window else intersect (P1,P2,I,xmin,xmax,ymin,ymax); if outside(p1) CS(I,P2,xmin,xmax,ymin,ymax); else CS(P1,I,xmin,xmax,ymin,ymax);
18 Αποκοπή ευθείας σε 2Δ Αλγόριθμος Cohen-Sutherland Σημειώνεται ότι ο υπολογισμός των σχέσεων C 1 C 2 == 0000, C 1 C 2! = 0000 μπορεί να γίνει με τη βοήθεια ειδικών ρουτινών Η intersect υπολογίζει στο Ī σημείο τομής μεταξύ των P 1 P 2 και μιας ευθείας του παραθύρου Η outside υπολογίζει αν το P 1 βρίσκεται στο ημιεπίπεδο εκείνο της ευθείας τομής στο οποίο βρίσκεται και το παράθυρο
19 Αποκοπή ευθείας σε 2Δ Αλγόριθμος Liang-Barsky Βασίζεται στην παραμετρική εξίσωση ευθείας Για P 1 (x 1, y 1 ) και P 2 (x 2, y 2 ), η παραμετρική εξίσωση των P 1, P 2 είναι P = P 1 + t ( P 2 P 1 ), t [0, 1] ή x = x 1 + t x, y = y 1 + t y με x = x 2 x 1, y = y 2 y 1 Για t [, + ] προκύπτει ολόκληρη η ευθεία που περνάει από τα P 1 και P 2
20 Αποκοπή ευθείας σε 2Δ Αλγόριθμος Liang-Barsky Για δοσμένο παράθυρο αποκοπής, θα ισχύει ή x min x 1 + t x x max, t x x 1 x min, y min y 1 + t y y max t y y 1 y min t x x max x 1, t y y max y 1
21 Αποκοπή ευθείας σε 2Δ Αλγόριθμος Liang-Barsky Οι προηγούμενες ανισότητες μπορούν να τεθούν στην κοινή μορφή t p i q i, i = 1, 2, 3, 4, όπου p 1 = x, q 1 = x 1 x min p 2 = x, q 2 = x max x i p 3 = y, q 3 = y 1 y min p 4 = y, q 4 = y max y 1
22 Εισαγωγή Αποκοπή ευθείας σε 2Δ Αποκοπή πολυγώνου σε 2Δ Αποκοπή σε 3Δ Αποκοπή ευθείας σε 2Δ Αλγόριθμος Liang-Barsky Αρίθμηση των ακμών Liang-Barsky (x = x min : 1, x = x max : 2, y = y min : 3, y = y max : 4) Ορισμός ορατού και μη ορατού ημιεπιπέδου ακμής
23 Αποκοπή ευθείας σε 2Δ Αλγόριθμος Liang-Barsky Κάθε πλευρά του παραθύρου ορίζει μια ημιευθεία, η οποία χωρίζει το επίπεδο σε δύο ημιεπίπεδα Ορατό ημιεπίπεδο: αυτό που περιέχει το παράθυρο Μη Ορατό ημιεπίπεδο: αυτό που δεν περιέχει το παράθυρο Το παράθυρο πλέον μπορεί να οριστεί ως η τομή των 4 ορατών ημιεπιπέδων
24 Αποκοπή ευθείας σε 2Δ Αλγόριθμος Liang-Barsky Κάθε μία ανισότητα δίνει την περιοχή τιμών του t η οποία αντιστοιχεί στο ορατό μέρος του ευθύγραμμου τμήματος αναφορικά με την αντίστοιχη ακμή Εάν p i 0, τότε το σημείο τομής της ευθείας που ορίζουν τα P 1, P 2 με την i πλευρά του παραθύρου δίνεται για t = q i p i, i = 1, 2, 3, 4 Το πρόσημο του q i καθορίζει το ημιεπίπεδο της πλευράς i στο οποίο βρίσκεται το P 1 q i 0 P 1 βρίσκεται στο ορατό ημιεπίπεδο q i < 0 P 1 βρίσκεται στο μη ορατό ημιεπίπεδο Εάν p i = 0, τότε η ευθεία είναι παράλληλη στην ακμή i, = 1, 2, 3, 4 Εάν p i < 0, τότε η προσανατολισμένη ευθεία P 1 P 2 μεταβαίνει από το μη ορατό προς το ορατό ημιεπίπεδο της πλευράς i Εάν p > 0, τότε η προσανατολισμένη ευθεία P P
25 Αποκοπή ευθείας σε 2Δ Αλγόριθμος Liang-Barsky Ο αλγόριθμος υπολογίζει δύο τιμές t 1 και t 2 της παραμέτρου t, οι οποίες καθορίζουν τα δύο άκρα του τμήματος του P 1 P 2 που βρίσκεται μέσα στο παράθυρο t 1 = max({ q i p i p i < 0, i = 1, 2, 3, 4} {0}) (1) και t 2 = min({ q i p i > 0, i = 1, 2, 3, 4} {1}) (2) p i Τα μονοσύνολα {0}, {1} εξασφαλίζουν την επιλογή των άκρων P 1, P 2 στην περίπτωση που τα σημεία τομής της ευθείας με τις πλευρές του παραθύρου βρίσκονται εκτός του P 1, P 2 Εάν t 1 > t 2, τότε το ευθύγραμμο τμήμα βρίσκεται εκτός του παραθύρου, διαφορετικά οι τιμές t 1, t 2 χρησιμοποιούνται για τον υπολογισμό Πανεπιστήμιο των σημείων Θεσσαλίας Τμήμα τομής Πληροφορικής
26 Αποκοπή πολυγώνου σε 2Δ Αποκοπή Πολυγώνων Η αποκοπή 2Δ πολυγώνων είναι βασική πράξη στα γραφικά Οι χρήσεις της περιλαμβάνουν Αλγόριθμους αντιτάυτισης (αποκοπή στα όρια του pixel) Αλγόριθμους απόκρυψης Χωρικό διαχωρισμό πολυγώνων σε συστήματα πολυεπεξεργασίας Οι 3Δ αλγόριθμοι αποκοπής είναι συνήθως γενικεύσεις των 2Δ αλγόριθμων αποκοπής Ο αλγόριθμος Sutherland-Hodgman είναι κατάλληλος για την αποκοπή οποιουδήποτε πολυγώνου με κυρτό πολύγωνο αποκοπής Ο αλγόριθμος Greiner-Hormann μπορεί να εφαρμοστεί για γενικευμένα πολύγωνα
27 Αποκοπή πολυγώνου σε 2Δ Αλγόριθμος Sutherland-Hodgman Ο αλγόριθμος Sutherland-Hodgman μπορεί να αποκόψει ένα κυρτό ή μη κυρτό πολύγωνο ως προς ένα κυρτό πολύγωνο (παράθυρο) αποκοπής Αν το παράθυρο έχει m πλευρές, ο αλγόριθμος αποτελείται από m βήματα Το βήμα i, i = 1, 2,, m, αφορά την αποκοπή του πολυγώνου ως προς την ευθεία που περιέχει την πλευρά i του παραθύρου Η είσοδος στο 1ο βήμα είναι το αρχικό πολύγωνο Η είσοδος στο i-οστό βήμα είναι το πολύγωνο που προκύπτει μετά την αποκοπή στο i-1-οστό βήμα
28 Εισαγωγή Αποκοπή ευθείας σε 2Δ Αποκοπή πολυγώνου σε 2Δ Αποκοπή σε 3Δ Αποκοπή πολυγώνου σε 2Δ Αλγόριθμος Sutherland-Hodgman Βήματα εφαρμογής του αλγορίθμου Sutherland-Hodgman
29 Αποκοπή πολυγώνου σε 2Δ Αλγόριθμος Sutherland-Hodgman Το πολύγωνο αρχικά ορίζεται από τις κορυφές του P 1, P 2, P 3,, P n Θεωρείται ότι η κίνηση κατά μήκος της περιμέτρου του πολυγώνου γίνεται με θετική φορά Οι κορυφές ορίζουν τις πλευρές P 1 P 2, P 2 P 3,, P n 1 P n, P n P 1 Για κάθε πλευρά S P του πολυγώνου το οποίο προέκυψε από το προηγούμενο βήμα αποκοπής, προστίθενται στη λίστα κορυφών του νέου πολυγώνου 0,1 ή 2 κορυφές, ανάλογα με τη θέση της πλευράς S P σε σχέση με την ευθεία αποκοπής
30 Εισαγωγή Αποκοπή ευθείας σε 2Δ Αποκοπή πολυγώνου σε 2Δ Αποκοπή σε 3Δ Αποκοπή πολυγώνου σε 2Δ Αλγόριθμος Sutherland-Hodgman Περιπτώσεις αποκοπής με την εφαρμογή του αλγορίθμου Sutherland-Hodgman
31 Αποκοπή πολυγώνου σε 2Δ Βήμα Αποκοπής Αλγορίθμου Sutherland-Hodgman Η θέση μιας κορυφής P(r, t) σε σχέση με την ευθεία που ορίζεται από την πλευρά K(x 1, y 1 ) L(x 2, y 2 ) ορίζεται ως Εάν η εξίσωση της ευθείας αποκοπής είναι y sx c = 0 με s = y 2 y 2 x 2 x 1, c = y 1x 2 y 2 x 1 x 2 x 1 τότε η κορυφή P θα είναι εσωτερική, αν t sr c < 0 εξωτερική, αν t sr c > 0
32 Αποκοπή πολυγώνου σε 2Δ Αλγόριθμος Sutherland-Hodgman Στην περίπτωση που η πλευρά του παραθύρου είναι παράλληλη με κάποιον άξονα, τότε ο παραπάνω έλεγχος απλουστεύεται σε μια σύγκριση Αποφεύγεται ο υπολογισμός των s, c Ο αλγόριθμος Sutherland-Hodgman είναι κατάλληλος για υλοποίηση σε hardware
33 Αποκοπή πολυγώνου σε 2Δ Αλγόριθμος Greiner-Hormann Ο αλγόριθμος των Greiner-Hormann είναι κατάλληλος για γενικευμένα πολύγωνα Το πολύγωνο αποκοπής C και το πολύγωνο προς αποκοπή S μπορεί να είναι οποιαδήποτε κλειστά πολύγωνα (ακόμη και μη κυρτά, αυτά που τέμνουν την περιφέρειά τους κλπ) Η απόφαση του εάν ένα σημείο είναι εντός ή εκτός του πολυγώνου είναι έυκολη στην περίπτωση που το πολύγωνο είναι κυρτό (Greiner-Hodgman) Για τη γενικευμένη περίπτωση, ο αλγόριθμος χρησιμοποιεί την έννοια του δείκτη περιστροφών
34 Αποκοπή πολυγώνου σε 2Δ Δείκτης Περιστροφών Για μια κλειστή καμπύλη γ και ένα σημείο Ā, ο αριθμός περιστροφών ω(γ, Ā) μετρά πόσες στροφές ολοκληρώνει μια ακτίνα που ξεκινά από το Ā και διαγράφει την περιφέρεια της καμπύλης γ μια φορά Για κάθε ολοκληρωμένη στροφή με τη φορά των δεικτών του ρολογιού, ο δείκτης μειώνεται κατά 1 Για κάθε ολοκληρωμένη στροφή με αντίθετη φορά από αυτή των δεικτών του ρολογιού, ο δείκτης αυξάνεται κατά 1 Ορίζεται ως ω(γ, Ā) = 1 2π dϕ
35 Αποκοπή πολυγώνου σε 2Δ Δείκτης Περιστροφών Ο δείκτης περιστροφής δεν αλλάζει εφόσον δεν μεταβάλλεται η τοπολογική σχέση του Ā με την γ Αν το Ā είναι εκτός της καμπύλης, τότε ω(γ, Ā) = 0 Αν το Ā μετακινηθεί και διασταυρώσει μία φορά την γ, τότε το ω(γ, Ā) αυξάνεται ή μειώνεται κατά 1 Αν το Ā βρίσκεται εντός της γ, τότε το ω(γ, Ā) είναι περιττός, αλλιώς είναι άρτιος
36 Αποκοπή πολυγώνου σε 2Δ Δείκτης Περιστροφών Από τα παραπάνω μπορεί να εξαχθεί το συμπέρασμα ότι κάθε φορά που το μονοπάτι του Ā τέμνει την γ, περνά είτε από το εξωτερικό στο εσωτερικό της, είτε αντίστροφα Αυτό είναι αντίστοιχο με το μέτρημα των τομών της γ με την ημιευθεία από το Ā προς το άπειρο
37 Εισαγωγή Αποκοπή ευθείας σε 2Δ Αποκοπή πολυγώνου σε 2Δ Αποκοπή σε 3Δ Αποκοπή πολυγώνου σε 2Δ Αλγόριθμος Greiner-Hormann - Παράδειγμα Έστω το πολύγωνο αποκοπής C και το πολύγωνο προς αποκοπή S
38 Αποκοπή πολυγώνου σε 2Δ Αλγόριθμος Greiner-Hormann - Βήμα 1 Εκκίνηση από μια κορυφή του S και ακολουθείται η περίμετρος του Χρησιμοποιείται μια γραφίδα (αναμμένη ή σβηστή) Αρχικά, είναι αναμμένη αν η κορυφή είναι εντός του C, σβηστή αν είναι εκτός του C Κάθε φορά που διασταυρώνεται με το C, αλλάζει κατάσταση Διαγράφονται τα τμήματα του S μέσα στο C
39 Εισαγωγή Αποκοπή ευθείας σε 2Δ Αποκοπή πολυγώνου σε 2Δ Αποκοπή σε 3Δ Αποκοπή πολυγώνου σε 2Δ Αλγόριθμος Greiner-Hormann - Βήμα 2 Το ίδιο με το βήμα 1, αλλάζει μόνο ο ρόλος των C, S Δημιουργούνται τα τμήματα του C που βρίσκονται μέσα στο S
40 Εισαγωγή Αποκοπή ευθείας σε 2Δ Αποκοπή πολυγώνου σε 2Δ Αποκοπή σε 3Δ Αποκοπή πολυγώνου σε 2Δ Αλγόριθμος Greiner-Hormann - Βήμα 3 Ενώνονται όλα τα τμήματα που προέκυψαν από τα βήματα 1 και 2 S
41 Αποκοπή πολυγώνου σε 2Δ Αλγόριθμος Greiner-Hormann Το αποτέλεσμα της αποκοπής μπορεί να αποτελείται από 1 ή περισσότερα μη συνεκτικά πολύγωνα Η αποκοπή ουσιαστικά βρίσκει την τομή των επιφανειών C,S (C S) Ο αλγόριθμος Greiner-Hormann εύκολα μετατρέπεται ώστε να υπολογίζει τα C S, C S, S C
42 Αποκοπή στις 3 Διαστάσεις Αποκοπή στις 3 Διαστάσεις Οι αλγόριθμοι που έχουν περιγραφεί εώς τώρα μπορούν να χρησιμοποιηθούν και για 3 διαστάσεις Θα περιγραφούν οι αλγόριθμοι Cohen-Sutherland και Sutherland-Hodgman Στις 3 διαστάσεις, το αντικείμενο αποκοπής είναι είτε η περιορισμένη πυραμίδα (προοπτική προβολή), είτε ο κύβος (παράλληλη προβολή) Προς το παρόν, θεωρούνται 6 επίπεδα αποκοπής, τα οποία και ορίζουν το 3Δ αντικείμενο αποκοπής
43 Αποκοπή στις 3 Διαστάσεις 3Δ Αλγόριθμος Cohen-Sutherland Απαιτείται χρήση κωδικών 6 bits για να κωδικοποιηθεί η θέση κάθε άκρου του P(x p y p z p ) σε σχέση με το αντικείμενο αποκοπής Θεωρείται ότι το αντικείμενο αποκοπής είναι κύβος με πλευρές κάθετες στους άξονες Τα επίπεδα αποκοπής θα είναι x = x min x = x max y = y min y = y max z = z min z = z max
44 Αποκοπή στις 3 Διαστάσεις 3Δ Αλγόριθμος Cohen-Sutherland Η σημασία κάθε bit του κώδικα είναι 01 1ο bit=1 z p > z max 02 2ο bit=1 z p < z min 03 3ο bit=1 y p > y max 04 4ο bit=1 y p < y min 05 5ο bit=1 x p > x max 06 6ο bit=1 x p < x min Όπως και στις 2Δ, αν C 1, C 2 οι κώδικες των δύο άκρων του ευθύγραμμου τμήματος, τότε C 1 C 2 = το ευθύγραμμο τμήμα είναι εντός του αντικειμένου αποκοπής C 1 C το ευθύγραμμο τμήμα είναι εκτός του αντικειμένου αποκοπής Διαφορετικά, το ευθύγραμμο τμήμα διασπάται ακριβώς όπως και στις 2Δ
45 Αποκοπή στις 3 Διαστάσεις 3Δ Αλγόριθμος Cohen-Sutherland Η εύρεση της τομής ευθύγραμμου τμήματος και επιπέδου γίνεται συνήθως με χρήση της παραμετρικής εξίσωσης του ευθυγράμμου τμήματος x(t) = x 1 + t(x 2 x 1 ) = x 1 + t x y(t) = y 1 + t(y 2 y 1 ) = y 1 + t y z(t) = z 1 + t(z 2 z 1 ) = z 1 + t z όπου t [0, 1] και P 1 (x 1, y 1, z 1 ), P 2 (x 2, y 2, z 2 ) τα άκρα του ευθύγραμμου τμήματος Για παράδειγμα, η τομή με το επίπεδο y = Y βρίσκεται ως εξής Y = y(t) = y 1 + t y t = Y y 1 y Αν t [0, 1], τότε υπάρχει σημείο τομής με συντεταγμένες (x 1 + t x, Y, z 1 + t z) = (x 1 + x y (y y 1), Y, z 1 + z y (y y 1))
46 Αποκοπή στις 3 Διαστάσεις 3Δ Αλγόριθμος Sutherland-Hodgman Ο αλγόριθμος Sutherland-Hodgman επεκτείνεται εύκολα στις 3 διαστάσεις, χρησιμοποιώντας 6 διαδοχικά στάδια αποκοπής αντί για 4 Κάθε στάδιο αποκόπτει με ένα από τα 6 επίπεδα του αντικειμένου αποκοπής Κάθε στάδιο λειτουργεί με τον ίδιο τρόπο, ακριβώς όπως και στη διδιάστατη περίπτωση με εξαίρεση τα εξής 01 Τον έλεγχο αν ένα σημείο P βρίσκεται στην εσωτερική ή εξωτερική πλευρά του επιπέδου αποκοπής Για επίπεδα κάθετα με τους άξονες, απλή σύγκριση Για τυχαίο επίπεδο με f(x, y, z) = ax + by + cz + d = 0, ελέγχεται το πρόσημο της f( P) 02 Τον υπολογισμό της τομής του ευθυγράμμου τμήματος με το επίπεδο αποκοπής Ένας τρόπος είναι αυτός που χρησιμοποιείται στον 3Δ Cohen-Sutherland
Τι είναι Αποκοπή (clip)?
 Αποκοπή Τι είναι Αποκοπή (clip)? Η διαδικασία απεικόνισης μόνο των τμημάτων των αντικειμένων που βρίσκονται μέσα σε μια περιοχή Από μεγαλύτερη 2Δ σκηνή στην οποία έχουμε ήδη τιμές για τα piels Κατά την
Αποκοπή Τι είναι Αποκοπή (clip)? Η διαδικασία απεικόνισης μόνο των τμημάτων των αντικειμένων που βρίσκονται μέσα σε μια περιοχή Από μεγαλύτερη 2Δ σκηνή στην οποία έχουμε ήδη τιμές για τα piels Κατά την
Αποκοπή 4.1. Εργα: : & ΣΚΕΠΣΙΣ (ΕΠΕΑΚ - ΥΠΕΠΘ) Τµήµα Πληροφορικής 1 2 (SCS) Θέση παρατηρητή. Θέσεις αντικειµένων και φωτεινών πηγών
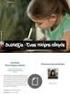 Αποκοπή Αποκοπή αντικειµένου (π.χ. πολυγώνου) ως προς αντικείµενο αποκοπής (π.χ. πολύγωνο, πυραµίδα, κύβος). Για αποφυγή αντεστραµµένης εµφάνισης αντικειµένων όπισθεν παρατηρητή. Για σηµαντική µείωση όγκου
Αποκοπή Αποκοπή αντικειµένου (π.χ. πολυγώνου) ως προς αντικείµενο αποκοπής (π.χ. πολύγωνο, πυραµίδα, κύβος). Για αποφυγή αντεστραµµένης εµφάνισης αντικειµένων όπισθεν παρατηρητή. Για σηµαντική µείωση όγκου
Διδάσκων: Φοίβος Μυλωνάς
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Χειμερινό εξάμηνο Γραφικά με υπολογιστές Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διάλεξη #08 Αποκοπή (εισαγωγή) Σημειακή Αποκοπή Αποκοπή Ευθύγραμμων Τμημάτων (line
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Χειμερινό εξάμηνο Γραφικά με υπολογιστές Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διάλεξη #08 Αποκοπή (εισαγωγή) Σημειακή Αποκοπή Αποκοπή Ευθύγραμμων Τμημάτων (line
Γραφικά με Η/Υ Αποκοπή
 Γραφικά με Η/Υ Αποκοπή Βασικές λειτουργίες απεικόνισης μετατροπή των φυσικών συντεταγμένων, ενός αντικειμένου, σε συντεταγμένες της συσκευής απεικόνισης (δημιουργία μετασχηματισμού απεικόνισης) αφαίρεση
Γραφικά με Η/Υ Αποκοπή Βασικές λειτουργίες απεικόνισης μετατροπή των φυσικών συντεταγμένων, ενός αντικειμένου, σε συντεταγμένες της συσκευής απεικόνισης (δημιουργία μετασχηματισμού απεικόνισης) αφαίρεση
Γραφικά Υπολογιστών: Εμφάνιση σε 2D
 1 ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Εμφάνιση σε 2D Πασχάλης Ράπτης http://aetos.it.teithe.gr/~praptis praptis@it.teithe.gr 2 Περιεχόμενα Έννοιες παραθύρων (windowing) Αποκοπή (clipping)
1 ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Εμφάνιση σε 2D Πασχάλης Ράπτης http://aetos.it.teithe.gr/~praptis praptis@it.teithe.gr 2 Περιεχόμενα Έννοιες παραθύρων (windowing) Αποκοπή (clipping)
Γραφικά με Η/Υ Αποκοπή
 Γραφικά με Η/Υ Αποκοπή Αποκοπή Οι αλγόριθμοι αποκοπής έχουν σχεδιαστεί έτσι ώστε να είναι αποτελεσματικοί στο να εντοπίζουν τα τμήματα μίας σκηνής ή ενός αντικειμένου σε συντεταγμένες προβολής που βρίσκονται
Γραφικά με Η/Υ Αποκοπή Αποκοπή Οι αλγόριθμοι αποκοπής έχουν σχεδιαστεί έτσι ώστε να είναι αποτελεσματικοί στο να εντοπίζουν τα τμήματα μίας σκηνής ή ενός αντικειμένου σε συντεταγμένες προβολής που βρίσκονται
Γραφικά Υπολογιστών & Εικονική Πραγματικότητα. Μετασχηματισμός απεικόνισης & Αλγόριθμοι αποκοπής
 Γραφικά Υπολογιστών & Εικονική Πραγματικότητα Μετασχηματισμός απεικόνισης & Αλγόριθμοι αποκοπής Βασικές λειτουργίες απεικόνισης μετατροπή του παγκόσμιου συστήματος συντεταγμένων, ενός αντικειμένου, σε
Γραφικά Υπολογιστών & Εικονική Πραγματικότητα Μετασχηματισμός απεικόνισης & Αλγόριθμοι αποκοπής Βασικές λειτουργίες απεικόνισης μετατροπή του παγκόσμιου συστήματος συντεταγμένων, ενός αντικειμένου, σε
Αποκοπή ευθυγράμμων τμημάτων
 Αλγόριθμος των Cohen-Sutherland Αποκοπή ευθυγράμμων τμημάτων Χαρακτηριστικά (Attrbutes LEFT : αριστερά της ευθείας LEFT RIGHT: δεξιά της ευθείας RIGHT ΤΟΡ : άνω της ευθείας TO BOTTO: κάτω της ευθείας BOTTO
Αλγόριθμος των Cohen-Sutherland Αποκοπή ευθυγράμμων τμημάτων Χαρακτηριστικά (Attrbutes LEFT : αριστερά της ευθείας LEFT RIGHT: δεξιά της ευθείας RIGHT ΤΟΡ : άνω της ευθείας TO BOTTO: κάτω της ευθείας BOTTO
Στο Κεφάλαιο 5 µελετώντας την προβολή του τρισδιάστατου χώρου στο επίπεδο της κάµερας εξετάστηκε
 Κεφάλαιο 6 Αποκοπή (clipping) Στο Κεφάλαιο 5 µελετώντας την προβολή του τρισδιάστατου χώρου στο επίπεδο της κάµερας εξετάστηκε η διαδικασία προβολής µεµονωµένων σηµείων και µόνο προς το τέλος του κεφαλαίου
Κεφάλαιο 6 Αποκοπή (clipping) Στο Κεφάλαιο 5 µελετώντας την προβολή του τρισδιάστατου χώρου στο επίπεδο της κάµερας εξετάστηκε η διαδικασία προβολής µεµονωµένων σηµείων και µόνο προς το τέλος του κεφαλαίου
Γραφικά Υπολογιστών: Αποκοπή στις 3D Διαστάσεις
 ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Αποκοπή στις 3D Διαστάσεις Πασχάλης Ράπτης ttp://aetos.it.teite.gr/~praptis praptis@it.teite.gr 2 Περιεχόμενα Θα δούμε μερικά demos προοπτικών προβολών
ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Αποκοπή στις 3D Διαστάσεις Πασχάλης Ράπτης ttp://aetos.it.teite.gr/~praptis praptis@it.teite.gr 2 Περιεχόμενα Θα δούμε μερικά demos προοπτικών προβολών
ΚΕΦΑΛΑΙΟ 5: ΑΠΕΙΚΟΝΙΣΗ ΚΑΙ ΑΠΟΚΟΠΗ
 ΚΕΦΑΛΑΙΟ 5: ΑΠΕΙΚΟΝΙΣΗ ΚΑΙ ΑΠΟΚΟΠΗ Ένα γεωμετρικό μοντέλο είναι μια αριθμητική περιγραφή ενός αντικειμένου, που περιλαμβάνει το μέγεθος, το σχήμα, καθώς και άλλες ιδιότητές του. Η περιγραφή του μοντέλου
ΚΕΦΑΛΑΙΟ 5: ΑΠΕΙΚΟΝΙΣΗ ΚΑΙ ΑΠΟΚΟΠΗ Ένα γεωμετρικό μοντέλο είναι μια αριθμητική περιγραφή ενός αντικειμένου, που περιλαμβάνει το μέγεθος, το σχήμα, καθώς και άλλες ιδιότητές του. Η περιγραφή του μοντέλου
5ο Μάθημα Αλγόριθμοι Σχεδίασης Βασικών Σχημάτων
 5ο Μάθημα Αλγόριθμοι Σχεδίασης Βασικών Σχημάτων Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Εισαγωγή Ευθεία Κύκλος Έλλειψη Σύνοψη του σημερινού μαθήματος 1 Εισαγωγή 2 Ευθεία 3 Κύκλος
5ο Μάθημα Αλγόριθμοι Σχεδίασης Βασικών Σχημάτων Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Εισαγωγή Ευθεία Κύκλος Έλλειψη Σύνοψη του σημερινού μαθήματος 1 Εισαγωγή 2 Ευθεία 3 Κύκλος
4ο Μάθημα Προβολές και Μετασχηματισμοί Παρατήρησης
 4ο Μάθημα Προβολές και Μετασχηματισμοί Παρατήρησης Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Εισαγωγή Προοπτική Προβολή Παράλληλη Προβολή Ορθογραφικές Προβολές Πλάγιες Παράλληλες
4ο Μάθημα Προβολές και Μετασχηματισμοί Παρατήρησης Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Εισαγωγή Προοπτική Προβολή Παράλληλη Προβολή Ορθογραφικές Προβολές Πλάγιες Παράλληλες
Απαραίτητες αφού 3Δ αντικείμενα απεικονίζονται σε 2Δ συσκευές. Θέση παρατηρητή. 3Δ Μετασχ/σμός Παρατήρησης
 Προβολές Προβολές Απαραίτητες αφού 3Δ αντικείμενα απεικονίζονται σε Δ συσκευές. Θέσεις αντικειμένων και φωτεινών πηγών Θέση παρατηρητή 3Δ Μαθηματικά Μοντέλα 3Δ Μετασχ/σμοί Μοντέλου 3Δ Μετασχ/σμός Παρατήρησης
Προβολές Προβολές Απαραίτητες αφού 3Δ αντικείμενα απεικονίζονται σε Δ συσκευές. Θέσεις αντικειμένων και φωτεινών πηγών Θέση παρατηρητή 3Δ Μαθηματικά Μοντέλα 3Δ Μετασχ/σμοί Μοντέλου 3Δ Μετασχ/σμός Παρατήρησης
Σχεδίαση με Ηλεκτρονικούς Υπολογιστές
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Σχεδίαση με Ηλεκτρονικούς Υπολογιστές Ενότητα # 13: Τεχνικές απεικόνισης στην οθόνη του ΗΥ Καθηγητής Ιωάννης Γ. Παρασχάκης Τμήμα Αγρονόμων
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Σχεδίαση με Ηλεκτρονικούς Υπολογιστές Ενότητα # 13: Τεχνικές απεικόνισης στην οθόνη του ΗΥ Καθηγητής Ιωάννης Γ. Παρασχάκης Τμήμα Αγρονόμων
Ένας απλός και γρήγορος αλγόριθμος για την αποκοπή γραμμών στο Scratch
 Ένας απλός και γρήγορος αλγόριθμος για την αποκοπή γραμμών στο Scratch Ματθές Δημήτριος 1, Μαγουλάς Αντώνιος 2 1 Εκπαιδευτικός Πληροφορικής ΠΕ86, dimmat@gmail.com 2 Εκπαιδευτικός Πληροφορικής ΠΕ03, amagul@yahoo.com
Ένας απλός και γρήγορος αλγόριθμος για την αποκοπή γραμμών στο Scratch Ματθές Δημήτριος 1, Μαγουλάς Αντώνιος 2 1 Εκπαιδευτικός Πληροφορικής ΠΕ86, dimmat@gmail.com 2 Εκπαιδευτικός Πληροφορικής ΠΕ03, amagul@yahoo.com
Γραφικά Υπολογιστών: Σχεδίαση γραμμών (Bresenham), Σχεδίασης Κύκλων, Γέμισμα Πολυγώνων
 1 ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Σχεδίαση γραμμών (Bresenham), Σχεδίασης Κύκλων, Γέμισμα Πολυγώνων Πασχάλης Ράπτης http://aetos.it.teithe.gr/~praptis praptis@it.teithe.gr 2 Περιγραφή
1 ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Σχεδίαση γραμμών (Bresenham), Σχεδίασης Κύκλων, Γέμισμα Πολυγώνων Πασχάλης Ράπτης http://aetos.it.teithe.gr/~praptis praptis@it.teithe.gr 2 Περιγραφή
Μετασχηματισμός Παρατήρησης
 Μετασχηματισμός Παρατήρησης Παγκόσμιο Σύστημα Συντεταγμένων Σύστημα Συντεταγμένων Παρατηρητή. Σύνθεση βασικών μετασχηματισμών. Καθορίζει όρια αποκοπής & παραμέτρους προβολής Θα εξετάσουμε ΜΠ Ι και Θέσεις
Μετασχηματισμός Παρατήρησης Παγκόσμιο Σύστημα Συντεταγμένων Σύστημα Συντεταγμένων Παρατηρητή. Σύνθεση βασικών μετασχηματισμών. Καθορίζει όρια αποκοπής & παραμέτρους προβολής Θα εξετάσουμε ΜΠ Ι και Θέσεις
Συνοπτική Θεωρία Μαθηματικών Α Γυμνασίου
 Web page: www.ma8eno.gr e-mail: vrentzou@ma8eno.gr Η αποτελεσματική μάθηση δεν θέλει κόπο αλλά τρόπο, δηλαδή ma8eno.gr Συνοπτική Θεωρία Μαθηματικών Α Γυμνασίου Αριθμητική - Άλγεβρα Γεωμετρία Άρτιος λέγεται
Web page: www.ma8eno.gr e-mail: vrentzou@ma8eno.gr Η αποτελεσματική μάθηση δεν θέλει κόπο αλλά τρόπο, δηλαδή ma8eno.gr Συνοπτική Θεωρία Μαθηματικών Α Γυμνασίου Αριθμητική - Άλγεβρα Γεωμετρία Άρτιος λέγεται
Εφαρμοσμένα Μαθηματικά ΙΙ 1ο Σετ Ασκήσεων (Λύσεις) Διανύσματα, Ευθείες Επίπεδα, Επιφάνειες 2ου βαθμού Επιμέλεια: Ι. Λυχναρόπουλος
 Εφαρμοσμένα Μαθηματικά ΙΙ ο Σετ Ασκήσεων (Λύσεις) Διανύσματα, Ευθείες Επίπεδα, Επιφάνειες ου βαθμού Επιμέλεια: Ι. Λυχναρόπουλος. Βρείτε το διάνυσμα με άκρα το Α(3,-,5) και Β(5,,-) ΑΒ=< 5 3, ( ), 5 >=
Εφαρμοσμένα Μαθηματικά ΙΙ ο Σετ Ασκήσεων (Λύσεις) Διανύσματα, Ευθείες Επίπεδα, Επιφάνειες ου βαθμού Επιμέλεια: Ι. Λυχναρόπουλος. Βρείτε το διάνυσμα με άκρα το Α(3,-,5) και Β(5,,-) ΑΒ=< 5 3, ( ), 5 >=
Γραφικά με υπολογιστές. Διδάσκων: Φοίβος Μυλωνάς. Διάλεξη #07
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Χειμερινό εξάμηνο Γραφικά με υπολογιστές Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διάλεξη #07 Γραμμές και Πολύγωνα: Εισαγωγή Αναπαράσταση 2D και 3D Χρωματισμός πολυγώνων
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Χειμερινό εξάμηνο Γραφικά με υπολογιστές Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διάλεξη #07 Γραμμές και Πολύγωνα: Εισαγωγή Αναπαράσταση 2D και 3D Χρωματισμός πολυγώνων
α) f(x(t), y(t)) = 0,
 Ρητές καμπύλες Μια επίπεδη αλγεβρική καμπύλη V (f) είναι το σύνολο όλων των σημείων του επιπέδου K 2 που μηδενίζουν κάποιο συγκεκριμένο ανάγωγο πολυώνυμο f K[x, y], δηλαδή V (f) = {(x 0, y 0 ) K 2 f(x
Ρητές καμπύλες Μια επίπεδη αλγεβρική καμπύλη V (f) είναι το σύνολο όλων των σημείων του επιπέδου K 2 που μηδενίζουν κάποιο συγκεκριμένο ανάγωγο πολυώνυμο f K[x, y], δηλαδή V (f) = {(x 0, y 0 ) K 2 f(x
Εργαστήριο Τεχνολογίας Πολυμέσων & Γραφικών, Τ.Ε.Π Π.Μ, Μάθημα: Γραφικά με Η/Υ
 ΓΡΑΦΙΚΑ Γέμισμα ΑΛΓΟΡΙΘΜΟΙ ΓΕΜΙΣΜΑΤΟΣ Για τις πλεγματικές οθόνες υπάρχουν: Αλγόριθμοι γεμίσματος:, που στηρίζονται στη συνάφεια των pixels του εσωτερικού ενός πολυγώνου Αλγόριθμοι σάρωσης: που στηρίζονται
ΓΡΑΦΙΚΑ Γέμισμα ΑΛΓΟΡΙΘΜΟΙ ΓΕΜΙΣΜΑΤΟΣ Για τις πλεγματικές οθόνες υπάρχουν: Αλγόριθμοι γεμίσματος:, που στηρίζονται στη συνάφεια των pixels του εσωτερικού ενός πολυγώνου Αλγόριθμοι σάρωσης: που στηρίζονται
Μετασχηματισμοί Μοντελοποίησης (modeling transformations)
 Μετασχηματισμοί Δ Μετασχηματισμοί Μοντελοποίησης (modeling trnformtion) Καθορισμός μετασχηματισμών των αντικειμένων Τα αντικείμενα περιγράφονται στο δικό τους σύστημα συντεταγμένων Επιτρέπει την χρήση
Μετασχηματισμοί Δ Μετασχηματισμοί Μοντελοποίησης (modeling trnformtion) Καθορισμός μετασχηματισμών των αντικειμένων Τα αντικείμενα περιγράφονται στο δικό τους σύστημα συντεταγμένων Επιτρέπει την χρήση
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ. Μια παράσταση που περιέχει πράξεις με μεταβλητές (γράμματα) και αριθμούς καλείται αλγεβρική, όπως για παράδειγμα η : 2x+3y-8
 ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
2ο Μάθημα Μετασχηματισμοί 2Δ/3Δ και Συστήματα Συντεταγμένων
 2ο Μάθημα Μετασχηματισμοί 2Δ/3Δ και Συστήματα Συντεταγμένων Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Σύνοψη του σημερινού μαθήματος 1 Εισαγωγή 2 Επανάληψη 3 Συσχετισμένοι 4 Γραμμικοί
2ο Μάθημα Μετασχηματισμοί 2Δ/3Δ και Συστήματα Συντεταγμένων Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Σύνοψη του σημερινού μαθήματος 1 Εισαγωγή 2 Επανάληψη 3 Συσχετισμένοι 4 Γραμμικοί
Η ΓΕΝΙΚΕΥΜΕΝΗ ΓΕΩΜΕΤΡΙΑ
 Η ΓΕΝΙΚΕΥΜΕΝΗ ΓΕΩΜΕΤΡΙΑ ΕΙΣΑΓΩΓΗ Η Γενικευμένη Γεωμετρία, που θα αναπτύξουμε στα παρακάτω κεφάλαια, είναι μία «Νέα Γεωμετρία», η οποία προέκυψε από την ανάγκη να γενικεύσει ορισμένα σημεία της Ευκλείδειας
Η ΓΕΝΙΚΕΥΜΕΝΗ ΓΕΩΜΕΤΡΙΑ ΕΙΣΑΓΩΓΗ Η Γενικευμένη Γεωμετρία, που θα αναπτύξουμε στα παρακάτω κεφάλαια, είναι μία «Νέα Γεωμετρία», η οποία προέκυψε από την ανάγκη να γενικεύσει ορισμένα σημεία της Ευκλείδειας
Γραφικά Υπολογιστών: Μέθοδοι Ανίχνευσης Επιφανειών (Surface Detection Methods)
 1 ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Μέθοδοι Ανίχνευσης Επιφανειών (Surface Detection Methods) Πασχάλης Ράπτης http://aetos.it.teithe.gr/~praptis praptis@it.teithe.gr 2 Περιεχόμενα
1 ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Μέθοδοι Ανίχνευσης Επιφανειών (Surface Detection Methods) Πασχάλης Ράπτης http://aetos.it.teithe.gr/~praptis praptis@it.teithe.gr 2 Περιεχόμενα
Απαλλακτική Εργασία Γραφικά & Εικονική Πραγματικότητα. Παπαπαύλου Χρήστος ΑΜ: 6609
 Απαλλακτική Εργασία Γραφικά & Εικονική Πραγματικότητα Παπαπαύλου Χρήστος ΑΜ: 6609 Αναπαράσταση μοντέλου Το 3D μοντέλο το αποθηκεύουμε στην μνήμη με τις εξής δομές δεδομένων: Λίστα κορυφών Λίστα τριγώνων
Απαλλακτική Εργασία Γραφικά & Εικονική Πραγματικότητα Παπαπαύλου Χρήστος ΑΜ: 6609 Αναπαράσταση μοντέλου Το 3D μοντέλο το αποθηκεύουμε στην μνήμη με τις εξής δομές δεδομένων: Λίστα κορυφών Λίστα τριγώνων
Διαφορικός Λογισμός πολλών μεταβλητών
 Διαφορικός Λογισμός πολλών μεταβλητών Πρόχειρες σημειώσεις Μιχάλης Παπαδημητράκης Τμήμα Μαθηματικών Πανεπιστήμιο Κρήτης 1η εβδομάδα. Τα στοιχεία του R n είναι όλα τα n-διάστατα διανύσματα ή, ισοδύναμα,
Διαφορικός Λογισμός πολλών μεταβλητών Πρόχειρες σημειώσεις Μιχάλης Παπαδημητράκης Τμήμα Μαθηματικών Πανεπιστήμιο Κρήτης 1η εβδομάδα. Τα στοιχεία του R n είναι όλα τα n-διάστατα διανύσματα ή, ισοδύναμα,
ΕΠΙΣΚΟΠΗΣΗ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ
 ΕΠΙΣΚΟΠΗΣΗ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΕΓΧΕΙΡΙΔΙΟ ΔΙΔΑΚΤΕΑΣ ΥΛΗΣ ΔΗΜΗΤΡΙΟΣ ΘΕΟΔΩΡΙΔΗΣ Κεφάλαιο 1.1 Ευθύγραμμη κίνηση 1. Τι ονομάζουμε κίνηση; Τι ονομάζουμε τροχιά; Ποια είδη τροχιών γνωρίζετε; Κίνηση ενός αντικειμένου
ΕΠΙΣΚΟΠΗΣΗ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΕΓΧΕΙΡΙΔΙΟ ΔΙΔΑΚΤΕΑΣ ΥΛΗΣ ΔΗΜΗΤΡΙΟΣ ΘΕΟΔΩΡΙΔΗΣ Κεφάλαιο 1.1 Ευθύγραμμη κίνηση 1. Τι ονομάζουμε κίνηση; Τι ονομάζουμε τροχιά; Ποια είδη τροχιών γνωρίζετε; Κίνηση ενός αντικειμένου
Οδηγίες για το Geogebra Μωυσιάδης Πολυχρόνης Δόρτσιος Κώστας
 Οδηγίες για το Geogebra Μωυσιάδης Πολυχρόνης Δόρτσιος Κώστας Η πρώτη οθόνη μετά την εκτέλεση του προγράμματος διαφέρει κάπως από τα προηγούμενα λογισμικά, αν και έχει αρκετά κοινά στοιχεία. Αποτελείται
Οδηγίες για το Geogebra Μωυσιάδης Πολυχρόνης Δόρτσιος Κώστας Η πρώτη οθόνη μετά την εκτέλεση του προγράμματος διαφέρει κάπως από τα προηγούμενα λογισμικά, αν και έχει αρκετά κοινά στοιχεία. Αποτελείται
1 x m 2. degn = m 1 + m m n. a(m 1 m 2...m k )x m 1
 1 Πολυώνυμα και συσχετικός χώρος Ορισμός 3.1 Ενα μονώνυμο N στις μεταβλητές x 1, x 2,..., x n είναι ένα γινόμενο της μορφής x m 1 2...x m n n, όπου όλοι οι εκθέτες είναι φυσικοί αριθμοί. Ο βαθμός του μονωνύμου
1 Πολυώνυμα και συσχετικός χώρος Ορισμός 3.1 Ενα μονώνυμο N στις μεταβλητές x 1, x 2,..., x n είναι ένα γινόμενο της μορφής x m 1 2...x m n n, όπου όλοι οι εκθέτες είναι φυσικοί αριθμοί. Ο βαθμός του μονωνύμου
Φύλλο Εργασίας για την y=αx 2
 Πρόβλημα Σε ένα τετραγωνικό περιβόλι πλευράς 10m πρόκειται να χτιστεί μια αποθήκη σχήματος ορθογωνίου, όπως φαίνεται στο διπλανό σχήμα. Α) Να βρεθούν οι διαστάσεις της αποθήκης συναρτήσει του x, αν γνωρίζετε
Πρόβλημα Σε ένα τετραγωνικό περιβόλι πλευράς 10m πρόκειται να χτιστεί μια αποθήκη σχήματος ορθογωνίου, όπως φαίνεται στο διπλανό σχήμα. Α) Να βρεθούν οι διαστάσεις της αποθήκης συναρτήσει του x, αν γνωρίζετε
2 Β Βάσεις παραλληλογράµµου Βαρύκεντρο Γ Γεωµετρική κατασκευή Γεωµετρικός τόπος (ς) Γωνία Οι απέναντι πλευρές του. Κέντρο βάρους τριγώνου, δηλ. το σηµ
 1 ΛΕΞΙΚΟ ΓΕΩΜΕΤΡΙΚΩΝ ΟΡΩΝ Α Ακτίνιο Ακτίνα κύκλου Ακτίνα σφαίρας Άκρα ευθύγραµµου τµήµατος Αµβλεία γωνία Αµβλυγώνιο Ανάλογα ευθύγραµµα τµήµατα Αντιδιαµετρικό σηµείο Αντικείµενες ηµιευθείες Άξονας συµµετρίας
1 ΛΕΞΙΚΟ ΓΕΩΜΕΤΡΙΚΩΝ ΟΡΩΝ Α Ακτίνιο Ακτίνα κύκλου Ακτίνα σφαίρας Άκρα ευθύγραµµου τµήµατος Αµβλεία γωνία Αµβλυγώνιο Ανάλογα ευθύγραµµα τµήµατα Αντιδιαµετρικό σηµείο Αντικείµενες ηµιευθείες Άξονας συµµετρίας
2. Ιδιότητες Συναρτήσεων
 Ιδιότητες Συναρτήσεων Μονοτονία Ακρότατα Συμμετρίες Συνάρτησης Πεδίο Ορισμού Το πρώτο βήμα για τη λύση μιας άσκησης που περιέει μια συνάρτηση είναι ο προσδιορισμός του πεδίου ορισμού της α) Κάθε πολυωνυμική
Ιδιότητες Συναρτήσεων Μονοτονία Ακρότατα Συμμετρίες Συνάρτησης Πεδίο Ορισμού Το πρώτο βήμα για τη λύση μιας άσκησης που περιέει μια συνάρτηση είναι ο προσδιορισμός του πεδίου ορισμού της α) Κάθε πολυωνυμική
Φροντιστηριακές Ασκήσεις Απεικόνισης - Αποκοπής
 Φροντιστηριακές Άσκηση Βρες τον πίνακα μετασχηματισμού που θα σχεδιάζει σημεία που περιέχονται σε ένα παράθυρο του οποίου η χαμηλότερη αριστερή γωνία είναι στο (3,3) και η ψηλότερη δεξιά γωνία είναι στο
Φροντιστηριακές Άσκηση Βρες τον πίνακα μετασχηματισμού που θα σχεδιάζει σημεία που περιέχονται σε ένα παράθυρο του οποίου η χαμηλότερη αριστερή γωνία είναι στο (3,3) και η ψηλότερη δεξιά γωνία είναι στο
Η διαδικασία Παραγωγής Συνθετικής Εικόνας (Rendering)
 Υφή Η διαδικασία Παραγωγής Συνθετικής Εικόνας (Rendering) Θέσεις αντικειμένων και φωτεινών πηγών Θέση παρατηρητή 3D Μοντέλα 3Δ Μετασχ/σμοί Μοντέλου 3Δ Μετασχ/σμός Παρατήρησης Απομάκρυνση Πίσω Επιφανειών
Υφή Η διαδικασία Παραγωγής Συνθετικής Εικόνας (Rendering) Θέσεις αντικειμένων και φωτεινών πηγών Θέση παρατηρητή 3D Μοντέλα 3Δ Μετασχ/σμοί Μοντέλου 3Δ Μετασχ/σμός Παρατήρησης Απομάκρυνση Πίσω Επιφανειών
Γραφικά Ι. Ενότητα 4: Προβολές και Μετασχηματισμοί Παρατήρησης. Θεοχάρης Θεοχάρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών
 Γραφικά Ι Ενότητα 4: Προβολές και Μετασχηματισμοί Παρατήρησης Θεοχάρης Θεοχάρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Ενότητα 4 Προβολές και Μετασχηματισμοί Παρατήρησης Εισαγωγή
Γραφικά Ι Ενότητα 4: Προβολές και Μετασχηματισμοί Παρατήρησης Θεοχάρης Θεοχάρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Ενότητα 4 Προβολές και Μετασχηματισμοί Παρατήρησης Εισαγωγή
Ειδικά θέματα Αλγορίθμων και Δομών Δεδομένων (ΠΛΕ073) Απαντήσεις 1 ου Σετ Ασκήσεων
 Ειδικά θέματα Αλγορίθμων και Δομών Δεδομένων (ΠΛΕ073) Απαντήσεις 1 ου Σετ Ασκήσεων Άσκηση 1 α) Η δομή σταθμισμένης ένωσης με συμπίεση διαδρομής μπορεί να τροποποιηθεί πολύ εύκολα ώστε να υποστηρίζει τις
Ειδικά θέματα Αλγορίθμων και Δομών Δεδομένων (ΠΛΕ073) Απαντήσεις 1 ου Σετ Ασκήσεων Άσκηση 1 α) Η δομή σταθμισμένης ένωσης με συμπίεση διαδρομής μπορεί να τροποποιηθεί πολύ εύκολα ώστε να υποστηρίζει τις
Περιεχόμενα. Κεφάλαιο 1 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΜΙΑ ΕΥΘΕΙΑ... 13 1.1 Οι συντεταγμένες ενός σημείου...13 1.2 Απόλυτη τιμή...14
 Περιεχόμενα Κεφάλαιο 1 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΜΙΑ ΕΥΘΕΙΑ... 13 1.1 Οι συντεταγμένες ενός σημείου...13 1.2 Απόλυτη τιμή...14 Κεφάλαιο 2 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΕΝΑ ΕΠΙΠΕΔΟ 20 2.1 Οι συντεταγμένες
Περιεχόμενα Κεφάλαιο 1 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΜΙΑ ΕΥΘΕΙΑ... 13 1.1 Οι συντεταγμένες ενός σημείου...13 1.2 Απόλυτη τιμή...14 Κεφάλαιο 2 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΕΝΑ ΕΠΙΠΕΔΟ 20 2.1 Οι συντεταγμένες
ΜΟΝΟΤΟΝΙΑ ΑΚΡΟΤΑΤΑ- ΣΥΝΟΛΟ ΤΙΜΩΝ ΚΟΙΛΟΤΗΤΑ ΣΗΜΕΙΑ ΚΑΜΠΗΣ. i) Για την εύρεση µονοτονίας µιας συνάρτησης υπολογίζω την f ( x )
 () Μονοτονία ΜΟΝΟΤΟΝΙΑ ΑΚΡΟΤΑΤΑ- ΣΥΝΟΛΟ ΤΙΜΩΝ ΚΟΙΛΟΤΗΤΑ ΣΗΜΕΙΑ ΚΑΜΠΗΣ i) Για την εύρεση µονοτονίας µιας συνάρτησης υπολογίζω την f ( ) και βρίσκω το πρόσηµό της ii) Αν προκύψει να είναι αύξουσα ή φθίνουσα,
() Μονοτονία ΜΟΝΟΤΟΝΙΑ ΑΚΡΟΤΑΤΑ- ΣΥΝΟΛΟ ΤΙΜΩΝ ΚΟΙΛΟΤΗΤΑ ΣΗΜΕΙΑ ΚΑΜΠΗΣ i) Για την εύρεση µονοτονίας µιας συνάρτησης υπολογίζω την f ( ) και βρίσκω το πρόσηµό της ii) Αν προκύψει να είναι αύξουσα ή φθίνουσα,
ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1 ΜΑΘΗΜΑ 1 ο +2 ο ΕΝΝΟΙΑ ΔΙΑΝΥΣΜΑΤΟΣ Διάνυσμα ορίζεται ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ένα ευθύγραμμο τμήμα
ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1 ΜΑΘΗΜΑ 1 ο +2 ο ΕΝΝΟΙΑ ΔΙΑΝΥΣΜΑΤΟΣ Διάνυσμα ορίζεται ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ένα ευθύγραμμο τμήμα
(Study Guide for Final Test)
 Homework #6, #7, #8 & #9 Analytic Geometry (Study Guide for Final Test) 1. Να βρείτε τις συντεταγμένες του κέντρου Κ του κύκλου, και την ακτίνα r του κύκλου: 1. Κ (, ) 2. r= 2. Να βρείτε τις εξισώσεις
Homework #6, #7, #8 & #9 Analytic Geometry (Study Guide for Final Test) 1. Να βρείτε τις συντεταγμένες του κέντρου Κ του κύκλου, και την ακτίνα r του κύκλου: 1. Κ (, ) 2. r= 2. Να βρείτε τις εξισώσεις
Συστήματα συντεταγμένων
 Κεφάλαιο. Για να δημιουργήσουμε τρισδιάστατα αντικείμενα, που μπορούν να παρασταθούν στην οθόνη του υπολογιστή ως ένα σύνολο από γραμμές, επίπεδες πολυγωνικές επιφάνειες ή ακόμη και από ένα συνδυασμό από
Κεφάλαιο. Για να δημιουργήσουμε τρισδιάστατα αντικείμενα, που μπορούν να παρασταθούν στην οθόνη του υπολογιστή ως ένα σύνολο από γραμμές, επίπεδες πολυγωνικές επιφάνειες ή ακόμη και από ένα συνδυασμό από
ΕΡΓΑΣΤΗΡΙΟ ΠΟΛΥΜΕΣΩΝ ΚΑΙ ΓΡΑΦΙΚΩΝ
 ΕΡΓΑΣΤΗΡΙΟ ΠΟΛΥΜΕΣΩΝ ΚΑΙ ΓΡΑΦΙΚΩΝ Εισαγωγή /4 Το σχήμα και το μέγεθος των δισδιάστατων αντικειμένων περιγράφονται με τις καρτεσιανές συντεταγμένες x, y. Με εφαρμογή γεωμετρικών μετασχηματισμών στο μοντέλο
ΕΡΓΑΣΤΗΡΙΟ ΠΟΛΥΜΕΣΩΝ ΚΑΙ ΓΡΑΦΙΚΩΝ Εισαγωγή /4 Το σχήμα και το μέγεθος των δισδιάστατων αντικειμένων περιγράφονται με τις καρτεσιανές συντεταγμένες x, y. Με εφαρμογή γεωμετρικών μετασχηματισμών στο μοντέλο
Για να παραστήσουμε ένα σύνολο χρησιμοποιούμε συνήθως έναν από τους παρακάτω τρόπους :
 ΚΕΦΑΛΑΙΟ Ο ΣΥΝΑΡΤΗΣΕΙΣ. Σύνολα ΠΑΡΑΣΤΑΣΗ ΣΥΝΟΛΟΥ ΓΡΑΦΗ ΣΥΝΟΛΟΥ Για να παραστήσουμε ένα σύνολο χρησιμοποιούμε συνήθως έναν από τους παρακάτω τρόπους : ) Παράσταση με αναγραφή των στοιχείων Όταν δίνονται
ΚΕΦΑΛΑΙΟ Ο ΣΥΝΑΡΤΗΣΕΙΣ. Σύνολα ΠΑΡΑΣΤΑΣΗ ΣΥΝΟΛΟΥ ΓΡΑΦΗ ΣΥΝΟΛΟΥ Για να παραστήσουμε ένα σύνολο χρησιμοποιούμε συνήθως έναν από τους παρακάτω τρόπους : ) Παράσταση με αναγραφή των στοιχείων Όταν δίνονται
ΘΕΩΡΙΑ Α ΓΥΜΝΑΣΙΟΥ. Η διαίρεση καλείται Ευκλείδεια και είναι τέλεια όταν το υπόλοιπο είναι μηδέν.
 ΑΛΓΕΒΡΑ 1 ο ΚΕΦΑΛΑΙΟ ΘΕΩΡΙΑ Α ΓΥΜΝΑΣΙΟΥ 1. Τι είναι αριθμητική παράσταση; Με ποια σειρά εκτελούμε τις πράξεις σε μια αριθμητική παράσταση ώστε να βρούμε την τιμή της; Αριθμητική παράσταση λέγεται κάθε
ΑΛΓΕΒΡΑ 1 ο ΚΕΦΑΛΑΙΟ ΘΕΩΡΙΑ Α ΓΥΜΝΑΣΙΟΥ 1. Τι είναι αριθμητική παράσταση; Με ποια σειρά εκτελούμε τις πράξεις σε μια αριθμητική παράσταση ώστε να βρούμε την τιμή της; Αριθμητική παράσταση λέγεται κάθε
ΜΑΘΗΜΑΤΙΚΑ ΙΙ ιδάσκων : Ε. Στεφανόπουλος 12 ιουνιου 2017
 Πανεπιστηµιο Πατρων Πολυτεχνικη Σχολη Τµηµα Μηχανικων Η/Υ & Πληροφορικης ΜΑΘΗΜΑΤΙΚΑ ΙΙ ιδάσκων : Ε. Στεφανόπουλος 12 ιουνιου 217 Θ1. Θεωρούµε την συνάρτηση f(x, y, z) = 1 + x 2 + 2y 2 z. (αʹ) Να ϐρεθεί
Πανεπιστηµιο Πατρων Πολυτεχνικη Σχολη Τµηµα Μηχανικων Η/Υ & Πληροφορικης ΜΑΘΗΜΑΤΙΚΑ ΙΙ ιδάσκων : Ε. Στεφανόπουλος 12 ιουνιου 217 Θ1. Θεωρούµε την συνάρτηση f(x, y, z) = 1 + x 2 + 2y 2 z. (αʹ) Να ϐρεθεί
Εφαρμοσμένα Μαθηματικά
 Εφαρμοσμένα Μαθηματικά ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ενότητα 6: Διπλά Ολοκληρώματα Δρ. Περικλής Παπαδόπουλος Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε Κάντε κλικ για
Εφαρμοσμένα Μαθηματικά ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ενότητα 6: Διπλά Ολοκληρώματα Δρ. Περικλής Παπαδόπουλος Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε Κάντε κλικ για
ΚΟΝΤΟΚΩΣΤΑΣ ΔΗΜΗΤΡΙΟΣ. ΠΑΡΑΔΕΙΓΜΑΤΑ-ΑΣΚΗΣΕΙΣ ΠΑΡΑΣΤΑΤΙΚΗΣ ΜΕ ΠΡΟΒΟΛΕΣ ΣΕ 2 ΕΠΙΠΕΔΑ (εκδοχή Σεπτεμβρίου 2014) Ε.Μ.Π.
 ΚΟΝΤΟΚΩΣΤΑΣ ΔΗΜΗΤΡΙΟΣ ΠΑΡΑΔΕΙΓΜΑΤΑ-ΑΣΚΗΣΕΙΣ ΠΑΡΑΣΤΑΤΙΚΗΣ ΜΕ ΠΡΟΒΟΛΕΣ ΣΕ ΕΠΙΠΕΔΑ (εκδοχή Σεπτεμβρίου 04) Ε.Μ.Π. (παρατηρήσεις για τη βελτίωση των σημειώσεων ευπρόσδεκτες) Παράσταση σημείου. Σχήμα Σχήμα
ΚΟΝΤΟΚΩΣΤΑΣ ΔΗΜΗΤΡΙΟΣ ΠΑΡΑΔΕΙΓΜΑΤΑ-ΑΣΚΗΣΕΙΣ ΠΑΡΑΣΤΑΤΙΚΗΣ ΜΕ ΠΡΟΒΟΛΕΣ ΣΕ ΕΠΙΠΕΔΑ (εκδοχή Σεπτεμβρίου 04) Ε.Μ.Π. (παρατηρήσεις για τη βελτίωση των σημειώσεων ευπρόσδεκτες) Παράσταση σημείου. Σχήμα Σχήμα
Γραφικά με Η/Υ Αλγόριθμοι σχεδίασης βασικών 22D D σχημάτων (ευθεία
 Γραφικά με Η/Υ Αλγόριθμοι σχεδίασης βασικών 2D σχημάτων (ευθεία) Σχεδίαση ευθείας θί με σάρωση (παρουσίαση προβλήματος) σχεδίαση ευθείας AB, με σάρωση, όπου A=(0,1) και B=(5,4) ποιο είναι το επόμενο pixel
Γραφικά με Η/Υ Αλγόριθμοι σχεδίασης βασικών 2D σχημάτων (ευθεία) Σχεδίαση ευθείας θί με σάρωση (παρουσίαση προβλήματος) σχεδίαση ευθείας AB, με σάρωση, όπου A=(0,1) και B=(5,4) ποιο είναι το επόμενο pixel
i=1 i=1 i=1 (x i 1, x i +1) (x 1 1, x k +1),
 Κεφάλαιο 6 Συμπάγεια 6.1 Ορισμός της συμπάγειας Οπως θα φανεί στην αμέσως επόμενη παράγραφο, υπάρχουν διάφοροι τρόποι με τους οποίους μπορεί κανείς να εισάγει την έννοια του συμπαγούς μετρικού χώρου. Ο
Κεφάλαιο 6 Συμπάγεια 6.1 Ορισμός της συμπάγειας Οπως θα φανεί στην αμέσως επόμενη παράγραφο, υπάρχουν διάφοροι τρόποι με τους οποίους μπορεί κανείς να εισάγει την έννοια του συμπαγούς μετρικού χώρου. Ο
Παραδείγματα διπλών oλοκληρωμάτων Γ. Λυχναρόπουλος
 Παραδείγματα διπλών oλοκληρωμάτων Γ. Λυχναρόπουλος Παράδειγμα Να υπολογισθεί με τρόπους το ολοκλήρωμα I d d 0 Η ολοκλήρωση, όπως φαίνεται από τα άκρα ολοκλήρωσης, γίνεται πάνω στο ορθογώνιο χωρίο R 0,,
Παραδείγματα διπλών oλοκληρωμάτων Γ. Λυχναρόπουλος Παράδειγμα Να υπολογισθεί με τρόπους το ολοκλήρωμα I d d 0 Η ολοκλήρωση, όπως φαίνεται από τα άκρα ολοκλήρωσης, γίνεται πάνω στο ορθογώνιο χωρίο R 0,,
 Β Γραφικές παραστάσεις - Πρώτο γράφημα Σχεδιάζοντας το μήκος της σανίδας συναρτήσει των φάσεων της σελήνης μπορείτε να δείτε αν υπάρχει κάποιος συσχετισμός μεταξύ των μεγεθών. Ο συνήθης τρόπος γραφικής
Β Γραφικές παραστάσεις - Πρώτο γράφημα Σχεδιάζοντας το μήκος της σανίδας συναρτήσει των φάσεων της σελήνης μπορείτε να δείτε αν υπάρχει κάποιος συσχετισμός μεταξύ των μεγεθών. Ο συνήθης τρόπος γραφικής
Παράλληλοι Αλγόριθμοι: Ανάλυση Εικόνας και Υπολογιστική Γεωμετρία. Πέτρος Ποτίκας CoReLab 4/5/2006
 Παράλληλοι Αλγόριθμοι: Ανάλυση Εικόνας και Υπολογιστική Γεωμετρία Πέτρος Ποτίκας CoReLab 4/5/2006 Επισκόπηση Ετικέτες σε συνιστώσες (Component labelling) Hough μετασχηματισμοί (transforms) Πλησιέστερος
Παράλληλοι Αλγόριθμοι: Ανάλυση Εικόνας και Υπολογιστική Γεωμετρία Πέτρος Ποτίκας CoReLab 4/5/2006 Επισκόπηση Ετικέτες σε συνιστώσες (Component labelling) Hough μετασχηματισμοί (transforms) Πλησιέστερος
Γραφικά με υπολογιστές
 Γραφικά με Υπολογιστές Ενότητα # 3: Εισαγωγή Φοίβος Μυλωνάς Τμήμα Πληροφορικής Φοίβος Μυλωνάς Γραφικά με υπολογιστές 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Γραφικά με Υπολογιστές Ενότητα # 3: Εισαγωγή Φοίβος Μυλωνάς Τμήμα Πληροφορικής Φοίβος Μυλωνάς Γραφικά με υπολογιστές 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Μορφές αποδείξεων Υπάρχουν πολλά είδη αποδείξεων. Εδώ θα δούμε τα πιο κοινά: Εξαντλητική μέθοδος ή μέθοδος επισκόπησης. Οταν το πρόβλημα έχει πεπερασμ
 Μαθηματικά Πληροφορικής 4ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Μορφές αποδείξεων Υπάρχουν πολλά είδη αποδείξεων. Εδώ θα δούμε τα πιο κοινά: Εξαντλητική μέθοδος ή μέθοδος επισκόπησης.
Μαθηματικά Πληροφορικής 4ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Μορφές αποδείξεων Υπάρχουν πολλά είδη αποδείξεων. Εδώ θα δούμε τα πιο κοινά: Εξαντλητική μέθοδος ή μέθοδος επισκόπησης.
α) Κύκλος από δύο δοσµένα σηµεία Α, Β. Το ένα από τα δύο σηµεία ορίζεται ως κέντρο αν το επιλέξουµε πρώτο. β) Κύκλος από δοσµένο σηµείο και δοσµένο ευ
 ΕΙΣΑΓΩΓΗ ΣΤΟ ΛΟΓΙΣΜΙΚΟ SKETCHPAD ΜΕΡΟΣ Α Μιλώντας για ένα λογισµικό δυναµικής γεωµετρίας καλό θα ήταν να διακρίνουµε αρχικά 3 οµάδες εργαλείων µε τα οποία µπορούµε να εργαστούµε µέσα στο συγκεκριµένο περιβάλλον.
ΕΙΣΑΓΩΓΗ ΣΤΟ ΛΟΓΙΣΜΙΚΟ SKETCHPAD ΜΕΡΟΣ Α Μιλώντας για ένα λογισµικό δυναµικής γεωµετρίας καλό θα ήταν να διακρίνουµε αρχικά 3 οµάδες εργαλείων µε τα οποία µπορούµε να εργαστούµε µέσα στο συγκεκριµένο περιβάλλον.
Σύντομος οδηγός αναφοράς Για Windows Έκδοση 4.0
 Σύντομος οδηγός αναφοράς Για Windows Έκδοση 4.0 Παράθυρα των εγγράφων Επιφάνεια του σχεδίου. Σχεδιάστε εδώ νέα αντικείμενα με τα εργαλεία σημείων, διαβήτη, σχεδίασης ευθύγραμμων αντικειμένων και κειμένου.
Σύντομος οδηγός αναφοράς Για Windows Έκδοση 4.0 Παράθυρα των εγγράφων Επιφάνεια του σχεδίου. Σχεδιάστε εδώ νέα αντικείμενα με τα εργαλεία σημείων, διαβήτη, σχεδίασης ευθύγραμμων αντικειμένων και κειμένου.
Γεωμετρία. 63. Σε περίπτωση που η αρχή, το σημείο Ο, βρίσκεται πάνω σε μια ευθεία χχ τότε η
 Γεωμετρία Κεφάλαιο 1: Βασικές γεωμετρικές έννοιες Β.1.1 61.Η ευθεία είναι βασική έννοια της γεωμετρίας που την αντιλαμβανόμαστε ως την γραμμή που αφήνει ο κανόνας (χάρακας).συμβολίζεται με μικρά γράμματα
Γεωμετρία Κεφάλαιο 1: Βασικές γεωμετρικές έννοιες Β.1.1 61.Η ευθεία είναι βασική έννοια της γεωμετρίας που την αντιλαμβανόμαστε ως την γραμμή που αφήνει ο κανόνας (χάρακας).συμβολίζεται με μικρά γράμματα
Το εγχειρίδιο αυτό, δεν είναι απλό τυπολόγιο αλλά μία εγκυκλοπαίδεια όλων των μαθηματικών του ενιαίου λυκείου.
 Τυπολόγιο Μαθηματικών Πρόλογος Το εγχειρίδιο αυτό, δεν είναι απλό τυπολόγιο αλλά μία εγκυκλοπαίδεια όλων των μαθηματικών του ενιαίου λυκείου. Π ε ρ ι ε χ ό μ ε ν α Λυκείου Άλγεβρα 001 018 Γεωμετρία 019
Τυπολόγιο Μαθηματικών Πρόλογος Το εγχειρίδιο αυτό, δεν είναι απλό τυπολόγιο αλλά μία εγκυκλοπαίδεια όλων των μαθηματικών του ενιαίου λυκείου. Π ε ρ ι ε χ ό μ ε ν α Λυκείου Άλγεβρα 001 018 Γεωμετρία 019
ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ
 1 ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Πότε µια συνάρτηση f σε ένα διάστηµα του πεδίου ορισµού της λέγεται γνησίως αύξουσα και πότε γνησίως φθίνουσα; 2. Να αποδείξετε ότι η παράγωγος
1 ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Πότε µια συνάρτηση f σε ένα διάστηµα του πεδίου ορισµού της λέγεται γνησίως αύξουσα και πότε γνησίως φθίνουσα; 2. Να αποδείξετε ότι η παράγωγος
7.1 ΜΕΛΕΤΗ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ
 7.1 ΜΕΛΕΤΗ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ f ( ) 1. Μορφή της συνάρτησης f ( ) Ιδιότητες Έχει πεδίο ορισµού ολο το R Είναι άρτια, άρα συµµετρική ως προς τον άξονα y y Είναι γνησίως φθίνουσα στο διάστηµα (,0] Είναι γνησίως
7.1 ΜΕΛΕΤΗ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ f ( ) 1. Μορφή της συνάρτησης f ( ) Ιδιότητες Έχει πεδίο ορισµού ολο το R Είναι άρτια, άρα συµµετρική ως προς τον άξονα y y Είναι γνησίως φθίνουσα στο διάστηµα (,0] Είναι γνησίως
7.7 Ασκήσεις σχολικού βιβλίου σελίδας 156
 1 7.7 σκήσεις σχολικού βιβλίου σελίδας 156 ρωτήσεις ατανόησης 1. Στα παρακάτω σχήματα να βρείτε τα x, ψ (α) ε 1 ε x 1 2 ε 2 ψ 6 ε 2 3 3 ε 4 ε 1 ε 2 ε 3 ε 4 ε 3 ε 2 ε 1 ε 2 4 x 1,5 ψ 3 4 ε 3 (β) (γ) ε 1
1 7.7 σκήσεις σχολικού βιβλίου σελίδας 156 ρωτήσεις ατανόησης 1. Στα παρακάτω σχήματα να βρείτε τα x, ψ (α) ε 1 ε x 1 2 ε 2 ψ 6 ε 2 3 3 ε 4 ε 1 ε 2 ε 3 ε 4 ε 3 ε 2 ε 1 ε 2 4 x 1,5 ψ 3 4 ε 3 (β) (γ) ε 1
Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα. Αντώνης Πουλιάσης Φυσικός M.Sc. 12 ο ΓΥΜΝΑΣΙΟ ΠΕΡΙΣΤΕΡΙΟΥ
 Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Αντώνης Πουλιάσης Φυσικός M.Sc. 12 ο ΓΥΜΝΑΣΙΟ ΠΕΡΙΣΤΕΡΙΟΥ Πουλιάσης Αντώνης Φυσικός M.Sc. 2 Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Γεωμετρική
Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Αντώνης Πουλιάσης Φυσικός M.Sc. 12 ο ΓΥΜΝΑΣΙΟ ΠΕΡΙΣΤΕΡΙΟΥ Πουλιάσης Αντώνης Φυσικός M.Sc. 2 Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Γεωμετρική
Να επιλύουμε και να διερευνούμε την εξίσωση αx + β = 0, βάση τη γραφική παράσταση της ευθείας y = ax + β.
 Ενότητα 1 Εξισώσεις Ανισώσεις α βαθμού Στην ενότητα αυτή θα μάθουμε: Να επιλύουμε και να διερευνούμε την εξίσωση αx + β = 0, με βάση τη γραφική παράσταση της ευθείας y = ax + β. Να επιλύουμε την ανίσωση
Ενότητα 1 Εξισώσεις Ανισώσεις α βαθμού Στην ενότητα αυτή θα μάθουμε: Να επιλύουμε και να διερευνούμε την εξίσωση αx + β = 0, με βάση τη γραφική παράσταση της ευθείας y = ax + β. Να επιλύουμε την ανίσωση
Μαθηματικά Α' Γυμ. - Ερωτήσεις Θεωρίας 1 ΕΡΩΤΗΣΕΙΣ. (1) Ποιοι είναι οι φυσικοί αριθμοί; Γράψε τέσσερα παραδείγματα.
 Μαθηματικά Α' Γυμ. - Ερωτήσεις Θεωρίας 1 ΕΡΩΤΗΣΕΙΣ (1) Ποιοι είναι οι φυσικοί αριθμοί; Γράψε τέσσερα παραδείγματα. (2) Ποιοι είναι οι άρτιοι και ποιοι οι περιττοί αριθμοί; Γράψε από τρία παραδείγματα.
Μαθηματικά Α' Γυμ. - Ερωτήσεις Θεωρίας 1 ΕΡΩΤΗΣΕΙΣ (1) Ποιοι είναι οι φυσικοί αριθμοί; Γράψε τέσσερα παραδείγματα. (2) Ποιοι είναι οι άρτιοι και ποιοι οι περιττοί αριθμοί; Γράψε από τρία παραδείγματα.
τριώνυμο Η εξίσωση δευτέρου βαθμού στην πλήρη της μορφή ονομάζεται τριώνυμο, γιατί αποτελείται από τρία μονώνυμα. Η γενική μορφή της είναι:
 κεφάλαιο 4 Α τριώνυμο επίλυση της εξίσωσης δευτέρου βαθμού Η εξίσωση δευτέρου βαθμού στην πλήρη της μορφή ονομάζεται τριώνυμο, γιατί αποτελείται από τρία μονώνυμα. Η γενική μορφή της είναι: αx + βx + γ
κεφάλαιο 4 Α τριώνυμο επίλυση της εξίσωσης δευτέρου βαθμού Η εξίσωση δευτέρου βαθμού στην πλήρη της μορφή ονομάζεται τριώνυμο, γιατί αποτελείται από τρία μονώνυμα. Η γενική μορφή της είναι: αx + βx + γ
Μετασχηµατισµοί 2 &3
 Μετασχηµατισµοί &3 Περιγράφονται σαν σύνθεση βασικών: µετατόπιση, αλλαγή κλίµακας,περιστροφή, στρέβλωση Χωρίζονται σε γεωµετρικούς (εδώ) και αξόνων (αντίστροφοι) Θέσεις αντικειµένων και φωτεινών πηγών
Μετασχηµατισµοί &3 Περιγράφονται σαν σύνθεση βασικών: µετατόπιση, αλλαγή κλίµακας,περιστροφή, στρέβλωση Χωρίζονται σε γεωµετρικούς (εδώ) και αξόνων (αντίστροφοι) Θέσεις αντικειµένων και φωτεινών πηγών
Λύκειο Παραλιμνίου Σχολική Χρονιά 2013-2014 Γενικές ασκήσεις επανάληψης Γ κατ
 Λύκειο Παραλιμνίου Σχολική Χρονιά 1-14 Γενικές ασκήσεις επανάληψης Γ κατ 1. Να βρείτε την παράγωγο της συνάρτησης y = e ημ + ln. Να βρείτε την παράγωγο της συνάρτησης y = τοξημ( ) d y y = ημ θ. Να βρείτε
Λύκειο Παραλιμνίου Σχολική Χρονιά 1-14 Γενικές ασκήσεις επανάληψης Γ κατ 1. Να βρείτε την παράγωγο της συνάρτησης y = e ημ + ln. Να βρείτε την παράγωγο της συνάρτησης y = τοξημ( ) d y y = ημ θ. Να βρείτε
Πρόλογος. Κατάλογος Σχημάτων
 Περιεχόμενα Πρόλογος Κατάλογος Σχημάτων v xv 1 ΜΔΕ πρώτης τάξης 21 1.1 Γενικότητες........................... 21 1.2 Εισαγωγή............................ 24 1.2.1 Γεωμετρικές θεωρήσεις στο πρόβλημα της
Περιεχόμενα Πρόλογος Κατάλογος Σχημάτων v xv 1 ΜΔΕ πρώτης τάξης 21 1.1 Γενικότητες........................... 21 1.2 Εισαγωγή............................ 24 1.2.1 Γεωμετρικές θεωρήσεις στο πρόβλημα της
ΣΤΕΡΕΟΜΕΤΡΙΑ Β ΓΥΜΝΑΣΙΟΥ - ΘΕΩΡΙΑ
 ΣΤΕΡΕΟΜΕΤΡΙΑ Β ΓΥΜΝΑΣΙΟΥ - ΘΕΩΡΙΑ Α. ΠΟΛΥΕ ΡΑ 1. ΟΡΙΣΜΟΙ 2. ΟΡΘΟΓΩΝΙΟ ΠΑΡΑΛΛΗΛΕΠΙΠΕ Ο α = µήκος β = πλάτος γ = ύψος δ = διαγώνιος = α. β. γ = Ε β. υ Ε ολ = 2. (αβ + αγ + βγ) 3. ΚΥΒΟΣ = α 3 Ε ολ = 6α 2
ΣΤΕΡΕΟΜΕΤΡΙΑ Β ΓΥΜΝΑΣΙΟΥ - ΘΕΩΡΙΑ Α. ΠΟΛΥΕ ΡΑ 1. ΟΡΙΣΜΟΙ 2. ΟΡΘΟΓΩΝΙΟ ΠΑΡΑΛΛΗΛΕΠΙΠΕ Ο α = µήκος β = πλάτος γ = ύψος δ = διαγώνιος = α. β. γ = Ε β. υ Ε ολ = 2. (αβ + αγ + βγ) 3. ΚΥΒΟΣ = α 3 Ε ολ = 6α 2
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΚΕΦΑΛΑΙΟ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΘΕΜΑ Α Άσκηση, μιγαδικοί αριθμοί να αποδείξετε ότι: Αν = Έχουμε: = ( ) ( ) ( ) ( ) = = =. Το τελευταίο ισχύει, άρα ισχύει και η ισοδύναμη αρχική σχέση.
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΘΕΜΑ Α Άσκηση, μιγαδικοί αριθμοί να αποδείξετε ότι: Αν = Έχουμε: = ( ) ( ) ( ) ( ) = = =. Το τελευταίο ισχύει, άρα ισχύει και η ισοδύναμη αρχική σχέση.
I. ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. math-gr
 I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
Γραφικά Ι. Ενότητα 2: Αλγόριθμοι Σχεδίασης. Θεοχάρης Θεοχάρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών
 Γραφικά Ι Ενότητα 2: Αλγόριθμοι Σχεδίασης Θεοχάρης Θεοχάρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Ενότητα 2 Αλγόριθμοι Σχεδίασης Σχεδίαση 2Δ οθόνες αποτελούνται από διακριτά πλέγματα
Γραφικά Ι Ενότητα 2: Αλγόριθμοι Σχεδίασης Θεοχάρης Θεοχάρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Ενότητα 2 Αλγόριθμοι Σχεδίασης Σχεδίαση 2Δ οθόνες αποτελούνται από διακριτά πλέγματα
Αντικείμενα και γεωμετρικοί μετασχηματισμοί
 Αντικείμενα και γεωμετρικοί μετασχηματισμοί Τα βασικά γεωμετρικά αντικείμενα και οι μεταξύ τους σχέσεις μπορούν να περιγραφούν με τρεις βασικές γεωμετρικές οντότητες: σημεία, βαθμωτά μεγέθη, διανύσματα
Αντικείμενα και γεωμετρικοί μετασχηματισμοί Τα βασικά γεωμετρικά αντικείμενα και οι μεταξύ τους σχέσεις μπορούν να περιγραφούν με τρεις βασικές γεωμετρικές οντότητες: σημεία, βαθμωτά μεγέθη, διανύσματα
ENOTHTA 1.1 ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ
 ENOTHTA. ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ ΜΕΡΟΣ ο. Πώς προσδιορίζουμε τη θέση των αντικειμένων; A O M B ' y P Ì(,y) Ð Για τον προσδιορισμό της θέσης πάνω σε μία ευθεία πρέπει να έχουμε ένα σημείο της
ENOTHTA. ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ ΜΕΡΟΣ ο. Πώς προσδιορίζουμε τη θέση των αντικειμένων; A O M B ' y P Ì(,y) Ð Για τον προσδιορισμό της θέσης πάνω σε μία ευθεία πρέπει να έχουμε ένα σημείο της
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΘΕΩΡΗΤΙΚΗ ΓΕΩΜΕΤΡΙΑ
 ΓΕΩΜΕΤΡΙΑ Α ΛΥΚΕΙΟΥ ΘΕΩΡΙΑ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΘΕΩΡΗΤΙΚΗ ΓΕΩΜΕΤΡΙΑ ΟΡΙΣΜΟΙ Ευθύγραμμο τμήμα είναι το κομμάτι της ευθείας που έχει αρχή και τέλος. Ημιευθεια Είναι το κομμάτι της ευθείας που έχει αρχή αλλά όχι
ΓΕΩΜΕΤΡΙΑ Α ΛΥΚΕΙΟΥ ΘΕΩΡΙΑ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΘΕΩΡΗΤΙΚΗ ΓΕΩΜΕΤΡΙΑ ΟΡΙΣΜΟΙ Ευθύγραμμο τμήμα είναι το κομμάτι της ευθείας που έχει αρχή και τέλος. Ημιευθεια Είναι το κομμάτι της ευθείας που έχει αρχή αλλά όχι
ΘΕΜΑΤΑ ΥΠΟΛΟΓΙΣΤΙΚΗΣ ΟΡΑΣΗΣ ΚΑΙ ΓΡΑΦΙΚΩΝ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΑΠΟΚΟΠΗ Ε. Θεοδωρίδης, Α. Τσακαλίδης
 ΘΕΜΑΤΑ ΥΠΟΛΟΓΙΣΤΙΚΗΣ ΟΡΑΣΗΣ ΚΑΙ ΓΡΑΦΙΚΩΝ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΑΠΟΚΟΠΗ 2013-2014 Ε. Θεοδωρίδης, Α. Τσακαλίδης Μετασχηματισμοί (1) Position, reshape, animate Objects, lights, cameras Linear transforms f(x)+f(y)=f(x+y)
ΘΕΜΑΤΑ ΥΠΟΛΟΓΙΣΤΙΚΗΣ ΟΡΑΣΗΣ ΚΑΙ ΓΡΑΦΙΚΩΝ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΑΠΟΚΟΠΗ 2013-2014 Ε. Θεοδωρίδης, Α. Τσακαλίδης Μετασχηματισμοί (1) Position, reshape, animate Objects, lights, cameras Linear transforms f(x)+f(y)=f(x+y)
Κεφάλαιο 3 Βασική Σχεδίαση και Επεξεργασία
 Περιεχόμενα Πρόλογος... 7 Εισαγωγή... 9 Κεφάλαιο 1: Στοιχεία Λειτουργίας του Υπολογιστή και του προγράμματος AutoCAD... 11 Κεφάλαιο 2: Στοιχεία Λειτουργικού Συστήματος... 15 Κεφάλαιο 3: Βασική Σχεδίαση
Περιεχόμενα Πρόλογος... 7 Εισαγωγή... 9 Κεφάλαιο 1: Στοιχεία Λειτουργίας του Υπολογιστή και του προγράμματος AutoCAD... 11 Κεφάλαιο 2: Στοιχεία Λειτουργικού Συστήματος... 15 Κεφάλαιο 3: Βασική Σχεδίαση
4.3 Δραστηριότητα: Θεώρημα Fermat
 4.3 Δραστηριότητα: Θεώρημα Fermat Θέμα της δραστηριότητας Η δραστηριότητα αυτή εισάγει το Θεώρημα Fermat και στη συνέχεια την απόδειξή του. Ακολούθως εξετάζεται η χρήση του στον εντοπισμό πιθανών τοπικών
4.3 Δραστηριότητα: Θεώρημα Fermat Θέμα της δραστηριότητας Η δραστηριότητα αυτή εισάγει το Θεώρημα Fermat και στη συνέχεια την απόδειξή του. Ακολούθως εξετάζεται η χρήση του στον εντοπισμό πιθανών τοπικών
1,y 1) είναι η C : xx yy 0.
 ΘΕΜΑ Α ΔΕΙΓΜΑΤΑ ΘΕΜΑΤΩΝ ΕΞΕΤΑΣΕΩΝ ΜΑΙΟΥ-ΙΟΥΝΙΟΥ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ο δείγμα Α. Αν α, β δύο διανύσματα του επιπέδου με συντελεστές διεύθυνσης λ και λ αντίστοιχα, να αποδείξετε ότι α β λ λ.
ΘΕΜΑ Α ΔΕΙΓΜΑΤΑ ΘΕΜΑΤΩΝ ΕΞΕΤΑΣΕΩΝ ΜΑΙΟΥ-ΙΟΥΝΙΟΥ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ο δείγμα Α. Αν α, β δύο διανύσματα του επιπέδου με συντελεστές διεύθυνσης λ και λ αντίστοιχα, να αποδείξετε ότι α β λ λ.
117 ΑΣΚΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ Μανώλη Ψαρρά. Μαθηματικού
 117 ΑΣΚΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ Μανώλη Ψαρρά Μαθηματικού Περιεχόμενα 1. Διανύσματα (47) ελ. - 9. Ευθεία (18) ελ. 10-1 3. Κύκλος (13).ελ. 13-15 4. Παραβολή (14) ελ. 16-18 5. Έλλειψη (18)..
117 ΑΣΚΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ Μανώλη Ψαρρά Μαθηματικού Περιεχόμενα 1. Διανύσματα (47) ελ. - 9. Ευθεία (18) ελ. 10-1 3. Κύκλος (13).ελ. 13-15 4. Παραβολή (14) ελ. 16-18 5. Έλλειψη (18)..
Στοιχεία Συναρτήσεων. 1. Να βρεθεί το πεδίο ορισμού των παρακάτω συναρτήσεων: στ. x 1
 Στοιχεία Συναρτήσεων 1. Να βρεθεί το πεδίο ορισμού των παρακάτω συναρτήσεων: 1 α. f() β. f() 3 6 8 3 1 γ. g() δ. g() ( 6)( 5) 4 ε. h() 4 στ. h() 4 ζ. ε. στ. 1 φ() η. 1 1 1 r() 5 6 1 r() 1 5 6 φ() 5. Στις
Στοιχεία Συναρτήσεων 1. Να βρεθεί το πεδίο ορισμού των παρακάτω συναρτήσεων: 1 α. f() β. f() 3 6 8 3 1 γ. g() δ. g() ( 6)( 5) 4 ε. h() 4 στ. h() 4 ζ. ε. στ. 1 φ() η. 1 1 1 r() 5 6 1 r() 1 5 6 φ() 5. Στις
δίου ορισμού, μέσου του τύπου εξαρτημένης μεταβλητής του πεδίου τιμών που λέγεται εικόνα της f για x α f α.
 3.1 Η έννοια της συνάρτησης Ορισμοί Συνάρτηση f από ένα συνόλου Α σε ένα σύνολο Β είναι μια αντιστοιχία των στοιχείων του Α στα στοιχεία του Β, κατά την οποία κάθε στοιχείο του Α αντιστοιχεί σε ένα μόνο
3.1 Η έννοια της συνάρτησης Ορισμοί Συνάρτηση f από ένα συνόλου Α σε ένα σύνολο Β είναι μια αντιστοιχία των στοιχείων του Α στα στοιχεία του Β, κατά την οποία κάθε στοιχείο του Α αντιστοιχεί σε ένα μόνο
ΑΣΚΗΣΕΙΣ. x + 5= 6 (1) και. x = 1, οπότε η (2) γίνεται 1 5x + 1= 7 x = 1 ΘΕΜΑ Β. Άσκηση 1. Να βρείτε τον αριθμό x R όταν. Λύση.
 ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i. ΙΔΙΟΤΗΤΕΣ
ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i. ΙΔΙΟΤΗΤΕΣ
b proj a b είναι κάθετο στο
 ΦΥΛΛΑ ΙΟ ΑΣΚΗΣΕΩΝ. Βρείτε όλα τα σηµεία P τέτοια ώστε η απόσταση του P από το A(, 5, 3) είναι διπλάσια από την απόσταση του P από το B(6, 2, 2). είξτε ότι το σύνολο όλων αυτών των σηµείων είναι σφαίρα.
ΦΥΛΛΑ ΙΟ ΑΣΚΗΣΕΩΝ. Βρείτε όλα τα σηµεία P τέτοια ώστε η απόσταση του P από το A(, 5, 3) είναι διπλάσια από την απόσταση του P από το B(6, 2, 2). είξτε ότι το σύνολο όλων αυτών των σηµείων είναι σφαίρα.
ΥΣ02 Τεχνητή Νοημοσύνη Χειμερινό Εξάμηνο
 ΥΣ02 Τεχνητή Νοημοσύνη Χειμερινό Εξάμηνο 2010-2011 Πρώτη Σειρά Ασκήσεων (20% του συνολικού βαθμού στο μάθημα, Άριστα = 390 μονάδες) Ημερομηνία Ανακοίνωσης: 6/10/2010 Ημερομηνία Παράδοσης: 15/11/2010 σύμφωνα
ΥΣ02 Τεχνητή Νοημοσύνη Χειμερινό Εξάμηνο 2010-2011 Πρώτη Σειρά Ασκήσεων (20% του συνολικού βαθμού στο μάθημα, Άριστα = 390 μονάδες) Ημερομηνία Ανακοίνωσης: 6/10/2010 Ημερομηνία Παράδοσης: 15/11/2010 σύμφωνα
Κεφάλαιο 1 ο. Βασικές γεωμετρικές έννοιες.
 Μαθηματικά A Γυμνασίου Κεφάλαιο 1 ο. Βασικές γεωμετρικές έννοιες. 1. Τι λέμε σημείο; Η άκρη του μολυβιού μας, οι κορυφές ενός σχήματος, η μύτη μιας βελόνας, μας δίνουν την έννοια του σημείου. 2. Τι λέμε
Μαθηματικά A Γυμνασίου Κεφάλαιο 1 ο. Βασικές γεωμετρικές έννοιες. 1. Τι λέμε σημείο; Η άκρη του μολυβιού μας, οι κορυφές ενός σχήματος, η μύτη μιας βελόνας, μας δίνουν την έννοια του σημείου. 2. Τι λέμε
Κατευθυνόμενα γραφήματα. Μαθηματικά Πληροφορικής 6ο Μάθημα. Βρόχοι. Μη κατευθυνόμενα γραφήματα. Ορισμός
 Κατευθυνόμενα γραφήματα Μαθηματικά Πληροφορικής 6ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Κατευθυνόμενο γράφημα G είναι ένα ζεύγος (V, E ) όπου V πεπερασμένο σύνολο του οποίου
Κατευθυνόμενα γραφήματα Μαθηματικά Πληροφορικής 6ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Κατευθυνόμενο γράφημα G είναι ένα ζεύγος (V, E ) όπου V πεπερασμένο σύνολο του οποίου
Τεχνολογία Παιγνίων. Τεχνολογία Παιγνίων. Τεχνολογία Παιγνίων. Εισαγωγή στο Easy Java Simulations (EJS)
 1. Σημεία και Γραμμές Ι.Παχουλάκης 1. Σημεία και Γραμμές Εισαγωγή στο Easy Java Simulations (EJS) Εγκατάσταση Εγκαταστήστε το πιο πρόσφατο JRE (Java Runtime Environment) από το σύνδεσμο https://www.oracle.com/technetwork/java/javase/downloads/jr
1. Σημεία και Γραμμές Ι.Παχουλάκης 1. Σημεία και Γραμμές Εισαγωγή στο Easy Java Simulations (EJS) Εγκατάσταση Εγκαταστήστε το πιο πρόσφατο JRE (Java Runtime Environment) από το σύνδεσμο https://www.oracle.com/technetwork/java/javase/downloads/jr
Κατευθυνόμενα γραφήματα. Μαθηματικά Πληροφορικής 6ο Μάθημα. Βρόχοι. Μη κατευθυνόμενα γραφήματα. Ορισμός
 Κατευθυνόμενα γραφήματα Μαθηματικά Πληροφορικής 6ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Κατευθυνόμενο γράφημα G είναι ένα ζεύγος (V, E ) όπου V πεπερασμένο σύνολο του οποίου
Κατευθυνόμενα γραφήματα Μαθηματικά Πληροφορικής 6ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Κατευθυνόμενο γράφημα G είναι ένα ζεύγος (V, E ) όπου V πεπερασμένο σύνολο του οποίου
Αλγόριθμοι Σχεδίασης
 Γραφικά & Οπτικοποίηση Κεφάλαιο 2 Αλγόριθμοι Σχεδίασης Σχεδίαση 2Δοθόνες αποτελούνται από διακριτά πλέγματα εικονοστοιχείων (pixels) Σχεδίαση: μετατροπή 2Δ στοιχειωδών σχημάτων σε διακριτή παράσταση εικονοστοιχείων
Γραφικά & Οπτικοποίηση Κεφάλαιο 2 Αλγόριθμοι Σχεδίασης Σχεδίαση 2Δοθόνες αποτελούνται από διακριτά πλέγματα εικονοστοιχείων (pixels) Σχεδίαση: μετατροπή 2Δ στοιχειωδών σχημάτων σε διακριτή παράσταση εικονοστοιχείων
ΓΥΜΝΑΣΙΟ ΑΠΟΣΤΟΛΟΥ ΑΝΔΡΕΑ ΕΜΠΑΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ ΕΞΕΤΑΣΤΙΚΟ ΔΟΚΙΜΙΟ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ ΙΟΥΝΙΟΥ ΧΡΟΝΟΣ : 2 Ώρες Υπογραφή :
 ΓΥΜΝΑΣΙΟ ΑΠΟΣΤΟΛΟΥ ΑΝΔΡΕΑ ΕΜΠΑΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2018 2019 ΕΞΕΤΑΣΤΙΚΟ ΔΟΚΙΜΙΟ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ ΙΟΥΝΙΟΥ 2019 ΜΑΘΗΜΑ : Μαθηματικά ΤΑΞΗ : Γ ΗΜΕΡΟΜΗΝΙΑ : 5 / 6 / 2019 ΧΡΟΝΟΣ : 2 Ώρες Βαθμός : Ολογράφως
ΓΥΜΝΑΣΙΟ ΑΠΟΣΤΟΛΟΥ ΑΝΔΡΕΑ ΕΜΠΑΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2018 2019 ΕΞΕΤΑΣΤΙΚΟ ΔΟΚΙΜΙΟ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ ΙΟΥΝΙΟΥ 2019 ΜΑΘΗΜΑ : Μαθηματικά ΤΑΞΗ : Γ ΗΜΕΡΟΜΗΝΙΑ : 5 / 6 / 2019 ΧΡΟΝΟΣ : 2 Ώρες Βαθμός : Ολογράφως
Μιχάλης Παπαδημητράκης. Μιγαδική Ανάλυση
 Μιχάλης Παπαδημητράκης Μιγαδική Ανάλυση Περιεχόμενα Οι μιγαδικοί αριθμοί.. Οι μιγαδικοί αριθμοί..................................2 Το Ĉ, η στερεογραφική προβολή και η σφαίρα του Riemann............ 0
Μιχάλης Παπαδημητράκης Μιγαδική Ανάλυση Περιεχόμενα Οι μιγαδικοί αριθμοί.. Οι μιγαδικοί αριθμοί..................................2 Το Ĉ, η στερεογραφική προβολή και η σφαίρα του Riemann............ 0
Προβολές. Απαραίτητες αφού 3 αντικείµενα απεικονίζονται σε 2 συσκευές.
 ροβολές Απαραίτητες αφού 3 αντικείµενα απεικονίζονται σε συσκευές. Θέσεις αντικειµένων και φωτεινών πηγών Θέση παρατηρητή 3 Μαθηµατικά Μοντέλα ΣΣΑ 3 Μετασχ/σµοί Μοντέλου ΣΣ (WCS) 3 Μετασχ/σµός αρατήρησης
ροβολές Απαραίτητες αφού 3 αντικείµενα απεικονίζονται σε συσκευές. Θέσεις αντικειµένων και φωτεινών πηγών Θέση παρατηρητή 3 Μαθηµατικά Μοντέλα ΣΣΑ 3 Μετασχ/σµοί Μοντέλου ΣΣ (WCS) 3 Μετασχ/σµός αρατήρησης
Ασκήσεις. Κεφάλαιο 6. a = a 0 + x 1 b 1 + x 2 b 2 + x 3 b 3, όπου b i = a i a 0, i = 1, 2, 3, P 2 = {(x, y, z) R 3 : x 2y + 3z = 2}.
 Κεφάλαιο 6 Ασκήσεις 1. (αʹ) ώστε δράση του Χ R 2 στο αφινικό επίπεδο P = {(x, y, z) R 3 : x = 2}. Επίσης, δώστε µία αφινική ϐάση τριών σηµείων (a 0, a 1, a 2 ) και ϐρείτε τις ϐαρυκεντρικές συντεταγµένες
Κεφάλαιο 6 Ασκήσεις 1. (αʹ) ώστε δράση του Χ R 2 στο αφινικό επίπεδο P = {(x, y, z) R 3 : x = 2}. Επίσης, δώστε µία αφινική ϐάση τριών σηµείων (a 0, a 1, a 2 ) και ϐρείτε τις ϐαρυκεντρικές συντεταγµένες
