REFLECTIONLESS POTENTIALS AND STOCHASTIC ANALYSIS. Setsuo TANIGUCHI. Faculty of Mathematics, Kyushu Univ.
|
|
|
- Φώτιος Φλέσσας
- 7 χρόνια πριν
- Προβολές:
Transcript
1 REFLECTIONLESS POTENTIALS AND STOCHASTIC ANALYSIS Setsuo TANIGUCHI Faculty of Mathematics, Kyushu Univ. 0
2 PDE and Stochastic Analysis 194 K.Itô; stoch. integral, Itô s formula R.Feynman; Feynman path integral ( d ) x dx 1944 R.Cameron-W.Martin; M.Kac; the Feynman-Kac formula Heat eq: u = u(x, t) ( L = 1 u t = Lxu, u(, 0) = f i,j aij x i x j + ) i bi x i + V u(x, t) = E [ f(x(t, x))e Φ(x;V )] ( X(t, x):l-diff.pr. ) Reflectionless potentials, generalized... n-solitons of the KdV eq. 1
3 Reflectionless potential us (s S); us(x) = (d/dx) log det(i + Gs(x)), where S = {{η j, m j } 1 j n n N, η j, m j > 0, η i η j } Gs(x) = ( m i m j e (η i+η j )x η i + η j ) 1 i,j n. Schrö Op. (d/dx) + u; Scattering data Ξ 0 = {us s S}, Ξ u µ > 0, un Ξ 0 s.t. Spec( (d/dx) + un) [ µ, ), n = 1,,... un u (unif on cpts)
4 Σ = {σ finite meas on R with cpt supp} W = {w : [0, ) R conti, w(0) = 0} X(x) : W R: X(x, w) = w(x), w W P σ : the prob meas on W under which {X(x)} is the centered Gaussian pr with cov fn e ζ(x+y) e ζ x y X(x)X(y)dP = σ(dζ). W R ζ a 1 X(x 1 ) +... a k X(x k ) N(0, ), (x j 0) G = {P σ σ Σ} (bij) Σ ) X(x) dp σ = W R e ζx 1 σ(dζ) ζ 3
5 ψ(p σ )(x) = 4 d dx W ( exp 1 x ) 0 X(y) dy dp, x 0 The Plan of talk G:Cen. Gauss P σ, σ Σ () G 0 : P σ, σ = j c j δ p j ψ (1) Ξ:gen. rl. pot u unif conv. on cpts Ξ 0 : rl pot us, s S Realization of P σ, Spelling out s S, Solitons 4
6 reflectionless potential and n-soliton Σ 0 = { σ = n j=1 c } j δ p j n N, p j R, p j p i, c j > 0 σ Σ 0. {b(x)} x 0 ; an n-dim B.m.on (Ω, F, P ) ξσ(x) = e xd σ x 0 e yd σdb(y) (Dσ =diag[p j ]) ξ i σ (x) = exp i x 0 e yp idb i (y), i = 1,..., n Xσ(x) = c, ξσ(x) (c = (c j )) P σ (A) = P (Xσ 1 (A)) Xσ : Ω ω Xσ(, ω) W σ Σ 0 ; m < n, 1 j(1) < < j(m) n s.t. p j p j+1, p j(l) > 0, p j(l)+1 = p j(l) #{ p 1,..., pn } = n m. 5
7 ψ : Σ 0 σ {η j, m j } S p 1 p n 1 {η 1 < < ηn} = {p j(1),..., p j(m), r 1,..., r n m } m i = (0 < r 1 < < r n m : n j=1 c j /(p j η i c j(l)+1 c j(l) η i k i k i η k + η i η k η i η k + η i η k η i n k=1 k j(l),j(l)+1 p k + η i p k η i, r) = 1) p k + η i p k η i, if i = j(l), otherwise. 6
8 Thm 1. Let P σ G 0 = {P σ σ Σ 0 }. Then ( ( 4 log exp 1 x W 0 X(y) dy )dp σ) ( ) = log det I + G (x) ψ(σ) ( ) + log det I + G (0) ψ(σ) x n (p i + η i ). i=1 In particular, ψ : G 0 Ξ 0 and ψ(p σ ) = u ψ(σ). Moreover, ψ : G 0 Ξ 0 is bijective. ψ(p σ ) = u ψ(σ) on [0, ); The real analyticity does the rest of job u ψ(σ) (x) = ψ(p µ )( x), x (, 0] (µ(a) = σ( A)) 7
9 The τ-function of the KdV hierarchy is τ (x, t) = 1 + p j=1 m ij η ij n p=1 1 i 1 < <i p n (η ij η ik ) [ p exp ζ η 1 j<k p ij +η ij ], ik j=1 where x R, t = (t j ) R N with #{t j 0} <, {η j, m j } Ξ 0, ζ j = ζ j (x, t) = xη j + α=1 tαη j α+1. If t = (t, 0,... ), then v(x, t) = x log τ (x, t) solves the KdV eq; v t = 3 vv x v xxx. 8
10 For σ Σ 0, let ψ(σ) = {η j, m j } Ξ 0 and Iσ(x, t) = Ω [ exp 1 x 0 X σ(y) dy + 1 ] (β t D σ)ξσ(x), ξσ(x) dp, where β t = ( ( xφ)φ 1) (0, t), ζ = diag[ζ j ], φ(x, t) = U { cosh(ζ) sinh(ζ)r 1 U 1 DσU } U 1, U O(n); D σ +c c = UR U 1 (R =diag[η j ]) Thm (i) log ( Iσ(x, t) ) = (1/) log τ (x, t) +(1/) log τ (0, t) (x/) n i=1 (p i + η i ) (ii) If t = (t, 0,... ), then vσ(x, t) = 4 x log( Iσ ) is an n-soliton of the KdV eq. 9
11 Change of variables formulae on W; Prop 1. Let φ(y) R n n be a sol of φ Eσφ = 0, where Eσ = D σ + c c. Let x > 0 and assume (A.1) det φ(y) 0, (A.) β(y) = (φ φ 1 )(y) is symm (0 y x). Then ( Ω exp 1 x 0 X σ(y) dy + 1 ) (β(0) D σ)ξσ(x), ξσ(x) dp = ( det φ(0) ) 1/ ( e xtrdσ det φ(x) ) 1/. 10
12 Pf of Thm 1: φ Eσφ = 0, φ(0) = I, φ (0) = Dσ; φ(y) = cosh(yeσ 1/ ) E 1/ sinh(yeσ 1/ )Dσ (Case1) p i < p i+1, i = 1,..., n 1. φ(y) = (1/)UV R 1 B { I + G ψ(σ) (y) } e yr B 1 XC, V = diag [ (D σ r j I) 1 c 1], R = diag[η j ], a(i) = sgn [ nβ=1 (p β η i ) ], { α i b(i) = a(i) η (η α η i ) } 1/, i nβ=1 (p β η i ) B = diag[b(j)], X ij = ( p j + η i ) 1. (Case) p ε j = p j ε m i=1 δ j,l(i)+1, ε 0. 11
13 Pf of Thm : φ(y) = φ(y, t); (A.1),(A.) are fulfilled (Case1) p i < p i+1, i = 1,..., n 1. φ(y, t) = 1 UR 1 V B{I + A(y, t)}e ζ(y,t) B 1 XC, where A(y, t) = ( mi m j e {ζ ) i(y,t)+ζ j (y,t)}. η i + η j 1 i,j n (Case) p ε j = p j ε m i=1 δ j,l(i)+1, ε 0. 1
14 ch of var formulae Dw; the Lebesgue meas on W n 1 (W n = {w : [0, ) R n conti, w(0) = 0}) ( fdp = f(w) exp 1 x W n W n 0 w ) Dw ( = f w ) ( Dw exp 1 x W n 0 w Dw ) Dw = e trd/ W n f (ch var w w Dw; Volterra) ( w ) Dw Itô s formula: Dw(x), w(x) = exp( 1 Dw(x), w(x) 1 x ) 0 Dw dp (w) x 0 Dw, w + trd 13
15 ξσ(x, w) = e xd σ x 0 e yd σdw(y) = w(y) + e xd σ x 0 e yd σdσw(y)dy ξσ(, w Dσw) = w Apply 1 with f(w) = g(ξσ( ; w)) ( exp 1 x W n 0 X σ(y) dy + 1 ) (γ(x) D σ)ξσ(x), ξσ(x) dp = e trd σ/ ( exp 1 x W n 0 E σw, w dy + 1 )dp γ(x)w(x), w(x) 14
16 ( 3 1 = exp 1 x W n 0 w ) Dw γ : [0, x] R n n ( = exp 1 x W n 0 w γw ) Dw. x x x γ(x)w(x), w(x) = 0 γ w, w + 0 γw, w + trγ. ( 0 1 = exp 1 x W n 0 (γ + γ )w, w + 1 ) γ(x)w(x), w(x) ( exp 1 x 0 w ) ( Dw exp 1 x ) 0 trγ ( x ) ( exp 1 0 trγ = exp 1 x W n 0 (γ + γ )w, w + 1 )dp γ(x)w(x), w(x) 4 γ + γ = Eσ, γ(x) = CH tr: γ(y) = (φ φ 1 )(x y), φ Eσφ = 0 15
17 Bijectivity Let u = us Ξ 0 (s S), and e + (x; ζ) be the right Jost sol of L = (d/dx) + us; Le + ( ; ζ) = ζ e + ( ; ζ), e + (x; ζ) e iζx (x ) Then λ j C (R; R), 1 j n, s.t. e + (x; ζ) = e 1ζx j Define κ : Ξ 0 Σ 0 by Then κ(s) = j ( λ j (0))δ λ j (0). ψ(κ(s)) = s, κ(ψ(σ)) = σ. ζ 1λ j (x) ζ+ 1η j. 16
18 generalized reflectionless potentials u Ξ µ > 0, un Ξ 0 s.t. Φσ(x) = Spec ( ( d dx ) + u n ) [ µ, ), n = 1,,... un u (unif on cpts) W ( exp 1 x ) 0 X(y) dy dp σ ψ(p σ ) = 4 ( d dx ) Φ σ G G 0 P σ ψ(p σ ) Ξ 0 Ξ : bijective Question: P σ n P σ un u, ψ(g) Ξ 17
19 Thm 3 (i) Φσ C ([0, )), σ Σ (ii) Let σn Σ 0, σ Σ. Suppose n N suppσ n [ β, β] ( β > 0), σn σ (vag). Then Φ (j) σ n Φ (j) σ (unif on cpts) (j = 0, 1, ). (iii) Let σ Σ and suppσ [ β, β]. Define σn(dξ) = n j= n { σ ([ jβn, (j+1)β n )) + n } δ jβ/n. Then n 0 N, λ 0 > 0 st Spec ( ( d dx ) + ψ(p σ n )) [ λ 0, ), n n 0. (iv) P σ G, u Ξ st ψ(p σ ) = u on [0, ). Conversely, u Ξ, P σ G st... u(x) = ψ(p µ )( x), x (, 0] (µ(a) = σ( A)) 18
20 Brownian sheet {W (p, x)} (p,x) [0, ) ; a 1 W (p 1, x 1 ) + + a k W (p k, x k ) N(0, ) W (p, x)w (q, y)dp = min{p, q} min{x, y} Ω Wiener integral s.t. L ([0, ) ) h [0, ) hdw L (P ) (isom) χ [0, ) [a,b) [c,d) dw = W (b, d) W (a, d) W (b, c) + W (a, c) d + c + a b 19
21 For σ = j c j δ p j and a > 0, a b < p 1, set q 0 = b + a, q k = q 0 + k j=1 p j p j 1, p 0 = b, ( W (qj,y) W (q Wq 0...q n (y) = j 1,y) ) {q j q j 1 } 1/ 1 j n. ξ a,b,σ (y) = e yd σ y 0 e zd σdwq 0...q n (z) X a,b,σ (y) = c, ξ a,b,σ (y) Xσ It holds that where X a,b,σ (y) = h(q, z; y) = n j=1 [0, ) h( ; y)dw, e (y z)pj c j χ [qj 1,q qj q j ) [0,y)(q, z). j 1 0
22 Gaussian filtering theory Let u Ξ and take P σ so that u = ψ(p σ ). {b(x)} x 0 : a 1-dim Bm indep of {Xσ(x)} x 0 Put Y (x) = x 0 Xσ(y)dy + b(x), Gx = σ{y (y) y x} ˆXσ(x) = E[Xσ(x) Gx] γ(x) = (X σ(x) ˆXσ(x)) dp Ω exp( 1 x Ω 0 X ) ( σ dp = exp 1 x 0 γ). K(x, y); K + 0 K(, z)r σ(z, )dz = Rσ γ(x) = K(x, x). u(x) = 4(d/dx) log ( exp( 1 x Ω 0 X ) ) σ dp = dx d ( K(x, x)). Marchenko s formula 1
23 quadratic Wiener functional For σ Σ 0 and symm β R n n, define qσ,x = 1 x 0 X σ(y) dy + 1 rl pot; β 0 KdV; β = β t Dσ. βξ σ(x), ξσ(x). Let A = qσ,x and Bσ(a) = Dσ + ac c. eζqσ,x dp = { j=1 (1 ζa Ω j ) } 1/ ( aj ;ev of A ) = exp ( R ( e ζx 1 ) fa (x)dx) ( f A (x) = 1 x = { e xtrd σ det [ cosh(xbσ(ζ) 1/ ) ) n;a n x>0 exp( x/a n) (ζβ + Dσ)Bσ(ζ) 1/ sinh(xbσ(ζ) 1/ ) ]} 1/.
Brownian sheet and the reflectionless potential. Setsuo TANIGUCHI. Faculty of Math., Kyushu Univ. Fukuoka , JAPAN
 Brownian sheet and the reflectionless potential Setsuo TANIGUCHI Faculty of Math., Kyushu Univ. Fukuoka 812-8581, JAPAN June 1, 24, at Keio Univ. http://www.math.kyushu-u.ac.jp/~taniguch/ Partially supported
Brownian sheet and the reflectionless potential Setsuo TANIGUCHI Faculty of Math., Kyushu Univ. Fukuoka 812-8581, JAPAN June 1, 24, at Keio Univ. http://www.math.kyushu-u.ac.jp/~taniguch/ Partially supported
D Alembert s Solution to the Wave Equation
 D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
SCHOOL OF MATHEMATICAL SCIENCES G11LMA Linear Mathematics Examination Solutions
 SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
On the Galois Group of Linear Difference-Differential Equations
 On the Galois Group of Linear Difference-Differential Equations Ruyong Feng KLMM, Chinese Academy of Sciences, China Ruyong Feng (KLMM, CAS) Galois Group 1 / 19 Contents 1 Basic Notations and Concepts
On the Galois Group of Linear Difference-Differential Equations Ruyong Feng KLMM, Chinese Academy of Sciences, China Ruyong Feng (KLMM, CAS) Galois Group 1 / 19 Contents 1 Basic Notations and Concepts
Laplace Expansion. Peter McCullagh. WHOA-PSI, St Louis August, Department of Statistics University of Chicago
 Laplace Expansion Peter McCullagh Department of Statistics University of Chicago WHOA-PSI, St Louis August, 2017 Outline Laplace approximation in 1D Laplace expansion in 1D Laplace expansion in R p Formal
Laplace Expansion Peter McCullagh Department of Statistics University of Chicago WHOA-PSI, St Louis August, 2017 Outline Laplace approximation in 1D Laplace expansion in 1D Laplace expansion in R p Formal
P AND P. P : actual probability. P : risk neutral probability. Realtionship: mutual absolute continuity P P. For example:
 (B t, S (t) t P AND P,..., S (p) t ): securities P : actual probability P : risk neutral probability Realtionship: mutual absolute continuity P P For example: P : ds t = µ t S t dt + σ t S t dw t P : ds
(B t, S (t) t P AND P,..., S (p) t ): securities P : actual probability P : risk neutral probability Realtionship: mutual absolute continuity P P For example: P : ds t = µ t S t dt + σ t S t dw t P : ds
Homework 8 Model Solution Section
 MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
Solutions to Exercise Sheet 5
 Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
 J J l 2 J T l 1 J T J T l 2 l 1 J J l 1 c 0 J J J J J l 2 l 2 J J J T J T l 1 J J T J T J T J {e n } n N {e n } n N x X {λ n } n N R x = λ n e n {e n } n N {e n : n N} e n 0 n N k 1, k 2,..., k n N λ
J J l 2 J T l 1 J T J T l 2 l 1 J J l 1 c 0 J J J J J l 2 l 2 J J J T J T l 1 J J T J T J T J {e n } n N {e n } n N x X {λ n } n N R x = λ n e n {e n } n N {e n : n N} e n 0 n N k 1, k 2,..., k n N λ
Gaussian related distributions
 Gaussian related distributions Santiago Aja-Fernández June 19, 009 1 Gaussian related distributions 1. Gaussian: ormal PDF: MGF: Main moments:. Rayleigh: PDF: MGF: Raw moments: Main moments: px = 1 σ π
Gaussian related distributions Santiago Aja-Fernández June 19, 009 1 Gaussian related distributions 1. Gaussian: ormal PDF: MGF: Main moments:. Rayleigh: PDF: MGF: Raw moments: Main moments: px = 1 σ π
Teor imov r. ta matem. statist. Vip. 94, 2016, stor
 eor imov r. ta matem. statist. Vip. 94, 6, stor. 93 5 Abstract. e article is devoted to models of financial markets wit stocastic volatility, wic is defined by a functional of Ornstein-Ulenbeck process
eor imov r. ta matem. statist. Vip. 94, 6, stor. 93 5 Abstract. e article is devoted to models of financial markets wit stocastic volatility, wic is defined by a functional of Ornstein-Ulenbeck process
12. Radon-Nikodym Theorem
 Tutorial 12: Radon-Nikodym Theorem 1 12. Radon-Nikodym Theorem In the following, (Ω, F) is an arbitrary measurable space. Definition 96 Let μ and ν be two (possibly complex) measures on (Ω, F). We say
Tutorial 12: Radon-Nikodym Theorem 1 12. Radon-Nikodym Theorem In the following, (Ω, F) is an arbitrary measurable space. Definition 96 Let μ and ν be two (possibly complex) measures on (Ω, F). We say
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
Second Order Partial Differential Equations
 Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
 y(t) S x(t) S dy dx E, E E T1 T2 T1 T2 1 T 1 T 2 2 T 2 1 T 2 2 3 T 3 1 T 3 2... V o R R R T V CC P F A P g h V ext V sin 2 S f S t V 1 V 2 V out sin 2 f S t x 1 F k q K x q K k F d F x d V
y(t) S x(t) S dy dx E, E E T1 T2 T1 T2 1 T 1 T 2 2 T 2 1 T 2 2 3 T 3 1 T 3 2... V o R R R T V CC P F A P g h V ext V sin 2 S f S t V 1 V 2 V out sin 2 f S t x 1 F k q K x q K k F d F x d V
Uniform Convergence of Fourier Series Michael Taylor
 Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
Parametrized Surfaces
 Parametrized Surfaces Recall from our unit on vector-valued functions at the beginning of the semester that an R 3 -valued function c(t) in one parameter is a mapping of the form c : I R 3 where I is some
Parametrized Surfaces Recall from our unit on vector-valued functions at the beginning of the semester that an R 3 -valued function c(t) in one parameter is a mapping of the form c : I R 3 where I is some
Local Approximation with Kernels
 Local Approximation with Kernels Thomas Hangelbroek University of Hawaii at Manoa 5th International Conference Approximation Theory, 26 work supported by: NSF DMS-43726 A cubic spline example Consider
Local Approximation with Kernels Thomas Hangelbroek University of Hawaii at Manoa 5th International Conference Approximation Theory, 26 work supported by: NSF DMS-43726 A cubic spline example Consider
On the summability of divergent power series solutions for certain first-order linear PDEs Masaki HIBINO (Meijo University)
 On the summability of divergent power series solutions for certain first-order linear PDEs Masaki HIBINO (Meijo University) 1 1 Introduction (E) {1+x 2 +β(x,y)}y u x (x,y)+{x+b(x,y)}y2 u y (x,y) +u(x,y)=f(x,y)
On the summability of divergent power series solutions for certain first-order linear PDEs Masaki HIBINO (Meijo University) 1 1 Introduction (E) {1+x 2 +β(x,y)}y u x (x,y)+{x+b(x,y)}y2 u y (x,y) +u(x,y)=f(x,y)
Ax = b. 7x = 21. x = 21 7 = 3.
 3 s st 3 r 3 t r 3 3 t s st t 3t s 3 3 r 3 3 st t t r 3 s t t r r r t st t rr 3t r t 3 3 rt3 3 t 3 3 r st 3 t 3 tr 3 r t3 t 3 s st t Ax = b. s t 3 t 3 3 r r t n r A tr 3 rr t 3 t n ts b 3 t t r r t x 3
3 s st 3 r 3 t r 3 3 t s st t 3t s 3 3 r 3 3 st t t r 3 s t t r r r t st t rr 3t r t 3 3 rt3 3 t 3 3 r st 3 t 3 tr 3 r t3 t 3 s st t Ax = b. s t 3 t 3 3 r r t n r A tr 3 rr t 3 t n ts b 3 t t r r t x 3
Solution Series 9. i=1 x i and i=1 x i.
 Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Jesse Maassen and Mark Lundstrom Purdue University November 25, 2013
 Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Partial Differential Equations in Biology The boundary element method. March 26, 2013
 The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
Empirical best prediction under area-level Poisson mixed models
 Noname manuscript No. (will be inserted by the editor Empirical best prediction under area-level Poisson mixed models Miguel Boubeta María José Lombardía Domingo Morales eceived: date / Accepted: date
Noname manuscript No. (will be inserted by the editor Empirical best prediction under area-level Poisson mixed models Miguel Boubeta María José Lombardía Domingo Morales eceived: date / Accepted: date
Every set of first-order formulas is equivalent to an independent set
 Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
DiracDelta. Notations. Primary definition. Specific values. General characteristics. Traditional name. Traditional notation
 DiracDelta Notations Traditional name Dirac delta function Traditional notation x Mathematica StandardForm notation DiracDeltax Primary definition 4.03.02.000.0 x Π lim ε ; x ε0 x 2 2 ε Specific values
DiracDelta Notations Traditional name Dirac delta function Traditional notation x Mathematica StandardForm notation DiracDeltax Primary definition 4.03.02.000.0 x Π lim ε ; x ε0 x 2 2 ε Specific values
M a t h e m a t i c a B a l k a n i c a. On Some Generalizations of Classical Integral Transforms. Nina Virchenko
 M a t h e m a t i c a B a l k a n i c a New Series Vol. 26, 212, Fasc. 1-2 On Some Generalizations of Classical Integral Transforms Nina Virchenko Presented at 6 th International Conference TMSF 211 Using
M a t h e m a t i c a B a l k a n i c a New Series Vol. 26, 212, Fasc. 1-2 On Some Generalizations of Classical Integral Transforms Nina Virchenko Presented at 6 th International Conference TMSF 211 Using
Vol. 37 ( 2017 ) No. 3. J. of Math. (PRC) : A : (2017) k=1. ,, f. f + u = f φ, x 1. x n : ( ).
 Vol. 37 ( 2017 ) No. 3 J. of Math. (PRC) R N - R N - 1, 2 (1., 100029) (2., 430072) : R N., R N, R N -. : ; ; R N ; MR(2010) : 58K40 : O192 : A : 0255-7797(2017)03-0467-07 1. [6], Mather f : (R n, 0) R
Vol. 37 ( 2017 ) No. 3 J. of Math. (PRC) R N - R N - 1, 2 (1., 100029) (2., 430072) : R N., R N, R N -. : ; ; R N ; MR(2010) : 58K40 : O192 : A : 0255-7797(2017)03-0467-07 1. [6], Mather f : (R n, 0) R
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
The circle theorem and related theorems for Gauss-type quadrature rules
 OP.circle p. / The circle theorem and related theorems for Gauss-type quadrature rules Walter Gautschi wxg@cs.purdue.edu Purdue University OP.circle p. 2/ Web Site http : //www.cs.purdue.edu/ archives/22/wxg/codes
OP.circle p. / The circle theorem and related theorems for Gauss-type quadrature rules Walter Gautschi wxg@cs.purdue.edu Purdue University OP.circle p. 2/ Web Site http : //www.cs.purdue.edu/ archives/22/wxg/codes
 l 0 l 2 l 1 l 1 l 1 l 2 l 2 l 1 l p λ λ µ R N l 2 R N l 2 2 = N x i l p p R N l p N p = ( x i p ) 1 p i=1 l 2 l p p = 2 l p l 1 R N l 1 i=1 x 2 i 1 = N x i i=1 l p p p R N l 0 0 = {i x i 0} R
l 0 l 2 l 1 l 1 l 1 l 2 l 2 l 1 l p λ λ µ R N l 2 R N l 2 2 = N x i l p p R N l p N p = ( x i p ) 1 p i=1 l 2 l p p = 2 l p l 1 R N l 1 i=1 x 2 i 1 = N x i i=1 l p p p R N l 0 0 = {i x i 0} R
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
 Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
Appendix to On the stability of a compressible axisymmetric rotating flow in a pipe. By Z. Rusak & J. H. Lee
 Appendi to On the stability of a compressible aisymmetric rotating flow in a pipe By Z. Rusak & J. H. Lee Journal of Fluid Mechanics, vol. 5 4, pp. 5 4 This material has not been copy-edited or typeset
Appendi to On the stability of a compressible aisymmetric rotating flow in a pipe By Z. Rusak & J. H. Lee Journal of Fluid Mechanics, vol. 5 4, pp. 5 4 This material has not been copy-edited or typeset
k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +
[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R + k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +](/thumbs/73/69566903.jpg) Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Mock Exam 7. 1 Hong Kong Educational Publishing Company. Section A 1. Reference: HKDSE Math M Q2 (a) (1 + kx) n 1M + 1A = (1) =
 Mock Eam 7 Mock Eam 7 Section A. Reference: HKDSE Math M 0 Q (a) ( + k) n nn ( )( k) + nk ( ) + + nn ( ) k + nk + + + A nk... () nn ( ) k... () From (), k...() n Substituting () into (), nn ( ) n 76n 76n
Mock Eam 7 Mock Eam 7 Section A. Reference: HKDSE Math M 0 Q (a) ( + k) n nn ( )( k) + nk ( ) + + nn ( ) k + nk + + + A nk... () nn ( ) k... () From (), k...() n Substituting () into (), nn ( ) n 76n 76n
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in
 Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
Chapter 5, 6 Multiple Random Variables ENCS Probability and Stochastic Processes
 Chapter 5, 6 Multiple Random Variables ENCS6161 - Probability and Stochastic Processes Concordia University ENCS6161 p.1/47 Vector Random Variables A vector r.v. X is a function X : S R n, where S is the
Chapter 5, 6 Multiple Random Variables ENCS6161 - Probability and Stochastic Processes Concordia University ENCS6161 p.1/47 Vector Random Variables A vector r.v. X is a function X : S R n, where S is the
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Graded Refractive-Index
 Graded Refractive-Index Common Devices Methodologies for Graded Refractive Index Methodologies: Ray Optics WKB Multilayer Modelling Solution requires: some knowledge of index profile n 2 x Ray Optics for
Graded Refractive-Index Common Devices Methodologies for Graded Refractive Index Methodologies: Ray Optics WKB Multilayer Modelling Solution requires: some knowledge of index profile n 2 x Ray Optics for
ECE Spring Prof. David R. Jackson ECE Dept. Notes 2
 ECE 634 Spring 6 Prof. David R. Jackson ECE Dept. Notes Fields in a Source-Free Region Example: Radiation from an aperture y PEC E t x Aperture Assume the following choice of vector potentials: A F = =
ECE 634 Spring 6 Prof. David R. Jackson ECE Dept. Notes Fields in a Source-Free Region Example: Radiation from an aperture y PEC E t x Aperture Assume the following choice of vector potentials: A F = =
Fractional Colorings and Zykov Products of graphs
 Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
THE SECOND ISOMORPHISM THEOREM ON ORDERED SET UNDER ANTIORDERS. Daniel A. Romano
 235 Kragujevac J. Math. 30 (2007) 235 242. THE SECOND ISOMORPHISM THEOREM ON ORDERED SET UNDER ANTIORDERS Daniel A. Romano Department of Mathematics and Informatics, Banja Luka University, Mladena Stojanovića
235 Kragujevac J. Math. 30 (2007) 235 242. THE SECOND ISOMORPHISM THEOREM ON ORDERED SET UNDER ANTIORDERS Daniel A. Romano Department of Mathematics and Informatics, Banja Luka University, Mladena Stojanovića
ω ω ω ω ω ω+2 ω ω+2 + ω ω ω ω+2 + ω ω+1 ω ω+2 2 ω ω ω ω ω ω ω ω+1 ω ω2 ω ω2 + ω ω ω2 + ω ω ω ω2 + ω ω+1 ω ω2 + ω ω+1 + ω ω ω ω2 + ω
 0 1 2 3 4 5 6 ω ω + 1 ω + 2 ω + 3 ω + 4 ω2 ω2 + 1 ω2 + 2 ω2 + 3 ω3 ω3 + 1 ω3 + 2 ω4 ω4 + 1 ω5 ω 2 ω 2 + 1 ω 2 + 2 ω 2 + ω ω 2 + ω + 1 ω 2 + ω2 ω 2 2 ω 2 2 + 1 ω 2 2 + ω ω 2 3 ω 3 ω 3 + 1 ω 3 + ω ω 3 +
0 1 2 3 4 5 6 ω ω + 1 ω + 2 ω + 3 ω + 4 ω2 ω2 + 1 ω2 + 2 ω2 + 3 ω3 ω3 + 1 ω3 + 2 ω4 ω4 + 1 ω5 ω 2 ω 2 + 1 ω 2 + 2 ω 2 + ω ω 2 + ω + 1 ω 2 + ω2 ω 2 2 ω 2 2 + 1 ω 2 2 + ω ω 2 3 ω 3 ω 3 + 1 ω 3 + ω ω 3 +
Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α
 Α Ρ Χ Α Ι Α Ι Σ Τ Ο Ρ Ι Α Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α Σ η µ ε ί ω σ η : σ υ ν ά δ ε λ φ ο ι, ν α µ ο υ σ υ γ χ ω ρ ή σ ε τ ε τ ο γ ρ ή γ ο ρ ο κ α ι α τ η µ έ λ η τ ο ύ
Α Ρ Χ Α Ι Α Ι Σ Τ Ο Ρ Ι Α Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α Σ η µ ε ί ω σ η : σ υ ν ά δ ε λ φ ο ι, ν α µ ο υ σ υ γ χ ω ρ ή σ ε τ ε τ ο γ ρ ή γ ο ρ ο κ α ι α τ η µ έ λ η τ ο ύ
( y) Partial Differential Equations
 Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate
Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate
MATHEMATICS. 1. If A and B are square matrices of order 3 such that A = -1, B =3, then 3AB = 1) -9 2) -27 3) -81 4) 81
 1. If A and B are square matrices of order 3 such that A = -1, B =3, then 3AB = 1) -9 2) -27 3) -81 4) 81 We know that KA = A If A is n th Order 3AB =3 3 A. B = 27 1 3 = 81 3 2. If A= 2 1 0 0 2 1 then
1. If A and B are square matrices of order 3 such that A = -1, B =3, then 3AB = 1) -9 2) -27 3) -81 4) 81 We know that KA = A If A is n th Order 3AB =3 3 A. B = 27 1 3 = 81 3 2. If A= 2 1 0 0 2 1 then
Łs t r t rs tø r P r s tø PrØ rø rs tø P r s r t t r s t Ø t q s P r s tr. 2stŁ s q t q s t rt r s t s t ss s Ø r s t r t. Łs t r t t Ø t q s
 Łs t r t rs tø r P r s tø PrØ rø rs tø P r s r t t r s t Ø t q s P r s tr st t t t Ø t q s ss P r s P 2stŁ s q t q s t rt r s t s t ss s Ø r s t r t P r røs r Łs t r t t Ø t q s r Ø r t t r t q t rs tø
Łs t r t rs tø r P r s tø PrØ rø rs tø P r s r t t r s t Ø t q s P r s tr st t t t Ø t q s ss P r s P 2stŁ s q t q s t rt r s t s t ss s Ø r s t r t P r røs r Łs t r t t Ø t q s r Ø r t t r t q t rs tø
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
Probability and Random Processes (Part II)
 Probability and Random Processes (Part II) 1. If the variance σ x of d(n) = x(n) x(n 1) is one-tenth the variance σ x of a stationary zero-mean discrete-time signal x(n), then the normalized autocorrelation
Probability and Random Processes (Part II) 1. If the variance σ x of d(n) = x(n) x(n 1) is one-tenth the variance σ x of a stationary zero-mean discrete-time signal x(n), then the normalized autocorrelation
SCITECH Volume 13, Issue 2 RESEARCH ORGANISATION Published online: March 29, 2018
 Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
1. If log x 2 y 2 = a, then dy / dx = x 2 + y 2 1] xy 2] y / x. 3] x / y 4] none of these
![1. If log x 2 y 2 = a, then dy / dx = x 2 + y 2 1] xy 2] y / x. 3] x / y 4] none of these 1. If log x 2 y 2 = a, then dy / dx = x 2 + y 2 1] xy 2] y / x. 3] x / y 4] none of these](/thumbs/52/30390275.jpg) 1. If log x 2 y 2 = a, then dy / dx = x 2 + y 2 1] xy 2] y / x 3] x / y 4] none of these 1. If log x 2 y 2 = a, then x 2 + y 2 Solution : Take y /x = k y = k x dy/dx = k dy/dx = y / x Answer : 2] y / x
1. If log x 2 y 2 = a, then dy / dx = x 2 + y 2 1] xy 2] y / x 3] x / y 4] none of these 1. If log x 2 y 2 = a, then x 2 + y 2 Solution : Take y /x = k y = k x dy/dx = k dy/dx = y / x Answer : 2] y / x
ENGR 691/692 Section 66 (Fall 06): Machine Learning Assigned: August 30 Homework 1: Bayesian Decision Theory (solutions) Due: September 13
 ENGR 69/69 Section 66 (Fall 06): Machine Learning Assigned: August 30 Homework : Bayesian Decision Theory (solutions) Due: Septemer 3 Prolem : ( pts) Let the conditional densities for a two-category one-dimensional
ENGR 69/69 Section 66 (Fall 06): Machine Learning Assigned: August 30 Homework : Bayesian Decision Theory (solutions) Due: Septemer 3 Prolem : ( pts) Let the conditional densities for a two-category one-dimensional
forms This gives Remark 1. How to remember the above formulas: Substituting these into the equation we obtain with
 Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
Mellin transforms and asymptotics: Harmonic sums
 Mellin tranform and aymptotic: Harmonic um Phillipe Flajolet, Xavier Gourdon, Philippe Duma Die Theorie der reziproen Funtionen und Integrale it ein centrale Gebiet, welche manche anderen Gebiete der Analyi
Mellin tranform and aymptotic: Harmonic um Phillipe Flajolet, Xavier Gourdon, Philippe Duma Die Theorie der reziproen Funtionen und Integrale it ein centrale Gebiet, welche manche anderen Gebiete der Analyi
Κεφάλαιο 1 Πραγματικοί Αριθμοί 1.1 Σύνολα
 x + = 0 N = {,, 3....}, Z Q, b, b N c, d c, d N + b = c, b = d. N = =. < > P n P (n) P () n = P (n) P (n + ) n n + P (n) n P (n) n P n P (n) P (m) P (n) n m P (n + ) P (n) n m P n P (n) P () P (), P (),...,
x + = 0 N = {,, 3....}, Z Q, b, b N c, d c, d N + b = c, b = d. N = =. < > P n P (n) P () n = P (n) P (n + ) n n + P (n) n P (n) n P n P (n) P (m) P (n) n m P (n + ) P (n) n m P n P (n) P () P (), P (),...,
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
Homework for 1/27 Due 2/5
 Name: ID: Homework for /7 Due /5. [ 8-3] I Example D of Sectio 8.4, the pdf of the populatio distributio is + αx x f(x α) =, α, otherwise ad the method of momets estimate was foud to be ˆα = 3X (where
Name: ID: Homework for /7 Due /5. [ 8-3] I Example D of Sectio 8.4, the pdf of the populatio distributio is + αx x f(x α) =, α, otherwise ad the method of momets estimate was foud to be ˆα = 3X (where
The Simply Typed Lambda Calculus
 Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
u = 0 u = ϕ t + Π) = 0 t + Π = C(t) C(t) C(t) = K K C(t) ϕ = ϕ 1 + C(t) dt Kt 2 ϕ = 0
 u = (u, v, w) ω ω = u = 0 ϕ u u = ϕ u = 0 ϕ 2 ϕ = 0 u t = u ω 1 ρ Π + ν 2 u Π = p + (1/2)ρ u 2 + ρgz ω = 0 ( ϕ t + Π) = 0 ϕ t + Π = C(t) C(t) C(t) = K K C(t) ϕ = ϕ 1 + C(t) dt Kt C(t) ϕ ϕ 1 ϕ = ϕ 1 p ρ
u = (u, v, w) ω ω = u = 0 ϕ u u = ϕ u = 0 ϕ 2 ϕ = 0 u t = u ω 1 ρ Π + ν 2 u Π = p + (1/2)ρ u 2 + ρgz ω = 0 ( ϕ t + Π) = 0 ϕ t + Π = C(t) C(t) C(t) = K K C(t) ϕ = ϕ 1 + C(t) dt Kt C(t) ϕ ϕ 1 ϕ = ϕ 1 p ρ
Math 446 Homework 3 Solutions. (1). (i): Reverse triangle inequality for metrics: Let (X, d) be a metric space and let x, y, z X.
 Math 446 Homework 3 Solutions. (1). (i): Reverse triangle inequalit for metrics: Let (X, d) be a metric space and let x,, z X. Prove that d(x, z) d(, z) d(x, ). (ii): Reverse triangle inequalit for norms:
Math 446 Homework 3 Solutions. (1). (i): Reverse triangle inequalit for metrics: Let (X, d) be a metric space and let x,, z X. Prove that d(x, z) d(, z) d(x, ). (ii): Reverse triangle inequalit for norms:
Credit Risk. Finance and Insurance - Stochastic Analysis and Practical Methods Spring School Jena, March 2009
 Credit Risk. Finance and Insurance - Stochastic Analysis and Practical Methods Spring School Jena, March 2009 1 IV. Hedging of credit derivatives 1. Two default free assets, one defaultable asset 1.1 Two
Credit Risk. Finance and Insurance - Stochastic Analysis and Practical Methods Spring School Jena, March 2009 1 IV. Hedging of credit derivatives 1. Two default free assets, one defaultable asset 1.1 Two
Computable error bounds for asymptotic expansions formulas of distributions related to gamma functions
 Computable error bounds for asymptotic expansions formulas of distributions related to gamma functions Hirofumi Wakaki (Math. of Department, Hiroshima Univ.) 20.7. Hiroshima Statistical Group Meeting at
Computable error bounds for asymptotic expansions formulas of distributions related to gamma functions Hirofumi Wakaki (Math. of Department, Hiroshima Univ.) 20.7. Hiroshima Statistical Group Meeting at
A Two-Sided Laplace Inversion Algorithm with Computable Error Bounds and Its Applications in Financial Engineering
 Electronic Companion A Two-Sie Laplace Inversion Algorithm with Computable Error Bouns an Its Applications in Financial Engineering Ning Cai, S. G. Kou, Zongjian Liu HKUST an Columbia University Appenix
Electronic Companion A Two-Sie Laplace Inversion Algorithm with Computable Error Bouns an Its Applications in Financial Engineering Ning Cai, S. G. Kou, Zongjian Liu HKUST an Columbia University Appenix
Nonlinear Fourier transform for the conductivity equation. Visibility and Invisibility in Impedance Tomography
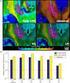 Nonlinear Fourier transform for the conductivity equation Visibility and Invisibility in Impedance Tomography Kari Astala University of Helsinki CoE in Analysis and Dynamics Research What is the non linear
Nonlinear Fourier transform for the conductivity equation Visibility and Invisibility in Impedance Tomography Kari Astala University of Helsinki CoE in Analysis and Dynamics Research What is the non linear
Solutions to Selected Homework Problems 1.26 Claim: α : S S which is 1-1 but not onto β : S S which is onto but not 1-1. y z = z y y, z S.
 Solutions to Selected Homework Problems 1.26 Claim: α : S S which is 1-1 but not onto β : S S which is onto but not 1-1. Proof. ( ) Since α is 1-1, β : S S such that β α = id S. Since β α = id S is onto,
Solutions to Selected Homework Problems 1.26 Claim: α : S S which is 1-1 but not onto β : S S which is onto but not 1-1. Proof. ( ) Since α is 1-1, β : S S such that β α = id S. Since β α = id S is onto,
 γ n ϑ n n ψ T 8 Q 6 j, k, m, n, p, r, r t, x, y f m (x) (f(x)) m / a/b (f g)(x) = f(g(x)) n f f n I J α β I = α + βj N, Z, Q ϕ Εὐκλείδης ὁ Ἀλεξανδρεύς Στοιχεῖα ἄκρος καὶ μέσος λόγος ὕδωρ αἰθήρ ϕ φ Φ τ
γ n ϑ n n ψ T 8 Q 6 j, k, m, n, p, r, r t, x, y f m (x) (f(x)) m / a/b (f g)(x) = f(g(x)) n f f n I J α β I = α + βj N, Z, Q ϕ Εὐκλείδης ὁ Ἀλεξανδρεύς Στοιχεῖα ἄκρος καὶ μέσος λόγος ὕδωρ αἰθήρ ϕ φ Φ τ
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
de Rham Theorem May 10, 2016
 de Rham Theorem May 10, 2016 Stokes formula and the integration morphism: Let M = σ Σ σ be a smooth triangulated manifold. Fact: Stokes formula σ ω = σ dω holds, e.g. for simplices. It can be used to define
de Rham Theorem May 10, 2016 Stokes formula and the integration morphism: Let M = σ Σ σ be a smooth triangulated manifold. Fact: Stokes formula σ ω = σ dω holds, e.g. for simplices. It can be used to define
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
 φ(t) TE 0 φ(z) φ(z) φ(z) φ(z) η(λ) G(z,λ) λ φ(z) η(λ) η(λ) = t CIGS 0 G(z,λ)φ(z)dz t CIGS η(λ) φ(z) 0 z
φ(t) TE 0 φ(z) φ(z) φ(z) φ(z) η(λ) G(z,λ) λ φ(z) η(λ) η(λ) = t CIGS 0 G(z,λ)φ(z)dz t CIGS η(λ) φ(z) 0 z
 1951 {0, 1} N = N \ {0} n m M n, m N F x i = (x i 1,..., xi m) x j = (x 1 j,..., xn j ) i j M M i j x i j m n M M M M T f : F m F f(m) f M (f(x 1 1,..., x1 m),..., f(x n 1,..., xn m)) T R F M R M R x
1951 {0, 1} N = N \ {0} n m M n, m N F x i = (x i 1,..., xi m) x j = (x 1 j,..., xn j ) i j M M i j x i j m n M M M M T f : F m F f(m) f M (f(x 1 1,..., x1 m),..., f(x n 1,..., xn m)) T R F M R M R x
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Fourier Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Math 5440 Problem Set 4 Solutions
 Math 5440 Math 5440 Problem Set 4 Solutions Aaron Fogelson Fall, 03 : (Logan,.8 # 4) Find all radial solutions of the two-dimensional Laplace s equation. That is, find all solutions of the form u(r) where
Math 5440 Math 5440 Problem Set 4 Solutions Aaron Fogelson Fall, 03 : (Logan,.8 # 4) Find all radial solutions of the two-dimensional Laplace s equation. That is, find all solutions of the form u(r) where
SPECIAL FUNCTIONS and POLYNOMIALS
 SPECIAL FUNCTIONS and POLYNOMIALS Gerard t Hooft Stefan Nobbenhuis Institute for Theoretical Physics Utrecht University, Leuvenlaan 4 3584 CC Utrecht, the Netherlands and Spinoza Institute Postbox 8.195
SPECIAL FUNCTIONS and POLYNOMIALS Gerard t Hooft Stefan Nobbenhuis Institute for Theoretical Physics Utrecht University, Leuvenlaan 4 3584 CC Utrecht, the Netherlands and Spinoza Institute Postbox 8.195
Differential equations
 Differential equations Differential equations: An equation inoling one dependent ariable and its deriaties w. r. t one or more independent ariables is called a differential equation. Order of differential
Differential equations Differential equations: An equation inoling one dependent ariable and its deriaties w. r. t one or more independent ariables is called a differential equation. Order of differential
Divergence for log concave functions
 Divergence or log concave unctions Umut Caglar The Euler International Mathematical Institute June 22nd, 2013 Joint work with C. Schütt and E. Werner Outline 1 Introduction 2 Main Theorem 3 -divergence
Divergence or log concave unctions Umut Caglar The Euler International Mathematical Institute June 22nd, 2013 Joint work with C. Schütt and E. Werner Outline 1 Introduction 2 Main Theorem 3 -divergence
w o = R 1 p. (1) R = p =. = 1
 Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 205 ιδάσκων : Α. Μουχτάρης Τριτη Σειρά Ασκήσεων Λύσεις Ασκηση 3. 5.2 (a) From the Wiener-Hopf equation we have:
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 205 ιδάσκων : Α. Μουχτάρης Τριτη Σειρά Ασκήσεων Λύσεις Ασκηση 3. 5.2 (a) From the Wiener-Hopf equation we have:
Τίτλος: Eνεργά δυναμικά στη θεωρία συναρτησιακών του πρώτου πίνακα πυκνότητας
 Τίτλος: Eνεργά δυναμικά στη θεωρία συναρτησιακών του πρώτου πίνακα πυκνότητας Μπουσιάδη Σοφία Τριμελής επιτροπή: Ν. Λαθιωτάκης (Ε.Ι.Ε) Ι. Λελίδης (Ε.Κ.Π.Α) Ι. Πετσαλάκης (Ε.Ι.Ε) Περιεχόμενα Εισαγωγή στην
Τίτλος: Eνεργά δυναμικά στη θεωρία συναρτησιακών του πρώτου πίνακα πυκνότητας Μπουσιάδη Σοφία Τριμελής επιτροπή: Ν. Λαθιωτάκης (Ε.Ι.Ε) Ι. Λελίδης (Ε.Κ.Π.Α) Ι. Πετσαλάκης (Ε.Ι.Ε) Περιεχόμενα Εισαγωγή στην
ADVANCED STRUCTURAL MECHANICS
 VSB TECHNICAL UNIVERSITY OF OSTRAVA FACULTY OF CIVIL ENGINEERING ADVANCED STRUCTURAL MECHANICS Lecture 1 Jiří Brožovský Office: LP H 406/3 Phone: 597 321 321 E-mail: jiri.brozovsky@vsb.cz WWW: http://fast10.vsb.cz/brozovsky/
VSB TECHNICAL UNIVERSITY OF OSTRAVA FACULTY OF CIVIL ENGINEERING ADVANCED STRUCTURAL MECHANICS Lecture 1 Jiří Brožovský Office: LP H 406/3 Phone: 597 321 321 E-mail: jiri.brozovsky@vsb.cz WWW: http://fast10.vsb.cz/brozovsky/
Προβολές και Μετασχηματισμοί Παρατήρησης
 Γραφικά & Οπτικοποίηση Κεφάλαιο 4 Προβολές και Μετασχηματισμοί Παρατήρησης Εισαγωγή Στα γραφικά υπάρχουν: 3Δ μοντέλα 2Δ συσκευές επισκόπησης (οθόνες & εκτυπωτές) Προοπτική απεικόνιση (προβολή): Λαμβάνει
Γραφικά & Οπτικοποίηση Κεφάλαιο 4 Προβολές και Μετασχηματισμοί Παρατήρησης Εισαγωγή Στα γραφικά υπάρχουν: 3Δ μοντέλα 2Δ συσκευές επισκόπησης (οθόνες & εκτυπωτές) Προοπτική απεικόνιση (προβολή): Λαμβάνει
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
f(w) f(z) = C f(z) = z z + h z h = h h h 0,h C f(z + h) f(z)
 Ω f: Ω C l C z Ω f f(w) f(z) z a w z = h 0,h C f(z + h) f(z) h = l. z f l = f (z) Ω f Ω f Ω H(Ω) n N C f(z) = z n h h 0 h z + h z h = h h C f(z) = z f (z) = f( z) f f: Ω C Ω = { z; z Ω} z, a Ω f (z) f
Ω f: Ω C l C z Ω f f(w) f(z) z a w z = h 0,h C f(z + h) f(z) h = l. z f l = f (z) Ω f Ω f Ω H(Ω) n N C f(z) = z n h h 0 h z + h z h = h h C f(z) = z f (z) = f( z) f f: Ω C Ω = { z; z Ω} z, a Ω f (z) f
ΠΑΡΟΡΑΜΑΤΑ ΕΚΔΟΣΗ 12 ΜΑΡΤΙΟΥ 2018
 ΝΙΚΟΛΑΟΣ M. ΣΤΑΥΡΑΚΑΚΗΣ: «Μερικές Διαφορικές Εξισώσεις & Μιγαδικές Συναρτήσεις: Θεωρία και Εφαρμογές» η Έκδοση, Αυτοέκδοση) Αθήνα, ΜΑΡΤΙΟΣ 06, Εξώφυλλο: ΜΑΛΑΚΟ, ΕΥΔΟΞΟΣ: 5084750, ISBN: 978-960-93-7366-
ΝΙΚΟΛΑΟΣ M. ΣΤΑΥΡΑΚΑΚΗΣ: «Μερικές Διαφορικές Εξισώσεις & Μιγαδικές Συναρτήσεις: Θεωρία και Εφαρμογές» η Έκδοση, Αυτοέκδοση) Αθήνα, ΜΑΡΤΙΟΣ 06, Εξώφυλλο: ΜΑΛΑΚΟ, ΕΥΔΟΞΟΣ: 5084750, ISBN: 978-960-93-7366-
Computing the Macdonald function for complex orders
 Macdonald p. 1/1 Computing the Macdonald function for complex orders Walter Gautschi wxg@cs.purdue.edu Purdue University Macdonald p. 2/1 Integral representation K ν (x) = complex order ν = α + iβ e x
Macdonald p. 1/1 Computing the Macdonald function for complex orders Walter Gautschi wxg@cs.purdue.edu Purdue University Macdonald p. 2/1 Integral representation K ν (x) = complex order ν = α + iβ e x
MÉTHODES ET EXERCICES
 J.-M. MONIER I G. HABERER I C. LARDON MATHS PCSI PTSI MÉTHODES ET EXERCICES 4 e édition Création graphique de la couverture : Hokus Pokus Créations Dunod, 2018 11 rue Paul Bert, 92240 Malakoff www.dunod.com
J.-M. MONIER I G. HABERER I C. LARDON MATHS PCSI PTSI MÉTHODES ET EXERCICES 4 e édition Création graphique de la couverture : Hokus Pokus Créations Dunod, 2018 11 rue Paul Bert, 92240 Malakoff www.dunod.com
Tridiagonal matrices. Gérard MEURANT. October, 2008
 Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Overview. Transition Semantics. Configurations and the transition relation. Executions and computation
 Overview Transition Semantics Configurations and the transition relation Executions and computation Inference rules for small-step structural operational semantics for the simple imperative language Transition
Overview Transition Semantics Configurations and the transition relation Executions and computation Inference rules for small-step structural operational semantics for the simple imperative language Transition
Homomorphism in Intuitionistic Fuzzy Automata
 International Journal of Fuzzy Mathematics Systems. ISSN 2248-9940 Volume 3, Number 1 (2013), pp. 39-45 Research India Publications http://www.ripublication.com/ijfms.htm Homomorphism in Intuitionistic
International Journal of Fuzzy Mathematics Systems. ISSN 2248-9940 Volume 3, Number 1 (2013), pp. 39-45 Research India Publications http://www.ripublication.com/ijfms.htm Homomorphism in Intuitionistic
Exercise 1.1. Verify that if we apply GS to the coordinate basis Gauss form ds 2 = E(u, v)du 2 + 2F (u, v)dudv + G(u, v)dv 2
 Math 209 Riemannian Geometry Jeongmin Shon Problem. Let M 2 R 3 be embedded surface. Then the induced metric on M 2 is obtained by taking the standard inner product on R 3 and restricting it to the tangent
Math 209 Riemannian Geometry Jeongmin Shon Problem. Let M 2 R 3 be embedded surface. Then the induced metric on M 2 is obtained by taking the standard inner product on R 3 and restricting it to the tangent
Takeaki Yamazaki (Toyo Univ.) 山崎丈明 ( 東洋大学 ) Oct. 24, RIMS
 Takeaki Yamazaki (Toyo Univ.) 山崎丈明 ( 東洋大学 ) Oct. 24, 2017 @ RIMS Contents Introduction Generalized Karcher equation Ando-Hiai inequalities Problem Introduction PP: The set of all positive definite operators
Takeaki Yamazaki (Toyo Univ.) 山崎丈明 ( 東洋大学 ) Oct. 24, 2017 @ RIMS Contents Introduction Generalized Karcher equation Ando-Hiai inequalities Problem Introduction PP: The set of all positive definite operators
6. MAXIMUM LIKELIHOOD ESTIMATION
 6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
Reminders: linear functions
 Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
Aquinas College. Edexcel Mathematical formulae and statistics tables DO NOT WRITE ON THIS BOOKLET
 Aquinas College Edexcel Mathematical formulae and statistics tables DO NOT WRITE ON THIS BOOKLET Pearson Edexcel Level 3 Advanced Subsidiary and Advanced GCE in Mathematics and Further Mathematics Mathematical
Aquinas College Edexcel Mathematical formulae and statistics tables DO NOT WRITE ON THIS BOOKLET Pearson Edexcel Level 3 Advanced Subsidiary and Advanced GCE in Mathematics and Further Mathematics Mathematical
Srednicki Chapter 55
 Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
6.642, Continuum Electromechanics, Fall 2004 Prof. Markus Zahn Lecture 8: Electrohydrodynamic and Ferrohydrodynamic Instabilities
 6.64, Continuum Electromechnics, Fll 4 Prof. Mrus Zhn Lecture 8: Electrohydrodynmic nd Ferrohydrodynmic Instilities I. Mgnetic Field Norml Instility Courtesy of MIT Press. Used with permission. A. Equilirium
6.64, Continuum Electromechnics, Fll 4 Prof. Mrus Zhn Lecture 8: Electrohydrodynmic nd Ferrohydrodynmic Instilities I. Mgnetic Field Norml Instility Courtesy of MIT Press. Used with permission. A. Equilirium
