6.642, Continuum Electromechanics, Fall 2004 Prof. Markus Zahn Lecture 8: Electrohydrodynamic and Ferrohydrodynamic Instabilities
|
|
|
- Ἠώς Ρόκας
- 7 χρόνια πριν
- Προβολές:
Transcript
1 6.64, Continuum Electromechnics, Fll 4 Prof. Mrus Zhn Lecture 8: Electrohydrodynmic nd Ferrohydrodynmic Instilities I. Mgnetic Field Norml Instility Courtesy of MIT Press. Used with permission. A. Equilirium ( ξ= ) = H = H ; 1 Poe Pod + H H = ρ gx + Pod x > Po ( x) = ρ gx + Poe x <. Perturtions: ( t yy zz) j e ω H = H i + h = + x, H H ix h 1 coth h c xc sinh Ψ = h 1 d xd coth Ψ sinh 1 coth h e xe sinh Ψ = h 1 f xf coth Ψ sinh 6.64, Continuum Electromechnics Lecture 8 Prof. Mrus Zhn Pge 1 of 13
2 C. oundry Conditions v = v = xc xf Ψ = Ψ = c f v xd,e = + vyd,e + vzd,e vxd = vxe = jωξ t y ix iy iz y z n = i i i y y x y z e i = ij j γ i pn T n nn n = + y i = x n = n = 1 i x P + P' = Txx nx + Txy ny + Txz ξ ξ nz + γ + y 1 perturtion perturtion Hh Hh x y x z Equilirium ( ξ= ) second order P = Txx P 1 od Poe = H H Perturtions 1 P P H h H h ' d ξ ' e ξ = ' d ξ ' e ξ γ ξ dp P P P P g P od ( ξ ) = ( ξ ) + = ξ + = ρ ξ + ' ' ' ' d od d d d x= dp P P P P g P oe ( ξ ) = ( ξ ) + = ξ + = ρ ξ + ' ' ' ' e oe e e e x= 6.64, Continuum Electromechnics Lecture 8 Prof. Mrus Zhn Pge of 13
3 1 coth c p v c jωρ sinh x = p 1 d d coth v sinh x 1 coth e p v e jωρ sinh x = p 1 f f coth v sinh x jωρ d ω ρ p = coth v = coth ξ d x jωρ e ω ρ Pe = coth v = coth ξ x h h xd xe d = coth Ψ e = coth Ψ ni = = i i i i ( ) i + ( h h ) i + ( h h ) i y x y z x xd xe x yd ye y + ( hzd hze) iz = = h = h xd xe n h = = ix iy iz ( H H ) ix + ( hxd hxe ) ix + ( hyd hye ) iy + ( hzd hze ) iz y = i h h i h h + H H i H H i y z yd ye y zd ze z y d ( e) hyd hye = H H + jy Ψ Ψ = jy H H ξ y d ( e) hzd hze = H H + jz Ψ Ψ = jz H H ξ ( H H ) Ψ Ψ = + ξ d e 6.64, Continuum Electromechnics Lecture 8 Prof. Mrus Zhn Pge 3 of 13
4 coth Ψ = coth Ψ coth Ψ d = Ψ coth d coth Ψe 1 = ( H H ) ξ coth H H ξ coth Ψ e = coth + Ψ d = + coth + e coth H H ξ coth coth e D. Dispersion Eqution ωρ ωρ ρgξ coth ξ+ρ gξ coth ξ H coth H H coth ξ H coth H H ξ coth = γ ξ coth + coth ω ( ) ( ) ( ρ coth + ρ coth ) = ( ρ ρ ) g + γ coth+ coth H H cothcoth H, H H H 1 1 ( ) = = = = ω ( ρ coth + ρ coth ) = g( ρ ρ ) + γ + tnh tnh E. Short Wvelength Limit ( 1, 1) tnh tnh 1 ( ) g f ω ( ρ + ρ ) = ( ρ ρ ) + γ = , Continuum Electromechnics Lecture 8 Prof. Mrus Zhn Pge 4 of 13
5 Incipience of Instility f = df d ( ) = = γc + c ( ) = γ + 1 g( ρ ρ ) + γ = γ + + γ ( ) = 4g ( ρ ρ) γ + 1 = 4g( ρ ρ ) γ = γ c g ( ρ ρ ) γ Courtesy of MIT Press. Used with permission. 6.64, Continuum Electromechnics Lecture 8 Prof. Mrus Zhn Pge 5 of 13
6 Courtesy of MIT Press. Used with permission. II. Electric Field Norml Instility A. Polriztion Forces Courtesy of MIT Press. Used with permission. ε ε D ω D ε ε ( ρ coth + ρ coth ) = g ( ρ ρ ) + γ + εε ε ε tnh tnh 6.64, Continuum Electromechnics Lecture 8 Prof. Mrus Zhn Pge 6 of 13
7 . Perfectly conducting lower fluid ( ε ) Courtesy of MIT Press. Used with permission. V coth coth g coth ω ( ρ + ρ ) = ( ρ ρ ) + γ ε Courtesy of MIT Press. Used with permission. 6.64, Continuum Electromechnics Lecture 8 Prof. Mrus Zhn Pge 7 of 13
8 III. Tngentil Grdient Fields Courtesy of MIT Press. Used with permission. 6.64, Continuum Electromechnics Lecture 8 Prof. Mrus Zhn Pge 8 of 13
9 A. Equilirium V V x V E= i i 1 + ;r R x;e = θ θ r θ r R θ R y i E x y 1 + R lim P x =ρ gx + P Po Po + Txx = o o P x =ρ gx + P o o T 1 εe 1 ε E xx = y = T = 1 ( ε ε ) E = P P xx o o. Perturtions 1 α e coth x α sinh Φ = β 1 coth β e Φ x sinh lim e e x x = Φ = Φ 1 coth α α p j sinh v ωρ x = β 1 p coth v β sinh x v α v β = = j ωξ x x P jωρ ω ρ = vx = ξ P jωρ ω ρ = vx = ξ 6.64, Continuum Electromechnics Lecture 8 Prof. Mrus Zhn Pge 9 of 13
10 C. oundry Conditions n = i i i y x y z n E = i i i x y z ( ex ex ) i + x ( ey ey ) i + y ( ez ez ) i = z y z ( y y ) ( z z ) i e e i e e = y e y = ey jy Φ = j y Φ Φ =Φ Φ e z = ez jz Φ = jz Φ ni εe = i i i i E ( ε ε ) i + ( ε e ε e ) i + ( ε e ε e ) i y + ( εez εez) i = z x y z y x x x y y y ε e ε e + j ξe ε ε = x x y Φ ε + ε + j E ε ε ξ = y ξ jy E ( ε ε) Φ= ( ε + ε ) ξ ξ pn = T n + γ + n y i ij j i i = x, nx = 1 p = T + T n + T n γ ξ xx xy y xz z Txx = 1 ε Ex Ey E 1 1 z Ey ey Ey Eey = ε + = ε + Txy = ε Ey ex T = ε e e xz x z 6.64, Continuum Electromechnics Lecture 8 Prof. Mrus Zhn Pge 1 of 13
11 T xy n second order y T xz n third order z 1 d ( ξ ) = ε ε T E ξ E e = xx y y x de = E ξ ε ε Eey de T =εe xx ξ ε Ee de =εe ξ j Φ ε E y T =( ε ε ) E ξ j E Φ ( ε ε ) xx de y y dp = ξ + = ρ ρ ξ p p P P g T de P P g ρ ρ ξ = ε ε E ξ jy ΦE ( ε ε) γ ξ ω ( ρ + ρ) ξ g( ρ ρ) ξ = de ( ε ε) E ξ γ ξ j E ( ε ε ) ( j E ) ( ε ε ) ξ y y ( ε + ε ) ω de E ε ( ) g( ) ( ) E + ε ρ + ρ = ρ ρ + γ + ε ε + ε ε E R y Uniform tngentil field lwys stilizes. Grdient field stilizes, if higher permittivity fluid is in stronger electric field. System stle even if hevier fluid ove if de ( ε ε ) E > g( ρ ρ ) 6.64, Continuum Electromechnics Lecture 8 Prof. Mrus Zhn Pge 11 of 13
12 Courtesy of MIT Press. Used with permission. 6.64, Continuum Electromechnics Lecture 8 Prof. Mrus Zhn Pge 1 of 13
13 Courtesy of MIT Press. Used with permission. 6.64, Continuum Electromechnics Lecture 8 Prof. Mrus Zhn Pge 13 of 13
6.642 Continuum Electromechanics
 MIT OpenCourseWre http://ocw.mit.edu 6.64 Continuum Electromechnics Fll 8 For informtion out citing these mterils or our Terms of Use, visit: http://ocw.mit.edu/terms. 6.64, Continuum Electromechnics,
MIT OpenCourseWre http://ocw.mit.edu 6.64 Continuum Electromechnics Fll 8 For informtion out citing these mterils or our Terms of Use, visit: http://ocw.mit.edu/terms. 6.64, Continuum Electromechnics,
Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α
 Α Ρ Χ Α Ι Α Ι Σ Τ Ο Ρ Ι Α Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α Σ η µ ε ί ω σ η : σ υ ν ά δ ε λ φ ο ι, ν α µ ο υ σ υ γ χ ω ρ ή σ ε τ ε τ ο γ ρ ή γ ο ρ ο κ α ι α τ η µ έ λ η τ ο ύ
Α Ρ Χ Α Ι Α Ι Σ Τ Ο Ρ Ι Α Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α Σ η µ ε ί ω σ η : σ υ ν ά δ ε λ φ ο ι, ν α µ ο υ σ υ γ χ ω ρ ή σ ε τ ε τ ο γ ρ ή γ ο ρ ο κ α ι α τ η µ έ λ η τ ο ύ
6.642 Continuum Electromechanics
 MIT OpenCourseWre http://ocw.mit.eu 6.64 Continuum Electromechnics Fll 8 For informtion out citing these mterils or our Terms of Use, visit: http://ocw.mit.eu/terms. 6.64, Continuum Electromechnics rof.
MIT OpenCourseWre http://ocw.mit.eu 6.64 Continuum Electromechnics Fll 8 For informtion out citing these mterils or our Terms of Use, visit: http://ocw.mit.eu/terms. 6.64, Continuum Electromechnics rof.
Α Ρ Ι Θ Μ Ο Σ : 6.913
 Α Ρ Ι Θ Μ Ο Σ : 6.913 ΠΡΑΞΗ ΚΑΤΑΘΕΣΗΣ ΟΡΩΝ ΔΙΑΓΩΝΙΣΜΟΥ Σ τ η ν Π ά τ ρ α σ ή μ ε ρ α σ τ ι ς δ ε κ α τ έ σ σ ε ρ ι ς ( 1 4 ) τ ο υ μ ή ν α Ο κ τ ω β ρ ί ο υ, η μ έ ρ α Τ ε τ ά ρ τ η, τ ο υ έ τ ο υ ς δ
Α Ρ Ι Θ Μ Ο Σ : 6.913 ΠΡΑΞΗ ΚΑΤΑΘΕΣΗΣ ΟΡΩΝ ΔΙΑΓΩΝΙΣΜΟΥ Σ τ η ν Π ά τ ρ α σ ή μ ε ρ α σ τ ι ς δ ε κ α τ έ σ σ ε ρ ι ς ( 1 4 ) τ ο υ μ ή ν α Ο κ τ ω β ρ ί ο υ, η μ έ ρ α Τ ε τ ά ρ τ η, τ ο υ έ τ ο υ ς δ
2. Α ν ά λ υ σ η Π ε ρ ι ο χ ή ς. 3. Α π α ι τ ή σ ε ι ς Ε ρ γ ο δ ό τ η. 4. Τ υ π ο λ ο γ ί α κ τ ι ρ ί ω ν. 5. Π ρ ό τ α σ η. 6.
 Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α 1. Ε ι σ α γ ω γ ή 2. Α ν ά λ υ σ η Π ε ρ ι ο χ ή ς 3. Α π α ι τ ή σ ε ι ς Ε ρ γ ο δ ό τ η 4. Τ υ π ο λ ο γ ί α κ τ ι ρ ί ω ν 5. Π ρ ό τ α σ η 6. Τ ο γ ρ α φ ε ί ο 1. Ε ι σ α γ ω
Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α 1. Ε ι σ α γ ω γ ή 2. Α ν ά λ υ σ η Π ε ρ ι ο χ ή ς 3. Α π α ι τ ή σ ε ι ς Ε ρ γ ο δ ό τ η 4. Τ υ π ο λ ο γ ί α κ τ ι ρ ί ω ν 5. Π ρ ό τ α σ η 6. Τ ο γ ρ α φ ε ί ο 1. Ε ι σ α γ ω
Κεφάλαιο 1 Πραγματικοί Αριθμοί 1.1 Σύνολα
 x 2 + 1 = 0 N = {1, 2, 3....}, Z Q a, b a, b N c, d c, d N a + b = c, a b = d. a a N 1 a = a 1 = a. < > P n P (n) P (1) n = 1 P (n) P (n + 1) n n + 1 P (n) n P (n) n P n P (n) P (m) P (n) n m P (n + 1)
x 2 + 1 = 0 N = {1, 2, 3....}, Z Q a, b a, b N c, d c, d N a + b = c, a b = d. a a N 1 a = a 1 = a. < > P n P (n) P (1) n = 1 P (n) P (n + 1) n n + 1 P (n) n P (n) n P n P (n) P (m) P (n) n m P (n + 1)
Προβολές και Μετασχηματισμοί Παρατήρησης
 Γραφικά & Οπτικοποίηση Κεφάλαιο 4 Προβολές και Μετασχηματισμοί Παρατήρησης Εισαγωγή Στα γραφικά υπάρχουν: 3Δ μοντέλα 2Δ συσκευές επισκόπησης (οθόνες & εκτυπωτές) Προοπτική απεικόνιση (προβολή): Λαμβάνει
Γραφικά & Οπτικοποίηση Κεφάλαιο 4 Προβολές και Μετασχηματισμοί Παρατήρησης Εισαγωγή Στα γραφικά υπάρχουν: 3Δ μοντέλα 2Δ συσκευές επισκόπησης (οθόνες & εκτυπωτές) Προοπτική απεικόνιση (προβολή): Λαμβάνει
Łs t r t rs tø r P r s tø PrØ rø rs tø P r s r t t r s t Ø t q s P r s tr. 2stŁ s q t q s t rt r s t s t ss s Ø r s t r t. Łs t r t t Ø t q s
 Łs t r t rs tø r P r s tø PrØ rø rs tø P r s r t t r s t Ø t q s P r s tr st t t t Ø t q s ss P r s P 2stŁ s q t q s t rt r s t s t ss s Ø r s t r t P r røs r Łs t r t t Ø t q s r Ø r t t r t q t rs tø
Łs t r t rs tø r P r s tø PrØ rø rs tø P r s r t t r s t Ø t q s P r s tr st t t t Ø t q s ss P r s P 2stŁ s q t q s t rt r s t s t ss s Ø r s t r t P r røs r Łs t r t t Ø t q s r Ø r t t r t q t rs tø
T : g r i l l b a r t a s o s Α Γ Ί Α Σ Σ Ο Φ Ί Α Σ 3, Δ Ρ Α Μ Α. Δ ι α ν ο μ έ ς κ α τ ο ί κ ο ν : 1 2 : 0 0 έ ω ς 0 1 : 0 0 π μ
 Α Γ Ί Α Σ Σ Ο Φ Ί Α Σ 3, Δ Ρ Α Μ Α g r i l l b a r t a s o s Δ ι α ν ο μ έ ς κ α τ ο ί κ ο ν : 1 2 : 0 0 έ ω ς 1 : 0 π μ Δ ι α ν ο μ έ ς κ α τ ο ί κ ο ν : 1 2 : 0 0 έ ω ς 0 1 : 0 0 π μ T ortiyas Σ ο υ
Α Γ Ί Α Σ Σ Ο Φ Ί Α Σ 3, Δ Ρ Α Μ Α g r i l l b a r t a s o s Δ ι α ν ο μ έ ς κ α τ ο ί κ ο ν : 1 2 : 0 0 έ ω ς 1 : 0 π μ Δ ι α ν ο μ έ ς κ α τ ο ί κ ο ν : 1 2 : 0 0 έ ω ς 0 1 : 0 0 π μ T ortiyas Σ ο υ
Note: Please use the actual date you accessed this material in your citation.
 MIT OpenCourseWre http://ocw.mit.edu 6.641 Electromgnetic Fields, Forces, nd Motion, Spring 005 Plese use the following cittion formt: Mrkus Zhn, 6.641 Electromgnetic Fields, Forces, nd Motion, Spring
MIT OpenCourseWre http://ocw.mit.edu 6.641 Electromgnetic Fields, Forces, nd Motion, Spring 005 Plese use the following cittion formt: Mrkus Zhn, 6.641 Electromgnetic Fields, Forces, nd Motion, Spring
(i) f(x, y) = xy + iy (iii) f(x, y) = e y e ix. f(z) = U(r, θ) + iv (r, θ) ; z = re iθ
 ΜΑΘΗΜΑΤΙΚΗ ΦΥΣΙΚΗ (ΜΕΤΑΠΤΥΧΙΑΚΟ) 6 Νοεμβρίου 07 Αναλυτικές συναρτήσεις Άσκηση (i) Δείξτε ότι η συνάρτηση f(z) είναι αναλυτική σε χωρίο D του μιγαδικού επιπέδου εάν και μόνο εάν η if(z) είναι αναλυτική
ΜΑΘΗΜΑΤΙΚΗ ΦΥΣΙΚΗ (ΜΕΤΑΠΤΥΧΙΑΚΟ) 6 Νοεμβρίου 07 Αναλυτικές συναρτήσεις Άσκηση (i) Δείξτε ότι η συνάρτηση f(z) είναι αναλυτική σε χωρίο D του μιγαδικού επιπέδου εάν και μόνο εάν η if(z) είναι αναλυτική
ΠΟΛΥΔΙΑΣΤΑΤΕΣ ΤΥΧΑΙΕΣ ΜΕΤΑΒΛΗΤΕΣ
 Δ.Φουσκάκης- Πολυδιάστατες Τυχαίες Μεταβλητές 1 ΠΟΛΥΔΙΑΣΤΑΤΕΣ ΤΥΧΑΙΕΣ ΜΕΤΑΒΛΗΤΕΣ Συνάρτηση Κατανομής: Έστω Χ=(Χ 1,,Χ ) T τυχαίο διάνυσμα (τ.δ). Ονομάζουμε συνάρτηση κατανομής πιθανότητας (σ.κ.π.) του τ.δ.
Δ.Φουσκάκης- Πολυδιάστατες Τυχαίες Μεταβλητές 1 ΠΟΛΥΔΙΑΣΤΑΤΕΣ ΤΥΧΑΙΕΣ ΜΕΤΑΒΛΗΤΕΣ Συνάρτηση Κατανομής: Έστω Χ=(Χ 1,,Χ ) T τυχαίο διάνυσμα (τ.δ). Ονομάζουμε συνάρτηση κατανομής πιθανότητας (σ.κ.π.) του τ.δ.
ΑΡΧΕΣ ΗΛΕΚΤΡΟΝΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Αγωγιμότητα σε ημιαγωγούς
 ΑΡΧΕΣ ΗΛΕΚΤΡΟΝΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Αγωγιμότητα σε ημιαγωγούς Required Text: Microelectronic Devices, Keith Leaver (1 st Chapter) Μέτρηση του μ e και προσδιορισμός του προσήμου των φορέων φορτίου Πρόβλημα: προσδιορισμός
ΑΡΧΕΣ ΗΛΕΚΤΡΟΝΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Αγωγιμότητα σε ημιαγωγούς Required Text: Microelectronic Devices, Keith Leaver (1 st Chapter) Μέτρηση του μ e και προσδιορισμός του προσήμου των φορέων φορτίου Πρόβλημα: προσδιορισμός
Κεφάλαιο 1 Πραγματικοί Αριθμοί 1.1 Σύνολα
 x + = 0 N = {,, 3....}, Z Q, b, b N c, d c, d N + b = c, b = d. N = =. < > P n P (n) P () n = P (n) P (n + ) n n + P (n) n P (n) n P n P (n) P (m) P (n) n m P (n + ) P (n) n m P n P (n) P () P (), P (),...,
x + = 0 N = {,, 3....}, Z Q, b, b N c, d c, d N + b = c, b = d. N = =. < > P n P (n) P () n = P (n) P (n + ) n n + P (n) n P (n) n P n P (n) P (m) P (n) n m P (n + ) P (n) n m P n P (n) P () P (), P (),...,
k = j + x 3 j + i + + f 2
 1 ΑΝΑΛΥΣΗ ΙΙ Διανυσματική Ανάλυση Κλίση-Απόκλιση-Στροβιλισμός Εστω f : D R 3 R μία βαθμωτή συνάρτηση και f : D R 3 R 3 μία διανυσματική συνάρτηση. Εισάγουμε τον διαφορικό τελεστή : = x 1 i + x 2 j + x
1 ΑΝΑΛΥΣΗ ΙΙ Διανυσματική Ανάλυση Κλίση-Απόκλιση-Στροβιλισμός Εστω f : D R 3 R μία βαθμωτή συνάρτηση και f : D R 3 R 3 μία διανυσματική συνάρτηση. Εισάγουμε τον διαφορικό τελεστή : = x 1 i + x 2 j + x
Second Order Partial Differential Equations
 Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
= df. f (n) (x) = dn f dx n
 Παράγωγος Συνάρτησης Ορισμός Παραγώγου σε ένα σημείο ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΗΣ σε ένα σημείο ξ είναι το όριο (αν υπάρχει!) Ορισμός Cauchy: f (ξ) = lim x ξ g(x, ξ), g(x, ξ) = f(x) f(ξ) x ξ ɛ > 0 δ(ɛ, ξ) > 0
Παράγωγος Συνάρτησης Ορισμός Παραγώγου σε ένα σημείο ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΗΣ σε ένα σημείο ξ είναι το όριο (αν υπάρχει!) Ορισμός Cauchy: f (ξ) = lim x ξ g(x, ξ), g(x, ξ) = f(x) f(ξ) x ξ ɛ > 0 δ(ɛ, ξ) > 0
F19MC2 Solutions 9 Complex Analysis
 F9MC Solutions 9 Complex Analysis. (i) Let f(z) = eaz +z. Then f is ifferentiable except at z = ±i an so by Cauchy s Resiue Theorem e az z = πi[res(f,i)+res(f, i)]. +z C(,) Since + has zeros of orer at
F9MC Solutions 9 Complex Analysis. (i) Let f(z) = eaz +z. Then f is ifferentiable except at z = ±i an so by Cauchy s Resiue Theorem e az z = πi[res(f,i)+res(f, i)]. +z C(,) Since + has zeros of orer at
 φ(t) TE 0 φ(z) φ(z) φ(z) φ(z) η(λ) G(z,λ) λ φ(z) η(λ) η(λ) = t CIGS 0 G(z,λ)φ(z)dz t CIGS η(λ) φ(z) 0 z
φ(t) TE 0 φ(z) φ(z) φ(z) φ(z) η(λ) G(z,λ) λ φ(z) η(λ) η(λ) = t CIGS 0 G(z,λ)φ(z)dz t CIGS η(λ) φ(z) 0 z
ΛΟΓΙΣΜΟΣ Συναρτήσεων µιας Μεταβλητής
 Σηµειωσεις: ΛΟΓΙΣΜΟΣ Συναρτήσεων µιας Μεταβλητής Θ. Κεχαγιάς Σεπτέµβρης 9 v..85 Περιεχόµενα Προλογος Εισαγωγη Βασικες Συναρτησεις. Θεωρια..................................... Λυµενα Προβληµατα.............................
Σηµειωσεις: ΛΟΓΙΣΜΟΣ Συναρτήσεων µιας Μεταβλητής Θ. Κεχαγιάς Σεπτέµβρης 9 v..85 Περιεχόµενα Προλογος Εισαγωγη Βασικες Συναρτησεις. Θεωρια..................................... Λυµενα Προβληµατα.............................
6.641, Electromagnetic Fields, Forces, and Motion Prof. Markus Zahn Lecture 7: Polarization and Conduction
 6.641, Electromgnetic Fiels, Forces, n Motion Prof. Mrkus Zhn Lecture 7: Polriztion n Conuction I. Experimentl Oservtion A. Fixe oltge - Switch Close ( v= o ) As n insulting mteril enters free-spce cpcitor
6.641, Electromgnetic Fiels, Forces, n Motion Prof. Mrkus Zhn Lecture 7: Polriztion n Conuction I. Experimentl Oservtion A. Fixe oltge - Switch Close ( v= o ) As n insulting mteril enters free-spce cpcitor
ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗ. Εµβαδά., x 1 x f
 ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗ Εµβαδά Θέµα 1 ίνεται η συνάρτηση x e e, x< 1 (x) = l nx, x 1 x Να δείξετε ότι η είναι συνεχής και να υπολογίσετε το εµβαδόν του χωρίου που περικλείεται από την C, τον άξονα
ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗ Εµβαδά Θέµα 1 ίνεται η συνάρτηση x e e, x< 1 (x) = l nx, x 1 x Να δείξετε ότι η είναι συνεχής και να υπολογίσετε το εµβαδόν του χωρίου που περικλείεται από την C, τον άξονα
(ii) x[y (x)] 4 + 2y(x) = 2x. (vi) y (x) = x 2 sin x
![(ii) x[y (x)] 4 + 2y(x) = 2x. (vi) y (x) = x 2 sin x (ii) x[y (x)] 4 + 2y(x) = 2x. (vi) y (x) = x 2 sin x](/thumbs/62/47493101.jpg) ΕΥΓΕΝΙΑ Ν. ΠΕΤΡΟΠΟΥΛΟΥ ΕΠΙΚ. ΚΑΘΗΓΗΤΡΙΑ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΑΣΚΗΣΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ «ΕΦΑΡΜΟΣΜΕΝΑ ΜΑΘΗΜΑΤΙΚΑ ΙΙΙ» ΠΑΤΡΑ 2015 1 Ασκήσεις 1η ομάδα ασκήσεων 1. Να χαρακτηρισθούν πλήρως
ΕΥΓΕΝΙΑ Ν. ΠΕΤΡΟΠΟΥΛΟΥ ΕΠΙΚ. ΚΑΘΗΓΗΤΡΙΑ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΑΣΚΗΣΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ «ΕΦΑΡΜΟΣΜΕΝΑ ΜΑΘΗΜΑΤΙΚΑ ΙΙΙ» ΠΑΤΡΑ 2015 1 Ασκήσεις 1η ομάδα ασκήσεων 1. Να χαρακτηρισθούν πλήρως
Note: Please use the actual date you accessed this material in your citation.
 MIT OpenCourseWre http://ocw.mit.edu 6.013/ESD.013J Electromgnetics nd Applictions, Fll 005 Plese use the following cittion formt: Mrkus Zhn, Erich Ippen, nd Dvid Stelin, 6.013/ESD.013J Electromgnetics
MIT OpenCourseWre http://ocw.mit.edu 6.013/ESD.013J Electromgnetics nd Applictions, Fll 005 Plese use the following cittion formt: Mrkus Zhn, Erich Ippen, nd Dvid Stelin, 6.013/ESD.013J Electromgnetics
CHAPTER (2) Electric Charges, Electric Charge Densities and Electric Field Intensity
 CHAPTE () Electric Chrges, Electric Chrge Densities nd Electric Field Intensity Chrge Configurtion ) Point Chrge: The concept of the point chrge is used when the dimensions of n electric chrge distriution
CHAPTE () Electric Chrges, Electric Chrge Densities nd Electric Field Intensity Chrge Configurtion ) Point Chrge: The concept of the point chrge is used when the dimensions of n electric chrge distriution
CHAPTER 70 DOUBLE AND TRIPLE INTEGRALS. 2 is integrated with respect to x between x = 2 and x = 4, with y regarded as a constant
 CHAPTER 7 DOUBLE AND TRIPLE INTEGRALS EXERCISE 78 Page 755. Evaluate: dxd y. is integrated with respect to x between x = and x =, with y regarded as a constant dx= [ x] = [ 8 ] = [ ] ( ) ( ) d x d y =
CHAPTER 7 DOUBLE AND TRIPLE INTEGRALS EXERCISE 78 Page 755. Evaluate: dxd y. is integrated with respect to x between x = and x =, with y regarded as a constant dx= [ x] = [ 8 ] = [ ] ( ) ( ) d x d y =
Note: Please use the actual date you accessed this material in your citation.
 MIT OpenCourseWare http://ocw.mit.edu 6.03/ESD.03J Electromagnetics and Applications, Fall 005 Please use the following citation format: Markus Zahn, 6.03/ESD.03J Electromagnetics and Applications, Fall
MIT OpenCourseWare http://ocw.mit.edu 6.03/ESD.03J Electromagnetics and Applications, Fall 005 Please use the following citation format: Markus Zahn, 6.03/ESD.03J Electromagnetics and Applications, Fall
MÉTHODES ET EXERCICES
 J.-M. MONIER I G. HABERER I C. LARDON MATHS PCSI PTSI MÉTHODES ET EXERCICES 4 e édition Création graphique de la couverture : Hokus Pokus Créations Dunod, 2018 11 rue Paul Bert, 92240 Malakoff www.dunod.com
J.-M. MONIER I G. HABERER I C. LARDON MATHS PCSI PTSI MÉTHODES ET EXERCICES 4 e édition Création graphique de la couverture : Hokus Pokus Créations Dunod, 2018 11 rue Paul Bert, 92240 Malakoff www.dunod.com
 10 20 X i a i (i, j) a ij (i, j, k) X x ijk j :j i i: R I J R K L IK JL a 11 a 12... a 1J a 21 a 22... a 2J = a I1 a I2... a IJ = [ 1 1 1 2 1 3... J L 1 J L ] R I K R J K IJ K = [ 1 1 2 2... K
10 20 X i a i (i, j) a ij (i, j, k) X x ijk j :j i i: R I J R K L IK JL a 11 a 12... a 1J a 21 a 22... a 2J = a I1 a I2... a IJ = [ 1 1 1 2 1 3... J L 1 J L ] R I K R J K IJ K = [ 1 1 2 2... K
z k z + n N f(z n ) + K z n = z n 1 2N
 Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά 6..5 Λύσεις Σειράς Ασκήσεων Άσκηση (α) Έστω z το όριο της ακολουθίας z n, δηλ. για κάθε ɛ > υπάρχει N(ɛ) ώστε z n z < ɛ για n > N. Για n > N(ɛ), είναι z n
Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά 6..5 Λύσεις Σειράς Ασκήσεων Άσκηση (α) Έστω z το όριο της ακολουθίας z n, δηλ. για κάθε ɛ > υπάρχει N(ɛ) ώστε z n z < ɛ για n > N. Για n > N(ɛ), είναι z n
Α Δ Ι. Παρασκευή 13 Δεκεμβρίου 2013
 Α Δ Ι Α - Φ 7 Δ : Ν. Μαρμαρίδης - Α. Μπεληγιάννης Ι Μ : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2013/asi2013.html, https://sites.google.com/site/maths4edu/home/algdom114 Παρασκευή 13 Δεκεμβρίου
Α Δ Ι Α - Φ 7 Δ : Ν. Μαρμαρίδης - Α. Μπεληγιάννης Ι Μ : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2013/asi2013.html, https://sites.google.com/site/maths4edu/home/algdom114 Παρασκευή 13 Δεκεμβρίου
ACTA MATHEMATICAE APPLICATAE SINICA Nov., ( µ ) ( (
 35 Þ 6 Ð Å Vol. 35 No. 6 2012 11 ACTA MATHEMATICAE APPLICATAE SINICA Nov., 2012 È ÄÎ Ç ÓÑ ( µ 266590) (E-mail: jgzhu980@yahoo.com.cn) Ð ( Æ (Í ), µ 266555) (E-mail: bbhao981@yahoo.com.cn) Þ» ½ α- Ð Æ Ä
35 Þ 6 Ð Å Vol. 35 No. 6 2012 11 ACTA MATHEMATICAE APPLICATAE SINICA Nov., 2012 È ÄÎ Ç ÓÑ ( µ 266590) (E-mail: jgzhu980@yahoo.com.cn) Ð ( Æ (Í ), µ 266555) (E-mail: bbhao981@yahoo.com.cn) Þ» ½ α- Ð Æ Ä
ΤΥΧΑΙΑ ΔΙΑΝΥΣΜΑΤΑ. 1. 0 F(x) 1, x n. 2. Η F είναι μη φθίνουσα και δεξιά συνεχής ως προς κάθε μεταβλητή. 3.
 ΤΥΧΑΙΑ ΔΙΑΝΥΣΜΑΤΑ Έστω Χ = (Χ 1,,Χ ) T τυχαίο διάνυσμα (τ.δ). Ονομάζουμε συνάρτηση κατανομής πιθανότητας (σ.κ.π.) του τ.δ. Χ την: F(x) = P(X 1 x 1,, X x ), x = (x 1,,x ) T 1. 0 F(x) 1, x.. Η F είναι μη
ΤΥΧΑΙΑ ΔΙΑΝΥΣΜΑΤΑ Έστω Χ = (Χ 1,,Χ ) T τυχαίο διάνυσμα (τ.δ). Ονομάζουμε συνάρτηση κατανομής πιθανότητας (σ.κ.π.) του τ.δ. Χ την: F(x) = P(X 1 x 1,, X x ), x = (x 1,,x ) T 1. 0 F(x) 1, x.. Η F είναι μη
Déformation et quantification par groupoïde des variétés toriques
 Défomation et uantification pa goupoïde de vaiété toiue Fédéic Cadet To cite thi veion: Fédéic Cadet. Défomation et uantification pa goupoïde de vaiété toiue. Mathématiue [math]. Univeité d Oléan, 200.
Défomation et uantification pa goupoïde de vaiété toiue Fédéic Cadet To cite thi veion: Fédéic Cadet. Défomation et uantification pa goupoïde de vaiété toiue. Mathématiue [math]. Univeité d Oléan, 200.
Differentiation exercise show differential equation
 Differentiation exercise show differential equation 1. If y x sin 2x, prove that x d2 y 2 2 + 2y x + 4xy 0 y x sin 2x sin 2x + 2x cos 2x 2 2cos 2x + (2 cos 2x 4x sin 2x) x d2 y 2 2 + 2y x + 4xy (2x cos
Differentiation exercise show differential equation 1. If y x sin 2x, prove that x d2 y 2 2 + 2y x + 4xy 0 y x sin 2x sin 2x + 2x cos 2x 2 2cos 2x + (2 cos 2x 4x sin 2x) x d2 y 2 2 + 2y x + 4xy (2x cos
ΚΑΤΑΝΟΜΕΣ Ι ΙΑΣΤΑΤΩΝ ΤΥΧΑΙΩΝ ΜΕΤΑΒΛΗΤΩΝ
 ΚΑΤΑΝΟΜΕΣ Ι ΙΑΣΤΑΤΩΝ ΤΥΧΑΙΩΝ ΜΕΤΑΒΛΗΤΩΝ Χαράλαµπος Α. Χαραλαµπίδης 21 εκεµβρίου 2009 ΑΝΕΞΑΡΤΗΣΙΑ ΤΥΧΑΙΩΝ ΜΕΤΑΒΛΗΤΩΝ Ορισµός (α) Εστω (X, Y) διακριτή διδιάστατη τυχαία µεταβλητή µε συνάρτηση πιθανότητας
ΚΑΤΑΝΟΜΕΣ Ι ΙΑΣΤΑΤΩΝ ΤΥΧΑΙΩΝ ΜΕΤΑΒΛΗΤΩΝ Χαράλαµπος Α. Χαραλαµπίδης 21 εκεµβρίου 2009 ΑΝΕΞΑΡΤΗΣΙΑ ΤΥΧΑΙΩΝ ΜΕΤΑΒΛΗΤΩΝ Ορισµός (α) Εστω (X, Y) διακριτή διδιάστατη τυχαία µεταβλητή µε συνάρτηση πιθανότητας
ΚΥΚΛΟΙ ΚΑΤΕΡΓΑΣΙΑΣ. κατά τον άξονα Ζ.
 ΚΥΚΛΟΙ ΚΑΤΕΡΓΑΣΙΑΣ Οι κύκλοι κατεργασίας χρησιµοποιούνται για ξεχόνδρισµα - φινίρισµα ενός προφίλ χωρίς να απαιτείται να προγραµµατίζουµε εµείς τα διαδοχικά πάσα της κατεργασίας. Έτσι, στο πρόγραµµα περικλείουµε
ΚΥΚΛΟΙ ΚΑΤΕΡΓΑΣΙΑΣ Οι κύκλοι κατεργασίας χρησιµοποιούνται για ξεχόνδρισµα - φινίρισµα ενός προφίλ χωρίς να απαιτείται να προγραµµατίζουµε εµείς τα διαδοχικά πάσα της κατεργασίας. Έτσι, στο πρόγραµµα περικλείουµε
SPECIAL FUNCTIONS and POLYNOMIALS
 SPECIAL FUNCTIONS and POLYNOMIALS Gerard t Hooft Stefan Nobbenhuis Institute for Theoretical Physics Utrecht University, Leuvenlaan 4 3584 CC Utrecht, the Netherlands and Spinoza Institute Postbox 8.195
SPECIAL FUNCTIONS and POLYNOMIALS Gerard t Hooft Stefan Nobbenhuis Institute for Theoretical Physics Utrecht University, Leuvenlaan 4 3584 CC Utrecht, the Netherlands and Spinoza Institute Postbox 8.195
Θεωρία Πιθανοτήτων, εαρινό εξάμηνο Λύσεις του όγδοου φυλλαδίου ασκήσεων.
 Θεωρία Πιθανοτήτων, εαρινό εξάμηνο 2017-. Λύσεις του όγδοου φυλλαδίου ασκήσεων. 1. Έστω F X, F Y οι συναρτήσεις κατανομής των τ.μ. X, Y και F X,Y η από κοινού συνάρτηση κατανομής τους. Αποδείξτε ότι (i)
Θεωρία Πιθανοτήτων, εαρινό εξάμηνο 2017-. Λύσεις του όγδοου φυλλαδίου ασκήσεων. 1. Έστω F X, F Y οι συναρτήσεις κατανομής των τ.μ. X, Y και F X,Y η από κοινού συνάρτηση κατανομής τους. Αποδείξτε ότι (i)
Gradient Descent for Optimization Problems With Sparse Solutions
 Gradient Descent for Optimization Problems With Sparse Solutions The Harvard community has made this article openly available. Please share how this access benefits you. Your story matters Citation Chen,
Gradient Descent for Optimization Problems With Sparse Solutions The Harvard community has made this article openly available. Please share how this access benefits you. Your story matters Citation Chen,
Τύπος TAYLOR. f : [a, b] R f (n 1) (x) συνεχής x [a, b] f (n) (x) x (a, b) ξ μεταξύ x και x 0. (x x 0 ) k k! f(x) = f (k) (x 0 ) + R n (x)
![Τύπος TAYLOR. f : [a, b] R f (n 1) (x) συνεχής x [a, b] f (n) (x) x (a, b) ξ μεταξύ x και x 0. (x x 0 ) k k! f(x) = f (k) (x 0 ) + R n (x) Τύπος TAYLOR. f : [a, b] R f (n 1) (x) συνεχής x [a, b] f (n) (x) x (a, b) ξ μεταξύ x και x 0. (x x 0 ) k k! f(x) = f (k) (x 0 ) + R n (x)](/thumbs/63/49057706.jpg) Τύπος TAYLOR f : [a, b] R f (n 1) (x) συνεχής x [a, b] f (n) (x) x (a, b) f(x) = ξ μεταξύ x και x 0 n 1 (x x 0 ) k f (k) (x 0 ) + R n (x) R n (x) = (x ξ)n p (x x 0 ) p p(n 1)! f (n) (ξ) υπόλοιπο Sclömlich-Roche
Τύπος TAYLOR f : [a, b] R f (n 1) (x) συνεχής x [a, b] f (n) (x) x (a, b) f(x) = ξ μεταξύ x και x 0 n 1 (x x 0 ) k f (k) (x 0 ) + R n (x) R n (x) = (x ξ)n p (x x 0 ) p p(n 1)! f (n) (ξ) υπόλοιπο Sclömlich-Roche
Zadatak 2 Odrediti tačke grananja, Riemann-ovu površ, opisati sve grane funkcije f(z) = z 3 z 4 i objasniti prelazak sa jedne na drugu granu.
 Kompleksna analiza Zadatak Odrediti tačke grananja, Riemann-ovu površ, opisati sve grane funkcije f(z) = z z 4 i objasniti prelazak sa jedne na drugu granu. Zadatak Odrediti tačke grananja, Riemann-ovu
Kompleksna analiza Zadatak Odrediti tačke grananja, Riemann-ovu površ, opisati sve grane funkcije f(z) = z z 4 i objasniti prelazak sa jedne na drugu granu. Zadatak Odrediti tačke grananja, Riemann-ovu
Παράγωγος Συνάρτησης. Ορισμός Παραγώγου σε ένα σημείο. ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΗΣ σε ένα σημείο ξ είναι το όριο (αν υπάρχει!) f (ξ) = lim.
 Παράγωγος Συνάρτησης Ορισμός Παραγώγου σε ένα σημείο ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΗΣ σε ένα σημείο ξ είναι το όριο (αν υπάρχει!) f (ξ) x ξ g(x, ξ), g(x, ξ) f(x) f(ξ) x ξ Ορισμός Cauchy: ɛ > 0 δ(ɛ, ξ) > 0 x x ξ
Παράγωγος Συνάρτησης Ορισμός Παραγώγου σε ένα σημείο ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΗΣ σε ένα σημείο ξ είναι το όριο (αν υπάρχει!) f (ξ) x ξ g(x, ξ), g(x, ξ) f(x) f(ξ) x ξ Ορισμός Cauchy: ɛ > 0 δ(ɛ, ξ) > 0 x x ξ
f a o gy s m a l nalg d co h n to h e y o m ia lalg e br coh the oogy lagebr
 - - - * k ˆ v ˆ k ˆ ˆ E x ˆ ˆ [ v ˆ ˆ ˆ ˆ ˆ E x ˆ ˆ ˆ ˆ v ˆ Ex U U ˆ ˆ ˆ ˆ ˆ ˆ v ˆ M v ˆ v M v ˆ ˆ I U ˆ I 9 70 k k ˆ ˆ - I I 9ˆ 70 ˆ [ ˆ - v - - v k k k ˆ - ˆ k ˆ k [ ˆ ˆ D M ˆ k k 0 D M k [ 0 M v M ˆ
- - - * k ˆ v ˆ k ˆ ˆ E x ˆ ˆ [ v ˆ ˆ ˆ ˆ ˆ E x ˆ ˆ ˆ ˆ v ˆ Ex U U ˆ ˆ ˆ ˆ ˆ ˆ v ˆ M v ˆ v M v ˆ ˆ I U ˆ I 9 70 k k ˆ ˆ - I I 9ˆ 70 ˆ [ ˆ - v - - v k k k ˆ - ˆ k ˆ k [ ˆ ˆ D M ˆ k k 0 D M k [ 0 M v M ˆ
 J J l 2 J T l 1 J T J T l 2 l 1 J J l 1 c 0 J J J J J l 2 l 2 J J J T J T l 1 J J T J T J T J {e n } n N {e n } n N x X {λ n } n N R x = λ n e n {e n } n N {e n : n N} e n 0 n N k 1, k 2,..., k n N λ
J J l 2 J T l 1 J T J T l 2 l 1 J J l 1 c 0 J J J J J l 2 l 2 J J J T J T l 1 J J T J T J T J {e n } n N {e n } n N x X {λ n } n N R x = λ n e n {e n } n N {e n : n N} e n 0 n N k 1, k 2,..., k n N λ
 ?=!! #! % &! & % (! )!! + &! %.! / ( + 0. 1 3 4 5 % 5 = : = ;Γ / Η 6 78 9 / : 7 ; < 5 = >97 :? : ΑΒ = Χ : ΔΕ Φ8Α 8 / Ι/ Α 5/ ; /?4 ϑκ : = # : 8/ 7 Φ 8Λ Γ = : 8Φ / Η = 7 Α 85 Φ = :
?=!! #! % &! & % (! )!! + &! %.! / ( + 0. 1 3 4 5 % 5 = : = ;Γ / Η 6 78 9 / : 7 ; < 5 = >97 :? : ΑΒ = Χ : ΔΕ Φ8Α 8 / Ι/ Α 5/ ; /?4 ϑκ : = # : 8/ 7 Φ 8Λ Γ = : 8Φ / Η = 7 Α 85 Φ = :
X x C(t) description lagrangienne ( X , t t t X x description eulérienne X x 1 1 v x t
 X 3 x 3 C Q y C(t) Q t QP t t C configuration initiale description lagrangienne x Φ ( X, t) X Y x X P x P t X x C(t) configuration actuelle description eulérienne (, ) d x v x t dt X 3 x 3 C(t) F( X, t)
X 3 x 3 C Q y C(t) Q t QP t t C configuration initiale description lagrangienne x Φ ( X, t) X Y x X P x P t X x C(t) configuration actuelle description eulérienne (, ) d x v x t dt X 3 x 3 C(t) F( X, t)
 γ n ϑ n n ψ T 8 Q 6 j, k, m, n, p, r, r t, x, y f m (x) (f(x)) m / a/b (f g)(x) = f(g(x)) n f f n I J α β I = α + βj N, Z, Q ϕ Εὐκλείδης ὁ Ἀλεξανδρεύς Στοιχεῖα ἄκρος καὶ μέσος λόγος ὕδωρ αἰθήρ ϕ φ Φ τ
γ n ϑ n n ψ T 8 Q 6 j, k, m, n, p, r, r t, x, y f m (x) (f(x)) m / a/b (f g)(x) = f(g(x)) n f f n I J α β I = α + βj N, Z, Q ϕ Εὐκλείδης ὁ Ἀλεξανδρεύς Στοιχεῖα ἄκρος καὶ μέσος λόγος ὕδωρ αἰθήρ ϕ φ Φ τ
2x 2 y x 4 +y 2 J (x, y) (0, 0) 0 J (x, y) = (0, 0) I ϕ(t) = (t, at), ψ(t) = (t, t 2 ), a ÑL<ÝÉ b, ½-? A? 2t 2 at t 4 +a 2 t 2 = lim
 9çB$ø`çü5 (-ç ) Ch.Ch4 b. è. [a] #8ƒb f(x, y) = { x y x 4 +y J (x, y) (, ) J (x, y) = (, ) I ϕ(t) = (t, at), ψ(t) = (t, t ), a ÑL
9çB$ø`çü5 (-ç ) Ch.Ch4 b. è. [a] #8ƒb f(x, y) = { x y x 4 +y J (x, y) (, ) J (x, y) = (, ) I ϕ(t) = (t, at), ψ(t) = (t, t ), a ÑL
Ν Κ Π 6Μ Θ 5 ϑ Μ % # =8 Α Α Φ ; ; 7 9 ; ; Ρ5 > ; Σ 1Τ Ιϑ. Υ Ι ς Ω Ι ϑτ 5 ϑ :Β > 0 1Φ ς1 : : Ξ Ρ ; 5 1 ΤΙ ϑ ΒΦΓ 0 1Φ ς1 : ΒΓ Υ Ι : Δ Φ Θ 5 ϑ Μ & Δ 6 6
 # % & ( ) +, %. / % 0 1 / 1 4 5 6 7 8 # 9 # : ; < # = >? 1 :; < 8 > Α Β Χ 1 ; Δ 7 = 8 1 ( 9 Ε 1 # 1 ; > Ε. # ( Ε 8 8 > ; Ε 1 ; # 8 Φ? : ;? 8 # 1? 1? Α Β Γ > Η Ι Φ 1 ϑ Β#Γ Κ Λ Μ Μ Η Ι 5 ϑ Φ ΒΦΓ Ν Ε Ο Ν
# % & ( ) +, %. / % 0 1 / 1 4 5 6 7 8 # 9 # : ; < # = >? 1 :; < 8 > Α Β Χ 1 ; Δ 7 = 8 1 ( 9 Ε 1 # 1 ; > Ε. # ( Ε 8 8 > ; Ε 1 ; # 8 Φ? : ;? 8 # 1? 1? Α Β Γ > Η Ι Φ 1 ϑ Β#Γ Κ Λ Μ Μ Η Ι 5 ϑ Φ ΒΦΓ Ν Ε Ο Ν
HMY 799 1: Αναγνώριση. συστημάτων. Διαλέξεις 6 7. Συνάφεια (συνέχεια) Μη παραμετρική αναγνώριση γραμμικών
 HMY 799 1: Αναγνώριση Συστημάτων Διαλέξεις 6 7 Συνάφεια (συνέχεια Συστήματα πολλαπλών εισόδων Μη παραμετρική αναγνώριση γραμμικών συστημάτων Εκτίμηση άσματος Ισχύος Περιοδόγραμμα, Bartlett/Welch, Παραμετρική
HMY 799 1: Αναγνώριση Συστημάτων Διαλέξεις 6 7 Συνάφεια (συνέχεια Συστήματα πολλαπλών εισόδων Μη παραμετρική αναγνώριση γραμμικών συστημάτων Εκτίμηση άσματος Ισχύος Περιοδόγραμμα, Bartlett/Welch, Παραμετρική
x3 + 1 (sin x)/x d dx (f(g(x))) = f ( g(x)) g (x). d dx (sin(x3 )) = cos(x 3 ) (3x 2 ). 3x 2 cos(x 3 )dx = sin(x 3 ) + C. d e (t2 +1) = e (t2 +1)
 x sin x cosx e x lnx x3 + (sin x)/x e x {}}{ (f(g(x))) = f ( g(x)) g (x). }{{}}{{} f(g(x)) 3x cos(x 3 ). 3x cos(x 3 ) x 3 3x sin(x 3 ) (sin(x3 )) = cos(x 3 ) (3x ). 3x cos(x 3 ) = sin(x 3 ) + C. e ( +).
x sin x cosx e x lnx x3 + (sin x)/x e x {}}{ (f(g(x))) = f ( g(x)) g (x). }{{}}{{} f(g(x)) 3x cos(x 3 ). 3x cos(x 3 ) x 3 3x sin(x 3 ) (sin(x3 )) = cos(x 3 ) (3x ). 3x cos(x 3 ) = sin(x 3 ) + C. e ( +).
ibemo Kazakhstan Republic of Kazakhstan, West Kazakhstan Oblast, Aksai, Pramzone, BKKS office complex Phone: ; Fax:

HMY 799 1: Αναγνώριση Συστημάτων
 HMY 799 : Αναγνώριση Συστημάτων Διάλεξη 5 Εκτίμηση φάσματος ισχύος Συνάφεια Παραδείγματα Στοχαστικά Διανύσματα Autoregressive model with exogenous inputs (ARX y( t + a y( t +... + a y( t n = bu( t +...
HMY 799 : Αναγνώριση Συστημάτων Διάλεξη 5 Εκτίμηση φάσματος ισχύος Συνάφεια Παραδείγματα Στοχαστικά Διανύσματα Autoregressive model with exogenous inputs (ARX y( t + a y( t +... + a y( t n = bu( t +...
Ε Π Ι Μ Ε Λ Η Τ Η Ρ Ι Ο Κ Υ Κ Λ Α Δ Ω Ν
 Ε ρ μ ο ύ π ο λ η, 0 9 Μ α ρ τ ί ο υ 2 0 1 2 Π ρ ο ς : Π ε ρ ιφ ε ρ ε ι ά ρ χ η Ν ο τ ίο υ Α ιγ α ί ο υ Α ρ ι θ. Π ρ ω τ. 3 4 2 2 κ. Ι ω ά ν ν η Μ α χ α ι ρ ί δ η F a x : 2 1 0 4 1 0 4 4 4 3 2, 2 2 8 1
Ε ρ μ ο ύ π ο λ η, 0 9 Μ α ρ τ ί ο υ 2 0 1 2 Π ρ ο ς : Π ε ρ ιφ ε ρ ε ι ά ρ χ η Ν ο τ ίο υ Α ιγ α ί ο υ Α ρ ι θ. Π ρ ω τ. 3 4 2 2 κ. Ι ω ά ν ν η Μ α χ α ι ρ ί δ η F a x : 2 1 0 4 1 0 4 4 4 3 2, 2 2 8 1
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Λογισμός Ι Ενότητα 4: Παράγωγοι Κ. Δασκαλογιάννης Τμήμα Μαθηματικών Α.Π.Θ. (Α.Π.Θ.) Λογισμός Ι 1 / 68 Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Λογισμός Ι Ενότητα 4: Παράγωγοι Κ. Δασκαλογιάννης Τμήμα Μαθηματικών Α.Π.Θ. (Α.Π.Θ.) Λογισμός Ι 1 / 68 Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Λογισμός ΙΙ Ενότητα 1: Λογισμός ΙΙ Κ. Δασκαλογιάννης Τμήμα Μαθηματικών Α.Π.Θ. (Α.Π.Θ.) Λογισμός ΙΙ 1 / 210 Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Λογισμός ΙΙ Ενότητα 1: Λογισμός ΙΙ Κ. Δασκαλογιάννης Τμήμα Μαθηματικών Α.Π.Θ. (Α.Π.Θ.) Λογισμός ΙΙ 1 / 210 Άδειες Χρήσης Το παρόν εκπαιδευτικό
Α θ ή ν α, 7 Α π ρ ι λ ί ο υ
 Α θ ή ν α, 7 Α π ρ ι λ ί ο υ 2 0 1 6 Τ ε ύ χ ο ς Δ ι α κ ή ρ υ ξ η ς Α ν ο ι κ τ ο ύ Δ ι ε θ ν ο ύ ς Δ ι α γ ω ν ι σ μ ο ύ 0 1 / 2 0 1 6 μ ε κ ρ ι τ ή ρ ι ο κ α τ α κ ύ ρ ω σ η ς τ η ν π λ έ ο ν σ υ μ
Α θ ή ν α, 7 Α π ρ ι λ ί ο υ 2 0 1 6 Τ ε ύ χ ο ς Δ ι α κ ή ρ υ ξ η ς Α ν ο ι κ τ ο ύ Δ ι ε θ ν ο ύ ς Δ ι α γ ω ν ι σ μ ο ύ 0 1 / 2 0 1 6 μ ε κ ρ ι τ ή ρ ι ο κ α τ α κ ύ ρ ω σ η ς τ η ν π λ έ ο ν σ υ μ
Μαθηµατικός Λογισµός ΙΙ
 Μαθηµατικός Λογισµός ΙΙ ΤΕΙ ΥΤΙΚΗΣ ΕΛΛΑ ΑΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ Η/Υ 2 Κ Ε Φ Α Λ Α Ι Ο 1 Ορια και Συνέχεια 1.1 Ορια Παράδειγµα 1.1. Να υπολογίσετε το x+y lim (x,y) (0,0) x y. Απάντηση: Παρατηρούµε ότι η συνάρτηση
Μαθηµατικός Λογισµός ΙΙ ΤΕΙ ΥΤΙΚΗΣ ΕΛΛΑ ΑΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ Η/Υ 2 Κ Ε Φ Α Λ Α Ι Ο 1 Ορια και Συνέχεια 1.1 Ορια Παράδειγµα 1.1. Να υπολογίσετε το x+y lim (x,y) (0,0) x y. Απάντηση: Παρατηρούµε ότι η συνάρτηση
Vol. 38 No Journal of Jiangxi Normal University Natural Science Nov. 2014
 38 6 Vol 38 No 6 204 Journal o Jiangxi Normal UniversityNatural Science Nov 204 000-586220406-055-06 2 * 330022 Nevanlinna 2 2 2 O 74 52 0 B j z 0j = 0 φz 0 0 λ - φ= C j z 0j = 0 ab 0 arg a arg b a = cb0
38 6 Vol 38 No 6 204 Journal o Jiangxi Normal UniversityNatural Science Nov 204 000-586220406-055-06 2 * 330022 Nevanlinna 2 2 2 O 74 52 0 B j z 0j = 0 φz 0 0 λ - φ= C j z 0j = 0 ab 0 arg a arg b a = cb0
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
Review-2 and Practice problems. sin 2 (x) cos 2 (x)(sin(x)dx) (1 cos 2 (x)) cos 2 (x)(sin(x)dx) let u = cos(x), du = sin(x)dx. = (1 u 2 )u 2 ( du)
 . Trigonometric Integrls. ( sin m (x cos n (x Cse-: m is odd let u cos(x Exmple: sin 3 (x cos (x Review- nd Prctice problems sin 3 (x cos (x Cse-: n is odd let u sin(x Exmple: cos 5 (x cos 5 (x sin (x
. Trigonometric Integrls. ( sin m (x cos n (x Cse-: m is odd let u cos(x Exmple: sin 3 (x cos (x Review- nd Prctice problems sin 3 (x cos (x Cse-: n is odd let u sin(x Exmple: cos 5 (x cos 5 (x sin (x
Homework 8 Model Solution Section
 MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
m i N 1 F i = j i F ij + F x
 N m i i = 1,..., N m i Fi x N 1 F ij, j = 1, 2,... i 1, i + 1,..., N m i F i = j i F ij + F x i mi Fi j Fj i mj O P i = F i = j i F ij + F x i, i = 1,..., N P = i F i = N F ij + i j i N i F x i, i = 1,...,
N m i i = 1,..., N m i Fi x N 1 F ij, j = 1, 2,... i 1, i + 1,..., N m i F i = j i F ij + F x i mi Fi j Fj i mj O P i = F i = j i F ij + F x i, i = 1,..., N P = i F i = N F ij + i j i N i F x i, i = 1,...,
ΠΑΡΟΡΑΜΑΤΑ ΕΚΔΟΣΗ 12 ΜΑΡΤΙΟΥ 2018
 ΝΙΚΟΛΑΟΣ M. ΣΤΑΥΡΑΚΑΚΗΣ: «Μερικές Διαφορικές Εξισώσεις & Μιγαδικές Συναρτήσεις: Θεωρία και Εφαρμογές» η Έκδοση, Αυτοέκδοση) Αθήνα, ΜΑΡΤΙΟΣ 06, Εξώφυλλο: ΜΑΛΑΚΟ, ΕΥΔΟΞΟΣ: 5084750, ISBN: 978-960-93-7366-
ΝΙΚΟΛΑΟΣ M. ΣΤΑΥΡΑΚΑΚΗΣ: «Μερικές Διαφορικές Εξισώσεις & Μιγαδικές Συναρτήσεις: Θεωρία και Εφαρμογές» η Έκδοση, Αυτοέκδοση) Αθήνα, ΜΑΡΤΙΟΣ 06, Εξώφυλλο: ΜΑΛΑΚΟ, ΕΥΔΟΞΟΣ: 5084750, ISBN: 978-960-93-7366-
1 Γραμμικές συναρτήσεις
 Γραμμικές συναρτήσεις Άσκηση. είξτε ότι η συνάρτηση f : R R, που ορίζεται με τη σχέση f(x, y, z) =(x y + z,x z), για κάθε (x, y, z) R, είναι μια γραμμική συνάρτηση, και να βρεθεί ο πυρήνας της. Απόδειξη.
Γραμμικές συναρτήσεις Άσκηση. είξτε ότι η συνάρτηση f : R R, που ορίζεται με τη σχέση f(x, y, z) =(x y + z,x z), για κάθε (x, y, z) R, είναι μια γραμμική συνάρτηση, και να βρεθεί ο πυρήνας της. Απόδειξη.
c(x 1)dx = 1 xf X (x)dx = (x 2 x)dx = 2 3 x3 x 2 x 2 2 (x 1)dx x 2 f X (x)dx = (x 3 x 2 )dx = 2 4 x4 2 3 x3
 Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών Θεωρία Πιθανοτήτων ιδάσκων : Π. Τσακαλίδης Λύσεις Τελικής Εξέτασης - 9 Ιανουαρίου 05 Θέµα. α Η γραφική παράσταση της σ.π.π. f X x ϕαίνεται στο σχήµα :
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών Θεωρία Πιθανοτήτων ιδάσκων : Π. Τσακαλίδης Λύσεις Τελικής Εξέτασης - 9 Ιανουαρίου 05 Θέµα. α Η γραφική παράσταση της σ.π.π. f X x ϕαίνεται στο σχήµα :
< = ) Τ 1 <Ο 6? <? Ν Α <? 6 ϑ<? ϑ = = Χ? 7 Π Ν Α = Ε = = = ;Χ? Ν !!! ) Τ 1. Ο = 6 Μ 6 < 6 Κ = Δ Χ ; ϑ = 6 = Σ Ν < Α <;< Δ Π 6 Χ6 Ο = ;= Χ Α
 # & ( ) ) +,. /, 1 /. 23 / 4 (& 5 6 7 8 8 9, :;< = 6 > < 6? ;< Β Γ Η. Ι 8 &ϑ Ε ; < 1 Χ6 Β 3 / Κ ;Χ 6 = ; Λ 4 ϑ < 6 Χ ; < = = Χ = Μ < = Φ ; ϑ =
# & ( ) ) +,. /, 1 /. 23 / 4 (& 5 6 7 8 8 9, :;< = 6 > < 6? ;< Β Γ Η. Ι 8 &ϑ Ε ; < 1 Χ6 Β 3 / Κ ;Χ 6 = ; Λ 4 ϑ < 6 Χ ; < = = Χ = Μ < = Φ ; ϑ =
Chapter 5, 6 Multiple Random Variables ENCS Probability and Stochastic Processes
 Chapter 5, 6 Multiple Random Variables ENCS6161 - Probability and Stochastic Processes Concordia University ENCS6161 p.1/47 Vector Random Variables A vector r.v. X is a function X : S R n, where S is the
Chapter 5, 6 Multiple Random Variables ENCS6161 - Probability and Stochastic Processes Concordia University ENCS6161 p.1/47 Vector Random Variables A vector r.v. X is a function X : S R n, where S is the
Note: Please use the actual date you accessed this material in your citation.
 MIT OpeCueWae hp://cw.m.eu 6.13/ESD.13J Elecmagec a pplca, Fall 5 Pleae ue he llwg ca ma: Maku Zah, Ech Ippe, a Dav Sael, 6.13/ESD.13J Elecmagec a pplca, Fall 5. (Maachue Iue Techlgy: MIT OpeCueWae). hp://cw.m.eu
MIT OpeCueWae hp://cw.m.eu 6.13/ESD.13J Elecmagec a pplca, Fall 5 Pleae ue he llwg ca ma: Maku Zah, Ech Ippe, a Dav Sael, 6.13/ESD.13J Elecmagec a pplca, Fall 5. (Maachue Iue Techlgy: MIT OpeCueWae). hp://cw.m.eu
Appendix A. Curvilinear coordinates. A.1 Lamé coefficients. Consider set of equations. ξ i = ξ i (x 1,x 2,x 3 ), i = 1,2,3
 Appendix A Curvilinear coordinates A. Lamé coefficients Consider set of equations ξ i = ξ i x,x 2,x 3, i =,2,3 where ξ,ξ 2,ξ 3 independent, single-valued and continuous x,x 2,x 3 : coordinates of point
Appendix A Curvilinear coordinates A. Lamé coefficients Consider set of equations ξ i = ξ i x,x 2,x 3, i =,2,3 where ξ,ξ 2,ξ 3 independent, single-valued and continuous x,x 2,x 3 : coordinates of point
D Alembert s Solution to the Wave Equation
 D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
Ó³ Ÿ , º 7(163).. 755Ä764 ˆ ˆŠ ˆ ˆŠ Š ˆ .. ± Î,. ˆ. ³. ƒ ˆ, Œμ ±
 Ó³ Ÿ. 2010.. 7, º 7(163).. 755Ä764 ˆ ˆŠ ˆ ˆŠ Š ˆ ˆ ƒ ˆ Šˆ ˆ ˆ ƒ Š.. ± Î,. ˆ. ³ ƒ ˆ, Œμ ± μí Ê μ ± É μ μ Êα Î ÉμÉ É É μ ÒÌ ±μ² Î É Í ³ Ö- É Ö - μ É Ì μé±²μ Ö μ ³ Ê²Ó Ê ( ² Î Ì μ³ É Î μ É ) ³ Ö ±Ê²μ- μ
Ó³ Ÿ. 2010.. 7, º 7(163).. 755Ä764 ˆ ˆŠ ˆ ˆŠ Š ˆ ˆ ƒ ˆ Šˆ ˆ ˆ ƒ Š.. ± Î,. ˆ. ³ ƒ ˆ, Œμ ± μí Ê μ ± É μ μ Êα Î ÉμÉ É É μ ÒÌ ±μ² Î É Í ³ Ö- É Ö - μ É Ì μé±²μ Ö μ ³ Ê²Ó Ê ( ² Î Ì μ³ É Î μ É ) ³ Ö ±Ê²μ- μ
(a) = lim. f y (a, b) = lim. (b) = lim. f y (x, y) = lim. g g(a + h) g(a) h g(b + h) g(b)
 1 ΑΝΑΛΥΣΗ ΙΙ Μερική Παράγωγος Μερικές Παράγωγοι Ορισμός 1: a) Εστω f(x y) : U R R μία συνάρτηση δύο μεταβλητών και (a b) ένα σημείο του U. Θεωρούμε ότι μεταβάλλεται μόνο το x ένω το y παραμένει σταθερό
1 ΑΝΑΛΥΣΗ ΙΙ Μερική Παράγωγος Μερικές Παράγωγοι Ορισμός 1: a) Εστω f(x y) : U R R μία συνάρτηση δύο μεταβλητών και (a b) ένα σημείο του U. Θεωρούμε ότι μεταβάλλεται μόνο το x ένω το y παραμένει σταθερό
ΜΑΘΗΜΑΤΙΚΑ κατεύθυνσης Γ ΛΥΚΕΙΟΥ
 ΕΞΕΤΑΣΕΙΣ 0 ΜΑΘΗΜΑΤΙΚΑ κατεύθυνσης Γ ΛΥΚΕΙΟΥ θεματα Α-Β-Γ-Δ Βαγγέλης Α Νικολακάκης Μαθηματικός ΠΕΡΙΕΧΟΜΕΝΑ ENOTHTA ΘΕΜΑ ΣΕΛΙΔΕΣ 0 ΣΥΝΟΠΤΙΚΗ ΜΕΘΟΔΟΛΟΓΙΑ 3-4 ΘΕΜΑΤΑ ΘΕΩΡΙΑΣ (ΘΕΜΑ Α) 5-7 ΑΣΚΗΣΕΙΣ (ΘΕΜΑ Β)
ΕΞΕΤΑΣΕΙΣ 0 ΜΑΘΗΜΑΤΙΚΑ κατεύθυνσης Γ ΛΥΚΕΙΟΥ θεματα Α-Β-Γ-Δ Βαγγέλης Α Νικολακάκης Μαθηματικός ΠΕΡΙΕΧΟΜΕΝΑ ENOTHTA ΘΕΜΑ ΣΕΛΙΔΕΣ 0 ΣΥΝΟΠΤΙΚΗ ΜΕΘΟΔΟΛΟΓΙΑ 3-4 ΘΕΜΑΤΑ ΘΕΩΡΙΑΣ (ΘΕΜΑ Α) 5-7 ΑΣΚΗΣΕΙΣ (ΘΕΜΑ Β)
Dark matter from Dark Energy-Baryonic Matter Couplings
 Dark matter from Dark Energy-Baryonic Matter Coulings Alejandro Avilés 1,2 1 Instituto de Ciencias Nucleares, UNAM, México 2 Instituto Nacional de Investigaciones Nucleares (ININ) México January 10, 2010
Dark matter from Dark Energy-Baryonic Matter Coulings Alejandro Avilés 1,2 1 Instituto de Ciencias Nucleares, UNAM, México 2 Instituto Nacional de Investigaciones Nucleares (ININ) México January 10, 2010
ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗ., x 1
 ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗ Τρόποι ολοκλήρωσης-θεµελειώδες θεώρηµα Θέµα lnx+, x > x ίνεται η συνάρτηση f(x) =. Να αποδειχθεί ότι η f είναι x, x x + ολοκληρώσιµη στο διάστηµα [,] και να υπολογιστεί
ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗ Τρόποι ολοκλήρωσης-θεµελειώδες θεώρηµα Θέµα lnx+, x > x ίνεται η συνάρτηση f(x) =. Να αποδειχθεί ότι η f είναι x, x x + ολοκληρώσιµη στο διάστηµα [,] και να υπολογιστεί
On the summability of divergent power series solutions for certain first-order linear PDEs Masaki HIBINO (Meijo University)
 On the summability of divergent power series solutions for certain first-order linear PDEs Masaki HIBINO (Meijo University) 1 1 Introduction (E) {1+x 2 +β(x,y)}y u x (x,y)+{x+b(x,y)}y2 u y (x,y) +u(x,y)=f(x,y)
On the summability of divergent power series solutions for certain first-order linear PDEs Masaki HIBINO (Meijo University) 1 1 Introduction (E) {1+x 2 +β(x,y)}y u x (x,y)+{x+b(x,y)}y2 u y (x,y) +u(x,y)=f(x,y)
 Καλώς ήρθατε στους Γραμμικούς Τελεστές! http://eclass.uoa.gr/courses/math122/ Εαρινό Εξάμηνο 2014-15 Χώροι με εσωτερικό γινόμενο Ορισμός Εστω E K-γραμμικός χώρος (K = R ή C). Ενα εσωτερικό γινόμενο (inner
Καλώς ήρθατε στους Γραμμικούς Τελεστές! http://eclass.uoa.gr/courses/math122/ Εαρινό Εξάμηνο 2014-15 Χώροι με εσωτερικό γινόμενο Ορισμός Εστω E K-γραμμικός χώρος (K = R ή C). Ενα εσωτερικό γινόμενο (inner
Ó³ Ÿ , º 1(130).. 7Ä ±μ. Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê
 Ó³ Ÿ. 006.. 3, º 1(130).. 7Ä16 Š 530.145 ˆ ƒ ˆ ˆŒ ˆŸ Š ƒ.. ±μ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê É μ ² Ö Ó μ μ Ö μ μ²õ μ É μ ÌÉ ±ÊÎ É ² ³ É μ - Î ±μ μ ÊÌ ±μ Ëμ ³ μ- ±² μ ÒÌ ³μ ²ÖÌ Ê ±. ³ É ÔÉμ μ μ μ Ö, Ö ²ÖÖ Ó ±μ³
Ó³ Ÿ. 006.. 3, º 1(130).. 7Ä16 Š 530.145 ˆ ƒ ˆ ˆŒ ˆŸ Š ƒ.. ±μ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê É μ ² Ö Ó μ μ Ö μ μ²õ μ É μ ÌÉ ±ÊÎ É ² ³ É μ - Î ±μ μ ÊÌ ±μ Ëμ ³ μ- ±² μ ÒÌ ³μ ²ÖÌ Ê ±. ³ É ÔÉμ μ μ μ Ö, Ö ²ÖÖ Ó ±μ³
Solutions to Exercise Sheet 5
 Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
 Molekulare Ebene (biochemische Messungen) Zelluläre Ebene (Elektrophysiologie, Imaging-Verfahren) Netzwerk Ebene (Multielektrodensysteme) Areale (MRT, EEG...) Gene Neuronen Synaptische Kopplung kleine
Molekulare Ebene (biochemische Messungen) Zelluläre Ebene (Elektrophysiologie, Imaging-Verfahren) Netzwerk Ebene (Multielektrodensysteme) Areale (MRT, EEG...) Gene Neuronen Synaptische Kopplung kleine
Constitutive Relations in Chiral Media
 Constitutive Relations in Chiral Media Covariance and Chirality Coefficients in Biisotropic Materials Roger Scott Montana State University, Department of Physics March 2 nd, 2010 Optical Activity Polarization
Constitutive Relations in Chiral Media Covariance and Chirality Coefficients in Biisotropic Materials Roger Scott Montana State University, Department of Physics March 2 nd, 2010 Optical Activity Polarization
y T - yy z x T + yy T + yz T + yx T + xy T + zy T - xz T - zx T - zz T - xx T + xx T + zx T + xz T + zz T - zy T - xy T - yx T - yz
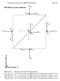 Συµπληρωµατικές Σηµειώσεις στα ΗΜ Πεδία (Κ. Χιτζανίδης Μάιος 2017 ΗΜ τάσεις σε υλικές επιφάνειες T + yy T + yz T + yx T + zy T + xy T - xx T - xz T - zx T - zz T + zz T + zx T + xz T + xx T - xy T - zy
Συµπληρωµατικές Σηµειώσεις στα ΗΜ Πεδία (Κ. Χιτζανίδης Μάιος 2017 ΗΜ τάσεις σε υλικές επιφάνειες T + yy T + yz T + yx T + zy T + xy T - xx T - xz T - zx T - zz T + zz T + zx T + xz T + xx T - xy T - zy
ΚΑΤΑΝΟΜΕΣ Ι ΙΑΣΤΑΤΩΝ ΤΥΧΑΙΩΝ ΜΕΤΑΒΛΗΤΩΝ (Συνέχεια)
 (Συνέχεια) Χαράλαµπος Α. Χαραλαµπίδης 23 εκεµβρίου 29 5.1. Στο τυχαίο πείραµα της ϱίψης δύο διακεκριµένων κύβων έστω X η ένδειξη του πρώτου κύβου και Y η µεγαλύτερη από τις δύο ενδείξεις. Να προσδιορισθούν
(Συνέχεια) Χαράλαµπος Α. Χαραλαµπίδης 23 εκεµβρίου 29 5.1. Στο τυχαίο πείραµα της ϱίψης δύο διακεκριµένων κύβων έστω X η ένδειξη του πρώτου κύβου και Y η µεγαλύτερη από τις δύο ενδείξεις. Να προσδιορισθούν
!"#! $%&'$% %(' ') '#*#(& ( #'##+,-'!$%(' & ('##$%(' &#' & ('##$%('. )!#)! ##%' " (&! #!$"/001
 !"#! $%&'$% %(' ') '#*#(& ( #'##+,-'!$%(' & ('##$%(' &#' & ('##$%('. ') '#*#(& )!#)! ##%' " (&! #!$"/001 ')!' &'# 2' '#)!( 3(&/004&' 5#(& /006 # '#)! 7!+8 8 8 #'%# ( #'## +,-'!$%(' & ('##$%('9&#' & ('##$%('9')
!"#! $%&'$% %(' ') '#*#(& ( #'##+,-'!$%(' & ('##$%(' &#' & ('##$%('. ') '#*#(& )!#)! ##%' " (&! #!$"/001 ')!' &'# 2' '#)!( 3(&/004&' 5#(& /006 # '#)! 7!+8 8 8 #'%# ( #'## +,-'!$%(' & ('##$%('9&#' & ('##$%('9')
ΕΦΑΡΜΟΣΜΕΝΗ ΣΤΑΤΙΣΤΙΚΗ I Παντελής Δημήτριος Τμήμα Μηχανολόγων Μηχανικών
 ΕΦΑΡΜΟΣΜΕΝΗ ΣΤΑΤΙΣΤΙΚΗ I Παντελής Δημήτριος Τμήμα Μηχανολόγων Μηχανικών ΤΥΧΑΙΕΣ ΜΕΤΑΒΛΗΤΕΣ Σε κάθε αποτέλεσμα του πειράματος αντιστοιχεί μία αριθμητική τιμή Μαθηματικός ορισμός: Τυχαία μεταβλητή X είναι
ΕΦΑΡΜΟΣΜΕΝΗ ΣΤΑΤΙΣΤΙΚΗ I Παντελής Δημήτριος Τμήμα Μηχανολόγων Μηχανικών ΤΥΧΑΙΕΣ ΜΕΤΑΒΛΗΤΕΣ Σε κάθε αποτέλεσμα του πειράματος αντιστοιχεί μία αριθμητική τιμή Μαθηματικός ορισμός: Τυχαία μεταβλητή X είναι
Dissertation for the degree philosophiae doctor (PhD) at the University of Bergen
 Dissertation for the degree philosophiae doctor (PhD) at the University of Bergen Dissertation date: GF F GF F SLE GF F D Ĉ = C { } Ĉ \ D D D = {z : z < 1} f : D D D D = D D, D = D D f f : D D
Dissertation for the degree philosophiae doctor (PhD) at the University of Bergen Dissertation date: GF F GF F SLE GF F D Ĉ = C { } Ĉ \ D D D = {z : z < 1} f : D D D D = D D, D = D D f f : D D
Α Ρ Η Θ Μ Ο : ΠΡΑΞΗ ΣΡΟΠΟΠΟΙΗΗ ΠΡΑΞΗ ΚΑΣΑΘΕΗ ΟΡΩΝ
 Α Ρ Η Θ Μ Ο : 6.984 ΠΡΑΞΗ ΣΡΟΠΟΠΟΙΗΗ ΠΡΑΞΗ ΚΑΣΑΘΕΗ ΟΡΩΝ ΔΙΑΓΩΝΙΜΟΤ η ε λ Π ά η ξ α ζ ή κ ε ξ α ζ η η ο ε ί θ ν ζ η κ ί α ( 2 1 ) η ν π κ ή λ α Μ α ξ η ί ν π, ε κ έ ξ α Γ ε π η έ ξ α, η ν π έ η ν π ο δ
Α Ρ Η Θ Μ Ο : 6.984 ΠΡΑΞΗ ΣΡΟΠΟΠΟΙΗΗ ΠΡΑΞΗ ΚΑΣΑΘΕΗ ΟΡΩΝ ΔΙΑΓΩΝΙΜΟΤ η ε λ Π ά η ξ α ζ ή κ ε ξ α ζ η η ο ε ί θ ν ζ η κ ί α ( 2 1 ) η ν π κ ή λ α Μ α ξ η ί ν π, ε κ έ ξ α Γ ε π η έ ξ α, η ν π έ η ν π ο δ
Αρµονική Ανάλυση. Ενότητα: Μετασχηµατισµός Fourier. Απόστολος Γιαννόπουλος. Τµήµα Μαθηµατικών
 Ενότητα: Μετασχηµατισµός Fourier Απόστολος Γιαννόπουλος Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που
Ενότητα: Μετασχηµατισµός Fourier Απόστολος Γιαννόπουλος Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που
P(Ο Χρήστος κερδίζει) = 1 P(Ο Χρήστος χάνει) = 1 P(X > Y ) = 1 2. P(Ο Χρήστος νικά σε 7 από τους 10 αγώνες) = 7
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-27: Πιθανότητες - Χειµερινό Εξάµηνο 28 ιδάσκων: Π. Τσακαλίδης Λύσεις Εβδοµης Σειράς Ασκήσεων Ηµεροµηνία Ανάθεσης: 3/2/28 Ηµεροµηνία Παράδοσης: 7/2/28
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-27: Πιθανότητες - Χειµερινό Εξάµηνο 28 ιδάσκων: Π. Τσακαλίδης Λύσεις Εβδοµης Σειράς Ασκήσεων Ηµεροµηνία Ανάθεσης: 3/2/28 Ηµεροµηνία Παράδοσης: 7/2/28
Basic Formulas. 8. sin(x) = cos(x π 2 ) 9. sin 2 (x) =1 cos 2 (x) 10. sin(2x) = 2 sin(x)cos(x) 11. cos(2x) =2cos 2 (x) tan(x) = 1 cos(2x)
 Bsic Formuls. n d =. d b = 3. b d =. sin d = 5. cos d = 6. tn d = n n ln b ln b b cos sin ln cos 7. udv= uv vdu. sin( = cos( π 9. sin ( = cos ( 0. sin( = sin(cos(. cos( =cos (. tn( = cos( sin( 3. sin(b
Bsic Formuls. n d =. d b = 3. b d =. sin d = 5. cos d = 6. tn d = n n ln b ln b b cos sin ln cos 7. udv= uv vdu. sin( = cos( π 9. sin ( = cos ( 0. sin( = sin(cos(. cos( =cos (. tn( = cos( sin( 3. sin(b
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ - ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΕΙΣΑΓΩΓΙΚΕΣ ΜΕΤΑΠΤΥΧΙΑΚΕΣ ΕΞΕΤΑΣΕΙΣ 26 ΙΟΥΛΙΟΥ 2008 ΕΥΤΕΡΟ ΜΕΡΟΣ :
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ - ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΑΛΓΕΒΡΑ - ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ ΑΝΑΛΥΣΗ ΑΡΙΘΜΗΤΙΚΗ ΑΝΑΛΥΣΗ ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΠΙΘΑΝΟΤΗΤΕΣ - ΣΤΑΤΙΣΤΙΚΗ ΕΙΣΑΓΩΓΙΚΕΣ ΜΕΤΑΠΤΥΧΙΑΚΕΣ ΕΞΕΤΑΣΕΙΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ - ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΑΛΓΕΒΡΑ - ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ ΑΝΑΛΥΣΗ ΑΡΙΘΜΗΤΙΚΗ ΑΝΑΛΥΣΗ ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΠΙΘΑΝΟΤΗΤΕΣ - ΣΤΑΤΙΣΤΙΚΗ ΕΙΣΑΓΩΓΙΚΕΣ ΜΕΤΑΠΤΥΧΙΑΚΕΣ ΕΞΕΤΑΣΕΙΣ
u = 0 u = ϕ t + Π) = 0 t + Π = C(t) C(t) C(t) = K K C(t) ϕ = ϕ 1 + C(t) dt Kt 2 ϕ = 0
 u = (u, v, w) ω ω = u = 0 ϕ u u = ϕ u = 0 ϕ 2 ϕ = 0 u t = u ω 1 ρ Π + ν 2 u Π = p + (1/2)ρ u 2 + ρgz ω = 0 ( ϕ t + Π) = 0 ϕ t + Π = C(t) C(t) C(t) = K K C(t) ϕ = ϕ 1 + C(t) dt Kt C(t) ϕ ϕ 1 ϕ = ϕ 1 p ρ
u = (u, v, w) ω ω = u = 0 ϕ u u = ϕ u = 0 ϕ 2 ϕ = 0 u t = u ω 1 ρ Π + ν 2 u Π = p + (1/2)ρ u 2 + ρgz ω = 0 ( ϕ t + Π) = 0 ϕ t + Π = C(t) C(t) C(t) = K K C(t) ϕ = ϕ 1 + C(t) dt Kt C(t) ϕ ϕ 1 ϕ = ϕ 1 p ρ
Discretization of Generalized Convection-Diffusion
 Discretization of Generalized Convection-Diffusion H. Heumann R. Hiptmair Seminar für Angewandte Mathematik ETH Zürich Colloque Numérique Suisse / Schweizer Numerik Kolloquium 8 Generalized Convection-Diffusion
Discretization of Generalized Convection-Diffusion H. Heumann R. Hiptmair Seminar für Angewandte Mathematik ETH Zürich Colloque Numérique Suisse / Schweizer Numerik Kolloquium 8 Generalized Convection-Diffusion
d 1 d 1
 É É d 1 d 1 n ; n ; x E x E Q 0 z db1 0 z W 0,( 0,d 0,1 ( (,W z 0 z 0 z 0 z z z z z z z z z z z z z z z z z z 0 Date 0 Date 1 Date 2 Borrowing Crisis Repayment Investment Consumption Date 0 Budget Constraint:
É É d 1 d 1 n ; n ; x E x E Q 0 z db1 0 z W 0,( 0,d 0,1 ( (,W z 0 z 0 z 0 z z z z z z z z z z z z z z z z z z 0 Date 0 Date 1 Date 2 Borrowing Crisis Repayment Investment Consumption Date 0 Budget Constraint:
Coupled Fluid Flow and Elastoplastic Damage Analysis of Acid. Stimulated Chalk Reservoirs
 Nazanin Jahani Coupled Fluid Flow and Elastoplastic Damage Analysis of Acid Stimulated Chalk Reservoirs Thesis for the degree of Philosophiae Doctor Trondheim, October 2015 Norwegian University of Science
Nazanin Jahani Coupled Fluid Flow and Elastoplastic Damage Analysis of Acid Stimulated Chalk Reservoirs Thesis for the degree of Philosophiae Doctor Trondheim, October 2015 Norwegian University of Science
# % % % % % # % % & %
 ! ! # % % % % % % % # % % & % # ( ) +,+.+ /0)1.2(3 40,563 +(073 063 + 70,+ 0 (0 8 0 /0.5606 6+ 0.+/+6+.+, +95,.+.+, + (0 5 +//5: 6+ 56 ;2(5/0 < + (0 27,+/ +.0 10 6+ 7 0, =7(5/0,> 06+?;, 6+ (0 +9)+ 5+ /50
! ! # % % % % % % % # % % & % # ( ) +,+.+ /0)1.2(3 40,563 +(073 063 + 70,+ 0 (0 8 0 /0.5606 6+ 0.+/+6+.+, +95,.+.+, + (0 5 +//5: 6+ 56 ;2(5/0 < + (0 27,+/ +.0 10 6+ 7 0, =7(5/0,> 06+?;, 6+ (0 +9)+ 5+ /50
Veliine u mehanici. Rad, snaga i energija. Dinamika. Meunarodni sustav mjere (SI) 1. Skalari. 2. Vektori - poetak. 12. dio. 1. Skalari. 2.
 Vele u ehc Rd, g eegj D. do. Sl. Veo 3. Tezo II. ed 4. Tezo IV. ed. Sl: 3 0 pod je jedc (ezo ulog ed). Veo: 3 3 pod je jedc (ezo pog ed) 3. Tezo dugog ed 3 9 pod je jedc 4. Tezoeog ed 3 4 8 pod je jedc
Vele u ehc Rd, g eegj D. do. Sl. Veo 3. Tezo II. ed 4. Tezo IV. ed. Sl: 3 0 pod je jedc (ezo ulog ed). Veo: 3 3 pod je jedc (ezo pog ed) 3. Tezo dugog ed 3 9 pod je jedc 4. Tezoeog ed 3 4 8 pod je jedc
 l 0 l 2 l 1 l 1 l 1 l 2 l 2 l 1 l p λ λ µ R N l 2 R N l 2 2 = N x i l p p R N l p N p = ( x i p ) 1 p i=1 l 2 l p p = 2 l p l 1 R N l 1 i=1 x 2 i 1 = N x i i=1 l p p p R N l 0 0 = {i x i 0} R
l 0 l 2 l 1 l 1 l 1 l 2 l 2 l 1 l p λ λ µ R N l 2 R N l 2 2 = N x i l p p R N l p N p = ( x i p ) 1 p i=1 l 2 l p p = 2 l p l 1 R N l 1 i=1 x 2 i 1 = N x i i=1 l p p p R N l 0 0 = {i x i 0} R
