GAŠENJE POŽAROV V VISOKOGORJU OSNOVNA PRIPOROČILA ZA ORGANIZIRANJE IN OPREMLJANJE GASILSKIH ENOT ZA GAŠENJE TOVRSTNIH POŽAROV
|
|
|
- Ἠσαῦ Ζωγράφου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 GAŠENJE POŽAROV V VISOKOGORJU OSNOVNA PRIPOROČILA ZA ORGANIZIRANJE IN OPREMLJANJE GASILSKIH ENOT ZA GAŠENJE TOVRSTNIH POŽAROV ORGAN DATUM PODPIS IZDELAL Delovna skupina 20 ODOBRIL SPREJEL Poveljnik GZS Matjaž Klarič Predsednik GZS Anton Koren
2 . UVOD Visokogorje je gorski svet nad 500 metrov nadmorske višine oziroma nad zgornjo gozdno mejo. Visokogorja so skalnata, slabo poraščena. Gozdna meja je nadmorska višina do koder seže strnjen gozd. Nad to mejo drevesa tako gosto ne morejo rasti zaradi prenizkih temperatur, preredkega ozračja, revne prsti ipd. Natančna višina gozdne meje je odvisna od podnebja širšega območja, kjer se nahajajo vzpetine. Nad gozdno mejo rastejo posamezna drevesa, zaradi pogojev največkrat pritlikave rasti in zgrbančena. Drevesna meja je nadmorska višina, nad katero tudi ta ne uspevajo. Požari v visokogorju predstavljajo pri nas posebno mesto in vlogo v gasilstvu, kajti samo gašenje takšnih požarov je popolnoma nekaj drugega kot gašenje požarov na kraškem območju. Predvsem gre tu zaradi konfiguracije in zahtevnosti terena za zelo zahtevno,nevarno in dolgotrajno gašenje. Omenjeno gradivo je prvenstveno namenjeno enotam, ki se srečujejo z visokogorjem oziroma terenom, ki ima vse značilnosti visokogorja nima pa zaradi nižje nadmorske višine tovrstnega statusa. 2. NAMEN IN VLOGA TAKIH ENOT Namen organiziranja takih enot je predvsem v tem, da se za gašenje požarov v visokogorju običajno ne uporablja mnogo-številčnih gasilskih enot ampak malo številčne enote predvsem pa morajo biti te enote, dobro usposobljene in opremljene. Organizirale naj bi se tam, kjer se gasilci srečujejo s požari v visokogorju. Delo enot je precej pogojeno tudi s sodelovanjem helikopterskih enot, ki opravljajo naloge gašenja požarov v visokogorju ter potrebne prevoze opreme in moštva. Gasilci takih enot, bi lahko pomenili tudi jedro sil za posredovanje ob zagotavljanju mednarodne pomoči v gašenju gozdnih požarov. Tovrstne enote se smiselno organizirajo na nivoju ene gasilske zveze enoto tvorijo pripadniki teritorialnih gasilskih društev v GZ. 3. GASILEC ZA GAŠENJE V VISOKOGORJU Sestavo enot je potrebno graditi z gasilci, ki so tudi v prostem času vešči gorništva in poznajo zakonitosti gibanja in premikanja v gorah (alpinisti, planinci, gorski reševalci,lovci itd.). Velik poudarek je potrebno nameniti tudi psiho-fizični pripravljenosti posameznika. 4. POVELJEVANJE, VODENJE IN AKTIVIRANJE GASILSKIH ENOT ZA GAŠENJE V VISOKOGORJU Vodenje intervencije se izvaja v skladu z Zakonom o gasilstvu ter Pravili gasilske službe. Vodenje velike intervencije temelji na uporabi Intervencijsko Poveljniškega Sistema IPS. IPS pomeni: - koordinacijo vseh sil in sredstev, ki se uporabljajo s ciljem zaščite življenja in ohranjanje materialnih in naravnih vrednosti v vseh postopkih na intervenciji.
3 - Uporablja preizkušene principe, ki so bili razviti za izboljšanje učinkovitosti sil in sredstev tako na področju načrtovanja intervencije kot na sami intervenciji. 5. TAKTIKA GAŠENJA IN CONE Noben požar v visokogorju ni enak. Pri načrtovanju taktičnih postopkov je potrebno predvsem upoštevati naslednje: - Kje je požar, - kam se bo širil, - kakšen je teren, - dostopnost in zahtevnost za gašenje požara. Vodja intervencije si mora natančno ogledati mesto požara in šele potem določiti cono, 2 in 3. Po opravljenih osnovnih korakov bomo z gasilsko enoto pristopili k gašenju požara. Pri načrtovanju intervencije je potrebno upoštevati tri pomembna pravila za pričetek gašenja: - PRIPRAVA ZAČETNE CONE ZA GAŠENJE / CONA - MESTO KJER SE BO ENOTA IZKRCALA / CONA 2 - MESTO NEPOSREDNEGA DELOVANJA / CONA 3 CONA V CONI se zbere vse gasilske enote in gasilsko opremo, ki se bo uporabila pri gašenju. Pripravi se vsa potrebna osebna in skupna oprema za intervencijo, gasilci v tej coni dobijo glavna navodila za pričetek akcije gašenja, nato se odpravijo na teren, bodisi peš, z gasilskimi vozili ali s helikopterjem. Ta cona se nahaja stran od mesta požara, praviloma tam, kjer imamo možnost preskrbe z vodo za gašenje oziroma polnjenje vodnega bazena ali helikopterske košare za gašenje PN in na mestu, kjer je omogočeno nemoteno delo helikopterskih enot. Za postavitev te cone je potrebno dobiti tudi soglasje vodje pilotov. V času, ko se pripravlja CONA je smiselno, da si vodja intervencije in vodja enote za visokogorje s helikopterjem ogleda požarišče. Potrebno je upoštevati vsa varnostna pravila. V Coni se formira štab za vodenje intervencije. Vodja intervencije (nivo GZ = vodja intervencije je poveljnik GZ, vodja enote za visokogorje je vodja operativnih sil na terenu oziroma v primeru ko imamo požar razdeljen na več sektorjev lahko tudi vodja sektorja na terenu) se nahaja v Coni in je v nenehnem kontaktu z vodjo operativnih sil na terenu oziroma vodji sektorjev.
4 CONA CONA 2 To je cona, kjer se bo gasilska enota izkrcala na samem terenu, vendar na varnem območju - v neposredni bližini samega požarišča. Tu si enota pripravi vso opremo za transport oziroma za gašenje požara. Na tem mestu se pripravi tudi poveljniško in logistično mesto-lokacija za vodjo operativnih sil oziroma vodjo sektorja na terenu, ter menjava ekip na terenu /služi tudi kot sprejemno mesto. V tej coni se namesti tudi logistik, vezist in bolničar. Potrebno je upoštevati vsa varnostna navodila in aktivnosti usklajevati z zračnimi silami.
5 CONA 3 To je mesto neposrednega delovanja oziroma gašenja požara. Tu gasilci skupaj s helikopterji gasijo požar. Opozoriti velja, da gasilci gasijo predvsem obrobje požara in se ne izpostavljajo nevarnostim ter se ne spuščajo v gašenje samega jedra požara,kjer bi lahko ogrožali svojo varnost. Jedro požara gasijo helikopterji. Strogo je potrebno upoštevati varnostna navodila - povelja vodje intervencije in posadk helikopterjev. Priprava mesta za zajemanje vode dostava Prva pomoč Vodja gašenja Mesto za postavitev opreme in bazena za gašenje Vezist Sprejemno mesto 2 Zajetje Sprejemno mesto Slike: Prikaz delovanja zračnih sil na terenu
6 Delo helikopterjev Transport opreme in gasilcev Gašenje in izvidovanje dostava HELIKOPTER 2 : - Gašenje - izvidovanje 2 transport HELIkOPTER : Transport gasilcev in opreme 6. LOGISTIKA Logistika predstavlja eno ključnih vej uspešnega posredovanja gasilskih enot na terenu tudi pri gašenju požarov v visokogorju. Če upoštevamo dejstvo, da bo gasilska enota delovala na terenu praktično cel dan in se zamenja šele zvečer, ko helikopterji odhajajo v bazo, je smiselno uporabiti dobro logistično podporo v CONI, kot tudi v CONI 2, tako za same gasilce, kot tudi za pripravo in oskrbo z gasilsko opremo, katero bodo enote potrebovale za nemoteno delovanje in gašenje. V CONI 2 je potrebno obvezno imeti vsaj enega gasilca, ki bo neposredno sodeloval z vodjo intervencije in vodjo operativnih sil na terenu in skrbel za opremo in ostalo logistično podporo. V CONI, kjer imamo organiziran tudi štab vodenja kot pomoč vodji intervencije, pa moramo organizirati logistični center, katerega vodi logistik. Na nivoju Občine, naj bi to mesto pripadalo štabu CZ oziroma osebi ki jo določi poveljnik OŠCZ občine, ta pa bi skrbel predvsem za prehrano,osnovna in materialna sredstva katere bi zahteval preko štaba vodja intervencije in vse ostalo kar spada zraven. Enako velja za nivo regije samo s to razliko, da tu lahko računamo na podporo regijskega štaba CZ. Kot poseben del gasilske logistike v CONI, pa je dejavnost, katero gasilci opravljamo pri delu s helikopterji. Potrebno je zagotoviti vsaj štiri gasilce, ponavadi so to iz domačega teritorialnega društva kjer je požar, ki predvsem skrbijo za nemoteno polnjenje vodnih rezervoarjev naj si bodi iz hidrantnega omrežja ali gasilskih vozil, nudijo pomoč oziroma suport posadkam helikopterjev, skrbijo za varnost v območju kjer delujejo plovila itd. 7. ALARMIRANJE ENOT ZA POŽARE V VISOKOGORJU. STOPNJA ALARMA Domače teritorialno PGD 2. STOPNJA ALARMA Gasilska enota za visokogorje v občini(gz) 3. STOPNJA ALARMA Gasilska enota za visokogorje iz najbližje sosednje občine(gz),nivo regije 4. STOPNJA ALARMA Gasilske enote za visokogorje iz države(gzs)
7 8. VODENJE INTERVENCIJE V prvi fazi alarmiranja prevzame vodenje domači poveljnik PGD, v kolikor oceni, da domače društvo ne bo sposobno izpeljati uspešne intervencije, zahteva vodja intervencije aktiviranje gasilske enote za gašenje požarov v visokogorju(gev) in njenega poveljnika. Ta tudi aktivira helikopter za gašenje preko ReCO v kolikor tega že ni storil poveljnik PGD (2 stopnja alarma). Vodenje intervencije prevzame poveljnik GZ, poveljnik enote za gašenje v visokogorju pa prevzame vodenje operativnih sil na terenu oziroma vodenje sektorja, če je ta posebej postavljen. Vodja intervencije organizira tudi štab vodenja. V kolikor vodja intervencije oceni, da se bo požar razširil in da bo potrebna dodatna pomoč gasilcev, ta aktivira dodatne sile iz sosednje občine oziroma GZ(3 stopnja alarma). Vodenje intervencije nadaljuje domači poveljnik gasilske zveze ob pomoči regijskega poveljnika. Ko se oceni da je požar prešel v zelo velik obseg in da bo potrebno enote na terenu menjati, svojih pa na nivoju regije ni dovolj na razpolago, se lahko vodja intervencije po posvetovanju z regijskim poveljnikom, poveljnikom Gasilske zveze Slovenije in poveljnikom CZ RS odloči za dodatno pomoč gasilskih enot za gašenje v visokogorju na nivoju celotne države. Vodenje intervencije tako naprej vodi domači poveljnik gasilske zveze ob pomoči regijskega poveljnika in poveljnika GZS.(4 stopnja alarma) DA ALGORITEM ZA DOLOČITEV POŽARA V VISOKOGORJU IN VODJO INTERVENCIJE Ali je do požara možno priti z vozilom? NE Ali je do požara možno priti z VT cevovodom? DA NE Ali lahko gasilci pridejo do požara v 30 minutah DA NE Požar v NARAVI Požar v VISOKOGORJU V osnovni pristojnosti PGD V osnovni pristojnosti GZ Aktiviranje helikopterja in GE za visokogorje POTEK ALARMIRANJA IN ODLOČANJA Zaznan požar in obvestilo na ReCO Aktiviranje poveljnika PGD Po algoritmu poveljnik PGD določi vrsto požara in osnovno pristojnost Požari v NARAVI Požar v VISOKOGORJU Pristojnost PGD Pristojnost GZ Seznanitev GZ o Aktiviranje poveljnika GZ in OŠCZ ter GEV dogajanju
8 Proženje PGD Odločitev o gašenju in uporabi helikopterja Gašenje DA Gašenje NE Helikopter DA Helikopter Vodenje Vodenje intervencije GZ NE intervencije Aktiviranje helikopterja??? CZ DA NE (ker je CZ Proženje prekinila GEV gašenje je Poveljnik GEV ona je vodja intervencije odgovorna) Ko in če se bo gasilo bo vodja GZ/GEV 9. FORMACIJA ENOTE IN MINIMALNA PRIPOROČLJIVA OSEBNA ZAŠČITNA IN SKUPNA OPREMA ZA OPREMLJANJE GASILSKIH ENOT ZA GAŠENJE POŽAROV V VISOKOGORJU Formacija enote:.) Oddelek: sestavljen iz 7 gasilcev Obrazložitev: oddelek je optimiziran za prevoz z večnamenskim transportnim helikopterjem Bell 42 Slovenske vojske oziroma Policije 2.) Enota: sestavljena iz 4 oddelkov + 4 Obrazložitev: enoto tvorijo 4 enaki oddelki + 4 gasilci, ki tvorijo poveljstvo enote Oddelek 7 gasilcev x 4 = 28 gasilcev + poveljnik enote + logistik + vezist za radio-veze + bolničar Σ = gasilcev Poveljstvo enote tvorijo: Poveljnik enote Radio-vezist Bolničar Logistik na terenu Vodje oddelkov Poveljnik enote: Poveljnik enote poveljuje enoti in je odgovoren za njeno delovanje. Prevzema vlogo vodje operativnih sil na požarišču. Če je postavljen sektor»visokogorje«prevzema vodenje v sektorju. Po gasilski usposobljenosti naj bi bil po činu vsaj
9 gasilski častnik priporočljivo pa VGČ, ter opravljeno usposabljanje za vodenje velikih intervencij. Radio vezist: Sodeluje v poveljstvu enote kot radio-vezist. Njegovo delovanje je na terenu, kjer ima nalogo, da je vzpostavljena brezhibna komunikacija med poveljnikom enote, helikopterjem in štabom v dolini. Opravljeno naj bi imel specialnost za radijske zveze. Čin vsaj NGČ. Bolničar: Je gasilec, ki ima nalogo, da ob morebitni poškodbi gasilcev na terenu z medicinsko opremo, ki jo ima s seboj nudi prvo pomoč. Sodeluje v poveljstvu enote na terenu. Imeti mora opravljen tečaj za bolničarja. Logistik Je gasilec, ki na terenu(požarišču) skrbi za logistiko. S poveljnikom enote načrtujeta cono 2, kjer se bo zbirala vsa oprema za gašenje. Skrbi za ureditev primernega mesta za dovoz opreme, jo pripravlja za transport, vodi zabeležke in je odgovoren za celotno opremo, katera se pripelje na teren. Sodeluje v poveljstvu enote. a) Osebna zaščitna oprema Št. Slika Naziv opreme količina 0 02 Kombinezon za gašenje požarov v naravi po tipizaciji Gasilske zveze Slovenije Priporočilo: material aramidna vlakna Zaščitna čelada izdelana za gašenje požarov v naravi 03 Plinska zaščitna očala 04 Varovalni pas - alpinistični 05 Gasilske zaščitne rokavice po tipizaciji Priporočilo: model z objetim
10 zapestjem Čelna baterijska luč Zaščitni filter za dim 08 Zaščitna podkapa 09 Gorniški škornji 0 Prva pomoč Bombažna ruta 2 Gorniški nahrbtnik (30-40l) z naslednjo vsebino: - torbica s prvo pomočjo (št.0) - plastenka za pijačo - priročno orodje - univerzalni nož - varovalni trak+2 vponki (alp. karabin) - rezervno perilo - zaščita za dež Skupna oprema Naziv blaga kom 0
11 Motorna žaga + zaščitne hlače pred urezi (oddelek) Varovalni komplet za strma pobočja: a) - osmica 30 kn b) ročna prižema c) vponka d) brezkončni trak e) 4- ali 6-zobe dereze f) pohodne palice z negorljivo transportno torbico (opcija) g) dinamična vrv debeline 0,3 mm h) statična vrv debeline 0,5 mm i) pomožna vrv debeline 8,0 mm j) pomožna vrvica debeline 6 mm 03 Zložljiva nosila za ponesrečenca 04 Nahrbtnik za prvo pomoč
12 05 Ročni GPS sprejemnik 06 Ročne radijske postaje ZARE 3 (oddelek) 5 (Enota) sestavljena iz 4 oddelkov Naglavne slušalke z mikrofonom c) Oprema za gašenje 0 Požarna metla 2 02 Grablje / motika 0 03 Izpihovalnik zraka z opcijo rezervoarja z vodo
13 04 Nahrbtna brenta / naprtnjača 8 05 Vodni rezervoar 000 l 06 Prenosna motorna črpalka + pripadajoča oprema (gorivo, sesalne cevi, D- cevi, armature) 07 Hruška za helikopter
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 5. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 22. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Funkcijske vrste. Matematika 2. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 2. april Gregor Dolinar Matematika 2
 Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Diferencialna enačba, v kateri nastopata neznana funkcija in njen odvod v prvi potenci
 Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Tretja vaja iz matematike 1
 Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 14. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 21. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Booleova algebra. Izjave in Booleove spremenljivke
 Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
IZPIT IZ ANALIZE II Maribor,
 Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
PONOVITEV SNOVI ZA 4. TEST
 PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK
 1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
Delovna točka in napajalna vezja bipolarnih tranzistorjev
 KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 15. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
ZASCITE IN RESEVANJA OB JEDRSKI NESRECI NA OBMOCJU LJUBLJANSKE REGIJE
 REGIJSKI N A C R T ZASCITE IN RESEVANJA OB JEDRSKI NESRECI NA OBMOCJU LJUBLJANSKE REGIJE Verzija 2.0 ORGAN Pripravil UPRAVA RS ZA ZASCITO IN RESEVANJE IZPOSTAVA LJUBLJANA Obravnaval in sprej el STAB cz
REGIJSKI N A C R T ZASCITE IN RESEVANJA OB JEDRSKI NESRECI NA OBMOCJU LJUBLJANSKE REGIJE Verzija 2.0 ORGAN Pripravil UPRAVA RS ZA ZASCITO IN RESEVANJE IZPOSTAVA LJUBLJANA Obravnaval in sprej el STAB cz
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 10. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK
 SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
Integralni račun. Nedoločeni integral in integracijske metrode. 1. Izračunaj naslednje nedoločene integrale: (a) dx. (b) x 3 +3+x 2 dx, (c) (d)
 Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου...
 ΑΠΟΖΗΜΙΩΣΗ ΘΥΜΑΤΩΝ ΕΓΚΛΗΜΑΤΙΚΩΝ ΠΡΑΞΕΩΝ ΣΛΟΒΕΝΙΑ 1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου... 3 1 1. Έντυπα αιτήσεων
ΑΠΟΖΗΜΙΩΣΗ ΘΥΜΑΤΩΝ ΕΓΚΛΗΜΑΤΙΚΩΝ ΠΡΑΞΕΩΝ ΣΛΟΒΕΝΙΑ 1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου... 3 1 1. Έντυπα αιτήσεων
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 12. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
Numerično reševanje. diferencialnih enačb II
 Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
13. Jacobijeva metoda za računanje singularnega razcepa
 13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
Osnove elektrotehnike uvod
 Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
Kontrolne karte uporabljamo za sprotno spremljanje kakovosti izdelka, ki ga izdelujemo v proizvodnem procesu.
 Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
Kotne in krožne funkcije
 Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
MATEMATIČNI IZRAZI V MAFIRA WIKIJU
 I FAKULTETA ZA MATEMATIKO IN FIZIKO Jadranska cesta 19 1000 Ljubljan Ljubljana, 25. marec 2011 MATEMATIČNI IZRAZI V MAFIRA WIKIJU KOMUNICIRANJE V MATEMATIKI Darja Celcer II KAZALO: 1 VSTAVLJANJE MATEMATIČNIH
I FAKULTETA ZA MATEMATIKO IN FIZIKO Jadranska cesta 19 1000 Ljubljan Ljubljana, 25. marec 2011 MATEMATIČNI IZRAZI V MAFIRA WIKIJU KOMUNICIRANJE V MATEMATIKI Darja Celcer II KAZALO: 1 VSTAVLJANJE MATEMATIČNIH
1. Definicijsko območje, zaloga vrednosti. 2. Naraščanje in padanje, ekstremi. 3. Ukrivljenost. 4. Trend na robu definicijskega območja
 ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
8. Diskretni LTI sistemi
 8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
Gimnazija Krˇsko. vektorji - naloge
 Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
Transformator. Delovanje transformatorja I. Delovanje transformatorja II
 Transformator Transformator je naprava, ki v osnovi pretvarja napetost iz enega nivoja v drugega. Poznamo vrsto različnih izvedb transformatorjev, glede na njihovo specifičnost uporabe:. Energetski transformator.
Transformator Transformator je naprava, ki v osnovi pretvarja napetost iz enega nivoja v drugega. Poznamo vrsto različnih izvedb transformatorjev, glede na njihovo specifičnost uporabe:. Energetski transformator.
Tipizacija gasilskih vozil_1/2003, dopolnitve
 GASILSKA ZVEZA SLOVENIJE Tržaška cesta 22 000 LJUBLJANA T I P I Z A C I J A G A S I L S K I H V O Z I L Tipizacija gasilskih vozil je bila sprejeta na seji predsedstva Gasilske zveze Slovenije dne.2.2000,
GASILSKA ZVEZA SLOVENIJE Tržaška cesta 22 000 LJUBLJANA T I P I Z A C I J A G A S I L S K I H V O Z I L Tipizacija gasilskih vozil je bila sprejeta na seji predsedstva Gasilske zveze Slovenije dne.2.2000,
Splošno o interpolaciji
 Splošno o interpolaciji J.Kozak Numerične metode II (FM) 2011-2012 1 / 18 O funkciji f poznamo ali hočemo uporabiti le posamezne podatke, na primer vrednosti r i = f (x i ) v danih točkah x i Izberemo
Splošno o interpolaciji J.Kozak Numerične metode II (FM) 2011-2012 1 / 18 O funkciji f poznamo ali hočemo uporabiti le posamezne podatke, na primer vrednosti r i = f (x i ) v danih točkah x i Izberemo
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
Logatherm WPL 14 AR T A ++ A + A B C D E F G A B C D E F G. kw kw /2013
 WP 14 R T d 9 10 11 53 d 2015 811/2013 WP 14 R T 2015 811/2013 WP 14 R T Naslednji podatki o izdelku izpolnjujejo zahteve uredb U 811/2013, 812/2013, 813/2013 in 814/2013 o dopolnitvi smernice 2010/30/U.
WP 14 R T d 9 10 11 53 d 2015 811/2013 WP 14 R T 2015 811/2013 WP 14 R T Naslednji podatki o izdelku izpolnjujejo zahteve uredb U 811/2013, 812/2013, 813/2013 in 814/2013 o dopolnitvi smernice 2010/30/U.
STANDARD1 EN EN EN
 PRILOGA RADIJSKE 9,000-20,05 khz naprave kratkega dosega: induktivne aplikacije 315 600 khz naprave kratkega dosega: aktivni medicinski vsadki ultra nizkih moči 4516 khz naprave kratkega dosega: železniške
PRILOGA RADIJSKE 9,000-20,05 khz naprave kratkega dosega: induktivne aplikacije 315 600 khz naprave kratkega dosega: aktivni medicinski vsadki ultra nizkih moči 4516 khz naprave kratkega dosega: železniške
p 1 ENTROPIJSKI ZAKON
 ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
T I P I Z A C I J A G A S I L S K I H V O Z I L
 GASILSKA ZVEZA SLOVENIJE Tržaška cesta 221 1000 LJUBLJANA T I P I Z A C I J A G A S I L S K I H V O Z I L Tipizacija gasilskih vozil je bila sprejeta na seji predsedstva Gasilske zveze Slovenije dne 11.2.2000,
GASILSKA ZVEZA SLOVENIJE Tržaška cesta 221 1000 LJUBLJANA T I P I Z A C I J A G A S I L S K I H V O Z I L Tipizacija gasilskih vozil je bila sprejeta na seji predsedstva Gasilske zveze Slovenije dne 11.2.2000,
POPIS DEL IN PREDIZMERE
 POPIS DEL IN PREDIZMERE ZEMELJSKI USAD v P 31 - P 32 ( l=18 m ) I. PREDDELA 1.1 Zakoličba, postavitev in zavarovanje prečnih profilov m 18,0 Preddela skupaj EUR II. ZEMELJSKA DELA 2.1 Izkop zemlje II.
POPIS DEL IN PREDIZMERE ZEMELJSKI USAD v P 31 - P 32 ( l=18 m ) I. PREDDELA 1.1 Zakoličba, postavitev in zavarovanje prečnih profilov m 18,0 Preddela skupaj EUR II. ZEMELJSKA DELA 2.1 Izkop zemlje II.
Primeri: naftalen kinolin spojeni kinolin
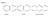 Primeri: naftalen kinolin spojeni kinolin 3 skupne strani 7 skupnih strani 5 skupnih strani 6 skupnih atomov 8 skupnih atomov 6 skupnih atomov orto spojen sistem orto in peri spojena sistema mostni kinolin
Primeri: naftalen kinolin spojeni kinolin 3 skupne strani 7 skupnih strani 5 skupnih strani 6 skupnih atomov 8 skupnih atomov 6 skupnih atomov orto spojen sistem orto in peri spojena sistema mostni kinolin
ΠΡΙΤΣΙΝΑΔΟΡΟΣ ΛΑΔΙΟΥ ΑΕΡΟΣ ΓΙΑ ΠΡΙΤΣΙΝΙΑ M4/M12 ΟΔΗΓΙΕΣ ΧΡΗΣΗΣ - ΑΝΤΑΛΛΑΚΤΙΚΑ
 GR ΠΡΙΤΣΙΝΑΔΟΡΟΣ ΛΑΔΙΟΥ ΑΕΡΟΣ ΓΙΑ ΠΡΙΤΣΙΝΙΑ M4/M12 ΟΔΗΓΙΕΣ ΧΡΗΣΗΣ - ΑΝΤΑΛΛΑΚΤΙΚΑ H OLJLAJNYOMÁSÚ SZEGECSELŐ M4/M12 SZEGECSEKHEZ HASZNÁLATI UTASÍTÁS - ALKATRÉSZEK SLO OLJNO-PNEVMATSKI KOVIČAR ZA ZAKOVICE
GR ΠΡΙΤΣΙΝΑΔΟΡΟΣ ΛΑΔΙΟΥ ΑΕΡΟΣ ΓΙΑ ΠΡΙΤΣΙΝΙΑ M4/M12 ΟΔΗΓΙΕΣ ΧΡΗΣΗΣ - ΑΝΤΑΛΛΑΚΤΙΚΑ H OLJLAJNYOMÁSÚ SZEGECSELŐ M4/M12 SZEGECSEKHEZ HASZNÁLATI UTASÍTÁS - ALKATRÉSZEK SLO OLJNO-PNEVMATSKI KOVIČAR ZA ZAKOVICE
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * NAVODILA ZA OCENJEVANJE. Sreda, 3. junij 2015 SPLOŠNA MATURA
 Državni izpitni center *M15143113* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sreda, 3. junij 2015 SPLOŠNA MATURA RIC 2015 M151-431-1-3 2 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor Naloga Odgovor
Državni izpitni center *M15143113* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sreda, 3. junij 2015 SPLOŠNA MATURA RIC 2015 M151-431-1-3 2 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor Naloga Odgovor
Na pregledni skici napišite/označite ustrezne točke in paraboli. A) 12 B) 8 C) 4 D) 4 E) 8 F) 12
 Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
Podobnost matrik. Matematika II (FKKT Kemijsko inženirstvo) Diagonalizacija matrik
 Podobnost matrik Matematika II (FKKT Kemijsko inženirstvo) Matjaž Željko FKKT Kemijsko inženirstvo 14 teden (Zadnja sprememba: 23 maj 213) Matrika A R n n je podobna matriki B R n n, če obstaja obrnljiva
Podobnost matrik Matematika II (FKKT Kemijsko inženirstvo) Matjaž Željko FKKT Kemijsko inženirstvo 14 teden (Zadnja sprememba: 23 maj 213) Matrika A R n n je podobna matriki B R n n, če obstaja obrnljiva
ČHE AVČE. Konzorcij RUDIS MITSUBISHI ELECTRIC SUMITOMO
 ČHE AVČE Konzorcij RUDIS MITSUBISHI ELECTRIC SUMITOMO MONTAŽA IN DOBAVA AGREGATA ČRPALKA / TURBINA MOTOR / GENERATOR S POMOŽNO OPREMO Anton Hribar d.i.s OSNOVNI TEHNIČNI PODATKI ČRPALNE HIDROELEKTRARNE
ČHE AVČE Konzorcij RUDIS MITSUBISHI ELECTRIC SUMITOMO MONTAŽA IN DOBAVA AGREGATA ČRPALKA / TURBINA MOTOR / GENERATOR S POMOŽNO OPREMO Anton Hribar d.i.s OSNOVNI TEHNIČNI PODATKI ČRPALNE HIDROELEKTRARNE
Iterativno reševanje sistemov linearnih enačb. Numerične metode, sistemi linearnih enačb. Numerične metode FE, 2. december 2013
 Numerične metode, sistemi linearnih enačb B. Jurčič Zlobec Numerične metode FE, 2. december 2013 1 Vsebina 1 z n neznankami. a i1 x 1 + a i2 x 2 + + a in = b i i = 1,..., n V matrični obliki zapišemo:
Numerične metode, sistemi linearnih enačb B. Jurčič Zlobec Numerične metode FE, 2. december 2013 1 Vsebina 1 z n neznankami. a i1 x 1 + a i2 x 2 + + a in = b i i = 1,..., n V matrični obliki zapišemo:
matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):
![matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij): matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):](/thumbs/87/96579490.jpg) 4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
Fazni diagram binarne tekočine
 Fazni diagram binarne tekočine Žiga Kos 5. junij 203 Binarno tekočino predstavljajo delci A in B. Ti se med seboj lahko mešajo v različnih razmerjih. V nalogi želimo izračunati fazni diagram take tekočine,
Fazni diagram binarne tekočine Žiga Kos 5. junij 203 Binarno tekočino predstavljajo delci A in B. Ti se med seboj lahko mešajo v različnih razmerjih. V nalogi želimo izračunati fazni diagram take tekočine,
Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba.
 1. Osnovni pojmi Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba. Primer 1.1: Diferencialne enačbe so izrazi: y
1. Osnovni pojmi Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba. Primer 1.1: Diferencialne enačbe so izrazi: y
SATCITANANDA. F = e E sila na naboj. = ΔW e. Rudolf Kladnik: Fizika za srednješolce 3. Svet elektronov in atomov
 Ruolf Klnik: Fizik z srenješolce Set elektrono in too Električno olje (11), gibnje elce električne olju Strn 55, nlog 1 Kolikšno netost or releteti elektron, se njego kinetičn energij oeč z 1 kev? Δ W
Ruolf Klnik: Fizik z srenješolce Set elektrono in too Električno olje (11), gibnje elce električne olju Strn 55, nlog 1 Kolikšno netost or releteti elektron, se njego kinetičn energij oeč z 1 kev? Δ W
Vaje iz MATEMATIKE 8. Odvod funkcije., pravimo, da je funkcija f odvedljiva v točki x 0 z odvodom. f (x f(x 0 + h) f(x 0 ) 0 ) := lim
 Študij AHITEKTURE IN URBANIZMA, šol l 06/7 Vaje iz MATEMATIKE 8 Odvod funkcije f( Definicija: Naj bo f definirana na neki okolici točke 0 Če obstaja lim 0 +h f( 0 h 0 h, pravimo, da je funkcija f odvedljiva
Študij AHITEKTURE IN URBANIZMA, šol l 06/7 Vaje iz MATEMATIKE 8 Odvod funkcije f( Definicija: Naj bo f definirana na neki okolici točke 0 Če obstaja lim 0 +h f( 0 h 0 h, pravimo, da je funkcija f odvedljiva
DISKRETNA FOURIERJEVA TRANSFORMACIJA
 29.03.2004 Definicija DFT Outline DFT je linearna transformacija nekega vektorskega prostora dimenzije n nad obsegom K, ki ga označujemo z V K, pri čemer ima slednji lastnost, da vsebuje nek poseben element,
29.03.2004 Definicija DFT Outline DFT je linearna transformacija nekega vektorskega prostora dimenzije n nad obsegom K, ki ga označujemo z V K, pri čemer ima slednji lastnost, da vsebuje nek poseben element,
NEPARAMETRIČNI TESTI. pregledovanje tabel hi-kvadrat test. as. dr. Nino RODE
 NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
ARHITEKTURA DETAJL 1, 1:10
 0.15 0.25 3.56 0.02 0.10 0.12 0.10 SESTV S2 polimer-bitumenska,dvoslojna(po),... 1.0 cm po zahtevah SIST DIN 52133 in nadstandardno, (glej opis v tehn.poročilu), npr.: PHOENIX STR/Super 5 M * GEMINI P
0.15 0.25 3.56 0.02 0.10 0.12 0.10 SESTV S2 polimer-bitumenska,dvoslojna(po),... 1.0 cm po zahtevah SIST DIN 52133 in nadstandardno, (glej opis v tehn.poročilu), npr.: PHOENIX STR/Super 5 M * GEMINI P
Definicija. definiramo skalarni produkt. x i y i. in razdaljo. d(x, y) = x y = < x y, x y > = n (x i y i ) 2. i=1. i=1
 Funkcije več realnih spremenljivk Osnovne definicije Limita in zveznost funkcije več spremenljivk Parcialni odvodi funkcije več spremenljivk Gradient in odvod funkcije več spremenljivk v dani smeri Parcialni
Funkcije več realnih spremenljivk Osnovne definicije Limita in zveznost funkcije več spremenljivk Parcialni odvodi funkcije več spremenljivk Gradient in odvod funkcije več spremenljivk v dani smeri Parcialni
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
*M * Osnovna in višja raven MATEMATIKA NAVODILA ZA OCENJEVANJE. Sobota, 4. junij 2011 SPOMLADANSKI IZPITNI ROK. Državni izpitni center
 Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
+105 C (plošče in trakovi +85 C) -50 C ( C)* * Za temperature pod C se posvetujte z našo tehnično službo. ϑ m *20 *40 +70
 KAIFLEX ST Tehnični podatki Material Izjemno fleksibilna zaprtocelična izolacija, fleksibilna elastomerna pena (FEF) Opis Uporaba Temperaturno območje Toplotna prevodnost W/(m K ) pri različnih srednjih
KAIFLEX ST Tehnični podatki Material Izjemno fleksibilna zaprtocelična izolacija, fleksibilna elastomerna pena (FEF) Opis Uporaba Temperaturno območje Toplotna prevodnost W/(m K ) pri različnih srednjih
PROCESIRANJE SIGNALOV
 Rešive pisega izpia PROCESIRANJE SIGNALOV Daum: 7... aloga Kolikša je ampliuda reje harmoske kompoee arisaega periodičega sigala? f() - -3 - - 3 Rešiev: Časova fukcija a iervalu ( /,/) je lieara fukcija:
Rešive pisega izpia PROCESIRANJE SIGNALOV Daum: 7... aloga Kolikša je ampliuda reje harmoske kompoee arisaega periodičega sigala? f() - -3 - - 3 Rešiev: Časova fukcija a iervalu ( /,/) je lieara fukcija:
Multivariatna analiza variance
 (MANOVA) MANOVA je multivariatna metoda za proučevanje odvisnosti med več odvisnimi (številskimi) in več neodvisnimi (opisnimi) spremenljivkami. (MANOVA) MANOVA je multivariatna metoda za proučevanje odvisnosti
(MANOVA) MANOVA je multivariatna metoda za proučevanje odvisnosti med več odvisnimi (številskimi) in več neodvisnimi (opisnimi) spremenljivkami. (MANOVA) MANOVA je multivariatna metoda za proučevanje odvisnosti
VEKTORJI. Operacije z vektorji
 VEKTORJI Vektorji so matematični objekti, s katerimi opisujemo določene fizikalne količine. V tisku jih označujemo s krepko natisnjenimi črkami (npr. a), pri pisanju pa s puščico ( a). Fizikalne količine,
VEKTORJI Vektorji so matematični objekti, s katerimi opisujemo določene fizikalne količine. V tisku jih označujemo s krepko natisnjenimi črkami (npr. a), pri pisanju pa s puščico ( a). Fizikalne količine,
Zaporedna in vzporedna feroresonanca
 Visokonapetostna tehnika Zaporedna in vzporedna feroresonanca delovanje regulacijskega stikala T3 174 kv Vaja 9 1 Osnovni pogoji za nastanek feroresonance L C U U L () U C () U L = U L () U C = ωc V vezju
Visokonapetostna tehnika Zaporedna in vzporedna feroresonanca delovanje regulacijskega stikala T3 174 kv Vaja 9 1 Osnovni pogoji za nastanek feroresonance L C U U L () U C () U L = U L () U C = ωc V vezju
Matematika 2. Diferencialne enačbe drugega reda
 Matematika 2 Diferencialne enačbe drugega reda (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) y 6y + 8y = 0, (b) y 2y + y = 0, (c) y + y = 0, (d) y + 2y + 2y = 0. Rešitev:
Matematika 2 Diferencialne enačbe drugega reda (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) y 6y + 8y = 0, (b) y 2y + y = 0, (c) y + y = 0, (d) y + 2y + 2y = 0. Rešitev:
POPLAVAH (predlog osnutek)
 OBČINA ŽALEC NAČRT ZAŠČITE IN REŠEVANJA OB POPLAVAH (predlog osnutek) Odobril Sprejel ODGOVORNA OSEBA DATUM PODPIS Poveljnik CZ PUNGARTNIK DUŠAN Župan POSEDEL LOJZE Skrbnik KOČEVAR MARJETA Datum: 24.08.2006
OBČINA ŽALEC NAČRT ZAŠČITE IN REŠEVANJA OB POPLAVAH (predlog osnutek) Odobril Sprejel ODGOVORNA OSEBA DATUM PODPIS Poveljnik CZ PUNGARTNIK DUŠAN Župan POSEDEL LOJZE Skrbnik KOČEVAR MARJETA Datum: 24.08.2006
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI)
 IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
Matematika 1. Gabrijel Tomšič Bojan Orel Neža Mramor Kosta
 Matematika Gabrijel Tomšič Bojan Orel Neža Mramor Kosta 6. november 200 Poglavje 2 Zaporedja in številske vrste 2. Zaporedja 2.. Uvod Definicija 2... Zaporedje (a n ) = a, a 2,..., a n,... je predpis,
Matematika Gabrijel Tomšič Bojan Orel Neža Mramor Kosta 6. november 200 Poglavje 2 Zaporedja in številske vrste 2. Zaporedja 2.. Uvod Definicija 2... Zaporedje (a n ) = a, a 2,..., a n,... je predpis,
CM707. GR Οδηγός χρήσης... 2-7. SLO Uporabniški priročnik... 8-13. CR Korisnički priručnik... 14-19. TR Kullanım Kılavuzu... 20-25
 1 2 3 4 5 6 7 OFFMANAUTO CM707 GR Οδηγός χρήσης... 2-7 SLO Uporabniški priročnik... 8-13 CR Korisnički priručnik... 14-19 TR Kullanım Kılavuzu... 20-25 ENG User Guide... 26-31 GR CM707 ΟΔΗΓΟΣ ΧΡΗΣΗΣ Περιγραφή
1 2 3 4 5 6 7 OFFMANAUTO CM707 GR Οδηγός χρήσης... 2-7 SLO Uporabniški priročnik... 8-13 CR Korisnički priručnik... 14-19 TR Kullanım Kılavuzu... 20-25 ENG User Guide... 26-31 GR CM707 ΟΔΗΓΟΣ ΧΡΗΣΗΣ Περιγραφή
IZZIVI DRUŽINSKE MEDICINE. U no gradivo zbornik seminarjev
 IZZIVI DRUŽINSKE MEDICINE Uno gradivo zbornik seminarjev študentov Medicinske fakultete Univerze v Mariboru 4. letnik 2008/2009 Uredniki: Alenka Bizjak, Viktorija Janar, Maša Krajnc, Jasmina Rehar, Mateja
IZZIVI DRUŽINSKE MEDICINE Uno gradivo zbornik seminarjev študentov Medicinske fakultete Univerze v Mariboru 4. letnik 2008/2009 Uredniki: Alenka Bizjak, Viktorija Janar, Maša Krajnc, Jasmina Rehar, Mateja
Analiza 2 Rešitve 14. sklopa nalog
 Analiza Rešitve 1 sklopa nalog Navadne diferencialne enačbe višjih redov in sistemi diferencialnih enačb (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) 6 + 8 0, (b)
Analiza Rešitve 1 sklopa nalog Navadne diferencialne enačbe višjih redov in sistemi diferencialnih enačb (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) 6 + 8 0, (b)
GASILSKA ZVEZA SLOVENIJE
 GASILSKA ZVEZA SLOVENIJE Tržaška cesta 221 1000 LJUBLJANA OSNUTEK ZA RAZPRAVO I. GASILSKA VOZILA ZA GOZDNE POŽARE AKTIVNOST ORGAN DATUM IZDELAL MENTOR, Andrej Ambrožič 02.04. 2013 Namestnik poveljnik gasilske
GASILSKA ZVEZA SLOVENIJE Tržaška cesta 221 1000 LJUBLJANA OSNUTEK ZA RAZPRAVO I. GASILSKA VOZILA ZA GOZDNE POŽARE AKTIVNOST ORGAN DATUM IZDELAL MENTOR, Andrej Ambrožič 02.04. 2013 Namestnik poveljnik gasilske
Vaja: Odbojnostni senzor z optičnimi vlakni. Namen vaje
 Namen vaje Spoznavanje osnovnih fiber-optičnih in optomehanskih komponent Spoznavanje načela delovanja in praktične uporabe odbojnostnega senzorja z optičnimi vlakni, Delo z merilnimi instrumenti (signal-generator,
Namen vaje Spoznavanje osnovnih fiber-optičnih in optomehanskih komponent Spoznavanje načela delovanja in praktične uporabe odbojnostnega senzorja z optičnimi vlakni, Delo z merilnimi instrumenti (signal-generator,
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri
 Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
1. Trikotniki hitrosti
 . Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
. Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
INTELIGENTNO UPRAVLJANJE
 INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
Spoznajmo sedaj definicijo in nekaj osnovnih primerov zaporedij števil.
 Zaporedja števil V matematiki in fiziki pogosto operiramo s približnimi vrednostmi neke količine. Pri numeričnemu računanju lahko npr. število π aproksimiramo s števili, ki imajo samo končno mnogo neničelnih
Zaporedja števil V matematiki in fiziki pogosto operiramo s približnimi vrednostmi neke količine. Pri numeričnemu računanju lahko npr. število π aproksimiramo s števili, ki imajo samo končno mnogo neničelnih
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
Matematika 1. Gregor Dolinar. 2. januar Fakulteta za elektrotehniko Univerza v Ljubljani. Gregor Dolinar Matematika 1
 Mtemtik 1 Gregor Dolinr Fkultet z elektrotehniko Univerz v Ljubljni 2. jnur 2014 Gregor Dolinr Mtemtik 1 Izrek (Izrek o povprečni vrednosti) Nj bo m ntnčn spodnj mej in M ntnčn zgornj mej integrbilne funkcije
Mtemtik 1 Gregor Dolinr Fkultet z elektrotehniko Univerz v Ljubljni 2. jnur 2014 Gregor Dolinr Mtemtik 1 Izrek (Izrek o povprečni vrednosti) Nj bo m ntnčn spodnj mej in M ntnčn zgornj mej integrbilne funkcije
PROCESIRANJE SIGNALOV
 Daum: 5.. 999. Izračuaje kompoee ampliudega spekra podaega periodičega sigala! Kolikša je osova frekveca ega sigala? Tabeliraje prvih šes ampliud! -,,,,3,4,5 - [ms]. Izračuaje Fourierjev rasform podaega
Daum: 5.. 999. Izračuaje kompoee ampliudega spekra podaega periodičega sigala! Kolikša je osova frekveca ega sigala? Tabeliraje prvih šes ampliud! -,,,,3,4,5 - [ms]. Izračuaje Fourierjev rasform podaega
PREDNAPETI BETON Primjer nadvožnjaka preko autoceste
 PREDNAPETI BETON Primjer nadvožnjaka preko autoceste 7. VJEŽBE PLAN ARMATURE PREDNAPETOG Dominik Skokandić, mag.ing.aedif. PLAN ARMATURE PREDNAPETOG 1. Rekapitulacija odabrane armature 2. Određivanje duljina
PREDNAPETI BETON Primjer nadvožnjaka preko autoceste 7. VJEŽBE PLAN ARMATURE PREDNAPETOG Dominik Skokandić, mag.ing.aedif. PLAN ARMATURE PREDNAPETOG 1. Rekapitulacija odabrane armature 2. Određivanje duljina
Funkcije več spremenljivk
 DODATEK C Funkcije več spremenljivk C.1. Osnovni pojmi Funkcija n spremenljivk je predpis: f : D f R, (x 1, x 2,..., x n ) u = f (x 1, x 2,..., x n ) kjer D f R n imenujemo definicijsko območje funkcije
DODATEK C Funkcije več spremenljivk C.1. Osnovni pojmi Funkcija n spremenljivk je predpis: f : D f R, (x 1, x 2,..., x n ) u = f (x 1, x 2,..., x n ) kjer D f R n imenujemo definicijsko območje funkcije
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Kvantni delec na potencialnem skoku
 Kvantni delec na potencialnem skoku Delec, ki se giblje premo enakomerno, pride na mejo, kjer potencial naraste s potenciala 0 na potencial. Takšno potencialno funkcijo zapišemo kot 0, 0 0,0. Slika 1:
Kvantni delec na potencialnem skoku Delec, ki se giblje premo enakomerno, pride na mejo, kjer potencial naraste s potenciala 0 na potencial. Takšno potencialno funkcijo zapišemo kot 0, 0 0,0. Slika 1:
Ovo nam govori da funkcija nije ni parna ni neparna, odnosno da nije simetrična ni u odnosu na y osu ni u odnosu na
 . Ispitati tok i skicirati grafik funkcij = Oblast dfinisanosti (domn) Ova funkcija j svuda dfinisana, jr nma razlomka a funkcija j dfinisana za svako iz skupa R. Dakl (, ). Ovo nam odmah govori da funkcija
. Ispitati tok i skicirati grafik funkcij = Oblast dfinisanosti (domn) Ova funkcija j svuda dfinisana, jr nma razlomka a funkcija j dfinisana za svako iz skupa R. Dakl (, ). Ovo nam odmah govori da funkcija
1 Fibonaccijeva stevila
 1 Fibonaccijeva stevila Fibonaccijevo število F n, kjer je n N, lahko definiramo kot število načinov zapisa števila n kot vsoto sumandov, enakih 1 ali Na primer, število 4 lahko zapišemo v obliki naslednjih
1 Fibonaccijeva stevila Fibonaccijevo število F n, kjer je n N, lahko definiramo kot število načinov zapisa števila n kot vsoto sumandov, enakih 1 ali Na primer, število 4 lahko zapišemo v obliki naslednjih
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
POROČILO 3.VAJA DOLOČANJE REZULTANTE SIL
 POROČILO 3.VAJA DOLOČANJE REZULTANTE SIL Izdba aje: Ljubjana, 11. 1. 007, 10.00 Jan OMAHNE, 1.M Namen: 1.Preeri paraeogramsko praio za doočanje rezutante nezporedni si s skupnim prijemaiščem (grafično)..dooči
POROČILO 3.VAJA DOLOČANJE REZULTANTE SIL Izdba aje: Ljubjana, 11. 1. 007, 10.00 Jan OMAHNE, 1.M Namen: 1.Preeri paraeogramsko praio za doočanje rezutante nezporedni si s skupnim prijemaiščem (grafično)..dooči
TOPNOST, HITROST RAZTAPLJANJA
 OPNOS, HIOS AZAPLJANJA Denja: onos (oz. nasčena razona) redsavlja sanje, ko je oljene (rdn, ekoč, lnas) v ravnoežju z razono (oljenem, razoljenm v olu). - kvanavn zraz - r določen - homogena molekularna
OPNOS, HIOS AZAPLJANJA Denja: onos (oz. nasčena razona) redsavlja sanje, ko je oljene (rdn, ekoč, lnas) v ravnoežju z razono (oljenem, razoljenm v olu). - kvanavn zraz - r določen - homogena molekularna
SISTEMI DIFERENCIJALNIH JEDNAČINA - ZADACI NORMALNI OBLIK
 SISTEMI DIFERENCIJALNIH JEDNAČINA - ZADACI NORMALNI OBLIK. Rši sism jdnačina: d 7 d d d Ršnj: Ša j idja kod ovih zadaaka? Jdnu od jdnačina difrniramo, o js nađmo izvod l jdnačin i u zamnimo drugu jdnačinu.
SISTEMI DIFERENCIJALNIH JEDNAČINA - ZADACI NORMALNI OBLIK. Rši sism jdnačina: d 7 d d d Ršnj: Ša j idja kod ovih zadaaka? Jdnu od jdnačina difrniramo, o js nađmo izvod l jdnačin i u zamnimo drugu jdnačinu.
OSNOVI ELEKTRONIKE VEŽBA BROJ 1 OSNOVNA KOLA SA DIODAMA
 ELEKTROTEHNIČKI FAKULTET U BEOGRADU KATEDRA ZA ELEKTRONIKU OSNOVI ELEKTRONIKE SVI ODSECI OSIM ODSEKA ZA ELEKTRONIKU LABORATORIJSKE VEŽBE VEŽBA BROJ 1 OSNOVNA KOLA SA DIODAMA Autori: Goran Savić i Milan
ELEKTROTEHNIČKI FAKULTET U BEOGRADU KATEDRA ZA ELEKTRONIKU OSNOVI ELEKTRONIKE SVI ODSECI OSIM ODSEKA ZA ELEKTRONIKU LABORATORIJSKE VEŽBE VEŽBA BROJ 1 OSNOVNA KOLA SA DIODAMA Autori: Goran Savić i Milan
1. TVORBA ŠIBKEGA (SIGMATNEGA) AORISTA: Največ grških glagolov ima tako imenovani šibki (sigmatni) aorist. Osnova se tvori s. γραψ
 TVORBA AORISTA: Grški aorist (dovršnik) izraža dovršno dejanje; v indikativu izraža poleg dovršnosti tudi preteklost. Za razliko od prezenta ima aorist posebne aktivne, medialne in pasivne oblike. Pri
TVORBA AORISTA: Grški aorist (dovršnik) izraža dovršno dejanje; v indikativu izraža poleg dovršnosti tudi preteklost. Za razliko od prezenta ima aorist posebne aktivne, medialne in pasivne oblike. Pri
8. Posplošeni problem lastnih vrednosti
 8. Posplošeni problem lastnih vrednosti Bor Plestenjak NLA 13. april 2010 Bor Plestenjak (NLA) 8. Posplošeni problem lastnih vrednosti 13. april 2010 1 / 15 Matrični šop Dani sta kvadratni n n matriki
8. Posplošeni problem lastnih vrednosti Bor Plestenjak NLA 13. april 2010 Bor Plestenjak (NLA) 8. Posplošeni problem lastnih vrednosti 13. april 2010 1 / 15 Matrični šop Dani sta kvadratni n n matriki
1. VAJA IZ TRDNOSTI. (linearna algebra - ponovitev, Kroneckerjev δ i j, permutacijski simbol e i jk )
 VAJA IZ TRDNOSTI (lnearna algebra - ponovtev, Kroneckerev δ, permutacsk smbol e k ) NALOGA : Zapš vektor a = [, 2,5,] kot lnearno kombnaco vektorev e = [,,,], e 2 = [,2,3,], e 3 = [2,,, ] n e 4 = [,,,]
VAJA IZ TRDNOSTI (lnearna algebra - ponovtev, Kroneckerev δ, permutacsk smbol e k ) NALOGA : Zapš vektor a = [, 2,5,] kot lnearno kombnaco vektorev e = [,,,], e 2 = [,2,3,], e 3 = [2,,, ] n e 4 = [,,,]
Statistična analiza. doc. dr. Mitja Kos, mag. farm. Katedra za socialno farmacijo Univerza v Ljubljani- Fakulteta za farmacijo
 Statistična analiza opisnih spremenljivk doc. dr. Mitja Kos, mag. arm. Katedra za socialno armacijo Univerza v Ljubljani- Fakulteta za armacijo Statistični znaki Proučevane spremenljivke: statistični znaki
Statistična analiza opisnih spremenljivk doc. dr. Mitja Kos, mag. arm. Katedra za socialno armacijo Univerza v Ljubljani- Fakulteta za armacijo Statistični znaki Proučevane spremenljivke: statistični znaki
Izpeljava Jensenove in Hölderjeve neenakosti ter neenakosti Minkowskega
 Izeljava Jensenove in Hölderjeve neenakosti ter neenakosti Minkowskega 1. Najosnovnejše o konveksnih funkcijah Definicija. Naj bo X vektorski rostor in D X konveksna množica. Funkcija ϕ: D R je konveksna,
Izeljava Jensenove in Hölderjeve neenakosti ter neenakosti Minkowskega 1. Najosnovnejše o konveksnih funkcijah Definicija. Naj bo X vektorski rostor in D X konveksna množica. Funkcija ϕ: D R je konveksna,
MERITVE LABORATORIJSKE VAJE. Študij. leto: 2011/2012 UNIVERZA V MARIBORU. Skupina: 9
 .cwww.grgor nik ol i c NVERZA V MARBOR FAKTETA ZA EEKTROTEHNKO, RAČNANŠTVO N NFORMATKO 2000 Maribor, Smtanova ul. 17 Študij. lto: 2011/2012 Skupina: 9 MERTVE ABORATORJSKE VAJE Vaja št.: 4.1 Določanj induktivnosti
.cwww.grgor nik ol i c NVERZA V MARBOR FAKTETA ZA EEKTROTEHNKO, RAČNANŠTVO N NFORMATKO 2000 Maribor, Smtanova ul. 17 Študij. lto: 2011/2012 Skupina: 9 MERTVE ABORATORJSKE VAJE Vaja št.: 4.1 Določanj induktivnosti
Inverzni problem lastnih vrednosti evklidsko razdaljnih matrik
 Univerza v Ljubljani Fakulteta za računalništvo in informatiko Fakulteta za matematiko in fiziko Peter Škvorc Inverzni problem lastnih vrednosti evklidsko razdaljnih matrik DIPLOMSKO DELO UNIVERZITETNI
Univerza v Ljubljani Fakulteta za računalništvo in informatiko Fakulteta za matematiko in fiziko Peter Škvorc Inverzni problem lastnih vrednosti evklidsko razdaljnih matrik DIPLOMSKO DELO UNIVERZITETNI
OSNOVE HIDROSTATIKE. - vede, ki preučuje mirujoče tekočine
 OSNOVE HIDROSTATIKE - vede, ki preučuje mirujoče tekočine HIDROSTATIKA Značilnost, da je sila na katero koli točko v tekočini enaka iz vseh smeri. Če ta pogoj o ravnovesju sil ne velja, se tekočina premakne
OSNOVE HIDROSTATIKE - vede, ki preučuje mirujoče tekočine HIDROSTATIKA Značilnost, da je sila na katero koli točko v tekočini enaka iz vseh smeri. Če ta pogoj o ravnovesju sil ne velja, se tekočina premakne
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
