Γεωργίου Κ. Λεοντάρη Καθηγητή Θεωρητικής Φυσικής. Μαθηματικές Μέθοδοι Φυσικής ΙΙ Πανεπιστημιακές Παραδόσεις. Πανεπιστήμιο Ιωαννίνων Ιωάννινα 2011
|
|
|
- Ἐφραίμ Ζερβός
- 8 χρόνια πριν
- Προβολές:
Transcript
1 1 Γεωργίου Κ. Λεοντάρη Καθηγητή Θεωρητικής Φυσικής. Μαθηματικές Μέθοδοι Φυσικής ΙΙ Πανεπιστημιακές Παραδόσεις Πανεπιστήμιο Ιωαννίνων Ιωάννινα 2011
2 2
3 Perieqìmena 1 Στοιχεία Διαϕορικών Εξισώσεων Συνήθεις Διαϕορικές Εξισώσεις Μια σύντομη ανασκόπιση στις Διαϕορικές Εξισώσεις πρώτης τάξης Ασκήσεις Ασκήσεις Δ.Ε. δεύτερης τάξης Ο τύπος του Liouville Η εύρεση της μερικής λύσης της μή ομογενούς Δ.Ε Ασκήσεις Διαϕορικές Εξισώσεις 2 ης τάξης με κανονικά ανώμαλα σημεία Γενική λύση της ΔΕ 2 ης τάξης στη γειτονιά κανονικού ανώμαλου σημείου Δ.Ε. με κανονικά ανώμαλα σημεία Η υπεργεωμετρική συνάρτηση Παραδείγματα Ασκήσεις Ολοκληρωτικές αναπαραστάσει της Υ.Σ Συρρέουσα Υπεργεωμετρική σειρά Εϕαρμογές
4 4 ΠΕΡΙΕΧ ΟΜΕΝΑ
5 Kefˆlaio 1 StoiqeÐa Diaforik n Exis sewn 1.1 Sun jeic Diaforikèc Exis seic Η μαθηματική ανάλυση πολλών προβλημάτων της Φυσικής οδηγεί στην επίλυση διαϕορικών εξίσωσεων (ΔΕ), μιας ή περισσοτέρων μεταβλητών. Μαθηματική επεξεργασία των πολυπροκότερων ΔΕ που περιέχουν μερικές παραγώγους και περισσότερες από μία μεταβλητές ανάγει το πρόβλημα στην επίλυση ΔΕ μιάς μεταβλητής. Θα μελετήσουμε τεχνικές διαχωρισμού των μεταβλητών σε επόμενα κεϕάλαια. Προς το παρόν θα ασχοληθούμε στη συνέχεια του κεϕαλαίου με ΔΕ μιάς μεταβλητής. Ονομάζουμε συνήθη Διαϕορική Εξίσωση (Δ.Ε.) N-τάξης, μιά εξίσωση η ο- ποία περιέχει άγνωστη συνάρτηση u(x) και τις παραγώγους αυτής u (k) (x) = dk u(x) k όπου k =, 1,..., N και x η μεταβλητή. Εν γένει, γράϕουμε F(x, u, u (1),, u (N) ) = 0 (1.1) Από το σύνολο των Δ.Ε. στο μεγαλύτερο μέρος της ανάλυσής μας θα επικεντρώσουμε το ενδιαϕέρον μας στην περίπτωση των Γραμμικών Δ.Ε., δηλαδή στην περίπτωση που η (1.1) είναι γραμμική συνάρτηση των u, u (1),, u (N), a N (x)u (N) (x) + a N 1 (x)u (N 1) (x) + + a 0 (x)u + b(x) = 0 (1.2) όπου b(x) και a k (x); k = 1,... N, είναι γνωστές συναρτήσεις της μεταβλητής x. Αν b(x) = 0 τότε η Δ.Ε. λέγεται ομογενής, ενώ αν b(x) 0 καλείται μήομογενής. Θα αναζητήσουμε λύσεις της (1.1) που είναι διαϕορίσιμες τουλάχιστον N- τάξης, δηλαδή ώστε να υπάρχουν παράγωγοι έως και N-οστού βαθμού. Η (1.1) 5
6 6 ΚΕΦ ΑΛΑΙΟ 1. ΣΤΟΙΧΕ ΙΑ ΔΙΑΦΟΡΙΚ ΩΝ ΕΞΙΣ ΩΣΕΩΝ δεν έχει πάντα λύση αλλά και όταν υπάρχει λύση u(x), αυτή δεν είναι μοναδικά προσδιορισμένη. Επιπρόσθετη πληροϕορία για την αναζητούμενη συνάρτηση u(x) λαμβάνεται από τις συνοριακές συνθήκες του προβλήματος. Αναϕέρουμε στη συνέχεια το θεώρημα ύπαρξης λύσης για μια γενική κατηγορία συνοριακών συνθηκών. Θεώρημα Cauchy Lipschitz. Εστω συνάρτηση f(y 1, y 2,, y N ) όπου οι y 1, y 2,, y N μεταβάλλονται στο διάστημα c i η y i c i + η, i = 1,, N (1.3) Οι c i είναι σταθερές και η θετικός αριθμός. Αν yi 1 και y2 i δύο αριθμοί που ανήκουν στο προαναϕερθέν διάστημα και υπάρχει θετικός αριθμός λ ώστε f(y 1, y 2 y 1 i y N ) f(y 1, y 2, y 2 i y N ) λ y 1 i y 2 i (1.4) τότε η f ικανοποιεί τις συνθήκες Lipschitz. Εστω ότι η Δ.Ε. (1.1) μπορεί να γραϕεί ως εξής και ότι οι συνοριακές συνθήκες είναι u(x 0 ) = c 0, d N u N = f(x, u, u(1),, u (N 1) ) (1.5) du x=x 0 = c 1, dn 1 u N 1 = c N 1 (1.6) όπου c i, i = 0, 1,..., N 1 είναι δοσμένες σταθερές. Τότε, ισχύει το ακόλουθο θεώρημα: Άν η συνάρτηση f(x) είναι συνεχής και υπάρχει αριθμός η τέτοιος ώστε για a x b, η f(x) ικανοποιεί τις συνθήκες Lipschitz για y i = u (i) d(i) u, i = i 0,... N 1, τότε η Δ.Ε. (1.5) έχει λύση γιά όλα x [a, b] και η λύση είναι μοναδική. 1.2 Mia sôntomh anaskìpish stic Diaforikèc Exis seic pr thc tˆxhc Η γενική μορϕή της Δ.Ε. πρώτης τάξης μπορεί να γραϕεί ως εξής du = g(u, x) h(u, x) (1.7) ή, ισοδύναμα h(u, x)du + g(u, x) = 0 (1.8) Στη συνέχεια θα κάνουμε μια σύντομη παρουσίαση των χαρακτηριστικότερων διαϕορικών εξισώσεων πρώτης τάξης που εμϕανίζονται συχνά στη Φυσική.
7 1.2. ΜΙΑ Σ ΥΝΤΟΜΗ ΑΝΑΣΚ ΟΠΙΣΗ ΣΤΙΣ ΔΙΑΦΟΡΙΚ ΕΣ ΕΞΙΣ ΩΣΕΙΣ ΠΡ ΩΤΗΣ Τ ΑΞΗΣ7 1. Διαχωρισμός των μεταβλητών. Στην ειδική περίπτωση που η (1.8) μπορεί να γραϕεί στη μορϕή a(u) du = b(x) (1.9) τότε ολοκληρώνουμε κατά μέλη, και επιλύουμε ως προς την u(x). 2. Τέλειο Διαϕορικό. Στην περίπτωση που οι συναρτήσεις στην (1.8) γρά- ϕονται ως οι παράγωγοι μιας κοινής συνάρτησης Φ(x, u) h(u, x) = f(u, x) = Φ(x, u) x Φ(x, u) u τότε, η (1.8) ταυτίζεται με τον τύπο του ολικού διαϕορικού dφ, dφ = Φ(x, u) + x Ολοκληρώνοντας προκύπτει Φ(x, u) = c, όπου c σταθερά. Φ(x, u) du = 0 (1.10) u 3. Αλλαγή μεταβλητής. Στην περίπτωση που η ΔΕ μπορεί να γραϕεί στην ακόλουθη μορϕή du(x) = f(au + bx) (1.11) εισάγουμε την νέα συνάρτηση z = au + bx, με dz = a du εξίσωση διαχωρίζεται ως προς τις μεταβλητές z, x ως εξής + b, οπότε η dz af(z) + b = (1.12) η οποία μπορεί να ολοκληρωθεί. Ομοίως, η Δ.Ε. της μορϕής du(x) = f( u x ) (1.13) με την αλλαγή μεταβλητής y = u/x, διαχωρίζεται ως εξής dy f(y) y = x (1.14) 4. Παραγοντική ολοκλήρωση Η εξίσωση du(x) + a(x)u(x) = b(x) (1.15)
8 8 ΚΕΦ ΑΛΑΙΟ 1. ΣΤΟΙΧΕ ΙΑ ΔΙΑΦΟΡΙΚ ΩΝ ΕΞΙΣ ΩΣΕΩΝ επιλύεται με τη μέθοδο της παραγοντικής ολοκλήρωσης. Πολλαπλασιάζουμε με κατάλληλη συνάρτηση h(x) έτσι ώστε h(x) du(x) + h(x)a(x)u(x) = h(x)b(x) (1.16) h(x)a(x) = dh(x) h(x) = h 0 e x a(x ) (1.17) Τότε η (1.15) μετασχηματίζεται στην d (h(x)u(x)) = h(x)b(x) h(x) u(x) = c 0 + h(x)b(x) οπότε η λύση γράϕεται u(x) = d 0 e x a(x ) (c 0 + ) b(x)e x a(x ) (1.18) 5. Η εξίσωση Bernoulli Ορισμένες μή-γραμμικές διαϕορικές εξισώσεις μπορούν να αναχθούν σε γραμμικές με κατάλληλο μετασχηματισμό. Χαρακτηριστική περίπτωση είναι η εξίσωση Bernoulli. y(x) = u k (x), du(x) du(x) + a(x)u(x) = b(x)un (x) (1.19) = 1 k y1/k 1 dy(x) 1 dy(x) n 1 + a(x)y(x) = b(x)y(x) k +1 k Επιλέγουμε k = 1 n και λαμβάνουμε dy(x) η οποία είναι της μορϕής (1.15). + (1 n)a(x)y(x) = b(x) 6. Η εξίσωση Lagrange. Η εξίσωση Lagrange γράϕεται u(x) = x f (p(x)) + g (p(x)), p(x) = du(x) Παραγωγίζοντας ως προς x, έχουμε du(x) p(x) = f(p) + ( x df(p) dp + dg(p) ) dp(x) dp (1.20)
9 1.2. ΜΙΑ Σ ΥΝΤΟΜΗ ΑΝΑΣΚ ΟΠΙΣΗ ΣΤΙΣ ΔΙΑΦΟΡΙΚ ΕΣ ΕΞΙΣ ΩΣΕΙΣ ΠΡ ΩΤΗΣ Τ ΑΞΗΣ9 από την οποία εϕόσον f(p) p, προκύπτει ( 1 df(p) = dp p f(p) dp x + dg(p) ) dp (1.21) Η τελευταία είναι μια γραμμική μή ομογενής εξίσωση της μορϕής (1.15) και επιλύεται ως προς x = x(p) με τη μέθοδο της εισαγωγής παράγοντα ολοκλήρωσης. Στην ειδική περίπτωση f(p) = p, έχουμε την εξίσωση Clairaut u(x) = x f (p(x)) + g (p(x)), p(x) = du(x) για την οποία εργαζόμαστε ανάλογα: du(x) p(x) = p(x) + ( x + dg(p) ) dp(x) dp (1.22) ή, απαλοίϕοντας το p(x) από τα δύο μέλη της εξίσωσης ( 0 = x + dg(p) ) dp(x) dp Διακρίνουμε δύο περιπτώσεις. Στην πρώτη dp(x) = 0 u(x) = c x + d (1.23) την οποία αντικαθιστούμε στην (1.22) και λαμβάνουμε Στη δεύτερη περίπτωση έχουμε u(x) = c x + g(c) x + dg(p) dp = 0 (1.24) Εϕόσον είναι γνωστή η συνάρτηση g(p), η τελευταία επιλύεται ως προς p και αντικατάσταση στην αρχική συνεπάγεται μια εξίσωση μόνον με u(x), x η οποία επιλύεται. 7. Η εξίσωση Riccati. Η εξίσωση Riccati είναι μή-γραμμική Δ.Ε. πρώτης τάξης της μορϕής du(x) = f(x) u(x) 2 + g(x) u(x) + h(x) (1.25) Η (1.26) μπορεί να μετατραπεί σε Δ.Ε. δεύτερης τάξης ως εξής. Πολλαπλασιάζοντας με f(x) f(x) du(x) = {f(x) u(x)} 2 + g(x) {f(x)u(x)} + f(x)h(x)
10 10 ΚΕΦ ΑΛΑΙΟ 1. ΣΤΟΙΧΕ ΙΑ ΔΙΑΦΟΡΙΚ ΩΝ ΕΞΙΣ ΩΣΕΩΝ και κάνοντας την αντικατάσταση w(x) = f(x)u(x), έχουμε dw = w 2 + (g + f ) w + fh (1.26) f Τέλος, γράϕοντας w(x) = v v d 2 v(x) 2 (g + f f, καταλήγουμε στην Δ.Ε. δεύτερης τάξης ) v(x) + fh v(x) = 0 Εάν είναι γνωστή μιά ειδική λύση της εξίσωσης (1.26) τότε είναι δυνατό να βρεθεί η γενική λύση ως εξής. Εστε u 0 (x) η μερική λύση, τότε γράϕουμε u(x) = u 0 (x) + 1 v(x) και αντικαθιστούμε στην (1.26) οπότε λαμβάνουμε (1.27) dv + (2f(x)u 0(x) + g(x))v(x) + h(x) = 0 (1.28) Η (1.28) είναι η γνωστή μορϕή (1.15) και λύνεται σύμϕωνα με τα εκτεθέντα ανωτέρω Ask seic 1. Κινούμενη λέμβος m δέχεται υδάτινη αντίσταση ανάλογη της n-οστής δύναμης της ταχύτητας, F res = kv n και συνεπώς από τον νόμο του Newton m dv dt + kvn = 0 (1.29) Να βρεθούν η ταχύτητα και η θέση ως συναρτήσεις του χρόνου t με αρχικές συνθήκες v(0) = v 0, x(0) = 0. Η Δ.Ε. διαχωρίζεται ως προς τις δύο μεταβλητές dv v n = k dt (1.30) m Ολοκληρώνουμε τα δύο μέλη και λαβάνοντας υπ όψη τη συνοριακή συνθήκη έχουμε v(t) = { v 0 (1+ k m (n 1)v 0 n 1 t) n 1 1 n 1 v 0 e k m t n = 1 (1.31) Ολοκληρώνοντας την (t) dt = v(t) έχουμε m k v 0 x(t) = m k v 2 n 0 n 2 ( m 1 e t) k, n = 1 m k ln ( 1 + k m v 0t ), n = 2 { (1 + k m (n 1)vn 1 0 t ) n 2 n 1 1 }, n 1, 2
11 1.2. ΜΙΑ Σ ΥΝΤΟΜΗ ΑΝΑΣΚ ΟΠΙΣΗ ΣΤΙΣ ΔΙΑΦΟΡΙΚ ΕΣ ΕΞΙΣ ΩΣΕΙΣ ΠΡ ΩΤΗΣ Τ ΑΞΗΣ11 2. Σε ηλεκτρικό κύκλωμα με αντίσταση και πηνείο από τον νόμο του Kirchhoff έχουμε την εξίσωση L d I(t) dt η οποία έχει τη μορϕή της (1.15). Επομένως, + R I(t) = V (t) (1.32) h(t) = e R L dt = e R L t (1.33) και η λύση γράϕεται I(t) = 1 L e R L (c t 0 + ) V (t)e R L t dt (1.34) 3. Στις υπερσυμμετρικές θεωρίες των στοιχειωδών σωματιδίων ή εξάρτηση των μαζών των βαθμωτών σωματιδίων από την ενεργειακή κλίμακα t ln E δίδεται από τις εξισώσεις d m 2 n dt N = g n (t) + f n (t) m 2 j(t) (1.35) j=1 όπου n = 1, 2,..., N και g n (t), f n (t) γνωστές συναρτήσεις των σταθερών σύζευξης. Να βρεθούν οι εκϕράσεις των μαζών ως συνάρτηση του t. Παρατηρούμε ότι αθροίζοντας τις εξισώσεις σχηματίζουμε μιά πρωτοβάθμια διαϕορική εξίσωση για το άθροισμα των μαζών Ορίζουμε d N N N N m 2 dt n(t) = g n (t) + f n (t) m 2 j(t) (1.36) n=1 M 2 (t) = n=1 N m 2 n(t), g(t) = n=1 n=1 N g n (t), h(t) = n=1 και η εξίσωση λαμβάνει την οικεία μορϕή d dt M 2 (t) = g(t) + f(t) M 2 (t) j=1 N h n (t) n=1 Από τη λύση της (1.15) έχουμε M 2 (t) = M 2 0 e t f(t )dt ( 1 c 0 ) g(t)e t f(t )dt dt (1.37) Αντικατάσταση του αθροίσματος από τη λύση αυτής στην αρχική εξίσωση δίδει μιά απλή εξίσωση η οποία επιλύεται για κάθε σωματίδιο ξεχωριστά.
12 12 ΚΕΦ ΑΛΑΙΟ 1. ΣΤΟΙΧΕ ΙΑ ΔΙΑΦΟΡΙΚ ΩΝ ΕΞΙΣ ΩΣΕΩΝ 4. Στην Κοσμολογία η παράμετρος διαστολής του Σύμπαντος a(t) διέπεται από την πρώτης τάξης διαϕορική εξίσωση (ȧ a ) 2 = 8πG 3 ρ k a 2 (1.38) όπου ρ η πυκνότητα μάζας του σύμπαντος, η οποία υπακούει στην εξίσωση ρ + 3ȧ (ρ + p ) a c 2 (1.39) G, c, k είναι σταθερές και p η πίεση. Να λυθούν οι εξισώσεις για k = 0 (επίπεδο σύμπαν), στην περίπτωση που η πίεση δίδεται από p = (γ 1)ρc 2. Η εξίσωση για την πυκνότητα γίνεται ρ + 3γ ȧ a ρ = 0 η οποία διαχωρίζεται ως προς τις δύο συναρτήσεις a(t), ρ(t) da a = 3γ dρ ρ και με ολοκλήρωση κατά μέλη ( a0 ) 3γ ρ = ρ 0 (1.40) a Στην εξίσωση (1.38 θέτουμε k = 0 και αντικαθιστούμε την ρ από την τελευταία οπότε έχουμε (ȧ a ) 2 = 8πG 3 ρ 0 ( a0 ) 3γ a Λαμβάνοντας την τετραγωνική ρίζα (ορίζοντας νέα σταθερά µ 0 ) ȧ a = µ 0 a 3γ/3 a 3γ/2 1 da = µ 0 dt η οποία μετά την ολοκλήρωση δίδει ( ) 2 t 3γ a(t) = a 0 t 0 (1.41) Αντικαθιστούμε στην (1.40) και ευρίσκουμε τη χρονική εξάρτηση της πυκνότητας ρ(t) = ρ 0 ( t0 t ) 2 (1.42)
13 1.3. ΑΣΚ ΗΣΕΙΣ Να λυθεί η ( ) du (1 + x) + e du/ u(x) + (1 x) = 0 (1.43) Λύση. Η εξίσωση γράϕεται u(x) = ( 1 + u + e du/ )x + (1 + u + e du/ ) η οποία είναι η μορϕή Lagrange, f(p) = 1 + u + e du/, g(p) = 1 + u + e du/, p = u 1.3 Ask seic 1. Να λυθού οι ΔΕ y = 1 2 (x y + y x ), y = x y + g(x)f(x y ) 2. Να λυθού οι ΔΕ y = e x y, y (cosx)y + cosx = 0 με αρχική συνθήκη y(0) = Να δοθούν παραδείγματα ΔΕ Ricatti, Bernoulli, Euler. 4. Να λυθεί η Δ.Ε. όπου α, β, γ σταθερές. dy = y(y2 + α β + γx ), 5. Να βρεθεί η μονοπαραμετρική οικογένεια λύσεων της εξίσωσης Clairaut 6. Να αναχθεί η px e p y = 0, p = dy xyy + x(y ) 2 yy = 0 σε ΔΕ πρώτης τάξης και να λυθεί. (Σημειώστε ότι οι δύο πρώτοι όροι είναι ίσοι με x(yy ) )
14 14 ΚΕΦ ΑΛΑΙΟ 1. ΣΤΟΙΧΕ ΙΑ ΔΙΑΦΟΡΙΚ ΩΝ ΕΞΙΣ ΩΣΕΩΝ 1.4 D.E. deôterhc tˆxhc. Θα μελετήσουμε στη συνέχεια εξισώσεις δεύτερης τάξης της μορϕής α(x) d2 d u(x) + β(x) u(x) + γ(x)u(x) = g(x) (1.44) 2 Στα ϕυσικά προβλήματα που μας ενδιαϕέρουν, οι συνοριακές συνθήκες που επιβάλλονται στις λύσεις έχουν πολυπροκότερη μορϕή από την (1.6). Αν x = [a, b] είναι το διάστημα στο οποίο αναζητείται η λύση u(x), τότε η γενική μορϕή των συνοριακών συνθηκών για την (1.44) είναι B 1 (u) α 1 u(a) + β 1 u (a) + γ 1 u(b) + δ 1 u (b) = σ 1 (1.45) B 2 (u) α 2 u(a) + β 2 u (a) + γ 2 u(b) + δ 2 u (b) = σ 2 (1.46) όπου α i, β i, γ i, δ i, σ i είναι σταθερές. Αν σ 1,2 0 τότε οι συνοριακές συνθήκες καλούνται μή-ομογενείς, ενώ όταν σ 1,2 = 0 τότε είναι ομογενείς. Η διαϕορική εξίσωση (1.44) είναι μή-ομογενής λόγω της ύπαρξης του μήμηδενικού όρου g(x) στο δεύτερο μέλος. Αν g(x) = 0 τότε η εξίσωση γράϕεται α(x) d2 u 2 + β(x)du + γ(x)u(x) = 0 (1.47) Η(1.47) καλείται ομογενής Δ.Ε. 2 ov βαθμού. Αν u 1 (x) και u 2 (x) είναι δύο γραμμικά ανεξάρτητες λύσεις τησ(1.47), τότε η γενική λύση u(x) μπορεί να εκϕραστεί ως γραμμικός συνδυασμός Οι u 1, u 2 είναι γραμμικά ανεξάρτητες όταν η σχέση u(x) = c 1 u 1 + c 2 u 2 (1.48) αu 1 + βu 2 = 0 (1.49) συνεπάγεται ότι α = β = 0. Λαμβάνοντας την παράγωγο της τελευταίας έχουμε επίσης αu 1 + βu 2 = 0 (1.50) Από την (1.49) και την παράγωγο αυτής συνάγουμε ότι οι u 1, u 2 είναι γραμμικά ανεξάρτητες αν η ορίζουσα W (u 1, u 2 ) = u ( ) 1 u 2 u 1 u = u du u du 1 2 d u2 u2 1 (1.51) u 1 είναι διάϕορη του μηδενός. Η W (u 1, u 2 ) καλείται W ronskian των λύσεων u 1,2. Αντίθετα, αν W (u 1, u 2 ) = 0, τότε ολοκληρώνοντας έχουμε u 1 (x) = cu 2 (x) (1.52) όπου c = σταθερά και επομένως πράγματι στην περίπτωση που η W ronskian μηδενίζεται οι λύσεις είναι γραμμικά εξαρτημένες. Θα διατυπώσουμε στη συνέχεια δύο θεωρήματα για τις λύσεις των εξισώσεων δεύτερης τάξης.
15 1.5. Ο Τ ΥΠΟΣ ΤΟΥ LIOUV ILLE 15 Θεώρημα 1 Η γενικώτερη λύση της ομογενούς διαϕορικής εξίσωσης (1.44) είναι u(x) = c 1 u 1 (x) + c 2 u 2 (x) (1.53) όπου c 1, c 2 αυθαίρετες μιγαδικές σταθερές και u 1, u 2 δύο γραμμικά ανεξάρτητες λύσεις της διαϕορικής εξίσωσης, δηλαδή ικανοποιούν τη συνθήκη W (u 1, u 2 ) 0 (1.54) Θεώρημα 2 Η γενικώτερη λύση της μή-ομογενούς διαϕορικής εξίσωσης (1.44) είναι u(x) = c 1 u 1 (x) + c 2 u 2 (x) + ũ(x) (1.55) όπου ũ(x) είναι οποιαδήποτε μερική λύση της (1.44), και u 1, u 2 λύσεις της αντίστοιχης ομογενούς Δ.Ε. που ικανοποιούν τη συνθήκη (1.54). 1.5 O tôpoc tou Liouville Αν είναι δυνατό να βρεθεί μια λύση u 1 (x) της ομογενούς διαϕορικής εξίσωσης (1.44), τότε η δεύτερη γραμμικά ανεξάρτητη λύση u 2 (x), μπορεί να εξαχθεί από την u 1 (x). Ας εκϕράσουμε την u 2 (x) ως εξής u 2 (x) = u 1 (x)h(x) (1.56) όπου h(x) άγνωστη συνάρτηση που θα προσδιοριστεί. Η W ronskian γράϕεται W (u 1, u 2 ) = u 1 u 2 u 2 u 1 = u 1 u 1h + u 1 u 1 h u 1 hu 1 = u 2 1h (1.57) Αντικατάσταση της u 2 = u 1 h, στη διαϕορική εξίσωση και κάνοντας χρήση του γεγονότος ότι η u 1 αποτελεί επίσης λύση, δίδει την ακόλουθη ΔΕ για την άγνωστη συνάρτηση h(x) d 2 h 2 + 2u 1 + p(x)u 1 dh u 1 = 0 (1.58) όπου p(x) = β(x) α(x) Ολοκληρώνοντας την (1.58) λαμβάνουμε για την παράγωγο h (x): (1.59) dh = c u 2 1 (x)e x x 0 p(x ) (1.60)
16 16 ΚΕΦ ΑΛΑΙΟ 1. ΣΤΟΙΧΕ ΙΑ ΔΙΑΦΟΡΙΚ ΩΝ ΕΞΙΣ ΩΣΕΩΝ όπου c σταθερά ολοκλήρωσης. Η h(x) προκύπτη με την ολοκλήρωση της τελευταίας x h(x) = c x x 0 u 2 1 (x ) e p(x ) x 0 (1.61) Συνεπώς, η δεύτερη λύση u 2 (x) γράϕεται συναρτήσει της πρώτης ως ακολούθως u 2 (x) = cu 1 (x) x x 0 u 2 1 (x ) e x x 0 p(x ) (1.62) Με τη χρήση της (1.60) η W ronskian (1.57) μπορεί να γραϕεί και ως εξής W (u 1, u 2 ) = u 2 d u 2 1 = u 2 u 1h = cu u 2 1 e x x 0 p(x ) W (x) = c e x x 0 β(x ) α(x ) (1.63) Η μορϕή (1.63) λέγεται τύπος του Liouville. Με τη χρήση αυτού, η λύση ξαναγράϕεται ως εξής W (x) u 2 (x) = c 0 u 1 (x) u 2 (1.64) 1 (x) Παραδείγματα. 1. Δίδεται η διαϕορική εξίσωση Να βρεθούν οι λύσεις αυτής. Διαπιστώνουμε ότι η u (x) + 2x u (x) + 2u(x) = 0 (1.65) u 1 (x) = e x2 αποτελεί λύση. Για να βρούμε τη δεύτερη υπολογίζουμε πρώτα τη W ronskian { } W (x) = c exp 2x = c e x2 και αντικαθιστούμε στον τύπο (1.64) e u 2 (x) = c x 2 u 1 (x) e 2x2 = c e x 2 e x2 π 2 2 e x Erf i(x) (1.66) όπου η Erf i(x) αντιστοιχεί στο τελευταίο ολοκλήρωμα (πολλαπλασιασμένο με 2 π ) και καλείται Imaginary error function 1. Οι δύο λύσεις σχεδιάζονται στο σχήμα H sunˆrthsh aut mporeð na jewrhjeð lôsh thc exðswshc u (x) 2xu (x) = 0 me arqikèc sun kec Erfi(0) = 0, derfi(x) = 2 0 π.
17 1.5. Ο Τ ΥΠΟΣ ΤΟΥ LIOUV ILLE Σχήμα 1.1: Οι δύο λύσεις της (1.65). 2. Η Δ.Ε. Legendre (1 x 2 ) d2 d Q(x) 2x Q(x) + n(n + 1)Q(x) = 0 2 για ακέραιες τιμές του n έχει ως λύση τα πολυώνυμα Legendre που όπως είδαμε δίδονται από τον τύπο του Rodriguez 2 P n (x) = n n! d n n (x2 1) n Η δεύτερη λύση επιτυγχάνεται με την παραπάνω μέθοδο. Γράϕουμε Q(x) = h(x)p n (x) η h(x) δίδεται από την (1.61) με p(x) = 2x h(x) = c = c Συνεπώς η δεύτερη λύση είναι Q n (z) = P n (z) [ Pn(x 2 ) exp 1 x 2, x x 0 P 2 n(x )(1 x 2 ) + c z ] 2x 1 x 2 dζ P 2 n(ζ)(ζ 2 1) (1.67) όπου έχει γίνει κατάλληλη επιλογή των σταθερών ολοκλήρωσης. Αποδεικνύεται ότι η Q n (z) λαμβάνει την μορϕή Q n (z) = 1 2 ln(z + 1 z 1 )P n(z) + Π n 1 (z). όπου Π n 1 (z) πολυώνυμο βαθμού n 1. 2 H sugkekrimmènh DE ja epilujeð epðshc me th mèdodo F robenious.
18 18 ΚΕΦ ΑΛΑΙΟ 1. ΣΤΟΙΧΕ ΙΑ ΔΙΑΦΟΡΙΚ ΩΝ ΕΞΙΣ ΩΣΕΩΝ 1.6 H eôresh thc merik c lôshc thc m o- mogenoôc D.E. Στο προηγούμενο εδάϕιο δείξαμε ότι η δεύτερη λύση της ομογενούς διαϕορικής εξίσωσης δεύτερης τάξης, ευρίσκεται εάν είναι γνωστή η μιά λύση. Στη συνέχεια θα δείξουμε ότι είναι δυνατό να κατασκευάσουμε και τη λύση της μή ομογενους με τη γνώση των δύο δύο λύσεων της αντίστοιχης ομογενούς Δ.Ε. Συνεπώς, το πρόβλημα εύρεσης των λύσεων της μή-ομογενούς (1.44) ανάγεται στην εύρεση των λύσεων της αντίστοιχης ομογενούς. Εστω λοιπόν ũ(x) η λύση της μη-ομογενούς η οποία γράϕεται ως εξής ũ(x) = υ(x)u 1 (x) (1.68) όπου u 1 (x) είναι λύση της αντίστοιχης ομογενούς Δ.Ε. Αντικαθιστούμε στην (1.44) και έχουμε u 1υ + 2υ u 1 + u 1 υ + pu 1υ + pu 1 υ + qu 1 υ = f(x) (1.69) όπου p = β(x)/α(x), q(x) = γ(x)/α(x) και f(x) = g(x)/α(x). Αναδιατάσουμε τους όρους στην (1.69) και έχουμε u 1 υ + 2υ u 1 + pu 1 υ + υ(u 1 + pu 1 + qu 1 ) = f(x) (1.70) Το άθροισμα των όρων στην παρένθεση συνιστούν την ομογενή ΔΕ και είναι μηδέν διότι η u 1 (x) είναι λύση της ομογενούς ΔΕ. Διαιρώντας με u 1 (x) την (1.70) λαμβάνουμε d 2 υ 2 + (2du p) dυ u 1 = f(x) (1.71) u 1 (x) Από την (1.63) επίσης έχουμε x ln w = p(x ) x 0 την οποία παραγωγίζουμε και λαμβάνουμε d ln w 1 dw = p(x) (1.72) w Η (1.71 ) τότε παίρνει τη μορϕή d 2 ( υ du 1 u 1 1 ) dw dυ w = f(x) u 1 (x) (1.73) ή d 2 υ 2 + d ln Q dυ = f(x) u 1 (x) (1.74)
19 1.6. Η Ε ΥΡΕΣΗ ΤΗΣ ΜΕΡΙΚ ΗΣ Λ ΥΣΗΣ ΤΗΣ Μ Η ΟΜΟΓΕΝΟ ΥΣ Δ.Ε.19 όπου Q(x) = = = = u 2 1(x) w(u 1, u 2 ) u 2 1(x) u 1 u 2 u 1 u 2 1 u 2 u u 1 u 1 2 u d [ u2 u 1 ] Πολλαπλασιάζοντας με Q(x) την (1.74) έχουμε { d 2 υ Q 2 + [ d } lnq(x)]dυ = Q { d 2 υ Q dq } dυ = Q d2 υ 2 + dq dυ = d { Q dυ } = Q f(x) u 1 (x) (1.75) (1.76) Ολοκληρώνουμε και παίρνουμε Q(x) dυ = x Διαιρώντας με Q(x) και κάνοντας χρήση της (1.75), x 0 Q(x ) f(x ) u 1 (x ) (1.77) dυ = d ( u2 u 1 = d {u 2(x) u 1 (x) ) x Q(x ) f(x ) x 0 u 1 (x ) x Στη συνέχεια ολοκληρώνουμε την (1.78) Q(x ) f(x ) x 0 u 1 (x ) } Q(x) f(x) u 1 (x) u 2 (x) u 1 (x) (1.78) υ(x) = u 2(x) u 1 (x) x Από την (1.79) έχουμε τη λύση ũ(x) u 1 (x)υ(x) = u 2 (x) x 0 Q(x ) f(x ) u 1 (x ) x x u 1 (x )f(x ) x 0 w(u 1, u 2 ) u 1 (x) Q(x ) f(x )u 2 (x ) x 0 u 2 1 (x ) x (1.79) u 2 (x )f(x ) x 0 w(u 1, u 2 ) (1.80) Επισημαίνουμε ότι η παραπάνω μέθοδος δεν μπορεί να γενικευθεί για ΔΕ μεγαλύτερης τάξης ή για ΔΕ με μερικές παραγώγους. Η επίλυση τέτοιων μορϕών μπορεί να γίνει με άλλες μεθόδους όπως εκείνη των συναρτήσεων Green που θα μελετηθούν σε επόμενα κεϕάλαια.
20 20 ΚΕΦ ΑΛΑΙΟ 1. ΣΤΟΙΧΕ ΙΑ ΔΙΑΦΟΡΙΚ ΩΝ ΕΞΙΣ ΩΣΕΩΝ 1. Παράδειγμα. Να λυθεί η ΔΕ u u = e x sinx Οι λύσεις της αντίστοιχης ομογενούς είναι u u = 0 u 1 e x, u 2 e x Είναι a(x) = 1, b(x) = 0 και επομένως η W ronskian δίδεται από { } 0 W (x) = c exp 1 = c Αντικαθιστούμε στον τύπο ũ(x) = e x e x (e x sin(x) c = 2 5c ex (2 cos(x) + sin(x)) Επιλέγουμε κατάλληλα τη σταθερά και έχουμε e x e x (e x sin(x) c ũ(x) = 1 5 ex (2 cos(x) + sin(x)) Ask seic 1. Να λυθεί η ΔΕ y + y = xcoshx 2. Να γραϕεί η κανονική μορϕή (δηλαδή χωρίς πρώτη παράγωγο) των ΔΕ x 2 y + xy + (x 2 n 2 )y = 0 y 2xy + λy = 0 xy + (1 x)y + λy = 0 (1.81)
21 1.7. ΔΙΑΦΟΡΙΚ ΕΣ ΕΞΙΣ ΩΣΕΙΣ 2 ης Τ ΑΞΗΣ ΜΕ ΚΑΝΟΝΙΚ Α ΑΝ ΩΜΑΛΑ ΣΗΜΕ ΙΑ Diaforikèc Exis seic 2 ης tˆxhc me kanonikˆ an mala shmeða Από τα παραπάνω εδάϕια διαπιστώσαμε ότι η μελέτη και εύρεση λύσεων μιας μεγάλης κατηγορίας Διαϕορικών Εξισώσεων δεύτερης τάξης με μή ομογενή όρο ανάγεται στην επίλυση της αντίστοιχης ομογενούς εξίσωσης που έχει τη μορϕή (1.47). Θα γενικεύσουμε την ανάλυση για μιγαδική μεταβλητή x z. Εισάγοντας τις ακόλουθες συναρτήσεις p(z) = β(z) γ(z), q(z) = α(z) α(z), η (1.47) γράϕεται d 2 u dz 2 + p(z)du + q(z)u = 0 (1.82) dz Περιοριζόμαστε στη συνέχεια στην περίπτωση που οι p(z), q(z) είναι αναλυτικές σε περιοχή R εκτός ενδεχομένως από κάποια σημεία. 3 Αν σε δεδομένο σημείο z 0, οι p(z), q(z) είναι αναλυτικές το z 0 καλείται ομαλό σημείο. Στη γειτονιά ομαλού σημείου, η ΔΕ (1.82) έχει πάντα δύο γραμμικά ανεξάρτητες λύσεις. Αν το σημείο z 0 είναι απομονωμένη ανωμαλία, για κάποια από τις συναρτήσεις p(z), q(z), τότε τουλαχιστο μια από τις δύο λύσεις θα εμϕανίζει ανωμαλία στο z 0. Ιδιαίτερα, αν η p(z) έχει πόλο το πολύ πρώτης τάξης και η q(z), το πολύ δεύτερης τάξης, τότε το σημείο z 0 καλείται κανονικό ανώμαλο σημείο. Στην περίπτωση αυτή, οι δύο λύσεις u 1, u 2, της ΔΕ έχουν τη μορϕή ή u 1 (z) = (z z 0 ) r 1 c n (z z 0 ) n u 2 (z) = (z z 0 ) r2 d n (z z 0 ) n, r 1 r 2 (1.83) u 1 (z) = (z z 0 ) r 1 c n (z z 0 ) n u 2 (z) = (z z 0 ) r2 d n (z z 0 ) n + κu 1 (z) ln(z z 0 ) (1.84) Σημειώνουμε τέλος ότι αν το z 0 είναι μή-κανονικό ανώμαλο σημείο, η λύση είναι της μορϕής u(x) c n (z z 0 ) n (1.85) n= 3 Sthn perðptwsh stajer n suntelest n thc omogenoôc D.E. oi lôseic mporoôn pˆnta na ekfrastoôn me stoiqei deic sunart seic. Ed exetˆzoume th genik terh perðptwsh me m stajeroôc suntelestèc ìpou oi lôseic ekfrˆzontai me morf apeiroseir n h kai oloklhrwmˆtwn.
22 22 ΚΕΦ ΑΛΑΙΟ 1. ΣΤΟΙΧΕ ΙΑ ΔΙΑΦΟΡΙΚ ΩΝ ΕΞΙΣ ΩΣΕΩΝ δηλαδή, το άθροισμα εκτείνεται από στο +. Πρίν επεκταθούμε στην γενική λύση της εξίσωσης με κανονικά ανώμαλα σημεία, θα δώσουμε ένα παράδειγμα εϕαμογής της μεθόδου στη γνωστή ΔΕ του Legendre η οποία γράϕεται ως εξής οι δε συναρτήσεις p, q γράϕονται (1 x 2 ) d2 u 2 2xdu + l(l + 1)u = 0 (1.86) p(x) = 2x l(l + 1), q(x) = 1 x2 1 x 2 και επομένως, θα αναζητήσουμε λύσεις σε μορϕή σειράς στο διάστημα x < 1. Εστω λοιπόν u 1 (x) = a n x n+r (1.87) Αντικαθιστούμε στη ΔΕ. (1.86) τη u 1 μαζί με τις παραγώγους du 1 = d 2 u 1 2 = (n + r) a n x n+r 1 (n + r)(n + r 1) a n x n+r 2 και λαμβάνουμε (n + r)(n + r 1)a n x n+r 2 = [(n + r)(n + r + 1) l(l + 1)] a n x n+r Γράϕουμε τον πρώτο όρο αυτής ως εξής (n + r)(n + r 1)a n x n+r 2 = r(r 1)a 0 x r 2 + (r + 1)ra 1 x r 1 + (n + r)(n + r 1)a n x n+r 2 n=2 Ορίζουμε τον νέο δείκτη n = n + 2 οπότε λαμβάνουμε (n + r)(n + r 1)a n x n+r 2 = n=2 (n + r + 2)(n + r + 1)a n +2x n +r n =0 (n + r + 2)(n + r + 1)a n+2 x n+r
23 1.7. ΔΙΑΦΟΡΙΚ ΕΣ ΕΞΙΣ ΩΣΕΙΣ 2 ης Τ ΑΞΗΣ ΜΕ ΚΑΝΟΝΙΚ Α ΑΝ ΩΜΑΛΑ ΣΗΜΕ ΙΑ23 όπου στην τελευταία γραμμή, αλλάξαμε την ονομασία του δείκτη n n. Συνδυάζοντας τα παραπάνω λαμβάνουμε την ισότητα r(r 1)a 0 x r 2 + (r + 1)ra 1 x r 1 + = (n + r + 2)(n + r + 1)a n+2 x n+r [(n + r)(n + r + 1) l(l + 1)] Εξισώνοντας τους συντελεστές ίσων δυνάμεων, προκύπτουν οι ακόλουθες ισότητες. Για τους δύο όρους εκτός των αθροισμάτων, δεν υπάρχουν αντίστοιχες δυνάμεις στο δεύτερο μέλος, επομένως r(r 1)a 0 = 0 r(r + 1)a 1 = 0 Μπορούμε να επιλέξουμε ένα από τα a 0, a 1 διάϕορο του μηδενός, έστω το a 0 0, και a 1 = 0. Τότε r = 0 ή r = 1, οπότε προκύπτουν οι περιπτώσεις a n+2 = = a n+2 = = n(n + 1) l(l + 1) a n (n + 1)(n + 2) (n l)(n + l + 1) a n (1.88) (n + 1)(n + 2) (n + 1)(n + 2) l(l + 1) a n (n + 2)(n + 3) (n + 1 l)(n + l + 2) a n (1.89) (n + 2)(n + 3) Συνεπώς η λύση της εξίσωσης θα έχει είτε άρτιες δυνάμεις του x (όταν r = 0) ή περιττές δυνάμεις (όταν r = 1). l(l + 1) a 2 = 1 2 a 0 (l 2)(l + 3) a 4 = a {l(l 2)} {(l + 1)(l + 3)} = ( 1) και γενικά ο συντελεστής ανάλογος του x 2n n {l(l 2) (l 2n + 2)} {(l + 1)(l + 3) (l + 2n)} a 2n = ( 1) (2n)! Ανάλογη έκϕραση λαμβάνουμε και για τους συντελεστές των περιττών δυνάμεων x 2n+1. Παρατηρούμε ότι αν η παράμετρος l ισούται με άρτιο l = 2N, τότε ο συντελεστής a 2N+2 = 0 και το ίδιο ισχύει για κάθε επόμενο συντελεστή. Αυτό σημαίνει a 0 a 0
24 24 ΚΕΦ ΑΛΑΙΟ 1. ΣΤΟΙΧΕ ΙΑ ΔΙΑΦΟΡΙΚ ΩΝ ΕΞΙΣ ΩΣΕΩΝ ότι η σειρά τερματίζεται το οποίο συνεπάγεται ότι η λύση των αρτίων δυνάμεων είναι πολυωνυμική. Η σειρά των περιττών δυνάμεων τερματίζεται αντίστοιχα για l = 2N + 1 διότι τότε a 2N+1 = 0 καθώς και για κάθε επόμενο συντελεστή. Επομένως, για κάθε ακέραια τιμή του l υπάρχει πολυωνυμική λύση η οποία επιπροσθέτως συγκλίνει και για τά άκρα του διαστήματος x = ±1. Μπορούμε να γράψουμε σε ενιαία ϕόρμουλα τη γενική πολυωνυμική (άρτια ή περιττή) λύση ως εξής P l (x) = [l/2] ( 1) k (2l 2k)! 2 l k!(l k)!(l 2k)! xl 2k (1.90) k=0 η οποία ταυτίζεται με τα γνωστά πολυώνυμα Legendre. 1.8 Genik lôsh thc DE 2 ης tˆxhc sth geitoniˆ kanonikoô an malou shmeðou Θα επαναλάβουμε την παραπάνω διαδικασία εύρεσης λύσης σε μορϕή σειράς για τις περιπτώσεις διαϕορικών εξισώσεων 2 ης τάξης που έχουν τουλάχιστο ένα κανονικό ανώμαλο σημείο. Θα αναζητηθούν λύσεις στη γειτονιά ενός τέτοιου σημείου. Ας ορίσουμε τον τελεστή L = d2 2 + p(z) d + q(z) Η ΔΕ γράϕεται Lu(z) d2 u 2 + p(z)du + q(z)u = 0 (1.91) Ας υποθέσουμε ότι το z 0 είναι κανονικό ανώμαλο σημείο. Τότε οι συναρτήσεις A(z) = (z z 0 )p(z), B(z) = (z z 0 ) 2 q(z) (1.92) είναι αναλυτικές στην περιοχή γύρω από το z 0 και συνεπώς αναπτύσσονται σε σειρά T aylor με a n = 1 2πi A(z) = a n (z z 0 ) n, B(z) = b n (z z 0 ) n (1.93) A(z ) (z z 0 ) n+1 dz, b n = 1 2πi όπου c δρόμος στην περιοχή αναλυτικότητας που περικύει το z 0. Δοκιμάζουμε στη συνέχεια λύση υπό μορϕή σειράς u(z) = (z z 0 ) r n= 0 B(z ) (z z 0 ) n+1 dz (1.94) c n (z z 0 ) n (1.95)
25 1.8. ΓΕΝΙΚ Η Λ ΥΣΗ ΤΗΣ ΔΕ 2 ης Τ ΑΞΗΣ ΣΤΗ ΓΕΙΤΟΝΙ Α ΚΑΝΟΝΙΚΟ Υ ΑΝ ΩΜΑΛΟΥ ΣΗΜΕ ΙΟΥ25 την οποία αντικαθιστούμε στη Δ.Ε.. Αντικαθιστούμε επίσης και τους συντελεστές υπό μορϕή σειράς από την (1.93) και κάνοντας χρήση της ιδιότητας f g = c n = ( ) b m z m = c n z n ( a n z n) m=0 n a n m b m m=0 λαμβάνουμε την ακόλουθη αναδρομική σχέση { } n (n + r)(n + r 1)c n + {(m + r)a n m + b n m }c m (z z 0 ) n = 0 m=0 (1.96) Για να είναι Lu(z) 0 πρέπει ο συντελεστής κάθε δύναμης (z z 0 ) της σειράς (1.96) να είναι μηδέν. Αυτό επιβάλει την ακόλουθη συνθήκη για τους συντελεστές c n και την παράμετρο r: {(n + r)(n + r 1) + (n + r)a 0 + b 0 }c n + n 1 {(m + r)a n m + b n m }c m = 0 m=0 Για διευκόλυνση στη συνέχεια ας ορίσουμε τις ακόλουθες συναρτήσεις ra 0 + b 0 + r(r 1) k = 0 f k (r) = ra k + b k k > 0 0 k < 0 Η εξίσωση τότε γράϕεται f 0 (r + n) c n = n 1 m=0 f n m (r + m) c m (1.97) Μέσω της (1.97) μπορούμε να υπολογίσουμε διαδοχικά τους συντελεστές c 1, c 2,..., c n συναρτήσει του πρώτου c 0 ο οποίος παραμένει απροσδιόριστος. Για n = 0 λαμβάνουμε την εξίσωση Υποθέτουμε c 0 0, άρα έχουμε n = 0 f 0 (r)c 0 = 0 c 0 0 f 0 (r) = 0 r 2 + (a 0 1)r + b 0 = 0. (1.98) Η εξίσωση για n = 0 καλείται δεικτική (indicial equation). Ονομάζουμε r 1, r 2 τις λύσεις αυτής με Rer 1 > Rr 2. Τότε από την εξίσωση προκύπτει 2Rer 1 > Re(1 a 0 ). Μπορούνε να δειχθούνε τα ακόλουθα: ι) Ψπάρχει πάντα μια λύση με r = r 1
26 26 ΚΕΦ ΑΛΑΙΟ 1. ΣΤΟΙΧΕ ΙΑ ΔΙΑΦΟΡΙΚ ΩΝ ΕΞΙΣ ΩΣΕΩΝ ιι) Η ρίζα r = r 2 παρέχει μια δεύτερη λύση εϕόσον η διαϕορά r 1 r 2 δεν είναι ακέραιος. Οι συντελεστές c n προκύπτουν από (1.97) διαιρώντας με f 0 (r + n): c n = n 1 m=0 f n m (r + m)c m f 0 (r + n) (1.99) Από την(1.99) προκύπτει πράγματι ότι όλοι οι c n μπορούν να εκϕραστούν συναρτήσει του πρώτου c D.E. me kanonikˆ an mala shmeða Θα μελετήσουμε στη συνέχεια Δ.Ε. με κανονικά ανώμαλα σημεία. Θα ασχοληθούμε με περιπτώσεις που έχουν το πολύ τρία τέτοια σημεία συμπεριλαμβανομένου και του απείρου. Στη γενικώτερη της (γνωστή ως μορϕή Riemann) η Δ.Ε. αυτή γράϕεται με τη συνθήκη u + ( 1 α α z z β β z z γ γ z z 3 )u + { (z 1 z 2 )(z 1 z 3 )αα z z 1 + (z 2 z 1 )(z 2 z 3 )ββ + (z 3 z 1 )(z 3 z 2 )γγ } z z 2 z z 3 1 (z z 1 )(z z 2 )(z z 3 ) u = 0 (1.100) Η δεικτική εξίσωση στο σημείο z 1 είναι με λύσεις α + α + β + β + γ + γ = 1 (1.101) r(r 1) + (1 α α )r + αα = 0 (1.102) r 1 = α, r 2 = α (1.103) Ομοια για τα σημεία z 2, z 3 έχουμε αντίστοιχα r 1 = β, γ και r 2 = β, γ. Ορίζουμε στη συνέχεια το σύμβολο P του Riemann το οποίο είναι z 1 z 2 z 3 P α β γ z (1.104) α β γ Το σύμβολο P του Riemann περιέχει εννέα παράμετρες οι οποίες μπορούν να μειωθούν σε τρείς με τους ακόλουθους μετασχηματισμούς u(z) = (z z 1 ) r (z z 2 ) s (z z 3 ) t υ(z)
27 1.9. Δ.Ε. ΜΕ ΚΑΝΟΝΙΚ Α ΑΝ ΩΜΑΛΑ ΣΗΜΕ ΙΑ 27 με τη συνθήκη r + s + t = 0, και τον μετασχηματισμό z = Az + B Cz + D Αντικαθιστούμε στη Δ.Ε., και ευρίσκουμε ότι το σύμβολο Riemann γράϕεται R(z) = P και με τον μετασχηματισμό z 1 z 2 z 3 α + r β + s γ + t z α + r β + s γ + t z i = Az i + B, i = 1, 2, 3 (1.105) Cz i + D R(z) = P z 1 z 2 z 3 α β γ z α β γ Εστω τώρα ότι και z 1 = 0 z 2 = z 3 = 1 r = α, s = α + γ, t = γ (1.106) Κάνοντας τις αντικαταστάσεις a = α + β + γ, b = α + γ + β, c = 1 + α + α μετά από λίγη άλγεβρα προκύπτει τελικά ( ) α ( ) γ z z1 z z3 R(z) = P z z 2 z z a 0 z 1 c b c a b (1.107) Συμπεραίνουμε ότι η λύση της γενικής εξίσωσης των εννέα παραμέτρων ανάγεται τελικά στην λύση μιας απλούστερης Δ.Ε. με κανονικά ανώμαλα σημεία και τρείς παραμέτρους a, b, c. z 1 = 0, z 2 = 1, z 3 =
28 28 ΚΕΦ ΑΛΑΙΟ 1. ΣΤΟΙΧΕ ΙΑ ΔΙΑΦΟΡΙΚ ΩΝ ΕΞΙΣ ΩΣΕΩΝ 1.10 H upergewmetrik sunˆrthsh Αν αντικαταστήσουμε τις τιμές των παραμέτρων του συμβόλου (1.107) στην Δ.Ε. (1.100) για τον συντελεστή του δεύτερο όρου (ανάλογου της πρώτης παραγώγου u ) έχουμε: 1 α α + 1 β β + 1 γ γ = c z z 1 z z 2 z z 3 z 0 + lim 1 a b a + b c z 2 z z 2 z 1 = c z a + b c z 1 Ανάλογα για τον συντετλεστή του τρίτου όρου λαμβάνουμε το αποτέλεσμα οπότε η Δ.Ε. γράϕεται ab z(z 1) z(1 z)u + {c (1 + a + b)z}u abu = 0 (1.108) Η Δ.Ε. (1.108) καλείται Υπεργεωμετρική Εξίσωση και οι λύσεις αυτής συμβολίζονται F (a, b; c; z) (1.109) Οι συναρτήσεις p(z), q(z) όπως ορίστηκαν στα προηγούμενα είναι p(z) = c (1 + a + b)z, q(z) = ab z(1 z) z(1 z) Αναζητούμε λύση γύρω από το κανονικό ανώμαλο σημείο z = 0, z < 1. Κατασκευάζουμε πρώτα τη δεικτική εξίσωση. Προς τούτο A(z) = zp(z) = c (a + b + 1)z z(1 z) B(z) = z 2 q(z) = abz + δηλαδή a 0 = c, b 0 = 0 και η δεικτική εξίσωση έχει λύσεις r(r 1) + rc = 0 r = 0, 1 c = c + ( 1 a b + c)z + Η F (a, b; c; z) είναι αναλυτική γύρω από το z 0 = 0, επομένως επιδιώκουμε λύση υπό μορϕή σειράς. Για την περίπτωση r = 0, η λύση γράϕεται F (a, b; c; z) = n c n z n, (c 0 = 1) (1.110) όπου με τη συνθήκη c 0 = 1 κανονικοποιήσαμε τον πρώτο όρο στη μονάδα. Αντικαθιστούμε στην (1.108) και παίρνουμε c n z n = 0 z(1 z)c n n(n 1)z n 2 + {c (1 + a + b)z}c n nz n 1 ab Διαχωρίζουμε τις δυνάμεις ως προς τη μεταβλητή {n(n 1) + cn}c n z n 1 = c n {n(n 1) + (1 + a + b)n + ab}z n (1.111) n n
29 1.10. Η ΥΠΕΡΓΕΩΜΕΤΡΙΚ Η ΣΥΝ ΑΡΤΗΣΗ 29 Ο συντελεστής του δεύτερου όρου γράϕεται q n = c n {n(n 1) + (1 + a + b)n + ab} = c n {n 2 + n(a + b) + ab} = (a + n)(b + n)c n και για n n 1 q n q n 1 = (a + n 1)(b + n 1)c n 1 Τότε από την (1.111) έχουμε την ακόλουθη αναδρομική σχέση c n = (a + n 1)(b + n 1) c n 1 (1.112) n(c + n 1) Οι συντελεστές υπολογίζονται διαδοχικά με τη χρήση της (1.112). Ετσι c 1 = ab c c 0 = ab c c 2 = (a + 1)(b + 1) c 1 = 2(c + 1) (a + 1)a(b + 1)b 2(c + 1)c (1.113) κ.ο.κ. Υπενθυμίζουμε τώρα την ιδιότητα της συνάρτησης Γάμμα Γ(z + 1) = zγ(z), Γ(z + 2) = (z + 1)zΓ(z),..., Γ(z + n) = (z + n 1) zγ(z) και την εϕαρμόζουμε για z = a, b και c. Συνεπώς για τον n-οστό όρο, χρησιμοποιούμε την ταυτότητα και ομοίως για b, c. Τελικά έχουμε c n = (a + n 1)... (a + 1)a = Γ(n + a) Γ(a) Άρα, η λύση γράϕεται ως εξής Γ(n + b) Γ(b) F (a, b; c; z) = 1 + Γ(c) Γ(a)Γ(b) n=1 Γ(c) = Γ(a)Γ(b) η οποία συγκλίνει για z < 1. Ας θεωρήσουμε την ειδική περίπτωση Γ(n + a) Γ(a) Γ(c), c n (1.114) Γ(n + 1)Γ(c + n) Γ(a + n)γ(b + n) Γ(c + n)γ(n + 1) zn Γ(a + n)γ(b + n) Γ(c + n)γ(n + 1) zn (1.115) a = 1, b = c (1.116)
30 30 ΚΕΦ ΑΛΑΙΟ 1. ΣΤΟΙΧΕ ΙΑ ΔΙΑΦΟΡΙΚ ΩΝ ΕΞΙΣ ΩΣΕΩΝ Τότε η (1.115) γράϕεται F (1, b; b; z) = 1 + Γ(b) Γ(1)Γ(b) n=1 = 1 + z n n=1 Γ(1 + n)γ(b + n) Γ(b + n)γ(n + 1) zn z n = 1, ( z < 1) (1.117) 1 z δηλαδή, το ανάπτυγμα (1.117) είναι η γνωστή υπεργεωμετρική σειρά. Η αντίστοιχη Δ.Ε. γράϕεται z(1 z)u + [c (2 + c)z]u cu = 0 (1.118) η οποία με αναδιάταξη των όρων γράϕεται z[(1 z)u u] + c[(1 z)u u] = 0 και η οποία ικανοποιείται από τη λύση (1.117) για κάθε τιμή της παραμέτρου c διότι (1 z)u u = 0. Υπάρχει μια σημαντική συμμετρία στην υπεργεωμετρική σειρά (ΥΣ) η οποία είναι εμϕανής ακόμη και στη διαϕορική εξίσωση. Η ΥΣ παραμένει αναλλοίωτη ως προς την εναλλαγή των a b F (a, b, c; z) = F (b, a, c; z) (1.119) Για να μελετήσουμε τη δεύτερη λύση, υπενθυμίζουμε ότι από τη δεικτική εξίσωση η δεύτερη ρίζα της είναι r = 1 c. Αν υποθέσουμε στη συνέχεια ότι ο (1 c) δεν είναι ακέραιος, τότε μπορούμε να βρούμε μια δεύτερη λύση της Δ.Ε. που είναι της μορϕής u(z) = z 1 c g 1 (z) (1.120) όπου g 1 (z) είναι δυναμοσειρά του z. Για να την προσδιορίσουμε αντικαθιστούμε στην (1.107) και έχουμε z(z 1)g 1 + [c 2 + z(3 + a + b 2c)]g 1 + (a c + 1)(b c + 1)g 1 = 0 (1.121) Η (1.121) είναι της ίδιας μορϕής με την (1.107). Πράγματι, από τον τρίτο όρο της (1.121) παρατηρούμε ότι αν κάνουμε την αντιστοιχία a a c + 1 (1.122) b b c + 1 τότε 1+a+b a+b 2c+3, που είναι ο συντελεστής του όρου zg 1 στην (1.121). Επίσης, ο συντελεστής του g 1 είναι c 2, συνεπώς αντιστοιχώντας c 2 c, έχουμε ότι η λύση της (1.121) είναι Συνεπώς η γενική λύση της Δ.Ε. είναι F (b c + 1, a c + 1; 2 c; z) (1.123) u = α F (a, b c z) + β z 1 c F (b c + 1, a c + 1; 2 c; z) (1.124)
31 1.10. Η ΥΠΕΡΓΕΩΜΕΤΡΙΚ Η ΣΥΝ ΑΡΤΗΣΗ ParadeÐgmata 1. Θεωρείστε την ανάπτυξη της ακόλουθης συνάρτησης σε σειρά (1 + z) a = f n z n, f n = 1 d n (1 + z)a n! dzn Οι συντελεστές είναι z=0 f n = a(a 1) (a n + 1) (1 + z) a n z=0 = Γ(a n) Γ(a) (1.125) και επομένως Παρατηρούμε ότι (1 + z) a = Γ(a n) n!γ(a) zn a(a 1) (a n+1) = ( a)(1 a) (n 1 a)( 1) n = επομένως ισοδύναμα γράϕουμε τη σειρά και ως εξής (1 + z) a = Γ(n a) n!γ( a) ( 1)n z n Γ(n a) Γ( a) ( 1)n Θεωρείστε στη συνέχεια την ειδική περίπτωση της υπεργεωμετρικής Άρα F ( a, b, b; z) = = Γ(n a) n!γ( a) ( z)n F ( a, b, b; z) = (1 + z) a Γ(n a) n!γ( a) ( 1)n z n (1.126) 2. Θα συσχετίσουμε την εξίσωση Legendre (1 z 2 ) d2 u du 2z + λ(λ + 1) = 0 dz2 dz που μελετήσαμε σε προηγούμενο παράδειγμα με την κατάλληλη λύση της υπεργεωμετρικής. Συγκρίνοντας τον δευτεροβάθμιο όρο με τον αντίστοιχο της υπεργεωμετρικής, εισάγουμε την νέα μεταβλητή w 1 z 2 = aw(1 w)
32 32 ΚΕΦ ΑΛΑΙΟ 1. ΣΤΟΙΧΕ ΙΑ ΔΙΑΦΟΡΙΚ ΩΝ ΕΞΙΣ ΩΣΕΩΝ όπου a κατάλληλη σταθερά. Επιλύοντας ως πρός w w = 1 ± 1 4 a (1 z2 ) 2 Κάνουμε τη βολική επιλογή a = 4 και έχουμε w = 1 z 2 Η διαϕορική εξίσωση Legendre γίνεται τότε w(1 w) d2 u du + (1 2w) + λ(λ + 1)u = 0 dw2 dw η οποία έχει τη μορϕή της υπεργεωμετρικής με Επιλύοντας ως προς a, b λαμβάνουμε (1 + a + b) = 2, ab = λ(λ + 1) a = λ, b = λ + 1, hb = λ, a = λ + 1 Επειδή η Υπεργεωμετρική έχει τη συμμετρία a b οι δύο λύσεις είναι ισοδύναμες. Επομένως η λύση της εξίσωσης Legendre δίδεται από την Υπεργεωμετρική σειρά u(z) = F ( λ, λ + 1, 1, 1 z 2 ) (1.127) η οποία καλείται συνάρτηση Legendre πρώτου είδους. Οταν ο λ είναι μή-αρνητικός ακέραιος, η σειρά τερματίζει και έχουμε τα αντίστοιχα πολυώνυμα Ask seic 1. Δείξτε ότι η Δ.Ε. u 2zu + 2ν u = 0 έχει πολυωνυμικές λύσεις (πολυώνυμα Hermite) για ν = 2N ή ν = 2N +1 ( όπου N ακέραιος) με συντελεστές 2. Δείξτε ότι 3. Επίσης, c n+2 = 2 ν (n + 1)(n + 2) c n F (1/2, 1/2, 3/2, z 2 ) = sin 1 z z F (1, 1, 2; z) = ln(1 + z) z (1.128) (1.129) 4. Δείξτε ότι όταν ένας από τους συντελεστές a, b της Δ.Ε. είναι μή-θετικός ακέραιος, η λύση (1.115) είναι πεπερασμένη σειρά.
33 1.11. ΟΛΟΚΛΗΡΩΤΙΚ ΕΣ ΑΝΑΠΑΡΑΣΤ ΑΣΕΙ ΤΗΣ Υ.Σ Oloklhrwtikèc anaparastˆsei thc U.S. Ας υποθέσουμε ότι η ΔΕ προς λύση έχει τη γενική μορϕή Στην περίπτωσή μας ο L z έχει τη μορϕή L z u = 0 (1.130) L z = z(1 z) d2 dz 2 + {c z(a + b + 1)} d ab (1.131) dz Η μέθοδος επίλυσης με ολοκληρωματική αναπαράσταση ανάγεται στην εύρεση `πυρήνα (Kernel) για το οποί ισχύει L z K(z, t) = M t K(z, t) (1.132) όπου K(z, t) ο πυρήνας και M t διαϕορικός τελεστής ως προς την παράμετρο t. Εστω υ(t) είναι συνάρτηση για την οποία ισχύει M + t υ(t) = 0 (1.133) όπου M + t είναι ο συναϕής του M t. Τότε η λύση της ΔΕ (1.130) δίδεται από u(z) = b Πράγματι, εϕαρμόζοντας τον L z στην (1.134) έχουμε L z u(z) = b Από την ταυτότητα Lagrange {L z K(z, t)}υ(t)dt a a a K(z, t)υ(t)dt (1.134) b {M t K(z, t)}υ(t)dt (1.135) υ(t){m t K(z, t)} K(z, t){m t + υ(t)} = [Q(K, υ)] (1.136) t όπου Q(K, υ) είναι επιϕανειακός όρος που περιέχει τις K, υ και διαϕορικά αυτών. Αντικαθιστώντας στην (1.135) έχουμε L z u(z) = b a Επιλέγοντας κατάλληλα όρια [a, b] έχουμε b K(z, t){m t + υ(t)}dt + [Q(K, υ)]dt (1.137) a t b a t [Q(K, υ)]dt = [Q(K, υ)]b a = 0 (1.138) και με τη χρήση της (1.133), η (1.137) αποδεικνύει την (1.130). Άρα η (1.134) αποτελεί λύση.
34 34 ΚΕΦ ΑΛΑΙΟ 1. ΣΤΟΙΧΕ ΙΑ ΔΙΑΦΟΡΙΚ ΩΝ ΕΞΙΣ ΩΣΕΩΝ Επιστρέϕοντας στην υπεργεωμετρική σειρά ας υποθέσουμε ότι η λύση είναι της μορϕής (1.134) με πυρήνα K(z, t) = (z t) λ (1.139) Ο (1.139) είναι γνωστός ως πυρήνας Euler. Δρώντας με τον τελεστή (1.131), στην u(z) για την περίπτωση της ΥΣ έχουμε L z u(z) = (λ(λ 1)z(1 z) + λ[c (a + b + 1)z](z t) ab(z t) 2) (z t) λ 2 υ(t)dt (1.140) Επιλέγουμε στη συνέχεια τον λ έτσι ώστε ο συντελεστής του z 2 στο προηγούμενο ολοκλήρωμα να είναι μηδέν. Εχουμε τότε την εξίσωση λ(λ 1) + λ(1 + a + b) + ab = 0 ή λ 2 + (a + b) + ab = 0 (1.141) με λύσεις λ = a, λ = b. Αν επιλέξουμε τη λύση λ = a τότε η (1.140) μετά από λίγες πράξεις λαμβάνει τη μορϕή ηέξεται L z u(z) = dtυ(t){[t(t 1) d2 dt 2 [(b a 1)t + (a c + 1)] d ]K} (1.142) dt όπου K = (z t) a. Συνεπώς ο M t είναι M t = t(t 1) d2 dt 2 [(b a 1)t + (a c + 1) d dt ] (1.143) Ενώ η υ(t) αποτελεί λύση της ΔΕ M t + υ(t) d2 dt 2 [t(t 1)υ(t)] + d [(b a 1)t + (a c + 1)]υ(t) = 0 (1.144) dt Για την επίλυση της (1.144) κάνουμε την αντικατάσταση w(t) = t(t 1)υ(t) (1.145) και λαμβάνουμε dw(t) w(t) a 1)t + (a c + 1) = (b dt (1.146) t(t 1) η οποία οδηγεί στη λύση όπου ρ είναι η σταθερά ολοκλήρωσης. υ(t) = ρt a c (t 1) c b 1 (1.147)
35 1.12. ΣΥΡΡ ΕΟΥΣΑ ΥΠΕΡΓΕΩΜΕΤΡΙΚ Η ΣΕΙΡ Α 35 Για να βρούμε τα όρια ολοκλήρωσης πρέπει να υπολογίσουμε τον ὲπιϕανειακό όρο Q(K, υ) και να ζητήσουμε να μηδενίζεται σύμϕωνα με την απαίτηση (1.138). Από την ταυτότητα Lagrange στη (1.136) έχουμε ότι Q(K, υ) = aρt a c+1 (t 1) c b (z t) a 1 (1.148) Η (1.148) μηδενίζεται στο t = 1 όταν Rec > Reb. Το άλλο σημείο είναι t =. Η απλούστερη επιλογή του δρόμου οκοκλήρωσης είναι ο πραγματικός άξονας από το 1 στο. Τότε η λύση είναι u(z) = = ρ 1 1 K(z, t)υ(t)dt (1.149) (t z) a t a c (t 1) c b 1 dt Η επιλογή της παραμέτρου ρ γίνεται σε συνδυασμό με τη λύση υπό μορϕή σειράς. Αναπτύσσοντας την (1.150) σε σειρά και συγκρίνοντας με την (1.115) έχουμε ρ = Γ(c) Γ(b)Γ(c b) 1.12 Surrèousa Upergewmetrik seirˆ Συρρέουσα (conf luent) Υπεργεωμετρική διαϕορική εξίσωση είναι x d2 y(x) d x 2 + (c x) d y(x) d x Η λύση προκύπτει με τη γνωστή μέθοδο επίλυσης των ΔΕ, 1F 1 (a, c; x) = Γ(c) Γ(a + n) x n Γ(a) Γ(c + n) n! = 1 + a c x 1! (1.150) a y(x) = 0 (1.151) + a(a + 1) c(c + 1) x 2 2! + (1.152) και καλείται Συρρέουσα Υπεργεωμετρική σειρά. Άν η παράμετρος a είναι αρνητικός ακέραιος, a = N, τότε η σειρά τερματίζεται και η λύση είναι πολυωνυμική βαθμού N. Πλήθος γνωστών συναρτήσεων αναπαρίστανται ως ειδικές περιπτώσεις της (1.152). Η δεύτερη γραμικά ανεξάρτητη λύση της ΔΕ δίδεται απο y(x) = x 1 c 2F 1 (a + 1 c, b + 1 c, 2 c; x) (1.153) Μια χρήσιμη μορϕή της ΔΕ (1.154) προκύπτει με την αντικατάσταση x = t 2. Λαμβάνοντας υπ όψη d y(x) = 1 d y(t 2 ) d x 2t d t d 2 y(x) d x 2 = 1 d 2 y(t 2 ) 4t 2 d t 2 1 d y(t 2 ) 4t 3 d t
36 36 ΚΕΦ ΑΛΑΙΟ 1. ΣΤΟΙΧΕ ΙΑ ΔΙΑΦΟΡΙΚ ΩΝ ΕΞΙΣ ΩΣΕΩΝ η (1.154) παίρνει τη μορϕή d 2 y(t 2 ( ) ) 2c 1 d y(t 2 ) d t 2 + 2t 4 a y(t 2 ) = 0 (1.154) t d t Efarmogèc 1. Θα δειχθεί ό,τι η διαϕορική εξίσωση d 2 u(x) d x 2 ( ) l(l + 1) x 2 + x 2 α u(x) = 0 (1.155) ανάγεται με κατάλληλο μετασχηματισμό στην (1.154). Κάνουμε τον μετασχηματισμό u(x) = x l+1 f(x) (1.156) u (x) = x l+1 f (x) + (l + 1)x l f(x) u (x) = x l+1 f (x) + 2(l + 1)x l f (x) + l(l + 1)x l 1 f(x) Αντικαθιστώντας, λαμβάνουμε f (x) + 2(l + 1) x Στη συνέχεια γράϕουμε την f(x) ως f (x) + (α x 2 ) f(x) = 0 (1.157) f(x) = e x2 /2 h(x) (1.158) συνεπώς η πρώτη και δεύτερη παράγωγος γράϕονται f (x) = e x2 /2 h (x) xe x2 /2 h(x) f (x) = e x2 /2 h (x) 2x e x2 /2 h (x) + (x 2 1) e x2 /2 h(x) Αντικαθιστώντας, καταλήγουμε στην ΔΕ d 2 ( ) h(x) (l + 1) d h(x) d x 2 + 2x (2(l + 1) + 1 α) h(x) = 0 x d x (1.159) η οποία είναι της ίδιας μορϕής με την (1.154). Συνεπώς η λύση της ΔΕ (1.155) είναι u(x) = x l+1 e x2 /2 1 F 1 ((2l + 3)/4 α/4, l + 3/2 ; x 2 ) (1.160) 2. Το ακτινικό μέρος της εξίσωσης Schroedinger παίρνει τη μορϕή d 2 R(ρ) d ρ ρ d R(ρ) d ρ ( l(l + 1) λ ρ 2 R(ρ) + ρ 1 ) R(ρ) = 0(1.161) 4
37 1.12. ΣΥΡΡ ΕΟΥΣΑ ΥΠΕΡΓΕΩΜΕΤΡΙΚ Η ΣΕΙΡ Α 37 όπου ρ = κάνουμε την αντικατάσταση 8µ E h, λ = Ze2 µ h 2 E (1.162) ρ = t 2, R(ρ) y(t) (1.163) και η διαϕορική εξίσωση λαμβάνει τη μορϕή d 2 y(t) d t ( ) d y(t) 4l(l + 1) t d t t 2 + t 2 4λ y(t) = 0 (1.164) Με στόχο να εξαλείψουμε την πρώτη παράγωγο στην ανωτέρω διαϕορική εξίσωση, κάνουμε την αντικατάσταση y(t) = t a u(t) u + 2a + 3 ( ) a(a + 2) 4l(l + 1) u + t t 2 t 2 + 4λ u = 0(1.165) Επιλέγοντας, a = 3/2 καταλήγουμε τελικά στην εξίσωση ( ) (4l + 3)(4l + 1) u + t 2 4λ u = 0 (1.166) που έχει την ίδια μορϕή με την (1.155). 3. Κλασσικά Πολυώνυμα t 2 Από την γενική εξίσωση (Surm Liouville) ( d p(x) d u ) + q(x) u(x) + λ w(x) u(x) = 0 (1.167) για συγκεκριμμένες επιλογές των p(x), q(x), w(x), λ, προκύπτουν τα κλασσικά πολυώνυμα. Laguerre Αντικαθιστουμε και λαμβάνουμε p(x) = x e x, q(x) = 0, w(x) = e x x u + (1 x) u + λ u = 0 (1.168) Συγκρίνοντας με την (1.154), διαπιστώνουμε ότι ταυτίζονται για c = 1, λ = a. Συνεπώς για ακέραιο λ = n λαμβάνουμε τα πολυώνυμα Laguerre Hermite L n (x) = 1 F 1 ( n, 1; x) (1.169) p(x) = e x2, q(x) = 0, w(x) = e x2
38 38 ΚΕΦ ΑΛΑΙΟ 1. ΣΤΟΙΧΕ ΙΑ ΔΙΑΦΟΡΙΚ ΩΝ ΕΞΙΣ ΩΣΕΩΝ Αντικαθιστουμε και λαμβάνουμε u 2x u + 2n u = 0 (1.170) Συγκρίνοντας με την (1.154), διαπιστώνουμε ότι ταυτίζονται για c = 1/2, λ = n. Συνεπώς λαμβάνουμε τα πολυώνυμα Hermite H 2n (x) = 1 F 1 ( n, 1/2; x 2 ) (1.171)
Γεωργίου Κ. Λεοντάρη Καθηγητή Θεωρητικής Φυσικής. Μαθηματικές Μέθοδοι Φυσικής ΙΙ Πανεπιστημιακές Παραδόσεις. Πανεπιστήμιο Ιωαννίνων Ιωάννινα 2013
 1 Γεωργίου Κ. Λεοντάρη Καθηγητή Θεωρητικής Φυσικής. Μαθηματικές Μέθοδοι Φυσικής ΙΙ Πανεπιστημιακές Παραδόσεις Πανεπιστήμιο Ιωαννίνων Ιωάννινα 2013 2 Περιεχόμενα 1 Στοιχεία Διαϕορικών Εξισώσεων 5 1.1 Συνήθεις
1 Γεωργίου Κ. Λεοντάρη Καθηγητή Θεωρητικής Φυσικής. Μαθηματικές Μέθοδοι Φυσικής ΙΙ Πανεπιστημιακές Παραδόσεις Πανεπιστήμιο Ιωαννίνων Ιωάννινα 2013 2 Περιεχόμενα 1 Στοιχεία Διαϕορικών Εξισώσεων 5 1.1 Συνήθεις
y 1 (x) f(x) W (y 1, y 2 )(x) dx,
 Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 07/1/017 Μέρος 1ο: Μη Ομογενείς Γραμμικές Διαφορικές Εξισώσεις Δεύτερης Τάξης Θεωρούμε τη γραμμική μή-ομογενή διαφορική εξίσωση y + p(x) y + q(x) y = f(x), x
Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 07/1/017 Μέρος 1ο: Μη Ομογενείς Γραμμικές Διαφορικές Εξισώσεις Δεύτερης Τάξης Θεωρούμε τη γραμμική μή-ομογενή διαφορική εξίσωση y + p(x) y + q(x) y = f(x), x
Συνήθεις Διαφορικές Εξισώσεις Ι ΣΔΕ Bernoulli, Riccati, Ομογενείς. Διαφορικές Εξισώσεις Bernoulli, Riccati και Ομογενείς
 Συνήθεις Διαφορικές Εξισώσεις Ι ΣΔΕ Bernoulli, Riccati, Ομογενείς Διαφορικές Εξισώσεις Bernoulli, Riccati και Ομογενείς Οι εξισώσεις Bernoulli αποτελούν την κλάση των μη γραμμικών διαφορικών εξισώσεων
Συνήθεις Διαφορικές Εξισώσεις Ι ΣΔΕ Bernoulli, Riccati, Ομογενείς Διαφορικές Εξισώσεις Bernoulli, Riccati και Ομογενείς Οι εξισώσεις Bernoulli αποτελούν την κλάση των μη γραμμικών διαφορικών εξισώσεων
Μέϑοδοι Εφαρμοσμένων Μαϑηματιϰών (ΜΕΜ 274) Φυλλάδιο 8
 Μέϑοδοι Εφαρμοσμένων Μαϑηματιϰών (ΜΕΜ 274) Φυλλάδιο 8 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΤΟΠΙΚΗ ΑΝΑΛΥΣΗ ΓΡΑΜΜΙΚΩΝ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ Θεωρούμε τη γενιϰή ομογενή γραμμιϰή διαφοριϰή εξίσωση τάξης n N στην ϰανονιϰή μορφή της
Μέϑοδοι Εφαρμοσμένων Μαϑηματιϰών (ΜΕΜ 274) Φυλλάδιο 8 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΤΟΠΙΚΗ ΑΝΑΛΥΣΗ ΓΡΑΜΜΙΚΩΝ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ Θεωρούμε τη γενιϰή ομογενή γραμμιϰή διαφοριϰή εξίσωση τάξης n N στην ϰανονιϰή μορφή της
(i) f(x, y) = xy + iy (iii) f(x, y) = e y e ix. f(z) = U(r, θ) + iv (r, θ) ; z = re iθ
 ΜΑΘΗΜΑΤΙΚΗ ΦΥΣΙΚΗ (ΜΕΤΑΠΤΥΧΙΑΚΟ) 6 Νοεμβρίου 07 Αναλυτικές συναρτήσεις Άσκηση (i) Δείξτε ότι η συνάρτηση f(z) είναι αναλυτική σε χωρίο D του μιγαδικού επιπέδου εάν και μόνο εάν η if(z) είναι αναλυτική
ΜΑΘΗΜΑΤΙΚΗ ΦΥΣΙΚΗ (ΜΕΤΑΠΤΥΧΙΑΚΟ) 6 Νοεμβρίου 07 Αναλυτικές συναρτήσεις Άσκηση (i) Δείξτε ότι η συνάρτηση f(z) είναι αναλυτική σε χωρίο D του μιγαδικού επιπέδου εάν και μόνο εάν η if(z) είναι αναλυτική
ΕΞΙΣΩΣΕΙΣ ΔΙΑΦΟΡΩΝ ΟΡΙΣΜΟΙ: διαφορές των αγνώστων συναρτήσεων. σύνολο τιμών. F(k,y k,y. =0, k=0,1,2, δείκτη των y k. =0 είναι 2 ης τάξης 1.
 ΕΞΙΣΩΣΕΙΣ ΔΙΑΦΟΡΩΝ ΟΡΙΣΜΟΙ: Οι Εξισώσεις Διαφορών (ε.δ.) είναι εξισώσεις που περιέχουν διακριτές αλλαγές και διαφορές των αγνώστων συναρτήσεων Εμφανίζονται σε μαθηματικά μοντέλα, όπου η μεταβλητή παίρνει
ΕΞΙΣΩΣΕΙΣ ΔΙΑΦΟΡΩΝ ΟΡΙΣΜΟΙ: Οι Εξισώσεις Διαφορών (ε.δ.) είναι εξισώσεις που περιέχουν διακριτές αλλαγές και διαφορές των αγνώστων συναρτήσεων Εμφανίζονται σε μαθηματικά μοντέλα, όπου η μεταβλητή παίρνει
Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 09/11/2017. Άσκηση 1. Να βρεθεί η γενική λύση της διαφορικής εξίσωσης. dy dx = 2y + x 2 y 2 2x
 Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 09/11/017 Άσκηση 1. Να βρεθεί η γενική λύση της διαφορικής εξίσωσης dx y + x y. x Παρατηρούμε ότι η δ.ε. είναι ομογενής. Πράγματι, dx y x + 1 x y x y x + 1 (
Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 09/11/017 Άσκηση 1. Να βρεθεί η γενική λύση της διαφορικής εξίσωσης dx y + x y. x Παρατηρούμε ότι η δ.ε. είναι ομογενής. Πράγματι, dx y x + 1 x y x y x + 1 (
Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 26/10/2017. Διαφορικές Εξισώσεις Bernoulli, Riccati και Ομογενείς
 Συνθεις Διαφορικές Εξισώσεις Ι Ασκσεις - 26/0/207 Διαφορικές Εξισώσεις Bernoulli, Riccati και Ομογενείς Οι εξισώσεις Bernoulli αποτελούν την κλάση των μη γραμμικών διαφορικών εξισώσεων πρώτης τάξης της
Συνθεις Διαφορικές Εξισώσεις Ι Ασκσεις - 26/0/207 Διαφορικές Εξισώσεις Bernoulli, Riccati και Ομογενείς Οι εξισώσεις Bernoulli αποτελούν την κλάση των μη γραμμικών διαφορικών εξισώσεων πρώτης τάξης της
9 Πολυώνυμα Διαίρεση πολυωνύμων
 4ο Κεφάλαιο 9 Πολυώνυμα Διαίρεση πολυωνύμων Α ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ορισμοί Μονώνυμο του x ονομάζουμε κάθε παράσταση της μορφής ν αx όπου α R, * ν N και x μια μεταβλητή που μπορεί να πάρει οποιαδήποτε
4ο Κεφάλαιο 9 Πολυώνυμα Διαίρεση πολυωνύμων Α ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ορισμοί Μονώνυμο του x ονομάζουμε κάθε παράσταση της μορφής ν αx όπου α R, * ν N και x μια μεταβλητή που μπορεί να πάρει οποιαδήποτε
Κεφάλαιο 1: Προβλήµατα τύπου Sturm-Liouville
 Κεφάλαιο : Προβλήµατα τύπου Stur-Liouvie. Ορισµός προβλήµατος Stur-Liouvie Πολλές τεχνικές επίλυσης µερικών διαφορικών εξισώσεων βασίζονται στην αναγωγή της µερικής διαφορικής εξίσωσης σε συνήθεις διαφορικές
Κεφάλαιο : Προβλήµατα τύπου Stur-Liouvie. Ορισµός προβλήµατος Stur-Liouvie Πολλές τεχνικές επίλυσης µερικών διαφορικών εξισώσεων βασίζονται στην αναγωγή της µερικής διαφορικής εξίσωσης σε συνήθεις διαφορικές
Διαφορικές Εξισώσεις.
 Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 05-6. Λύσεις δεύτερου φυλλαδίου ασκήσεων.. Βρείτε όλες τις λύσεις της εξίσωσης Bernoulli x y = xy + y 3 καθορίζοντας προσεκτικά το διάστημα στο οποίο ορίζεται καθεμιά
Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 05-6. Λύσεις δεύτερου φυλλαδίου ασκήσεων.. Βρείτε όλες τις λύσεις της εξίσωσης Bernoulli x y = xy + y 3 καθορίζοντας προσεκτικά το διάστημα στο οποίο ορίζεται καθεμιά
2ογελ ΣΥΚΕΩΝ 2ογελ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β Λυκει(ου ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ
 ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β Λυκει(ου ο ΓΕΛ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β ΛΥΚΕΙΟΥ ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΣΧΟΛΙΚΟ ΕΤΟΣ -4 ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Επιμέλεια: ΧΑΛΑΤΖΙΑΝ ΠΑΥΛΟΣ
ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β Λυκει(ου ο ΓΕΛ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β ΛΥΚΕΙΟΥ ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΣΧΟΛΙΚΟ ΕΤΟΣ -4 ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Επιμέλεια: ΧΑΛΑΤΖΙΑΝ ΠΑΥΛΟΣ
Πολυωνυμικές εξισώσεις και ανισώσεις Εξισώσεις και ανισώσεις που ανάγονται σε πολυωνυμικές
 0 Πολυωνυμικές εξισώσεις και ανισώσεις Εξισώσεις και ανισώσεις που ανάγονται σε πολυωνυμικές Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Για να λύσουμε μια πολυωνυμική εξίσωση P(x) 0 (ή μια πολυωνυμική ανίσωση P(x)
0 Πολυωνυμικές εξισώσεις και ανισώσεις Εξισώσεις και ανισώσεις που ανάγονται σε πολυωνυμικές Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Για να λύσουμε μια πολυωνυμική εξίσωση P(x) 0 (ή μια πολυωνυμική ανίσωση P(x)
Μέϑοδοι Εφαρμοσμένων Μαϑηματιϰών (ΜΕΜ 274) Φυλλάδιο 2
 Μέϑοδοι Εφαρμοσμένων Μαϑηματιϰών (ΜΕΜ 274) Φυλλάδιο 2 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΕΝΝΟΙΑ ΤΗΣ ΑΣΥΜΠΤΩΤΙΚΗΣ ΣΕΙΡΑΣ Εστω μη ϰενά διαστήματα J, I R, με 0 Ī. Ονομάζουμε μεταβλητή το x J ϰαι ασυμπτωτιϰή (ή διαταραϰτιϰή) παράμετρο
Μέϑοδοι Εφαρμοσμένων Μαϑηματιϰών (ΜΕΜ 274) Φυλλάδιο 2 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΕΝΝΟΙΑ ΤΗΣ ΑΣΥΜΠΤΩΤΙΚΗΣ ΣΕΙΡΑΣ Εστω μη ϰενά διαστήματα J, I R, με 0 Ī. Ονομάζουμε μεταβλητή το x J ϰαι ασυμπτωτιϰή (ή διαταραϰτιϰή) παράμετρο
ΚΕΦΑΛΑΙΟ 3 ΤΟ ΔΙΩΝΥΜΙΚΟ ΘΕΩΡΗΜΑ
 ΚΕΦΑΛΑΙΟ 3 ΤΟ ΔΙΩΝΥΜΙΚΟ ΘΕΩΡΗΜΑ Εισαγωγή Οι αριθμοί που εκφράζουν το πλήθος των στοιχείων ανά αποτελούν ίσως τους πιο σημαντικούς αριθμούς της Συνδυαστικής και καλούνται διωνυμικοί συντελεστές διότι εμφανίζονται
ΚΕΦΑΛΑΙΟ 3 ΤΟ ΔΙΩΝΥΜΙΚΟ ΘΕΩΡΗΜΑ Εισαγωγή Οι αριθμοί που εκφράζουν το πλήθος των στοιχείων ανά αποτελούν ίσως τους πιο σημαντικούς αριθμούς της Συνδυαστικής και καλούνται διωνυμικοί συντελεστές διότι εμφανίζονται
ΚΕΦ. 1. ΣΥΝΗΘΕΙΣ ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ Εισαγωγή.
 1 ΚΕΦ. 1. ΣΥΝΗΘΕΙΣ ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ 1.1. Εισαγωγή. Σε ότι ακολουθεί με τον όρο συνάρτηση θα εννοούμε μια πραγματική συνάρτηση πραγματικής μεταβλητής, ορισμένη σε ένα διάστημα πραγματικών αριθμών. Σε
1 ΚΕΦ. 1. ΣΥΝΗΘΕΙΣ ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ 1.1. Εισαγωγή. Σε ότι ακολουθεί με τον όρο συνάρτηση θα εννοούμε μια πραγματική συνάρτηση πραγματικής μεταβλητής, ορισμένη σε ένα διάστημα πραγματικών αριθμών. Σε
Δηλαδή η ρητή συνάρτηση είναι πηλίκο δύο ακέραιων πολυωνύμων. Επομένως, το ζητούμενο ολοκλήρωμα είναι της μορφής
 D ολοκλήρωση ρητών συναρτήσεων Το θέμα μας στην ενότητα αυτή είναι η ολοκλήρωση ρητών συναρτήσεων. Ας θυμηθούμε πρώτα ποιες συναρτήσεις ονομάζονται ρητές. Ορισμός: Μία συνάρτηση ονομάζεται ρητή όταν μπορεί
D ολοκλήρωση ρητών συναρτήσεων Το θέμα μας στην ενότητα αυτή είναι η ολοκλήρωση ρητών συναρτήσεων. Ας θυμηθούμε πρώτα ποιες συναρτήσεις ονομάζονται ρητές. Ορισμός: Μία συνάρτηση ονομάζεται ρητή όταν μπορεί
ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 8: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ [Ενότητα Μονοτονία Συνάρτησης του κεφ.2.6 Μέρος Β του σχολικού βιβλίου].
![ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 8: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ [Ενότητα Μονοτονία Συνάρτησης του κεφ.2.6 Μέρος Β του σχολικού βιβλίου]. ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 8: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ [Ενότητα Μονοτονία Συνάρτησης του κεφ.2.6 Μέρος Β του σχολικού βιβλίου].](/thumbs/52/29746903.jpg) ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 8: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ [Ενότητα Μονοτονία Συνάρτησης του κεφ..6 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα 1. ΘΕΜΑ Β Να μελετηθούν ως προς την μονοτονία
ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 8: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ [Ενότητα Μονοτονία Συνάρτησης του κεφ..6 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα 1. ΘΕΜΑ Β Να μελετηθούν ως προς την μονοτονία
Μέϑοδοι Εφαρμοσμένων Μαϑηματιϰών (ΜΕΜ 274) Λύσεις Θεμάτων Εξέτασης Ιούνη 2019
 Μέϑοδοι Εφαρμοσμένων Μαϑηματιϰών ΜΕΜ 74 Λύσεις Θεμάτων Εξέτασης Ιούνη 9 Ζήτημα Α Α. Δείξτε ότι αν p, q πραγματιϰά πολυώνυμα ίδιου βαϑμού, τότε p q ϰαϑώς ±. Λύση. Αρϰεί να δείξουμε ότι για με αρϰετά μεγάλο
Μέϑοδοι Εφαρμοσμένων Μαϑηματιϰών ΜΕΜ 74 Λύσεις Θεμάτων Εξέτασης Ιούνη 9 Ζήτημα Α Α. Δείξτε ότι αν p, q πραγματιϰά πολυώνυμα ίδιου βαϑμού, τότε p q ϰαϑώς ±. Λύση. Αρϰεί να δείξουμε ότι για με αρϰετά μεγάλο
1.1 Βασικές Έννοιες των Διαφορικών Εξισώσεων
 Κεφάλαιο 1 Εισαγωγικά Στο κεφάλαιο αυτό θα παρουσιάσουμε τις βασικές έννοιες και ορισμούς των Διαφορικών Εξισώσεων. Στο εδάφιο 1.1 παρουσιάζονται οι βασικές έννοιες και ορισμοί των διαφορικών εξισώσεων
Κεφάλαιο 1 Εισαγωγικά Στο κεφάλαιο αυτό θα παρουσιάσουμε τις βασικές έννοιες και ορισμούς των Διαφορικών Εξισώσεων. Στο εδάφιο 1.1 παρουσιάζονται οι βασικές έννοιες και ορισμοί των διαφορικών εξισώσεων
f (x) dx = f (x) + c a f (x) f (x) cos 2 (f (x)) f (x) dx = tan(f (x)) + c 1 sin 2 (f (x)) f (x) dx = cot(f (x)) + c e f (x) f (x) dx = e f (x) + c
 Ασκήσεις στα Μαθηματικά Ι Τμήμα Χημ. Μηχανικών ΑΠΘ Μουτάφη Ευαγγελία Θεσσαλονίκη 208-209 Ορισμοί ΤΟ ΑΟΡΙΣΤΟ ΟΛΟΚΛΗΡΩΜΑ Αντιπαράγωγος συνάρτησης Εστω συνάρτηση f : R, R διάστημα. Αν για τη συνάρτηση F :
Ασκήσεις στα Μαθηματικά Ι Τμήμα Χημ. Μηχανικών ΑΠΘ Μουτάφη Ευαγγελία Θεσσαλονίκη 208-209 Ορισμοί ΤΟ ΑΟΡΙΣΤΟ ΟΛΟΚΛΗΡΩΜΑ Αντιπαράγωγος συνάρτησης Εστω συνάρτηση f : R, R διάστημα. Αν για τη συνάρτηση F :
1.1. Διαφορική Εξίσωση και λύση αυτής
 Εισαγωγή στις συνήθεις διαφορικές εξισώσεις 9 Διαφορική Εξίσωση και λύση αυτής Σε ότι ακολουθεί με τον όρο συνάρτηση θα εννοούμε μια πραγματική συνάρτηση μιας πραγματικής μεταβλητής, ορισμένη σε ένα διάστημα
Εισαγωγή στις συνήθεις διαφορικές εξισώσεις 9 Διαφορική Εξίσωση και λύση αυτής Σε ότι ακολουθεί με τον όρο συνάρτηση θα εννοούμε μια πραγματική συνάρτηση μιας πραγματικής μεταβλητής, ορισμένη σε ένα διάστημα
a (x)y a (x)y a (x)y' a (x)y 0
 Γραμμικές Διαφορικές εξισώσεις Ανώτερης Τάξης Έστω ότι έχουμε μια γραμμική διαφορική εξίσωση τάξης n a (x) a (x) a (x)' a (x) f (x) () (n) (n) n n 0 όπου a i(x),i 0,...,n και f(x) είναι συνεχείς συναρτήσεις
Γραμμικές Διαφορικές εξισώσεις Ανώτερης Τάξης Έστω ότι έχουμε μια γραμμική διαφορική εξίσωση τάξης n a (x) a (x) a (x)' a (x) f (x) () (n) (n) n n 0 όπου a i(x),i 0,...,n και f(x) είναι συνεχείς συναρτήσεις
Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 19/10/2017. Ακριβείς Διαφορικές Εξισώσεις-Ολοκληρωτικοί Παράγοντες. Η πρώτης τάξης διαφορική εξίσωση
 Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 19/10/2017 Ακριβείς Διαφορικές Εξισώσεις-Ολοκληρωτικοί Παράγοντες Η πρώτης τάξης διαφορική εξίσωση M(x, y) + (x, y)y = 0 ή ισοδύναμα, γραμμένη στην μορφή M(x,
Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 19/10/2017 Ακριβείς Διαφορικές Εξισώσεις-Ολοκληρωτικοί Παράγοντες Η πρώτης τάξης διαφορική εξίσωση M(x, y) + (x, y)y = 0 ή ισοδύναμα, γραμμένη στην μορφή M(x,
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής Φυσική Σημασία του Μετασχηματισμού Fourier Ο μετασχηματισμός Fourier
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής Φυσική Σημασία του Μετασχηματισμού Fourier Ο μετασχηματισμός Fourier
10 ΣΥΝΗΘΕΙΣ ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ
 SECTION 0 ΣΥΝΗΘΕΙΣ ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ 0. Ορισµοί Συνήθης διαφορική εξίσωση (Σ Ε) καλείται µια εξίσωση της µορφής f [y (n), y (n ),..., y'', y', y, x] 0 όπου y', y'',..., y (n ), y (n) είναι οι παράγωγοι
SECTION 0 ΣΥΝΗΘΕΙΣ ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ 0. Ορισµοί Συνήθης διαφορική εξίσωση (Σ Ε) καλείται µια εξίσωση της µορφής f [y (n), y (n ),..., y'', y', y, x] 0 όπου y', y'',..., y (n ), y (n) είναι οι παράγωγοι
12. ΑΝΙΣΩΣΕΙΣ Α ΒΑΘΜΟΥ. είναι δύο παραστάσεις μιας μεταβλητής x πού παίρνει τιμές στο
 ΓΕΝΙΚΑ ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Έστω f σύνολο Α, g Α ΒΑΘΜΟΥ είναι δύο παραστάσεις μιας μεταβλητής πού παίρνει τιμές στο Ανίσωση με έναν άγνωστο λέγεται κάθε σχέση της μορφής f f g g ή, η οποία αληθεύει για ορισμένες
ΓΕΝΙΚΑ ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Έστω f σύνολο Α, g Α ΒΑΘΜΟΥ είναι δύο παραστάσεις μιας μεταβλητής πού παίρνει τιμές στο Ανίσωση με έναν άγνωστο λέγεται κάθε σχέση της μορφής f f g g ή, η οποία αληθεύει για ορισμένες
1 GRAMMIKES DIAFORIKES EXISWSEIS DEUTERAS TAXHS
 1 GRAMMIKES DIAFORIKES EXISWSEIS DEUTERAS TAXHS Γραμμικές μη ομογενείς διαφορικές εξισώσεις δευτέρας τάξης λέγονται οι εξισώσεις τύπου y + p(x)y + g(x)y = f(x) (1.1) Οταν f(x) = 0 η εξίσωση y + p(x)y +
1 GRAMMIKES DIAFORIKES EXISWSEIS DEUTERAS TAXHS Γραμμικές μη ομογενείς διαφορικές εξισώσεις δευτέρας τάξης λέγονται οι εξισώσεις τύπου y + p(x)y + g(x)y = f(x) (1.1) Οταν f(x) = 0 η εξίσωση y + p(x)y +
Κεφάλαιο 3 ΠΑΡΑΓΩΓΟΣ. 3.1 Η έννοια της παραγώγου. y = f(x) f(x 0 ), = f(x 0 + x) f(x 0 )
 Κεφάλαιο 3 ΠΑΡΑΓΩΓΟΣ 3.1 Η έννοια της παραγώγου Εστω y = f(x) µία συνάρτηση, που συνδέει τις µεταβλητές ποσότητες x και y. Ενα ερώτηµα που µπορεί να προκύψει καθώς µελετούµε τις δύο αυτές ποσοτήτες είναι
Κεφάλαιο 3 ΠΑΡΑΓΩΓΟΣ 3.1 Η έννοια της παραγώγου Εστω y = f(x) µία συνάρτηση, που συνδέει τις µεταβλητές ποσότητες x και y. Ενα ερώτηµα που µπορεί να προκύψει καθώς µελετούµε τις δύο αυτές ποσοτήτες είναι
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Ολοκλήρωση Εισαγωγή Έστω ότι η f είναι μία φραγμένη συνάρτηση στο πεπερασμένο
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Ολοκλήρωση Εισαγωγή Έστω ότι η f είναι μία φραγμένη συνάρτηση στο πεπερασμένο
Διαφορικές Εξισώσεις Πρώτης Τάξης
 Κεφάλαιο 2 Διαφορικές Εξισώσεις Πρώτης Τάξης Στο κεφάλαιο αυτό θα μελετήσουμε διαφορικές εξισώσεις πρώτης τάξης και θα διατυπώσουμε χωρίς απόδειξη βασικά θεωρήματα αυτών. Το εδάφιο 2.1 ασχολείται με γραμμικές
Κεφάλαιο 2 Διαφορικές Εξισώσεις Πρώτης Τάξης Στο κεφάλαιο αυτό θα μελετήσουμε διαφορικές εξισώσεις πρώτης τάξης και θα διατυπώσουμε χωρίς απόδειξη βασικά θεωρήματα αυτών. Το εδάφιο 2.1 ασχολείται με γραμμικές
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Αντίστροφος Μετασχηματισμός Laplace Στην
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Αντίστροφος Μετασχηματισμός Laplace Στην
M. J. Lighthill. g(y) = f(x) e 2πixy dx, (1) d N. g (p) (y) =
 Εισαγωγή στην ανάλυση Fourier και τις γενικευμένες συναρτήσεις * M. J. Lighthill μετάφραση: Γ. Ευθυβουλίδης ΚΕΦΑΛΑΙΟ 2 Η ΘΕΩΡΙΑ ΤΩΝ ΓΕΝΙΚΕΥΜΕΝΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΚΑΙ ΤΩΝ ΜΕΤΑΣΧΗΜΑΤΙΣΜΩΝ ΤΟΥΣ FOURIER 2.1. Καλές
Εισαγωγή στην ανάλυση Fourier και τις γενικευμένες συναρτήσεις * M. J. Lighthill μετάφραση: Γ. Ευθυβουλίδης ΚΕΦΑΛΑΙΟ 2 Η ΘΕΩΡΙΑ ΤΩΝ ΓΕΝΙΚΕΥΜΕΝΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΚΑΙ ΤΩΝ ΜΕΤΑΣΧΗΜΑΤΙΣΜΩΝ ΤΟΥΣ FOURIER 2.1. Καλές
Παράδειγμα 14.2 Να βρεθεί ο μετασχηματισμός Laplace των συναρτήσεων
 Κεφάλαιο 4 Μετασχηματισμός aplace 4. Μετασχηματισμός aplace της εκθετικής συνάρτησης e Είναι Άρα a a a u( a ( a ( a ( aj F( e e d e d [ e ] [ e ] ( a e (c ji, με a (4.9 a a a [ e u( ] a, με a (4.3 Η σχέση
Κεφάλαιο 4 Μετασχηματισμός aplace 4. Μετασχηματισμός aplace της εκθετικής συνάρτησης e Είναι Άρα a a a u( a ( a ( a ( aj F( e e d e d [ e ] [ e ] ( a e (c ji, με a (4.9 a a a [ e u( ] a, με a (4.3 Η σχέση
Μερικές Διαφορικές Εξισώσεις
 Πανεπιστήμιο Πατρών, Τμήμα Μαθηματικών Μερικές Διαφορικές Εξισώσεις Χειμερινό εξάμηνο ακαδημαϊκού έτους 24-25, Διδάσκων: Α.Τόγκας ο φύλλο προβλημάτων Ονοματεπώνυμο - ΑΜ: ΜΔΕ ο φύλλο προβλημάτων Α. Τόγκας
Πανεπιστήμιο Πατρών, Τμήμα Μαθηματικών Μερικές Διαφορικές Εξισώσεις Χειμερινό εξάμηνο ακαδημαϊκού έτους 24-25, Διδάσκων: Α.Τόγκας ο φύλλο προβλημάτων Ονοματεπώνυμο - ΑΜ: ΜΔΕ ο φύλλο προβλημάτων Α. Τόγκας
Ο μαθητής που έχει μελετήσει το κεφάλαιο αυτό θα πρέπει:
 Ο μαθητής που έχει μελετήσει το κεφάλαιο αυτό θα πρέπει: Να αναγνωρίζει πότε μια αλγεβρική παράσταση της πραγματικής μεταβλητής x, είναι πολυώνυμο και να διακρίνει τα στοιχεία του: όροι, συντελεστές, σταθερός
Ο μαθητής που έχει μελετήσει το κεφάλαιο αυτό θα πρέπει: Να αναγνωρίζει πότε μια αλγεβρική παράσταση της πραγματικής μεταβλητής x, είναι πολυώνυμο και να διακρίνει τα στοιχεία του: όροι, συντελεστές, σταθερός
Παράρτημα Αʹ. Ασκησεις. Αʹ.1 Ασκήσεις Κεϕαλαίου 1: Εισαγωγή στη κβαντική ϕύση του ϕωτός.
 Παράρτημα Αʹ Ασκησεις Αʹ.1 Ασκήσεις Κεϕαλαίου 1: Εισαγωγή στη κβαντική ϕύση του ϕωτός. Άσκηση 1. Συμβατικά στην περιοχή του ηλεκτρομαγνητικού ϕάσματος μακρινό υπέρυθρο (far infrared, FIR) έχουμε μήκος
Παράρτημα Αʹ Ασκησεις Αʹ.1 Ασκήσεις Κεϕαλαίου 1: Εισαγωγή στη κβαντική ϕύση του ϕωτός. Άσκηση 1. Συμβατικά στην περιοχή του ηλεκτρομαγνητικού ϕάσματος μακρινό υπέρυθρο (far infrared, FIR) έχουμε μήκος
Λ. Ζαχείλας. Επίκουρος Καθηγητής Εφαρμοσμένων Μαθηματικών Τμήμα Οικονομικών Επιστημών Πανεπιστήμιο Θεσσαλίας. Οικονομική Δυναμική 29/6/14
 1 Λ. Ζαχείλας Επίκουρος Καθηγητής Εφαρμοσμένων Μαθηματικών Τμήμα Οικονομικών Επιστημών Πανεπιστήμιο Θεσσαλίας Οικονομική Δυναμική 9 Συνεχή δυναμικά συστήματα Μέρος 1 ο Λουκάς Ζαχείλας Ορισμός Διαφορικής
1 Λ. Ζαχείλας Επίκουρος Καθηγητής Εφαρμοσμένων Μαθηματικών Τμήμα Οικονομικών Επιστημών Πανεπιστήμιο Θεσσαλίας Οικονομική Δυναμική 9 Συνεχή δυναμικά συστήματα Μέρος 1 ο Λουκάς Ζαχείλας Ορισμός Διαφορικής
Μερικές Διαφορικές Εξισώσεις
 Πανεπιστήμιο Πατρών, Τμήμα Μαθηματικών Μερικές Διαφορικές Εξισώσεις Χειμερινό εξάμηνο ακαδημαϊκού έτους 14-15, Διδάσκων: Α.Τόγκας ο φύλλο προβλημάτων Ονοματεπώνυμο - ΑΜ: Πρόβλημα 1. Για κάθε μια από τις
Πανεπιστήμιο Πατρών, Τμήμα Μαθηματικών Μερικές Διαφορικές Εξισώσεις Χειμερινό εξάμηνο ακαδημαϊκού έτους 14-15, Διδάσκων: Α.Τόγκας ο φύλλο προβλημάτων Ονοματεπώνυμο - ΑΜ: Πρόβλημα 1. Για κάθε μια από τις
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ - ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΕΙΣΑΓΩΓΙΚΕΣ ΜΕΤΑΠΤΥΧΙΑΚΕΣ ΕΞΕΤΑΣΕΙΣ 26 ΙΟΥΛΙΟΥ 2008 ΕΥΤΕΡΟ ΜΕΡΟΣ :
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ - ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΑΛΓΕΒΡΑ - ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ ΑΝΑΛΥΣΗ ΑΡΙΘΜΗΤΙΚΗ ΑΝΑΛΥΣΗ ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΠΙΘΑΝΟΤΗΤΕΣ - ΣΤΑΤΙΣΤΙΚΗ ΕΙΣΑΓΩΓΙΚΕΣ ΜΕΤΑΠΤΥΧΙΑΚΕΣ ΕΞΕΤΑΣΕΙΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ - ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΑΛΓΕΒΡΑ - ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ ΑΝΑΛΥΣΗ ΑΡΙΘΜΗΤΙΚΗ ΑΝΑΛΥΣΗ ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΠΙΘΑΝΟΤΗΤΕΣ - ΣΤΑΤΙΣΤΙΚΗ ΕΙΣΑΓΩΓΙΚΕΣ ΜΕΤΑΠΤΥΧΙΑΚΕΣ ΕΞΕΤΑΣΕΙΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ - ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΕΙΣΑΓΩΓΙΚΕΣ ΜΕΤΑΠΤΥΧΙΑΚΕΣ ΕΞΕΤΑΣΕΙΣ 26 ΙΟΥΛΙΟΥ 2009 ΕΥΤΕΡΟ ΜΕΡΟΣ :
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ - ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΑΛΓΕΒΡΑ-ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ ΑΝΑΛΥΣΗ ΑΡΙΘΜΗΤΙΚΗ ΑΝΑΛΥΣΗ ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΠΙΘΑΝΟΤΗΤΕΣ-ΣΤΑΤΙΣΤΙΚΗ ΕΙΣΑΓΩΓΙΚΕΣ ΜΕΤΑΠΤΥΧΙΑΚΕΣ ΕΞΕΤΑΣΕΙΣ 26
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ - ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΑΛΓΕΒΡΑ-ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ ΑΝΑΛΥΣΗ ΑΡΙΘΜΗΤΙΚΗ ΑΝΑΛΥΣΗ ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΠΙΘΑΝΟΤΗΤΕΣ-ΣΤΑΤΙΣΤΙΚΗ ΕΙΣΑΓΩΓΙΚΕΣ ΜΕΤΑΠΤΥΧΙΑΚΕΣ ΕΞΕΤΑΣΕΙΣ 26
ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΕΙΑ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ
 ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΕΙΑ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ.Καρτάλη 8 Βόλος Τηλ. 43598 ΠΊΝΑΚΑΣ ΠΕΡΙΕΧΟΜΈΝΩΝ 3. Η ΕΝΝΟΙΑ ΤΗΣ ΠΑΡΑΓΩΓΟΥ... 5 ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ...
ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΕΙΑ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ.Καρτάλη 8 Βόλος Τηλ. 43598 ΠΊΝΑΚΑΣ ΠΕΡΙΕΧΟΜΈΝΩΝ 3. Η ΕΝΝΟΙΑ ΤΗΣ ΠΑΡΑΓΩΓΟΥ... 5 ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ...
f f 2 0 B f f 0 1 B 10.3 Ακρότατα υπό συνθήκες Πολλαπλασιαστές του Lagrange
 Μέγιστα και ελάχιστα 39 f f B f f yx y x xy Οι ιδιοτιμές του πίνακα Β είναι λ =-, λ =- και οι δυο αρνητικές, άρα το κρίσιμο σημείο (,) είναι σημείο τοπικού μεγίστου. Εφαρμογή 6: Στο παράδειγμα 3 ο αντίστοιχος
Μέγιστα και ελάχιστα 39 f f B f f yx y x xy Οι ιδιοτιμές του πίνακα Β είναι λ =-, λ =- και οι δυο αρνητικές, άρα το κρίσιμο σημείο (,) είναι σημείο τοπικού μεγίστου. Εφαρμογή 6: Στο παράδειγμα 3 ο αντίστοιχος
ΜΕΡΙΚΕΣ ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ
 ΜΑΣ 3: Συνήθεις Διαφορικές Εξισώσεις, Εαρινό Εξάμηνο 4 ΜΕΡΙΚΕΣ ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ Να ταξινομηθούν οι πιο κάτω ΣΔΕ με βάση τα εξής: τάξη, γραμμική ή μή Να δοθούν επίσης οι ανεξάρτητες και εξαρτημένες μεταβλητές
ΜΑΣ 3: Συνήθεις Διαφορικές Εξισώσεις, Εαρινό Εξάμηνο 4 ΜΕΡΙΚΕΣ ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ Να ταξινομηθούν οι πιο κάτω ΣΔΕ με βάση τα εξής: τάξη, γραμμική ή μή Να δοθούν επίσης οι ανεξάρτητες και εξαρτημένες μεταβλητές
ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ Κεφ. 1 - Συστήματα 1
 ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ Κεφ. 1 - Συστήματα 1 1.1 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Η εξίσωση α + βy = γ 1. Υπάρχουν προβλήματα που η επίλυση τους οδηγεί σε μια γραμμική εξίσωση με δύο αγνώστους, y και η οποία είναι της μορφής
ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ Κεφ. 1 - Συστήματα 1 1.1 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Η εξίσωση α + βy = γ 1. Υπάρχουν προβλήματα που η επίλυση τους οδηγεί σε μια γραμμική εξίσωση με δύο αγνώστους, y και η οποία είναι της μορφής
α) f(x(t), y(t)) = 0,
 Ρητές καμπύλες Μια επίπεδη αλγεβρική καμπύλη V (f) είναι το σύνολο όλων των σημείων του επιπέδου K 2 που μηδενίζουν κάποιο συγκεκριμένο ανάγωγο πολυώνυμο f K[x, y], δηλαδή V (f) = {(x 0, y 0 ) K 2 f(x
Ρητές καμπύλες Μια επίπεδη αλγεβρική καμπύλη V (f) είναι το σύνολο όλων των σημείων του επιπέδου K 2 που μηδενίζουν κάποιο συγκεκριμένο ανάγωγο πολυώνυμο f K[x, y], δηλαδή V (f) = {(x 0, y 0 ) K 2 f(x
ΑΚΡΟΤΑΤΑ ΣΥΝΑΡΤΗΣΕΩΝ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ
 6 KΕΦΑΛΑΙΟ 3 ΑΚΡΟΤΑΤΑ ΣΥΝΑΡΤΗΣΕΩΝ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ Η θεωρία μεγίστων και ελαχίστων μιας πραγματικής συνάρτησης με μια μεταβλητή είναι γνωστή Στο κεφάλαιο αυτό θα δούμε τη θεωρία μεγίστων και ελαχίστων
6 KΕΦΑΛΑΙΟ 3 ΑΚΡΟΤΑΤΑ ΣΥΝΑΡΤΗΣΕΩΝ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ Η θεωρία μεγίστων και ελαχίστων μιας πραγματικής συνάρτησης με μια μεταβλητή είναι γνωστή Στο κεφάλαιο αυτό θα δούμε τη θεωρία μεγίστων και ελαχίστων
- ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ
 ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ R - ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΣΤΟ ΑΠΕΙΡΟ - ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΑΚΟΛΟΥΘΙΑΣ [Κεφ..6: Μη Πεπερασμένο Όριο στο R - Κεφ..7: Όρια Συνάρτησης
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ R - ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΣΤΟ ΑΠΕΙΡΟ - ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΑΚΟΛΟΥΘΙΑΣ [Κεφ..6: Μη Πεπερασμένο Όριο στο R - Κεφ..7: Όρια Συνάρτησης
u x = 2uu y u y = 0 ϕ x = x t h (t), ϕ xx = x2 t 3 h (t) και ϕ y = y t h (t), ϕ yy = y2 t 3 h (t). t 2 h (t) + x2
 ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ & ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΟΜΕΑΣ ΜΑΘΗΜΑΤΙΚΩΝ Εξετάσεις στη Μιγαδική Ανάλυση ΟΜΑΔΑ: Β 9 Ιουνίου, 07 Θ. αʹ) Αν το G είναι ένας τόπος, δηλαδή ένα ανοικτό και συνεκτικό σύνολο στο
ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ & ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΟΜΕΑΣ ΜΑΘΗΜΑΤΙΚΩΝ Εξετάσεις στη Μιγαδική Ανάλυση ΟΜΑΔΑ: Β 9 Ιουνίου, 07 Θ. αʹ) Αν το G είναι ένας τόπος, δηλαδή ένα ανοικτό και συνεκτικό σύνολο στο
A N A B P Y T A ΑΣΚΗΣΕΙΣ ΠΟΛΥΩΝΥΜΩΝ. 1 (α + β + γ) [(α-β) 2 +(α-γ) 2 +(β-γ) 2 ] και τις υποθέσεις
![A N A B P Y T A ΑΣΚΗΣΕΙΣ ΠΟΛΥΩΝΥΜΩΝ. 1 (α + β + γ) [(α-β) 2 +(α-γ) 2 +(β-γ) 2 ] και τις υποθέσεις A N A B P Y T A ΑΣΚΗΣΕΙΣ ΠΟΛΥΩΝΥΜΩΝ. 1 (α + β + γ) [(α-β) 2 +(α-γ) 2 +(β-γ) 2 ] και τις υποθέσεις](/thumbs/93/111356738.jpg) ΑΣΚΗΣΕΙΣ ΠΟΛΥΩΝΥΜΩΝ ΑΣΚΗΣΗ η Αν α +β +γ = αβγ και α + β + γ, να δείξετε ότι το πολυώνυμο P()=(α β) +(β γ) + γ α είναι το μηδενικό πολυώνυμο. Από την ταυτότητα του Euler α +β +γ -αβγ = (α + β + γ)[(α-β)
ΑΣΚΗΣΕΙΣ ΠΟΛΥΩΝΥΜΩΝ ΑΣΚΗΣΗ η Αν α +β +γ = αβγ και α + β + γ, να δείξετε ότι το πολυώνυμο P()=(α β) +(β γ) + γ α είναι το μηδενικό πολυώνυμο. Από την ταυτότητα του Euler α +β +γ -αβγ = (α + β + γ)[(α-β)
I. ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. math-gr
 I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 2: ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΗΣ - ΚΑΝΟΝΕΣ ΠΑΡΑΓΩΓΙΣΗΣ - ΠΑΡΑΓΩΓΟΣ ΣΥΝΘΕΤΗΣ ΣΥΝΑΡΤΗΣΗΣ
 ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ : ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΗΣ - ΚΑΝΟΝΕΣ ΠΑΡΑΓΩΓΙΣΗΣ - ΠΑΡΑΓΩΓΟΣ ΣΥΝΘΕΤΗΣ ΣΥΝΑΡΤΗΣΗΣ [Κεφ..: Παραγωγίσιμες Συναρτήσεις Παράγωγος Συνάρτηση - Κεφ..: Κανόνες Παραγώγισης του
ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ : ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΗΣ - ΚΑΝΟΝΕΣ ΠΑΡΑΓΩΓΙΣΗΣ - ΠΑΡΑΓΩΓΟΣ ΣΥΝΘΕΤΗΣ ΣΥΝΑΡΤΗΣΗΣ [Κεφ..: Παραγωγίσιμες Συναρτήσεις Παράγωγος Συνάρτηση - Κεφ..: Κανόνες Παραγώγισης του
Κεφάλαιο 1 Συστήματα γραμμικών εξισώσεων
 Κεφάλαιο Συστήματα γραμμικών εξισώσεων Παραδείγματα από εφαρμογές Γραμμική Άλγεβρα Παράδειγμα : Σε ένα δίκτυο (αγωγών ή σωλήνων ή δρόμων) ισχύει ο κανόνας των κόμβων όπου το άθροισμα των εισερχόμενων ροών
Κεφάλαιο Συστήματα γραμμικών εξισώσεων Παραδείγματα από εφαρμογές Γραμμική Άλγεβρα Παράδειγμα : Σε ένα δίκτυο (αγωγών ή σωλήνων ή δρόμων) ισχύει ο κανόνας των κόμβων όπου το άθροισμα των εισερχόμενων ροών
2 (3x2 1) 5x 1 ) 5x 3 4x 3 )= 1 2 (5x3 3x) 7x 1 2 (5x3 3x) 3 ) + 48x ) 16x 3 )= 1 8 (63x5 70x 3 +15x)
 1 Prìblhma 4 Η αναδρομική σχέση γράφεται στη μορφή Για n =1 P n+1 = 1 n +1 [2n +1)xP n np n 1 ] P 2 = 1 2 3xP 1 P )= 1 2 3x2 1) Για n =2 P 3 = 1 3 5xP 2 2P 1 )= 1 3 = 1 2 5x3x2 3 5x 1 ) 2 3x2 1) 2x 5x
1 Prìblhma 4 Η αναδρομική σχέση γράφεται στη μορφή Για n =1 P n+1 = 1 n +1 [2n +1)xP n np n 1 ] P 2 = 1 2 3xP 1 P )= 1 2 3x2 1) Για n =2 P 3 = 1 3 5xP 2 2P 1 )= 1 3 = 1 2 5x3x2 3 5x 1 ) 2 3x2 1) 2x 5x
ΠΟΛΥΩΝΥΜΑ ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ
 ΠΟΛΥΩΝΥΜΑ ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ Έννοια του πολυωνύμου. Ας υποθέσουμε ότι έχουμε μια μεταβλητή x που μπορεί να πάρει κάθε πραγματική τιμή. Μονώνυμο του x, είναι κάθε παράσταση της μορφής : x όπου α είναι
ΠΟΛΥΩΝΥΜΑ ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ Έννοια του πολυωνύμου. Ας υποθέσουμε ότι έχουμε μια μεταβλητή x που μπορεί να πάρει κάθε πραγματική τιμή. Μονώνυμο του x, είναι κάθε παράσταση της μορφής : x όπου α είναι
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 1 η Ημερομηνία Αποστολής στον Φοιτητή: 20 Οκτωβρίου 2008
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 0 Οκτωβρίου 008 Ημερομηνία παράδοσης της Εργασίας: Νοεμβρίου 008 Πριν
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 0 Οκτωβρίου 008 Ημερομηνία παράδοσης της Εργασίας: Νοεμβρίου 008 Πριν
Εφαρμοσμένα Μαθηματικά ΙΙ Εξέταση Σεπτεμβρίου 25/9/2017 Διδάσκων: Ι. Λυχναρόπουλος
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Εξέταση Σεπτεμβρίου 5/9/07 Διδάσκων: Ι. Λυχναρόπουλος Άσκηση (Μονάδες ) Να δειχθεί ότι το πεδίο F( x, y) = y cos x + y,sin x
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Εξέταση Σεπτεμβρίου 5/9/07 Διδάσκων: Ι. Λυχναρόπουλος Άσκηση (Μονάδες ) Να δειχθεί ότι το πεδίο F( x, y) = y cos x + y,sin x
Διαφορικές Εξισώσεις.
 Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 2015-16. Λύσεις του τρίτου φυλλαδίου ασκήσεων. 1. Λύστε τις παρακάτω διαφορικές εξισώσεις. Αν προκύψει αλγεβρική σχέση ανάμεσα στις μεταβλητές x, y η οποία δεν λύνεται
Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 2015-16. Λύσεις του τρίτου φυλλαδίου ασκήσεων. 1. Λύστε τις παρακάτω διαφορικές εξισώσεις. Αν προκύψει αλγεβρική σχέση ανάμεσα στις μεταβλητές x, y η οποία δεν λύνεται
v y = 12x 2 y + 4y v(x, y) = 6x 2 y 2 + y 4 + y + c(x). f(z) = u(z, 0) + iv(z, 0) = z + i(z 4 + c), f(z) = iz 4 + z i.
 ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ & ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΟΜΕΑΣ ΜΑΘΗΜΑΤΙΚΩΝ Εξετάσεις στη Μιγαδική Ανάλυση ΟΜΑΔΑ: Α 0 Ιουλίου, 0 Θέμα. (αʹ) Να βρεθεί η τιμή του a R για την οποία η συνάρτηση u(x, y) ax 3 y +4xy
ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ & ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΟΜΕΑΣ ΜΑΘΗΜΑΤΙΚΩΝ Εξετάσεις στη Μιγαδική Ανάλυση ΟΜΑΔΑ: Α 0 Ιουλίου, 0 Θέμα. (αʹ) Να βρεθεί η τιμή του a R για την οποία η συνάρτηση u(x, y) ax 3 y +4xy
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α. ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 5: ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΥΠΟΧΩΡΟΙ ΓΡΑΜΜΙΚΗ ΑΝΕΞΑΡΤΗΣΙΑ ΒΑΣΕΙΣ & ΔΙΑΣΤΑΣΗ Δ.Χ. ΣΗΜΕΙΩΣΕΙΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α. ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 5: ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΥΠΟΧΩΡΟΙ ΓΡΑΜΜΙΚΗ ΑΝΕΞΑΡΤΗΣΙΑ ΒΑΣΕΙΣ & ΔΙΑΣΤΑΣΗ Δ.Χ. ΣΗΜΕΙΩΣΕΙΣ
Απειροστικός Λογισμός ΙΙ, εαρινό εξάμηνο Φυλλάδιο ασκήσεων επανάληψης.
 Απειροστικός Λογισμός ΙΙ, εαρινό εξάμηνο 2016-17. Φυλλάδιο ασκήσεων επανάληψης. 1. Για καθεμία από τις παρακάτω συναρτήσεις ελέγξτε βάσει του ορισμού της παραγωγισιμότητας αν είναι παραγωγίσιμη στο αντίστοιχο
Απειροστικός Λογισμός ΙΙ, εαρινό εξάμηνο 2016-17. Φυλλάδιο ασκήσεων επανάληψης. 1. Για καθεμία από τις παρακάτω συναρτήσεις ελέγξτε βάσει του ορισμού της παραγωγισιμότητας αν είναι παραγωγίσιμη στο αντίστοιχο
ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 2014
 ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Γ ΛΥΚΕΙΟΥ 04 ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 04 ΘΕΜΑ ο : * Θεωρούμε τους μιγαδικούς αριθμούς της μορφής xxi,
ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Γ ΛΥΚΕΙΟΥ 04 ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 04 ΘΕΜΑ ο : * Θεωρούμε τους μιγαδικούς αριθμούς της μορφής xxi,
ΕΝΟΤΗΤΑ 1: ΟΡΙΣΜΟΣ ΠΕΔΙΟ ΟΡΙΣΜΟΥ ΠΡΑΞΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Α
 ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 1: ΟΡΙΣΜΟΣ ΠΕΔΙΟ ΟΡΙΣΜΟΥ ΠΡΑΞΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΛΥΜΕΝΑ ΘΕΜΑΤΑ Ερώτηση θεωρίας 1 ΘΕΜΑ Α Τι ονομάζουμε πραγματική συνάρτηση
ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 1: ΟΡΙΣΜΟΣ ΠΕΔΙΟ ΟΡΙΣΜΟΥ ΠΡΑΞΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΛΥΜΕΝΑ ΘΕΜΑΤΑ Ερώτηση θεωρίας 1 ΘΕΜΑ Α Τι ονομάζουμε πραγματική συνάρτηση
Κλασική Ηλεκτροδυναμική Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΤΕΧΝΙΚΕΣ ΥΠΟΛΟΓΙΣΜΟΥ ΗΛΕΚΤΡΙΚΟΥ ΔΥΝΑΜΙΚΟΥ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΤΕΧΝΙΚΕΣ ΥΠΟΛΟΓΙΣΜΟΥ ΗΛΕΚΤΡΙΚΟΥ ΔΥΝΑΜΙΚΟΥ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
x y z xy yz zx, να αποδείξετε ότι x=y=z.
 ΑΣΚΗΣΕΙΣ ΣΤΗΝ ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ ΚΕΦ. ο A. Ταυτότητες, ιδιότητες δυνάμεων, διάταξη.1 Να παραγοντοποιήσετε τις παρακάτω παραστάσεις: 1. 15a x 15a y 5a x 5a y. a x a x a x a x 3 3 4 3 3 3 3. x 4xy 16 4 y
ΑΣΚΗΣΕΙΣ ΣΤΗΝ ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ ΚΕΦ. ο A. Ταυτότητες, ιδιότητες δυνάμεων, διάταξη.1 Να παραγοντοποιήσετε τις παρακάτω παραστάσεις: 1. 15a x 15a y 5a x 5a y. a x a x a x a x 3 3 4 3 3 3 3. x 4xy 16 4 y
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Αντίστροφος Μετασχηματισμός Laplace Στην
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Αντίστροφος Μετασχηματισμός Laplace Στην
ΣΥΣΤΗΜΑΤΑ. 6.1 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ (Επαναλήψεις-Συμπληρώσεις)
 6 ΣΥΣΤΗΜΑΤΑ 6.1 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ (Επαναλήψεις-Συμπληρώσεις) Η εξίσωση αx βy γ Στο Γυμνάσιο διαπιστώσαμε με την βοήθεια παραδειγμάτων ότι η εξίσωση αx βy γ, με α 0 ή β 0, που λέγεται γραμμική εξίσωση,
6 ΣΥΣΤΗΜΑΤΑ 6.1 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ (Επαναλήψεις-Συμπληρώσεις) Η εξίσωση αx βy γ Στο Γυμνάσιο διαπιστώσαμε με την βοήθεια παραδειγμάτων ότι η εξίσωση αx βy γ, με α 0 ή β 0, που λέγεται γραμμική εξίσωση,
Πολυωνυμική εξίσωση βαθμού ν ονομάζεται κάθε εξίσωση της μορφής α ν x ν +α ν-1 x ν α 1 x+α 0 =0,με α 0,α 1,...
 3 0 ΛΥΚΕΙΟ ΚΕΡΑΤΣΙΝΙΟΥ Λ. ΒΟΥΛΓΑΡΗ ΜΑΘΗΜΑΤΙΚΟΣ ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΕΞΙΣΩΣΕΙΣ ΠΟΥ ΑΝΑΓΟΝΤΑΙ ΣΕ ΠΟΛΥΩΝΥΜΙΚΕΣ Πολυωνυμική εξίσωση βαθμού ν ονομάζεται κάθε εξίσωση της μορφής α ν x ν +α ν-1 x ν-1 +...+α
3 0 ΛΥΚΕΙΟ ΚΕΡΑΤΣΙΝΙΟΥ Λ. ΒΟΥΛΓΑΡΗ ΜΑΘΗΜΑΤΙΚΟΣ ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΕΞΙΣΩΣΕΙΣ ΠΟΥ ΑΝΑΓΟΝΤΑΙ ΣΕ ΠΟΛΥΩΝΥΜΙΚΕΣ Πολυωνυμική εξίσωση βαθμού ν ονομάζεται κάθε εξίσωση της μορφής α ν x ν +α ν-1 x ν-1 +...+α
α. y = y x 2 β. x + 5x = e x γ. xy (xy + y) = 2y 2 δ. y (4) + xy + e x = 0 η. x 2 (y ) 4 + xy + y 5 = 0 θ. y + ln y + x 2 y 3 = 0 d 3 y dy + 5y
 Ασκήσεις στα Μαθηματικά ΙΙΙ Τμήμα Χημ. Μηχανικών ΑΠΘ Μουτάφη Ευαγγελία Θεσσαλονίκη 2018-2019 ΣΥΝΗΘΕΙΣ ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΕΙΣΑΓΩΓΗ 1. Στις παρακάτω Δ.Ε. να προσδιορίσετε: α) την ανεξάρτητη και την εξαρτημένη
Ασκήσεις στα Μαθηματικά ΙΙΙ Τμήμα Χημ. Μηχανικών ΑΠΘ Μουτάφη Ευαγγελία Θεσσαλονίκη 2018-2019 ΣΥΝΗΘΕΙΣ ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΕΙΣΑΓΩΓΗ 1. Στις παρακάτω Δ.Ε. να προσδιορίσετε: α) την ανεξάρτητη και την εξαρτημένη
1 of 79 ΘΕΜΑ 2. Δίνεται η συνάρτηση f(x) = x 2 4x + 5, x R
 1 of 79 Δίνεται η συνάρτηση f(x) = x 2 4x + 5, x R α) Να αποδείξετε ότι η f γράφεται στη μορφή f(x) = (x- 2) 2 + 1. (Μονάδες 12) β) Στο σύστημα συντεταγμένων που ακολουθεί, να παραστήσετε γραφικά τη συνάρτηση
1 of 79 Δίνεται η συνάρτηση f(x) = x 2 4x + 5, x R α) Να αποδείξετε ότι η f γράφεται στη μορφή f(x) = (x- 2) 2 + 1. (Μονάδες 12) β) Στο σύστημα συντεταγμένων που ακολουθεί, να παραστήσετε γραφικά τη συνάρτηση
Σήματα και Συστήματα. Διάλεξη 1: Σήματα Συνεχούς Χρόνου. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 1: Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Εισαγωγή στα Σήματα 1. Σκοποί της Θεωρίας Σημάτων 2. Κατηγορίες Σημάτων 3. Χαρακτηριστικές Παράμετροι
Σήματα και Συστήματα Διάλεξη 1: Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Εισαγωγή στα Σήματα 1. Σκοποί της Θεωρίας Σημάτων 2. Κατηγορίες Σημάτων 3. Χαρακτηριστικές Παράμετροι
(a + b) + c = a + (b + c), (ab)c = a(bc) a + b = b + a, ab = ba. a(b + c) = ab + ac
 Σημειώσεις μαθήματος Μ1212 Γραμμική Άλγεβρα ΙΙ Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2014 Κεφάλαιο 1 Διανυσματικοί Χώροι Στο εισαγωγικό μάθημα Γραμμικής Άλγεβρας ξεκινήσαμε μελετώντας
Σημειώσεις μαθήματος Μ1212 Γραμμική Άλγεβρα ΙΙ Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2014 Κεφάλαιο 1 Διανυσματικοί Χώροι Στο εισαγωγικό μάθημα Γραμμικής Άλγεβρας ξεκινήσαμε μελετώντας
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Παραγώγιση Εισαγωγή Ορισμός 7. Αν y f x είναι μια συνάρτηση ορισμένη σε ένα διάστημα
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Παραγώγιση Εισαγωγή Ορισμός 7. Αν y f x είναι μια συνάρτηση ορισμένη σε ένα διάστημα
Μ Α Θ Η Μ Α Τ Α Γ Λ Υ Κ Ε Ι Ο Υ
 Μ Α Θ Η Μ Α Τ Α Γ Λ Υ Κ Ε Ι Ο Υ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ (Α ΜΕΡΟΣ: ΣΥΝΑΡΤΗΣΕΙΣ) Επιμέλεια: Καραγιάννης Ιωάννης, Σχολικός Σύμβουλος Μαθηματικών
Μ Α Θ Η Μ Α Τ Α Γ Λ Υ Κ Ε Ι Ο Υ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ (Α ΜΕΡΟΣ: ΣΥΝΑΡΤΗΣΕΙΣ) Επιμέλεια: Καραγιάννης Ιωάννης, Σχολικός Σύμβουλος Μαθηματικών
2.2 ιαίρεση Πολυωνύμων
 ιαίρεση Πολυωνύμων 1 Να γίνουν οι διαιρέσεις: α) (x 5 - x + x - 9) : (x - 1) β) (x 4-7x + x - 15) : (x + 5) γ) (x - 4αx + α ) : (x - α) δ) [7x - (9α + 7α ) x + 9α ] : (x - α) Με τη βοήθεια του σχήματος
ιαίρεση Πολυωνύμων 1 Να γίνουν οι διαιρέσεις: α) (x 5 - x + x - 9) : (x - 1) β) (x 4-7x + x - 15) : (x + 5) γ) (x - 4αx + α ) : (x - α) δ) [7x - (9α + 7α ) x + 9α ] : (x - α) Με τη βοήθεια του σχήματος
(ii) x[y (x)] 4 + 2y(x) = 2x. (vi) y (x) = x 2 sin x
![(ii) x[y (x)] 4 + 2y(x) = 2x. (vi) y (x) = x 2 sin x (ii) x[y (x)] 4 + 2y(x) = 2x. (vi) y (x) = x 2 sin x](/thumbs/62/47493101.jpg) ΕΥΓΕΝΙΑ Ν. ΠΕΤΡΟΠΟΥΛΟΥ ΕΠΙΚ. ΚΑΘΗΓΗΤΡΙΑ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΑΣΚΗΣΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ «ΕΦΑΡΜΟΣΜΕΝΑ ΜΑΘΗΜΑΤΙΚΑ ΙΙΙ» ΠΑΤΡΑ 2015 1 Ασκήσεις 1η ομάδα ασκήσεων 1. Να χαρακτηρισθούν πλήρως
ΕΥΓΕΝΙΑ Ν. ΠΕΤΡΟΠΟΥΛΟΥ ΕΠΙΚ. ΚΑΘΗΓΗΤΡΙΑ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΑΣΚΗΣΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ «ΕΦΑΡΜΟΣΜΕΝΑ ΜΑΘΗΜΑΤΙΚΑ ΙΙΙ» ΠΑΤΡΑ 2015 1 Ασκήσεις 1η ομάδα ασκήσεων 1. Να χαρακτηρισθούν πλήρως
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής Μετασχηματισμός Fourier Στο κεφάλαιο αυτό θα εισάγουμε και θα μελετήσουμε
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής Μετασχηματισμός Fourier Στο κεφάλαιο αυτό θα εισάγουμε και θα μελετήσουμε
Κεφάλαιο 4: Διαφορικός Λογισμός
 ΣΥΓΧΡΟΝΗ ΠΑΙΔΕΙΑ ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Κεφάλαιο 4: Διαφορικός Λογισμός Μονοτονία Συνάρτησης Tζουβάλης Αθανάσιος Κεφάλαιο 4: Διαφορικός Λογισμός Περιεχόμενα Μονοτονία συνάρτησης... Λυμένα παραδείγματα...
ΣΥΓΧΡΟΝΗ ΠΑΙΔΕΙΑ ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Κεφάλαιο 4: Διαφορικός Λογισμός Μονοτονία Συνάρτησης Tζουβάλης Αθανάσιος Κεφάλαιο 4: Διαφορικός Λογισμός Περιεχόμενα Μονοτονία συνάρτησης... Λυμένα παραδείγματα...
Συνέχεια συνάρτησης σε διάστημα. Η θεωρία και τι προσέχουμε. x, ισχύει: lim f (x) f ( ).
 Κεφάλαιο 4 Συνέχεια συνάρτησης σε διάστημα 411 Ερώτηση θεωρίας 1 Η θεωρία και τι προσέχουμε Πότε μια συνάρτηση f θα λέμε ότι είναι συνεχής σε ένα ανοικτό διάστημα (, ) αβ; Απάντηση Μια συνάρτηση f θα λέμε
Κεφάλαιο 4 Συνέχεια συνάρτησης σε διάστημα 411 Ερώτηση θεωρίας 1 Η θεωρία και τι προσέχουμε Πότε μια συνάρτηση f θα λέμε ότι είναι συνεχής σε ένα ανοικτό διάστημα (, ) αβ; Απάντηση Μια συνάρτηση f θα λέμε
Ενότητα 9: Ασκήσεις. Άδειες Χρήσης
 Μηχανική των Ρευστών Ενότητα 9: Ασκήσεις Βασίλειος Λουκόπουλος, Επίκουρος Καθηγητής Τμήμα Φυσικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Μηχανική των Ρευστών Ενότητα 9: Ασκήσεις Βασίλειος Λουκόπουλος, Επίκουρος Καθηγητής Τμήμα Φυσικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Μιχάλης Παπαδημητράκης. Μερικές Διαφορικές Εξισώσεις
 Μιχάλης Παπαδημητράκης Μερικές Διαφορικές Εξισώσεις Περιεχόμενα 1 Γενικά. 1 1.1 Μερικές διαφορικές εξισώσεις............................ 1 1.2 Διαφορικοί τελεστές................................. 2 1.3
Μιχάλης Παπαδημητράκης Μερικές Διαφορικές Εξισώσεις Περιεχόμενα 1 Γενικά. 1 1.1 Μερικές διαφορικές εξισώσεις............................ 1 1.2 Διαφορικοί τελεστές................................. 2 1.3
Λύσεις Εξετάσεων Φεβρουαρίου Ακ. Έτους
 ΜΑΘΗΜΑΤΙΚΑ, 6-7 ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΕΠΙΚ. ΚΑΘ. ΣΤΑΥΡΟΣ ΤΟΥΜΠΗΣ Λύσεις Εξετάσεων Φεβρουαρίου Ακ. Έτους 6-7. Περιοδικές Συναρτήσεις) Έστω συνεχής συνάρτηση f : R R περιοδική
ΜΑΘΗΜΑΤΙΚΑ, 6-7 ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΕΠΙΚ. ΚΑΘ. ΣΤΑΥΡΟΣ ΤΟΥΜΠΗΣ Λύσεις Εξετάσεων Φεβρουαρίου Ακ. Έτους 6-7. Περιοδικές Συναρτήσεις) Έστω συνεχής συνάρτηση f : R R περιοδική
ΑΣΚΗΣΕΙΣ. 2. ίνεται το Ρ(x) αν το ρ είναι ρίζα Ρ(2x) 2x τότε το ρ είναι ρίζα του Ρ( Ρ(2x)) 2x.
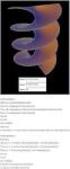 ΑΣΚΗΣΕΙΣ. ίνονται τα πολυώνυµα Ρ (x), Ρ (x), Ρ (x) αν τα πολυώνυµα Ρ (x) και Ρ (x) δεν έχουν κοινή ρίζα και ισχύει : ( Ρ (x)) + (Ρ (x)) = (Ρ (x)) για κάθε x R να δείξετε ότι το Ρ (x) δεν έχει πραγµατική
ΑΣΚΗΣΕΙΣ. ίνονται τα πολυώνυµα Ρ (x), Ρ (x), Ρ (x) αν τα πολυώνυµα Ρ (x) και Ρ (x) δεν έχουν κοινή ρίζα και ισχύει : ( Ρ (x)) + (Ρ (x)) = (Ρ (x)) για κάθε x R να δείξετε ότι το Ρ (x) δεν έχει πραγµατική
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ. Μαθηματικά 2. Σταύρος Παπαϊωάννου
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ Μαθηματικά Σταύρος Παπαϊωάννου Ιούνιος Τίτλος Μαθήματος Περιεχόμενα Χρηματοδότηση. Σφάλμα! Δεν έχει οριστεί σελιδοδείκτης. Σκοποί Μαθήματος
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ Μαθηματικά Σταύρος Παπαϊωάννου Ιούνιος Τίτλος Μαθήματος Περιεχόμενα Χρηματοδότηση. Σφάλμα! Δεν έχει οριστεί σελιδοδείκτης. Σκοποί Μαθήματος
Συνήθεις Διαφορικές Εξισώσεις
 Π Δ Μ Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Συνήθεις Διαφορικές Εξισώσεις Δρ. Θεόδωρος Ζυγκιρίδης 28 Δεκεμβρίου 211 2 Περιεχόμενα 1 Εισαγωγή 1 1.1 Ορισμοί.........................................
Π Δ Μ Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Συνήθεις Διαφορικές Εξισώσεις Δρ. Θεόδωρος Ζυγκιρίδης 28 Δεκεμβρίου 211 2 Περιεχόμενα 1 Εισαγωγή 1 1.1 Ορισμοί.........................................
4.1. Πολυώνυμα. Η έννοια του πολυωνύμου
 4.1 Πολυώνυμα Η έννοια του πολυωνύμου ΟΡΙΣΜΟΙ 1. Μονώνυμο του x ονομάζουμε κάθε παράσταση της μορφής αx ν, όπου α R, ν N (σταθερές) και x R (μεταβλητή). 2. Πολυώνυμο του x ονομάζουμε κάθε παράσταση της
4.1 Πολυώνυμα Η έννοια του πολυωνύμου ΟΡΙΣΜΟΙ 1. Μονώνυμο του x ονομάζουμε κάθε παράσταση της μορφής αx ν, όπου α R, ν N (σταθερές) και x R (μεταβλητή). 2. Πολυώνυμο του x ονομάζουμε κάθε παράσταση της
Kεφάλαιο 4. Συστήματα διαφορικών εξισώσεων. F : : F = F r, όπου r xy
 4 Εισαγωγή Kεφάλαιο 4 Συστήματα διαφορικών εξισώσεων Εστω διανυσματικό πεδίο F : : F = Fr, όπου r x, και είναι η ταχύτητα στο σημείο πχ ενός ρευστού στο επίπεδο Εστω ότι ψάχνουμε τις τροχιές κίνησης των
4 Εισαγωγή Kεφάλαιο 4 Συστήματα διαφορικών εξισώσεων Εστω διανυσματικό πεδίο F : : F = Fr, όπου r x, και είναι η ταχύτητα στο σημείο πχ ενός ρευστού στο επίπεδο Εστω ότι ψάχνουμε τις τροχιές κίνησης των
ΚΕΦΑΛΑΙΟ 2: ΟΡΙΖΟΥΣΕΣ
 ΚΕΦΑΛΑΙΟ ΚΕΦΑΛΑΙΟ :. ΕΙΣΑΓΩΓΗ Σε κάθε τετραγωνικό πίνακα ) τάξης n θα αντιστοιχίσουμε έναν πραγματικό ( ij αριθμό, τον οποίο θα ονομάσουμε ορίζουσα του πίνακα. Η ορίζουσα θα συμβολίζεται det ή Α ή n n
ΚΕΦΑΛΑΙΟ ΚΕΦΑΛΑΙΟ :. ΕΙΣΑΓΩΓΗ Σε κάθε τετραγωνικό πίνακα ) τάξης n θα αντιστοιχίσουμε έναν πραγματικό ( ij αριθμό, τον οποίο θα ονομάσουμε ορίζουσα του πίνακα. Η ορίζουσα θα συμβολίζεται det ή Α ή n n
ΜΑΣ 203: Συνήθεις Διαφορικές Εξισώσεις, Εαρινό Εξάμηνο 2017 ΑΣΚΗΣΕΙΣ
 ΜΑΣ 3: Συνήθεις Διαφορικές Εξισώσεις, Εαρινό Εξάμηνο 17 ΑΣΚΗΣΕΙΣ 1. Να ταξινομηθούν οι πιο κάτω ΣΔΕ με βάση τα εξής: τάξη, γραμμική ή μή. Να δοθούν επίσης οι ανεξάρτητες και εξαρτημένες μεταβλητές. 3 d
ΜΑΣ 3: Συνήθεις Διαφορικές Εξισώσεις, Εαρινό Εξάμηνο 17 ΑΣΚΗΣΕΙΣ 1. Να ταξινομηθούν οι πιο κάτω ΣΔΕ με βάση τα εξής: τάξη, γραμμική ή μή. Να δοθούν επίσης οι ανεξάρτητες και εξαρτημένες μεταβλητές. 3 d
ΣΗΜΕΙΩΣΕΙΣ. x A αντιστοιχίζεται (συσχετίζεται) με ένα μόνο. = ονομάζεται εξίσωση της
 ΚΕΦΑΛΑΙΟ 2ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 1: ΕΝΝΟΙΑ ΠΡΑΓΜΑΤΙΚΗΣ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ ΣΥΝΑΡΤΗΣΗΣ. IΣΟΤΗΤΑ ΣΥΝΑΡΤΗΣΕΩΝ - ΠΡΑΞΕΙΣ ΜΕ ΣΥΝΑΡΤΗΣΕΙΣ - ΣΥΝΘΕΣΗ ΣΥΝΑΡΤΗΣΕΩΝ [Ενότητα
ΚΕΦΑΛΑΙΟ 2ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 1: ΕΝΝΟΙΑ ΠΡΑΓΜΑΤΙΚΗΣ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ ΣΥΝΑΡΤΗΣΗΣ. IΣΟΤΗΤΑ ΣΥΝΑΡΤΗΣΕΩΝ - ΠΡΑΞΕΙΣ ΜΕ ΣΥΝΑΡΤΗΣΕΙΣ - ΣΥΝΘΕΣΗ ΣΥΝΑΡΤΗΣΕΩΝ [Ενότητα
> ln 1 + ln ln n = ln(1 2 3 n) = ln(n!).
 η Διάλεξη: Άρρητοι αριθμοί Το σύνολο Q των ρητών αριθμών είναι το Q = { m n : m Z, n N}. αριθμός που δεν είναι ρητός λέγεται άρρητος. Ενας πραγματικός Ασκηση: Αποδείξτε ότι το άθροισμα και το γινόμενο
η Διάλεξη: Άρρητοι αριθμοί Το σύνολο Q των ρητών αριθμών είναι το Q = { m n : m Z, n N}. αριθμός που δεν είναι ρητός λέγεται άρρητος. Ενας πραγματικός Ασκηση: Αποδείξτε ότι το άθροισμα και το γινόμενο
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ. Μαθηματικά 2. Σταύρος Παπαϊωάννου
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ Μαθηματικά Σταύρος Παπαϊωάννου Ιούνιος 015 Τίτλος Μαθήματος Περιεχόμενα Χρηματοδότηση... Error! ookmark not defined. Σκοποί Μαθήματος (Επικεφαλίδα
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ Μαθηματικά Σταύρος Παπαϊωάννου Ιούνιος 015 Τίτλος Μαθήματος Περιεχόμενα Χρηματοδότηση... Error! ookmark not defined. Σκοποί Μαθήματος (Επικεφαλίδα
Περί εξισώσεων με ένα άγνωστο
 1 ο ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΧΑΝΙΩΝ 19 Φεβρουαρίου 013 ΤΑΞΗ Α Σημειώσεις Άλγεβρας Περί εξισώσεων με ένα άγνωστο Εξίσωση με ένα άγνωστο λέμε την ισότητα δύο παραστάσεων μιας μεταβλητής. Πχ f(x) = g(x) όπου x μεταβλητή
1 ο ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΧΑΝΙΩΝ 19 Φεβρουαρίου 013 ΤΑΞΗ Α Σημειώσεις Άλγεβρας Περί εξισώσεων με ένα άγνωστο Εξίσωση με ένα άγνωστο λέμε την ισότητα δύο παραστάσεων μιας μεταβλητής. Πχ f(x) = g(x) όπου x μεταβλητή
Πρόλογος Εισαγωγή στη δεύτερη έκδοση Εισαγωγή... 11
 Περιεχόμενα Πρόλογος... 9 Εισαγωγή στη δεύτερη έκδοση... 0 Εισαγωγή... Ε. Εισαγωγή στην έννοια της Αριθμητικής Ανάλυσης... Ε. Ταξινόμηση των θεμάτων που απασχολούν την αριθμητική ανάλυση.. Ε.3 Μορφές σφαλμάτων...
Περιεχόμενα Πρόλογος... 9 Εισαγωγή στη δεύτερη έκδοση... 0 Εισαγωγή... Ε. Εισαγωγή στην έννοια της Αριθμητικής Ανάλυσης... Ε. Ταξινόμηση των θεμάτων που απασχολούν την αριθμητική ανάλυση.. Ε.3 Μορφές σφαλμάτων...
Μιγαδικός λογισμός και ολοκληρωτικοί Μετασχηματισμοί
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μιγαδικός λογισμός και ολοκληρωτικοί Μετασχηματισμοί ΑΝΩΜΑΛΑ ΣΗΜΕΙΑ, ΠΟΛΟΙ ΚΑΙ ΤΟ ΘΕΩΡΗΜΑ ΤΩΝ ΟΛΟΚΛΗΡΩΤΙΚΩΝ ΥΠΟΛΟΙΠΩΝ Διδάσκων : Επίκ. Καθ. Κολάσης Χαράλαμπος
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μιγαδικός λογισμός και ολοκληρωτικοί Μετασχηματισμοί ΑΝΩΜΑΛΑ ΣΗΜΕΙΑ, ΠΟΛΟΙ ΚΑΙ ΤΟ ΘΕΩΡΗΜΑ ΤΩΝ ΟΛΟΚΛΗΡΩΤΙΚΩΝ ΥΠΟΛΟΙΠΩΝ Διδάσκων : Επίκ. Καθ. Κολάσης Χαράλαμπος
Ασκήσεις3 Διαγωνίσιμες Γραμμικές Απεικονίσεις
 Ασκήσεις 5 Βασικά σημεία Ιδιότητες ιδιόχωρων: Έστω,, Ισχύουν τα εξής Ασκήσεις Διαγωνίσιμες Γραμμικές Απεικονίσεις κάποιες διακεκριμένες ιδιοτιμές της γραμμικής απεικόνισης : V V, όπου o Αν v v 0, όπου
Ασκήσεις 5 Βασικά σημεία Ιδιότητες ιδιόχωρων: Έστω,, Ισχύουν τα εξής Ασκήσεις Διαγωνίσιμες Γραμμικές Απεικονίσεις κάποιες διακεκριμένες ιδιοτιμές της γραμμικής απεικόνισης : V V, όπου o Αν v v 0, όπου
ΚΕΦΑΛΑΙΟ 2 Ο ΠΟΛΥΩΝΥΜΑ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ - ΑΣΚΗΣΕΙΣ
 ΚΕΦΑΛΑΙΟ Ο ΠΟΛΥΩΝΥΜΑ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ - ΑΣΚΗΣΕΙΣ ΚΕΦΑΛΑΙΟ Ο ΠΟΛΥΩΝΥΜΑ 10 ΕΠΑΝΑΛΗΨΕΙΣ ΑΠΟ ΠΡΟΗΓΟΥΜΕΝΕΣ ΤΑΞΕΙΣ α ) Ταυτότητες 1. (a-β)(a+β)=a - b. (a ± b ) = a ± ab + b 3 3 3 3. (a ± b ) = a ± 3a b + 3ab
ΚΕΦΑΛΑΙΟ Ο ΠΟΛΥΩΝΥΜΑ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ - ΑΣΚΗΣΕΙΣ ΚΕΦΑΛΑΙΟ Ο ΠΟΛΥΩΝΥΜΑ 10 ΕΠΑΝΑΛΗΨΕΙΣ ΑΠΟ ΠΡΟΗΓΟΥΜΕΝΕΣ ΤΑΞΕΙΣ α ) Ταυτότητες 1. (a-β)(a+β)=a - b. (a ± b ) = a ± ab + b 3 3 3 3. (a ± b ) = a ± 3a b + 3ab
ΜΕΜ251 Αριθμητική Ανάλυση
 ΜΕΜ251 Αριθμητική Ανάλυση Διάλεξη 10, 12 Μαρτίου 2018 Μιχάλης Πλεξουσάκης Τμήμα Μαθηματικών και Εφαρμοσμένων Μαθηματικών Περιεχόμενα 1. Παρεμβολή 2. Παράσταση και υπολογισμός του πολυωνύμου παρεμβολής
ΜΕΜ251 Αριθμητική Ανάλυση Διάλεξη 10, 12 Μαρτίου 2018 Μιχάλης Πλεξουσάκης Τμήμα Μαθηματικών και Εφαρμοσμένων Μαθηματικών Περιεχόμενα 1. Παρεμβολή 2. Παράσταση και υπολογισμός του πολυωνύμου παρεμβολής
Ακρότατα πραγματικών συναρτήσεων
 Ακρότατα πραγματικών συναρτήσεων Ορισμός Έστω U R, U και f : U R R συνάρτηση τότε: )Το λέγεται τοπικό ελάχιστο της f αν υπάρχει περιοχή V του ώστε f f για κάθε V U Το λέγεται τοπικό μέγιστο της f αν υπάρχει
Ακρότατα πραγματικών συναρτήσεων Ορισμός Έστω U R, U και f : U R R συνάρτηση τότε: )Το λέγεται τοπικό ελάχιστο της f αν υπάρχει περιοχή V του ώστε f f για κάθε V U Το λέγεται τοπικό μέγιστο της f αν υπάρχει
