ΚΕΦΑΛΑΙΟ 7: Αναπαραστάσεις Πεπερασμένων Ομάδων Ι
|
|
|
- Δωρόθεος Φαίδρος Αναγνώστου
- 6 χρόνια πριν
- Προβολές:
Transcript
1 ΚΕΦΑΛΑΙΟ 7: Αναπαραστάσεις Πεπερασμένων Ομάδων Ι Χρησιμοποιώντας το θεώρημα του Weddebu για ημιαπλούς δακτυλίους, αναπτύσσουμε εδώ τις πρώτες προτάσεις από τη θεωρία των αναπαραστάσεων και αρακτήρων πεπερασμένων ομάδων υπέρ του Αυτές εφαρμόζονται στο επόμενο κεφάλαιο όπου αποδεικνύουμε ένα θεμελιώδες θεώρημα του Bude που αφορά στην επιλυσιμότητα ομάδων τάξης p a q b ( p, q πρώτοι) 7 Αναπαραστάσεις Έστω G ομάδα και k σώμα Μια αναπαράσταση της G υπέρ του k είναι ένας ομομορφισμός ομάδων ρ : G GL ( k), για κάποιο, όπου GL (k) είναι η ομάδα των αντιστρέψιμων πινάκων με στοιεία από το k Το ονομάζεται ο βαθμός της αναπαράστασης Αν ρ : G GL ( k) είναι μια αναπαράσταση της G, τότε θέτοντας V : k και ορίζοντας v ( )( v) λαμβάνουμε ένα k[g]-πρότυπο Αντίστροφα αν V είναι ένα k[g]-πρότυπο διάστασης, τότε σταθεροποιώντας μια βάση του V έουμε Aut( V) GL ( k ) και ορίζεται ένας ομομορφισμός ομάδων ρ : G GL ( k), όπου ρ () είναι ο πίνακας της γραμμικής απεικόνισης V v v V ως προς τη συγκεκριμένη επιλογή βάση Έτσι, στις σημειώσεις αυτές, θα ρησιμοποιούμε τους όρους αναπαράσταση της G και k[g]-πρότυπο ωρίς να γίνεται ιδιαίτερη διάκριση μεταξύ της ρ και του V 7 Παράδειγμα Για κάθε ομάδα G έουμε την αναπαράσταση : G GL ( k), όπου ( ) για κάθε G Αυτή λέγεται η τετριμμένη αναπαράσταση της G Για τη συμμετρική ομάδα G S έουμε την αναπαράσταση : G GL ( k), όπου ( ) ( ) για κάθε S Αυτή λέγεται η αναπαράσταση προσήμου της S Έστω G η ομάδα D 8 που δίνεται με γεννήτορες και σέσεις από 8 a, b : a b, D ab ba (Κάθε στοιείο της D 8 γράφεται μοναδικά στη μορφή Ειδικά, η D8 έει ab με 0, 0 τάξη 8 Είναι μία από μια οικογένεια ομάδων που ονομάζονται διεδρικές Γεωμετρικά, η D8 περιγράφει τις συμμετρίες του τετραγώνου) Θέτουμε 0 0 A, B 0 0 Ελέγουμε ότι A B I, AB BA Συνεπώς ορίζεται μία αναπαράσταση G πάνω από το, : G GL ( ), από τις σέσεις ρ( a b ) A B, 0,, 0, Γεωμετρικά το Α παριστάνει στροφή 90 ο γύρω από την αρή των αξόνων και το Β ανάκλαση ως προς τον άξονα των x όπως φαίνεται στο παρακάτω σήμα Έτσι η συγκεκριμένη αναπαράσταση ρ αναπαριστάνει τη G ως ομάδα μετασηματισμών του επιπέδου
2 6 A: B : Δύο αναπαραστάσεις ρ, ρ : G GL ( k) λέγεται ισοδύναμες αν υπάρει T GL (k) με την ιδιότητα ρ ( ) T ρ( ) T για κάθε G Για παράδειγμα η αναπαράσταση : D8 GL( ) του προηγούμενου παραδείγματος είναι ισοδύναμη με την : D8 GL( ) που ορίζεται από τις σέσεις 0 0 ρ ( a) και ρ (b) 0 0 Εδώ Τ είναι πίνακας που διαγωνοποιεί τον Α, δηλαδή πίνακας των ιδιοδιανυσμάτων του Α, T Έστω ρ, ρ : G GL ( k) δύο αναπαραστάσεις της G με αντίστοια k[g]-πρότυπα V, V Τότε οι ρ, ρ είναι ισοδύναμες αν και μόνο αν υπάρει ισομορφισμός k[g]-προτύπων V V (άσκηση) Μία αναπαράσταση ρ : G GL ( k) λέγεται ανάγωγη αν το αντίστοιο k[g]-πρότυπο V είναι απλό 7 Παράδειγμα Έστω G S η συμμετρική ομάδα των μεταθέσεων στοιείων Έστω V k και μια βάση { v,, v } του V Το V είναι S -πρότυπο με δράση v v () Δεν είναι απλό όταν, γιατί ένα υποπρότυπό του είναι το v v Πράγματι, έουμε, το κυκλικό υποπρότυπο του V που παράγεται από το v v v v v v για κάθε () ( ) S v v Ένα k[g]-πρότυπο V λέγεται πλήρως αναλύσιμο αν είναι ευθύ άθροισμα απλών υποπροτύπων του Το θεώρημα του Machke μας δίνει το εξής αποτέλεσμα 7 Πόρισμα Έστω G μια πεπερασμένη ομάδα τάξης Αν η αρακτηριστική του k είναι μηδέν, ή αν η αρακτηριστική του k είναι p με p, τότε κάθε k[g]-πρότυπο είναι πλήρως αναλύσιμο Στα παρακάτω θα ασοληθούμε αποκλειστικά με την περίπτωση k πόρισμα Επίσης, G θα είναι πάντα πεπερασμένη ομάδα, οπότε ισύει το προηγούμενο
3 Στο κεφάλαιο είδαμε ότι υπάρει ισομορφισμός αλγεβρών διαστάσεις υπεράνω του έουμε G 6 [ G] M ( ) M ( ) Λαμβάνοντας Υπενθυμίζουμε ότι το είναι το πλήθος των ανά δυο μη ισόμορφων απλών [ G] -προτύπων Στη συνέεια θα αρακτηρίσουμε τον αριθμό ρησιμοποιώντας ομαδοθεωρητικές έννοιες Υπενθυμίζουμε ότι η κλάση συζυγίας του G είναι το σύνολο { x x x G} και ότι δύο κλάσεις συζυγίας είτε ταυτίζονται είτε είναι ξένες Έστω C μία κλάση συζυγίας Θέτουμε C [ G] C Θα δείξουμε ότι κάθε C ανήκει στο κέντρο της άλγεβρας [ G ] Έστω C { x x,, x x } και h G Έουμε C x x, οπότε γιατί καθώς το h Ch x διατρέει τα στοιεία h x x h C, () x το h x xh x,, διατρέει τα στοιεία του C (αφού h x x h h x x h x x x x x x λόγω του ορισμού των x στο σύνολο C) Από την () συνάγουμε ότι C C( [ G]) 7 Πρόταση Έστω C,,Cm οι (ανά δύο διάφορες) κλάσεις συζυγίας της G Τότε μία βάση του - διανυσματικού ώρου C( [ G ]) είναι η { C,, C m } Απόδειξη: Είδαμε πριν ότι C C( [ G]) για κάθε ) Γραμμική ανεξαρτησία: Αν λ C λ m Cm 0 με παίρνουμε λ λm 0, γιατί τα C,,C m είναι ανά δύο ξένα υποσύνολα βάσης ) Παράγουν το C( [ G ]) : Έστω C( [ G]) Τότε για κάθε h G ισύει λh h επομένως οπότε παίρνουμε συζυγίας λ hxh x λ x λ, xg hxh λ για κάθε x G Με άλλα λόγια, καθώς το διατρέει τα στοιεία μια κλάσης C ο συντελεστής λ παραμένει σταθερός Παράδειγμα Οι κλάσεις συζυγίας της συμμετρικής ομάδας οι κύκλοι μήκους δύο και, είναι οι κύκλοι μήκους, είναι C C C λ λ Έτσι γράφουμε λ λ C λ {}, {,, }, {, } G S λ mcm {,,,,, }, όπου και,, είναι (Γενικά ξέρουμε ότι δύο μεταθέσεις της S είναι συζυγή στοιεία αν και μόνο αν έουν τον ίδιο τύπο στην ανάλυση σε γινόμενο ξένων ανά δύο κύκλων) Άρα μια βάση του κέντρου της -άλγεβρας [ G ] είναι C, C C,
4 6 75 Πόρισμα Το πλήθος των ανά δύο μη ισόμορφων απλών [ G] -προτύπων είναι το πλήθος των κλάσεων συζυγίας της G Απόδειξη: Έουμε [ G] M ( ) M ( ) όπου είναι το πλήθος των ανά δύο μη ισόμορφων απλών [ G] -προτύπων Υπολογίζοντας κέντρα παίρνουμε C( [ G ]) Το ζητούμενο προκύπτει από την Πρόταση 7 76 Πόρισμα Μια πεπερασμένη ομάδα G είναι αβελιανή αν και μόνο αν κάθε απλό [ G] -πρότυπο έει διάσταση ένα Απόδειξη: Αν G αβελιανή, τότε η G έει G κλάσεις συζυγίας, οπότε η σέση Αντίστροφα αν, τότε από τη σέση οπότε η G έει G κλάσεις συζυγίας και άρα είναι αβελιανή G G δίνει έπεται ότι G 77 Παράδειγμα (Οι ανάγωγες αναπαραστάσεις αβελιανών ομάδων) Έστω G (πεπερασμένη, όπως πάντα) αβελιανή ομάδα τάξης Από το θεώρημα ταξινόμησης των πεπερασμένων αβελιανών ομάδων γνωρίζουμε ότι η G είναι ισόμορφη με ευθύ γινόμενο κυκλικών ομάδων, G, όπου είναι θετικοί ακέραιοι Μια παρουσίαση της G με γεννήτορες και σέσεις είναι: G,, :,, Έστω,, με λ Ορίζουμε την αναπαράσταση : G λ λ ( ) λ ρ λ Το σύνολο { ρλ λ λ,,, } έει ακριβώς στοιεία και αποτελεί το σύνολο των αναγώγων αναπαραστάσεων της G υπέρ του *, 7 Χαρακτήρες Ορισμός Έστω ρ : G GL ( k) αναπαράσταση της G Ο αρακτήρας του ρ είναι η απεικόνιση όπου T( A ) συμβολίζει το ίνος αρακτήρας της αντίστοιης αναπαράστασης ρ a του πίνακα A a : G k, ρ ( ) T( ρ( )), Ο αρακτήρας ενός k [G] -προτύπου είναι ο Επειδή όμοιοι πίνακες έουν το ίδιο ίνος, παρατηρούμε ότι ισοδύναμες αναπαραστάσεις έουν τον ίδιο αρακτήρα Επιπλέον η τιμή ρ () εξαρτάται μόνο από τη κλάση συζυγίας του (και όι από το αυτό καθευατό) Παράδειγμα Μετά από μερικές πράξεις με υπολογισμούς πινάκων και ινών, βλέπουμε ότι ο αρακτήρας της αναπαράστασης : D8 GL( ) του Παραδείγματος 7 είναι a a a b ab a b a b ( )
5 Παρατηρούμε ότι αν είναι ο αρακτήρας μιας αναπαράστασης ρ υπέρ του : G GL ( ), τότε: ) Ο βαθμός της ρ είναι η τιμή () ) Αν m είναι η τάξη του στοιείου G, τότε το () είναι άθροισμα m-στών ριζών της μονάδας m Πράγματι, αφού ισύει ρ( ) m I οπότε οι ιδιοτιμές του πίνακα ρ () είναι m-στές ρίζες της μονάδας Το ίνος του ρ () είναι το άθροισμα των ιδιοτιμών του ) Ισύει ( ) ( ) (ο συζυγής του () ), γιατί αν ( ) ω ω με ω ( ) ω ω και ω ω για κάθε v) ( ) αν και ( ) ( ) ( ) είναι συζυγή Πράγματι, αν και m 6, τότε είναι συζυγή τότε ισύει Ορισμός Έστω : G GL m ( ), : G GL ( ) δύο αναπαραστάσεις της G βαθμού m και αντίστοια Το ευθύ άθροισμα των ρ και ρ είναι η αναπαράσταση : G GL m ( ) βαθμού m που ορίζεται από ρ( ) 0 ( ρ ρ)( ) 0 ρ( ) Παρατήρηση Συνεπώς αν V, V είναι τα αντίστοια [ G] -πρότυπα των ρ, ρ του παραπάνω ορισμού, τότε το αντίστοιο [ G] -πρότυπο της αναπαράστασης ρ ρ είναι το V V Θεωρώντας ίνη παίρνουμε ρρ (όπου στο δεξί μέλος έουμε τη συνήθη πρόσθεση συναρτήσεων G, δηλαδή ρ ρ ( )( ) ( ) ( ) για κάθε G) Σημειώνουμε ότι η αναπαράσταση : G GL ( ) είναι ανάγωγη αν και μόνο αν δεν υπάρουν αναπαραστάσεις : ( ) G GL, : ( ) G GL, με και (άσκηση) Ορισμός Έστω, :G συναρτήσεις (όι αναγκαστικά αρακτήρες) Ορίζουμε το εσωτερικό γινόμενο των και ψ, ψ ( ) ψ( ) G Παρατηρούμε ότι ),, ), είναι γραμμική στην πρώτη μεταβλητή, και ), 0 αν 0 Επίσης, λ ψ λψ λ, ψ λ, ψ για κάθε, και,, : G Σε κάθε περίπτωση οι αποδείξεις είναι άμεσες Για αρακτήρες μπορούμε να πούμε κάτι ισυρότερο: 7 Πρόταση Έστω και ψ αρακτήρες της G και,, ανιιπρόσωποι των κλάσεων συζυγίας της G Με C ( ) συμβολίζουμε την κεντροποιούσα ομάδα του, C( ) { x G x x} Τότε
6 (),, ( ) ( ) G, και 65 () ( ) ψ( ), ψ C( ) Απόδειξη: ) Έουμε, ψ Αφού, ) ) Έστω G ( ) ψ( ) G ( ) ψ( ) G ( ) ψ( ), ψ ψ,, παίρνουμε, ψ, ψ και άρα, (θα δούμε παρακάτω ότι ισύει C η κλάση συζυγίας του ψ, Επειδή ) ( ) και ψ( ) ψ( ) για κάθε C έουμε ( C, ψ ( ) ψ( ) ( ) ψ( ) G Θυμόμαστε από τις ομάδες (π δράσεις ομάδων) ότι C [ G : C( G )] (ο πληθάριθμος μιας τροιάς είναι ο δείκτης της αντίστοιης σταθεροποιούσας ομάδας) Έτσι ψ( h Μια συνάρτηση h) ψ( ) για κάθε C C( ) : G ονομάζεται συνάρτηση κλάσεων αν για κάθε G ισύει h G, δηλαδή αν η ψ είναι σταθερή σε κάθε κλάση συζυγίας Κάθε αρακτήρας είναι συνάρτηση κλάσεων Το -διανυσματικό ώρο των συναρτήσεων κλάσεων συμβολίζουμε με cf (G) Θα αποδείξουμε στη συνέεια το σημαντικό αποτέλεσμα ότι οι αρακτήρες των αναγώγων αναπαραστάσεων της G αποτελούν ορθοκανονική βάση του cf (G) ως προς το εσωτερικό γινόμενο, Αν : G είναι συνάρτηση, θα συμβολίζουμε πάλι με : [ G] τη γραμμική επέκταση της G στο [ G] Έστω αντίστοια Οι V,,V τα ανά δύο μη ισόμορφα απλά [ G] -πρότυπα και,, οι αρακτήρες τους ονομάζονται ανάγωγοι αρακτήρες της G Από την άσκηση 9 υπάρουν κεντρικά αυτοδύναμα στοιεία e,, [ ] e G με την ιδιότητα e e και e e 0 για Επιπλέον e για κάθε R και e R 0 για κάθε και e e 0 για κάθε, όπου R είναι οι απλές συνιστώσες του [ G ], [ G] R R Συνεπώς ισύει και ev v για κάθε v V και e V 0 για κάθε 7 Λήμμα Με τους προηγούμενους συμβολισμούς έουμε ( e dm V ) 0 αν αν
7 66 Απόδειξη: Για έουμε e V 0 και άρα το ίνος της δράσης του e στο V είναι μηδέν, δηλαδή ( e ) 0 Γράφοντας τώρα e e παίρνουμε ( ) ( e ) ( e ) dm V ( e ) 7 Λήμμα Έστω e ο αρακτήρας του [ G] -προτύπου [ G ] (με δράση αριστερό πολλαπλασιασμό) Διατηρώντας τους προηγούμενους συμβολισμούς έουμε: ) e ( ) και e ( ) 0 για κάθε G, ) ) () e ( Απόδειξη: ) e () dm [ G] G Έστω G, Θεωρούμε τη βάση G,,, } του { [ G ] Ο αντίστοιος πίνακας της δράσης του έει μη μηδενικό στοιείο πάνω στη διαγώνιο αν και μόνο αν, δηλαδή αν ) Το ζητούμενο προκύπτει αμέσως από τον ισομορφισμό [ G] V V (βλ κεφάλαιο ) και το γεγονός ότι dm V () 7 Πρόταση Με τους προηγούμενους συμβολισμούς ισύει e () ( ) Απόδειξη: Έστω e το Λήμμα 7 ) Έστω G λ h G Από το Λήμμα 7 ) έουμε, Θεωρώντας τον αρακτήρα e της υπολογίζουμε σύμφωνα με G ( h e ) λ ( h ) λ e e G e ( h e ) () x ( h e ) Επειδή e R 0 για, έουμε ( h e ) 0 για Για έουμε ev v v R και άρα x ( h e ) ( h απ όπου προκύπτει το ζητούμενο ) Τελικά αντικαθιστώντας έουμε λ h () ( h e ) h () ( h Είμαστε τώρα έτοιμοι να αποδείξουμε το πρώτο κύριο αποτέλεσμα αυτού του κεφαλαίου 75 Θεώρημα Οι ανάγωγοι αρακτήρες της G πάνω από το αποτελούν ορθοκανονική βάση του - διανυσματικού ώρου cf (G) ως προς το εσωτερικό γινόμενο, Απόδειξη: Έστω,, οι ανάγωγοι αρακτήρες Θα δείξουμε πρώτα ότι οι,, αποτελούν βάση του cf (G) Γνωρίζουμε ότι είναι το πλήθος των κλάσεων συζυγίας της G (Πόρισμα 75) Επειδή η διάσταση του cf (G) είναι (μια βάση του cf (G) είναι οι αρακτηριστικές συναρτήσεις f : G που ορίζονται από f ( ) 0 για και f ( ) για κάθε C ) αρκεί να δείξουμε ότι οι,, είναι C γραμμικώς ανεξάρτητες Έστω λ 0 Από το Λήμμα 7 παίρνουμε τότε λ ( e ) 0, δηλαδή λ dm V 0, οπότε λ 0 (Η γραμμική ανεξαρτησία των έπεται και από το γεγονός ),, δ
8 που θα δείξουμε αμέσως παρακάτω) Θα δείξουμε τώρα ότι, Από τον τύπο της Πρότασης 7 συμπεραίνουμε ότι ο συντελεστής του G στο e είναι () ( ) ( ) G G που είναι (λόγω της Πρότασης 7 )) ίσος με (), Όμως e e οπότε ο συντελεστής του στο e είναι ίσος με (Πρόταση 7) Συγκρίνοντας τις δύο τελευταίες εκφράσεις παίρνουμε, Θα δείξουμε τώρα ότι, 0 για Από τη σέση e e 0 παίρνουμε λόγω της Πρότασης 7 ότι Ο συντελεστής του, hg () ( ) ( h ) h 0 G στην προηγούμενη ισότητα δίνει G οπότε, 0 από την πρόταση 7 ) ( ) ( ) 0 76 Πόρισμα Έστω V ένα [ G] -πρότυπο με αρακτήρα Τότε το V είναι ανάγωγο αν και μόνο αν, Απόδειξη: Αν V είναι ανάγωγο τότε, από το προηγούμενο θεώρημα Αντίστροφα, έστω m m, Γράφοντας το V ως ευθύ άθροισμα αναγώγων προτύπων V V V λαμβάνουμε m m οπότε η σέση, δίνει mm,, Από το προηγούμενο θεώρημα έουμε, και, 0 για, οπότε m m Συνεπώς m για κάποιο και m 0 για Άρα V V Το προηγούμενο πόρισμα είναι ιδιαίτερα ρήσιμο σε υπολογισμούς Για παράδειγμα, ο αρακτήρας της αναπαράστασης : D8 GL( ) του Παραδείγματος 7 υπολογίστηκε στην αρή της παρούσας παραγράφου και βρήκαμε a a a b ab a b a b ( ) Εύκολα επαληθεύουμε ότι, και άρα η ρ είναι ανάγωγη 67 Το ακόλουθο αποτέλεσμα δείνει ότι οι αρακτήρες αναπαραστάσεων επί του αναπαραστάσεις αρακτηρίζουν τις
9 68 77 Πόρισμα Δύο αναπαραστάσεις της G επί του είναι ισοδύναμες αν και μόνο αν οι αρακτήρες τους ταυτίζονται Απόδειξη: Έστω ρ και ρ αναπαραστάσεις με αντίστοιους αρακτήρες και Αν ρ και ρ είναι ισοδύναμες τότε όπως είπαμε στην αρή της παραγράφου Αντίστροφα, έστω Για τα m m m m αντίστοια [ G] -πρότυπα γράφουμε V V V, V V V όπου V,,V είναι ανά δύο μη ισόμορφα ανάγωγα [ G] -πρότυπα Από,, παίρνουμε m m, m, m,,, οπότε το Θεώρημα 75 δίνει m m για κάθε Άρα V V 78 Πόρισμα Έστω V, V [ G] -πρότυπα με αρακτήρες, αντίστοια Τότε, dm Hom [ ]( VV G, ) m m m m Απόδειξη: Γράφοντας V V V και V V V, το θεώρημα δίνει, mm mm Από την άλλη μεριά έουμε από το Λήμμα του Schu για αλγεβρικά κλειστά σώματα ότι, αν Hom [ G] ( VV, ) 0, αν Από την Πρόταση παίρνουμε dm Hom [ G] ( V, V) mm mm Τονίζουμε ότι στην ειδική περίπτωση που στο προηγούμενο πόρισμα ο αρακτήρας είναι ανάγωγος, τότε ο μη αρνητικός ακέραιος, ισούται με την πολλαπλότητα του στην παράσταση του ως -γραμμικός συνδυασμός αναγώγων αρακτήρων 7 Σέσεις Ορθογωνιότητας και Πίνακες Χαρακτήρων Έστω IG {,, } το σύνολο των αναγώγων αρακτήρων της G,,, αντιπρόσωποι των κλάσεων συζυγίας της G και C ( ) { xg x x} η κεντροποιούσα ομάδα του Με συμβολίζουμε το δέλτα του Koecke, δ 0 εκτός αν α β οπότε δ 7 Θεώρημα Με τους προηγούμενους συμβολισμούς έουμε: α ( ) β ( ) ) (ορθογώνιες σέσεις γραμμών) δαβ C( ) αβ ) (ορθογώνιες σέσεις στηλών) ( ) ( ) δ C( ) α β αβ Απόδειξη: ) Από το Θεώρημα 75 έουμε, οπότε το ζητούμενο προκύπτει από την Πρόταση 7 ) α αα δ αβ
10 ) Έστω ψ cf (G) που ορίζεται από ψ β ( α ) δαβ Λόγω του Θεωρήματος 75 γράφουμε ψ β λ λ οπότε παίρνουμε, ( ) ( ) Ισύει ψ β ( ) αν το είναι συζυγές του β και ψ β ( ) 0 διαφορετικά Επειδή επιπλέον ο πληθάριθμος της κλάσης συζυγίας του δ αβ ψ β G β είναι / C( β ), παίρνουμε λ ( β ) Άρα C( ) ( α ) ( β ) ( α ) λ ( α ) λ ( α ) C( ) Έστω IG,, } και,, αντιπρόσωποι των κλάσεων συζυγίας της G Ο πίνακας { αρακτήρων της G είναι ένας Παραδείγματα Ο πίνακας αρακτήρων της κυκλικής ομάδας πίνακας που στη θέση (, ) υπάρει η τιμή ) β β ( {, aa, } τάξης είναι (Παράδειγμα 79), όπου ω με ω, δηλαδή ω ω 0 Οι ορθογώνιες σέσεις γραμμών a ω ω a ω ω ω ω για τις πρώτες δύο γραμμές δίνουν 0, και ωω ω ω για τη δεύτερη γραμμή με τον εαυτό της δίνουν Οι ορθογώνιες σέσεις στηλών για τις δύο τελευταίες στήλες δίνουν ω ω ω ω 0 Οι ορθογώνιες σέσεις επιτρέπουν συνά τον προσδιορισμό ολόκληρου του πίνακα αρακτήρων αν γνωρίζουμε μόνο κάποιο τμήμα του Για παράδειγμα, ας υποθέσουμε ότι για μια ομάδα G τάξης που έει κλάσεις συζυγίας γνωρίζουμε το ακόλουθο τμήμα του πίνακα αρακτήρων C( ) ω ω ω ω όπου,, είναι αντιπρόσωποι των κλάσεων συζυγίας και ω ω 0 Από τη σέση () () (θεώρημα 75 ή θεώρημα 7 ) για α β ) παίρνουμε () Οι 69
11 ορθογώνιες σέσεις στηλών για τις στήλες και δίνουν 70 ( ) ( ) 0 ( ) 0 ( ) Οι ορθογώνιες σέσεις στηλών για τις στήλες και δίνουν και για τις στήλες και δίνουν ( ) ( ) 0 ω ω ( ) 0 ( ) 0 ( ) ( ) 0 ω ω ( ) 0 ( ) 0 Προσδιορίζεται κατά αυτόν τον τρόπο όλος ο πίνακας αρακτήρων της G Παρατηρήσεις ) Ο προηγούμενος πίνακας αρακτήρων είναι αυτός της ομάδας A ) Ήδη επισημάναμε ότι το Θεώρημα 75 περιέεται στο Θεώρημα 7 ) για α β Παρόμοια, το Λήμμα 7 περιέεται στο Θεώρημα 7 ) για α Ως άλλο παράδειγμα ας θεωρήσουμε τη G S που έει τρεις κλάσεις συζυγίας { }, {(, (), ()}, {( ), ()} Το Πόρισμα 75 δίνει οπότε,, Μια ανάγωγη αναπαράσταση της S είναι * η : S ( ) που έει αρακτήρα, που δίνεται από (), (), () Συνεπώς ο πίνακας αρακτήρων της S έει τη μορφή C( ) 6 () a () b Οι ορθογώνιες σέσεις στηλών για τις στήλες και δίνουν ( ) a 0 οπότε a 0 Για τις στήλες και δίνουν b 0 b
12 Ασκήσεις 7 Στις παρακάτω ασκήσεις με G συμβολίζουμε μια πεπερασμένη ομάδα Το μη μηδενικό cf (G) είναι αρακτήρας αν και μόνο αν, για κάθε ανάγωγο αρακτήρα Αν για τον αρακτήρα ισύει ( ) 0 G,, τότε ο είναι της μορφής m, m Υπόδ: Υπολογίστε το, όπου ανάγωγος αρακτήρας και ρησιμοποιείστε το Λήμμα 7) Συμπληρώσετε τον πίνακα αρακτήρων της D 8 C( 5 ) 8 ) Οι ορθογώνιες σέσεις γραμμών είναι ισοδύναμες με τις ορθογώνιες σέσεις στηλών a ) Έστω Μ ο πίνακας αρακτήρων της G Δείξετε ότι αντιπρόσωποι των κλάσεων συζυγίας της G a b ab det M C( ) Υπόδειξη: από τις σέσεις ορθογωνιότητας προκύπτει ότι ο πίνακας e, όπου,, είναι t MM είναι διαγώνιος ) Έστω I( G) {,, } Τότε C( G) G ( ) ( ) 7 Έστω αρακτήρας της G Θέτουμε ke { G ( ) ()} Τότε ke είναι κανονική υποομάδα της G Αντίστροφα κάθε κανονική υποομάδα της G είναι της μορφής αρακτήρα Επιπλέον αν όπου το,, είναι οι ανάγωγοι αρακτήρες τότε ke ke ke για κάποιο διατρέει τους ανάγωγους αρακτήρες που έουν την ιδιότητα, 0 Συμπέρασμα: από τον πίνακα αρακτήρων της G μπορούμε να βρούμε όλες τις κανονικές υποομάδες της G Βρείτε τώρα όλες τις κανονικές υποομάδες της D 8 από την άσκηση 8 Η G δεν είναι απλή αν και μόνο αν ( ) () για κάποιον μη τετριμμένο ανάγωγο αρακτήρα και κάποιο G, (Βλ προηγούμενη άσκηση) 9 Για κάθε αρακτήρα αβελιανής ομάδας ισύει, () Αληθεύει το συμπέρασμα για μη αβελιανές ομάδες; 0 Έστω ανάγωγος αρακτήρας της G βαθμού ) Για κάθε C( G) ισύει ( ) ) Ισύει [ G : C( G)] Έστω H αβελιανή υποομάδα της G Τότε κάθε ανάγωγος αρακτήρας της G έει βαθμό [ G : H] Κατά συνέπεια κάθε ανάγωγος αρακτήρας της διεδρικής ομάδας D a, b : a b, ab ba έει βαθμό ή Έστω [ G] -πρότυπα V, W με αντίστοιους αρακτήρες, ψ Τότε ο αρακτήρας του V W είναι το
13 γινόμενο ψ (Η δράση είναι ( v w) ( v) ( w) ) Υπόδειξη: υπολογίσετε το ίνος της δράσης του παίρνοντας βάσεις των V, W που αποτελούνται από ιδιοδιανύσματα Αν, I( G) και de, τότε I( G) (Βλ προηγούμενη άσκηση και Πόρισμα 76) Έστω ο μοναδικός ανάγωγος αρακτήρας της S βαθμού Βρείτε την ανάλυση του άθροισμα αναγώγων αρακτήρων 5 Έστω : G GL ( ) αναπαράσταση ) Αν υπάρει G με det( ( )), δείξτε ότι η G δεν είναι απλή 7 σε ) Αν το G έει τάξη, τότε ισύει ένα από τα εξής συμπεράσματα: a) ( ) ()mod b) η G έει κανονική υποομάδα δείκτη Υπόδειξη: Αν V είναι το αντίστοιο πρότυπο της, μπορούμε να επιλέξουμε βάση του V τέτοια ώστε ο πίνακας της γραμμικής απεικόνισης V V, v v, είναι διαγώνιος με στη διαγώνιο 6 Έστω VWδυο, ανάγωγα [ G] -πρότυπα Δείξτε ότι το V W (άσκηση) εμφυτεύεται στην κανονική αναπαράσταση της G Υπόδειξη: αρκεί να δειτεί ότι αν,, I( G), τότε, () 7 Με το συμβολισμό του Παραδείγματος 7 έστω k ) Δείξτε ότι το [ S ]-πρότυπο V v v είναι ανάγωγο ) Δείξτε ότι, V όπου είναι ο τετριμμένος αρακτήρας της S 8 Να βρεθούν όλες οι ομάδες με ακριβώς, ή ανάγωγους αρακτήρες 9 Έστω G πεπερασμένη υποομάδα της GL ( ) Αποδείξτε ότι αν T( ) 0, τότε 0 0 Έστω : G GL ( ) μια αναπαράσταση τέτοια ώστε το είναι ιδιοτιμή του ( ) για κάθε G Δείξτε ότι η δεν είναι ανάγωγη Υπόδειξη: Υπολογίστε το,, όπου είναι ο αρακτήρας της και ο τετριμμένος αρακτήρας της G, συναρτήσει των ιδιοτιμών των ( ) Αποδείξτε ότι κάθε πεπερασμένη απλή ομάδα με τάξη όι δύναμη πρώτου δεν έει ανάγωγη αναπαράσταση βαθμού Έστω V ένας -διανυσματικός ώρος με dm V και v,, v } μια βάση του V Ο V Με είναι [ S ]-πρότυπο με δράση v v (), Θέτουμε Fx( ) { {,, } ( ) } ) Δείξτε ότι ( ) Fx( ) V ) Στο ερώτημα αυτό υποθέτουμε ότι a Υπολογίστε το εσωτερικό γινόμενο S G { G V συμβολίζουμε το αρακτήρα του V, και με βάση αυτό αποδείξτε ότι ο V V είναι άθροισμα δύο ανάγωγων αρακτήρων της S Υπολογίστε τους αρακτήρες αυτούς V b Βρείτε το αρακτήρα του V V και παραστήστε τον ως άθροισμα ανάγωγων αρακτήρων της S ) Θεωρούμε τους υπόωρους U { av av a a 0} και W { a( v v) a } του V a Δείξτε ότι οι παραπάνω υπόωροι είναι [ S ]-υποπρότυπα του V και ότι V U W b Δείξτε ότι για κάθε,, ισύει v v U Με βάση αυτό δείξτε ότι το U είναι απλό [ S ]-πρότυπο Έστω A ένας -διανυσματικός ώρος με dm A 9 και { v, } μια βάση του A Ο A
14 είναι [ S] -πρότυπο με δράση v v ( ) ( ), S Για παράδειγμα, αν (), τότε v v Δείξτε ότι A [ S] V, όπου V είναι το [ S] -πρότυπο της προηγούμενης άσκησης Έστω άρτιος θετικός ακέραιος, m Ο διανυσματικός ώρος [ m m] είναι [ ] πρότυπο με εξωτερικό πολλαπλασιασμό που ορίζεται από ([ a],([ x],[ y] ) ([ a x],[ a y] ) Παραστήστε m m m m το αρακτήρα του [ ] ως γραμμικό συνδυασμό των ανάγωγων αρακτήρων της m m Υπόδειξη: Ίσως είναι ρήσιμο να λύσετε αναλυτικά πρώτα την περίπτωση m 5 Οι αναπαραστάσεις της δικυκλικής ομάδας a Έστω : G GL ( ) μια αναπαράσταση τέτοια ώστε για κάποια, h G έουμε ( ) ( h) ( h) ( ) Αποδείξτε ότι η δεν είναι ανάγωγη b Θεωρούμε την ομάδα ( δικυκλική ) T a, b : a, a b, b ab a που έει τάξη Έστω ένας ακέραιος και e Δείξτε τα εξής 0 0 Η αντιστοιία a, b ορίζει μια αναπαράσταση της T 0 0 Η είναι ανάγωγη αν (Υπόδειξη: ένας τρόπος είναι με το a) Οι,, είναι ανά δυο μη ισοδύναμες v Οι υπόλοιπες ανάγωγες ανά δυο μη ισοδύναμες αναπαραστάσεις της T είναι βαθμού 6 Υπολογίστε τον πίνακα αρακτήρων της S ως εξής a Υπολογίστε τον αριθμό των κλάσεων συζυγίας ρησιμοποιώντας την ανάλυση μεταθέσεων σε γινόμενο ξένων κύκλων Υπολογίστε τον πληθάριθμο κάθε κλάσης συζυγίας C και το C( ) [ G : C ] b Έστω, ο τετριμμένος αρακτήρας και ο αρακτήρας προσήμου αντίστοια Έστω ο αρακτήρας V όπου V ο αρακτήρας του προτύπου στο παράδειγμα 7 για Υπολογίστε τον και δείξτε ότι είναι ανάγωγος c Στη συνέεια θέστε 5 (που είναι ανάγωγος από την άσκηση ) και υπολογίστε τον Βρείτε τον τελευταίο αρακτήρα από τις ορθογώνιες σέσεις Δίνεται ο πίνακας αρακτήρων της S για επαλήθευση () () ()() () C ( )
ΚΕΦΑΛΑΙΟ 7: Αναπαραστάσεις Πεπερασµένων Οµάδων Ι
 ΚΕΦΑΛΑΙΟ 7: Αναπαραστάσεις Πεπερασµένων Οµάδων Ι Χρησιµοποιώντας το θεώρηµα του Weddebu για ηµιαπλούς δακτυλίους αναπτύσσουµε εδώ τις πρώτες προτάσεις από τη θεωρία των αναπαραστάσεων και αρακτήρων πεπερασµένων
ΚΕΦΑΛΑΙΟ 7: Αναπαραστάσεις Πεπερασµένων Οµάδων Ι Χρησιµοποιώντας το θεώρηµα του Weddebu για ηµιαπλούς δακτυλίους αναπτύσσουµε εδώ τις πρώτες προτάσεις από τη θεωρία των αναπαραστάσεων και αρακτήρων πεπερασµένων
ΚΕΦΑΛΑΙΟ 2: Ημιαπλοί Δακτύλιοι
 ΚΕΦΑΛΑΙΟ : Ημιαπλοί Δακτύλιοι Είδαμε στο κύριο θεώρημα του προηγούμενου κεφαλαίου ότι κάθε δακτύλιος διαίρεσης έχει την ιδιότητα κάθε πρότυπο είναι ευθύ άθροισμα απλών προτύπων Εδώ θα χαρακτηρίσουμε όλους
ΚΕΦΑΛΑΙΟ : Ημιαπλοί Δακτύλιοι Είδαμε στο κύριο θεώρημα του προηγούμενου κεφαλαίου ότι κάθε δακτύλιος διαίρεσης έχει την ιδιότητα κάθε πρότυπο είναι ευθύ άθροισμα απλών προτύπων Εδώ θα χαρακτηρίσουμε όλους
ΚΕΦΑΛΑΙΟ 9: Επαγόµενοι Χαρακτήρες και το Θεώρηµα του Frobenius
 ΚΕΦΑΛΑΙΟ 9: Επαγόµενοι Χαρακτήρες και το Θεώρηµα του Frobenus Στο κεφάλαιο αυτό εισάγουµε τους επαγόµενους αρακτήρες µε τη βοήθεια των οποίων αποδεικνύουµε το θεώρηµα των συµπληρωµάτων του Frobenus Οι
ΚΕΦΑΛΑΙΟ 9: Επαγόµενοι Χαρακτήρες και το Θεώρηµα του Frobenus Στο κεφάλαιο αυτό εισάγουµε τους επαγόµενους αρακτήρες µε τη βοήθεια των οποίων αποδεικνύουµε το θεώρηµα των συµπληρωµάτων του Frobenus Οι
ΚΕΦΑΛΑΙΟ 8: Εφαρμογή: Το θεώρημα του Burnside
 ΚΕΦΑΛΑΙΟ 8: Εφαρμογή: Το θεώρημα του Bursde a b Θα αποδείξουμε εδώ ότι κάθε ομάδα τάξης pq ( p, q πρώτοι) είναι επιλύσιμη Το θεώρημα αυτό αποδείχτηκε από τον Bursde το 904 ο οποίος χρησιμοποίησε τη νέα
ΚΕΦΑΛΑΙΟ 8: Εφαρμογή: Το θεώρημα του Bursde a b Θα αποδείξουμε εδώ ότι κάθε ομάδα τάξης pq ( p, q πρώτοι) είναι επιλύσιμη Το θεώρημα αυτό αποδείχτηκε από τον Bursde το 904 ο οποίος χρησιμοποίησε τη νέα
ΚΕΦΑΛΑΙΟ 1: Πρότυπα. x y x z για κάθε x, y, R με την ιδιότητα 1R. x για κάθε x R, iii) υπάρχει στοιχείο 1 R. ii) ( x y) z x ( y z)
 ΚΕΦΑΛΑΙΟ 1: Πρότυπα Στο κεφάλαιο αυτό θα υπενθυμίσουμε τις βασικές έννοιες που αφορούν πρότυπα πάνω από ένα δακτύλιο Θα περιοριστούμε στα πλέον απαραίτητα για αυτά που ακολουθούν στα άλλα κεφάλαια Η κατευθυντήρια
ΚΕΦΑΛΑΙΟ 1: Πρότυπα Στο κεφάλαιο αυτό θα υπενθυμίσουμε τις βασικές έννοιες που αφορούν πρότυπα πάνω από ένα δακτύλιο Θα περιοριστούμε στα πλέον απαραίτητα για αυτά που ακολουθούν στα άλλα κεφάλαια Η κατευθυντήρια
Κεφάλαιο 1 Πρότυπα. Στο κεφάλαιο αυτό εισάγουμε την έννοια του προτύπου πάνω από δακτύλιο.
 Κεφάλαιο Πρότυπα Στο κεφάλαιο αυτό εισάγουμε την έννοια του προτύπου πάνω από δακτύλιο Ορισμοί και Παραδείγματα Παραδοχές Στo βιβλίο αυτό θα κάνουμε τις εξής παραδοχές Χρησιμοποιούμε προσθετικό συμβολισμό
Κεφάλαιο Πρότυπα Στο κεφάλαιο αυτό εισάγουμε την έννοια του προτύπου πάνω από δακτύλιο Ορισμοί και Παραδείγματα Παραδοχές Στo βιβλίο αυτό θα κάνουμε τις εξής παραδοχές Χρησιμοποιούμε προσθετικό συμβολισμό
Ασκήσεις3 Διαγωνίσιμες Γραμμικές Απεικονίσεις
 Ασκήσεις 5 Βασικά σημεία Ιδιότητες ιδιόχωρων: Έστω,, Ισχύουν τα εξής Ασκήσεις Διαγωνίσιμες Γραμμικές Απεικονίσεις κάποιες διακεκριμένες ιδιοτιμές της γραμμικής απεικόνισης : V V, όπου o Αν v v 0, όπου
Ασκήσεις 5 Βασικά σημεία Ιδιότητες ιδιόχωρων: Έστω,, Ισχύουν τα εξής Ασκήσεις Διαγωνίσιμες Γραμμικές Απεικονίσεις κάποιες διακεκριμένες ιδιοτιμές της γραμμικής απεικόνισης : V V, όπου o Αν v v 0, όπου
ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων
 ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων Μελετάμε εδώ τη συνθήκη της αύξουσας αλυσίδας υποπροτύπων και τη συνθήκη της φθίνουσας αλυσίδας υποπροτύπων Αυτές συνδέονται μεταξύ τους με την έννοια της συνθετικής σειράς
ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων Μελετάμε εδώ τη συνθήκη της αύξουσας αλυσίδας υποπροτύπων και τη συνθήκη της φθίνουσας αλυσίδας υποπροτύπων Αυτές συνδέονται μεταξύ τους με την έννοια της συνθετικής σειράς
Ασκήσεις2 8. ; Αληθεύει ότι το (1, 0, 1, 2) είναι ιδιοδιάνυσμα της f ; b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα της γραμμικής απεικόνισης 3 3
 Ασκήσεις 8 Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμων και ιδιοδιανυσμάτων, υπολογισμός τους Σε διακεκριμένες ιδιοτιμές αντιστοιχούν γραμμικά ανεξάρτητα ιδιοδιανύσματα Αν ΑΧ=λΧ,
Ασκήσεις 8 Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμων και ιδιοδιανυσμάτων, υπολογισμός τους Σε διακεκριμένες ιδιοτιμές αντιστοιχούν γραμμικά ανεξάρτητα ιδιοδιανύσματα Αν ΑΧ=λΧ,
Ασκήσεις3 Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα.
 Ασκήσεις 0 Ασκήσεις Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα o H -στήλη του P P είναι E αν και μόνο αν η -στήλη του P είναι ιδιοδιάνυσμα του που αντιστοιχεί στην ιδιοτιμή
Ασκήσεις 0 Ασκήσεις Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα o H -στήλη του P P είναι E αν και μόνο αν η -στήλη του P είναι ιδιοδιάνυσμα του που αντιστοιχεί στην ιδιοτιμή
Δακτύλιοι και Πρότυπα Ασκήσεις 6. Η ύλη των ασκήσεων αυτών είναι η Ενότητα6, Εφαρμογές Θεωρημάτων Δομής στη Γραμμική Αλγεβρα.
 Δακτύλιοι και Πρότυπα 0-7 Ασκήσεις Η ύλη των ασκήσεων αυτών είναι η Ενότητα, Εφαρμογές Θεωρημάτων Δομής στη Γραμμική Αλγεβρα Βρείτε τη ρητή κανονική μορφή και μια κανονική μορφή Jorda του M( ) 0 0 Έστω
Δακτύλιοι και Πρότυπα 0-7 Ασκήσεις Η ύλη των ασκήσεων αυτών είναι η Ενότητα, Εφαρμογές Θεωρημάτων Δομής στη Γραμμική Αλγεβρα Βρείτε τη ρητή κανονική μορφή και μια κανονική μορφή Jorda του M( ) 0 0 Έστω
ΚΕΦΑΛΑΙΟ 2: Ηµιαπλοί ακτύλιοι
 ΚΕΦΑΛΑΙΟ 2: Ηµιαπλοί ακτύλιοι Είδαµε στο κύριο θεώρηµα του προηγούµενου κεφαλαίου ότι κάθε δακτύλιος διαίρεσης έχει την ιδιότητα κάθε πρότυπο είναι ευθύ άθροισµα απλών προτύπων. Εδώ θα χαρακτηρίσουµε όλους
ΚΕΦΑΛΑΙΟ 2: Ηµιαπλοί ακτύλιοι Είδαµε στο κύριο θεώρηµα του προηγούµενου κεφαλαίου ότι κάθε δακτύλιος διαίρεσης έχει την ιδιότητα κάθε πρότυπο είναι ευθύ άθροισµα απλών προτύπων. Εδώ θα χαρακτηρίσουµε όλους
Πορίσματα της Κανονικής Μορφής Smith (συμπλήρωμα για την Ενότητα 4)
 Πορίσματα της Κανονικής Μορφής Smh (συμπλήρωμα για την Ενότητα 4 Θα δείξουμε εδώ ότι από την κανονική μορφή Smh πινάκων πάνω από περιοχή κυρίων ιδεωδών R, έπονται τα εξής Το Θεώρημα Βάσεων Το Θεώρημα Ανάλυσης
Πορίσματα της Κανονικής Μορφής Smh (συμπλήρωμα για την Ενότητα 4 Θα δείξουμε εδώ ότι από την κανονική μορφή Smh πινάκων πάνω από περιοχή κυρίων ιδεωδών R, έπονται τα εξής Το Θεώρημα Βάσεων Το Θεώρημα Ανάλυσης
a = a a Z n. a = a mod n.
 Αλγεβρα Ι Χειμερινο Εξαμηνο 2017 18 Διάλεξη 1 Ενότητα 1. Πράξεις: Πράξεις στο σύνολο S, ο πίνακας της πράξης, αντιμεταθετικές πράξεις. Προσεταιριστικές πράξεις, το στοιχείο a 1 a 2 a n. Η πράξη «σύνθεση
Αλγεβρα Ι Χειμερινο Εξαμηνο 2017 18 Διάλεξη 1 Ενότητα 1. Πράξεις: Πράξεις στο σύνολο S, ο πίνακας της πράξης, αντιμεταθετικές πράξεις. Προσεταιριστικές πράξεις, το στοιχείο a 1 a 2 a n. Η πράξη «σύνθεση
Δακτύλιοι και Πρότυπα Ασκήσεις 2. όπου a (4 i) (1 2 i), b i. Στη συνέχεια βρείτε κάθε τέτοιο d. b. Δείξτε ότι [ i] (4 i)
![Δακτύλιοι και Πρότυπα Ασκήσεις 2. όπου a (4 i) (1 2 i), b i. Στη συνέχεια βρείτε κάθε τέτοιο d. b. Δείξτε ότι [ i] (4 i) Δακτύλιοι και Πρότυπα Ασκήσεις 2. όπου a (4 i) (1 2 i), b i. Στη συνέχεια βρείτε κάθε τέτοιο d. b. Δείξτε ότι [ i] (4 i)](/thumbs/62/47831736.jpg) 6 Δακτύλιοι και Πρότυπα 016-17 Ασκήσεις Η ύλη των ασκήσεων αυτών είναι η Ενότητα, Περιοχές κυρίων ιδεωδών. 1. Θεωρούμε το δακτύλιο [ i]. a. Βρείτε ένα d [ i] με ( a, b) d, όπου a (4 i) (1 i), b 16 1 i.
6 Δακτύλιοι και Πρότυπα 016-17 Ασκήσεις Η ύλη των ασκήσεων αυτών είναι η Ενότητα, Περιοχές κυρίων ιδεωδών. 1. Θεωρούμε το δακτύλιο [ i]. a. Βρείτε ένα d [ i] με ( a, b) d, όπου a (4 i) (1 i), b 16 1 i.
g (v + W ) = gv + W gv = 0.
 Ασκήσεις #1 Σε ότι ακολουθεί, G είναι πεπερασμένη ομάδα και V είναι C-διανυσματικός χώρος πεπερασμένης διάστασης. 1. Δείξτε ότι η απεικόνιση G G G που ορίζεται θέτοντας g x = gxg 1 για g, x G αποτελεί
Ασκήσεις #1 Σε ότι ακολουθεί, G είναι πεπερασμένη ομάδα και V είναι C-διανυσματικός χώρος πεπερασμένης διάστασης. 1. Δείξτε ότι η απεικόνιση G G G που ορίζεται θέτοντας g x = gxg 1 για g, x G αποτελεί
ΚΕΦΑΛΑΙΟ 6: Κεντρικές Απλές Άλγεβρες
 ΚΕΦΑΛΑΙΟ 6: Κεντρικές Απλές Άλγεβρες Χρησιμοποιώντας τανυστικά γινόμενα και εφαρμόζοντας το θεώρημα των Wedderbur-Art ( 33) θα αποδείξουμε δύο θεμελιώδη θεωρήματα που αφορούν κεντρικές απλές άλγεβρες *
ΚΕΦΑΛΑΙΟ 6: Κεντρικές Απλές Άλγεβρες Χρησιμοποιώντας τανυστικά γινόμενα και εφαρμόζοντας το θεώρημα των Wedderbur-Art ( 33) θα αποδείξουμε δύο θεμελιώδη θεωρήματα που αφορούν κεντρικές απλές άλγεβρες *
βαθμού 1 με A 2. Υπολογίστε τα χαρακτηριστικά και ελάχιστα πολυώνυμα των
 Ασκήσεις 6 Ασκήσεις Ελάχιστο Πολυώνυμο Βασικά σημεία Ορισμός ελαχίστου πολυωνύμου πίνακα και ιδιότητές του Ορισμός ελαχίστου πολυωνύμου γραμμικής απεικόνισης και ιδιότητές του Κριτήριο διαγωνισιμότητας
Ασκήσεις 6 Ασκήσεις Ελάχιστο Πολυώνυμο Βασικά σημεία Ορισμός ελαχίστου πολυωνύμου πίνακα και ιδιότητές του Ορισμός ελαχίστου πολυωνύμου γραμμικής απεικόνισης και ιδιότητές του Κριτήριο διαγωνισιμότητας
ΚΕΦΑΛΑΙΟ 4: Ριζικό του Jacobson
 ΚΕΦΑΛΑΙΟ 4: Ριζικό του Jacobso Στο κεφάλαιο αυτό μελετάμε δακτυλίους του Art χρησιμοποιώντας το ριζικό του Jacobso. Ως εφαρμογή αποδεικνύουμε ότι κάθε δακτύλιος του Art είναι και της Noether. 4.1. Δακτύλιοι
ΚΕΦΑΛΑΙΟ 4: Ριζικό του Jacobso Στο κεφάλαιο αυτό μελετάμε δακτυλίους του Art χρησιμοποιώντας το ριζικό του Jacobso. Ως εφαρμογή αποδεικνύουμε ότι κάθε δακτύλιος του Art είναι και της Noether. 4.1. Δακτύλιοι
b. Για κάθε θετικό ακέραιο m και για κάθε A. , υπάρχουν άπειρα το πλήθος πολυώνυμα ( x) [ x] m και ( A) 0.
![b. Για κάθε θετικό ακέραιο m και για κάθε A. , υπάρχουν άπειρα το πλήθος πολυώνυμα ( x) [ x] m και ( A) 0. b. Για κάθε θετικό ακέραιο m και για κάθε A. , υπάρχουν άπειρα το πλήθος πολυώνυμα ( x) [ x] m και ( A) 0.](/thumbs/63/49387122.jpg) Ασκήσεις4 46 Ασκήσεις 4 Τριγωνίσιμες γραμμικές απεικονίσεις, Θεώρημα των Cayley-Hamilton Βασικά σημεία Ορισμός τριγωνίσιμου πίνακα, ορισμός τριγωνίσιμης γραμμικής απεικόνισης Κριτήριο τριγωνισιμότητας
Ασκήσεις4 46 Ασκήσεις 4 Τριγωνίσιμες γραμμικές απεικονίσεις, Θεώρημα των Cayley-Hamilton Βασικά σημεία Ορισμός τριγωνίσιμου πίνακα, ορισμός τριγωνίσιμης γραμμικής απεικόνισης Κριτήριο τριγωνισιμότητας
1. a. Έστω b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα του A Έστω A και ( x) [ x]
![1. a. Έστω b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα του A Έστω A και ( x) [ x] 1. a. Έστω b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα του A Έστω A και ( x) [ x]](/thumbs/77/75945202.jpg) σκήσεις Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμών και ιδιοδιανυσμάτων, υπολογισμός τους Ιδιόχωροι, διάσταση ιδιόχωρου, εύρεση βάσης ιδιόχωρου Σε διακεκριμένες ιδιοτιμές αντιστοιχούν
σκήσεις Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμών και ιδιοδιανυσμάτων, υπολογισμός τους Ιδιόχωροι, διάσταση ιδιόχωρου, εύρεση βάσης ιδιόχωρου Σε διακεκριμένες ιδιοτιμές αντιστοιχούν
bca = e. H 1j = G 2 H 5j = {f G j : f(0) = 1}
 Αλγεβρα Ι, Χειμερινο Εξαμηνο 2017 18 Ασκησεις που συζητηθηκαν στο φροντιστηριο Το [Α] συμβολίζει το φυλλάδιο ασκήσεων που θα βρείτε στην ιστοσελίδα του μαθήματος επιλέγοντας «Άλλες Ασκήσεις». 1. Πόσες
Αλγεβρα Ι, Χειμερινο Εξαμηνο 2017 18 Ασκησεις που συζητηθηκαν στο φροντιστηριο Το [Α] συμβολίζει το φυλλάδιο ασκήσεων που θα βρείτε στην ιστοσελίδα του μαθήματος επιλέγοντας «Άλλες Ασκήσεις». 1. Πόσες
,..., v n. W πεπερασμένα παραγόμενοι και dimv. Τα ακόλουθα είναι ισοδύναμα f είναι ισομορφιμός. f είναι 1-1. f είναι επί.
 Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις7: Γραμμικές Απεικονίσεις Βασικά σημεία Ορισμός και παραδείγματα γραμμικών απεικονίσεων Σύνθεση γραμμικών απεικονίσεων, ισομορφισμοί Κάθε γραμμική απεικόνιση f : V W, όπου
Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις7: Γραμμικές Απεικονίσεις Βασικά σημεία Ορισμός και παραδείγματα γραμμικών απεικονίσεων Σύνθεση γραμμικών απεικονίσεων, ισομορφισμοί Κάθε γραμμική απεικόνιση f : V W, όπου
Δακτύλιοι και Πρότυπα Ασκήσεις 3. Στις παρακάτω ασκήσεις κάθε δακτύλιος είναι μη τετριμμένος μεταθετικός δακτύλιος. N ( a)
 11 Δακτύλιοι και Πρότυπα 2016-17 Ασκήσεις 3 Η ύλη των ασκήσεων αυτών είναι η Ενότητα3, Ελεύθερα πρότυπα Στις παρακάτω ασκήσεις κάθε δακτύλιος είναι μη τετριμμένος μεταθετικός δακτύλιος 1 Δείξτε ότι το
11 Δακτύλιοι και Πρότυπα 2016-17 Ασκήσεις 3 Η ύλη των ασκήσεων αυτών είναι η Ενότητα3, Ελεύθερα πρότυπα Στις παρακάτω ασκήσεις κάθε δακτύλιος είναι μη τετριμμένος μεταθετικός δακτύλιος 1 Δείξτε ότι το
ΚΕΦΑΛΑΙΟ 8: Εφαρµογή: Το θεώρηµα του Burnside
 ΚΕΦΑΛΑΙΟ 8: Εφαρµογή: Το θεώρηµα του Bursde Θα αποδείξουµε εδώ ότι κάθε οµάδα τάξης a q b (, q πρώτοι) είναι επιλύσιµη. Το θεώρηµα αυτό αποδείχτηκε από τον Bursde το 904 ο οποίος χρησιµοποίησε τη νέα τότε
ΚΕΦΑΛΑΙΟ 8: Εφαρµογή: Το θεώρηµα του Bursde Θα αποδείξουµε εδώ ότι κάθε οµάδα τάξης a q b (, q πρώτοι) είναι επιλύσιµη. Το θεώρηµα αυτό αποδείχτηκε από τον Bursde το 904 ο οποίος χρησιµοποίησε τη νέα τότε
ΚΕΦΑΛΑΙΟ 5: Τανυστικά Γινόµενα
 ΚΕΦΑΛΑΙΟ 5: Τανυστικά Γινόµενα Στο κεφάλαιο αυτό εισάγουµε την έννοια του τανυστικού γινοµένου προτύπων. Θα είµαστε συνοπτικοί καθώς αναπτύσσουµε µόνο εκείνες τις στοιχειώδεις προτάσεις που θα βρουν εφαρµογές
ΚΕΦΑΛΑΙΟ 5: Τανυστικά Γινόµενα Στο κεφάλαιο αυτό εισάγουµε την έννοια του τανυστικού γινοµένου προτύπων. Θα είµαστε συνοπτικοί καθώς αναπτύσσουµε µόνο εκείνες τις στοιχειώδεις προτάσεις που θα βρουν εφαρµογές
1. Για καθένα από τους ακόλουθους διανυσματικούς χώρους βρείτε μια βάση και τη διάσταση. 3. U x y z x y z x y. {(,, ) } a b. c d
 Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις6: Βάση και Διάσταση Βασικά σημεία Βάση διανυσματικού χώρου (ορισμός, παραδείγματα, μοναδικότητα συντελεστών) Θεώρημα (ύπαρξη, πρώτη μορφή) Έστω V K μη μηδενικός με K πεπερασμένο
Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις6: Βάση και Διάσταση Βασικά σημεία Βάση διανυσματικού χώρου (ορισμός, παραδείγματα, μοναδικότητα συντελεστών) Θεώρημα (ύπαρξη, πρώτη μορφή) Έστω V K μη μηδενικός με K πεπερασμένο
ΚΕΦΑΛΑΙΟ 6: Κεντρικές Απλές Άλγεβρες
 ΚΕΦΑΛΑΙΟ 6: Κεντρικές Απλές Άλγεβρες Χρησιμοποιώντας τανυστικά γινόμενα και εφαρμόζοντας το θεώρημα των Wedderbur-rt ( 33) θα αποδείξουμε δύο θεμελιώδη θεωρήματα που αφορούν κεντρικές απλές άλγεβρες θεώρημα
ΚΕΦΑΛΑΙΟ 6: Κεντρικές Απλές Άλγεβρες Χρησιμοποιώντας τανυστικά γινόμενα και εφαρμόζοντας το θεώρημα των Wedderbur-rt ( 33) θα αποδείξουμε δύο θεμελιώδη θεωρήματα που αφορούν κεντρικές απλές άλγεβρες θεώρημα
Γραμμική Άλγεβρα II Εαρινό εξάμηνο
 Γραμμική Άλγεβρα II Εαρινό εξάμηνο 0-0 Υποδείξεις/Απαντήσεις των Ασκήσεων Περιεχόμενα Ασκήσεις Πολυώνυμα Ασκήσεις Ιδιοτιμές-Ιδιοδιανύσματα 6 Ασκήσεις Διαγωνίσιμες γραμμικές απεικονίσεις 9 Ασκήσεις4 Τριγωνίσιμες
Γραμμική Άλγεβρα II Εαρινό εξάμηνο 0-0 Υποδείξεις/Απαντήσεις των Ασκήσεων Περιεχόμενα Ασκήσεις Πολυώνυμα Ασκήσεις Ιδιοτιμές-Ιδιοδιανύσματα 6 Ασκήσεις Διαγωνίσιμες γραμμικές απεικονίσεις 9 Ασκήσεις4 Τριγωνίσιμες
A, και εξετάστε αν είναι διαγωνίσιμη.
 Ασκήσεις 6 Ασκήσεις Ελάχιστο Πολυώνυμο Βασικά σημεία Ορισμός ελαχίστου πολυωνύμου πίνακα και ιδιότητές του Θεώρημα (Κριτήριο διαγωνισιμότητας) Ένας είναι διαγωνίσιμος αν και μόνο αν ( x) γινόμενο διακεκριμένων
Ασκήσεις 6 Ασκήσεις Ελάχιστο Πολυώνυμο Βασικά σημεία Ορισμός ελαχίστου πολυωνύμου πίνακα και ιδιότητές του Θεώρημα (Κριτήριο διαγωνισιμότητας) Ένας είναι διαγωνίσιμος αν και μόνο αν ( x) γινόμενο διακεκριμένων
Ε Μέχρι 18 Μαΐου 2015.
 Ε Μέχρι 18 Μαΐου 2015. 1 Αντικείμενα: δακτύλιοι Fraleigh, 4.1. Ορισμός έννοιας «δακτυλίου». Χαρακτηρισμοί δακτυλίων και στοιχείων αυτών: Δακτύλιος R Στοιχεία δακτυλίου R / (= δεν έχει μηδενοδιαιρέτες άρα
Ε Μέχρι 18 Μαΐου 2015. 1 Αντικείμενα: δακτύλιοι Fraleigh, 4.1. Ορισμός έννοιας «δακτυλίου». Χαρακτηρισμοί δακτυλίων και στοιχείων αυτών: Δακτύλιος R Στοιχεία δακτυλίου R / (= δεν έχει μηδενοδιαιρέτες άρα
Ασκήσεις4 48. P AP τριγωνικό. Αφού δείξτε ότι ο A δεν είναι διαγωνίσιμος, βρείτε αντιστρέψιμο A 1 3 1
 Ασκήσεις4 48 Ασκήσεις4 Τριγωνισιμότητα Βασικά σημεία Ορισμός τριγωνίσιμου πίνακα, ορισμός τριγωνίσιμης γραμμικής απεικόνισης Θεώρημα: είναι τριγωνίσιμος αν και μόνο αν ( x ) γινόμενο πρωτοβάθμιων παραγόντων
Ασκήσεις4 48 Ασκήσεις4 Τριγωνισιμότητα Βασικά σημεία Ορισμός τριγωνίσιμου πίνακα, ορισμός τριγωνίσιμης γραμμικής απεικόνισης Θεώρημα: είναι τριγωνίσιμος αν και μόνο αν ( x ) γινόμενο πρωτοβάθμιων παραγόντων
12. ΑΝΙΣΩΣΕΙΣ Α ΒΑΘΜΟΥ. είναι δύο παραστάσεις μιας μεταβλητής x πού παίρνει τιμές στο
 ΓΕΝΙΚΑ ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Έστω f σύνολο Α, g Α ΒΑΘΜΟΥ είναι δύο παραστάσεις μιας μεταβλητής πού παίρνει τιμές στο Ανίσωση με έναν άγνωστο λέγεται κάθε σχέση της μορφής f f g g ή, η οποία αληθεύει για ορισμένες
ΓΕΝΙΚΑ ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Έστω f σύνολο Α, g Α ΒΑΘΜΟΥ είναι δύο παραστάσεις μιας μεταβλητής πού παίρνει τιμές στο Ανίσωση με έναν άγνωστο λέγεται κάθε σχέση της μορφής f f g g ή, η οποία αληθεύει για ορισμένες
Θεωρία Galois. Πρόχειρες σημειώσεις (εκδοχή )
 Θεωρία Galos Πρόχειρες σημειώσεις 0- (εκδοχή -7-0) Περιεχόμενα 0 Υπενθυμίσεις και συμπληρώματα Ανάγωγα πολυώνυμα Ανάγωγα πολυώνυμα και σώματα Χαρακτηριστική σώματος Απλές ρίζες πολυωνύμων Ασκήσεις 0 Επεκτάσεις
Θεωρία Galos Πρόχειρες σημειώσεις 0- (εκδοχή -7-0) Περιεχόμενα 0 Υπενθυμίσεις και συμπληρώματα Ανάγωγα πολυώνυμα Ανάγωγα πολυώνυμα και σώματα Χαρακτηριστική σώματος Απλές ρίζες πολυωνύμων Ασκήσεις 0 Επεκτάσεις
Ασκήσεις6 Διαγωνοποίηση Ερμιτιανών Πινάκων
 7 Βασικά σημεία Ασκήσεις6 Διαγωνοποίηση Ερμιτιανών Πινάκων Το σύνηθες εσωτερικό γινόμενο στο και Ορθοκανονικές βάσεις και η μέθοδος Gram-Schmidt Ορισμός, Ερμιτιανού πίνακα και μοναδιαίου πίνακα Ιδιότητες
7 Βασικά σημεία Ασκήσεις6 Διαγωνοποίηση Ερμιτιανών Πινάκων Το σύνηθες εσωτερικό γινόμενο στο και Ορθοκανονικές βάσεις και η μέθοδος Gram-Schmidt Ορισμός, Ερμιτιανού πίνακα και μοναδιαίου πίνακα Ιδιότητες
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 1 η Ημερομηνία Αποστολής στον Φοιτητή: 17 Οκτωβρίου 2011
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 7 Οκτωβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 5 Νοεμβρίου 0 Οι ασκήσεις
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 7 Οκτωβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 5 Νοεμβρίου 0 Οι ασκήσεις
ΜΑΣ121: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ I Εαρινό εξάμηνο , Διδάσκων: Γιώργος Γεωργίου ΕΝΔΙΑΜΕΣΗ ΕΞΕΤΑΣΗ, Διάρκεια: 2 ώρες 18 Νοεμβρίου, 2017
 ΜΑΣ: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ I Εαρινό εξάμηνο 07-08, Διδάσκων: Γιώργος Γεωργίου ΕΝΔΙΑΜΕΣΗ ΕΞΕΤΑΣΗ, Διάρκεια: ώρες 8 Νοεμβρίου, 07 Δίνονται 4 προβλήματα που αντιστοιχούν σε 0 μονάδες με άριστα το 00! ΟΝΟΜΑ: Αρ.
ΜΑΣ: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ I Εαρινό εξάμηνο 07-08, Διδάσκων: Γιώργος Γεωργίου ΕΝΔΙΑΜΕΣΗ ΕΞΕΤΑΣΗ, Διάρκεια: ώρες 8 Νοεμβρίου, 07 Δίνονται 4 προβλήματα που αντιστοιχούν σε 0 μονάδες με άριστα το 00! ΟΝΟΜΑ: Αρ.
Ασκήσεις1 Πολυώνυμα. x x c. με το. b. Να βρεθούν όλες οι τιμές των a, Να βρεθεί ο μκδ και το εκπ τους
 Aσκήσεις1 1 Βασικά σημεία Ευκλείδεια διαίρεση πολυωνύμων Ορισμός και ιδιότητες μκδ και εκπ Ιδιότητες σχετικών πρώτων πολυωνύμων Τα ανάγωγα πολυώνυμα στο [ ] και [ ] Ασκήσεις1 Πολυώνυμα Ανάλυση πολυωνύμου
Aσκήσεις1 1 Βασικά σημεία Ευκλείδεια διαίρεση πολυωνύμων Ορισμός και ιδιότητες μκδ και εκπ Ιδιότητες σχετικών πρώτων πολυωνύμων Τα ανάγωγα πολυώνυμα στο [ ] και [ ] Ασκήσεις1 Πολυώνυμα Ανάλυση πολυωνύμου
8.1 Διαγωνοποίηση πίνακα
 Κεφάλαιο 8 Κανονικές μορφές από 6 Κεφάλαιο 8 Κ Α Ν Ο Ν Ι Κ Ε Σ Μ Ο Ρ Φ Ε Σ 8. Διαγωνοποίηση πίνακα Ορισμός 8.α Ένας πίνακας M n ( ) oνομάζεται διαγωνοποιήσιμος στο αν υπάρχει αντιστρέψιμος πίνακας P M
Κεφάλαιο 8 Κανονικές μορφές από 6 Κεφάλαιο 8 Κ Α Ν Ο Ν Ι Κ Ε Σ Μ Ο Ρ Φ Ε Σ 8. Διαγωνοποίηση πίνακα Ορισμός 8.α Ένας πίνακας M n ( ) oνομάζεται διαγωνοποιήσιμος στο αν υπάρχει αντιστρέψιμος πίνακας P M
1 Η εναλλάσσουσα ομάδα
 Η εναλλάσσουσα ομάδα Η εναλλάσσουσα ομάδα Όπως είδαμε η συνάρτηση g : S { } είναι ένας επιμορφισμός ομάδων. Ο πυρήνας Ke g {σ S / g σ } του επιμορφισμού συμβολίζεται με A περιέχει όλες τις άρτιες μεταθέσεις
Η εναλλάσσουσα ομάδα Η εναλλάσσουσα ομάδα Όπως είδαμε η συνάρτηση g : S { } είναι ένας επιμορφισμός ομάδων. Ο πυρήνας Ke g {σ S / g σ } του επιμορφισμού συμβολίζεται με A περιέχει όλες τις άρτιες μεταθέσεις
Βασική Άλγεβρα. Ασκήσεις (εκδοχή )
 Βασική Άλγεβρα Ασκήσεις 0-4 (εκδοχή 5--04) Βασική Άλγεβρα Ασκήσεις Υποδείξεις/Απαντήσεις Περιεχόµενα σελίδα Ασκήσεις ιαιρετότητα στους ακέραιους, ισοτιµίες Ασκήσεις Ακέραιοι odulo, Θεώρηµα του Euler 7
Βασική Άλγεβρα Ασκήσεις 0-4 (εκδοχή 5--04) Βασική Άλγεβρα Ασκήσεις Υποδείξεις/Απαντήσεις Περιεχόµενα σελίδα Ασκήσεις ιαιρετότητα στους ακέραιους, ισοτιµίες Ασκήσεις Ακέραιοι odulo, Θεώρηµα του Euler 7
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 2 η Ημερομηνία Αποστολής στον Φοιτητή: 28 Νοεμβρίου 2011
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 8 Νοεμβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 6 Ιανουαρίου 0 Οι ασκήσεις
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 8 Νοεμβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 6 Ιανουαρίου 0 Οι ασκήσεις
Βασική Άλγεβρα. Ασκήσεις (εκδοχή )
 Βασική Άλγεβρα Ασκήσεις 05-6 (εκδοχή 8--05) Βασική Άλγεβρα Ασκήσεις Υποδείξεις/Απαντήσεις Περιεχόμενα σελίδα Ασκήσεις Διαιρετότητα στους ακέραιους, ισοτιμίες Ασκήσεις Ακέραιοι odulo, Θεώρημα του Euler
Βασική Άλγεβρα Ασκήσεις 05-6 (εκδοχή 8--05) Βασική Άλγεβρα Ασκήσεις Υποδείξεις/Απαντήσεις Περιεχόμενα σελίδα Ασκήσεις Διαιρετότητα στους ακέραιους, ισοτιμίες Ασκήσεις Ακέραιοι odulo, Θεώρημα του Euler
Γραμμική Άλγεβρα II. Ασκήσεις με Υποδείξεις - Απαντήσεις. Περιεχόμενα
 Γραμμική Άλγεβρα II Ασκήσεις με Υποδείξεις - Απαντήσεις ΜΜ Περιεχόμενα Ασκήσεις0: Όμοιοι Πίνακες Ασκήσεις: Πολυώνυμα 6 Ασκήσεις: Ιδιοτιμές και Ιδιοδιανύσματα Ασκήσεις: Διαγωνισιμότητα Ασκήσεις4: Τριγωνισιμότητα
Γραμμική Άλγεβρα II Ασκήσεις με Υποδείξεις - Απαντήσεις ΜΜ Περιεχόμενα Ασκήσεις0: Όμοιοι Πίνακες Ασκήσεις: Πολυώνυμα 6 Ασκήσεις: Ιδιοτιμές και Ιδιοδιανύσματα Ασκήσεις: Διαγωνισιμότητα Ασκήσεις4: Τριγωνισιμότητα
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α. ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 5: ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΥΠΟΧΩΡΟΙ ΓΡΑΜΜΙΚΗ ΑΝΕΞΑΡΤΗΣΙΑ ΒΑΣΕΙΣ & ΔΙΑΣΤΑΣΗ Δ.Χ. ΣΗΜΕΙΩΣΕΙΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α. ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 5: ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΥΠΟΧΩΡΟΙ ΓΡΑΜΜΙΚΗ ΑΝΕΞΑΡΤΗΣΙΑ ΒΑΣΕΙΣ & ΔΙΑΣΤΑΣΗ Δ.Χ. ΣΗΜΕΙΩΣΕΙΣ
Κεφάλαιο 7 Ορθογώνιοι Πίνακες
 Κεφάλαιο 7 Ορθογώνιοι Πίνακες Εσωτερικό Γινόμενο και ορθογωνιότητα Έστω V ένας διανυσματικός χώρος, υπόχωρος του n. Κάθε συνάρτηση ορισμένη στο VV (την οποία θα συμβολίζουμε με ) ορίζει ένα εσωτερικό γινόμενο
Κεφάλαιο 7 Ορθογώνιοι Πίνακες Εσωτερικό Γινόμενο και ορθογωνιότητα Έστω V ένας διανυσματικός χώρος, υπόχωρος του n. Κάθε συνάρτηση ορισμένη στο VV (την οποία θα συμβολίζουμε με ) ορίζει ένα εσωτερικό γινόμενο
Παρασκευή 6 Δεκεμβρίου 2013
 Α Δ Ι Α - Φ 6 Δ : Ν. Μαρμαρίδης - Α. Μπεληγιάννης Ι Μ : http://users.uoi.gr/abeligia/algebraicstructuresi/asi20/asi20.html, https://sites.google.com/site/mathsedu/home/algdom Παρασκευή 6 Δεκεμβρίου 20
Α Δ Ι Α - Φ 6 Δ : Ν. Μαρμαρίδης - Α. Μπεληγιάννης Ι Μ : http://users.uoi.gr/abeligia/algebraicstructuresi/asi20/asi20.html, https://sites.google.com/site/mathsedu/home/algdom Παρασκευή 6 Δεκεμβρίου 20
G 1 = G/H. I 3 = {f R : f(1) = 2f(2) ή f(1) = 3f(2)}. I 5 = {f R : f(1) = 0}.
 Αλγεβρα ΙΙ, Εαρινο Εξαμηνο 2017 18 Ασκησεις που συζητηθηκαν στο φροντιστηριο Φροντιστήριο 1. 1. Δίνεται η ομάδα G = Z 4 Z 8, το στοιχείο a = (1, 2) της G, και η υποομάδα H =< a > της G. Εστω G 1 = G/H.
Αλγεβρα ΙΙ, Εαρινο Εξαμηνο 2017 18 Ασκησεις που συζητηθηκαν στο φροντιστηριο Φροντιστήριο 1. 1. Δίνεται η ομάδα G = Z 4 Z 8, το στοιχείο a = (1, 2) της G, και η υποομάδα H =< a > της G. Εστω G 1 = G/H.
ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων
 ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων Μελετάµε εδώ τη συνθήκη της αύξουσας αλυσίδας υποπροτύπων και τη συνθήκη της φθίνουσας αλυσίδας υποπροτύπων. Αυτές συνδέονται µεταξύ τους µε την έννοια της συνθετικής σειράς
ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων Μελετάµε εδώ τη συνθήκη της αύξουσας αλυσίδας υποπροτύπων και τη συνθήκη της φθίνουσας αλυσίδας υποπροτύπων. Αυτές συνδέονται µεταξύ τους µε την έννοια της συνθετικής σειράς
(a + b) + c = a + (b + c), (ab)c = a(bc) a + b = b + a, ab = ba. a(b + c) = ab + ac
 Σημειώσεις μαθήματος Μ1212 Γραμμική Άλγεβρα ΙΙ Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2014 Κεφάλαιο 1 Διανυσματικοί Χώροι Στο εισαγωγικό μάθημα Γραμμικής Άλγεβρας ξεκινήσαμε μελετώντας
Σημειώσεις μαθήματος Μ1212 Γραμμική Άλγεβρα ΙΙ Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2014 Κεφάλαιο 1 Διανυσματικοί Χώροι Στο εισαγωγικό μάθημα Γραμμικής Άλγεβρας ξεκινήσαμε μελετώντας
Κεφάλαιο 5 Γραμμικοί Μετασχηματισμοί
 Κεφάλαιο 5 Γραμμικοί Μετασχηματισμοί 5 Γενικά Γραμμικοί Μετασχηματισμοί Μία σχέση μεταξύ των στοιχείων δύο συνόλων Α,Β αντιστοιχίζει στοιχεία του Α με στοιχεία του Β άλλου μέσω ενός κανόνα που μπορεί να
Κεφάλαιο 5 Γραμμικοί Μετασχηματισμοί 5 Γενικά Γραμμικοί Μετασχηματισμοί Μία σχέση μεταξύ των στοιχείων δύο συνόλων Α,Β αντιστοιχίζει στοιχεία του Α με στοιχεία του Β άλλου μέσω ενός κανόνα που μπορεί να
Τίτλος Μαθήματος: Θεωρία Ομάδων. Ενότητα: Θεωρία Sylow. Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης. Τμήμα: Μαθηματικών
 Τίτλος Μαθήματος: Θεωρία Ομάδων Ενότητα: Θεωρία Sylow Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης Τμήμα: Μαθηματικών Κεφάλαιο 2 Θεωρία Sylow 21 Τα Θεωρήματα Sylow Ορισμός 211 Μια ομάδα (G, ) τάξης p α, όπου
Τίτλος Μαθήματος: Θεωρία Ομάδων Ενότητα: Θεωρία Sylow Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης Τμήμα: Μαθηματικών Κεφάλαιο 2 Θεωρία Sylow 21 Τα Θεωρήματα Sylow Ορισμός 211 Μια ομάδα (G, ) τάξης p α, όπου
Γραμμική Αλγεβρα ΙΙ Διάλεξη 1 Εισαγωγή Χρήστος Κουρουνιώτης Πανεπισ τήμιο Κρήτης 19/2/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 1 19/2/ / 13
 Γραμμική Άλγεβρα ΙΙ Διάλεξη 1 Εισαγωγή Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 19/2/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 1 19/2/2014 1 / 13 Εισαγωγή Τι έχουμε μάθει; Στο πρώτο μάθημα Γραμμικής Άλγεβρας
Γραμμική Άλγεβρα ΙΙ Διάλεξη 1 Εισαγωγή Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 19/2/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 1 19/2/2014 1 / 13 Εισαγωγή Τι έχουμε μάθει; Στο πρώτο μάθημα Γραμμικής Άλγεβρας
Μεταθέσεις και πίνακες μεταθέσεων
 Παράρτημα Α Μεταθέσεις και πίνακες μεταθέσεων Το παρόν παράρτημα βασίζεται στις σελίδες 671 8 του βιβλίου: Γ. Χ. Ψαλτάκης, Κβαντικά Συστήματα Πολλών Σωματιδίων (Πανεπιστημιακές Εκδόσεις Κρήτης, Ηράκλειο,
Παράρτημα Α Μεταθέσεις και πίνακες μεταθέσεων Το παρόν παράρτημα βασίζεται στις σελίδες 671 8 του βιβλίου: Γ. Χ. Ψαλτάκης, Κβαντικά Συστήματα Πολλών Σωματιδίων (Πανεπιστημιακές Εκδόσεις Κρήτης, Ηράκλειο,
Κεφάλαιο 7 Βάσεις και ιάσταση
 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα από 9 Κεφάλαιο 7 Βάσεις και ιάσταση n Στο Κεφάλαιο 5 είδαµε την έννοια της βάσης στο και στο Κεφάλαιο 6 µελετήσαµε διανυσµατικούς χώρους. Στο παρόν κεφάλαιο θα ασχοληθούµε
Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα από 9 Κεφάλαιο 7 Βάσεις και ιάσταση n Στο Κεφάλαιο 5 είδαµε την έννοια της βάσης στο και στο Κεφάλαιο 6 µελετήσαµε διανυσµατικούς χώρους. Στο παρόν κεφάλαιο θα ασχοληθούµε
ΠΛΗ ΛΥΣΕΙΣ ΕΡΓ_2 ΣΕΛ. 1/11
 ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: Νοεμβρίου 007 Ημερομηνία παράδοσης της Εργασίας: 4 Δεκεμβρίου 007 Πριν από την λύση κάθε άσκησης καλό
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: Νοεμβρίου 007 Ημερομηνία παράδοσης της Εργασίας: 4 Δεκεμβρίου 007 Πριν από την λύση κάθε άσκησης καλό
Ποιες από τις παρακάτω προτάσεις είναι αληθείς; Δικαιολογήστε την απάντησή σας.
 Ποιες από τις παρακάτω προτάσεις είναι αληθείς; Δικαιολογήστε την απάντησή σας. 1. Κάθε πολυώνυμο ανάγωγο επί του Z είναι ανάγωγο επί του Q. Σωστό. 2. Κάθε πολυώνυμο ανάγωγο επί του Q είναι ανάγωγο επί
Ποιες από τις παρακάτω προτάσεις είναι αληθείς; Δικαιολογήστε την απάντησή σας. 1. Κάθε πολυώνυμο ανάγωγο επί του Z είναι ανάγωγο επί του Q. Σωστό. 2. Κάθε πολυώνυμο ανάγωγο επί του Q είναι ανάγωγο επί
Γραμμική Άλγεβρα ΙΙ Εξέταση Σεπτεμβρίου Όνομα συνοπτικές ενδεικτικές λύσεις
 Γραμμική Άλγεβρα ΙΙ Εξέταση Σεπτεμβρίου 009 Όνομα συνοπτικές ενδεικτικές λύσεις ΑΜ Ημ/ία Αίθουσα 1 Σύνολο Η εξέταση αποτελείται από θέματα. Κάθε θέμα αξίζει 4 μονάδες. Το άριστα είναι μονάδες και η βάση
Γραμμική Άλγεβρα ΙΙ Εξέταση Σεπτεμβρίου 009 Όνομα συνοπτικές ενδεικτικές λύσεις ΑΜ Ημ/ία Αίθουσα 1 Σύνολο Η εξέταση αποτελείται από θέματα. Κάθε θέμα αξίζει 4 μονάδες. Το άριστα είναι μονάδες και η βάση
με Τέλος πάντων, έστω ότι ξεκινάει ένα άλλο υποθετικό σενάριο που απλά δεν διευκρινίζεται. Για το i) θα έχουμε , 2
 Άσκηση 75 Σε έναν οργανισμό, αρχικά υπάρχουν 04800 βακτήρια. Μετά από 1 ώρα υπάρχουν 10400 βακτήρια, μετά από ώρες 5100 βακτήρια, και γενικά ο αριθμός των βακτηρίων υποδιπλασιάζεται κάθε μια ώρα. α) Πόσα
Άσκηση 75 Σε έναν οργανισμό, αρχικά υπάρχουν 04800 βακτήρια. Μετά από 1 ώρα υπάρχουν 10400 βακτήρια, μετά από ώρες 5100 βακτήρια, και γενικά ο αριθμός των βακτηρίων υποδιπλασιάζεται κάθε μια ώρα. α) Πόσα
Κεφάλαιο 6 Ιδιοτιμές και Ιδιοδιανύσματα
 Κεφάλαιο 6 Ορισμοί Έστω Α ένας πίνακας με πραγματικά στοιχεία Ο πραγματικός ή μιγαδικός αριθμός λ καλείται ιδιοτιμή του πίνακα Α εάν υπάρχει μη μηδενικό διάνυσμα v με πραγματικά ή μιγαδικά στοιχεία τέτοιο
Κεφάλαιο 6 Ορισμοί Έστω Α ένας πίνακας με πραγματικά στοιχεία Ο πραγματικός ή μιγαδικός αριθμός λ καλείται ιδιοτιμή του πίνακα Α εάν υπάρχει μη μηδενικό διάνυσμα v με πραγματικά ή μιγαδικά στοιχεία τέτοιο
f(t) = (1 t)a + tb. f(n) =
 Παράρτημα Αʹ Αριθμήσιμα και υπεραριθμήσιμα σύνολα Αʹ1 Ισοπληθικά σύνολα Ορισμός Αʹ11 (ισοπληθικότητα) Εστω A, B δύο μη κενά σύνολα Τα A, B λέγονται ισοπληθικά αν υπάρχει μια συνάρτηση f : A B, η οποία
Παράρτημα Αʹ Αριθμήσιμα και υπεραριθμήσιμα σύνολα Αʹ1 Ισοπληθικά σύνολα Ορισμός Αʹ11 (ισοπληθικότητα) Εστω A, B δύο μη κενά σύνολα Τα A, B λέγονται ισοπληθικά αν υπάρχει μια συνάρτηση f : A B, η οποία
2. Ιδιότητες Συναρτήσεων
 Ιδιότητες Συναρτήσεων Μονοτονία Ακρότατα Συμμετρίες Συνάρτησης Πεδίο Ορισμού Το πρώτο βήμα για τη λύση μιας άσκησης που περιέει μια συνάρτηση είναι ο προσδιορισμός του πεδίου ορισμού της α) Κάθε πολυωνυμική
Ιδιότητες Συναρτήσεων Μονοτονία Ακρότατα Συμμετρίες Συνάρτησης Πεδίο Ορισμού Το πρώτο βήμα για τη λύση μιας άσκησης που περιέει μια συνάρτηση είναι ο προσδιορισμός του πεδίου ορισμού της α) Κάθε πολυωνυμική
Αλγεβρικές Δομές Ι. 1 Ομάδα I
 Αλγεβρικές Δομές Ι 1 Ομάδα I Ά σ κ η σ η 1.1 Έστω G μια προσθετική ομάδα S ένα μη κενό σύνολο και M(S G το σύνολο όλων των συναρτήσεων f : S G. Δείξτε ότι το σύνολο M(S G είναι ομάδα με πράξη την πρόσθεση
Αλγεβρικές Δομές Ι 1 Ομάδα I Ά σ κ η σ η 1.1 Έστω G μια προσθετική ομάδα S ένα μη κενό σύνολο και M(S G το σύνολο όλων των συναρτήσεων f : S G. Δείξτε ότι το σύνολο M(S G είναι ομάδα με πράξη την πρόσθεση
Δώδεκα Αποδείξεις του. Θεμελιώδους Θεωρήματος της Άλγεβρας
 Δώδεκα Αποδείξεις του Θεμελιώδους Θεωρήματος της Άλγεβρας Mία εκδοχή της αρχικής απόδειξης του Gauss f ( z) = T ( z) + iu ( z) T = r cos φ + Ar 1 cos(( 1) φ + α) + + L cosλ U = r si φ + Ar 1 si(( 1) φ
Δώδεκα Αποδείξεις του Θεμελιώδους Θεωρήματος της Άλγεβρας Mία εκδοχή της αρχικής απόδειξης του Gauss f ( z) = T ( z) + iu ( z) T = r cos φ + Ar 1 cos(( 1) φ + α) + + L cosλ U = r si φ + Ar 1 si(( 1) φ
1 Επανάληψη εννοιών από τον Απειροστικό Λογισμό
 1 Επανάληψη εννοιών από τον Απειροστικό Λογισμό 1.1 Όρια ακολουθιών Λέμε ότι η ακολουθία { n } συγκλίνει με όριο R αν για κάθε ϵ > 0 υπάρχει ακέραιος N = N(ϵ) τέτοιος ώστε (1.1) n < ϵ για κάθε n > N, και
1 Επανάληψη εννοιών από τον Απειροστικό Λογισμό 1.1 Όρια ακολουθιών Λέμε ότι η ακολουθία { n } συγκλίνει με όριο R αν για κάθε ϵ > 0 υπάρχει ακέραιος N = N(ϵ) τέτοιος ώστε (1.1) n < ϵ για κάθε n > N, και
ΤΕΤΥ Εφαρμοσμένα Μαθηματικά 1. Τελεστές και πίνακες. 1. Τελεστές και πίνακες Γενικά. Τι είναι συνάρτηση? Απεικόνιση ενός αριθμού σε έναν άλλο.
 ΤΕΤΥ Εφαρμοσμένα Μαθηματικά 1 Τελεστές και πίνακες 1. Τελεστές και πίνακες Γενικά Τι είναι συνάρτηση? Απεικόνιση ενός αριθμού σε έναν άλλο. Ανάλογα, τελεστής είναι η απεικόνιση ενός διανύσματος σε ένα
ΤΕΤΥ Εφαρμοσμένα Μαθηματικά 1 Τελεστές και πίνακες 1. Τελεστές και πίνακες Γενικά Τι είναι συνάρτηση? Απεικόνιση ενός αριθμού σε έναν άλλο. Ανάλογα, τελεστής είναι η απεικόνιση ενός διανύσματος σε ένα
Α Δ Ι. Παρασκευή 15 Νοεμβρίου Ασκηση 1. Να ευρεθεί η τάξη τού στοιχείου a τής ομάδας (G, ), όπου. (4) a = ( 1 + i 3)/2, (G, ) = (C, ),
 Α Δ Ι Α - Φ 4 Δ : Ν. Μαρμαρίδης - Α. Μπεληγιάννης Ι Μ : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2013/asi2013.html, https://sites.google.com/site/maths4edu/home/algdom114 Παρασκευή 15 Νοεμβρίου
Α Δ Ι Α - Φ 4 Δ : Ν. Μαρμαρίδης - Α. Μπεληγιάννης Ι Μ : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2013/asi2013.html, https://sites.google.com/site/maths4edu/home/algdom114 Παρασκευή 15 Νοεμβρίου
ΑΛΓΕΒΡΙΚΕΣ ΟΜΕΣ Ι. Ασκησεις - Φυλλαδιο 3
 ΑΛΓΕΒΡΙΚΕΣ ΟΜΕΣ Ι Τµηµα Β Ασκησεις - Φυλλαδιο 3 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2017/asi2017.html Παρασκευή 31 Μαρτίου 2017 Υπενθυµίζουµε
ΑΛΓΕΒΡΙΚΕΣ ΟΜΕΣ Ι Τµηµα Β Ασκησεις - Φυλλαδιο 3 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2017/asi2017.html Παρασκευή 31 Μαρτίου 2017 Υπενθυµίζουµε
Α Δ Ι. Παρασκευή 29 Νοεμβρίου 2013 & K =
 Α Δ Ι Α - Φ 5 Δ : Ν. Μαρμαρίδης - Α. Μπεληγιάννης Ι Μ : http://users.uoi.gr/abeligia/algebraicstructuresi/asi.html, https://sites.google.com/site/maths4edu/home/algdom114 Παρασκευή 29 Νοεμβρίου 2013 Ασκηση
Α Δ Ι Α - Φ 5 Δ : Ν. Μαρμαρίδης - Α. Μπεληγιάννης Ι Μ : http://users.uoi.gr/abeligia/algebraicstructuresi/asi.html, https://sites.google.com/site/maths4edu/home/algdom114 Παρασκευή 29 Νοεμβρίου 2013 Ασκηση
Ε Μέχρι 31 Μαρτίου 2015.
 Ε Μέχρι 31 Μαρτίου 2015. 1 Αντικείμενα: δακτύλιοι Fraleigh, 4.1. Ορισμός έννοιας «δακτυλίου». Χαρακτηρισμοί δακτυλίων και στοιχείων αυτών: Δακτύλιος R Στοιχεία δακτυλίου R / (= δεν έχει μηδενοδιαιρέτες
Ε Μέχρι 31 Μαρτίου 2015. 1 Αντικείμενα: δακτύλιοι Fraleigh, 4.1. Ορισμός έννοιας «δακτυλίου». Χαρακτηρισμοί δακτυλίων και στοιχείων αυτών: Δακτύλιος R Στοιχεία δακτυλίου R / (= δεν έχει μηδενοδιαιρέτες
Κεφάλαιο 0. Μεταθετικοί ακτύλιοι, Ιδεώδη
 Κεφάλαιο 0 Μεταθετικοί ακτύλιοι, Ιδεώδη Το κεφάλαιο αυτό έχει προπαρασκευαστικό χαρακτήρα Θα καθιερώσουµε συµβολισµούς και θα υπενθυµίσουµε ορισµούς και στοιχειώδεις προτάσεις για δακτύλιους και ιδεώδη
Κεφάλαιο 0 Μεταθετικοί ακτύλιοι, Ιδεώδη Το κεφάλαιο αυτό έχει προπαρασκευαστικό χαρακτήρα Θα καθιερώσουµε συµβολισµούς και θα υπενθυµίσουµε ορισµούς και στοιχειώδεις προτάσεις για δακτύλιους και ιδεώδη
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
Τίτλος Μαθήματος: Θεωρία Ομάδων. Ενότητα: Ευθέα Γινόμενα Ομάδων. Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης. Τμήμα: Μαθηματικών
 Τίτλος Μαθήματος: Θεωρία Ομάδων Ενότητα: Ευθέα Γινόμενα Ομάδων Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης Τμήμα: Μαθηματικών Κεφάλαιο 3 Ευθέα Γινόμενα Ομάδων Για την περαιτέρω ανάπτυξη τής θεωρίας θα χρειαστούμε
Τίτλος Μαθήματος: Θεωρία Ομάδων Ενότητα: Ευθέα Γινόμενα Ομάδων Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης Τμήμα: Μαθηματικών Κεφάλαιο 3 Ευθέα Γινόμενα Ομάδων Για την περαιτέρω ανάπτυξη τής θεωρίας θα χρειαστούμε
Κεφάλαιο 4 Διανυσματικοί Χώροι
 Κεφάλαιο Διανυσματικοί Χώροι Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: Διανυσματικοί Χώροι α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο
Κεφάλαιο Διανυσματικοί Χώροι Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: Διανυσματικοί Χώροι α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο
Μία απεικόνιση από ένα διανυσματικό χώρο V στον εαυτό του, L : V V την ονομάζουμε γραμμικό τελεστή στο V (ή ενδομορφισμό του V ). Ορισμός. L : V V γρα
 Γραμμική Άλγεβρα ΙΙ Διάλεξη 15 Αναλλοίωτοι Υπόχωροι, Ιδιόχωροι Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 2/5/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 15 2/5/2014 1 / 12 Μία απεικόνιση από ένα διανυσματικό
Γραμμική Άλγεβρα ΙΙ Διάλεξη 15 Αναλλοίωτοι Υπόχωροι, Ιδιόχωροι Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 2/5/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 15 2/5/2014 1 / 12 Μία απεικόνιση από ένα διανυσματικό
1 1 A = x 1 x 2 x 3. x 4. R 2 3 : a + b + c = x + y + z = 0. R 2 3 : a + x = b + y = c + z = 0
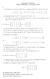 Γραμμική Άλγεβρα Ι Θέματα Εξετάσεων Ιανουαρίου 6. (α Υπολογίστε τον πίνακα X R και την ορίζουσα det(x 5 αν AX = B + C και ( ( ( 3 3 A = B = C =. 4 3 (β Θεωρούμε πίνακα A R n n τέτοιον ώστε A = 4A 4I n.
Γραμμική Άλγεβρα Ι Θέματα Εξετάσεων Ιανουαρίου 6. (α Υπολογίστε τον πίνακα X R και την ορίζουσα det(x 5 αν AX = B + C και ( ( ( 3 3 A = B = C =. 4 3 (β Θεωρούμε πίνακα A R n n τέτοιον ώστε A = 4A 4I n.
Ασκήσεις6 Το σύνηθες εσωτερικό γινόμενο στο
 Ασκήσεις6 7 Ασκήσεις6 Το σύνηθες εσωτερικό γινόμενο στο και Βασικά σημεία Το σύνηθες εσωτερικό γινόμενο στο και (ορισμοί και ιδιότητες) Ορθοκανονικές βάσεις και η μέθοδος Gram-Schmidt Ορθογώνιο συμπλήρωμα
Ασκήσεις6 7 Ασκήσεις6 Το σύνηθες εσωτερικό γινόμενο στο και Βασικά σημεία Το σύνηθες εσωτερικό γινόμενο στο και (ορισμοί και ιδιότητες) Ορθοκανονικές βάσεις και η μέθοδος Gram-Schmidt Ορθογώνιο συμπλήρωμα
ETY-202 ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΕΡΓΑΛΕΙΑ ΤΗΣ ΚΒΑΝΤΟΜΗΧΑΝΙΚΗΣ ETY-202 ΎΛΗ & ΦΩΣ 02. ΜΑΘΗΜΑΤΙΚΑ ΕΡΓΑΛΕΙΑ. Στέλιος Τζωρτζάκης 1/11/2013
 stzortz@iesl.forth.gr 1396; office Δ013 ΙΤΕ 2 ΎΛΗ & ΦΩΣ 02. ΜΑΘΗΜΑΤΙΚΑ ΕΡΓΑΛΕΙΑ ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΕΡΓΑΛΕΙΑ ΤΗΣ ΚΒΑΝΤΟΜΗΧΑΝΙΚΗΣ Στέλιος Τζωρτζάκης 1 3 4 Ο διανυσματικός χώρος των φυσικών καταστάσεων Η έννοια
stzortz@iesl.forth.gr 1396; office Δ013 ΙΤΕ 2 ΎΛΗ & ΦΩΣ 02. ΜΑΘΗΜΑΤΙΚΑ ΕΡΓΑΛΕΙΑ ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΕΡΓΑΛΕΙΑ ΤΗΣ ΚΒΑΝΤΟΜΗΧΑΝΙΚΗΣ Στέλιος Τζωρτζάκης 1 3 4 Ο διανυσματικός χώρος των φυσικών καταστάσεων Η έννοια
Έντυπο Yποβολής Αξιολόγησης ΓΕ
 Έντυπο Yποβολής Αξιολόγησης ΓΕ O φοιτητής συμπληρώνει την ενότητα «Υποβολή Εργασίας» και αποστέλλει το έντυπο σε δύο μη συρραμμένα αντίγραφα (ή ηλεκτρονικά) στον Καθηγητή-Σύμβουλο Ο Καθηγητής-Σύμβουλος
Έντυπο Yποβολής Αξιολόγησης ΓΕ O φοιτητής συμπληρώνει την ενότητα «Υποβολή Εργασίας» και αποστέλλει το έντυπο σε δύο μη συρραμμένα αντίγραφα (ή ηλεκτρονικά) στον Καθηγητή-Σύμβουλο Ο Καθηγητής-Σύμβουλος
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (Εξ. Ιουνίου - 02/07/08) ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ
 Ονοματεπώνυμο:......... Α.Μ....... Ετος... ΑΙΘΟΥΣΑ:....... I. (περί τις 55μ. = ++5++. Σωστό ή Λάθος: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (Εξ. Ιουνίου - //8 ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ (αʹ Αν AB = BA όπου A, B τετραγωνικά και
Ονοματεπώνυμο:......... Α.Μ....... Ετος... ΑΙΘΟΥΣΑ:....... I. (περί τις 55μ. = ++5++. Σωστό ή Λάθος: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (Εξ. Ιουνίου - //8 ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ (αʹ Αν AB = BA όπου A, B τετραγωνικά και
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ. ΕΝΟΤΗΤΑ: Άλγεβρα των Πινάκων (2) ΔΙΔΑΣΚΩΝ: Βλάμος Παναγιώτης ΙΟΝΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΕΝΟΤΗΤΑ: Άλγεβρα των Πινάκων (2) ΙΟΝΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΔΙΔΑΣΚΩΝ: Βλάμος Παναγιώτης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΕΝΟΤΗΤΑ: Άλγεβρα των Πινάκων (2) ΙΟΝΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΔΙΔΑΣΚΩΝ: Βλάμος Παναγιώτης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
ΚΕΦΑΛΑΙΟ 6: Κεντρικές Απλές Άλγεβρες
 ΚΕΦΑΛΑΙΟ 6: Κεντρικές Απλές Άλγεβρες Χρησιµοποιώντας τανυστικά γινόµενα και εφαρµόζοντας το θεώρηµα των Wedderbur-rt ( 33) θα αποδείξουµε δύο θεµελιώδη θεωρήµατα που αφορούν κεντρικές απλές άλγεβρες *
ΚΕΦΑΛΑΙΟ 6: Κεντρικές Απλές Άλγεβρες Χρησιµοποιώντας τανυστικά γινόµενα και εφαρµόζοντας το θεώρηµα των Wedderbur-rt ( 33) θα αποδείξουµε δύο θεµελιώδη θεωρήµατα που αφορούν κεντρικές απλές άλγεβρες *
ΣΗΜΕΙΩΣΕΙΣ. Από προηγούμενες τάξεις γνωρίζουμε ότι το τετράγωνο οποιουδήποτε πραγματικού αριθμού
 ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i ΙΔΙΟΤΗΤΕΣ
ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i ΙΔΙΟΤΗΤΕΣ
ΚΕΦΑΛΑΙΟ 4: Ριζικό του Jacobson
 ΚΕΦΑΛΑΙΟ 4: Ριζικό του Jacobso Είδαµε στο προηγούµενο κεφάλαιο ότι κάθε ηµιαπλός δακτύλιος είναι δακτύλιος του Art. Επειδή υπάρχουν παραδείγµατα δακτυλίων του Art που δεν είναι ηµιαπλοί, πχ Z 2, > 1, τίθεται
ΚΕΦΑΛΑΙΟ 4: Ριζικό του Jacobso Είδαµε στο προηγούµενο κεφάλαιο ότι κάθε ηµιαπλός δακτύλιος είναι δακτύλιος του Art. Επειδή υπάρχουν παραδείγµατα δακτυλίων του Art που δεν είναι ηµιαπλοί, πχ Z 2, > 1, τίθεται
Αλγεβρικες οµες Ι Ασκησεις - Φυλλαδιο 4 1 2
 Αλγεβρικες οµες Ι Ασκησεις - Φυλλαδιο 4 1 2 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi.html Πέµπτη 27 εκεµβρίου 2012 Ασκηση
Αλγεβρικες οµες Ι Ασκησεις - Φυλλαδιο 4 1 2 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi.html Πέµπτη 27 εκεµβρίου 2012 Ασκηση
Παραδείγματα Ιδιοτιμές Ιδιοδιανύσματα
 Παραδείγματα Ιδιοτιμές Ιδιοδιανύσματα Παράδειγμα Να βρείτε τις ιδιοτιμές και τα αντίστοιχα ιδιοδιανύσματα του πίνακα A 4. Επίσης να προσδιοριστούν οι ιδιοχώροι και οι γεωμετρικές πολλαπλότητες των ιδιοτιμών.
Παραδείγματα Ιδιοτιμές Ιδιοδιανύσματα Παράδειγμα Να βρείτε τις ιδιοτιμές και τα αντίστοιχα ιδιοδιανύσματα του πίνακα A 4. Επίσης να προσδιοριστούν οι ιδιοχώροι και οι γεωμετρικές πολλαπλότητες των ιδιοτιμών.
, b, έχει λύση αν και μόνο αν rank( A) rank( A b) είναι οι συνήθεις διατεταγμένες βάσεις των,
 Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις8: Γραμμικές Απεικονίσεις και Πίνακες Βασικά σημεία Ορισμός πίνακα γραμμικής απεικόνισης, παραδείγματα Ανάκτηση γραμμικής απεικόνισης από πίνακά της Ιδιότητες (πίνακας
Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις8: Γραμμικές Απεικονίσεις και Πίνακες Βασικά σημεία Ορισμός πίνακα γραμμικής απεικόνισης, παραδείγματα Ανάκτηση γραμμικής απεικόνισης από πίνακά της Ιδιότητες (πίνακας
a b b < a > < b > < a >.
 Θεωρια Δακτυλιων και Modules Εαρινο Εξαμηνο 2016 17 Διάλεξη 1 Ενότητα 1. Επανάληψη: Προσθετικές ομάδες, δακτύλιοι, αντιμεταθετικοί δακτύλιοι, δακτύλιοι με μοναδιαίο στοιχείο, παραδείγματα. Συμφωνήσαμε
Θεωρια Δακτυλιων και Modules Εαρινο Εξαμηνο 2016 17 Διάλεξη 1 Ενότητα 1. Επανάληψη: Προσθετικές ομάδες, δακτύλιοι, αντιμεταθετικοί δακτύλιοι, δακτύλιοι με μοναδιαίο στοιχείο, παραδείγματα. Συμφωνήσαμε
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΠΙΜΕΛΕΙΑ : ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ
 ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΠΙΜΕΛΕΙΑ : ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΕΥΡΙΠΙΔΟΥ 80 ΝΙΚΑΙΑ ΝΕΑΠΟΛΗ ΤΗΛΕΦΩΝΟ 0965897 ΔΙΕΥΘΥΝΣΗ ΣΠΟΥΔΩΝ ΒΡΟΥΤΣΗ ΕΥΑΓΓΕΛΙΑ ΜΠΟΥΡΝΟΥΤΣΟΥ ΚΩΝ/ΝΑ ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Η έννοια του μιγαδικού
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΠΙΜΕΛΕΙΑ : ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΕΥΡΙΠΙΔΟΥ 80 ΝΙΚΑΙΑ ΝΕΑΠΟΛΗ ΤΗΛΕΦΩΝΟ 0965897 ΔΙΕΥΘΥΝΣΗ ΣΠΟΥΔΩΝ ΒΡΟΥΤΣΗ ΕΥΑΓΓΕΛΙΑ ΜΠΟΥΡΝΟΥΤΣΟΥ ΚΩΝ/ΝΑ ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Η έννοια του μιγαδικού
ΧΑΡΑΚΤΗΡΙΣΤΙΚΟ ΠΟΛΥΩΝΥΜΟ ΠΙΝΑΚΑ: Έστω Α ένας n nπίνακας επί ενός σώματος F. Για χ στο F, ορίζεται το πολυώνυμο ( ως προς χ ) : h ( x) = det( A- xi ).
 1 ΧΑΡΑΚΤΗΡΙΣΤΙΚΟ ΠΟΛΥΩΝΥΜΟ ΠΙΝΑΚΑ: Έστω Α ένας n nπίνακας επί ενός σώματος F. Για χ στο F, ορίζεται το πολυώνυμο ( ως προς χ ) : h ( x) = det( A- xi ). A n Πόρισμα 1: Ο βαθμός του χαρ/κου πολυωνύμου ενός
1 ΧΑΡΑΚΤΗΡΙΣΤΙΚΟ ΠΟΛΥΩΝΥΜΟ ΠΙΝΑΚΑ: Έστω Α ένας n nπίνακας επί ενός σώματος F. Για χ στο F, ορίζεται το πολυώνυμο ( ως προς χ ) : h ( x) = det( A- xi ). A n Πόρισμα 1: Ο βαθμός του χαρ/κου πολυωνύμου ενός
Κεφάλαιο 4. Ευθέα γινόµενα οµάδων. 4.1 Ευθύ εξωτερικό γινόµενο οµάδων. i 1 G 1 G 1 G 2, g 1 (g 1, e 2 ), (4.1.1)
 Κεφάλαιο 4 Ευθέα γινόµενα οµάδων Στο Παράδειγµα 1.1.2.11 ορίσαµε το ευθύ εξωτερικό γινόµενο G 1 G 2 G n των οµάδων G i, 1 i n. Στο κεφάλαιο αυτό ϑα ασχοληθούµε λεπτοµερέστερα µε τα ευθέα γινόµενα οµάδων
Κεφάλαιο 4 Ευθέα γινόµενα οµάδων Στο Παράδειγµα 1.1.2.11 ορίσαµε το ευθύ εξωτερικό γινόµενο G 1 G 2 G n των οµάδων G i, 1 i n. Στο κεφάλαιο αυτό ϑα ασχοληθούµε λεπτοµερέστερα µε τα ευθέα γινόµενα οµάδων
Μαθηματικά Γ Γυμνασίου
 Α λ γ ε β ρ ι κ έ ς π α ρ α σ τ ά σ ε ι ς 1.1 Πράξεις με πραγματικούς αριθμούς (επαναλήψεις συμπληρώσεις) A. Οι πραγματικοί αριθμοί και οι πράξεις τους Διδακτικοί στόχοι Θυμάμαι ποιοι αριθμοί λέγονται
Α λ γ ε β ρ ι κ έ ς π α ρ α σ τ ά σ ε ι ς 1.1 Πράξεις με πραγματικούς αριθμούς (επαναλήψεις συμπληρώσεις) A. Οι πραγματικοί αριθμοί και οι πράξεις τους Διδακτικοί στόχοι Θυμάμαι ποιοι αριθμοί λέγονται
Κεφάλαιο 4 Διανυσματικοί Χώροι
 Κεφάλαιο Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο συμβολίζουμε με Σε αυτό το σύνολο γνωρίζουμε
Κεφάλαιο Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο συμβολίζουμε με Σε αυτό το σύνολο γνωρίζουμε
Α Δ Ι. Δευτέρα 13 Ιανουαρίου 2014
 Α Δ Ι Α - Φ 9 Δ : Ν. Μαρμαρίδης - Α. Μπεληγιάννης Ι Μ : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2013/asi2013.html, https://sites.google.com/site/maths4edu/home/algdom114 Δευτέρα 13 Ιανουαρίου
Α Δ Ι Α - Φ 9 Δ : Ν. Μαρμαρίδης - Α. Μπεληγιάννης Ι Μ : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2013/asi2013.html, https://sites.google.com/site/maths4edu/home/algdom114 Δευτέρα 13 Ιανουαρίου
ΕΝΔΕΙΚΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑ ΠΙΝΑΚΩΝ. (ii) Αν ο Β m+1, με m N, αντιστρέφεται, τότε και ο Β αντιστρέφεται
 ΕΝΔΕΙΚΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑ ΠΙΝΑΚΩΝ 1) Έστω A, Β Μ n (R) τέτοιοι, ώστε A + Β = Ι n. Να δείξετε ότι : A = A 2 κκκ Β = Β 2 ΑΑ = Ο 2) Έστω A, Β Μ n (R), με A = A 2 και ΑΑ + ΒΒ = Ο. Να δειχθεί ότι ΑΑ = ΒΒ
ΕΝΔΕΙΚΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑ ΠΙΝΑΚΩΝ 1) Έστω A, Β Μ n (R) τέτοιοι, ώστε A + Β = Ι n. Να δείξετε ότι : A = A 2 κκκ Β = Β 2 ΑΑ = Ο 2) Έστω A, Β Μ n (R), με A = A 2 και ΑΑ + ΒΒ = Ο. Να δειχθεί ότι ΑΑ = ΒΒ
ΚΕΦΑΛΑΙΟ 2. Γραμμικοί Κώδικες. 2.1 Η έννοια του Γραμμικού κώδικα
 ΚΕΦΑΛΑΙΟ 2 Γραμμικοί Κώδικες 2.1 Η έννοια του Γραμμικού κώδικα Μέχρι τώρα θεωρούσαμε έναν κώδικα C με παραμέτρους (n, M, d) απλώς ως ένα υποσύνολο του συνόλου A n, όπου A είναι ένα αλφάβητο. Είχαμε, όμως,
ΚΕΦΑΛΑΙΟ 2 Γραμμικοί Κώδικες 2.1 Η έννοια του Γραμμικού κώδικα Μέχρι τώρα θεωρούσαμε έναν κώδικα C με παραμέτρους (n, M, d) απλώς ως ένα υποσύνολο του συνόλου A n, όπου A είναι ένα αλφάβητο. Είχαμε, όμως,
Κεφάλαιο 0 Μιγαδικοί Αριθμοί
 Κεφάλαιο 0 Μιγαδικοί Αριθμοί 0 Βασικοί ορισμοί και πράξεις Είναι γνωστό ότι δεν υπάρχει πραγματικός αριθμός που επαληθεύει την εξίσωση x Η ανάγκη επίλυσης τέτοιων εξισώσεων οδηγεί στο σύνολο των μιγαδικών
Κεφάλαιο 0 Μιγαδικοί Αριθμοί 0 Βασικοί ορισμοί και πράξεις Είναι γνωστό ότι δεν υπάρχει πραγματικός αριθμός που επαληθεύει την εξίσωση x Η ανάγκη επίλυσης τέτοιων εξισώσεων οδηγεί στο σύνολο των μιγαδικών
ΑΛΓΕΒΡΙΚΕΣ ΟΜΕΣ Ι. Ασκησεις - Φυλλαδιο 8
 ΑΛΓΕΒΡΙΚΕΣ ΟΜΕΣ Ι Τµηµα Β Ασκησεις - Φυλλαδιο 8 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi07/asi07.html Παρασκευή 9 Μαίου 07 Για κάθε µετάθεση
ΑΛΓΕΒΡΙΚΕΣ ΟΜΕΣ Ι Τµηµα Β Ασκησεις - Φυλλαδιο 8 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi07/asi07.html Παρασκευή 9 Μαίου 07 Για κάθε µετάθεση
