DESCRIEREA CULORILOR ACHIZITIA IMAGINILOR COLOR CU CAMERE FOTO DIGITALE
|
|
|
- Ἐφραίμ Αυγερινός
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Cursul 2 DESCRIEREA CULORILOR ACHIZITIA IMAGINILOR COLOR CU CAMERE FOTO DIGITALE
2 Sistemul vizual uman: perceptia vizuala Descrierea culorilor Camera digitala color: structura de baza
3 Sectiune laterala prin craniul uman nerv optic cortex vizual ochi obiect din campul vizual retina CGL : corp geniculat lateral
4 Sectiune transversala prin craniul uman cortex vizual Fiecare ramura a nervului optic are fascicule separate pentru campurile vizuale. CGL : corp geniculat lateral chiasma ochi optica nerv optic camp vizual temporal camp vizual nazal
5 Iris Pupila Ochiul uman : vedere exterioara Iris - muschi circular de control al deschiderii pupilei Pleoapa (protectie mecanica) Pozitia ochiului este reglata prin sase muschi. Fanta reglabila pentru captarea luminii
6 Sclerotica Ochiul uman : structura Coroida Cornee Pupila Retina Fovee Lentila oculara (umoare sticloasa) Iris Corp cilar (muschi pentru controlul formei lentilei oculare) Nerv optic
7 Retina fovea nerv optic Vedere la microscop Retina ochiului uman Vedere prin oftalmoscop Celulele fotoreceptoare : conuri si bastonase
8 Structura retinei Celulele fotoreceptoare : conuri si bastonase Flux celule orizontale informatie celule bipolare celule amacrine lumina celule ganglionare (on-off) fibre ale nervului optic
9 conuri pentru vederea diurna sensibilitate luminoasa mica rezolutie spatiala mare adaptate la diferite lungimi de unda a radiatiei luminoase (S, M, L) bastonase Structura retinei : celule receptoare pentru vederea nocturna sensibilitate luminoasa mare rezolutie spatiala mica
10
11 Cateva numere : aria retinei : 5 x 5 mm numar conuri : 5 milioane numar bastonase : 100 milioane numar fibre ale nervului optic : 1,6 milioane densitate maxima conuri : 0,16 milioane / mm 2 Structura retinei
12 Trebuie realizata o specificare numerica a culorii : uniformitatea denumirii repetabilitatea crearii senzatiei de culoare pastrarea principiului de diferenta de culoare (culori opuse) incorporarea unei semnificatii fizice
13 Lumina vizibila : portiune a spectrului electromagnetic din domeniul lungimilor de unda de [360 nm, 830 nm] (sau [380 nm, 780 nm]). O radiatie luminoasa este caracterizata de distributia spectrala de energie f(λ). Dupa cum am vazut, fiecare tip de fotoreceptor din retina (con) are o caracteristica spectrala proprie C i (λ) ; raspunsul unui con la radiatia luminoasa f este : c i = λ λ max min C i ( λ ) f ( λ ) dλ
14 Young, Grassman, Maxwell : Teoria tricromaticitatii orice culoare poate fi reprodusa ca amestec (aditiv sau substractiv) a trei culori primare porneste de la realitatea biologica a fiziologiei sistemului vizual are suport matematic O culoare este un triplet de numere, corespunzand proiectiei spectrului radiatiei luminoase pe functiile caracteristice ale spectrelor primare.
15 culoare sintetizata prin amestec aditiv S(λ) culoare de test C(λ) A(λ) B(λ) Amestec aditiv a b S(λ) = aa(λ) + bb(λ) +cc(λ) S = (a, b, c) c surse de lumina primara reglare intensitate
16 culoare sintetizata prin amestec aditiv S(λ) culoare de test aditivata cu culoare primara C(λ) A(λ) B(λ) Amestec substractiv a b c S(λ)+ cc(λ) = aa(λ) + bb(λ) S(λ) = aa(λ) + bb(λ) - cc(λ) S = (a, b, c) reglare intensitate surse de lumina primara
17 In practica: spectrele luminoase sunt esantionate la interval de cel mult 10 nm; ecuatiile capata forma discreta. a b c = = = λ max A( ) f ( )d λ λ λ λ = min λ max B( ) f ( )d λ λ λ λ = min λ max C( ) f ( )d λ λ λ λ = min j j j A j f B j f C j f Reprezentarea unei culori prin tripletul (a, b, c) este univoca si universala daca A(λ), B(λ), C(λ), sunt standardizate. j j j
18 Tipuri de sisteme colorimetrice : sisteme primare de reprezentare (RGB, XYZ) sisteme tehnice derivate liniar (NTSC, PAL, SECAM) sisteme perceptuale derivate liniar (culori opuse, Ohta) sisteme cu cromaticitate uniforma (Lab) sisteme perceptuale neliniare (HSV, Munsell)
19 CIE - Comité International de l Eclairage Standardizarea Sisteme colorimetrice de reprezentare - recomandarea CIE 1931 stabileste doua sisteme primare de reprezentare: RGB si XYZ. RGB - (Red, Green, Blue) : culorile primare sunt spectre monocromatice de lungimi de unda de 700 nm, 546,1 nm si 435,8 nm. intensitatile sunt asfel alese incat valorile tristimulus asociate luminii albe sunt egale si unitare.
20 g Functii de corespondenta a culorilor CIE RGB
21 Cubul RGB LABORATORUL DE ANALIZA ŞI PRELUCRAREA IMAGINILOR
22 Culorile fizic realizabile prin amestecul aditiv de culori primare (gamut-ul de culoare) RGB sunt situate intr-un cub (valorile tristimulus sunt asociate unor coordonate carteziene). RGB Desi culorile primare sunt fizic realizabile, nu toate valorile tristimulus sunt pozitive (exista culori fizice ce nu pot fi sintetizate prin amestecul aditiv al componentelor primare RGB). Spatiul este cu variatie neuniforma - distantele euclidiene intre reprezentarile tristimulus nu corespund distantelor perceptuale dintre culorile corespunzatoare. :-) Calcularea valorilor tristimulus prin folosirea de adunari si scaderi alternate nu era exacta din cauza erorilor operatorilor umani ce operau masinile de calcul - s-a dorit deci gasirea unor alte primare, pentru care valorile tristimulus sa fie doar pozitive.
23 XYZ - transformare liniara a valorilor tristimuls RGB astfel incat : orice culoare fizica monocromatica sa fie caracterizata de valori tristimulus pozitive componenta Y sa fie o masura a eficientei luminoase (deci a luminantei culorii) pentru o lumina alba valorile tristimulus sa fie egale. X 0,490 Y = 0,177 Z 0,000 0,310 0,813 0,010 0,200 R 0,011 G 0,990 B
24 X Y Z Functii de corespondenta a culorilor CIE XYZ
25 X Y Z = 0,490 0,177 0,000 0,310 0,813 0,010 0,200 R 0,011 G 0,990 B XYZ Matricea transformarii nu este unitara, si deci transformarea nu este o rotatie a cubului RGB cu tot cu sistemul de coordonate. Gamut-ul de culoare XYZ este un paraleliped inclinat
26 Coordonate de cromaticitate Normalizare a valorilor tristimulus (T 1, T 2, T 3 ): T T T T t + + = T T T T t + + = T T T T t + + = 1 t t t = + + cele trei valori sunt liniar dependente; pot fi pastrate doar doua, coordonatele de cromaticitate.
27 Coordonate r g b = = = R R + G + B G R + G + B B R + G + B r + g +b = 1 G 1 (r, g, b) de cromaticitate (R, G, B) 1 RGB R Triunghiul Maxwell 1 B
28 Coordonate de cromaticitate XYZ x = y = z = X X X X + Y + Z Y + Y + Z Z + Y + Z x + y + z = 1
29 Gamut-ul reprezentabil culori primare culori realizabile prin amestec aditiv
30 NTSC receptor SMPTE (Society of Motion Picture and Television Engineers) Standarde de televiziune corespunde culorilor primare realizate de afisajele cu fosfor (tuburi catodice) R G B r r r 0,842 = 0,129 0,008 0,156 1,319 0,069 0,091 R 0,203 G 0,897 B
31 NTSC National Television Standard Committee (Never Twice the Same Color) Y 0,299 I = 0,147 Q 0,615 0,597 0,289 0,515 Standarde de 0,114 R 0,437 G 0,100 B televiziune Y este componenta de luminanta; I, Q sunt diferente cromatice Y I Q = = 0,3R 0,493 0, ,6G + ( B Y ) ( R Y ) 0,1B
32 PAL Phase Alternating Lines (Peace At Last) Y U V = 0,299 0,196 0,211 0,597 0,274 0,523 Standarde de televiziune 0,114 R 0,322 G 0,312 B Y este componenta de luminanta; U, V sunt diferente cromatice Componentele de crominanta se pot subesantiona (1:2) Y U V = = 0,3R 0, 74 0,48 + 0,6G + 0,1B ( R Y ) 0,27( B Y ) ( R Y ) + 0,41( B Y )
33 SECAM Sequentiel à Memoire Standarde de televiziune Y 0,299 Cb = 0,169 Cr 0,500 0,597 0,331 0,418 0,114 R 0,500 G 0,031 B Y este componenta de luminanta; Cb, Cr sunt diferente cromatice Componentele de crominanta se pot subesantiona (1:2) Se foloseste si in compresia JPEG
34 Experimentele lui Hering : aranjarea de catre observatori pe un cerc in plan a unor esantioane de culoare, a. i. culorile similare sa fie vecine. Jumatati opuse ale cercului contin rosu si respectiv verde, sau galben si respectiv albastru. rosu Nici o culoare nu este descrisa ca fiind simultan ; albastru rosie si verde, galbena si albastra. Spatiul culorilor opuse galben verde
35 Culorile opuse sunt : rosu - verde galben - albastru [alb - negru] (prin extensie) Spatiul culorilor opuse Experimentul e sustinut de fenomenul de post-imagine (afterimage). Codare : cat rosu / verde, galben / albastru si alb contine culoarea. Y O O 1 2 = 0,333 0,500 0,250 0,333 0,500 0,250 0,333 R 0,000 G 0,500 B O alta varianta foloseste pentru codarea componentelor opuse raspunsul perceptual (logaritmat) al culorilor primare.
36 Sisteme colorimetrice neliniare: Motivatie Exista neliniaritati intrinseci in mecanismul perceptiei umane (fotodetectorii din retina au o caracteristica logaritmica) si in dispozitivele de achizitie (corectia de γ). Trebuie tinut cont de pragul de sensibilitate la culoare a sistemului vizual uman (culori diferite ce arata similar) si trebuie introdusa o distanta intre culori care sa fie proportionala cu distanta perceptuala dintre respectivele culori. Trebuie folosita o descriere de culoare similara cu descrierea semantica si perceptuala utilizata de observatorii umani.
37 Elipsele MacAdams Locul geometric al culorilor perceptual nediscriminabile fata de culoarea centrului elipsei (raport 1:20 pentru factorul de aspect si dimensiuni absolute). JND - Just Noticeable Difference Dorim ca elipsele sa devina cercuri.
38 Spatiu de cromaticitate uniforma (UCS) : elipsele MacAdams devin aproape circulare (1:1-1:2) si aproape egale in tot spatiul de cromaticitate. 4X u = X + 15Y + 3Z 6Y v = X + 15Y + 3Z Spatiul Yuv Distantele Euclidiene dintre numerele (u,v) si respectiv (U,V,W) sunt in continuare diferite de distantele perceptuale dintre culori.
39 Spatiul U * V * W * Spatiul de cromaticitate uniforma modificat (UCS modificat): translatie cu originea in albul de referinta neliniaritate a coordonatei de luminanta ( stralucire ) W * = 116Y 1/ 3 17 U V * * = 13W = 13W * * ( u u ) ( v v ) 0 0
40 CIE Lab 1976 = = = Z Z f Y Y f 200 b Y Y f X X f 500 a 16 Y Y f 116 L unde albul de referinta este (X 0, Y 0, Z 0 ) si functia neliniara de transformare a stralucirii este ca la CIE Luv 1976: + =,in rest x x, x x ) ( f 3 1/
41 CIE Lab 1976 L
42 Coordonatele de cromaticitate (diferente cromatice) a si b sunt independente de luminanta L. Se poate face o definire perceptuala a culorilor prin definirea unei nuante H si a unei saturatii C prin exprimarea coordonatelor de cromaticitate intr-un sistem polar de coordonate H C = arctan = a 2 + b b a 2 CIE Lab 1976 H C
43 Distantea euclidiana in spatiul Lab corespunde distantei perceptuale dintre culori: ab = ( ΔL ) + ( Δa ) ( Δb ) Δ + CIE Lab 1976 In spatiul Lab, diferenta dintre doua culori abia perceptibile este definita de o distanta maxima de 2,3. Spatiul Lab este utilizat in majoritatea aplicatiilor de analiza automata a imaginilor.
44 Spatii perceptuale : familia HSV Descrierea culorilor in limbaj natural foloseste o terminologie specifica: nuanta - ce fel de culoare (verde, rosu, galben,.) saturatia - cat de pura este culoarea, cu cat alb a fost amestecata culoarea pura din care aceasta provine luminozitatea - luminanta, stralucire luminoasa Este deci un sistem de reprezentare de tipul celui utilizat de Munsell, dar cu o specificare numerica a nuantei.
45 Spatii perceptuale : familia HSV spatiul de culoare este modelat ca un dublu con exita variante cu model de cilindru, dubla prisma
46 Componenta de intensitate (V sau I) R + G + B V = 3 V = 0.3R + 0.6G + 0.1B = Y max( R,G,B ) min( R,G,B ) V = 2 Componenta de saturatie S Componenta de nuanta H H ( R G ) ( R B )) S = 1 S = arccos,b > G 2 ( R G ) ( R B )( B G ) = 0.5 ( R G ) ( R B )) 2π arccos,b < G 2 ( R G ) ( R B )( B G ) Spatii perceptuale : familia HSV 3min( R, G, B) R + G + B min( R, G, B) max( R, G, B)
47 Sisteme de achizitie a imaginilor color: Achizitie digitala camera digitala senzori imagine Tehnologie: CMOS CCD Parametru esential: numarul de pixeli
48 CCD Sarcina acumulata in celule este proportionala cu intensitatea radiatiei (luminoase) incidente.
49 CCD interline frame transfer read noise
50 CCD shot noise
51 CCD dark noise
52 Cazul tri-ccd trei CCD, dispozitive de filtrare si separare a fluxului optic un CCD, set de filtre optice mobile ce se interpun pe rand in fluxul optic la fiecare poza
53 Cazul mono-ccd Bayer pattern (CFA Color Filter Array)
54 Schema operatiilor la achizitia imaginii in camera digitala
55 Imagine supraexpusa Controlul expunerii Imagine subexpusa Imagine normala partitionarea imaginii pentru masurarea luminantei medii
56 Controlul focalizarii
57 Gray world model: toate canalele se scaleaza la fel, astfel incat valoarea maxima sa corespunda culorii albe. Controlul punctului de alb
58 Refacerea unui triplet RGB pt fiecare pixel De-mozaicarea color aliasing
59 Prelucrarea imaginilor color prin extinderea metodelor de prelucrare scalare 1. Abordarea marginala : descompunere RGB R G B Scalar processing Scalar processing Scalar processing R G B
60 Prelucrarea imaginilor color prin extinderea metodelor de prelucrare scalare 2. Abordarea tranformarii colorimetrice liniare fixe (luminanta + crominante) R G B Direct transform Y C 1 C 2 Scalar processing Scalar processing Scalar processing Y C 1 C 2 Inverse transform R G B
61 Prelucrarea imaginilor color prin extinderea metodelor de prelucrare scalare 3. Abordarea tranformarii colorimetrice liniare adaptive (decorelare) R G B Decorrelation I 1 I 2 I 3 Scalar processing Scalar processing Scalar processing I 1 I 2 I 3 Recorrelation R G B
62 Prelucrarea imaginilor color prin extinderea metodelor de prelucrare scalare 4. Transformare neliniara R G B Direct transform S H V Scalar processing Y Inverse transform R G B
Spatii de reprezentare a culorilor
 Spatii de reprezentare a culorilor Culoarea = calitate a perceptiei determinata de compozitia spectrala a luminii (radiatiei electromagnetice) primite de ochi Lumina vizibila e compusa dintr-o banda relativ
Spatii de reprezentare a culorilor Culoarea = calitate a perceptiei determinata de compozitia spectrala a luminii (radiatiei electromagnetice) primite de ochi Lumina vizibila e compusa dintr-o banda relativ
Analiza și Prelucrarea Digitală a Semnalelor Video
 Analiza și Prelucrarea Digitală a Semnalelor Video Conf. dr. ing. Radu Ovidiu Preda radu@comm.pub.ro Ș.l. dr. ing. Ionuţ Pirnog ionut@comm.pub.ro Site disciplină: www.comm.pub.ro/preda/apdsv Analiza și
Analiza și Prelucrarea Digitală a Semnalelor Video Conf. dr. ing. Radu Ovidiu Preda radu@comm.pub.ro Ș.l. dr. ing. Ionuţ Pirnog ionut@comm.pub.ro Site disciplină: www.comm.pub.ro/preda/apdsv Analiza și
Captura imaginilor. este necesară o sursă de lumină (λ: lungimea de undă a sursei)
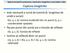 Captura imaginilor este necesară o sursă de lumină (λ: lungimea de undă a sursei) E(x, y, z, λ): lumina incidentă într-un punct (x, y, z coordonatele spațiale) fiecare punct din scenă are o funcție de
Captura imaginilor este necesară o sursă de lumină (λ: lungimea de undă a sursei) E(x, y, z, λ): lumina incidentă într-un punct (x, y, z coordonatele spațiale) fiecare punct din scenă are o funcție de
Metode iterative pentru probleme neliniare - contractii
 Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
MARCAREA REZISTOARELOR
 1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate.
 Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Planul determinat de normală şi un punct Ecuaţia generală Plane paralele Unghi diedru Planul determinat de 3 puncte necoliniare
 1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
(a) se numeşte derivata parţială a funcţiei f în raport cu variabila x i în punctul a.
 Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
R R, f ( x) = x 7x+ 6. Determinați distanța dintre punctele de. B=, unde x și y sunt numere reale.
 5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
5.5. REZOLVAREA CIRCUITELOR CU TRANZISTOARE BIPOLARE
 5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
a n (ζ z 0 ) n. n=1 se numeste partea principala iar seria a n (z z 0 ) n se numeste partea
 Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Sisteme diferenţiale liniare de ordinul 1
 1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
Definiţia generală Cazul 1. Elipsa şi hiperbola Cercul Cazul 2. Parabola Reprezentari parametrice ale conicelor Tangente la conice
 1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
V O. = v I v stabilizator
 Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor
 Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor X) functia f 1
 Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Conice. Lect. dr. Constantin-Cosmin Todea. U.T. Cluj-Napoca
 Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
Subiecte Clasa a VII-a
 lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
Curs 1 Şiruri de numere reale
 Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
5. FUNCŢII IMPLICITE. EXTREME CONDIŢIONATE.
 5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
Seminariile Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reziduurilor
 Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Curs 14 Funcţii implicite. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi"
 Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Percepţia vizuală umană. Percepţia vizuală umană Teoria culorii Percepţi culorilor. Procesarea informaţiei vizuale. Ochiul uman.
 (2008-1 (2008-2 Percepţia vizuală umană Teoria culorii Percepţi culorilor Percepţia vizuală umană http://sorana.academicdirect.ro/pages/doc/imag-iii.php (2008-3 (2008-4 Procesarea informaţiei vizuale Ochiul
(2008-1 (2008-2 Percepţia vizuală umană Teoria culorii Percepţi culorilor Percepţia vizuală umană http://sorana.academicdirect.ro/pages/doc/imag-iii.php (2008-3 (2008-4 Procesarea informaţiei vizuale Ochiul
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE
 DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM 1 electronica.geniu.ro
 Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Metode de interpolare bazate pe diferenţe divizate
 Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
Ecuaţia generală Probleme de tangenţă Sfera prin 4 puncte necoplanare. Elipsoidul Hiperboloizi Paraboloizi Conul Cilindrul. 1 Sfera.
 pe ecuaţii generale 1 Sfera Ecuaţia generală Probleme de tangenţă 2 pe ecuaţii generale Sfera pe ecuaţii generale Ecuaţia generală Probleme de tangenţă Numim sferă locul geometric al punctelor din spaţiu
pe ecuaţii generale 1 Sfera Ecuaţia generală Probleme de tangenţă 2 pe ecuaţii generale Sfera pe ecuaţii generale Ecuaţia generală Probleme de tangenţă Numim sferă locul geometric al punctelor din spaţiu
RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii transversale, scrisă faţă de una dintre axele de inerţie principale:,
 REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
COLEGIUL NATIONAL CONSTANTIN CARABELLA TARGOVISTE. CONCURSUL JUDETEAN DE MATEMATICA CEZAR IVANESCU Editia a VI-a 26 februarie 2005.
 SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
Subiecte Clasa a VIII-a
 Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Sisteme de culoare * Complemente Fiziologia vederii umane
 Sisteme de culoare * Complemente Fiziologia vederii umane Ochiul uman Retina rods cones bipolar ganglion horizontal amacrine light Fotoreceptorii retinei Distributia si tipurile de conuri Mai putin sensibile
Sisteme de culoare * Complemente Fiziologia vederii umane Ochiul uman Retina rods cones bipolar ganglion horizontal amacrine light Fotoreceptorii retinei Distributia si tipurile de conuri Mai putin sensibile
Laborator 11. Mulţimi Julia. Temă
 Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Asupra unei inegalităţi date la barajul OBMJ 2006
 Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
III. Serii absolut convergente. Serii semiconvergente. ii) semiconvergentă dacă este convergentă iar seria modulelor divergentă.
 III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
prin egalizarea histogramei
 Lucrarea 4 Îmbunătăţirea imaginilor prin egalizarea histogramei BREVIAR TEORETIC Tehnicile de îmbunătăţire a imaginilor bazate pe calculul histogramei modifică histograma astfel încât aceasta să aibă o
Lucrarea 4 Îmbunătăţirea imaginilor prin egalizarea histogramei BREVIAR TEORETIC Tehnicile de îmbunătăţire a imaginilor bazate pe calculul histogramei modifică histograma astfel încât aceasta să aibă o
Aplicaţii ale principiului I al termodinamicii la gazul ideal
 Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Integrala nedefinită (primitive)
 nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].
![Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].](/thumbs/72/67648751.jpg) Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
Esalonul Redus pe Linii (ERL). Subspatii.
 Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile
 Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Zgomotul se poate suprapune informaţiei utile în două moduri: g(x, y) = f(x, y) n(x, y) (6.2)
 Lucrarea 6 Zgomotul în imagini BREVIAR TEORETIC Zgomotul este un semnal aleator, care afectează informaţia utilă conţinută într-o imagine. El poate apare de-alungul unui lanţ de transmisiune, sau prin
Lucrarea 6 Zgomotul în imagini BREVIAR TEORETIC Zgomotul este un semnal aleator, care afectează informaţia utilă conţinută într-o imagine. El poate apare de-alungul unui lanţ de transmisiune, sau prin
 4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
2 Transformări liniare între spaţii finit dimensionale
 Transformări 1 Noţiunea de transformare liniară Proprietăţi. Operaţii Nucleul şi imagine Rangul şi defectul unei transformări 2 Matricea unei transformări Relaţia dintre rang şi defect Schimbarea matricei
Transformări 1 Noţiunea de transformare liniară Proprietăţi. Operaţii Nucleul şi imagine Rangul şi defectul unei transformări 2 Matricea unei transformări Relaţia dintre rang şi defect Schimbarea matricei
a. 11 % b. 12 % c. 13 % d. 14 %
 1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
T R A I A N ( ) Trigonometrie. \ kπ; k. este periodică (perioada principală T * =π ), impară, nemărginită.
 Trignmetrie Funcţia sinus sin : [, ] este peridică (periada principală T * = ), impară, mărginită. Funcţia arcsinus arcsin : [, ], este impară, mărginită, bijectivă. Funcţia csinus cs : [, ] este peridică
Trignmetrie Funcţia sinus sin : [, ] este peridică (periada principală T * = ), impară, mărginită. Funcţia arcsinus arcsin : [, ], este impară, mărginită, bijectivă. Funcţia csinus cs : [, ] este peridică
Curs 4 Serii de numere reale
 Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Să se arate că n este număr par. Dan Nedeianu
 Primul test de selecție pentru juniori I. Să se determine numerele prime p, q, r cu proprietatea că 1 p + 1 q + 1 r 1. Fie ABCD un patrulater convex cu m( BCD) = 10, m( CBA) = 45, m( CBD) = 15 și m( CAB)
Primul test de selecție pentru juniori I. Să se determine numerele prime p, q, r cu proprietatea că 1 p + 1 q + 1 r 1. Fie ABCD un patrulater convex cu m( BCD) = 10, m( CBA) = 45, m( CBD) = 15 și m( CAB)
Componente şi Circuite Electronice Pasive. Laborator 3. Divizorul de tensiune. Divizorul de curent
 Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
riptografie şi Securitate
 riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
Toate subiectele sunt obligatorii. Timpul de lucru efectiv este de 3 ore. Se acordă din oficiu 10 puncte. SUBIECTUL I.
 Modelul 4 Se acordă din oficiu puncte.. Fie numărul complex z = i. Calculaţi (z ) 25. 2. Dacă x şi x 2 sunt rădăcinile ecuaţiei x 2 9x+8 =, atunci să se calculeze x2 +x2 2 x x 2. 3. Rezolvaţi în mulţimea
Modelul 4 Se acordă din oficiu puncte.. Fie numărul complex z = i. Calculaţi (z ) 25. 2. Dacă x şi x 2 sunt rădăcinile ecuaţiei x 2 9x+8 =, atunci să se calculeze x2 +x2 2 x x 2. 3. Rezolvaţi în mulţimea
Valori limită privind SO2, NOx şi emisiile de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili
 Anexa 2.6.2-1 SO2, NOx şi de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili de bioxid de sulf combustibil solid (mg/nm 3 ), conţinut de O 2 de 6% în gazele de ardere, pentru
Anexa 2.6.2-1 SO2, NOx şi de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili de bioxid de sulf combustibil solid (mg/nm 3 ), conţinut de O 2 de 6% în gazele de ardere, pentru
Reflexia şi refracţia luminii.
 Reflexia şi refracţia luminii. 1. Cu cat se deplaseaza o raza care cade sub unghiul i =30 pe o placa plan-paralela de grosime e = 8,0 mm si indicele de refractie n = 1,50, pe care o traverseaza? Caz particular
Reflexia şi refracţia luminii. 1. Cu cat se deplaseaza o raza care cade sub unghiul i =30 pe o placa plan-paralela de grosime e = 8,0 mm si indicele de refractie n = 1,50, pe care o traverseaza? Caz particular
Orice izometrie f : (X, d 1 ) (Y, d 2 ) este un homeomorfism. (Y = f(x)).
 Teoremă. (Y = f(x)). Orice izometrie f : (X, d 1 ) (Y, d 2 ) este un homeomorfism Demonstraţie. f este continuă pe X: x 0 X, S Y (f(x 0 ), ε), S X (x 0, ε) aşa ca f(s X (x 0, ε)) = S Y (f(x 0 ), ε) : y
Teoremă. (Y = f(x)). Orice izometrie f : (X, d 1 ) (Y, d 2 ) este un homeomorfism Demonstraţie. f este continuă pe X: x 0 X, S Y (f(x 0 ), ε), S X (x 0, ε) aşa ca f(s X (x 0, ε)) = S Y (f(x 0 ), ε) : y
Profesor Blaga Mirela-Gabriela DREAPTA
 DREAPTA Fie punctele A ( xa, ya ), B ( xb, yb ), C ( xc, yc ) şi D ( xd, yd ) în planul xoy. 1)Distanţa AB = (x x ) + (y y ) Ex. Fie punctele A( 1, -3) şi B( -2, 5). Calculaţi distanţa AB. AB = ( 2 1)
DREAPTA Fie punctele A ( xa, ya ), B ( xb, yb ), C ( xc, yc ) şi D ( xd, yd ) în planul xoy. 1)Distanţa AB = (x x ) + (y y ) Ex. Fie punctele A( 1, -3) şi B( -2, 5). Calculaţi distanţa AB. AB = ( 2 1)
1.7. AMPLIFICATOARE DE PUTERE ÎN CLASA A ŞI AB
 1.7. AMLFCATOARE DE UTERE ÎN CLASA A Ş AB 1.7.1 Amplificatoare în clasa A La amplificatoarele din clasa A, forma de undă a tensiunii de ieşire este aceeaşi ca a tensiunii de intrare, deci întreg semnalul
1.7. AMLFCATOARE DE UTERE ÎN CLASA A Ş AB 1.7.1 Amplificatoare în clasa A La amplificatoarele din clasa A, forma de undă a tensiunii de ieşire este aceeaşi ca a tensiunii de intrare, deci întreg semnalul
2. Sisteme de forţe concurente...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...3
 SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
Problema a II - a (10 puncte) Diferite circuite electrice
 Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
2.1 Sfera. (EGS) ecuaţie care poartă denumirea de ecuaţia generală asferei. (EGS) reprezintă osferă cu centrul în punctul. 2 + p 2
 .1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
.1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
Conice - Câteva proprietǎţi elementare
 Conice - Câteva proprietǎţi elementare lect.dr. Mihai Chiş Facultatea de Matematicǎ şi Informaticǎ Universitatea de Vest din Timişoara Viitori Olimpici ediţia a 5-a, etapa I, clasa a XII-a 1 Definiţii
Conice - Câteva proprietǎţi elementare lect.dr. Mihai Chiş Facultatea de Matematicǎ şi Informaticǎ Universitatea de Vest din Timişoara Viitori Olimpici ediţia a 5-a, etapa I, clasa a XII-a 1 Definiţii
VII.2. PROBLEME REZOLVATE
 Teoria Circuitelor Electrice Aplicaţii V PROBEME REOVATE R7 În circuitul din fiura 7R se cunosc: R e t 0 sint [V] C C t 0 sint [A] Se cer: a rezolvarea circuitului cu metoda teoremelor Kirchhoff; rezolvarea
Teoria Circuitelor Electrice Aplicaţii V PROBEME REOVATE R7 În circuitul din fiura 7R se cunosc: R e t 0 sint [V] C C t 0 sint [A] Se cer: a rezolvarea circuitului cu metoda teoremelor Kirchhoff; rezolvarea
Proiectarea filtrelor prin metoda pierderilor de inserţie
 FITRE DE MIROUNDE Proiectarea filtrelor prin metoda pierderilor de inserţie P R Puterea disponibila de la sursa Puterea livrata sarcinii P inc P Γ ( ) Γ I lo P R ( ) ( ) M ( ) ( ) M N P R M N ( ) ( ) Tipuri
FITRE DE MIROUNDE Proiectarea filtrelor prin metoda pierderilor de inserţie P R Puterea disponibila de la sursa Puterea livrata sarcinii P inc P Γ ( ) Γ I lo P R ( ) ( ) M ( ) ( ) M N P R M N ( ) ( ) Tipuri
Seminar 5 Analiza stabilității sistemelor liniare
 Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Eleonora SCHILLER FIZIOLOGIA ŞI PATOLOGIA CROMATICII DENTARE
 Anca VÂLCEANU Constantin VÂRLAN Eleonora SCHILLER FIZIOLOGIA ŞI PATOLOGIA CROMATICII DENTARE Descrierea CIP a Bibliotecii Naţionale a României VÂLCEANU, ANCA Fiziologia şi patologia cromaticii dentare
Anca VÂLCEANU Constantin VÂRLAN Eleonora SCHILLER FIZIOLOGIA ŞI PATOLOGIA CROMATICII DENTARE Descrierea CIP a Bibliotecii Naţionale a României VÂLCEANU, ANCA Fiziologia şi patologia cromaticii dentare
Examen AG. Student:... Grupa: ianuarie 2016
 16-17 ianuarie 2016 Problema 1. Se consideră graful G = pk n (p, n N, p 2, n 3). Unul din vârfurile lui G se uneşte cu câte un vârf din fiecare graf complet care nu-l conţine, obţinându-se un graf conex
16-17 ianuarie 2016 Problema 1. Se consideră graful G = pk n (p, n N, p 2, n 3). Unul din vârfurile lui G se uneşte cu câte un vârf din fiecare graf complet care nu-l conţine, obţinându-se un graf conex
Geometrie computationala 2. Preliminarii geometrice
 Platformă de e-learning și curriculă e-content pentru învățământul superior tehnic Geometrie computationala 2. Preliminarii geometrice Preliminarii geometrice Spatiu Euclidean: E d Spatiu de d-tupluri,
Platformă de e-learning și curriculă e-content pentru învățământul superior tehnic Geometrie computationala 2. Preliminarii geometrice Preliminarii geometrice Spatiu Euclidean: E d Spatiu de d-tupluri,
Algebra si Geometrie Seminar 9
 Algebra si Geometrie Seminar 9 Decembrie 017 ii Equations are just the boring part of mathematics. I attempt to see things in terms of geometry. Stephen Hawking 9 Dreapta si planul in spatiu 1 Notiuni
Algebra si Geometrie Seminar 9 Decembrie 017 ii Equations are just the boring part of mathematics. I attempt to see things in terms of geometry. Stephen Hawking 9 Dreapta si planul in spatiu 1 Notiuni
3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...4
 SEMINAR 3 MMENTUL FRŢEI ÎN RAPRT CU UN PUNCT CUPRINS 3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere...1 3.1. Aspecte teoretice...2 3.2. Aplicaţii rezolvate...4 3. Momentul forţei
SEMINAR 3 MMENTUL FRŢEI ÎN RAPRT CU UN PUNCT CUPRINS 3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere...1 3.1. Aspecte teoretice...2 3.2. Aplicaţii rezolvate...4 3. Momentul forţei
Compresia de imagini. Standardul JPEG
 Tehnici de Compresie a Semnalelor Multimedia Lucrare de laborator Compresia de imagini. Standardul JPEG I. Obiectivul lucrării Lucrarea îşi propune familiarizarea cu metodele şi algoritmii utilizaţi în
Tehnici de Compresie a Semnalelor Multimedia Lucrare de laborator Compresia de imagini. Standardul JPEG I. Obiectivul lucrării Lucrarea îşi propune familiarizarea cu metodele şi algoritmii utilizaţi în
BARAJ DE JUNIORI,,Euclid Cipru, 28 mai 2012 (barajul 3)
 BARAJ DE JUNIORI,,Euclid Cipru, 8 mi 0 (brjul ) Problem Arătţi că dcă, b, c sunt numere rele cre verifică + b + c =, tunci re loc ineglitte xy + yz + zx Problem Fie şi b numere nturle nenule Dcă numărul
BARAJ DE JUNIORI,,Euclid Cipru, 8 mi 0 (brjul ) Problem Arătţi că dcă, b, c sunt numere rele cre verifică + b + c =, tunci re loc ineglitte xy + yz + zx Problem Fie şi b numere nturle nenule Dcă numărul
Erori si incertitudini de măsurare. Modele matematice Instrument: proiectare, fabricaţie, Interacţiune măsurand instrument:
 Erori i incertitudini de măurare Sure: Modele matematice Intrument: proiectare, fabricaţie, Interacţiune măurandintrument: (tranfer informaţie tranfer energie) Influente externe: temperatura, preiune,
Erori i incertitudini de măurare Sure: Modele matematice Intrument: proiectare, fabricaţie, Interacţiune măurandintrument: (tranfer informaţie tranfer energie) Influente externe: temperatura, preiune,
Spatii liniare. Exemple Subspaţiu liniar Acoperire (înfăşurătoare) liniară. Mulţime infinită liniar independentă
 Noţiunea de spaţiu liniar 1 Noţiunea de spaţiu liniar Exemple Subspaţiu liniar Acoperire (înfăşurătoare) liniară 2 Mulţime infinită liniar independentă 3 Schimbarea coordonatelor unui vector la o schimbare
Noţiunea de spaţiu liniar 1 Noţiunea de spaţiu liniar Exemple Subspaţiu liniar Acoperire (înfăşurătoare) liniară 2 Mulţime infinită liniar independentă 3 Schimbarea coordonatelor unui vector la o schimbare
5.4. MULTIPLEXOARE A 0 A 1 A 2
 5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
5.1. Noţiuni introductive
 ursul 13 aitolul 5. Soluţii 5.1. oţiuni introductive Soluţiile = aestecuri oogene de două sau ai ulte substanţe / coonente, ale căror articule nu se ot seara rin filtrare sau centrifugare. oonente: - Mediul
ursul 13 aitolul 5. Soluţii 5.1. oţiuni introductive Soluţiile = aestecuri oogene de două sau ai ulte substanţe / coonente, ale căror articule nu se ot seara rin filtrare sau centrifugare. oonente: - Mediul
Functii Breviar teoretic 8 ianuarie ianuarie 2011
 Functii Breviar teoretic 8 ianuarie 011 15 ianuarie 011 I Fie I, interval si f : I 1) a) functia f este (strict) crescatoare pe I daca x, y I, x< y ( f( x) < f( y)), f( x) f( y) b) functia f este (strict)
Functii Breviar teoretic 8 ianuarie 011 15 ianuarie 011 I Fie I, interval si f : I 1) a) functia f este (strict) crescatoare pe I daca x, y I, x< y ( f( x) < f( y)), f( x) f( y) b) functia f este (strict)
CONCURSUL DE MATEMATICĂ APLICATĂ ADOLF HAIMOVICI, 2017 ETAPA LOCALĂ, HUNEDOARA Clasa a IX-a profil științe ale naturii, tehnologic, servicii
 Clasa a IX-a 1 x 1 a) Demonstrați inegalitatea 1, x (0, 1) x x b) Demonstrați că, dacă a 1, a,, a n (0, 1) astfel încât a 1 +a + +a n = 1, atunci: a +a 3 + +a n a1 +a 3 + +a n a1 +a + +a n 1 + + + < 1
Clasa a IX-a 1 x 1 a) Demonstrați inegalitatea 1, x (0, 1) x x b) Demonstrați că, dacă a 1, a,, a n (0, 1) astfel încât a 1 +a + +a n = 1, atunci: a +a 3 + +a n a1 +a 3 + +a n a1 +a + +a n 1 + + + < 1
1.3 Baza a unui spaţiu vectorial. Dimensiune
 .3 Baza a unui spaţiu vectorial. Dimensiune Definiţia.3. Se numeşte bază a spaţiului vectorial V o familie de vectori B care îndeplineşte condiţiile de mai jos: a) B este liniar independentă; b) B este
.3 Baza a unui spaţiu vectorial. Dimensiune Definiţia.3. Se numeşte bază a spaţiului vectorial V o familie de vectori B care îndeplineşte condiţiile de mai jos: a) B este liniar independentă; b) B este
IV. CUADRIPOLI SI FILTRE ELECTRICE CAP. 13. CUADRIPOLI ELECTRICI
 V. POL S FLTE ELETE P. 3. POL ELET reviar a) Forma fundamentala a ecuatiilor cuadripolilor si parametrii fundamentali: Prima forma fundamentala: doua forma fundamentala: b) Parametrii fundamentali au urmatoarele
V. POL S FLTE ELETE P. 3. POL ELET reviar a) Forma fundamentala a ecuatiilor cuadripolilor si parametrii fundamentali: Prima forma fundamentala: doua forma fundamentala: b) Parametrii fundamentali au urmatoarele
Transformata Radon. Reconstructia unei imagini bidimensionale cu ajutorul proiectiilor rezultate de-a lungul unor drepte.
 Problema Tranformaa Radon Reconrucia unei imaini bidimenionale cu auorul roieciilor rezulae de-a lunul unor dree. Domeniul de uilizare: Prelucrarea imainilor din domeniul medical Prelucrarea imainilor
Problema Tranformaa Radon Reconrucia unei imaini bidimenionale cu auorul roieciilor rezulae de-a lunul unor dree. Domeniul de uilizare: Prelucrarea imainilor din domeniul medical Prelucrarea imainilor
prin operaţii punctuale
 Lucrarea 3 Îmbunătăţirea imaginilor prin operaţii punctuale BREVIAR TEORETIC Termenul general de îmbunătăţire a imaginilor se referă la o clasă largă de operaţii, ce au ca scop mărirea detectabilităţii
Lucrarea 3 Îmbunătăţirea imaginilor prin operaţii punctuale BREVIAR TEORETIC Termenul general de îmbunătăţire a imaginilor se referă la o clasă largă de operaţii, ce au ca scop mărirea detectabilităţii
Lectia VI Structura de spatiu an E 3. Dreapta si planul ca subspatii ane
 Subspatii ane Lectia VI Structura de spatiu an E 3. Dreapta si planul ca subspatii ane Oana Constantinescu Oana Constantinescu Lectia VI Subspatii ane Table of Contents 1 Structura de spatiu an E 3 2 Subspatii
Subspatii ane Lectia VI Structura de spatiu an E 3. Dreapta si planul ca subspatii ane Oana Constantinescu Oana Constantinescu Lectia VI Subspatii ane Table of Contents 1 Structura de spatiu an E 3 2 Subspatii
Cursul Măsuri reale. D.Rusu, Teoria măsurii şi integrala Lebesgue 15
 MĂSURI RELE Cursul 13 15 Măsuri reale Fie (,, µ) un spaţiu cu măsură completă şi f : R o funcţie -măsurabilă. Cum am văzut în Teorema 11.29, dacă f are integrală pe, atunci funcţia de mulţime ν : R, ν()
MĂSURI RELE Cursul 13 15 Măsuri reale Fie (,, µ) un spaţiu cu măsură completă şi f : R o funcţie -măsurabilă. Cum am văzut în Teorema 11.29, dacă f are integrală pe, atunci funcţia de mulţime ν : R, ν()
CURS MECANICA CONSTRUCŢIILOR
 CURS 10+11 MECANICA CONSTRUCŢIILOR Conf. Dr. Ing. Viorel Ungureanu CINEMATICA SOLIDULUI RIGID In cadrul cinematicii punctului material s-a arătat ca a studia mişcarea unui punct înseamnă a determina la
CURS 10+11 MECANICA CONSTRUCŢIILOR Conf. Dr. Ing. Viorel Ungureanu CINEMATICA SOLIDULUI RIGID In cadrul cinematicii punctului material s-a arătat ca a studia mişcarea unui punct înseamnă a determina la
y y x x 1 y1 Elemente de geometrie analiticã 1. Segmente 1. DistanŃa dintre douã puncte A(x 1,y 1 ), B(x 2,y 2 ): AB = 2. Panta dreptei AB: m AB =
 Elemente de geometrie analiticã. Segmente. DistanŃa dintre douã puncte A(, ), B(, ): AB = ) + ( ) (. Panta dreptei AB: m AB = +. Coordonatele (,) ale mijlocului segmentului AB: =, =. Coordonatele punctului
Elemente de geometrie analiticã. Segmente. DistanŃa dintre douã puncte A(, ), B(, ): AB = ) + ( ) (. Panta dreptei AB: m AB = +. Coordonatele (,) ale mijlocului segmentului AB: =, =. Coordonatele punctului
CONCURSUL INTERJUDEȚEAN DE MATEMATICĂ TRAIAN LALESCU, 1998 Clasa a V-a
 CONCURSUL INTERJUDEȚEAN DE MATEMATICĂ TRAIAN LALESCU, 998 Clasa a V-a. La gara Timișoara se eliberează trei bilete de tren: unul pentru Arad, altul pentru Deva și al treilea pentru Reșița. Cel pentru Deva
CONCURSUL INTERJUDEȚEAN DE MATEMATICĂ TRAIAN LALESCU, 998 Clasa a V-a. La gara Timișoara se eliberează trei bilete de tren: unul pentru Arad, altul pentru Deva și al treilea pentru Reșița. Cel pentru Deva
TRANSFORMATOARE MONOFAZATE DE SIGURANŢĂ ŞI ÎN CARCASĂ
 TRANSFORMATOARE MONOFAZATE DE SIGURANŢĂ ŞI ÎN CARCASĂ Transformatoare de siguranţă Este un transformator destinat să alimenteze un circuit la maximum 50V (asigură siguranţă de funcţionare la tensiune foarte
TRANSFORMATOARE MONOFAZATE DE SIGURANŢĂ ŞI ÎN CARCASĂ Transformatoare de siguranţă Este un transformator destinat să alimenteze un circuit la maximum 50V (asigură siguranţă de funcţionare la tensiune foarte
CONCURSUL DE MATEMATICĂ APLICATĂ ADOLF HAIMOVICI, 2016 ETAPA LOCALĂ, HUNEDOARA Clasa a IX-a profil științe ale naturii, tehnologic, servicii
 ADOLF HAIMOVICI, 206 Clasa a IX-a profil științe ale naturii, tehnologic, servicii. Se consideră predicatul binar p(x, y) : 4x + 3y = 206, x, y N și mulțimea A = {(x, y) N N 4x+3y = 206}. a) Determinați
ADOLF HAIMOVICI, 206 Clasa a IX-a profil științe ale naturii, tehnologic, servicii. Se consideră predicatul binar p(x, y) : 4x + 3y = 206, x, y N și mulțimea A = {(x, y) N N 4x+3y = 206}. a) Determinați
Capitolul 4. Integrale improprii Integrale cu limite de integrare infinite
 Capitolul 4 Integrale improprii 7-8 În cadrul studiului integrabilităţii iemann a unei funcţii s-au evidenţiat douăcondiţii esenţiale:. funcţia :[ ] este definită peintervalînchis şi mărginit (interval
Capitolul 4 Integrale improprii 7-8 În cadrul studiului integrabilităţii iemann a unei funcţii s-au evidenţiat douăcondiţii esenţiale:. funcţia :[ ] este definită peintervalînchis şi mărginit (interval
Cum folosim cazuri particulare în rezolvarea unor probleme
 Cum folosim cazuri particulare în rezolvarea unor probleme GHEORGHE ECKSTEIN 1 Atunci când întâlnim o problemă pe care nu ştim s-o abordăm, adesea este bine să considerăm cazuri particulare ale acesteia.
Cum folosim cazuri particulare în rezolvarea unor probleme GHEORGHE ECKSTEIN 1 Atunci când întâlnim o problemă pe care nu ştim s-o abordăm, adesea este bine să considerăm cazuri particulare ale acesteia.
Semnale 3D. Prelucrarea Semnalelor Video. Concept general:
 Semnale 3D Prelucrarea Semnalelor Video Extensie a teoriei semnalelor și sistemelor 1D la 3 dimensiuni Concept general: Achiziție (de la 3D la 2D, lentile, senzori, multiplexoare) Transmisie (1D) Reproducere
Semnale 3D Prelucrarea Semnalelor Video Extensie a teoriei semnalelor și sistemelor 1D la 3 dimensiuni Concept general: Achiziție (de la 3D la 2D, lentile, senzori, multiplexoare) Transmisie (1D) Reproducere
Seria Balmer. Determinarea constantei lui Rydberg
 Seria Balmer. Determinarea constantei lui Rydberg Obiectivele lucrarii analiza spectrului in vizibil emis de atomii de hidrogen si determinarea lungimii de unda a liniilor serie Balmer; determinarea constantei
Seria Balmer. Determinarea constantei lui Rydberg Obiectivele lucrarii analiza spectrului in vizibil emis de atomii de hidrogen si determinarea lungimii de unda a liniilor serie Balmer; determinarea constantei
Dreapta in plan. = y y 0
 Dreapta in plan 1 Dreapta in plan i) Presupunem ca planul este inzestrat cu un reper ortonormat de dreapta (O, i, j). Fiecarui punct M al planului ii corespunde vectorul OM numit vector de pozitie al punctului
Dreapta in plan 1 Dreapta in plan i) Presupunem ca planul este inzestrat cu un reper ortonormat de dreapta (O, i, j). Fiecarui punct M al planului ii corespunde vectorul OM numit vector de pozitie al punctului
CURS 11: ALGEBRĂ Spaţii liniare euclidiene. Produs scalar real. Spaţiu euclidian. Produs scalar complex. Spaţiu unitar. Noţiunea de normă.
 Sala: 2103 Decembrie 2014 Conf. univ. dr.: Dragoş-Pătru Covei CURS 11: ALGEBRĂ Specializarea: C.E., I.E., S.P.E. Nota: Acest curs nu a fost supus unui proces riguros de recenzare pentru a fi oficial publicat.
Sala: 2103 Decembrie 2014 Conf. univ. dr.: Dragoş-Pătru Covei CURS 11: ALGEBRĂ Specializarea: C.E., I.E., S.P.E. Nota: Acest curs nu a fost supus unui proces riguros de recenzare pentru a fi oficial publicat.
Seminar Algebra. det(a λi 3 ) = 0
 Rezolvari ale unor probleme propuse "Matematica const în a dovedi ceea ce este evident în cel mai puµin evident mod." George Polya P/Seminar Valori si vectori proprii : Solutie: ( ) a) A = Valorile proprii:
Rezolvari ale unor probleme propuse "Matematica const în a dovedi ceea ce este evident în cel mai puµin evident mod." George Polya P/Seminar Valori si vectori proprii : Solutie: ( ) a) A = Valorile proprii:
Capitolul 14. Asamblari prin pene
 Capitolul 14 Asamblari prin pene T.14.1. Momentul de torsiune este transmis de la arbore la butuc prin intermediul unei pene paralele (figura 14.1). De care din cotele indicate depinde tensiunea superficiala
Capitolul 14 Asamblari prin pene T.14.1. Momentul de torsiune este transmis de la arbore la butuc prin intermediul unei pene paralele (figura 14.1). De care din cotele indicate depinde tensiunea superficiala
Examen AG. Student:... Grupa:... ianuarie 2011
 Problema 1. Pentru ce valori ale lui n,m N (n,m 1) graful K n,m este eulerian? Problema 2. Să se construiască o funcţie care să recunoască un graf P 3 -free. La intrare aceasta va primi un graf G = ({1,...,n},E)
Problema 1. Pentru ce valori ale lui n,m N (n,m 1) graful K n,m este eulerian? Problema 2. Să se construiască o funcţie care să recunoască un graf P 3 -free. La intrare aceasta va primi un graf G = ({1,...,n},E)
GEOMETRIE PLANĂ TEOREME IMPORTANTE ARII. bh lh 2. abc. abc. formula înălţimii
 GEOMETRIE PLNĂ TEOREME IMPORTNTE suma unghiurilor unui triunghi este 8º suma unghiurilor unui patrulater este 6º unghiurile de la baza unui triunghi isoscel sunt congruente într-un triunghi isoscel liniile
GEOMETRIE PLNĂ TEOREME IMPORTNTE suma unghiurilor unui triunghi este 8º suma unghiurilor unui patrulater este 6º unghiurile de la baza unui triunghi isoscel sunt congruente într-un triunghi isoscel liniile
* K. toate K. circuitului. portile. Considerând această sumă pentru toate rezistoarele 2. = sl I K I K. toate rez. Pentru o bobină: U * toate I K K 1
 FNCȚ DE ENERGE Fie un n-port care conține numai elemente paive de circuit: rezitoare dipolare, condenatoare dipolare și bobine cuplate. Conform teoremei lui Tellegen n * = * toate toate laturile portile
FNCȚ DE ENERGE Fie un n-port care conține numai elemente paive de circuit: rezitoare dipolare, condenatoare dipolare și bobine cuplate. Conform teoremei lui Tellegen n * = * toate toate laturile portile
III. Reprezentarea informaţiei în sistemele de calcul
 Metode Numerice Curs 3 III. Reprezentarea informaţiei în sistemele de calcul III.1. Reprezentarea internă a numerelor întregi III. 1.1. Reprezentarea internă a numerelor întregi fără semn (pozitive) Reprezentarea
Metode Numerice Curs 3 III. Reprezentarea informaţiei în sistemele de calcul III.1. Reprezentarea internă a numerelor întregi III. 1.1. Reprezentarea internă a numerelor întregi fără semn (pozitive) Reprezentarea
Grafuri planare Colorarea grafurilor. Curs 12. Grafuri planare. Colorarea grafurilor. Polinoame cromatice. 23 decembrie 2016.
 Grafuri planare Polinoame cromatice 23 decembrie 2016 Definiţii şi exemple Grafuri planare Un graf G este planar dacă poate fi desenat în plan astfel încât muchiile să nu se intersecteze decât în nodurile
Grafuri planare Polinoame cromatice 23 decembrie 2016 Definiţii şi exemple Grafuri planare Un graf G este planar dacă poate fi desenat în plan astfel încât muchiile să nu se intersecteze decât în nodurile
Microscopie optica. Masuratori cu microscopul optic
 . Masuratori cu microscopul optic Tehnici de microscopie de transmisie Microscopie de baleiaj utilizand lasere Microscopie confocala Microscopie in camp apropiat Microscopie electronica Microscopie Microscopie
. Masuratori cu microscopul optic Tehnici de microscopie de transmisie Microscopie de baleiaj utilizand lasere Microscopie confocala Microscopie in camp apropiat Microscopie electronica Microscopie Microscopie
