Poglavje 10. Izbira re ima deviznega tečaja Evrope
|
|
|
- Ἀριστείδης Τρικούπη
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Poglavje 10 Izbira re ima deviznega tečaja Evrope
2 Neobstojna trojica (impossible trinity) S fiksnim tečajem je neodvisnost monetarne politike izgubljena. Kaj to pomeni? Na dolgi rok je monetarna politika nevtralna v vsakem primeru, Inflacija torej ni več determinirana od domačih oblasti včasih to celo zaželeno. Neodvisna monetarna politika se lahko obdrži z omejevanjem mobilnosti kapitala.
3 Neobstojna trojica (impossible trinity) Načelo neobstojne trojice: Le dve od spodnjih kategorij sta istočasno obstojni! Fiksen devizni tečaj Fiksen devizni tečaj in avtonomna monetarna politika Fiksen devizni tečaj in mobilnost kapitala Monetarna neodvisnost Mobilnost kapitala in avtonomna monetarna politika Mobilnost kapitala
4 Izbira režima deviznega tečaja Kašen režim deviznega tečaja izbrati? Staro in kontroverzno vprašanje. Ni enoznačnega odgovora. Ni najboljše rešitve, vse vsebujejo prednosti in slabosti, ki se razlikujejo glede na okoliščine, države in obdobje.
5 Izbira režima deviznega tečaja Je devizni tečaj sploh pomemben? Pomemben je le, če ima (nominalni) tečaj vpliv na realno ekonomijo. Torej le na kratki rok: Spremembe v E se odražajo na λ = EP/P*: P in P* so lepljive. Na dolgi rok, pa je λ konstanten in neodvisen od E: P se prilagajajo
6 Izbira režima deviznega tečaja Pomembno je tudi, da kratek rok traja nekaj let. (2-3 leta ali več) Zaradi počasnega spreminjanja cen in plač. Izbira režima deviznega tečaja je torej pomembna na kratek rok, zaradi lepljivosti cen in plač.
7 Izbira režima deviznega tečaja Kaj je na voljo (1) Prosto drseči tečaj (Free floating). Uravnavano drseči tečaj (Managed floating). Ciljni razpon (Target zones). Plezajoča pritrditev (Crawling pegs). Fiksni in prilagodljivi tečaj (Fixed and adjustable).
8 Izbira režima deviznega tečaja Kaj je na voljo (2) Valutni odbor (Currency boards). Dolarizacija/Evroizacija in monetarna unija (Dollarization/euroization and Monetary union).
9 Izbira režima deviznega tečaja Kaj upoštevati pri iskanju režima? Ohranjanje avtonomne monetarne politike: Koristen instrument na kratek rok. Lahko povzroča inflacijo (kvaliteta domačih institucij). Velikost države. Fleksibilen tečaj izolira državo od zunanjih vplivov (vpliv na konkurenčnost). Volatilnost tečaja.
10 Izbira režima deviznega tečaja Stabilnost deviznega tečaja: Fleksibilni tečaj se preveč premika, Fiksni tečaj pa po določenem času postane nevzdržen.
11 Večno vprašanje: fiksen ali fleksibilen tečaj? Razlogi ZA fleksibilen tečaj: Ob lepljivih cenah, fleksibilen tečaj omogoča prilagajanje po ekonomskih šokih. Fleksibilen tečaj ni pod vplivom politike. Ohranitev avtonomne monetarne politike.
12 Večno vprašanje: fiksen ali fleksibilen tečaj? Razlogi ZA fiksen tečaj: Finančni trgi so podvrženi nepopolnim informacijam in neracionalnemu obnašanju akterjev (panika). Fleksibilen tečaj je lahko zelo volatilen, kar ima za posledico veliko negotovost. S fiksiranjem tečaja se skuša disciplinirati monetarno politiko. Ko se pojavijo šoki, se še vedno lahko zamenja pariteto tečaja.
13 Nova rešitev: Dva ekstrema Le prosto drseči tečaj (pure float) ali trdna pritrditev (hard peg) sta zanesljiva: Pri nekaj vmes (soft pegs) vedno lahko prihaja do zlorab s strani države, do preoz. pod- cenjenega tečaja in do špekulativnih napadov, Prosto drseči tečaj politika se z njim sploh ne ukvarja Trdna pritrditev pa je nepovratna (pa je res?)
14 Nova rešitev: Dva ekstrema V skladu s teorijo: soft pegs: monetarna politika se le na pol zaveže k cilju deviznega tečaja, V času prostega pretoka kapitala je to v nasprotju z načelom neobstojne trojice, In obsojeno na propad. V Evropi se je večino držav odločilo za enega od ekstremov, vendar ne drži za vse države sveta.
15 Pregled monetarne zgodovine Evrope Monetarna unija je kontroverzni rezultat dolgega procesa. Pregled zgodovine pripomore k razumevanju. Od uvedbe papirnatega denarja je bila monetarna zgodovina Evrope razburkana. Iz vsake slabe izkušnje se nekaj pomembnega naučimo. Pred uvedbo papirnatega denarja je bila Evropa de facto monetarna unija. Mehanizem pomaga razumeti njeno delovanje danes.
16 Kovinski denar Evropa kot monetarna unija Zlati in srebrni denar, Vsak vladar je koval svoj denar, Devizni tečaj le razmerje med vsebnostjo kovine med različnimi valutami. Torej je bil le en pravi denar: zlato (srebro). Evropa delovala kot monetarna unija
17 Zlati standard in Humov mehanizem Mehanizem opisuje osnove delovanja monetarne unije. Temelji na načelih nevtralnosti denarja na dolgi rok, PPP in na kratkoročnem vplivu denarja na obrestne mere Humov mehanizem: količina denarja se avtomatično prilagodi za dosego uravnotežene plačilne bilance.
18 Zlati standard in Humov mehanizem (tekoči račun) Trgovinska (plačilna) bilanca vpliva na tokove denarja.
19 Zlati standard in Humov mehanizem (tekoči račun) Količina denarja določa P (na dolgi rok), P pa vpliva na trgovinsko bilanco.
20 Zlati standard in Humov mehanizem (finančni račun) Količina denarja vpliva na obrestno mero, obrestna mera pa na tokove denarja.
21 Zlati standard in Humov mehanizem Vračanje v položaj uravnotežene plačilne bilance je samodejno. Prilagajanje preko cen je počasno, preko finančnega trga pa zelo hitro. Zlati standard je bil torej v osnovi stabilen. Ni potrebe po vmešavanju ekonomske politike, saj je količina zlatega denarja določena endogeno.
22 Zlati standard in monetarna unija danes Podobno deluje kot zlati standard. Namesto zlata evro. V države s presežkom pritekajo evri, iz držav s primanjkljajem evri odtekajo. Države ne morejo devalvirati/depreciirati tečaja. Sprijazniti se morajo s padcem (počasnejšo rastjo) cen. Pomembno, da pravila igre držijo (prosti pretok blaga in kapitala).
23 Zlati konvertibilni standard Uveden papirnati denar (19. stoletje). Stabilnost se ohrani le pod tremi pogoji: bankovci zamenljivi za zlato po fiksni ceni (torej le kot substitut za zlato) Popolna pokritost. Centralna banka ima (vsaj) toliko zlata kot je izdala bankovcev. S pritoki/odtoki zlata izdaja/ odvzema papirnati denar. Popolna mobilnost trgovine in kapitala, da je mehanizem prilagoditve mogoč.
24 Obdobje med vojnama: najslabše vseh svetov Ob začetku vojne 1914 zlati standard ukinjen. Po vojni so oblasti imele v mislih vrnitev na zlati standard, vendar: Ni bilo konsenza po kakšnih paritetah vzpostaviti devizne tečaje, Zelo kaotičen začetek s posledicami prve svetovne vojne zelo visoka javnofinančna zadolženost visoka inflacija. In kasneje še gospodarska kriza.
25 Obdobje med vojnama: trije primeri Velika Britanija: predolgo zavračanje devalvacije precenjenega funta: desetletje nizke gospodarske rasti. Francija: devalvacija, podcenjenost franka, dokler ostali ne devalvirajo svojih valut; sledi precenjenost franka. Nemčija: hiperinflacija, devalvacija in dvigovanje ovir prosti trgovini in prostemu pretoku kapitala.
26 Lekcije za Evropo Po razpadu zlatega standarda so bili tečaji prosto drseči. Države so pustile svoje valute depreciirati za izboljšanje konkurenčnosti na račun drugih. To je začelo ovirati trgovino. In spodbujalo protekcionizem. Kar je še poglobilo depresijo.
27 Lekcije za Evropo Zaključki: Drseči tečaji povzročajo neravnovesja in spodbujajo trgovinske ovire in znižujejo prosperiteto. Veliko Evropskih držav je razvilo strah pred drsečim tečajem. Tečaje je treba fiksirati, vendar ne zelo trdno. Določanje paritet deviznih tečajev ne morejo biti prepuščeni vsaki državi po svoje. Vzpostavljen mora biti mednarodni sistem.
28 Povojna ureditev: Bretton Woods Vzpostavitev mednarodnega denarnega sistema. Na zlato vezan le dolar. Tečaji so bili fiksni in prilagodljivi (fixed and adjustable). Ustanovljen MDS (IMF) za nadzor in pomoč državam v težavah. Ovire gibanju kapitala so bile dovoljene, in veliko držav jih je uporabljalo. ZDA ekonomski in politični garantor sistema.
29 Razpad BW sistema in Evropska kača 1971 v ZDA ukinejo konvertibilnost dolarja za zlato fiksni in prilagodljivi tečaji uradno ukinjeni. Evropski devizni tečaji so se spet pričeli oddaljevati.
30 Razpad BW sistema in Evropska kača Evropa se je znašla brez sistema. Zaradi medvojne izkušnje je iskala rešitev: Kača Sporazum o stabiliziranju intra-evropskih tečajev znotraj ozkih mej. Ovire za mobilnost kapitala so se večkrat uporabljale, a niso bile striktne; ni omejitev za nacionalne monetarne politike. Zelo krhek sistem, brez trdnih zavez in brez ukrepov v primeru kriz.
31 Razpad BW sistema in Evropska kača
32 Razpad BW sistema in Evropska kača Ob prvem naftnem šoku so centralne banke reagirale različno. Nekatere države uspejo zadržati inflacijo, druge ne. Sistem ni imel mehanizmov za reagiranje v krizah. Nekatere države so zapustile sistem.
33 Razpad BW sistema in Evropska kača Evropska kača je pokazala, da obstaja determiniranost za fiksiranje intraevropskih deviznih tečajev, brez zunanje reference (zlato, dolar), se morajo evropske valute fiksirati druga na drugo.
34 Evropski monetarni sistem Mehanizem deviznih tečajev (ERM) ERM: medsebojno uravnavani fiksni in prilagodljivi tečaji. Nestabilni začetki: ni formalnih restrikcij za nacionalne monetarne politike, zaradi globalizacije vedno bolj prost pretok kapitala. Devizni tečaji divergirajo. Pogoste menjave paritet. Neformalna zaveza načelu neobstojne trojice : države se zavežejo k zmanjšanju razlik v stopnjah inflacije.
35 Evropski monetarni sistem Bundesbank in DM postaneta center sistema. Valute se vežejo na DM. Le Nemčija ohrani avtonomno monetarno politiko. Vendar preveč neformalen sistem, da bi zdržal krizo. Ob združitvi Nemčije, Bundesbank vodi restriktivno monetarno politiko. Ostale države ne sledijo. ERM skoraj razpade , razpon gibanja tečajev se razširi.
36 K Monetarni uniji Vedno bolj prost pretok kapitala. Potreben bolj trden sistem. Maastricht 1991: rojstvo EU in program za vzpostavitev EMU. 1999: tečaji 11 držav nepovratno zamrznjeni. ESCB s sedežem v Frankfurtu začne delovati. 2002: v obtok pridejo tudi evro kovanci in bankovci. Januar 2009: 16 držav evroobmočja.
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 5. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 21. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 22. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Funkcijske vrste. Matematika 2. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 2. april Gregor Dolinar Matematika 2
 Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Monetarna ekonomija. Mednarodni denarni sistem. Igor Masten. Univerza v Ljubljani - Ekonomska fakulteta
 Monetarna ekonomija Mednarodni denarni sistem Igor Masten Univerza v Ljuljani - Ekonomska fakulteta 2010 igor.masten@ef.uni-lj.si (EF) Monetarna ekonomija 2010 1 / 21 Model mednarodne menjave Model mednarodne
Monetarna ekonomija Mednarodni denarni sistem Igor Masten Univerza v Ljuljani - Ekonomska fakulteta 2010 igor.masten@ef.uni-lj.si (EF) Monetarna ekonomija 2010 1 / 21 Model mednarodne menjave Model mednarodne
Tretja vaja iz matematike 1
 Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Booleova algebra. Izjave in Booleove spremenljivke
 Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
Diferencialna enačba, v kateri nastopata neznana funkcija in njen odvod v prvi potenci
 Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK
 1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
Delovna točka in napajalna vezja bipolarnih tranzistorjev
 KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 14. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK
 SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
Kotne in krožne funkcije
 Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
p 1 ENTROPIJSKI ZAKON
 ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
PONOVITEV SNOVI ZA 4. TEST
 PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 15. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου...
 ΑΠΟΖΗΜΙΩΣΗ ΘΥΜΑΤΩΝ ΕΓΚΛΗΜΑΤΙΚΩΝ ΠΡΑΞΕΩΝ ΣΛΟΒΕΝΙΑ 1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου... 3 1 1. Έντυπα αιτήσεων
ΑΠΟΖΗΜΙΩΣΗ ΘΥΜΑΤΩΝ ΕΓΚΛΗΜΑΤΙΚΩΝ ΠΡΑΞΕΩΝ ΣΛΟΒΕΝΙΑ 1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου... 3 1 1. Έντυπα αιτήσεων
13. Jacobijeva metoda za računanje singularnega razcepa
 13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
Numerično reševanje. diferencialnih enačb II
 Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):
![matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij): matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):](/thumbs/87/96579490.jpg) 4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
*M * Osnovna in višja raven MATEMATIKA NAVODILA ZA OCENJEVANJE. Sobota, 4. junij 2011 SPOMLADANSKI IZPITNI ROK. Državni izpitni center
 Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
NEPARAMETRIČNI TESTI. pregledovanje tabel hi-kvadrat test. as. dr. Nino RODE
 NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
8. Diskretni LTI sistemi
 8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
1. Definicijsko območje, zaloga vrednosti. 2. Naraščanje in padanje, ekstremi. 3. Ukrivljenost. 4. Trend na robu definicijskega območja
 ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 10. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
IZPIT IZ ANALIZE II Maribor,
 Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
Monetarna ekonomija. Cenovna presenečenja. Igor Masten. Univerza v Ljubljani - Ekonomska fakulteta
 Monetarna ekonomija Cenovna presenečenja Igor Masten Univerza v Ljubljani - Ekonomska fakulteta 2013 igor.masten@ef.uni-lj.si (EF) Monetarna ekonomija 2013 1 / 22 Stilizirana empirična dejstva Kaj pravijo
Monetarna ekonomija Cenovna presenečenja Igor Masten Univerza v Ljubljani - Ekonomska fakulteta 2013 igor.masten@ef.uni-lj.si (EF) Monetarna ekonomija 2013 1 / 22 Stilizirana empirična dejstva Kaj pravijo
Transformator. Delovanje transformatorja I. Delovanje transformatorja II
 Transformator Transformator je naprava, ki v osnovi pretvarja napetost iz enega nivoja v drugega. Poznamo vrsto različnih izvedb transformatorjev, glede na njihovo specifičnost uporabe:. Energetski transformator.
Transformator Transformator je naprava, ki v osnovi pretvarja napetost iz enega nivoja v drugega. Poznamo vrsto različnih izvedb transformatorjev, glede na njihovo specifičnost uporabe:. Energetski transformator.
Osnove elektrotehnike uvod
 Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
Devizno tržište. Mart 2010 Ekonomski fakultet, Beograd Irena Janković
 Devizno tržište Devizni urs i devizno tržište Devizni urs - cena jedne valute izražena u drugoj valuti Promene deviznog ursa utiču na vrednost ative i pasive oje su izražene u stranoj valuti Devizni urs
Devizno tržište Devizni urs i devizno tržište Devizni urs - cena jedne valute izražena u drugoj valuti Promene deviznog ursa utiču na vrednost ative i pasive oje su izražene u stranoj valuti Devizni urs
CM707. GR Οδηγός χρήσης... 2-7. SLO Uporabniški priročnik... 8-13. CR Korisnički priručnik... 14-19. TR Kullanım Kılavuzu... 20-25
 1 2 3 4 5 6 7 OFFMANAUTO CM707 GR Οδηγός χρήσης... 2-7 SLO Uporabniški priročnik... 8-13 CR Korisnički priručnik... 14-19 TR Kullanım Kılavuzu... 20-25 ENG User Guide... 26-31 GR CM707 ΟΔΗΓΟΣ ΧΡΗΣΗΣ Περιγραφή
1 2 3 4 5 6 7 OFFMANAUTO CM707 GR Οδηγός χρήσης... 2-7 SLO Uporabniški priročnik... 8-13 CR Korisnički priručnik... 14-19 TR Kullanım Kılavuzu... 20-25 ENG User Guide... 26-31 GR CM707 ΟΔΗΓΟΣ ΧΡΗΣΗΣ Περιγραφή
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * NAVODILA ZA OCENJEVANJE. Sreda, 3. junij 2015 SPLOŠNA MATURA
 Državni izpitni center *M15143113* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sreda, 3. junij 2015 SPLOŠNA MATURA RIC 2015 M151-431-1-3 2 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor Naloga Odgovor
Državni izpitni center *M15143113* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sreda, 3. junij 2015 SPLOŠNA MATURA RIC 2015 M151-431-1-3 2 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor Naloga Odgovor
Podobnost matrik. Matematika II (FKKT Kemijsko inženirstvo) Diagonalizacija matrik
 Podobnost matrik Matematika II (FKKT Kemijsko inženirstvo) Matjaž Željko FKKT Kemijsko inženirstvo 14 teden (Zadnja sprememba: 23 maj 213) Matrika A R n n je podobna matriki B R n n, če obstaja obrnljiva
Podobnost matrik Matematika II (FKKT Kemijsko inženirstvo) Matjaž Željko FKKT Kemijsko inženirstvo 14 teden (Zadnja sprememba: 23 maj 213) Matrika A R n n je podobna matriki B R n n, če obstaja obrnljiva
MATEMATIČNI IZRAZI V MAFIRA WIKIJU
 I FAKULTETA ZA MATEMATIKO IN FIZIKO Jadranska cesta 19 1000 Ljubljan Ljubljana, 25. marec 2011 MATEMATIČNI IZRAZI V MAFIRA WIKIJU KOMUNICIRANJE V MATEMATIKI Darja Celcer II KAZALO: 1 VSTAVLJANJE MATEMATIČNIH
I FAKULTETA ZA MATEMATIKO IN FIZIKO Jadranska cesta 19 1000 Ljubljan Ljubljana, 25. marec 2011 MATEMATIČNI IZRAZI V MAFIRA WIKIJU KOMUNICIRANJE V MATEMATIKI Darja Celcer II KAZALO: 1 VSTAVLJANJE MATEMATIČNIH
Kontrolne karte uporabljamo za sprotno spremljanje kakovosti izdelka, ki ga izdelujemo v proizvodnem procesu.
 Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
ZADACI 18. Blanchard. 3. Pretpostavite slijedeće IS-LM jednadžbe: M P. E pri čemu je E
 1 ZDCI 18 Blanchard 1. Nominalni devizni tečaj, realni devizni tečaj, strana i domaća inflacija Koristeći definiciju realnog deviznog tečaja (i matematički dodatak u knjizi) možete, pokazati da vrijedi
1 ZDCI 18 Blanchard 1. Nominalni devizni tečaj, realni devizni tečaj, strana i domaća inflacija Koristeći definiciju realnog deviznog tečaja (i matematički dodatak u knjizi) možete, pokazati da vrijedi
1. Trikotniki hitrosti
 . Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
. Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
Iterativno reševanje sistemov linearnih enačb. Numerične metode, sistemi linearnih enačb. Numerične metode FE, 2. december 2013
 Numerične metode, sistemi linearnih enačb B. Jurčič Zlobec Numerične metode FE, 2. december 2013 1 Vsebina 1 z n neznankami. a i1 x 1 + a i2 x 2 + + a in = b i i = 1,..., n V matrični obliki zapišemo:
Numerične metode, sistemi linearnih enačb B. Jurčič Zlobec Numerične metode FE, 2. december 2013 1 Vsebina 1 z n neznankami. a i1 x 1 + a i2 x 2 + + a in = b i i = 1,..., n V matrični obliki zapišemo:
Matematika 1. Gregor Dolinar. 2. januar Fakulteta za elektrotehniko Univerza v Ljubljani. Gregor Dolinar Matematika 1
 Mtemtik 1 Gregor Dolinr Fkultet z elektrotehniko Univerz v Ljubljni 2. jnur 2014 Gregor Dolinr Mtemtik 1 Izrek (Izrek o povprečni vrednosti) Nj bo m ntnčn spodnj mej in M ntnčn zgornj mej integrbilne funkcije
Mtemtik 1 Gregor Dolinr Fkultet z elektrotehniko Univerz v Ljubljni 2. jnur 2014 Gregor Dolinr Mtemtik 1 Izrek (Izrek o povprečni vrednosti) Nj bo m ntnčn spodnj mej in M ntnčn zgornj mej integrbilne funkcije
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 12. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
Integralni račun. Nedoločeni integral in integracijske metrode. 1. Izračunaj naslednje nedoločene integrale: (a) dx. (b) x 3 +3+x 2 dx, (c) (d)
 Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba.
 1. Osnovni pojmi Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba. Primer 1.1: Diferencialne enačbe so izrazi: y
1. Osnovni pojmi Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba. Primer 1.1: Diferencialne enačbe so izrazi: y
Poglavje 7. Poglavje 7. Poglavje 7. Regulacijski sistemi. Regulacijski sistemi. Slika 7. 1: Normirana blokovna shema regulacije EM
 Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
PROCESIRANJE SIGNALOV
 Rešive pisega izpia PROCESIRANJE SIGNALOV Daum: 7... aloga Kolikša je ampliuda reje harmoske kompoee arisaega periodičega sigala? f() - -3 - - 3 Rešiev: Časova fukcija a iervalu ( /,/) je lieara fukcija:
Rešive pisega izpia PROCESIRANJE SIGNALOV Daum: 7... aloga Kolikša je ampliuda reje harmoske kompoee arisaega periodičega sigala? f() - -3 - - 3 Rešiev: Časova fukcija a iervalu ( /,/) je lieara fukcija:
Kvantni delec na potencialnem skoku
 Kvantni delec na potencialnem skoku Delec, ki se giblje premo enakomerno, pride na mejo, kjer potencial naraste s potenciala 0 na potencial. Takšno potencialno funkcijo zapišemo kot 0, 0 0,0. Slika 1:
Kvantni delec na potencialnem skoku Delec, ki se giblje premo enakomerno, pride na mejo, kjer potencial naraste s potenciala 0 na potencial. Takšno potencialno funkcijo zapišemo kot 0, 0 0,0. Slika 1:
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
Splošno o interpolaciji
 Splošno o interpolaciji J.Kozak Numerične metode II (FM) 2011-2012 1 / 18 O funkciji f poznamo ali hočemo uporabiti le posamezne podatke, na primer vrednosti r i = f (x i ) v danih točkah x i Izberemo
Splošno o interpolaciji J.Kozak Numerične metode II (FM) 2011-2012 1 / 18 O funkciji f poznamo ali hočemo uporabiti le posamezne podatke, na primer vrednosti r i = f (x i ) v danih točkah x i Izberemo
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
Logatherm WPL 14 AR T A ++ A + A B C D E F G A B C D E F G. kw kw /2013
 WP 14 R T d 9 10 11 53 d 2015 811/2013 WP 14 R T 2015 811/2013 WP 14 R T Naslednji podatki o izdelku izpolnjujejo zahteve uredb U 811/2013, 812/2013, 813/2013 in 814/2013 o dopolnitvi smernice 2010/30/U.
WP 14 R T d 9 10 11 53 d 2015 811/2013 WP 14 R T 2015 811/2013 WP 14 R T Naslednji podatki o izdelku izpolnjujejo zahteve uredb U 811/2013, 812/2013, 813/2013 in 814/2013 o dopolnitvi smernice 2010/30/U.
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
Izpeljava Jensenove in Hölderjeve neenakosti ter neenakosti Minkowskega
 Izeljava Jensenove in Hölderjeve neenakosti ter neenakosti Minkowskega 1. Najosnovnejše o konveksnih funkcijah Definicija. Naj bo X vektorski rostor in D X konveksna množica. Funkcija ϕ: D R je konveksna,
Izeljava Jensenove in Hölderjeve neenakosti ter neenakosti Minkowskega 1. Najosnovnejše o konveksnih funkcijah Definicija. Naj bo X vektorski rostor in D X konveksna množica. Funkcija ϕ: D R je konveksna,
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
Αναλυτικά περιεχόμενα
 Αναλυτικά περιεχόμενα Μέρος Α : Βασικές έννοιες Το χάος των χρηματοοικονομικών εξελίξεων 3 1.1 Εισαγωγή 3 1.2 Η κρίση που άλλαξε τον κόσμο 5 1.3 Το χάος των χρηματοοικονομικών εξελίξεων 14 Μεγάλος αριθμός
Αναλυτικά περιεχόμενα Μέρος Α : Βασικές έννοιες Το χάος των χρηματοοικονομικών εξελίξεων 3 1.1 Εισαγωγή 3 1.2 Η κρίση που άλλαξε τον κόσμο 5 1.3 Το χάος των χρηματοοικονομικών εξελίξεων 14 Μεγάλος αριθμός
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
SEMINAR - 4. LETNIK. Veliki pok. Avtor: Daša Rozmus. Mentor: dr. Anže Slosar in prof. dr. Tomaž Zwitter. Ljubljana, Marec 2011
 SEMINAR - 4. LETNIK Veliki pok Avtor: Daša Rozmus Mentor: dr. Anže Slosar in prof. dr. Tomaž Zwitter Ljubljana, Marec 2011 Povzetek Že stoletja pred našim štetjem so se ljudje spraševali kaj nas obdaja,
SEMINAR - 4. LETNIK Veliki pok Avtor: Daša Rozmus Mentor: dr. Anže Slosar in prof. dr. Tomaž Zwitter Ljubljana, Marec 2011 Povzetek Že stoletja pred našim štetjem so se ljudje spraševali kaj nas obdaja,
ΠΡΙΤΣΙΝΑΔΟΡΟΣ ΛΑΔΙΟΥ ΑΕΡΟΣ ΓΙΑ ΠΡΙΤΣΙΝΙΑ M4/M12 ΟΔΗΓΙΕΣ ΧΡΗΣΗΣ - ΑΝΤΑΛΛΑΚΤΙΚΑ
 GR ΠΡΙΤΣΙΝΑΔΟΡΟΣ ΛΑΔΙΟΥ ΑΕΡΟΣ ΓΙΑ ΠΡΙΤΣΙΝΙΑ M4/M12 ΟΔΗΓΙΕΣ ΧΡΗΣΗΣ - ΑΝΤΑΛΛΑΚΤΙΚΑ H OLJLAJNYOMÁSÚ SZEGECSELŐ M4/M12 SZEGECSEKHEZ HASZNÁLATI UTASÍTÁS - ALKATRÉSZEK SLO OLJNO-PNEVMATSKI KOVIČAR ZA ZAKOVICE
GR ΠΡΙΤΣΙΝΑΔΟΡΟΣ ΛΑΔΙΟΥ ΑΕΡΟΣ ΓΙΑ ΠΡΙΤΣΙΝΙΑ M4/M12 ΟΔΗΓΙΕΣ ΧΡΗΣΗΣ - ΑΝΤΑΛΛΑΚΤΙΚΑ H OLJLAJNYOMÁSÚ SZEGECSELŐ M4/M12 SZEGECSEKHEZ HASZNÁLATI UTASÍTÁS - ALKATRÉSZEK SLO OLJNO-PNEVMATSKI KOVIČAR ZA ZAKOVICE
ZLATO KOT SESTAVNI DEL PREMOŽENJA
 UNIVERZA V LJUBLJANI EKONOMSKA FAKULTETA MAGISTRSKO DELO ZLATO KOT SESTAVNI DEL PREMOŽENJA Ljubljana, februar 2015 BARBARA BREG IZJAVA O AVTORSTVU Spodaj podpisana Barbara Breg, študentka Ekonomske fakultete
UNIVERZA V LJUBLJANI EKONOMSKA FAKULTETA MAGISTRSKO DELO ZLATO KOT SESTAVNI DEL PREMOŽENJA Ljubljana, februar 2015 BARBARA BREG IZJAVA O AVTORSTVU Spodaj podpisana Barbara Breg, študentka Ekonomske fakultete
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri
 Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
BANK OF SLOVENIA Slovenska Ljubljana Slovenia Tel: Fax: Telex: BS LJB SI
 BANK OF SLOVENIA Slovenska 35 1505 Ljubljana Slovenia Tel: +386 1 47 19 325 Fax: +386 1 47 19 727 Telex: 31214 BS LJB SI E-mail: bsl@bsi.si WWW: http://www.bsi.si SWIFT: BS LJ SI 2X Variabilnost deviznega
BANK OF SLOVENIA Slovenska 35 1505 Ljubljana Slovenia Tel: +386 1 47 19 325 Fax: +386 1 47 19 727 Telex: 31214 BS LJB SI E-mail: bsl@bsi.si WWW: http://www.bsi.si SWIFT: BS LJ SI 2X Variabilnost deviznega
Zaporedna in vzporedna feroresonanca
 Visokonapetostna tehnika Zaporedna in vzporedna feroresonanca delovanje regulacijskega stikala T3 174 kv Vaja 9 1 Osnovni pogoji za nastanek feroresonance L C U U L () U C () U L = U L () U C = ωc V vezju
Visokonapetostna tehnika Zaporedna in vzporedna feroresonanca delovanje regulacijskega stikala T3 174 kv Vaja 9 1 Osnovni pogoji za nastanek feroresonance L C U U L () U C () U L = U L () U C = ωc V vezju
Konvencijo Št. prej. dok.: CONV 820/1/03 REV 1, CONV 847/03 CONV 848/03 Zadeva: Osnutek Pogodbe o Ustavi za Evropo
 EVROPSKA KONVENCIJA Sekretariat Bruselj, 18. julija 2003 NAOVNA OPOMBA Od: Sekretariata Za: Konvencijo Št. prej. dok.: CONV 820/1/03 REV 1, CONV 847/03 CONV 848/03 Zadeva: Osnutek Pogodbe o Ustavi za Evropo
EVROPSKA KONVENCIJA Sekretariat Bruselj, 18. julija 2003 NAOVNA OPOMBA Od: Sekretariata Za: Konvencijo Št. prej. dok.: CONV 820/1/03 REV 1, CONV 847/03 CONV 848/03 Zadeva: Osnutek Pogodbe o Ustavi za Evropo
STANDARD1 EN EN EN
 PRILOGA RADIJSKE 9,000-20,05 khz naprave kratkega dosega: induktivne aplikacije 315 600 khz naprave kratkega dosega: aktivni medicinski vsadki ultra nizkih moči 4516 khz naprave kratkega dosega: železniške
PRILOGA RADIJSKE 9,000-20,05 khz naprave kratkega dosega: induktivne aplikacije 315 600 khz naprave kratkega dosega: aktivni medicinski vsadki ultra nizkih moči 4516 khz naprave kratkega dosega: železniške
Effect of Fibre Fineness on Colour and Reflectance Value of Dyed Filament Polyester Fabrics after Abrasion Process Izvirni znanstveni članek
 Učinek finosti filamentov na barvne vrednosti in odbojnost svetlobe 8 Učinek finosti filamentov na barvne vrednosti in odbojnost svetlobe barvanih poliestrskih filamentnih tkanin po drgnjenju July November
Učinek finosti filamentov na barvne vrednosti in odbojnost svetlobe 8 Učinek finosti filamentov na barvne vrednosti in odbojnost svetlobe barvanih poliestrskih filamentnih tkanin po drgnjenju July November
Gimnazija Krˇsko. vektorji - naloge
 Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
1. TVORBA ŠIBKEGA (SIGMATNEGA) AORISTA: Največ grških glagolov ima tako imenovani šibki (sigmatni) aorist. Osnova se tvori s. γραψ
 TVORBA AORISTA: Grški aorist (dovršnik) izraža dovršno dejanje; v indikativu izraža poleg dovršnosti tudi preteklost. Za razliko od prezenta ima aorist posebne aktivne, medialne in pasivne oblike. Pri
TVORBA AORISTA: Grški aorist (dovršnik) izraža dovršno dejanje; v indikativu izraža poleg dovršnosti tudi preteklost. Za razliko od prezenta ima aorist posebne aktivne, medialne in pasivne oblike. Pri
Mesečni pregled makroekonomskih podatkov
 Mesečni pregled makroekonomskih podatkov november 2016 NLB d.d. Jaka Erpič Samostojni analitik za finančne trge 01 476 91 70 jaka.erpic@nlb.si EMU BDP (YoY) Inflacija (YoY) Industrijska proizvodnja (YoY)
Mesečni pregled makroekonomskih podatkov november 2016 NLB d.d. Jaka Erpič Samostojni analitik za finančne trge 01 476 91 70 jaka.erpic@nlb.si EMU BDP (YoY) Inflacija (YoY) Industrijska proizvodnja (YoY)
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE)
 (Enegane) List: PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE) Na mjestima gdje se istovremeno troši električna i toplinska energija, ekonomičan način opskrbe energijom
(Enegane) List: PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE) Na mjestima gdje se istovremeno troši električna i toplinska energija, ekonomičan način opskrbe energijom
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
Kotni funkciji sinus in kosinus
 Kotni funkciji sinus in kosinus Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z oznako cos x, DEFINICIJA V PRAVOKOTNEM TRIKOTNIKU: Kotna funkcija sinus je definirana kot razmerje
Kotni funkciji sinus in kosinus Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z oznako cos x, DEFINICIJA V PRAVOKOTNEM TRIKOTNIKU: Kotna funkcija sinus je definirana kot razmerje
!"#ά%&'( 21 To )*+,-&./ό 1(2'32&4'/ό 5ύ3472& /&' 4( )*+ώ
 L'ώ+;(? I%(;(3/(ύ#7?, =->?1ή7 @-(+1+,-(ή!"#ά%&'( 21 To )*+,-&./ό 1(2'32&4'/ό 5ύ3472& /&' 4( )*+ώ 9( )*+,-&./ό 1(2'32&4'/ό 5ύ3472& ()15) :72'(*+;ή=7/" 2"4ά 47> /&4ά++"*37 4(* 3*34ή2&4(? 34&="+ώ> '3(4'2'ώ>
L'ώ+;(? I%(;(3/(ύ#7?, =->?1ή7 @-(+1+,-(ή!"#ά%&'( 21 To )*+,-&./ό 1(2'32&4'/ό 5ύ3472& /&' 4( )*+ώ 9( )*+,-&./ό 1(2'32&4'/ό 5ύ3472& ()15) :72'(*+;ή=7/" 2"4ά 47> /&4ά++"*37 4(* 3*34ή2&4(? 34&="+ώ> '3(4'2'ώ>
Statistična analiza. doc. dr. Mitja Kos, mag. farm. Katedra za socialno farmacijo Univerza v Ljubljani- Fakulteta za farmacijo
 Statistična analiza opisnih spremenljivk doc. dr. Mitja Kos, mag. arm. Katedra za socialno armacijo Univerza v Ljubljani- Fakulteta za armacijo Statistični znaki Proučevane spremenljivke: statistični znaki
Statistična analiza opisnih spremenljivk doc. dr. Mitja Kos, mag. arm. Katedra za socialno armacijo Univerza v Ljubljani- Fakulteta za armacijo Statistični znaki Proučevane spremenljivke: statistični znaki
POROČILO 3.VAJA DOLOČANJE REZULTANTE SIL
 POROČILO 3.VAJA DOLOČANJE REZULTANTE SIL Izdba aje: Ljubjana, 11. 1. 007, 10.00 Jan OMAHNE, 1.M Namen: 1.Preeri paraeogramsko praio za doočanje rezutante nezporedni si s skupnim prijemaiščem (grafično)..dooči
POROČILO 3.VAJA DOLOČANJE REZULTANTE SIL Izdba aje: Ljubjana, 11. 1. 007, 10.00 Jan OMAHNE, 1.M Namen: 1.Preeri paraeogramsko praio za doočanje rezutante nezporedni si s skupnim prijemaiščem (grafično)..dooči
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
ARHITEKTURA DETAJL 1, 1:10
 0.15 0.25 3.56 0.02 0.10 0.12 0.10 SESTV S2 polimer-bitumenska,dvoslojna(po),... 1.0 cm po zahtevah SIST DIN 52133 in nadstandardno, (glej opis v tehn.poročilu), npr.: PHOENIX STR/Super 5 M * GEMINI P
0.15 0.25 3.56 0.02 0.10 0.12 0.10 SESTV S2 polimer-bitumenska,dvoslojna(po),... 1.0 cm po zahtevah SIST DIN 52133 in nadstandardno, (glej opis v tehn.poročilu), npr.: PHOENIX STR/Super 5 M * GEMINI P
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
SISTEMI NELINEARNIH JEDNAČINA
 SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
NAPOVEDI MAKROEKONOMSKIH GIBANJ V SLOVENIJI
 BANKA SLOVENIJE EVROSISTEM NAPOVEDI MAKROEKONOMSKIH GIBANJ V SLOVENIJI DECEMBER 17 Naslov: Izdajatelj: Napovedi makroekonomskih gibanj v Sloveniji Številka: december 17 BANKA SLOVENIJE Slovenska 35 155
BANKA SLOVENIJE EVROSISTEM NAPOVEDI MAKROEKONOMSKIH GIBANJ V SLOVENIJI DECEMBER 17 Naslov: Izdajatelj: Napovedi makroekonomskih gibanj v Sloveniji Številka: december 17 BANKA SLOVENIJE Slovenska 35 155
МЕХАНИКА НА ФЛУИДИ (AFI, TI, EE)
 Zada~i za program 2 po predmetot МЕХАНИКА НА ФЛУИДИ (AFI, TI, EE) Предметен наставник: Проф. д-р Методија Мирчевски Асистент: Виктор Илиев (rok za predavawe na programot - 07. i 08. maj 2010) (во термини
Zada~i za program 2 po predmetot МЕХАНИКА НА ФЛУИДИ (AFI, TI, EE) Предметен наставник: Проф. д-р Методија Мирчевски Асистент: Виктор Илиев (rok za predavawe na programot - 07. i 08. maj 2010) (во термини
Na pregledni skici napišite/označite ustrezne točke in paraboli. A) 12 B) 8 C) 4 D) 4 E) 8 F) 12
 Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
VEKTORJI. Operacije z vektorji
 VEKTORJI Vektorji so matematični objekti, s katerimi opisujemo določene fizikalne količine. V tisku jih označujemo s krepko natisnjenimi črkami (npr. a), pri pisanju pa s puščico ( a). Fizikalne količine,
VEKTORJI Vektorji so matematični objekti, s katerimi opisujemo določene fizikalne količine. V tisku jih označujemo s krepko natisnjenimi črkami (npr. a), pri pisanju pa s puščico ( a). Fizikalne količine,
Mesečni pregled makroekonomskih podatkov
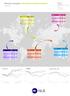 Mesečni pregled makroekonomskih podatkov marec 2017 NLB d.d. Jaka Erpič Samostojni analitik za finančne trge 01 476 91 70 jaka.erpic@nlb.si EMU BDP (YoY) Inflacija (YoY) Industrijska proizvodnja (YoY)
Mesečni pregled makroekonomskih podatkov marec 2017 NLB d.d. Jaka Erpič Samostojni analitik za finančne trge 01 476 91 70 jaka.erpic@nlb.si EMU BDP (YoY) Inflacija (YoY) Industrijska proizvodnja (YoY)
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
1 Fibonaccijeva stevila
 1 Fibonaccijeva stevila Fibonaccijevo število F n, kjer je n N, lahko definiramo kot število načinov zapisa števila n kot vsoto sumandov, enakih 1 ali Na primer, število 4 lahko zapišemo v obliki naslednjih
1 Fibonaccijeva stevila Fibonaccijevo število F n, kjer je n N, lahko definiramo kot število načinov zapisa števila n kot vsoto sumandov, enakih 1 ali Na primer, število 4 lahko zapišemo v obliki naslednjih
Izdala: BANKA SLOVENIJE Slovenska Ljubljana Tel.: Fax.: This publication is also available in English.
 SEPTEMBER 1 Izdala: BANKA SLOVENIJE Slovenska 3 1 Ljubljana Tel.: 1 7 19 Fax.: 1 1 1 This publication is also available in English. ISSN 3-99 MAKROEKONOMSKA GIBANJA IN PROJEKCIJE, september 1 Pregled vsebine
SEPTEMBER 1 Izdala: BANKA SLOVENIJE Slovenska 3 1 Ljubljana Tel.: 1 7 19 Fax.: 1 1 1 This publication is also available in English. ISSN 3-99 MAKROEKONOMSKA GIBANJA IN PROJEKCIJE, september 1 Pregled vsebine
Vaje: Električni tokovi
 Barbara Rovšek, Bojan Golli, Ana Gostinčar Blagotinšek Vaje: Električni tokovi 1 Merjenje toka in napetosti Naloga: Izmerite tok, ki teče skozi žarnico, ter napetost na žarnici Za izvedbo vaje potrebujete
Barbara Rovšek, Bojan Golli, Ana Gostinčar Blagotinšek Vaje: Električni tokovi 1 Merjenje toka in napetosti Naloga: Izmerite tok, ki teče skozi žarnico, ter napetost na žarnici Za izvedbo vaje potrebujete
DISKRETNA FOURIERJEVA TRANSFORMACIJA
 29.03.2004 Definicija DFT Outline DFT je linearna transformacija nekega vektorskega prostora dimenzije n nad obsegom K, ki ga označujemo z V K, pri čemer ima slednji lastnost, da vsebuje nek poseben element,
29.03.2004 Definicija DFT Outline DFT je linearna transformacija nekega vektorskega prostora dimenzije n nad obsegom K, ki ga označujemo z V K, pri čemer ima slednji lastnost, da vsebuje nek poseben element,
Obrada signala
 Obrada signala 1 18.1.17. Greška kvantizacije Pretpostavka je da greška kvantizacije ima uniformnu raspodelu 7 6 5 4 -X m p x 1,, za x druge vrednosti x 3 x X m 1 X m = 3 x Greška kvantizacije x x x p
Obrada signala 1 18.1.17. Greška kvantizacije Pretpostavka je da greška kvantizacije ima uniformnu raspodelu 7 6 5 4 -X m p x 1,, za x druge vrednosti x 3 x X m 1 X m = 3 x Greška kvantizacije x x x p
S t r a n a 1. 1.Povezati jonsku jačinu rastvora: a) MgCl 2 b) Al 2 (SO 4 ) 3 sa njihovim molalitetima, m. za so tipa: M p X q. pa je jonska jačina:
 S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
Postavitev hipotez NUJNO! Milena Kova. 10. januar 2013
 Postavitev hipotez NUJNO! Milena Kova 10. januar 2013 Osnove biometrije 2012/13 1 Postavitev in preizku²anje hipotez Hipoteze zastavimo najprej ob na rtovanju preizkusa Ob obdelavi jih morda malo popravimo
Postavitev hipotez NUJNO! Milena Kova 10. januar 2013 Osnove biometrije 2012/13 1 Postavitev in preizku²anje hipotez Hipoteze zastavimo najprej ob na rtovanju preizkusa Ob obdelavi jih morda malo popravimo
www.absolualarme.com met la disposition du public, via www.docalarme.com, de la documentation technique dont les rιfιrences, marques et logos, sont
 w. ww lua so ab me lar m.co t me la sit po dis ion du c, bli pu via lar ca do w. ww me.co m, de la ion nta t do cu me on t ed hn iqu tec les en ce s, rι fιr ma rq ue se t lo go s, so nt la pr op riι tι
w. ww lua so ab me lar m.co t me la sit po dis ion du c, bli pu via lar ca do w. ww me.co m, de la ion nta t do cu me on t ed hn iqu tec les en ce s, rι fιr ma rq ue se t lo go s, so nt la pr op riι tι
INTELIGENTNO UPRAVLJANJE
 INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
DEVIZNO TRŽIŠTE I DEVIZNI TEČAJ
 DEVIZNO TRŽIŠTE I DEVIZNI TEČAJ 1 DEVIZNO TRŽIŠTE U međunarodnoj razmjeni transakcije se obračunavaju i plaćaju u različitim valutama Svako potraživanje u stranoj valuti naziva se devizama Trgovanje stranim
DEVIZNO TRŽIŠTE I DEVIZNI TEČAJ 1 DEVIZNO TRŽIŠTE U međunarodnoj razmjeni transakcije se obračunavaju i plaćaju u različitim valutama Svako potraživanje u stranoj valuti naziva se devizama Trgovanje stranim
