2 M Prazna stran
|
|
|
- Λαύρα Μπότσαρης
- 7 χρόνια πριν
- Προβολές:
Transcript
1
2 2 M Prazna stran
3 3 M IZPITNA POLA Naloga Odgovor Naloga Odgovor Naloga Odgovor Naloga Odgovor C E 2 C 3 C 2 E 2 C 22 B 32 E 3 B 3 C 23 D 33 C 4 D 4 C 24 B 34 E 5 B 5 B 25 C 35 D 6 D 6 C 26 C 36 E 7 A 7 B 27 E 37 A 8 C 8 B 28 A 38 C 9 A 9 A 29 B 39 D 0 E 20 B 30 B 40 A Za vsak pravilen odgovor točka. Skupaj 40 točk
4 4 M IZPITNA POLA 2. naloga: Proizvodni dejavniki. Proizvodnja je materialno preoblikovanje proizvodnih dejavnikov v produkte. Preoblikovanje inputov v outpute. Za smiselno opredelitev točka..2 3 Primer proizvodnega dejavnika v Proizvodni dejavnik proizvodnji pohištva delo npr. delavci za tekočim trakom, vzdrževalci narava (zemlja) npr. les, lesne plošče, električna energija kapital npr. stroji, roboti, naprave, zgradbe Za vsak pravilen proizvodni dejavnik s primerom točka. Za pravilno naštete le proizvodne dejavnike točka. Za pravilno naštete le primere točka..3 Delo je zavestna, premišljena uporaba človekovih umskih in fizičnih sposobnosti za proizvodnjo bogastva v obliki novih proizvodov in storitev. Delo je premišljena uporaba človekovih sposobnosti..4 Produktivnost dela je razmerje med ustvarjenim proizvodom in količino dela, ki smo ga vložili v proizvodnjo..5 celotni prihodki produktivnost dela število delavcev EUR na delavca V podjetju Pohištvo, d. o. o., je v letu 20 zaposlen delavec v povprečju ustvaril EUR celotnega prihodka.
5 5 M dve od: povečanje delavčevih spretnosti: usposabljanje delavcev v lakirnici tehnična uporabnost izumov: novi proizvodni procesi, novi materiali, novi proizvodi v proizvodnji pohištva boljša družbena kombinacija proizvodnega procesa: boljše usklajevanje vseh sodelujočih podjetij v proizvodni verigi obseg in učinkovitost proizvodnih sredstev: boljša tehnična opremljenost dela v proizvodnji pohištva (nova strojna linija) motivacija: višja plača, stimulacije, dodatki Kandidat lahko navaja tudi druge smiselne ukrepe. En smiselno utemeljen ukrep točka.
6 6 M naloga: Tržno ravnotežje 2. 2 število kupcev in prodajalcev stopnja razlikovanja blaga mobilnost proizvodnih dejavnikov racionalnost ravnanja tržnih osebkov Za 4 navedene dejavnike 2 točki, za tri ali dva navedena dejavnika točka. 2.2 So vse tržne sile, ki po prodajalcih vplivajo na ravnotežno ceno in količino na trgu. 2.3 tri od: proizvodni stroški tehnologija cena proizvoda cene drugih proizvodov pričakovana cena število ponudnikov vremenske razmere zaloge likvidna sredstva 2.4 Za pravilno vrisano in označeno krivuljo ponudbe točka.
7 7 M povpraševanje,.800 Za vsako pravilno navedbo točka. ponudba,.900 Za pravilno vrisan premik krivulje ponudbe točka. Skupaj ηs= Q P ,25 P Q zviša Za obe pravilni navedbi, vključno z 2,5 % odstotkom, točka.
8 8 M naloga: Dobiček 3. Dobiček je razlika med celotnimi prihodki in celotnimi stroški. 3.2 dve od: samofinanciranje merilo investiranja merilo uspešnosti poslovanja ena od: samofinanciranje: Podjetje si prizadeva kar najbolj povečati dobiček in del dobička ali dobiček v celoti prihraniti za vlaganje v naložbe. merilo investiranja: Ko se podjetja odločajo o vlaganju v različne investicijske projekte, je pričakovana profitna stopnja pogosto glavni dejavnik odločitve. merilo uspešnosti poslovanja: Podjetje lahko na podlagi višine pričakovanega dobička učinkovito izbira različne trge, poslovne procese, poslovne lokacije oziroma obrate.
9 9 M Za tri pravilne navedbe 2 točki, za dve pravilni navedbi točka. 400 Skupaj 5 Obrazec: profitna mera dobiček 00 kapital Izračun: profitna mera ,5% 6000 Rezultat: 2,5 % ena od: znižanje stroškov poslovanja z nabavo surovin po ugodnejših cenah povečanje prodaje z uvedbo akcij (kupiš pet, dobiš eno zastonj) zvišanje cene zaradi boljše kakovosti Za smiseln predlog točka. 3.4 ena od: glavnica obr. mera ,6 obresti 896 EUR obrestna mera obresti ,25 % glavnica 6000 ena od: Ugodnejša je ponudba podjetniškega sklada, saj bo v tem primeru plačal 56 EUR manj obresti, kakor če bi najel posojilo pri banki. Ugodnejša je ponudba podjetniškega sklada, saj ponuja posojilo po 5,25-odstotni obrestni meri, banka pa po 5,6- odstotni obrestni meri. Za smiselno utemeljitev.
10 0 M naloga: Denar 4. ena od: Denar je kovina, ki trajno opravlja vlogo splošnega ekvivalenta in menjalnega posrednika. Denar je blago, s katerim lahko v vsakem trenutku plačamo, ker ga vsi radi sprejemajo kot plačilo. Denar je vse, kar služi kot splošni ekvivalent (menjalni posrednik), ter je splošno sprejemljiv v zameno za dobrine in storitve. 4.2 kovanci, bankovci (papirnati denar) in knjižni denar 4.3 štiri od: menjalni posrednik splošno merilo vrednosti (mera vrednosti) hranilec vrednosti plačilno sredstvo svetovni denar Skupaj 3 2 dve od: Menjalni posrednik (posrednik v menjavi): denar omogoča menjavo, prodajo in nakup dobrin (lažja menjava, omogoča hitrejše transakcije). Splošno merilo vrednosti (mera vrednosti): vsako blago na trgu ima v denarju izraženo vrednost oz. vsako blago ima svojo ceno. Hranilec vrednosti: denar omogoča varčevanje in posojanje (se ne pokvari, likvidna oblika premoženja). Plačilno sredstvo: z denarjem plačujemo obveznosti brez neposredne materialne protivrednosti, (prodaja ali nakup na posojilo, plačilo položnic, plačilo davčnih obveznosti). Svetovni denar: v času zlate valute denar omogoča plačevanje po vsem svetu (le nekatere valute omogočajo menjavo in plačila po vsem svetu, npr. dolar, jen, evro, funt in juan). Za štiri navedbe točka. Za vsako pojasnilo točka.
11 M Inflacija je zvišanje splošne ravni cen. Inflacija nastane, če kupni skladi presegajo blagovne sklade. 4.5 Deflacija (znižanje splošne ravni cen) vpliva zaviralno na nadaljnjo proizvodnjo, saj bodo proizvajalci prodajali blago po nižjih cenah, dosegli manjši dohodek od načrtovanega, ki ne bo spodbujal naložbe, ampak zmanjšal obseg proizvodnje. V gospodarstvu se zaradi zmanjševanja proizvodnje poveča brezposelnost, najmanj učinkoviti proizvajalci, ki prodajajo blago po nižjih cenah od proizvodnih stroškov, lahko gredo v stečaj. V gospodarstvu je recesija. Za smiselno ugotovitev, ki vključuje vsaj dve podčrtani navedbi točka. Za smiselno ugotovitev, ki vključuje vsaj dve podčrtani navedbi točka. 4.6 Delnica je lastniški vrednostni papir, saj daje imetniku trajno solastnino v podjetju. Obveznica je dolžniški vrednostni papir, saj se izdajatelj obveže, da bo njenemu imetniku v določenem času vrnil izposojeni znesek, povečan za obresti. Delnica je tvegana naložba kapitala, saj daje spremenljiv donos (dividendo), ki je odvisen od uspešnosti poslovanja podjetja. Obveznica je varnejša (netvegana) naložba kapitala, saj daje poleg izplačila v določenem obdobju še fiksen donos (določena obrestna mera).
12 2 M naloga: Bruto domači proizvod 5. BDP je seštevek tržnih vrednost vseh končnih proizvodov in storitev, proizvedenih v državi v določenem obdobju. 5.2 metoda dodane vrednosti metoda dohodkov metoda izdatkov ena od: metoda dodane vrednosti: BDP izračunamo tako, da od prihodka vseh proizvajalcev dobrin in storitev odštejemo stroške (ali: odštejemo vmesno proizvodnjo ali vmesno porabo). metoda dohodkov: BDP izračunamo tako, da seštejemo vse dohodke od dela in kapitala ter neto posredne davke. metoda izdatkov: BDP izračunamo tako, da seštejemo potrošne izdatke (osebno potrošnjo), naložbe, državne izdatke in neto izvoz (ali: prištejemo izvoz in odštejemo uvoz) največji večji ,00 EUR,87 % ,46 EUR Skupaj 3
13 3 M ,4 % BDP držav EMU se je leta 202 zmanjšal glede na BDP leta 20. 0, % BDP držav EMU se je leta 203 povečal glede na BDP leta 202. Za obe pravilno navedeni stopnji rasti BDP točka.
14 4 M naloga: Vloga države in fiskalna politika Vpr. Točke Rešitev Še sprejemljiv odgovor Dodatna navodila 6. 2 gospodarski razvoj stabilna raven cen nizka stopnja brezposelnosti uravnoteženi odnosi s tujino Za štiri ali tri pravilne navedbe 2 točki, za dve navedbi točka. Vpr. Točke Rešitev Še sprejemljiv odgovor Dodatna navodila 6.2 Je organizirana akcija nosilcev ekonomska politike, ki poskušajo s pomočjo sredstev (instrumentov) doseči najpomembnejše ekonomske cilje. Vpr. Točke Rešitev Še sprejemljiv odgovor Dodatna navodila 6.3 parlament (državni zbor), vlada Za obe navedbi točka. 6.4 Cilj je enakomernejša porazdelitev dohodka in bogastva. S (progresivno) obdavčitvijo dohodkov bogatejših del dohodka preusmerja k socialno šibkejšim prebivalcem v obliki transferjev. 6.5 Pri investicijskih odhodkih gre za nakupe države za naložbene namene. Investicijski odhodki povečujejo realno premoženje države, investicijski transferji pa povečujejo premoženje prejemnikov sredstev.
15 5 M Vpr. Točke Rešitev Še sprejemljiv odgovor Dodatna navodila dva od: zvišanje DDV uvedba nepremičninskega davka ukinitev regresa za upokojence s pokojnino nad 600 EUR znižanje in časovna omejitev izplačila nadomestil za brezposelne znižanje nadomestila za čas porodniškega dopusta ukinitev ali omejitev subvencij za prehrano dijakov in študentov znižanje plač v javnem sektorju Kandidat lahko navede kateri koli primer davkov, drugih prihodkov ali odhodkov, katerih učinek je sestavni del restriktivne fiskalne politike.
*M * Osnovna in višja raven MATEMATIKA NAVODILA ZA OCENJEVANJE. Sobota, 4. junij 2011 SPOMLADANSKI IZPITNI ROK. Državni izpitni center
 Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Križna elastičnost: relativna sprememba povpraševane količine dobrine X, do katere pride zaradi relativne spremembe
 2. POGLAVJE φ Elastičnost povpraševanja: E x, Px = % Q x / % P x % Q x > % sprememba Q % P x > % sprememba P Ex, Px = ( Q x / Q x ) / ( P x /P x ) = (P x / Q x ) * ( Q x / P x ) Linearna funkcija povpraševanja:
2. POGLAVJE φ Elastičnost povpraševanja: E x, Px = % Q x / % P x % Q x > % sprememba Q % P x > % sprememba P Ex, Px = ( Q x / Q x ) / ( P x /P x ) = (P x / Q x ) * ( Q x / P x ) Linearna funkcija povpraševanja:
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 22. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Diferencialna enačba, v kateri nastopata neznana funkcija in njen odvod v prvi potenci
 Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Posameznikovo in tr no povpraševanje
 Posameznikovo in tr no povpraševanje Posameznikovo povpraševanje po dobrini Sprememba cene blaga Krivulja povpraševanja x i =f(p i ) in y, p j = const., j i. y = 60 EUR p 2 = 1 EUR p 1 = 12, 6, 3, 2 EUR
Posameznikovo in tr no povpraševanje Posameznikovo povpraševanje po dobrini Sprememba cene blaga Krivulja povpraševanja x i =f(p i ) in y, p j = const., j i. y = 60 EUR p 2 = 1 EUR p 1 = 12, 6, 3, 2 EUR
EKONOMIJA. Mag. Božena Kramar
 EKONOMIJA Mag. Božena Kramar KAJ JE EKONOMIKA Ekonomika je preučevanje evanje ravnanja ljudi v vsakdanjem življenju. ivljenju. (Alfred Marshall) Glavni cilj politične ekonomije v vsaki deželi eli je povečati
EKONOMIJA Mag. Božena Kramar KAJ JE EKONOMIKA Ekonomika je preučevanje evanje ravnanja ljudi v vsakdanjem življenju. ivljenju. (Alfred Marshall) Glavni cilj politične ekonomije v vsaki deželi eli je povečati
Proizvodnja in stroški
 Proizvodnja in stroški Teorija podjetja Proizvodnja je dejavnost, ki ustvarja sedanjo ali bodočo korist. S sedanjo koristnostjo razumemo proizvodnjo dobrin za končno potrošnjo, z bodočo koristnostjo pa
Proizvodnja in stroški Teorija podjetja Proizvodnja je dejavnost, ki ustvarja sedanjo ali bodočo korist. S sedanjo koristnostjo razumemo proizvodnjo dobrin za končno potrošnjo, z bodočo koristnostjo pa
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 5. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 21. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Državni izpitni center *M * SPOMLADANSKI IZPITNI ROK EKONOMIJA NAVODILA ZA OCENJEVANJE. Petek, 28. maj 2010 SPLOŠNA MATURA
 Državni izpitni center *M10170113* EKONOMIJA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Petek, 28. maj 2010 SPLOŠNA MATURA RIC 2010 2 M101-701-1-3 IZPITNA POLA 1 PRAVILNI ODGOVORI IZBIRNIH NALOG
Državni izpitni center *M10170113* EKONOMIJA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Petek, 28. maj 2010 SPLOŠNA MATURA RIC 2010 2 M101-701-1-3 IZPITNA POLA 1 PRAVILNI ODGOVORI IZBIRNIH NALOG
Funkcijske vrste. Matematika 2. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 2. april Gregor Dolinar Matematika 2
 Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Proizvajalna funkcija
 Proizvajalna funkcija in računovodske informacije za odločanje o proizvajanju učinkov mag. Darjana Vidic Vsebina predavanja 1. Opredelitev proizvajalne funkcije 2. Računovodske informacije za odločanje
Proizvajalna funkcija in računovodske informacije za odločanje o proizvajanju učinkov mag. Darjana Vidic Vsebina predavanja 1. Opredelitev proizvajalne funkcije 2. Računovodske informacije za odločanje
EKONOMSKI VIDIKI MANAGEMENTA ZAPISKI PEDAVANJ
 EKONOMSKI VIDIKI MANAGEMENTA ZAPISKI PEDAVANJ Študijsko leto 2009/2010 Valter Ilenič KAZALO UVOD V EKONOMIJO...4 1. EKONOMSKA ZNANOST...4 2. TEMELJNI PROBLEM EKONOMIJE...5 3. MIKROEKONOMIJA...6 3.1. Proizvodnja...7
EKONOMSKI VIDIKI MANAGEMENTA ZAPISKI PEDAVANJ Študijsko leto 2009/2010 Valter Ilenič KAZALO UVOD V EKONOMIJO...4 1. EKONOMSKA ZNANOST...4 2. TEMELJNI PROBLEM EKONOMIJE...5 3. MIKROEKONOMIJA...6 3.1. Proizvodnja...7
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 14. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Tretja vaja iz matematike 1
 Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 10. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * NAVODILA ZA OCENJEVANJE. Sreda, 3. junij 2015 SPLOŠNA MATURA
 Državni izpitni center *M15143113* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sreda, 3. junij 2015 SPLOŠNA MATURA RIC 2015 M151-431-1-3 2 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor Naloga Odgovor
Državni izpitni center *M15143113* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sreda, 3. junij 2015 SPLOŠNA MATURA RIC 2015 M151-431-1-3 2 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor Naloga Odgovor
Vaje iz predmeta UPRAVLJANJE IN RAVNANJE PODJETJA. 5. vaje 1
 Vaje iz predmeta UPRAVLJANJE IN RAVNANJE PODJETJA 5. vaje 1 5. Vaje: Planiranje in vloga analize poslovanja 5. vaje 2 1. Podjetje upravljajo. lastniki Kaj že vemo? 2. Ker je vir moči, lastnina imajo managerji
Vaje iz predmeta UPRAVLJANJE IN RAVNANJE PODJETJA 5. vaje 1 5. Vaje: Planiranje in vloga analize poslovanja 5. vaje 2 1. Podjetje upravljajo. lastniki Kaj že vemo? 2. Ker je vir moči, lastnina imajo managerji
Ekonomska fakulteta Visoka poslovna šola. PRIIMEK IN IME: Datum: Izpit iz predmeta UVOD V GOSPODARSTVO I.del S 1 P 1 Q Q
 RIIMEK IN IME: Datum: Izpit iz predmeta UVOD V GOSODARSTVO I.del Neugodne vremenske razmere v poletnih mesecih bodo neugodno vplivale na letošnji pridelek slovenskih vinarjev. Tako se pričakuje precej
RIIMEK IN IME: Datum: Izpit iz predmeta UVOD V GOSODARSTVO I.del Neugodne vremenske razmere v poletnih mesecih bodo neugodno vplivale na letošnji pridelek slovenskih vinarjev. Tako se pričakuje precej
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * FIZIKA NAVODILA ZA OCENJEVANJE. Petek, 10. junij 2016 SPLOŠNA MATURA
 Državni izpitni center *M16141113* SPOMLADANSKI IZPITNI ROK FIZIKA NAVODILA ZA OCENJEVANJE Petek, 1. junij 16 SPLOŠNA MATURA RIC 16 M161-411-3 M161-411-3 3 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor
Državni izpitni center *M16141113* SPOMLADANSKI IZPITNI ROK FIZIKA NAVODILA ZA OCENJEVANJE Petek, 1. junij 16 SPLOŠNA MATURA RIC 16 M161-411-3 M161-411-3 3 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor
NEPARAMETRIČNI TESTI. pregledovanje tabel hi-kvadrat test. as. dr. Nino RODE
 NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
Integralni račun. Nedoločeni integral in integracijske metrode. 1. Izračunaj naslednje nedoločene integrale: (a) dx. (b) x 3 +3+x 2 dx, (c) (d)
 Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
Politična ekonomija. 3. Menjava in potrošnja ponudba in povpraševanje. 4. Proizvodnja in stroški. 5. Delitev Trg delovne sile in ekonomske blaginje
 Politična ekonomija En kolokvij obvezen za pristop k izpitu (kar nad 15 točk se šteje k končnem izpitu) in dva neobvezna kolokvija. Izpit 8 vprašanj, pol strani na vprašanje, 2 do 3 so računske naloge
Politična ekonomija En kolokvij obvezen za pristop k izpitu (kar nad 15 točk se šteje k končnem izpitu) in dva neobvezna kolokvija. Izpit 8 vprašanj, pol strani na vprašanje, 2 do 3 so računske naloge
Kontrolne karte uporabljamo za sprotno spremljanje kakovosti izdelka, ki ga izdelujemo v proizvodnem procesu.
 Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
Organizacija in struktura trga
 Organizacija in struktura trga Uvod: učinkovitost, tržne strukture, tržna moč Predmet obravnave Analiza podjetij in trgov Strateška konkurenca na različnih osnovah Cene Diferenciacija Oglaševanje Kako
Organizacija in struktura trga Uvod: učinkovitost, tržne strukture, tržna moč Predmet obravnave Analiza podjetij in trgov Strateška konkurenca na različnih osnovah Cene Diferenciacija Oglaševanje Kako
IZPIT IZ ANALIZE II Maribor,
 Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου...
 ΑΠΟΖΗΜΙΩΣΗ ΘΥΜΑΤΩΝ ΕΓΚΛΗΜΑΤΙΚΩΝ ΠΡΑΞΕΩΝ ΣΛΟΒΕΝΙΑ 1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου... 3 1 1. Έντυπα αιτήσεων
ΑΠΟΖΗΜΙΩΣΗ ΘΥΜΑΤΩΝ ΕΓΚΛΗΜΑΤΙΚΩΝ ΠΡΑΞΕΩΝ ΣΛΟΒΕΝΙΑ 1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου... 3 1 1. Έντυπα αιτήσεων
PONOVITEV SNOVI ZA 4. TEST
 PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
Gimnazija Krˇsko. vektorji - naloge
 Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
Dejavniki ekonomičnosti: potroški poslovnih prvin, cene za enoto poslovnih prvin. Če upoštevamo E = P/O potem še: prodajne cene proizvodov.
 Časovne metode amortiziranja: metoda enakih letnih zneskov metoda naraščajočih letnih zneskov metoda padajočih letnih zneskov linearna metoda s spremenjenimi stopnjami Izhajajo iz podmene, da ekonomska
Časovne metode amortiziranja: metoda enakih letnih zneskov metoda naraščajočih letnih zneskov metoda padajočih letnih zneskov linearna metoda s spremenjenimi stopnjami Izhajajo iz podmene, da ekonomska
SPTE V OBRATU PRIPRAVE LESA
 Laboratorij za termoenergetiko SPTE V OBRATU PRIPRAVE LESA Avditorna demonstracijska vaja Ekonomska in energijska analiza kotla in SPTE v sušilnici lesa Cilj vaje analiza proizvodnje toplote za potrebe
Laboratorij za termoenergetiko SPTE V OBRATU PRIPRAVE LESA Avditorna demonstracijska vaja Ekonomska in energijska analiza kotla in SPTE v sušilnici lesa Cilj vaje analiza proizvodnje toplote za potrebe
Ekonomika 1. dr. Mićo Mrkaić
 Ekonomika 1 dr. Mićo Mrkaić Email: mico.mrkaic@fov.uni-mb.si Kaj je cilj tega predmeta? Pridobiti znanje za dobro gospodarjenje Pridobiti razumevanje za inteligentno branje novic Poglobiti razumevanje
Ekonomika 1 dr. Mićo Mrkaić Email: mico.mrkaic@fov.uni-mb.si Kaj je cilj tega predmeta? Pridobiti znanje za dobro gospodarjenje Pridobiti razumevanje za inteligentno branje novic Poglobiti razumevanje
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * NAVODILA ZA OCENJEVANJE. Petek, 12. junij 2015 SPLOŠNA MATURA
 Državni izpitni center *M543* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Petek,. junij 05 SPLOŠNA MATURA RIC 05 M543 M543 3 IZPITNA POLA Naloga Odgovor Naloga Odgovor Naloga Odgovor Naloga Odgovor
Državni izpitni center *M543* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Petek,. junij 05 SPLOŠNA MATURA RIC 05 M543 M543 3 IZPITNA POLA Naloga Odgovor Naloga Odgovor Naloga Odgovor Naloga Odgovor
EKONOMIKA ZA INŽENIRJE VAJE 3
 Univerza v Novi Gorici Poslovno-tehniška fakulteta Program: Gospodarski inženiring II. stopnje EKONOMIKA ZA INŽENIRJE VAJE 3 asist. Drago Papler, mag. gosp. inž. Program: Gospodarski inženiring II. stopnje
Univerza v Novi Gorici Poslovno-tehniška fakulteta Program: Gospodarski inženiring II. stopnje EKONOMIKA ZA INŽENIRJE VAJE 3 asist. Drago Papler, mag. gosp. inž. Program: Gospodarski inženiring II. stopnje
Booleova algebra. Izjave in Booleove spremenljivke
 Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK
 1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
Direktorica mag. Brigita Šen Kreže
 Elaborat o oblikovanju cen storitev obvezne občinske gospodarske javne službe varstva okolja V OBČINI VRHNIKA Direktorica mag. Brigita Šen Kreže Vrhnika, januar 2016 KAZALO: 1 UVOD... 4 1.1 Pravne podlage
Elaborat o oblikovanju cen storitev obvezne občinske gospodarske javne službe varstva okolja V OBČINI VRHNIKA Direktorica mag. Brigita Šen Kreže Vrhnika, januar 2016 KAZALO: 1 UVOD... 4 1.1 Pravne podlage
SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK
 SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
FIZIKA NAVODILA ZA OCENJEVANJE
 Dr`avni izpitni center *M0441113* JESENSKI ROK FIZIKA NAVODILA ZA OCENJEVANJE Torek, 31. avgust 004 SPLO[NA MATURA C RIC 004 M04-411-1-3 Rešitve: POLA 1 VPRAŠANJA IZBIRNEGA TIPA REŠITVE 1. C 1. D. B. A
Dr`avni izpitni center *M0441113* JESENSKI ROK FIZIKA NAVODILA ZA OCENJEVANJE Torek, 31. avgust 004 SPLO[NA MATURA C RIC 004 M04-411-1-3 Rešitve: POLA 1 VPRAŠANJA IZBIRNEGA TIPA REŠITVE 1. C 1. D. B. A
EKONOMIJA: Q&A II. MIKROEKONOMIJA
 II. Mikroekonomija 1. Uvod 2. Vedenje potrošnika v tržnem okolju 3. opolna konkurenca 4. Ravnotežje na konkurenčnem trgu 5. Elastičnost 6. premembe tržnega ravnotežja 7. odjetja in teorija produkcije 8.
II. Mikroekonomija 1. Uvod 2. Vedenje potrošnika v tržnem okolju 3. opolna konkurenca 4. Ravnotežje na konkurenčnem trgu 5. Elastičnost 6. premembe tržnega ravnotežja 7. odjetja in teorija produkcije 8.
1. Definicijsko območje, zaloga vrednosti. 2. Naraščanje in padanje, ekstremi. 3. Ukrivljenost. 4. Trend na robu definicijskega območja
 ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 12. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
1. Kaj v računovodskem pristopu pomenita obdelava in zajemanje opredmetenih osnovnih sredstev?
 1 Kaj v računovodskem pristopu pomenita obdelava in zajemanje opredmetenih osnovnih sredstev? OPREDMETENA OSNOVNA SREDSTVA (OOS) So vedno premoženje podjetja To premoženje ima lahko podjetje : v lasti
1 Kaj v računovodskem pristopu pomenita obdelava in zajemanje opredmetenih osnovnih sredstev? OPREDMETENA OSNOVNA SREDSTVA (OOS) So vedno premoženje podjetja To premoženje ima lahko podjetje : v lasti
Mesečni pregled makroekonomskih podatkov
 Mesečni pregled makroekonomskih podatkov november 2016 NLB d.d. Jaka Erpič Samostojni analitik za finančne trge 01 476 91 70 jaka.erpic@nlb.si EMU BDP (YoY) Inflacija (YoY) Industrijska proizvodnja (YoY)
Mesečni pregled makroekonomskih podatkov november 2016 NLB d.d. Jaka Erpič Samostojni analitik za finančne trge 01 476 91 70 jaka.erpic@nlb.si EMU BDP (YoY) Inflacija (YoY) Industrijska proizvodnja (YoY)
Monetarna ekonomija. Cenovna presenečenja. Igor Masten. Univerza v Ljubljani - Ekonomska fakulteta
 Monetarna ekonomija Cenovna presenečenja Igor Masten Univerza v Ljubljani - Ekonomska fakulteta 2013 igor.masten@ef.uni-lj.si (EF) Monetarna ekonomija 2013 1 / 22 Stilizirana empirična dejstva Kaj pravijo
Monetarna ekonomija Cenovna presenečenja Igor Masten Univerza v Ljubljani - Ekonomska fakulteta 2013 igor.masten@ef.uni-lj.si (EF) Monetarna ekonomija 2013 1 / 22 Stilizirana empirična dejstva Kaj pravijo
UČINKOVITOST, USPEŠNOST IN FINANCIRANJE PODJETJA UVOD. Finančne odločitve in investicijske odločitve. Finančne/investicijske odločitve 2/24/12
 UČINKOVITOST, USPEŠNOST IN FINANCIRANJE PODJETJA UVOD doc. dr. Boštjan Aver Februar 2012 Finančne odločitve in investicijske odločitve Podjetje se mora ukvarjati s finančnimi odločitvami (pasiva) in investicijskimi
UČINKOVITOST, USPEŠNOST IN FINANCIRANJE PODJETJA UVOD doc. dr. Boštjan Aver Februar 2012 Finančne odločitve in investicijske odločitve Podjetje se mora ukvarjati s finančnimi odločitvami (pasiva) in investicijskimi
Numerično reševanje. diferencialnih enačb II
 Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
Gospodarjenje je zavestna človekova dejavnost, njen namen je zmanjšati omejenost dobrin s katerimi ljudje zadovoljujejo svoje potrebe.
 Poslovni proces: Poslovni učinki - proizvodi ali opravljene storitve Poslovni proces - proces opravljanja dejavnosti podjetja, rezultati so poslovni učinki (proizvodnja, storitvena in trgovska podjetja,
Poslovni proces: Poslovni učinki - proizvodi ali opravljene storitve Poslovni proces - proces opravljanja dejavnosti podjetja, rezultati so poslovni učinki (proizvodnja, storitvena in trgovska podjetja,
Matematika 1. Gregor Dolinar. 2. januar Fakulteta za elektrotehniko Univerza v Ljubljani. Gregor Dolinar Matematika 1
 Mtemtik 1 Gregor Dolinr Fkultet z elektrotehniko Univerz v Ljubljni 2. jnur 2014 Gregor Dolinr Mtemtik 1 Izrek (Izrek o povprečni vrednosti) Nj bo m ntnčn spodnj mej in M ntnčn zgornj mej integrbilne funkcije
Mtemtik 1 Gregor Dolinr Fkultet z elektrotehniko Univerz v Ljubljni 2. jnur 2014 Gregor Dolinr Mtemtik 1 Izrek (Izrek o povprečni vrednosti) Nj bo m ntnčn spodnj mej in M ntnčn zgornj mej integrbilne funkcije
Mesečni pregled makroekonomskih podatkov
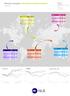 Mesečni pregled makroekonomskih podatkov marec 2017 NLB d.d. Jaka Erpič Samostojni analitik za finančne trge 01 476 91 70 jaka.erpic@nlb.si EMU BDP (YoY) Inflacija (YoY) Industrijska proizvodnja (YoY)
Mesečni pregled makroekonomskih podatkov marec 2017 NLB d.d. Jaka Erpič Samostojni analitik za finančne trge 01 476 91 70 jaka.erpic@nlb.si EMU BDP (YoY) Inflacija (YoY) Industrijska proizvodnja (YoY)
Slovenska oskrbna veriga z žiti in izdelki iz žit
 Zbornica kmetijskih in živilskih podjetij Slovenska oskrbna veriga z žiti in izdelki iz žit doc. dr. Aleš KUHAR Univerza v Ljubljani Biotehniška fakulteta VSEBINA - Pridelava žit v Sloveniji - Mednarodna
Zbornica kmetijskih in živilskih podjetij Slovenska oskrbna veriga z žiti in izdelki iz žit doc. dr. Aleš KUHAR Univerza v Ljubljani Biotehniška fakulteta VSEBINA - Pridelava žit v Sloveniji - Mednarodna
- Geodetske točke in geodetske mreže
 - Geodetske točke in geodetske mreže 15 Geodetske točke in geodetske mreže Materializacija koordinatnih sistemov 2 Geodetske točke Geodetska točka je točka, označena na fizični površini Zemlje z izbrano
- Geodetske točke in geodetske mreže 15 Geodetske točke in geodetske mreže Materializacija koordinatnih sistemov 2 Geodetske točke Geodetska točka je točka, označena na fizični površini Zemlje z izbrano
Splošno o interpolaciji
 Splošno o interpolaciji J.Kozak Numerične metode II (FM) 2011-2012 1 / 18 O funkciji f poznamo ali hočemo uporabiti le posamezne podatke, na primer vrednosti r i = f (x i ) v danih točkah x i Izberemo
Splošno o interpolaciji J.Kozak Numerične metode II (FM) 2011-2012 1 / 18 O funkciji f poznamo ali hočemo uporabiti le posamezne podatke, na primer vrednosti r i = f (x i ) v danih točkah x i Izberemo
Delovna točka in napajalna vezja bipolarnih tranzistorjev
 KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
8. Diskretni LTI sistemi
 8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 15. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
EKONOMIJA ALENKA BRADAČ
 EKONOMIJA ALENKA BRADAČ Višješolski strokovni program: Ekonomist Učbenik: Ekonomija Gradivo za 1. letnik Avtorica: Mag. Alenka Bradač, univ. dipl. ekon. Zavod IRC Višja strokovna šola Strokovna recenzentka:
EKONOMIJA ALENKA BRADAČ Višješolski strokovni program: Ekonomist Učbenik: Ekonomija Gradivo za 1. letnik Avtorica: Mag. Alenka Bradač, univ. dipl. ekon. Zavod IRC Višja strokovna šola Strokovna recenzentka:
matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):
![matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij): matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):](/thumbs/87/96579490.jpg) 4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
2. RAČUNOVODSKE KATEGORIJE IN METODE
 2. RAČUNOVODSKE KATEGORIJE IN METODE 1. Ekonomske kategorije in odločanje -dinamične -statične Te kategorije vplivajo na finančni in poslovni izid. Nekatere kategorije so bolj pomembne, nekatere manj.
2. RAČUNOVODSKE KATEGORIJE IN METODE 1. Ekonomske kategorije in odločanje -dinamične -statične Te kategorije vplivajo na finančni in poslovni izid. Nekatere kategorije so bolj pomembne, nekatere manj.
PROCESIRANJE SIGNALOV
 Rešive pisega izpia PROCESIRANJE SIGNALOV Daum: 7... aloga Kolikša je ampliuda reje harmoske kompoee arisaega periodičega sigala? f() - -3 - - 3 Rešiev: Časova fukcija a iervalu ( /,/) je lieara fukcija:
Rešive pisega izpia PROCESIRANJE SIGNALOV Daum: 7... aloga Kolikša je ampliuda reje harmoske kompoee arisaega periodičega sigala? f() - -3 - - 3 Rešiev: Časova fukcija a iervalu ( /,/) je lieara fukcija:
vezani ekstremi funkcij
 11. vaja iz Matematike 2 (UNI) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 ekstremi funkcij več spremenljivk nadaljevanje vezani ekstremi funkcij Dana je funkcija f(x, y). Zanimajo nas ekstremi nad
11. vaja iz Matematike 2 (UNI) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 ekstremi funkcij več spremenljivk nadaljevanje vezani ekstremi funkcij Dana je funkcija f(x, y). Zanimajo nas ekstremi nad
PREDSTAVITEV SPTE SISTEMOV GOSPEJNA IN MERCATOR CELJE
 TOPLOTNO ENERGETSKI SISTEMI TES d.o.o. GREGORČIČEVA 3 2000 MARIBOR IN PREDSTAVITEV SPTE SISTEMOV GOSPEJNA IN MERCATOR CELJE Saša Rodošek December 2011, Hotel BETNAVA, Maribor TES d.o.o. Energetika Maribor
TOPLOTNO ENERGETSKI SISTEMI TES d.o.o. GREGORČIČEVA 3 2000 MARIBOR IN PREDSTAVITEV SPTE SISTEMOV GOSPEJNA IN MERCATOR CELJE Saša Rodošek December 2011, Hotel BETNAVA, Maribor TES d.o.o. Energetika Maribor
13. Jacobijeva metoda za računanje singularnega razcepa
 13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
CM707. GR Οδηγός χρήσης... 2-7. SLO Uporabniški priročnik... 8-13. CR Korisnički priručnik... 14-19. TR Kullanım Kılavuzu... 20-25
 1 2 3 4 5 6 7 OFFMANAUTO CM707 GR Οδηγός χρήσης... 2-7 SLO Uporabniški priročnik... 8-13 CR Korisnički priručnik... 14-19 TR Kullanım Kılavuzu... 20-25 ENG User Guide... 26-31 GR CM707 ΟΔΗΓΟΣ ΧΡΗΣΗΣ Περιγραφή
1 2 3 4 5 6 7 OFFMANAUTO CM707 GR Οδηγός χρήσης... 2-7 SLO Uporabniški priročnik... 8-13 CR Korisnički priručnik... 14-19 TR Kullanım Kılavuzu... 20-25 ENG User Guide... 26-31 GR CM707 ΟΔΗΓΟΣ ΧΡΗΣΗΣ Περιγραφή
EKONOMIKA IN MENEDŽMENT PODJETJA MARIJA TURNŠEK MIKAČIĆ
 EKONOMIKA IN MENEDŽMENT PODJETJA MARIJA TURNŠEK MIKAČIĆ Višješolski strokovni program: Urejanje podeželja in krajine Učbenik: Ekonomika in menedžment podjetja Gradivo za 1. letnik Avtorica: mag. Marija
EKONOMIKA IN MENEDŽMENT PODJETJA MARIJA TURNŠEK MIKAČIĆ Višješolski strokovni program: Urejanje podeželja in krajine Učbenik: Ekonomika in menedžment podjetja Gradivo za 1. letnik Avtorica: mag. Marija
Abanka d.d. Ljubljana
 Letno poročilo 2000 Abanka d.d. Ljubljana Vsebina POMEMBNEJŠI PODATKI IN KAZALCI POSLOVANJA 2 Vodstvo UPRAVA BANKE 6 MNENJE UPRAVE 7 NADZORNI SVET 8 MNENJE NADZORNEGA SVETA 9 Poslovno poročilo SPLOŠNO
Letno poročilo 2000 Abanka d.d. Ljubljana Vsebina POMEMBNEJŠI PODATKI IN KAZALCI POSLOVANJA 2 Vodstvo UPRAVA BANKE 6 MNENJE UPRAVE 7 NADZORNI SVET 8 MNENJE NADZORNEGA SVETA 9 Poslovno poročilo SPLOŠNO
p 1 ENTROPIJSKI ZAKON
 ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
Statistična analiza. doc. dr. Mitja Kos, mag. farm. Katedra za socialno farmacijo Univerza v Ljubljani- Fakulteta za farmacijo
 Statistična analiza opisnih spremenljivk doc. dr. Mitja Kos, mag. arm. Katedra za socialno armacijo Univerza v Ljubljani- Fakulteta za armacijo Statistični znaki Proučevane spremenljivke: statistični znaki
Statistična analiza opisnih spremenljivk doc. dr. Mitja Kos, mag. arm. Katedra za socialno armacijo Univerza v Ljubljani- Fakulteta za armacijo Statistični znaki Proučevane spremenljivke: statistični znaki
EKONOMIJA MAJDA BUKOVNIK BRANKA LIKON JADRANKA PRODNIK VERA MERCINA ŠEGINA KARMEN VIRC
 EKONOMIJA MAJDA BUKOVNIK BRANKA LIKON JADRANKA PRODNIK VERA MERCINA ŠEGINA KARMEN VIRC Višješolski strokovni program: Ekonomist Učbenik: Gradivo za 1. letnik Avtorji: mag. Majda Bukovnik, univ. dipl. ekon.
EKONOMIJA MAJDA BUKOVNIK BRANKA LIKON JADRANKA PRODNIK VERA MERCINA ŠEGINA KARMEN VIRC Višješolski strokovni program: Ekonomist Učbenik: Gradivo za 1. letnik Avtorji: mag. Majda Bukovnik, univ. dipl. ekon.
ZLATO KOT SESTAVNI DEL PREMOŽENJA
 UNIVERZA V LJUBLJANI EKONOMSKA FAKULTETA MAGISTRSKO DELO ZLATO KOT SESTAVNI DEL PREMOŽENJA Ljubljana, februar 2015 BARBARA BREG IZJAVA O AVTORSTVU Spodaj podpisana Barbara Breg, študentka Ekonomske fakultete
UNIVERZA V LJUBLJANI EKONOMSKA FAKULTETA MAGISTRSKO DELO ZLATO KOT SESTAVNI DEL PREMOŽENJA Ljubljana, februar 2015 BARBARA BREG IZJAVA O AVTORSTVU Spodaj podpisana Barbara Breg, študentka Ekonomske fakultete
IZZIVI DRUŽINSKE MEDICINE. U no gradivo zbornik seminarjev
 IZZIVI DRUŽINSKE MEDICINE Uno gradivo zbornik seminarjev študentov Medicinske fakultete Univerze v Mariboru 4. letnik 2008/2009 Uredniki: Alenka Bizjak, Viktorija Janar, Maša Krajnc, Jasmina Rehar, Mateja
IZZIVI DRUŽINSKE MEDICINE Uno gradivo zbornik seminarjev študentov Medicinske fakultete Univerze v Mariboru 4. letnik 2008/2009 Uredniki: Alenka Bizjak, Viktorija Janar, Maša Krajnc, Jasmina Rehar, Mateja
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba.
 1. Osnovni pojmi Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba. Primer 1.1: Diferencialne enačbe so izrazi: y
1. Osnovni pojmi Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba. Primer 1.1: Diferencialne enačbe so izrazi: y
Na pregledni skici napišite/označite ustrezne točke in paraboli. A) 12 B) 8 C) 4 D) 4 E) 8 F) 12
 Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
Kotni funkciji sinus in kosinus
 Kotni funkciji sinus in kosinus Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z oznako cos x, DEFINICIJA V PRAVOKOTNEM TRIKOTNIKU: Kotna funkcija sinus je definirana kot razmerje
Kotni funkciji sinus in kosinus Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z oznako cos x, DEFINICIJA V PRAVOKOTNEM TRIKOTNIKU: Kotna funkcija sinus je definirana kot razmerje
POPIS DEL IN PREDIZMERE
 POPIS DEL IN PREDIZMERE ZEMELJSKI USAD v P 31 - P 32 ( l=18 m ) I. PREDDELA 1.1 Zakoličba, postavitev in zavarovanje prečnih profilov m 18,0 Preddela skupaj EUR II. ZEMELJSKA DELA 2.1 Izkop zemlje II.
POPIS DEL IN PREDIZMERE ZEMELJSKI USAD v P 31 - P 32 ( l=18 m ) I. PREDDELA 1.1 Zakoličba, postavitev in zavarovanje prečnih profilov m 18,0 Preddela skupaj EUR II. ZEMELJSKA DELA 2.1 Izkop zemlje II.
1. člen (vsebina) 2. člen (pomen izrazov)
 Na podlagi 64.e člena Energetskega zakona (Uradni list RS, št. 27/07 uradno prečiščeno besedilo in 70/08) in za izvrševanje četrte alinee tretjega odstavka 42. člena Zakona o spremembah in dopolnitvah
Na podlagi 64.e člena Energetskega zakona (Uradni list RS, št. 27/07 uradno prečiščeno besedilo in 70/08) in za izvrševanje četrte alinee tretjega odstavka 42. člena Zakona o spremembah in dopolnitvah
Izdala: BANKA SLOVENIJE Slovenska Ljubljana Tel.: Fax.: This publication is also available in English.
 SEPTEMBER 1 Izdala: BANKA SLOVENIJE Slovenska 3 1 Ljubljana Tel.: 1 7 19 Fax.: 1 1 1 This publication is also available in English. ISSN 3-99 MAKROEKONOMSKA GIBANJA IN PROJEKCIJE, september 1 Pregled vsebine
SEPTEMBER 1 Izdala: BANKA SLOVENIJE Slovenska 3 1 Ljubljana Tel.: 1 7 19 Fax.: 1 1 1 This publication is also available in English. ISSN 3-99 MAKROEKONOMSKA GIBANJA IN PROJEKCIJE, september 1 Pregled vsebine
Iterativno reševanje sistemov linearnih enačb. Numerične metode, sistemi linearnih enačb. Numerične metode FE, 2. december 2013
 Numerične metode, sistemi linearnih enačb B. Jurčič Zlobec Numerične metode FE, 2. december 2013 1 Vsebina 1 z n neznankami. a i1 x 1 + a i2 x 2 + + a in = b i i = 1,..., n V matrični obliki zapišemo:
Numerične metode, sistemi linearnih enačb B. Jurčič Zlobec Numerične metode FE, 2. december 2013 1 Vsebina 1 z n neznankami. a i1 x 1 + a i2 x 2 + + a in = b i i = 1,..., n V matrični obliki zapišemo:
Gradivo pripravila: Klara Golja LJUDSKA UNIVERZA NOVA GORICA. Program: EKONOMSKI TEHNIK (SSI) prejšnji program. POSLOVNA MATEMATIKA 3.
 LJUDSKA UNIVERZA NOVA GORICA Program: EKONOMSKI TEHNIK (SSI) prejšnji program POSLOVNA MATEMATIKA 3. Letnik Program: EKONOMSKI TEHNIK (SSI) prenovljen program EKONOMIKA POSLOVANJA 2. 1. Sklop: Poslovno
LJUDSKA UNIVERZA NOVA GORICA Program: EKONOMSKI TEHNIK (SSI) prejšnji program POSLOVNA MATEMATIKA 3. Letnik Program: EKONOMSKI TEHNIK (SSI) prenovljen program EKONOMIKA POSLOVANJA 2. 1. Sklop: Poslovno
Kotne in krožne funkcije
 Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
Nerevidirani konsolidirani računovodski izkazi skupine Krka in nerevidirani računovodski izkazi družbe Krka, d. d., Novo mesto za leto 2016 s
 Nerevidirani konsolidirani računovodski izkazi skupine Krka in nerevidirani računovodski izkazi družbe Krka, d. d., Novo mesto za leto 2016 s pomembnejšimi pojasnili Novo mesto, marec 2017 VSEBINA Podatki
Nerevidirani konsolidirani računovodski izkazi skupine Krka in nerevidirani računovodski izkazi družbe Krka, d. d., Novo mesto za leto 2016 s pomembnejšimi pojasnili Novo mesto, marec 2017 VSEBINA Podatki
IRENA VIHER 1 OCENJEVANJE VREDNOSTI PODJETJA
 IRENA VIHER 1 OCENJEVANJE VREDNOSTI PODJETJA 1. UVOD Poznamo: - Knjigovodsko vrednost podjetja (je razlika med celotnimi sredstvi in celotnimi obveznostmi podjetja, kot izhaja bilance stanja) lastniški
IRENA VIHER 1 OCENJEVANJE VREDNOSTI PODJETJA 1. UVOD Poznamo: - Knjigovodsko vrednost podjetja (je razlika med celotnimi sredstvi in celotnimi obveznostmi podjetja, kot izhaja bilance stanja) lastniški
NAVODILA ZA IZPOLNJEVANJE OBRAZCA ZA POROČANJE USPEŠNOSTI Z NALOŽBO ZA UKREP»POVEČANJE GOSPODARSKE VREDNOSTI GOZDOV«
 MINISTRSTVO ZA KMETIJSTVO, GOZDARSTVO IN PREHRANO REPUBLIKA SLOVENIJA www.mkgp.gov.si, e: gp.mkgp@gov.si Dunajska cesta 58, 1000 Ljubljana t: 01 478 90 00, f: 01 478 90 21 NAVODILA ZA IZPOLNJEVANJE OBRAZCA
MINISTRSTVO ZA KMETIJSTVO, GOZDARSTVO IN PREHRANO REPUBLIKA SLOVENIJA www.mkgp.gov.si, e: gp.mkgp@gov.si Dunajska cesta 58, 1000 Ljubljana t: 01 478 90 00, f: 01 478 90 21 NAVODILA ZA IZPOLNJEVANJE OBRAZCA
1. VAJA IZ TRDNOSTI. (linearna algebra - ponovitev, Kroneckerjev δ i j, permutacijski simbol e i jk )
 VAJA IZ TRDNOSTI (lnearna algebra - ponovtev, Kroneckerev δ, permutacsk smbol e k ) NALOGA : Zapš vektor a = [, 2,5,] kot lnearno kombnaco vektorev e = [,,,], e 2 = [,2,3,], e 3 = [2,,, ] n e 4 = [,,,]
VAJA IZ TRDNOSTI (lnearna algebra - ponovtev, Kroneckerev δ, permutacsk smbol e k ) NALOGA : Zapš vektor a = [, 2,5,] kot lnearno kombnaco vektorev e = [,,,], e 2 = [,2,3,], e 3 = [2,,, ] n e 4 = [,,,]
Tehnika za življenje SOLUTIONS KTS 560 / KTS 590. Diagnostika ECU z ESI[tronic]
![Tehnika za življenje SOLUTIONS KTS 560 / KTS 590. Diagnostika ECU z ESI[tronic] Tehnika za življenje SOLUTIONS KTS 560 / KTS 590. Diagnostika ECU z ESI[tronic]](/thumbs/91/105389415.jpg) Tehnika za življenje SOLUTIONS KTS 560 / KTS 590 Diagnostika ECU z ESI[tronic] Visokotehnološka diagnoza ECU za optimalno učinkovitost Nova trpežna modula KTS KTS 560 in KTS 590 sta osnovana na Boschevi
Tehnika za življenje SOLUTIONS KTS 560 / KTS 590 Diagnostika ECU z ESI[tronic] Visokotehnološka diagnoza ECU za optimalno učinkovitost Nova trpežna modula KTS KTS 560 in KTS 590 sta osnovana na Boschevi
Revidirano letno poročilo za leto 2008 za Delniški vzajemni sklad MP-TECH.SI
 Revidirano letno poročilo za leto 2008 za Delniški vzajemni sklad MP-TECH.SI PREGLED VSEBINE stran 1. POROČILO O POSLOVANJU DELNIŠKEGA VZAJEMNEGA SKLADA MP-TECH.SI ZA LETO 2008 2 1.1 PREGLED POSLOVANJA
Revidirano letno poročilo za leto 2008 za Delniški vzajemni sklad MP-TECH.SI PREGLED VSEBINE stran 1. POROČILO O POSLOVANJU DELNIŠKEGA VZAJEMNEGA SKLADA MP-TECH.SI ZA LETO 2008 2 1.1 PREGLED POSLOVANJA
Kvadratne forme. Poglavje XI. 1 Definicija in osnovne lastnosti
 Poglavje XI Kvadratne forme V zadnjem poglavju si bomo ogledali še eno vrsto preslikav, ki jih tudi lahko podamo z matrikami. To so tako imenovane kvadratne forme, ki niso več linearne preslikave. Kvadratne
Poglavje XI Kvadratne forme V zadnjem poglavju si bomo ogledali še eno vrsto preslikav, ki jih tudi lahko podamo z matrikami. To so tako imenovane kvadratne forme, ki niso več linearne preslikave. Kvadratne
Osnove elektrotehnike uvod
 Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
*N * MATEMATIKA. razred NAVODILA ZA VREDNOTENJE. Sreda, 4. maj Državni izpitni center. NACIONALNO PREVERJANJE ZNANJA v 9.
 Državni izpitni center *N1614012* 9. razred MATEMATIKA Sreda, 4. maj 2016 NAVODILA ZA VREDNOTENJE NACIONALNO PREVERJANJE ZNANJA v 9. razredu RIC 2016 2 N161-401--2 SPLOŠNA NAVODILA Prosimo, da najprej
Državni izpitni center *N1614012* 9. razred MATEMATIKA Sreda, 4. maj 2016 NAVODILA ZA VREDNOTENJE NACIONALNO PREVERJANJE ZNANJA v 9. razredu RIC 2016 2 N161-401--2 SPLOŠNA NAVODILA Prosimo, da najprej
MODERIRANA RAZLIČICA
 Dr`avni izpitni center *N07143132* REDNI ROK KEMIJA PREIZKUS ZNANJA Maj 2007 NAVODILA ZA VREDNOTENJE NACIONALNO PREVERJANJE ZNANJA b kncu 3. bdbja MODERIRANA RAZLIČICA RIC 2007 2 N071-431-3-2 NAVODILA
Dr`avni izpitni center *N07143132* REDNI ROK KEMIJA PREIZKUS ZNANJA Maj 2007 NAVODILA ZA VREDNOTENJE NACIONALNO PREVERJANJE ZNANJA b kncu 3. bdbja MODERIRANA RAZLIČICA RIC 2007 2 N071-431-3-2 NAVODILA
( , 2. kolokvij)
 A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
Vaja: Odbojnostni senzor z optičnimi vlakni. Namen vaje
 Namen vaje Spoznavanje osnovnih fiber-optičnih in optomehanskih komponent Spoznavanje načela delovanja in praktične uporabe odbojnostnega senzorja z optičnimi vlakni, Delo z merilnimi instrumenti (signal-generator,
Namen vaje Spoznavanje osnovnih fiber-optičnih in optomehanskih komponent Spoznavanje načela delovanja in praktične uporabe odbojnostnega senzorja z optičnimi vlakni, Delo z merilnimi instrumenti (signal-generator,
A N A L I S I S K U A L I T A S A I R D I K A L I M A N T A N S E L A T A N S E B A G A I B A H A N C A M P U R A N B E T O N
 I N F O T E K N I K V o l u m e 1 5 N o. 1 J u l i 2 0 1 4 ( 61-70) A N A L I S I S K U A L I T A S A I R D I K A L I M A N T A N S E L A T A N S E B A G A I B A H A N C A M P U R A N B E T O N N o v i
I N F O T E K N I K V o l u m e 1 5 N o. 1 J u l i 2 0 1 4 ( 61-70) A N A L I S I S K U A L I T A S A I R D I K A L I M A N T A N S E L A T A N S E B A G A I B A H A N C A M P U R A N B E T O N N o v i
Monetarna ekonomija. Mednarodni denarni sistem. Igor Masten. Univerza v Ljubljani - Ekonomska fakulteta
 Monetarna ekonomija Mednarodni denarni sistem Igor Masten Univerza v Ljuljani - Ekonomska fakulteta 2010 igor.masten@ef.uni-lj.si (EF) Monetarna ekonomija 2010 1 / 21 Model mednarodne menjave Model mednarodne
Monetarna ekonomija Mednarodni denarni sistem Igor Masten Univerza v Ljuljani - Ekonomska fakulteta 2010 igor.masten@ef.uni-lj.si (EF) Monetarna ekonomija 2010 1 / 21 Model mednarodne menjave Model mednarodne
Državni izpitni center. Višja raven MATEMATIKA. Izpitna pola 1. Torek, 25. avgust 2009 / 90 minut
 Š i f r a k a n d i d a t a : Državni izpitni center *M094011* Višja raven MATEMATIKA Izpitna pola 1 JESENSKI IZPITNI ROK Torek, 5. avgust 009 / 90 minut Dovoljeno gradivo in pripomočki: Kandidat prinese
Š i f r a k a n d i d a t a : Državni izpitni center *M094011* Višja raven MATEMATIKA Izpitna pola 1 JESENSKI IZPITNI ROK Torek, 5. avgust 009 / 90 minut Dovoljeno gradivo in pripomočki: Kandidat prinese
Državni izpitni center. Višja raven MATEMATIKA. Izpitna pola 2. Sobota, 4. junij 2011 / 90 minut
 Š i f r a k a n d i d a t a : Državni izpitni center *M111401* Višja raven MATEMATIKA Izpitna pola SPOMLADANSKI IZPITNI ROK Sobota, 4. junij 011 / 90 minut Dovoljeno gradivo in pripomočki: Kandidat prinese
Š i f r a k a n d i d a t a : Državni izpitni center *M111401* Višja raven MATEMATIKA Izpitna pola SPOMLADANSKI IZPITNI ROK Sobota, 4. junij 011 / 90 minut Dovoljeno gradivo in pripomočki: Kandidat prinese
1. Trikotniki hitrosti
 . Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
. Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
NAPOVEDI MAKROEKONOMSKIH GIBANJ V SLOVENIJI
 BANKA SLOVENIJE EVROSISTEM NAPOVEDI MAKROEKONOMSKIH GIBANJ V SLOVENIJI DECEMBER 17 Naslov: Izdajatelj: Napovedi makroekonomskih gibanj v Sloveniji Številka: december 17 BANKA SLOVENIJE Slovenska 35 155
BANKA SLOVENIJE EVROSISTEM NAPOVEDI MAKROEKONOMSKIH GIBANJ V SLOVENIJI DECEMBER 17 Naslov: Izdajatelj: Napovedi makroekonomskih gibanj v Sloveniji Številka: december 17 BANKA SLOVENIJE Slovenska 35 155
Logatherm WPL 14 AR T A ++ A + A B C D E F G A B C D E F G. kw kw /2013
 WP 14 R T d 9 10 11 53 d 2015 811/2013 WP 14 R T 2015 811/2013 WP 14 R T Naslednji podatki o izdelku izpolnjujejo zahteve uredb U 811/2013, 812/2013, 813/2013 in 814/2013 o dopolnitvi smernice 2010/30/U.
WP 14 R T d 9 10 11 53 d 2015 811/2013 WP 14 R T 2015 811/2013 WP 14 R T Naslednji podatki o izdelku izpolnjujejo zahteve uredb U 811/2013, 812/2013, 813/2013 in 814/2013 o dopolnitvi smernice 2010/30/U.
