IV. STATICA SISTEMELOR DE CORPURI RIGIDE. GRINZI CU ZĂBRELE
|
|
|
- Υγίνος Λιακόπουλος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 IV. STATICA SISTEMELOR DE CORPURI RIGIDE. GRINZI CU ZĂBRELE 4.1 Consideraţii generale În numeroase probleme de echilibru corpurile rigide interacţionează mecanic, formând sisteme de corpuri rigide între care există legături exterioare şi legături interioare. Studiul echilibrului sistemelor de corpuri se efectuează ţinând seama că în legăturile exterioare apar reacţiuni care, împreună cu forţele direct aplicate, constituie forţe exterioare pentru sistemul respectiv. În legăturile interioare, datorită interacţiunii dintre corpurile sistemului, apar forţe (cupluri de forţe) de legătură interioare. Conform principiului egalităţii între acţiune şi reacţiune forţele de legătură interioare au module egale şi sensuri opuse, deci suma lor la nivelul întregului sistem este nulă. 4.2 Metode folosite la studiul echilibrului sistemelor de corpuri Pentru studiul echilibrului sistemelor de corpuri se folosesc următoarele metode : a. Metoda izolării (separării) corpurilor Această metodă se bazează pe constatarea că dacă sub acţiunea unui sistem de forţe, sistemul de copuri este în echilibru atunci fiecare corp din sistem se află în echilibru. Sistemul se separă în corpuri componente iar pentru fiecare corp se introduc forţele exterioare direct aplicate, reacţiunile exterioare şi forţele de legătură interioare, sub acţiunea cărora corpul respectiv trebuie să fie în echilibru. 120
2 STATICA SISTEMELOR DE CORPURI RIGIDE. GRINZI CU ZĂBRELE Pentru fiecare corp se scriu apoi ecuaţiile de echilibru static, din care se determină necunoscutele problemei: parametrii geometrici care determină poziţia de echilibru a sistemului; reacţiunile exterioare şi cele interioare. Este de remarcat faptul că forţele de legătură interioare au, două câte două, module egale şi sensuri opuse pentru corpurile care înaintea separării au fost în interacţiune. Dacă sistemul este compus din n corpuri, atunci se pot scrie 6n ecuaţii de echilibru în cazul forţelor spaţiale şi 3n ecuaţii în cazul forţelor coplanare, din care se pot determina 6n, respectiv 3n necunoscute. În cazul când numărul necunoscutelor depăşeşte numărul ecuaţiilor, problema devine static nedeterminată. Aplicarea metodei izolării corpurilor are dezavantajul că sistemul obţinut are multe ecuaţii şi un număr mare de necunoscute. b. Metoda solidificării (rigidizării) corpurilor Această metodă se bazează pe principiul solidificării conform căruia, dacă un sistem alcătuit din corpuri rigide se află în echilibru sub acţiunea unui sistem de forţe direct aplicate, el rămâne în echilibru sub acţiunea acestor forţe şi în cazul în care ar deveni rigid (nedeformabil) păstrându-se legăturile exterioare iniţiale. În metoda solidificării întregul sistem se consideră ca un singur corp rigid în echilibru sub acţiunea forţelor direct aplicate şi a reacţiunilor din legăturile exterioare (forţele de legătură interioare nu se iau în considerare deoarece corpurile din sistem nu sunt izolate). În acest fel se pot scrie un număr de 6 ecuaţii de echilibru în spaţiu şi 3 ecuaţii de echilibru în plan. Aceste ecuaţii de echilibru nu sunt însă întotdeauna suficiente pentru determinarea forţelor de legătură exterioare (reacţiunilor) ori a poziţiei de echilibru şi, de aceea, metoda nu este aplicabilă oricărui sistem de corpuri. De asemenea, se remarcă faptul că forţele de legătură interioare nu se pot determina, deoarece ele nu intervin în ecuaţiile de echilibru. 121
3 FUNDAMENTE DE MECANICĂ - Teorie şi Aplicaţii c. Metoda mixtă (echilibrul părţilor) Această metodă se bazează pe teorema echilibrului părţilor, conform căreia dacă un sistem de corpuri se găseşte în echilibru atunci şi o parte oarecare din sistem, considerată ca rigid, este de asemenea în echilibru sub acţiunea forţelor ce acţionează asupra ei. În cazul unor sisteme care conţin mai multe corpuri, metoda mixtă, rezultată din combinaţia celor două metode expuse anterior, presupune mai întâi separarea unor grupuri de corpuri asupra cărora se aplică metoda izolării, apoi asupra acestor grupuri se aplică metoda solidificării. Metoda mixtă se utilizează de obicei pentru determinarea mai comodă a unor necunoscute sau, în scopul verificării valorilor acestora. Observaţii : * Se remarcă faptul că ecuaţiile de echilibru obţinute prin metodele prezentate nu sunt independente. Astfel, ecuaţiile de echilibru rezultate prin aplicarea teoremei solidificării şi echilibrului părţilor, reprezintă combinaţii liniare ale ecuaţiilor obţinute prin aplicarea metodei izolării. * Numărul total de ecuaţii independente pentru un sistem de n corpuri este de 6n în cazul sistemelor spaţiale şi de 3n pentru sistemele plane. Dacă în rezolvarea anumitor probleme ecuaţiile de echilibru nu sunt suficiente, acestora li se adaugă relaţii suplimentare, independente, de natură geometrică, relaţii din care rezultă mărimea forţelor şi momentelor de frecare, etc. Dacă şi în această situaţie numărul necunoscutelor depăşeşte numărul ecuaţiilor, sistemul se numeşte static nedeterminat. 122
4 STATICA SISTEMELOR DE CORPURI RIGIDE. GRINZI CU ZĂBRELE 4.3 Grinzi cu zăbrele Aspecte generale Dintre sistemele particulare de corpuri, frecvent întâlnite în practică, fac parte sistemele de bare articulate. Aceste sisteme, alcătuite din bare rigide legate între ele prin articulaţii în nodurile situate la extremităţi, sunt numite grinzi cu zăbrele. În funcţie de modul lor de alcătuire, grinzile cu zăbrele pot fi : - plane, când toate barele sunt situate într-un plan iar forţele exterioare ce acţionează asupra lor se află în acelaşi plan ; - spaţiale, când barele articulate ale sistemului au nodurile poziţionate în spaţiu. În continuare se vor studia numai grinzi cu zăbrele plane (cum sunt, de exemplu, cele din fig.4.1a-d) pentru care se acceptă următoarele ipoteze simplificatoare : a. b. 123
5 FUNDAMENTE DE MECANICĂ - Teorie şi Aplicaţii c. d. Fig.4.1 Tipuri de grinzi cu zăbrele plane barele sunt drepte, au secţiunea neglijabilă în raport cu lungimea lor şi au extremităţile articulate în noduri; articulaţiile sunt punctiforme şi astfel frecările din articulaţii sunt neglijabile (în practică, barele unei grinzi cu zăbrele sunt îmbinate prin sudură sau nituire); forţele exterioare acţionează numai în noduri ; legăturile cu exteriorul ale unei grinzi cu zăbrele se realizează numai prin noduri; greutatea barelor este neglijabilă în comparaţie cu forţele exterioare ( dacă în anumite cazuri se cere să se ţină seama şi de greutatea proprie a barei, aceasta se repartizează în părţi egale în nodurile de la extremităţile barei respective ). În condiţiile ipotezelor simplificatoare prezentate, forţa care acţionează fiecare bară are direcţia coliniară cu bara respectivă, adică barele unei grinzi cu zăbrele sunt solicitate numai la eforturi axiale. În funcţie de orientarea efortului, bara poate fi solicitată la : - întindere, când efortul are sensul marcat în fig.4.2a, adică efortul iese din nod; - compresiune, când efortul are sensul indicat în fig.4.2b, adică efortul intră din nod. a. b. Fig.4.2 Solicitări în barele unei grinzi cu zăbrele. Convenţii de notare La rezolvarea grinzilor cu zăbrele se întâlnesc două tipuri de necunoscute : forţele de legătură exterioare (reacţiunile); eforturile din bare, care sunt forţe interioare. Pentru calculul forţelor de legătură exterioare se aplică metoda solidificării: se consideră grinda cu zăbrele ca un singur corp rigid, încărcat cu forţele exterioare şi supus forţelor de legătură din reazeme. Se scriu apoi ecuaţiile de echilibru, din rezolvarea cărora rezultă forţele de legătură căutate. 124
6 STATICA SISTEMELOR DE CORPURI RIGIDE. GRINZI CU ZĂBRELE Pentru determinarea eforturilor din barele unei grinzi cu zăbrele se pot aplica atât metode analitice cât şi metode grafice. Dintre metodele analitice, mai des utilizate sunt: metoda izolării nodurilor şi metoda secţiunilor (Ritter), precum şi metodele de calcul automat iar dintre metodele grafice: planul (epura) Cremona şi metoda Culmann. Oricare ar fi metoda folosită pentru aflarea eforturilor din bare, în prima etapă de calcul este necesar să se verifice dacă grinda cu zăbrele este static determinată. În acest scop, se consideră că grinda are un număr b de bare şi n noduri. Deoarece pentru echilibrul fiecărui nod se pot scrie 2 ecuaţii de proiecţii, rezultă că pentru nodurile întregii grinzi se vor putea scrie 2n ecuaţii independente de echilibru. Dintre acestea, un număr de 3 ecuaţii sunt necesare determinării forţelor de legătură (reacţiunilor). În consecinţă, pentru determinarea eforturilor necunoscute din barele grinzii, rămân la dispoziţie un număr de (2n-3) ecuaţii independente. Cum fiecare bară introduce câte o necunoscută - efortul din bara respectivă - iar grinda cu zăbrele are b bare, vor trebui determinate b necunoscute. Din acest raţionament, rezultă condiţia ca grinda cu zăbrele să fie static determinată : (4.1) b = 2n Metoda izolării nodurilor Această metodă reprezintă aplicarea la studiul grinzilor cu zăbrele a metodei separării corpurilor. Astfel, se consideră că dacă întreaga grindă este în echilibru, atunci fiecare nod al ei trebuie să fie de asemenea în echilibru. Metoda constă în izolarea succesivă a tuturor nodurilor şi studierea echilibrului acestora, ca puncte materiale supuse la legături fără frecare în plan. Ordinea de izolare a nodurilor se alege astfel, încât pe nodul izolat să fie necunoscute cel mult două eforturi din bare ( deoarece pe fiecare nod se pot scrie două ecuaţii de echilibru). Forţele care acţionează într-un nod sunt : a) forţele exterioare direct aplicate şi reacţiunile din legăturile exterioare, (forţe cunoscute) ; b) eforturile în bare (forţe necunoscute) care se introduc pe direcţia barelor secţionate, ca forţe ce ies din nod. Prin aceasta se face ipoteza că toate eforturile din bare sunt de întindere. 125
7 FUNDAMENTE DE MECANICĂ - Teorie şi Aplicaţii În consecinţă, eforturile care se obţin din calcule ca fiind pozitive sunt eforturi de întindere, iar cele care din calcul rezultă negative, sunt eforturi de compresiune (deoarece în realitate sensul lor corect din punct de vedere mecanic este opus celui presupus iniţial). După aplicarea principiului acţiunii şi reacţiunii pentru eforturile calculate, se trece la izolarea următorului nod, urmărind ca numărul de necunoscute să fie 2. În acest fel, se scriu cele 2n ecuaţii din care un număr de (2n-3) ecuaţii se utilizează efectiv pentru calculul eforturilor din bare iar celelalte 3 se folosesc pentru verificare. Astfel, la penultimul nod studiat, una dintre ecuaţii va putea fi utilizată pentru verificare iar la ultimul nod, ambele ecuaţii sunt de verificare. Ca dezavantaje ale metodei izolării nodurilor se menţionează : - volumul relativ mare de calcule necesare, îndeosebi la grinzile cu zăbrele de dimensiuni mari, care au mai multe noduri; - posibilitatea transmiterii de la un nod la altul a unor eforturi calculate eronat, fapt ce poate deveni evident doar pe penultimul, sau pe ultimul nod al grinzii cu zăbrele studiate. Aplicaţie: Exemplificarea aplicării metodei izolării nodurilor este prezentată în continuare pentru grinda cu zăbrele din fig.4.3, prin parcurgerea următoarelor etape : 126 Fig.4.3 Grinda cu zăbrele plană
8 STATICA SISTEMELOR DE CORPURI RIGIDE. GRINZI CU ZĂBRELE Verificarea condiţiei ca grinda cu zăbrele (care are un număr de b =7 bare şi n =5 noduri ) să fie static determinată: b = 2n - 3, şi, deoarece 7=2. 5-3, rezultă că această condiţie este îndeplinită. * Determinarea reacţiunilor şi verificarea acestora : ΣFix = 0 ; -3 F + F + HB = 0 ; HB = 2 F ΣMA= 0 ; ΣMB = 0 ; 3 F. a - F. 2 a - 2 F. 2 a + VB. a - 2 F. a = 0 ; VB = 5 F - VA. a - 3 F. a = 0 ; VA = -3 F Observaţie: Pentru reacţiunea VA, ce a rezultat din calcul ca fiind negativă, este necesar a se modifica sensul presupus iniţial, aşa cum este marcat în fig.4.3. Ecuaţia de echilibru pentru verificarea reacţiunilor: ΣFix = 0 ; - VA + VB - 2 F = 0 ; - 3 F + 5 F - 2 F = 0 ; Determinarea eforturilor axiale din barele grinzii cu zăbrele Ordinea de izolare a nodurilor este stabilită după cum urmează : - nodul A, din izolarea căruia se calculează eforturile din barele 1 şi 2; - nodul D, din izolarea căruia se calculează eforturile din barele 3 şi 4; - nodul C, din izolarea căruia se calculează eforturile din barele 5 şi 6; - nodul E, penultimul nod, din izolarea căruia se calculează efortul din bara 7 şi se poate verifica efortul din bara 6; - nodul B, ultimul nod, din izolarea căruia se pot verifica eforturile din barele notate 4,5 şi 7, concurente în acest nod. Observaţie: Pe fiecare nod izolat, eforturile deja cunoscute din izolarea precedentă a altui nod, sunt marcate în paranteză. 127
9 FUNDAMENTE DE MECANICĂ - Teorie şi Aplicaţii ΣFix = 0 ; N2 cos 45 o = 0 ; N2 = 0 ΣFiy = 0 ; - 3 F + N1 = 0 ; N1 = 3 F ΣFix = 0 ; F + N4 = 0 ; N4 = - F ΣFiy = 0 ; - N3 = 0 ; N3 = 0 ΣFiy = 0 ; - 3 F + N5 sin 45 o = 0 ; N5 = 6 F 2 ΣFix = 0 ; - 3 F + N5 cos 45 o + N6 = 0 ; N6 = 0 ΣFix = 0 ; N6 = 0 ( ecuaţie de verificare ) ΣFiy = 0 ; N7-2 F = 0 ; N7 = 2 F 128
10 STATICA SISTEMELOR DE CORPURI RIGIDE. GRINZI CU ZĂBRELE ΣFix = 0 ; N4 + HB - N5. cos 45 o = 0 ; 6 F 2 F + 2 F -. = 0 ; = 0 ΣFiy = 0 ; VB - N7 - N5. cos 45 o = 0 ; 6 F 2 5 F - 2 F -. = 0 ; = 0 Eforturile calculate prin izolarea succesivă a nodurilor, sunt marcate pe barele grinzii cu zăbrele în fig.4.4. Fig.4.4 Grinda cu zăbrele plană. Eforturi în bare 129
11 FUNDAMENTE DE MECANICĂ - Teorie şi Aplicaţii Observaţie: determinate prin metoda izolării nodurilor Barele unei grinzi cu zăbrele în care efortul axial a rezultat nul nu se pot suprima, deoarece, în funcţie de configuraţia grinzii, pot apare situaţiile : - nu se mai îndeplineşte condiţia ca grinda să fie static determinată; - grinda cu zăbrele se transformă într-un mecanism ; - condiţiile de verificare la stabilitate ale altor bare din grinda cu zăbrele impun menţinerea barelor în care efortul este nul Metoda secţiunilor (Ritter) Această metodă reprezintă aplicarea teoriei echilibrului părţilor la studiul grinzilor cu zăbrele: se secţionează grinda în două părţi şi se studiază echilibrul uneia dintre ele, ca un rigid în plan. Traseul de secţionare se alege în aşa fel, încât acesta să nu traverseze mai mult de 3 bare cu eforturi necunoscute, deoarece, sistemul fiind plan, se pot scrie doar 3 ecuaţii de echilibru. Prin urmare se pot determina maxim 3 necunoscute, şi acestea cu condiţia ca barele secţionate să nu fie toate concurente ( în acest caz obţinându-se izolarea nodul respectiv) ori toate paralele între ele. Studiul echilibrului se efectuează asupra uneia din cele două părţi obţinute prin secţionare, în locul barelor secţionate fiind introduse eforturile necunoscute respective, presupuse ca fiind eforturi de întindere. Se scriu apoi cele trei ecuaţii de echilibru, iar din rezolvarea sistemului algebric obţinut rezultă eforturile din barele secţionate. În scopul simplificării calculelor şi obţinerii unor ecuaţii cu o singură necunoscută, se recomandă ca dintre cele trei ecuaţii de echilibru se scrie mai întâi ecuaţia de momente în raport cu punctul în care sunt concurente două dintre barele secţionate ( cu eforturi necunoscute ). Se menţionează că atât metoda izolării nodurilor cât şi metoda secţiunilor se aplică după ce au fost calculat reacţiunile exterioare din reazeme. Aplicaţie: Exemplificarea utilizării metodei secţiunilor este prezentată în continuare pentru grinda cu zăbrele din fig.4.5a, pentru care verificarea 130
12 STATICA SISTEMELOR DE CORPURI RIGIDE. GRINZI CU ZĂBRELE condiţiei ca grinda să fie static determinată precum şi calculul reacţiunilor, au fost efectuate în paragraful , astfel încât: Grinda cu zăbrele, care are un număr de b =7 bare şi n =5 noduri, este static determinată, deoarece cu b = 2n - 3 rezultă 7= şi condiţia dată este îndeplinită. * Reacţiunile din reazemele grinzii, fig. 4.5a, sunt: HB = 2 F, orientată spre dreapta; VB = 5 F, orientată în sus; VA = 3 F, orientată în jos Pentru determinarea eforturilor axiale din cele 7 bare ale grinzii cu zăbrele, se stabilesc traseele de secţionare, prezentate în fig. 4.5b - d, după cum urmează: 131
13 FUNDAMENTE DE MECANICĂ - Teorie şi Aplicaţii Fig.4.5 Grinda cu zăbrele plană. Trasee de secţionare pentru determinarea eforturilor axiale în bare - traseul marcat I-I, care secţionează grinda cu zăbrele astfel încât se pot determina eforturile din barele 1, 6 şi 7 ; 132
14 STATICA SISTEMELOR DE CORPURI RIGIDE. GRINZI CU ZĂBRELE - traseul marcat II-II, care secţionează grinda cu zăbrele astfel încât se pot determina eforturile rămase necunoscute din barele 2, 4 şi 5; - traseul marcat III-III, care secţionează grinda cu zăbrele astfel încât se poate determina efortul rămas necunoscut, respectiv cel din bara 3, şi se pot verifica eforturile determinate anterior în alte două dintre barele 2, 5, 6. Observaţie: Pentru fiecare secţiune efectuată, eforturile deja cunoscute din condiţia de echilibru a unei părţi secţionate printr-un traseu anterior, sunt marcate în paranteză. ΣME = 0 ; - N1. a + 3 F. a = 0 ; N1 = 3 F ΣFix = 0 ; - N6 = 0 ; N6 = 0 ΣFiy = 0 ; - 3 F + N1 + N7-2F= 0 ; N7 = 2F ΣMB = 0 ; N2. d = 0 ; N2 = 0 ΣFiy = 0 ; 5 F - N5. cos45 o - 2F = 0 ; 6 F N5 = 2 ΣFix = 0 ; - N4 +HB -N5. cos45 o -N2. cos45 o -N6 = 0 N4 = - F 133
15 FUNDAMENTE DE MECANICĂ - Teorie şi Aplicaţii ΣFiy = 0 ; N3 + N5. cos45 o - N2. cos45 o -3 F = 0 N3 = 0 Eforturile din alte două bare, de exemplu din barele 2 şi 5, se pot verifica din ecuaţiile de echilibru : ΣMC = 0 ; N2. d = 0 ; N2 = 0 ΣFix = 0; N5. cos45 o + N6 + N2. cos45 o - 3 F = 0 6 F N5 = 2 Eforturile calculate sunt marcate în fig.4.6. Fig.4.6 Grinda cu zăbrele plană. Eforturi în bare determinate prin metoda secţiunilor 134
16 4.3.4 Metode grafice STATICA SISTEMELOR DE CORPURI RIGIDE. GRINZI CU ZĂBRELE Dintre metodele grafice care au fost frecvent utilizate în analiza statică a structurilor plane alcătuite din bare articulate se menţionează planul (epura) Cremona şi metoda Culmann. Metoda grafică (epura) Cremona reprezintă corespondentul grafic al metodei izolării nodurilor şi constă în studierea succesivă, pe cale grafică, a echilibrului fiecărui nod. În metoda Culmann, se aplică interpretarea grafică a metodei secţiunilor. Odată cu dezvoltarea şi perfecţionarea mijloacelor de calcul automat dedicate, metodele grafice de rezolvare sunt actualmente mai puţin utilizate în analiza structurilor şi sistemelor Metode de calcul automat Evoluţia sistemelor de calcul automat şi a produselor de software a condus la includerea rapidă a programelor informatice în categoria mijloacelor eficiente de utilizare a calculatoarelor în rezolvarea aplicaţiilor inginereşti din mecanica structurilor. În acest sens, analiza comportării structurilor în general şi, în particular, a celor alcătuite din elemente sub formă de bare, beneficiază de numeroase programe de calcul automat elaborate, în cea mai mare parte, pe baza metodei elementelor finite. Utilizarea unor astfel de programe permite calculul eforturilor şi al deplasărilor în secţiunile şi punctele caracteristice ale structurii, precum şi dimensionarea şi alcătuirea elementelor structurale. Ca element comun programelor de calcul, se menţionează necesitatea alcătuirii blocului datelor de intrare, care trebuie să conţină elemente referitoare la : * topologia structurii analizate : geometria structurii propriu-zise şi poziţionarea prin coordonate a nodurilor şi elementelor componente; * date referitoare la acţiunile exterioare: modulul, direcţia, sensul şi poziţia în care sunt aplicate; * date care definesc din punct de vedere mecanic elementele structurale: - caracteristicile de material, ca de exemplu modulul de elasticitate longitudinal şi transversal, coeficientul de contracţie transversală ; 135
17 FUNDAMENTE DE MECANICĂ - Teorie şi Aplicaţii - caracteristicile geometrice: aria secţiunii transversale a elementelor analizate, momentele de inerţie, modulele de rezistenţă ; * elementele definitorii pentru legăturile exterioare ale elementelor (reazeme) precum şi pentru legăturile dintre elementele structurii, prin declararea gradelor de libertate, libere respectiv blocate, de la nivelul fiecărei legături. Dintre programele de calcul automat de o mai mare complexitate se pot enumera : SAP-05, COSMOS, ALGOR, ANSYS, PEP-MICRO, ROBOT- STRUCTURE. Alte programe, ca de exemplu MDSolids, GRIDCAD-FRAMES, GRIDCAD-TRUSS, necesitând un volum mai redus de informaţii în blocul datelor de intrare, permit calculul mai rapid al structurilor plane alcătuite din bare cu diverse tipuri de legături exterioare, precum şi calculul structurilor din bare articulate. Utilizarea unui astfel de program este exemplificată în continuare, pentru cazul unei grinzi cu zăbrele plane. Aplicaţie: a. Utilizarea programului de calcul automat MDSolids pentru calculul eforturilor din barele unei grinzi cu zăbrele plane, static determinate. MDSolids este un program educaţional pentru studiul solidelor deformabile. Modulele de analiză sunt grupate tematic şi dedicate unor tipuri particulare de probleme de mecanică şi rezistenţă. MDSolids conţine 12 module, pentru rezolvarea grinzilor cu zăbrele utilizându-se modulul Truss Analysis Module. Declararea geometriei structurii şi a acţiunilor mecanice se efectuează după accesarea comenzii New Truss (fig.4.7a) şi definirea caroiajului în caseta de dialog Define Grid (fig.4.7b). Declararea barelor grinzii cu zăbrele (Create;Members), a reazemelor (Create;Supports) şi a încărcărilor exterioare (Create;Loads) se realizează cu ajutorul opţiunilor de desenare selectând succesiv, prin intermediul mouse-ului, butoanele radio aferente prezentate în partea stângă a ecranului de lucru (fig.4.8a, b, c). Dacă se doreşte ştergerea unei bare, unui reazem sau a unei încărcări, se activează butonul Erase şi apoi una din opţiunile Members, Supports sau Loads (fig.4.8d) şi mouse-ul, cu butonul stâng menţinut apăsat, se trece peste elementul care se doreşte a fi şters. 136
18 STATICA SISTEMELOR DE CORPURI RIGIDE. GRINZI CU ZĂBRELE b. a. c. Figura 4.7 Programul MdSolids. Ecran demarare. Modul Truss Analysis a. b. c. d. Fig.4.8 Opţiuni de desenare a barelor (a), reazemelor (b), încărcărilor exterioare (c) şi de ştergere a acestora (d) Pentru a crea reazemele grinzii cu zăbrele, se declară prin tragere cu mouse-ul direcţiile deplasărilor blocate de reazeme, programul alegând apoi tipul acestuia (fig.4.9a). Definirea încărcărilor exterioare se face desenându-le pe fiecare în parte în nodul dorit, specificând direcţia, sensul şi valoarea acestora în caseta exemplificată în fig.4.9b. 137
19 FUNDAMENTE DE MECANICĂ - Teorie şi Aplicaţii a. b. Figura 4.9 Tipuri de reazeme (a). Declararea încărcărilor exterioare (b). După introducerea completă a datelor iniţiale ale problemei, se obţine schema geometrică şi de încărcare a grinzii şi se poate solicita programului efectuarea calculelor, prin acţionarea comenzii Compute devenită activă în bara de opţiuni afişată în partea stângă a ecranului de lucru. În urma acestei operaţiuni se realizează analiza statică a grinzii cu zăbrele, iar pe grindă vor fi afişate (fig. 4.10a,b): eforturile în bare, colorate în funcţie de natura acestui efort, astfel: barele supuse la compresiune, (C), în roşu, cele supuse la tracţiune, (T), în magenta, iar cele cu efort nul (0), cu verde. reacţiunile din reazeme, colorate în albastru. Valorile reacţiunilor şi a eforturilor din bare pot fi vizualizate şi in cele două casete derulante din partea de sus a ecranului de lucru. casetă eforturi în casetă reacţiuni a. b. Fig.4.10 Afişarea rezultatelor analizei statice a unei grinzi cu zăbrele, în programul MdSolids 138
20 STATICA SISTEMELOR DE CORPURI RIGIDE. GRINZI CU ZĂBRELE b. Rezolvarea unui exemplu de calcul a eforturilor în barele unei grinzi cu zăbrele cu ajutorul programului MdSolids. Se cere determinarea eforturilor din barele grinzii cu zăbrele reprezentată în fig.4.11 utilizând programul MdSolids. Încărcările exterioare, marcate Fi (i=1,...,4), au valorile: F1 = 280kN; F2 = 210kN ; F3 = 280kN ; F4 = 360kN. Fig Grinda cu zăbrele plană. Geometrie şi încărcări Efectuând operaţiunile de introducere a datelor geometrice ale problemei conform procedurilor detaliate în paragraful anterior, se obţine schema geometrică şi de încărcare din fig.4.12 iar în bara de comenzi din partea stângă a ecranului butonul Compute devine activ: Fig.4.12 Schema geometrică şi de încărcare a grinzii cu zăbrele, în programul MdSolids 139
21 FUNDAMENTE DE MECANICĂ - Teorie şi Aplicaţii Analiza statică a structurii este efectuată la acţionarea butonului Compute (fig. 4.13) : Fig Analiza statică a structurii grinzii cu zăbrele Ca rezultat al rulării, (fig.4.14), eforturile sunt afişate pe bare şi înscrise în caseta derulantă Member Forces, iar reacţiunile, în nodurile de reazem A şi G, respectiv în caseta Reactions. 140 Fig Rezultatele analizei statice efectuate în programul MdSolids
14. Grinzi cu zăbrele Metoda secţiunilor...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...3
 SEMINAR GRINZI CU ZĂBRELE METODA SECŢIUNILOR CUPRINS. Grinzi cu zăbrele Metoda secţiunilor... Cuprins... Introducere..... Aspecte teoretice..... Aplicaţii rezolvate.... Grinzi cu zăbrele Metoda secţiunilor
SEMINAR GRINZI CU ZĂBRELE METODA SECŢIUNILOR CUPRINS. Grinzi cu zăbrele Metoda secţiunilor... Cuprins... Introducere..... Aspecte teoretice..... Aplicaţii rezolvate.... Grinzi cu zăbrele Metoda secţiunilor
13. Grinzi cu zăbrele Metoda izolării nodurilor...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...
 SEMINAR GRINZI CU ZĂBRELE METODA IZOLĂRII NODURILOR CUPRINS. Grinzi cu zăbrele Metoda izolării nodurilor... Cuprins... Introducere..... Aspecte teoretice..... Aplicaţii rezolvate.... Grinzi cu zăbrele
SEMINAR GRINZI CU ZĂBRELE METODA IZOLĂRII NODURILOR CUPRINS. Grinzi cu zăbrele Metoda izolării nodurilor... Cuprins... Introducere..... Aspecte teoretice..... Aplicaţii rezolvate.... Grinzi cu zăbrele
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM 1 electronica.geniu.ro
 Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
CUPRINS 9. Echilibrul sistemelor de corpuri rigide... 1 Cuprins..1
 CURS 9 ECHILIBRUL SISTEMELOR DE CORPURI RIGIDE CUPRINS 9. Echilibrul sistemelor de corpuri rigide........... 1 Cuprins..1 Introducere modul.1 Obiective modul....2 9.1. Generalităţi. Legături intermediare...2
CURS 9 ECHILIBRUL SISTEMELOR DE CORPURI RIGIDE CUPRINS 9. Echilibrul sistemelor de corpuri rigide........... 1 Cuprins..1 Introducere modul.1 Obiective modul....2 9.1. Generalităţi. Legături intermediare...2
Planul determinat de normală şi un punct Ecuaţia generală Plane paralele Unghi diedru Planul determinat de 3 puncte necoliniare
 1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii transversale, scrisă faţă de una dintre axele de inerţie principale:,
 REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
2. Sisteme de forţe concurente...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...3
 SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
Metode iterative pentru probleme neliniare - contractii
 Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
(a) se numeşte derivata parţială a funcţiei f în raport cu variabila x i în punctul a.
 Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Curs 14 Funcţii implicite. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi"
 Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...4
 SEMINAR 3 MMENTUL FRŢEI ÎN RAPRT CU UN PUNCT CUPRINS 3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere...1 3.1. Aspecte teoretice...2 3.2. Aplicaţii rezolvate...4 3. Momentul forţei
SEMINAR 3 MMENTUL FRŢEI ÎN RAPRT CU UN PUNCT CUPRINS 3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere...1 3.1. Aspecte teoretice...2 3.2. Aplicaţii rezolvate...4 3. Momentul forţei
5. FUNCŢII IMPLICITE. EXTREME CONDIŢIONATE.
 5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate.
 Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
MARCAREA REZISTOARELOR
 1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
Metode de interpolare bazate pe diferenţe divizate
 Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile
 Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Curs 4 Serii de numere reale
 Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Aplicaţii ale principiului I al termodinamicii la gazul ideal
 Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
5.5. REZOLVAREA CIRCUITELOR CU TRANZISTOARE BIPOLARE
 5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
Sisteme diferenţiale liniare de ordinul 1
 1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE
 DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
5.4. MULTIPLEXOARE A 0 A 1 A 2
 5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
Seminar 5 Analiza stabilității sistemelor liniare
 Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Esalonul Redus pe Linii (ERL). Subspatii.
 Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
IV. CUADRIPOLI SI FILTRE ELECTRICE CAP. 13. CUADRIPOLI ELECTRICI
 V. POL S FLTE ELETE P. 3. POL ELET reviar a) Forma fundamentala a ecuatiilor cuadripolilor si parametrii fundamentali: Prima forma fundamentala: doua forma fundamentala: b) Parametrii fundamentali au urmatoarele
V. POL S FLTE ELETE P. 3. POL ELET reviar a) Forma fundamentala a ecuatiilor cuadripolilor si parametrii fundamentali: Prima forma fundamentala: doua forma fundamentala: b) Parametrii fundamentali au urmatoarele
a n (ζ z 0 ) n. n=1 se numeste partea principala iar seria a n (z z 0 ) n se numeste partea
 Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
III. Serii absolut convergente. Serii semiconvergente. ii) semiconvergentă dacă este convergentă iar seria modulelor divergentă.
 III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
2.1 Sfera. (EGS) ecuaţie care poartă denumirea de ecuaţia generală asferei. (EGS) reprezintă osferă cu centrul în punctul. 2 + p 2
 .1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
.1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
VII.2. PROBLEME REZOLVATE
 Teoria Circuitelor Electrice Aplicaţii V PROBEME REOVATE R7 În circuitul din fiura 7R se cunosc: R e t 0 sint [V] C C t 0 sint [A] Se cer: a rezolvarea circuitului cu metoda teoremelor Kirchhoff; rezolvarea
Teoria Circuitelor Electrice Aplicaţii V PROBEME REOVATE R7 În circuitul din fiura 7R se cunosc: R e t 0 sint [V] C C t 0 sint [A] Se cer: a rezolvarea circuitului cu metoda teoremelor Kirchhoff; rezolvarea
Curs 1 REZISTENTA SI STABILITATEA ELEMENTELOR STRUCTURILOR DIN OTEL
 Curs 1 REZISTENTA SI STABILITATEA ELEMENTELOR STRUCTURILOR DIN OTEL Rezistenta elementelor structurale din otel o Calcul la nivelul secţiunii elementelor structurale (rezistenta secţiunilor) Stabilitatea
Curs 1 REZISTENTA SI STABILITATEA ELEMENTELOR STRUCTURILOR DIN OTEL Rezistenta elementelor structurale din otel o Calcul la nivelul secţiunii elementelor structurale (rezistenta secţiunilor) Stabilitatea
 4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
Subiecte Clasa a VIII-a
 Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Conice. Lect. dr. Constantin-Cosmin Todea. U.T. Cluj-Napoca
 Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
R R, f ( x) = x 7x+ 6. Determinați distanța dintre punctele de. B=, unde x și y sunt numere reale.
 5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
SOLICITAREA DE TRACŢIUNE COMPRESIUNE
 CPITOLUL 4 SOLICITRE DE TRCŢIUE COMPRESIUE 4.1. Forţe axiale Dacă asupra unei bare drepte se aplică forţe dirijate în lungul axei longitudinale bara este solicitată la tracţiune (Fig.4.1.a) sau la compresiune
CPITOLUL 4 SOLICITRE DE TRCŢIUE COMPRESIUE 4.1. Forţe axiale Dacă asupra unei bare drepte se aplică forţe dirijate în lungul axei longitudinale bara este solicitată la tracţiune (Fig.4.1.a) sau la compresiune
2.1.1 Grindă dreaptă simplu rezemată încărcată cu o sarcină concentrată
 Seminar. Calculul forțelor de legătură (reacțiunilor) la bare drepte simplu rezemate. Introducere Calculul forțelor de legătură reprezintă primul pas (obligatoriu), din algoritmul de abordare al oricărei
Seminar. Calculul forțelor de legătură (reacțiunilor) la bare drepte simplu rezemate. Introducere Calculul forțelor de legătură reprezintă primul pas (obligatoriu), din algoritmul de abordare al oricărei
Integrala nedefinită (primitive)
 nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor X) functia f 1
 Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor
 Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
SEMINAR 14. Funcţii de mai multe variabile (continuare) ( = 1 z(x,y) x = 0. x = f. x + f. y = f. = x. = 1 y. y = x ( y = = 0
 Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
Asupra unei inegalităţi date la barajul OBMJ 2006
 Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
Curs 1 Şiruri de numere reale
 Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
MECANICA CORP DEFORMABIL - NOŢIUNI GENERALE
 MECANICA CORP DEFORMABIL - NOŢIUNI GENERALE 1. Obiectul mecanicii corpului deformabil În mecanica generală corpul solid - este considerat rigid nedeformabil. Această ipoteză este adecvată şi suficientă
MECANICA CORP DEFORMABIL - NOŢIUNI GENERALE 1. Obiectul mecanicii corpului deformabil În mecanica generală corpul solid - este considerat rigid nedeformabil. Această ipoteză este adecvată şi suficientă
Definiţia generală Cazul 1. Elipsa şi hiperbola Cercul Cazul 2. Parabola Reprezentari parametrice ale conicelor Tangente la conice
 1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
FORŢE INTERIOARE. EFORTURI. DIAGRAME DE EFORTURI.
 2.1.Metoda secţiunilor CAPITOLUL 2 FORŢE INTERIOARE. EFORTURI. DIAGRAME DE EFORTURI. În orice corp solid există forţe interioare, de structură, care asigură păstrarea formei şi dimensiunilor corpului.
2.1.Metoda secţiunilor CAPITOLUL 2 FORŢE INTERIOARE. EFORTURI. DIAGRAME DE EFORTURI. În orice corp solid există forţe interioare, de structură, care asigură păstrarea formei şi dimensiunilor corpului.
CUPRINS 8. Statica solidului rigid... 1 Cuprins..1
 CURS 8 STATICA SOLIDULUI RIGID CUPRINS 8. Statica solidului rigid.......... 1 Cuprins..1 Introducere modul.1 Obiective modul....2 8.1. Generalităţi...2 8.2. Echilibrul solidului rigid liber...4 Test de
CURS 8 STATICA SOLIDULUI RIGID CUPRINS 8. Statica solidului rigid.......... 1 Cuprins..1 Introducere modul.1 Obiective modul....2 8.1. Generalităţi...2 8.2. Echilibrul solidului rigid liber...4 Test de
Problema a II - a (10 puncte) Diferite circuite electrice
 Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
Ecuatii trigonometrice
 Ecuatii trigonometrice Ecuatiile ce contin necunoscute sub semnul functiilor trigonometrice se numesc ecuatii trigonometrice. Cele mai simple ecuatii trigonometrice sunt ecuatiile de tipul sin x = a, cos
Ecuatii trigonometrice Ecuatiile ce contin necunoscute sub semnul functiilor trigonometrice se numesc ecuatii trigonometrice. Cele mai simple ecuatii trigonometrice sunt ecuatiile de tipul sin x = a, cos
riptografie şi Securitate
 riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
CUPRINS 5. Reducerea sistemelor de forţe (continuare)... 1 Cuprins..1
 CURS 5 REDUCEREA SISTEMELOR DE FORŢE (CONTINUARE) CUPRINS 5. Reducerea sistemelor de forţe (continuare)...... 1 Cuprins..1 Introducere modul.1 Obiective modul....2 5.1. Teorema lui Varignon pentru sisteme
CURS 5 REDUCEREA SISTEMELOR DE FORŢE (CONTINUARE) CUPRINS 5. Reducerea sistemelor de forţe (continuare)...... 1 Cuprins..1 Introducere modul.1 Obiective modul....2 5.1. Teorema lui Varignon pentru sisteme
a. 11 % b. 12 % c. 13 % d. 14 %
 1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
Profesor Blaga Mirela-Gabriela DREAPTA
 DREAPTA Fie punctele A ( xa, ya ), B ( xb, yb ), C ( xc, yc ) şi D ( xd, yd ) în planul xoy. 1)Distanţa AB = (x x ) + (y y ) Ex. Fie punctele A( 1, -3) şi B( -2, 5). Calculaţi distanţa AB. AB = ( 2 1)
DREAPTA Fie punctele A ( xa, ya ), B ( xb, yb ), C ( xc, yc ) şi D ( xd, yd ) în planul xoy. 1)Distanţa AB = (x x ) + (y y ) Ex. Fie punctele A( 1, -3) şi B( -2, 5). Calculaţi distanţa AB. AB = ( 2 1)
Laborator 11. Mulţimi Julia. Temă
 Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Exemple de probleme rezolvate pentru cursurile DEEA Tranzistoare bipolare cu joncţiuni
 Problema 1. Se dă circuitul de mai jos pentru care se cunosc: VCC10[V], 470[kΩ], RC2,7[kΩ]. Tranzistorul bipolar cu joncţiuni (TBJ) este de tipul BC170 şi are parametrii β100 şi VBE0,6[V]. 1. să se determine
Problema 1. Se dă circuitul de mai jos pentru care se cunosc: VCC10[V], 470[kΩ], RC2,7[kΩ]. Tranzistorul bipolar cu joncţiuni (TBJ) este de tipul BC170 şi are parametrii β100 şi VBE0,6[V]. 1. să se determine
Ecuaţia generală Probleme de tangenţă Sfera prin 4 puncte necoplanare. Elipsoidul Hiperboloizi Paraboloizi Conul Cilindrul. 1 Sfera.
 pe ecuaţii generale 1 Sfera Ecuaţia generală Probleme de tangenţă 2 pe ecuaţii generale Sfera pe ecuaţii generale Ecuaţia generală Probleme de tangenţă Numim sferă locul geometric al punctelor din spaţiu
pe ecuaţii generale 1 Sfera Ecuaţia generală Probleme de tangenţă 2 pe ecuaţii generale Sfera pe ecuaţii generale Ecuaţia generală Probleme de tangenţă Numim sferă locul geometric al punctelor din spaţiu
Algebra si Geometrie Seminar 9
 Algebra si Geometrie Seminar 9 Decembrie 017 ii Equations are just the boring part of mathematics. I attempt to see things in terms of geometry. Stephen Hawking 9 Dreapta si planul in spatiu 1 Notiuni
Algebra si Geometrie Seminar 9 Decembrie 017 ii Equations are just the boring part of mathematics. I attempt to see things in terms of geometry. Stephen Hawking 9 Dreapta si planul in spatiu 1 Notiuni
3. REPREZENTAREA PLANULUI
 3.1. GENERALITĂŢI 3. REPREZENTAREA PLANULUI Un plan este definit, în general, prin trei puncte necoliniare sau prin o dreaptă şi un punct exterior, două drepte concurente sau două drepte paralele (fig.3.1).
3.1. GENERALITĂŢI 3. REPREZENTAREA PLANULUI Un plan este definit, în general, prin trei puncte necoliniare sau prin o dreaptă şi un punct exterior, două drepte concurente sau două drepte paralele (fig.3.1).
Seminariile Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reziduurilor
 Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Lucrul mecanic. Puterea mecanică.
 1 Lucrul mecanic. Puterea mecanică. In acestă prezentare sunt discutate următoarele subiecte: Definitia lucrului mecanic al unei forţe constante Definiţia lucrului mecanic al unei forţe variabile Intepretarea
1 Lucrul mecanic. Puterea mecanică. In acestă prezentare sunt discutate următoarele subiecte: Definitia lucrului mecanic al unei forţe constante Definiţia lucrului mecanic al unei forţe variabile Intepretarea
Capitolul 14. Asamblari prin pene
 Capitolul 14 Asamblari prin pene T.14.1. Momentul de torsiune este transmis de la arbore la butuc prin intermediul unei pene paralele (figura 14.1). De care din cotele indicate depinde tensiunea superficiala
Capitolul 14 Asamblari prin pene T.14.1. Momentul de torsiune este transmis de la arbore la butuc prin intermediul unei pene paralele (figura 14.1). De care din cotele indicate depinde tensiunea superficiala
1.7. AMPLIFICATOARE DE PUTERE ÎN CLASA A ŞI AB
 1.7. AMLFCATOARE DE UTERE ÎN CLASA A Ş AB 1.7.1 Amplificatoare în clasa A La amplificatoarele din clasa A, forma de undă a tensiunii de ieşire este aceeaşi ca a tensiunii de intrare, deci întreg semnalul
1.7. AMLFCATOARE DE UTERE ÎN CLASA A Ş AB 1.7.1 Amplificatoare în clasa A La amplificatoarele din clasa A, forma de undă a tensiunii de ieşire este aceeaşi ca a tensiunii de intrare, deci întreg semnalul
Functii Breviar teoretic 8 ianuarie ianuarie 2011
 Functii Breviar teoretic 8 ianuarie 011 15 ianuarie 011 I Fie I, interval si f : I 1) a) functia f este (strict) crescatoare pe I daca x, y I, x< y ( f( x) < f( y)), f( x) f( y) b) functia f este (strict)
Functii Breviar teoretic 8 ianuarie 011 15 ianuarie 011 I Fie I, interval si f : I 1) a) functia f este (strict) crescatoare pe I daca x, y I, x< y ( f( x) < f( y)), f( x) f( y) b) functia f este (strict)
STATICA CONSTRUCȚIILOR CADRE STATIC NEDETERMINATE
 Nicolae CHIRA Ioana MUREȘAN Roxana BÂLC Cristian MOJOLIC STATICA CONSTRUCȚIILOR CADRE STATIC NEDETERMINATE - Teorie și aplicații - U.T. PRESS Cluj-Napoca, 2015 ISBN 978-606-737-138-3 Editura U.T.PRESS
Nicolae CHIRA Ioana MUREȘAN Roxana BÂLC Cristian MOJOLIC STATICA CONSTRUCȚIILOR CADRE STATIC NEDETERMINATE - Teorie și aplicații - U.T. PRESS Cluj-Napoca, 2015 ISBN 978-606-737-138-3 Editura U.T.PRESS
Principiul Inductiei Matematice.
 Principiul Inductiei Matematice. Principiul inductiei matematice constituie un mijloc important de demonstratie in matematica a propozitiilor (afirmatiilor) ce depind de argument natural. Metoda inductiei
Principiul Inductiei Matematice. Principiul inductiei matematice constituie un mijloc important de demonstratie in matematica a propozitiilor (afirmatiilor) ce depind de argument natural. Metoda inductiei
SERII NUMERICE. Definiţia 3.1. Fie (a n ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0
 SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
Activitatea A5. Introducerea unor module specifice de pregătire a studenţilor în vederea asigurării de şanse egale
 Investeşte în oameni! FONDUL SOCIAL EUROPEAN Programul Operaţional Sectorial pentru Dezvoltarea Resurselor Umane 2007 2013 Axa prioritară nr. 1 Educaţiaşiformareaprofesionalăînsprijinulcreşteriieconomiceşidezvoltăriisocietăţiibazatepecunoaştere
Investeşte în oameni! FONDUL SOCIAL EUROPEAN Programul Operaţional Sectorial pentru Dezvoltarea Resurselor Umane 2007 2013 Axa prioritară nr. 1 Educaţiaşiformareaprofesionalăînsprijinulcreşteriieconomiceşidezvoltăriisocietăţiibazatepecunoaştere
1. STATICA SISTEMELOR DE CORPURI
 1 1. STATICA SISTEELOR DE CORPURI 1.1. ECHILIBRUL SOLIDULUI RIGID ACŢIONAT DE FORŢE Interacţiunea dintre corpuri se poate manifesta prin contact direct sau la distanţă. Acţiunea forţelor la distanţă se
1 1. STATICA SISTEELOR DE CORPURI 1.1. ECHILIBRUL SOLIDULUI RIGID ACŢIONAT DE FORŢE Interacţiunea dintre corpuri se poate manifesta prin contact direct sau la distanţă. Acţiunea forţelor la distanţă se
I. NOŢIUNI FUNDAMENTALE DIVIZIUNILE MECANICII. PRINCIPIILE MECANICII CLASICE SISTEME ŞI UNITĂŢI DE MĂSURĂ
 I. NOŢIUNI FUNDAMENTALE DIVIZIUNILE MECANICII. PRINCIPIILE MECANICII CLASICE SISTEME ŞI UNITĂŢI DE MĂSURĂ 1.1 Noţiuni fundamentale Mecanica este una dintre ştiinţele fundamentale ale naturii, având ca
I. NOŢIUNI FUNDAMENTALE DIVIZIUNILE MECANICII. PRINCIPIILE MECANICII CLASICE SISTEME ŞI UNITĂŢI DE MĂSURĂ 1.1 Noţiuni fundamentale Mecanica este una dintre ştiinţele fundamentale ale naturii, având ca
CUPRINS 7. Statica punctului material... 1 Cuprins..1
 CURS 7 STATICA UNCTULUI MATERIAL CURINS 7. Statica punctului material.......... 1 Cuprins..1 Introducere modul.1 Obiective modul....2 7.1. Generalităţi...2 7.2. Echilibrul punctului material liber...3
CURS 7 STATICA UNCTULUI MATERIAL CURINS 7. Statica punctului material.......... 1 Cuprins..1 Introducere modul.1 Obiective modul....2 7.1. Generalităţi...2 7.2. Echilibrul punctului material liber...3
9. Statica solidului rigid...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...3
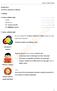 SEMINAR 9 STATICA SOLIDULUI RIGID CUPRINS 9. Statica solidului rigid...1 Curins...1 Introducere...1 9.1. Asecte teoretice...2 9.2. Alicaţii rezolvate...3 9. Statica solidului rigid În acest seminar se
SEMINAR 9 STATICA SOLIDULUI RIGID CUPRINS 9. Statica solidului rigid...1 Curins...1 Introducere...1 9.1. Asecte teoretice...2 9.2. Alicaţii rezolvate...3 9. Statica solidului rigid În acest seminar se
Criptosisteme cu cheie publică III
 Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
COLEGIUL NATIONAL CONSTANTIN CARABELLA TARGOVISTE. CONCURSUL JUDETEAN DE MATEMATICA CEZAR IVANESCU Editia a VI-a 26 februarie 2005.
 SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
Ecuatii exponentiale. Ecuatia ce contine variabila necunoscuta la exponentul puterii se numeste ecuatie exponentiala. a x = b, (1)
 Ecuatii exponentiale Ecuatia ce contine variabila necunoscuta la exponentul puterii se numeste ecuatie exponentiala. Cea mai simpla ecuatie exponentiala este de forma a x = b, () unde a >, a. Afirmatia.
Ecuatii exponentiale Ecuatia ce contine variabila necunoscuta la exponentul puterii se numeste ecuatie exponentiala. Cea mai simpla ecuatie exponentiala este de forma a x = b, () unde a >, a. Afirmatia.
STATICA CONSTRUCȚIILOR STRUCTURI STATIC DETERMINATE - Îndrumător pentru lucrări -
 Nicolae CHIRA Roxana BÂLC Alexandru CĂTĂRIG Aliz MÁTHÉ Cristian CIPLEA Cristian MOJOLIC Ioana MUREȘAN Cristian CUCEU Radu HULEA Daniela PETRIC STATICA CONSTRUCȚIILOR STRUCTURI STATIC DETERMINATE - Îndrumător
Nicolae CHIRA Roxana BÂLC Alexandru CĂTĂRIG Aliz MÁTHÉ Cristian CIPLEA Cristian MOJOLIC Ioana MUREȘAN Cristian CUCEU Radu HULEA Daniela PETRIC STATICA CONSTRUCȚIILOR STRUCTURI STATIC DETERMINATE - Îndrumător
Tranzistoare bipolare şi cu efect de câmp
 apitolul 3 apitolul 3 26. Pentru circuitul de polarizare din fig. 26 se cunosc: = 5, = 5, = 2KΩ, = 5KΩ, iar pentru tranzistor se cunosc următorii parametrii: β = 200, 0 = 0, μa, = 0,6. a) ă se determine
apitolul 3 apitolul 3 26. Pentru circuitul de polarizare din fig. 26 se cunosc: = 5, = 5, = 2KΩ, = 5KΩ, iar pentru tranzistor se cunosc următorii parametrii: β = 200, 0 = 0, μa, = 0,6. a) ă se determine
STATICA CONSTRUCȚIILOR STRUCTURI STATIC NEDETERMINATE
 Nicolae CHIRA Roxana BÂLC Alexandru CĂTĂRIG Aliz MÁTHÉ Cristian MOJOLIC Ioana MUREȘAN STATICA CONSTRUCȚIILOR STRUCTURI STATIC NEDETERMINATE - Îndrumător pentru lucrări - U.T. PRESS Cluj-Napoca, 2014 ISBN
Nicolae CHIRA Roxana BÂLC Alexandru CĂTĂRIG Aliz MÁTHÉ Cristian MOJOLIC Ioana MUREȘAN STATICA CONSTRUCȚIILOR STRUCTURI STATIC NEDETERMINATE - Îndrumător pentru lucrări - U.T. PRESS Cluj-Napoca, 2014 ISBN
- Grinzile sprijină (se descarcă) pe diafragme, stâlp şi pe alte grinzi.
 GRNA Grinda este un element structural, orizontal sau înclinat, liniar (b,h
GRNA Grinda este un element structural, orizontal sau înclinat, liniar (b,h
Laborator 6. Integrarea ecuaţiilor diferenţiale
 Laborator 6 Integrarea ecuaţiilor diferenţiale Responsabili: 1. Surdu Cristina(anacristinasurdu@gmail.com) 2. Ştirbăţ Bogdan(bogdanstirbat@yahoo.com) Obiective În urma parcurgerii acestui laborator elevul
Laborator 6 Integrarea ecuaţiilor diferenţiale Responsabili: 1. Surdu Cristina(anacristinasurdu@gmail.com) 2. Ştirbăţ Bogdan(bogdanstirbat@yahoo.com) Obiective În urma parcurgerii acestui laborator elevul
Transformări de frecvenţă
 Lucrarea 22 Tranformări de frecvenţă Scopul lucrării: prezentarea metodei de inteză bazate pe utilizarea tranformărilor de frecvenţă şi exemplificarea aceteia cu ajutorul unui filtru trece-jo de tip Sallen-Key.
Lucrarea 22 Tranformări de frecvenţă Scopul lucrării: prezentarea metodei de inteză bazate pe utilizarea tranformărilor de frecvenţă şi exemplificarea aceteia cu ajutorul unui filtru trece-jo de tip Sallen-Key.
Determinarea eforturilor din barele unei grinzi cu zabrele
 Determinarea efrturilr din barele unei inzi cu zabrele I. Scpul lucrarii Se determina reactiunile si efrturile din barele unei inzi cu zabrele. II. Tema lucrarii Se da inda cu zabrele din figura slicitata
Determinarea efrturilr din barele unei inzi cu zabrele I. Scpul lucrarii Se determina reactiunile si efrturile din barele unei inzi cu zabrele. II. Tema lucrarii Se da inda cu zabrele din figura slicitata
Lectia VI Structura de spatiu an E 3. Dreapta si planul ca subspatii ane
 Subspatii ane Lectia VI Structura de spatiu an E 3. Dreapta si planul ca subspatii ane Oana Constantinescu Oana Constantinescu Lectia VI Subspatii ane Table of Contents 1 Structura de spatiu an E 3 2 Subspatii
Subspatii ane Lectia VI Structura de spatiu an E 3. Dreapta si planul ca subspatii ane Oana Constantinescu Oana Constantinescu Lectia VI Subspatii ane Table of Contents 1 Structura de spatiu an E 3 2 Subspatii
 10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
Capitolul 4. Integrale improprii Integrale cu limite de integrare infinite
 Capitolul 4 Integrale improprii 7-8 În cadrul studiului integrabilităţii iemann a unei funcţii s-au evidenţiat douăcondiţii esenţiale:. funcţia :[ ] este definită peintervalînchis şi mărginit (interval
Capitolul 4 Integrale improprii 7-8 În cadrul studiului integrabilităţii iemann a unei funcţii s-au evidenţiat douăcondiţii esenţiale:. funcţia :[ ] este definită peintervalînchis şi mărginit (interval
Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25
 Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25 LAGĂRELE CU ALUNECARE!" 25.1.Caracteristici.Părţi componente.materiale.!" 25.2.Funcţionarea lagărelor cu alunecare.! 25.1.Caracteristici.Părţi componente.materiale.
Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25 LAGĂRELE CU ALUNECARE!" 25.1.Caracteristici.Părţi componente.materiale.!" 25.2.Funcţionarea lagărelor cu alunecare.! 25.1.Caracteristici.Părţi componente.materiale.
Laborator 1: INTRODUCERE ÎN ALGORITMI. Întocmit de: Claudia Pârloagă. Îndrumător: Asist. Drd. Gabriel Danciu
 INTRODUCERE Laborator 1: ÎN ALGORITMI Întocmit de: Claudia Pârloagă Îndrumător: Asist. Drd. Gabriel Danciu I. NOŢIUNI TEORETICE A. Sortarea prin selecţie Date de intrare: un şir A, de date Date de ieşire:
INTRODUCERE Laborator 1: ÎN ALGORITMI Întocmit de: Claudia Pârloagă Îndrumător: Asist. Drd. Gabriel Danciu I. NOŢIUNI TEORETICE A. Sortarea prin selecţie Date de intrare: un şir A, de date Date de ieşire:
Lectia VII Dreapta si planul
 Planul. Ecuatii, pozitii relative Dreapta. Ecuatii, pozitii relative Aplicatii Lectia VII Dreapta si planul Oana Constantinescu Oana Constantinescu Lectia VII Planul. Ecuatii, pozitii relative Dreapta.
Planul. Ecuatii, pozitii relative Dreapta. Ecuatii, pozitii relative Aplicatii Lectia VII Dreapta si planul Oana Constantinescu Oana Constantinescu Lectia VII Planul. Ecuatii, pozitii relative Dreapta.
Examen AG. Student:... Grupa: ianuarie 2016
 16-17 ianuarie 2016 Problema 1. Se consideră graful G = pk n (p, n N, p 2, n 3). Unul din vârfurile lui G se uneşte cu câte un vârf din fiecare graf complet care nu-l conţine, obţinându-se un graf conex
16-17 ianuarie 2016 Problema 1. Se consideră graful G = pk n (p, n N, p 2, n 3). Unul din vârfurile lui G se uneşte cu câte un vârf din fiecare graf complet care nu-l conţine, obţinându-se un graf conex
2. STATICA FLUIDELOR. 2.A. Presa hidraulică. Legea lui Arhimede
 2. STATICA FLUIDELOR 2.A. Presa hidraulică. Legea lui Arhimede Aplicația 2.1 Să se determine ce masă M poate fi ridicată cu o presă hidraulică având raportul razelor pistoanelor r 1 /r 2 = 1/20, ştiind
2. STATICA FLUIDELOR 2.A. Presa hidraulică. Legea lui Arhimede Aplicația 2.1 Să se determine ce masă M poate fi ridicată cu o presă hidraulică având raportul razelor pistoanelor r 1 /r 2 = 1/20, ştiind
Subiecte Clasa a VII-a
 lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
FLUXURI MAXIME ÎN REŢELE DE TRANSPORT. x 4
 FLUXURI MAXIME ÎN REŢELE DE TRANSPORT Se numeşte reţea de transport un graf în care fiecărui arc îi este asociat capacitatea arcului şi în care eistă un singur punct de intrare şi un singur punct de ieşire.
FLUXURI MAXIME ÎN REŢELE DE TRANSPORT Se numeşte reţea de transport un graf în care fiecărui arc îi este asociat capacitatea arcului şi în care eistă un singur punct de intrare şi un singur punct de ieşire.
Progresii aritmetice si geometrice. Progresia aritmetica.
 Progresii aritmetice si geometrice Progresia aritmetica. Definitia 1. Sirul numeric (a n ) n N se numeste progresie aritmetica, daca exista un numar real d, numit ratia progresia, astfel incat a n+1 a
Progresii aritmetice si geometrice Progresia aritmetica. Definitia 1. Sirul numeric (a n ) n N se numeste progresie aritmetica, daca exista un numar real d, numit ratia progresia, astfel incat a n+1 a
2. Circuite logice 2.4. Decodoare. Multiplexoare. Copyright Paul GASNER
 2. Circuite logice 2.4. Decodoare. Multiplexoare Copyright Paul GASNER Definiţii Un decodor pe n bits are n intrări şi 2 n ieşiri; cele n intrări reprezintă un număr binar care determină în mod unic care
2. Circuite logice 2.4. Decodoare. Multiplexoare Copyright Paul GASNER Definiţii Un decodor pe n bits are n intrări şi 2 n ieşiri; cele n intrări reprezintă un număr binar care determină în mod unic care
2.3 Geometria analitică liniarăînspaţiu
 2.3 Geometria analitică liniarăînspaţiu Pentru început sădefinim câteva noţiuni de bază în geometria analitică. Definitia 2.3.1 Se numeşte reper în spaţiu o mulţime formată dintr-un punct O (numit originea
2.3 Geometria analitică liniarăînspaţiu Pentru început sădefinim câteva noţiuni de bază în geometria analitică. Definitia 2.3.1 Se numeşte reper în spaţiu o mulţime formată dintr-un punct O (numit originea
Componente şi Circuite Electronice Pasive. Laborator 3. Divizorul de tensiune. Divizorul de curent
 Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
Asemănarea triunghiurilor O selecție de probleme de geometrie elementară pentru gimnaziu Constantin Chirila Colegiul Naţional Garabet Ibrãileanu,
 Asemănarea triunghiurilor O selecție de probleme de geometrie elementară pentru gimnaziu Constantin Chirila Colegiul Naţional Garabet Ibrãileanu, Iaşi Repere metodice ale predării asemănării în gimnaziu
Asemănarea triunghiurilor O selecție de probleme de geometrie elementară pentru gimnaziu Constantin Chirila Colegiul Naţional Garabet Ibrãileanu, Iaşi Repere metodice ale predării asemănării în gimnaziu
Capitolul 30. Transmisii prin lant
 Capitolul 30 Transmisii prin lant T.30.1. Sa se precizeze domeniile de utilizare a transmisiilor prin lant. T.30.2. Sa se precizeze avantajele si dezavantajele transmisiilor prin lant. T.30.3. Realizati
Capitolul 30 Transmisii prin lant T.30.1. Sa se precizeze domeniile de utilizare a transmisiilor prin lant. T.30.2. Sa se precizeze avantajele si dezavantajele transmisiilor prin lant. T.30.3. Realizati
III. Statica III. Statica. Echilibrul mecanic al corpurilor. 1. Sistem de forțe concurente. Sistemul de forțe
 III. Statica III. Statica. Echilibrul mecanic al corpurilor. 1. Sistem de forțe concurente. Sistemul de forțe reprezintă totalitatea forțelor care acționează simultan asupra unui corp, Fig. 1. În Fig.
III. Statica III. Statica. Echilibrul mecanic al corpurilor. 1. Sistem de forțe concurente. Sistemul de forțe reprezintă totalitatea forțelor care acționează simultan asupra unui corp, Fig. 1. În Fig.
V O. = v I v stabilizator
 Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R. 4.1 Proprietăţi topologice ale lui R Puncte de acumulare
 Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R În cele ce urmează, vom studia unele proprietăţi ale mulţimilor din R. Astfel, vom caracteriza locul" unui punct în cadrul unei mulţimi (în limba
Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R În cele ce urmează, vom studia unele proprietăţi ale mulţimilor din R. Astfel, vom caracteriza locul" unui punct în cadrul unei mulţimi (în limba
z a + c 0 + c 1 (z a)
 1 Serii Laurent (continuare) Teorema 1.1 Fie D C un domeniu, a D şi f : D \ {a} C o funcţie olomorfă. Punctul a este pol multiplu de ordin p al lui f dacă şi numai dacă dezvoltarea în serie Laurent a funcţiei
1 Serii Laurent (continuare) Teorema 1.1 Fie D C un domeniu, a D şi f : D \ {a} C o funcţie olomorfă. Punctul a este pol multiplu de ordin p al lui f dacă şi numai dacă dezvoltarea în serie Laurent a funcţiei
