d 1 d 1

1%(5:25.,1*3$3(56(5,(6,17(51$7,21$//,48,',7<,//86,21217+(5,6.62)67(5,/,=$7,21 5L DUGR-&DEDOOHUR $UYLQG.ULVKQDPXUWK\

1%(5:25.,1*3$3(56(5,(6,17(51$7,21$//,48,',7

TeSys contactors a.c. coils for 3-pole contactors LC1-D

References a.c. coils for 3-pole contactors LC1-D Control circuit voltage Average resistance Inductance of Reference (1) Weight Uc at 0 C ± 10 % closed circuit For 3-pole " contactors LC1-D09...D38 and

Κεφάλαιο 1 Πραγματικοί Αριθμοί 1.1 Σύνολα

x 2 + 1 = 0 N = {1, 2, 3....}, Z Q a, b a, b N c, d c, d N a + b = c, a b = d. a a N 1 a = a 1 = a. < > P n P (n) P (1) n = 1 P (n) P (n + 1) n n + 1 P (n) n P (n) n P n P (n) P (m) P (n) n m P (n + 1)

CHAPTER (2) Electric Charges, Electric Charge Densities and Electric Field Intensity

CHAPTE () Electric Chrges, Electric Chrge Densities nd Electric Field Intensity Chrge Configurtion ) Point Chrge: The concept of the point chrge is used when the dimensions of n electric chrge distriution

2?nom. Bacc. 2 nom. acc. S <u. >nom. 7acc. acc >nom < <

K+P K+P PK+ K+P - _+ l Š N K - - a\ Q4 Q + hz - I 4 - _+.P k - G H... /.4 h i j j - 4 _Q &\\ \\ ` J K aa\ `- c -+ _Q K J K -. P.. F H H - H - _+ 4 K4 \\ F &&. P H.4 Q+ 4 G H J + I K/4 &&& && F : ( -+..

Homework 8 Model Solution Section

MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx

o-r sub ff i-d m e s o o t h-e i-l mtsetisequa tob t-h-colon sub t e b x c u t-n n g dmenson.. ndp a

M M - - - - q -- x - K - W q - - x x - M q j x j x K W D M K q 6 W x x A j ˆ K ė j x ˆ D M [ 6 C ˆ j ˆ ˆ ˆ ˆ j M ˆ x ˆ A - D ˆ ˆ D M ˆ ˆ K x [ 6 ˆ C + M D ˆ ˆ + + D ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ + x 9 M S C : 4 R 9

m i N 1 F i = j i F ij + F x

N m i i = 1,..., N m i Fi x N 1 F ij, j = 1, 2,... i 1, i + 1,..., N m i F i = j i F ij + F x i mi Fi j Fj i mj O P i = F i = j i F ij + F x i, i = 1,..., N P = i F i = N F ij + i j i N i F x i, i = 1,...,

ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ

3/5/016 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΑΣΥΡΜΑΤΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Παραδείγματα Κεραιών Αθανάσιος Κανάτας Καθηγητής Παν/μίου Πειραιώς Δίπολο Hetz L d

d 1 d 1

É É d 1 d 1 n n ;,x E ; x E X0 X X)0 0Ld 0Ld 0Ld 0Ld 0Ld 0Ld 1 0Ld 0Ld 0 0 0 1 ' 0 0d 0 0d 0 0d 0 0 0 0 0 0 0d 0 0 0 0d 0 0 0 0 0d 0 0 0Ld 0 0Ld 0d 0 0 0 0 0 0 0 0 0 0 \g 0,Q 0 i 0)( 0)( 0 0 0 0d 0 0

f(w) f(z) = C f(z) = z z + h z h = h h h 0,h C f(z + h) f(z)

Ω f: Ω C l C z Ω f f(w) f(z) z a w z = h 0,h C f(z + h) f(z) h = l. z f l = f (z) Ω f Ω f Ω H(Ω) n N C f(z) = z n h h 0 h z + h z h = h h C f(z) = z f (z) = f( z) f f: Ω C Ω = { z; z Ω} z, a Ω f (z) f

_YkR${R x(eu 7BjZ$BtR B VRR$t8 t '1

_YR{R xeu 7BjZBtR B VRRt t tr Z{B U stt +st *Z Is U stzs ; _ BAj Mn wsd ]YBBR s {stzjs {BB Its RR by? }s sjj j B Y R } sjbt Y RI r } } ti{zjs B Y R } sti sjbt Y jt N w, n D ) Ã 7w>D A Y RZ Ps{ {Z t I tr

22 .5 Real consumption.5 Real residential investment.5.5.5 965 975 985 995 25.5 965 975 985 995 25.5 Real house prices.5 Real fixed investment.5.5.5 965 975 985 995 25.5 965 975 985 995 25.3 Inflation

P AND P. P : actual probability. P : risk neutral probability. Realtionship: mutual absolute continuity P P. For example:

(B t, S (t) t P AND P,..., S (p) t ): securities P : actual probability P : risk neutral probability Realtionship: mutual absolute continuity P P For example: P : ds t = µ t S t dt + σ t S t dw t P : ds

f a o gy s m a l nalg d co h n to h e y o m ia lalg e br coh the oogy lagebr

- - - * k ˆ v ˆ k ˆ ˆ E x ˆ ˆ [ v ˆ ˆ ˆ ˆ ˆ E x ˆ ˆ ˆ ˆ v ˆ Ex U U ˆ ˆ ˆ ˆ ˆ ˆ v ˆ M v ˆ v M v ˆ ˆ I U ˆ I 9 70 k k ˆ ˆ - I I 9ˆ 70 ˆ [ ˆ - v - - v k k k ˆ - ˆ k ˆ k [ ˆ ˆ D M ˆ k k 0 D M k [ 0 M v M ˆ

: Ω F F 0 t T P F 0 t T F 0 P Q. Merton 1974 XT T X T XT. T t. V t t X d T = XT [V t/t ]. τ 0 < τ < X d T = XT I {V τ T } δt XT I {V τ<t } I A

2012 4 Chinese Journal of Applied Probability and Statistics Vol.28 No.2 Apr. 2012 730000. :. : O211.9. 1..... Johnson Stulz [3] 1987. Merton 1974 Johnson Stulz 1987. Hull White 1995 Klein 1996 2008 Klein

y T - yy z x T + yy T + yz T + yx T + xy T + zy T - xz T - zx T - zz T - xx T + xx T + zx T + xz T + zz T - zy T - xy T - yx T - yz

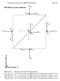Συµπληρωµατικές Σηµειώσεις στα ΗΜ Πεδία (Κ. Χιτζανίδης Μάιος 2017 ΗΜ τάσεις σε υλικές επιφάνειες T + yy T + yz T + yx T + zy T + xy T - xx T - xz T - zx T - zz T + zz T + zx T + xz T + xx T - xy T - zy

! " # $ % & $ % & $ & # " ' $ ( $ ) * ) * +, -. / # $ $ ( $ " $ $ $ % $ $ ' ƒ " " ' %. " 0 1 2 3 4 5 6 7 8 9 : ; ; < = : ; > : 0? @ 8? 4 A 1 4 B 3 C 8? D C B? E F 4 5 8 3 G @ H I@ A 1 4 D G 8 5 1 @ J C

ΑΡΧΕΣ ΗΛΕΚΤΡΟΝΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Αγωγιμότητα σε ημιαγωγούς

ΑΡΧΕΣ ΗΛΕΚΤΡΟΝΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Αγωγιμότητα σε ημιαγωγούς Required Text: Microelectronic Devices, Keith Leaver (1 st Chapter) Μέτρηση του μ e και προσδιορισμός του προσήμου των φορέων φορτίου Πρόβλημα: προσδιορισμός

Τυπολογίο Μαθηµατικών Μεθόδων Φυσικής ΙΙ

. Μέθοδος Frobenius Τυπολογίο Μαθηµατικών Μεθόδων Φυσικής ΙΙ d w Γενική µορφή της γραµµικής.ε. ης τάξης: dz + P (z)dw + Q(z)w = dz Μορφή της.ε. όταν το σηµείο z = z είναι κανονικό ανώµαλο σηµείο d w dz

Z L L L N b d g 5 * " # $ % $ ' $ % % % ) * + *, - %. / / + 3 / / / / + * 4 / / 1 " 5 % / 6, 7 # * $ 8 2. / / % 1 9 ; < ; = ; ; >? 8 3 " #

Z L L L N b d g 5 * " # $ % $ ' $ % % % ) * + *, - %. / 0 1 2 / + 3 / / 1 2 3 / / + * 4 / / 1 " 5 % / 6, 7 # * $ 8 2. / / % 1 9 ; < ; = ; ; >? 8 3 " # $ % $ ' $ % ) * % @ + * 1 A B C D E D F 9 O O D H

.. ntsets ofa.. d ffeom.. orp ism.. na s.. m ooth.. man iod period I n open square. n t s e t s ofa \quad d ffeom \quad orp ism \quad na s \quad m o

G G - - -- - W - - - R S - q k RS ˆ W q q k M G W R S L [ RS - q k M S 4 R q k S [ RS [ M L ˆ L [M O S 4] L ˆ ˆ L ˆ [ M ˆ S 4 ] ˆ - O - ˆ q k ˆ RS q k q k M - j [ RS ] [ M - j - L ˆ ˆ ˆ O ˆ [ RS ] [ M

CHAPTER 70 DOUBLE AND TRIPLE INTEGRALS. 2 is integrated with respect to x between x = 2 and x = 4, with y regarded as a constant

CHAPTER 7 DOUBLE AND TRIPLE INTEGRALS EXERCISE 78 Page 755. Evaluate: dxd y. is integrated with respect to x between x = and x =, with y regarded as a constant dx= [ x] = [ 8 ] = [ ] ( ) ( ) d x d y =

!"# '1,2-0- +,$%& &-

"#.)/-0- '1,2-0- "# $%& &'()* +,$%& &- 3 4 $%&'()*+$,&%$ -. /..-. " 44 3$*)-),-0-5 4 /&30&2&" 4 4 -&" 4 /-&" 4 6 710& 4 5 *& 4 # 1*&.. #"0 4 80*-9 44 0&-)* %&9 4 %&0-:10* &1 0)%&0-4 4.)-0)%&0-44 )-0)%&0-4#

ETS i =1 ETS i = 0 Y it (1) Y it (0) α AT T = E[Y i1 (1) Y i1 (0) ETS i =1], α AT T E[Y i1 (1) ETS i =1] [Y i1 (0) ETS i =1] α AT T α biased AT T = E[ Y i (1) ETS i =1]+E[Y 0i ETS i =1] E[Y 0i ETS i =0].

ΑΣΥΡΜΑΤΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ

ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΑΣΥΡΜΑΤΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Εισαγωγή στα Η/Μ Κύματα Αθανάσιος Κανάτας Καθηγητής Παν/μίου Πειραιώς Ιδιότητες των μέσων

Major Concepts. Multiphase Equilibrium Stability Applications to Phase Equilibrium. Two-Phase Coexistence

Major Concepts Multiphase Equilibrium Stability Applications to Phase Equilibrium Phase Rule Clausius-Clapeyron Equation Special case of Gibbs-Duhem wo-phase Coexistence Criticality Metastability Spinodal

1 String with massive end-points

1 String with massive end-points Πρόβλημα 5.11:Θεωρείστε μια χορδή μήκους, τάσης T, με δύο σημειακά σωματίδια στα άκρα της, το ένα μάζας m, και το άλλο μάζας m. α) Μελετώντας την κίνηση των άκρων βρείτε

φ(t) TE 0 φ(z) φ(z) φ(z) φ(z) η(λ) G(z,λ) λ φ(z) η(λ) η(λ) = t CIGS 0 G(z,λ)φ(z)dz t CIGS η(λ) φ(z) 0 z

Ακτινοβολίες και Ακτινοπροστασία Ενότητα 2η: Απορρόφηση ραδιενεργών ακτινοβολιών, επιπτώσεις στην υγεία, δοσιμετρία

Ακτινοβολίες και Ακτινοπροστασία Ενότητα 2η: Απορρόφηση ραδιενεργών ακτινοβολιών, επιπτώσεις στην υγεία, δοσιμετρία Μιχάλης Φωτάκης και Τσικριτζής Λάζαρος Τμήμα Μηχανικών Περιβάλλοντος και Μηχανικών Αντιρρύπανσης

Ηλεκτρονικοί Υπολογιστές IV

ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ηλεκτρονικοί Υπολογιστές IV Δυναμική του χρέους και του ελλείμματος Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης Άδειες Χρήσης Το παρόν εκπαιδευτικό

ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα. Ξένη Ορολογία. Ενότητα 6: Working Capital

ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ξένη Ορολογία Ενότητα 6: Working Capital Ευαγγελία Κουτσογιάννη Τμήμα Λογιστικής & Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό

! " #$% & '()()*+.,/0.

! " #$% & '()()*+,),--+.,/0. 1!!" "!! 21 # " $%!%!! &'($ ) "! % " % *! 3 %,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,0 %%4,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,5

ΚΕΦΑΛΑΙΟ 1 Ο 1.1. ΕΛΑΣΤΙΚΟ ΣΤΕΡΕΟ

ΚΕΦΑΛΑΙΟ Ο.. ΕΛΑΣΤΙΚΟ ΣΤΕΡΕΟ Ο Robert Hooke έγρψε το 678, "he power of any spring is in the same proportion with the tension thereof". Αυτή η δήλωση είνι η βάση του πρώτου ρεολογικού νόµου γι ιδνικά ελστικά

) * +, -. + / - 0 1 2 3 4 5 6 7 8 9 6 : ; < 8 = 8 9 >? @ A 4 5 6 7 8 9 6 ; = B? @ : C B B D 9 E : F 9 C 6 < G 8 B A F A > < C 6 < B H 8 9 I 8 9 E ) * +, -. + / J - 0 1 2 3 J K 3 L M N L O / 1 L 3 O 2,

Managing Economic Fluctuations. Managing Macroeconomic Fluctuations 1

Managing Economic Fluctuations -Keynesian macro: - -term nominal interest rates. - - P. - - P. Managing Macroeconomic Fluctuations 1 Review: New Keynesian Model -run macroeconomics: - π = γ (Y Y P ) +

Ó³ Ÿ , º 1(130).. 7Ä ±μ. Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê

Ó³ Ÿ. 006.. 3, º 1(130).. 7Ä16 Š 530.145 ˆ ƒ ˆ ˆŒ ˆŸ Š ƒ.. ±μ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê É μ ² Ö Ó μ μ Ö μ μ²õ μ É μ ÌÉ ±ÊÎ É ² ³ É μ - Î ±μ μ ÊÌ ±μ Ëμ ³ μ- ±² μ ÒÌ ³μ ²ÖÌ Ê ±. ³ É ÔÉμ μ μ μ Ö, Ö ²ÖÖ Ó ±μ³

6.642, Continuum Electromechanics, Fall 2004 Prof. Markus Zahn Lecture 8: Electrohydrodynamic and Ferrohydrodynamic Instabilities

6.64, Continuum Electromechnics, Fll 4 Prof. Mrus Zhn Lecture 8: Electrohydrodynmic nd Ferrohydrodynmic Instilities I. Mgnetic Field Norml Instility Courtesy of MIT Press. Used with permission. A. Equilirium

+ z, όπου I x, I y, I z είναι οι ροπές αδράνειας

r Έστω κβαντικός περιστροφέας ολικής στροφορμής J, που περιγράφεται από Jx J y J τη Χαμιλτονιανή H = z, όπου I x, I y, I z είναι οι ροπές αδράνειας I x I y I z του περιστροφέα ως προς τους άξονες x,y,z,

1. Ηλεκτρικό Φορτίο. Ηλεκτρικό Φορτίο και Πεδίο 1

. Ηλεκτρικό Φορτίο Το ηλεκτρικό φορτίο είναι ένα από τα βασικά χαρακτηριστικά των σωματιδίων από τα οποία οικοδομείται η ύλη. Υπάρχουν δύο είδη φορτίου (θετικό αρνητικό). Κατά την φόρτιση το φορτίο δεν

ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Οικονομία. Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών

ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Τέλος Ενότητας Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί

DOCUMENTS DE TRAVAIL / WORKING PAPERS

DOCUMENTS DE TRAVAIL / WORKING PAPERS 2017-66 How shifting investment towards low-carbon sectors impacts employment: three determinants under scrutiny Quentin Perrier 1, *, Philippe Quirion 1,2 September

APPLICATIONS TECHNOLOGY. Leaded Discs N.03 N.06 N.09

NC Disc hermistors ND 03/06/09 NE 03/06/09 NV 06/09 APPLICAIONS ND or NE: Commerical, Industrial and Automotive Applications AEC-Q200 Qualified NV: Professional Applicationsl Alarm and temperature measurement

%78 (!*+$&%,+$&*+$&%,-. /0$12*343556

! %78 ( 9 :: "#$% $&'"(" )!*$&%,$&*$&%,-. /$*343556 $ $& %$&.;$& $(# $"*("$# $ "$?, !* $&,#$"&::> $&( &$#, #$&# $"#&"& @($&%%>A!" #$ % µ & ' (#$ )! ) * ' "!)!,-./.' ) " $ &

ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ - Θ. BOLZANO - Θ. ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ. , ώστε η συνάρτηση. æ η γραφική της παράσταση να διέρχεται από το σημείο Mç

Να βρεθούν τα α και β Î R, ώστε η συνάρτηση ì 4 ημ - + = í - î α + β < ³ να είναι συνεχής και æ η γραφική της παράσταση να διέρχεται από το σημείο Mç è,- ö ø Να βρείτε τα α, β, γ Î R, ώστε να είναι συνεχής

.5 Real consumption.5 Real residential investment.5.5.5 965 975 985 995 25.5 965 975 985 995 25.5 Real house prices.5 Real fixed investment.5.5.5 965 975 985 995 25.5 965 975 985 995 25.3 Inflation rate.3

Eaton 1987 Roldos Eaton Roldos Galor and Lin Shimomura 1993 Nakanishi Turnovsky 1997, Chap. 4

Eaton 987 Roldos 99 Eaton 987 Galor and Lin 997 Roldos 99 Shimomura 993 Nakanishi 000 Turnovsky 997, Chap. 4 8 5 004 004 i i 004 3 3 4 ODA 5 ii 004 3 i heterogeneous capital joint production iii Ikemoto

!!" # $!!" %% &% $ : () *"++,- ; 4 % < & & / % % & / % 1 " #. % % 6

!!" # $!!" %% &% ' $ () *"++,- % &. % % & %/ % % / # % 2 3 / / ' / / / 45 ( & % / % 6 / / 3 / / 3 / 7 /7 7 $ 8"7 87 9" $ : () *"++,- ; 4 % < & & / % % & / % " #. % % 6 5/ %!!". 5 5 ' = % = % % #% 5 5 //

Ηλεκτρονικοί Υπολογιστές IV

ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ηλεκτρονικοί Υπολογιστές IV Η δυναμική ενός μοντέλου Keynsian Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης Άδειες Χρήσης Το παρόν εκπαιδευτικό

Εισαγωγή στις Φυσικές Επιστήμες (ΦΥΕ14) Περίοδος ΕΡΓΑΣΙΑ 1 η. Τότε r r b c. και ( )

Εισαγωγή στις Φυσικές Επιστήμες (ΦΥΕ4) Περίοδος 8-9 ΕΡΓΑΣΙΑ η Θέμα (μονάδες ) i. Δείξτε ότι ( a b) c a ( b c ) + b( a c ). a b c+ c a b+ b c a ii. Δείξτε την ταυτότητα Jacobi : ( ) ( ) ( ) Απάντηση i.

Parts Manual. Trio Mobile Surgery Platform. Model 1033

Trio Mobile Surgery Platform Model 1033 Parts Manual For parts or technical assistance: Pour pièces de service ou assistance technique : Für Teile oder technische Unterstützung Anruf: Voor delen of technische

Ηλεκτρονικοί Υπολογιστές IV

ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ηλεκτρονικοί Υπολογιστές IV Το μοντέλο Cobweb για την δυναμική των τιμών Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης Άδειες Χρήσης Το παρόν εκπαιδευτικό

Dissertation for the degree philosophiae doctor (PhD) at the University of Bergen

Dissertation for the degree philosophiae doctor (PhD) at the University of Bergen Dissertation date: GF F GF F SLE GF F D Ĉ = C { } Ĉ \ D D D = {z : z < 1} f : D D D D = D D, D = D D f f : D D

means ) ( )- 4 ) ;2 2 , < =- >?6 2 AB )4 AB ) $17,495,00 IJ 0'7 (3- &' ( - KK9 ( ()G ( <). ('2) 100% )7 )!

ارائه شده توسط: سايت ه فا مرجع جديد مقا ت ه شده از ن ت معت K- : means (+ $% &' ( *'.#! ( (.. ( /.0 # 1' 2 1 ('3-2 15 06 7. 8 ( - 4 0 ;2 2 : ('2 9 2.2.# @ < =- >?6 5 ('2 &' / ( 100 m4- xlarge Amazon EC2

X x C(t) description lagrangienne ( X , t t t X x description eulérienne X x 1 1 v x t

X 3 x 3 C Q y C(t) Q t QP t t C configuration initiale description lagrangienne x Φ ( X, t) X Y x X P x P t X x C(t) configuration actuelle description eulérienne (, ) d x v x t dt X 3 x 3 C(t) F( X, t)

Για τον ορισμό της ισχύος θα χρησιμοποιηθεί η παρακάτω διάταξη αποτελούμενη από ένα κύκλωμα Κ και μία πηγή Π:

1. Ηλεκτρικό ρεύμα Το ηλεκτρικό ρεύμα ορίζεται ως ο ρυθμός μιας συνισταμένης κίνησης φορτίων. Δηλαδή εάν στα άκρα ενός μεταλλικού αγωγού εφαρμοστεί μια διαφορά δυναμικού, τότε το παραγόμενο ηλεκτρικό πεδίο

ADVANCED STRUCTURAL MECHANICS

VSB TECHNICAL UNIVERSITY OF OSTRAVA FACULTY OF CIVIL ENGINEERING ADVANCED STRUCTURAL MECHANICS Lecture 1 Jiří Brožovský Office: LP H 406/3 Phone: 597 321 321 E-mail: jiri.brozovsky@vsb.cz WWW: http://fast10.vsb.cz/brozovsky/

, 11 1 / 49

ÍÚÈÔ (È È È Ï Ê Ø2017 ÏÑ) Ñ(1) È 2017 10 4, 11 1 / 49 ÏÑÒ ØËÌÙ Õ Õ Ø 2 / 49 ÏÑÒ ØËÌÙ ÏÑÒ ØËÌÙ Õ Õ Ø (I) Í(Ù ) ØÙ Ù ÚÓ (II) Black-Scholes-Merton Ð Ú ÌÑØÎÔ Ð Ô Black-Scholes (III) ØÕÊÔ ÕÚÔÍ(ÓÙÊØ Ú ) È ÎÑØÎÔ

CMOS Technology for Computer Architects

CMOS Technology for Computer Architects Iakovos Mavroidis Giorgos Passas Manolis Katevenis Lecture 13: On chip SRAM Technology FORTH ICS / EURECCA & UoC GREECE ABC A A E F A BCDAECF A AB C DE ABCDAECF

(1) P(Ω) = 1. i=1 A i) = i=1 P(A i)

Χρηματοοικονομικά Μαθηματικά Το συνεχές μοντέλο συνεχούς χρόνου Σ. Ξανθόπουλος Παν. Αιγαίου Χειμερινό Εξάμηνο 2015-2016 Χειμερινό Εξάμηνο 2015-2016 1 / Σύνοψη 1 Προκαταρκτικά 2 Διαδικασία Wiener ή Κίνηση

Κρίση και Κατάρρευση στην Ελλάδα του Μεσοπολέµου: Πεπρωµένο ή ολέθρια σφάλµατα? Νίκος Χριστοδουλάκης

Κρίση και Κατάρρευση στην Ελλάδα του Μεσοπολέµου: Πεπρωµένο ή ολέθρια σφάλµατα? Νίκος Χριστοδουλάκης Μάϊος 212 Γιατί θεωρούν µοιραία την έξοδο από το Ευρώ? Roubini (211): «Με την σηµερινή λιτότητα και

' ( )* * +,,, ) - ". &!: &/#&$&0& &!& $#/&! 1 2!#&, #/&2!#&3 &"&!3, #&- &2!#&, "#4&#3 $!&$3% 2!% #!.1 & &!" //! &-!!

..!! "#$% #&" 535.34 ' ( )* *,,, ) - ". &!: 1.4.7 &/#&$&& &!&11 5.7.1 $#/&! 1!#&, #/&!#&3 &"&!3, #&- &!#&, "#4&#3 $!&$3%!% #!.1 & &!" //! &-!!% 3 #&$&/!: /&!&# &-!!%, "#&&# 56$.., //! &-!!% ).. &$ 13 .

RS306 High Speed Fuse for Semiconductor Protection

Product Information Standard square body fuse, comply with GB13539/IEC60269/UL-248/VDE-0636 Protection: ar (GB\IEC), short circuit or backup Rated : 250-4000VAC Very low I 2 t/high current-limiting/high

Teor imov r. ta matem. statist. Vip. 94, 2016, stor

eor imov r. ta matem. statist. Vip. 94, 6, stor. 93 5 Abstract. e article is devoted to models of financial markets wit stocastic volatility, wic is defined by a functional of Ornstein-Ulenbeck process

ΕΦΗΜΕΡΙΣ ΤΗΣ ΚΥΒΕΡΝΗΣΕΩΣ

901 ΕΦΗΜΕΡΙΣ ΤΗΣ ΚΥΒΕΡΝΗΣΕΩΣ ΤΗΣ ΕΛΛΗΝΙΚΗΣ ΔΗΜΟΚΡΑΤΙΑΣ ΤΕΥΧΟΣ ΔΕΥΤΕΡΟ Αρ. Φύλλου 82 27 Ιανουαρίου 2006 ΑΠΟΦΑΣΕΙΣ Αριθμ. 012582 Απόφαση της ΡΑΕ για την έγκριση του Εγχειριδίου Δι αχείρισης Μετρήσεων και

ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ ΚΑΤΑΝΟΜΕΣ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ

ΚΑΤΑΝΟΜΕΣ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ 1 Θέμα 1 α) Προσδιορίστε τον όγκο V ιδανικού αερίου, στον οποίο η σχετική διακύμανση είναι α = 10-6 και η συγκέντρωση των σωματιδίων είναι n =,7 10 19 cm -3. β) Προσδιορίστε

The mass and anisotropy profiles of nearby galaxy clusters from the projected phase-space density

The mass and anisotropy profiles of nearby galaxy clusters from the projected phase-space density 5..29 Radek Wojtak Nicolaus Copernicus Astronomical Center collaboration: Ewa Łokas, Gary Mamon, Stefan

(iii) Να βρεθεί το δεσμευμένο στάσιμο της συνάρτησης f(x, y) = x + y με τον περιορισμό:

ΔΙΑΓΩΝΙΣΜΑ 1 (3 μονάδες) (i) Δίνονται οι παραμετρικές εξισώσεις: = ln(t+ 1), y= t + t. Να υπολογιστεί η παράγωγος του ως προς y, όταν t= 0. (ii) Δίνεται η συνάρτηση: f() = p+. Να διερευνηθεί αν είναι κυρτή

"!$#&%('*),+.- /,0 +/.1),032 #4)5/ /.0 )80/ 9,: A B C <ED<8;=F >.<,G H I JD<8KA C B <=L&F8>.< >.: M <8G H I

"!$#&%('*),+.- /,0 +/.1),032 #4)5/.-076 4/.0 )80/ 9,: ;=@?4: A B C

w 1, z = 2 και r = 1

ΑΣΚΗΣΗ ΥΠΟΛΟΓΙΣΤΙΚΕΣ ΜΕΘΟΔΟΙ, 008-009, 5 Ο ΕΞΑΜΗΝΟ ΕΡΓΑΣΙΑ #4: ΠΑΡΑΒΟΛΙΚΑ ΠΡΟΒΛΗΜΑΤΑ ΗΜΕΡΟΜΗΝΙΑ ΠΑΡΑΔΟΣΗΣ: 0..009 ΔΙΔΑΣΚΩΝ: Δ. Βαλουγεώργης Δίδεται η διαφορική εξίσωση Επιμέλεια απαντήσεων: Ιωάννης Λυχναρόπουλος

6.642 Continuum Electromechanics

MIT OpenCourseWre http://ocw.mit.edu 6.64 Continuum Electromechnics Fll 8 For informtion out citing these mterils or our Terms of Use, visit: http://ocw.mit.edu/terms. 6.64, Continuum Electromechnics,

Ó³ Ÿ , º 7(205) Ä1540 ˆ ˆŠ ˆ ˆŠ Š ˆ. .. ŠÊ Íμ,.. Ê ±μ,.. ² μ 1. Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê

Ó³ Ÿ. 016.. 13 º 7(05).. 1533Ä1540 ˆ ˆŠ ˆ ˆŠ Š ˆ œ Š ˆ NICA ˆ ˆˆ ƒ ƒ.. ŠÊ Íμ.. Ê ±μ.. ² μ 1 Ñ Ò É ÉÊÉ Ö ÒÌ ² μ Ê ² Î ² Ö μ É ÉμÎ μ μ ±Êʳ μ ± ³ μí Ê ±μ Ö ÉÖ ²ÒÌ μ μ Ö ²Ö É Ö μ μ Î μé É μ É Ê ±μ É ². μ

1 Ο ΣΕΤ ΑΣΚΗΣΕΩΝ (Ενδεικτικές Λύσεις)

ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΙΣΑΓΩΓΗ ΣΤΟ ΔΙΑΔΙΚΑΣΤΙΚΟ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟ (2009-2010) ΥΠΕΥΘΥΝΟΙ ΔΙΔΑΣΚΟΝΤΕΣ ΕΡΓΑΣΤΗΡΙΟΥ: Α. ΦΩΚΑ, K. ΣΤΑΜΟΣ

(f,g) f(x,y,v, w) = xy v= 0 x (v,y) = = = = = 3. g(x,y,v,w) = x+ 2y w= 0. (x,y) g g 1 2. Λύση 2. Με πλεγμένη παραγώγιση ως προς v, με σταθερό w :

ΤΕΣΤ Β.λύσεις ΟΜΑΔΑ Ι Οι εξισώσεις: {=, + = w} ορίζουν πλεγμένα τα {,} ως συναρτήσεις των {,w}. Να βρεθεί η μερική παράγωγος του ως προς. Λύση. Με τους τύπους πλεγμένης παραγώγισης: (,g) (,,, w) = = (,)

Ρεύμα. n q dx da dt dt. Ροή (γενικά):

ΡΕΥΜΑ (KΕΦ 25) Ροή (γενικά): Ρεύμα Η ποσότητα ενός μεγέθους που διέρχεται από μία επιφάνεια (ανά μονάδα χρόνου για κλασσικές ροές όπως εδώ). q v n η πυκνότητα n των φορτίων q: n=αριθμ. φορτίων ανά μονάδα

Š Œ Š, ƒˆ ƒ ˆ ˆ Œ.. Œμ μ μ

ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 016.. 47.. 5 Š Œ Š, ƒˆ ƒ ˆ ˆ Œ.. Œμ μ μ ˆ É ÉÊÉ μ ² ³ Î Ëμ ³ Í, Œμ ± Í μ ²Ó Ò ² μ É ²Ó ± Ö Ò Ê É É Œˆ ˆ, Œμ ± ˆ 149 Š Œ Ÿ ˆŸ Ÿ 1440 ƒ - ˆ 1484 ˆŸ ˆ ˆ ƒ œ ƒ 1505 ˆŸ Ä Œ 1518 Š ˆ 1538 ˆ

HONDA. Έτος κατασκευής

Accord + Coupe IV 2.0 16V (CB3) F20A2-A3 81 110 01/90-09/93 0800-0175 11,00 2.0 16V (CB3) F20A6 66 90 01/90-09/93 0800-0175 11,00 2.0i 16V (CB3-CC9) F20A8 98 133 01/90-09/93 0802-9205M 237,40 2.0i 16V

X Y 5 Z 2404 [0\0 234 ] = \ ] Y^\_ 054 ] ` 0_\04 4 a = ] 8 b 8b 8 c d X e e \0] 4 `4Z e \ 5023 f \ 5 g h i] 50] 5 `0 4 j k lmn l m

!" # $ % % & "# ' ( " & ) ' ' * "!"'+,, + - "!"'.!& +!, / 01 234 53 67 899 86: ; < 0 4 2 = >? @ A B C D E D C F A GHII DCAFJ HH K F I B HIL F KH D MND K BO I ADPD KH L F KGHG FAF E HQHL BRS FADS FA H ND

Εισαγωγή στη Μικροηλεκτρονική 1. Στοιχειακοί ηµιαγωγοί

Εισαγωγή στη Μικροηλεκτρονική 1 Στοιχειακοί ηµιαγωγοί Εισαγωγή στη Μικροηλεκτρονική Οµοιοπολικοί δεσµοί στο πυρίτιο Κρυσταλλική δοµή Πυριτίου ιάσταση κύβου για το Si: 0.543 nm Εισαγωγή στη Μικροηλεκτρονική

!"#ά%&'( 17 ) *+&,-,+ό/'(0 1+(23'(+'24ό0 5(- 6-/(%'7(ύ 9'2(3ή4&5(0 7&' 5;0 6-/&%%&<4&5'7ή0 =2(5'4ί&0

N'ώ+

QBER DISCUSSION PAPER No. 8/2013. On Assortative and Disassortative Mixing in Scale-Free Networks: The Case of Interbank Credit Networks

QBER DISCUSSION PAPER No. 8/2013 On Assortative and Disassortative Mixing in Scale-Free Networks: The Case of Interbank Credit Networks Karl Finger, Daniel Fricke and Thomas Lux ss rt t s ss rt t 1 r t

ΜΑΘΗΜΑ ΤEΤΑΡΤΟ ΜΑΘΗΜΑΤΙΚΩΝ ΓΙΑ ΟΙΚΟΝΟΜΟΛΟΓΟΥΣ ΑΣΚΗΣΕΙΣ ( ΙΑΦΟΡΙΚΟ-ΜΕΛΕΤΗ ΣΥΝΑΡΤΗΣΕΩΣ- ΕΦΑΡΜΟΓΕΣ ΣΤΑ ΟΙΚΟΝΟΜΙΚΑ)

ΜΑΘΗΜΑ ΤEΤΑΡΤΟ ΜΑΘΗΜΑΤΙΚΩΝ ΓΙΑ ΟΙΚΟΝΟΜΟΛΟΓΟΥΣ ΑΣΚΗΣΕΙΣ ( ΙΑΦΟΡΙΚΟ-ΜΕΛΕΤΗ ΣΥΝΑΡΤΗΣΕΩΣ- ΕΦΑΡΜΟΓΕΣ ΣΤΑ ΟΙΚΟΝΟΜΙΚΑ) A. Κανόνας de L Hospital (Συνέχεια από το προηγούµενο µάθηµα) Παράδειγµα 1. Να βρεθεί το

( ) ( ) ( ) ( ) ( ) 槡 槡 槡 ( ) 槡 槡 槡 槡 ( ) ( )

3 3 Vol.3.3 0 3 JournalofHarbinEngineeringUniversity Mar.0 doi:0.3969/j.isn.006-7043.0.03.0 ARIMA GARCH,, 5000 :!""#$%&' *+&,$-.,/0 ' 3$,456$*+7&'89 $:;,/0 ?4@A$ ARI MA GARCHBCDE FG%&HIJKL$ B

x E[x] x xµº λx. E[x] λx. x 2 3x +2

¾ λ¹ ÐÓÒ Ó ÙÖ ½ ¼ º õ ¹ ¹ ÙÖ ¾ ÙÖ º ÃÐ ¹ ½ ¼º ¹ Ð Ñ ÐÙÐÙ µ λ¹ λ¹ ÐÙÐÙ µº λ¹ º ý ½ ¼ ø λ¹ ÃÐ º λ¹ ÌÙÖ Ò ÌÙÖ º ÌÙÖ Ò ÚÓÒ Æ ÙÑ ÒÒ ¹ ÇÊÌÊ Æ Ä Çĺ ý λ¹ ¹ º Ö ÙØ ÓÒ Ñ Ò µ Ø ¹ ÓÛ ÓÑÔÙØ Ö µ ¹ λ¹ º λ¹ ÙÒØ ÓÒ Ð

ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΤΑΞΗ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ:28/05/2012

ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΤΑΞΗ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ:8/5/ ΘΕΜΑ Α Α. Θεωρία. Σελίδα σχολικού βιβλίου 53 Α. Θεωρία. Σελίδα σχολικού βιβλίου 9 Α3. Θεωρία. Σελίδα σχολικού βιβλίου 58

ΚΛΕΜΜΕΣ WAGO ΑΙΣΘΗΤΗΡΙΩΝ-ΕΝΕΡΓΟΠΟΙΗΤΩΝ

VER. DATE: 20/10/2013 ΠΑΝΑΓΙΩΤΗΣ ΣΠ. ΔΗΜΟΥΛΑΣ ΒΑΙΑ ΣΠ. ΔΗΜΟΥΛΑ E.E. ΔΗΜΟΥΛΑΣ ΑΥΤΟΜΑΤΙΣΜΟΙ ΣΥΣΤΗΜΑΤΑ ΜΕΤΡΗΣΕΩΝ ΚΑΙ ΑΥΤΟΜΑΤΙΣΜΟΥ ΚΡΗΤΗΣ 26 10439 ΑΘΗΝΑ ΤΗΛ: 210 8833337 ΦΑΞ: 210 8834436 SITE: www.dimoulas.com.gr

z k z + n N f(z n ) + K z n = z n 1 2N

Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά 6..5 Λύσεις Σειράς Ασκήσεων Άσκηση (α) Έστω z το όριο της ακολουθίας z n, δηλ. για κάθε ɛ > υπάρχει N(ɛ) ώστε z n z < ɛ για n > N. Για n > N(ɛ), είναι z n

ΚΕΦΑΛΑΙΟ 6. Τιμολόγηση Δικαιωμάτων σε συνεχή χρόνο Το μοντέλο των Black and Scholes

ΚΕΦΑΛΑΙΟ 6 Τιμολόγηη Δικαιωμάτων ε υνεχή χρόνο Το μοντέλο των Blk nd ol 6.. Το Μοντέλο των Blk ol ή Blk ol Mon Έτω μια χρηματοοικονομική αγορά εξεταζόμενη το χρονικό διάτημα [ ] για κάποιο δεδομένο Τ.

Οικονομική Πολιτική Ι: Σταθερές Συναλλαγματικές Ισοτιμίες χωρίς Κίνηση Κεφαλαίου

Κεφάλαιο 6 Οικονομική Πολιτική Ι: Σταθερές Συναλλαγματικές Ισοτιμίες χωρίς Κίνηση Κεφαλαίου 6.1 Σύνοψη Στο έκτο κεφάλαιο του συγγράμματος ξεκινάει η ανάλυση της μακροοικονομικής πολιτικής. Περιγράφονται

Dickey Rural Networks. Proof of Performance Report Summer 2017 Warm Weather Test. August 14-15, 2017

Dickey Rural Networks Proof of Performance Report Summer 2017 Warm Weather Test August 14-15, 2017 ENGINEERING FOR TELECOMMUNICATIONS 244 West Pioneer Road P.O. BOX 1003 Fond du Lac, WI 54936-1003 920.923.1034

NBER WORKING PAPER SERIES EQUILIBRIUM ASSET PRICES UNDER IMPERFECT CORPORATE CONTROL. James Dow Gary Gorton Arvind Krishnamurthy

NBER WORKING PAPER SERIES EQUILIBRIUM ASSET PRICES UNDER IMPERFECT CORPORATE CONTROL James Dow Gary Gorton Arvind Krishnamurthy Working Paper 9758 http://www.nber.org/papers/w9758 NATIONAL BUREAU OF ECONOMIC

γ n ϑ n n ψ T 8 Q 6 j, k, m, n, p, r, r t, x, y f m (x) (f(x)) m / a/b (f g)(x) = f(g(x)) n f f n I J α β I = α + βj N, Z, Q ϕ Εὐκλείδης ὁ Ἀλεξανδρεύς Στοιχεῖα ἄκρος καὶ μέσος λόγος ὕδωρ αἰθήρ ϕ φ Φ τ

l 0 l 2 l 1 l 1 l 1 l 2 l 2 l 1 l p λ λ µ R N l 2 R N l 2 2 = N x i l p p R N l p N p = ( x i p ) 1 p i=1 l 2 l p p = 2 l p l 1 R N l 1 i=1 x 2 i 1 = N x i i=1 l p p p R N l 0 0 = {i x i 0} R

http://www.mathematica.gr/forum/viewtopic.php?f=109&t=15584

Επιμέλεια: xr.tsif Σελίδα 1 ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΓΙΑ ΜΑΘΗΤΙΚΟΥΣ ΔΙΑΓΩΝΙΣΜΟΥΣ ΕΚΦΩΝΗΣΕΙΣ ΤΕΥΧΟΣ 5ο ΑΣΚΗΣΕΙΣ 401-500 Αφιερωμένο σε κάθε μαθητή που ασχολείται ή πρόκειται να ασχοληθεί με Μαθηματικούς διαγωνισμούς

Appendix A. Curvilinear coordinates. A.1 Lamé coefficients. Consider set of equations. ξ i = ξ i (x 1,x 2,x 3 ), i = 1,2,3

Appendix A Curvilinear coordinates A. Lamé coefficients Consider set of equations ξ i = ξ i x,x 2,x 3, i =,2,3 where ξ,ξ 2,ξ 3 independent, single-valued and continuous x,x 2,x 3 : coordinates of point

C F E E E F FF E F B F F A EA C AEC

Proceedings of the International Multiconference on Computer Science and Information Technology pp. 767 774 ISBN 978-83-60810-27-9 ISSN 1896-7094 CFEEEFFFEFBFFAEAC AEC EEEDB DACDB DEEE EDBCD BACE FE DD

Mantel & Haenzel (1959) Mantel-Haenszel

Mantel-Haenszel 2008 6 12 1 / 39 1 (, (, (,,, pp719 730 2 2 2 3 1 4 pp730 746 2 2, i j 3 / 39 Mantel & Haenzel (1959 Mantel N, Haenszel W Statistical aspects of the analysis of data from retrospective

ΗΥ118 Διακριτά Μαθηματικά. Εαρινό Εξάμηνο 2017

ΗΥ118 Διακριτά Μαθηματικά Εαρινό Εξάμηνο 2017 2 η Σειρά Ασκήσεων Λύσεις Άσκηση 2.1 [1 μονάδα] Έστω F(x,y) = «Το αυτοκίνητο x έχει μέγιστη ταχύτητα μεγαλύτερη από αυτή του αυτοκινήτου y», με Π.Ο. των x,y

Βραχυπρόθεσμες οικονομικές διακυμάνσεις

Βραχυπρόθεσμες οικονομικές διακυμάνσεις Συναθροιστική ζήτηση και συναθροιστική προσφορά Βραχυπρόθεσμες οικονομικές διακυμάνσεις Η οικονομική δραστηριότητα μεταβάλλεται από χρόνο σε χρόνο. Τις περισσότερες

J J l 2 J T l 1 J T J T l 2 l 1 J J l 1 c 0 J J J J J l 2 l 2 J J J T J T l 1 J J T J T J T J {e n } n N {e n } n N x X {λ n } n N R x = λ n e n {e n } n N {e n : n N} e n 0 n N k 1, k 2,..., k n N λ