Kovalentna veza , CO 2. U molekulima H 2
|
|
|
- Βερενίκη Δυοβουνιώτης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Kovalentna veza U molekulima H 2, N 2, O 2, CO 2, NH 3, H 2 O,... ili molekulima organskih jedinjenja ne postoje joni. To je veza između atoma i ona se bitno razlikuje od jonske veze a naziva se kovalentnom vezom. Luis je prvi objasnio ovu vezu. Teorije koje objašnjavaju kovalentnu vezu: Luisova oktetna teorija elektronska teorija valence KOVALENTNA VEZA Kvantno mehanička teorija - polarna, nepolarna, koordinativna - jednostruka, dvostruka i trostruka Teorija valentne veze Teorija molekulskih orbitala
2 Luisova oktetna teorija Po Luisu atomi postižu stabilnu elektronsku konfiguraciju (plemenitog gasa) stvaranjem jednog ili više zajedničkih elektronskih parova što čini kovalentnu ili atomsku vezu. Ti elektronski parovi su: - zajednički i povezuju dva jezgra - mogu biti samo iz spoljašnjih valentnih orbitala - elektroni koji ne učestvuju u stvaranju veze čine slobodne elektronske parove Reakcije se mogu prikazati - pomoću Luisovih simbola i strukturnih formula - elektronski parovi se često obilježavaju crticom.
3 Jednostruka kovalentna veza: Cl ili P Cl Cl H ili H C H H
4 Dvostruka kovalentna veza: Trostruka kovalentna veza:
5 Izuzeci od oktetnog pravila 1. Jedinjenja u kojima je centralni atom okruţen sa manje od 8 valentnih elektrona. Npr. - BeCl 2 gde oko Be ima ukupno 4 e - ( 2 elektronska para) - BF 3 gde imamo 6 elektrona (3 elektro. para) I u ovom slučaju možemo napisati Luisove formule: - gdje je zadovoljeno pravilo okteta za sve atome - formalno pozitivno naelektrisanje nalazi na atomu fluora (najelektronegativniji atom) - zato su ove strukturne formule malo vjerovatne
6 2.Jedinjenja u kojima je centralni atom okružen sa više od 8 e - Npr. :PCl 5, SF 4, SF 6, AsF 6, XeF 4, ICl 4 PCl 5 - oko atoma P imamo 10 elektrona - ove elektrone ne mogu primiti 3s i 3p orbitale fosfora - za vezu se moraju koristiti prazne 3d orbitale P koje su sljedeće po E 3. Jedinjenja sa neparnim brojem valentnih e - Primjer su: NO, NO 2, Cl 2 O 7N 1s 2 2s 2 2p 3 NO 5 v.e v.e - = 11 v.e - 8O 1s 2 2s 2 2p 4 NO 2-17 v.e - ; Cl 2 O - 19 v.e - Ovi molekuli se veoma reaktivni i obično grade dimere
7 Formalno naelektrisanje (naboj) Formalno naelektrisanje = N 1,e- - N 2, e- N 1e- - broj e - koji pripadaju atomu iz svakog elektronskog para u vezi + slobodni elektronski parovi N 2e- - broj valentnih elektrona Rezonantne strukture HNO 3 N (Z = 7; 5 v.e) 1s 2 2s 2 p 3 O(Z = 8 ; 6 v.e.) -1s 2 2s 2 p 4 => N - pripada 4 e - iz 4 elektr.para (nedostaje mu 1 e - pa je on pozitivan) => O - pripada 7 e - iz 1 elektr.para + 6 slobod. e - (ima 1 e - višak pa je on negativan)
8 Ovo naelektrisanje atoma je samo formalno jer je raspodjela stvarnog nealektrisanja određena razlikama u elektronegativnostima između atoma NO 3 - NH 4 +
9
10
11 Rezonantne strukturne formule Kod nekih jedinjenja Luisovim simbolima i formulama ne može se prikazati kov. veza kao što je to slučaj kod: O 3, NO 2, NO 3- itd. Npr. kod ozona struktura molekule može se predstaviti: Očekivani ugao 60 o Stvarni ugao
12 O 3 se može da prikaže rezonantnim strukturama - R. S. predstavljaju međustanje između hipotetičkih graničnih struktura - ove strukture se povezuju dvosmjernom strelicom O 3 NO 3 -
13 Prostorna usmerenost kovalentne veze odgovara pravcu u kome su atomske orbitale preklopljene. Teorija valentne veze Ova teorija za nastajanje hemijske veze koristi - teoriju talasno-mehaničkog modela elek. strukture atoma - prva tumačenja dali su Hajtler i London na atomu vodonika: kovalentna veza nastaje preklapanjem atomskih orbitala to jest preklapanjem talasnih funkcija ( ) dva elektrona sa suprotnim spinom Funkcija predstavlja orbitalu u kojoj se mogu naći maksimalno dva elektrona sa suprotnim spinom Ako elektroni imaju paralelni spin dolazi do njihovog odbijanja što onemogućava preklapanje atomskih orbitala (ne stvara se kovalentne veze među atomima)
14 T. V. V. objašnjava nastajanje kovalentne veze porastom vjerovat. nalaženja e - ( 2 ) u djelu prostora između dva atom. jezgra usled interakcije valent. e - i atoms. jezgara vez. atoma Funkcija predstavlja orbitalu u kojoj se mogu naći maksimalno dva elektrona sa suprotnim spinom = A (1) B (2) + A (2) B (1) + A (1) A (2) + B (1) B (2) koeficijent < 1 jzegra A jzegra B Pri preklapanju atomskih orbitala dolazi do porasta verovatnoće nalaţenja elektrona ( 2 ) u djelu prostora između jezgara A i B
15 Vjerovatnoća nalaţenja e - preklopljene orbitale za Vjerovatnoća nalaţenja e - za nepreklopljene orbitale Za stvaranja kovalentne veze moraju se preklopiti «bregovi» talasnih funkcija i njihove «doline». Tako nastaje nova talasna funkcija sa većom amplitudom (veća je vjerovatnoća nalaženja e - između spojenih atoma) Kada se preklope «brjeg» i «dolina» tada amplituda rezultujuće talasne funkcije ima manju vrijednost i ne dolazi do stvaranja kovalentne veze
16 Preklapanjem atomskih orbitala mogu nastati dvije vrste kovalentnih veza: -veza (primarna) i -veza (sekundarna) -veza -veza nastaje preklapanjem - dviju atomskih orbitala duţ međunuklearne ose (osa koja prolazi kroz jezgra dva atoma) - dvije s-orbitale, ili dvije p-orbitale ili s- i p-orbitala
17 Preklapanje orbitala
18 - veza u molekuli HCl - veza u molekuli Cl 2
19 -veza - veze nastaje bočnim preklapanjem - dviju p-orbitala - p- i d-orbitale ili - dviju d-orbitala iste simetrije (p y sa p y ili d yz sa d yz ) Do stvaranja -veze dolazi tek pošto se uspostavi -veza između dva atoma.
20 Usmjerenost kovalentnih veza Ugao koje zaklapaju -veza uglavnom je: - veći od ugla atomskih orbitala od kojih su nastale (zbog odbijanja «elektronskih oblaka» ) - ista situacija je i sa duţinom veza. Npr. u molekulu vode O gradi dvije -veze sa H i H - 1s 1 Dvije -veze nastaju preklapanjem po jedne p-orbitale kiseonika sa po jednom s-orbitalom atoma vdonika Te dve -veze bi trebalo da stoje pod uglom od 90 jer se pod tim uglom nalaze p-orbitale u O-atomu Ispitivanja su pokazala da je ugao između -veza 105.
21 H 2 O 105 o 92 o Kod amonijaka - NH 3 imamo 3 -veze pod uglom od 107 o
22 Hibridizacija Analizirajući molekul metana (CH 4 ) očekivali bi da ugljenik gradi: - dvije kovalentne veze nastale preklapanjem s-s orbitale C i H - dvije kovalentne veze nastale preklapanjem s-p orbitale H i C - ove veze bi trebalo da budu različite dužine Strukturnom analizom ovog molekula utvrđeno je: - da su sve četiri -veze iste - da su sve veze pod uglom od 109 (što znači da valentne s- i p-orbitale C sadržale isti nivo energije) Neslaganja eksperimentalnih rezultata i T. V. V. u CH 4 može se objasniti hibridizacijom predstavlja pojavu kombinovanja (mješanja) atomskih orbitala pri čemu nastaju nove degenerisane hibridne orbitale sa istim sadrţajem energije
23 Pri tumačenju hibridizacije potrebno je imati na umu: 1.hibridizacija je mješanje najmanje dvije različite AO 2. hibridizirati se mogu samo one orbitale koje se malo razlikuju u energiji 3. broj nastalih h.o. jednak je broju AO iz kojih su nastale 4. hibridizacija zahtjeva dodatnu energiju koja se vrati nakon nastajanja veze 5. hibridizacija se nikad ne primjenjuje na izolovani atom, koristi se samo za objašnjenje postojeće strukture molekule
24 Postojanje h.o. u izolovanom atomu nije dokazano i zato se pretpost. da one «nastaju» samo u trenutku stvara. molek. Tipovi hibridizacije: Tip hibridizacije Geometrija molekula Prostorni razmještaj Valentni ugao Broj energijski istih veza Primjeri sp- linearna pravac BeH 2, CO 2, C 2 H 2 sp 2 - trigonalna (trougaona) trougao AlH 3, SO 3, CO 2 3, NO 3, BF 3 sp 3 - tetraedarska tetraedar 109,5 4 SiH 4, NH 4+, H 2 O, HF, NH 3, CCl 4 dsp 2 - kvadrat 90 o 4 dsp 3 - trigonalnobipiramidalna 90 i PF 5, AsF 5, PCl 5 d 2 sp 3 - oktaedarska 90 6 SF 6, AsF 6 d 4 sp 3 - dodekaedar 8
25 sp- hibridizacija
26 Preklapanje orbitala Be
27 sp 2 - hibridizacija
28 F 120 o B F B sp 2- h.o. B p-orbit. F F
29 sp 3 - hibridizacija
30 C
31 NH 33 H 2 O H 2 O
32 Zavisnost vrijednosti ugla između σ - veza od broja slobodnih elektronskih parova u molekuli Zavisnost vrijednosti ugla između σ - veza od poluprečnika centralnog atoma
33 sp3d (dsp3 )- hibridizacija :PCl5, SF4, BrF3
34 sp3d2 (d2sp3 )- hibridizacija : SF6, XeF4, ClF5,PF6
35 Višestruke veze DVOSTRUKA eten - C 2 H 4
36
37 TROSTRUKA etin - C 2 H 2 + -
38
39 Teorija molekulskih orbitala Stanje e - u: - atomu definisano je talasnom funkcijom A koja predstavlja atomsku orbitalu - u molekulu određeno je talasnom funkcijom MO koja predstavlja molekulsku orbitalu Po T.M.O. kovalentna veza je rezultat kombinacije svih a.o. atoma koji čine odgovarajući molekul, dok prema Po T.V.V. kovalentna veza nastaje preklapanjem (kombinovanjem) samo atomskih orbitala valentnih elektrona. Linearnom kombinacijom atomskih orbitala (LCAO) nastaju dvije molekuske orbitale i to vezujuća ( MO ) i antivezujuća ( * MO ) MO = C 1 A + C 2 B i * MO = C 1 A - C 2 B - C 1 i C 2 koeficijent koji određuju udio svake od AO u MO
40 Interakcijom između atoma A i B povećava se vjerovatnoća nalaženja e - ( 2 MO ) u MO 2 MO 2 * MO 2 A 2 B 2 A 2 B Vjerovatnoća nalaženja e - u Vjerovatnoća nalaženja e - u vezujućoj MO - antivezujućoj MO - * MO MO
41 Vrste molekulskih orbitala Kombinovanjem orbitale dva atoma 1. s - s-orbitalom, 2. s - p-orbitalom ili 3. p p- orbitale duž međunuklearne ose, nastaju jedna -vezna MO i jedna *-antivezna MO Bočnim preklapanjem (kombinov.) p-orbitale jednog ato. sa: 1. p-orbitalom ili 2. d-orbitalom drugog atoma nastaju jedna -vezna MO i jedna *-antivezna MO MO svojim oblikom podsjećaju na atomske orbitale Kombinuju se samo AO koje imaju sličan sadržaj energije. Ostale AO jednog atoma, koje se ne kombinuju sa AO drugog atoma, predstavljaju nevezne molekulske orbitale. Obeleţavaju se simbolima n i n.
42 a) preklapanje s- orbitala i nastajanje σ i σ* MO u H 2 c) preklapanje p- orbitala i nastajanje i * MO b) preklapanje p- orbitala i nastajanje σ i σ* MO
43 Oznaka odgovarajuće molekulske orbitale sadrži - vrstu molekulske orbitale (, *, n,, * ili n ), - vrstu atomskih orbitala (1s, 2s, 2p, itd.) i - broj elektrona koji se nalazi u datoj MO. Npr. 2s 1 - predstavlja -veznu MO -koja je nastala kombinovanjem dvije 2s-orbitale - u njoj se nalazi jedan elektron. *2p y2 (ili y *2p 2 ) predstavlja - antiveznu *-molekulsku orbitalu - koja je nastala kombinovanjem dvije 2p y -AO - u njoj se nalaze dva elektrona. Za prikazivanje elektronske konfiguracije molekula na osnovu TMO koriste se energetski dijagrami - oni pokazuju energetske nivoe MO - prema energetskom nivou AO čijim kombin. nastaju.
44 s Dijagram energetskih nivoa MO σ 1s i σ*1s koje nastaju kombinovanjem 1s orbitala Šematski prikaz MO σ 1s i σ*1s koje nastaju kombinovanjem 1s orbitala p U molekulima elemenata druge periode PS sa Z = 5, 6 i 7 (B 2, C 2 i N 2 ), zbog odbijanja koje postoji između MO energija 2p z - MO u tim molekulima je veća od energije degenerisanih 2p x - i 2p y -MO.
45
46 Elektroni se u molekulu raspoređuju u odgovarajuće MO na isti način kao što se raspoređuju u odgovarajuće AO Pravila za crtanje dijagrama MO: 1.Broj nastalih MO mora biti jednak broju kombinovanih AO 2. Da bi se AO mogle kombinovati moraju biti bliskih energija i moraju imati odgovarajuću simetriju 3. Efikasnost kombinovanja AO je proporcionalna njihovom prekapanju što je bolje preklapanje vezna MO će imati nižu energiju a antivezivna MO višu 4. Prvo se popunjava MO sa najnižom energijom 5. Svaka MO može da primi maksimalno dva e - suprotnih spinova 6. Ako su dvije ili više MO degenerisane (imaju iste energije) popunjavaće se u skladu sa Hundovim pravilom
47 Ako je zbir e - u veznim MO (vezni elektroni) veći od zbira e - u antiveznim MO (antivezni elektroni) tada dolazi do stvaranja hemijske veze Nastajanje veze određuje se preko vrijednosti koji se naziva RED VEZE: 1 red veze : RV = ( N vez.elek. N antivez.elek. ) 2 Ako je RV : - jednak - nuli neće doći do stvaranj hem. veze - jednak - 1/2 veza se uspostavlja sa jednim e - - jednak jedan uspostavlja se jednostruka veza Teorija MO daje objašnjenja i za magnetna svojstva molekula, a koja se mogu i praktično izmjeriti.
48 Joni, atomi i molekule koji sadrže: 1. nesparene elektrone -u magnetnom polju, privlače linije sila polja i ponašaju se kao paramagnetici 2. sve sparene elektrone - odbijaju linije sila magnetnog polja i ponašaju se kao dijamagnetici H 2 2H(1s 1 ) H 2 [( 1s 2 )] r H o = -435 kj/mol - RV = 1 - diamagnetična molekula H 2 + H(1s 1 ) + H + (1s 0 ) H 2+ [( 1s 1 )] r H o =-256 kj/mol - RV = 1 - paramagnnetična molekula
49 He 2 2He(1s 2 ) He 2 [( 1s 2 ) ( *1s 2 )] RV = 0 He 2 + He(1s 2 ) + He + (1s 1 ) He 2+ [( 1s 2 ) ( *1s 1 )] - r H o = -242 kj/mol - RV = ½ - paramagnetičns molekula Li 2 2Li(1s 2 2s 1 ) Li 2 [( 1s 2 ) ( *1s 2 ) ( 2s 2 )] - r H o = -110 kj/mol - RV = 1 - diamagnetična molekula
50 B 2 2 B(1s 2 2s 2 2p 1 ) B 2 [( 1s 2 ) ( *1s 2 ) ( 2s 2 ) ( *2s 2 ) ( 2p x1 ) ( 2p y1 )] - r H o = -272 kj/mol - RV = 1 - paramagnetična molekula
51 C 2 2 C(1s 2 2s 2 2p 2 ) C 2 [( 1s 2 )( *1s 2 )( 2s 2 )( *2s 2 )( 2p x2 )( 2p y2 )] ili C 2 [ KK ( 2s 2 )( *2s 2 )( 2p x2 )( 2p y2 )] - r H o = -593 kj/mol - RV = 2 - diamagnetična molekula N 2 2 N(1s 2 2s 2 2p 3 ) N 2 [( 1s 2 ) ( *1s 2 ) ( 2s 2 ) ( *2s 2 )( 2p x2 ) ( 2p y2 )( 2p z2 )] ili N 2 [ KK( 2s 2 ) ( *2s 2 )( 2p x2 ) ( 2p y2 )( 2p z2 )] - r H o = -946 kj/mol - RV = 3 - diamagnetična molekula
52 O 2 2 O(1s 2 2s 2 2p 4 ) O 2 [( 1s 2 )( *1s 2 )( 2s 2 )( *2s 2 )( 2p z2 )( 2p x2 )( 2p y2 ) ( *2p x1 )( *2p y1 )] O 2 [KK( 2s 2 )( *2s 2 )( 2p z2 )( 2p x2 )( 2p y2 )( *2p x1 ) ( *2p y1 )] - r H o = -498 kj/mol - RV = 2 - paramagnetična molekula F 2 2 F(1s 2 2s 2 2p 5 ) F 2 [( 1s 2 )( *1s 2 )( 2s 2 )( *2s 2 )( 2p z2 )( 2p x2 )( 2p y2 ) ( *2p x2 )( *2p y2 )] F 2 [KK( 2s 2 )( *2s 2 )( 2p z2 )( 2p x2 )( 2p y2 )( *2p x2 ) ( *2p y2 )] - r H o = -158 kj/mol - RV = 1 - diamagnetična molekula
53 Heteronuklearni molekuli Dijagrami energetskih nivoa MO kada su razlike u elektronegativnosti između atoma A i B a) jako male b) veće i c) znatne
54 H (1s 1 ) + F(K2s 2 2p 5 ) HF [ KK ( 2p z2 ) ( n 2s 2 ) ( n 2p x2 ) ( n 2p y2 )] - RV = 1 - diamagnetična molekula
55 NO [ KK ( 2s 2 ) ( *2 s 2 ) ( 2p 2 ) ( 2p x2 ) ( 2p y2 ) ( * p z1 )]
56 C (K 2s 2 2p 2 )+O(K2s 2 2p 4 ) CO[ KK( n 1 2 ) ( 22 ) ( p x2 ) ( p y2 ) ( n 3 2 ) ]
57 CO 2 [ KKK ( n s 2 ) ( n s 2 ) ( s2 ) ( z2 ) ( p x2 ) ( p y2 ) ( n p x2 ) ( n p y2 ) ]
58 Polarnost kovalentne veze K. V. nepolarna polarna H 2, O 2, N 2, H 2 O 2, N 2 H 4, CCl 4, H 2 O, HCl, HBr... Nepolarna kovalentna veza moţe se očekivati - između atoma istih elemenata (H 2, O 2, N 2 ) ili - u slučajevima kada je u MO podjednak udio AO oba atoma (elektronski par se nalazi na podjednakoj udaljenosti od oba jezgra (CCl 4, N 2 H 4, H 2 O 2 ) Polarna kovalentna veza moţe se očekivati: - između atoma koji imaju veliku razliku u elektronegativnosti - kada jedan od atoma više privlači sebi elektronski par - polarnost molek. izražava se preko dipolnog momenta - µ
59 Dipolni momenat - je vektorska veličina usmjerena od pozitivnog ka negativnom naelektrisanju gdje je: Q - naelektrisanje (C) l - rastojanje između + i centra naelektrisanja Npr. - CO 2 je linearan molekul, sabiranjem dva vektora istog intenzitetai pravca, a suprotnog smera, dobije se da je µ = 0, molekul jenepolaran - CCl 4 (µ = 0, iako je pojedinačno C- Cl veza polarana )
60 Smanjenje polarsnosti
61 Ponašanje polarnih molek. u električnom polju
62 Vrijednosti dipol. momenta i udjela jonske veze u halogenovodonicima Elektronegativnost Pauling je definisao elektronegativnost : kao mjeru sposobnosti za privlačenje elektrona od strane nekog atoma, pri uspostavljanju hemijske veze, naziva se elektronegativnost (i obeležava sa χ (grčko slovo hi ) ili EN). Eksperimentalno je utvrđeno da je : E pol. K.V. >E nepol. K.V za E A-B E A-B = k (χ B - χ A ) 2 Miliken je elektronegativnost definisao kao:
63 Najveću elektronegativnost ima :- fluor, x = 4 Najmanju elektronegativnost :- alkalni metali, francijum χ = 0,7 tipični metali od 1 do 2 metaloidi oko 2 nemetali veći od 2 Tablica koeficijenata elektronegativnosti po Paulingu
64 Razlika elektronegativnosti sluţi za procjenu karaktera hemijske veze 1. ako je χ B - χ A = 0 molekula je nepolarna 2. ako je χ B - χ A >1,9 udio jonske veze je veći od 50 % 3. ako je χ B - χ A < 1,9 udio kovalentne veze je veći od 50 %
65 Svojstva kovalentne veze DUŢINOM K.V. Se definiše ENERGIJOM USMJERENOŠĆU U PROSTORU 1. Dužina kovalentne veze je rastojanje između atoma vezanih K.V. i odgovara zbiru kovalentnih poluprečnika Kovalentni poluprečnici i duţina kovalentne veze Duţina jednostruke veze > duţine dvostruke > duţine trostruke.
66 2. Energija kovalentne veze Energija K.V. je E koja je potrebna da se u 1 molu molekule AB u gasovitom stanju raskine kovalentna veza i dobije po 1mol A (g) i B (g) Energija nepolarne K.V. E A-B = 1/2 E A-A - 1/2 E B-B = k (χ B - χ A ) 2 Energija npolarne K.V. Kod polarnih molekula usljed jačeg privlačenja elektronegativnijih atoma E je veća od izračunate E za nepolarnu molekulu (E A-B ) E A-B = E * A-B - E A-B 3. Usmjerenost kovalentne veze Kovalentna veza je usmjerena u prostoru (u pravacu usmjerenja atomskih orbitala ) i vektorska je veličina
67 Karakteristike jedinjenja sa kovalentnom vezom 1. Molekule zbog usmjerenosti i krutosti K.V.i maju : - definisanu strukturu i geometrijski oblik, - atomi ne mogu ni izaći iz molekula ni promjeniti svoj položaj u molekulu a da se pri tom ne razori molekula 2. Privlačne sile između molekula sa K.V. su slabe, pa su zbog toga ta jedinjenja obično - gasovi (CH 4, N 2, SF 6...), - tečnosti (CCl 4, Br 2, benzen.. ) ili - čvrste supstance (I 2, S 8, P 4..) koje lako sublimišu ili imaju relativno niske t t i t k 3. Jedinjenja sa kovalentnom vezom najčešće se: - tope na temperaturi nižoj od 300 C a - ključaju na temperaturi nižoj od 500 C.
68 Izuzeci od ovog pravila javljaju se kod - jedinjenja koje grade atomsku kristalnu rešetku sa kovalentnom vezom (kod kvarca i dijamanta ) - ova jedinjenja izgrađena su od velikog broja jedinica a ne molekule Kristalna rešetka kod ova dva jedinjeja ima tetraedarsku strukturu što uslovljava i ponašanje tih jedinjenja (karakteristika ove strukture je dobra provodljivost toplote, slaba provodljivost električne struje, hemijska inertnost: kvarc : t t = C i t k = C dijamant : t t = C i t k = C 4. Jedinjenja sa K.V. najčešće se slabo rastvaraju u vodi 5. Jedinjenja sa kovalentnom vezom koja se u vodi dobro rastvaraju je usljed hemijske reakcije sa vodom ( NH 3, HCl i dr.) 6. Jedinjenja sa K.V. razlikuju se od jonskih jedinjenja i po tome što slabo ili nikako ne provode električnu struju u tečnom ili čvrstom stanju ili u vodenom rastvoru (rastvori neelektrolita).
HEMIJSKA VEZA TEORIJA VALENTNE VEZE
 TEORIJA VALENTNE VEZE Kovalentna veza nastaje preklapanjem atomskih orbitala valentnih elektrona, pri čemu je region preklapanja između dva jezgra okupiran parom elektrona. - Nastalu kovalentnu vezu opisuje
TEORIJA VALENTNE VEZE Kovalentna veza nastaje preklapanjem atomskih orbitala valentnih elektrona, pri čemu je region preklapanja između dva jezgra okupiran parom elektrona. - Nastalu kovalentnu vezu opisuje
Pri međusobnom spajanju atoma nastaje energetski stabilniji sistem. To se postiže:
 HEMIJSKE VEZE Pri međusobnom spajanju atoma nastaje energetski stabilniji sistem. To se postiže: - prelaskom atoma u pozitivno i negativno naelektrisane jone koji se međusobno privlače, jonska veza - sparivanjem
HEMIJSKE VEZE Pri međusobnom spajanju atoma nastaje energetski stabilniji sistem. To se postiže: - prelaskom atoma u pozitivno i negativno naelektrisane jone koji se međusobno privlače, jonska veza - sparivanjem
SEKUNDARNE VEZE međumolekulske veze
 PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
HEMIJSKA VEZA ŠTA DRŽI STVARI (ATOME) ZAJEDNO?
 HEMIJSKA VEZA ŠTA DRŽI STVARI (ATOME) ZAJEDNO? U OKVIRU OVOG POGLAVLJA ĆEMO RADITI Jonska i kovalentna veza. Metalna veza. Elektronska teorija hemijske veze. Struktura molekula. Međumolekulske interakcije.
HEMIJSKA VEZA ŠTA DRŽI STVARI (ATOME) ZAJEDNO? U OKVIRU OVOG POGLAVLJA ĆEMO RADITI Jonska i kovalentna veza. Metalna veza. Elektronska teorija hemijske veze. Struktura molekula. Međumolekulske interakcije.
U stvaranju hemijske veze među atomima učestvuju samo elektroni u najvišem energetskom nivou valentni elektroni
 HEMIJSKA VEZA ELEKTRONSKA TEORIJA VALENCE U stvaranju hemijske veze među atomima učestvuju samo elektroni u najvišem energetskom nivou valentni elektroni Atomi teže da postignu oktet elektrona na poslednjem
HEMIJSKA VEZA ELEKTRONSKA TEORIJA VALENCE U stvaranju hemijske veze među atomima učestvuju samo elektroni u najvišem energetskom nivou valentni elektroni Atomi teže da postignu oktet elektrona na poslednjem
1. razred gimnazije- opšti i prirodno-matematički smer STRUKTURA MOLEKULA HEMIJSKA VEZA
 EMIJSKE VEZE 1 razred gimnazije- opšti i prirodno-matematički smer STRUKTURA MLEKULA Molekul je najsitnija čestica koja se sastoji od dva ili više istih atoma, a to su molekuli elemenata: Cl 2, 2, N 2,
EMIJSKE VEZE 1 razred gimnazije- opšti i prirodno-matematički smer STRUKTURA MLEKULA Molekul je najsitnija čestica koja se sastoji od dva ili više istih atoma, a to su molekuli elemenata: Cl 2, 2, N 2,
Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze:
 Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze: Jonska, Kovalentna i Metalna Luisovi simboli veoma zgodan
Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze: Jonska, Kovalentna i Metalna Luisovi simboli veoma zgodan
Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze:
 Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze: Jonska, Kovalentna i Metalna Luisovi simboli veoma zgodan
Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze: Jonska, Kovalentna i Metalna Luisovi simboli veoma zgodan
Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne
 Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne metode (rentgenska kristalografija, NMR spektroskopija...)
Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne metode (rentgenska kristalografija, NMR spektroskopija...)
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne
 Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne metode (rentgenska kristalografija, NMR spektroskopija...)
Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne metode (rentgenska kristalografija, NMR spektroskopija...)
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
1s 2 2s 2 2p 2. C-atom. Hibridne atomske orbitale. sp 3 hibridizacija. sp 3. Elektronska konfiguracija ugljenika: aktivacija. ekscitovano stanje
 PREAVAJE 2. Ugljenik je u organskim jedinjenjima četvorovalentan. Elektronska konfiguracija ugljenika: 1s 2 2 2p 2 dva nesparena elektrona -atom oc.dr Mirjana Abramović 2p osnovno stanje aktivacija 2p
PREAVAJE 2. Ugljenik je u organskim jedinjenjima četvorovalentan. Elektronska konfiguracija ugljenika: 1s 2 2 2p 2 dva nesparena elektrona -atom oc.dr Mirjana Abramović 2p osnovno stanje aktivacija 2p
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
Teorija molekulskoi orbitala linearna kombinacija atomskih orbitala(lcao)
 Teorija molekulskoi orbitala linearna kombinacija atomskih orbitala(lcao) Kada je elektron u blizini jezgre jednog atoma onda njegova valna funkcija sliči atomskoj orbitali tog atoma. Zbrajanjem atomskih
Teorija molekulskoi orbitala linearna kombinacija atomskih orbitala(lcao) Kada je elektron u blizini jezgre jednog atoma onda njegova valna funkcija sliči atomskoj orbitali tog atoma. Zbrajanjem atomskih
n (glavni ) 1, 2, 3,.. veličina orbitale i njena energija E= -R(1/n 2 )
 Kvantni brojevi Jedna atomska orbitala je definisana sa tri kvantna broja n l m l Elektroni su rasporedjeni u nivoima i podnivoima n l definiše nivo definiše podnivo ukupni broj orbitala u podnivou: 2
Kvantni brojevi Jedna atomska orbitala je definisana sa tri kvantna broja n l m l Elektroni su rasporedjeni u nivoima i podnivoima n l definiše nivo definiše podnivo ukupni broj orbitala u podnivou: 2
3. razred gimnazije- opšti i prirodno-matematički smer ALKENI. Aciklični nezasićeni ugljovodonici koji imaju jednu dvostruku vezu.
 ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
dr.sc. M. Cetina, doc. Tekstilno-tehnološki fakultet, Zavod za primijenjenu kemiju
 Kovalentna veza Za razliku od ionske veze gdje se veza ostvaruje prijenosom elektrona, kod kovalentne veze ona se ostvaruje tako da u toj vezi atomi dijele jedan ili više zajedničkih elektronskih parova.
Kovalentna veza Za razliku od ionske veze gdje se veza ostvaruje prijenosom elektrona, kod kovalentne veze ona se ostvaruje tako da u toj vezi atomi dijele jedan ili više zajedničkih elektronskih parova.
MEĐUMOLEKULSKE SILE JON-DIPOL DIPOL VODONIČNE NE VEZE DIPOL DIPOL-DIPOL DIPOL-INDUKOVANI INDUKOVANI JON-INDUKOVANI DISPERZNE SILE
 MEĐUMLEKULSKE SILE JN-DIPL VDNIČNE NE VEZE DIPL-DIPL JN-INDUKVANI DIPL DIPL-INDUKVANI INDUKVANI DIPL DISPERZNE SILE MEĐUMLEKULSKE SILE jake JNSKA VEZA (metal-nemetal) KVALENTNA VEZA (nemetal-nemetal) METALNA
MEĐUMLEKULSKE SILE JN-DIPL VDNIČNE NE VEZE DIPL-DIPL JN-INDUKVANI DIPL DIPL-INDUKVANI INDUKVANI DIPL DISPERZNE SILE MEĐUMLEKULSKE SILE jake JNSKA VEZA (metal-nemetal) KVALENTNA VEZA (nemetal-nemetal) METALNA
STRUKTURA ATOMA. Dalton (1803) Tomson (1904) Raderford (1911) Bor (1913) Šredinger (1926)
 Dalton (1803) Tomson (1904) Raderford (1911) Bor (1913) Šredinger (1926) TALASNO MEHANIČKI MODEL ATOMA Hipoteza de Brolja Elektroni i fotoni imaju dvojnu prirodu: talasnu i korpuskularnu. E = hν E = mc
Dalton (1803) Tomson (1904) Raderford (1911) Bor (1913) Šredinger (1926) TALASNO MEHANIČKI MODEL ATOMA Hipoteza de Brolja Elektroni i fotoni imaju dvojnu prirodu: talasnu i korpuskularnu. E = hν E = mc
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
JONSKA VEZA (metal-nemetal) KOVALENTNA VEZA (nemetal-nemetal) METALNA VEZA (metal-metal) jake H N. prelazne VODONIČNA VEZA H F
 HEMIJSKE VEZE HEMIJSKE VEZE I GRAĐA JEDINJENJA,, I deo Postoje tri osnovna tipa veza (primarne veze) i one imaju najveći uticaj na svojstva jedinjenja. Pored njih postoje i dopunske (sekundarne) veze između
HEMIJSKE VEZE HEMIJSKE VEZE I GRAĐA JEDINJENJA,, I deo Postoje tri osnovna tipa veza (primarne veze) i one imaju najveći uticaj na svojstva jedinjenja. Pored njih postoje i dopunske (sekundarne) veze između
S t r a n a 1. 1.Povezati jonsku jačinu rastvora: a) MgCl 2 b) Al 2 (SO 4 ) 3 sa njihovim molalitetima, m. za so tipa: M p X q. pa je jonska jačina:
 S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
NOMENKLATURA ORGANSKIH SPOJEVA. Imenovanje aromatskih ugljikovodika
 NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
Teorijske osnove informatike 1
 Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
5. Karakteristične funkcije
 5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
( ) ( ) 2 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET. Zadaci za pripremu polaganja kvalifikacionog ispita iz Matematike. 1. Riješiti jednačine: 4
 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
I HEMIJSKI ZAKONI I STRUKTURA SUPSTANCI
 dr Ljiljana Vojinović-Ješić I HEMIJSKI ZAKONI I STRUKTURA SUPSTANCI ZAKON STALNIH MASENIH ODNOSA (I stehiometrijski zakon, Prust, 1799) Maseni odnos elemenata u datom jedinjenju je stalan, bez obzira na
dr Ljiljana Vojinović-Ješić I HEMIJSKI ZAKONI I STRUKTURA SUPSTANCI ZAKON STALNIH MASENIH ODNOSA (I stehiometrijski zakon, Prust, 1799) Maseni odnos elemenata u datom jedinjenju je stalan, bez obzira na
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
RIJEŠENI ZADACI I TEORIJA IZ
 RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
OBRTNA TELA. Vladimir Marinkov OBRTNA TELA VALJAK
 OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
Ĉetverokut - DOMAĆA ZADAĆA. Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke.
 Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
Riješeni zadaci: Nizovi realnih brojeva
 Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
elektronskog para samo jednog od atoma u vezi
 KOMPLEKSNI SPOJEVI Spojevi u kojima se nalaze skupine atoma koji su povezani u više ili manje stabilne jedinice u krutom, tekućem, otopljenom i plinovitom stanju. Koordinacijski spojevi jer imaju koordinacijsku
KOMPLEKSNI SPOJEVI Spojevi u kojima se nalaze skupine atoma koji su povezani u više ili manje stabilne jedinice u krutom, tekućem, otopljenom i plinovitom stanju. Koordinacijski spojevi jer imaju koordinacijsku
Osnove elektrotehnike I popravni parcijalni ispit VARIJANTA A
 Osnove elektrotehnike I popravni parcijalni ispit 1..014. VARIJANTA A Prezime i ime: Broj indeksa: Profesorov prvi postulat: Što se ne može pročitati, ne može se ni ocijeniti. A C 1.1. Tri naelektrisanja
Osnove elektrotehnike I popravni parcijalni ispit 1..014. VARIJANTA A Prezime i ime: Broj indeksa: Profesorov prvi postulat: Što se ne može pročitati, ne može se ni ocijeniti. A C 1.1. Tri naelektrisanja
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
 TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI)
 IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
KERAMIKA, BETON I DRVO
 VJEŽBE: četvrtak, 12:15-14:00 KERAMIKA, BETON I DRVO Vježba 1. Ionske i kovalentne strukture Prof.dr.sc. Lidija Ćurković STRUKTURA ČVRSTIH (krutih) TVARI ovisi o: 1. VRSTI VEZA IZMEĐU STRUKTURNIH JEDINICA
VJEŽBE: četvrtak, 12:15-14:00 KERAMIKA, BETON I DRVO Vježba 1. Ionske i kovalentne strukture Prof.dr.sc. Lidija Ćurković STRUKTURA ČVRSTIH (krutih) TVARI ovisi o: 1. VRSTI VEZA IZMEĐU STRUKTURNIH JEDINICA
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Zavrxni ispit iz Matematiqke analize 1
 Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
 Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
III VEŽBA: FURIJEOVI REDOVI
 III VEŽBA: URIJEOVI REDOVI 3.1. eorijska osnova Posmatrajmo neki vremenski kontinualan signal x(t) na intervalu definisati: t + t t. ada se može X [ k ] = 1 t + t x ( t ) e j 2 π kf t dt, gde je f = 1/.
III VEŽBA: URIJEOVI REDOVI 3.1. eorijska osnova Posmatrajmo neki vremenski kontinualan signal x(t) na intervalu definisati: t + t t. ada se može X [ k ] = 1 t + t x ( t ) e j 2 π kf t dt, gde je f = 1/.
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
( , 2. kolokvij)
 A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
Funkcije dviju varjabli (zadaci za vježbu)
 Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
Linearna algebra 2 prvi kolokvij,
 1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
INTEGRALNI RAČUN. Teorije, metodike i povijest infinitezimalnih računa. Lucija Mijić 17. veljače 2011.
 INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
DIMENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE
 TEORIJA ETONSKIH KONSTRUKCIJA T- DIENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE 3.5 f "2" η y 2 D G N z d y A "" 0 Z a a G - tačka presek koja određje položaj sistemne
TEORIJA ETONSKIH KONSTRUKCIJA T- DIENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE 3.5 f "2" η y 2 D G N z d y A "" 0 Z a a G - tačka presek koja određje položaj sistemne
Strukture podataka i algoritmi 1. kolokvij 16. studenog Zadatak 1
 Strukture podataka i algoritmi 1. kolokvij Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i službeni šalabahter. Predajete samo papire koje ste dobili. Rezultati i uvid u kolokvije: ponedjeljak,
Strukture podataka i algoritmi 1. kolokvij Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i službeni šalabahter. Predajete samo papire koje ste dobili. Rezultati i uvid u kolokvije: ponedjeljak,
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Matematička analiza 1 dodatni zadaci
 Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Otpornost R u kolu naizmjenične struje
 Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
4.7. Zadaci Formalizam diferenciranja (teorija na stranama ) 343. Znajući izvod funkcije x arctg x, odrediti izvod funkcije x arcctg x.
 4.7. ZADACI 87 4.7. Zadaci 4.7.. Formalizam diferenciranja teorija na stranama 4-46) 340. Znajući izvod funkcije arcsin, odrediti izvod funkcije arccos. Rešenje. Polazeći od jednakosti arcsin + arccos
4.7. ZADACI 87 4.7. Zadaci 4.7.. Formalizam diferenciranja teorija na stranama 4-46) 340. Znajući izvod funkcije arcsin, odrediti izvod funkcije arccos. Rešenje. Polazeći od jednakosti arcsin + arccos
Verovatnoća i Statistika I deo Teorija verovatnoće (zadaci) Beleške dr Bobana Marinkovića
 Verovatnoća i Statistika I deo Teorija verovatnoće zadaci Beleške dr Bobana Marinkovića Iz skupa, 2,, 00} bira se na slučajan način 5 brojeva Odrediti skup elementarnih dogadjaja ako se brojevi biraju
Verovatnoća i Statistika I deo Teorija verovatnoće zadaci Beleške dr Bobana Marinkovića Iz skupa, 2,, 00} bira se na slučajan način 5 brojeva Odrediti skup elementarnih dogadjaja ako se brojevi biraju
Elektronska struktura atoma
 Elektronska struktura atoma Raderfordov atomski model jezgro u sredini pozitivno naelektrisano skoro sva masa u jezgru veoma malo Elektroni kruže oko jezgra elektrostatičke interakcije ih drže da ne napuste
Elektronska struktura atoma Raderfordov atomski model jezgro u sredini pozitivno naelektrisano skoro sva masa u jezgru veoma malo Elektroni kruže oko jezgra elektrostatičke interakcije ih drže da ne napuste
SISTEMI NELINEARNIH JEDNAČINA
 SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE
 **** MLADEN SRAGA **** 011. UNIVERZALNA ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE SKUP REALNIH BROJEVA α Autor: MLADEN SRAGA Grafički urednik: BESPLATNA - WEB-VARIJANTA Tisak: M.I.M.-SRAGA
**** MLADEN SRAGA **** 011. UNIVERZALNA ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE SKUP REALNIH BROJEVA α Autor: MLADEN SRAGA Grafički urednik: BESPLATNA - WEB-VARIJANTA Tisak: M.I.M.-SRAGA
Osnovne teoreme diferencijalnog računa
 Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
7 Algebarske jednadžbe
 7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
Osnovne veličine, jedinice i izračunavanja u hemiji
 Osnovne veličine, jedinice i izračunavanja u hemiji Pregled pojmova veličina i njihovih jedinica koje se koriste pri osnovnim izračunavanjima u hemiji dat je u Tabeli 1. Tabela 1. Veličine i njihove jedinice
Osnovne veličine, jedinice i izračunavanja u hemiji Pregled pojmova veličina i njihovih jedinica koje se koriste pri osnovnim izračunavanjima u hemiji dat je u Tabeli 1. Tabela 1. Veličine i njihove jedinice
XI dvoqas veжbi dr Vladimir Balti. 4. Stabla
 XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
Pismeni ispit iz matematike GRUPA A 1. Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj, zatim naći 4 z.
 Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
, 81, 5?J,. 1o~",mlt. [ BO'?o~ ~Iel7L1 povr.sil?lj pt"en:nt7 cf~ ~ <;). So. r~ ~ I~ + 2 JA = (;82,67'11:/'+2-[ 4'33.10'+ 7M.
 J r_jl v. el7l1 povr.sl?lj pt"en:nt7 cf \ L.sj,,;, ocredz' 3 Q),sof'stvene f1?(j'me")7e?j1erc!je b) po{o!.aj 'i1m/' ce/y11ra.[,p! (j'j,a 1lerc!/e
J r_jl v. el7l1 povr.sl?lj pt"en:nt7 cf \ L.sj,,;, ocredz' 3 Q),sof'stvene f1?(j'me")7e?j1erc!je b) po{o!.aj 'i1m/' ce/y11ra.[,p! (j'j,a 1lerc!/e
TEORIJA KRISTALNOG POLJA TEORIJA LIGANDNOG POLJA. ili ELETRONSKA STRUKTURA KOORDINACIONIH JEDINJENJA
 TEORIJA KRISTALNOG POLJA TEORIJA LIGANDNOG POLJA ili ELETRONSKA STRUKTURA KOORDINACIONIH JEDINJENJA Alfred Verner otac modere neorganske hemije Prusko plavo - Fe 4 [Fe(CN) 6 ] 3, je prvo poznati sintetisani
TEORIJA KRISTALNOG POLJA TEORIJA LIGANDNOG POLJA ili ELETRONSKA STRUKTURA KOORDINACIONIH JEDINJENJA Alfred Verner otac modere neorganske hemije Prusko plavo - Fe 4 [Fe(CN) 6 ] 3, je prvo poznati sintetisani
Elektronska struktura atoma
 Elektronska struktura atoma Raderfordov atomski model jezgro u sredini pozitivno naelektrisano skoro sva masa jezgru veoma malo Elektroni kruže oko jezgra elektrostatičke interakcije ih drže da ne napuste
Elektronska struktura atoma Raderfordov atomski model jezgro u sredini pozitivno naelektrisano skoro sva masa jezgru veoma malo Elektroni kruže oko jezgra elektrostatičke interakcije ih drže da ne napuste
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
Linearna algebra 2 prvi kolokvij,
 Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f
 IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
radni nerecenzirani materijal za predavanja R(f) = {f(x) x D}
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Rad, snaga, energija. Tehnička fizika 1 03/11/2017 Tehnološki fakultet
 Rad, snaga, energija Tehnička fizika 1 03/11/2017 Tehnološki fakultet Rad i energija Da bi rad bio izvršen neophodno je postojanje sile. Sila vrši rad: Pri pomjeranju tijela sa jednog mjesta na drugo Pri
Rad, snaga, energija Tehnička fizika 1 03/11/2017 Tehnološki fakultet Rad i energija Da bi rad bio izvršen neophodno je postojanje sile. Sila vrši rad: Pri pomjeranju tijela sa jednog mjesta na drugo Pri
PRIMJER 3. MATLAB filtdemo
 PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
TRIGONOMETRIJSKE FUNKCIJE I I.1.
 TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
Grafičko prikazivanje atributivnih i geografskih nizova
 Grafičko prikazivanje atributivnih i geografskih nizova Biserka Draščić Ban Pomorski fakultet u Rijeci 17. veljače 2011. Grafičko prikazivanje atributivnih nizova Atributivni nizovi prikazuju se grafički
Grafičko prikazivanje atributivnih i geografskih nizova Biserka Draščić Ban Pomorski fakultet u Rijeci 17. veljače 2011. Grafičko prikazivanje atributivnih nizova Atributivni nizovi prikazuju se grafički
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE GODINE 8. RAZRED TOČNI ODGOVORI
 21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
Svojstva veze. Duljina Energija disocijacije Konstanta sile Dipolni moment
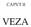 CAPVT II VEZA Svojstva veze Duljina Energija disocijacije Konstanta sile Dipolni moment Duljina veze 1. Udaljenost između jezgara 2. Udaljenost između maksimumâ elektronske gustoće 3. Ravnotežna duljina
CAPVT II VEZA Svojstva veze Duljina Energija disocijacije Konstanta sile Dipolni moment Duljina veze 1. Udaljenost između jezgara 2. Udaljenost između maksimumâ elektronske gustoće 3. Ravnotežna duljina
MEHANIKA FLUIDA. Isticanje kroz otvore sa promenljivim nivoom tečnosti
 MEHANIKA FLUIDA Isticanje kroz otvore sa promenljivim nivoom tečnosti zadatak Prizmatična sud podeljen je vertikalnom pregradom, u kojoj je otvor prečnika d, na dve komore Leva komora je napunjena vodom
MEHANIKA FLUIDA Isticanje kroz otvore sa promenljivim nivoom tečnosti zadatak Prizmatična sud podeljen je vertikalnom pregradom, u kojoj je otvor prečnika d, na dve komore Leva komora je napunjena vodom
INTELIGENTNO UPRAVLJANJE
 INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
Cauchyjev teorem. Postoji više dokaza ovog teorema, a najjednostvniji je uz pomoć Greenove formule: dxdy. int C i Cauchy Riemannovih uvjeta.
 auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
MATEMATIKA 2. Grupa 1 Rexea zadataka. Prvi pismeni kolokvijum, Dragan ori
 MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
