Περιεχόμενα. A(x 1, x 2 )

Transcript

1 Περιεχόμενα A(x 1, x 2

2

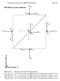
3 7 Ολοκληρώματα της Μαγνητοϋδροδυναμικής και Μαγνητοϋδροδυναμικά Κύματα Σχήμα 7.1: Οι τριδιάστατες ελικοειδείς μαγνητικές γραμμές στις οποίες εφάπτεται το διάνυσμα του μαγνητικού πεδίου B(x 1, x 2, αντιστοιχούν σε συγκεκριμένη τιμή της μαγνητικής ροής A(x 1, x 2 = σταθ. Επίσης, οι ελικοειδείς γραμμές ροής στις οποίες εφάπτεται το διάνυσμα του πεδίου ταχυτήτων V (x 1, x 2, αντιστοιχούν σε συγκεκριμένη τιμή της ροής μάζας, Ψ(x 1, x 2 = Ψ(A = σταθ. Οι δύο αυτές γραμμές B(x 1, x 2 και B(x 1, x 2 τυλίγονται γύρω από την ίδια χωανοειδή επιφάνεια η οποία προκύπτει από την περιστροφή της καμπύλης A(x 1, x 2 = σταθ. γύρω από τον άξονα z της αξονικής συμμετρίας του συστήματος που εκφράζεται απο την αγνοήσιμη συντεταγμένη x 3 = φ.

4 7.1. Μη σχετικιστική μαγνητοϋδροδυναμική Μη σχετικιστική Μαγνητοϋδροδυναμική ρ t + (ρ V = 0, B = E = 0 (Gauss, ( V B = B t (F araday Ohm, B = 4π c J (Ampere, [ V ρ t + ( V V ] = P + 1 4π ( B B ρ V, T = m p P 2 ρ, P = K(Aρ γ,

5 5 Κεφάλαιο 7: ΜΥΔ ολοκληρώματα και ΜΥΔ κύματα (ρ V = 0, B = 0, ( V B = 0, ρ( V V = P + 1 ( B B ρ V, 4π P = K(Aρ γ, T = m p 2 P ρ. 1 ( V P P Γ V Γ 1 ρ ρ = E H + E c ρ 2 Λ(T ρ q t. ρdq/dt E H E c ρ 2 Λ(T Q = E + P V, q = ϵ + P (1/ρ. ϵ = P ρ(γ 1 = 3 T 2, Γ = c p /c v ρ q = 1 ( P Γ P Γ 1 ρ ρ, ρ q t = 1 ( V P P Γ V Γ 1 ρ ρ = P Γ 1 ( P t ρ Γ.

6 7.1. Μη σχετικιστική μαγνητοϋδροδυναμική 6 A q = 0 P = K(Aρ Γ K(A γ γ P ρ γ γ = 1 γ = 3/2 γ = 5/3 (x 1, x 2, x 3 ˆx 1, ˆx 2, ˆx 3 g ij, g ij x 3 = 0. ˆx 3 ˆx 3 ˆx 3 = a + b r, b = 0 / z = 0 a = 0 / ϕ = 0 a 0, b 0 / u = 0 u

7 7 Κεφάλαιο 7: ΜΥΔ ολοκληρώματα και ΜΥΔ κύματα 7.2 Καμπυλόγραμμες συντεταγμένες t (x 1, x 2, x 3 (x, y, z (ϖ, φ, z (r, θ, φ (x, y, z (x 1, x 2, x 3 x = x(x 1, x 2, x 3, y = y(x 1, x 2, x 3, z = z(x 1, x 2, x 3. Σχήμα 7.2: Σύστημα ορθογώνιων καμπυλόγραμμων συντεταγμένων (x 1, x 2, x 3. r = xˆx + yŷ + zẑ = x 1ˆx 1 + x 2ˆx 2 + x 3ˆx 3, r = r x 1 x 1 + r x 2 x 2 + r x 3 x 3 = h 1 x 1 ˆx 1 + h 2 x 2 ˆx 2 + h 3 x 3 ˆx 3,

8 7.2. Καμπυλόγραμμες συντεταγμένες 8 ˆx 1, ˆx 2, ˆx 3 h 1, h 2, h 3 h 1ˆx 1 = r x 1, h 2ˆx 2 = r x 2, ˆx 1, ˆx 2, ˆx 3 h 3ˆx 3 = r x 3. h i = r, ˆx i = r/ x i, i = 1, 2, 3. x i r/ x 1 s 2 = r r = h 2 1 x h 2 2 x h 2 3 x 2 3, V = h 1 h 2 h 3 x 1 x 2 x 3. Σχήμα 7.3: (α Σύστημα κυλινδρικών συντεταγμένων (ϖ, φ, z. (β Σύστημα σφαιρικών συντεταγμένων (r, φ, θ. Παράδειγμα 7.1 (ϖ, φ, z x = ϖ φ, y = ϖ φ, z = z h 1 = 1, h 2 = ϖ, h 3 = 1 ˆϖ = φˆx + φŷ ˆφ = φˆx + φŷ ẑ = ẑ

9 9 Κεφάλαιο 7: ΜΥΔ ολοκληρώματα και ΜΥΔ κύματα (r, θ, φ h 1 = 1, h 2 = r, h 3 = r θ r = r θ φˆx + r θ φ ŷ + r θẑ ˆr = θ φˆx + θ φŷ + θẑ ˆθ = θ φˆx + θ φŷ θẑ ˆφ = φˆx + φŷ Κλίση, απόκλιση, στροφή και Λαπλασιανή σε ορθόγωνες καμπυλόγραμμες συντεταγμένες f f(x 1, x 2, x 3 (x 1, x 2, x 3 f = f = ˆx 1 h 1 f x 1 + ˆx 2 h 2 f x 2 + ˆx 3 h 3 f x 3. A A(x 1, x 2, x 3 = A 1ˆx 1 + A 2ˆx 2 + A 3ˆx 3 (x 1, x 2, x 3 A = A = 1 [ (h 2 h 3 A 1 + h 1 h 2 h 3 x 1 x 2 (h 3 h 1 A 2 + ] (h 1 h 2 A 3. x 3 A A(x 1, x 2, x 3 = A 1ˆx 1 +A 2ˆx 2 + A 3ˆx 3 (x 1, x 2, x 3 A = A 1 h 1ˆx 1 h 2ˆx 2 h 3ˆx 3 = h 1 h 2 h 3 x 1 x 2 x 3 h 1 A 1 h 2 A 2 h 3 A 3 2 f f(x 1, x 2, x 3 (x 1, x 2, x 3 2 f = 1 [ ( h2 h 3 h 1 h 2 h 3 x 1 h 1 f + ( h3 h 1 x 1 x 2 h 2 f + ( h1 h 2 x 2 x 3 h 3 f ]. x Επιφάνειες μαγνητικής ροής (r, θ, ϕ h r = 1, h θ = r, h ϕ = r θ

10 7.3. Επιφάνειες μαγνητικής ροής 10 ϕ, ϕ = 0 (z, ϖ, ϕ h z = 1, h ϖ = 1, h ϕ = ϖ (x 1, x 2 B 3 x 3 B = B(x 1, x 2 = B p (x 1, x 2 + B 3 (x 1, x 2, x 1, x 2 B = 0 B = ( A ˆx3 + B h 3 (x 1, x 2. 3 B = ( 1 h 2 h 3 A x 2, 1 h 1 h 3 A x 1, B 3. (r, θ, φ (ϖ, φ, z ( 1 A B = r 2 θ θ, 1 A ( 1 r θ r, B A ϕ = ϖ ϖ, 1 A ϖ z, B ϕ. h 1 x 1 B 1 = h 2 x 2 B 2 x 1 A/ x 2 = x 2 A/ x 1 x 1 A x 1 + x 2 A x 2 = 0 A(x 1, x 2 = 0 A(x 1, x 2 =. A A = x 3 = ϕ 1 2 F B = B S ( A = ˆϕ S, h 3 A ϕ = 2πA γρ, S C A γρ A F B S F B = 4πA γρ A(x 1, x 2

11 11 Κεφάλαιο 7: ΜΥΔ ολοκληρώματα και ΜΥΔ κύματα 7.4 Επιφάνειες ροής μάζας ˆx 3 ρ V = 0 ρ V = ( Ψ ˆx3 4 π h 3 + ρ V 3 = ρ V p (x 1, x 2 + ρ V 3 (x 1, x 2. 4 π ρ V = ( 1 h 3 h 2 Ψ x 2, 1 h 1 h 3 Ψ x 1, 4πρV 3. h 1 x 1 4 π ρv 1 = h 2 x 2 4 π ρv 2 x 1 Ψ/ x 2 = x 2 Ψ/ x 1 x 1 Ψ x 1 + x 2 Ψ x 2 = 0 Ψ(x 1, x 2 = 0 Ψ(x 1, x 2 =. Ψ(x 1, x 2 A γρ Ψ(x 1, x 2 = 1 2Ṁ = S ρv p S = S ( Ψ ˆϕ S 4 π h = 3 c Ψ 4 π ϕ = 1 2 Ψ γρ Ψ γρ Ṁ Ṁ = Ψ γρ Ψ(x 1, x Πρώτο ολοκλήρωμα: λόγος ροής μάζας και μαγνητικής ροής E = V B c.

12 7.5. 1o ολοκλήρωμα: λόγος ροής μάζας και μαγνητικής ροής 12 E = 0 ( V B = 0 V B = c Φ, Φ E = Φ Φ(x 1, x 2 δφ Φ r r Φ Φ V B V Φ = B Φ = 0, Φ V B Φ Ψ Φ Ψ = x 1 x 2 x 2 x 1 [ ] Φ, Ψ [ ] Φ, Ψ = 0, Φ A Φ A [ ] = Φ, A = 0, x 1 x 2 x 2 x 1 Φ Ψ [ ] Φ, A Φ Φ Φ = Φ(Ψ, Φ = Φ(A, Ψ = Ψ(A. Ψ(A V B ( V P + V ϕ ( BP + B ϕ = c Φ(x1, x 2 V p B p + V }{{} p B ϕ + V }{{} ϕ B p + V }{{} ϕ B ϕ = }{{}}{{} c Φ. ˆϕ ˆp ˆp 0 ˆp ˆϕ V p B p = 0 V p // B p ρ V p = α B p α α = ρv p B p = 1 4 π A p Ψ p = 1 4 π Ψ A A p A p = 1 Ψ 4 π A = Ψ A(A = 4 π

13 13 Κεφάλαιο 7: ΜΥΔ ολοκληρώματα και ΜΥΔ κύματα Ψ A = 4πρV p B p, 7.6 Δεύτερο ολοκλήρωμα: νόμος της ισοπεριστροφής V p B ϕ + V ϕ B p = c Φ } V p = Ψ A 4πρ B p, c da dφ Ω(A Ψ A 4πρ ( B p B ϕ B p V ϕ = Ω(A A B p = A ˆϕ h 3 Ω(A Φ V p B p A Ψ AB ϕ ( A 4πρh ˆϕ ˆϕ V ϕ ( A 3 }{{} h ˆϕ ˆϕ = Ω(A A. 3 }{{} A A ( A B C = B( A C A( B C V ϕ = h 3 Ω(A + Ψ A 4πρ B ϕ. V p = Ψ A 4πρ B p, V = Ψ A 4πρ B p + V ϕ = Ψ A 4πρ B p + Ψ A 4πρ B ϕ + h 3 Ω(A ˆϕ = Ψ A 4πρ B + h 3 Ω ˆϕ h 3 = ϖ = r θ

14 7.7. Στροφορμή του ηλεκτρομαγνητικού πεδίου 14 A = Ω(A V = h 3 Ω = ϖ Ω = r θω. V = h 3 Ω = ϖω = r θω Ω(A V B 7.7 Στροφορμή του ηλεκτρομαγνητικού πεδίου q = e g (x, y, z = (0, 0, 0 (0, 0, s E B 0 E = q r 2 ( θẑ + θ ˆϖ B = g r 2 ( θ ẑ + θ ˆϖ S = c E B 4π = cqg 4πr 2 r 2 (θ θ ˆϕ, d p dv = S c 2 θ θ z Σ(r, θ, ϕ q g z s dv L V p = r V = r E B 4 π c = g q (θ θ r 2 r 2 r 4 π c ˆθ. L z L z = 2 π r 2 q g θ θ r 4 π c r 2 r 2 (θ θ θr.

15 15 Κεφάλαιο 7: ΜΥΔ ολοκληρώματα και ΜΥΔ κύματα Σχήμα 7.4: Η στροφορμή του Η/Μ πεδίου L V και οι συνιστώσες της, L V ẑ και L V ˆϖ. r 2 = r 2 + s 2 2 r s θ, θ r = (θ θ = s r θ θ > θ L z = q g s 2 c 0 θ, θ = r θ s r r, π θ 3 θ r r 0 (r 2 + s 2 2 r s θ 3/2. x x I = ( α x 2 + b x + c 3/2 = 2 (2 a x + b ( 4 α c b 2 αx 2 + bx + c, L z = q g/c s L z = nh/2π L z = n h 2 π = e g c α = 2 π e2 = 1 h c 137 g = n h c 2 π e = n e h c 2 π e 2 g = n 137 e. g = 137 e. g 2 e 2 =

16 7.8. 3ο ολοκλήρωμα: Διατήρηση της συνολικής στροφορμής Τρίτο ολοκλήρωμα: διατήρηση της συνολικής στροφορμής A B ( A B = ( B A + ( A B + B A + A B. A = B = V ( V V = ( V 2 2 V ( V. ˆϕ ( ( V V P B = ρ + B V, 4 π ρ ( V V ( B B =. ϕ 4πρ ϕ [ ( ( V p + V ] ϕ ( V p + V ϕ = ( V p V p + ( }{{} V p V ϕ + ( }{{} V ϕ V p + ( }{{} V ϕ V ϕ. }{{} ˆp 0 ˆϕ ˆp ˆϕ ˆϕ ( V ϕ V p = ( B ϕ B p 4πρ V p = Ψ A Bp /4πρ V ϕ = (h 3 V ϕ ˆϕ h 3, B ϕ = (h 3 B ϕ ˆϕ h 3..

17 17 Κεφάλαιο 7: ΜΥΔ ολοκληρώματα και ΜΥΔ κύματα ( A B C = B( A C A( B C A = (h 3 V ϕ B = ˆϕ C = V p ˆϕ[ Vp ( Bp h 3 V ϕ 4πρ ( ] h 3 B ϕ = ˆϕ [ Vp ( Vp h 3 V ϕ Ψ ( ] h 3 B ϕ = 0, A V p ( h 3 V ϕ h 3 B [( ϕ = 0, h 3 V ϕ h 3 B ] ϕ, A = 0, Ψ A Ψ A V p f = 0 f(x 1, x 2 f = f(ψ = f(a h 3 V ϕ h 3B ϕ Ψ A = L(A L(A h 3 V ϕ V ϕ = L h 3 h 2 3 Ω L M 2 1 M 2 B ϕ = L h 2 Ω 3 L 1 Ψ A h 3 1 M 2 Ψ A (A Ω(A L(A M Πρόβλημα 7.1 M 2 = Ψ 2 A /4πρ = V p 2 /VA 2 << 1 V A 2 = B2 p/4πρ V ϕ,o Ωϖ o Ω(A A(r, θ = V ϕ

18 7.9. 4ο ολοκλήρωμα: διατήρηση ενέργειας για πολυτροπική εξίσωση 18 Ω(A V // B Πρόβλημα 7.2 J J d J dt = L(AρV p ds. S I z ϖ I z I z = c 2 ϖb ϕ = c 2 LΨ A 1 ϖ2 ϖ 2 A 1 M Τέταρτο ολοκλήρωμα: διατήρηση συνολικής ενέργειας υποθέτοντας μια πολυτροπική εξίσωση P = Kρ γ, h h = ϵ + P ρ = P (γ 1ρ + P ρ = γ P γ 1 ρ. H H = V h + V = V h G M. r ( ( V V = V 2 + ( 2 V V, H H + ( V V ( B B 4πρ = 0.

19 19 Κεφάλαιο 7: ΜΥΔ ολοκληρώματα και ΜΥΔ κύματα ( ˆp, A A, ˆϕ, ˆp ˆp H [ ( ] + V V ˆp [ ( ( V p + V ] ϕ ( V p + V ϕ = [ ( B B 4πρ ] ˆp = 0. ( V ϕ V ϕ + ( }{{} V p V p + ( }{{} V p V ϕ + ( }{{} V ϕ V p, }{{} ˆp ˆp 0 ˆϕ [ ] [ ( V V ˆp = ( Vϕ V ] [ ϕ ˆp + ( Vp V }{{} ] ϕ ˆp [ ( B B ] ˆp 4 π ρ = 1 4 π ρ ˆϕ } {{ } 0 + [ ( V p V ] p ˆp + [ ( }{{} V ϕ ] V p ˆp }{{} 0 0 { [( Bϕ B ] [ ϕ ˆp + ( Bp B }{{} ] ϕ ˆp ˆϕ } {{ } 0 + [ ( B p B ] p ˆp + [ ( }{{} B ϕ ] B p ˆp }{{} 0 0 ˆp H + [ ( V ϕ V ] [ ( Bϕ B ] ϕ ϕ ˆp ˆp = 0. 4πρ V ϕ = 1 (ϖv ϖ ϕ ˆϕ, Bϕ = 1 (ϖb ϖ ϕ ˆϕ ˆp H + 1 [ ( (ϖvϕ ϖ ˆϕ ] V ϕ ˆp 1 [ ( (ϖbϕ 4πρϖ ˆϕ B ] ϕ ˆp = 0 }

20 7.9. 4ο ολοκλήρωμα: διατήρηση ενέργειας για πολυτροπική εξίσωση 20 V ϕ = ϖω + Ψ A 4πρ B ϕ, L = ϖv ϕ ϖb ϕ Ψ A ϖb ϕ = ϖv ϕ Ψ A LΨ A. f(ϖ, z g(a [ f(ϖ, zg(a ] = g f + f g A { [ (f } { [(g } g ˆϕ] ˆϕ ˆp = f + f g A ˆϕ] ˆϕ ˆp { [(g } { [f ] = f ˆϕ] ˆϕ ˆp + g A ˆϕ ˆϕ} ˆp }{{} }{{} 0 { [ (f } { [(g } g ˆϕ] ˆϕ ˆp = f ˆϕ] ˆϕ ˆp. g(a ˆp H + 1 {[ ( ϖbϕ ϖ Ψ ˆϕ ] } V ϕ ˆp A Ψ {[ ( A ϖbϕ 4πρϖ Ψ ˆϕ ] } B ϕ ˆp = 0, A ˆp H + 1 {[ ( ϖbϕ ϖ Ψ ˆϕ ] } V ϕ ˆp } A {{} 1 {[ ( ϖbϕ ϖ Ψ ˆϕ ] (V ϕ ϖω ˆϕ } ˆp = 0 } A {{} ˆp H {[ ( + ϖωbϕ Ψ ˆϕ A ] ˆp ˆϕ } ˆp = 0. ( A B C = B( A C A( B C A = (ϖωb ϕ /Ψ A B = ˆϕ = C { ( ˆp H ϖωbϕ } ( ˆp = 0 ˆp H ϖωb ϕ = 0 H ϖωb ϕ = E(A, Ψ A Ψ A Ψ A 1 2 V 2 + γ γ 1 P ρ + V h 3B ϕ Ω Ψ = E(A A

21 21 Κεφάλαιο 7: ΜΥΔ ολοκληρώματα και ΜΥΔ κύματα Πρόβλημα 7.3 ( E, B S = c( E B 4π E = ( V B/c S z /ρv z V = V z ẑ + V ϖ ˆϖ + V ϕ ˆϕ B = B z ẑ + B ϖ ˆϖ + B ϕ ˆϕ z Ω Ψ A S z ρv z = ϖωb ϕ Ψ A., Πρόβλημα 7.4 Ω(A

22 ο ολοκλήρωμα: γενικότερη περίπτωση διατήρησης της ενέργειας 22 E = 1 2 V p (V ϕ ϖω 2 + γ P γ 1 ρ + V ϖ2 Ω 2 2 = E ΩL. Ω(AL(A 7.10 Τέταρτο ολοκλήρωμα: γενικότερη περίπτωση διατήρηση της ενέργειας P = Kρ γ γ q q = ρv ( h P, ρ h q = 0 P h = ρ. q ( = h P ˆp, ρv p ρ ˆp P ρ ˆp = ( P ρ h ˆp + h ˆp = q + h ρv ˆp. p ˆr [ ( ˆp 1 2 V 2 + V h 3 B ϕ Ω ] P + Ψ A ρ [ ( ˆp 1 2 V 2 + V h 3 B ϕ Ω ] q Ψ A [ ( ˆp 1 2 V 2 + h + V h 3 B ϕ Ω Ψ A ˆp = 0, + h ρv ˆp = 0 p o q ρv p l p ] = 0,

23 23 Κεφάλαιο 7: ΜΥΔ ολοκληρώματα και ΜΥΔ κύματα dl p 1 2 V 2 + h + V h 3B ϕ Ω Ψ A o o q ρv p dl p = E(A. q q h l p = h = γ P ρv p γ 1 ρ, h = Γ P Γ 1 ρ, Γ Γ = 5/ Τελική διαφορική εξίσωση για τη συνάρτηση της μαγνητικής ροής A(x 1, x 2 Ω(A Ψ(A L(A E(A A(x 1, x 2 E(A A(x 1, x 2 p p 1 [ 1 d(lψ A 2 A Ψ A Ψ + 2(1 Ψ 2 A /4πρ h 2 3 da 1 [ 1 (LΨ A 2 ] + 2(1 Ψ 2 A /4πρ2 h 2 + h 2 3 4πρ 3Ω 2 2ΩL + 4πρh 2 dω 2 3 ] da 8πρd(ΩL da + 4πρ de da = 0, A 1 [ h 2 A + h 1 A ] = ˆx 3 h 1 h 2 h 3 x 1 h 1 h 3 x 1 x 2 h 2 h 3 x 2 h B 3 Ψ 1 [ h 2 1 h 1 h 2 h 3 x 1 h 1 h 3 4πρ Ψ + x 1 h 1 1 x 2 h 2 h 3 4πρ Ψ ] x 2 = ˆx 3 h 3 V. Ω(A Ψ(A L(A E(A A(x 1, x 2

24 7.12. Σύνοψη Σύνοψη x 3 (x 1, x 2, x 3 A(x 1, x 2 Ψ(x 1, x 2 Ψ = Ψ(A 4πρV p = Ψ ABp V B c Φ Φ = Φ(A cφ A Ω V ϕ = ϖω + (Ψ A /4πρB ϕ L = ϖv ϕ + ϖb ϕ /Ψ A B V Ψ A (A Ω(A L(A B V A(x 1, x 2 Ψ A (A Ω(A L(A E(A

25 25 Κεφάλαιο 7: ΜΥΔ ολοκληρώματα και ΜΥΔ κύματα Σχήμα 7.5: Μαγνητοϋδροδυναμικά κύματα στο πλάσμα. (α Κάθετα σε ένα μαγνητικό πεδίο διαδίδονται διαμήκη ηχητικά κύματα με ταχύτητα V 2 A + C2 s. (β Παράλληλα στο μαγνητικό πεδίο διαδίδονται εγκάρσια κύματα Alfvén με ταχύτητα V A και διαμήκη ηχητικά κύματα με ταχύτητα C s. Σε τυχούσα γωνία ως προς τη διεύθυνση ενός μαγνητικού πεδίου διαδίδονται τρία ΜΥΔ κύματα: τα κύματα Alfvén και τα αργά και γρήγορα ΜΥΔ κύματα Ηλεκτρομαγνητικά κύματα J = 0, ρ = 0, E = 0, E = 1 c B = 0, B = 1 c / t 1 c 2 2 B t 2 = 1 c B t, E t. t ( E = 1 c E t.

26 7.13. Ηλεκτρομαγνητικά κύματα 26 1 c 2 2 B t 2 = ( B = ( B 2 B. 2 B 1 2 B c 2 = 0. t2 E 2 E 1 2 E c 2 = 0. t2 c B = B 0 i( k r ωt, E = E 0 i( k r ωt, k = k î + l ĵ + m ˆk, k r = k x + l y + m z. E B ω 2 = (k 2 + l 2 + m 2 c 2 ω = k 2 + l 2 + m 2 c k E = 0, k B = 0, k E = ω B c E B = 0,

27 27 Κεφάλαιο 7: ΜΥΔ ολοκληρώματα και ΜΥΔ κύματα k E = k E ˆn, ˆn B = B ˆn ω/ k = c Παράδειγμα 7.2 E = E y (x, t ĵ, B = B z (x, t ˆk 1 B z c t 1 E y c t 2 B z t 2 = E y x, = B z x, = c 2 2 B z x 2. B z = B 0 ( kx ωt, E y = E 0 ( kx ωt, ω=, = E 0, ˆx 7.14 Ηχητικά κύματα ρ V t + ρ( V V = P, ρ t + (ρ V = 0, P = RρT,

28 7.14. Ηχητικά κύματα 28 R V = 0 P 0 ρ 0 P 0 = R ρ 0 T δp = p 1 δ v = v 1 δρ = ρ 1 p 1 ( r, t, v ( r, t, ρ 1 ( r, t P 0 ρ 0 p 1 P 0, ρ 1 ρ 0 ρ = ρ 0 + ρ 1, P = P 0 + p 1 ( ( v 1 ρ0 + ρ 1 t + ( v 1 v 1 = ( P 0 + p 1, (ρ 0 + ρ 1 + [( ] ρ 0 + ρ 1 v1 = 0, t P 0 + p 1 = R T ( ρ 0 + ρ 1. P 0 ρ 0 1 ρ 0 t = p 1, ρ 1 t + ρ 0 1 = 0, p 1 = Cs 2 ρ 1, Cs 2 = R T C s = 300 / C s = 270 / C s = 1410 / C s = 5600 / 1 p 1 ρ 1 2 ρ 1 t 2 = C2 s 2 ρ 1. ρ 1 = ρ 1 (x, t 2 ρ 1 t 2 = C2 s 2 ρ 1 x 2,

29 29 Κεφάλαιο 7: ΜΥΔ ολοκληρώματα και ΜΥΔ κύματα x C s ρ 1 = ρ i ( k x ωt, ρ ω 2 = k 2 C 2 s. ρ 1 = ρ i ( k x + l ψ + m z ω t. k k = ( k, l, m k = k 2 + l 2 + m 2. ω 2 = ( k 2 + l 2 + m 2 C 2 S. ωρ 0 v 1 = kp 1, v 1 k 7.15 Κύματα Alfvén B 0 ρ 0 P = 0 ρ/ t = 0 V = v 1 B = B 0 + b 1 ρ V = ( B B, 4 π B t = ( V B,

30 7.15. Κύματα Alfvén 30 v 1 ρ 0 t = ( b 1 B 0, 4 π b 1 t = ( v 1 B 0, b 1 = 0. A i( k r ω t = A i(k x + l y + m z ω t, A 4 π ρ 0 ω v 1 = ( k b1 B0 = ( k B0 b1 ( B0 b 1 k, ω b 1 = k ( v 1 B 0 = ( k B0 v1 ( k v1 B0, ( A B C = B( A C A( B C v 1 = 0 k v 1 = 0, b 1 = 0 k b 1 = 0. v 1 B 1 k B 0 b 1 = 0 ( k B0 b1 ρ 0 ω v 1 = 4π ω b 1 = ( k B0 v1. ω ω 2 = ( k B0 2 4 π ρ 0, ω 2 = k 2 V 2 A 2 θ, θ B 0 k V A V A = B 0 4 π ρ0,

31 31 Κεφάλαιο 7: ΜΥΔ ολοκληρώματα και ΜΥΔ κύματα θ ω/ k Πρόβλημα 7.5 B 0 k

32 7.16. Μαγνητοϋδροδυναμικά κύματα 32 E = ( V B/c + J/σ σ ω 2 = k 2 V 2 A 2 θ i ω k 2 c 2 4 π σ. V 0 = 0 B 0 = B 0 ẑ ρ 0 P 0 ρ 1 = 0 p 1 = 0 v 1 ŷ b 1 ŷ [ i(ωt k r ] k = k θẑ + k θˆx J = c B/4π ω kv A θ ω kv A θ i k2 c 2 8 π σ. τ = 8 π σ k 2 c Μαγνητοϋδροδυναμικά κύματα

33 33 Κεφάλαιο 7: ΜΥΔ ολοκληρώματα και ΜΥΔ κύματα ρ t + ρ V = 0. ρ ( V t + P B B = 0. 4 π B t + ( V B = 0. ( P t ρ Γ = 0. 0 ρ t + ρ 0 v = 0, ( v ρ 0 t + p b B0 = 0, 4 π b t + ( v B 0 = 0, ( p Γρ = 0. t P 0 ρ 0 ρ 0 p 0 B 0 i ( k r ωt ω ρ + ρ 0 k v = 0, ( k ω ρ 0 v + b B0 k p = 0, 4 π ω b + k ( v B 0 = 0, ( p ω Γρ = 0. P 0 ρ 0

34 7.16. Μαγνητοϋδροδυναμικά κύματα 34 ω 0 ρ = ρ 0 k v ω, p = ΓP 0 k v ω, ( k v B0 ( k B0 v b =. ω { ( k 2 { ω 2 B0 } (Γ P0 B v = k ( k B } 0 B0 ( 4 π ρ 0 ρ 0 4π ρ 0 4 π ρ k v 0 ( ( k B0 v B0 4 π ρ 0 k. B 0 ẑ k x z B 0 k v x v y v z = 0, ω 2 k 2 VA 2 k2 CS 2 2 θ 0 k 2 C 2 S θ θ = 0 ω 2 k 2 VA 2 2 θ 0 k 2 CS 2 θ θ 0 ω2 k 2 CS 2 2 θ B0 2 V =, 4πρ 0 C S = Γp 0 ρ ( ω 2 k 2 VA 2 2 θ ( ω 4 ω 2 k 2 ( VA 2 + CS 2 + k 4 VA 2 CS 2 2 θ = 0.

35 35 Κεφάλαιο 7: ΜΥΔ ολοκληρώματα και ΜΥΔ κύματα ω = k V A θ. v x = v z = 0 ω = k V A θ ( 0, v y, 0 k v = 0 v B 0 = 0 ω = k v +, ω = k v, v ± = { 1 ( V 2 2 A + CS 2 ± (VA 2 + C2 S 2 4 VA 2 C2 S 2 θ } 1 2. v + v v y = 0 ( v x, 0, v z k v 0 v B 0 = 0 v v k v v 180

36 7.16. Μαγνητοϋδροδυναμικά κύματα 36 p ( B 0 b/4 π z p v z ω ρ 0 v z = k p θ. B 2 δ( B = 0 b 8 π 4 π = ( k v B0 2 ( ( k B0 B0 v. 4 π ω B 0 b 4 π = ρ V A 2 k2 VA 2 2 θ ω 2 p = V A 2 ( CS 2 1 k2 CS 2 2 θ ω 2 p. p ( B 0 b/4 π v > C S θ v < C S θ v = ω/k v + > C S θ v < C S θ ( v x, 0, v z k v 0 v B0 0 v k B 0 k C S ω = k V A. V A C S β = 8πP /B 2 ω k C S θ.

37 37 Κεφάλαιο 7: ΜΥΔ ολοκληρώματα και ΜΥΔ κύματα x z Πρόβλημα 7.6 α 1 n = 10 5 B = 0.5 α 2 n = B = 10 α 3 n = 10 B = 10 2 α 4 n = B = v v k v v 180 θ

38 7.16. Μαγνητοϋδροδυναμικά κύματα 38 Χαµηλό Ηλιακό Στέµµ Σχήμα 7.6: Διάγραμμα ταχυτήτων φάσης για τα τρία χαρακτηριστικά ΜΥΔ κύματα στο Ηλιακό Στέμμα: το παρατηρούμενο αργό ΜΥΔ κύμα διαδίδεται σε γωνία 85 c irc ως προς το ηλιακό μαγνητικό πεδίο με ταχύτητα 14 km/s km (Απο το άρθρο Extreme Ultraviolet Observations and Analysis of Micro-Eruptions and Their Associated Coronal Waves, O. Podladchikova et al. 2010, ApJ 709, 369.

39 39 Κεφάλαιο 7: ΜΥΔ ολοκληρώματα και ΜΥΔ κύματα Σχήμα 7.7: Διάγραμμα ταχυτήτων φάσης V ϕ = ω/k για τα τρία χαρακτηριστικά ΜΥΔ κύματα: Γρήγορο (εξωτερικό, Alfvén και αργό (εσωτερικό, όταν V A = 0.5 > C s = 0.4. Στη διεύθυνση του άξονα x, η φασική ταχύτητα του γρήγορου κύματος είναι V + = V 2 A + Cs 2 = Σχήμα 7.8: Διάγραμμα ταχυτήτων ομάδος V g = dω/dk για τα τρία χαρακτηριστικά ΜΥΔ κύματα: Alfvén (μαύρα σημάδια, αργό (εσωτερική καμπύλη και γρήγορο (εξωτερική καμπύλη όταν V A = 0.5 > C s = 0.4. Στη διεύθυνση του άξονα x, η ταχύτητα ομάδος του γρήγορου κύματος είναι V + = VA 2 + C2 s = Τα δύο σφαιρικά τρίγωνα τερματίζονται εσωτερικά στη χαρακτηριστική ταχύτητα C T = (V A C s / VA 2 + C2 s = 0.31.

40 7.16. Μαγνητοϋδροδυναμικά κύματα 40 Σχήμα 7.9: Διάγραμμα ταχυτήτων φάσης V ϕ = ω/k για τα τρία χαρακτηριστικά ΜΥΔ κύματα: Γρήγορο (εξωτερική καμπύλη Alfvén και αργό (εσωτερική καμπύλη, όταν V A = C s = 0.5. Στη διεύθυνση του άξονα x, η φασική ταχύτητα του γρήγορου κύματος είναι V + = VA 2 + C2 s = Η χαρακτηριστική ταχύτητα είναι C T = (V A C s/ VA 2 + C2 s = Σχήμα 7.10: Διάγραμμα ταχυτήτων ομάδος V g = dω/dk για τα τρία χαρακτηριστικά ΜΥΔ κύματα: Alfvén (μαύρα σημάδια, αργό (συνεχής καμπύλες και γρήγορο (εξωτερική καμπύλη, όταν V A = C s = 0.5. Στη διεύθυνση του άξονα x, η ταχύτητα ομάδος του γρήγορου κύματος είναι V + = VA 2 + C2 s =

41 41 Κεφάλαιο 7: ΜΥΔ ολοκληρώματα και ΜΥΔ κύματα 0,75 0,5 0,25 z 0 0,25 0,5 0,75 0,75 0,5 0,25 0 0,25 0,5 0,75 Σχήμα 7.11: Διάγραμμα ταχυτήτων φάσης V ϕ = ω/k για τα τρία χαρακτηριστικά ΜΥΔ κύματα: Αργό, Alfvén και γρήγορο, όταν V A = 0.5 < C s = 0.8. Στη διεύθυνση του άξονα x, η φασική ταχύτητα του γρήγορου κύματος είναι V + = V 2 A + C2 s = x Σχήμα 7.12: Διάγραμμα ταχυτήτων ομάδος V g = dω/dk για τα τρία χαρακτηριστικά ΜΥΔ κύματα: Αlfvén (μαύρα σημάδια, αργό (συνεχείς καμπύλες και γρήγορο (εξωτερική καμπύλη, όταν V A = 0.5 < C s = 0.8. Στη διεύθυνση του άξονα x, η ταχύτητα ομάδος του γρήγορου κύματος είναι V + = V 2 A + C2 s = Τα δύο σφαιρικά τρίγωνα τερματίζονται εσωτερικά στη χαρακτηριστική ταχύτητα C T = (V A C s / V 2 A + C2 s =