dr 1...dp N exp [ βh ({p}, {r})], (1) p 2 i 2m +Φ(r 1,..., r N ). (2) Z id = N!Λ 3N Z = Q(N,V,T). (6) Z = Z id
|
|
|
- Πήγασος Μακρής
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Física de Líquidos L. Mederos Instituto de Ciencia de Materiales de Madrid Consejo Superior de Investigaciones Científicas 5 de abril de 2004 Índice. Descripción microscópica de un líquido. 2.. Conceptos básicos Diagramas Funciones de distribución en el colectivo canónico Funciones de distribución en el colectivo grancanónico Factor de estructura Función de correlación directa y ecuación de Ornstein-Zernike Teorías aproximadas Desarrollo del virial Ecuaciones integrales Teorías de perturbaciones Apéndice: Desarrollo en cumulantes. 43
2 . Descripción microscópica de un líquido... Conceptos básicos. Supongamos un sistema de partículas clásicas que interactúan unas con otras. Empecemos considerando el caso canónico; es decir, suponemos que el sistema ocupa un volumen V y que está en contacto con un baño térmico de temperatura T. Bajo estas circunstancias la función de partición del sistema es Z =! h 3 dp...dp dr...dp exp [ βh ({p}, {r})], () donde h es la constante de Planck, β =/k B T y H ({p}, {r}) es el hamiltoniano del sistema que depende de los momentos y las posiciones de cada una de las partículas. El factor /! tiene en cuenta la indistinguibilidad de las partículas y su inclusión en la Mecánica Estadística clásica se hace de manera ad hoc (téngase en cuenta que clásicamente las partículas son distinguibles) de manera que se resuelva la paradoja de Gibbs. Supongamos ahora que las partículas del fluido son suficientemente simétricas como para que sus únicos grados de libertad sean los traslacionales (esto es lo que se conoce como un líquido simple). Entonces el hamiltoniano del sistema es H = i= p 2 i 2m +Φ(r,..., r ). (2) m es la masa de cada una de las partículas y Φ(r,..., r ) es la energía potencial de interacción. Después de introducir (2) en () las integrales en momentos se pueden resolver analíticamente obteniéndose Z =!Λ 3 dr...dr exp [ βφ(r,..., r )], (3) ( βh 2 ) /2es donde Λ 2mπ la longitud de onda térmica de de Broglie.Enel caso particular de un sistema de partículas que no interactúan la energía potencial Φ(r,..., r )=0y las integrales en posiciones dan simplemente V con lo que la función de partición (3) se reduce al conocido resultado para el gas ideal Z id = V (4)!Λ 3 a partir de la cual se obtiene la energía libre y la ecuación de estado de manera trivial. En el caso general de partículas interactuantes para las que la energía potencial no es nula llamamos integral de configuración Q(,V,T) a Q(,V,T) dr...dr exp [ βφ(r,..., r )], (5) con lo que la función de partición clásica se escribe finalmente como Z = Q(,V,T). (6)!Λ3 Utilizando el resultado (4) la función de partición se puede escribir como Z = Z id Q(,V,T) V. (7) La aproximación clásica que estamos haciendo es válida cuando Λ 3 /V, según hemos discutido en la introducción del curso. Esto significa, por tanto, altas temperaturas y partículas pesadas y se satisface bastante bien para la mayoría de líquidos en los que estamos interesados. Excepciones son el helio y el hidrógeno debido a la poca masa de sus partículas. 2
3 Si ahora tomamos logaritmos en ambos lados de esta última ecuación obtenemos el interesante resultado de que la energía libre se separa de manera natural en dos contribuciones, la ideal y el exceso debido a las interacciones: donde F = F id + F ex, (8) y βf id =lnρ +3lnΛ (9) F ex = k B T ln Q(,V,T) V. (0) La parte de exceso contiene toda la contribución a la energía libre debida a las interacciones entre las partículas. En la obtención de la ecuación (9) hemos hecho uso de la aproximación de Stirling para el logaritmo de! y hemos introducido la densidad numérica de partículas ρ /V.Por otra parte, es evidente ahora que cualquier otra magnitud termodinámica que se obtenga a partir de la energía libre F mediante derivación (con respecto a sus variables naturales V y T ) quedará automáticamente separada también en una contribución ideal y un exceso. Por ejemplo, la energía interna del sistema, U, se obtiene a partir de la energía libre F mediante la ecuación ( ) (F/T) U = (/T ) que conduce junto con (8) al resultado V U = U id + Uex U id = 3 2 k BT U ex = dr...dr Φ(r,..., r )exp[ βφ(r,..., r )] Q(,V,T) Φ(r,..., r ). () ótese que la expresión (2) para el hamiltoniano del sistema supone que no existe campo externo actuando sobre las partículas. Sólo en ese caso la integral de configuración de un gas ideal se reduce a V, su función de partición viene dada por (4) y su densidad de partículas es constante (e igual a /V, evidentemente) lo que significa que existe la misma probabilidad de encontrar una partícula dentro de un elemento de volumen del sistema independientemente de la posición del elemento de volumen dentro del sistema. Esto es lo que llamaremos un sistema uniforme 2.Enel caso de un gas ideal no uniforme (por ejemplo, un gas ideal en presencia del campo gravitatorio) las cosas son más complicadas y resultarán más fácilmente tratables en el marco del formalismo del funcional de la densidad al que dedicaremos una parte importante de este curso. Los resultado anteriores son completamente generales. En los casos en los que el potencial de interacción entre las partículas es a dos cuerpos (a los que nosotros nos restringiremos en este curso), o sea, el potencial es aditivo a pares, la energía potencial se escribe como: Φ(r,..., r )= i<j φ( r i r j ), (2) j= 2 Algunos autores utilizan el término homogéneo en lugar de uniforme. Sin embargo, es preferible el segundo: Un sólido cristalino en equilibrio es un sistema claramente no uniforme miestras que desde el punto de vista macroscópico (termodinámico) es un sistema homogéneo. 3
4 donde φ(r) es el potencial de interacción entre un par de partículas que se encuentran a una distancia r. Se define la función de Mayer f(r) como f(r) e βφ(r) (3) mediante la cual se puede expresar la integral de configuración de la siguiente manera Q(,V,T)= dr...dr exp [ β (φ(r 2 )+φ(r 3 )+...)] = dr...dr ( + f(r ij )), (4) i<j donde el producto se extiende sobre todos los pares de partículas y f(r ij ) f ( r i r j ) es la función de Mayer correspondiente al par de partículas i y j. Desarrollando el producto obtenemos Q(,V,T) = dr...dr [ + (f 2 + f )+(f 2 f 3 + f 2 f )+...]. (5) ótese que trabajar con la función de Mayer en lugar de hacerlo con el potencial es especialmente apropiado porque la función de Mayer permanece finita siempre, incluso cuando el potencial diverge (como es el caso del potencial de esferas duras para el que f(r) es simplemente una función escalón o, también, el potencial de Lennard-Jones cuando la separación entre las partículas tiende a cero). Además, como veremos a continuación, permite un estudio sistemático, mediante diagramas, de integrales como la que aparece en la ecuación anterior, muy frecuentes en Mecánica Estadística..2. Diagramas. Existe una manera conveniente (por lo compacta) de representar todos los términos que aparecen en la ecuación (5) y es mediante el uso de diagramas. Conviene observar, sin embargo, que el uso de estos diagramas no supone la introducción de ningún concepto físico nuevo ni ningún tipo de aproximación. Se trata sólo de una notación interesante que merece ser tratada brevemente porque es útil también en otros campos de la Mecánica Estadística. Un diagrama de partículas es una colección de círculos distintos, numerados, 2,...,, con cualquier número (incluido el cero) de líneas uniéndolos con la condición de que cualquier par de círculos no puede estar conectado por más una línea. Ahora se puede asociar una expresión algebraica del tipo de las que aparecen en (5) con un diagrama de partículas simplemente asignando un factor f ij a cada par ij de círculos numerados que están conectados por una línea. Así, por ejemplo, el siguiente es un diagrama de 6 partículas: que representa gráficamente a la expresión algebraica f 34 f 25 f 26. Dos diagramas de un mismo número de partículas son diferentes si sus círculos están conectados de diferente manera. Por ejemplo, los diagramas
5 son diferentes pero estos dos son iguales. Con esta definición de diagrama es evidente que el integrando en la expresión (5) para la integral de configuración es, simplemente, la suma de todos los diagramas distintos de partículas, de modo que Q(,V,T)= dr...dr {todos los diagramas distintos de particulas}. (6) Por ejemplo, el sumando que aparece en el integrando de (5) no es más que un diagrama de partículas formado por círculos sin conectar. Por supuesto, cada círculo de un diagrama sin conectar da lugar a un factor V cuando el diagrama es integrado sobre todas las coordenadas de las partículas y, en particular, el diagrama formado por círculos no conectados da un factor V al realizar la integración. ótese que aunque los dos diagramas de tres partículas de la figura anterior son diferentes de acuerdo con nuestra definición, la integral (con respecto a las posiciones de las tres partículas) de estos dos diagramas tienen el mismo valor, así que su contribución a una expresión del tipo (6) es la misma. Algunos autores incluyen la integración con respecto a las posiciones de todas las partículas en la definición del diagrama (de modo que los dos diagramas de tres partículas de arriba serían entonces idénticos). Otros autores definen incluso dos tipos de círculos -rellenos y sin rellenar, por ejemplo-utilizando uno de los tipos para indicar variables con respecto a las que se integra y el otro tipo para variables con respecto a las que no se integra. Una propiedad interesante de los diagramas es su posibilidad de factorización. Es claro que la mayoría de los diagramas se pueden descomponer en diagramas más simples que reproducen al original cuando se multiplican unos por otros. Evidentemente, estos diagramas más simples son aquellas partes del diagrama original que no están conectadas al resto mediante línea alguna. Cada uno de estos diagramas-factores se pueden integrar separadamente. Por ejemplo, consideremos el diagrama de 0 partículas siguiente: que representa a la expresión f 2 f 39 f 67 f 68 f 6,0 f 78 f 8,0. Este diagrama se puede descomponer en cinco factores más simples: de modo que la integral sobre las posiciones de las 0 partículas es, entonces, 5
6 dr...dr 0 f 2 f 39 f 67 f 68 f 6,0 f 78 f 8,0 = V 2 dr dr 2 f 2 dr3 dr 9 f 39 dr6 dr 7 dr 8 dr 0 f 67 f 68 f 6,0 f 78 f 8,0 = V 2 V 2 dr 2 f 2 dr39 f 39 dr6 dr 7 dr 8 dr 0 f 67 f 68 f 6,0 f 78 f 8,0 = V 4 ( dr 2 f 2 ) 2 dr6 dr 7 dr 8 dr 0 f 67 f 68 f 6,0 f 78 f 8,0. Esta propiedad muestra que es conveniente definir un l-clúster como un diagrama de l partículas en el que de cada círculo sale al menos una línea (es decir, cada círculo está unido al menos a otro círculo) y cada círculo está unido directa o indirectamente al resto de los l círculos del clúster. Por tanto, en un l-clúster es posible llegar a cualquiera de sus círculos siguiendo de manera continua líneas entre círculos. Con esta definición es obvio que cada uno de los factores en los que se descompone un diagrama complejo como el del ejemplo anterior es un clúster. ótese que:. Cada círculo no conectado da lugar a un factor V al integrar. 2. La integral de un clúster cualquiera es proporcional a V. Esto, que se ve fácilmente teniendo en cuenta que f ij depende de la distancia r i r j y haciendo un cambio de variables, corresponde al hecho de integrar sobre la posición del centro de masas del clúster o, en otras palabras, a que el clúster puede estar en cualquier lugar de la caja. Por ejemplo, considérese el clúster G de tres partículas siguiente: G = 2 3 Su integral es dr dr 2 dr 3 [G] = dr dr 2 f(r 2 ) dr 3 f(r 3 )f(r 23 ), que, haciendo los cambios de variables r 2 = r + r 2 y r 3 = r + r 3 en las dos últimas integrales y teniendo en cuenta que r 23 = r 3 r 2, podemos escribir como dr dr 2 dr 3 [G] = dr dr 2 f(r 2 ) dr 3 f(r 3 )f(r 23 ) = V dr 2 f(r 2 ) dr 3 f(r 3 )f( r 3 r 2 ). Como segundo ejemplo, considérese el diagrama siguiente: G = 2 3 En este caso, la integral es 6
7 dr dr 2 f(r 2 ) dr dr 2 dr 3 [G ]= dr dr 2 f(r 2 ) dr 3 f(r 3 )= [ 2 [ ] 2 dr 3 f(r 3 )=V dr 2 f(r 2 )] = V dr 2 [ ] [ 2 [ 2 = V dr [ ]] = V dr 2 [ ]]. Volveremos posteriormente en este capítulo a retomar el uso de los diagramas y los clústeres. Sin embargo, conviene terminar ahora esta primera sección del capítulo, referente a la descripción mecano-estadística formal de un líquido, con un apartado dedicado a introducir el concepto de funciones de distribución ya que juegan un papel crucial en prácticamente todas las aproximaciones existentes..3. Funciones de distribución en el colectivo canónico. Seguimos pues considerando un fluido en equilibrio formado por partículas ocupando un volumen V y en contacto con un baño térmico de temperatura T. Bajo estas circunstancias, la probabilidad P (r, r 2,..., r )dr dr 2...dr de encontrar a la partícula dentro del elemento de volumen dr centrado en r, a la partícula 2 en el elemento de volumen dr 2 centrado en r 2,... y a la partícula en el elemento dr centrado en r, independientemente de sus momentos, es P (r, r 2,..., r )dr dr 2...dr = exp [ βφ(r,..., r )] dr dr 2...dr Q(,V,T). (7) ótese que no estamos incluyendo el factor! que consideramos en la definición de la función de partición () puesto que en la definición de P (r, r 2,..., r ) estamos considerando a las partículas como distinguibles. Esta probabilidad representa la descripción microscópica más detallada que podemos imaginar. Si, por la razón que sea, estamos interesados sólo en un subconjuntos de partículas, no tenemos más que integrar P (r, r 2,..., r ) sobre las coordenadas de aquellas partículas que no nos interesan. Así, la probabilidad de que la partícula esté en dr,la2 esté en dr 2,...ylam (m ) esté en el elemento dr m centrado en r m, independientemente de la posición de las restantes ( m) partículas y de los momentos de todas las, será: [ ] P (m) (r,..., r m ) dr...dr m = dr m+...dr P (r, r 2,..., r ) dr...dr m O sea que ρ (m) P (m) (r drm+...dr exp [ βφ(r,..., r )],..., r m )=. (8) Q(,V,T) Definimos una jerarquía de funciones de distribución ρ (m) (r,..., r m ) de tal manera que (r,..., r m ) dr...dr m sea la probabilidad de encontrar una partícula cualquiera del sistema (no la precisamente) en dr, otra cualquiera en dr 2,... y otra en dr m, independientemente de la posición del resto de las partículas. Esta probabilidad se obtendrá a partir de P (m) (r,..., r m ) sin más que tener en cuanta cuántas posibilidades hay de seleccionar un subconjunto de m partículas de entre de ellas 3. Evidentemente, 3! En realidad, existen maneras de elegir un subconjunto de m partículas de entre de ellas. Pero en el m!( m)! segundo miembro de (8) estamos tratando las partículas como distinguibles (es la la que está en dr etc.) asi que, además de las diferentes maneras de eligir m partículas de entre, hemos de tener en cuenta las m! permutaciones de los elementos de cada uno de estos subconjuntos de m partículas con lo que obtenemos finalmente el factor!/( m)! que aparece en (9). 7
8 ρ (m) (r,..., r m )=! ( m)! P (m) (r,..., r m ). (9) ótese que ρ (m) (r,..., r m ) tiene unidades de [distancia] 3m, pero el verdadero significa físico reside en la probabilidad ρ (m) (r,..., r m ) dr...dr m que es obviamente adimensional. ρ (m) Si integramos (9) sobre todas sus variables es evidente que la condición de normalización de (r,..., r m ) es dr...dr m ρ (m) (r,..., r m )=! ( m)!. (20) En el caso de un gas ideal (de nuevo en ausencia de campo externo), para el que Φ(r,..., r )=0 y Q(,V,T) =V, las expresiones (8) y (9) conducen inmediatamente al resultado siguiente: ρ (m),id (r,..., r m )=ρ m! m ( m)!, (2) donde ρ = /V es, de nuevo, la densidad (constante) del gas ideal. De toda esta jerarquía de funciones de distribución ρ (m) (r,..., r m ) las más importantes en la teoría de fluidos son las primeras (entre otras cosas, porque, como veremos, son las únicas que finalmente conseguimos aproximar de alguna manera y para las que podemos obtener información experimental). Más concretamente, ρ () (r ) y ρ (2) (r, r 2 ) que vamos a discutir en más detalle a continuación: ρ () (r ) dr es la probabilidad de encontrar una partícula cualquiera del sistema en el elemento dr. La condición de normalización (20) es en este caso dr ρ () (r )=, que indica que ρ () (r ) es la densidad numérica de partículas, es decir, el número medio de partículas del sistema por unidad de volumen en el punto r. Si el sistema es uniforme entonces ρ () (r ) es constante y su valor es, de acuerdo con la condición de normalización (o a partir de (2), /V ρ 0, como es obvio. os referiremos frecuentemente a ρ () (r ) como el perfil de densidad o, simplemente, la densidad. La discusión de ρ (2) (r, r 2 ) es más complicada: De acuerdo con la definición, ρ (2) (r, r 2 ) dr dr 2 es la probabilidad de encontrar simultáneamente una partícula cualquiera del sistema en r y otra en r 2. Es decir, se trata de una probabilidad condicionada 4 que describe las correlaciones a pares que existen en el sistema. La condición de normalización es dr dr 2 ρ (2) (r, r 2 )=( ). En el caso de un gas ideal la ecuación (2) da como resultado ρ (2),id (r, r 2 )=ρ 2 ( ). (22) ótese que la aparición del término en / está reflejando el hecho de que, en un sistema que tiene el número de partículas fijo, la probabilidad de encontrar una partícula en r 2 cuando tenemos una fija en r (y esta es la definición de ρ (2) (r, r 2 )) es proporcional a ( )/V ynoa/v. Así que el resultado (22) para ρ (2),id (r, r 2 ) se podía haber anticipado utilizando directamente su definición: Probabilidad de encontrar una partícula en r (o sea, ρ) multiplicada por la probabilidad de que, fijada una partícula en r,encontremos otra en r 2 (o sea, ( )/V ). 4 Condicionada porque la probabilidad de encontrar dos partículas simultáneamente es la probabilidad de encontrar la primera por la probabilidad de encontrar la segunda cuando la primera está donde queremos. 8
9 ρ (2) En el caso de un sistema uniforme (que es isótropo) en general, es decir, aunque no sea ideal, (r, r 2 ) sólo puede depender de la distancia entre la partícula yla2. Por tanto, se tiene: ρ (2) (r, r 2 ) ρ (2) ( r r 2 ) ρ (2) (r 2). Definimos en este caso la función de distribución radial (fdr) g(r 2 ) del líquido escribiendo ρ (2) (r 2) ρ 2 g (r 2 ), (23) donde ρ /V es la densidad constante del fluido uniforme. La condición de normalización de la fdr se escribe entonces, ρ 2 dr dr 2 g (r 2 )=( ) ρ 2 V dr 2 g (r 2 )=( ) dr ρg (r) =. (24) ótese que, de acuerdo con el significado físico de la función de distribución de dos cuerpos que acabos de discutir arriba, ρg (r)dr es la probabilidad de encontrar una partícula en el elemento de volumen dr a una distancia r (en cualquier dirección) de una partícula fija en el origen. Por tanto, podemos interpretar ρg (r) como la función de distribución de un cuerpo (la densidad) ρ (r) vista desde una partícula fija en el origen. Este resultado es interesante: Aunque estamos en un sistema uniforme que, en consecuencia, tiene una función de distribución de un cuerpo constante, el hecho de fijar una partícula en el origen equivale a la existencia de un potencial externo sobre el resto de partículas, así que el fluido formado por este resto de partículas con una de ellas fija en el origen no tiene un perfil de densidad constante sino que, por el contrario, se distribuye según indica ρ (r) =ρg (r) que, evidentemente, tiene simetría esférica. Esta idea es particularmente importante porque permitirá obtener la función de distribución radial de un fluido uniforme utilizando técnicas que veremos en los capítulos siguientes (basadas en el formalismo del funcional de la densidad) y que han sido diseñadas para el estudio de sistemas no uniformes. Finalmente, para terminar esta llamada de atención, nótese que entonces ρg (r)4πr 2 dr es el número medio de partículas contenidas en una cáscara esférica de espesor dr y colocada a una distancia r de una partícula fija en el origen. Si integramos tal cantidad a todo el sistema hemos de obtener, por tanto, todas las partículas del sistema menos la que tenemos fija en el origen; es decir, obtenemos la condición de normalización tal como está escrita en la tercera de las ecuaciones (24). En pocas palabras, la fdr describe la estructura media del líquido según la veríamos si nos montamos sobre una partícula y miramos a nuestro alrededor. Para un gas ideal las ecuaciones (22) y (23) indican que g,id (r) =. Si el sistema no es ideal, lo que cabe esperar es que cuando la separación entre las partículas sea mucho más grande que el alcance del potencial g (r) tienda al límite ideal, así que tenemos el comportamiento asintótico siguiente g (r) r. (25) El término / es despreciable en el límite termodinámico 5 (recordemos, y V pero manteniendo ρ /V constante) así que a efectos de cálculos prácticos la fdr de un gas ideal es 5 Sin embargo, en ciertos casos no es irrelevante la existencia del término en / ni siquiera en el límite termodinámico pues si integramos ese término sobre todo el volumen del sistema (que es infinito en este límite) obtenemos una cantidad finita. La dificultad que esto ocasiona en determinados casos puede evitarse, como veremos más adelante, trabajando en el colectivo grancanónico. 9
10 simplemente ylag (r) de cualquier líquido uniforme tiende a para r suficientemente grande. El comportamiento de g (r) cuando r es comparable con el alcance del potencial depende sin embargo de la forma de éste, aunque existen ciertas similitudes cualitativas entre las fdr de todos ellos. La figura muestra la función de distribución radial de un fluido uniforme de esferas duras (para varios valores de la densidad) que puede calcularse de manera cuasi-exacta y la fdr obtenida experimentalmente (veremos más adelante brevemente de que manera) mediante scattering de neutrones para argon líquido a 85K 6 La figura de la izquierda corresponde a un sistema uniforme de esferas duras de diámetro σ a tres densidades diferentes. Como es obvio, a cualquier densidad, g (r) es estrictamente cero para distancias menores que el diámetro de una esfera pues el potencial de interacción es infinito en ese rango de modo que dos esferas no pueden acercar sus centros a menos de r = σ. Existe por tanto un volumen excluido alrededor de cada partícula en el que no puede encontrarse el centro de ninguna otra. Cuando la densidad es muy baja, la distancia media entre las partículas del líquido es muy grande así que podemos esperar que se comporte como un gas ideal (excepto por la exclusión debida al tamaño finito de las partículas que acabamos de comentar) y tengamos g (r) = para todo r>σsea cual sea el potencial de interacción. A medida que aumenta la densidad las partículas se empaquetan y lo que indica la figura es que lo hacen en una estructura de capas concéntricas a distancias de, aproximadamente, r = σ, r = 2σ, etc., mostrando que en un líquido denso existe un cierto tipo de orden de corto alcance. Cuando la distancia a la partícula del origen aumenta se pierde tal orden (pues no existe orden de largo alcance en un líquido) y la fdr tiende de nuevo al límite de gas ideal como hemos comentado anteriormente. El hecho de que el potencial de interacción entre dos esferas duras sea una función discontinua se traduce en la discontinuidad de la fdr de este sistema. La figura de la derecha representa la fdr del argón. Presenta exactamente las mismas características cualitativas que el caso de las esferas duras, si bien se trata de una función continua. Esta similitud será de gran interés en el desarrollo de aproximaciones en la teoría de líquidos pues indica que la estructura del argón líquido está esencialmente determinada por la parte fuertemente repulsiva a cortas distancias de su potencial de interacción (que puede aproximarse adecuadamente por un potencial de esferas duras de diámetro apropiado). Esta es la idea crucial que existe detrás de las teorías de perturbaciones para líquidos: La parte repulsiva de corto alcance del potencial se trata como esferas duras y la contribución de la cola del potencial se calcula (como veremos seguidamente, conocida la fdr se obtiene fácilmente la termodinámica de un sistema uniforme) suponiendo que la estructura (o sea, la fdr) del líquido es la determinada por ese sistema de esferas duras de referencia. 6 El potencial de interacción entre átomos de gases nobles es, con muy buena aproximación, el potencial Lennard- Jones, así que podemos considerar esa figura una representación de la fdr experimental de este potencial. 0
11 Las funciones de distribución de órdenes más altos en la jerarquía, por ejemplo ρ (3), describen probabilidades de encontrar simultáneamente partículas en más de dos sitios, así que describen correlaciones de más alto orden (entre más partículas) en el sistema. El punto importante es que si el potencial de interacción es aditivo a pares, entonces las propiedades termodinámicas (macroscópicas) del fluido pueden expresarse en términos de la función de distribución a dos cuerpos. Si, además, el fluido es uniforme, entonces las propiedades termodinámicas se expresan, como vamos a ver a continuación, en términos de la fdr g (r), siendo esta la razón fundamental que hace de la fdr una magnitud clave en la teoría de líquidos. En efecto, el exceso de energía interna de puede escribir como 7 : U ex = 2 dr dr 2 ρ (2) (r, r 2 )φ(r 2 ) (26) ótese que, aunque estamos suponiendo que el líquido es uniforme, en realidad tal suposición no se ha utilizado en la obtención de la ecuación anterior, así que (26) es general, siendo válida también para un sistema no uniforme. En realidad, esta ecuación se podía haber obtenido intuitivamente de manera directa utilizando el significado físico de ρ (2) (r, r 2 ): La energía de interacción será la suma (doble integral) a todos los pares de partículas (una en r y otra en r 2 ) de la energía de interacción del par φ(r 2 ) multiplicada por la probabilidad de que efectivamente el par exista (o sea ρ (2) (r, r 2 )) y dividido por 2 para no contar los pares dos veces. En el caso de un líquido uniforme utilizamos la definición de la fdr y obtenemos fácilmente: U ex = ρ2 2 dr dr 2 g (r 2 )φ(r 2 )= 2π2 V que se conoce como la ecuación de la energía. Para la presión se obtiene 8 : 7 La ecuación (2) para la energía potencial se puede escribir como Φ(r,..., r )= φ(r ij ). 2 i j Por tanto, la ecuación () para U ex conduce a U ex = dr...dr φ(r ij ) exp [ βφ(r,..., r )]. Q(, V, T) 2 i j dr r 2 g (r)φ(r), (27) La doble suma en i y j da lugar a ( ) términos los cuales son todos iguales después de integrar. Así que la 2 integral puede escribirse como ( ) veces el resultado de integrar uno de estos sumandos. Por tanto, 2 U ex = 2 ( ) [ dr dr 2 φ(r 2 ) Q(, V, T) ] dr 3...dr exp [ βφ(r,..., r )] = 2 dr dr 2 ρ (2) (r, r 2 )φ(r 2 ) 8 Supongamos que nuestro sistema está contenido en un cubo de lado L de modo que V = L 3. Suponemos, además, que la caja es lo suficientemente grande como para despreciar los efectos de las paredes (esto es rigurosamente cierto en el límite termodinámico). La presión puede entonces obtenerse como P = k B T ( V ) ( ln Z(, V, T) = k B T T, V = k BTL 3V ) ln Q(, V, T) ( ln Q(, V, T) L T, ). T, Por otro lado, haciendo el cambio de variables r i = Lq i,laintegral de configuración se puede escribir como Q(, V, T) =V... dq...dq 3 exp [ βφ(lq,..., Lq ]. 0 0 La derivada con respecto a L da
12 P k B T = V β 6V dr dr 2 r 2 φ(r 2) r 2 ρ (2) (r, r 2 ). (28) De nuevo, en el caso uniforme esta ecuación se puede escribir fácilmente en términos de la fdr: P k B T = V β 6 ρ2 dr 4πr 2 r φ(r) r g (r), (29) conocida como la ecuación de la presión o, también, como la ecuación del virial. o existe, sin embargo, una ecuación análoga para la entropía. Las ecuaciones anteriores son bastante simples: Consiguen expresar las propiedades termodinámicas de un líquido mediante una integral simple. Sin embargo, esta simplicidad es sólo aparente pues el problema ahora se ha trasladado a obtener la fdr del líquido (a cualquier densidad y temperatura) conocido únicamente el potencial de interacción entre un par de sus partículas. En realidad, este es el objetivo de cualquier teoría de líquidos y, como veremos a lo largo del curso, se trata de una tarea en general muy complicada que requiere el uso de aproximaciones no triviales. El problema se complica aun más si el potencial de interacción no es a pares pues ello hace aparecer funciones de distribución de órdenes superiores. Por otra parte, la ecuación (29) para la presión implica el uso de la derivada del potencial interatómico. Esto representa un problema cuando el modelo de potencial es discontinuo, como es el caso del sistema de esferas duras. Para resolver tal problema se define la función y (r) como y (r) =g (r)exp[βφ(r)]. (30) Se puede demostrar que y (r) es una función continua incluso en los casos en que tanto el potencial como la frd presentan discontinuidades. Introduciendo esta definición en la ecuación (29) podemos reescribir la presión de un sistema uniforme como βp ρ =+2 3 πβρ 0 dr r 3 y (r) d {exp [ βφ(r)]}. (3) dr En el caso particular de un sistema de esferas duras de diámetro σ el factor de Boltzmann que aparece en la ecuación anterior es, simplemente, la función escalón centrara en r = σ cuya derivada es una función δ. Es trivial entonces obtener el siguiente resultado: βp HS ρ =+ 2 πρ lím r 3 y (r) =+ 2 3 r σ + 3 πρσ3 g (σ), (32) donde el subíndice HS se ha utilizado para indicar que este resultado es exclusivo del sistema de esferas duras. La ecuación anterior muestra que la presión de un sistema uniforme de esferas duras está determinada enteramente por el valor de la fdr a la distancia de contacto entre dos esferas. Para finalizar la discusión de las funciones de distribución en el colectivo canónico vamos a incluir algunas expresiones de estas funciones en términos de promedios de funciones delta. Tales expresiones resultarán de gran utilidad con posterioridad. Para ello, comenzamos notando que: βv dq...dq 3 ( Φ(Lq,..., Lq ) L Si ahora tenemos en cuenta que ( ) Φ(Lq,..., Lq ) = L 2 (ij) ( ) Q(, V, T) = 3 Q(, V, T) L T, L ) exp [ βφ(lq,..., Lq ] r ij L φ(r ij) r ij = 2L (ij) r ij φ(r ij) r ij, resulta evidente llegar a la ecuacion (28) utilizando la denfinición de la función de distribución. 2
13 δ(r r ) = dr...dr δ(r r )exp[ βφ(r,..., r )] Q(,V,T) = dr 2...dr exp [ βφ(r, r 2,..., r )]. Q(,V,T) Este promedio es una función de la posición r pero es evidente que es independiente de la partícula concreta (la en nuestro caso) que utilicemos para su obtención. Por tanto, si sumamos sobre todas las partículas lo que obtendremos es veces el resultado anterior. Utilizando entonces la definición de las funciones de distribución es evidente que ρ () (r) = δ(r r i ). (33) De manera análoga se encuentra que ρ (2) (r, r )= i= δ(r r i )δ(r r j ). (34) i= j i Finalmente, las propiedades de la función δ junto con las definiciones de esta sección permiten encontrar el siguiente resultado para un sistema uniforme: = dr = δ(r + r j r i ) i= j i δ(r + r r i )δ(r r j ) i= j i dr ρ (2) (r + r, r )=ρg (r). (35).4. Funciones de distribución en el colectivo grancanónico. Ahora nuestro sistema ocupa un volumen V y está en contacto con un baño térmico de temperatura T y un baño de partículas de potencial químico µ. El sistema puede intercambiar energía y partículas con el baño así que el volumen y la temperatura son fijos pero el número de partículas no. La probabilidad P ( i,e i ) de encontrar al sistema con i partículas y energía E i (es decir, la probabilidad de que el sistema se encuentre en el microestado i de número de partículas i y energía E i ) está dada por la distribución grancanónica: P ( i,e i )= donde Ξ(µV, T ) es la gran función de partición: Ξ= {microestados} Ξ(µ, V, T ) exp [ β (E i µ i )], exp [ β (E i µ i )] = e βµ Z(,V,T). (36) donde Z(,V,T) es la función de partición canónica del sistema con partículas. Si existen Ω(E,,V ) microestados en los que el sistema tiene partículas y energía E, entonces la probabilidad de encontrar al sistema con exactamente partículas y energía E será P (,E) = Ω(E,,V ) Ξ(µ, V, T ) =0 exp [ β (E µ)]. 3
14 Por consiguiente, la probabilidad de que el sistema tenga exactamente partículas, P, sin más restricciones, será P = {E} P (,E) = Ξ(µ, V, T ) Ω(E,,V )exp[ β (E µ)] {E} = eβµ Z(,V,T) Ξ(µ, V, T ) = z Z(,V,T) Ξ(µ, V, T ), (37) donde se entiende que las sumas en energía se extienden sobre aquellos microestados compatibles con que el sistema tenga exactamente partículas. Hemos, además, introducido la actividad (también llamada afinidad) z definida como z =exp[βµ]. La función de distribución ρ (m) (r,..., r m ) vendrá, por tanto, dada por 9 = Ξ(µ, V, T ) m ρ (m) (r,..., r m )= z Λ 3 ( m)! m P ρ (m) (r,..., r m ) dr m+...dr e βφ(r,...,r ) (38) La condición de normalización se obtiene fácilmente integrando sobre todas sus variables: dr...dr m ρ (m)! (r,..., r m )=. (39) ( m)! En particular, para los casos m =y m =2obtenemos: drρ () (r) = (40) dr dr 2 ρ (2) (r, r 2 )= 2 (4) Si el sistema es uniforme, la primera de estas ecuaciones muestra que su perfil de densidad (que es constante en ese caso) es, simplemente /V, como era obvio. Por otra parte, para un gas ideal es fácil, utilizando los resultados de esta sección y de la anterior, encontrar que 0 ρ (m) id (r,..., r m )=ρ m. (42) ótese como ahora no aparece el término proporcional a m/ que aparecía en la ecuación (2) para esta misma magnitud en el colectivo canónico. Como vamos a ver seguidamente, esto tiene consecuencias importantes sobre el comportamiento de la fdr en este colectivo. En particular, para un sistema que no es ideal, ρ (2) (r, r 2 ) tenderá al comportamiento ideal cuando la separación entre las dos partículas sea suficientemente grande (es decir; tiende a ρ 2 ). En consecuencia, la función de distribución radial para un fluido uniforme ahora tiende exactamente a (sin la corrección / que teníamos en el colectivo canónico) cuando r tiende a infinito: 9 Esta ecuación es intuitiva: El grancanónico puede considerarse como una serie de canónicos (cada uno de diferente número de partículas recorriendo todas las posibilidades para ) pesados por la probabilidad de que el sistema grancanónico real tenga ese número de partículas. 0 En efecto, combinando las ecuaciones (4), (2), (36), (37) y (38) tenemos: ρ (m) id (r,..., r m)= =0 z V!Λ 3 m z V m Λ 3 ( m)! = ( z Λ 3 ) m. Pero la expresión para el potencial químico de un gas ideal permite ver inmediatamente que el contenido del paréntesis de la ecuación anterior no es más que la densidad constante del gas ideal. 4
15 g(r). (43) r Otra propiedad interesante es el límite de baja densidad de la función de distribución radial. Para un sistema uniforme generalizamos a definición de la fdr al caso de m partículas escribiendo ρ (m) (r,..., r m ) ρ m g (m) (r,..., r m ). (44) Introduciendo (38) en esta ecuación encontramos que, para un sistema uniforme, Ξρ m g (m) (r,..., r m )= = zm Λ 3m e βφ(r,...,rm) + m =m+ = zm Λ 3m e βφ(r,...,rm) + zm Λ 3m z Λ 3 ( m)! z dr m+...dr e βφ(r,...,r ) Λ 3 dr m+...dr e βφ(r,...,r ) ( m)! z k Λ 3k dr m+...dr m+k e βφ(r,...,r m+k) k! k= Ahora, en el límite de baja densidad, ρ 0, se tiene que z z/λ 3 0 y Ξ pero ρ/z. Por tanto, solo el primer término del segundo miembro de esta ecuación contribuye. Obtenemos, entonces, g (m) (r,..., r m ) ρ 0 exp [ βφ(r,..., r m )], que, el caso m =2, conduce al interesante resultado g(r) ρ 0 exp [ βφ(r)] (45) Es decir, en el límite de baja densidad la fdr es, simplemente, el factor de Boltzmann del potencial de interacción ente un par de partículas. Evidentemente, en el caso de un gas ideal esto es verdad a cualquier densidad obteniéndose g(r) =. Finalizaremos este apartado recuperando la conexión con la termodinámica. Aunque las ecuaciones de la energía (27) y de la presión (29) fueron obtenidas utilizando el colectivo canónico, es fácil demostrar que se obtienen resultados enteramente equivalentes para el colectivo grancanónico. Es decir, eliminando el subíndice en esas ecuaciones obtenemos las correspondientes al colectivo grancanónico. Sin embargo, existe una nueva ecuación, la ecuación de la compresibilidad, que es válida únicamente en el grancanónico, no teniendo sentido su planteamiento en el colectivo canónico. Esta ecuación relaciona la compresibilidad isotérmica del sistema uniforme con cierta integral de la fdr y la razón de que sólo tenga sentido en el grancanónico es evidente: La compresibilidad, como sabemos, está relacionada con fluctuaciones del número departículas que no existen en el colectivo canónico. Para obtenerla basta con combinar las dos ecuaciones de normalización de arriba para obtener inmediatamente que ] dr dr 2 [ρ (2) (r, r 2 ) ρ () (r )ρ () (r 2 ) = 2 2. Esta ecuación es válida incluso para sistemas no uniformes. Si el sistema es uniforme entonces conduce a +ρ 2 2 dr [g(r) ] = = ρk B Tχ T. (46) Esto no quiere decir, evidentemente, que la compresibilidad de un sistema que tiene un número fijo de partículas sea nula. La compresibilidad de tal sistema se obtendrá termodinámicamente (como la derivada apropiada de la magnitud termodinámica apropiada). Lo que significa es que en tal sistema no existe una relación entre su compresibilidad y su fdr. 5
16 donde χ T es la compresibilidad isotérmica del sistema uniforme. ótese que esta ecuación, al contrario de las ecuaciones para la energía y la presión, es válida incluso cuando la interacción entre las partículas no es aditiva a pares. Definimos ahora la función de correlación total h(r) como h(r) =g(r). (47) Con esta definición, la ecuación de la compresibilidad se reescribe como ρk B Tχ T =+ρ dr h(r). (48) El nombre de la función h(r) se debe a que esta función contiene toda la información posible sobre las correlaciones entre dos partículas que se encuentran a una distancia r una de otra. Esto será obvio más adelante pero, de momento, observemos que como la compresibilidad isotérmica diverge cuando nos aproximamos al punto crítico, la integral de h(r) diverge y esto significa que la función de correlación total ha de ser de muy largo alcance cuando nos aproximamos a tal punto..5. Factor de estructura. El factor de estructura S(k) de un líquido uniforme se define como: S(k) =+ρ dr e ik r 2 sin kr [g(r) ] = + 4πρ dr r [g(r) ]. (49) kr Es decir, es esencialmente la transformada de Fourier de g(r). ótese que S(k) es una magnitud adimensional. En el límite de número de ondas k =0encontramos, utilizando la ecuación de la compresibilidad, que S(k =0)=+ρ dr [g(r) ] = ρk B Tχ T. (50) El factor de estructura S(k) de un líquido se puede medir experimentalmente utilizando difracción de rayos X o de neutrones. Aunque una teoría que relacione de manera rigurosa el factor de estructura con la intensidad del haz difractado para cada número de ondas k no es sencilla a y, además, está fuera de los objetivos de este curso, se puede entender de manera aproximada esta relación utilizando el argumento que vamos a dar a continuación, argumento que permitirá de paso obtener algunas relaciones útiles que involucran al factor de estructura y otras funciones utilizadas en la descripción del líquido. Supongamos un haz de rayos X que incide sobre una muestra de líquido. En el experimento medimos la intensidad I(θ) del haz difractado formando un ángulo θ con el haz incidente. Este scattering puede considerarse, con muy buena aproximación, elástico ya que las energías típicas de los rayos X son 0 4 ev k B T. Así que representando los haces incidente y difractado por ondas planas de vectores de onda q y q, respectivamente, tendremos q = q + k y el hecho de que el scattering sea elástico implica que se conserva la energía lo que significa que q = q q que, junto con la ecuación anterior, conduce a que k k =2qsin (θ/2). El número de ondas q vendrá determinado por la longitud de onda de los rayos X utilizados en el experimento mientras que k es la transferencia de momento entre el haz incidente y la muestra. Imaginemos ahora que los átomos de la muestra se encuentran fijos ocupando el conjunto de posiciones {R i },i=,...,. Laintensidad difractada I f (θ) por esta distribución fija de átomos es 2 I f (θ) dr e iq r n(r) e iq r, 0 6
17 donde n(r) es la densidad electrónica total. Supongamos ahora que n(r) se puede expresar como la suma de las contribuciones de cada átomo de la muestra, n(r) = n a ( r R i ), i= donde ahora n a (r), que suponemos con simetría esférica, describe la densidad electrónica de un átomo individual. Entonces la intensidad difractada por la distribución fija de átomos la podemos escribir como: = i= e ik Ri 2 I f (θ) dr e ik r n a ( r R i ) i= 2 dr e ik (r Ri) 2 n a ( r R i ) = e ik Ri n a (k) 2, i= donde n a (k) dr n a (r)exp[ ik r], es decir, la transformada de Fourier de la densidad electrónica de un átomo, es el factor de forma de un átomo individual. Ahora hemos de tener en cuenta que en la muestra real los átomos no están fijos en posiciones determinadas. Por tanto, en el experimento real la intensidad observada será el promedio estadístico (mecanoestadístico) sobre todas las posiciones de los átomos. En consecuencia, podemos escribir I(θ) = I f (θ) c = e ik (Ri Rj) n a (k) 2, (5) i= j= donde hemos factorizado la parte estructural, que depende del promedio... c sobre el colectivo mecanoestadístico, de la parte no estructural que depende de las propiedades de un sólo átomo 2. El punto clave ahora es ver que la parte estructural de la ecuación anterior es esencialmente el factor de estructura del líquido. En efecto, consideremos la función G(k) definida como G(k) e ik Ri e ik Rj. i= j= Esta función se puede reescribir de la siguiente manera: c =+ i j i G(k) =+ e ik (Ri Rj) i= j i dr dr δ(r R i )δ(r R j ) e ik (r r ) =+ dr dr ρ (2) (r, r ) e ik (r r ), donde hemos hecho uso de las propiedades de la función δ y de la ecuación (34) que es válida también en el colectivo grancanónico (como puede demostrarse fácilmente). Si el sistema es uniforme podemos reescribir el resultado anterior en términos de la fdr: 2 En el caso de difracción de neutrones se encuentra una expresión equivalente pero con n a(k) sustituido por una parámetro constante. La razón es que un neutrón siente un potencial tipo δ debido al núcleo atómico mientras que los rayos X ven toda la distribución de carga electrónica del átomo. 7
18 G(k) =+ρ dr g(r) e ik r =+ρ dr [g(r) ] e ik r + ρ dr e ik r. El último sumando es cero a menos que k =0en cuyo caso la integral da como resultado el volumen del sistema. Por tanto, utilizando la definición del factor de estructura, tenemos: S(k) =G(k) δ k,0. (52) Por tanto, midiendo la intensidad difractada podemos obtener el factor de estructura. El punto interesante ahora es discutir el significado físico de esta función S(k) y eso es lo que haremos a continuación. El factor de estructura S(k) es una medida de la correlación entre fluctuaciones (de número de onda k) de densidad en dos puntos del fluido. Para entender el significado preciso de esta afirmación empezamos por introducir el operador densidad, ρ(r) (no confundir con la función de distribución de un cuerpo ρ () (r) de los apartados anteriores) definido como ρ(r) δ(r R i ), (53) i= es decir, un conjunto de funciones delta localizadas en las posiciones atómicas. De acuerdo con la ecuación (33), el promedio del operador densidad es la función de distribución de un cuerpo, ρ(r) = ρ () (r), que, en el límite uniforme, es simplemente ρ /V. La transformada de Fourier del operador densidad es ρ(k) = dr ρ(r) e ik r = e ik Ri. Consideremos ahora un fluido uniforme. Su densidad es constante e igual a ρ. La fluctuación de la densidad en el punto r está dada por ρ(r ) ρ y la fluctuación en el punto r 2 por ρ(r ) ρ. La correlación entre tales fluctuaciones 3 es descrita por la función χ( r r 2 ) definida como i= χ( r r 2 ) ρ ( ρ(r ) ρ)( ρ(r 2 ) ρ) = ρ ρ(r ) ρ(r 2 ) ρ, (54) donde, como de costumbre,... significa promedio sobre el colectivo, es decir, en el colectivo canónico, O = dr...dr O(r,..., r ) e βφ(r,...,r). Q(,V,T) Utilizando la definición de arriba para el operador densidad es fácil demostrar entonces que, para el sistema uniforme, 4 χ(r 2 )=ρ [g(r 2 ) ] + δ(r r 2 ) Transformando Fourier esta ecuación obtenemos directamente, χ(k) =S(k). 3 Evidentemente, si promediamos estadísticamente cada una de estas fluctuaciones obtenermos 0. 4 En efecto, ρ(r ) ρ(r 2 ) = δ(r R i ) δ(r 2 R j ) i= j= = δ(r R i )δ(r 2 R j ) + δ(r R i )δ(r 2 R i ) i= j i El primer sumando de esta última expresión es, según la ecuación (34) la función de distribución de dos cuerpos i= 8
19 Este resultado en realidad no es sorprendente pues para k =0ya lo habíamos obtenido al demostrar que S(k =0)es esencialmente la compresibilidad isotérmica que, como sabemos, mide fluctuaciones (más precisamente, correlación entre fluctuaciones) en el número de partículas. El factor de estructura nos da, por tanto, el espectro en número de ondas de estas fluctuaciones. Cuando las condiciones termodinámicas a las que está sometido el sistema uniforme se varían de forma que este se aproxima a su punto crítico, las fluctuaciones de longitud de onda larga se hacen cada vez más importantes y divergen en el punto crítico. Esta conducta quedará reflejada en el factor de estructura en el comportamiento de S(k 0). En particular, a medida que nos aproximamos al punto crítico se generará un pico en el origen que acaba por diverger. Esto se ve claramente en la siguiente figura que muestra resultados experimentales para el factor de estructura del rubidio líquido a diferentes temperaturas a lo largo de la curva de coexistencia con su vapor. Otros resultados para el factor de estructura se muestran en la figura siguiente. La parte de la izquierda muestra el resultado para esferas duras (puntos) y el correspondiente al potencial de Lennard-Jones (línea). De nuevo, al igual que ocurría con la función de distribución radial, es claro el hecho de que el potencial de esferas duras reproduce excelentemente la estructura del líquido Lennard-Jones, un hecho que, como se comentó anteriormente, será la base de una clase de aproximación conocida como teoríasdeperturbaciones. La figura de la derecha muestra el factor de estructura del sodio líquido a 00 o C (temperatura cercana a su punto triple). Los puntos son resultados experimentales obtenidos mediante difracción de rayos X mientras que la curva continua son los resultados de una simulación Monte Carlo utilizando un modelo de potencial tipo /r 4. Es evidente el magnífico acuerdo entre simulaciones y experimento lo que pone de manifiesto que este tipo de técnica es extremadamente útil a la hora de extraer información acerca del potencial de interacción entre las partículas del sistema. ρ (2) (r, r 2 ) que en el límite uniforme escribimos como ρ 2 g(g). El segundo sumando se puede reescribir δ(r R i )δ(r 2 R i ) i= = dr...dr δ(r R i )δ(r 2 R i )e βφ(r,...,r ) Q(, V, T) i= = dr...dr δ(r R )δ(r 2 R )e βφ(r,...,r ) Q(, V, T) = δ(r r 2 ) dr 2...dR e βφ(r,...,r ) = ρ(r )δ(r r 2 ) Q(, V, T) que conduce al resultado de arriba en el límite uniforme. 9
20 .6. Función de correlación directa y ecuación de Ornstein-Zernike. Hemos visto anteriormente que la función h(r) g(r) debe ser de largo alcance y que su integral diverge al aproximarnos al punto crítico. Ornstein y Zernike introdujeron la idea de descomponer esta función en una parte de corto alcance y otra de largo alcance. Para ello definieron en un líquido uniforme la función de correlación directa, c(r) de manera implícita escribiendo h(r) mediante la siguiente ecuación integral (conocida como ecuación de Ornstein-Zernike (OZ)) : h(r 2 )=c(r 2 )+ρ dr 3 c(r 3 ) h(r 32 ). (55) El primer sumando del segundo miembro (es decir, c(r 2 )) representa la correlación directa entre las partículas y 2. Elsegundo sumando tiene en cuenta todas las correlaciones indirectas que existen entre las partículas y 2 por intermediación del resto de partículas. De ahí los nombres para h(r) y c(r). Para ver esto más claramente reescribimos la ecuación de OZ de manera recurrente: expresamos h(r 32 ) en la forma (55) y la introducimos en la integral del segundo miembro. Si repetimos sucesivamente este proceso llegamos a h(r 2 )=c(r 2 )+ρ dr 3 c(r 3 )c(r 32 )+ρ 2 dr 3 dr 4 c(r 3 )c(r 34 )c(r 42 )+... (56) Podemos introducir una representación diagramática de esta ecuación (de manera análoga a como hemos hecho anteriormente). Para ello definimos diagramas formados por círculos abiertos (puntos raíz) que representan posiciones de partículas con respecto a las que no se integra, círculos rellenos (puntos campo) que implican integración a todo el espacio con respecto a la posición de esa partícula (pesada la integral con un factor ρ) y, finalmente, líneas uniendo círculos que en este caso representan enlaces vía la correspondiente c(r ij ).Esevidente entonces que la ecuación anterior para la función de correlación total se puede representar diagramáticamente como se muestra en la figura c c c c c c h(r ) = La razón para estos nombres (función de correlación total y función de correlación directa) resulta ahora evidente. 20
21 Cuál es la razón primordial que justifica la introducción de esta nueva función de correlación c(r) cuando, según hemos visto en los apartados anteriores, en un líquido uniforme el sólo conocimiento de g(r) (o sea, h(r)) basta (para potenciales a pares) para describir totalmente el sistema?. Ornstein y Zernike sugirieron que c(r) debía ser una función mucho más simple que g(r) que, como hemos visto, presenta fuertes oscilaciones y es de largo alcance (es decir, su alcance es mucho mayor que el alcance del potencial de interacción entre dos partículas). Es más, OZ argumentaron que la función de correlación directa debe tener el mismo alcance que el potencial de interacción y asintóticamente debe comportarse como: c(r) φ(r). (57) r k B T Esto es interesante pues tenido en cuenta con la expansión diagramática de arriba explica el largo alcance de g(r): Se debe, simplemente a la interacción indirecta entre las partículas y 2 por intermediación de un número cada vez mayor de partículas intermedias. Si (57) es cierta, entonces será más fácil encontrar una aproximación razonable 5 para la función simple c(r) que hacerlo para la fdr. Introduciendo entonces esa aproximación para c(r) en la ecuación de OZ debe ser posible obtener g(r) que luego utilizamos para obtener las propiedades termodinámicas del sistema. Muchas de las modernas teorías de líquidos se basan precisamente en esta idea, como veremos en su momento. Por tanto, probar el resultado (57) es importante. En el límite de muy baja densidad es fácil de demostrar: La ecuación de OZ muestra que, a orden más bajo en densidad, h(r) =c(r). Por otra parte, la ecuación (45) muestra que, en este límite, g(r) exp [ βφ(r)] así que c(r) =h(r) exp [ βφ(r)]. Si el potencial decae suficientemente rápido, en el límite r el argumento de la exponencial es muy pequeño y podemos desarrollarla en serie, obteniendo directamente el resultado (57). Es mucho más difícil probar que el resultado (57) es cierto también en líquidos densos, es decir, a todos los órdenes en la densidad, y no lo vamos a hacer aquí 6, conformándonos con mostrarlo gráficamente en la figura siguiente donde se representan h(r) y c(r) para un líquido simple típico cerca del punto triple (es decir, a densidad muy alta). La diferencia entre ambas funciones así como las propiedades de ambas (especialmente la diferencia en alcance) son evidentes. 5 Al final siempre tendremos que recurrir a buscar aproximaciones cuando nos planteemos el estudio de líquidos reales. 6 Una discusión detallada de este punto ha sido hecha por G. Stell en el libro Modern Theoretical Chemistry (Volumen5, 977), editado por B. J. Berne. El resultado solo deja de ser válidoenelpunto crítico. 2
Métodos Matemáticos en Física L4F. CONDICIONES de CONTORNO+Fuerzas Externas (Cap. 3, libro APL)
 L4F. CONDICIONES de CONTORNO+Fuerzas Externas (Cap. 3, libro Condiciones de contorno. Fuerzas externas aplicadas sobre una cuerda. condición que nos describe un extremo libre en una cuerda tensa. Ecuación
L4F. CONDICIONES de CONTORNO+Fuerzas Externas (Cap. 3, libro Condiciones de contorno. Fuerzas externas aplicadas sobre una cuerda. condición que nos describe un extremo libre en una cuerda tensa. Ecuación
TEMA IV: FUNCIONES HIPERGEOMETRICAS
 TEMA IV: FUNCIONES HIPERGEOMETRICAS 1. La ecuación hipergeométrica x R y α, β, γ parámetros reales. x(1 x)y + [γ (α + β + 1)x]y αβy 0 (1.1) Dividiendo en (1.1) por x(1 x) obtenemos (x 0, x 1) y + γ (α
TEMA IV: FUNCIONES HIPERGEOMETRICAS 1. La ecuación hipergeométrica x R y α, β, γ parámetros reales. x(1 x)y + [γ (α + β + 1)x]y αβy 0 (1.1) Dividiendo en (1.1) por x(1 x) obtenemos (x 0, x 1) y + γ (α
την..., επειδή... Se usa cuando se cree que el punto de vista del otro es válido, pero no se concuerda completamente
 - Concordar En términos generales, coincido con X por Se usa cuando se concuerda con el punto de vista de otro Uno tiende a concordar con X ya Se usa cuando se concuerda con el punto de vista de otro Comprendo
- Concordar En términos generales, coincido con X por Se usa cuando se concuerda con el punto de vista de otro Uno tiende a concordar con X ya Se usa cuando se concuerda con el punto de vista de otro Comprendo
TRIGONOMETRIA. hipotenusa L 2. hipotenusa
 TRIGONOMETRIA. Calcular las razones trigonométricas de 0º, º y 60º. Para calcular las razones trigonométricas de º, nos ayudamos de un triángulo rectángulo isósceles como el de la figura. cateto opuesto
TRIGONOMETRIA. Calcular las razones trigonométricas de 0º, º y 60º. Para calcular las razones trigonométricas de º, nos ayudamos de un triángulo rectángulo isósceles como el de la figura. cateto opuesto
SOLUCIONES DE LAS ACTIVIDADES Págs. 101 a 119
 Página 0. a) b) π 4 π x 0 4 π π / 0 π / x 0º 0 x π π. 0 rad 0 π π rad 0 4 π 0 π rad 0 π 0 π / 4. rad 4º 4 π π 0 π / rad 0º π π 0 π / rad 0º π 4. De izquierda a derecha: 4 80 π rad π / rad 0 Página 0. tg
Página 0. a) b) π 4 π x 0 4 π π / 0 π / x 0º 0 x π π. 0 rad 0 π π rad 0 4 π 0 π rad 0 π 0 π / 4. rad 4º 4 π π 0 π / rad 0º π π 0 π / rad 0º π 4. De izquierda a derecha: 4 80 π rad π / rad 0 Página 0. tg
Escenas de episodios anteriores
 Clase 09/10/2013 Tomado y editado de los apuntes de Pedro Sánchez Terraf Escenas de episodios anteriores objetivo: estudiar formalmente el concepto de demostración matemática. caso de estudio: lenguaje
Clase 09/10/2013 Tomado y editado de los apuntes de Pedro Sánchez Terraf Escenas de episodios anteriores objetivo: estudiar formalmente el concepto de demostración matemática. caso de estudio: lenguaje
1 La teoría de Jeans. t + (n v) = 0 (1) b) Navier-Stokes (conservación del impulso) c) Poisson
 1 La teoría de Jeans El caso ás siple de evolución de fluctuaciones es el de un fluído no relativista. las ecuaciones básicas son: a conservación del núero de partículas n t + (n v = 0 (1 b Navier-Stokes
1 La teoría de Jeans El caso ás siple de evolución de fluctuaciones es el de un fluído no relativista. las ecuaciones básicas son: a conservación del núero de partículas n t + (n v = 0 (1 b Navier-Stokes
Lógica Proposicional. Justificación de la validez del razonamiento?
 Proposicional educción Natural Proposicional - 1 Justificación de la validez del razonamiento? os maneras diferentes de justificar Justificar que la veracidad de las hipótesis implica la veracidad de la
Proposicional educción Natural Proposicional - 1 Justificación de la validez del razonamiento? os maneras diferentes de justificar Justificar que la veracidad de las hipótesis implica la veracidad de la
Lógica Proposicional
 Proposicional educción Natural Proposicional - 1 Justificación de la validez del razonamiento os maneras diferentes de justificar Justificar que la veracidad de las hipótesis implica la veracidad de la
Proposicional educción Natural Proposicional - 1 Justificación de la validez del razonamiento os maneras diferentes de justificar Justificar que la veracidad de las hipótesis implica la veracidad de la
PÁGINA 106 PÁGINA a) sen 30 = 1/2 b) cos 120 = 1/2. c) tg 135 = 1 d) cos 45 = PÁGINA 109
 PÁGINA 0. La altura del árbol es de 8,5 cm.. BC m. CA 70 m. a) x b) y PÁGINA 0. tg a 0, Con calculadora: sß 0,9 t{ ««}. cos a 0, Con calculadora: st,8 { \ \ } PÁGINA 05. cos a 0,78 tg a 0,79. sen a 0,5
PÁGINA 0. La altura del árbol es de 8,5 cm.. BC m. CA 70 m. a) x b) y PÁGINA 0. tg a 0, Con calculadora: sß 0,9 t{ ««}. cos a 0, Con calculadora: st,8 { \ \ } PÁGINA 05. cos a 0,78 tg a 0,79. sen a 0,5
Académico Introducción
 - Σε αυτήν την εργασία/διατριβή θα αναλύσω/εξετάσω/διερευνήσω/αξιολογήσω... general para un ensayo/tesis Για να απαντήσουμε αυτή την ερώτηση, θα επικεντρωθούμε πρώτα... Para introducir un área específica
- Σε αυτήν την εργασία/διατριβή θα αναλύσω/εξετάσω/διερευνήσω/αξιολογήσω... general para un ensayo/tesis Για να απαντήσουμε αυτή την ερώτηση, θα επικεντρωθούμε πρώτα... Para introducir un área específica
Academic Opening Opening - Introduction Greek Spanish En este ensayo/tesis analizaré/investigaré/evaluaré...
 - Introduction Σε αυτήν την εργασία/διατριβή θα αναλύσω/εξετάσω/διερευνήσω/αξιολογήσω... General opening for an essay/thesis En este ensayo/tesis analizaré/investigaré/evaluaré... Για να απαντήσουμε αυτή
- Introduction Σε αυτήν την εργασία/διατριβή θα αναλύσω/εξετάσω/διερευνήσω/αξιολογήσω... General opening for an essay/thesis En este ensayo/tesis analizaré/investigaré/evaluaré... Για να απαντήσουμε αυτή
Filipenses 2:5-11. Filipenses
 Filipenses 2:5-11 Filipenses La ciudad de Filipos fue nombrada en honor de Felipe II de Macedonia, padre de Alejandro. Con una pequeña colonia judía aparentemente no tenía una sinagoga. El apóstol fundó
Filipenses 2:5-11 Filipenses La ciudad de Filipos fue nombrada en honor de Felipe II de Macedonia, padre de Alejandro. Con una pequeña colonia judía aparentemente no tenía una sinagoga. El apóstol fundó
Nro. 01 Septiembre de 2011
 SOL Cultura La Tolita, de 400 ac. a 600 dc. En su representación se sintetiza toda la mitología ancestral del Ecuador. Trabajado en oro laminado y repujado. Museo Nacional Banco Central del Ecuador Dirección
SOL Cultura La Tolita, de 400 ac. a 600 dc. En su representación se sintetiza toda la mitología ancestral del Ecuador. Trabajado en oro laminado y repujado. Museo Nacional Banco Central del Ecuador Dirección
Ventiladores helicoidales murales o tubulares, versión PL equipados con hélice de plástico y versión AL equipados con hélice de aluminio.
 HCH HCT HCH HCT Ventiladores helicoidales murales o tubulares, de gran robustez Ventiladores helicoidales murales o tubulares, versión PL equipados con hélice de plástico y versión AL equipados con hélice
HCH HCT HCH HCT Ventiladores helicoidales murales o tubulares, de gran robustez Ventiladores helicoidales murales o tubulares, versión PL equipados con hélice de plástico y versión AL equipados con hélice
Catálogodegrandespotencias
 www.dimotor.com Catálogogranspotencias Índice Motores grans potencias 3 Motores asíncronos trifásicos Baja Tensión y Alta tensión.... 3 Serie Y2 Baja tensión 4 Motores asíncronos trifásicos Baja Tensión
www.dimotor.com Catálogogranspotencias Índice Motores grans potencias 3 Motores asíncronos trifásicos Baja Tensión y Alta tensión.... 3 Serie Y2 Baja tensión 4 Motores asíncronos trifásicos Baja Tensión
μέλλων τελευτᾶν 0,25 puntos καὶ βουλόμενος 0,25 puntos τοὺς αὐτοῦ παῖδας ἐμπείρους εἶναι τῆς γεωργίας, 0,5 puntos
 Materia: GRIEGO II. EvAU CURSO 17/18 CRITERIOS ESPECÍFICOS DE CORRECCIÓN PROPUESTA A: EL LABRADOR Y SUS HIJOS 1.- Traducción íntegra del texto: (4 puntos). Se ponderará, ante todo: - La recta adecuación
Materia: GRIEGO II. EvAU CURSO 17/18 CRITERIOS ESPECÍFICOS DE CORRECCIÓN PROPUESTA A: EL LABRADOR Y SUS HIJOS 1.- Traducción íntegra del texto: (4 puntos). Se ponderará, ante todo: - La recta adecuación
La transformada de ondícula continua y algunas clases de operadores de localización
 La transformada de ondícula continua y algunas clases de operadores de localización Gerardo Ramos Vázquez Dr. Egor Maximenko Instituto Politécnico Nacional, ESFM diciembre 2016 Contenido El grupo afín
La transformada de ondícula continua y algunas clases de operadores de localización Gerardo Ramos Vázquez Dr. Egor Maximenko Instituto Politécnico Nacional, ESFM diciembre 2016 Contenido El grupo afín
ΑΡΧΗ 1 ης ΣΕΛΙΔΑΣ KΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΠΑΡΑΣΚΕΥΗ 24 ΙΟΥΝΙΟΥ 2005 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΑ ΙΣΠΑΝΙΚΑ
 ΑΡΧΗ 1 ης ΣΕΛΙΔΑΣ KΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΠΑΡΑΣΚΕΥΗ 24 ΙΟΥΝΙΟΥ 2005 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΑ ΙΣΠΑΝΙΚΑ Α. Να αποδώσετε στο τετράδιό σας στην ελληνική γλώσσα το παρακάτω κείμενο,
ΑΡΧΗ 1 ης ΣΕΛΙΔΑΣ KΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΠΑΡΑΣΚΕΥΗ 24 ΙΟΥΝΙΟΥ 2005 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΑ ΙΣΠΑΝΙΚΑ Α. Να αποδώσετε στο τετράδιό σας στην ελληνική γλώσσα το παρακάτω κείμενο,
ΕΙΣΑΓΩΓΗ INTRODUCCIÓN
 ΕΝΗΜΕΡΩΣΗ ΚΑΙ ΔΙΑΒΟΥΛΕΥΣΗ ΣΤΑ ΕΥΡΩΠΑΙΚΑ ΣΥΜΒΟΥΛΙΑ ΕΡΓΑΖΟΜΕΝΩΝ (ΕΣΕ) KAI Η ΚΟΙΝΟΤΙΚΗ ΟΔΗΓΙΑ 2009/38 INFORMACIÓN Y CONSULTA EN LOS COMITÉS DE EMPRESA EUROPEOS (CEE) Y LA DIRECTIVA COMUNITARIA 2009/38 Αθανάσιος
ΕΝΗΜΕΡΩΣΗ ΚΑΙ ΔΙΑΒΟΥΛΕΥΣΗ ΣΤΑ ΕΥΡΩΠΑΙΚΑ ΣΥΜΒΟΥΛΙΑ ΕΡΓΑΖΟΜΕΝΩΝ (ΕΣΕ) KAI Η ΚΟΙΝΟΤΙΚΗ ΟΔΗΓΙΑ 2009/38 INFORMACIÓN Y CONSULTA EN LOS COMITÉS DE EMPRESA EUROPEOS (CEE) Y LA DIRECTIVA COMUNITARIA 2009/38 Αθανάσιος
FUNCIONES Y FÓRMULAS TRIGONOMÉTRICAS
 5 FUNCIONES Y FÓRMULAS TRIGONOMÉTRICAS Página PARA EMPEZAR, REFLEXIONA Y RESUELVE. Aunque el método para resolver las siguientes preguntas se sistematiza en la página siguiente, puedes resolverlas ahora:
5 FUNCIONES Y FÓRMULAS TRIGONOMÉTRICAS Página PARA EMPEZAR, REFLEXIONA Y RESUELVE. Aunque el método para resolver las siguientes preguntas se sistematiza en la página siguiente, puedes resolverlas ahora:
Tema 3. Espazos métricos. Topoloxía Xeral,
 Tema 3. Espazos métricos Topoloxía Xeral, 2017-18 Índice Métricas en R n Métricas no espazo de funcións Bólas e relacións métricas Definición Unha métrica nun conxunto M é unha aplicación d con valores
Tema 3. Espazos métricos Topoloxía Xeral, 2017-18 Índice Métricas en R n Métricas no espazo de funcións Bólas e relacións métricas Definición Unha métrica nun conxunto M é unha aplicación d con valores
Inmigración Estudiar. Estudiar - Universidad. Indicar que quieres matricularte. Indicar que quieres matricularte en una asignatura.
 - Universidad Me gustaría matricularme en la universidad. Indicar que quieres matricularte Me quiero matricular. Indicar que quieres matricularte en una asignatura en un grado en un posgrado en un doctorado
- Universidad Me gustaría matricularme en la universidad. Indicar que quieres matricularte Me quiero matricular. Indicar que quieres matricularte en una asignatura en un grado en un posgrado en un doctorado
TEMA 6.- BIOMOLÉCULAS ORGÁNICAS IV: ÁCIDOS NUCLEICOS
 TEMA 6.- BIMLÉCULAS RGÁNICAS IV: ÁCIDS NUCLEICS A.- Características generales de los Ácidos Nucleicos B.- Nucleótidos y derivados nucleotídicos El esqueleto covalente de los ácidos nucleicos: el enlace
TEMA 6.- BIMLÉCULAS RGÁNICAS IV: ÁCIDS NUCLEICS A.- Características generales de los Ácidos Nucleicos B.- Nucleótidos y derivados nucleotídicos El esqueleto covalente de los ácidos nucleicos: el enlace
TEST DE INDEPENDENCIA EN SERIES TEMPORALES
 TEST DE INDEPENDENCIA EN SERIES TEMPORALES Titulación: Doctorado en Tecnologías Industriales Alumno/a: Salvador Vera Nieto Director/a/s: José Salvador Cánovas Peña Antonio Guillamón Frutos Cartagena, 10
TEST DE INDEPENDENCIA EN SERIES TEMPORALES Titulación: Doctorado en Tecnologías Industriales Alumno/a: Salvador Vera Nieto Director/a/s: José Salvador Cánovas Peña Antonio Guillamón Frutos Cartagena, 10
Análisis de las Enneadas de Plotino. Gonzalo Hernández Sanjorge A Parte Rei 20
 Análisis de las Enneadas de Plotino, Tratado Cuarto de la Enneada Primera Acerca de la felicidad1 Gonzalo Hernández Sanjorge La felicidad vinculada al vivir bien: la sensación y la razón. Identificar qué
Análisis de las Enneadas de Plotino, Tratado Cuarto de la Enneada Primera Acerca de la felicidad1 Gonzalo Hernández Sanjorge La felicidad vinculada al vivir bien: la sensación y la razón. Identificar qué
Metrología Cuántica e Información Cuántica de Fisher.
 Metrología Cuántica e Información Cuántica de Fisher. Entrelazamiento y Distinguibilidad en Interferometría Atómica. Diego Alejandro Lancheros Seminario de Óptica Cuántica. Universidad de Los Andes. Table
Metrología Cuántica e Información Cuántica de Fisher. Entrelazamiento y Distinguibilidad en Interferometría Atómica. Diego Alejandro Lancheros Seminario de Óptica Cuántica. Universidad de Los Andes. Table
Revista de Filosofía Vol. XXV, N 1, 2013 pp Platão, Filebo -
 Revista de Filosofía Vol. XXV, N 1, 2013 pp. 163-181 Platão, Filebo - - - Filebo 164 1 Filebo 2, me resulta especialmente útil la - i.e. interpre- en particular. 1. II 2 Filebo - 3 : ) vêm do um e do múltiplo,
Revista de Filosofía Vol. XXV, N 1, 2013 pp. 163-181 Platão, Filebo - - - Filebo 164 1 Filebo 2, me resulta especialmente útil la - i.e. interpre- en particular. 1. II 2 Filebo - 3 : ) vêm do um e do múltiplo,
FORMULARIO DE ELASTICIDAD
 U. D. Resistencia de Mateiales, Elasticidad Plasticidad Depatamento de Mecánica de Medios Continuos Teoía de Estuctuas E.T.S. Ingenieos de Caminos, Canales Puetos Univesidad Politécnica de Madid FORMULARIO
U. D. Resistencia de Mateiales, Elasticidad Plasticidad Depatamento de Mecánica de Medios Continuos Teoía de Estuctuas E.T.S. Ingenieos de Caminos, Canales Puetos Univesidad Politécnica de Madid FORMULARIO
Académico Introducción
 - Σε αυτήν την εργασία/διατριβή θα αναλύσω/εξετάσω/διερευνήσω/αξιολογήσω... general para un ensayo/tesis In this essay/paper/thesis I shall examine/investigate/evaluate/analyze Για να απαντήσουμε αυτή
- Σε αυτήν την εργασία/διατριβή θα αναλύσω/εξετάσω/διερευνήσω/αξιολογήσω... general para un ensayo/tesis In this essay/paper/thesis I shall examine/investigate/evaluate/analyze Για να απαντήσουμε αυτή
FL/STEM Σχεδιασμός/Πρότυπο μαθήματος (χημεία) 2015/2016. Μάθημα (τίτλος) Οξυγόνο. Παραγωγή οξυγόνου Επίπεδο επάρκειας γλώσσας < Α1 Α2 Β1 Β2 C1
 Μάθημα (τίτλος) Οξυγόνο. Παραγωγή οξυγόνου Επίπεδο επάρκειας γλώσσας < Α1 Α2 Β1 Β2 C1 Τάξη/βαθμίδα: 6η Αριθμός μαθητών στην τάξη: 8 Περιεχόμενο μαθήματος: Οξυγόνο. Θέμα: Άνθρωπος και φύση Ουσίες Προϋποθέσεις
Μάθημα (τίτλος) Οξυγόνο. Παραγωγή οξυγόνου Επίπεδο επάρκειας γλώσσας < Α1 Α2 Β1 Β2 C1 Τάξη/βαθμίδα: 6η Αριθμός μαθητών στην τάξη: 8 Περιεχόμενο μαθήματος: Οξυγόνο. Θέμα: Άνθρωπος και φύση Ουσίες Προϋποθέσεις
PAU XUÑO 2011 MATEMÁTICAS II
 PAU XUÑO 2011 MATEMÁTICAS II Código: 26 (O alumno/a debe responder só os exercicios dunha das opcións. Puntuación máxima dos exercicios de cada opción: exercicio 1= 3 puntos, exercicio 2= 3 puntos, exercicio
PAU XUÑO 2011 MATEMÁTICAS II Código: 26 (O alumno/a debe responder só os exercicios dunha das opcións. Puntuación máxima dos exercicios de cada opción: exercicio 1= 3 puntos, exercicio 2= 3 puntos, exercicio
CAPÍTULO 6: EL PRONOMBRE DEMOSTRATIVO Y RELATIVO
 CAPÍTULO 6: EL PRONOMBRE DEMOSTRATIVO Y RELATIVO I. EL PRONOMBRE DEMOSTRATIVO Hay dos tipos de pronombres demostrativos: cercanos y lejanos. 1 Normalmente sirven para señalar la cercanía o lejanía de alguien/algo
CAPÍTULO 6: EL PRONOMBRE DEMOSTRATIVO Y RELATIVO I. EL PRONOMBRE DEMOSTRATIVO Hay dos tipos de pronombres demostrativos: cercanos y lejanos. 1 Normalmente sirven para señalar la cercanía o lejanía de alguien/algo
Una visión alberiana del tema. Abstract *** El marco teórico. democracia, república y emprendedores; alberdiano
 Abstract Una visión alberiana del tema - democracia, república y emprendedores; - - alberdiano El marco teórico *** - 26 LIBERTAS SEGUNDA ÉPOCA - - - - - - - - revolución industrial EMPRENDEDORES, REPÚBLICA
Abstract Una visión alberiana del tema - democracia, república y emprendedores; - - alberdiano El marco teórico *** - 26 LIBERTAS SEGUNDA ÉPOCA - - - - - - - - revolución industrial EMPRENDEDORES, REPÚBLICA
f) cotg 300 ctg 60 2 d) cos 5 cos 6 Al ser un ángulo del primer cuadrante, todas las razones son positivas. Así, tenemos: tg α 3
 .9. Calcula el valor de las siguientes razones trigonométricas reduciéndolas al primer cuadrante. a) sen 0 c) tg 0 e) sec 0 b) cos d) cosec f) cotg 00 Solucionario a) sen 0 sen 0 d) cosec sen sen b) cos
.9. Calcula el valor de las siguientes razones trigonométricas reduciéndolas al primer cuadrante. a) sen 0 c) tg 0 e) sec 0 b) cos d) cosec f) cotg 00 Solucionario a) sen 0 sen 0 d) cosec sen sen b) cos
LUGARES XEOMÉTRICOS. CÓNICAS
 LUGARES XEOMÉTRICOS. CÓNICAS Páxina REFLEXIONA E RESOLVE Cónicas abertas: parábolas e hipérboles Completa a seguinte táboa, na que a é o ángulo que forman as xeratrices co eixe, e, da cónica e b o ángulo
LUGARES XEOMÉTRICOS. CÓNICAS Páxina REFLEXIONA E RESOLVE Cónicas abertas: parábolas e hipérboles Completa a seguinte táboa, na que a é o ángulo que forman as xeratrices co eixe, e, da cónica e b o ángulo
A proba constará de vinte cuestións tipo test. As cuestións tipo test teñen tres posibles respostas, das que soamente unha é correcta.
 Páxina 1 de 9 1. Formato da proba Formato proba constará de vinte cuestións tipo test. s cuestións tipo test teñen tres posibles respostas, das que soamente unha é correcta. Puntuación Puntuación: 0.5
Páxina 1 de 9 1. Formato da proba Formato proba constará de vinte cuestións tipo test. s cuestións tipo test teñen tres posibles respostas, das que soamente unha é correcta. Puntuación Puntuación: 0.5
TEMA 3. Lípidos. Bioq. Juan Pablo Rodríguez
 TEMA 3 Lípidos Bioq. Juan Pablo Rodríguez Lípidos - Definición Bajo el término Lípidos se agrupan un gran número de compuestos, de estructura química variada, que tienen la propiedad común de ser solubles
TEMA 3 Lípidos Bioq. Juan Pablo Rodríguez Lípidos - Definición Bajo el término Lípidos se agrupan un gran número de compuestos, de estructura química variada, que tienen la propiedad común de ser solubles
Tema de aoristo. Morfología y semántica
 Tema de aoristo Morfología y semántica El verbo politemático Cada verbo griego tiene 4 temas principales. La diferencia semántica entre ellos es el aspecto, no el tiempo. Semántica de los temas verbales
Tema de aoristo Morfología y semántica El verbo politemático Cada verbo griego tiene 4 temas principales. La diferencia semántica entre ellos es el aspecto, no el tiempo. Semántica de los temas verbales
Για να ρωτήσετε αν κάποιος μπορεί να σας βοηθήσει να γεμίσετε μια φόρμα
 - Γενικά Dónde tengo que pedir el formulario/impreso para? Για να ρωτήσετε που μπορείτε να βρείτε μια φόρμα Dónde tengo que pedir el formulario/impreso para? Cuál es la fecha de expedición de su (documento)?
- Γενικά Dónde tengo que pedir el formulario/impreso para? Για να ρωτήσετε που μπορείτε να βρείτε μια φόρμα Dónde tengo que pedir el formulario/impreso para? Cuál es la fecha de expedición de su (documento)?
Το ίκτυο Βιβλιοθηκών του Τµήµατος Κοινωνικού Έργου της Caja Madrid. La Red de Bibliotecas de Obra Social Caja Madrid
 Το ίκτυο Βιβλιοθηκών του Τµήµατος Κοινωνικού Έργου της Caja Madrid La Red de Bibliotecas de Obra Social Caja Madrid Το ίκτυο Βιβλιοθηκών αποτελεί τµήµα ενός Χρηµατοπιστωτικού Φορέα που προορίζει ποσοστό
Το ίκτυο Βιβλιοθηκών του Τµήµατος Κοινωνικού Έργου της Caja Madrid La Red de Bibliotecas de Obra Social Caja Madrid Το ίκτυο Βιβλιοθηκών αποτελεί τµήµα ενός Χρηµατοπιστωτικού Φορέα που προορίζει ποσοστό
Los Determinantes y los Pronombres
 Los Determinantes y los Pronombres Englobamos dentro de los determinantes al artículo y a todos los adjetivos determinativos (demostrativos, posesivos, numerales, indefinidos, interrogativos y exclamativos).
Los Determinantes y los Pronombres Englobamos dentro de los determinantes al artículo y a todos los adjetivos determinativos (demostrativos, posesivos, numerales, indefinidos, interrogativos y exclamativos).
EXERCICIOS DE REFORZO: RECTAS E PLANOS
 EXERCICIOS DE REFORZO RECTAS E PLANOS Dada a recta r z a) Determna a ecuacón mplícta do plano π que pasa polo punto P(,, ) e é perpendcular a r Calcula o punto de nterseccón de r a π b) Calcula o punto
EXERCICIOS DE REFORZO RECTAS E PLANOS Dada a recta r z a) Determna a ecuacón mplícta do plano π que pasa polo punto P(,, ) e é perpendcular a r Calcula o punto de nterseccón de r a π b) Calcula o punto
ΚΑΙΝΟΤΟΜΙΑ ΚΑΙ ΑΠΛΟΤΗΤΑ. Innovación y simplicidad
 pro ima pro ima Innovación y simplicidad PROXIMA es la última innovación de Serrature Meroni, un producto diseñado tanto para aquellos que ya disponen de un pomo PremiApri Meroni en su puerta, como para
pro ima pro ima Innovación y simplicidad PROXIMA es la última innovación de Serrature Meroni, un producto diseñado tanto para aquellos que ya disponen de un pomo PremiApri Meroni en su puerta, como para
AXIAL ES SU MEJOR ELECCIÓN. MÁXIMA CALIDAD ALTA TECNOLOGÍA VARIEDAD DE MODELOS PRESTACIONES SERVICIO. La plegadora de la serie PSE, le ofrece
 PLEGADORA SERIE PSE AXIAL ES SU MEJOR ELECCIÓN. MÁXIMA CALIDAD ALTA TECNOLOGÍA VARIEDAD DE MODELOS PRESTACIONES SERVICIO La plegadora de la serie PSE, le ofrece una gran variedad de modelos, que comprende
PLEGADORA SERIE PSE AXIAL ES SU MEJOR ELECCIÓN. MÁXIMA CALIDAD ALTA TECNOLOGÍA VARIEDAD DE MODELOS PRESTACIONES SERVICIO La plegadora de la serie PSE, le ofrece una gran variedad de modelos, que comprende
Algunas integrales impropias con límites de integración infinitos que involucran a la generalización τ de la función hipergeométrica de Gauss
 Ingeniería y Ciencia, ISSN 794 965 Volumen 3, número 5, páginas 67-85, junio de 27 Algunas integrales impropias con límites de integración infinitos que involucran a la generalización de la función hipergeométrica
Ingeniería y Ciencia, ISSN 794 965 Volumen 3, número 5, páginas 67-85, junio de 27 Algunas integrales impropias con límites de integración infinitos que involucran a la generalización de la función hipergeométrica
NÚMEROS REAIS. Páxina 27 REFLEXIONA E RESOLVE. O paso de Z a Q. O paso de Q a Á
 NÚMEROS REAIS Páxina 7 REFLEXIONA E RESOLVE O paso de Z a Q Di cales das seguintes ecuacións se poden resolver en Z e para cales é necesario o conxunto dos números racionais, Q. a) x 0 b) 7x c) x + d)
NÚMEROS REAIS Páxina 7 REFLEXIONA E RESOLVE O paso de Z a Q Di cales das seguintes ecuacións se poden resolver en Z e para cales é necesario o conxunto dos números racionais, Q. a) x 0 b) 7x c) x + d)
Το παρόν σχέδιο μαθήματος δημιουργήθηκε από την κα. Radost Mazganova, καθηγήτρια Ισπανικών και την κα. Yordanka Yordanova, καθηγήτρια χημείας
 Μάθημα (τίτλος) Καθαρές ουσίες και μείγματα Επίπεδο γλωσσικής επάρκειας Α1 Α2 Β1 Β2 C1 Τάξη/βαθμίδα: πέμπτη Αριθμός μαθητών στην τάξη: 15 Θέμα: Άνθρωπος και φύση / Ουσίες και οι ιδιότητές τους Προϋποθέσεις
Μάθημα (τίτλος) Καθαρές ουσίες και μείγματα Επίπεδο γλωσσικής επάρκειας Α1 Α2 Β1 Β2 C1 Τάξη/βαθμίδα: πέμπτη Αριθμός μαθητών στην τάξη: 15 Θέμα: Άνθρωπος και φύση / Ουσίες και οι ιδιότητές τους Προϋποθέσεις
2 ÍNDICE GENERAL A Modelo de Wess Zumino Witten. 109 A.1 Propiedades del modelo de WZW B Orden normal y relaciones entre OP
 Índice General 1 Introducción. 3 2 Teor as masivas y ecuaciones de Toda no abelianas. 11 2.1 Ecuaciones de Toda no abelianas....................... 11 2.2 Teor as con acción real y positiva.......................
Índice General 1 Introducción. 3 2 Teor as masivas y ecuaciones de Toda no abelianas. 11 2.1 Ecuaciones de Toda no abelianas....................... 11 2.2 Teor as con acción real y positiva.......................
PAU XUÑO 2010 MATEMÁTICAS II
 PAU XUÑO 010 MATEMÁTICAS II Código: 6 (O alumno/a deber responder só aos eercicios dunha das opcións. Punuación máima dos eercicios de cada opción: eercicio 1= 3 punos, eercicio = 3 punos, eercicio 3 =
PAU XUÑO 010 MATEMÁTICAS II Código: 6 (O alumno/a deber responder só aos eercicios dunha das opcións. Punuación máima dos eercicios de cada opción: eercicio 1= 3 punos, eercicio = 3 punos, eercicio 3 =
Κυρ. Ιωάννου Οδ. Δωριέων 34 Τ.Κ 8068, Λάρνακα. Adam Smith 8 Crossfield Road Selly Oak Birmingham West Midlands B29 1WQ
 - Dirección Κυρ. Ιωάννου Οδ. Δωριέων 34 Τ.Κ 8068, Λάρνακα Formato de dirección de México: Colonia Código postal + Estado, Ciudad. Jeremy Rhodes 212 Silverback Drive California Springs CA 92926 Formato
- Dirección Κυρ. Ιωάννου Οδ. Δωριέων 34 Τ.Κ 8068, Λάρνακα Formato de dirección de México: Colonia Código postal + Estado, Ciudad. Jeremy Rhodes 212 Silverback Drive California Springs CA 92926 Formato
Εμπορική αλληλογραφία Ηλεκτρονική Αλληλογραφία
 - Εισαγωγή ελληνικά Αξιότιμε κύριε Πρόεδρε, ισπανικά Distinguido Sr. Presidente: Εξαιρετικά επίσημη επιστολή, ο παραλήπτης έχει ένα ειδικό τίτλο ο οποίος πρέπει να χρησιμοποιηθεί αντί του ονόματος του
- Εισαγωγή ελληνικά Αξιότιμε κύριε Πρόεδρε, ισπανικά Distinguido Sr. Presidente: Εξαιρετικά επίσημη επιστολή, ο παραλήπτης έχει ένα ειδικό τίτλο ο οποίος πρέπει να χρησιμοποιηθεί αντί του ονόματος του
Universidad Nacional del Sur
 Universidad Nacional del Sur Tesis de Magister en Matemática Reductos hilbertianos de las álgebras de Lukasiewicz-Moisil de orden 3 Juan Sebastián Slagter Director: Dr. Aldo Figallo Orellano Bahía Blanca
Universidad Nacional del Sur Tesis de Magister en Matemática Reductos hilbertianos de las álgebras de Lukasiewicz-Moisil de orden 3 Juan Sebastián Slagter Director: Dr. Aldo Figallo Orellano Bahía Blanca
Εμπορική αλληλογραφία Επιστολή
 - Διεύθυνση Sr. J. Rhodes Rhodes & Rhodes Corp. 212 Silverback Drive California Springs CA 92926 Sr. J. Rhodes Rhodes & Rhodes Corp. 212 Silverback Drive California Springs CA 92926 Αμερικανική γραφή διεύθυνσης:
- Διεύθυνση Sr. J. Rhodes Rhodes & Rhodes Corp. 212 Silverback Drive California Springs CA 92926 Sr. J. Rhodes Rhodes & Rhodes Corp. 212 Silverback Drive California Springs CA 92926 Αμερικανική γραφή διεύθυνσης:
KΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΤΕΤΑΡΤΗ 20 ΙΟΥΝΙΟΥ 2007 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΑ ΙΣΠΑΝΙΚΑ
 ΑΡΧΗ 1ης ΣΕΛΙ ΑΣ KΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΤΕΤΑΡΤΗ 20 ΙΟΥΝΙΟΥ 2007 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΑ ΙΣΠΑΝΙΚΑ Α. Να αποδώσετε στο τετράδιό σας στην ελληνική γλώσσα το παρακάτω κείμενο, προσδίδοντάς
ΑΡΧΗ 1ης ΣΕΛΙ ΑΣ KΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΤΕΤΑΡΤΗ 20 ΙΟΥΝΙΟΥ 2007 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΑ ΙΣΠΑΝΙΚΑ Α. Να αποδώσετε στο τετράδιό σας στην ελληνική γλώσσα το παρακάτω κείμενο, προσδίδοντάς
BCE. Compra y Venta de divisas negociadas en el país por el Sistema Financiero privado. banco central del ecuador
 BCE DIRECCIÓN DE ESTADÍSTICA ECONÓMICA Compra y Venta de divisas negociadas en el país por el Sistema Financiero privado banco central del ecuador www.bce.fin.ec Nro. 11 Resumen anual 2012 SOL Cultura
BCE DIRECCIÓN DE ESTADÍSTICA ECONÓMICA Compra y Venta de divisas negociadas en el país por el Sistema Financiero privado banco central del ecuador www.bce.fin.ec Nro. 11 Resumen anual 2012 SOL Cultura
NÚMEROS COMPLEXOS. Páxina 147 REFLEXIONA E RESOLVE. Extraer fóra da raíz. Potencias de. Como se manexa k 1? Saca fóra da raíz:
 NÚMEROS COMPLEXOS Páxina 7 REFLEXIONA E RESOLVE Extraer fóra da raíz Saca fóra da raíz: a) b) 00 a) b) 00 0 Potencias de Calcula as sucesivas potencias de : a) ( ) ( ) ( ) b) ( ) c) ( ) 5 a) ( ) ( ) (
NÚMEROS COMPLEXOS Páxina 7 REFLEXIONA E RESOLVE Extraer fóra da raíz Saca fóra da raíz: a) b) 00 a) b) 00 0 Potencias de Calcula as sucesivas potencias de : a) ( ) ( ) ( ) b) ( ) c) ( ) 5 a) ( ) ( ) (
Negocios Carta. Carta - Dirección
 - Dirección Mr. J. Rhodes Rhodes & Rhodes Corp. 212 Silverback Drive California Springs CA 92926 Mr. J. Rhodes Rhodes & Rhodes Corp. 212 Silverback Drive California Springs CA 92926 Formato de dirección
- Dirección Mr. J. Rhodes Rhodes & Rhodes Corp. 212 Silverback Drive California Springs CA 92926 Mr. J. Rhodes Rhodes & Rhodes Corp. 212 Silverback Drive California Springs CA 92926 Formato de dirección
PROPIEDADES Y APLICACIONES DE LA FAMILIA DE DISTRIBUCIONES SKEW-NORMAL MULTIVARIADA
 PONTIFICIA UNIVERSIDAD CATÓLICA DE CHILE FACULTAD DE MATEMÁTICA DEPARTAMENTO DE ESTADÍSTICA PROPIEDADES Y APLICACIONES DE LA FAMILIA DE DISTRIBUCIONES SKEW-NORMAL MULTIVARIADA POR GABRIELA VALDÉS Tesis
PONTIFICIA UNIVERSIDAD CATÓLICA DE CHILE FACULTAD DE MATEMÁTICA DEPARTAMENTO DE ESTADÍSTICA PROPIEDADES Y APLICACIONES DE LA FAMILIA DE DISTRIBUCIONES SKEW-NORMAL MULTIVARIADA POR GABRIELA VALDÉS Tesis
Inmigración Documentos
 - General Πού μπορώ να βρω τη φόρμα για ; Pedir un formulario Πότε εκδόθηκε το [έγγραφο] σας; Pedir la fecha de expedición de un documento Πού εκδόθηκε το [έγγραφο] σας; Pedir el lugar de expedición de
- General Πού μπορώ να βρω τη φόρμα για ; Pedir un formulario Πότε εκδόθηκε το [έγγραφο] σας; Pedir la fecha de expedición de un documento Πού εκδόθηκε το [έγγραφο] σας; Pedir el lugar de expedición de
Inmigración Documentos
 - General Dónde tengo que pedir el formulario/impreso para? Pedir un formulario Cuál es la fecha de expedición de su (documento)? Pedir la fecha de expedición de un documento Cuál es el lugar de expedición
- General Dónde tengo que pedir el formulario/impreso para? Pedir un formulario Cuál es la fecha de expedición de su (documento)? Pedir la fecha de expedición de un documento Cuál es el lugar de expedición
-νω. - νω. -σκω. - σκω
 TEMA DE PRESENTE -1- PRESENTES TEMÁTICOS ATEMÁTICOS RADICALES SUFIJADOS RADICALES SUFIJADOS SIN -νω SIN -ν -µι -ν -µαι CON - νω -σκω CON -νη-µι -ν -µαι - σκω - A) Temáticos radicales sin reduplicación
TEMA DE PRESENTE -1- PRESENTES TEMÁTICOS ATEMÁTICOS RADICALES SUFIJADOS RADICALES SUFIJADOS SIN -νω SIN -ν -µι -ν -µαι CON - νω -σκω CON -νη-µι -ν -µαι - σκω - A) Temáticos radicales sin reduplicación
Τραγwδούμενα. EDICIÓN CRÍTICA, TRADUCCIÓN Y COMENTARIO DE LOS FRAGMENTOS ATRIBUIDOS A ASCLEPÍADES DE TRAGILO
 Tesis doctoral Τραγwδούμενα. EDICIÓN CRÍTICA, TRADUCCIÓN Y COMENTARIO DE LOS FRAGMENTOS ATRIBUIDOS A ASCLEPÍADES DE TRAGILO Nereida Villagra Hidalgo Τραγῳδούμενα. EDICIÓN CRÍTICA, TRADUCCIÓN Y COMENTARIO
Tesis doctoral Τραγwδούμενα. EDICIÓN CRÍTICA, TRADUCCIÓN Y COMENTARIO DE LOS FRAGMENTOS ATRIBUIDOS A ASCLEPÍADES DE TRAGILO Nereida Villagra Hidalgo Τραγῳδούμενα. EDICIÓN CRÍTICA, TRADUCCIÓN Y COMENTARIO
PARTICIPIO DE PRESENTE
 EL PARTICIPIO MORFOLOGÍA PARTICIPIO DE PRESENTE ACTIVA MEDIA PASIVA λύ- ων, -ουσα, -ον λύ- οντος, -ουσης,-οντος λύ- ο - µενος, -η, -ον λύ- ο - µενου, -ης, -ου λύ- ο - µενος, -η, -ον λύ- ο - µενου, -ης,
EL PARTICIPIO MORFOLOGÍA PARTICIPIO DE PRESENTE ACTIVA MEDIA PASIVA λύ- ων, -ουσα, -ον λύ- οντος, -ουσης,-οντος λύ- ο - µενος, -η, -ον λύ- ο - µενου, -ης, -ου λύ- ο - µενος, -η, -ον λύ- ο - µενου, -ης,
ε x = du dx ε(x) = ds ds = du(x) dx
 Capítulo 8 ECUCIONES DIFERENCIES Cálculo de desplazamientos Dr. Fernando Flores 8.. INTRODUCCIÓN En este capítulo se sistematizan las ecuaciones que gobiernan el comportamiento de vigas. En general se
Capítulo 8 ECUCIONES DIFERENCIES Cálculo de desplazamientos Dr. Fernando Flores 8.. INTRODUCCIÓN En este capítulo se sistematizan las ecuaciones que gobiernan el comportamiento de vigas. En general se
1ª y 2ª DECLINACIONES. PRESENTE INDICATIVO ACTIVO. CASOS. ORACIONES SIMPLES Y COMPUESTAS COORDINADAS.
 TEMA 3: 1ª y 2ª DECLINACIONES. PRESENTE INDICATIVO ACTIVO. CASOS. ORACIONES SIMPLES Y COMPUESTAS COORDINADAS. a) Morfología nominal: 1ª (femeninos) y 2ª declinaciones (masculinos). b) Morfología verbal:
TEMA 3: 1ª y 2ª DECLINACIONES. PRESENTE INDICATIVO ACTIVO. CASOS. ORACIONES SIMPLES Y COMPUESTAS COORDINADAS. a) Morfología nominal: 1ª (femeninos) y 2ª declinaciones (masculinos). b) Morfología verbal:
Tema 1. Espazos topolóxicos. Topoloxía Xeral, 2016
 Tema 1. Espazos topolóxicos Topoloxía Xeral, 2016 Topoloxía e Espazo topolóxico Índice Topoloxía e Espazo topolóxico Exemplos de topoloxías Conxuntos pechados Topoloxías definidas por conxuntos pechados:
Tema 1. Espazos topolóxicos Topoloxía Xeral, 2016 Topoloxía e Espazo topolóxico Índice Topoloxía e Espazo topolóxico Exemplos de topoloxías Conxuntos pechados Topoloxías definidas por conxuntos pechados:
ln x, d) y = (3x 5 5x 2 + 7) 8 x
 EXERCICIOS AUTOAVALIABLES: CÁLCULO DIFERENCIAL. Deriva: a) y 7 6 + 5, b) y e, c) y e) y 7 ( 5 ), f) y ln, d) y ( 5 5 + 7) 8 n e ln, g) y, h) y n. Usando a derivada da función inversa, demostra que: a)
EXERCICIOS AUTOAVALIABLES: CÁLCULO DIFERENCIAL. Deriva: a) y 7 6 + 5, b) y e, c) y e) y 7 ( 5 ), f) y ln, d) y ( 5 5 + 7) 8 n e ln, g) y, h) y n. Usando a derivada da función inversa, demostra que: a)
Electrodinámica Cuántica
 Electrodinámica Cuántica L 0 = ψ i m)ψ Reemplazo minimal: D µ = µ iea µ Lagrangiano de la electrodinámica cuántica. L = ψ id m)ψ 1 4 F µνf µν Propagador del electrón L 0 = ψ i m)ψ + j ψ + ψ j S F x y)
Electrodinámica Cuántica L 0 = ψ i m)ψ Reemplazo minimal: D µ = µ iea µ Lagrangiano de la electrodinámica cuántica. L = ψ id m)ψ 1 4 F µνf µν Propagador del electrón L 0 = ψ i m)ψ + j ψ + ψ j S F x y)
PAU XUÑO 2011 MATEMÁTICAS II
 PAU XUÑO 2011 MATEMÁTICAS II Código: 26 (O alumno/a debe responder só os exercicios dunha das opcións. Puntuación máxima dos exercicios de cada opción: exercicio 1= 3 puntos, exercicio 2= 3 puntos, exercicio
PAU XUÑO 2011 MATEMÁTICAS II Código: 26 (O alumno/a debe responder só os exercicios dunha das opcións. Puntuación máxima dos exercicios de cada opción: exercicio 1= 3 puntos, exercicio 2= 3 puntos, exercicio
Negocios Encabezamiento e introducción
 - Encabezamiento e introducción Español Griego Distinguido Sr. Presidente: Αξιότιμε κύριε Πρόεδρε, Muy formal, el destinatario recibe un título especial que debe ser usado junto a su nombre o sustituyéndolo.
- Encabezamiento e introducción Español Griego Distinguido Sr. Presidente: Αξιότιμε κύριε Πρόεδρε, Muy formal, el destinatario recibe un título especial que debe ser usado junto a su nombre o sustituyéndolo.
LA TERCERA DECLINACIÓN O DECLINACIÓN ATEMÁTICA
 LA TERCERA DECLINACIÓN O DECLINACIÓN ATEMÁTICA Comprende sustantivos de género masculino y femenino (animados) y neutro (inanimados). Esta declinación recibe el nombre de atemática porque entre la raíz
LA TERCERA DECLINACIÓN O DECLINACIÓN ATEMÁTICA Comprende sustantivos de género masculino y femenino (animados) y neutro (inanimados). Esta declinación recibe el nombre de atemática porque entre la raíz
ΕΞΕΤΑΣΗ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΗΝ ΙΣΠΑΝΙΚΗ ΓΛΩΣΣΑ
 ΑΡΧΗ ΣΕΛΙ ΑΣ 1 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΔΙΑ ΒΙΟΥ ΜΑΘΗΣΗΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΞΕΤΑΣΕΩΝ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΕΛΛΗΝΩΝ ΕΞΩΤΕΡΙΚΟΥ ΕΞΕΤΑΣΗ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΗΝ ΙΣΠΑΝΙΚΗ ΓΛΩΣΣΑ Πέμπτη, 15 Σεπτεμβρίου 2011
ΑΡΧΗ ΣΕΛΙ ΑΣ 1 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΔΙΑ ΒΙΟΥ ΜΑΘΗΣΗΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΞΕΤΑΣΕΩΝ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΕΛΛΗΝΩΝ ΕΞΩΤΕΡΙΚΟΥ ΕΞΕΤΑΣΗ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΗΝ ΙΣΠΑΝΙΚΗ ΓΛΩΣΣΑ Πέμπτη, 15 Σεπτεμβρίου 2011
MATEMÁTICAS APLICADAS A LA ECONOMÍA CUADERNO DE EJERCICIOS SOLUCIONES. Dra. Lorena Zogaib Departamento de Matemáticas ITAM
 MATEMÁTICAS APLICADAS A LA ECONOMÍA CUADERNO DE EJERCICIOS SOLUCIONES Dra. Lorena Zogaib Departamento de Matemáticas ITAM Agosto 4, 4 INTRODUCCIÓN Este documento constituye un material de apoyo para el
MATEMÁTICAS APLICADAS A LA ECONOMÍA CUADERNO DE EJERCICIOS SOLUCIONES Dra. Lorena Zogaib Departamento de Matemáticas ITAM Agosto 4, 4 INTRODUCCIÓN Este documento constituye un material de apoyo para el
XEOMETRÍA NO ESPAZO. - Se dun vector se coñecen a orixe, o módulo, a dirección e o sentido, este está perfectamente determinado no espazo.
 XEOMETRÍA NO ESPAZO Vectores fixos Dos puntos do espazo, A e B, determinan o vector fixo AB, sendo o punto A a orixe e o punto B o extremo, é dicir, un vector no espazo é calquera segmento orientado que
XEOMETRÍA NO ESPAZO Vectores fixos Dos puntos do espazo, A e B, determinan o vector fixo AB, sendo o punto A a orixe e o punto B o extremo, é dicir, un vector no espazo é calquera segmento orientado que
Ταξίδι Τρώγοντας έξω. Τρώγοντας έξω - Στην είσοδο. Τρώγοντας έξω - Παραγγελία φαγητού
 - Στην είσοδο Me gustaría reservar una mesa para _[número de personas]_ a las _[hora]_. Για να κάνετε κράτηση Una mesa para _[número de personas]_, por favor. Για να ζητήσετε τραπέζι Aceptan tarjetas de
- Στην είσοδο Me gustaría reservar una mesa para _[número de personas]_ a las _[hora]_. Για να κάνετε κράτηση Una mesa para _[número de personas]_, por favor. Για να ζητήσετε τραπέζι Aceptan tarjetas de
La experiencia de la Mesa contra el Racismo
 La experiencia de la Mesa contra el Racismo Informe Di icultad para identi icarse como discriminado Subsistencia de mecanismos individuales para enfrentar el racismo Las propuestas de las organizaciones
La experiencia de la Mesa contra el Racismo Informe Di icultad para identi icarse como discriminado Subsistencia de mecanismos individuales para enfrentar el racismo Las propuestas de las organizaciones
Problemas resueltos del teorema de Bolzano
 Problemas resueltos del teorema de Bolzano 1 S e a la fun ción: S e puede af irm a r que f (x) está acotada en el interva lo [1, 4 ]? P or no se r c ont i nua f (x ) e n x = 1, la f unció n no e s c ont
Problemas resueltos del teorema de Bolzano 1 S e a la fun ción: S e puede af irm a r que f (x) está acotada en el interva lo [1, 4 ]? P or no se r c ont i nua f (x ) e n x = 1, la f unció n no e s c ont
Las Funciones Trigonométricas
 Caítulo 3 Las Funciones Trigonométricas 3.. El círculo trigonométrico Vamos a suoner conocido el sistema cartesiano en lo que se refiere a concetos fundamentales como son los de abscisa y ordenada de un
Caítulo 3 Las Funciones Trigonométricas 3.. El círculo trigonométrico Vamos a suoner conocido el sistema cartesiano en lo que se refiere a concetos fundamentales como son los de abscisa y ordenada de un
PRUEBA INICIAL DE CLASIFICACIÓN CURSO Documento para adjuntar a la Solicitud de plaza
 PRUEBA INICIAL DE CLASIFICACIÓN CURSO 2017-18 Documento para adjuntar a la Solicitud de plaza Yo con DNI, número de teléfono y dirección de correo electrónico, solicitante del idioma, nivel, declaro bajo
PRUEBA INICIAL DE CLASIFICACIÓN CURSO 2017-18 Documento para adjuntar a la Solicitud de plaza Yo con DNI, número de teléfono y dirección de correo electrónico, solicitante del idioma, nivel, declaro bajo
δικαιοσύνης διδασκαλεῖα. ἀλλ οἱ µὲν δυνάµενοι τρέφειν τοὺς παῖδας
 Instrucciones: a) Duración: 1 hora y 30 minutos. b) Se podrá hacer uso del diccionario y de su apéndice gramatical. c) El alumno elegirá y desarrollará en su totalidad una de las dos opciones propuestas,
Instrucciones: a) Duración: 1 hora y 30 minutos. b) Se podrá hacer uso del diccionario y de su apéndice gramatical. c) El alumno elegirá y desarrollará en su totalidad una de las dos opciones propuestas,
ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΗΝ ΙΣΠΑΝΙΚΗ ΓΛΩΣΣΑ
 ΑΡΧΗ ΣΕΛΙ ΑΣ 1 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΔΙΑ ΒΙΟΥ ΜΑΘΗΣΗΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΗΝ ΙΣΠΑΝΙΚΗ ΓΛΩΣΣΑ Πέμπτη, 16 Ιουνίου 2011 ΟΔΗΓΙΕΣ ΓΙΑ ΤΟΥΣ ΥΠΟΨΗΦΙΟΥΣ
ΑΡΧΗ ΣΕΛΙ ΑΣ 1 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΔΙΑ ΒΙΟΥ ΜΑΘΗΣΗΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΗΝ ΙΣΠΑΝΙΚΗ ΓΛΩΣΣΑ Πέμπτη, 16 Ιουνίου 2011 ΟΔΗΓΙΕΣ ΓΙΑ ΤΟΥΣ ΥΠΟΨΗΦΙΟΥΣ
Sólido deformable: cables
 Sólido deformable: cables Mariano Vázquez Espí Madrid (España), 15 de marzo de 2017. Robert Hooke (1635 1703) Físico, astrónomo y naturalista Entre otras cosas, introdujo el concepto de célula y analizó
Sólido deformable: cables Mariano Vázquez Espí Madrid (España), 15 de marzo de 2017. Robert Hooke (1635 1703) Físico, astrónomo y naturalista Entre otras cosas, introdujo el concepto de célula y analizó
bab.la Φράσεις: Προσωπική Αλληλογραφία Ευχές ελληνικά-ισπανικά
 Ευχές : Γάμος Συγχαρητήρια. Σας ευχόμαστε όλη την ευτυχία του κόσμου. Felicitaciones. Les deseamos a ambos toda la felicidad del mundo. νιόπαντρο ζευγάρι Θερμά συγχαρητήρια για τους δυο σας αυτήν την ημέρα
Ευχές : Γάμος Συγχαρητήρια. Σας ευχόμαστε όλη την ευτυχία του κόσμου. Felicitaciones. Les deseamos a ambos toda la felicidad del mundo. νιόπαντρο ζευγάρι Θερμά συγχαρητήρια για τους δυο σας αυτήν την ημέρα
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΟΙΚΟΝΟΜΙΚΩΝ REPÚBLICA HELÉNICA MINISTERIO DE FINANZAS
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΟΙΚΟΝΟΜΙΚΩΝ HELLENIC REPUBLIC MINISTRY OF FINANCE REPÚBLICA HELÉNICA MINISTERIO DE FINANZAS 1ο αντίγραφο για την Ελληνική Φορολογική Αρχή 1 st copy for the Hellenic Tax Authority
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΟΙΚΟΝΟΜΙΚΩΝ HELLENIC REPUBLIC MINISTRY OF FINANCE REPÚBLICA HELÉNICA MINISTERIO DE FINANZAS 1ο αντίγραφο για την Ελληνική Φορολογική Αρχή 1 st copy for the Hellenic Tax Authority
ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΗΝ ΙΣΠΑΝΙΚΗ ΓΛΩΣΣΑ
 ΑΡΧΗ ΣΕΛΙΔΑΣ 1 ΥΠΟΥΡΓΕΙΟ ΠΟΛΙΤΙΣΜΟΥ ΠΑΙΔΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΗΝ ΙΣΠΑΝΙΚΗ ΓΛΩΣΣΑ Σάββατο, 20 Ιουνίου 2015 ΟΔΗΓΙΕΣ ΓΙΑ ΤΟΥΣ ΥΠΟΨΗΦΙΟΥΣ
ΑΡΧΗ ΣΕΛΙΔΑΣ 1 ΥΠΟΥΡΓΕΙΟ ΠΟΛΙΤΙΣΜΟΥ ΠΑΙΔΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΗΝ ΙΣΠΑΝΙΚΗ ΓΛΩΣΣΑ Σάββατο, 20 Ιουνίου 2015 ΟΔΗΓΙΕΣ ΓΙΑ ΤΟΥΣ ΥΠΟΨΗΦΙΟΥΣ
Unos cambios de la pronunciación
 Unos cambios de la pronunciación desde griego moderno al griego clásico (según Erasmo) por El profesor Don Potter Cambios de la pronunciación recomendados de parte del Maestro Don Potter para El Griego
Unos cambios de la pronunciación desde griego moderno al griego clásico (según Erasmo) por El profesor Don Potter Cambios de la pronunciación recomendados de parte del Maestro Don Potter para El Griego
KIT DE DRENAJE DE CONDENSADOS
 KIT DE DRENAJE DE CONDENSADOS Estas instrucciones forman parte integrante del manual que acompaña el aparato en el cual está instalado este Kit. Este manual se refiere a ADVERTENCIAS GENERALES y REGLAS
KIT DE DRENAJE DE CONDENSADOS Estas instrucciones forman parte integrante del manual que acompaña el aparato en el cual está instalado este Kit. Este manual se refiere a ADVERTENCIAS GENERALES y REGLAS
EXERCICIOS AUTOAVALIABLES: RECTAS E PLANOS. 3. Cal é o vector de posición da orixe de coordenadas O? Cales son as coordenadas do punto O?
 EXERCICIOS AUTOAVALIABLES: RECTAS E PLANOS Representa en R os puntos S(2, 2, 2) e T(,, ) 2 Debuxa os puntos M (, 0, 0), M 2 (0,, 0) e M (0, 0, ) e logo traza o vector OM sendo M(,, ) Cal é o vector de
EXERCICIOS AUTOAVALIABLES: RECTAS E PLANOS Representa en R os puntos S(2, 2, 2) e T(,, ) 2 Debuxa os puntos M (, 0, 0), M 2 (0,, 0) e M (0, 0, ) e logo traza o vector OM sendo M(,, ) Cal é o vector de
Procedementos operatorios de unións non soldadas
 Procedementos operatorios de unións non soldadas Técnicas de montaxe de instalacións Ciclo medio de montaxe e mantemento de instalacións frigoríficas 1 de 28 Técnicas de roscado Unha rosca é unha hélice
Procedementos operatorios de unións non soldadas Técnicas de montaxe de instalacións Ciclo medio de montaxe e mantemento de instalacións frigoríficas 1 de 28 Técnicas de roscado Unha rosca é unha hélice
Ευρύτερη περιοχή χαράδρας ποταμού Αράχθου
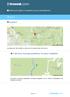 Ruta por Epiro: Ioannina y sus alrededores Día 1 Kostitsi La población de Kostitsi se ubica en la región Epiro de Grecia. Ευρύτερη περιοχή χαράδρας ποταμού Αράχθου Ευρύτερη περιοχή χαράδρας ποταμού Αράχθου
Ruta por Epiro: Ioannina y sus alrededores Día 1 Kostitsi La población de Kostitsi se ubica en la región Epiro de Grecia. Ευρύτερη περιοχή χαράδρας ποταμού Αράχθου Ευρύτερη περιοχή χαράδρας ποταμού Αράχθου
IV FESTIVAL LEA. Concurso entre escuelas de aprendizaje del español
 IV FESTIVAL LEA El IV Festival Iberoamericano Literatura En Atenas, organizado por la revista Cultural Sol Latino, el Instituto Cervantes de Atenas y la Fundación María Tsakos, dura este año dos semanas:
IV FESTIVAL LEA El IV Festival Iberoamericano Literatura En Atenas, organizado por la revista Cultural Sol Latino, el Instituto Cervantes de Atenas y la Fundación María Tsakos, dura este año dos semanas:
Αιτήσεις Συνοδευτική Επιστολή
 - Εισαγωγή Αξιότιμε κύριε, Επίσημη επιστολή, αρσενικός αποδέκτης, όνομα άγνωστο Αξιότιμη κυρία, Επίσημη επιστολή, θηλυκός αποδέκτης, όνομα άγνωστο Αξιότιμε κύριε/ κυρία, Distinguido Señor: Distinguida
- Εισαγωγή Αξιότιμε κύριε, Επίσημη επιστολή, αρσενικός αποδέκτης, όνομα άγνωστο Αξιότιμη κυρία, Επίσημη επιστολή, θηλυκός αποδέκτης, όνομα άγνωστο Αξιότιμε κύριε/ κυρία, Distinguido Señor: Distinguida
EL MOVIMIE TO DEL U IVERSO Y SUS CARACTERÍSTICAS E LA COSMOLOGÍA DE PLATÓ
 EL MOVIMIE TO DEL U IVERSO Y SUS CARACTERÍSTICAS E LA COSMOLOGÍA DE PLATÓ Resumen Se analiza la constitución del universo tal como es desarrollado en los diálogos de Platón Parménides, Timeo y Teeteto.
EL MOVIMIE TO DEL U IVERSO Y SUS CARACTERÍSTICAS E LA COSMOLOGÍA DE PLATÓ Resumen Se analiza la constitución del universo tal como es desarrollado en los diálogos de Platón Parménides, Timeo y Teeteto.
CENTRIFUGAL AIR COOLED CONDENSERS CONDENSADORES DE AIRE CENTRÍFUGOS. GPC, GMC and GSC Series. Series GPC, GMC y GSC
 CENTRIFUGAL AIR COOLED CONDENSERS GPC, GMC and GSC Series CONDENSADORES DE AIRE CENTRÍFUGOS Series GPC, GMC y GSC Key Example / Ejemplo de nomenclatura de modelos GP Direct Drive 900/100 rpm / Transmisión
CENTRIFUGAL AIR COOLED CONDENSERS GPC, GMC and GSC Series CONDENSADORES DE AIRE CENTRÍFUGOS Series GPC, GMC y GSC Key Example / Ejemplo de nomenclatura de modelos GP Direct Drive 900/100 rpm / Transmisión
ÁCIDOS ORGÁNICOS MAS COMUNES
 ÁCIDOS ORGÁNICOS MAS COMUNES Los nombres triviales de los ácidos carboxílicos se designan según la fuente natural de la que inicialmente se aislaron. Se clasificaron así: Nombres de los ácidos carboxílicos
ÁCIDOS ORGÁNICOS MAS COMUNES Los nombres triviales de los ácidos carboxílicos se designan según la fuente natural de la que inicialmente se aislaron. Se clasificaron así: Nombres de los ácidos carboxílicos
Κυρ. Ιωάννου Οδ. Δωριέων 34 Τ.Κ 8068, Λάρνακα. Adam Smith 8 Crossfield Road Selly Oak Birmingham West Midlands B29 1WQ
 - Dirección Av. Galileo 110 Colonia Polanco C.P. 12560 México, D.F. Formato de dirección de México: Colonia Código postal + Estado, Ciudad. Av. Galileo 110 12560 Madrid (Madrid) Formato de dirección de
- Dirección Av. Galileo 110 Colonia Polanco C.P. 12560 México, D.F. Formato de dirección de México: Colonia Código postal + Estado, Ciudad. Av. Galileo 110 12560 Madrid (Madrid) Formato de dirección de
ACTIVIDADES INICIALES
 Solucionario Trigonometría ACTIVIDADES INICIALES.I. En una recta r hay tres puntos: A, B y C, que distan, sucesivamente, y cm. Por esos puntos se trazan rectas paralelas que cortan otra, s, en M, N y P.
Solucionario Trigonometría ACTIVIDADES INICIALES.I. En una recta r hay tres puntos: A, B y C, que distan, sucesivamente, y cm. Por esos puntos se trazan rectas paralelas que cortan otra, s, en M, N y P.
Código: 25 XUÑO 2016 PAU FÍSICA OPCIÓN A OPCIÓN B
 PAU Código: 5 XUÑO 016 FÍSICA Puntuación máxima: Cuestiones 4 puntos (1 cada cuestión, teórica o práctica). Problemas 6 puntos (1 cada apartado). No se valorará la simple anotación de un ítem cómo solución
PAU Código: 5 XUÑO 016 FÍSICA Puntuación máxima: Cuestiones 4 puntos (1 cada cuestión, teórica o práctica). Problemas 6 puntos (1 cada apartado). No se valorará la simple anotación de un ítem cómo solución
Gonzalo Hernández Sanjorge
 Análisis de las Enneadas de Plotino. Tratado Segundo de la Enneada Primera Acerca de las virtudes 1 Gonzalo Hernández Sanjorge La virtud como forma de semejanza con la divinidad. En este tratado Plotino
Análisis de las Enneadas de Plotino. Tratado Segundo de la Enneada Primera Acerca de las virtudes 1 Gonzalo Hernández Sanjorge La virtud como forma de semejanza con la divinidad. En este tratado Plotino
